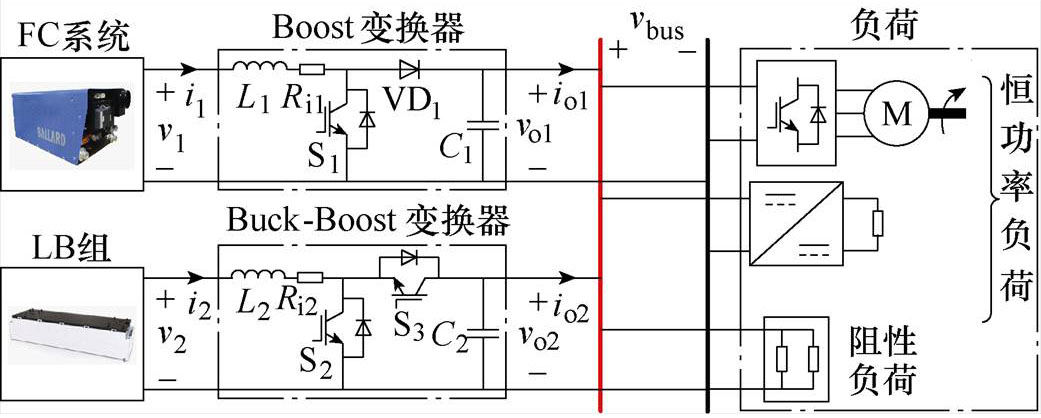
图1 燃料电池-锂电池混合供电系统结构
Fig.1 Structure diagram of FC-LB HPSS
摘要 多源混合供电技术可有效地利用不同供电单元性能,在电气化交通系统中得到广泛应用。然而,随着越来越多的恒功率特性及强脉动特性负载接入供电系统,系统的稳定性难以得到保证。针对传统线性控制方法难以保证系统的大信号稳定性,而现有非线性控制的研究仍缺乏兼顾稳定性和动态性能的控制参数设计方法的问题,该文对燃料电池-锂电池混合供电系统设计基于无源控制和扩张高增益状态观测器的复合控制方法,并对控制器和观测器参数进行了设计,有效地保证了系统的动静态性能。在实验室搭建一套额定功率为3 kW的燃料电池-锂电池混合供电系统实验平台进行测试,结果验证了所提控制策略和参数设计方法的有效性和正确性。
关键词:无源控制 参数设计 扩张高增益状态观测器 混合供电系统
近年来,交通行业持续推进能源供给侧改革,对清洁、高效、无污染的能源需求比例越来越高,研究和发展交通绿色供电技术刻不容缓。以氢燃料电池为代表的氢能技术凭借其低噪声、高能量密度等优势受到了学术界和工业界的广泛关注[1-4]。然而,燃料电池(Fuel Cell, FC)存在动态响应较慢、不能进行能量回收、难以适应交通系统的多工况用能需求,需辅以电池(Batterry, BAT)或超级电容(Supercapacitor, SC)等响应较快的储能单元结合电力电子变换器构成混合供电系统(Hybrid Power Supply System, HPSS),以提升供电灵活性。
混合供电系统的核心技术之一是通过对电力电子变换器控制器的设计实现母线电压稳定及负载功率在不同供电源间的动态分配。然而,随着越来越多的新型多时间尺度(ms-s-min)、强脉动(电磁武器、飞行器舵面)、恒功率(伺服驱动系统)电气化负荷接入HPSS,大量跨时间尺度、跨功率等级的源荷交织在一起,采用常规线性控制方法(如PID控制)难以保证系统的大信号稳定性。此外,传统集中式功率分配控制方法也难以满足多场景用电条件下热插拔、冗余拓展以及再生能量的无损消纳等需求。
针对集中式功率分配的不足,国内外学者相继提出了基于频域解耦[5-6]和基于混合下垂控制[7-10]的分散式控制方法。频域控制通过对各个供电电源端口变换器施加相互独立的控制,实现动态功率分配。混合下垂控制利用虚拟电阻、虚拟电感、虚拟电容的组合实现对供电源端口变换器的输出阻抗设计,使得动态功率按频率范围自动地分配到各个供电源上。文献[10]针对燃料电池-蓄电池-超级电容混合供电系统,基于改进混合下垂控制方法,提出了一种高可靠的分散式动态功率分配策略,实现了脉动负荷功率在供电单元间优化分配、储能单元荷电状态调节和再生能量回收。本文所研究的燃料电池-锂电池(Lithium Battery, LB)HPSS亦采用此功率分配控制策略。
针对HPSS的致稳控制问题,国内外学者基于非线性控制理论,提出了模型预测控制[11-13]、滑模控制[14-16]、反步法[17-19]、有源阻尼控制[20-21]、无源控制(Passivity-Based Control, PBC)[22-26]等先进控制方法。然而,模型预测控制难以在理论层次证明系统的全局稳定性,难以指导控制器参数设计。滑模控制器应用于电力电子变换器时会产生抖振,易受到电磁干扰,且现有研究未考虑兼顾动态性能的控制器参数设计问题。反步法的设计过程在系统阶数较高时较为繁琐,且在设计时未考虑系统的可控性。相较于上述控制方法,无源控制因控制器设计简单、物理意义清晰,近年来在直流电源系统的控制中得到了广泛关注。文献[22-24]针对单个供电源中由恒功率负载(Constant Power Load, CPL)、未知扰动等引起的系统不稳定、存在稳态误差等问题设计了基于扰动观测器的无源控制,有效地解决了稳态误差、系统不稳等问题,但未进行系统化的控制器参数设计以兼顾系统动态性能。文献[25]提出了一种采用非支配排序遗传算法Ⅲ的参数多目标优化,对无源控制器控制参数进行了优化,获得了更好的动静态性能,但未考量优化参数对系统稳定性的影响。文献[26]针对燃料电池-锂电池混合供电系统设计了基于扰动观测器的无源控制,但同样未对控制参数进行优化设计,使得系统性能未能进一步提升。此外,现有研究在设计控制器时通常要对负载建模,引入了非线性项,当负载模型发生变化时,原有的控制器可能保证不了稳定性。在对控制器进行参数设计时,传统线性控制设计方法通常要将系统中的非线性项转化为平衡点附近的线性项,在直流电源系统中这个非线性项通常为恒功率负载,难以保证系统的大信号稳定性。无源控制本质上是一种非线性控制,相关参数设计方法鲜有文献报道,尤其是满足动态性能的设计方法。总体而言,已有研究大都未考虑兼顾系统动态性能及稳定性的参数设计问题。
针对上述问题,本文在现有研究基础上,针对燃料电池-锂电池HPSS控制参数设计展开了研究,主要工作及创新点如下:
(1)设计了针对Boost变换器的无需考虑负荷类型的无源控制器,将参数不确定性视为扰动并用观测器进行估计并补偿,运用经典控制理论建立端口变换器、PBC控制器、扩张高增益状态观测器(Extended High Gain State Observer, EHGSO)的小信号模型。
(2)分析了系统参数与系统动态性能、稳定性的关联关系,在无需考虑负载模型的前提下以线性控制器设计方法设计了非线性控制器参数,提出了兼顾系统动态性能的参数整定方法,并通过实验验证了所提方法的有效性。
图1为典型的燃料电池-锂电池混合供电系统结构,图中,vx(x=1, 2)和ix分别为燃料电池和锂电池的输出电压和输出电流,vox和iox分别为端口变换器的输出电压和输出电流;vbus为母线电压,Lx和Cx分别为端口变换器的滤波电感和滤波电容,Rix为滤波电感的内阻,VD1为二极管,S1、S2和S3为功率开关器件。

图1 燃料电池-锂电池混合供电系统结构
Fig.1 Structure diagram of FC-LB HPSS
根据图1,综合考虑参数的不确定性(滤波电容的内阻、二极管/开关管的导通内阻等引起的不确定建模误差)及测量噪声,端口变换器数学模型[26]可表示为
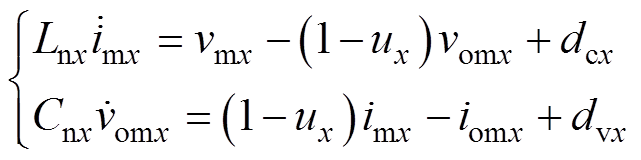 (1)
(1)
其中
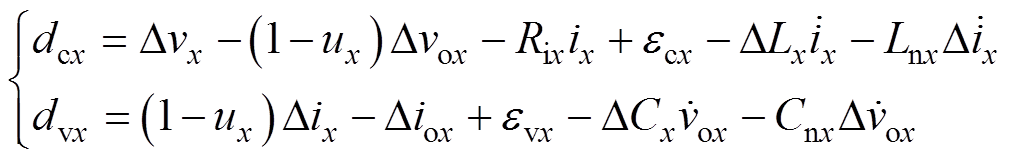 (2)
(2)
式中,Lnx和Cnx分别为Lx和Cx的标称值;vmx、imx、vomx和iomx分别为vx、ix、vox和iox的测量值;Dvx、Dix、Dvox和Diox分别为vx、ix、vox和iox的不确定测量噪声;DLx和DCx分别为Lx和Cx的不确定变化量;dcx和dvx为由不确定的系统参数和测量噪声等引起的不确定扰动;ux为开关管PWM的占空比。
令x=[im1vom1 im2vom2]T,则式(1)可整理为Euler-Lagrange形式[22]。即
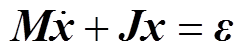 (3)
(3)
其中
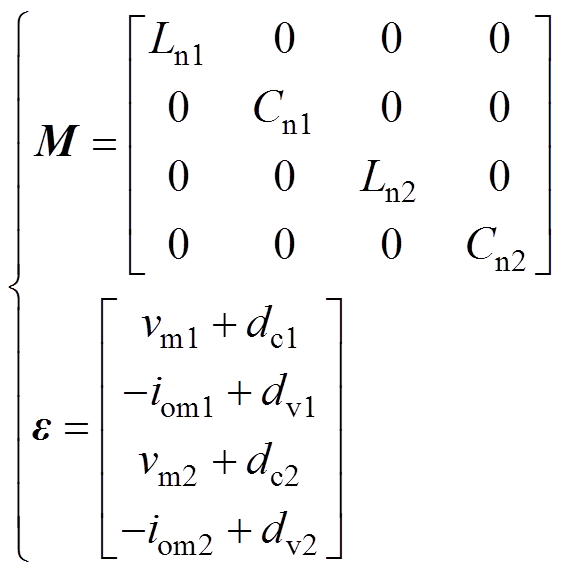 (4)
(4)
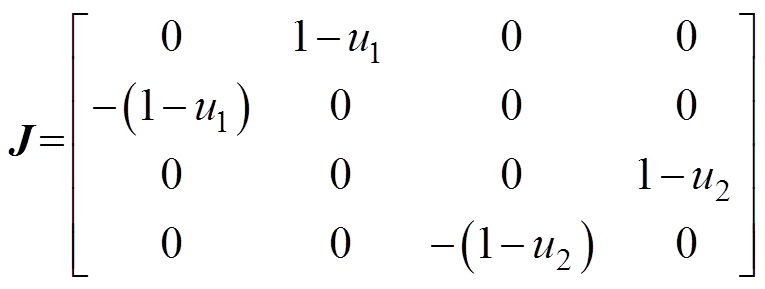 (5)
(5)
式中,M为正定矩阵;J为反对称矩阵;e 为外部输入矩阵。
设基准状态向量xd=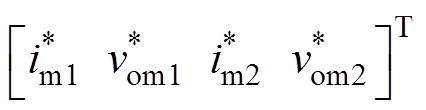 ,则系统的跟踪误差向量e=x-xd。为提升系统的动态跟踪性能,PBC控制器通常通过反馈控制引入耗散阻尼矩阵Rd以加快跟踪误差能量的耗散。因此,系统的动态跟踪误差可表示为
,则系统的跟踪误差向量e=x-xd。为提升系统的动态跟踪性能,PBC控制器通常通过反馈控制引入耗散阻尼矩阵Rd以加快跟踪误差能量的耗散。因此,系统的动态跟踪误差可表示为
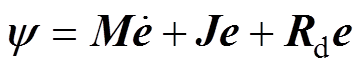 (6)
(6)
式中,耗散阻尼矩阵Rd=diag(Rd1, Gd1, Rd2, Gd2)为正定矩阵。
根据PBC控制器的设计方法[27],令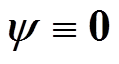 ,则式(3)的PBC控制器可设计为
,则式(3)的PBC控制器可设计为
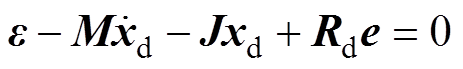 (7)
(7)
即
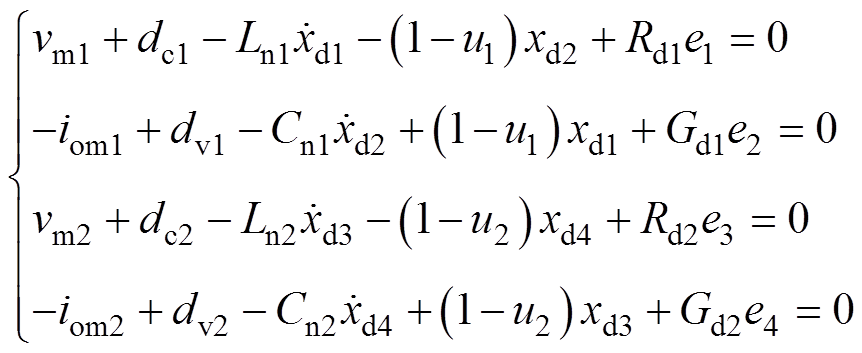 (8)
(8)
根据式(8),可得PBC控制器的控制律为
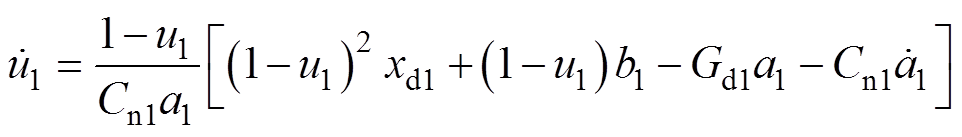 (9)
(9)
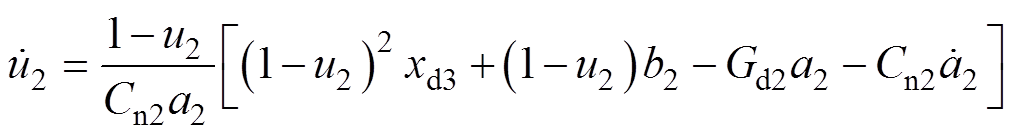 (10)
(10)
其中
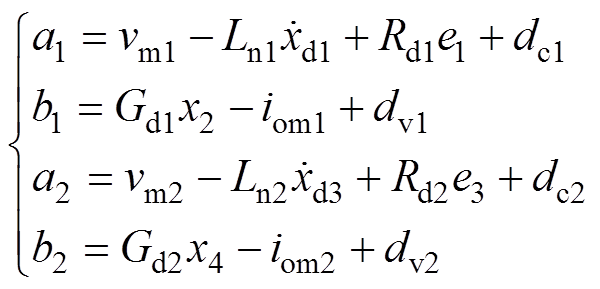 (11)
(11)
对于系统式(3),候选李雅普诺夫函数选为
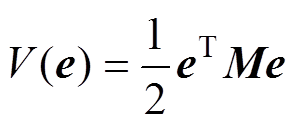 (12)
(12)
结合式(6)、式(7)和式(12),候选李雅普诺夫函数的导数满足
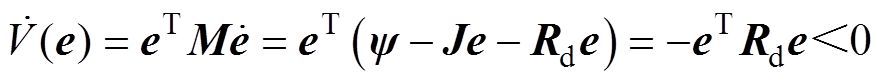 (13)
(13)
因此系统式(3)是全局渐近稳定的。
由式(9)和式(10)可知,PBC控制器依赖于扰动dc1、dc2、dv1和dv2的准确值。然而,在实际工程中,它们通常是不可测量的未知扰动,在其作用下,系统性能变差甚至失稳。因此,本文采用EHGSO技术[28]观测扰动dc1、dc2、dv1和dv2,以补偿其对系统性能的影响,从而提高系统的控制性能和鲁棒性。具体而言,本文为扰动dc1、dv1、dc2和dv2设计的EHGSO分别为
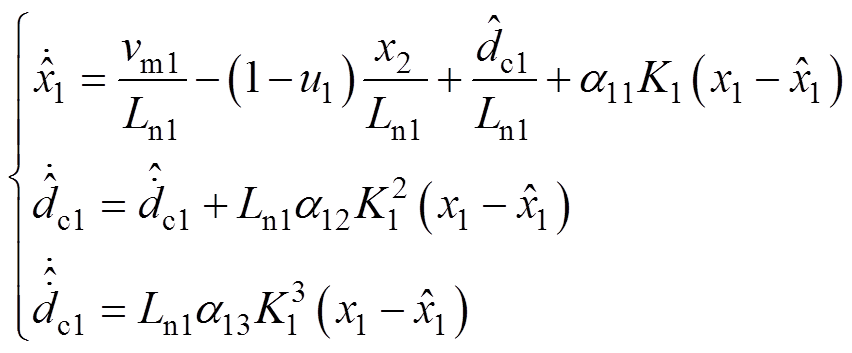 (14)
(14)
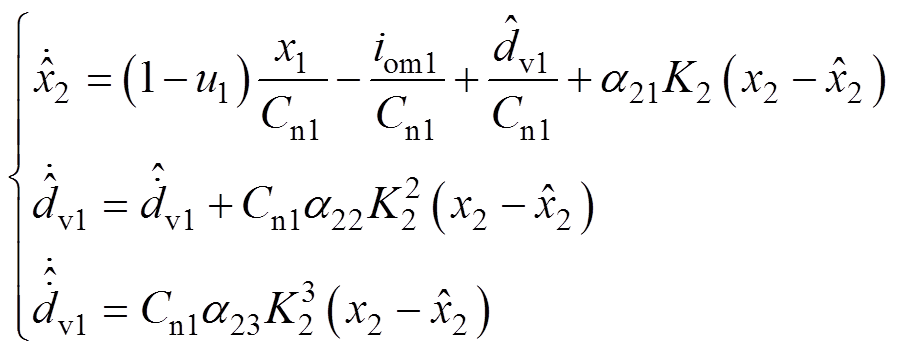 (15)
(15)
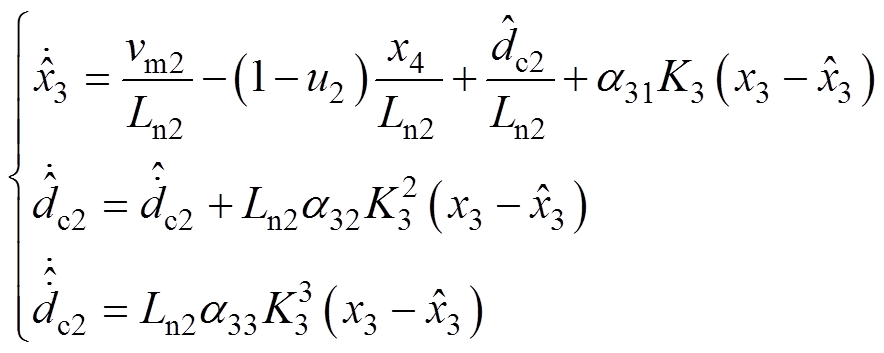 (16)
(16)
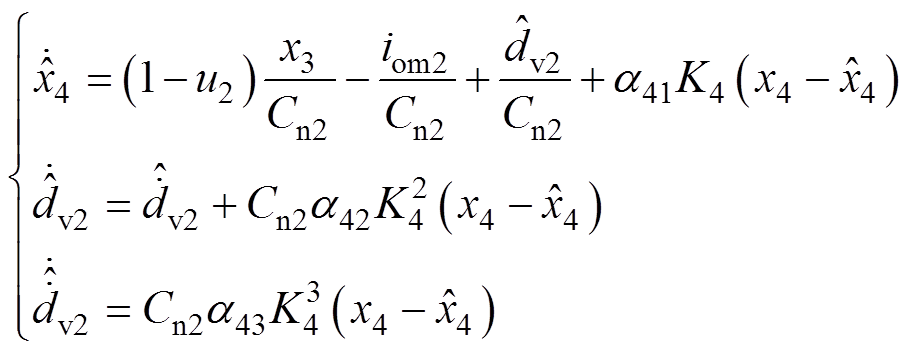 (17)
(17)
式中,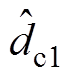 、
、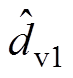 、
、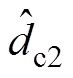 和
和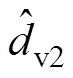 分别为扰动dc1、dv1、dc2和dv2的观测值;
分别为扰动dc1、dv1、dc2和dv2的观测值;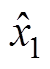 ~
~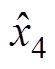 分别为状态x1~x4的观测值;K1~K4均为大于1的正比例增益;a11~a13、a21~a23、a31~a33和a41~a43为观测器增益,其分别对应Hurwitz多项式h1(s)=s3+a11s2+a12s+a13,h2(s)=s3+a21s2+a22s+a23,h3(s)=s3+a31s2+a32s+a33和h4(s)=s3+a41s2+a42s+a43的系数。
分别为状态x1~x4的观测值;K1~K4均为大于1的正比例增益;a11~a13、a21~a23、a31~a33和a41~a43为观测器增益,其分别对应Hurwitz多项式h1(s)=s3+a11s2+a12s+a13,h2(s)=s3+a21s2+a22s+a23,h3(s)=s3+a31s2+a32s+a33和h4(s)=s3+a41s2+a42s+a43的系数。
由于篇幅受限,观测器的稳定性证明不再赘述,相关证明过程可参考文献[26]。结合混合下垂控制,以及所设计的无源控制器和扩张高增益观测器,FC-LB HPSS控制架构如图2所示,图中,Vnom为母线电压标称值,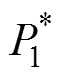 =(Vnom-vom1)/m,
=(Vnom-vom1)/m,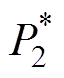 =(Vnom-vom2)/n。
=(Vnom-vom2)/n。
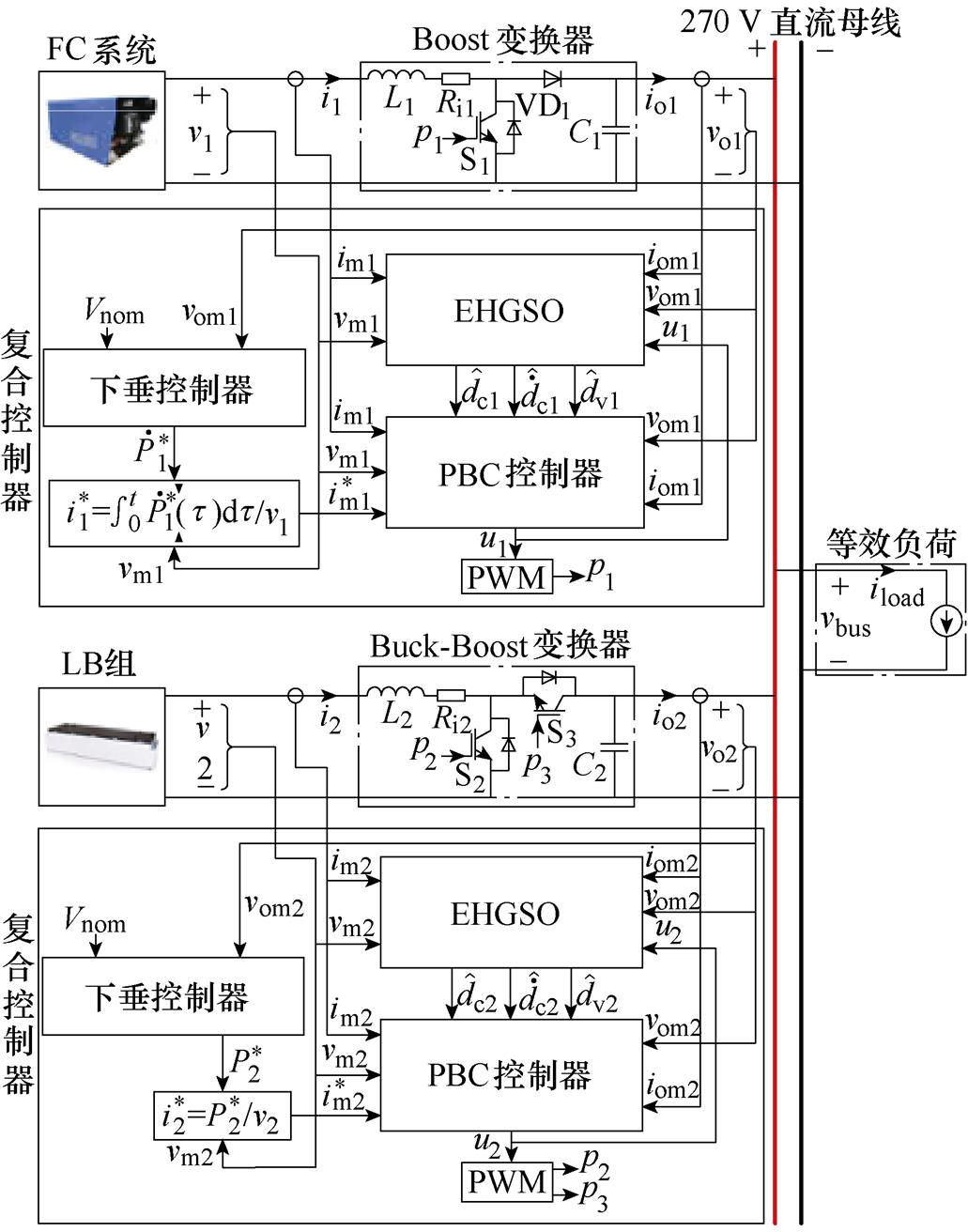
图2 燃料电池-锂电池混合供电系统控制架构
Fig.2 Control architecture of FC-LB HPSS
由式(9)和式(10)可知,所提出的无源控制器与负荷类型无关,即负荷类型不会影响系统的全局稳定性。因此,本文以FC端口变换器带阻性负荷为例,结合小信号模型研究复合控制器参数设计方法。
2.1.1 FC端口变换器带阻性负荷的小信号模型
根据式(1),FC端口变换器带阻性负荷的小信号模型可推导为
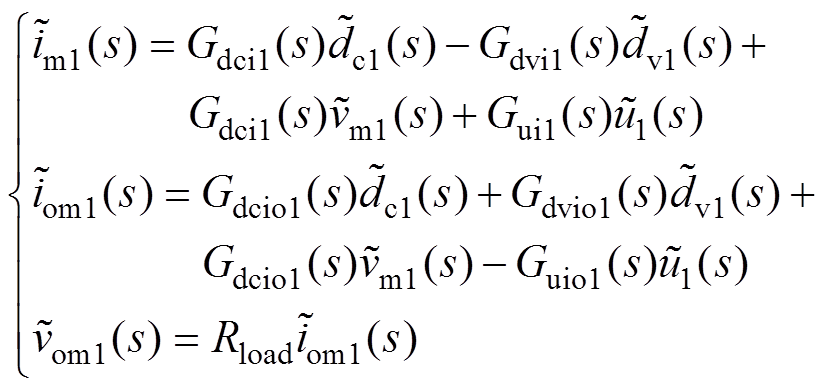 (18)
(18)
式中,Gdci1(s)、Gdvi1(s)、Gui1(s)、Gdcio1(s)、Gdvio1(s)、Guio1(s)详见附录式(A1)~式(A6);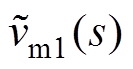 、
、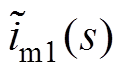 、
、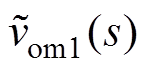 、
、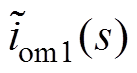 和
和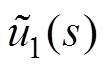 分别为vm1、im1、vom1、iom1和u1小信号值对应的频域函数。
分别为vm1、im1、vom1、iom1和u1小信号值对应的频域函数。
2.1.2 PBC控制器的小信号模型
根据式(8),FC端口变换器PBC控制器的小信号模型可推导为
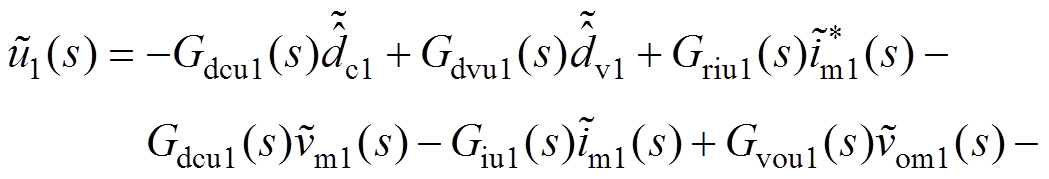
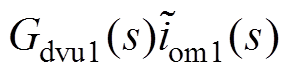 (19)
(19)
式中,Gdcu1(s)、Gdvu1(s)、Griu1(s)、Giu1(s)、Gvou1(s)详见附录式(A7)~式(A11)。
2.1.3 EHGSO的小信号模型
根据式(14),扰动dc1和dv1 EHGSO的小信号模型可推导为
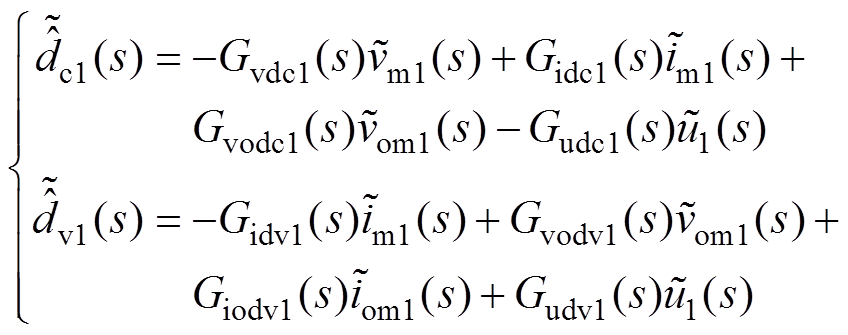 (20)
(20)
式中,Gvdc1(s)、Gidc1(s)、Gvodc1(s)、Gudc1(s)、Gidv1(s)、Gvodv1(s)、Giodv1(s)、Gudv1(s)详见附录式(A12)~式(A19)。
综上所述,FC供电单元带阻性负荷的小信号模型如图3所示,图中,PBC控制器和EHGSO所使用的电压和电流信号均经过了滤波环节Gs(s),Gs(s)=1/(Tss+1),Ts为开关周期。
为简化设计过程,本节在设计PBC控制器参数时,忽略外部扰动和EHGSO的影响,即令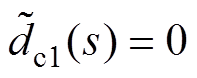 ,
,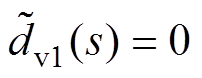 ,
,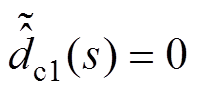 ,
,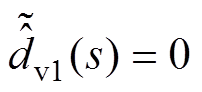 ,系统仅在PBC控制器的控制下运行。结合图3,系统的闭环传递函数可推导为
,系统仅在PBC控制器的控制下运行。结合图3,系统的闭环传递函数可推导为
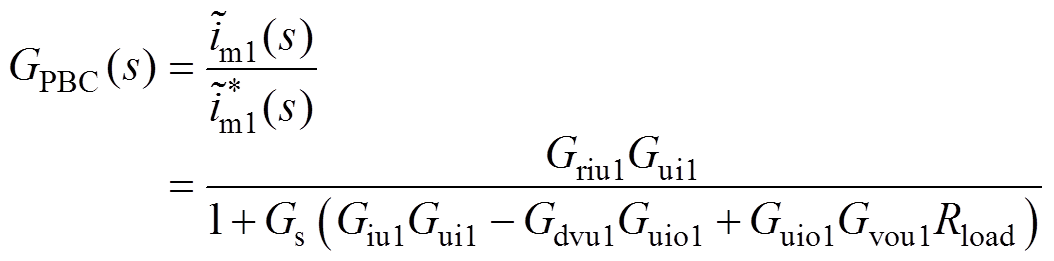 (21)
(21)
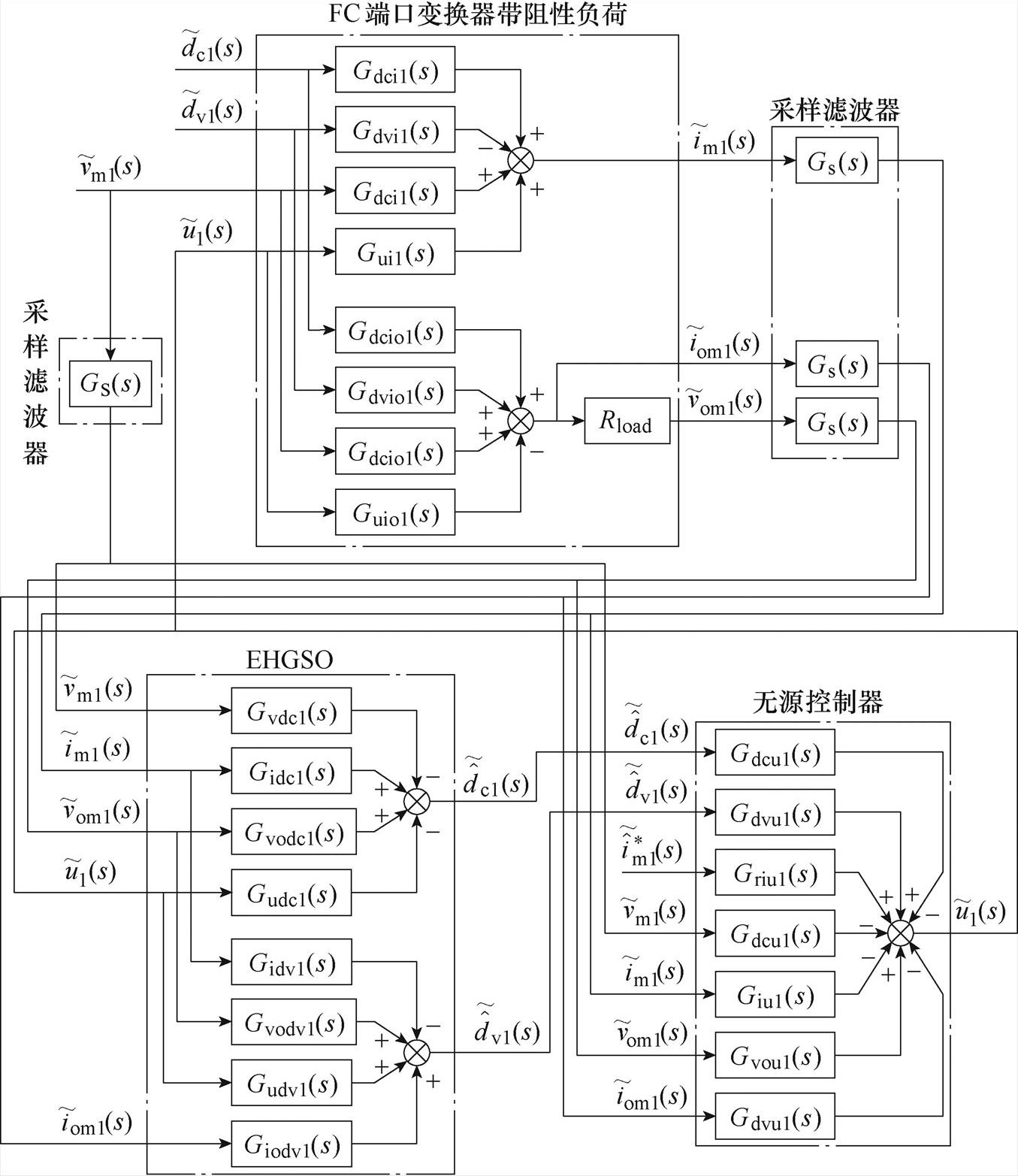
图3 FC供电单元带阻性负荷小信号模型
Fig.3 Small-signal model of the FC power supply unit with resistive load
式中,GPBC(s)为系统仅在PBC控制器控制下的闭环传递函数。
若不考虑采样滤波器Gs(s),即采样滤波器的时间常数Ts=0时,结合稳态关系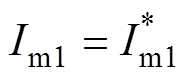 和
和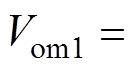
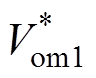 ,由式(21)可推导出,系统仅在PBC控制器控制下的闭环传递函数恒为
,由式(21)可推导出,系统仅在PBC控制器控制下的闭环传递函数恒为
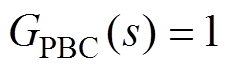 (22)
(22)
由式(22)可知,在理想情况下,即不考虑采样滤波器Gs(s)时,PBC控制器的闭环控制带宽无穷大。因此,FC端口变换器的输入电流可完全复现其对应的输入电流基准,但PBC控制器无法抑制系统中的高频干扰。在实际工程应用中,为消除电压/电流信号中高频干扰对系统性能的影响,需先对采集信号进行滤波处理再代入控制算法进行运算,从而获得相应的控制信号。需要说明的是,Gs(s)的截止频率通常设为端口变换器开关频率的1/10。
对于稳定的高阶系统,其动态性能主要由闭环主导极点决定。因此,通过分析系统参数对系统闭环传递函数主导极点的影响,即可定性说明系统参数与动态性能的关联关系。基于表1中初选的系统参数,根据式(21)可得,在考虑采样滤波器Gs(s)后,系统闭环传递函数GPBC(s)的零极点见表2。由表2可知,零点z3、z4和极点s3、s4可近似相消,且远大于零点z1、z2和极点s1、s2。因此,系统动态性能主要由闭环主导极点s1、s2和闭环主导零点z1、z2决定。
表1 FC/LB HPSS的参数
Tab.1 Parameters of the FC/LB HPSS

单元参 数数 值 FC供电单元额定电压V1/V105.6 额定功率P1max/kW3 最大功率变化率bpcr/(kW/s)0.3 滤波电感Ln1/mH1 滤波电容Cn1/mF220 开关频率fs/kHz20 下垂系数m3.18×10–3
(续)
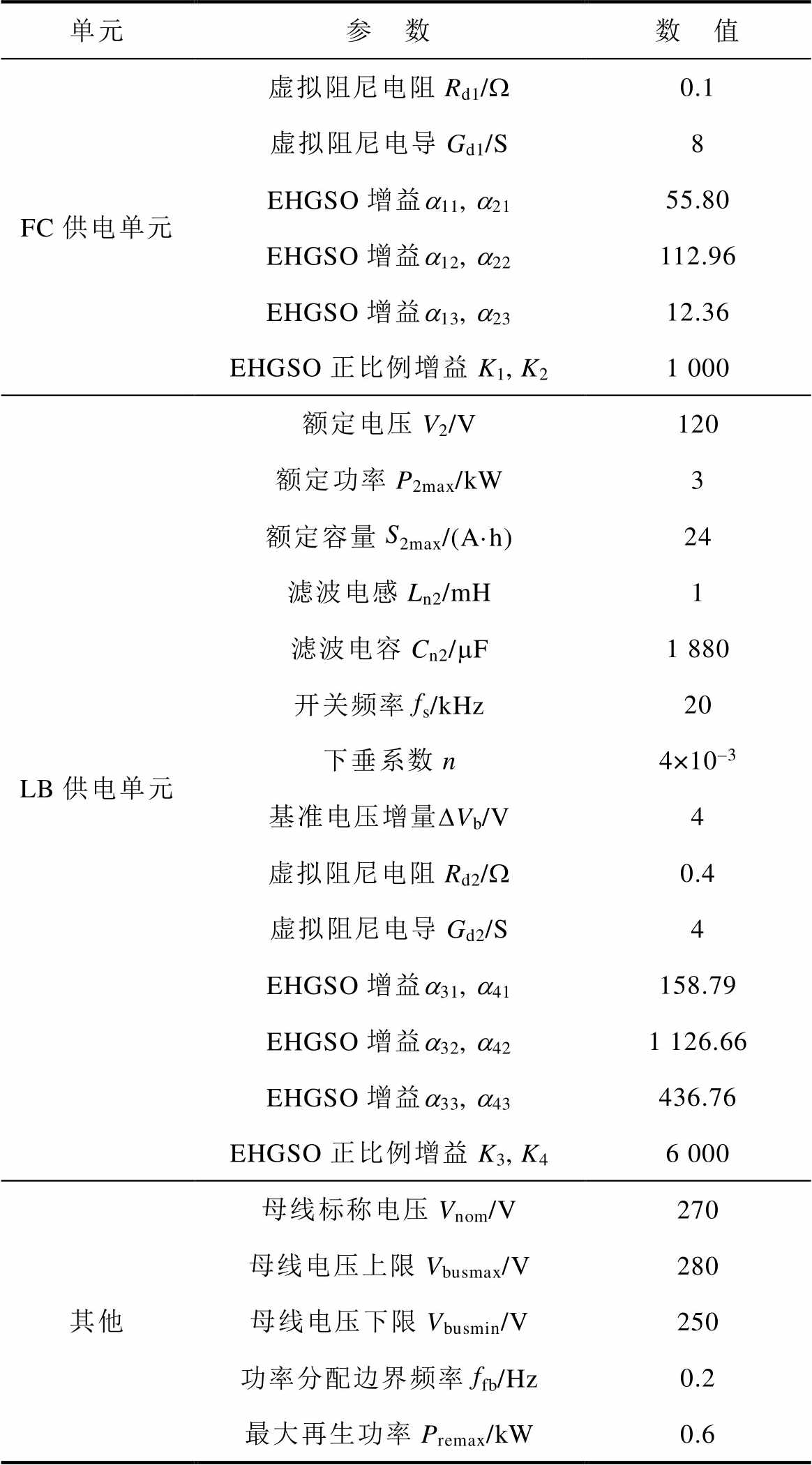
单元参 数数 值 FC供电单元虚拟阻尼电阻Rd1/W0.1 虚拟阻尼电导Gd1/S8 EHGSO增益a11, a2155.80 EHGSO增益a12, a22112.96 EHGSO增益a13, a2312.36 EHGSO正比例增益K1, K21 000 LB供电单元额定电压V2/V120 额定功率P2max/kW3 额定容量S2max/(A·h)24 滤波电感Ln2/mH1 滤波电容Cn2/mF1 880 开关频率fs/kHz20 下垂系数n4×10–3 基准电压增量DVb/V4 虚拟阻尼电阻Rd2/W0.4 虚拟阻尼电导Gd2/S4 EHGSO增益a31, a41158.79 EHGSO增益a32, a421 126.66 EHGSO增益a33, a43436.76 EHGSO正比例增益K3, K46 000 其他母线标称电压Vnom/V270 母线电压上限Vbusmax/V280 母线电压下限Vbusmin/V250 功率分配边界频率ffb/Hz0.2 最大再生功率Premax/kW0.6
表2 GPBC(s)的零极点
Tab.2 Zeros and poles of GPBC(s)
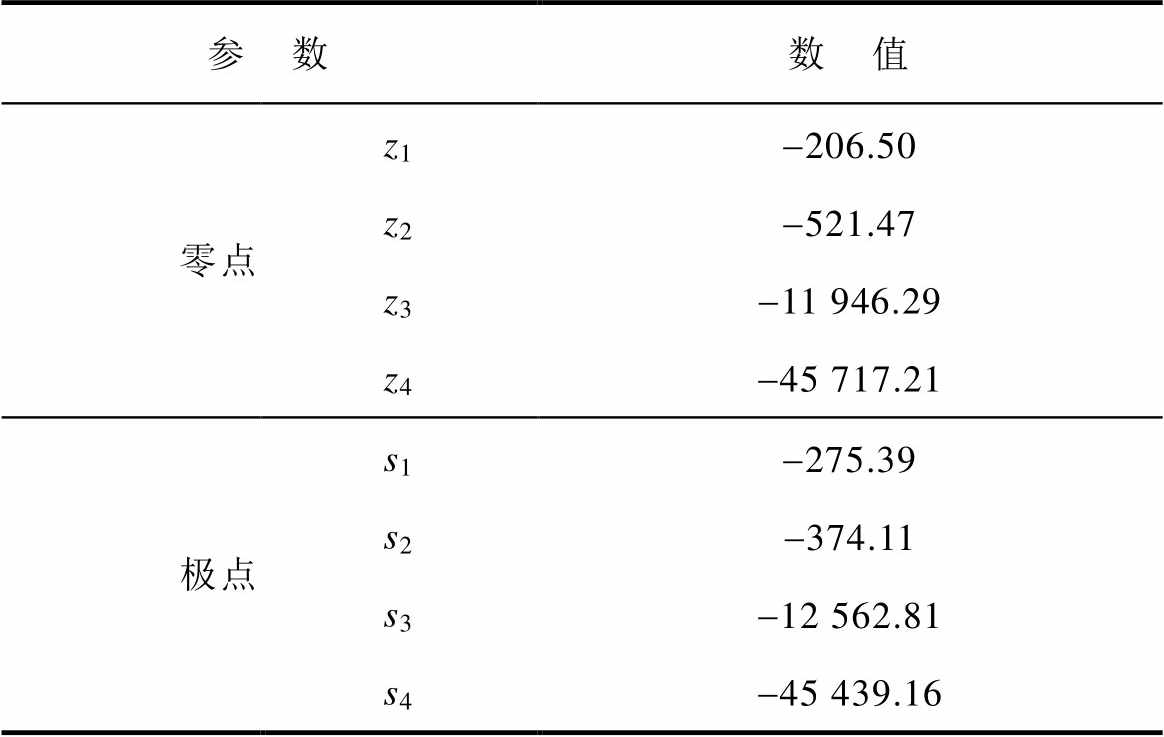
参 数数 值 零点z1-206.50 z2-521.47 z3-11 946.29 z4-45 717.21 极点s1-275.39 s2-374.11 s3-12 562.81 s4-45 439.16
图4所示为系统闭环传递函数GPBC(s)的零极点分布,图中除调节的参数外,其余参数见表1。从图4a中可以看出,主导极点s2实部的模比主导极点s1实部的模大一倍左右,故主导极点s1对系统动态性能的影响更大。随着时间常数Ts的增大,主导极点s1往靠近虚轴的方向移动,系统的动态响应速度变慢。从图4b中可以看出,随着虚拟耗散电阻Rd1的增大,主导极点s1和s2均往远离虚轴的方向移动,系统动态响应速度变快。从图4c、图4d和图4e中可以看出,随着虚拟耗散电导Gd1、滤波电感Ln1和滤波电容Cn1的增大,主导极点s1和s2均往靠近虚轴的方向移动,系统动态响应速度变慢。综上所述,系统参数的整定方法可归纳为:若需加快系统动态响应速度,则可适当减小采样滤波器时间常数Ts、虚拟耗散电导Gd1、滤波电感Ln1、滤波电容Cn1或增大虚拟耗散电阻Rd1;若需降低系统动态响应速度,则可适当增大采样滤波器时间常数Ts、虚拟耗散电导Gd1、滤波电感Ln1、滤波电容Cn1或减小虚拟耗散电阻Rd1。
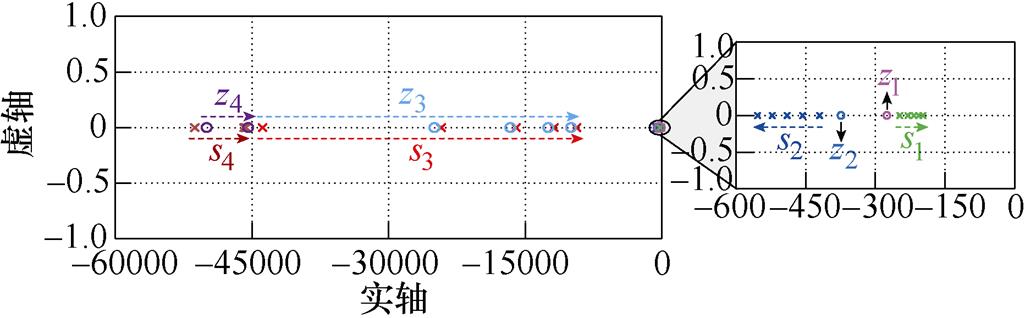
(a)Ts由2×10-5 s增大至1×10-4 s
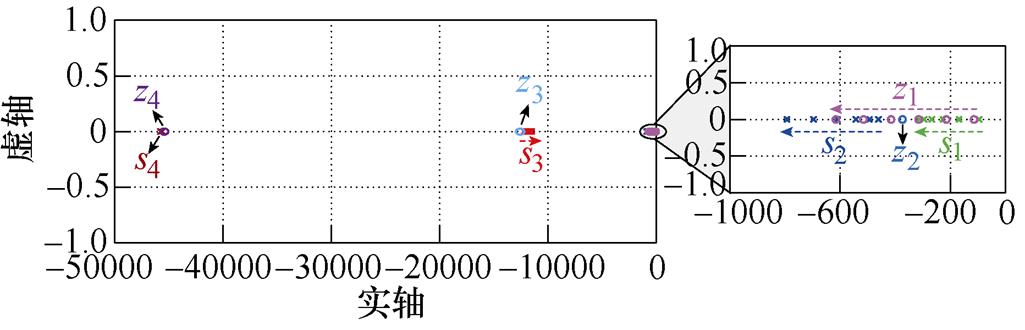
(b)Rd1由0.1 W 增大至0.6 W
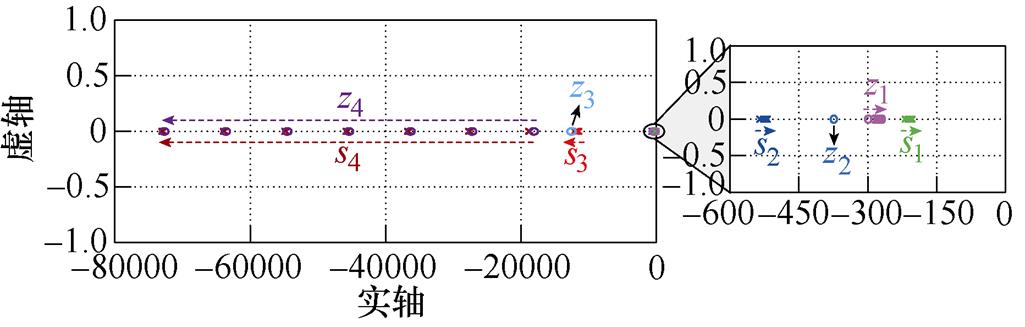
(c)Gd1由4 S增大至16 S
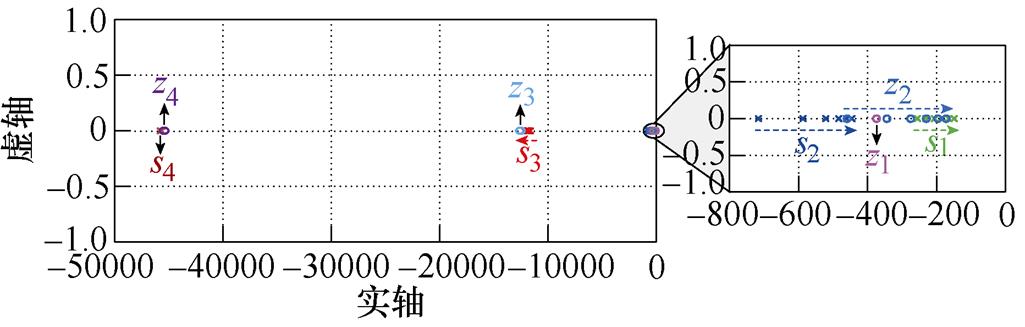
(d)Ln1由0.6 mH增大至1.6 mH
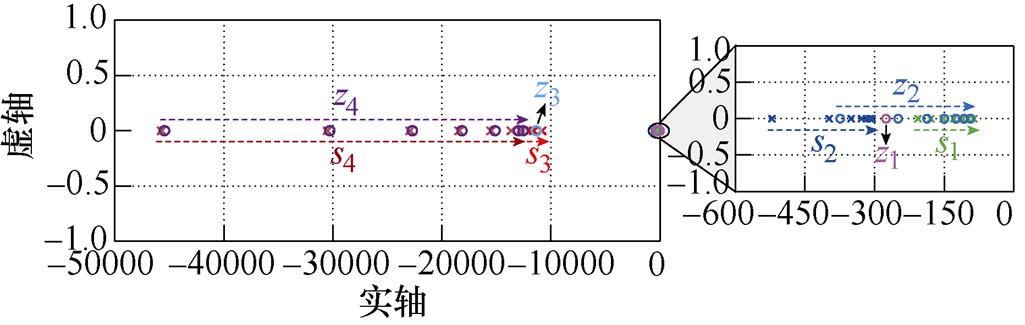
(e)Cn1由220 mF增大至880 mF
图4 GPBC(s)的零极点分布
Fig.4 Pole-zero location of GPBC(s)
为保证FC供电单元仅提供低频负荷功率而LB供电单元缓冲所有的高频脉动功率,LB端口变换器的动态响应速度应远快于FC端口变换器。根据这一准则,本文将FC和LB端口变换器在10 %负载和满载之间阶跃跳变的调节时间(误差带取2 %)分别设置为20 ms和1 ms,超调量均不超过3 %。图5所示为FC端口变换器在不同控制参数下对应的动态性能。通过对比不同控制参数对应的动态性能,从图5中可以看出,随着虚拟耗散电阻Rd1的增大,FC端口变换器的调节时间缩短,动态响应速度变快,但超调量增大;随着虚拟耗散电导Gd1的增大,FC端口变换器的调节时间变长,动态响应速度变慢,超调量略微增大。这说明FC端口变换器控制参数与动态响应速度的关联关系符合上述分析结果。由于LB端口变换器控制参数的设计过程与FC端口变换器类似,在此不再赘述。根据设定的动态性能指标,FC和LB端口变换器的PBC控制器参数Rd1、Gd1和Rd2、Gd2最终选取为0.1 W、8 S和0.4 W、4 S,见表1。在此控制参数下,FC和LB端口变换器对应的调节时间(误差带取2 %)分别为20.66 ms和1.04 ms,超调量分别为1.46 %和2.97 %,均基本满足设计要求。
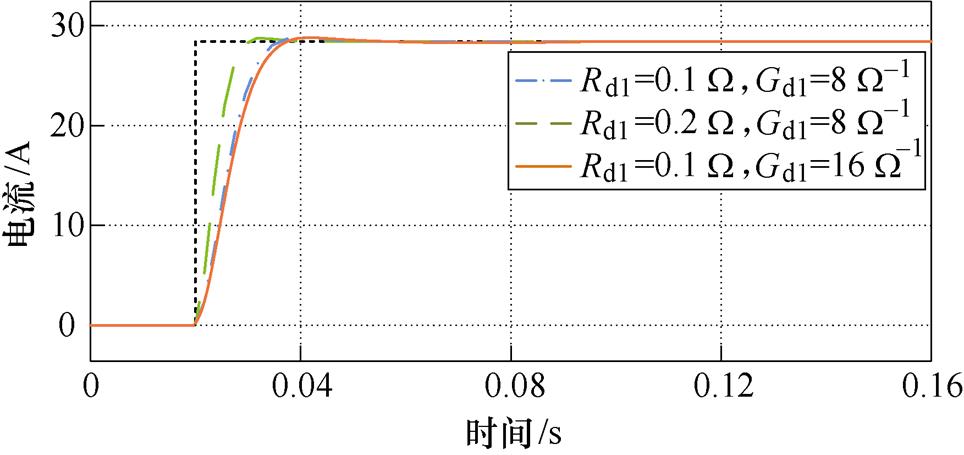
图5 FC端口变换器的动态性能
Fig.5 Dynamic performance of the FC converter
结合图3及式(18)~式(20),EHGSO的扰动观测值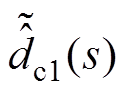 对扰动
对扰动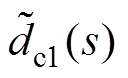 的闭环传递函数Gc1(s)可推导为
的闭环传递函数Gc1(s)可推导为
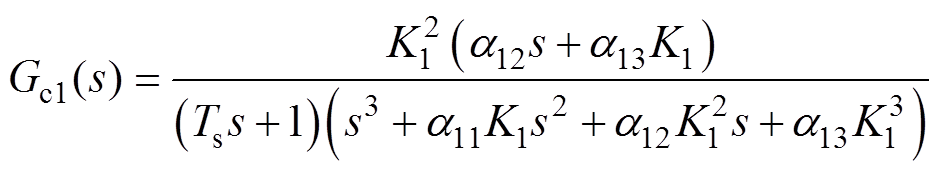 (23)
(23)
由于采样滤波器Gs(s)的时间常数Ts通常很小,则Gc1(s)的极点-1/Ts远离虚轴,其所对应的响应分量衰减很快,可忽略不计。因此,可将闭环传递函数Gc1(s)近似为
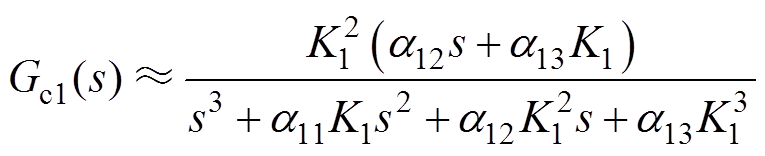 (24)
(24)
在工程实践中,通常要求控制系统既要具有较快的响应速度,又要具有一定的阻尼程度。为此,高阶系统参数常常调整到使系统具有一对闭环共轭主导极点。此时,高阶系统的动态性能可用二阶系统的动态性能指标来估算。因此,闭环传递函数Gc1(s)可设计为
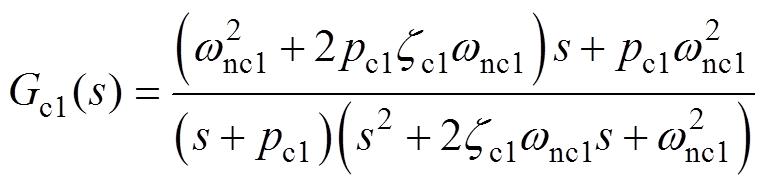 (25)
(25)
式中,pc1为Gc1(s)非主导极点实部的模;zc1为Gc1(s)近似二阶系统的阻尼比(或相对阻尼系数);wnc1为Gc1(s)近似二阶系统的自然频率(或无阻尼振荡频率)。
若保证Gc1(s)具有一对共轭复数主导极点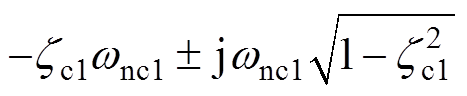 (0<zc1<1
(0<zc1<1 ,且闭环零点
,且闭环零点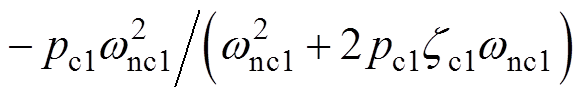 不在主导极点附近,非主导极点-pc1实部的模比主导极点实部的模大3倍以上(pc1≥3zc1wnc1),则可将Gc1(s)进一步近似为
不在主导极点附近,非主导极点-pc1实部的模比主导极点实部的模大3倍以上(pc1≥3zc1wnc1),则可将Gc1(s)进一步近似为
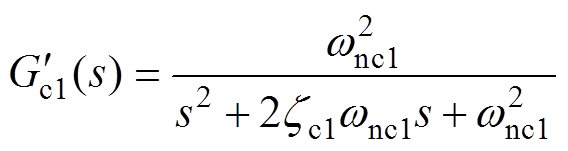 (26)
(26)
式中,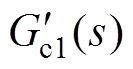 为Gc1(s)的近似二阶系统的传递函数。
为Gc1(s)的近似二阶系统的传递函数。
根据经典控制理论可知,二阶系统式(26)单位阶跃响应的超调量sc1 %和调节时间tsc1分别为
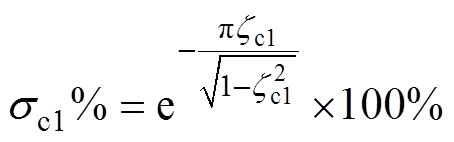 (27)
(27)
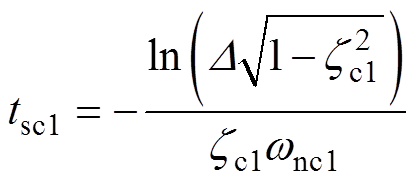 (28)
(28)
式中, 为系统实际响应与稳态输出之间的误差带,本文取
为系统实际响应与稳态输出之间的误差带,本文取 =2 %。
=2 %。
为保证EHGSO及时补偿不确定扰动对系统性能的影响,EHGSO的动态响应速度应远快于PBC控制器。根据这一准则,本文将FC和LB端口变换器所采用的EHGSO的调节时间分别设置为10 ms和0.5 ms,超调量不超过5 %。因此,二阶系统式(26)单位阶跃响应的调节时间设置为tsc1=10 ms,超调量满足sc1 %≤5 %。
一般而言,为确保二阶系统单位阶跃响应的振荡特性适度且调节时间较短,系统的阻尼比通常设定为0.4~0.8。首先,考虑到系统的超调量设计要求,本文将二阶系统式(26)的阻尼比设置为zc1= 0.707,则其对应的超调量为4.33 %,满足设计要求。其次,将zc1=0.707和tsc1=0.01 s代入式(28),即 可求解出二阶系统式(26)的自然频率为wnc1= 602.33 rad/s。再次,根据条件pc1≥3zc1wnc1选取合适的pc1,确保Gc1(s)的零点不在主导极点附近(若选取的pc1无法保证Gc1(s)的零点不在主导极点附近,则需根据条件pc1≥3zc1wnc1重新选取pc1)。本节取pc1=100zc1wnc1=42 584.46,则Gc1(s)的零点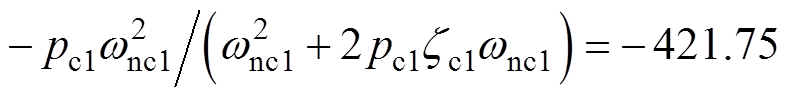 不在主导极点
不在主导极点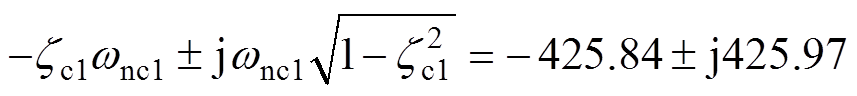 附近,满足Gc1(s)的简化条件。最后,通过合理选择dc1 EHGSO的正比例增益K1,结合式(24)和式(25),求解出dc1 EHGSO的观测增益a11、a12和a13,并验证其能否保证h1(s)=s3+a11s2+a12s+a13为Hurwitz多项式,即能否保证条件式(29)成立。同理,若h1(s)不是Hurwitz多项式,则需重复上述步骤直至h1(s)为Hurwitz多项式为止。
附近,满足Gc1(s)的简化条件。最后,通过合理选择dc1 EHGSO的正比例增益K1,结合式(24)和式(25),求解出dc1 EHGSO的观测增益a11、a12和a13,并验证其能否保证h1(s)=s3+a11s2+a12s+a13为Hurwitz多项式,即能否保证条件式(29)成立。同理,若h1(s)不是Hurwitz多项式,则需重复上述步骤直至h1(s)为Hurwitz多项式为止。
若h1(s)=s3+a11s2+a12s+a13为Hurwitz多项式,则根据劳斯判据可得,观测增益a11、a12和a13满足
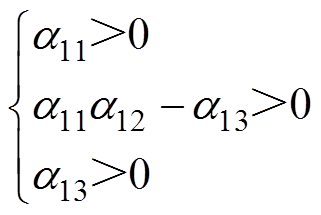 (29)
(29)
由式(24)和式(25)可得,EHGSO参数满足
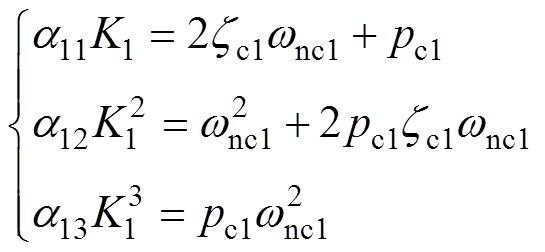 (30)
(30)
本文取K1=1 000,则根据式(30)求解出EHGSO的观测增益a11、a12和a13分别为a11=43.44、a12= 36.63和a13=15.45,满足条件式(29)。
图6所示为Gc1(s)在不同观测增益下对应的动态性能。从图6中可以看出,原传递函数Gc1(s)的超调量与设定的超调量指标相差太大,不满足设计要求。为此,本文将在设计参数的基础上适当调节dc1 EHGSO的观测增益a11、a12和a13,以保证原传递函数Gc1(s)的动态性能满足设定指标。通过对比Gc1(s)在不同观测增益下对应的动态性能可以发现,当观测增益a12和a13保持不变时,增大观测增益a11,Gc1(s)的超调量将稍微增大,调节时间将变长;当观测增益a11和a13保持不变时,增大观测增益a12,Gc1(s)的超调量将显著减小,调节时间将变长;当观测增益a11和a12保持不变时,增大观测增益a13,Gc1(s)的超调量将增大,调节时间明显变长。因此,根据上述规律,本节在设计参数的基础上适当增大a11、a12以及适当减小a13,使原传递函数Gc1(s)的超调量显著减小,调节时间适当变长,从而满足预设指标。EHGSO式(14)的观测增益a11、a12和a13最终设定为a11=55.80、a12=112.96和a13=12.36,满足条件式(29)。在此参数下,dc1 EHGSO单位阶跃响应的调节时间(误差带取2 %)为9.98 ms,超调量为4.25 %,满足设计要求。参照dc1 EHGSO的参数设计过程,dv1 EHGSO最终选取的参数与dc1 EHGSO参数完全相同,而dc2和dv2 EHGSO的正比例增益最终设定为K3=K4=6 000,观测增益最终设定为a31=a41=158.79、a32=a42=1 126.66和a33=a43= 436.76。在此参数下,dc2和dv2 EHGSO单位阶跃响应的调节时间(误差带取2 %)为0.48 ms,超调量为4.32 %,满足设计要求。
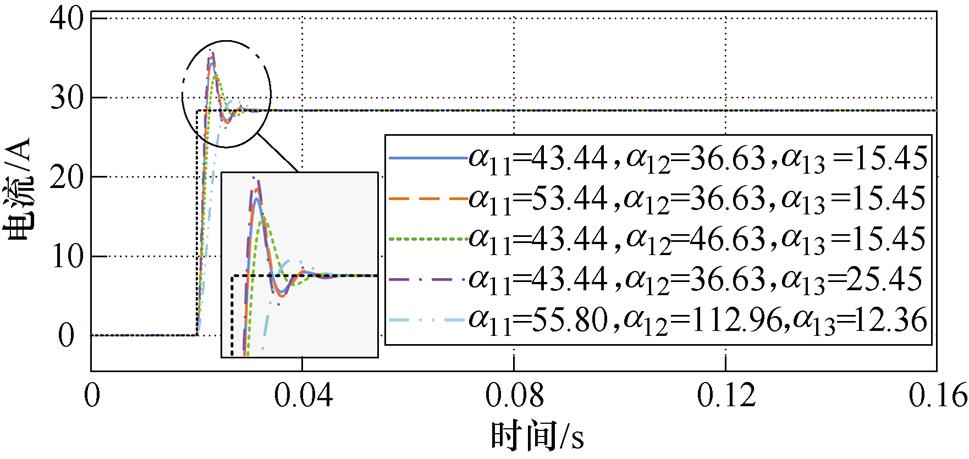
图6 Gc1(s)的动态性能
Fig.6 Dynamic performance of Gc1(s)
为验证所提控制策略的有效性和可行性,搭建了FC/LB HPSS的实验平台如图7所示,系统参数详见表1。负荷部分采用可编程电子负载来模拟。

图7 燃料电池-锂电池混合供电系统实验平台
Fig.7 FC-LB HPSS experiment platform
图8所示为FC端口变换器仅在PBC控制器控制下带阻性负荷的仿真结果。在此仿真中,不确定扰动dc1和dv1设为0,输入电流基准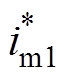 在10 %负载(2.84 A)和满载(28.41 A)之间阶跃跳变。从图8a中可以看出,当虚拟耗散电阻Gd1=8 S保持不变时,FC端口变换器输入电流的动态响应速度随着虚拟耗散电阻Rd1的增大而变快。从图8b中可以看出,当虚拟耗散电阻Rd1=0.1 W 保持不变时,虚拟耗散电导Gd1越大,FC端口变换器输入电流的动态响应速度越慢。这与PBC控制器的参数分析结果相一致,验证了PBC控制器参数设计的正确性。
在10 %负载(2.84 A)和满载(28.41 A)之间阶跃跳变。从图8a中可以看出,当虚拟耗散电阻Gd1=8 S保持不变时,FC端口变换器输入电流的动态响应速度随着虚拟耗散电阻Rd1的增大而变快。从图8b中可以看出,当虚拟耗散电阻Rd1=0.1 W 保持不变时,虚拟耗散电导Gd1越大,FC端口变换器输入电流的动态响应速度越慢。这与PBC控制器的参数分析结果相一致,验证了PBC控制器参数设计的正确性。
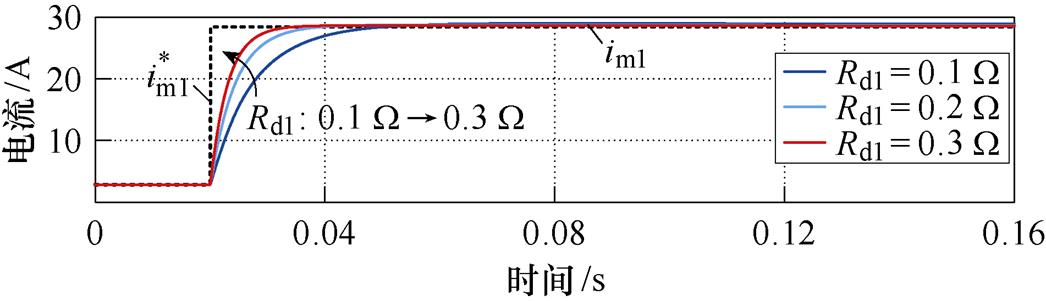
(a)Rd1由0.1 W 增大至0.3 W
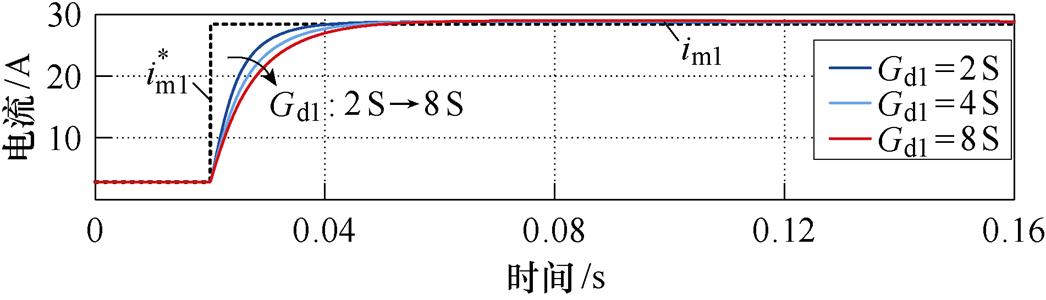
(b)Gd1由2 S增大至8 S
图8 FC端口变换器带阻性负荷的仿真结果
Fig.8 Simulation results of the FC converter with resistive load
图9所示为FC和LB端口变换器仅在PBC控制器控制下的动态特性,图中ts1和ts2分别为FC和LB端口变换器的调节时间,s1 %和s2 %分别为FC和LB端口变换器的超调量。在此实验中,不确定扰动dc1、dv1、dc2和dv2均设为0,输入电流基准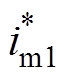 和
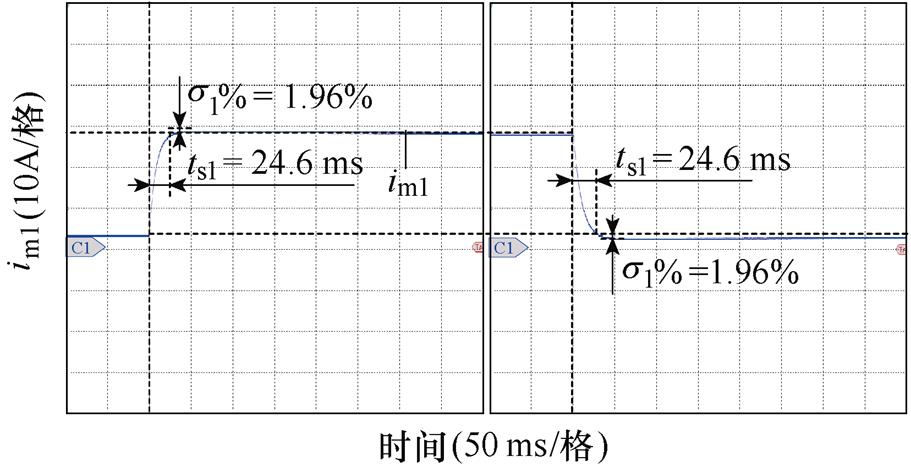
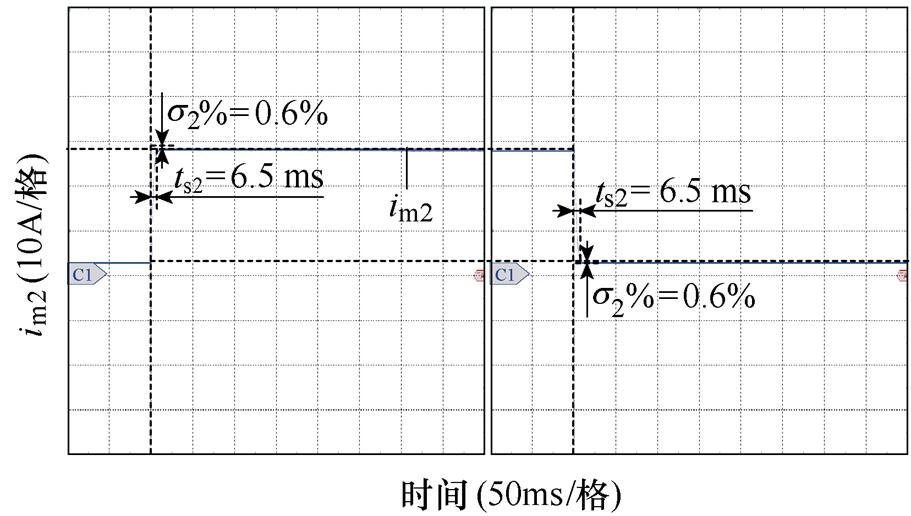
和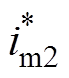 在10 %负载(2.84 A)和满载(28.41 A)之间阶跃跳变。从图9中可以看出,FC和LB端口变换器实际的调节时间分别为24.6 ms和6.5 ms(误差带取2 %),超调量分别为1.96 %和0.6 %。尽管FC和LB端口变换器在PBC控制器控制下实际的动态性能指标与设计值存在一定的差异,但LB端口变换器的动态响应速度远快于FC端口变换器,满足PBC控制器参数设计要求。
在10 %负载(2.84 A)和满载(28.41 A)之间阶跃跳变。从图9中可以看出,FC和LB端口变换器实际的调节时间分别为24.6 ms和6.5 ms(误差带取2 %),超调量分别为1.96 %和0.6 %。尽管FC和LB端口变换器在PBC控制器控制下实际的动态性能指标与设计值存在一定的差异,但LB端口变换器的动态响应速度远快于FC端口变换器,满足PBC控制器参数设计要求。
(a)FC端口变换器
(b)LB端口变换器
图9 FC和LB端口变换器仅在PBC控制下的动态特性
Fig.9 Dynamic characteristics of FC and LB converters under the control of PBC controllers
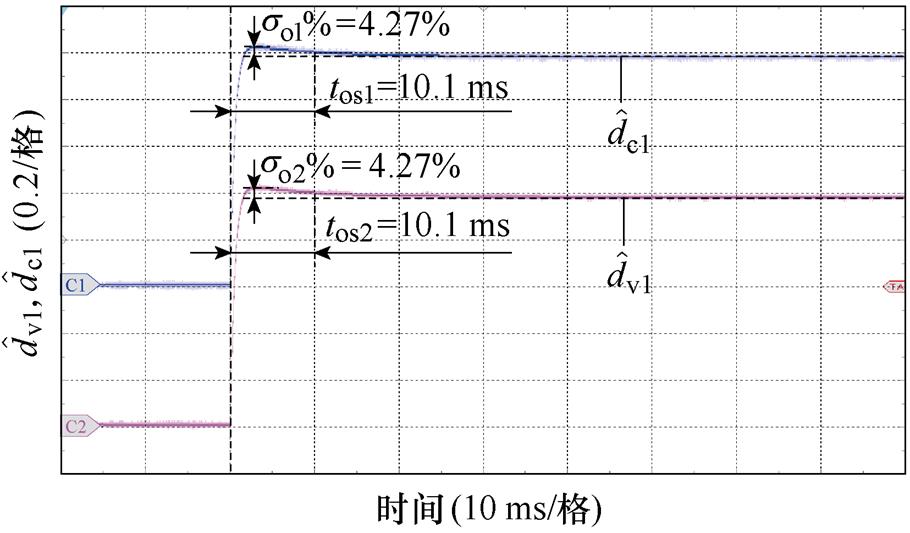
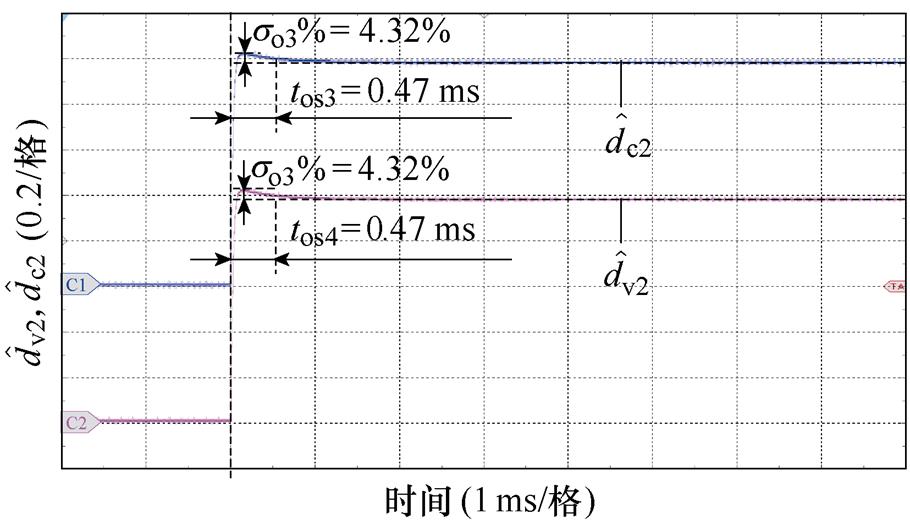
图10所示为FC和LB端口变换器EHGSO的动态特性,其中tos1~tos4和so1 %~so4 %分别为dc1、dv1、dc2和dv2 EHGSO的调节时间和超调量。在此实验中,FC和LB端口变换器带阻性满载负荷,扰动dc1、dv1、dc2和dv2由0阶跃突变为1。需要说明的是,由式(1)可知,可将不确定扰动dc1和dc2等效为端口变换器输入侧电压不确定的电压源,不确定扰动dv1和dv2等效为端口变换器输出侧电流不确定的电流源。因此,为简单起见,本文通过在端口变换器的输入侧或输出侧外加电压源或电流源以实现不确定扰动的等效注入。从图10中可以看出,FC端口变换器dc1和dv1 EHGSO实际的调节时间为10.1 ms,超调量为4.27 %;LB端口变换器dc2和dv2 EHGSO实际的调节时间为0.47 ms,超调量为4.32 %。因此,FC和LB端口变换器EHGSO实际的动态性能指标与设计值基本一致,满足设计要求。
图11所示为FC端口变换器不采用或采用EHGSO的实验结果。在此实验中,FC端口变换器带阻性满载负荷,不确定扰动dv1设为0,而不确定扰动dc1设为随机扰动。从图11中可以看出,若FC端口变换器不采用EHGSO,当不确定扰动dc1和dv1均为0时,FC端口变换器的输出电压稳定在设定值270 V,然而随着不确定扰动dc1随机变化,FC端口变换器的输出电压也将随机波动。当FC端口变换器采用EHGSO后,无论不确定扰动dc1和dv1如何变化,所设计的EHGSO均能跟踪上不确定扰动dc1和dv1,FC端口变换器的输出电压始终稳定在设定值270 V。因此,所设计的EHGSO能够较好地提升端口变换器的抗干扰能力。
(a)FC端口变换器
(b)LB端口变换器
图10 FC和LB端口变换器EHGSO的动态特性
Fig.10 Dynamic characteristics of EHGSOs of FC and LB converters
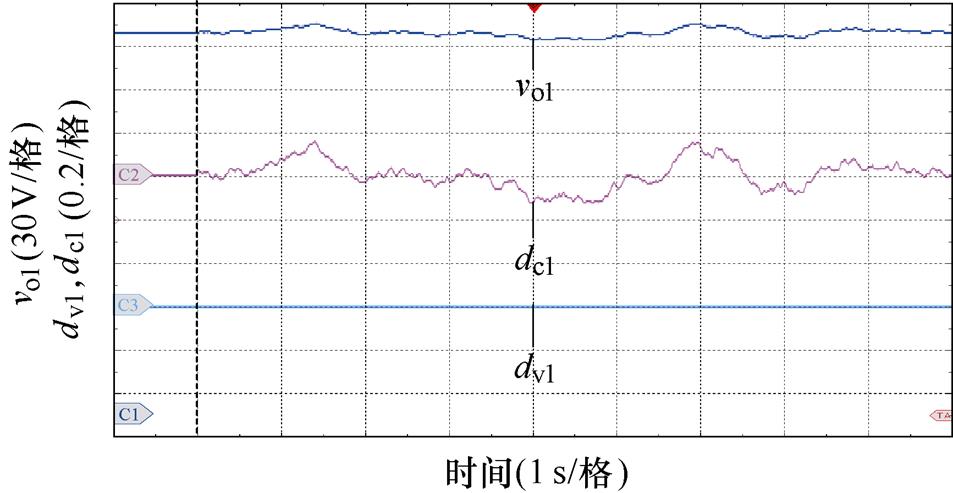
(a)FC端口变换器未采用EHGSO
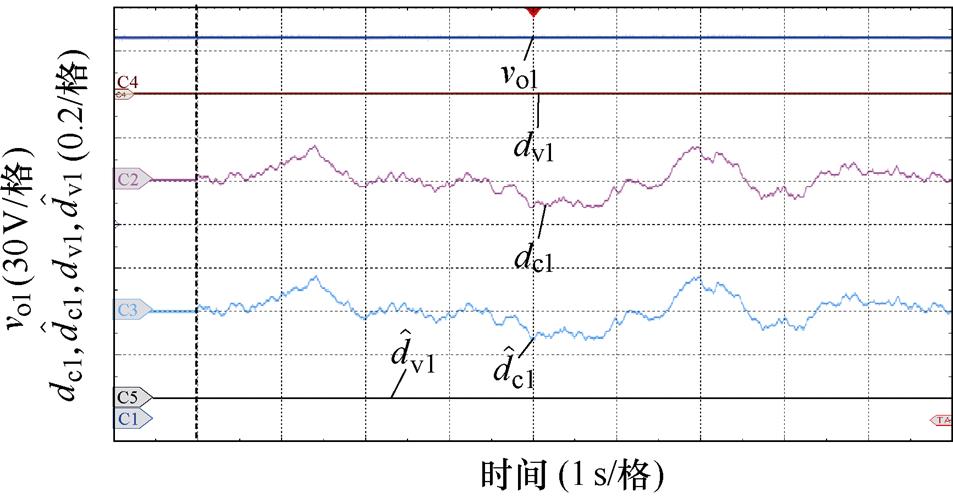
(b)FC端口变换器采用EHGSO
图11 FC端口变换器不采用或采用EHGSO的实验结果
Fig.11 Experimental results of the FC converter without or with EHGSOs
图12所示为FC端口变换器在PBC控制器和PI控制器控制下带CPL的仿真结果。在此仿真中,输入电压叠加随机扰动,输出侧从第3 s开始叠加随机扰动,输入电流基准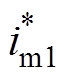 从第12 s由10 %负载(2.84 A)跳变到满载(28.41 A)。从图12中可以看出,在轻载条件下,输入测电压叠加扰动时,两个控制器性能无明显差距,当输出侧叠加电流扰动时,PI控制器易出现突变,使得母线电压出现较大波动甚至振荡,满载时,该现象消失,但母线电压的平滑性劣于无源控制器。
从第12 s由10 %负载(2.84 A)跳变到满载(28.41 A)。从图12中可以看出,在轻载条件下,输入测电压叠加扰动时,两个控制器性能无明显差距,当输出侧叠加电流扰动时,PI控制器易出现突变,使得母线电压出现较大波动甚至振荡,满载时,该现象消失,但母线电压的平滑性劣于无源控制器。
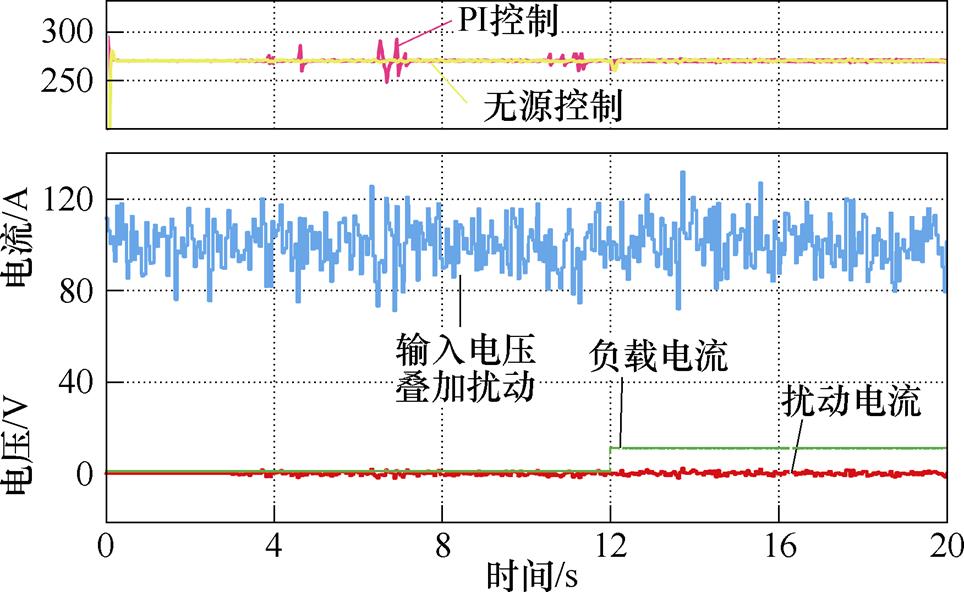
图12 无源控制器与PI控制器仿真结果
Fig.12 Simulation results of passivity-based controller and PI controller
图13所示为FC/LB HPSS带CPL的实验结果。在此实验中,CPL功率在0.3 kW(10 %负载)和3 kW(满载)间阶跃跳变,不确定扰动dv1和dv2设为0,而不确定扰动dc1和dc2设为随机扰动。从图13中可以看出,无论FC和LB端口变换器是否采用EHGSO,当CPL功率阶跃跳变时,FC供电单元缓慢响应负荷功率变化,最终提供所有的负荷功率,而LB供电单元快速响应负荷功率突变,其稳态输出功率为0 kW。此外,直流母线电压始终处于设定范围内,并且系统在整个过程中始终是稳定的。然而,通过对比图10b和图13a可以发现,若FC和LB端口变换器均不采用EHGSO,随着不确定扰动dc1和dc2随机变化,直流母线电压随机波动,FC和LB供电单元的稳态输出功率也将随机波动;而FC和LB端口变换器采用EHGSO后,无论扰动dc1、dv1、dc2和dv2如何变化,所设计的EHGSO均能跟踪上相应的扰动,并且直流母线电压始终稳定在设定值270 V,FC和LB供电单元的稳态输出功率也将稳定在稳态值。因此,所提策略不仅实现了直流母线电压调节、动态功率分配等控制目标,还能保证系统稳定运行,并且所设计的EHGSO极大地提升了系统的鲁棒性,验证了所提策略的有效性。
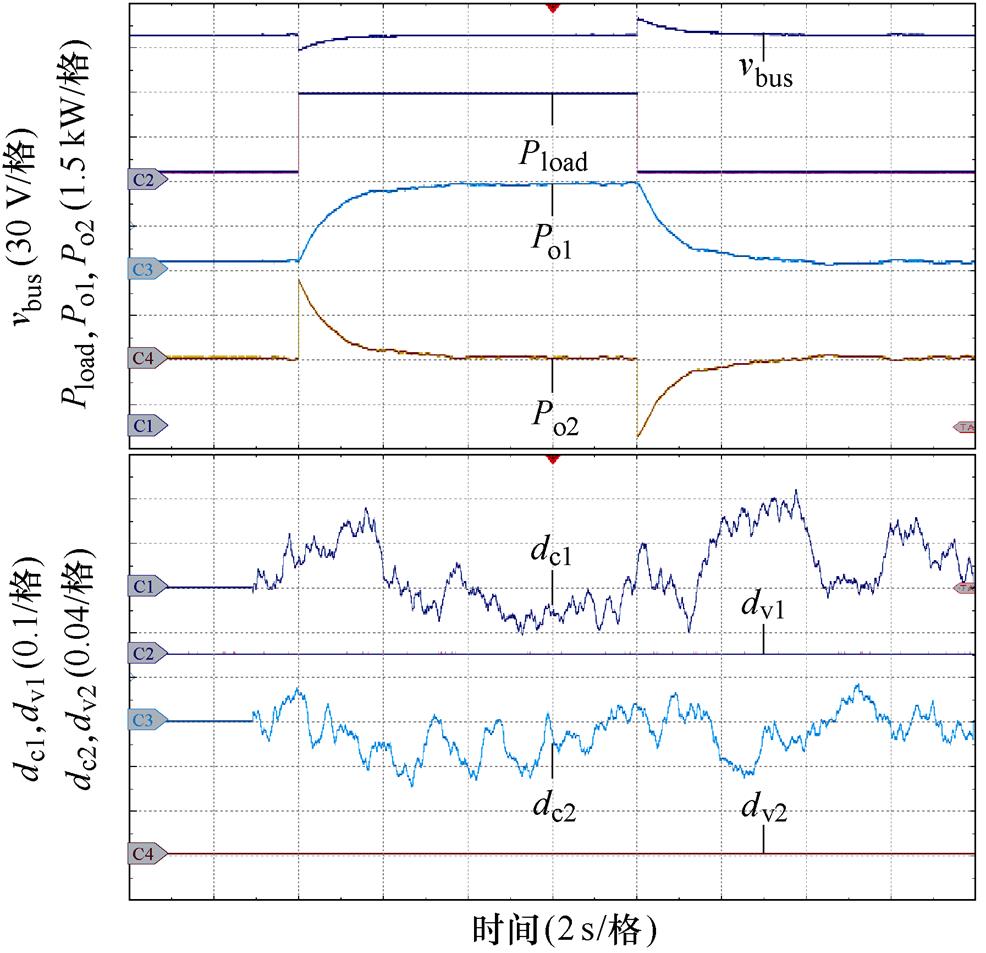
(a)FC和LB端口变换器未采用EHGSO
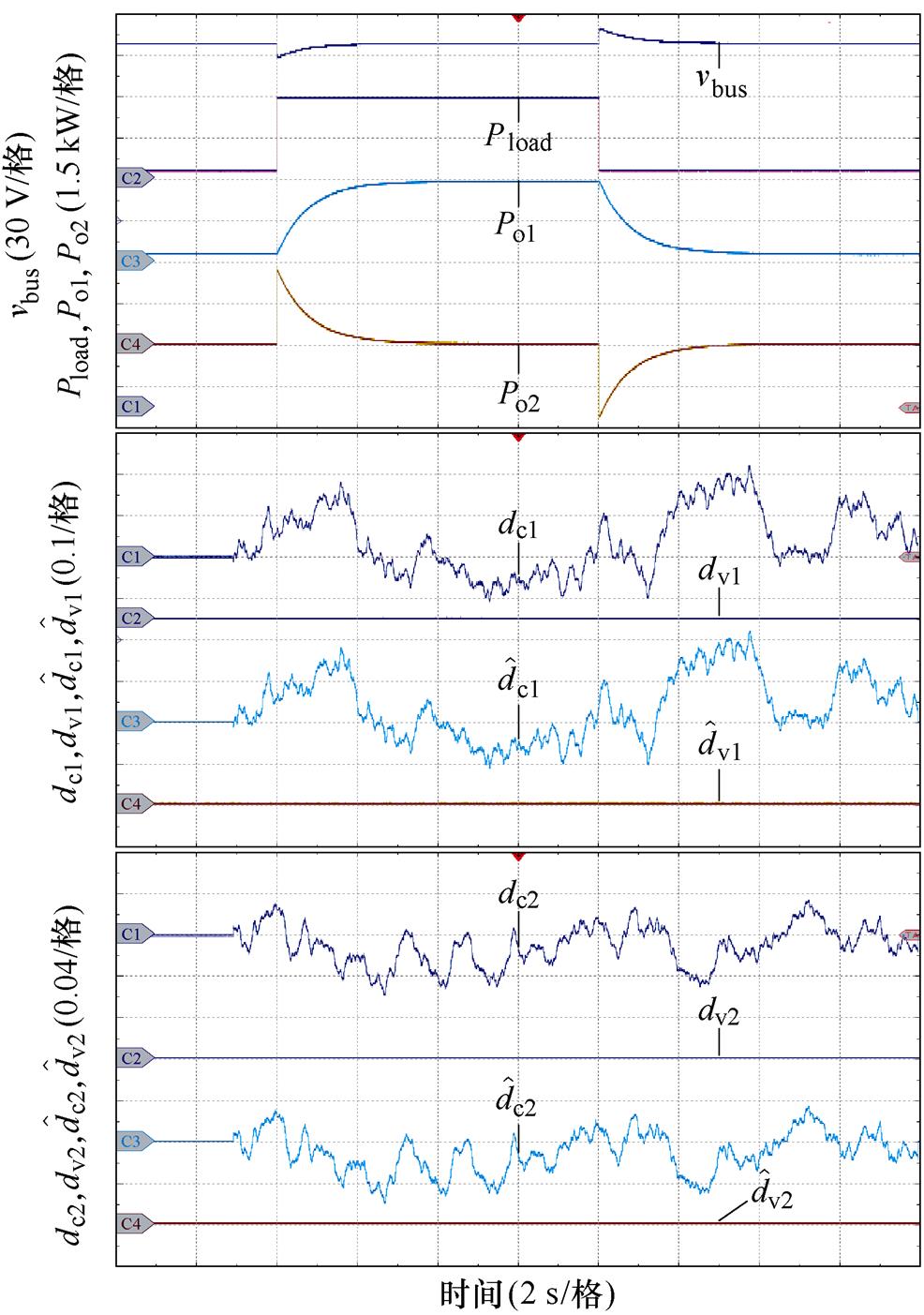
(b)FC和LB端口变换器采用EHGSO
图13 FC/LB HPSS带CPL的实验结果
Fig.13 Experimental results of the FC/LB HPSS with CPL
图14所示为FC/LB HPSS带脉冲负荷的半实物实验结果。在此实验中,脉冲功率负荷功率在-2~3 kW间随机变化,不确定扰动dv1和dv2设为0,而不确定扰动dc1和dc2设为随机扰动。从图14可以看出,功率分配正常。通过对比图11b和图14a可以发现,若FC和LB端口变换器采用EHGSO后,FC供电单元的输出功率更平滑,并且无论扰动dc1、dv1、dc2和dv2如何随机变化,所设计的EHGSO均能跟踪上相应的扰动。
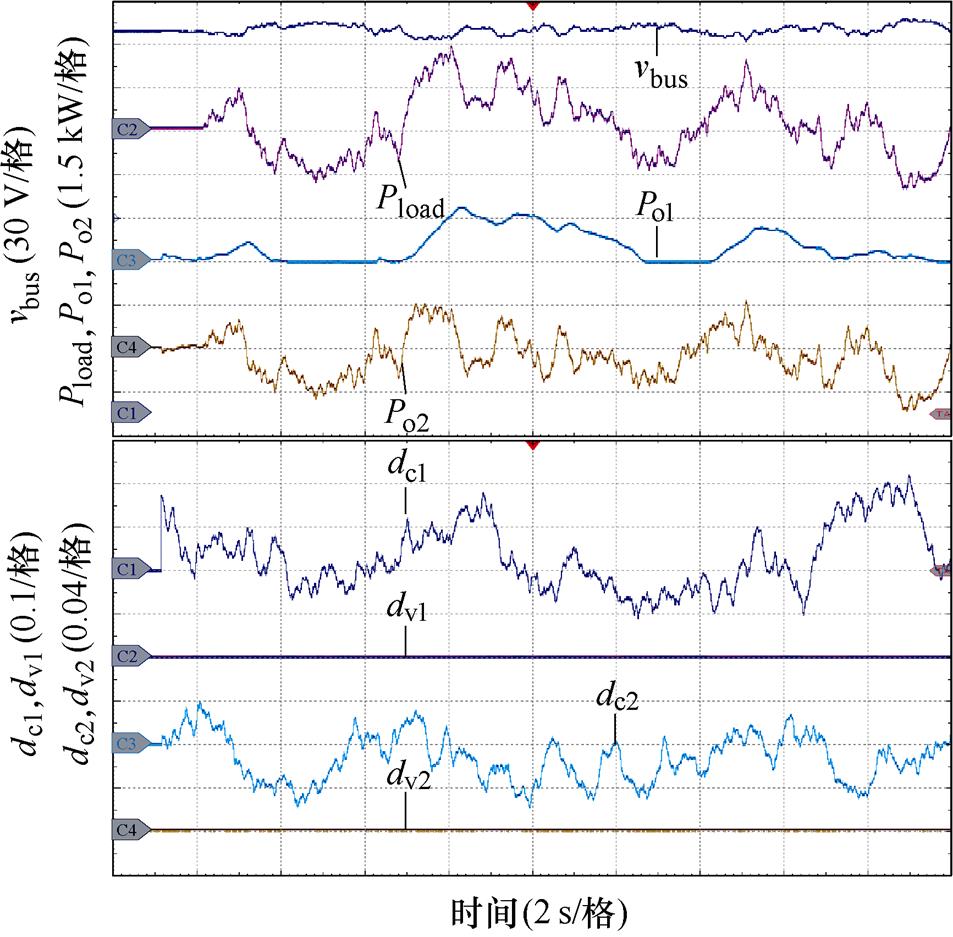
(a)FC和LB端口变换器未采用EHGSO
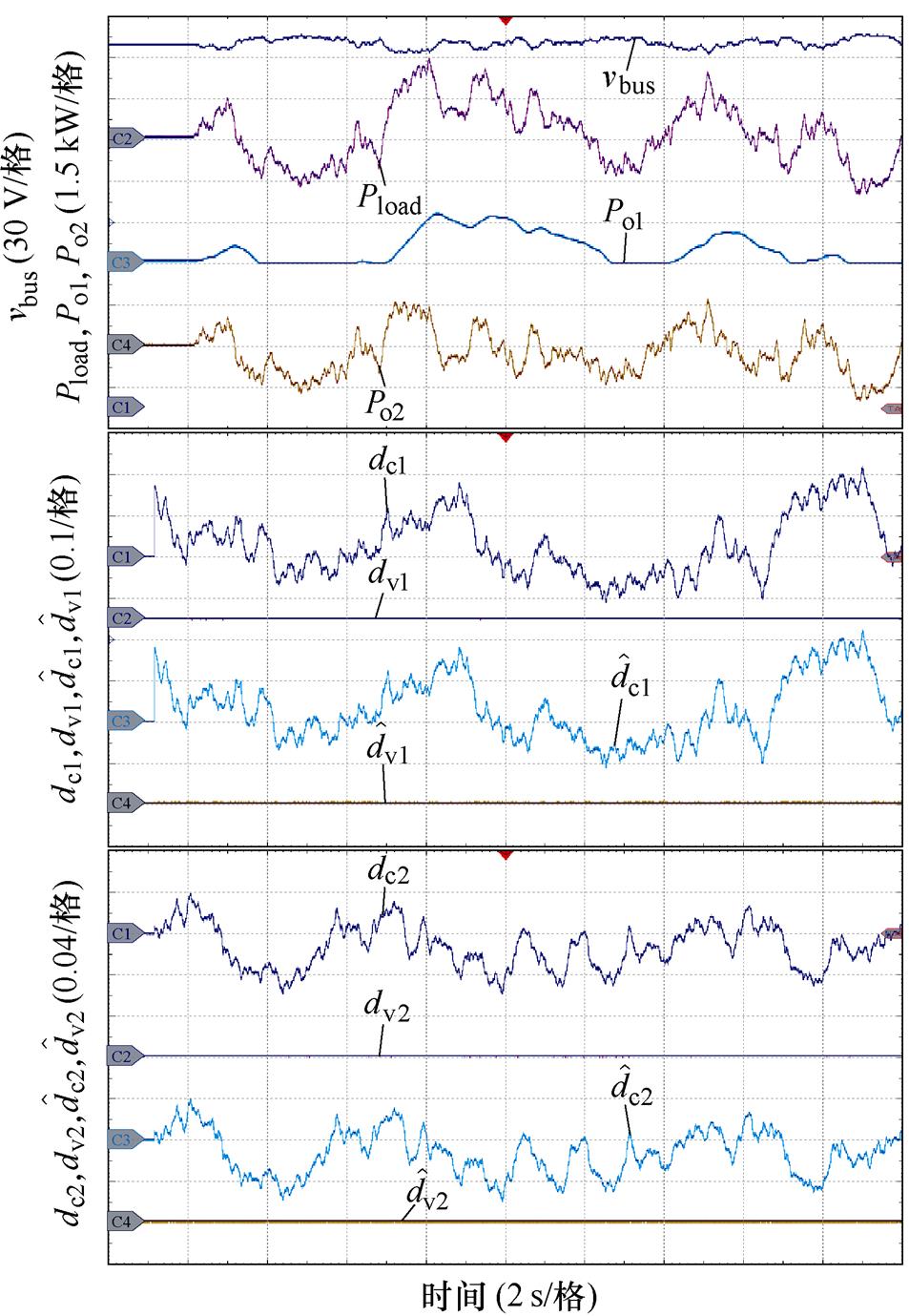
(b)FC和LB端口变换器采用EHGSO
图14 FC/LB HPSS带脉动负荷的实验结果
Fig.14 Experiment results of the FC/LB HPSS with pulsating load
针对采用无源控制结合扩张高增益观测器的燃料电池-锂电池混合供电系统,本文提出了一种兼顾系统动态性能的无需考虑负荷模型的复合控制器参数整定方法。实验结果表明,实际的动态性能指标与设计值基本一致,系统的动态性能与抗干扰能力、稳定性指标得到了兼顾。以这种方式去整定复合控制器的参数,可满足未来多场景用电条件下对混合供电系统稳定性、动态功率分配、动态性能等需求,所提参数整定方法在以燃料电池为主动力源的混合供电系统中具有较好的应用前景。后续研究将考虑各个控制参数之间的耦合关系,简化设计步骤,综合考虑源-荷-控制器-观测器进行优化设计。
附 录
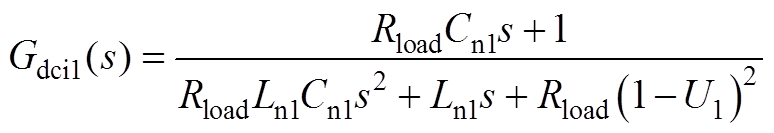 (A1)
(A1)
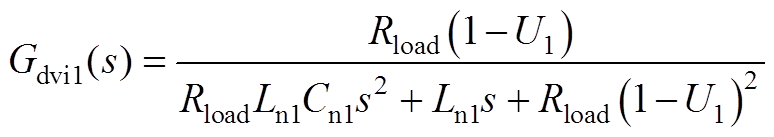 (A2)
(A2)
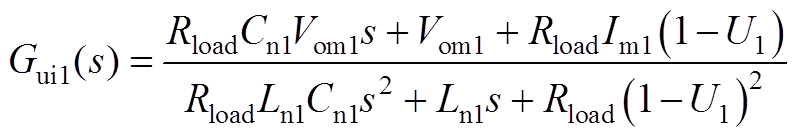 (A3)
(A3)
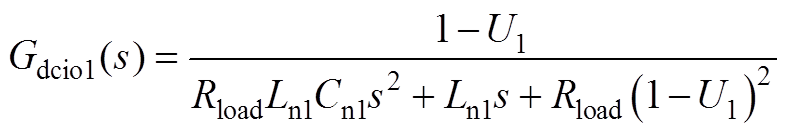 (A4)
(A4)
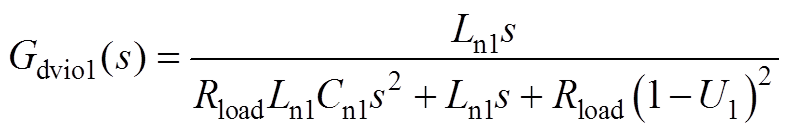 (A5)
(A5)
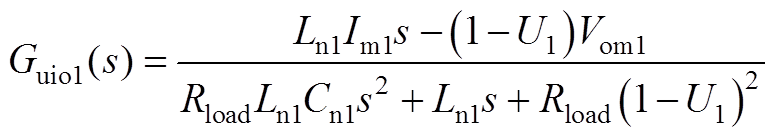 (A6)
(A6)
式中,Im1、Vom1和U1分别为im1、vom1和u1对应的稳态值;Rload为阻性负荷的电阻值。
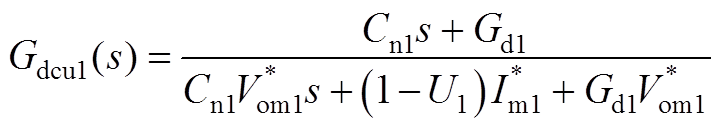 (A7)
(A7)
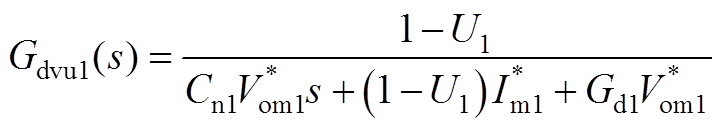 (A8)
(A8)
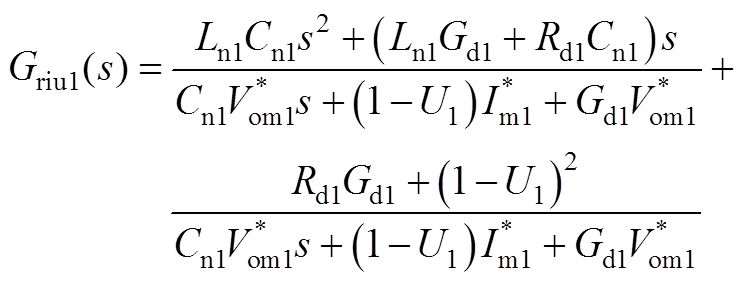 (A9)
(A9)
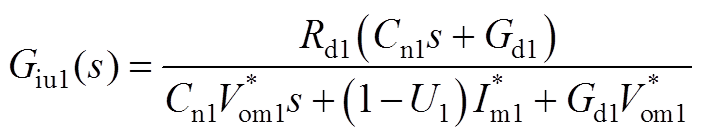 (A10)
(A10)
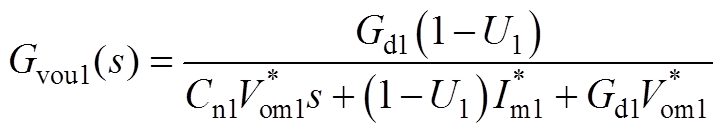 (A11)
(A11)
式中,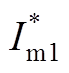 和
和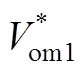 分别为FC端口变换器的输入电流基准和输出电压基准;Gd1和Rd1为虚拟阻尼。
分别为FC端口变换器的输入电流基准和输出电压基准;Gd1和Rd1为虚拟阻尼。
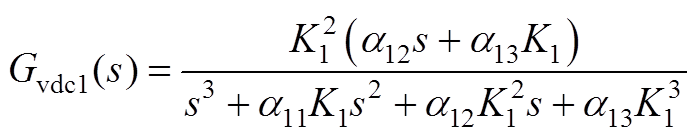 (A12)
(A12)
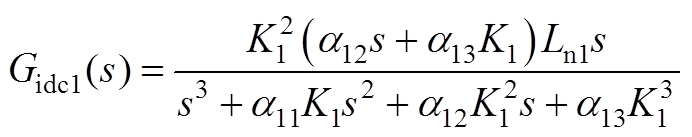 (A13)
(A13)
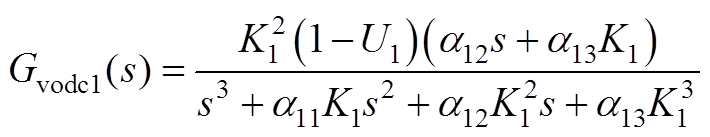 (A14)
(A14)
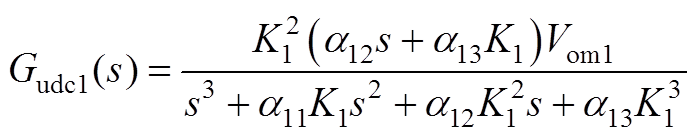 (A15)
(A15)
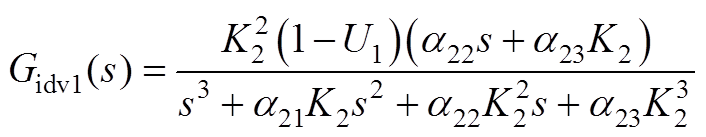 (A16)
(A16)
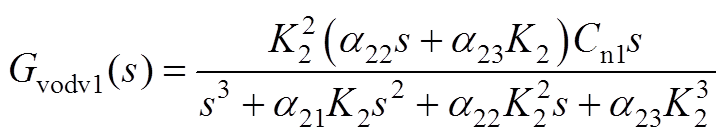 (A17)
(A17)
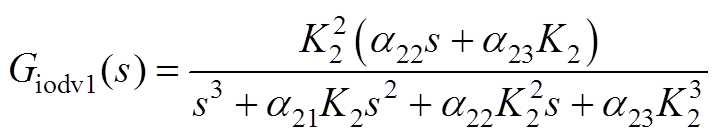 (A18)
(A18)
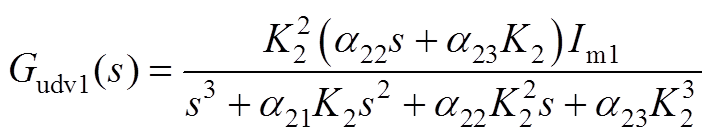 (A19)
(A19)
式中,K1、K2均为大于1的正比例增益;a11~a13和a21~a23为观测器增益,其分别对应Hurwitz多项式h1(s)=s3+ a11s2+a12s+a13、h2(s)=s3+a21s2+a22s+a23的系数。
参考文献
[1] Cano Z P, Banham D, Ye Siyu, et al. Batteries and fuel cells for emerging electric vehicle markets[J]. Nature Energy, 2018, 3(4): 279-289.
[2] 高锋阳, 高翾宇, 张浩然, 等. 全局与瞬时特性兼优的燃料电池有轨电车能量管理策略[J/OL]. 电工技术学报: 1-17[2022-10-25]. DOI: 10.19595/j.cnki. 1000-6753.tces.221297.
Gao Fengyang, Gao Xuanyu, Zhang Haoran, et al. Management strategy for fuel cell trams with both global and transient characteristics[J]. Transactions of China Electrotechnical Society, 1-17[2022-10-25]. DOI: 10.19595/j.cnki.1000-6753.tces.221297.
[3] 高锋阳, 张浩然, 王文祥, 等. 氢燃料电池有轨电车混合储能系统的节能运行优化[J]. 电工技术学报, 2022, 37(3): 686-696.
Gao Fengyang, Zhang Haoran, Wang Wenxiang, et al. Energy saving operation optimization of hybrid energy storage system for hydrogen fuel cell tram[J]. Transactions of China Electrotechnical Society, 2022, 37(3): 686-696.
[4] 邵志刚, 衣宝廉. 氢能与燃料电池发展现状及展望[J]. 中国科学院院刊, 2019, 34(4): 469-477.
Shao Zhigang, Yi Baolian. Development status and prospect of hydrogen energy and fuel cell[J]. Bulletin of the Chinese Academy of Sciences, 2019, 34(4): 469-477.
[5] Turpin C, Morin B, Bru E, et al. Power for aircraft emergencies: a hybrid proton-exchange membrane H2/O2 fuel cell and ultracapacitor system[J]. IEEE Electrification Magazine, 2017, 5(4): 72-85.
[6] Azib T, Bethoux O, Remy G, et al. An innovative control strategy of a single converter for hybrid fuel cell/supercapacitor power source[J]. IEEE Transa- ctions on Industrial Electronics, 2010, 57(12): 4024- 4031.
[7] Gu Yunjie, Li Wuhua, He Xiangning. Frequency- coordinating virtual impedance for autonomous power management of DC microgrid[J]. IEEE Transactions on Power Electronics, 2015, 30(4): 2328-2337.
[8] Zhang Yuru, Li Yunwei. Energy management strategy for supercapacitor in droop-controlled DC microgrid using virtual impedance[J]. IEEE Transactions on Power Electronics, 2017, 32(4): 2704-2716.
[9] Xu Qianwen, Xiao Jianfang, Hu Xiaolei, et al. A decentralized power management strategy for hybrid energy storage system with autonomous bus voltage restoration and state-of-charge recovery[J]. IEEE Transactions on Industrial Electronics, 2017, 64(9): 7098-7108.
[10] 宋清超, 陈家伟, 蔡坤城, 等. 多电飞机用燃料电池-蓄电池-超级电容混合供电系统的高可靠动态功率分配技术[J]. 电工技术学报, 2022, 37(2): 445- 458.
Song Qingchao, Chen Jiawei, Cai Kuncheng, et al. A highly reliable power allocation technology for the fuel cell-battery-supercapacitor hybrid power supply system of a more electric aircraft[J]. Transactions of China Electrotechnical Society, 2022, 37(2): 445- 458.
[11] 杨兴武, 杨帆, 薛花, 等. 基于占空比调制的模块化多电平换流器模型预测控制[J]. 电力系统自动化, 2021, 45(17): 134-142.
Yang Xingwu, Yang Fan, Xue Hua, et al. Duty-cycle modulation based model predictive control of modular multilevel converter[J]. Automation of Electric Power Systems, 2021, 45(17): 134-142.
[12] 赵冬冬, 李海言, 夏磊, 等. 航空燃料电池用馈流式半桥DC/DC变换器预测优化控制研究[J]. 中国电机工程学报, 2022, 42(17): 6436-6449.
Zhao Dongdong, Li Haiyan, Xia Lei, et al. Research on predictive optimization control of current-fed half-bridge DC/DC converter for aerospace fuel cells[J]. Proceedings of the CSEE, 2022, 42(17): 6436-6449.
[13] Wang Daming, Shen Z J, Yin Xin, et al. Model predictive control using artificial neural network for power converters[J]. IEEE Transactions on Industrial Electronics, 2022, 69(4): 3689-3699.
[14] 许加柱, 王家禹, 刘裕兴, 等. 引入负载扰动观测的Boost变换器定频滑模控制[J/OL]. 电源学报, 2022: 1-10 [2022-06-23]. http://kns.cnki.net/kcms/ detail/12.1420.TM.20220622.1342.002.html.
Xu Jiazhu, Wang Jiayu, Liu Yuxing, et al. Fixed- frequency sliding mode control with load disturbance observation for boost converter[J]. Journal of Power Supply, 2022: 1-10 [2022-06-23]. https://kns.cnki.net/ kcms/detail/12.1420.TM.20220622.1342.002.html.
[15] Hao Xinyang, Salhi I, Laghrouche S, et al. Observer- based adaptive sliding mode control of interleaved boost converter for fuel cell vehicles[C]//47th Annual Conference of the IEEE Industrial Electronics Society, Toronto, ON, Canada, 2021: 1-5.
[16] Babes B, Mekhilef S, Boutaghane A, et al. Fuzzy approximation-based fractional-order nonsingular terminal sliding mode controller for DC-DC buck converters[J]. IEEE Transactions on Power Elec- tronics, 2022, 37(3): 2749-2760.
[17] Hao Xinyang, Salhi I, Laghrouche S, et al. Back- stepping supertwisting control of four-phase inter- leaved Boost converter for PEM fuel cell[J]. IEEE Transactions on Power Electronics, 2022, 37(7): 7858-7870.
[18] Xu Qianwen, Xu Yan, Zhang Chuanlin, et al. A robust droop-based autonomous controller for decentralized power sharing in DC microgrid considering large- signal stability[J]. IEEE Transactions on Industrial Informatics, 2020, 16(3): 1483-1494.
[19] Xu Qianwen, Jiang Wentao, Blaabjerg F, et al. Back- stepping control for large signal stability of high boost ratio interleaved converter interfaced DC microgrids with constant power loads[J]. IEEE Transactions on Power Electronics, 2020, 35(5): 5397-5407.
[20] 陈鹏伟, 刘奕泽, 阮新波, 等. 电力电子化电力系统随机电磁暂态仿真算法[J]. 中国电机工程学报, 2021, 41(11): 3829-3841.
Chen Pengwei, Liu Yize, Ruan Xinbo, et al. Stochastic electromagnetic transient simulation algo- rithm applied to power electronics dominated power system[J]. Proceedings of the CSEE, 2021, 41(11): 3829-3841.
[21] 陈鹏伟, 姜文伟, 阮新波, 等. 直流配电系统有源阻尼控制的阻抗释义与谐振点灵敏度参数调节方法[J]. 中国电机工程学报, 2021, 41(19): 6616-6630.
Chen Pengwei, Jiang Wenwei, Ruan Xinbo, et al. Impedance explanation and resonance point sensitivity- based parameter design method of active damping applied to DC distribution system[J]. Proceedings of the CSEE, 2021, 41(19): 6616-6630.
[22] 李史玉, 李建国, 张雅静, 等. 基于扩张状态观测器补偿的Boost变换器无源控制[J]. 电力系统及其自动化学报, 2022, 34(6): 34-41.
Li Shiyu, Li Jianguo, Zhang Yajing, et al. Passivity- based control of boost converter based on extended state observer compensation[J]. Proceedings of the CSU-EPSA, 2022, 34(6): 34-41.
[23] 王勉, 唐芬, 陈麒宇, 等. DC-DC变换器并联系统无源控制及大信号稳定性研究[J]. 中国电机工程学报, 2022, 42(18): 6789-6803.
Wang Mian, Tang Fen, Chen Qiyu, et al. Passivity- based control and large signal stability of DC-DC converter parallel system[J]. Proceedings of the CSEE, 2022, 42(18): 6789-6803.
[24] 崔健, 王久和, 李建国, 等. 基于扩张状态观测器估计补偿的Buck变换器带恒功率负载无源控制[J]. 电工技术学报, 2019, 34(增刊1): 171-180.
Cui Jian, Wang Jiuhe, Li Jianguo, et al. Research on passivity-based control of buck converter with constant power load based on extend state observer estimating and compensating[J]. Transactions of China Electrotechnical Society, 2019, 34(S1): 171- 180.
[25] 王路, 王久和, 赵燕, 等. Buck-Boost变换器PI+ PBC控制器参数的多目标优化[J]. 电力系统及其自动化学报, 2022, 34(11): 84-91, 99.
Wang Lu, Wang Jiuhe, Zhao Yan, et al. Multi- objective optimization of PI+PBC controller para- meters for buck-boost converter[J]. Proceedings of the CSU-EPSA, 2022, 34(11): 84-91, 99.
[26] Song Qingchao, Wang Lei, Chen Jiawei. A decentra- lized energy management strategy for a fuel cell- battery hybrid electric vehicle based on composite control[J]. IEEE Transactions on Industrial Elec- tronics, 2021, 68(7): 5486-5496.
[27] Ortega R, Loría A, Nicklasson P J, et al. Passivity- based control of Euler-Lagrange systems: mechanical, electrical, and electromechanical applications[M]. London: Springer-Verlag, 1998.
[28] Freidovich L B, Khalil H K. Performance recovery of feedback-linearization-based designs[J]. IEEE Transa- ctions on Automatic Control, 2008, 53(10): 2324- 2334.
Passivity-Based Control Strategy and Parameter Design Method for Fuel Cell-Lithium Battery Hybrid Power Supply System
Abstract Multi-source hybrid power supply technology can effectively utilize the performance of different power supply units and is widely used in electrified transportation systems. However, as more and more loads with constant power characteristics and strong pulsation characteristics are connected to the system, the system's large-signal stability and dynamic performance are hard to guarantee. Recently, some nonlinear control methods were presented to enhance the stability and dynamic performance of the power supply. However, most existing studies have yet to consider the parameter design that takes into account the dynamic performance and stability of the system. Therefore, this paper designs a composite control method based on passivity-based control (PBC) and extended high-gain state observer (EHGSO) for the fuel cell (FC)-lithium battery (LB) hybrid power supply system (HPSS). The detailed design of the controller and observer parameters is provided, effectively ensuring the system's dynamic and static performance.
First, a mathematical model of the Boost converter considering parameter uncertainty is established. The proposed mixed droop controller is employed and designed for decentralized power allocation. Then the PBC was designed, and its stability was strictly proved based on the Lyapunov stability theory. Due to parameter uncertainties, an EHGSO was employed to enhance the system’s ability to cancel uncertainties. A general system parameter tuning method, which considers the converter's static and dynamic requirements, is finally proposed based on the small-signal analysis method.
The simulation model and experimental platform are designed and established. Simulation and experimental results verify the composite controller and the proposed parameter design method. Specifically, the simulation results show that the dynamic response of the FC converter increases with the increase of virtual dissipation resistance and decreases with the rise of virtual dissipation conductance (both of which are adjustable parameters of the PBC controller). The rising time and overshoot are approximately 20 ms and 2% for the FC converter, 6 ms and 1% for the LB converter, and 10 ms and 4% for the EHGSO, respectively. In addition, the experimental results of the FC/LB HPSS with step-changing constant power load (CPL) show that when the CPL steps up from 0.3 kW (10% of full load) to 3 kW (full load), the FC unit responds slowly to load power changes and eventually provides all the load power. In contrast, the LB unit reacts quickly to sudden load power changes with a steady-state output power of 0 kW. In the process, the bus voltage is stable and smooth in the presence of the EHGSO. Similarly, in the case of pulsation load, the LB and FC units automatically supply power to high- and low-frequency loads, respectively. The output power of the FC unit is smoother with EHGSO.
In summary, the following conclusions can be made: (1) The composite controller, composed of a PBC and an EHGSO, can allocate the load power to the FC and LB units in a decentralized way; (2) The small-signal modeling and analysis method can be employed to design the parameters of nonlinear controllers to satisfy the system’s dynamic requirements. (3) The proposed parameter design method can be used as a general guideline for designing system parameters of HPSS when nonlinear controllers are adopted.
keywords:Passivity-based control, parameter design, extended high gain state observer, hybrid power supply system
中图分类号:TM46; TM911
DOI: 10.19595/j.cnki.1000-6753.tces.222389
国家自然科学基金资助项目(51877019)。
收稿日期 2023-01-03
改稿日期 2023-02-22
敖文杰 男,1996年生,博士研究生,研究方向为多源混合供电系统及其控制。E-mail: wenjieao@cqu.edu.cn
陈家伟 男,1986年生,教授,博士生导师,研究方向为电气化交通技术、新能源发电与微电网技术等。E-mail: echenjw@cqu.edu.cn(通信作者)
(编辑 陈 诚)