摘要 针对锁相环、电网阻抗与并网逆变器相互耦合所引发的系统稳定性下降问题。首先,建立考虑电网阻抗的锁相环控制结构模型,通过分析锁相环闭环传递函数可知,电网阻抗会使锁相环系统产生右半平面闭环极点,严重影响锁相环与逆变器系统的稳定性。其次,通过分析逆变器系统输出阻抗,说明锁相环所引入的负阻抗是逆变器系统稳定裕度下降的主要原因。鉴于此,该文提出一种新型锁相环设计方法,理论分析表明,所提方法既能够保证高渗透率下锁相环具有高鲁棒性,又能够对逆变器系统输出阻抗进行重塑,有效拓宽系统对电网阻抗的适应范围。最后,通过仿真与实验验证所提新型锁相环设计方法的有效性。
关键词:高渗透率 并网逆变器 锁相环 阻抗重塑 鲁棒性
目前,随着光伏、风电等新能源发电技术与装机容量的不断提高,高渗透率新能源发电已成为必然趋势,此时,电网往往表现出低短路比的弱电网特性甚至极弱电网特性,即含有不可忽略的电网阻抗,因此,通常可以由最大短路比(Short Circuit Ratio, SCR)的大小来判断出电网的强弱,从而间接地判断出新能源发电系统渗透率的高低[1-3]。基于锁相环(Phase-Locked Loop, PLL)同步控制的并网逆变器是新能源发电的重要组成部分,其稳定性往往受到电网阻抗与PLL的影响[4-5]。因此,高渗透率下PLL对并网逆变器稳定性影响的分析与研究是十分必要的。
弱电网下,并网公共耦合点(Point of Common Coupling, PCC)电压作为PLL的输入信号,由于其受电网阻抗的影响,间接导致PLL稳定性受电网阻抗的影响[6]。高渗透率下PLL对并网逆变器稳定性影响的研究可分为两个方面:一是对PLL控制结构而言,电网阻抗的存在使PLL结构引入了额外的反馈回路,对PLL自身鲁棒性产生影响;二是逆变器系统考虑PLL时,系统输出阻抗会引入与PLL相关的负阻抗,此负阻抗直接影响系统输出阻抗的幅值、相位,导致并网逆变器系统稳定裕度下降。
目前,针对上述问题,许多学者采用不同的分析方法进行了研究。文献[7-8]通过对并网逆变器系统阻抗模型进行分析,提出了在传统PLL前串联二阶低通滤波器或复数滤波器的设计方法,从而降低逆变器输出阻抗分母中与锁相环相关的附加项对逆变器稳定性的影响。但上述两种方法会引入额外的相位补偿或滤波能力不足的问题。文献[9-10]提出了一种基于电网阻抗在线测量的自适应控制策略,可有效解决电网阻抗较大时并网系统的失稳问题,但此方法过度依赖电网阻抗在线测量的准确性。在文献[11]所提对称PLL结构基础上,文献[12]提出了一种基于复数滤波器的对称锁相环同步结构,所提方案在不增加额外控制补偿和调整系统控制参数前提下,实现了并网逆变系统频率解耦控制。文献[13]通过对文献[7]所提新型PLL结构进行分析,提出了一种基于电流二阶校正的阻抗重塑方法,该方法通过约束二阶校正环节参数,实现了并网逆变器单位功率因数并网与稳定运行。文献[14-15]对逆变器系统等效输出阻抗进行重塑,提高其与电网阻抗交截频率处的相位裕度。上述研究表明,弱电网下,虽然基于传统PLL的改进型PLL结构与控制策略多种多样,但电网阻抗所导致的PLL自身鲁棒性下降问题仍未被充分研究,因此,高渗透率下PLL系统与逆变器系统稳定性的交互影响仍需进一步研究。
基于上述研究现状,本文以弱电网下单相LCL滤波并网逆变器为研究对象,通过深入揭示锁相环自身鲁棒性与逆变器系统稳定裕度下降的原因,提出了一种以并网点电压、并网点电流为输入信号的新型锁相环控制结构,所提新型锁相环控制结构不仅自身具有高鲁棒性,而且能够对系统输出阻抗相位特性进行重塑,极大地提高了并网逆变器系统在弱电网甚至极弱电网下的稳定性。最后,通过仿真与实验验证了本文理论分析的正确性以及所提新型锁相环设计方法的有效性。
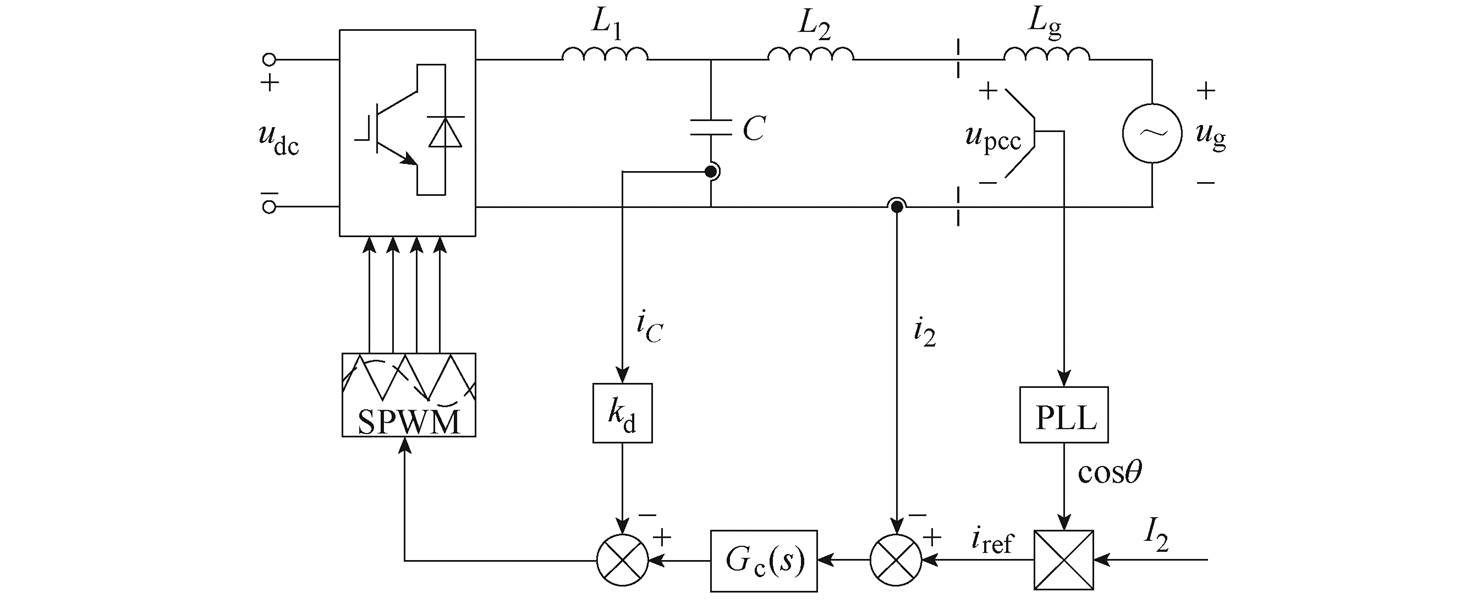
图1为采用并网电流反馈和电容电流有源阻尼策略的单相并网逆变器的拓扑结构和控制框图。

(a)拓扑结构
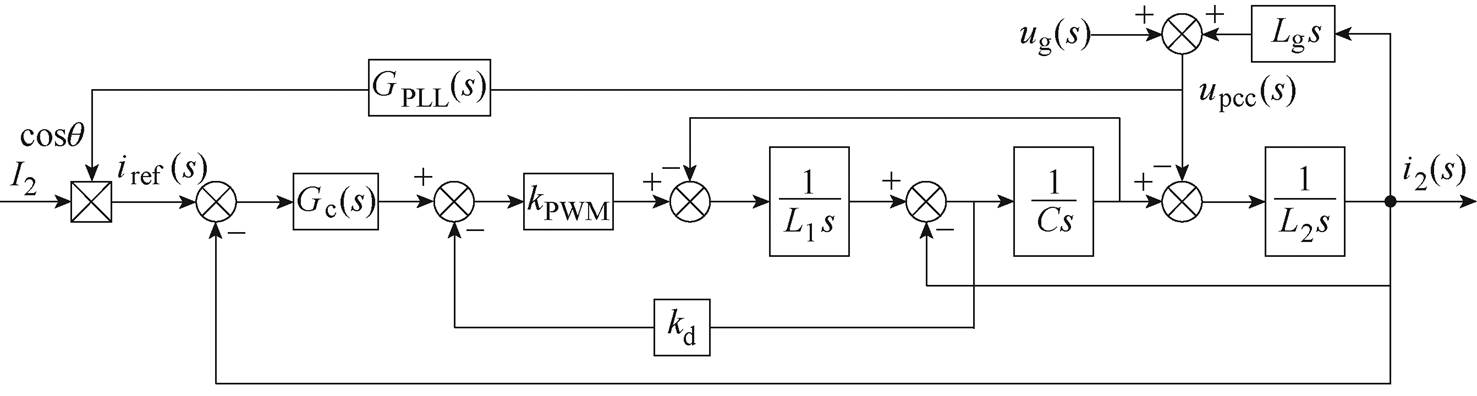
(b)系统控制框图
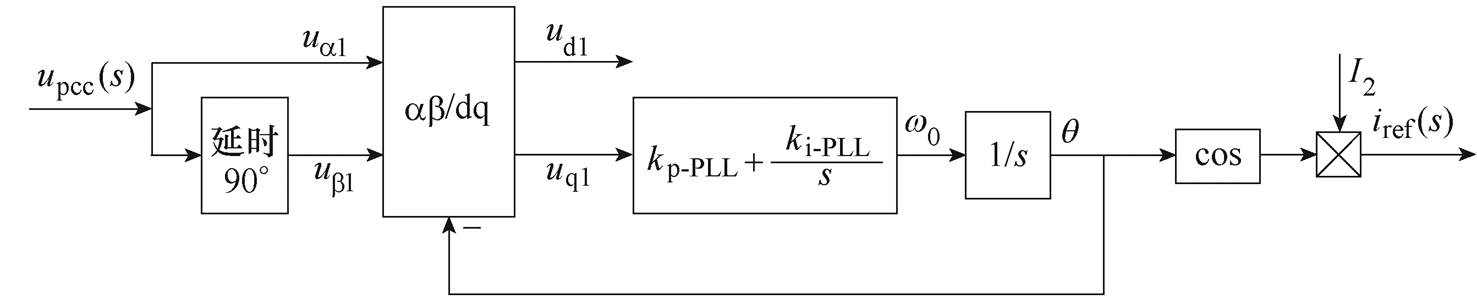
(c)传统PLL控制结构
图1 单相并网逆变器的拓扑结构和控制框图
Fig.1 Topology structure and control block diagram of single-phase grid-connected inverter
图1中,逆变侧电感L1、滤波电容C和网侧电感L2构成LCL滤波器;电网等效为电压源与电网阻抗串联的等效模型,ug为电网电压,Lg为电网阻抗(本文考虑最恶劣情况,即电网阻抗为纯电感);udc、upcc分别为直流母线电压、PCC处电压;i1、i2、iC分别为逆变器机侧电流、并网电流、滤波电容电流;iref、I2分别为并网电流基准值、给定幅值;q 为PLL输出相位(PCC处相位),kp-PLL、ki-PLL分别为PLL控制器的比例系数、积分系数;kd为电容电流有源阻尼系数;Gc(s)为电流控制器,本文采用准比例谐振(Quasi Proportional Resonant, QPR)控制器对电流进行控制。
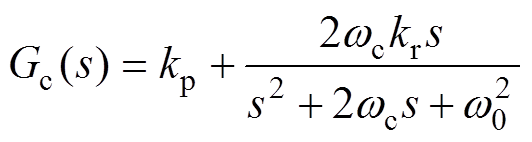 (1)
(1)
式中,kp、kr、w0、wc分别为QPR控制器的比例系数、谐振系数、谐振角频率和控制带宽。
此外通过文献[8]可知,传统PLL控制环节的传递函数表达式为
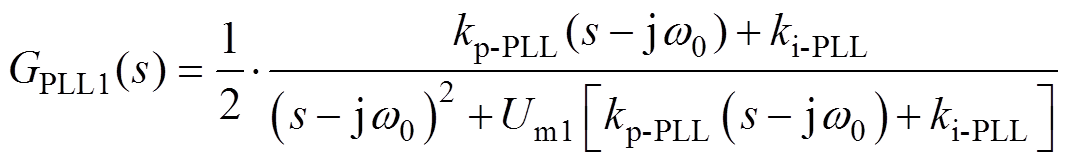 (2)
(2)
式中,Um1为并网点电压upcc的幅值。
弱电网下,由于电网阻抗不可忽略,当并网逆变器系统考虑锁相环时,为保证系统稳定性,不仅要考虑锁相环自身的稳定性,还需要考虑系统输出阻抗在交截频率范围内的稳定裕度。
根据图1a可知,强电网下,PLL输入信号为电网电压ug(s),弱电网下,由于受电网阻抗的影响,PLL输入信号为并网点电压upcc(s),即
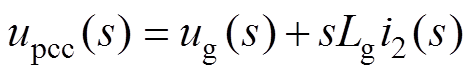 (3)
(3)
根据式(3)并结合图1c可得,PLL输入信号upcc(s)与ua1、ub1之间的时域关系表达式为
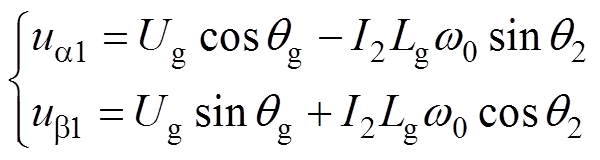 (4)
(4)
式中,Ug、qg为ug(s)的幅值和相位;q2为并网电流i2相位;Lgw0为电网阻抗模值。
进一步地,对式(4)进行ab-dq坐标变换可得
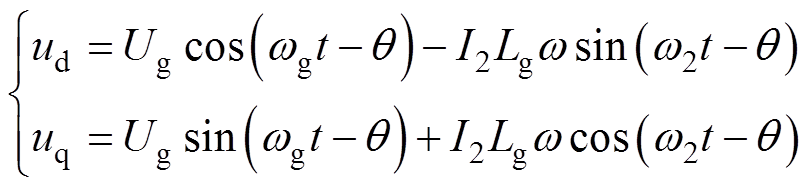 (5)
(5)
式中,wg、w2分别为电网电压和并网电流的角频率,且有wgt =qg、w2t =q2。
考虑到系统稳定运行时,PCC与电网电压相位差较小,与并网电流相位一致,即wgt-q≈0,w2t-q =0,因此,式(5)中分量uq1可简化为
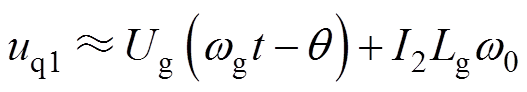 (6)
(6)
根据式(6)和图1b可得如图2所示的弱电网下传统PLL控制系统框图。
由图2可知,弱电网下传统PLL输出相位q 对参考输入相位qg的闭环传递函数G1(s)表达式为
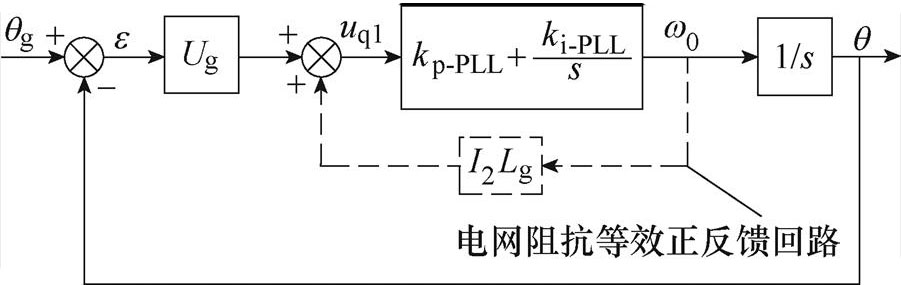
图2 弱电网下传统PLL控制系统框图
Fig.2 Block diagram of traditional PLL control system under weak power grid
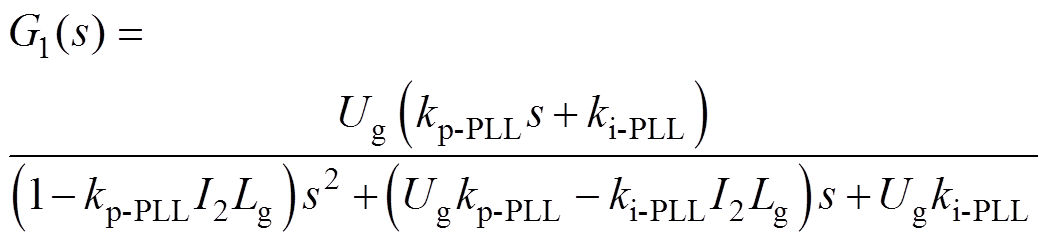 (7)
(7)
通过式(7)可以分析出:PLL控制系统的闭环极点分布受电网阻抗影响,当电网阻抗宽范围变化时,PLL控制系统会产生右半平面的闭环极点,从而导致PLL系统失稳。此外,结合式(3)和图2分析可知,正是由于PLL输入信号中存在分量sLgi2,导致PLL控制环路中引入一条与电网阻抗有关的正反馈回路,此反馈回路直接改变了传统PLL的控制结构,进而影响了PLL输入输出闭环传递函数及其自身稳定性。
由图1b所示的系统控制框图可以推导出并网电流i2(s)表达式为
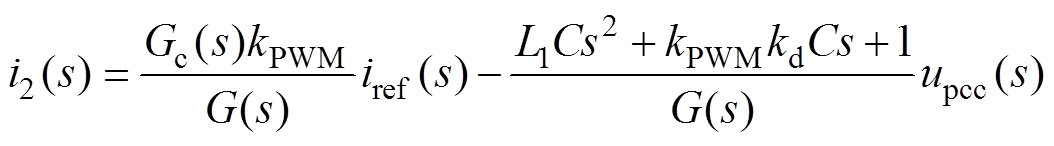 (8)
(8)
其中
G(s)=L1L2Cs3+kPWMkdCL2s2+(L1+L2)s+Gc(s)kPWM
此外,考虑PLL因素时,由于参考电流iref(s)= I2GPLL1(s)upcc(s),将其代入式(8)化简可得
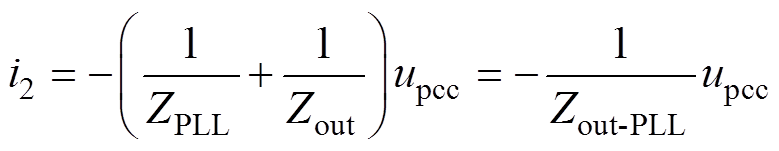 (9)
(9)
式中,ZPLL为考虑PLL时所引入的负阻抗;Zout为不考虑PLL时的系统输出阻抗;Zout-PLL为考虑PLL时的系统输出阻抗。
根据式(9)可得,考虑PLL时的并网逆变器等效电路,Zout-PLL(s)、ZPLL(s)的表达式分别为
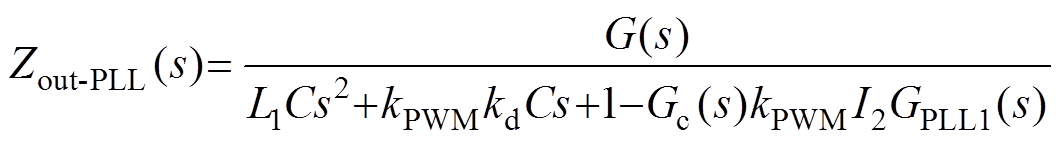 (10)
(10)
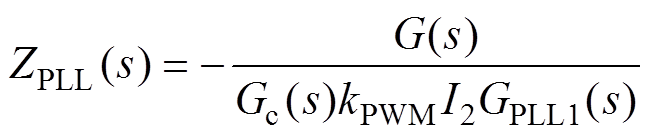 (11)
(11)
令式(10)中的GPLL1(s)=0即为不考虑PLL时的系统输出阻抗Zout。
由文献[16]可知,并网逆变器系统稳定条件为系统相位裕度(Phase Margin, PM)大于0 °,即要求系统输出阻抗在交截频率处的相位必须大于-90 °。根据式(10)、式(11)并结合表1所示参数,可绘制Zout-PLL、Zout和ZPLL的伯德图如图3所示。
表1 并网逆变器相关参数
Tab.1 Relevant parameters of grid-connected inverter

参 数数 值 额定功率Pout/kW2 直流母线电压udc/V300 滤波器参数L1/mH3 L2/mH1 C/mF15 有源阻尼系数kd0.1 脉宽调制系kPWM300 锁相环kp-PLL4.36 电网电压ugrms/V140 电网频率f0/Hz50 控制器参数kp0.057 kr7.2 wc/(rad/s)p 开关频率fsw/kHz10 采样频率fs/kHz20 锁相环ki-PLL1 884.2
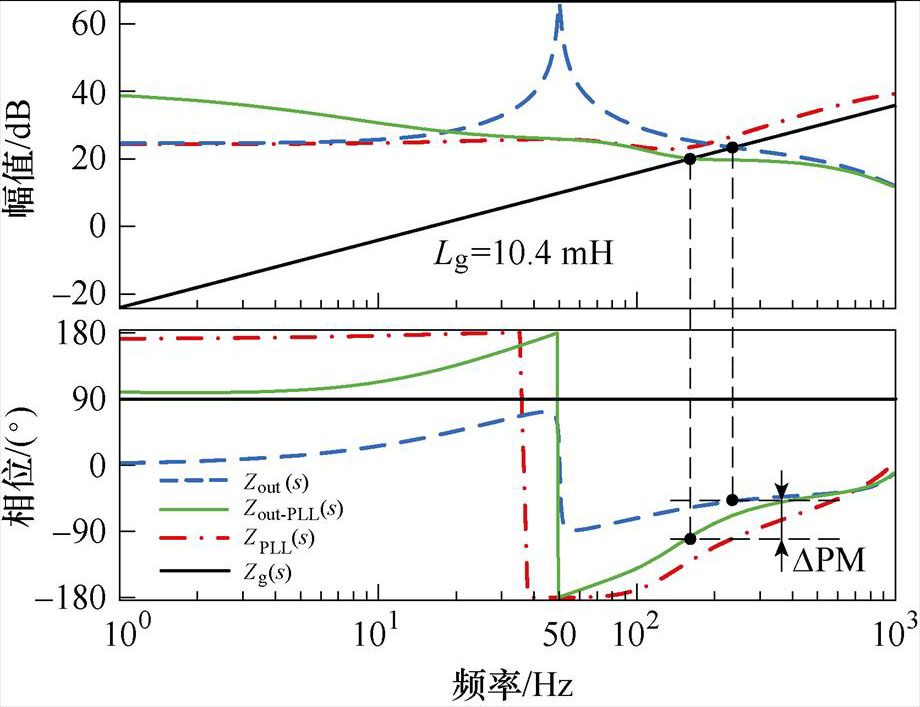
图3 Zout(s)、Zout-PLL(s)、ZPLL(s)的伯德图
Fig.3 Bode diagrams of Zout(s)、Zout-PLL(s)、ZPLL(s)
根据式(9)可知,阻抗Zout-PLL等效为负阻抗ZPLL与阻抗Zout二者并联所得。由图3可以看出,在50~1 000 Hz频率范围内,负阻抗ZPLL的相位均小于阻抗Zout的相位,因此,相较于阻抗Zout,阻抗Zout-PLL在交截频率处的相位大幅下降,且下降角度为DPM。
考虑PLL时的并网逆变器等效电路如图4所示。基于上述分析可知,当电网阻抗宽范围变化时,考虑PLL时所引入的负阻抗ZPLL会导致系统在中低频段稳定裕度大幅降低甚至失稳。为降低负阻抗ZPLL对系统稳定性的影响,本文提出以下两种方法:
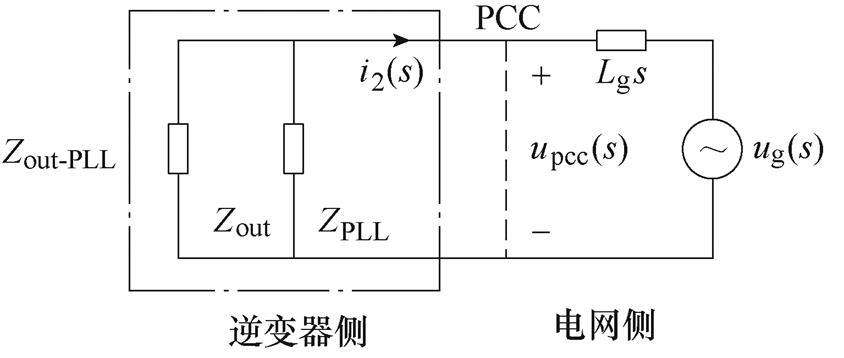
(a)未阻抗重塑
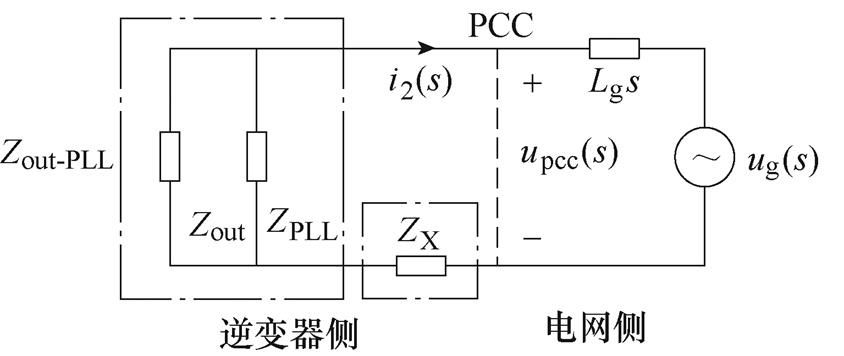
(b)通过串联阻抗进行阻抗重塑
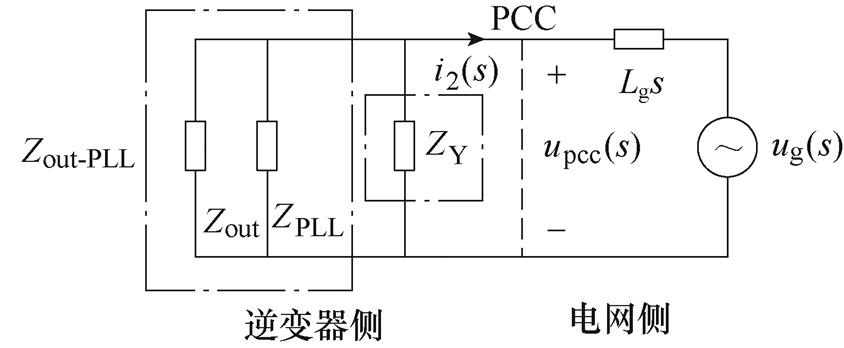
(c)通过并联阻抗进行阻抗重塑
图4 考虑PLL时的并网逆变器等效电路
Fig.4 Equivalent circuit of grid-connected inverter considering PLL
(1)从并网电流i2到参考电流iref之间引入一条传递函数为GX(s)的支路,此时,iref(s)=I2GPLL1(s)upcc(s)+ GX(s)i2(s),等效为在并网逆变器输出端串联一个阻抗ZX,以对输出阻抗进行重塑,如图4b所示,其中,阻抗ZX可以通过合理设计传递函数GX(s)进行配置。
(2)从并网点电流i2到并网点电压upcc之间引入一条传递函数为GY(s)的支路,等效为在并网逆变器输出端并联阻抗ZY,以对系统输出阻抗进行重塑,如图4c所示,其中,阻抗ZY可以通过合理地设计传递函数GY(s)进行配置。
上述两种方法均可以对输出阻抗Zout-PLL进行重塑,提升其在交截频率范围内的稳定裕度,从而达到减小甚至消除ZPLL的影响。结合本文新型PLL的设计方法,为避免引入额外的电流支路或相位补偿环节,只考虑方法(1),方法(2)暂不考虑。
基于第1节分析,本文提出了一种以并网点电压、并网点电流为输入信号的新型PLL设计方法,具体控制结构如图5所示。图5中,Gv(s)为微分环节,Gw(s)为阻抗重塑环节,Gq(s)为相位补偿环节。
由图5可以看出,根据输入信号的不同,新型PLL控制结构可分为两部分:第一部分为基于并网点电压upcc(s)为输入信号的锁相功能部分;第二部分为基于并网点电流i2(s)为输入信号的提高PLL鲁棒性部分,这两部分均为基频信号输入。以下分别从新型PLL高鲁棒性、阻抗重塑环节和相位矫正环节三个角度进行分析与设计。
本节暂不考虑阻抗重塑环节与相位补偿环节。为提高PLL自身鲁棒性,降低传统PLL输入信号中所含分量sLgi2对PLL自身稳定性的影响,如图5所示,可采用小信号注入法对电网阻抗进行在线测量[17-18],即利用电网阻抗测量值Lg0与微分环节 Gv(s)对新型PLL中并网电流i2(s)支路进行动态调整,进而实现对传统PLL输入信号中所含分量sLgi2的限制。
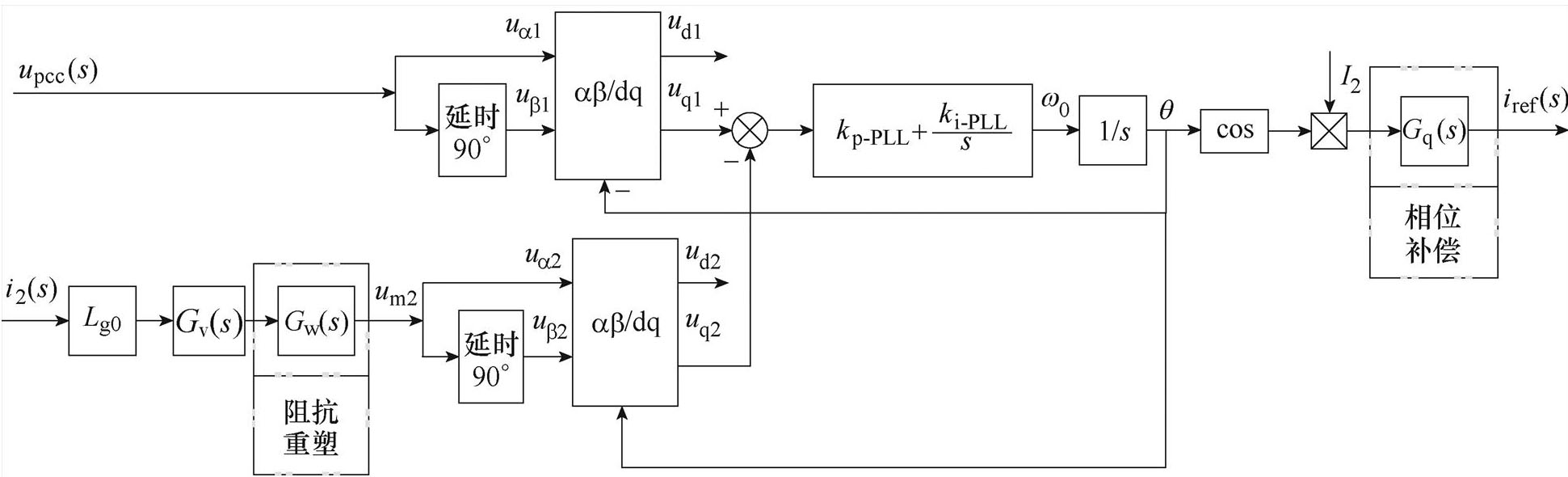
图5 新型PLL控制结构
Fig.5 New PLL control block diagram
由于二阶线性微分跟踪器在实际工程中易于实现,且具有良好的高频噪声抑制能力[19],本文使用二阶线性微分跟踪器代替传统微分环节Gv0(s)=s,其中,二阶线性微分跟踪器的表达式Gv(s)为
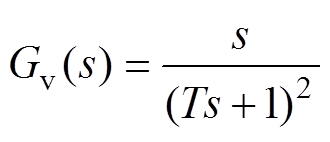 (12)
(12)
式中,T为二阶线性微分跟踪器的时间常数。
图6给出了二阶线性微分跟踪器Gv(s)与传统微分环节Gv0(s)的伯德图。
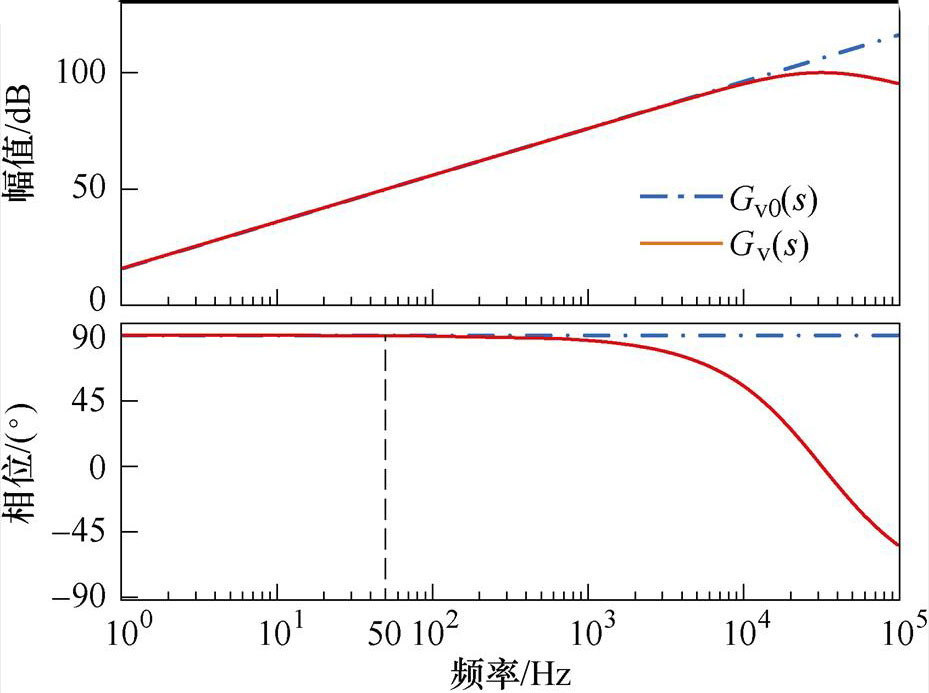
图6 不同微分环节伯德图
Fig.6 Bode diagrams with different differential links
图6中,对于时间常数T的取值,只需二阶线性微分跟踪器的转折频率1/T大于系统开关频率即可,结合表1参数,本文取T=5 ms。
从图6中可以看出,二阶线性微分跟踪器与传统微分环节在低于1 kHz频率范围内几乎重合,虽然高频处有一定差别,但高频信号对并网电流i2(s)支路的输入信号影响很小,可忽略不计。
结合图5和式(2)可以推导出,新型PLL中参考电流iref(s)对并网电流i2(s)支路的传递函数表达式GPLL2(s)为
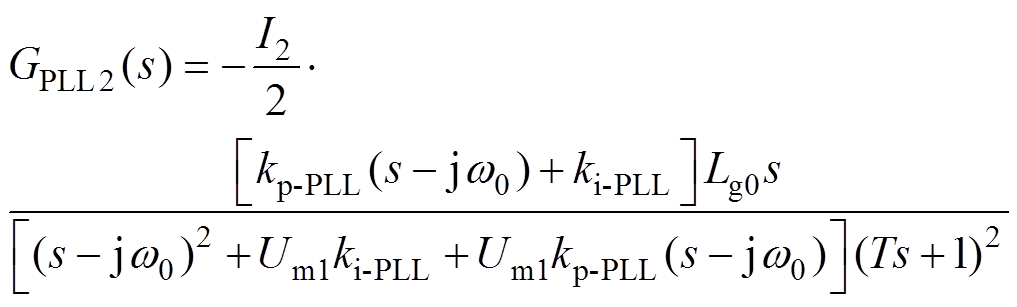 (13)
(13)
为进一步揭示新型PLL的高鲁棒性,根据图5可得并网电流i2(s)支路中等效电压um2(s)和并网电流i2(s)之间的相量关系为
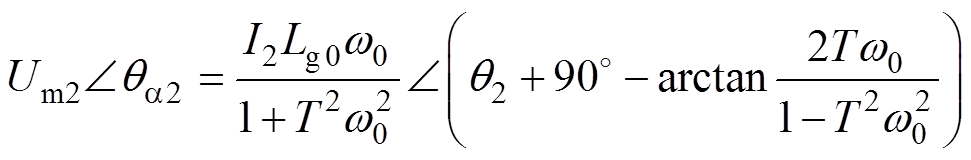 (14)
(14)
式中,Um2、qa2为um2(s)的幅值、相位;Lg0w0为在线测量电网阻抗模值。
借鉴式(4)~式(6)的分析方法,对式(14)进行分析与化简,同时,考虑时间常数T的取值,可得简化后的分量uq2为
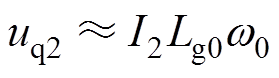 (15)
(15)
结合式(6)、式(15)和图2可得新型PLL控制系统框图,如图7所示。
根据图7可得新型PLL输出相位q 对参考输入相位qg的闭环传递函数表达式G2(s)为
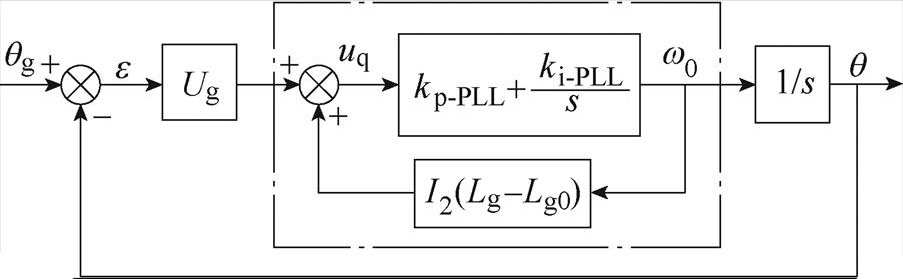
图7 弱电网下新型PLL控制系统框图
Fig.7 Block diagram of new PLL control system under weak grid
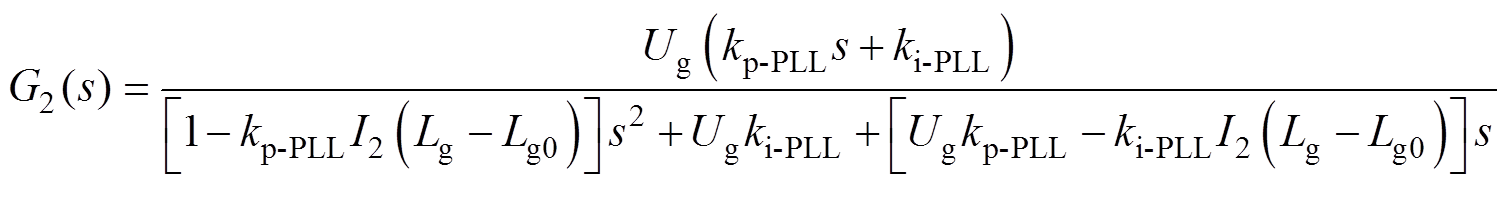 (16)
(16)
由于Lg0为在线测量值,具有一定误差,其误差范围通常在±20 %之间,考虑其误差最大情况即Lg0=0.8Lg,若系统在此情况下PLL依旧具有稳定性,则说明Lg0在误差范围内无论取何值,均可以保证PLL稳定运行。结合表1参数并考虑电网阻抗宽范围变化情况,当电网阻抗Lg=31.2 mH(SCR=1)时,新型PLL控制系统仍未产生右半平面闭环极点,即PLL系统保持稳定,有效降低了弱电网下传统PLL输入信号中所含分量sLgi2对PLL自身稳定性影响。
在上述分析基础上,为降低负阻抗ZPLL对系统稳定性的影响,可在新型PLL中并网点电流i2(s)支路上串联超前校正器Gw(s),其等效为1.3节所述第(1)种方法,即通过串联阻抗对系统输出阻抗Zout-PLL进行重塑,具体分析与设计过程如下。
对于Gw(s)的设计,首先应满足Gw(s)在基频处的幅值与相位为0,以保证新型PLL的高鲁棒性;其次Gw(s)环节在交截频率范围内应具有较高相位,以提高输出阻抗Zout-PLL在交截频率处的稳定裕度。超前校正器Gw(s)的[20]表达式为
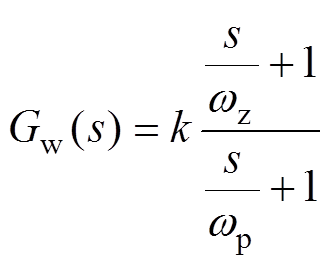 (17)
(17)
式中,k为超前校正器的开环增益。
结合表1参数,系统输出阻抗Zout-PLL的交截频率介于fz=100 Hz与fp=250 Hz之间时,系统稳定裕度较低,由此可得
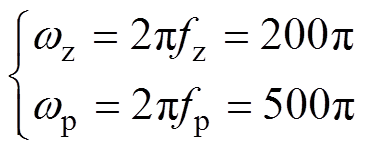 (18)
(18)
结合式(13)、式(17)和图5可得不考虑相位补偿时,新型PLL中参考电流iref(s)对并网电流i2(s)支路的传递函数GZPLL2(s)为
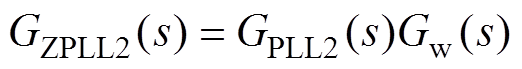 (19)
(19)
图8所示为传递函数GPLL2(s)和GZPLL2(s)的伯德图。对比GPLL2(s)和GZPLL2(s)可以看出,相较于GPLL2(s),考虑阻抗重塑时GZPLL2(s)会在50 Hz基频处产生很小的相位偏差,但对锁相功能无影响。此外,GZPLL2(s)的基频幅值与Gw(s)中的系数k有关,出于减小误差考虑,本文选择k=1,此时基频幅值无误差。
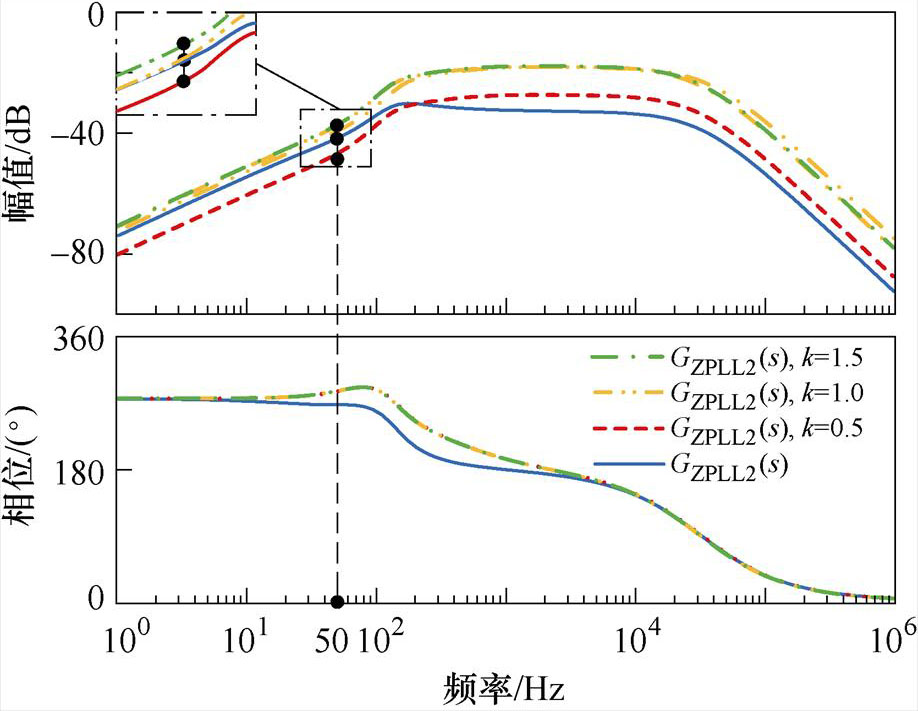
图8 不同k值下GPLL2(s)、GZPLL2(s)伯德图
Fig.8 Bode diagrams of GPLL2(s) and GZPLL2(s) under different k values
进一步地,结合式(19)与图5可知,参考电流iref(s)=I2GPLL1(s)upcc(s)+GZPLL2(s)i2(s)。将iref(s)代入式(8)可得,阻抗重塑后的系统输出阻抗Zout-ZPLL为
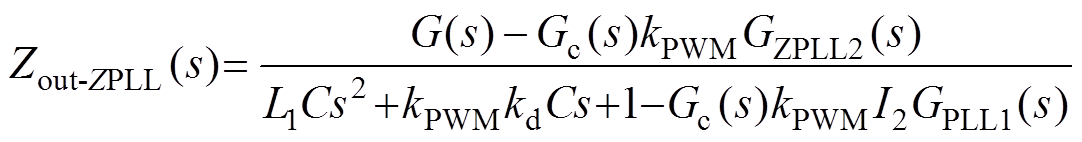
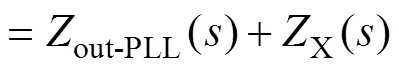 (20)
(20)
根据图4b可知,在输出阻抗支路串联的阻抗ZX为
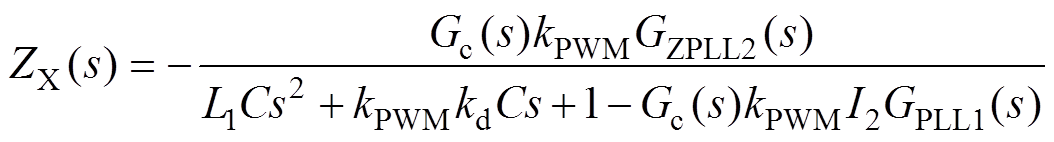 (21)
(21)
根据式(10)、式(20)、式(21)可以绘制Zout-PLL、Zout、ZX和Zout-ZPLL的伯德图,如图9所示。
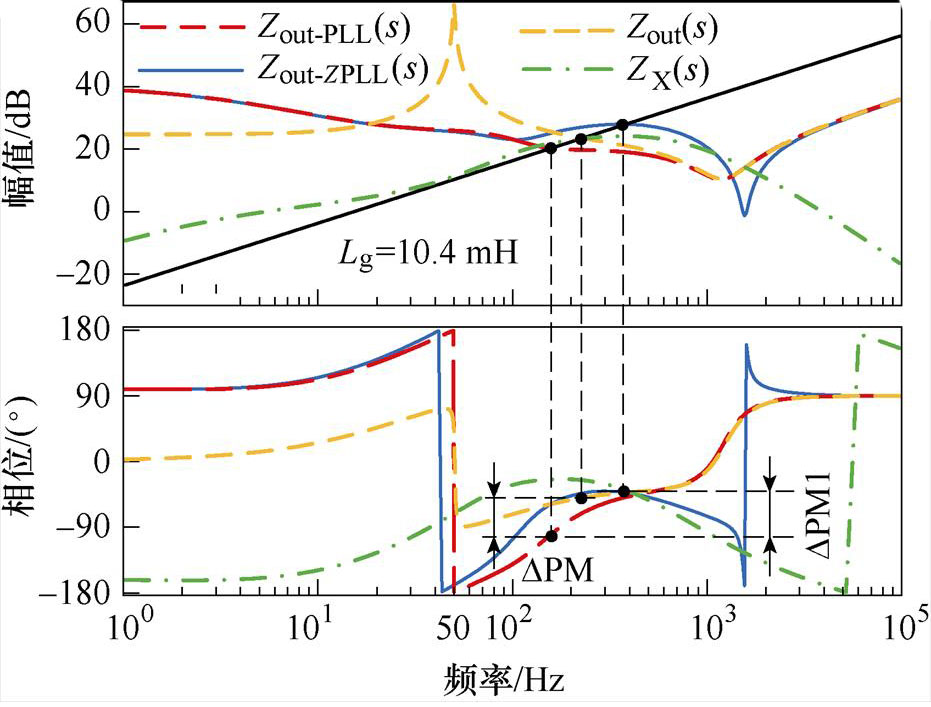
图9 Zout、Zout-PLL、Zout-ZPLL和ZX的伯德图
Fig.9 Bode diagrams of Zout、Zout-PLL、Zout-ZPLL、ZX
根据式(20)可知重塑后的系统输出阻抗Zout-ZPLL是由阻抗ZX与阻抗Zout-PLL串联所得。分析图9,阻抗ZX在交截频率范围内相位较高,且大于阻抗Zout-PLL的相位,因此,相较于阻抗Zout-PLL,阻抗Zout-ZPLL在交截频率处的相位大幅提升,且提升角度为DPM1,同时,系统稳定裕度显著提高,系统鲁棒性得到保证。
此外,由于新型PLL控制结构改变了传统PLL的输入信号,所以会导致新型PLL的输出相位q 与并网点电压upcc(s)之间存在相位偏差。从图9也可以看出,阻抗重塑后的Zout-ZPLL与阻抗未重塑时的Zout-PLL在50 Hz基频处相位不同步,因此需要进行必要的基频相位矫正。
由于逆变器稳定运行时,PCC电压与电网电压相位差较小,且与并网电流相位一致,即wgt-q≈0,w2t-q =0,进而得出w2t≈wgt。
根据上述分析,传统PLL下,式(5)中的q轴信号分量可化简为信号uqc,即
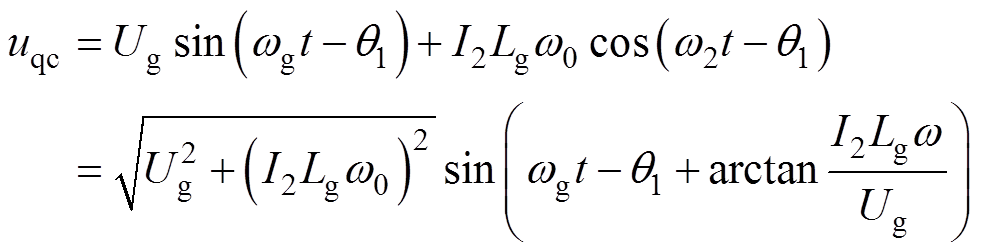 (22)
(22)
由式(22)可得,传统PLL输出的相位q1为
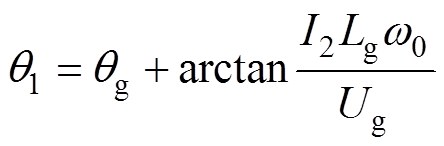 (23)
(23)
同理,结合式(5)、式(14)、式(15)可得新型PLL下化简后的q轴信号分量uqx为
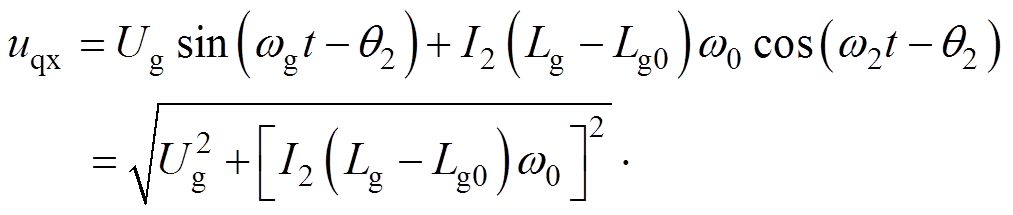
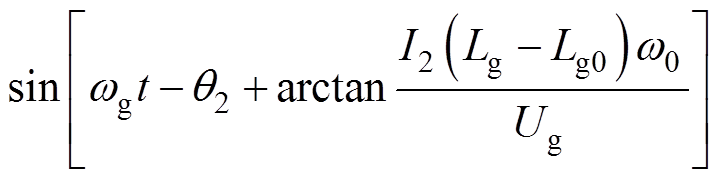 (24)
(24)
由式(24)可得,新型PLL输出的相位q2为
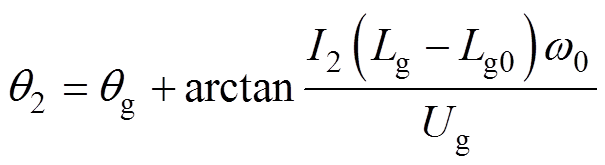 (25)
(25)
将式(23)与式(25)作差可得,传统PLL与新型PLL输出的相位误差Dq1为
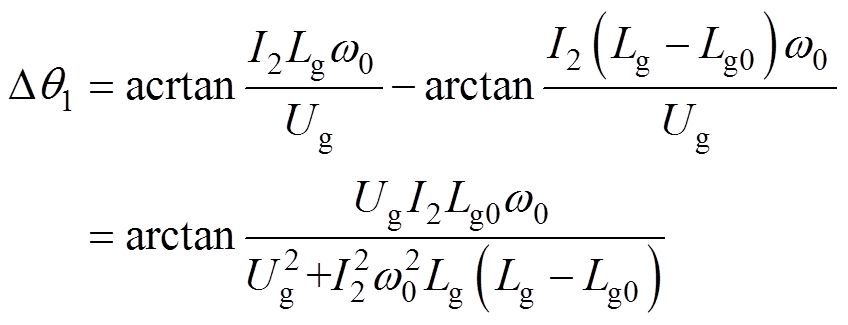 (26)
(26)
式(26)为新型PLL需要进行相位矫正的相位大小,由于含有未知量电网电感Lg和电网电压幅值Ug,所以使用在线测量信号近似代替未知信号,即Lg0≈Lg和Upcc≈Ug,则相位近似矫正j1为
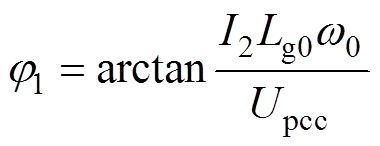 (27)
(27)
为证明相位近似矫正的可行性,令式(26)与式(27)作差可得相位近似矫正的误差大小Dq2为
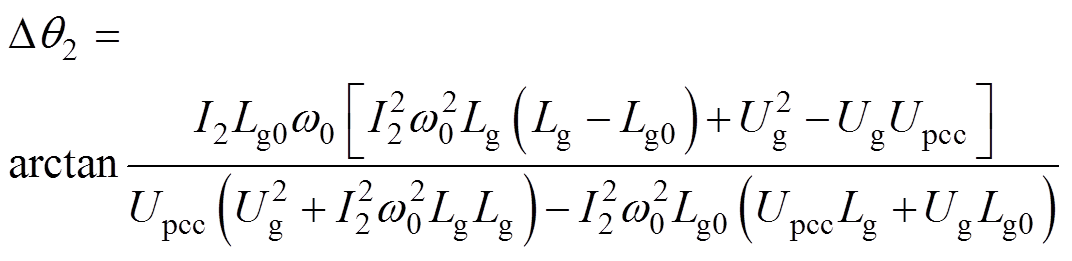 (28)
(28)
将表1所示参数代入式(28),可得相位近似矫正的误差数量级为10-3,对于反三角函数而言,可忽略不计,所以相位偏差可按j1进行矫正。
为便于在实际工程中进行相位矫正,考虑到全通滤波器只会从转折频率处改变相位,并且不会改变原有信号的幅值,因此在新型PLL后串联一阶全通滤波器Gq(s)环节用于相位矫正[21],Gq(s)表达式为
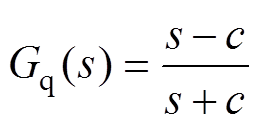 (29)
(29)
式中,c为Gq(s)的转折频率。
令s=jw0,并代入式(29)中可以推导出全通滤波器Gq(s)在基频处的相位表达式为
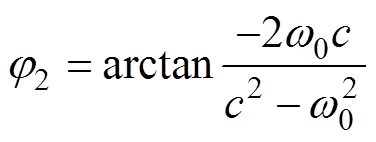 (30)
(30)
令式(27)与式(30)相等,即j1=j2。则有
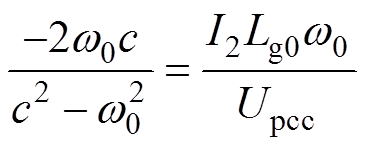 (31)
(31)
由式(31)即可得到全通滤波器的转折频率c,进而实现相位矫正。
并网逆变器控制系统的鲁棒性可通过推导其输出阻抗并借助阻抗稳定判据进行分析,鉴于此,本节首先给出了基于新型PLL控制时的系统输出阻抗与控制框图,然后通过设计示例从理论层面说明本文所提新型PLL的有效性。
当采用图5所示新型PLL时,考虑式(2)、式(19)、式(29),可得参考电流iref(s)到并网点电压upcc(s)和并网电流i2(s)的函数关系表达式为
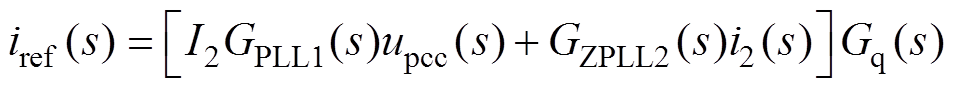
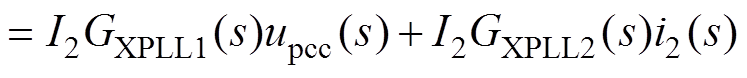 (32)
(32)
式中,GXPLL1(s)、GXPLL2(s)分别为新型PLL环节中并网点电压和并网点电流的等效传递函数。
根据上述分析可得如图10所示的基于新型PLL的系统控制框图。
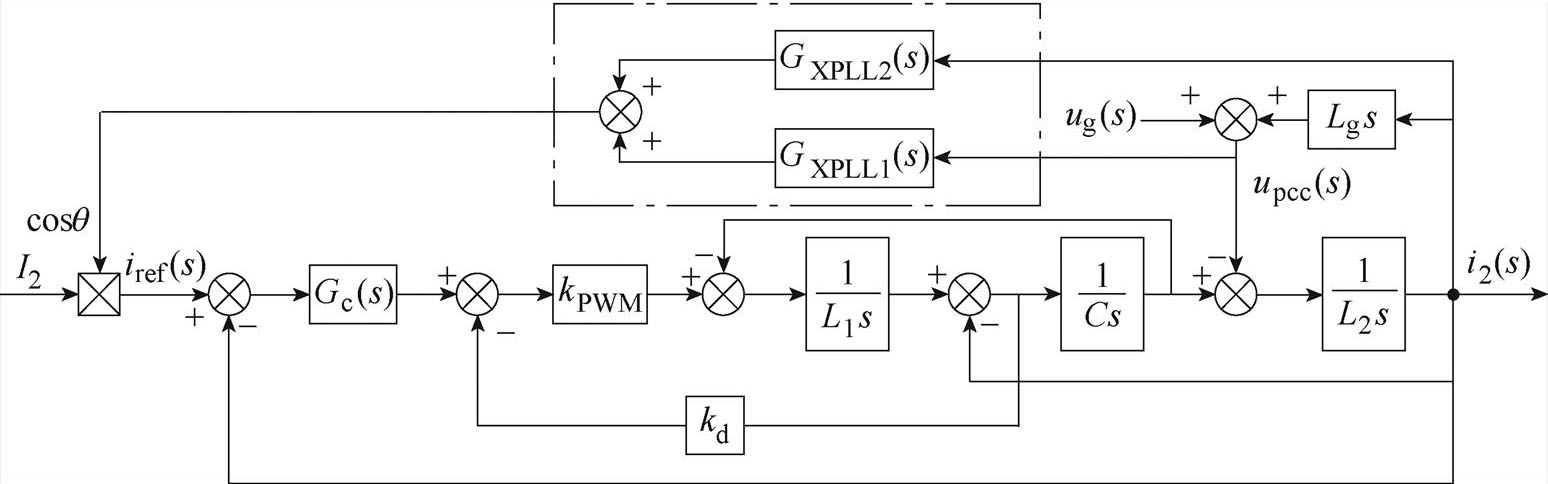
图10 新型PLL的系统控制框图
Fig.10 System control block diagram under the new PLL
将式(32)代入式(8),可得考虑新型PLL时系统的输出阻抗Zout-XPLL(s)为
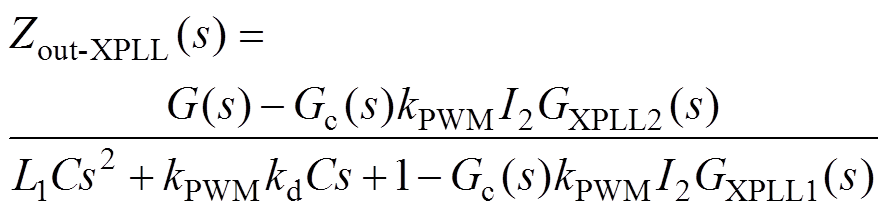 (33)
(33)
为了便于对比分析,给出并网逆变器的相关参数见表1。此外,为了保证PLL具有较好的动态响应能力,本文以PLL带宽fBW=250 Hz为例进行设计[16]。
图11给出了考虑传统PLL控制时的系统输出阻抗Zout-PLL的伯德图。从图中可以看出,采用传统PLL控制时,随着电网阻抗Lg的增大,系统输出阻抗Zout-PLL与Lg在交截频率范围内的相位裕度逐渐减小,系统鲁棒性逐渐下降直至失稳。
图12为不同电网阻抗、不同短路比时,新型PLL下有无考虑误差时的系统输出阻抗Zout-XPLL的伯德图。
由图12a可知,采用新型PLL控制时,弱电网下,当电网阻抗Lg=10.4 mH(SCR=3)时,系统相位裕度提升了57.8 °,相位裕度为47.8 °,系统鲁棒性得到保证;极弱电网下,即使当电网阻抗Lg= 20.8 mH(SCR=1.5)或Lg=31.2 mH(SCR=1)时,系统的相位裕度分别提升了101.3 °、120.4 °,相位裕度分别为54.3 °、58.4 °,系统依旧具有极高的鲁棒性。此外,考虑到新型PLL中电网阻抗测量值Lg0存在一定误差,且误差范围通常在±20 %之间。以SCR=1.5时为例,图12b给出了考虑误差时的系统输出阻抗Zout-PLL伯德图。从图中可以看出,系统相位裕度依然大于50 °,满足实际工程要求。
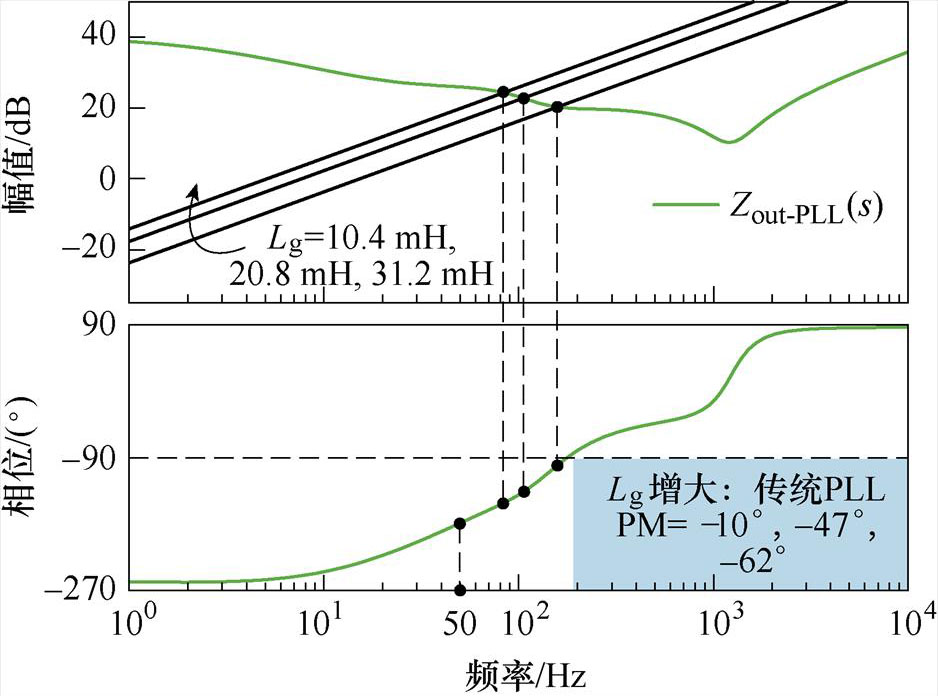
图11 不同电网阻抗下Zout-PLL的伯德图
Fig.11 Bode plot of Zout-PLL under different grid impedances
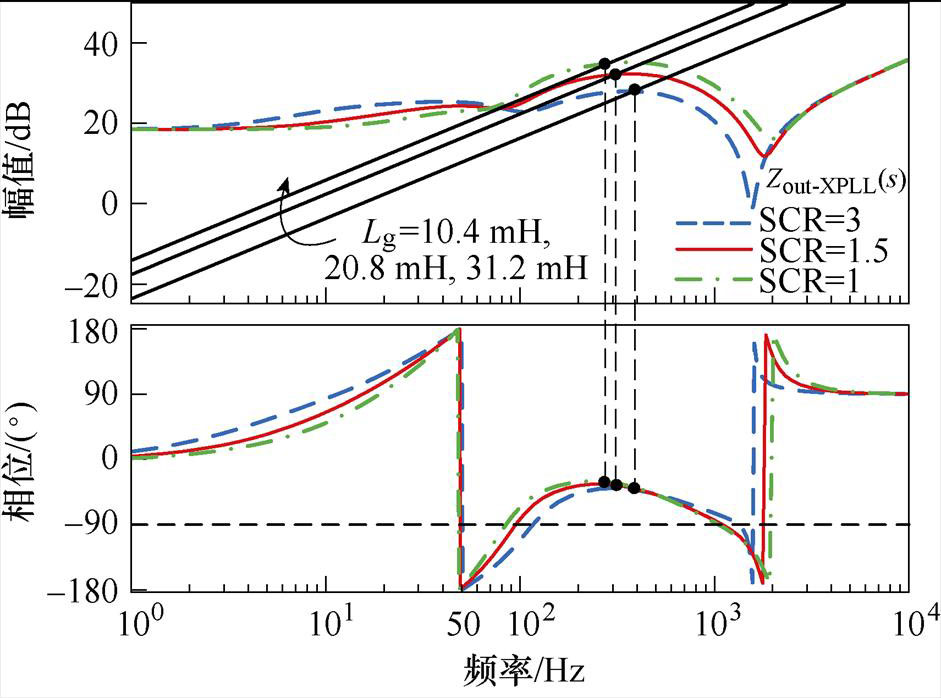
(a)不同电网阻抗下Zout-XPLL的伯德图
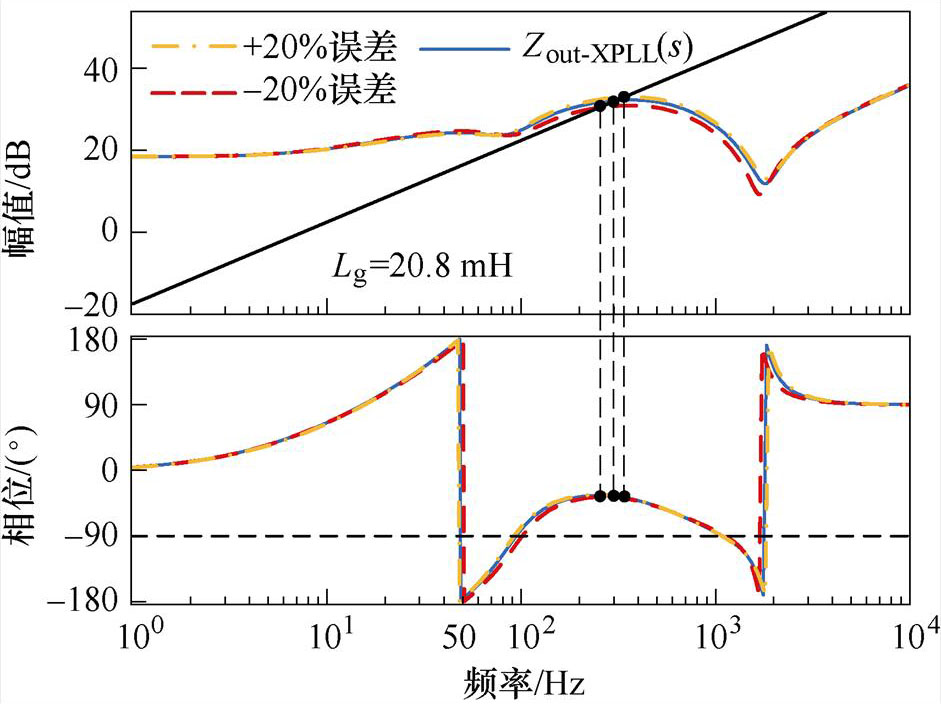
(b)考虑误差下Zout-XPLL的伯德图
图12 Zout-XPLL的伯德图
Fig.12 Bode plot of Zout-XPLL
为验证所提新型PLL的有效性,在Matlab/ Simulink中搭建了单相LCL型并网逆变器仿真模型,参数见表1。
图13为采用传统PLL和新型PLL控制时的系统仿真波形。采用传统PLL控制时,如图13a所示,当电网阻抗Lg=2.6 mH(SCR=12)时,并网电流波形稳定;当电网阻抗Lg=5.2 mH(SCR=6)时,并网电流总谐波畸变率(Total Harmonic Distortion, THD)为4.93 %,已处于并网标准的临界值;当电网阻抗Lg=10.4 mH(SCR=3)时,并网电流发生严重振荡,且已无法满足并网要求。采用新型PLL控制时,如图13b所示,并网电流质量得到了明显改善,并且在极弱电网下,如电网阻抗Lg=31.2 mH(SCR=1)时,并网电流THD为1.47 %,依然满足并网要求。此外,如图13c所示,采用新型PLL控制时,并网点电压、电流不存在相位偏差,满足并网点单位功率因数并网的要求。
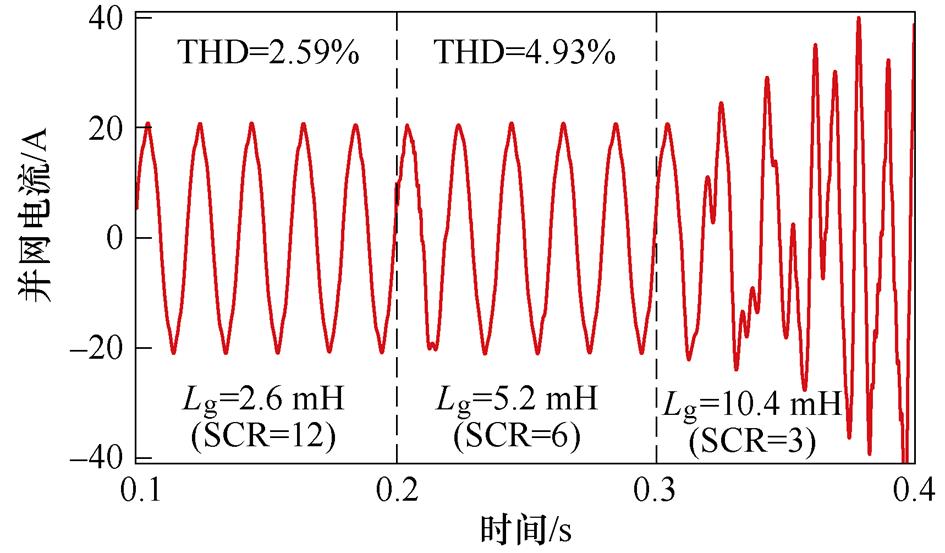
(a)传统PLL控制时并网电流仿真波形
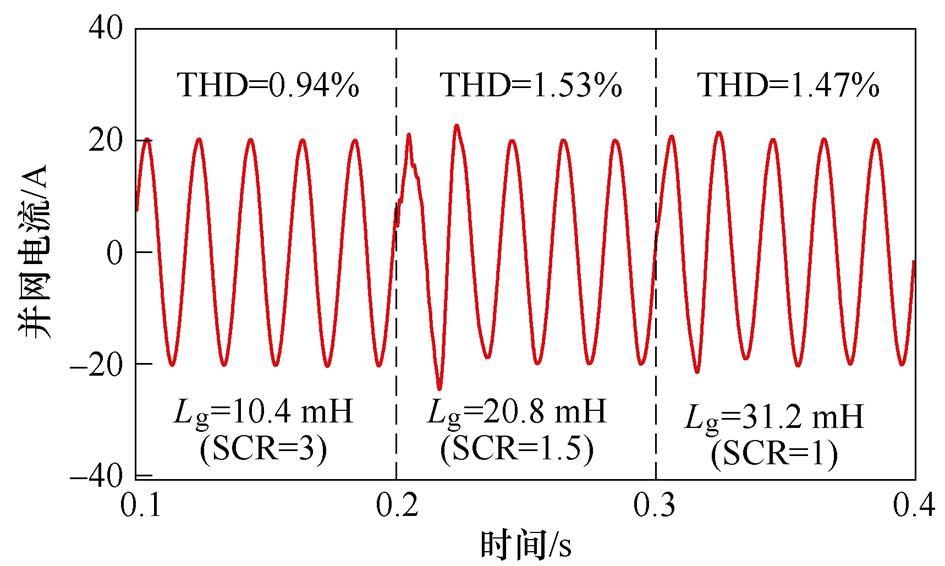
(b)新型PLL控制时并网电流仿真波形
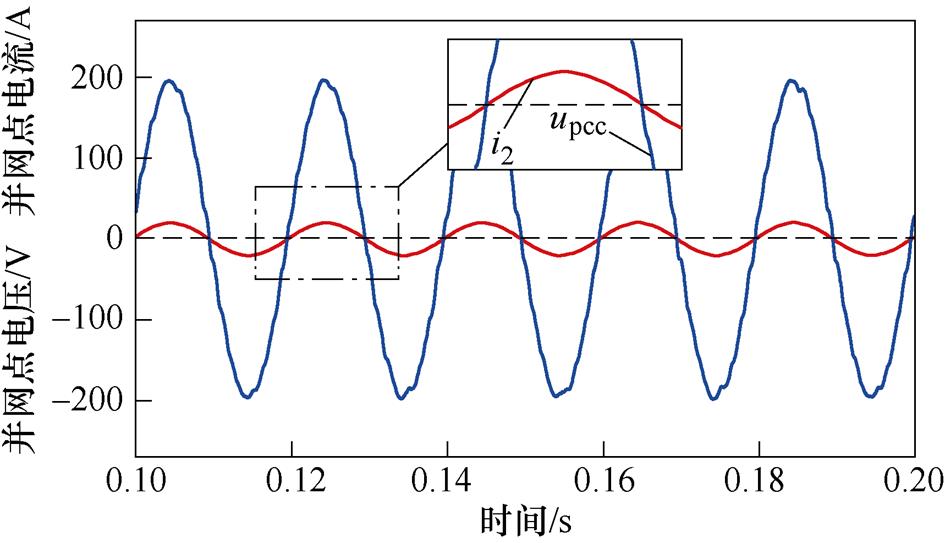
(c)新型PLL控制时并网点电流、电压仿真波形
图13 传统PLL与新型PLL控制时系统仿真波形
Fig.13 System simulation waveforms of traditional PLL and new PLL control
为进一步验证本文所提新型PLL的有效性,采用实时数字控制器RTU-BOX204控制平台,搭建了如图14所示的2 kW单相LCL型并网逆变器实验平台,具体实验参数与表1一致。
图15为采用传统PLL控制时并网点电压、电流实验波形。从图15可以看出,当电网阻抗Lg= 5.2 mH时,并网电流出现较大畸变,当Lg继续增大时,并网电流会出现严重畸变甚至发生振荡,实验样机自动保护,系统断开。
图16为采用新型PLL控制时的系统并网点电压、电流实验波形。从图中可以看出,当电网阻抗Lg=10.4 mH(SCR=3)和Lg=20.8 mH(SCR=1.5)时,并网电流保持稳定运行,系统鲁棒性得到加强;当电网阻抗Lg=31.2 mH(SCR=1)时,并网电流仍能稳定运行且畸变较小。并且并网电压与并网电流同时过零点,无相位偏差。以上实验结论与4.1节仿真验证结论一致,但是需要指出的是,由于电网阻抗的存在,并网点电压不可避免地受到影响,并且随着电网阻抗Lg的增大,并网电压出现了明显的低频谐波失真,同时,电网电压的相位与并网点电压相位偏差的逐渐增大,导致并网点电压幅值下降。

图14 实验平台示意图
Fig.14 Schematic diagram of experimental platform
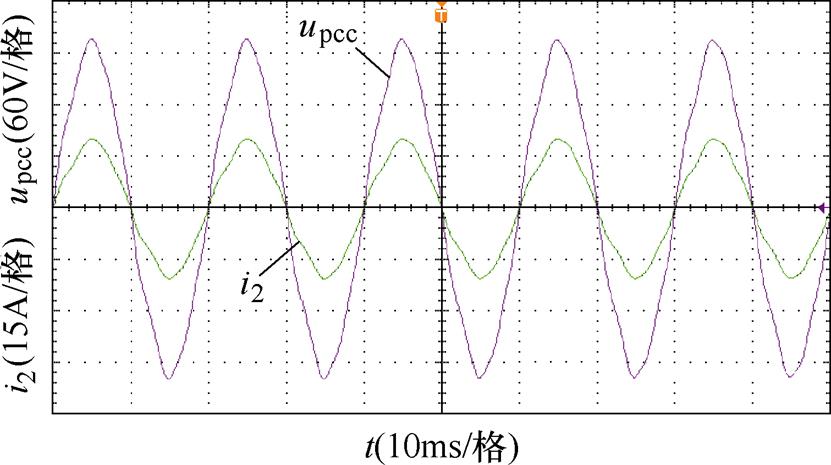
图15 传统PLL控制时并网点电压、电流实验波形(Lg=5.2 mH)
Fig.15 Experimental waveforms of voltage and current under traditional PLL control with Lg=5.2 mH
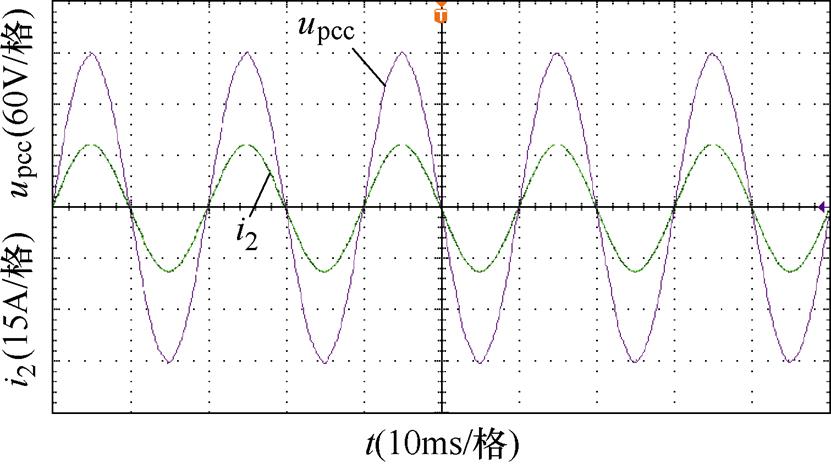
(a)Lg=10.4 mH
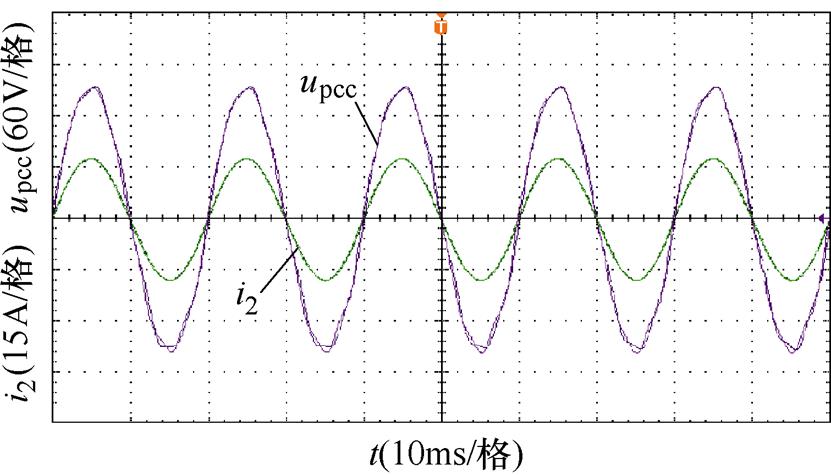
(b)Lg=20.8 mH
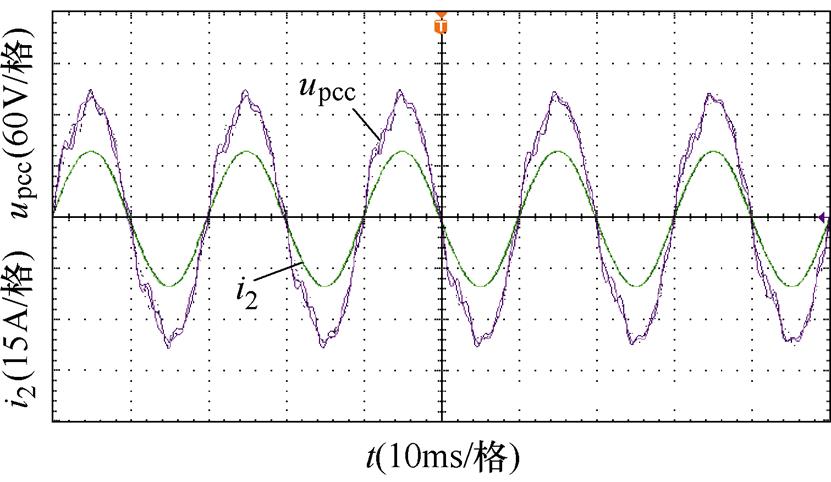
(c)Lg=31.2 mH
图16 新型PLL控制时并网点电压、电流波形
Fig.16 Experimental waveforms of voltage and current under new PLL control
此外,图17给出了新型PLL控制时系统并网电流跳变时的动态实验波形,为使动态实验波形更加清晰直观,此实验选择在电网阻抗Lg=5.2 mH的情况下进行,此时并网点电压、电流畸变率均较小。如图17所示,当实验设置参考电流由满载到半载跳变时,并网电流在跳变瞬间出现短暂的调节过程,并在半个工频周期内进入稳态,说明基于新型PLL控制时系统具有良好的动态性能。
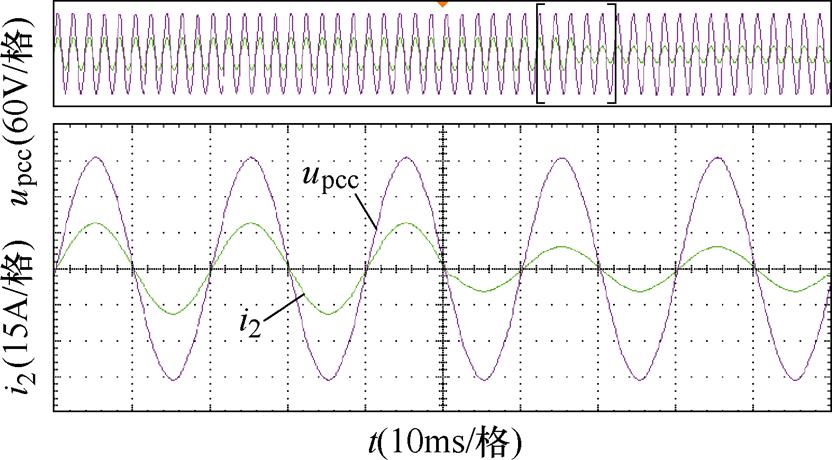
图17 新型PLL控制时并网点电压、电流动态实验波形
Fig.17 Dynamic experimental waveforms of voltage and current under new PLL control
基于上述仿真与实验结果表明,提出的新型PLL控制结构可以有效解决高渗透率下系统鲁棒性下降甚至失稳问题,拓宽了弱电网甚至极弱电网下系统对电网阻抗宽范围变化的适应能力。
本文以LCL滤波单相并网逆变器为例,提出了一种新型PLL控制结构,该结构能够有效解决高渗透率下PLL与系统鲁棒性下降问题,并得到以下几点结论:
1)高渗透率下,PLL与电网阻抗之间存在耦合,等效为在PLL控制环路中引入了一条与电网阻抗有关的正反馈回路,此反馈回路直接影响了PLL输出及其自身稳定性。
2)从阻抗角度分析,PLL的引入降低了并网逆变器输出阻抗的相位,并且系统的交截频率随着电网阻抗的增大而减小,二者共同作用导致系统稳定裕度降低甚至系统失稳。
3)所提新型PLL控制结构通过对系统输出阻抗进行重塑和相位校正,即使是在极弱电网下,依旧可以准确提取电压相位并确保系统高鲁棒性,拓宽了高渗透率下并网逆变器电流控制系统对电网阻抗的适应范围。
4)下一步将在本文1.3节所提串并联阻抗重塑的基础上,通过对并网逆变器控制框图的等效变换,推导得到可以完全消除负阻抗ZPLL对输出阻抗影响的电网电压前馈函数,并基于电网电压前馈控制实现对逆变器输出阻抗相位特性进行重塑。
参考文献
[1] 沈姝衡, 方天治, 章益凡. 高带宽数字控制LCL型并网逆变器及其提高并网系统鲁棒性的谐振抑制技术研究[J]. 电工技术学报, 2022, 37(21): 5548- 5561.
Shen Shuheng, Fang Tianzhi, Zhang Yifan. A high- bandwidth digital-control LCL-type grid-tied inverter and resonance-suppressing technique for improving the robustness of grid-connected system[J]. Transa- ctions of China Electrotechnical Society, 2022, 37(21): 5548-5561.
[2] Wang Xiongfei, Blaabjerg F, Loh P C. Grid-current- feedback active damping for LCL resonance in grid- connected voltage-source converters[J]. IEEE Transa- ctions on Power Electronics, 2016, 31(1): 213-223.
[3] 李明. 高渗透率新能源发电并网逆变器阻抗自适应双模式控制研究[D]. 合肥: 合肥工业大学, 2020.
[4] 郭小强, 朱铁影. 新型非隔离型三相三电平光伏并网逆变器及其漏电流抑制研究[J]. 电工技术学报, 2018, 33(1): 26-37.
Guo Xiaoqiang, Zhu Tieying. Research on leakage current suppression of novel three-phase three-level non-isolated PV inverter[J]. Transactions of China Electrotechnical Society, 2018, 33(1): 26-37.
[5] Davari M, Mohamed Y A R I. Robust vector control of a very weak-grid-connected voltage-source converter considering the phase-locked loop dynamics[J]. IEEE Transactions on Power Electronics, 2017, 32(2): 977- 994.
[6] 张兴, 李明, 郭梓暄, 等. 新能源并网逆变器控制策略研究综述与展望[J]. 全球能源互联网, 2021, 4(5): 506-515.
Zhang Xing, Li Ming, Guo Zixuan, et al. Review and perspectives on control strategies for renewable energy grid-connected inverters[J]. Journal of Global Energy Interconnection, 2021, 4(5): 506-515.
[7] 许津铭, 卞申一阳, 钱浩, 等. 弱电网下单相并网逆变器延时锁相环的鲁棒控制及优化方法[J]. 中国电机工程学报, 2020, 40(7): 2062-2070, 2386.
Xu Jinming, Bian Shenyiyang, Qian Hao, et al. Robust control and optimization of delay-based phase-locked loop of single-phase grid-connected inverters under weak grid conditions[J]. Proceedings of the CSEE, 2020, 40(7): 2062-2070, 2386.
[8] 涂春鸣, 高家元, 李庆, 等. 具有复数滤波器结构锁相环的并网逆变器对弱电网的适应性研究[J]. 电工技术学报, 2020, 35(12): 2632-2642.
Tu Chunming, Gao Jiayuan, Li Qing, et al. Research on adaptability of grid-connected inverter with com- plex coefficient-filter structure phase locked loop to weak grid[J]. Transactions of China Electrotechnical Society, 2020, 35(12): 2632-2642.
[9] Cespedes M, Sun Jian. Adaptive control of grid- connected inverters based on online grid impedance measurements[J]. IEEE Transactions on Sustainable Energy, 2014, 5(2): 516-523.
[10] 许津铭, 谢少军, 唐婷. 弱电网下LCL滤波并网逆变器自适应电流控制[J]. 中国电机工程学报, 2014, 34(24): 4031-4039.
Xu Jinming, Xie Shaojun, Tang Ting. An adaptive current control for grid-connected LCL-filtered inver- ters in weak grid case[J]. Proceedings of the CSEE, 2014, 34(24): 4031-4039.
[11] 钱一涛, 赵晋斌, 马俊清, 等. 弱电网基于对称PLL结构的并网逆变器频率耦合消除与稳定性增强方法[J]. 电网技术, 2022, 46(10): 3893-3901.
Qian Yitao, Zhao Jinbin, Ma Junqing, et al. Gird- connected inverter frequency coupling elimination and stability enhancement method based on sym- metrical PLL structure under weak grid[J]. Power System Technology, 2021, 46(10): 3893-3901.
[12] Yang Dongsheng, Wang Xiongfei, Liu Fangcheng, et al. Symmetrical PLL for SISO impedance modeling and enhanced stability in weak grids[J]. IEEE Transa- ctions on Power Electronics, 2019, 35(2): 1473-1483.
[13] 杜燕, 言明明, 杨向真, 等. 多目标约束下逆变器阻抗的电流矫正方法[J]. 控制理论与应用, 2022, 39(4): 701-710.
Du Yan, Yan Mingming, Yang Xiangzhen, et al. Current correction method for grid-connected inverter impedance under multi-objective constraints[J]. Con- trol Theory & Applications, 2022, 39(4): 701-710.
[14] 高家元, 肖凡, 姜飞, 等. 弱电网下具有新型PLL结构的并网逆变器阻抗相位重塑控制[J]. 中国电机工程学报, 2020, 40(20): 6682-6694.
Gao Jiayuan, Xiao Fan, Jiang Fei, et al. Grid- connected inverter impedance phase reshaping control with novel PLL structure in weak grid[J]. Proceedings of the CSEE, 2020, 40(20): 6682-6694.
[15] 张烨, 田慕琴, 宋建成, 等. 弱电网下计及锁相环影响的并网逆变器输出阻抗重塑[J]. 高电压技术, 2021, 47(11): 4033-4044.
Zhang Ye, Tian Muqin, Song Jiancheng, et al. Recon- struction of the output impedance of grid-connected inverter considering PLL effect in weak grids[J]. High Voltage Engineering, 2021, 47(11): 4033-4044.
[16] 吴恒, 阮新波, 杨东升. 弱电网条件下锁相环对LCL型并网逆变器稳定性的影响研究及锁相环参数设计[J]. 中国电机工程学报, 2014, 34(30): 5259- 5268.
Wu Heng, Ruan Xinbo, Yang Dongsheng. Research on the stability caused by phase-locked loop for LCL- type grid-connected inverter in weak grid condition[J]. Proceedings of the CSEE, 2014, 34(30): 5259-5268.
[17] 涂春鸣, 高家元, 赵晋斌, 等. 弱电网下具有定稳定裕度的并网逆变器阻抗重塑分析与设计[J]. 电工技术学报, 2020, 35(6): 1327-1335.
Tu Chunming, Gao Jiayuan, Zhao Jinbin, et al. Analysis and design of grid-connected inverter impedance remodeling with fixed stability margin in weak grid[J]. Transactions of China Electrotechnical Society, 2020, 35(6): 1327-1335.
[18] 李杨, 帅智康, 方俊彬, 等. 基于阻抗测量的多逆变器系统稳定性校验方法[J]. 电力系统自动化, 2021, 45(11): 95-101.
Li Yang, Shuai Zhikang, Fang Junbin, et al. Stability check method for multi-inverter system based on impedance measurement[J]. Automation of Electric Power Systems, 2021, 45(11): 95-101.
[19] 邓吉鸽. 高阶线性跟踪微分器性能研究[J]. 舰船电子工程, 2012, 32(4): 68-70.
Deng Jige. Study on high order linear tarcking differentlator[J]. Ship Electronic Engineering, 2012, 32(4): 68-70.
[20] 方天治, 黄淳, 陈乃铭, 等. 一种提高弱电网下LCL型并网逆变器鲁棒性的相位超前补偿策略[J]. 电工技术学报, 2018, 33(20): 4813-4822.
Fang Tianzhi, Huang Chun, Chen Naiming, et al. A phase-lead compensation strategy on enhancing robustness of LCL-type grid-tied inverters under weak grid conditions[J]. Transactions of China Elec- trotechnical Society, 2018, 33(20): 4813-4822.
[21] 张莉华. 全通IIR数字滤波器的设计和应用[D]. 杭州: 杭州电子科技大学, 2015.
A Phase-Locked Loop Design Method Based on Impedance Remodeling of Grid-Connected Inverter under High Permeability
Abstract Under high permeability, the phase-locked loop (PLL), grid impedance, and grid-connected inverter are coupled, seriously impacting the stable operation of the grid-connected inverter system based on synchronous control of PLL. Firstly, for the PLL control structure, grid impedance leads to the introduction of additional feedback loops in the PLL structure. When the grid impedance changes in a wide range, the PLL system will generate the right half plane pole, decreasing the stability of the PLL or even instability. Secondly, for the grid-connected inverter system, when PLL is considered, the additional negative impedance will be introduced into the output impedance of the system, which directly affects the amplitude and phase of the output impedance of the system, decreasing the stability margin of the grid-connected inverter system.
Therefore, this paper takes the single-phase LCL filter grid-connected inverter under the weak current network as the research object and proposes a new PLL control structure with the dot connection current and dot connection voltage as input signals. The new PLL control structure uses the grid impedance measurement value and differential link to dynamically adjust the grid-connected current branch in the new PLL, limiting the grid impedance component in the PLL input signal. Meanwhile, the advance corrector is used to reshape the phase characteristics of the system output impedance. The influence of additional negative impedance on system stability was reduced. Then, the output phase Angle of the new PLL was corrected using an all-pass filter to ensure that the fundamental frequency phase was consistent before and after impedance remodeling.
The robustness analysis of the grid-connected inverter system based on the new PLL control shows that the new PLL structure has high robustness and can reshape the output impedance of the inverter system to improve the phase angle of the output impedance at the intercept frequency. When the system is in a weak grid, the phase margin is greater than 30o, and the system robustness is guaranteed. In addition, the simulation and experimental verification show that the quality of the grid-connected current of the system is improved when the new PLL control is adopted. The voltage and current of the grid connection point do not have phase deviation, which meets the requirements of the grid connection point unit power factor. Moreover, the system has good dynamic performance, and effectively expands the adaptive range of the grid-connected inverter electrical system to the grid impedance under high permeability.
In the next step, the grid voltage feedforward function, which can eliminate the influence of PLL, will be obtained by an equivalent transformation of the control block diagram of the grid-connected inverter. The phase characteristics of the output impedance of the inverter will be reshaped using grid voltage feedforward control to improve the stability of the grid-connected inverter system under high permeability.
keywords:High permeability, grid-connected inverters, phase-locked loop, impedance remodeling, robustness
中图分类号:TM464
DOI: 10.19595/j.cnki.1000-6753.tces.222018
国家自然科学基金资助项目(U1804143)。
收稿日期 2022-10-26
改稿日期 2023-01-08
杨 明 男,1982年生,博士,副教授,研究方向为新能源并网发电技术、电能质量控制、虚拟同步发电机等。E-mail: yangming0391@163.com
杨 倬 男,1999年生,硕士研究生,研究方向为并网逆变器控制及稳定性分析。E-mail: 1135229637@qq.com(通信作者)
(编辑 陈 诚)