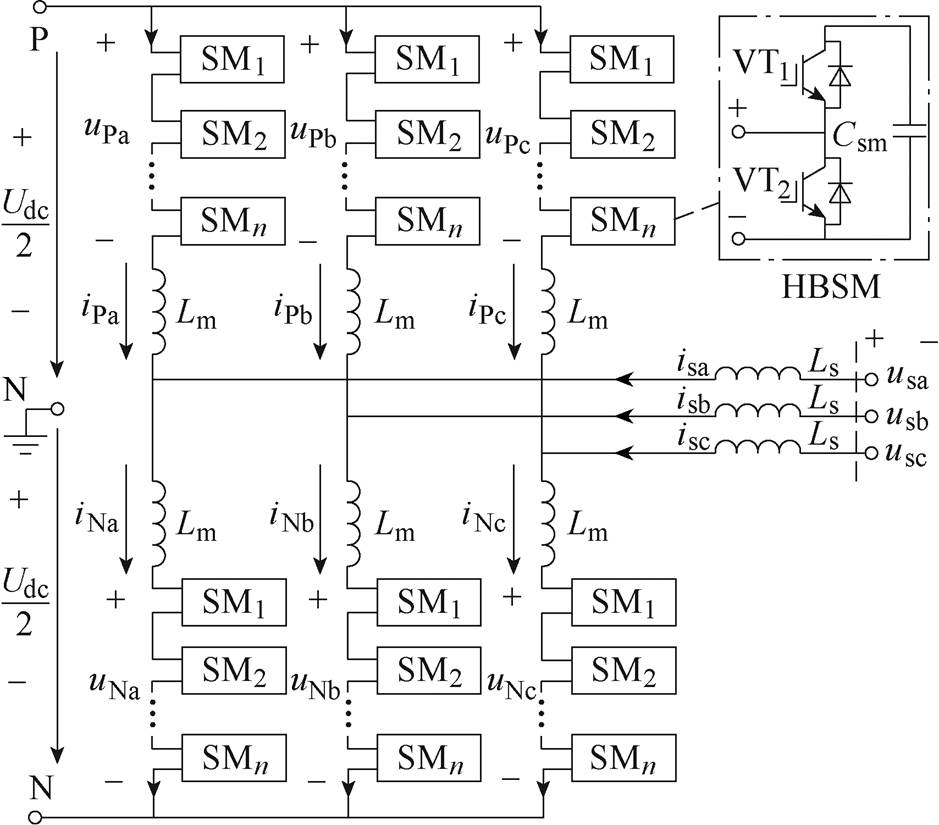
图1 模块化多电平换流器拓扑
Fig.1 Configuration of modular multilevel converter
摘要 不平衡电网下模块化多电平换流器（MMC）存在三相直流环流不均衡问题，易导致相间电流应力和热应力差异，降低其在不平衡工况下安全运行能力。该文从桥臂功率角度分析不平衡电网下三相MMC直流环流不均衡现象和基于零序电压注入的直流环流均衡机理。提出一种零序电压注入的直流环流均衡方法，通过网侧电流与直流环流偏差量计算得到零序电压相位，经过比例谐振控制器生成零序电压注入量，进而实现直流环流的快速、有效均衡。在所提出的控制策略的基础上，研究该方法对MMC桥臂电流峰值、有效值及子模块电容电压纹波的影响规律。仿真与实验结果验证了该文理论分析与控制策略的有效性。
关键词：不平衡电网 模块化多电平换流器 直流环流 零序电压注入 桥臂电流 子模块电容电压
模块化多电平换流器（Modular Multilevel Converter, MMC）具有模块化程度高、扩展性强、输出谐波含量低等优势，在柔性直流输电、新能源并网、电能路由器等中高压大功率领域获得广泛应用[1-3]。由于MMC储能电容分布于各功率单元，三相桥臂并联于公共直流母线的结构特点，桥臂间电压难以实现完全一致，不可避免会存在环流问题[4]。
通常情况下，MMC桥臂环流主要由二倍频负序性质的交流分量与三相平衡的直流分量构成。然而当电网电压不平衡时，MMC桥臂电压波动变得复杂且相间功率分配难以均衡[5]，随之而来的正、负、零序环流分量和不对称的直流环流势必会加剧MMC相间电流应力与热应力差异。过大的电流应力与热应力是MMC安全运行的首要隐患，轻则增大系统损耗、缩短功率器件寿命，严重时将触发闭锁保护甚至直接导致功率单元过电流损坏[6-7]。因此必须对不平衡的MMC桥臂环流采取有效控制措施。
国内外众多专家学者开展了不平衡网压下的MMC桥臂环流控制研究[8-15]。为降低桥臂电流峰值和损耗，正、负、零序交流环流抑制策略率先得到关注并进行了广泛研究，文献[8]提出在正、负序双dq坐标系下基于比例积分（Proportional Integral, PI）调节器的环流抑制方法，但未考虑零序环流分量的控制。文献[9]在两相静止坐标系下，利用比例谐振（Proportional Resonant, PR）调节器实现正、负、零序环流抑制。文献[10]则在abc坐标系下采用准PR调节器完成了交流环流分相控制，无需坐标变换，原理简单。为提升交流环流抑制性能，文献[11]提出了PI与准PR双回路环流抑制策略，增加了直流分量控制回路且需额外计算三相直流环流参考值。类似地，文献[12]在abc坐标系下采用比例积分和矢量比例积分调节器并联方法实现了交流环流控制，然而同样需要计算直流环流参考值。文献[13]则提出基于重复控制的桥臂电流多层控制策略，间接实现正、负、零序交流环流抑制，物理意义较为直观但参数整定困难。上述交流环流控制虽成效显著，但由于不平衡的直流环流未得到有效控制，相间电流应力与热应力失衡的隐患仍然存在。为此，文献[14]提出一种基于零序电压注入的直流环流均衡开环算法，在交流环流抑制的基础上实现了直流环流均衡，但控制效果依赖于输入量的准确度，且开环算法动态性能欠佳。文献[15]提出一种基于平均损耗预测的直流环流控制策略，通过控制零序电压注入实现相单元损耗与器件结温的均衡，但运算过程繁琐且未考虑零序电压可能对子模块电容电压纹波等内特性造成的影响。现有的不平衡网压MMC桥臂环流控制研究大多针对交流环流展开，而对直流环流控制方法及其潜在影响研究并不深入。因此，研究一种快速有效的直流环流均衡策略并分析其对MMC内特性的影响规律将是本文的研究重点。
本文首先分析了不平衡电网下MMC三相直流环流不均衡现象的产生机理，基于零序电压注入的MMC并网等效模型求解得到直流环流均衡目标下的零序电压幅值、相位表达式。以此为基础，提出一种零序电压注入的直流环流均衡方法，通过网侧电流与直流环流偏差量计算得到零序电压相位，利用PR控制器调节幅值生成零序电压注入量，原理简单且实用性强。接着重点研究零序电压注入对MMC桥臂电流峰值、有效值及子模块电容电压纹波的影响规律。最后通过仿真与实验结果对本文理论分析与所提策略进行了验证。
图1是典型n+1电平三相MMC拓扑，包含6个桥臂，每个桥臂由n个半桥型子模块（Half-Bridge Submodule, HBSM）和桥臂电感Lm级联而成。HBSM由两个开关管VT1、VT2与子模块电容Csm并联组成。此外，图1中，Udc为公共直流电压，uPj、uNj分别为MMC第j相的上、下桥臂电压，iPj、iNj分别为对应的桥臂电流；usj、isj分别为网侧电压和电流，j为相数，j=a, b, c。
图1 模块化多电平换流器拓扑
Fig.1 Configuration of modular multilevel converter
根据基尔霍夫电压定律，MMC的j相上、下桥臂回路方程满足
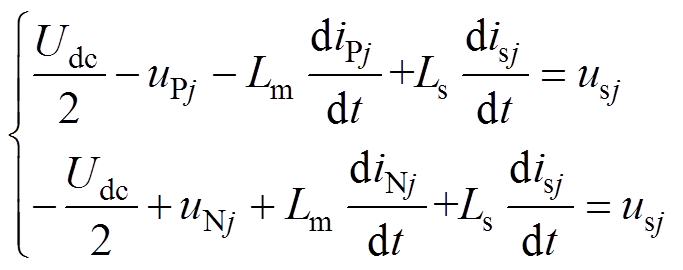（1）
式中，Ls为并网电感。由基尔霍夫电流定律可求得MMC网侧等效数学模型为
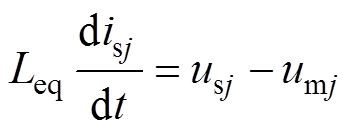（2）
式中，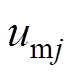
为MMC交流电压，
；
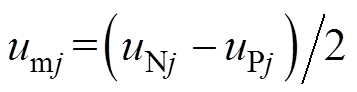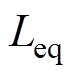为等效电感，
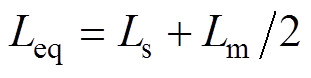。由式（2）可知，通过控制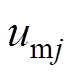即可实现对MMC网侧电流及功率的调节。
MMC通常通过星-三角形变压器接入电网，实现交流电压匹配的同时避免向电网注入零序电流[16]，此时不平衡电网电压可表示为仅含正序、负序分量，即
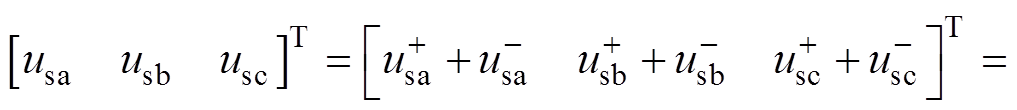
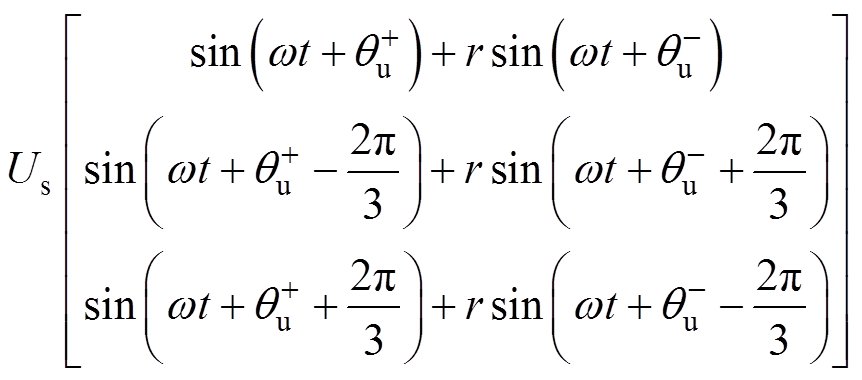（3）
式中，电网电压不平衡度r定义为负序电压与正序电压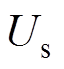
的幅值之比；
、
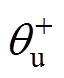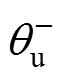分别为电网电压的正、负序分量初相角；
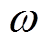为额定角频率。
与传统并网逆变器类似，在电网电压不平衡工况发生时，MMC通常需要选取有功功率恒定、无功功率恒定或网侧电流平衡作为其控制目标[17]。实际上，考虑到负序电流可能导致的线路设备过电流保护现象以及MMC内部桥臂电流应力失衡[18]，网侧电流平衡是最常采用的控制目标之一[19]。在网侧电流平衡控制下，由于负序电流得到抑制，MMC三相网侧电流满足
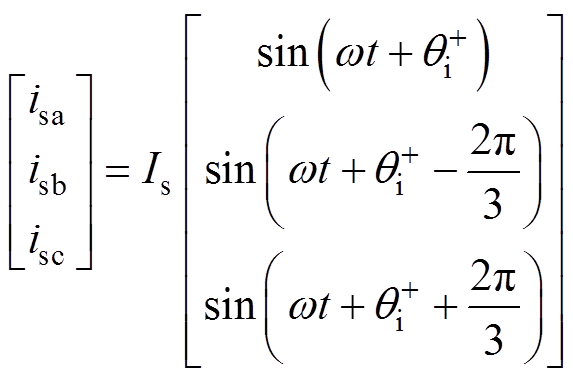（4）
式中，
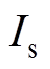和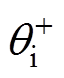
分别为网侧电流幅值与初相角。
此时MMC三相并网有功功率Psj可表示为
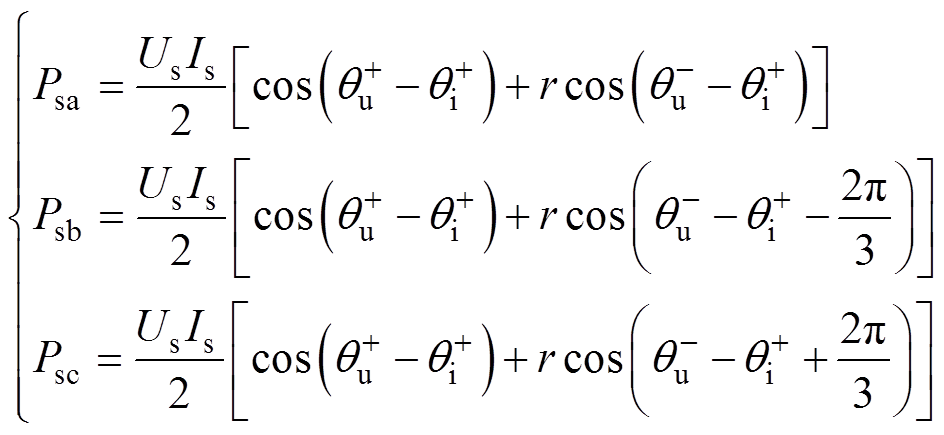（5）
式中，正序电网电压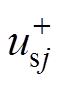
与网侧电流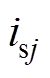
乘积将决定MMC的并网总有功功率Ps；而负序电网电压
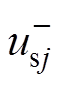与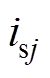乘积由于其三相之和为零，仅影响MMC的相间有功功率分布。
若忽略系统损耗，MMC各相交直流功率守恒，定义Idcj为桥臂直流环流，Idcj应满足
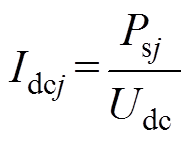（6）
通过上述分析可知，负序网压分量使得部分有功功率在MMC三相分配不均，进而造成桥臂直流环流差异。直流环流差异将导致热应力失衡、桥臂电流峰值增大及子模块电容电压波动加剧等一系列问题，因此采取有效的直流环流均衡措施至关重要。
根据叠加原理，为实现网侧电流平衡控制，MMC交流电压中的负序分量应等于电网负序电压分量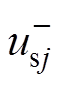。而正序电压分量由传输功率大小决定。因此，仅零序分量可作为自由控制维度。
在交流侧不存在零序电流回路的前提下，注入零序电压只会重新分配MMC相间有功功率，而不会对三相网侧电流及整体并网功率产生影响。设注入零序电压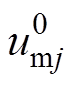
的幅值、相位分别为
、
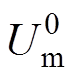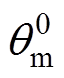，得到零序电压注入后的MMC的等效电路如图2所示。
此时MMC上、下桥臂电压应满足
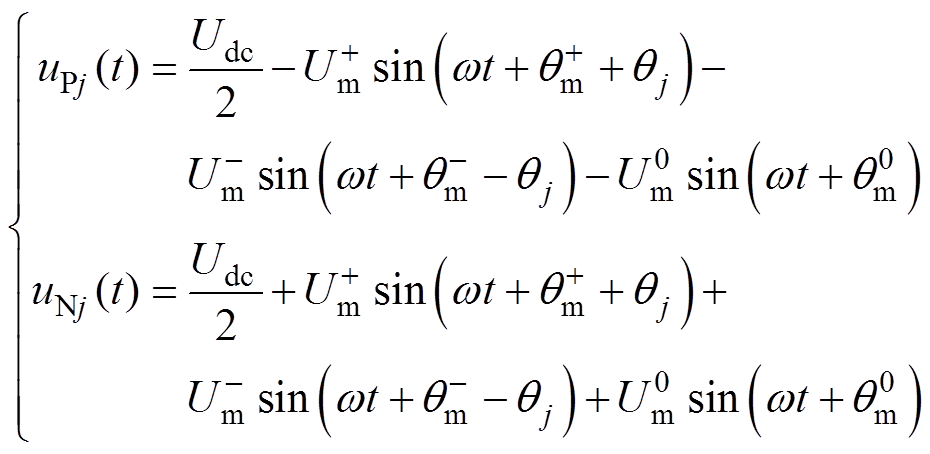（7）
式中，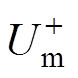
、
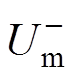分别为MMC输出正、负序电压幅值；
、
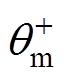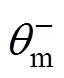分别为MMC输出正、负序电压初相角；
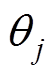为第j相电压初相角。。
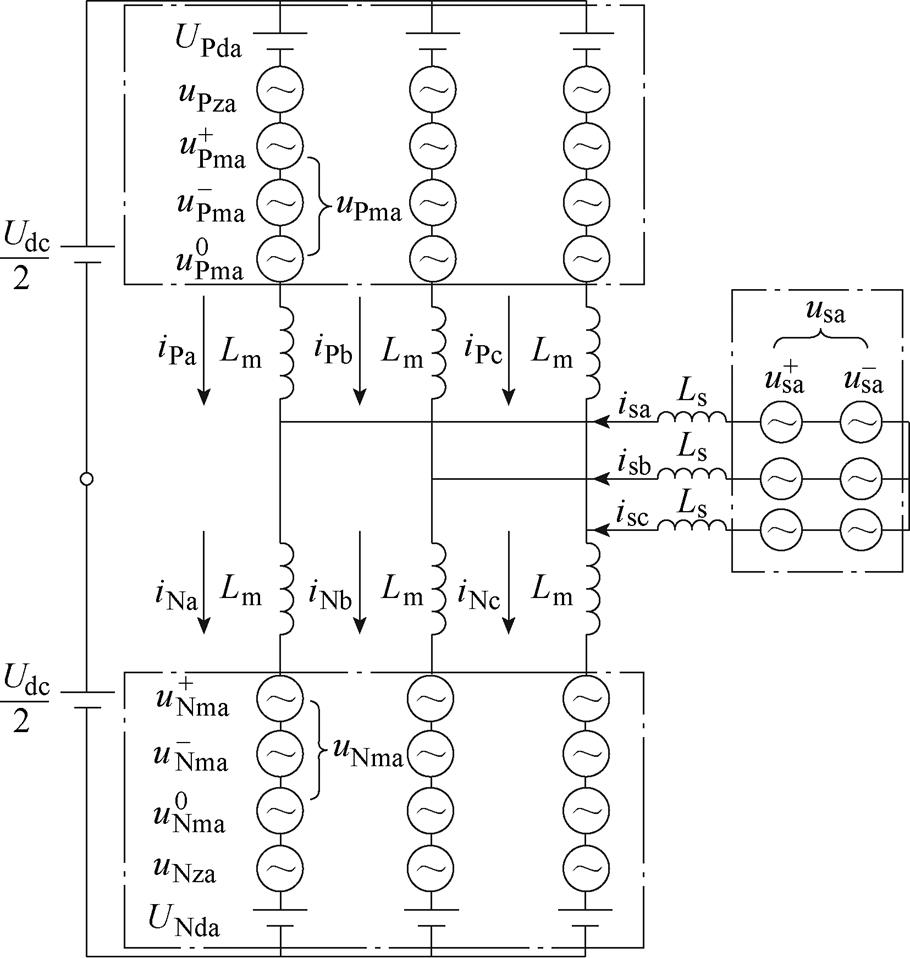
图2 零序电压注入的MMC并网等效电路
Fig.2 Equivalent circuit of grid-connected MMC with zero sequence voltage injection
MMC的桥臂电流由直流环流分量、基频网侧电流分量以及正、负、零序交流环流分量组成。
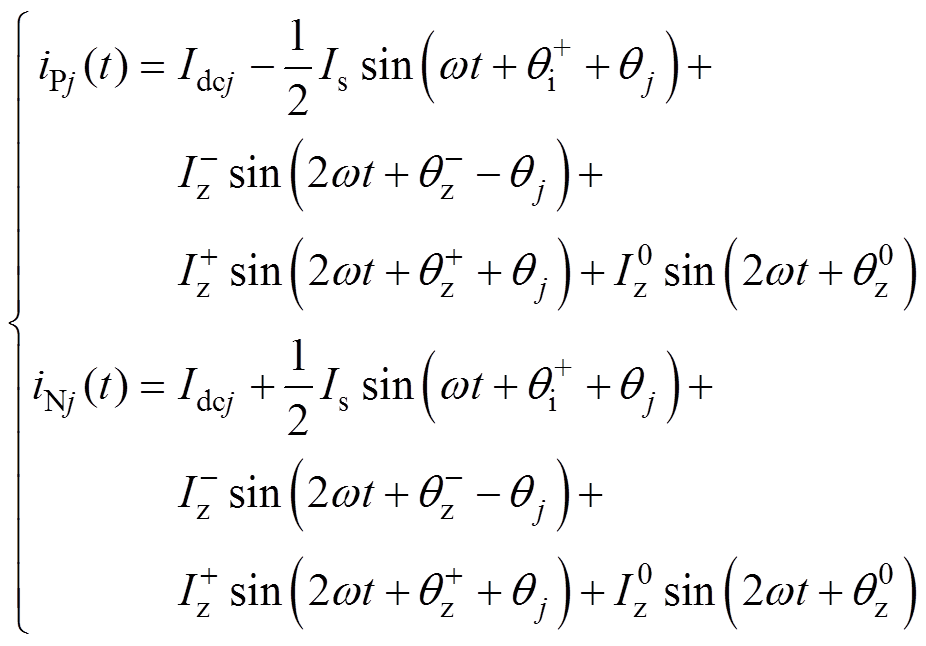（8）
式中，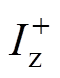
、
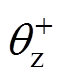分别为正序交流环流分量的幅值与相位；
、
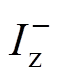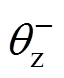分别为负序交流环流分量的幅值与相位；
、
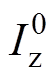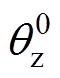分别为零序交流环流分量的幅值与相位。
假设MMC子模块电容电压均衡，忽略桥臂阻抗压降，j相平均功率满足
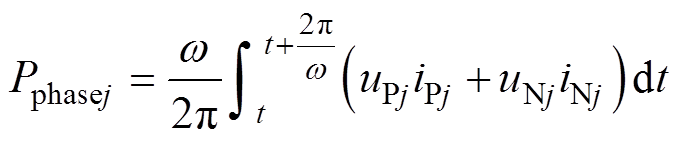（9）
由于二倍频环流分量不会对式（9）中平均功率计算产生影响，因此可忽略，得到
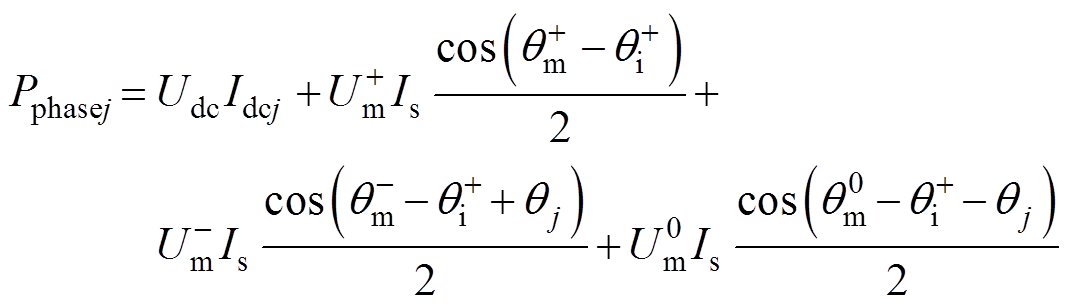（10）
根据式（10）可知，j相平均功率包含直流环流导致的直流功率，以及由正序网侧电流导致的交流功率。结合桥臂功率守恒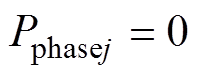
，取三相直流环流均衡作为零序电压注入目标，即满足等式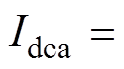
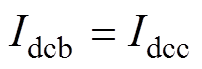，可计算零序电压幅值、相位分别为
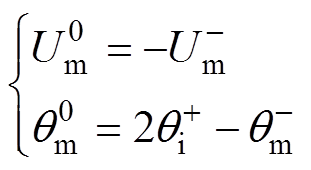（11）
根据2.1节分析不难发现，实现三相直流环流均衡目标的关键在于获取幅值、相位关系满足式（11）的零序电压注入量。本文所提零序电压注入的直流环流均衡方法主要控制思路如下：将直流环流偏差作为被控量，设置其参考值为0；接着引入网侧电流进行相位补偿，得到满足零序电压注入相位条件的控制中间量；最后利用PR调节器调节幅值，生成适宜的零序电压注入量。
结合式（5）、式（6）可得各相直流环流偏差量DIdcj表达式为
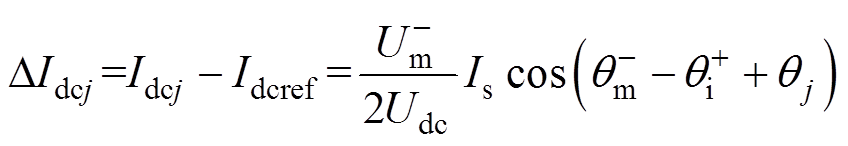（12）
式中，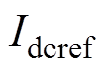
为直流环流参考值，
。
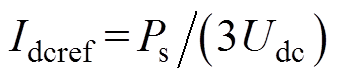为得到式（11）中所需的零序电压相位，引入网侧电流乘积环节进行相位补偿，生成控制中间量uZSV的表达式为
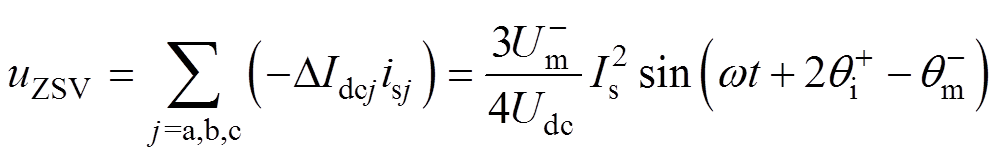（13）
从式（13）中不难发现，其相位与式（11）所需零序电压注入量一致。
接着需对中间量uZSV幅值进行调节。值得说明的是，为避免由于MMC功率指令切换等因素引发网侧电流幅值变化影响所提直流环流均衡控制性能，在中间量uZSV输入到PR调节器之前，对其进行电流幅值归一化处理得
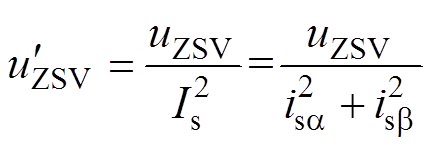（14）
式中，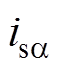
、
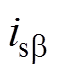分别为网侧电流在a、b 坐标系下的分量。
幅值归一化处理后的中间控制量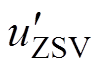
经过PR调节器生成零序电压注入量
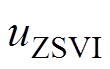，叠加于MMC参考调制波。PR调节器传递函数表达式为
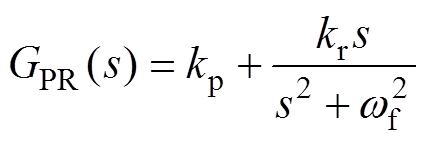（15）
式中，kp为比例系数；kr为谐振增益；wf为基频谐振角频率。
图3为本文所提出的直流环流均衡控制框图。该方法仅通过系统已采样（三相环流与网侧电流）计算生成零序电压注入量，无需正负序分离环节，简单易于实现。通过合理配置PR调节器即可获得理想的控制性能，实用性较强。
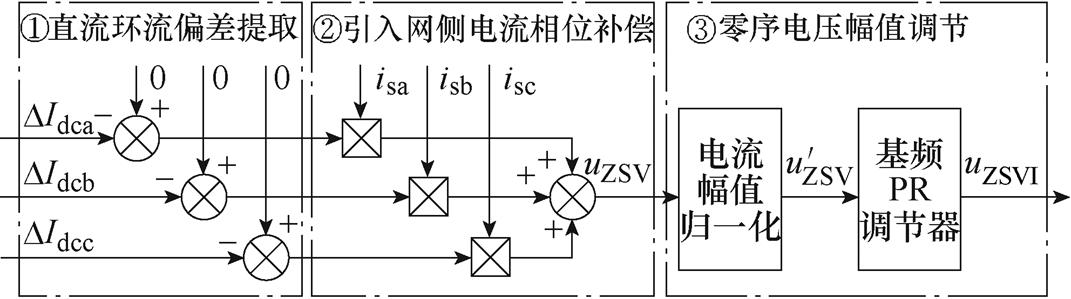
图3 零序电压注入的直流环流均衡控制框图
Fig.3 DC circulating current balancing control block diagram based on zero sequence voltage injection
桥臂电流峰值大小与MMC保护阈值密切相关，在确保MMC安全裕度的前提下，减小桥臂电流峰值可降低误保护动作概率。此外，桥臂电流有效值是决定桥臂热应力的关键因素，三相桥臂间不均衡的温升分布会影响MMC在不平衡工况下的长时间运行能力，同时威胁开关器件的安全。考虑到MMC结构的对称性，不失一般性，本节将以典型单相电压跌落工况为例，从理论角度分析零序电压注入对不平衡电网下MMC桥臂电流峰值及有效值的影响。
单相电压跌落工况下的不平衡电压表达式为
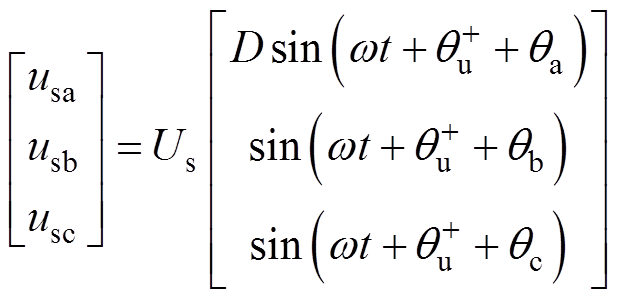（16）
式中，定义电压跌落度D以表示单相电压跌落程度，D∈[0, 1]，其数值越小表明单相电压跌落越严重。
根据正负零序分解法则[14]，正、负序电网电压表达式为
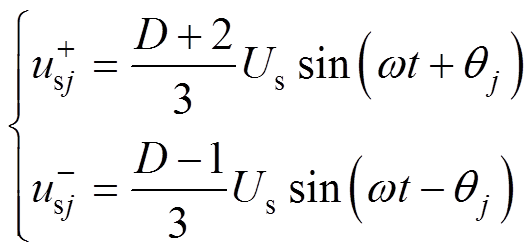（17）
为简化分析，假设电网电压正序分量初相角为0，此时各相直流环流表达式为
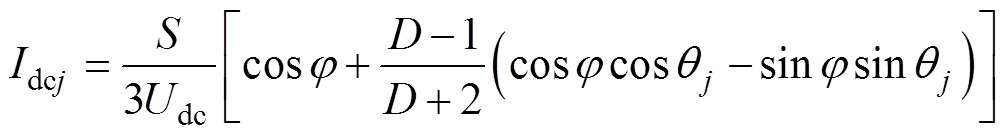（18）
式中，S为MMC额定容量；j 为功率因数角。
假设正、负、零序交流环流分量被有效抑制，此时MMC桥臂电流可视作仅由直流环流与基频网侧电流分量组成，式（8）可重写为
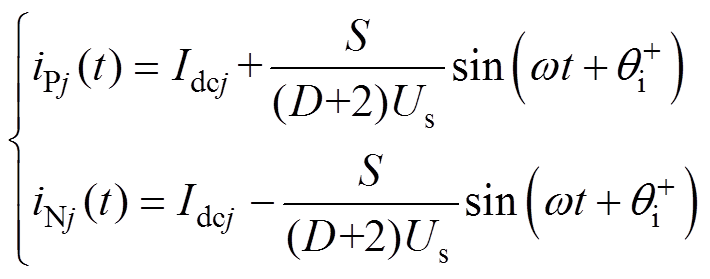（19）
桥臂电流峰值计算可以转化为最大绝对值问题，即
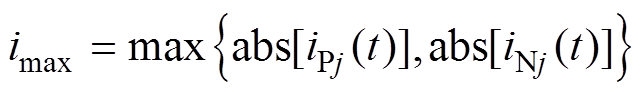（20）
式（20）求解过程涉及三维多变量函数的极值问题，为简化计算过程，本文采用编程遍历求解方法。图4展示了零序电压注入前后桥臂电流峰值imax与相电压跌落度D、功率因数角j 关系。本文理论计算与仿真验证中的MMC并网模型参数均见表1。
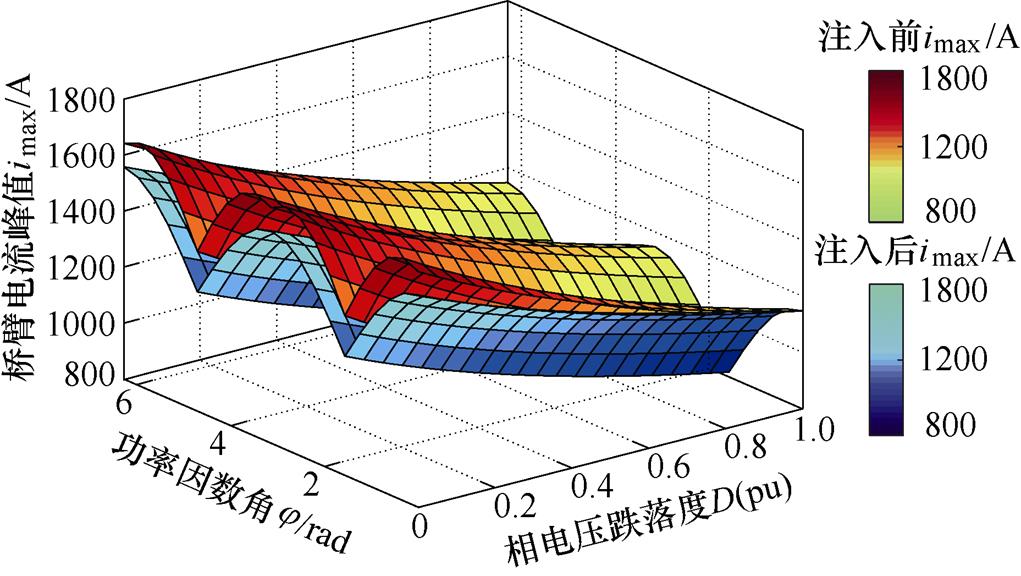
图4 零序电压注入前后桥臂电流峰值
Fig.4 The arm current peak with and without zero-sequence voltage injection
表1 MMC并网模型参数
Tab.1 Parameters of MMC simulation model
参 数数 值 额定容量/(MV·A)20 直流电压/kV20 交流线电压有效值/kV10 单桥臂子模块数4 交流侧电感/mH20 子模块电容/mF5.6 桥臂电感/mH4
由图4可知，MMC桥臂电流峰值与功率因数角j 密切相关，且随着电压跌落度D减小而增大。对比零序电压注入前后的波形不难发现，任一功率因数角下注入零序电压均可降低MMC桥臂电流峰值，在相电压幅值跌落至零时，零序电压注入后的桥臂电流峰值最大可下降10.9 %，有利于MMC不平衡电网下安全运行。
桥臂电流有效值则可以转化为对式（19）的函数积分问题。为使得对比更直观，本文以桥臂电流有效值的标准差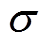
来表征桥臂电流有效值差异，得
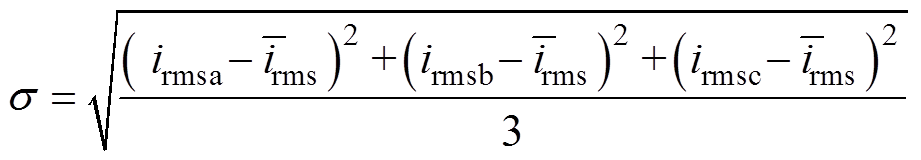（21）
式中，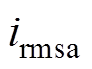
、
、
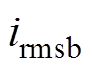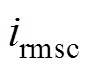为各相桥臂电流有效值，其平均值
。
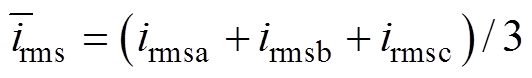零序电压注入前后桥臂电流有效值标准差如图5所示。图5表明，未注入零序电压时，MMC桥臂电流有效值标准差与功率因数角有关。在相同的功率因数下，三相桥臂电流有效值的不平衡程度随着相电压跌落度D降低而逐渐加剧。在网侧电流平衡控制及交流环流抑制理想前提下，零序电压注入可实现桥臂电流有效值完全均衡，避免不平衡的桥臂温升分布，有利于MMC在不对称网压下较长时间运行。
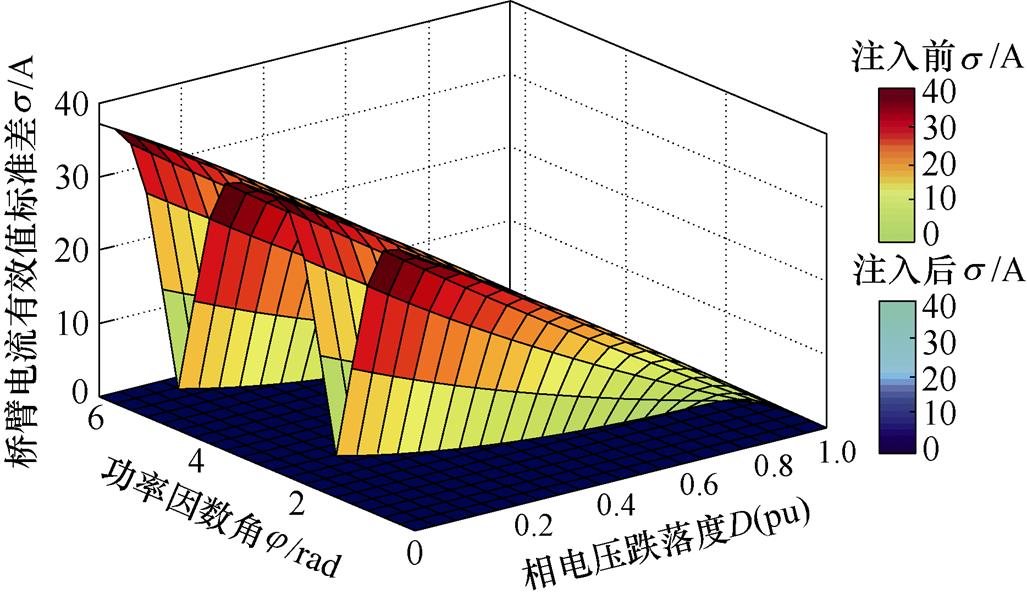
图5 零序电压注入前后桥臂电流有效值标准差
Fig.5 Standard deviation of arm current RMS with and without zero-sequence voltage injection
MMC固有的非线性与强耦合动态特性源于桥臂电流对子模块电容的周期性充放电，不平衡电网电压使得该耦合过程更为复杂，三相桥臂中的子模块电容电压纹波呈现不平衡状态[20]。而电容电压纹波是子模块电容成本、体积的决定因素，降低不平衡电网下最大子模块电容电压纹波不仅可以扩大MMC安全运行范围，还有助于提升MMC功率密度、降低成本[21]。因此，本节同样以单相电压跌落为例，分析不平衡电网下注入零序电压对MMC子模块电容电压纹波的影响。
若环流抑制参数选取适宜，叠加于三相调制波上的环流抑制修正量幅值较小可忽略[22]。得到考虑零序电压注入后MMC的j相上、下桥臂等效开关函数SPj、SNj满足
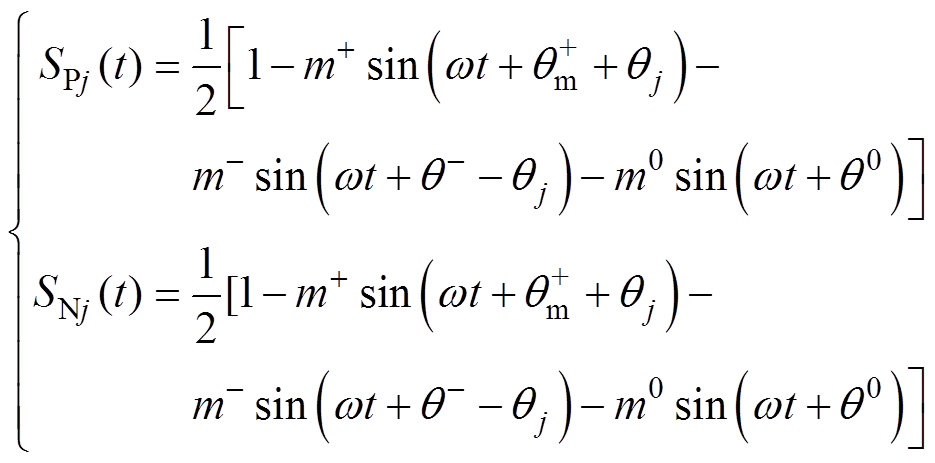（22）
式中，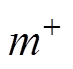
、
、
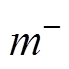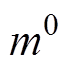分别为MMC交流电压正、负、零序调制比，其中负序、零序分量的幅值、相位关系已于2.1节中介绍，在此仅对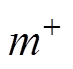的计算展开说明。对于如图6所示的不平衡交流系统，根据交流系统功率传输理论，MMC从电网吸收的平均有功、无功功率为
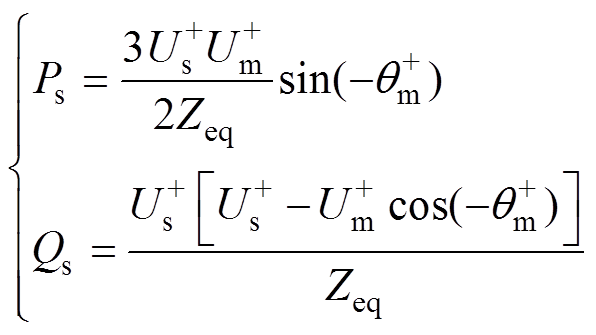（23）
式中，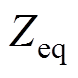
为MMC并网等效阻抗。
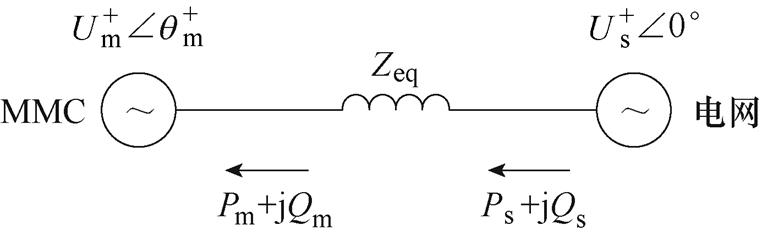
图6 MMC并网功率传输简化示意图
Fig.6 Simplified schematic diagram of grid-connected MMC power transmission
根据式（23），可得MMC输出电压正序调制比及其相位满足
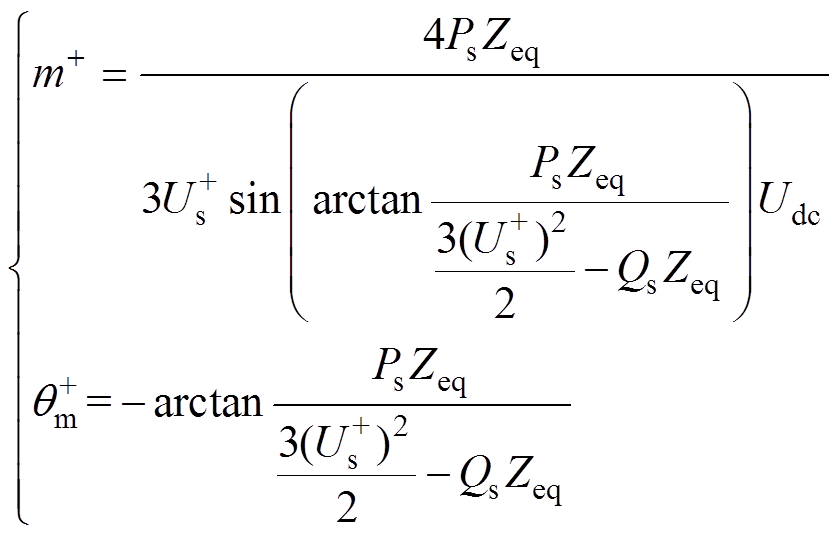（24）
将式（24）代入式（22）后，结合桥臂电流表达式（19）可得上、下桥臂子模块电容充放电电流满足
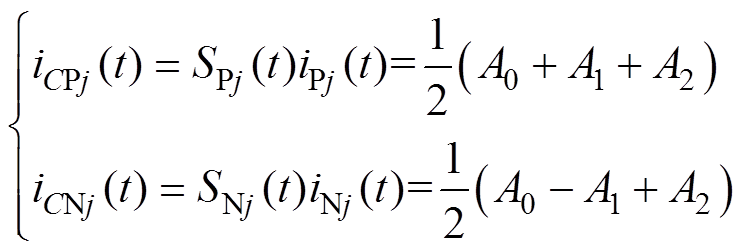（25）
其中
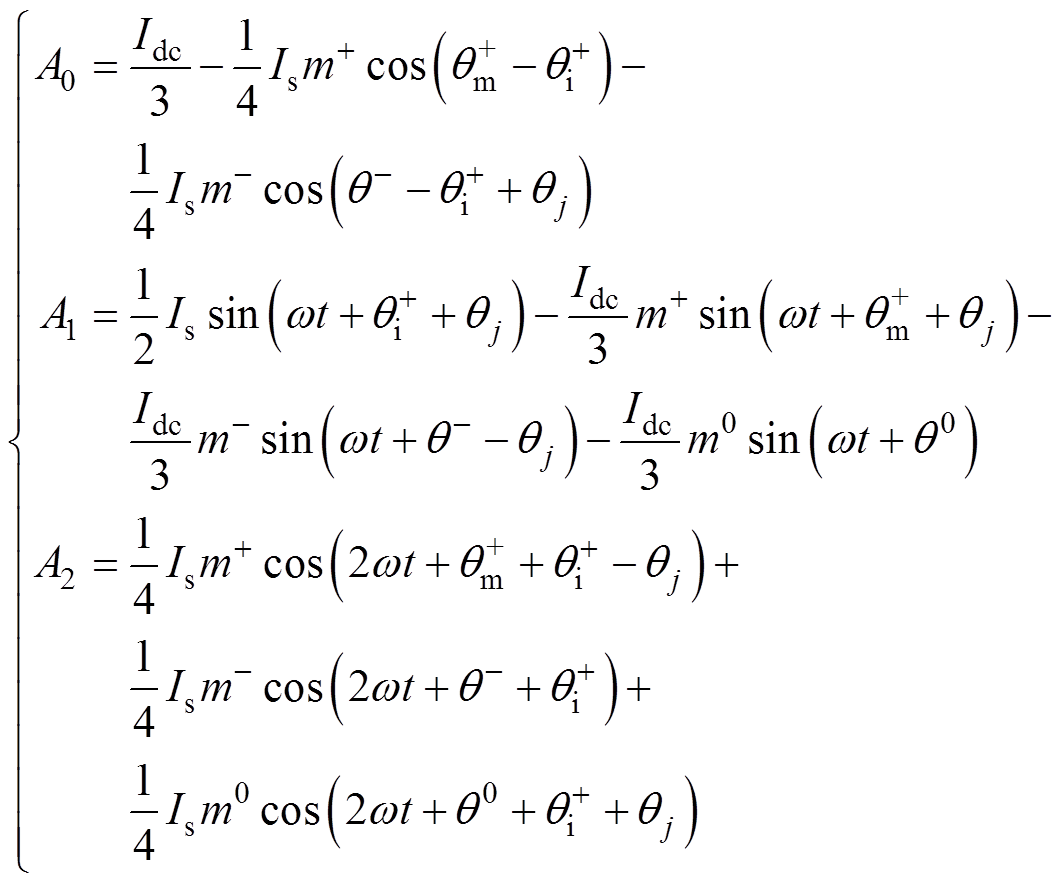（26）
根据式（25）、式（26）及子模块电容充放电关系，可以计算出以基频和二倍频为主的MMC上、下桥臂子模块电容电压波动表达式分别为
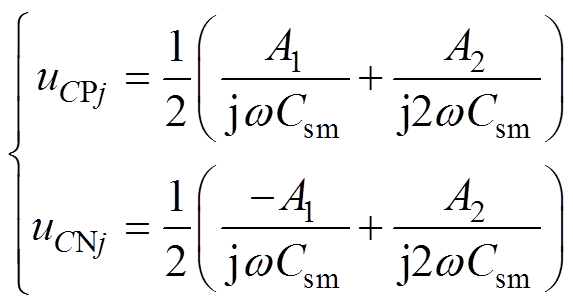（27）
图7展示了零序电压注入前后桥臂中子模块电容电压纹波最大值分布。由图7可知，子模块电容电压纹波大小与功率因数密切相关，整体趋势表现为传输无功功率越大，子模块电容电压纹波越大。此外，在相同功率因数下，子模块电容电压纹波最大值随着D减小而增大，存在严重不对称电网下电容电压纹波越限的风险。注入零序电压后子模块电容电压纹波最大值减小，在相电压幅值跌落至零时，最大下降超过8 %，有利于确保不平衡电网下MMC的安全裕度。
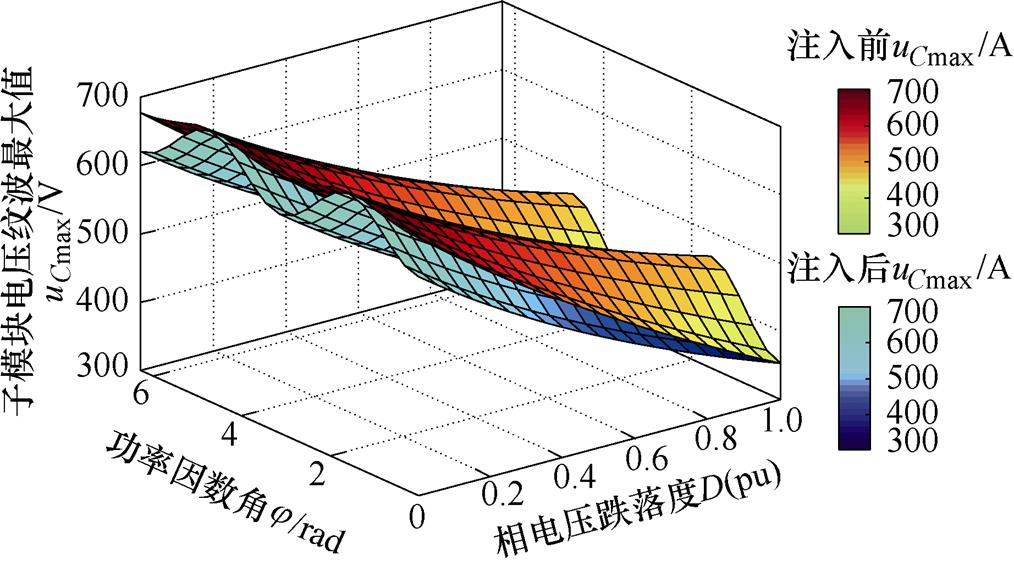
图7 零序电压注入前后子模块电容电压纹波最大值
Fig.7 Maximum SM capacitor voltage ripple with and without zero-sequence voltage injection
为验证上述理论分析与所提控制策略的有效性，本文在Matlab/Simulink环境下搭建三相五电平MMC模型，模型参数与表1一致。
MMC的环流抑制采用文献[10]中准PR控制的二倍频环流抑制。MMC控制系统参数见表2。
表2 MMC控制系统参数
Tab.2 Parameters of MMC control system
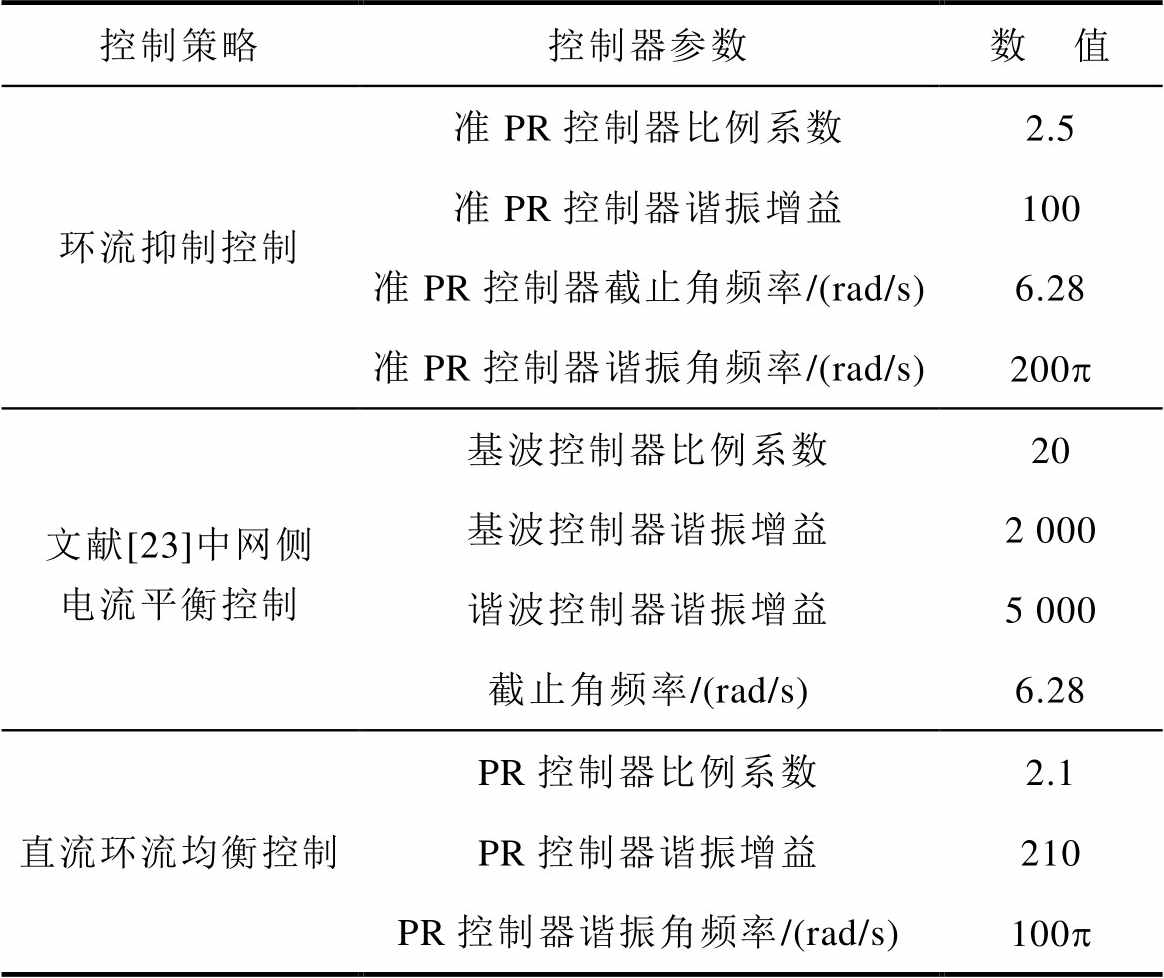
控制策略控制器参数数 值 环流抑制控制准PR控制器比例系数2.5 准PR控制器谐振增益100 准PR控制器截止角频率/(rad/s)6.28 准PR控制器谐振角频率/(rad/s)200p 文献[23]中网侧电流平衡控制基波控制器比例系数20 基波控制器谐振增益2 000 谐波控制器谐振增益5 000 截止角频率/(rad/s)6.28 直流环流均衡控制PR控制器比例系数2.1 PR控制器谐振增益210 PR控制器谐振角频率/(rad/s)100p
4.1.1 单相电压跌落工况
本节在单相电压跌落工况下验证所提直流环流均衡策略的有效性并对比零序电压注入前后MMC内特性变化趋势。本节中MMC采用文献[23]中网侧电流平衡控制，该方法无需电压、电流正负序分离，易于实现。
MMC运行于整流工况，分别在功率因数为1与0.8下进行仿真证明。整体仿真时长1.2 s，0.2 s时a相电压跌落至额定电压40 %（D=0.4），0.7 s时加入图3中直流环流均衡策略，分别得到两种功率因数下仿真结果如图8a、图8b所示。
仿真结果表明，0.2 s前MMC运行于对称网压工况，三相环流中交流分量几乎抑制为0，而直流分量呈三相均衡。0.2 s发生单相电压跌落后，MMC网侧电流在短暂波动后恢复三相平衡，幅值增大至2.0 kA以维持额定的功率传输。此时三相直流环流出现差异，同时三相桥臂电流峰值、子模块电容电压纹波显著增大，威胁MMC安全运行。
（a）功率因数为1
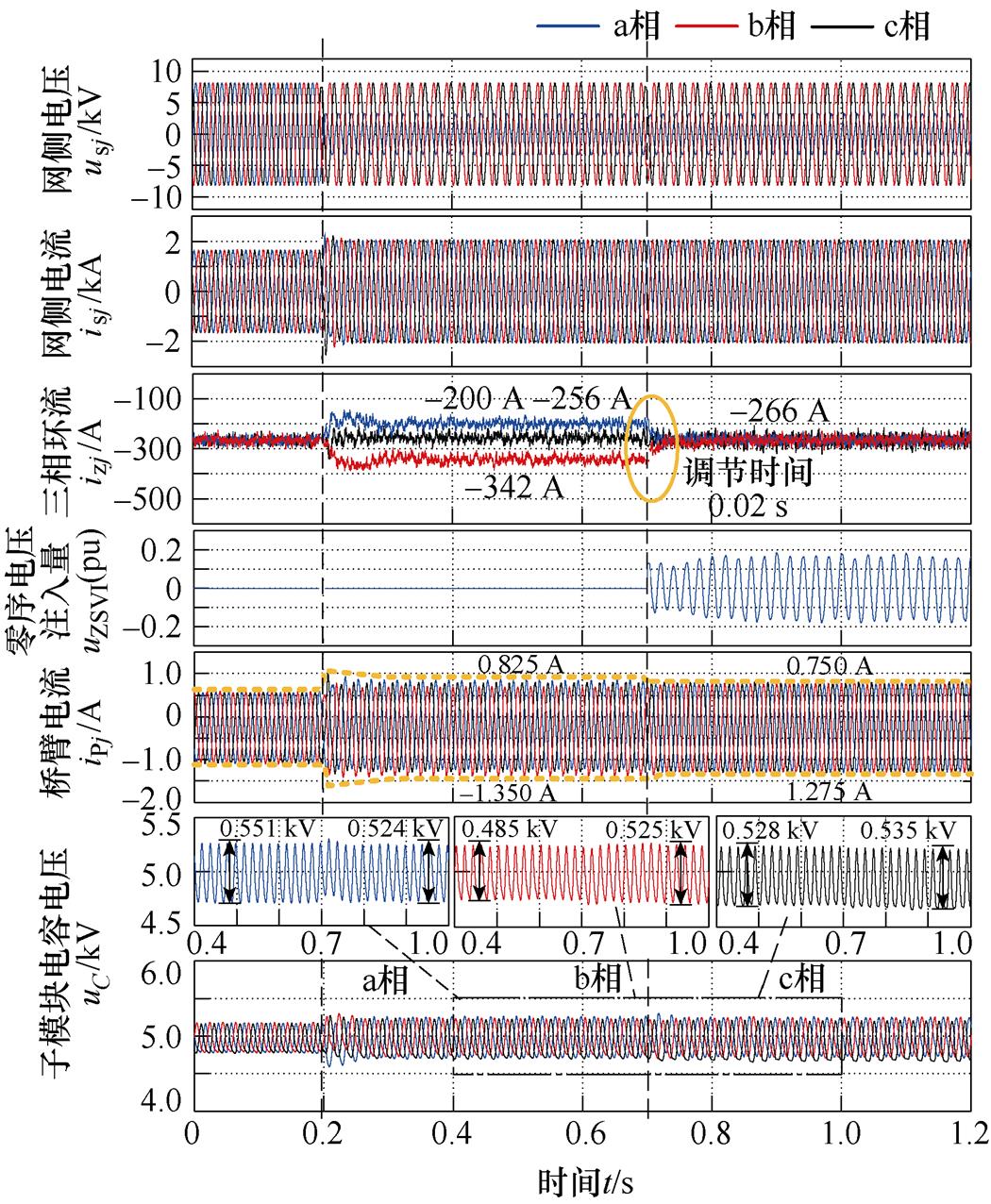
（b）功率因数为0.8
图8 a相电压跌落工况不同功率因数下直流环流均衡仿真结果
Fig.8 Simulation results of proposed control under different power factors when a-phase voltage drop occurs
图8a表明，0.7 s加入直流环流均衡策略后，三相直流环流分别由-248、-375、-376 A快速均衡至额定值-333 A，调节时间约0.03 s，桥臂电流有效值标准差下降了22.2。图8a中桥臂电流与子模块电容电压波形表明，0.7 s零序电压注入前、后MMC桥臂电流峰值分别为1 400 A和1 350 A，降低约3.6 %；子模块电容电压纹波最大值在零序电压注入前、后分别为532 V和485 V，三相子模块电容电压纹波趋于均衡且纹波最大值降低了47 V，相比零序电压注入前约降低了8.8 %。
图8b为功率因数0.8下的仿真结果，与图8a类似，当a相电压跌落后三相直流环流同样存在差异，各相直流环流分别为-200、-256、-342 A，桥臂电流有效值标准差为21.1，加入直流环流均衡策略后约0.02 s实现快速均衡。此外，图8b中桥臂电流与子模块电容电压波形表明，随着零序电压注入，MMC桥臂电流峰值由1 350 A降低至1 275 A，减小约5.6 %；而子模块电容电压纹波最大值由551 V降低至535 V，降低了16 V，相比零序电压注入前约降低了3.0 %。
上述仿真结果表明，在不同功率因数下本文所提策略均能有效均衡三相直流环流。此外，随着零序电压注入，MMC桥臂电流有效值实现均衡，桥臂电流峰值与子模块电容电压纹波最大值均有所减小。将仿真结果与理论计算结果进行对比，如图9所示，其结果进一步验证了理论分析的准确性。
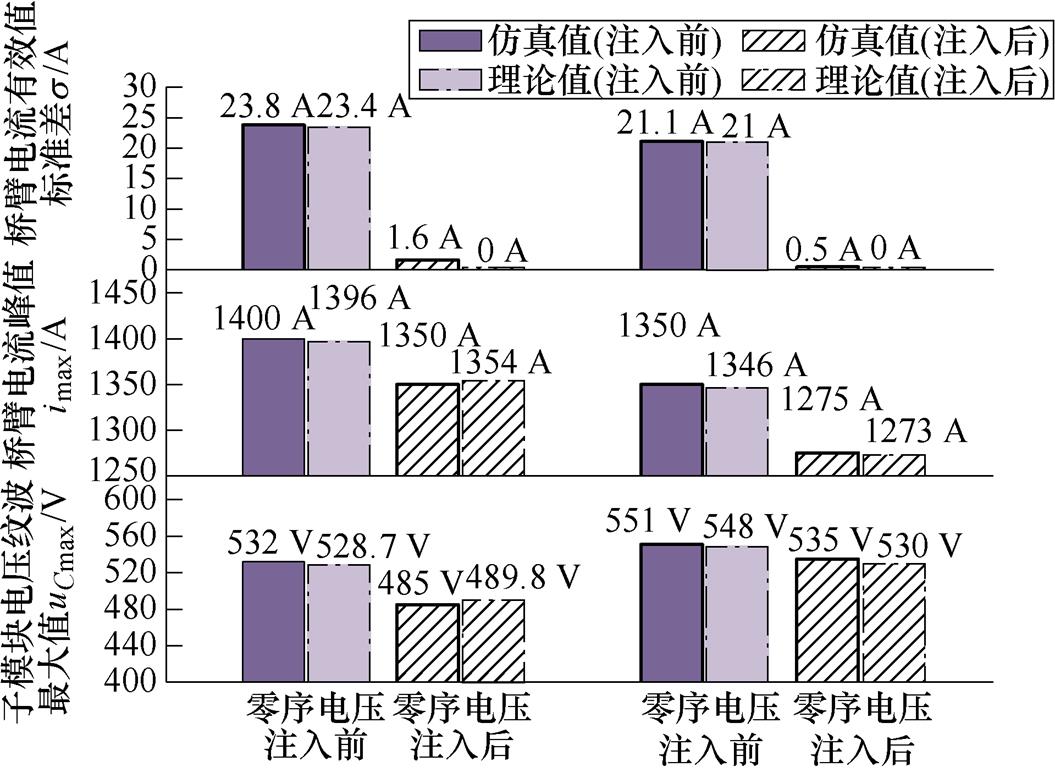
（a）功率因数为1 （b）功率因数为0.8
图9 仿真值与理论值对比结果
Fig.9 Comparison of simulation and theory values
4.1.2 与已有策略动态性能对比
为验证本文所提控制策略动态性能，与文献[14]所提开环直流环流均衡策略进行仿真对比。本节中仿真模型均采用基于正、负序双dq坐标系的网侧电流平衡控制[14]，其控制参数见表2。不平衡故障工况设置也与文献[14]中一致：分别在a相接地短路故障与a、b两相接地短路故障下开展对比验证，故障发生点均设置于星-三角形变压器一次侧。以a相接地短路故障工况为例，仿真示意图如图10所示，图10中，Ls1为电网等效电感，ugj为电网电压，仿真模型采用表1中参数。
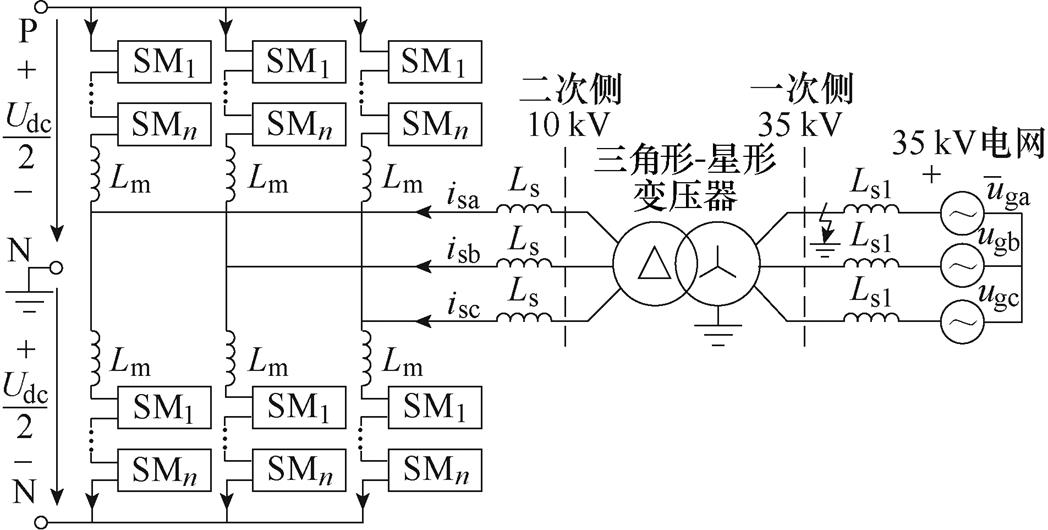
图10 不平衡故障工况仿真示意图
Fig10 Structure of the simulation model under unbalanced grid faults condition
仿真过程如下：MMC运行于整流工况，功率因数为1，电网吸收有功功率1.0(pu)，无功功率0(pu)，0.2 s时电网发生单相/两相接地短路故障，0.7 s时分别加入本文所提策略（见①）与文献[14]策略（见②），对比两者的动态响应性能，仿真结果如图11a、图11b所示。
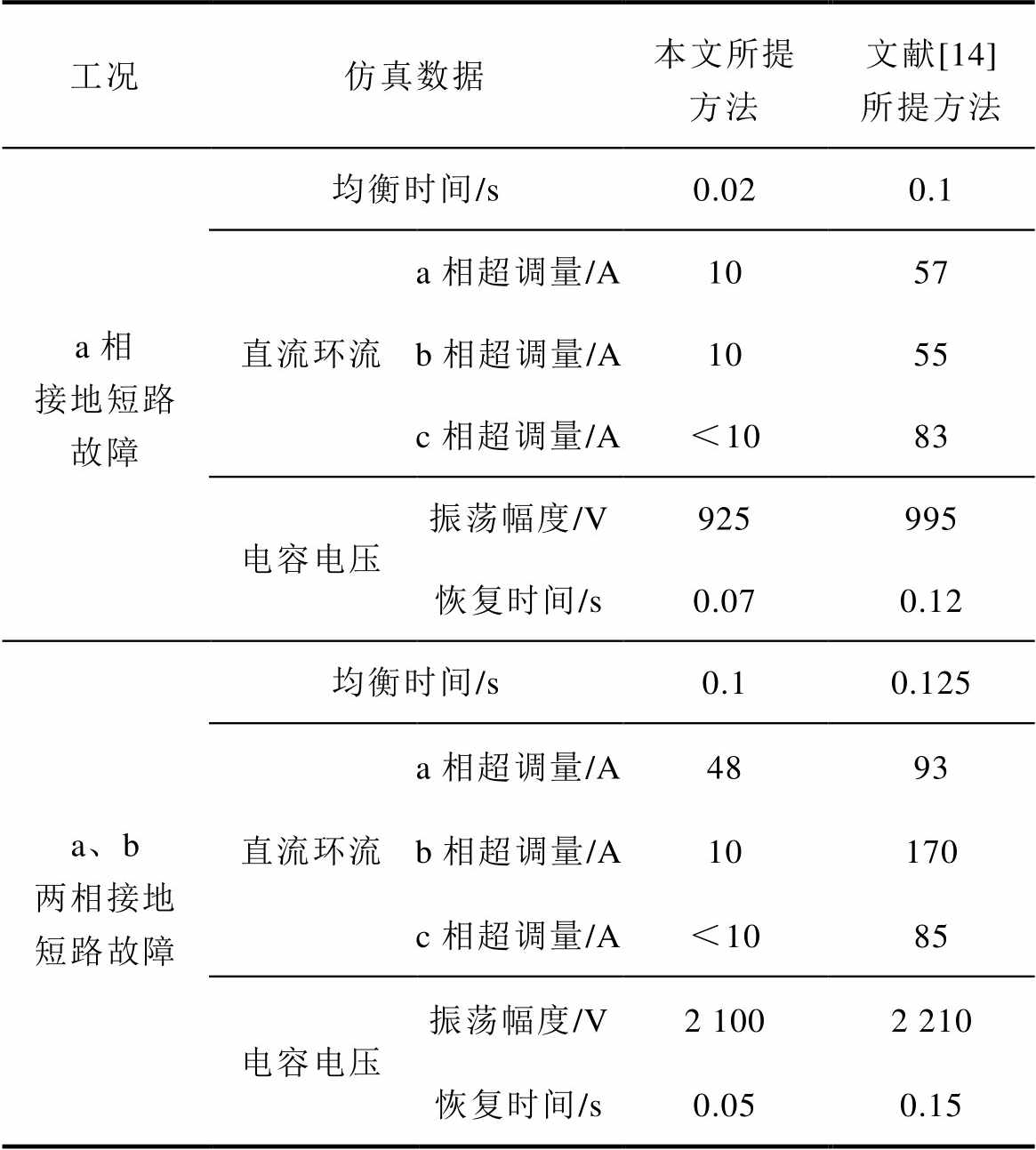
图11a仿真结果表明，在单相接地短路故障工况下，文献[14]所提策略调节时间约为0.1 s，调节过程中三相直流环流最大超调量约为83 A，本文所提直流环流均衡策略调节时间约0.02 s，调节过程中超调较小。同样也可以发现本文所提直流环流均衡策略调节过程中MMC子模块电容电压振荡程度小、恢复稳态较快，具有较好的动态响应性能。
（a）a相接地短路故障
（b）a、b两相接地短路故障
图11 两种不对称故障工况下本文所提策略与文献[14]所提策略动态性能对比
Fig.11 Comparison of dynamic performance between the proposed method and the method proposed in literature Ref.[14] under two unbalanced grid faults condiction
图11b仿真结果表明，在两相接地短路故障下文献[14]所提策略调节时间约为0.125 s，调节过程中三相直流环流最大超调量约为170 A，而本文所提直流环流均衡策略调节时间约0.1 s，最大超调量约为48 A。此外，在两相接地短路故障下本文所提控制策略同样存在MMC子模块电容电压振荡幅度小、恢复稳态时间短的优势。
对上述仿真结果开展详细数据对比见表3，对比结果显示，本文所提直流环流均衡策略调节速度较快且超调量较小，同时子模块电容电压能较快恢复稳态，具有较优的动态性能。
为进一步验证零序电压注入的直流环流均衡策略及理论分析的有效性，进行单相电压跌落工况实验验证。图12为三相五电平MMC实验平台，其参数见表4。
表3 与已有方法的动态性能对比
Tab.3 Comparison of dynamic performance with existing method proposed
工况仿真数据本文所提方法文献[14]所提方法 a相接地短路故障均衡时间/s0.020.1 直流环流a相超调量/A1057 b相超调量/A1055 c相超调量/A＜1083 电容电压振荡幅度/V925995 恢复时间/s0.070.12 a、b两相接地短路故障均衡时间/s0.10.125 直流环流a相超调量/A4893 b相超调量/A10170 c相超调量/A＜1085 电容电压振荡幅度/V2 1002 210 恢复时间/s0.050.15
设置a相电压跌落至额定值的60 %，MMC运行于逆变工况，分别设置稳态工作点为：输出有功功率1(pu)，无功功率0(pu)；输出有功功功率0.8(pu)，无功功率0.6(pu)两种工况下进行验证。鉴于网侧电流平衡控制、环流抑制等控制有效性，实验过程中MMC输出电流三相平衡，交流环流抑制效果理想且子模块电容电压维持均衡。
图12 三相五电平MMC实验台
Fig.12 Three-phase MMC experimental prototype
表4 MMC实验台参数
Tab.4 Parameters of MMC experimental prototype
参 数数 值 额定功率/(V·A)1 500 直流电压/V250 交流线电压有效值/V125 单桥臂子模块数4 子模块电容/mF1 桥臂电感/mH3 交流侧滤波电感/mH2.5
如图13所示为两种工况下实验波形，其结果表明未加入直流环流均衡控制时，三相直流环流存在差异，同时桥臂电流、子模块电容电压纹波三相不均衡，随着电网电压不平衡程度加剧可能会引起MMC保护动作甚至发生故障。在加入本文所提直流环流均衡策略后，图13a表明约40 ms后三相直流环流快速均衡至额定值2.0 A，且桥臂电流峰值与子模块电容电压纹波最大值均有所下降；图13b实验结果表明，随着零序电压注入约35 ms后三相直流环流均衡至额定值1.6 A，桥臂电流峰值与子模块电容电压纹波最大值变化趋势同样与理论分析一致，验证了本文理论分析与控制策略有效性。
（a）输出有功功率1(pu)，无功功率0(pu)
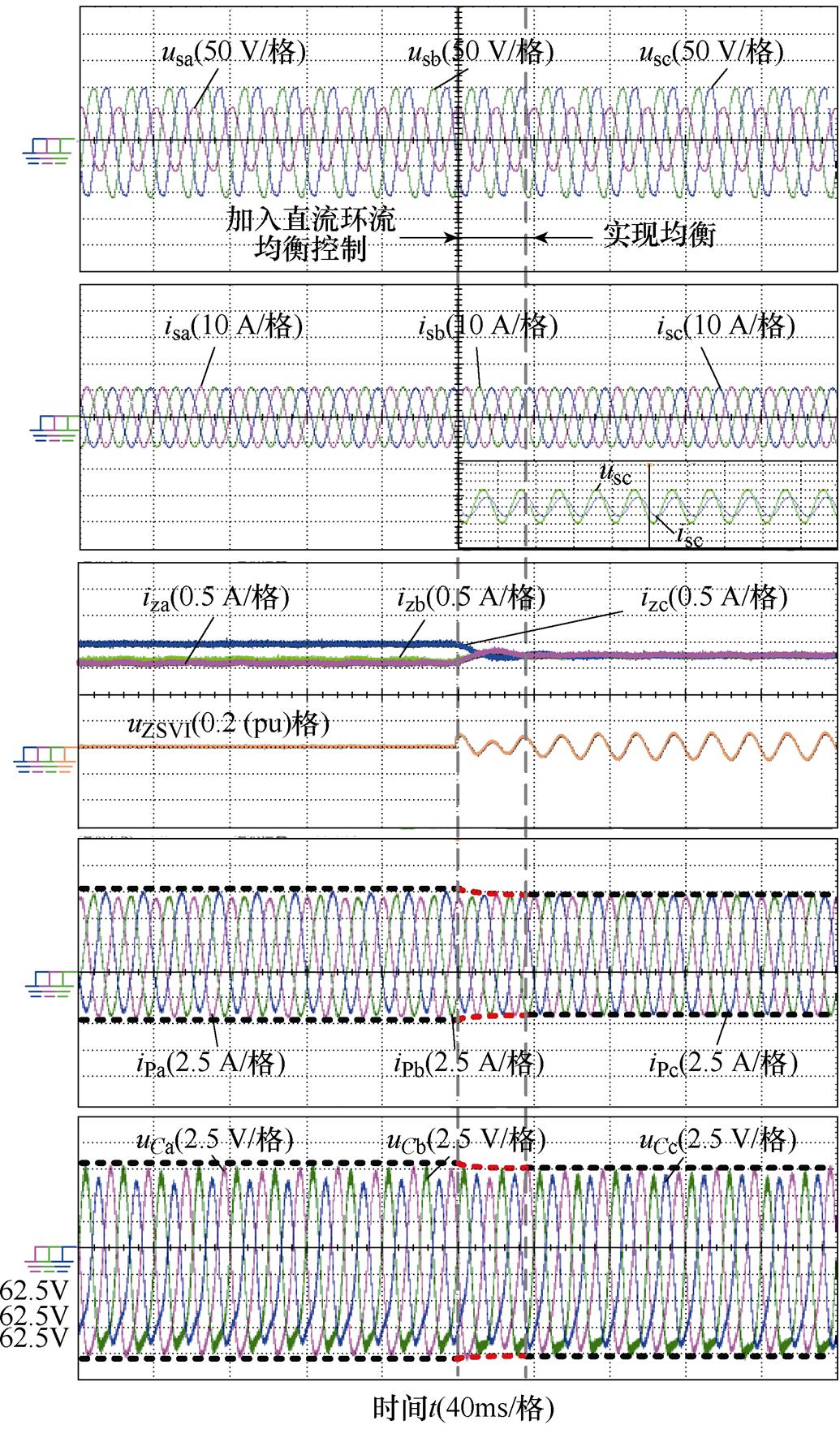
（b）输出有功功率0.8(pu)，无功功率0.6(pu)
图13 a相电压跌落工况下直流环流均衡实验结果
Fig.13 Experiment results of proposed control under the unbalanced condition of a-phase voltage drop
本文建立了零序电压注入的不平衡电网MMC等效电路模型，并提出了一种基于零序电压注入的直流环流均衡策略，在此基础上详细总结了该策略对MMC桥臂电流、子模块电容电压的影响规律，并开展了仿真和实验验证。研究结果表明：
1）零序电压注入可减小MMC桥臂电流峰值，均衡桥臂电流有效值，减小相间的电流应力与热应力差异。理论推导结果显示，单相电压跌落工况下桥臂电流峰值最大可下降10.9 %，有效值标准差可降低至零。
2）零序电压注入后MMC子模块电容电压纹波最大值有所减小，有利于扩大其安全运行范围，降低子模块电容体积与成本。单相电压跌落工况下，三相子模块电容电压纹波最大可下降超过8 %。
3）本文所提基于零序电压注入的直流环流均衡策略无需正负序分离，原理简单易于实现，在不同功率因数和不平衡工况下均具有较好的动态性能，对于不平衡网压下MMC的安全运行具有一定实际应用意义。
参考文献
[1] 茆美琴, 程德健, 袁敏, 等. 基于暂态能量流的模块化多电平高压直流电网接地优化配置[J]. 电工技术学报, 2022, 37(3): 739-749.
Mao Meiqin, Cheng Dejian, Yuan Min, et al. Optimal allocation of grounding system in high voltage direct current grid with modular multi-level converters based on transient energy flow[J]. Transactions of China Electrotechnical Society, 2022, 37(3): 739-749.
[2] 束洪春, 代月, 安娜, 等. 基于线性回归的柔性直流电网纵联保护方法[J]. 电工技术学报, 2022, 37(13): 3213-3226, 3288.
Shu Hongchun, Dai Yue, An Na, et al. Pilot protection method of flexible DC grid based on linear regression[J]. Transactions of China Electrotechnical Society, 2022, 37(13): 3213-3226, 3288.
[3] 江畅, 程启明, 马信乔, 等. 不平衡电网电压下基于模块化多电平变流器的统一电能质量调节器的微分平坦控制[J]. 电工技术学报, 2021, 36(16): 3410-3421.
Jiang Chang, Cheng Qiming, Ma Xinqiao, et al. Differential flat control for unified power quality controller based on modular multilevel converter under unbalanced grid voltage[J]. Transactions of China Electrotechnical Society, 2021, 36(16): 3410- 3421.
[4] 梁营玉, 张涛, 刘建政, 等. 不平衡电网电压下模块化多电平换流器的环流抑制策略[J]. 电工技术学报, 2016, 31(9): 120-128.
Liang Yingyu, Zhang Tao, Liu Jianzheng, et al. A circulating current suppressing method for modular multilevel converter under unbalanced grid voltage[J]. Transactions of China Electrotechnical Society, 2016, 31(9): 120-128.
[5] Shi Xiaojie, Wang Zhiqiang, Liu Bo, et al. Steady- state modeling of modular multilevel converter under unbalanced grid conditions[J]. IEEE Transactions on Power Electronics, 2017, 32(9): 7306-7324.
[6] Hahn F, Andresen M, Buticchi G, et al. Thermal analysis and balancing for modular multilevel con- verters in HVDC applications[J]. IEEE Transactions on Power Electronics, 2018, 33(3): 1985-1996.
[7] Bakhshizadeh M K, Ma Ke, Loh P C, et al. Indirect thermal control for improved reliability of modular multilevel converter by utilizing circulating current[C]// 2015 IEEE Applied Power Electronics Conference and Exposition (APEC), 2015, Charlotte, NC, USA, 2015: 2167-2173.
[8] 卓谷颖, 江道灼, 连霄壤. 模块化多电平换流器不平衡环流抑制研究[J]. 电力系统保护与控制, 2012, 40(24): 118-124.
Zhuo Guying, Jiang Daozhuo, Lian Xiaorang. Study of unbalanced circular current suppressing for modular multilevel converter[J]. Power System Protection and Control, 2012, 40(24): 118-124.
[9] Zhou Yuebin, Jiang Daozhuo, Guo Jie, et al. Analysis and control of modular multilevel converters under unbalanced conditions[J]. IEEE Transactions on Power Delivery, 2013, 28(4): 1986-1995.
[10] 李金科, 金新民, 吴学智, 等. 不平衡交流电网模块化多电平变流器特性分析及环流抑制方法[J]. 中国电机工程学报, 2017, 37(12): 3535-3544, 3682.
Li Jinke, Jin Xinmin, Wu Xuezhi, et al. Characteristic analysis and a circulating current control method in modular multilevel converters under unbalanced grid conditions[J]. Proceedings of the CSEE, 2017, 37(12): 3535-3544, 3682.
[11] 张臣, 叶华, 韦凌霄, 等. 不平衡状态下MMC双回路环流抑制策略[J]. 电工技术学报, 2019, 34(9): 1924-1933.
Zhang Chen, Ye Hua, Wei Lingxiao, et al. Double- loop circulating current suppressing strategy for modular multilevel converter under unbalanced con- ditions[J]. Transactions of China Electrotechnical Society, 2019, 34(9): 1924-1933.
[12] Liang Yingyu, Liu Jianzheng, Zhang Tao, et al. Arm current control strategy for MMC-HVDC under unbalanced conditions[J]. IEEE Transactions on Power Delivery, 2017, 32(1): 125-134.
[13] 赖锦木, 尹项根, 王要强, 等. 基于桥臂电流控制的MMC改进电容电压均衡控制策略研究[J]. 高电压技术, 2022, 48(8): 3132-3145.
Lai Jinmu, Yin Xianggen, Wang Yaoqiang, et al. Improved capacitor voltage balancing control strategy for modular multilevel converter with arm current control[J]. High Voltage Engineering, 2022, 48(8): 3132-3145.
[14] Wang Jinyu, Tang Yi, Liu Xiong. Arm current balancing control for modular multilevel converters under unbalanced grid conditions[J]. IEEE Transa- ctions on Power Electronics, 2020, 35(3): 2467- 2479.
[15] Xu Jianzhong, Yu Yongjie, Zhao Chengyong. The predictive closed-loop averaging control of MMC phase-unit losses under unbalanced conditions[J]. IEEE Transactions on Power Delivery, 2019, 34(1): 198-207.
[16] 孟沛彧, 向往, 潘尔生, 等. 分址建设直流输电系统拓扑方案与运行特性研究[J]. 电工技术学报, 2022, 37(19): 4808-4822.
Meng Peiyu, Xiang Wang, Pan Ersheng, et al. Research on topology and operation characteristics of HVDC transmission system based on site-division construction[J]. Transactions of China Electro- technical Society, 2022, 37(19): 4808-4822.
[17] Rodriguez P, Timbus A V, Teodorescu R, et al. Flexible active power control of distributed power generation systems during grid faults[J]. IEEE Transactions on Industrial Electronics, 2007, 54(5): 2583-2592.
[18] Hao Quanrui, Li Bowei, Sun Yifan, et al. Operating region and boundary control of modular multilevel converter station under unbalanced grid conditions[J]. IEEE Transactions on Power Delivery, 2020, 35(3): 1146-1157.
[19] 薛花, 田广平, 扈曾辉, 等. 电网不平衡下模块化多电平变换器无源一致性控制方法[J]. 电力系统自动化, 2022, 46(3): 85-95.
Xue Hua, Tian Guangping, Hu Zenghui, et al. Passivity-consensus based control method for modu- lar multilevel converter in unbalanced power grid[J]. Automation of Electric Power Systems, 2022, 46(3): 85-95.
[20] 施恩泽, 吴学智, 荆龙, 等. 网压不平衡下环流注入对模块化多电平换流器的影响分析[J]. 电工技术学报, 2018, 33(16): 3719-3731.
Shi Enze, Wu Xuezhi, Jing Long, et al. Analysis of the impact on modular multilevel converter with circulating current injection under unbalanced grid voltage[J]. Transactions of China Electrotechnical Society, 2018, 33(16): 3719-3731.
[21] Zhao Cong, Luan Kedong, Zhang Hang, et al. Enhancement of ZSVI by circulating current injection for full-bridge MMC with low energy storage require- ments[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2020, 8(4): 4075- 4085.
[22] 杨晓峰, 李泽杰, 郑琼林. 基于虚拟阻抗滑模控制的MMC环流抑制策略[J]. 中国电机工程学报, 2018, 38(23): 6893-6904, 7123.
Yang Xiaofeng, Li Zejie, Zheng Trillion Q. A novel MMC circulating current suppressing strategy based on virtual impedance sliding mode control[J]. Pro- ceedings of the CSEE, 2018, 38(23): 6893-6904, 7123.
[23] 王逸超, 欧名勇, 陈燕东, 等. 不平衡电压下并网逆变器的功率波动抑制与电流平衡协调控制方法[J]. 中国电机工程学报, 2017, 37(23): 6981-6987, 7089.
Wang Yichao, Ou Mingyong, Chen Yandong, et al. Coordinate control of power fluctuation suppression and current balance under unbalanced voltage conditions[J]. Proceedings of the CSEE, 2017, 37(23): 6981-6987, 7089.
DC Circulating Current Balancing Control of Modular Multilevel Converter under Unbalanced Power Grid
Abstract Under an unbalanced power grid, the circulating current of a modular multilevel converter (MMC) contains double-line frequency positive, negative and zero sequence components, and unbalanced DC components, leading to unbalanced arm currents. Consequently, asymmetrical electrical stresses and nonuniform temperature distributions exist. However, traditional circulating current control methods generally take the AC components suppression as the control objective and ignore the potential impact of unequal DC components. Therefore, this paper considers unbalanced DC circulating current and proposes a zero-sequence voltage injection method to equalize DC circulating current. In addition, the effects of this method on the arm current and sub-module (SM) capacitor voltage are discussed in detail.
Firstly, the DC circulating current equalization mechanism based on zero-sequence voltage injection is analyzed from the arm power transmission perspective. The expression of the amplitude and phase of the zero-sequence voltage is obtained. Then, a zero-sequence voltage injection method is proposed to equalize DC circulating current. The phase of zero-sequence voltage is obtained from the grid current and the deviation of DC circulating current, and a proportional resonant controller is added to adjust its amplitude. After that, the effects of this method on the arm current and SM capacitor voltage are quantitatively studied. The analysis results show that when a single-phase voltage drop occurs, the arm current peak can be reduced by 10.9 % at most, and the standard deviation of the arm current root-mean-square (RMS) value can be reduced to zero. Besides, the maximum SM capacitor voltage ripple can drop by more than 8 % under the above condition.
Simulation and experiment are performed on Matlab/Simulink platform and a three-phase five-level MMC prototype. In the simulation, the proposed method is first applied when single-phase voltage drops to 40 %, which shows that the DC circulating current becomes balanced, and both the arm current peak and the maximum SM capacitance voltage ripple are reduced. The simulation results are quantitatively compared with theoretical analysis results, further verifying the accuracy of the theoretical analysis. Then, for dynamic performance comparison with the existing method, the proposed method is enabled under single-phase-to-ground and two-phase-to-ground faults. The results indicate that the method proposed in this paper has better dynamic performance, such as shorter compensation time and smaller overshoot. Additionally, the SM capacitor voltage can recover to a stable state more quickly. As for the experiment, when the proposed control method is added under a-phase voltage drop condition, DC circulating current achieves equalization in barely 40ms under different power factors. The trend of the arm current peak and the SM capacitor voltage ripple is also consistent with the analysis above.
The following conclusions can be drawn from this paper: (1) The proposed method can reduce the arm current peak and equalize the arm current RMS value, thereby reducing the difference in electrical and thermal stress among phase units. (2) The maximum SM capacitor voltage ripple can also be reduced, which is beneficial to expand the MMC operation range and reduce both SM capacitance volume and cost. (3) The method proposed in this paper does not require positive-negative sequence separation and is convenient to implement, which has better dynamic performance than existing methods under different grid faults.
keywords：Unbalanced power grid, modular multilevel converter, DC circulating current, zero-sequence voltage injection, arm current, sub-module capacitor voltage
中图分类号：TM46
DOI: 10.19595/j.cnki.1000-6753.tces.222180
中央高校基本科研业务费专项资金资助项目（2019JBM058）。
收稿日期 2022-11-21
改稿日期 2023-01-12
潘子迅 男，1998年生，硕士研究生，研究方向为模块化多电平换流器控制技术与应用。E-mail: 20121478@bjtu.edu.cn
杨晓峰 男，1980年生，副教授，博士生导师，研究方向为多电平变换器、柔性直流输电、宽禁带半导体及电力电子技术在轨道交通中的应用等。E-mail: xfyang@bjtu.edu.cn（通信作者）
（编辑 陈 诚）