摘要 针对新型并联谐振直流环节软开关逆变器的辅助电路运行过程中电流应力高、导通损耗大的问题,提出一种基于不连续的脉冲宽度调制且采用斜率正负交替锯齿载波的改进调制策略。与原调制策略相比,首先,该文所提调制策略在保留辅助电路动作频率最小化优点的基础上,不仅实现了全部开关管的软开关,而且将第二辅助开关管的电流应力降为谐振电流峰值。然后,通过合理的参数设计,进一步降低辅助电路电流应力,从而减少辅助电路损耗。然后,根据所提调制策略分析工作原理、对比不同文献、规划参数设计、进行损耗分析。最后,使用SiC MOSFET制作一台5 kW/40 kHz通用样机,通过实验验证所提调制策略对原拓扑效率提升与电流应力降低的有效性。
关键词:并联谐振直流环节 辅助电路 调制策略 电流应力 导通损耗
高效率、高功率密度一直以来都是电力电子逆变器研究人员所追寻的目标。特别是,随着以SiC MOSFET为代表的宽禁带器件的出现,与Si基器件相比,其拥有更快的开关速度、更高的结温以及更高的电压等级,更加助力于上述目标的实现[1]。在这些优点中,宽禁带器件开关速度的提升是减少其开关损耗、提高其开关频率的关键,但也带来了严重的电磁干扰问题[2],同时当开关频率提高到一定程度时,开关损耗亦会大幅提升。软开关逆变技术的提出,为实现高频化下宽禁带逆变器的高效、高功率密度提供了一条切实可行的道路,并在电机驱动[3-4]、并网逆变器[5]以及无线电能传输[6]等领域取得了成功应用。
经过几十年的研发,软开关逆变拓扑种类繁多,其分类依据也有多种,即可按照开关器件的使用与否,划分为有源软开关逆变器与无源软开关逆变器[3];也可按照主逆变电路拓扑结构的不同划分为两电平软开关逆变器与三电平软开关逆变器[7];还可按照辅助电路位置的不同划分为辅助谐振换流极型软开关逆变器(Auxiliary Resonant Commutated Pole Soft-switching Inverter, ARCPSI)[4,8]和谐振直流环节型软开关逆变器(Resonant DC Link Soft- switching Inverter, RDCLSI)[9-16]。考虑到软开关效果及主逆变电路拓扑结构应用的普遍性,本文选取依据辅助电路位置分类的方式,介绍软开关逆变器。
ARCPSI的每相桥臂均拥有各自独立的辅助电路,其位于直流母线与交流电输出点之间,特点是控制独立、易于应用多种脉冲宽度调制(Pulse Width Modulation, PWM)策略,辅助元器件数量较多,更适用于硬件成本不敏感且可靠性要求较高的50 kW以上大功率应用场合。而在20 kW以下的中小功率应用场合,辅助电路位于直流母线侧的RDCLSI则更为适用,其特点是拓扑结构简单、硬件成本较低,但须经特殊处理方可应用多种PWM。
RDCLSI源起于文献[9],经过有源钳位RDCLSI(Active Clamed RDCLSI, ACRDCLSI)的发展[5,10],过渡到并联RDCLSI(Parallel RDCLSI, PRDCLSI)[11-14],然而现有此类拓扑仍有一些问题值得商榷,例如,有的需设定谐振电感电流阈值,对于电感电流的检测与控制降低了拓扑的实用性与可靠性[11];有的需要使用大容量电容作为辅助电源,高频工作下中性点电位漂移且使用寿命受限[12];有的需要使用耦合电感或变压器,耦合磁性元件的存在使参数设计变得复杂且功率密度受限[13];有的谐振电感工作时电感电流双向流动,磁滞损耗产生的热量会耗散于电感且缩短其寿命[14]。
文献[15]提出了具有能量回馈功能的新型PRDCLSI,避免了上述问题,但原调制策略还存在以下问题:①辅助电路电流应力过大。由于谐振参数未经优化,导致辅助电路正常运行时,其电流应力至少2倍于负载电流峰值,增加损耗的同时易于损毁器件;②辅助电路动作频率过高。在传统空间矢量脉宽调制(Space Vector Pulse Width Modulation, SVPWM)策略下,一个开关周期时间内,辅助电路需要动作6次,形成6个直流母线零电压凹槽,用于实现6个主开关管的软切换。显然,6倍于开关频率的辅助电路动作频率将会大幅增加其损耗。同时,大幅降低直流母线电压利用率。为了解决问题②,文献[16]提出了基于斜率正负交替锯齿载波的自适应调制策略,其将辅助电路动作频率降为文献[15]的1/6,即在一个开关周期内,辅助电路仅需动作1次即可实现全部开关管的软切换。然而对于问题①,第二辅助开关管Sa2的电流应力却从原调制策略下的谐振电流峰值,上升为与第一辅助开关管Sa1的电流应力一致的谐振电流峰值与负载电流峰值之和,一定程度上削减了辅助电路动作频率降低所带来的优势。
为了解决上述辅助电路电流应力与动作频率的矛盾,本文提出一种基于不连续的脉冲宽度调制(Discontinuous PWM, DPWM),且采用斜率正负交替锯齿载波的改进调制策略,其在保留辅助电路动作频率最小化的基础上,将第二辅助开关管电流应力降为谐振电流峰值,然后通过合理的参数设计进一步降低辅助电路电流应力,在减少损耗的同时提升逆变器的效率。
改进调制策略由DPWM和斜率正负交替锯齿载波两部分组成。具体内容如下:
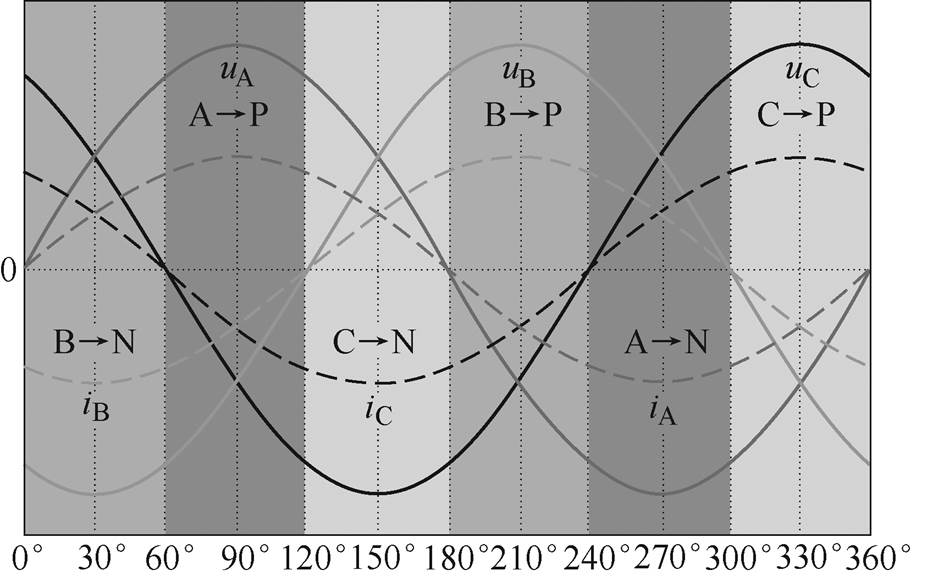
DPWM[17],又名母线钳位脉宽调制,其特点是:任意时刻,三相逆变桥中总有一相的上桥臂主开关管钳位至直流母线正极或下桥臂主开关管钳位至直流母线负极,钳位相持续区间为120 °电角度。本文所提DPWM的钳位规则是:钳位相为三相负载电流绝对值最大相,若该相负载电流为正(规定负载电流从逆变器侧流向负载侧为正;反之,则为负),则该相上桥臂主开关管钳位至直流母线正极,持续导通120 °电角度;反之,则该相下桥臂主开关管钳位至直流母线负极,持续导通120 °电角度。工频周期内本文所提DPWM的钳位规则如图1a所示。以0 °~30 °区间为例进行说明,在此区间B相负载电流绝对值最大且其值为负,故B相下桥臂主开关管被钳位到直流母线负极,如图1b所示,其在图1a中表示为“B→N”。

(a)工频周期内钳位规则
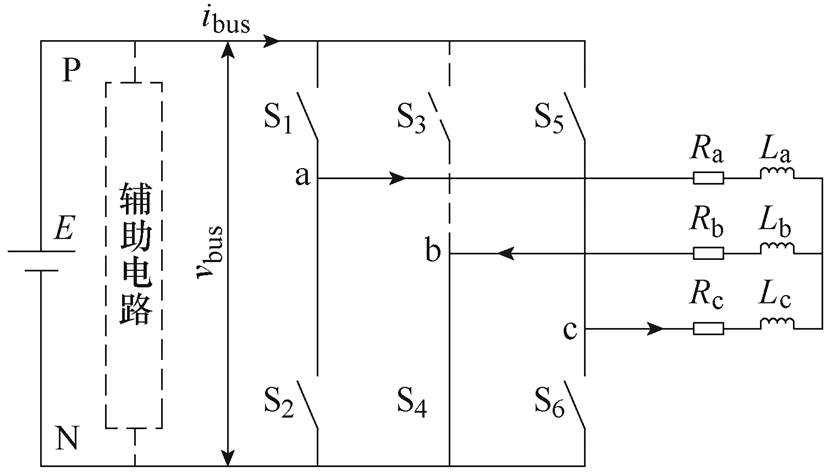
(b)0 °~30 °区间内钳位电路
图1 DPWM下钳位规则及钳位电路
Fig.1 The clamped rule and circuit under DPWM
在本文所提DPWM下,三相逆变桥的主开关管在一个开关周期内有4次开关动作,包括2次开关管向同一桥臂对侧的二极管换相和2次二极管向同一桥臂对侧的开关管换相过程,其中前者可以借助并联缓冲电容线性充放电自然实现准零电压软开关(Zero Voltage Switching, ZVS)关断,但由于后者存在二极管反向恢复过程,必须通过辅助电路转移二极管反向恢复能量,并将主开关管两端电压下降至零,方可实现主开关管零电压零电流软开关(Zero Voltage and Zero Current Switching, ZVZCS)开通[5, 10]。通过采用斜率正负交替锯齿载波(锯齿载波斜率变化的依据是:若负载电流为正,则锯齿载波斜率为正;反之,则锯齿载波斜率为负)可以将2次二极管向开关管换相动作统一于锯齿载波垂直沿处,此时辅助电路运行,转移二极管反向恢复能量后将主开关管两端电压降为零,实现主开关管ZVZCS开通的同时辅助电路仅需动作1次[16],大幅降低辅助电路频繁动作带来的损耗及直流母线电压丢失。0 °~30 °区间内各开关矢量及导通电路如图2所示,仍以0 °~30 °区间为例进行说明,在此区间开关矢量变化如图2a所示,在不同开关矢量下主逆变电路导通情况如图2b所示。由图2可知,开关矢量101向001转换和001向000转换时,主开关管S1、S5均可以借助负载电流iA、iC对并联缓冲电容C1和C2、C5和C6线性充放电,自然实现准ZVS关断,但当开关矢量000向101转换时,即二极管VD2、VD6向S1、S5换流时,由于VD2、VD6存在反向恢复过程,则必须启动辅助电路转移VD2、VD6的反向恢复能量,而后将C1、C5两端电压降为零,进而实现S1、S5的ZVZCS开通。在一个开关周期内,当且仅当此时需要辅助电路动作1次。
仍以0 °~30 °区间为例,具体介绍本文所提调制策略。在此区间内单位开关周期内的调制策略如图3所示,图中,tdead为死区时间,S1~S6中实线表示上桥臂主开关管驱动信号,虚线表示下桥臂主开关管驱动信号。通过采用DPWM与斜率正负交替的锯齿载波,在此区间内主逆变电路中开关矢量的切换顺序为001→000→101→001。结合图2分析可知,101向001切换与001向000切换,辅助电路无需动作,直流母线电压保持为E,直至000向101切换时,辅助电路开始运行。在000开关矢量内母线开关管SL关断的同时第二辅助开关管Sa2开通。为使主开关管S1、S2、S5、S6在直流母线零电压凹槽期间切换,Sa2开通d1时间后S2与S6关断,S2与S6关断d2时间后Sa2关断,S2与S6关断tdead时间后S1与S5开通,电路进入101开关矢量状态,此时直流母线电压仍为零。S1与S5开通d3时间后第一辅助开关管Sa1开通,Sa1开通d4时间后SL开通,SL开通d5时间后Sa1关断。
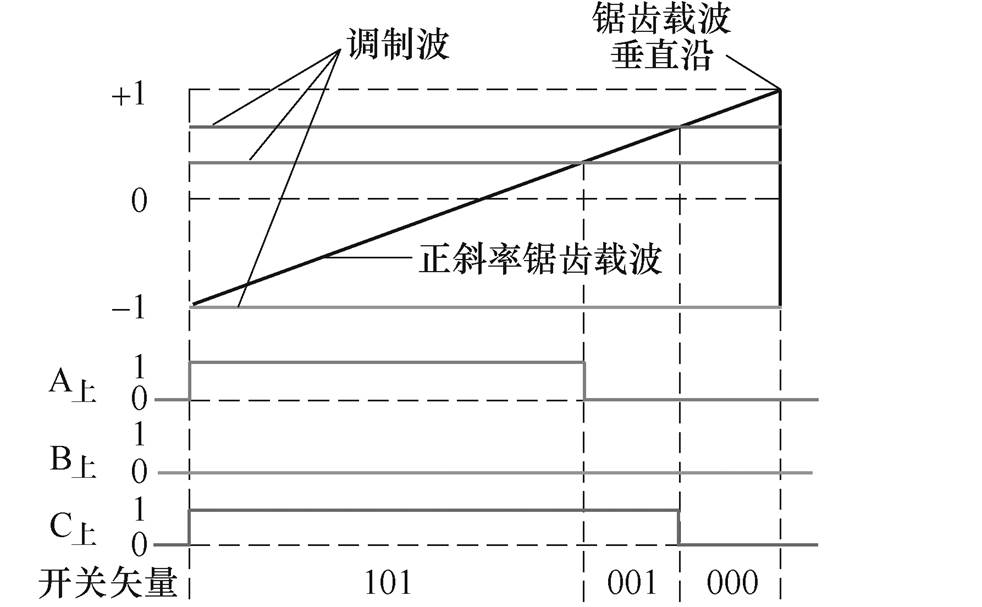
(a)0 °~30 °区间内开关矢量生成与分布
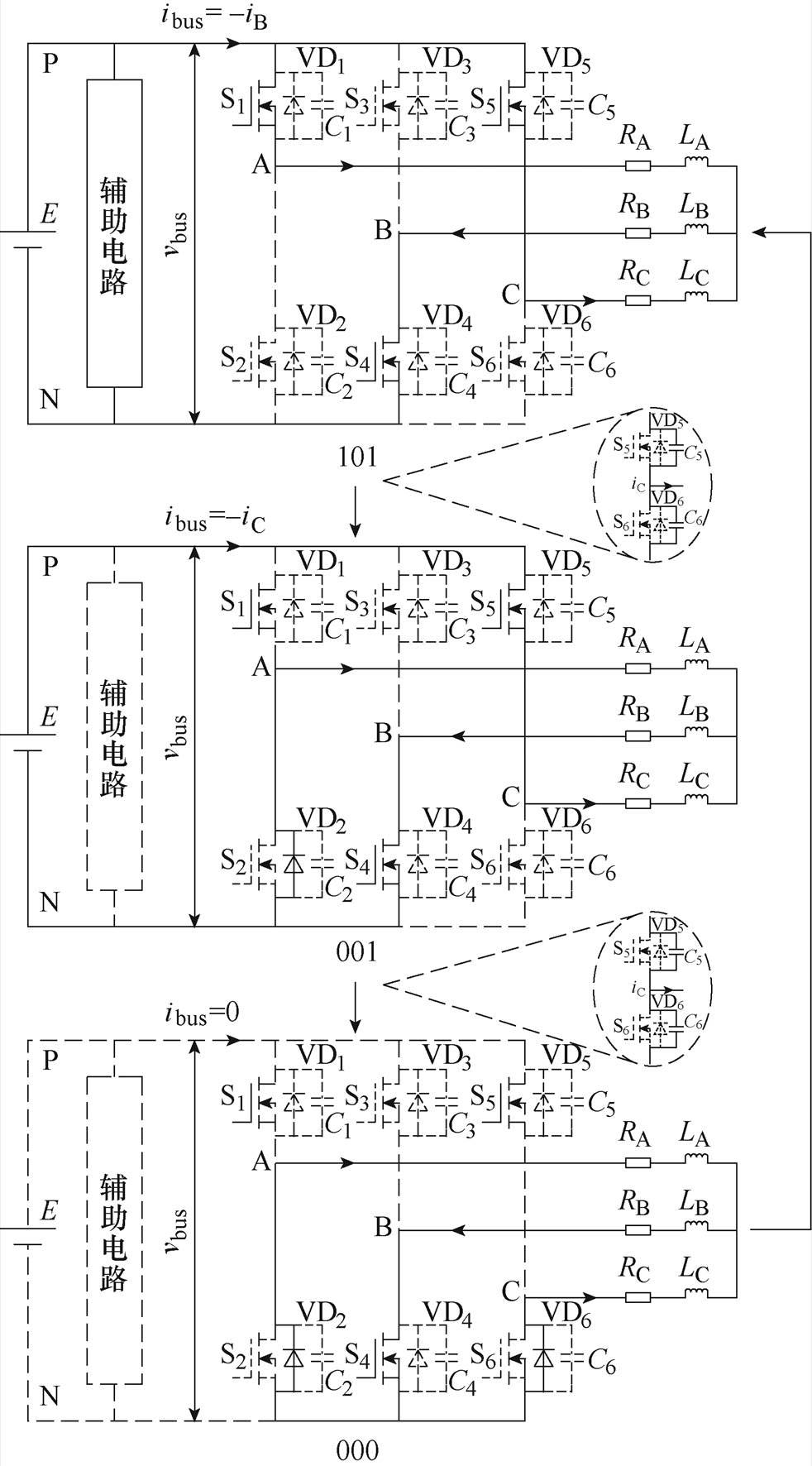
(b)0 °~30 °区间内各开关矢量下导通电路
图2 0 °~30 °区间内各开关矢量及导通电路
Fig.2 Switching vector and conduction circuit in 0 °~30 ° interval
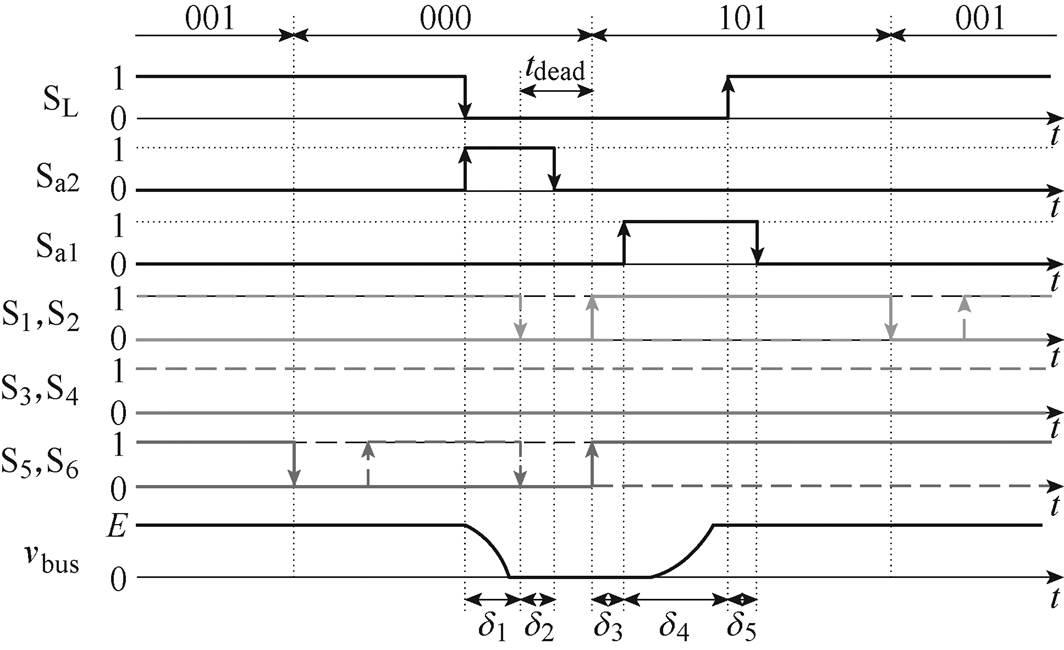
图3 单位开关周期内的调制策略
Fig.3 Modulation strategy in one switching period
结合图2b与图3进一步分析可知:母线电压vbus下降时母线电流ibus=0,而母线电压vbus上升时母线电流ibus=-iB。以此类推,可以得到整个工频周期内母线电流ibus的变化规律,如图4所示。图中加粗虚线表示母线电流ibus。由图4可知,母线电流ibus最大值为负载电流峰值、最小值为零。
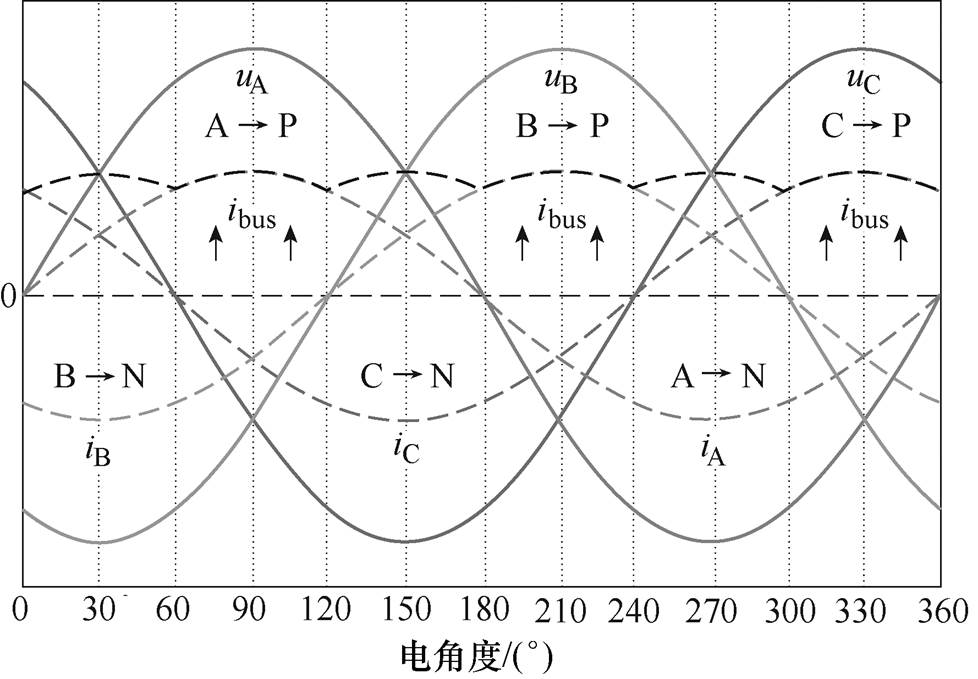
图4 母线电流ibus变化规律
Fig.4 Change rule of bus current ibus
新型PRDCLSI拓扑结构如图5所示,规定图中箭头所指方向即为各谐振电容电压、谐振电感电流的参考正方向。为了便于分析,做如下假设:①新型PRDCLSI中所采用的元器件均工作在理想条件下,忽略寄生参数对换相过程所造成的影响;②新型PRDCLSI所选开关频率fs远大于输出交流电频率fo,故在一个开关矢量中母线电流ibus保持恒定不变;③新型PRDCLSI各主开关管并联缓冲电容相等记为Cs,且CL=3Cs=Ca、Ca1=Ca2=Cb、La1=La2=L。
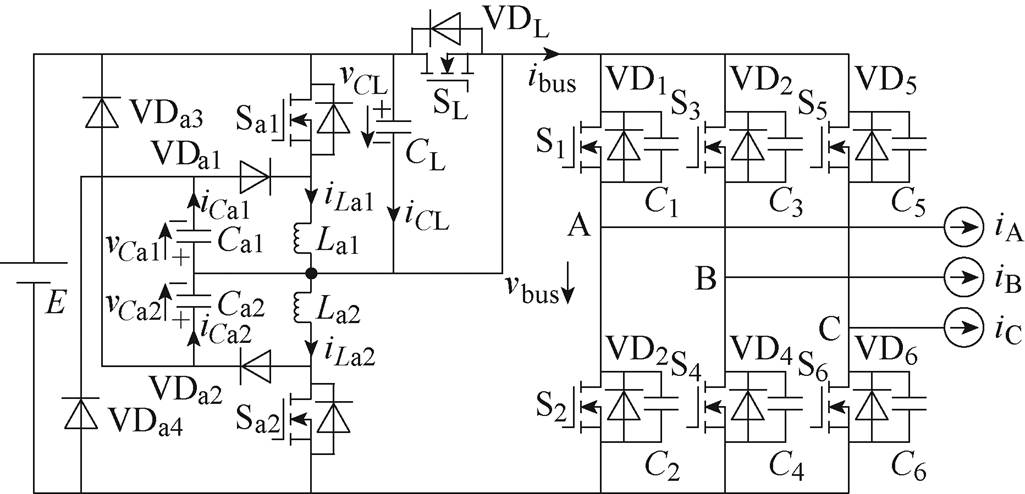
图5 新型PRDCLSI拓扑结构
Fig.5 Topological structure of novel PRDCLSI
图6和图7分别展示了新型PRDCLSI在所提调制策略下的关键工作波形以及据此划分工作模式的等效电路。图6中,实线为上桥臂主开关管驱动信号,虚线为下桥臂主开关管驱动信号;iresmax为谐振电流峰值,iresmax=iLa2max。仍以0 °~30 °区间为例对各工作模式加以描述。
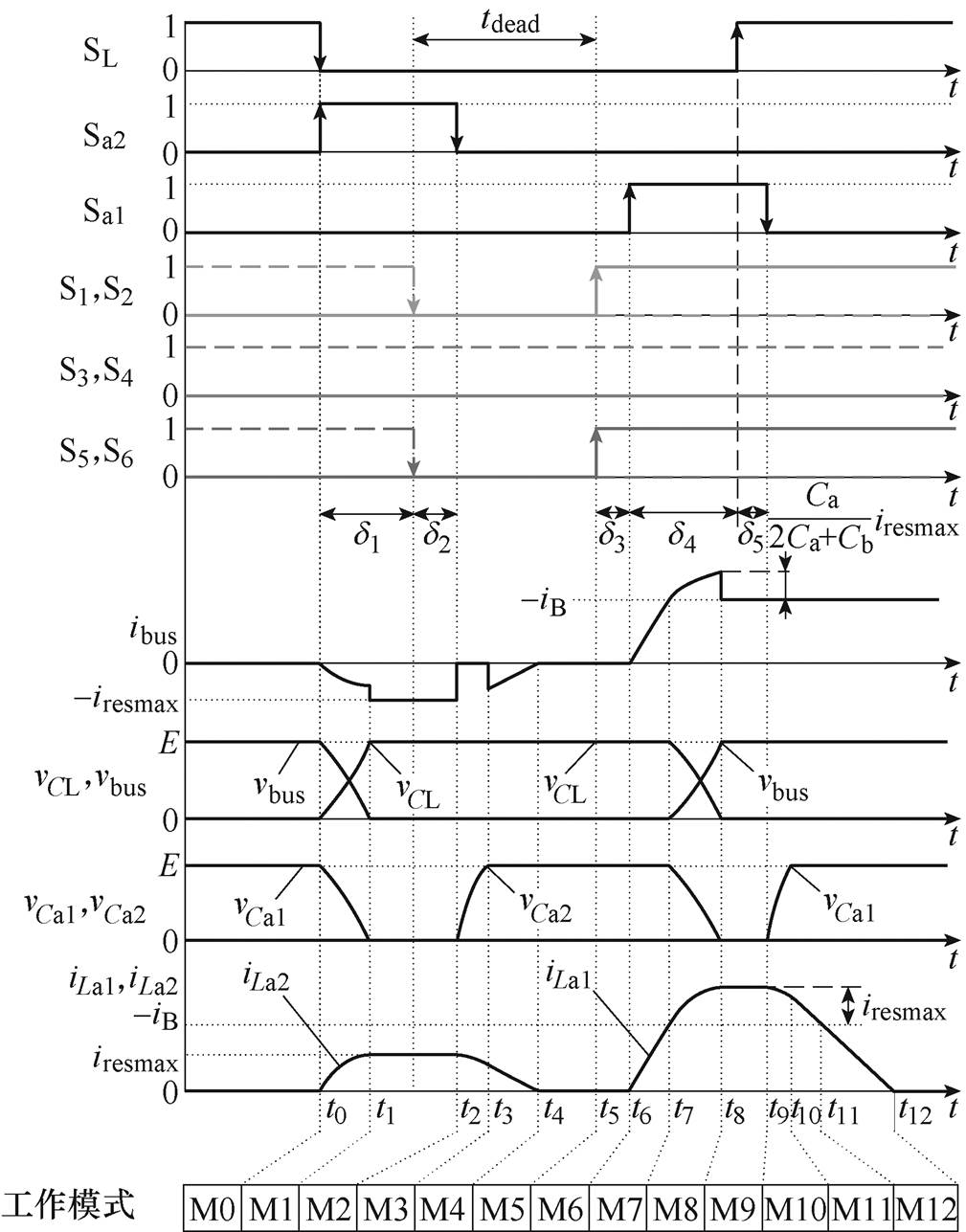
图6 新型PRDCLSI关键工作波形
Fig.6 Key working waveforms of novel PRDCSI

(a)M0
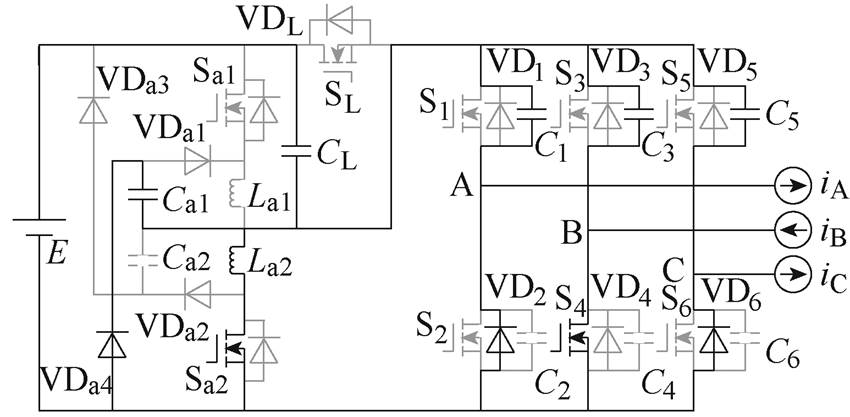
(b)M1
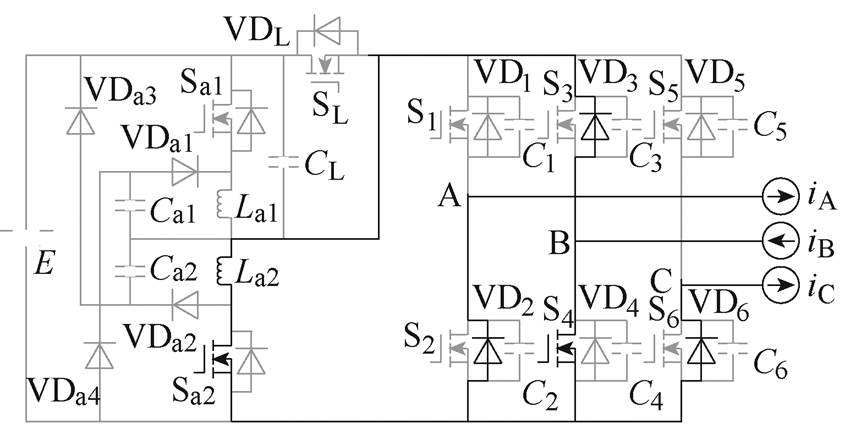
(c)M2
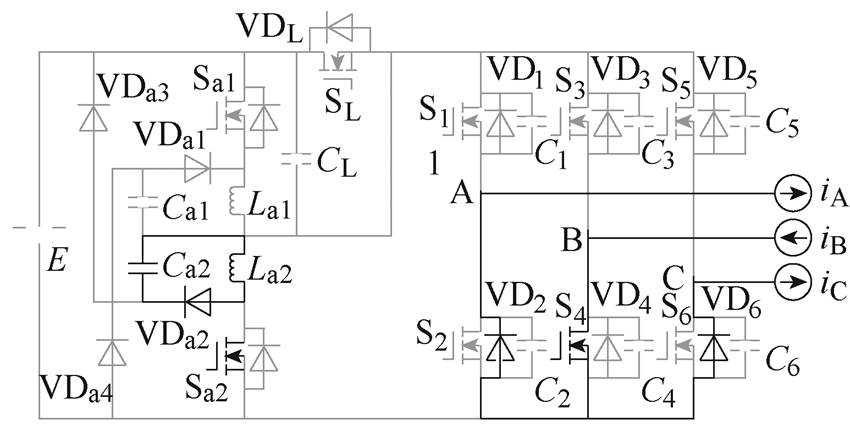
(d)M3

(e)M4
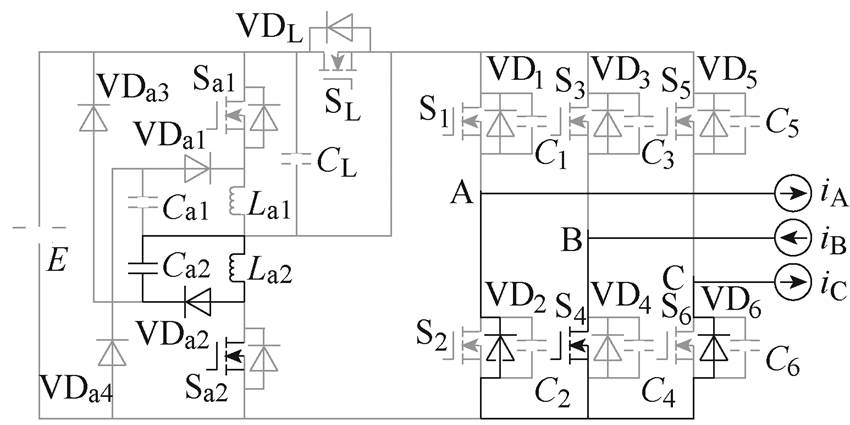
(f)M5
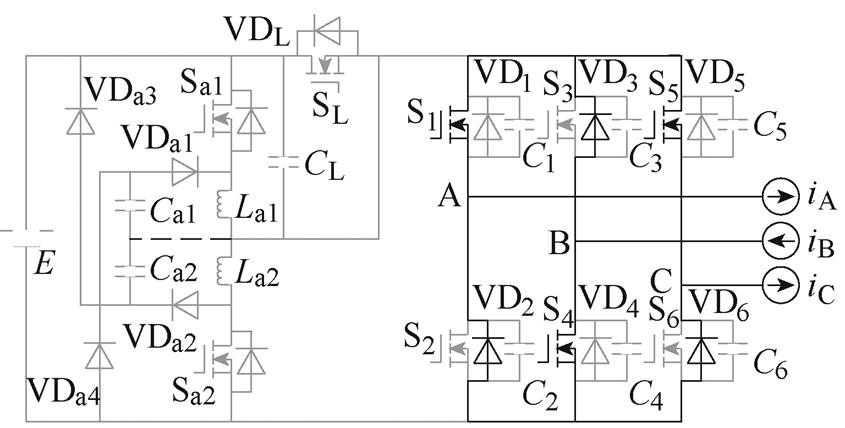
(g)M6
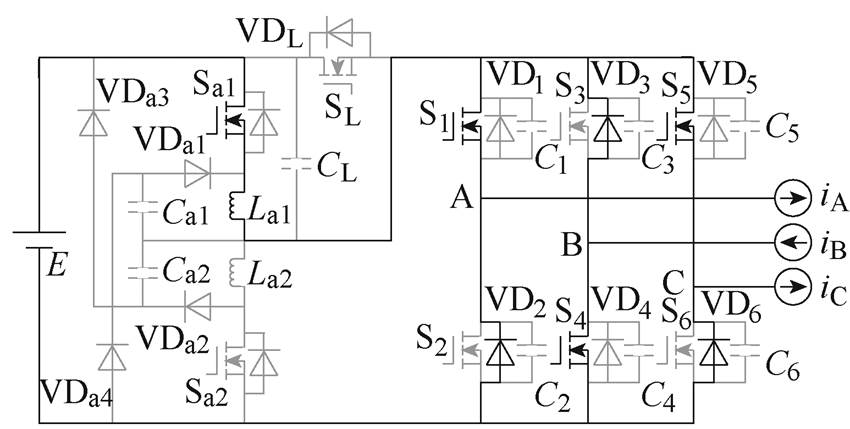
(h)M7
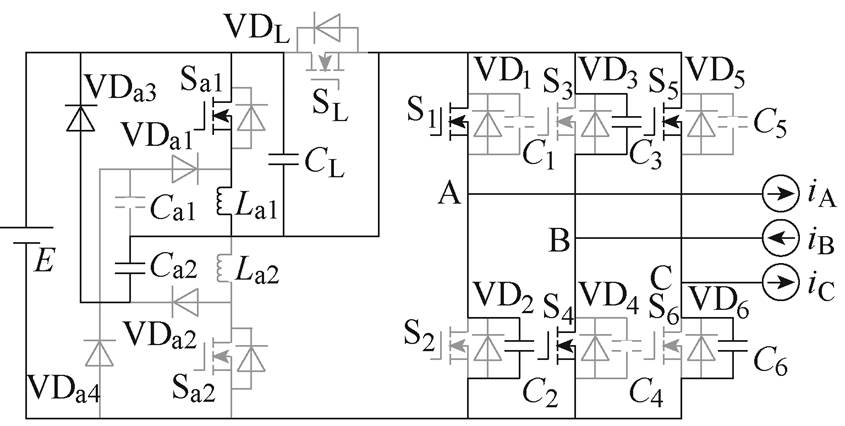
(i)M8

(j)M9
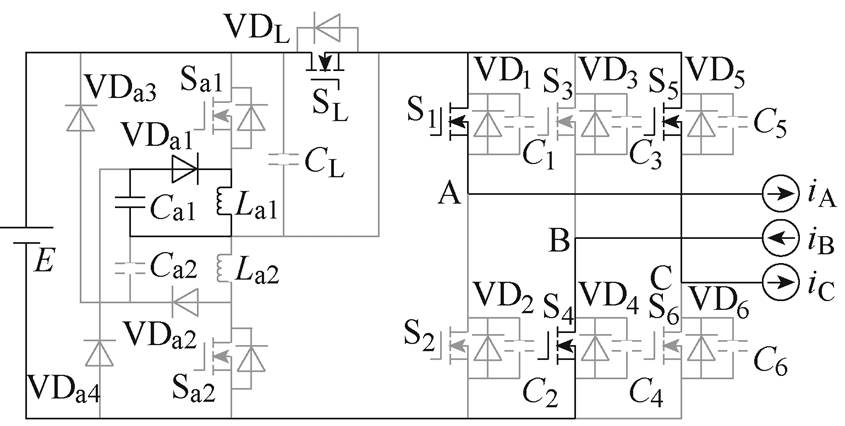
(k)M10
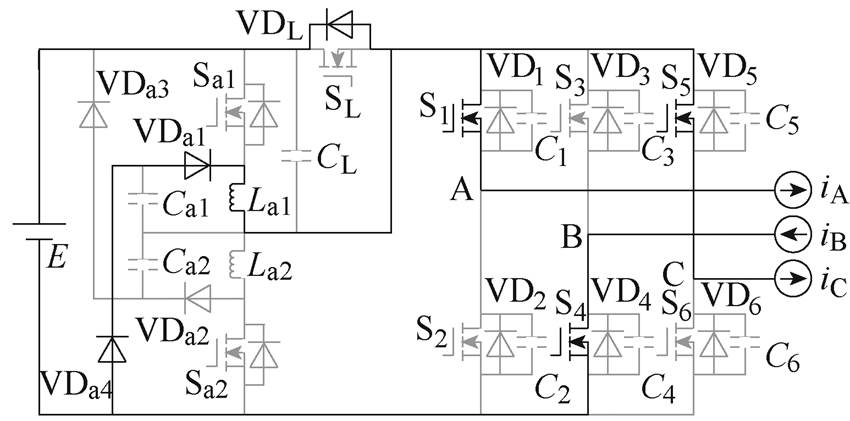
(l)M11
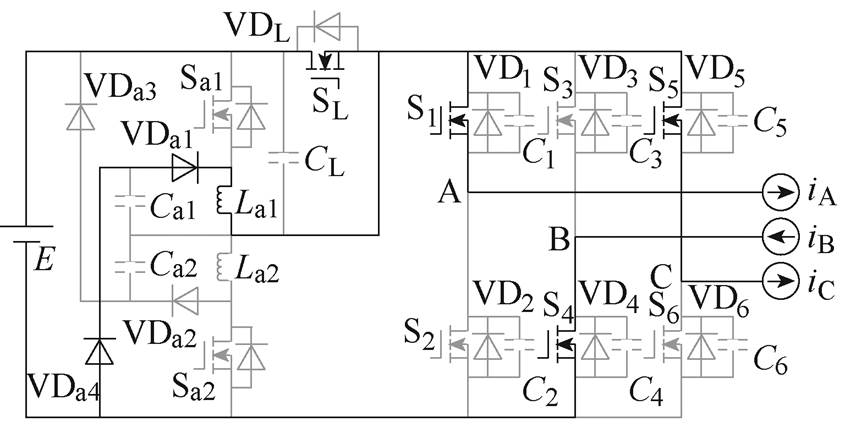
(m)M12
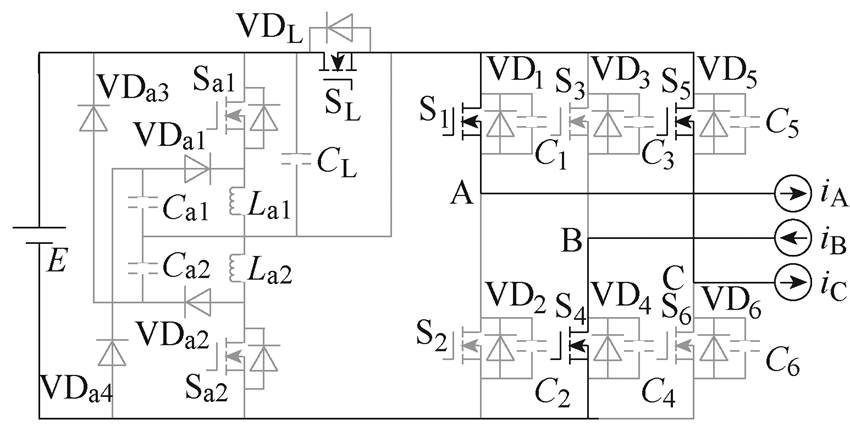
(n)M13
图7 各工作模式等效电路
Fig.7 Equivalent circuit in different working mode
(1)M0 (t0 :Sa1、Sa2关断,虽然SL开通,但电路处于000开关矢量,直流电源不向负载传输能量。此时vCL(t0)=vCa2(t0)=0,vCa1(t0)=vC1(t0)=vC3(t0)=vC5(t0)=E,iSL(t0)=ibus(t0)=0。
:Sa1、Sa2关断,虽然SL开通,但电路处于000开关矢量,直流电源不向负载传输能量。此时vCL(t0)=vCa2(t0)=0,vCa1(t0)=vC1(t0)=vC3(t0)=vC5(t0)=E,iSL(t0)=ibus(t0)=0。
(2)M1 [t0, t1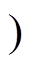 :SL关断的同时Sa2开通,La2与CL、Ca1、C1、C3、C5谐振。该模式中SL实现ZVZCS关断,Sa2实现准ZCS开通。关键元件电流和电压表达式分别为
:SL关断的同时Sa2开通,La2与CL、Ca1、C1、C3、C5谐振。该模式中SL实现ZVZCS关断,Sa2实现准ZCS开通。关键元件电流和电压表达式分别为
 (1)
(1)
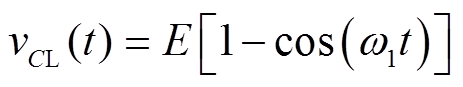 (2)
(2)
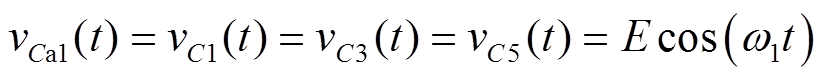 (3)
(3)
其中
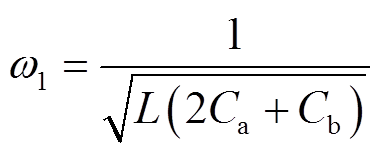
当vC1/3/5下降至零时,M1结束,其续时间为
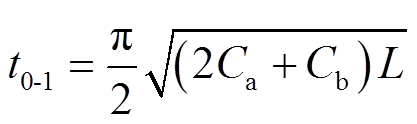 (4)
(4)
(3)M2 [t1, t2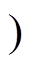 :vC1、vC3、vC5放电至零,VD3导通。iLa2通过Sa2、S4、VD3和La2续流,负载电流通过VD2、S4、VD6续流。该模式中S2与S6实现ZVZCS关断。当Sa2关断时,M2结束,其持续时间为
:vC1、vC3、vC5放电至零,VD3导通。iLa2通过Sa2、S4、VD3和La2续流,负载电流通过VD2、S4、VD6续流。该模式中S2与S6实现ZVZCS关断。当Sa2关断时,M2结束,其持续时间为
 (5)
(5)
(4)M3 [t2, t3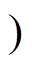 :Sa2关断,La2和Ca2谐振,负载电流继续通过VD2、S4、VD6续流。该模式中Sa2实现准ZVS关断。关键元件电流和电压表达式分别为
:Sa2关断,La2和Ca2谐振,负载电流继续通过VD2、S4、VD6续流。该模式中Sa2实现准ZVS关断。关键元件电流和电压表达式分别为
 (6)
(6)
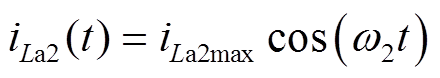 (7)
(7)
其中
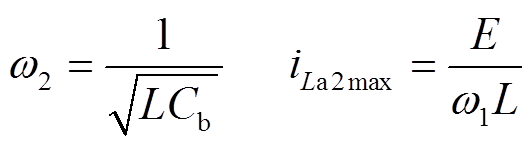
当vCa2上升至E时,M3结束,其持续时间为
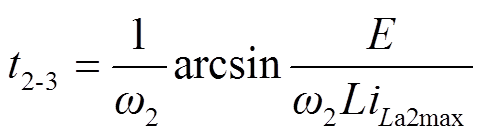 (8)
(8)
(5)M4 [t3, t4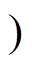 :vCa2充电至E,VDa3导通,iLa2通过VDa2、VDa3、S4、VD3、La2向电源线性回馈能量。电感电流为
:vCa2充电至E,VDa3导通,iLa2通过VDa2、VDa3、S4、VD3、La2向电源线性回馈能量。电感电流为
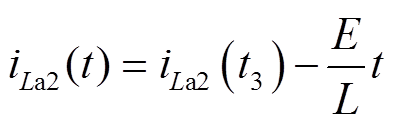 (9)
(9)
当iLa2下降至零时,M4结束,其续时间为
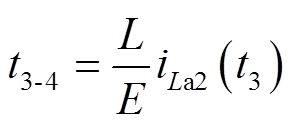 (10)
(10)
(6)M5 [t4, t5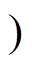 iLa2放电至零。负载电流继续通过VD2、S4、VD6续流。当S1与S5开通时,M5结束,其持续时间为
iLa2放电至零。负载电流继续通过VD2、S4、VD6续流。当S1与S5开通时,M5结束,其持续时间为
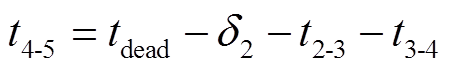 (11)
(11)
(7)M6 [t5, t6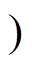 :S1与S5开通。负载电流通过S1、VD2、VD3、S4、S5、VD6续流。该模式中S1与S5实现ZVZCS开通。当Sa1开通时,M6结束,其持续时间为
:S1与S5开通。负载电流通过S1、VD2、VD3、S4、S5、VD6续流。该模式中S1与S5实现ZVZCS开通。当Sa1开通时,M6结束,其持续时间为
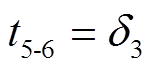 (12)
(12)
(8)M7 [t6, t7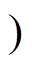 :Sa1开通,VD2、VD3、VD6依次向La1换相,iLa1线性上升。该模式中Sa1实现准ZCS开通。关键元件电流表达式为
:Sa1开通,VD2、VD3、VD6依次向La1换相,iLa1线性上升。该模式中Sa1实现准ZCS开通。关键元件电流表达式为
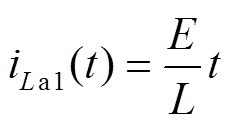 (13)
(13)
当iLa1上升至-iB时,M7结束,其持续时间为
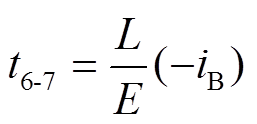 (14)
(14)
(9)M8 [t7, t8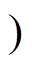 :iLa1上升至-iB,La1与CL、Ca2、C2、C3、C6谐振。关键元件电流和电压表达式分别为
:iLa1上升至-iB,La1与CL、Ca2、C2、C3、C6谐振。关键元件电流和电压表达式分别为
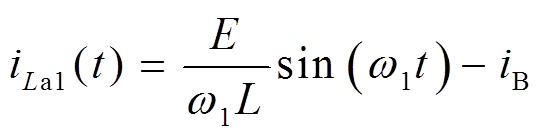 (15)
(15)
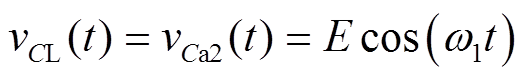 (16)
(16)
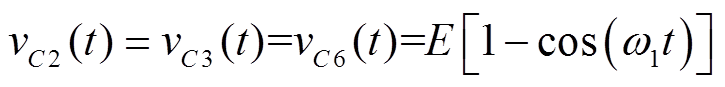 (17)
(17)
当vCL放电至零时,M8结束,其持续时间为
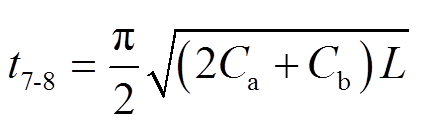 (18)
(18)
(10)M9 [t8, t9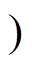 :vCL下降至零,VDL导通。iLa1通过Sa1、La1和VDL续流。该模式中SL实现ZVZCS开通。当Sa1关断时,M9结束,其持续时间为
:vCL下降至零,VDL导通。iLa1通过Sa1、La1和VDL续流。该模式中SL实现ZVZCS开通。当Sa1关断时,M9结束,其持续时间为
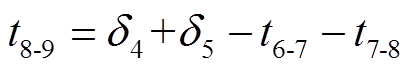 (19)
(19)
(11)M10 [t9, t10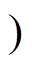 :Sa1关断,VDa1导通,La1和Ca1开始谐振,直流电源通过SL向负载传输能量。该模式中Sa1实现准ZVS关断。关键元件电流和电压表达式分别为
:Sa1关断,VDa1导通,La1和Ca1开始谐振,直流电源通过SL向负载传输能量。该模式中Sa1实现准ZVS关断。关键元件电流和电压表达式分别为
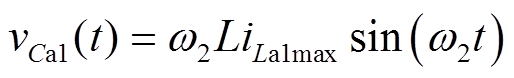 (20)
(20)
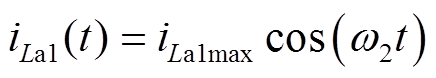 (21)
(21)
其中
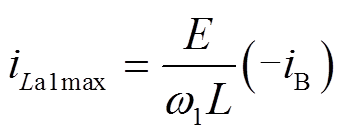
当vCa1充电至E时,M10结束,其持续时间为
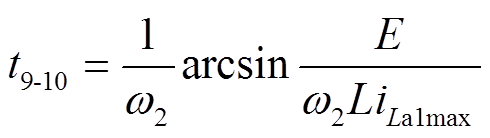 (22)
(22)
(12)M11 [t10, t11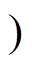 :vCa1充电至E,VDa4导通。La1通过VDa1、VDa4和VDL向直流电源线性回馈能量,iLa1线性下降。关键元件电流表达式为
:vCa1充电至E,VDa4导通。La1通过VDa1、VDa4和VDL向直流电源线性回馈能量,iLa1线性下降。关键元件电流表达式为
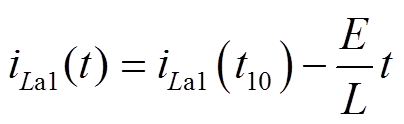 (23)
(23)
当iLa1减小到-iB时,M11结束,其持续时间为
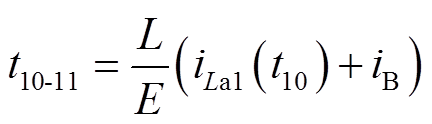 (24)
(24)
(13)M12 [t11, t12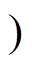 :iLa1继续线性下降,iLa1从La1向SL换相。关键元件电流表达式为
:iLa1继续线性下降,iLa1从La1向SL换相。关键元件电流表达式为
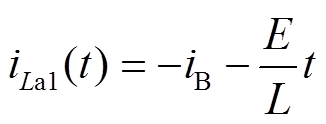 (25)
(25)
当iLa1下降到零时,M12结束,其持续时间为
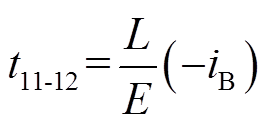 (26)
(26)
(14)M13 [t12,~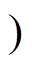 :iLa1向SL换相完毕后,电路进入101开关矢量,直流电源经SL向负载稳定供能,此时vCL(~)=vCa2(~)=0,vCa1(~)=vC2(~)=vC3(~)=vC6(~)=E,iSL(~)=ibus(~)=-iB(~),为下一次换相过程做好准备。
:iLa1向SL换相完毕后,电路进入101开关矢量,直流电源经SL向负载稳定供能,此时vCL(~)=vCa2(~)=0,vCa1(~)=vC2(~)=vC3(~)=vC6(~)=E,iSL(~)=ibus(~)=-iB(~),为下一次换相过程做好准备。
表1为文献[15-16]和本文所提调制策略下新型PRDCLSI中辅助开关管电流应力以及辅助电路动作次数对比。
在三种调制策略下,第一辅助开关管Sa1的电流应力均为iresmax与负载电流Iomax之和。在文献[15]和本文所提调制策略下,第二辅助开关管Sa2的电流应力均为iresmax,而在文献[16]所提调制策略下依旧为iresmax与Iomax之和,这说明本文所提调制策略保持了Sa2的低电流应力特性。
关于辅助电路动作次数,在文献[16]和本文所提调制策略下,一个开关周期时间内辅助电路只动作1次,而文献[15]则需要动作6次完成相应的软切换需求,这说明本文所提调制策略保持了辅助电路动作频率的最小化。
表1 不同文献中辅助开关管电流应力及辅助电路动作次数对比
Tab.1 Comparison of auxiliary switch current stresses and auxiliary circuit operation times in different references

对比项文献[15]文献[16]本文 Sa1电流应力 Sa2电流应力 辅助电路动作次数611
综上所述,在对比文献中,本文所提调制策略同时兼顾了辅助电路电流应力与动作次数的优化。
在本文所提调制策略下主线、母线、辅助开关管借助外并联电容均实现了软关断,且SiC MOSFET的开通损耗远大于关断损耗[18],故本文在进行参数设计时仅对软开通条件进行约束,具体内容如下:
1)延迟时间d1与死区时间tdead的选择
为了保证主开关管的软开通。首先,M1须在d1延迟时间内完成并联缓冲电容的谐振放电,由式(4)可得
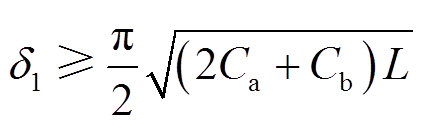 (27)
(27)
M3与M4须在tdead死区时间内结束,而后主开关管实现软开通,由式(8)和式(10)可得
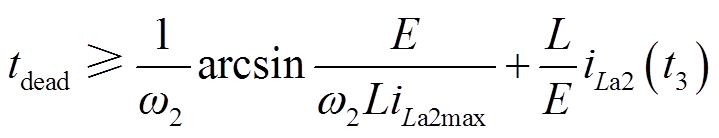 (28)
(28)
2)延迟时间d4的选择
为了保证母线开关管的软开通,M7与M8须在d4延迟时间内完成,由式(14)和式(18)可得
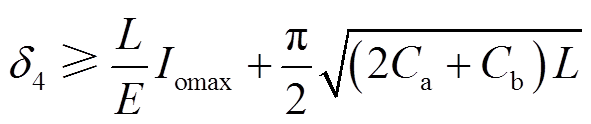 (29)
(29)
3)辅助谐振电感L的设计
为了减小辅助开关管的开通损耗,式(13)须不大于辅助开关管开通后的预设电流变化率(di/dt)set,即
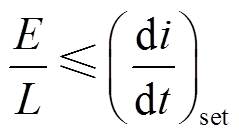 (30)
(30)
4)辅助谐振电容Ca和Cb的设计
为了减小辅助电路的电流应力及导通损耗,规定式(7)所代表的iresmax须不大于0.2Iomax,即
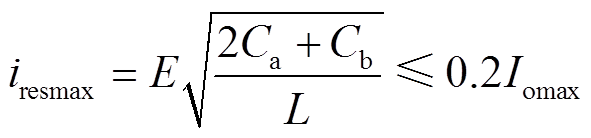 (31)
(31)
在本设计举例中规定:E=200 V,Iomax=40 A,(di/dt)set=50 A/ms。根据式(30)求得L≥4 mH,取L=5 mH。因为iresmax≤8 A,根据式(31)求得2Ca+Cb≤8nF;考虑到电容值的不连续性,取Ca= 3 nF、Cb=1 nF。将L=5 µH、Ca=3 nF、Cb=1 nF代入式(27)~式(29)可得:d1≥0.29 ms、tdead≥0.2 ms、d4≥1.29 ms;取d1=0.5 ms、tdead=0.5 ms、d4=1.5 ms。
不考虑寄生参数的影响,在本文所提调制策略下,PRDCLSI的损耗包括主逆变电路的损耗PMI及辅助电路的损耗PAC,其具体组成如下:
PMI又可以进一步划分为主开关管的开关损耗Psw(main)和导通损耗Pcon(main)。由图1a可知,在本文所提调制策略下,主开关管的工况具有1/4工频周期对称性。
1)主开关管的开关损耗Psw(main)
在本文所提调制策略下,主开关管S1可以实现ZVZCS开通和准ZVS关断,S1的体二极管VD1可以实现软切换,故其开关损耗Psw(main)仅包含S1的关断损耗,即
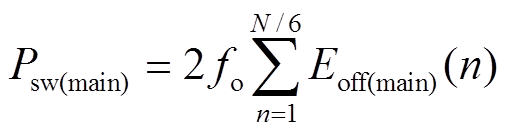 (32)
(32)
式中,fo为工频;N为一个工频周期内S1的切换次数;Eoff(main)(n)为第n个开关周期内S1产生的关断损耗,其值在并联缓冲电容Cs、关断时刻电流为iA(n)条件下通过实验测得(n∈[1, 1/6N]);关于关断损耗的测定方法与此相同,具体测试条件参照工作原理所述,不再重复。
2)主开关管的导通损耗Pcon(main)
忽略辅助电路短时工作对主开关管电流波形的影响,则所提调制策略下PRDCLSI的主开关管导通过程与采用DPWM的硬开关逆变器相似。考虑到SiC MOSFET同步整流效应的影响,S1(VD1)的导通损耗Pcon(main)可以表示为
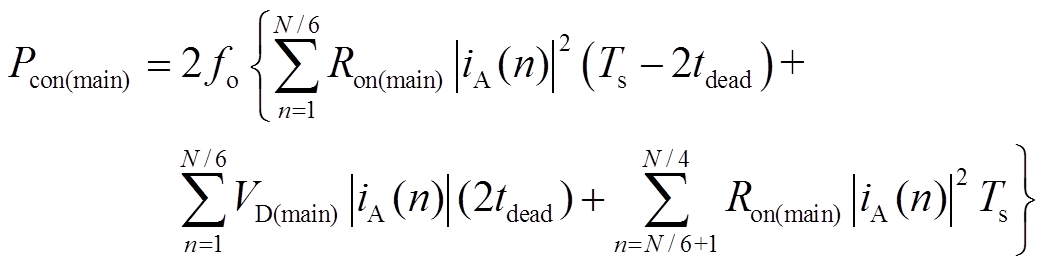 (33)
(33)
式中,Ron(main)为S1的导通电阻;VD(main)为VD1的导通压降。
PAC可进一步划分为母线开关管的损耗PSL、辅助开关管的损耗PAS、辅助二极管的损耗PDa、谐振电感的损耗PLr与谐振电容的损耗PCr。由图4可知,在本文所提调制策略下,辅助电路的工况具有1/12工频周期对称性。
1)母线开关管的损耗PSL
由于SL实现ZVZCS开通和关断,SL的体二极管VDL实现了软切换,故其仅包含导通损耗Pcon(SL),可以表示为
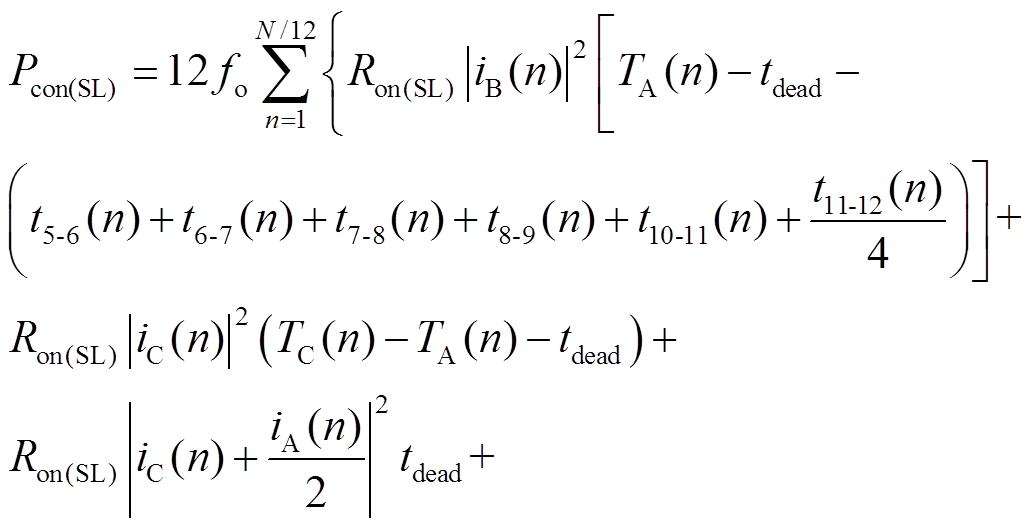
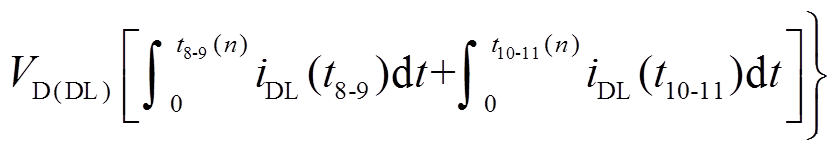 (34)
(34)
式中,Ron(SL)为SL的导通电阻;VD(DL)为VDL的导通压降;TA(n)和TC(n)分别为第n个开关周期内S1和S5的导通时间,其值可以通过调制波与载波的比例关系计算获得;t5-6(n)、t6-7(n)、t7-8(n)、t8-9(n)、t10-11(n)和t11-12(n)分别为第n个开关周期内,模式M6、M7、M8、M9、M11和M12的持续时间,可分别由式(12)、式(14)、式(18)、式(19)、式(24)和式(26)得到;iDL(t8-9)和iDL(t10-11)分别为第n个开关周期内,模式M9和M11中VDL所流过的电流,可分别由式(15)和式(23)得到。
2)辅助开关管的损耗PAS
Sa1和Sa2的损耗由两部分组成:一部分是开关损耗;另一部分是导通损耗。由于Sa1和Sa2实现了准ZCS开通和准ZVS关断,故二者开关损耗Psw(aux)可以表示为
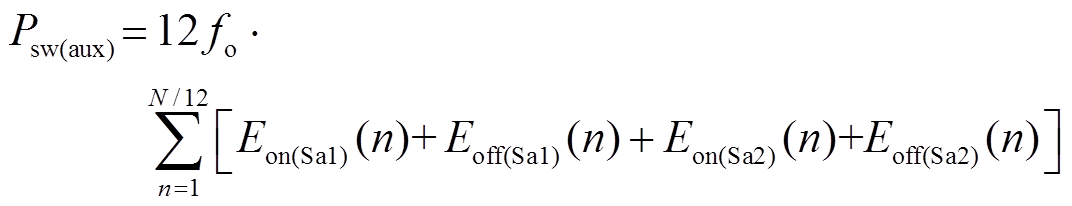 (35)
(35)
式中,Eon(Sa1)(n)和Eon(Sa2)(n)分别为第n个开关周期内Sa1和Sa2产生的开通损耗,其值在串联谐振电感La1和La2,开通时刻电压为直流电源电压E条件下通过实验测得;Eoff(Sa1)(n)和Eoff(Sa2)(n)为第n个开关周期内Sa1和Sa2产生的关断损耗。
二者导通损耗Pcon(aux)可以表示为
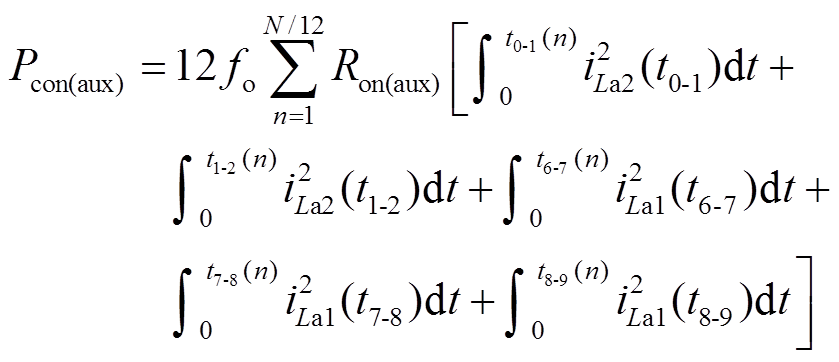 (36)
(36)
式中,Ron(aux)为Sa1和Sa2的导通电阻;t0-1(n)和t1-2(n)分别为第n个开关周期内,模式M1和M2的持续时间,可分别由式(4)和式(5)得到;iLa2(t0-1)、iLa2(t1-2)、iLa1(t6-7)、iLa1(t7-8)、iLa1(t8-9)分别为第n个开关周期内,模式M1、M2、M7、M8、M9中La2和La1所流过的电流,可分别由式(1)、式(1)、式(13)、式(15)、式(15)得到。
3)辅助二极管的损耗PDa
由于VDa1~VDa4实现了软切换,故其损耗仅包括导通损耗Pcon(Da),表示为
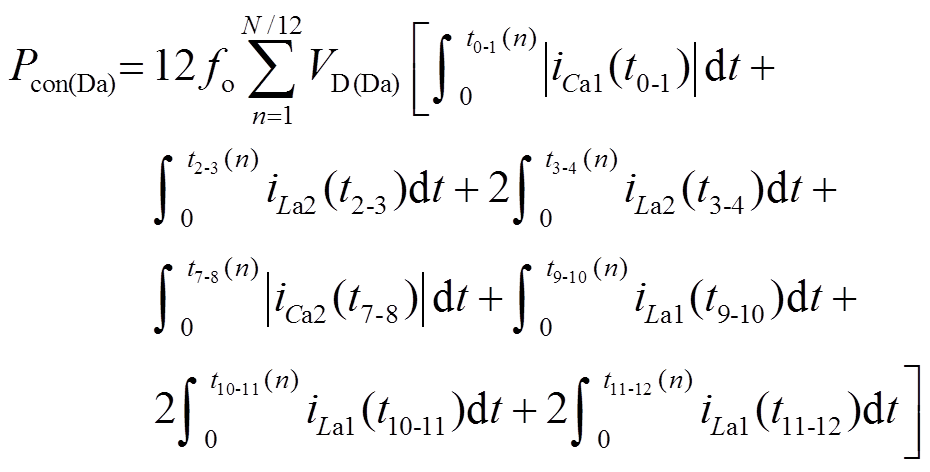 (37)
(37)
式中,VD(Da)为VDa1~VDa4的导通压降;t2-3(n)、t3-4(n)、t9-10(n)分别为第n个开关周期内,模式M3、M4、M10的持续时间,可由式(8)、式(10)、式(22)得到;iCa1(t0-1)和iCa2(t7-8)为第n个开关周期内,模式M1中Ca1和模式M8中Ca2所流过的电流,可分别由式(3)和式(16)得到;iLa2(t2-3)、iLa2(t3-4)、iLa1(t9-10)、iLa1(t10-11)、iLa1(t11-12)分别为第n个开关周期内,模式M3、M4、M10、M11、M12中La2和La1所流过的电流,可分别由式(7)、式(9)、式(21)、式(23)、式(25)得到。
4)谐振电感的损耗PLr与谐振电容的损耗PCr
PLr和PCr包括直流损耗和交流损耗,其中直流损耗占比较小,可忽略不计。交流损耗是由邻近效应和趋肤效应引起的,其分析非常复杂。为简化分析,本节仅考虑所选开关频率下谐振电感和谐振电容中等效串联电阻引起的交流损耗,其表达式分别为
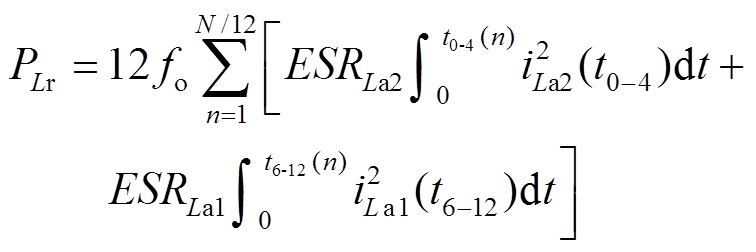 (38)
(38)
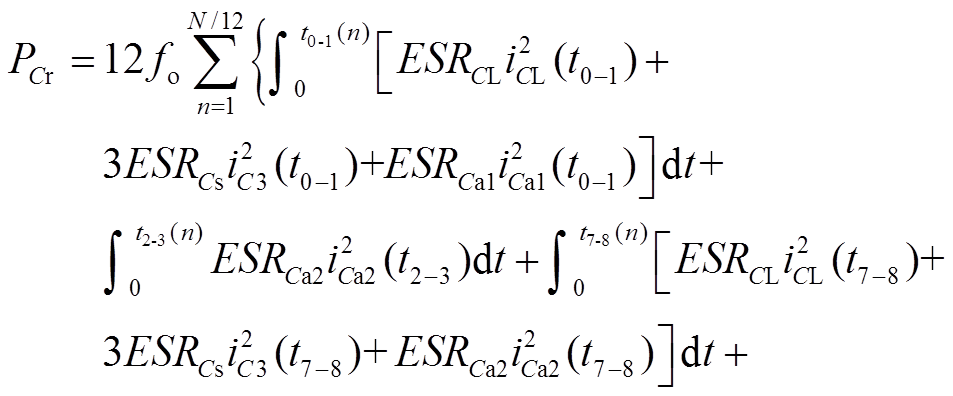
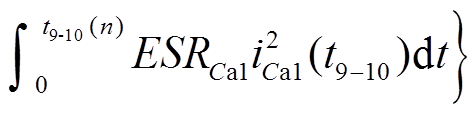 (39)
(39)
式中,ESRLa2、ESRLa1、ESRCL、ESRCs、ESRCa2、ESRCa1分别为La2、La1、CL、Cs、Ca2、Ca1在所选开关频率下的等效串联电阻,其值由LCR表测得;iCL(t0-1)、iC3(t0-1)为第n个开关周期内,模式M1中CL、C3所流过的电流,可分别由式(2)、式(3)得到;iCa2(t2-3)为第n个开关周期内,模式M3中Ca2所流过的电流,可由式(6)得到;iCL(t7-8)、iC3(t7-8)为第n个开关周期内,模式M8中CL、C3所流过的电流,可由式(16)和式(17)得到;iCa1(t9-10)为第n个开关周期内,模式M10中Ca1所流过的电流,可由式(20)得到。
为验证本文分析结果的正确性,研制一台5 kW/40 kHz的实验样机,实验平台如图8a所示,控制板如图8b所示,功率板正、反面分别如图8c和8d所示。样机设计参数与器件选型见表2。

(a)实验样机 (b)控制板

(c)功率板正面 (d)功率板反面
图8 逆变器样机照片
Fig.8 Photographs of inverter prototype
表2 样机器件选型和参数设计
Tab.2 Devices selection and parameters design

参 数数值 (型号) 控制芯片Xilinx Zynq-7020 (FPGA+ARM) 驱动芯片Ti UCC21521 E/V200 Iomax/A40 fs/kHz40 S1(VD1)~S6(VD6), SL(VDL),Sa1, Sa2Rohm SCT3022AL (650 V, 93 A) VDa1~VDa4ST STBR6012Y (1 200 V, 60 A) C1~C6, Ca1, Ca2STE B22G102JJ1B0100060035EOZ (400 V, 1 nF) CLSRD MPP332J4130407LC (400 V, 3.3 nF) La1, La2自制(50 A, 5 mH) d1, tdead/ms0.5 d4/ms1.5
在相同负载电流条件下,图9a~图9c分别为本文、文献[15-16]所提调制策略下,工频周期内第二辅助谐振电感电流iLa2波形和开关周期内第一辅助谐振电感电流iLa1波形。对比三者可知:文献[16]与本文所提调制策略下辅助电路均在一个开关周期内动作1次,最小化辅助电路动作次数带来导通损耗,并且本文所提调制策略下辅助谐振电感电流峰值较文献[15-16]均大幅降低,即辅助电路电流应力大幅降低,从而进一步减小辅助电路损耗。
图10为各开关管开通与关断时的电压电流波形,图10a、图10c、图10e和图10g分别为S1、SL、Sa1、Sa2开通时的电压和电流波形;图10b、图10d、图10f和图10h分别为S1、SL、Sa1、Sa2关断时的电压和电流波形。由图10可知,S1实现ZVZCS开通与准ZVS关断;SL实现ZVZCS开通与关断;Sa1和Sa2均实现准ZCS开通与准ZVS关断。
图11为本文所提改进调制策略下新型PRDCLSI输出的负载电流及其谐波分析,从图11中可以看出,改进调制策略下新型PRDCLSI的负载电流波形较为平滑且畸变较小,满足相关应用需求。
图12为本文和文献[16]所提调制策略下新型PRDCLSI仿真损耗分布对比(fs=40 kHz),考虑到文献[15]中辅助电路动作频率为开关频率的6倍,即达到240 kHz(4.17 ms),在如此短暂的时间里辅助电路难以完成软开关切换,并且极易对实验平台造成损毁,故未对其损耗分布进行评估,下文实测效率亦同。由图12可知,无论轻载还是重载,本文所提调制策略下各项损耗均照文献[16]有所下降。与文献[16]相比,当输出功率Po=1.0 kW时,本文总损耗下降38.10 W,效率提升3.50 %;当输出功率Po=5.0 kW时,本文总损耗下降76.94W,效率提升1.46 %。

(a)本文 (b)文献[16] (c)文献[15]
图9 辅助谐振电感电流波形对比
Fig.9 Comparison of auxiliary resonant inductor current
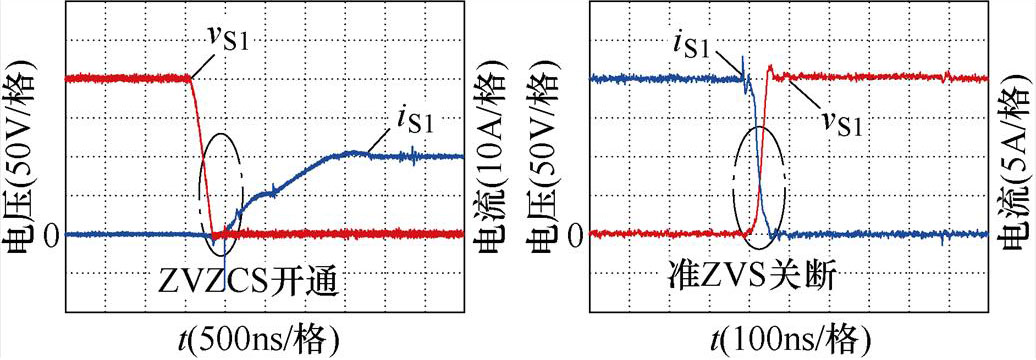
(a)主开关管S1的开通波形 (b)主开关管S1的关断波形
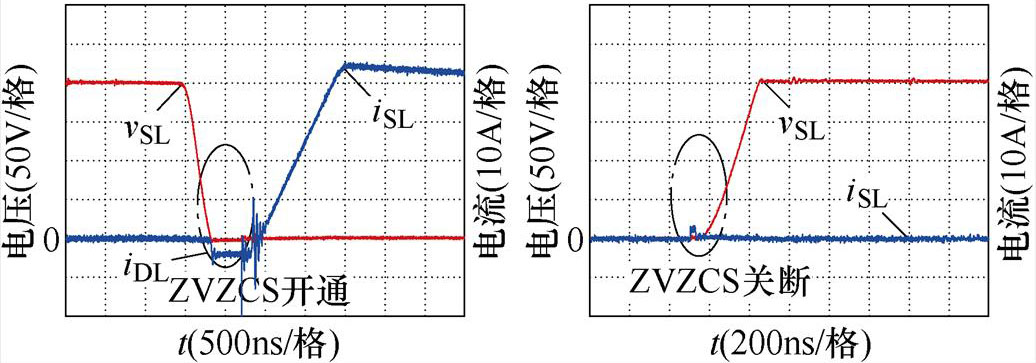
(c)母线开关管SL的开通波形(d)母线开关管SL的关断波形

(e)辅助开关管Sa1的开通波形(f)辅助开关管Sa1的关断波形
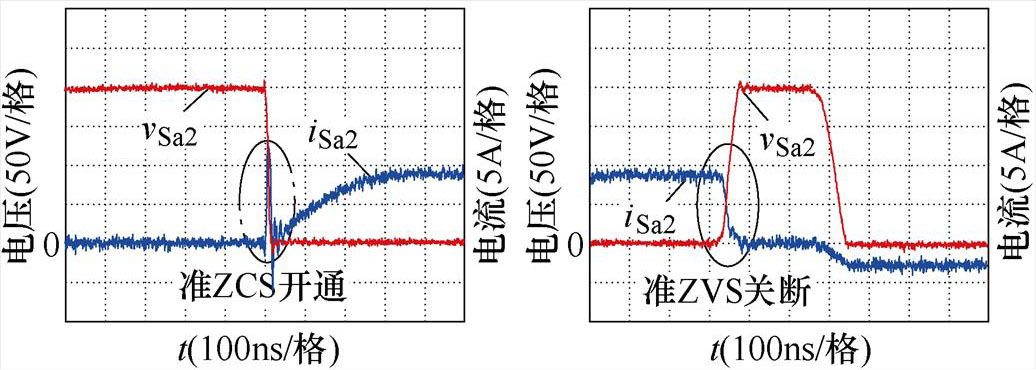
(g)辅助开关管Sa2的开通波形(h)辅助开关管Sa2的关断波形
图10 开通与关断波形
Fig.10 Waveforms during turn-on and turn-off transition
图13为本文和文献[16]所提调制策略下新型PRDCLSI实测效率曲线与硬开关条件下实测效率曲线对比(fs=40 kHz)。由图13可知,在全负载范围内,本文所提调制策略下新型PRDCLSI效率高于文献[16],且越是轻负载,这种效率优势越明显;其与文献[16]效率曲线相对于硬开关效率曲线的变化趋势相同,不同之处在于文献[16]效率提升有限。结合图13分析可知,在轻负载范围内仿真效率与实测效率相接近,随着输出功率提升,电路中寄生电阻与导线电阻损耗增加,导致实测效率低于仿真效率,同时由于文献[16]中辅助电路电流应力远大于本文,其影响更大,故二者在重载范围内的效率差进一步增大。在本文所提改进调制策略下,新型PRDCLSI在额定负载5.0 kW处可获得97.97 %的效率,比文献[16]提高1.70 %,比硬开关提高1.92 %;在轻负载1.0 kW处也可获得97.63 %的效率,比文献[16]提高3.47 %,比硬开关提高4.16 %。故可认为本文所提改进调制策略维持了新型PRDCLSI较高的能量变换效率。
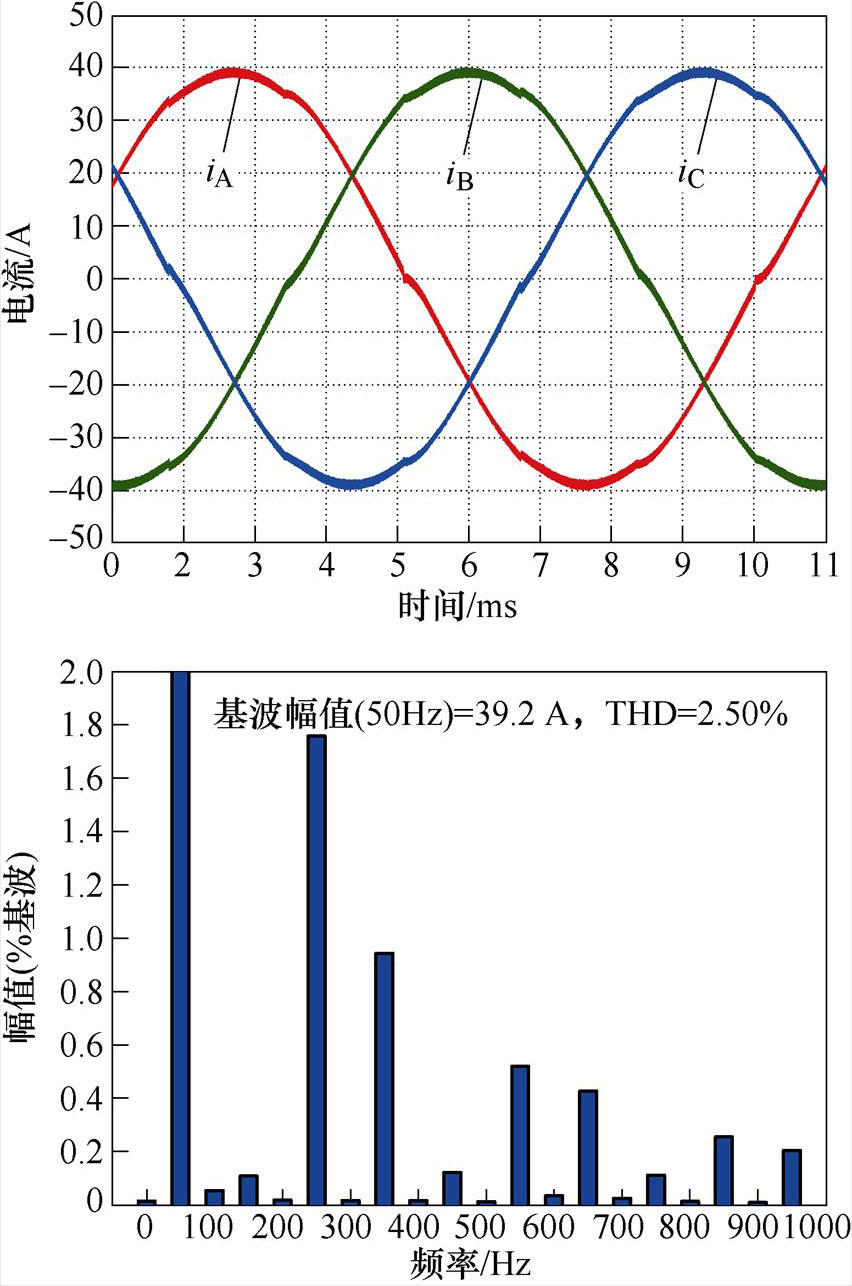
图11 负载电流及其谐波分析
Fig.11 Load current and their harmonic analysis

图12 仿真损耗分布
Fig.12 Simulation loss distribution
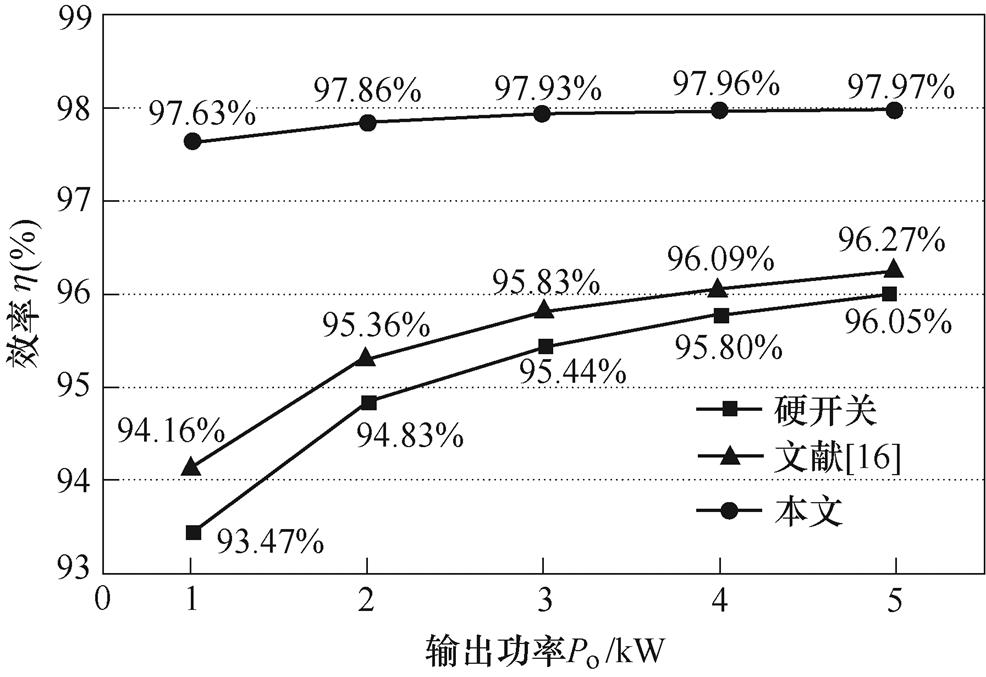
图13 效率曲线
Fig.13 Efficiency curves
本文针对一种性能优良的新型PRDCLSI,提出了一种由DPWM与锯齿载波组成的改进调制策略。通过理论分析和实验研究得出如下结论:
1)主开关管实现了ZVZCS开通和准ZVS关断;母线开关管实现了ZVZCS开通和关断;辅助开关管实现了准ZCS开通和准ZVS关断。
2)本文辅助电路动作频率与文献[16]保持一致,仅为文献[15]的1/6,即在一个开关周期内,辅助电路仅需动作一次,即可实现全部开关管的软切换。
3)与文献[15-16]相比,通过改进调制策略的实施与合理的参数设计,第一与第二辅助开关管的电流应力大幅降低,有效地降低辅助电路导通损耗。
4)fs=40 kHz时,文献[15]不适用于高频化逆变电路;此时与文献[16]相比,本文在全负载范围内取得效率优势,峰值效率达到97.97 %,且越是轻负载,这种效率优势越明显。
参考文献
[1] Zhou Wenzhi, Diab M, Yuan Xibo, et al. Mitigation of motor overvoltage in SiC-based drives using soft-switching voltage slew-rate (dv/dt) profiling[J]. IEEE Transactions on Power Electronics, 2022, 37(8): 9612-9628.
[2] 成林, 欧宏, 毕闯, 等. 基于SiC MOSFET的同步Buck变换器电磁干扰噪声分析及预测[J]. 电工技术学报, 2021, 36(增刊2): 627-634, 643.
Cheng Lin, Ou Hong, Bi Chuang, et al. Analysis and prediction of electromagnetic interference noise in synchronous Buck converter with SiC MOSFET[J]. Transactions of China Electrotechnical Society, 2021, 36(S2): 627-634, 643.
[3] Pulsinelli F, di Benedetto M, Lidozzi A, et al. Power losses distribution in SiC inverter based electric motor drives[J]. IEEE Transactions on Industry Applications, 2019, 55(6): 7843-7853.
[4] 胡伟涛, 孙鹏纬. 55kW软开关模块化逆变器在高温混合动力电动汽车应用上的效率评估[J]. 电工技术学报, 2011, 26(增刊1): 97-101.
Hu Weitao, Sun Pengwei. Efficiency evaluation of a 55kW soft-switching module based inverter for high temperature hybrid electric vehicle drives appli- cation[J]. Transactions of China Electrotechnical Society, 2011, 26(S1): 97-101.
[5] Wu Yuying, He Ning, Chen Mili, et al. Generalized space-vector-modulation method for soft-switching three-phase inverters[J]. IEEE Transactions on Power Electronics, 2021, 36(5): 6030-6045.
[6] 张少腾, 赵晋斌, 吴月宝, 等. 基于自互感调节的无线电能传输用E类逆变器软开关技术研究[J]. 电工技术学报, 2021, 36(21): 4558-4566.
Zhang Shaoteng, Zhao Jinbin, Wu Yuebao, et al. Research on soft switching technology of class E inverter based on self mutual-inductance regulation in wireless power transfer[J]. Transactions of China Electrotechnical Society, 2021, 36(21): 4558-4566.
[7] 姚修远, 吴学智, 杜宇鹏, 等. T型中点钳位三电平逆变器的零电流转换软开关技术[J]. 电工技术学报, 2016, 31(23): 179-188.
Yao Xiuyuan, Wu Xuezhi, Du Yupeng, et al. The zero-current-transition soft-switching technique for T-type neutral-point-clamped inverter[J]. Transa- ctions of China Electrotechnical Society, 2016, 31(23): 179-188.
[8] Cai Minyu, Wasynczuk O, Saeedifard M. A voltage- edge-rate-limiting soft-switching inverter based on auxiliary resonant pole[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2019, 7(2): 736-744.
[9] Divan D M. The resonant DC link converter-a new concept in static power conversion[J]. IEEE Transa- ctions on Industry Applications, 1989, 25(2): 317- 325.
[10] Du Chengrui, Xu Dehong, He Ning, et al. Modeling and optimization of a zero-voltage switching inverter for high efficiency and miniaturization[J]. IEEE Transactions on Power Electronics, 2017, 32(1): 150-163.
[11] Turzynski M, Chrzan P J. Reducing common-mode voltage and bearing currents in quasi-resonant DC-link inverter[J]. IEEE Transactions on Power Electronics, 2020, 35(9): 9553-9562.
[12] Turzynski M, Chrzan P J, Kolincio M, et al. Quasi- resonant DC-link voltage inverter with enhanced zero-voltage switching control[C]//European Conference on Power Electronics and Applications, Warsaw, 2017: 1-8.
[13] Wang Qiang, Guo Guoxian, Wang Youzheng, et al. An efficient three- phase resonant DC-link inverter with low energy consumption[J]. IEEE Transactions on Power Electronics, 2021, 36(1): 702-715.
[14] 王强, 王天施, 孙海军, 等. 新型高效率并联谐振直流环节软开关逆变器[J]. 电工技术学报, 2013, 28(5): 219-226.
Wang Qiang, Wang Tianshi, Sun Haijun, et al. Novel high efficiency parallel resonant DC link soft- switching inverter[J]. Transactions of China Elec- trotechnical Society, 2013, 28(5): 219-226.
[15] Chu Enhui, Xie Haolin, Chen Zhifang, et al. Parallel resonant DC link inverter topology and analysis of its operation principle[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2020, 8(3): 3124-3138.
[16] Chu Enhui, Li Si, Xie Haolin, et al. RDCL three- phase inverter and load adaptive commutation control[J]. IET Power Electronics, 2019, 12(3): 505- 514.
[17] An Shaoliang, Sun Xiangdong, Zhang Qi, et al. Study on the novel generalized discontinuous SVPWM strategies for three-phase voltage source inverters[J]. IEEE Transactions on Industrial Informatics, 2013, 9(2): 781-789.
[18] Son G, Huang Zhengrong, Li Qiang. Light load efficiency improvement for two-channel paralleled soft-switching three-phase inverter using phase shedding control[J]. 2022, IEEE Transactions on Power Electronics, 2022, 37(9): 10200-10212.
Improved Modulation Strategy of Novel Parallel Resonant DC Link Soft-Switching Inverter
Abstract With the continuous development of wide band gap devices represented by SiC MOSFET, the problems of high switching loss and strong electromagnetic interference of wide band gap inverters under high frequency have become increasingly prominent. To solve these problems, researchers put forward soft-switching inverter technology. In medium and small power applications, the resonant DC link soft-switching inverter (RDCLSI) is the first choice. After years of development, RDCLSI gradually transited to parallel RDCLSI (PRDCLSI), but the existent PRDCLIs have the following problems. Using two electrolytic capacitors as auxiliary power supply leads to the change of neutral point potential. The coupled inductor is used to replace the split capacitor, but the existence of coupled inductor makes the parameter design very complicated. Setting the inductor current threshold increases control complexity. The topology proposed in the reference “Parallel resonance DC link inverter topology and analysis of its operation principle” (Ref. [15]) and the reference “RDCL three-phase inverter and load adaptive commutation control” (Ref. [16]) can solve the above problems well. However, it is not perfect, and its auxiliary circuit has the problem that the current stress and operation times cannot be optimized at the same time. Therefore, this paper proposes an improved modulation strategy based on discontinuous pulse width modulation (DPWM) and adopting sawtooth carriers with alternating slopes.
Firstly, the composition of the improved modulation strategy is introduced. The clamped basis of DPWM is that the phase with the largest absolute value of load current is clamped. If the load current of this phase is positive, the main switch of the upper bridge leg of this phase will keep conducting. Otherwise, the main switch of the lower bridge leg will keep conducting. The changing basis of the sawtooth carrier slope is that if the load current is also positive, the sawtooth carrier slope is positive. Otherwise, the sawtooth carrier slope is negative. Secondly, according to the proposed improved modulation strategy, 14 working modes are divided, their equivalent circuits are given, and important theoretical working waveforms are drawn. Thirdly, compared with Ref. [15] and Ref. [16], the proposed improved modulation strategy considers the optimization of current stress and operation times of the auxiliary circuit. Fourthly, considering the switching loss characteristics of SiC MOSFET, the delay time is designed, and resonance parameters are selected. Fifthly, the theoretical loss of the soft-switching inverter circuit under the proposed improved modulation strategy is analyzed, which mainly includes the loss of the main switch, bus switch, auxiliary switches, auxiliary diodes, resonant inductors, and capacitors. Finally, according to the parameter design, a 5 kW/40 kHz experimental prototype is built with SiC MOSFET as the switching device to verify the characteristics of the auxiliary circuit, the realization of soft switching, the load current waveform, and the efficiency improvement.
Through theoretical analysis and experimental research, the following conclusions are drawn. (1) The main switch realizes ZVZCS turn-on and quasi-ZVS turn-off. The bus switch realizes ZVZCS turn-on and turn-off. The auxiliary switches realize quasi-ZCS turn-on and quasi-ZVS turn-off. (2) The operating frequency of the auxiliary circuit in this paper is consistent with that of Ref. [16], which is only 1/6 of that of Ref. [15]. That is, in one switching period, the auxiliary circuit only needs to operate once to realize the soft switching of all switches. (3) Compared with Ref. [15] and Ref. [16], by adopting the improved modulation strategy and reasonable parameter design, the current stress of the first and the second auxiliary switch is greatly reduced, and the conduction loss of the auxiliary circuit is effectively reduced. (4) When the switching frequency is 40 kHz, the Ref. [15] is unsuitable for the high-frequency inverter circuit. Compared with Ref. [16], the efficiency advantage of this paper is achieved in the full load range, with the peak efficiency reaching 97.97 %, and the lighter the load, the more noticeable this efficiency advantage will become.
keywords:Parallel resonant DC link, auxiliary circuit, modulation strategy, current stress, conduction loss
中图分类号:TM464
DOI: 10.19595/j.cnki.1000-6753.tces.221944
国家自然科学基金资助项目(52277038)。
收稿日期 2022-10-12
改稿日期 2022-12-14
李 思 男,1993年生,博士研究生,研究方向为基于宽禁带器件的高效、高功率密度软开关电机驱动技术。E-mail: 13080819608@163.com
杨 明 男,1978年生,教授,博士生导师,研究方向为电力电子技术及应用、交流永磁伺服系统和智能控制应用。E-mail: yangming@hit.edu.cn(通信作者)
(编辑 陈 诚)