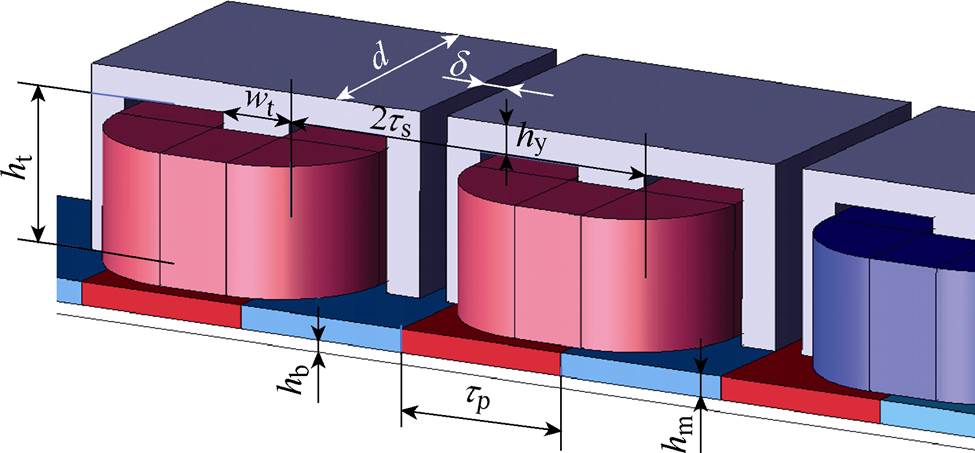
图1 18S20P MPMLSM拓扑结构示意图
Fig.1 Topology diagram of 18S20P MPMLSM
摘要 模块化永磁直线同步电机(MPMLSM)具有效率与推力密度高、可靠性和可加工性好等优点,非常适用于长行程运输系统;缺点是批量生产中性能易受到加工公差的影响。针对这一问题,该文提出了一种考虑制造公差的综合多目标鲁棒优化设计方法。首先,基于六西格玛设计方法建立了鲁棒优化模型;其次,采用拉丁超立方采样方法在尺寸公差范围内根据正态分布规律进行抽样,模拟大规模生产时电机尺寸受公差影响可能会出现的各种变化;再次,在尺寸优化范围内均匀抽样构成足够的训练样本,由有限元软件仿真这些抽样方案的推力性能,并基于反向传播神经网络建立电机设计代理模型;然后,应用该代理模型对拉丁超立方采样得到的样本进行电机性能的计算,求解样本整体对应的各优化目标的均值与方差,进而计算多目标优化的适应度;最后,采用非支配排序遗传算法Ⅱ进行全局优化,得到鲁棒优化方案,与不考虑公差的确定性优化方案相比,验证了该方法的有效性。鲁棒优化方案虽然略微增加了电机体积和推力波动,但是其失效概率低,受公差影响小,更加符合产品批量生产过程中的质量要求。
关键词:模块化永磁直线同步电机(MPMLSM) 制造公差 鲁棒优化设计 六西格玛设计 代理模型
永磁直线同步电机(Permanent Magnet Linear Synchronous Motor, PMLSM)作为一种具有高效率、高推力密度、高可靠性的电机,近年来受到了广泛的关注与应用[1-2]。同时,由于永磁材料含有昂贵的稀土元素,学者们通过采用初级励磁型电机结构[3]、模块化结构以及使用较低最大磁能积永磁材料等手段,实现节约资源、降低成本的目的。模块化永磁直线同步电机(Modular Permanent Magnet Linear Synchronous Motor, MPMLSM)在初级插入隔磁间隙(磁隙),不仅有利于简化绕线制造过程,还能够提高电机的性能与容错率[4-5]。
在实际工程应用中,电机驱动系统的最终质量很大程度上取决于制造技术、材料多样性、加工公差、装配误差等因素。因此,为保证低产品报废率,应当将这些不确定因素考虑在初期设计中,以满足相应性能指标,实现更高的系统可靠性[6-10]。文献[7]考虑了软磁材料B-H特性在制造过程中的劣化对电机性能的影响,并将该制造影响作为优化设计的一部分,保证了优化设计方案对制造影响的低灵敏度,但是软磁材料的劣化程度随不同材料、不同加工过程而异,为确定对应的数值变化需进行大量的实验模拟,耗时耗力。文献[8]考虑了电机尺寸误差对产品生产缺陷率的影响,基于六西格玛设计(Design for Six Sigma, DFSS)与蒙特卡罗模拟对内嵌式永磁电机进行了鲁棒性优化,并与确定性优化方案对比,验证了鲁棒设计方案的有效性。文献[9]通过极限学习机求解了PMLSM气隙对称度误差、平行度误差、直线度误差与推力性能的非线性关系,根据设计要求,采用遗传算法求解气隙的几何公差范围,并将公差分配至相关零件上。文献[10]同时考虑了电机尺寸参数与控制参数对电机性能的影响,保证了系统静态与动态性能的鲁棒性,并通过多级框架解决了高维优化问题。无论电机推力、尺寸大抑或小,公差对电机性能的影响都不可忽略,文献[11]对推力可达数百牛顿的高温超导直线同步电机进行了鲁棒优化设计,同时对传统田口参数设计法进行了改进,在增加平均推力、降低推力波动的同时提升了制造质量,提高了求解效率。
由上可见,采用考虑公差的电机优化算法成为了一个研究热点。MPMLSM由于模块化结构更容易受到加工公差的影响,为了提高电机性能,需要采用鲁棒性优化方法进行优化设计。然而,现在鲜有文献对此进行研究。因此,本文针对18槽20极(18S20P)MPMLSM提出了考虑公差的推力鲁棒性优化方法。在介绍拓扑结构与结构参数后,建立了考虑公差的鲁棒性优化模型,包括优化目标函数、优化变量、约束条件与优化方法等。通过全局优化获得了鲁棒性优化方案,并与不考虑公差的确定性优化方案对比,验证了鲁棒优化方法的有效性。研究能为MPMLSM优化设计与推广应用提供帮助。
图1为典型的MPMLSM拓扑结构,其极槽配合为18槽20极(18S20P),采用端部非重叠式隔齿绕组[12-13],相关性能指标与结构参数见表1。这种隔齿绕组电机不仅具有线圈端部短、效率高、推力密度大等优点,而且平均推力高、容错能力强[14-15]。模块化结构下,电机采用单一铁心就可以实现多种极槽配合,增强了制造灵活性,降低了加工难度。可以看到,在该模块化结构中模块与模块之间存在隔磁间隙,此时相应减小槽的宽度,从而保证齿宽及极距不变。研究表明,该间隙不仅方便了安装,而且在某些结构下还能提高电机的性能[15-16]。

图1 18S20P MPMLSM拓扑结构示意图
Fig.1 Topology diagram of 18S20P MPMLSM
MPMLSM的特点是将多个独立模块组装成一个整体,拼装的模式使得电机性能容易受到公差的影响,包括加工误差与安装误差,若设计时没有考虑公差,优化方案的性能可能不是最优的,其原因可通过图2确定性优化设计与鲁棒性优化设计的对比来解释。图中,A点为确定性优化中系统的最优解,即范围内输出最小值对应的点,但是当公差(噪声因子)Dx出现时,可能会引起输出量较大的波动;B点为鲁棒性优化解,相比之下,虽然B点对应的输出值不是全局最小,但是B点受到公差的影响较小,具有较高的鲁棒性,有利于生产加工。也就是说,在传统不考虑公差的优化(确定性优化)过程中最优解是A,而若考虑加工误差,则最优解将是B。由此可见,两种优化方法出现了不同,显然后者更适用于MPMLSM,因此建立鲁棒性优化设计模型至关重要,图3为详细的设计流程,具体步骤如下所述。
表1 MPMLSM性能指标与结构参数
Tab.1 Performance index and structure parameters of MPMLSM
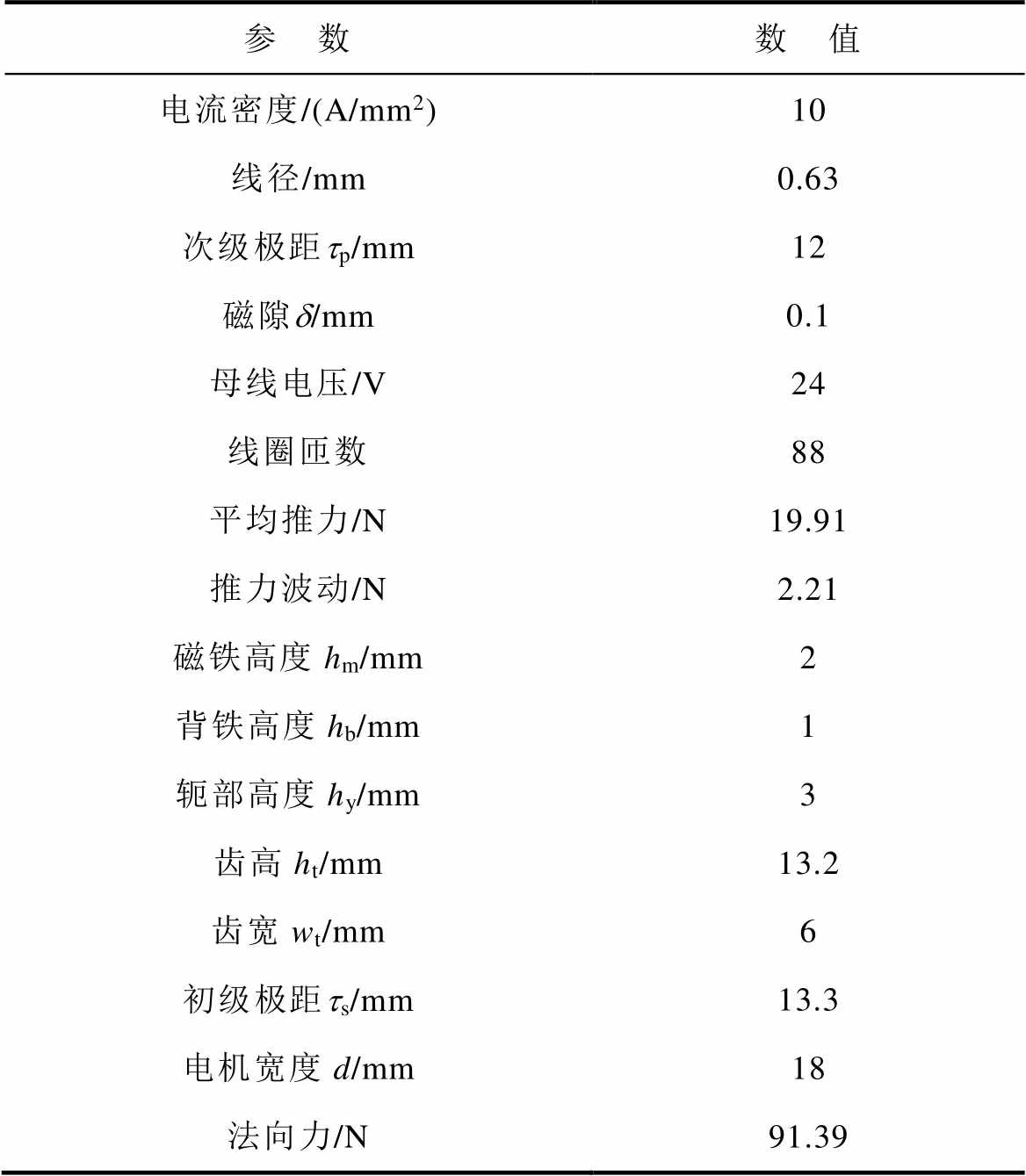
参 数数 值 电流密度/(A/mm2)10 线径/mm0.63 次级极距tp/mm12 磁隙d/mm0.1 母线电压/V24 线圈匝数88 平均推力/N19.91 推力波动/N2.21 磁铁高度hm/mm2 背铁高度hb/mm1 轭部高度hy/mm3 齿高ht/mm13.2 齿宽wt/mm6 初级极距ts/mm13.3 电机宽度d/mm18 法向力/N91.39
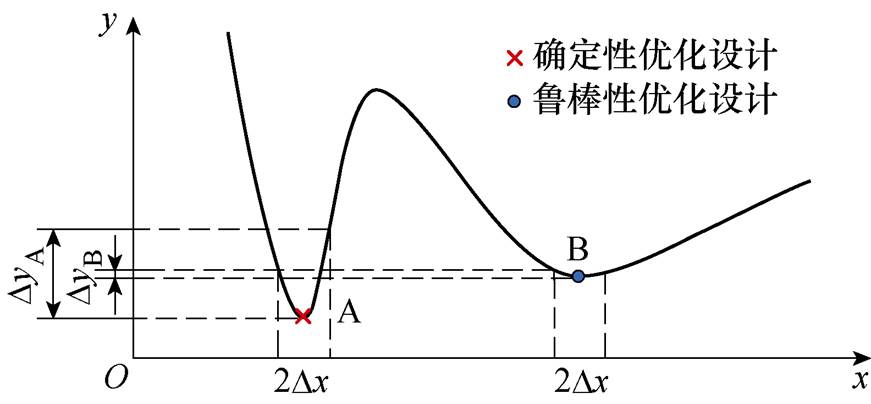
图2 确定性优化设计与鲁棒性优化设计的区别
Fig.2 The difference between deterministic optimization design and robust optimization design
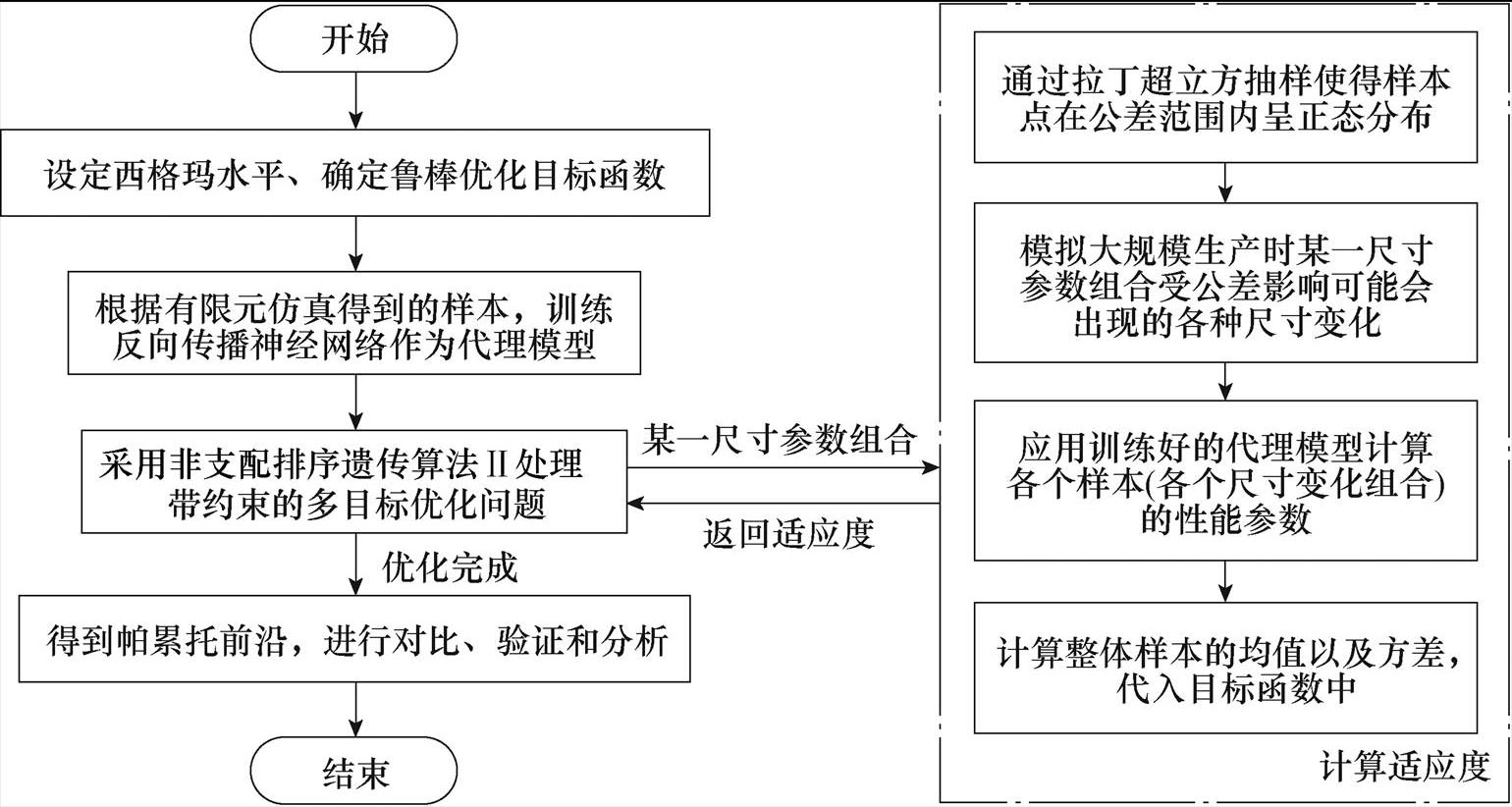
图3 MPMLSM鲁棒性优化设计流程
Fig.3 Flow chart of MPMLSM robust optimization design
第一步,设定西格玛水平并确定优化目标函数。
第二步,为快速、便捷地计算后续优化所需的电机性能,本文先基于有限元软件仿真计算相应的训练样本(该训练样本无需呈正态分布,在尺寸优化范围内通过均匀抽样获取),然后通过反向传播神经网络建立代理模型。
第三步,采用非支配排序遗传算法Ⅱ[17]处理带约束的多目标优化问题,优化过程主要包括抽样与适应度计算:①抽样,为计算目标函数所包含的样本均值与方差,首先需要使样本点在公差范围内呈正态分布,本文采用拉丁超立方抽样方法[18]实现上述目标,以模拟大规模生产时受公差影响可能会出现的电机尺寸组合;②适应度计算,采用第二步训练完成的代理模型计算各个样本对应的电机性能参数,进而计算样本整体的均值与方差,用于代入目标函数之中,得到适应度计算值。
根据适应度计算值得到帕累托前沿,选取最优解,并与确定性优化方案的失效概率进行比较,验证鲁棒性优化设计方案的有效性。
传统优化模型包括了优化目标以及约束条件,有
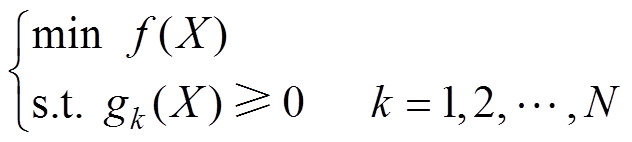 (1)
(1)
式中,f为优化目标函数;X为输入变量;gk为部分电机性能的约束条件;N为约束条件的个数。
传统优化模型通常不考虑公差,MPMLSM为了显著降低批量生产中的缺陷率,需要将不可避免的公差(噪声因素)考虑在内,称为考虑制造公差的鲁棒性优化设计,此时优化目标与约束条件需要采用六西格玛设计(DFSS)方法确定[19]。
六西格玛起初主要针对制造业,通过数据收集、研究分布规律,利用正态分布分析每百万次生产中的产品缺陷率(Defects Per Million Opportunities, DPMO),后来在服务业也有相关应用。6s 从统计意义上就是百万分之三点四,即西格玛水平由DPMO定义,当不合格品率达到3.4DPMO时,产品已经达到了6s 水平。表2为不同西格玛水平与DPMO的转换关系[20]。由于长期数据分布与短期数据分布之间存在1.5s 的水平偏移,4s 只能符合短期要求,6s 才能满足实际工程长期制造的需求。
表2 西格玛水平、合格率与DPMO的转换
Tab.2 The conversion of Sigma level, qualified rate and DPMO
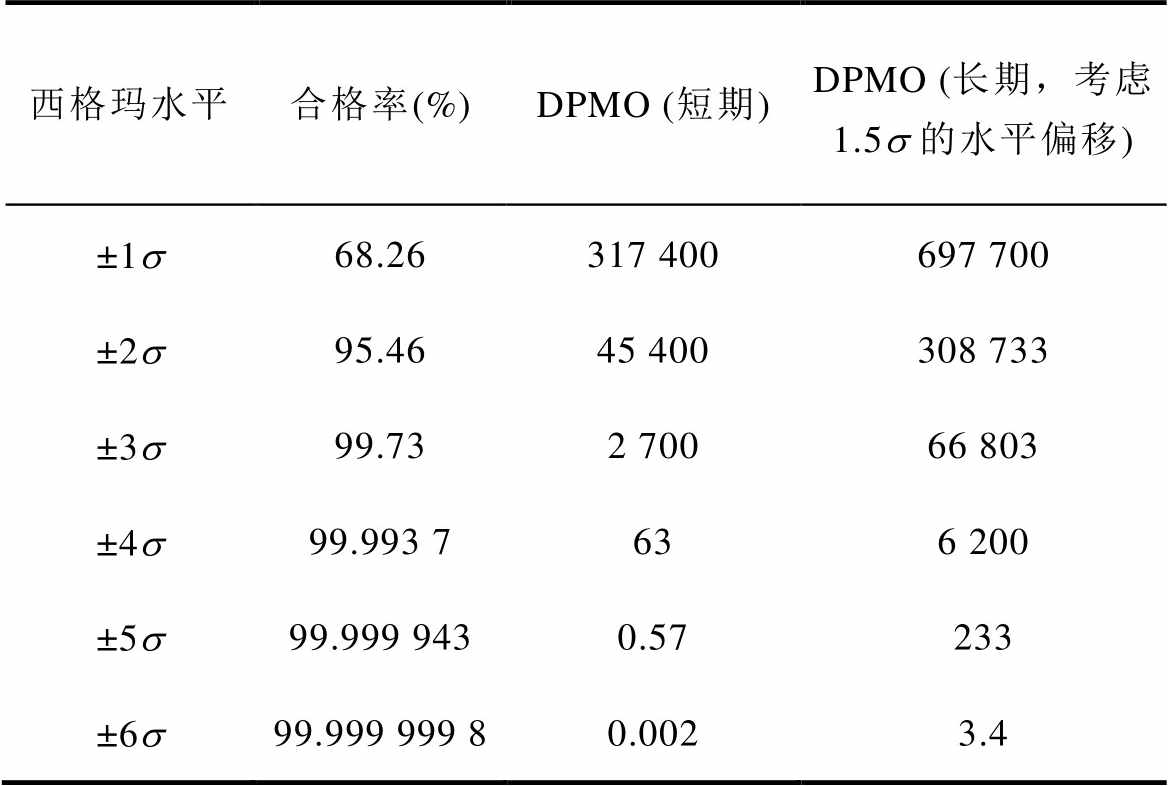
西格玛水平合格率(%)DPMO (短期)DPMO (长期,考虑1.5s 的水平偏移) ±1s68.26317 400697 700 ±2s95.4645 400308 733 ±3s99.732 70066 803 ±4s99.993 7636 200 ±5s99.999 9430.57233 ±6s99.999 999 80.0023.4
采用六西格玛设计方法考虑公差(扰动)后,就可以得到MPMLSM鲁棒性优化的优化目标与约束条件,式(1)转变为
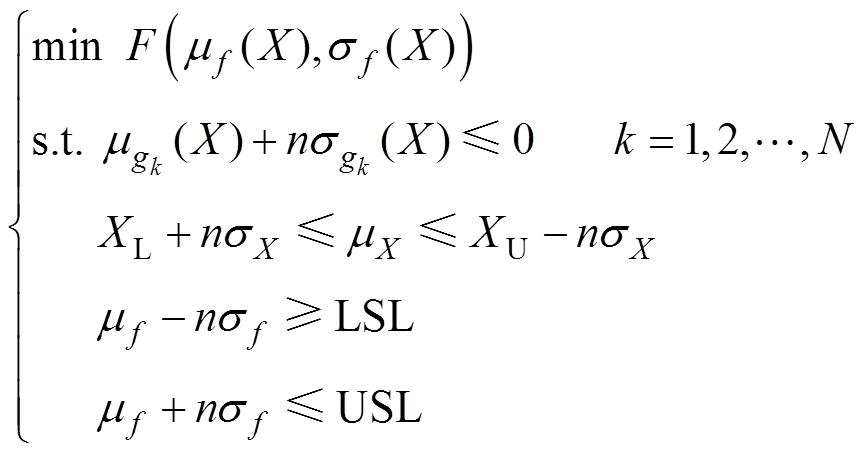 (2)
(2)
式中,LSL、USL、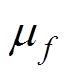 和
和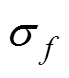 分别为原函数f(X)的下界、上界、均值和标准差;
分别为原函数f(X)的下界、上界、均值和标准差;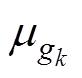 、
、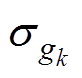 分别为原约束条件gk的均值与标准差;
分别为原约束条件gk的均值与标准差;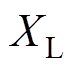 、
、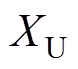 、
、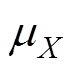 、
、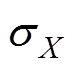 分别为变量的下界、上界、均值和标准差;n为西格玛水平,本文采用六西格玛设计因此n=6。
分别为变量的下界、上界、均值和标准差;n为西格玛水平,本文采用六西格玛设计因此n=6。
对于目标函数最大最小化的情况,目标函数表示为
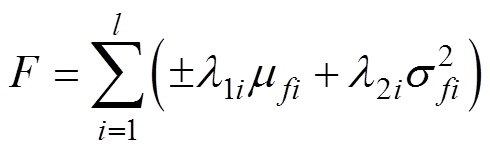 (3)
(3)
式中,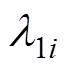 、
、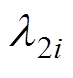 分别为目标函数均值、最小方差的权重因子;l为原目标函数的数量。目标最小化时式中采用“+”,最大化时式中采用“-”。式(3)实质上是将待优化的多个目标通过加权得到单目标,从而简化优化过程,其目的是实现目标均值的最小化(或最大化)以及方差的最小化。
分别为目标函数均值、最小方差的权重因子;l为原目标函数的数量。目标最小化时式中采用“+”,最大化时式中采用“-”。式(3)实质上是将待优化的多个目标通过加权得到单目标,从而简化优化过程,其目的是实现目标均值的最小化(或最大化)以及方差的最小化。
MPMLSM在保持平均推力基本不变的条件下,需要优化的主要是推力波动与体积,因此以这两者为优化目标,将式(3)转变为多目标优化目标函数,即
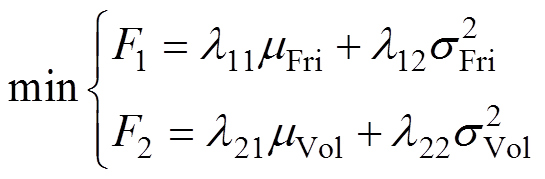 (4)
(4)
式中,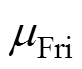 为推力波动的均值;
为推力波动的均值;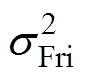 为推力波动的方差;
为推力波动的方差;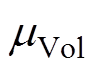 为电机体积的均值;
为电机体积的均值;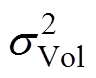 为电机体积的方差;
为电机体积的方差;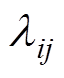 (i=1, 2, j=1, 2)为加权系数,可以根据优化目标的重要性进行选择。MPMLSM优化设计中,两者同样重要,因此均设置为1。
(i=1, 2, j=1, 2)为加权系数,可以根据优化目标的重要性进行选择。MPMLSM优化设计中,两者同样重要,因此均设置为1。
MPMLSM结构参数中与性能紧密相关的是齿宽、齿高、磁隙、背铁高度、磁铁高度和初级极距,因此将这6个变量作为优化变量,表3为这些优化变量的取值范围。
对于MPMLSM,其优化需要满足以下条件:
(1)在确定性优化结果中次级高度被优化到了约束的临界位置,且六西格玛设计使得约束条件增倍,为使得鲁棒性优化结果收敛,设定磁铁高度以及背铁高度的公差均为负公差。
表3 各优化变量取值范围
Tab.3 The range of optimization variables (单位: mm)
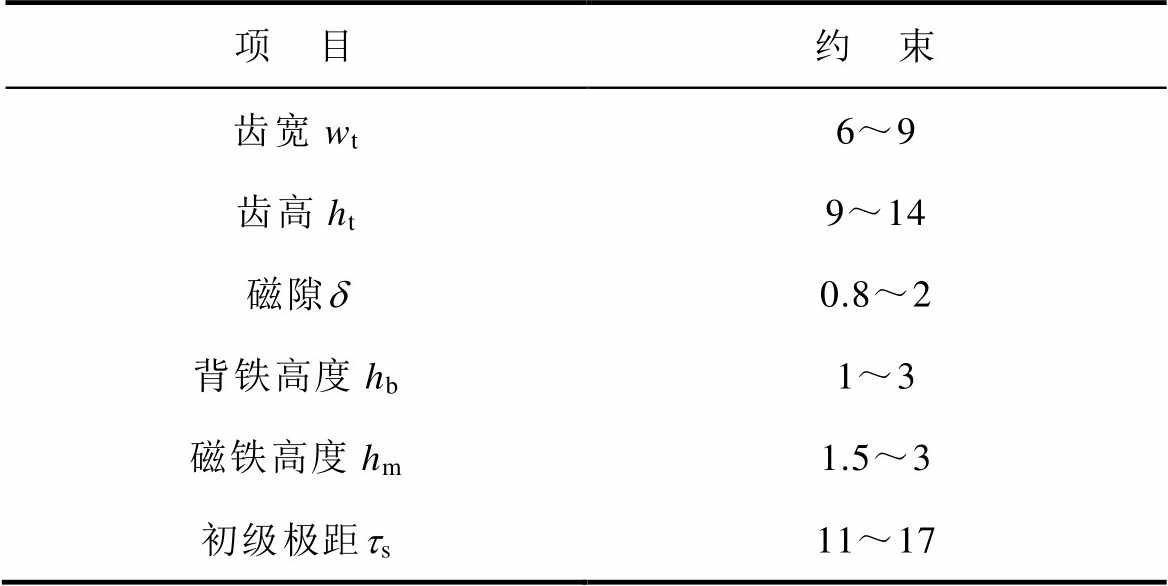
项 目约 束 齿宽wt6~9 齿高ht9~14 磁隙d0.8~2 背铁高度hb1~3 磁铁高度hm1.5~3 初级极距ts11~17
(2)认定设计变量在其公差范围内呈正态分布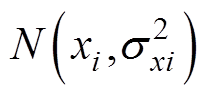 ((1)所述公差取正态分布的左侧),其中
((1)所述公差取正态分布的左侧),其中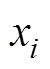 为优化设计值,
为优化设计值,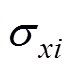 为尺寸变量的方均差,借鉴文献[8]的做法,
为尺寸变量的方均差,借鉴文献[8]的做法,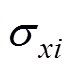 可设定为制造公差的1/3。
可设定为制造公差的1/3。
(3)在代理模型中,轭部高度设置为齿宽的一半,为满足代理模型的计算要求、便于优化计算,设定前者公差同样为后者的一半。
(4)考虑组合件的公差累计问题时,采用方均根法(Root Sum Square, RSS)作为公差叠加分析模型,将公差二次方和的根作为累计公差。
(5)优化时电机槽满率增加至50%,以改善电机性能。
根据以上假设条件,就可以得到MPMLSM鲁棒性优化设计的约束条件,有
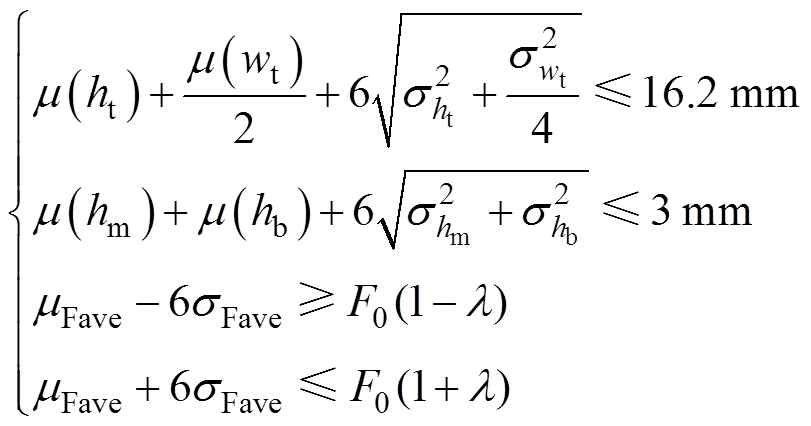 (5)
(5)
式中,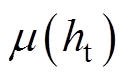 为齿高均值;
为齿高均值;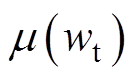 为齿宽均值;
为齿宽均值;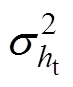 为齿高尺寸的方差;
为齿高尺寸的方差;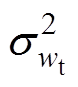 为齿宽尺寸的方差;μ(hm)为磁铁高度均值;
为齿宽尺寸的方差;μ(hm)为磁铁高度均值;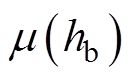 为背铁高度均值;
为背铁高度均值;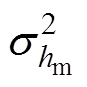 为磁铁高度的方差;
为磁铁高度的方差;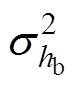 为背铁高度的方差;
为背铁高度的方差;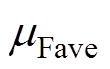 为推力平均值的样本均值;
为推力平均值的样本均值;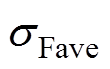 为推力平均值的样本方均差;F0为设定的电机推力固定值;
为推力平均值的样本方均差;F0为设定的电机推力固定值;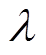 为推力平均值可允许的变化范围。为了便于工程应用,在原样机的基础上进行改进,要求优化后的电机能纳入原有框架中,因此对初级、次级总高度进行限制。为了便于优化计算,同时考虑到代理模型与实际仿真计算结果也存在一定误差,因此将推力约束在原推力平均值附近。
为推力平均值可允许的变化范围。为了便于工程应用,在原样机的基础上进行改进,要求优化后的电机能纳入原有框架中,因此对初级、次级总高度进行限制。为了便于优化计算,同时考虑到代理模型与实际仿真计算结果也存在一定误差,因此将推力约束在原推力平均值附近。
MPMLSM优化目标函数中的推力波动、约束条件中的推力平均值都由电机设计模型计算得到。传统优化方法中电机设计模型主要为解析算法、等效磁路法及磁网络法等,计算时间短,但是传统方法会对电机结构进行简化,其计算结果无法满足鲁棒优化的模型精度需求。为了提高计算的快速性与适用性,本文采用了基于代理模型的电机设计模型,虽然增加了抽取样本以及训练模型的时间,但训练完成后代理模型的计算速度堪比传统电机设计模型,且精度接近于有限元[21-23]。
在电机尺寸允许范围内均匀采样获得样本库,通过有限元软件仿真计算相应的电机性能参数。接着,通过机器学习的方法对样本库进行训练与学习,得到基于代理模型的电机模型。本文选择反向传播神经网络(Back Propagation Neural Network, BPNN)[24]对样本进行训练,其具有高效、高精度的优点。
MPMLSM代理模型基于8 100个有限元样本训练得到,采用了一层隐含层,决定系数R2=0.999 9,方均误差MSE=1.76×10-3,可见代理模型精度很高。图4为代理模型与有限元的推力平均值和波动值对比结果,可以看出所采用的神经网络对推力及推力波动的高维曲线具有足够的学习和表征能力。
对于图1的MPMLSM,考虑了背铁高度、磁钢高度、齿高、磁隙宽度、齿宽与初级极距6个优化变量的制造公差,在推力平均值与设定值有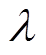 偏差、初级和次级总高度均小于初始高度的约束条件下,选择电机体积与推力波动作为优化目标进行了鲁棒性优化设计。
偏差、初级和次级总高度均小于初始高度的约束条件下,选择电机体积与推力波动作为优化目标进行了鲁棒性优化设计。
根据实际工艺要求,设定磁钢高度的制造公差为0.1 mm,考虑到轭部高度公差为齿宽制造公差的一半,避免轭部高度制造公差过小,设定齿宽公差为0.1 mm,其余关键尺寸的公差同时设置为0.1 mm或0.05 mm。通过六西格玛设计,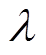 与鲁棒性优化可行解的关系如图5所示。
与鲁棒性优化可行解的关系如图5所示。
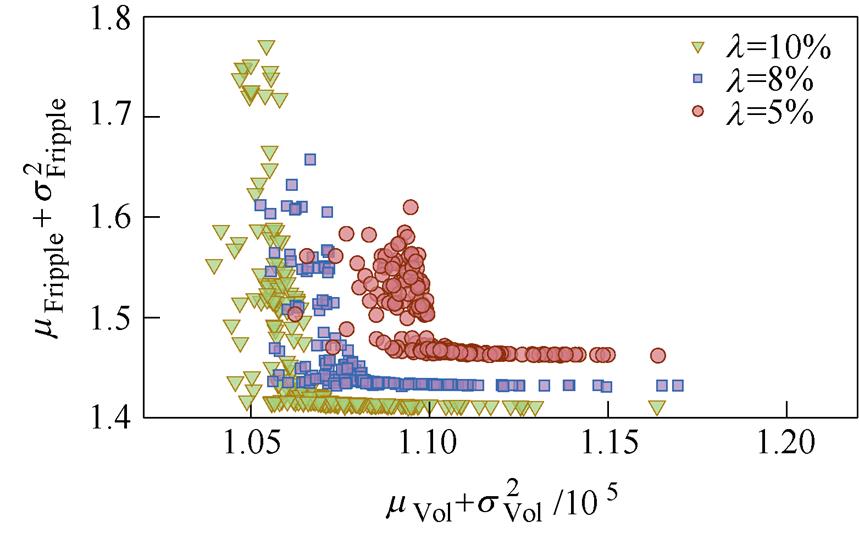
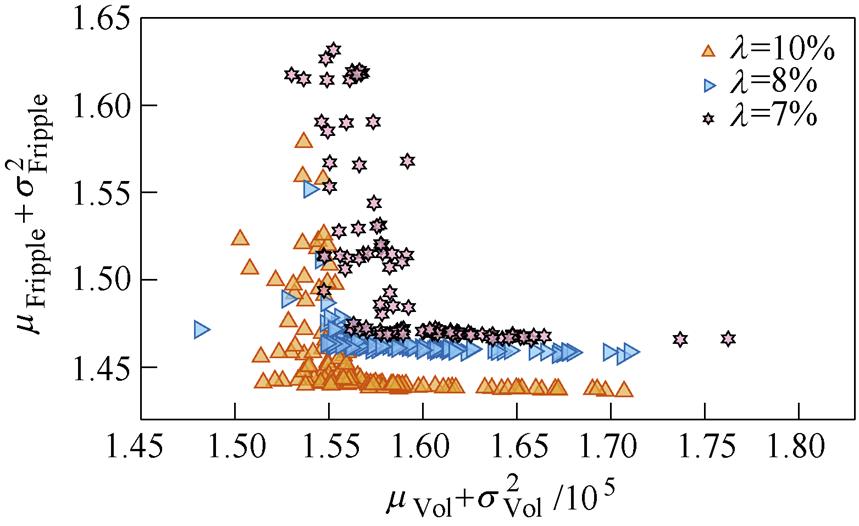
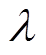 以1%为步长进行仿真扫描,发现制造公差均为0.1 mm(称条件一)的情况下,
以1%为步长进行仿真扫描,发现制造公差均为0.1 mm(称条件一)的情况下,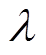 <7%时优化不收敛,也就是说推力平均值跟设定值差异达7%;当磁钢与齿宽制造公差保持0.1 mm,而其余为0.05 mm(称条件二)时,
<7%时优化不收敛,也就是说推力平均值跟设定值差异达7%;当磁钢与齿宽制造公差保持0.1 mm,而其余为0.05 mm(称条件二)时,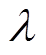 <5%优化无法收敛,即推力平均值跟设定值差异可减小至5%,说明鲁棒性优化收敛的前提下减小制造公差能够使电机推力更接近于设定值。结合图5可知:减小制造公差能有效减小体积,但也会使得制造成本增加;
<5%优化无法收敛,即推力平均值跟设定值差异可减小至5%,说明鲁棒性优化收敛的前提下减小制造公差能够使电机推力更接近于设定值。结合图5可知:减小制造公差能有效减小体积,但也会使得制造成本增加;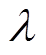 主要影响推力波动,对体积影响较小,在相同体积条件下推力波动值随
主要影响推力波动,对体积影响较小,在相同体积条件下推力波动值随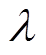 增加而提升。
增加而提升。
表4列举了两种条件下的可行解,可以发现,优化过程中主要通过改变齿高和初级极距适应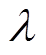 的变化,其余变量已经优化到了稳定值。其中,条件一对应的
的变化,其余变量已经优化到了稳定值。其中,条件一对应的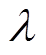 为7%的方案以及条件二对应的
为7%的方案以及条件二对应的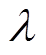 为5%的方案将作为最终的鲁棒优化方案。
为5%的方案将作为最终的鲁棒优化方案。
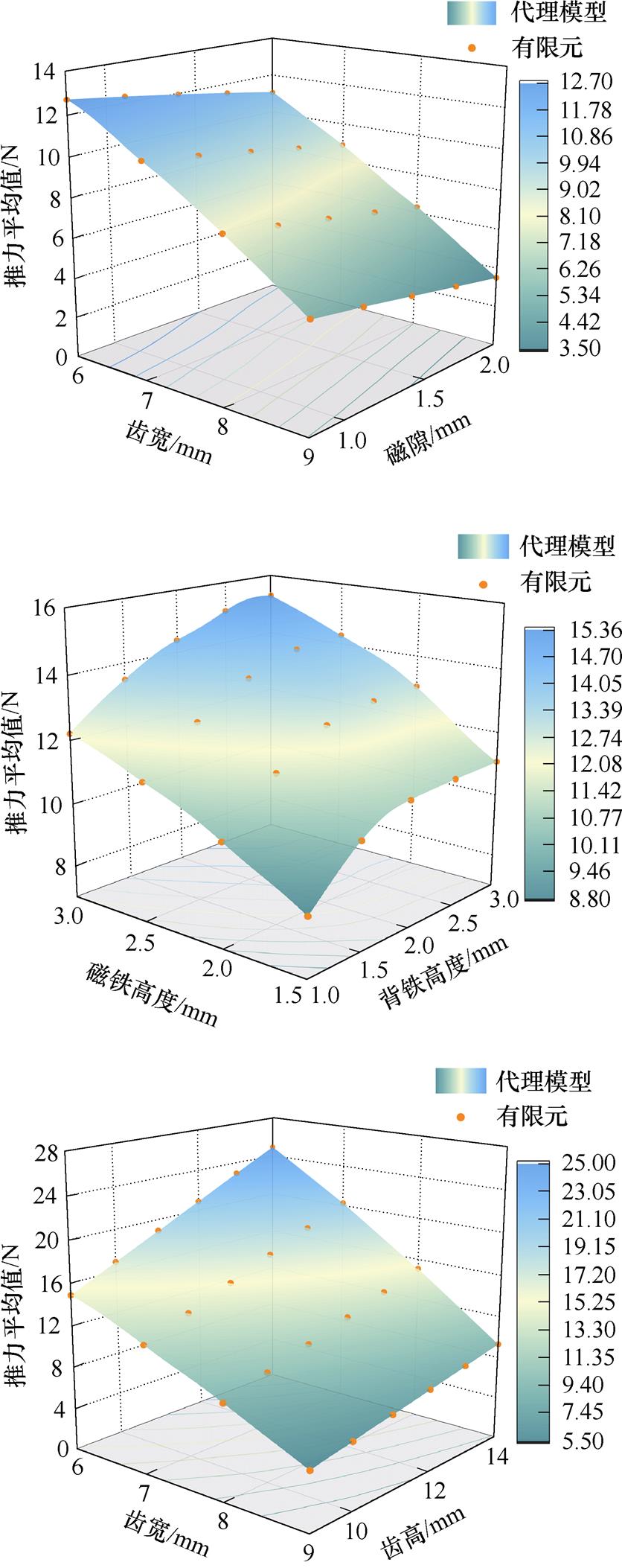
(a)推力平均值
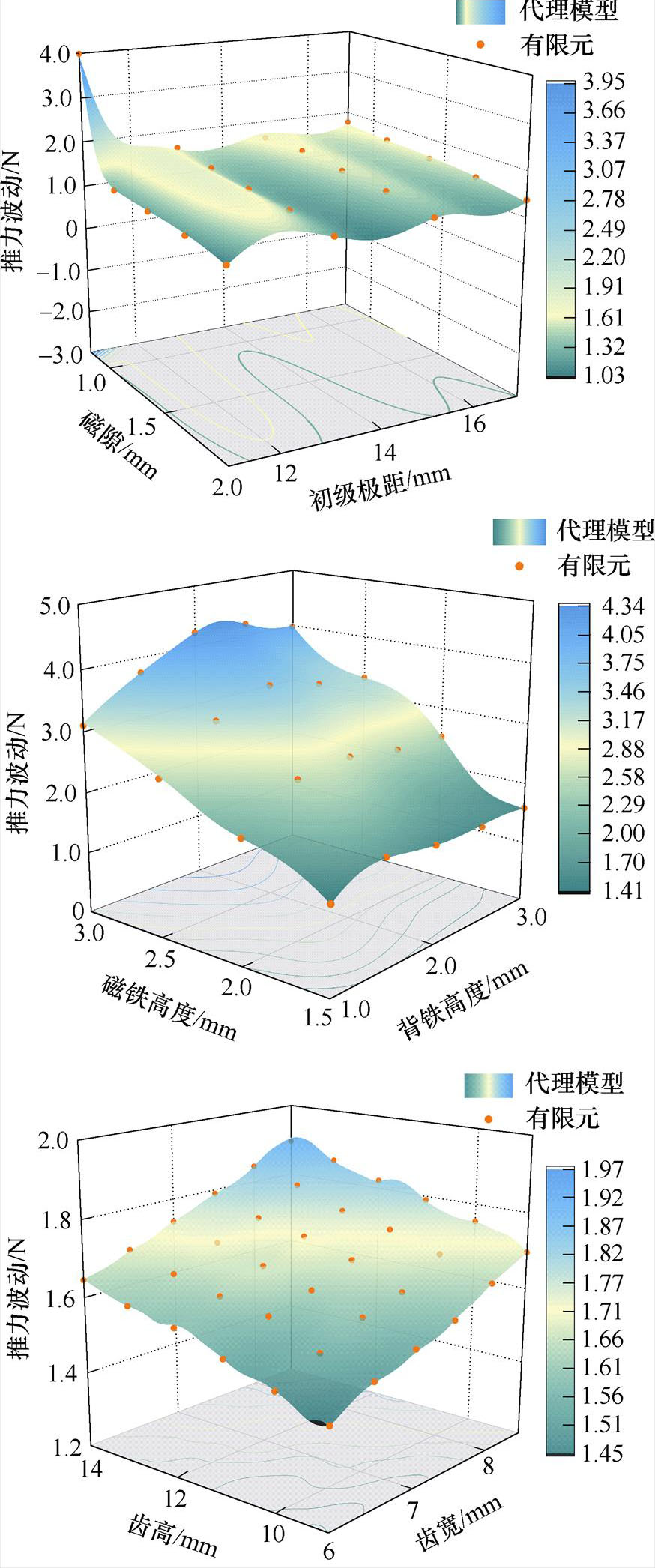
(b)推力波动值
图4 代理模型与有限元计算结果的对比
Fig.4 Comparison between surrogate model results and finite element calculation results
(a)磁钢高度/齿宽制造公差0.1 mm,其余0.05 mm
(b)制造公差均为0.1 mm
图5 不同公差、不同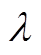 对应的鲁棒性优化可行解
对应的鲁棒性优化可行解
Fig.5 The feasible robust optimization solution corresponding to different tolerances and different 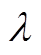
表4 不同条件下的鲁棒优化可行解
Tab.4 The feasible solution of robust optimization under different conditions
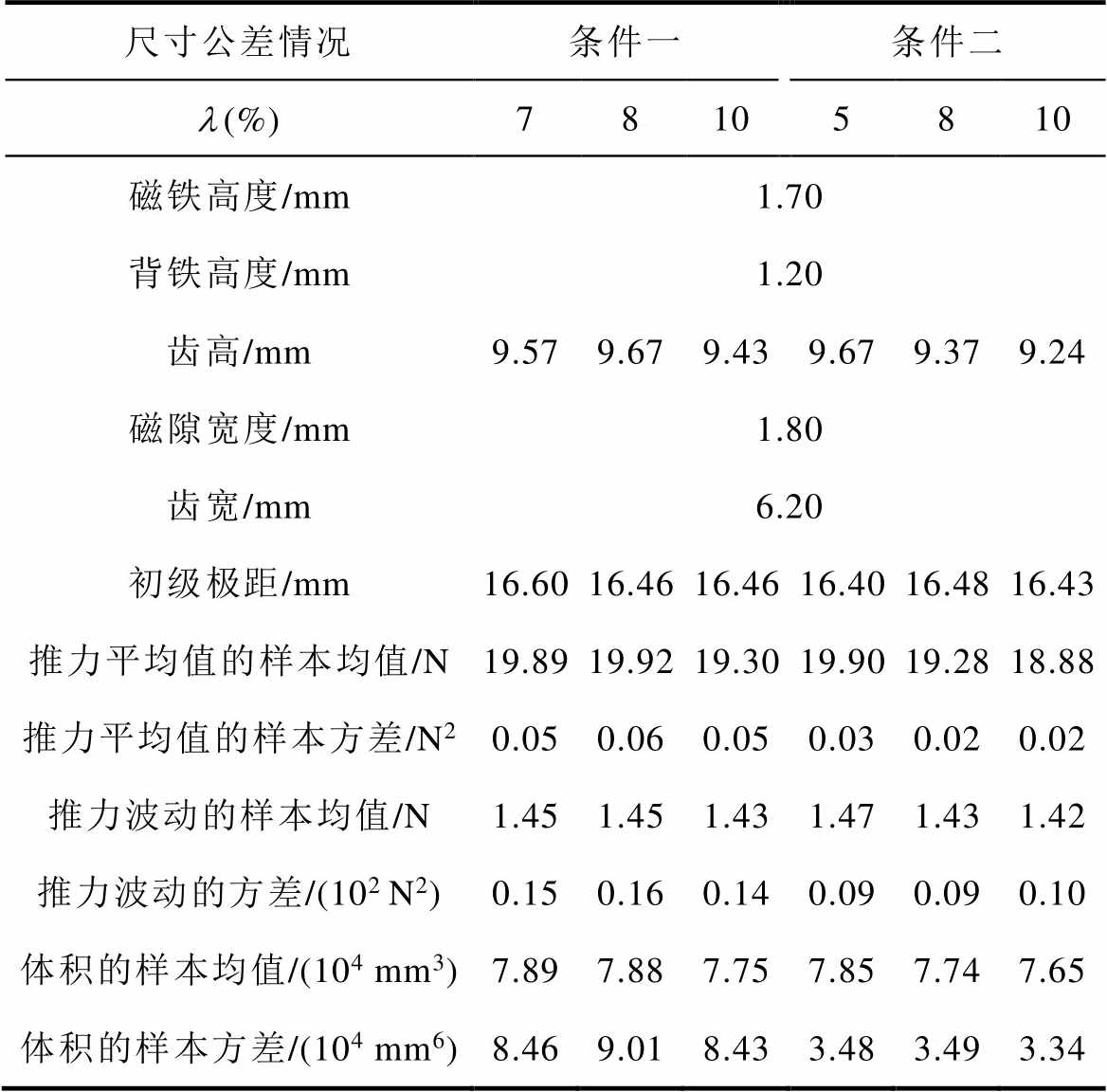
尺寸公差情况条件一条件二 l(%)78105810 磁铁高度/mm1.70 背铁高度/mm1.20 齿高/mm9.579.679.439.679.379.24 磁隙宽度/mm1.80 齿宽/mm6.20 初级极距/mm16.6016.4616.4616.4016.4816.43 推力平均值的样本均值/N19.8919.9219.3019.9019.2818.88 推力平均值的样本方差/N20.050.060.050.030.020.02 推力波动的样本均值/N1.451.451.431.471.431.42 推力波动的方差/(102 N2)0.150.160.140.090.090.10 体积的样本均值/(104 mm3)7.897.887.757.857.747.65 体积的样本方差/(104 mm6)8.469.018.433.483.493.34
在建立的优化模型中,如果不考虑公差,优化目标函数直接是推力波动与体积,无需进行抽样模拟,无需考虑样本的均值与方差,全局优化后得到的结果即为确定性优化方案。MPMLSM确定性优化方案与原样机的对比见表5。
对比表4与表5可以看出,18S20P MPMLSM的鲁棒性优化方案的体积与推力波动比确定性优化方案略有增高。但计算发现,确定性优化方案在条件一情况下,推力平均值可允许的变化范围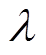 需扩大到10%才能满足六西格玛设计,而鲁棒性优化方案只需7%;条件二情况下,确定性优化结果对应的
需扩大到10%才能满足六西格玛设计,而鲁棒性优化方案只需7%;条件二情况下,确定性优化结果对应的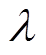 需达到7%才能满足六西格玛设计,而鲁棒性优化方案对应的
需达到7%才能满足六西格玛设计,而鲁棒性优化方案对应的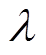 只需5%即可。显然,鲁棒性优化方案鲁棒性增强。
只需5%即可。显然,鲁棒性优化方案鲁棒性增强。
表5 MPMLSM确定性优化方案与原样机对比
Tab.5 Comparison between deterministic optimization design and original design of MPMLSM

参 数数 值 确定性优化原样机 磁铁高度/mm1.52.0 背铁高度/mm1.481.00 齿高/mm9.6113.2 磁隙/mm2.000.40 齿宽/mm6.006.00 极距/mm15.9312.00 总体积/mm375 39282 631 推力平均值/N19.7119.91 推力波动/N1.262.21 法向力/N109.0591.39 加速度/(m/s2)0.130.12
图6为不同公差条件下确定性优化结果与鲁棒性优化结果的推力平均值分布情况。显然,推力曲线均呈正态分布规律,但两个鲁棒性优化方案的曲线均值更接近于设定值。
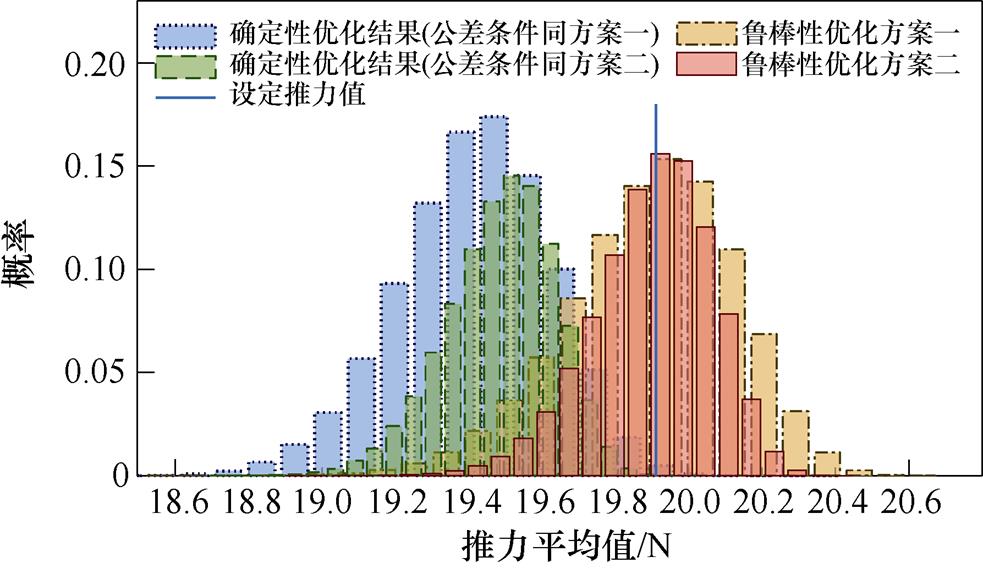
图6 不同公差条件下确定性优化结果与鲁棒性优化结果的推力平均值分布情况
Fig.6 Mean thrust distribution of deterministic and robust optimization results under different tolerances
为了验证鲁棒优化的有效性,对确定性优化结果与鲁棒性优化结果的失效概率(Probability of Failure, POF)进行对比,结果见表6。抽取100 000个样本计算后发现,鲁棒性优化方案的失效概率比确定性优化方案更低,尤其在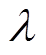 较小的时候,所以鲁棒优化方案具有更好的稳健性。
较小的时候,所以鲁棒优化方案具有更好的稳健性。
表6 确定性与鲁棒性优化结果的失效概率对比
Tab.6 POF comparison between deterministic and robust optimization results (%)
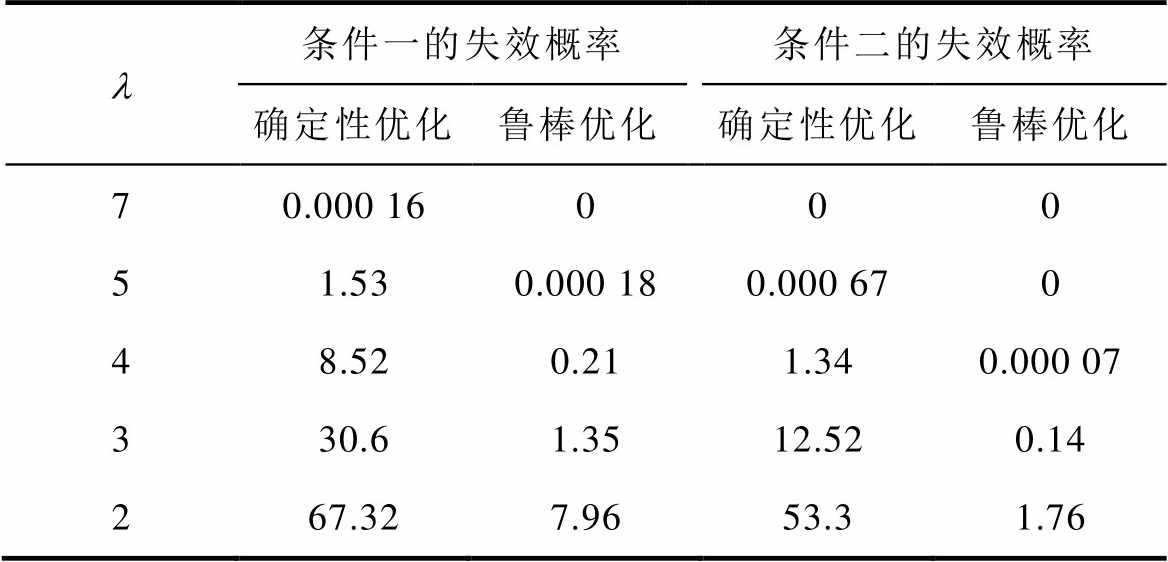
l条件一的失效概率条件二的失效概率 确定性优化鲁棒优化确定性优化鲁棒优化 70.000 16000 51.530.000 180.000 670 48.520.211.340.000 07 330.61.3512.520.14 267.327.9653.31.76
对优化后的MPMLSM电机进行测试,验证所提出的优化设计方案。图7为实验样机,对应条件二且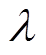 为5%的优化方案。
为5%的优化方案。

图7 实验样机
Fig.7 Experimental prototype
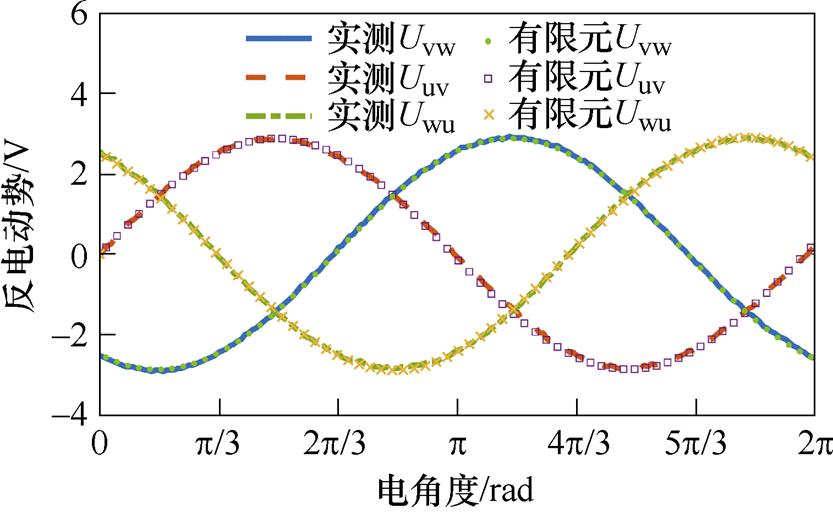
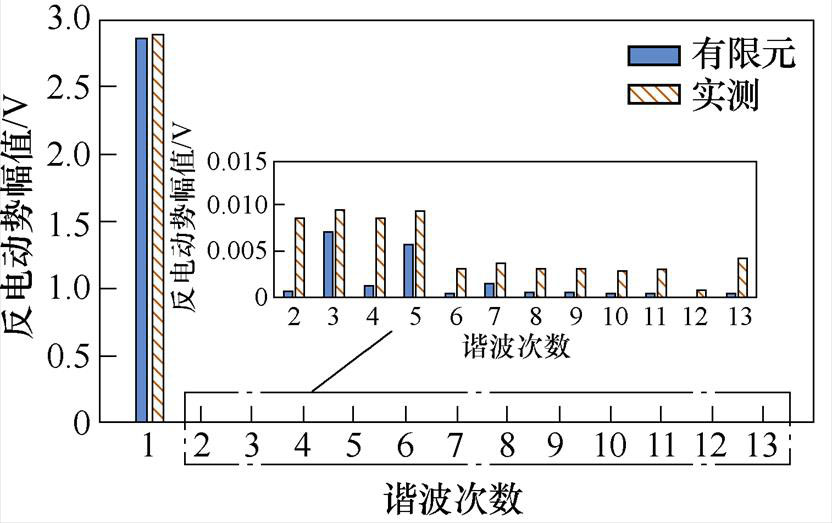
图8为MPMLSM在0.43 m/s速度下反电动势波形的实测与有限元结果对比。如图8所示,测得的反电动势基波含量与有限元仿真结果基本保持一致,而谐波分析结果略有差异,这可能是磁钢质量差异性与装配误差导致的。由于基波幅值远远高于谐波幅值,因此谐波的差异对反电动势波形的影响不大。
基于图9所示的推力测试平台,测量id=0控制方案下电机推力平均值与q轴电流的关系。首先,在A轴通入直流电,使得A轴与次级d轴吸合;然后,将电机向前移动1/2极距的距离,以对准q轴位置;最后,在此基础上,根据所测q轴电流,给三相各通入相应大小的直流电,模拟交流电的瞬时状态,并记录推力计测得的推力值。图10为推力平均值与q轴电流的对应关系,有限元仿真结果与实验测量结果基本保持一致,且两者误差低于5%,除样机本体外直流电源输出的不稳定性、测力计测量误差等因素也可能使结果产生偏差。
(a)单位周期内的波形
(b)傅里叶分解结果
图8 空载反电动势的实测与有限元结果
Fig.8 Comparison between measured and finite element results of no-load back electromotive force

图9 推力测试平台
Fig.9 The thrust test platform of prototype
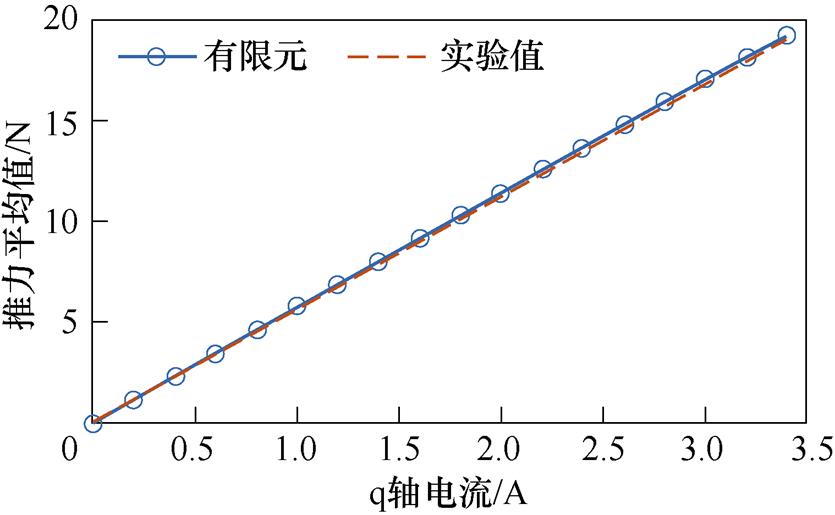
图10 推力平均值与q轴电流的关系
Fig.10 The relationship between mean thrust and q-axis current
考虑到MPMLSM不可避免的公差因素,本文提出了一种考虑公差的鲁棒性优化设计模型,其优化目标函数与约束条件中都加入了样本整体对应的各优化目标的均值与方差。为模拟大规模生产时MPMLSM尺寸受公差影响会发生的变化,采用LHS建立样本库,保证样本在公差范围内呈正态分布;通过BPNN建立电机设计代理模型,经过有限元验证,该代理模型的决定系数为0.999 9,方均误差为1.76×10-3,通过该模型计算出电机性能,进而计算样本整体的均值与方差,得到多目标优化的适应度。最后,采用非支配排序遗传算法Ⅱ全局优化算法得到了鲁棒优化设计方案,解决了带约束的多目标优化问题。
对比不考虑公差的确定性优化方案,鲁棒优化设计方案虽然略微增加了电机体积与推力波动,但是在推力允许变化值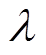 为2%的苛刻条件下,条件一对应的鲁棒优化方案能将失效概率从确定性优化的67.32%降低至7.96%,条件二对应的鲁棒优化方案能将失效概率从53.3%降低至1.76%。同时可以推断出,条件一对应的鲁棒优化方案在
为2%的苛刻条件下,条件一对应的鲁棒优化方案能将失效概率从确定性优化的67.32%降低至7.96%,条件二对应的鲁棒优化方案能将失效概率从53.3%降低至1.76%。同时可以推断出,条件一对应的鲁棒优化方案在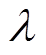 ≥7%时失效概率都为0,条件二对应的鲁棒优化方案在
≥7%时失效概率都为0,条件二对应的鲁棒优化方案在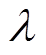 ≥5%时失效概率都为0。失效概率降低表明,MPMLSM鲁棒优化方案在大规模生产中合格率更高,受公差影响更小,更好地满足了产品大量生产过程中所需的质量要求。
≥5%时失效概率都为0。失效概率降低表明,MPMLSM鲁棒优化方案在大规模生产中合格率更高,受公差影响更小,更好地满足了产品大量生产过程中所需的质量要求。
考虑到安装误差同样会对磁隙、气隙等参数产生影响,今后可以在本文优化结果的基础上,进一步针对安装误差对电机进行优化,以提升电机性能的鲁棒性,提高产品制造质量。
参考文献
[1] 蒋钱, 卢琴芬, 李焱鑫. 双三相永磁直线同步电机的推力波动及抑制[J]. 电工技术学报, 2021, 36(5): 883-892.
Jiang Qian, Lu Qinfen, Li Yanxin. Thrust ripple and depression method of dual three-phase permanent magnet linear synchronous motors[J]. Transactions of China Electrotechnical Society, 2021, 36(5): 883- 892.
[2] Cui Fengrui, Sun Zhaolong, Xu Wei, et al. Com- parative analysis of bilateral permanent magnet linear synchronous motors with different structures[J]. CES Transactions on Electrical Machines and Systems, 2020, 4(2): 142-150.
[3] 沈燚明, 卢琴芬. 初级励磁型永磁直线电机研究现状与展望[J]. 电工技术学报, 2021, 36(11): 2325- 2343.
Shen Yiming, Lu Qinfen. Overview of permanent magnet linear machines with primary excitation[J]. Transactions of China Electrotechnical Society, 2021, 36(11): 2325-2343.
[4] 丁文, 李可, 付海刚. 一种12/10极模块化定子混合励磁开关磁阻电机分析[J]. 电工技术学报, 2022, 37(8): 1948-1958.
Ding Wen, Li Ke, Fu Haigang. Analysis of a 12/10- pole modular-stator hybrid-excited switched relu- ctance machine[J]. Transactions of China Electro- technical Society, 2022, 37(8): 1948-1958.
[5] 王宇, 张成糕, 郝雯娟. 永磁电机及其驱动系统容错技术综述[J]. 中国电机工程学报, 2022, 42(1): 351-372.
Wang Yu, Zhang Chenggao, Hao Wenjuan. Overview of fault-tolerant technologies of permanent magnet brushless machine and its control system[J]. Pro- ceedings of the CSEE, 2022, 42(1): 351-372.
[6] Lei Gang, Bramerdorfer G, Liu Chengcheng, et al. Robust design optimization of electrical machines: a comparative study and space reduction strategy[J]. IEEE Transactions on Energy Conversion, 2021, 36(1): 300-313.
[7] Bramerdorfer G. Effect of the manufacturing impact on the optimal electric machine design and perfor- mance[J]. IEEE Transactions on Energy Conversion, 2020, 35(4): 1935-1943.
[8] Xu Gaohong, Jia Zexin, Zhao Wenxiang, et al. Multi- objective optimization design of inset-surface per- manent magnet machine considering deterministic and robust performances[J]. Chinese Journal of Elec- trical Engineering, 2021, 7(3): 73-87.
[9] Yao Zheng, Zhao Jiwen, Song Juncai, et al. Research on selection criterion of design tolerance for air-core permanent magnet synchronous linear motor[J]. IEEE Transactions on Industrial Electronics, 2021, 68(4): 3336-3347.
[10] Lei Gang, Wang Tianshi, Zhu Jianguo, et al. Robust multiobjective and multidisciplinary design optimi- zation of electrical drive systems[J]. CES Transa- ctions on Electrical Machines and Systems, 2018, 2(4): 409-416.
[11] Lei Gang, Liu Chengcheng, Li Yanbin, et al. Robust design optimization of a high-temperature supercon- ducting linear synchronous motor based on taguchi method[J]. IEEE Transactions on Applied Supercon- ductivity, 2019, 29(2): 1-6.
[12] Sun Ke, Tian Shaopeng. Multiobjective optimization of IPMSM with FSCW applying rotor Notch design for torque performance improvement[J]. IEEE Transa- ctions on Magnetics, 2022, 58(5): 1-9.
[13] Skarmoutsos G A, Gyftakis K N, Mueller M. Analyti- cal prediction of the MCSA signatures under dynamic eccentricity in PM machines with concentrated non- overlapping windings[J]. IEEE Transactions on Energy Conversion, 2022, 37(2): 1011-1019.
[14] 丁强, 王晓琳, 邓智泉, 等. 大气隙磁通切换无轴承永磁电机径向力绕组设计与比较[J]. 电工技术学报, 2018, 33(11): 2403-2413.
Ding Qiang, Wang Xiaolin, Deng Zhiquan, et al. Design and comparison of radial force winding configurations for wide air-gap flux-switching bearingless permanent-magnet motor[J]. Transactions of China Electrotechnical Society, 2018, 33(11): 2403-2413.
[15] 隋义, 尹佐生, 郑萍, 等. 单双层混合绕组型低互感五相容错永磁电机的电磁问题研究[J]. 中国电机工程学报, 2022, 42(1): 329-340.
Sui Yi, Yin Zuosheng, Zheng Ping, et al. Research on electromagnetic problems of low-mutual-inductance five-phase fault-tolerant PMSM with hybrid single/ double-layer FSCW[J]. Proceedings of the CSEE, 2022, 42(1): 329-340.
[16] Mehta S, Kabir M A, Pramod P, et al. Segmented rotor mutually coupled switched reluctance machine for low torque ripple applications[J]. IEEE Transa- ctions on Industry Applications, 2021, 57(4): 3582- 3594.
[17] Deb K, Pratap A, Agarwal S, et al. A fast and elitist multiobjective genetic algorithm: NSGA-Ⅱ[J]. IEEE Transactions on Evolutionary Computation, 2002, 6(2): 182-197.
[18] Ma Yiming, Xiao Yang, Wang Jin, et al. Multicriteria optimal Latin hypercube design-based surrogate- assisted design optimization for a permanent-magnet vernier machine[J]. IEEE Transactions on Magnetics, 2022, 58(2): 1-5.
[19] Koch P N, Yang R, Gu L. Design for six sigma through robust optimization[J]. Structural and Multi- disciplinary Optimization, 2004, 26(3): 235-248.
[20] 唐晓芬主编, 上海质量管理科学研究院编著. 六西格玛核心教程: 黑带读本[M]. 修订版. 北京: 中国标准出版社, 2006.
[21] 谢冰川, 张岳, 徐振耀, 等. 基于代理模型的电机多学科优化关键技术综述[J]. 电工技术学报, 2022, 37(20): 5117-5143.
Xie Bingchuan, Zhang Yue, Xu Zhenyao, et al. Review on multidisciplinary optimization key tech- nology of electrical machine based on surrogate models[J]. Transactions of China Electrotechnical Society, 2022, 37(20): 5117-5143.
[22] Wu Jiangling, Sun Xiaodong, Zhu Jianguo. Accurate torque modeling with PSO-based recursive robust LSSVR for a segmented-rotor switched reluctance motor[J]. CES Transactions on Electrical Machines and Systems, 2020, 4(2): 96-104.
[23] 李雄松, 崔鹤松, 胡纯福, 等. 平板型永磁直线同步电机推力特性的优化设计[J]. 电工技术学报, 2021, 36(5): 916-923.
Li Xiongsong, Cui Hesong, Hu Chunfu, et al. Optimal design of thrust characteristics of flat-type permanent magnet linear synchronous motor[J]. Transactions of China Electrotechnical Society, 2021, 36(5): 916-923.
[24] 何海婷, 柳亦兵, 巴黎明, 等. 基于BP神经网络的飞轮储能系统主动磁轴承非线性动力学模型[J]. 中国电机工程学报, 2022, 42(3): 1184-1198.
He Haiting, Liu Yibing, Ba Liming, et al. Nonlinear dynamic model of active magnetic bearing in flywheel system based on BP neural network[J]. Proceedings of the CSEE, 2022, 42(3): 1184-1198.
Thrust Robustness Optimization of Modular Permanent Magnet Linear Synchronous Motor Accounting for Manufacture Tolerance
Abstract The modular structure of modular permanent magnet linear synchronous motor (MPMLSM) is beneficial to simplify the winding manufacturing process and improve the motor performance and fault tolerance rate. As a motor with high efficiency, high thrust density, and high reliability, it has received extensive attention and application in recent years. However, in mass production, the modular structure is more susceptible to machining tolerances. In order to improve the motor performance and better meet the quality requirements, this paper proposes a thrust robustness optimization method considering manufacturing tolerance, which provides help for the optimization design and application of MPMLSM.
First, a robust optimization model is established based on design for six Sigma (DFSS), and the optimization objective function is determined according to the sigma level. Then, the Latin Hypercube Sampling (LHS) method is used to sample within the dimensional tolerance range according to the normal distribution law to simulate possible variations in motor dimensions in mass production. A motor design surrogate model based on the Back Propagation Neural Network (BPNN) can calculate the motor performance required for subsequent optimization quickly and conveniently. The training samples of the model are obtained by uniform sampling, and the thrust performance of the samples is simulated by finite element software. Subsequently, the motor performance of the samples obtained by LHS is calculated by the trained surrogate model, and the mean and variance of the whole sample are solved and substituted into the objective function to obtain the fitness value. Finally, Non-dominated Sorting Genetic Algorithm Ⅱ is used for global optimization to obtain the Pareto front and robust optimization schemes. Compared with the deterministic optimization scheme, the effectiveness of the method is verified.
Through finite element verification, the determination coefficient of the surrogate model established by BPNN is 0.999 9, and the mean square error is 1.76×10-3. Thus, the motor performance can be calculated quickly and accurately. Under the harsh condition that the allowable thrust variation range (l) is 2%, the robust optimization scheme can reduce the probability of failure (POF) from 67.32% to 7.96% under condition 1, and from 53.3% to 1.76% under condition 2. Compared with the deterministic optimization scheme without considering tolerance, although the robust optimization design slightly increases the motor volume and thrust ripple, the robustness is improved. At the same time, it can be inferred that the POF of the robust optimization scheme is 0 when l≥7% under condition 1 or l≥5% under condition 2. The reduction of failure probability indicates that the MPMLSM robust optimization schemes have higher qualification rates in mass production and are less affected by tolerances.
The following conclusions can be drawn: (1) Under the premise of convergence, reducing manufacturing tolerance can reduce the motor volume and make the motor thrust closer to the set value. However, the manufacturing cost is increased. (2) l mainly affects the thrust fluctuation, and little affects the volume. Under the same volume condition, the thrust fluctuation increases with the increase of l. (3) In the optimization results, the tooth height and primary polar distance vary with different tolerance conditions, while the remaining variables are optimized to optimum values. (4) The POF of the robust optimization scheme is lower than that of the deterministic optimization scheme, especially when l is small. Therefore, the robust optimization scheme has better robustness and is more in line with the quality requirement in mass production.
keywords:Modular permanent magnet linear synchronous motor (MPMLSM), manufacture tolerance, robust optimization design, design for six Sigma, surrogate model
中图分类号:TM351
DOI: 10.19595/j.cnki.1000-6753.tces.221956
国家自然科学基金面上资助项目(52177061, 52107060)。
收稿日期 2022-10-14
改稿日期 2022-11-03
龚夕霞 女,1997年生,硕士,研究方向为模块化永磁直线同步电机设计与优化。E-mail: gongxixia@zju.edu.cn
李焱鑫 男,1988年生,副研究员,硕士生导师,研究方向为新型直线电机与永磁电机的建模分析与优化分析。E-mail: eeliyanxin@zju.edu.cn(通信作者)
(编辑 崔文静)