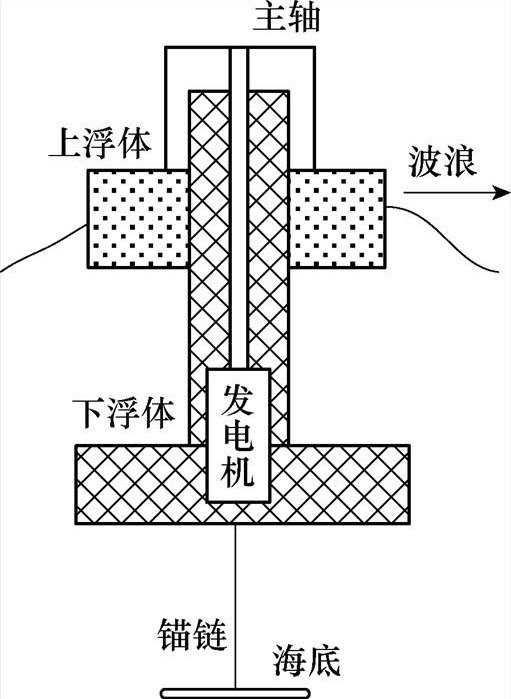
图1 双浮体直驱波浪发电装置示意图
Fig.1 Diagram of two-body direct drive WEC
摘要 基于振荡浮体结构的直驱波浪发电装置具有损耗低、控制灵活等优点，近年来，逐渐成为波浪发电领域的研究热点。双浮体直驱波浪发电装置不需要海上固定平台，能够通过锚系结构在海水中工作，是一种工程可行的直驱波浪发电方案，但其动力学模型更为复杂，相关控制算法缺少实际装置测试。该文通过等效电路的方法对双浮体装置进行建模分析，指出采用张力锚结构可将双浮体装置等效为单浮体装置进行分析，简化控制器的分析与设计，从而建立基于模型预测控制的高效波浪能提取问题。提出一种结合波浪激励力辨识、预测与快速模型预测求解的控制算法，并且设计了双浮体直驱波浪发电装置，在不同波浪条件下进行了相关实验测试。实验结果表明，所提控制算法能够在有效降低运算复杂度的前提下提高装置的波浪能提取效率。
关键词：双浮体直驱波浪发电 能量提取优化算法 装置建模分析 波浪水槽 模型预测控制
我国海域辽阔，波浪能资源储量可观，波浪发电可用于海工平台供电、海水淡化、海岛供电等多个领域。作为绿色可再生能源，发展波浪发电对国家“双碳目标”也有重大意义。直驱波浪发电装置（Wave Energy Converter, WEC）是一种利用海洋波浪中的振荡浮体并采用直驱能量提取系统的波浪发电装置，相较于传统的气压型和液压型波浪发电装置，其传动损耗低、控制自由度高，通过采用合适的控制算法能够在不同海况下控制浮体与波浪的相互运动匹配，从而大幅提高对波浪能的提取效率[1]。据统计，在2020年处于建造或运行测试状态的波浪发电项目中，采用直驱系统的项目数量最多，占总量的40%左右。由此可以看出，直驱波浪发电装置正受到全球波浪发电研究较大的关注，已经成为极具发展前景的技术方案之一[2]。
直驱波浪发电装置的实现形式可分为单浮体结构和双浮体结构两种。单浮体装置由一个浮体和发电系统组成，浮体漂浮在水面，发电系统固定在平台上，在波浪作用下浮体驱动发电机发电。中国海洋大学研制了单浮体装置并在水槽实验室和海洋环境均做了测试[3]。单浮体装置结构简单，但在海洋实际应用中受限于固定平台建设成本太高，需要依靠已有的海工平台做支撑，也难以在波浪能资源更为丰富的深远海区域部署。为了解决这一问题，双浮体装置采用上下浮体结构，上浮体漂浮在海面，下浮体通过锚链与海底连接，两者通过发电系统相连，在波浪作用下，上下浮体产生相对运动进而可驱动发电机发电。中科院广州能源所和东南大学都研制了采用直线发电机的双浮体装置样机并进行了海试[4]。针对波浪发电用的直线发电机，不少学者提出了基于Halbalch拓扑[5]来优化发电机磁路以及针对波浪发电应用的低速大推力工况优化直线发电机的功率密度及发电效率[6]，但目前直线发电机的成本还较为高昂，采用旋转电机-滚珠丝杠的直驱发电结构是一种更可行的方案，美国OPT公司研制的PB3型双浮体装置就采用了旋转电机-滚珠丝杠的方案，且完成了海试并应用于美国海军项目，已开始了商业化进程。
直驱波浪发电装置的一大特点是可以通过合适的控制算法来提升波浪能转化的效率。从机械学角度看，波浪发电系统本质上是浮体（发电机）和波浪振动的一个系统，由此J. Falnes指出，在两者发生谐振时，发电机能够从波浪获取最大的能量转 化[7]，即浮体的自然振动频率与波浪的频率一致时，能最大化提取波浪能，此时浮体的运动同波浪激励力同相位，且幅值满足谐振比例。然而，浮体的自然振动频率是固定值，取决于其固有的机械参数，而波浪的频率会发生变化，因此若不采取功率优化控制方法，波浪发电装置仅能高效提取对应谐振频率的海浪能，而在其他频率范围会有明显能量损失。
研究者最早采取的方式是电阻控制方法，这是最简单的波浪发电装置功率控制方法，即在发电机的三相输出直接连接三相电阻负载或是经过不控整流在直流母线上挂载电阻，通过改变电阻以改变装置特性，从而改变系统的波浪能提取特性。但这种控制方式只能用于装置驱动固定负载，无法将电能进一步传输，应用受限。随着发电机控制技术的进步，在矢量控制下，发电机的电磁力能够人为控制，通过控制发电机电磁推力和浮体速度成正比，使得发电机等效为一个阻尼可调的机械负载，从而可以灵活地对装置进行控制，这种控制方法被称作阻尼控制[8]。电阻控制和阻尼控制本质上都是改变了装置的等效机械阻尼来改变发电特性，但只改变机械振动系统的阻尼无法改变自然谐振频率，导致这两种控制方法的波浪能提取效率较低。闭锁控制在一段时间内封锁浮体，在特定时间释放浮体，从而改变浮体振动的相位，近似实现了浮体与波浪谐振的同相位条件，等价于改变了装置的固有谐振频率，相比于阻尼控制，理论上具备更高的波浪能提取效 率[9]，但因其无法控制谐振的幅值条件，本质上是一种次优的功率提取控制。阻抗匹配控制通过控制发电机推力是速度和位移的线性组合，可以满足谐振条件从而实现最大化的波浪能提取，因在运行中会产生无功功率，又称为无功控制，也需要发电机和变换器具备能量双向流动的能力[8]。阻抗匹配要求控制参数和模型参数相匹配，但实际系统难免存在模型误差，基于阻抗匹配控制的思路，可采取最大功率跟踪控制实现参数的自适应[10]。
以上几种控制方法从机械谐振的角度出发，本质是从频域分析得到的控制方法，近些年来众多研究工作者提出从时域模型结合模型预测控制（Model Predictive Control, MPC）来解决波浪发电的能量提取优化控制，其核心思路是预测未来一段时间的装置状态信息，建立发电机推力控制序列和提取能量的数学模型，求解最大化提取波浪能量的最优化问题，通过在线滚动优化给发电机推力控制指令[11]。基于模型预测控制的控制方法理论上能够实现在不规则波浪工况下的最大化波浪能提取，并且可以将装置位置、速度、电压电流等约束条件考虑进去[12]，结合非线性模型预测还能考虑模型非线性因素的最优化控制[13]。但模型预测主要面临的问题是求解复杂度高、模型精度要求高、所需控制反馈量多等缺点。
双浮体装置由于没有固定的海上平台约束，理论上其会在海水中产生六个自由度的运动，整体的动力学特性更加复杂，虽然在锚系作用的约束下，只需考虑装置垂直方向的运动，但双浮体装置的输出功率和上下浮体的相对运动相关，相比单浮体装置更为复杂，且锚链作用也会影响装置的能量提取性能。在已有的直驱波浪发电装置测试中，测试更多聚焦于装置的水动力学特性，针对发电机的控制算法，只采用了电阻控制或是阻尼控制，并没有深入研究能量提取算法对波浪能转换效率的提升作用。为此，本文将详细分析双浮体装置的动力学模型，设计能够满足高效能量提取算法的双浮体装置样机，提出一种基于模型预测控制的高效波浪能提取控制算法。并搭建实验测试装置，在波浪水槽实验室展开详细测试，在规则波工况下测试不同能量提取控制算法的实际效果，为直驱波浪发电装置高效能量提取算法的应用提供实验测试结果。
图1为双浮体直驱波浪发电装置的结构示意图，装置由上下两个浮体组成，其中上浮体漂浮在水面上，下浮体通过锚链作用浸没在水下，发电机固定安装在下浮体上，上浮体通过主轴与发电机直接连接，通过这样的结构，当波浪作用在装置上时，上下浮体运动不一致产生相对运动进而可以驱动发电机发电。
图1 双浮体直驱波浪发电装置示意图
Fig.1 Diagram of two-body direct drive WEC
双浮体装置由于没有固定平台，在波浪环境下理论上会产生六个自由度的运动。实际上浮体受到自身结构的约束以及锚链的牵引，装置主要的运动状态是上下浮体沿着主轴作相对运动，整体产生小幅的平移或摇荡。考虑到波浪对装置水平方向上的作用力会远小于垂直方向，因此装置提取波浪能主要是在垂直方向上，为简化建模分析，只需考虑垂直方向自由度的动力学方程。
考虑垂直方向的受力状况，双浮体装置上下浮体各自受到与波浪相互作用的力、浮力、自身重力、主轴上的机械阻力，以及大小相等、方向相反的发电机推力分别作用于上浮体和下浮体，除此之外下浮体额外受到锚链拉力的约束作用。不妨设在静水时浮体平衡状态的上下浮体位置为各自的平衡位置，此时浮体的重力与浮力、锚链拉力抵消，为简化锚链模型，本文将其简化为具有固定刚度系数的弹性模型，因此可以得到双浮体装置的动力学模型为
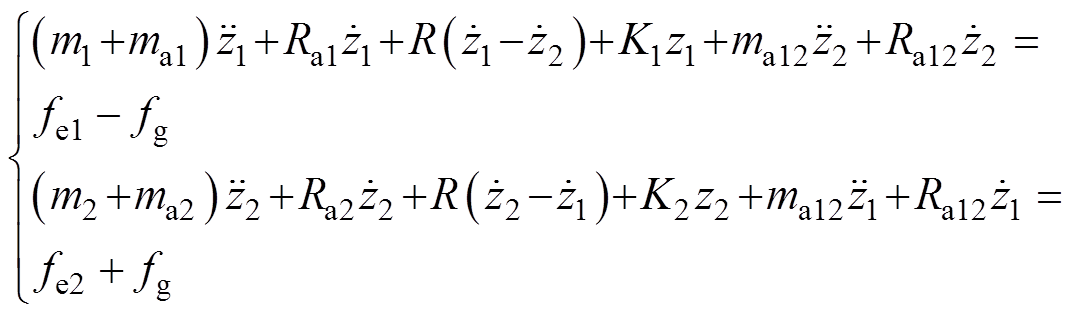（1）
式中，zi为浮体相对平衡位置的位移；mi为浮体质量；mai为附加质量；Rai为附加阻尼；R为主轴机械阻尼；K1为上浮体浮力系数；K2为锚链刚度系数；ma12和Ra12分别为耦合附加质量和附加阻尼；fg为电磁推力；fei为浮体激励力；下标i取1代表下浮体，2代表上浮体。附加质量和附加阻尼是表征浮体和波浪间的辐射作用力的水动力学系数，由浮体的形状决定，与波浪频率w 相关，可由有限元分析软件计算得到。由此可知，发电机输出的瞬时功率及一段时间内提取的波浪能分别为
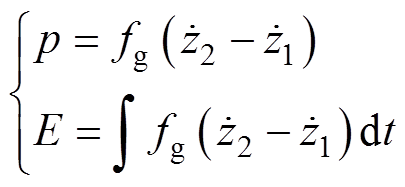（2）
由于装置的瞬时功率会随着波浪的波动而不断变化，因此最大化波浪能提取的数学问题可描述为在装置动力学方程的约束下控制发电机电磁推力fg，使得一段时间内提取到的波浪能E最大化。对于规则波浪而言，最大化波浪能提取即是最大化一个波浪周期内的平均功率。
由式（1）和式（2）可以看出，发电机提取的波浪能取决于发电机推力和双浮体装置上下浮体的相对运动速度，为了提高波浪能的提取效率，则需要考虑上下浮体的运动状态，理论分析的复杂度大幅增加，但利用单浮体装置等效电路进行最优能量提取条件的分析的思路[14]，将波浪对浮体的激励力作用等效为有效值为
、相位为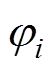
的交流电源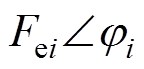
，浮体速度等效为电流，质量、阻尼、弹性等机械变量统一等价为阻抗，再将发电机等效为一阻抗可调的负载，则双浮体直驱波浪发电装置的动力学模型等效电路如图2a所示，等效电路中相关电路元件和装置动力学模型中的对应参数关系为
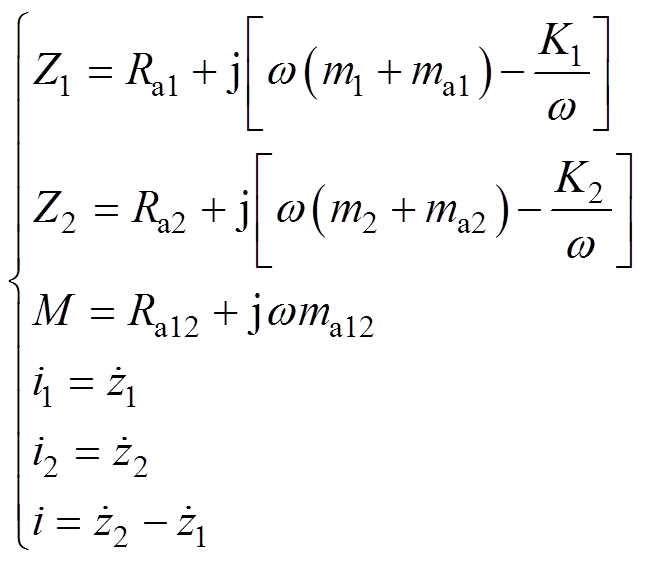（3）
式中，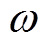
为角频率；i、i1和i2为等效模型各支路电流。
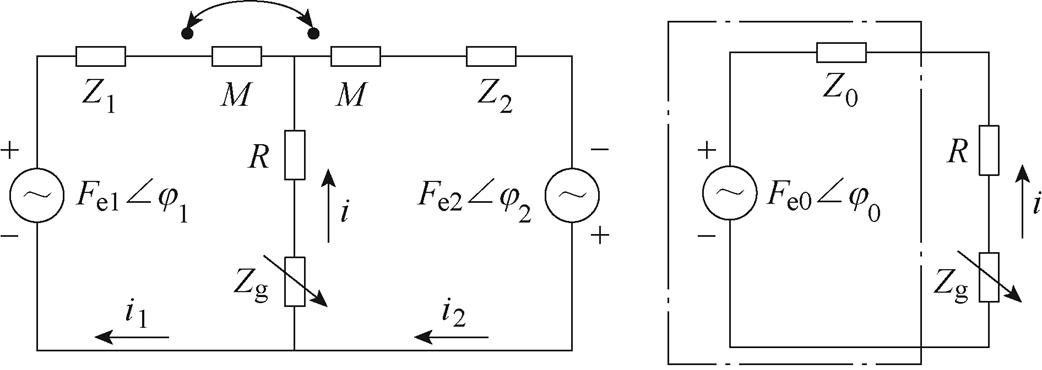
（a）双电源模型 （b）等效单电源模型
图2 双浮体直驱波浪发电装置等效电路模型
Fig.2 Equivalent circuit of two-body direct drive WEC
由双电源等效电路可以看出，质量、附加质量、附加阻尼、浮力系数、锚链刚度等物理量可等价为两个电源的内阻抗Z1和Z2，耦合附加质量与附加阻尼等价为双电源的互阻抗M，主轴机械阻尼等价为外部固有电阻R，发电机提取的波浪能即是发电机等效负载Zg受到双电源并联作用下的电功率。根据戴维南定理，可将图2a所示的双电源模型进一步简化等效为单电源模型，等效单电源的电压有效值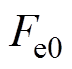
、相位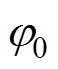
与内阻Z0可由式（4）计算，等效模型如图2b所示。
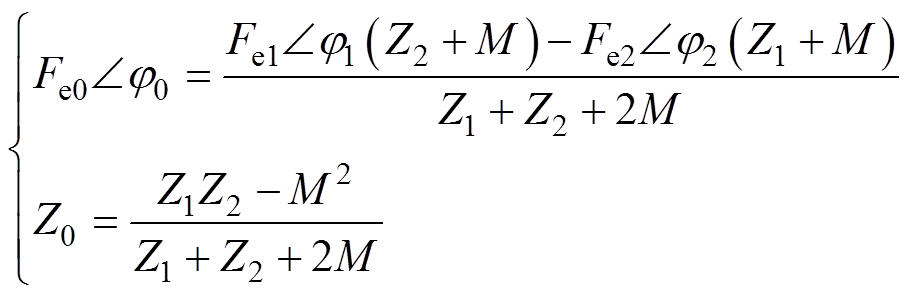（4）
经过等效后，可以看出，系统已和上下浮体各自的运动状态无关，仅和两者的相对运动状态有关，即发电机的位置与速度。因此，只需在发电机上安装位置传感器即可，免去了对上下浮体运动状态的测量，从而简化实际装置的设计。发电机的位置传感器也利于对发电机实现更精确的推力控制，从而实现期望的能量提取控制算法。同时由图2b也可以直观地看出，当电路谐振时，Z0可从电源提取的能量最大化，即波浪能的提取效率最大化。
双浮体装置的设计初衷是为了实现锚系结构布放，解决单浮体装置需要海上平台作为固定支撑的限制，从而能够应用于深远海等区域。从理论构想上看，双浮体装置中上浮体等价于单浮体装置的浮体，下浮体及锚链等价于单浮体装置所需要的稳定平台，但不同的是单浮体装置的动力学特性只取决于其浮体结构，而基于1.2节的分析，双浮体装置的下浮体会对整体的动力学特性乃至发电特性产生影响。不难看出，上下浮体存在三种可能的运动状态：①上下浮体同方向运动；②下浮体静止不动；③上下浮体反方向运动。对于状态②而言，此时双浮体装置退化为单浮体装置，但实际中无法实现，对于状态③而言，此时两者的相对运动大于单浮体的独立运动，进而装置的波浪能提取效率将增加，而对于状态①，上下浮体运动同方向将减小相对运动的趋势，必然导致装置吸收波浪能的效率下降。
对于已有的一些双浮体直驱波浪发电装置，一般会设计在装置处静水平衡状态时，下浮体的浮力和自重基本平衡，此时锚链基本处在松弛状态，对装置的主要作用是防止波浪横向冲击导致装置平移，并没有对下浮体垂直方向上的运动做过多的约束，等效为锚链的刚度系数很小。假设某一时刻在波浪的作用下，上浮体向上运动，此时发电机为提取波浪能，会对上浮体施加向下的作用力，因而会对下浮体产生一个大小相等的向上作用力。由于下浮体处在水下受到的波浪激励力较小，此时发电机推力起到了影响下浮体运动的主要作用，从而导致下浮体向上运动，使得上下浮体具有相同的运动趋势，即状态①，导致双浮体波浪发电装置的波浪能效率提取降低，小于同上浮体尺寸的单浮体波浪发电装置。
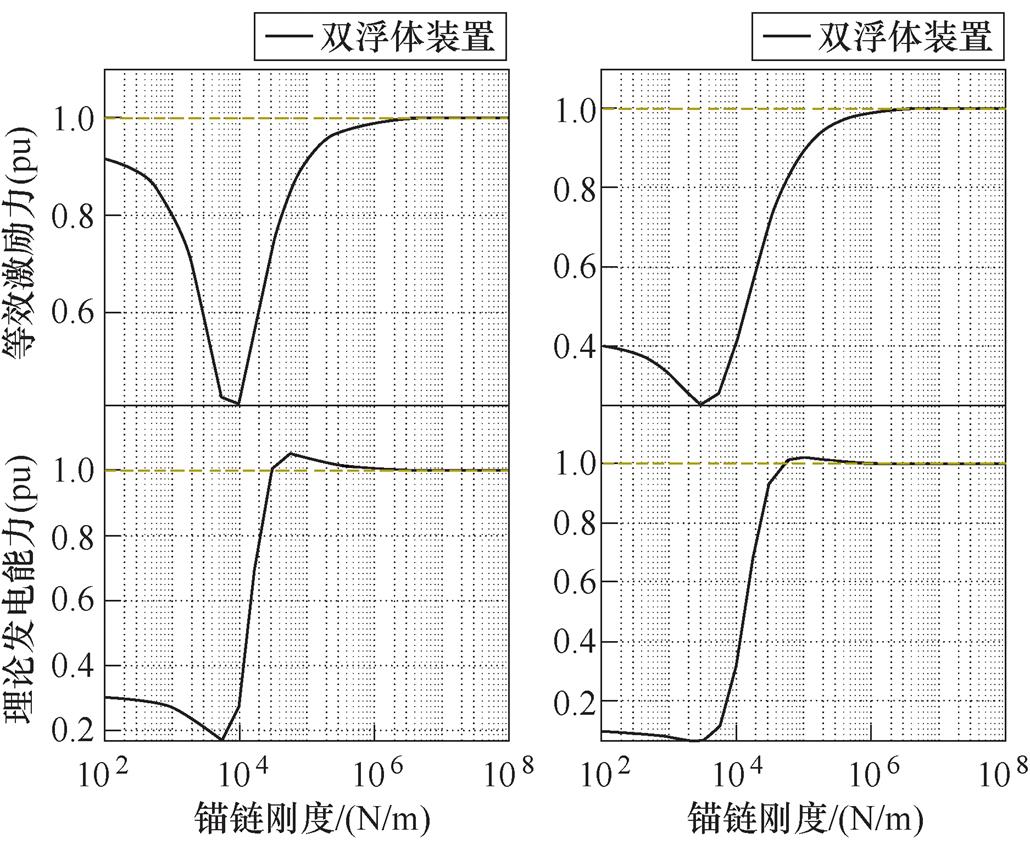
图3为结合装置有限元水动力学数据分析和等效电路模型分析，不同锚链刚度下双浮体直驱波浪发电装置等效激励力和理论发电能力影响的特性曲线。可以看出，在低锚链刚度的情形下，相对于单浮体装置的激励力，双浮体装置的等效激励力明显减小，导致所能提取的波浪能也大幅下降，在锚链松弛状态下发电性能仅为同尺寸单浮体装置的30%；随着锚链刚度增加，在一个小范围内双浮体装置的理论发电能力略高于单浮体装置，随着锚链刚度进一步增加，双浮体装置的发电性能几乎与单浮体装置一致。因此，针对双浮体装置，有必要设计高刚度锚链来优化装置的波浪能提取特性。在锚链刚度较大时，根据等效电路和式（4）有
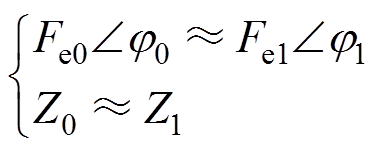（5）
此时双浮体装置的波浪能提取特性与单浮体基本一致，从而可以直接使用基于单浮体装置的相关控制算法。
（a）波浪周期3 s （b）波浪周期4 s
图3 锚链刚度对装置发电性能的影响
Fig.3 Influence of mooring stiffness on WEC performance
锚链的特性决定了其仅能够提供向下的拉力，且仅能在绷紧状态下等效为线性弹簧系统，而双浮体装置会在上下两个方向运动，需要锚系结构为其提供向上方向的等效弹性约束，因此参考张力腿平台结构，本文针对双浮体直驱波浪发电装置提出了一种改进方案，即设计下浮体排水体积大于自身重力，在完成装置安装后，锚链处在紧绷状态并且使预紧拉力大于发电机最大输出推力，保证在运行状态中锚链始终处在紧绷状态，满足双向弹性约束，以提高装置提取波浪能的效率。
基于以上分析，本文设计了一个双浮体直驱波浪发电装置实验测试样机，其结构设计关键参数见表1。
表1 装置关键参数
Tab.1 Key of the designed prototype
参 数数 值 上浮体外径/m1.5 上浮体内径/m0.3 上浮体吃水深度/m0.3 上浮体水上长度/m0.3 上浮体质量/kg508 主轴行程/m0.6 下浮体排水体积/m31.2 下浮体质量/kg745 下浮体水下长度/m2.85 阻尼盘直径/m1.6 锚链预紧拉力/N4 795 发电机最大推力/N4 000 最大速度/(m/s)0.4
设系统的状态变量为x，采样周期为Ts，根据式（1）和单电源等效模型，可以得到系统动力学方程的离散状态空间表达为
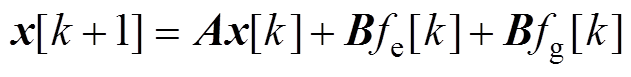（6）
式中，k为离散时刻；A和B为状态空间矩阵。系统的状态变量x的第一个元素x1为浮体速度，第二个元素x2为浮体位置，其余元素为辐射力状态，5的阶数一般为六阶，状态矩阵A可通过Prony方法[15]离散化求得。
基于模型预测算法最大化波浪能提取的问题可描述为在任一时刻，从某个状态x出发，给定未来一段时间T=NTs内的波浪激励力预测序列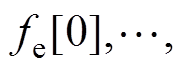
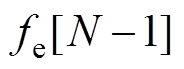，求解对应的预测控制序列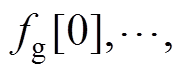
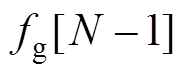，使得系统在该时间内提取的波浪能最大化，同时满足浮体位移x2不超出最大行程zm的约束条件。该问题的数学形式为
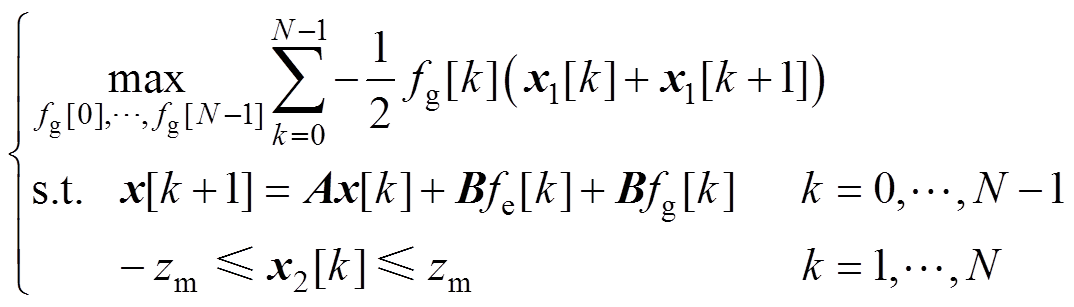（7）
记
，
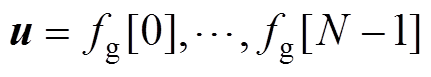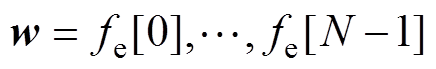，定义向量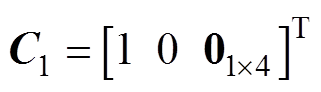
，
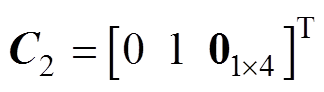，上述问题可以表达为含参数二次规划问题形式，有
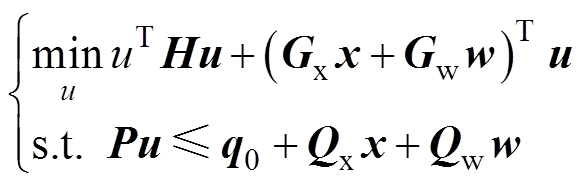（8）
式中，矩阵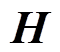
、
、
、
、
、
、
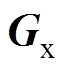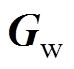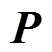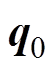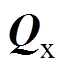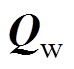计算分别为
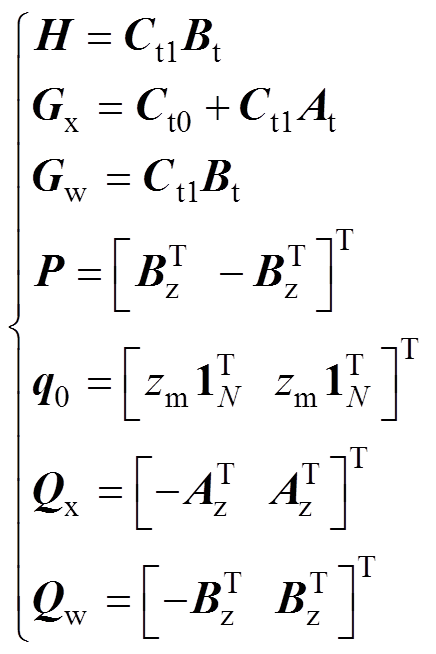（9）
其中，辅助矩阵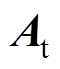
、
、
、
、
、
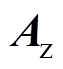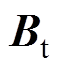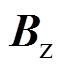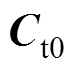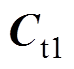分别为
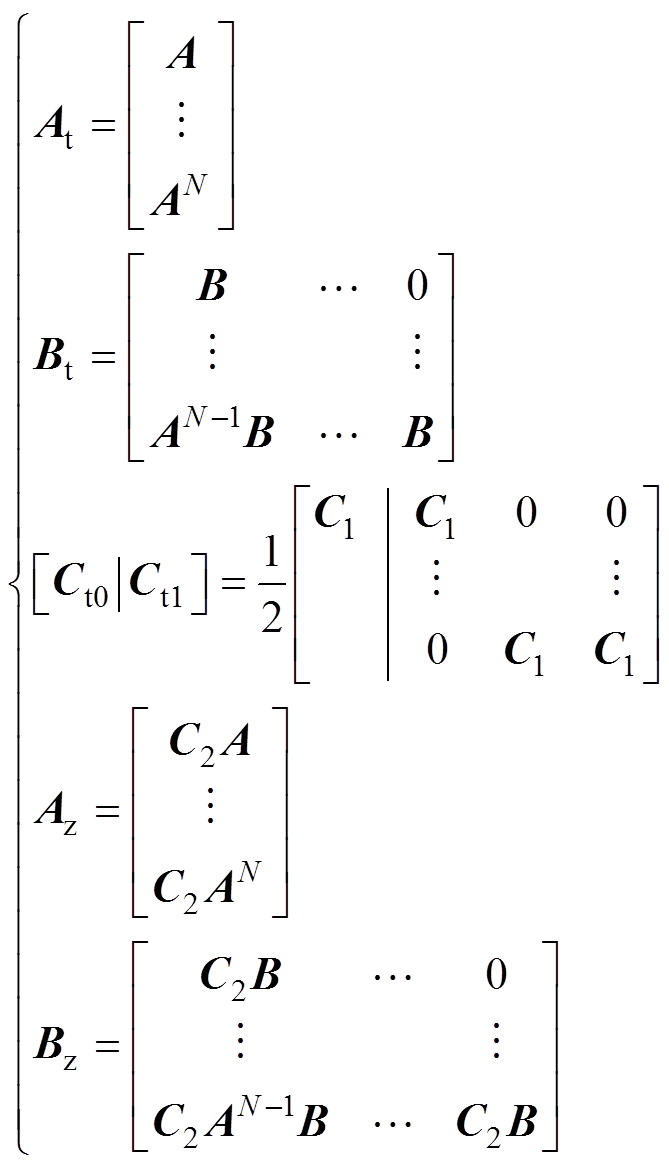（10）
在求解式（8）得到预测控制序列后，模型预测控制只采用其第一步控制；在下一时刻获得更新的状态和波浪信息后重新求解上述问题——即运行在“滚动优化”模式下。
由式（8）～式（10）可以看出，在最大化波浪能提取的模型预测控制问题中，系统状态x和波浪激励力预测序列w是可变的问题参数，需要在线获得；其余矩阵均为固定参数，可通过离线一次性计算得到。但模型预测控制中所需要的波浪激励力信息无法直接观测得到，需要根据系统模型进行辨识。将波浪激励力作为随机过程进行考虑，得到扩展的系统方程为
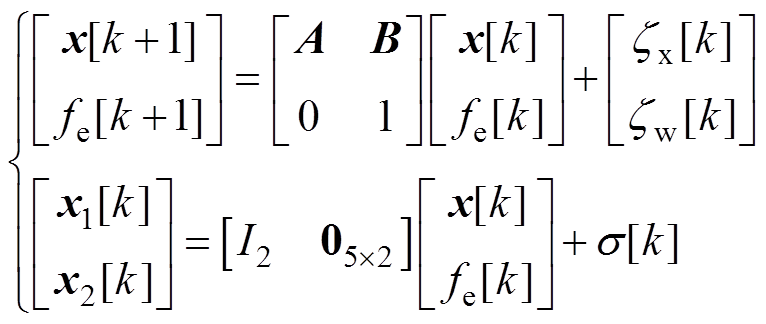（11）
式中，
、
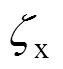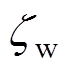和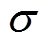
分别为过程噪声和测量噪声。对此系统使用经典卡尔曼滤波算法即可由所施加的发电机推力和测量得到的浮体位置和速度估计出实时波浪激励力。
进一步地，使用线性自回归模型对波浪激励力的变化过程进行建模，从而基于其历史数值预测未来数值。线性自回归模型表示为
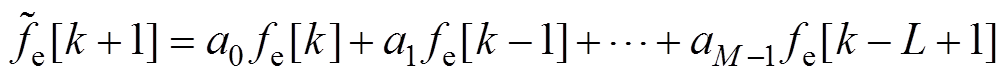（12）
式中，L为历史数值长度；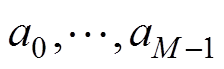
为自回归系数；
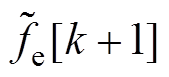为预测得到的激励力。在所预测数值的基础上迭代使用该式，即可获得所需的波浪激励力预测序列。
由于模型预测控制需要实时求解二次规划问题，需要考虑计算加速方法使之能够满足实际控制器的算力限制，因此可采用内点法求解，记g=Gxx+ Gww，q=Qxx+Qww+q0，内点法将含约束问题转化为无约束问题，有
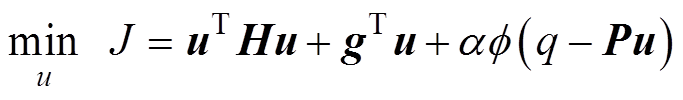（13）
其中
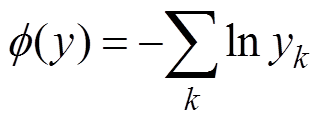（14）
式中，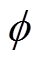
为对数形式的障碍函数；
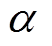为障碍因子。在传统内点法中，需要令障碍因子逐次减小，并对每个障碍因子都使用多次牛顿迭代求解无约束问题——即一个双重循环过程。为进一步加速求解，可继承上一步所得解作为本步初始解，随后只在一个固定障碍因子下进行一次牛顿迭代，从而大大减小计算量。
牛顿法迭代过程如下：从某个初始解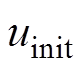
出发，计算中间变量，有
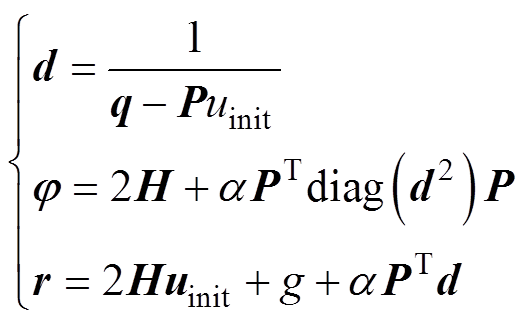（15）
则牛顿方向为
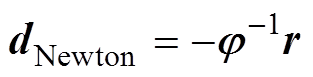（16）
在该方向上进行线搜索以确定满足约束条件的迭代步长，记为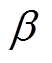
，最后得到更新后的解
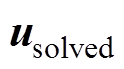为
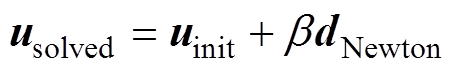（17）
由于只需进行一次迭代计算，相较于传统算法需进行3～5次迭代，求解所需的时间理论上可降低80%。
本文所设计的双浮体装置在加工装配完毕后，在国家海洋技术中心的波浪水槽实验室进行相关测试。该水槽尺寸长100 m、宽18 m、最大水深5 m。波浪水槽持续稳定可造周期2～4 s，最大波高0.25 m的波浪。装置采用配重块方案进行固定：在安装过程中，先运输装置本体至测试点，躺放漂浮在水面上，随后吊装配重块至测试点，由工作人员通过锚链将下浮体和配重块连接，如图4a所示，随后控制吊装机缓慢放下配重块直至沉入水底，并将装置姿态拉正，最终安装完毕装置在水中的平衡状态如图4b所示。
（a）装置安装 （b）静水平衡状态
（c）整体测试环境示意
图4 装置实物与测试环境
Fig.4 Device and test enviroment
实验操作台在装置测试点一侧的水槽上方。实验仪器设备主要包括双向直流电源、发电机驱动器、控制器和上位机，装置和驱动器通过电缆相连，如图4c所示，相关实验操作通过上位机给控制器下达指令，由控制器控制驱动器实现对发电机的控制。
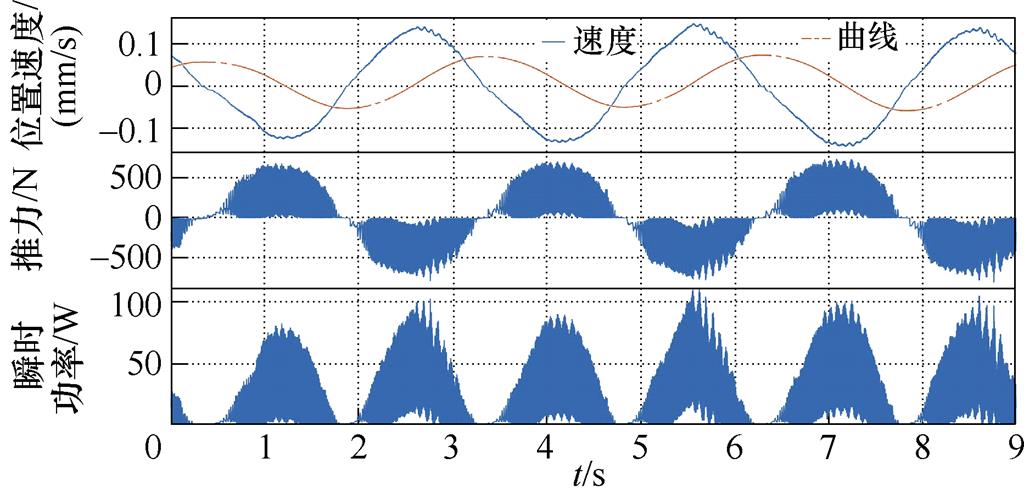
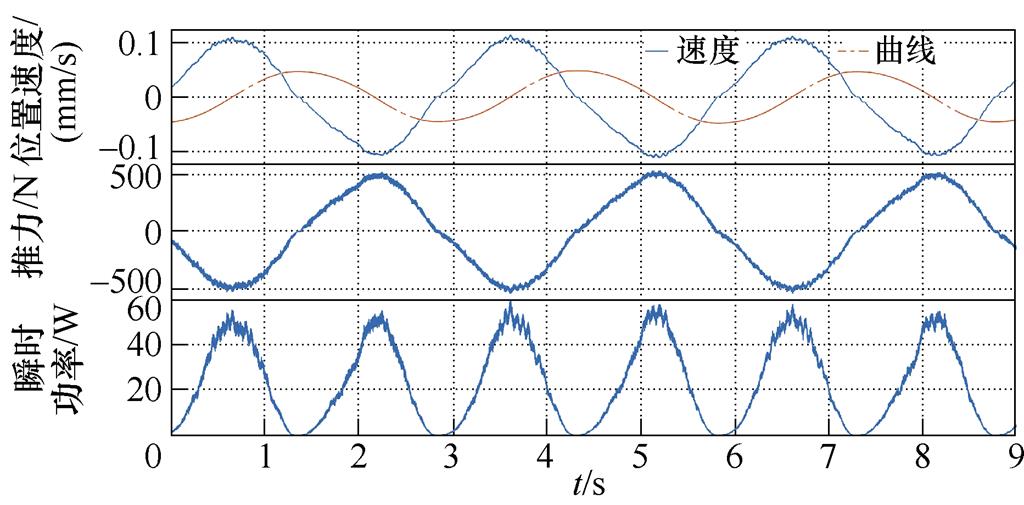
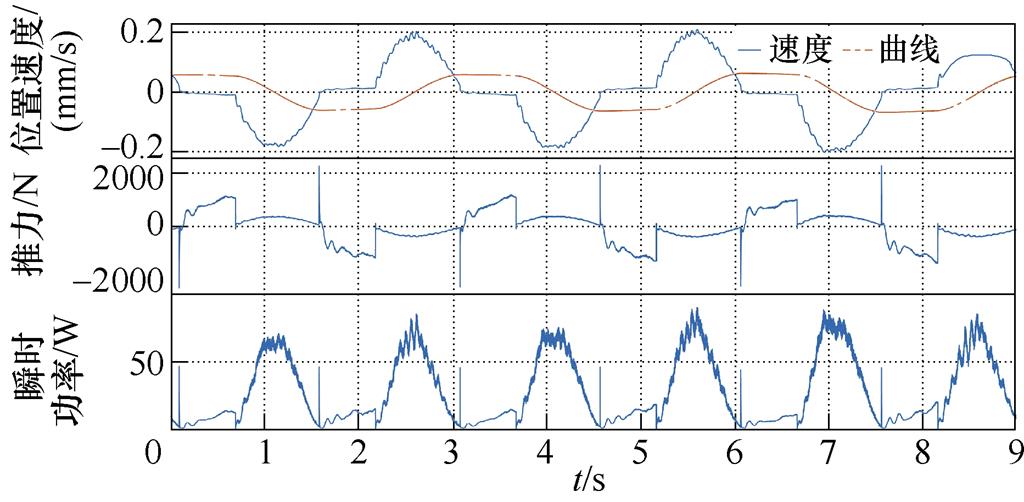
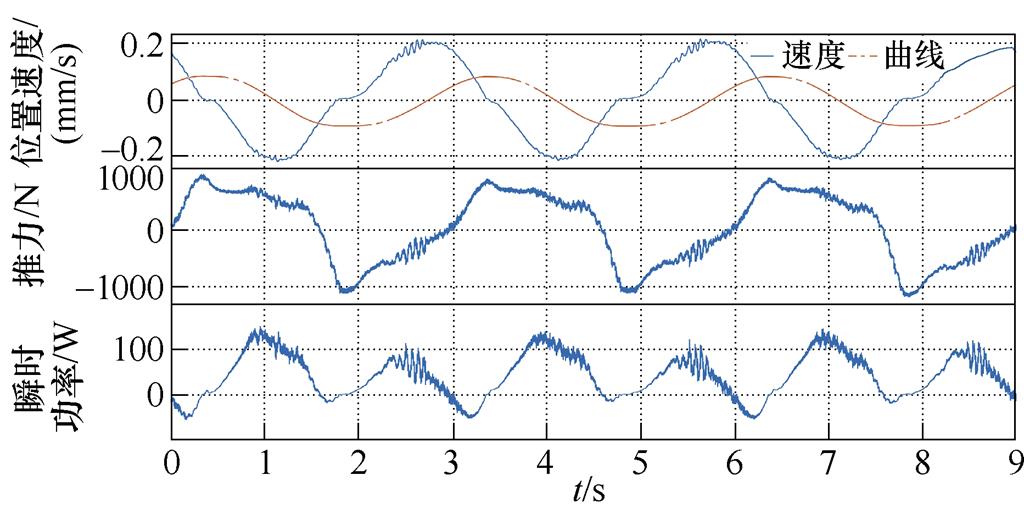
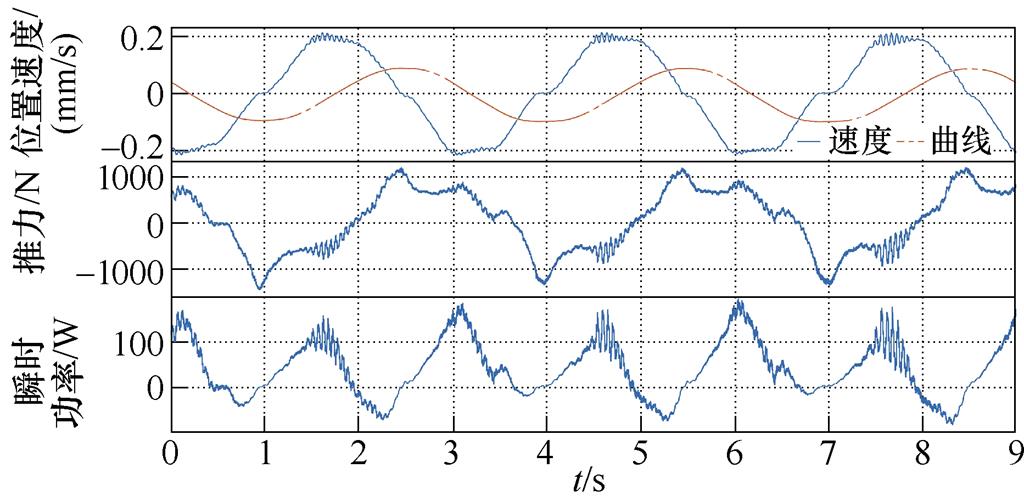
经过装置测试与控制参数调试，在波高0.2 m、周期3 s的工况下，测试了所提的采用快速求解算法的改进MPC和未采取快速求解算法的传统MPC，并与传统的电阻控制、阻尼控制和闭锁控制进行了对比，不同控制方法稳态下装置浮体的速度位置、发电机推力和装置吸收的瞬时波浪功率如图5所示。表2列出了各控制方法的关键性能指标。
由实验测试结果可以看出，阻尼控制和闭锁控制下装置的速度、位置、推力、功率基本呈现正弦特征，与规则波浪特性匹配，电阻控制、闭锁控制和模型预测控制的装置响应出现了明显的非线性特征。本次测试的电阻控制采取了三相不控整流带电阻的方案，发电机的实际推力有明显的脉动，导致提取的波浪功率也有明显波动；可以看出，闭锁控制实现了预期的行为，即在速度过零后停止运动一定时间后再释放，过零的一瞬间为实现闭锁发电机推力产生了较大的尖峰；模型预测控制的发电机推力呈现了比较明显的非线性，由于设置了0.1 m的位置限幅条件，在运行至0.1 m附近时装置产生了短暂的停顿，说明模型预测控制有效实现了位置的约束。
（a）电阻控制
（b）阻尼控制
（c）闭锁控制
（d）传统MPC
（e）改进MPC
图5 不同控制方法下装置的运行状态曲线
Fig.5 WEC operation curves under different control methods
表2 不同控制方法下装置运行关键参数对比
Tab.2 Comparison of key operation parameters of WEC under different control methods
控制算法峰值位移/m峰值速度/ (m/s)峰值推力/N峰值功率/W平均功率/W峰值负功率/W 电阻控制0.0750.152723111.724.60 阻尼控制0.0460.11154360.223.10 闭锁控制0.0610.2092 33090.527.10 传统MPC0.0970.2241 19215140.7-56.79 改进MPC0.0990.2171 414.719739.4-85.2
从波浪能提取的效果来看，电阻控制和阻尼控制的效果基本一致，但阻尼控制的峰值位置、速度、推力、功率均小于电阻控制，且电阻控制带来的发电机推力波动长时间运行下对装置的主轴等机械结构也会产生负面影响；理论上闭锁控制相较阻尼控制应该有更高的波浪能提取效率，但实际测试的提升却只有17%，且在闭锁的瞬间需要较大的瞬时发电机推力，导致波浪效率提升不明显的原因可能是实际装置的模型参数与理论不匹配导致所设置的控制参数与理论最佳有偏差，另一个可能的原因是文献[9]给出的闭锁控制的最优控制参数规则也是定性给出，并没有基于严格的最优条件数学推导，从而导致实际测试中效率提升有限；控制器的底层控制周期为100 ms以满足发电机矢量控制的需求，由于MPC算法无法在100 ms内完成计算，因此实验将MPC的求解拆分成多个任务分散在多个控制周期内计算，最终实现了MPC的等效控制周期为10 ms。实验测试结果表明，传统MPC的平均功率为40.7 W，单次求解总用时为3 753 ms，所提的改进MPC算法求解时间缩减至1 579 ms，实现了39.4 W的平均功率，与传统MPC基本一致，同时也保证了0.1 m的位移限幅。可以看出，模型预测控制下，装置出现了负功率，即说明波浪和装置之间产生了双向的能量流动，同时峰值功率也更高。
在波高0.25 m、周期2.5 s的波浪工况下重复了对比实验，电阻控制、阻尼控制、闭锁控制和传统MPC与改进MPC算法下装置的波浪能提取平均功率分别为20.9、20.7、20.9、28.1、27.0 W，所提的模型预测控制算法依然能实现波浪能提取效率提升。
本文详细分析了双浮体直驱波浪发电装置的动力学模型及其波浪能提取特性，指出锚链的等效刚度对装置的发电性能有重要的影响，创新性提出了采用类张力腿结构的双浮体装置结构，使之可以简化为单浮体装置进行设计和控制，且不会因为缺乏大型固定平台造成波浪能提取效率损失，减少了系统的安装成本。进一步地，本文设计并制造了双浮体装置的原型实验样机，提出了一种基于模型预测控制的优化能量提取算法，并在波浪水槽实验室对装置进行了测试，主要结论如下：
1）注入适当的负功率可以有效提高装置的波浪能提取效率，原因是负功率可以提高浮体的振动幅度，从而更好地和波浪相互作用提取波浪能。因此，电阻控制、阻尼控制、闭锁控制三种控制的浮体位移幅度都较小，平均功率也较小，而模型预测控制存在负功率，浮体位移幅度更大，从而可以获取更多的波浪能。
2）模型预测控制要求较高的建模精度，但实际波浪工况下的装置与理论模型会存误差，且实验装置未采用额外的传感器，仅通过算法进行波浪激励力辨识和预测，在控制算法执行时间降低50%的前提下，所提的改进MPC在实际装置测试中能够稳定工作，取得了与传统MPC一样的能量提取效率，且保证了浮体行程的限幅，相比其他算法能量提取效率显著提升，表现出了很好的鲁棒性和性能。
参考文献
[1] 洪岳, 潘剑飞, 刘云, 等. 直驱波浪能发电系统综述[J]. 中国电机工程学报, 2019, 39(7): 1886-1900.
Hong Yue, Pan Jianfei, Liu Yun, et al. Summary of direct drive wave power generation system[J]. Proceedings of the CSEE, 2019, 39(7): 1886-1900.
[2] Ahamed R, McKee K, Howard I. Advancements of wave energy converters based on power take off (PTO) systems: a review[J]. Ocean Engineering, 2020, 204: 107248.
[3] 张家明, 黎明, 刘臻, 等. 10kW组合型振荡浮子波浪发电装置的电力变换与控制系统[J]. 中国海洋大学学报(自然科学版), 2018, 48(4): 126-133.
Zhang Jiaming, Li Ming, Liu Zhen, et al. Power conversion and control system for 10kW oscillating buoy array wave energy converter[J]. Periodical of Ocean University of China, 2018, 48(4): 126-133.
[4] 路晴, 史宏达. 中国波浪能技术进展与未来趋势[J]. 海岸工程, 2022, 41(1): 1-12.
Lu Qing, Shi Hongda. Progress and future trend of wave energy technology in China[J]. Coastal Engin- eering, 2022, 41(1): 1-12.
[5] 刘娜, 谭亦旻, 莫伟强, 等. 基于模拟退火算法的Halbach直线发电机优化设计[J]. 电工技术学报, 2021, 36(6): 1210-1218.
Liu Na, Tan Yimin, Mo Weiqiang, et al. Optimization design of Halbach linear generator with simulated annealing algorithm[J]. Transactions of China Elec- trotechnical Society, 2021, 36(6): 1210-1218.
[6] 张静, 余海涛, 施振川. 一种波浪发电装置用低速双动子永磁直线电机运行机理研究[J]. 电工技术学报, 2018, 33(19): 4553-4562.
Zhang Jing, Yu Haitao, Shi Zhenchuan. Research on a tubular linear permanent magnet machines with dual translators for low speed wave energy conversion[J]. Transactions of China Electrotechnical Society, 2018, 33(19): 4553-4562.
[7] Falnes J. Ocean waves and oscillating systems: linear interactions including wave-energy extraction[M]. Cambridge: Cambridge University Press, 2020.
[8] 康庆, 肖曦, 聂赞相, 等. 直驱型海浪发电系统输出功率优化控制策略[J]. 电力系统自动化, 2013, 37(3): 24-29.
Kang Qing, Xiao Xi, Nie Zanxiang, et al. An optimal control strategy for output power of the directly driven wave power generation system[J]. Automation of Electric Power Systems, 2013, 37(3): 24-29.
[9] Temiz I, Leijon J, Ekergård B, et al. Economic aspects of latching control for a wave energy con- verter with a direct drive linear generator power take-off[J]. Renewable Energy, 2018, 128: 57-67.
[10] Xiao Xi, Huang Xuanrui, Kang Qing. A hill-climbing- method-based maximum-power-point-tracking strategy for direct-drive wave energy converters[J]. IEEE Transactions on Industrial Electronics, 2016, 63(1): 257-267.
[11] Li Guang, Belmont M R. Model predictive control of sea wave energy converters-partⅠ: a convex approach for the case of a single device[J]. Renewable Energy, 2014, 69: 453-463.
[12] Zhan Siyuan, Na Jing, Li Guang, et al. Adaptive model predictive control of wave energy converters[J]. IEEE Transactions on Sustainable Energy, 2020, 11(1): 229-238.
[13] Haider A S, Brekken T K A, McCall A. Application of real-time nonlinear model predictive control for wave energy conversion[J]. IET Renewable Power Generation, 2021, 15(14): 3331-3340.
[14] 方红伟, 宋如楠, 姜茹, 等. 振荡浮子式波浪能转换装置的全电气化模拟研究[J]. 电工技术学报, 2019, 34(14): 3059-3065.
Fang Hongwei, Song Runan, Jiang Ru, et al. An oscillating buoy type wave energy converter with all-electrical analogue method[J]. Transactions of China Electrotechnical Society, 2019, 34(14): 3059- 3065.
[15] Sahraoui M, Cardoso A J M, Ghoggal A. The use of a modified prony method to track the broken rotor bar characteristic frequencies and amplitudes in three- phase induction motors[J]. IEEE Transactions on Industry Applications, 2015, 51(3): 2136-2147.
Modelling and Analysis of the Two-Body Direct-Drive Wave Energy Converter and Optimal Energy Extraction Method Based on Model Predictive Control
Abstract With low loss and flexible control, a direct-drive wave energy converter (WEC) based on oscillating body structure has become a research hotspot in wave energy. Through the mooring system, two-body direct-drive WEC, independent of off-shore fixed platforms, is a promising solution to wave energy utilization. However, the two-body WEC utilizes relative motion between upper and lower float to generate electricity, which makes modelling and optimal energy extraction control more difficult. A two-body WEC can be regarded as two power sources with different voltages and resistance paralleled to output electricity through the equivalent method. Furthermore, this two-paralleled power source can be equivalent to a single source model, similar to a single-body WEC. Therefore, modelling and energy extraction characteristics of two-body WEC are simplified. The stiffness of mooring has a great effect on maximum wave energy extraction. The results show that the mooring should be as stiff as possible to avoid energy extraction loss. In this case, the two-body WEC can be equivalent to a single-body WEC: the upper float harnesses wave energy, and the lower float along with the mooring system acts as a fixed base. Moreover, the design of a two-body WEC with a pretension mooring system is put forward.
Model predictive control (MPC) is a state-of-the-art method for optimal energy extraction in wave energy. Based on the equivalent model, the MPC problem for maximizing wave energy extraction considering generator force and float displacement constraints is formulated. For wave excitation force prediction, the Kalman filter is used to achieve excitation force identification, and the autoregressive model is used for excitation force prediction. Considering the computation complexity of the MPC solution, a fast solution algorithm is put forward, and the previous step is set as the initial iteration of the current step. Thus, only one iteration is required. Compared with the conventional MPC that requires 3～5 interactions, the proposed fast solution algorithm can save up to 80% computing time.
A two-body direct-drive WEC prototype with an upper float of 1.5 m diameter is designed for experimental test in the wave tank lab with a dimension of 100 m×18 m×5 m. This lab can generate waves with periods from 2～3 m and 0.25 m maximum wave height. Different power control methods include resistive control, damping control, latching control, conventional MPC, and proposed MPC. The results show that MPC can extract 70% more energy than traditional methods. The proposed MPC with the fast solution algorithm has the same energy extraction efficiency, and only 50% CPU operation time is required.
The following conclusions can be drawn. (1) Pretension mooring has no adverse effect on energy extraction, and two-body WEC can be equivalent to one-body WEC through the equivalent circuit method, which will simplify control modelling significantly. (2) Compared with conventional methods, MPC has more energy extraction efficiency by injecting reactive power to increase the oscillation amplitude while limiting it within preset constraints. (3) The experimental results indicate that the proposed MPC is stable, considering modelling errors in the experiment. Besides, excitation force prediction is achieved by software algorithms, and the proposed MPC method only requires 50% computation time. The proposed method is promising for practical implementation without additional sensors and a high-performance control system.
keywords：Two-body direct-drive wave energy converter, energy extraction control algorithm, prototype modelling and analysis, wave tank, model predictive control
中图分类号：TM619
DOI: 10.19595/j.cnki.1000-6753.tces.221998
国家自然科学基金资助项目（U1806224）。
收稿日期 2022-10-21
改稿日期 2022-12-30
黄宣睿 男，1991年生，博士，研究方向为永磁电机控制与直驱波浪发电优化控制。E-mail: huangxr16@tsinghua.org.cn
肖 曦 男，1973年生，教授，博士生导师，主要研究方向为交流伺服电机控制、新能源发电与电力储能、波浪发电等。E-mail: xiao_xi@tsinghua.edu.cn（通信作者）
（编辑 崔文静）