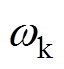 为旋转角频率),以定子电流矢量is、转子磁链矢量
为旋转角频率),以定子电流矢量is、转子磁链矢量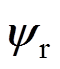 为状态变量,定子电压矢量us为输入变量的连续域电压方程为
为状态变量,定子电压矢量us为输入变量的连续域电压方程为摘要 在大功率和高速电机驱动领域,电机控制系统将运行于低载波比工况。传统的一阶欧拉、二阶双线性等降阶离散化模型在低载波比下由于离散化误差过大,对应的状态观测将出现幅值和相位的稳态误差,严重时甚至出现发散不收敛现象。针对上述问题,该文提出了感应电机特征根离散化模型。通过构建感应电机的复矢量模型状态空间方程,将满秩的状态转移矩阵进行对角化,得到状态转移矩阵的精确离散化结果,该模型在低载波比时仍具有较高的离散化精度。同时,提出了一种基于伯德图的离散化误差定量分析方法,通过定量对比不同离散化模型和连续域模型之间观测变量的幅值和相位误差,从理论上证明了提出方法的优越性。最后,通过仿真和实验验证了上述感应电机特征根离散化模型在低载波比下均具有良好的稳态精度与暂态跟随性能。
关键词:感应电机 离散化模型 传递函数 伯德图 低载波比
在电机驱动系统中,电机离散模型的精度在状态观测器设计、无位置/无速度传感器算法、电流控制器设计等方面均具有重要意义。离散模型的准确度依赖于电磁关系的建模、参数的准确度、离散化误差的大小等几个重要方面。其中,参数的离线测量和在线辨识已有国内外学者对其进行了大量的研究工作,且目前仍在继续深入[1-5]。而在离散化方面,随着高速电机、大功率牵引电机的研究持续深入,离散化误差对控制系统的影响被越来越多学者所关注[6-8]。
在大功率牵引电机驱动系统中,当电机进入中高速区域时控制系统的开关频率与电频率的比值(“载波比”)将逐渐下降,随着高性能同步调制策略的应用,载波比将低至3,最后甚至进入方波工况。在低载波比工况下,传统降阶的离散化模型由于离散化误差过大,无法适用于低载波工况的控制系统[9]。文献[10]从状态矩阵的角度分析了一阶欧拉、二阶双线性变换的离散化误差,但未在低载波比工况下进行分析。文献[11]提出变坐标系的离散化方法,将定子方程在静止坐标系下离散化,转子方程在转子旋转坐标系下离散化,大大降低了离散化误差,然而在极低载波比下仍然无法满足高性能要求。文献[12]对比了一阶欧拉、二阶龙格库塔法、双线性变换离散化方法对无速度传感器算法的影响,分析了弱磁区域的无速度观测器稳态精度及动态性能。文献[13]研究了一种基于电流源的永磁同步电机预测转矩控制,但仅采用一阶欧拉离散化方法,没有在低载波比情况下研究其离散化误差。文献[14-15]提出在连续域下采用复数域模型进行电流控制器设计,该方法未考虑离散化误差的影响,在载波比较低时性能较差。因此,文献[16]提出直接在离散域下进行建模,提升了高速下的解耦性能,然而受限于模型精度的影响,极低载波比下的性能提升依旧困难。文献[17-18]研究了低载波比下永磁同步电机离散模型的近似误差,文献[8, 19]在此基础上研究了考虑转子位置补偿的离散模型,该模型对预测电流控制器性能有显著改善。文献[20]分析了感应电机混合型磁链观测器在离散域内的实现问题,通过考虑转子偏转角,提出了改进的数字实现方案。文献[21]提出了一种基于状态空间拆分重组的离散化方法,将状态矩阵拆分成动态系数矩阵和常量系数矩阵,仅对动态系数矩阵进行离散化,该方法在2 kHz的离散化频率下具有较高的精度,但并没有在更低的离散化频率下验证其离散化精度。文献[22]以定子电流和转子磁链作为状态变量构建感应电机的状态空间方程,实现了对状态转移矩阵的精确离散化,但是缺少在极低载波比工况下开展定量的离散化误差分析。
本文以感应电机为例,研究了连续域下感应电机的传递函数和极点分布轨迹,推导了零阶保持离散化数学模型,分析了传统包括二阶双线性变换在内的降阶离散化模型在低载波比工况下的局限性,提出了特征根离散化模型,该模型在低载波比下仍具有良好的稳态精度和暂态跟随性能。同时,提出了基于伯德图的离散化误差定量分析方法,通过推导不同离散模型的磁链观测z域传递函数,绘制其伯德图,以连续模型的伯德图为评判标准,对比了传统的离散化模型和提出的特征根离散化模型在磁链观测幅值和相位上的误差大小。最后,仿真和实验验证了所提出方法的有效性。
假定定子三相绕组对称,铁心磁路不饱和,忽略磁滞损耗和涡流损耗的影响,在任意旋转坐标系下(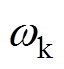 为旋转角频率),以定子电流矢量is、转子磁链矢量
为旋转角频率),以定子电流矢量is、转子磁链矢量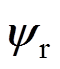 为状态变量,定子电压矢量us为输入变量的连续域电压方程为
为状态变量,定子电压矢量us为输入变量的连续域电压方程为
 (1)
(1)
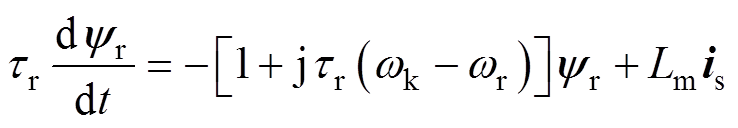 (2)
(2)
其中
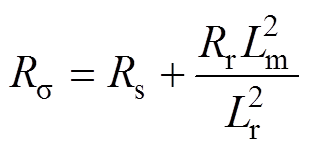
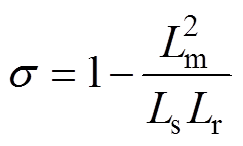
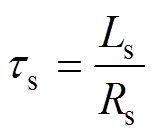
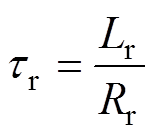
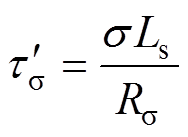
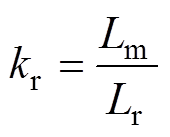
式中,Rs、Rr分别为定子电阻、转子电阻;Lm、Ls、Lr分别为励磁电感、定子电感、转子电感;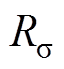 为定子等效电阻;
为定子等效电阻;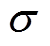 为总漏磁系数;
为总漏磁系数;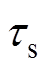 、
、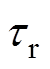 分别为定、转子时间常数;
分别为定、转子时间常数;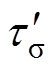 为等效定子瞬态时间常数;
为等效定子瞬态时间常数;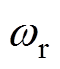 、
、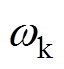 分别为转子电角频率、参考坐标系角频率;
分别为转子电角频率、参考坐标系角频率;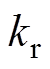 为转子磁耦合因数。
为转子磁耦合因数。
式(1)和式(2)分别为描述定子电流和转子磁链变化模态的复数微分方程,可将该系统看作一个单输入、双输出,定转子间具有强耦合特性的二阶系统。
为进一步分析该系统的稳态特性,在静止坐标系下,即令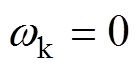 ,将式(1)和式(2)取拉氏变换,可分别获得定子电压对定子电流、定子电压对转子磁链的传递函数,分别为
,将式(1)和式(2)取拉氏变换,可分别获得定子电压对定子电流、定子电压对转子磁链的传递函数,分别为
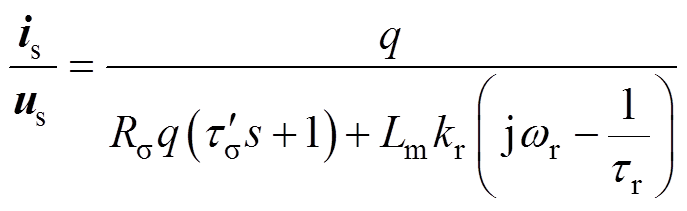 (3)
(3)
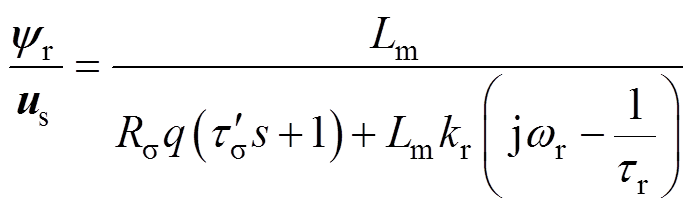 (4)
(4)
其中
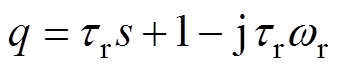
式中,s为拉普拉斯算子。再将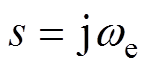 代入化简后,易得到系统的频率特性,且满足
代入化简后,易得到系统的频率特性,且满足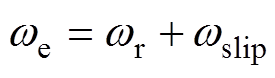 的约束,其中,
的约束,其中,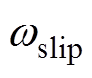 和
和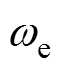 分别为转差角频率和同步角频率。
分别为转差角频率和同步角频率。
绘制由式(3)和式(4)化简后的系统频率响应在空载和满载时的伯德图,能更直观地分析输入输出变量的稳态特性。感应电机连续域传递函数的伯德图如图1所示,电机系统是一个幅值衰减剧烈,相位滞后严重的系统。以连续系统的伯德图为基准能精确地定量对比不同离散化模型对系统描述精度的影响,后文将以此为手段进行离散化误差的相关分析。
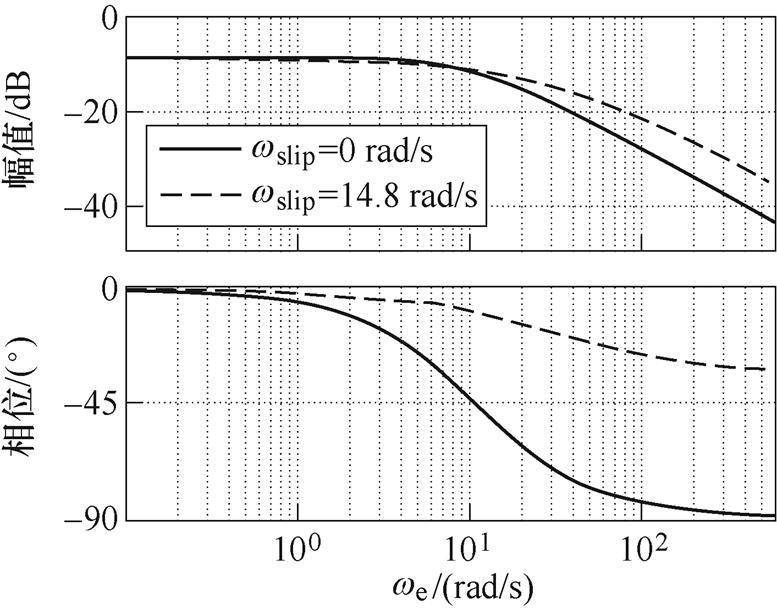
(a)is/us伯德图
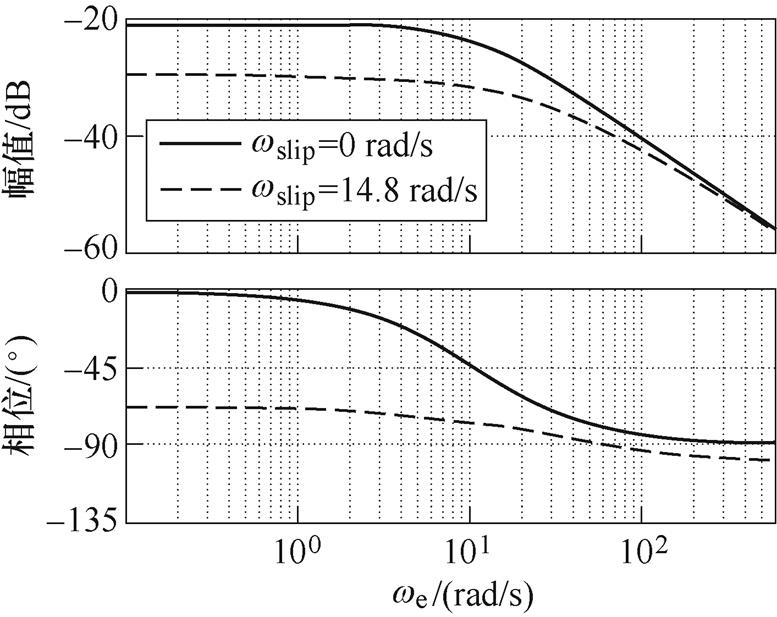
(b)yr/us伯德图
图1 感应电机连续域传递函数的伯德图
Fig.1 The Bode plot of induction machine in continous domain
传统的离散化方法可以分为基于数值积分的降阶离散化方法(也叫近似法)和输入响应不变的离散化方法两类。基于数值积分的降阶离散化是将s与z的无理关系近似地化为有理关系,即
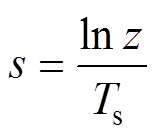 (5)
(5)
式中,Ts为离散化频率。常用的近似法包括一阶前向欧拉、后向欧拉、双线性变换法、二阶龙格库塔法等。其中,一阶前向欧拉模型具有实现简单、计算量小的优点,而双线性变换在以上降阶的离散化方法中具有最小的离散化误差,本文以此两种典型离散化模型为参考,在后文分析其在低载波比下的局限性。基于数值积分的离散化方法等效于对状态量在一拍范围内的变化进行线性近似,变化的斜率示意图如图2所示。状态变量在tk-1~tk之间的变化斜率在一阶前向欧拉模型中为k1,该斜率只与tk-1时刻的状态量和输入电压有关。对后向欧拉和双线性变化,斜率则分别为k2和(k1+k2)/2。具体而言,一阶前向欧拉离散模型Gfir(z)和双线性变换离散模型Gsecd(z)分别为
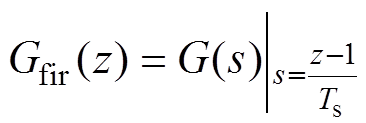 (6)
(6)
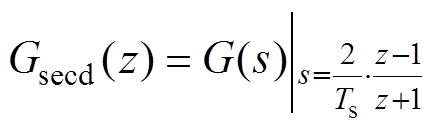 (7)
(7)
式中,G(s)为连续域下定子电压到转子磁链的传递函数yr/us,如式(4)所示。当控制系统处于低载波比工况时,由于忽略了高阶项的影响,基于数值积分的降阶离散化方法会出现明显的离散化误差,对应的状态观测将出现幅值和相位的稳态误差。
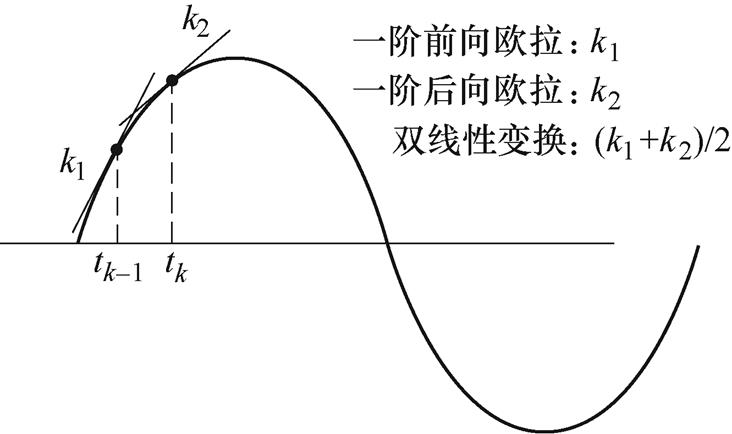
图2 降阶离散模型状态变量变化斜率示意图
Fig.2 The change slope diagram of state variable in traditional discrete model reduced order
输入响应不变的离散化方法具有离散化前后连续系统和离散系统对输入信号的响应不变这一特性,通常可分为Z变换(冲击响应不变离散化)、零阶保持离散化(阶跃响应不变离散化)和一阶保持离散化(脉冲响应不变离散化)三种。考虑到实际的电压指令由电压型逆变器基于一个开关周期内的伏秒平衡等效作用于电机系统;而零阶保持离散化方法假定输入量在一拍内维持恒定,和实际电压的作用方式一致,能保证在采样处连续系统和离散系统的状态变量尽可能一致。因此,本文也将零阶保持离散化方法作为参考,感应电机的零阶保持离散化模型Gzoh(z)为
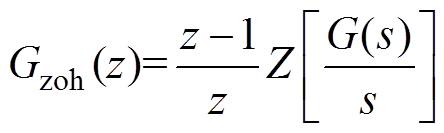 (8)
(8)
式中,Z[ ]为Z变换。
该离散模型具有较高的稳态观测精度,然而在转速动态以及转矩发生突变时,传递函数式(4)中的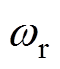 与
与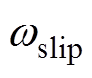 为时变量,基于频域下传递函数的设计方法无法考虑时变系统,因此将时变量近似为定常量进行分析和设计得到的零阶保持离散模型在暂态时将出现跟踪误差。
为时变量,基于频域下传递函数的设计方法无法考虑时变系统,因此将时变量近似为定常量进行分析和设计得到的零阶保持离散模型在暂态时将出现跟踪误差。
感应电机通过气隙磁场切割转子,在转子内感应出电流,从而产生电磁转矩。转差频率在暂态时为时变量,因此严格意义上传递函数无法准确描述这一时变系统。
为更准确地描述系统的暂态特性,采取状态空间描述的方式对系统进行建模[11],有
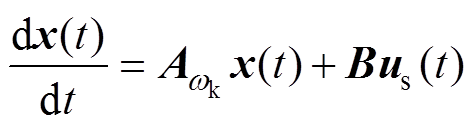 (9)
(9)
其中
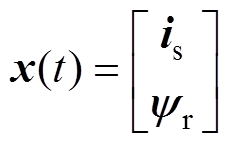
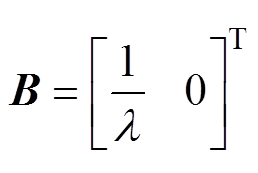
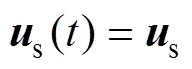
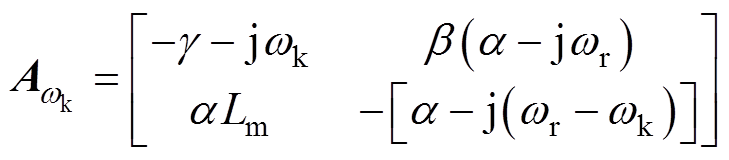
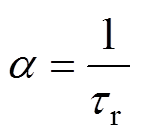
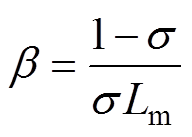
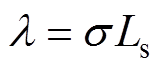
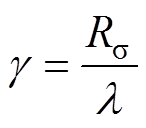
式中,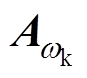 为任意参考坐标系下的状态矩阵。
为任意参考坐标系下的状态矩阵。
假定电气时间常数远小于机械时间常数,wr为定值,则状态方程式(9)为线性定常系统。在静止坐标系下,由线性控制理论,状态变量x(t)的精确解为
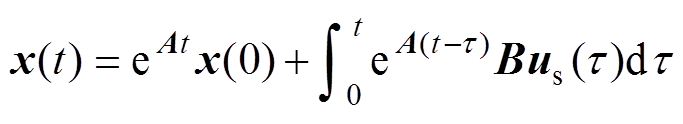 (10)
(10)
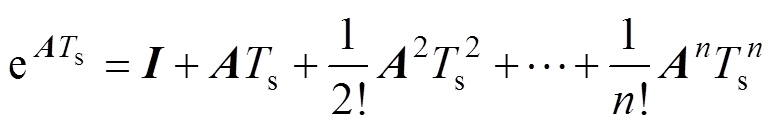 (11)
(11)
其中,在两相静止ab 参考坐标系下有
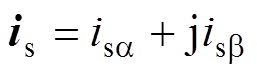
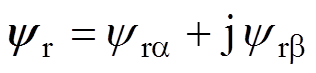
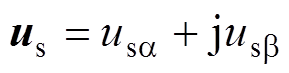
式中,I为单位矩阵;下标“a”和“b”分别为相应矢量在a 轴与b 轴上的投影;静止坐标系下的状态矩阵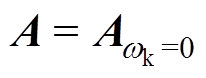 ;状态矩阵的矩阵指数
;状态矩阵的矩阵指数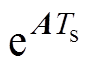 也称为状态转移矩阵,其麦克劳林级数如式(11)所示。传统的降阶离散方法等价于对矩阵指数
也称为状态转移矩阵,其麦克劳林级数如式(11)所示。传统的降阶离散方法等价于对矩阵指数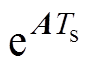 取降阶的近似,在低载波比下必然存在较大的离散化误差;如果对矩阵指数
取降阶的近似,在低载波比下必然存在较大的离散化误差;如果对矩阵指数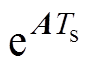 做更高阶的近似,则需要对状态矩阵A进行大量的幂运算,占用微处理器的大量计算资源,进而影响电机实时控制[21]。后文提出的特征根离散化方法可以很好地平衡计算量与离散化误差的关系。
做更高阶的近似,则需要对状态矩阵A进行大量的幂运算,占用微处理器的大量计算资源,进而影响电机实时控制[21]。后文提出的特征根离散化方法可以很好地平衡计算量与离散化误差的关系。
在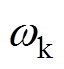 旋转参考坐标系下,系统的特征根方程为
旋转参考坐标系下,系统的特征根方程为
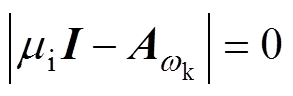 (12)
(12)
将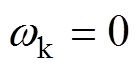 代入式(12)可得静止坐标系下的特征根
代入式(12)可得静止坐标系下的特征根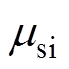 ,有
,有
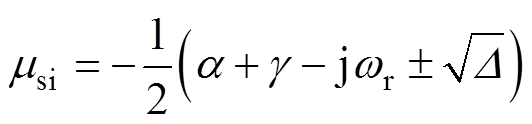 (13)
(13)
其中
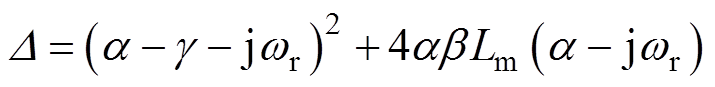
转子坐标系下的特征根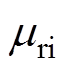 为静止坐标系下特征根减去转子旋转因子项,有
为静止坐标系下特征根减去转子旋转因子项,有
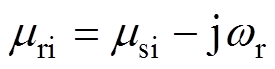 (14)
(14)
根据式(13)和式(14),静止坐标系和转子旋转参考系下的感应电机极点分布分别如图3中轨迹所示。当转速趋近于零时,主导极点离虚轴较近,系统的响应带宽较窄。而随着转速的升高,在任意坐标系下总有一簇极点的虚部迅速增大,极点的模不断增大表征系统状态变量的变化频率加快。由式(9)和式(11)可知,状态矩阵A与转子电角频率wr有关,在离散化频率一定时,随着转速的升高,状态转移矩阵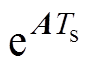 的展开式中高阶项的影响越大,降阶后的状态转移矩阵则难以在高速时准确地反映状态向量的变化,因此传统的降阶离散化方法在低载波比工况将出现过大的离散误差。
的展开式中高阶项的影响越大,降阶后的状态转移矩阵则难以在高速时准确地反映状态向量的变化,因此传统的降阶离散化方法在低载波比工况将出现过大的离散误差。
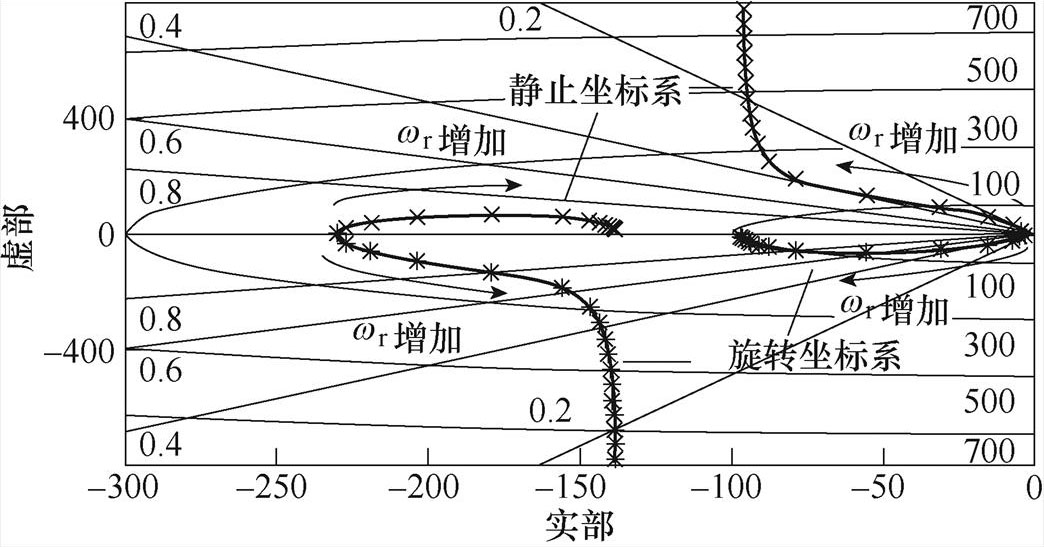
图3 感应电机在静止坐标系和转子旋转参考系下的极点分布轨迹
Fig.3 The root locus of induction machine in stationary and rotor reference frame
为了得到状态转移矩阵的精确解,在离散域下式(10)可以写成式(15)的形式,离散域下状态变量的精确解包含零输入响应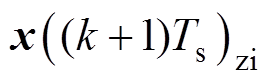 和零状态响应
和零状态响应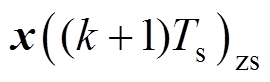 两部分,表示为
两部分,表示为
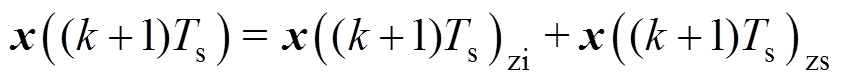 (15)
(15)
其中
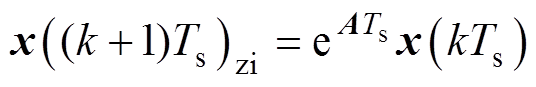 (16)
(16)
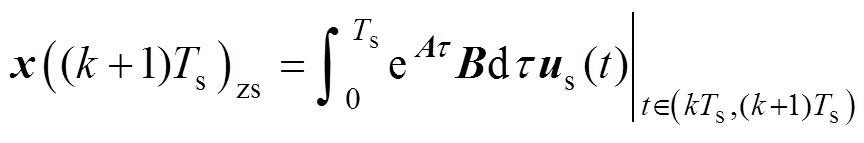 (17)
(17)
为了获得完全离散化的感应电机数学模型,需对离散状态方程中的系统矩阵F和输入矩阵G精确求解,有
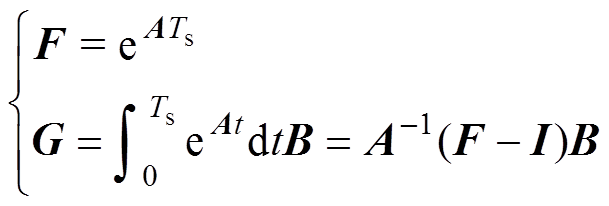 (18)
(18)
该方程本质是对系统矩阵F的精确求解。系统矩阵F的定义如式(11)所示,是关于转子速度的非线性矩阵函数,传统降阶近似计算不可避免引入近似误差,且随着转速升高而不断增加,而通过定义式完全求解该系统矩阵十分困难。
通过线性系统理论,矩阵指数精确求解有拉氏变换法、凯莱-哈密顿法和特征根法。拉氏变换法的计算如式(19)所示,其中,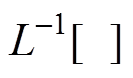 表示拉普拉斯反变换。该方法和凯莱-哈密顿法的实时求解较为复杂,具体方法本文不予展开。下面详细介绍特征根法的矩阵指数精确求解方法。
表示拉普拉斯反变换。该方法和凯莱-哈密顿法的实时求解较为复杂,具体方法本文不予展开。下面详细介绍特征根法的矩阵指数精确求解方法。
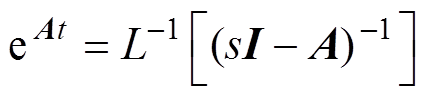 (19)
(19)
满秩的状态矩阵A可通过变换矩阵P进行对角化,对角矩阵对角线上的元素即为相应定转子电压方程的特征根如式(20)所示,分别为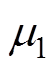 和
和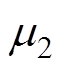 ,其解析解如式(13)所示。对角化后,状态矩阵A的矩阵指数的求解,可通过变换矩阵P和特征根矩阵指数进行求解,如式(21)所示。
,其解析解如式(13)所示。对角化后,状态矩阵A的矩阵指数的求解,可通过变换矩阵P和特征根矩阵指数进行求解,如式(21)所示。
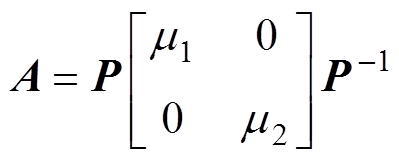 (20)
(20)
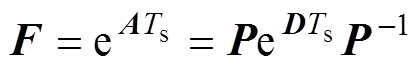 (21)
(21)
其中
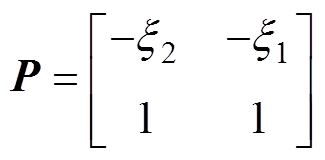
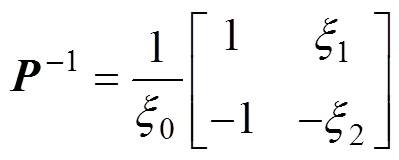
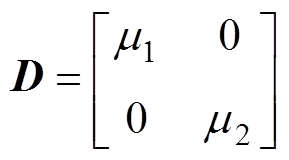
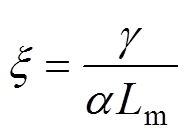
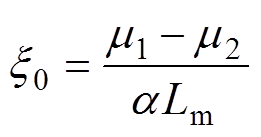
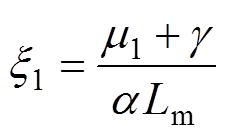
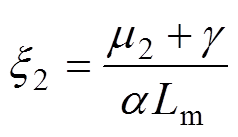
将上述中间参数代入式(21),可得状态矩阵指数和输入矩阵的精确解分别为
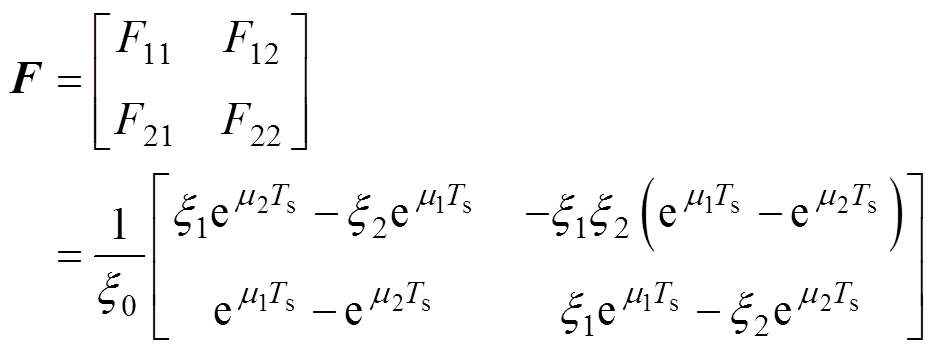 (22)
(22)
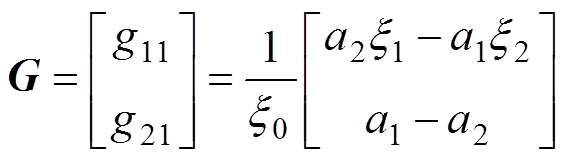 (23)
(23)
其中
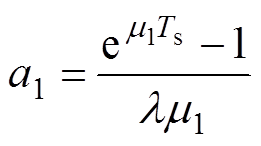
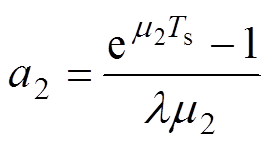
因此,结合式(15)~式(18)、式(22)和式(23)最终获得感应电机特征根离散化数学模型为
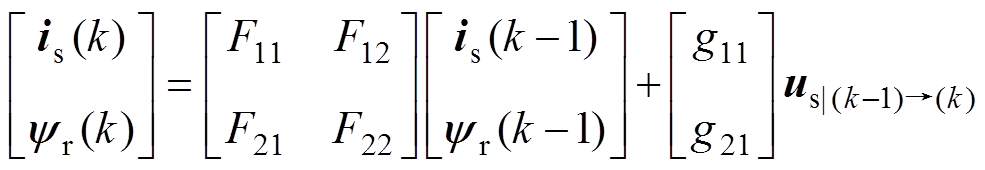 (24)
(24)
式中,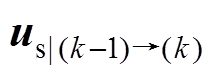 为从k-1时刻到k时刻的平均电压矢量。对式(24)进行Z变换,按行展开消去定子电流is(z),可求取z域的转子磁链的传递函数如式(25)所示,后文将依此进行离散精度的分析。其中,考虑控制系统的调制环节将引入半拍的延时,因此将输入的电压矢量us(z)乘以旋转因子
为从k-1时刻到k时刻的平均电压矢量。对式(24)进行Z变换,按行展开消去定子电流is(z),可求取z域的转子磁链的传递函数如式(25)所示,后文将依此进行离散精度的分析。其中,考虑控制系统的调制环节将引入半拍的延时,因此将输入的电压矢量us(z)乘以旋转因子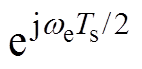 进行半拍的延时补偿,以抵消电压脉冲宽度调制(Pulse Width Modulation, PWM)延时带来的影响。
进行半拍的延时补偿,以抵消电压脉冲宽度调制(Pulse Width Modulation, PWM)延时带来的影响。
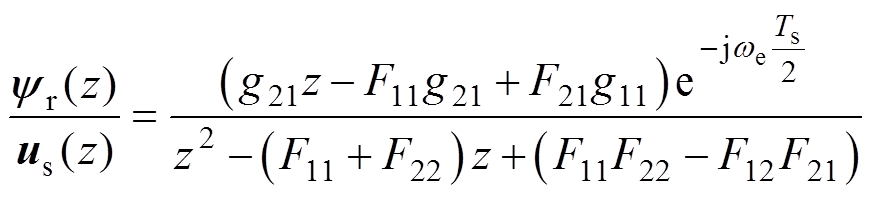 (25)
(25)
以Frobenius范数来表征矩阵数字特征,通过状态矩阵指数的近似程度进行定量分析[21],传统的离散化误差分析方法为
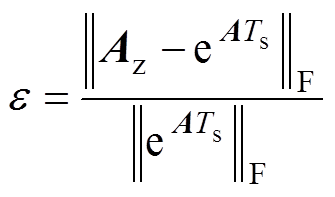 (26)
(26)
式中,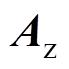 为
为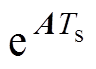 的近似解。
的近似解。
然而上述方法无法确定离散化误差对观测状态量的幅值和角度的影响。伯德图作为连续时间系统的一种分析方法,同样可以用于离散时间系统的分析,一种简化的分析手段是先通过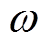 变换[23]将z平面的单位圆内部映射到
变换[23]将z平面的单位圆内部映射到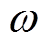 平面的整个左半平面,它等效于是将原本s左半平面的主带映射到了
平面的整个左半平面,它等效于是将原本s左半平面的主带映射到了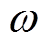 平面的整个左半平面,可在
平面的整个左半平面,可在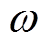 平面对关于
平面对关于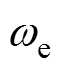 的传递函数进行频率特性分析,其中
的传递函数进行频率特性分析,其中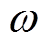 变换的定义式如(27)所示,但这种变换方式在
变换的定义式如(27)所示,但这种变换方式在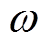 平面距离实轴越远的地方存在的失真越大。z平面和s平面存在准确的映射关系如(28)所示,将其代入到式(25)后,再将
平面距离实轴越远的地方存在的失真越大。z平面和s平面存在准确的映射关系如(28)所示,将其代入到式(25)后,再将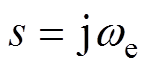 代入,可得到转子磁链从离散域映射到连续域的传递函数,通过Matlab绘图即可得到离散化模型的转子磁链的伯德图。本文提出基于伯德图的离散化误差分析方法,以转子磁链观测为例,将连续域数学模型的伯德图作为衡量标准,通过比较不同离散化模型的转子磁链幅值和角度偏差,从理论上验证了传统离散化模型的局限性和提出的特征根离散化模型的有效性。
代入,可得到转子磁链从离散域映射到连续域的传递函数,通过Matlab绘图即可得到离散化模型的转子磁链的伯德图。本文提出基于伯德图的离散化误差分析方法,以转子磁链观测为例,将连续域数学模型的伯德图作为衡量标准,通过比较不同离散化模型的转子磁链幅值和角度偏差,从理论上验证了传统离散化模型的局限性和提出的特征根离散化模型的有效性。
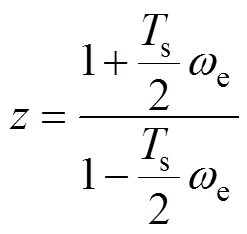 (27)
(27)
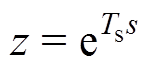 (28)
(28)
以图1为参考标准,通过传统离散模型的z域传递函数式(6)和式(7),零阶保持离散模型的传递函数式(8)和特征根离散模型的z域传递函数式(25)。在满载和空载时,分别绘出离散化频率为1 kHz时的伯德图,如图4和图5所示。
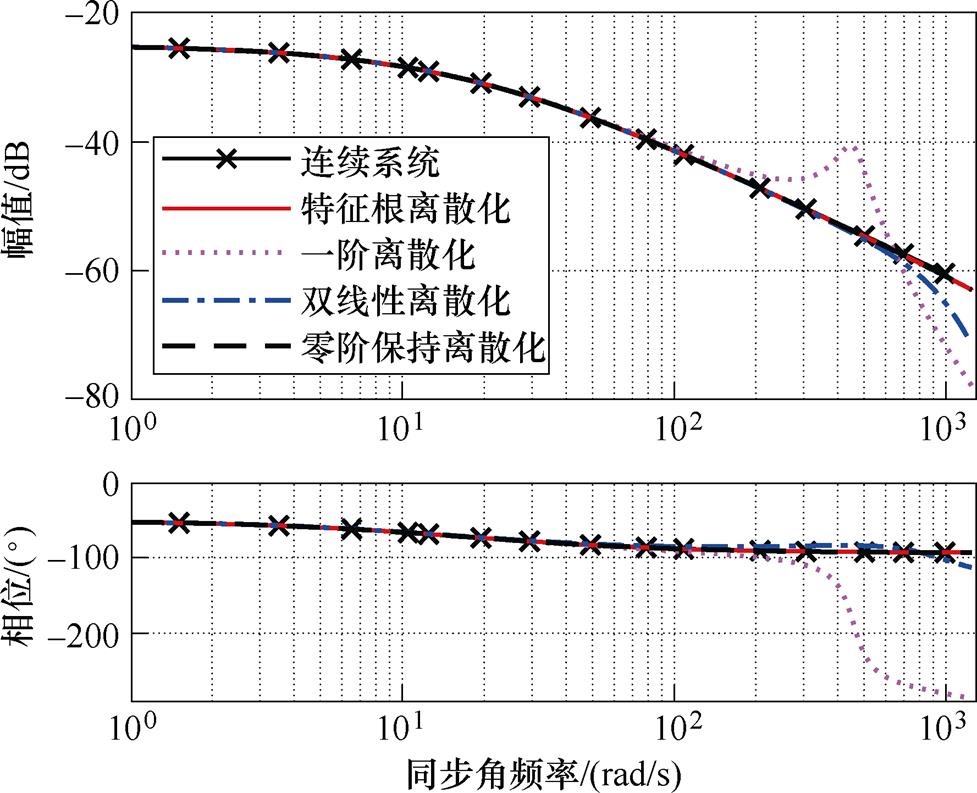
图4 1 kHz离散化频率下满载时不同离散化模型的伯德图对比
Fig.4 The comparative results of Bode plots between different discretization models under full load at 1 kHz discretization frequency
在图4和图5中,随着电频率的上升,不同离散化模型的误差在满载与空载的情况下,表现出相同的变化规律。随着转速的上升,传统一阶离散化模型与二阶离散化模型在幅值和相位曲线和连续系统相比均出现较大的偏差,且随着频率增加逐渐恶化,同样无法适用于低载波比的场合,而提出的特征根离散化模型仍然和连续系统模型高度吻合,离散化误差较小。
基于Matlab/Simulink对本文的研究内容进行了仿真验证,仿真和实验所用感应电机参数见表1,逆变器允许的最大开关频率为500 Hz,采用非对称采样模式,故采样频率为1 kHz,所有观测器及控制算法均在PWM中断中进行。
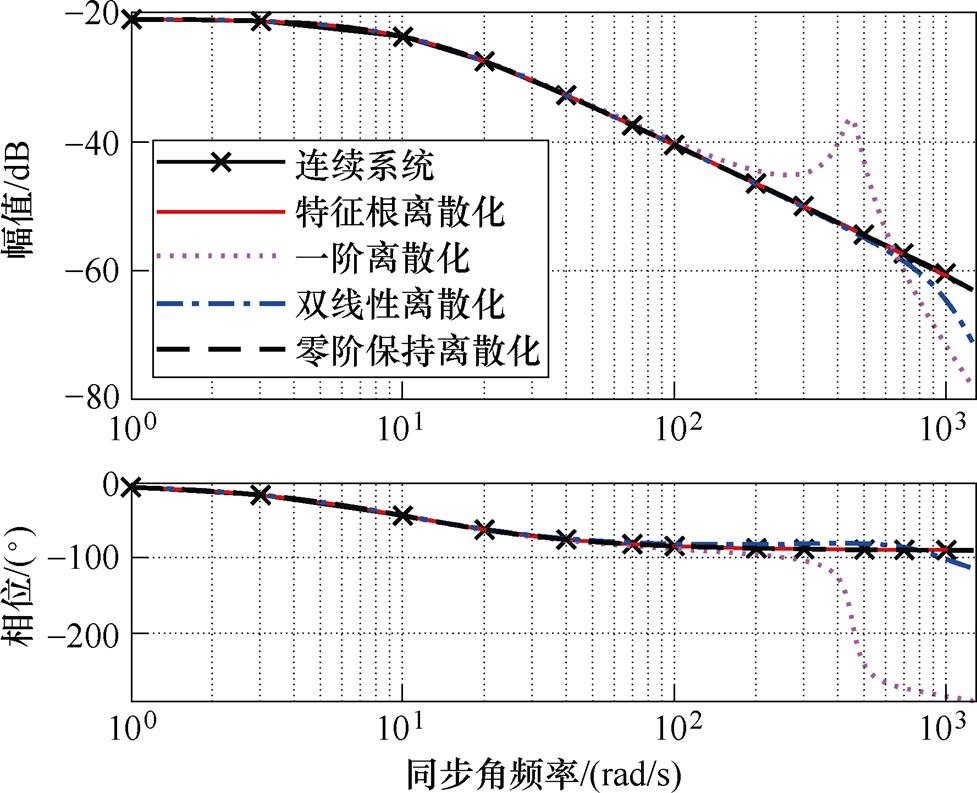
图5 1 kHz离散化频率下空载时不同离散化模型的伯德图对比
Fig.5 The comparative results of Bode plots between different discretization models under no-load at 1 kHz discretization frequency
表1 2.2 kW感应电机参数
Tab.1 The parameters of 2.2 kW induction machine
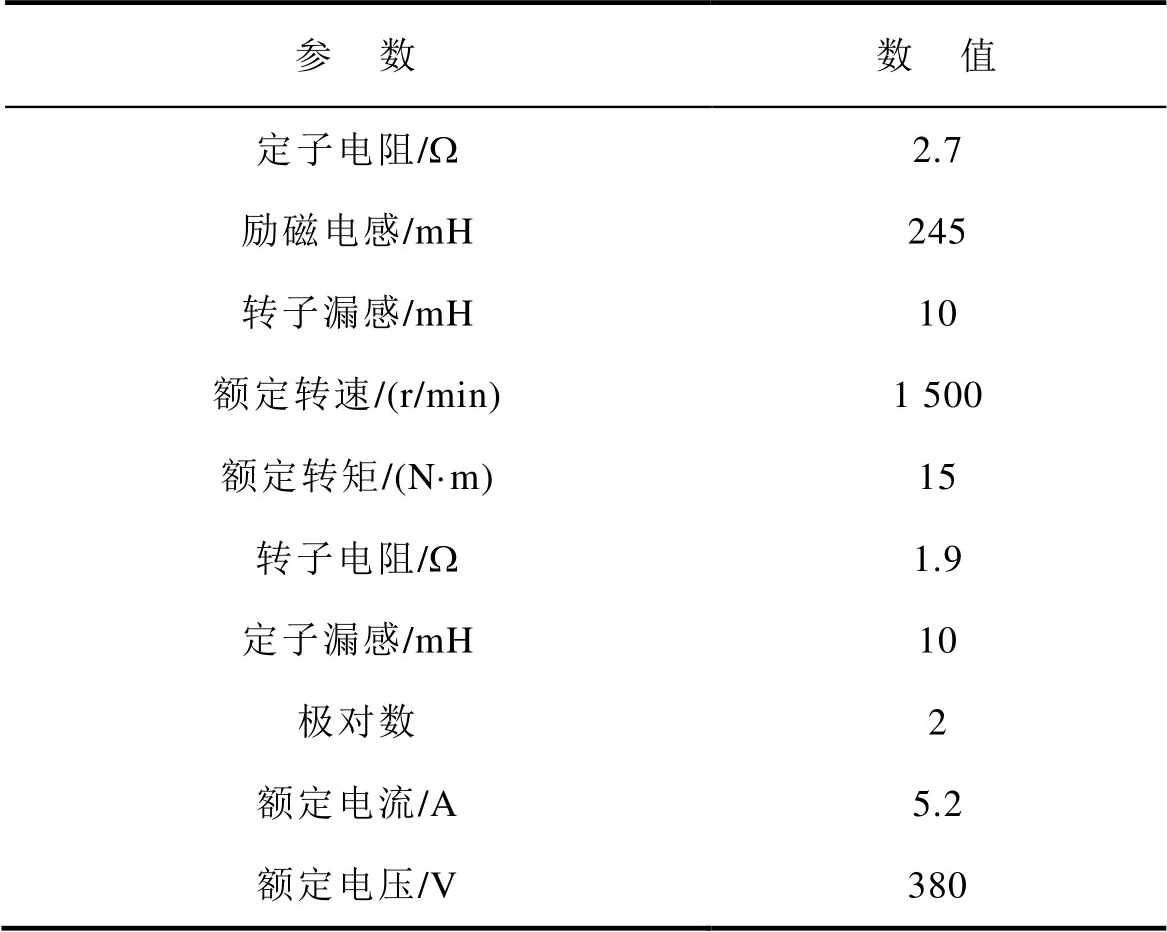
参 数数 值 定子电阻/W2.7 励磁电感/mH245 转子漏感/mH10 额定转速/(r/min)1 500 额定转矩/(N·m)15 转子电阻/W1.9 定子漏感/mH10 极对数2 额定电流/A5.2 额定电压/V380
图6为电机升速过程中一阶欧拉离散化模型的观测波形。图中,ia为a相电流,Dqe为转子磁场角度误差,fe为电频率,在所有仿真结果中均表示此含义。在中高速时电流观测出现发散不收敛趋势。随着转速的上升,观测的转子磁场角度和真实角度的偏差越来越大。
图7为不同离散模型观测的转子磁场角度和真实转子磁场角度的误差对比波形,在载波比为5时,二阶双线性离散化模型转子磁场角度和真实值偏差高达20°,而零阶保持离散化和特征根离散化模型观测得到的转子磁场角度稳态误差较小,磁场角度误差均在1°左右。
图8为在高速3 000 r/min,载波比低至5时的稳态观测电流对比。传统的二阶双线性离散化模型观测电流幅值和相位均出现了较大的稳态误差,而零阶保持离散化模型和特征根离散化模型的观测电流和真实电流基本一致。
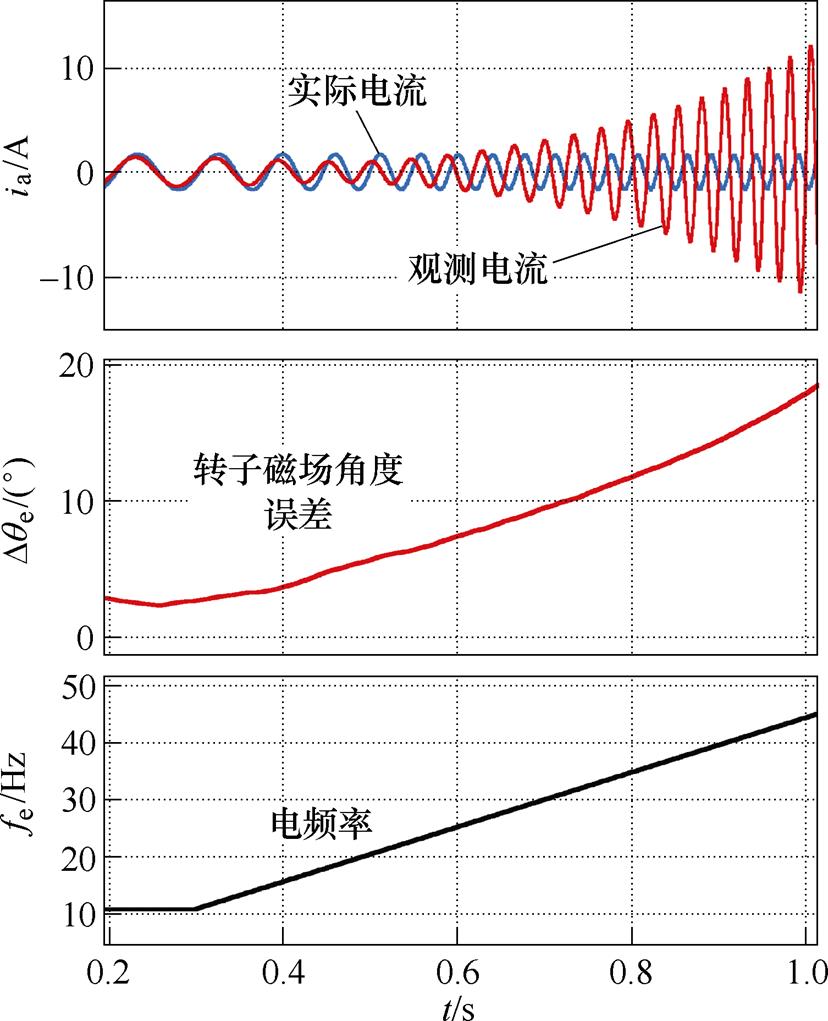
图6 一阶欧拉离散化模型在升速时的观测波形
Fig.6 The observed waveforms of the first order Euler discretized model during acceleration
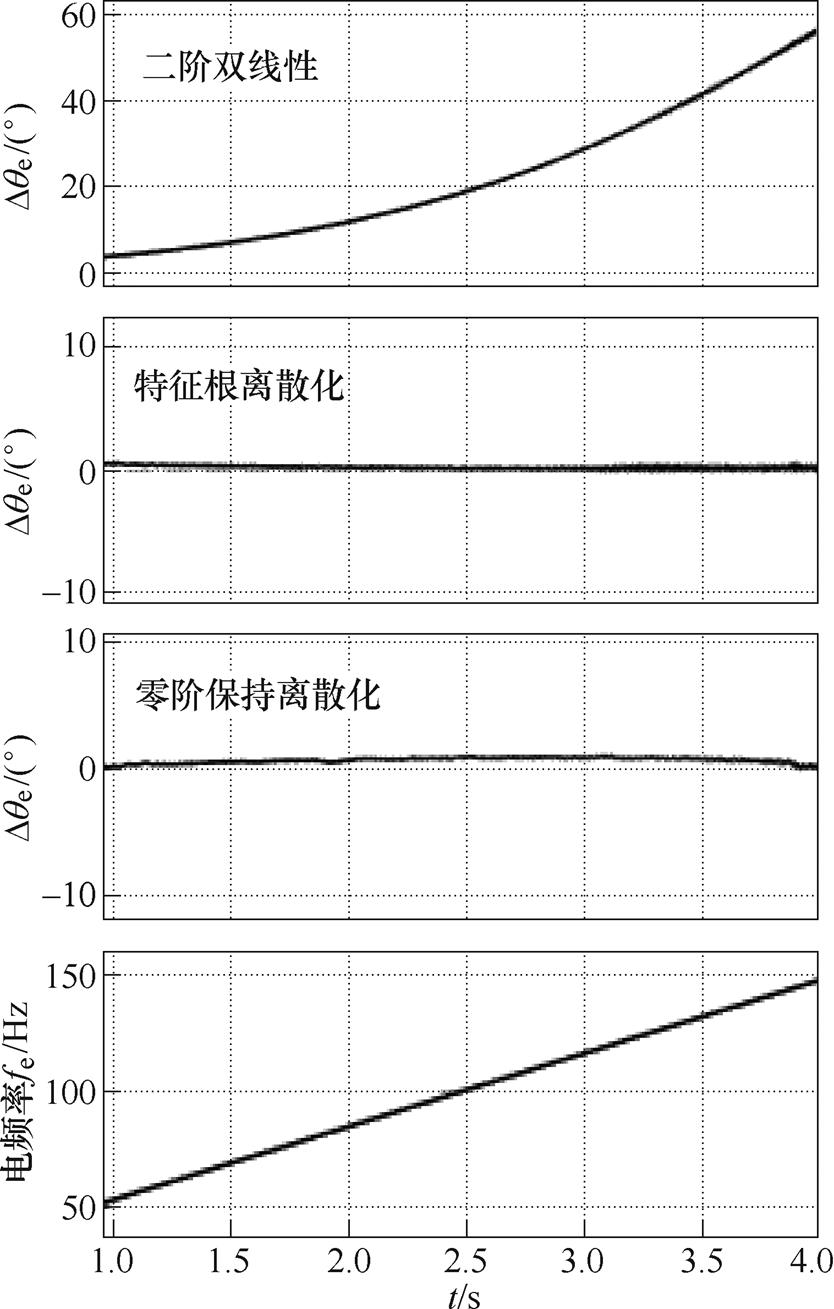
图7 不同离散化模型观测磁链角度的误差大小对比
Fig.7 Comparison of rotor flux angle errors predicted between different discrete models
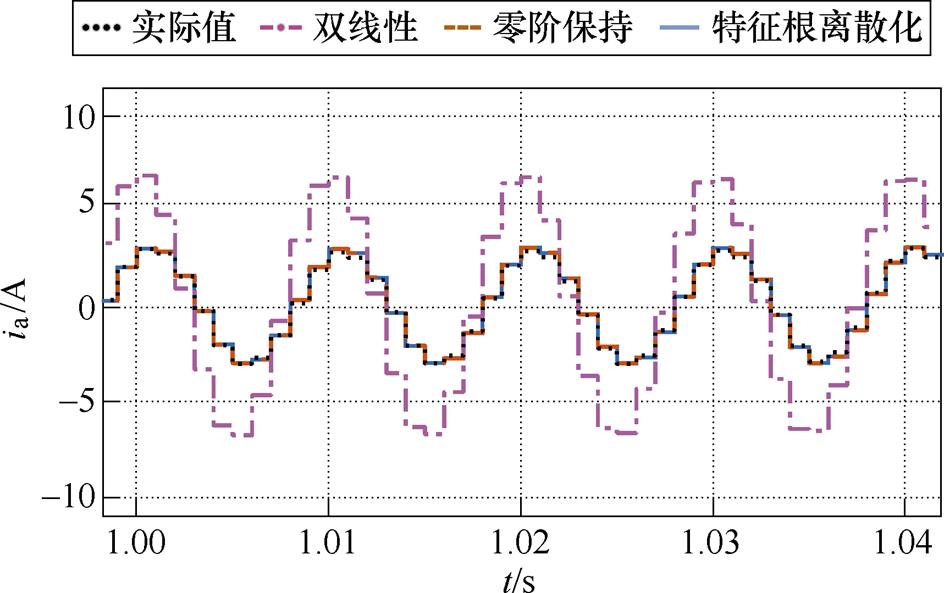
图8 不同离散模型稳态电流波形对比(3 000 r/min)
Fig.8 Steady-state current waveform comparison between different discrete models at 3 000 r/min
图9为转速为2 160 r/min,在0.8 s时刻转矩从1 N·m阶跃上升至3 N·m时,不同离散化模型观测的电流与实际电流ireal对比。在转矩暂态工况时,二阶双线性模型的观测电流isecd出现了明显的幅值误差与相位误差,而零阶保持模型的观测电流izoh与特征根离散化模型的观测电流ieigen也受到了转矩突变带来的影响,产生了电流幅值的观测误差。产生电流观测误差的原因在于转矩突变带来了转差频率的突变,时变量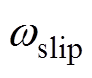 不仅会影响基于频域下的传递函数推导得到的零阶保持模型,同时也会影响采用状态空间方式描述的特征根离散化模型。
不仅会影响基于频域下的传递函数推导得到的零阶保持模型,同时也会影响采用状态空间方式描述的特征根离散化模型。
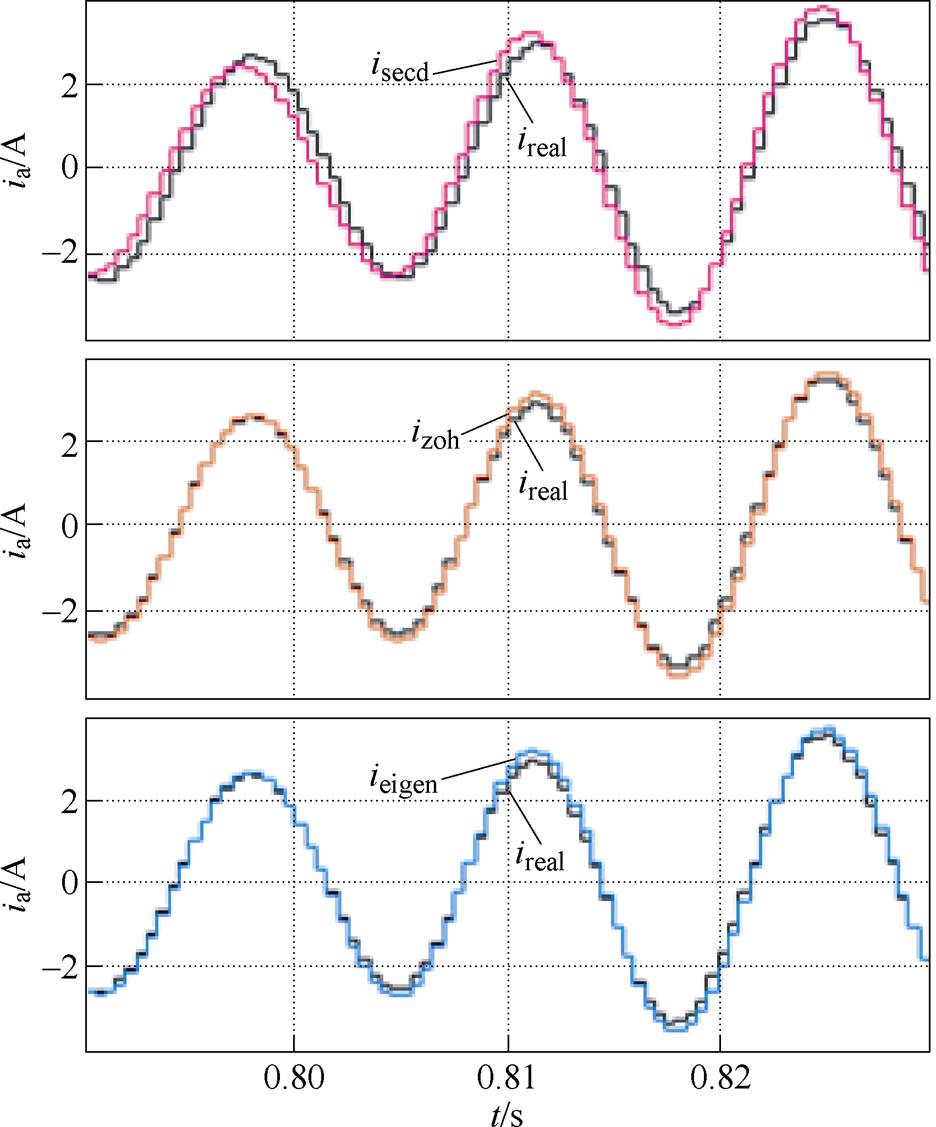
图9 不同离散化模型在转矩阶跃时的电流波形对比(2 160 r/min)
Fig.9 Comparison of current waveforms of different discrete models during torque step at 2 160 r/min
图10为降速过程的暂态电流波形对比。在转速暂态工况时,零阶保持离散化模型在电流观测上出现了一定的幅值和相位偏差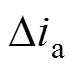 ,幅值偏差最大高达30%,速度进入稳态后,偏差消失。而特征根离散化模型在暂态和稳态均具有良好性能。其原因在于在速度变化过程中,传递函数式(3)中的
,幅值偏差最大高达30%,速度进入稳态后,偏差消失。而特征根离散化模型在暂态和稳态均具有良好性能。其原因在于在速度变化过程中,传递函数式(3)中的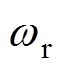 为时变变量,基于频域下的传递函数推导得到的零阶保持模型,无法考虑这种时变性,且当
为时变变量,基于频域下的传递函数推导得到的零阶保持模型,无法考虑这种时变性,且当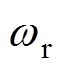 变化率越大时,这种由时变性导致的误差就越大。图9与图10的仿真结果也进一步体现了从状态空间角度设计的特征根离散化模型在暂态跟踪效果相对于零阶保持模型要更好,且更多地体现在降速过程中,特征根离散化模型具有更优的暂态观测结果。
变化率越大时,这种由时变性导致的误差就越大。图9与图10的仿真结果也进一步体现了从状态空间角度设计的特征根离散化模型在暂态跟踪效果相对于零阶保持模型要更好,且更多地体现在降速过程中,特征根离散化模型具有更优的暂态观测结果。
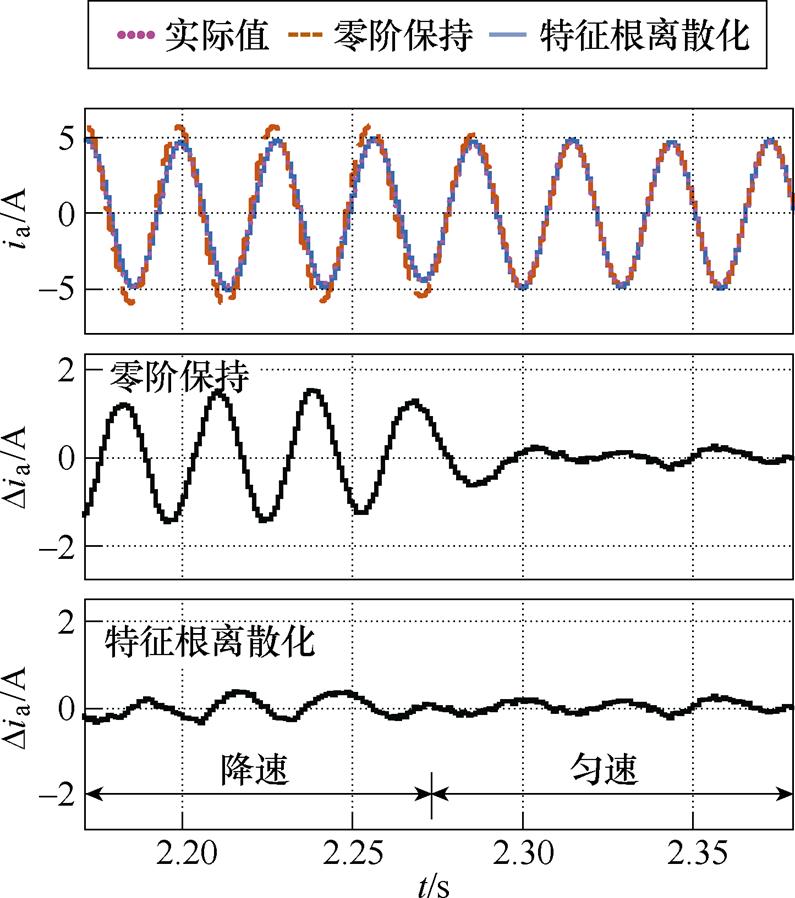
图10 零阶保持和特征根离散模型在降速时的电流波形对比
Fig.10 Comparison of current waveforms between zero-order hold model and full discrete model at deceleration condition
为进一步验证本文的分析结果,采用dSPACE公司MicroLabBox控制器对文中的离散化数学模型进行了实验验证,小功率异步电机实验平台如图11所示,包括被试电机及其驱动器和控制器、陪试电机、高压电源、低压电源、调试计算机、示波器、变频器等。电机运行在基于特征根离散化模型设计的无差拍预测控制策略下,开关频率为500 Hz,采用非对称采样方式,计算和采样频率为1 kHz。离散化模型计算均由PWM中断同步触发运行,观测器输出的电流、转子磁链、磁场角度、电频率等变量通过D-A转换输出,实际电流通过录波仪实时记录。

图11 小功率异步电机实验平台
Fig.11 Small power asynchronous motor experimental platform
图12为升速实验中一阶欧拉离散化模型在中高速下的观测波形。在频率为20 Hz左右,一阶离散化模型观测的电流ifir出现明显观测误差,且随着转速的上升,观测的电流开始出现发散趋势,和仿真(见图6)基本一致,而特征根离散化模型的观测电流ieigen观测误差较小。
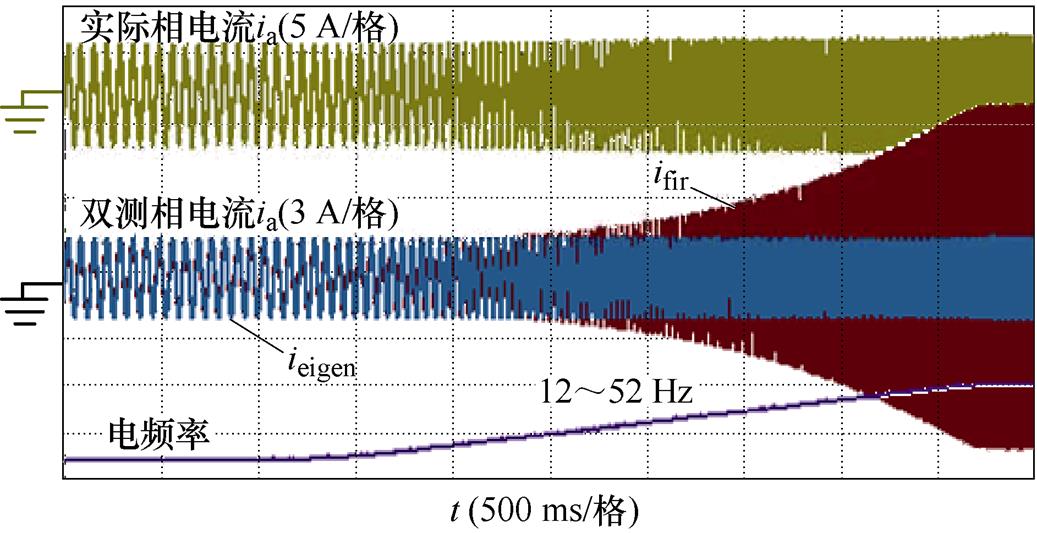
图12 一阶欧拉离散化模型在中高速下的观测波形
Fig.12 Observed waveforms of first-order Euler discretized model at medium and high speeds
图13为高速下,载波比为7时,不同观测器的观测电流稳态对比波形。图中,ia为电流探头采样的电流信号,同步采样电流ia_syn为A-D在PWM中断中采样的真实A相电流信号,再通过D-A从3个通道输出作为其他观测器的参考波形。其中,二阶双线性模型观测电流isecd在低载波比下能维持稳定,但观测的电流幅值和相位出现了较大误差,提出的零阶保持观测电流izoh和特征根离散化模型观测电流ieigen均能很好地跟踪实际同步采样电流。
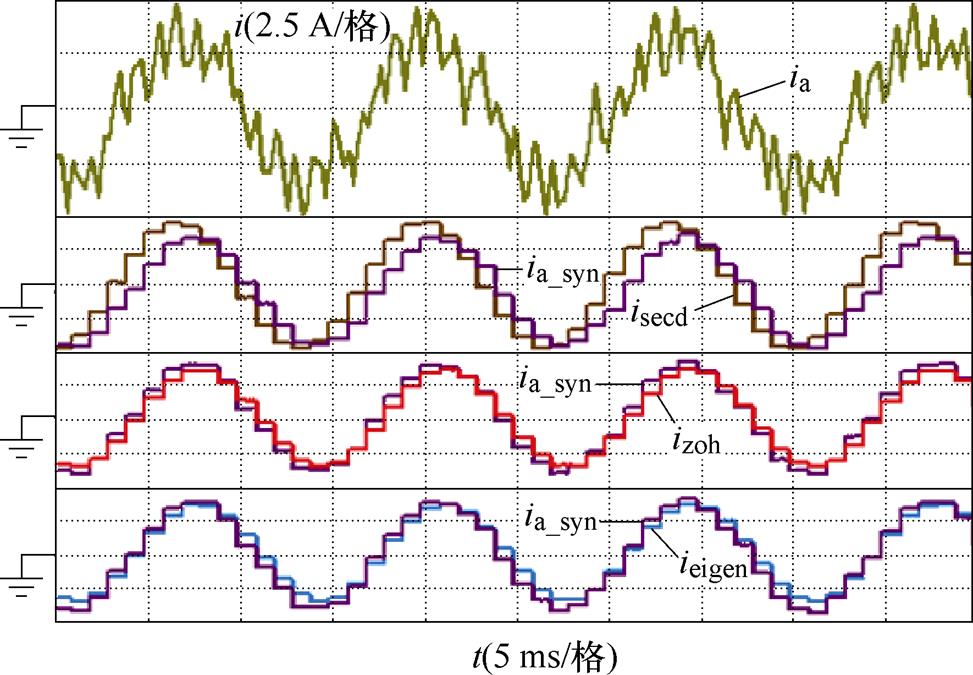
图13 不同离散化模型的稳态电流波形(2 160 r/min)
Fig.13 Steady-state current observation waveforms between different discrete models at 2 160 r/min
图14为2 160 r/min时,转矩从1 N·m升至3 N·m再降至1 N·m时的暂态电流波形对比,转矩阶跃时,二阶双线性离散化模型的观测电流出现了明显的相位误差,而零阶保持模型和特征根离散化模型的观测电流也出现了一定的观测误差,与仿真结果图9一致,但相比于二阶双线性离散化模型具有更好的动态跟随性能。
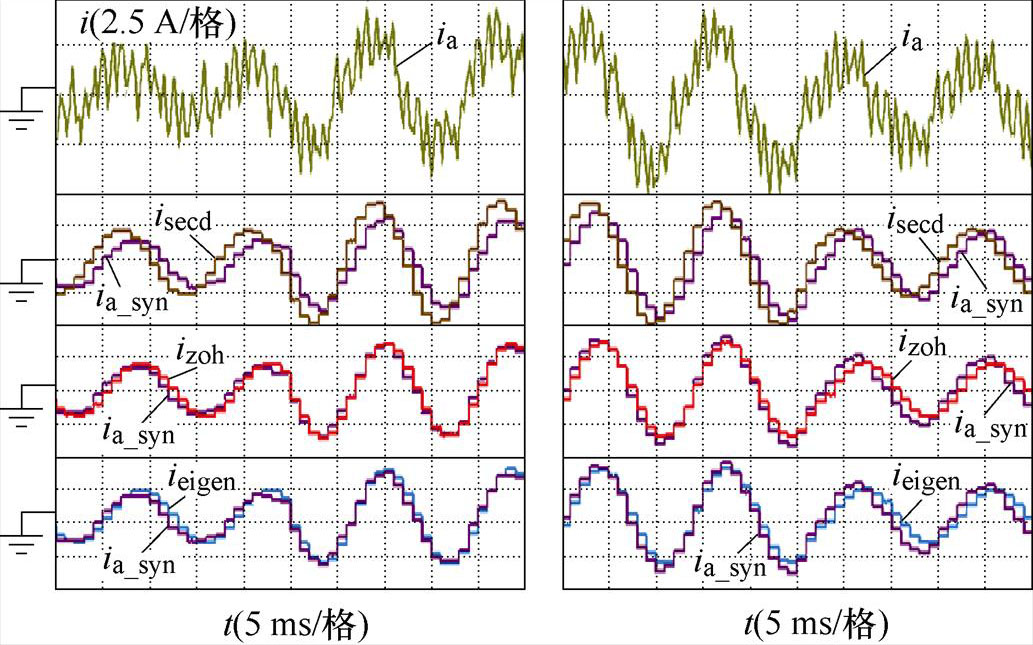
(a)转矩突增 (b)转矩突减
图14 转矩阶跃时的观测波形对比(2 160 r/min)
Fig.14 Comparison of observed waveforms during torque step at 2 160 r/min
图15为三种离散模型的转子磁场角度在稳态下的对比波形,由于真实的磁场角度未知,各个模型的磁场角度通过互相印证进行说明。在2 400 r/min时,特征根离散化模型和零阶保持器模型所对应的磁场角度具有较好的一致性,而二阶双线性模型和其他模型相比存在较大的偏差,约为10°,和仿真图7在80 Hz时二阶双线性模型对应的角度误差结果基本一致。
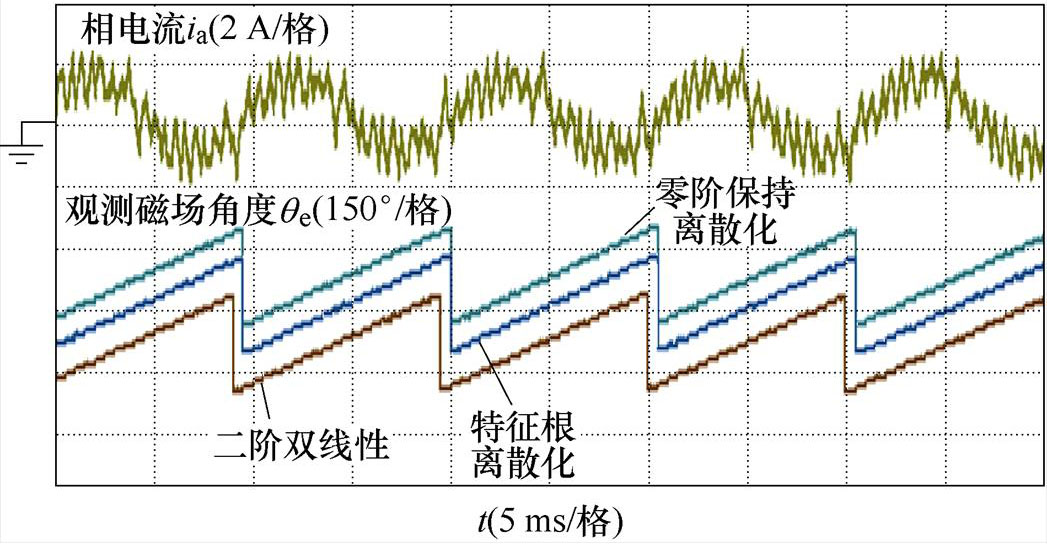
图15 2 400 r/min时的转子磁场角度对比
Fig.15 Comparison of rotor magnetic field angles at 2 400 r/min
本文对低载波比下的感应电机离散模型和离散化误差分析方法展开了研究,主要取得了以下成果:
1)提出了感应电机特征根离散化模型,该模型在全速度范围内均能实现高精度的转子磁链和定子电流观测,在载波比低至5时,磁链角度观测误差小于1°,相比于传统二阶双线性模型高达20°的角度偏差,大大提升了模型的稳态精度,同时仿真和实验也验证了该模型具有良好的稳态精度和暂态跟随性能。
2)推导了不同离散模型的z域传递函数,提出了基于伯德图的离散误差定量分析方法。该方法克服了传统基于矩阵误差的方法无法分析离散误差对状态量的幅值和相位影响的缺点,通过对比不同离散模型和连续模型的伯德图,从理论上验证了传统方法的局限性和提出方法的优越性。
参考文献
[1] Odhano S A, Pescetto P, Ali Awan H A, et al. Parameter identification and self-commissioning in AC motor drives: a technology status review[J]. IEEE Transactions on Power Electronics, 2019, 34(4): 3603-3614.
[2] Zhao Lihang, Huang Jin, Chen Jiahao, et al. A parallel speed and rotor time constant identification scheme for indirect field oriented induction motor drives[J]. IEEE Transactions on Power Electronics, 2016, 31(9): 6494-6503.
[3] 李婕, 杨淑英, 谢震, 等. 基于有效信息迭代快速粒子群优化算法的永磁同步电机参数在线辨识[J]. 电工技术学报, 2022, 37(18): 4604-4613.
Li Jie, Yang Shuying, Xie Zhen, et al. Online para- meter identification of permanent magnet syn- chronous motor based on fast particle swarm optimization algorithm with effective information iterated[J]. Transactions of China Electrotechnical Society, 2022, 37(18): 4604-4613.
[4] 徐伟, 董定昊, 葛健, 等. 基于在线参数辨识补偿的直线感应电机低开关频率模型预测控制策略[J]. 电工技术学报, 2022, 37(16): 4116-4133.
Xu Wei, Dong Dinghao, Ge Jian, et al. Low switching frequency model predictive control strategy based on online parameter identification compensation of linear induction motor for urban rail application[J]. Transa- ctions of China Electrotechnical Society, 2022, 37(16): 4116-4133.
[5] 黄科元, 周佳新, 刘思美, 等. 考虑逆变器非线性永磁同步电机高频注入电感辨识方法[J]. 电工技术学报, 2021, 36(8): 1607-1616.
Huang Keyuan, Zhou Jiaxin, Liu Simei, et al. Indu- ctance identification method of permanent magnet synchronous motor considering inverter nonlinearity based on high-frequency injection[J]. Transactions of China Electrotechnical Society, 2021, 36(8): 1607-1616.
[6] 刘亚静, 段超. 全数字自适应滤波器不同离散结构的性能对比分析[J]. 电工技术学报, 2021, 36(20): 4339-4349.
Liu Yajing, Duan Chao. Performance comparison and analysis of all-digital adaptive filter with different discrete methods[J]. Transactions of China Electro- technical Society, 2021, 36(20): 4339-4349.
[7] Xu Yang, Morito C, Lorenz R D. Accurate discrete- time modeling for improved torque control accuracy for induction machine drives at very low sampling- to-fundamental frequency ratios[J]. IEEE Transa- ctions on Transportation Electrification, 2020, 6(2): 668-678.
[8] 孙建业, 王志强, 谷鑫, 等. 高速低载波比下永磁同步电机预测电流控制[J]. 中国电机工程学报, 2020, 40(11): 3663-3672.
Sun Jianye, Wang Zhiqiang, Gu Xin, et al. Predictive current control of permanent magnet synchronous motor under high speed and low carrier ratio[J]. Proceedings of the CSEE, 2020, 40(11): 3663-3672.
[9] 李杰, 詹榕, 宋文祥. 感应电机低采样频率的磁链观测器离散化模型研究[J]. 电工技术学报, 2019, 34(15): 3136-3146.
Li Jie, Zhan Rong, Song Wenxiang. Improved discrete observer model of induction motor at low sampling frequency[J]. Transactions of China Electrotechnical Society, 2019, 34(15): 3136-3146.
[10] 罗慧. 感应电机全阶磁链观测器和转速估算方法研究[D]. 武汉: 华中科技大学, 2009.
[11] Diao Lijun, Sun Danan, Dong Kan, et al. Optimized design of discrete traction induction motor model at low-switching frequency[J]. IEEE Transactions on Power Electronics, 2013, 28(10): 4803-4810.
[12] Wang Bo, Zhao Yongzheng, Yu Yong, et al. Speed- sensorless induction machine control in the field- weakening region using discrete speed-adaptive full- order observer[J]. IEEE Transactions on Power Elec- tronics, 2016, 31(8): 5759-5773.
[13] 李昱, 郭宏, 平朝春, 等. 基于电流源变流器的永磁同步电机驱动系统全状态变量预测转矩控制[J]. 电工技术学报, 2021, 36(1): 15-26.
Li Yu, Guo Hong, Ping Zhaochun, et al. A full-state variable predictive torque control of current source converter fed permanent magnet synchronous motor drives[J]. Transactions of China Electrotechnical Society, 2021, 36(1): 15-26.
[14] Holtz J, Quan Juntao, Pontt J, et al. Design of fast and robust current regulators for high-power drives based on complex state variables[J]. IEEE Transactions on Industry Applications, 2004, 40(5): 1388-1397.
[15] 国敬, 范涛, 章回炫, 等. 高速低载波比下永磁同步电机电流环稳定性分析[J]. 中国电机工程学报, 2019, 39(24): 7336-7346, 7506.
Guo Jing, Fan Tao, Zhang Huixuan, et al. Stability analysis of permanent magnet synchronous motor current loop control at high speed and low carrier ratio[J]. Proceedings of the CSEE, 2019, 39(24): 7336-7346, 7506.
[16] Kim H, Degner M, Guerrero J M, et al. Discrete-time current regulator design for AC machine drives[C]// 2009 IEEE Energy Conversion Congress and Expo- sition, San Jose, CA, USA, 2009: 1317-1324.
[17] Jarzebowicz L. Errors of a linear current approxi- mation in high-speed PMSM drives[J]. IEEE Transa- ctions on Power Electronics, 2017, 32(11): 8254- 8257.
[18] Jarzebowicz L. Quasi-discrete modelling of PMSM phase currents in drives with low switching-to- fundamental frequency ratio[J]. IET Power Electro- nics, 2019, 12(12): 3280-3285.
[19] Dai Shangjian, Wang Jiabin, Sun Zhigang, et al. Deadbeat predictive current control for high-speed permanent magnet synchronous machine drives with low switching-to-fundamental frequency ratios[J]. IEEE Transactions on Industrial Electronics, 2022, 69(5): 4510-4521.
[20] West N T, Lorenz R D. Digital implementation of stator and rotor flux-linkage observers and a stator- current observer for deadbeat direct torque control of induction machines[J]. IEEE Transactions on Industry Applications, 2009, 45(2): 729-736.
[21] 赵雷廷, 刁利军, 董侃, 等. 基于状态空间拆分重组的牵引异步电机闭环离散全阶转子磁链观测器[J]. 电工技术学报, 2013, 28(10): 103-112.
Zhao Leiting, Diao Lijun, Dong Kan, et al. A novel discretized closed-loop full-order rotor flux observer for induction motor based on re-organization of state space[J]. Transactions of China Electrotechnical Society, 2013, 28(10): 103-112.
[22] Jean C A. Direct eigen control for induction machines and synchronous motors[M]. United Kingdom: John Wiley&Sons, 2013.
[23] 尾形克彦 (Katsuhiko Ogata). 离散时间控制系统[M]. 陈杰, 蔡涛, 张娟, 等译. 北京: 机械工业出版社, 2006.
Research on Discretization Model of Induction Motor for Low Switching-to-Fundamental Frequency Ratio Traction System
Abstract In high-power and high-speed motor drives, the control system will operate in low switching- to-fundamental frequency ratio conditions. Due to the large discretization error, the traditional reduced-order discrete model cannot be applied to the control system. Therefore, this paper proposes an eigenvalue-based discrete induction motor model, which still has good steady-state accuracy and transient tracking performance under a low switching-to-fundamental frequency ratio. At the same time, a quantitative analysis method of discretization error based on the Bode diagram is proposed.
Firstly, the mathematical model of the induction motor is modeled in the continuous domain using state space description. The full-rank state matrix is diagonalized through the transformation matrix. The elements on the diagonal of the diagonal matrix are the characteristic roots of the corresponding stator and rotor voltage equations of the induction motor. Then, the exact solution of the system matrix can be obtained through the transformation matrix and the diagonal matrix, and the eigenvalue-based discrete model of the induction motor is derived. Moreover, by deducing the z-domain transfer function of flux linkage observation of different discrete models, the Bode diagram is drawn. Taking the Bode diagram of the continuous model as the evaluation standard, the traditional and the proposed discrete models’ errors in the magnitude and phase of flux linkage observation is compared.
The simulation and experimental results show that in terms of the steady-state observation accuracy, at the electric frequency of about 20 Hz, the observed current of the first-order discretization model has an obvious observation error. In contrast, the observed current of the eigenvalue-based discrete model has a small observation error. When the switching-to-fundamental frequency ratio is seven, the observed current of the second-order bilinear model can maintain stability. However, the observed current amplitude and phase have large errors, while the observed current of the characteristic root discretization model can track the actual synchronous sampling current. Regarding dynamic observation accuracy, in speed reduction, the zero-order holder discrete model has a specific amplitude and phase deviation in current observation. The maximum amplitude deviation is up to 30%, and the deviation disappears after the speed enters the steady state. The eigenvalue-based discrete model has good performance in both transient and steady speeds.
The following conclusions can be drawn: (1) The proposed discrete model of the characteristic root of the induction motor can achieve high-precision rotor flux and stator current observation in the full-speed range. When the switching-to-fundamental frequency ratio is as low as five, the observation error of the flux angle is less than 1°. (2) Compared with the zero-order holder discretization model, the proposed eigenvalue-based discrete model has higher current observation accuracy in speed reduction.
keywords:Induction machine, discretization method, transfer function, Bode plot, low switching-to- fundamental frequency ratio
DOI: 10.19595/j.cnki.1000-6753.tces.222046
中图分类号:TM301.2
收稿日期 2022-10-28
改稿日期 2023-01-19
张钦培 男,1998年生,硕士研究生,主要研究方向为感应电机数学模型与控制策略。E-mail: zqp@hust.edu.cn
李 健 男,1982年生,研究员,博士生导师,主要研究方向为大功率牵引变流器控制方面的理论和技术开发。E-mail: jianli@hust.edu.cn(通信作者)
(编辑 崔文静)