
图1 V型定子HPLUM结构示意图
Fig.1 Configuration of the HPLUM with V-shape stator
摘要 物理场分析对于大功率直线超声波电机的设计与优化至关重要,该文提出一种基于场路结合的超声波电机压电-热-结构多物理场解耦分析方法,解决了超声波电机传统多物理场分析方法无法兼顾分析效率与计算精度的问题。基于场的观点建立压电-结构耦合以及热-结构耦合有限元模型,基于路的观点构建定子电-振-热耦合损耗计算模型及其二维热网络模型,在此基础上通过超声波电机内部固有的电-振-热耦合效应实现压电-热-结构多物理场耦合分析,并实现了对多场耦合作用下电机作动性能、电气特性、温升特性以及关键部件机械强度的快速同步评估。利用该方法对一台V型定子大功率直线超声波电机进行理论建模与分析,仿真和实验结果表明,所提出的方法可为大功率直线超声波电机的多物理场分析及多场耦合优化设计提供理论参考。
关键词:超声波电机 多物理场 场路结合 性能评估
超声波电机是一种利用压电陶瓷逆压电效应激发弹性体(定子)机械共振,并通过定转(动)子的接触与摩擦直接输出动力的一种新型特种电机,具有结构简单紧凑、断电自锁、抗磁场干扰能力强等独特优点[1-2]。而大功率直线超声波电机(High- Power Linear Ultrasonic Motor, HPLUM)兼具高速大推力、直接输出直线运动等优点,在航空航天、半导体制造等需要较大功率的场合,相较于传统mW级直线超声波电机更具优势。然而,为了获得较大的输出功率,HPLUM通常需要较高驱动电压[3],这使得电机关键部件(如压电陶瓷)的机械强度、温升与电机机械特性之间的矛盾愈加突出,已成为高性能HPLUM优化设计亟待解决的问题。
精准高效的多物理场分析对于电机的设计与优化至关重要,而基于传统有限元法的超声波电机多物理场分析方法无法兼顾分析效率与计算精度的问题[4-6]。Zhou Lifeng等[7]基于能量原理建立了V型定子HPLUM的压电-热-结构耦合解析动力学模型,分析了电机的热-机-电耦合动力学,相比传统的有限元法更具时效性,但该方法普适性较差,不易推广。王鑫等[8]采用传递矩阵法建立一款贴片式直线超声波电机定子的压电-结构耦合动力学模型,并对定子结构进行了优化设计,拓展了超声波电机多场耦合建模方法,但此方法需要进行结构离散化,构建过程较为繁琐。场路结合方法已在电磁电机多物理场优化设计方面取得了显著成效[9-12],其基本思路是:基于“场”的观点建立电机电磁耦合特性的精确计算模型,基于“路”的观点建立计算电机各部件温升的热路模型,实现电机内部电磁惯性(ms级)与热惯性(min级)的解耦计算。赵能桐等[13]基于场路结合法分析了大功率超磁致伸缩电声换能器的阻抗特性,对该型换能器的电-声耦合分析与结构优化设计具有重要的指导意义。Li Xiang等[14]基于场路结合思想,建立了HPLUM的快速温升预测模型,为超声波电机的热分析提供了新的思路,但并未对热-机-电耦合作用下电机的输出性能进行深入研究。
为了解决超声波电机传统多物理场分析方法无法兼顾分析效率与计算精度的问题,提出一种基于场路结合的超声波电机压电-热-结构多物理场分析方法,基于“场”的观点建立压电-结构耦合以及热-结构耦合有限元模型,基于“路”的观点构建定子电-振-热耦合损耗计算模型以及电机二维热路模型,同时将电机几何-机-电多域参数作为输入,通过超声波电机内部固有的电-振-热耦合效应实现压电-热-结构多物理场耦合分析,并实现对多场耦合作用下电机作动性能、电气特性、温升特性以及关键部件机械强度的快速同步评估。最后,利用该方法对一台V型定子HPLUM进行多场耦合建模与分析,并通过搭建实验平台进行验证,结果表明,所提出的多物理场分析方法可为HPLUM的多场耦合分析及优化设计提供理论参考与技术支撑。
图1为V型定子HPLUM的结构示意图,主要由V型定子、夹持装置以及粘有摩擦条的动子构成,其定子为电机的核心机电能量转换器件,主要由一对采用螺栓预紧的夹心式兰杰文压电换能器(Langevin Piezoelectric Transducer, LPT)通过柔性铰链连接而成,具体尺寸参数可参见文献[15]。图2为电机的工作原理示意图,当施加于定子两组压电陶瓷(Piezoelectric Ceramics, PZT)的A、B两相高频正弦激励电压信号的频率接近定子对称振动模态与反对称振动模态的频率时,就会同时激发定子的这两种振动模态,从而在驱动足处合成微观椭圆运动,进而在预压力作用下通过定、动子之间的接触摩擦实现动子的宏观直线运动与动力输出。电机基本参数见表1。

图1 V型定子HPLUM结构示意图
Fig.1 Configuration of the HPLUM with V-shape stator

图2 V型定子HPLUM工作原理示意图
Fig.2 Working principle of the HPLUM with V-shape stator
表1 电机基本参数
Tab.1 Basic parameters of the motor

参 数数 值 额定功率/W12 最大推力/N58 最大推重比/(N/kg)337 额定驱动电压/V300 额定驱动频率/kHz40 额定预压力/N200
考虑到电机的热惯性(min级)远远大于电机的“电振”惯性(ms级),将超声波电机内部的压电-热-结构耦合多物理场分析分解为压电-结构耦合分析与热-结构耦合分析。图3所示为本文所提出的基于场路结合的HPLUM压电-热-结构多物理场解耦分析方法框图,其中将电机几何-机-电(Geometry- Mechanical-Electrical, GME)多域参数作为多物理场分析的输入参数。基于“场”的观点建立定子的压电-结构耦合有限元模型及热-结构耦合有限元模型,基于“路”的观点构建计算定子损耗的等效电路模型以及电机温升的二维热路模型,进而通过超声波电机内部固有的电-振-热耦合效应实现超声波电机压电-热-结构多物理场耦合分析。
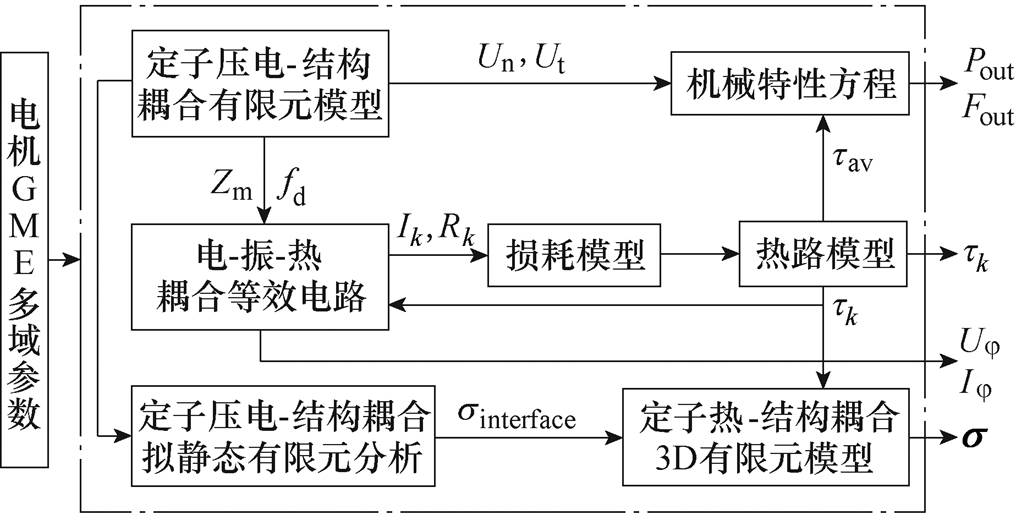
图3 基于场路结合的压电-热-结构多场耦合分析框图
Fig.3 Diagram of piezo-thermal-structure coupling analysis based on field-circuit combination
具体地,通过压电-结构耦合有限元模型计算出定子的工作频率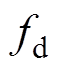 以及机械阻抗
以及机械阻抗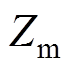 ,将其作为定子电-振-热耦合等效电路的输入,并结合定、动子摩擦损耗,计算出电机各种损耗,输入到电机的二维热路模型,计算出电机各部分的温升
,将其作为定子电-振-热耦合等效电路的输入,并结合定、动子摩擦损耗,计算出电机各种损耗,输入到电机的二维热路模型,计算出电机各部分的温升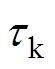 ,再将温升反馈至定子损耗计算模型和定子热-结构耦合3D有限元模型,同时将定子平均稳态温升
,再将温升反馈至定子损耗计算模型和定子热-结构耦合3D有限元模型,同时将定子平均稳态温升 反馈至电机机械特性方程中,以表征电机工作频率的温漂特性;通过对定子进行压电-结构耦合拟静态有限元分析,获得定子压电陶瓷与金属基体接触界面处的应力分布,并将其作为压电-热-结构耦合分析的集中载荷加载到定子3D有限元模型中,进而结合计算出的定子各部件温升,实现对电机关键部件机械强度的分析;对定子压电-结构耦合有限元模型进行谐响应分析,计算出定子驱动足的法向振幅
反馈至电机机械特性方程中,以表征电机工作频率的温漂特性;通过对定子进行压电-结构耦合拟静态有限元分析,获得定子压电陶瓷与金属基体接触界面处的应力分布,并将其作为压电-热-结构耦合分析的集中载荷加载到定子3D有限元模型中,进而结合计算出的定子各部件温升,实现对电机关键部件机械强度的分析;对定子压电-结构耦合有限元模型进行谐响应分析,计算出定子驱动足的法向振幅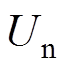 和切向振幅
和切向振幅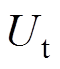 ,并结合电机的机械特性方程与定子平均温升,计算出多场耦合作用下电机的输出功率
,并结合电机的机械特性方程与定子平均温升,计算出多场耦合作用下电机的输出功率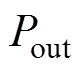 与推力
与推力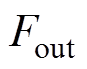 。此外,通过定子等效电路还可以分析电-振-热耦合作用下电机的相电压Uj 及相电流Ij,进而实现对多场耦合作用下电机作动性能、电气特性、温升特性以及关键部位机械强度的快速同步评估。
。此外,通过定子等效电路还可以分析电-振-热耦合作用下电机的相电压Uj 及相电流Ij,进而实现对多场耦合作用下电机作动性能、电气特性、温升特性以及关键部位机械强度的快速同步评估。
基于图3所示的场路结合思想,对V型定子HPLUM进行压电-热-结构多物理场耦合建模。
图4所示为基于Ansys软件(Ansys Inc, Canonsburg, PA)建立的考虑了电学和力学边界条件的V型定子HPLUM的有限元模型,其中45钢金属基体采用solid 45单元,PZT-8压电陶瓷采用solid 98耦合场单元,并对该部分的网格划分进行加密处理。定子材料属性见表2。
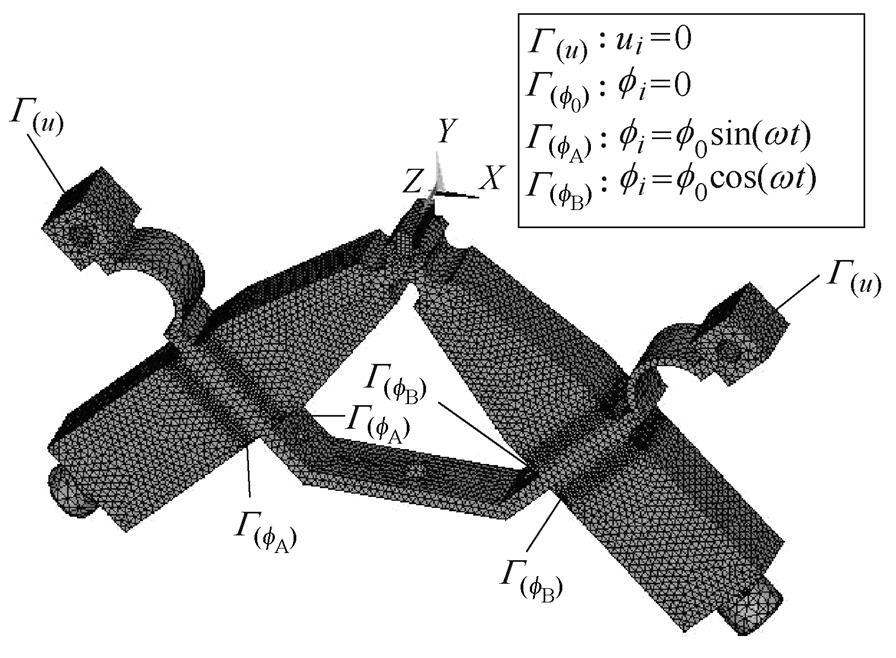
图4 定子压电-结构耦合三维有限元模型
Fig.4 Piezo-structure coupling 3D FEM of the stator
压电陶瓷本构关系由第二类压电方程描述[1],有
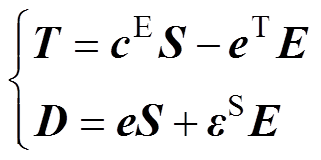 (1)
(1)
表2 定子材料属性
Tab.2 Material property of the stator

参 数数 值 45钢密度/(kg/m3)7 800 45钢杨氏模量/GPa200 45钢泊松比0.3 PZT-8密度/(kg/m3)7 600 PZT-8杨氏模量/GPa PZT-8压电常数/(C/m2) PZT-8介电常数/(F/m)
式中,T为机械应力矢量;D为电位移矢量;S为机械应变矢量;E为电场强度矢量;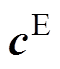 为保持电场强度不变的条件下测得的压电陶瓷的刚度矩阵;
为保持电场强度不变的条件下测得的压电陶瓷的刚度矩阵; 为保持机械应变不变的条件下测得的压电陶瓷的介电矩阵;
为保持机械应变不变的条件下测得的压电陶瓷的介电矩阵;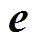 和
和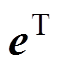 分别为压电应力矩阵及其转置。
分别为压电应力矩阵及其转置。
由压电陶瓷的本构方程可知,其力场参数应力不仅与应变有关,还与电场的分布有关,而电场参数电位移不仅与电场有关,还与力场参数应变的分布情况有关,即存在压电-结构耦合效应。因此,对压电陶瓷需要求解的结构场参数为位移、应力和应变,电场参数为电动势、电场和电位移,采用有限元对定子压电-结构耦合场求解的顺序如图5所示。
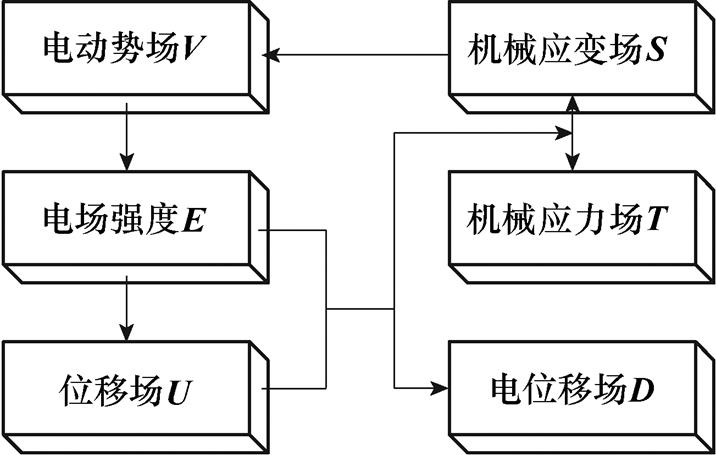
图5 压电-结构耦合场求解顺序
Fig.5 Solution procedure of piezo-structure coupling field of the stator
直线超声波电机损耗主要包括:定子机械阻尼损耗、PZT迟滞损耗[16](压电损耗、介电损耗及机械损耗)以及定动子之间的摩擦损耗,而超声波电机系统中固有的压电/逆压电效应以及电机材料参数温度依赖性的共同作用,使得其电气特性、振动特性以及温升特性三者之间存在相互耦合作用,故超声波电机损耗计算须考虑电-振-热耦合影响因素。
为此,本文采用如图6所示的LPT六端口等效网络[14],并考虑电-振-热耦合效应对定子PZT迟滞损耗的影响,其中前端盖、后端盖以及预紧螺栓的等效机械阻抗Zfk、Zek、Zbk(k=1, 2, 3),可由压电-结构耦合有限元分析获得。

图6 定子单支LPT六端口等效网络
Fig.6 Six-terminal equivalent network for single LPT
考虑温升特性的PZT等效电路机电转换系数、等效电容、等效电阻及电抗参数可通过下列公式解析计算得到。
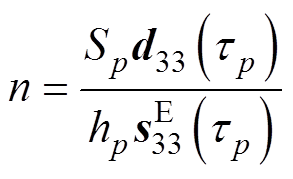 (2)
(2)
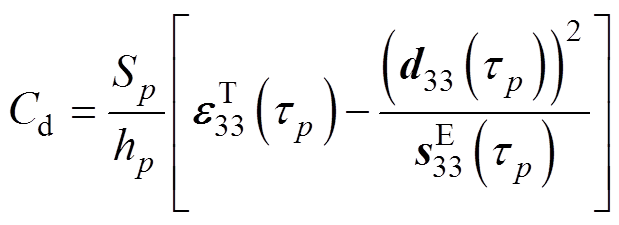 (3)
(3)
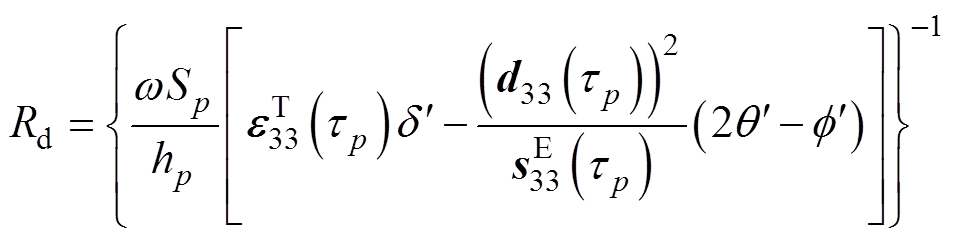 (4)
(4)
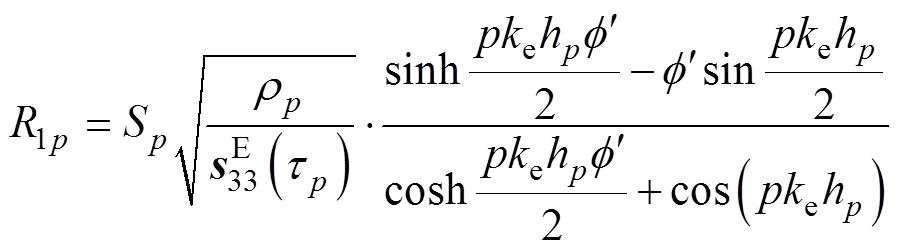 (5)
(5)

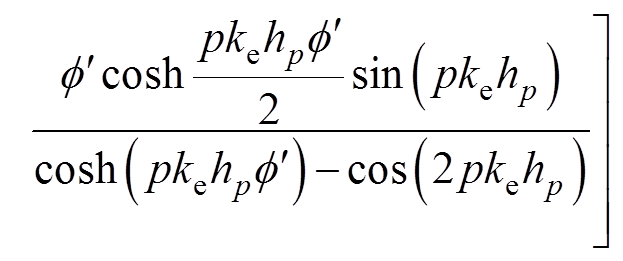 (6)
(6)
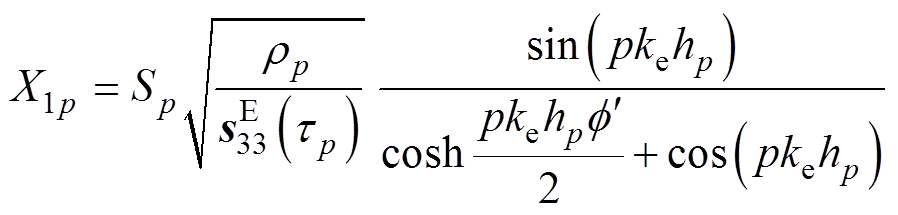 (7)
(7)
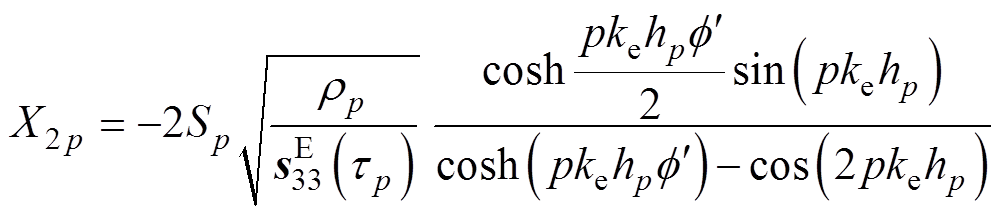 (8)
(8)
式中,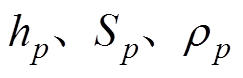 分别为压电陶瓷片的高、横截面积和密度;p为并联的压电陶瓷个数,
分别为压电陶瓷片的高、横截面积和密度;p为并联的压电陶瓷个数,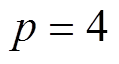 ;
; 为压电陶瓷的温升;
为压电陶瓷的温升;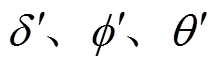 分别为压电陶瓷的介电损耗、弹性损耗以及压电损耗的损耗角,可通过压电材料的损耗因子求得;
分别为压电陶瓷的介电损耗、弹性损耗以及压电损耗的损耗角,可通过压电材料的损耗因子求得;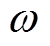 为激励电压的角频率。需要注意的是,以上等效电路参数解析表达式中的压电陶瓷参数
为激励电压的角频率。需要注意的是,以上等效电路参数解析表达式中的压电陶瓷参数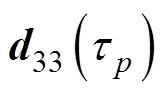 、
、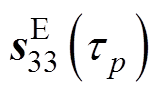 、
、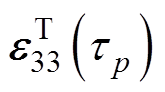 均随着温升的变化而变化,可以用Taylor公式进行展开得到
均随着温升的变化而变化,可以用Taylor公式进行展开得到
 (9)
(9)
式中,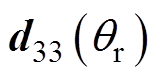 、
、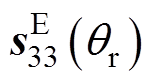 、
、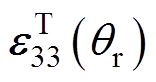 为在参考温度
为在参考温度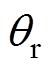 下的压电参数;
下的压电参数;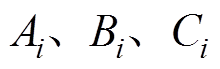 为系数,可根据利用阻抗分析仪与恒温箱测试的不同温升条件下压电参数的实验数据进行拟合获得。
为系数,可根据利用阻抗分析仪与恒温箱测试的不同温升条件下压电参数的实验数据进行拟合获得。
则定子单支LPT的前、后端盖、预紧螺栓以及PZT部分的损耗总和可计算为
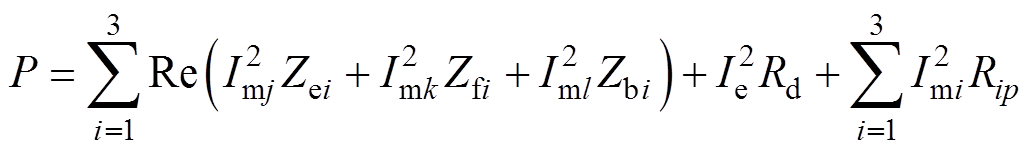 (10)
(10)
式中,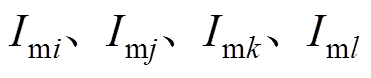 为等效电路中各机械支路的电流;
为等效电路中各机械支路的电流;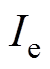 为电气支路的电流。
为电气支路的电流。
为快速评估定子各部件的温升,这里采用一个26节点的二维热路模型,如图7所示,其中仅考虑了单支LPT的轴向热传导。定子各部分损耗用电流源表示,热路模型中的热阻则由热量在定子同种材料部件中传递时所定义的传导热阻、热量在两种不同材料部件接触界面传递时所定义的接触热阻以及定子表面热量与周围空气热对流所定义的对流热阻三大类构成,且各热阻的具体计算公式可参见文献[14],这里不再赘述。

图7 定子二维热网络拓扑
Fig.7 2D thermal network for the stator
基于上述热网络模型,电机的节点温度可由以下微分方程描述。
 (11)
(11)
式中,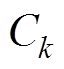 为定子各部分的热容,
为定子各部分的热容, ,其值由各部件的质量
,其值由各部件的质量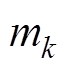 与材料比热容
与材料比热容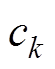 的乘积决定;
的乘积决定;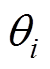 (
( )为节点温度;
)为节点温度; (
(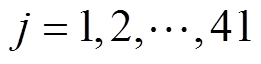 )为各类热阻;Ik为电流源,
)为各类热阻;Ik为电流源,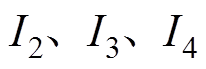 分别为前端盖损耗、两片压电陶瓷的损耗以及后端盖损耗(计入了预紧螺栓损耗),其值可由等效电路进行计算;
分别为前端盖损耗、两片压电陶瓷的损耗以及后端盖损耗(计入了预紧螺栓损耗),其值可由等效电路进行计算;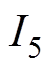 为夹持件的损耗,其值可以根据定子损耗进行估算,约占总损耗的
为夹持件的损耗,其值可以根据定子损耗进行估算,约占总损耗的 。
。
电流源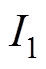 为定动子摩擦功率损耗传导至定子驱动足的分量,其值[17]为
为定动子摩擦功率损耗传导至定子驱动足的分量,其值[17]为
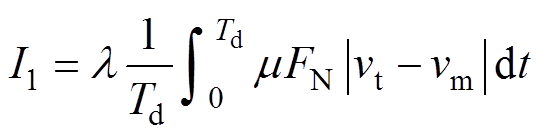 (12)
(12)
式中,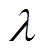 为热分配因子,即摩擦损耗传导至定子部分的比例系数,其值主要与摩擦副材料的导热系数相关,这里设置为0.6;
为热分配因子,即摩擦损耗传导至定子部分的比例系数,其值主要与摩擦副材料的导热系数相关,这里设置为0.6;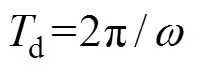 为一个驱动周期;
为一个驱动周期;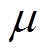 为定动子摩擦副的滑动摩擦系数;
为定动子摩擦副的滑动摩擦系数;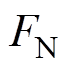 为定动子之间的法向接触力,其在一个驱动周期内的平均值可以近似地认为等于施加的预压力;
为定动子之间的法向接触力,其在一个驱动周期内的平均值可以近似地认为等于施加的预压力;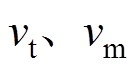 分别为驱动足的切向振动速度和动子的直线运动速度,前者可由压电-结构耦合有限元模型的谐响应分析得到,后者可通过实验测得。
分别为驱动足的切向振动速度和动子的直线运动速度,前者可由压电-结构耦合有限元模型的谐响应分析得到,后者可通过实验测得。
大功率超声波电机运行过程中,定子受到电场、高频机械振动以及温度场的共同耦合作用,再加上不同材质膨胀系数不同以及力学边界条件约束,会产生较大的热应力,而热应力是诱发定子各部件连接部位及压电陶瓷发生疲劳断裂的主要原因之一,故分析定子关键部件的热应力情况,对电机的服役性能及故障诊断具有重要意义。
通过建立定子三维全域有限元模型,并采用热-结构间接耦合分析方法实现对定子热应力的快速分析,图8所示为施加了边界条件的求解域物理模型。网格剖分则采用混合型网格,以提高计算精度,其中45钢金属基体采用solid 70单元,PZT-8压电陶瓷采用solid 98耦合场单元,将定子驱动足前端的力学边界条件设置为铰支边界,夹持两端的力学边界条件设置为固支边界。载荷分为力学载荷与热学载荷两大类,其中不同材料之间接触界面的力学载荷可通过对定子压电-结构耦合有限元模型进行拟静态分析得到,并将计算得到的拟静态应力
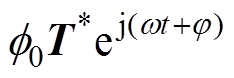 以面载荷的形式施加到PZT与金属基体的接触界面以及PZT与PZT的接触界面处,螺栓预紧力产生的力学载荷则通过预应力单元PRETS 179施加;热学载荷则先通过前述热路模型计算出的定子驱动足、前后端盖、预紧螺栓、PZT组件以及夹持等部件的稳态温度
以面载荷的形式施加到PZT与金属基体的接触界面以及PZT与PZT的接触界面处,螺栓预紧力产生的力学载荷则通过预应力单元PRETS 179施加;热学载荷则先通过前述热路模型计算出的定子驱动足、前后端盖、预紧螺栓、PZT组件以及夹持等部件的稳态温度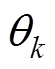 (
(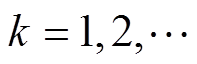 ),再以体载荷
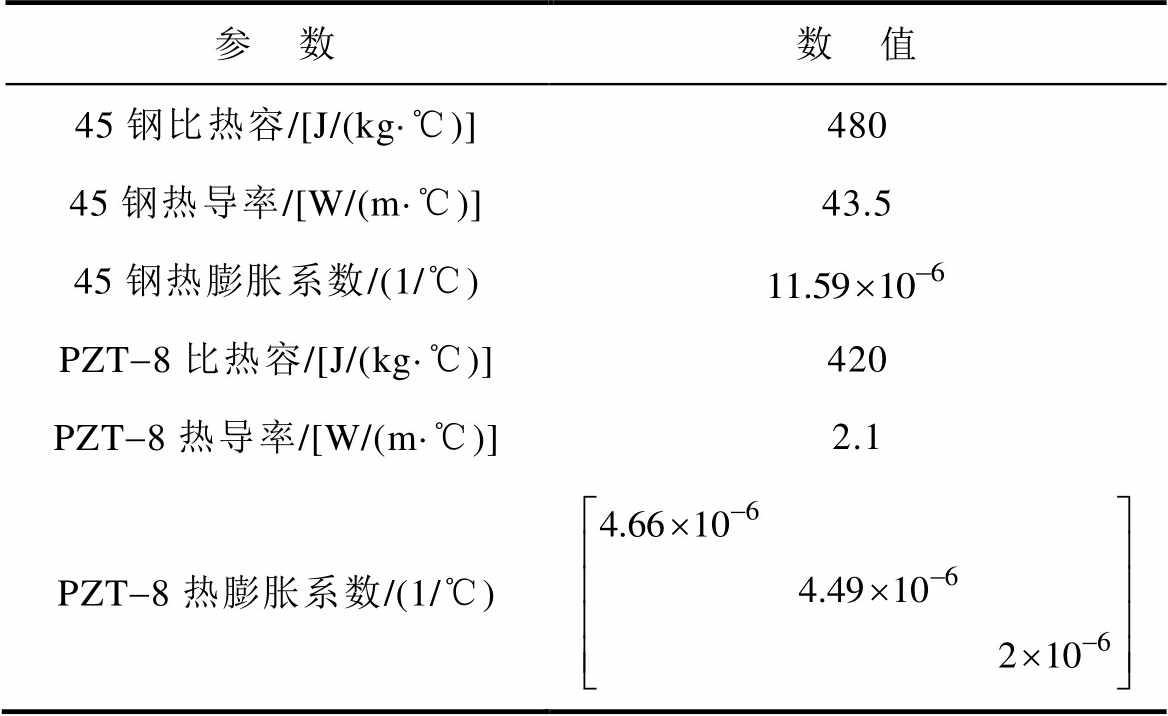
),再以体载荷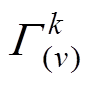 的形式施加到定子各个部件中。定子各部分材料热力学参数见表3。
的形式施加到定子各个部件中。定子各部分材料热力学参数见表3。

图8 施加了边界条件及载荷的求解域物理模型
Fig.8 Physical model of solving domain with boundary conditions and loads
若仅考虑热应力对定子各部件的受力影响,其静力学方程[18]为
表3 定子材料热力学参数
Tab.3 Thermodynamic parameters of stator material
参 数数 值 45钢比热容/[J/(kg·℃)]480 45钢热导率/[W/(m·℃)]43.5 45钢热膨胀系数/(1/℃) PZT-8比热容/[J/(kg·℃)]420 PZT-8热导率/[W/(m·℃)]2.1 PZT-8热膨胀系数/(1/℃)
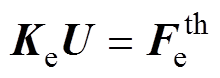 (13)
(13)
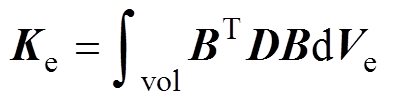 (14)
(14)
 (15)
(15)
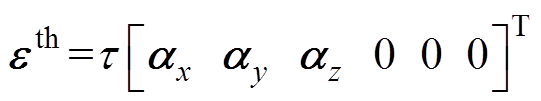 (16)
(16)
 (17)
(17)
 (18)
(18)
 (19)
(19)
式中,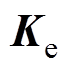 为单元刚度矩阵;
为单元刚度矩阵;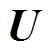 为节点位移矢量矩阵;
为节点位移矢量矩阵; 为单元热载荷矢量矩阵;
为单元热载荷矢量矩阵;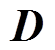 为弹性刚度矩阵;
为弹性刚度矩阵;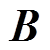 为基于单元形状函数的应变-位移矩阵;
为基于单元形状函数的应变-位移矩阵;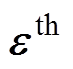 为热应变矢量矩阵;
为热应变矢量矩阵;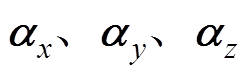 分别为材料在
分别为材料在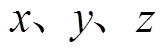 方向上的热膨胀系数;
方向上的热膨胀系数;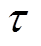 为温升值;
为温升值;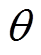 为节点的当前温度;
为节点的当前温度;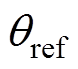 为参考温度值(当物质为该温度时其应变为0);
为参考温度值(当物质为该温度时其应变为0);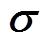 为热应力矢量;
为热应力矢量;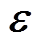 为全应变矢量。
为全应变矢量。
为分析电-振-热多场耦合作用下电机的输出功率、推力等作动性能,需要考虑超声波电机谐振频率的温漂特性[19],其原理如图9所示,即超声波电机定子的幅频特性曲线会随温度升高而向左漂移,造成电机谐振频率降低(向左发生偏移,由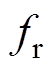 变为
变为 ,进而造成定子振幅在原工作频率处下降的现象,即由
,进而造成定子振幅在原工作频率处下降的现象,即由 下降为
下降为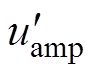 )。
)。
为考虑超声波电机谐振频率的温漂特性所造成的驱动频率处驱动足振幅下降的现象,首先基于压电-结构耦合有限元模型对定子进行谐响应分析,获得定子驱动足处关键点的法向(Y方向)振幅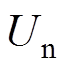 和切向(X方向)振幅
和切向(X方向)振幅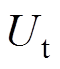 与激励频率之间的函数关系,再结合电机频率温漂实验结果[7],利用线性近似的方法,可得考虑超声波电机谐振频率温漂特性的驱动足振幅-温升函数关系为
与激励频率之间的函数关系,再结合电机频率温漂实验结果[7],利用线性近似的方法,可得考虑超声波电机谐振频率温漂特性的驱动足振幅-温升函数关系为
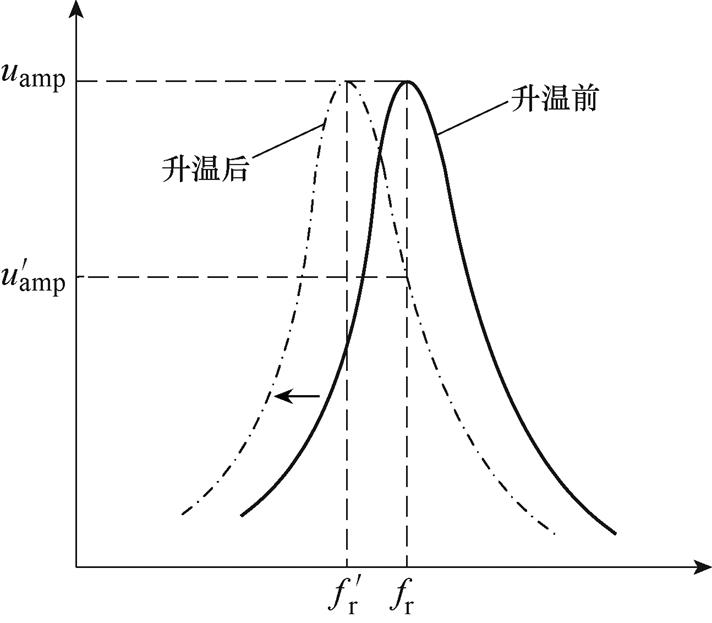
图9 超声波电机谐振频率温漂特性示意图
Fig.9 Schematics for resonant frequency drift of ultrasonic motors
 (20)
(20)
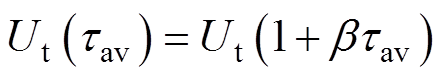 (21)
(21)
式中,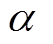 、
、 分别为法向和切向温漂系数。
分别为法向和切向温漂系数。
进一步地,将以上振幅函数代入Shi Yunlai等[20]提出的直线超声波电机机械特性方程得
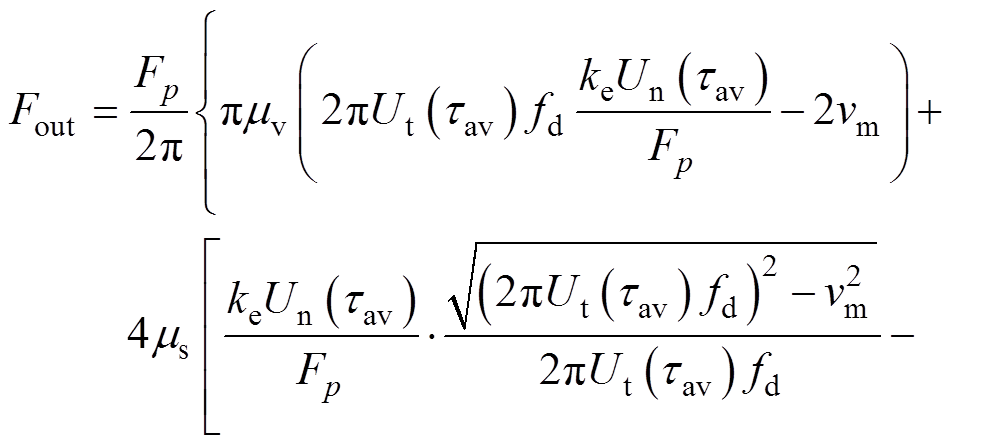
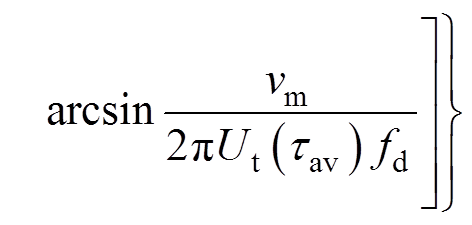 (22)
(22)
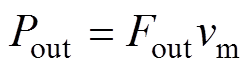 (23)
(23)
式中,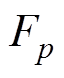 为预压力;
为预压力; 、
、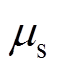 分别为定、动子接触界面的粘性摩擦系数与静摩擦系数;
分别为定、动子接触界面的粘性摩擦系数与静摩擦系数; 为定动子接触界面的法向等效接触刚度,其值采用考虑正压力的改进Hertz接触理论[21]进行计算,有
为定动子接触界面的法向等效接触刚度,其值采用考虑正压力的改进Hertz接触理论[21]进行计算,有
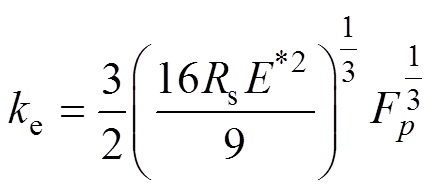 (24)
(24)
其中

式中,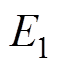 、
、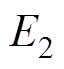 分别为驱动足与摩擦条的弹性模量;
分别为驱动足与摩擦条的弹性模量;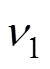 、
、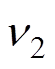 分别为驱动足与摩擦条的泊松比;
分别为驱动足与摩擦条的泊松比;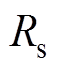 为驱动足前端面粗糙微凸体平均半径,其值可由如图10所示的驱动足表面实测微观形貌特征参数获得,
为驱动足前端面粗糙微凸体平均半径,其值可由如图10所示的驱动足表面实测微观形貌特征参数获得,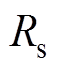 =2.43 mm。
=2.43 mm。

图10 实测的驱动足三维表面微观形貌
Fig.10 Measured 3D surface topology of driving tip
图11所示为所搭建的V型定子大功率直线超声波电机连续运行工况下的输出特性测试平台,其中直流电源用于给电机驱动器供电,并利用安装于直线导轨两侧的一对限位开关,通过电机控制器实现电机动子的连续往复运行。电机运行过程中定子相电压、相电流分别通过示波器与电流传感器测得,电机空载速度则由激光位移传感器(LK-H150,Keyence,日本)测得,同时电机表面温度可通过粘贴于定子左侧后端盖的贴片式温度传感器实时测得。此外,定子表面的温度分布通过红外热像仪(FLIR-i5, FLIR Systems, Inc,美国)实时测量。图12所示为实验测得的电机连续运行工况下定子压电陶瓷(PZT)部位的温升、电机空载速度以及定子相电流的实时变化情况,可以发现,在压电-热-结构多场耦合作用下,电机表现出明显的热-机-电耦合特性,即随着电机温度升高,其空载速度和定子相电流呈现出明显的下降趋势,这主要是由于超声波电机系统中固有的压电/逆压电效应以及电机材料参数温度依赖性共同作用,使其电气特性、振动特性以及温升特性三者之间相互耦合作用。仿真部分所用参数见表4,其他输入参数取额定值。

图11 连续运行工况下电机输出特性测试平台
Fig.11 Test platform for output characteristics of the motor under continuous operation condition
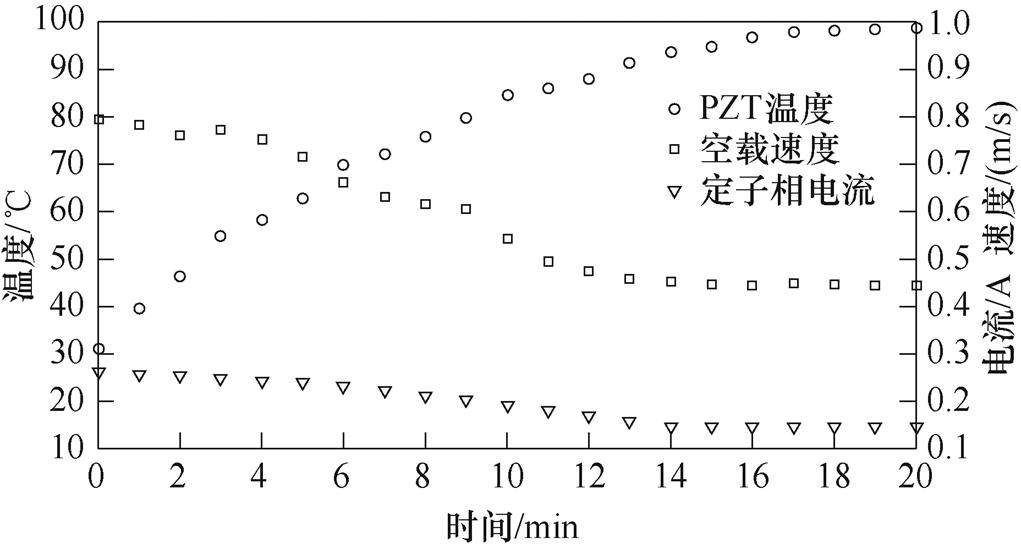
图12 电机热-机-电耦合输出特性实测结果
Fig.12 Measurement results for thermal-mechanical-electrical output characteristics of the motor
表4 仿真参数设置
Tab.4 Simulation parameter settings
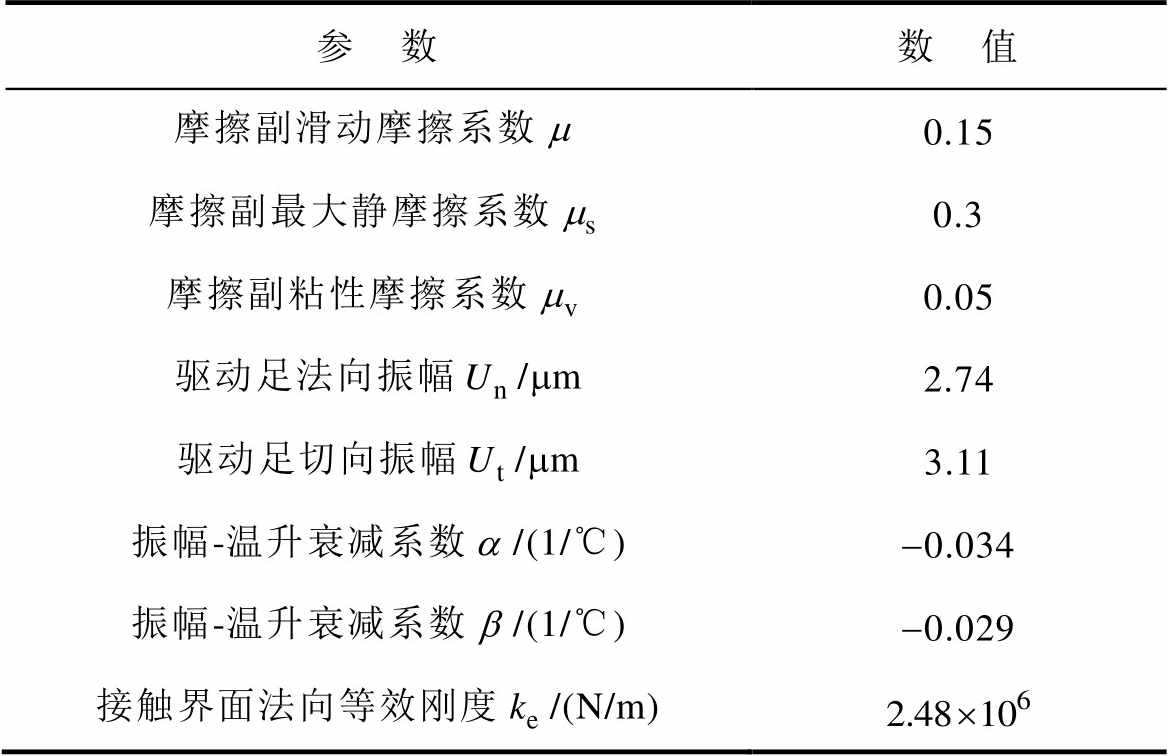
参 数数 值 摩擦副滑动摩擦系数0.15 摩擦副最大静摩擦系数0.3 摩擦副粘性摩擦系数0.05 驱动足法向振幅/mm2.74 驱动足切向振幅/mm3.11 振幅-温升衰减系数/(1/℃)-0.034 振幅-温升衰减系数/(1/℃)-0.029 接触界面法向等效刚度/(N/m)
图13所示为电机连续运行20 min的过程中,定子驱动足(A点)、前端盖(B点)、夹持件(C点)、PZT(D点)、后端盖(E点)五个不同部位的瞬态温升计算值与实验测试值的对比,其中图13a所示为定子的热像图,环境参考温度为31℃。由图13b可见,本文所建立的热路模型可较为准确地预测电机不同部位的温升,且定子PZT部分为电机温升最为剧烈的部位(温升超过60℃,最终稳态温度可达98℃),这主要与其内部的迟滞损耗总量较大有关;定子前端盖及定子驱动足处的温升次之,这主要与采用变幅杆设计的前端盖振幅较大有关;而定子夹持部位为温升最小的部位(仅20℃左右的温升),这主要与其位于定子振动的节面处有关。
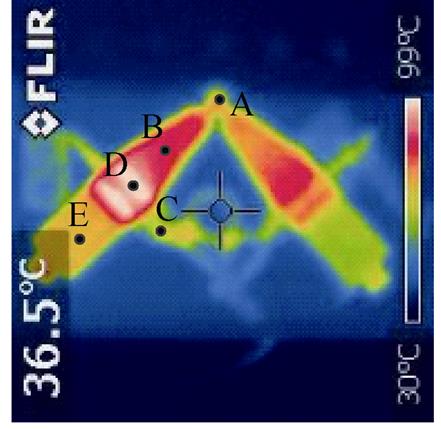
(a)定子热像图

(b)不同部位温升
图13 电机连续运行工况下定子温升
Fig.13 Temperature rise of the stator under continuous operation condition
利用定子单支LPT六端口等效网络可对不同温升下定子的电气特性进行仿真预测。图14所示为定子相电压与相电流随定子后端盖温度升高而变化的仿真与实测对比,可见仿真计算出的电气特性与实测的趋势基本吻合,且相电压随温度升高而变大,相电流则随温度升高而降低,同时两者与电机温升之间均呈现出明显的非线性关系,再次验证了大功率直线超声波电机连续运行工况下存在复杂的热-机-电耦合动力学行为。
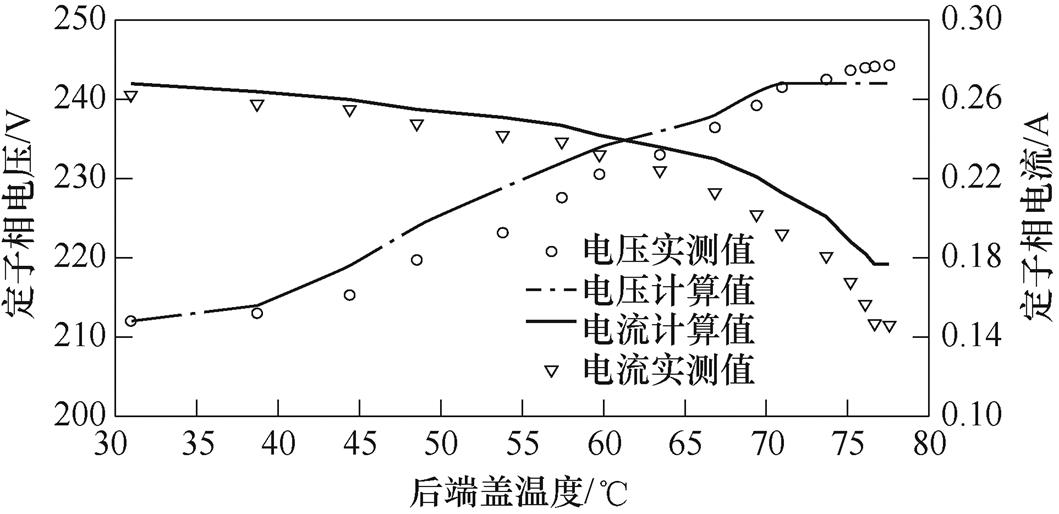
图14 不同温度下电机的电气特性
Fig.14 Electrical characteristics of the motor under different temperature rise
利用解析的作动性能计算公式,可对电机不同温升条件下的作动性能进行评估,图15a和图15b分别为不同温升条件下电机输出速度-推力特性曲线与输出功率-推力特性曲线的仿真结果与实验结果对比。结果表明,仿真结果与实验结果趋势基本一致,造成误差的主要原因是由于实验过程中不同负载下电机温升存在一定范围的波动。不难发现,随着电机温升的增加,其机械特性明显下降,这主要是由电机谐振频率的温漂特性导致的,可通过频率跟踪控制的方法抑制这种不利的现象[22]。
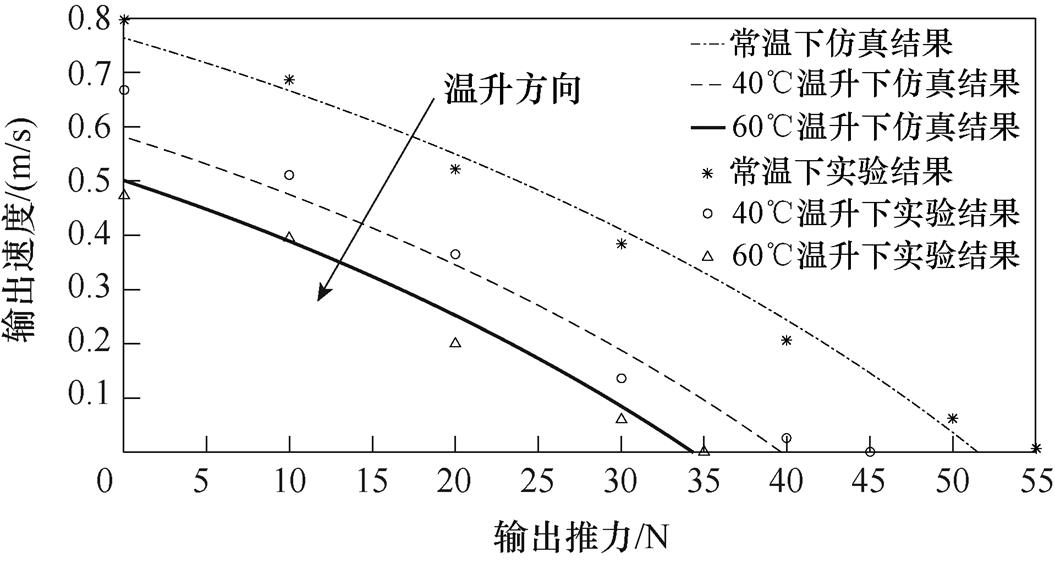
(a)速度-推力曲线

(b)功率-推力曲线
图15 电机不同温升下的机械特性仿真与实验结果
Fig.15 Simulation and experimental results for mechanical characteristics of the motor under different temperature rise conditions
由于热应力的大小与温升成正比,文中只分析电机定子温升稳定时的热应力分布情况,图16所示为电机额定工况下温升达到稳态时的V型定子Von- Mises热应力云图。可以看出,夹持部件连接处以及定子驱动足处的热应力表现为最大,这是因为夹持两端与驱动足处受到结构条件以及力学条件约束。同时,压电陶瓷处的热应力要大于定子前后端盖处的热应力,这主要是由于压电陶瓷处的温升明显高于前后端盖的温升所致。此外,可以发现压电陶瓷与金属基体接触部位的热应力要高于压电陶瓷与前后端盖处的热应力,这主要是由于不同材料之间的热膨胀系数不同以及压电-结构耦合效应在该部位所产生的内部应力所致。因此,热应力是诱发大功率直线超声波电机中定子不同材料交界处压电陶瓷断裂以及夹持连接处疲劳的主要原因之一,应在此类型电机的优化设计中得到足够重视。

图16 V型定子Von-Mises 热应力云图
Fig.16 Von-Mises stress distribution of V-shape stator
本文提出一种基于场路结合的HPLUM压电-热-结构高效多物理场分析方法,并利用仿真与实验结果验证了该方法的有效性,本文主要结论如下:
1)实现了多场耦合作用下电机电气特性、机械特性以及温度特性的快速同步评估,仿真与实验结果均表明,由于超声波电机系统中固有的压电/逆压电效应以及材料参数温度依赖性的共同作用,电机运行过程中表现出明显的热-机-电耦合动力学特性,且电气特性与温升特性呈现出复杂的非线性关系,可考虑采用LLCC谐振网络的驱动电路拓扑,以满足驱动电压不随负载和驱动频率变化而改变的要求,提高热-机-电耦合作用下电机运行的稳定性。
2)定子表面的温度场分布不均匀,且压电陶瓷的温升最为剧烈,定子前端盖与驱动足处的温升次之,夹持部件的温升最小,但由于受结构和力的约束,夹持部件连接处以及定子驱动足处的热应力表现为最大,压电陶瓷与金属基体接触部位热应力次之,定子前、后端盖以及夹持中部的热应力最小,可考虑采用更利于压电陶瓷部件散热的,导热性能更好的铜制夹持部件,以降低压电陶瓷的温升。
3)基于考虑电机谐振频率温漂特性的机械特性方程,对不同温升下电机的机械特性进行仿真与实验对比分析,结果表明,机械特性随电机温升的增加而显著下降,有必要在今后的工作中对HPLUM开展损耗最小意义下的最优频率跟踪控制研究。
参考文献
[1] Zhao Chunsheng. Ultrasonic motors: technologies and applications[M]. Berlin, Heidelberg: Springer Berlin Heidelberg, 2011.
[2] 蒋春容, 赵子龙, 陆旦宏, 等. 环形行波超声波电机动态接触摩擦特性建模与分析[J]. 电工技术学报, 2023, 38(8): 2036-2047.
Jiang Chunrong, Zhao Zilong, Lu Danhong, et al. Modeling and analysis on dynamic contact and friction characteristics of ring type traveling wave ultrasonic motors[J]. Transactions of China Electro- technical Society, 2023, 38(8): 2036-2047.
[3] Liu Yingxiang, Chen Weishan, Liu Junkao, et al. A high-power linear ultrasonic motor using bending vibration transducer[J]. IEEE Transactions on Indu- strial Electronics, 2013, 60(11): 5160-5166.
[4] Lu Xiaolong, Hu Junhui, Zhao Chunsheng. Analyses of the temperature field of traveling-wave rotary ultrasonic motors[J]. IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, 2011, 58(12): 2708-2719.
[5] 王光庆, 岳玉秋, 展永政. 纵-弯复合旋转式超声波电动机的优化设计与性能分析[J]. 电工技术学报, 2015, 30(22): 33-41.
Wang Guangqing, Yue Yuqiu, Zhan Yongzheng. Optimum design and performances analysis of the longitudinal-bending hybrid rotating type ultrasonic motor[J]. Transactions of China Electrotechnical Society, 2015, 30(22): 33-41.
[6] 白洋, 王剑, 郭吉丰. 基于复损耗的杆式超声波电机定子建模及其仿真[J]. 电工技术学报, 2012, 27(12): 185-190.
Bai Yang, Wang Jian, Guo Jifeng. Odeling and simulation of a bar-type ultrasonic motor based on loss coefficients[J]. Transactions of China Electro- technical Society, 2012, 27(12): 185-190.
[7] Zhou Lifeng, Yao Zhiyuan, Li Xiaoniu, et al. Modeling and verification of thermal-mechanical- electric coupling dynamics of a V-shape linear ultrasonic motor[J]. Sensors and Actuators A: Physical, 2019, 298: 111580.
[8] 王鑫, 王亮, 于鹏鹏, 等. 贴片式纵弯复合型直线超声电机的理论建模与实验研究[J]. 中国电机工程学报, 2021, 41(14): 5014-5024.
Wang Xin, Wang Liang, Yu Pengpeng, et al. Theoretical modeling and experiment studies of a bonded type longitudinal-bending hybrid linear ultrasonic motor[J]. Proceedings of the CSEE, 2021, 41(14): 5014-5024.
[9] Akiki P, Hassan M H, Bensetti M, et al. Multiphysics design of a V-shape IPM motor[J]. IEEE Transactions on Energy Conversion, 2018, 33(3): 1141-1153.
[10] 鲁炳林, 徐衍亮. 步进电机新型场路结合分析方法: 齿层计算转矩法[J]. 电机与控制学报, 2018, 22(5): 11-18.
Lu Binglin, Xu Yanliang. Field-circuit coupled method of stepping motors-tooth-layer calculated torque method[J]. Electric Machines and Control, 2018, 22(5): 11-18.
[11] 唐钊, 刘轩东, 陈铭. 考虑流体动力学的干式变压器热网络模型仿真分析[J]. 电工技术学报, 2022, 37(18): 4777-4787.
Tang Zhao, Liu Xuandong, Chen Ming. Simulation analysis of dry-type transformer thermal network model considering fluid dynamics[J]. Transactions of China Electrotechnical Society, 2022, 37(18): 4777- 4787.
[12] 师蔚, 骆凯传, 张舟云. 基于热网络法的永磁电机温度在线估计[J]. 电工技术学报, 2023, 38(10): 2686-2697.
Shi Wei, Luo Kaichuan, Zhang Zhouyun. On-line temperature estimation of permanent magnet motor based on lumped parameter thermal network method[J]. Transactions of China Electrotechnical Society, 2023, 38(10): 2686-2697.
[13] 赵能桐, 杨鑫, 陈钰凯, 等. 考虑超磁致伸缩材料非均匀性的大功率电声换能器阻抗特性[J]. 电工技术学报, 2021, 36(10): 1999-2006.
Zhao Nengtong, Yang Xin, Chen Yukai, et al. The impedance characteristics of high power electro- acoustic transducer considering the inhomogeneity of giant magnetostrictive material[J]. Transactions of China Electrotechnical Society, 2021, 36(10): 1999- 2006.
[14] Li Xiang, Kan Chaohao, Ren Taian, et al. Deve- lopment of thermal network for a high power linear ultrasonic motor with V-shape stator[C]//2021 13th International Symposium on Linear Drives for Indu- stry Applications (LDIA), Wuhan, China, 2021: 1-6.
[15] Li Xiang, Kan Chaohao, Ren Taian, et al. Thermal network modeling and thermal stress evaluation for a high-power linear ultrasonic motor[J]. IEEE Transa- ctions on Industry Applications, 2022, 58(6): 7181- 7191.
[16] 董晓霄, 黄肖肖, 夏博, 等. 超声波电机夹心式定子结构含损耗机电等效电路建模与分析[J]. 电工技术学报, 2022, 37(22): 5756-5764.
Dong Xiaoxiao, Huang Xiaoxiao, Xia Bo, et al. Electromechanical equivalent model of sandwich stator of ultrasonic motors considering losses[J]. Transactions of China Electrotechnical Society, 2022, 37(22): 5756-5764.
[17] Li Shiyang, Yang Ming. Analysis of the temperature field distribution for piezoelectric plate-type ultrasonic motor[J]. Sensors and Actuators A: Physical, 2010, 164(1/2): 107-115.
[18] Cook R D. Finite element modeling for stress analysis[M]. New York: Wiley, 1995.
[19] Qi Xue, Shi Weijia, Wang Shaokai, et al. Com- pensating nonlinear temperature dependence of ultrasonic motor[J]. Ultrasonics, 2021, 117: 106522.
[20] Shi Yunlai, Zhao Chunsheng, Zhang Jianhui. Contact analysis and modeling of standing wave linear ultrasonic motor[J]. Journal of Wuhan University of Technology-Materials Science Edition, 2011, 26(6): 1235-1242.
[21] Shi Xi, Polycarpou A A. Measurement and modeling of normal contact stiffness and contact damping at the meso scale[J]. Journal of Vibration and Acoustics, 2005, 127(1): 52-60.
[22] Shi Weijia, Zhao Hui, Ma Jie, et al. An optimum- frequency tracking scheme for ultrasonic motor[J]. IEEE Transactions on Industrial Electronics, 2017, 64(6): 4413-4422.
Abstract Due to high-voltage excitation, high-frequency mechanical vibration, and friction drive principle, high-power linear ultrasonic motors (HPLUMs) demonstrate complicated thermal-mechanical-electrical coupling dynamics under continuous operating conditions. Traditional field-based simulation methods and lumped parameter-based analytical methods are difficult to balance calculation accuracy and analysis efficiency when addressing the multi-physics coupled issues of ultrasonic motors. Existing multi-physics models for ultrasonic motors focus on stator performance rather than the comprehensive performance of motors under the multi-field coupling effect. Therefore, this paper proposes a field-circuit combination analysis methodology to analyze the piezo-thermal-structure multi-physics coupling of ultrasonic motors, considering the inherent electrical- vibration-thermal coupled effect. Furthermore, the electrical characteristics, temperature rise characteristics, actuating performance, and mechanical strength of critical components in HPLUMs under multi-field coupling effects can be evaluated.
Firstly, the piezo-structure coupled finite element model (FEM) and thermal-structure coupled FEM for a V-shape HPLUM are constructed from the field viewpoint. Secondly, the stator’s electrical-vibration-thermal coupled loss model and a 2D thermal network model (TNM) are constructed from the circuit viewpoint. Thirdly, considering temperature-caused resonant frequency drifting behavior and real roughness at the contact interface, an analytical actuating performance model (APM) of the HPLUM is constructed. Finally, the results from modal and harmonic response analysis based on the piezo-structure coupled FEM are used as inputs into thermal- structure coupled FEM, circuit-based loss model and 2D TNM, and APM. The temperature rise for different stator components based on TNM is coupled to the thermal-structure coupled FEM, circuit-based loss model, and APM, forming a field-circuit combination calculation loop.
Simulation results show complex nonlinear relationships between electrical characteristics (input voltage and current) and temperature rise characteristics. The rise in temperature for different stator parts shows considerable differences, and the peak temperature occurs at piezoelectric ceramics (PZT). The driving tip and the joint of the clamping end encounter maximum thermal stress, and the nominal thermal stress exceeds 60 MPa at the interface between PZT and metal caps. Actuating performance remarkably decreases with the rise in temperature due to resonant frequency drift. Comparison between the simulation and the experimental results verifies the multi-field model.
The following conclusions can be drawn from the simulation and experimental analysis: (1) Compared with traditional multi-physics analysis methods, the proposed field-circuit combination method effectively reduces computational costs and evaluates the comprehensive performance of HPLUMs under multi-field coupling effects. Therefore, applying the proposed method for the multi-physics optimization design of HPLUMs is appropriate. (2) The calculation loop clarifies the electrical-vibration-thermal two-way coupled dynamics in ultrasonic motors, providing valuable insights for design optimization and performance evaluation.
keywords:Ultrasonic motor, multi-physics, field-circuit combination, performance evaluation
中图分类号:TM35
DOI: 10.19595/j.cnki.1000-6753.tces.220675
国家自然科学基金资助项目(52105092)。
收稿日期2022-04-27
改稿日期 2022-11-28
李 响 男,1986年生,副教授,硕士生导师,研究方向为超声电机动力学建模与驱动控制技术、压电换能器设计等。E-mail: lixiang@hfut.edu.cn(通信作者)
郭鹏涛 男,1999年生,硕士研究生,研究方向为超声电机。E-mail: A15690864573@163.com
(编辑 崔文静)