摘要 第二代高温超导带材因其较高的临界电流密度以及良好的机械特性，近年来在超导研究领域得到极大关注。由REBCO带材组成的高温超导导体在液氮温度下的零电阻特性使其在超导输电领域具有巨大的潜力。从安全角度看，高温超导导体的失超保护研究是其获得广泛应用的一个关键。该文建立了准各向同性超导股线的三维失超仿真模型，耦合了电场、磁场和温度场，模拟了不同运行电流以及不同点状热干扰能量下超导股线的失超行为，求解出股线的温度、电流密度以及磁场分布，得到了准各向同性高温超导股线的最小失超能（MQE）以及失超传播速度（QPV），对超导装置的失超保护具有重要意义。该文对准各向同性超导股线建立的三维失超模型，也可以应用到其他结构的高温超导导体的失超研究中。
关键词：准各向同性超导股线 失超行为 最小失超能 失超传播速度
近年来，随着超导电力技术的研究和发展[1-6]，以REBCO为载流层的第二代高温超导带材[7]因其载流能力强、交流损耗低，在超导电力领域获得了极大关注，被广泛应用于超导电缆、超导限流器、超导变压器等超导电力设备中。基于第二代高温超导带材的超导电缆导体，例如RACC（roebel assembled coated conductor）导体/电缆[8-10]、CORC（conductor on round core）导体/电缆[11-12]，TSTC（twisted stacked-tapes cable）导体/电缆[13]以及准各向同性超导股线（Quasi-Isotropic Superconducting, Q-IS）导体/电缆[14]等被相继提出，其中，Q-IS采用REBCO二代高温超导带材，在制作时将四股堆叠带材（每股都是正方形截面）组装起来，且每股堆叠带材都相对于相邻股旋转90°，外覆金属填充物和金属包套，这种结构使Q-IS具有通流密度大、受外场影响小的优点，在超导电力应用中具有广阔的前景。
高温超导装置在电网中运行时，易受到电力系统故障，如短路故障、电流不平衡的影响，严重时可能会使超导导体因大电流或机械应力而发生失超行为。详细来讲，故障处超导体会由超导态转变为正常态，发生局部失超，电流从超导区域分流到金属区域，由于高温超导体的传输电流很高，此时在金属区域产生大量焦耳热，使得超导体温度持续上升，当焦耳热的积累量高于导体与液氮热交换导出的热量时，失超会继续扩散，不仅有可能损坏高温超导装置，甚至影响整个电力系统的稳定运行，因此超导体的失超特性是目前超导装置实用化过程中需要重点解决的关键技术之一。
目前单根超导带材失超特性已被大量研究，例如，W. K. Chan等通过建立由多个高纵横比薄层组成的数值混合电热模型（2D-3D）来模拟超导带材的失超行为[15-16]，F. Roy等通过建立三维磁热模型对不同基底的高温超导带材的失超特性进行了详细的研究[17]。基于第二代高温超导带材的超导导体的失超特性也被研究，如Wang Yawei等建立了基于T-A的三维磁热模型对CORC导体在不同接触电阻下的失超特性进行了研究[18]。Kang Rui等建立了热-电-力模型，得到了影响液氦温度下TSTC导体的失超特性的因素[19]。
本文将通过建立三维电磁热模型对液氮温度下的准各向同性超导股线（Q-IS）的失超特性进行研究，得到准各向同性超导股线在自场下通以不同运行电流以及施加不同热干扰的磁场、电流密度和温度分布，进而计算出该股线的最小失超能[20]以及失超传播速度。
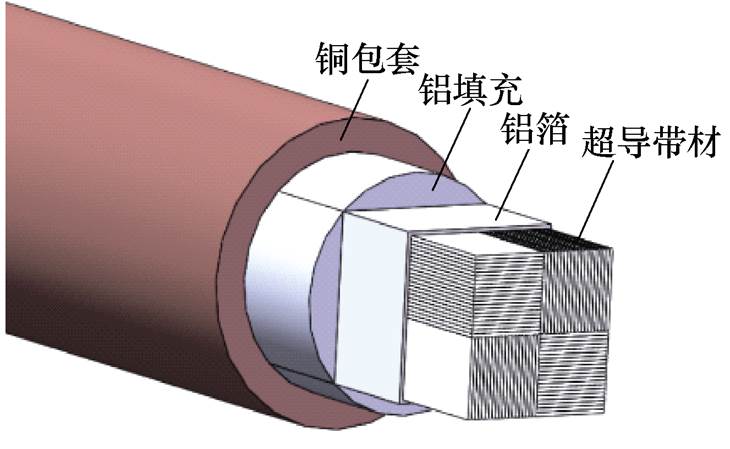
准各向同性超导股线结构如图1所示，由超导线芯、铝箔、铝填充、铜包套构成，其中超导线芯是由四股超导带材依次旋转90°堆叠而成，超导线芯外侧包裹铝箔、铝填充以及铜包套。
（a）准各向同性超导股线结构
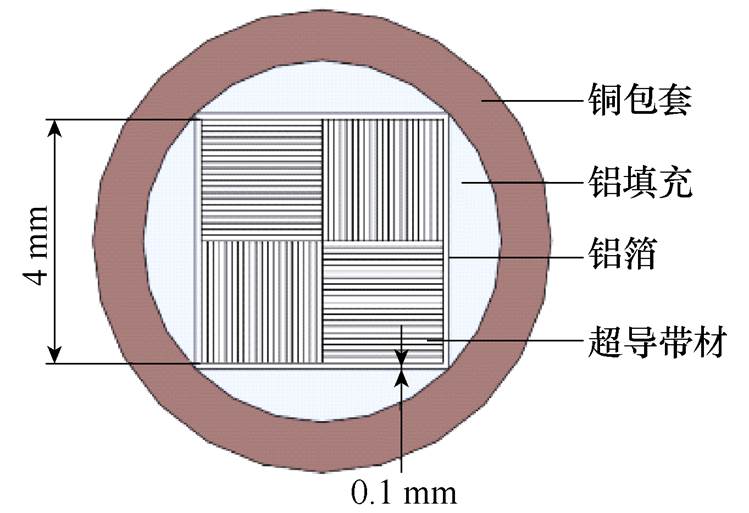
（b）股线横截面图
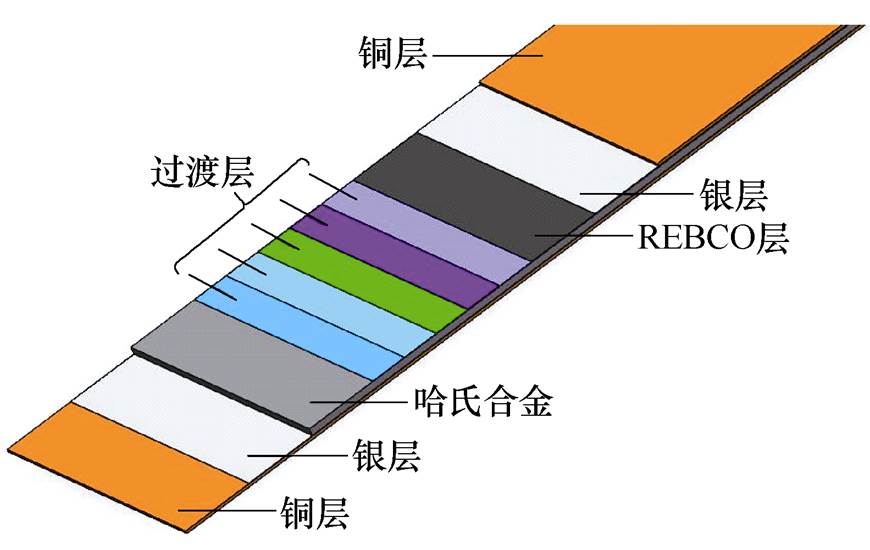
（c）超导带材放大图
图1 准各向同性股线示意图
Fig.1 Schematic diagram of the quasi-isotropic superconducting strand
股线的主要参数见表1，REBCO超导带材由上海超导有限公司提供，忽略过渡层的超导带材主要尺寸见表2。
表1 股线的主要参数
Tab.1 Main parameters of the cable
参 数数 值 超导带材厚度/mm0.1 超导带材宽度/mm2 股线中所含超导带材数量80 铝箔厚度/mm0.1 铝箔层数/层1 铜包套内径/mm5.9 铜包套外径/mm7 单根带材临界电流@77K, 自场/A90 临界温度/K92 股线长度/mm40
表2 超导带材的主要尺寸
Tab.2 Main parameters of the tape
成分厚度/mm体积占比fi 铜基体～400.43 银层～20.021 5 REBCO层～10.010 75 哈氏合金～500.537 6
因股线具有对称性，为减少计算量，根据对称性仅对股线的一半（7 cm）进行仿真，将上述准各向同性股线在有限元分析软件中建立几何模型如图2所示，尺寸见表1，其中股线外部表示液氮浴。对该几何模型进行网格划分，划分结果如图3所示。
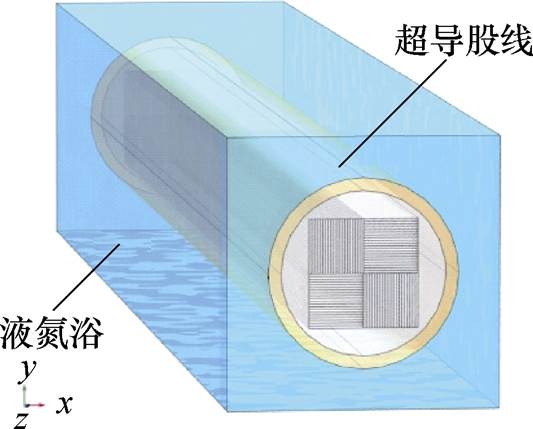
图2 准各向同性股线几何模型的建立
Fig.2 Diagram of the quasi-isotropic superconducting strand
为实现股线电磁场与温度场的耦合，采用H方法[21-22]求解股线的磁场，在有限元软件中通过PDE模块与固体传热模块的耦合实现股线电磁热模型的求解[23]。
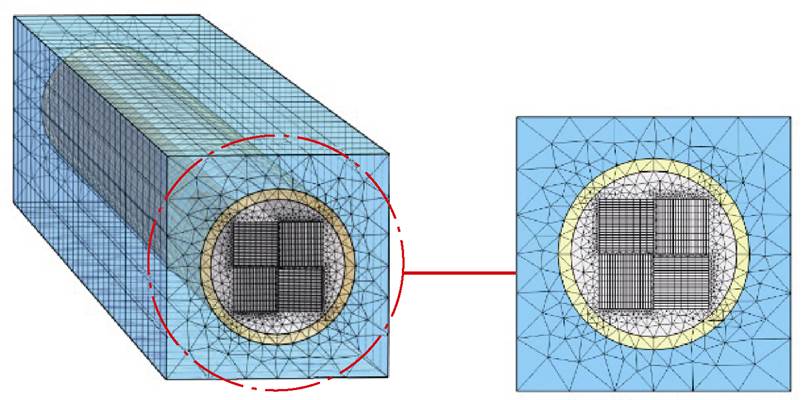
图3 准各向同性股线几何模型的网格划分
Fig.3 Grid map of the quasi-isotropic superconducting strand
1.2.1 电磁场仿真模块的建立
基于H法求解股线的磁场部分，自变量为磁场强度变量H，其控制方程为
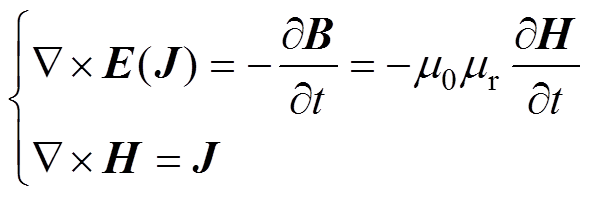（1）
式中，m0为真空中的磁导率；mr为相对磁导率。
对于三维问题，上述控制方程可以写为分量形式，即
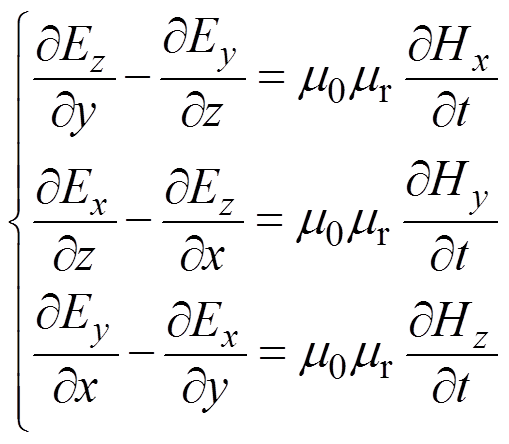（2）
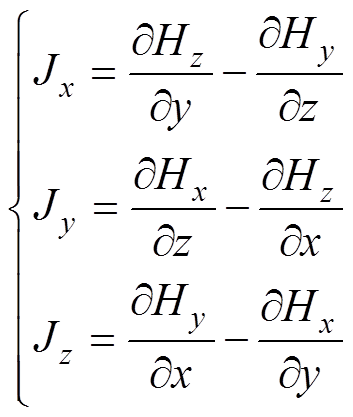（3）
第二代超导体的电阻率满足E-J指数规律，即
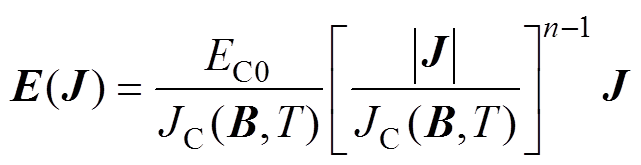（4）
式中，EC0为临界电场强度（10-4 V/m）；n为反映E-J曲线陡度的指数，在本模型中取值为21；JC为临界电流密度，其值的大小受磁场强度以及温度的影响[24]，即
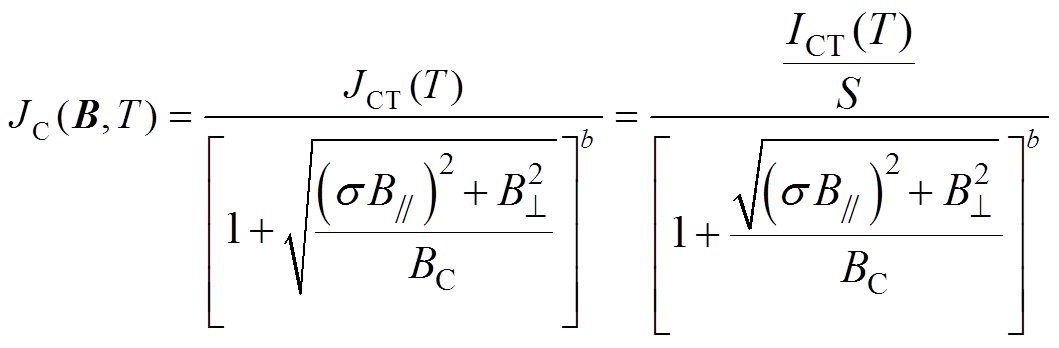（5）
式中，
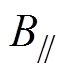与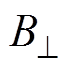
分别为平行于超导带材表面的磁场分量和垂直于带材表面的磁场分量；
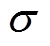、b和BC均为REBCO导体各向异性特征的拟合参数，其值的大小由实验中股线所测临界电流大小拟合而成，在本篇文章中取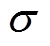=0.225，b=0.55，BC=47.5 mT；S为股线上流通电流的截面积；ICT为股线的临界电流，可根据式（6）计算。
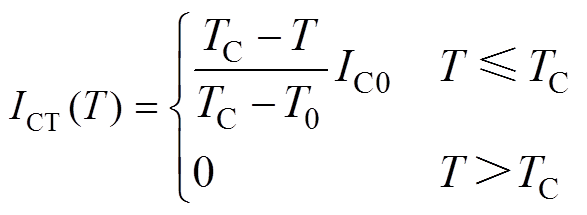（6）
式中，TC为临界转变温度，本文取90 K；IC0为80根单根超导带材在自场下77 K时的临界电流叠加值，即
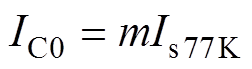（7）
式中，m为超导带材的根数（80）；Is77K为单根带材在77 K温度下的临界电流（90 A）。
由于本文模拟股线在零场液氮冷却条件下，因此本模型的磁场初始条件为
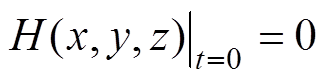（8）
当准各向同性超导股线通电流时，对股线横截面采用积分约束的方式施加电流，如式（9）所示。可通过有限元软件中PDE模块中的逐点约束实现此功能。
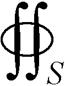
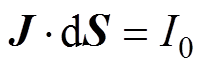（9）
式中，I0为准各向同性超导股线所通的运行电流。
1.2.2 传热模块的建立
为了求解股线的温度分布，需建立股线的传热模型。式（5）中的未知变量除了磁场强度H还有温度T，通过传热模块与磁场模块的联合求解即可得到股线的2个未知量：磁场强度与温度。本文对超导带材的热力学参数采用均一化策略，以点热源的形式添加热脉冲，建立仿真模型。热源的添加如图4所示，热源是Z=0截面处以中心点为圆点，热脉冲周期为200 ms。
传热模块的控制方程为
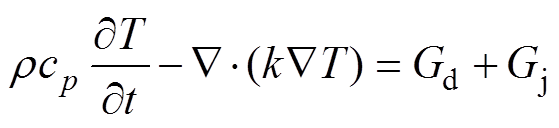（10）
式中，r 为密度（kg/m3）；cp和k分别为比定压热容（J∙kg-1∙K-1）和热导率（W∙m-1∙K-1）；Gd和Gj分别为外加的热脉冲（W/m3）以及单位体积的铜每秒产生的焦耳热（W/m3）。
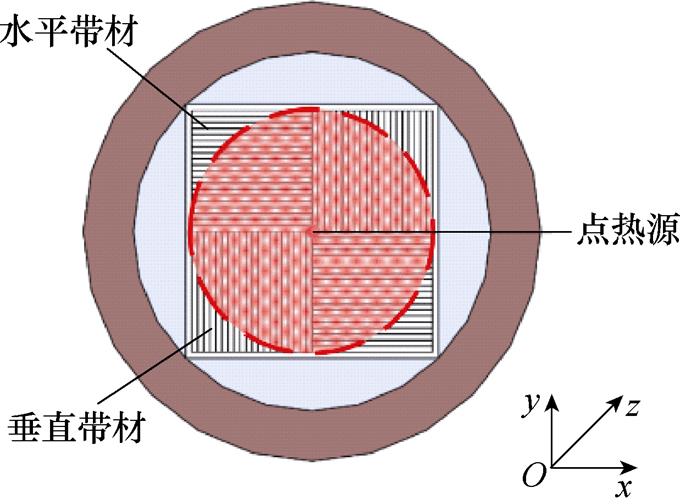
图4 准各向同性超导股线的热脉冲施加
Fig.4 The view of heat pulse of the quasi-isotropic superconducting strand
由图4可以看出，超导线芯的带材可以分为两部分：一部分是与XZ平面平行的平行带材，另一部分是与XZ平面垂直的垂直带材。由于超导带材的热导率k为各向异性[25]，股线超导线芯部分的热导率可写成矩阵形式为
（11）
式中，
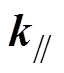与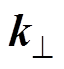
分别为平行带材和垂直带材的热导率，如图4所示。kab与kc可以表示为
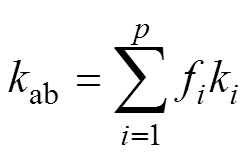（12）
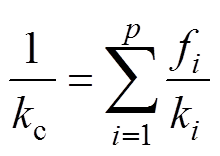（13）
式中，fi为单根超导带材中不同材料的体积占比，见表2；ki为超导带材中不同材料的热导率。
由于本文模拟的是股线在零场液氮冷却条件下的失超特性，传热模块初始条件可写为
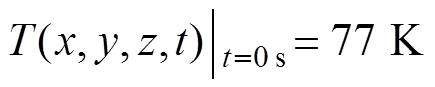（14）
超导股线的长度为L=140 mm，为减小计算量，仿真计算时仅需研究股线的一半（L/2=70 mm），股线的中点位置为z=0 mm，边界条件为
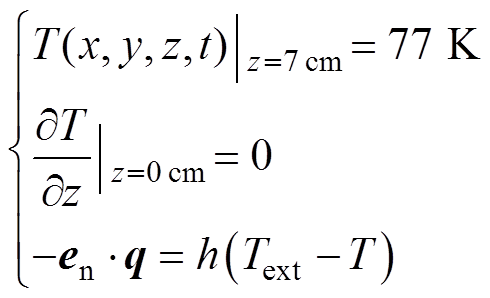（15）
式中，en=[enx eny enz]为垂直于铜包套外表面的单位法向量；q为热流密度（J×m-2×s-1）；h为液氮与铜的换热系数[26]（W∙m-2∙K-1）；Text为液氮温度（77 K）。
本节利用上述失超模型研究了外界热干扰下股线的失超特性。仿真过程中作了如下假设：
（1）股线各处的界面接触热阻（TCR）为0，即界面热接触为理想接触。
（2）超导带材温度高于临界温度（90 K）时其电阻率视为铜的电阻率，且铜的电阻率随温度的变化而变化[27]。
（3）不考虑超导带材终端接触电阻对失超特性的影响。
仿真过程如下：首先，对准各向同性超导股线施加运行电流（100 ms后增加到3 000 A），经过一段时间待股线稳定后，在股线的中央以点热源的方式施加一个热脉冲。热脉冲周期为200 ms，热脉冲期间加热功率恒定。
未施加热干扰时，通过仿真得出该股线临界电流为4 188 A，之后给股线施加3 000 A的运行电流，待其稳定后对股线进行分析，此时股线的磁场强度分布如图5所示。
自场下对此超导股线施加热脉冲，当干扰热量为1.40 J/mm3时，所施加的热干扰未达到最小失超能，股线发生失超恢复行为。准各向同性超导股线被施加热干扰后5 s内的温度分布（x=0 mm, y= 0 mm）如图6所示，从图中可以看出，随着时间的增长，股线的失超区域逐步缩小直至整根股线恢复超导状态。
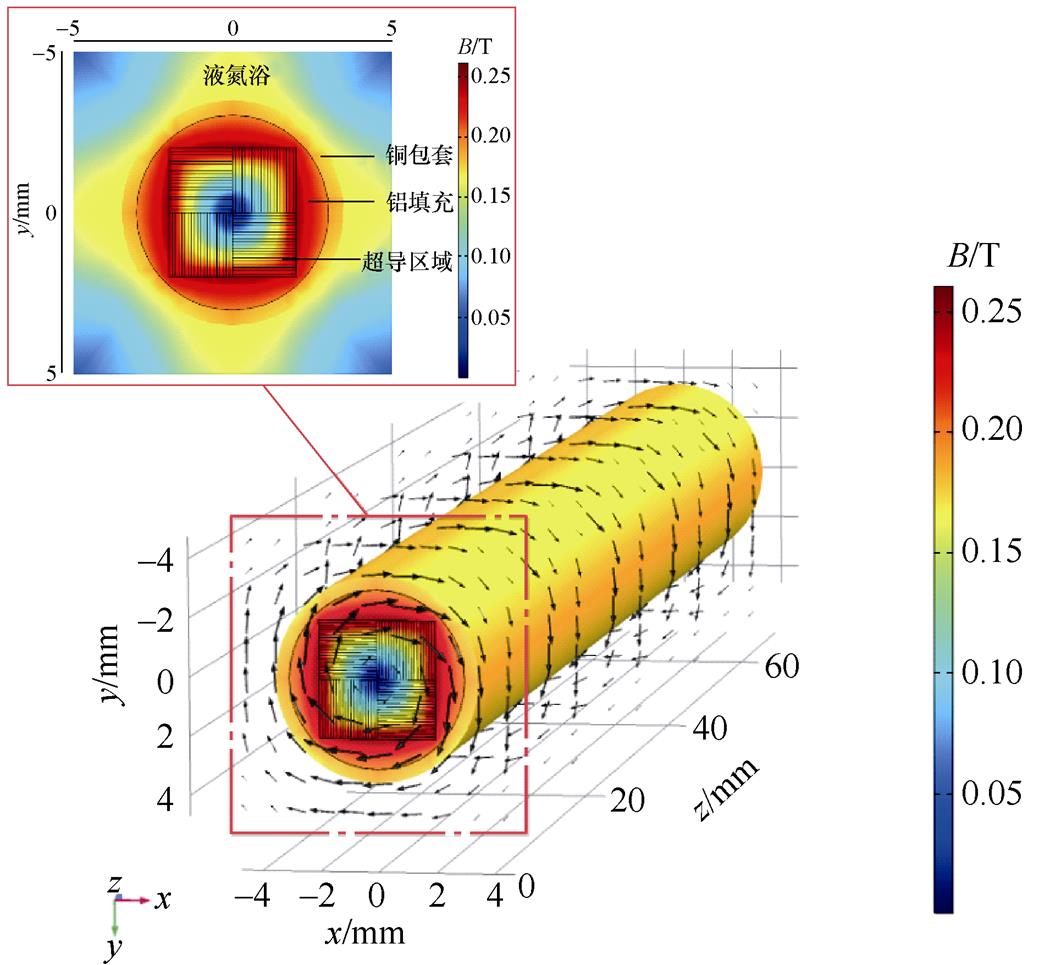
图5 准各向同性超导股线通流3 000 A的磁感应强度分布
Fig.5 The magnetic field distribution of the quasi- isotropic cable at the operating current of 3 000 A
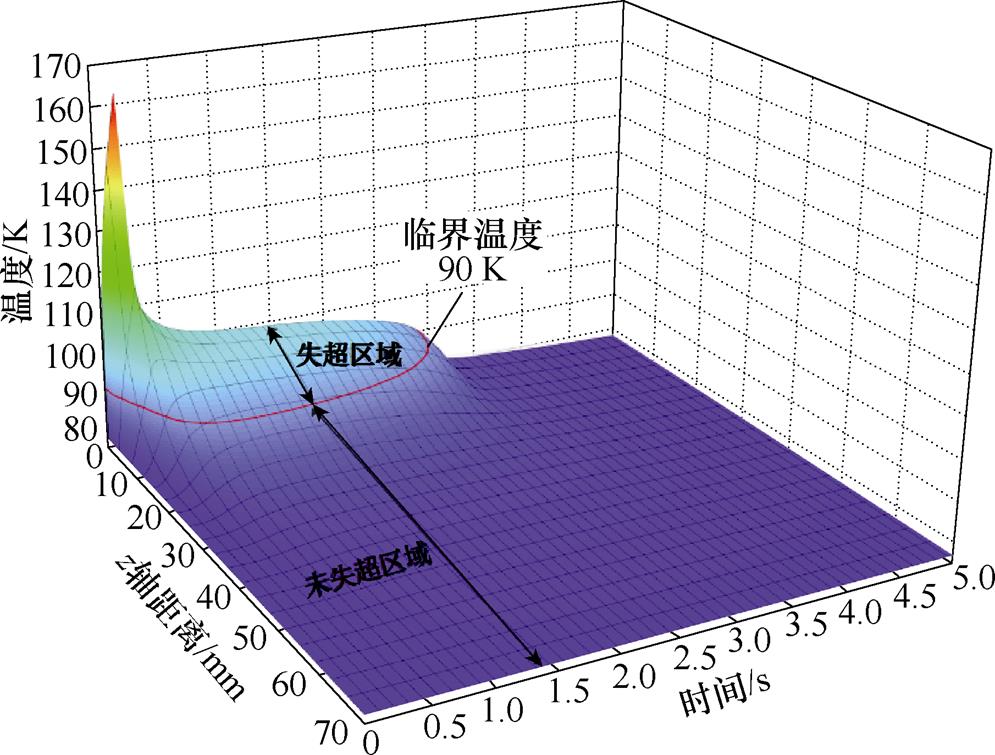
图6 超导股线通流3 000 A施加1.40 J/mm3干扰热量后5 s内的温度分布
Fig.6 The temperature field with the operating current of 3 000 A and the heat energy of 1.40 J/mm3 in 5 s
股线通3 000 A电流时在z=0 mm处径向的温度、电流密度及磁场分布如图7所示。从图中可以看出，0.2 s时z=0 mm处的股线温度高于临界温度，超导股线发生失超，电流转移到铜基底层和铜包套，磁场分布也相应发生变化。当t=5 s时z=0 mm处的股线发生失超恢复行为，温度降低至临界温度以下，电流重新全部转回超导层内。
逐步增加干扰热量至1.48 J/mm3时，股线发生失超传播行为，12 s内的温度分布（x=0 mm, y= 0 mm）如图8所示，失超区域随着时间增大不断扩散，故此时超导股线的最小失超能为1.48 J/mm3。
由于此时发生了失超传播行为，需对除热源施加位置z=0 mm处以外其他位置的温度、电流密度进行观测，这里选择股线模型的中点z=35 mm处，以反映股线的失超传播过程。股线通流3 000 A时在z=35 mm处径向的温度、电流密度以及磁场分布如图9所示。
从图9中可以看出，0.2 s时股线z=35 mm处还未发生失超，电流集中在超导层。当t=10 s时，失超区域已从热点所在区域扩散到z=35 mm处，股线发生失超传播行为。在此，记录该处发生失超的开始时刻为t=10 s，后续将以此为基础计算股线失超传播速度。
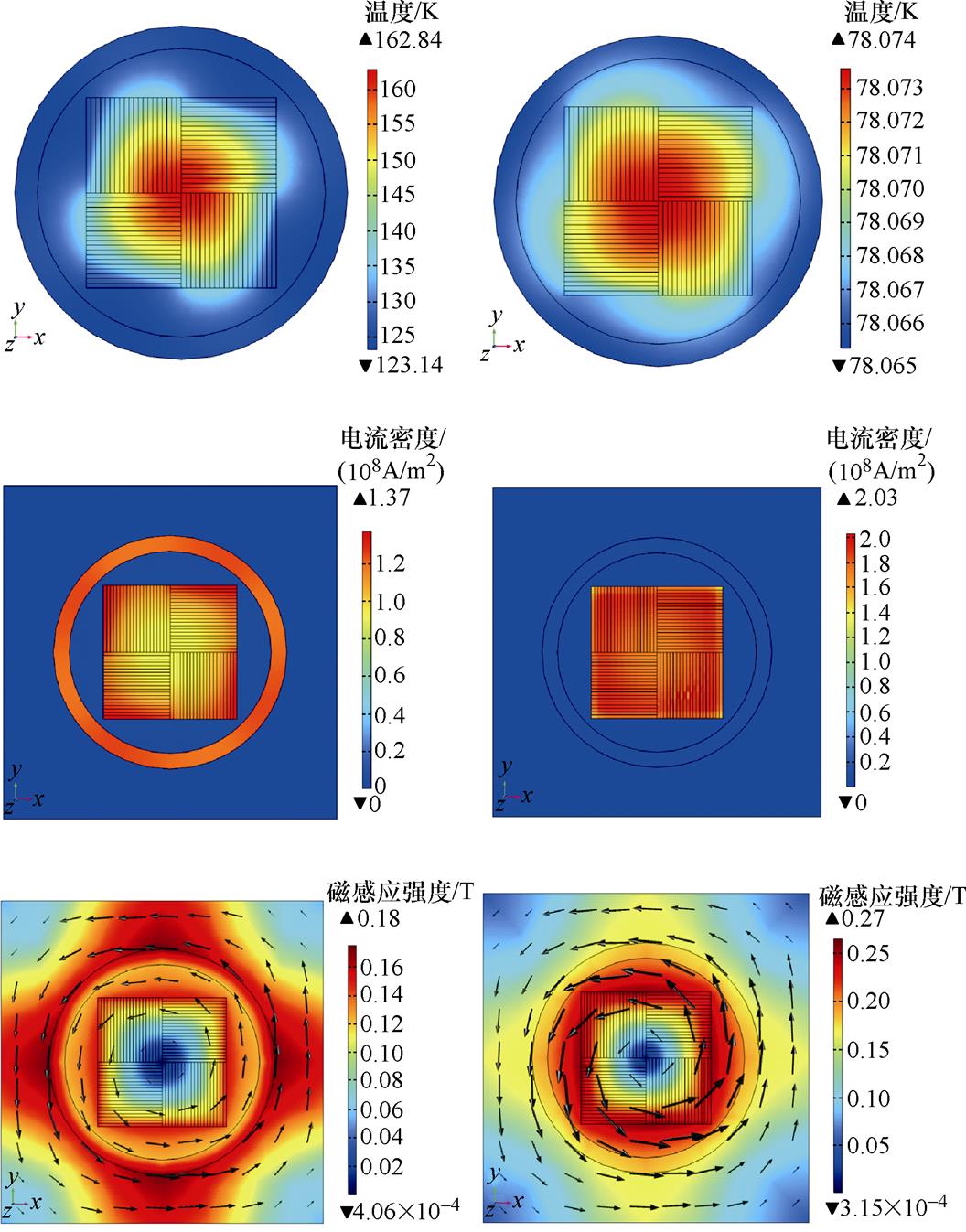
（a）t=0.2 s （b）t=5 s
图7 施加1.40 J/mm3干扰热量后超导股线Z=0 mm处径向温度、电流密度及磁场分布
Fig.7 The temperature field, current distribution and magnetic field of the quasi-isotropic strand under the heat energy of 1.40 J/mm3
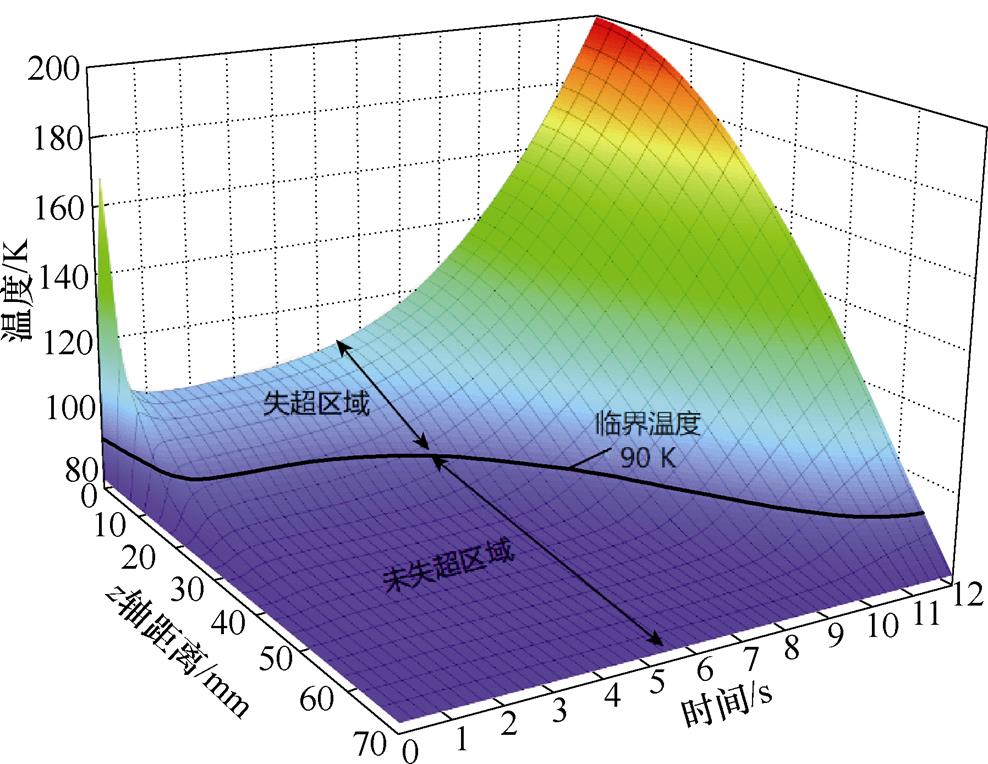
图8 超导股线通流3 000 A施加1.48 J/mm3干扰热量后12 s内的温度分布
Fig.8 The temperature field with the operating current of 3 000 A and the heat energy of 1.48 J/mm3 in 12 s
超导体在正常运行时，外界施加在超导体上的干扰热量会诱发超导体失超，此时正常态下的超导带电阻急剧增大，运行电流转移到金属基体中产生焦耳热，如果这部分焦耳热较小可以沿着超导股线进行热扩散并通过液氮与铜包套的热交换被直接导出，失超区域不会扩散。而当股线中焦耳热的积累大于热扩散散失的热量时，热量逐渐积累，进而导致相邻的超导体温度随之升高而发生失超现象，失超区域扩大，超导股线出现失超传播行为。
（a）t=0.2 s （b）t=10 s
图9 施加1.48 J/mm3干扰热量后超导股线Z=35 mm处径向温度、电流密度及磁场分布图
Fig.9 The temperature field, current distribution and magnetic field of the quasi-isotropic strand under the heat energy of 1.48 J/mm3
由此可见，外界施加在超导体上的干扰热量的大小会影响股线是否发生失超行为。能够引起超导股线失超的最小干扰热量即被定义为最小失超能（Minimum Quench Energy, MQE）。
本文所建立的失超模型中，外界所施加的干扰热量Qd为
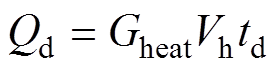（16）
式中，Gheat为热脉冲功率体密度（W×m-3）；Vh为加热区域（半径为2 mm的球体）的体积；td为热脉冲的持续时间（0.2 s）。
增大干扰热量Qd的值直至超导股线失超，MQE可被表示为
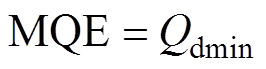（17）
式中，Qdmin为诱发超导股线发生失超的最小干扰 热量。
失超传播速度（QPV）可表示为
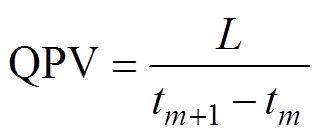（18）
式中，L为股线Z轴上两不同位置间的距离（cm）；tm+1和tm分别为两位置的温度达到临界温度所需的时间。MQE与QPV随运行电流的变化曲线如图10所示。
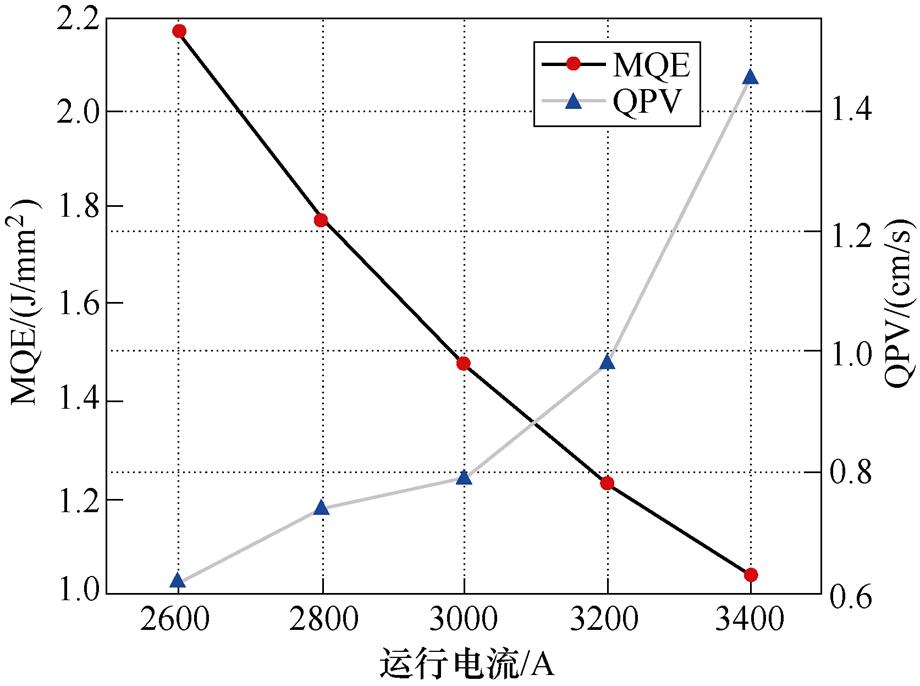
图10 股线MQE与QPV随运行电流的变化曲线
Fig.10 MQEs and QPVs of the strand at different operating currents
由图10可以看出，准各向同性超导股线在运行电流为2 600～3 400 A时其最小失超能由2.17 J/mm3降至1.04 J/mm3，失超传播速度由0.61 cm/s增加到1.45 cm/s。股线的最小失超能随运行电流的增大而减小，失超传播速度随运行电流的增大而增大。当运行电流为2 600 A时，即归一化电流为0.59时，MQE可达到2.17 J/mm3，此时股线最高热点温度已达190 K，然而在实际应用中REBCO超导带材临界热应力[28]所对应的温度约为200 K[29]，因此股线在低电流运行时尽管不易发生失超行为，一旦由于外界干扰发生失超传播，过高的热点温度非常可能会损坏股线，同时低电流下股线的失超传播速度极慢，不利于失超保护装置的及时检测，因此超导股线的运行电流大小极大地影响失超保护装置参数的设置。为了减小股线的热点温度，可采取增加股线中铜的含量[30]，利用其高热导率，将热量在股线径向方向上及时将热量传导出去，然而铜含量的增加会减缓失超传播速度，不利于失超检测。另外，减小股线内部的界面热接触电阻也会降低热点温度，同增加股线中铜含量一样，会减缓失超传播速度[31]。
本文对点状热干源扰诱导的准各向同性超导股线（Q-IS）的失超特性建立了三维电磁热模型，仿真了股线的失超行为及恢复过程，得到了不同运行电流下的最小失超能与失超传播速度，结论如下：
股线的最小失超能随运行电流的增大而减小，失超传播速度随运行电流的增大而增大。铜包套的存在使得股线的热稳定性有了显著提高，铜包套通过及时分流避免超导体因热点温度过高而造成自身不可逆的损坏，矛盾的是，缓慢的失超传播速度不利于对股线的失超检测与失超保护，因此设计股线的铜包套尺寸时不仅要考虑降低超导体热点的温度，还要考虑其失超传播速度不可过低，以避免超过失超保护装置的失超检测时间。
本文所建立的针对准各向同性超导股线考虑自场的三维磁热失超模型可推广应用到其他超导导体失超特性的研究中去。
参考文献
[1] 党卫军, 孙奇珍, 薛艺为, 等. 施工缺陷对超导电缆中间接头内电场分布的影响[J]. 江苏电机工程, 2020, 39(5): 23-29.
Dang Weijun, Sun Qizhen, Xue Yiwei, et al. Influ- ence of construction defects on electric field distri- bution of superconducting cable intermediate joints[J]. Jiangsu Electrical Engineering, 2020, 39(5): 23-29.
[2] 李显皓, 徐颖, 任丽, 等. 非均匀高温超导带材对CORC电缆失超特性的影响研究[J]. 电工技术学报, 2022, 37(19): 5044-5055.
Li Xianhao, Xu Ying, Ren Li, et al. Influence of non-uniform high temperature superconducting tapes on quench characteristics of CORC cable[J]. Transa- ctions of China Electrotechnical Society, 2022, 37(19): 5044-5055.
[3] 张国民, 陈建辉, 邱清泉, 等. 超导直流能源管道的研究进展[J]. 电工技术学报, 2021, 36(21): 4389- 4398, 4428.
Zhang Guomin, Chen Jianhui, Qiu Qingquan, et al. Research progress on the superconducting DC energy pipeline[J]. Transactions of China Electrotechnical Society, 2021, 36(21): 4389-4398, 4428.
[4] 祝乘风, 厉彦忠, 谭宏博, 等. 热扰动冲击下的高温超导电缆失超恢复特性[J]. 电工技术学报, 2021, 36(18): 3884-3890.
Zhu Chengfeng, Li Yanzhong, Tan Hongbo, et al. Numerical analysis on the quench and recovery of the high temperature superconducting cable subjected to thermal disturbance[J]. Transactions of China Elec- trotechnical Society, 2021, 36(18): 3884-3890.
[5] 秦伟, 马育华, 吕刚, 等. 一种可用于低真空管道的高温超导无铁心直线感应磁悬浮电机[J]. 电工技术学报, 2022, 37(16): 4038-4046.
Qin Wei, Ma Yuhua, Lü Gang, et al. Analyzing and designing a novel coreless linear induction maglev motor for low vacuum pipeline[J]. Transactions of China Electrotechnical Society, 2022, 37(16): 4038-4046.
[6] 龚珺, 诸嘉慧, 方进, 等. 电阻型高温超导限流器暂态电阻特性分析[J]. 电工技术学报, 2018, 33(9): 2130-2138.
Gong Jun, Zhu Jiahui, Fang Jin, et al. Transient resistance analysis of resistive high temperature superconducting current limiter[J]. Transactions of China Electrotechnical Society, 2018, 33(9): 2130- 2138.
[7] 夏芳敏, 王醒东. 实用化高温超导带材的应用进展[J]. 新材料产业, 2014(4): 48-52.
Xia Fangmin, Wang Xingdong. Progress in the application of practical HTS tapes[J]. Advanced Materials Industry, 2014(4): 48-52.
[8] Fleiter J, Ballarino A, Bottura L, et al. Charac- terization of roebel cables for potential use in high-field magnets[J]. IEEE Transactions on Applied Superconductivity, 2015, 25(3): 1-4.
[9] Goldacker W, Grilli F, Pardo E, et al. Roebel cables from REBCO coated conductors: a one-century-old concept for the superconductivity of the future[J]. Superconductor Science and Technology, 2014, 27(9): 093001.
[10] Komeda T, Amemiya N, Tsukamoto T, et al. Experimental comparison of AC loss in REBCO roebel cables consisting of six strands and ten strands[J]. IEEE Transactions on Applied Super- conductivity, 2014, 24(3): 1-5.
[11] van der Laan D C. YBa2Cu3O7-d coated conductor cabling for low ac-loss and high-field magnet applications[J]. Superconductor Science and Tech- nology, 2009, 22(6): 065013.
[12] van der Laan D C, Weiss J D, Noyes P, et al. Record current density of 344 A mm-2 4.2 K and 17 T in CORC® accelerator magnet cables[J]. Superconductor Science and Technology, 2016, 29(5): 055009.
[13] Takayasu M, Chiesa L, Bromberg L, et al. Cabling method for high current conductors made of HTS tapes[J]. IEEE Transactions on Applied Super- conductivity, 2011, 21(3): 2340-2344.
[14] Wang Yinshun, Baasansuren S, Xue Chi, et al. Development of a quasi-isotropic strand stacked by 2G wires[J]. IEEE Transactions on Applied Super- conductivity, 2016, 26(4): 1-6.
[15] Chan W K, Masson P J, Luongo C, et al. Three- dimensional micrometer-scale modeling of quenching in high-aspect-ratio YBa2Cu3O7-d coated conductor tapes-part I: Model development and validation[J]. IEEE Transactions on Applied Superconductivity, 2010, 20(6): 2370-2380.
[16] Chan W K, Schwartz J. Three-dimensional micrometer- scale modeling of quenching in high-aspect-ratio YBa2Cu3O7-d coated conductor tapes-part II: Influ- ence of geometric and material properties and impli- cations for conductor engineering and magnet design[J]. IEEE Transactions on Applied Super- conductivity, 2011, 21(6): 3628-3634.
[17] Roy F, Therasse M, Dutoit B, et al. Numerical studies of the quench propagation in coated conductors for fault current limiters[J]. IEEE Transactions on Applied Superconductivity, 2009, 19(3): 2496-2499.
[18] Wang Yawei, Zheng Jinxing, Zhu Zixuan, et al. Quench behavior of high-temperature superconductor (RE) Ba2Cu3Ox CORC cable[J]. Journal of Physics D: Applied Physics, 2019, 52(34): 345303.
[19] Kang Rui, Uglietti D, Wesche R, et al. Quench simulation of REBCO cable-in-conduit conductor with twisted stacked-tape cable[J]. IEEE Transactions on Applied Superconductivity, 2020, 30(1): 1-7.
[20] 林良真. 超导电性及其应用[M]. 北京: 北京工业大学出版社, 1998.
[21] Hong Z, Campbell A M, Coombs T A. Numerical solution of critical state in superconductivity by finite element software[J]. Superconductor Science and Technology, 2006, 19(12): 1246-1252.
[22] Brambilla R, Grilli F, Martini L. Development of an edge-element model for AC loss computation of high-temperature superconductors[J]. Superconductor Science and Technology, 2007, 20(1): 16-24.
[23] Ma Jun, Geng Jianzhao, Chan Wan kan, et al. A temperature-dependent multilayer model for direct current carrying HTS coated-conductors under per- pendicular AC magnetic fields[J]. Superconductor Science and Technology, 2020, 33(4): 045007.
[24] Grilli F, Sirois F, Zermeño V M R, et al. Self- consistent modeling of the Ic of HTS devices: how accurate do models really need to be?[J]. IEEE Transa- ctions on Applied Superconductivity, 2014, 24(6): 1-8.
[25] Bagrets N, Goldacker W, Jung A, et al. Thermal properties of ReBCO copper stabilized supercon- ducting tapes[J]. IEEE Transactions on Applied Superconductivity, 2013, 23(3): 6600303.
[26] Li Tingting, Wang Yinshun, Shi Chenjie, et al. Thermal stability of a quasi-isotropic strand made from coated conductors[J]. IEEE Transactions on Applied Superconductivity, 2016, 26(4): 1-5.
[27] Casali M, Breschi M, Ribani P L. Two-dimensional anisotropic model of YBCO coated conductors[J]. IEEE Transactions on Applied Superconductivity, 2015, 25(1): 1-12.
[28] Duan Yujie, Gao Yuanwen. Delamination and current-carrying degradation behavior of epoxy- impregnated superconducting coil winding with 2G HTS tape caused by thermal stress[J]. AIP Advances, 2020, 10(2): 1-13.
[29] Marinucci C, Bottura L, Calvi M, et al. Quench analysis of a high-current forced-flow HTS conductor model for fusion magnets[J]. IEEE Transactions on Applied Superconductivity, 2011, 21(3): 2445-2448.
[30] Kang Rui, Uglietti D, Song Yuntao. To the opti- mization of quench performance for a large REBCO cable-in-conduit conductor[J]. IEEE Transactions on Applied Superconductivity, 2021, 31(2): 1-9.
[31] Kang Rui, Uglietti D, Wesche R, et al. Quench simulation of REBCO cable-in-conduit conductor with twisted stacked-tape cable[J]. IEEE Transactions on Applied Superconductivity, 2020, 30(1): 1-7.
Quench Characteristics of Quasi-Isotropic Superconducting Strand Triggered by Point Thermal Disturbance
Abstract With the development of second-generation (2G) high-temperature superconductors (HTS) and the progress in cryogenic technology, 2G HTS has been widely applied in superconducting power technology due to its excellent mechanical properties, complete diamagnetism, and zero resistance characteristic at liquid nitrogen temperatures. However, the practical applications of HTS face a key issue: the quench behavior of HTS, mainly embodied in the minimum quench energy (MQE) and quench propagation velocity (QPV). This paper studies the quench characteristics of quasi-isotropic superconducting (Q-IS) strands when subjected to a point thermal disturbance and the influence of different operating currents for quench detection and protection of HTS devices in power systems.
Firstly, the structure and parameters of the superconducting strand used in the simulation model are described in detail, and the geometric model of a 140 mm long Q-IS strand immersed in liquid nitrogen is established. Considering the effect of the self-magnetic field, a 3D electric-magnetic-thermal simulation model is established to analyze the thermal stability of the strand using the finite element method (FEM). At the beginning of the simulation, the operating current is applied to the HTS strand until the strand operates stably. Then, a thermal pulse is added to the strand’s center to simulate a point thermal disturbance. The thermal disturbance power is constant during the 200 ms duration of the thermal disturbance application.
The thermal stability simulation results show that when the operating current is 3 000 A and the disturbance energy is 1.40 J/mm3, the strand exhibits an apparent quench recovery behavior, suggesting that 1.40 J/mm3 does not reach the MQE of the strand. As the disturbance energy increases to 1.48 J/mm3, the quench region diffuses continuously over time, resulting in quench propagation with the strand. Under this operating current, the MQE of the superconducting strand is 1.48 J/mm3, and the QPV is 0.79 cm/s. Then, MQEs and QPVs under various operating currents are simulated by the same method. The MQE of the Q-IS strand decreases from 2.17 J/mm3 to 1.04 J/mm3, and the QPV increases from 0.61 cm/s to 1.45 cm/s as the operating current increases from 2 600 A to 3 400 A.
It is also shown that the MQE of the Q-IS strand decreases and the QPV increases with the increase of operating current. The current sharing of the copper sheath can significantly improve the thermal stability of the Q-IS strand. However, it is essential to consider the size design of the copper sheath to ensure it is manageable, potentially causing a delay in quench detection by the protection device. The electric-magnetic-thermal simulation model established in this paper can also be extended to study the thermal stability of Q-IS strands in external fields and other superconducting strands.
keywords：Quasi-isotropic superconducting strand, quench behavior, minimum quench energy (MQE), quench propagation velocity (QPV)
中图分类号：TM26
DOI: 10.19595/j.cnki.1000-6753.tces.221990
国家自然科学基金资助项目（52277025, 51877083）。
收稿日期 2022-10-18
改稿日期 2022-12-19
王起悦 女，1999年生，硕士研究生，研究方向为超导电力技术。E-mail: superyue990826@163.com
皮 伟 男，1979年生，副教授，研究方向为超导电力技术。E-mail: ppiiwei@ncepu.edu.cn（通信作者）
（编辑 郭丽军）