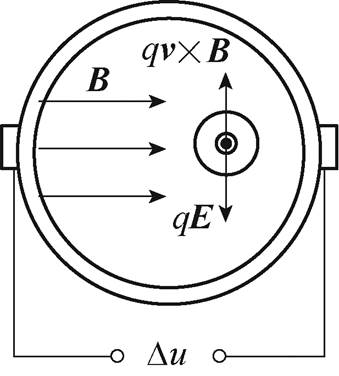
图1 磁场与血流耦合电效应原理
Fig.1 Principle of magnetic field and blood flow coupling electrical effect
摘要 基于磁电耦合效应的血流检测及血管成像是实现心血管疾病早期诊疗的有效方法之一。该文基于磁场与血流耦合电效应,设计一种用于动脉血管扫描成像的组合线圈结构,产生带有零磁场线(FFL)区域的线性梯度磁场;在此结构的基础上,通过控制激励电流驱动FFL实现成像区域双向扫描;结合卷积神经网络(CNN)实现磁电耦合信号与血管信息的非线性映射,进而提出一种基于线性零磁场的动脉血管扫描成像新方法。采用多物理场仿真软件COMSOL对基于线性零磁场的血管扫描成像方法进行建模,求解磁电耦合信号,验证了所提出方法的合理性和有效性。结果表明,线性梯度磁场模式下的磁电耦合信号含有血管位置、半径等信息;CNN重建血管位置误差平均值为1.569 4 mm,重建血管半径的方均误差(MSE)和相关系数(CC)平均值分别为0.054 8和0.987 0。研究结果可用于血管成像装置设计及后续相关临床应用提供研究支撑。
关键词:心血管疾病 磁场与血流耦合电效应 零磁场线 线性梯度磁场 卷积神经网络 COMSOL
据世界卫生组织(World Health Organization, WHO)官网的统计数据显示[1]:缺血性心脏病和中风是全球范围内的第一大死亡原因,2016年共造成1 520万例死亡。而引发心脑血管疾病的主要诱因是心脏或脑部的供血动脉狭窄导致供血不足。目前临床常用的动脉血管病变诊断方法有数字减影血管造影、磁共振血管造影、CT血管造影和超声检查[2]。这些方法由于其创伤性、诊断成本、辐射问题、操作及分析难度等因素,仍无法作为常规的血管疾病初期诊断手段[3]。因此,研究低成本、普及型的血管病变早期诊断方法对于预警心脑血管疾病至关 重要。
近年来,电阻抗成像、磁感应成像、磁声成像等无创功能成像技术在医学影像学领域的研究取得很大进展[4-6],研究成果表明,基于电磁的生理信息检测及功能成像技术在疾病早期诊断和监测方面具有优势。随着微弱信号检测技术的发展[7-8],电磁血流测量方法受到研究学者的关注。2013年,S. Mikami等[9]应用电磁流量计对肢体血流进行了测量采集。2014年,H. Nakagawa等[10]将电磁流量计应用于一种人工血液循环系统和用于改善血液流动的医疗装置设计过程中。2016年,S. Tanveer等[11]提出了在周期性体加速度和磁场作用下,倾斜管内脉动血液通过多孔介质的重力流动问题。2017年,D. Yamamoto等[12]在利用区域动脉自旋标记评估围手术期颈内动脉灌注区变化与重建术后脑血流的关系问题中,应用电磁流量计测量颈动脉内膜切除术前后的颈内动脉流量。H. Boccalon等[13]利用麦克斯韦方程组建立了肢体血流理论模型,将流动诱发电位与血流联系起来。H. Kanai等[14]开发了一种靠近皮肤表面测量的非侵入式动脉血流计。张俊[15]研究一种基于旋转磁场的多电极电磁流量测量方法,对非对称流流速测量、流型可视化等问题进行了相关探索。赵宇洋等[16]基于Shercliff权函数提出了区域权函数的概念,并设计了一种基于区域权函数理论的多电极电磁流量计。以上工作集中在匀强磁场激励下通过电极测量肢体皮肤表面电压,获取血液流速或血流量信息的研究。在前期学者研究的基础上,2020年,刘晏君等[17]分析均匀强磁场下血流磁电耦合效应,并利用奇异值分解法进行血液流速反演血管断层图像,说明了磁场与血流耦合电效应在动脉血管成像及狭窄率预测方面的潜在应用。
本课题组在前期研究已经证明了均匀强磁场激励下的动脉血流成像方法的可行性[18],并发现了较大范围的匀强磁场产生,不利于血管成像实验工作的展开。为了改善该问题,设计了一种组合线圈结构,用于产生线性梯度零磁场[19],分析了线性梯度零磁场对血流磁电耦合信号的影响,研究了组合线圈结构、激励磁场特点对零磁场线(Field Free Line, FFL)的影响;建立了血管成像模型,通过卷积神经网络(Convolutional Neural Networks, CNN)实现双向磁电耦合信号与血管位置及半径的非线性映射,对所提血管扫描成像新思路的进行了验证。研究工作为后续动脉血流实时成像乃至血管狭窄早期诊断等奠定基础。
磁场与血流耦合电效应原理如图1所示。人体血液兼具流动性和导电性,当垂直于血管血液流速方向施加一外部磁场B时,血管血液可等效为一导体沿垂直于磁场方向作切割磁感线运动,则血液中的正、负电荷粒子将受到洛伦兹力qv×B的作用,发生极化分离,最终在电场力qE的作用下达到平衡,进而在导电目标体内形成电势场。

图1 磁场与血流耦合电效应原理
Fig.1 Principle of magnetic field and blood flow coupling electrical effect
利用紧贴在目标体表面的电极即可检测到相应的感应电压信号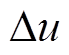 。电压信号携带了目标体内血管血流位置和速度等信息,可用于探测血管血流分布情况。根据欧姆定律微分方程,整个层析平面内的电流密度J满足
。电压信号携带了目标体内血管血流位置和速度等信息,可用于探测血管血流分布情况。根据欧姆定律微分方程,整个层析平面内的电流密度J满足
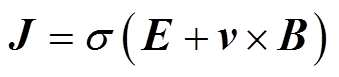 (1)
(1)
式中,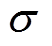 为电导率;
为电导率;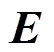 为电场强度矢量;
为电场强度矢量;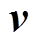 为血流速度矢量;
为血流速度矢量;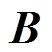 为磁感应强度矢量。引入标量电势
为磁感应强度矢量。引入标量电势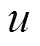 ,得到标量电势
,得到标量电势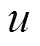 与血流矢量流速
与血流矢量流速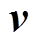 、矢量磁场
、矢量磁场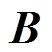 数值关系的泊松方程为
数值关系的泊松方程为
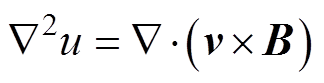 (2)
(2)
当血液流速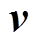 和磁场
和磁场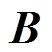 已知时,利用式(2)求解待测区域内的电势场分布,进而获得体表两电极间的电势差信号。当通过测量电压
已知时,利用式(2)求解待测区域内的电势场分布,进而获得体表两电极间的电势差信号。当通过测量电压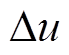 后,同样能够计算出动脉血液流速
后,同样能够计算出动脉血液流速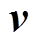 ,获得血管内血流速度分布。
,获得血管内血流速度分布。
基于互易定理[20],边界电压的积分表达式为
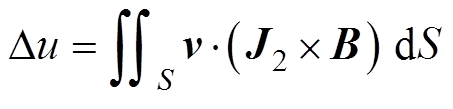 (3)
(3)
式中,J2为互易场中的电流密度矢量;S为闭合曲面面积。
式(3)说明感应电压Δu与动脉血液流速v之间的近似线性关系。当激励磁场随时间t变化时,有
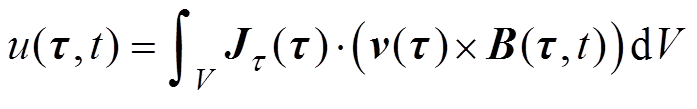 (4)
(4)
式中,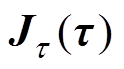 为互易电流密度矢量;
为互易电流密度矢量;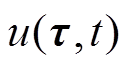 为电压信号;
为电压信号;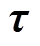 为动脉血流区域空间位置;V为血管血流区域体积。此时电压信号由血管中血液流速分布与时变激励磁场共同作用产生,血液流速分布则受血管位置、半径表征信息的影响,于是所得感应电压信号与血管位置及半径相关。
为动脉血流区域空间位置;V为血管血流区域体积。此时电压信号由血管中血液流速分布与时变激励磁场共同作用产生,血液流速分布则受血管位置、半径表征信息的影响,于是所得感应电压信号与血管位置及半径相关。
基于线性零磁场的血管扫描成像主要利用带有零磁场区域的线性梯度磁场,驱动FFL在待测区域内扫描,获得包含不同方向血管表征信息的感应电压信号,进而通过非线性映射实现血管断层图像重建。其基本过程如图2所示,具体步骤如下。
首先,通过组合线圈结构设计构建线性梯度磁场的FFL,具体设计思路将在后续第2节将展开详细讨论。
然后,调控组合线圈的激励电流,驱动FFL先沿着y轴扫描,获得感应电压信号Uy(t);再沿着z轴扫描,获得感应电压信号Uz(t)。由式(4)可知,当血流区域的磁场随时间连续变化时,感应电压为一组时变电压信号。对其进一步分析,由于血管内径很小,其径向方向上的互易电流密度和磁场变化不大。因此,将血管径向(FFL扫描方向)上的参数值用中心线处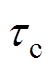 的参数值代替;同时,对于血管轴向
的参数值代替;同时,对于血管轴向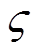 各点参数,采用轴向参数的平均值代替。根据向量运算规则,式(4)可近似转换为
各点参数,采用轴向参数的平均值代替。根据向量运算规则,式(4)可近似转换为
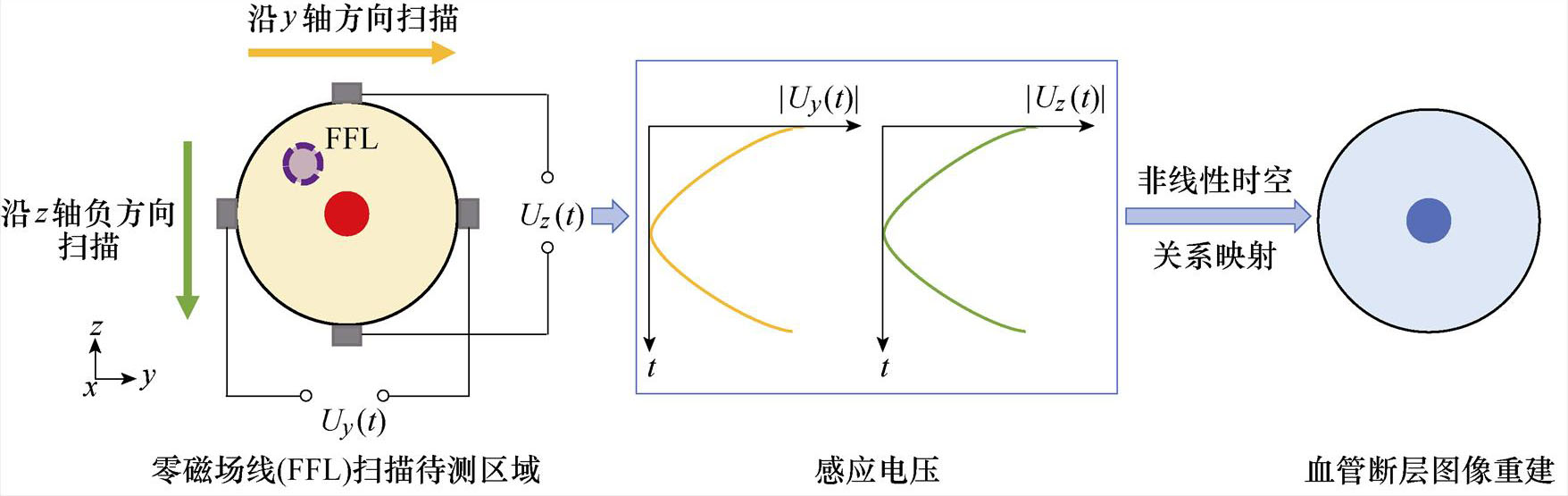
图2 基于FFL的血管断层扫描成像原理
Fig.2 Principle diagram of zero magnetic field line based tomography imaging of blood vessels
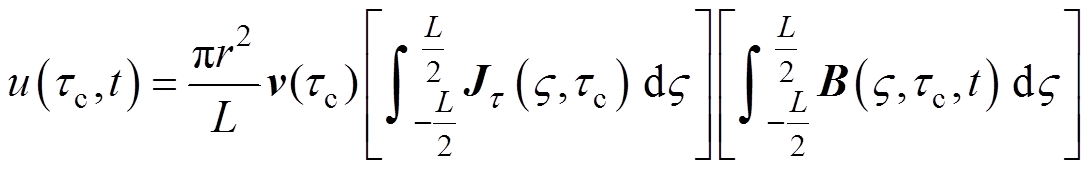 (5)
(5)
式中,r为血管半径;L为血管血流区域长度。
由式(5)可得,时变感应电压信号与血管中心位置和血管半径呈非线性关系。并且,经过FFL分别沿y、z方向扫描,感应电压信号中将包含血管中心位置y坐标、血管中心位置z坐标和血管半径的信息。
由于血管的中心位置和半径信息能够表征血管的分布与形态。这使得通过提取感应电压信号中的血管表征信息重建血管断层图像存在可能。
深度学习算法在复杂非线性问题中的数据处理具有优势[21]。本文提出利用CNN能够拟合输入与输出数据之间非线性关系的特点,建立感应电压信号与血管中心位置y、z坐标和血管半径之间的非线性时空映射关系。
所采用的CNN具有3个“卷积层+池化层”顺次相接、最后一个池化层后连接一个全连接层的结构。CNN以时变感应电压信号作为输入,以血管中心位置y、z坐标及半径作为输出。
输入感应电压数据后,先通过卷积计算提取其表征信息,经过第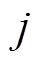 层卷积的输出
层卷积的输出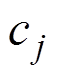 为
为
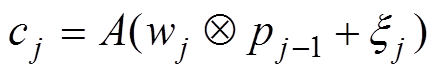 (6)
(6)
式中,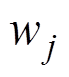 和
和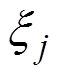 分别为第
分别为第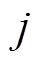 层卷积计算中的权重和偏置项;
层卷积计算中的权重和偏置项;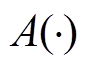 为激活函数;
为激活函数;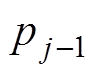 为第
为第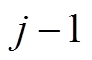 层的输出;
层的输出; 表示卷积计算。
表示卷积计算。
卷积计算的结果接入最大池化层,表征信息经过最大池化操作后变为
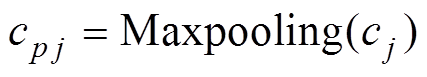 (7)
(7)
式中,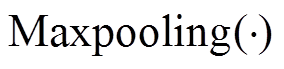 为最大池化操作。
为最大池化操作。
重复以上操作后,最后一层池化层处理后的特征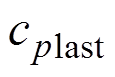 被输入全连接层进行特征整合,则有
被输入全连接层进行特征整合,则有
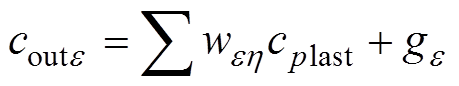 (8)
(8)
式中,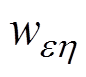 为上层第
为上层第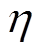 个节点数据对应全连接层第
个节点数据对应全连接层第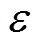 个节点数据的权重;
个节点数据的权重;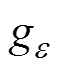 为第
为第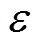 个节点数据的偏置项;
个节点数据的偏置项;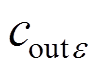 为全连接层第
为全连接层第 个节点的输出数据,即血管中心位置y、z坐标值或半径值。
个节点的输出数据,即血管中心位置y、z坐标值或半径值。
当通过全连接层的所有节点输出血管中心位置坐标和半径后,可由血管中心位置的y、z坐标确定血管在yz平面内的位置,并根据血管半径值进行血管断层图像重建。
为了保证零磁场的均匀性[22],用于产生线性梯度磁场的组合线圈结构如图3所示。作为一种开放式组合线圈结构,其包括四个尺寸相同的梯度线圈(GC1、GC2、GC3、GC4)和三个驱动线圈(DC1、DC2、DC3,DC2与DC3尺寸相同),被测目标放置于中央空隙区域。其中,驱动线圈采用非对称结构的设计。这是由于对称的FFL双向扫描驱动线圈结构虽然能够产生较大且稳定的磁场梯度,但其会构成封闭式组合线圈结构,对被测对象体积大小有所限制[23]。而非对称驱动线圈结构则降低了该局限性,且减少了线圈个数,有利于组合线圈结构的简化。
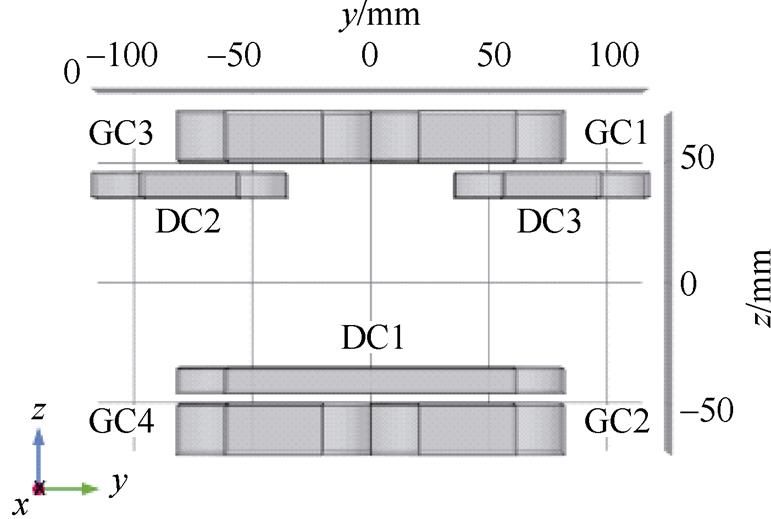
(a)yz视图
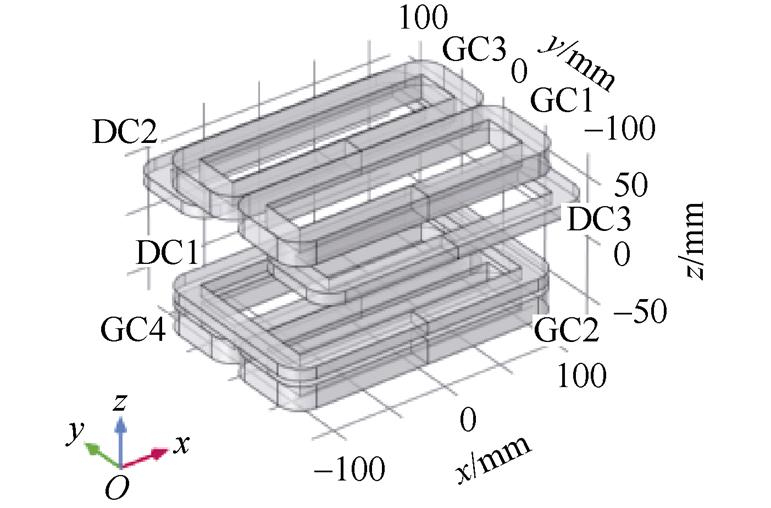
(b)三维视图
图3 设计的开放式组合线圈结构
Fig.3 The design of open combination coil structure
梯度线圈用于产生线性梯度磁场,分别对同轴的梯度线圈通入相同的直流电流,对异轴梯度线圈通入大小相同但方向相反的直流电流,即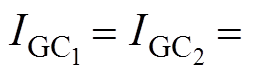
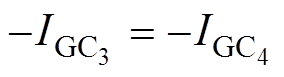 ,由于对称磁场的相互叠加,在x轴方向上(y=z=0)将会产生一个磁场强度近似为0的线型区域,即FFL。
,由于对称磁场的相互叠加,在x轴方向上(y=z=0)将会产生一个磁场强度近似为0的线型区域,即FFL。
由空间向量分解定理,一个通电线圈离轴处任意一点P磁场可分解为互相正交的x、y、z方向磁场分量。当四个梯度线圈如图4a方式排列时,GC1(GC2)和GC3(GC4)、GC1(GC3)和GC2(GC4)分别关于xOz、xOy平面呈镜像几何关系。各梯度线圈磁场分量Bij满足
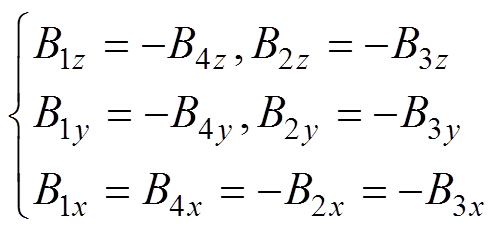 (9)
(9)
式中,Bij(i=1, 2, 3, 4,j=x, y, z)中i为梯度线圈序号,j为磁场分量方向。
于是,在z=y=0线附近沿x轴方向的磁场消失,产生x轴方向的零磁场区域,如图4b所示。
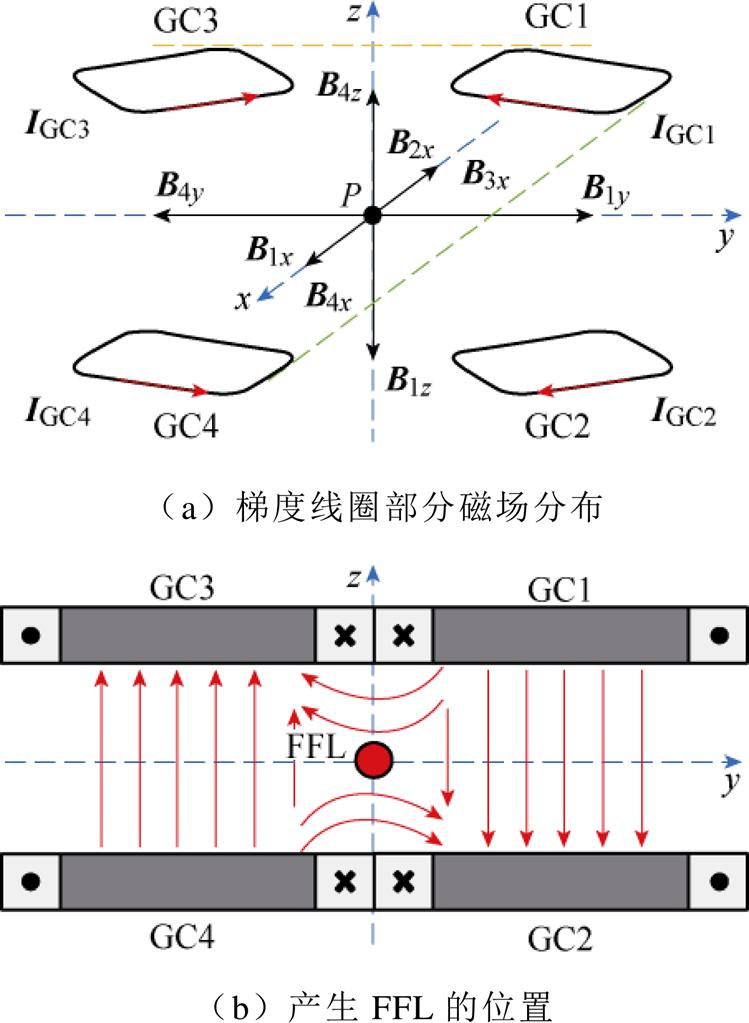
图4 FFL的产生原理
Fig.4 The principle of FFL generation
空间内的梯度磁场强度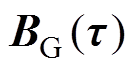 与磁场梯度
与磁场梯度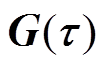 的关系可以表示为
的关系可以表示为
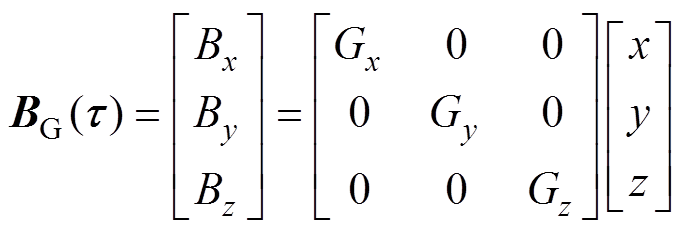 (10)
(10)
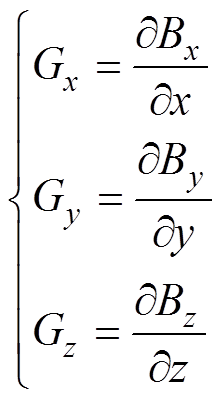 (11)
(11)
式中,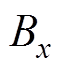 、
、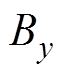 、
、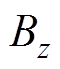 为磁场B在x、y、z方向上的分量;
为磁场B在x、y、z方向上的分量;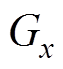 、
、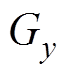 、
、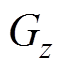 为磁场梯度
为磁场梯度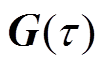 在x、y、z方向上的分量。
在x、y、z方向上的分量。
为驱动FFL在被测区域内进行平移扫描,向驱动线圈通入驱动电流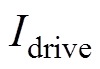 以产生交变的驱动磁场
以产生交变的驱动磁场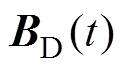 为
为
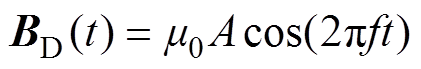 (12)
(12)
式中,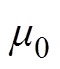 为真空中的磁导率;
为真空中的磁导率;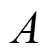 为驱动电流
为驱动电流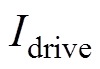 产生的磁场幅值,决定FFL扫描的最大位移;
产生的磁场幅值,决定FFL扫描的最大位移;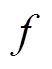 为驱动频率,决定了FFL扫描速度。FFL对被测目标扫描一次的时间为扫描周期
为驱动频率,决定了FFL扫描速度。FFL对被测目标扫描一次的时间为扫描周期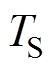 ,即驱动电流
,即驱动电流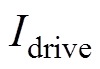 由
由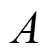 变为
变为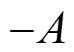 的时间,则
的时间,则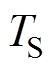 与驱动频率
与驱动频率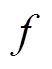 的关系为
的关系为
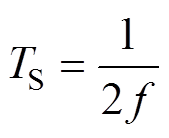 (13)
(13)
梯度线圈与驱动线圈分别通入直流与驱动电流后,产生梯度磁场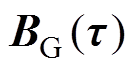 和交变磁场
和交变磁场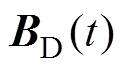 ,二者产生的磁场相互叠加形成复合磁场
,二者产生的磁场相互叠加形成复合磁场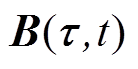 ,同时由位置和时间决定,如式(14)所示。
,同时由位置和时间决定,如式(14)所示。
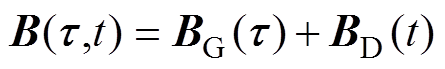 (14)
(14)
由式(10)~式(12)可知,在三维空间中,区域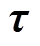 内与时间
内与时间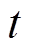 相关的磁场可以表示为
相关的磁场可以表示为
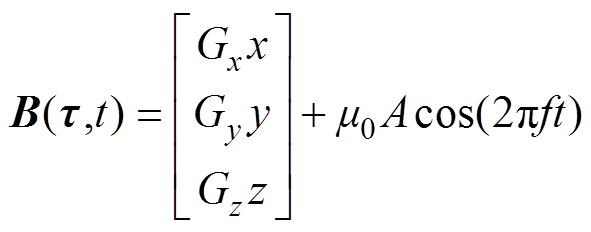 (15)
(15)
通过改变驱动线圈通电方式实现FFL的双向扫描。将驱动线圈分为两组,一组为DC1,另一组为DC2和DC3,电流起始通电方向如图5所示。
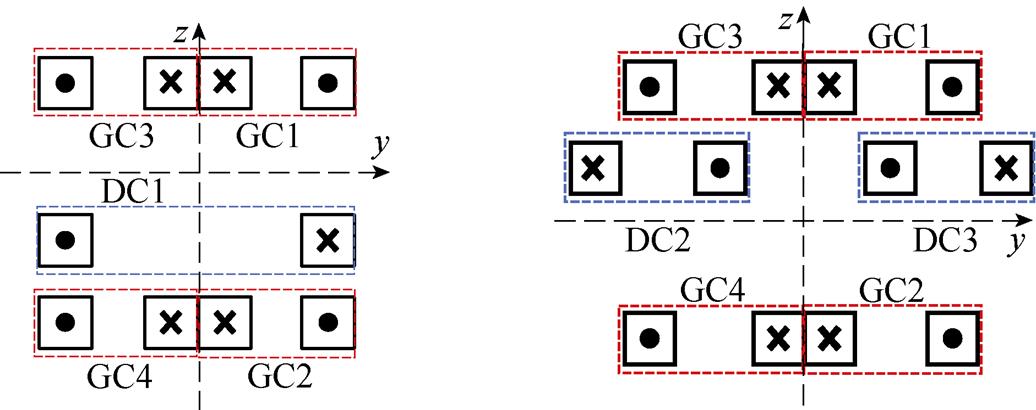
(a)DC1 (b)DC2与DC3
图5 驱动线圈起始通入电流方向
Fig.5 Direction of the starting incoming current of the drive coil
如图5a所示,向DC1中通入式(12)所示交流电流时,将在被测区域内产生主要沿z轴方向的外加驱动交变磁场。通过磁场叠加,可使FFL沿y轴方向进行扫描,获取血管在xy平面内的表征信息。
如图5b所示,DC2与DC3采用对称通电方式,即通入幅值、频率相同,方向相反的交流电流,产生的外加驱动交变磁场主要沿y轴方向,从而驱动FFL沿z轴方向进行扫描。由测量电极便可得到包含xz平面内血管表征信息的感应电压信号。
通过梯度与两组驱动线圈叠加生成复合磁场,可以完成对xy平面和xz平面内线型零磁场的平移式扫描,进行两个维度的血管表征信息提取,进而实现血管断层扫描成像。
本文所设计组合线圈结构在FFL沿y轴方向扫描时,驱动磁场仅由DC1线圈产生。由磁通连续性定理可得,此时在被测区域的驱动磁场虽然主要沿z轴方向分布(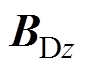 ),但仍有一定的y轴方向磁场分量
),但仍有一定的y轴方向磁场分量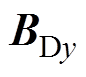 存在,如图6a所示。这导致驱动磁场均匀性较差,在yz平面上FFL沿y轴的扫描轨迹产生偏移高度h,进而其轨迹曲率增大,并呈弧形,如图6b所示。因此,本文通过给梯度线圈GC1和GC3的通电电流添加一个矫正系数a来补偿FFL的中心位置高度偏移量,从而达到矫正FFL轨迹的目标。
存在,如图6a所示。这导致驱动磁场均匀性较差,在yz平面上FFL沿y轴的扫描轨迹产生偏移高度h,进而其轨迹曲率增大,并呈弧形,如图6b所示。因此,本文通过给梯度线圈GC1和GC3的通电电流添加一个矫正系数a来补偿FFL的中心位置高度偏移量,从而达到矫正FFL轨迹的目标。
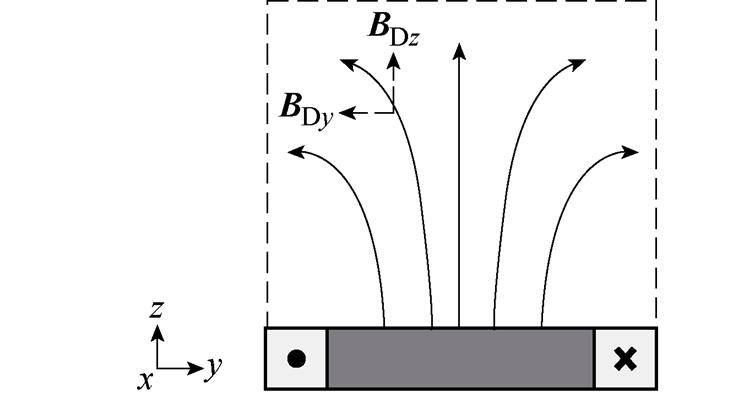
(a)仅由DC1产生外加驱动交变磁场分布
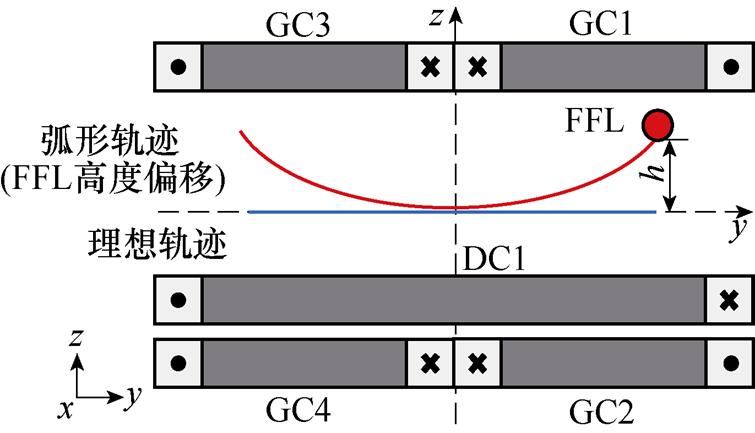
(b)FFL沿y轴扫描弧形轨迹
图6 FFL沿y轴扫描轨迹偏移示意图
Fig.6 Schematic of the scan trajectory offset along the y-axis
FFL轨迹偏移与磁场强度B、线圈通电电流I和扫描时刻t相关。而FFL中心的偏移高度h主要受B与I影响,此影响能够由FFL中心的y轴坐标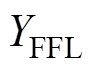 和t直观反映。因此,矫正系数a应描述h、
和t直观反映。因此,矫正系数a应描述h、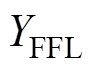 和t之间的关系,从而实现随扫描时刻t的变化对偏移高度h的动态补偿。
和t之间的关系,从而实现随扫描时刻t的变化对偏移高度h的动态补偿。
为了拟合FFL中心y轴坐标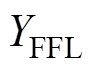 与t、偏移高度h与
与t、偏移高度h与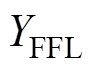 的关系,对图6b所示驱动磁场模式的FFL扫描轨迹进行分析。FFL中心的y轴坐标
的关系,对图6b所示驱动磁场模式的FFL扫描轨迹进行分析。FFL中心的y轴坐标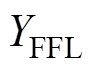 随扫描时刻t的变化可用线性关系
随扫描时刻t的变化可用线性关系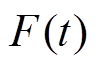 表示,有
表示,有
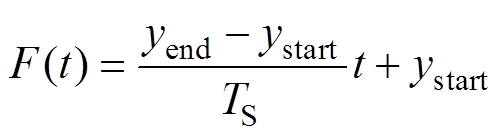 (16)
(16)
式中,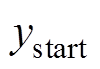 、
、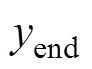 分别为FFL扫描起始与结束时中心y轴坐标值。
分别为FFL扫描起始与结束时中心y轴坐标值。
随着扫描时刻t变化,每个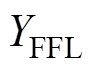 均与一个偏移高度h对应。由于FFL的轨迹呈弧形,二者之间的关系可由m阶多项式
均与一个偏移高度h对应。由于FFL的轨迹呈弧形,二者之间的关系可由m阶多项式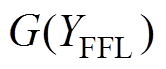 表示,有
表示,有
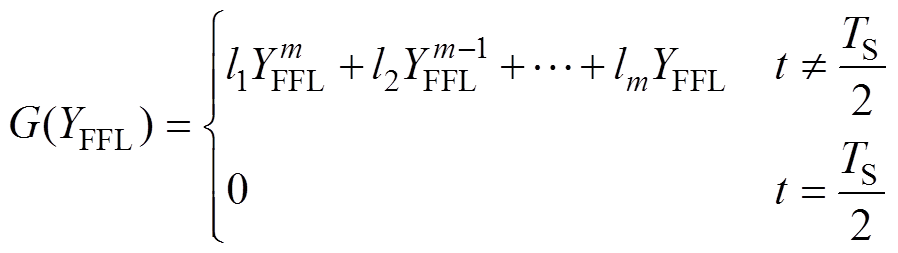 (17)
(17)
式中,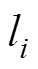 为多项式系数,
为多项式系数,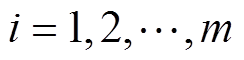 。
。
由于矫正系数a改变线圈通电电流I的大小时,磁场强度B也随之变化。所以,偏移高度h也间接受到矫正系数a的影响,二者之间的对应关系可由n阶多项式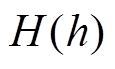 表示,有
表示,有
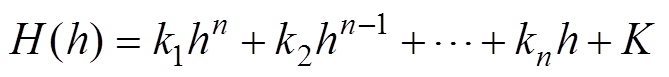 (18)
(18)
式中,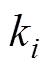 为多项式系数,其与偏移高度h有关,i= 1, 2,…, n;K为常数项。
为多项式系数,其与偏移高度h有关,i= 1, 2,…, n;K为常数项。
矫正系数a存在时,通过上述各个变量拟合关系,可知其与FFL的扫描时刻t的关系为mn阶多项式。即
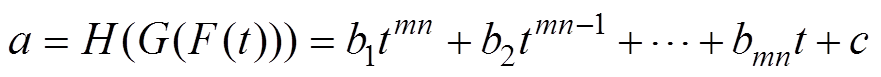 (19)
(19)
式中,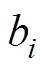 为多项式系数,其由
为多项式系数,其由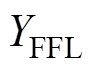 、h和t共同决定,i=1, 2,…, mn;c为常数项。
、h和t共同决定,i=1, 2,…, mn;c为常数项。
由式(16)~式(19)可知,通过调整矫正系数a,实现FFL轨迹偏移的矫正。
在COMSOL中建立如图3所示的组合线圈的三维有限元模型。线圈材料设置为铜,梯度线圈与驱动线圈匝数均为500匝。根据2.1节中的激励方式仅对梯度线圈通入幅值为IGC的直流电流,产生线性梯度磁场与FFL。
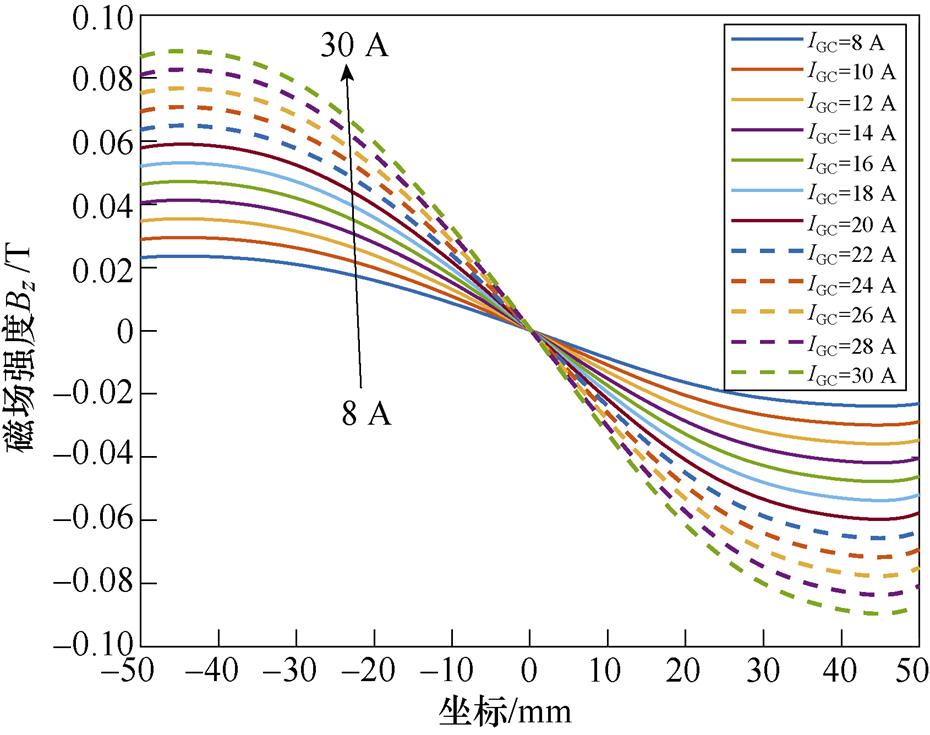
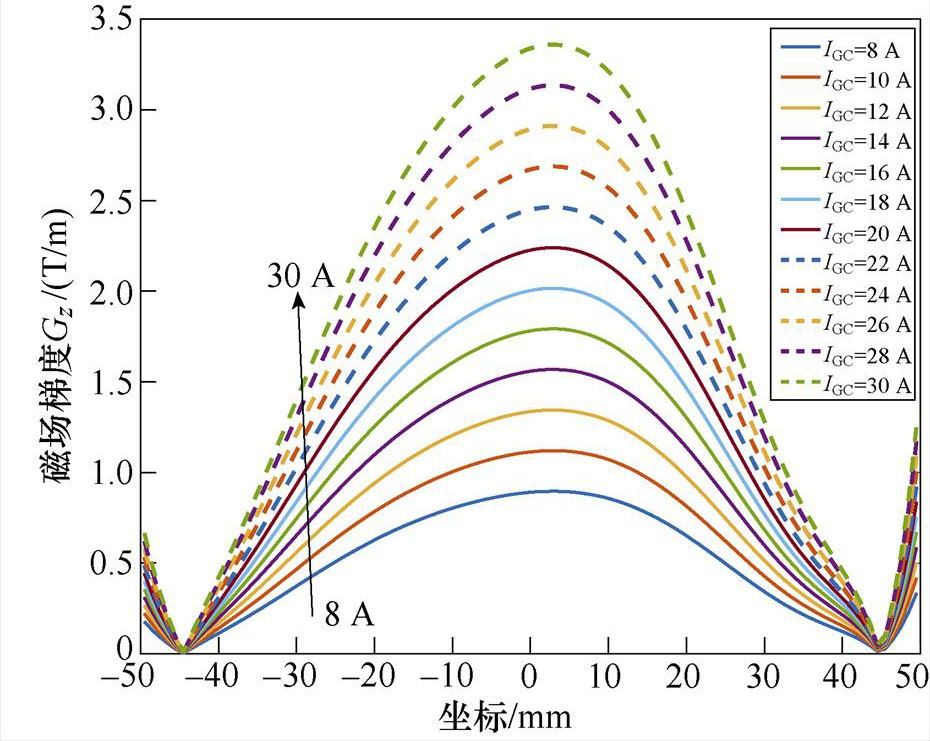
为探讨激励电流与磁场的关系,分别向梯度线圈通入不同幅值的直流电流IGC,取x=0时y轴z方向的磁感应强度Bz和磁场梯度Gz分布进行分析,Bz及Gz与不同IGC之间的关系曲线如图7所示。
图7表明,梯度线圈产生的磁场沿y轴方向呈正弦波状分布,在梯度线圈轴心附近达到峰值,且激励电流大小与磁场峰值呈线性关系。随着梯度线圈电流幅值IGC由8 A变化至30 A时,y轴z方向的磁场强度Bz的峰值由0.024 T增大至0.089 T,磁场梯度Gz也随之增大。磁场梯度Gz越大,FFL半径越小,有利于得到更精确的感应电压信号。而磁场过大会使生物神经受到刺激而感到不适[24-25],因此,选取IGC=10 A。此时,线圈中央气隙内的磁通密度模分布如图8所示。
(a)磁场强度Bz
(b)磁场梯度Gz
图7 梯度线圈IGC大小与y轴z方向磁场强度Bz和磁场梯度Gz关系
Fig.7 Gradient coil size versus y-axis z-direction magnetic field strength and magnetic field gradient
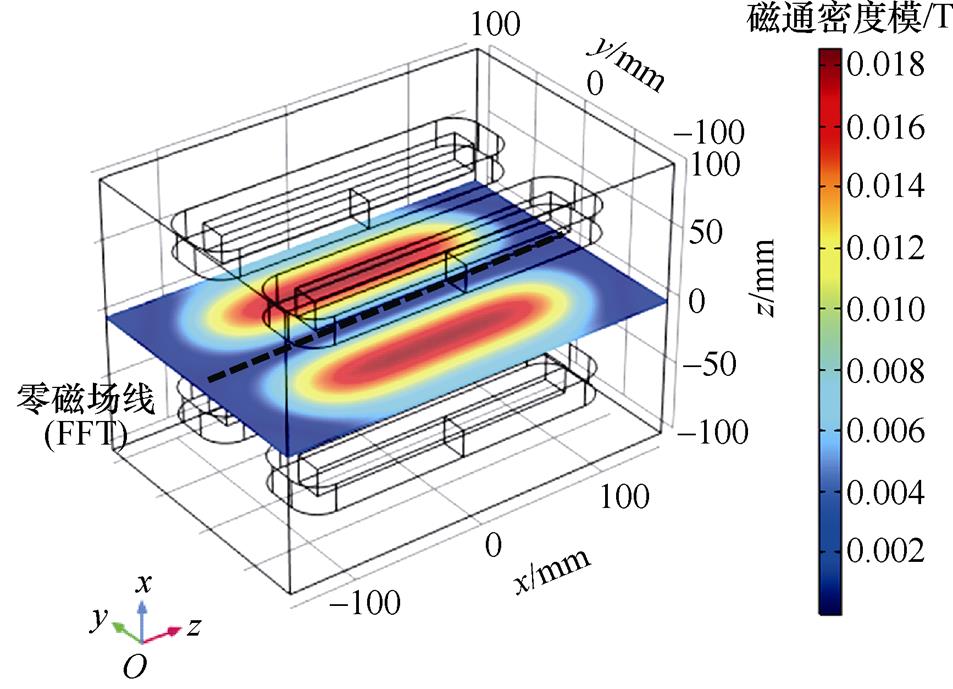
图8 IGC=10 A时梯度磁场分布
Fig.8 Gradient magnetic field distribution when IGC=10 A
如图8所示,FFL两侧磁通密度模对称分布,靠近梯度线圈轴心的位置磁通密度模最大。另外,磁场峰值之间的区域即成像所需要线性梯度磁场,被测目标将被放置在该区域内。
在线性梯度磁场的基础上,根据图5a所示激励模式,向组合线圈中通入电流。其中,DC1按照式(12)通入幅值为15 A、频率为100 Hz的交流电,驱动磁场强度的模值将逐渐减小至零再反向增大。所以,通过交变驱动磁场与线性梯度磁场叠加可实现FFL沿y轴方向扫描,扫描周期TS为5 ms。
FFL沿y轴扫描具体实现过程对应磁通密度等值线结果如图9a所示。
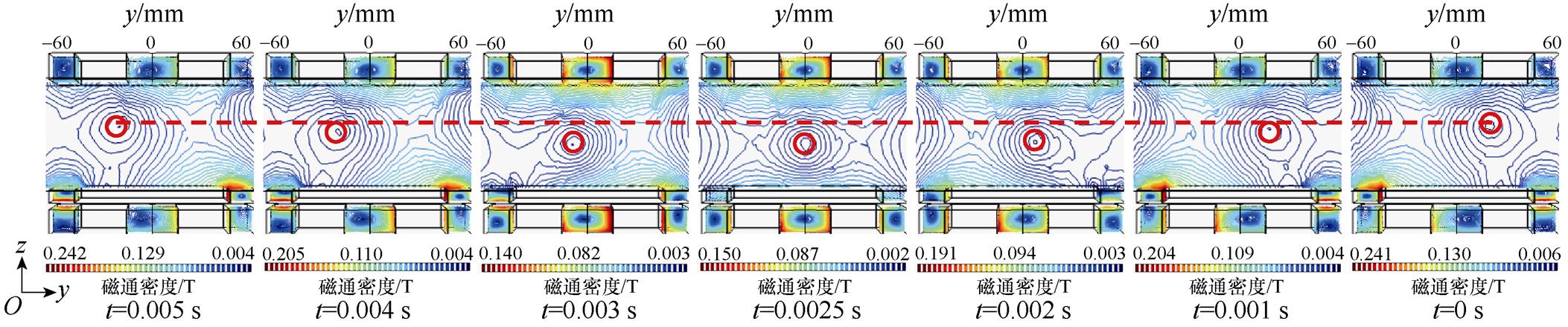
(a)矫正前
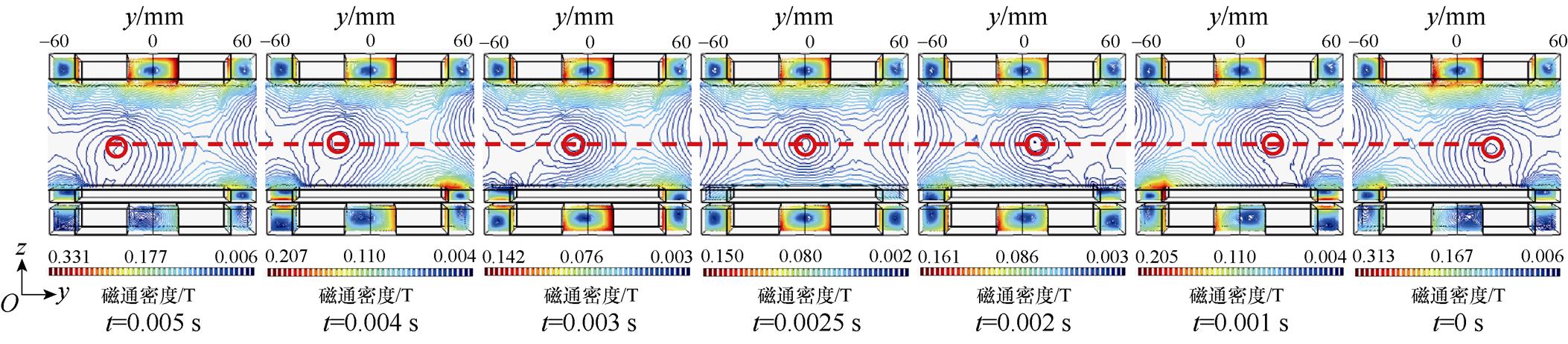
(b)矫正后
图9 FFL轨迹矫正前后磁通密度等值线结果(yz平面视图)
Fig.9 Results of magnetic flux density contour before and after FFL trajectory correction (yz-plane view)
如图9a所示,红色圆圈突出显示为FFL,其在半个余弦周期内完成对待测区域的一次沿y轴方向的扫描。而在此过程中,其并未保持直线扫描。于是,需对FFL沿y轴扫描轨迹进行矫正。
首先将yz平面(x=0)中y坐标范围为[-50 mm, 50 mm]、z坐标范围为[-30 mm, 44 mm]的区域以步长为2 mm划分为多个栅格,共1 938个坐标点;再记录该区域各时刻的磁场强度数据,取磁场强度绝对值最小处的坐标位置,获取FFL中心位置。如2.2节所述,拟合所提取的数据,对式(19)中的m、n均取2,得到a与t之间的关系函数曲线,矫正后的FFL沿y轴扫描轨迹对应磁通密度等值线结果如图9b所示。
图9b表明,添加矫正系数a,使FFL的中心位置在z方向上的高度偏移量得以补偿,矫正后的FFL扫描轨迹较矫正前更接近于直线,且y轴z方向上磁通密度为零的区域覆盖y坐标范围为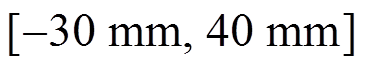 。
。
根据图5b所示激励模式,向组合线圈中通入电流。其中,DC2、DC3按照式(12)通入幅值为25 A、频率为100 Hz的交流电,可驱动FFL沿z轴方向扫描。对应的具体过程如图10所示。
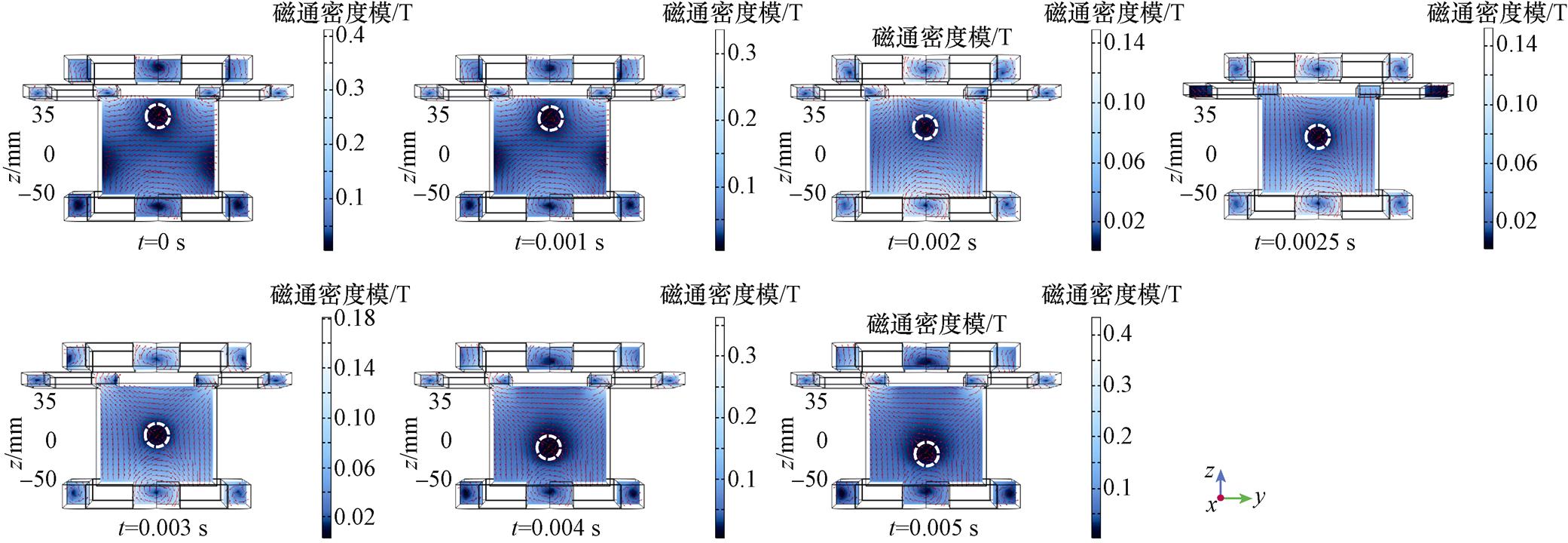
图10 FFL沿z轴扫描轨迹(yz平面视图)
Fig.10 FFL scan trajectory along z-axis (yz-plane view)
图10表明,FFL沿z轴扫描的过程中,其中心位置始终沿着中心轴线进行扫描,轨迹未发生偏移,因此不需进行轨迹矫正,且z轴y方向磁场强度为零的区域覆盖z坐标范围为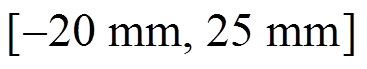 。
。
为进一步利用FFL完成血管断层扫描成像,在COMSOL中建立血管扫描成像仿真模型,如图11所示。设置血管中心位置为x=0 mm,y=dy mm,z= dz mm;设置无血流组织半径为35 mm,血管半径为5 mm,血液流速为0.7 m/s,血液沿x轴流动;血液电导率设置为1.09 S/m,无血流组织区域电导率设置为0.2 S/m[26-28];设置感应电极材料为铜,电导率为5.998´107 S/m,相对磁导率为1,用于检测不同轴向上的边界电压信号变化。
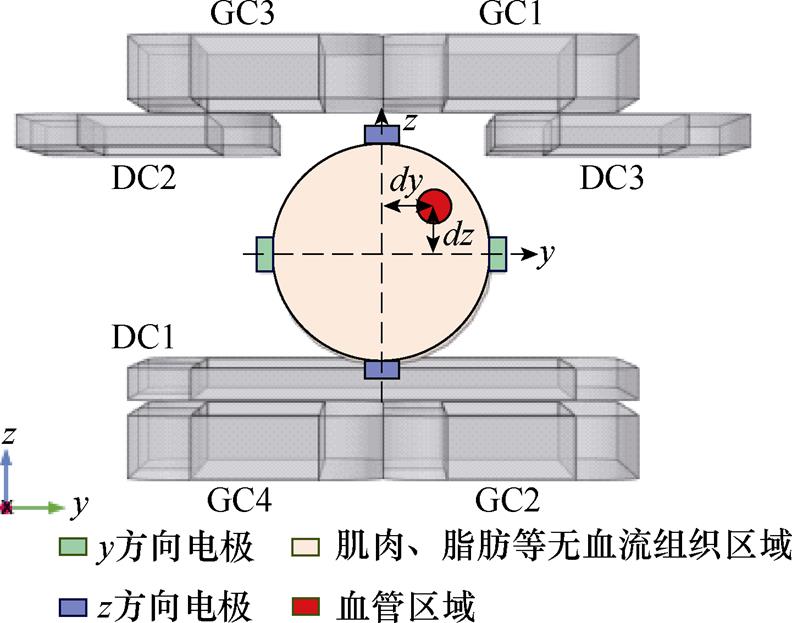
图11 基于FFL的血管扫描成像仿真模型
Fig.11 FFL-based vascular scanning imaging simulation model
获得具有血管中心位置和半径信息的感应电压信号后,本文利用CNN根据感应电压信号对血管断层图像进行重建。
分别改变图11所示仿真模型的血管中心位置y坐标dy、z坐标dz与血管半径r的值生成数据集。dy和dz变化范围为[-10 mm, 10mm],变化步长为1 mm,r变化范围为[1 mm, 5 mm],变化步长为1 mm,共生成2 205个样本,每个样本包含一个尺寸为1×162的感应电压信号和血管中心位置y坐标、z坐标及血管半径r值组成的标签。将2 205个数据集分成训练集与测试集,训练集为1 746个样本,测试集为441个样本。将感应电压信号输入至训练完成的CNN网络中,经过非线性时空关系映射,输出血管中心位置y坐标、z坐标和血管半径r值。CNN网络具体结构参数见表1。
设置CNN网络学习率为0.000 1,迭代次数为5 000次,批次设置为21。本文的网络的结构是在开源Python发行版本软件PyCharm Community Edition 2021.3.3中,基于TensorFlow 1.10.0并通过编程语言Python 3.5实现的。网络训练与测试环境在处理器为AMD Ryzen 7 5700G with Radeon Graphics 3.80 GHz,系统类型为64位,内存为16.0 GB,计算机操作系统为Win10的个人计算机上实现。
表1 CNN网络具体结构参数
Tab.1 Specific structural parameters of CNN network
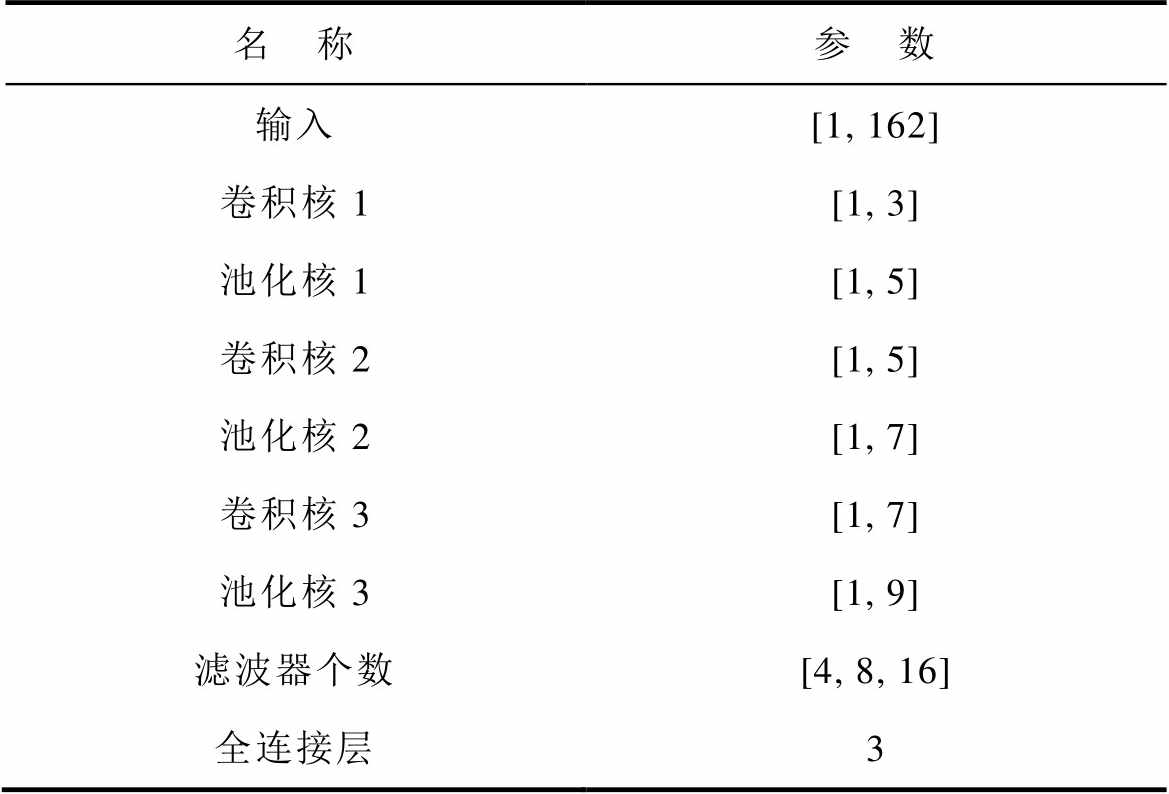
名 称参 数 输入[1, 162] 卷积核1[1, 3] 池化核1[1, 5] 卷积核2[1, 5] 池化核2[1, 7] 卷积核3[1, 7] 池化核3[1, 9] 滤波器个数[4, 8, 16] 全连接层3
随着迭代次数的增加,待训练集与测试集的损失函数曲线逐渐收敛,且损失函数值基本不变时,CNN网络模型训练完成。
在测试集中随机选取21个样本,其基于CNN的血管断层成像结果如图12所示。
图12中,红色区域为血管重建结果,蓝色虚线为原始血管区域,重建血管基本与原始血管区域重合。利用重建与原始血管中心位置之间的距离对成像结果进行量化评价,该距离D定义为
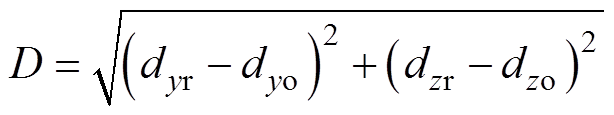 (20)
(20)
式中,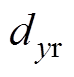 、
、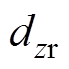 分别为重建的y、z坐标值;
分别为重建的y、z坐标值;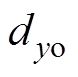 、
、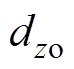 分别为原始的y、z坐标值。
分别为原始的y、z坐标值。
利用式(20)计算CNN重建与原始血管中心位置距离,结果见表2。
表2中,样本7、10、13、17重建与原始血管中心位置距离超过2 mm,误差较大。这可能是由于血管位置距离坐标中心较远(如样本7、10),FFL扫描该位置血管时零磁场区域磁感应强度不足以接近0 T,或血管半径过小(如样本13、17),导致感应电压信号包含血管表征信息不足引起的。总的来说,所有测试集样本的重建与原始血管位置距离的平均值为1.569 4 mm,重建结果能够较准确地反应原始血管位置。
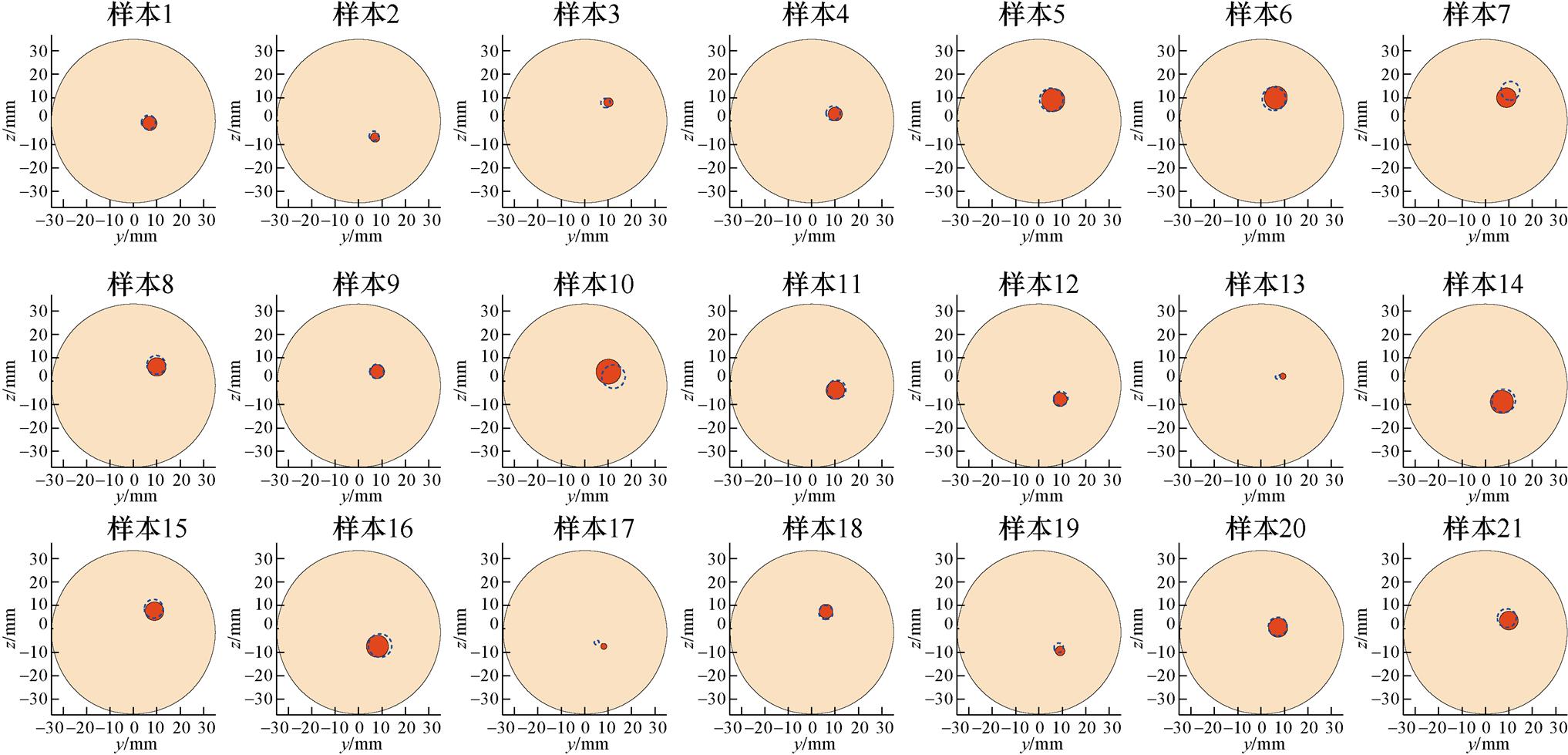
图12 基于CNN的血管断层成像结果
Fig.12 CNN-based vascular tomography results
表2 CNN重建与原始血管中心位置距离误差
Tab.2 Distance error between CNN reconstruction and original vessel center position

样本编号D/mm 10.702 4 20.862 3 31.261 0 41.007 0 50.781 8 60.957 0 73.343 0 80.875 7 90.312 6 103.032 0 110.611 1 120.528 7 132.125 0 140.911 8 151.111 0 161.162 0 173.494 0 180.520 9 191.533 0 200.470 4 211.385 0
利用相对误差err对各样本血管半径重建效果进行评价,有
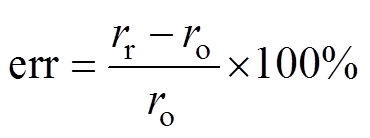 (21)
(21)
式中,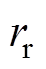 、
、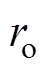 分别为重建、原始的血管半径值。
分别为重建、原始的血管半径值。
各样本重建与原始血管半径数值进行对比,结果如图13所示。
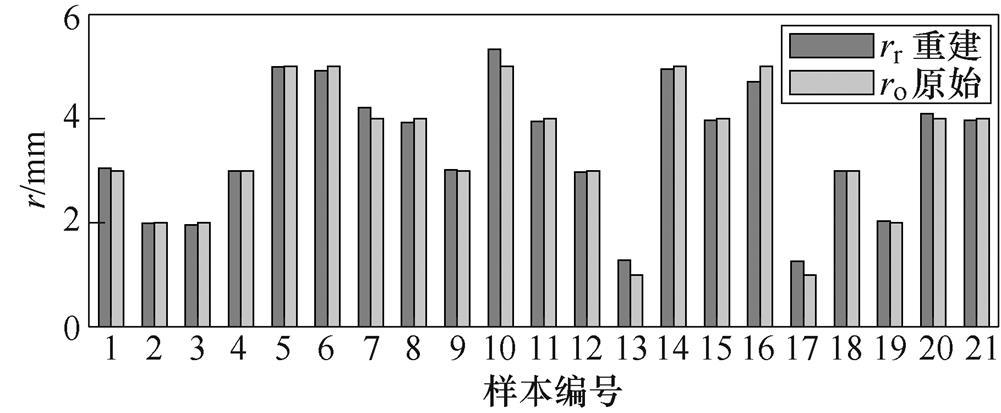
(a)各样本血管半径数值
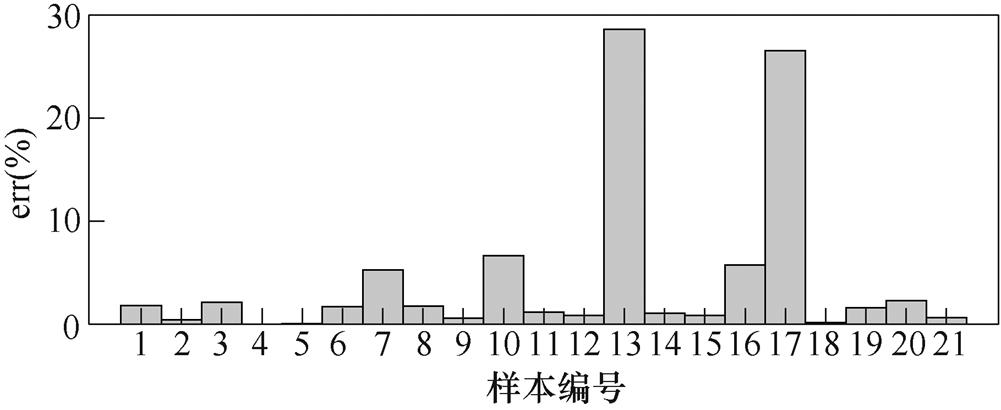
(b)各样本血管半径数值相对误差
图13 CNN重建与原始血管半径数值对比结果
Fig.13 Comparison results of CNN reconstruction and original vessel radius values
图13表明,血管重建半径与真实半径具有较高的一致性,除样本13和17因半径较小而相对误差较大以外,其余样本的相对误差均较小,均小于8%,其中样本4、5、18的误差几乎接近于0。
分别用方均误差(Mean Squared Error, MSE)和相关系数(Correlation Coefficient, CC)对CNN重建血管半径进行整体量化评价,即
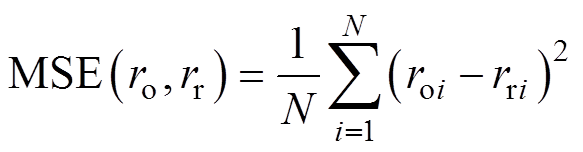 (22)
(22)
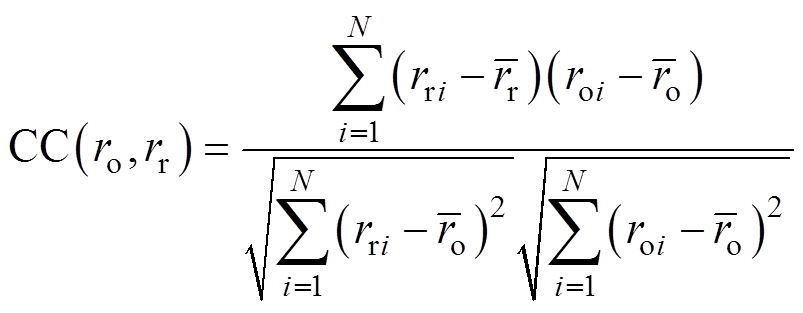 (23)
(23)
式中,N为样本总个数;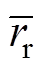 、
、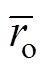 分别为重建、原始血管半径值的平均值;
分别为重建、原始血管半径值的平均值;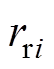 、
、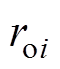 分别为第
分别为第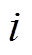 (
(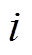 =1, 2,…, N)个重建、原始血管半径值。
=1, 2,…, N)个重建、原始血管半径值。
从整体测试集角度来看,CNN重建血管半径的MSE和CC平均值分别为0.054 8和0.987 0,重建结果能够较准确地反映原始血管半径。
本文提出了一种基于线性零场的动脉血管扫描成像方法,设计实现FFL双向扫描的组合线圈结构,重点研究驱动FFL沿特定方向扫描的线圈激励方式、针对FFL轨迹偏移的矫正方法、血管表征参数对感应电压信号的影响与零磁场下血管断层成像方法。主要结论如下:
1)本文所提组合线圈结构能够产生FFL,改变驱动线圈通电方式,在余弦交流电的激励下驱动FFL沿y、z轴方向双向扫描。
2)通过建立受磁场强度与线圈通电电流影响的FFL中心y轴坐标、偏移高度与扫描时刻之间的关系,设计FFL轨迹矫正系数。采用向梯度线圈GC1、GC3的通电电流中引入矫正系数的方式,对FFL偏移高度进行动态补偿,进而实现对FFL弧形轨迹的线性矫正。
3)建立线性零场激励下的血流磁电耦合模型,利用CNN的非线性拟合特点,实现零场激励下血流磁电耦合信号与血管位置及半径信息的非线性映射,重构动脉血管的剖面图像。
结果表明,本文所提组合线圈结构在通入频率为100 Hz的交流驱动电流时,能够保持单扫描周期为0.005 s,其远小于动脉血流变化周期,理论上可满足实时成像的要求,同时无需大量反演计算。该方法有助于血管断层图像监测手段的研究,为FFL双向扫描血管成像装置的实现提供了思路。而在实际成像系统设计中,可能出现线圈匝数较多、线圈间间距过小,导致的线圈不能严格按照所提尺寸和位置排布摆放的问题。在后续研究中,将进一步对各个线圈的位置进行调整或对组合线圈的结构进行优化。
参考文献
[1] 世界卫生组织. 全球十大死亡原因[EB/OL]. http:// www.who.int/mediacentre/factsheets/fs310/en/, 2018.
World Health Organization. The top 10 causes of death[OL]. http://www.who.int/mediacentre/factsheets/ fs310/en/, 2018.
[2] 冯焕, 姜晖, 王雪梅. 功能磁共振成像在肿瘤学领域的应用[J]. 电工技术学报, 2021, 36(4): 705-716.
Feng Huan, Jiang Hui, Wang Xuemei. Application of functional magnetic resonance imaging in the field of oncology[J]. Transactions of China Electrotechnical Sosiety, 2021, 36(4): 705-716.
[3] Sun Z, Choo G H, Ng K H. Coronary CT angiography: current status and continuing challenges[J]. British Journal of Radiology, 2012, 85(1013): 495-510.
[4] 张帅, 侯琬姣, 张雪莹, 等. 基于真实乳腺模型的感应式磁声成像正问题[J]. 电工技术学报, 2016, 31(24): 126-133, 149.
Zhang Shuai, Hou Wanjiao, Zhang Xueying, et al. Forward problem in magnetoacoustic tomography with magnetic induction based on real model of breast[J]. Transactions of China Electrotechnical Sosiety, 2016, 31(24): 126-133, 149.
[5] 李彩莲, 李元园, 刘国强. 基于磁声电技术的肺部组织成像仿真研究[J]. 电工技术学报, 2021, 36(4): 732-737.
Li Cailian, Li Yuanyuan, Liu Guoqiang. Simulation of lung tissue imaging based on magneto-acousto- electrical technology[J]. Transactions of China Elec- trotechnical Society, 2021, 36(4): 732-737.
[6] 丁晓迪, 柯丽, 杜强. 大脑脉动血流电导率孔隙导电模型仿真[J]. 电工技术学报, 2021, 36(4): 738- 746.
Ding Xiaodi, Ke Li, Du Qiang. Simulation on pore conductivity model of cerebral pulsating blood flow conductivity[J]. Transactions of China Electrotech- nical Society, 2021, 36(4): 738-746.
[7] 赵吉祥, 陈超婵, 王欢, 等. 微弱电信号检测方法回顾[J]. 中国计量学院学报, 2009, 20(3): 201-210.
Zhao Jixiang, Chen Chaochan, Wang Huan, et al. A review on weak electrical signal detection[J]. Journal of China University of Metrology, 2009, 20(3): 201- 210.
[8] 刘向龙, 刘泽, 朱盛. 电磁层析成像图像重建中的修正Landweber迭代算法[J]. 中国电机工程学报, 2019, 39(13): 3971-3980.
Liu Xianglong, Liu Ze, Zhu Sheng. The modified landweber iteration algorithm in the reconstruction of electromagnetic tomography image reconstruction[J]. Proceedings of the CSEE, 2019, 39(13): 3971-3980.
[9] Mikami S, Nakashima A, Nakagawa K, et al. Autologous bone-marrow mesenchymal stem cell implantation and endothelial function in a rabbit ischemic limb model[J]. PloS one, 2013, 8(7): e67739.
[10] Nakagawa H, Ohuchi M, Kawase H, et al. Extremely low-frequency electromagnetic control of bloodstream on imitative blood-circulation system[J]. IEEE Transactions on Magnetics, 2014, 50(11): 1-4.
[11] Tanveer S, Rathod V P. Gravity flow of pulsatile blood through a porous medium under periodic body acceleration and magnetic field in an inclined tube[J]. International Journal of Biomathematics, 2016, 9(2): 1650025.
[12] Yamamoto D, Hosoda K, Uchihashi Y, et al. Perioperative changes in cerebral perfusion territories assessed by arterial spin labeling magnetic resonance imaging are associated with postoperative increases in cerebral blood flow in patients with carotid stenosis[J]. World Neurosurgery, 2017, 102: 477- 486.
[13] Boccalon H, Lozes A, Newman W, et al. Noninvasive electromagnetic blood flowmeter: theoretical aspects and technical evaluation[J]. Medical and Biological Engineering and Computing, 1982, 20: 671-680.
[14] Kanai H, Yamano E, Nakayama K, et al. Trans- cutaneous blood flow measurement by electro- magnetic induction[J]. IEEE Transactions on Biomedical Engineering, 1974 (2): 144-151.
[15] 张俊. 一种基于旋转磁场的多电极电磁流量测量方法的研究[D]. 太原: 中北大学, 2012.
[16] 赵宇洋, 张涛, LUCAS G, 等. 基于区域权函数理论的多电极电磁流量计电极设计[J]. 传感器与微系统, 2014, 33(2): 94-97.
Zhao Yuyang, Zhang Tao, Lucas G, et al. Electrode design of multi-electrode electromagnetic flow meter based on region weight function theory[J]. Transducer and Microsystem Technologies, 2014, 33(2): 94-97.
[17] Liu Yanjun, Yang Dan, Duo Yunhui, et al. Numerical model and finite element simulation of arterial blood flow profile reconstruction in a uniform magnetic field[J]. Journal of Physics D: Applied Physics, 2020, 53(19): 195402.
[18] Yang Dan, Wang Yuchen, Xu Bin, et al. A deep neural network method for arterial blood flow profile reconstruction[J]. Entropy, 2021, 23(9): 1114.
[19] 祖婉妮, 柯丽, 杜强, 等. 开放式磁性纳米粒子断层成像线型旋转零磁场设计[J]. 电工技术学报, 2020, 35(19): 4161-4170.
Zu Wanni, Ke Li, Du Qiang, et al. Electronically rotated field-free line generation for open bore magnetic particle tomography imaging[J]. Transa- ctions of China Electrotechnical Society, 2020, 35(19): 4161-4170.
[20] Guo Liang, Liu Guoqiang, Xia Hui. Magneto- acousto-electrical tomography with magnetic indu- ction for conductivity reconstruction[J]. IEEE Transactions on Biomedical Engineering, 2014, 62(9): 2114-2124.
[21] 金亮, 闫银刚, 杨庆新, 等. 小样本条件下永磁同步电机深度迁移学习性能预测方法[J]. 电工技术学报, 2023, 38(18): 4921-4931.
Jin Liang, Yan Yingang, Yang Qingxin, et al. Predi- ction method of deep transfer learning performance of permanent magnet synchronous motor under the condition of few-shot[J]. Transactions of China Electrotechnical Society, 2023, 38(18): 4921-4931.
[22] Top C B, Güngör A. Tomographic field free line magnetic particle imaging with an open-sided scanner configuration[J]. IEEE Transactions on Medical Imaging, 2020, 39(12): 4164-4173.
[23] Bakenecker A C, Ahlborg M, Debbeler C, et al. Magnetic particle imaging in vascular medicine[J]. Innovative Surgical Sciences, 2018, 3(3): 179-192.
[24] Schaefer D J, Bourland J D, Nyenhuis J A. Review of patient safety in time-varying gradient fields[J]. Journal of Magnetic Resonance Imaging, 2000, 12(1): 20-29.
[25] Saritas E U, Goodwill P W, Zhang G Z, et al. Magnetostimulation limits in magnetic particle imaging[J]. IEEE Transactions on Medical Imaging, 2013, 32(9): 1600-1610.
[26] Italian national research council institute for applied physics/Andreuccetti D, Fossi R, Petrucci C, et al. An internet resource for the calculation of the dielectric properties of body tissues in the frequency range 10 Hz-100 GHz[DB/OL]. (1997)[2021-12-31]. http:// niremf.ifac.cnr.it/tissprop/.
[27] 申华. 动脉血流电导率和电阻抗的血流动力学建模与分析[D]. 大连: 大连理工大学, 2020.
[28] Abdalla S, Al-Ameer S S, Al-Magaishi S H. Electrical properties with relaxation through human blood[J]. Biomicrofluidics, 2010, 4(3): 034101.
Abstract Cardiovascular diseases, such as coronary artery stenosis and coronary heart disease, have become prominent in human health. Nowadays, existing diagnostic techniques in clinical practice are unsuitable for early cardiovascular disease prediction and monitoring due to trauma, high cost, radiation problems, and operation complexity. In this paper, the coupling electric effect of magnetic field and blood flow is studied, and slow imaging speed caused by an extensive range of uniform magnetic fields is considered. Then, a linear gradient magnetic field for arterial scanning imaging method is proposed.
Firstly, the topology of a combined coil for arterial vascular scanning imaging is proposed for generating a linear gradient magnetic field with a field-free line (FFL) configuration. Secondly, FFL is moved by adjusting the excitation current to realize a two-directional electronic scan of the imaging region. In addition, the curved FFL scanning trajectory is corrected. Then, the numerical simulation model of arterial scanning imaging is established by COMSOL, and the voltage signals of magnetoelectric coupling are solved by the finite element method (FEM). Finally, convolutional neural networks (CNN) are used to realize the nonlinear mapping between the magnetoelectric coupled signals and the vascular information. The coordinates of the center position and the radius of the blood vessel are obtained to reconstruct the arterial vascular image.
When the current amplitude of the gradient coil changes from 8 A to 30 A, the peak value of the magnetic field intensity in the Y-axis z direction varies from 0.024 T to 0.089 T, and the magnetic field gradient increases accordingly. The FFL is generated by superimposing the alternating driving field and the linear gradient magnetic field line. Injecting cosine alternating currents into the driving coil, FFL is electronically scanned in the yz-plane. The translated range of FFL is -30 mm to 40 mm in the y-direction and -20 mm to 25 mm in the z-direction. The CNN is trained by simulation datasets, and nonlinear mapping between the induced voltage signal and the vascular information is established. The average error of the vessel position reconstructed is 1.569 4 mm. The mean squared error (MSE) and correlation coefficient (CC) of the reconstructed vascular radius are 0.054 8 and 0.987 0, respectively.
The proposed topology of the combined coil for generating FFL has shown the potential advantage in real-time imaging of arteries. By adopting the correction coefficient in the gradient coil current, the FFL offset height can be dynamically compensated, and the linear correction of the FFL trajectory has been realized. Using CNN, a nonlinear mapping between the magneto-electric coupling signal of blood flow in linear gradient zero field excitation and the vascular information can be established, thereby obtaining the arterial vessel profile image. However, in the practical design of the imaging system, several factors must be considered, such as coil turns, coil group geometry, FFL translating the field of view (FOV), imaging speed, and image resolution. Further studies will focus on adjusting the position of each coil or optimizing the structure of combined coils for the clinical requirements of blood vessel images.
keywords:Cardiovascular disease, magnetic field and blood flow coupling electrical effect, field free line, linear gradient magnetic field, convolutional neural networks, COMSOL
中图分类号:TM12
DOI: 10.19595/j.cnki.1000-6753.tces.221991
国家自然科学基金项目(U22A20221, 61836011, 71790614)、教育部中央高校基础科研业务费项目(2020GFZD008)、辽宁省自然科学基金资助项目(2021-MS093, 2022-MS-119, 2021-BS-054)、辽宁省教育厅基础科学研究项目2021(LJKZ0014)和111项目(B16009)资助。
收稿日期 2022-10-18
改稿日期 2023-01-09
杨 丹 女,1979年生,博士,副教授,研究方向为生物电磁检测及成像。E-mail: yangdan@mail.neu.edu.cn(通信作者)
王雨忱 女,1998年生,硕士研究生,研究方向为电磁探测和成像技术。E-mail: 2070802@stu.neu.edu.cn
(编辑 郭丽军)