Tab.1 FTPMF parameters that have been mainly implemented
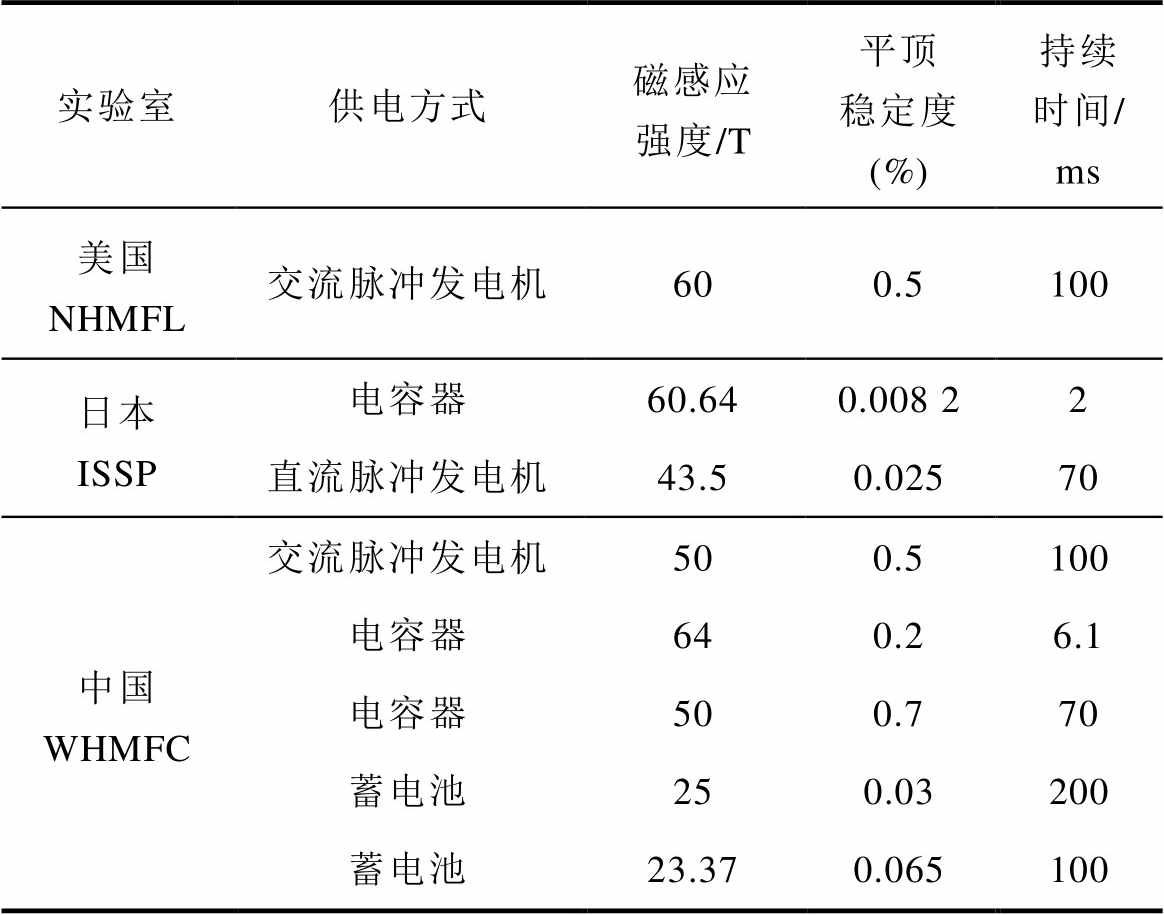
实验室供电方式磁感应强度/T平顶稳定度 (%)持续时间/ ms 美国 NHMFL交流脉冲发电机600.5100 日本 ISSP电容器60.640.008 22 直流脉冲发电机43.50.02570 中国WHMFC交流脉冲发电机500.5100 电容器640.26.1 电容器500.770 蓄电池250.03200 蓄电池23.370.065100
摘要 平顶脉冲磁场具备脉冲磁场强度高和稳态磁场稳定度高的双重优势，是现代物理科学研究的重要工具。为满足脉冲场核磁共振、I-V测量等科学实验对平顶脉冲磁场高稳定度的需求，该文提出基于双电容器回路耦合放电和线性补偿的平顶磁场调控方案。为此，理论分析双电容器回路耦合放电过程，建立配置主/辅回路电容电压和放电时序的优化方法，基于IGBT有源区的流控特性，设计线性调节补偿回路和前馈反馈相结合的控制器，研制与主磁体解耦的1 T补偿磁体，对双电容器回路耦合放电产生的背景磁场进行高精度调控，最终实现了强度为45.2 T、持续时间为8 ms以及稳定度为0.02%的平顶脉冲磁场，满足相关固态核磁共振等科学实验需求。
关键词：平顶脉冲磁场 双电容器耦合 磁场补偿 线性调控 高稳定度
强磁场对物质磁矩有强烈作用，能够改变核自旋和电子结构，进而改变物质特性，是研究物理现象和机理的重要极端条件[1]。高磁场强度是引发材料发生奇特物理现象的关键环境因素，而排除磁场变化引发的感应加热和涡流效应的影响，精准测出材料物性的变化过程，必须使磁场在材料的弛豫时间内保持稳定[2]。平顶脉冲磁场（Flat-Top Pulsed Magnetic Field, FTPMF）兼具脉冲磁场高场强和稳态磁场高稳定度的双重优点，是进行高场核磁共振（Nuclear Magnetic Resonance, NMR）和I-V测量，开展磁化效应、磁阻效应、电输运等凝聚态物理研究，发现新物理现象的重要工具[3]。
中国武汉国家脉冲强磁场科学中心（WHMFC）建设了脉冲强磁场NMR、I-V测量实验站，其要求磁感应强度大于40 T，平顶稳定度在0.01%量级[4-5]。为了一次放电测量多次共振信号，平顶持续时间越长越好[6]，初步建设目标平顶持续时间大于5 ms。但是，产生大于20 T脉冲磁场的电流值一般大于10 kA，大电流作用下平顶期间磁体内阻在0.1 s内变化幅度高达2～7倍，故实现平顶磁场的0.01%高精度量级难度极大。
美国国家强磁场实验室（NHMFL）、日本东京大学物性研究所（ISSP）、WHMFC采用脉冲发电机、电容器、蓄电池等电源供电，通过各类调控手段实现了不同参数的FTPMF，见表1[2]。综述文献[2]对实现FTPMF的各类方法进行了详细分析。其中，仅有ISSP实现了磁感应强度大于40 T，稳定度在0.01%量级的FTPMF，并据此大力发展脉冲场比热测量、脉冲场NMR等技术[7-8]。ISSP采用的方法是利用电容器或直流脉冲发电机提供一个无纹波的背景磁场，然后在主磁体内嵌入小线圈，通过小线圈补偿背景磁场变化实现高精度平顶磁场。然而，利用电容器提供背景磁场，可调节的平顶持续时间较短，ISSP在40 T和60 T下分别仅实现了3 ms和2 ms的平顶持续时间[7]。ISSP建有储能210 MJ、功率51.3 MW的大型直流脉冲发电机，用其提供背景磁场实现了43.5 T/0.025%/70 ms的FTPMF[8]。然而，大型直流脉冲发电机建造、运行与维护成本过高，难以适用于常态化实验。
表1 目前已实现的主要FTPMF参数
Tab.1 FTPMF parameters that have been mainly implemented
实验室供电方式磁感应强度/T平顶稳定度 (%)持续时间/ ms 美国 NHMFL交流脉冲发电机600.5100 日本 ISSP电容器60.640.008 22 直流脉冲发电机43.50.02570 中国WHMFC交流脉冲发电机500.5100 电容器640.26.1 电容器500.770 蓄电池250.03200 蓄电池23.370.065100
WHMFC建有交流脉冲发电机、蓄电池和电容器三种类型脉冲电源，综合各电源类型在能量密度、功率密度和纹波特性等方面的优缺点[2]，在双电容器耦合放电方案的基础上，进一步进行高精度补偿调控为最佳建设方案。2014年WHMFC提出了双电容器耦合放电产生FTPMF的方案[9]，并于2019年实现了最高64 T/0.2%/6 ms的参数指标[10]，但其为开环调控，实验中需反复调节主/辅回路电容器充电电压和触发时序，调节精度和实验效率相对较低，进一步提升平顶稳定度难度较大，难以满足高场NMR对磁场0.01%量级稳定度的需求。
为此，为实现脉冲强磁场NMR实验站建设目标，本文提出了结合双电容器耦合放电方案和补偿调控方案，利用前者提供背景磁场，通过在主磁体内部嵌入补偿磁体实现磁场的0.01%量级高精度调控。本文首先对双电容耦合放电的机理进行了深入分析，达到在已知系统硬件参数时，给定目标参考平顶磁场或磁体电流即可实现计算出主/辅回路电容器充电电压和触发时序的目的；然后，设计了补偿磁体，利用IGBT有源区实现了补偿磁体电流的线性调节，并研发了调控系统；最后，搭建了实验系统，实现了最高参数为45 T/0.02%/8 ms的FTPMF，并在40 T下成功实现了93Nb的NMR信号测量，可满足NMR等实验站建设需求。
本文所提出的平顶脉冲磁场方案原理如图1所示，主要由主回路、辅助回路和线性补偿回路构成。主回路和辅助回路采用高压电容器组C1和C2作为储能电源分别对主回路和辅助回路放电，主磁体串联在主回路中，主回路和辅助回路通过空心变压器相互耦合。在t0时刻控制器触发主回路晶闸管VT1、电容器C1放电，主回路电流快速上升；经过一定延时，在主回路磁体电流到达峰值之前的t1时刻，控制器触发辅助回路晶闸管VT2、电容器C2开始放电，辅助回路电流变化经过耦合变压器在主回路产生感应电压U21，辅助回路开始放电时U21最大，主回路由上升转为平顶，平顶阶段U21逐渐变小抵消磁体内阻电压增量及主回路电容器电压下降，两个回路通过时序配合在主磁体中产生稳定度1%级的平顶磁场作为背景磁场，系统放电过程波形示意图如图2所示。双电容器耦合放电等效原理如图3所示。
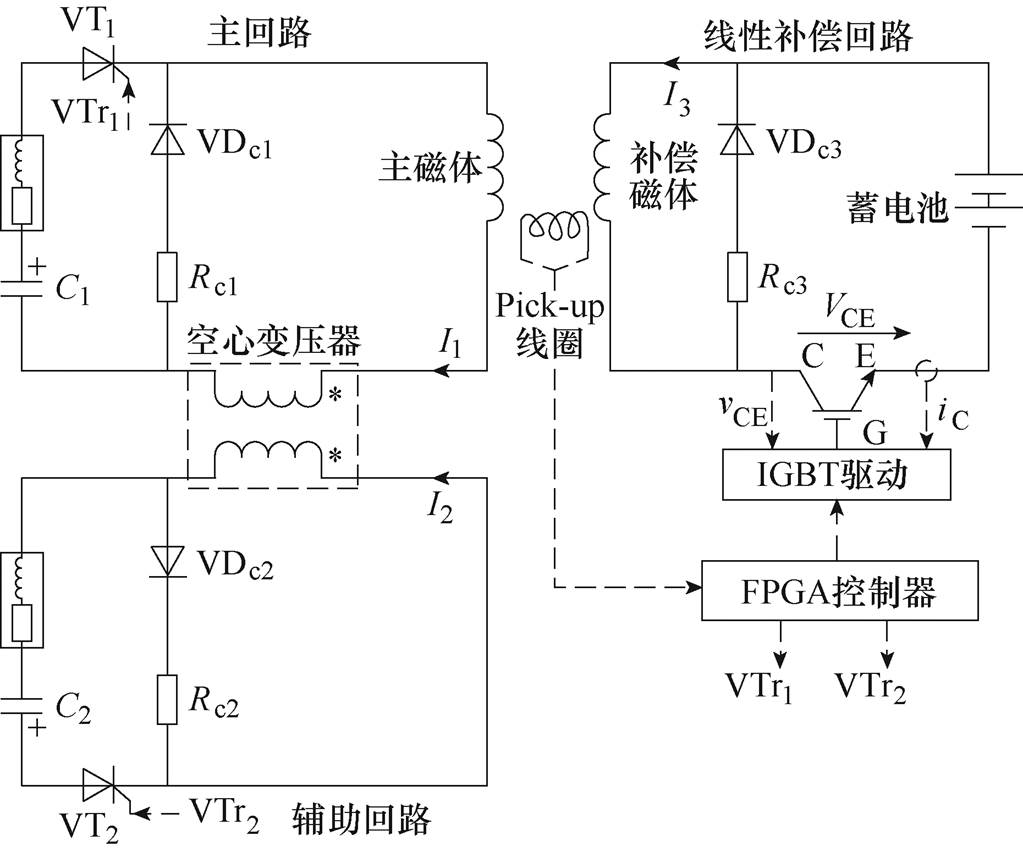
图1 系统原理
Fig.1 Schematic diagram of the system
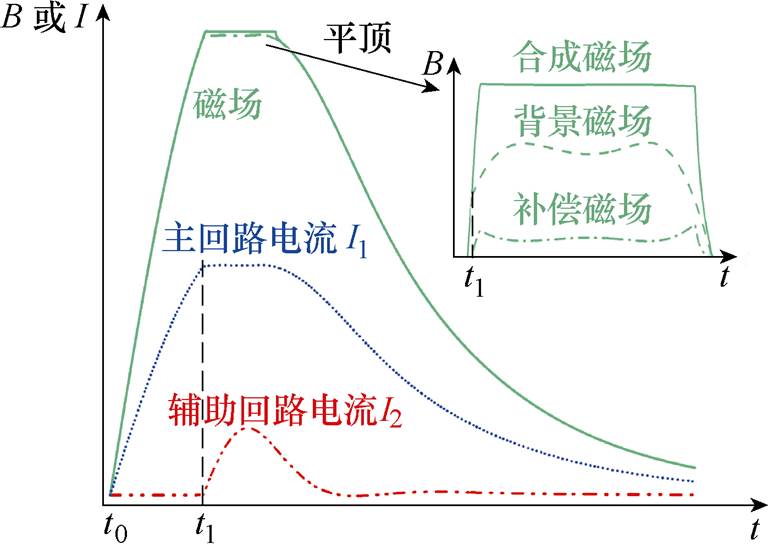
图2 系统工作原理波形示意图
Fig.2 Sketch of the waveforms for the system principle
线性补偿回路由蓄电池为补偿磁体供电，补偿磁体嵌入在主磁体中，通过结构设计消除补偿磁体与主磁体的电磁耦合，具体见下文。线性补偿回路中IGBT工作在有源区用以控制线性补偿回路的电流大小。放电时，在触发辅助回路的同时开启线性补偿回路，Pick-up线圈探测合成磁场微分信号，并在控制器中进行积分得到合成磁场，通过PI控制器控制有源区IGBT的门极电压，连续调节线性补偿回路电流大小，产生可以补偿背景磁场波动的补偿磁场，根据磁场叠加原理，最终形成0.01%量级高稳定度平顶脉冲磁场。
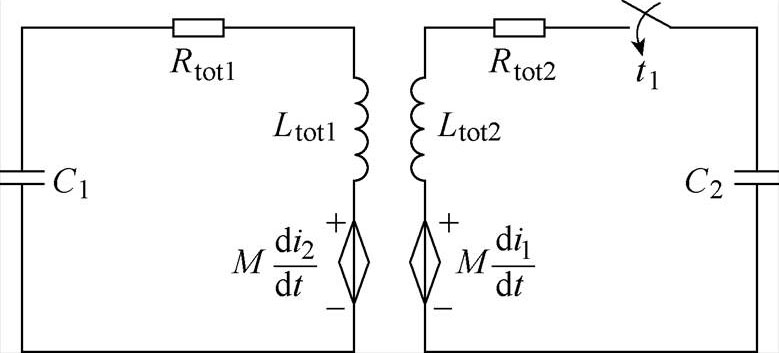
图3 双电容器耦合放电等效电路
Fig.3 Equivalent circuit of the coupled discharge based on two capacitor banks
VDc1与Rc1、VDc2与Rc2和VDc3与Rc3分别为主回路、辅助回路和线性补偿回路的续流支路，平顶结束后各回路的磁场能量经续流回路释放。
主磁体在大电流作用下产生焦耳热，使得主磁体内阻呈现非线性变化，如式（1）所示[11]。由于不能对非线性时变微分方程直接解析计算，本节根据双电容器耦合放电等效电路，厘清双电容器耦合放电的过程，通过合理简化和假设，分析得出辅助回路闭合的换路条件，然后通过寻优算法，实现给定磁场目标即可得到主/辅回路电容器充电电压和触发时序参数配置的目的。
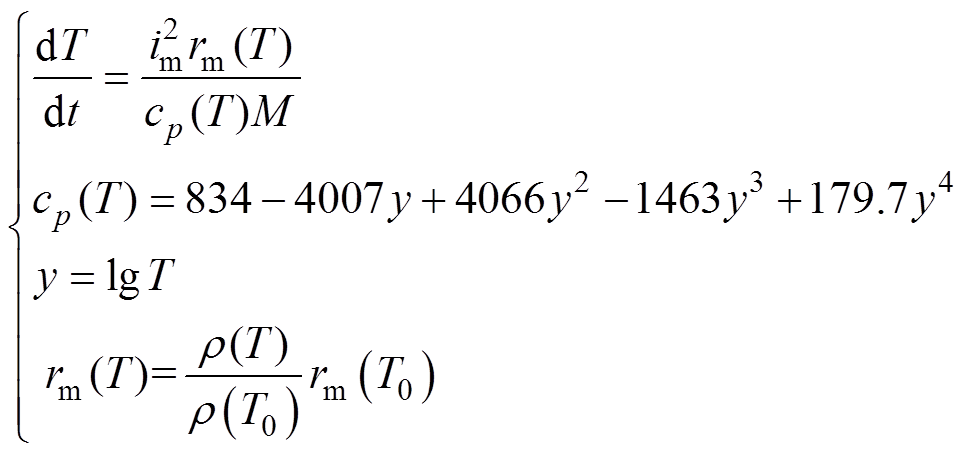（1）
式中，im为流经磁体的电流；T为磁体温度（K）；rm(T)为磁体电阻；M为磁体内导体质量；cp(T)和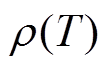
分别为导体材料在温度T下的比定压热容和电阻率；T0为磁体初始温度。
磁体内阻变化和磁体通流密度、通流时间、导体材料特性有关，对于电容器型平顶脉冲磁场系统而言，电流上升阶段磁体电流有效值较小，磁体温升导致的内阻变化大约1%，故可以忽略内阻变化进行解析计算。
t0～t1时间段内仅有主回路工作，辅助回路和补偿回路开路。在t0触发主回路控制晶闸管VT1，电容器C1对磁体和耦合变压器一次侧放电，其电路方程为二阶微分方程，易得辅助回路闭合前主回路电流和电容器电压时域表达式[12]为
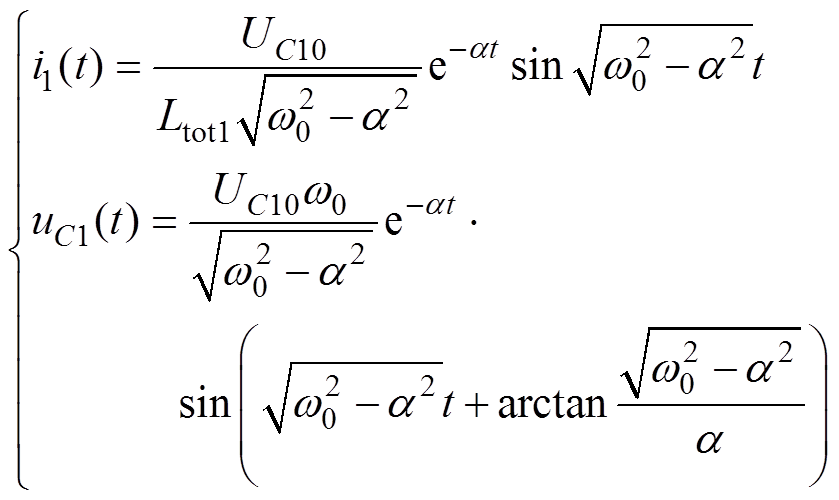（2）
式中，a =Rtot1/(2Ltot1)；w0=1/(Ltot1C1)1/2；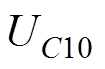
为电容器C1充电电压；Rtot1和Ltot1分别为主回路中保护电感、磁体和空心变压器一次侧的内阻之和及电感值之和；i1为主回路电流，也是磁体电流。
主回路电流在峰值之前达到某一参考电流值Iref（主磁体对应磁感应强度为Bref）时触发辅助回路开始平顶调节，若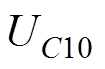配置已知，则可求出辅助回路触发时刻t1为
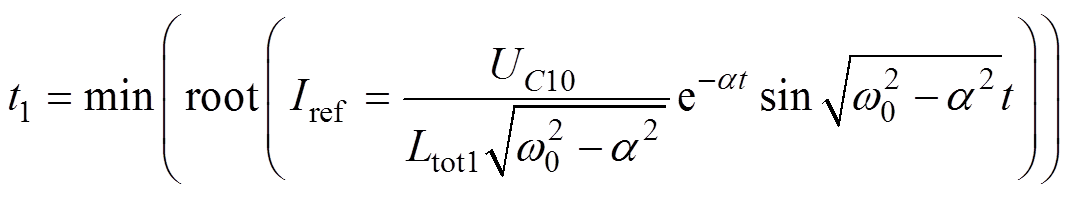（3）
式中，root( · )和min( · )分别为方程求根函数和集合最小值函数。
辅助回路闭合换路时刻t1的双电容器放电回路等效原理如图3所示，换路后主回路和辅助回路电路方程和初始状态为
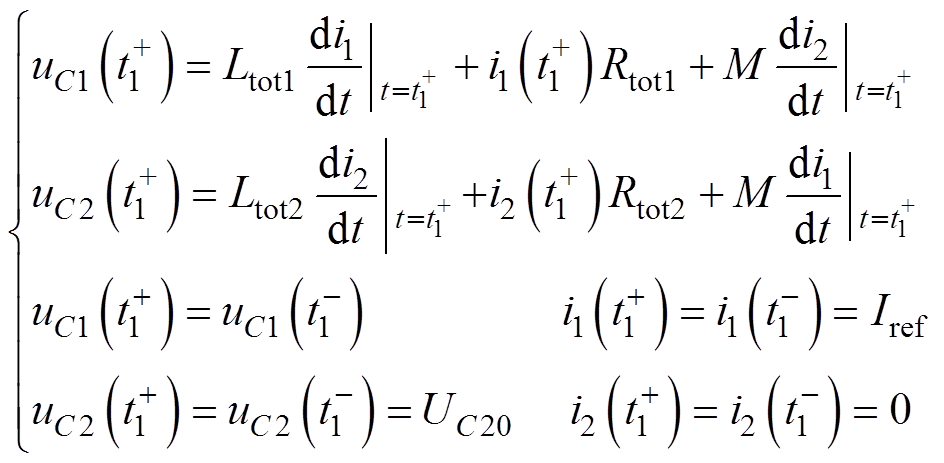（4）
式中，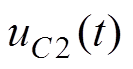
为电容器C2电压；
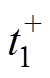和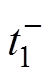
分别为辅助回路闭合的前、后时刻；Rtot2和Ltot2分别为辅助回路中保护电感和空心变压器二次侧的内阻之和及电感值之和；i2为辅助回路电流；M为空心变压器一次侧和二次侧的互感；
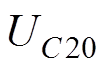为辅助回路电容器C2充电电压。
若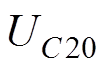和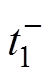时刻主回路电路状态已知，则可以进一步求出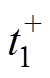时刻主回路和辅助回路电流变化率，从而完全确定平顶阶段初始状态。
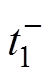时刻主回路电路状态可由式（2）和式（3）求得，下面来分析得到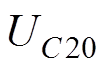的约束条件。理想情况下，辅助回路闭合后主回路电流进入理想平顶状态，主回路电流i1的变化率为0，由式（4）可得
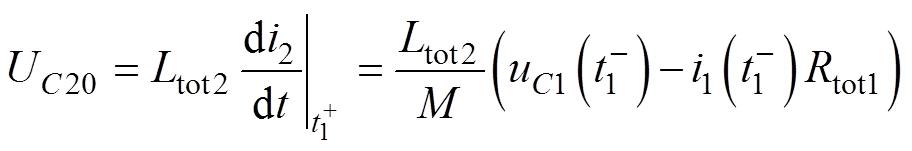（5）
假如平顶期间磁体电流保持不变，则主回路互感器电压变化必须与主回路内阻变化和电容器放电引起的电压变化相等，即有
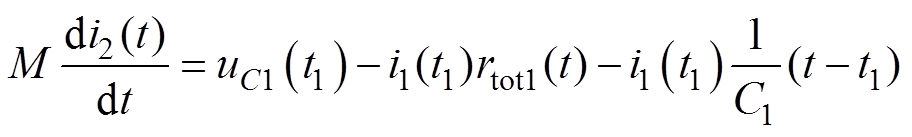（6）
式中，rtot1(t)为平顶期间主回路内阻，其因焦耳热而逐渐变大。然而，式（6）等号左边为近似正弦波形，等号右边为近似线性变化，故式（6）不可能完全成立。为了得到更高的平顶稳定度，利用主回路电感的电流保持能力，辅助回路触发后让主回路电流的变化率保持一定的正值，故需要适当减小式（5）确定的辅助回路电容器充电电压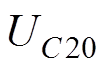，其表达式为
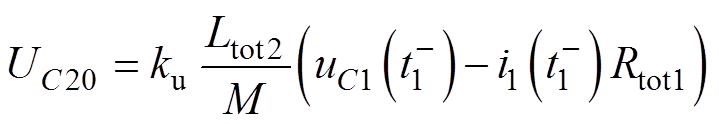（7）
式中，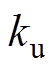
为调整系数。减小幅度和平顶器件主回路内阻变化幅度有关，难以解析确定，后续可以通过优化算法计算得到。
平顶期间的主回路和辅助回路同时工作，两个回路通过耦合变压器相互耦合，忽略续流支路导通，系统电路微分方程为
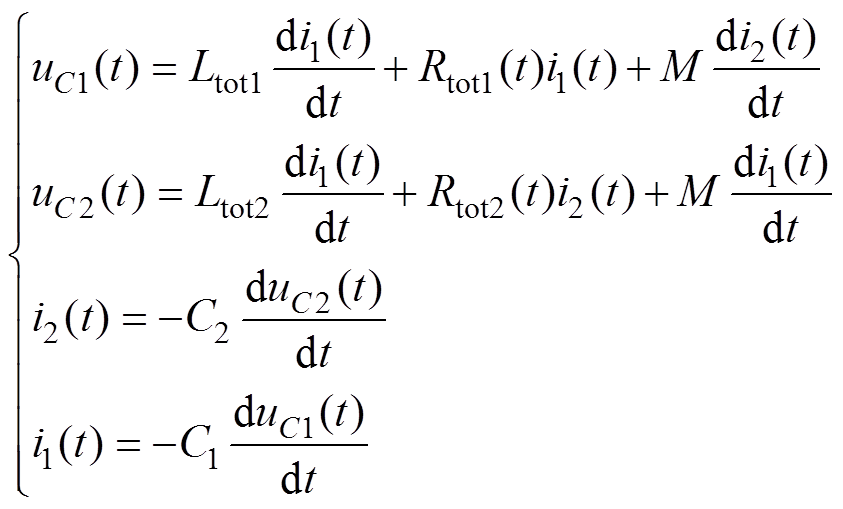（8）
式（8）为非线性时变微分方程，难以求出时域通解，故此只能通过实验系统参数代入方程进行数值计算。
由2.1节和2.2节可知，对于某一磁场目标主辅回路电容器充电电压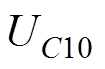和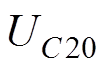的解不唯一，而且无法通过解析获得最优配置，因此需要采用优化算法进行优化计算。
系统配置的优化目标函数可用最小化平顶期间的主回路电流波动表示为
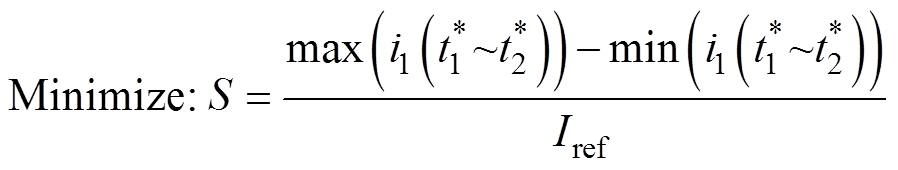（9）
式中，max( · )和min( · )分别为最大值和最小值函数；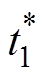
、
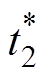分别为优化时预设的平顶开始与结束时刻。根据WHMFC的电容器电源电压范围，约束条件设置为
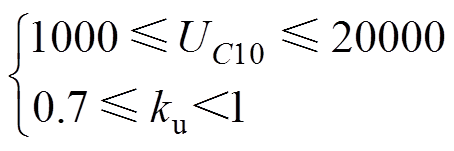（10）
优化算法方面，采用常规的粒子群算法进行优化计算得到全局最优解[13]。
双电容器耦合放电克服了单回路电容器放电时电容器电压快速跌落和磁体内阻大幅上升的问题，但是其为开环调控方法在磁场稳定度上有局限性，即上文所述式（6）不可能完全成立。这也是本文在此基础上对其进行高精度线性补偿的原因。
双电容器耦合放电系统可产生平顶持续时间约10 ms、稳定度1%～0.1%级、磁场强度大于60 T的无纹波平顶脉冲磁场。但是，其稳定度仍需进一步提升，以满足NMR等精密科学测量实验的需求。本文根据磁场叠加原理，在主磁体内部嵌入一个与其同心的补偿磁体，通过闭环反馈控制补偿磁体产生的磁场以补偿主磁体的磁场波动，最终形成高稳定度平顶脉冲磁场。下面对补偿磁体设计及其电流的高稳定度控制进行分析。
补偿磁体仅需提供磁场强度1 T范围以内的可调控磁场即可补偿主磁体磁场波动实现高稳定度的平顶磁场。然而，补偿磁体内嵌于主磁体中，采用简单的单线圈结构会与主磁体产生较强的磁耦合关系，最终导致回路相互耦合，难以形成高稳定度合成磁场。为此，本文设计了如图4所示的补偿磁体，其包括三个线圈：中间为补偿线圈用于调控磁场，两侧为解耦线圈，绕制方向与补偿线圈相反。三个线圈串联与主磁体的耦合电压相互抵消，两个补偿线圈对称分布不影响中心处磁场的均匀度。
（a）补偿磁体
（b）Zylon纤维加固后的补偿磁体
图4 补偿磁体结构实物
Fig.4 Structure of the magnet for field compensation
补偿磁体内置在主磁体内，且中心孔内需容纳绝热杜瓦和样品杆等科学实验器件，因此其内外径受到严格限制。WHMFC已有的主磁体内孔径为20 mm，绝热杜瓦外径16 mm，故选择内径16 mm、外径17 mm的环氧管作为骨架，0.45 mm线径漆包铜线进行绕制。补偿线圈和解耦线圈分别设计为160匝和80匝，分两层绕制，权衡解耦线圈对补偿磁场的减弱效应以及与主磁体的解耦程度，解耦线圈和主补偿线圈之间的间隔设计为5 mm，最外层采用0.25 mm厚度的环氧树脂浸渍的Zylon纤维进行加固，防止承受电磁应力而损坏。补偿磁体电磁参数见表2：液氮77 K温度下内阻为0.7 W，自感为300 mH；电流磁场系数约为200 A/T；若无解耦线圈，补偿磁体与主磁体之间的互感超过100 mH，而在加入解耦线圈后其降低至10 mH。
表2 补偿磁体参数
Tab.2 Parameters of the magnet for field compensation
参 数数 值 电阻/W0.7 (77 K) 电感/mH300 与主磁体的互感/mH10 电流磁场系数/(A/T)200 磁体中心10 mm3范围内的磁场相对不均匀度(%)0.3
通过有限元仿真对其温升和电磁力进行校核，10 ms通流200 A，绝热条件下其导线从77 K温升到157 K，小于其绝缘破坏温度450 K；导线承受的最大应力为60 MPa，远小于铜材在77 K时的抗拉强度345 MPa。
通过补偿磁体的结构设置，其与主磁体的耦合效应可以忽略，线性补偿回路等效电路及控制框图如图5所示，主电路是蓄电池、补偿磁体和IGBT的串联回路，回路方程为
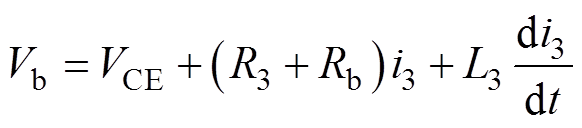（11）
式中，Vb和Rb分别为蓄电池的开路电压和内阻；L3和R3分别为补偿磁体电感和内阻；i3为线性补偿回路电流；VCE为IGBT的集射极电压。其中IGBT与常规的开关工作方式不同，本电路中IGBT工作在有源区，由半导体理论可知，IGBT有源区的静态特性为受控电流源[14]。
（12）
式中，IC为IGBT集电极电流；a 为电流增益；k为玻耳兹曼常数；VGEth为门极导通阈值电压；VCEth为饱和区和有源区阈值电压；VCES为IGBT击穿电压临界值。因此，通过IGBT门极电压可以连续调节线性补偿回路电流稳态值，避免产生开关纹波。但是，由于回路中补偿磁体为感性元件，故回路电流的动态响应不是由IGBT决定，难以理论计算，本文通过实验法得到IGBT驱动输入至其集电极电流输出环节的传递函数[15]。
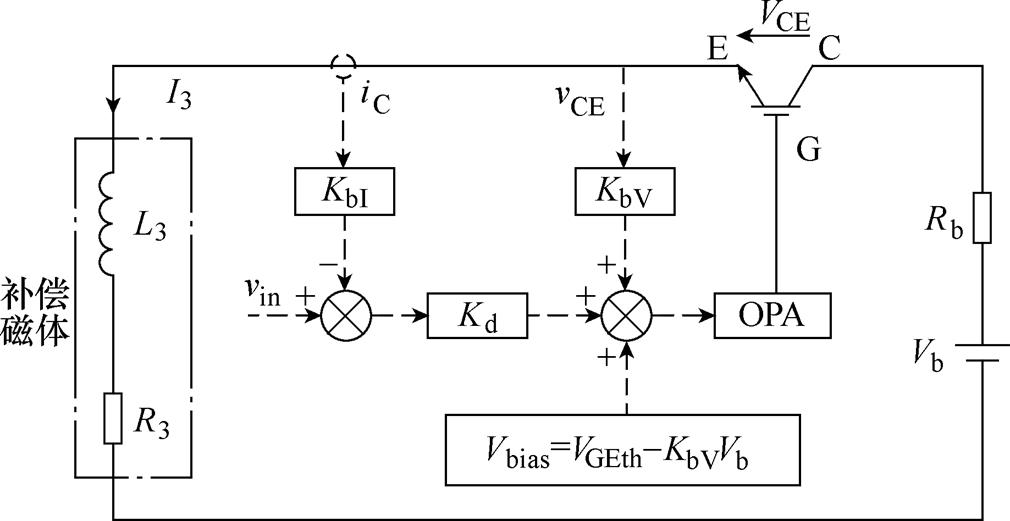
图5 线性补偿回路等效原理
Fig.5 Schematic of the linear circuit for field compensation
图5中，vin为输入控制电压，IGBT线性驱动采用电压内环、电流外环的双闭环控制结构，其中电压内环可提高控制速度抑制超调，电流外环改善IGBT转移特性线性度及其负温度特性。其中KbI和KbV分别为电流传感器和电压传感器系数。设置偏置电压Vbias=VGEth-KbVVb，此时在补偿回路开路时IGBT门极电压为开启电压VGEth，从而使IGBT门极输入vin和电流输出IC成正比例关系。
本文采用的补偿回路蓄电池组输出电压约为150 V，其内阻约为0.1 W，IGBT模块为FZ3600R17- HP4，功率驱动器OPA为OPA544，驱动板通过6路光纤接受数字信号，再经由DAC转换模拟驱动电压vin，实现和FPGA控制器高压隔离。KbI、KbV和Kd分别取0.004 4、0.01和1，偏置电压Vbias设为4.5 V。以驱动电压vin为输入信号，集电极电流IC为输出信号，测得其小信号阶跃响应如图6所示，其等效传递函数可拟合为
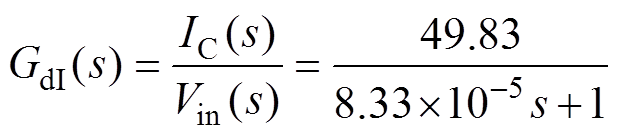（13）
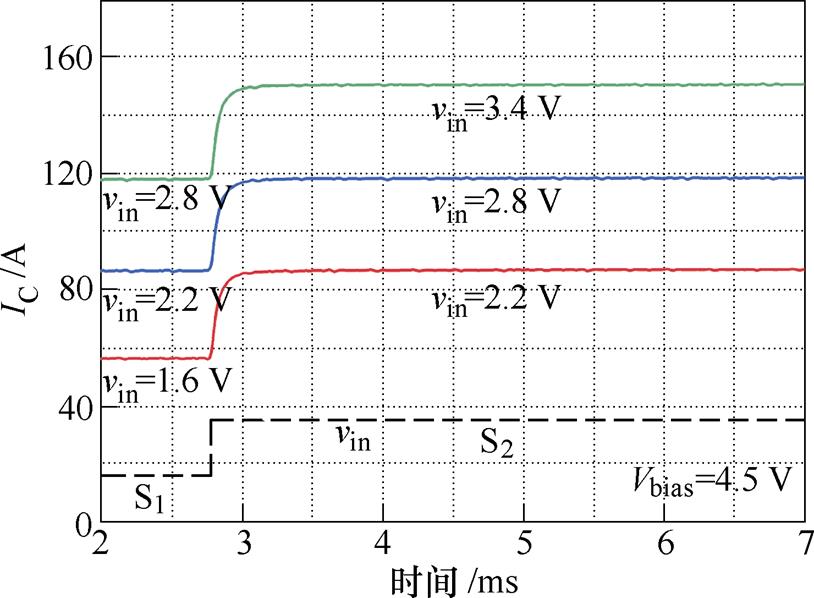
图6 线性补偿回路小信号阶跃响应测试
Fig.6 Small-signal step responses of the linear circuit
控制系统采用反馈和前馈控制，等效控制框图如图7所示。图7中，Bref为合成磁场设定值，Bb为双电容器耦合放电产生的背景磁场，Btot为合成磁场；Gc(s)和Gf (s)分别为PI反馈控制器和背景磁场前馈补偿控制器；经测试，数字控制系统产生延时为40 ms，可用一阶惯性环节近似等效；Km为补偿磁体的电流磁场系数，Km=0.005 T/A。前馈控制器采用超前滞后补偿器形式[16]为
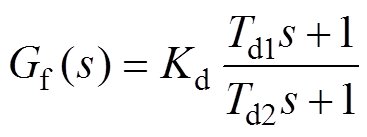（14）
由图7可知，前馈控制器的输入即为补偿磁体需要输出的磁场值，故使Gf(s)GT(s)的稳态增益为1，Kd取值为4.21。为补偿控制器延时，超前时间常数Td1取值40 ms，同时滞后时间常数Td2比GdI(s)的时间常数小10倍以上，取为1 ms。反馈控制器采用常规PI控制器[16]为
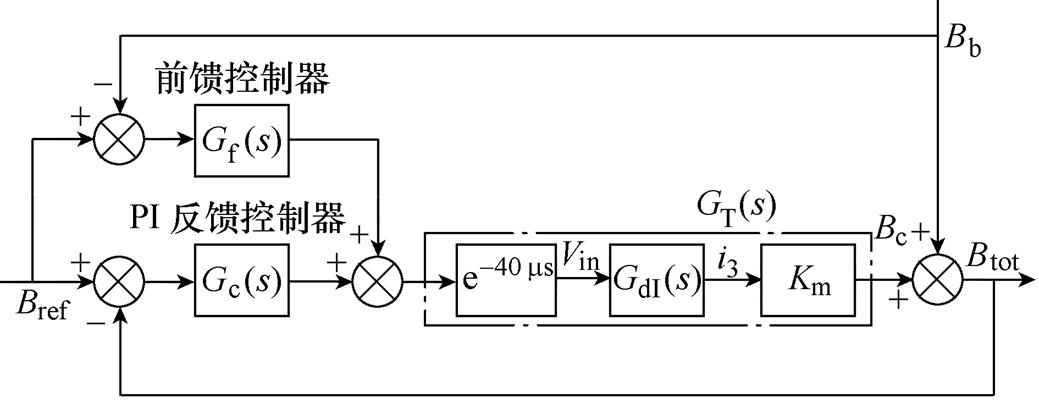
图7 平顶磁场系统等效控制框图
Fig.7 Block diagram of the FTPMF control
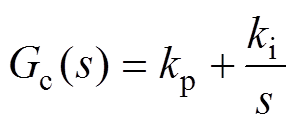（15）
式中，kp和ki分别为反馈控制器的比例和积分系数。
令PI控制器零点与延时环节相消，保证开环传函相位裕度大于30°，则取ki=1×105，kp=4，经分析开环传函的相位裕度为38°，幅值裕度超过50 dB，满足稳定性要求。
WHMFC现有可用的电源模块为20个1.2 MJ的高压电容器组，其每组电容值和最大充电电压分别为3.84 mF和25 kV[17]。为了尽可能地延长脉冲磁场脉宽以增加平顶时长，应选择多个电容器组并联为主回路和辅助回路供电。考虑到磁体温升限制和模块工作冗余需求，主回路采用8个电容器组并联供电，辅助回路采用6个电容器组并联供电。
主磁体采用WHMFC研制的60 T标准用户脉冲磁体进行实验，如图8a所示。该磁体由高强度CuNb合金导线绕制，并采用环氧树脂浸渍的Zylon纤维进行分层加固，降低导线所受应力。磁体内径为20 mm，磁体高度为150 mm。为了降低磁体内阻，减少焦耳热，将该磁体放入液氮环境（77 K）中进行冷却，在77 K时的磁体内阻为30 mW。电感为3.48 mH。磁体电流与中心磁场磁感应强度之比约为460 A/T，即产生1 T的中心磁场需要通流460 A。用于主回路和辅助回路耦合的空心变压器如图8b所示[10]。为了提高空心变压器的能量利用率以实现初步的平顶磁场，其一次侧和二次侧的互感应尽可能地较大。为此，空心变压器被设计具有较大的体积，其内径约为500 mm，高度约为660 mm。相比主磁体，变压器所受电磁应力较低，因此可采用Cu导线绕制；由于变压器导线体积较大、电流密度低，故可在室温下工作，脉冲放电后最大温升仅约为10 K。变压器一次侧在300 K时的稳态内阻约为34 mW，自感约为2.46 mH；二次侧的稳态内阻约为31 mW，自感约为2.21 mH；一次侧和二次侧的互感约为2.19 mH。在考虑电容器保护电感为0.1 mH的基础上，用于优化计算和仿真的主回路和辅助回路电参数总结见表3。
（a）主磁体 （b）空心变压器实物
图8 主磁体和空心变压器实物
Fig.8 Photo of the main magnet and air-core transformer
表3 双电容器耦合放电系统电路参数
Tab.3 Parameters of the coupled two capacitor bank circuits
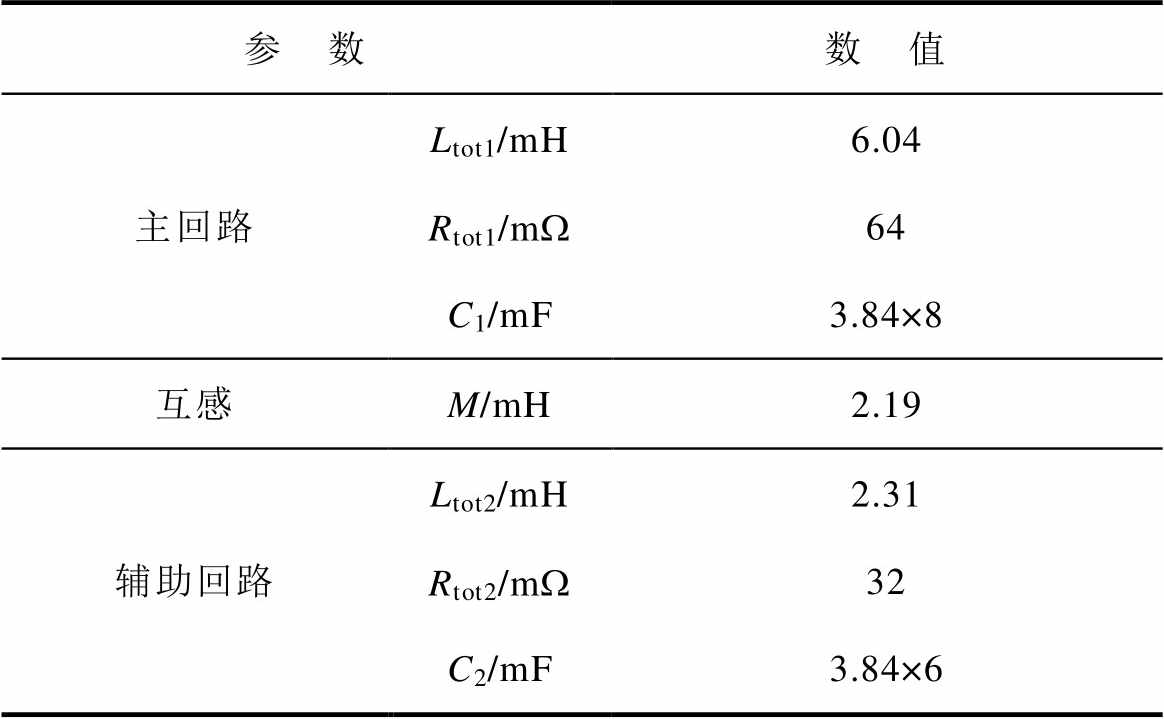
参 数数 值 主回路Ltot1/mH6.04 Rtot1/mW64 C1/mF3.84×8 互感M/mH2.19 辅助回路Ltot2/mH2.31 Rtot2/mW32 C2/mF3.84×6
图9为线性补偿装置机柜实物。蓄电池组由12个12 V的铅酸蓄电池串联而成；在线性补偿回路中串联了机械断路器和固态开关进行短路保护；采用闭环霍尔电流传感器和高压隔离探头分别采集IGBT集电极电流iC和集射级电压vCE进行闭环反馈；控制器采用基于现场可编程逻辑门阵列（Field Programmable Gate Array, FPGA）的嵌入式控制器cRIO-9030进行系统控制，其搭载了NI-9401数字I/O模块输出指令信号和NI-9215模拟输入模块采集磁场信号，控制周期为10 ms。
图9 线性补偿装置机柜
Fig.9 Photo of the linear circuit for field compensation
4.2.1 双电容器耦合放电
双电容器耦合放电参数优化计算结果见表4。在参考磁场Bref分别为20 T、30 T和44 T下进行优化计算，得到主/辅回路充电电压和触发时序。在优化过程中，选择辅助回路触发时刻1 ms后的10 ms区间作为计算平顶稳定度的时间段。在上述设定参数下采用第2节中的分析与优化方法，计算得到的系统放电参数配置在表4中列出。随着参考磁场的增加，主/辅回路电容器充电电压非线性增加，而辅助回路触发时间延时呈减小趋势。优化计算中辅助回路电容器充电电压调整系数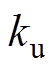保持在0.80～0.81范围内，说明在同一电路参数下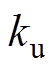基本保持不变，因此只需优化主回路电容器充电电压，即可解析计算得出辅助回路放电配置。
表4 双电容器耦合放电优化结果
Tab.4 Optimized discharging results of the coupled two capacitor bank circuits
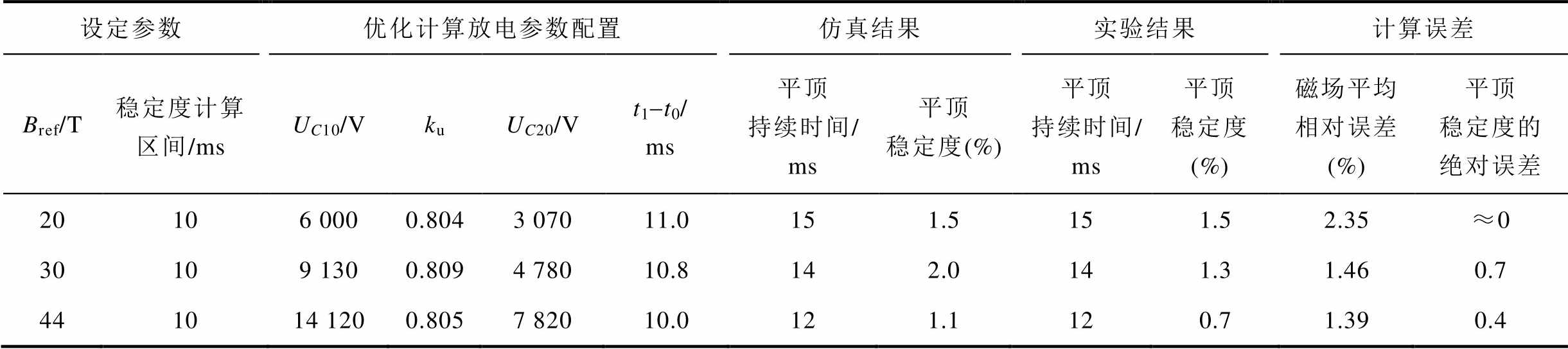
设定参数优化计算放电参数配置仿真结果实验结果计算误差 Bref/T稳定度计算区间/msUC10/VkuUC20/Vt1-t0/ms平顶持续时间/ms平顶稳定度(%)平顶持续时间/ms平顶稳定度(%)磁场平均相对误差 (%)平顶稳定度的绝对误差 20106 0000.8043 07011.0151.5151.52.35≈0 30109 1300.8094 78010.8142.0141.31.460.7 441014 1200.8057 82010.0121.1120.71.390.4
采用该优化计算放电参数配置得到的仿真和实验磁场波形如图10所示，相应的平顶磁场时长和稳定度参数也在表4中列出。可见仿真波形和实验波形基本一致，磁场上升和平顶阶段的磁场最大相对误差为4%，平均相对误差小于3%，平均相对误差的计算方法为
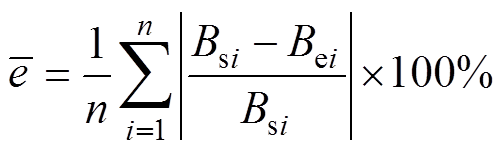（16）
式中，Bsi和Bei分别为仿真和实验在第i个时间点的磁感应强度；n为0～30 ms范围内波形点数。
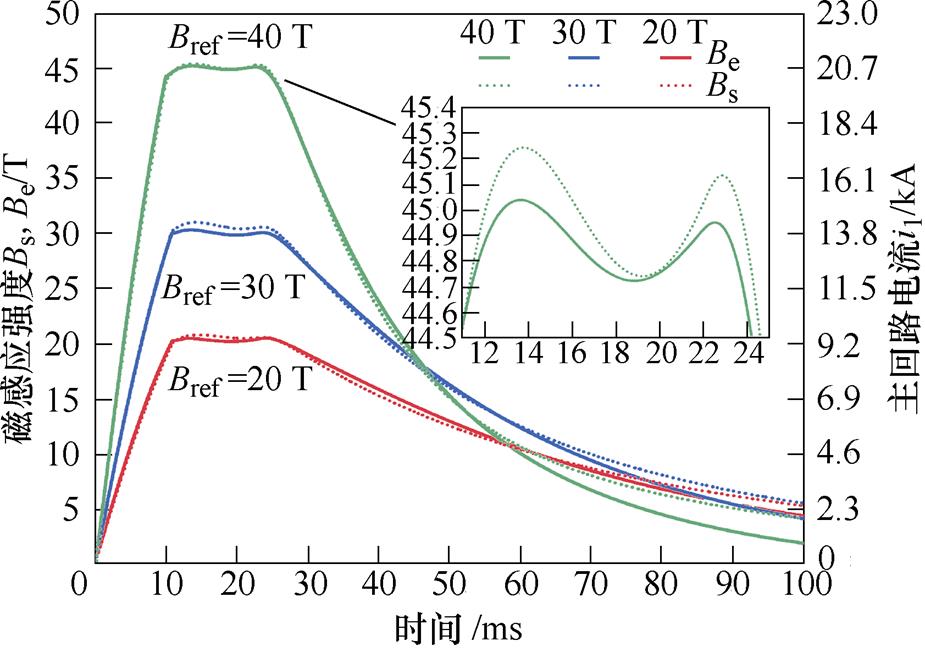
图10 双电容器耦合放电磁场波形
Fig.10 Discharging waveforms of the coupled two capacitor bank circuits
由于电路参数和磁体热模型误差导致仿真平顶阶段稳定度略低于实验结果[18]，但优化计算得到的放电参数配置，可使背景磁场平顶期间的波动在补偿磁体的补偿能力之内，满足了补偿环节的要求。仿真与实验结果表明，按照本文提出的优化配置方法，双电容器耦合放电系统能够实现40 T以上、10 ms平顶时长、1%级稳定度的背景磁场，为后续补偿磁体高精度线性调控奠定了基础。
4.2.2 高稳定度平顶实验
为实现平顶稳定度在0.01%量级的平顶磁场，需要通过补偿磁体线性回路对背景磁场进行高精度调控。图11展示了基于本文方案的高稳定度平顶磁场实验波形，其在4.2.1节产生的背景磁场基础上进一步反馈调控，实现了持续时间为8 ms、稳定度为0.02%、强度为45.2 T的高精度平顶磁场，能够满足相关固态NMR实验需求。平顶开始时由于超调振荡导致了11～13 ms的磁场波动范围超过了稳定度要求，后期可采用变PID或加入预测算法进行优化，并减小系统延迟，进一步延长平顶时间。
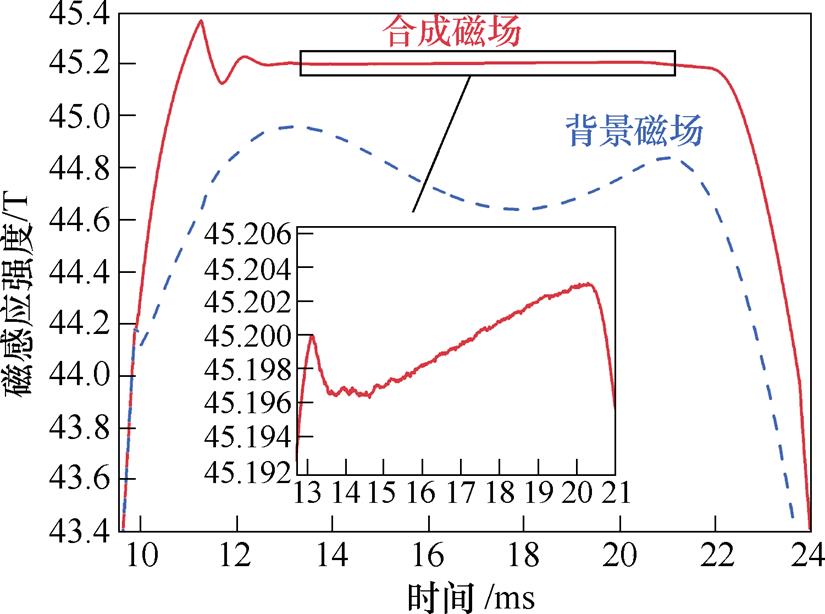
图11 45 T高稳定度平顶磁场实验波形
Fig.11 Experimental waveforms of the 45 T FTPMF with high stability
此外，从图11中还可以看出：合成磁场在21 ms后开始出现跌落，然而此时待补偿的磁场仍在预计的调控范围内。为了分析该现象，绘制了线性补偿回路电流和IGBT集射级电压波形，如图12所示。可见IGBT集射级电压在21 ms后由70 V迅速衰减，在22 ms后IGBT从有源区进入饱和区后完全导通，此时IGBT调控能力失效；由3.1节可知，由于主磁体孔径的限制，补偿磁体只能采用0.45 mm线径的导线绕制，导致其内阻较大，为0.7 W，因而其焦耳热效应明显，温升较大。本文方案中采用的蓄电池组输出电压为150 V，实验过程中随着补偿磁体内阻的增加，补偿回路所能提供的最大电流也随之减小，导致补偿回路电流在增加至150 A后达到极限，限制了补偿磁体的磁场值。后续实验中，一方面可以设计孔径更大的主磁体，采用线径更大的导线绕制补偿磁体以降低其内阻和温升；另一方面可也提升补偿回路蓄电池组供电电压，从而进一步延长平顶时间至10～15 ms。
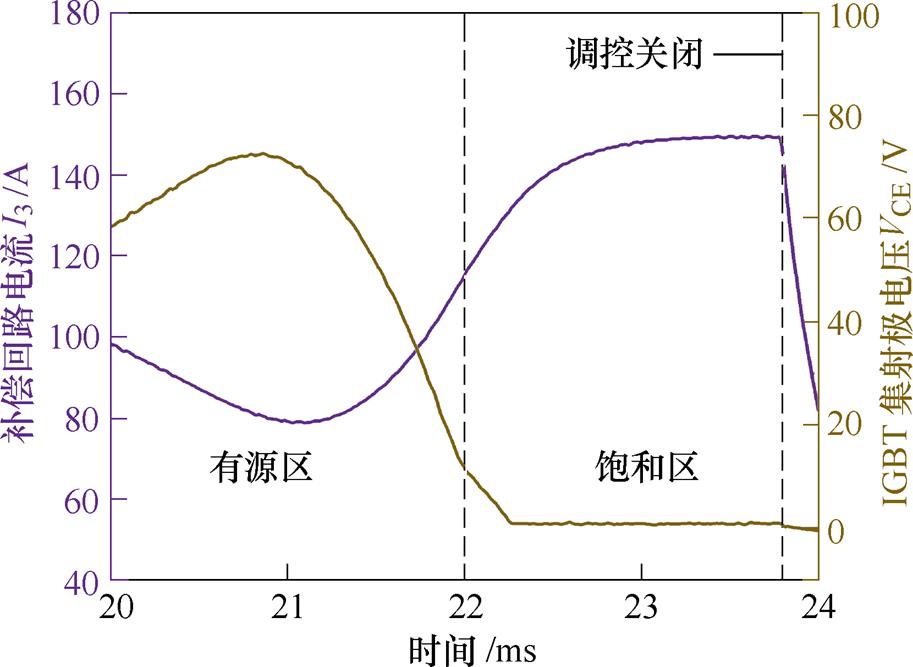
图12 补偿回路电流I3和IGBT集射级电压VCE波形
Fig.12 Experimental waveforms of the I3 and VCE
平顶脉冲强磁场是凝聚态物理重要的极端实验环境，为满足脉冲场NMR、I-V测量等科学实验对平顶脉冲强磁场性能要求，本文提出基于双电容器耦合放电和线性补偿的平顶脉冲磁场实现方案。首先，对双电容器耦合放电调控过程进行了理论分析，得到了特定系统下配置主/辅回路电容电压和放电时序的方法，并通过实验验证了其正确性；其次，设计出了与主磁体解耦的补偿磁体，研制了连续调节IGBT有源区集电极电流的线性驱动以对补偿磁场进行线性控制，设计了前馈和反馈补偿控制器。据此，实现了最高参数为45.2 T/0.02%/8 ms的平顶脉冲磁场，表明本文所提方案切实可行。最后，通过实验结果分析，指出了优化平顶持续时间的方向。
参考文献
[1] Battesti R, Beard J, Böser S, et al. High magnetic fields for fundamental physics[J]. Physics Reports, 2018, 765/766: 1-39.
[2] 韩小涛, 张绍哲, 魏文琦, 等. 平顶脉冲强磁场技术及其应用[J]. 电工技术学报, 2022, 37(19): 5021- 5034.
Han Xiaotao, Zhang Shaozhe, Wei Wenqi, et al. Flat- top pulsed high magnetic field technology and its application[J]. Transactions of China Electrotechnical Society, 2022, 37(19): 5021-5034.
[3] Han Xiaotao, Peng Tao, Ding Hongfa, et al. The pulsed high magnetic field facility and scientific research at Wuhan National High Magnetic Field Center[J]. Matter and Radiation at Extremes, 2017, 2(6): 278-286.
[4] 刘沁莹. 平顶脉冲强磁场核磁共振技术研究[D]. 武汉: 华中科技大学, 2022.
[5] Wei Wenqi, Yang Ming, Jin Shimin, et al. The current-voltage measurements under flat-top pulsed magnetic fields for non-ohmic transport study[J]. Review of Scientific Instruments, 2022, 93(8): 085102.
[6] Liu Qinying, Liu Shiyu, Luo Yongkang, et al. Pulsed- field nuclear magnetic resonance: Status and pro- spects[J]. Matter and Radiation at Extremes, 2021, 6(2): 24201.
[7] Kohama Y, Kindo K. Generation of flat-top pulsed magnetic fields with feedback control approach[J]. Review of Scientific Instruments, 2015, 86(10): 104701.
[8] Imajo S, Dong Chao, Matsuo A, et al. High-resolution calorimetry in pulsed magnetic fields[J]. Review of Scientific Instruments, 2021, 92(4): 43901.
[9] Jiang Fan, Peng Tao, Xiao Houxiu, et al. Design and test of a flat-top magnetic field system driven by capacitor banks[J]. Review of Scientific Instruments, 2014, 85(4): 45106.
[10] Wang Shuang, Peng Tao, Jiang Fan, et al. Upgrade of the pulsed magnetic field system with flat-top at the WHMFC[J]. IEEE Transactions on Applied Super- conductivity, 2020, 30(4): 1-4.
[11] Zhang Shaozhe, Wang Zhenglei, Ding Tonghai, et al. Realization of high-stability flat-top pulsed magnetic fields by a bypass circuit of IGBTs in the active region[J]. IEEE Transactions on Power Electronics, 2020, 35(3): 2436-2444.
[12] 王莹. 高功率脉冲电源[M]. 北京: 原子能出版社, 1991.
[13] 潘峰, 李位星, 高琪. 粒子群优化算法与多目标优化[M]. 北京: 北京理工大学出版社, 2013.
[14] (美)贾扬·巴利加 (B. Jayant Baliga) 著. 韩雁, 丁扣宝, 张世峰, 等译. IGBT器件: 物理、设计与应用[M]. 北京: 机械工业出版社, 2018.
[15] 张绍哲. 蓄电池供电的高稳定度平顶脉冲磁场关键技术研究[D]. 武汉: 华中科技大学, 2020.
[16] 胡寿松. 自动控制原理[M]. 7版. 北京: 科学出版社, 2019.
[17] Xie Jianfeng, Wan Hao, Zhang Shaozhe, et al. Analysis and design of the control sequence for an ultrahigh magnetic field system[J]. IEEE Transactions on Applied Superconductivity, 2022, 32(6): 1-5.
[18] 肖后秀, 李亮. 脉冲磁体的电感计算[J]. 电工技术学报, 2010, 25(1): 14-18.
Xiao Houxiu, Li Liang. Inductance calculation for pulsed magnets[J]. Transactions of China Electro- technical Society, 2010, 25(1): 14-18.
Analysis and Design of a High-Stability Flat-Top Pulsed Magnetic Field Based on the Coupled Double Capacitor Bank Circuits and the Linear Compensation
Abstract Due to its high strength and stability, the flat-top pulsed magnetic field (FTPMF) is one of the most significant tools for studying the magnetization effect, magneto resistance effect, and electrical transport. The Wuhan National High Magnetic Field Center (WHMFC) in China has built experimental stations of nuclear magnetic resonance (NMR) and current voltage (I-V) based on FTPMF. It requires FTPMF strength exceeding 40 T, flat-top stability within 0.01%, and a flat-top duration exceeding 5 ms. Until now, only the institute of solid-state physics (ISSP) in Japan has achieved an FTPMF of this level based on a DC pulsed generator. However, constructing a large DC pulsed generator is costly and time-consuming. This paper proposes a high-stability FTPMF scheme to meet the requirements of NMR and I-V measurements, combined with coupled double capacitor bank circuits and linear magnetic field compensation. The coupled double capacitor bank circuits generate FTPMF with stability of about 1%, and the linear compensation circuit precisely adjusts the magnetic field to achieve high stability.
Firstly, the circuit topology is expounded, including two capacitor circuits coupled by an air-core transformer, a main magnet, a compensating magnet embedded into the main magnet, and a linear regulating circuit of the compensating magnet. Then, the discharge process of the double capacitors is discussed based on circuit state equations. An optimized method for charging voltage and discharge sequence is proposed to generate the background magnetic field. A field-compensation magnet of 1 T is designed with three windings and two decoupling windings to reduce mutual inductance between the main magnet and the compensation magnet from 100 mH to 10 mH. A linear power supply is proposed based on the current control characteristics of the IGBT in the active region. The IGBT is connected in series with the compensation magnet. An IGBT driver with current and voltage feedback is designed to control the loop current through the gate voltage of the IGBT in the active region. A corresponding controller with feedback and feed forward is designed for high-precision compensation of the background magnetic field, with a detailed discussion of controller parameters and system stability analysis. The system’s phase degree and amplitude margin are 38°and 50 dB, respectively.
Finally, a system of FTPMF is constructed. The optimized method of the charging voltage and discharge sequence of the two capacitors is verified. The average relative error between the experimental and simulation waveforms is about 3%. The dual-capacitor coupled discharge system can realize a background magnetic field with a strength of 40 T, flat-top duration of 10 ms, and stability of 1%, laying a foundation for high-precision linear regulation. A FTPMF with a strength of 45.2 T/8 ms/0.02% is achieved by linear compensation, meeting the requirements of solid-state NMR experiments. The method of prolonging the flat-top duration is also pointed out.
keywords：Flat-top pulsed magnetic field, coupled double capacitor bank circuits, magnet for field compensation, linear regulation, high stability
中图分类号：TM15
DOI: 10.19595/j.cnki.1000-6753.tces.230087
国家自然科学基金重点项目（U21A20458）、国家自然科学基金青年基金项目（52107152）、国家自然科学基金-创新群体项目（51821005）和国家重点研发计划项目（2021YFA1600301）资助。
收稿日期 2023-01-17
改稿日期 2023-02-22
张绍哲 男，1991年生，讲师，研究方向为强电磁技术及其应用、大功率脉冲电源技术。E-mail: szzhang@.hust.edu.cn
韩小涛 男，1974年生，教授，博士生导师，研究方向为强磁场产生与调控、电磁测量与信号处理。E-mail: xthan@mail.hust.edu.cn（通信作者）
（编辑 郭丽军）