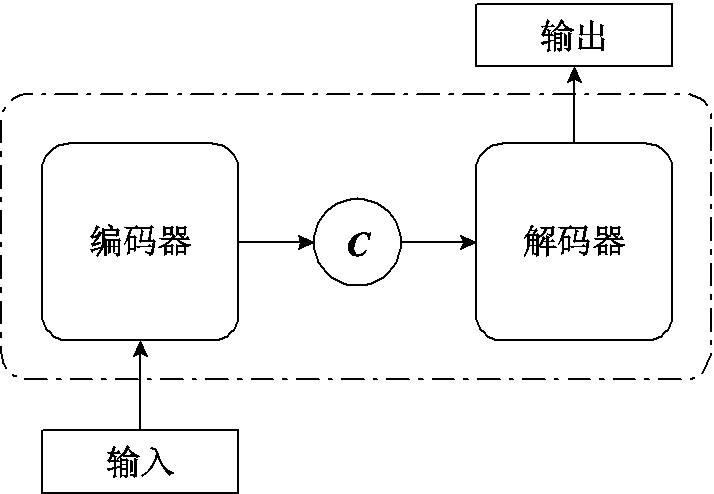
图1 Seq2Seq模型
Fig.1 Seq2Seq model
摘要 锂电池荷电状态(SOC)的准确估算是新能源技术发展中的一项关键技术,由于难以直接获取SOC准确数值,而面对此长序列预测问题,采用传统深度学习方法,其估算效果不佳。对此,该文提出一种对抗性的权重注意力序列到序列(AWAS)模型以估算SOC,其中权重注意力机制通过引入额外的线性变换增强了注意力机制提取长序列依赖的能力。该模型由门控循环单元(GRU)作为编码器和解码器的基本构建模块。首先利用编码器提取特征间的相关信息;其次将包含特征信息的隐藏向量交由权重注意力处理,以深化特征间的关联性学习;再次由GRU进行解码;最后与生成对抗网络(GAN)中的鉴别器联合,提高模型估算能力。通过多步SOC估算任务的测试实验,该文提出的模型估算SOC的方均根误差及平均绝对百分比误差分别达到0.1695%和0.2096%;同时,在不同数据集的单步估算任务测试中,平均绝对误差和方均根误差达到0.141 2%和0.109 4%;相比稀疏化Informer模型在平均绝对误差评估指标上降低了45.7%。
关键词:锂电池荷电状态 序列到序列模型 对抗生成网络 稀疏化Informer 注意力
近年来,随着新能源的迅速发展,锂电池作为一种重要的储能产品,已经广泛地应用在各种场景,目前锂电池的各项关键技术问题已成为新能源汽车发展的核心问题[1]。为了保证新能源汽车的可靠性和持久性,监测锂电池的荷电状态(State of Charge, SOC)[2-3]是锂电池寿命保护的关键。由于SOC无法直接测量,传统基于物理模型的SOC估计方法存在许多缺点:例如,放电实验法[4]和开路电压法[5]只能用于静止的电池,并不适合行驶中的新能源汽车;安时积分法[6]在电流测量中存在的误差导致SOC计算误差累积越来越大,同样不适合用于在激烈工况中行驶的电动汽车。
因此,基于数据驱动[7-8]方法逐渐走入研究者的视野中,其利用电池的历史数据进行训练,可以更加准确地得到SOC的预测值。近年来,深度学习方法在时间序列预测领域得到普遍应用,基于循环神经网络(Recurrent Neural Network, RNN)[9-13]的预测算法成为近年来研究热点。Informer[14]通过改进注意力机制[15]的计算复杂度,减少训练的参数量,并通过蒸馏操作提高计算速度,在多温度预测的平均绝对误差(Mean Absolute Error, MAE)和方均根误差(Root Mean Square Error, RMSE)分别达到0.427%和0.501%。何滢婕等[16]在Informer的基础上使用基于彩票假设的幅值迭代剪枝方法对其进行优化,使得模型的MAE和RMSE分别达到0.278%和0.380%。
上述的部分RNN及其改进模型在短序列预测中能够取得不错的效果,但是涉及长序列预测以及多步预测模型收敛的效果会明显地降低。注意力机制可以有效地增加模型的依赖提取能力,现有的许多模型为了防止梯度爆炸和梯度消失的问题完全舍弃了RNN结构,在Transformer结构上进行改进取得了非常好的效果,但是使用多层编码器[17]和解码器融合自注意力机制使模型的参数冗余非常严重。Informer及类似的Sparse Transformers[18]等模型旨在降低Transformer的参数冗余,但是对于估计精度却没有很好的提升。
Transformer类模型由于多层编码器、解码器及多头注意力机制产生了大量的自由参数,导致模型过拟合风险提高,在增加了模型训练成本的同时无法保证训练的稳定性,降低了模型的泛化能力。在时间序列的随机性和复杂性的影响下,过多的参数冗余会使多头注意力机制难以准确地提取特征之间的依赖。因此在对注意力机制进行改进的同时可以在RNN结构上引入生成对抗网络的思想,通过训练生成器和鉴别器网络,能够更好地学习到数据分布特征,从而减轻梯度消失的问题,使模型的损失函数对于梯度爆炸问题更具鲁棒性。
本文提出一种对抗性的权重注意力机制序列到序列模型(Adversarial Weighted Attention Seq2Seq, AWAS),主要贡献如下:
1)在以门控循环单元(Gated Recurrent Units, GRU)作为编码器、解码器的Seq2Seq模型基础上,提出一种权重注意力机制(Weighed Attention),在解码器中使用时,实验表明效果优于未改进的多头注意力机制。
2)模型引入对抗性训练的思想,联合生成对抗网络(Generative Adversarial Network, GAN)的鉴别器进行训练,其鉴别器由三层一维卷积融合多头注意力机制组成。生成式模型具备一次性预测多步SOC值的能力,以减少滚动预测的误差,且单层编码器和解码器可以大幅度减少数据冗余。
3)在三个公开数据集上对不同温度和工况进行实验,在单步预测任务和多步预测任务上的平均绝对误差、最大误差(Maximum Error, MAX)、方均根误差、平均绝对百分比误差(Mean Absolute Percentage Error, MAPE)均有明显降低,证明了本文模型的性能。
本文提出的模型增强了模型的长序列依赖提取能力、泛化能力及表达能力。实验在三种电池的不同温度下对不同工况进行测试,无论是单步预测还是多步预测都取得了非常好的结果。
本文提出的是一种对抗性的权重注意力机制Seq2Seq模型,由于相关模型在时间序列预测方面的应用和性能评估的综合讨论相对较少,本节主要描述Seq2Seq模型和GAN模型的基本内容。
Seq2Seq模型是一种全新的端到端的映射方法,如图1所示,其核心是编码器-解码器(Encoder-Decoder)架构。编码器负责将长度可变的输入序列转换成形状固定的上下文向量,并且将输入的序列信息在该上下文变量中进行编码,这个向量就可以看成是这个序列的语义向量C。解码器则负责根据语义向量C生成指定的序列,这个过程也称为解码。

图1 Seq2Seq模型
Fig.1 Seq2Seq model
若输入序列为{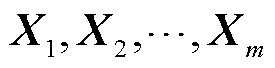 },
},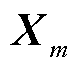 为输入序列的第m个标记,在时间步m时,循环神经网络将
为输入序列的第m个标记,在时间步m时,循环神经网络将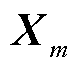 和上一时间步的隐藏状态
和上一时间步的隐藏状态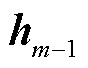 通过函数f转换成当前隐藏状态
通过函数f转换成当前隐藏状态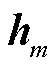 ,如式(1)所示。而后编码器通过函数q将所有时间步的隐藏状态转换为语义向量C,如式(2)所示。若训练集的输出序列为
,如式(1)所示。而后编码器通过函数q将所有时间步的隐藏状态转换为语义向量C,如式(2)所示。若训练集的输出序列为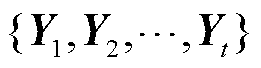 ,对于每个时间步t,解码器输出
,对于每个时间步t,解码器输出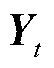 的条件概率分布P都取决于先前输出的子序列{
的条件概率分布P都取决于先前输出的子序列{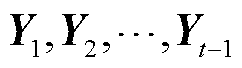 }和语义向量C,如式(3)所示。
}和语义向量C,如式(3)所示。
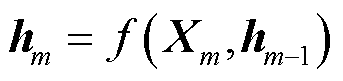 (1)
(1)
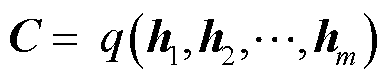 (2)
(2)
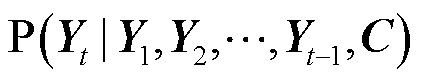 (3)
(3)
Seq2Seq同样使用一种循环神经网络作为解码器使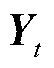 的条件概率分布模型化。在输出序列上的任何时间步t,循环神经网络都将来自上一时间步的输出
的条件概率分布模型化。在输出序列上的任何时间步t,循环神经网络都将来自上一时间步的输出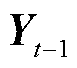 和语义向量C作为输入,然后将当前时间步t的这些输入与上一个隐藏状态
和语义向量C作为输入,然后将当前时间步t的这些输入与上一个隐藏状态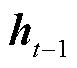 通过函数g转换为新的隐藏状态
通过函数g转换为新的隐藏状态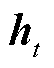 ,如式(4)所示,用函数g来表示解码器隐藏层变换。
,如式(4)所示,用函数g来表示解码器隐藏层变换。
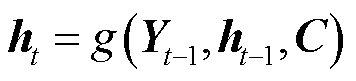 (4)
(4)
Seq2Seq通常以GRU或者长短期记忆网络(Long Short-Term Memory, LSTM)作为编码器和解码器,有学者对这两种神经网络进行了大量的实验[19],表明在不同任务下GRU的收敛情况明显好于LSTM,故本文使用GRU作为Seq2Seq的编码器和解码器,其单元结构如图2所示。
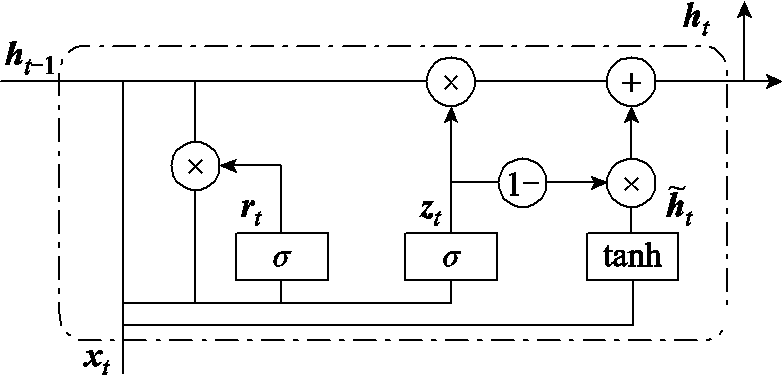
图2 GRU单元结构
Fig.2 GRU cell structure
图2中,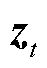 为GRU的更新门,用来控制当前
为GRU的更新门,用来控制当前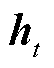 状态需要从上一时刻的
状态需要从上一时刻的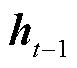 状态中保留多少信息,以及从候选状态
状态中保留多少信息,以及从候选状态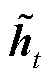 中能接受多少信息;重置门
中能接受多少信息;重置门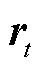 用来控制候选状态
用来控制候选状态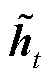 的计算是否依赖上一时刻状态
的计算是否依赖上一时刻状态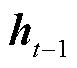 ;
;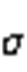 为激活函数;b为偏置值;时间步参数对应权重矩阵为
为激活函数;b为偏置值;时间步参数对应权重矩阵为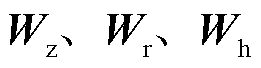 ;隐藏状态对应参数为
;隐藏状态对应参数为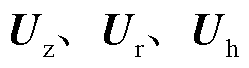 计算过程如式(5)~式(8)所示。
计算过程如式(5)~式(8)所示。
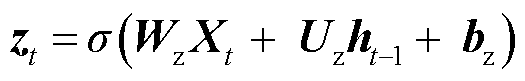 (5)
(5)
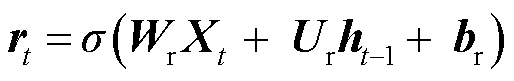 (6)
(6)
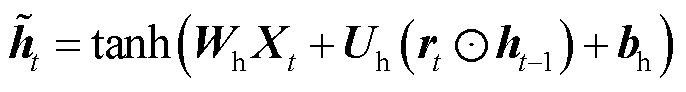 (7)
(7)
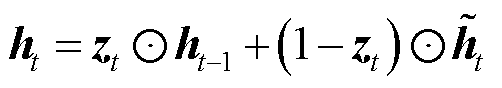 (8)
(8)
Seq2Seq模型在时间序列预测中的应用是将历史观测序列作为输入,并生成未来一段时间的预测序列作为输出。该模型通过编码器、解码器结构捕捉序列之间的依赖关系和模式,能够有效地学习序列的演化趋势。Seq2Seq模型可以适应不同长度的输入和输出序列,具有可以处理变长序列的能力,使其适用于各种时间序列的预测任务。但是基于传统循环神经网络的Seq2Seq模型依然保留了循环神经网络的缺点,在模型解码过程中使用注意力机制可以有效地增加模型提取长序列依赖的能力。
GAN模型如图3所示,GAN[20]是由生成器G和鉴别器D两部分组成的模型。
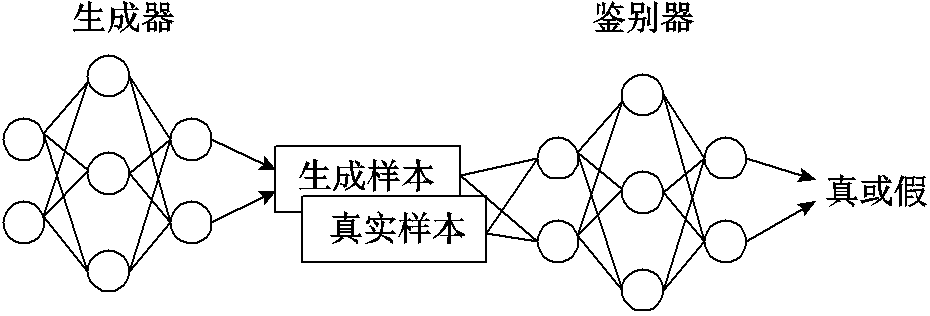
图3 GAN模型
Fig.3 GAN model
生成器G可以是任意一种神经网络,鉴别器D主要为了解决传统二分类问题。生成器的本质是希望用某一种具体的分布形式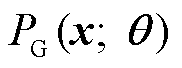 得到生成的分布
得到生成的分布 ,使其尽可能逼近真实分布
,使其尽可能逼近真实分布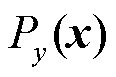 。由于高斯分布的拟合能力不佳,所以生成器采用神经网络生成数据,如式(9)所示。
。由于高斯分布的拟合能力不佳,所以生成器采用神经网络生成数据,如式(9)所示。
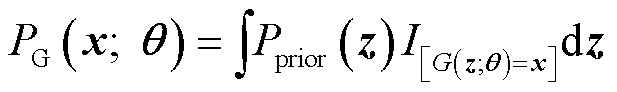 (9)
(9)
式中,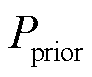 为先验分布;指示函数
为先验分布;指示函数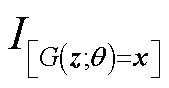 表示
表示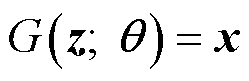 的条件为真时取1,反之取0。
的条件为真时取1,反之取0。
首先从先验分布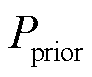 中采样z作为神经网络G的输入,通过这种方式构建生成分布
中采样z作为神经网络G的输入,通过这种方式构建生成分布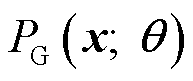 ,其采样x的概率是所有能够使
,其采样x的概率是所有能够使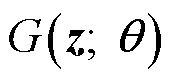 =x成立的z出现的概率之和。显然
=x成立的z出现的概率之和。显然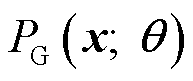 的计算是非常复杂的,因此引入鉴别器D。鉴别器D负责对生成器生成的序列和真实序列分别进行判别,评估分布
的计算是非常复杂的,因此引入鉴别器D。鉴别器D负责对生成器生成的序列和真实序列分别进行判别,评估分布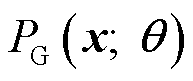 和
和 之间的差异。因此GAN的核心思想是生成器通过历史数据得到生成样本,鉴别器则判断生成样本和真实样本的真伪。GAN的最终目标是得到使
之间的差异。因此GAN的核心思想是生成器通过历史数据得到生成样本,鉴别器则判断生成样本和真实样本的真伪。GAN的最终目标是得到使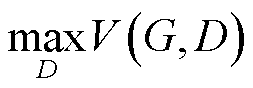 最小的生成器
最小的生成器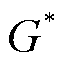 ,有
,有
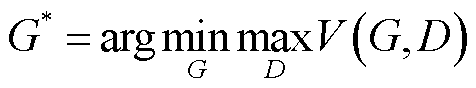 (10)
(10)
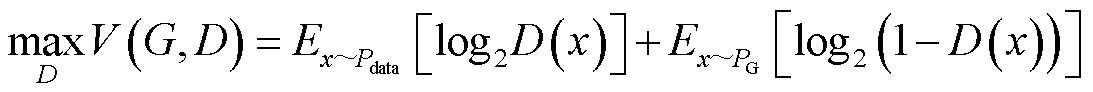 (11)
(11)
式(11)所示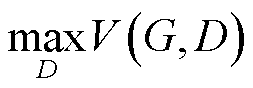 用于衡量分布
用于衡量分布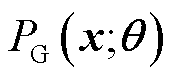 和
和 之间的差异,训练过程中G需要减少
之间的差异,训练过程中G需要减少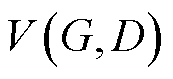 的值,让自己生成的样本无法被D识别,而D希望增大
的值,让自己生成的样本无法被D识别,而D希望增大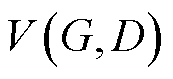 的值更高效地判断数据的真假类别。
的值更高效地判断数据的真假类别。
通过生成器和鉴别器的对抗训练,GAN模型能够学习并且生成逼近未来真实序列的预测结果。同时GAN模型能够捕获时间序列中的多模态特征,生成器可以生成多样性的预测序列,涵盖了不同可能的序列趋势与变化,这些序列通过鉴别器进行评估,使模型能够生成更准确、可靠的预测结果,并对其进行优化。但是由于GAN训练的复杂性,容易出现模式坍塌的问题,生成器和鉴别器对模型收敛和稳定性的影响非常大,所以选择合适的生成器和鉴别器是非常具有挑战性的问题。
本节提出的AWAS模型主要由权重注意力的Seq2Seq模型和GAN网络的鉴别器组成。权重注意力的Seq2Seq模型由编码器和解码器组成,在解码器中引入了改进的权重注意力机制,并且在解码器的顶部加入了鉴别器引入对抗训练的思想。
AWAS模型如图4所示。图中 表示拼接。模型的Seq2Seq部分在数据输入编码器之前需要进行预处理,然后将预处理的数据输入编码器,得到编码器输出和编码器隐藏层向量;再经过权重注意力机制处理后,得到结果与输入拼接,作为解码器GRU的输入;最后将预测值与对应特征值拼接,得到预测序列
表示拼接。模型的Seq2Seq部分在数据输入编码器之前需要进行预处理,然后将预处理的数据输入编码器,得到编码器输出和编码器隐藏层向量;再经过权重注意力机制处理后,得到结果与输入拼接,作为解码器GRU的输入;最后将预测值与对应特征值拼接,得到预测序列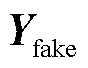 ,对应的标签矩阵
,对应的标签矩阵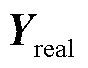 ,作为GAN的鉴别器训练数据,通过GAN训练后,能够提升其对序列的鉴别能力,从而提高整个模型的预测能力。
,作为GAN的鉴别器训练数据,通过GAN训练后,能够提升其对序列的鉴别能力,从而提高整个模型的预测能力。
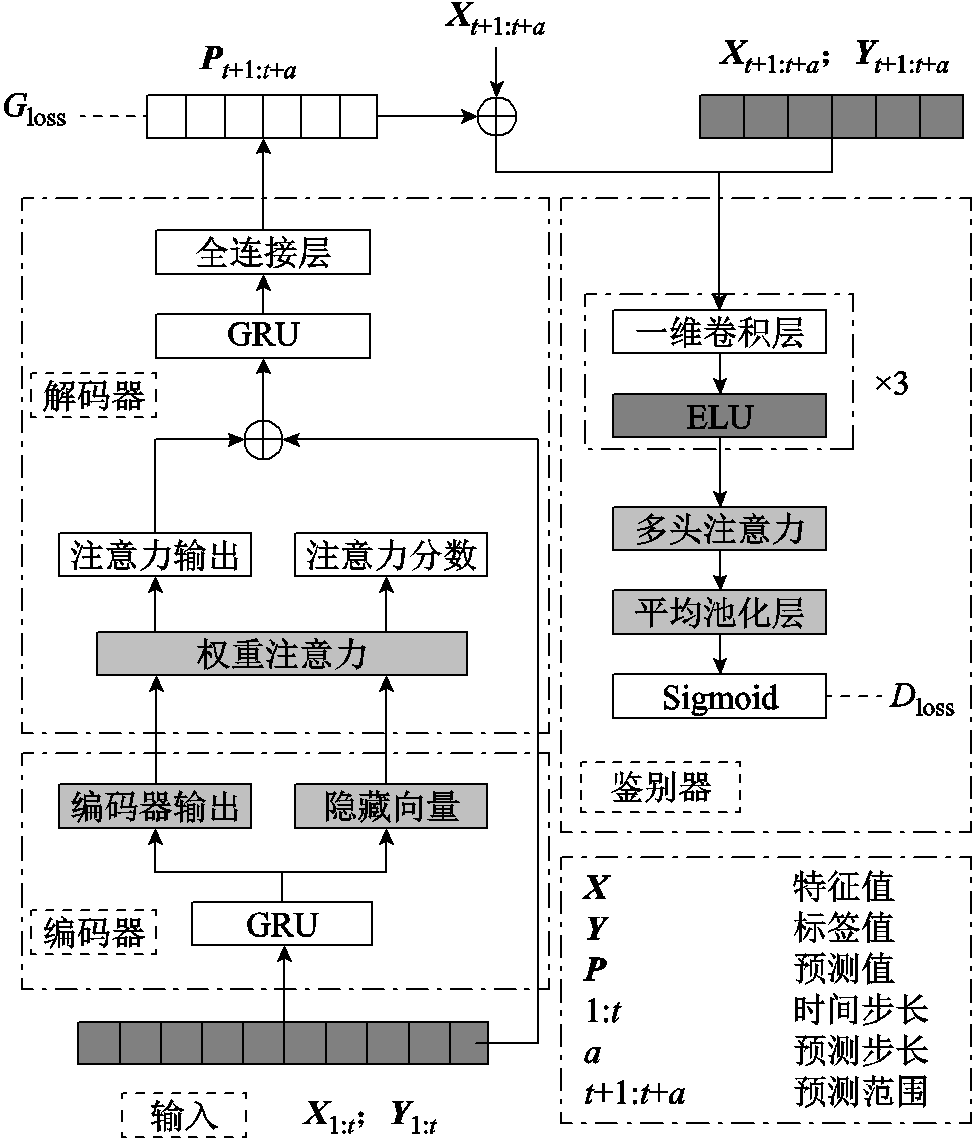
图4 AWAS模型
Fig.4 AWAS model
如图4所示的左半部分是Seq2Seq模型,其由编码器和解码器组成,本文在解码器中引入一个权重注意机制,形成一个权重注意力机制的Seq2Seq模型。整个模型的输入序列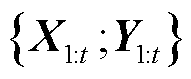 包含了所需数据的特征及其对应的标签,以GRU作为编码器。编码器接受输入序列,得到包含每个时间步的输出状态,以及编码器在最后一个时间步的隐藏状态。接着经过权重注意力机制得到权重注意力输出,将输入序列与权重注意力输出拼接作为解码器中GRU的输入,构成本文提出的权重注意力机制的Seq2Seq模型。
包含了所需数据的特征及其对应的标签,以GRU作为编码器。编码器接受输入序列,得到包含每个时间步的输出状态,以及编码器在最后一个时间步的隐藏状态。接着经过权重注意力机制得到权重注意力输出,将输入序列与权重注意力输出拼接作为解码器中GRU的输入,构成本文提出的权重注意力机制的Seq2Seq模型。
在Seq2Seq模型的解码器部分引入权重注意力机制,如图4所示。权重注意力机制的主要作用是增强模型的长序列依赖提取能力。
普通的多头注意力机制接收三个输入,分别为查询(Q)、键(K)、值(V),然后将三个输入经过简单的线性变换,再通过给定的注意力头的数量,将查询、键和值分别映射到不同的表示空间,相比自注意力机制具有更丰富的表达能力。但是在面对时间序列复杂的输入特征时,这种方法不能很好地捕捉序列的多样性和复杂关系。
为了提升模型的预测能力,本文在多头注意力机制的基础上引入额外的线性层计算,用于计算头数相关的权重矩阵W,权重注意力机制如图5所示。其中额外线性层的输出大小与注意力的头数相同,便于对查询、键和值进行额外的线性变换后将其映射到多个注意力头的权重空间中。每个注意力头都可以自适应地学习权重,不同的线性变换增强了模型捕捉输入序列中不同特征和关系的能力,同时引入W权重矩阵投影,使模型可以更灵活地计算注意力得分。经过W权重矩阵投影与加权后的查询、键和值可以在更细粒度的特征空间上计算注意力,以增强不同头在不同表示空间的信息交流,使模型获得更大的表征能力,提高模型的性能和泛化能力。
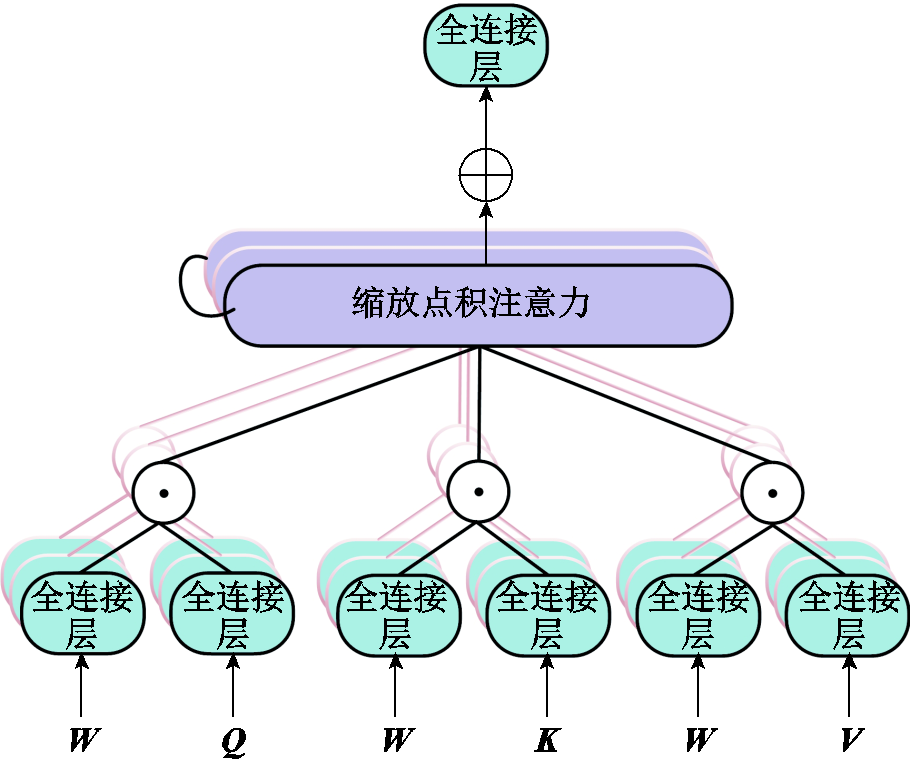
图5 权重注意力机制
Fig.5 Weighed attention mechanism
查询、键、值都需要经过线性变换得到最终的Q、K、V,其中K和V矩阵初始状态为编码器的输出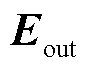 ,W与Q的初始状态为编码器输出的隐藏层向量
,W与Q的初始状态为编码器输出的隐藏层向量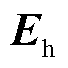 ,与普通多头注意力机制不同,这里额外使用了线性层
,与普通多头注意力机制不同,这里额外使用了线性层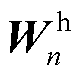 ,计算得到头数相关的权重矩阵
,计算得到头数相关的权重矩阵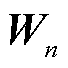 ,并依次与
,并依次与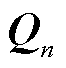 、
、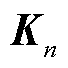 、
、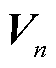 相乘,其计算方法为
相乘,其计算方法为
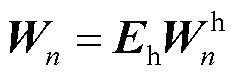 (12)
(12)
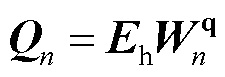 (13)
(13)
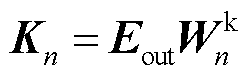 (14)
(14)
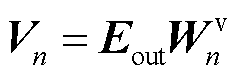 (15)
(15)
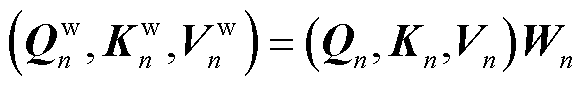 (16)
(16)
后续计算用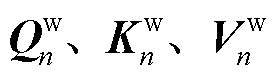 代替原来的
代替原来的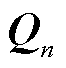 、
、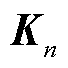 、
、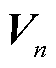 计算注意力输出,其中
计算注意力输出,其中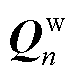 和
和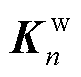 相乘后除以缩放因子
相乘后除以缩放因子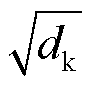 ,再经过softmax激活函数得到注意力分数
,再经过softmax激活函数得到注意力分数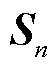 ,
,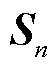 与
与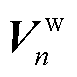 相乘得到各个头的注意力输出
相乘得到各个头的注意力输出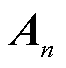 ,最后将所有注意力分数拼接得到注意力输出
,最后将所有注意力分数拼接得到注意力输出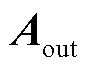 为
为
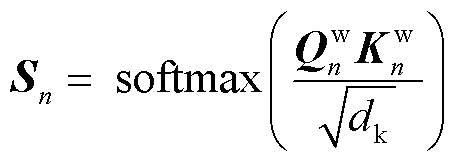 (17)
(17)
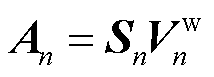 (18)
(18)
 (19)
(19)
式中,Concat表示拼接。
如图4所示,在模型的右边加入鉴别器网络D。大部分用来预测时间序列的模型都有一个特定的目标,例如最小化损失函数。但是由于无法处理时间序列存在于真实世界的随机性,从而影响了模型的性能。同时预测长时间序列的误差积累也会对实验结果造成很大的影响。本文使用对抗性的训练方法使模型能更好地学习序列表示,提高模型的预测精度。
AWAS模型的算法中设置了 和
和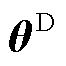 作为Seq2Seq网络和鉴别器网络的参数集,在训练过程中不断更新参数集,提升模型的预测能力。
作为Seq2Seq网络和鉴别器网络的参数集,在训练过程中不断更新参数集,提升模型的预测能力。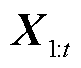 表示历史样本第一个时间步特征到第t个时间步特征的合集,t为时间步长的大小,
表示历史样本第一个时间步特征到第t个时间步特征的合集,t为时间步长的大小,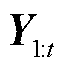 则是包含了t个时间步的对应标签集,将
则是包含了t个时间步的对应标签集,将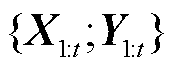 作为编码器GRU的输入,表示为
作为编码器GRU的输入,表示为
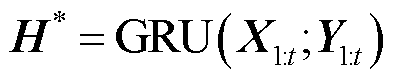 (20)
(20)
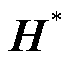 包含了GRU的隐藏层向量和编码器输出,如式(12)~式(19)所示,隐藏层向量作为权重注意力机制中权重线性层
包含了GRU的隐藏层向量和编码器输出,如式(12)~式(19)所示,隐藏层向量作为权重注意力机制中权重线性层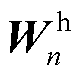 和查询线性层
和查询线性层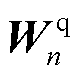 的输入,编码器输出则作为键线性层
的输入,编码器输出则作为键线性层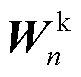 和值线性层
和值线性层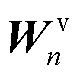 的输入,
的输入,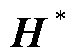 经过权重注意力机制计算后得到注意力输出,即
经过权重注意力机制计算后得到注意力输出,即
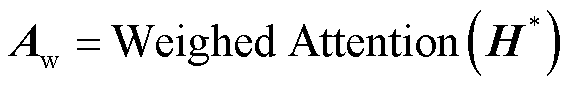 (21)
(21)
权重注意力机制可以帮助模型更好地关注不同时间点上电池荷电状态的变化模式。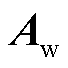 是权重注意力的输出,可以被视为一个关注的权重分布,显示了模型在生成单个或者多个预测值时,对输入序列中各个时间步的编码信息关注程度。此时将
是权重注意力的输出,可以被视为一个关注的权重分布,显示了模型在生成单个或者多个预测值时,对输入序列中各个时间步的编码信息关注程度。此时将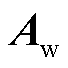 和
和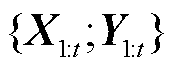 拼接作为解码器GRU的输入,得到的输出
拼接作为解码器GRU的输入,得到的输出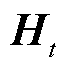 经过全连接层就是权重注意力Seq2Seq模型的预测的序列
经过全连接层就是权重注意力Seq2Seq模型的预测的序列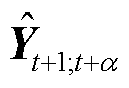 ,如式(22)所示。
,如式(22)所示。
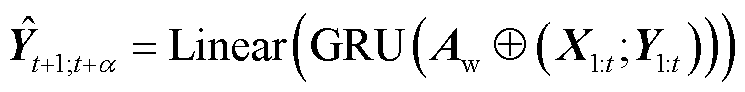 (22)
(22)
式中,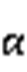 为多步预测任务需要预测的步数。Seq2Seq模型引入了对抗训练的思想,将
为多步预测任务需要预测的步数。Seq2Seq模型引入了对抗训练的思想,将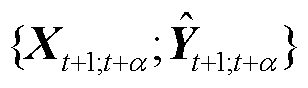 作为鉴别器的假样本,
作为鉴别器的假样本,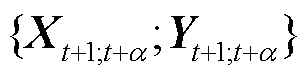 则为鉴别器的真样本,分别输入鉴别器中,如式(23)所示。
则为鉴别器的真样本,分别输入鉴别器中,如式(23)所示。
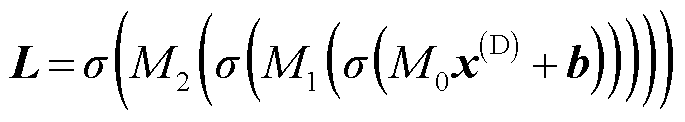 (23)
(23)
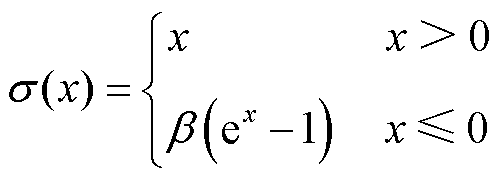 (24)
(24)
式中,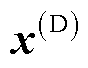 为鉴别器输入的真假样本;b为偏置值向量;
为鉴别器输入的真假样本;b为偏置值向量;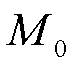 、
、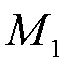 、
、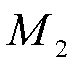 分别表示三个一维卷积的卷积核。最终映射得到输出
分别表示三个一维卷积的卷积核。最终映射得到输出 。
。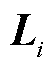 经过多头注意力机制得到输出
经过多头注意力机制得到输出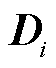 ,增强了鉴别器的网络感知能力和特征提取能力,有助于识别输入数据中的重要特征,以便更好地判断数据的真伪,如式(25)所示。
,增强了鉴别器的网络感知能力和特征提取能力,有助于识别输入数据中的重要特征,以便更好地判断数据的真伪,如式(25)所示。
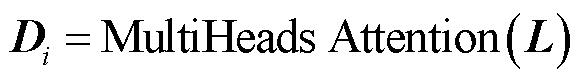 (25)
(25)
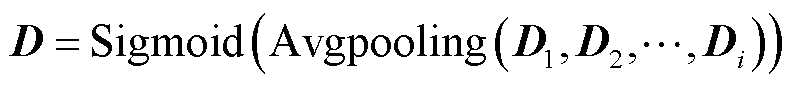 (26)
(26)
如式(26)所示,在多头注意力之后使用平均池化层来降低特征的维度。平均池化层可以减少数据的空间维度,从而提取出更高级别的特征,提高了鉴别器判断数据真伪的能力。最后使用Sigmoid函数输出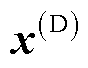 样本为真实数据的概率D。
样本为真实数据的概率D。
算法过程如算法1所示。

算法1 AWAS模型计算过程 输入:特征集X,标签集Y,全1矩阵,全0矩阵输出:预测序列,样本类别随机初始化和参数集For each training iteration doFor k steps do= GRU//编码器GRU计算输出集=Weighed Attention//计算注意力输出集=GRU//计算输出=Predict//得到预测的序列=//鉴别器假样本//鉴别器真样本//鉴别器判断//鉴别器判断//随机梯度更新和参数End ForEnd For
AWAS模型的Seq2seq部分损失函数如式(27)所示,Y为Seq2Seq模型的真实值序列,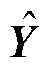 为Seq2Seq模型的预测值序列。鉴别器部分的损失函数分为两个部分,输入
为Seq2Seq模型的预测值序列。鉴别器部分的损失函数分为两个部分,输入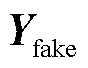 、
、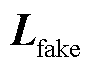 与
与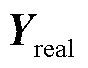 、
、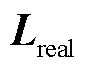 分别得到损失函数
分别得到损失函数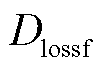 和
和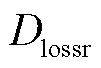 ,如式(28)、式(29)所示。
,如式(28)、式(29)所示。
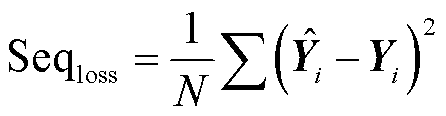 (27)
(27)
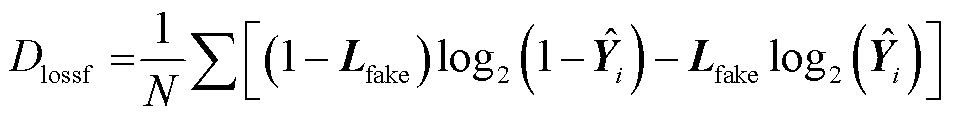 (28)
(28)
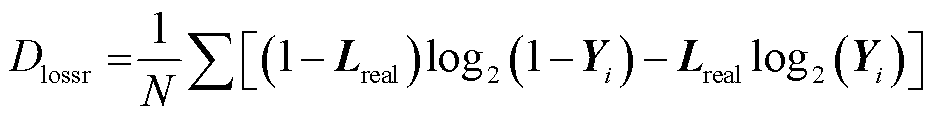 (29)
(29)
鉴别器的损失为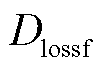 与
与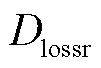 损失之和,模型总损失为
损失之和,模型总损失为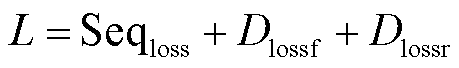 。如式(10)所示,鉴别器通过最小化交叉熵损失函数来判断输入的序列是预测值还是真实值,Seq2Seq网络通过最小化预测序列和真实值之间的均方损失与鉴别器交叉熵损失互补。将Seq2Seq网络引入权重注意力机制,有利于模型捕获时间序列的整体模式和时间依赖关系,使预测值尽可能和真实值贴近,从而防止鉴别器因为快速收敛而停止优化,使鉴别器可以从全局角度判别预测序列的生成情况。
。如式(10)所示,鉴别器通过最小化交叉熵损失函数来判断输入的序列是预测值还是真实值,Seq2Seq网络通过最小化预测序列和真实值之间的均方损失与鉴别器交叉熵损失互补。将Seq2Seq网络引入权重注意力机制,有利于模型捕获时间序列的整体模式和时间依赖关系,使预测值尽可能和真实值贴近,从而防止鉴别器因为快速收敛而停止优化,使鉴别器可以从全局角度判别预测序列的生成情况。
实验使用的数据集是Panasonic18650PF[21]、LG-HG2[22]及CACLE[23]锂电池数据集。前两个数据集分别包含了HWFET、UDDS、LA92、US06四种常见的汽车行驶工况,以及四种工况随机混合的实验记录,其中UDDS、LA92、US06作为测试集,HWFET作为验证集,其余作为训练集。
三个数据集的基本参数见表1,其中Panasonic 18650PF数据集在25、10、0、-10、-20℃的温度下分别进行(0.5C、1C、2C、4C、6C)五次脉冲放电,每次测试后电池以1 C倍率充电至4.2 V,电池温度为12℃以上。LG-HG2数据集在不同温度下进行四次脉冲测试(以1C、2C、4C和6C的倍率放电,以及0.5C、1C、1.5C、2C的倍率充电),每次测试后电池以1C倍率充电至4.2 V,电池温度为22℃以上,这两个数据集单步预测周期为0.1 s,多步预测周期为1.2 s。来自马里兰大学高级生命周期工程中心的CACLE作为迁移测试的数据集,在0~50℃的温度条件下进行低电流放电测试后以1C的倍率充电至3.6 V,放电测试的温度间隔为10℃,单步预测周期为5 s,多步预测周期为60 s。
表1 锂电池数据集基本参数
Tab.1 Lithium-ion battery dataset basic parameters
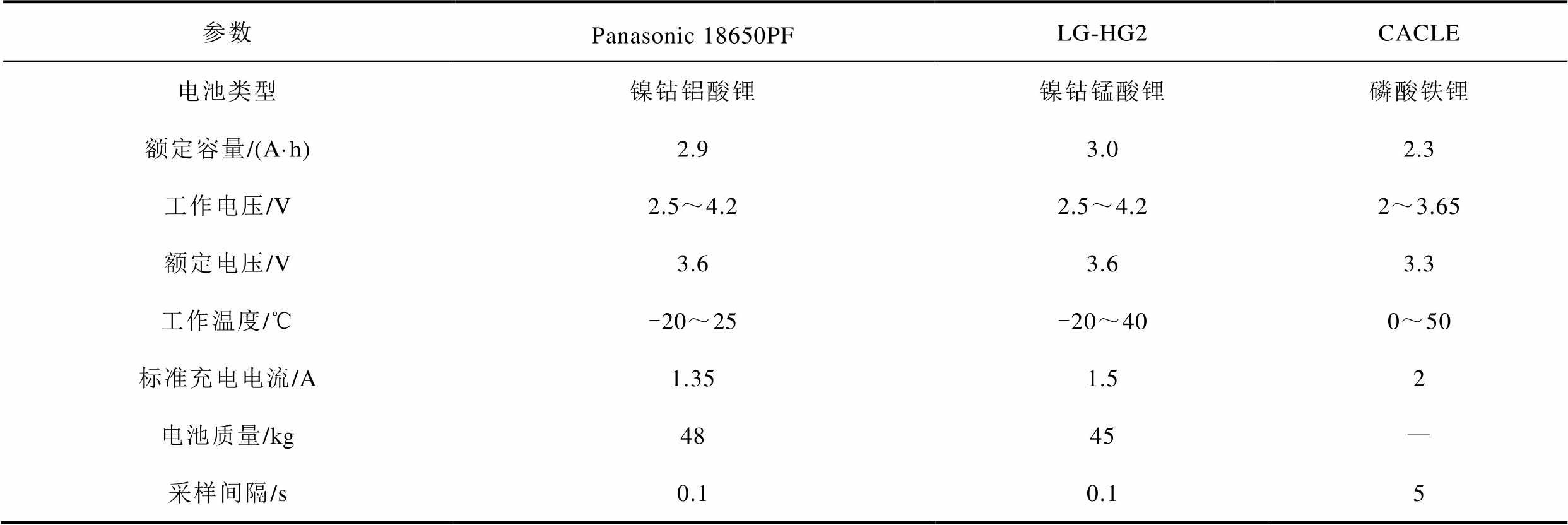
参数Panasonic 18650PFLG-HG2CACLE 电池类型镍钴铝酸锂镍钴锰酸锂磷酸铁锂 额定容量/(A·h)2.93.02.3 工作电压/V2.5~4.22.5~4.22~3.65 额定电压/V3.63.63.3 工作温度/℃-20~25-20~400~50 标准充电电流/A1.351.52 电池质量/kg4845— 采样间隔/s0.10.15
实验选取数据集中的电流I、电压V及电池温度T作为特征,SOC真实值作为标签。对训练集进行压缩再扩充操作,适当增加数据集泛化能力,最后使用Minmax Scare对数据进行归一化预处理。
实验在Pycharm上使用Pytorch框架,搭载RTX3070显卡。AWAS模型进行单步预测时,30 000条数据所需预测时间约为51 s,进行12步预测所需时间约为5 s。采用权重衰减[24]技术降低模型过拟合风险,经过多次实验,模型选取的最佳超参数见表2。
表2 AWAS超参数
Tab.2 Hyperparameters of AWAS

超参数锂电池数据集 Panasonic18650PFLG-HG2 输入节点44 隐藏节点6464 输出节点1/121 优化算法AdamAdam 计算步长9696 迭代次数3030 损失函数MSE/BCEMSE/BCE 注意力头数88 批量大小3232 评价函数MAPE/RMSE/MAEMAX/MAE/RMSE
表2中MAX、MAE、RMSE、MAPE的计算公式为
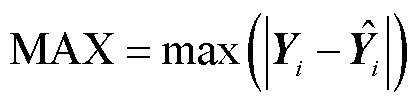 (30)
(30)
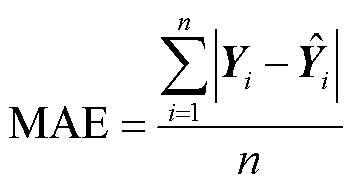 (31)
(31)
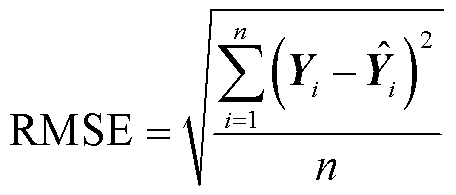 (32)
(32)
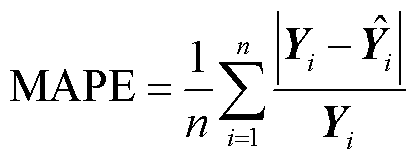 (33)
(33)
式中,i为样本序列编号;n为样本序列的总数;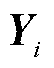 为真实值;
为真实值;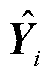 为预测值。
为预测值。
实验选择MAE、RMSE和MAX评估模型预测性能。由于电池在不同温度、不同工况的状态下放电和充电的能力会出现较大的差异,所以在多种温度和工况下进行测试可以验证模型的泛化能力。AWAS的单步预测结果见表3。可见无论在何种温度和工况,AWAS模型的预测误差都非常低,精度十分稳定。
表3 LG-HG2数据集AWAS模型单步预测结果
Tab.3 Single-step prediction results of AWAS model for the LG-HG2 dataset
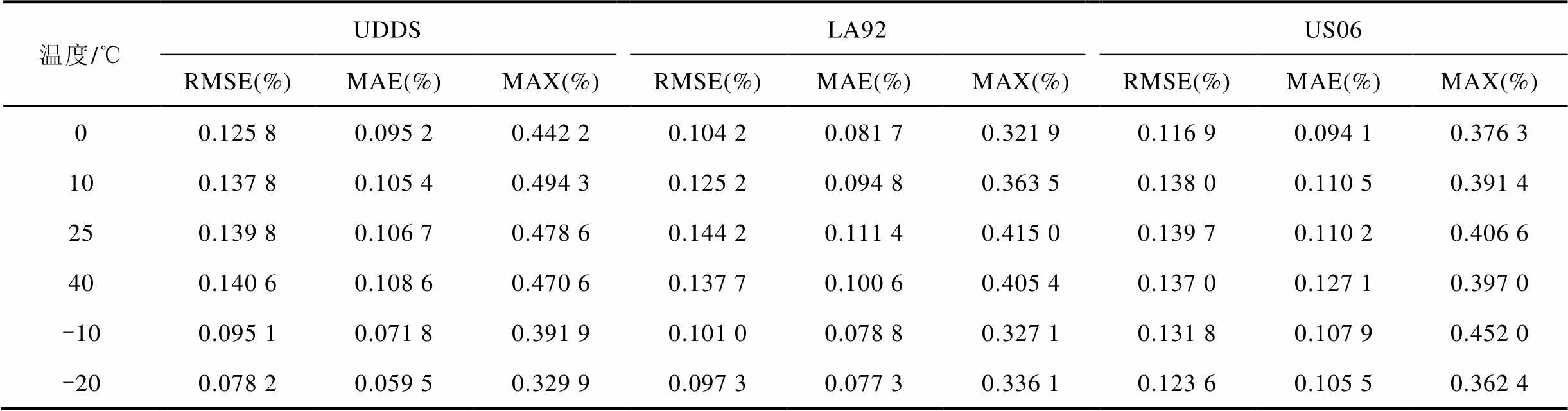
温度/℃UDDSLA92US06 RMSE(%)MAE(%)MAX(%)RMSE(%)MAE(%)MAX(%)RMSE(%)MAE(%)MAX(%) 00.125 80.095 20.442 20.104 20.081 70.321 90.116 90.094 10.376 3 100.137 80.105 40.494 30.125 20.094 80.363 50.138 00.110 50.391 4 250.139 80.106 70.478 60.144 20.111 40.415 00.139 70.110 20.406 6 400.140 60.108 60.470 60.137 70.100 60.405 40.137 00.127 10.397 0 -100.095 10.071 80.391 90.101 00.078 80.327 10.131 80.107 90.452 0 -200.078 20.059 50.329 90.097 30.077 30.336 10.123 60.105 50.362 4
LG-HG2单步预测不同模型误差比较见表4,包括长短期趋势网络(Long-Short-Term Time-series Network, LSTNet)、双向长短期记忆网络(Bi-directional Long Short-Term Memory, BiLSTM)、双向门控循环单元(Bi-directional Gated Recurrent Unit, BiGRU)。结果表明,AWAS模型的预测能力全面优于Informer和稀疏化Informer。在实际使用过程中,由于大倍率放电使电池本身的温度经常超过25℃,因此图6分别展示了AWAS模型在40℃下LA92工况、40℃下UDDS工况以及25℃下US06工况的单步预测曲线和真实值的对比曲线。由图6可知,即使在高温情况下,本文提出的模型在单步预测任务依然展现了非常高的精度。
表4 LG-HG2单步预测不同模型误差比较
Tab.4 Comparison of error for single-step predictions using different models on the LG-HG2 dataset
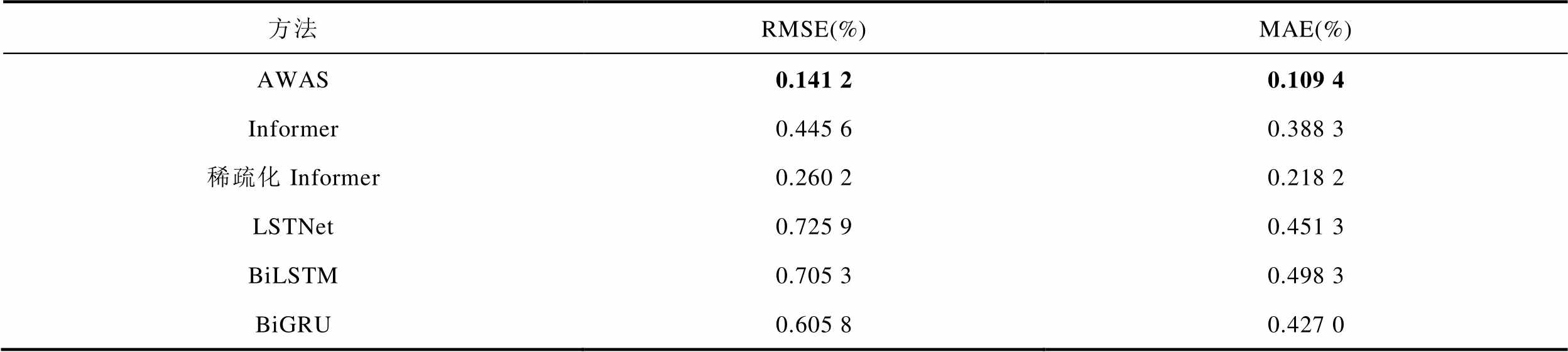
方法RMSE(%)MAE(%) AWAS0.141 20.109 4 Informer0.445 60.388 3 稀疏化Informer0.260 20.218 2 LSTNet0.725 90.451 3 BiLSTM0.705 30.498 3 BiGRU0.605 80.427 0
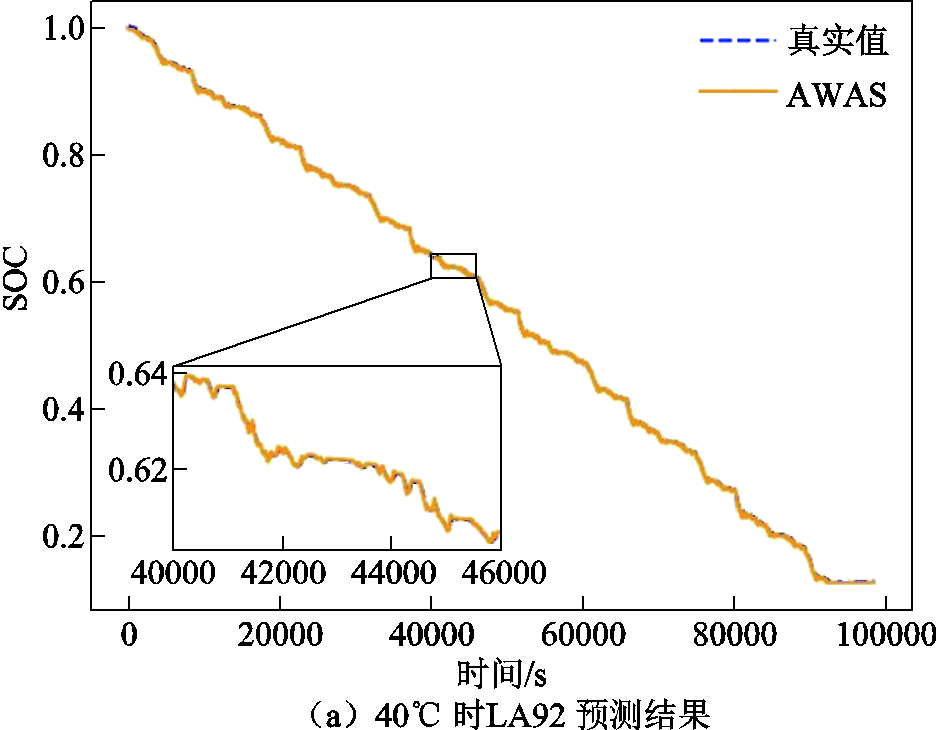
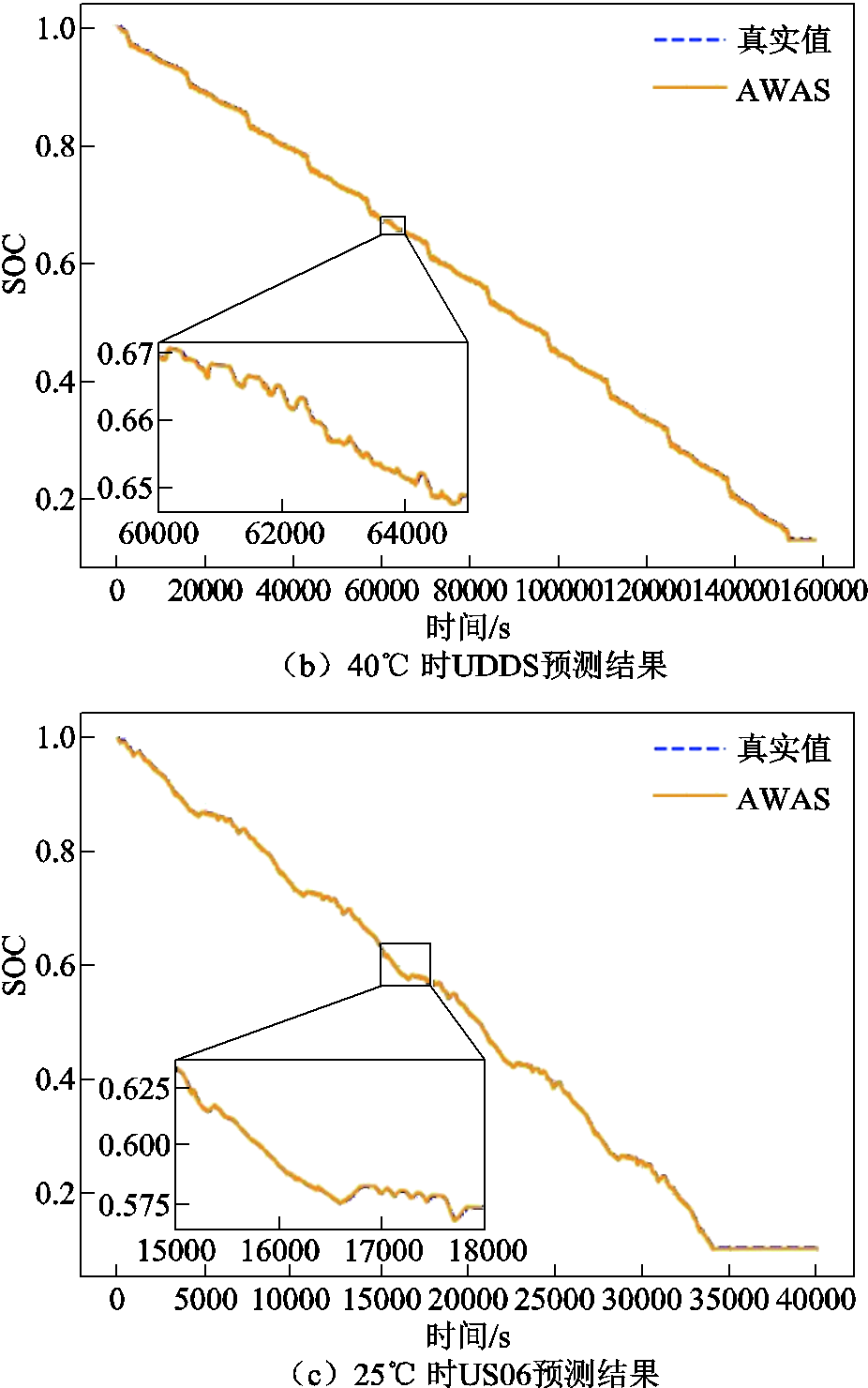
图6 LG-HG2数据集下不同温度在不同工况下的预测结果
Fig.6 Predicted results for different operating conditions at various temperatures in the LG-HG2 dataset
不同种类的电池放电能力也有差异,为了验证模型在不同电池的泛化能力,对Panasonic数据集进行单步预测和多步预测任务测试。
25℃下AWAS与Informer预测结果对比见表5。在室温25℃条件下,AWAS模型在MAE和RMSE两种误差评估上达到最低的0.101 0%和0.122 2%,相比Informer降低了很多。Informer在US06工况上误差相比其他两种工况出现较大幅度的上升,而AWAS模型在三种工况的精度都非常稳定。
表5 25℃下AWAS与Informer预测结果对比
Tab.5 Comparison of AWAS and Informer predictions at 25℃

工况AWASInformer RMSE(%)MAE(%)RMSE(%)MAE(%) UDDS0.122 20.106 40.375 00.297 8 LA920.151 50.140 70.394 40.315 9 US060.123 20.101 00.582 70.454 7
表6为AWAS模型在Panasonic数据集三种工况、不同温度下单步预测任务的误差均值与不同模型预测结果对比。无论是RNN结构及其优化模型,还是Transformer结构及其优化模型,AWAS模型在RMSE和MAE两项误差评估结果上都取得了明显的提升。
表6 Panasonic数据集单步预测不同模型误差比较
Tab.6 Comparison of error for single-step predictions using different models on the Panasonic dataset
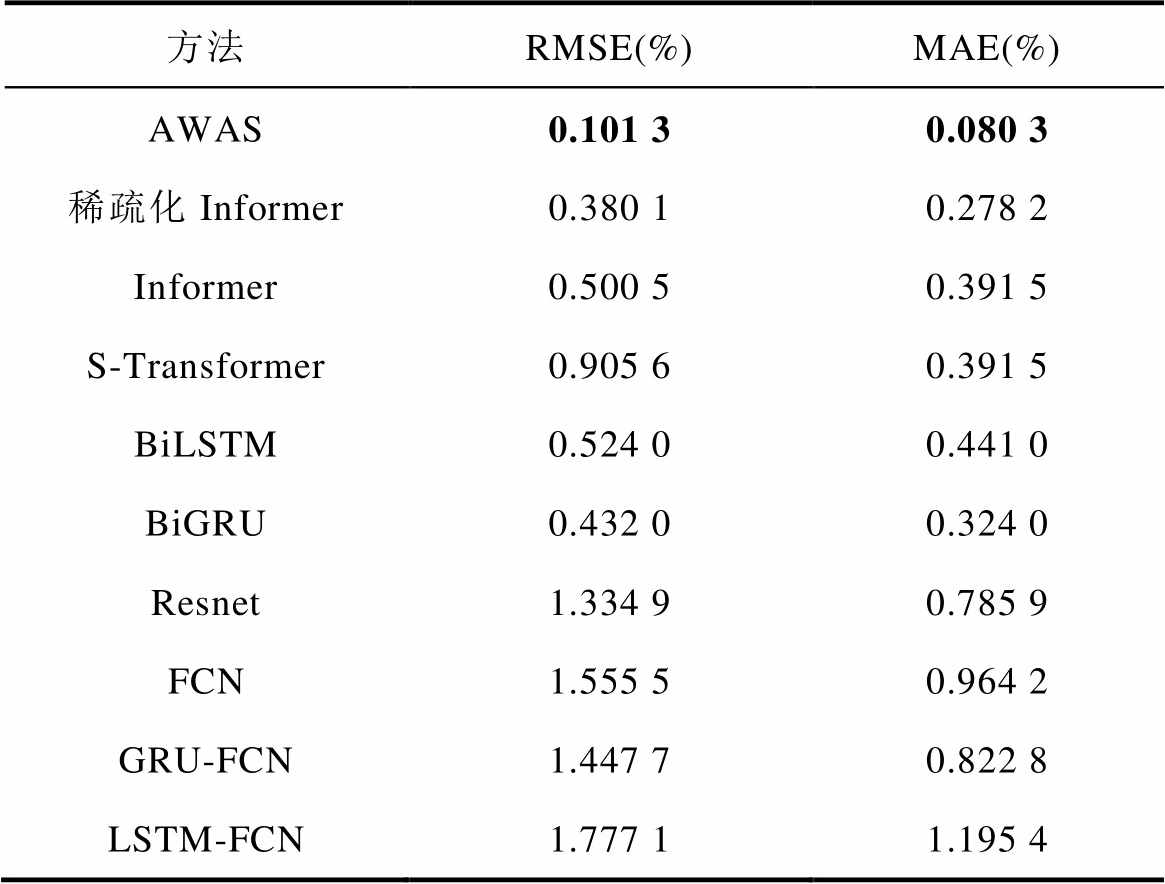
方法RMSE(%)MAE(%) AWAS0.101 30.080 3 稀疏化Informer0.380 10.278 2 Informer0.500 50.391 5 S-Transformer0.905 60.391 5 BiLSTM0.524 00.441 0 BiGRU0.432 00.324 0 Resnet1.334 90.785 9 FCN1.555 50.964 2 GRU-FCN1.447 70.822 8 LSTM-FCN1.777 11.195 4
同时对于多步预测任务,本文在相同条件下进行12步预测,表7展示了在该数据集下对SOC的12步预测结果。在多温度下AWAS模型的平均MAPE、RMSE和MAE分别达到了0.3818%,0.2199%和0.1666%,图7展示了不同温度下不同工况的多步预测任务下部分模型与AWAS的预测结果对比,AWAS在多步预测任务下也能得到误差非常低的预测结果。可见AWAS模型可以适应不同锂电池在不同温度、不同工况的多步预测任务,并能取得更高的精度,证明了模型的泛化能力。
表7 Panasonic数据集AWAS模型多步预测结果
Tab.7 Multi-step prediction results of the AWAS model on the Panasonic dataset
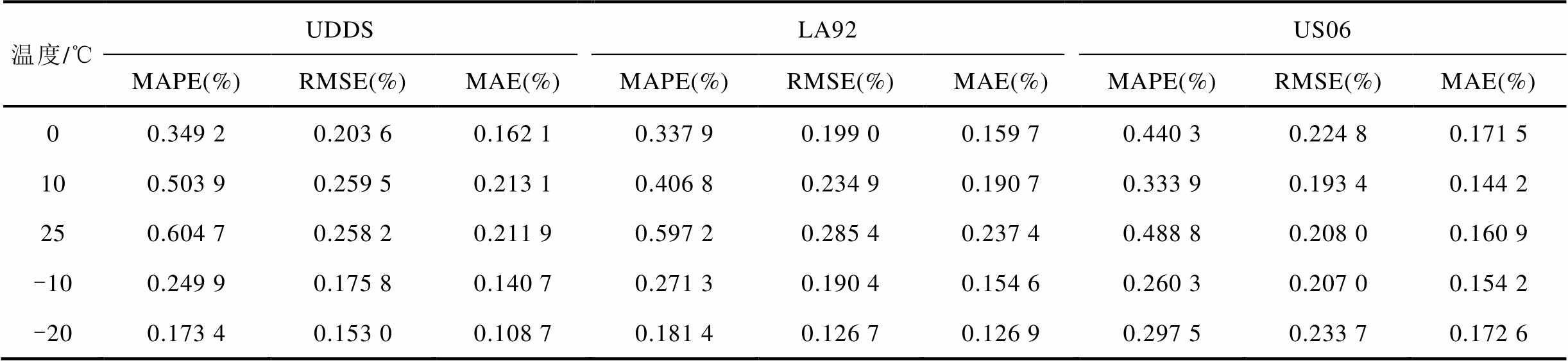
温度/℃UDDSLA92US06 MAPE(%)RMSE(%)MAE(%)MAPE(%)RMSE(%)MAE(%)MAPE(%)RMSE(%)MAE(%) 00.349 20.203 60.162 10.337 90.199 00.159 70.440 30.224 80.171 5 100.503 90.259 50.213 10.406 80.234 90.190 70.333 90.193 40.144 2 250.604 70.258 20.211 90.597 20.285 40.237 40.488 80.208 00.160 9 -100.249 90.175 80.140 70.271 30.190 40.154 60.260 30.207 00.154 2 -200.173 40.153 00.108 70.181 40.126 70.126 90.297 50.233 70.172 6
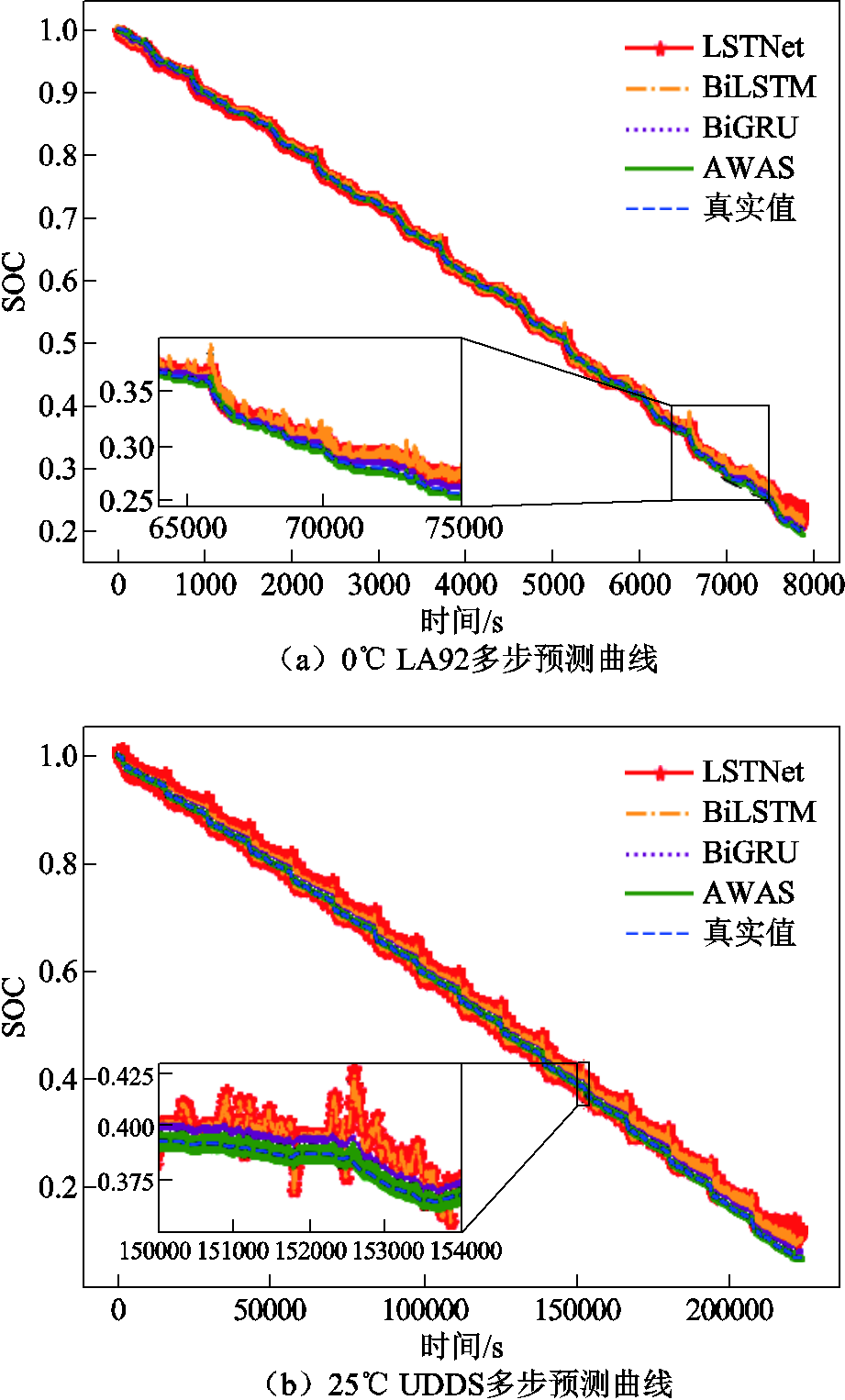
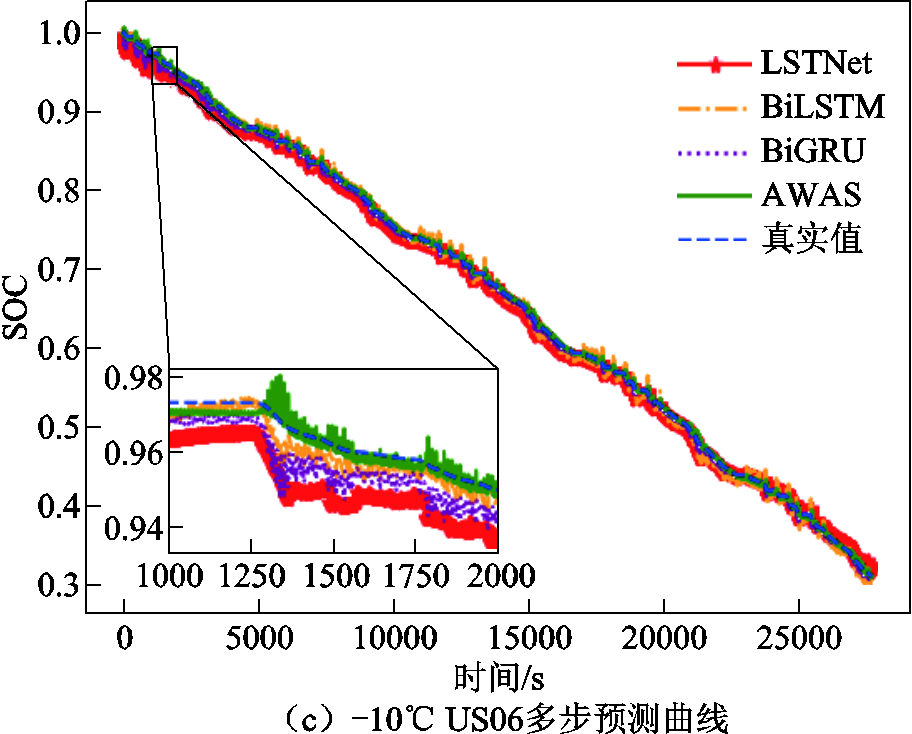
图7 Panasoni数据集下在不同温度、不同工况中的多步预测结果
Fig.7 Multi-step prediction results for different operating conditions at various temperatures in the Panasonic dataset
为了验证AWAS模型的普适性,本节使用Panasonic 18650PF数据集训练的模型参数对CACLE数据集直接进行迁移测试。数据集使用了007和008两块磷酸铁锂电池,分别在30、40、50℃进行放电测试。对比实验选取了同样条件的数据集训练的BiLSTM模型和BiGRU模型作为对比实验,结果见表8。可见,单步预测时,AWAS模型平均MAPE、RMSE、MAE分别达到0.1225%、0.0881%和0.0628%,多步预测的误差也远比BiGRU低。对CACLE数据集进行迁移测试时,AWAS模型能保持非常稳定的预测能力,在具备高精度预测能力的同时,不同温度条件下的各种指标的误差评估不会出现非常大的波动。
表8 CACLE数据集迁移测试实验对比
Tab.8 Comparison of data set migration testing experiments for CACLE
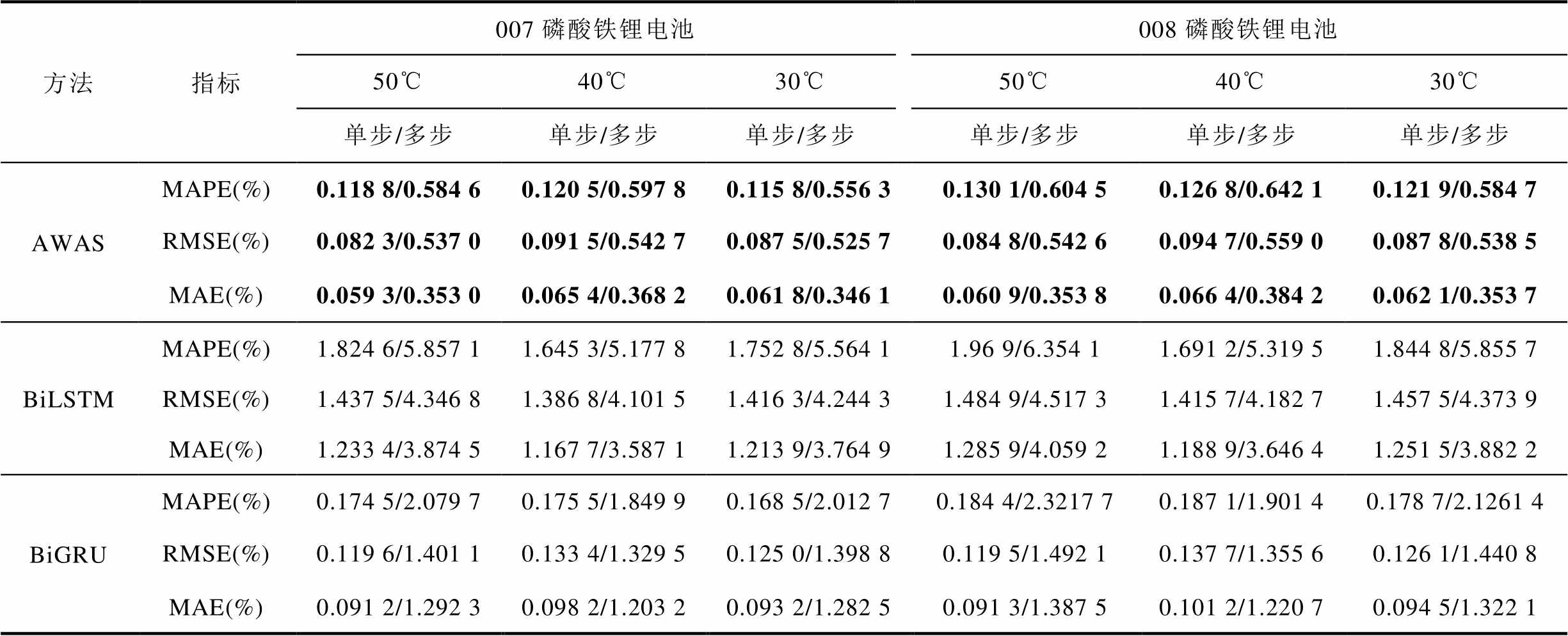
方法指标007磷酸铁锂电池008磷酸铁锂电池 50℃40℃30℃50℃40℃30℃ 单步/多步单步/多步单步/多步单步/多步单步/多步单步/多步 AWASMAPE(%)0.118 8/0.584 60.120 5/0.597 80.115 8/0.556 30.130 1/0.604 50.126 8/0.642 10.121 9/0.584 7 RMSE(%)0.082 3/0.537 00.091 5/0.542 70.087 5/0.525 70.084 8/0.542 60.094 7/0.559 00.087 8/0.538 5 MAE(%)0.059 3/0.353 00.065 4/0.368 20.061 8/0.346 10.060 9/0.353 80.066 4/0.384 20.062 1/0.353 7 BiLSTMMAPE(%)1.824 6/5.857 11.645 3/5.177 81.752 8/5.564 11.96 9/6.354 11.691 2/5.319 51.844 8/5.855 7 RMSE(%)1.437 5/4.346 81.386 8/4.101 51.416 3/4.244 31.484 9/4.517 31.415 7/4.182 71.457 5/4.373 9 MAE(%)1.233 4/3.874 51.167 7/3.587 11.213 9/3.764 91.285 9/4.059 21.188 9/3.646 41.251 5/3.882 2 BiGRUMAPE(%)0.174 5/2.079 70.175 5/1.849 90.168 5/2.012 70.184 4/2.3217 70.187 1/1.901 40.178 7/2.1261 4 RMSE(%)0.119 6/1.401 10.133 4/1.329 50.125 0/1.398 80.119 5/1.492 10.137 7/1.355 60.126 1/1.440 8 MAE(%)0.091 2/1.292 30.098 2/1.203 20.093 2/1.282 50.091 3/1.387 50.101 2/1.220 70.094 5/1.322 1
分别对AWAS模型的鉴别器、权重注意力进行消融实验,结果见表9。在单步预测的情况下AWAS模型的平均RMSE和MAE都达到最低的0.0966%和0.0837%,比基础的Seq2Seq模型在平均RMSE和MAE误差评估上精度分别提高了2.8%和6.8%。消融实验还进行了多步预测,实验预测12步,消融后的所有模型效果精度和单步预测相比下降了非常多,但是本文提出的AWAS模型依然能够保持较高的精度,平均MAPE、RMSE和MAE分别达到0.3472%、0.2096%和0.1695%,比消融实验精度最高的Without GAN在三种误差评估指标上分别降低了47.6%、49.6%和52.8%。
表9 消融实验结果
Tab.9 Results of ablation study

方法单步/多步 MAPE(%)RMSE(%)MAE(%) AWAS0.192 2/0.347 20.096 6/0.209 60.083 7/0.169 5 Without GAN0.202 4/0.663 10.146 1/0.416 60.116 4/0.359 2 Without WA0.246 7/0.721 40.124 1/0.478 20.101 0/0.393 8 Seq2Seq0.189 1/0.836 30.099 4/0.423 40.089 9/0.401 5
不同温度下注意力机制对比如图8所示,为了证明改进的权重注意力有效果,将AWAS的解码器部分的权重注意力机制替换为未改进多头注意力,并比较了不同温度不同工况下、多步预测的MAPE、RMSE、MAE的均值误差。图8中实线为AWAS模型使用权重注意力时在每种温度下预测误差的均值,虚线为使用未改进的多头注意力在每种温度下预测误差的均值。除了0℃下权重注意力误差会稍微偏高,其余温度使用权重注意力的预测误差都比普通的多头注意力低,且普通多头注意力的MAPE随着温度升高呈大幅上升的趋势,改进的权重注意力有效地抑制了上升的误差,验证了权重注意力机制对多头注意力机制的改进是有效的。
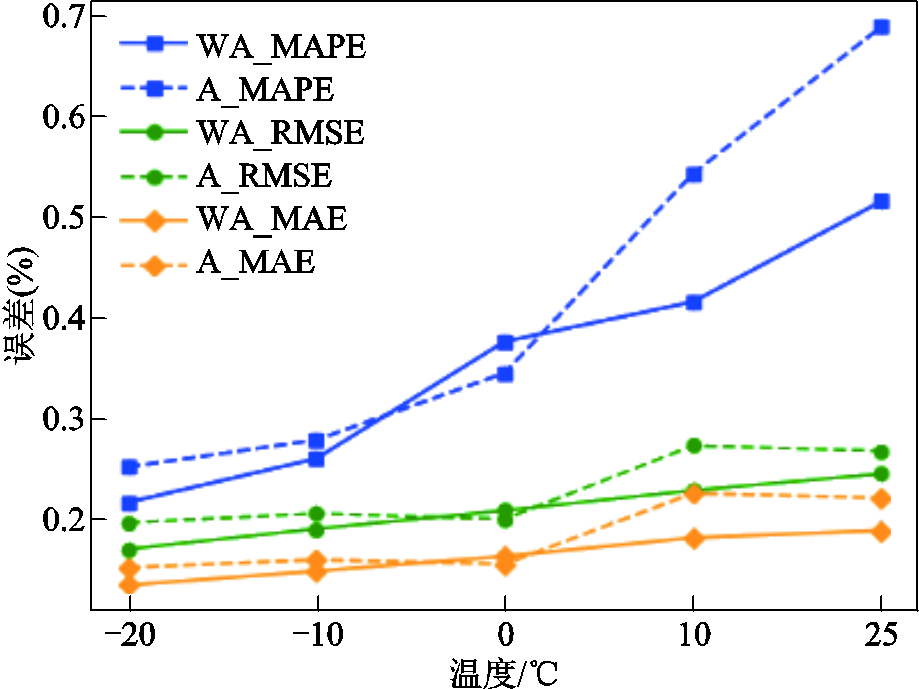
图8 不同温度下注意力机制对比
Fig.8 Comparison of attention mechanisms at different temperatures
本文在普通的序列到序列模型的基础上进行改进。首先在模型的解码器结构上引入了多头注意力机制,并且对传统多头注意力机制进行改进,为了提升模型特征提取的能力引入额外的权重线性层计算多头注意力机制;然后引入对抗训练的思想,利用三层一维卷积引入多头注意力机制作为鉴别器,通过比较,判断模型的输出和标签的差异,提高模型的预测能力。AWAS模型在单步预测任务下RMSE与MAE均值能够达到最低的0.0966%和0.0837%,而在12步预测任务下MAPE、RMSE和MAE均值分别达到0.347 2%、0.209 6%和0.169 5%。相比于循环神经网络、卷积神经网络、Informer及其优化模型等,即使在不同体系的锂电池数据集测试中AWAS模型也能够取得更高的预测精度。
本文在大量数据的基础上进行实验,并在多步预测任务中取得了良好的结果。但是还存在部分待优化的问题。在3.5节中-20、-10、10和25℃的环境下,模型使用权重注意力的预测误差对比使用普通多头注意力降低了许多,但是在0℃的环境下效果却不明显。这是因为锂电池数据集存在的数据过于庞大,导致数据集存在许多异常数据和噪声,而权重注意力提取特征的能力比普通注意力更强,对数据集的质量更为敏感。因此后续工作中需要针对0℃数据集进行去噪或者缩放处理,选取适当的去噪技术,监控去噪过程,在不丢失重要信息的同时提高数据集的质量。
在本文的实验中,随着预测步数的增加,模型的误差逐渐增大。这是因为注意力机制更加强调特征之间的点积计算,而对于局部信息的敏感性较低。尽管本文引入了权重注意力以增强特征提取能力,但仍然存在改进的空间,为了解决这个问题,将着重改进两个方面:①对权重注意力机制进行改进,用局部注意力或者稀疏注意力替换基础注意力模型。局部注意力机制在处理长序列或大量时间步任务时,通常会赋予距离查询向量较近的时间步更高的权重,以增强模型对局部信息的感知。而稀疏注意力机制的目标是在降低注意力机制的计算和存储复杂度的同时,最小化不必要的冗余计算对预测结果的影响。②对输入序列的处理进行优化,可以采用截断长序列的方法来提高多步预测的精度。这意味着将长序列分割成较短的子序列,分别进行预测,然后合并这些预测结果以获得整体预测结果,降低模型预测误差。
参考文献
[1] 高德欣, 郑晓雨, 王义, 等. 电动汽车充电状态监测与多级安全预报警方法[J]. 电工技术学报, 2022, 37(9): 2252-2262.
Gao Dexin, Zheng Xiaoyu, Wang Yi, et al. A state monitoring and multi-level safety pre-warning method for electric vehicle charging process[J]. Transactions of China Electrotechnical Society, 2022, 37(9): 2252-2262.
[2] 武龙星, 庞辉, 晋佳敏, 等. 基于电化学模型的锂离子电池荷电状态估计方法综述[J]. 电工技术学报, 2022, 37(7): 1703-1725.
Wu Longxing, Pang Hui, Jin Jiamin, et al. A review of SOC estimation methods for lithium-ion batteries based on electrochemical model[J]. Transactions of China Electrotechnical Society, 2022, 37(7): 1703-1725.
[3] 王义军, 左雪. 锂离子电池荷电状态估算方法及其应用场景综述[J]. 电力系统自动化, 2022, 46(14): 193-207.
Wang Yijun, Zuo Xue. Review on estimation methods for state of charge of lithium-ion battery and their application scenarios[J]. Automation of Electric Power Systems, 2022, 46(14): 193-207.
[4] Zhou Wenlu, Zheng Yanping, Pan Zhengjun, et al. Review on the battery model and SOC estimation method[J]. Processes, 2021, 9(9): 1685.
[5] Al Hadi A M R, Ekaputri C, Reza M. Estimating the state of charge on lead acid battery using the open circuit voltage method[J]. Journal of Physics: Conference Series, 2019, 1367(1): 012077.
[6] Zhang Mingyue, Fan Xiaobin. Design of battery management system based on improved ampere-hour integration method[J]. International Journal of Electric and Hybrid Vehicles, 2022, 14(1/2): 1.
[7] Masmoudi A, Hamdi J, Hadrich Belguith L. Deep learning for sentiment analysis of Tunisian dialect[J]. Computación y Sistemas, 2021, 25(1): 129-148.
[8] 刘素贞, 袁路航, 张闯, 等. 基于超声时域特征及随机森林的磷酸铁锂电池荷电状态估计[J]. 电工技术学报, 2022, 37(22): 5872-5885.
Liu Suzhen, Yuan Luhang, Zhang Chuang, et al. State of charge estimation of LiFeO4 batteries based on time domain features of ultrasonic waves and random forest[J]. Transactions of China Electrotechnical Society, 2022, 37(22): 5872-5885.
[9] 李超然, 肖飞, 樊亚翔, 等. 基于门控循环单元神经网络和Huber-M估计鲁棒卡尔曼滤波融合方法的锂离子电池荷电状态估算方法[J]. 电工技术学报, 2020, 35(9): 2051-2062.
Li Chaoran, Xiao Fei, Fan Yaxiang, et al. A hybrid approach to lithium-ion battery SOC estimation based on recurrent neural network with gated recurrent unit and Huber-M robust Kalman filter[J]. Transactions of China Electrotechnical Society, 2020, 35(9): 2051-2062.
[10] Wei Meng, Ye Min, Li Jiabo, et al. State of charge estimation of lithium-ion batteries using LSTM and NARX neural networks[J]. IEEE Access, 2020, 8: 189236-189245.
[11] 潘锦业, 王苗苗, 阚威, 等. 基于Adam优化算法和长短期记忆神经网络的锂离子电池荷电状态估计方法[J]. 电气技术, 2022, 23(4): 25-30.
Pan Jinye, Wang Miaomiao, Kan Wei, et al. State of charge estimation of lithium-ion battery based on Adam optimization algorithm and long short-term memory neural network[J]. Electrical Engineering, 2022, 23(4): 25-30.
[12] 李宁, 何复兴, 马文涛, 等. 基于经验模态分解的门控循环单元神经网络的锂离子电池荷电状态估计[J]. 电工技术学报, 2022, 37(17): 4528-4536.
Li Ning, He Fuxing, Ma Wentao, et al. State-of-charge estimation of lithium-ion battery based on gated recurrent unit using empirical mode decomposition[J]. Transactions of China Electrotechnical Society, 2022, 37(17): 4528-4536.
[13] Jiao Meng, Wang Dongqing, Qiu Jianlong. A GRU-RNN based momentum optimized algorithm for SOC estimation[J]. Journal of Power Sources, 2020, 459: 228051.
[14] Zhou Haoyi, Zhang Shanghang, Peng Jieqi, et al. Informer: beyond efficient transformer for long sequence time-series forecasting[J]. Proceedings of the AAAI Conference on Artificial Intelligence, 2021, 35(12): 11106-11115.
[15] Liu Xiaowei, Li Kenli, Li Keqin. Attentive semantic and perceptual faces completion using self-attention generative adversarial networks[J]. Neural Processing Letters, 2020, 51(1): 211-229.
[16] 何滢婕, 刘月峰, 边浩东, 等. 基于Informer的电池荷电状态估算及其稀疏优化方法[J]. 电子学报, 2023, 51(1): 50-56.
He Yingjie, Liu Yuefeng, Bian Haodong, et al. State-of-charge estimation of lithium-ion battery based on Informer and its sparse optimization method[J]. Acta Electronica Sinica, 2023, 51(1): 50-56.
[17] Luo Tao, Cao Xudong, Li Jin, et al. Multi-task prediction model based on ConvLSTM and encoder-decoder[J]. Intelligent Data Analysis, 2021, 25(2): 359-382.
[18] Liu Di, Li Qiang, Li Sen, et al. Non-autoregressive sparse transformer networks for pedestrian trajectory prediction[J]. Applied Sciences, 2023, 13(5): 3296.
[19] Abumohsen M, Owda A Y, Owda M. Electrical load forecasting using LSTM, GRU, and RNN algorithms[J]. Energies, 2023, 16(5): 2283.
[20] Wang Jinrui, Han Baokun, Bao Huaiqian, et al. Data augment method for machine fault diagnosis using conditional generative adversarial networks[J]. Proceedings of the Institution of Mechanical Engineers, Part D: Journal of Automobile Engineering, 2020, 234(12): 2719-2727.
[21] Chemali E, Kollmeyer P J, Preindl M, et al. Long short-term memory networks for accurate state-of-charge estimation of Li-ion batteries[J]. IEEE Transactions on Industrial Electronics, 2018, 65(8): 6730-6739.
[22] Vidal C, Kollmeyer P, Chemali E, et al. Li-ion battery state of charge estimation using long short-term memory recurrent neural network with transfer learning[C]//2019 IEEE Transportation Electrification Conference and Expo (ITEC), Detroit, MI, USA, 2019: 1-6.
[23] Xing Yinjiao, He Wei, Pecht M, et al. State of charge estimation of lithium-ion batteries using the open-circuit voltage at various ambient temperatures[J]. Applied Energy, 2014, 113: 106-115.
[24] Nakamura K, Hong B W. Adaptive weight decay for deep neural networks[J]. IEEE Access, 2019, 7: 118857-118865.
SOC Prediction of Lithium-Ion Batteries Based on Sequence-to-Sequence Model with Adversarial Weighted Attention Mechanism
Abstract In practical use, lithium-ion batteries often face extreme temperatures, and the behavior of different battery systems varies under different discharge conditions. Traditional state of charge (SOC) prediction methods, based on physical models, often overlook these differences, resulting in significant prediction errors. In recent years, as deep learning techniques, including recurrent neural networks (RNNs) and Transformers, have gained attention in time series forecasting, most of these methods have shown limited progress in improving prediction accuracy. To address these challenges, this paper introduces an adversarial weighted attention sequence-to-sequence (AWAS) model to enhance SOC prediction.
First, features are extracted from the lithium-ion battery dataset to create an input matrix. This matrix is then sent through an encoder with gated recurrent units (GRU) to capture feature correlations. Next, on top of the multi-head attention mechanism, an additional linear layer is introduced to compute a weight matrix W related to the number of attention heads. The output of this linear layer matches the number of attention heads, facilitating extra linear transformations of queries, keys, and values, and mapping them into the weight space of the multi-head attention. This enhances the computational flexibility of the attention mechanism. Then, the relevant information extracted by the GRU is input into the improved weight attention mechanism and is then passed to the GRU in the decoder. This process strengthens the extraction of correlated information among the features. Finally, the concept of adversarial training is introduced, using a three-layer convolutional layer as the core of the discriminator. The output of the decoder's GRU is considered as sequence 1, while the corresponding SOC values for the given time period are treated as sequence 2. The truthfulness of sequence 1 and sequence 2 is evaluated using the sigmoid function. Adversarial training mitigates the issue of gradient vanishing in the GRU, resolving long-term dependencies. Ultimately, the encoder's output is processed through a fully connected layer to obtain the SOC prediction. The results show that for single-step prediction tasks, our proposed model achieved significantly reduced root mean square error (RMSE) and mean absolute error (MAE) on the LG-HG2 dataset, with values of 0.1412% and 0.1094% respectively. On the Panasonic dataset, the errors further decreased to 0.1013% and 0.0803%. The Sparse Informer model, which outperformed others in control experiments, achieved errors of 0.260 2%, 0.218 2%, 0.380 1%, and 0.278 2%. In the case of a 12-step prediction task, our model achieved the lowest average MAE of 0.108 7% and mean absolute percentage error (MAPE) of 0.1734% on the Panasonic dataset at -20℃.The results of ablation experiments indicated that the average MAPE for 12-step predictions decreased to 0.3472%, while the average RMSE and MAE for single-step predictions reduced to 0.0966% and 0.0837%, respectively. These findings validate the effectiveness of our model architecture.
The experiments lead to these conclusions: (1) Compared to numerous RNN and transformer models, the incorporation of adversarial training into the Seq2Seq model effectively mitigates the issues of gradient vanishing and exploding. Across various prediction tasks, the error evaluations for the three different datasets consistently yielded the lowest values. Thus, the introduction of adversarial training is deemed appropriate. (2) Conventional multi-head attention mechanisms exhibit a substantial increase in MAPE as the lithium battery temperature rises. In contrast, the proposed weight attention mechanism reduces errors and curbs the upward trend in errors. From the experimental results, it is evident that the weight attention mechanism is more practical.
keywords:State of charge, sequence-to-sequence model, generative adversarial network,sparse informer, attention
中图分类号:TM912
DOI:10.19595/j.cnki.1000-6753.tces.231338
国家自然科学基金(62172095)、福建省自然科学基金(2023J01349)和福建省创新资金(2022C0022)资助项目。
收稿日期 2023-08-17
改稿日期 2023-10-23
陈治铭 男,1998年生,硕士研究生,研究方向为时间序列预测和机器学习。
E-mail:c1198832099@163.com
刘建华 男,1967年生,教授,博士,硕士生导师,研究方向为机器学习、智能计算、自然语言处理等。
E-mail:656095080@qq.com(通信作者)
(编辑 赫 蕾)