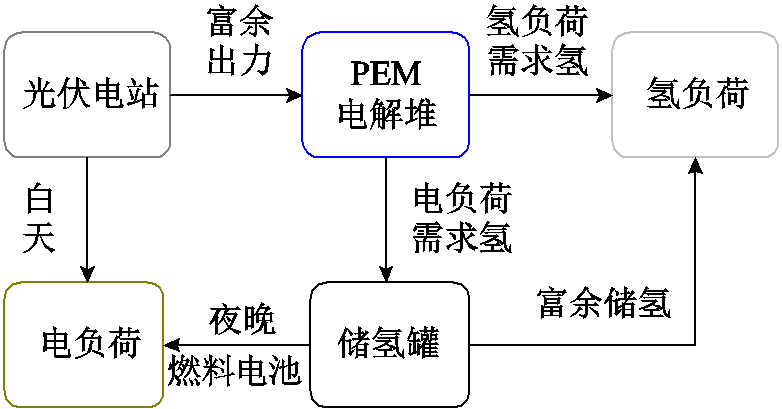
图1 孤立网电解制氢消纳光伏出力场景
Fig.1 Scenery diagram of isolated grid electrolysis hydrogen production and PV output consumption
摘要 电解水制氢可用于光伏出力消纳和绿氢制备,但目前尚缺乏模拟测试光伏电解水制氢电解堆典型应用场景下的工作模式,即电解堆典型工况,无法为电解堆性能衰减测试提供输入条件。该文提出了一种电解水制氢典型工况的提取方法,首先采用经验小波变换对光伏出力进行时频域分析,提取分时波动特征。然后用改进加权模糊聚类方法获得典型的光伏出力曲线。最后利用工况指标重构出简化工况曲线,并得到对电解堆运行场景模拟的循环工况谱。以我国“三北”地区某光伏电解水制氢系统作为算例,通过波动特征提取,获得了电解堆的典型工况。经初步仿真分析,提取的典型工况较好地刻画了电解堆的性能衰减过程。
关键词:电解水制氢 经验小波变换 模糊聚类 典型工况
随着“双碳”目标的提出,可再生能源发电在我国电力系统电源结构中的比重越来越高,对电力系统惯性减小的影响也越来越严重[1]。其中光伏电站的发展尤为迅猛,2021年我国光伏电站新增装机容量5 488.0万kW,累计装机容量达到30 598.7万kW[2]。然而光伏发电量受日照、云层等天气因素影响较大,具有min级别的波动性。
电解水制氢是一种绿色制氢技术[3],氢能可实现长时间、大容量存储,对于季节和日波动特性明显的光伏出力具有很好的契合性。光伏电解水产生的“绿氢”,是实现绿色低碳转型的重要载体,将成为国家能源体系的重要部分[4]。氢能在未来具有非常广阔的市场前景,随着《“十四五”能源领域科技创新规划》的提出,我国将构建完善的“制储运用”一体化的氢能产业链[5],并积极建设支撑中国能源安全的电氢耦合系统形态[6]。
质子交换膜(Proton Exchange Membrane, PEM)水电解制氢具有min级甚至s级的功率响应能力,且运行的功率范围能覆盖5%~150%额定功率,更能够适应光伏出力的强波动性,因此在光伏制氢领域应用广泛[6-8],但是PEM制氢存在的问题是电解堆材料成本高,产业化较为困难[9]。目前研究对可再生能源电解制氢的分析主要侧重于电解堆的功率-效率特性[10-11],并未考虑电解堆在波动性电源输入下的性能衰减,在涉及长时间的优化计算时会对分析结果产生较大的误差。
目前考虑电解堆在动态功率输入条件下的性能变化的相关研究较少。文献[12]主要分析在模拟的风速环境下风能碱性水制氢的电解堆工作性能,通过实物仿真验证了间歇性输入条件下的响应。文献[13]评价了氢能利用系统在晴天和部分阴天的太阳能辐照度下模拟光伏功率不同变化下的动态响应、制氢性能和系统整体性能等动态反应。文献[14]通过实验证明了在变化幅度相当大的光伏波动输入以及频繁的启停下,电解制氢PEM电解堆会产生性能退化的现象,例如,膜的降解与催化剂的活性下降,这会导致制氢效率的下降。文献[15]用手动改变电解电流密度的方法,在模拟的暂态波动行为下,观察氢气产生浓度等电解槽各项参数的变化,验证了动态行为对电解槽造成的负面影响。文献[16]考虑了电解堆的动态功率区间,计算功率波动下的最优制氢效率,构建优化模型以最大化制氢系统的经济性。文献[17]考虑了电解设备的退化率并考虑电网调峰需求,求得制氢系统的最佳容量。上述文献对电解堆源侧波动输入产生的影响缺少系统性的分析,对电解堆的性能衰减测试指导意义有限。
电解堆的典型工况是指模拟测试电解堆典型应用场景下的工作模式。目前,对于储能电池、电动汽车等设备的典型工况分析已经有相应的研究[18-20],但是对于PEM电解堆在光伏制氢场景的典型工况研究尚未设定相关标准,相关的研究较少[21]。考虑计算效率,光伏典型场景的生成多以聚类的方式得到。文献[22]基于密度峰值聚类算法求解出典型的光伏出力场景,再分别对不同类别场景下的数据进行训练并预测出力,得到了较为准确的结果。文献[23]利用自组织映射(Self-Organizing Maps, SOM)算法对某光伏电站四季出力进行聚类分析,生成了典型光伏场景,并将其应用于光伏-储能联合运行的优化计算。文献[24]用表征光伏波动性的符号特征序列,并以粗粒度描述方法提取特征序列中的特征量,聚类后得到了典型的光伏出力曲线,并将其用作气象预测的标签样本。然而现阶段的输入工况生成方法应用在光伏电解水制氢场景的效果较差。现有的聚类算法生成的光伏输入工况曲线多以区分光伏出力的峰值大小为基准,得到的聚类结果为最大出力值不同的平滑曲线。而众多研究表明,电解堆在输入波动下会对材料性能产生较大的影响[25-27]。所以现有的聚类算法难以精确刻画光伏出力曲线的波动情况,得到的典型工况未能体现波动输入下的电解堆性能衰减情况,在电解制氢应用层面不具有典型性。适用于光伏电解制氢场景下的电解制氢典型工况,能够分解出差异明显的波动特征与性能衰减因素,为实验室条件下电解堆波动适应性分析与材料寿命衰减规律探究提供测试输入条件,从而构建得到波动适应性评价体系,有利于规范相关行业准则,加快可再生能源制氢的发展。
本文提出了一种典型工况生成方法,能够将光伏出力曲线的波动特性分解并提取特征,再根据特征重构测试工况曲线。相比之前的研究,本文具有如下创新点:
1)依据光伏出力特有的波动特性,对出力大小进行时频域分析,提取出与PEM电解堆工作特性相关的特征指标并进行聚类分析。
2)提出的聚类方法可以有效地区分各类典型工况曲线的波动特征,提取的波动特征比一般的聚类方法更为显著。
3)根据电解堆功率特性得到简化工况曲线,突出了对电解堆性能影响较大的因素,更有利于电解堆的性能与衰减测试。
本文研究偏远地区光伏电站制氢场景下不同类型光伏出力输入下对应电解堆的典型工况,孤立网电解制氢消纳光伏出力场景如图1所示。假设该偏远地区的制氢场景如下:
(1)在偏远地区,电网延伸的成本较高,采用光伏离网制氢的模式,即制氢所需的能量全部来自光伏电站。
(2)考虑该地区负荷容量小,氢能的利用方向主要为供给其他氢负荷使用,即电氢转化。剩余部分存储在储氢罐中,用于氢电转化。
(3)采用光伏直接耦合电解堆的设计,忽略变流器的功率误差,即假设光伏功率全部转换为电解堆的输入功率。

图1 孤立网电解制氢消纳光伏出力场景
Fig.1 Scenery diagram of isolated grid electrolysis hydrogen production and PV output consumption
本文光伏场站出力曲线的数据分辨率为1 min,在细微时间尺度下的测量往往会出现较大的误差,并且电源输入的高纹波会降低电解堆的工作效率,所以对光伏出力曲线的初步平滑处理是必要的。
以往的研究对光伏波动特征的刻画多是单一的时域分析或频域分析,而光伏出力的时频特性明显,不同的时间段具有不同的波动频率。并且对电解堆来说,在不同时间段下基准功率不同,产生功率波动会对电解堆功率特性造成不同的影响。所以本文采用经验小波变换(Empirical Wavelet Transform, EWT)对光伏出力曲线进行多个模态的分解。
经验小波变换是J. Gilles于2013年提出的一种变换方法[28]。该方法的优点是结合了小波变换严谨的数学公式推导和完备的理论分析,以及经验模态分解的自适应基函数形成,是一种有效的时频域分析手段。其核心思想是将傅里叶变换后的频谱划分为N个连续的区间,再在每个区间上搭建相应的小波滤波器,最后通过信号重构的方法得出调幅调频分量,自适应地获取不同频率下的信号成分。在本文中,输入是光伏出力原始数据,输出是根据需求滤波后的数据曲线与各个频率的分量。对EWT应用的具体推导过程见附录。EWT中变量与参数的定义见附表1。
为了得到电解堆的典型运行工况,需要在众多工况场景下选取具有代表特征的场景。场景削减的方法通常使用聚类分析,如K-means法和K-mediods法。但是,对以1 min为时间尺度的光伏出力日曲线(1440维)进行聚类会因维数过多而导致聚类效果较差。因此本文采用特征指标聚类的方法对光伏出力曲线降维分析。
不同于风电,光伏具有特有的出力特性,日特性与季节特性明显。其中,日特性可以依据太阳光照强度的大小和变化过程分为三个时段:上午时段即7:00—11:00;中午时段即11:00—13:00;下午时段即13:00—17:00。因此将分解后的曲线分为三个时段再进行特征提取。
以2.1节中提取到的光伏出力低频分量为基础,定义如下两类特征指标(下标a=1、2、3分别代表上午时段、中午时段、下午时段;上标t表示时段内的第t个时间点,tmax为时段的时间点总数):
1)中午平均值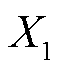 的表达式如式(1)所示,它能够反映最大光伏出力时段的平均值,对应工况指标的工况水平。
的表达式如式(1)所示,它能够反映最大光伏出力时段的平均值,对应工况指标的工况水平。
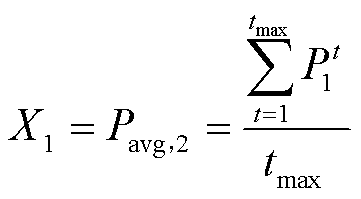 (1)
(1)
式中,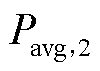 为光伏出力在中午时段的平均值;
为光伏出力在中午时段的平均值;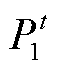 为上午时段内第t个时间点的光伏出力值。
为上午时段内第t个时间点的光伏出力值。
2)上午、下午爬坡率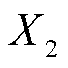 、
、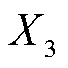 ,能够反映光伏出力在上午、下午时段内的光伏出力变化速率
,能够反映光伏出力在上午、下午时段内的光伏出力变化速率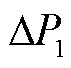 和
和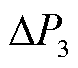 ,对应工况指标的变载速率。
,对应工况指标的变载速率。
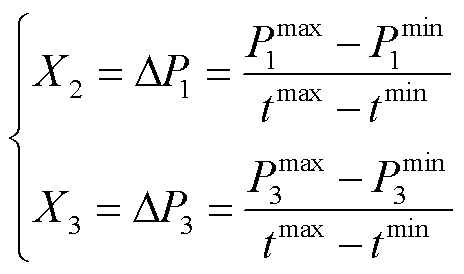 (2)
(2)
式中,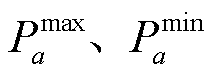 分别为第a个时段内的最大、最小值;
分别为第a个时段内的最大、最小值;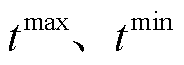 分别为最大、最小值对应的时间点。
分别为最大、最小值对应的时间点。
以2.1节中提取到的中频分量为基础,定义如下两类特征指标:
3)上午、中午、下午波动幅值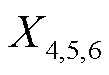 ,衡量提取出的中频分量的平均峰谷差
,衡量提取出的中频分量的平均峰谷差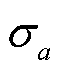 ,对应工况指标的波动率。
,对应工况指标的波动率。
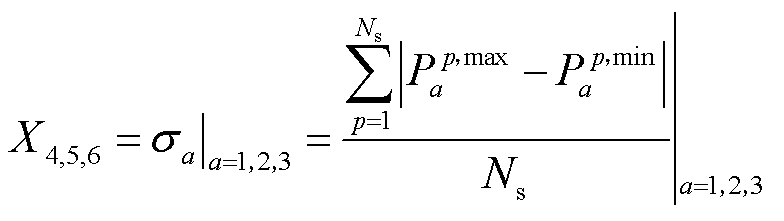 (3)
(3)
式中,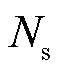 为每个时段内的峰谷波动数;
为每个时段内的峰谷波动数;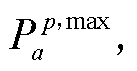
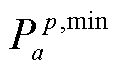 分别为第a个时段内第p个峰谷波动的峰值与谷值。
分别为第a个时段内第p个峰谷波动的峰值与谷值。
4)上午、中午、下午波动频率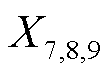 ,衡量提取出第a个时段内中频分量的平均峰谷波动数Aa。对应工况指标的波动率。
,衡量提取出第a个时段内中频分量的平均峰谷波动数Aa。对应工况指标的波动率。
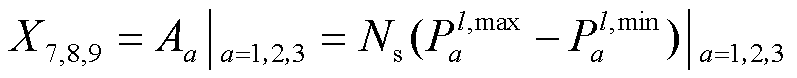 (4)
(4)
以上四类特征指标,构成9维的特征序列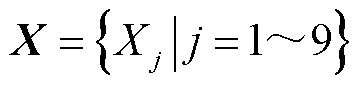 ,且该9个特征指标与电解制氢工况联系紧密,在一定程度上能够反映电解制氢的变载、恒载过程。
,且该9个特征指标与电解制氢工况联系紧密,在一定程度上能够反映电解制氢的变载、恒载过程。
上述定义的各类特征指标在聚类中的分离度不同,若直接进行聚类,则聚类效果不能达到最优。本文参考文献[29],采取带权重的模糊C均值(Fuzzy C-Means, FCM)聚类方法处理,通过原数据自适应地分配各个指标的权重,使在聚类过程中计算得到的聚类中心会更倾向于分开权值高的指标,使得分离效果更为出色。
对特征权重进行配置,本文采用客观赋权法[30],先把光伏出力特征序列归一化,再用指标变异性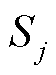 和指标冲突性
和指标冲突性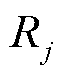 评价该特征序列,根据评价结果分配相应权重,得到权重矩阵
评价该特征序列,根据评价结果分配相应权重,得到权重矩阵 。
。
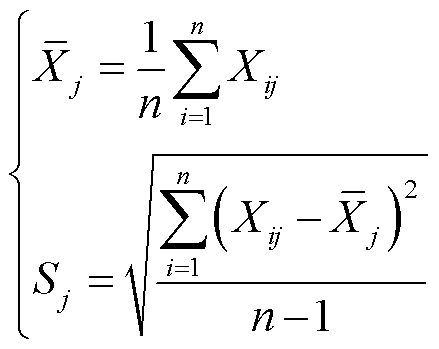 (5)
(5)
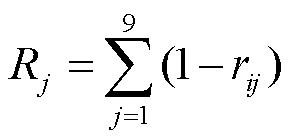 (6)
(6)
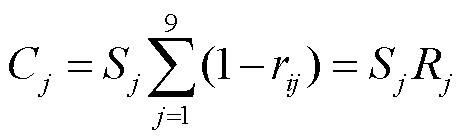 (7)
(7)
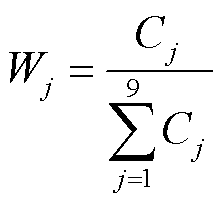 (8)
(8)
式中,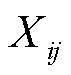 为光伏特征指标,下标i为第i个样本的特征序列,下标j表示该样本特征序列的第j个特征指标;
为光伏特征指标,下标i为第i个样本的特征序列,下标j表示该样本特征序列的第j个特征指标;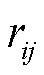 为光伏特征指标
为光伏特征指标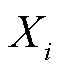 与
与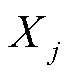 之间的相关系数;n为样本数量;
之间的相关系数;n为样本数量;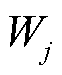 为权重矩阵中第j个分量;
为权重矩阵中第j个分量;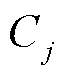 为第j个特征指标的评价值。
为第j个特征指标的评价值。
再对光伏特征指标应用加权FCM聚类法迭代公式,即
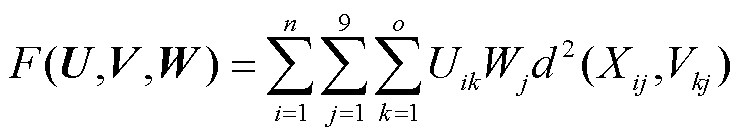 (9)
(9)
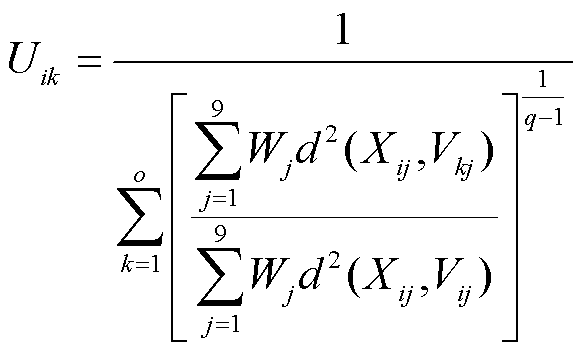 (10)
(10)
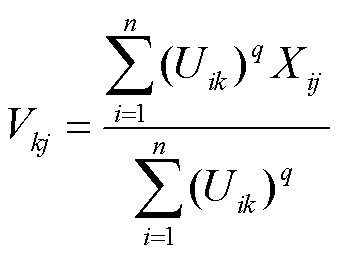 (11)
(11)
式中,下标k为聚类簇类别;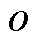 为聚类数;
为聚类数;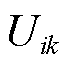 为第i个样本中对第k类聚类中心的隶属度函数;
为第i个样本中对第k类聚类中心的隶属度函数;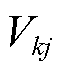 为第k类聚类中心中对应的光伏特征序列中第j类特征指标;
为第k类聚类中心中对应的光伏特征序列中第j类特征指标;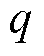 为常数2;d(
为常数2;d(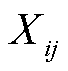 ,
,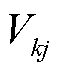 )为所选光伏特征指标与聚类中心之间的欧式距离。
)为所选光伏特征指标与聚类中心之间的欧式距离。
一般FCM聚类需要人为定义聚类数,为避免选择聚类数的主观性,采用改进的聚类有效性函数来确定最佳聚类数。聚类的有效性评价主要是两个方面:一个是评价每一类内样本之间的聚拢程度;另一个是评价类与类之间的分离程度。本文参考文献[31],使用一种涵盖上述两类评价的聚类有效性函数,该函数能够在聚类海量光伏特征序列的过程中抑制部分离散点与坏数据对聚类结果的影响,最终确定合适的聚类数目。
首先确定PEM电解堆的电压模型[26]。一种被广泛使用的电压模型是由开路电压Voc、活化过电压Vact、欧姆过电压和扩散过电压四部分构成,因扩散过电压对整个电压模型的贡献很小,通常对其忽略不计。
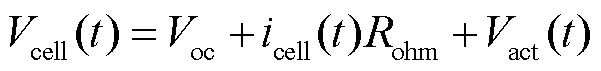 (12)
(12)
式中,Vcell为电解堆电压;icell为电解堆电流;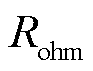 为欧姆过电压对应的欧姆电阻。
为欧姆过电压对应的欧姆电阻。
开路电压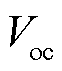 是用于水分解的热力学最小能量的体现,由能斯特方程表示。
是用于水分解的热力学最小能量的体现,由能斯特方程表示。
 (13)
(13)
式中,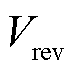 为可逆过电压;R为理想气体常数;T为反应温度;F为法拉第常数;
为可逆过电压;R为理想气体常数;T为反应温度;F为法拉第常数;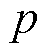 为各分量的蒸汽分压;
为各分量的蒸汽分压;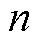 为反应过程的电子转移数。对氢、氧、水的蒸汽分压的计算则是基于阴极阳极的流场压力、饱和蒸气压与电极内气体演化引起的电流相关压力,考虑膜厚度与氢、氧渗透性的变化,蒸汽分压也会随着膜降解而变化。
为反应过程的电子转移数。对氢、氧、水的蒸汽分压的计算则是基于阴极阳极的流场压力、饱和蒸气压与电极内气体演化引起的电流相关压力,考虑膜厚度与氢、氧渗透性的变化,蒸汽分压也会随着膜降解而变化。
活化过电压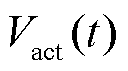 可以由Butler-Volmer方程概括表示,并且主要考虑阳极的贡献。
可以由Butler-Volmer方程概括表示,并且主要考虑阳极的贡献。
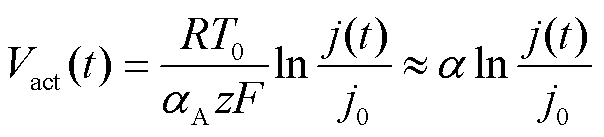 (14)
(14)
式中,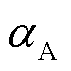 为电荷转移系数;
为电荷转移系数;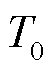 为标准温度,
为标准温度,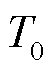 =25℃;z为活化反应的转移电子数;
=25℃;z为活化反应的转移电子数;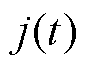 为t时刻的电流密度值;
为t时刻的电流密度值;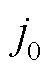 为交换电流密度;
为交换电流密度;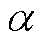 为塔菲尔斜率。
为塔菲尔斜率。
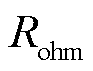 的表达式为
的表达式为
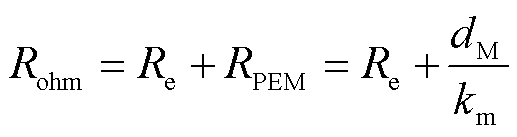 (15)
(15)
式中,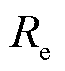 为膜电极、双极板、多孔传输层的等效欧姆电阻;
为膜电极、双极板、多孔传输层的等效欧姆电阻;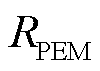 为膜电阻;
为膜电阻;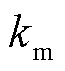 为膜电导率;
为膜电导率;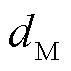 为膜厚度。
为膜厚度。
电解制氢电解堆受波动输入影响的主要衰减现象是膜降解与催化剂降解[27]。本文对上述两个组件的衰减过程进行建模,再动态修改电压模型参数得到性能衰减后的电解堆电压值。
3.2.1 膜降解
质子交换膜在机械应力与化学反应的作用下导致膜降解[32-34]。本文主要研究氢交叉下产生过氧化氢自由基并攻击膜中氟化物的降解过程[32]。
阳极生成的氧气在膜内出现浓度梯度,并因扩散过程影响其在阴极的量,氧交叉现象引起过氧化氢与羟基自由基的生成。
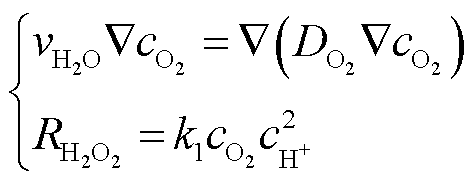 (16)
(16)
式中, 表示膜中电子交换方向的梯度运算;
表示膜中电子交换方向的梯度运算;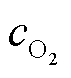 为氧气的物种浓度;
为氧气的物种浓度;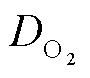 为氧气在膜中的扩散系数;
为氧气在膜中的扩散系数;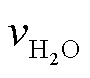 为膜内水流速度,与输入的电流密度有关;
为膜内水流速度,与输入的电流密度有关;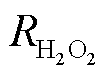 为过氧化氢的生成速率;k1为该反应的一阶动力学常数;
为过氧化氢的生成速率;k1为该反应的一阶动力学常数;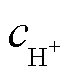 为质子浓度。
为质子浓度。
再考虑活性金属离子下以自由基反应机理进行过氧化氢的分解过程。自由基反应存在多个步骤,不同物种的浓度随时间的变化根据摩尔质量平衡方程得到。
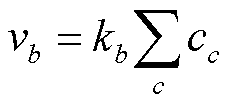 (17)
(17)
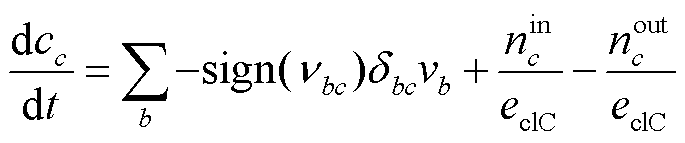 (18)
(18)
式中,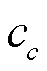 为参与反应的物种c的浓度;
为参与反应的物种c的浓度;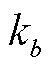 为物种浓度与反应速率之间的转换系数;
为物种浓度与反应速率之间的转换系数;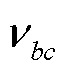 为参与反应的化学计量系数;
为参与反应的化学计量系数;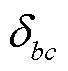 为0-1变量,若物种c参与反应b则其值为1,反之为0;
为0-1变量,若物种c参与反应b则其值为1,反之为0;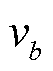 为反应速率;
为反应速率; 、
、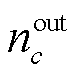 为流入、流出阴极催化剂层的物种c的量;
为流入、流出阴极催化剂层的物种c的量;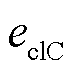 为催化剂层厚度。
为催化剂层厚度。
最后是自由基攻击膜离聚物,引起氟化物降解、膜变薄的现象。模型的膜厚度、膜电导率、参数随膜厚度降低而变化。
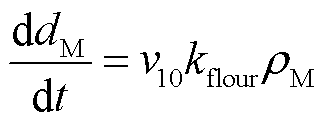 (19)
(19)
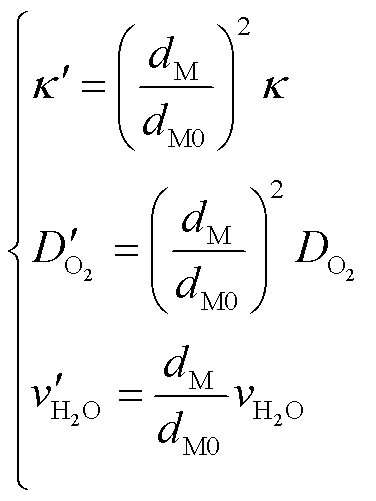 (20)
(20)
式中,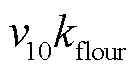 为自由基反应机理中氟化物释放的步骤对应速率;
为自由基反应机理中氟化物释放的步骤对应速率;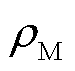 为膜的单位厚度密度;
为膜的单位厚度密度;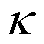 为膜电导率;
为膜电导率;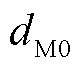 为衰减前膜的初始厚度。
为衰减前膜的初始厚度。
2)催化剂降解。电解堆在高电流密度、电位频繁突变过后的膜电极表面上的Ir颗粒的氧化和溶解是阳极催化剂的主要降解因素[35-37],而催化剂活性越好,反应所需的标准自由能越低,交换电流密度的值也越大[38-39]。
本文采用文献[40]的衰减模型对阳极催化剂颗粒进行建模,该模型基于催化剂颗粒半径分布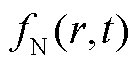 在溶解与沉积的作用下随时间动态改变,进而影响催化剂活性表面积(Electrochemical Active Surface Area, ECSA)的大小,最终影响电解堆活化过电位的大小。
在溶解与沉积的作用下随时间动态改变,进而影响催化剂活性表面积(Electrochemical Active Surface Area, ECSA)的大小,最终影响电解堆活化过电位的大小。
催化剂颗粒半径分布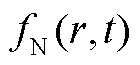 随时间的变化如式(21)所示,等式右边第一项表示奥斯特瓦尔德熟化过程第二项、第三项表示颗粒的凝聚现象。
随时间的变化如式(21)所示,等式右边第一项表示奥斯特瓦尔德熟化过程第二项、第三项表示颗粒的凝聚现象。
第四项表示颗粒失活,其中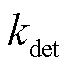 为失活系数。
为失活系数。
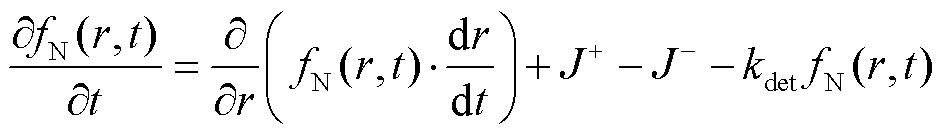 (21)
(21)
式中,r为颗粒半径;J+表示颗粒凝聚;J-表示颗粒脱落。
催化剂颗粒半径随时间的变化量如式(22)所示,颗粒半径的变化主要由催化剂颗粒的溶解与再沉积有关。
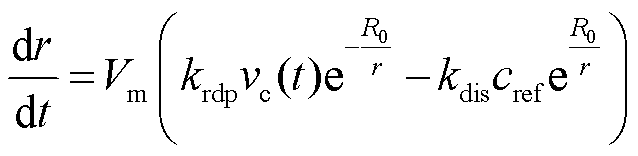 (22)
(22)
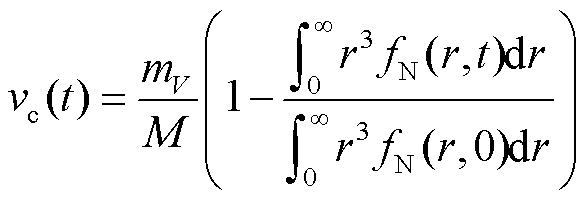 (23)
(23)
 (24)
(24)
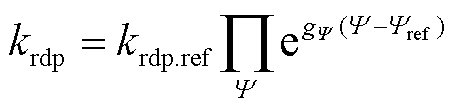 (25)
(25)
式中,下标ref表示相应量的参考值;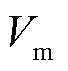 为颗粒体积;
为颗粒体积;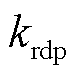 为再沉积参数;
为再沉积参数;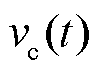 为再沉积速率;
为再沉积速率;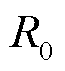 为参考半径;kdis为溶解参数;cref为催化剂浓度;
为参考半径;kdis为溶解参数;cref为催化剂浓度;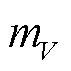 为单位体积催化剂质量;M为催化剂相对分子质量;Θ、Ω、Ψ表示电解操作,其中Θ包含快速电位变化、高操作时长,Ω包含出现高电位、出现低电位;Y包含出现高电位等操作;g为换算系数,反映不同电解操作对催化剂溶解速率的贡献,系数的下标表示电解操作类型。
为单位体积催化剂质量;M为催化剂相对分子质量;Θ、Ω、Ψ表示电解操作,其中Θ包含快速电位变化、高操作时长,Ω包含出现高电位、出现低电位;Y包含出现高电位等操作;g为换算系数,反映不同电解操作对催化剂溶解速率的贡献,系数的下标表示电解操作类型。
催化剂归一化电化学活性表面积 的计算式如式(26)所示,该值体现降解前后电化学活性的变化情况。
的计算式如式(26)所示,该值体现降解前后电化学活性的变化情况。
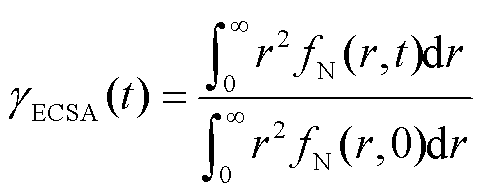 (26)
(26)
催化剂电化学活性的变化对交换电流密度项的修正式为
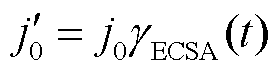 (27)
(27)
为了着重突出测试用典型工况的可用性,本文提出一维衰减模型与零维电压模型相结合的综合模型,既表明了波动输入下电解堆材料组件的衰减过程,又能直观地用模型的电压值衡量性能衰减程度。
本文为了方便后续电解堆衰减性能测试的等效试验方法实现,需要对工况模式的几个参数和指标进行初步的定义。
本文所选光伏电站的容量为20MW,PEM电解堆的总容量为10 MW。为了保证不同规模下工况测试的适用性,后续的研究将以百分值讨论各个分量的大小。参考PEM电解堆的工作特性[41]以及PEM燃料电池的工况曲线制订方案[42],对PEM电解堆的工况指标定义如下:
1)工况出力水平:工况曲线的最大出力值,并定义工况范围,过载工况范围是额定值的100%~150%,正常工况范围是额定值的30%~100%,低载工况范围是额定输入的5%~30%。
2)变载速率:单位时间内工况输入大小的变化值,单位为%/min。
3)恒定工况时间:工况曲线在其最大工况范围内所持续的时间,单位为min。
4)波动率:工况曲线波动部分(矩形波)的波动幅值与波动频率的乘积,单位为%·次。
在3.3节已经提到与电解堆衰减因素相关的工况指标。本节的内容是根据工况指标重构得到简化电解制氢典型工况曲线。
2.1节已经介绍,原始的光伏出力曲线可分解成低频分量与中频分量。2.2节将这两种分量转换为相应的指标。而对电解堆的输入测试通常以矩形波、三角波等简单波形,所以本文根据2.2节提出的特征指标按如下步骤生成简化工况曲线:
1)利用原始曲线低频分量提取出的最大出力指标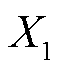 ,在对应工况时段内维持该值出力。上述两个步骤形成简化低频分量。
,在对应工况时段内维持该值出力。上述两个步骤形成简化低频分量。
2)利用原始曲线低频分量提取出的爬坡率指标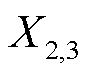 ,在整个工况区间范围内都以该速率爬坡。
,在整个工况区间范围内都以该速率爬坡。
3)利用原始曲线中频分量特征提取出的每个出力时段下波动幅值指标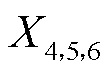 与波动频率指标
与波动频率指标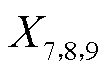 ,构造出相同幅值与频率的矩形波,即简化中频分量。
,构造出相同幅值与频率的矩形波,即简化中频分量。
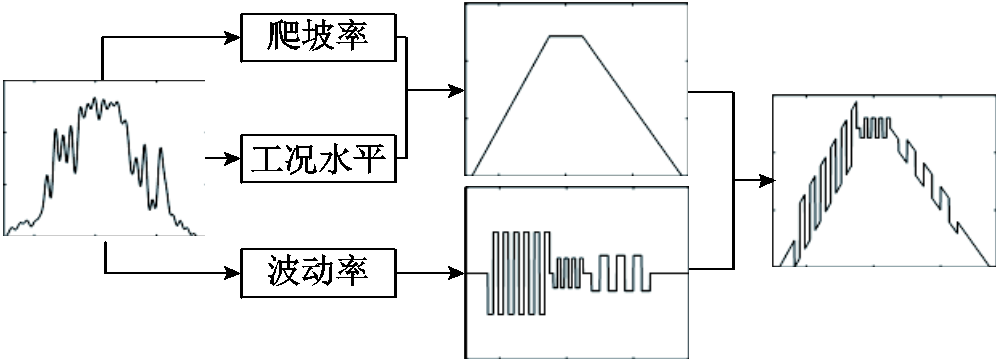
图2 工况曲线重构方法
Fig.2 Working condition curve reconstruction method
4)将简化的低频分量与中频分量信号叠加,即为所需的简化典型光伏输出功率工况曲线。
简化的工况曲线由基础波形的组合构成,功率指令容易由功率电源实现,便于在实验室环境开展电解堆工况输入测试。
光伏场站直接耦合电解制氢场景下,电力电子器件以光伏输出功率作为参考,跟踪功率变化,以调整输入电解堆的电流大小[14]。因此电解堆的电流工况曲线与光伏输出功率曲线具有相同的走势。考虑到电解堆的功率范围5%~150%额定功率,电解堆电流输入工况在非停机状态下应保持5%以上的输入,以避免多次启停带来的额外性能衰减。
本文选取三北地区某偏远光伏电站3年的出力数据(day=1 095)作为基础数据,其中剔除了一些场站维护或者极小概率出现的极端天气对应的数据。
首先对整体光伏出力曲线数据进行频域分析,采取locmaxmin的频带划分方法将曲线频谱分解[28],频带检测边界示意图如图3所示。为确定分解频带数N,在保证N尽量小的情况下,前N-1个频带覆盖的频谱分量能够达到95%以上。用试探法得出EWT方法的最优区间数N=5,即初步分解成五种分量。
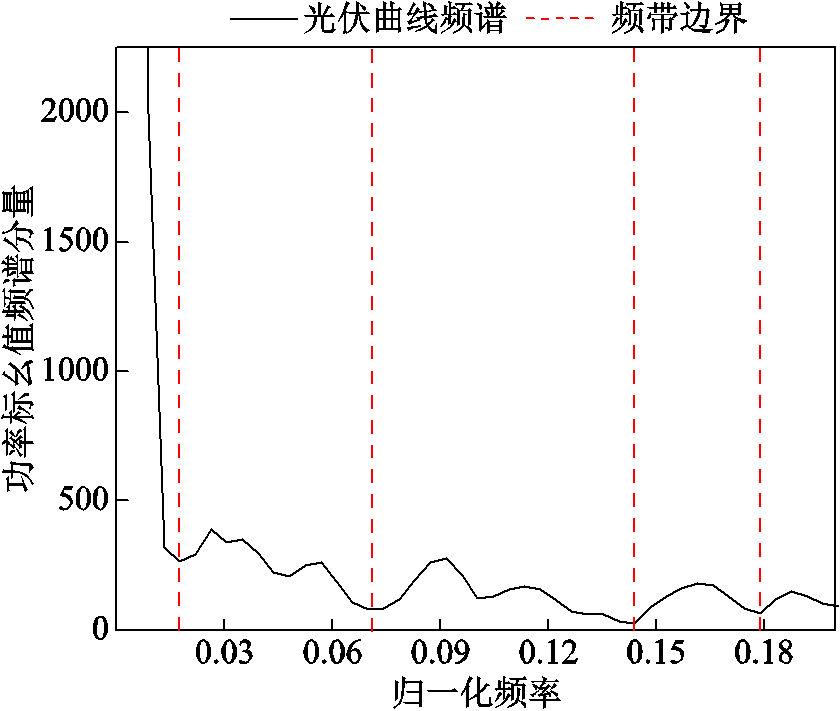
图3 光伏出力曲线频带检测边界示意图
Fig.3 Boundary diagram of photovoltaic output curve band detection
本文根据光伏曲线数据波动特性设定频率分量阈值,具体的频率分量阈值确定在附录第2小节中介绍。根据上述设定的阈值,将滤波器频带分量进一步划分为相对应的低频、中频、高频分量。低频分量反映曲线的整体走势;中频分量反映曲线的波动程度;高频分量反映出力曲线的误差与电力电子设备的纹波,电解堆无需承担该部分,以滤波方式去除。光伏出力曲线经验小波分解分量图(N=5)如图4所示。由图4可知,不同的滤波器将对应的频域分量反变换为时域分量,再根据式(1)~式(4),在时域分量的基础上提取分时特征指标 。
。
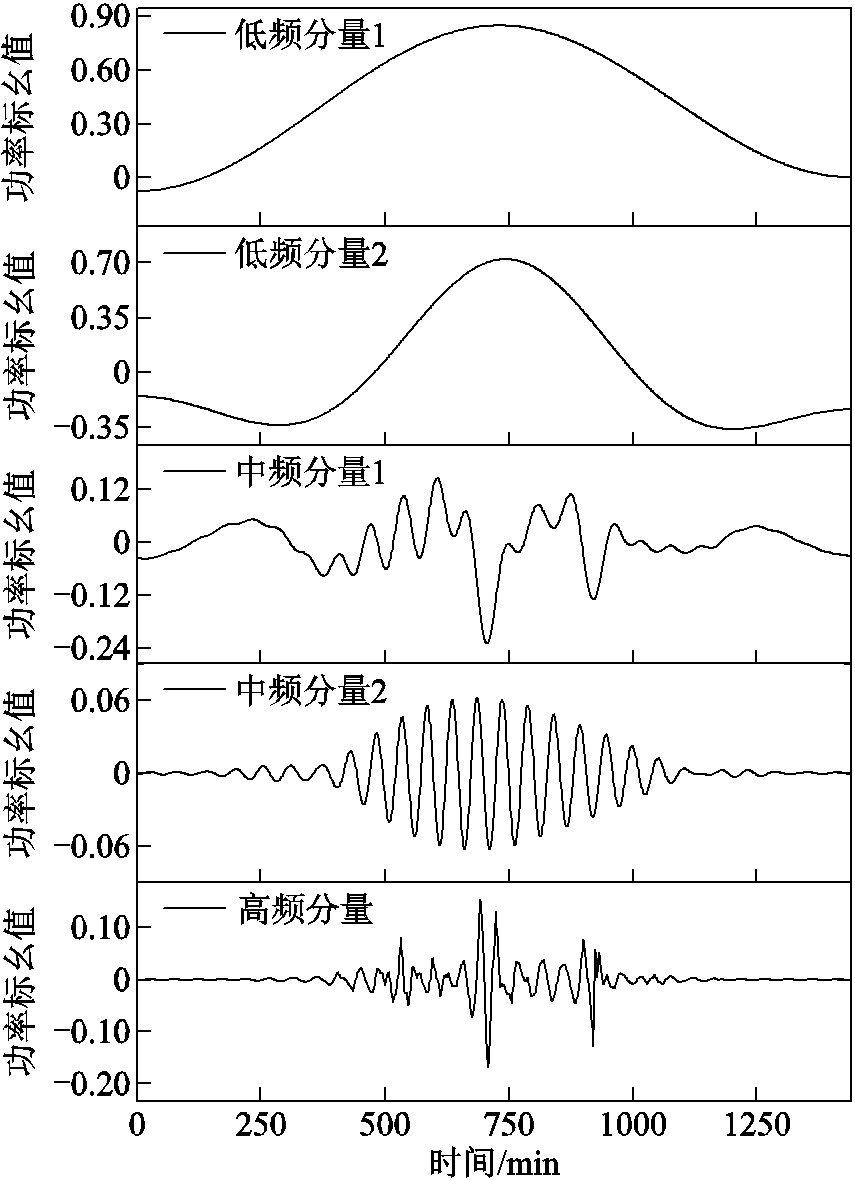
图4 光伏出力曲线经验小波分解分量图(N=5)
Fig.4 Empirical wavelet decomposition componentdiagram of PV output curves (N=5)
对指标聚类前先进行赋权。采用2.3节的权重赋值方法后得到各个特征指标的赋权结果见表1。
表1 对各个波动特征指标的赋权结果
Tab.1 Weighting each fluctuation characteristic index

波动特征指标权值 中午平均值W10.246 5 上午爬坡率W20.055 3 下午爬坡率W30.085 1 上午波动幅值W40.081 9 中午波动幅值W50.099 6 中午波动幅值W60.083 5 上午波动频率W70.106 3 中午波动频率W80.099 2 下午波动频率W90.142 6
赋权后进行聚类数的确定。根据文献[31],聚类有效性指标的衡量方式为类内相似度和类间离散度之差,该值越小说明聚类的效果越好。聚类有效性函数与聚类数的函数关系如图5所示,可以得到最适合的聚类数为4。
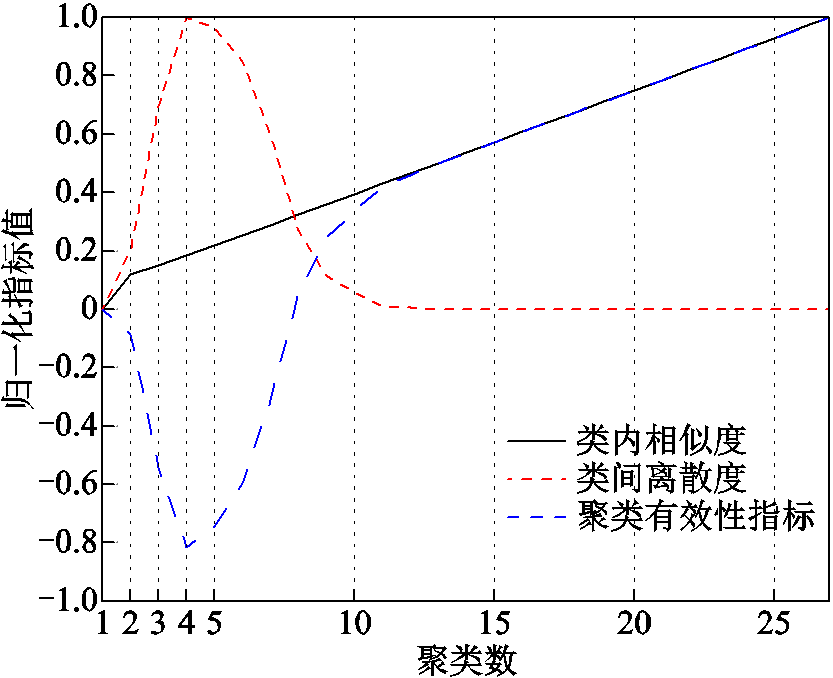
图5 聚类有效性指标与聚类数的函数关系
Fig.5 Function of cluster validity index and cluster number
确定聚类数后根据2.3节提出的带权模糊聚类方法处理特征指标,得到四类典型光伏出力曲线。再根据4.2节的原则生成相应的电解堆输入电流曲线,如图6所示。因本文未考虑停机,所以输入电流曲线的最小值保持在额定值的5%。
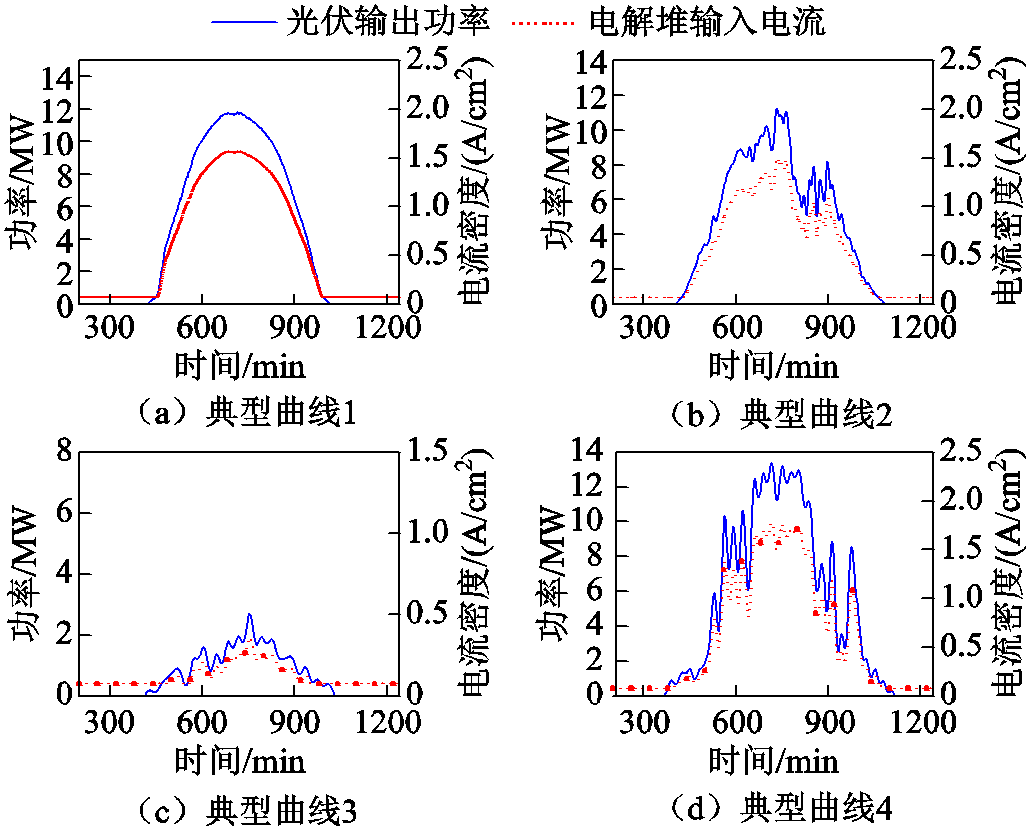
图6 典型光伏功率曲线与典型电解制氢电流曲线
Fig.6 Typical PV power curves and typical electrolytic hydrogen production current curves
分析四类电解堆输入电流曲线,典型工况曲线1是晴天下的电解堆工作曲线,大致以均匀的速率变载到过载工况,再以均匀的速率变载至停机。典型工况曲线2是阴天小波动下的电解堆工作曲线,爬坡过程中叠加了低频率高幅值的分量。典型工况曲线3是雨雪天下的电解堆工作曲线,基本处于低载工况范围。典型工况曲线4是阴天大波动下的电解堆工作曲线,爬坡过程中叠加了高频率低幅值的分量。每一种工况曲线的占比如图7所示,工况指标见附表2~附表5。
5.2.1 电解堆模型仿真测试
本文对电解堆的仿真电压模型构建参考了文献[26]的电解堆半经验电压模型,并结合3.2节内容,添加了电解堆材料性能衰减模型,以动态修改电压模型的参数,最终得到电压模型与衰减模型相结合的综合模型,该模型的搭建在Matlab/Simulink上完成。其中电压模型的参数由表2给出,并设定电解过程配备有水体控温系统,电解环境温度维持在75℃。
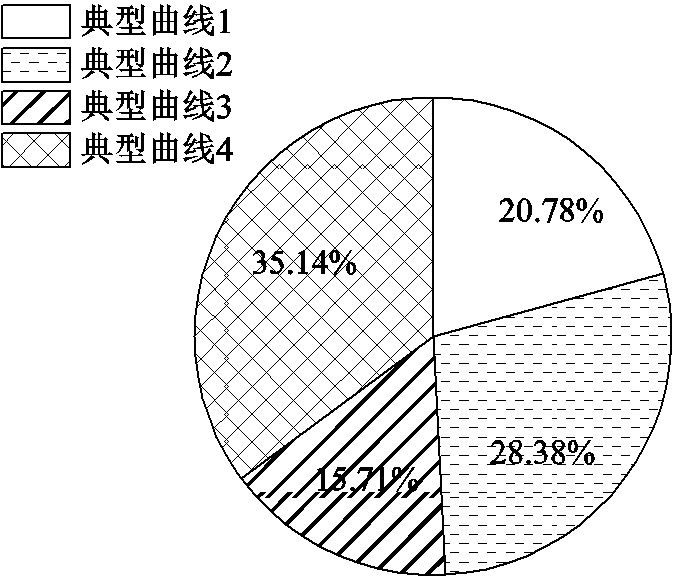
图7 四种典型曲线的占比
Fig.7 Proportion of four typical curves
表2 电解堆仿真模型参数
Tab.2 Simulation model parameters of electrolytic cell

参数数值(材料) 额定电流密度/(A/cm2)2 阴极催化剂含量/(mg/cm2)0.5 阳极催化剂含量/(mg/cm2)3 膜面积/cm217.64 多孔传输层阳极配置结构铱烧结钛 交换电流密度/(A/cm2)2.641×10-6 膜电导率/(S/cm2)0.160 3 膜厚度/mm0.02 组件欧姆电阻/(mΩ/cm2)29 多孔传输层阴极配置结构Toray纸
在衡量性能衰减程度上,通常采用电压退化率(单位μV/h)这一指标[25],该值越小,则电解堆性能衰减程度越低。为了验证生成的典型工况提取不同衰减因素的能力,本文利用实际电解堆测试平台,先在多种波动测试曲线输入下得到电解堆的电压退化率,再利用上述数据对提出的衰减模型进行参数拟合,电解堆性能衰减模型的参数见附表6。确定参数后,持续输入循环长度为300天(7 200 h)的各类工况曲线,再输入额定电流,测量模型中膜部分的电压退化率VPEM、催化剂部分的电压退化率Vact与整个电解堆电压的电压退化率Vel,用于量化电解堆各部分的性能衰减程度。
5.2.2 聚类方法对比分析
为验证本文提出聚类方法的有效性,利用文献[22]提出的密度峰值聚类法(Density Peaks Clustering, DPC)法、文献[23]提出的自组织映射网络(SOM)聚类法以及文献[24]提出的符号特征序列直方图(Symbolic Sequence Histogram, SSH)聚类法,与本文提出的EWT分解配合特征指标降维的模糊聚类方法进行对比,得到的聚类中心如图8所示。
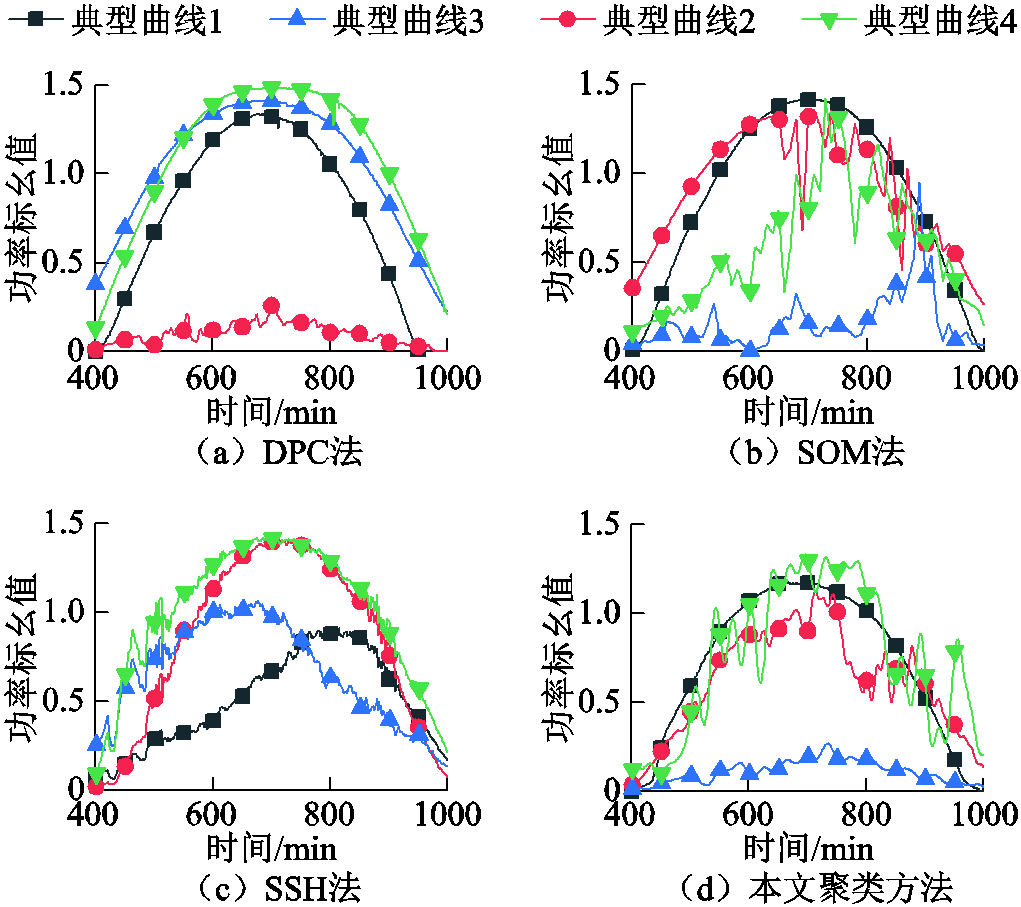
图8 不同聚类方法得到的聚类中心
Fig.8 Clustering centers obtained by different clustering methods
为了验证本文方法的有效性,将各类方法生成四条聚类中心曲线,并输入电解堆衰减模型中,得到质子交换膜与阳极催化剂层的性能衰减情况如图9和图10所示。在工况使用层面,不同工况下电解堆响应结果差异越大,则说明选取的工况区分效果越好,越具有典型性。分析图9和图10的衰减结果可以得知,DPC法得到的典型工况曲线测试结果具有一定的质子交换膜衰减量区分效果,但是在催化剂衰减量的区分效果较差。SOM法因计算聚类中心的能力较差,所以两类材料的衰减量区分效果都较差。SSH法虽然具有较好的催化剂衰减区分效果,但是相比较本文方法,在质子交换膜的衰减量区分效果上稍有不足。
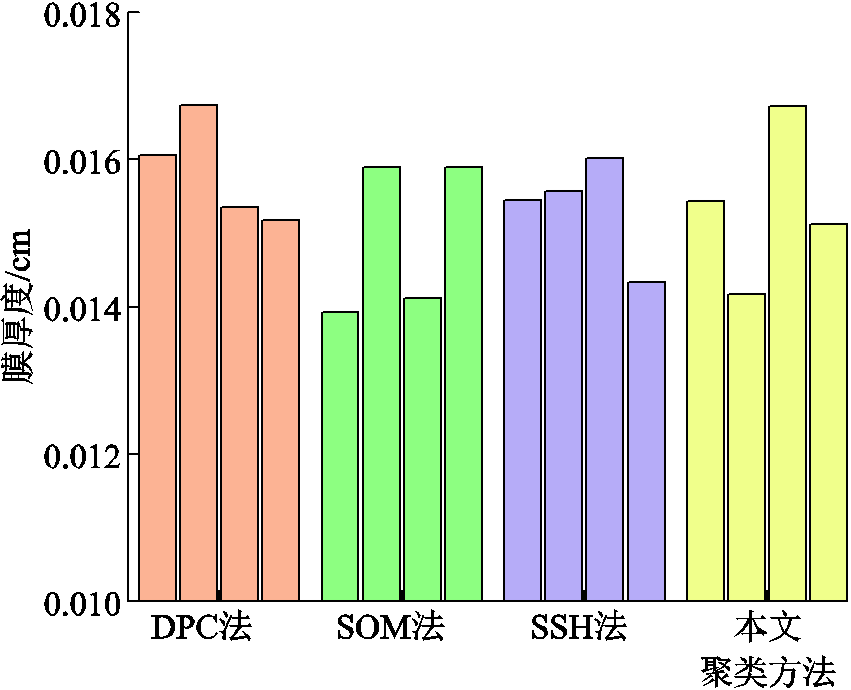
图9 不同聚类结果的质子交换膜厚度
Fig.9 Comparison of thickness of PEM by different clustering methods
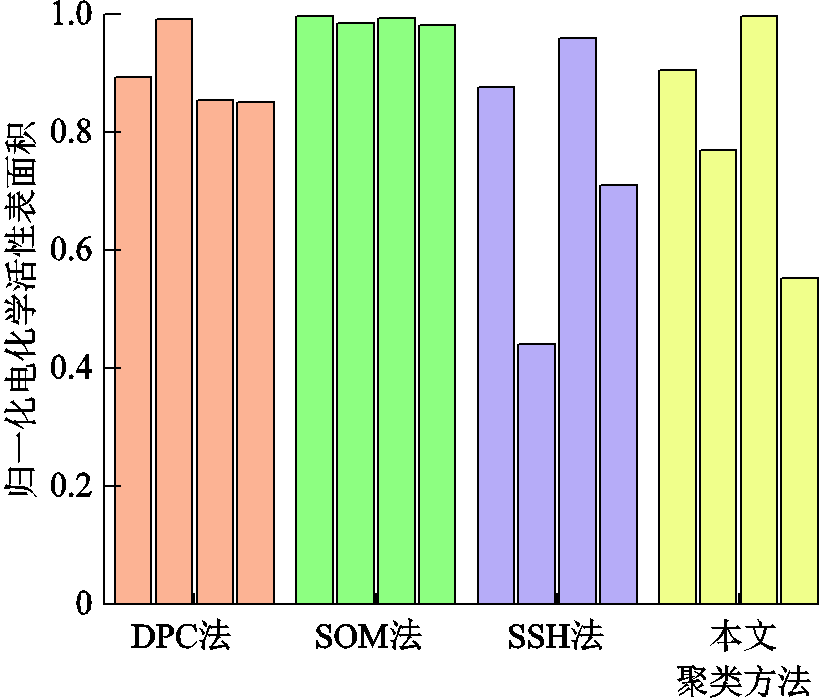
图10 不同聚类结果的催化剂归一化电化学活性表面积
Fig.10 Normalized ECSA of catalysts with different clustering results
为了进一步量化衡量聚类中心的分离效果,通常使用分隔度(Seperation, SP)这一指标,分隔度越大,说明聚类簇之间的间隔越远,聚类中心对应的曲线越典型。
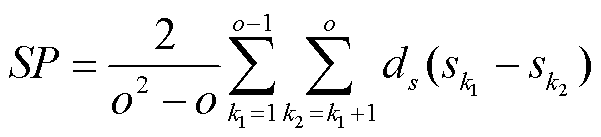 (28)
(28)
式中,s为聚类中心,本文计算SP时用衰减后的材料剩余量表示聚类中心数据;k1、k2为选取的两类聚类中心序号;o为聚类中心的数目,ds(·)为距离度量函数,本文选取相对距离计算。
计算各个方法的SP见表3。可以发现,DPC法、SOM法的聚类结果主要对光伏出力值的大小聚类,对催化剂活性区分能力较小;SSH法虽然考虑了光伏波动,但是在质子交换膜厚度变化的区分能力最小,得出的聚类结果不是最优的,并且该方法在样本较多的情况下聚类时间较长,效率难以保证。
表3 不同聚类方法的结果计算的SP值
Tab.3 SP value calculated from the results of different clustering methods
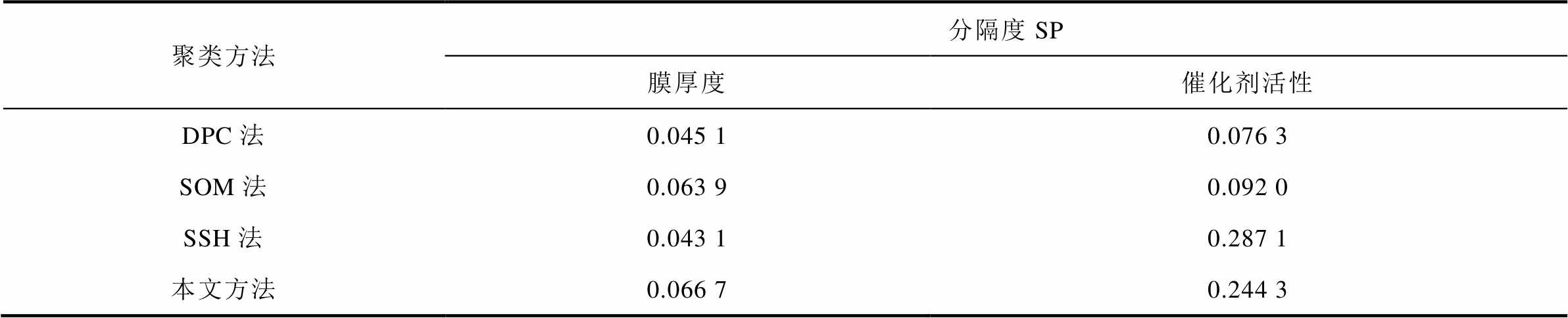
聚类方法分隔度SP 膜厚度催化剂活性 DPC法0.045 10.076 3 SOM法0.063 90.092 0 SSH法0.043 10.287 1 本文方法0.066 70.244 3
综合来看,本文提出的方法具有最优的分隔度,得到聚类中心的效果最好。
5.2.3 简化工况有效性验证
利用提取得的工况指标重构的简化典型光伏功率工况曲线与原出力曲线在图11展示。为了验证简化后的典型光伏出力曲线的有效性,将简化前后的典型工况曲线输入电解堆仿真模型进行验证,得到简化工况误差见表4。四类典型工况参数见附表2~附表5。分析仿真结果,可以证明本文提出的简化工况与原始曲线对电解堆的性能衰减影响效果非常相近,计算得到的电压退化率的相对误差均小于10%。
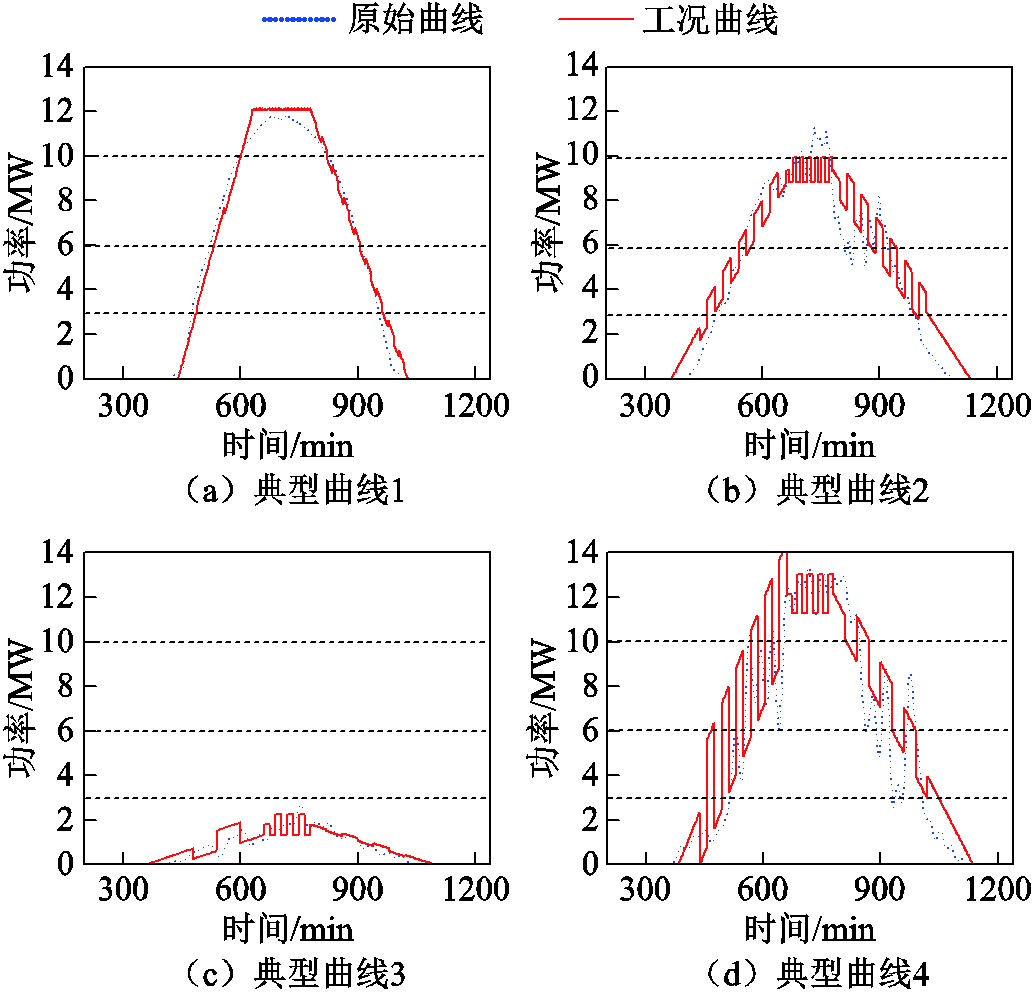
图11 简化后的四类光伏出力曲线
Fig.11 Simplified four PV output curves
表4 简化工况电压退化率及误差
Tab.4 Voltage degradation rate and error of simplification method

工况电压退化率/(μV/h)相对误差(%) 简化前简化后 典型曲线113.710 214.266 24.055 4 典型曲线218.930 720.152 66.454 6 典型曲线38.709 49.024 43.616 8 典型曲线416.493 516.136 72.163 3
5.2.4 典型工况的性能衰减特征
本节将四类典型工况曲线输入仿真模型中,对比分析各个材料组件的性能衰减特征。
四类典型的运行工况下,第一类是晴天场景下的低波动、高出力工况。该工况下的膜降解速率中等,催化剂降解速率低。该工况对应的性能衰减特征是非波动因素下高电流密度生成的氧化欧姆电阻。
第二类是阴天小波动场景下的中等波动、中等出力的工况。该工况下膜降解速率高,催化剂降解速率中等。该工况下对应的性能衰减特征是膜组件的大幅降解。
第三类是雨雪天场景下的低波动、低出力工况。该工况下具有最小的膜降解速率与催化剂降解速率。该工况对应的性能衰减特征则是低出力下的电解堆在5%额定功率上下浮动而频繁启停造成的额外影响。
第四类是阴天大波动场景下的高波动、高出力工况。该工况下膜降解速率中等,催化剂降解速率高。该工况对应的性能衰减特征是催化剂组件的大幅降解。
表5展示了四类典型工况循环输入后在额定电流密度测试下的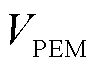 、
、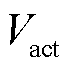 、
、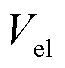 的电压退化率。通过表5可以进一步验证本文提出的光伏制氢典型工况生成方法能够体现出每一类工况下不同材料组件的性能衰减特征,生成的结果具有典型性。
的电压退化率。通过表5可以进一步验证本文提出的光伏制氢典型工况生成方法能够体现出每一类工况下不同材料组件的性能衰减特征,生成的结果具有典型性。
表5 四类典型工况循环输入下的电压退化率
Tab.5 Voltage degradation rate under four typical working conditions under cyclic input

工况电压退化率/(μV/h) 典型曲线113.931 90.311 213.710 2 典型曲线219.227 80.411 818.930 7 典型曲线39.064 20.012 58.709 4 典型曲线415.173 31.896 016.493 5
图12展示了典型工况循环输入下电解堆的极化曲线。极化曲线越上翘,说明电解堆性能衰减现象越严重,电压效率越低。
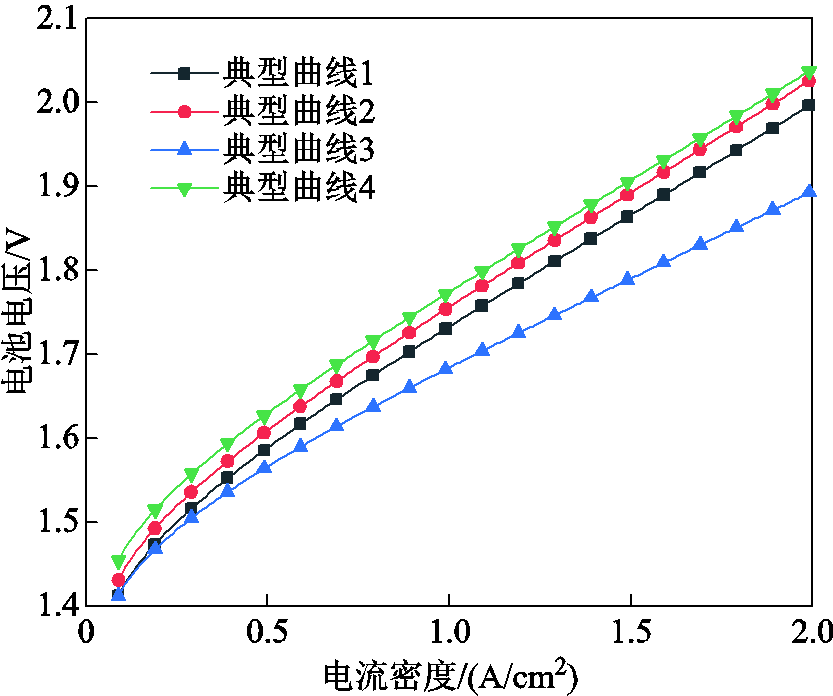
图12 不同类型工况曲线循环输入下电解堆极化曲线
Fig.12 Polarization curves of electrolytic stacks under cyclic input of different working condition curves
根据5.1节得到的各类典型光伏出力曲线的比例,得到实验室测试用的工况循环曲线如图13所示。该曲线体现了不同典型光伏出力曲线的发生概率,可以模拟PEM电解堆在光伏输入下的实际应用场景。
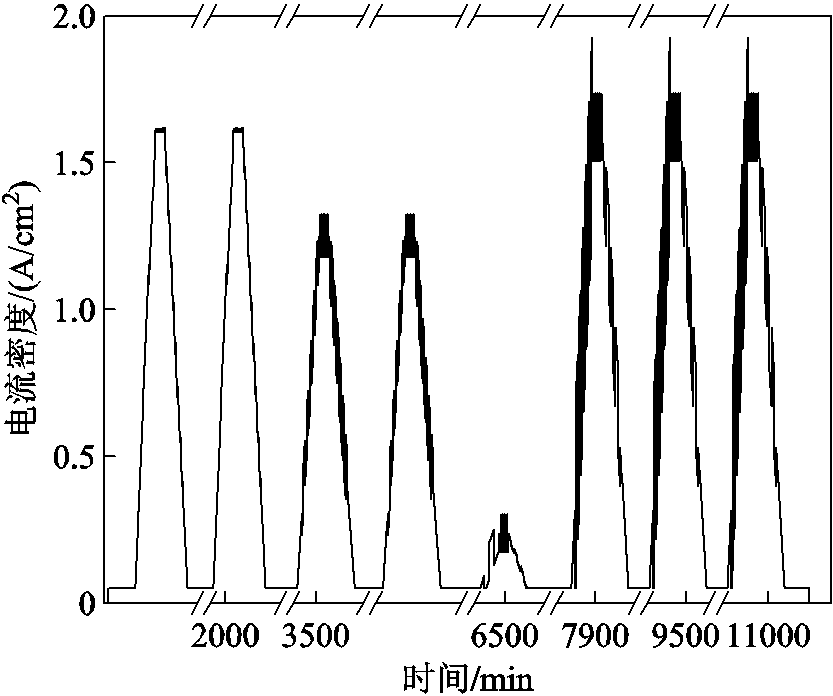
图13 光伏电解制氢工况
Fig.13 Working condition of PV hydrogen production
根据光伏电站-电解制氢设备的安装地点,可以用本文方法提取出力曲线的特征并聚类缩减出相应场景,再依比例拼接成实验室测试工况,以研究当地光伏资源制氢对电解堆的性能影响。也可以针对电解堆的某一组件的性能衰减测试,选取具有该组件最大电压退化率的的某一类典型工况进行循环测试。
本文的工作重心在于提出光伏离网制氢工况曲线的刻画方法,仿真实验仅涉及对典型工况有效性的验证。后续工作需要将工况曲线输入实物电解堆中循环测试,以验证其对电解堆的实际影响。
本文针对偏远地区光伏制氢场景,对光伏出力曲线进行时频域分析,结合电解堆的性能衰减,分解并提取不同时段下体现出力大小与出力波动的指标,生成特点鲜明的工况曲线。经过算例计算,得到如下结论:
1)在选取的数据集下,根据提取的指标进行聚类可以将众多出力场景削减成四类,每一类工况曲线根据其不同出力大小与出力波动对应着不同天气情况:第一类曲线对应晴天;第二类曲线对应阴天小波动;第三类曲线对应雨雪天;第四类曲线对应阴天大波动。因此本文提出的聚类方法能够有效地反映不同天气类型下的光伏出力特征。
2)仿真测试了每一类典型工况下电解堆的衰减特性。对于膜厚度衰减,晴天出力以及高、中等出力水平下的阴天波动出力工况具有较大的影响;对于催化剂降解,阴天的波动工况降解程度较大,而晴天出力的降解程度较小;特别地,雨雪天低出力模式对电解堆元件性能衰减影响最小。上述结果体现了本文提取的典型工况在电解堆性能测试实验中的有效性。
3)本文得到的电解堆典型工况谱为后续光伏电解水制氢场景下电解堆性能衰减提供了基础测试数据,对电解堆性能衰减规律的探究具有重要意义。
附 录
1. 经验小波变换处理光伏数据步骤
首先,对各个变量、参数进行定义,见附表1。
附表1 变量与参数的定义
App.Tab.1 Definition of variables and parameters

变量定义 第q个频带区间 第q个区间的经验小波函数 第q个区间的经验尺度函数 小波多项式 第q个区间频带缓冲宽度 细节系数 逼近系数 P原光伏出力曲线 曲线的第u个单分量 第q个区间边界值
其次,将光伏出力曲线 的频域频带划分为
的频域频带划分为
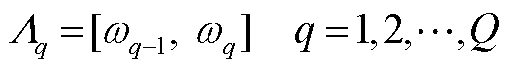 (A1)
(A1)
在归一化后的傅里叶频率轴的支撑区间为
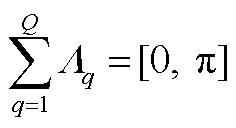 (A2)
(A2)
划分频带的方法有很多,较常用的方法是locmaxmin法,即根据频谱曲线之间的局部极小值点作为分界。设定频带划分数N后,需要对每个频带设计相应的滤波器,以提取光伏曲线不同波动频率的差异。
再次,滤波器由经验小波函数与经验尺度函数组成,经验小波函数与经验尺度函数分别为
 (A3)
(A3)
 (A4)
(A4)
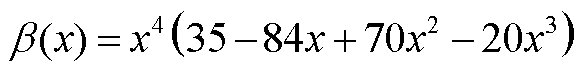 (A5)
(A5)
最后,细节系数和逼近系数分别用经验小波函数和经验尺度函数与原出力曲线进行内积计算得到,可以根据滤波需求选择相应的曲线分量组合重构出新的光伏出力曲线。
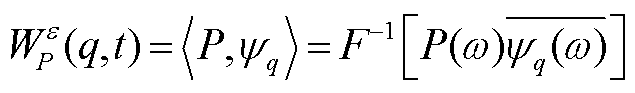 (A6)
(A6)
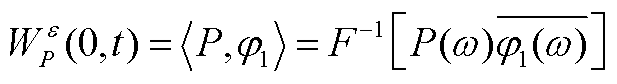 (A7)
(A7)
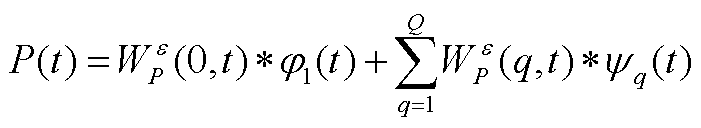 (A8)
(A8)
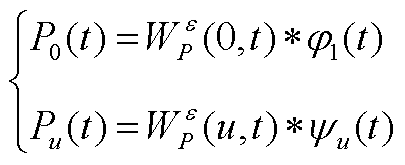 (A9)
(A9)
2. 频率分量阈值的设定
频率分量的阈值是根据光伏出力曲线的波动特性设定的。光伏曲线的整体趋势是随着太阳辐照度大小而变化的,辐照度随时间的变化关系可以近似看作[0, π]内的正弦曲线,所以低频分量的设置是以分量中正向单峰的长度作为标准的。
本文的频带划分法是将光伏出力曲线频谱横坐标归一化到[0,2π]并取[0, π]部分的单边谱,原数据分辨率为 1 min,所以横坐标为[0, 144 0],且单个数据点在归一化后的单位频率为π/1440=0.004 4 min-1。本文的光伏出力曲线数据集中,数据处理方法是将一天600个数据点分为上午、中午、下午三个时段,平均每个时段200个数据点。而光伏的低频分量通常为正弦波单峰的形式,所以低频分量的划分在每个时段内不能出现双峰以上的形式,即正弦曲线的数据点长度至少需要200/2=100 min。低频分量阈值的上限可按上述讨论计算得到(1440/100´ 0.0044=0.064 min-1)。
高频分量的阈值设置则是根据电解堆消纳光伏波动的能力决定,该值可以自行设定。若阈值设定过高,则电解堆需要承担的功率波动频率值越高,对电解槽性能衰减的影响越大;若阈值设定过低,则PEM电解堆的承担波动的能力无法体现。考虑PEM电解堆中单个槽的启停时间限制(设定为10min),而出现单峰的情况会引起电解堆单槽的一次启动与停止过程,需要20 min的启停时间。所以高频分量的正弦波曲线的数据点长度至多为20´2=40 min,高频分量阈值的下限可按上述讨论计算为[1440/(20´2)] ´0.0044=0.158 min-1)。
在规定的范围内,本文取低频分量阈值为0.05 min-1,高频分量阈值为0.2 min-1。
3.各类典型工况相应参数
各类典型工况下参数分别见附表2~附表5。
附表2 典型曲线1(晴天)
App.Tab.2 Typical curve 1(sunny)

参数数值 上爬坡/(%/min)0.454 下爬坡/(%/min)-0.397 工况水平(%)120.09(过载工况) 恒定工况时间/(min)208 上午波动率/(%·次)0.028×2 中午波动率/(%·次)0.006×36 下午波动率/(%·次)0.017×16
附表3 典型曲线2(阴天小波动)
App.Tab.3 Typical curve 2(cloudy with small fluctuation)

参数数值 上爬坡/(%/min)0.319 下爬坡/(%/min)-0.266 工况水平(%)93.79(额定工况) 恒定工况时间/min547 上午波动率/(%·次)0.059×11 中午波动率/(%·次)0.054×12 下午波动率/(%·次)0.085×12
附表4 典型曲线3(雨雪天)
App.Tab.4 Typical curve 3(rainy)

参数数值 上爬坡/(%/min)0.059 下爬坡/(%/min)-0.057 工况水平(%)17.93(低载工况) 恒定工况时间/min513 上午波动率/(%·次)0.046×3 中午波动率/(%·次)0.048×7 下午波动率/(%·次)0.006×5
附表5 典型曲线4(阴天大波动)
App.Tab.5 Typical curve 4(cloudy with great fluctuation)

参数数值 上爬坡/(%/min)0.437 下爬坡/(%/min)-0.340 工况水平(%)121.53(过载工况) 恒定工况时间/min238 上午波动率/(%·次)0.238×12 中午波动率/(%·次)0.086×8 下午波动率/(%·次)0.103×7
4. 电解堆衰减模型拟合参数
电解堆衰减模型拟合参数见附表6。衰减模型的参数需要拟合的部分是提出线性化处理后经验模型的比例系数项。拟合后线性经验模型的性能衰减程度与实际电解堆性能衰减程度相近。
附表6 电解堆衰减模型拟合参数
App.Tab.6 Fitting parameters of electrolytic stacks degradation model

参数数值 膜中初始质子浓度/(mol/cm3)2.06 过氧化氢分解反应动力学常数2.56×10-5 质子交换膜降解速率系数3.60 催化剂颗粒溶解速率系数4.00×10-11 催化剂颗粒再沉积速率系数2.00×10-10 钝化电阻增长速率系数8.73×10-5
参考文献
[1] Hamada H, Kusayanagi Y, Tatematsu M, et al. Challenges for a reduced inertia power system due to the large-scale integration of renewable energy[J]. Global Energy Interconnection, 2022, 5(3): 266-273.
[2] 国家能源局. 2021年光伏发电建设运行情况[EB/OL]. (2022-03-09)[2023-09-27]. www.nea.gov.cn.
[3] Badwal S P S, Giddey S S, Munnings C, et al. Emerging electrochemical energy conversion and storage technologies[J]. Frontiers in Chemistry, 2014, 2: 79.
[4] 刘玮, 万燕鸣, 熊亚林, 等. 碳中和目标下电解水制氢关键技术及价格平准化分析[J]. 电工技术学报, 2022, 37(11): 2888-2896.
Liu Wei, Wan Yanming, Xiong Yalin, et al. Key technology of water electrolysis and levelized cost of hydrogen analysis under carbon neutral vision[J]. Transactions of China Electrotechnical Society, 2022, 37(11): 2888-2896.
[5] 黄嘉豪, 田志鹏, 雷励斌, 等. 氢储运行业现状及发展趋势[J]. 新能源进展, 2023, 11(2): 162-173.
Huang Jiahao, Tian Zhipeng, Lei Libin, et al. Advances and development trends of hydrogen storage and refueling industry[J]. Advances in New and Renewable Energy, 2023, 11(2): 162-173.
[6] 郜捷, 宋洁, 王剑晓, 等. 支撑中国能源安全的电氢耦合系统形态与关键技术[J]. 电力系统自动化, 2023, 47(19): 1-15.
Gao Jie, Song Jie, Wang Jianxiao, et al. Form and key technologies of integrated electricity-hydrogen system supporting energy security in China[J]. Automation of Electric Power Systems, 2023, 47(19): 1-15.
[7] 刘语忱, 闫群民, 郭阳, 等. 基于完备局部均值分解和相关分析的光伏发电侧电-氢混合储能优化配置[J]. 电气技术, 2022, 23(11): 21-29.
Liu Yuchen, Yan Qunmin, Guo Yang, et al. Optimal configuration of electricity-hydrogen hybrid energy storage on photovoltaic generation side based on ensemble local mean decomposition and correlation analysis[J]. Electrical Engineering, 2022, 23(11): 21-29.
[8] 李建林, 李光辉, 梁丹曦, 等. “双碳目标”下可再生能源制氢技术综述及前景展望[J]. 分布式能源, 2021, 6(5): 1-9.
Li Jianlin, Li Guanghui, Liang Danxi, et al. Review and prospect of hydrogen production technology from renewable energy under targets of carbon peak and carbon neutrality[J]. Distributed Energy, 2021, 6(5): 1-9.
[9] 郭秀盈, 李先明, 许壮, 等. 可再生能源电解制氢成本分析[J]. 储能科学与技术, 2020, 9(3): 688-695.
Guo Xiuying, Li Xianming, Xu Zhuang, et al. Cost analysis of hydrogen production by electrolysis of renewable energy[J]. Energy Storage Science and Technology, 2020, 9(3): 688-695.
[10] 袁铁江, 计力, 田雪沁,等. 考虑燃料电池汽车加氢负荷的电-氢系统协同优化运行[J]. 电力系统自动化, 2023, 47(5): 16-25.
Yuan Tiejiang, Ji Li, Tian Xueqin, et al. Synergistic optimal operation of electricity-hydrogen systems considering hydrogen refueling loads for fuel cell vehicles[J]. Automation of Electric Power Systems, 2023, 47(5): 16-25.
[11] 杨紫娟, 田雪沁, 吴伟丽, 等. 考虑电解槽组合运行的风电-氢能-HCNG耦合网络容量优化配置[J]. 电力系统自动化, 2023, 47(12): 76-85.
Yang Zijuan, Tian Xueqin, Wu Weili, et al. Optimal capacity configuration of wind-hydrogen-HCNG coupled network considering combined electrolyzer operation[J]. Automation of Electric Power Systems, 2023, 47(12): 76-85.
[12] Gandía L M, Oroz R, Ursúa A, et al. Renewable hydrogen production: performance of an alkaline water electrolyzer working under emulated wind conditions[J]. Energy & Fuels, 2007, 21(3): 1699-1706.
[13] Bhogilla S S, Ito H, Kato A, et al. Experimental study on a laboratory scale Totalized Hydrogen Energy Utilization System for solar photovoltaic application[J]. Applied Energy, 2016, 177: 309-322.
[14] Clarke R E, Giddey S, Ciacchi F T, et al. Direct coupling of an electrolyser to a solar PV system for generating hydrogen[J]. International Journal of Hydrogen Energy, 2009, 34(6): 2531-2542.
[15] Kim H, Park M, Lee K S. One-dimensional dynamic modeling of a high-pressure water electrolysis system for hydrogen production[J]. International Journal of Hydrogen Energy, 2013, 38(6): 2596-2609.
[16] 李军舟, 赵晋斌, 陈逸文, 等. 考虑动态功率区间和制氢效率的电转氢(P2H)设备容量配置优化[J]. 电工技术学报, 2023, 38(18): 4864-4874, 4920.
Li Junzhou, Zhao Jinbin, Chen Yiwen, et al. Optimal capacity configuration of P2H equipment considering dynamic power range and hydrogen production efficiency[J]. Transactions of China Electrotechnical Society, 2023, 38(18): 4864-4874, 4920.
[17] 孔令国, 陈钥含, 万燕鸣, 等. 计及调峰辅助服务的风电场/群经济制氢容量计算[J]. 电工技术学报, 2023, 38(16): 4406-4420.
Kong Lingguo, Chen Yuehan, Wan Yanming, et al. Calculation of economics of power-to-gas capacity for wind farms/clusters with peak regulation auxiliary service response[J]. Transactions of China Electro- technical Society, 2023, 38(16): 4406-4420.
[18] 赵礼辉, 王震, 冯金芝, 等. 基于用户大数据的电动汽车驱动系统可靠性试验循环工况构建方法[J]. 机械工程学报, 2021, 57(14): 129-140.
Zhao Lihui, Wang Zhen, Feng Jinzhi, et al. Construction method for reliability test driving cycle of electric vehicle drive system based on users' big data[J]. Journal of Mechanical Engineering, 2021, 57(14): 129-140.
[19] 杜旭浩, 李秉宇, 苗俊杰, 等. 分布式储能电池运行工况及性能检测分析[J]. 中国电力, 2021, 54(9): 119-124.
Du Xuhao, Li Bingyu, Miao Junjie, et al. Operation condition and performance test analysis of distributed energy storage battery[J]. Electric Power, 2021, 54(9): 119-124.
[20] 赵安新, 张智晟. 考虑电-气综合需求响应的综合能源系统低碳经济调度[J]. 电气工程学报, 2022, 17(4): 226-232.
Zhao Anxin, Zhang Zhisheng. Low-carbon economic dispatch of integrated energy system considering integrated power demand response[J]. Journal of Electrical Engineering, 2022, 17(4): 226-232.
[21] Xu Yanhui, Xu Yijia, Huang Yan. Generation of typical operation curves for hydrogen storage applied to the wind power fluctuation smoothing mode[J]. Global Energy Interconnection, 2022, 5(4): 353-361.
[22] 姚宏民, 杜欣慧, 秦文萍. 基于密度峰值聚类及GRNN神经网络的光伏发电功率预测方法[J]. 太阳能学报, 2020, 41(9): 184-190.
Yao Hongmin, Du Xinhui, Qin Wenping. PV power forecasting approach based on density peaks clustering and general regression neural network[J]. ActaEnergiae Solaris Sinica, 2020, 41(9): 184-190.
[23] 董雪, 赵宏伟, 赵生校, 等. 基于SOM聚类和二次分解的BiGRU超短期光伏功率预测[J]. 太阳能学报, 2022, 43(11): 85-93.
Dong Xue, Zhao Hongwei, Zhao Shengxiao, et al. Ultra-short-term forecasting method of photovoltaic power based on SOM clustering, secondary decomposition and BiGRU[J]. Acta Energiae Solaris Sinica, 2022, 43(11): 85-93.
[24] Zheng Lingwei, Su Ran, Sun Xinyu, et al. Historical PV-output characteristic extraction based weather-type classification strategy and its forecasting method for the day-ahead prediction of PV output[J]. Energy, 2023, 271: 127009.
[25] Kojima H, Nagasawa K, Todoroki N, et al. Influence of renewable energy power fluctuations on water electrolysis for green hydrogen production[J]. International Journal of Hydrogen Energy, 2023, 48(12): 4572-4593.
[26] Koponen J, Ruuskanen V, Hehemann M, et al. Effect of power quality on the design of proton exchange membrane water electrolysis systems[J]. Applied Energy, 2020, 279: 115791.
[27] Khatib F N, Wilberforce T, Ijaodola O, et al. Material degradation of components in polymer electrolyte membrane (PEM) electrolytic cell and mitigation mechanisms: a review[J]. Renewable and Sustainable Energy Reviews, 2019, 111: 1-14.
[28] Gilles J. Empirical wavelet transform[J]. IEEE Transactions on Signal Processing, 2013, 61(16): 3999-4010.
[29] 吕伟杰, 方一帆, 程泽. 基于模糊C均值聚类和样本加权卷积神经网络的日前光伏出力预测研究[J]. 电网技术, 2022, 46(1): 231-238.
Lü Weijie, Fang Yifan, Cheng Ze. Prediction of day-ahead photovoltaic output based on FCM- WS-CNN[J]. Power System Technology, 2022, 46(1): 231-238.
[30] 张立军, 张潇. 基于改进CRITIC法的加权聚类方法[J]. 统计与决策, 2015, 31(22): 65-68.
Zhang Lijun, Zhang Xiao. Weighted clustering method based on improved CRITIC method[J]. Statistics & Decision, 2015, 31(22): 65-68.
[31] 朴尚哲, 超木日力格, 于剑. 模糊C均值算法的聚类有效性评价[J]. 模式识别与人工智能, 2015, 28(5): 452-461.
Piao Shangzhe, Chao Murilige, Yu Jian. Cluster validity indexes for FCM clustering algorithm[J]. Pattern Recognition and Artificial Intelligence, 2015, 28(5): 452-461.
[32] Chandesris M, Médeau V, Guillet N, et al. Membrane degradation in PEM water electrolyzer: Numerical modeling and experimental evidence of the influence of temperature and current density[J]. International Journal of Hydrogen Energy, 2015, 40(3): 1353- 1366.
[33] Frensch S H, Serre G, Fouda-Onana F, et al. Impact of iron and hydrogen peroxide on membrane degradation for polymer electrolyte membrane water electrolysis: computational and experimental investigation on fluoride emission[J]. Journal of Power Sources, 2019, 420: 54-62.
[34] Siracusano S, Trocino S, Briguglio N, et al. Analysis of performance degradation during steady-state and load-thermal cycles of proton exchange membrane water electrolysis cells[J]. Journal of Power Sources, 2020, 468: 228390.
[35] Siracusano S, Hodnik N, Jovanovic P, et al. New insights into the stability of a high performance nanostructured catalyst for sustainable water electrolysis[J]. Nano Energy, 2017, 40: 618-632.
[36] Alia S M, Rasimick B, Ngo C, et al. Activity and durability of iridium nanoparticles in the oxygen evolution reaction[J]. Journal of the Electrochemical Society, 2016, 163(11): F3105-F3112.
[37] Zheng Yao, Jiao Yan, Jaroniec M, et al. Advancing the electrochemistry of the hydrogen-evolution reaction through combining experiment and theory[J]. Angewandte Chemie International Edition, 2015, 54(1): 52-65.
[38] Guo Mingming, Ji Mingjuan, Cui Wei. Theoretical investigation of HER/OER/ORR catalytic activity of single atom-decorated graphyne by DFT and comparative DOS analyses[J]. Applied Surface Science, 2022, 592: 153237.
[39] Bystron T, Vesely M, Paidar M, et al. Enhancing PEM water electrolysis efficiency by reducing the extent of Ti gas diffusion layer passivation[J]. Journal of Applied Electrochemistry, 2018, 48(6): 713-723.
[40] Bernhard D, Kadyk T, Kirsch S, et al. Model-assisted analysis and prediction of activity degradation in PEM-fuel cell cathodes[J]. Journal of Power Sources, 2023, 562: 232771.
[41] Zhang Liqiang, Lin Junyu, Li Ming. Research on the typical working condition of energy storage batteries for a wave energy converter[C]//2018 IEEE Inter- national Power Electronics and Application Conference and Exposition (PEAC), Shenzhen, China, 2018: 1-6.
[42] 国家市场监督管理总局, 国家标准化管理委员会. 车用质子交换膜燃料电池堆使用寿命测试评价方法: GB/T 38914—2020[S]. 北京: 中国标准出版社, 2020.
Abstract The photovoltaic (PV) power generation is greatly influenced by weather factors and has great fluctuation. Hydrogen production equipment by electrolysis of water, especially proton exchange membrane (PEM) electrolytic stacks, has the characteristics of fast power response and wide power range, and is very suitable for absorbing PV output with strong fluctuation and preparing green hydrogen. However, at present, there is little research on the performance change of electrolytic stacks under fluctuation power input, and there is a lack of working modes to simulate and test the typical application scenario of electrolytic stacks, which can not provide typical input conditions for the performance attenuation test of electrolytic stacks. Therefore, an extraction method of typical working conditions of PV electrolytic water hydrogen production was put forward in this paper, which can obtain the typical working conditions curve reflecting the performance attenuation characteristics of electrolytic stacks under PV fluctuation input.
Firstly, empirical wavelet transform (EWT) was used to analyze the initial PV output curves in time and frequency domain, and PV output components with different fluctuation frequencies were separated. Secondly, the fluctuation characteristics of different time periods weredefined and extracted to reduce the dimension of the output curves. Thirdly, the weighted fuzzy clustering method was used to reduce the scenes of many fluctuation feature sequences, and typical PV output scenes were obtained. Finally, according to the characteristic sequence, the working condition indexes are set and the simplified working condition curves are reconstructed, and the cycle working condition spectrum of the electrolytic stacks was obtained.
A PV water electrolysis hydrogen production system in the "Three North" area of China was selected as an example, and the PV output data with 1 minute resolution in three years were analyzed. The frequency band number N of EWT was selected as 5, and the initial data curves were decomposed into five components. According to the characteristics of feature sequence data, the optimal clustering number was 4 for scene reduction. In order to compare the advantages of clustering results, the attenuation model of electrolytic stack was introduced to calculate the change values of membrane thickness and catalyst activity of electrolytic stack under different PV input scenarios. The results show that compared with the typical working conditions obtained by other clustering methods, this method has taken into account the degradation of electrolytic stacks, and the separation (SP) index values, containing thickness of PEM and normalized electrochemical active surface area of catalyst, are 0.066 7 and 0.244 3 respectively, which are better than the other three methods. Compared with four kinds of typical original curves, the typical operating curve obtained by the simplification method in this paper has a difference of 4.055 4%, 6.454 6%, 3.616 8% and 2.163 3% respectively in voltage degradation rate, which proves the feasibility of the simplification method.
Through simulation analysis, the conclusions are following: (1) the typical working conditions have a good role in describing the performance attenuation of electrolytic stacks. (2) Compared with other methods, the typical working condition curves of PV electrolytic hydrogen production generated by this method can distinguish the performance attenuation of electrolytic stacks, which is more effective in the performance test experiment of electrolytic stacks. (3) For voltage degradation of electrolytic stacks, the difference between the typical working conditions and the actual curves is less than 10%, which is of testing significance.
Keywords:Hydrogen production by electrolysis of water, empirical wavelet transforms, fuzzy clustering, typical working condition
中图分类号:TM615;TK91
DOI: 10.19595/j.cnki.1000-6753.tces.231400
国家重点研发计划资助项目(2021YFB4000104)。
收稿日期 2023-08-28
改稿日期 2023-09-07
徐衍会 男,1978年生,教授,博士生导师,研究方向为新能源电力系统宽频振荡与氢能领域。
E-mail:xuyanhui23@sohu.com(通信作者)
陈浩维 男,1999年生,硕士研究生,研究方向为可再生能源电解水制氢源侧波动性研究。
E-mail:chw1999827@163.com
(编辑 郭丽军)