图1 隔离开关切合短母线流注分叉现象
Fig.1 Streamer bifurcation phenomenon in opening and closing process of disconnect switch
摘要 近年来，在特高压气体绝缘开关设备（GIS）的操作过程中发现，隔离开关在切合短母线时会在断口间产生流注分叉对地二次击穿现象。传统有限元-通量修正（FEM-FCT）方法和粒子网格-蒙特卡罗（PIC-MCC）方法在仿真此类长距离气体流注放电分叉现象时，会因高昂的计算成本而难以应用。针对这一问题，该文提出了一种基于相场法的流注放电仿真方法，实现了双阳极流注放电过程中流注分叉现象的模拟，仿真结果与PIC-MCC方法对比证明了该方法的合理性。最后，采用该方法对特高压GIS隔离开关切合短母线过程中的流注分叉现象及其引起的二次击穿现象进了模拟，结果表明，屏蔽罩的屏蔽区域与二次击穿现象有直接关系，减小第一次击穿时的触头间距以及增大屏蔽罩的屏蔽区域，均可以有效地抑制隔离开关对地二次击穿现象。
关键词：特高压 气体绝缘开关设备（GIS） 隔离开关 二次击穿 相场法
特高压输电技术因其优异的输电效率与超远的输电距离，在保障中国能源安全、推动绿色发展、促进雾霾治理中发挥了重大作用[1]。特高压气体绝缘开关设备（Gas Insulated Switchgear, GIS）作为特高压输电工程中的核心设备，其可靠性及安全性直接关系到全国范围内电网的安全稳定运行[2-3]。
近年来，在特高压GIS的操作过程中发现了隔离开关断口对地二次击穿现象[4-6]，即GIS隔离开关在切合短母线过程中，除了动静触头间的正常放电通道外，还形成了断口对地的二次击穿放电通道，进而引发故障预警。其试验观测结果如图1所示[4]。这一问题已经严重影响了特高压设备的安全稳定运行。
由于气体击穿过程中组分复杂、持续时间短暂（ns级）等特点，完全依赖试验方法探究此类长距离击穿过程中的流注分叉及其引起的二次击穿问题较为困难。因此，数值仿真方法成为研究该问题的重要手段。目前，研究高压电力设备中电击穿问题的仿真手段主要有三种：①有限元-通量修正（Finite Element-Flux Corrected Transport, FEM-FCT）方法；②粒子网格-蒙特卡罗（Particle in Cell-Monte Carlo Collision, PIC-MCC）方法；③相场（phase-field）法。
图1 隔离开关切合短母线流注分叉现象
Fig.1 Streamer bifurcation phenomenon in opening and closing process of disconnect switch
FEM-FCT方法将流注发展过程看作一种流体中的带电粒子输运过程，并通过修正流体控制方程中的通量源项以反映电离碰撞等化学反应的影响。R. Morrow首次通过FEM方法对氧气环境中的电晕放电过程进行了一维数值模拟[7]；N. L. Aleksandrov等采用改进后的FEM-FCT方法对空气中的流注发展过程进行了一维数值模拟[8]；A. Bourdon等在FEM-FCT方法的基础上添加了光电离模型[9]；D. V. Beloplotov等对负流注的形成和发展进行了数值模拟[10]；还有许多其他学者采用FEM-FCT方法对不同气体环境中的流注放电问题进行了仿真探究[11-14]。FEM-FCT方法计算成本较低，但当涉及粒子种类较多时，该方法计算成本也会迅速攀升，且在仿真长距离击穿时会由于处理流注区与非流注区界面需要大量计算网格，导致计算时间急剧上升，难以模拟流注分叉问题。
PIC-MCC方法的原理是通过计算大量微观粒子在电磁环境中的碰撞过程以模拟气体击穿过程中流注发展的宏观现象。J. Dawson于1962年首次提出采用粒子方法模拟等离子体[15]，并于1964年通过粒子方法验证了静电波的朗道阻尼效应，证实了该方法的可信性[16]。在此基础上引入离散网格用于计算泊松方程，形成了现代广泛采用的粒子网格（Particle-in-Cell, PIC）方法。P. C. Liewer等开发了通用并行PIC（General Concurrent PIC, GCPIC）算法以实现PIC方法在分布式内存中的并行处理[17]；V. Vahedi在PIC方法的基础上添加了一种包含零碰撞方法的蒙特卡罗（Monte Carlo Collision, MCC）算法，并对Ar和O2中的放电过程进行了模拟[18]；国内学者段韶峰采用PIC-MCC方法对隔离开关电弧进行了一维模拟[19]。尽管PIC-MCC方法基于第一性原理，有着较高的准确性，但由于其网格剖分必须与德拜长度相适应，导致该方法在模拟长距离击穿时，其所需计算网格数量会达到现有计算机硬件无法承受的程度。
相场法以Ginzburg-Landau理论为基础，通过微分方程模拟体系中特定物理过程的扩散和热力学驱动的综合作用。Z. Suo根据电击穿与断裂问题的相似性提出采用相场法模拟固体问题中的电击穿问题[20]；H. G. Beom等研究了电击穿中导电通道与电流密度J积分的关系[21]；K. Chaitanya Pitike等采用相场法建立固体材料中的电击穿模型[22]；沈忠慧等在固体电击穿模型的基础上添加应力、电热模型，对薄膜击穿问题进行了模拟[23]；米章等在固体电击穿模型的基础上添加了铁磁相变模型[24]；李进等在固体电击穿模型的基础上增加热应力模型，并对GIS盆式绝缘子在不同温度下的击穿特性进行了仿真分析[25]。
相场法在处理界面变化问题方面具有优势，在求解时对网格剖分没有绝对尺度的要求，可以大幅度降低长距离气体击穿仿真所需网格数量及计算时间。因此，本文提出一种基于相场法的气体击穿仿真方法，实现了特高压GIS隔离开关中的流注分叉及对地二次击穿现象的模拟。首先，将气体击穿过程中的流注发展过程等效假设为气体由绝缘相转变为导电相的相变过程；其次，对固体击穿的相场法放电方法进行了相应的修改，使之适用于气体击穿模拟，并通过PIC-MCC方法仿真验证了方法的合理性；最后，采用基于相场法的气体击穿仿真方法对特高压GIS隔离开关流注分叉及二次击穿放电现象进行了模拟，并对影响二次击穿现象的因素进行了探究。
特高压GIS中充气压力一般会达到0.45 MPa以上，气体较为稠密，其击穿现象与固体和液体中的击穿现象有一定相似性。同时试验结果表明，特高压GIS隔离开关在切合短母线时击穿时间为ns级，气体流动对流注发展的影响可以忽略。因此，该情形下的流注发展过程可按上述特点进行等效假设。
以典型的针板放电模型为例，其流注放电过程示意图如图2所示。当针板两极间施加足够大的电位差时，针极附近的气体会产生一定的局部电离，电离产生的自由电荷在电场强度的作用下形成流注，流注内部的阳离子和电子在电场作用下产生德拜屏蔽作用，使得流注表面形成等位面。此时流注头表面的电位接近针极电位，进而驱动流注进一步发展。
此外，由于阳离子大多为迁移率较低的重粒子，流注发展过程中形成的阳离子在整个击穿过程中不会出现明显的扩散、迁移现象，也就是说流注发展形成的电离区域在气体放电的先导阶段（ns级）能够保持其形态。
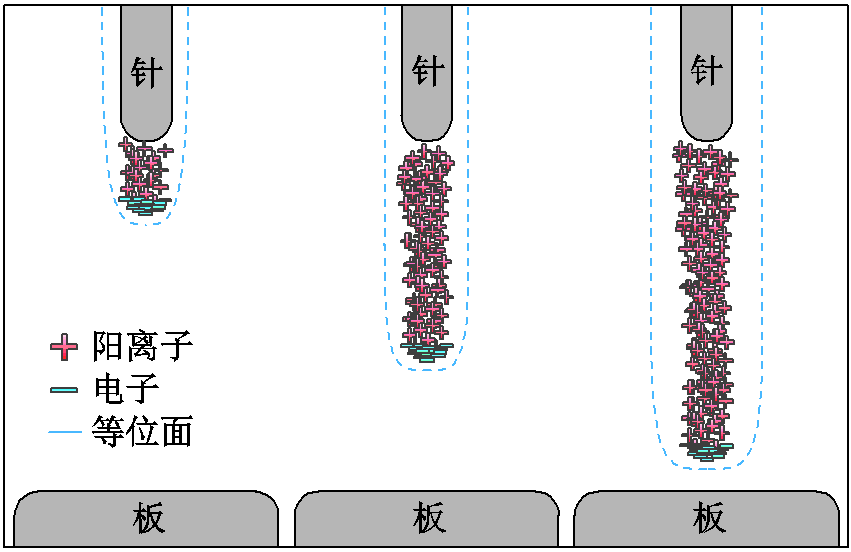
图2 针板模型流注放电过程示意图
Fig.2 Schematic diagram of streamer discharge process of needle plate model
依据1.1节的分析可知，流注发展过程中形成的导电通道具有德拜屏蔽特性以及短时间（ns级）内的形态稳定性。这一特点与固体击穿过程中导电通道的静电屏蔽效应及固体导电通道的形态稳定性具有较高的相似性。因此，本文将先导阶段的流注发展过程也等效为一种物质连续相变的过程，如图3所示，具体细节如下。
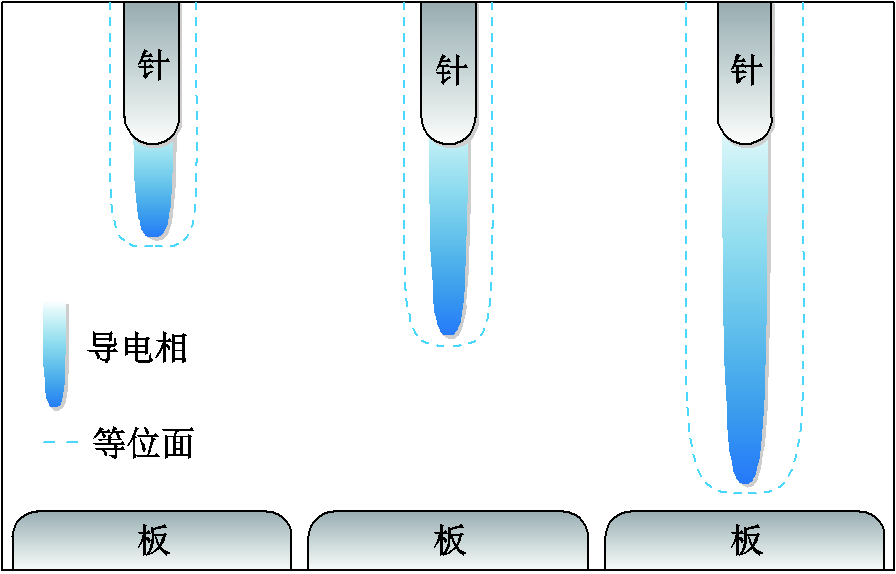
图3 相变假设下流注放电过程示意图
Fig.3 Schematic diagram of the streamer discharge process under the phase transition assumption
1）将等离子体的德拜屏蔽效应近似等价为导体的静电屏蔽效应，从而可以将未电离区域视为气体的绝缘相，将电离区域视为导电相。
2）将电离过程视为一种气体由绝缘相转换为导电相的相变过程。
为了更加直观地说明1.2节中的等效假设在正负流注中的合理性，本节采用FEM-FCT方法对双头流注模型的流注放电过程进行模拟。
1.3.1 双头流注仿真模型及边界条件
二维轴对称简化后的双头流注模型及其网格剖分情况如图4所示，其中涉及的边界条件见表1。表中，反应物M涉及的碰撞截面以及中心位置初始电子密度设置来自文献[9]。
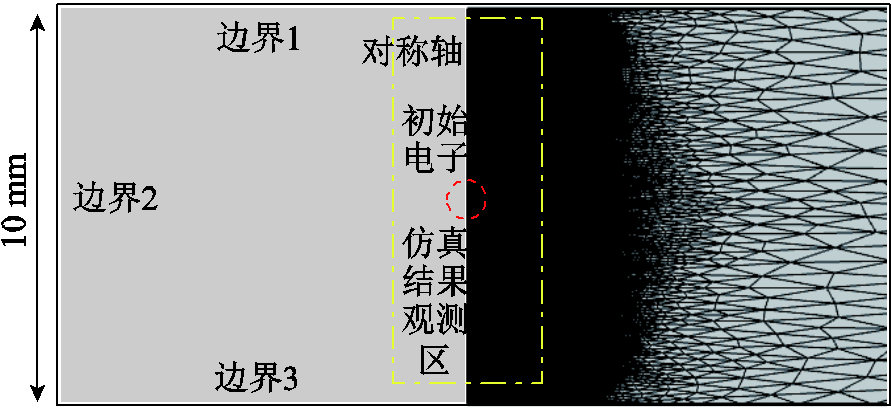
图4 双头流注模型及边界条件
Fig.4 Double-head streamer model and boundary conditions
表1 FEM-FCT流注放电仿真边界条件
Tab.1 Boundary conditions of FEM-FCT streamer discharge simulation
边界扩散方程反应方程电位方程 边界1壁面M+→M（阴极）52 kV 边界2壁面M+→M（阴极）绝缘 边界3电子出口开放边界接地 计算域—e+M→2e+M+—
1.3.2 FEM-FCT流注放电仿真结果
由于本节的仿真是为了说明相变假设的合理性，因此，这里仅展示正负流注放电过程中的阳离子分布和电场强度分布，观测区内的仿真结果如图5所示。从仿真结果中可以看出，正负流注发展过程中的阳离子密集区域内存在明显的德拜屏蔽效应（类似于导体中的静电屏蔽效应），使得该区域电场强度明显低于未电离区域，这与本文提出的相变假设一致，可以证明该假设的合理性。此外，文献[9, 26-28]中流注内电场强度的仿真结果也能说明本文假设的合理性。
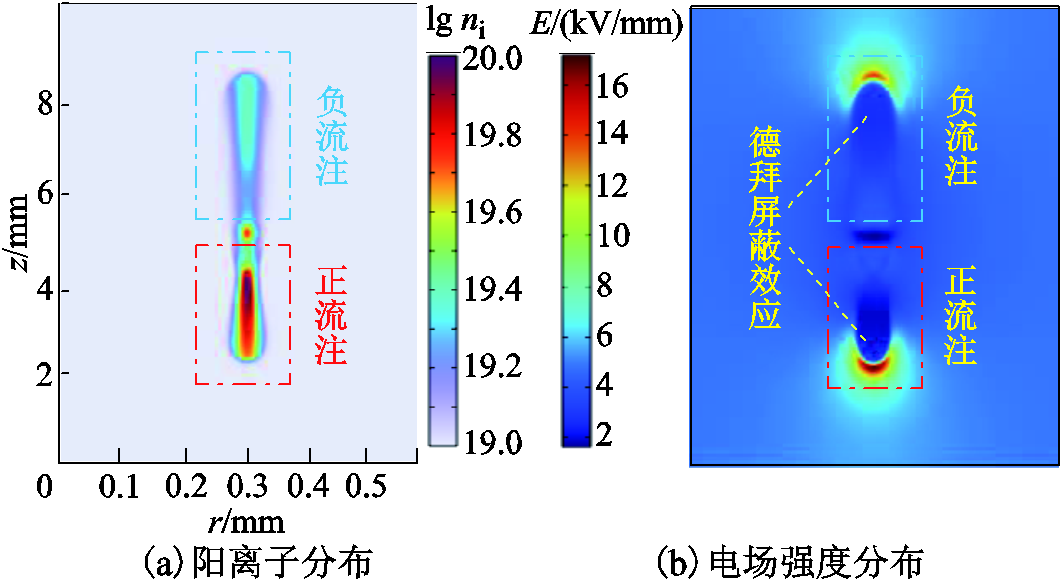
图5 双头流注仿真结果
Fig.5 Results of two-head streamer discharge simulation
2.1.1 序参量
依据1.2节中的相变假设，可以将气体击穿过程中的流注发展视为一种气体在强电场下的由绝缘相转变为导电相的相变现象。为了能够对相变的过程进行量化分析，本文采用序参量s表示其物态，s=1表示气体处于完全的绝缘相；s=0表示气体处于完全的导电相。序参量s是空间和时间的函数。
为了能采用统一的控制方程约束绝缘相和导电相的序参量变化，本文采用文献[22]中的数学方法，构建的气体介电常数表达式为
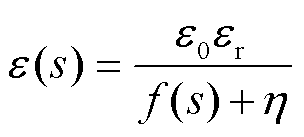（1）
式中，e0为真空介电常数；er为气体处于绝缘相时的相对介电常数；h为无量纲小量，本文取h=1×10-4；f (s)为连续可导函数。只要f (s)满足f (0)=0、f (1)=1，则e(s)即可表示从绝缘相到导电相的介电常数；进一步地，若f (s)还同时满足
、
，则可以确保序参量不影响其他热力学量。依据上述要求，本节最终采用的表达式[22]为
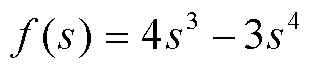（2）
2.1.2 静电能密度
在一个准静电体系中，考虑内部静电能和表面静电能的情况下，其静电能积分表达式可写为
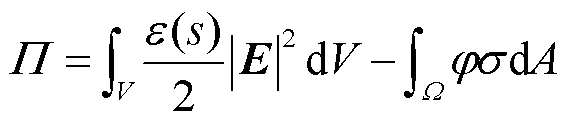（3）
式中，P为体系总静电能；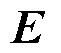
为空间电场强度；
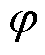为体系表面电位；σ为表面电荷密度；V为体积分对应的体系空间；Ω为面积分对应的体系表面。
根据高斯定理，式（3）可变换为
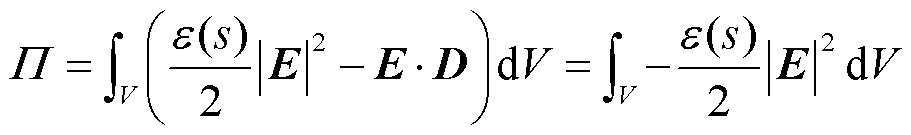（4）
式中，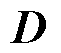
为电位移矢量。
因此，最终的静电能密度函数We可以写为
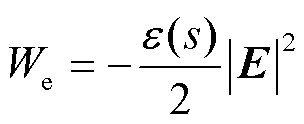（5）
2.1.3 击穿能密度
在相场法击穿模型中[20-24]，当击穿能密度写作式（6）形式时，可使推导出的控制方程满足：当局部空间静电能大于临界击穿能时，介质自然发生“绝缘-导电”相变。
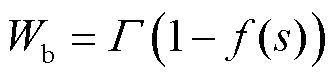（6）
式中，Wb为击穿能密度函数；Γ为气体的临界击穿能密度。
在固体介质击穿过程中，临界击穿能密度由固体材料的临界击穿场强和固体材料的结构内应力共同决定；而在气体介质中，该临界击穿能则完全由临界击穿场强决定。因此，本文中的临界击穿能密度可以表示为
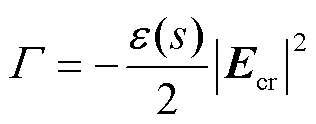（7）
式中，Ecr为临界击穿场强。
2.1.4 梯度能密度
和其他情形下的相场法模型相似，梯度能密度函数可以进一步描述导电通道的演化过程。
（8）
式中，Wi为梯度能密度函数；l为导电通道的特征长度。
2.1.5 能量泛函和控制方程
在获得静电能密度、击穿能密度和梯度能密度的基础上，体系的总能量G可以描述为
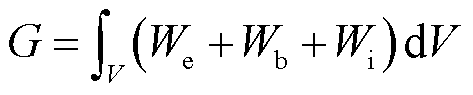（9）
根据能量最低原则，即数学形式上的变分原则，总能量G(s, f)取最小值时，可以推导出相平衡时的欧拉方程为
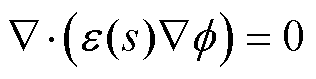（10）
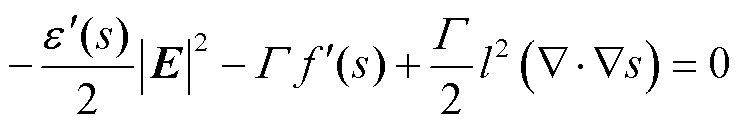（11）
其中，式（10）为泊松方程，式（11）为相守恒方程。
从式（7）中可以看出，计算击穿能密度还需要相应的气体临界击穿场强。
通过求解一阶近似Boltzmann方程计算气体的电子能量分布函数，进而计算得到电离反应速率和吸附反应速率，二者的交点即为临界约化击穿场强，具体流程如图6所示。
获得气体临界约化击穿场强后，可以通过式（12）计算相应的临界击穿场强。
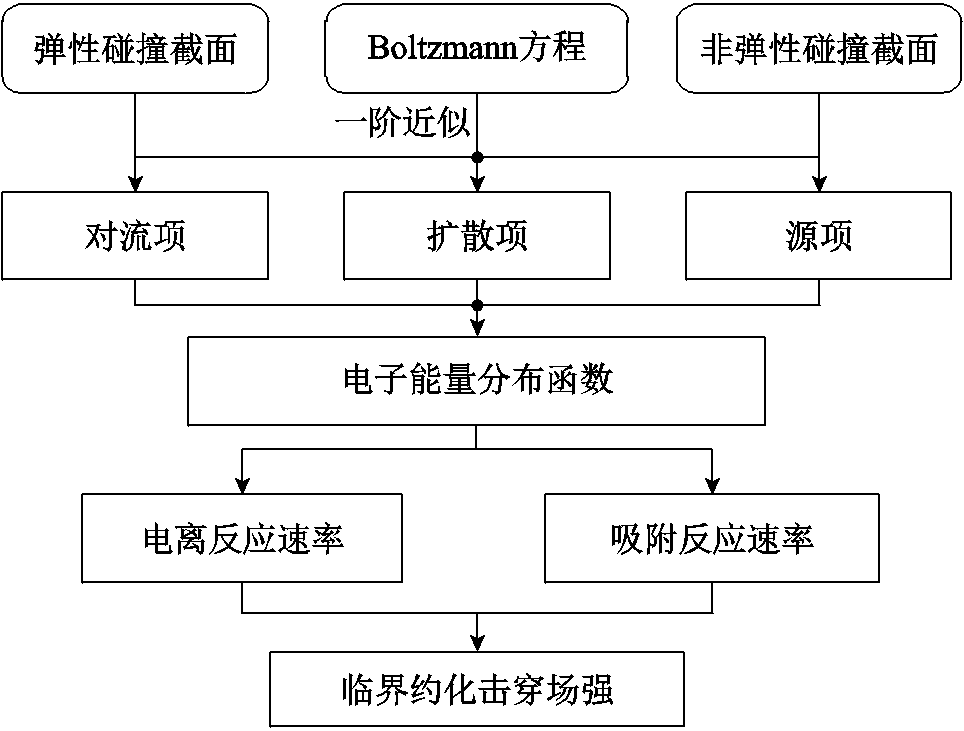
图6 临界约化击穿场强计算流程
Fig.6 Flow chart of critical breakdown approximate field strength calculation
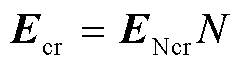（12）
式中，ENcr为临界约化击穿场强；N为气体的粒子数密度。
本文中计算SF6临界击穿场强所考虑的反应见表2；计算得到的电离反应速率和吸附反应速率如图7所示。从图7中可以看出，SF6的临界约化击穿场强约为360 Td（1 Td=10-17 V·cm2），与文献[29-30]中一致。
表2 SF6中的碰撞反应及其碰撞截面
Tab.2 Collision reactions and collision cross sections in SF6 gas
反应类型反应方程碰撞截面 电离e + SF6 = 2e +文献[31] 电离e + SF6 = 2e +文献[31] 电离e + SF6 = 2e + SF+文献[31] 吸附e + SF6 =文献[32] 吸附e + SF6 =文献[32] 吸附e + SF6 =文献[32] 激发e + SF6 = e + SF6(v4)文献[31] 激发e + SF6 = e + SF6(v1)文献[31] 激发e + SF6 = e + SF6(v3)文献[31]
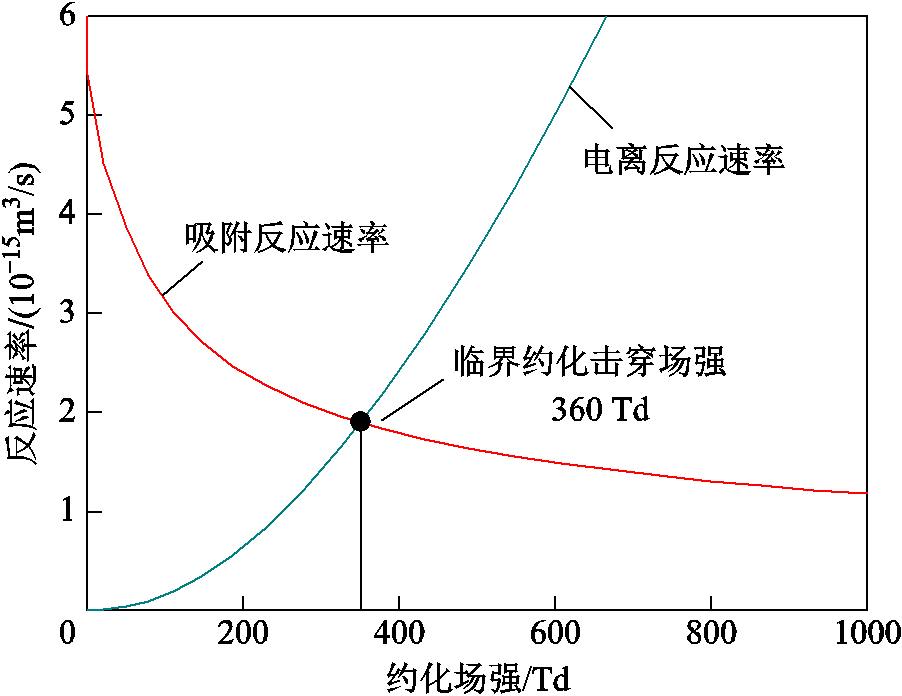
图7 SF6中的反应速率曲线
Fig.7 Reaction rate curves in SF6 gas
从式（8）中可以看出，计算梯度能密度还需要相应的导电通道特征长度。在固体击穿过程中，该参数可以依据放电模型的尺寸进行合理设置，并无绝对的尺寸要求。然而，由于本文中的气体导电通道是流注通道的等效假设，因此该通道特征长度应当大于德拜半径，即
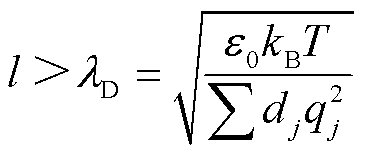（13）
式中，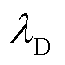
为德拜半径；kB为玻耳兹曼常数；T为气体温度；dj为带电粒子j的数密度；qj为带电粒子j的电荷量。
为了进一步说明本方法中导电通道特征长度的作用，这里将放电体系退化为一维，则梯度能密度（式（8））简化为
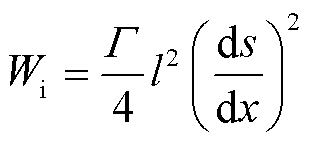（14）
在导电通道外部，气体状态不发生改变，有ds/dx=0；在导电通道内部，即相变区域，有ds/dx≠0。
即为导电通道的半径，若将序参量的梯度近似为平均变化，则式（14）可以写作
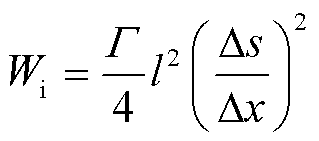（15）
可以看出：当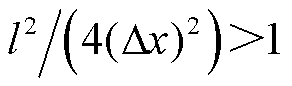
时，通道内的梯度能Wi更高；当
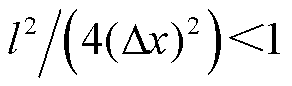时，通道内的梯度能Wi更低。
根据能量最低原则可知，直径大于特征长度的流注分支能量更低，更容易产生；而直径小于特征长度的流注分支能量更高，不易产生。因此，导电通道特征长度可以视为该方法的一种“抑制器”，使得小于特征长度的流注分支不易发生，通过调节导电通道特征长度，可以减少流注分叉的产生，降低计算成本。
需要说明的是，上述特征是在仅考虑梯度能情况下的分析，考虑到静电能和击穿能的影响，并不是直径小于特征长度的流注分支就绝对不会存在，如在静电能较低（电场强度较大）的位置仍能产生。
为验证基于相场法的气体击穿仿真的合理性，分别采用PIC-MCC方法和本文提出的方法对典型的小尺寸双阳极放电模型进行模拟，对比其流注分叉现象仿真结果的差异。二维双阳极放电模型如图8所示，阴极施加-10 kV电位，阳极施加+10 kV电位，背景气体为气压为1.0 atm（1 atm=101.3 kPa）的SF6。
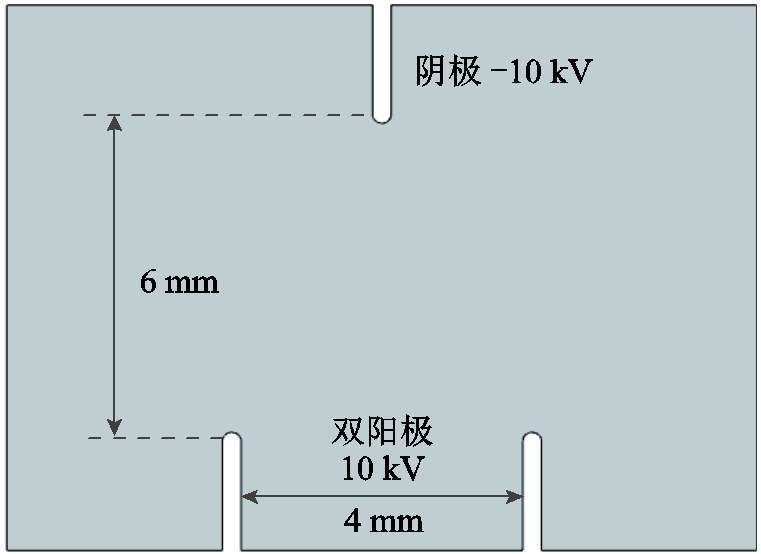
图8 双阳极放电模型
Fig.8 Double anode discharge model
PIC-MCC方法仿真中的电场边界条件按图8设置，其中涉及的碰撞反应参考表2。由于PIC-MCC方法模拟流注放电时所考虑的粒子种类越多，其计算成本会越高昂，本文PIC-MCC方法仿真中涉及的粒子仅考虑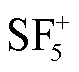
、
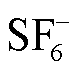及e，表2中其余电离、吸附反应均以激发碰撞的形式参与计算。PIC-MCC方法模拟该流注放电过程需要内存资源11.4 GB，计算时间约为16.30 h。
采用PIC-MCC方法模拟的双阳极流注放电过程如图9所示。在前期阶段（0～5.0 ns），流注茎在双阳极的影响下产生了明显的分叉；在中期阶段（5.0～7.0 ns），流注茎之间的差异导致左侧流注头电场强度高于右侧流注头，左侧支流注茎发展初始速度明显高于右侧流注茎；在后期阶段（7.0～7.7 ns），随着最左侧的流注头接近左阳极，流注头表面电场强度显著上升，进而迅速发展直至完成击穿；击穿后（7.7～8.3 ns），最左侧流注茎通道内电场强度略有上升。
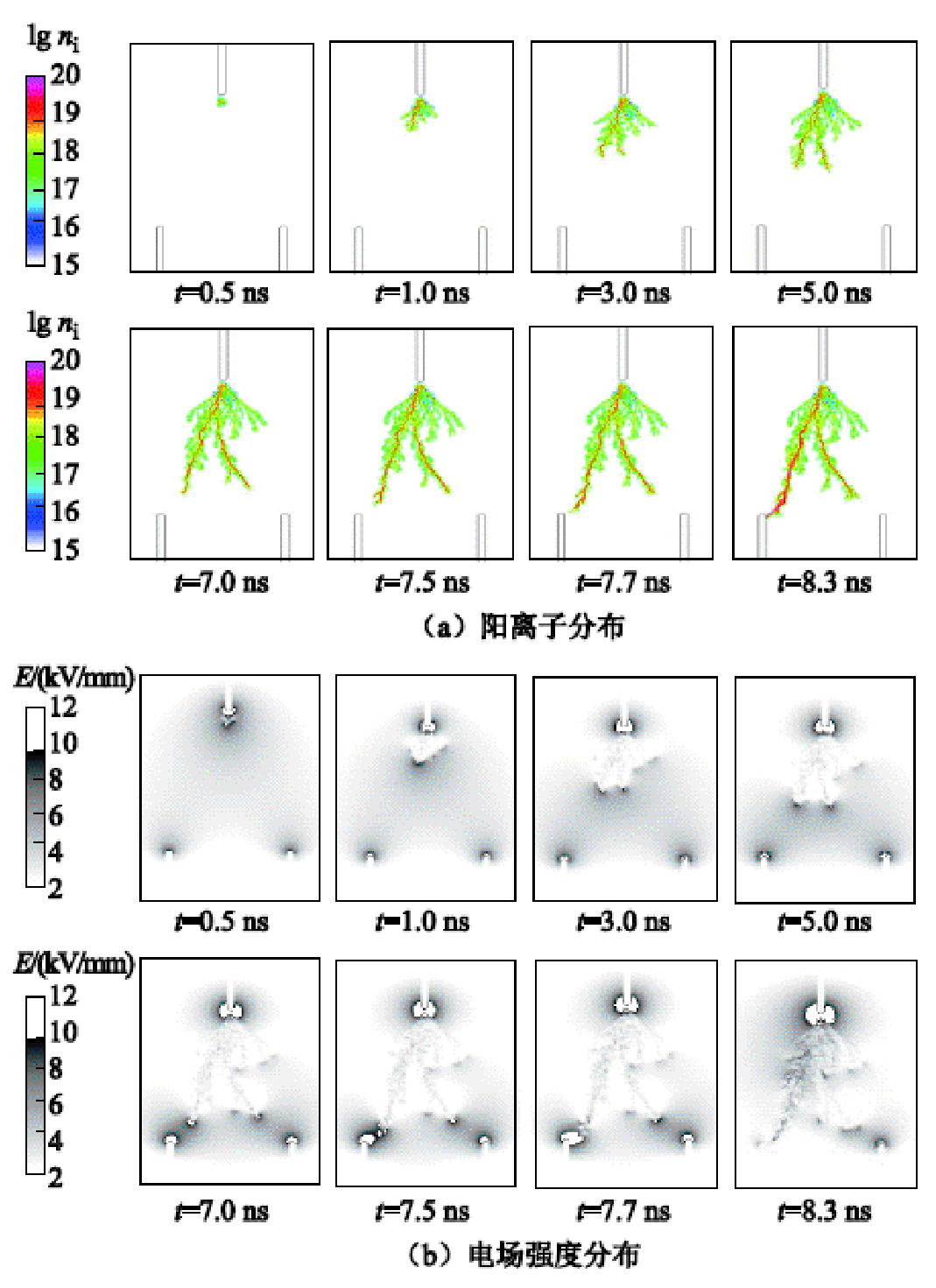
图9 阳离子分布和电场强度
Fig.9 Cation distribution and electric field strength
按图8设置基于相场法的气体击穿模拟方法的电场边界条件，采用泊松方程计算电场分布；碰撞反应及其碰撞截面参考表2设置；并按照第2节方法计算序参量分布等。模拟过程中所需内存资源为3.83 GB，计算时间为1.88 h。
基于相场法的气体击穿模拟方法计算的双阳极流注放电过程如图10所示。在前期阶段（0～5.0 ns），流注茎分叉并向两个阳极同时发展；在中期阶段（5.0～7.0 ns），流注茎之间的差异导致最左侧流注头电场强度高于其他次级流注头，该支流注茎发展速度开始明显高于其他次级流注；在后期阶段（7.0～7.8 ns），随着最左侧的流注头接近左阳极，流注头表面电场强度显著上升，进而迅速发展直至完成击穿；击穿后（7.8～8.5 ns），最左侧流注茎通道内电场强度略有上升。整个发展过程符合放电基本规律，且有明显的流注茎分叉行为。整个放电过程中流注茎的分叉趋势与图9较为相似，这表明相场法放电模型在模拟流注茎分叉行为时具有一定的合理性。
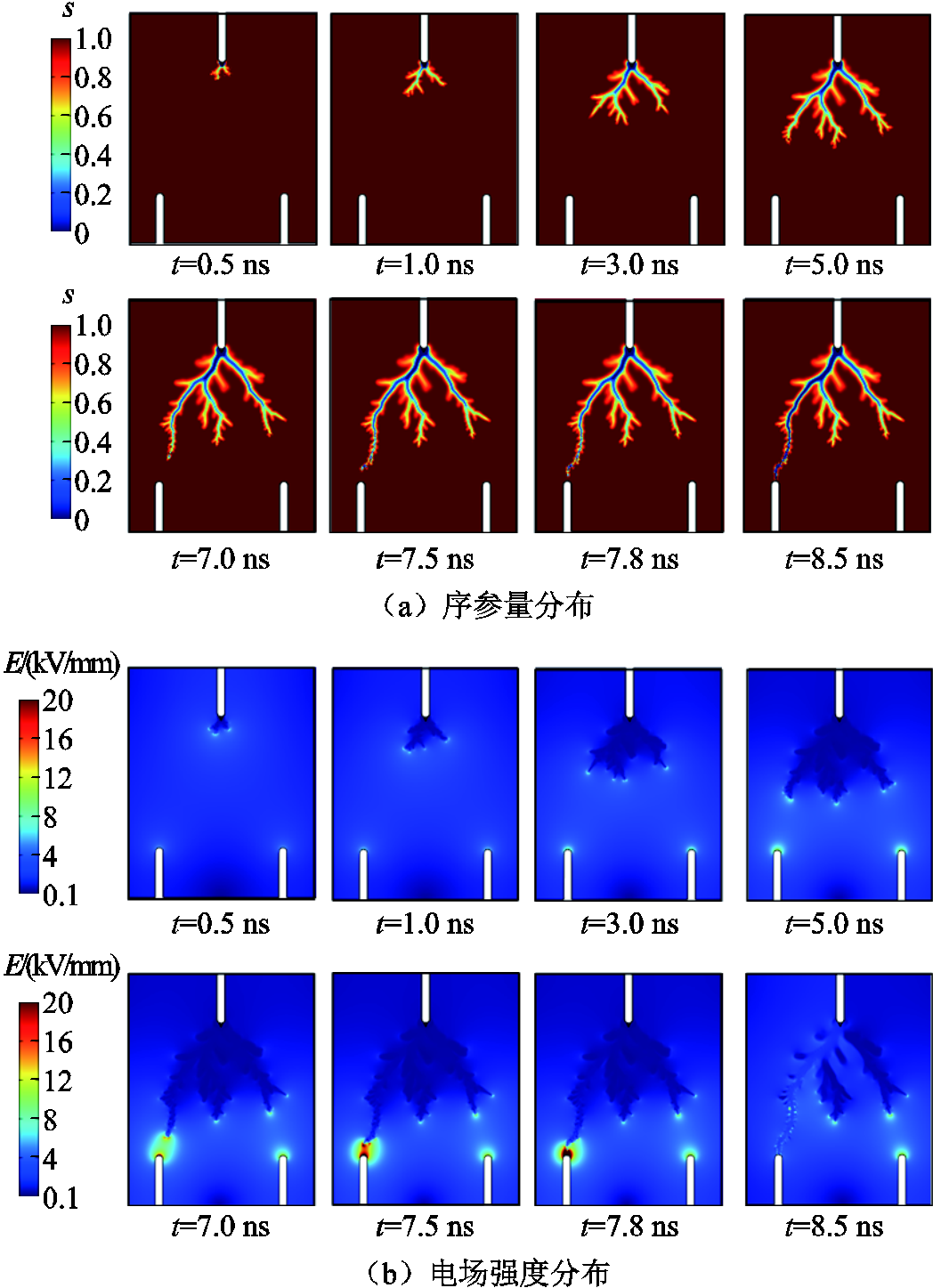
图10 序参量分布和电场强度分布
Fig.10 Order parameter distribution and electric field intensity distribution
由于PIC-MCC方法与本文提出的方法本身具有一定的随机性，因此需要对两种方法进行多次重复仿真，并对结果进行对比。分别采用本文提出的方法和PIC-MCC方法对图8的双阳极放电模型进行10次模拟，并对仿真结果中的三个流注特征进行对比：①主流注头（最先击穿的流注）发展路径；②次级流注头（头部电场强度仅次于主流注的流注）发展路径；③主流注头运动速度。
主流注头发展路径的对比如图11所示，次级流注头发展路径的对比如图12所示，主流注头发展速度的对比如图13所示。从图11～图13中可以看出，两种方法计算结果具有较高的一致性，主流注头发展路径区域重叠面积约为90%，次级流注头发展路径区域重叠面积约为70%，主流注发展速度均呈现击穿前速度陡增的趋势，且平均击穿时间约相差10.3%，验证了本文所提出相场法放电模型的合理性。
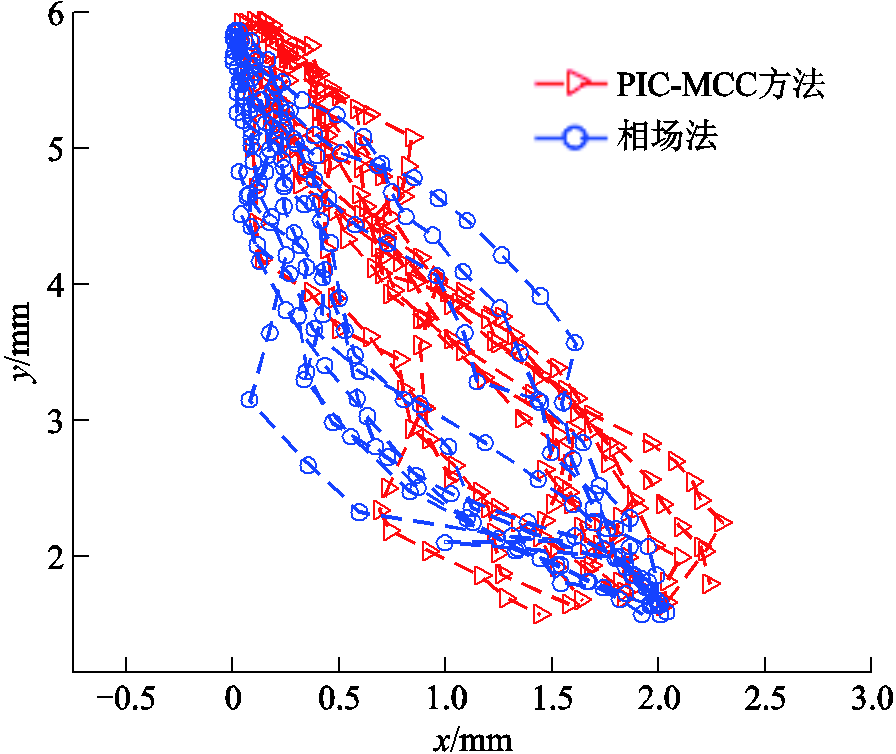
图11 主流注头发展路径
Fig.11 Main stream head development path
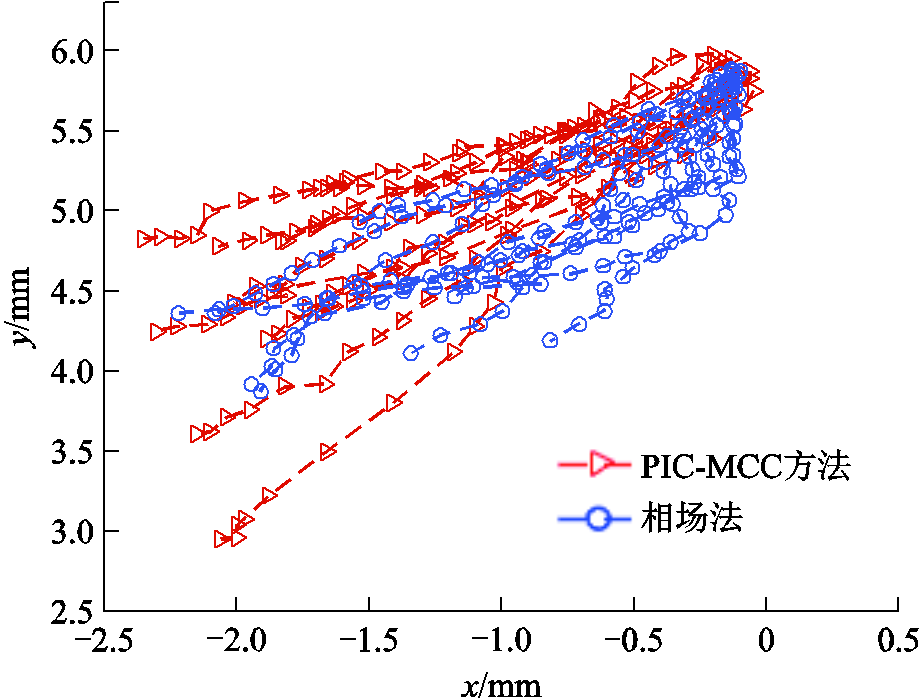
图12 次级流注头发展路径
Fig.12 Secondary streamer head development path
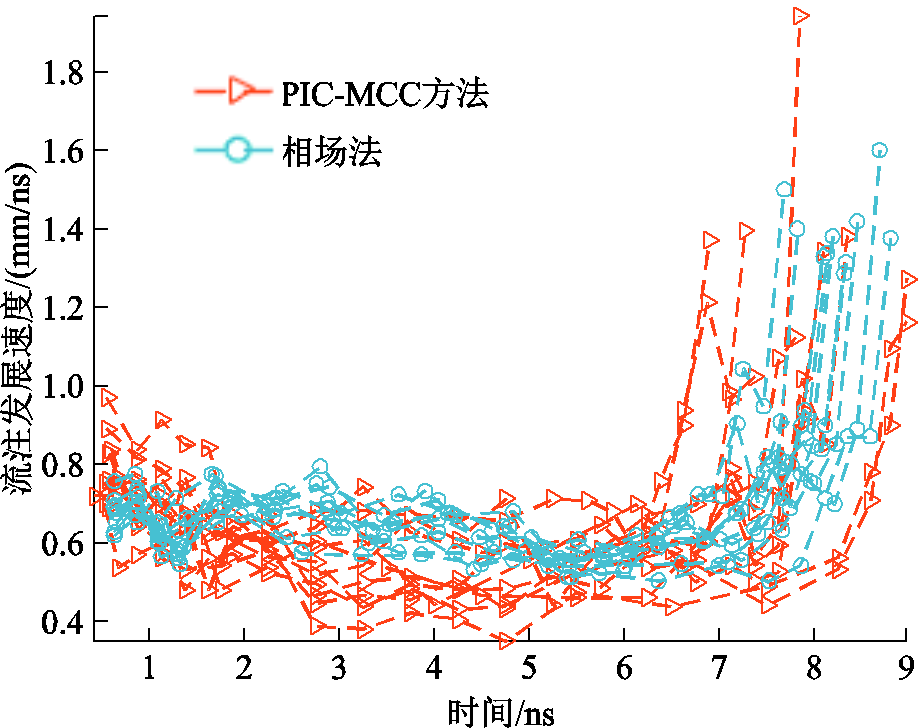
图13 主流注头发展速度
Fig.13 Main stream head movement speed
为说明本文方法的优越性，本节对PIC-MCC方法与本文建立的基于相场法的气体击穿模拟方法在不同尺寸的双阳极模型中所需的网格资源进行了对比。两种方法的网格剖分条件如下：
1）由于PIC-MCC方法在模拟流注问题时，需要模拟单个粒子在网格中的运动，因此其网格尺寸不能远大于德拜半径，这里按德拜半径的尺寸进行网格剖分。
2）基于相场法的气体击穿模拟方法依据3.2节中的导电通道特征长度的四分之一进行网格剖分。
3）两种方法中均采用四边形网格剖分。
不同比例下两种方法的网格剖分结果见表3。可以看出，随着模型绝对尺寸的增加，PIC-MCC方法受限于德拜半径的约束，其所需网格数量会急剧上升，而本文提出的方法可以通过忽略与模型尺度相比十分微小的流注分支，从而依然保持相对较低的网格数量。
表3 网格剖分结果对比
Tab.3 Comparison of mesh sectioning results
模型尺寸/(mm×mm)PIC-MCC网格数量本文方法网格数量 9×106 300 000 110 000 90×100630 000 000110 000 900×1 00063 000 000 000110 000
值得说明的是，本文提出的基于相场法的流注放电模型，不仅可以用于特高压GIS环境中的放电过程，也可以用于其他流注内部德拜屏蔽效应足够强的长气隙击穿过程。
为了研究特高压GIS隔离开关切合短母线过程中对地二次击穿现象的产生机理，采用本文提出的方法对1 100 kV特高压GIS隔离开关切合短母线放电过程进行模拟。
特高压GIS隔离开关在切合短母线过程中的第一次击穿（动静触头间的击穿）仅与隔离开关结构及空间电位分布相关，考虑到动静触头间的击穿时间在100 ns以内，该阶段的击穿过程可以视为静电模型下的放电过程。此外，由于一次击穿后断口间产生的特快速暂态过电压（Very Fast Transient Overvoltage, VFTO）及壳体表面产生的暂态地电压（Transient Earth Voltage, TEV）十分复杂，难以实现与基于相场法的流注放电方法的耦合。因此，本文仅对隔离开关结构本身与二次击穿现象的关系进行探究。
为避免电位变化对探究隔离开关结构与二次击穿关系的干扰，本节后续仿真所用特高压GIS隔离开关流注放电模型如图14所示，所涉及电位条件统一为：设置动触头为-1 000 kV悬浮电位，静触头为-600 kV固定电位，GIS壳体接地。此外，环境压力为0.45 MPa，屏蔽罩直径约为525 mm，触头间距为80～200 mm。需要说明的是，为了方便后续探究不同间距下的击穿过程，图14的模型在动触头表面统一设置了一个角度为30°、高度约为2 mm的三角形缺陷，以确保不同间距下都能发生击穿。
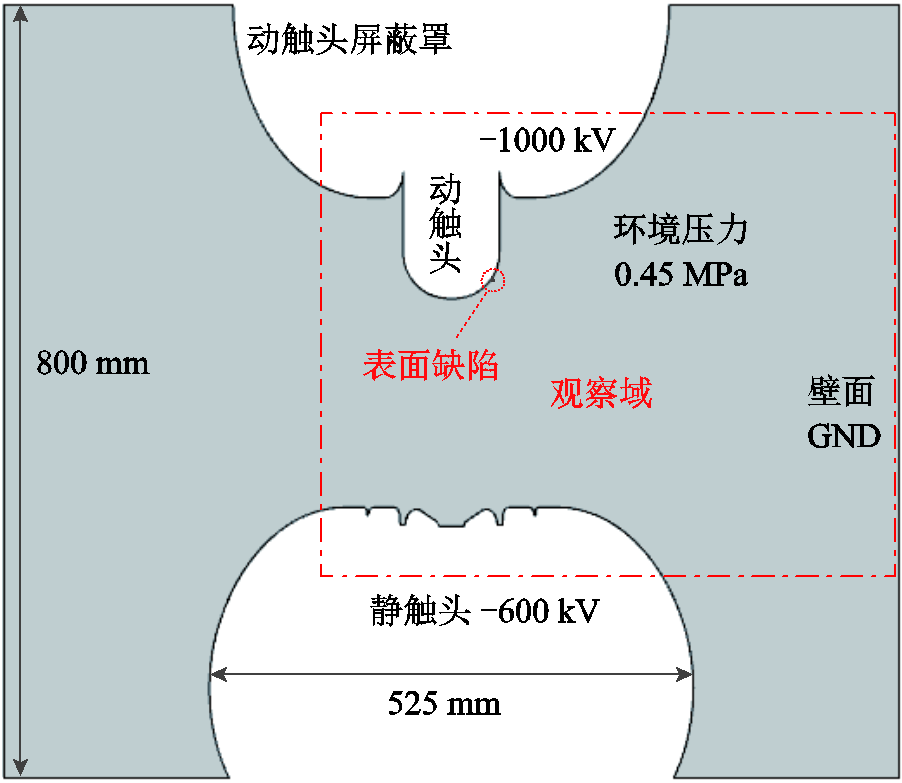
图14 特高压GIS隔离开关流注放电模型
Fig.14 Streamer discharge model in UHV GIS disconnect switch
4.2.1 发生二次击穿的隔离开关气隙击穿过程
图15为特高压GIS隔离开关在200 mm触头间距下发生击穿过程的序参量分布、电场强度分布及电位分布。从图15中可以看出，在t=25 ns时，流注在动触头、静触头和壳体三者共同构建的三电极空间电场影响下开始出现明显分叉；t=25～55 ns期间，主流注头P1向着静触头发展，次级流注头P2在向静触头发展的过程中逐渐向屏蔽罩外偏离；当t=61 ns时，主流注头P1击穿动静触头气隙，动触头悬浮电位迅速与静触头平衡，空间电场由动触头、静触头和壳体的三电极模式转变为动静触头和壳体的双电极模式，此时次级流注头P2刚好发展超过屏蔽罩影响区域（下文简称屏蔽区域），其表面电场强度约为40.2 kV/mm，仍略大于SF6的临界击穿场强，因此，该次级流注P2在双电极模式空间电场（径向方向）的作用下继续向壳体方向发展，由于双电极模式下的空间电场方向与三电极模式下相比发生突变，次级流注头P2的发展轨迹也在t=61 ns时刻发生偏转；随后在t=61～309 ns内，次级流注头P2完成对壳体的击穿，最终形成动触头对壳体的二次击穿。
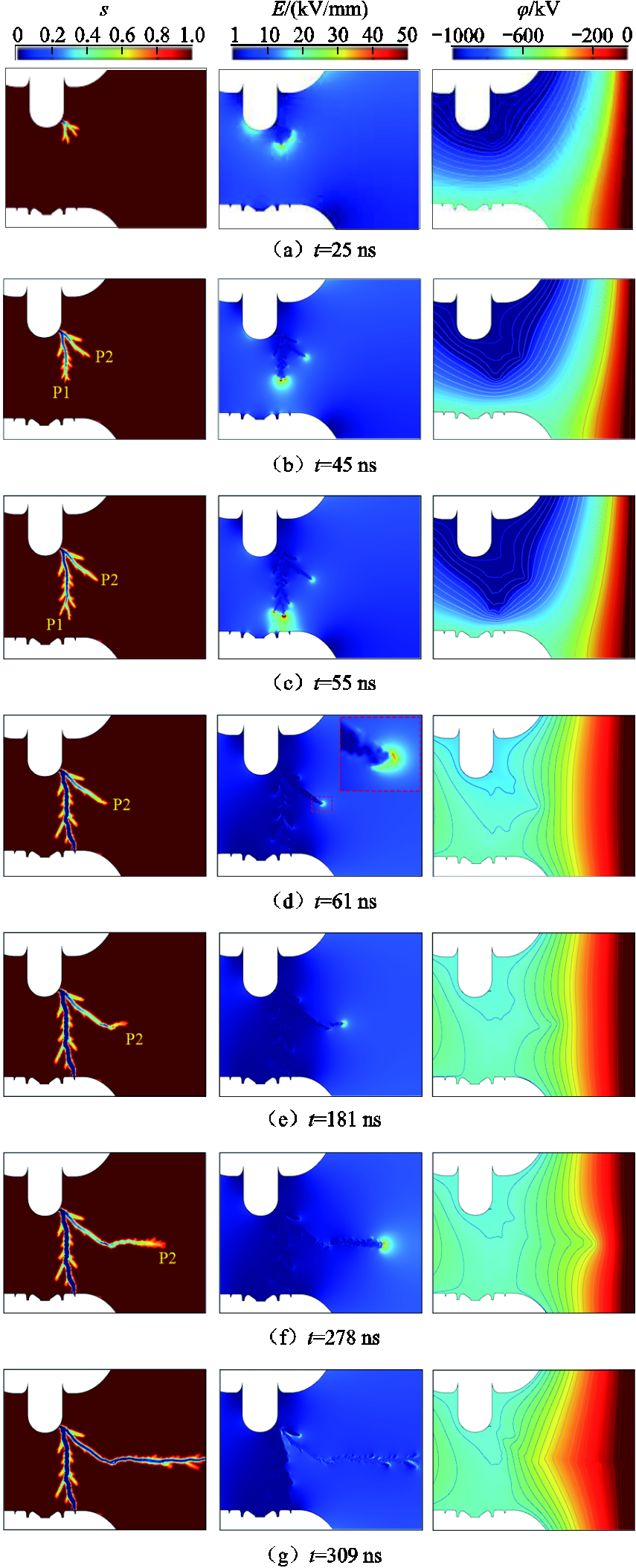
图15 特高压GIS隔离开关二次击穿流注放电仿真结果
Fig.15 Simulation results of streamer discharge with secondary breakdown in UHV GIS disconnecting switch
4.2.2 未发生二次击穿的隔离开关气隙击穿过程
气体击穿过程中，由于一些粒子的无规则碰撞会导致相同条件下的击穿过程也有些许差异，而图15中的二次击穿与一次击穿过程中次级流注头的空间位置有着直接关系，因此需要对图15相同条件下的一次击穿过程进行重复仿真。重复仿真发现，在与图15相同条件下也存在一次击穿完成后未发生动触头对壳体二次击穿的气体击穿过程，如图16所示。从图16中可以看出，当静触头与动触头完成击穿时（t=51 ns），尽管次级流注头P2也显著地向屏蔽罩外侧偏离，但由于其并未超过屏蔽区域，其表面电场强度也未达到SF6的临界击穿场强，因此，该次级流注头P2并未在动静触头电位平衡后向壳体方向发展。
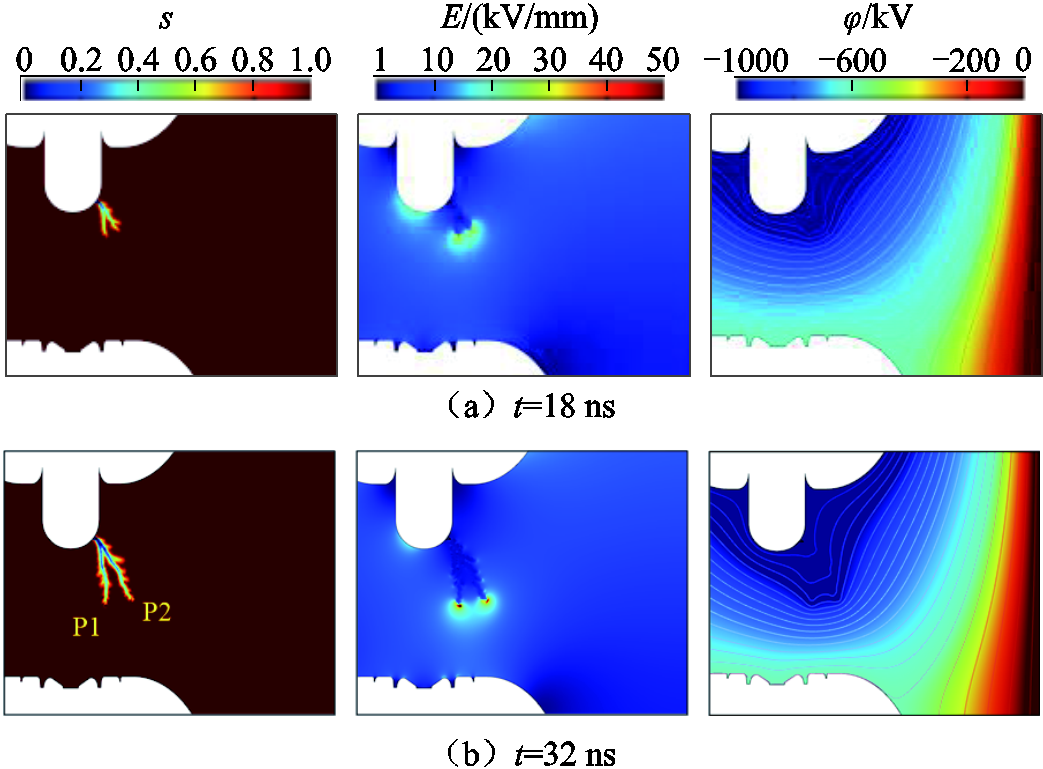
图16 特高压GIS隔离开关未发生二次击穿的流注放电仿真结果
Fig.16 Simulation results of streamer discharge without secondary breakdown in UHV GIS disconnecting switch
为方便分析特高压GIS隔离开关在气隙击穿过程中发生二次击穿的机理，需要对“屏蔽区域”这一概念进行介绍。当动静触头等电位时，动静触头间会由于屏蔽罩的存在而形成一层层鞍形的等电位线，且电场强度（电位降）沿着径向方向逐渐增大，如图17所示。以某一等位线L为例，L内部的电场强度（电位降）明显低于其外部，为方便下文叙述，本文将这种电场强度较低的区域简称为“屏蔽区域”。需要说明的是，当流注头处于屏蔽区域内时，其表面电场强度会受到一定程度的影响而降低；而当流注头超出屏蔽区域时，其表面电场强度则受屏蔽区域的影响较小。
图15、图16分别分析了相同结构、相同电位条件下的特高压GIS隔离开关气隙击穿过程中发生两次击穿和仅发生一次击穿的情形。为更直观地说明引起两次击穿的机理，本节对两次气隙击穿过程中动静触头间完成第一次击穿时次级流注头P2的空间位置进行了对比，如图18所示。图中红色“×”符号表示图15中次级流注头P2在动静触头间发生击穿时（t=61 ns）的空间位置，紫色“〇”符号表示图16中相同情况下P2的位置，蓝色虚线所囊括的区域表示屏蔽罩的屏蔽区域。可以看出，图15中发生二次击穿的直接原因是：动静触头间第一次击穿完成时，某个次级流注头已经发展至屏蔽区域外，该次级流注头受到的屏蔽作用较弱，其表面电场强度在动触头与壳体的电位差下可能会超过气体的临界击穿场强，进而发生动触头与壳体间的二次击穿，形成两条放电通道；反之，若动静触头间第一次击穿完成时，次级流注头仍在屏蔽区域内，其受到屏蔽作用较强，表面电场强度仍保持较低水平，则二次击穿现象不容易发生。
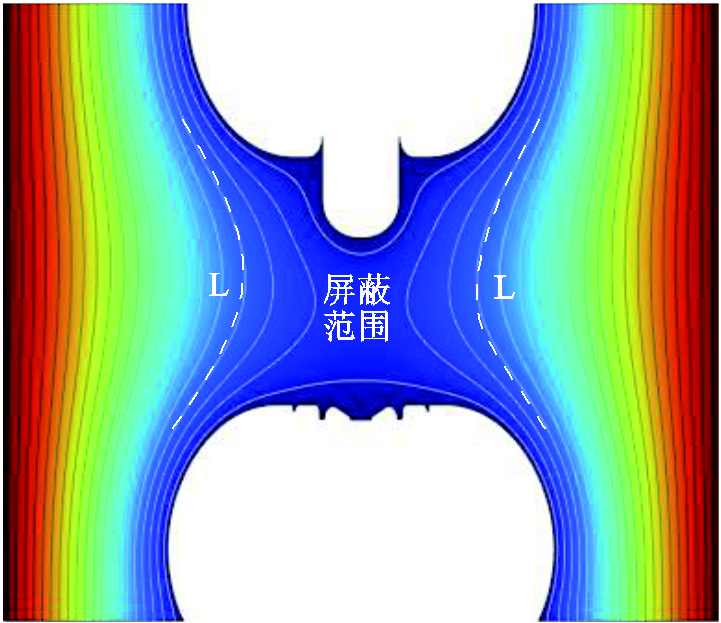
图17 “屏蔽区域”概念说明
Fig.17 Description of the concept of "shielding area"
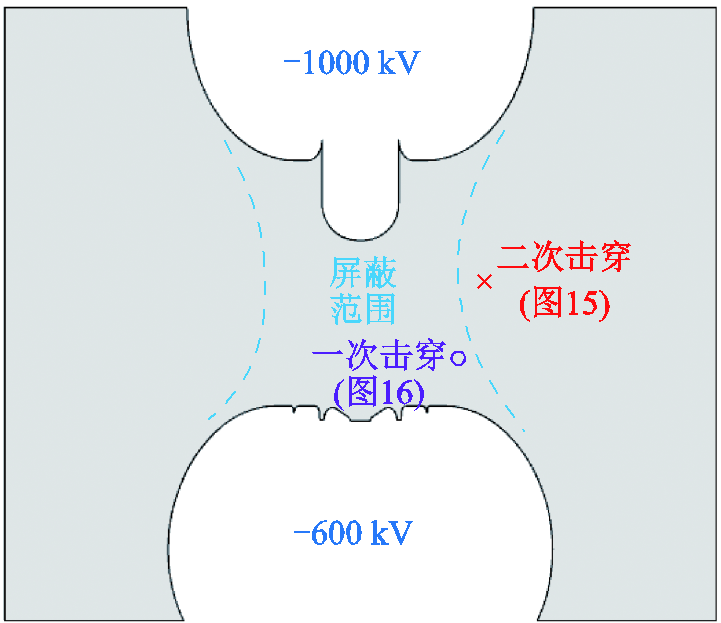
图18 二次击穿机理示意图
Fig.18 Diagram of secondary breakdown mechanism
根据4.3节中的分析可知，在特高压GIS隔离开关放电过程中，若确保次级流注头P2在第一次击穿完成时不超出屏蔽区域，则可以有效地避免二次击穿的发生。根据这一结论，本节对200、120、80 mm间距下的击穿过程分别进行了仿真。当动静触头间第一次击穿完成时，三种间距下次级流注头P2的发展状态如图19所示。触头的间距越小，第一次击穿发生时次级流注头的空间位置P2越不容易超出屏蔽区域，甚至在触头间距为80 mm时，流注的分叉行为也会消失，进而抑制了二次击穿现象的产生。
对200 mm和120 mm间距下第一次击穿完成时P2的位置进行多次仿真和统计，结果如图20所示。可以发现在120 mm间距下，第一次击穿完成时P2位置均未超出屏蔽区域；而在200 mm间距下，P2位置有两次超过屏蔽区域（进而发生二次击穿）。这主要是因为较短的动静触头间距提高了轴向电场强度分量（动触头指向静触头方向），且缩短了第一次击穿所需的时间，从而导致次级流注头P2没有足够的径向空间电场强度和时间发展超过屏蔽区域，因而不会发生二次击穿现象。
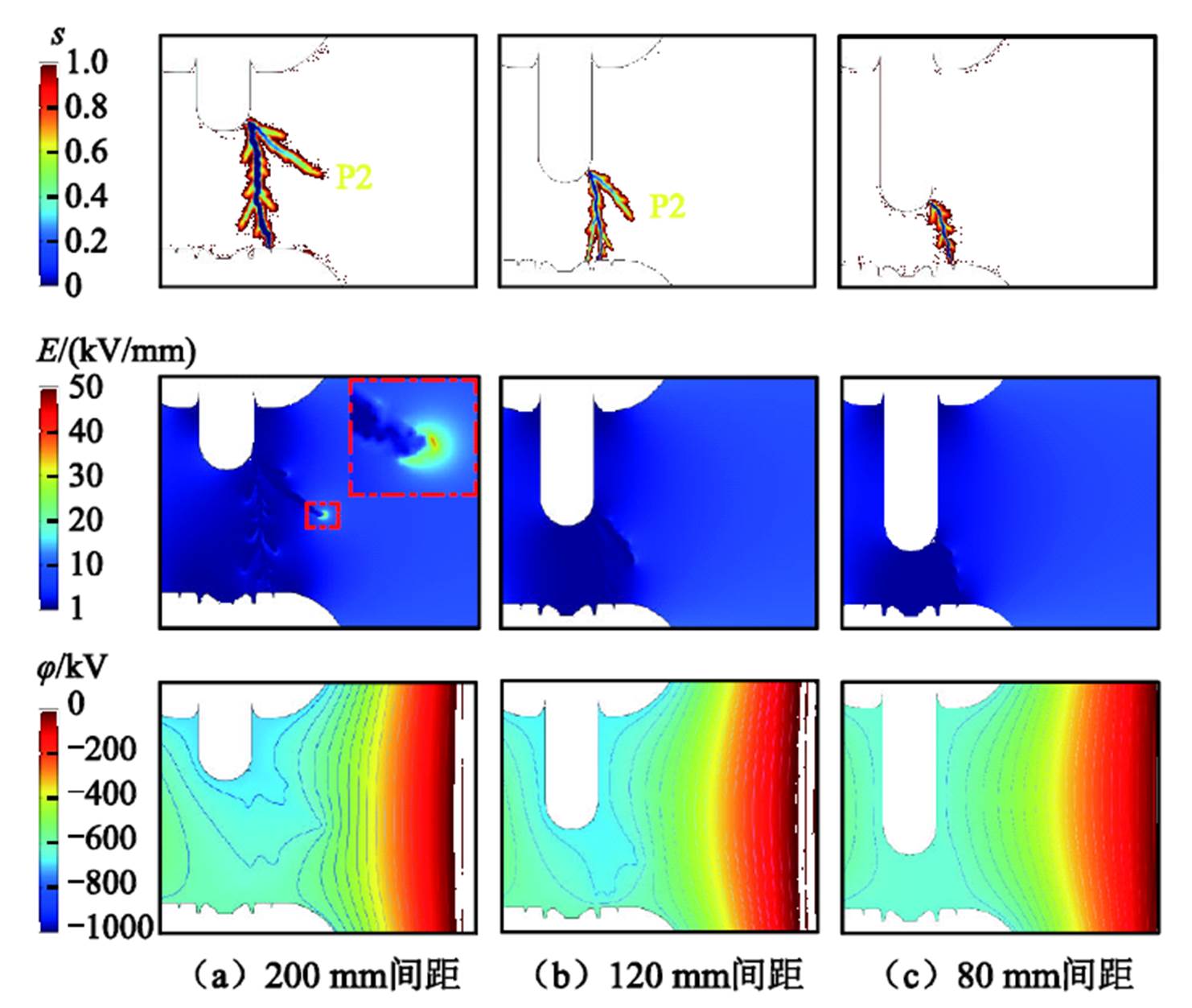
图19 不同间距下次级流注发展对比
Fig.19 Comparison of secondary streamer development at different distances
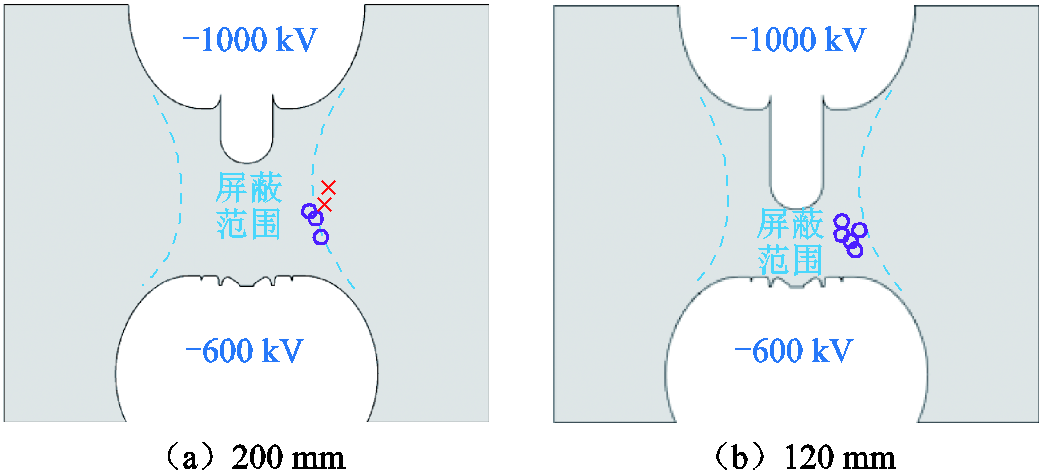
图20 不同间距下一次击穿完成时次级流注头位置分布
Fig.20 Distribution of secondary streamer head position at the completion of the first breakdown at different distances
除了降低第一次击穿时的动静触头间距，还可以通过增大屏蔽区域来抑制二次击穿现象的发生。为了更直观地说明这一措施，本节对788 mm直径屏蔽罩、200 mm触头间距情况下的特高压隔离开关放电过程进行了模拟，电位条件同图14，其一次击穿完成时的仿真结果与图15过程的对比如图21所示，多次重复仿真过程中统计的第一次击穿时刻次级流注头P2位置对比如图22所示。从图21和图22中可以看出，由于屏蔽区域的扩大，动静触头间第一次击穿完成时次级流注头P2难以超过屏蔽区域，因而难以发生二次击穿现象。
图21 不同屏蔽罩结构次级流注发展对比
Fig.21 Comparison of secondary streamer development at different shield
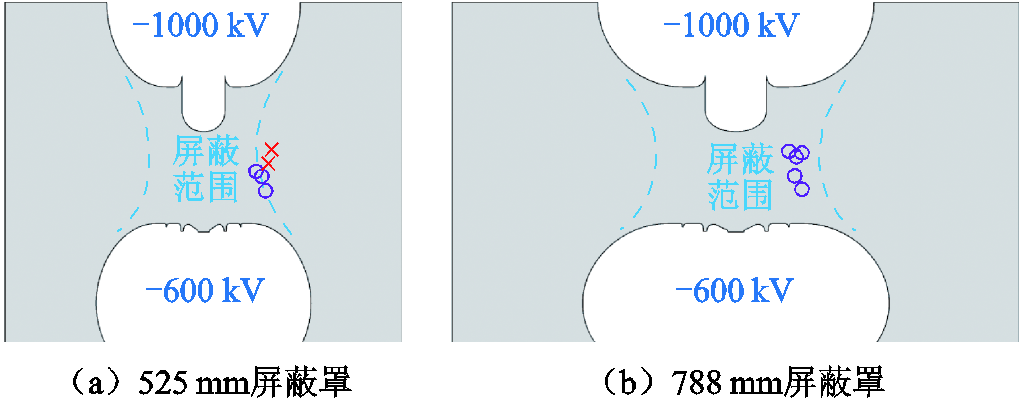
图22 不同屏蔽罩一次击穿完成时次级流注头位置分布
Fig.22 Distribution of secondary streamer head position at the completion of the first breakdown at different shield
针对特高压GIS隔离开关中的流注分叉及其引起的对地二次击穿现象模拟困难的问题，本文提出了一种基于相场法的气体击穿模拟方法。首先，将流注发展过程等效为气体由绝缘相转变为导电相的相变过程；其次，通过求解一阶近似Boltzmann方程构建击穿能密度函数，进而建立适用于气体击穿的长距离气体击穿模拟方法，并与PIC-MCC方法计算小尺寸双阳极流注放电模型的仿真结果进行对比，验证本文方法的有效性；最后，采用基于相场法的气体击穿模拟方法对特高压GIS隔离开关切合短母线过程中产生二次击穿的机理进行了探究。结果表明：
1）将流注放电等效为气体的“绝缘-导电”相变过程，避免了对气体组分中大量粒子的碰撞进行模拟，极大地节约了计算成本；与PIC-MCC方法相比，网格数减少了98%以上，大大降低了计算机的内存占用和计算时间。
2）基于相场法的流注放电模型可以较好地模拟流注茎的发展路径及流注头的发展速度，与PIC-MCC方法计算结果相比，主流注头路径区域重叠面积约为90%，次级流注头路径区域重叠面积约为70%，击穿时间差异小于11%。
3）特高压GIS隔离开关在切合短母线过程中，当动静触头间第一次击穿完成时，若存在某一次级流注头发展至屏蔽罩的屏蔽区域外，则会出现动触头与壳体之间的二次击穿现象。
4）增大动触头表面的曲率半径，减少动触头表面的毛刺缺陷，进而降低第一次击穿时的动静触头间距，可以有效地限制次级流注的发展，控制其流注头不超过屏蔽罩的屏蔽区域，以抑制特高压GIS隔离开关对地二次击穿现象的发生。
5）增加屏蔽罩的尺寸以扩大其屏蔽区域，也可以有效地抑制特高压GIS隔离开关对地二次击穿现象的发生。
参考文献
[1] 刘振亚. 特高压电网[M]. 北京: 中国经济出版社, 2005.
[2] 韩先才, 孙昕, 陈海波, 等. 中国特高压交流输电工程技术发展综述[J]. 中国电机工程学报, 2020, 40(14): 4371-4386, 4719.
Han Xiancai, Sun Xin, Chen Haibo, et al. The overview of development of UHV AC transmission technology in China[J]. Proceedings of the CSEE, 2020, 40(14): 4371-4386, 4719.
[3] 刘鹏, 郭伊宇, 吴泽华, 等. 特高压换流站大尺寸典型电极起晕特性的仿真与试验[J]. 电工技术学报, 2022, 37(13): 3431-3440.
Liu Peng, Guo Yiyu, Wu Zehua, et al. Simulation and experimental study on corona characteristics of large size typical electrodes used in UHV converter station[J]. Transactions of China Electrotechnical Society, 2022, 37(13): 3431-3440.
[4] 苏春强, 丁登伟, 李强, 等. GIS隔离开关方式1试验中断口对地击穿时光电暂态过程监测与分析[J]. 高压电器, 2022, 58(5): 56-62.
Su Chunqiang, Ding Dengwei, Li Qiang, et al. Monitoring and analysis of optical and electric transient process induced by breakdown-to-ground during type test duty 1 of GIS disconnector[J]. High Voltage Apparatus, 2022, 58(5): 56-62.
[5] 申萌, 丁登伟, 李强, 等. GIS隔离开关开合短母线型式试验方式1中VFTO测量系统构建及波形解析[J]. 高压电器, 2022, 58(7): 207-213.
Shen Meng, Ding Dengwei, Li Qiang, et al. Construction of VFTO measurement system and waveform analysis for switching test duty 1 of short busbar by GIS disconnector[J]. High Voltage Apparatus, 2022, 58(7): 207-213.
[6] 王安琪. 1100 kV GIS特快速暂态过电压研究[D]. 厦门: 厦门理工学院, 2020.
Wang Anqi. Research on very fast transient overvoltage of 1100 kV GIS[D]. Xiamen: Xiamen University of Technology, 2020.
[7] Morrow R. Theory of negative corona in oxygen[J]. Physical Review A, General Physics, 1985, 32(3): 1799-1809.
[8] Aleksandrov N L, Bazelyan E M. Simulation of long-streamer propagation in air at atmospheric pressure[J]. Journal of Physics D: Applied Physics, 1996, 29(3): 740-752.
[9] Bourdon A, Pasko V P, Liu N Y, et al. Efficient models for photoionization produced by non-thermal gas discharges in air based on radiative transfer and the Helmholtz equations[J]. Plasma Sources Science Technology, 2007, 16(3): 656-678.
[10] Beloplotov D V, Sorokin D A, Lomaev M I, et al. Formation of a negative streamer in a sharply nonuniform electric field and the time of generation of runaway electrons[J]. Russian Physics Journal, 2020, 62(11): 1967-1975.
[11] 臧奕茗, 钱勇, 刘伟, 等. C4F7N/CO2混合气体中尖端缺陷的流注放电仿真研究[J]. 电工技术学报, 2020, 35(1): 34-42.
Zang Yiming, Qian Yong, Liu Wei, et al. Simulation study on streamer of tip defects in C4F7N/CO2 mixed gas[J]. Transactions of China Electrotechnical Society, 2020, 35(1): 34-42.
[12] He Wei, Liu Xinghua, Yang Fan, et al. Numerical simulation of direct current glow discharge in air with experimental validation[J]. Japanese Journal of Applied Physics, 2012, 51(2R): 026001.
[13] Gao Qingqing, Niu Chunping, Adamiak K, et al. Numerical simulation of negative point-plane corona discharge mechanism in SF6 gas[J]. Plasma Sources Science and Technology, 2018, 27(11): 115001.
[14] Zeng F, Zhang M, Yang D, et al. Hybrid numerical simulation of decomposition of SF6 under negative DC partial discharge process[J]. Plasma Chemistry and Plasma Processing, 2019, 39(1): 205-226.
[15] Dawson J. One-dimensional plasma model[J]. Physics of Fluids, 1962, 5(4): 445-459.
[16] Dawson J M. Thermal relaxation in a one-species, one-dimensional plasma[J]. The Physics of Fluids, 1964, 7(3): 419-425.
[17] Liewer P C, Decyk V K. A general concurrent algorithm for plasma particle-in-cell simulation codes[J]. Journal of Computational Physics, 1989, 85(2): 302-322.
[18] Vahedi V, Surendra M. A Monte Carlo collision model for the particle-in-cell method: applications to argon and oxygen discharges[J]. Computer Physics Communications, 1995, 87(1/2): 179-198.
[19] 段韶峰. GIS隔离开关瞬态电弧的建模与仿真[D]. 北京: 华北电力大学, 2016.
Duan Shaofeng. Modeling and simulation of very fast transient spark in disconnecting switch of gas insulated switchgear[D]. Beijing: North China Electric Power University, 2016.
[20] Suo Z. Models for breakdown-resistant dielectric and ferroelectric ceramics[J]. Journal of the Mechanics and Physics of Solids, 1993, 41(7): 1155-1176.
[21] Beom H G, Kim Y H. Application of J integral to breakdown analysis of a dielectric material[J]. International Journal of Solids and Structures, 2008, 45(24): 6045-6055.
[22] Chaitanya Pitike K, Hong Wei. Phase-field model for dielectric breakdown in solids[J]. Journal of Applied Physics, 2014, 115(4): 044101.
[23] Shen Zhonghui, Wang Jianjun, Jiang Jianyong, et al. Phase-field modeling and machine learning of electric-thermal-mechanical breakdown of polymer-based dielectrics[J]. Nature Communications, 2019, 10(1): 1843.
[24] Mi Zhang, Zhang Yong, Hou Xu, et al. Phase field modeling of dielectric breakdown of ferroelectric polymers subjected to mechanical and electrical loadings[J]. International Journal of Solids and Structures, 2021, 217: 123-133.
[25] Li Jin, Wang Yufan, Liu Songtao, et al. Thermal-elastic free energy driven electrical tree breakdown process in epoxy resin under temperature gradient[J]. Materials Today Communications, 2022, 33: 104951.
[26] 李长云, 李岩青, 于永进. 大气条件下厘米级棒-板间隙负极性电晕放电中流注的产生与发展机制[J]. 电工技术学报, 2024, 39(3): 887-900.
Li Changyun, Li Yanqing, Yu Yongjin. The generation and development mechanism of streamers in centimeter-level rod-plate gap negative corona discharge under atmospheric conditions[J]. Transactionsof China Electrotechnical Society, 2024, 39(3): 887-900.
[27] 彭长志, 董旭柱, 赵彦普, 等. 正极性先导起始与发展过程中的等离子体特征[J]. 电工技术学报, 2023, 38(2): 533-541.
Peng Changzhi, Dong Xuzhu, Zhao Yanpu, et al. Plasma characteristics of positive leader inception and development[J]. Transactions of China Electrotechnical Society, 2023, 38(2): 533-541.
[28] Morrow R. A survey of the electron and ion transport properties of SF6[J]. IEEE Transactions on Plasma Science, 1986, 14(3): 234-239.
[29] 赵虎, 李兴文, 贾申利. SF6及其混合气体临界击穿场强计算与特性分析[J]. 西安交通大学学报, 2013, 47(2): 109-115.
Zhao Hu, Li Xingwen, Jia Shenli. Calculation and characteristic analysis of critical breakdown field strength of SF6 and the mixtures[J]. Journal of Xi’an Jiaotong University, 2013, 47(2): 109-115.
[30] Yousfi M, Robin-Jouan P, Kanzari Z. Breakdown electric field calculations of hot SF6 for high voltage circuit breaker applications[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2005, 12(6): 1192-1200.
[31] The LXCat Team. Biagi (transcription of data from SF Biagi's Fortran code, Magboltz) database[DB/OL]. (2021-02-11)[2023-10-16]. https://www.lxcat.net/Biagi.
[32] Christophorou L G, Olthoff J K. Electron interactions with SF6[J]. Journal of Physical and Chemical Reference Data, 2000, 29(3): 267-330.
Abstract Gas insulated switchgear (GIS) is the core equipment in ultra-high voltage (UHV) transmission engineering, and its reliability is directly related to the safe and stable operation of the power system. In recent years, the phenomenon of secondary breakdown to ground has been observed during the process of closing short busbar in the UHV GIS disconnector: In the disconnector, besides the discharge channel between the static and dynamic contacts, a discharge channel from the electrode to the ground is formed, which then lead to a fault warning. This problem poses a serious insulation threat to the UHV GIS equipment and affects the stable operation of the UHV GIS equipment. However, since previous studies were mainly concerned with the very fast transient overvoltage (VFTO) generated during the operation of the disconnector, and insufficient attention has been paid to the breakdown characteristics during the operation of the disconnector. Therefore, the current understanding of the mechanism of secondary breakdown during the process of closing short busbar in the UHV GIS disconnector is weak. To address this problem, the simulation work for the secondary breakdown phenomenon during the process of closing short busbar in the UHV GIS disconnector are carried out and analyzed.
Firstly, a method for simulating the long distance stream discharge bifurcation with low computational cost is proposed, which solves the problem that the traditional stream discharge simulation methods require too much computational cost to simulate the long distance (hundreds millimeters or more) stream discharge bifurcation. Subsquently, the proposed method is compared with the particle in cell-Monte Carlo collision (PIC-MCC) method by taking a small size (several millimeters) model as an example, which proves the rationality of the proposed method. Compared with the calculation results of PIC-MCC method, the overlap area of the main streamer development path is about 90%, the overlap area of the secondary streamer development path is about 70%, the breakdown time difference is less than 11%, and the grid resources required for the proposed method are only 2% of the PIC-MCC method. Finally, the breakdown phenomenon during the process of closing short busbar in the UHV GIS disconnector was repeatedly simulated by using the long distance stream discharge bifurcation simulation method based on the phase field method. The mechanism of the secondary breakdown was revealed and the factors affecting the secondary breakdown were explored.
The results of the study reveal that if there exists a certain secondary streamer head develops outside of the shielding area of the shielding cover, when the first breakdown between the static and dynamic contacts is finished during the process of closing short busbar in the UHV GIS disconnector, the secondary breakdown between the contacts and the shell will occur. Increasing the curvature radius of the contact surface and reducing the burr defects on the contact surface, which can reduce the spacing between the static and dynamic contacts at the time of the first breakdown, will effectively limit the development of the secondary streamer, and then prevent the head of secondary streamer exceeding the shielding area of the shielding cover, and finally inhibit the occurrence of the secondary breakdown phenomenon during the process of closing short busbar in the UHV GIS disconnector. Increasing the size of the shielding cover to enhance its shielding area can also effectively inhibit the occurrence of the secondary breakdown phenomenon during the process of closing short busbar in the UHV GIS disconnector.
keywords：Ultra-high voltage, gas insulated switchgear (GIS), disconnector, secondary breakdown, phase field method
中图分类号：TM561
DOI: 10.19595/j.cnki.1000-6753.tces.231381
国家电网有限公司科技资助项目（5500-202255135A-1-1-ZN）。
收稿日期 2023-08-25
改稿日期 2023-10-10
崔建男，1992年生，博士研究生，研究方向为电弧等离子体及其输运现象。
E-mail：cuijian_bachelor@stu.xjtu.edu.cn
张国钢 男，1976年生，教授，博士生导师，研究方向为智能电器理论与工程、储能与新能源电力系统以及电弧等离子体与电接触等。
E-mail：ggzhang@mail.xjtu.edu.cn（通信作者）
（编辑 李 冰）