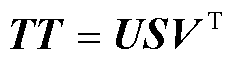（1）
摘要 为了提高油浸式电力变压器绕组瞬态温升的计算效率，提出了一种基于离散监测点的温度场降阶计算方法。该方法以绕组内部若干离散监测点的温度信息为输入，以基于本征正交分解的降阶算法为载体，建立瞬态过程中温度场的快速反演模型，从而实现从监测点数据到温度场全域的快速计算。首先分析了本征正交分解算法的降阶特性，在此基础上建立了从场域内离散监测点数据到降阶模态，再到温度场全域的快速计算策略。为了验证算法的有效性，该文根据油浸式电力变压器绕组结构特点建立二维八分区分匝绕组传热模型，并对比了所提出的降阶计算方法与全阶计算方法的精度和效率，结果表明，二者的最大平均计算偏差仅为1.03 K，摄氏温标下温升的最大平均相对误差不超过5%，且降阶计算时间仅为0.18 s，相较于全阶计算获得了较高的效率提升。最后，依靠110 kV油浸式变压器绕组温升试验平台，通过测量绕组实际的温升情况，对算法的性能进一步验证，相关结果表明所提算法各时刻的计算结果与测量结果相比最大误差不超过4.67 K，且各测量线饼的平均误差不超过1.02 K，在工程上属于可接受的范围。同时，所提算法对绕组瞬态温升全过程的计算时间仅为3.40 s，初步实现了实际工程场景下对于绕组瞬态温升快速计算的要求。
关键词：油浸式电力变压器 本征正交分解 离散监测点 快速计算方法
油浸式电力变压器是电网实现电压变换和电能传输的关键核心设备，对其状态的准确评估及在此基础上的可靠运行是电网安全稳定的基础。随着变压器投运年限的增长，设备内部结构长期承受复杂多物理场的联合作用，使得各类运行故障频发，其中绕组过热是引发变压器诸多故障的主要诱因之一[1-3]。油浸式电力变压器绕组温升是一个涉及流场和温度场的耦合问题，对于绕组温度的计算，在当前的解决方案中，较为常见的是采用数值计算方法求解流热耦合控制方程，如：谢裕清等[4]采用最小二乘有限元法与迎风有限元法对油浸式电力变压器的流热耦合问题进行了计算；彭丽丹[5]采用QUICK格式的有限体积法确定了电力变压器油的速度场分布及绕组的温度场分布。然而，由于油浸式电力变压器的结构复杂、材料类型及边界多、实景尺寸大，使得流热耦合问题形成的离散方程组具有高阶数、非线性、强耦合等特点[6-7]，采用数值方法计算的时间成本一般较高，无法满足当下对于变压器状态数字化实时性要求。
为了快速获得绕组的温度场信息，随着计算机技术的高速发展，人工神经网络、支持向量机回归等机器学习算法开始应用于绕组温度计算领域，如：邓永清等[6]分析了变压器内部热流扩散规律，通过提取流经绕组热点区域与外壳散热区域的典型热流流线，并采用网格搜索法优化的支持向量回归机构建特征测温点温度与绕组热点温度间的多维非线性和模糊神经网络算法的油浸式变压器热点温度反演模型，通过T-S模糊神经网络算法预测变压器绕组热点温度值。这类基于机器学习算法的代理模型通过等效或者智能寻优的方式，简化了流热耦合中流场与温度场之间复杂的隐性关系，跳过了大规模非线性方程组的低效计算，从而达到快速获得温度场信息的目的。然而，上述算法一般只能针对场域内有限个特殊点构造代理模型，无法获得绕组上全场域的温度分布，且高精度的代理模型一般要求较多的样本数据作为训练集，其训练的时间成本较高，很难应用于实际工程环境。
因此，为了能够在低构建成本的前提下快速获得绕组温度分布，从20世纪90年代开始[9-10]，降阶计算方法（Reduced Order Method, ROM）逐渐应用于各工程领域的数值计算当中[11-13]。该方法通过构建降阶计算模型，降低复杂系统的计算维度，在保留高维或无限维系统重要特征的前提下，实现高效计算，其中本征正交分解方法（Proper Orthogonal Decomposition, POD）是目前为止较为有效且数值稳定性较强的方法之一[14-16]。在油浸式电力变压器绕组温度计算领域，已有采用POD方法及其衍生方案进行快速计算的报道，如：刘刚等[17]采用POD方法基于最小二乘有限元离散方程对变压器绕组的瞬态温升进行了计算；胡万君等[18]结合POD方法与离散经验插值方法（Discrete Empirical Interpolation Method, DEIM）构造了变压器绕组稳态温度计算的降阶计算模型并实现了快速获得单分区绕组温度。但是，考虑到工程级油浸式电力变压器规模较大，空间离散之后的网格与节点数量较多，现有基于物理方程构造的降阶模型也很难做到快速计算，这是限制降阶技术发展的瓶颈之一。
综上所述，降阶技术是当前快速获得变压器绕组温度分布的有效方法之一，为了进一步提高基于本征正交分解方法的降阶模型计算效率，本文考虑充分利用POD方法的降阶特性，提出一种采用场域内若干离散监测点的温度信息快速反演物理场的计算方法。文章通过推导场域内离散监测点与降阶计算模型的对应关系，构造从监测点数据到降阶模态再到全场温度的计算流程，从而跳过传统降阶计算中需要进行复杂非线性迭代的效率瓶颈，进而实现变压器绕组瞬态温升的快速计算。为了验证方法的有效性，本文依靠110 kV变压器绕组温升试验平台开展瞬态温升试验，通过将文章所提算法的计算结果与试验过程中绕组的温升记录结果做对比，讨论算法的精度、效率等相关性能。
为了建立场域内部离散监测点与全场温度分布的关系，首先需要通过降阶算法构造高阶模型的低维计算空间，本文采用的是本征正交分解方法。对于油浸式电力变压器绕组的瞬态温升计算，假设前m个时间步的计算结果为[T1 T2 … Tm]∈Rn×m，该计算结果可以通过全场域的数值计算获得（将其称之为全阶数据），将这些全阶结果组成快照矩阵（snapshot）TT=[T1 T2 … Tm]，对快照矩阵进行奇异值分解为
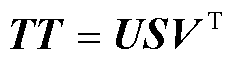（1）
式中，U、V分别为通过奇异值分解得到左、右正交矩阵；S为对角矩阵，对角线上元素为快照矩阵TT的奇异值，且按照从大到小的顺序依次排列。由于S中前d个奇异值的大小往往远大于其后的奇异值，因此可以将快照矩阵TT近似表示为
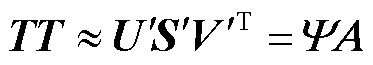（2）
式中，U'∈Rn×d，S'∈Rd×d，V'∈Rm×d，Ψ=[φ1 φ2 … φd]∈Rn×d，A=[α1 α2 … αm]∈Rd×m，d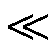
n。这样,原矩阵中表示每一时步温度场分布的全阶列向量T∈Rn×1，可通过阶数较低的列向量α∈Rd×1结合降阶正交基Ψ获得，从而达到降低计算阶数的目的。降阶阶数d的取值通过式（3）得到。
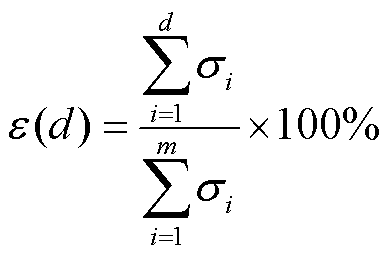（3）
一般情况下，当ε(d)≥99.9%时，即可通过前d阶奇异值及对应的正交基矩阵近似表示原全阶矩阵，且能够保证降阶误差较小。综上，即通过POD方法建立了全场域温度分布与降阶模态及其系数的对应关系（如式（4）为第k时间步温度场的降阶表示），在此基础上本文进一步构建从离散监测点温度信息到温度场全域分布的快速计算策略。
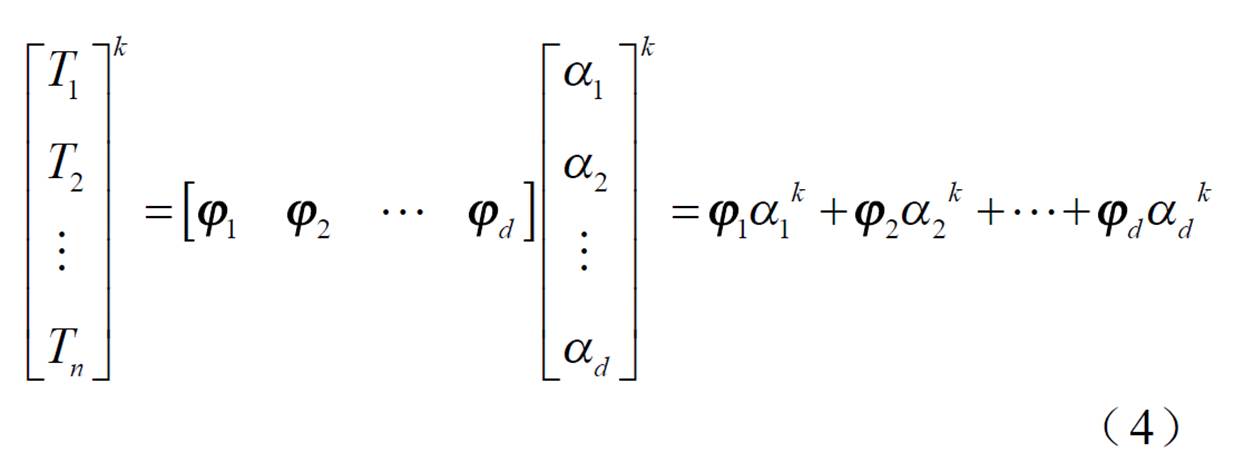
假设某一时刻能够通过场域内部的测量装置获得若干监测点的温度信息为
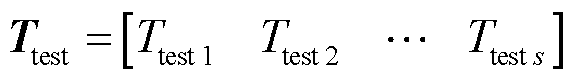（5）
考虑利用POD降阶模型建立监测点与全场域温度分布之间的关系。若利用POD模态重构这s个点位的温度，则需要满足
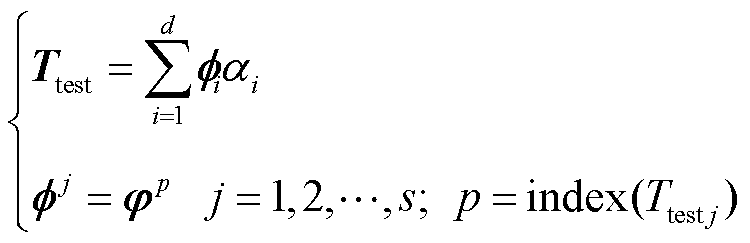（6）
式中，上角标j表示矩阵中的行号，下角标i表示监测点序号，矩阵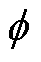
共有s行，其第j行（
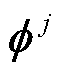）对应POD模态矩阵φ中的第p行（
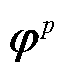），这里p又指第j个测量点位的节点标号（如图1所示）。
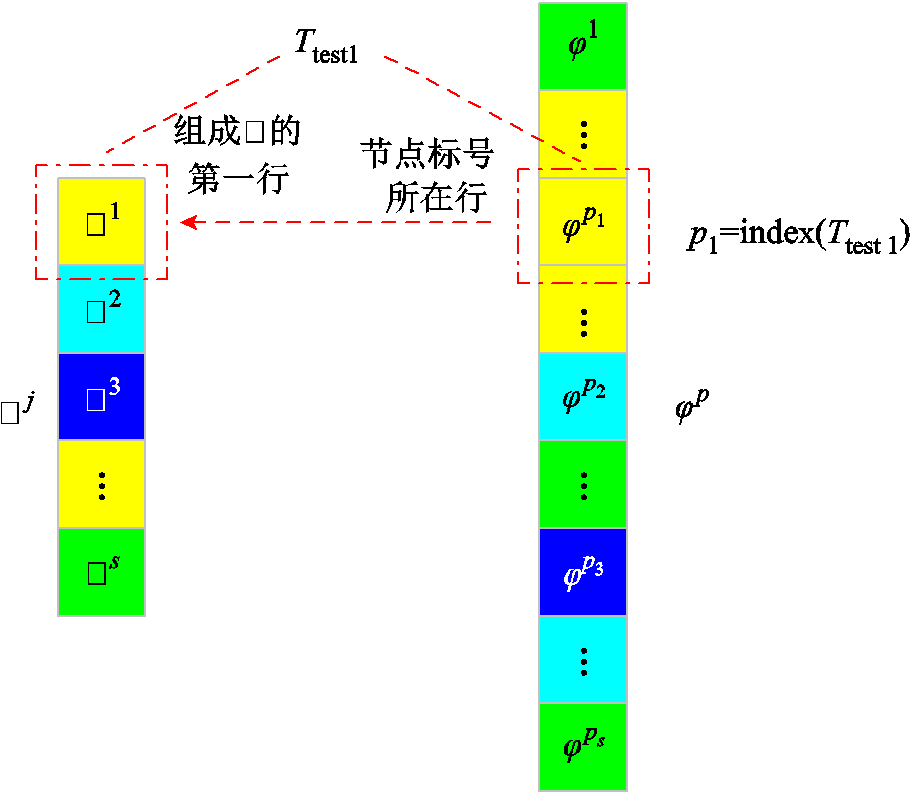
图1 矩阵元素对应关系
Fig.1 Matrix element correspondence
式（6）是一个包含s个未知数的方程组，当s=d时，α存在精确解为
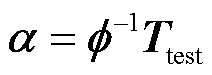（7）
当s≠d时，其存在最小二乘解为
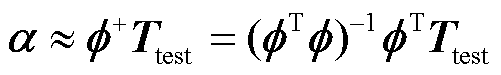（8）
式中，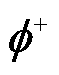
表示Moore-Penrose伪逆。通过式（8）即可获得温度场降阶模型中的POD模态系数α，其即可结合POD模态矩阵φ快速获得绕组温度全场域分布，即
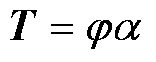（9）
为了保证温度场反演的准确性，场域内部监测点位置的选取至关重要。根据式（6）可以看出，基于离散测量点的温度场反演本质上是通过有限个已知点对未知点进行离散插值，因此，为了提高计算精度，本文引入一种基于列主元QR分解的离散点选取策略[19]，对降阶模态矩阵φ进行列主元QR分解，得到
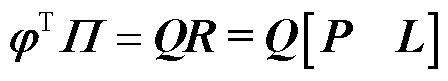（10）
式中，列主元置换矩阵Π的前r列中元素1所在位置即为监测点选取位置，由于上三角矩阵R中对角线上各元素遵循绝对值从大到小排列，因此，可以通过置换矩阵Π选取φ的前r行，以较小误差近似反映原矩阵。基于Matlab编程语言的监测点选取策略伪代码段见表1。
表1 监测点选取的步骤
Tab.1 Steps for selecting discrete points
输入：φ∈Rn×d 输出：监测点位置矩阵index 1. [n,m]=size(φ); 2. [Q,R,E]=qr [φ', ’vector’]; 3. index=E(:,1:m); end
如表1所示，在算例中，对降阶模态矩阵的转置φT进行列主元QR分解（即式（10）），因此，获得的最佳监测点数量不超过降阶模态矩阵的阶数，即若降阶模态矩阵阶数为3，那么通过式（10）即可获得3个最佳监测点位置。根据文献[19]中的相关推导能够得知，采用这3个监测点位置对应的温度对全场域温度进行反演具有较好的误差上限[19]，即
（11）
综上所述，即建立了从离散监测点的温度信息反演绕组温度分布的快速计算方法。算法流程如图2所示，该方法中，POD模态矩阵φ可以通过对快照矩阵的一次计算得到，模态系数α则经由式（7）通过离散监测点的温度信息获得，而瞬态过程中每一时步的绕组温度分布则可以在此基础上通过以上二者的乘积T=φα得到。由于该方法不存在复杂的非线性计算及大规模的方程组迭代过程，因此，理论上具有较高的计算效率。
图2 算法流程
Fig.2 Flow chart of the algorithm
为了验证本文所提算法在油浸式电力变压器绕组瞬态温升计算中的正确性，本文基于变压器饼式绕组基本结构，建立了八分区分匝绕组数值计算模型，并在该模型中对算法性能进行讨论。
二维八分区分匝绕组模型如图3所示。本文建立的油浸式电力变压器绕组模型包含66个线饼，74条油道以及7个挡板，将相邻两个挡板之间的部分划分为一个分区。其中，分区1～3包含7个线饼，其余分区包含9个线饼，油流在每个分区中以S形运动轨迹充分与绕组表面接触并带走热量。为了便于分析讨论，将线饼从上至下编号为线饼1～66，将油道从上至下编号为油道1～74。其中，每个线饼包含30个线匝，将每个线饼的线匝从左至右编号为线匝1～30。模型经网格剖分后共2 022 371个节点，网格已经过独立性验证，由于油道和线饼、油道和挡板边界间的速度变化剧烈，且线匝与绝缘纸边界间的温度变化剧烈，因此为了保证有限元方法的计算精度，这部分网格采用更为精细的边界层剖分。非边界区域网格尺寸为0.5 mm，边界层设置为2层，区域第一层高度为0.1 mm，网格高度增长率为1.1。模型的结构如图3所示。采用的物性参数见表2[20]。
图3 二维八分区分匝绕组模型
Fig.3 2-D eight zone split turn winding model
表2 物性参数[20]
Tab.2 Physical parameters[20]
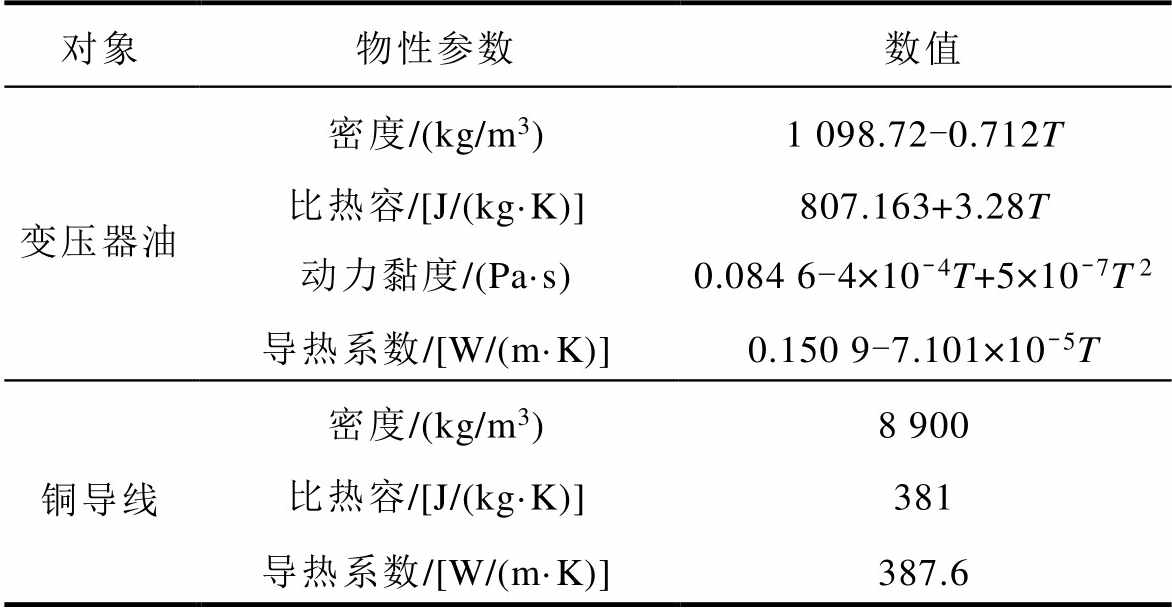
对象物性参数数值 变压器油密度/(kg/m3)1 098.72-0.712T 比热容/[J/(kg·K)]807.163+3.28T 动力黏度/(Pa·s) 0.084 6-4×10-4T+5×10-7T2 导热系数/[W/(m·K)]0.150 9-7.101×10-5T 铜导线密度/(kg/m3)8 900 比热容/[J/(kg·K)]381 导热系数/[W/(m·K)]387.6
（续）
对象物性参数数值 绝缘油纸密度/(kg/m3)980 比热容/[J/(kg·K)]2 000 导热系数/[W/(m·K)]0.25 挡板密度/(kg/m3)700 比热容/[J/(kg·K)]2 310 导热系数/[W/(m·K)]0.17
油浸式电力变压器绕组温升计算是一个涉及流场及温度场的耦合问题，其控制方程为[20]
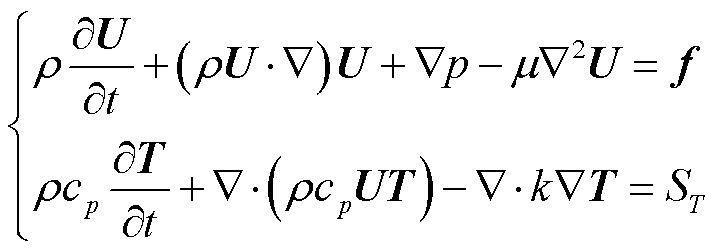（12）
式中，ρ为密度；μ为流体动力粘度系数；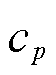
为比定压热容；k为热导率；U为流体速度矢量，由横向速度u及纵向速度v两个分量构成；p为流体压强；T为温度；f为外力密度矢量，当不考虑重力时，其为0；ST为热源密度。
根据上述控制方程，设置模型在数值计算中的边界条件如下：
（1）入口油流速度：入口横向速度u=0 m/s；入口纵向速度v=0.1 m/s。
（2）出口油流压强：出口压强p=0 Pa。
（3）挡板及绝缘筒：u=v=0 m/s。
（4）环境温度：Ta=290 K。
（5）绕组热源：参考文献[4]，以热源密度ST为单位，将其设置为随温度变化的函数为
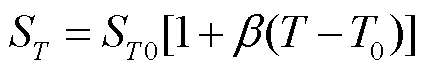（13）
式中，ST0为温度等于T0时的热源密度，热源密度通过绕组损耗与绕组导热体积相除得到；β为绕组导体温度系数，可取0.003 93 K-1。
模型初始条件为：①绕组和油流的初始温度T0=290 K；②绝缘筒内变压器油初始速度u=v=0 m/s。
模型瞬态计算参数为：①时间步长：初始设置为∆t=0.02 s，当流场稳定之后，设置为∆t=10 s；②仿真时间：设置仿真计算总时间为tmax=2 000 s；③收敛判据：流场的收敛判据为∆U＜0.000 1 m/s，温度场的收敛判据为∆T＜0.001 K。
建立POD降阶模型首先需要获得快照矩阵，通过全阶计算（Fluent仿真计算）获得0～200 s温度场各节点的温升情况，并将计算结果组成快照矩阵TT=[T10T20…T200]。根据式（1）与式（3）对快照矩阵进行奇异值分解并获得其奇异值分布情况，如图4所示。
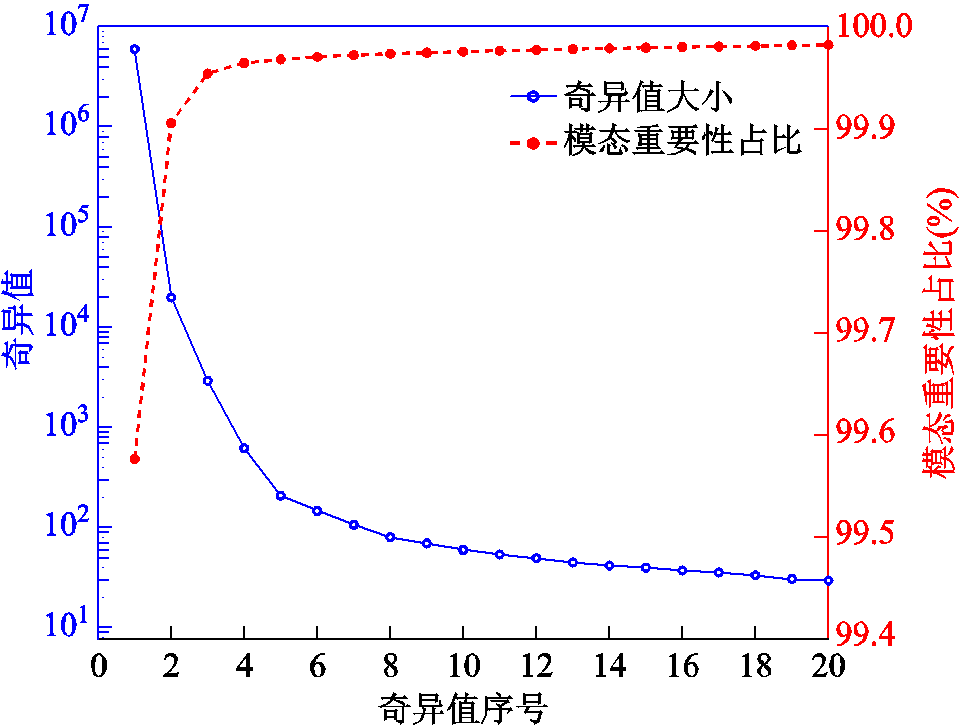
图4 奇异值大小及模态重要性占比
Fig.4 Singular value size and mode importance proportion
从图4中可以看出，快照矩阵前三阶奇异值大小远远大于其后的所有奇异值，且前三阶奇异值根据式（3）计算得到的重要性占比已经超过99.9%，因此理论上能够通过POD的前3阶主要模态近似还原全阶温度场。为了进一步说明这一点，绘制第200 s温度场在不同模态下的云图如图5a所示，可以看出POD的第一模态已经包含了场域的绝大部分温度场分布信息，第二、第三模态反映的温度场信息逐渐减少。如图5b所示，当采用前2阶POD模态还原第200 s的温度场时，场域最大误差超过0.5 K；而当采用前3阶POD模态还原时，场域最大误差仅为0.35 K，如图5c所示。因此，本文通过前3阶POD模态构建的降阶计算模型能够较为精确地反映原全阶模型温度场分布。
完成降阶模型的构建之后，通过式（10）获得最佳监测点位置。由于降阶模态矩阵φ的行数与模型节点数相等，且各行与模型节点序号相对应，因此根据表1的输出结果，输出矩阵index中的每个元素即对应着模型的节点序号。根据该序号在节点坐标矩阵中找到监测点所在位置，本文选取监测点数量为3个，其分布如图6所示，分别位于线饼7的线匝29（节点序号843 277），线饼47的线匝1（节点序号421 069）和线饼59的线匝1（节点序号374 757）。
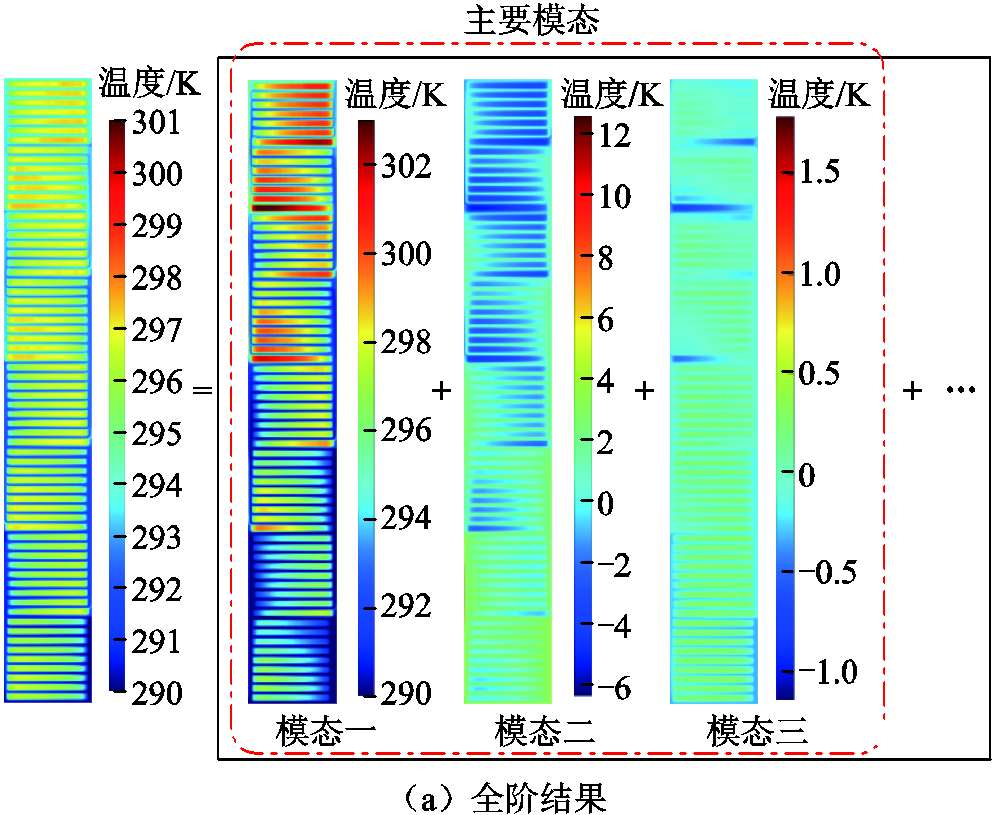
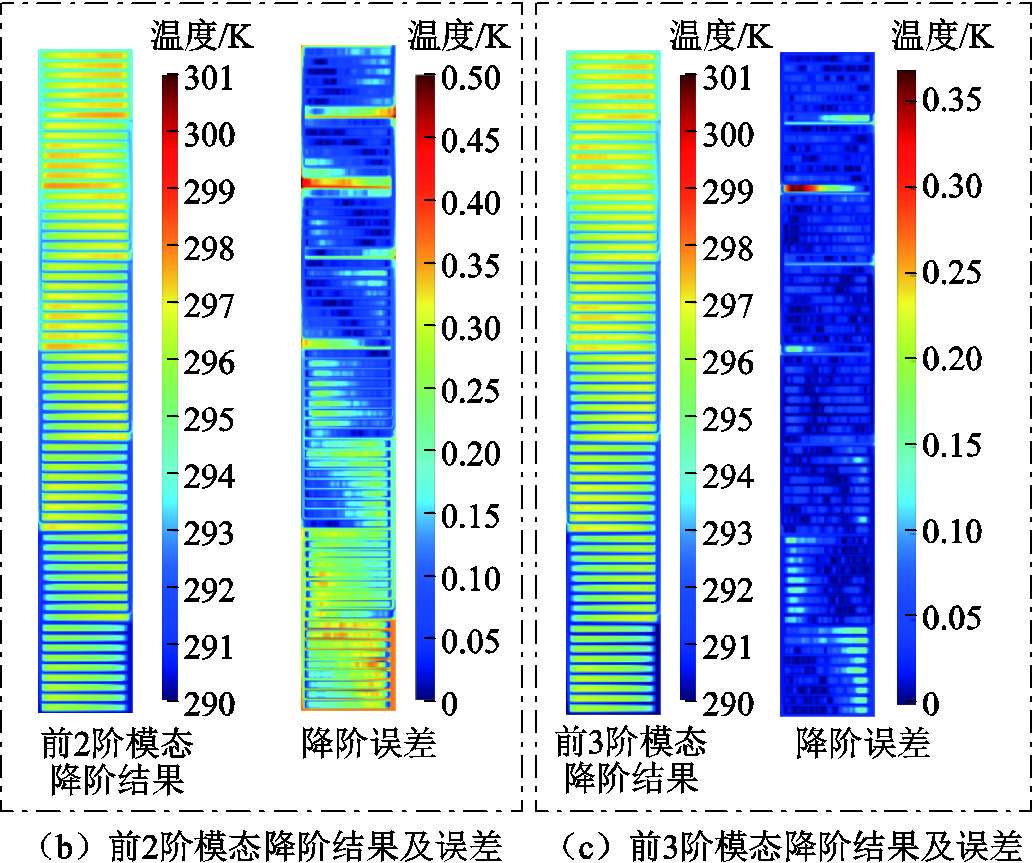
图5 第200 s温度场模态构成情况及各阶模态反演结果
Fig.5 Modal composition of the temperature field in the 200 s and inversion results of various modes
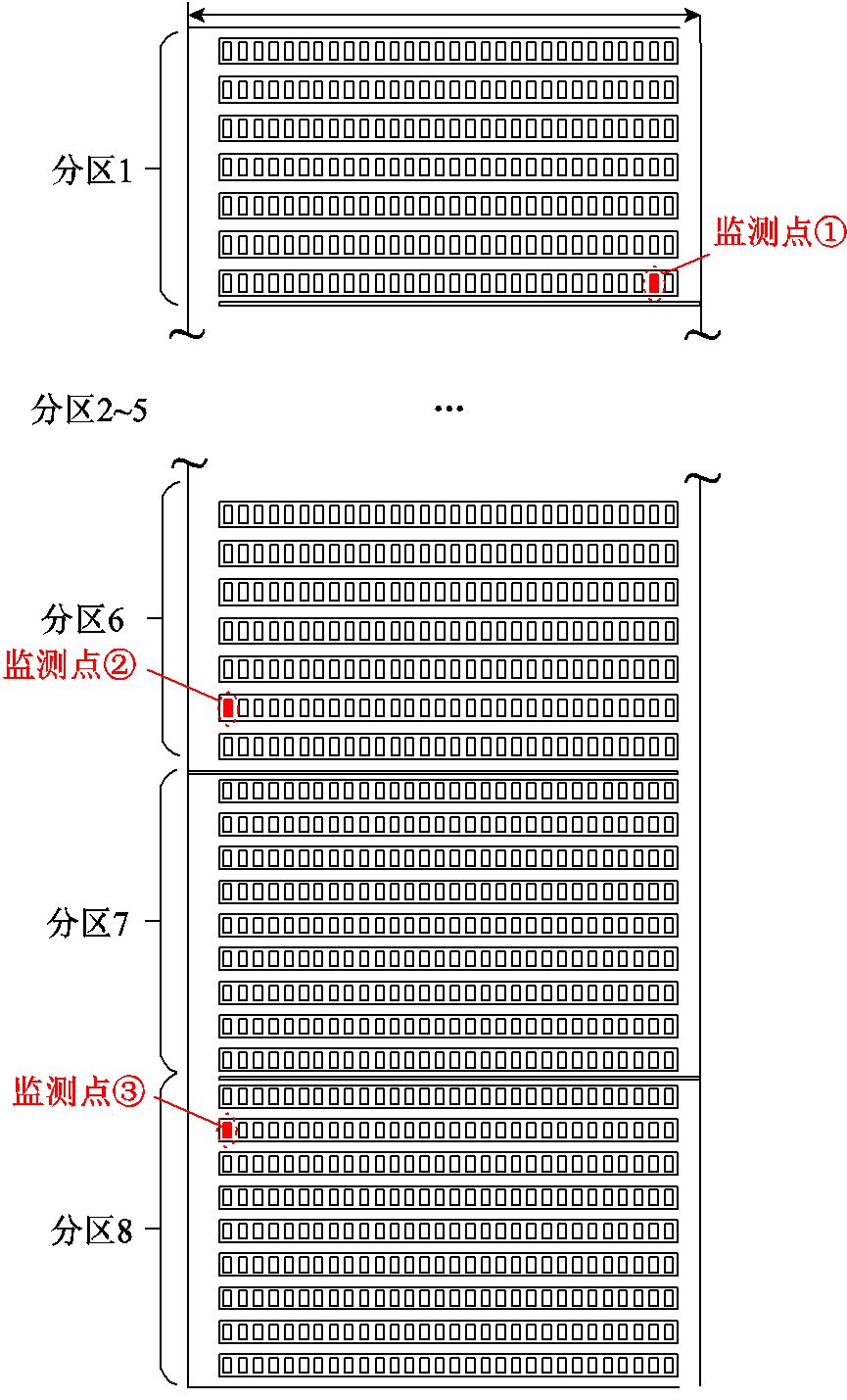
图6 监测点分布情况
Fig.6 Distribution of monitoring points in windings
根据式（7）与式（8）以降阶模型为桥梁建立监测点测量数据与全阶模型的映射关系，在本算例中，由于本文所提算法需要所选监测点的测量数据，在工程场景下该数据可以通过热电偶、光纤等测量装置获得，但算例模型无法通过这些方式获取监测结果，因此，文章通过Fluent仿真软件对所建立的绕组八分区模型进行了瞬态温度场计算，获得了0～2 000 s时段内绕组各节点的温度分布结果，并将各时刻对应监测点的温度提取用于所提算法的计算，模型仿真的边界条件、初始条件以及计算参数已在前文给出。通过监测点的测量数据快速计算各时刻绕组全域温度场分布，定义计算误差为
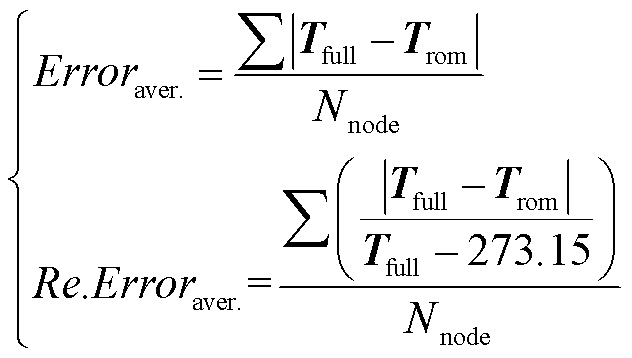（14）
式中，Erroraver.为场域内部所有节点温升的平均计算偏差；Re.Erroraver.为场域内部所有节点摄氏温标下温升的平均相对误差；Tfull为全阶计算结果；Trom为降阶计算结果；Nnode为场域内的所有节点数。绘制200 s以后各时刻全场域平均计算误差的变化曲线如图7所示。
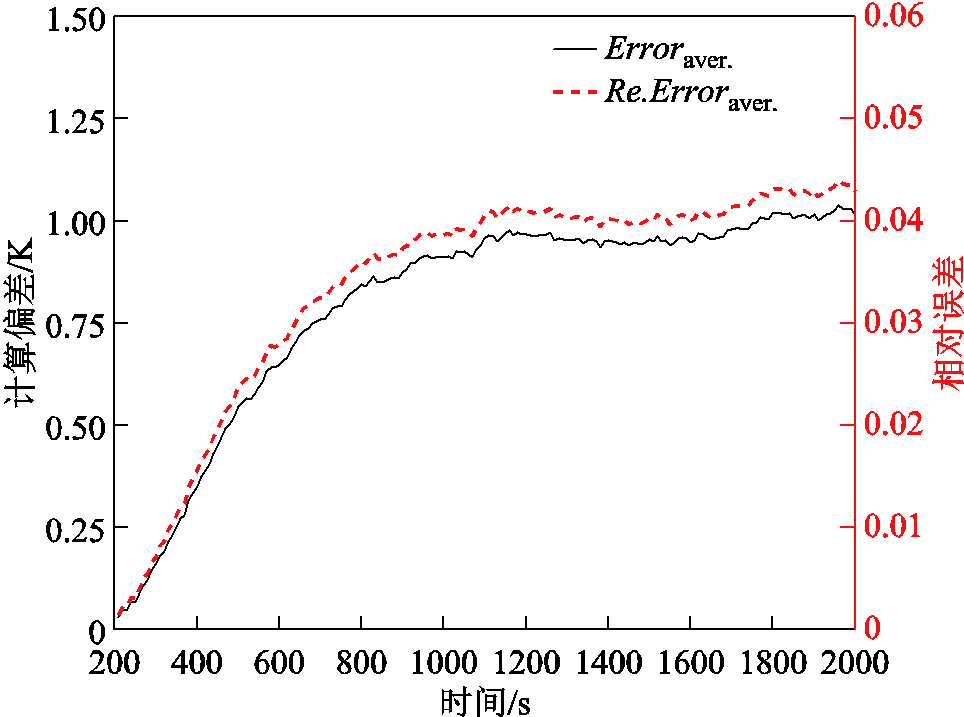
图7 全场域平均计算误差变化曲线
Fig.7 Curves of variation of average calculation error in the whole field
从图7中可以看出，通过3个离散监测点的测量数据重构的温度场结果在200～2 000 s的仿真时间中，最大平均计算偏差仅为1.03 K，摄氏温标下温升的最大平均相对误差不超过5%，计算精度处于合理的范围以内。为了进一步说明算法的正确性，分别选取温度较高的分区6、分区7、分区8的热点作为测试点，绘制降阶计算与全阶计算过程中热点温升误差的变化，并绘制分区7热点的温度变化，如图8所示。
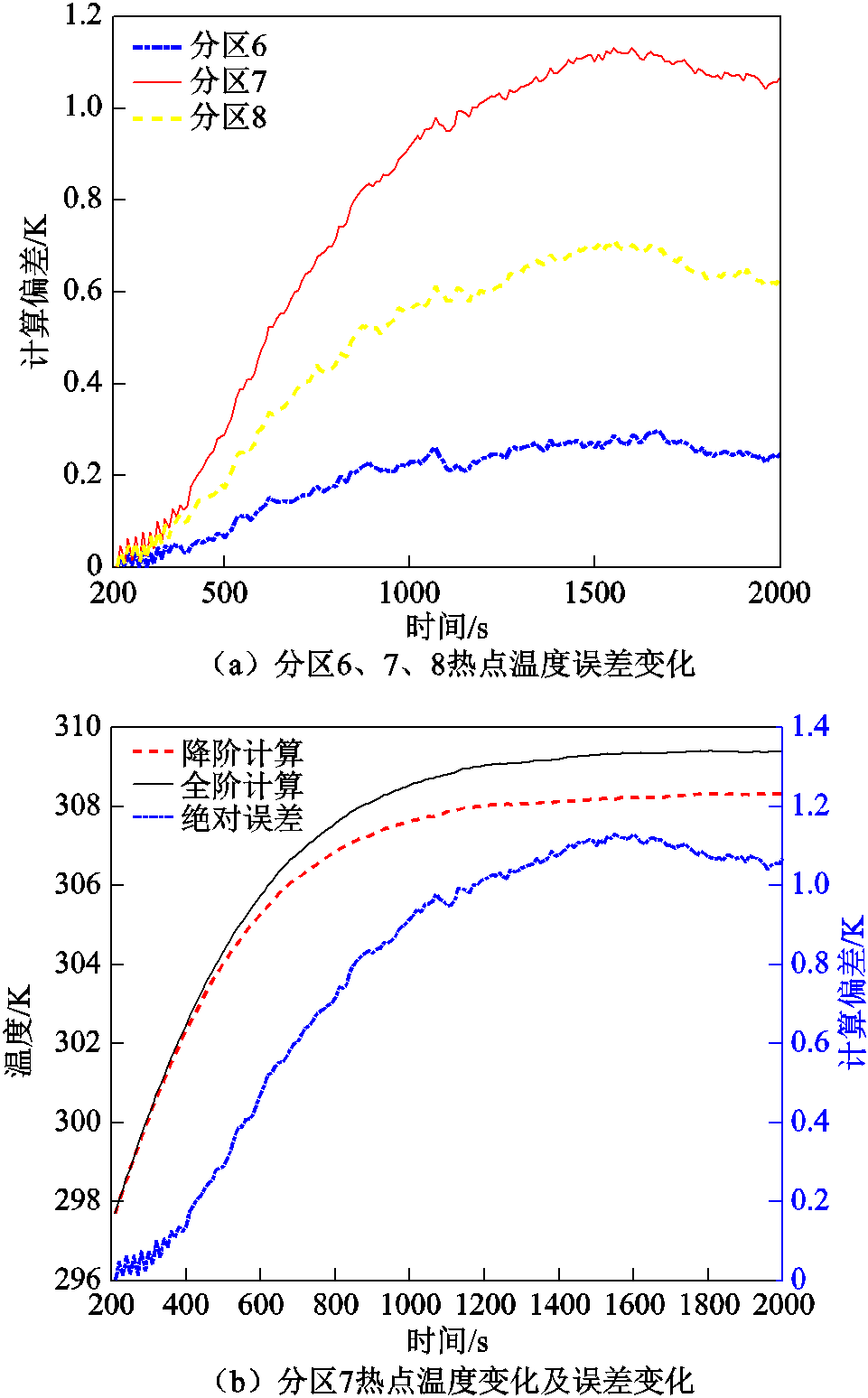
图8 分区热点温度对比
Fig.8 Comparison of hot spot temperatures in different zones
由图8可知，三个分区热点温度的误差在计算过程中最大不超过1.2 K，同时，对于其中误差较大的分区7热点，随着计算时间的增加，当温度逐渐达到平衡之后，误差不会持续增大，这是由于POD算法本质上是提取了系统中主要模态的变化特征，因此在保证快照矩阵精度的前提下，降阶计算的温升变化理论上与全阶计算一致，即当全阶计算温升达到稳定时，降阶计算也能够稳定，且降阶误差不会进一步扩大。上述内容验证了本文所提算法的准确性。
同时，监测点的数量对计算精度显然存在影响，为了探究影响规律，且考虑到最大插值点数量等于降阶模态，因此重新设置降阶模态，分别选取监测点数量为1、2、3、4、5、6对温度场进行快速计算，监测点位置的选取基于式（10），并根据式（13）计算场域内部所有节点摄氏温标下温升的平均相对误差，如图9所示。
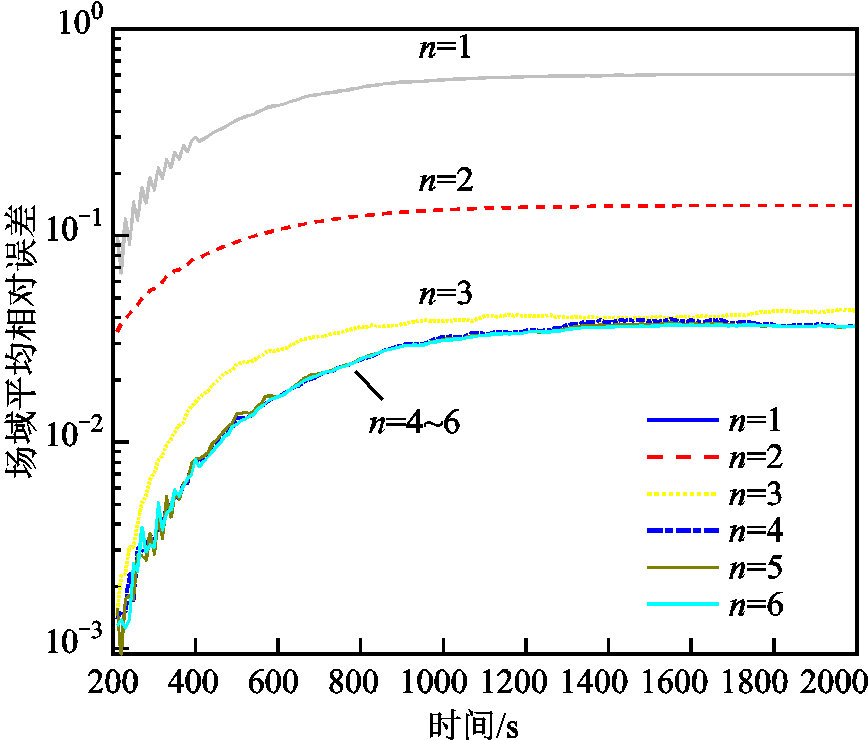
图9 不同监测点数量下场域平均计算误差
Fig.9 Average calculation error of field under different number of monitoring points
从图9中可以看出，随着监测点数量的增加，全场域的平均相对误差逐点减小，这是因为本文所提算法本质上是利用POD降阶技术对温度场进行插值，随着插值点数量的增多，插值精度逐渐提高，二者结论相符。且根据表1可知，每多一个降阶模态，就多了一个监测点，而降阶模态的重要程度依次递减，因此，监测点的重要程度依次递减，即与第一降阶模态对应的第一监测点最为重要，这点也能够从上三角矩阵R的形式中看出，R中对角线上各元素遵循绝对值从大到小排列，即象征着对应监测点的重要性依次减小。结合图9，当插值点数量大于3时，计算误差降低至5%以下，此后虽然会随着监测点数量的增多继续减小但幅度并不大，考虑到监测点数量的增加会导致在实际工程应用时需要预先埋设的传感器数量增加，对于相应的经济成本及内部物理场分布存在一定影响，因此监测点数以少量为宜，对于该模型，最优插值点数量应为3个。
同时，从图4和图9可知，当降阶模态大于3时POD降阶模型计算精度几乎不再变化，当监测点数量大于3时，模型的计算精度也几乎不变。因此可以看出，本文所采用模型的监测点数量对精度的影响与降阶模态数量对精度影响变化近似相同，可以基于式（3）在获得最佳降阶模态数量的基础上判断该模型的最优监测点数量。
本文所提算法的一个显著特点在于能够以较高的效率计算瞬态过程中的温度场分布，为了验证这一点，将200～2 000 s的仿真时间中本文所提算法的计算时间与全阶计算时间进行对比，将二者时间统计见表3。
表3 计算效率对比
Tab.3 Comparison of computational efficiency
计算方法快照矩阵形成时间/s预处理时间/s降阶计算时间/s总时间/s 基于监测点降阶计算65.630.810.1866.62 全阶计算———638.81
表3中，预处理时间主要指获得快照矩阵之后，进行POD降阶与离散点选取的时间，即原文中式（1）～式（10）的过程；全阶计算通过商业仿真软件Fluent实现，采用单线程计算。算法效率统计使用的计算平台配置为：CPU i9-12900 KF，内存128 GB，自编程算法基于Matlab R2021a软件实现。从表3中数据可以看出，在0～2 000 s的瞬态温度场计算中，全阶计算所需时间为638.81 s，而对于基于监测点的降阶计算，总计算时间为66.62 s，计算效率提高9.59倍，且在获得0～200 s的快照矩阵之后，本文所提算法计算200～2 000 s的瞬态温度场分布仅需0.18 s，平均单步时间不超过0.001 s，相较于全阶计算效率提升约3 184倍，这充分说明了本文算法的高效性。
为了验证算法的工程应用价值，本文依靠110 kV变压器绕组温升试验平台开展了瞬态温升试验，测试所提算法在实际工程场景下的相关性能，试验平台的基本结构如图10所示。
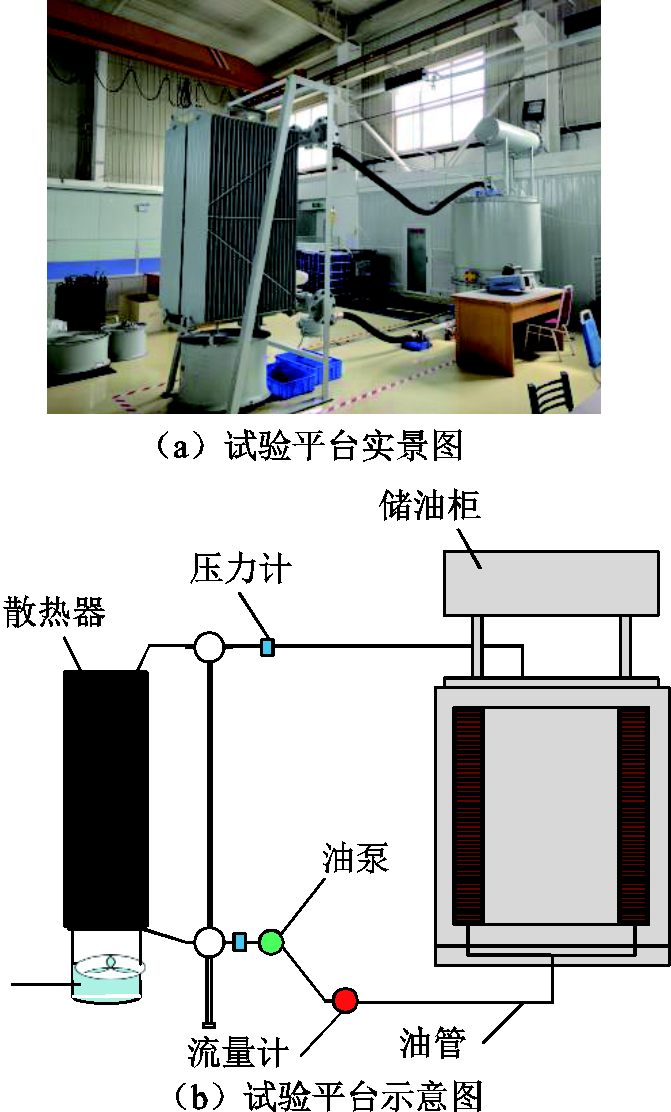
图10 温升试验平台
Fig.10 Temperature rise test platform
平台主要部件包括饼式空心无感绕组、油箱、散热器等，测量装置包含流量计、功率测试仪、热电偶等。试验通过控制绕组功率改变热源密度，通过油泵实现入口油流速度恒定的强迫油循环散热。绕组温度的测量装置为铜-康铜热电偶，分别布置于线饼12、线饼20、线饼30、线饼38上，其中线饼38的热电偶放置位置为线匝1、4、7、10、16、19、22、25、28、30，其余线饼热电偶的放置位置为线匝1、4、7、10、13、16、19、22、25、28、30。试验工况设置如下：绕组功率为25.000 4 kW；蝶阀控制入口油流流量为14.4 m3/h，折算成速度为0.117 3 m/s；绕组初始温度为289.43 K。判断瞬态温升试验达到稳定的标志为顶层油温变化率小于1 K/h并持续2 h，试验过程中通过温度记录仪每10 s记录一次各测量点温度。
通过上述试验平台验证本文所提基于监测点的降阶算法有效性，试验中绕组的二维等效模型的结构参数及物性参数同前文算例验证中的图3、表1所示。对于监测点的选取问题，考虑到更一般的工程场景中监测点的布置无法提前拟定，因此，试验中根据已有测量装置热电偶的布置情况选取算法中采用的监测点，分别选取线饼12的线匝19、线饼20的线匝4以及线饼38的线匝10三个位置的热电偶测量结果作为算法输入以充分提取绕组中温度场整体的数据特征，其余测量点位的结果作为算法验证。试验共进行了7.66 h（27 580 s），记录了2 758组数据。
首先，根据0～1 000 s的仿真数据建立降阶计算模型；其次，将1 000 s后各个时刻监测点的测量温度作为算法输入，快速获得各时刻全场域温度分布，并通过布置的测量装置结果进行验证。当绕组温升达到稳态时，各线饼测量点的降阶计算误差如图11所示。从图中可以看出，达到稳态时，各线饼的降阶计算误差均不超过3 K，且线饼12、线饼20、线饼38上绝大部分测量点的误差小于1 K，初步说明了本文所提算法的正确性。为进一步研究绕组温升过程中的误差变化，以线饼12的线匝1、线饼20的线匝22、线饼30的线匝10以及线饼38的线匝28为例，绘制其温升曲线及误差变化曲线如图12所示。
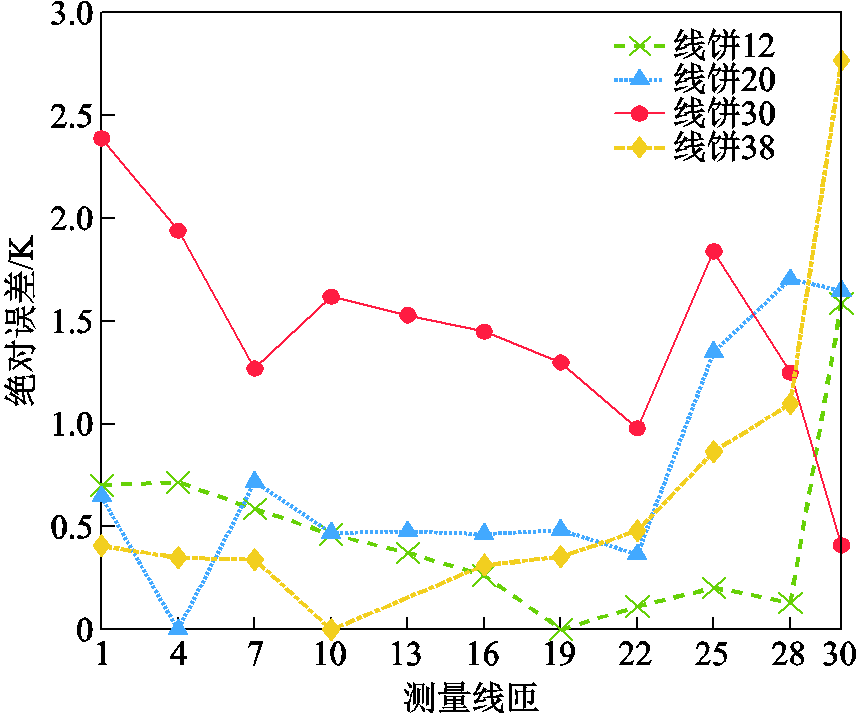
图11 各测量线饼稳态误差
Fig.11 Steady state error of each measurement line cake
从图12中可以看出，通过基于监测点数据的降阶计算得到的各测试点温度与实际测量温度大致相同，且温升变化曲线二者趋势相同，这与前文的算例分析结论一致。造成图12中误差的可能原因包括算法误差与随机误差，其中前者来源于算法本身理论上会使得计算误差逐渐增加并达到稳定（见图13所示），而后者可能来源于环境变化、测量装置灵敏度的影响，使得误差呈现不规律的随机变化，二者共同作用使得误差呈现为图12中所表现的形式。
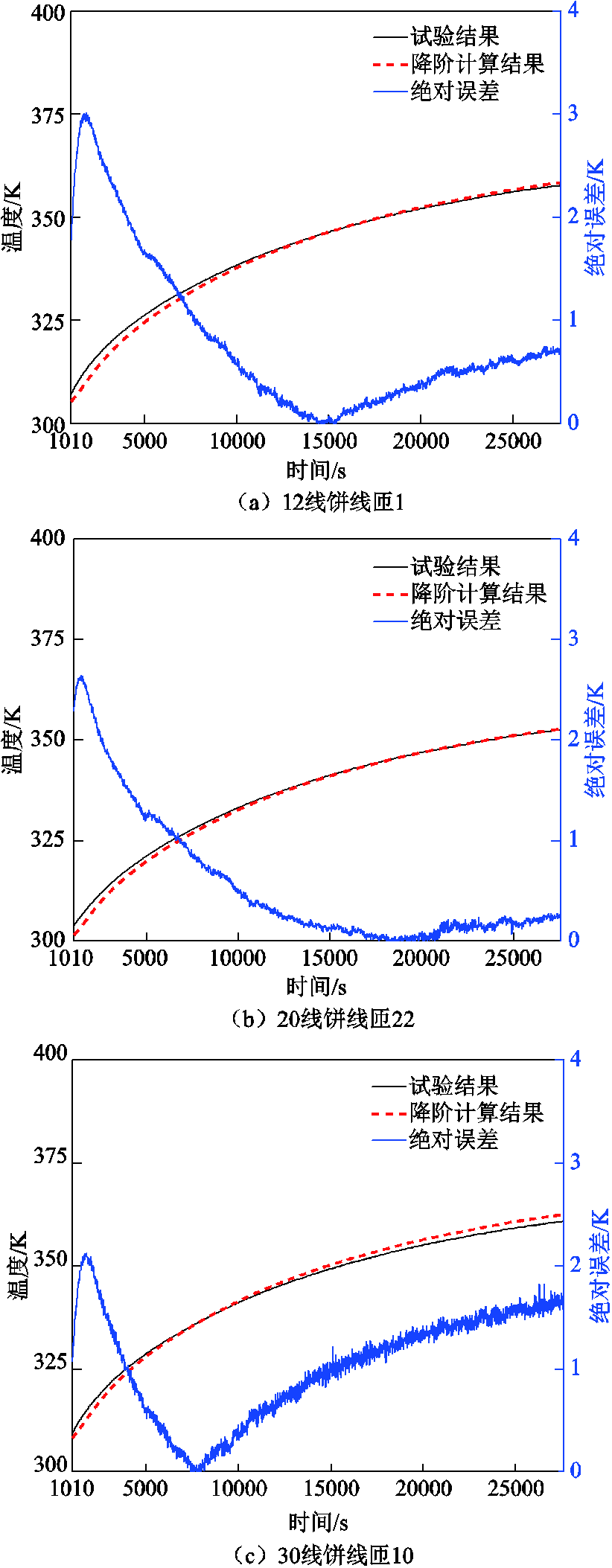
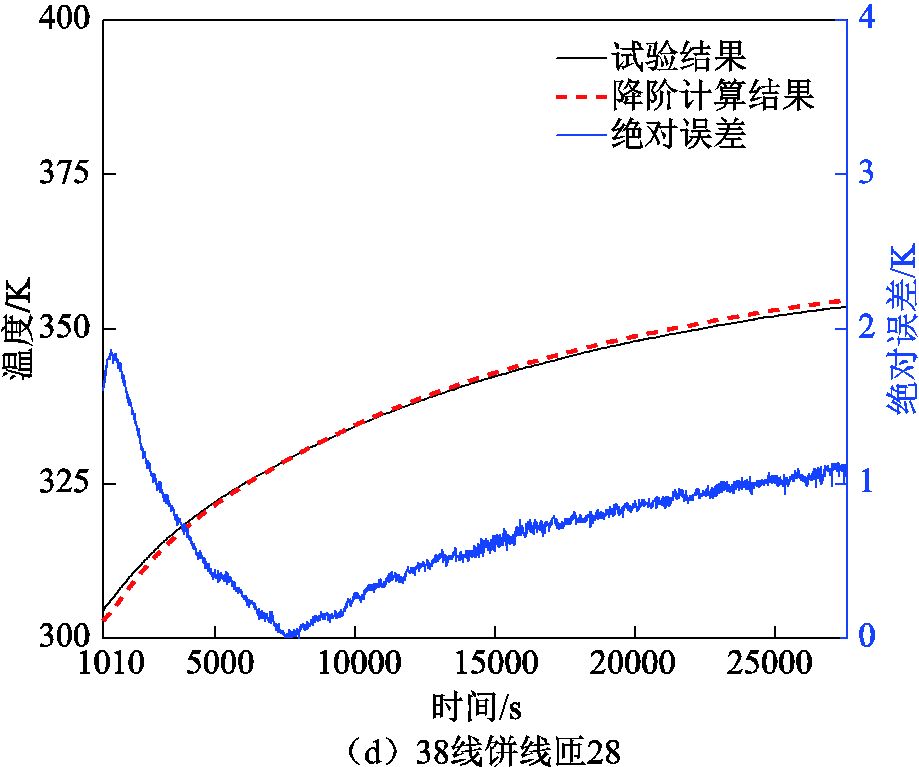
图12 测量点温升变化曲线及误差曲线
Fig.12 Temperature rise variation curve and error curve of measuring points
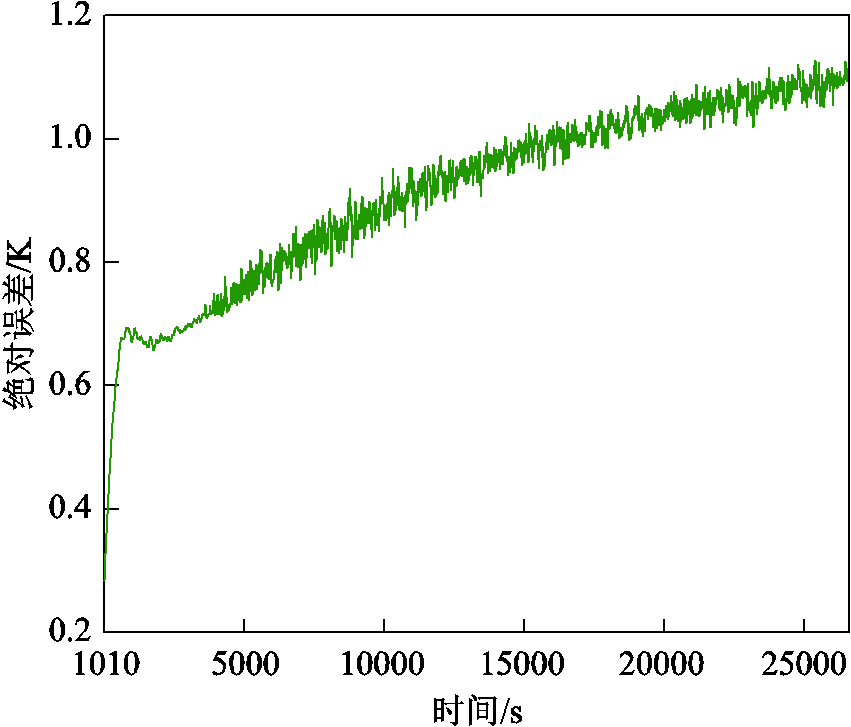
图13 全场域最大误差变化
Fig.13 Maximum error change in the entire field
同时，记录各测量线饼在试验过程中的误差情况见表4。
表4 各测量线饼瞬态计算误差
Tab.4 Transient calculation error of each measurement pie
位置最大误差/K热点误差/K平均误差/K 线饼124.673.171.00 线饼203.362.600.81 线饼303.312.121.02 线饼383.143.040.66
表4中，最大误差表示线饼上各测量点的降阶计算结果与实际结果在绕组温升过程中的最大误差；热点误差表示各线饼最热测量点的最大计算误差；平均误差表示线饼上各测量点各时刻的误差之和除以时间步数。从表中可以看出，采用本文所提算法计算得到的温度场分布与实际测量结果的最大误差不超过4.67 K，且热点误差不超过3.17 K，各测量线饼的平均误差不超过1.02 K，在工程上属于可接受的范围。为了进一步说明本文所提算法在试验工况下对于绕组全场域温度计算的准确性，本文将基于监测点数据的降阶计算结果与全阶仿真结果进行对比，记录了计算过程中二者场域内最大误差变化情况如图13所示，同时，绘制了二者达到稳态时的温度云图及误差云图如图14所示。
图14 稳态时全场域云图对比
Fig.14 Comparison of full field cloud images at steady state
根据文献[3,17]中的前期研究结论，可以认为在本文所进行的试验中，基于Fluent的仿真结果与试验结果相差不大，可以用作结果对比。从图13可以看出，数据驱动算法的计算结果与仿真结果的全场域最大误差变化曲线呈现缓慢上升并逐渐达到稳定的趋势，这是由于本文所提出的数据驱动算法基于POD降阶计算，且提取的数据特征仅基于0～1 000 s的仿真数据，因此随着计算时间的延伸，误差会逐渐变大并最终随着温升稳定而逐渐稳定。图13与图14表明在试验工况下，场域最大误差不超过1.2 K，且计算达到稳定时，全域各节点的摄氏温标相对误差不超过1.29%，这充分说明了本文所提算法在计算绕组全域温升方面的准确性。
由于绕组热点温度的变化趋势及温升大小对变压器安全运行具有十分重要的意义，因此，为了说明文章所提算法的工程应用价值，将热点温度的变化与误差记录如图15所示。
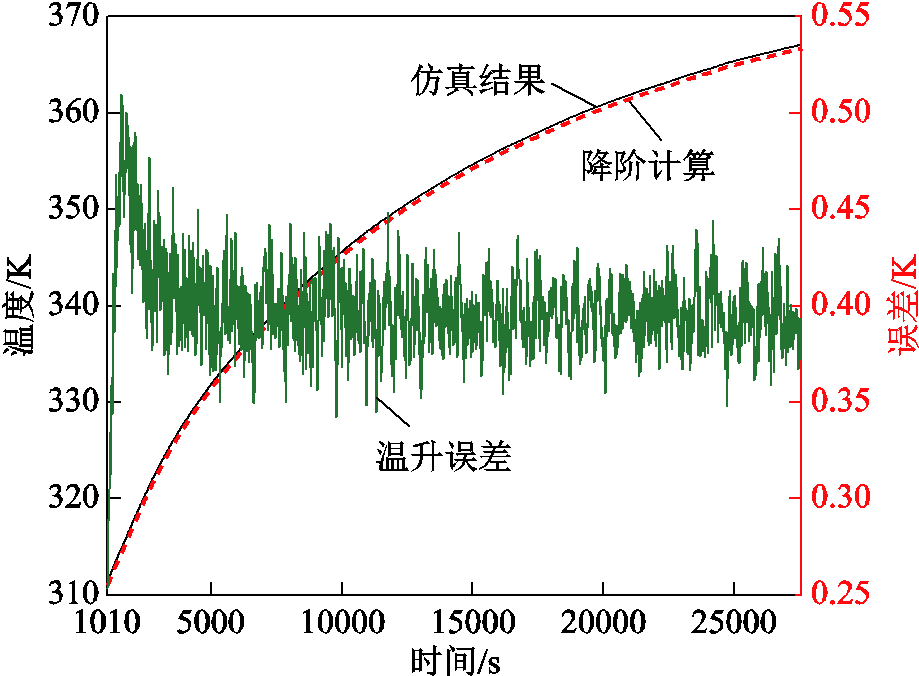
图15 热点温度变化与误差
Fig.15 Changes and errors in hot spot temperature
从图15中可以看出，基于数据驱动降阶算法得到的热点温度与仿真结果相比有较高的精度，最大误差不超过0.6 K，摄氏温标下的相对误差不超过1.3%，且从图14所示的云图可以看出，二者得到的热点位置基本相同，均处于第7线饼的28线匝处，达到稳定时的温度分别为366.7 K与367.08 K。由此可说明本文所提算法面向工程中对绕组热点温升的预测具有一定的应用价值。
考虑到试验中用于算法输入的监测点是根据测量装置所在位置选择的，假若能够通过式（10）自由选择最佳监测点位置，那么理论上本文所提算法能够具有更高的计算精度，能够更贴合实际测量结果。同时，从计算效率的角度上看，考虑预处理时间在内，本文所提算法计算1 010 s～27 580 s的绕组温度场仅需3.40 s，远远小于当前主流数值方法的计算时间，能够实现在实际场景下较为快速的绕组温升计算。
本文提出了一种基于监测点测量数据的油浸式变压器绕组温升降阶计算方法，该方法能够跳过传统数值计算中求解大规模、强非线性离散方程组的效率瓶颈，通过绕组内部若干离散监测点的温度数据，以POD降阶算法为载体快速重构温度场全域。本文通过数值算例及温升试验验证了算法的可行性和有效性，相关结论表明：
1）本文所提算法包含一种监测点选取策略，通过基于列主元的正交三角分解选取场域中较为重要的节点作为监测点，从而以较小的误差近似反映原矩阵。本文采用的算例表明，以该方法选取的监测点作为算法输入时，对于绕组温度场的计算具有较好的精度。
2）为了验证算法的可行性，本文基于油浸式电力变压器绕组基本结构建立了八分区分匝绕组模型，降阶模型建立所需监测点数据及快照矩阵通过Fluent仿真软件获得，计算结果表明：本文所提算法在200～2 000 s的仿真时间中，最大平均计算偏差仅为1.03 K，最大平均相对误差不超过5%，计算精度处于合理的范围以内，且计算时间仅为0.18 s，相较于全阶计算获得了较高的效率提升。
3）为了进一步说明本文所提算法的应用价值，论文基于110 kV油浸式变压器绕组温升试验平台开展试验，通过实际测量装置获得算法所需监测点数据，并将其作为算法输入对绕组温升过程中各时间点的温度场进行计算，试验及计算结果表明：本文所提算法各时刻的计算结果与测量结果相比最大误差不超过4.67 K，且各测量线饼的平均误差不超过1.02 K，在工程上属于可接受的范围。同时，算法计算1 010 s～27 580 s的绕组温度场仅需3.40 s，远远小于当前主流数值方法的计算时间，可初步实现实际场景下绕组温升的快速计算。
4）本文将算法应用于试验中时，监测点的选取受到了实际测量装置已有热电偶布置位置的限制，假若能够实现基于最佳监测点选取策略布置热电偶，理论上能够取得更好的计算精度。
综上所述，本文所提算法已在油浸式电力变压器绕组流热耦合场中验证了其可行性，然而，实际工程场景下，在复杂多物理场联合作用下绕组温度的分布表现可能与文中不同，监测点数量和位置的选取也需要根据实际情形具体考虑。同时需要注意的是，本文所提算法的计算精度关键在于能否获得高精度的温度场数据或仿真数据，因此只要保证数值仿真贴近工程实际，即可从中充分提取数据特征，建立高精度的降阶模型，从而实现快速可靠的降阶计算。
参考文献
[1] 谭又博, 余小玲, 臧英, 等. 谐波电流对换流变压器绕组损耗及温度分布特性的影响[J]. 电工技术学报, 2023, 38(2): 542-553.
Tan Youbo, Yu Xiaoling, Zang Ying, et al. The influence of harmonic current on the loss and temperature distribution characteristics of a converter transformer winding[J]. Transactions of China Electro-technical Society, 2023, 38(2): 542-553.
[2] 刘刚, 郝世缘, 朱章宸等. 基于动态模态分解-自适应变步长油浸式电力变压器绕组瞬态温升快速计算方法[J].电工技术学报, 2024, 39(12): 3895-3906.
Liu Gang, Hao Shiyuan, Zhu Zhangchen, et al. Research on rapid calculation method of transient temperature rise of winding of dynamic mode decomposition-adaptive time stepping oil-immersed power transformer[J]. Transactions of China Electro-technical Society, 2024, 39(12): 3895-3906
[3] 杜志叶, 肖湃, 郝兆扬, 等. 基于绕组热点温度反馈的特高压交流变压器低频加热干燥方法研究[J]. 电工技术学报, 2022, 37(15): 3888-3896.
Du Zhiye, Xiao Pai, Hao Zhaoyang, et al. Study on low-frequency heating and drying method of UHVAC transformer based on temperature feedback of winding hot spots[J]. Transactions of China Electrotechnical Society, 2022, 37(15): 3888-3896.
[4] 谢裕清, 李琳, 宋雅吾, 等. 油浸式电力变压器绕组温升的多物理场耦合计算方法[J]. 中国电机工程学报, 2016, 36(21): 5957-5965, 6040.
Xie Yuqing, Li Lin, Song Yawu, et al. Multi-physical field coupled method for temperature rise of winding in oil-immersed power transformer[J]. Proceedings of the CSEE, 2016, 36(21): 5957-5965, 6040.
[5] 彭丽丹. 电力变压器温度场数值计算研究[D]. 北京: 华北电力大学, 2016.
Peng Lidan.Study on numerical calculation of temperature field of power transformer[D]. Beijing: North China Electric Power University, 2016.
[6] 邓永清, 阮江军, 董旭柱, 等. 基于流线分析的 10 kV油浸式变压器绕组热点温度反演模型建立及验证研究[J]. 中国电机工程学报, 2023, 43(8): 3191-3203.
Deng Yongqing, Ruan Jiangjun, Dong Xuzhu, et al. Establishment and verification of 10 kV oil immersed transformer winding hot spot temperature inversion model based on streamline analysis[J]. Proceedings of the CSEE, 2023, 43(8): 3191-3203.
[7] 程书灿, 赵彦普, 张军飞, 等. 电力设备多物理场仿真技术及软件发展现状[J]. 电力系统自动化, 2022, 46(10): 121-137.
Cheng Shucan, Zhao Yanpu, Zhang Junfei, et al. State of the art of multiphysics simulation technology and software development for power equipment[J]. Automation of Electric Power Systems, 2022, 46(10): 121-137.
[8] 骆小满, 阮江军, 邓永清, 等. 基于多物理场计算和模糊神经网络算法的变压器热点温度反演[J]. 高电压技术, 2020, 46(3): 860-866.
Luo Xiaoman, Ruan Jiangjun, Deng Yongqing, et al. Transformer hot-spot temperature inversion based on multi-physics calculation and fuzzy neural network algorithm[J]. High Voltage Engineering, 2020, 46(3): 860-866.
[9] Dowell E H. Eigenmode analysis in unsteady aerodynamics-Reduced-order models[J]. AIAA Journal, 1996, 34(8): 1578-1583.
[10] Silva W A. Identification of linear and nonlinear aerodynamic impulse responses using digital filter technique[C]//22nd Atmospheric Flight Mechanics Conference, New Orleans, LA, USA, 1997: 584-597.
[11] Antoulas A C. Approximation of Large-scale dynamicalsystems (advances in design and control)[M]. Philadelphia: Society for Industrial and Applied Mathematics, 2005.
[12] 齐凯, 韩玉兵, 盛卫星. 基于快速近似幂迭代子空间跟踪算法的自适应分集接收技术[J]. 南京理工大学学报, 2017, 41(1): 90-94.
Qi Kai, Han Yubing, Sheng Weixing. Adaptive diversity reception technique based on fast approximated power iteration subspace tracking[J]. Journal of Nanjing University of Science and Technology, 2017, 41(1): 90-94.
[13] 丁永龙, 胡琳萍, 张瑞勤. 一种基于迭代子空间直接求逆算法的高效子空间混合算法[J]. 计算物理, 2021, 38(4): 418-422.
Ding Yonglong, Hu Linping, Zhang Ruiqin. An efficient subspace hybrid algorithm based on direct inversion in iterative subspace algorithm[J]. Chinese Journal of Computational Physics, 2021, 38(4): 418-422.
[14] Maulik R, Lusch B, Balaprakash P. Reduced-order modeling of advection-dominated systems with recurrent neural networks and convolutional autoencoders[J]. Physics of Fluids, 2021, 33(3): 037106.
[15] 魏代同, 陈星, 陈玉刚, 等. 基于本征正交分解的叶片碰摩系统降阶方法[J]. 航空动力学报, 2022, 37(4): 711-720.
Wei Daitong, Chen Xing, Chen Yugang, et al. Reduced order method of blade rubbing system based on proper orthogonal decomposition[J]. Journal of Aerospace Power, 2022, 37(4): 711-720.
[16] 张宇娇, 赵志涛, 徐斌, 等. 基于U-net卷积神经网络的电磁场快速计算方法[J]. 电工技术学报, 2024, 39(9): 2730-2742.
Zhang Yujiao, Zhao Zhitao, Xu Bin, et al. Fast calculation method of electromagnetic field based on U-net convolutional neural network[J]. Transactions ofChina Electrotechnical Society, 2024, 39(9): 2730-2742.
[17] 刘刚, 荣世昌, 武卫革, 等. 基于混合有限元法和降阶技术的油浸式变压器绕组2维瞬态流-热耦合场分析[J]. 高电压技术, 2022, 48(5): 1695-1705.
Liu Gang, Rong Shichang, Wu Weige, et al. Two-dimensional transient flow-thermal coupling field analysis of oil-immersed transformer windings based on hybrid finite element method and reduced-order technology[J]. High Voltage Engineering, 2022, 48(5): 1695-1705.
[18] 胡万君, 刘刚, 朱章宸, 等. 油浸式电力变压器绕组稳态温升降阶计算方法研究[J]. 中国电机工程学报, 2023, 43(16): 6505-6517.
Hu Wanjun, Liu Gang, Zhu Zhangchen, et al. Reduced order calculation method of steady temperature rise of oil immersed power transformer[J]. Proceedings of the CSEE, 2023, 43(16): 6505-6517.
[19] Drmač Z, Gugercin S. A new selection operator for the discrete empirical interpolation method - improved a priori error bound and extensions[J]. SIAM Journal on Scientific Computing, 2016, 38(2): A631-A648.
[20] 刘刚, 郝世缘, 胡万君, 等. 基于子循环自适应串行交错时间匹配算法的油浸式变压器绕组瞬态温升计算[J]. 电工技术学报, 2024, 39(4): 1185-1197.
Liu Gang, Hao Shiyuan, Hu Wanjun, et al. Transient temperature rise calculation of oil immersed transformer winding based on sub cyclic adaptive staggered time matching algorithm[J]. Transactions of China Electrotechnical Society, 2024, 39(4): 1185-1197.
Abstract In order to improve the calculation efficiency of transient temperature rise in oil immersed power transformer windings, order reduction technology is one of the most effective methods in current research. This paper considers fully utilizing the order reduction characteristics of POD method and proposes a calculation method that uses temperature information from several discrete monitoring points in the field to quickly invert the physical field.
Firstly, the article derives the reduced expression of the full order temperature field of transformers based on the POD method, and on this basis, establishes the relationship between discrete monitoring points and the temperature distribution in the entire field. In this method, the POD modal matrix can be obtained through a single calculation of the snapshot matrix, the modal coefficients are obtained through the temperature information of discrete monitoring points, and the temperature distribution of the winding at each step in the transient process can be obtained by multiplying the above two on this basis. Due to the absence of complex nonlinear calculations and large-scale equation iteration processes, this method theoretically has high computational efficiency. At the same time, in order to ensure the accuracy of temperature field inversion, the selection of monitoring point positions within the field is crucial. Therefore, in order to improve computational accuracy, this paper introduces a discrete point selection strategy based on column principal component QR decomposition. Relevant research results show that using this method for temperature inversion in the entire field has a good upper limit of error.
In order to verify the correctness of the method proposed in this article, based on the basic structure of transformer cake windings, an eight zone winding numerical calculation model and corresponding temperature rise test platform were established. The performance of the method was discussed through numerical simulation and experimental results. The relevant results showed that the maximum average calculation deviation of the method proposed in this article in numerical simulation was only 1.03 K, The maximum average relative error does not exceed 5%, the calculation accuracy is within a reasonable range, and the calculation time is only 0.18 s, which has achieved a higher efficiency improvement compared to full order calculations; In the experimental analysis, the maximum error between the calculation results of the method proposed in this article and the measurement results at each time point does not exceed 4.67 K, and the average error of each measurement line cake does not exceed 1.02 K, which is within an acceptable range in engineering. Meanwhile, the algorithm only takes 3.40 s to calculate the corresponding winding temperature field at the corresponding time, which is much shorter than the calculation time of current mainstream numerical methods.
keywords：Oil immersed power transformer, proper orthogonal decomposition(POD), discrete monitoring points, fast calculation method
中图分类号：TM411
DOI: 10.19595/j.cnki.1000-6753.tces.231247
国家重点研发计划（2021YFB2401700）和中央高校基本科研业务费专项资金（2022MS073）资助项目。
收稿日期 2023-08-01
改稿日期 2023-11-13
刘 刚 男，1985年生，副教授，硕士生导师，研究方向为电气设备多物理场建模和仿真、基于多物理场的结构优化、电力设备数字孪生仿真模型以及电力系统时域仿真技术研究。
E-mail：liugang_em@163.com（通信作者）
胡万君 男，1999 年生，硕士研究生，研究方向为电力设备多物理场建模和仿真。
E-mail：1366320104@qq.com
（编辑 郭丽军）