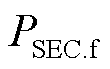 为送端换流站有功功率,
为送端换流站有功功率,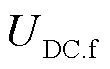 和
和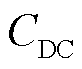 分别为VSC-HVDC的直流电压和等效电容,
分别为VSC-HVDC的直流电压和等效电容,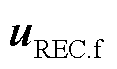 为受端换流站交流母线电压矢量,
为受端换流站交流母线电压矢量,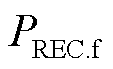 和
和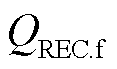 分别为受端换流站有功功率和无功功率,
分别为受端换流站有功功率和无功功率,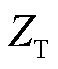 为联接变压器的等效阻抗,
为联接变压器的等效阻抗,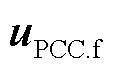 为VSC-HVDC与受端电网的公共耦合点即等效故障点的电压矢量,
为VSC-HVDC与受端电网的公共耦合点即等效故障点的电压矢量,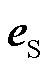 和
和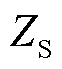 分别为等效无穷大系统电势矢量和正常运行时受端电网等值阻抗,
分别为等效无穷大系统电势矢量和正常运行时受端电网等值阻抗,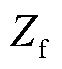 为等效故障过渡阻抗。
为等效故障过渡阻抗。摘要 受端电网三相故障下柔性直流输电(VSC-HVDC)的直流电压骤升,可能引发过电压闭锁并威胁电网稳定。现有基于卸荷的VSC-HVDC故障穿越方法大多以直流电压为投切条件,未计及受端换流站交流母线电压和无功功率对直流电压安全的影响,可能因投切条件不合理或受端换流站无功功率过大引发卸荷非必要投入,对交直流系统造成额外冲击并增加能量损失。为此,该文建立了受端换流站功率可行域,以刻画受端电网故障下受端换流站的功率控制能力;分析发现了受端换流站功率可行域的缩减特征,进而提出避免直流电压越限的受端电网故障极限切除时间的概念和计算方法;通过解析引发直流电压越限的门槛电压,提出基于最大限度避免直流电压越限的协调控制点的VSC-HVDC故障穿越控制方法。算例表明,所提方法在受端强电网或VSC-HVDC卸荷风险较高的场景中,能够兼顾VSC-HVDC的直流电压安全和对受端电网的无功功率支撑,在最大限度避免卸荷投入的同时,尽可能地为受端电网提供无功功率。
关键词:柔性直流输电 交流故障穿越 直流电压 无功功率
与常规直流输电系统相比,柔性直流输电(Voltage Source Converter based High Voltage Direct Current, VSC-HVDC)采用可控关断器件,从根本上避免了换相失败的问题,被广泛应用于异步电网互联[1]、接入孤岛或无源电网[2]等场景。电压源换流器具有两个控制自由度,通过VSC-HVDC有功功率和无功功率的解耦控制,调节交流电网频率和电压已成为交直流混联电网高效运行的重要手段[3-4]。然而,受端电网三相故障导致受端换流站交流母线全相电压跌落,受端换流站有功功率送出严重受阻,不平衡功率使直流电容充电,造成直流电压上升,可能诱发VSC-HVDC过电压闭锁乃至交流电网暂态失稳[5]。因此,受端电网故障下VSC-HVDC的安全运行成为业界关注的焦点。
调节送端电网馈入VSC-HVDC的有功功率与受端换流站有功功率再次平衡是VSC-HVDC故障穿越的思路之一。文献[6-7]借助电力通信链路,送端换流站在检测直流电压超过规定阈值后向送端发电机组发送减载指令,但其有效性受通信传输延时的影响。文献[8-9]提出降压法,根据直流电压偏差调节送端新能源并网点电压,通过触发新能源低电压穿越,减小馈入VSC-HVDC的有功功率。文献[10-11]提出升频法,通过直流电压与送端电网频率的映射,使送端新能源感受直流电压变化而降低有功功率。降压和升频法利用新能源的响应特性实现VSC-HVDC故障穿越,但降压法大幅增加了机组应力,升频法的响应速度欠佳。此外,联接有源电网的送端换流站采用定有功功率控制,升频法或降压法不适用。直接降低送端换流站有功功率使受端电网故障的影响范围扩大至送端电网,有违直流异步联网以隔离故障的初衷。
卸荷使不平衡功率在制动电阻中以热能形式耗散,通常不改变送端换流站有功功率的参考值,是VSC-HVDC交流故障穿越的常用方法[12]。然而,卸荷投切对交直流系统产生冲击,增加散热成本且不利于有功功率消纳[13]。在直流电压安全的前提下,应最大程度地避免卸荷的投入。受端电网故障期间,受端换流站有功电流在定直流电压控制作用下增加,以抑制直流电压升高。然而,受制于功率变换器件能承受的最大电流应力,维持直流电压稳定所需的受端换流站有功电流不能随着交流母线电压跌落程度的增加而无限制增大。当交流母线电压跌落较大,受端换流站交流电流受到内环控制器限幅作用时,受端换流站有功功率无法恢复至故障前的初始值,直流电压随故障持续不断升高,常需投入卸荷以避免直流电压越限。现有卸荷方法以直流电压作为卸荷投切的条件,并在传统集中式直流卸荷的基础上,就安装位置[14-15]、拓扑结构[16-17]和控制算法[18-19]等方面进行改进。当受端换流站交流母线电压跌落较轻时,受端换流站有功功率可恢复至故障前的初始值,受端电网故障期间直流电压无越限风险。此时,直流电压在受端换流站定直流电压控制下可能先升高,乃至达到卸荷投入阈值后下降并稳定,仅以直流电压作为卸荷投切条件可能引起卸荷的非必要投入。
现有VSC-HVDC故障穿越的部分研究参考新能源并网规范,受端电网故障期间控制受端换流站根据电压跌落深度提供无功功率[20]。当交流母线电压跌落较为严重时,受端换流站提供无功功率将以降低有功功率为代价,进一步增大直流电压变化率。受端电网短路比较大时,受端换流站提供无功功率对受端电网电压的抬升作用非常有限[21],却使受端换流站有功功率显著降低,直流电压快速上升导致卸荷高频投切,对换流设备和交直流系统产生冲击。特别地,VSC-HVDC作为大容量通道时,牺牲有功功率以提供无功功率支撑的代价和风险不容忽视;根据查阅到的有限资料,暂无强制性标准规定受端换流站无功功率数值。因此,VSC-HVDC的故障穿越应根据应用场景确定,VSC-HVDC用于受端电网较强等场景中应兼顾直流电压安全和无功功率支撑。
针对受端电网三相故障,本文通过推导直流电压和交流母线电压关于受端换流站有功功率和无功功率的解析式,提出了最大允许交流电流限制下保证直流电压安全的受端换流站功率可行域,以刻画受端电网故障下受端换流站的功率控制能力。通过分析发现受端换流站功率可行域的缩减特征,提出了避免直流电压越限的受端电网故障极限切除时间的概念和计算方法。通过解析引发直流电压越限的交流电压跌落深度作为切换门槛电压,提出了卸荷的闭锁判据;通过刻画最大限度避免直流电压越限的协调控制点,提出了兼顾直流电压安全与无功支撑的VSC-HVDC故障穿越控制方法。当故障持续时间小于故障极限切除时间时,所提控制方法可不启动卸荷;即使故障持续时间大于故障极限切除时间,所提方法也能够减小卸荷的投切次数和能量耗散。因此,所提方法可在避免卸荷非必要动作的同时,为受端电网提供尽可能避免直流电压越限前提下的最大无功功率。
VSC-HVDC由电压源换流器和直流线路组成。一般由送端换流站控制馈入VSC-HVDC的有功功率,受端换流站控制直流电压。受端换流站通过直流电压的负反馈PI环节调节有功电流,维持送端和受端换流站有功功率相等以稳定直流电压。受端电网故障导致受端换流站交流母线电压跌落,定直流电压控制下受端换流站有功电流增加,以抑制直流电压升高。然而,受端换流站交流母线电压跌落越严重,为维持直流电压稳定所需的受端换流站有功电流越大。由于受端换流站的交流电流不能超过一定限值,故障下受端换流站有功功率可能无法恢复至故障前的初始有功功率。不平衡功率积蓄使得VSC-HVDC的直流电容充电,直流电压逐步上升。
与正常运行时受端电网拓扑相比,故障下受端电网拓扑存在经故障过渡电阻的短路支路,则受端电网故障前后的等值阻抗有所变化。由于高压交流线路阻抗以感性为主,故当受端换流站交流母线远区发生三相故障时,等效至交流母线处的过渡阻抗设置多为感性[22];而当受端换流站交流母线近区发生三相故障时,等效至交流母线处的过渡阻抗性质及数值取决于实际故障的位置和过渡电阻。根据戴维南定理,以受端换流站交流母线电压跌落程度不变为条件,将发生内部故障的受端电网等值为由恒定电压源、串联阻抗与并联等效故障过渡阻抗构成的二端口网络,如图1所示。恒定电压源和串联阻抗分别为受端电网等效无穷大系统和正常运行时受端电网等值阻抗;并联等效故障过渡阻抗接于VSC-HVDC与受端电网的公共耦合点,用以等效短路支路对受端电网等值阻抗的影响。图1中,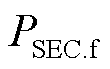 为送端换流站有功功率,
为送端换流站有功功率,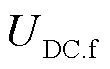 和
和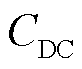 分别为VSC-HVDC的直流电压和等效电容,
分别为VSC-HVDC的直流电压和等效电容,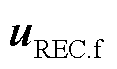 为受端换流站交流母线电压矢量,
为受端换流站交流母线电压矢量,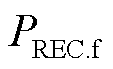 和
和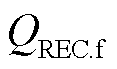 分别为受端换流站有功功率和无功功率,
分别为受端换流站有功功率和无功功率,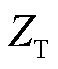 为联接变压器的等效阻抗,
为联接变压器的等效阻抗,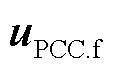 为VSC-HVDC与受端电网的公共耦合点即等效故障点的电压矢量,
为VSC-HVDC与受端电网的公共耦合点即等效故障点的电压矢量,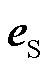 和
和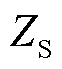 分别为等效无穷大系统电势矢量和正常运行时受端电网等值阻抗,
分别为等效无穷大系统电势矢量和正常运行时受端电网等值阻抗,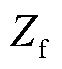 为等效故障过渡阻抗。
为等效故障过渡阻抗。
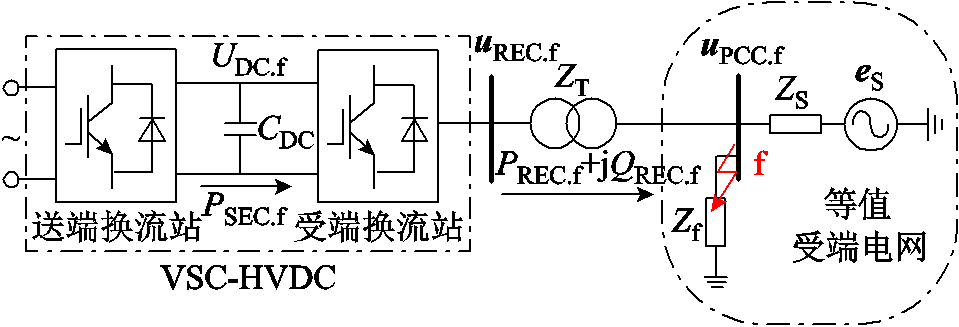
图1 受端电网故障下VSC-HVDC等值模型
Fig.1 Equivalence model of VSC-HVDC under the receiving-end grid fault
联接变压器的铜耗和铁耗较小,且励磁电抗远大于绕组电抗,故联接变压器可等效为电抗[23]。高压交流线路电抗远大于电阻,故可将正常运行时受端电网等值阻抗近似为电抗[24]。受端电网故障前,受端换流站的交流母线电压矢量和等效无穷大系统电势矢量满足
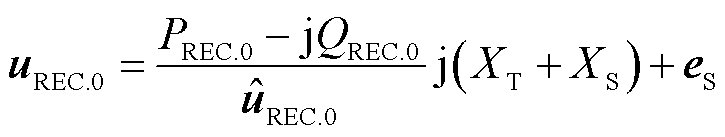 (1)
(1)
式中,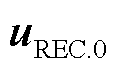 和
和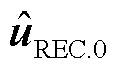 分别为故障发生前受端换流站的交流母线电压矢量及其共轭;
分别为故障发生前受端换流站的交流母线电压矢量及其共轭;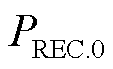 和
和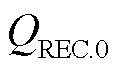 分别为故障发生前受端换流站的有功功率和无功功率;
分别为故障发生前受端换流站的有功功率和无功功率;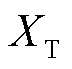 为联接变压器等效电抗;XS为正常运行时受端电网等值电抗。
为联接变压器等效电抗;XS为正常运行时受端电网等值电抗。
根据矢量幅值相等原理,将式(1)改写为标量,即
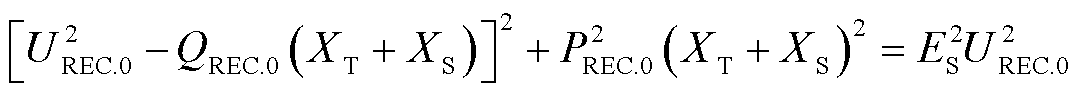 (2)
(2)
式中,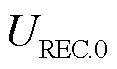 为故障前受端换流站交流母线电压幅值;
为故障前受端换流站交流母线电压幅值;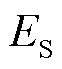 为等效无穷大系统电势,受端电网故障前后近似恒定[25]。
为等效无穷大系统电势,受端电网故障前后近似恒定[25]。
求解式(2)可得
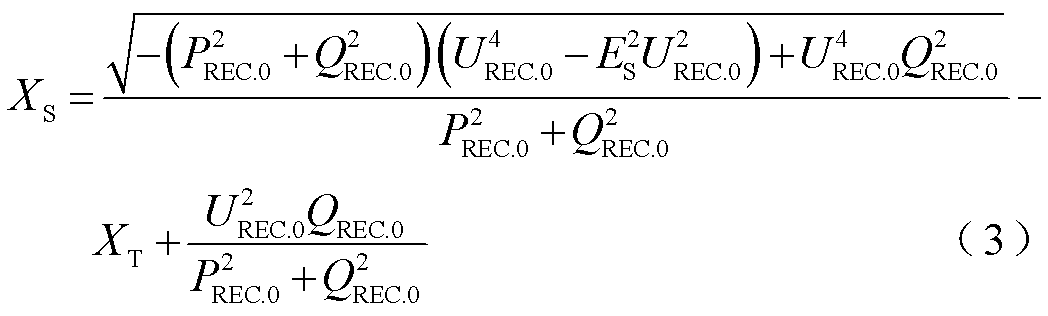
故障前受端换流站交流母线电压、有功功率和无功功率可在受端换流站就地测量;联接变压器等值电抗值取决于设备型号,为常数。因此,受端换流站可利用式(3)和故障前运行参数计算正常运行时受端电网等值阻抗,作为受端电网故障等值模型的串联阻抗。
受端电网故障下,受端换流站交流母线和等效故障点的电压矢量满足
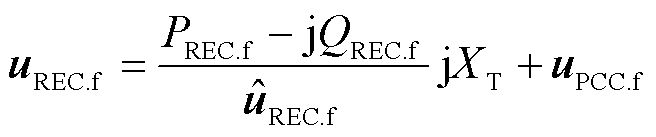 (4)
(4)
式中,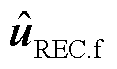 为受端换流站交流母线电压矢量的共轭。
为受端换流站交流母线电压矢量的共轭。
根据基尔霍夫定律,等效故障点的电压矢量满足
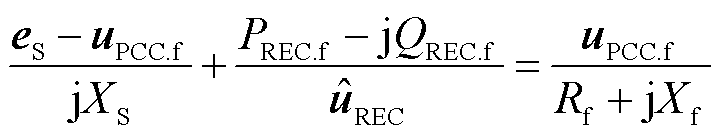 (5)
(5)
式中,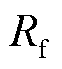 和
和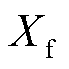 分别为受端电网等效故障过渡电阻和电抗。
分别为受端电网等效故障过渡电阻和电抗。
联立式(4)和式(5),消去等效故障点的电压矢量,受端换流站交流母线电压矢量可表示为
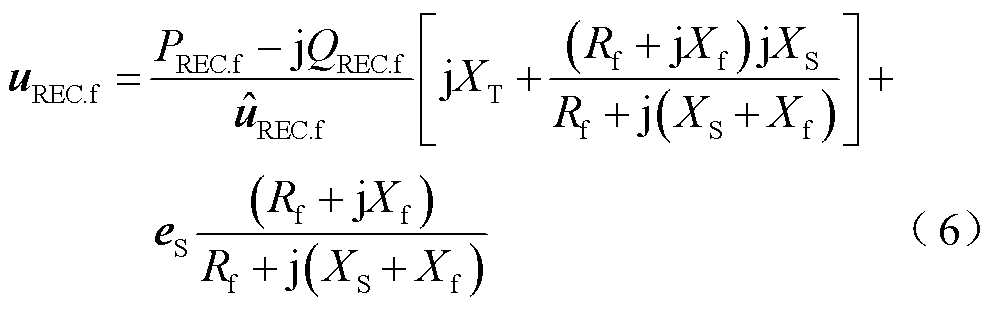
根据式(6)中矢量的模和相位相等,构造等效故障过渡电阻和电抗关于受端换流站交流母线电压幅值和相位、受端换流站有功功率和无功功率的代数方程。求解式(7)可得等效故障过渡阻抗。
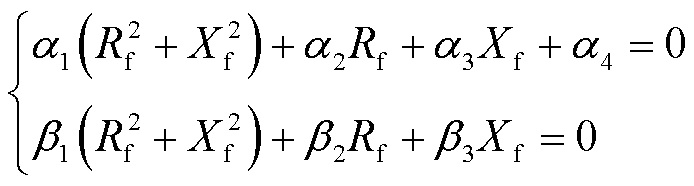 (7)
(7)
其中
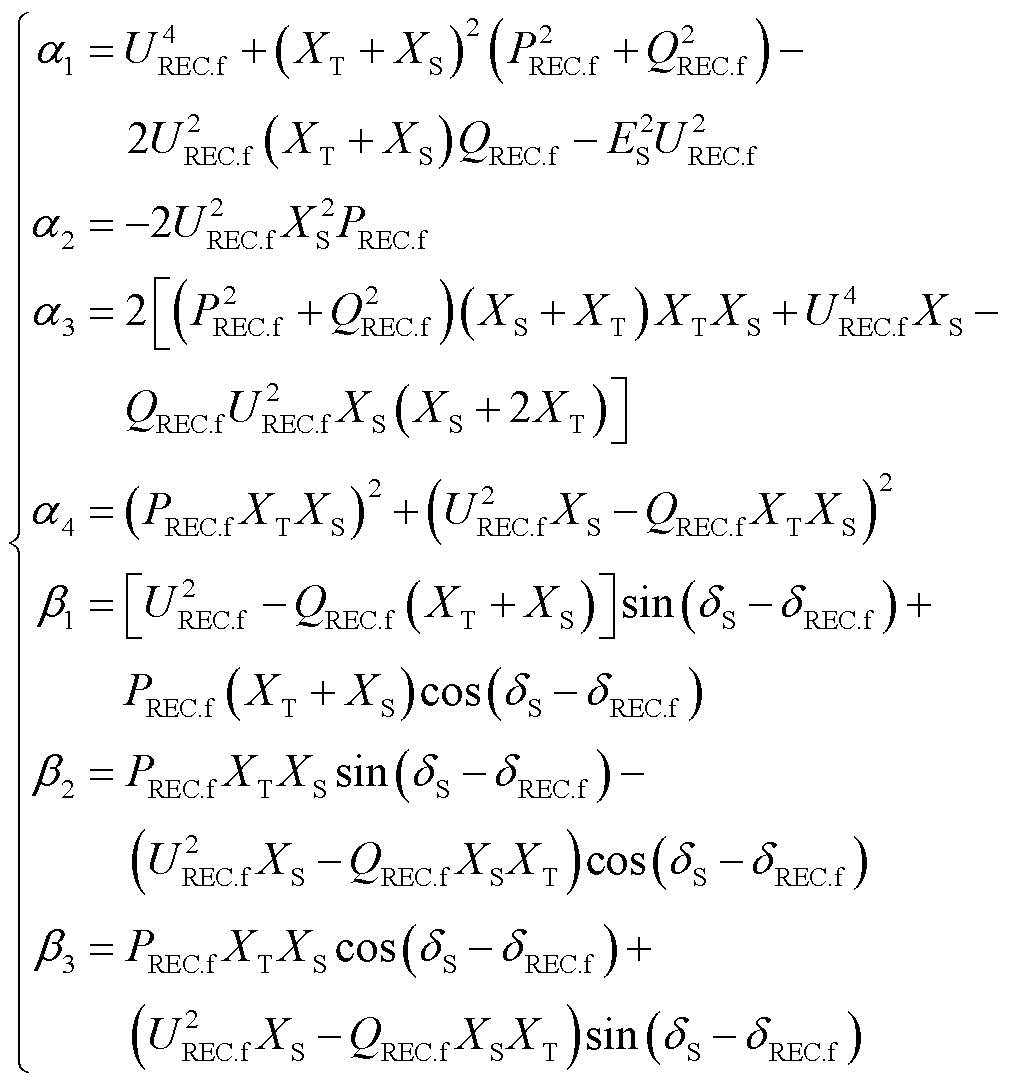
式中,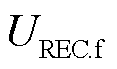 和
和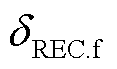 分别为故障下受端换流站交流母线电压的幅值和相位;
分别为故障下受端换流站交流母线电压的幅值和相位;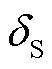 为等效无穷大系统的相位,故障前后保持不变。
为等效无穷大系统的相位,故障前后保持不变。
因此,将故障前后受端换流站运行参数分别代入式(3)和式(7),计算受端电网故障等值模型的串联阻抗和并联等效故障过渡阻抗,可建立与实际故障受端电网具有相同外特性的受端电网故障等值模型。
受端换流站有功和无功电流不得超过最大允许交流电流限制,即满足
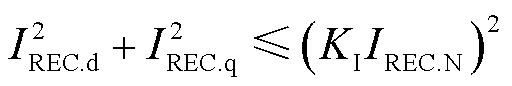 (8)
(8)
式中,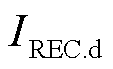 和
和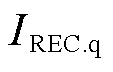 分别为受端换流站有功和无功电流;
分别为受端换流站有功和无功电流;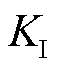 为受端换流站最大允许交流电流系数;
为受端换流站最大允许交流电流系数;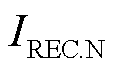 为受端换流站额定交流电流。
为受端换流站额定交流电流。
受端换流站采用交流母线电压矢量定向的同步旋转坐标系作为控制器的参考坐标系,同步旋转坐标系下受端换流站交流母线电压q轴分量为0。根据瞬时功率理论,将式(8)两侧同时乘以受端换流站交流母线电压,最大允许交流电流限制下的受端换流站有功功率和无功功率满足
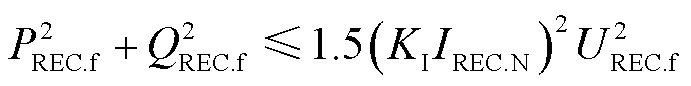 (9)
(9)
根据瞬时功率理论确定的最大允许交流电流限制下受端换流站有功功率和无功功率可行范围,与受端换流站交流母线电压有关。式(6)表征了受端换流站与等值故障受端电网的潮流耦合关系。式(6)和式(9)均含有受端换流站有功功率和无功功率、受端换流站交流母线电压三个变量。通过联立消去受端换流站交流母线电压,可得仅含受端换流站有功功率和无功功率两个变量的可行范围,即
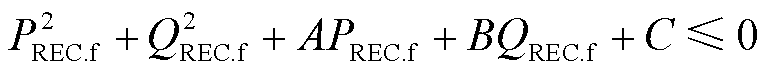 (10)
(10)
其中
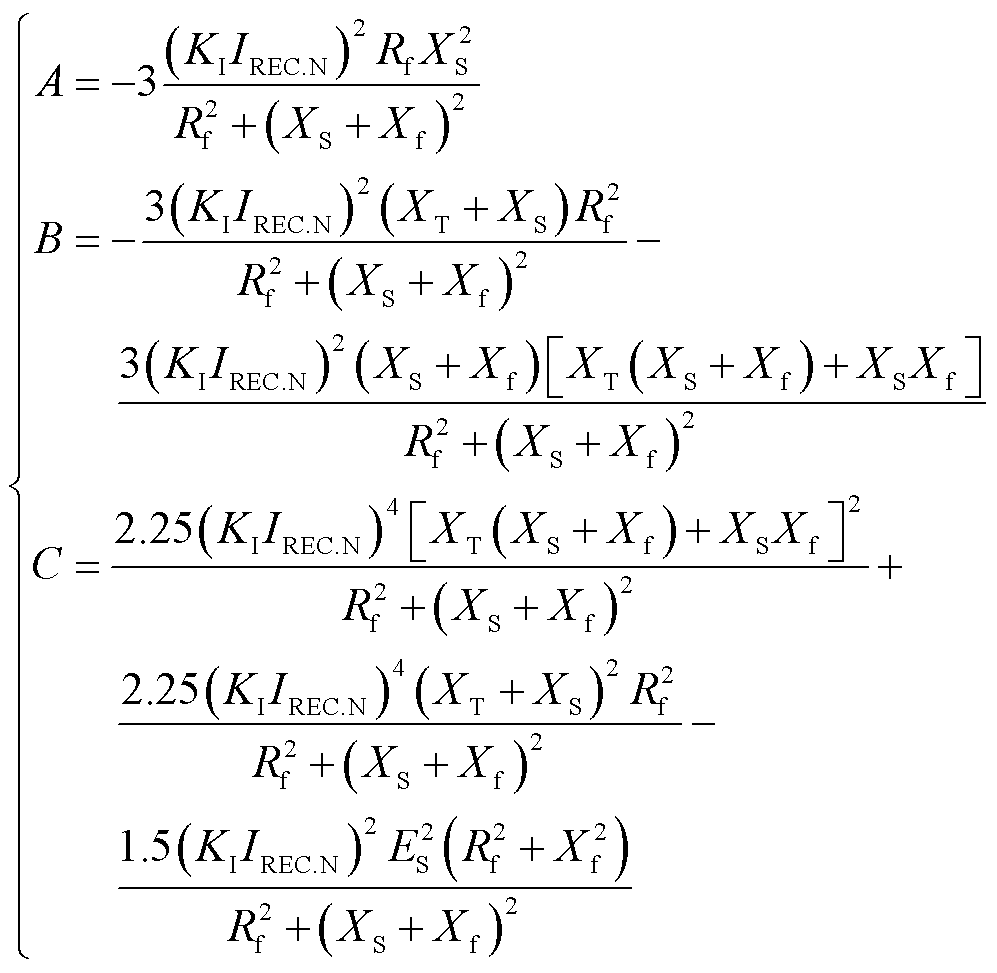
换流器拓扑影响VSC-HVDC直流电容和最大允许直流系数[26],但VSC-HVDC故障穿越期间直流电压变化与送端和受端换流站有功功率之差始终满足直流电容的充放电方程。为避免电压应力超过器件所能承受极限,不平衡功率所积蓄的能量应小于直流电压上升至最大允许直流电压时VSC-HVDC电容的能量变化量,即
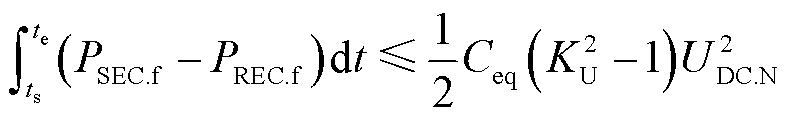 (11)
(11)
式中,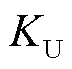 为最大允许直流电压系数;
为最大允许直流电压系数;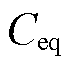 为VSC-HVDC的直流电容,二者根据换流器拓扑和阀组级调制策略确定;
为VSC-HVDC的直流电容,二者根据换流器拓扑和阀组级调制策略确定;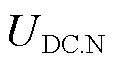 为额定直流电压;
为额定直流电压;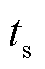 为故障发生时刻即积分零时刻;
为故障发生时刻即积分零时刻;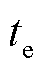 为故障切除时刻。
为故障切除时刻。
不改变送端换流站有功功率参考值时,送端电网馈入VSC-HVDC的有功功率在故障期间近似为常数。换流站控制器暂态响应时间远小于故障时间尺度,可近似认为受端换流站有功功率无差跟踪控制参考值变化[27]。在受端换流站有功功率控制参考值恒定的条件下,式(11)可化简为
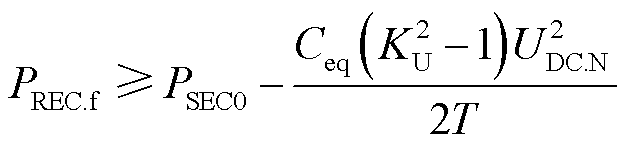 (12)
(12)
式中,T为故障持续时间,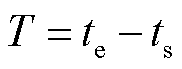 ;
;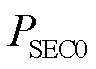 为故障前送端换流站的初始有功功率。
为故障前送端换流站的初始有功功率。
式(10)和式(12)分别刻画了最大允许交流电流、最大允许直流电压限制下受端换流站有功功率和无功功率的范围。令式(10)取等时受端换流站有功功率和无功功率恰好满足最大允许交流电流限制。当受端换流站有功或无功功率进一步增大时,受端换流站交流电流将超过限值,故恰好满足最大允许交流电流限制的受端换流站有功功率和无功功率的组合构成了受端换流站功率范围的上边界。式(12)取等号时,满足式(12)的受端换流站有功功率恰好使得故障切除时刻的直流电压等于最大允许直流电压,为避免直流过电压的受端换流站最小有功功率。因此,恰好满足最大允许直流电压限制的受端换流站有功功率构成了受端换流站功率范围的下边界。式(10)和式(12)的交集表征了受端电网故障下保证VSC-HVDC交流电流和直流电压安全的受端换流站有功功率和无功功率的范围,定义为受端换流站功率可行域。
受端换流站向受端电网提供有功功率,且不应在交流母线电压跌落期间吸收无功功率。因此,受端电网故障下受端换流站功率可行域仅位于有功-无功功率坐标系的第1象限。受端换流站功率可行域如图2所示,红色曲线为受端换流站功率范围的上边界,红色斑点状阴影为满足式(10)的受端换流站有功功率和无功功率的范围。蓝色直线为受端换流站功率范围的下边界。若受端换流站有功功率能恢复至故障前的初始有功功率,受端电网故障期间直流电压能维持稳定。因此,当受端换流站有功功率无穷大时,式(12)必然成立。最大允许直流电压限制下受端换流站有功功率的范围无上界,如图2中蓝色线条状阴影区域所示。蓝色线条状阴影区域和红色斑点状阴影区域的交集a0b0e为受端换流站功率可行域。
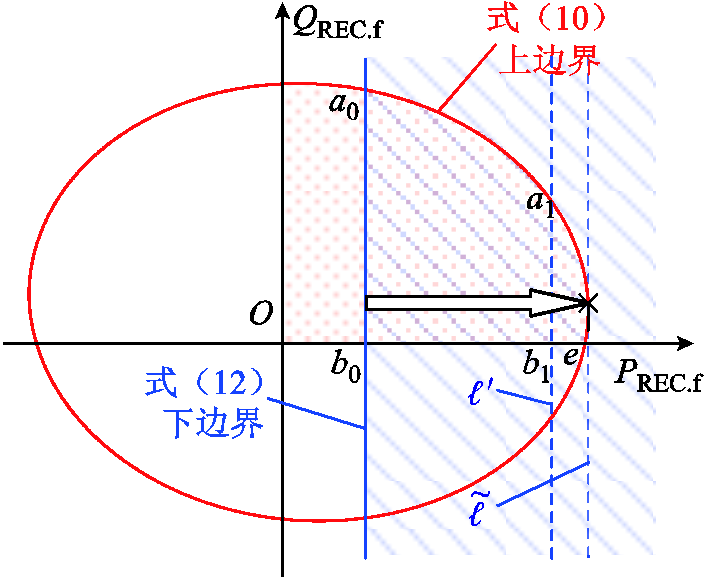
图2 受端换流站功率可行域
Fig.2 Power feasible region of REC
式(10)仅含受端换流站有功功率和无功功率两个变量;式(12)除受端换流站有功功率外,还含有故障持续时间。因此,受端换流站功率可行域与故障持续时间有关。恰好保证直流电压安全的受端换流站最小有功功率随故障持续时间的增加而增加,受端换流站功率范围的下边界逐步右移。由于满足最大允许交流电流限制的受端换流站有功功率和无功功率的范围恒定,故受端换流站功率可行域随故障持续时间的增加呈现缩减特征。如图2所示,区域a0b0e为故障持续时间T0对应的受端换流站功率可行域。随着故障持续时间增加至T1,受端换流站功率范围的下边界可能移动至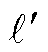 ,受端换流站功率可行域变为区域a1b1e,区域a1b1e的面积小于区域a0b0e。
,受端换流站功率可行域变为区域a1b1e,区域a1b1e的面积小于区域a0b0e。
若某个故障持续时间下受端换流站功率范围的上、下边界在有功-无功功率坐标系第1象限有且仅有1个交点,该故障持续时间为受端电网故障极限切除时间。当故障持续时间大于极限切除时间,受端换流站功率范围的下边界超过上边界,不存在同时避免直流电压和交流电流越限的受端换流站有功功率和无功功率的组合。如图2所示,当受端换流站功率范围的下边界移动至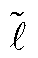 时,受端换流站功率范围的上、下边界相切,切点为受端换流站功率可行域内唯一的有功功率和无功功率的组合。受端换流站功率范围的下边界
时,受端换流站功率范围的上、下边界相切,切点为受端换流站功率可行域内唯一的有功功率和无功功率的组合。受端换流站功率范围的下边界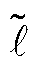 对应的故障持续时间Tmax为极限切除时间。令式(10)和式(12)取等并联立,受端换流站功率范围的上、下边界的交点满足
对应的故障持续时间Tmax为极限切除时间。令式(10)和式(12)取等并联立,受端换流站功率范围的上、下边界的交点满足
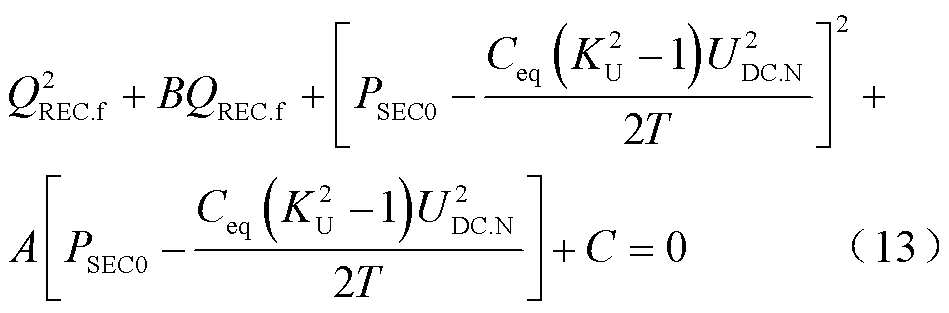
式(13)是关于受端换流站无功功率的二次函数,根的形式取决于故障持续时间。极限切除时间为使得式(13)仅有1个根的故障持续时间。根据一元二次方程根的判别式构造极限切除时间的等式为
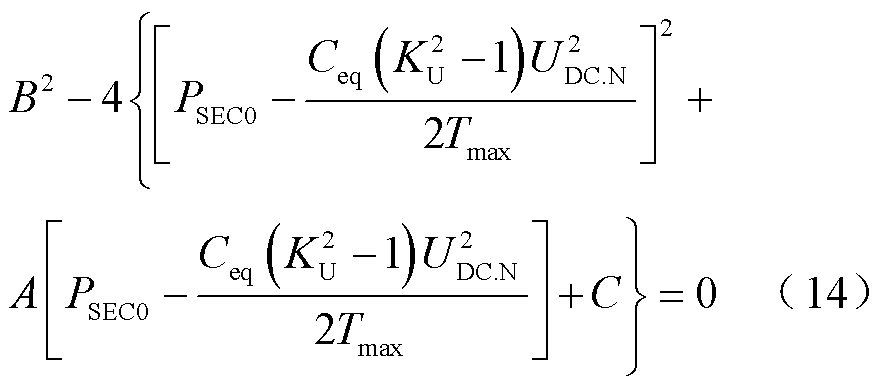
求解式(14)可得极限切除时间为
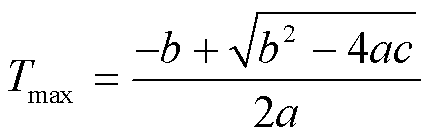 (15)
(15)
其中
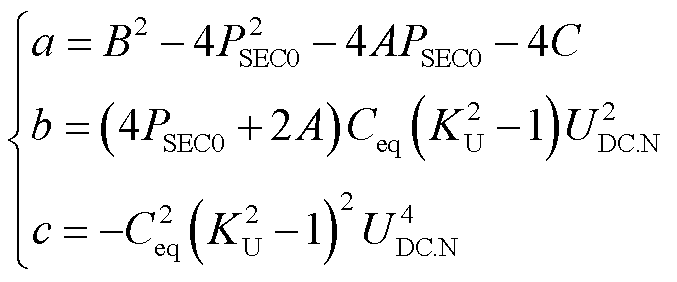
受端换流站有功功率越大,不平衡功率越小,直流电压上升至最大允许直流电压的时间越长。当故障持续时间小于极限切除时间时,提高受端换流站有功功率即可避免直流电压越限;当故障持续时间等于极限切除时间时,最大允许交流电流限制下的受端换流站有功功率最大值与避免直流过电压的最小受端换流站有功功率相等,故障切除时刻的直流电压处于最大允许直流电压的极限状态。若大于极限切除时间时清除受端电网故障,保证直流电压安全所需的受端换流站有功功率将导致交流电流越限。由于受端换流站至多能提供避免交流电流越限前提下的最大有功功率,直流电压将于极限切除时间越限。因此,受端电网故障极限切除时间表征了受端电网故障下直流电压的安全裕度。
维持直流电压稳定所需的受端换流站有功电流不能随着交流母线电压跌落程度的增加而无限制增加。受端换流站功率控制参考值需适应不同的受端电网故障严重程度。若受端换流站在提供某一无功电流的同时能够确保受端换流站有功功率恢复至故障前的初始值,直流电压可维持稳定,受端换流站继续采用定直流电压控制。当受端电网故障较严重,受端换流站提供无功功率导致有功功率降低时,直流电压会随着故障持续时间增加而不断上升,受端换流站应切换至定有功功率和无功功率控制并与卸荷配合,在最大限度保证直流电压安全的同时,尽可能为受端电网提供无功功率。若某一受端换流站交流母线电压下受端换流站在提供无功电流的同时,其有功电流恰好可保证受端换流站有功功率等于故障前的初始值,则VSC-HVDC处于直流电压越限的临界状态。该交流母线电压为受端换流站由定直流电压控制切换至定有功功率和无功功率控制的切换门槛。
故障持续时间取决于受端电网继电保护动作时间,具有未知性。由式(15)可知,极限切除时间与等效故障过渡阻抗等参数有关。当受端换流站交流母线电压跌落严重时,受端换流站有功功率显著降低,不平衡功率较大,极限切除时间较小并可能小于故障持续时间,受端电网故障将导致直流电压越限。受端换流站交流母线电压跌落较轻时,极限切除时间则较大,若极限切除时间大于故障持续时间,受端电网故障期间直流电压小于最大允许直流电压。
若故障持续时间小于极限切除时间,某一预期故障持续时间对应的受端换流站功率范围上、下边界的交点对应着此时功率可行域内受端换流站最大无功功率。控制受端换流站运行于该交点可避免直流电压越限,并最大限度地提供无功功率。然而,由于功率可行域随故障持续时间的增加而缩减,一旦故障未能按预期故障持续时间切除,将导致直流电压越限。兼顾直流电压安全与无功支撑的故障穿越原理如图3所示,V点和C点分别为任一小于极限切除时间的故障持续时间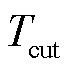 和极限切除时间对应的受端换流站功率范围的上、下边界的交点和切点。V点位于大于
和极限切除时间对应的受端换流站功率范围的上、下边界的交点和切点。V点位于大于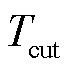 的故障持续时间对应的功率可行域外,故障持续时间大于
的故障持续时间对应的功率可行域外,故障持续时间大于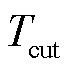 时控制受端换流站运行于V点必然导致直流电压越限。极限切除时间对应的受端换流站功率范围的上、下边界相切,切点C是可最长时间承受功率不平衡的受端换流站运行点。故障持续时间小于极限切除时间时,控制受端换流站运行于切点,可始终保证直流电压在故障切除时刻小于最大允许直流电压。因此,当故障持续时间小于极限切除时间时,C点的有功功率和无功功率应作为受端换流站的控制参考值。
时控制受端换流站运行于V点必然导致直流电压越限。极限切除时间对应的受端换流站功率范围的上、下边界相切,切点C是可最长时间承受功率不平衡的受端换流站运行点。故障持续时间小于极限切除时间时,控制受端换流站运行于切点,可始终保证直流电压在故障切除时刻小于最大允许直流电压。因此,当故障持续时间小于极限切除时间时,C点的有功功率和无功功率应作为受端换流站的控制参考值。
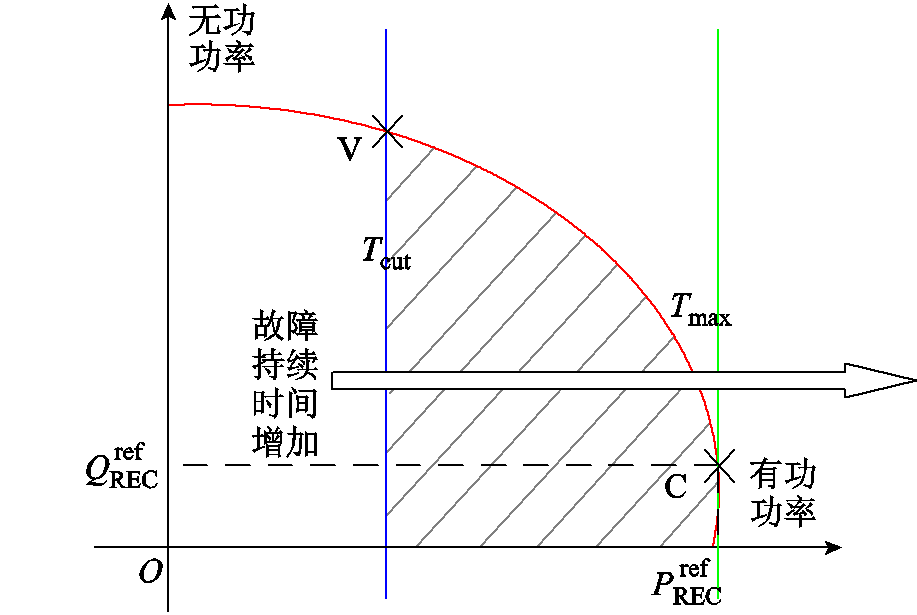
图3 兼顾直流电压安全与无功支撑的故障穿越原理
Fig.3 Fault ride-through principle balancing between DC voltage security and reactive power support
若故障持续时间大于极限切除时间,不存在避免直流电压越限的受端换流站有功功率和无功功率,需通过受端换流站与卸荷配合以保证直流电压安全。由于受端换流站运行于C点时可最大限度地延长直流电压越限所需时间,故不平衡功率最小,相同故障持续时间下为保证直流电压安全所需耗散的能量最小。单次卸荷耗散的能量等于直流电压从卸荷投入阈值降低到卸荷切除阈值期间的VSC-HVDC电容能量变化量,为常数。故障持续期间卸荷的投切次数与故障持续期间需耗散的能量正相关。因此,故障持续时间大于极限切除时间时,控制受端换流站运行于C点可最大限度地降低卸荷耗散的能量并减少卸荷投切次数。
C点可兼顾直流电压安全和无功功率支撑,故称C点为协调控制点。因此,无论故障持续多长时间,当故障后受端换流站交流母线电压低于切换门槛电压时,均应控制受端换流站运行于协调控制点,并根据极限切除时间投入卸荷。所提方法执行过程中:若控制器欠阻尼响应,响应过程中受端换流站有功功率将大于控制参考值,实际不平衡功率小于忽略了控制器动态过程的理想不平衡功率,根据理想不平衡功率计算的控制参考值不会导致直流过电压。即使当受端换流站有功功率因控制器过阻尼响应而略小于控制参考值时,实际不平衡功率可能略大。所提方法控制受端换流站运行于协调控制点,当故障持续时间小于极限切除时间,理想情况下直流电压小于最大允许直流电压。因此,所提方法根据理想不平衡功率计算的控制参考值留有一定的直流电压安全裕度,亦有助于耐受因控制器过阻尼响应造成的直流电压控制误差。
兼顾直流电压安全与无功支撑的VSC-HVDC故障穿越控制的框图如图4所示。
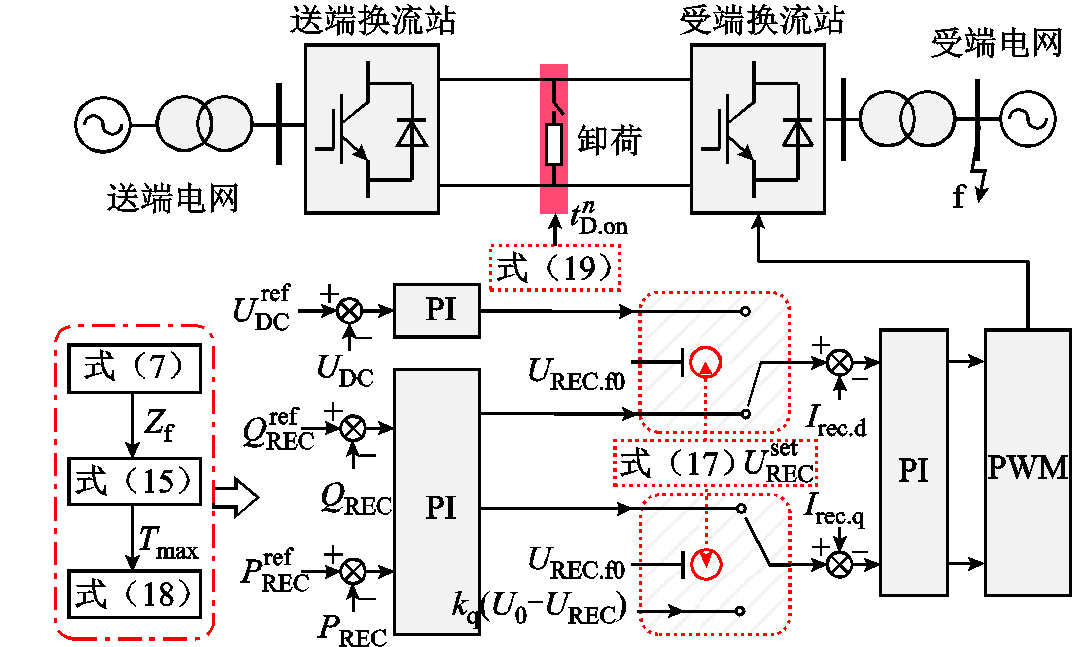
图4 所提VSC-HVDC故障穿越的控制框图
Fig.4 Control diagram of fault ride-through for VSC-HVDC of the proposed method
在受端换流站控制器上增加有功功率和无功功率控制参考值计算单元和切换门槛单元,如红色线条状阴影区域。当受端换流站交流母线电压跌落时,采集故障瞬间受端换流站交流母线电压幅值,比较受端换流站交流母线电压跌落程度与切换门槛电压的大小。当故障下受端换流站交流母线电压幅值低于切换门槛电压时,闭锁受端换流站直流电压控制外环,有功电流控制参考值由有功功率控制外环确定。当受端换流站交流母线电压跌落至切换门槛电压时,最大允许交流电流限制下的计及无功电流影响的受端换流站有功功率恰好受限。当受端换流站无功电流控制参考值依据电压跌落程度确定时,根据瞬时功率理论,切换门槛电压满足
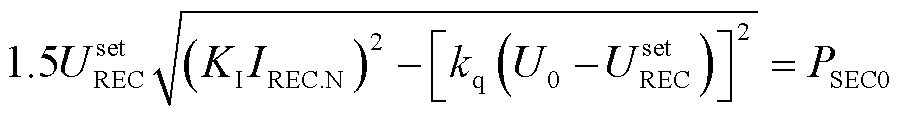 (16)
(16)
式中,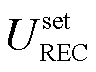 为切换门槛电压;
为切换门槛电压;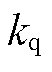 为无功电流系数;
为无功电流系数;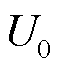 为受端换流站注入无功电流的启动电压。
为受端换流站注入无功电流的启动电压。
求解式(16)可得切换门槛电压为
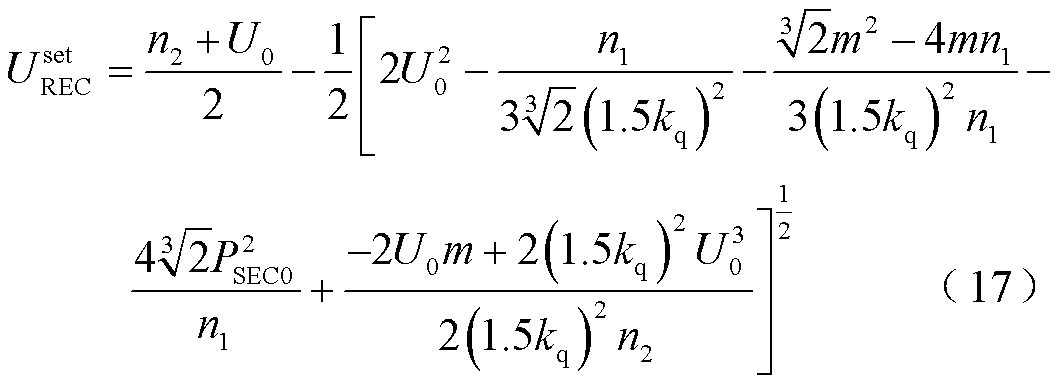
其中
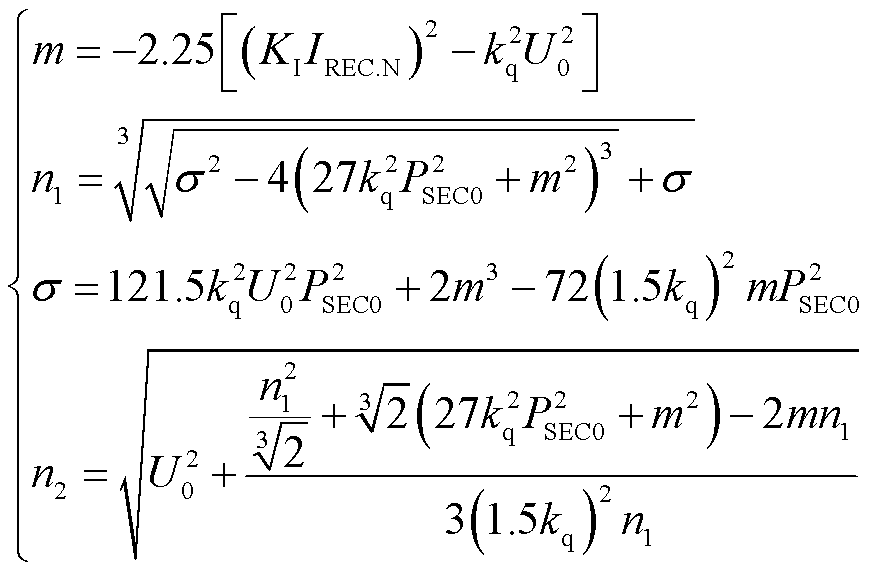
若故障下受端换流站交流母线电压幅值高于切换门槛电压,受端换流站维持定直流电压控制,由于直流电压不存在越限风险,卸荷闭锁;若故障下受端换流站交流母线电压幅值低于切换门槛电压,受端换流站切换为定有功功率和无功功率控制。进一步采集故障瞬间受端换流站交流母线电压相位、受端换流站有功功率和无功功率,代入式(7)求解等效故障过渡阻抗。受端电网的等效无穷大系统电势矢量在故障前后基本保持不变。串联阻抗可在故障前通过式(3)获得。因此,受端电网故障等值模型的建立仅需利用受端换流站内的电气量,避免了受端电网故障信息上传至受端换流站带来的延时。将等值故障受端电网的参数代入式(15),计算得到受端电网故障极限切除时间。将极限切除时间分别代入式(10)和式(12),受端换流站有功功率和无功功率控制参考值分别为
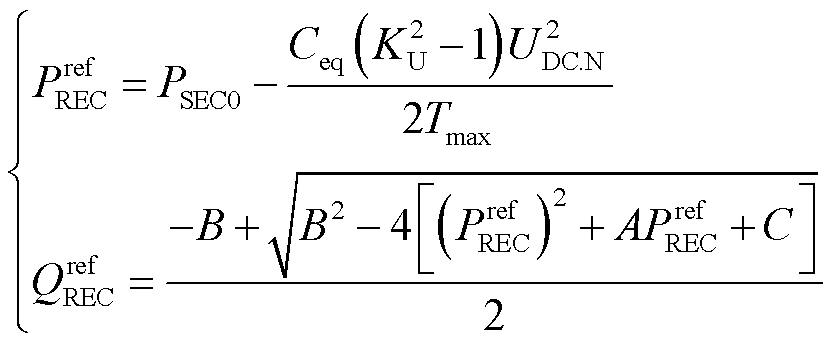 (18)
(18)
受端换流站联接强电网或VSC-HVDC卸荷风险较高时,为避免卸荷高频投切,受端电网故障下应在最大限度避免直流电压越限的前提下,尽可能地向受端电网提供无功功率。为此,所提方法充分利用最大交流电流限制下受端换流站有功功率和无功功率裕度,令受端换流站控制参考值在故障持续期间保持为协同控制点对应的有功功率和无功功率。根据式(18)可知,协同控制点对应的有功功率和无功功率仅与直流电容等常数、送端换流站有功功率和极限切除时间有关。所提方法为最大限度地避免将受端电网故障影响传播至送端电网,借助卸荷耗散不平衡功率,故设定故障期间送端换流站有功功率不变。由式(15)可知,极限切除时间仅与故障参数和VSC-HVDC额定参数有关,受端电网故障发生后极限切除时间随即确定。因此,故障期间受端换流站有功功率和无功功率参考值为常数。所提方法的控制参考值非时变,尽可能避免直流电压控制效果受控制器影响。
若受端电网故障在极限切除时间之前切除,定有功功率和无功功率控制下直流电压不会越限。若故障发生后极限切除时间时刻,受端换流站交流母线电压仍未恢复,应即刻投入卸荷,并于直流电压下降至额定值后切除。卸荷切除后,不平衡功率再次对VSC-HVDC的直流电容充电,直流电压变化趋势与故障发生后一致,故应在卸荷切除后的极限切除时间再次投入卸荷,在直流电压下降至额定值再次切除,不断重复直至受端电网故障切除。因此,卸荷的投入时间为
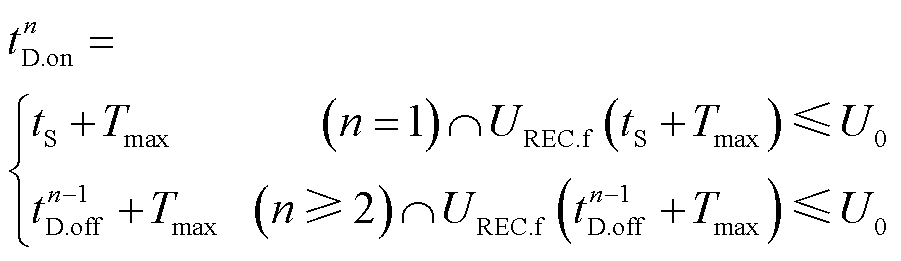 (19)
(19)
式中,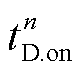 为第n次卸荷的投入时间;
为第n次卸荷的投入时间;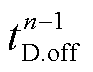 为第n-1次卸荷的切除时间;
为第n-1次卸荷的切除时间;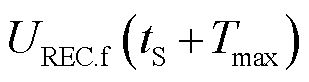 和
和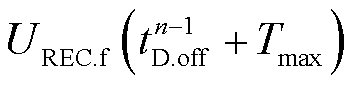 分别为
分别为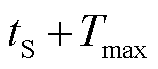 和
和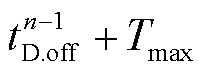 时刻的受端换流站交流母线电压。
时刻的受端换流站交流母线电压。
所提方法延续现有卸荷惯例,不调整送端换流站有功功率参考值,故所提方法效果和直流过电压水平不受送端电网的短路容量影响。受端电网故障参数一定时,受端换流站交流母线电压跌落程度随受端电网短路容量减小而增大。受制于受端换流站最大容许交流电流,故障前后受端换流站有功功率减小量随受端电网短路容量的减小而增大。因此,受端电网短路容量越小,相同故障场景下VSC-HVDC不平衡功率越大,直流过电压水平越高。然而,根据式(18),所提方法的控制参考值与受端电网故障等值模型的串联阻抗有关,串联阻抗反映了正常运行时受端电网的短路容量。因此,所提方法可适应不同的受端电网短路容量,始终能在最大限度避免卸荷的同时,尽可能地为受端电网提供无功功率。
建立如图5所示的仿真模型。受端换流站通常接入高压交流网络,一般难以建立详细模型。本文参考文献[28]利用2区4机系统等值实际受端电网。受端电网短路比为9,额定电压为220 kV。VSC-HVDC采用对称单极拓扑,配置常规直流集中卸荷,额定电压和传输容量分别为±100 kV和200 MV·A,最大允许直流电压系数和最大允许交流电流系数分别为1.1和1.2。送端换流站始终采用定有功功率和无功功率控制,控制参考值分别为1.0(pu)和0(pu)。正常运行时,受端换流站采用定直流电压和无功功率控制,控制参考值分别为1.0(pu)和0(pu)。其他参数详见附录。
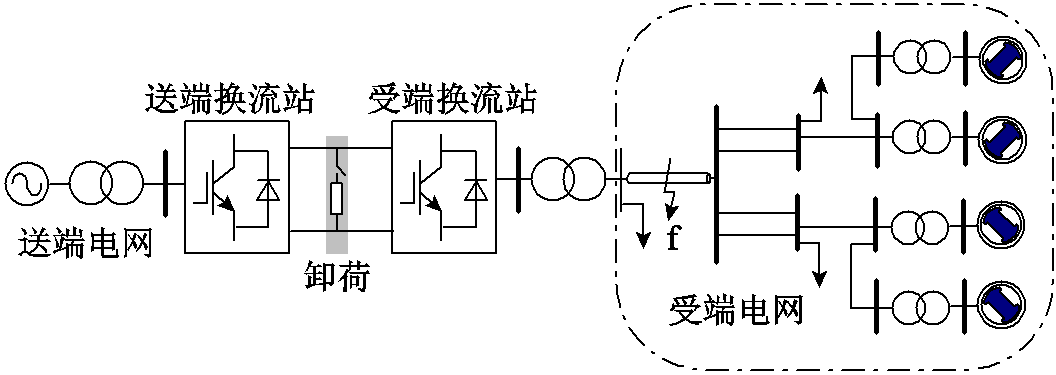
图5 仿真模型
Fig.5 Simulation model
设2.2 s于f点发生三相短路故障。故障瞬间受端换流站交流母线电压为0.78(pu),受端换流站有功功率和无功功率分别为0.94(pu)和0(pu)。根据故障瞬间受端换流站电气量和式(7),可得等效故障过渡电阻为11.6 Ω。由式(15)可得,受端电网故障极限切除时间为133 ms。设置故障持续时间分别为100 ms和极限切除时间,并令受端换流站的有功功率和无功功率参考值分别为100 ms和极限切除时间对应的受端换流站功率范围的上、下边界的交点和切点。将100 ms和极限切除时间代入式(13)可得有功功率参考值分别为0.89(pu)和0.93(pu),无功功率参考值分别为0.32(pu)和0.14(pu)。仿真可得不同故障持续时间下直流电压、受端换流站有功功率和无功功率,以及受端换流站交流母线电压、交流侧瞬时值分别如图6中红色实线和蓝色虚线所示。
图6a中,直流电压随故障持续时间增加而抬升,红色实线和蓝色虚线分别于100 ms和133 ms达到1.1(pu),证明控制受端换流站运行于功率范围的上、下边界的交点可使直流电压在故障切除时刻恰好达到最大允许直流电压。蓝色虚线在100 ms时的直流电压小于红线,并在极限切除时间取得峰值,表明受端换流站运行于协调控制点可以最大限度地延长直流电压越限所需时间,在极限切除时间前切除受端电网故障均可保证直流电压安全。
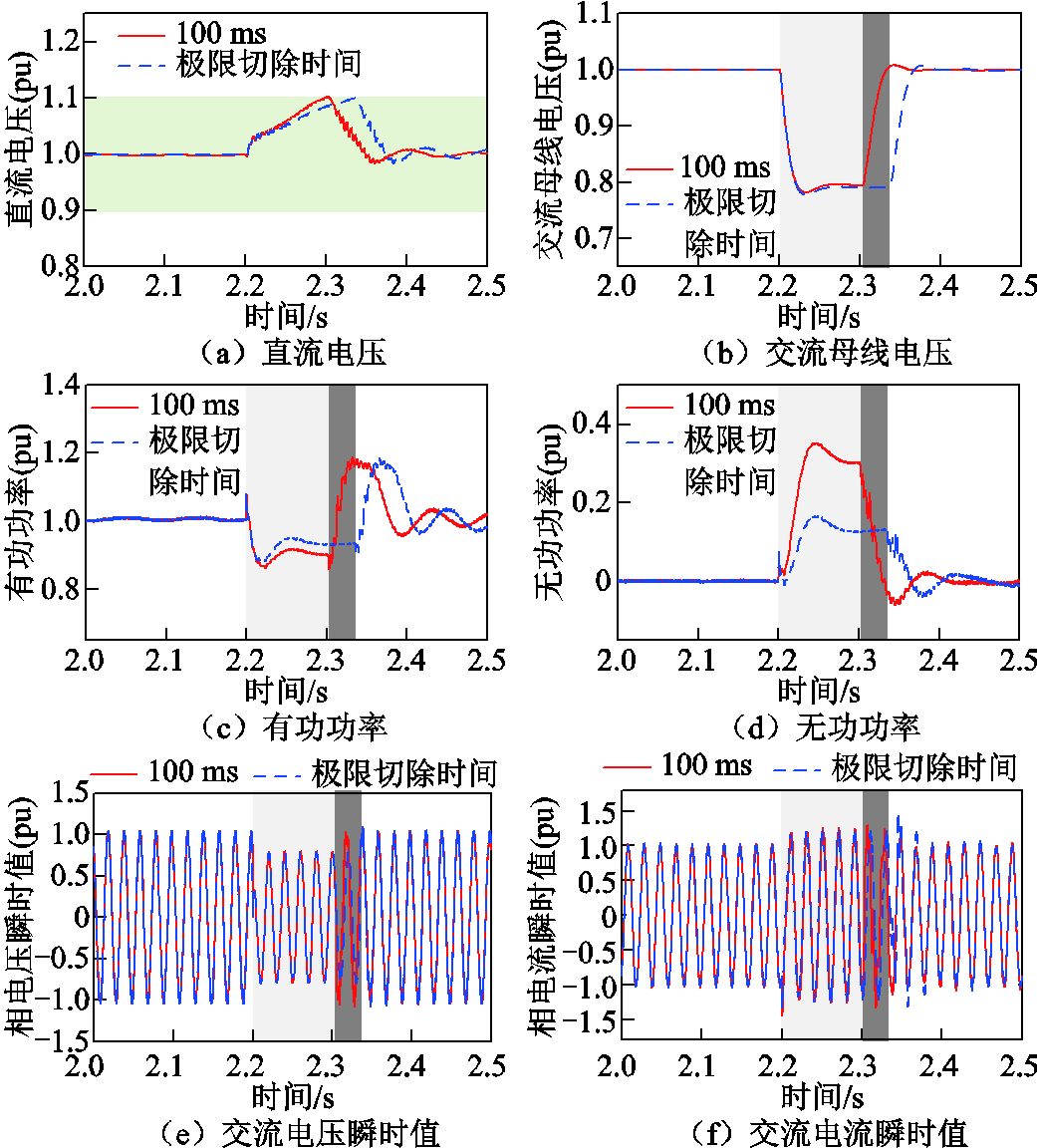
图6 故障持续时间不确定影响的验证
Fig.6 Verification of the impact of uncertain fault duration
当控制受端换流站运行于100 ms对应的受端换流站功率范围的上、下边界的交点时,交流母线电压抬升效果略优于运行于协调控制点,如图6b所示。然而,一旦故障未在100 ms时切除,红色实线的直流电压将超过安全限值。由图6c和图6d可见,随着故障持续时间增加,受端换流站功率范围的上、下边界的交点对应的有功功率增加,无功功率减小,证明受端换流站功率范围的下边界随故障持续时间增加向有功功率增大方向移动,使受端换流站功率可行域不断缩减。如图6e和图6f,受端电网故障发生和切除瞬间,受端换流站交流电压和电流发生跳变,但均位于安全界限内。
根据受端换流站交流母线电压跌落程度和切换门槛电压的大小关系设计两种场景。其中,当受端换流站交流母线电压低于切换门槛电压时,根据极限切除时间和故障持续时间的大小关系分为两种场景,并设置受端换流站有功功率送出严重受阻的场景4、实际工程参数的场景5。对以下两种控制方法进行比较:方法1根据交流电压跌落程度控制受端换流站向电网提供无功功率[29],无功电流控制参考值为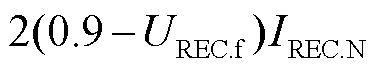 ,有功功率控制参考值取维持直流电压稳定所需有功功率与交流电流限幅下受端换流站最大有功功率中的较小者,并在直流电压超过1.05(pu)时候投入卸荷;方法2为本文所提的故障穿越控制方法。
,有功功率控制参考值取维持直流电压稳定所需有功功率与交流电流限幅下受端换流站最大有功功率中的较小者,并在直流电压超过1.05(pu)时候投入卸荷;方法2为本文所提的故障穿越控制方法。
5.2.1 电压跌落程度小于切换门槛电压
场景1:2.2 s时f点发生三相短路故障,故障持续时间为200 ms。根据式(7)可得等效故障过渡电阻为14.8 Ω。根据式(17)可得切换门槛电压为0.83(pu),小于故障瞬间的受端换流站交流母线电压0.85(pu)。方法1和2的受端换流站无功电流控制参考值均为0.11(pu),有功功率控制参考值均为故障前的初始有功功率。方法2相较于方法1闭锁卸荷。仿真可得方法1和2下的VSC-HVDC电气量分别如图7中红色实线和蓝色虚线所示。
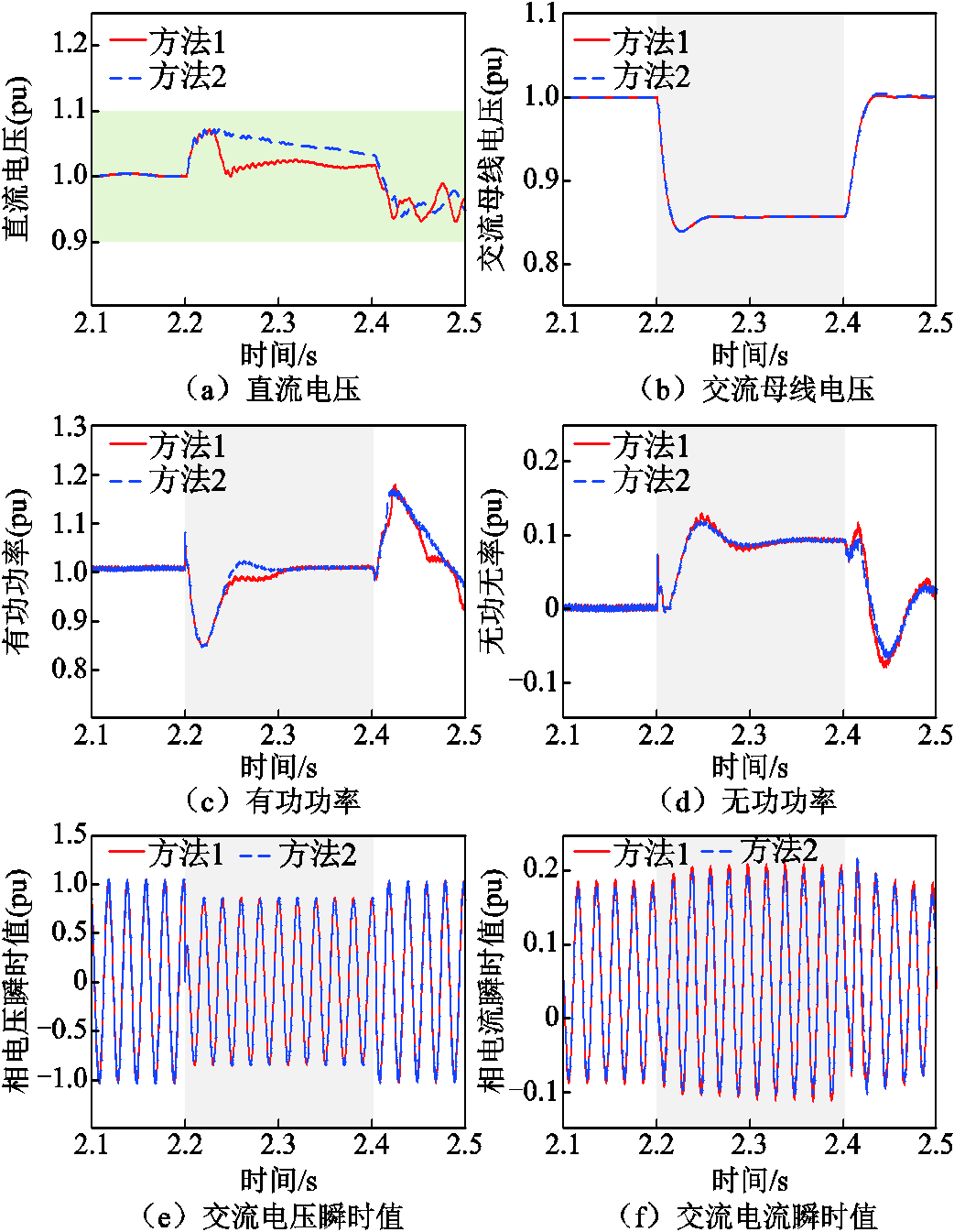
图7 场景1下VSC-HVDC电气量
Fig.7 Electrical quantities under scenario 1
由图7a可知,受端电网故障下受端换流站有功功率在定直流电压控制下恢复至初始有功功率,直流电压先升高后降低。当直流电压超过1.05(pu)时,方法1立即投入卸荷。然而,直流电压在达到1.05(pu)后不断减小,并逐步稳定至额定值,最大直流电压未超过安全限制1.1(pu),方法1造成卸荷的非必要投入。方法2的切换门槛电压小于故障瞬间的受端换流站交流母线电压,故判定受端电网故障期间直流电压不越限,从而闭锁了卸荷。方法1和2下受端换流站无功功率均为0.08(pu),交流母线电压抬升程度近似,如图7b~图7d所示。两种方法对受端电网的电压支撑效果相同,但本文所提方法避免了卸荷的非必要投入。方法1和2下受端换流站交流电流均小于最大允许值1.2(pu),不会导致换流站过流闭锁,如图7e和图7f所示。
5.2.2 电压跌落程度大于切换门槛电压
场景2:改变故障严重程度,2.2 s时f点发生三相短路故障,故障持续时间为100 ms。故障瞬间受端换流站交流母线电压跌落至0.76(pu),小于切换门槛电压。根据式(7),等效故障过渡电阻为11.5 Ω。方法2中受端换流站切换为定有功功率和无功功率控制并与卸荷配合,根据式(15)可得受端电网故障极限切除时间为104 ms,根据式(18)可得方法2的有功功率和无功功率控制参考值分别为0.91(pu)和0.12(pu)。仿真可得不同控制方法下电气量如图8所示。
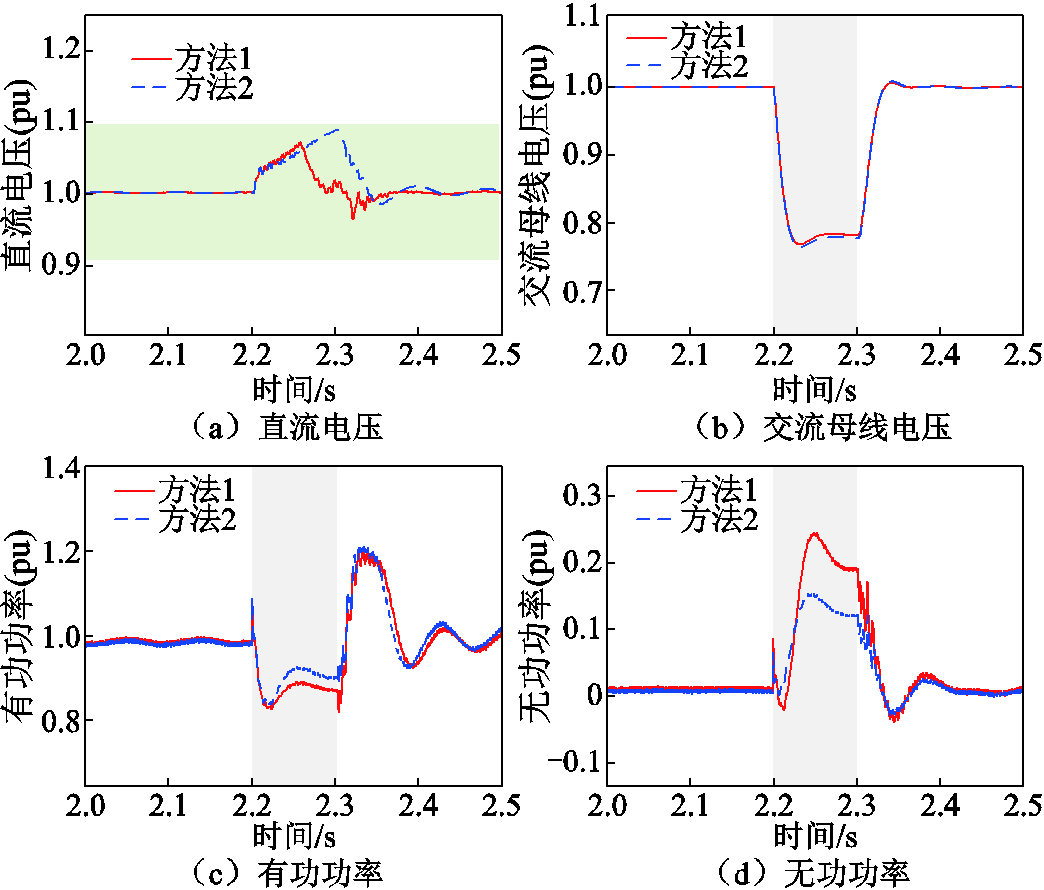
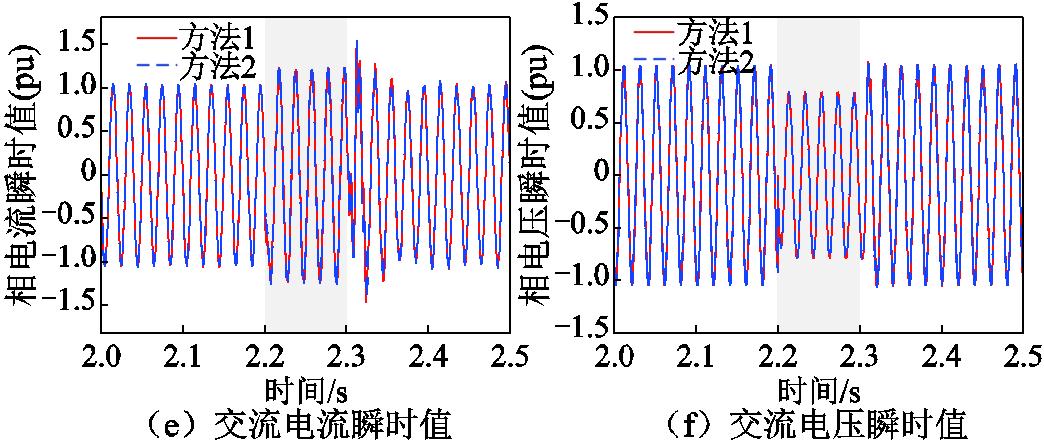
图8 场景2下VSC-HVDC电气量(故障持续时间小于故障极限切除时间)
Fig.8 Electrical quantities under scenario 2 (fault duration less than critical clearing time)
方法1根据交流母线电压跌落程度确定控制参考值,为受端电网提供了更大的无功功率,但却以牺牲有功功率为代价,故障前后有功功率变化量达到24 MW,造成受端电网故障期间直流电压快速上升。方法1作用下,故障发生后52 ms直流电压达到卸荷投入门槛值,如图8a~图8c红色实线所示。方法2通过适度降低无功功率,减缓了直流电压的变化率。方法2作用下,故障切除时刻直流电压未超过最大允许直流电压,避免了卸荷投切。如图8b所示,方法1和2的交流母线电压基本重合。方法2的受端换流站无功功率减小对受端电网电压的影响十分有限,但避免了直流电压越限,也证明了VSC-HVDC故障穿越兼顾受端换流站无功功率与直流电压安全的必要性。
场景3:改变故障持续时间为200 ms。根据式(7)和式(18),可得等效故障过渡电阻为10 Ω,协调控制点的有功功率和无功功率分别为0.85(pu)和0.12(pu)。根据式(19)可得方法2下卸荷的首次投入时间为2.26 s。仿真可得两种控制方法下的VSC-HVDC电气量如图9所示。
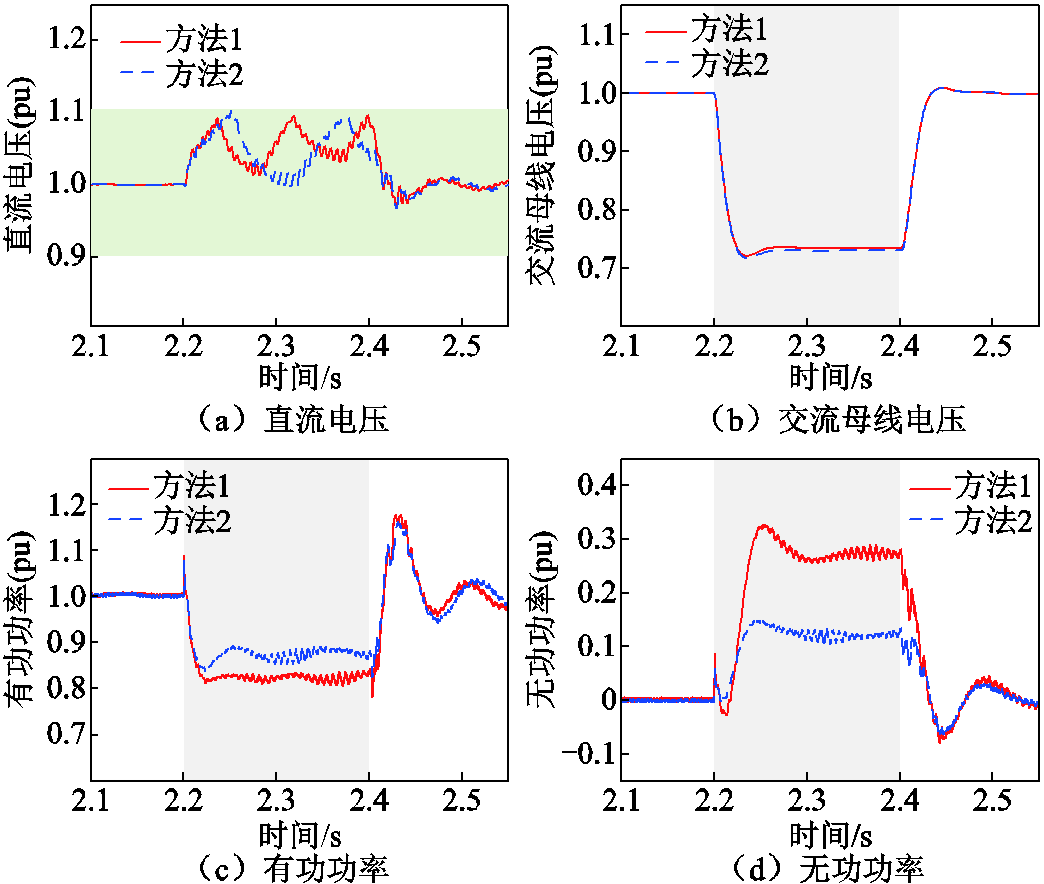
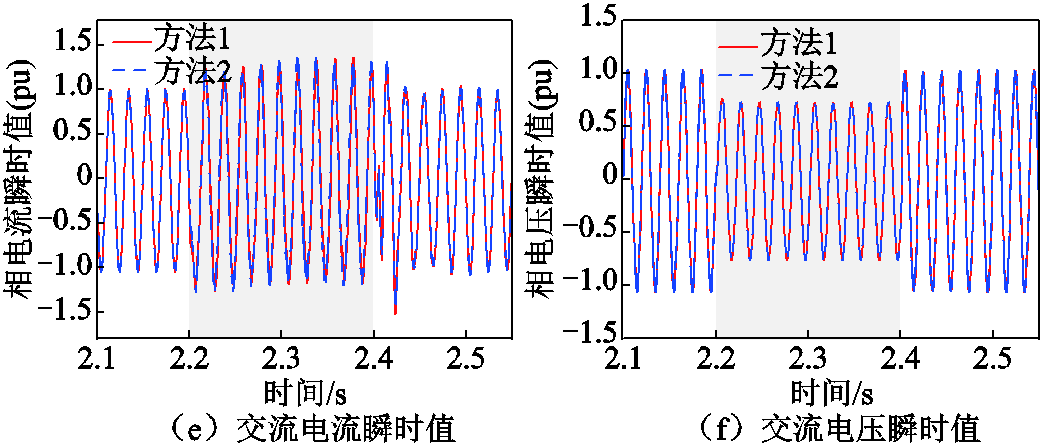
图9 场景3下VSC-HVDC电气量(受端电网故障极限切除时间小于故障持续时间)
Fig.9 Electrical quantities under scenario 3 (fault duration more than critical clearing time)
故障持续时间为200 ms,极限切除时间为61.2 ms,故受端电网故障期间仅依靠受端换流站控制无法避免直流电压越限。图9a中,两种控制方法下直流电压均超过卸荷启动门槛值。然而,方法1下受端换流站有功功率和无功功率分别为0.82(pu)和0.26(pu)。由于方法1的控制参考值仅根据交流母线电压确定,导致直流电压上升斜率显著大于方法2。方法1作用下,卸荷于故障后37 ms首次投入;方法2的卸荷在故障后61 ms时首次投入。受端电网故障期间,方法1下总计卸荷3次,方法2卸荷2次,所提方法的卸荷投切次数降低。如图9b~图9d所示,两种方法下的交流母线电压相近,但所提方法有效地降低了卸荷投切对换流设备和交直流系统造成的冲击。
场景4:改变实际故障位置。根据式(7)和式(18),可得等效故障过渡电感为13.0 mH,协调控制点的有功功率和无功功率分别为0.33(pu)和0.10(pu)。根据式(19)可得方法2下卸荷的首次投入时间为2.21 s。仿真可得两种控制方法下的电气量如图10所示。
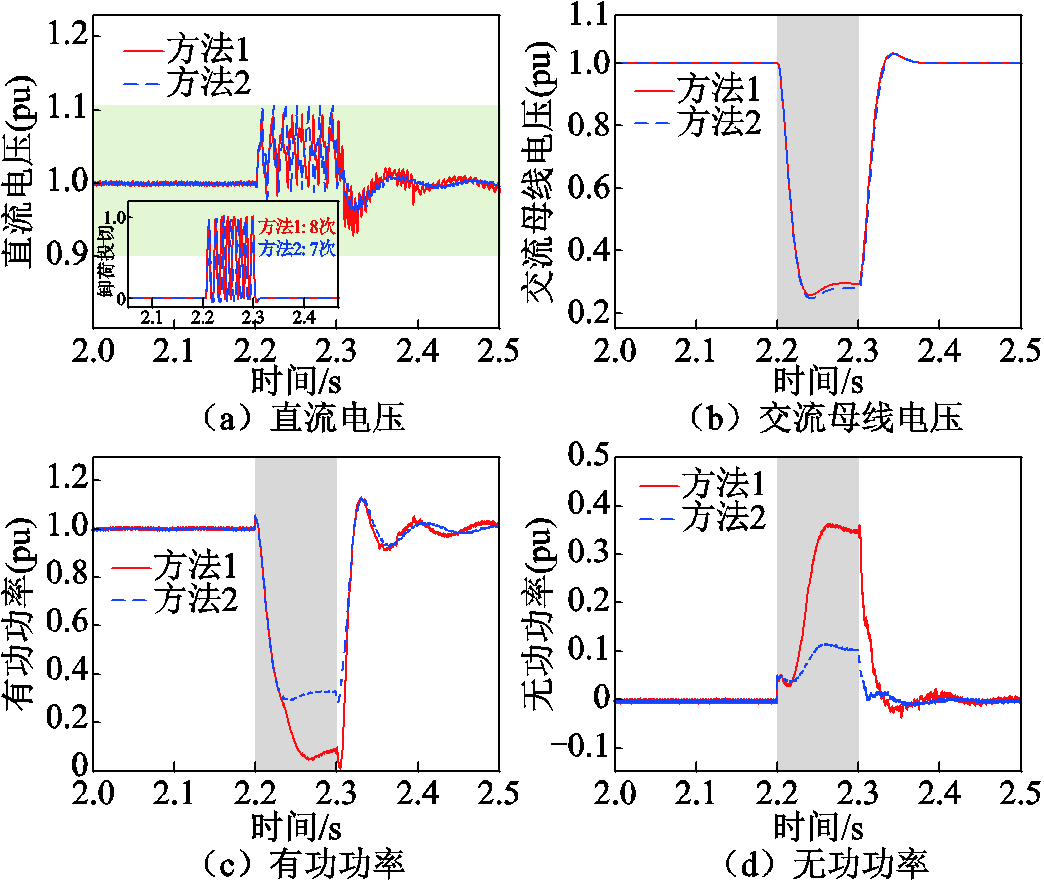
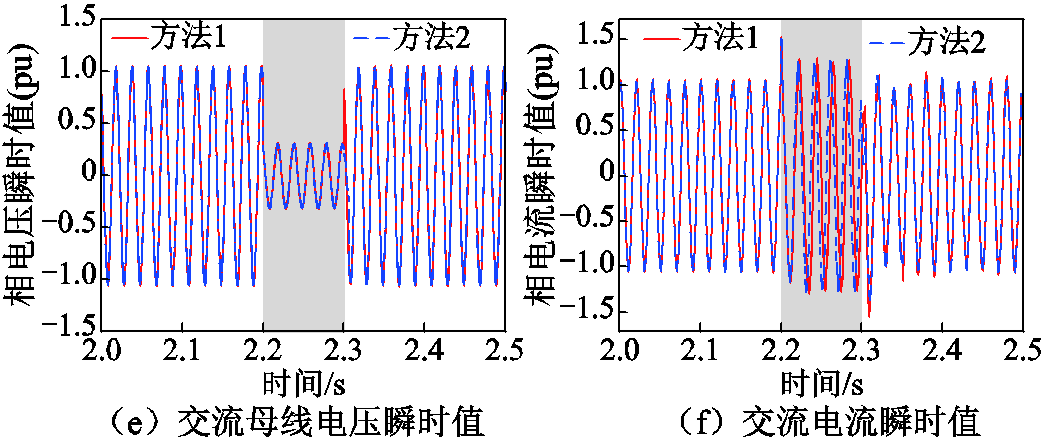
图10 场景4下VSC-HVDC电气量(经电感接地的三相严重故障)
Fig.10 Electrical quantities under scenario 4 (severe three-phase fault via inductive grounding)
方法1根据交流母线电压跌落程度确定控制参考值,为受端电网多提供了0.23(pu)的无功功率,但与方法2相比交流母线电压抬升效果增幅微弱。方法1以牺牲有功功率为代价,故障后有功功率大幅减小至0.07(pu),造成受端电网故障期间直流电压的快速上升。在方法1作用下,故障发生后6.8 ms直流电压达到卸荷投入门槛值,如图10a~图10c红色实线所示。故障下方法2的受端换流站有功功率仍保持0.33(pu),有利于降低受端电网造成的VSC-HVDC功率不平衡,保障直流电压安全所需的卸荷投切次数和能量耗散量均降低,如图10a~10d蓝色虚线所示。相较于经电阻接地故障,受端换流站交流电压和电流在故障发生和切除时的突变更显著,如图10e和图10f所示。
场景5:进一步以鲁西背靠背VSC-HVDC工程参数为条件,以故障过渡阻抗为测试场景,验证所提方法的有效性。鲁西背靠背VSC-HVDC采用对称单极拓扑,额定电压和传输容量分别为±350 kV和1 000 MV·A。等效故障过渡电阻和电感分别为7.2 Ω和30.6 mH,方法1和2均配置常规直流集中卸荷以耗散不平衡功率。方法2的协同控制点的有功功率和无功功率分别为726 MW和133 Mvar,卸荷的首次投入时间为2.230 s。仿真可得两种控制方法下的VSC-HVDC电气量如图11所示。
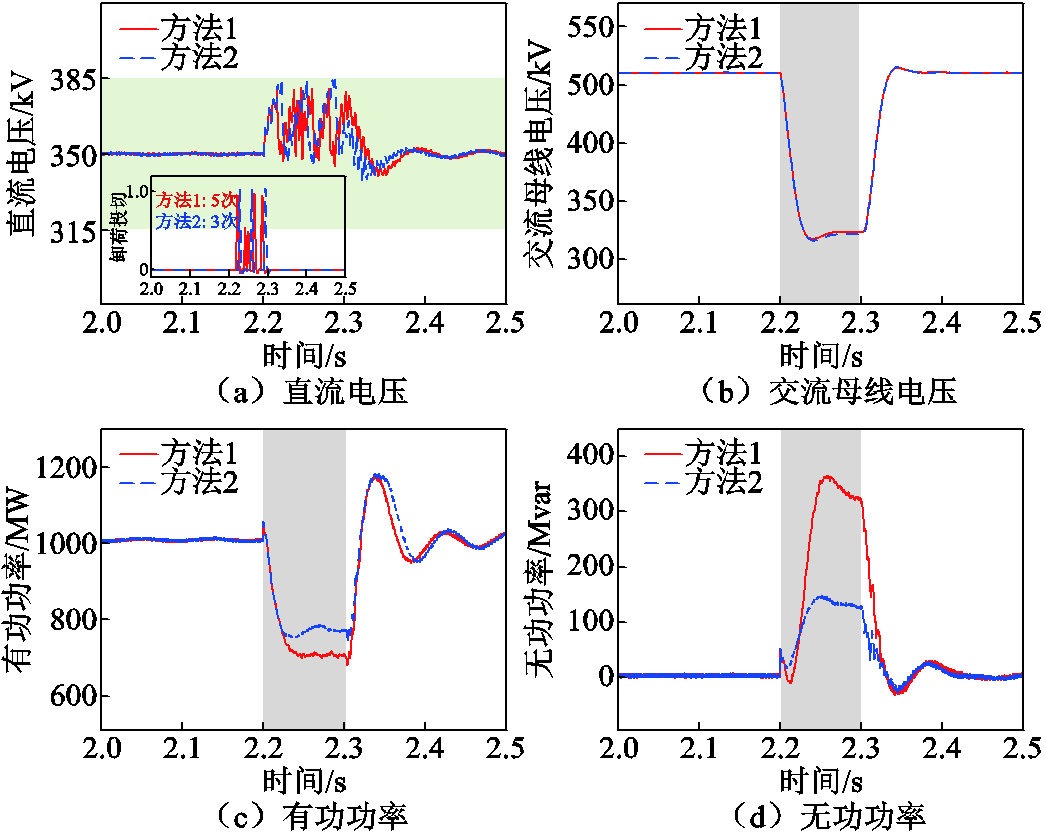
图11 场景5下VSC-HVDC电气量(实际工程参数下经故障阻抗接地)
Fig.11 Electrical quantities under scenario 5 (real engineering parameters when short-circuited by impedance)
方法1根据交流母线电压跌落程度确定控制参考值,为受端电网多提供了194.4 Mvar的无功功率,但却以牺牲有功功率为代价,故障前后有功功率变化量达到322 MW,造成受端电网故障期间直流电压的快速上升;方法2通过适度降低无功功率,减缓了直流电压的变化率。方法2的受端换流站交流母线电压抬升程度与方法1相似,但却能降低16.3%的有功功率跌落。因此,方法2的受端换流站无功功率减小对受端电网电压的影响十分有限,但使得不平衡功率降低,保障直流电压安全所需的卸荷投切次数和卸荷量均降低,如图11所示。结合场景1~5可知,本文所提方法的有效性不受故障阻抗性质、故障持续时间和交流母线电压跌落程度影响。
装设卸荷的VSC-HVPC中,卸荷投入门槛单一且与受端换流站无功功率控制缺乏配合,可能造成卸荷非必要投入。本文通过推导令直流电压越限的受端换流站交流母线作为切换门槛,提出了卸荷闭锁判据。通过建立避免直流电压和交流电流越限的受端换流站功率可行域,提出了表征直流电压安全裕度的受端电网故障极限切除时间的概念和计算方法。考虑到不同故障持续时间下受端换流站功率可行域的变化,提出了VSC-HVDC故障穿越控制方法。所提出的方法计及交流母线电压和受端换流站无功功率对直流电压安全的影响,在尽可能减少卸荷的同时,使受端换流站最大限度地支撑受端电网电压。
与三相故障不同,单相故障下受端换流站存在负序电流,受端换流站有功功率产生2倍工频分量,造成直流电压波动。单相故障下,当受端换流站的交流母线电压正序分量大于式(17)的切换门槛电压时,定直流电压控制作用下健全相有功功率增大,送端换流站与受端换流站的有功功率直流分量之差为0,直流电压不会随着故障持续而抬升,仅因受端换流站有功功率的2倍频分量而波动,直流电压不存在越限风险。因此,当受端电网发生单相故障时,若受端换流站的交流母线电压正序分量大于切换门槛电压,所提出的方法依然适用,受端换流站维持定直流电压控制,闭锁卸荷。若受端换流站的交流母线电压正序分量小于切换门槛电压,直流电压波动上升,此时所提出的方法不再适用,受端换流站功率可行域、受端电网故障极限切除时间以及控制参考值的计算还需进一步研究。
附 录
1. 仿真模型参数
附表1 仿真模型主接线参数
App.Tab.1 Electrical wiring parameters of simulation model
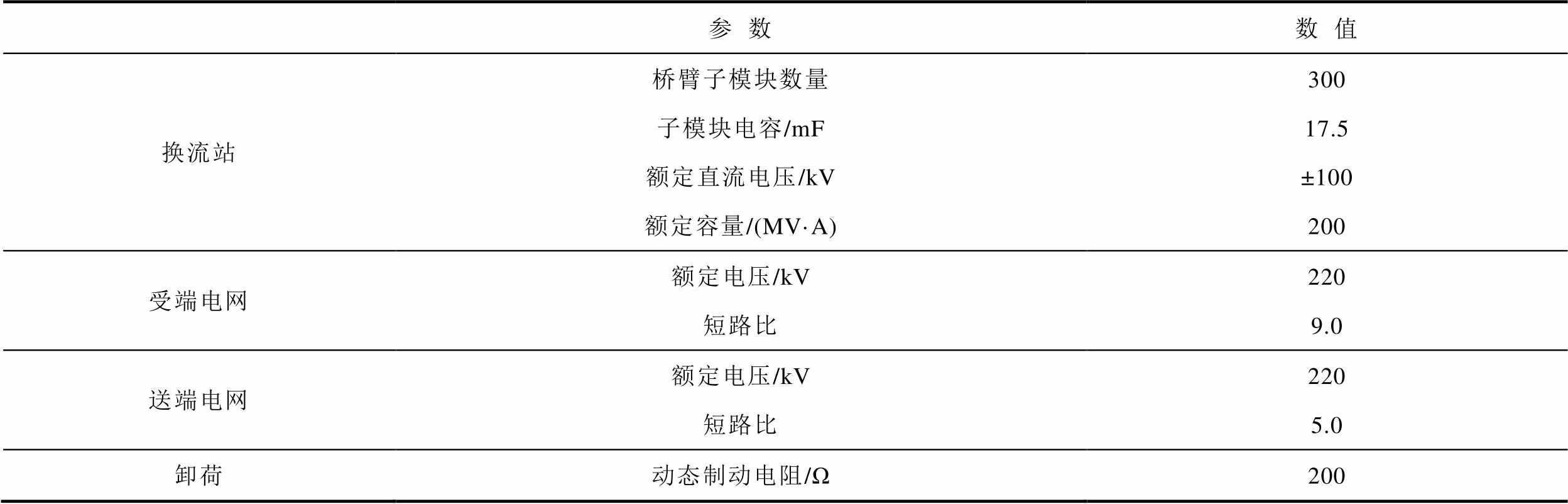
参数数值 换流站桥臂子模块数量300 子模块电容/mF17.5 额定直流电压/kV±100 额定容量/(MV·A)200 受端电网额定电压/kV220 短路比9.0 送端电网额定电压/kV220 短路比5.0 卸荷动态制动电阻/Ω200
附表2 换流站控制器参数
App.Tab.2 Converter controller parameters of simulation model

换流站参数数值 受端换流站外环控制量UDC, QREC 外环的比例和积分系数2.0, 40.0 内环的比例和积分系数0.6, 6.0 内环限幅系数1.2 送端换流站外环控制量PSEC, QSEC 外环的比例和积分系数3.0, 3.0 内环的比例和积分系数0.6, 6.0 内环限幅系数1.2
2. 所提方法实例计算
以第5.2.2节场景3中受端电网故障极限切除时间小于故障持续时间为例,受端换流站功率可行域的上边界可表示为
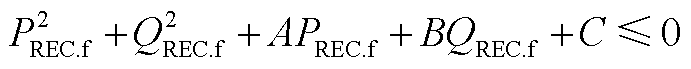 (A1)
(A1)
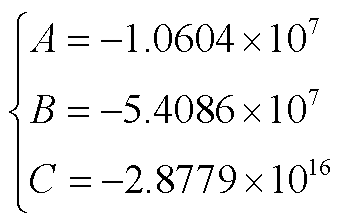 (A2)
(A2)
受端换流站功率可行域的下边界的解析式为
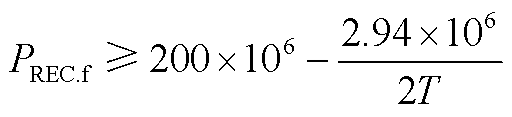 (A3)
(A3)
受端电网故障极限切除时间可表示为
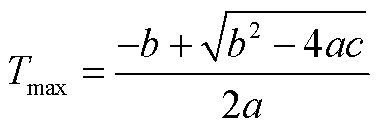 (A4)
(A4)
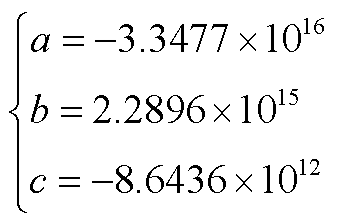 (A5)
(A5)
因此,受端电网故障极限切除时间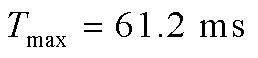 ,代入式(18),可得受端换流站有功功率参考值
,代入式(18),可得受端换流站有功功率参考值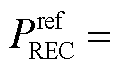
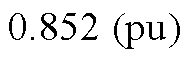 ,无功功率参考值
,无功功率参考值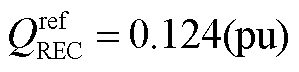 。
。
参考文献
[1] 孟沛彧, 向往, 潘尔生, 等. 分址建设直流输电系统拓扑方案与运行特性研究[J]. 电工技术学报, 2022, 37(19): 4808-4822.
Meng Peiyu, Xiang Wang, Pan Ersheng, et al. Research on topology and operation characteristics of HVDC transmission system based on site-division construction[J]. Transactions of China Electrotechnical Society, 2022, 37(19): 4808-4822.
[2] 马富艺龙, 辛焕海, 刘晨曦, 等. 新能源基地柔性直流送出系统小扰动电压支撑强度评估[J]. 电工技术学报, 2023, 38(21): 5758-5770, 5938.
Ma Fuyilong, Xin Huanhai, Liu Chenxi, et al. Small-disturbance system voltage support strength assessmentmethod for renewables VSC-HVDC delivery system[J]. Transactions of China Electrotechnical Society, 2023, 38(21): 5758-5770, 5938.
[3] 束洪春, 代月, 安娜, 等. 基于线性回归的柔性直流电网纵联保护方法[J]. 电工技术学报, 2022, 37(13): 3213-3226, 3288.
Shu Hongchun, Dai Yue, An Na, et al. Pilot protection method of flexible DC grid based on linear regression[J]. Transactions of China Electrotechnical Society, 2022, 37(13): 3213-3226, 3288.
[4] 束洪春, 邵宗学, 赵伟, 等. 含柔性直流的交直流混联电力系统紧急频率控制研究[J]. 电工技术学报, 2023, 38(20): 5590-5604.
Shu Hongchun, Shao Zongxue, Zhao Wei, et al. Research on emergency power control of AC-DC hybrid power system with flexible DC[J]. Transa-ctions of China Electrotechnical Society, 2023, 38(20): 5590-5604.
[5] 陈明泉, 林国栋, 晁武杰, 等. 厦门柔直工程交流故障穿越失败事件分析及改进措施[J]. 电气技术, 2023, 24(2): 71-76.
Chen Mingquan, Lin Guodong, Chao Wujie, et al. Analysis and improvement for AC fault ride-through failure event in Xiamen flexible HVDC transmission project[J]. Electrical Engineering, 2023, 24(2): 71-76.
[6] 江守其, 李国庆, 辛业春, 等. 提升柔性直流电网盈余功率消纳能力的协调控制策略[J]. 高电压技术, 2021, 47(12): 4471-4482.
Jiang Shouqi, Li Guoqing, Xin Yechun, et al. Coordinated control strategies to enhance the capability of surplus power consumption for DC grid[J]. High Voltage Engineering, 2021, 47(12): 4471-4482.
[7] 张钦智, 王宾, 李琰, 等. 风电场经柔性直流输电系统故障穿越协调控制研究[J]. 电力系统保护与控制, 2020, 48(10): 131-138.
Zhang Qinzhi, Wang Bin, Li Yan, et al. Research on fault crossing coordination control of a wind farm via a flexible direct current transmission system[J]. Power System Protection and Control, 2020, 48(10): 131-138.
[8] 杨仁炘, 王霄鹤, 陈晴, 等. 机组协同-分布卸荷的风电场-柔直并网系统故障穿越方法[J]. 电力系统自动化, 2021, 45(21): 103-111.
Yang Renxin, Wang Xiaohe, Chen Qing, et al. Fault ride-through method of flexible HVDC transmission system for wind farm integration based on coordination of wind turbines and distributed braking resistors[J]. Automation of Electric Power Systems, 2021, 45(21): 103-111.
[9] 董旭, 张峻榤, 王枫, 等. 风电经架空柔性直流输电线路并网的交直流故障穿越技术[J]. 电力系统自动化, 2016, 40(18): 48-55.
Dong Xu, Zhang Junjie, Wang Feng, et al. AC and DC fault ride-through technology for wind power integration via VSC-HVDC overhead lines[J]. Automation of Electric Power Systems, 2016, 40(18): 48-55.
[10] 厉璇, 宋强, 刘文华, 等. 风电场柔性直流输电的故障穿越方法对风电机组的影响[J]. 电力系统自动化, 2015, 39(11): 31-36, 125.
Li Xuan, Song Qiang, Liu Wenhua, et al. Impact of fault ride-through methods on wind power generators in a VSC-HVDC system[J]. Automation of Electric Power Systems, 2015, 39(11): 31-36, 125.
[11] Silva B, Moreira C L, Leite H, et al. Control strategies for AC fault ride through in multiterminal HVDC grids[J]. IEEE Transactions on Power Delivery, 2014, 29(1): 395-405.
[12] 梅念, 周杨, 李探, 等. 张北柔性直流电网盈余功率问题的耗能方法[J]. 电网技术, 2020, 44(5): 1991-1999.
Mei Nian, Zhou Yang, Li Tan, et al. Energy consumption method for power surplus in Zhangbei VSC-based DC grid[J]. Power System Technology, 2020, 44(5): 1991-1999.
[13] Xu Bin, Gao Chong, Zhang Jing, et al. A novel DC chopper topology for VSC-based offshore wind farm connection[J]. IEEE Transactions on Power Electronics, 2021, 36(3): 3017-3027.
[14] 曹帅, 向往, 左文平, 等. 风电经柔性直流电网外送系统的交流故障诊断与穿越控制策略[J]. 中国电机工程学报, 2021, 41(4): 1295-1306.
Cao Shuai, Xiang Wang, Zuo Wenping, et al. AC fault diagnosis and ride-trough control strategy for the wind power delivery system via HVDC grid[J]. Proceedings of the CSEE, 2021, 41(4): 1295-1306.
[15] 张福轩, 郭贤珊, 汪楠楠, 等. 接入新能源孤岛系统的双极柔性直流系统盈余功率耗散策略[J]. 电力系统自动化, 2020, 44(5): 154-160.
Zhang Fuxuan, Guo Xianshan, Wang Nannan, et al. Surplus power dissipation strategy for bipolar VSC-HVDC system with integration of islanded renewable energy generation system[J]. Automation of Electric Power Systems, 2020, 44(5): 154-160.
[16] 蔡婷婷, 穆钢, 严干贵, 等. 提高海上风电场经MMC联网系统故障穿越能力的柔性泄能电阻控制策略[J]. 电网技术, 2020, 44(1): 166-173.
Cai Tingting, Mu Gang, Yan Gangui, et al. A flexible control strategy of breaking resistor to enhance fault-ride-through ability for offshore wind farms integrated to grid via MMC[J]. Power System Technology, 2020, 44(1): 166-173.
[17] 曹帅, 刘东, 赵成功. 适用于风电经柔性直流并网系统的柔性耗能装置及控制策略[J]. 电力系统保护与控制, 2022, 50(23): 51-62.
Cao Shuai, Liu Dong, Zhao Chenggong. A flexible energy dissipation device with control strategy for an HVDC wind power integration system[J]. Power System Protection and Control, 2022, 50(23): 51-62.
[18] 陈晴, 严佳男, 谢瑞, 等. 半/全桥混合型DC Chopper拓扑及其控制策略[J]. 高电压技术, 2021, 47(11): 4013-4022.
Chen Qing, Yan Jianan, Xie Rui, et al. Half/full bridge hybrid DC Chopper topology and its control strategy[J]. High Voltage Engineering, 2021, 47(11): 4013-4022.
[19] 张静, 高冲, 许彬, 等. 海上风电直流并网工程用新型柔性直流耗能装置电气设计研究[J]. 中国电机工程学报, 2021, 41(12): 4081-4091.
Zhang Jing, Gao Chong, Xu Bin, et al. Research on electrical design of novel flexible DC energy consuming device for offshore wind power DC grid connection project[J]. Proceedings of the CSEE, 2021, 41(12): 4081-4091.
[20] 贾科, 董学正, 毕天姝, 等. 功率精准匹配的海上风电柔直并网系统电网侧故障穿越方法[J]. 中国电机工程学报, 2023, 43(增刊1): 84-93.
Jia Ke, Dong Xuezheng, Bi Tianshu, et al. A grid side fault ride-through method based on precise matching power for offshore wind farms connected MMC-HVDC[J]. Proceedings of the CSEE, 2023, 43(S1): 84-93.
[21] 周瑀涵, 辛焕海, 鞠平. 基于广义短路比的多馈入系统强度量化原理与方法:回顾、探讨与展望[J]. 中国电机工程学报, 2023, 43(10): 3794-3811.
Zhou Yuhan, Xin Huanhai, Ju Ping. System strength quantification principle and method of multi-infeed systems based on generalized short-circuit ratio: reviews, discussions and outlooks[J]. Proceedings of the CSEE, 2023, 43(10): 3794-3811.
[22] 朱海, 郝亮亮, 和敬涵, 等.HVDC送端交流系统故障引起换相失败的机理分析[J]. 电工技术学报, 2023, 38(16): 4465-4478.
Zhu Hai, Hao Liangliang, He Jinghan, et al. Mechanism analysis of commutation failure caused by fault of HVDC sending end AC system[J]. Tran-sactions of China Electrotechnical Society, 2023, 38(16): 4465-4478.
[23] Ouyang Jinxin, Pang Mingyu, Zheng Di, et al. Improved voltage control method of power system based on doubly fed wind farm considering power coupling under grid short-circuit fault[J]. IET Renewable Power Generation, 2020, 14(13): 2429-2436.
[24] 郝晓宇, 郭春义, 蒋雯, 等. 基于无功功率注入的MMC-HVDC交流电网等值阻抗识别方法[J]. 电力系统自动化, 2023, 47(9): 184-192.
Hao Xiaoyu, Guo Chunyi, Jiang Wen, et al. Identification method for equivalent impedance of AC power grid connected to MMC-HVDC system based on reactive power injection[J]. Automation of Electric Power Systems, 2023, 47(9): 184-192.
[25] Huang Sen, Yao Jun, Pei Jinxin, et al. Transient synchronization stability improvement control strategy for grid-connected VSC under symmetrical grid fault[J]. IEEE Transactions on Power Electronics, 2022, 37(5): 4957-4961.
[26] 向往, 文劲宇, 张浩博, 等. 柔性直流输电系统三维度控制[J]. 电网技术, 2023, 47(8): 3385-3397.
Xiang Wang, Wen Jinyu, Zhang Haobo, et al. Three-degree control of MMC based high voltage direct current transmission system[J]. Power System Technology, 2023, 47(8): 3385-3397.
[27] 袁小明, 张美清, 迟永宁, 等. 电力电子化电力系统动态问题的基本挑战和技术路线[J]. 中国电机工程学报, 2022, 42(5): 1904-1917.
Yuan Xiaoming, Zhang Meiqing, Chi Yongning, et al. Basic challenges of and technical roadmap to power-electronized power system dynamics issues[J]. Proceedings of the CSEE, 2022, 42(5): 1904-1917.
[28] Chakravarthi K, Bhui P, Sharma N K, et al. Real time congestion management using generation re-dispatch: modeling and controller design[J]. IEEE Transactions on Power Systems, 2023, 38(3): 2189-2203.
[29] 齐金玲, 李卫星, 晁璞璞, 等. 直驱风机故障穿越全过程的通用电磁暂态建模方法[J]. 中国电机工程学报, 2022, 42(4): 1428-1443.
Qi Jinling, Li Weixing, Chao Pupu, et al. Generic electromagnetic transient modeling method for complete fault ride-through processes of direct-driven wind turbine generators[J]. Proceedings of the CSEE, 2022, 42(4): 1428-1443.
Abstract Voltage source converter-based high voltage direct current (VSC-HVDC) is essential for building modern power systems. The rapid rise of DC voltage under the three-phase fault in the receiving-end grid may trigger overvoltage blocking and threaten grid stability. The existing fault ride-through method based on the dynamic braking resistor (DBR) for VSC-HVDC uses DC voltage as the activation condition. It does not take into account the impact of the AC bus voltage and reactive power of the receiving-end converter (REC) on DC voltage security, which may lead to non-essential activation of DBR due to unreasonable activation conditions or excessive reactive power of REC, causing extra shocks to the AC-DC system and increasing energy dissipation.
According to Davina's theorem, the faulty receiving-end grid is equated to a two-port network. Among them, the ideal voltage source and series impedance are the equivalent potential and the equivalent impedance of the receiving-end grid during normal operation, respectively. The parallel equivalent fault transition impedance is used to equate the effect of a short-circuited branch circuit on the equivalent impedance of the receiving-end grid. The analytical equations of the DC voltage and AC bus voltage of REC concerning the active and reactive power of REC are deduced. The power feasible domain of REC under the limitation of the maximum permissible AC current with the guarantee of DC voltage security is established to depict the power control capability of REC under the receiving-end grid fault.
The minimum active power of REC that precisely guarantees DC voltage security increases with the increase in fault duration, and the range of active and reactive power of REC under the limitation of the maximum permissible AC current is constant, so that the power feasible domain of REC exhibits a shrinking characteristic. If the power feasible domain of REC under a certain fault duration has only one point, the fault duration is the critical clearing time of the receiving-end grid fault. Since REC can provide the maximum active power under the limitation of the maximum permissible AC current, the DC voltage will exceed its maximum permissible value at the critical clearing time. Therefore, the critical clearing time characterizes the security margin of the DC voltage under the receiving-end grid fault.
The active current of REC required to maintain DC voltage stabilization cannot be increased without limit as the degree of AC bus voltage drop increases. The control reference value of REC shall be adapted to the different fault severities in the receiving-end grid. Suppose REC can provide a certain reactive current while restoring its active power to its initial value before the fault. In that case, the DC voltage can be kept stable, and REC can continue to use constant DC voltage control. When the receiving-end grid fault is more severe and the active power decreases due to the reactive power provided by REC, the DC voltage will continue to rise with the increase in fault duration. REC should be switched to the fixed active and reactive power control and cooperate with DBR.
The coordination control point is the operating point of REC that can withstand the power imbalance for the longest time. The time required for DC overvoltage can be maximized when REC is operated at the coordination control point. If the critical clearing time exceeds the fault duration, the DC voltage during the receiving-end grid fault is less than the maximum permissible DC voltage. If the fault duration exceeds the critical clearing time, the unbalanced power is minimized, and the energy dissipated to ensure DC voltage security is minimized. Therefore, no matter how long the fault duration is, when the AC bus voltage of REC is lower than the switching threshold voltage, REC should be controlled to operate at the coordination control point and activate DBR according to the critical clearing time.
keywords:Voltage source converter based high voltage direct current (VSC-HVDC), AC fault ride-through, DC voltage, reactive power
中图分类号:TM721
DOI: 10.19595/j.cnki.1000-6753.tces.231447
国家重点研发计划资助项目(2023YFB2406800)。
收稿日期 2023-09-01
改稿日期 2024-03-19
欧阳金鑫 男,1984年生,副教授,博士生导师,研究方向为电力系统故障分析、保护与控制。
E-mail:jinxinoy@163.com(通信作者)
陈纪宇 男,1999年生,博士研究生,研究方向为柔性直流输电的故障分析、保护与控制。
E-mail:chenjiyve@163.com
(编辑 赫 蕾)