图1 需求响应原理
Fig.1 The principle of DR
摘要 为提高在需求响应情境下,综合能源系统的多元负荷短期预测精度,基于消费者心理学、响应不确定性原理、耦合响应原理,构建了考虑综合需求响应的Transformer-图神经网络(Trans-GNN)预测模型。通过响应不确定性随电价差产生的变化规律和消费者心理学原理,量化在不同概率条件下的电力需求响应结果。通过耦合响应原理,求解包含冷、热耦合响应的综合需求响应信号,最终利用注意力机制将综合需求响应信号引入Trans-GNN预测模型,提高网络模型在需求响应情境下的多元负荷预测能力。算例分析结果表明,该模型能有效地提高预测精度,为计及综合需求响应的多元负荷预测研究提供了一定的理论基础。
关键词:综合能源系统 综合需求响应 耦合响应 图神经网络 Transformer模型 多元负荷短期预测
伴随着能源系统高效、低碳化需求的日益增长,综合能源系统(Integrated Energy System, IES)已成为世界能源行业的研究热点[1]。综合能源系统以电力系统为核心,集成了多种能源的转换、存储设备,协调不同能源在同一区域内的运用[2]。而综合能源系统的多元负荷预测是实现多种能源协调运行、保证系统安全与稳定的前提[3]。
伴随着电力市场改革的推进,以及智能电网技术的不断发展,需求响应技术(Demand Response, DR)在能源领域得到了更多的研究和应用。需求响应通过在负荷侧进行能耗调节,降低峰值负荷,提高能源的供需平衡,实现更高的能源利用效率,加强能源系统的稳定性[4]。需求响应的激励与价格政策将影响用户的一般用能习惯,为整个能源系统增加了更多的复杂度与不确定性,进一步加大了负荷预测等工作的难度[5]。
目前,关于IES的多元负荷预测研究主要围绕多元负荷之间存在的耦合关系,采用深度学习等人工智能技术进行预测。在电力系统领域,已有部分研究在考虑需求响应的条件下进行负荷预测,并取得了良好的预测结果。但在综合能源系统领域,缺乏考虑综合需求响应(Integrated Demand Response, IDR)[6-7]的多元负荷预测研究[8]。文献[9-10]针对IES内存在的多元负荷强耦合性,应用深度学习模型提取多元负荷之间的耦合关系并做出多元负荷预测,未考虑需求响应对用户侧产生的影响。文献[11]建立了反映用户模糊需求响应的函数,并通过半梯形隶属度将模糊响应转换为精确响应,在考虑需求响应的基础上对纯电力系统进行了单一负荷预测。文献[12]应用统计学原理建立了考虑不确定性的需求响应模型,在不同的响应区间内使用分段线性函数描述用户响应程度。文献[13]通过电力需求响应推导IES的需求耦合响应特性,并将所得模型应用于IES优化运行领域,提高了系统运行的经济性。
本文首先根据消费者心理学原理[14]建立了基于tanh函数的电力需求响应中心曲线,并通过响应不确定性与电价差之间的关系,应用统计学原理量化在不同响应区间、概率条件下的电力需求响应波动值,求解考虑不确定性的电力需求响应信号;其次,结合上述信号以及耦合响应原理,求解冷、热负荷的需求耦合响应信号,完成对综合需求响应信号的求解;最后,通过Transformer注意力机制,将不同概率条件下的综合需求响应信号以输入特征的形式引入预测模型,从而建立考虑综合需求响应的Transformer-图神经网络(Transformer-Graph Neural Networks, Trans-GNN)模型。在预测模型方面,模型采用Transformer[15]神经网络对历史用能数据进行动态提取与筛选,采用图神经网络(Graph Neural Networks, GNN)[16]完成对输入数据的进一步分析和负荷预测工作,模型输入为历史用能数据、气象数据、综合需求响应信号。算例分析结果表明,本文所提出模型考虑了综合需求响应,能有效提高模型预测精度。
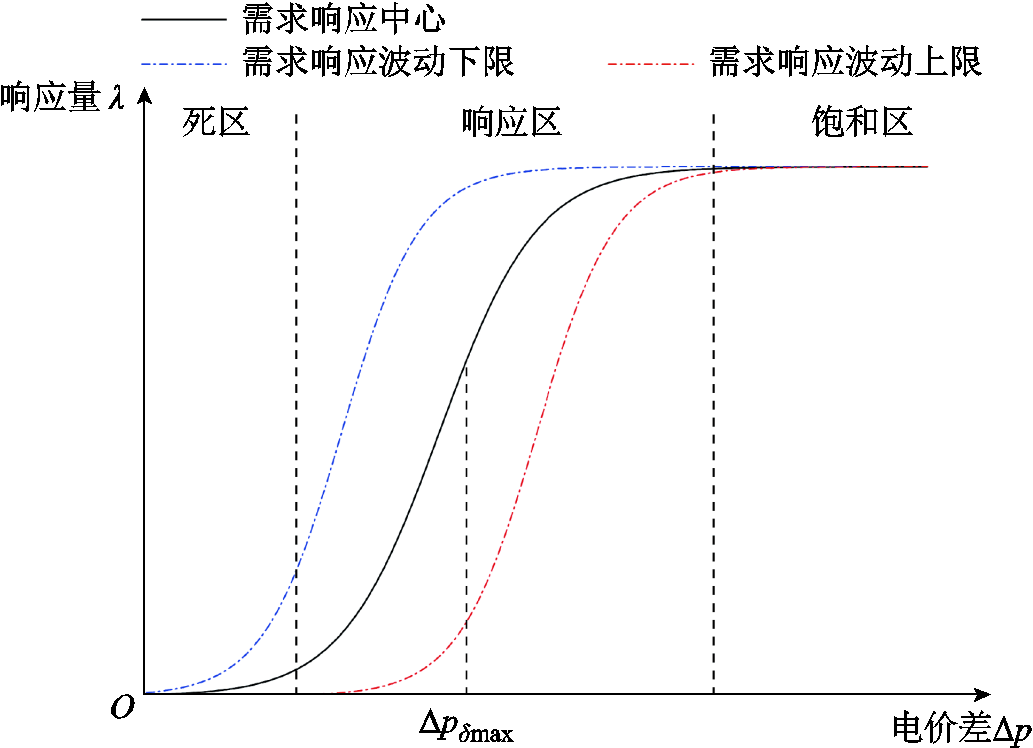
在需求响应过程中,用户会根据自身需求及电力价格的高低来自主选择响应量,可以依据消费者心理学原理,采用tanh函数对上述响应过程进行描述。在实际操作中,用户的用能行为、消费行为等因素存在的随机性会导致需求响应结果产生不确定性,该不确定性可以被描述为在一定范围内的需求响应波动。基于tanh函数的需求响应原理如图1所示。

图1 需求响应原理
Fig.1 The principle of DR
需求响应曲线基于消费者心理学,通过tanh函数将需求响应划分为死区、响应区、饱和区,描述在不同电价激励程度下用户产生的响应情况。死区意味着电价激励过低,不足以产生明显的响应结果;响应区内的电价差处于合理范围,用户将产生较为明显的响应结果;饱和区内的用户需求响应能力已开发完全,响应值将不再产生显著变化。需求响应过程中所存在的不确定性范围,可以通过设置响应波动的上下限进行描述。需求响应中心曲线的计算原理为
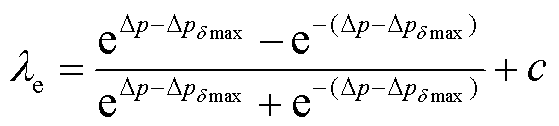 (1)
(1)
式中,λe为中心曲线响应量;Δp为电价差;c为用于平移曲线的常数;![]() 为响应区内产生最大波动
为响应区内产生最大波动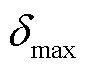 对应的电价差值,为响应区Δp的中值点。
对应的电价差值,为响应区Δp的中值点。
尽管需求响应具有不确定性,但在不同响应区间内的不确定性会随着电价差产生规律性变化[17],且不同概率条件下的需求响应波动结果可以基于统计学实现量化。如果能计算不同概率条件下需求响应指定电价差对应的波动值,则可实现对不确定性需求响应结果的求解。
需求响应的不确定性由用户心理、环境等多个独立微小因素所引起,该随机变量总体服从正态分布[18],可以通过正态分布函数求解在给定概率条件下的需求响应波动值,计算式为
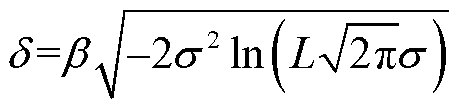 (2)
(2)
式中,δ为需求响应波动量的绝对值;β用于缩放波动值的计算结果;L为概率条件;σ为不确定性,其数学意义为响应波动值的标准差,通过波动值的分布情况反映波动所具有的不确定性。σ增加,需求响应波动的分布将更加发散,具有更高的不确定性;反之,则响应波动值会更加集中,不确定性降低。
需求响应的不确定性会随着电价差的改变而发生变化,可通过需求响应波动值在各响应区间内的概率密度分布来表现,不同响应区间内的需求响应波动值如图2所示。死区、饱和区内的响应结果不确定性低,波动值多集中分布在零值附近;响应区内的不确定性较高,分布更加发散。
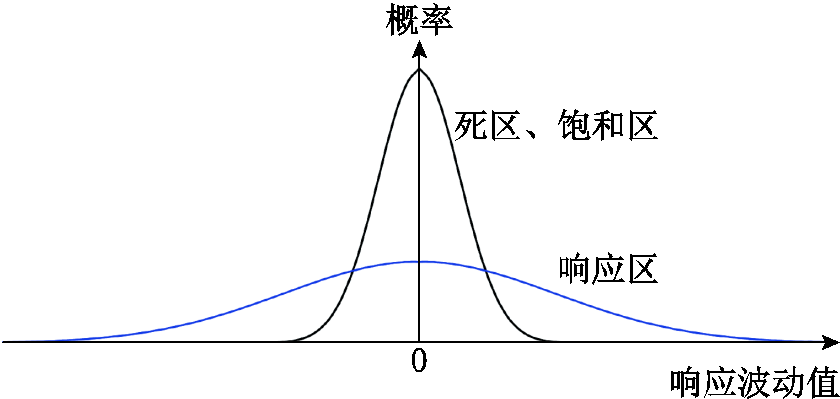
图2 不同响应区间内的需求响应波动值
Fig.2 DR fluctuation in different response intervals
将响应不确定性σ以电价差Δp为变量来描述上述规律,需求响应不确定性随电价差的变化特性可用图3进行描述。
依据响应不确定性与电价差之间的关系,以及在不同概率条件下的响应波动性计算公式,可推导出考虑不确定性的电力需求响应结果,计算原理如式(3)所示。不同概率条件下的需求响应结果如图4所示。
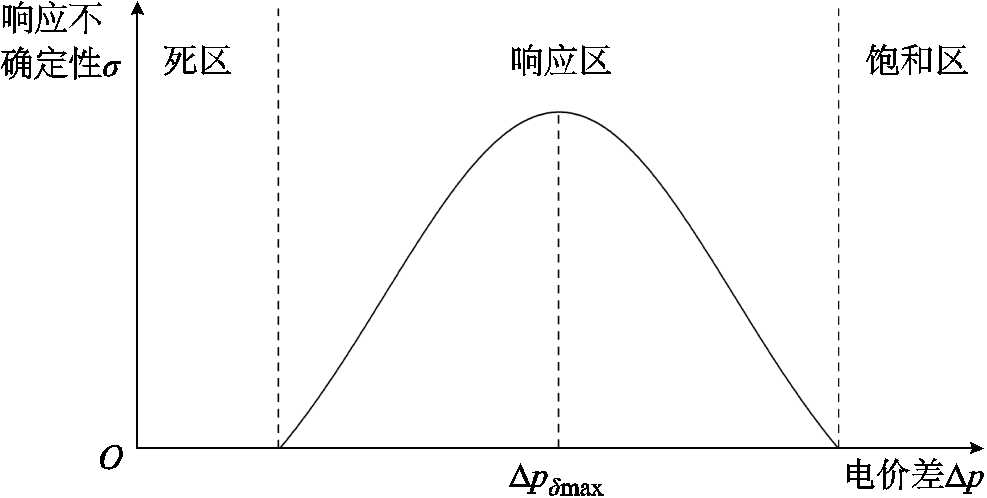
图3 需求响应的不确定性与电价差的关系
Fig.3 The relationship between the uncertainty of DR and the electricity price difference
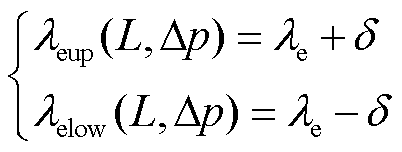 (3)
(3)
式中,λeup、λelow分别为在指定概率条件L下响应波动的上界和下界。
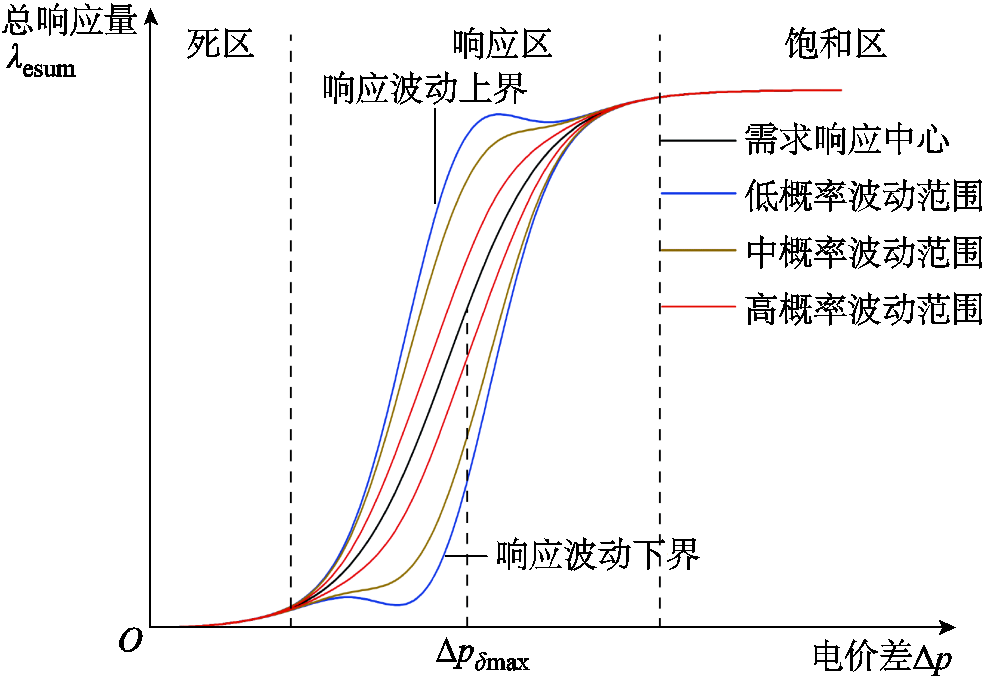
图4 不确定性需求响应原理
Fig.4 Uncertainty demand response principle
不确定性需求响应结果λesum由响应中心λe与响应波动量δ进行求解,在指定的概率条件L下计算不同电价差Δp对应的响应结果。后续神经网络求解过程中,将对不同概率条件下的响应结果施加等值的注意力权重,实现模型对不确定性响应结果的概率化认识,在优先把握大概率响应可能性的前提下,结合其他输入影响因素,考虑可能发生的中等与小概率情况,提高模型考虑问题的全面性,进而提高最终预测精度。
在IES用户对电价进行需求响应的同时,为弥补电负荷响应带来的用能空缺,用户的用能特性会向冷负荷与热负荷迁移,发生耦合响应[13],该过程在实际情况中主要表现为热负荷、冷负荷伴随电价差发生变化。在确定电价差与电负荷之间存在的需求响应结果之后,通过式(4)和式(5)可以对冷负荷、热负荷所产生的耦合响应结果进行计算。式(6)为综合需求响应信号。
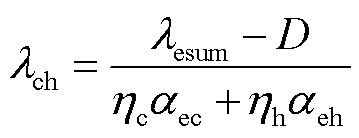 (4)
(4)
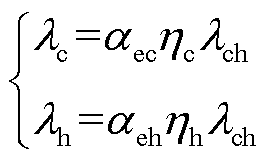 (5)
(5)
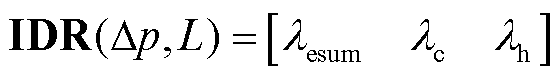 (6)
(6)
式中,λch为耦合响应总量;λc、λh分别为冷、热负荷响应量;D为耦合响应偏移量;ηc、ηh分别为冷、热负荷设备运行效率;αec、αeh分别为冷、热负荷耦合响应分配比例。D、αec、αeh将作为模型训练过程中的待优化参数,伴随每次误差更新进行寻优,使模型不断学习耦合响应存在的规律。
综上所述,由考虑不确定性的电力需求响应以及耦合响应所组成的综合需求响应信号结构如图5所示。
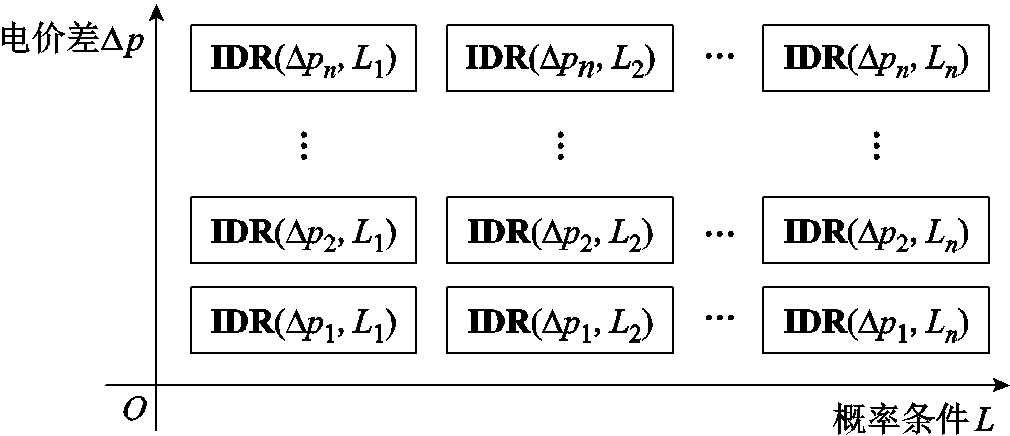
图5 综合需求响应信号结构
Fig.5 Signal structure of IDR
本文所提出的模型预测流程如图6所示。模型的输入数据为一周时间范围内的历史多元负荷数据、气象数据以及需求响应分时电价;输出为未来一定时间范围内的电、冷、热负荷。
Trans-GNN模型通过Transformer注意力机制实现对综合需求响应中各响应信号的概率化认识。注意力机制通过对输入数据施加注意力矩阵,模拟人类决策时优先考虑关键影响因素的行为。依据概率条件,赋予各IDR信号与概率条件值相等的注意力值,提高模型对高概率值信号的计算权重。经注意力矩阵处理后的综合需求响应信号如图7所示。
除了通过直接施加注意力矩阵来处理输入数据外,Transformer的多头自注意力机制还可以从多个不同角度对输入的历史数据进行分析,实现对重要输入数据的提取和筛选,计算原理为
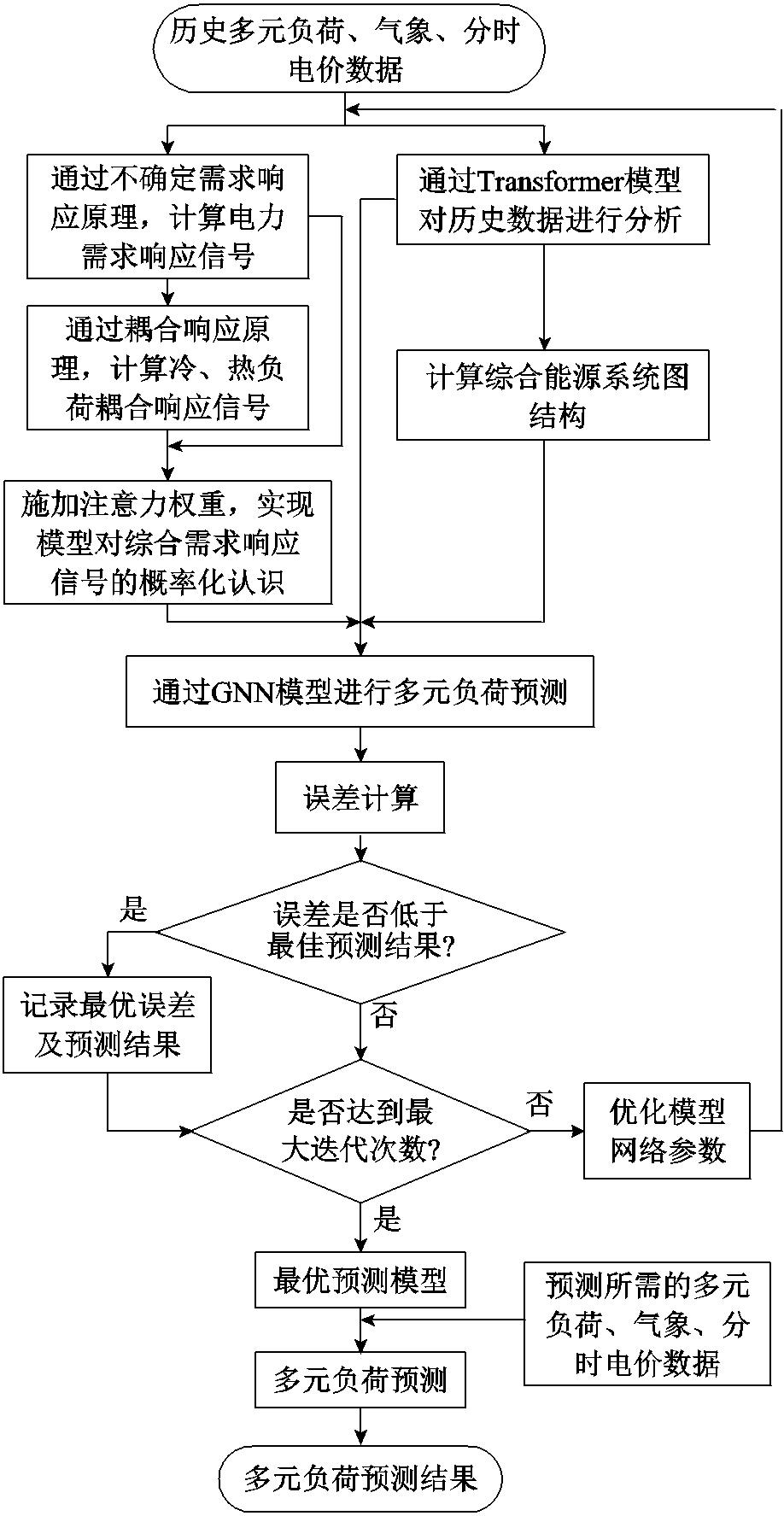
图6 模型预测流程
Fig.6 The predictive flow chart of the model
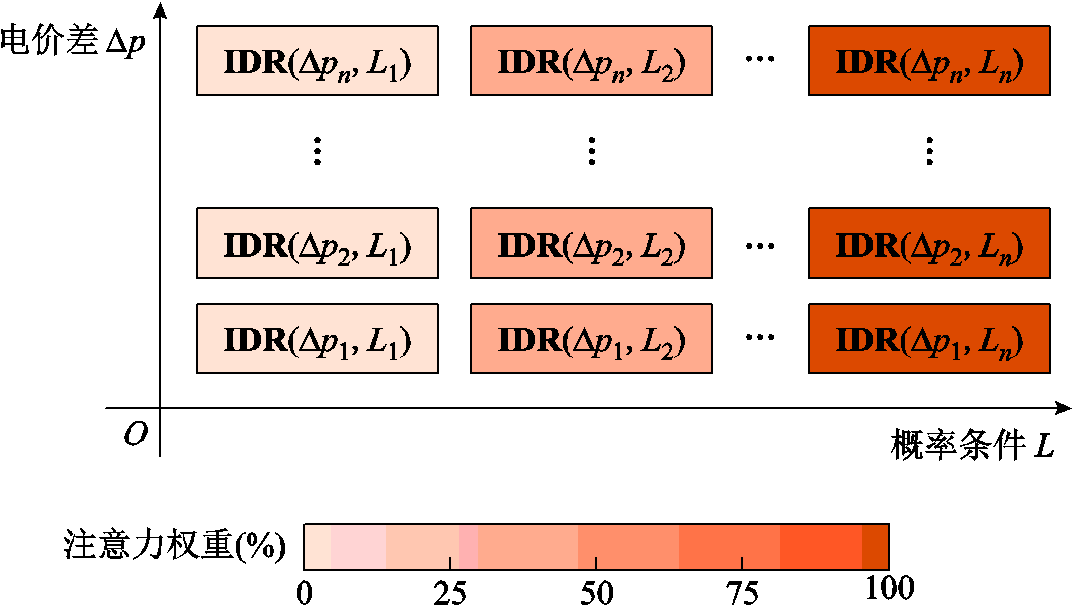
图7 施加注意力权重后的综合需求响应信号
Fig.7 The IDR signal after applied attention weight
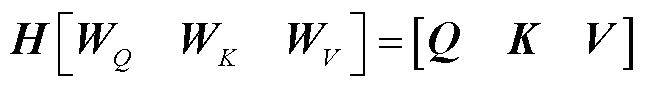 (7)
(7)
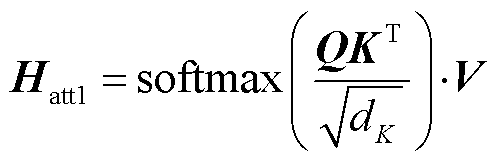 (8)
(8)
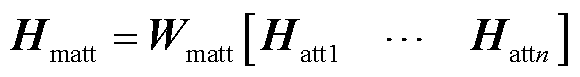 (9)
(9)
式中,Q和K分别为查询向量和键向量,用于计算数据间的相关度,通过对预测前一周时间范围内的历史数据H进行分析,得出各时间点能耗数据间存在的关联性,提高对强关联性数据的注意力值;dK为K的维数,与softmax函数共同对注意力值进行归一化,归一化后的注意力值与表征历史数据的值向量V相乘,完成对用能关联性注意力值Hatt1的计算;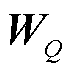 、
、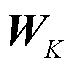 、
、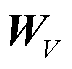 分别为Q、K、V的参数矩阵。从共计n个注意力角度完成对各时间点之间能耗关联性的分析后,通过汇总矩阵Wmatt对上述能耗关联性中存在的系统用能规律进行总结,推测出在预测时需要模型重点关注的历史输入数据Hmatt。
分别为Q、K、V的参数矩阵。从共计n个注意力角度完成对各时间点之间能耗关联性的分析后,通过汇总矩阵Wmatt对上述能耗关联性中存在的系统用能规律进行总结,推测出在预测时需要模型重点关注的历史输入数据Hmatt。
图作为一种高效的信息结构,在表达与推理数据间的复杂联系上具有良好效果,为此本文通过图结构来分析IES内电、冷、热负荷之间的复杂耦合关系,并利用能有效分析图结构的GNN模型做出预测。图结构G可表达为G=(VG, EG),其中,VG为顶点,表示构建关系网的主体;EG为边,表示主体之间的联系。以电、冷、热负荷和气象因素为节点,以它们相互之间的耦合关系为边建立综合能源系统图结构如图8所示。
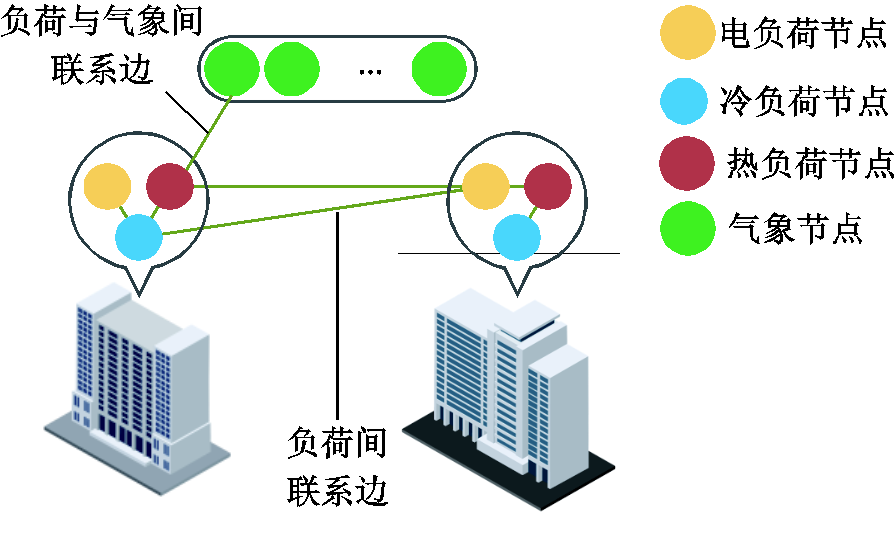
图8 综合能源系统图结构
Fig.8 Diagram structure of the integrated energy system
通过神经网络对历史用能数据和气象数据进行分析计算,可以实现对上述综合能源系统图结构的数据化构建,计算原理为
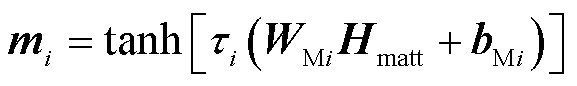 (10)
(10)
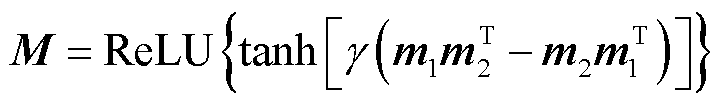 (11)
(11)
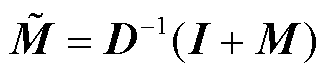 (12)
(12)
式中,![]() 为第i个网络寻优结果,i=1, 2;WMi、bMi为将具有重点关联性的历史数据计算为图数据的神经网络参数矩阵;τi、γ为控制超参数,用于控制tanh激活函数的饱和率;M为邻接矩阵形式的图结构,由网络寻优结果mi经tanh以及ReLU线性修正函数计算获得;式(12)为归一化过程,
为第i个网络寻优结果,i=1, 2;WMi、bMi为将具有重点关联性的历史数据计算为图数据的神经网络参数矩阵;τi、γ为控制超参数,用于控制tanh激活函数的饱和率;M为邻接矩阵形式的图结构,由网络寻优结果mi经tanh以及ReLU线性修正函数计算获得;式(12)为归一化过程,![]() 为M归一化结果;矩阵D的对角线元素由对M的行元素求和获得,其余元素为零;I为单位矩阵。
为M归一化结果;矩阵D的对角线元素由对M的行元素求和获得,其余元素为零;I为单位矩阵。
GNN通过对图结构内多元负荷、气象耦合关系的学习,在融合时序数据特征与图信息的基础上,强化模型对多元负荷数据动态变化过程的理解。GNN融合各项时序数据与综合能源系统图结构的多元负荷预测原理为
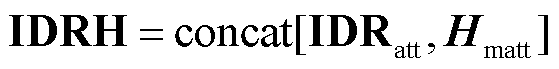 (13)
(13)
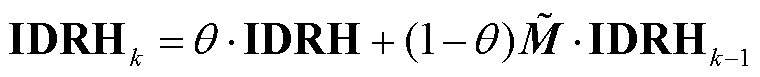 (14)
(14)
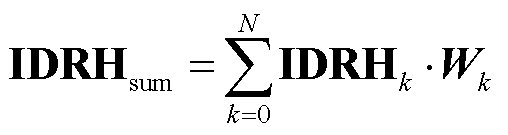 (15)
(15)
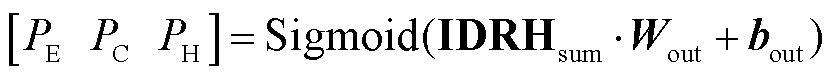 (16)
(16)
式中,IDRH为注意力机制处理后的综合需求响应信号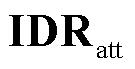 与历史数据
与历史数据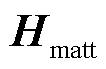 经矩阵拼接concat[·]后形成的时序特征矩阵。式(14)为信息融合过程,通过N次递归、比例求和的方式分析图数据与时序特征数据,深度学习所求问题;θ为递归信息保留比例;k为学习深度。式(15)用于完成对不同学习深度下所得结论的筛选,Wk为筛选矩阵;IDRHsum为各多元负荷在高维度的预测结果。式(16)通过降维计算以及Sigmoid函数激活,输出电、冷、热负荷预测结果分别为PE、PC、PH,其中
经矩阵拼接concat[·]后形成的时序特征矩阵。式(14)为信息融合过程,通过N次递归、比例求和的方式分析图数据与时序特征数据,深度学习所求问题;θ为递归信息保留比例;k为学习深度。式(15)用于完成对不同学习深度下所得结论的筛选,Wk为筛选矩阵;IDRHsum为各多元负荷在高维度的预测结果。式(16)通过降维计算以及Sigmoid函数激活,输出电、冷、热负荷预测结果分别为PE、PC、PH,其中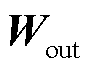 和
和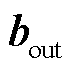 分别为输出层的参数矩阵和偏置向量。
分别为输出层的参数矩阵和偏置向量。
本文采用美国亚利桑那州立大学Tempe校区公开数据集为仿真算例[19],数据类型包括电、冷、热负荷。气象数据来自太阳能辐射全球数据基地[20],数据类型包括温度、相对湿度、可降水量、太阳辐射强度等,数据时间尺度为1 h,以2019年7月1日0:00—2020年6月30日23:00为训练集,2020年7月1日0:00—2020年7月7日23:00为测试集。仿真使用Python 3.9.7为编程语言,Pytorch 1.10.0为框架搭建模型。
本文采用平均绝对百分比误差(Mean Absolute Percentage Error, MAPE)、方均根误差(Root Mean Square Error, RMSE)、加权平均绝对百分比误差(Weighted Mean Absolute Percentage Error, WMAPE)来评估模型的预测精度。各评价指标的计算表达式分别为
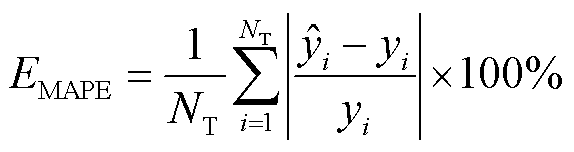 (17)
(17)
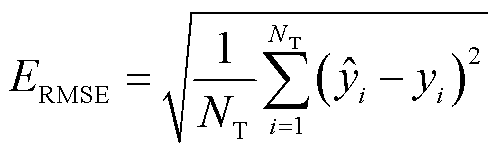 (18)
(18)
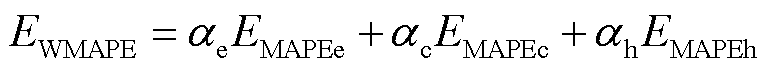 (19)
(19)
式中,yi为实际值;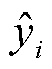 为预测值;NT为预测时间样本数;
为预测值;NT为预测时间样本数;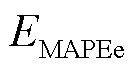 、
、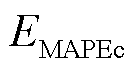 和
和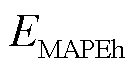 分别为电、冷热负荷的MAPE;αe、αc、αh分别为电、冷、热负荷MAPE求和权重,由电、冷、热负荷在算例IES中的能源占比所确定。为凸显高占比负荷在IES内的重要性,本文αe、αc、αh分别取0.4、0.4、0.2。
分别为电、冷热负荷的MAPE;αe、αc、αh分别为电、冷、热负荷MAPE求和权重,由电、冷、热负荷在算例IES中的能源占比所确定。为凸显高占比负荷在IES内的重要性,本文αe、αc、αh分别取0.4、0.4、0.2。
本文以预测精度为前提,利用网格搜索法通过多次实验确定所需的超参数。模型的训练超参数设置为:训练次数为200次,训练批次为24,学习率为1×10-4,训练设置dropout环节,防止过拟合现象,dropout比例为0.2。其余网络模型内的主要超参数见表1。
表1 Trans-GNN模型的主要超参数
Tab.1 The main hyperparameters of Trans-GNN

网络层名称子网络其他超参数 名称神经元数 Transformer多头自注意力层512注意力角度数:n=8 全连接层1 024— GNN图构建层256控制超参数:τi=0.05, γ =3 负荷预测层256信息保留比例:θ=0.4学习深度:k =3
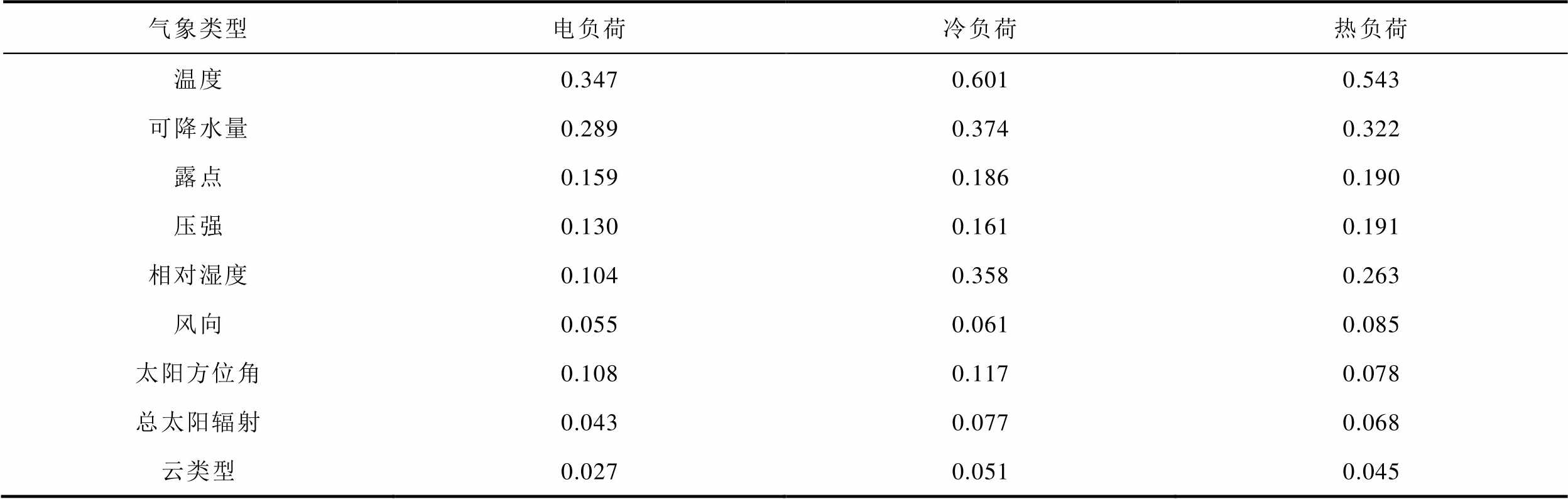
为提高模型对气象信息的利用效率,需筛选出与各种类型负荷具有强相关性的气象数据来构成输入。本文采用最大信息系数法[21]对气象数据和多元负荷特征之间的相关性进行分析,该方法能有效地检测数据之间的线性与非线性关联度,分析结果见表2。从表2中可以看出,温度、可降水量、相对湿度对该地区的能耗情况影响较大,且温度与冷负荷间具有很高的相关性。本文针对不同类型的负荷选择与其具有高相关性的气象数据为输入,对应输入关系为:电负荷——输入温度、可降水量;冷负荷——输入温度、可降水量、相对湿度;热负荷——输入温度、可降水量、相对湿度。
表2 多元负荷与气象数据的相关性分析结果
Tab.2 Correlation analysis between multi load data and meteorological data
气象类型电负荷冷负荷热负荷 温度0.3470.6010.543 可降水量0.2890.3740.322 露点0.1590.1860.190 压强0.1300.1610.191 相对湿度0.1040.3580.263 风向0.0550.0610.085 太阳方位角0.1080.1170.078 总太阳辐射0.0430.0770.068 云类型0.0270.0510.045
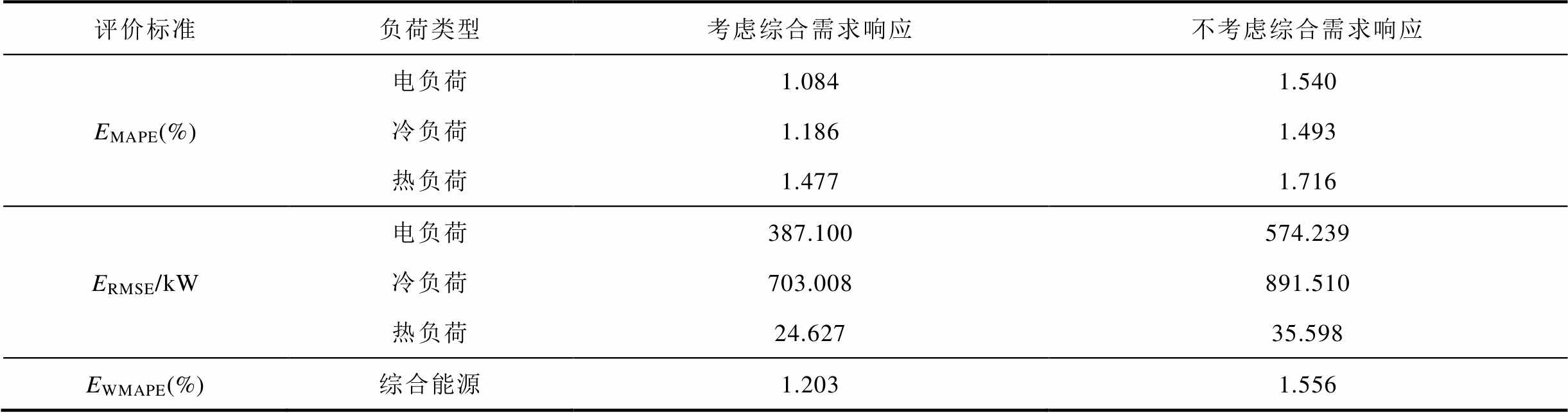
为验证考虑综合需求响应对多元负荷预测的积极作用,本文对比分析了Trans-GNN模型在考虑以及未考虑综合需求响应信号情况下的预测性能,所得预测误差统计结果见表3。从表3中可以看出,在考虑综合需求响应信号的情况下,模型各项预测误差均低于未考虑综合需求响应信号的情况,说明考虑综合需求响应因素能加强模型对综合能源系统运行方式的理解,并可有效地提高模型的预测精度和预测稳定性。
表3 考虑及不考虑综合需求响应预测误差对比
Tab.3 Comparison of prediction error with IDR and without IDR
评价标准负荷类型考虑综合需求响应不考虑综合需求响应 EMAPE(%)电负荷1.0841.540 冷负荷1.1861.493 热负荷1.4771.716 ERMSE/kW电负荷387.100574.239 冷负荷703.008891.510 热负荷24.62735.598 EWMAPE(%)综合能源1.2031.556
为验证Trans-GNN模型中Transformer动态提取方式的有效性,本文对模型分析历史数据的注意力结果进行了可视化输出,如图9所示。
该注意力热图能反映模型对历史输入数据的选取方式,若模型对该时间点的数据特征所施加的注意力权重值越大,则模型认为该输入数据的重要性越强,对应热图颜色越亮;反之越暗。图9横轴代表历史负荷的不同时间点,时间跨度为从预测目标时间点往前1~168 h,纵轴为该时间点的电、冷、热负荷在高维度层面的特征数值,用于数字化描述多元负荷的特点,该特征数值量由神经网络对历史负荷数据、历史气象数据分析得出。从图9中能明显看出,模型将注意力集中在以24 h为倍数的历史数据上,与IES用户的用能周期性规律相符合。模型通过提高对重要时间点数据的关注程度,实现对IES用户周期性用能规律的把握。
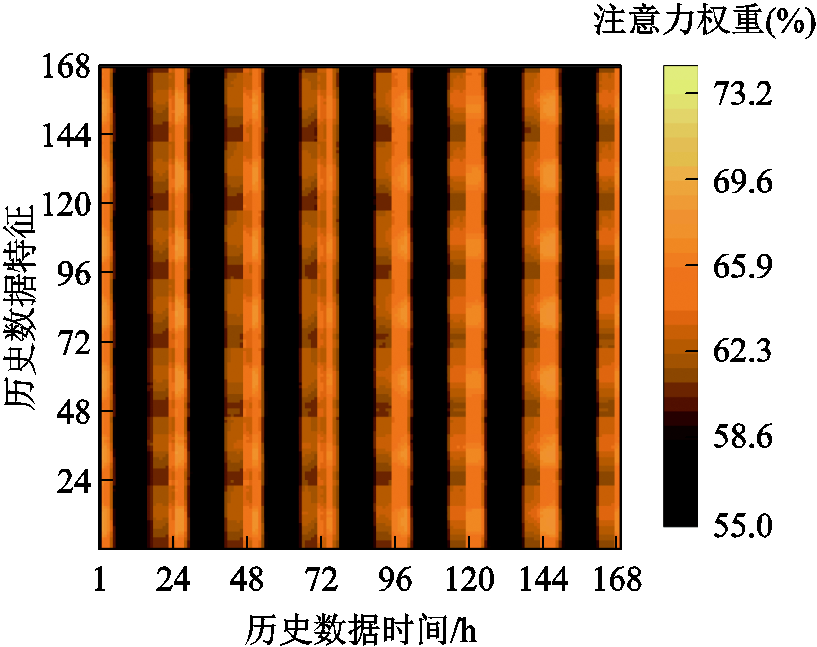
图9 历史数据注意力热图
Fig.9 Heat map of attention with historical data
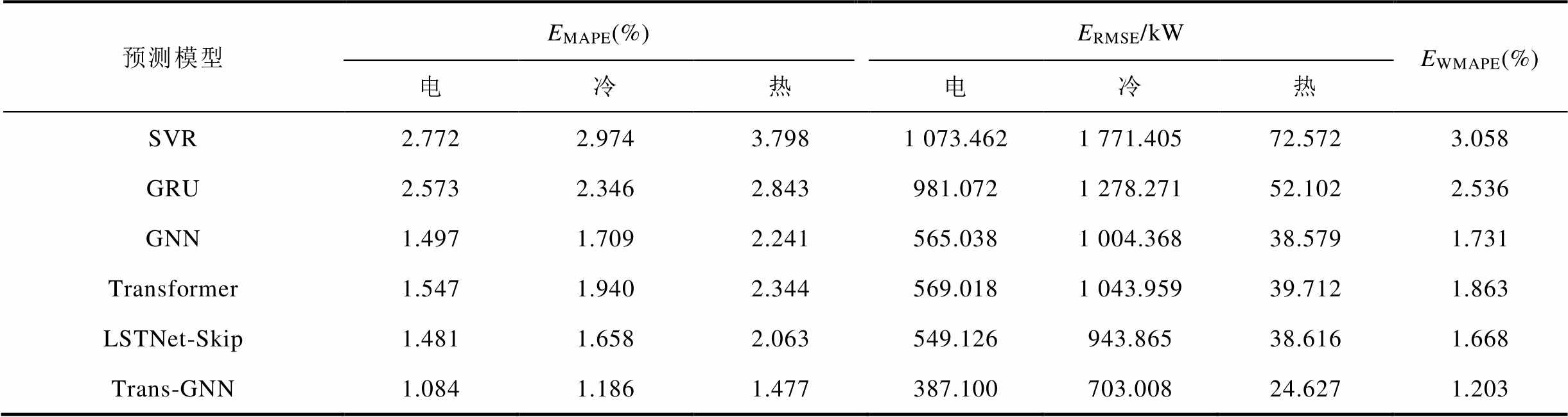
本文使用支持向量回归(Support Vector Regression, SVR)、门控循环单元神经网络(Gate Recurrent Unit, GRU)、GNN、Transformer、LSTNet-Skip、Trans-GNN六种模型对算例IES中2020年7月1日—7日内的电、冷、热负荷进行预测,时间单位为1 h,输入量为一周时间范围内的多元负荷、气象数据及综合需求响应信号。上述对比分析模型的基本预测流程与Trans-GNN模型一致,最终用于对比分析的模型均为训练所得的误差最优模型,且均通过输入综合需求响应信号的方式考虑综合能源系统的需求响应过程。通过基于传统机器学习的SVR和在时序预测领域应用广泛的GRU验证本文所提出模型的时序预测性能;通过对比针对IES多元负荷预测问题而设计的LSTNet-Skip与Trans-GNN,验证本文所提出模型在IES多元负荷预测问题上的有效性以及对综合需求响应信号的分析优势。各模型的预测数据评价结果见表4,预测误差分布的统计结果如图10所示。预测误差分布描述了各模型预测结果的总体误差分布情况,如果在低误差区间范围内的误差概率密度值更大,则说明模型不仅有更高的预测精度,同时还具备更好的预测稳定性。
表4 不同模型预测误差对比
Tab.4 Comparison of prediction errors of different models
预测模型EMAPE(%)ERMSE/kWEWMAPE(%) 电冷热电冷热 SVR2.7722.9743.7981 073.4621 771.40572.5723.058 GRU2.5732.3462.843981.0721 278.27152.1022.536 GNN1.4971.7092.241565.0381 004.36838.5791.731 Transformer1.5471.9402.344569.0181 043.95939.7121.863 LSTNet-Skip1.4811.6582.063549.126943.86538.6161.668 Trans-GNN1.0841.1861.477387.100703.00824.6271.203
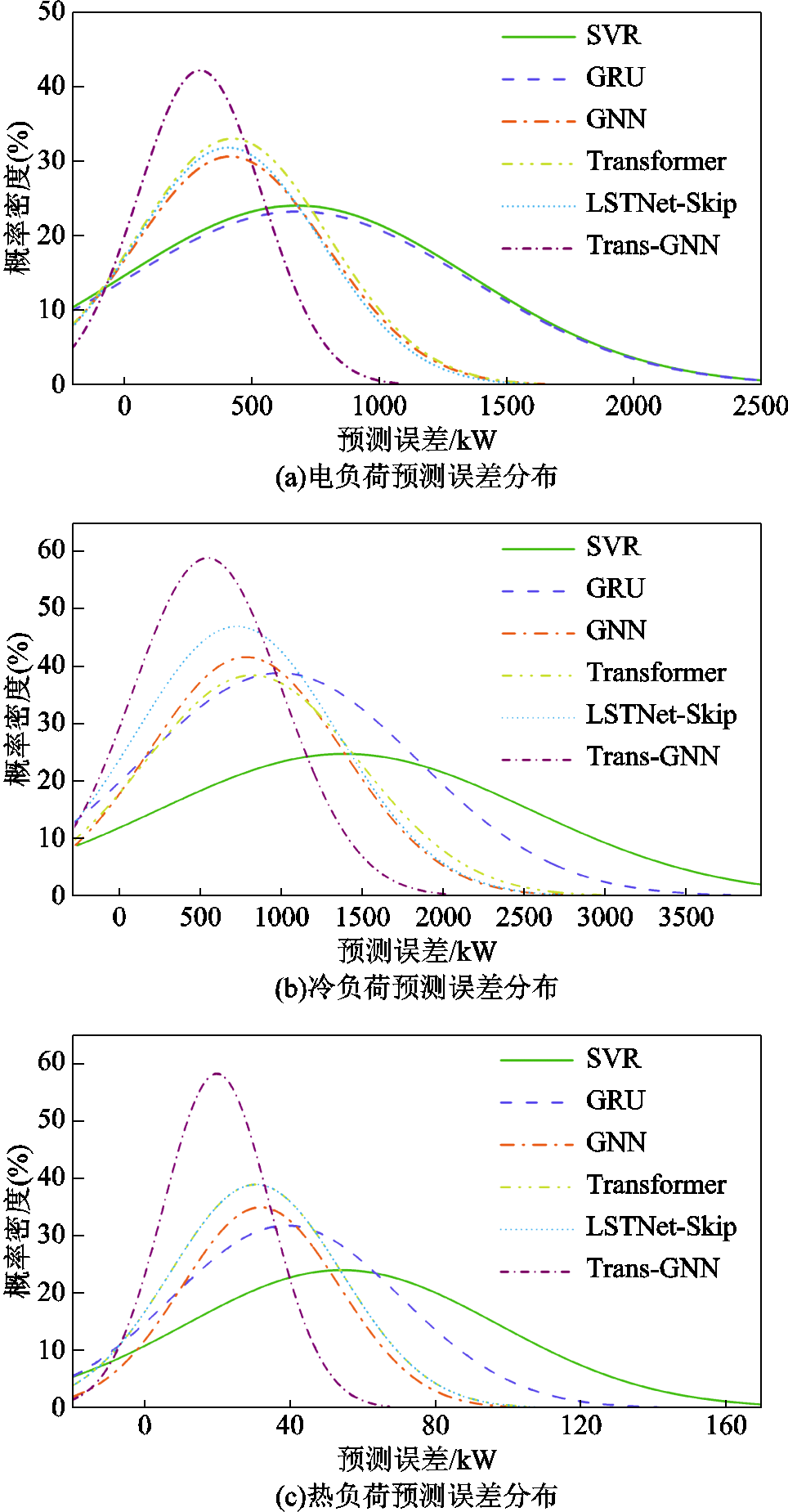
图10 各模型预测误差概率密度分布
Fig.10 The prediction error distribution of each model
通过预测统计结果可以发现,相较于SVR、GRU,本文所采用的GNN、Transformer基础模型具有更优的预测结果,验证了本文所采用的理论基础模型在该问题上的性能优势。进一步分析可以发现,GNN的预测精度高于Transformer,其EWMAPE降低了7.09%。Transformer模型侧重于提取关键的历史能耗数据信息,寻求用能周期性规律,而GNN更倾向于分析各能源数据间存在耦合关系,侧面验证了分析多元负荷间存在的耦合关系对提高模型预测精度的重要性。
采用注意力机制以及图理论的Trans-GNN模型的预测性能有了明显的提高,其EWMAPE相较于Transformer、GNN模型分别降低了35.43%、30.50%,可见Trans-GNN模型能够结合上述两种基础模型在用能周期性规律及耦合关系分析方面的理论优势,从而进一步提高预测性能。Trans-GNN的EWMAPE相较于LSTNet-Skip模型降低了27.88%,且电、冷、热负荷的预测评价指标均优于LSTNet-Skip,可见Trans-GNN模型通过注意力机制矩阵对具有不确定性需求响应的输入数据得出了更好的分析结论,也进一步验证了本文所提出模型在分析综合需求响应信号方面的优势。从图10来看,Trans-GNN模型的电、冷、热负荷预测误差均处于更低的误差区间范围内,且分布明显更加集中,说明本文所提出模型的预测结果更加接近真实情况,且模型预测结果的波动性更小,具备更好的预测稳定性以及可靠性。从上述统计数据中还可以发现,Trans-GNN模型即使在不考虑综合需求响应的情况下,仍能取得相较于部分人工智能方法在考虑综合需求响应时更优的预测性能,这与模型的设计理念与结构有关。首先,Trans-GNN模型通过图神经网络强化了模型对综合能源运行模式、能源间耦合关系的认识。而传统人工智能时序预测方法侧重于捕获数据时间上的前后关联性,相对缺乏对系统用能规律、耦合特性的提取能力。其次,传统预测模型未通过注意力机制等方法来实现对综合需求响应信号的概率化认知,导致综合需求响应信号对其精度的提高较为有限,这也从侧面印证了Trans-GNN对综合需求响应问题的设计针对性。
本文针对综合能源系统多元负荷短期预测问题,提出一种基于Transformer-图神经网络的深度学习模型,在考虑综合需求响应条件下,以美国亚利桑那州立大学Tempe校区的真实数据集进行算例分析与验证,得到主要结论如下:
1)根据消费者心理学、响应不确定性原理、耦合响应原理建立的综合需求响应信号能有效提高模型在综合需求响应情境下的多元负荷短期预测精度。
2)注意力机制的合理应用能提高模型对输入信息重要性的认识能力,通过提取关键时间点的历史数据,使模型更好地把握用户用能规律,并可有效地分析综合需求响应信号存在的不确定性。
3)图神经网络及图结构的应用,使模型能更充分地分析综合能源系统运行模式以及多元负荷之间存在的耦合联系性,提高预测性能。
参考文献
[1] 李响, 牛赛. 双碳目标下源-网-荷多层评价体系研究[J]. 中国电机工程学报, 2021, 41(增刊1): 178-184.
Li Xiang, Niu Sai. Study on multi-layer evaluation system of source-grid-load under carbon-neutral goal[J]. Proceedings of the CSEE, 2021, 41(S1): 178-184.
[2] 刘英培, 黄寅峰. 考虑碳排权供求关系的多区域综合能源系统联合优化运行[J]. 电工技术学报, 2023, 38(13): 3459-3472.
Liu Yingpei, Huang Yinfeng. Joint optimal operation of multi-regional integrated energy system considering the supply and demand of carbon emission rights[J]. Transactions of China Electrotechnical Society, 2023, 38(13): 3459-3472.
[3] 余晓丹, 徐宪东, 陈硕翼, 等. 综合能源系统与能源互联网简述[J]. 电工技术学报, 2016, 31(1): 1-13.
Yu Xiaodan, Xu Xiandong, Chen Shuoyi, et al. A brief review to integrated energy system and energy Internet[J]. Transactions of China Electrotechnical Society, 2016, 31(1): 1-13.
[4] 代心芸, 陈皓勇, 肖东亮, 等. 电力市场环境下工业需求响应技术的应用与研究综述[J]. 电网技术, 2022, 46(11): 4169-4186.
Dai Xinyun, Chen Haoyong, Xiao Dongliang, et al. Review of applications and researches of industrial demand response technology under electricity market environment[J]. Power System Technology, 2022, 46(11): 4169-4186.
[5] 张沈习, 王丹阳, 程浩忠, 等. 双碳目标下低碳综合能源系统规划关键技术及挑战[J]. 电力系统自动化, 2022, 46(8): 189-207.
Zhang Shenxi, Wang Danyang, Cheng Haozhong, et al. Key technologies and challenges of low-carbon integrated energy system planning for carbon emission peak and carbon neutrality[J]. Automation of Electric Power Systems, 2022, 46(8): 189-207.
[6] 徐成司, 董树锋, 华一波, 等. 基于改进一致性算法的工业园区分布式综合需求响应[J]. 电工技术学报, 2022, 37(20): 5175-5187.
Xu Chengsi, Dong Shufeng, Hua Yibo, et al. Distributed integrated demand response of industrial park based on improved consensus algorithm[J]. Transactions of China Electrotechnical Society, 2022, 37(20): 5175-5187.
[7] 孙毅, 李飞, 胡亚杰, 等. 计及条件风险价值和综合需求响应的产消者能量共享激励策略[J]. 电工技术学报, 2023, 38(9): 2448-2463.
Sun Yi, Li Fei, Hu Yajie, et al. Energy sharing incentive strategy of prosumers considering conditional value at risk and integrated demand response[J]. Transactions of China Electrotechnical Society, 2023, 38(9): 2448-2463.
[8] 韩富佳, 王晓辉, 乔骥, 等. 基于人工智能技术的新型电力系统负荷预测研究综述[J]. 中国电机工程学报, 2023, 43(22): 8569-8592.
Han Fujia, Wang Xiaohui, Qiao Ji, et al. Review on artificial intelligence based load forecasting research for the new-type power system[J]. Proceedings of the CSEE, 2023, 43(22): 8569-8592.
[9] 王琛, 王颖, 郑涛, 等. 基于ResNet-LSTM网络和注意力机制的综合能源系统多元负荷预测[J]. 电工技术学报, 2022, 37(7): 1789-1799.
Wang Chen, Wang Ying, Zheng Tao, et al. Multi-energy load forecasting in integrated energy system based on ResNet-LSTM network and attention mechanism[J]. Transactions of China Electrotechnical Society, 2022, 37(7): 1789-1799.
[10] 鲁斌, 霍泽健, 俞敏. 基于LSTNet-Skip的综合能源系统多元负荷超短期预测[J]. 中国电机工程学报, 2023, 43(6): 2273-2283.
Lu Bin, Huo Zejian, Yu Min. Multi load ultra short-term forecasting of integrated energy system based on LSTNet-skip[J]. Proceedings of the CSEE, 2023, 43(6): 2273-2283.
[11] 张智晟, 于道林. 考虑需求响应综合影响因素的RBF-NN短期负荷预测模型[J]. 中国电机工程学报, 2018, 38(6): 1631-1638, 1899.
Zhang Zhisheng, Yu Daolin. RBF-NN based short-term load forecasting model considering comprehensive factors affecting demand response[J]. Proceedings of the CSEE, 2018, 38(6): 1631-1638, 1899.
[12] 王蓓蓓, 胥鹏, 王宣元, 等. 需求响应分布鲁棒建模及其大规模潜力推演方法[J]. 电力系统自动化, 2022, 46(3): 33-41.
Wang Beibei, Xu Peng, Wang Xuanyuan, et al. Distributionally robust modeling of demand response and its large-scale potential deduction method[J]. Automation of Electric Power Systems, 2022, 46(3): 33-41.
[13] 赵海彭, 苗世洪, 李超, 等. 考虑冷热电需求耦合响应特性的园区综合能源系统优化运行策略研究[J]. 中国电机工程学报, 2022, 42(2): 573-589.
Zhao Haipeng, Miao Shihong, Li Chao, et al. Research on optimal operation strategy for park-level integrated energy system considering cold-heat-electric demand coupling response characteristics[J]. Proceedings of the CSEE, 2022, 42(2): 573-589.
[14] 范添圆, 王海云, 王维庆, 等. 计及主/被动需求响应下基于合作博弈的微网-配电网协调优化调度[J]. 电网技术, 2022, 46(2): 453-463.
Fan Tianyuan, Wang Haiyun, Wang Weiqing, et al. Coordinated optimization scheduling of microgrid and distribution network based on cooperative game considering active/passive demand response[J]. Power System Technology, 2022, 46(2): 453-463.
[15] Vaswani A, Shazeer N, Parmar N, et al. Attention is all you need[C]//Proceedings of the 31st International Conference on Neural Information Processing Systems, Long Beach, California, USA, 2017: 6000-6010.
[16] Wu Zonghan, Pan Shirui, Long Guodong, et al. Connecting the dots: multivariate time series forecasting with graph neural networks[C]// Proceedings of the 26th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, Virtual Event, CA, USA, 2020: 753-763.
[17] 林俐, 张玉. 激励型需求响应参与主动配电网优化调度的不确定性分析[J]. 华北电力大学学报(自然科学版), 2020, 47(5): 10-20.
Lin Li, Zhang Yu. Uncertainty analysis of incentive demand response participating in optimal scheduling of active distribution network[J]. Journal of North China Electric Power University (Natural Science Edition), 2020, 47(5): 10-20.
[18] Paterakis N G, Erdinç O, Catalão J P S. An overview of demand response: key-elements and international experience[J]. Renewable and Sustainable Energy Reviews, 2017, 69: 871-891.
[19] Arizona State University. AUS campus metabolism [DB/OL]. [2023-04-13]. http://cm.asu.edu/.
[20] National Renewable Energy Laboratory. National solar radiation database[DB/OL]. [2023-04-13]. https://nsrdb.nrel.gov/.
[21] 郑睿程, 顾洁, 金之俭, 等. 数据驱动与预测误差驱动融合的短期负荷预测输入变量选择方法研究[J]. 中国电机工程学报, 2020, 40(2): 487-500.
Zheng Ruicheng, Gu Jie, Jin Zhijian, et al. Research on short-term load forecasting variable selection based on fusion of data driven method and forecast error driven method[J]. Proceedings of the CSEE, 2020, 40(2): 487-500.
Transformer Based Multi Load Short-Term Forecasting of Integrated Energy System Considering Integrated Demand Response
Abstract The accurate forecasting of multi load in an integrated energy system is imperative for ensuring the efficient and secure operation of diverse energy sources. Demand response technology not only enhances the equilibrium between energy supply and demand but also induces changes in users' general energy consumption habits, thereby amplifying the complexity and uncertainty of load forecasting. While existing research explores the coupling relationships among different energy sources in integrated energy systems and employs artificial intelligence methods for predictions, there is a noticeable gap in research concerning multi load forecasting that incorporates integrated demand response. To address these issues, this paper presents a Trans-GNN prediction model that incorporates integrated demand response considerations. Through the mathematical modeling of integrated demand response signals and their incorporation as input variables into the deep learning model, the accuracy of load predictions in demand response scenarios is improved.
Firstly, adhering to consumer psychology principles, we establish the power demand response center curve. By statistically calculating the fluctuation value of power demand response under various probability conditions, considering the correlation between response uncertainty and electricity price difference, we derive the power demand response signal with due consideration to uncertainty. Employing this signal and the coupling response principle, we ascertain the demand coupling response signal for cold and heat loads, culminating in the derivation of a integrated demand response signal. Then the Trans-GNN model integrates this signal, historical energy consumption data, and meteorological data for prediction. Through Transformer 's attention mechanism, the model realizes the probabilistic understanding of the integrated demand response signal, and dynamically extracts and filters the historical energy consumption data. Finally, the graph neural network is used to complete the further analysis of the input data and load forecasting.
In this paper, the data set of Tempe campus of Arizona State University in the United States is used as a simulation example to predict the multi load in a week, and the validity of the model is verified. The proposed model yields mean absolute percentage error (MAPE) values of 1.084%, 1.186%, and 1.477% for electric load, cooling load, and heat load, respectively. Corresponding root mean square error (RMSE) values are 387.100 kW, 703.008 kW, and 24.627 kW, while the weighted mean absolute percentage error (WMAPE) is 1.203%. Through the attention heat map, the way in which the model analyzes the input data is visualized, and the rationality of the model structure is verified. The error distribution of the model is statistically analyzed by the prediction error distribution, and the prediction stability of the model is further analyzed.
The following conclusions can be drawn from the simulation analysis: (1) The integrated demand response signal can effectively improve the short-term prediction accuracy of the model in the context of integrated demand response. (2) The reasonable application of attention mechanism can improve model 's ability to understand the importance of input information. By extracting historical data at critical time points, the model can grasp the regularity of load forecasting problems and effectively analyze the uncertainty of integrated demand response signals. (3) The application of graph neural network can make the model effectively analyze the coupling relationship between the operation mode of the integrated energy system and the multi load, and improve the prediction performance.
keywords:Integrated energy system, integrated demand response, coupling response, graph neural network, Transformer model, multi load short-term forecasting
中图分类号:TM715
DOI: 10.19595/j.cnki.1000-6753.tces.231267
国家自然科学基金资助项目(52077108)。
收稿日期 2023-08-06
改稿日期 2023-11-06
李云松 男,1999年生,硕士研究生,研究方向为区域综合能源系统多元负荷预测。
E-mail:1012413565@qq.com
张智晟 男,1975年生,教授,博士,研究方向为电力系统和综合能源系统负荷预测、经济调度等。
E-mail:slnzzs@126.com(通信作者)
(编辑 李 冰)