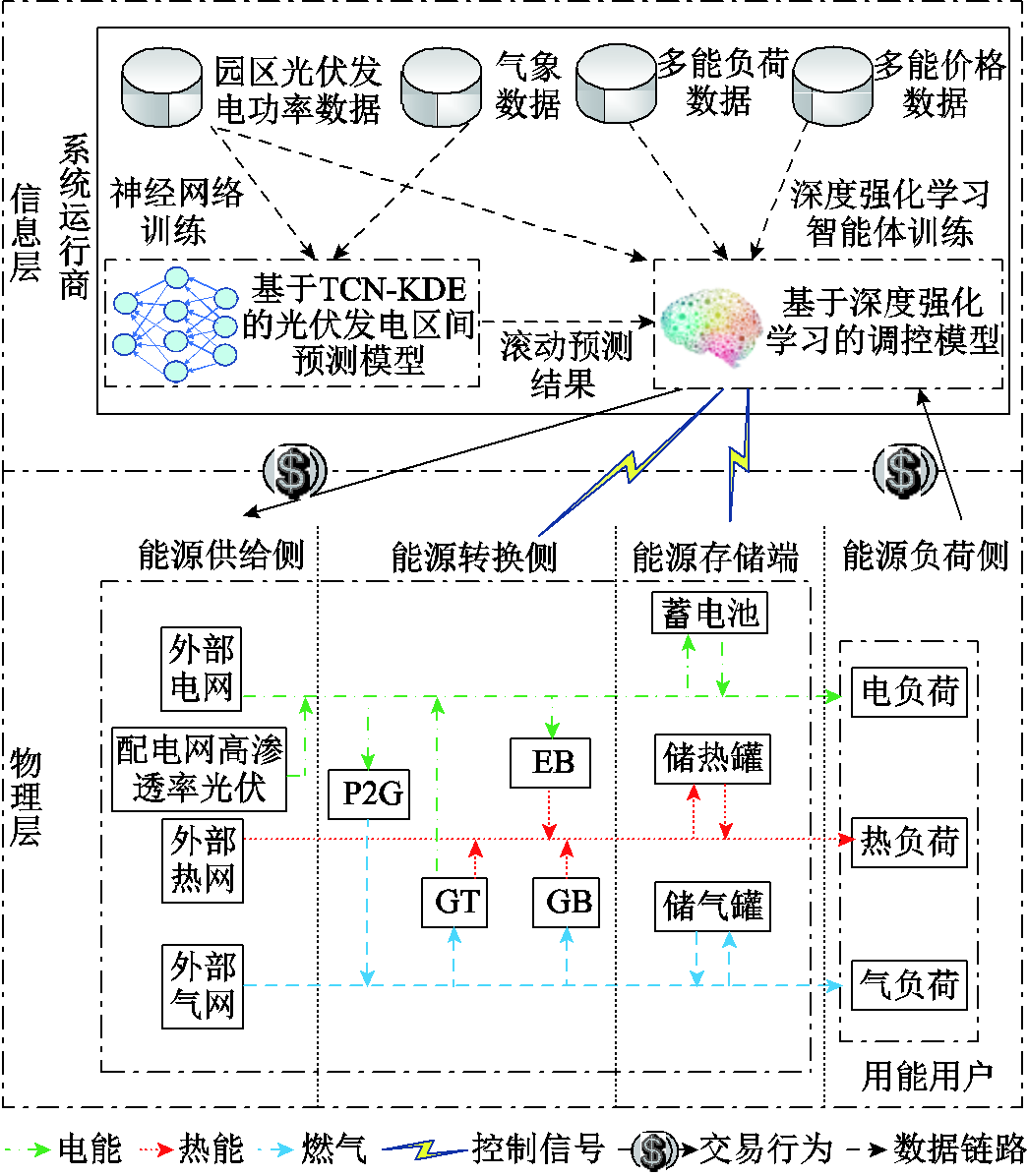
图1 园区综合能源系统预测调控架构
Fig.1 The predictive-control structure for PIES model
摘要 深度强化学习(DRL)是支撑园区综合能源系统(PIES)自适应调控其多能转换与存储设备,以消纳光伏发电及满足用户多能需求的重要技术。然而,DRL智能体通常利用其与PIES的实时环境-动作交互来调控其设备运行状态,难以在高渗透率光伏场景下考虑尖峰光伏发电并预留充足的储能资源。基于模型预测控制理论,该文提出了一种基于DRL与光伏发电区间预测的PIES优化调控方法。该方法面向电-气-热园区综合能源系统,利用时序卷积网络与核密度估计得到光伏发电区间预测结果,并采用柔性Actor-Critic(SAC)算法构建PIES预测优化调控模型。该模型将光伏发电预测区间构建为SAC智能体状态空间,通过迭代试错训练获得PIES多能存储与转换的动态调节策略,从而优化光伏消纳率和运行成本。仿真实验表明,所提方法通过动态调节电、气、热三种能源转换设备的运行功率和预留三种储能设备的储能量,可有效提升PIES在高渗透率光伏场景下的消纳率,优化其运行经济效益。
关键词:综合能源系统 深度强化学习 柔性“行动器-判别器” 时序卷积网络 模型预测控制
光伏发电在构建“清洁低碳、安全高效”的能源体系中发挥着越来越重要的作用。当前我国光伏装机量已突破4.71亿kW[1],仅依靠电力系统调节已无法有效消纳光伏出力。园区综合能源系统(Park Integrated Energy System, PIES)作为连接配电网与多能用户的纽带,通过相互转换电力、热力、燃气等能源,不仅可以提升不同类型能源的利用效率与系统经济效益,还可以提升分布式光伏发电的就地消纳率[2-3]。建立高效、经济、灵活的园区电-气-热综合能源系统调控方法,挖掘其对于配电网高渗透率光伏发电的消纳潜力,对于促进新型电力系统发展具有重要意义。
当前,国内外的综合能源系统(Integrated Energy System, IES)/PIES优化调控方法整体上可划分为基于模型的规划优化方法与无模型的数据驱动方法。其中,基于模型的随机优化、鲁棒优化等IES/PIES调控方法通常基于特定调控规则、随机规划、鲁棒优化等数学解析理论,构建IES/PIES调控问题的确定性数学模型或单/多目标优化问题。例如,ChenRuijun等[4]提出一种改进多目标优化算法来提升电-热-氢-冷综合能源系统的运行经济性、能效和碳排放水平;曾艾东等[5]针对IES内热力管网的能量惯性,设计一种双层时间尺度的电-热IES调控模型;L. R. Robert等[6]基于改进量子行为轻量搜索算法来调控水力-热力-风力混合发电系统,在服从机组爬坡与调控时间尺度差异的约束下,提升风力发电消纳率与系统经济性。然而,这类方法依赖对能源转换、存储、管网等设备能量模型的精细化建模,增加了IES/PIES的模型复杂度。例如,文献[5]为了精确地分析IES热能潮流分布特性而构建了基于二阶迎风隐式的供热管网动态模型,根据管网深度、Boussinesq近似式、环境温度等高纬参量来计算热能在管网中传输所损失的能量。因此,基于模型与规划理论的传统IES/PIES调控方法存在建模复杂度高、灵活性差、计算困难等弊端。同时,随着IES/PIES异质能源类型与耦合设备种类的增加,这些智能搜索算法所需的求解时延将不断增长,并容易陷入局部最优解。
相反,作为机器学习的前沿方向和一种“黑盒”模型,深度学习/深度强化学习(Deep Learning/Deep Reinforcement Learning, DL/DRL)通过构建代表IES/PIES运营商的智能体模型来动态调控其运行状态,并凭借其卓越的感知、学习、自动决策能力进行智能体迭代试错训练以获得最优调控策略[7]。目前,已有不少研究工作尝试使用不同DL/DRL算法实现IES/PIES经济优化调控。例如,文献[8]提出一种基于表格Q学习算法、计及光热的IES调度方法;文献[9]以经济优化为目标,设计一种多智能体深度Q网络的分布式PIES优化调度架构;杨挺等[10]利用深度策略性梯度(Deep Deterministic Policy Gradient, DDPG)算法实现电-热-气综合能源系统的动态调控;文献[11-12]面向PIES与社区综合能源系统的隐私保护需求,分别提出基于模仿学习与联邦学习的经济优化调度策略。
相比于随机优化、鲁棒优化等传统基于模型的调控方法,基于DL/DRL的调控方法能够克服对于IES及其设备进行精细化模型的依赖性,且具有面向IES动态运行状态而作出自适应调控动作的优势。基于DL/DRL的调控方法首先构建DRL调控智能体;其次,面向PIES实时运行环境执行智能体所选定的动作,并根据环境状态转移结果反馈智能体特定奖励结果。然而,这一模式要求智能体每次选定和执行动作时通常考虑的PIES是当前运行环境,而难以考虑高渗透率光伏发电的不确定性及PIES的消纳能力[13]。因此,现有基于深度强化学习的PIES调度方法难以克服在高渗透率光伏部署场景下的出力波动性,并难以消纳尖峰光伏发电。
为准确地评估光伏发电的就地消纳需求,很多学者提出了不同时间尺度下的光伏发电预测方法,并尝试不断减小其预测误差。同时,很多研究工作基于模型预测控制理论(Model Predictive Control, MPC)提出利用光伏预测结果支撑微电网/IES/PIES,挖掘其光伏消纳潜力[14-15]。舒晓欣等[16]提出一种基于微电网光伏发电与负荷预测结果的双层预测调控模型,通过动态调节柴油发电机发电功率与蓄电池储/放能动作,在满足用户用能需求的同时提升微电网光伏消纳率;文献[17-18]以经济效益为优化目标,提出一种包含光伏-光热-热泵的电-热综合能源系统预测调控方法;王阳等[19]采用门控循环单元(Gate Recurrent Unit, GRU)对分布式光伏发电进行预测,并构建光储电站日前-日内两阶段预测优化控制模型,实现光伏出力与负荷需求的滚动跟踪平衡。然而,由于光伏发电功率受到天气条件、设备材质等高维因素的耦合影响,且每种预测方法对于光伏发电影响因素的建模评估均是有限的,因此现有的光伏发电点预测方法不可避免地存在预测误差。这使得PIES基于光伏发电预测结果而制定的能源转换和存储调控动作不够合理,且这一情况会随着配电网光伏部署渗透率的不断增长而不断恶化。
综上所述,本文面向高渗透率光伏消纳及PIES经济效益优化的需求,考虑光伏发电不确定性,提出一种结合SAC深度强化学习与光伏发电区间预测的PIES优化调控方法(Probabilistic Forecasting of Photovoltaic-Power-Soft Actor Critic, PFP-SAC)。该方法以电-气-热PIES的多能转换与存储设备为调控对象,构建基于时序卷积网络-核密度估计(Temporal Convolutional Network-Kernel Density Estimation, TCN-KDE)的PIES光伏发电区间预测模型,滚动得到所接入光伏的短期发电功率区间;同时基于MPC理论,将光伏发电区间预测结果作为智能体运行环境,滚动输入基于SAC的PIES优化调控模型,以调控多能转换与存储设备运行状态。PIES调控模型通过动态购买、转换、储/放其电、气、热三种能源的功率,维持系统供需平衡并优化其经济效益与光伏消纳率。仿真表明,PFP-SAC方法可得到高渗透率光伏发电的区间预测结果,且光伏发电预测结果可用于训练调控PIES的SAC智能体,最终提升系统整体运行经济效益与光伏消纳率。
本文研究的园区综合能源系统预测优化调控架构如图1所示。作为连通外部能源主网与多能负荷的桥梁,PIES负责进行电力、热力、燃气三种能源的动态传输、转换及存储,其运行优化模型可分为物理层和信息层。
物理层主要包括能源供给侧、转换侧、存储端及负荷侧四个部分。具体而言,能源供给侧利用外部电网和气网为PIES提供能源输入,同时PIES接入其所属配电网的高渗透率光伏发电单元以消纳其发电出力;能源转换侧利用电转气(Power to Gas, P2G)、电热锅炉(Electric Boiler, EB)、燃气轮机(Gas Turbine, GT)和燃气锅炉(Gas Boiler, GB)四种设备实现三种能源的动态转换;能源存储端的蓄电池、储热罐与储气罐用于平衡三种能源子系统的供需差异,并为光伏发电提供消纳空间;PIES通过向用户提供三种异质能源来获取收益,能源负荷侧将用能用户分别聚合并统一表征为电负荷、气负荷及热负荷。PIES各类型设备的能量模型如附录所示。

图1 园区综合能源系统预测调控架构
Fig.1 The predictive-control structure for PIES model
信息层的作用是存储从物理层所量测到的多能负荷、光伏发电、气象等数据;将上述数据用于训练光伏发电预测模型和基于DRL的PIES优化调控模型,部署的调控模型通过发送控制信号以动态调整多能耦合与存储设备的运行状态。
1.2.1 PIES调控问题
由于任意时隙t下PIES电、热、气能的负荷大小、购能价格、能源转换与存储设备运行状态都是确定的,因此PIES调控问题本质上是一个时序的马尔可夫决策过程(Markov Decision Process, MDP),即PIES可面向当前多能需求,通过调整其能源转换设备运行功率和储能设备的储/放能功率,在满足多能供需平衡的同时转换为新的运行状态,并根据当前能源价格量化所选择动作的经济成本。
DRL首先构建代表PIES运行商的人工智能体,通过与PIES环境进行迭代和交互式的试错学习训练,获取动态调控PIES的相关“知识”。训练完成的DRL智能体即可在离线模式下,承担运行商时序滚动调控PIES设备运行状态的角色。
1.2.2 SAC算法
本文采用SAC算法构建PIES调控模型,滚动制定其系统运行调控方案。作为Actor-Critic架构的新型DRL算法,SAC既克服了双延迟深度确定性策略梯度(Twin Delayed Deep Deterministic policy gradient, TD3)等确定性策略算法存在的动作选择局限性,也克服了近端策略优化(Proximal Policy Optimization, PPO)等在线学习算法对于样本规模和采样有效性的依赖。
SAC是一种离线学习算法,其主要改进之处在于引入最大熵来训练得到一个既能最大化预期收益,又能得到最大动作熵的智能体策略。这种做法使得SAC能够提升其对于优秀策略的探索能力,以及已获得策略的鲁棒性。任意时隙t下,SAC的折扣累积奖励函数J和目标函数![]() 为
为
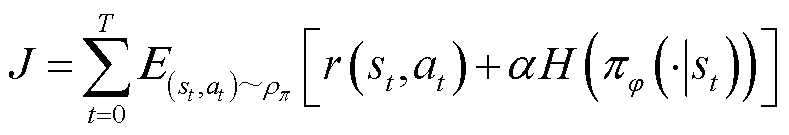 (1)
(1)
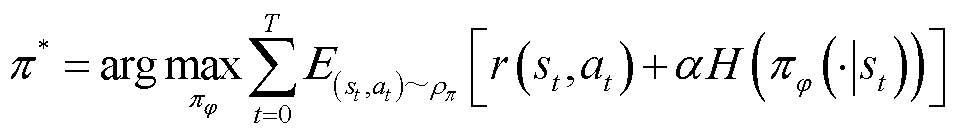 (2)
(2)
式中,π为智能体动作策略,其本质是智能体动作选择的概率分布;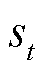 、
、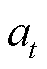 和
和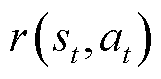 分别为当前智能体所处的环境状态、策略所输出动作及环境反馈给智能体的奖励值;α为动作熵的温度系数,用于表征动作熵对于奖励的影响程度;
分别为当前智能体所处的环境状态、策略所输出动作及环境反馈给智能体的奖励值;α为动作熵的温度系数,用于表征动作熵对于奖励的影响程度;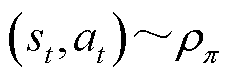 为策略π的动作轨迹;
为策略π的动作轨迹;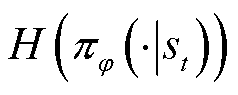 为策略π在状态
为策略π在状态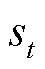 下的动作熵;φ为代表策略π的网络参数。
下的动作熵;φ为代表策略π的网络参数。
动作熵用于表征策略π对于动作选择的不确定性。SAC通过引入动作熵最大化,使其策略π在迭代训练过程中所输出的动作尽可能分散,从而使得智能体能够考虑更多的选择行为而不遗漏任何可能有用的动作选择。动作熵定义式为
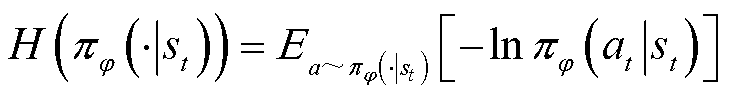 (3)
(3)
作为一种Actor-Critic算法,SAC的Actor网络负责对动作策略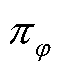 进行建模,Critic网络利用值函数
进行建模,Critic网络利用值函数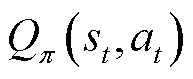 来评估Actor网络所得到策略,即Q值函数用于表征智能体从状态-动作
来评估Actor网络所得到策略,即Q值函数用于表征智能体从状态-动作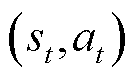 开始一直执行策略
开始一直执行策略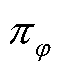 直至结束时所获得的预期折扣奖励与动作熵的期望值之和。SAC的Q值函数和状态值函数分别定义为
直至结束时所获得的预期折扣奖励与动作熵的期望值之和。SAC的Q值函数和状态值函数分别定义为
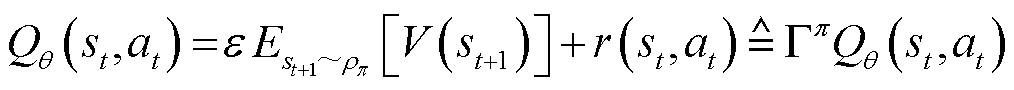 (4)
(4)
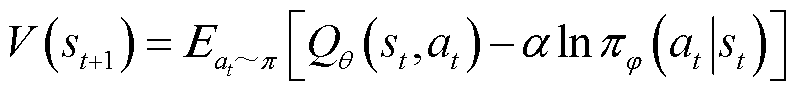 (5)
(5)
式中,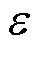 为奖励折扣因子;
为奖励折扣因子;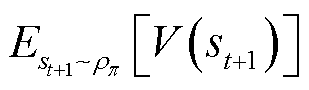 表示轨迹
表示轨迹![]() 下所有状态
下所有状态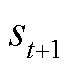 的期望值之和;
的期望值之和;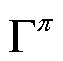 为策略π的贝尔曼算子。
为策略π的贝尔曼算子。
SAC分别对Actor和Critic网络的参数(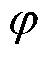 和
和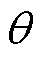 )进行梯度反向更新,从而得到最优的运行策略和Q值函数。
)进行梯度反向更新,从而得到最优的运行策略和Q值函数。
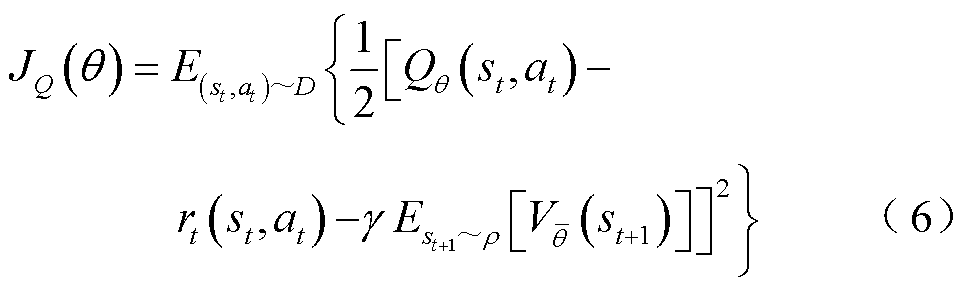
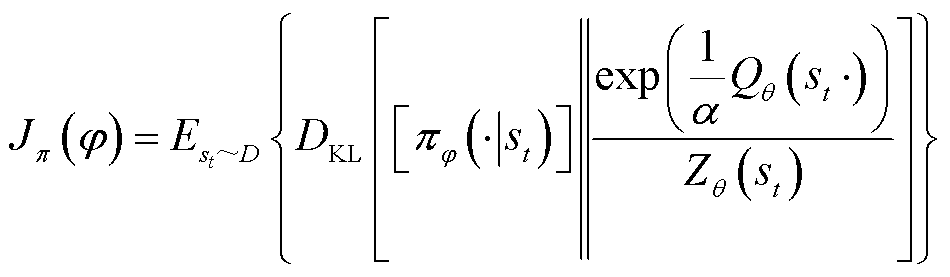 (7)
(7)
式中,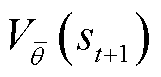 为Critic网络更新后的新状态值函数;
为Critic网络更新后的新状态值函数;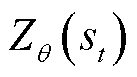 为用于归一化的分配函数;
为用于归一化的分配函数;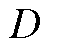 为更新样本集合;
为更新样本集合;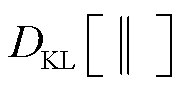 表示KullbackLeibler(KL)散度计算,以表征两个分布之间的距离。
表示KullbackLeibler(KL)散度计算,以表征两个分布之间的距离。
对于光伏发电功率具有较强作用的因素称为特征。现有研究通常采用Pearson等相关性系数来衡量不同特征因素与光伏发电功率之间的相关性。本文基于文献[20]研究结果,选取历史光伏发电功率、辐照度、平均风速、温度及降水量五种时序连续特征,以及硅板材质、季节、天气条件三种离散特征数据,构建光伏发电特征数据矩阵。同时,本文利用时序卷积网络(Temporal Convolutional Network, TCN)算法,训练并得到光伏发电功率预测结果。
2.1.1 时序连续特征的数据归一化
时序连续数据需要进行最大-最小归一化处理,以便对TCN预测模型进行训练。对于光伏发电功率、辐照度、风速、温度及降水量的历史数据,分别进行最大-最小归一化处理,有
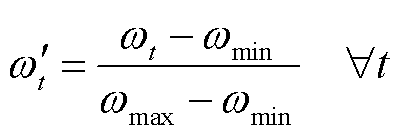 (8)
(8)
式中,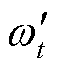 、
、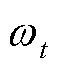 、
、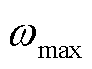 和
和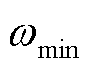 分别为任意时隙t下元素x的归一化值、原始值、最大值及最小值。
分别为任意时隙t下元素x的归一化值、原始值、最大值及最小值。
任意时隙t下,构建时序连续特征数据的矩阵为
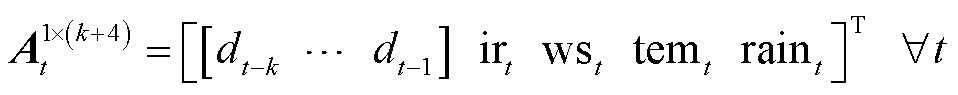 (9)
(9)
式中,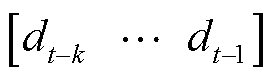 为时隙t前k个时隙内的光伏功率数据;
为时隙t前k个时隙内的光伏功率数据;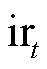 、
、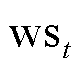 、
、![]() 和
和 分别为时隙t下的辐照度、风速、温度及降水量数据。
分别为时隙t下的辐照度、风速、温度及降水量数据。
2.1.2 离散特征的数据编码
由于离散特征是有限的,因此需要制定特定的编码规则将其离散数据映射到对应的数字元组,从而使其适合输入TCN网络并运算。
作为当前离散特征数据的主流编码规则,One-Hot编码为离散特征的每个实例分别创建一个特定的二进制码组[21-22]。例如,若某类离散特征的实例值属于其第i类特征值时,则码组的第i位二进制值对应为1,其他位赋为0。One-Hot编码结果见表1,则任意时隙t下,硅板材质、季节、天气条件这三种离散特征的编码输出序列为
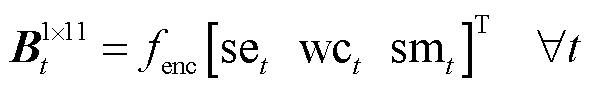 (10)
(10)
式中,![]() 、
、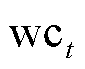 和
和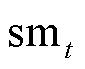 分别为季节、天气条件与硅板材质特征值;
分别为季节、天气条件与硅板材质特征值;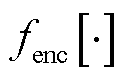 表示One-Hot编码操作。
表示One-Hot编码操作。
表1 利用One-Hot编码对三种离散特征编码结果
Tab.1 The rule of One-Hot encoding for three kinds of discrete features
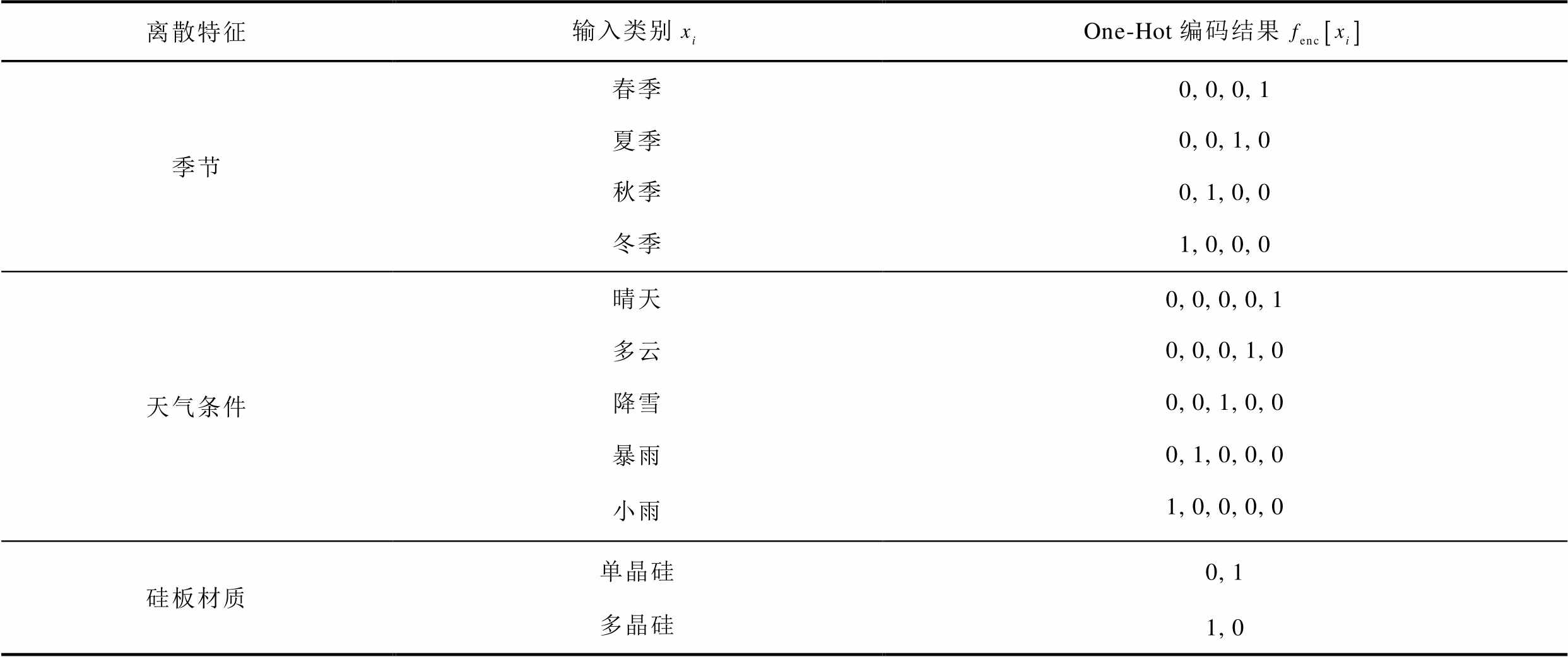
离散特征输入类别One-Hot编码结果 季节春季0, 0, 0, 1 夏季0, 0, 1, 0 秋季0, 1, 0, 0 冬季1, 0, 0, 0 天气条件晴天0, 0, 0, 0, 1 多云0, 0, 0, 1, 0 降雪0, 0, 1, 0, 0 暴雨0, 1, 0, 0, 0 小雨1, 0, 0, 0, 0 硅板材质单晶硅0, 1 多晶硅1, 0
2.1.3 构建光伏发电预测的特征数据矩阵
任意时隙t,基于TCN的光伏发电预测模型的数据矩阵构建为
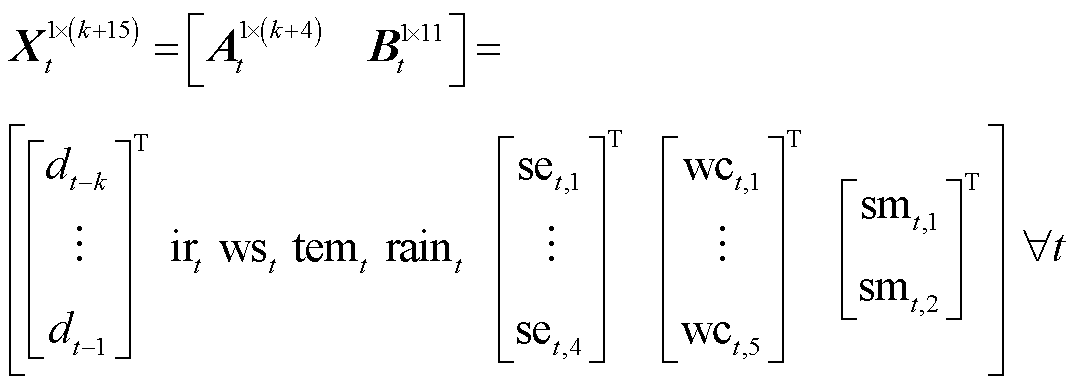 (11)
(11)
式中,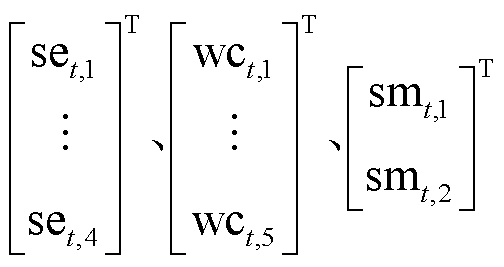 分别为三种离散特征数据的编码输出。
分别为三种离散特征数据的编码输出。
为挖掘特征数据的时序相关性,本文采用时序卷积网络对PIES光伏发电进行精准点预测。由于式(11)中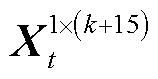 只包含时隙t下特征数据,因此采用一维卷积将其进行特征融合,其中卷积核大小为1×(k+15)。
只包含时隙t下特征数据,因此采用一维卷积将其进行特征融合,其中卷积核大小为1×(k+15)。
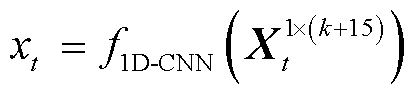 (12)
(12)
式中,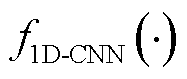 表示一维卷积处理。
表示一维卷积处理。
作为针对时间序列的卷积神经网络,TCN被证明能够在光伏出力预测和电力负荷波动预测等领域取得很好的效果[23-24]。相比传统卷积神经网络(Convolutional Neural Networks, CNN),TCN引入了因果卷积、扩张卷积和残差网络,使其具备处理任意长度时间序列的能力。TCN结构示意图如图2所示。
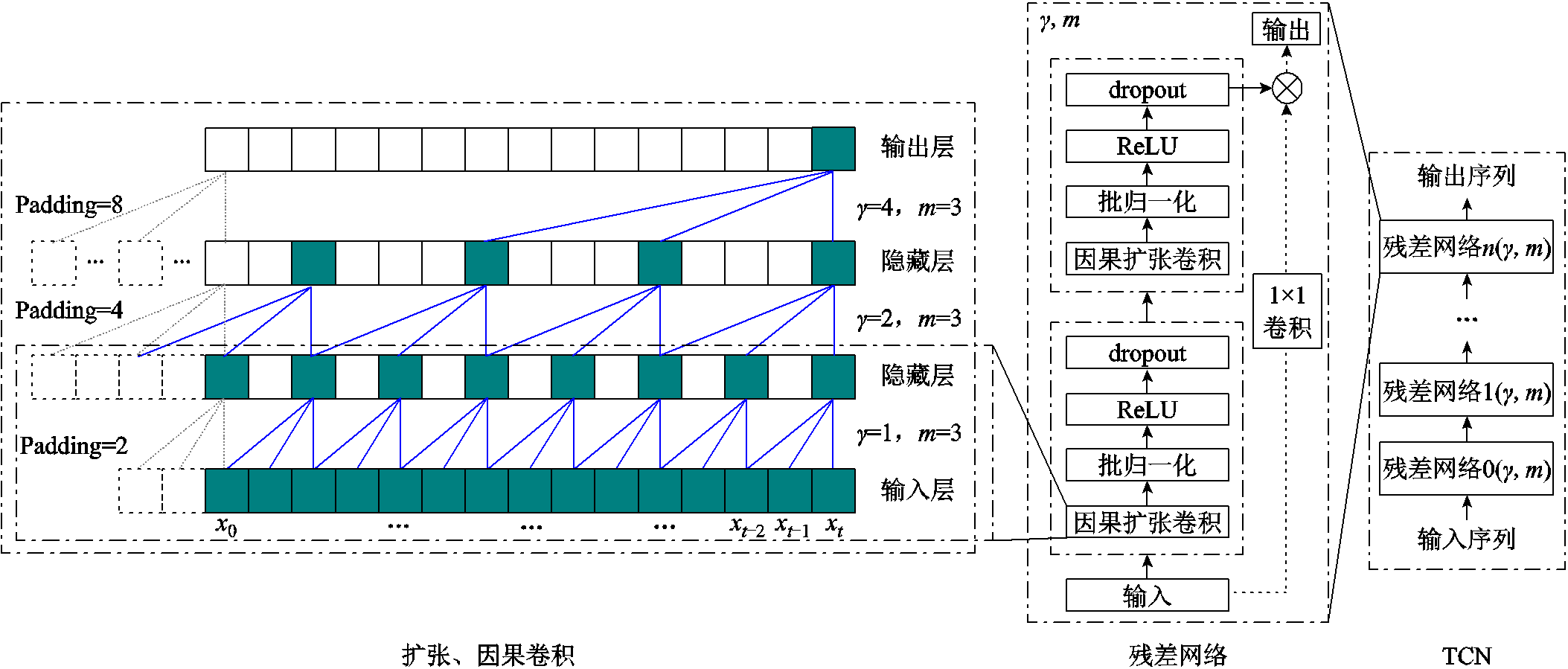
图2 时序卷积网络模型结构示意图
Fig.2 The illustration of the structure of temporal convolutional network
1)因果卷积是指TCN的输出结果只与当前时隙输入及更早时隙数据有关,而不考虑未来时隙数据的影响。如图2所示,网络最终输出结果由多个隐藏层所映射得到,并随着隐藏层层数的增多而能够考虑更久的时间序列数据。以大小为m的核函数为例,每个隐藏层的输出由其前一个隐藏层的对应位置数据和前m-1个位置的数据进行卷积得到。
2)可发现当m较小时,若想考虑较长的时序输入数据,TCN需构建较多隐藏层。为克服这一问题,TCN引入扩张卷积来平衡网络深度与卷积计算的感受野范围。如图2所示,扩张系数d随着隐藏层的增加而以指数增长,扩张卷积就是在每个隐藏层中以扩张系数值为步长进行卷积计算。因此,扩张卷积能以较少的隐藏层层数和网络复杂度获得较大的输入数据感受野。
3)TCN采用残差网络来克服网络在训练过程中由于隐藏层层数增加和网络复杂化所引起的梯度消失、梯度爆炸等问题。如图2所示,残差网络在因果扩张卷积层后增加了批归一化、dropout、ReLU激活函数等模块,从而避免卷积层在特征提取过程中丢失过多信息。
TCN中第n个残差块第s个神经元的输出为
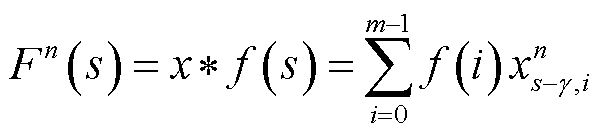 (13)
(13)
式中,*和m分别为卷积运算和卷积核大小;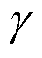 为第n个残差块扩张系数;
为第n个残差块扩张系数;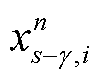 为第n个残差块第s-
为第n个残差块第s-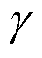 个位置与卷积核第i个元素对应相乘的元素。为提取感受野内所有时刻信息则m不能小于
个位置与卷积核第i个元素对应相乘的元素。为提取感受野内所有时刻信息则m不能小于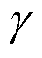 。残差块数为n的TCN所具有的感受野w为
。残差块数为n的TCN所具有的感受野w为
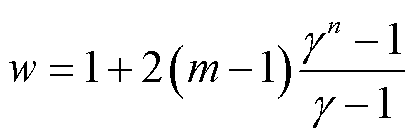 (14)
(14)
时隙t下,TCN最终输出的PIES光伏发电点预测结果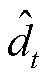 为
为
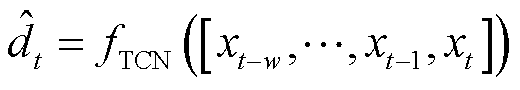 (15)
(15)
式中, 表示TCN网络进行点预测计算。
表示TCN网络进行点预测计算。
由于光伏发电点预测模型只将相关性较高的特征数据作为TCN网络输入,因此其同样存在预测误差。为评估光伏发电不确定性并指导PIES实现准确合理的调控,本文引入核密度估计将光伏发电点预测结果拟合为特定置信度下的预测区间。
时隙t下,TCN网络的光伏发电点预测值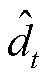 与特征预测数据相结合,递归地构造式(11)的预测数据矩阵并输入TCN网络,得到未来H个时隙的光伏发电点预测结果并构成序列
与特征预测数据相结合,递归地构造式(11)的预测数据矩阵并输入TCN网络,得到未来H个时隙的光伏发电点预测结果并构成序列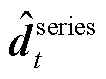 ,即
,即
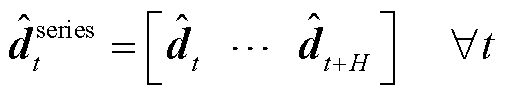 (16)
(16)
显然序列的预测误差将不断累计并偏离实际光伏发电功率值。因此,利用KDE计算光伏发电预测序列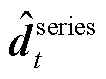 在t+H时隙下的概率密度函数
在t+H时隙下的概率密度函数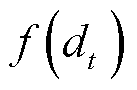 ,有
,有
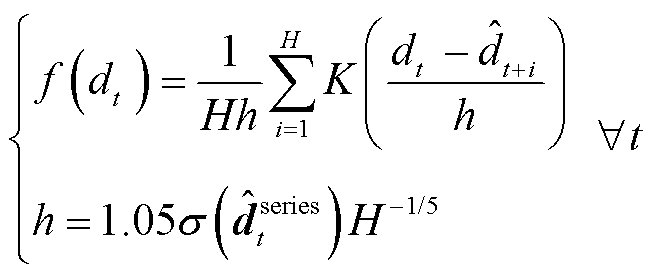 (17)
(17)
式中,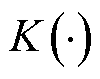 、h和
、h和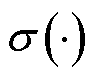 分别为核函数、采样带宽和序列
分别为核函数、采样带宽和序列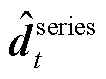 的标准差。其中,核函数选用抗噪声能力较强的高斯核函数[25]。基于光伏发电概率密度函数
的标准差。其中,核函数选用抗噪声能力较强的高斯核函数[25]。基于光伏发电概率密度函数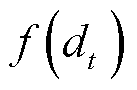 可计算出置信水平
可计算出置信水平![]() 下的光伏发电区间
下的光伏发电区间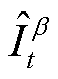 为
为
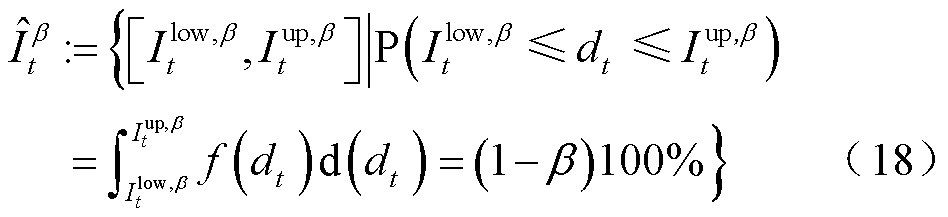
式中,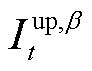 和
和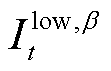 分别为预测区间上、下界的分位数。
分别为预测区间上、下界的分位数。
在一定程度上,交互试错的训练机制、SAC的最大期望回报和动作熵能帮助智能体量化所选动作的优劣并得到其最优的动作策略。然而,由于大多数研究在SAC状态空间中仅考虑PIES实时运行状态(例如,设备运行功率、储能荷电状态、负荷大小等),因此智能体难以了解未来光伏发电及其消纳需求。
针对这一问题,如图3所示,本文提出一种基于SAC与光伏发电区间预测的PIES优化调控方法。该方法利用PIES光伏发电区间预测结果构建SAC智能体的状态空间,从而利用光伏发电预测结果训练智能体,使其理解PIES未来光伏消纳需求,并“前瞻性”地调节储能设备的储能量和多能转换设备的运行状态,进而提升PIES在高渗透率光伏发电场景下的消纳能力和经济效益。
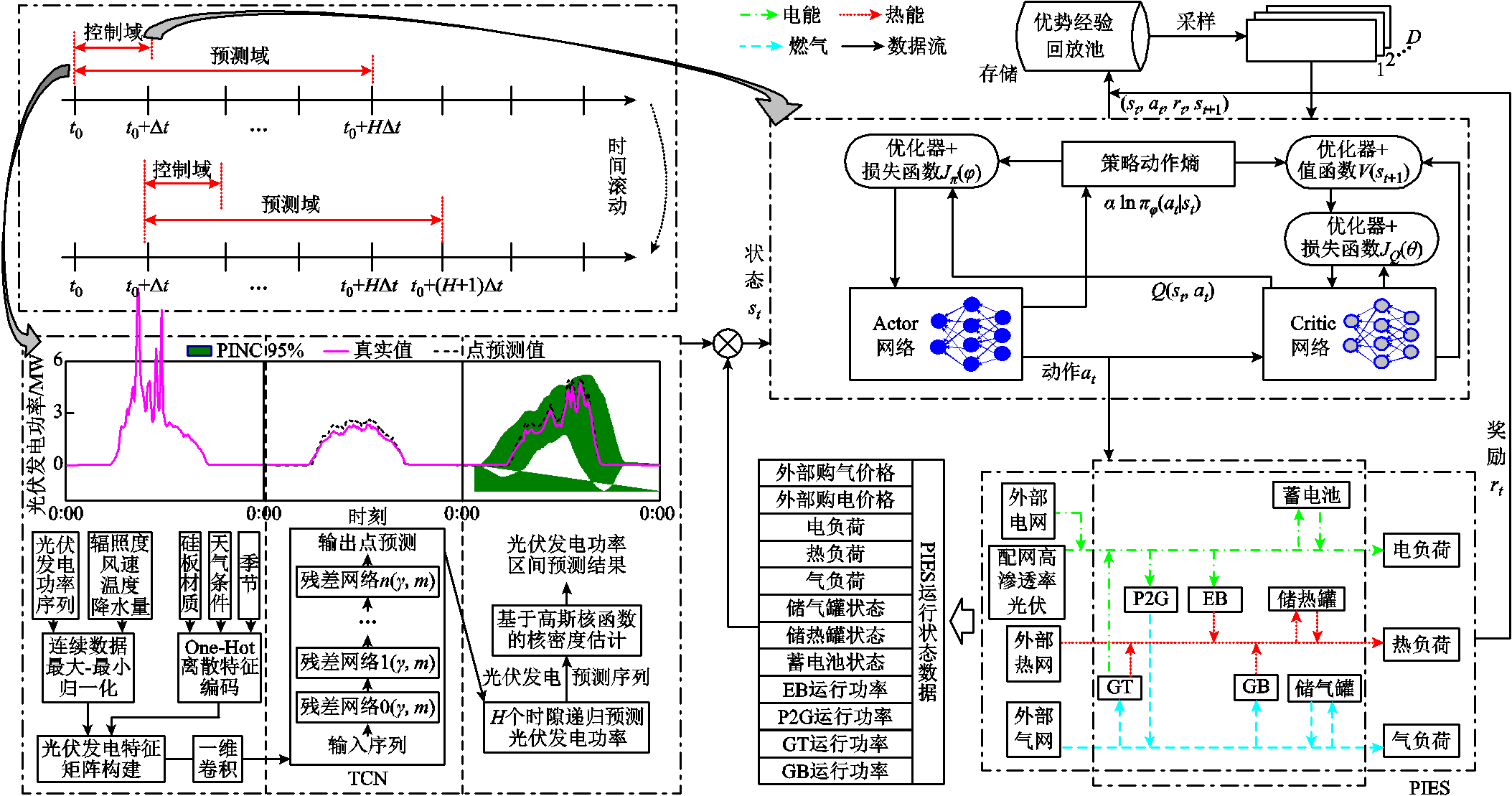
图3 基于SAC与光伏发电区间预测的PIES预测优化调控方法示意图
Fig.3 The illustration of the proposed predictive-control optimization method for PIES based on SAC and probabilistic photovoltaic power forecasting
作为连接多能供给与用户需求的桥梁,PIES在调控设备运行时需要同时考虑用户多能负荷大小及设备运行状态。同时,将光伏发电区间预测结果引入SAC智能体状态空间中,指导智能体了解未来光伏消纳需求。任意时隙t下,SAC状态空间为
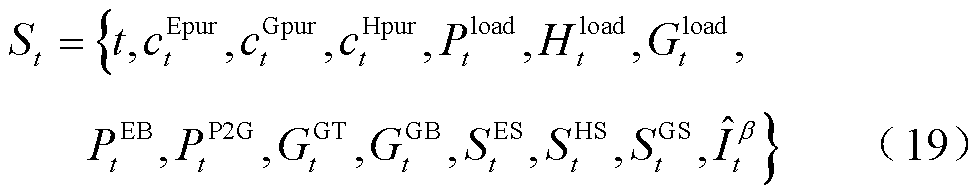
式中,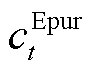 、
、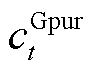 和
和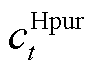 分别为外部电网、气网和热网购能价格;
分别为外部电网、气网和热网购能价格;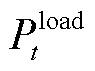 、
、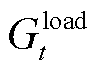 和
和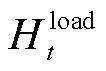 分别为电、气、热负荷大小;
分别为电、气、热负荷大小;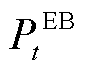 、
、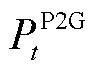 、
、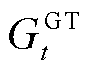 和
和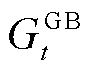 分别为EB和P2G的用电功率及GT和GB的耗气等效功率;
分别为EB和P2G的用电功率及GT和GB的耗气等效功率;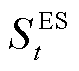 、
、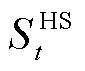 和
和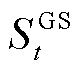 分别为蓄电池荷电状态及储热罐与储气罐的储能量。
分别为蓄电池荷电状态及储热罐与储气罐的储能量。
面向时隙t下环境状态,SAC智能体通过调节能源转换设备的运行功率和能源存储设备的储/放能功率来消纳光伏和优化经济效益,其动作空间为
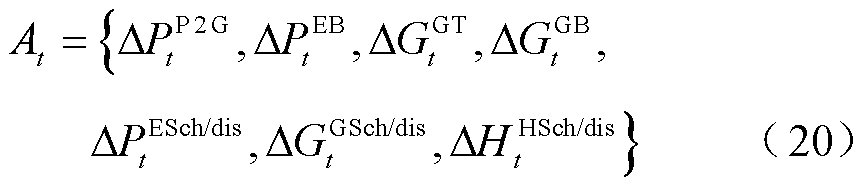
式中,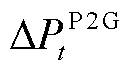 、
、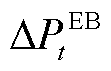 、
、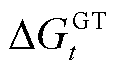 和
和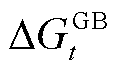 分别为EB和P2G的用电功率调节量及GT和GB的耗气等效功率调节量;
分别为EB和P2G的用电功率调节量及GT和GB的耗气等效功率调节量;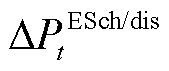 、
、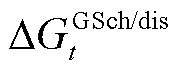 和
和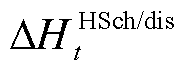 分别为蓄电池、储气罐与储热罐的储/放电、气、热等效功率。
分别为蓄电池、储气罐与储热罐的储/放电、气、热等效功率。
SAC智能体动作空间的约束条件为
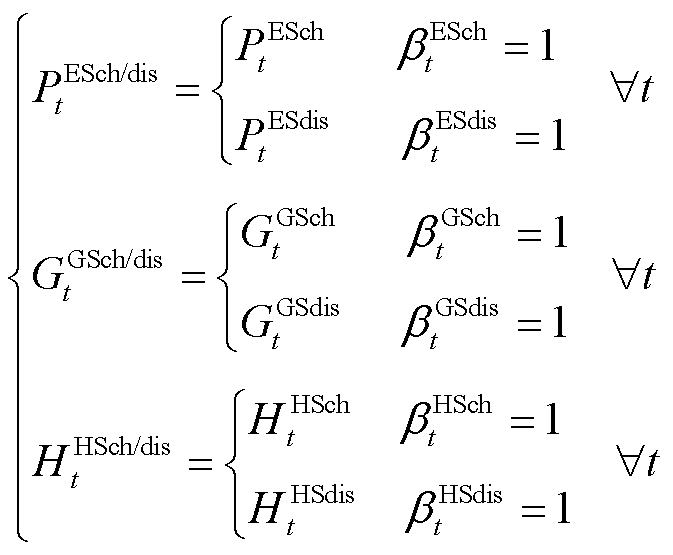 (21)
(21)
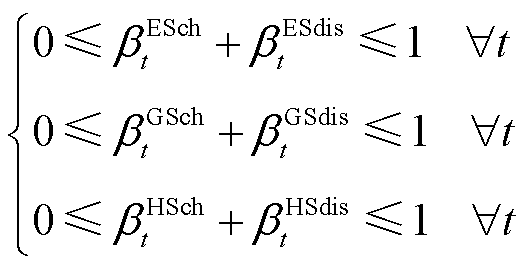 (22)
(22)
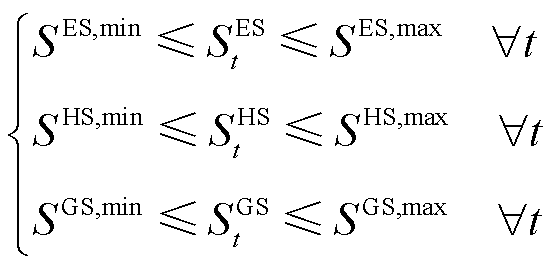 (23)
(23)
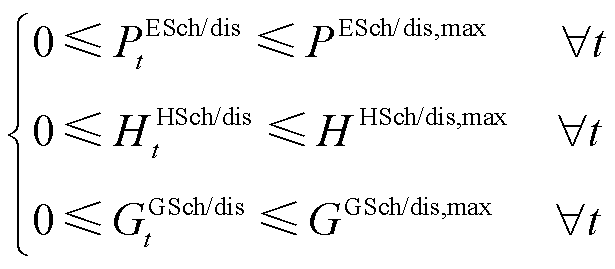 (24)
(24)
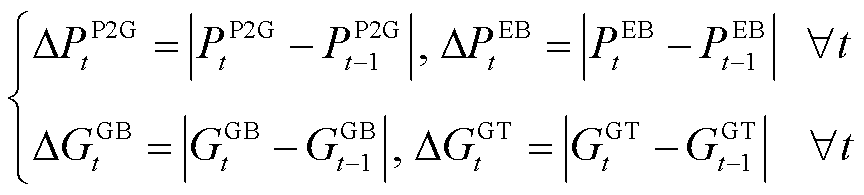 (25)
(25)
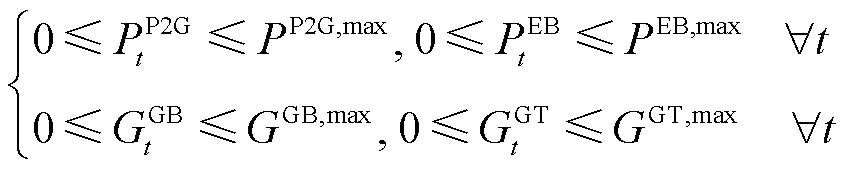 (26)
(26)
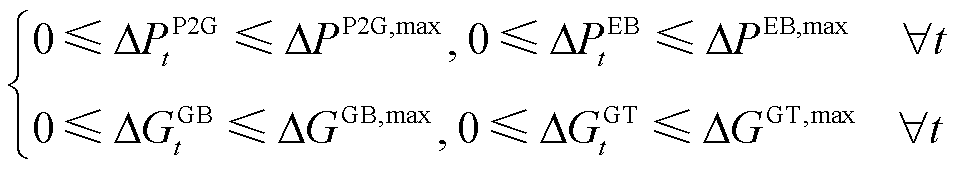 (27)
(27)
式(21)和式(22)是储能设备动作状态约束,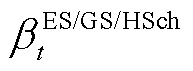 和
和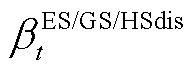 分别为表征时隙t下蓄电池、储热罐与储气罐储、放能状态的0-1变量,即储能设备在任意时隙下只能储能或放能。式(23)是储能设备的储能量上下限约束,
分别为表征时隙t下蓄电池、储热罐与储气罐储、放能状态的0-1变量,即储能设备在任意时隙下只能储能或放能。式(23)是储能设备的储能量上下限约束,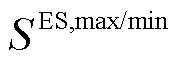 、
、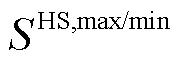 和
和![]() 分别为三种储能设备的最大/最小储能量。式(24)是储能设备储/放能功率约束,
分别为三种储能设备的最大/最小储能量。式(24)是储能设备储/放能功率约束,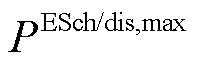 、
、 和
和 分别为蓄电池最大充/放电功率、储热罐最大储/放热功率与储气罐最大储/放气等效功率。式(25)是能源耦合设备运行功率调节量的定义式。式(26)和式(27)分别是四种能源耦合设备的最大运行功率和爬坡率约束,
分别为蓄电池最大充/放电功率、储热罐最大储/放热功率与储气罐最大储/放气等效功率。式(25)是能源耦合设备运行功率调节量的定义式。式(26)和式(27)分别是四种能源耦合设备的最大运行功率和爬坡率约束,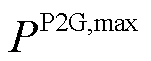 、
、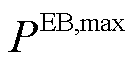 、
、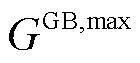 和
和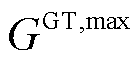 分别为P2G、EB、GB与GT最大运行功率;
分别为P2G、EB、GB与GT最大运行功率;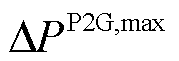 、
、 、
、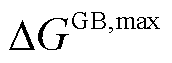 和
和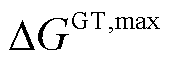 分别为其最大爬坡率。
分别为其最大爬坡率。
SAC智能体以系统经济效益为目标,动态调节能源耦合与存储设备的运行状态。由于PIES在提升光伏发电消纳水平的同时可减少其与外部电、气、热网的购能功率,因此优化PIES的光伏消纳能力及其经济效益的目标是一致的。为此,本文将PIES购能成本和弃光惩罚成本相结合作为其运行调控目标函数,从而引导SAC智能体最小化PIES总成本。
3.3.1 购能成本
在任意时隙t下,PIES的电、热、气三种能源子系统都需要服从能量供需平衡约束,即任意能源系统在任意时隙下,其购买、储能释放及转换输入该能源母线的能源总量要等于系统当前用户消耗、储能存储及转换输出的能源总量。由于某一时隙下用户用能负荷的大小是确定的,而异质能源之间的转换与存储量又是智能体在该时隙下决策动作,因此根据能量供需平衡约束即可计算出各子系统的能源购买量与对应购能成本。PIES电、热、气三种能源的供需平衡约束为
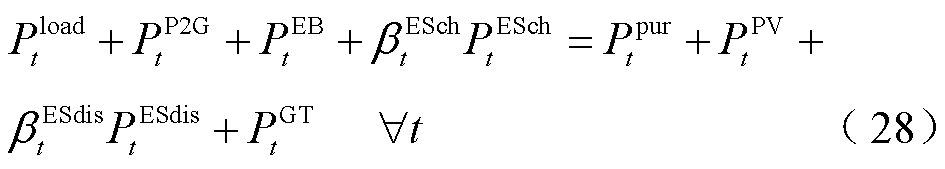
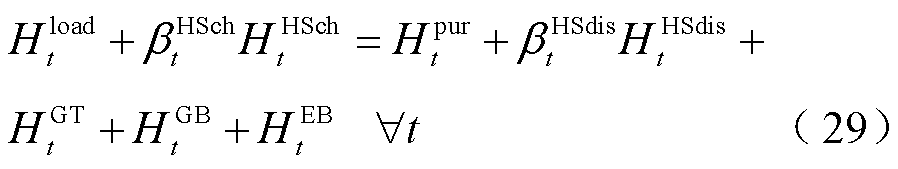
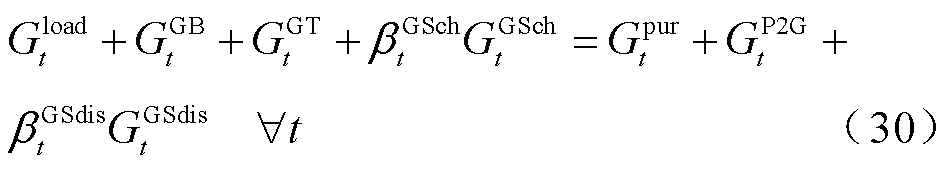
式中,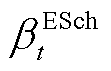 、
、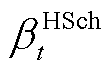 和
和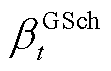 分别为表征时隙t下蓄电池、储热罐与储气罐储/放能状态的0-1变量;
分别为表征时隙t下蓄电池、储热罐与储气罐储/放能状态的0-1变量;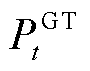 、
、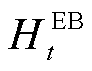 、
、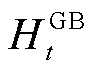 、
、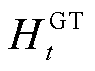 和
和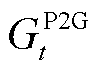 由附录中能量模型计算得到。
由附录中能量模型计算得到。
由式(28)~式(30)分别计算出时隙t下PIES外部购电功率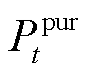 、购气等效功率
、购气等效功率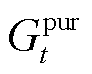 和购热等效功率
和购热等效功率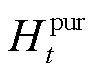 ,则该时隙的PIES购能成本为
,则该时隙的PIES购能成本为
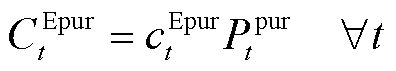 (31)
(31)
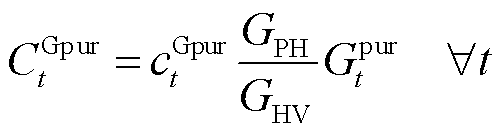 (32)
(32)
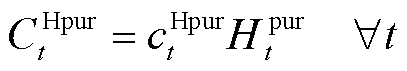 (33)
(33)
式中,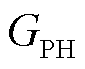 和
和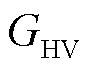 分别为燃气等效功率与热能转换系数、燃气燃烧高位热值。
分别为燃气等效功率与热能转换系数、燃气燃烧高位热值。
3.3.2 弃光成本
尽管式(28)假定PIES优先使用光伏出力(存在能源供给缺口时才从外部网络购能),但是随着配电网光伏建设渗透率的不断上升,光伏发电尖峰时段仍可能存在消纳缺口。此时,PIES运行商将不得不舍弃多余光伏出力以维持能源供给平衡。即PIES的电母线功率平衡式(28)重述为
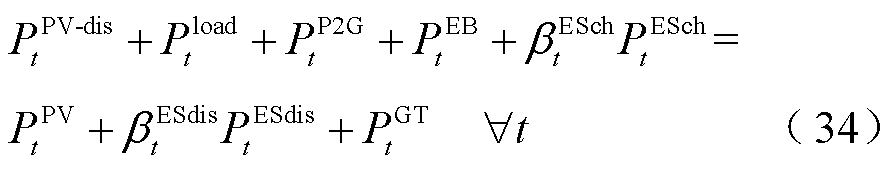
式中,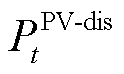 为PIES弃光量。因此,任意时隙t下的弃光惩罚成本为
为PIES弃光量。因此,任意时隙t下的弃光惩罚成本为
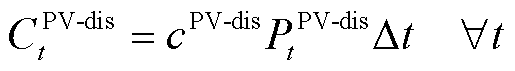 (35)
(35)
式中,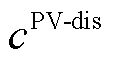 为弃光惩罚单价;
为弃光惩罚单价;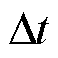 为单位时隙长度。
为单位时隙长度。
综上所述,任意时隙t下,SAC智能体基于状态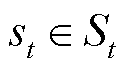 执行动作
执行动作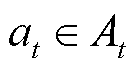 后获得的奖励值为
后获得的奖励值为
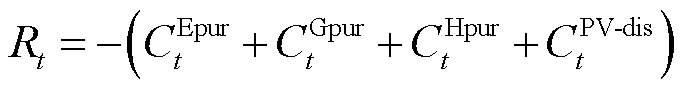 (36)
(36)
为验证本文所提出PFP-SAC方法的有效性,本文分别对所提出基于TCN-KDE的PIES光伏发电区间预测方法,以及将光伏发电区间预测与SAC相结合的优化调控方法进行验证分析。
光伏发电及对应天气、材质等数据来源于澳大利亚DKA Solar Center开源数据平台(采用2020—2021年间数据、数据分辨率为5 min)。PIES调控所用数据如附录所示,其中,附表1给出图1所示PIES的设备能量模型参数与调控约束;附图1和附图2分别给出PIES从外部电、气、热网购买能源的分时价格及其电、气、热负荷曲线(燃气与热能分别利用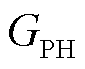 :1Nm3=36 MJ和
:1Nm3=36 MJ和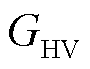 :3.6 MJ=1 kW·h统一转换为kW)。所有仿真实验在一台配置Inter Core i7-10800 CPU和8GB RAM的计算机上进行,仿真实验软件环境为Pycharm2022.1、Python3.8和Pytorch1.4.0。
:3.6 MJ=1 kW·h统一转换为kW)。所有仿真实验在一台配置Inter Core i7-10800 CPU和8GB RAM的计算机上进行,仿真实验软件环境为Pycharm2022.1、Python3.8和Pytorch1.4.0。
为验证PFP-SAC的光伏发电功率点预测精度,本文以文献[24]所提出的结合注意力机制的时序卷积网络(Temporal Convolutional Network-Attention, TCN-AT)和文献[26]所提出的基于长短时记忆网络与卷积神经网络(Long Short Term Memory-Convolutional Neural Networks, LSTM-CNN)的光伏发电预测方法相对比,采用平均绝对百分比误差(Mean Absolute Percentage Error, MAPE)、方均根误差(Root Mean Squared Error, RMSE)和平均绝对误差(Mean Absolute Error, MAE)来评估光伏发电的点预测准确度。此外,引入平均覆盖误差(Average Coverage Error, ACE)和平均区间宽度(Average Width, AW)来衡量PFP-SAC所得到光伏发电区间预测结果的有效性[27-28],有
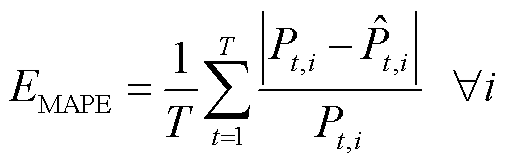 (37)
(37)
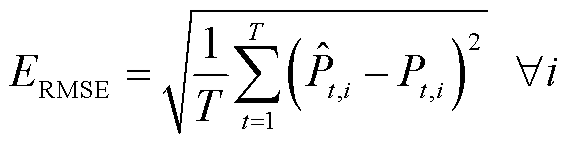 (38)
(38)
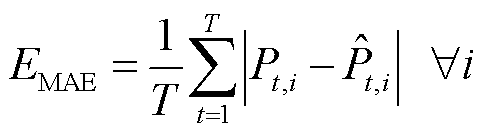 (39)
(39)
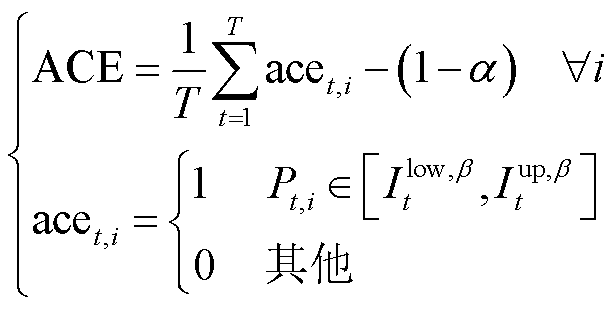 (40)
(40)
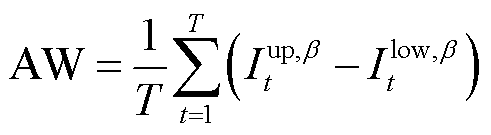 (41)
(41)
4.2.1 PIES光伏发电点预测与区间预测结果
基于TCN与离散特征编码的光伏发电点预测方法与TCN-AT、LSTM-CNN两种对比方法的预测准确度及在不同季节下连续3日的预测曲线分别如表2和附图3所示。观察发现,TCN-OHE(Temporal Convolutional Network-One-Hot Encoding)在不同季节、多次实验下的多数指标都取得了准确性的优化。这一情况与附图3结果相一致。相比TCN-AT和LSTM-CNN,TCN-OHE在春季分别获得了20.83%、27.70%的RMSE增益和26.14%、34.76%的MAE增益;在夏季分别获得了31.76%、75.46%的MAPE增益和6.7%、39.68%的MAE增益;在秋季分别获得了0.56%、55.17%的MAPE增益,47.3%、66.4%的RMSE增益和43.27%、63.03%的MAE增益;在冬季分别获得了9.86%、25.65%的MAPE增益和13.62%、69.51%的RMSE增益。
表2 PIES光伏发电点预测结果对比
Tab.2 Comparison results of point PV forecasting for PIES
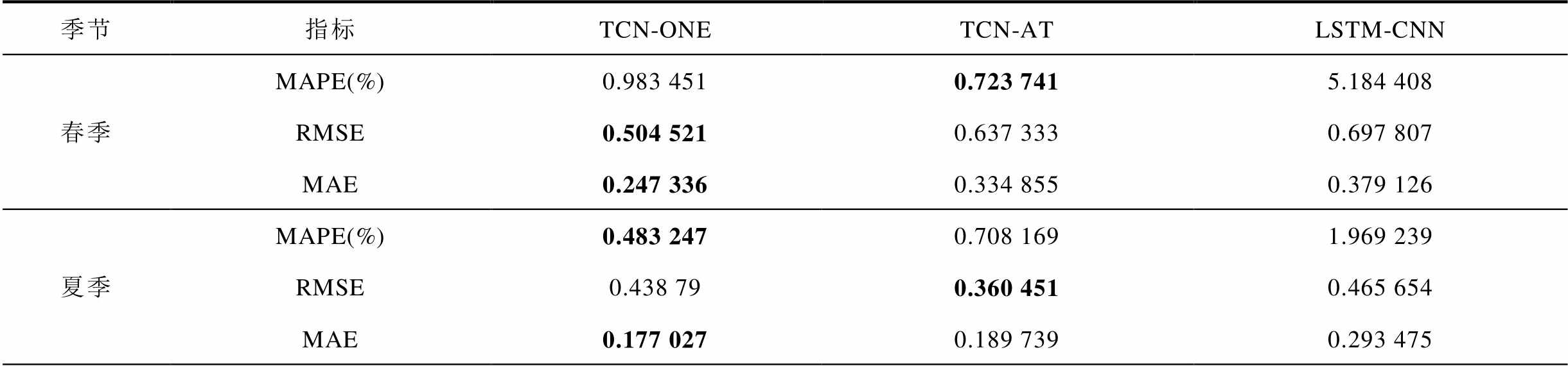
季节指标TCN-ONETCN-ATLSTM-CNN 春季MAPE(%)0.983 4510.723 7415.184 408 RMSE0.504 5210.637 3330.697 807 MAE0.247 3360.334 8550.379 126 夏季MAPE(%)0.483 2470.708 1691.969 239 RMSE0.438 790.360 4510.465 654 MAE0.177 0270.189 7390.293 475
(续)
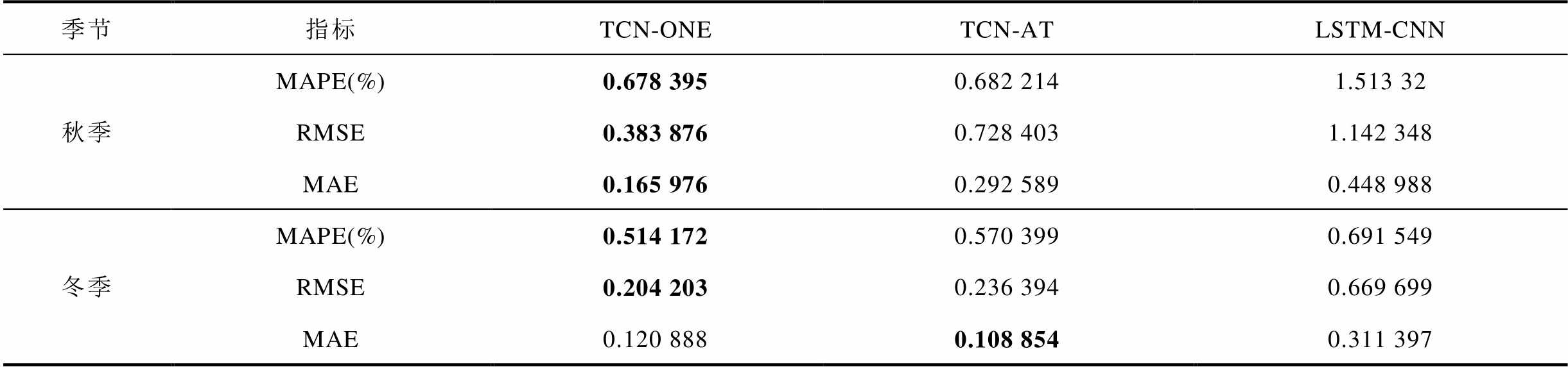
季节指标TCN-ONETCN-ATLSTM-CNN 秋季MAPE(%)0.678 3950.682 2141.513 32 RMSE0.383 8760.728 4031.142 348 MAE0.165 9760.292 5890.448 988 冬季MAPE(%)0.514 1720.570 3990.691 549 RMSE0.204 2030.236 3940.669 699 MAE0.120 8880.108 8540.311 397
相比TCN-AT,TCN-OHE能够提升光伏发电预测精度的原因在于:独热编码机制将离散特征信息输入TCN预测模型,从而为其提供了季节、硅板材质等更高维的关联信息;然而,由于两者主体均为相同结构的TCN网络,因此预测准确度的优化效果相对有限。相比LSTM-CNN,TCN-OHE获得较高预测精度的原因在于:TCN采用的因果扩张卷积使其在不显著增加网络规模下能够感受比LSTM更长的输入序列,并从中提取更多时间关联信息。
基于TCN-OHE输出的光伏发电点预测序列,利用核密度估计计算其预测区间。KDE在不同季节连续3日下拟合得到的两种光伏发电置信区间(置信度为90%和95%)及其有效性结果分别如附图4和表3所示。如表3所示,KDE基于光伏发电点预测序列所拟合的概率区间能够接近甚至超过置信区间准确度(四个季节下90%和95%置信区间的平均ACE为87.13%和94.69%)。
表3 PIES光伏发电区间预测结果
Tab.3 Results of probabilistic PV forecasting for PIES

季节ACEAW 90%95%90%95% 春季0.852 9710.929 0161.078 3081.612 997 夏季0.877 9170.959 9291.389 0841.701 841 秋季0.893 7130.968 0471.455 9771.796 483 冬季0.860 5350.930 5931.221 2541.593 414
4.2.2 SAC智能体迭代训练结果
本节验证PFP-SAC的SAC智能体训练效果。SAC智能体在4次训练过程中的平均奖励函数收敛曲线及波动区间分别为图4中的实线与阴影区域。如图4所示,SAC智能体能够在587~723次迭代训练后收敛到[-3.94×107, -4.01×107]的奖励值区间中。这一结果证明了SAC智能体能通过与PIES运行环境的迭代交互学习,获得基于多能价格、光伏发电预测区间及用户需求动态变化环境下能量转换与存储设备的优化调控知识。同时,该结果说明了利用光伏预测区间作为智能体状态空间及训练的可行性。
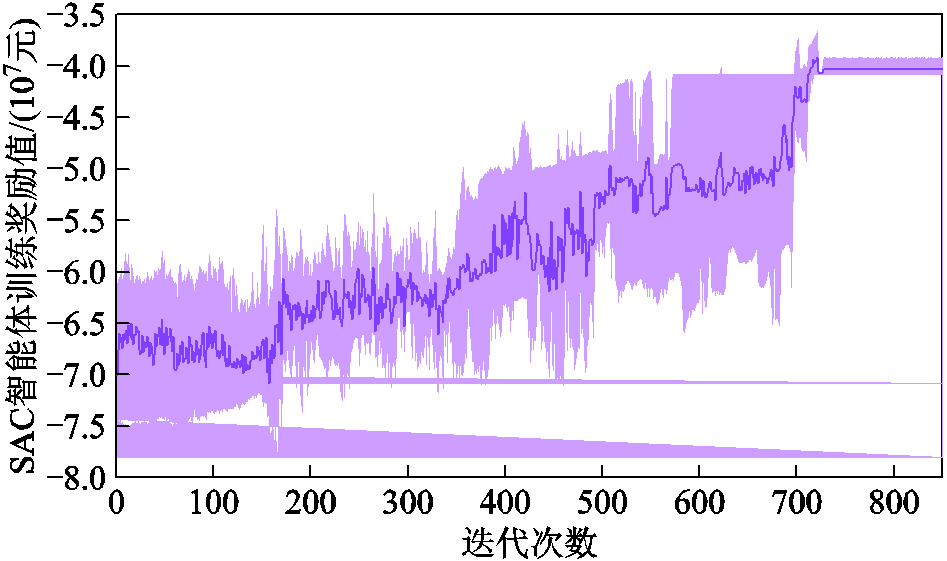
图4 SAC奖励函数的平均收敛曲线及波动区间
Fig.4 The average convergence curve and fluctuation of the SAC agent’s reward
4.2.3 低渗透与高渗透率光伏发电场景下PIES运行调控结果
通过部署训练好的SAC智能体,PIES动态调控能源转换设备的运行功率与储能设备的储/放能功率。PIES在低、高渗透率光伏场景下的设备运行情况分别如图5a和图5b所示。低、高渗透率光伏场景指PIES所接入光伏的额定发电功率分别占其最大电负荷与耗电设备额定功率之和的50%和100%。
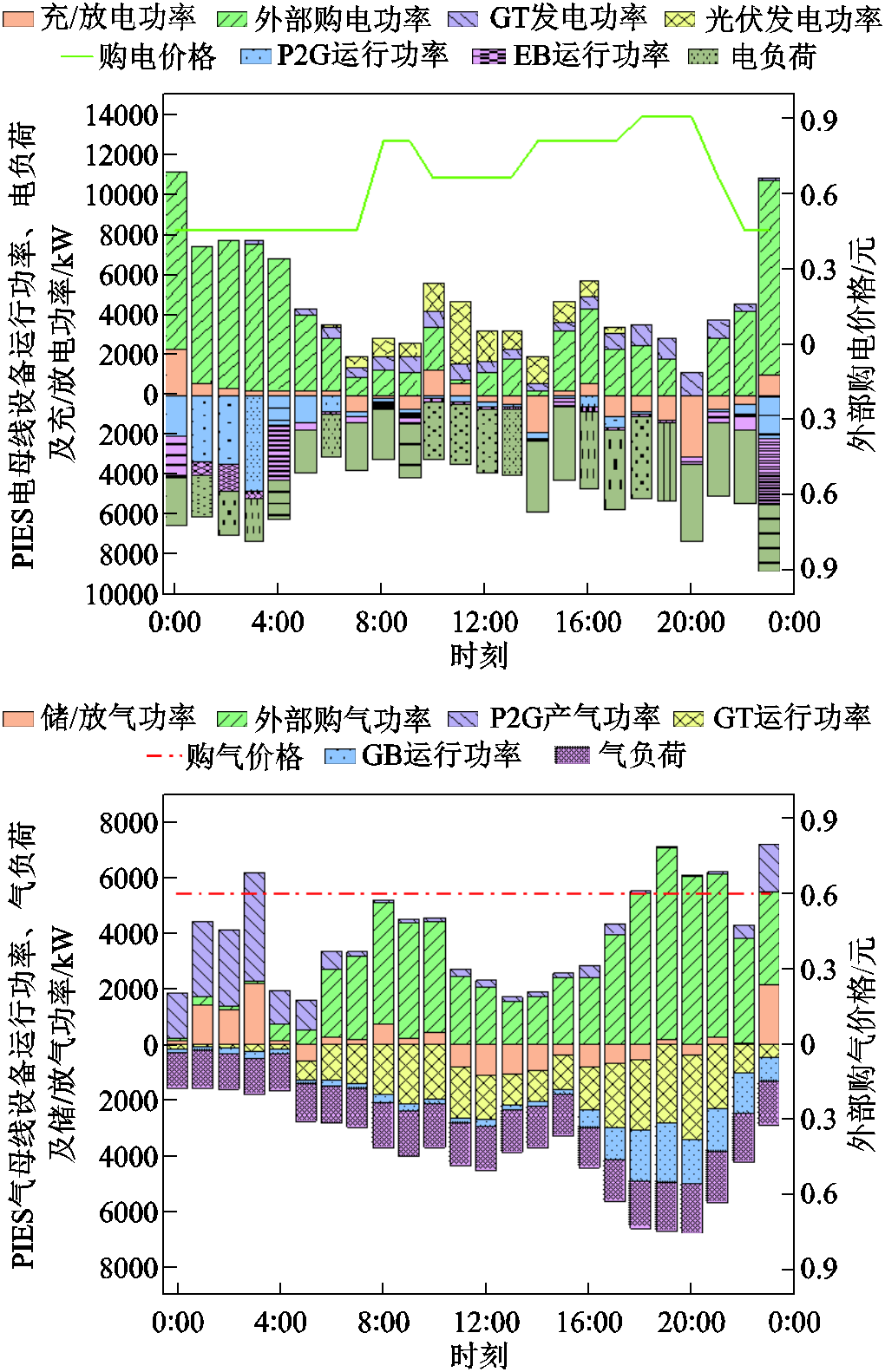

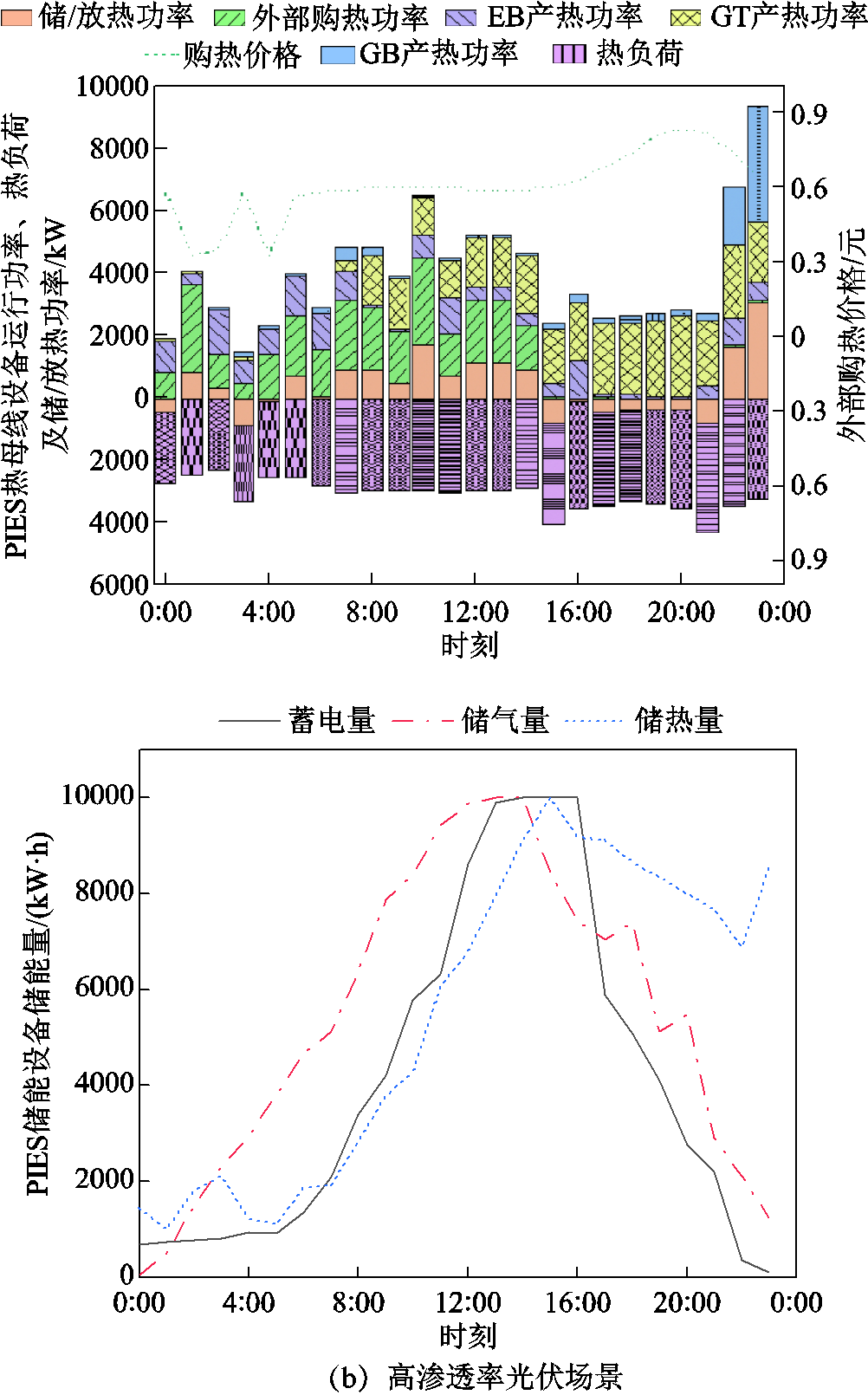
图5 SAC在低、高渗透率光伏部署场景下得到的PIES日内调控方案
Fig.5 The intraday control schemes for PIES obtained by SAC agent in the scenario of low and high penetration of PV
从图5a展示的PIES运行调控结果发现,在低渗透率光伏发电场景下,能源分时价格是驱动PIES耦合设备调控进行能源转换的动力。例如,电母线P2G和EB设备在0:00—7:00和21:00—24:00的电价低谷时段将廉价的电能转换为昂贵的气能和热能;气母线的GT和GB设备在电价高峰阶段(8:00—22:00)和热价高峰阶段(16:00—22:00)增大运行功率,以减少从外部电网与热网中购买昂贵的电能和热能。
同时,在低渗透率光伏发电场景下,储能设备的储/放能动作也是由能源分时价格来引导的。即PIES储能设备通常在能源价格较低时储能并在能源价格较高时放能,以节约购能成本。例如,蓄电池和储热罐分别在0:00—7:00、0:00—5:00的电价、热价低谷时段储能;在8:00—21:00的高峰时段放能。储热罐在17:00—20:00热价高峰期未放能的原因在于:由于此时热价和电价均较高,PIES增加了
GT运行功率以同时增加电、热供给量,将廉价的氢能同时转换为电能和热能,弥补了热母线的供热缺口而无须储热罐放热。由于外部气网采用固定价格,因此气母线储气罐的储/放能动作是由另外两种能源的转换情况所决定的。例如,储气罐在0:00—5:00存储了P2G利用廉价电能转换来的氢能,并在后续调度中逐步释放以节约PIES的购气成本。
图5b展示了在高渗透率光伏部署下SAC智能体训练得到的PIES优化调控方案。相比于低渗透率光伏部署,高渗透率场景的电母线在白天出现了光伏发电高峰。由于SAC奖励函数式(35)需要同时考虑PIES的购能成本与弃光成本,因此在高渗透率光伏部署场景,三种能源的价格差和光伏发电的消纳需求共同对PIES能源转换设备的运行功率及储能设备的储/放能功率进行调节。
PIES的光伏发电尖峰主要出现在9:00—15:00。在此期间,电母线通过降低联络线购电功率、增大蓄电池储能量、增加P2G和EB运行功率以尽可能地消纳光伏发电;气母线则降低外部购气功率并增大储气量,以尽可能地存储P2G为消纳光伏发电所带来的额外气能供给;热母线同样增大储热罐储热量以存储由于EB、GT和GB运行功率增长所增加的热能供给。尽管消纳光伏发电是PIES调控的目标,但是三种能源之间的价格差仍是影响其调控方案的重要因素。例如,由于购气价较高,气母线GT设备在0:00—7:00仍以较低功率运行;电母线P2G和EB设备在17:00—21:00的运行功率也处于低位,因为此时PIES的光伏消纳需求较低且购电价较高。
对比图5a和图5b发现,PIES三种储能设备的储/放能动作在高渗透率光伏发电场景下将优先考虑光伏消纳需求。在高渗透率光伏部署场景下,三种储能设备的储能量在夜晚阶段(18:00—7:00)将尽可能维持低位,并在白天阶段(8:00—17:00)随着光伏发电功率的增长而尽可能地将电能转换为热能和气能,并充分利用其储能潜力以消纳光伏发电。
4.2.4 PIES储能量对比结果
为对比验证本文PFP-SAC方法相比于现有PIES优化调控方法在消纳高渗透率光伏发电的优势,引入文献[29-30]基于DDPG和传统SAC算法所分别提出的PIES优化调控方法。相比本文采用光伏发电区间预测结果来构成SAC智能体状态空间,两种对比方法均采用实时光伏发电量来分别构成其DDPG和SAC智能体状态空间并进行训练。图6展示了PFP-SAC与所对比DDPG和传统SAC方法得到的PIES三种储能设备的储能量日内变化情况。
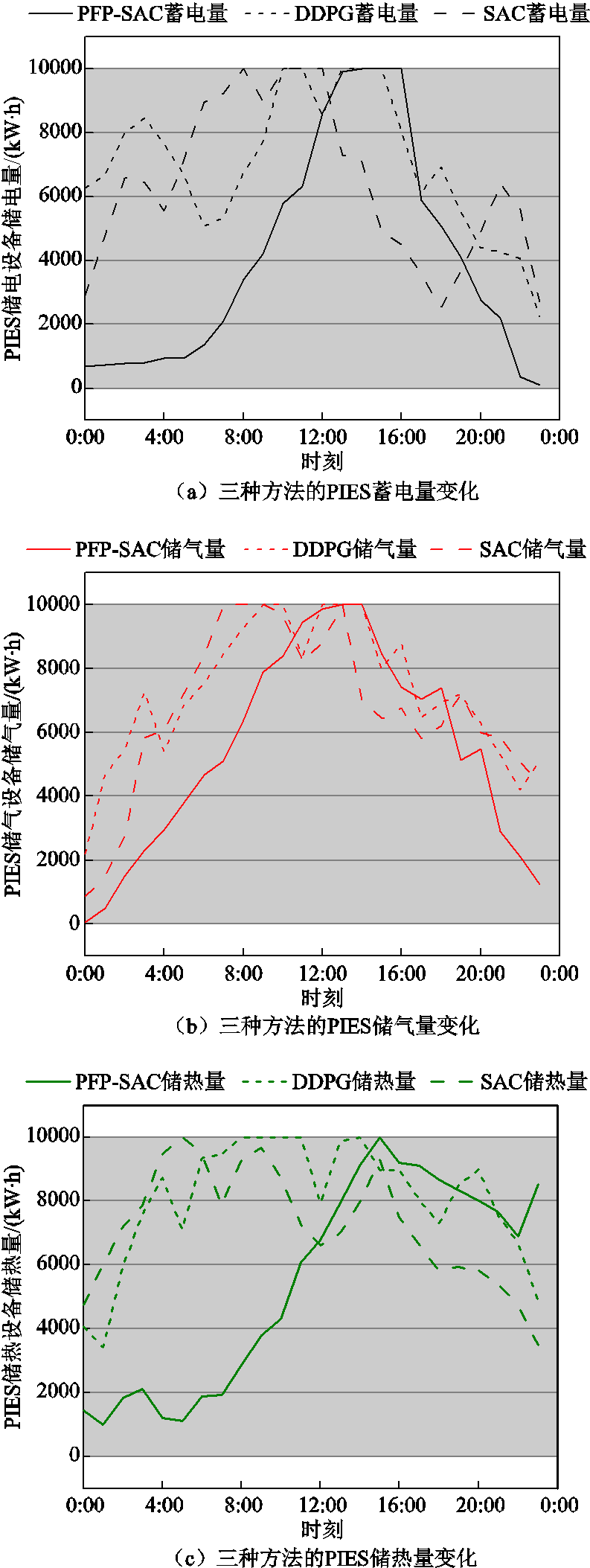
图6 PFP-SAC及对比方法得到的PIES日内异质储能量变化
Fig.6 The intra-day variation of heterogeneous storage for PIES under proposed PFP-SAC and benchmarks
图6中阴影区域为PIES储能设备储能量的约束范围。如3.3节所述,如果PIES由于蓄电池容量限制而无法存储光伏发电电能,或由于储气罐和储热罐容量限制而无法存储P2G、EB设备消纳光伏发电而转换的气能和热能时,PIES须舍弃剩余光伏以维持供需功率平衡,并由此造成弃光惩罚。观察图6发现,DDPG和传统SAC智能体的电、气、热储能设备分别在11:00、10:00、9:00和9:00、8:00、7:00达到最大储能量,而本文PFP-SAC方法直至15:00、14:00、16:00才达到最大储能量。这是因为本文所提出PFP-SAC方法利用光伏发电区间预测结果构建智能体状态空间,使得智能体可以在训练过程中学习并研判未来光伏发电情况,并通过预留出足够的储能资源以提升PIES在高渗透率光伏部署场景下的消纳率。而DDPG和传统SAC智能体由于将实时光伏发电量作为其状态空间,因此其调控方案只能针对实时光伏发电功率,而无法通过预留其储能资源来满足未来光伏发电波动及消纳需求。因此,DDPG和传统SAC智能体的储能设备倾向于在购能价格较低(0:00—7:00)时购买、转换和存储廉价能源并在购能价格较高(16:00—20:00)时段放能来降低PIES运行成本。
4.2.5 PIES运行成本对比结果
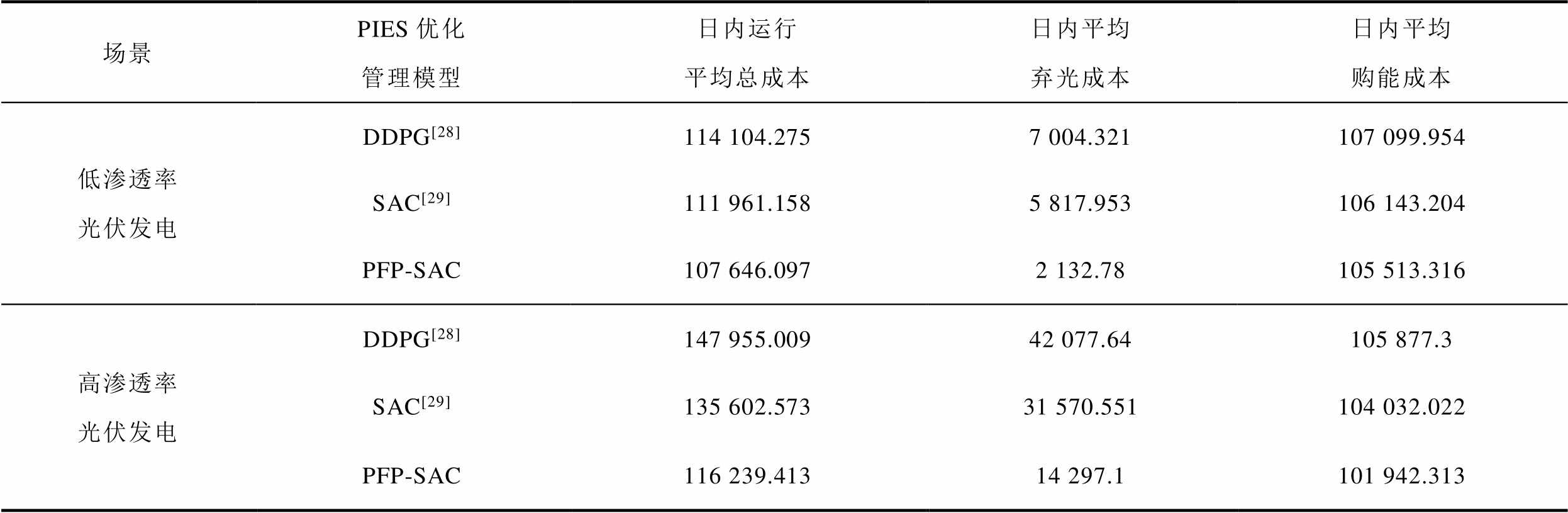
表4给出了本文PFP-SAC方法与DDPG和传统SAC方法的运行成本对比结果。在低渗透率光伏部署场景下,PFP-SAC相比DDPG和传统SAC方法分别节省了5.66%和3.85%;相反在高渗透率光伏部署场景下,本文PFP-SAC方法则能够实现21.44%和14.28%的PIES运行成本优化。
表4 调控方法经济效益比较
Tab.4 Benefit comparison among control methods (单位:元)
场景PIES优化管理模型日内运行平均总成本日内平均弃光成本日内平均购能成本 低渗透率光伏发电DDPG[28]114 104.2757 004.321107 099.954 SAC[29]111 961.1585 817.953106 143.204 PFP-SAC107 646.0972 132.78105 513.316 高渗透率光伏发电DDPG[28]147 955.00942 077.64105 877.3 SAC[29]135 602.57331 570.551104 032.022 PFP-SAC116 239.41314 297.1101 942.313
整体而言,三种方法在高渗透光伏部署场景下的购能成本均低于低渗透率光伏部署场景,这是由于更多清洁、廉价的光伏电能有效地降低了PIES的外部购能量。然而,高渗透光伏部署的更强发电间歇性和正午尖峰发电带来了高昂的弃光成本,进而使得PIES的总运行成本高于低渗透率场景。在低、高渗透率光伏部署场景下,本文PFP-SAC相比DDPG和传统SAC方法分别节省69.55%、63.34%和66.02%、54.71%的弃光成本。这一结果验证了本文采用光伏发电区间预测结果来构建智能体状态空间,能够帮助智能体在调控PIES运行状态时辨识未来光伏消纳需求,进而通过优化电、气、热能的转换与存储来尽可能地挖掘其光伏消纳潜力,进而降低其日内运行的平均弃光与购能成本。
为充分挖掘PIES的多能耦合优势及其储能设备在配电网高渗透率光伏部署场景下具备的消纳潜力,本文提出一种结合光伏发电区间预测与SAC深度强化学习的PIES优化调控方法。该方法利用时序卷积网络和核密度估计得到配电网光伏发电区间预测结果,并将光伏区间预测结果作为柔性Actor-Critic智能体优化调控模型的状态空间,以挖掘PIES支撑配电网光伏消纳的潜力并优化其运行经济效益。仿真结果验证了本文PFP-SAC方法能够基于光伏区间预测结果研判未来光伏消纳需求,并通过动态调节PIES多能转换设备运行功率和储能设备储能量来尽可能地消纳光伏出力和降低系统运行成本。
仿真结果表明,当光伏渗透率较低时,不同能源之间的价格差是PIES进行能源动态转换以获得成本节约的驱动力;相反,在高渗透率光伏部署场景,PIES的日内多能转换与存储动作需要同时兼顾光伏消纳需求与多能价格差,并通过尽可能预留储能资源以提升其光伏发电消纳能力。
同时本文研究发现,PIES作为连接配电网多能供给与负荷的桥梁,其电、气、热能转换与存储的优化调控动作不仅需要考虑光伏等新能源出力的波动性,还需要同时考虑其用户多能需求的不确定性。因此,后续研究需要在本文基础上,进一步针对用户用能行为特性展开分析,实现PIES新能源发电-用户负荷的供需联合预测,并反馈指导其动态调控能源转换与存储动作,进一步优化其经济效益。
附 录
任意时隙t下,能源转换侧GT、GB、P2G及EB的运行特性分别为
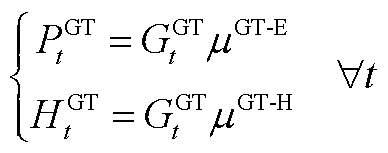 (A1)
(A1)
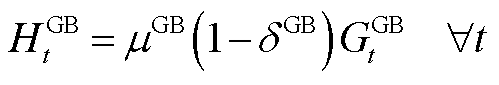 (A2)
(A2)
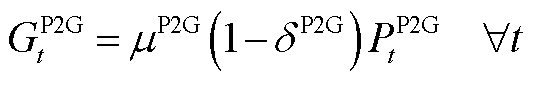 (A3)
(A3)
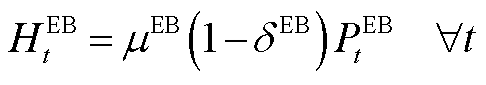 (A4)
(A4)
式中,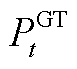 和
和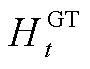 分别为GT等效发电和产热功率;
分别为GT等效发电和产热功率;![]() 与
与![]() 分别为GT的气能与电能、热能间转换效率;
分别为GT的气能与电能、热能间转换效率;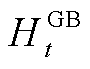 和
和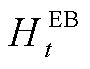 分别为GB和EB的产热功率;
分别为GB和EB的产热功率;![]() 与
与![]() 分别为GB气-热转换效率及EB电制热效率[8];
分别为GB气-热转换效率及EB电制热效率[8];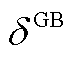 与
与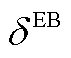 分别为两种设备的燃气损耗系数和电能损耗系数;
分别为两种设备的燃气损耗系数和电能损耗系数;![]() 与
与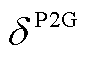 分别为P2G电-气转换效率及电能损耗系数。
分别为P2G电-气转换效率及电能损耗系数。
任意时隙t下,能源存储端蓄电池、储热罐及储气罐的运行特性分别为
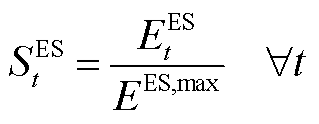 (A5)
(A5)
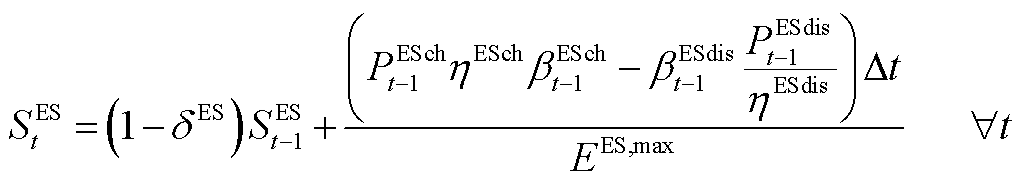 (A6)
(A6)
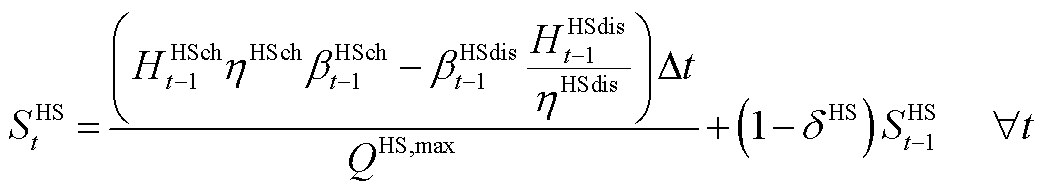 (A7)
(A7)
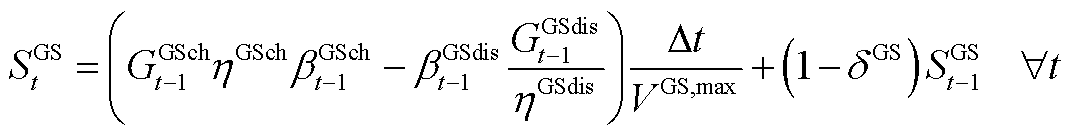 (A8)
(A8)
式中,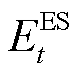 和
和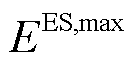 分别为电池蓄电量和最大蓄电量;
分别为电池蓄电量和最大蓄电量;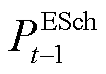 、
、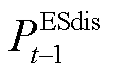 、
、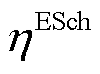 与
与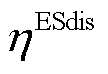 分别为蓄电池在时隙t-1下充、放电功率和充、放电效率;
分别为蓄电池在时隙t-1下充、放电功率和充、放电效率;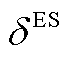 为蓄电池损耗系数;
为蓄电池损耗系数;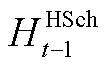 、
、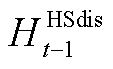 、
、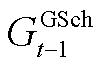 和
和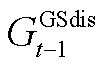 分别为时隙t-1下储热罐储热、放热功率和储气罐储气、放气等效功率;
分别为时隙t-1下储热罐储热、放热功率和储气罐储气、放气等效功率;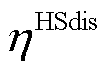 、
、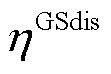 、
、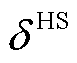 和
和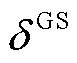 分别为储热罐与储气罐放能效率和自损耗系数;
分别为储热罐与储气罐放能效率和自损耗系数;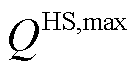 和
和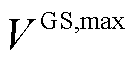 分别为储热罐与储气罐最大储能量。
分别为储热罐与储气罐最大储能量。
附表1 仿真其他参数设定
App.Tab.1 The setting of other simulation parameters

参数数值 k,48, 24 (%)95 (%)38, 36 (%)85, 88, 80 (%)7, 5, 25 (%)0.5, 1, 0.6 /(kW·h)12 500 15 /[元/(kW·h)]5 (%)96, 92, 93 (%)105, 110, 115 (%)80/0 /kW1 000, 500, 750 /kW5 000 /kW800 0.7 0.92 0.04 中更新样本数量1 500 2 880 SAC隐藏层神经元数量(Actor, Critic)128, 128 SAC学习率(Actor, Critic, Q-value)/10-520, 16, 14 SAC训练优化器Adam SAC经验缓存池容量80 000 TCN卷积核大小、数量3, 16 TCN训练轮次500 TCN损失及激活函数MSE,ReLU TCN训练优化器Adam TCN批次大小128 TCN残差块数量3
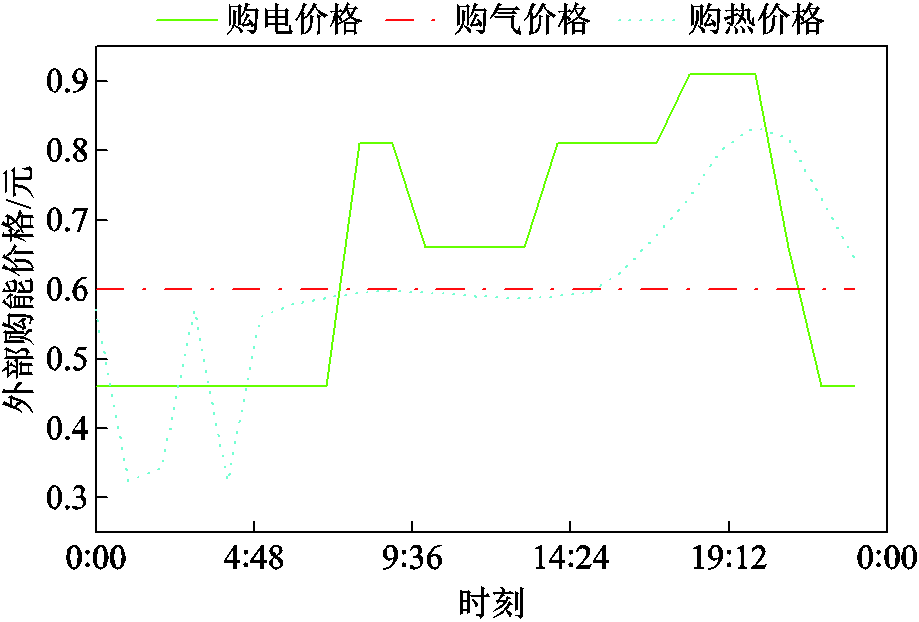
附图1 PIES的三种能源购能价格曲线
App.Fig.1 The price of electricity, gas, and heat for PIES
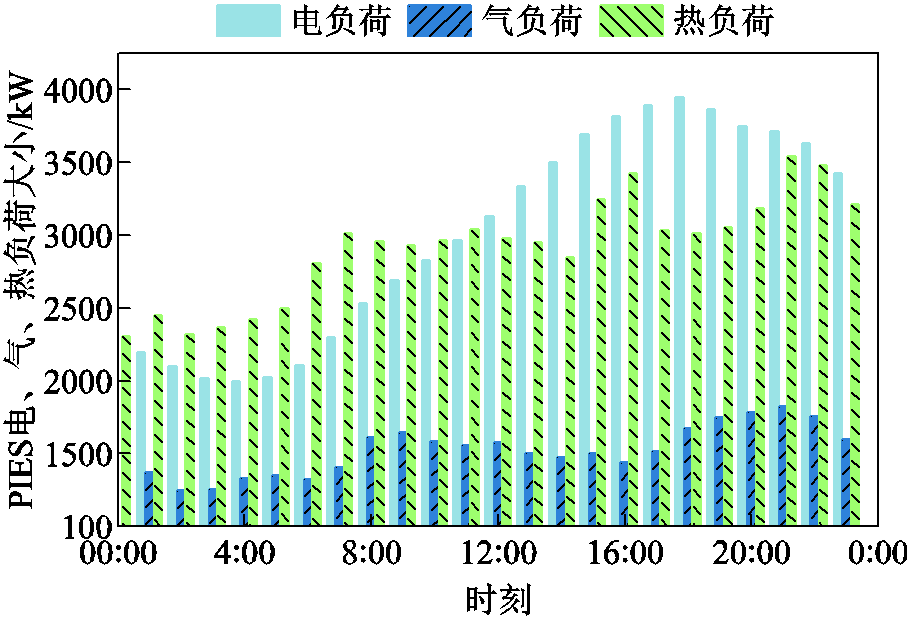
附图2 PIES的三种能源负荷曲线
App.Fig.2 The user’s demand of electricity, gas, and heat for PIES
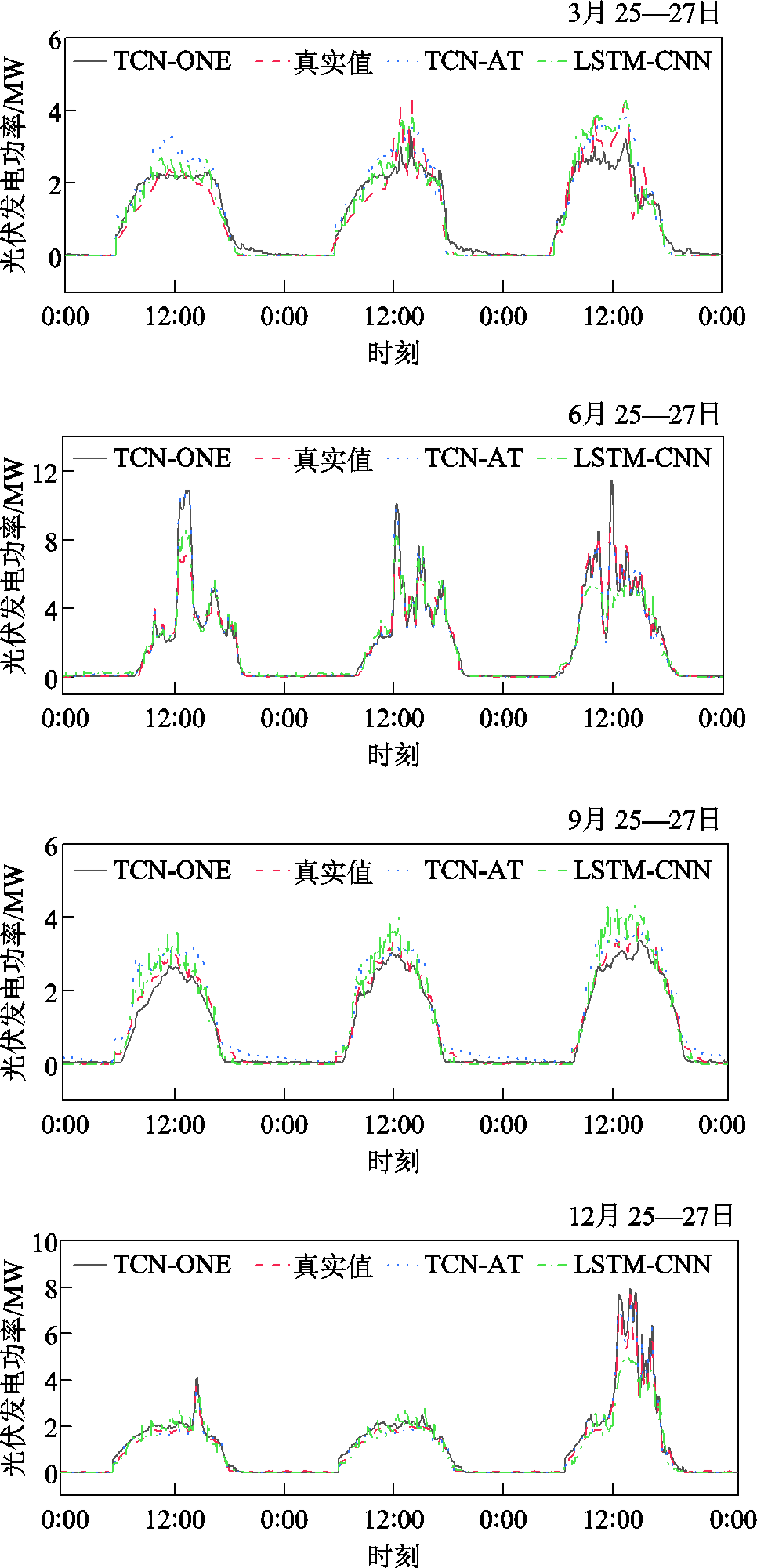
附图3 时序卷积网络得到的PIES连续三日光伏发电预测曲线
App.Fig.3 The point-forecasting curves of PV for PIES in three days based on TCN
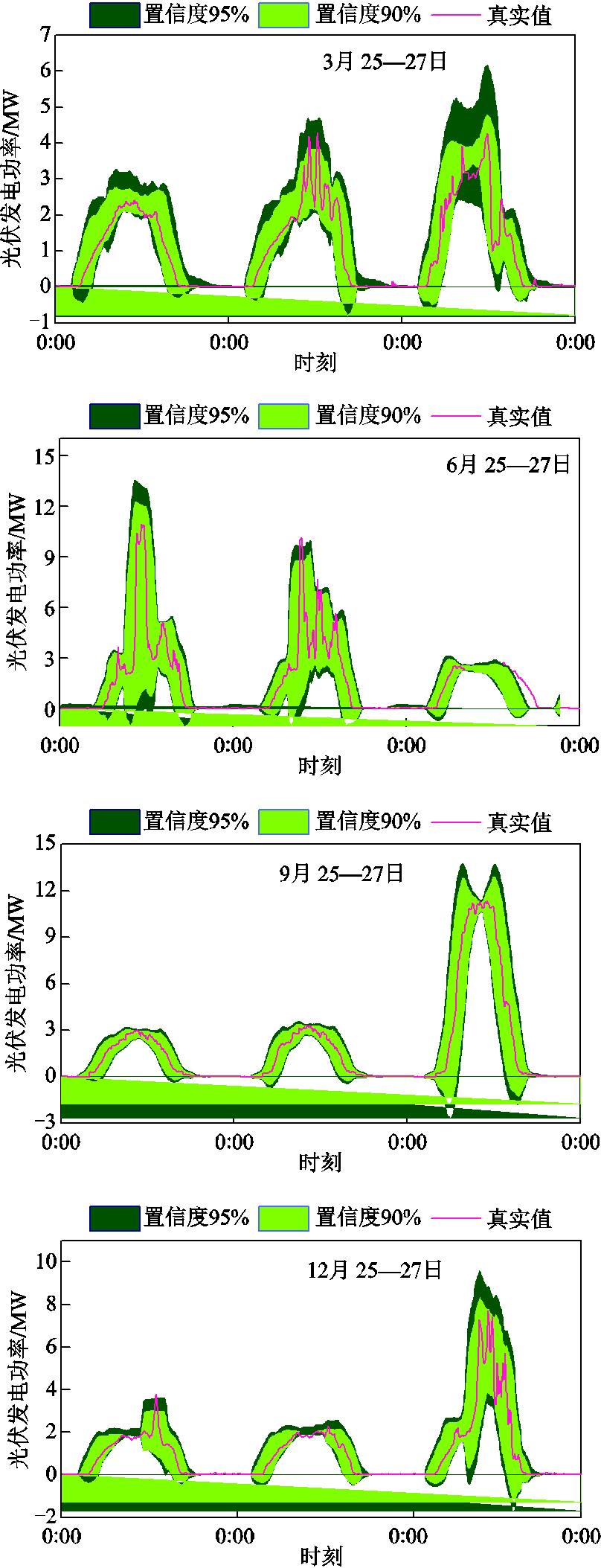
附图4 核密度估计得到的PIES连续三日光伏发电预测区间
App.Fig.4 The prediction intervals of PV for PIES in three days based on KDE
本文所提出结合光伏发电区间预测与SAC深度强化学习的PIES优化调控方法的伪代码如下:

初始化PIES物理层能量模型;初始化SAC智能体Actor和Critic网络(和)、经验回放池D 1while 达到最大训练回合数do 2for每一时隙do
(续)

参考文献
[1] 国家能源局.我国可再生能源发电总装机突破13亿kW[EB/OL]. [2023-11-18]. http:// www.nea.gov.cn/ 2023-07/19/c_1310733273.htm.
[2] 吴孟雪, 房方. 计及风光不确定性的电-热-氢综合能源系统分布鲁棒优化[J]. 电工技术学报, 2023, 38(13): 3473-3485.
Wu Mengxue, Fang Fang. Distributionally robust optimization of electricity-heat-hydrogen integrated energy system with wind and solar uncertainties[J]. Transactions of China Electrotechnical Society, 2023, 38(13): 3473-3485.
[3] 罗潇, 任洲洋, 温紫豪, 等. 考虑氢能系统热回收的电氢区域综合能源系统日前优化运行[J]. 电工技术学报, 2023, 38(23): 6359-6372.
Luo Xiao, Ren Zhouyang, Wen Zihao, et al. A day-ahead dispatching method of regional integrated electric-hydrogen energy systems considering the heat recycle of hydrogen systems[J]. Transactions of China Electrotechnical Society, 2023, 38(23): 6359-6372.
[4] Chen Ruijun, Tsay Y S, Zhang Ting. A multi-objective optimization strategy for building carbon emission from the whole life cycle perspective[J]. Energy, 2023, 262: 125373.
[5] 曾艾东, 王佳伟, 邹宇航, 等. 考虑供热管网储热的综合能源系统多时间尺度优化调度[J]. 高电压技术, 2023, 49(10): 4192-4202.
Zeng Aidong, Wang Jiawei, Zou Yuhang, et al. Multi-time-scale optimal scheduling of integrated energy system considering heat storage characteristics of heating network[J]. High Voltage Engineering, 2023, 49(10): 4192-4202.
[6] Robert L R, Ravi Singh L R S. Economic emission dispatch of hydro-thermal-wind using CMQLSPSN technique[J]. IET Renewable Power Generation, 2020, 14(14): 2680-2692.
[7] 黄文杰, 崔雪, 陈君, 等. 基于多智能体Q学习算法的能源互联园区协调调度[J]. 武汉大学学报(工学版), 2022, 55(11): 1141-1148.
Huang Wenjie, Cui Xue, Chen Jun, et al. Coordinated scheduling of energy interconnected parks based on multi-agent Q-learning algorithm[J]. Engineering Journal of Wuhan University, 2022, 55(11): 1141-1148.
[8] Correa-Jullian C, López Droguett E, Cardemil J M. Operation scheduling in a solar thermal system: a reinforcement learning-based framework[J]. Applied Energy, 2020, 268: 114943.
[9] 张帆, 武东昊, 陈玉萍, 等. 多智能体深度强化学习的分布式园区综合能源系统经济调度策略[J]. 电力系统及其自动化学报, 2022, 34(12): 18-26.
Zhang Fan, Wu Donghao, Chen Yuping, et al. Economic scheduling strategy for integrated energy system in distributed parks based on multi-agent deep reinforcement learning[J]. Proceedings of the CSU-EPSA, 2022, 34(12): 18-26.
[10] 杨挺, 赵黎媛, 刘亚闯, 等. 基于深度强化学习的综合能源系统动态经济调度[J]. 电力系统自动化, 2021, 45(5): 39-47.
Yang Ting, Zhao Liyuan, Liu Yachuang, et al. Dynamic economic dispatch for integrated energy system based on deep reinforcement learning[J]. Automation of Electric Power Systems, 2021, 45(5): 39-47.
[11] 程义, 李更丰. 基于双层模仿学习的多园区综合能源系统分布式协同优化调度[J]. 电力系统自动化, 2022, 46(24): 16-25.
Cheng Yi, Li Gengfeng. Distributed collaborative optimal dispatch of multi-park integrated energy system based on bilayer imitation learning[J]. Automation of Electric Power Systems, 2022, 46(24): 16-25.
[12] 陈明昊, 孙毅, 胡亚杰, 等. 基于纵向联邦强化学习的居民社区综合能源系统协同训练与优化管理方法[J]. 中国电机工程学报, 2022, 42(15): 5535-5549.
Chen Minghao, Sun Yi, Hu Yajie, et al. The collaborative training and management-optimized method for residential integrated energy system based on vertical federated reinforcement learning[J]. Proceedings of the CSEE, 2022, 42(15): 5535-5549.
[13] Bag A, Subudhi B, Ray P K. A combined reinforcement learning and sliding mode control scheme for grid integration of a PV system[J]. CSEE Journal of Power and Energy Systems, 2019, 5(4): 498-506.
[14] 刘自发, 张婷, 王岩. 基于模型预测控制的主动配电网多场景变时间尺度优化调度[J]. 电力自动化设备, 2022, 42(4): 121-128.
Liu Zifa, Zhang Ting, Wang Yan. Multi-scenario variable time scale optimal scheduling of active distribution network based on model predictive control[J]. Electric Power Automation Equipment, 2022, 42(4): 121-128.
[15] 余洋, 贾浩, 陈启维, 等. 基于改进模型预测控制的电-气系统新能源功率波动平滑策略[J]. 电力建设, 2021, 42(9): 65-73.
Yu Yang, Jia Hao, Chen Qiwei, et al. Fluctuation smoothing strategy of new energy power for electricity-gas interconnected system based on improved model predictive control[J]. Electric Power Construction, 2021, 42(9): 65-73.
[16] 舒晓欣, 林其友, 张健, 等. 基于双层模型预测控制的微电网经济调度[J]. 浙江工业大学学报, 2023, 51(3): 324-329.
Shu Xiaoxin, Lin Qiyou, Zhang Jian, et al. A Two-stage model predictive control strategy for economical operation of microgrid[J]. Journal of Zhejiang University of Technology, 2023, 51(3): 324-329.
[17] 吴梦丹, 张俊礼, 吴嘉峰, 等. 基于经济模型预测控制的光伏光热一体化热泵系统动态能效优化[J]. 中国电机工程学报, 2023, 43(6): 2119-2130.
Wu Mengdan, Zhang Junli, Wu Jiafeng, et al. Dynamic energy efficiency optimization of photovoltaic/ thermal integrated heat pump system based on economic model predictive control[J]. Proceedings of the CSEE, 2023, 43(6): 2119-2130.
[18] 杨海涛, 江晶晶, 赵敏, 等. 基于模型预测控制的区域综合能源系统运行优化方法[J]. 电气技术, 2022, 23(4): 7-13.
Yang Haitao, Jiang Jingjing, Zhao Min, et al. Operational optimization method of regional integrated energy system based on model predictive control[J]. Electrical Engineering, 2022, 23(4): 7-13.
[19] 王阳, 刘希喆. 基于GRU-MPC的光储充电站日前- 日内两阶段优化控制[J]. 电力自动化设备, 2022, 42(10): 177-183.
Wang Yang, Liu Xizhe. Day-ahead and intra-day two-stage optimal control of photovoltaic-energy storage charging station based on GRU-MPC[J]. Electric Power Automation Equipment, 2022, 42(10): 177-183.
[20] 王晓霞, 俞敏, 霍泽健, 等. 基于近邻传播聚类与LSTNet的分布式光伏电站群短期功率预测[J]. 电力系统自动化, 2023, 47(6): 133-141.
Wang Xiaoxia, Yu Min, Huo Zejian, et al. Short-term power forecasting of distributed photovoltaic station clusters based on affinity propagation clustering and long short-term time-series network[J]. Automation of Electric Power Systems, 2023, 47(6): 133-141.
[21] Zhang Qingyong, Chen Jiahua, Xiao Gang, et al. TransformGraph: a novel short-term electricity net load forecasting model[J]. Energy Reports, 2023, 9: 2705-2717.
[22] Blad C, Bøgh S, Kallesøe C S. Data-driven offline reinforcement learning for HVAC-systems[J]. Energy, 2022, 261: 125290.
[23] 陈柘, 刘嘉华, 赵斌, 等. 基于GCN和TCN的多因素城市路网出租车需求预测[J]. 控制与决策, 2023, 38(4): 1031-1038.
Chen Zhe, Liu Jiahua, Zhao Bin, et al. Multi-factor taxi demand forecasting for urban road network based on GCN and TCN[J]. Control and Decision, 2023, 38(4): 1031-1038.
[24] 邢晨, 张照贝. 基于改进时间卷积网络的短期光伏出力概率预测方法[J]. 太阳能学报, 2023, 44(2): 373-380.
Xing Chen, Zhang Zhaobei. Short-term probabilistic forecasting method of photovoltaic output power based on improved temporal convolutional network[J]. Acta Energiae Solaris Sinica, 2023, 44(2): 373-380.
[25] 宋绍剑, 姜屹远, 刘斌. 一种TCN的改进模型及其在短期光伏功率区间预测的应用[J]. 计算机应用研究, 2023, 40(10): 3064-3069.
Song Shaojian, Jiang Yiyuan, Liu Bin. Improved TCN model and its application in short-term photovoltaic power interval prediction[J]. Application Research of Computers, 2023, 40(10): 3064-3069.
[26] Wang Kejun, Qi Xiaoxia, Liu Hongda. Photovoltaic power forecasting based LSTM-convolutional Network[J]. Energy, 2019, 189: 116225.
[27] 万灿, 崔文康, 宋永华. 新能源电力系统概率预测:基本概念与数学原理[J]. 中国电机工程学报, 2021, 41(19): 6493-6509.
Wan Can, Cui Wenkang, Song Yonghua. Probabilistic forecasting for power systems with renewable energy sources: basic concepts and mathematical principles[J]. Proceedings of the CSEE, 2021, 41(19): 6493-6509.
[28] Cheng Lilin, Zang Haixiang, Xu Yan, et al. Probabilistic residential load forecasting based on micrometeorological data and customer consumption pattern[J]. IEEE Transactions on Power Systems, 2021, 36(4): 3762-3775.
[29] 陈明昊, 孙毅, 谢志远. 基于双层深度强化学习的园区综合能源系统多时间尺度优化管理[J]. 电工技术学报, 2023, 38(7): 1864-1881.
Chen Minghao, Sun Yi, Xie Zhiyuan. The multi-time-scale management optimization method for park integrated energy system based on the Bi-layer deep reinforcement learning[J]. Transactions of China Electrotechnical Society, 2023, 38(7): 1864-1881.
[30] 朱振山, 陈哲盛, 盛明鼎. 基于柔性行动器-评判器的园区综合能源系统运行优化[J]. 高电压技术, 2022, 48(12): 4949-4958.
Zhu Zhenshan, Chen Zhesheng, Sheng Mingding. Operation optimization of park-level integrated energy system based on soft actor-critic[J]. High Voltage Engineering, 2022, 48(12): 4949-4958.
The Predictive-Control Optimization Method for Park Integrated Energy System Considering the High Penetration of Photovoltaics and Deep Reinforcement Learning
Abstract As the interface between different energy infrastructures and users, park integrated energy system (PIES) has gained universal recognition for improving the reliability, resiliency, and profitability of multi-carrier energy systems by adaptively scheduling fast energy conversion units (e.g., combined heat and power (CHP), gas boiler (GB), and electric boiler (EB)) and participating in the various energy markets (e.g., electricity, heat, and natural gas). As a promising technology for replacing the rule-based decision-making in PIES, deep reinforcement learning (DRL) is a practical solution to identify the optimal control for energy conversion equipment. However, as PIES’s customers perform more casual energy-consumption behaviors, the intermittency and volatility of demands make managing multi-energy supply and storage much harder for DRL agents. To tackle this task, focusing on the utilization of high penetration photovoltaic and the optimization of PIES’s benefits, this article proposes an optimization scheduling method for PIES that combines the deep reinforcement learning and the interval prediction of photovoltaic power generation, considering the uncertainty of photovoltaic power generation.
Firstly, taking the equipment of energy conversion and storage as the scheduling objects, we design the predictive-control optimization structure, which can be divided into the facility level and information level, of PIES with electricity, gas, and heat, introducing the coordination between different sub-models. Secondly, the continuous and discrete feature data are respectively normalized and encoded for deterministic and probabilistic predicting the photovoltaic power generation based on temporal convolutional networks and kernel density estimation. Thirdly, based on the theory of model predictive control, the iteratively obtained intervals of photovoltaic power generation are used to construct the operating environment state of the control agent of soft actor critic (SAC) and to obtain the scheduling actions for PIES’s equipment of energy conversion and storage.
Numerical results show that the proposed PFP-SAC method is able to identify the generation of photovoltaic power, improve the utilization of PV generation, and optimize the benefit of PIES by dynamic scheduling these conversion and storage equipment and increasing their operation efficiency. Meanwhile, these results prove that the gaps of energy purchasing price is the motivation of multi-energy conversion for PIES and its cost-saving. On the contrast, in the scenario of high penetration of photovoltaic power, the multi-energy conversion and storage of PIES need to simultaneously consider the consumption demand for photovoltaic power and the price-gaps of multi energy, and improve its utilization of photovoltaic power generation as much as possible by reserving energy storage resources. Finally, taking the traditional SAC and deep deterministic policy gradient (DDPG) as the benchmarks, the same datasets are utilized to verify the performance of proposed method and benchmarks, including the scheduling benefit and SOC of storage. The results show that our proposed method is superior for each index.
The following conclusions can be drawn from the simulation analysis: (1) A PIES model with multiple kinds of energy conversion and storage units are constructed, accompanying the uncertainty of renewable generation, demands, and energy purchasing prices. In this sense, it is closer to reality than existing PIES models. (2) Model predictive control theory and deep reinforcement learning algorithm are employed to cope with the intermittent nature of multi-energy demands. This paper constructs the state space of DRL models with prediction intervals of multi-energy demands of PIES, which is obtained by TCN and KDE. (3) Taking the operating cost saving as the prioritize objective and the generation utilization of photovoltaic power as secondary goal of PIES scheduling, soft actor critic, which is a promising DRL algorithm, is applied to reduce the operational expenditures and improve the usage of multi-energy storage capacity as much as possible. Compared with traditional DRL algorithms, it owns the advantages of predicting accuracy and the economic benefits of PIES management.
keywords: Integrated energy system, deep reinforcement learning, soft actor-critic, temporal convolutional network, model predictive control
中图分类号:TM73
DOI:10.19595/j.cnki.1000-6753.tces.231320
国家电网有限公司科技项目资助(52130X230008)。
收稿日期 2023-08-16
改稿日期 2023-11-19
陈明昊 男,1997年生,博士研究生,研究方向为电力信息与通信系统、综合能源系统管理。
E-mail:120212101090@ncepu.edu.cn
孙 毅 男,1972年生,教授,博士生导师,研究方向为需求侧管理、电力系统自动化与信息化。
E-mail:sy@ncepu.edu.cn(通信作者)
(编辑 赫 蕾)