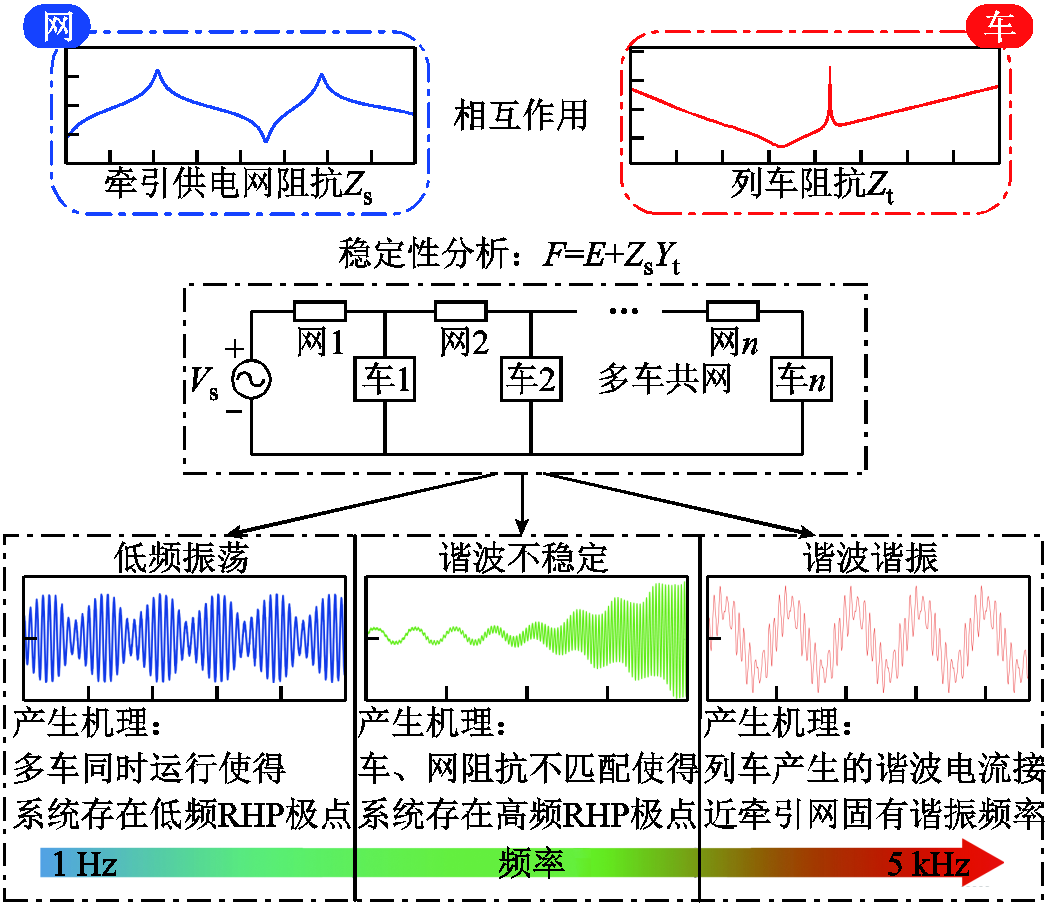
图1 基于阻抗测量信息的稳定性分析示意图
Fig.1 Schematic diagram of stability analysis based on impedance measurement information
摘要 阻抗测量技术能够准确地获取“牵引供电网-列车”（简称“车-网”）系统的宽频阻抗特性，但在阻抗测量信息的利用方面目前多是针对单车系统的稳定性分析，缺少对“多车共网”系统宽频稳定性问题的分析。因此，该文提出一种基于牵引供电网与列车阻抗测量信息的“多车共网”系统稳定性分析方法。首先，利用阻抗测量的方式获取牵引供电网节点阻抗矩阵与列车阻抗信息；然后，建立“多车共网”系统模型，采用基于阻抗回差矩阵行列式的稳定性分析方法，分别从低频到高频分析了电气化铁路中低频振荡、谐波谐振和谐波不稳定三类典型振荡问题，并给出相关的振荡信息，实现多类稳定性问题的统一分析；最后，利用Matlab/Simulink仿真验证了所提稳定性分析方法的有效性。
关键词：电气化铁路 多车共网 阻抗测量 阻抗回差矩阵 稳定性分析
四象限变流器（Four-Quadrant Converter, 4QC）作为CRH系列动车组与HXD系列电力机车（后文统称为列车）牵引传动系统的核心变流设备，具有能量转换效率高、动态响应快、主动可控性强等优点。然而，这些恒功率变流设备控制系统呈现出来的负阻抗特性易引发列车4QC控制系统振荡或失稳，给“车-网”系统造成一系列宽频带振荡问题，严重威胁列车的运行安全[1-3]。现有研究表明，各类稳定性问题是由牵引供电网与列车的宽频带阻抗特性不匹配造成的[3]。目前，对电气化铁路“车-网”系统稳定性的分析方法大多是采用频域阻抗分析方法。但由于车、网详细参数动态变化且难以完全获取，使得小信号频域阻抗建模难以在实际工程中应用。因此，近年来，阻抗测量技术成为精确获取“车-网”系统阻抗的重要手段。
阻抗测量技术在电气化铁路“车-网”系统中已得到广泛研究[4-11]。在牵引供电网的阻抗测量方面，已有研究通过单频主动测量法获取牵引供电网阻抗特性[4-5]，其利用级联H桥向牵引供电网注入单频的扰动电流，具有较高的信噪比，能够准确地获取牵引供电网的阻抗特性。然而，单频主动测量法需要耗费大量时间，测量效率低。为提高阻抗测量的速度，基于多频点注入的宽频主动测量法在牵引供电网阻抗测量领域得到广泛研究[6-8]。文献[6]提出利用方波信号投切电阻的方法快速测量牵引供电网阻抗，但是其频谱能量会随着频率的增大而衰减，频谱可控性较差。为了实现注入扰动频带的精确控制，基于Chirp-PWM信号的蝶形扰动电路被用于牵引供电网的阻抗测量[7]，但其产生的扰动信号能量分布不均匀，信噪比较低。在此基础上，一种基于分段Chirp-PWM信号的模块化电路被用于产生高信噪比的宽频谐波扰动[8]，使得阻抗测量结果更为准确。然而，对于列车4QC的阻抗测量，为避免4QC频率耦合效应对阻抗测量结果的干扰，大多采用单频主动测量法来精确获取其阻抗特性[9-11]。
在稳定性分析方面，已有相关研究通过将“车- 网”系统等效为一个单节点级联系统，采用基于车网阻抗比特征值的广义Nyquist判据（General Nyquist Criterion, GNC）进行分析[12-13]。该方法可有效分析单车接入牵引供电网时的稳定性，但对于多车系统，没有考虑实际运行中每辆列车接入牵引供电网的位置不同，忽略了车与车之间的线路阻抗，其稳定性分析结果可能并不准确[13]。此外，单节点级联系统通常认为线路上并联的多辆列车具有相同的阻抗特性，并用一个等效阻抗替代多辆列车，而实际电气化铁路中接入牵引供电网的列车因参数不同，其阻抗存在差异，因此该方法具有一定局限性。考虑列车实际位置的不同，已有研究通过搭建仿真模型给出了时域仿真结果，但却没有进行振荡机理分析[14]。文献[15]采用阻抗建模的方式对多车系统稳定性进行了理论分析，但其阻抗信息来源于数学建模，过于理想化，实际难以获取。此外，现有基于阻抗的“车-网”系统稳定性分析理论通常只关注单一的振荡问题，且使用的分析方法各有不同，没有对“车-网”系统多类典型振荡问题进行统一分析。例如：在低频振荡研究方面，首先通过阻抗建模的方式获取车、网低频阻抗特性，然后采用基于特征值的GNC法分析“车-网”系统的低频稳定性[12,16]。在高频方面，“车-网”系统的稳定性问题可分为谐波谐振与谐波不稳定，其中谐波谐振可以通过模态分析来获取牵引供电网的固有谐振频率[17]；而谐波不稳定则是由于闭环系统存在高频不稳定极点，可通过求解闭环传递函数的零极点进行分析[15]。以上稳定性分析方法仅针对某一类型的振荡问题，缺乏对“车-网”系统宽频带振荡问题的统一分析。
因此，针对上述问题，本文提出一种基于阻抗测量信息的“多车共网”系统稳定性分析方法。通过主动测量法分别获取牵引供电网与列车的阻抗信息，采用基于行列式的稳定性分析方法对“多车共网”系统的阻抗回差矩阵进行分析，简化了分析过程。在此基础上，提出通过寻找其右半平面（Right-Half Plane, RHP）零点的方法识别系统的振荡频率，实现对“多车共网”系统常见的低频振荡、谐波谐振和谐波不稳定问题的统一分析，如图1所示。最后，基于Matlab/Simulink仿真验证了所提分析方法的正确性与有效性，可为实际电气化铁路中的宽频带振荡问题分析提供技术参考。
全并联自耦变压器（Auto Transformer, AT）牵引供电系统结构示意图如图2所示。牵引变压器从220 kV/110 kV的三相电网取电并转换成2×27.5 kV单相交流电。列车从+27.5 kV的接触线取电，其流出的牵引电流通过钢轨形成回路。AT的两端接头分别与接触线、正馈线-27.5 kV相连，中间线接地并与钢轨相连。AT所沿铁路间距通常为10～15 km，且在相邻牵引变电所之间设置有分区所。在AT所和分区所，横连线将上、下行线路进行并联连接。全并联AT牵引供电系统具有减小线路电流、降低电压损失等优势，已在电气化高速铁路中广泛应用[5-6]。
图1 基于阻抗测量信息的稳定性分析示意图
Fig.1 Schematic diagram of stability analysis based on impedance measurement information
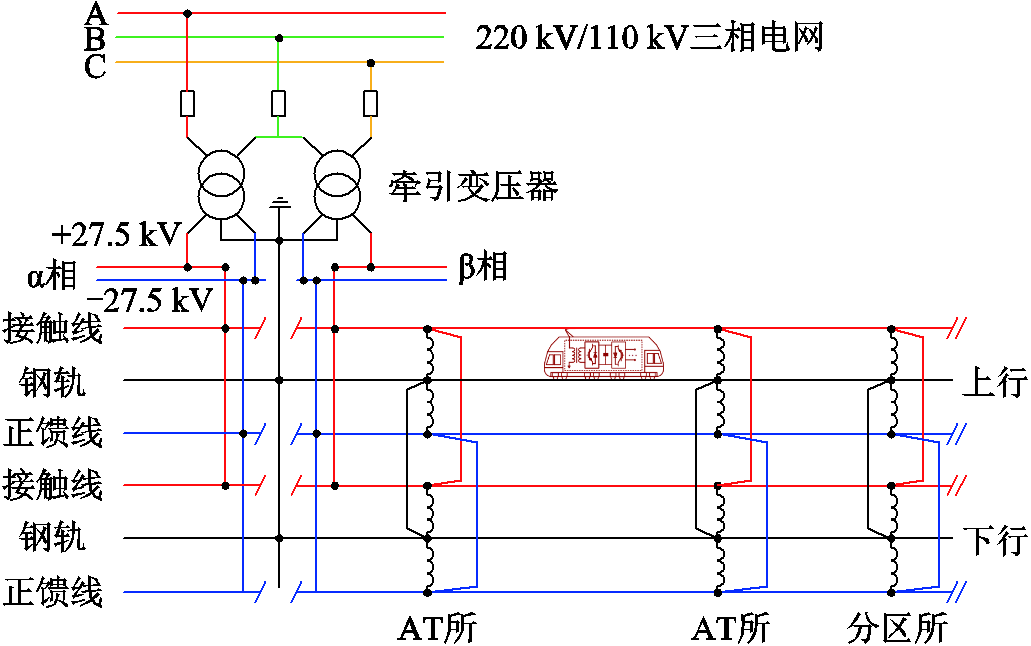
图2 AT牵引供电系统结构示意图
Fig.2 Schematic diagram of AT traction power supply system
对于牵引供电网（含外部三相电源、牵引变压器、牵引网）的阻抗测量，往往采用并联电流扰动注入的方式。传统牵引供电网阻抗测量方法只在谐波注入节点处采集响应电压与电流数据，通过计算得到注入节点处的等效阻抗[6]。该方法虽然能够得到测量节点处的等效阻抗，但却难以获取不同节点之间的互阻抗。因此，为了能准确分析“多车共网”系统的稳定性，需要测量牵引供电网多个节点的阻抗矩阵信息。
由于“多车共网”系统的振荡问题多出现在列车升弓整备状态，因此本文主要开展对多车整备运行工况的测量分析。将列车升弓整备接入点设为牵引供电网节点，考虑系统中有n个节点，则牵引供电网等效测量模型如图3所示。其中，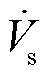
为牵引供电网等效电压源，R0与L0为外部电源与牵引变压器等效电阻与电感，Ri、Li与Ci（i=1, 2, …, n）分别为每段线路的等效电阻、电感与对地电容，
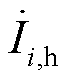为节点i处注入的扰动电流源，
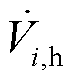为节点i处的扰动响应电压。
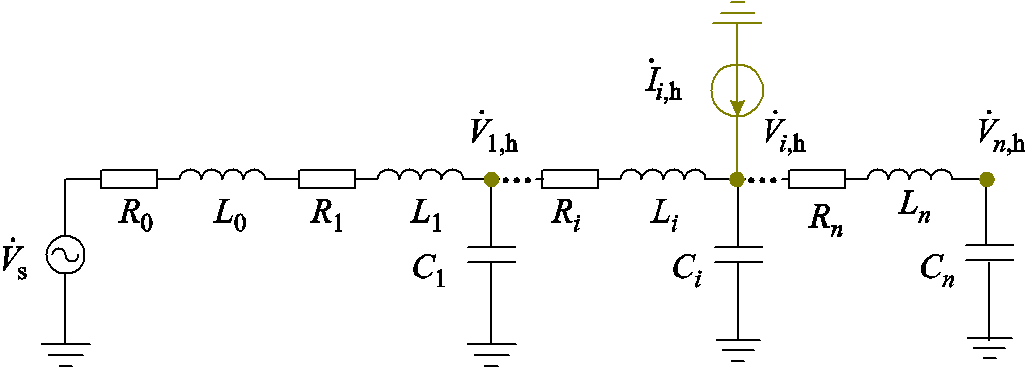
图3 牵引供电网节点阻抗矩阵测量模型
Fig.3 Measurement model of the impedance matrix of traction power supply network nodes
扰动注入下牵引供电网的节点阻抗矩阵[18]为
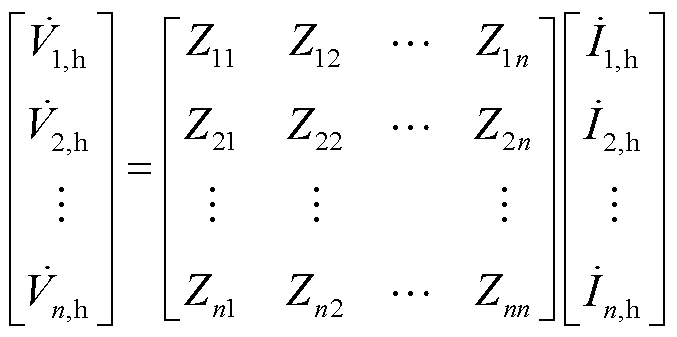（1）
式中，矩阵对角线元素Zii为节点i的自阻抗；非对角线元素Zij为节点i与j之间的互阻抗，i, j=(1, 2, 
, n；j¹i)。
测量时，每次只有一个节点注入电流，假设节点i处有扰动电流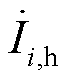注入，而在其余节点j处无电流注入，即
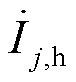= 0。此时，自阻抗Zii与互阻抗Zji满足
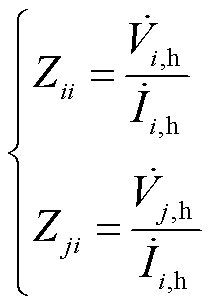（2）
为消除背景谐波影响，牵引供电网节点阻抗矩阵的完整测量步骤为：
1）在扰动注入之前，先采集无扰动时牵引供电网各个节点的响应电压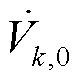
（k=1, 2,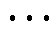, n）。
2）节点i处注入扰动电流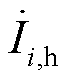，并采集节点i处的响应电压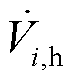及其余节点j处的响应电压
。
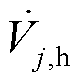3）通过式（3）计算出扰动频率下节点i的自阻抗Zii(jw)及节点i与j之间的互阻抗Zji(jw)。
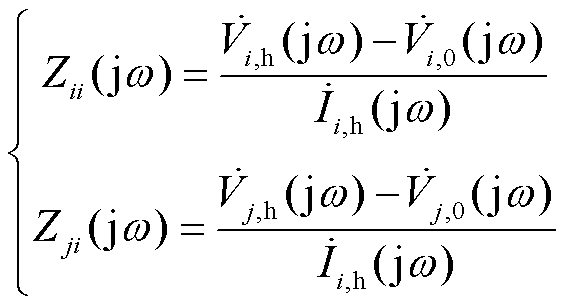（3）
式中，
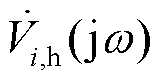和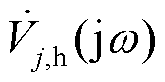
分别为扰动注入后节点i和j的频域响应电压；
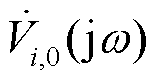和
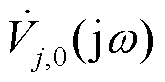分别为扰动注入前节点i和j的频域响应电压；
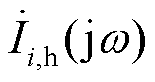为频域下的扰动电流。
4）在节点i处完成测量后，在下一节点i+1处重复步骤2）与步骤3），直到所有节点的自阻抗与互阻抗元素均被测量。
根据牵引供电网节点阻抗矩阵性质，式（1）中互阻抗元素Zij=Zji。因此，为了减少阻抗测量时间，互阻抗Zij和Zji只需在某一个节点处进行采集计算。此外，获取牵引供电网静止坐标系阻抗后，可通过坐标变换将其阻抗转换为dq阻抗[16]。
对于列车阻抗的测量，通常采用串联电压扰动注入方式。本文以CRH5型动车组为例进行分析，控制系统采用dq解耦电流控制策略，图4为列车等效阻抗测量模型。其中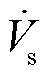，为等效电压源，Zs为牵引供电网等效阻抗，Rn与Ln分别为车载变压器等效电阻与电感，Cd为4QC直流侧支撑电容，Rd为等效负载，Vdc为直流侧电压，
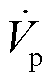为扰动电压源。4QC作为列车的核心变流设备，其控制环节由锁相环、电流环、电压环、PWM调制模块共同构成[12]。
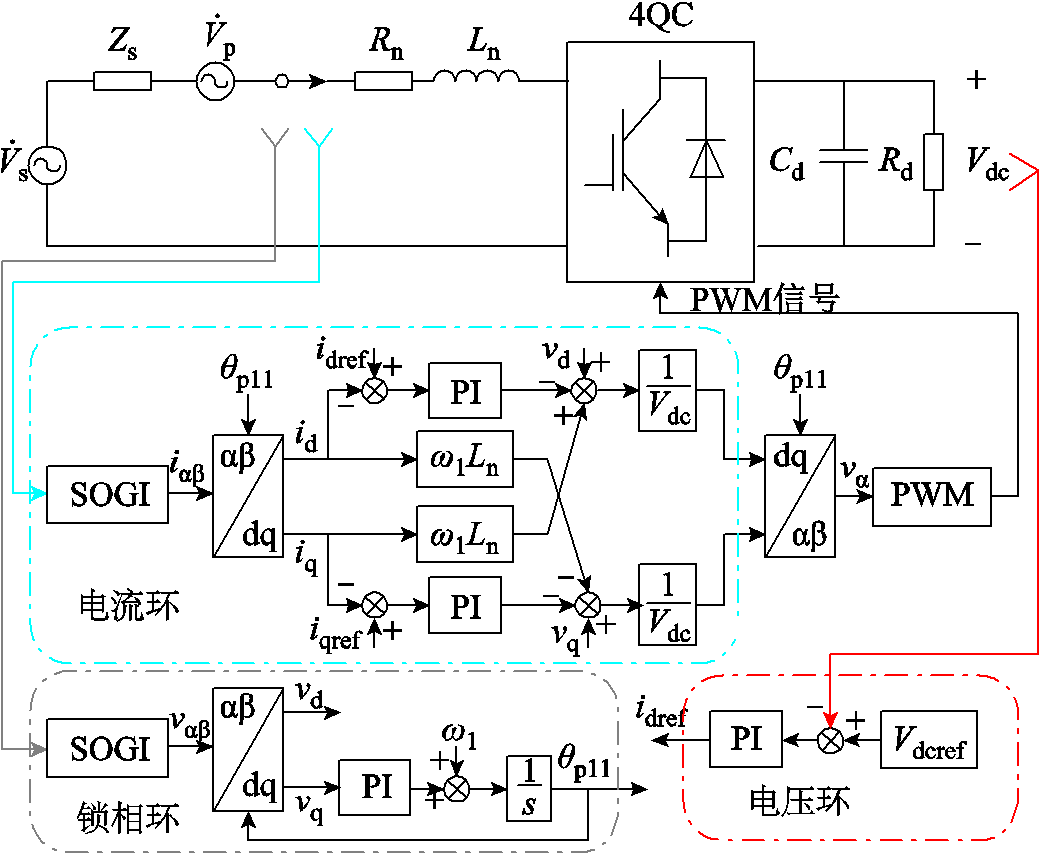
图4 列车等效阻抗测量模型
Fig.4 Equivalent impedance measurement model of train
为了能够体现4QC的不对称控制、非线性等特性，采用dq阻抗来表征列车阻抗，其表达式为
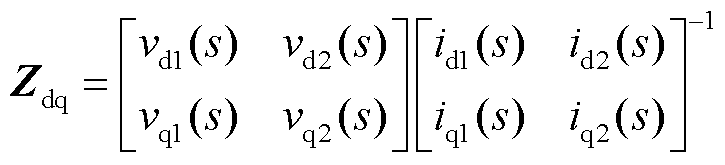（4）
列车dq阻抗矩阵Zdq具有四个元素Zdd(s)、Zdq(s)、Zqd(s)、Zqq(s)。因此，为测量出列车的dq阻抗，需要依次注入两组线性无关的扰动电压，然后通过两组响应电压[vd1 vq1]T和[vd2 vq2]T，以及响应电流[id1 iq1]T和[id2 iq2]T进行阻抗计算。
列车4QC的dq阻抗测量步骤为：①在牵引变电所出口馈线与列车之间串联接入谐波扰动源，当列车处于升弓整备状态，4QC稳定运行时依次注入两组线性无关的单频扰动电压；②采集列车端口电压与电流响应数据，记为va、ia，并利用Hilbert变换得到与之正交的另一组分量vb、ib；③利用一种非对称Park变换将静止坐标系下的αβ分量变换至dq旋转坐标系下[9]，得到vd、vq、id、iq分量；④利用式（4）计算出列车的dq阻抗测量信息。
已有研究通常将“车-网”系统模型等效为一个单节点的级联系统，该模型虽然能准确分析单车接入牵引供电网时的系统稳定性，但却无法适用于考虑不同列车之间线路阻抗的多车系统稳定性。因此，本文建立了一种基于多节点的“多车共网”系统模型，其示意图如图5所示，可用于分析多辆列车同时接入牵引供电网时的系统稳定性。
图5 “多车共网”系统示意图
Fig.5 Schematic diagram of multiple train-network system
假设有n辆列车接入牵引供电网，每个接入点看作一个牵引供电网节点，考虑不同列车之间的线路阻抗，此时可将整个系统等效为图6所示的电路。其中，Vs为等效电压源；Rsk与Lsk（k=1, 2,, n）为每段牵引等效电阻与电感，Rs1与Ls1不仅包含线路阻抗，还包含外部电源与牵引变压器阻抗；Csk为每段线路的对地电容。根据诺顿定理，每辆列车可以等效为一个谐波电流源Itk和等效导纳Ytk并联。Ik为第k辆列车的输出电流；Vk为第k辆列车接入牵引供电网处的节点电压。
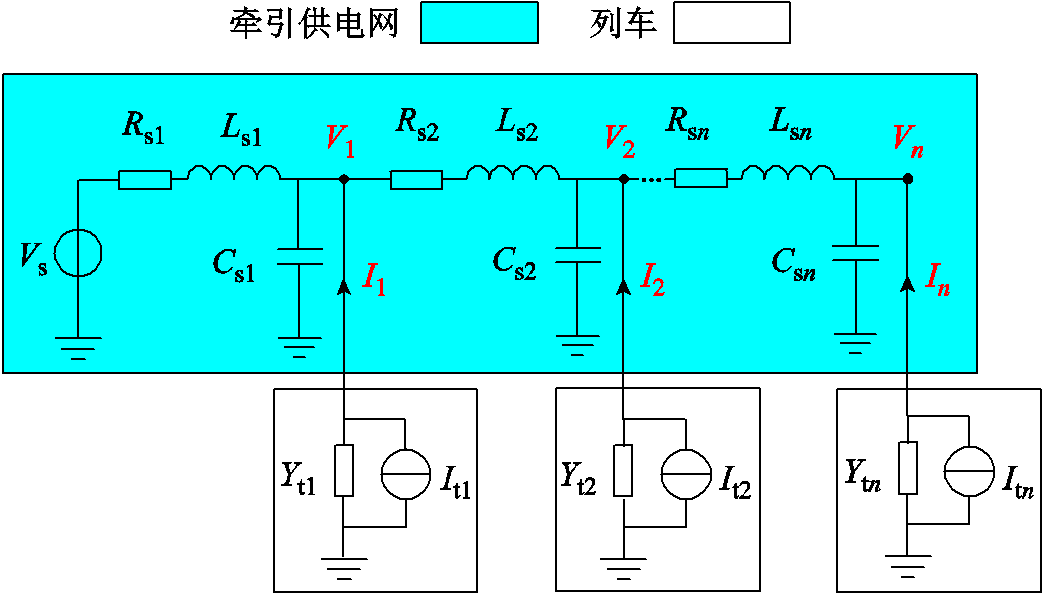
图6 “多车共网”系统等效电路
Fig.6 Equivalent circuit of multiple train-network system
对于牵引供电网，其节点电压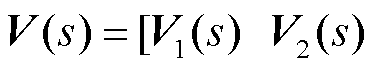
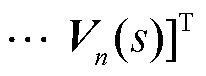与列车输入电流
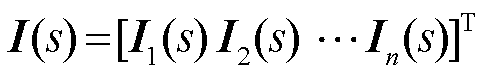的关系为
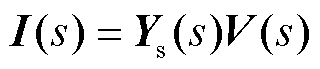（5）
式中，节点电压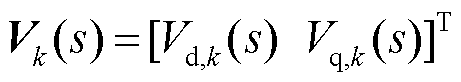
与节点输入电流
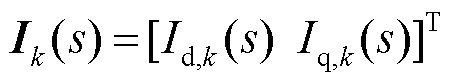均为dq坐标系下的变量；Ys(s)为dq坐标系下的牵引供电网节点导纳矩阵，为2n阶矩阵，如式（6）所示。
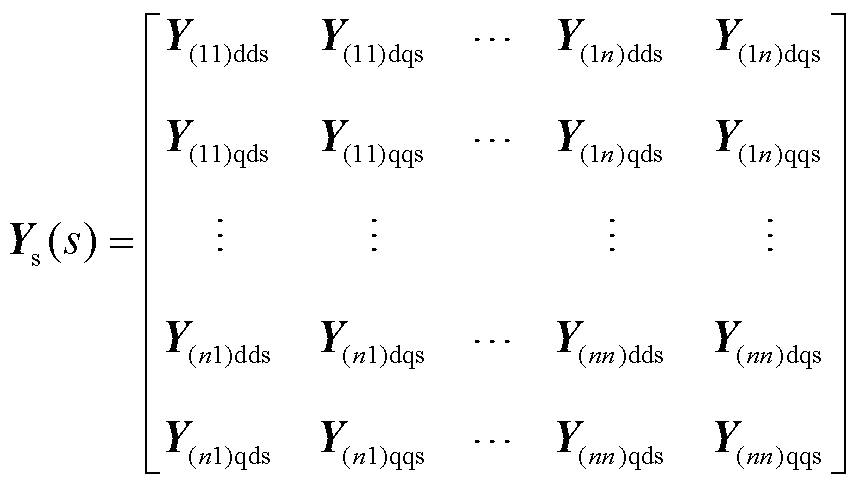（6）
式中，矩阵中的对角元素矩阵Y(ii)s(s)为节点i的dq自导纳；非对角元素矩阵Y(ij)s(s)（i, j = 1, 2,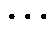 
, n；i¹j）为节点i与j之间的dq互导纳。
对于接入牵引供电网的列车而言，其等效输出电流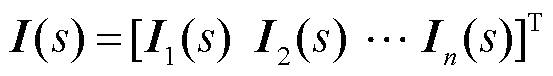
与等效谐波电流源
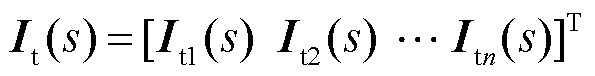满足
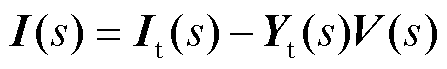（7）
式中，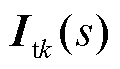
为dq坐标系变量，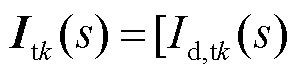
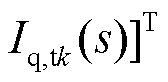；Yt(s)为电力机车的等效dq导纳矩阵，如式（8）所示。
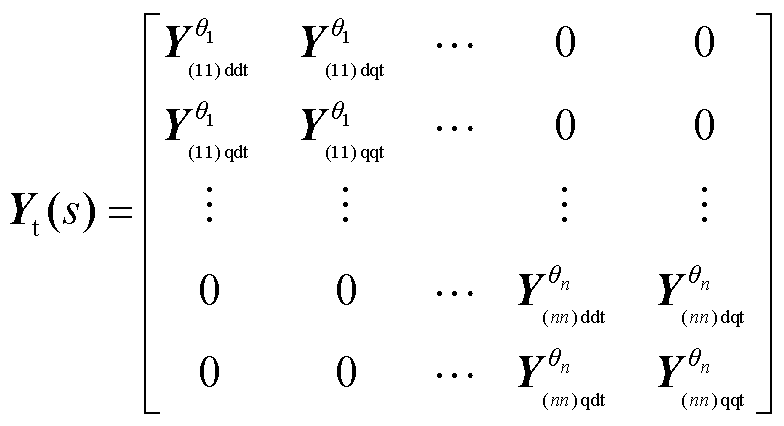（8）
式中，qi为列车接入节点处的不同稳态相位，可通过车-网等效电路方程组求解并转换至同一相位参考系下[19]；对角元素矩阵Y(ii)t(s)为第i辆机车的dq导纳，其余元素均为零[15]。
结合式（5）与式（7），可将整个2n阶“多车共网”系统推导为
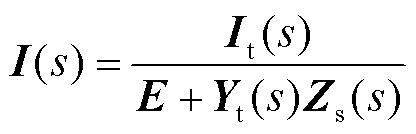（9）
式中，E为2n阶单位矩阵；Zs(s)为牵引供电网节点dq阻抗矩阵，即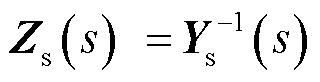
。
由式（9）可知，“多车共网”系统可等效为一个多输入多输出（Multi-Input Multi-Output, MIMO）的负反馈系统，如图7所示。此时，系统稳定性只由牵引供电网节点阻抗矩阵Zs(s)与列车导纳矩阵Yt(s)决定。因此，可通过车网阻抗比矩阵L(s)=Yt(s)Zs(s)或阻抗回差矩阵F(s)=E+Yt(s)Zs(s)来分析系统的稳定性。Zs(s)和Yt(s)可通过第1节提出的阻抗测量方法得到，无需进行额外的理论推导或模型辨识。
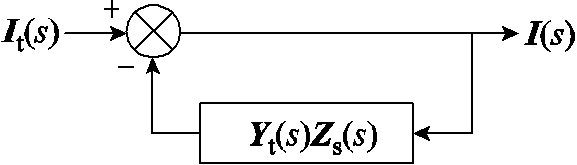
图7 等效MIMO负反馈系统
Fig.7 Equivalent MIMO negative feedback system
需要注意的是，阻抗/导纳的阶数受接入牵引供电网的列车数量和测量阻抗形式的影响。在本文中，有n辆列车接入牵引供电网，测量的阻抗形式为dq阻抗，因此，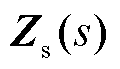
与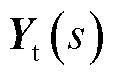
均为2n阶矩阵，后续分析均在dq坐标系下进行。
单节点“车-网”级联系统忽略了车与车之间的线路阻抗，可利用车网阻抗比矩阵L(s)的特征值对该系统进行稳定性分析，此时“车-网”系统的稳定条件[20-21]为：L(s)特征值的Nyquist曲线在复平面上不包围临界点(-1，j0)。而对于考虑车间线路阻抗的“多车共网”系统而言，其车网阻抗比矩阵L(s)的阶数较大，想要完整获取系统的频率特性信息，需要对每一个特征值的Nyquist曲线都进行检查。但由于不同特征值的频率特性曲线相互纠缠，往往难以计算Nyquist曲线包围(-1，j0)点的圈数，使得多车系统的稳定性难以判断，如图8所示。
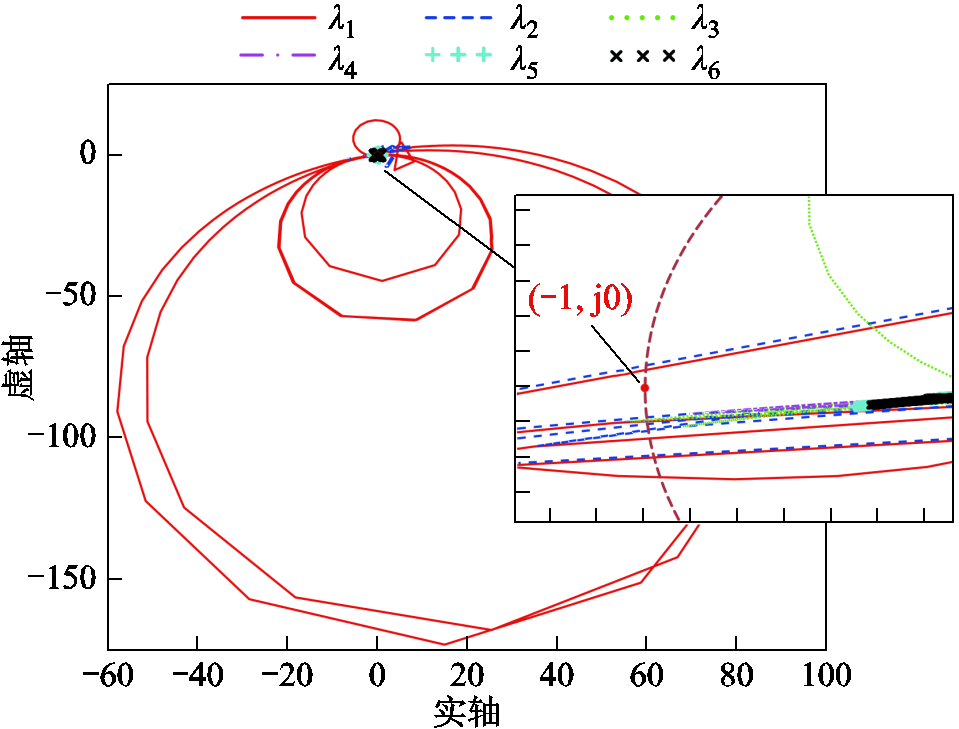
图8 基于L(s)特征值的Nyquist图
Fig.8 Nyquist diagram based on L(s) eigenvalues
因此，本文使用一种基于阻抗回差矩阵F(s)行列式的稳定性分析方法对“多车共网”系统进行稳定性的统一分析，可将高维的阻抗矩阵等效为一个单维的行列式进行分析，大大简化了分析过程。阻抗回差矩阵F(s)的行列式定义为
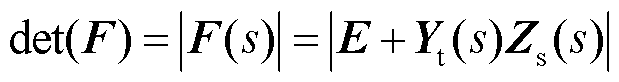（10）
基于阻抗回差矩阵F(s)行列式的稳定性分析法的有效性已经得到证明[22-23]，其稳定性判据为
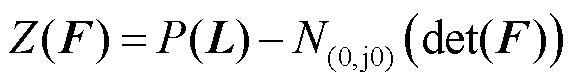（11）
式中，Z(×)为RHP零点的数量；P(×)为RHP极点的数量；N(0,j0)(×)为围绕(0，j0)点的逆时针包围圈的数量。Z(F) = 0代表系统稳定，Z(F)¹0表示系统不稳定。
由于牵引供电网与列车自身设计是稳定的，所以Zs(s)和Yt(s)均没有RHP极点，即P(L)=0。此时，系统稳定的充分必要条件可由式（12）表示，当且仅当N(0,j0)(det(F)) = 0时系统稳定。
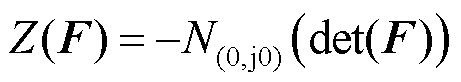（12）
为了便于观察包围(0,j0)点的圈数，使用det(F)的Bode图来获取N(0，j0)(det(F))的数量[22]。其稳定条件为：如果det(F)的Bode图在整个正频率范围内的相位减小为0°，则闭环系统不包含任何RHP极点，此时系统稳定；如果det(F)的相位减小n ´ 180°，意味着顺时针围绕(0，j0)点n次，闭环系统含有n个RHP极点，此时系统不稳定。图9显示了两种情况下det(F)的Bode图。情况1中相位变化量为0°，说明此时“车-网”系统稳定；情况2中相位减小了2´180°，“车-网”系统不稳定，且系统具有2个RHP极点。对于实际的测量系统而言，测量出系统在整个正频率范围内的阻抗特性不可能实现，因此可以选择将测量终止频率降低为Nyquist频率或其他适当频率[24-25]。
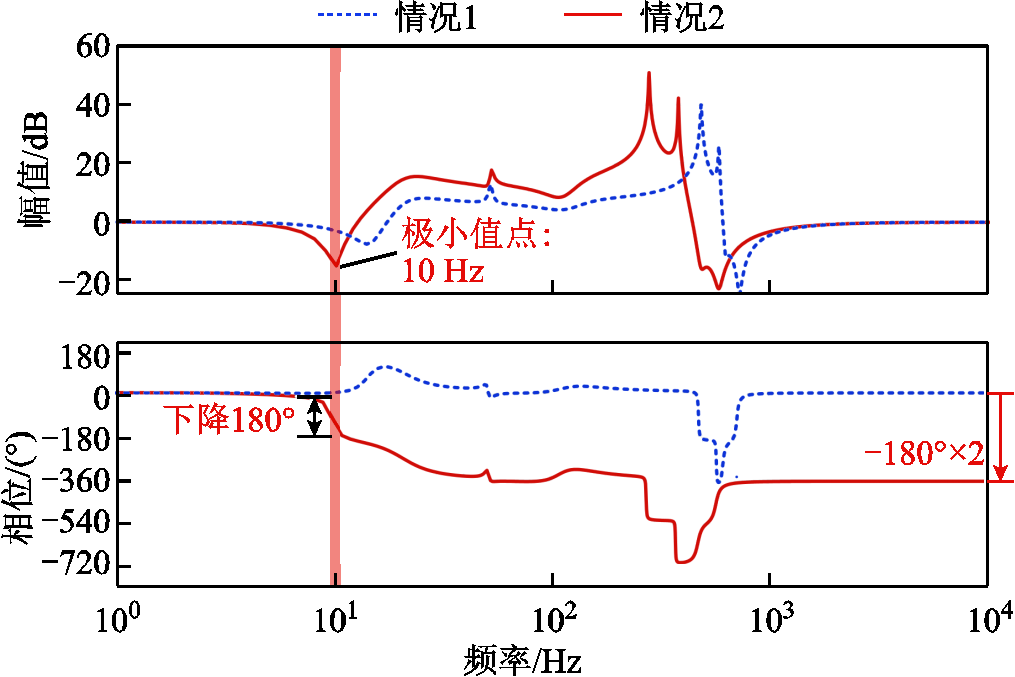
图9 不同情况下det(F)的Bode图
Fig.9 Bode diagrams for det(F) under different conditions
基于阻抗回差矩阵F(s)行列式的分析方法虽然可以判断系统的稳定性，但由于其只关注起始频率和终止频率的相位信息，没有充分利用det(F)的整个宽频信息，无法进一步分析闭环系统的RHP极点，难以获取其振荡频率信息。因此，提出一种基于阻抗回差矩阵行列式RHP零点的“车-网”系统振荡频率识别方法。
MIMO系统稳定需要其传递函数矩阵没有RHP极点。由式（9）可知，车网阻抗回差矩阵F(s)的零点即为“多车共网”系统的极点，此时系统的稳定条件可等效为：系统的特征多项式det(F)不存在RHP零点，或系统的特征方程det(F) = 0不存在RHP的根[26]。因此，det(F)的RHP零点等价于整个“车-网”系统的RHP极点，通过识别det(F)的RHP零点便可直接获取系统的振荡频率。
对于RHP零点的频率特性，其在Bode图上表现为幅值曲线存在某一极小值且对应频率下的相位曲线下降180°[27]。此时，若det(F)存在一对共轭RHP零点，则det(F)的Bode图中会存在某一频率下的幅值极小值，且对应相位下降180°，对于整个“车-网”系统而言，即存在一对共轭RHP极点，且该频率为系统的振荡频率。
从图9可以看出，情况1下det(F)的Bode图不存在幅值为极小值且对应相位下降180°的频率点，即不存在RHP零点，说明“车-网”系统稳定。而在情况2中，其Bode图幅值曲线在10 Hz左右存在极小值且对应相位下降180°，说明det(F)在该频率下存在一对主导RHP零点，“车-网”系统存在一对RHP极点，系统不稳定，可能会发生频率为10 Hz的低频振荡。通过对比两种情况下det(F)的Bode图可以看出，导致其相位减小的根本原因正是det(F)存在RHP零点。因此，如果可以在det(F)的Bode图中识别出RHP零点，则可直接说明系统不稳定，从而进一步减小测量的终止频率。
在电气化铁路“车-网”系统中，目前报道的宽频带振荡问题主要有三类：低频振荡、谐波谐振与谐波不稳定[13]。本节利用测量的车、网阻抗信息对这三类稳定性问题分别进行分析，通过统一分析det(F)的Bode图，将车、网阻抗的低频与高频信息全面应用于“车-网”系统的稳定性评估。
为了验证提出的车、网阻抗测量信息的正确性，本文以“三车共网”系统为例，分别建立了如图3所示的牵引供电网节点阻抗矩阵测量模型及图4所示的列车阻抗测量模型。牵引供电网等效测量参数见表1，三辆列车等效测量参数见表2，采用宽频主动测量法获取牵引供电网节点dq阻抗矩阵，单频主动测量法获取列车dq阻抗。将此时的车、网参数作为案例1，后续分析案例均与该案例作对比。
表1 牵引供电网阻抗测量参数
Tab.1 Impedance measurement parameters of traction power supply network
参数数值 等效电压源Vs/V1 770 牵引等效电阻Rs1, Rs2, Rs3/Ω0.113 5, 0.1, 0.1 牵引等效电感Ls1, Ls2, Ls3/mH0.8, 0.6, 0.6 对地电容Cs1, Cs2, Cs3/mF30, 25, 25 扰动电流Ii,h/A2
表2 列车阻抗测量参数
Tab.2 Impedance measurement parameters of train
参数数值 等效电压源Vs/V1 770 车载变压器等效电阻Rn/Ω0.12 车载变压器等效电感Ln/mH5 直流侧支撑电容Cd/mF9 直流侧等效负载Rd/kΩ1 直流侧参考电压Vdcref/V3 600 锁相环PI参数Kppll, Kipll0.2, 0.9
（续）
参数数值 电流环PI参数Kpi, Kii1.5, 5 电压环PI参数Kpv, Kiv0.5, 6.5 开关频率fs/Hz1 250 扰动电压Vp/V100
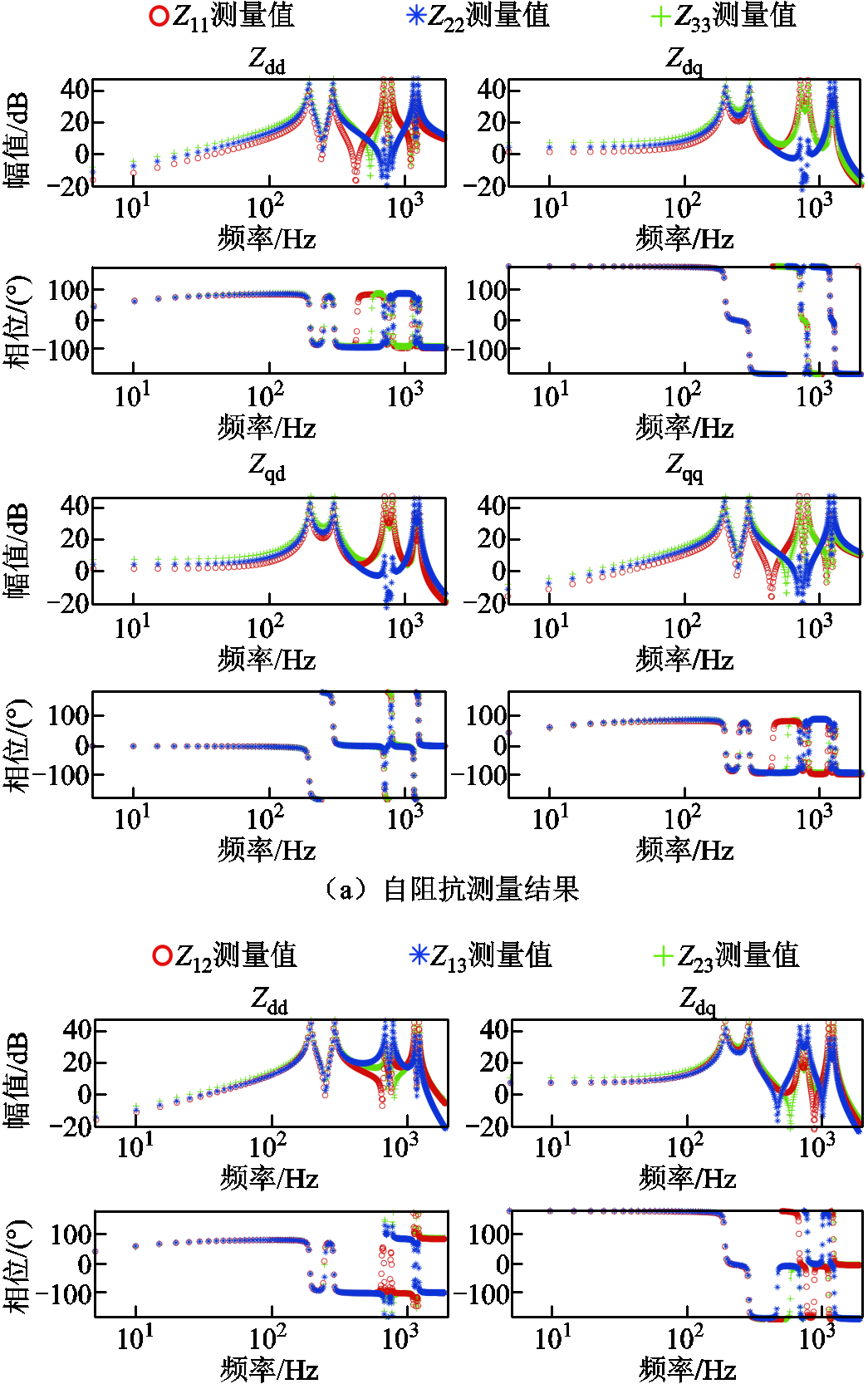
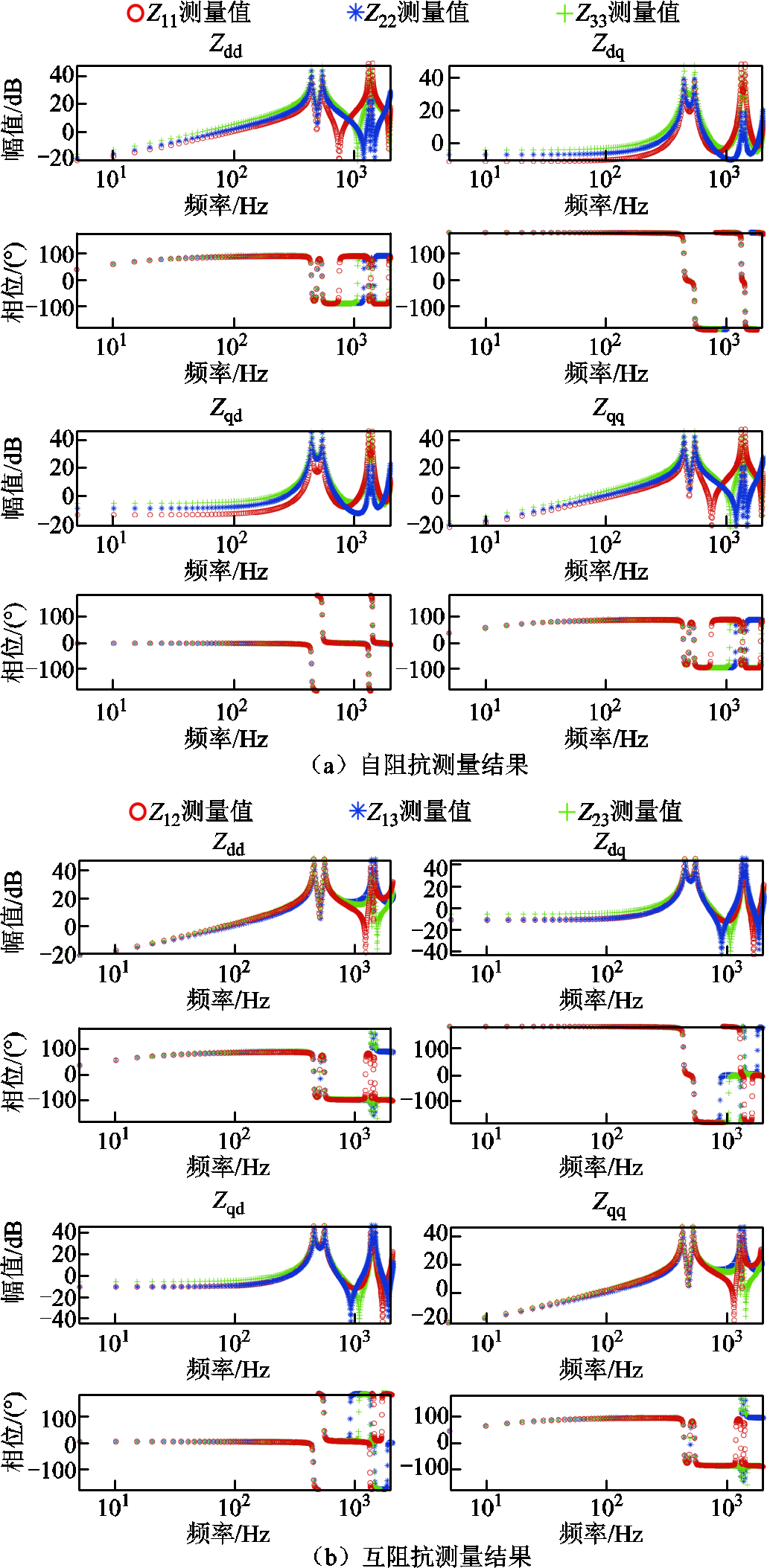
图10a与图10b分别为案例1中牵引供电网节点阻抗矩阵的自阻抗与互阻抗测量结果。对于牵引供电网互阻抗元素Z21、Z31、Z32，其分别与Z12、Z13、Z23相等。案例1中列车的dq阻抗测量结果如图11所示。
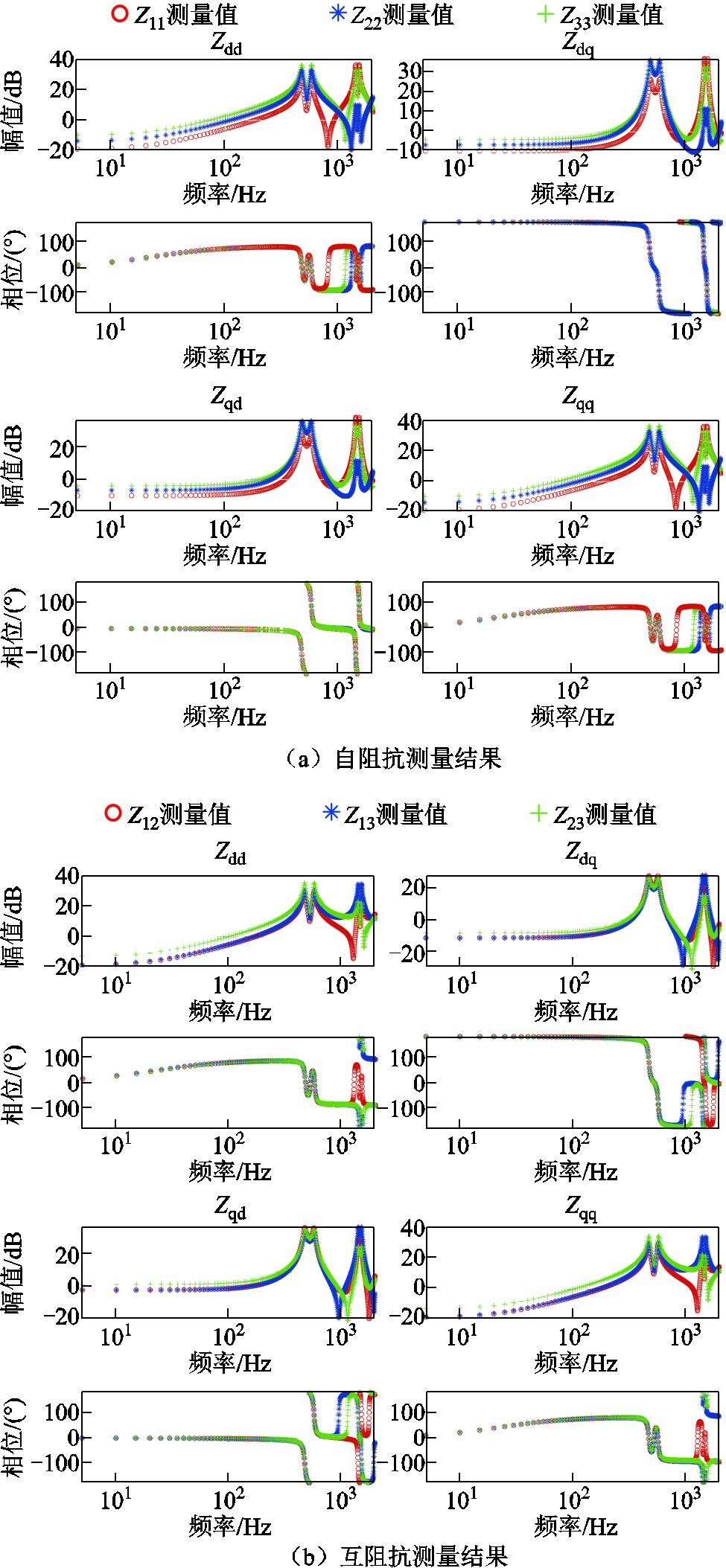
图10 案例1牵引供电网dq阻抗测量结果
Fig.10 Measurement results ofdq-frame impedance for traction power supply network in case 1
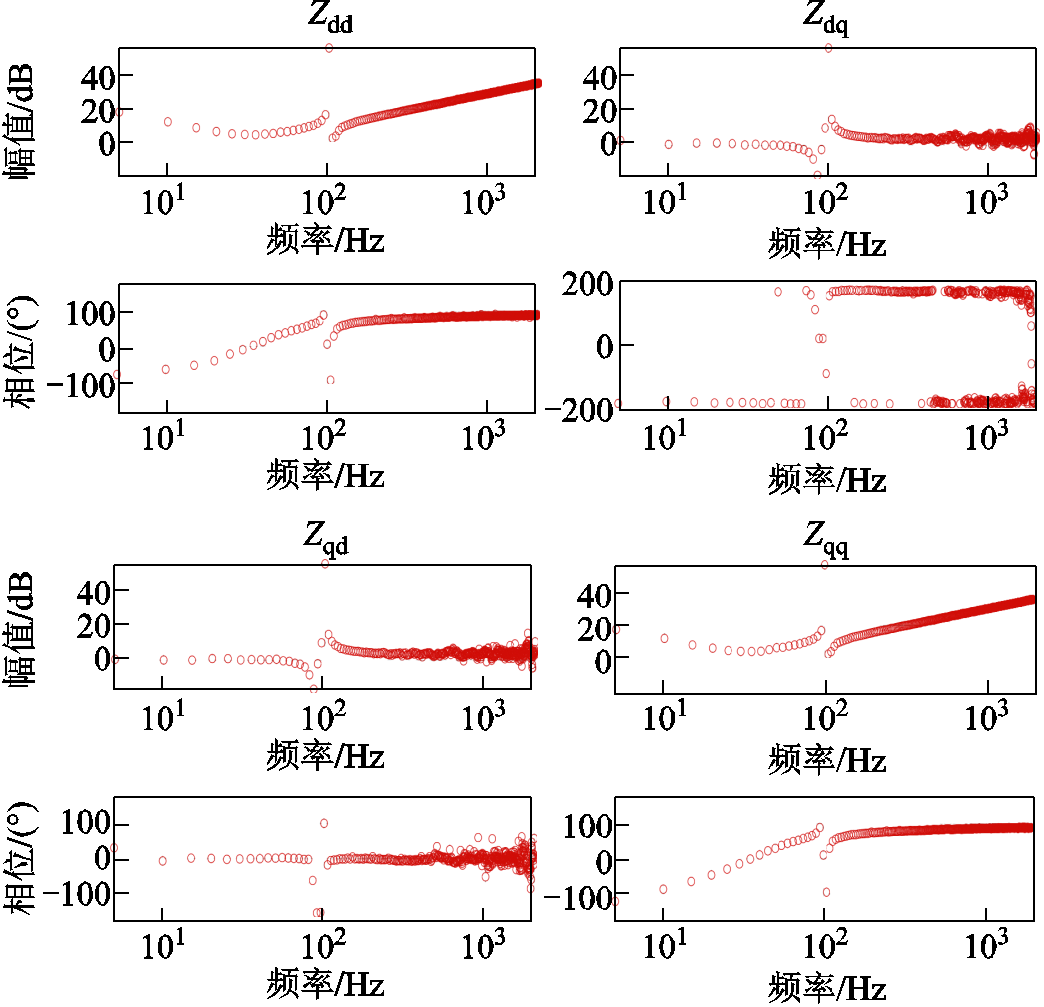
图11 案例1列车dq阻抗测量结果
Fig.11 Measurement results ofdq-frame impedance for train in case 1
获取牵引供电网与列车阻抗测量结果后，利用所提方法对“三车共网”系统进行稳定性分析，得到案例1参数下det(F)的Bode图，如图12所示。
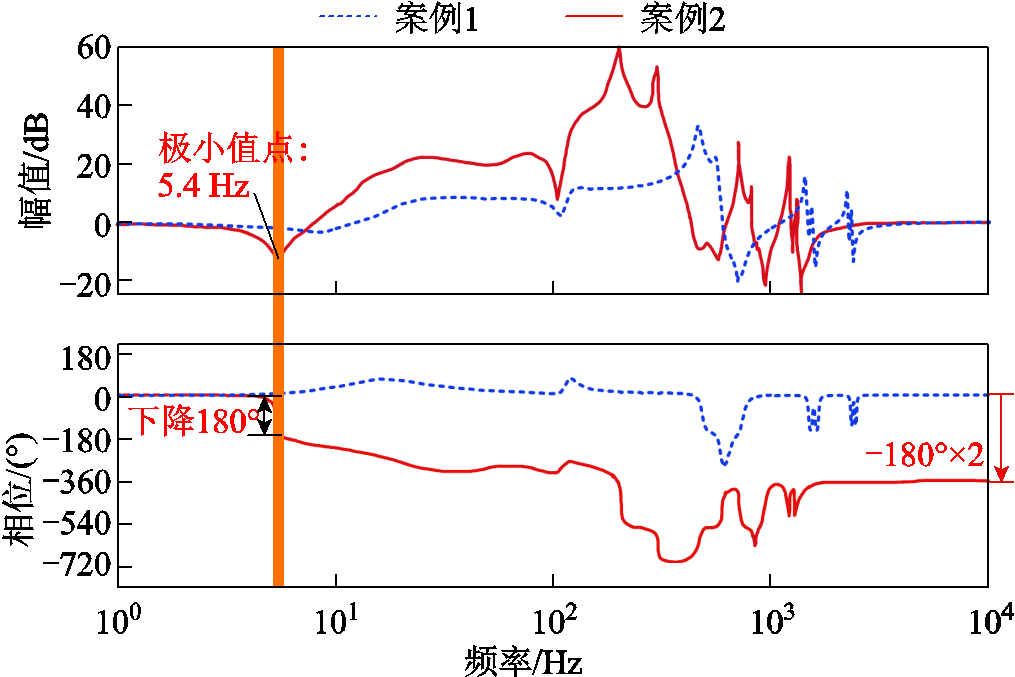
图12 案例1与案例2中det(F)的Bode图
Fig.12 Bode diagrams of det(F) in case 1 and case 2
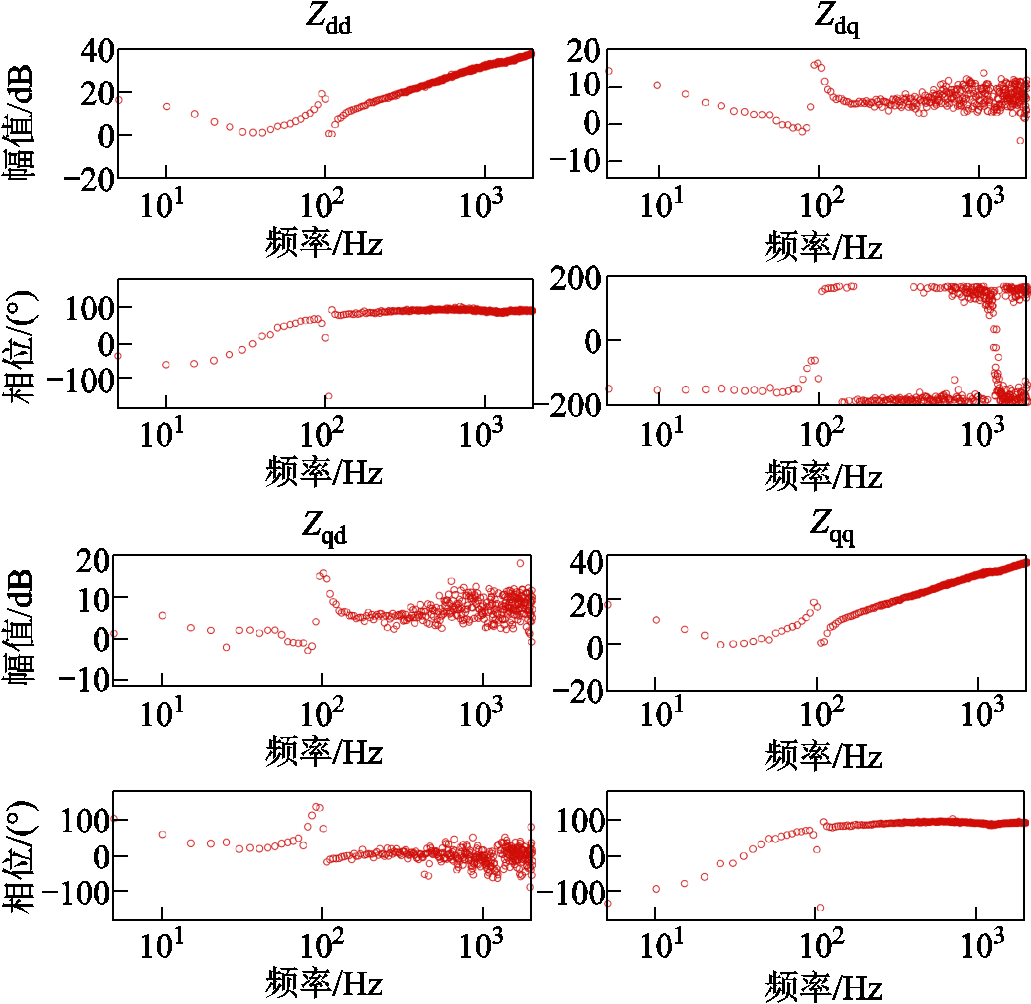
改变表1中牵引供电网电感参数Ls1、Ls2、Ls3为4、2、2 mH，其阻抗测量结果如附图1所示。列车参数保持不变，得到案例2中det(F)的Bode图，并与案例1对比，如图12所示。从图12可以看出，案例1中det(F)Bode图的相位变换为0°，此时“三车共网”系统稳定；而案例2中相位减小了2´180°，此时系统不稳定。并且，通过寻找det(F)的RHP零点发现，案例1中不存在RHP零点，也能够说明“三车共网”系统稳定。而案例2中det(F)的Bode图幅值曲线在5.4 Hz存在幅值极小值且对应相位下降180°，说明det(F)存在一对共轭RHP零点，对于整个系统而言，即存在一对主导RHP极点。由此可知，案例2中“三车共网”系统可能会发生约5.4 Hz的低频振荡。
从上述两种案例可以看出，如果车、网阻抗不匹配，det(F)的低频特性区域则会出现RHP零点，从而导致“车-网”系统发生低频振荡。
改变案例1中牵引供电网与列车部分参数见表3，其余参数保持不变，牵引供电网与列车阻抗测量结果如附图2与附图3所示。此时，得到案例3参数下det(F)的Bode图，并与案例1对比。案例1与案例3中det(F)的Bode图在高频下的分析结果分别如图13与图14所示。
表3 改变的列车、供电网参数
Tab.3 Modified parameters of train and network
参数数值 牵引等效电阻Rs1, Rs2, Rs3/W0.035, 0.03, 0.03 牵引等效电感Ls1, Ls2, Ls3/mH0.9, 0.7, 0.7 车载变压器等效电阻Rn/Ω0.01 车载变压器等效电感Ln/mH6 直流侧等效负载Rd/Ω50 锁相环PI参数Kppll, Kipll1.5, 60 电流环PI参数Kpi, Kii1.5, 5 电压环PI参数Kpv, Kiv0.15, 2
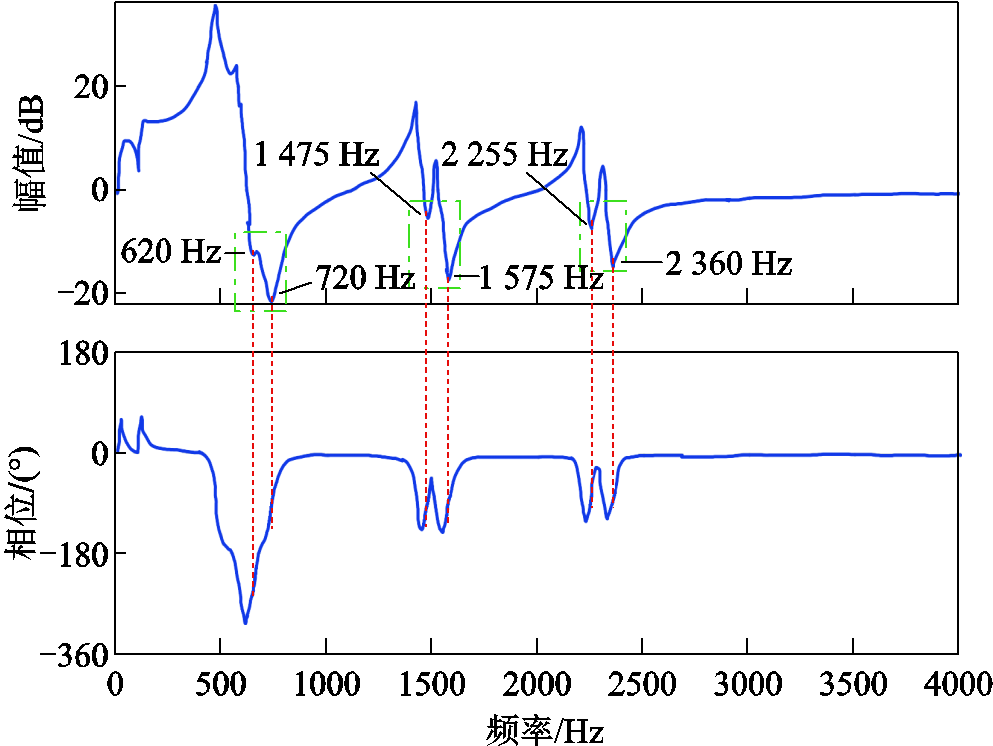
图13 案例1“车-网”系统高频谐波稳定性分析
Fig.13 High-frequency harmonic stability analysis of train-network system in case 1
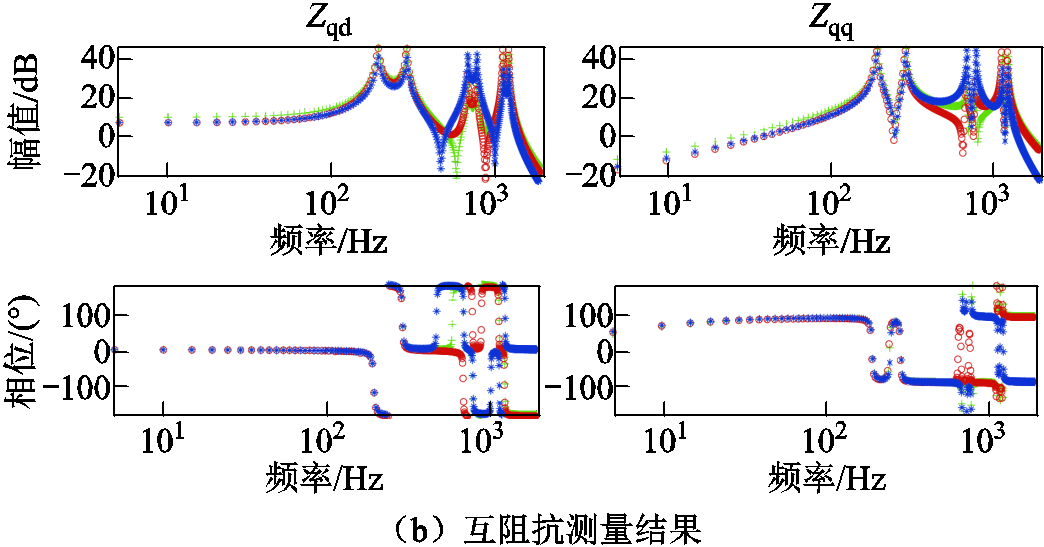
从图13可以看出，案例1中的车、网阻抗交互点共有三处，由绿色点画线框标出。以第一处阻抗交互区域为例进行分析，其共有两处幅值极小值点，对应频率分别约为620 Hz与720 Hz，相差100 Hz。再观察相位发现，两处频率下的相位均有突变，720 Hz对应相位上升了大约180°，而620 Hz处相位上升略小于180°。这是因为此时车、网阻抗的交互点在det(F)中表现为左半平面（Left-HalfPlane, LHP）零点，其与牵引供电网固有谐振频率相互影响，削弱了LHP零点原有的频率特性。其余两处阻抗交互点的频率分别为1 475 Hz与1 575 Hz、2 255 Hz与2 360 Hz，且对应相位上升均小于180°。第一处阻抗交互区域的LHP零点频率特性最为突出，说明系统在此处的谐波含量最大。
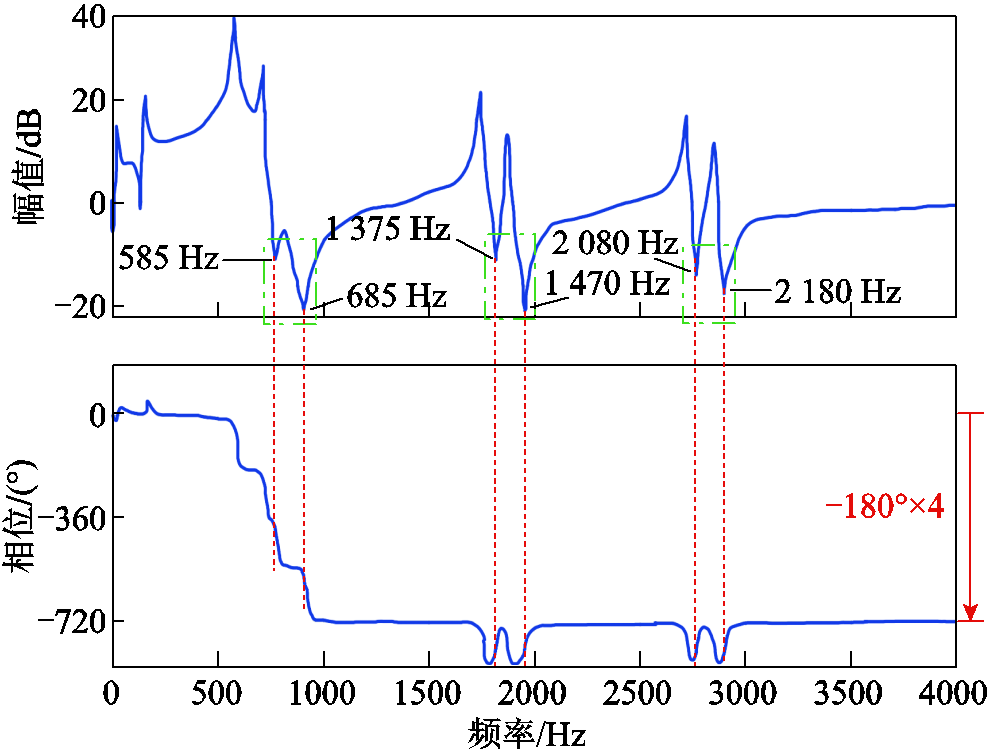
图14 案例3“车-网”系统高频谐波稳定性分析
Fig.14 High-frequency harmonic stability analysis of train-network system in case 3
由图14可以看出，案例3中“三车共网”系统运行不稳定，有2对共轭RHP极点。与图13对比，相同的是系统依然有三处阻抗交互点，其幅值极小值点处的频率分别为585 Hz与685 Hz、1 375 Hz与1 470 Hz、2 080 Hz与2 180 Hz。不同的是，585 Hz与685 Hz处的相位变成了下降180°，说明此时车、网阻抗交互点在det(F)中不再为LHP零点，而是变为RHP零点。因此，系统将会存在2对高频共轭RHP极点，可能会将此处的高频谐波放大，最终发生谐波不稳定。
由det(F)的Bode图分析“车-网”系统高频谐波稳定性的方法可归结如下：寻找幅值曲线中车、网阻抗交互区域，得到该区域中相差约100 Hz的两处幅值极小值点；观察其对应频率下的相位变换，若对应相位均呈现上升趋势，则可认为此处的高频谐波不会出现不稳定现象；若对应相位呈现180°的下降趋势，则说明det(F)具有RHP零点，系统可能会发生谐波不稳定。
此外，将“三车共网”系统等效为单节点级联系统进行稳定性分析[28-29]，并与所提方法进行了对比，上述三种不同案例的分析结果对比见表4。
通过表4可以看出，案例1中本文所提方法与级联系统分析方法结果一致，但案例2中分析结果却不一致，案例3中稳定性分析结果虽然都是不稳定，但两者不稳定的谐波频率却不相同。这是由于传统“车-网”级联系统未考虑列车之间的线路阻抗，而这些线路阻抗自身也是牵引供电网阻抗的一部分，若忽略线路阻抗便会导致牵引供电网的阻抗特性不完整，因此在某些情况下便可能会导致错误的分析结果，如线路阻抗较大或在进行高频谐波分析时。
表4 稳定性分析结果对比
Tab.4 Comparison of stability analysis results
案例所提分析方法级联系统分析方法 1稳定稳定 2不稳定，频率约5.4 Hz稳定 3不稳定，频率约585 Hz与685 Hz不稳定，频率约1 120 Hz与1 217 Hz
与低频振荡、谐波不稳定不同，谐波的谐振频率由牵引供电网自身参数决定[13]。为与其他两类稳定性问题在频率特性上进行统一分析，本文依然通过det(F)的Bode图曲线获取牵引供电网的谐振频率。图15显示了dq坐标系下案例1通过det(F)的Bode图分析谐振频率的结果。
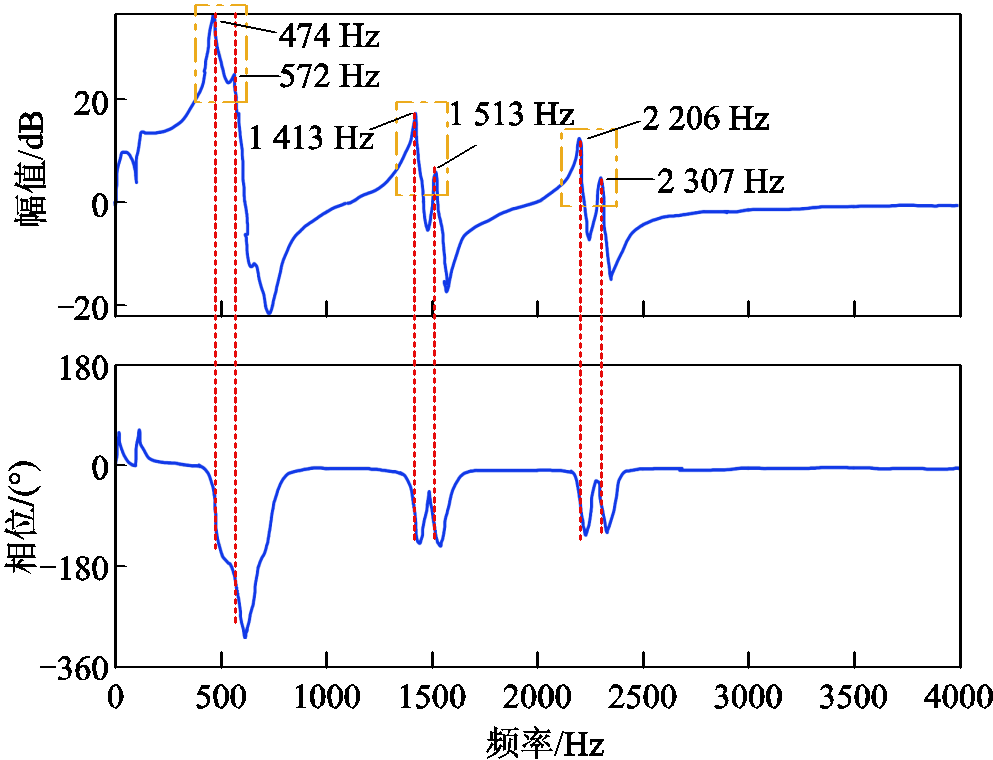
图15 dq坐标系下案例1的谐振频率分析
Fig.15 Resonance frequency analysis of case 1 in dq coordinate system
从图15可以看出，det(F)的Bode图幅值曲线有三处峰值区域，由黄色点画线框标出。每处峰值区域均有两个峰值点，对应频率分别为474 Hz与572 Hz、1 413 Hz与1 513 Hz、2 206 Hz与2 307 Hz，频率相差均为100 Hz左右。在第一处峰值区域中，峰值点474 Hz下的对应相位下降了180°，符合谐振频率点的分布规律，而572 Hz下的相位下降程度不足180°。这是因为谐振频率点与车、网阻抗交互点相近，使得谐振点的频率特性被车、网阻抗交互点的频率特性削弱。这种规律在第二、三峰值区域较为明显，其峰值点对应相位的下降程度均不足180°。
为了进一步说明利用det(F)的Bode图分析谐振频率的可行性，给出了案例1中牵引供电网在静止坐标系下的谐振频率分析结果，如图16所示。从图16可以看出，牵引供电网共有三个谐振峰值点：524、1 465和2 262 Hz，且谐振点相位均下降180°，符合牵引供电网谐振频率分布规律。将这三处谐振频率点转换到dq坐标系下，正好与图15中分析的峰值频率点对应，说明det(F)的Bode图曲线依然能够体现出牵引供电网谐振频率信息。
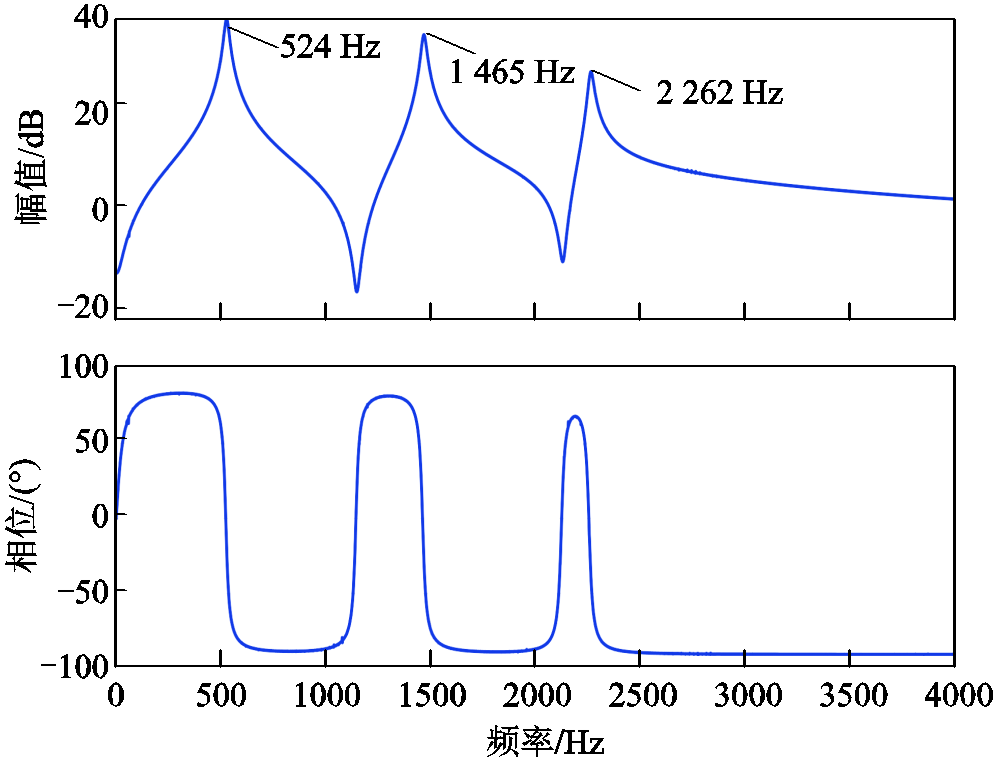
图16 静止坐标系下案例1的谐振频率分析
Fig.16 Resonance frequency analysis of case 1 in stationary coordinate system
因此，在dq坐标系下通过det(F)的Bode图获取谐振频率的方法可总结如下：首先寻找幅值曲线中的峰值区域，得到该区域中相差大约100 Hz的两处频率点；然后，观察这两处频率下的相位变换是否呈现下降趋势，如果两处相位均有明显的下降，无论下降程度是否有180°，则可认为此处的峰值频率点为谐振频率。
为了验证所提方法对“多车共网”系统稳定性分析的正确性，基于Matlab/Simulink搭建了“三车共网”系统仿真模型。图17显示了“三车共网”系统在不同案例下的仿真分析结果。图17a为牵引供电网节点处的交流电压U1、U2、U3，图17b为三辆列车直流侧电压Udc1、Udc2、Udc3，图17c为对牵引供电网电压进行快速傅里叶变换后得到的频谱分析结果。图17中第1、2、3行分别为在案例1、2、3下的仿真结果，第4行为改变列车开关频率为250 Hz时的仿真结果。
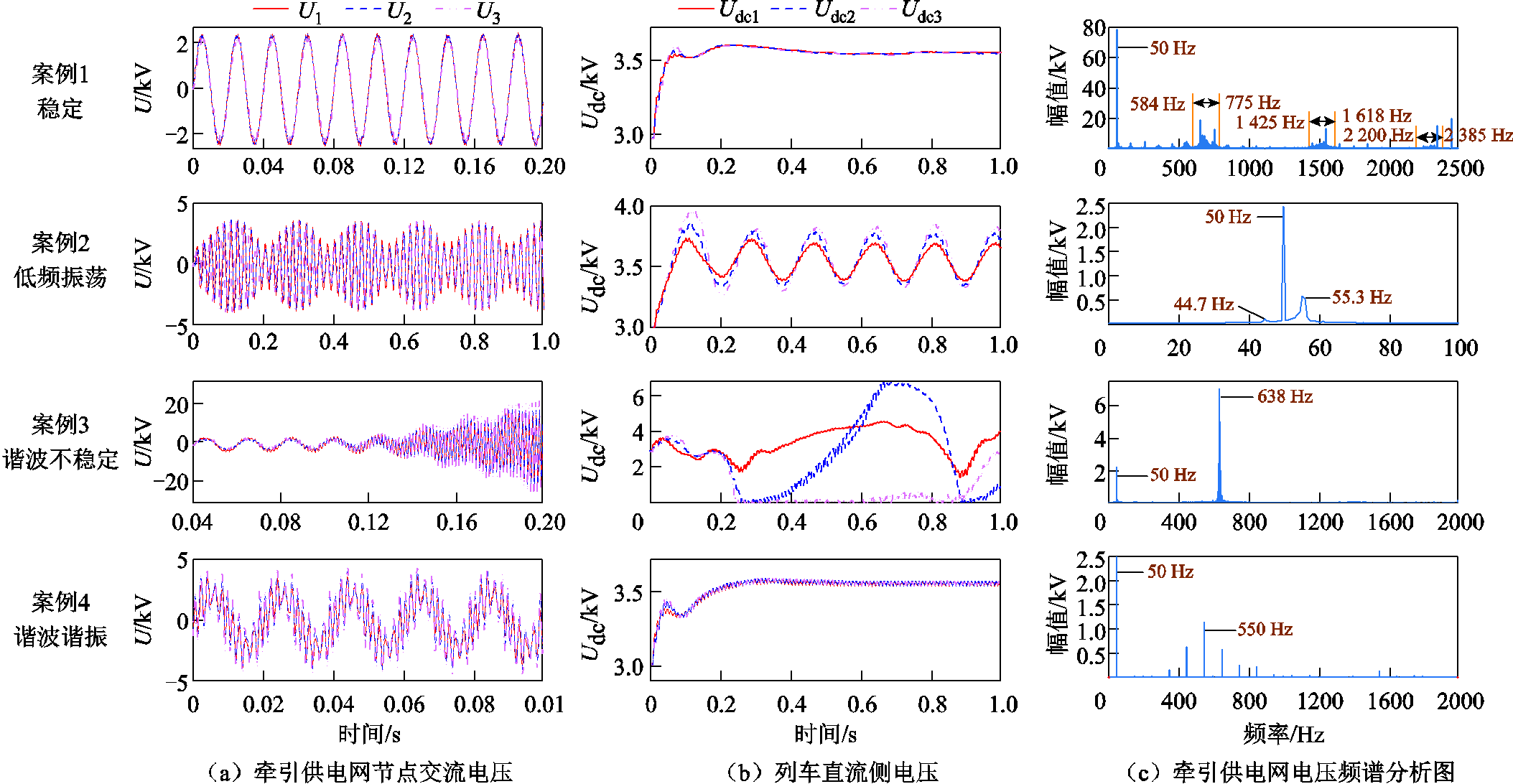
图17 不同案例下的仿真分析结果
Fig.17 Simulation analysis results in different cases
从图17中第1行可以看出，案例1中“车-网”系统能够稳定运行，与稳定性分析结果一致。且从图17c可以看出，系统的高频谐波在三处频率段内较为集中且幅值较大，图中由黄色线条标出。第一处频率范围约为584～775 Hz，将其转换为dq坐标系，正好与3.3节中620 Hz和720 Hz对应的阻抗交互区域一致。另外两处的谐波频率范围分别为1 425～1 618 Hz、2 200～2 385 Hz，也与其余两处阻抗分析的交互区域对应。并且，从频谱图中可以看出，三处频率段中第一处谐波含量最大，与3.3节中的分析一致。
从图17中第2行可以看出，案例2中牵引供电网电压与列车直流侧电压均出现了明显的低频振荡，“车-网”系统不再稳定。从频谱分析图可以看出，牵引供电网电压存在明显的低频分量：55.3 Hz和44.7 Hz，转换至dq坐标系下为5.3 Hz，与3.2节的分析结果5.4 Hz对应，证明了所提方法对“车-网”系统低频振荡分析的正确性。
从图17中第3行可以看出，此时牵引供电网的电压出现了明显的谐波放大现象，并且列车直流侧电压已不能维持在3 600 V左右，系统不稳定。观察牵引供电网电压频谱分析图可知，其电压在638 Hz处存在一个很大的谐波分量，转换到dq坐标系下正好与3.3节分析的585 Hz与685 Hz对应，证明了所提方法对系统高频谐波不稳定分析的正确性。
从图17中第4行可以看出，此时牵引供电网电压出现了谐波谐振现象，电压峰值已超出正常值，严重影响列车的运行安全。且通过电压频谱分析结果可知，列车产生的550 Hz左右特征谐波被明显放大，这与牵引供电网固有谐振频率524 Hz接近，证明了利用det(F)的Bode图进行牵引供电网谐振频率分析的有效性。
综上所述，各案例的稳定性分析和仿真结果对比见表5，相关频率已转换至静止坐标系下。
表5 不同案例下的稳定性分析与仿真结果对比
Tab.5 Comparison of stability analysis and simulation results in different cases
案例分析结果仿真结果 1. 稳定稳定，幅值极小值处：570～770 Hz稳定，谐波含量最大集中处：584～775 Hz 2. 低频振荡不稳定，振荡频率为5.4 Hz不稳定，振荡频率为5.3 Hz 3. 谐波不稳定不稳定，谐波不稳定频率为635 Hz不稳定，谐波不稳定频率为638 Hz 4. 谐波谐振谐振频率：524 Hz左右谐波谐振频率：550 Hz左右
不同案例下的仿真结果均与稳定性分析结果一致，证明了所提出的基于阻抗测量信息的“多车共网”系统稳定性统一分析方法的有效性。
本文提出了一种基于阻抗测量信息的电气化铁路“多车共网”系统稳定性分析方法。利用测量的牵引供电网节点dq阻抗矩阵与列车dq阻抗矩阵，采用基于阻抗回差矩阵行列式的稳定性分析方法将电气化铁路中的三类振荡问题统一分析，该方法具有以下优点：
1）利用测量的车、网宽频带阻抗信息可将三类稳定性问题在频域上进行统一，弥补了以往只分析单一振荡问题的不足。
2）稳定性分析过程简单，且通过寻找阻抗回差矩阵行列式的RHP零点便可直接识别系统的振荡频率，避免了对每个特征值Nyquist曲线校验的繁琐过程。
3）相较于基于理论建模的稳定性分析方法，该方法仅需要阻抗测量数据，无需掌握牵引供电网和列车详细参数便可以预测“多车共网”系统的稳定性，对预估实际系统的稳定性具有重要意义。
附 录
附图1 案例2牵引供电网dq阻抗测量结果
App.Fig.1 Measurement results ofdq-frame impedance for traction power supply network in case 2
附图2 案例3牵引供电网dq阻抗测量结果
App.Fig.2 Measurement results ofdq-frame impedance for traction power supply network in case 3
附图3 案例3列车dq阻抗测量结果
App.Fig.3 Measurement results of dq-frame impedance for train in case 3
参考文献
[1] 陶海东, 胡海涛, 姜晓锋, 等. 牵引供电低频网压振荡影响规律研究[J]. 电网技术, 2016, 40(6): 1830-1838.
Tao Haidong, Hu Haitao, Jiang Xiaofeng, et al. Research on low frequency voltage oscillation in traction power supply system and its affecting factors[J]. Power System Technology, 2016, 40(6): 1830-1838.
[2] 陶海东, 胡海涛, 朱晓娟, 等. 车网耦合下的牵引供电系统谐振不稳定机理分析[J]. 中国电机工程学报, 2019, 39(8): 2315-2324, 14.
Tao Haidong, Hu Haitao, Zhu Xiaojuan, et al. Mechanism on resonance instability of traction power supply system considering interaction between trains and networks[J]. Proceedings of the CSEE, 2019, 39(8): 2315-2324, 14.
[3] Zhou Yi, Hu Haitao, Yang Xiaowei, et al. Low frequency oscillation traceability and suppression in railway electrification systems[J]. IEEE Transactions on Industry Applications, 2019, 55(6): 7699-7711.
[4] 刘秋降, 吴命利, 张俊骐, 等. 基于分层控制策略的牵引供电系统谐波阻抗测试装置[J]. 电工技术学报, 2018, 33(13): 3098-3108.
Liu Qiujiang, Wu Mingli, Zhang Junqi, et al. Harmonic impedance measuring apparatus of traction power supply system based on hierarchical control strategy[J]. Transactions of China Electrotechnical Society, 2018, 33(13): 3098-3108.
[5] Liu Qiujiang, Wu Mingli, Li Jing, et al. Frequency-scanning harmonic generator for (inter)harmonic impedance tests and its implementation in actual 2×25kV railway systems[J]. IEEE Transactions on Industrial Electronics, 2021, 68(6): 4801-4811.
[6] Pan Pengyu, Hu Haitao, Yang Xiaowei, et al. Impedance measurement of traction network and electric train for stability analysis in high-speed railways[J]. IEEE Transactions on Power Electronics, 2018, 33(12): 10086-10100.
[7] Hu Haitao, Pan Pengyu, Song Yitong, et al. A novel controlled frequency band impedance measurement approach for single-phase railway traction power system[J]. IEEE Transactions on Industrial Electronics, 2020, 67(1): 244-253.
[8] Pan Pengyu, Hu Haitao, Xiao Donghua, et al. An improved controlled-frequency-band impedance mea-surement scheme for railway traction power system[J]. IEEE Transactions on Industrial Electronics, 2021, 68(3): 2184-2195.
[9] 肖冬华, 胡海涛, 潘鹏宇, 等. 高速列车dq阻抗测量方法及其装置设计[J]. 中国电机工程学报, 2020, 40(22): 7230-7240.
Xiao Donghua, Hu Haitao, Pan Pengyu, et al. dq impedance measurement method and its device design of high-speed train[J]. Proceedings of the CSEE, 2020, 40(22): 7230-7240.
[10] 刘方平, 葛兴来, 余思儒, 等. 一种高速列车-牵引网阻抗测量方法及其稳定性分析[J]. 电力自动化设备, 2020, 40(8): 154-159, 178, 160-161.
Liu Fangping, Ge Xinglai, Yu Siru, et al. Impedance measurement method and stability analysis of high-speed train-traction network[J]. Electric Power Automation Equipment, 2020, 40(8): 154-159, 178, 160-161.
[11] 潘鹏宇, 胡海涛, 肖冬华, 等. 高速列车变流器“扫频式”dq阻抗测量中的频率耦合干扰机理及抑制策略[J]. 电工技术学报, 2022, 37(4): 990-999, 1009.
Pan Pengyu, Hu Haitao, Xiao Donghua, et al. Frequency coupling interference mechanism and suppression strategy for frequency-sweeping-based dq impedance measurement of high-speed train converter[J]. Transactions of China Electrotechnical Society, 2022, 37(4): 990-999, 1009.
[12] 廖一橙. 高速铁路多车并联系统低频稳定性研究[D]. 成都: 西南交通大学, 2018.
Liao Yicheng. Research on low-frequency stability of high-speed railway system with multiple vehicles paralleled multi-vehicle parallel[D]. Chengdu: South-west Jiaotong University, 2018.
[13] Hu Haitao, Tao Haidong, Wang Xiongfei, et al. Train–network interactions and stability evaluation in high-speed railways—part II: influential factors and verifications[J]. IEEE Transactions on Power Electronics, 2018, 33(6): 4643-4659.
[14] 刘诗慧. 基于阻抗分析的电气化铁路车-网-车耦合作用及系统稳定性研究[D]. 北京: 北京交通大学, 2020.
Liu Shihui. Research on coupling effect and system stability of train-network-train in electrified railway based on impedance analysis[D]. Beijing: Beijing Jiaotong University, 2020.
[15] Tao Haidong, Hu Haitao, Wang Xiongfei, et al. Impedance-based harmonic instability assessment in a multiple electric trains and traction network interaction system[J]. IEEE Transactions on Industry Applications, 2018, 54(5): 5083-5096.
[16] Hu Haitao, Zhou Yi, Li Xin, et al. Low-frequency oscillation in electric railway depot: a comprehensive review[J]. IEEE Transactions on Power Electronics, 2021, 36(1): 295-314.
[17] 胡海涛. 高速铁路牵引供电系统谐波传输及谐振规律研究[D]. 成都: 西南交通大学, 2014.
Hu Haitao. Harmonic propagation and resonance analysis for traction power supply system of high-speed railway[D]. Chengdu: Southwest Jiaotong University, 2014.
[18] 孟昭斐. 含多类型变流器的高速铁路“车—网”耦合供电系统稳定性分析[D]. 成都: 西南交通大学, 2022.
Meng Zhaofei. Stability analysis of “vehicle-network” coupled power supply system of high-speed railway with multiple types of converters[D]. Chengdu: Southwest Jiaotong University, 2022.
[19] 涂春鸣, 邹凯星, 高家元, 等. 基于不对称正负反馈效应的PQ功率控制并网逆变器稳定性分析[J]. 电工技术学报, 2023, 38(2): 496-509.
Tu Chunming, Zou Kaixing, Gao Jiayuan, et al. Stability analysis of grid-connected inverter under PQ power control based on asymmetric positive-negative-feedback effects[J]. Transactions of China Electro-technical Society, 2023, 38(2): 496-509.
[20] 王晴, 刘增, 韩鹏程, 等. 基于变流器输出阻抗的直流微电网下垂并联系统振荡机理与稳定边界分析[J]. 电工技术学报, 2023, 38(8): 2148-2161.
Wang Qing, Liu Zeng, Han Pengcheng, et al. Analysis of oscillation mechanism and stability boundary of droop-controlled parallel converters based on output impedances of individual converters in DC micro-grids[J]. Transactions of China Electrotechnical Society, 2023, 38(8): 2148-2161.
[21] Cao Wenchao, Ma Yiwei, Yang Liu, et al. D-Q impedance based stability analysis and parameter design of three-phase inverter-based AC power systems[J]. IEEE Transactions on Industrial Electronics, 2017, 64(7): 6017-6028.
[22] Zhang Haitao, Mehrabankhomartash M, Saeedifard M, et al. Stability analysis of a grid-tied interlinking converter system with the hybrid AC/DC admittance model and determinant-based GNC[J]. IEEE Transactions on Power Delivery, 2022, 37(2): 798-812.
[23] Jiang Shan, Zhu Ye, Konstantinou G. Settling angle-based stability criterion for power-electronics-dominated power systems[J]. IEEE Transactions on Power Electronics, 2023, 38(3): 2972-2984.
[24] Fan Lingling, Miao Zhixin. Admittance-based stability analysis: Bode plots, nyquist diagrams or eigenvalue analysis?[J]. IEEE Transactions on Power Systems, 2020, 35(4): 3312-3315.
[25] Liao Yicheng, Wang Xiongfei. Impedance-based stability analysis for interconnected converter systems with open-loop RHP poles[J]. IEEE Transactions on Power Electronics, 2020, 35(4): 4388-4397.
[26] 李杨, 帅智康, 方俊彬, 等. 基于阻抗测量的多逆变器系统稳定性校验方法[J]. 电力系统自动化, 2021, 45(11): 95-101.
Li Yang, Shuai Zhikang, Fang Junbin, et al. Stability check method for multi-inverter system based on impedance measurement[J]. Automation of Electric Power Systems, 2021, 45(11): 95-101.
[27] 洪芦诚, 徐佳裕, 唐润悦, 等. 三相LCL型逆变器序阻抗简化建模方法及并网稳定性分析[J]. 电力系统自动化, 2023, 47(7): 150-157.
Hong Lucheng, Xu Jiayu, Tang Runyue, et al. Simplified modeling method of sequence impedance and grid-connected stability analysis for three-phase LCL inverter[J]. Automation of Electric Power Systems, 2023, 47(7): 150-157.
[28] 徐少博, 徐永海, 陶顺, 等. 计及边带分量频率耦合的电压源型换流器输入导纳建模[J]. 电工技术学报, 2023, 38(11): 2883-2893.
Xu Shaobo, Xu Yonghai, Tao Shun, et al. Voltage source converter input admittance model considering frequency coupling of sideband components[J]. Transactions of China Electrotechnical Society, 2023, 38(11): 2883-2893.
[29] 韩应生, 孙海顺, 秦世耀, 等. 电压源型双馈风电并网系统小扰动低频稳定性分析[J]. 电工技术学报, 2023, 38(5): 1312-1324, 1374.
Han Yingsheng, Sun Haishun, Qin Shiyao, et al. Low-frequency stability analysis of voltage-sourced doubly-fed wind power grid-connected system under small disturbance[J]. Transactions of China Electro-technical Society, 2023, 38(5): 1312-1324, 1374.
Stability Analysis of Electrified Railway Multiple Train-Network System Based on Impedance Measurement Information
Abstract With the increasing investment of electric trains in electrified railways, the wide-band oscillation phenomenon frequently occurs in the electric train-traction power supply network (train-network) system. The use of impedance measurement technology to accurately obtain the wide-band impedance characteristics of the traction power supply network and electric train has become an important way to reveal the wide-band oscillation problem of the electrified railway train-network system. However, the utilization of impedance measurement information is mainly focused on the stability analysis of single train system, lacking the wide-band stability analysis of multiple train system that consider the impedance of traction lines between difference trains. Moreover, existing analyses often focus on a single stability issue, only analyzing impedance measurement information in a specific frequency band, and have not fully applied the entire wide-band impedance information of train and network. Therefore, this paper presents a stability analysis method for the multiple train-network system based on impedance measurement information, which can conduct a unified analysis of typical wide-band oscillation problems in train-network system.
Firstly, an active measurement method for the dq-frame impedance matrix of traction power supply network nodes and train is provided, which is used to obtain the impedance information of train and network required for stability analysis. Secondly, considering the impedance of traction lines between different trains, a multiple train-network system model based on multi-nodes is established and its impedance transfer function matrix is derived, which can be equivalent to a multi-input multi-output (MIMO) negative feedback system. The stability of multi-train system is evaluated by the determinant of impedance return-difference matrix of the train and network system, and the oscillation frequency of system can be obtained by identifying its right half plane (RHP) zero, extremely simplifying the analysis process of the multiple train-network system. The proposed method is used to analyze three typical oscillation problems: low-frequency oscillation, harmonic resonance and harmonic instability in electrified railway, and compared with the cascaded system analysis method based on a single node. The results indicate that ignoring the impedance of the traction line may lead to incorrect analysis results. Finally, the analysis method is simulated and verified based on Matlab/Simulink. The simulation results of the multiple train-network system under different conditions are basically consistent with the stability analysis results, which proves the effectiveness of the proposed method.
The following conclusions can be drawn from the simulation analysis: (1) The three types of stability problems of electrified railways can be unified in the frequency domain by utilizing the measured train and network wide-band impedance information, which compensates for the shortcomings of only analyzing single oscillation problems. (2) The stability analysis process is simple, and the oscillation frequency of system can be directly identified by finding the RHP zero point of the determinant of impedance return-difference matrix, avoiding the tedious process of verifying the Nyquist curve for each eigenvalue. (3) Compared to stability analysis methods based on theoretical modeling, the proposed method only requires impedance measurement data and can predict the stability of multiple train-network system, without the need to master detailed parameters of the network and train.
keywords：Electrified railway, multiple train-network, impedance measurement, impedance return-difference matrix, stability analysis
中图分类号：TM922
DOI:10.19595/j.cnki.1000-6753.tces.231294
国家电网公司总部科技项目资助（5108-202218280A-2-270-XG）。
收稿日期 2023-08-09
改稿日期 2024-03-04
唐圣德 男，2000年生，硕士研究生，研究方向为电气化铁路“车- 网”系统频域阻抗测量及其应用。
E-mail：tsd_swjtu@163.com
胡海涛 男，1987年生，教授，博士生导师，研究方向为牵引供电/ 电力系统电能质量与稳定性。
E-mail：hht@swjtu.edu.cn（通信作者）
（编辑 赫 蕾）