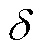 且频率耦合的次同步和超同步分量,分别以下标“0”、“sub”和“sup”表示。用
且频率耦合的次同步和超同步分量,分别以下标“0”、“sub”和“sup”表示。用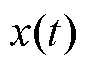 表示电压或电流的瞬时值有
表示电压或电流的瞬时值有摘要 大量新能源发电和电力电子设备引起的次同步振荡(SSO)严重影响了电力系统稳定性。基于广域测量系统(WAMS)和相量测量单元(PMU)提供的基波同步相量辨识次/超同步振荡参数具有广域同步和高刷新率的核心优势,可实现次/超同步振荡的动态在线监测。该文从基波同步相量在次/超同步振荡下的复数域频谱特性出发,综述并分析了目前已有次/超同步振荡参数辨识方法的参数辨识特性及关键问题。首先,根据同步相量频谱分析了频率辨识范围、各分量叠加耦合特性及相位翻转特性;其次,分析了参数辨识的关键问题在于振荡分量耦合关系、基波分量耦合关系的解耦问题及频谱泄漏问题,并围绕复数域频谱分析方法分析了在解决以上问题时的三个关键难点:针对次/超同步分量的耦合关系有效地辨识超同步分量的问题、不同同步相量采样频率下进行参数辨识的适应性问题,以及如何处理频谱泄漏从而缩短数据窗长的难题;对此,综述了相应解决方法并展望了未来可能的技术突破点;最后,通过仿真数据和实际PMU数据对比分析验证了该文观点。
关键词:同步相量 次/超同步振荡 参数辨识 广域测量系统 频谱分析
电力系统正形成“高比例可再生能源”和“高比例电力电子设备”的“双高”发展趋势[1]。光伏、风电等高比例可再生能源和高比例电力电子设备的接入改变了传统电力系统的动态行为和稳定特性[2-5]。相较于传统同步发电机,电力电子设备惯性小,控制频带宽且耦合效应明显,非线性特性显著[6],可能引发机理更为复杂的新型次同步振荡(Subsynchronous Oscillation, SSO)问题[7]。这种次同步振荡往往发生速度快、传播范围广[8],且可能同时存在频率与次同步振荡耦合的超同步振荡,严重影响系统传输能力和新能源消纳,甚至可能引起系统失稳[9-10]。因此,需要准确辨识电压电流的次/超同步分量参数以动态监测SSO的产生和传播[11],从而对其进行有效的抑制[12-14]。
近年来,广域测量系统(Wide Area Measurement System, WAMS)和相量测量单元(Phasor Measurement Unit, PMU)已经在电力系统中大范围应用,其提供的基波同步相量数据报告率高且广域同步,可有效实现电网动态在线监测。在WAMS和PMU提供的基波同步相量中,振荡分量信息主要以频谱泄漏的方式出现[15-16],利用此信息可以进行基于同步相量的次/超同步振荡参数辨识[15,17-19]。而数字故障录波仪(Digital Fault Recorder, DFR)记录的瞬时信号波形数据虽然采样率更高,且利用Hilbert-Huang变换[20]、递归最小二乘法[21]、瞬时值Prony法[22]等方法也可获得SSO参数,但是不同母线和节点的瞬时信号很难及时采集,且测量数据没有统一时标,所以无法形成对次同步振荡的动态全局观测。
在研究初期,文献[23]利用同步相量辨识次同步振荡频率进而实现在线监测预警,部分成果已在华北电力调度中心应用。然而前期研究也发现,受基波同步相量计算的影响,同步相量的频谱分析并不能直接得到次同步分量的幅值[24-27]。文献[28]研究了谐波、间谐波对同步相量中次同步分量的影响。文献[29]利用补零快速傅里叶变换(Fast Fourier Transform, FFT)实现次/超同步参数辨识,但计算误差较大。文献[17]通过建立同步相量幅值频谱和标准波形频谱的等比关系,首先解决了次同步分量幅值辨识的难题。然而,为保证必要的频率分辨率,其使用了长达10 s的数据窗,而实际的次同步振荡模式几乎不可能在10 s内保持不变,这导致该方法因假设条件过强而使实用性大打折扣;该方法的另一个显著局限是仅对同步相量幅值进行频谱分析而并未充分利用相位信息。作为对上述探索性方法的一个重要改进,文献[18]提出一种基于插值离散傅里叶变换(Discrete Fourier Transform, DFT)和汉宁窗的同步相量复频谱分析方法以辨识次同步分量的频率和幅值,该方法有效解决了频率分辨率受限的问题,将数据窗缩短至2 s。文献[19]在此思路基础上提出加阻尼Rife-Vincent M(RV-M)阶窗函数的插值DFT方法,有效地提升了辨识精度。文献[14]使用了非DFT方法,将次同步振荡参数辨识转换为模态参数提取(Model Parameter Extraction, MPE)问题,并且使用了两个经典的MPE方法,即Prony方法和矩阵束法(Matrix Pencil Method, MPM)提取次同步分量的参数,进而计算次同步频率的阻抗和功率以在线辨识次同步振荡源。文献[30]通过人工智能方法改善了多支持向量机(Support Vector Machine, SVM)模型,开发了一种数据驱动的次同步振荡参数辨识方法。文献[31]提出一种针对同步相量实部的变分模态分解(Variational Mode Decomposition, VMD)与Hilbert变换次同步分量参数辨识,两种方法将数据窗减小到1 s。以上方法的一个显著缺点是无法辨识与次同步分量耦合存在的超同步分量,而实际的次同步振荡事件中往往伴随着超同步分量。为此,文献[32]提出一种基于频谱幅值的超同步分量检测方法以判断是否存在超同步分量,但该方法并不可靠(参见3.1节)。文献[15]在文献[18]的基础上考虑次/超同步分量频率耦合关系,实现了对基波分量、频率耦合的次/超同步分量的参数辨识。文献[33]提出一种基于同步相量轨迹拟合的次/超同步振荡参数辨识方法,尽管该方法将数据窗大幅缩短至100 ms,但代价是求解难度高、计算量大、易受测量噪声影响,且不适用于存在多对振荡分量的场景。文献[34]同样基于同步相量旋转特性并利用频谱偏移检测次/超同步分量并辨识参数。此外,针对基波同步相量能否有效辨识超同步分量的问题,目前业界观点仍未完全统一。由于我国省级调度中心的WAMS主站既有采用100 Hz报告率的,也有采用50 Hz报告率的(即同步相量的数据分辨率或采样频率为50 Hz),有必要分析研究同步相量采样率(即报告率)对次/超同步振荡参数辨识的影响,而现有方法均未对此进行深入研究。
目前实现次/超同步振荡同步监测的另一种方案是宽频测量方法[35-37]和装置,其核心是基于瞬时信号的自适应频率检测方法实时测量宽频信号。例如,南瑞继保的PCS-993C[38]以及四方继保的CSD-361-WF[39]宽频测量装置,可有效检测次/超同步振荡及100 Hz以上振荡,测量精度高[40],且相较于故障录波器具有同步性和实时性[41-44]。但宽频测量装置在实际应用中存在一定局限性:①相较于WAMS,宽频测量装置通信规约发生变化,带宽需求显著增大,带宽的限制导致实时通信速率较低(通常为10~100 Hz);②装置的部署需要软硬件系统的升级改造,且针对宽频振荡检测这单一应用场景全面布置整套测量系统的经济性较低。相对地,WAMS已广泛部署且其数据传输速率快,未来与部署在关键节点的宽频测量装置结合可实现高低搭配。
本文从次同步振荡下的同步相量特性出发,以频谱分析为基本工具,通过综述和分析已有主要技术方法,对基于基波同步相量测量的次/超同步振荡参数辨识特性、难点、方法进行了总结,探究了次同步振荡参数辨识研究过程中面临的困难与挑战,并展望了未来可能的技术突破点。具体包括:
1)分析了基波同步相量可辨识的振荡分量频率范围,从复数域频谱分析的数学解析和奈奎斯特定理两个角度解释了同步相量采样频率以及辨识范围之间的关系。同时,结合实际WAMS的同步相量数据特点,分析了实际同步相量数据的相位翻转及其修正方法。
2)探讨了同步相量采样频率为100 Hz和50 Hz条件下的参数辨识可行性,进一步分析了同步相量复数域频谱的特性,包括同步相量频谱尖峰位置以及各分量的叠加特性,并综述和分析了基于频谱分析法的次/超同步参数辨识应用范围、限制条件以及解决方法。
3)分析了数据窗长与辨识精度之间的矛盾,探究能够用来进行次同步振荡辨识的最小数据窗长,并分析了在存在多对振荡分量的场景下使用此方法进行参数辨识的特性及其影响因素,以及未来在此方向的进一步研究展望。
在电力系统次同步振荡过程中的电压或电流瞬时信号通常建模为三个分量之和,即基波分量以及一对具有相同阻尼因子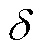 且频率耦合的次同步和超同步分量,分别以下标“0”、“sub”和“sup”表示。用
且频率耦合的次同步和超同步分量,分别以下标“0”、“sub”和“sup”表示。用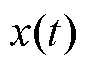 表示电压或电流的瞬时值有
表示电压或电流的瞬时值有
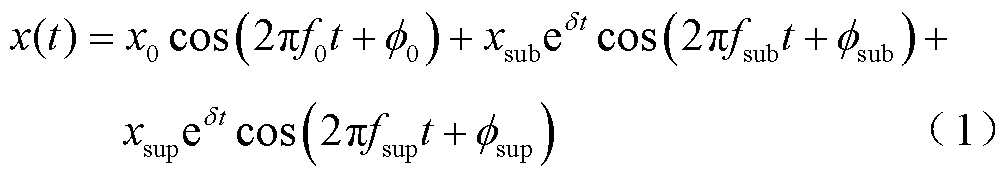
式中,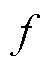 、
、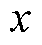 和
和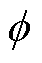 分别为各分量频率、幅值和相位。次同步和超同步分量统称为振荡分量。
分别为各分量频率、幅值和相位。次同步和超同步分量统称为振荡分量。
瞬时信号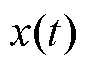 的同步相量为
的同步相量为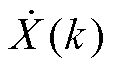 ,表示额定频率的基波相量,可由DFT算法计算得到[15,45],其中,
,表示额定频率的基波相量,可由DFT算法计算得到[15,45],其中, 为PMU上报同步相量数据的频率(即报告率或采样频率),
为PMU上报同步相量数据的频率(即报告率或采样频率),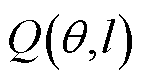 中
中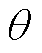 为考虑阻尼因子时的角频率,l为DFT计算结果中频率分量的索引,
为考虑阻尼因子时的角频率,l为DFT计算结果中频率分量的索引,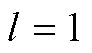 表示同步相量是对应于标称频率
表示同步相量是对应于标称频率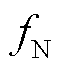 的DFT结果。
的DFT结果。
以次同步分量为例,其在基波同步相量中的分量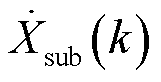 如式(2)所示,其中
如式(2)所示,其中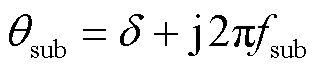 ,上标*表示共轭计算。
,上标*表示共轭计算。
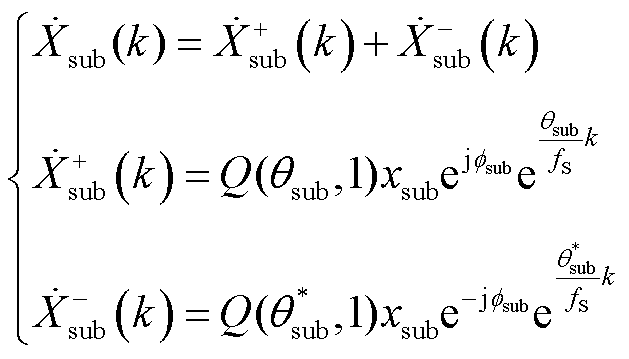 (2)
(2)
同样地,可以计算同步相量中超同步分量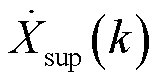 和基波分量
和基波分量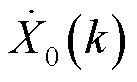 [15],其中
[15],其中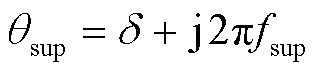 ,
,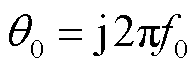 。
。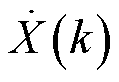 由以上三个分量组成,如式(3)所示,各分量均包括正、负频率两部分。
由以上三个分量组成,如式(3)所示,各分量均包括正、负频率两部分。
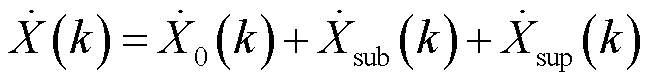 (3)
(3)
在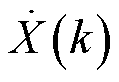 引入如式(4)所示的
引入如式(4)所示的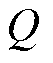 函数来表示
函数来表示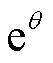 的DFT算法计算同步相量过程,其中
的DFT算法计算同步相量过程,其中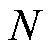 是计算过程中瞬时信号数据点数。
是计算过程中瞬时信号数据点数。
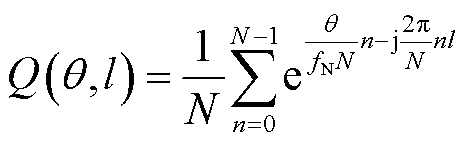 (4)
(4)
Q的意义是同步相量计算的频谱泄漏因子,由于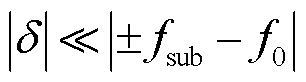 且
且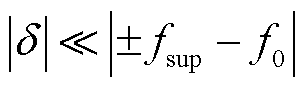 ,因此
,因此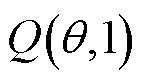 主要取决于
主要取决于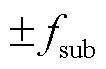 与
与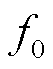 或
或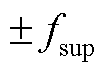 与f0之间的距离,如图1所示。在图1中引入距离参数
与f0之间的距离,如图1所示。在图1中引入距离参数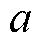 以描述
以描述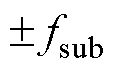 、
、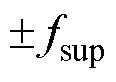 的位置关系。
的位置关系。
综上所述,由于PMU的同步相量是对应额定频率的基波同步相量,振荡分量的同步相量分量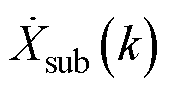 和
和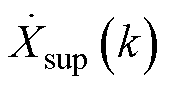 并非实际的次、超同步相量,而分别是在DFT同步相量计算过程中次、超同步分量在额定频率下的频谱泄漏,如图1中Q函数图像所示。因此,基于WAMS和PMU提供的同步相量进行次/超同步振荡参数辨识的关键难点在于如何基于同步相量序列中泄漏的信息
并非实际的次、超同步相量,而分别是在DFT同步相量计算过程中次、超同步分量在额定频率下的频谱泄漏,如图1中Q函数图像所示。因此,基于WAMS和PMU提供的同步相量进行次/超同步振荡参数辨识的关键难点在于如何基于同步相量序列中泄漏的信息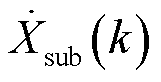 和
和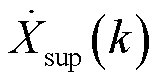 还原出如式(1)所示的瞬时值参数。
还原出如式(1)所示的瞬时值参数。
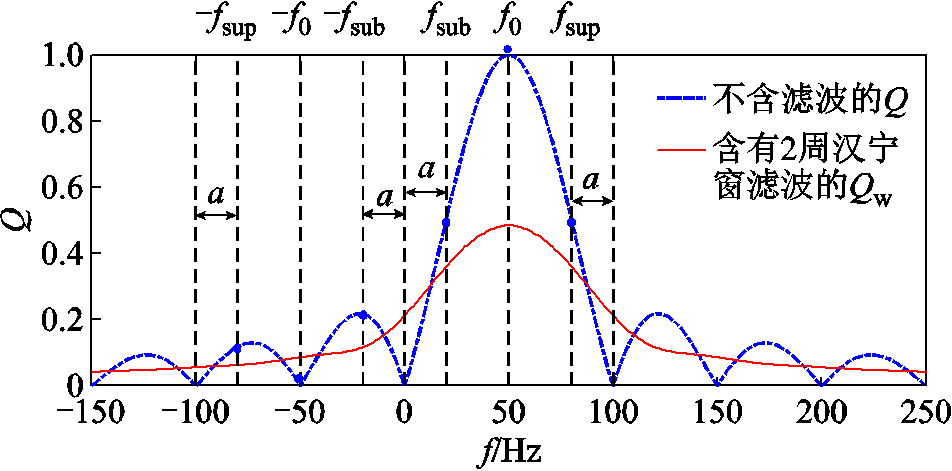
图1 含有及不含滤波的情况下,不同频率的频谱泄漏因子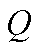
Fig.1 Spectral leakage factor Q for different frequencies with and without filtering
在辨识次/超同步分量参数时可认为次/超同步分量频率的耦合关系为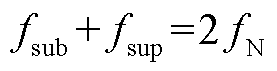 ,尽管两者的实际关系为
,尽管两者的实际关系为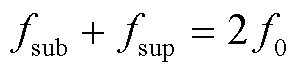 [46]。一方面,实际电力系统中发生次同步振荡时的系统频率
[46]。一方面,实际电力系统中发生次同步振荡时的系统频率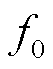 往往非常接近
往往非常接近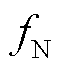 ,且
,且 的取值通常为
的取值通常为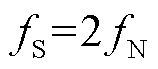 或
或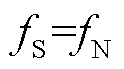 ,因此
,因此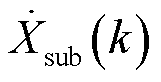 和
和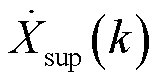 中变量存在关系为
中变量存在关系为
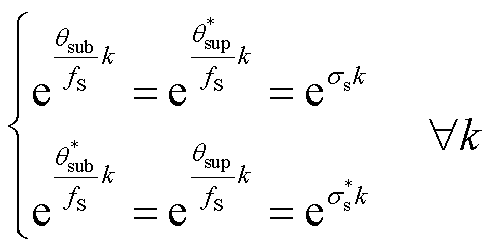 (5)
(5)
令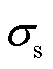 和
和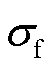 分别表示振荡分量和基波分量的衰减因子和频率,其取值分别为
分别表示振荡分量和基波分量的衰减因子和频率,其取值分别为
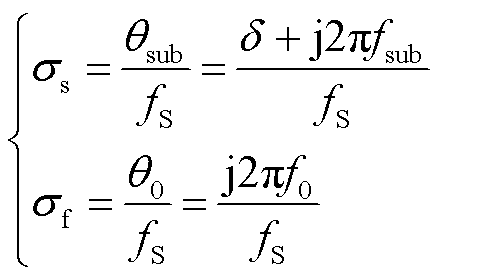 (6)
(6)
可以看到,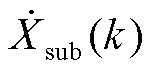 的正/负频率部分分别与
的正/负频率部分分别与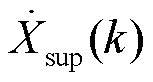 的负/正频率部分因频率相同而互相叠加,进而可得出振荡分量的正负频率部分分别为
的负/正频率部分因频率相同而互相叠加,进而可得出振荡分量的正负频率部分分别为
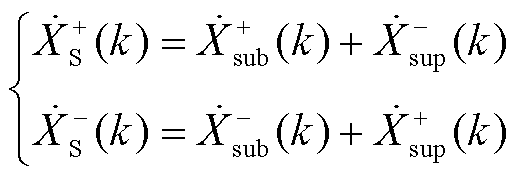 (7)
(7)
可见,当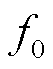 非常接近
非常接近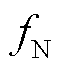 时,频率耦合关系将导致
时,频率耦合关系将导致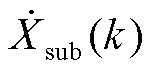 和
和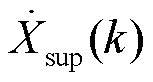 互相叠加,因此必须在参数辨识时进一步处理二者的耦合关系,这将导致参数辨识问题显著复杂化,也是次/超同步振荡参数辨识的难点之一,如2.2节所述。
互相叠加,因此必须在参数辨识时进一步处理二者的耦合关系,这将导致参数辨识问题显著复杂化,也是次/超同步振荡参数辨识的难点之一,如2.2节所述。
另一方面,如果系统频率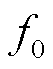 偏离
偏离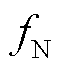 很多,则由于
很多,则由于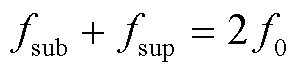 ,在同步相量中如式(5)所示的次/ 超同步耦合关系将不再存在,次同步分量和超同步分量可以轻易地分别作为独立分量进行辨识。
,在同步相量中如式(5)所示的次/ 超同步耦合关系将不再存在,次同步分量和超同步分量可以轻易地分别作为独立分量进行辨识。
因此,本文在此后分析和探究次/超同步分量耦合关系的影响时认为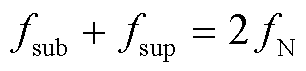 ,而针对基波分量的辨识时并不受
,而针对基波分量的辨识时并不受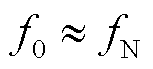 的假设限制。
的假设限制。
为了进一步深入探究基波同步相量序列的时序特性及其中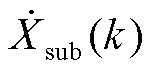 和
和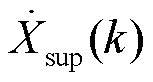 的影响,本文使用复数域DFT频谱分析方法进行研究。用“
的影响,本文使用复数域DFT频谱分析方法进行研究。用“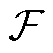 ”和“
”和“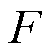 ”分别表示复数域频谱分析的计算过程和结果,即
”分别表示复数域频谱分析的计算过程和结果,即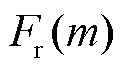 表示
表示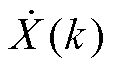 的复数域频谱,共包括三个分量,表示为
的复数域频谱,共包括三个分量,表示为
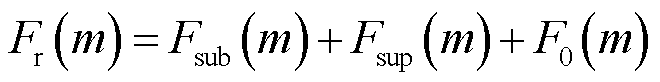 (8)
(8)
式中,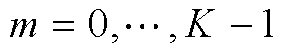 ,
,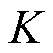 为频谱分析的数据点总数。如式(9)所示为振荡分量正频率部分的DFT频谱分析,其负频率部分及基波分量表达式同理[15]。
为频谱分析的数据点总数。如式(9)所示为振荡分量正频率部分的DFT频谱分析,其负频率部分及基波分量表达式同理[15]。
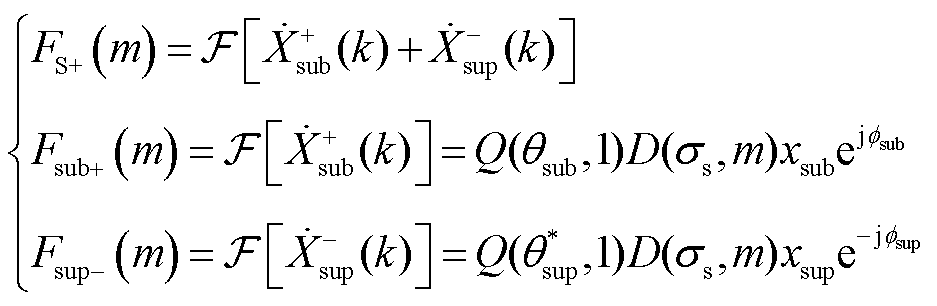 (9)
(9)
其中
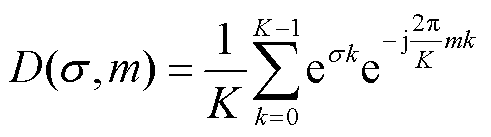 (10)
(10)
同步相量各分量及其频谱合成示意图如图2所示,左侧为旋转的同步相量,根据文献[32]可知振荡分量的正、负频率部分叠加后以椭圆轨迹旋转;右侧为同步相量所对应的频谱幅值。
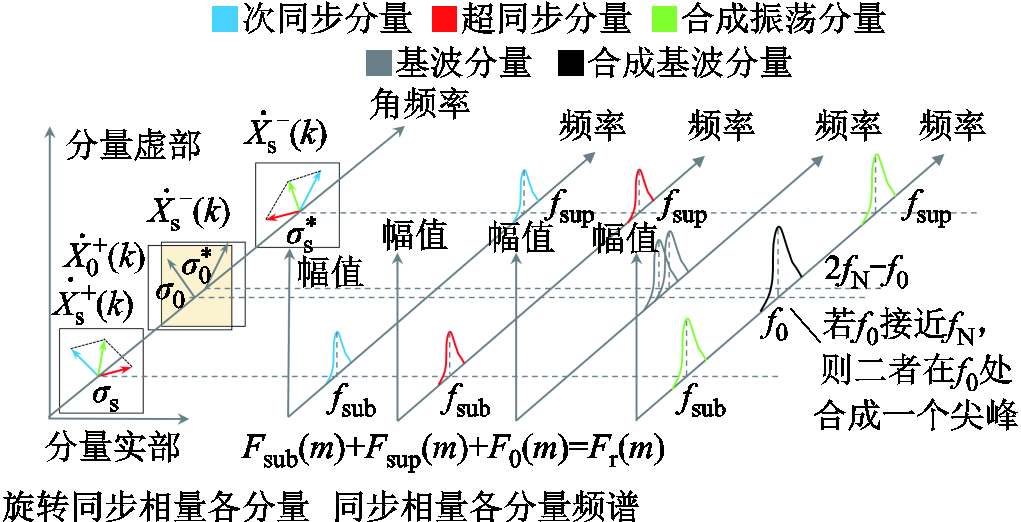
图2 旋转同步相量及其频谱
Fig.2 Rotating synchrophasors and their spectrum
此外,工程上应用的PMU往往含有滤波算法滤除高频分量,从而提高同步相量精度,如南瑞继保的PCS-996[47]以及四方继保的CSD-360-CG[39]型PMU,使用2周汉宁窗滤波函数[48]。在同步相量计算过程中,滤波过程影响了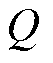 函数的计算而不会影响其他推导过程。将考虑滤波影响的
函数的计算而不会影响其他推导过程。将考虑滤波影响的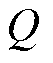 函数以
函数以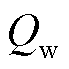 表示,加入2周汉宁窗后的
表示,加入2周汉宁窗后的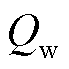 如式(11)所示,其图像如图1所示。
如式(11)所示,其图像如图1所示。
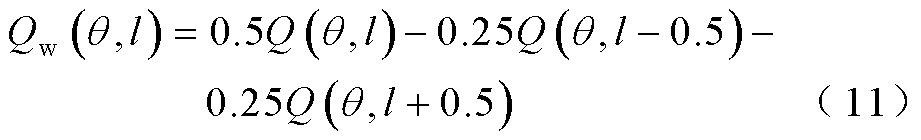
由于Q函数变化,滤波过程将影响参数辨识精度。对于实际工程应用,必须知道同步相量计算的细节,在已知滤波算法的情况下可以利用滤波后的同步相量数据进行参数辨识。现有研究并未考虑滤波过程对同步相量及基于同步相量的参数辨识的影响[14-15,17-19,23-34],故此问题可能是未来研究中的重点之一。
PMU上报同步相量的报告率 决定了由同步相量可辨识出的各分量的频率范围。利用报告率为
决定了由同步相量可辨识出的各分量的频率范围。利用报告率为 (即采样频率)的同步相量序列可以对频率在
(即采样频率)的同步相量序列可以对频率在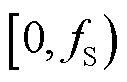 范围内的分量进行参数辨识。
范围内的分量进行参数辨识。
一方面,这一结论可由奈奎斯特采样定理得出。实数域的奈奎斯特采样定理的采样对象是实数,因此可辨识最大频率为采样频率的一半;而若采样对象为复数,等效的采样频率变为实际的2倍,因此可辨识的频率范围等于复数序列的采样频率。
另一方面,如果从频谱分析角度看,实数信号的频谱左右两侧共轭,只有一半的频谱能提供有效信息(如瞬时信号的频谱),因此实数信号的可辨识频率范围是采样频率的一半,即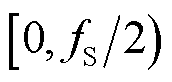 ;然而,对复数域的同步相量序列进行频谱分析时,其频谱的左右两侧非共轭,如图3所示,频谱在整个
;然而,对复数域的同步相量序列进行频谱分析时,其频谱的左右两侧非共轭,如图3所示,频谱在整个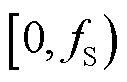 范围都可以提供非重复的有效信息,因此可辨识的频率范围是
范围都可以提供非重复的有效信息,因此可辨识的频率范围是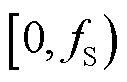 。另外,由于频谱泄漏,同步相量频谱图中各尖峰的频率值f并非同步相量实际频率值。
。另外,由于频谱泄漏,同步相量频谱图中各尖峰的频率值f并非同步相量实际频率值。
由于频谱分析得到的频谱范围是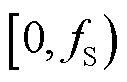 ,不在此范围内的频率分量会被映射到此频率范围中,即映射后的频率
,不在此范围内的频率分量会被映射到此频率范围中,即映射后的频率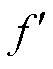 为
为
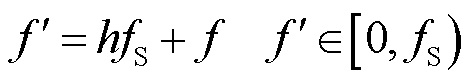 ,
,
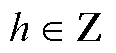 (12)
(12)
式中,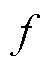 为实际的频率值;
为实际的频率值;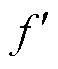 为实际频率
为实际频率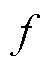 映射到
映射到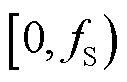 之后的频率。如图4b中的频谱示意图所示,在
之后的频率。如图4b中的频谱示意图所示,在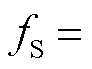 50 Hz、
50 Hz、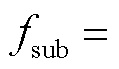 20 Hz时,次同步分量正频率20 Hz映射后为20 Hz,负频率
20 Hz时,次同步分量正频率20 Hz映射后为20 Hz,负频率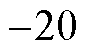 Hz映射后为30 Hz;超同步分量正频率80 Hz映射为30 Hz,负频率
Hz映射后为30 Hz;超同步分量正频率80 Hz映射为30 Hz,负频率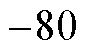 Hz映射为20 Hz。
Hz映射为20 Hz。
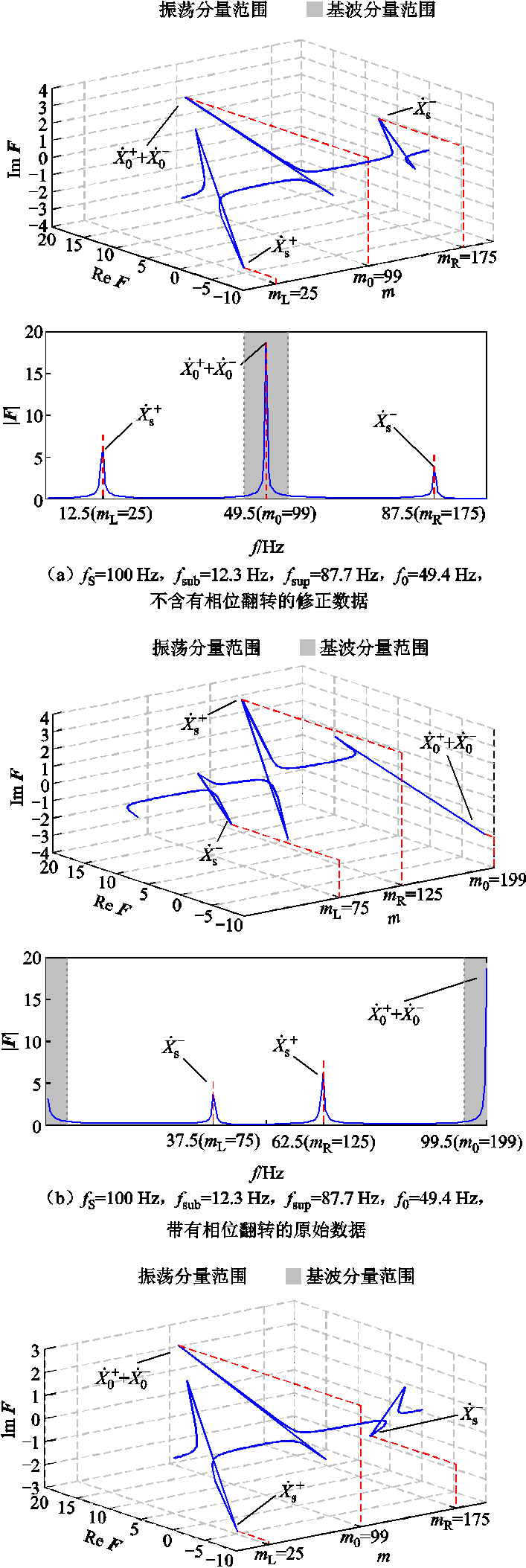
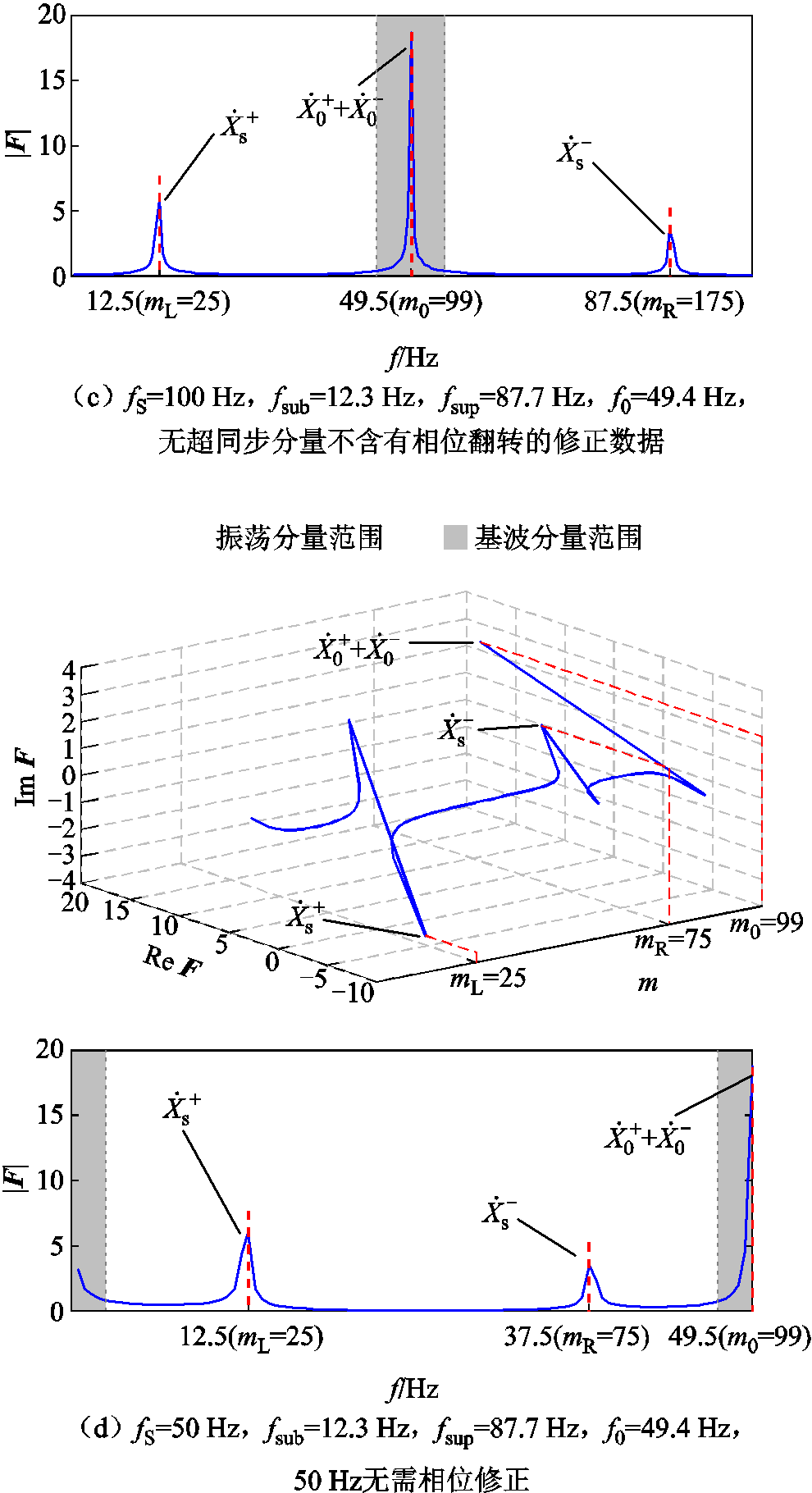
图3 同步相量频谱F以及同步相量频谱的幅值|F|
Fig.3 Spectral of synchrophasor F and spectral magnitude of synchrophasor |F|
此外,除次/超同步振荡外,在宽频振荡的场景中可能存在频率为100 Hz以上的分量,这些分量同样会映射到同步相量频谱中。同步相量频谱中的峰值可能会对应多个实际值,例如,若映射后的峰值频率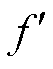 =20 Hz,当
=20 Hz,当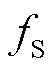 =100 Hz时,实际频率
=100 Hz时,实际频率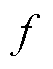 可能取值为
可能取值为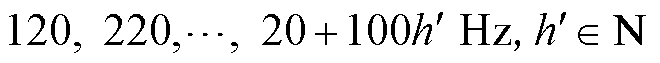 ;当
;当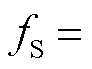 50 Hz时,
50 Hz时,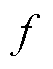 可能取值为
可能取值为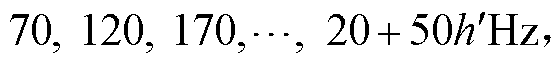
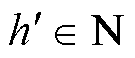 。对于此情况,在风电集群等多节点场景下,个别少量节点如安装宽频测量装置[38]则可以提供该节点的精确频率值,而其他安装PMU的节点即可以此频率值为参考确定
。对于此情况,在风电集群等多节点场景下,个别少量节点如安装宽频测量装置[38]则可以提供该节点的精确频率值,而其他安装PMU的节点即可以此频率值为参考确定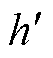 的取值,进而得到本节点的实际频率值。
的取值,进而得到本节点的实际频率值。
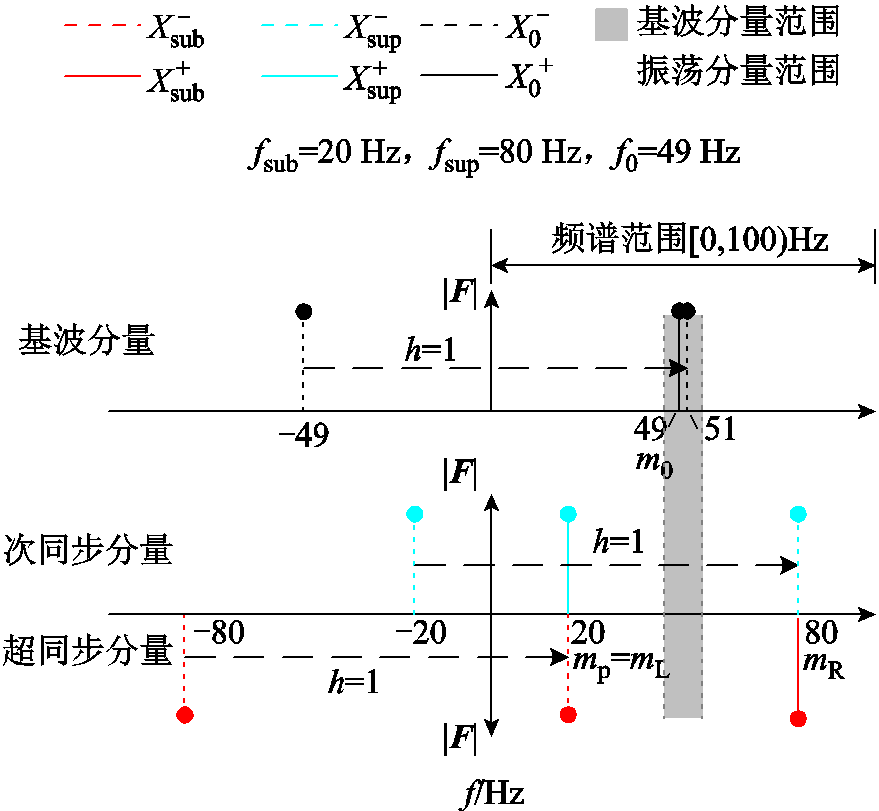
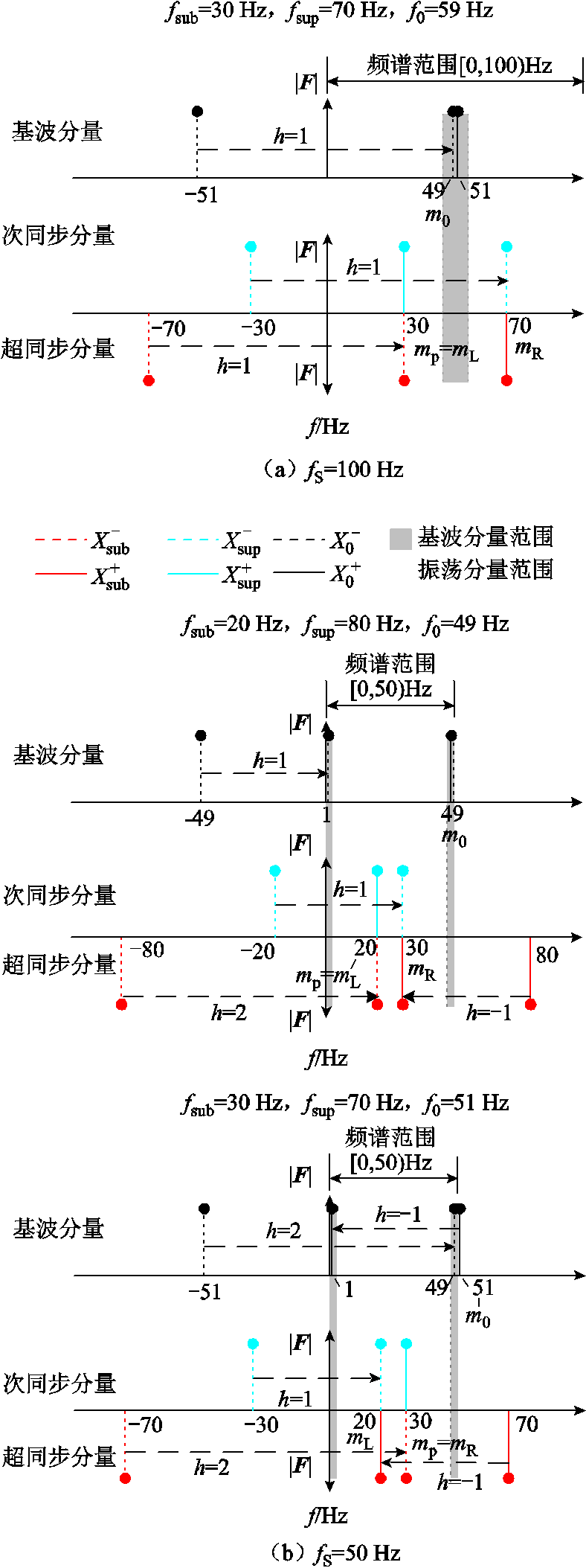
图4 不同采样频率下同步相量频谱的频率映射关系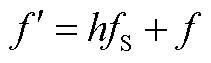 和叠加特性示意图
和叠加特性示意图
Fig.4 Schematic diagram of the frequency folding relationship 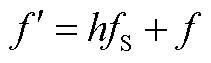 and aliasing characteristics of the synchrophasor spectrum at different sampling frequencies
and aliasing characteristics of the synchrophasor spectrum at different sampling frequencies
PMU实测的同步相量由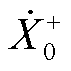 、
、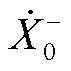 、
、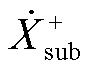 、
、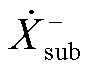 、
、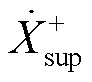 、
、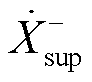 各分量叠加和耦合产生,且当
各分量叠加和耦合产生,且当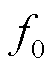 接近
接近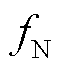 时,
时,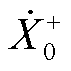 和
和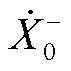 、
、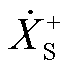 和
和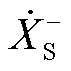 分别存在频率耦合关系。基于同步相量的参数辨识过程即为拆分叠加关系、解耦耦合关系的过程。
分别存在频率耦合关系。基于同步相量的参数辨识过程即为拆分叠加关系、解耦耦合关系的过程。
本节使用最基本的频谱分析方法,从频域角度对上述叠加和耦合特性进行直观分析。典型的同步相量复数域频谱如图3所示,通常包含三个尖峰。
1)基波分量存在一个尖峰,对应于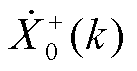 和
和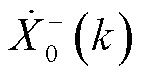 二者的叠加。对于基波分量,其正、负频率分别为
二者的叠加。对于基波分量,其正、负频率分别为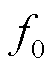 和
和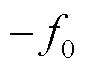 ,频率特征映射到
,频率特征映射到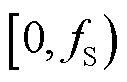 中,映射关系受
中,映射关系受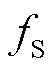 取值影响,具体如3.2节所述。对于一般情况,当频谱分析的数据窗较短导致频谱分辨率较低时(数据窗长的影响在3.3节详细讨论),由于
取值影响,具体如3.2节所述。对于一般情况,当频谱分析的数据窗较短导致频谱分辨率较低时(数据窗长的影响在3.3节详细讨论),由于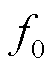 非常接近
非常接近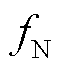 ,因此
,因此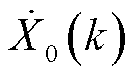 的两个互相耦合的正、负频率部分
的两个互相耦合的正、负频率部分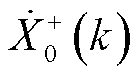 和
和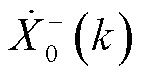 会叠加为一个尖峰。
会叠加为一个尖峰。
此外,从图1可以看出,对于正、负频率分别为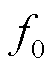 、
、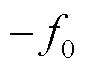 的基波分量恒有
的基波分量恒有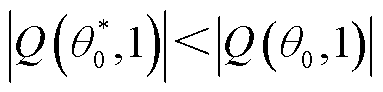 ,即在同步相量中有
,即在同步相量中有
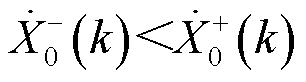 (13)
(13)
且二者数值相差较大,因此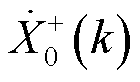 为基波分量的主导分量。
为基波分量的主导分量。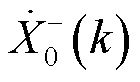 频谱幅值很小,其不会对
频谱幅值很小,其不会对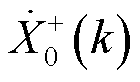 的频谱幅值尖峰位置造成影响,因此基波分量尖峰仍位于
的频谱幅值尖峰位置造成影响,因此基波分量尖峰仍位于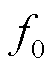 处,对应于
处,对应于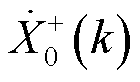 ,位置索引为
,位置索引为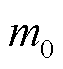 。
。
2)振荡分量存在两个尖峰,分别对应于振荡分量正频率部分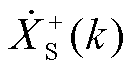 和负频率部分
和负频率部分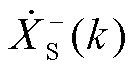 。采样频率
。采样频率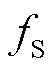 会影响尖峰的位置,令此两个尖峰中左尖峰的位置索引为
会影响尖峰的位置,令此两个尖峰中左尖峰的位置索引为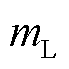 、右尖峰的位置索引为
、右尖峰的位置索引为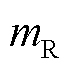 ,振荡分量的两个尖峰与其正/负频率部分的具体对应关系的分析如3.2节所述。当
,振荡分量的两个尖峰与其正/负频率部分的具体对应关系的分析如3.2节所述。当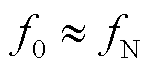 时,次、超同步分量频率满足
时,次、超同步分量频率满足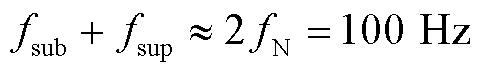 ,无论采样频率为
,无论采样频率为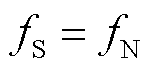 还是
还是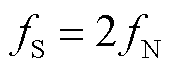 ,如图4所示,
,如图4所示,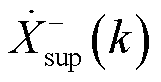 的频率
的频率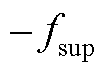 总会与
总会与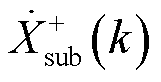 的频率
的频率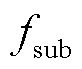 映射到同一位置,称为正尖峰,即振荡分量的正频率
映射到同一位置,称为正尖峰,即振荡分量的正频率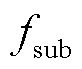 处,位置索引为
处,位置索引为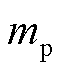 ;
;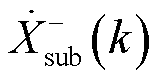 的频率
的频率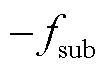 总会与
总会与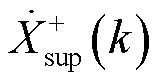 的频率
的频率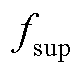 映射到同一位置,称为负尖峰,即振荡分量的负频率
映射到同一位置,称为负尖峰,即振荡分量的负频率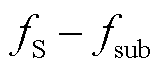 处,位置索引为
处,位置索引为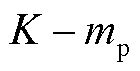 ,其中
,其中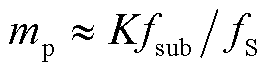 。
。
上述对同步相量各分量叠加及耦合特性的分析反映了基于同步相量进行参数辨识的关键环节和难点,可以概括为一个基本问题及两个解耦问题:即频谱泄漏的基本问题、振荡分量耦合关系的解耦问题以及基波分量耦合关系的解耦问题。
WAMS和PMU提供的同步相量序列为保证数据的连续性,分别存在以下两种形式的相位翻转。
1)相位超出范围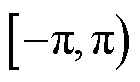 时的翻转。同步相量测量标准[45]中规定相位的取值范围为
时的翻转。同步相量测量标准[45]中规定相位的取值范围为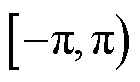 ,因此在同步相量的相位变化超出此范围时会将其翻转回此范围内,并产生大小为
,因此在同步相量的相位变化超出此范围时会将其翻转回此范围内,并产生大小为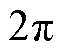 的相位差。但是由于同步相量序列为复数域数据序列,此类相位翻转并不会影响同步相量序列的时间连续性,也不会影响参数辨识计算,如复数域DFT频谱分析[15,18]、矩阵束算法[14,16]等。
的相位差。但是由于同步相量序列为复数域数据序列,此类相位翻转并不会影响同步相量序列的时间连续性,也不会影响参数辨识计算,如复数域DFT频谱分析[15,18]、矩阵束算法[14,16]等。
2)同步相量数据采样频率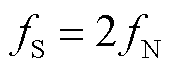 时相邻两个同步相量间的相位翻转。当
时相邻两个同步相量间的相位翻转。当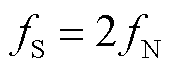 时,同步相量序列中相邻两个同步相量点计算得到的相位差接近
时,同步相量序列中相邻两个同步相量点计算得到的相位差接近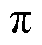 。为保证同步相量序列的连续性,PMU往往额外间隔地附加补偿一个相位差
。为保证同步相量序列的连续性,PMU往往额外间隔地附加补偿一个相位差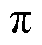 。前文的分析并未考虑这种额外附加的相位翻转的影响,因此直接使用这种附加相位翻转的同步相量数据进行分析,将得到图3b所示的频谱,其中的基波分量峰值点将位于频谱两侧、振荡分量峰值点将位于
。前文的分析并未考虑这种额外附加的相位翻转的影响,因此直接使用这种附加相位翻转的同步相量数据进行分析,将得到图3b所示的频谱,其中的基波分量峰值点将位于频谱两侧、振荡分量峰值点将位于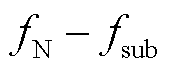 和
和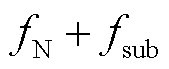 。
。
为了保证参数辨识算法的统一性,如果原始同步相量序列 已附加相位翻转(即稳态时,相邻两个同步相量点的相位差接近0,应用时需要根据实际情况来确定),则需要对其进行相位修正预处理得到修正的同步相量序列
已附加相位翻转(即稳态时,相邻两个同步相量点的相位差接近0,应用时需要根据实际情况来确定),则需要对其进行相位修正预处理得到修正的同步相量序列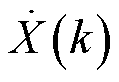 ,有
,有
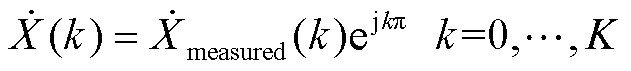 (14)
(14)
相比于相位翻转修正前的图3b,相位翻转修正后的频谱如图3a所示,相位翻转修正后的基波分量正负尖峰叠加为一个尖峰,更便于特性分析。
根据第2节中的同步相量特性分析可知,同步相量包含各分量之间的叠加,即次/超同步分量之间的耦合叠加、基波分量自身正负分量的耦合叠加以及振荡分量与基波分量之间的频谱泄漏叠加影响。因此,参数辨识过程中需要根据同步相量信息拆解各分量的叠加关系。基于同步相量数据进行参数辨识的过程中均会面临以下问题,具体为一个基本问题和两个解耦问题。
1)频谱泄漏的基本问题,即分解不同频的振荡分量和基波分量的基本问题。当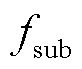 越大,即
越大,即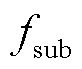 越接近
越接近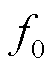 时,两个振荡尖峰越靠近基波尖峰,这代表着振荡分量的变化特征越接近基波分量的变化特征,此时振荡分量和基波分量之间的频谱泄漏问题越难处理。需要说明的是,即使是非DFT参数辨识方法,由于振荡分量和基波分量的变化特征更接近,
时,两个振荡尖峰越靠近基波尖峰,这代表着振荡分量的变化特征越接近基波分量的变化特征,此时振荡分量和基波分量之间的频谱泄漏问题越难处理。需要说明的是,即使是非DFT参数辨识方法,由于振荡分量和基波分量的变化特征更接近,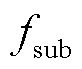 大的情况也比
大的情况也比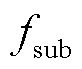 小时更难处理。此外,在数据窗变短时将导致基波分量与振荡分量之间频谱泄漏加剧,如3.3节所述,非DFT参数辨识方法也面临此问题[33]。例如,当使用2 s数据窗时,文献[18-19]中
小时更难处理。此外,在数据窗变短时将导致基波分量与振荡分量之间频谱泄漏加剧,如3.3节所述,非DFT参数辨识方法也面临此问题[33]。例如,当使用2 s数据窗时,文献[18-19]中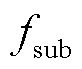 =45 Hz下的参数辨识误差明显高于
=45 Hz下的参数辨识误差明显高于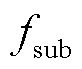 =5 Hz时的情况,而这一现象在采用100 ms数据窗时更为突出[33];文献[14]尽管测试了
=5 Hz时的情况,而这一现象在采用100 ms数据窗时更为突出[33];文献[14]尽管测试了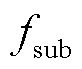 为5~45 Hz的辨识精度,但并未明确给出
为5~45 Hz的辨识精度,但并未明确给出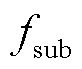 接近45 Hz时的辨识精度。作者谨慎怀疑其中所用的扩展至复数域而未作其他改进的MPM算法在40 dB测量噪声下不能保证对
接近45 Hz时的辨识精度。作者谨慎怀疑其中所用的扩展至复数域而未作其他改进的MPM算法在40 dB测量噪声下不能保证对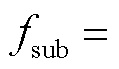 45 Hz的次同步振荡参数的辨识精度。综上所述,更短的数据窗将带来更高的参数辨识结果更新率和更好的动态监测性能,也将显著加剧参数辨识难度,因此如何有效地解决基波分量与振荡分量之间的频谱泄漏问题是参数辨识过程中的一个基本问题,也是关键核心问题。
45 Hz的次同步振荡参数的辨识精度。综上所述,更短的数据窗将带来更高的参数辨识结果更新率和更好的动态监测性能,也将显著加剧参数辨识难度,因此如何有效地解决基波分量与振荡分量之间的频谱泄漏问题是参数辨识过程中的一个基本问题,也是关键核心问题。
2)振荡分量耦合关系的解耦问题。根据前文所述,频率耦合关系将导致次同步分量和超同步分量的正、负部分互相叠加。这种叠加关系是由次/超同步频率耦合关系造成的,并不能作为频谱泄漏对其进行近似或忽略处理,因此必须在参数辨识时进一步处理次同步分量和超同步分量的耦合关系对其解耦。早期研究因认识不足,均假设不存在频率耦合的超同步分量而仅存在次同步分量,并未能有效地处理次/超同步分量的频率耦合关系,进而无法辨识超同步分量的参数,如文献[15,18-19,32]。最新的一系列研究成果已关注到这一问题[15,32-33],例如,文献[32]认为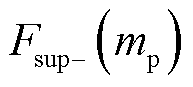 很小,在
很小,在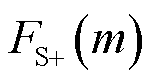 处将其忽略,基于这一假设前提检测超同步分量的存在。然而,这种近似或忽略的处理方法并不可靠。综上可见,次/超同步分量的解耦是基于同步相量进行参数辨识的另一个难点和重点。
处将其忽略,基于这一假设前提检测超同步分量的存在。然而,这种近似或忽略的处理方法并不可靠。综上可见,次/超同步分量的解耦是基于同步相量进行参数辨识的另一个难点和重点。
3)基波分量耦合关系的解耦问题。与次/超频率耦合导致的次/超同步两个分量变化特性耦合不同,基波分量的正/负频率分量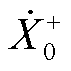 、
、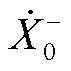 由基波分量自身产生,且两者的耦合由参数辨识数据窗较短引起。文献[15]中对此进行了详细分析并提出了解耦方法。虽然基波分量的辨识并不是次/超同步振荡参数辨识中的关键问题,但基波分量的辨识精度会严重影响次/超同步分量参数的辨识精度[15,33],因此基波分量自身的正负频率分量解耦问题仍需给以一定关注。
由基波分量自身产生,且两者的耦合由参数辨识数据窗较短引起。文献[15]中对此进行了详细分析并提出了解耦方法。虽然基波分量的辨识并不是次/超同步振荡参数辨识中的关键问题,但基波分量的辨识精度会严重影响次/超同步分量参数的辨识精度[15,33],因此基波分量自身的正负频率分量解耦问题仍需给以一定关注。
频谱分析方法是最基本的、研究最深入的方法,因此本节以同步相量的复数域频谱分析参数辨识法为基准,分析探讨了复数域频谱分析方法在解决以上三个问题时的三个关键难点:①针对次/超同步分量的耦合关系,检测是否存在超同步分量的方法,以及如何有效地辨识超同步分量;②不同的同步相量采样频率下进行参数辨识的适应性问题;③如何处理频谱泄漏来缩短数据窗长以解决数据窗长与辨识精度之间的矛盾难题。
超同步分量由于存在与次同步分量的频率耦合关系,因此检测是否存在超同步分量及其辨识需要针对次/超同步频率耦合关系进行深入分析。
文献[32]提出了一种检测超同步分量是否存在的方法,首先认为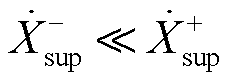 ,即在振荡分量中有
,即在振荡分量中有
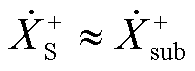 (15)
(15)
其次,根据振荡分量正频率峰值的频谱位置计算出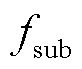 ,进而计算若仅含有频率为此的次同步分量时,振荡分量频谱的负正尖峰幅值比值的理论值为
,进而计算若仅含有频率为此的次同步分量时,振荡分量频谱的负正尖峰幅值比值的理论值为
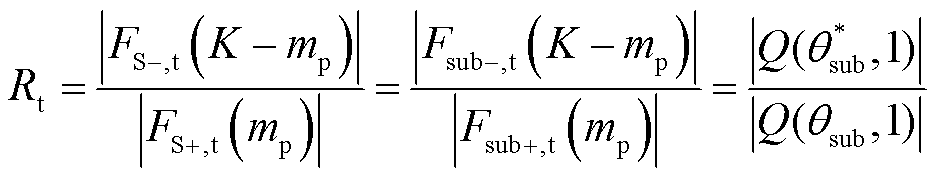 (16)
(16)
式中,下标t表示理论值。
实际测量的比值为
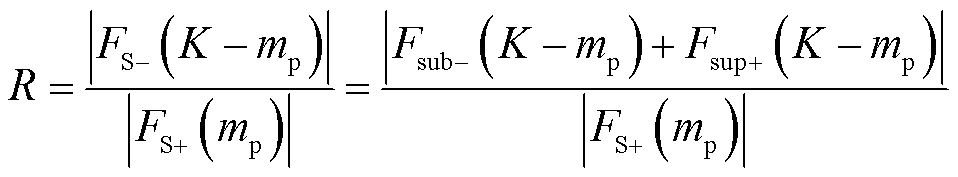 (17)
(17)
最后将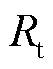 与
与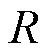 进行对比,若二者误差在所设定的阈值范围内,则不存在超同步分量;反之,则存在超同步分量。但此方法遗漏了两个重要问题。
进行对比,若二者误差在所设定的阈值范围内,则不存在超同步分量;反之,则存在超同步分量。但此方法遗漏了两个重要问题。
(1)认为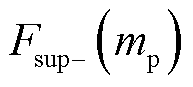 很小而在
很小而在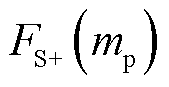 处将其忽略。然而,根据图1所示,虽然有
处将其忽略。然而,根据图1所示,虽然有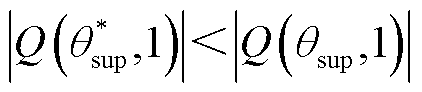 ,但是二者仍在同一数量级,
,但是二者仍在同一数量级,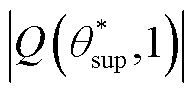 相对于
相对于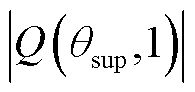 仍不可忽略,即不可忽略
仍不可忽略,即不可忽略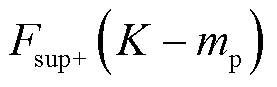 。
。
(2)复数域的频谱不仅包含频谱幅值信息,频谱相位信息同样重要。当实测得到的同步相量复数域频谱满足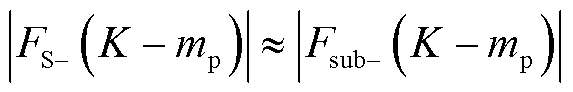 时有
时有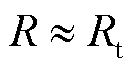 ,根据该方法的判断条件,将判定不存在超同步分量。然而,如图5所示,由于
,根据该方法的判断条件,将判定不存在超同步分量。然而,如图5所示,由于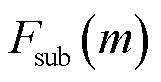 与
与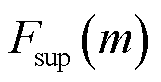 之间是矢量叠加的,存在不唯一的超同步分量,其所对应的
之间是矢量叠加的,存在不唯一的超同步分量,其所对应的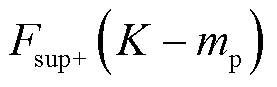 叠加
叠加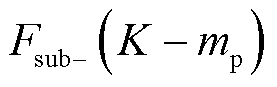 后得到新的
后得到新的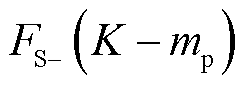 将等于原始的
将等于原始的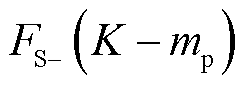 旋转某一角度
旋转某一角度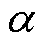 ,且保持
,且保持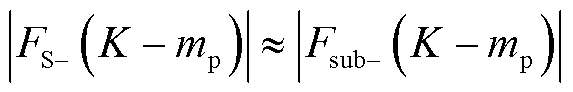 这一条件仍然成立,而此时的判定结果显然是错的。例如,如图3所示,图3a为有超同步分量的场景,而图3c为不含超同步分量的场景,两者的复数域频谱幅值几乎完全一致,均满足文献[32]方法判定不存在超同步分量的条件,此时判定结果错误。综上所述,尽管此方法判定存在超同步分量的结果是可靠的,但所有被判定为不存在超同步分量的场景实际上均可能存在某一超同步分量,从而针对该方法的准确性分析也无从可谈。此外,该方法仅能检测超同步分量的存在而不能辨识超同步分量参数。造成该方法存在显著局限性和不可靠的根本原因在于仅利用了频谱幅值信息而忽略了相位信息。
这一条件仍然成立,而此时的判定结果显然是错的。例如,如图3所示,图3a为有超同步分量的场景,而图3c为不含超同步分量的场景,两者的复数域频谱幅值几乎完全一致,均满足文献[32]方法判定不存在超同步分量的条件,此时判定结果错误。综上所述,尽管此方法判定存在超同步分量的结果是可靠的,但所有被判定为不存在超同步分量的场景实际上均可能存在某一超同步分量,从而针对该方法的准确性分析也无从可谈。此外,该方法仅能检测超同步分量的存在而不能辨识超同步分量参数。造成该方法存在显著局限性和不可靠的根本原因在于仅利用了频谱幅值信息而忽略了相位信息。
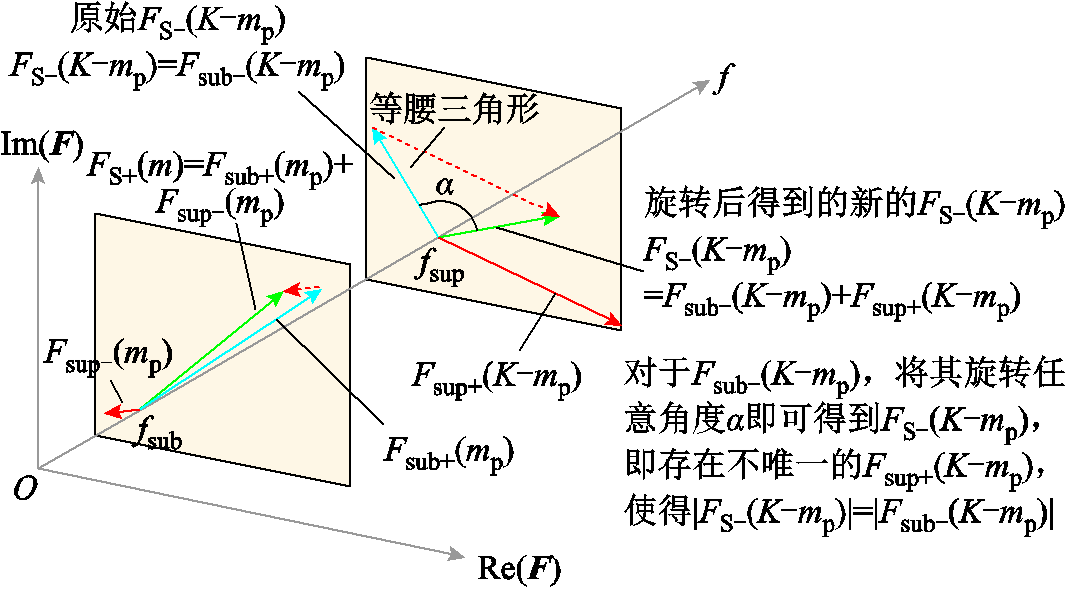
图5 文献[32]中超同步检测方法适应性分析
Fig.5 Adaptation analysis of supersynchronous detection method in Ref.[32]
目前可准确判定超同步分量是否存在的方法是直接辨识超同步分量参数。例如,后文基于复数域频谱分析的参数辨识方法可直接辨识超同步分量参数,当超同步分量幅值很小时可近似认为不存在超同步分量,这一方法具有更好的准确性和实用性。
采样频率影响了复数域频谱分析的频率辨识范围,不在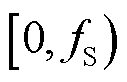 范围内的分量会映射到此范围内。目前WAMS采用的主流采样频率为
范围内的分量会映射到此范围内。目前WAMS采用的主流采样频率为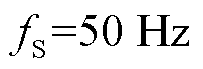 和
和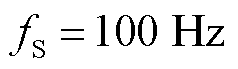 ,因此,本节从数学解析角度分别分析了这两种采样频率下的同步相量复数域频谱特性及其对参数的影响。
,因此,本节从数学解析角度分别分析了这两种采样频率下的同步相量复数域频谱特性及其对参数的影响。
频谱分析方法以尖峰位置为依据来计算各分量,需要首先确定各尖峰和各分量的对应关系,然后即可根据尖峰位置反推出各分量的频率。对于振荡分量,同步相量的复数域频谱中存在相应的两个尖峰,令其中左尖峰的位置索引为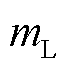 、右尖峰的位置索引为
、右尖峰的位置索引为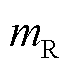 ,则有
,则有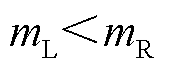 且
且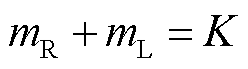 ;在不同采样频率
;在不同采样频率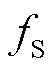 的情况下,确定左右尖峰索引
的情况下,确定左右尖峰索引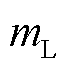 、
、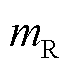 与正负尖峰索引
与正负尖峰索引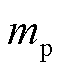 、
、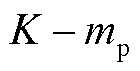 之间的对应关系是参数辨识的重要环节。不同采样频率下振荡分量的正负尖峰位置见表1。
之间的对应关系是参数辨识的重要环节。不同采样频率下振荡分量的正负尖峰位置见表1。
表1 同步相量频谱中振荡分量各分量尖峰位置
Tab.1 The peak position of each component of the oscillatory component in the synchrophasor spectrum

采样频率/Hz的频率范围/Hz振荡分量所含分量振荡分量正频谱振荡分量负频谱 尖峰所对应频率尖峰位置索引尖峰所对应频率尖峰位置索引 100(0,50)存在次同步和超同步分量 50(0,25]存在次同步和超同步分量 (25,50)存在次同步和超同步分量 (0,50)仅存在次同步分量①
①若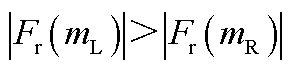 ,则
,则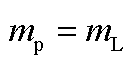 ;若
;若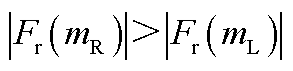 ,则
,则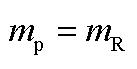 。
。
3.2.1 采样频率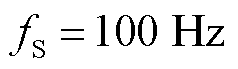
1)振荡分量
根据式(12),在采样频率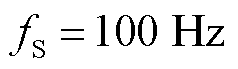 时,振荡分量的正、负频率
时,振荡分量的正、负频率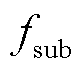 、
、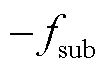 映射到
映射到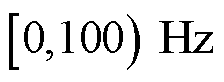 范围内为
范围内为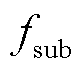 和
和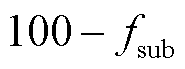 ,分别对应于
,分别对应于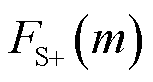 和
和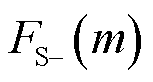 的两个尖峰。如图4a所示,由于
的两个尖峰。如图4a所示,由于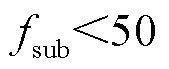 Hz,则
Hz,则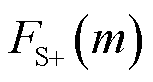 尖峰在
尖峰在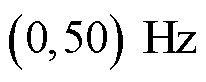 范围内,
范围内,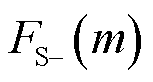 尖峰在
尖峰在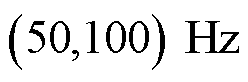 范围内。由于振荡分量正、负频谱的尖峰分别位于50 Hz位置的左右两侧,因此容易确定左尖峰对应的是
范围内。由于振荡分量正、负频谱的尖峰分别位于50 Hz位置的左右两侧,因此容易确定左尖峰对应的是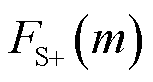 ,右尖峰对应的是
,右尖峰对应的是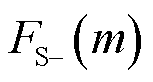 ,有
,有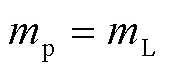 ,可进一步由此计算振荡分量的频率
,可进一步由此计算振荡分量的频率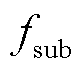 和
和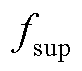 。
。
进而可辨识次/超同步分量的幅值和相位,分别在正负尖峰处建立方程并联立为方程组,即
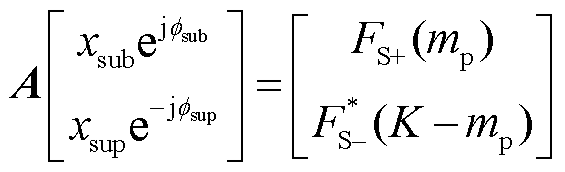 (18)
(18)
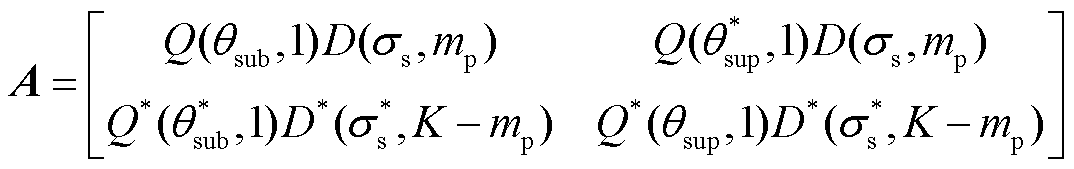 (19)
(19)
该方程组中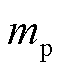 有唯一取值,且该方程组满足
有唯一取值,且该方程组满足
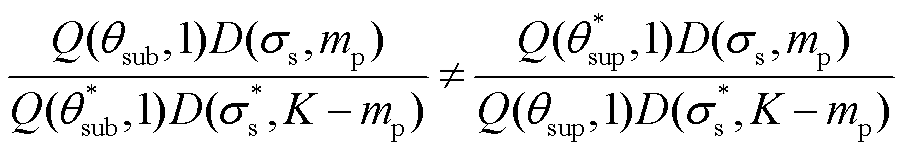 (20)
(20)
因此,该方程组有且仅有唯一解。该方程组的建立和求解即为频率耦合的次/超同步分量解耦过程。综上所述,采样频率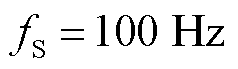 时可直接辨识
时可直接辨识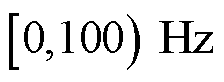 范围的各振荡分量参数。
范围的各振荡分量参数。
2)基波分量
在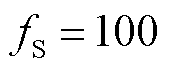 Hz时,基波分量的正、负频率
Hz时,基波分量的正、负频率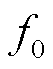 、
、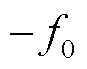 映射到
映射到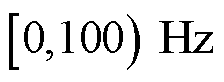 范围内为
范围内为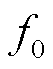 、
、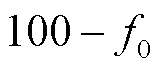 ,均在 50 Hz附近,分别对应于基波分量正、负频谱
,均在 50 Hz附近,分别对应于基波分量正、负频谱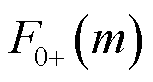 、
、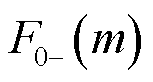 的两个尖峰。根据2.2节中的分析,这两个尖峰在
的两个尖峰。根据2.2节中的分析,这两个尖峰在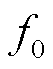 处合成一个尖峰,此尖峰可以列出唯一方程组式(21)、式(22),该方程组有且仅有唯一解[15]。
处合成一个尖峰,此尖峰可以列出唯一方程组式(21)、式(22),该方程组有且仅有唯一解[15]。
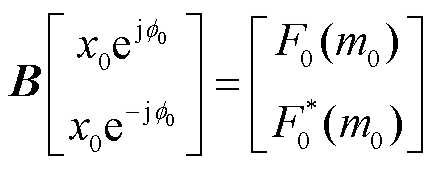 (21)
(21)
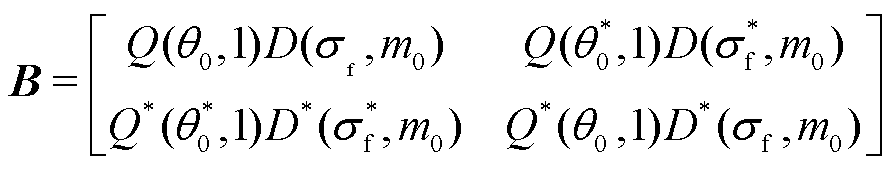 (22)
(22)
式(21)、式(22)即为基波分量的正、负分量解耦过程。
3.2.2 采样频率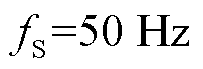
1)振荡分量
使用采样频率50 Hz无法直接对含有超同步分量的振荡分量进行辨识,需提供额外信息进行参数辨识。具体地:在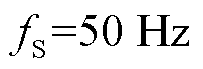 时,振荡分量的正、负频率
时,振荡分量的正、负频率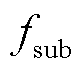 、
、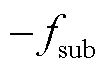 映射到
映射到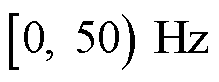 范围内后的频率为
范围内后的频率为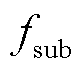 、
、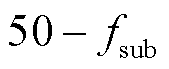 ,分别对应于
,分别对应于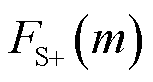 和
和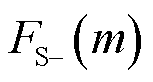 的两个尖峰。由于
的两个尖峰。由于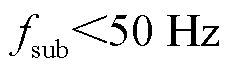 ,
,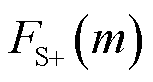 正尖峰和
正尖峰和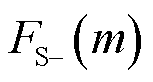 负尖峰均落在
负尖峰均落在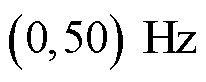 范围内,因此,无法确定左右尖峰和正负尖峰的对应关系。此时,对于一个频谱结果,存在两种可能的实际情况而分别对应两种完全不同的参数结果:若
范围内,因此,无法确定左右尖峰和正负尖峰的对应关系。此时,对于一个频谱结果,存在两种可能的实际情况而分别对应两种完全不同的参数结果:若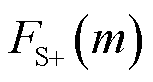 尖峰在左侧,
尖峰在左侧,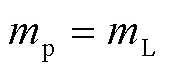 ;若
;若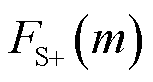 尖峰在右侧,
尖峰在右侧,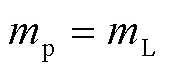 ,两种情况分别对应图4b中的上、下两图。与3.2.1节相似,在频谱的左右尖峰处仍可列出方程组式(18),但方程组中参数
,两种情况分别对应图4b中的上、下两图。与3.2.1节相似,在频谱的左右尖峰处仍可列出方程组式(18),但方程组中参数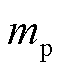 有两个可能的取值,进而该方程组可得到两个解。
有两个可能的取值,进而该方程组可得到两个解。
综上所述,在采样频率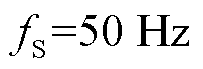 时仅凭同步相量的复数域频谱无法进行含有超同步分量的次/超同步振荡参数辨识,此结论与2.1节的分析一致。
时仅凭同步相量的复数域频谱无法进行含有超同步分量的次/超同步振荡参数辨识,此结论与2.1节的分析一致。
若要实现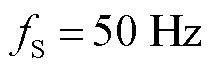 时的次/超同步振荡参数辨识,需给定额外条件。条件1:给定SSO中次同步分量频率是否低于25 Hz;条件2:所辨识的SSO只含有次同步分量而不含有超同步分量。给定这两个条件之一,即可用50 Hz采样频率的同步相量进行次/超同步振荡参数辨识。具体地:
时的次/超同步振荡参数辨识,需给定额外条件。条件1:给定SSO中次同步分量频率是否低于25 Hz;条件2:所辨识的SSO只含有次同步分量而不含有超同步分量。给定这两个条件之一,即可用50 Hz采样频率的同步相量进行次/超同步振荡参数辨识。具体地:
条件1:给定SSO中次同步分量频率是否低于25 Hz。次同步分量频率不同决定了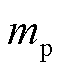 的取值不同,由于频谱的左右尖峰分别位于25 Hz位置的左右两侧,已知次同步频率的范围即可确定
的取值不同,由于频谱的左右尖峰分别位于25 Hz位置的左右两侧,已知次同步频率的范围即可确定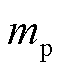 :当
:当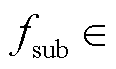
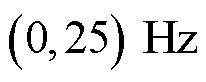 时,方程组式(18)中
时,方程组式(18)中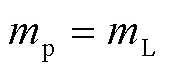 ;当
;当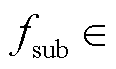
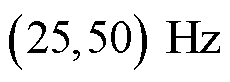 时,方程组式(18)中
时,方程组式(18)中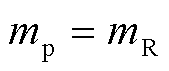 。
。
条件2:所辨识的SSO中只含有次同步分量而不含有超同步分量,或超同步分量幅值很小可将其忽略。当只有次同步分量的时候,尽管振荡分量的复数域频谱依然包含左右两个尖峰,但由于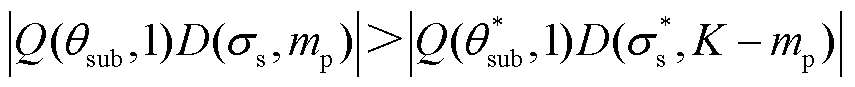 (即
(即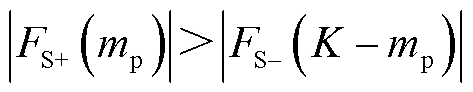 ),可根据尖峰的幅值大小来确定
),可根据尖峰的幅值大小来确定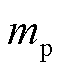 。若
。若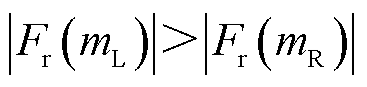 ,则
,则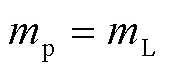 ;若
;若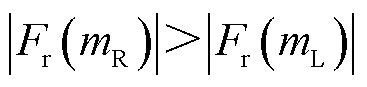 ,则
,则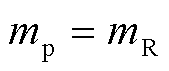 。在振荡分量正频率处(即
。在振荡分量正频率处(即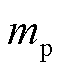 对应的尖峰处)建立方程为
对应的尖峰处)建立方程为
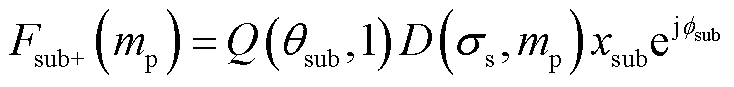 (23)
(23)
可得到唯一方程并进一步求解得到唯一解及其对应的次同步振荡参数。特别地,当次同步分量频率为25 Hz时,次同步分量的正负频率与超同步分量的正负频率这四个部分耦合在一起,在频谱中叠加为一个尖峰,无法对其进行解耦求解。
2)基波分量
在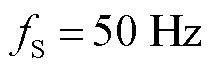 的情况下,基波分量的尖峰将受频谱分析的频率映射关系影响而被拆分为0 Hz附近和50 Hz附近两部分,在分析过程中,需先将
的情况下,基波分量的尖峰将受频谱分析的频率映射关系影响而被拆分为0 Hz附近和50 Hz附近两部分,在分析过程中,需先将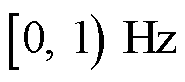 范围的频谱右移至
范围的频谱右移至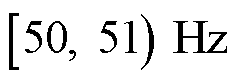 ,重新拼接出基波尖峰进行分析。若
,重新拼接出基波尖峰进行分析。若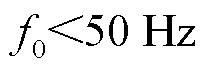 ,则
,则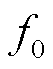 、
、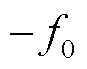 映射后为
映射后为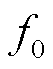 和
和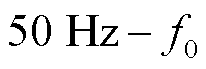 ;若
;若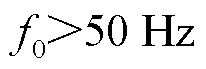 ,则
,则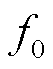 、
、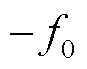 映射后为
映射后为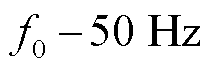 和
和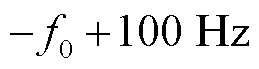 ,两种情况下基波均只有一个尖峰。实际上,这与100 Hz采样频率的情况本质上是相同的,是一个尖峰被分在了频谱的左右两侧。因此可以在此尖峰处列出参数辨识方程,与式(21)、式(22)相同。
,两种情况下基波均只有一个尖峰。实际上,这与100 Hz采样频率的情况本质上是相同的,是一个尖峰被分在了频谱的左右两侧。因此可以在此尖峰处列出参数辨识方程,与式(21)、式(22)相同。
综上所述,采样频率与频率辨识范围之间关系的结论与复数域范围内的奈奎斯特定理吻合,即在复数域范围内,以采样频率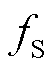 进行频谱分析能够辨识的频率范围也是
进行频谱分析能够辨识的频率范围也是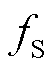 。使用不同采样频率所能辨识的频率范围见表2。
。使用不同采样频率所能辨识的频率范围见表2。
表2 不同采样频率所能辨识的振荡分量频率范围
Tab.2 The frequency range that different sampling frequencies can recognize
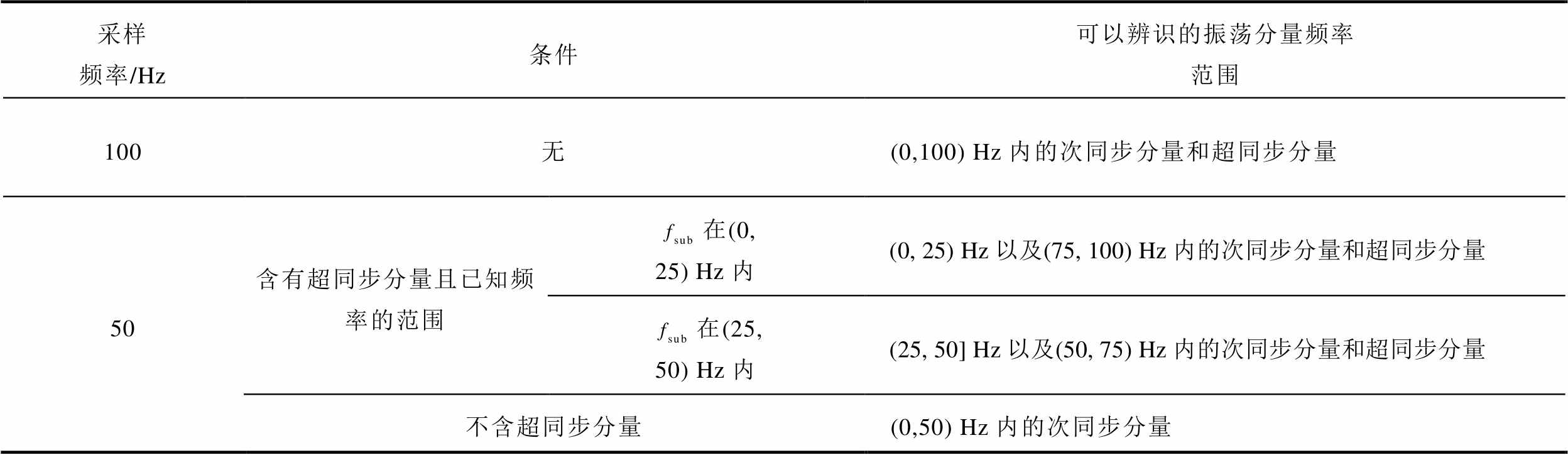
采样频率/Hz条件可以辨识的振荡分量频率范围 100无(0,100) Hz内的次同步分量和超同步分量 50含有超同步分量且已知频率的范围在(0,25) Hz内(0, 25) Hz以及(75, 100) Hz内的次同步分量和超同步分量 在(25,50) Hz内(25, 50] Hz以及(50, 75) Hz内的次同步分量和超同步分量 不含超同步分量(0,50) Hz内的次同步分量
需要注意的是,在确定了尖峰索引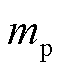 以及
以及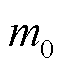 后,分别求解方程组式(18)及式(21)时仅分别解决了2.2节所述难点2的次/超同步振荡分量的耦合问题以及难点3的基波正负频率分量的耦合问题,要实现准确的参数辨识,还需要解决难点1中的频谱泄漏问题。对于频率,由于频谱泄漏的存在,不能直接根据
后,分别求解方程组式(18)及式(21)时仅分别解决了2.2节所述难点2的次/超同步振荡分量的耦合问题以及难点3的基波正负频率分量的耦合问题,要实现准确的参数辨识,还需要解决难点1中的频谱泄漏问题。对于频率,由于频谱泄漏的存在,不能直接根据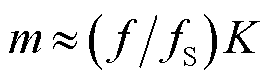 计算频率;对于幅值,由于频谱泄漏的存在导致
计算频率;对于幅值,由于频谱泄漏的存在导致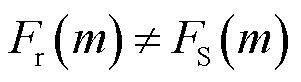 ,不能使用方程组式(18)及式(21)计算幅值,需要使用3.3节所述的方法解决频谱泄漏问题。
,不能使用方程组式(18)及式(21)计算幅值,需要使用3.3节所述的方法解决频谱泄漏问题。
3.3.1 数据窗长的选择
在基于同步相量的次/超同步振荡参数辨识过程中,选取的同步相量序列数据窗长度是一个关键问题,这是因为数据窗长度和参数辨识精度存在固有矛盾难题,具体体现在:
1)频谱分析所使用的数据窗太短,会显著增加参数辨识算法的复杂度并影响辨识精度。造成这一现象的原因有两点:①频谱分析的数据窗太短会降低频谱的频率分辨率,加重频谱混叠效应;②在一定的采样频率下数据窗越短则采样点数越少,会增加窗函数主瓣的宽度而导致更大的频谱泄漏。此处必须强调的一个事实是,缩短数据窗带来的算法复杂和辨识精度难题并不仅仅是频谱分析类方法的问题,而是所有参数辨识方法所面临的共同难题。因为数据窗短则数据序列中所蕴含的低频信息就少,次/超同步振荡与基波之间的特征区分度越低,需要以更复杂的算法和更大的计算量为代价保证参数辨识精度[14,16,33]。此外,传统基于DFR瞬时值的次/超同步振荡参数辨识方法由于采样频率高(往往高于4 kHz甚至10 kHz),而频谱泄漏和混叠问题并不显著[20-21,49-55],因此传统方法并不能简单直接用于以同步相量为计算对象的次/超同步振荡参数辨识中。
2)数据窗太长会显著降低参数辨识算法的可行性和实用性。造成这一现象的原因同样有两点:①参数辨识的假设前提是数据窗内的振荡模式和参数不变,而数据窗越大则实际振荡模式越可能变化,越无法真实反映实际的次/超同步振荡特性,进而显著降低参数辨识结果的可靠度和可信度[15,18];②更重要的是,这会导致参数辨识结果的实时性较差,而基于同步相量的次/超同步振荡监测的核心优势就是广域同步和高刷新率的高实时性在线监测[33]。因此,为了更充分地发挥同步相量测量数据的核心优势,需要参数辨识算法在保证辨识精度的前提下尽可能地缩短数据窗长。事实上,推动基于同步相量的次/超同步振荡监测研究的一个最重要实际问题就是高比例新能源接入后电网中出现的快速响应、广泛传播的次/超同步振荡,这种次/超同步振荡甚至在200 ms内已经振荡发散并广泛传播,与传统汽轮机轴系扭振的次同步振荡特性完全不同[13,56-57]。
综上所述,如何缩短同步相量序列数据窗是次/超同步振荡参数辨识最为关键和重要的基本问题。如3.3.2节所述,文献[15,18]中使用了汉宁窗和插值DFT方法减小频谱泄漏的影响,相比于未做任何处理直接使用DFT频谱结果[17],将数据窗由10 s缩短至2 s且提高了参数辨识精度。文献[19]的RV-M窗在使用2 s数据窗时,辨识精度有所改进。此外,文献[33]提出了一种同步相量轨迹拟合的非DFT参数辨识方法,克服了频谱分析方法的频谱分辨率受限问题,在保证参数辨识精度的前提下将数据窗缩短至100 ms,但由于文中并未提及40 dB下次/超同步分量相位的辨识结果,如辨识精度较低则可能需要将窗长加至200 ms甚至更多。
3.3.2 频谱分析中的频谱泄漏及其处理方法
在实际应用中,由于采用较短的同步相量序列数据窗进行复数域频谱分析,频谱泄漏问题较为严重而不能直接忽略,即2.2节所述的“基本问题”。频谱泄漏就是信号频谱中各谱线之间的相互影响,将导致频谱结果偏离实际值且在真实谱线两侧频率点上出现一些较小的假谱。某一分量的频谱泄漏即为其频谱在非其自身频率点的取值,可用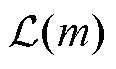 来表示。由于频谱泄漏,因此在振荡分量正、负频谱部分以及基波分量正、负频谱部分的频谱位置分别有来自其他三个分量在此处的频谱泄漏影响。例如,
来表示。由于频谱泄漏,因此在振荡分量正、负频谱部分以及基波分量正、负频谱部分的频谱位置分别有来自其他三个分量在此处的频谱泄漏影响。例如,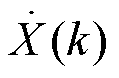 的频谱
的频谱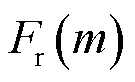 在
在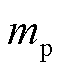 处的值为
处的值为
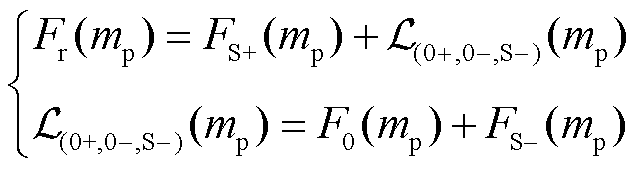 (24)
(24)
即在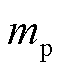 处包含振荡分量负频谱和基波分量正负频谱在此位置的频谱泄漏
处包含振荡分量负频谱和基波分量正负频谱在此位置的频谱泄漏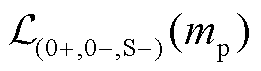 ,基波分量同理。
,基波分量同理。
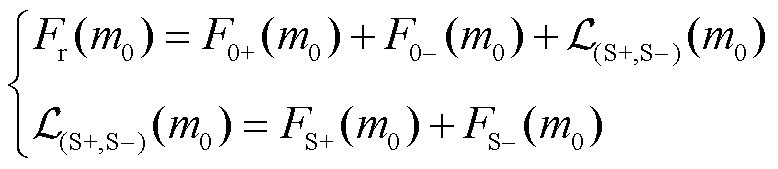 (25)
(25)
文献[18]在公式中混用了同步相量频谱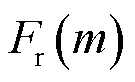 与振荡分量频谱
与振荡分量频谱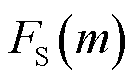 而没有详细区分二者的意义,实际上由于存在频谱泄漏,二者的意义完全不同,并不适宜将频谱中的振荡尖峰简化等效为振荡分量频谱,有必要对两者进行区分[15]。
而没有详细区分二者的意义,实际上由于存在频谱泄漏,二者的意义完全不同,并不适宜将频谱中的振荡尖峰简化等效为振荡分量频谱,有必要对两者进行区分[15]。
文献[15,18]中分别使用汉宁窗和插值DFT辨识次同步振荡的频率和幅值。在计算频率和阻尼因子时,使用插值DFT解决频谱泄漏的影响。以振荡分量为例,引入参数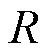 表示二阶差分之比,其中
表示二阶差分之比,其中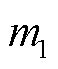 、
、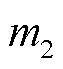 、
、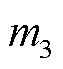 、
、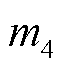 为峰值点的索引
为峰值点的索引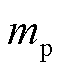 附近频谱幅值最大的四个点,从而得到
附近频谱幅值最大的四个点,从而得到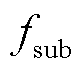 如式(26)所示。基波分量同理,在此不做赘述。
如式(26)所示。基波分量同理,在此不做赘述。
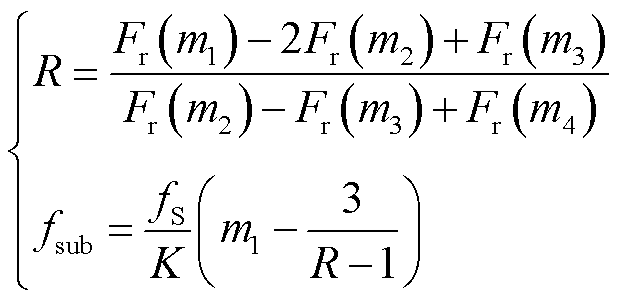 (26)
(26)
在计算幅值和相位时,插值DFT不能有效地减少频谱泄漏对幅值的影响[18],因此使用汉宁窗进行幅值和相位辨识。以振荡分量为例,使用汉宁窗的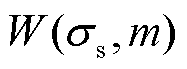 函数替代
函数替代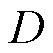 函数,即
函数,即
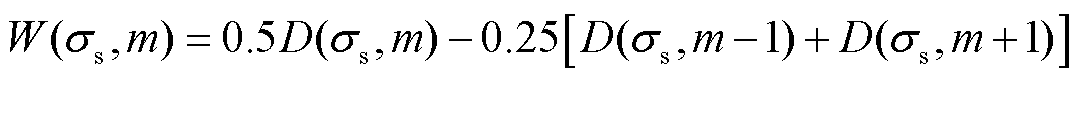 (27)
(27)
在方程组式(18)及式(21)中使用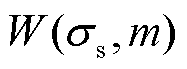 代替
代替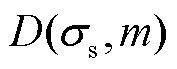 进行计算后,频谱泄漏
进行计算后,频谱泄漏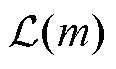 足够小而可忽略,进而可以使用不同频谱尖峰的
足够小而可忽略,进而可以使用不同频谱尖峰的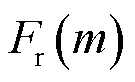 代替
代替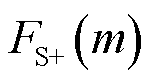 或
或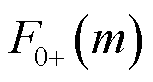 进行次/超同步分量幅值与相位的辨识,基波分量同理。文献[19]针对窗函数进行了优化,使用RV-M窗计算频谱并进行参数辨识,能更好地抑制频谱泄漏和栅栏效应。
进行次/超同步分量幅值与相位的辨识,基波分量同理。文献[19]针对窗函数进行了优化,使用RV-M窗计算频谱并进行参数辨识,能更好地抑制频谱泄漏和栅栏效应。
需要注意的是:首先,频谱泄漏在频谱分析中难以避免,处理频谱泄漏是频谱分析方法的重要问题;其次,频谱泄漏严重影响参数辨识精度,如果不能有效处理频谱泄漏,就不能利用频谱结果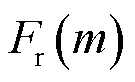 代替
代替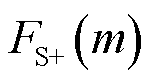 或者
或者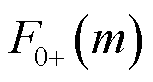 进行分析,进而不能准确辨识参数;最后,后续研究可能提出更好的频谱泄漏解决方案,如性能更好的窗函数等。
进行分析,进而不能准确辨识参数;最后,后续研究可能提出更好的频谱泄漏解决方案,如性能更好的窗函数等。
3.3.3 阻尼因子的引入
在对瞬时信号进行数学表达式建模时,需要根据同步相量数据的数据窗长来确定是否引入振荡分量的阻尼因子(即式(1)中的参数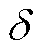 )。一方面,阻尼因子参数的辨识精度往往是所有参数中最差的,但是由于阻尼因子一般仅用于判断振荡发散或衰减速度而不直接用于扰动源定位、振荡抑制控制,其稍差的辨识精度并不会产生显著影响[14-16,18,58]。
)。一方面,阻尼因子参数的辨识精度往往是所有参数中最差的,但是由于阻尼因子一般仅用于判断振荡发散或衰减速度而不直接用于扰动源定位、振荡抑制控制,其稍差的辨识精度并不会产生显著影响[14-16,18,58]。
文献[17]在最早尝试基于同步相量幅值频谱进行次同步分量的幅值辨识时并未考虑阻尼因子,由于其使用了长达10 s的数据窗以减轻频谱泄漏的影响,导致若振荡模式存在衰减或发散时计算得到的次同步分量幅值误差显著[18]。因此,文献[15,17]在2 s数据窗长条件下,引入了阻尼因子以准确计算次同步分量的幅值。对于频谱分析方法,由于难以采用短于1 s的数据窗,有必要在瞬时值模型中加入阻尼因子。而对于更短的数据窗,如文献[33]所使用的100 ms数据窗,数据窗内的次/超同步振荡衰减变化可近似忽略而对幅值精度影响有限,且可根据辨识的幅值结果进一步计算阻尼因子,其结果与在瞬时值中考虑阻尼因子的结果一致[33]。
3.3.4 存在多对振荡分量时的参数辨识
实际电网的次/超同步振荡存在一种多对频率耦合的次/超同步振荡分量同时出现的复杂场景[59-60]。在这种场景下,数据窗长的影响更加显著,由于数据窗短导致频谱分辨率低,不同耦合关系的振荡分量可能相互混叠而导致参数辨识更加复杂。
文献[19]基于RV-M窗实现参数辨识,在仅存一个次同步分量时数据窗长2 s即可;而存在多个次同步分量时,为提高频率分辨率而需要使用10 s数据窗才可满足辨识精度。文献[33]中的轨迹拟合方法在存在多对振荡分量场景下的局限性显著:①在振荡分量数未知时无法针对多对振荡分量确定所需方程数量而无法进行参数拟合;②多对振荡分量的辨识会增加轨迹拟合方程组数量,导致需要更长的数据窗而失去了其数据窗短的核心优势,且算法求解的计算量将显著增加,因此轨迹拟合法并不适用于这种场景。本文在文献[15]的基础上,测试了插值DFT和汉宁窗方法在存在多对振荡分量场景下的适应性。与仅存在一对振荡分量时的参数辨识过程一致,仅需在不同峰值处依次计算参数即可。但需要注意的是,在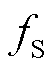 =50 Hz时同样需要额外条件,由于多对振荡分量之间往往是同一因素造成,互相之间为谐波关系[59-60],针对频谱幅值最高的第一对振荡分量尖峰给出额外条件即可,即条件1的次同步频率范围或条件2是否存在超同步分量。本文将在第4节的算例中验证这种方法的可行性。
=50 Hz时同样需要额外条件,由于多对振荡分量之间往往是同一因素造成,互相之间为谐波关系[59-60],针对频谱幅值最高的第一对振荡分量尖峰给出额外条件即可,即条件1的次同步频率范围或条件2是否存在超同步分量。本文将在第4节的算例中验证这种方法的可行性。
此外,若存在多个因素产生的振荡主分量及其相应的谐波,则很可能会出现频谱混叠的现象。多个振荡之间的相互频谱泄漏影响较大,因此为了确保辨识精度需要使用更长的数据窗来减少频谱泄漏的影响。
综上所述,尽管频谱分析方法在解决数据窗长与参数辨识精度这一矛盾问题上相比于非频谱分析方法[14,16,33]仅存在计算量优势而并不存在辨识精度优势,且2 s数据窗几乎已达到频谱方法的极限;但频谱分析结果可清晰直观地反映出多对振荡分量,在这种短数据窗无法适应的场景下具有显著优势。
3.3.5 其他影响因素
一种通常的影响因素是噪声。主要是瞬时值中的噪声,即在式(1)中叠加白噪声。通常,PMU所测同步相量的信噪比为45 dB左右[61]。大部分文献针对信噪比40 dB的测量噪声进行了测试[14-16,18],文献[14,16]还利用奇异值分解进行了降噪预处理。若噪声的信噪比更低,则需要加长数据窗。
另一种对次/超同步振荡参数辨识影响显著的情况是同步相量序列中的坏数据或丢数据。目前,绝大多数基于同步相量的次/超同步振荡参数辨识方法均未考虑这一问题。该问题的主要难点在于,次/超同步振荡分量的同步相量轨迹为椭圆轨迹[33],与基波分量叠加后特性更加复杂。针对同步相量幅值和相位分别进行线性插值的传统坏数据修复方法不仅不能补偿数据缺失,反而会引入更多的错误信息导致参数辨识错误。因此,同步相量序列中坏数据或丢数据的处理将是未来研究中值得关注的一个重点。
此外,针对次/超同步分量相位的辨识正在逐渐引起越来越多的重视。因为次/超同步分量的相位与幅值辨识结果相结合,可以进一步计算次/超同步潮流和等效阻抗,进而实现次/超同步振荡源的定位监测[13]。早期研究[17-18,33]并未对相位辨识给予足够重视,近期相关研究已将相位的辨识精度纳入考量[14-16,19]。
为了验证前文对基于同步相量数据参数辨识的特性,本节分别在不同场景下进行了次/超同步振荡参数辨识和对比分析,见表3。场景一和场景三由PSCAD仿真生成,场景二是实际次同步振荡事件中的PMU数据,三个场景均对电流参数进行辨识。本节采用文献[15]所用的基于插值DFT和汉宁窗的复数域频谱分析方法进行辨识,同步相量数据窗长为2 s。
表3 不同场景下的次/超同步振荡
Tab.3 Sub/supersynchronous oscillations in different cases
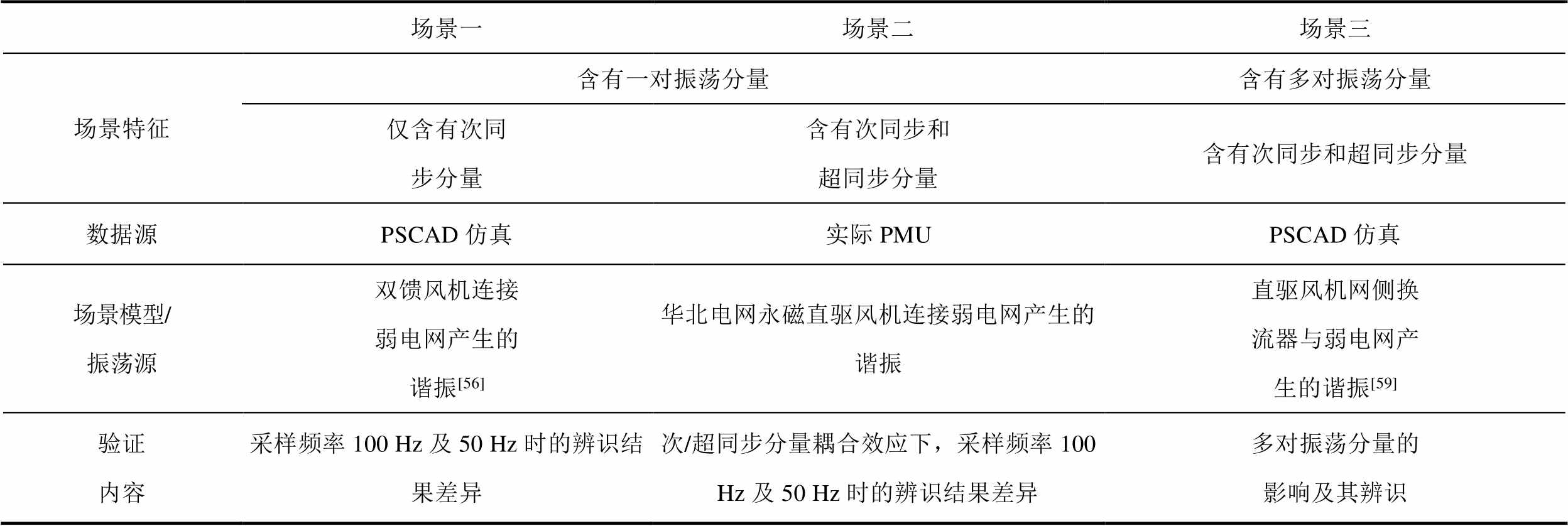
场景一场景二场景三 场景特征含有一对振荡分量含有多对振荡分量 仅含有次同步分量含有次同步和超同步分量含有次同步和超同步分量 数据源PSCAD仿真实际PMUPSCAD仿真 场景模型/振荡源双馈风机连接弱电网产生的谐振[56]华北电网永磁直驱风机连接弱电网产生的谐振直驱风机网侧换流器与弱电网产生的谐振[59] 验证内容采样频率100 Hz及50 Hz时的辨识结果差异次/超同步分量耦合效应下,采样频率100 Hz及50 Hz时的辨识结果差异多对振荡分量的影响及其辨识
本文分析了同步相量采样频率分别为100 Hz和50 Hz下的辨识结果,并与另外两种方法进行了对比分析:一种是基于同步相量的原始插值DFT法[18],该方法仅能辨识次同步分量参数而未考虑次/超同步分量之间的耦合关系;另一种是基于瞬时信号的Prony分析法[62],此方法被广泛用于振荡模式辨识,并以此作为基准。需要说明的是,尽管Prony分析法易受到噪声的影响,但本文算例验证所用的场景噪声含量很小,且瞬时信号数据采样频率高,因此对于Prony分析法的计算结果影响极小,可以忽略。
场景一是双馈风力发电机(Doubly Fed Induction Generator, DFIG)带并联补偿器并通过弱传输线连接到大电网的仿真系统。双馈感应发电机作为风力发电的常用机型之一,其定子侧与电网直接相连[63]。当风速下降时,DFIG和并联补偿器发生次同步谐振,振荡机理和仿真参数与文献[56]一致。这种SSO只包含次同步分量,超同步分量很小可近似忽略。场景一中电流瞬时值和对应的基波同步相量幅值如图6所示。针对88~90 s的2 s数据窗进行参数辨识,得到的辨识结果如图7所示,包括不同方法辨识的各分量频率和幅值。图7中的频谱是瞬时值的频谱,由于受频谱泄漏影响严重,仅作为峰值位置的参考,并非准确参数。
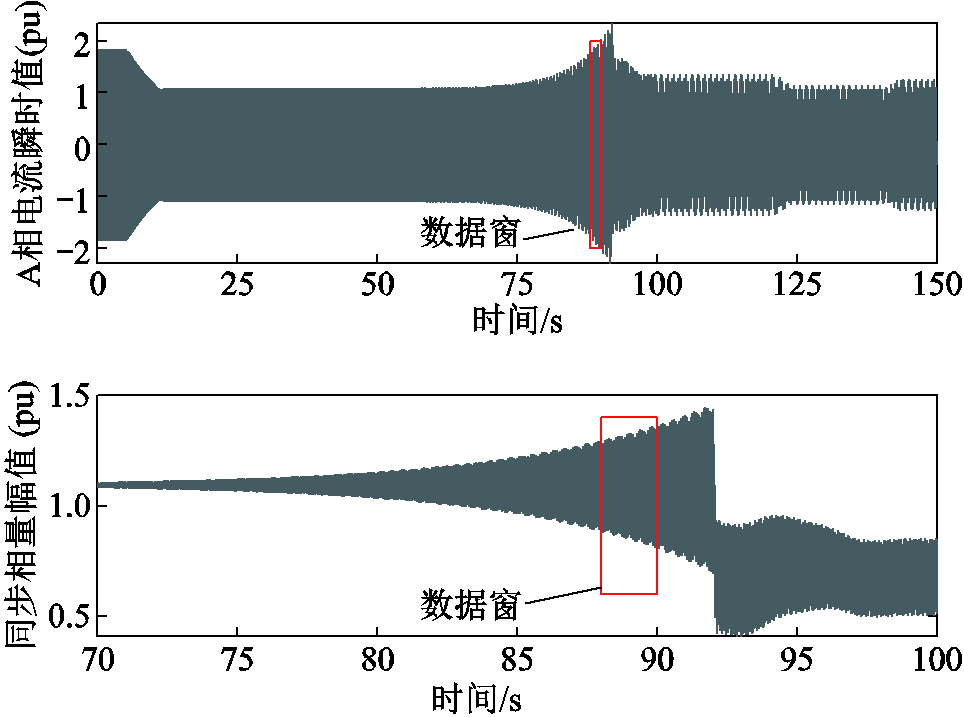
图6 场景一中的A相电流瞬时值和其对应的同步相量序列的幅值
Fig. 6 The instantaneous signal of A-phase current and the amplitudes of the corresponding synchrophasor sequence in Case 1
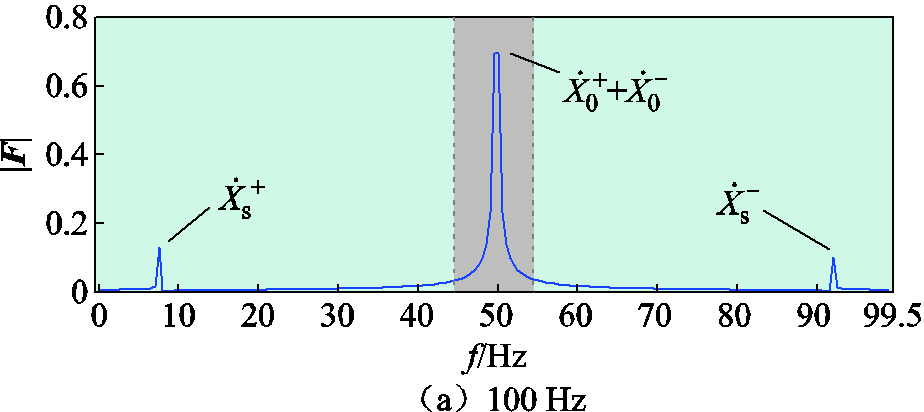
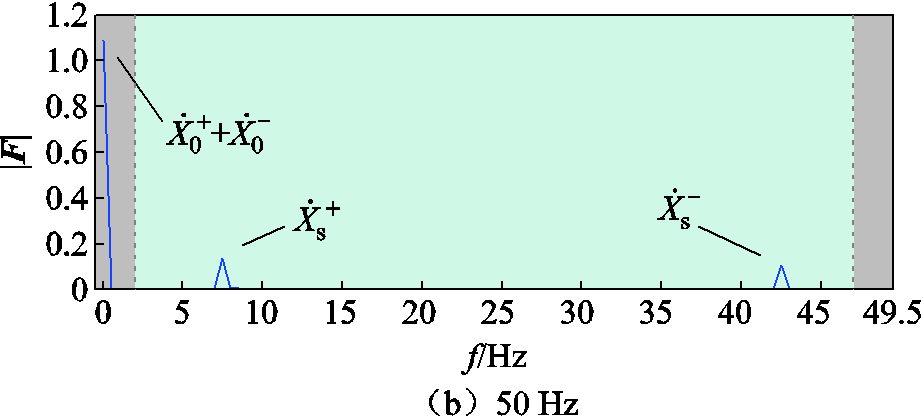
图7 场景一中100 Hz及50 Hz采样频率下同步相量频谱幅值
Fig.7 Synchronized phasor spectrum amplitudes at 100 Hz and 50 Hz sampling frequencies in Case 1
具体参数辨识结果见表4,包括基波分量的频率、幅值、相位以及次/超同步分量的频率、幅值、相位、阻尼因子。
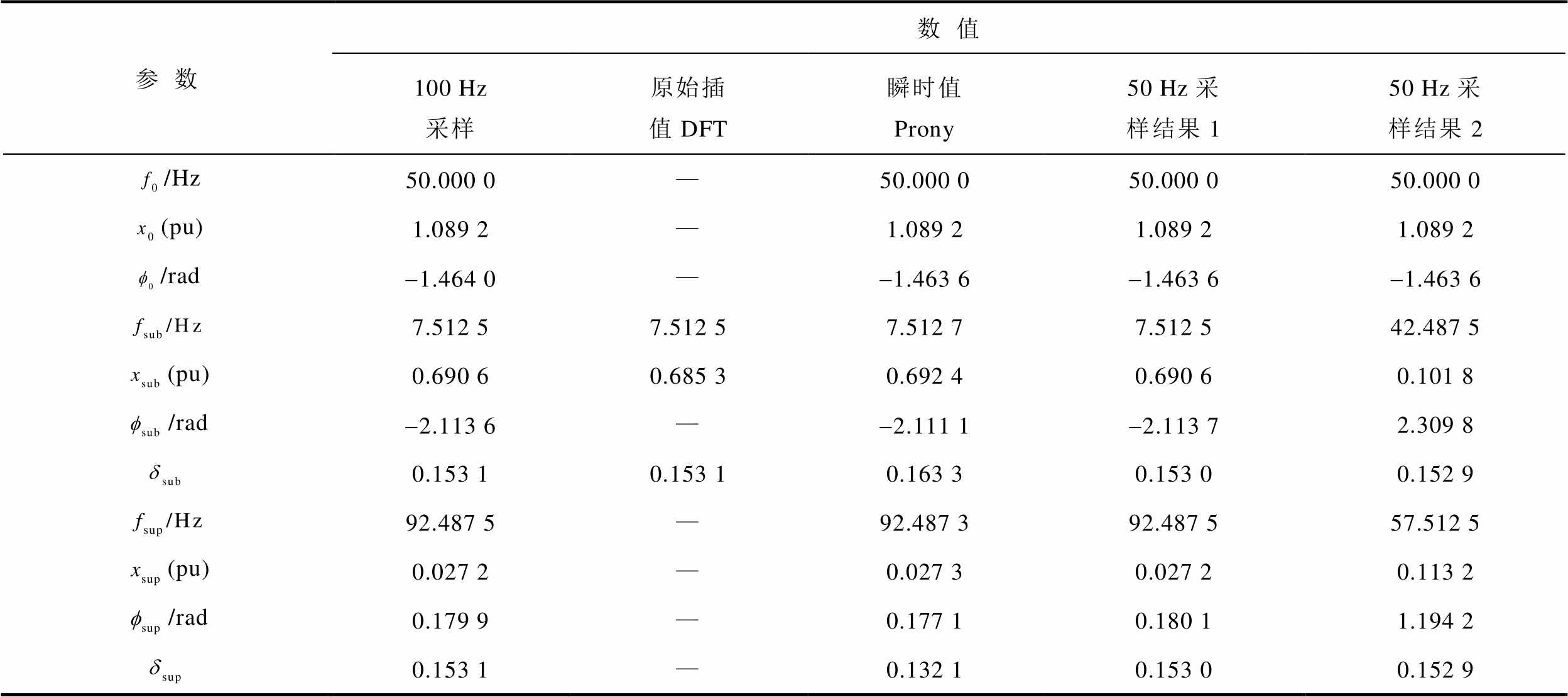
表4 场景一中用不同方法辨识出的参数
Tab. 4 Parameters identified by different methods in Case 1
参数数值 100 Hz采样原始插值DFT瞬时值Prony50 Hz采样结果150 Hz采样结果2 /Hz50.000 0—50.000 050.000 050.000 0 (pu)1.089 2—1.089 21.089 21.089 2 /rad-1.464 0—-1.463 6-1.463 6-1.463 6 7.512 57.512 57.512 77.512 542.487 5 (pu)0.690 60.685 30.692 40.690 60.101 8 /rad-2.113 6—-2.111 1-2.113 72.309 8 0.153 10.153 10.163 30.153 00.152 9 92.487 5—92.487 392.487 557.512 5 (pu)0.027 2—0.027 30.027 20.113 2 /rad0.179 9—0.177 10.180 11.194 2 0.153 1—0.132 10.153 00.152 9
从辨识结果来看,由于场景一几乎不包含超同步分量,尽管原始插值DFT法未考虑次/超同步分量之间的耦合关系,但仍能准确计算结果;本文方法在考虑次/超同步分量之间的耦合关系基础上计算出超同步分量幅值几乎为0,可准确判断不存在超同步分量。综上所述,本文方法和原始插值DFT法都与作为基准的Prony方法接近,验证了使用100 Hz采样频率可以对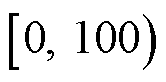 Hz内的次同步分量进行有效辨识。
Hz内的次同步分量进行有效辨识。
此外,本文方法在采样频率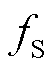 =50 Hz的情况下会辨识出两个结果,如3.2节所示,将
=50 Hz的情况下会辨识出两个结果,如3.2节所示,将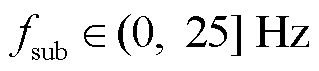 时的辨识结果标记为结果1,
时的辨识结果标记为结果1,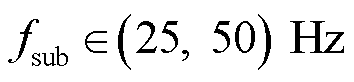 时的辨识结果标记为结果2(后文均以此标记)。场景一中实际频率为
时的辨识结果标记为结果2(后文均以此标记)。场景一中实际频率为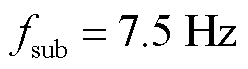 ,根据第3.2的分析,若给定条件1,即给定
,根据第3.2的分析,若给定条件1,即给定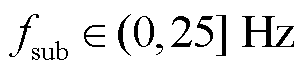 ,则可知结果1为正确结果,结果2错误;若不给定
,则可知结果1为正确结果,结果2错误;若不给定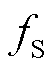 的范围,则无法排除错误结果2。若给定条件2,即给定场景一中只含有次同步分量而几乎不含有超同步分量,则根据如图7b所示的
的范围,则无法排除错误结果2。若给定条件2,即给定场景一中只含有次同步分量而几乎不含有超同步分量,则根据如图7b所示的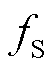 =50 Hz时的同步相量频谱幅值图像可知
=50 Hz时的同步相量频谱幅值图像可知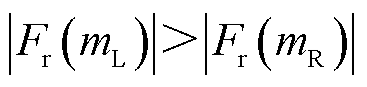 ,即
,即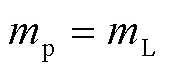 ,从而可以计算得到正确结果,验证了使用50 Hz采样频率下参数辨识特性的正确性。
,从而可以计算得到正确结果,验证了使用50 Hz采样频率下参数辨识特性的正确性。
场景二的数据是华北电网永磁直驱风机(Permanent Magnetic Synchronous Generator, PMSG)与弱电网间的SSO事件中由PMU实录的同步相量,其中既包括次同步分量也包括超同步分量。场景二中的电流瞬时值和对应同步相量幅值如图8所示,使用4~6 s的2 s数据窗进行参数辨识,与场景一中结果相似,得到的频谱结果如图9所示,具体参数辨识结果见表5,包括各方法辨识的各分量频率和幅值。
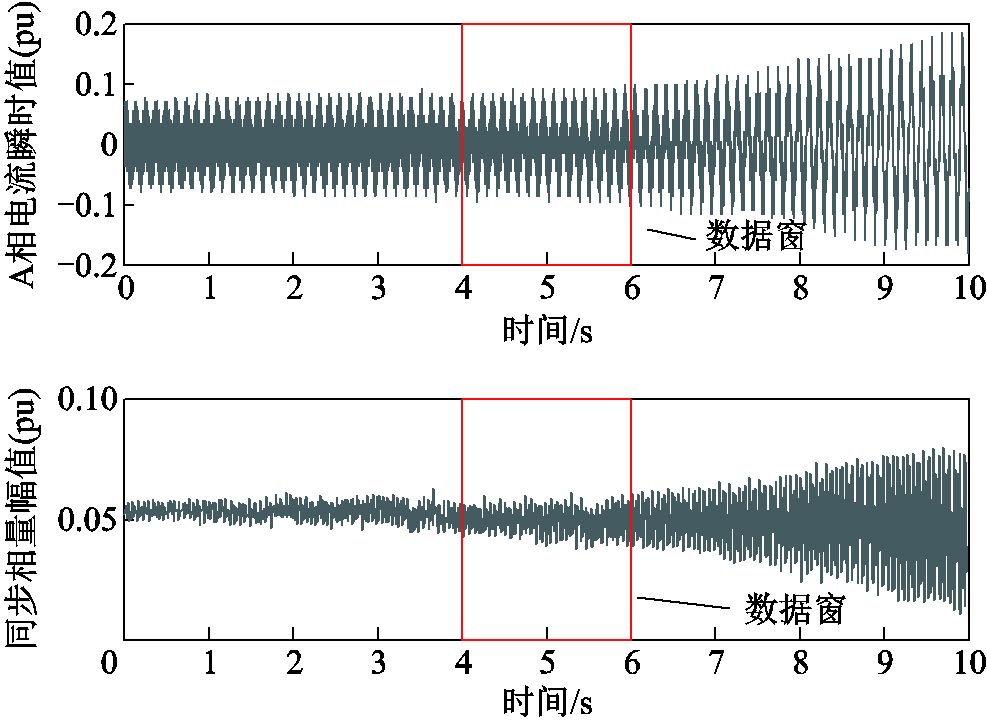
图8 场景二中的A相电流瞬时值和其对应的同步相量序列的幅值
Fig. 8 The instantaneous signal of A-phase current and the amplitudes of the corresponding synchrophasor sequence in Case 2
从辨识结果来看,在同时存在耦合的次同步分量和超同步分量的场景二中,原始插值DFT法由于没有考虑次/超同步分量间的耦合关系,仅能准确计算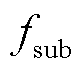 ,而
,而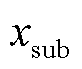 和
和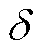 的辨识结果是错误的。本文方法由于考虑了此耦合关系,辨识结果与作为基准的Prony方法辨识结果接近。
的辨识结果是错误的。本文方法由于考虑了此耦合关系,辨识结果与作为基准的Prony方法辨识结果接近。
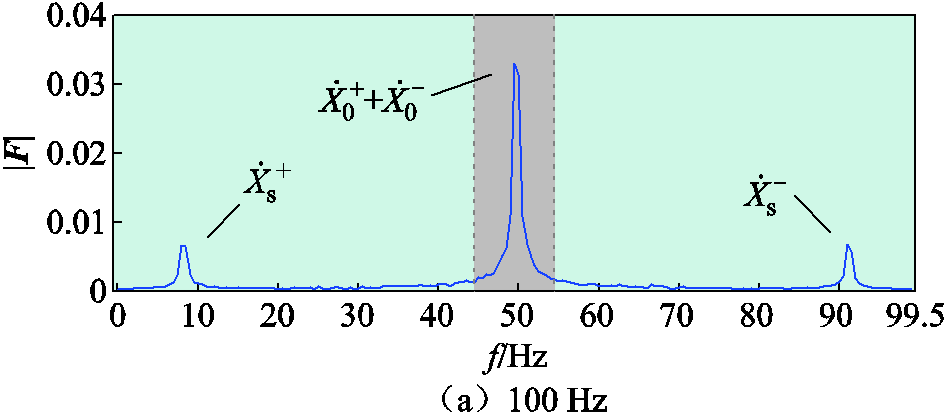
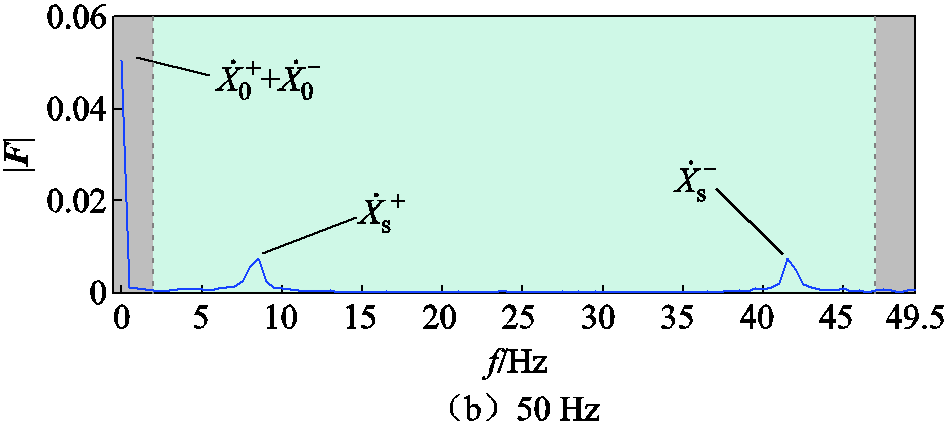
图9 场景二中100 Hz及50 Hz采样频率下同步相量频谱幅值
Fig.9 Synchronized phasor spectrum amplitudes at 100 Hz and 50 Hz sampling frequencies in Case 2
表5 场景二中用不同方法辨识出的参数
Tab. 5 Parameters identified by different methods in Case 2
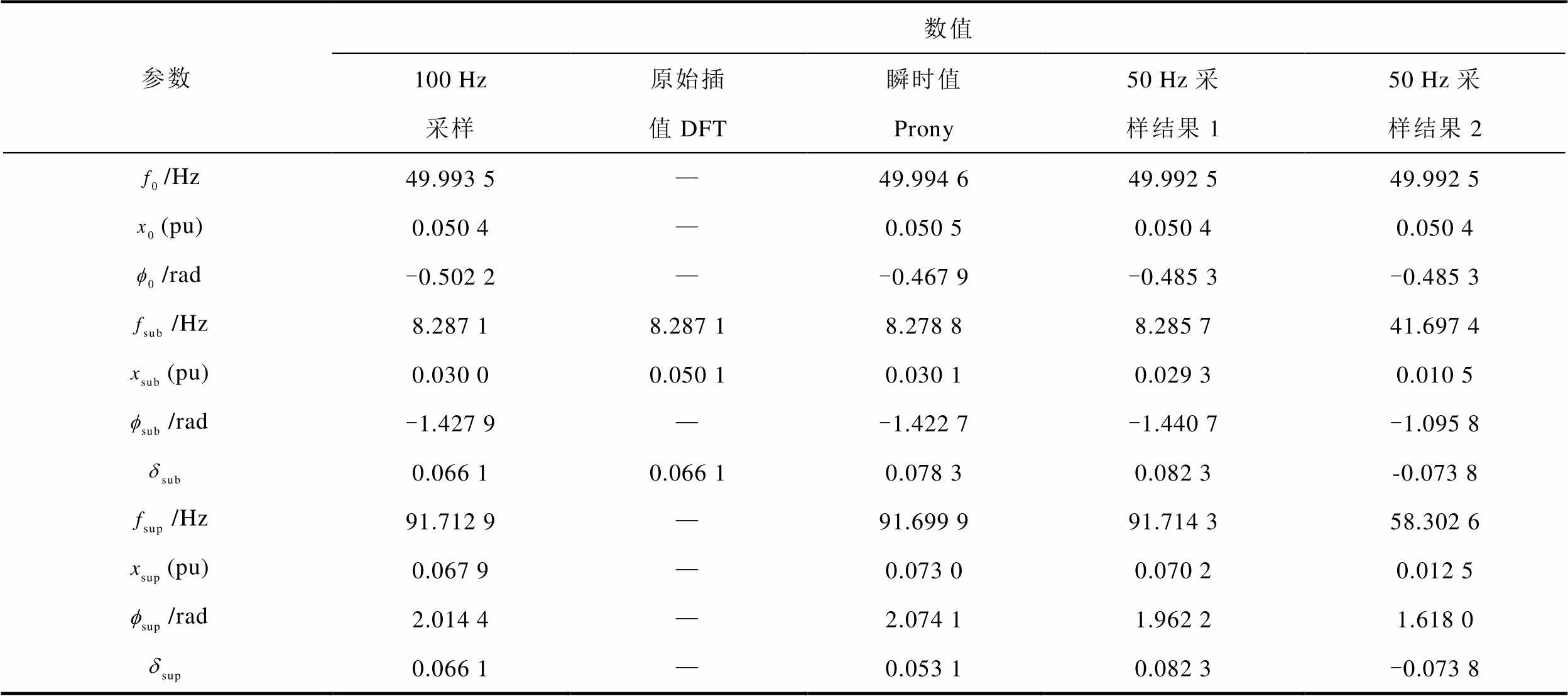
参数数值 100 Hz采样原始插值DFT瞬时值Prony50 Hz采样结果150 Hz采样结果2 /Hz49.993 5—49.994 649.992 549.992 5 (pu)0.050 4—0.050 50.050 40.050 4 /rad-0.502 2—-0.467 9-0.485 3-0.485 3 /Hz8.287 18.287 18.278 88.285 741.697 4 (pu)0.030 00.050 10.030 10.029 30.010 5 /rad-1.427 9—-1.422 7-1.440 7-1.095 8 0.066 10.066 10.078 30.082 3-0.073 8 /Hz91.712 9—91.699 991.714 358.302 6 (pu)0.067 9—0.073 00.070 20.012 5 /rad2.014 4—2.074 11.962 21.618 0 0.066 1—0.053 10.082 3-0.073 8
与场景一中相似,在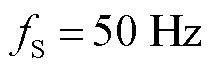 的条件下,如果给定条件1,即给定
的条件下,如果给定条件1,即给定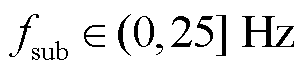 ,则可知结果1正确,结果2错误。此场景不满足条件2,因此无法作为仅存在次同步分量的情况进行计算。此场景验证了使用100 Hz采样频率可以对
,则可知结果1正确,结果2错误。此场景不满足条件2,因此无法作为仅存在次同步分量的情况进行计算。此场景验证了使用100 Hz采样频率可以对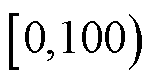 Hz内的次同步振荡进行有效辨识,而使用50 Hz采样频率时,在补充频率范围后即可进行参数辨识。
Hz内的次同步振荡进行有效辨识,而使用50 Hz采样频率时,在补充频率范围后即可进行参数辨识。
场景三是直驱风机网侧换流器控制系统对电网谐波响应过程引发的次/超同步振荡,其中包括基波分量及多对振荡分量,振荡机理和仿真系统参数与文献[59]一致。
场景三中的电流瞬时值和同步相量幅值如图10所示,使用2 ~4 s的2 s数据窗进行参数辨识。与场景一中结果相似,得到的频谱结果如图11所示,辨识结果如图12所示,包括各方法辨识的各分量频率和幅值。
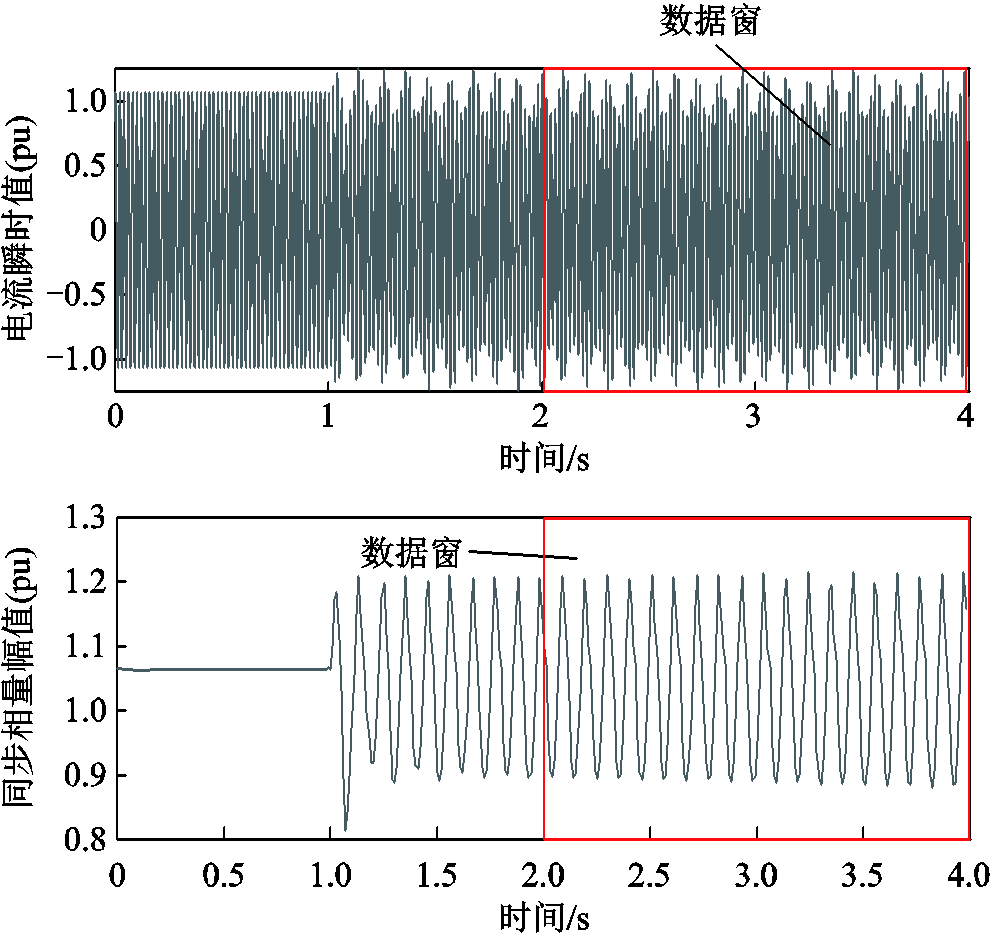
图10 场景三中的电流瞬时值和其对应的同步相量序列的幅值
Fig. 10 The instantaneous signal of current and the amplitudes of the corresponding synchrophasor sequence in Case 3
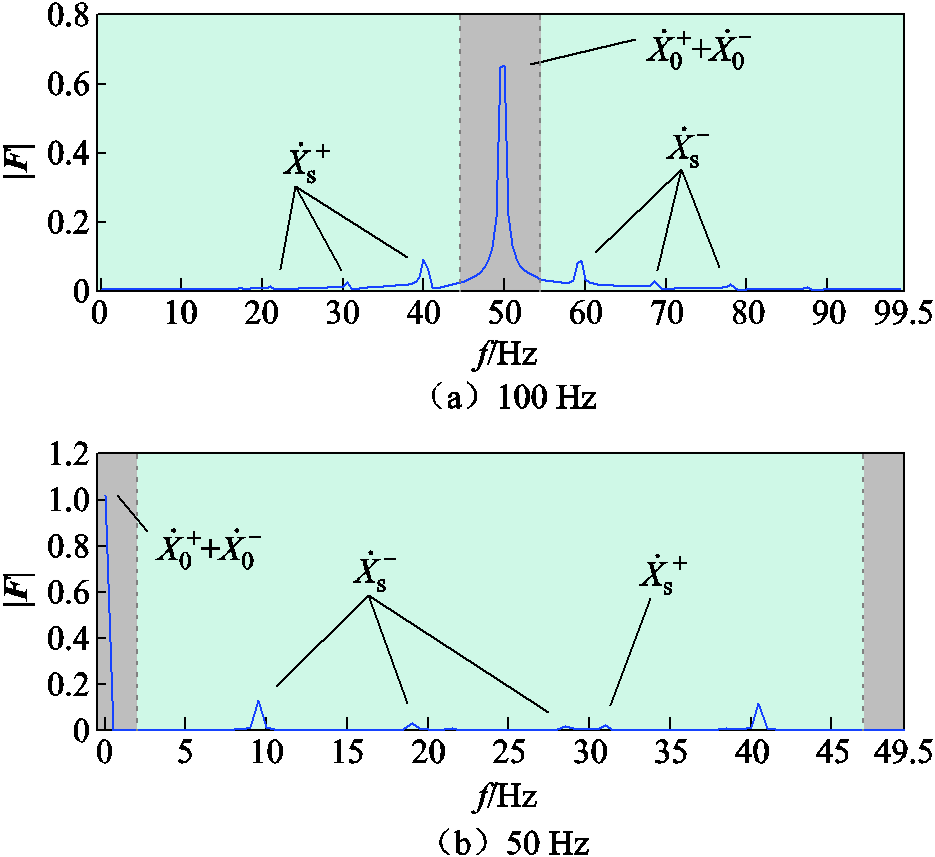
图11 场景三中100 Hz及50 Hz采样频率下同步相量频谱幅值
Fig.11 Synchronized phasor spectrum amplitudes at 100 Hz and 50 Hz sampling frequencies in Case 3
数据中主要包括三对振荡分量,它们的频率在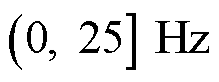 及
及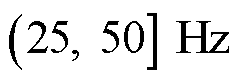 内均有分布。在采样频率为50 Hz时,对于某一对振荡分量,其辨识结果中包含一个正确和一个错误的计算结果,若给定各对振荡分量频率的范围条件,即可得出其正确计算结果。在图11中,若给定第一对次/超同步分量中次同步频率在
内均有分布。在采样频率为50 Hz时,对于某一对振荡分量,其辨识结果中包含一个正确和一个错误的计算结果,若给定各对振荡分量频率的范围条件,即可得出其正确计算结果。在图11中,若给定第一对次/超同步分量中次同步频率在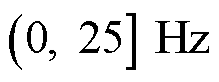 范围内(频谱峰值在40 Hz附近),则50 Hz采样中的正确结果与其他方法的计算结果接近。在采样频率为100 Hz时,其计算结果与作为标准的Prony方法计算结果接近,100 Hz的同步相量更适用于多对振荡分量的有效辨识。此场景验证了在多对振荡的情况下,使用100 Hz采样频率及在给定适用范围条件下使用50 Hz采样频率可以有效进行参数辨识,同前文所述特性相符合。
范围内(频谱峰值在40 Hz附近),则50 Hz采样中的正确结果与其他方法的计算结果接近。在采样频率为100 Hz时,其计算结果与作为标准的Prony方法计算结果接近,100 Hz的同步相量更适用于多对振荡分量的有效辨识。此场景验证了在多对振荡的情况下,使用100 Hz采样频率及在给定适用范围条件下使用50 Hz采样频率可以有效进行参数辨识,同前文所述特性相符合。
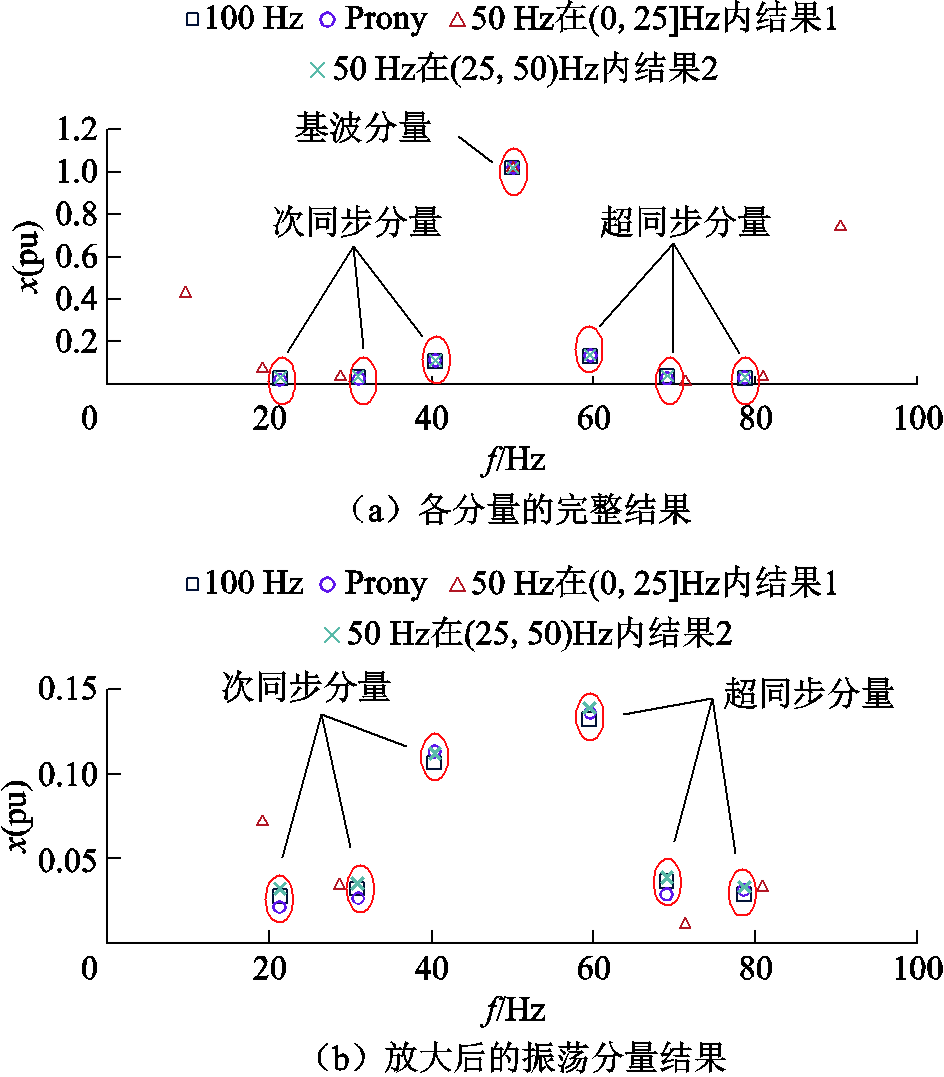
图12 场景三中各分量的频率和幅值辨识结果对比
Fig. 12 Comparison of frequency and amplitude identification results for each component in Case 3
为充分发挥广域同步相量测量的广域同步和高刷新率的核心优势,实现次/超同步振荡的高实时性在线监测,本文分析了基波同步相量在次/超同步振荡下的变化特性及其复数域频谱特征。以频谱分析为工具,综述并分析了目前已有次/超同步振荡参数辨识方法的适用范围、关键难题、解决方法及新问题,尤其是围绕复数域频谱分析方法分析了其特点、优势和局限。最终,本文利用仿真数据和实际PMU数据进行了验证和对比分析,得到了以下结论:
1)基波同步相量的次/超同步振荡参数辨识受同步相量的采样频率(即报告率)影响,可辨识频率范围满足复数的采样定理。具体地,采样频率为100 Hz的基波同步相量数据序列可辨识出所有次/超同步分量的参数而无需额外信息;采样频率为 50 Hz时,需要在额外条件的辅助下才能区分错误结果进而有效辨识次/超同步振荡参数。
2)基波同步相量的次/超同步振荡参数辨识的基本问题和核心问题是如何使用更短的同步相量序列数据窗实现高精度的参数辨识。由于频率分辨率与数据窗长之间存在固有矛盾,所有的参数辨识方法均面临这一共同问题,这也是未来参数辨识方法的突破点之一。
3)有必要计及次/超同步振荡之间的频率耦合关系对参数辨识的影响。原因是,绝大多数新能源接入引发的次同步振荡事件中均存在与次同步分量耦合的超同步分量。而次/超同步分量之间的耦合是振荡正/负频率的完全耦合而并不能简单认为它是互相的频谱泄漏,这与基波和次/超同步分量之间的影响是完全不同的问题。此外,仅从复数域频谱幅值并不能准确可靠地检测是否存在超同步分量,直接辨识超同步分量的参数是更行之有效的方法。
4)基于DFT频谱分析方法的显著优点是原理简单、计算复杂度低、计算量小,尤其是频谱结果直观而适用于存在多对振荡分量的情况。但频谱分析类方法在处理频谱泄漏时需将其做近似处理,导致目前尽管使用性能更好的窗函数也难以进一步缩短数据窗长度,而非DFT方法在这一问题上可能有所突破。
5)对参数辨识算法的适应性分析有必要考虑瞬时值中测量噪声的影响。而同步相量序列中的丢数据和坏数据问题在实际应用中可能存在而有必要进一步考虑,目前已有方法均依赖同步相量序列的连续性而未有相关深入研究,这将是基于基波同步相量的次/超同步振荡参数辨识方法在实用性方面的另一重要突破点。
参考文献
[1] 谢小荣, 贺静波, 毛航银, 等. “双高”电力系统稳定性的新问题及分类探讨[J]. 中国电机工程学报, 2021, 41(2): 461-475.
Xie Xiaorong, He Jingbo, Mao Hangyin, et al. New issues and classification of power system stability with high shares of renewables and power electronics[J]. Proceedings of the CSEE, 2021, 41(2): 461-475.
[2] 占颖, 吴琛, 谢小荣, 等. 风电并网系统次同步振荡的频域模式分析[J]. 电力系统自动化, 2020, 44(18): 90-97.
Zhan Ying, Wu Chen, Xie Xiaorong, et al. Frequency domain modal analysis of subsynchronous oscillation in grid-connected wind power system[J]. Automation of Electric Power Systems, 2020, 44(18): 90-97.
[3] 占颖, 谢小荣, 柴炜, 等. 风电次/超同步振荡的安全域分析[J]. 中国电机工程学报, 2022, 42(23): 8446-8454.
Zhan Ying, Xie Xiaorong, Chai Wei, et al. Analyzing the security region of sub/super-synchronous oscillation in wind power integrated systems[J]. Proceedings of the CSEE, 2022, 42(23): 8446-8454.
[4] 肖湘宁, 罗超, 廖坤玉. 新能源电力系统次同步振荡问题研究综述[J]. 电工技术学报, 2017, 32(6): 85-97.
Xiao Xiangning, Luo Chao, Liao Kunyu. Review of the research on subsynchronous oscillation issues in electric power system with renewable energy sources[J]. Transactions of China Electrotechnical Society, 2017, 32(6): 85-97.
[5] 李明节, 于钊, 许涛, 等. 新能源并网系统引发的复杂振荡问题及其对策研究[J]. 电网技术, 2017, 41(4): 1035-1042.
Li Mingjie, Yu Zhao, Xu Tao, et al. Study of complex oscillation caused by renewable energy integration and its solution[J]. Power System Technology, 2017, 41(4): 1035-1042.
[6] 马宁宁, 谢小荣, 亢朋朋, 等. 高比例风电并网系统次同步振荡的广域监测与分析[J]. 中国电机工程学报, 2021, 41(1): 65-74, 398.
Ma Ningning, Xie Xiaorong, Kang Pengpeng, et al. Wide-area monitoring and analysis of subsynchronous oscillation in power systems with high-penetration of wind power[J]. Proceedings of the CSEE, 2021, 41(1): 65-74, 398.
[7] 谢小荣, 刘华坤, 贺静波, 等. 电力系统新型振荡问题浅析[J]. 中国电机工程学报, 2018, 38(10): 2821-2828, 3133.
Xie Xiaorong, Liu Huakun, He Jingbo, et al. On new oscillation issues of power systems[J]. Proceedings of the CSEE, 2018, 38(10): 2821-2828, 3133.
[8] Shair J, Xie Xiaorong, Yang Jianjun, et al. Adaptive damping control of subsynchronous oscillation in DFIG-based wind farms connected to series-compensated network[J]. IEEE Transactions on Power Delivery, 2022, 37(2): 1036-1049.
[9] 张路, 陈军, 赵启, 等. 新疆电网次同步振荡控制系统及其测试方法研究[J]. 电气技术, 2022, 23(12): 31-37.
Zhang Lu, Chen Jun, Zhao Qi, et al. Research on sub-synchronous oscillation control system for Xinjiang power grid and its test method[J]. Electrical Engineering, 2022, 23(12): 31-37.
[10] 邵冰冰, 赵峥, 肖琪, 等. 多直驱风机经柔直并网系统相近次同步振荡模式参与因子的弱鲁棒性分析[J]. 电工技术学报, 2023, 38(3): 754-769.
Shao Bingbing, Zhao Zheng, Xiao Qi, et al. Weak robustness analysis of close subsynchronous oscillation modes’ participation factors in multiple direct-drive wind turbines with the VSC-HVDC system[J]. Transactions of China Electrotechnical Society, 2023, 38(3): 754-769.
[11] Xie Xiaorong, Zhan Ying, Liu Huakun, et al. Wide-area monitoring and early-warning of subsynchronous oscillation in power systems with high-penetration of renewables[J]. International Journal of Electrical Power & Energy Systems, 2019, 108: 31-39.
[12] Mahish P, Pradhan A K. Mitigating subsynchronous resonance using synchrophasor data based control of wind farms[J]. IEEE Transactions on Power Delivery, 2020, 35(1): 364-376.
[13] Xie Xiaorong, Zhan Ying, Shair J, et al. Identifying the source of subsynchronous control interaction via wide-area monitoring of sub/super-synchronous power flows[J]. IEEE Transactions on Power Delivery, 2020, 35(5): 2177-2185.
[14] Wang Yang, Jiang Xiaolong, Xie Xiaorong, et al. Identifying sources of subsynchronous resonance using wide-area phasor measurements[J]. IEEE Transactions on Power Delivery, 2021, 36(5): 3242-3254.
[15] Zhang Fang, Li Jiaxin, Liu Jun, et al. An improved interpolated DFT-based parameter identification for sub-/super-synchronous oscillations with synchro-phasors[J]. IEEE Transactions on Power Systems, 2023, 38(2): 1714-1727.
[16] 王杨, 晁苗苗, 谢小荣, 等. 基于同步相量数据的次同步振荡参数辨识与实测验证[J]. 中国电机工程学报, 2022, 42(3): 899-909.
Wang Yang, Chao Miaomiao, Xie Xiaorong, et al. Identification of subsynchronous oscillation parameters and field tests based on PMU data[J]. Proceedings of the CSEE, 2022, 42(3): 899-909.
[17] Zhang Fang, Cheng Lin, Gao Wenzhong, et al. Synchrophasors-based identification for subsynchronous oscillations in power systems[J]. IEEE Transactions on Smart Grid, 2019, 10(2): 2224-2233.
[18] Yang Xiaomei, Zhang Jianing, Xie Xiaorong, et al. Interpolated DFT-based identification of sub-synchronous oscillation parameters using synchrophasor data[J]. IEEE Transactions on Smart Grid, 2020, 11(3): 2662-2675.
[19] 马钺, 蔡东升, 黄琦. 基于Rife-Vincent窗和同步相量测量数据的风电次同步振荡参数辨识[J]. 中国电机工程学报, 2021, 41(3): 790-803.
Ma Yue, Cai Dongsheng, Huang Qi. Parameter identification of wind power sub-synchronous oscillation based on Rife-Vincent window and synchrophasor data[J]. Proceedings of the CSEE, 2021, 41(3): 790-803.
[20] Laila D S, Messina A R, Pal B C. A refined Hilbert-Huang transform with applications to inter-area oscillation monitoring[C]//2009 IEEE Power & Energy Society General Meeting, Calgary, AB, Canada, 2009: 1.
[21] Zhou Ning, Trudnowski D J, Pierre J W, et al. Electromechanical mode online estimation using regularized robust RLS methods[J]. IEEE Transactions on Power Systems, 2008, 23(4): 1670-1680.
[22] 董青迅, 李兴源, 穆子龙, 等. 基于Prony算法的次同步谐振检测方法[J]. 电力系统及其自动化学报, 2012, 24(2): 1-4, 34.
Dong Qingxun, Li Xingyuan, Mu Zilong, et al. New method for detection of sub-synchronous resonance based on Prony algorithm[J]. Proceedings of the Chinese Society of Universities for Electric Power System and Its Automation, 2012, 24(2): 1-4, 34.
[23] 王茂海, 高洵, 王蓓, 等. 基于广域测量系统的次同步振荡在线监测预警方法[J]. 电力系统自动化, 2011, 35(6): 98-102.
Wang Maohai, Gao Xun, Wang Bei, et al. Online early-warning of sub-synchronous oscillations based on wide area measurement system[J]. Automation of Electric Power Systems, 2011, 35(6): 98-102.
[24] 张敏, 沈健, 侯明国, 等. 相量测量单元实现次同步振荡在线辨识和告警的探讨[J]. 电力系统自动化, 2016, 40(16): 143-146, 152.
Zhang Min, Shen Jian, Hou Mingguo, et al. Discussion on on-line identification and warning of subsynchronous oscillation for phasor measuring unit[J]. Automation of Electric Power Systems, 2016, 40(16): 143-146, 152.
[25] Wang Maohai, Sun Yuanzhang. A practical, precise method for frequency tracking and phasor estimation[J]. IEEE Transactions on Power Delivery, 2004, 19(4): 1547-1552.
[26] 王茂海, 齐霞. 电力系统次同步振荡分量的快速在线检测算法[J]. 电力系统自动化, 2016, 40(18): 149-154.
Wang Maohai, Qi Xia. Fast online detection method for power system sub-synchronous oscillation components[J]. Automation of Electric Power Systems, 2016, 40(18): 149-154.
[27] Rauhala T, Gole A M, Järventausta P. Detection of subsynchronous torsional oscillation frequencies using phasor measurement[J]. IEEE Transactions on Power Delivery, 2016, 31(1): 11-19.
[28] Liu Hao, Bi Tianshu, Chang Xiqiang, et al. Impacts of subsynchronous and supersynchronous frequency components on synchrophasor measurements[J]. Journal of Modern Power Systems and Clean Energy, 2016, 4(3): 362-369.
[29] 刘灏, 李珏, 毕天姝, 等. 基于PMU相量的次/超同步间谐波识别方法[J]. 电网技术, 2017, 41(10): 3237-3245.
Liu Hao, Li Jue, Bi Tianshu, et al. Subsynchronous and supersynchronous inter-harmonic identification method based on phasor measurements[J]. Power System Technology, 2017, 41(10): 3237-3245.
[30] Liu Hao, Qi Yuan, Zhao Junbo, et al. Data-driven subsynchronous oscillation identification using field synchrophasor measurements[J]. IEEE Transactions on Power Delivery, 2022, 37(1): 165-175.
[31] 王渝红, 王宏宇, 于光远, 等. 基于同步相量数据的次同步振荡检测与模态参数辨识方法[J]. 高电压技术, 2023, 49(6): 2557-2568.
Wang Yuhong, Wang Hongyu, Yu Guangyuan, et al. Sub-synchronous oscillation detection and modal parameter identification method based on synchrophasor [J]. High Voltage Engineering, 2023, 49(6): 2557-2568.
[32] 张放, 刘军, 李佳欣, 等. 基于同步相量轨迹拟合的电力系统次同步/超同步振荡的实时参数辨识[J]. 中国电机工程学报, 2023, 43(4): 1413-1426.
Zhang Fang, Liu Jun, Li Jiaxin, et al. Real-time parameter identification with synchrophasor trajectory fitting technique for subsynchronous/supersynchronous oscillations in power systems[J]. Proceedings of the CSEE, 2023, 43(4): 1413-1426.
[33] Yang Xiaomei, Yang Lin, Xiao Xianyong, et al. A novel detection method for supersynchronous resonance from synchrophasor data[J]. IEEE Transactions on Power Systems, 2023, 38(4): 3694-3706.
[34] Wang Yuhong, Wang Hongyu, Song Yuyan, et al. Parameter identification of sub-synchronous/super-synchronous oscillations based on synchrophasor rotation and spectral shift[J]. International Journal of Electrical Power & Energy Systems, 2023, 149: 109044.
[35] Wu Chen, Sheng Jie, Cheng Guangying, et al. Wide-band phasor measurement unit: design and test[C]// 2019 IEEE Innovative Smart Grid Technologies-Asia (ISGT Asia), Chengdu, China, 2019: 1116-1120.
[36] 樊陈, 姚建国, 常乃超, 等. 面向电力电子化电网的宽频测量技术探讨[J]. 电力系统自动化, 2019, 43(16): 1-8, 57.
Fan Chen, Yao Jianguo, Chang Naichao, et al. Discussion on wide-frequency measurement technology for power electronized power grid[J]. Automation of Electric Power Systems, 2019, 43(16): 1-8, 57.
[37] 吴艳平, 姚建国, 常乃超, 等. 多功能宽频测量装置的设计与实现[J]. 电力系统自动化, 2020, 44(20): 136-141.
Wu Yanping, Yao Jianguo, Chang Naichao, et al. Design and implementation of multi-functional wide-frequency measurement device[J]. Automation of Electric Power Systems, 2020, 44(20): 136-141.
[38] 南京南瑞继保电气有限公司. PCS-993C振荡监测与控制装置[EB/OL]. https://nrec.com/cn/index.php/ product/list/21/37.
[39] 北京四方继保自动化股份有限公司. CSD-360系列同步相量测量装置[EB/OL]. https://www.sf-auto.com/ productDetail/3155.html.
[40] 徐衍会, 成蕴丹, 刘慧, 等. 基于瞬时功率的次同步振荡频率提取及振荡源识别方法[J]. 电工技术学报, 2023, 38(11): 2894-2907.
Xu Yanhui, Cheng Yundan, Liu Hui, et al. Subsynchronous oscillation frequency extraction and oscillation source identification method based on instantaneous power[J]. Transactions of China Electrotechnical Society, 2023, 38(11): 2894-2907.
[41] 樊陈, 姚建国, 常乃超, 等. 电力系统宽频测量装置技术规范解读及应用展望[J]. 电力系统自动化, 2023, 47(5): 190-199.
Fan Chen, Yao Jianguo, Chang Naichao, et al. Interpretation of technical specification for wide-frequency measurement device of power system and prospect of its application[J]. Automation of Electric Power Systems, 2023, 47(5): 190-199.
[42] 刘灏, 任小伟, 田建南, 等. 基于K-ESPRIT的快速宽频测量方法[J]. 电力系统自动化, 2020, 44(10): 186-192.
Liu Hao, Ren Xiaowei, Tian Jiannan, et al. Fast wide-frequency measurement method based on kurtosis-estimation of signal parameters via rotation invariance technique[J]. Automation of Electric Power Systems, 2020, 44(10): 186-192.
[43] 刘灏, 李进生, 毕天姝, 等. 基于改进Prony的动态宽频测量算法[J]. 电网技术, 2023, 47(5): 2119-2128.
Liu Hao, Li Jinsheng, Bi Tianshu, et al. Dynamic wide-frequency measurement algorithm based on improved Prony[J]. Power System Technology, 2023, 47(5): 2119-2128.
[44] 马宁宁, 谢小荣, 唐健, 等. “双高”电力系统宽频振荡广域监测与预警系统[J]. 清华大学学报(自然科学版), 2021, 61(5): 457-464.
Ma Ningning, Xie Xiaorong, Tang Jian, et al. Wide-area measurement and early warning system for wide-band oscillations in “double-high” power systems[J]. Journal of Tsinghua University (Science and Technology), 2021, 61(5): 457-464.
[45] IEEE standard for synchrophasor measurements for power systems: IEEE Std C37.118.1—2011 (Revision of IEEE Std C37.118-2005)[S]. IEEE, 2011.
[46] Ren Wei, Larsen E. A refined frequency scan approach to sub-synchronous control interaction (SSCI) study of wind farms[J]. IEEE Transactions on Power Systems, 2016, 31(5): 3904-3912.
[47] 南京南瑞继保电气有限公司. PCS-996-H2同步相量测量系统[EB/OL]. https://www.nrec.com/cn/index. php/product/list/21/65.
[48] 余高旺, 方陈, 樊占峰, 等. 基于汉宁窗的配电网同步相量测量装置算法及应用[J]. 中国电力, 2022, 55(6): 18-24.
Yu Gaowang, Fang Chen, Fan Zhanfeng, et al. Research and application of algorithm for distribution network synchronous phasor measurement unit based on hanning window[J]. Electric Power, 2022, 55(6): 18-24.
[49] Netto M, Mili L. A robust prony method for power system electromechanical modes identification[C]// 2017 IEEE Power & Energy Society General Meeting, Chicago, IL, USA, 2018: 1-5.
[50] Khalilinia H, Venkatasubramanian V. Subsynchronous resonance monitoring using ambient high speed sensor data[J]. IEEE Transactions on Power Systems, 2016, 31(2): 1073-1083.
[51] Bertocco M, Frigo G, Narduzzi C, et al. Resolution enhancement by compressive sensing in power quality and phasor measurement[J]. IEEE Transactions on Instrumentation and Measurement, 2014, 63(10): 2358-2367.
[52] Jain S K, Singh S N. Exact model order ESPRIT technique for harmonics and interharmonics estimation[J]. IEEE Transactions on Instrumentation and Measurement, 2012, 61(7): 1915-1923.
[53] Bertocco M, Frigo G, Narduzzi C, et al. Compressive sensing of a Taylor-Fourier multifrequency model for synchrophasor estimation[J]. IEEE Transactions on Instrumentation and Measurement, 2015, 64(12): 3274-3283.
[54] Narduzzi C, Bertocco M, Frigo G, et al. Fast-TFM—multifrequency phasor measurement for distribution networks[J]. IEEE Transactions on Instrumentation and Measurement, 2018, 67(8): 1825-1835.
[55] Arrieta Paternina M R, Tripathy R K, Zamora Mendez A, et al. Identification of electromechanical oscillatory modes based on variational mode decomposition[J]. Electric Power Systems Research, 2019, 167: 71-85.
[56] Wang Liang, Xie Xiaorong, Jiang Qirong, et al. Investigation of SSR in practical DFIG-based wind farms connected to a series-compensated power system[J]. IEEE Transactions on Power Systems, 2015, 30(5): 2772-2779.
[57] Liu Huakun, Xie Xiaorong, He Jingbo, et al. Subsynchronous interaction between direct-drive PMSG based wind farms and weak AC networks[J]. IEEE Transactions on Power Systems, 2017, 32(6): 4708-4720.
[58] Wang Liang, Xie Xiaorong, Jiang Qirong, et al. Mitigation of multimodal subsynchronous resonance via controlled injection of supersynchronous and subsynchronous currents[J]. IEEE Transactions on Power Systems, 2014, 29(3): 1335-1344.
[59] 徐衍会, 曹宇平. 直驱风机网侧换流器引发次/超同步振荡机理研究[J]. 电网技术, 2018, 42(5): 1556-1564.
Xu Yanhui, Cao Yuping. Research on mechanism of sub/sup-synchronous oscillation caused by GSC controller of direct-drive permanent magnetic synchronous generator[J]. Power System Technology, 2018, 42(5): 1556-1564.
[60] 李景一, 毕天姝, 于钊, 等. 直驱风机变流控制系统对次同步频率分量的响应机理研究[J]. 电网技术, 2017, 41(6): 1734-1740.
Li Jingyi, Bi Tianshu, Yu Zhao, et al. Study on response characteristics of grid converter control system of permanent magnet synchronous generators (PMSG) to subsynchronous frequency component[J]. Power System Technology, 2017, 41(6): 1734-1740.
[61] Brown M, Biswal M, Brahma S, et al. Characterizing and quantifying noise in PMU data[C]//2016 IEEE Power and Energy Society General Meeting (PESGM), Boston, MA, USA, 2016: 1-5.
[62] Almunif A, Fan Lingling, Miao Zhixin. A tutorial on data-driven eigenvalue identification: Prony analysis, matrix pencil, and eigensystem realization algorithm [J]. International Transactions on Electrical Energy Systems, 2020, 30(4): e12283.1-e12283.17.
[63] 孙东阳, 孟繁易, 王南, 等. 基于反步自适应准谐振控制的双馈风机次同步振荡抑制策略[J]. 电工技术学报, 2023, 38(9): 2375-2390, 2434.
Sun Dongyang, Meng Fanyi, Wang Nan, et al. DFIG sub-synchronous oscillation suppression strategy based on backstepping adaptive quasi-resonant control[J]. Transactions of China Electrotechnical Society, 2023, 38(9): 2375-2390, 2434.
Abstract Subsynchronous oscillations (SSO) caused by considerable renewable generation and power electronic equipment seriously affect the stability of power systems. The parameter identification of sub/supersynchronous oscillations based on fundamental synchrophasors, which are provided by the wide-area measurement system (WAMS) and phasor measurement units (PMU), has the core advantages of wide-area synchronization and high refresh rate. These advantages will enhance the dynamic monitoring of sub/supersynchronous oscillations significantly. Based on the complex spectrum characteristics of the fundamental synchrophasors under sub/supersynchronous oscillations, this paper summarizes and analyzes the parameter identification characteristics and essential issues of the existing parameter identification techniques for sub/supersynchronous oscillations. First, the identified frequency range, the coupling characteristics of each component, and the phase reversal characteristics are analyzed according to the spectrum of synchrophasors. Then, the essential issues of the parameter identification are analyzed, including the spectrum leakage problem, the decoupling problems of the coupled relationship of the oscillational component and the coupled relationship of the fundamental component, respectively. Focusing on the spectrum-based techniques, three essential difficulties in solving the above problems are concluded and analyzed: the problem of effectively identifying the supersynchronous component considering the coupled relationship between the sub/supersynchronous components, the adaptability of parameter identification under different synchrophasor refresh frequencies, and the issue of dealing with spectrum leakages to shorten the data window. Thus, this paper summarizes the corresponding solutions and looks forward to the possible technological breakthroughs in the future.
The results of simulation data and actual PMU data in different cases show that in the case of a single subsynchronous oscillation component, a couple of sub/supersynchronous oscillation components, and multiple couples of sub/supersynchronous oscillation components, spectrum-based techniques can effectively identify parameters using a sampling frequency of 100 Hz or under a given applicable range using a sampling frequency of 50 Hz.
The following conclusions can be drawn:
(1) The sub/super-synchronous oscillation parameter identification with synchrophasors is affected by the synchrophasor sampling frequency (i.e., the reporting rate), and the identifiable frequency range conforms to the sampling theorem with complex numbers. Specifically, using synchrophasors with a sampling frequency of 100 Hz can identify the parameters of all sub/supersynchronous components without additional information; When the sampling frequency of synchrophasors is 50 Hz, additional conditions are needed to distinguish the wrong results to identify the sub/supersynchronous oscillation parameters.
(2) The most essential problem of sub/supersynchronous oscillation parameter identification based on synchrophasors is how to use a shorter synchrophasor sequence to achieve high-precision parameter identification, which may also be one of the breakthroughs in future parameter identification techniques.
(3)The influence of the frequency coupled relationship between the sub/supersynchronous oscillations on the parameter identification needs to be considered. The coupled relationship between the sub/supersynchronous components is the coupling of the positive/negative frequencies of the oscillation rather than the mutual spectrum leakage, which is completely different from the influence between the fundamental component and the sub/supersynchronous component.
(4) The advantages of the spectrum-based techniques are simple with low computational complexity. The spectrum results are especially suitable for the case of multiple pairs of oscillational components. However, the DFT-based methods need to approximate the spectrum leakage, which makes it difficult to further shorten the data window even if a better window function is used, and the non-DFT-based methods may make a breakthrough in this problem.
(5) The problem of data loss and bad data in the synchrophasor sequence may exist in practical applications and needs to be considered. The existing methods rely on the continuity of the synchronous phasor sequence without an in-depth study of the above problems, and it will be another breakthrough point in the practical application of the sub/supersynchronous oscillation parameter identification method based on the synchronous phasor.
Keywords:Synchrophasor, sub/supersynchronous oscillation, parameter identification, wide-area measurement system (WAMS), spectral analysis
中图分类号:TM712
DOI:10.19595/j.cnki.1000-6753.tces.231270
国家自然科学基金资助项目(52077004)。
收稿日期 2023-08-08
改稿日期 2023-12-19
张 放 男,1988年生,博士,教授,研究方向为电力系统动态分析、交通能源系统优化运行与控制、电力系统同步相量测量技术、基于同步相量的电力系统动态监测及控制等。
E-mail:fangzhang@bjtu.edu.cn(通信作者)
李佳欣 女,2000年生,硕士研究生,研究方向为基于同步相量的电力系统次/超同步振荡参数辨识及分析。
E-mail:21121437@bjtu.edu.cn
(编辑 赫 蕾)