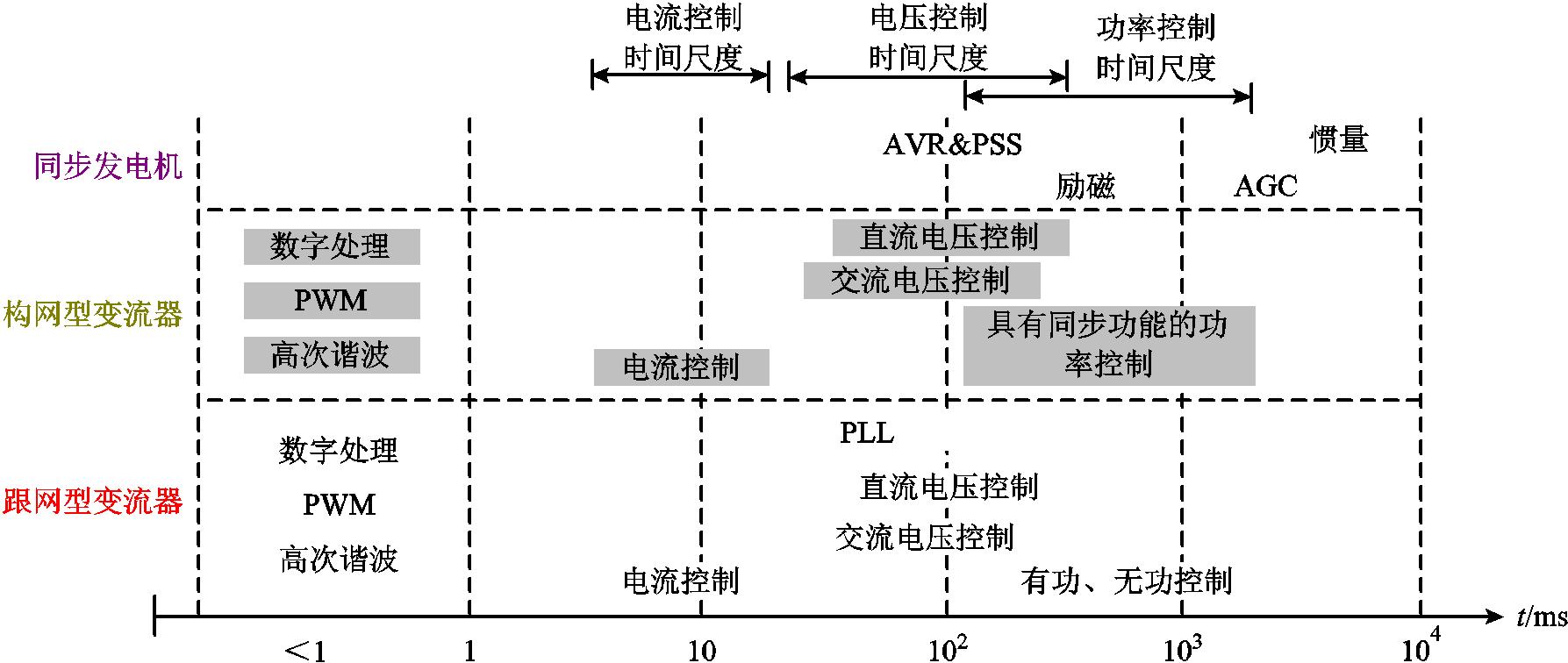
图1 并网变流器多时间尺度控制环与多时间尺度动态
Fig.1 Multi-time scale control loop and multi-time scale dynamics of grid-connected converters
摘要 电力电子并网变流器是新能源并网的关键接口装备,系统的稳定运行受电力电子多时间尺度控制影响。控制主导下的电力电子并网变流器运行非线性强、耐受能力弱,给电力电子化电力系统同步稳定性带来挑战。该文首先对多时间尺度控制下的电力电子并网变流器同步稳定性研究进行梳理,分别综述同步控制时间尺度、多时间尺度交互、多机多时间尺度交互下并网系统的建模与稳定分析技术;然后,从同步性能的全局设计到分散实现视角,提出考虑资源和网络约束的新能源并网系统同步机制构建思路;最后,对电力电子化电力系统同步技术现状和发展进行了总结与展望。
关键词:并网变流器 跟网型控制 构网型控制 同步稳定性 同步机制
随着我国沙漠、戈壁、荒漠新能源大基地建设和海上风电、分布式光伏等应用发展,大量可再生能源发电和储能装置通过电力电子变流器并入交流电网。在这些高比例新能源、高比例电力电子接入交流电网场景下,传统以同步发电机为主导的电力系统将逐渐转变为以变流器为主导的电力电子化电力系统[1]。然而,新能源通过电力电子并网变流器接入电网,电力电子装备的低惯量、强非线性、弱抗扰性等特性给新能源并网系统的稳定运行和高效送出消纳带来了极大挑战。
与电网保持同步是新能源发电装备向电网稳定传输功率的基本条件。但是,高比例新能源电力系统中装备与电网同步、多装备同步都将由电力电子控制主导[2-3]。现有并网装备一般采用多时间尺度控制架构,包括跟网型(grid-following)和构网型(grid-forming)同步环节,以及电压、电流、限幅等自身功率控制环节,时间尺度覆盖ms~s级范围,并且部分控制环节有时间尺度的重叠,并网变流器多时间尺度控制环与多时间尺度动态如图1所示。电力电子并网变流器多时间尺度的共同作用形成新能源并网系统的同步特性,与同步发动机的自动电压调节(Automatic Voltage Regulator, AVR)、电力系统稳定器(Power System Stabilizer, PSS)、自动发电控制(Automatic Generation Control, AGC)等环节时间尺度有较大差别。
相比于同步发动机,电力电子控制主导下的新能源并网系统交互作用更加复杂。特别是新能源装备规模化接入弱电网时,装备内多时间尺度交互和装备间的多机交互极易引发并网系统稳定问题。2016、2017年美国加州电网曾多次出现因线路故障导致的光伏电站中跟网型并网逆变器跳闸,事故报告阐明其原因是锁相环(Phase Locked Loop, PLL)的同步失稳[4]。我国张北柔性直流工程中次、超同步振荡问题仍时有发生[5]。因此,有必要重点关注新能源并网系统的同步稳定性,厘清电力电子控制环节对同步稳定性的影响。
现有文献[6]将新能源并网系统的同步失稳问题归纳为三类:①系统无平衡点;②平衡点存在发生小扰动失稳;③无法过渡至新的可行平衡点。其中,平衡点存在问题与控制无关,在系统分析时需要通过合适的调度保证平衡点存在;而后两类同步失稳现象均由控制主导,对系统稳定性的影响可分为小扰动和大扰动同步稳定性两方面。

图1 并网变流器多时间尺度控制环与多时间尺度动态
Fig.1 Multi-time scale control loop and multi-time scale dynamics of grid-connected converters
新能源并网装备中,跟网型变流器主要采用锁相环控制实现同步。由于变流器端电压受到干扰,锁相环在弱电网下的同步稳定性受到了广泛关注。文献[7-15]基于阻抗模型、状态空间模型等小扰动方法分析了并网变流器中PLL环路增益和带宽的影响。其中,针对工况变化下的PLL准稳态运行,文献[13]基于环路分析,识别了PLL在弱电网下的“自同步环”和“电网同步环”,解析了PLL与弱电网交互的机理;文献[14]分析了电网短路比对PLL环路阻尼比的影响,得出准稳态下小信号稳定边界。采用构网型控制的并网变流器对弱电网有较好的适应性,但研究也指出,构网型与跟网型控制结构存在对偶性,构网型变流器在强电网下有失稳风险,阻感特性的线路阻抗会造成功率耦合、多机功率振荡等问题[16-18]。尽管现有小扰动分析已取得一些结果,但现有分析缺乏对交流系统动态过程的分析,特别是在多时间尺度控制下,并网系统中存在宽频带振荡,系统在稳态工作点附近的状态周期性变化对同步稳定性影响难以体现。
在同步稳定性的大扰动(暂态)分析方面,跟网/构网型控制中的非线性、限幅保护、切换控制的影响更为明显。特别是在高比例电力电子接入的电力系统中,故障扰动下并网变流器运行直接影响系统的同步稳定性。文献[19]基于相位图法分析了电力电子并网变流器的暂态特性,但无法通过解析计算定量给出变流器的暂态稳定判据及边界。文献[20]应用等面积法则(Equal Area Criterion, EAC),通过比较加速面积和最大减速面积,量化分析在低电压穿越过程中新能源并网系统的暂态稳定性,并直观地给出了暂态失稳判据。针对构网型变流器,文献[21]基于惯性中心的概念构造了构网型变流器多机系统的能量函数,进而研究了多机系统的暂态稳定性。这些方法大都针对同步控制环,对并网变流器中其他控制环节,如无功控制、电流控制等做了一定简化。
实际上,由于新能源并网变流器多时间尺度控制耦合,控制主导下的并网系统同步稳定机理有待深入梳理。因此,本文针对新能源并网系统同步稳定问题,对现有文献进行综述,从多类型同步控制稳定性、多时间尺度交互稳定性、多机交互稳定性对当前研究成果进行总结。在此基础上,从新能源并网变流器同步性能的全局设计到分散实现视角,提出考虑资源和网络约束的新能源并网系统同步机制构建思路,并对新能源并网系统同步技术现状和发展进行总结与展望。
常见的跟网型变流器(Grid-Following controlled-Voltage Source Converter, GFL-VSC)结构如图2所示,包含PLL、直流电压环、交流电压/电流环等,其中θPLL为PLL输出相角。PLL通过对公共耦合点(Point of Common Coupling, PCC)电压相位的追踪,实现被动同步。直流电压环通过控制变流器有功输出(d轴电流参考值),实现变流器输入输出功率的平衡。交流电流环则根据直流电压环输出的电流参考值实现快速的电流追踪。
文献[7]对微电网系统中变流器的每个子模块分别建立状态空间模型,分析系统参数在不同频段下的灵敏性。采用阻抗模型可以直观地从频域的角度理解变流器的动态,并且阻抗模型具有可测量的特点,在实际中即使系统参数未知,也能对其阻抗进行测量。传统的正负序阻抗法基于谐波线性化理论[22],将系统解耦为正序和负序两个阻抗模型,并利用奈奎斯特判据分析系统的稳定性。然而,该方法在中低频段存在较大误差,甚至可能对系统的同步稳定性产生误判。为解决上述问题,文献[23]采用修正序阻抗法对阻抗矩阵中的耦合项进行精确建模,形成考虑耦合项的正序和负序阻抗判据。广义阻抗分析法基于极坐标进行阻抗建模,并通过特征方程矩阵的Schur补变换,将幅值阻抗回路折算到相位回路,形成聚焦系统相位交互动态的阻抗判据[24]。该方法的优势在于阻抗矩阵在任意功率因数下都具有解耦性,锁相环的动态集中在前向传递函数通道中,适合分析由锁相环引起的变流器失稳问题[25]。
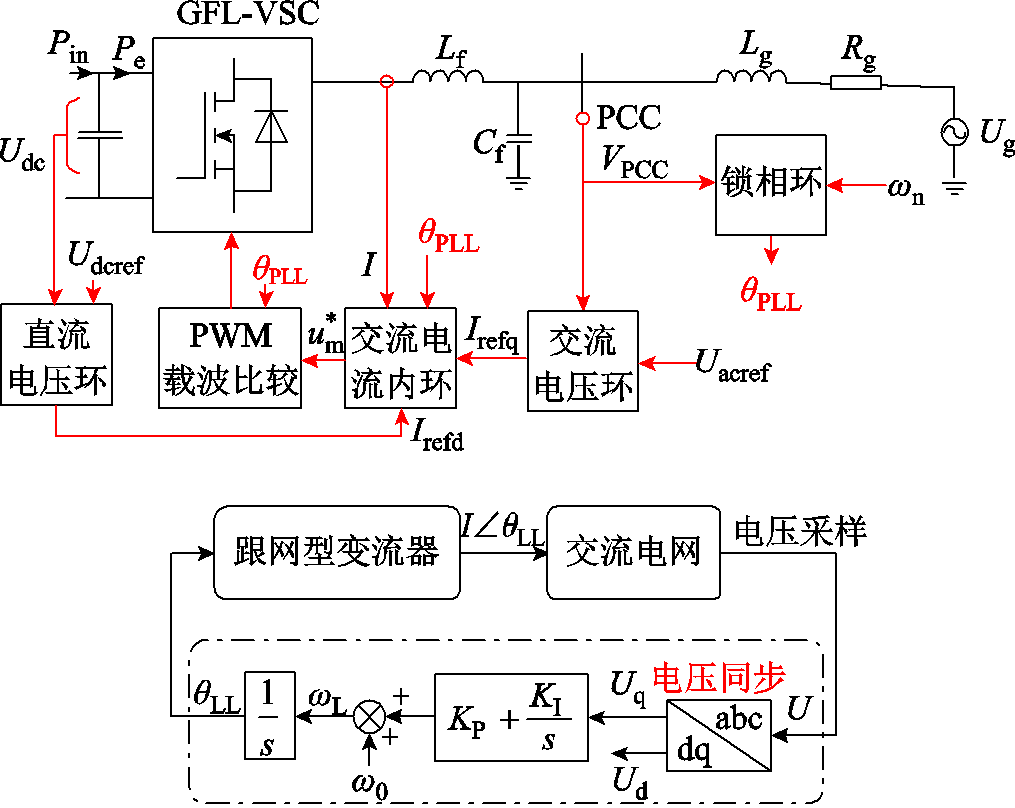
图2 并网变流器及其跟网型控制[14](a)整体控制框图(b)跟网型同步控制框图
Fig.2 Grid-connected converter and grid-following control
跟网型变流器大扰动下的同步稳定运行首先受PLL二阶动态主导,因此,较多文献对PLL在大扰动下的建模与稳定分析方法进行了研究。文献[20]推导了跟网型变流器接入弱电网的二阶简化非线性模型,通过与同步发电机转子摇摆方程类比,推导了虚拟功角摇摆方程,即
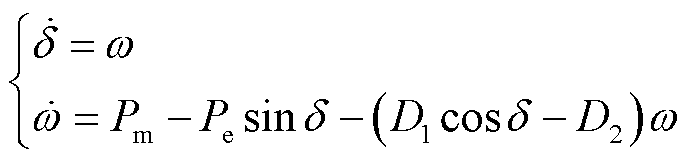 (1)
(1)
式中,Pm为等效机械功率;Pesinδ为等效电磁功率;Deq=(D1cosδ-D2)ω为等效阻尼系数;δ为虚拟功角,也为锁相环输出相位θPLL与电网相位θg之差;w为变流器输出电压的角频率。由于其数学结构与同步发动机摇摆方程具有相似性,式(1)被广泛应用于跟网型控制下并网系统的暂态同步稳定性分析。值得注意的是,式(1)包含可为负的非线性阻尼系数Deq,当δ>δd=arccos(D2/D1)时,Deq为负。文献[26]尝试应用非线性振动平均法对PLL动态进行解析,得出了保证PLL稳定的电流限幅值范围。
一般来说,大扰动稳定性分析可以采用Lyapunov第二法(直接法)。Lyapunov第二法是非线性系统稳定性分析的一种通用方法。其基本原理是针对所分析的非线性系统构建Lyapunov函数V(δ,ω),满足
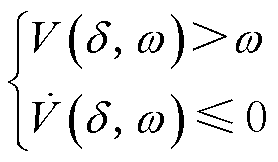 (2)
(2)
满足式(2)的区域内部的最大闭合等能量面即为δ-ω平面的稳定边界估计。
文献[27-28]使用Lyapunov直接法分析了跟网型控制下并网系统的稳定性。类比同步发动机,系统(1)的等效动能Ek和势能Ep(保守力积分)如式(3)所示,并定义系统Lyapunov函数V(δ,ω)为势能和动能之和,即
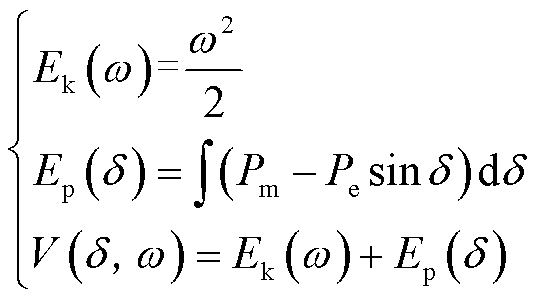 (3)
(3)
其耗散条件dV/dt<0的解析解为-δd<δ<δd。
文献[29]基于Port-Hamilton理论推导了跟网型变流器的模型和稳定边界,因为完全舍去了负阻尼区间,文献[24-26]中结果的保守性均较大。文献[30]通过待定系数法改进能量函数,得到了一个扩大的耗散区域(包含了部分的负阻尼区域)以及一个保守性部分改进的吸引域估计,但其Lyapunov函数不像式(1)一样拥有明确的物理意义,不利于分析系统失稳机理。
等面积法则(EAC)广泛应用于同步发动机主导的传统电力系统暂态稳定性判断。文献[31]对摇摆方程归一化,将所有参数整合为三个参数,分析了在整个相空间内的分岔行为以及相应的吸引域的变化,并基于EAC分析了系统失稳机理。文献[32]基于EAC方法,迭代求解了不同故障深度下的临界故障切除角。文献[33]运用EAC定量地分析锁相环带宽、故障点的端口特性及电网短路比等因素对全功率机组暂态稳定裕度的影响,并近似计算了临界切除时间。前述EAC方法均忽略了非线性阻尼对稳定性的不利影响,导致所得分析结果可能过于乐观,存在误判风险。文献[34]指出负阻尼的不利影响不应在EAC分析中被忽略,并提出了一种基于动态有功平衡的暂态稳定增强方法。
实际上,无论是类比机械系统构建能量函数,还是采用等面积法则,本质上都是能量守恒在电力电子系统暂态同步过程中的体现。但是,跟网型变流器中阻尼做功随PLL虚拟功角变化的特点给系统稳定分析带来了挑战。
常见的构网型变流器(Grid-forming controlled- voltage source converter, GFM-VSC)结构如图3所示,包含同步控制、有功/无功功率控制、直流电压环、电流内环等,其中θ为同步控制环输出相角。以功率同步控制为例,构网型变流器通过有功功率环实现同步,其时间尺度与锁相环近似。但是,强电网中使用功率同步控制策略时,变流器与电网之间相位差的微小变化都可能引起明显的功率波动,容易导致同步失稳[35-36]。
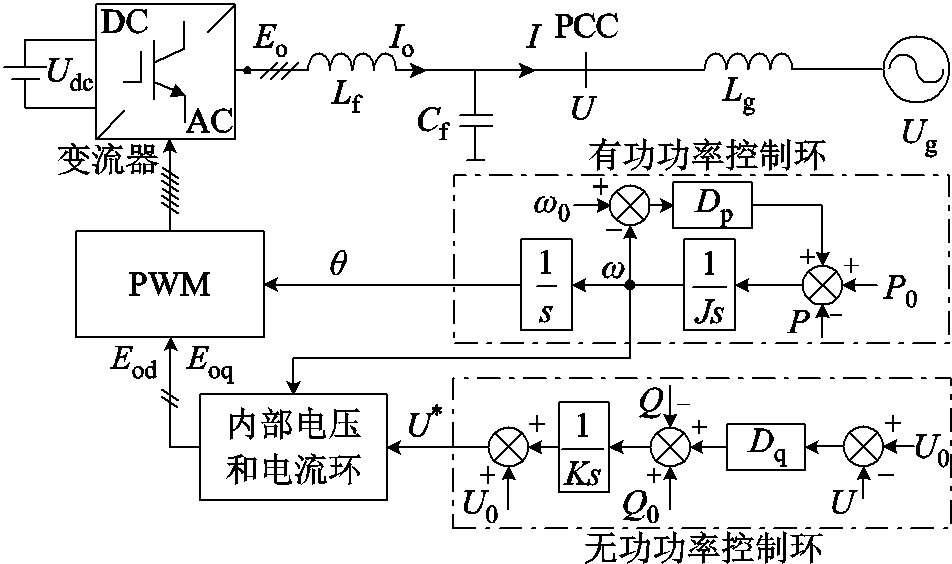
图3 功率同步控制的构网型变流器[18]
Fig.3 Grid-forming converter with power synchronization control[18]
小扰动稳定性分析方法着重于分析构网型变流器在工作点附近存在扰动后的稳定性和稳定裕度。文献[37]分别分析了采用功率同步控制、电压同步控制的构网型变流器小扰动稳定性,并揭示了阻尼控制对小扰动稳定的改善能力。强电网中的构网型变流器的同步不稳定现象可分为边带振荡与同步振荡。边带振荡可以通过调整控制参数解决,如降低功率回路控制增益[38],或降低电压反馈解耦增益[39]。同步振荡可以通过附加阻尼法解决,文献[40]通过虚拟阻抗控制,将同步电机控制结构转为PID控制器,并根据同步电机的参数调整增益,能够有效抑制频率不平衡时的功率振荡问题。文献[41]中使用交叉前馈补偿方法,调整了两个比例阻尼项,能够更好地解决构网型变流器并网的同步振荡问题。
构网型控制在大扰动下也面临同步稳定问题,其中,动态下的功率耦合也将给模型带来较大的复杂性。因此,可假设暂态下构网型变流器端电压恒定,构网型控制可简化为有功-功角二阶微分方程模型,同时认为无功环响应较快,可作为代数方程。在此假设下,文献[42-43]分别采用Lyapunov直接法、非线性分岔分析法对构网型变流器大扰动下的同步稳定性进行了分析。功率耦合相关问题将在2.3节进行详细说明。
多时间尺度控制交互主要体现在同步控制与电压环、电流环交互。其中,跟网型变流器在弱电网工况下的交互尤为显著。此外,构网型变流器中的有功和无功控制环由于时间尺度接近,也存在不可忽略的交互作用。
一般分析中认为在时间尺度上,电流环动态远快于PLL和电压环,可近似认为其处于准稳态,即输出电流与参考电流相等。然而,并网变流器电流动态通过并网点电压影响锁相跟踪,从而影响跟网型变流器同步稳定性,有较多文献对小扰动下的锁相环-电流环交互开展了研究。例如,文献[7]基于并网变流器的dq阻抗模型研究了锁相环与电流环的交互作用,结果表明锁相环影响阻抗模型中的q-q通道,使其表现出负阻抗效应,降低了稳定性。文献[44]基于正负序阻抗概念,推导了考虑电流环和锁相环交互的并网变流器模型,将系统解耦成正序和负序子系统,揭示了交互带来的振荡机理。
以上研究基于并网变流器在工作点附近的线性化假设。实际上,交流系统工作点定义存疑,交流瞬时值以及dq轴电气量并非直接表征系统能量存储水平的状态变量和工作点,造成系统动态过程分析的基本原理过于简化。文献[45]以跟网型变流器小扰动分析为例,基于内电动势幅值/频率和有功/无功电流工作点,提出了描述变换器/网络的内电动势幅值/频率和有功/无功电流间的激励-响应小扰动线性化方法,即:从电压、电流的原始非线性关系出发,通过函数展开构建小扰动线性化关系。该方法精确地揭示了小扰动动态过程初期交流信号复指数函数调制的演化机制。
在大扰动方面,文献[46]分析了跟网型变流器在电流环不同带宽影响下围绕平衡点振荡的同宿分岔行为,并提出了电流高/低带宽可以触发周期轨道的鞍结分岔或避免同宿分岔来保证同步稳定性。文献[47]建立了跟网型变流器模拟同步机模型,考虑了电流环和锁相环的动态性能,结合等面积法则和小信号分析揭示了低电流环带宽会恶化并网变流器的稳定性。文献[48]利用奇异摄动理论建立了跟网型变流器锁相环和电流环时间尺度的快/慢非线性模型,并利用Lyapunov间接法和直接法分别分析了这两个模型的暂态同步稳定性,结果表明减小电流环比例系数有利于快模型的稳定。文献[49]进一步应用时域解析法研究了电流限幅和环形限幅器对跟网型变流器系统同步稳定性的影响。
构网型变流器采用电流限幅策略,以防止变流器故障穿越过程中超过其过电流能力,这种非线性控制也表现出明显的交互行为,造成变流器工作模式变化,增加了变流器失去同步的风险[50]。基于此,文献[51]通过等面积法则揭示了控制策略的切换会降低系统的暂态同步稳定性,并且也会牺牲变流器的电压支撑能力。为了避免上述情况的发生,文献[52-53]从虚拟阻抗、电压补偿等通过调节无功环输出电压的方法间接实现电流限幅。文献[54]分析不同电流限值下构网型变流器的暂态同步稳定性,提出了动态电流限幅策略来增强稳定性。
锁相环和外环控制间的动态交互对系统小扰动稳定性有较大影响,文献[55]基于复转矩系数法研究了锁相环和交流电压控制环的交互作用,指出电网强度越弱,交流电压控制导致的负阻尼越明显,系统小干扰稳定性越差;文献[56]基于模式分析法指出,当锁相环和直流电压环的固有频率接近时,两者会发生强相互作用且固有频率低的振荡模式更容易失稳。
大扰动方面,文献[57]在直流母线电压控制时间尺度,建立了锁相环和直流电压环的非线性模型,分析了不同电网强度下暂态同步稳定性的影响,发现忽略直流电压环的动态性会导致过于乐观的稳定估计,提出可以通过增加直流电压环的比例系数或者减小积分系数来提升系统阻尼,从而减小直流电压环的不利影响。
构网型变流器中包含功率同步控制和端电压控制这两个慢尺度动态环节,可以建立包含这两个环节的四阶系统来分析控制交互作用,如图4所示,其中φ为同步控制环输出相角。文献[58]通过比较强弱电网下构网型变流器系统四阶模型和二阶模型的小扰动与大扰动稳定性,分析端电压控制外环对功率同步控制环的影响,发现在弱电网下,功率同步环节自身的固有同步转矩和端电压控制引入的附加同步转矩都很小,导致系统总的同步转矩不足,系统发生单调失稳;而在强电网下,端电压控制引入了过大的负阻尼转矩,导致系统的阻尼转矩不足,系统发生振荡失稳。
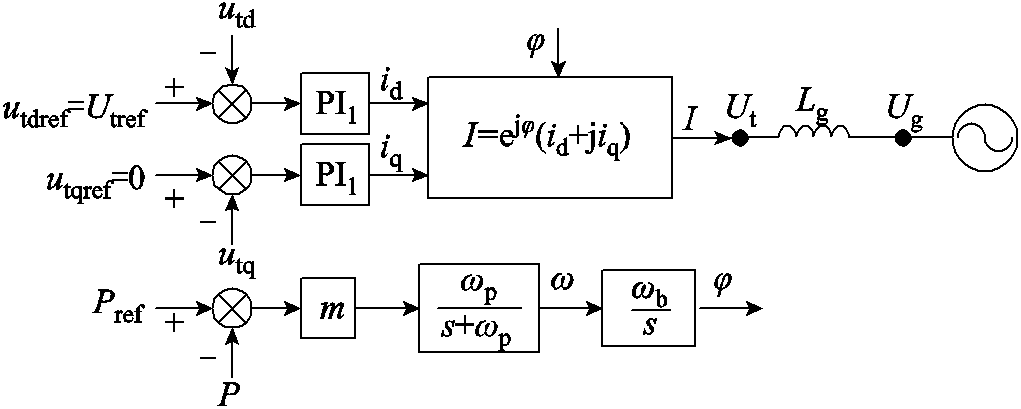
图4 包含端电压控制的构网型变流器四阶模型[58]
Fig.4 Fourth-order model of grid-forming converter with terminal voltage control[58]
另一类构网型变流器采用电压同步控制,能够使直流侧电压稳定的同时实现变流器自同步。文献[59]分析发现直流电压同步相比于功率同步会引入更多相位滞后,叠加交流电压环相位滞后,使系统环路在低频高增益区产生低频振荡。
跟网型变流器在电网故障下引入无功功率控制增强支撑能力,然而无功环通过PLL影响变流器功率输出。文献[60]基于变流器的同步主导回路模型分析了锁相环和无功控制环的交互作用,指出当变流器采用无功-电压下垂控制时,降低锁相环的带宽可以提高系统小干扰稳定性;而当变流器采用定无功功率控制时,足够低或者足够高的锁相环带宽均可以保证变流器的稳定性。
构网型变流器的基本思想是通过调节变流器的电压幅值和频率(相位)来控制其输出功率。并网控制的基础是输电线路功率潮流的解耦特性,即在变流器和电网之间的阻抗为感性且功角非常小的情况下,有功功率主要由功角控制,而无功功率主要由电压幅值控制。然而在许多情况下,纯感性线路阻抗和小功角这两个前提条件通常不满足。这样,控制变量(输出电压的频率和幅值)与输出变量(逆变器输出的有功功率和无功功率)之间就会产生不必要的交叉耦合,这会使上述独立控制的方式不再有效,并进一步恶化并网逆变器的动态性和稳定性。为了解决这个问题,在过去下垂控制和微电网的研究中有许多功率解耦方法被提出,主要可分为以下四类:虚拟阻抗方法、虚拟功率方法、虚拟频率和电压方法、功率前馈补偿方法。这些方法都是基于小功角假设条件,且只针对于基频下的稳态特性进行解耦。
构网型变流器在电压源运行下的有功无功计算公式如式(4)所示,其功率耦合机制如图5所示。可以看出,在无功下垂环路通过输出电压影响有功环路的功角动态,而有功环路通过其输出功角动态进一步影响输出电压。在无功-电压下垂控制的影响下,构网型变流器平衡点移动,且伴随着功率传输极限的减小,意味着减速面积的减小,构网型变流器暂态同步稳定裕度恶化[18]。
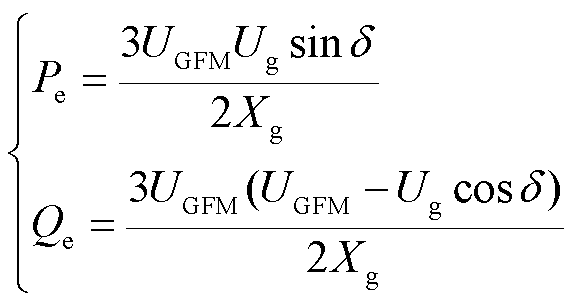 (4)
(4)
式中,Pe和Qe分别为变流器输出的有功功率和无功功率;UGFM和Ug分别为变流器的输出电压和电网电压;Xg为线路阻抗;δ为功角。
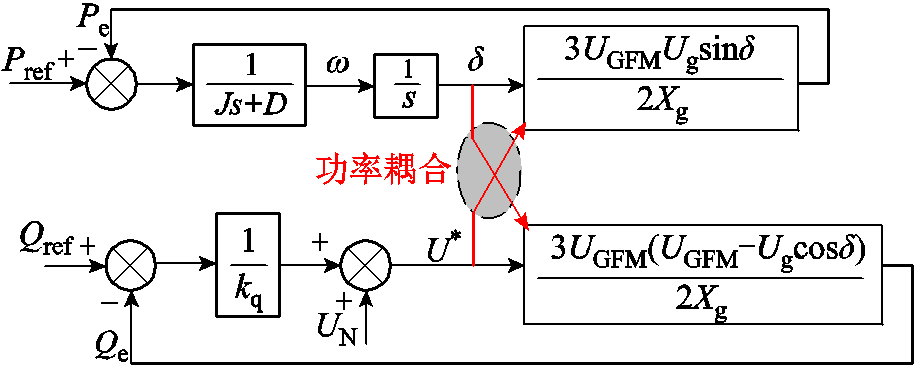
Fig.5 Power coupling mechanism[62]
因此,面向大扰动下的有功-无功控制交互问题,文献[61]在功率控制时间尺度下建立了构网型变流器的二阶暂态同步模型,考虑构网型变流器来自稳态无功环的耦合影响,进而得到了提高阻尼系数和减小惯性时间常数有利于系统暂态同步稳定提升的结论,同时也分析了不同控制参数的影响,说明减小同步环节的等效惯量可以减小变流器对电网的频率支撑能力,从而能够提升自身的暂态同步稳定。文献[41]建立了无功环约束下构网型变流器的能量函数,揭示了无功环交互会通过降低输出电压来恶化并网变流器的暂态同步稳定的机制,并在此基础上发现了阻尼系数和电压下垂系数的提升有利于吸引域的增加。文献[62]考虑构网型变流器功率耦合和限幅下的三阶微分方程,将输出电压作为状态变量,建立了构网型变流器的能量函数模型,结果表明功率耦合和电流限幅分别通过影响等效势能和阻尼分布削弱变流器的暂态同步稳定性。
在新能源场站等应用中,多台并网变流器并联接入PCC。在非理想弱电网工况下,并联接入的多台并网变流器的控制环路之间发生交互作用,不仅有相同时间尺度的同步-同步控制交互,也包括多机不同时间尺度之间的交互,在系统中形成复杂动态过程。
以构网型控制下的分布式发电单元(Distributed Generator, DG)两机并联系统为例,其电路结构如图6a所示,该系统被认为是由同质或异质构网设备组成的电力系统原型[63],可用于表示输配电网络。串联阻抗Z1和Z2包括传输线路阻抗和变压器阻抗等,ZL是系统等效恒定阻抗负载,ZF是系统发生三相接地故障时的等效接地阻抗。为降低计算复杂度和简化分析过程,在暂态分析中,原型系统通常收缩至发电单元节点,等效电路如图6b所示,包含对地等效导纳支路Y11、Y22和两机间等效导纳支路Y12。
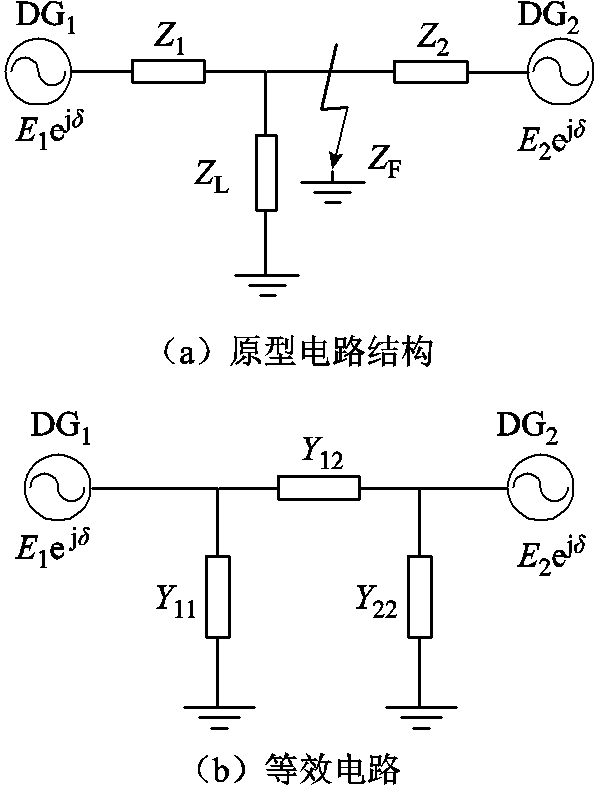
图6 构网型控制的两机并联系统
Fig.6 Parallel system of two DGs with GFM control
两机并联系统中的发电单元i(i=1, 2)可以是构网型变流器,采用经典二阶模型,其摇摆方程为
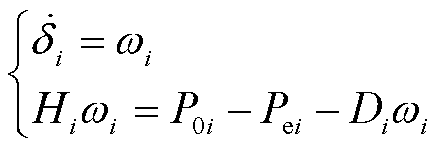 (5)
(5)
式中,P0i和Pei分别为给定机械功率和输出有功功率;δi为变流器的功角;ωi为角速度与同步转速的偏差,Di和Hi分别为阻尼系数和惯性时间常数。根据图6,有功功率输出可表示为
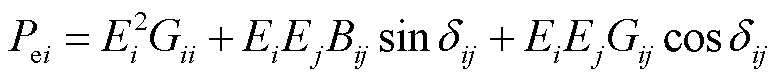 (6)
(6)
式中,E为变流器内电动势;δij为构网型变流器i和j的功角差,δij=δi−δj;Yij、Gij、Bij为两机系统的节点导纳矩阵元素,且Gij+ jBij= Yij。
文献[64]对电网故障下基于锁相环同步的多并联风机系统耦合机制进行研究,主要从保证系统在面临大扰动或电网故障后具备稳态运行点的角度评价多风机并联系统暂态稳定性。稳定性分析侧重的是通过矩阵运算保证系统稳态运行点,而不针对大扰动下系统从一个稳态运行点移动到另一个稳态运行点的动态过程,是多机并联系统保持暂态稳定的必要不充分条件。针对暂态扰动下的稳定性问题,文献[65]分析了两台跟网型变流器并联系统静态和动态交互现象,量化了动态交互对两机不平衡功率的影响,识别了变流器之间的联锁失稳过程,如图7所示。
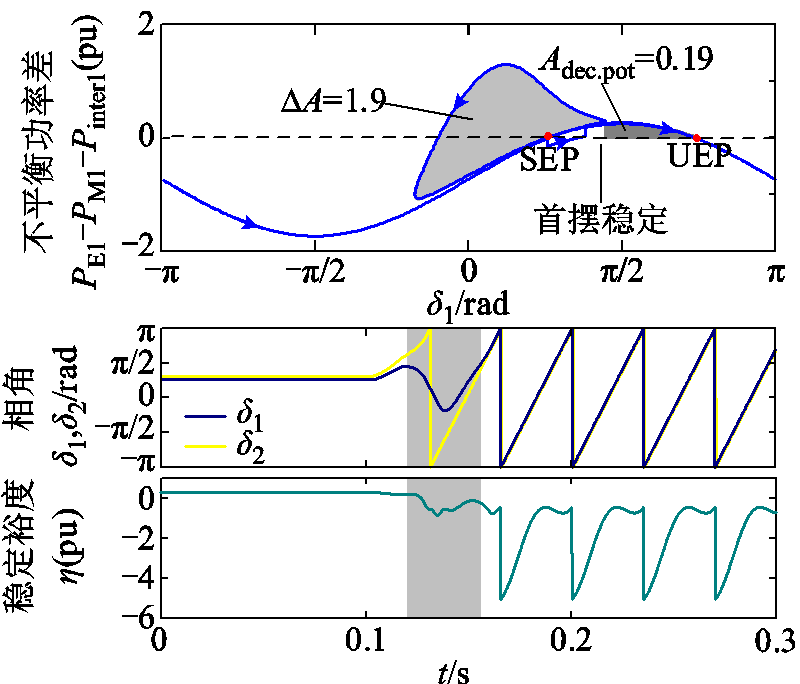
图7 两机动态交互引发的连锁失稳现象[65]
Fig.7 Chain instability phenomenon caused by dynamic interaction between two generators[65]
针对两台虚拟同步机(Virtual Synchronous Generator, VSG)控制的并网变流器并联运行工况,文献[66-67]推导其小信号模型,并根据负荷暂态特性平均分配虚拟惯量。当负荷波动时,会使双机系统产生有功功率振荡,这会影响并网系统的安全运行。文献[68]简化跟网型变流器和虚拟同步机并联并网系统,建立二阶模型,使用扩展等面积法则对系统暂态稳定性进行分析。所建立的简化模型是典型的准稳态模型,忽略了变流器控制内环和线路动态的影响,所建立的简化二阶模型仍然是将多机系统整合成等效的单机无穷大形式进行分析。文献[69]分别对孤岛微网中同步机和虚拟同步机组成的并联系统,以及双虚拟同步机组成的并联系统建立等效二阶摇摆方程,通过对比摇摆方程发现,同步机和虚拟同步机组成的并联系统相对于单独虚拟同步机组成的并联系统,由于调速器差异而更容易引发暂态失稳,并且分别建立了两种并联系统的全阶状态空间模型,基于T-S模糊模型推导Lyapunov函数定量确定系统吸引域。
针对跟网型、构网型变流器混联场景的稳定性,较多研究人员已经注意到其中的理论挑战。文献[70]基于小增益-小相位理论提出了大规模多机异构混联系统稳定判据,克服了常规小信号分析复杂度高的问题。文献[71]提出了阻抗传递函数法,用于大规模多机系统判稳和失稳溯源。
和前述场景类似,虽然小信号分析可以得到线性化过后的系统稳定判据,但是并未直接反映系统的同步特性。因此,针对大扰动下的混联系统问题,文献[68]分析了跟网型变流器电流注入对构网型变流器暂态同步稳定性的影响。文献[72]针对孤岛模式下的混联系统,重点研究了孤岛条件下系统频率变化影响,构建了一种二次型 Lyapunov 函数分析了系统暂态同步稳定性。文献[73]针对含跟网型、构网型变流器以及同步发动机的混联并网系统场景,利用空间矢量图示法与相平面法分析了跟网型变流器注入电流、锁相环参数以及构网型变流器有功控制环参数等因素对混联系统内各发电单元暂态同步稳定性的影响规律。
考虑多并网装备间的同步-电压控制交互研究较少,研究主要集中在小扰动稳定性建模与分析方面。文献基于dq阻抗模型研究了多整流器并联系统的低频振荡,显示直流电压环增益对稳定边界有较大影响。文献[74]以跟网/构网型光伏配置构网型储能构成的新能源场站为例,在频域下构建了跟网型和构网型设备的同步模型,基于多变量频域理论,根据频域下输入输出端口与特征函数的相关因子,形成了从小扰动稳定性到特征轨迹/函数再到输入输出端口的关联关系,提出了主导失稳设备辨识的方法。在弱同步系统实例中,通过修改主导失稳设备的控制参数有效地改善了系统的稳定性。文献[75]也建立了类似的跟网型变流器直流电压时间尺度频域模型,采用有功和无功功率作为输入,内电动势的幅值和相位作为输出。
文献[76]考虑了构网型变流器中的端电压控制,在dq坐标系下建立了端口特性模型,并分析了孤岛工况下的多机稳定性。然而,由于时间尺度接近,大扰动下多机同步-电压控制交互更加复杂,现有研究尚不多见。
以两台跟网型变流器并网系统为例,其电路结构如图8所示。图中,Z1和Z2为传输线路阻抗;Zg为电网阻抗;I为变流器输出电流。
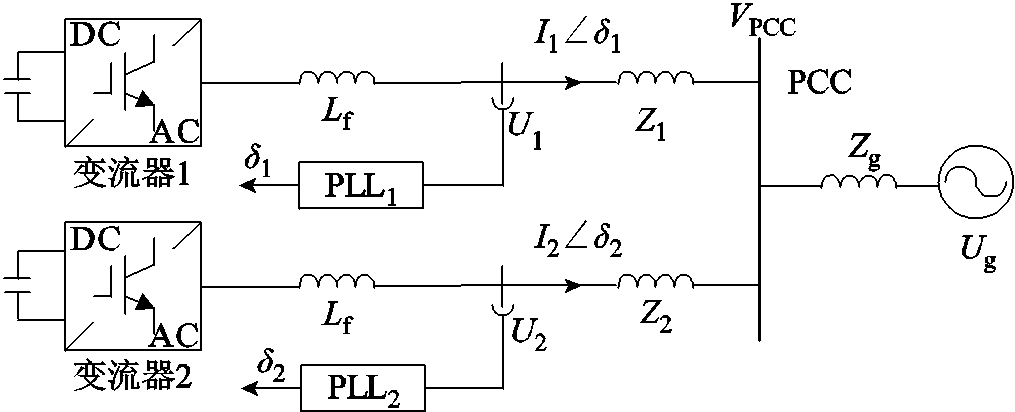
图8 跟网型变流器并网系统
Fig.8 Grid-connected system with grid-following converters
跟网型变流器的锁相环输入(以变流器1为例)可表示为
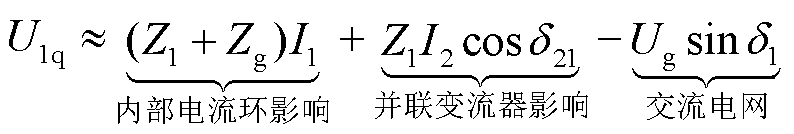 (7)
(7)
式中,d21为相位差,δ21=δ2-δ1。
通过式(7)可知,跟网型变流器的锁相环输入受到自身电流环和并联变流器的状态变量的影响,并且影响程度也与两机相位差相关,这意味着变流器不仅同步环节之间存在交互作用,变流器同步环和电流环之间也有控制交互行为。需要说明的是,由于功率控制环的时间尺度远大于电流环和锁相环,因此构网型变流器的接入可通过网络阻抗矩阵等效换算成对系统自阻抗和互阻抗的影响,从而可以仅在跟网型变流器多机系统中研究同步-电流控制交互作用影响。
文献[77-78]假设电流环为单位增益环节,考虑锁相环输入关于电流环的状态变量为其指令值,从而通过简化的多机暂态同步模型分析系统的暂态行为。在此假设的基础上,仅有变流器同步控制交互,稳定性分析结果与3.1节类似。
为了研究电流环动态在变流器同步过程中的参与机制,文献[79]利用单输入单输出的传递函数模型考虑电流环的交互影响,发现可以通过增加电流环的比例系数来部分抑制同步-电流控制交互的不利影响。文献[80]采用路径级数展开法分析了多变流器装备之间的相互作用,可用于解析同步环和电流环之间的交互作用路径,但是其分析模型的复杂程度较高。文献[81]将同步-电流控制交互区分为静态和动态交互项,利用稳定域中的吸引子范围来量化来自电流环状态量动态过程的影响。
实际上,考虑电压、电流控制之后,系统同步过程中的网络动态(特别是线路电感元件)也不应忽略。文献[82]以瞬时幅值和瞬时频率描述动态过程中的电压、电流电气量,推导了线路传输的功率特性方程,为多机系统研究提供了参考。
从以上文献可以发现,近年来,工程和研究人员面向系统同步稳定性,在单机并网、多机组网等场景开展了大量研究,电力电子化电力系统的同步稳定性的内涵、方法都有发展和深化。参考传统电力系统稳定性分类,可以对现有研究进行分类和梳理,结果如图9所示。
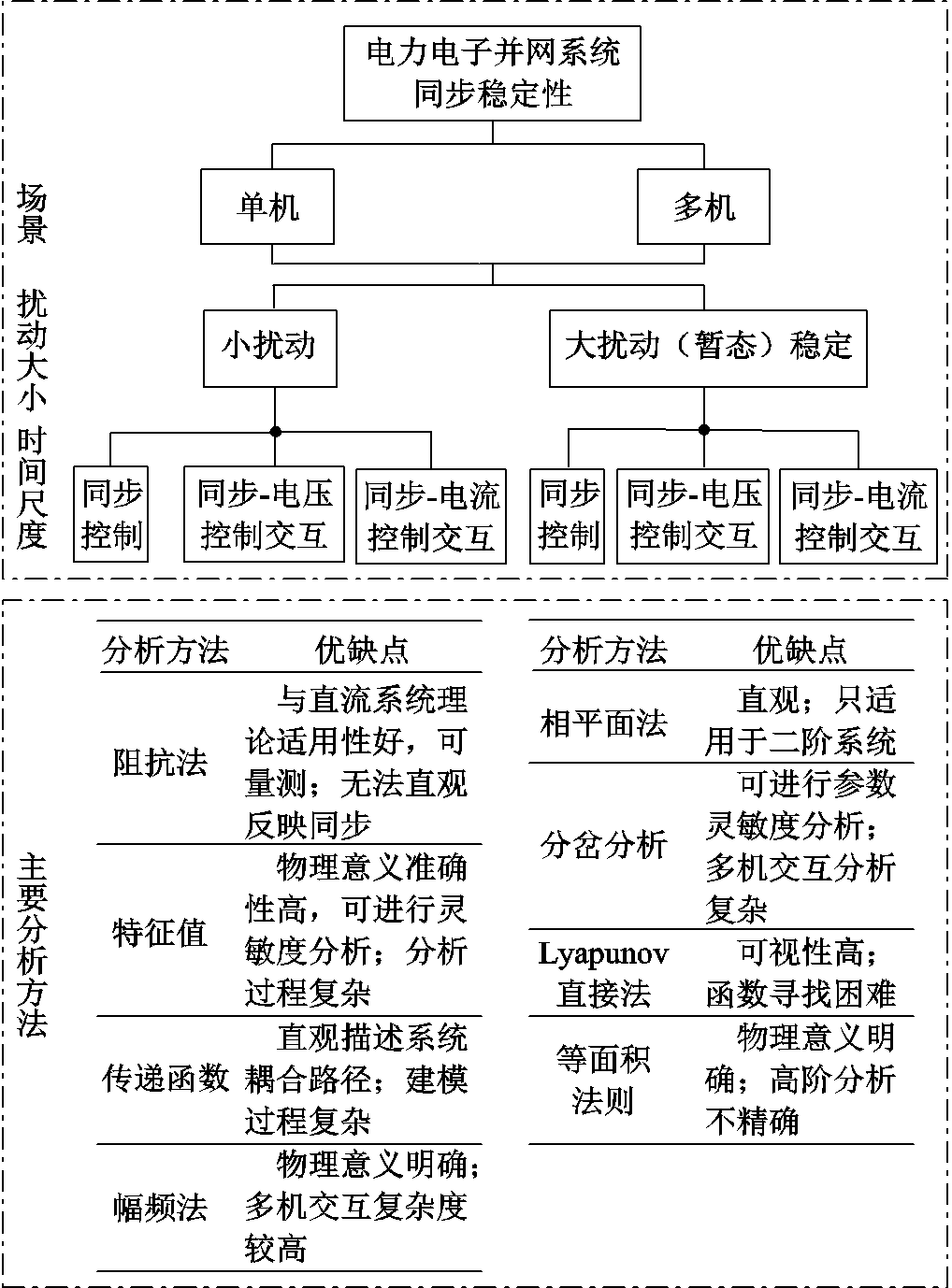
图9 电力电子并网系统同步稳定性分类和主要分析方法
Fig.9 Catalog and analysis methods of synchronous stability for grid-connected system
在多时间尺度及海量分散分布的并网变流器系统中,大量变流器同时向电网输送功率,需要考虑在系统动态特性复杂条件下实现变流器的协同控制。海量分散分布变流器的协同控制需要先进的控制策略,以实现系统整体的稳定控制与功率分配。传统方法大多基于单机无穷大简化模型进行同步控制策略优化或参数最优整定工作,未考虑实际工况下变流器接入互联网络时,海量变流器多时间尺度动态交互导致的系统整体协调性恶化,严重危害系统整体稳定同步运行。
文献[83]采用主从控制,根据变流器输出频率与惯量中心的偏差计算得到变流器需要提供的功率。惯量中心频率是各频率在虚拟惯量加权下的平均值,采用惯量中心频率能够将多机系统的频率趋于一致,增强系统的鲁棒性。文献[21]将每台变流器的频率传输给集中控制器,计算惯量中心频率,然后将其分配给每台变流器,每台机组对各自的频偏差进行PID控制,形成频率反馈并作用于有功输出参考值。然而上述变流器协同控制依赖实时通信。当通信延时严重时,实时性和可靠性都存在一定的问题,会影响控制效果[84]。依靠通信实现多机整体控制本质上仍是因为没有找到网络功率响应机制所蕴含的泛函变分机制,只能依靠人为通信通道实现网络内机组间的协调控制。
最早提出的依据网络物理特性构建的分散自治控制为下垂控制,其无需依靠中央控制器和联络信号即可实现全网功率平衡[85],具备即插即用功能,简化了控制系统的复杂程度,提高了控制的可靠性[86]。但由于传统下垂控制对线路阻抗的限制[87]及并联环流问题[88],下垂控制需要进行诸多改进。实际应用中由于功率匹配的问题,下垂控制的应用场景具有局限性。传统下垂控制的弊端主要是因为采用两个单输入单输出(有功-频率和无功-电压)控制器对具备多输入多输出特性的网络进行控制。因此,文献[89]提出了一种新的具有(几乎)全局渐近稳定保证的耦合振荡器分散控制方法,并探讨了其在并网逆变器控制中的应用,该方法充分考虑了网络在功率扰动下平衡恢复过程中的有功-无功耦合特性。文献[90]提出了一种可调度的虚拟振荡器控制(dispatchable Virtual Oscillator Control, dVOC)策略,并验证了其在变流器主导电网中的构网功能。仅使用本地信息,dVOC逆变器实现几乎瞬时的动态同步和负载共享。进一步地,随着复频率概念的提出[91],文献[92]提出一种在微网和并网场景下均可实现全局渐近稳定的复下垂控制,如图10所示。
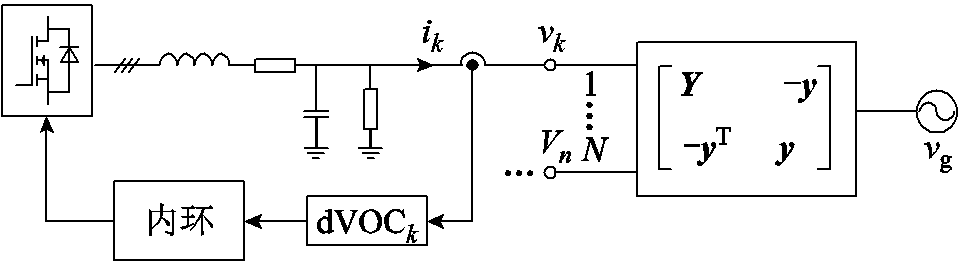
图10 复下垂控制[92]
Fig.10 Complex droop control[92]
针对现有变流装备到系统的同步控制方式存在的问题,需要考虑构建从系统到变流装备的同步机制,以解决高比例新能源电力系统静态和暂态条件下海量并网变流器多时间尺度控制及其对系统状态行为同步协调性的影响问题。一个可行的思路是由系统级的功率平衡需求建立并网变流器同步协调控制目标。在此基础上,基于最优控制理论体系,将系统同步稳定性和功率振荡等工程问题转换为系统控制问题的目标函数;由系统的功率平衡关系、系统状态行为及其驱动控制动力学规律,生成系统功率平衡调控机制中隐含的系统泛函变分过程;通过变分方法得到泛函极值,建立系统的状态运动方程和控制方程。
同时,可将电力电子化电力系统理解为海量电力电子变流器相互连接的系统,将并网变流器控制问题等效地转换为其连接边界参量或参变量待定问题[93]。借助连接边界参量或参变量的确定,将系统功率平衡机制中隐含的系统状态泛函变分过程表达成各个变流器状态变分过程之和,由此解决资源分散分布条件下并网变流器状态行为的同步协调控制问题。基于参量变分的并网变流器互联系统如图11所示。
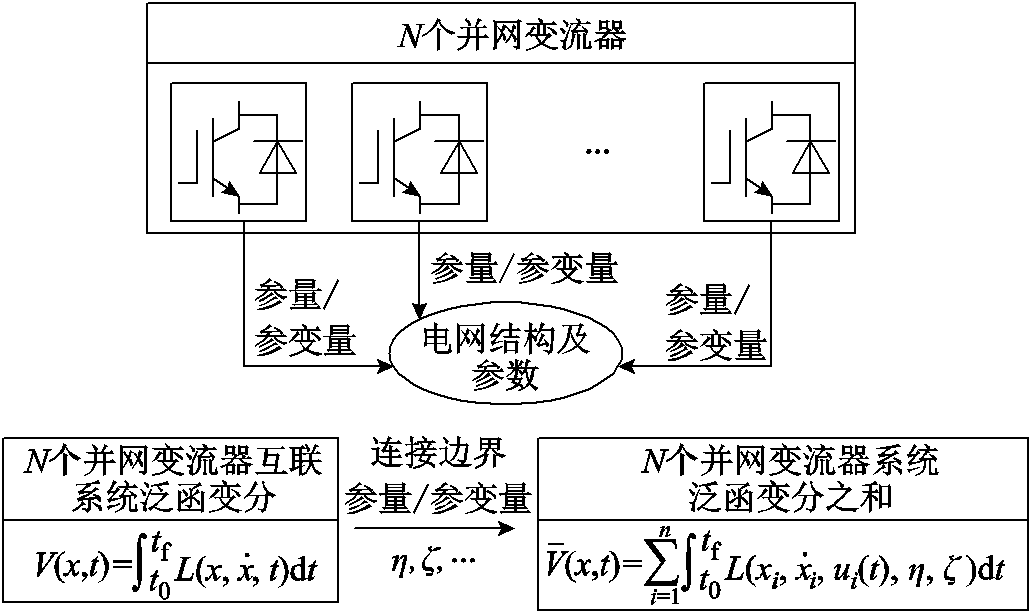
图11 基于参量变分的并网变流器互联系统
Fig.11 Grid-connected converter interconnection system based on parametric variational
电力电子化电力系统中同步电源支撑能力弱,海量电力电子并网变流器通过同步控制协调运行是系统安全稳定的关键。现有研究初步揭示了电力电子同步控制自身和多时间尺度交互下的系统同步稳定机理。然而,电力电子化电力系统这类高阶非线性系统分析仍不成熟,在传统交流电力系统理论框架下的诸多技术挑战亟待突破。特别是在同步运行方面,同步稳定是交流电力系统稳定的基础,控制主导下的同步运行机理和方法亟待进一步探索,包括但不限于以下方面:
1)电力电子化电力系统建模与分析方法。电力电子控制自身具有非线性、多时间尺度的交互特征,对并网变流器同步运行的影响不容忽视。同步稳定性分析时,如何有效地考虑电力电子控制影响而不过多地提升模型和稳定分析的复杂性,是同步稳定性研究面临的主要挑战之一。
2)基于人工智能、边缘计算的电力电子并网装备的状态感知和稳定分析技术。面向海量电力电子装备并网等复杂应用场景,数据驱动的感知和稳定分析技术将弥补机理模型、解析性稳定判据的不足。随着人工智能技术的发展和边缘计算芯片的广泛应用,电力电子装备对于复杂电网环境的感知和判断能力将进一步提升。
3)面向同步稳定性的系统控制技术。现有电力电子装备广泛使用的锁相环是基于强电网假设,采用信号处理的方式进行同步,而构网同步方式更多地是模拟传统交流系统同步机运行,同步机制并未体现电力电子装备特性。因此,理论化、系统性的同步机制构建仍然存在许多挑战,相应的控制理论和实现方法亟待突破。
参考文献
[1] 舒印彪, 陈国平, 贺静波, 等. 构建以新能源为主体的新型电力系统框架研究[J]. 中国工程科学, 2021, 23(6): 61-69.
Shu Yinbiao, Chen Guoping, He Jingbo, et al. Building a new electric power system based on new energy sources[J]. Strategic Study of CAE, 2021, 23(6): 61-69.
[2] 唐王倩云, 周保荣, 胡家兵, 等. 锁相同步型风机-同步机互联电力系统转子转速尺度暂态同步稳定性分析[J]. 中国电机工程学报, 2021, 41(20): 6900-6916.
Tang Wangqianyun, Zhou Baorong, Hu Jiabing, et al. Transient synchronous stability of PLL-based wind power-synchronous generation interconnected power system in rotor speed control timescale[J]. Proceedings of the CSEE, 2021, 41(20): 6900-6916.
[3] 王成山, 武震, 李鹏. 微电网关键技术研究[J]. 电工技术学报, 2014, 29(2): 1-12.
Wang Chengshan, Wu Zhen, Li Peng. Research on key technologies of microgrid[J]. Transactions of China Electrotechnical Society, 2014, 29(2): 1-12.
[4] NERC Joint and WECC Staff Report. 900 MW Fault Induced Solar Photovoltaic Resource Interruption Disturbance Report[N]. NERC Atlanta and GA USA Tech. Rep. , 2018-02.
[5] 郑少明, 刘一民, 董鹏, 等. 张北工程风电柔直汇集系统次、超同步振荡分析[J]. 全球能源互联网, 2023, 6(6): 608-617.
Zheng Shaoming, Liu Yimin, Dong Peng, et al. Analysis of sub/super-synchronous oscillation between wind farm and MMC in Zhangbei Project[J]. Journal of Global Energy Interconnection, 2023, 6(6): 608-617.
[6] 张宇, 蔡旭, 张琛, 等. 并网变换器的暂态同步稳定性研究综述[J]. 中国电机工程学报, 2021, 41(5): 1687-1702.
Zhang Yu, Cai Xu, Zhang Chen, et al. Transient synchronization stability analysis of voltage source converters: a review[J]. Proceedings of the CSEE, 2021, 41(5): 1687-1702.
[7] Wen Bo, Boroyevich D, Burgos R, et al. Analysis of D-Q small-signal impedance of grid-tied inverters[J]. IEEE Transactions on Power Electronics, 2016, 31(1): 675-687.
[8] 朱军, 曲玉博, 刘鹏辉, 等. 电网频率小扰动下虚拟同步发电机统一模型关键参数辨识[J]. 电气技术, 2022, 23(7): 26-33, 41.
Zhu Jun, Qu Yubo, Liu Penghui, et al. Identification of key parameters of virtual synchronous generator unified model under small frequency disturbance of power grid[J]. Electrical Engineering, 2022, 23(7): 26-33, 41.
[9] Wang Xiongfei, Harnefors L, Blaabjerg F. Unified impedance model of grid-connected voltage-source converters[J]. IEEE Transactions on Power Electronics, 2018, 33(2): 1775-1787.
[10] Harnefors L, Wang Xiongfei, Yepes A G, et al. Passivity-based stability assessment of grid-connected VSCs—an overview[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2016, 4(1): 116-125.
[11] Hu Jiabing, Wang Bo, Wang Weisheng, et al. Small signal dynamics of DFIG-based wind turbines during riding through symmetrical faults in weak AC grid[J]. IEEE Transactions on Energy Conversion, 2017, 32(2): 720-730.
[12] Göksu Ö, Teodorescu R, Bak C L, et al. Instability of wind turbine converters during current injection to low voltage grid faults and PLL frequency based stability solution[J]. IEEE Transactions on Power Systems, 2014, 29(4): 1683-1691.
[13] Dong Dong, Wen Bo, Boroyevich D, et al. Analysis of phase-locked loop low-frequency stability in three- phase grid-connected power converters considering impedance interactions[J]. IEEE Transactions on Industrial Electronics, 2015, 62(1): 310-321.
[14] Zhao Jiantao, Huang Meng, Zha Xiaoming. Nonlinear analysis of PLL damping characteristics in weak-grid-tied inverters[J]. IEEE Transactions on Circuits and Systems II: Express Briefs, 2020, 67(11): 2752-2756.
[15] 李红, 梁军杨, 王振民, 等. 跟网型变换器的小扰动同步稳定机理分析与致稳控制[J]. 电工技术学报, 2024, 39(12):3802-3815.
Li Hong, Liang Junyang, Wang Zhenmin, et al. Small signal synchronization stability analysis and improved control strategy for grid following converter[J]. Transactions of China Electrotechnical Society, 2024, 39(12):3802-3815.
[16] Li Yitong, Gu Yunjie, Green T C. Revisiting grid-forming and grid-following inverters: a duality theory[J]. IEEE Transactions on Power Systems, 2022, 37(6): 4541-4554.
[17] 谢震, 杨曙昕, 代鹏程, 等. 构网型全功率风电机组网侧变流器耦合分析及抑制策略[J]. 电工技术学报, 2023, 38(14):3745-3758, 3768.
Xie Zhen, Yang Shuxin, Dai Pengcheng, et al. Grid-side coupling analysis and suppression strategy of grid-forming full-power wind turbines[J]. Transactions of China Electrotechnical Society, 2023, 38(14): 3745-3758, 3768.
[18] 黄萌, 凌扬坚, 耿华, 等. 功率同步控制的构网型变流器多机交互分析与稳定控制研究综述[J]. 高电压技术, 2023, 49(11): 4571-4583.
Huang Meng, Ling Yangjian, Geng Hua, et al. An overview on multi-VSCs interaction analysis and stability controls of grid-forming converters with power synchronization control[J]. High Voltage Engineering, 2023, 49(11): 4571-4583.
[19] Wu Heng, Wang Xiongfei. Design-oriented transient stability analysis of grid-connected converters with power synchronization control[J]. IEEE Transactions on Industrial Electronics, 2019, 66(8): 6473-6482.
[20] Hu Qi, Fu Lijun, Ma Fan, et al. Large signal synchronizing instability of PLL-based VSC connected to weak AC grid[J]. IEEE Transactions on Power Systems, 2019, 34(4): 3220-3229.
[21] Choopani M, Hosseinian S H, Vahidi B. New transient stability and LVRT improvement of multi- VSG grids using the frequency of the center of inertia[J]. IEEE Transactions on Power Systems, 2020, 35(1): 527-538.
[22] Sun Jian, Wang Guoning, Du Xiong, et al. A theory for harmonics created by resonance in converter-grid systems[J]. IEEE Transactions on Power Electronics, 2019, 34(4): 3025-3029.
[23] Rygg A, Molinas M, Zhang Chen, et al. On the equivalence and impact on stability of impedance modeling of power electronic converters in different domains[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2017, 5(4): 1444-1454.
[24] 辛焕海, 李子恒, 董炜, 等. 三相变流器并网系统的广义阻抗及稳定判据[J]. 中国电机工程学报, 2017, 37(5): 1277-1293.
Xin Huanhai, Li Ziheng, Dong Wei, et al. Generalized-impedance and stability criterion for grid-connected converters[J]. Proceedings of the CSEE, 2017, 37(5): 1277-1293.
[25] Xu Luyao, Xin Huanhai, Huang Linbin, et al. Symmetric admittance modeling for stability analysis of grid-connected converters[J]. IEEE Transactions on Energy Conversion, 2020, 35(1): 434-444.
[26] Zhao Jiantao, Huang Meng, Yan Han, et al. Nonlinear and transient stability analysis of phase-locked loops in grid-connected converters[J]. IEEE Transactions on Power Electronics, 2021, 36(1): 1018-1029.
[27] Fu Xikun, Sun Jianjun, Huang Meng, et al. Large-signal stability of grid-forming and grid- following controls in voltage source converter: a comparative study[J]. IEEE Transactions on Power Electronics, 2021, 36(7): 7832-7840.
[28] 李锡林, 查晓明, 田震, 等. 频率突变影响下基于Lyapunov法的孤岛微电网暂态稳定性分析[J]. 电工技术学报, 2023, 38(增刊1): 18-31.
Li Xilin, Zha Xiaoming, Tian Zhen, et al. lyapunov based transient stability analysis of islanded microgrid under the influence of frequency abrupt change[J]. Transactions of China Electrotechnical Society, 2023, 38(S1): 18-31.
[29] Tian Zhen, Tang Yingjie, Zha Xiaoming, et al. Hamilton-based stability criterion and attraction region estimation for grid-tied inverters under large-signal disturbances[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2022, 10(1): 413-423.
[30] Zhang Yu, Zhang Chen, Cai Xu. Large-signal grid-synchronization stability analysis of PLL-based VSCs using Lyapunov’s direct method[J]. IEEE Transactions on Power Systems, 2022, 37(1): 788- 791.
[31] Ma Rui, Li Jinxin, Kurths J, et al. Generalized swing equation and transient synchronous stability with PLL-based VSC[J]. IEEE Transactions on Energy Conversion, 2022, 37(2): 1428-1441.
[32] Zhang Chen, Cai Xu, Rygg A, et al. Modeling and analysis of grid-synchronizing stability of a Type-IV wind turbine under grid faults[J]. International Journal of Electrical Power & Energy Systems, 2020, 117: 105544.
[33] 张琛, 蔡旭, 李征. 全功率变换风电机组的暂态稳定性分析[J]. 中国电机工程学报, 2017, 37(14): 4018-4026, 4280.
Zhang Chen, Cai Xu, Li Zheng. Transient stability analysis of wind turbines with full-scale voltage source converter[J]. Proceedings of the CSEE, 2017, 37(14): 4018-4026, 4280.
[34] He Xiuqiang, Geng Hua, Li Ruiqi, et al. Transient stability analysis and enhancement of renewable energy conversion system during LVRT[J]. IEEE Transactions on Sustainable Energy, 2020, 11(3): 1612-1623.
[35] 许诘翊, 刘威, 刘树, 等. 电力系统变流器构网控制技术的现状与发展趋势[J]. 电网技术, 2022, 46(9): 3586-3595.
Xu Jieyi, Liu Wei, Liu Shu, et al. Current state and development trends of power system converter grid-forming control technology[J]. Power System Technology, 2022, 46(9): 3586-3595.
[36] 熊小玲, 李昕悦, 周琰, 等. 基于陷波器的构网型换流器同步频率谐振抑制策略[J]. 电工技术学报, 2024, 39(12):3827-3839.
Xiong Xiaoling, Li Xinyue, Zhou Yan, et al. Synchronous frequency resonance suppression of grid-forming converter based on notch filter[J]. Transactions of China Electrotechnical Society, 2024, 39(12):3827-3839.
[37] Wang Xiongfei, Taul M G, Wu Heng, et al. Grid-synchronization stability of converter-based resources—an overview[J]. IEEE Open Journal of Industry Applications, 2020, 1: 115-134.
[38] Wang Shike, Liu Zeng, Liu Jinjun, et al. Small-signal modeling and stability prediction of parallel droop-controlled inverters based on terminal characteristics of individual inverters[J]. IEEE Transactions on Power Electronics, 2020, 35(1): 1045-1063.
[39] Guillaume D. From grid-following to grid-forming: the new strategy to build 100% power-electronics interfaced transmission system with enhanced transient behavior[D]. Lille: Ecole Centrale de Lille, 2017.
[40] Zhang Lidong, Harnefors L, Nee H P. Power- synchronization control of grid-connected voltage- source converters[J]. IEEE Transactions on Power Systems, 2010, 25(2): 809-820.
[41] Wang Jinhua, Wang Yuxiang, GuYunjie, et al. Synchronous frequency resonance of virtual synchronous generators and damping control[C]// 2015 9th International Conference on Power Electronics and ECCE Asia (ICPE-ECCE Asia), Seoul, Korea (South), 2015: 1011-1016.
[42] Shuai Zhikang, Shen Chao, Liu Xuan, et al. Transient angle stability of virtual synchronous generators using Lyapunov’s direct method[J]. IEEE Transactions on Smart Grid, 2019, 10(4): 4648-4661.
[43] Yang Jingxi, Tse C K, Huang Meng, et al. Homoclinic bifurcation of a grid-forming voltage source converter[J]. IEEE Transactions on Power Electronics, 2021, 36(11): 13176-13187.
[44] Cespedes M, Sun Jian. Impedance modeling and analysis of grid-connected voltage-source converters[J]. IEEE Transactions on Power Electronics, 2014, 29(3): 1254-1261.
[45] 王思成, 袁小明. 基于内电势幅值/频率和网络有功/无功电流工作点的变换器并网交流系统小扰动线性化方法[J]. 中国电机工程学报, 2024, 44(3): 1081-1094.
Wang Sicheng, Yuan Xiaoming. Small-disturbance linearization method for converter interfaced AC power systems based on operating points of internal-voltage amplitude/frequency and networks' active/ reactive current[J]. Proceedings of the CSEE, 2024, 44(3): 1081-1094.
[46] Liu C C, Yang Jingxi, Tse C K, et al. Transient synchronization stability of grid-following converters considering nonideal current loop[J]. IEEE Transactions on Power Electronics, 2023, 38(11): 13757-13769.
[47] Hu Qi, Fu Lijun, Ma Fan, et al. Analogized synchronous-generator model of PLL-based VSC and transient synchronizing stability of converter dominated power system[J]. IEEE Transactions on Sustainable Energy, 2021, 12(2): 1174-1185.
[48] 张梓钦, 朱东海, 马玉梅, 等. 弱电网故障下新能源并网变换器的奇异摄动模型与暂态稳定性分析[J]. 中国电机工程学报, 2023, 43(2): 454-466.
Zhang Ziqin, Zhu Donghai, Ma Yumei, et al. Singular perturbation model and transient stability analysis of grid-connected converter under weak grid faults[J]. Proceedings of the CSEE, 2023, 43(2): 454-466.
[49] Wu Tianhao, Jiang Qirong, Huang Meng, et al. Synchronization stability of grid-following converters governed by saturation nonlinearities[J]. IEEE Transactions on Power Systems, 2022, 37(5): 4102-4105.
[50] Rokrok E, Qoria T, Bruyere A, et al. Transient stability assessment and enhancement of grid-forming converters embedding current reference saturation as current limiting strategy[J]. IEEE Transactions on Power Systems, 2022, 37(2): 1519- 1531.
[51] Taul M G, Wang Xiongfei, Davari P, et al. Current limiting control with enhanced dynamics of grid-forming converters during fault conditions[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2020, 8(2): 1062-1073.
[52] 刘航, 王跃, 刘永慧, 等. 基于定量设计虚拟阻抗的VSG低电压穿越策略[J]. 高电压技术, 2022, 48(1): 245-256.
Liu Hang, Wang Yue, Liu Yonghui, et al. The LVRT strategy for VSG based on the quantitatively designed virtual impedance[J]. High Voltage Engineering, 2022, 48(1): 245-256.
[53] 葛平娟, 肖凡, 涂春鸣, 等. 考虑故障限流的下垂控制型逆变器暂态控制策略[J]. 电工技术学报, 2022, 37(14):3676-3687.
GePingjuan, Xiao Fan, Tu Chunming, et al. Transient control strategy of droop-controlled inverter considering fault current limitation[J]. Transactions of China Electrotechnical Society, 2022, 37(14):3676-3687.
[54] Liu Yushuang, Geng Hua, Huang Meng, et al. Dynamic current limiting of grid-forming converters for transient synchronization stability enhancement[J]. IEEE Transactions on Industry Applications, 2024, 60(2): 2238-2248.
[55] Huang Yunhui, Yuan Xiaoming, Hu Jiabing, et al. DC-bus voltage control stability affected by AC-bus voltage control in VSCs connected to weak AC grids[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2016, 4(2): 445-458.
[56] Wang Dong, Liang Liang, Shi Lei, et al. Analysis of modal resonance between PLL and DC-link voltage control in weak-grid tied VSCs[J]. IEEE Transactions on Power Systems, 2019, 34(2): 1127-1138.
[57] Luo Cheng, Liu Teng, Wang Xiongfei, et al. Design-oriented analysis of DC-link voltage control for transient stability of grid-forming inverters[J]. IEEE Transactions on Industrial Electronics, 2024, 71(4): 3698-3707.
[58] 洪镇堃, 占萌. 构网型变流器并网系统在强弱电网下的分岔分析[J]. 电力自动化设备, 2023, 43(9): 27-32, 54.
Hong Zhenkun, Zhan Meng. Bifurcation analysis of grid-forming converter system connected with stiff or weak AC grids[J]. Electric Power Automation Equipment, 2023, 43(9): 27-32, 54.
[59] 姜鑫, 易皓, 卓放, 等. 基于直流电压同步的构网型变流器低频振荡分析与阻尼控制[J]. 电力系统自动化, 2024, 48(16): 30-39.
Jiang Xin, Yi Hao, Zhuo Fang, et al. Low-frequency oscillation analysis and damping control of grid-based converter based on DC voltage synchronization[J]. Automation of Electric Power Systems, 2024, 48(16): 30-39.
[60] HuangLinbin, Xin Huanhai, Li Zhiyi, et al. Grid-synchronization stability analysis and loop shaping for PLL-based power converters with different reactive power control[J]. IEEE Transactions on Smart Grid, 2020, 11(1): 501-516.
[61] Pan Donghua, Wang Xiongfei, Liu Fangcheng, et al. Transient stability of voltage-source converters with grid-forming control: a design-oriented study[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2020, 8(2): 1019-1033.
[62] 付熙坤, 黄萌, 凌扬坚, 等. 功率耦合和电流限幅影响下构网型变流器的暂态同步稳定分析[J]. 中国电机工程学报, 2024, 44(7): 2815-2024.
Fu Xikun, Huang Meng, Ling Yangjian, et al. Transient synchronization stability analysis of grid-forming converterinfluenced by power-coupling and current-limiting[J]. Proceedings of the CSEE, 2024, 44(7): 2815-2024..
[63] He Xiuqiang, Pan Sisi, Geng Hua. Transient stability of hybrid power systems dominated by different types of grid-forming devices[J]. IEEE Transactions on Energy Conversion, 2022, 37(2): 868-879.
[64] Chen Shiyue, Yao Jun, Liu Yuan, et al. Coupling mechanism analysis and transient stability assessment for multiparalleled wind farms during LVRT[J]. IEEE Transactions on Sustainable Energy, 2021, 12(4): 2132-2145.
[65] Fu Xikun, Huang Meng, Pan Shangzhi, et al. Cascading synchronization instability in multi-VSC grid-connected system[J]. IEEE Transactions on Power Electronics, 2022, 37(7): 7572-7576.
[66] Hou Xiaochao, Sun Yao, Zhang Xin, et al. Improvement of frequency regulation in VSG-based AC microgrid via adaptive virtual inertia[J]. IEEE Transactions on Power Electronics, 2020, 35(2): 1589-1602.
[67] 于彦雪, 马慧敏, 陈晓光, 等. 弱电网下基于准静态模型的混合控制微电网逆变器同步稳定性研究[J]. 电工技术学报, 2022, 37(1): 152-164.
Yu Yanxue, Ma Huimin, Chen Xiaoguang, et al. Synchronous stability research of inverters in hybrid microgrid based on the quasi-static models under weak grid[J]. Transactions of China Electrotechnical Society, 2022, 37(1): 152-164.
[68] Shen Chao, Shuai Zhikang, Shen Yang, et al. Transient stability and current injection design of paralleled current-controlled VSCs and virtual synchronous generators[J]. IEEE Transactions on Smart Grid, 2021, 12(2): 1118-1134.
[69] Cheng Huijie, Shuai Zhikang, Shen Chao, et al. Transient angle stability of paralleled synchronous and virtual synchronous generators in islanded microgrids[J]. IEEE Transactions on Power Electronics, 2020, 35(8): 8751-8765.
[70] Huang Linbin, Wang Dan, Wang Xiongfei, et al. Gain and phase: decentralized stability conditions for power electronics-dominated power systems[J]. IEEE Transactions on Power Systems, 2024, http://doi.org/ 10.48550/arxiv.2309.0837.
[71] Gu Yunjie, Li Yitong, Zhu Yue, et al. Impedance-based whole-system modeling for a composite grid via embedding of frame dynamics[J]. IEEE Transactions on Power Systems, 2021, 36(1): 336-345.
[72] Tian Zhen, Li Xilin, Zha Xiaoming, et al. Transient synchronization stability of an islanded AC microgrid considering interactions between grid-forming and grid-following converters[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2023, 11(4): 4463-4476.
[73] 黄森, 姚骏, 钟勤敏, 等. 含跟网和构网型新能源发电单元的混联电力系统暂态同步稳定分析[J/OL]. 中国电机工程学报, 1-14[2024-09-25]. http://kns.cnki.net/kcms/detail/11.2107.TM.20230801. 1732.002.html.
Huang Sen, Yao Jun, Zhong Qinmin, et al. Transient synchronization stability analysis of hybrid power system with grid-following and grid-forming renewable energy generation units[J]. Proceedings of the CSEE, 1-14[2024-09-25]. http://kns.cnki.net/kcms/ detail/11.2107.TM.20230801.1732.002.html.
[74] 杨子千. 直流电压时间尺度下电压源型变换器并网系统同步稳定建模与分析[D]. 武汉: 华中科技大学, 2022.
Yang Ziqian. Synchronization stability modeling and analysis of VSC-tied systems under DC-link voltage timescale[D]. Wuhan: Huazhong University of Science and Technology, 2022.
[75] Yuan Hao, Yuan Xiaoming, Hu Jiabing. Modeling of grid-connected VSCs for power system small-signal stability analysis in DC-link voltage control time scale[J]. IEEE Transactions on Power Systems, 2017, 32(5): 3981-3991.
[76] Yu Jiajun, Wang Shike, Liu Zeng, et al. Accurate small-signal terminal characteristic model and SISO stability analysis approach for parallel grid-forming inverters in islanded microgrids[J]. IEEE Transactions on Power Electronics, 2023, 38(5): 6597-6612.
[77] 易相彤, 黄文, 沈超, 等. 锁相环同步型变流器并联系统暂态同步稳定分析[J]. 中国电机工程学报, 2022, 42(17): 6338-6347.
Yi Xiangtong, Huang Wen, Shen Chao, et al. Transient synchronization stability analysis of paralleled converter systems with phase-locked loop[J]. Proceedings of the CSEE, 2022, 42(17): 6338-6347.
[78] He Xiuqiang, Geng Hua. PLL synchronization stability of grid-connected multiconverter systems[J]. IEEE Transactions on Industry Applications, 2022, 58(1): 830-842.
[79] Gong Hong, Wang Xiongfei, Harnefors L. Rethinking current controller design for PLL-synchronized VSCs in weak grids[J]. IEEE Transactions on Power Electronics, 2022, 37(2): 1369-1381.
[80] 张美清, 袁小明, 胡家兵. 基于自稳/致稳性的路径级数展开方法及其在含多样化电力电子装备电力系统稳定性分析中的应用[J]. 中国电机工程学报, 2021, 41(5): 1637-1655.
Zhang Meiqing, Yuan Xiaoming, Hu Jiabing. Path series expansion method based on self-/en-stabilizing properties and its application in the stability analysis of power systems with diversified power electronic devices[J]. Proceedings of the CSEE, 2021, 41(5): 1637-1655.
[81] FuXikun, Huang Meng, Tse C K, et al. Synchronization stability of grid-following VSC considering interactions of inner current loop and parallel-connected converters[J]. IEEE Transactions on Smart Grid, 2023, 14(6): 4230-4241.
[82] 杨晖, 袁小明. 电力系统机电动态过程中时变幅频内电势激励下的功率特性[J]. 中国电机工程学报, 2021, 41(9): 3079-3090.
Yang Hui, Yuan Xiaoming. Power characteristics with excitation of time-varying amplitude-frequency internal voltages during electromechanical dynamic process in power systems[J]. Proceedings of the CSEE, 2021, 41(9): 3079-3090.
[83] Bianchi F D, Domnguez-Garca J L. Coordinated frequency control using MT-HVDC grids with wind power plants[J]. IEEE Transactions on Sustainable Energy, 2016, 7(1): 213-220.
[84] 刘永辉, 张国澎, 孙新迪, 等. 基于PCS变主从协同控制的微电网平滑离网技术[J]. 电气工程学报, 2023, 18(4): 310-319.
Liu Yonghui, Zhang Guopeng, Sun Xindi, et al. Microgrid smooth off grid technology based on PCS variable master-slave cooperative control[J]. Journal of Electrical Engineering, 2023, 18(4): 310-319.
[85] 余墨多, 黄文焘, 邰能灵, 等. 逆变型分布式电源并网运行暂态稳定机理与评估方法[J]. 电工技术学报, 2022, 37(10):2596-2610.
Yu Moduo, Huang Wentao, Tai Nengling, et al. Transient stability mechanism and judgment for inverter interfaced distributed generators connected with public grids[J]. Transactions of China Electrotechnical Society, 2022, 37(10):2596-2610.
[86] 刘子文, 苗世洪, 范志华, 等. 基于自适应下垂特性的孤立直流微电网功率精确分配与电压无偏差控制策略[J]. 电工技术学报, 2019, 34(4): 795-806.
Liu Ziwen, Miao Shihong, Fan Zhihua, et al. Accurate power allocation and zero steady-state error voltage control of the islanding DC microgird based on adaptive droop characteristics[J]. Transactions of China Electrotechnical Society, 2019, 34(4): 795-806.
[87] 谢沁园, 王瑞田, 林克文, 等. 基于端口电压积分与变下垂系数的逆变器并联下垂控制策略[J]. 电工技术学报, 2023, 38(6):1596-1607.
XieQinyuan, Wang Ruitian, Lin Kewen, et al. Droop control strategy of parallel lnverters based on port voltage integration and variable droop coefficient[J]. Transactions of China Electrotechnical Society, 2023, 38(6):1596-1607.
[88] 方红伟, 陶月, 肖朝霞, 等. 并网逆变器并联系统的鲁棒控制与环流分析[J]. 电工技术学报, 2017, 32(18): 248-258.
Fang Hongwei, Tao Yue, Xiao Zhaoxia, et al. Robust control and circulating current analysis for grid- connected parallel inverters[J]. Transactions of China Electrotechnical Society, 2017, 32(18): 248-258.
[89] Colombino M, Groß D, Brouillon J S, et al. Global phase and magnitude synchronization of coupled oscillators with application to the control of grid-forming power inverters[J]. IEEE Transactions on Automatic Control, 2019, 64(11): 4496-4511.
[90] Seo G S, Colombino M, Subotic I, et al. Dispatchable virtual oscillator control for decentralized inverter- dominated power systems: analysis and experiments [C]//2019 IEEE Applied Power Electronics Conference and Exposition (APEC), Anaheim, CA, USA, 2019: 561-566.
[91] Milano Federico. Complex frequency[J]. IEEE Transa-ctions on Power Systems, 2022, 37(2): 1230-1240.
[92] He Xiuqiang, Häberle V, Subotić I, et al. Nonlinear stability of complex droop control in converter-based power systems[J]. IEEE Control Systems Letters, 2023, 7: 1327-1332.
[93] 钟万勰. 参变量变分原理及其在工程中的应用[M]. 北京: 科学出版社,1997.
Abstract With the integration of a large amount of renewable energy generation into the AC power grid through power electronic equipment, the dynamic characteristics of the system are influenced by the multi-timescale control of these electronic devices. The grid-connected converters, operated under various types of controls, exhibit strong nonlinearity and low inertia during operation, posing synchronization stability issues for power grids with a high proportion of renewable energy.Especially when large-scale renewable energydevicesare connected to the weak grid, the multi-time scale and the multi-machine interaction between the devices are easy to cause the stability problem of the grid-connected system. For the grid-following converters, the synchronization stability of PLL under weak grid has received much attention due to the disturbance of the converter terminal voltage. Thegrid-formingconvertershave the risk of instability in strong grid, due the line impedance of resistive characteristics will cause power coupling and multi-machine power oscillation. In the large-disturbance analysis of synchronous stability, the influence of nonlinearity, limiting protection and switching control of grid-following/grid-forming converters is more obvious.The synchronous stability mechanism of the grid-connected converter system under control needs to be further sorted out.
This article provides an overview of the research on the synchronization stability of renewable energy grid-connected systems under multi-time scale control. It comprehensively reviews the modeling and stability analysis techniques for grid-connected systems under single-time scale synchronization control, multi-time scale interaction, and multi-machine multi-time scale interaction. Firstly, under the synchronous control time scale, the synchronous stability analysis methods of grid-following and grid-forming converters are summarized. Secondly, The multi-time scale control interaction is mainly embodied in the interaction between synchronization control andvoltage/current loop. The interaction of grid-following converters is particularly significant under the condition of weak grid. The non-negligible interactionis existed between the active and reactive power control loops in the grid-forming converter due to their close time scale.Thirdly, in new energy plants and stations, there is a complex dynamic process of multi-machine multi-time scale interaction. Under the condition of non-ideal weak grid, the interaction between the control loops of multiple grid-connected converters in parallel has synchronous- synchronous control interaction of the same time scale, and the interaction of different time scales between voltage/current loops.
On this basis, a construction framework for the synchronization mechanism of renewable energy grid-connected systems is proposed. In the grid-connected converter system with multi-time scale and mass distributed generation, it is not considered in the traditional methods that the deterioration of the overall coordination of the system caused by the dynamic interaction of multi-timescale massive converters. Based on this, a construction framework for the synchronization mechanism of renewable energy grid-connected systems is proposed, considering both global design and distributed implementation of synchronization performance, while taking into account resource and network constraints.
The analysis and review of synchronization technology in renewable energy grid-connected systems in this article provide a systematic overview of the current state of research on analysis methods. Moreover, a reliable outlook on the direction of synchronous operation mechanism and method, especially high-order nonlinear system analysis is presented.
keywords:Grid-connected converter, grid-following control, grid-forming control, synchronization stability, synchronization mechanism
中图分类号:TM464
DOI: 10.19595/j.cnki.1000-6753.tces.240569
国家电网有限公司科技项目资助(4000-202399470A-3-2-ZN)。
收稿日期 2024-04-10
改稿日期 2024-04-18
黄 萌 男,1984年生,教授,博士生导师,研究方向为新能源并网系统稳定分析与控制。
E-mail:meng.huang@whu.edu.cn(通信作者)
舒思睿 女,1998年生,博士研究生,研究方向为新能源并网系统稳定分析与控制。
E-mail: ssr5dd@stu.xjtu.edu.cn
(编辑 郭丽军)