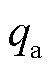占总热量q的比值，称为电枢侧热分配系数[12]，则单位时间内传导进沉积层轨道的热量为
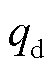=(1-α)q，传导进电枢的热量为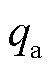=αq。摘要 维持良好的滑动电接触性能是实现电磁轨道发射高频率和高效率工作的重要保证。重复发射时，轨道表面沉积层影响电枢表面熔化特性，进而改变接触状态，从而影响滑动电接触性能，因此有必要对沉积层作用下的电枢熔化特性进行分析。首先，通过分析沉积层受热过程，建立了沉积层熔化判断模型，并提出沉积层熔化判断条件；其次，基于沉积层熔化特性，建立了沉积层作用下的电枢熔化磨损计算模型，分析不同电流条件下沉积层熔化特性发现，载流量越大，沉积层熔化范围越大，并且启动低速阶段沉积层能够发生熔化，高速阶段沉积层不容易发生熔化；最后，开展重复发射试验，通过理论分析结合试验验证对电枢熔化的抑制特性进行研究。结果表明：沉积层厚度随着发射次数逐渐增加，沉积层全部熔化状态下，电枢最大熔化深度随发射次数呈逐渐减小的趋势。模型计算结果与试验测量结果变化趋势相同，说明沉积层熔化对电枢熔化有抑制效应。该文所建立模型及分析结果对深入理解重复发射时枢轨界面熔化磨损机理、提高滑动电接触性能具有重要意义。
关键词：重复发射 滑动电接触 沉积层熔化 电枢熔化
维持良好的滑动电接触性能是实现电磁轨道发射（Electromagnetic Launch, EML）高频率和高效率工作的重要保证[1-4]。大电流高速滑动电接触环境下，随着电枢在轨道上高速滑动，电接触界面上会产生很大的焦耳热和摩擦热[5]。首次发射（轨道出厂/清理后）时，电枢在光洁轨道表面滑动，在巨大的焦耳热和摩擦热作用下，低熔点电枢表面产生熔化磨损，熔化后的材料最终凝固在轨道表面上形成百微米厚的铝沉积层[6]。重复发射时，电枢在轨道表面沉积层上滑动，沉积层表面材料受热发生熔化，其熔化状态影响电枢表面熔化磨损过程，进而改变接触状态，从而影响滑动电接触性能。因此，研究沉积层作用下的电枢熔化特性，对深入理解界面熔化磨损机理、提高滑动电接触性能具有重要意义。
文献[7]通过开展重复发射试验发现，在重复发射过程中沉积层发生了重新熔化现象，但是没有从理论上对沉积层熔化特性及其熔化机理进行研究。文献[8]开展了低速大电流条件下电枢熔化磨损试验，获得了电枢熔化扩展规律，但是重复发射试验时轨道表面沉积层被打磨去除，没有考虑沉积层对电枢熔化特性的影响。文献[9]通过理论分析和数值仿真对高速滑动电接触电枢表面熔化磨损过程进行了研究，但未涉及沉积层作用下的电枢熔化磨损计算。文献[10-11]基于小口径发射装置开展连续发射试验，发现沉积层的存在可以缩短电枢的启动时间，认为可能是沉积层在焦耳热的作用下发生了熔化，熔化液具有润滑效应，减小了枢轨间的摩擦力，但是没有对沉积层熔化特性及其对电枢熔化的影响进行更深入的理论分析。
基于上述分析，本文建立了沉积层熔化判断模型，获得了沉积层熔化时刻和熔化厚度计算方程，提出了沉积层熔化判断条件。基于沉积层熔化特性，建立了沉积层作用下的电枢熔化磨损计算模型。分析了不同电流条件下沉积层的熔化特性，并通过理论分析结合试验验证对电枢熔化的抑制特性进行了研究，获得了沉积熔化范围及其对电枢熔化的抑制效果，对于后续研究沉积层控制技术、提高重复发射时的枢轨接触性能具有重要意义。
电磁轨道发射（EML）依靠脉冲大电流形成强磁场推动载流电枢在轨道表面高速滑动，滑动电接触界面产生巨大的焦耳热和摩擦热。轨道表面打磨后首次发射时，铝电枢在光洁铜轨道表面滑动，在界面热源作用下，低熔点电枢表面会产生熔化磨损，熔化后的材料最终凝固在轨道表面上形成百微米厚的铝沉积层。电枢-沉积层滑动电接触模型如图1所示。重复发射时，电枢在轨道表面沉积层上滑动。由于电枢滑动时间较短，与空气的对流换热可以忽略不计，不考虑界面上热量损失，认为界面热源全部被沉积层轨道和电枢吸收。图1中，α（0≤α≤1）定义为电枢侧吸收的热量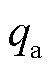占总热量q的比值，称为电枢侧热分配系数[12]，则单位时间内传导进沉积层轨道的热量为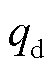=(1-α)q，传导进电枢的热量为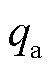=αq。
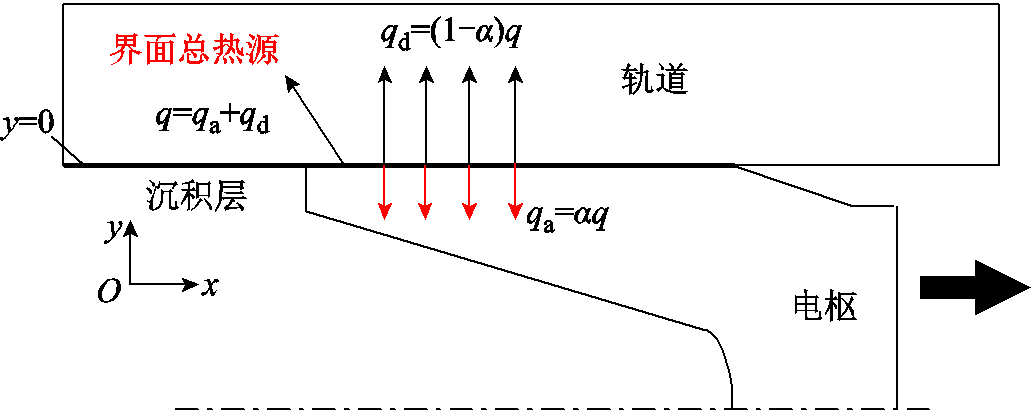
图1 电枢-沉积层滑动电接触模型
Fig.1 Sliding electrical contacts modeling of armature-deposited rail
在滑动过程中，界面热源持续加热接触界面。界面热源相对于电枢是静止热源；相对于沉积层轨道来说，只有接触区域存在热源，所以是运动热源。重复发射过程中，电枢与轨道侧铝沉积层直接接触，由于滑动时间较短，热量在接触界面的透入深度远小于电枢和轨道侧沉积层的尺寸，可以将电枢和沉积层轨道看作半无限大固体[13]，并且初始温度分布均为室温。为了方便分析，沉积层受热过程示意图如图2所示。
将图2中黄色沉积层作为研究对象，电枢和轨道沉积层开始接触的时间为tin，则离开时间为tr=tin+tc，tc=la/Uav为接触时间，la为接触长度，Uav为接触时间内电枢平均运动速度，定义为Uav=[U(tin)+ U(tr)]/2，U(t)为电枢运动速度。假定轨道沉积层只有在接触时间内才会受热，不考虑电枢离开后沉积层受焦耳热加热影响，从tin时刻开始，沉积层受持续热源加热升温进而发生熔化，到tr时刻电枢离开沉积层，该区域内沉积层不再受热源加热，进入自然冷却状态。接触时间内流入沉积层的热流量可以看作恒定静止热源并均匀分布在接触面上，沉积层受恒定静止热源持续加热产生温升进而发生熔化。
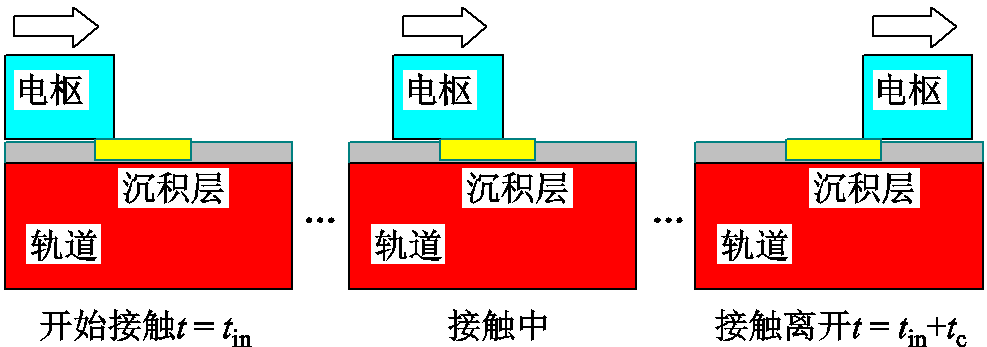
图2 沉积层受热过程示意图
Fig.2 Schematic diagram of the heating process of the deposited layer
在小口径低能级发射工况下，枢轨间接触电阻值对界面焦耳热的影响较为显著。接触电阻与接触面积、电磁压力、接触材料参数有关，计算模型见文献[9]。
为方便分析，认为界面热源均匀分布在接触区域，并且在滑动过程中接触区域面积保持不变。若驱动电流为I，接触面积为A，接触电阻为Rc，则单位面积上产生的焦耳热流速率可以写为
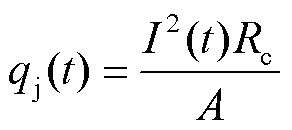（1）
一体C形电枢尾翼提供的电磁接触压力示意图如图3所示。流经电枢尾翼的电流I在电流产生的磁场B作用下产生电磁力F，电磁力垂直于轨道的分力即为电枢/轨道电磁接触压力FEM。
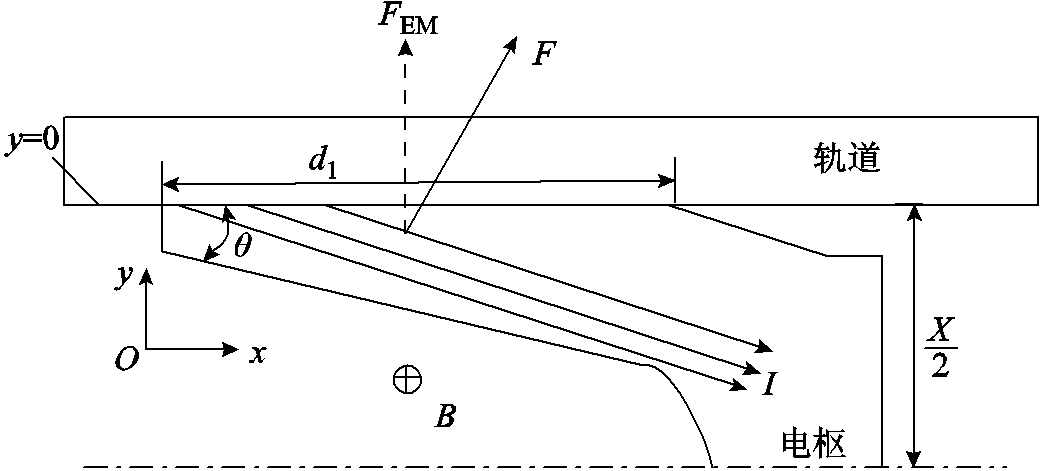
图3 电枢/轨道电磁接触压力示意图
Fig.3 Schematic diagram of armature/rail electromagnetic contact pressure
假设电枢后部炮膛中的磁场分布均匀并且轨道电流从电枢尾翼端部流入电枢内部，可以得到电枢尾翼电磁接触压力为
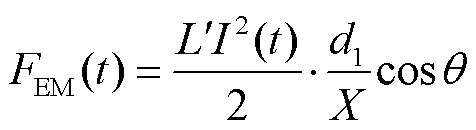（2）
式中，d1为电枢尾翼长度；X为轨道间距；θ为尾翼倾角；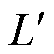
为电感梯度。若发射质量为M，在电磁推力和滑动摩擦共同作用下的电枢滑动速度可以写为[14]
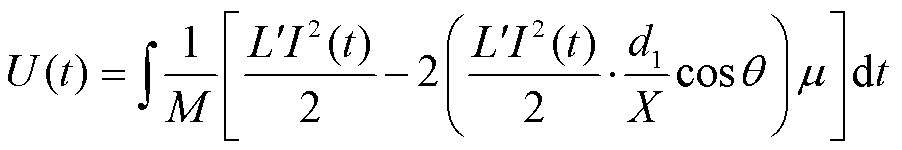（3）
式中，μ为动摩擦系数，文中取为0.1[15]。则单位面积单位时间内界面产生的摩擦热为
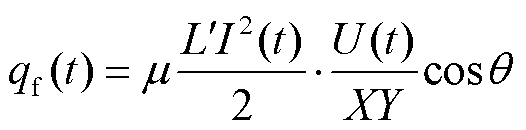（4）
式中，Y为电枢宽度。
假设接触时间内驱动电流取平均值并保持不变，则接触时间内平均电流Iav为
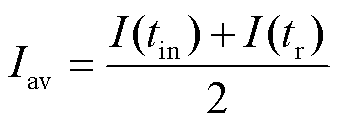（5）
令速度为接触时间内平均值Uav，则接触时间内界面焦耳热和摩擦热一起构成界面恒定热源，可以近似写为
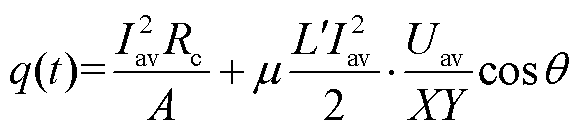（6）
不考虑接触界面结构的改变，在滑块静止状态下，界面热源在电枢和轨道间的热分配系数仅与材料热参数有关[16]。由于电枢和沉积层材料主要成分均为铝，材料热参数相同，在电枢启动阶段，即滑动速度近似为0，可以认为界面总热量的50%将进入沉积层轨道，另一半热量会传导进入电枢。当电枢沿着沉积轨道滑动时，随着滑动速度的增加，由于两个滑动表面的温差增大，更多的热量将流入温度较低的沉积层。极限状态下，所有界面热量都会流入沉积轨道。因此，沉积轨道的热分配系数变化范围为
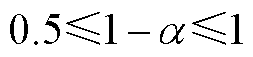（7）
若沉积层厚度足够厚，远大于接触时间内的热透入深度，则沉积层可以视为半无限大固体。接触时间内，假如接触界面热流量恒定，沉积层受热过程可以等效为初始温度为T0的一半无限大物体在y=0位置处界面突然受到恒定热流密度加热的物理模型。由于界面温度处处相等，温度梯度只存在于沉积层厚度方向，所以接触时间内沉积层的热传导可近似看作一维模型，则相应的一维热传导方程可以写为
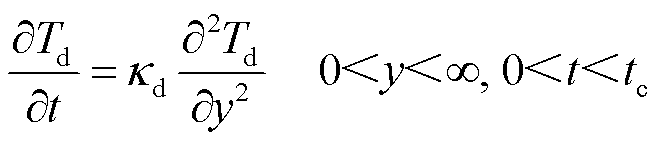（8）
式中，κd为沉积层轨道的热扩散率，定义为κd= kd/(cdρd)，kd为沉积层轨道热导率，cd为沉积层比热容，ρd为沉积层密度；Td(y, t)为沉积层温度分布。
沉积层初始温度为T0，当y趋于无穷大时沉积层温度也为T0，接触界面边界条件为
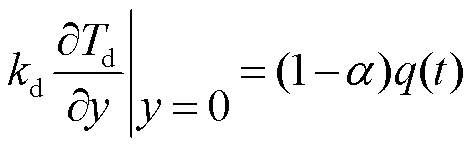（9）
结合边界条件式（9），采用拉普拉斯变换求解一维热传导偏微分方程式（8），可以获得接触时间内沉积层温度分布方程为
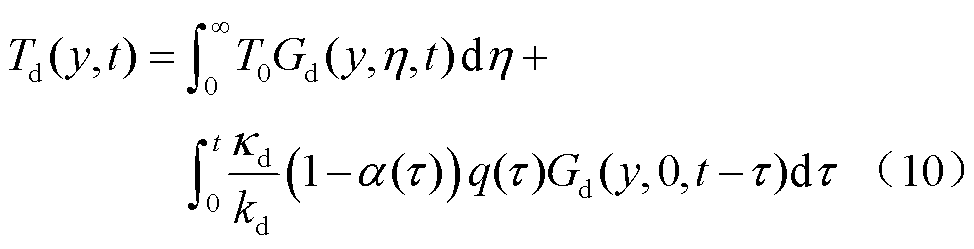
式中，η为y轴方向无量纲变量；Gd(y, η, t)为半格林函数，定义为
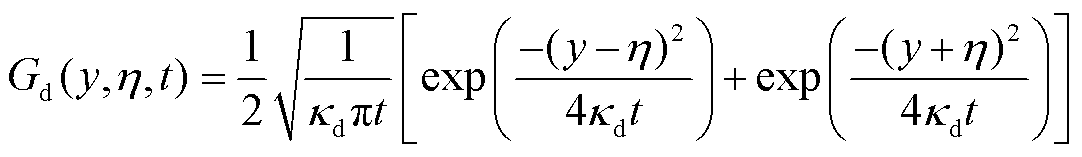（11）
假设界面材料熔化后不随着电枢运动，而是在轨道作用下立即被移走并沉积在轨道表面。令沉积层在界面处温度为沉积层熔点Tm，即Td(0, tm)=Tm，即可获得沉积层达到熔点时对应的时刻tm为
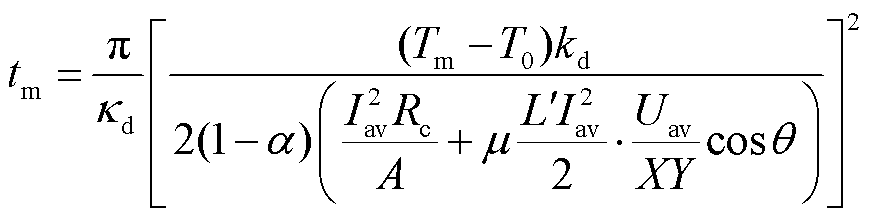（12）
在接触时间内，如果界面热源持续加热沉积层到达熔化时刻tm，沉积层温度达到熔点开始熔化，继续吸收潜热沉积发生相变。因此，如果沉积层受热时间tc≥tm，则接触时间内沉积层会发生熔化。为方便分析，定义沉积层熔化时间系数λ为
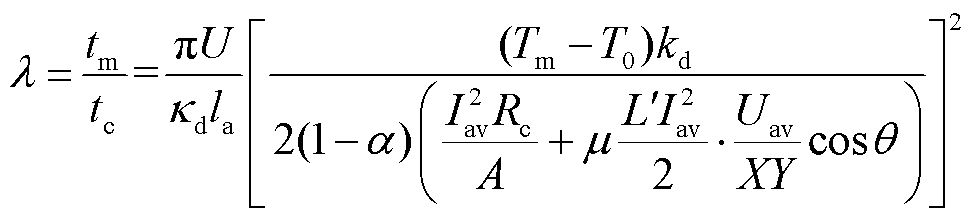（13）
则接触期间界面热源作用下沉积层发生熔化的条件可以写为
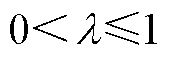（14）
从式（13）可以看出，在速度和电流已知的情况下，沉积层熔化时间系数仅为界面热分配系数的函数。由热分配系数变化范围式（7）可知，当1-α=0.5时，界面热源流入沉积层的热量最小，熔化时间系数最大为λmax。如果当沉积层轨道侧吸收热量最小时，沉积层熔化时间系数依然能小于1，即λmax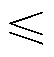
1，则在实际发射条件下，沉积层必然会发生熔化。因此，沉积层能够发生熔化的条件变为
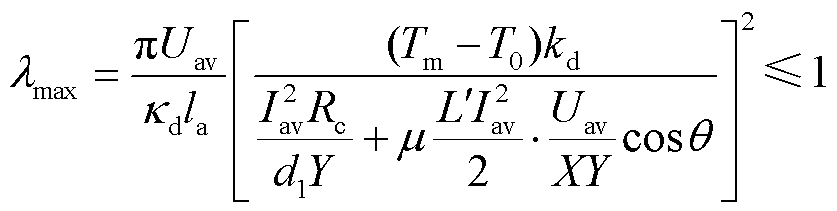（15）
极限状态下，界面热源最终全部进入沉积层轨道侧，即沉积层轨道侧热分配系数1-α取最大值1，对应沉积层熔化时间系数取最小值λmin。如果沉积层在吸热最大情况下的熔化时间系数依然能大于或等于1，即λmin≥1，则沉积层不会发生熔化。故沉积层不会发生熔化的极限条件为
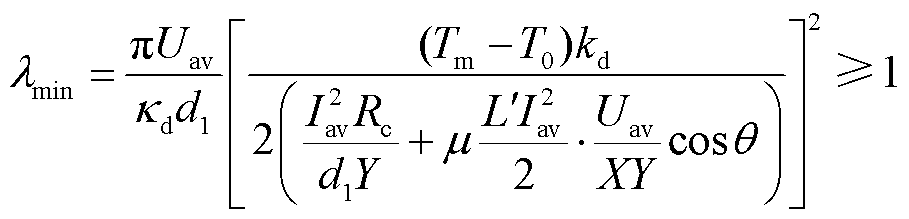（16）
沉积层熔化后，由于枢轨接触荷载较大，熔化的液态沉积铝无法在枢轨间形成完整液化层，熔化过程中电枢仍与未熔化的固态沉积层直接接触，界面热源焦耳热和摩擦热占主导，在摩擦学中称为边界润滑状态[17]。边界润滑建模分析时可以等效为摩擦系数减小的固-固摩擦[18]。
电枢和轨道沉积层接触时间内，流入沉积层的热流量为(1-α)q(t)，取一个沉积层体积元，长度为l，宽度为Y（即电枢宽度），厚度为d0。由于电枢和沉积层接触时间很短，沉积层自身焦耳热及其向轨道和周围空气的传热可以忽略，则沉积层体积元熔化热平衡方程为
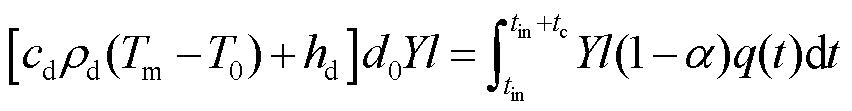（17）
式中，hd为沉积层单位体积熔化潜热。
此时接触面积A=d1Y，考虑界面恒定热源计算表达式（6），接触时间tc内界面沉积层熔化厚度可以写为
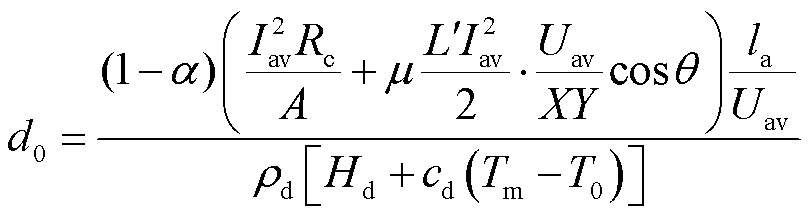（18）
式中，Hd为沉积层单位质量熔化潜热，Hd=hd/ρd。
在电流、速度等其他发射参数确定的情况下，沉积层熔化厚度与沉积层侧热分配系数成正比。当1-α=0.5时，界面热源流入沉积层热量最小，沉积层熔化厚度为最小值dmin，即
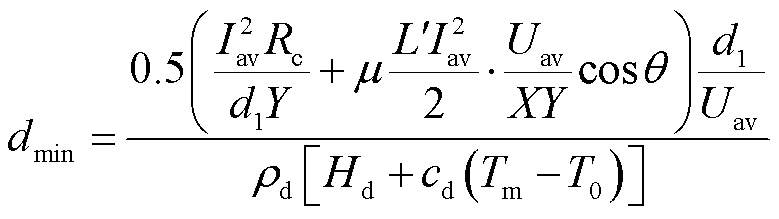（19）
假设电枢与沉积层接触时间内界面热源全部被沉积层吸收，则接触时间内沉积层能够熔化的厚度应为沉积层最大重熔厚度值，此时1-α=1，即
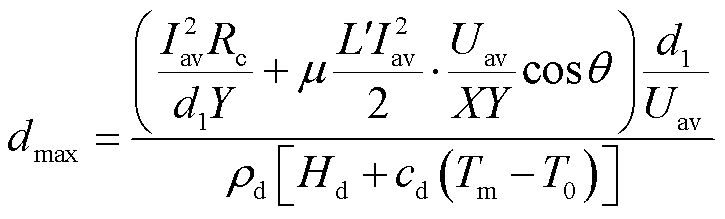（20）
根据式（19）和式（20）可以分别求出不同发射位置处沉积层熔化厚度的最小值和最大值，则在电枢熔化后沉积层在不同发射位置处能够熔化的厚度范围为
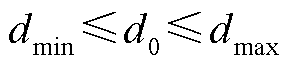（21）
为了对比分析沉积层轨道对电枢熔化磨损的影响，首先计算光洁轨道下电枢熔化磨损特性。此处光洁轨道为铜轨道，熔点远高于铝电枢，铝电枢和沉积层材料近似相同，熔点相同均为Tm。电枢熔化后，不考虑液化层存在的情况下，可认为铜轨道表面不会发生熔化，最大温度为熔点Tm。这种情况下轨道侧热流量可以写为[19]
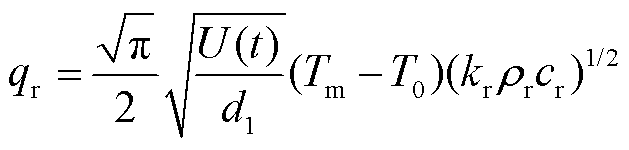（22）
式中，kr为光洁轨道热导率；cr为光洁轨道比热容；ρr为光洁轨道密度。
电枢达到熔点后，继续吸收热量会使材料熔化，设电枢熔化平均磨损速率为vma（m/s），忽略电枢材料本身的焦耳温升以及与周围空气的对流换热，电枢界面处的热流量可以近似写为
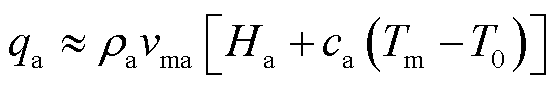（23）
式中，Ha为电枢材料熔化潜热；ca为电枢材料比热容。
不考虑界面上热量损失，界面焦耳热和摩擦热全部流向电枢和轨道，根据界面热量守恒，电枢侧热流量又可以写为
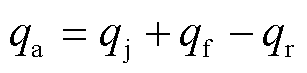（24）
则电枢平均熔化磨损速度为
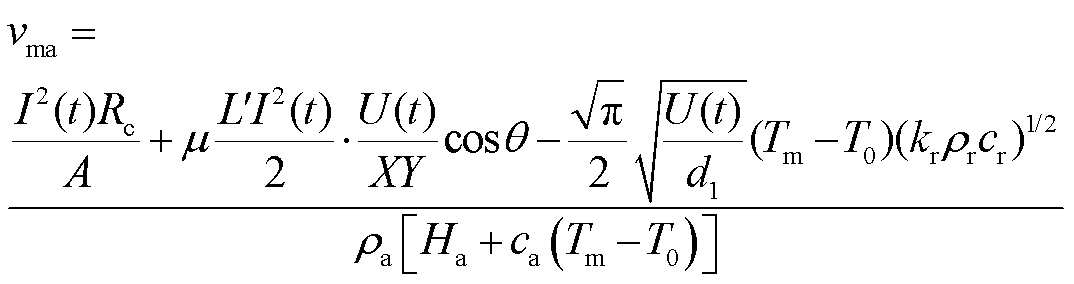（25）
电枢与沉积层开始接触的时间为tin，假设在开始接触后的tg时间内沉积层全部熔化（0＜tg＜tc），则经过tg时间后电枢和轨道直接接触传热，单位时间单位面积内光洁轨道吸收的热量qr如式（22）所示。设沉积层厚度为d0，在经历tg时间全部熔化，则有
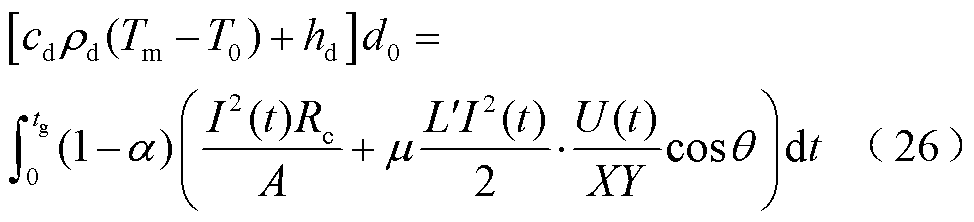
若0～tg时间内电流和速度均取平均值即Iav和Uav，则沉积层全部熔化时刻为
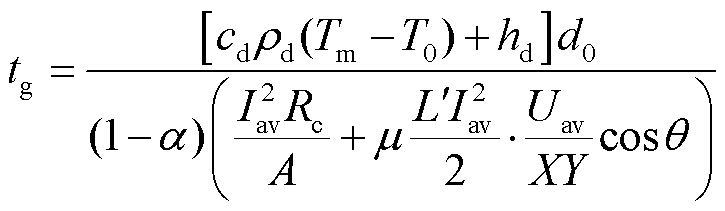（27）
则接触时间tc内沉积层和轨道吸收总热量为
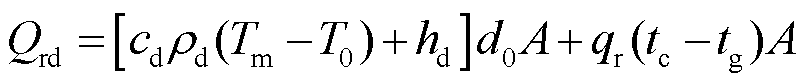（28）
所以接触时间内轨道和沉积层侧吸收的热流量为
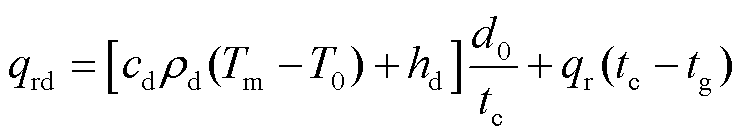（29）
则接触时间内焦耳热和摩擦热产生的总热量减去沉积层和轨道吸收的热量即为电枢侧发生熔化磨损所需的热流量，表示为
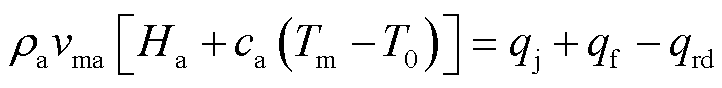（30）
则沉积层全部熔化情形下电枢熔化磨损速度为
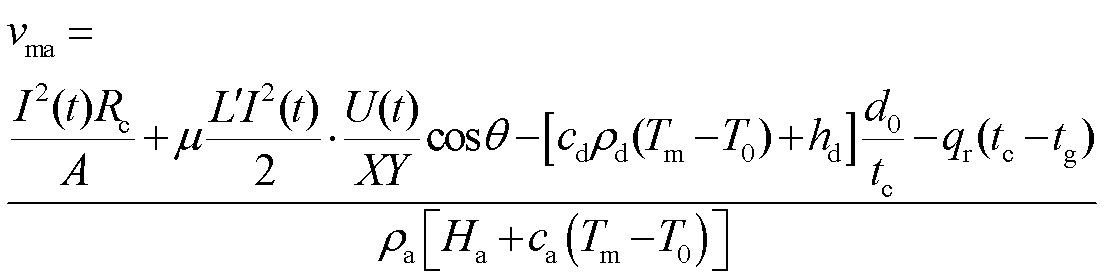（31）
典型电流波形如图4所示，电流幅值IM=400 kA。电枢口径为20 mm×20 mm、尾翼接触长度d1=20 mm，发射质量为30 g，对应电枢运动速度和位移曲线如图5所示。电枢材料为6061铝合金，轨道为铜轨道，由于沉积层主要成分为铝，近似认为沉积层材料与电枢材料相同，均为铝合金材料，材料参数见表1。
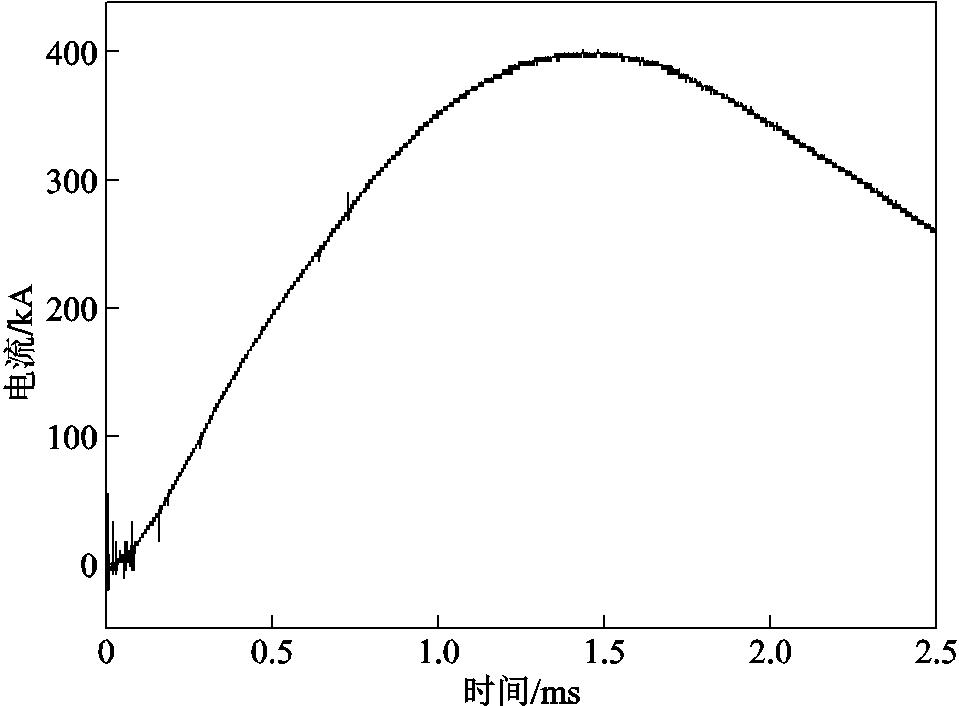
图4 电流波形
Fig.4 Current waveform
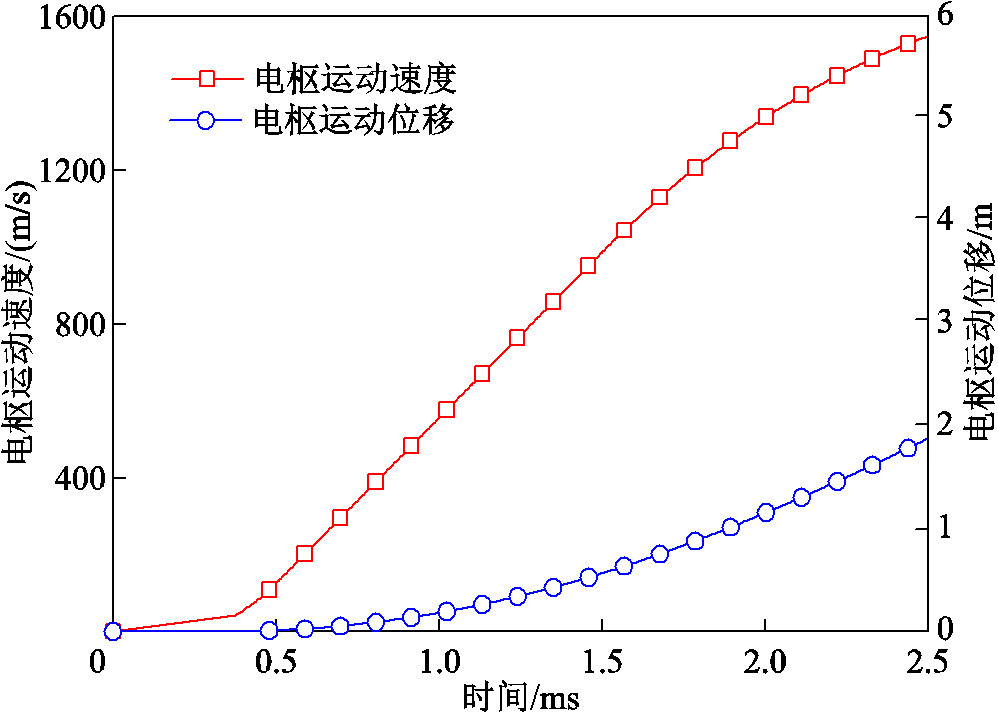
图5 电枢运动速度及位移曲线
Fig.5 Armature’s velocity and displacement curves
表1 材料参数
Tab.1 Material parameters
材料熔点/K密度/(kg/m3)热导率/[W/(m·K)]比热容/[J/(kg·K)] 铝合金9332 758170900 铜1 3588 950400400
为了更准确地衡量沉积层熔化范围，相同电流波形下，可引入载流量G进行衡量，表示为
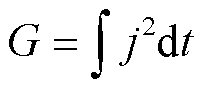（32）
式中，j为电流密度。相同电流波形情况下，不同电流幅值对应的载流量见表2。
表2 不同电流幅值对应的载流量
Tab.2 Current carrying capacity for different current amplitudes
电流幅值/kAG/(kA2·ms/m2) 350420 400524 500723 600909 7001 080
根据本文沉积层熔化条件分析模型，电流幅值为400 kA，载流量对应为524 kA2·ms/m2，计算轨道表面上沉积层熔化范围如图6所示。当流入沉积层热量最小时，熔化时间系数取最大值λmax，λmax随位移变化曲线如图6中红色实线所示，曲线与λ=1交点为(Lmin, 1)。可以发现，在发射范围[0, Lmin]内，满足沉积层熔化的极限条件式（15），这说明沉积层在[0, Lmin]范围内肯定会发生熔化，此位移区间为沉积层熔化区，Lmin为沉积层熔化范围的最小值。
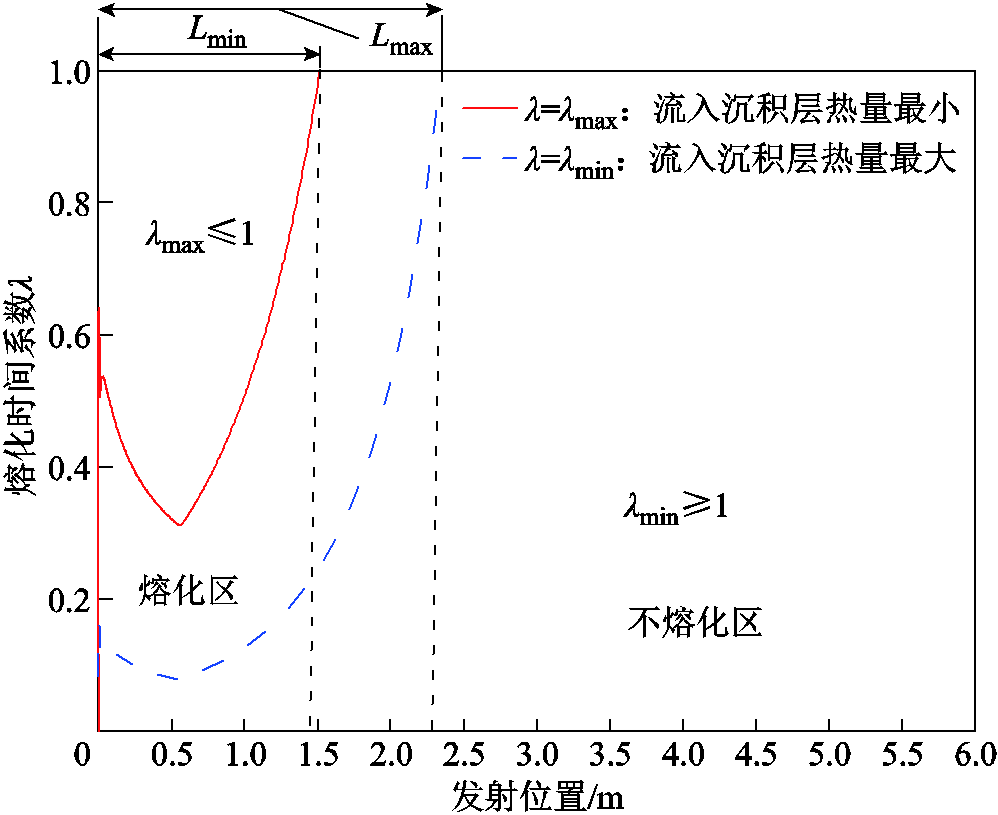
图6 沉积层熔化范围
Fig.6 Melting range of the deposited layer
当流入沉积层热量为最大时，熔化时间系数取最小值为λmin，λmin随位移变化曲线如图6中蓝色虚线所示，曲线与λ=1交点为(Lmax, 1)。可以看到，在发射范围[Lmax, 6]内，满足沉积层不熔化的极限条件式（16），这说明沉积层在[Lmax, 6]范围内肯定不会发生熔化，此位移区间为沉积层不熔化区，Lmax称为沉积层能够熔化的最大范围，即超过此范围沉积层不会发生熔化。如图6中所示，在电流幅值为400 kA、载流量为524 kA2·ms/m2发射条件下，最小熔化范围约为0～1.5 m。
图7为不同电流下沉积层熔化范围，其中图7a为熔化时间系数最大值，图7b为熔化时间系数最小值。可以发现，随着发射位移的增加，λmax和λmin在初始阶段均小于1，在高速阶段位移较大处出现大于或等于1的情况，并且电流幅值越大，载流量越大，熔化时间系数越小，沉积层越容易发生熔化。
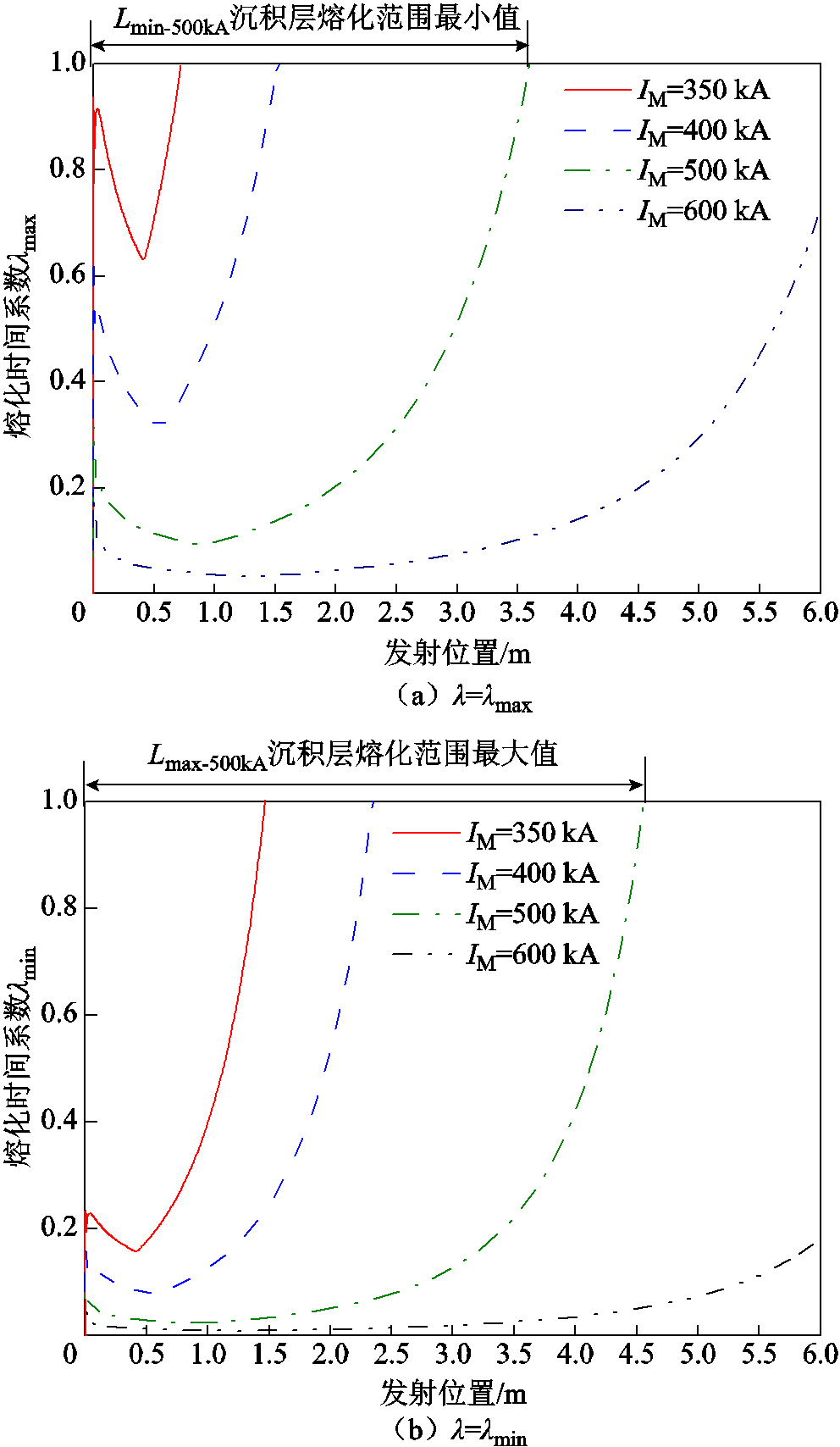
图7 不同电流下沉积层熔化范围
Fig.7 Melting range of deposited layers at different currents
当电流幅值为350 kA时，对应载流量为 420 kA2·ms/m2，炮膛长度如果为2 m，Lmin≈0.7 m，Lmax≈1.5 m，即发射范围0～0.7 m内沉积层都能够发生熔化，而当电枢位移大于1.5 m时，图7b中对应的沉积层最小熔化系数开始出现大于1的情形，即1.5 m位移之后沉积层不会发生熔化，这说明启动低速阶段沉积层能够发生熔化，高速阶段沉积层不容易发生熔化。
当电流幅值增加至500 kA时，对应载流量增加至723 kA2·ms/m2，Lmin≈3.5 m，Lmax≈4.5 m，即发射范围0～3.5 m内沉积层都能够发生熔化，而当电枢位移大于4.5 m时，图7b中对应的沉积层最小熔化系数大于1，即4.5 m位移之后沉积层不会发生熔化。如果炮膛长度为2 m，则在整个发射范围内，沉积层均能够发生熔化。可以看到，载流量对沉积层熔化范围有很大影响，载流量越大，沉积层熔化范围越大。
保持电流波形不变，改变电流幅值从400～700 kA变化，发射质量仍为30 g，其他参数保持不变，则不同电流幅值下沉积层熔化厚度随着发射位置的变化曲线如图8所示。可以发现，沉积层熔化厚度在起始位置较大，然后迅速减小，在电流平顶阶段沉积层熔化厚度变化较为缓慢，呈现稳定分布状态，到电流下降时刻，沉积层熔化厚度曲线出现转折点，沉积层熔化厚度开始近似直线减小趋势。随着电流幅值的增大，不同位置处熔化厚度均有所增加，增加量与电流幅值的增大量近似成正比关系。
通过测量实际发射后沉积层的厚度分布发现，如果沉积层厚度分布在最小熔化厚度曲线之下，说明沉积层能够发生全部熔化；如果沉积层厚度分布在最大熔化厚度曲线之上，则沉积层不会发生全部熔化。
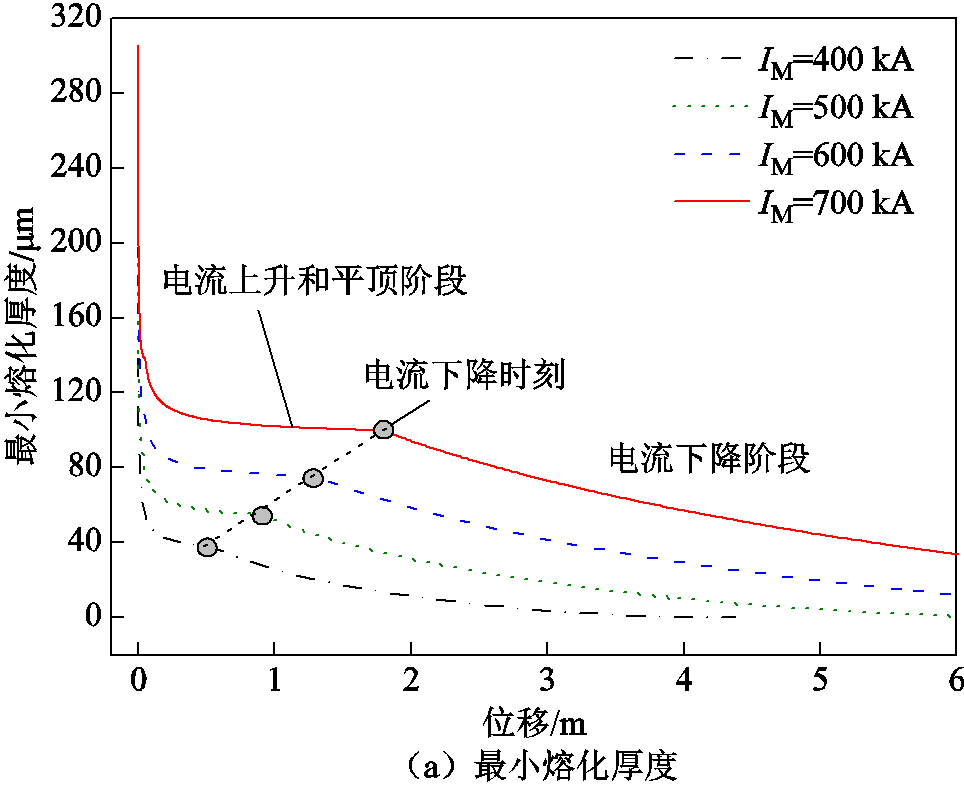
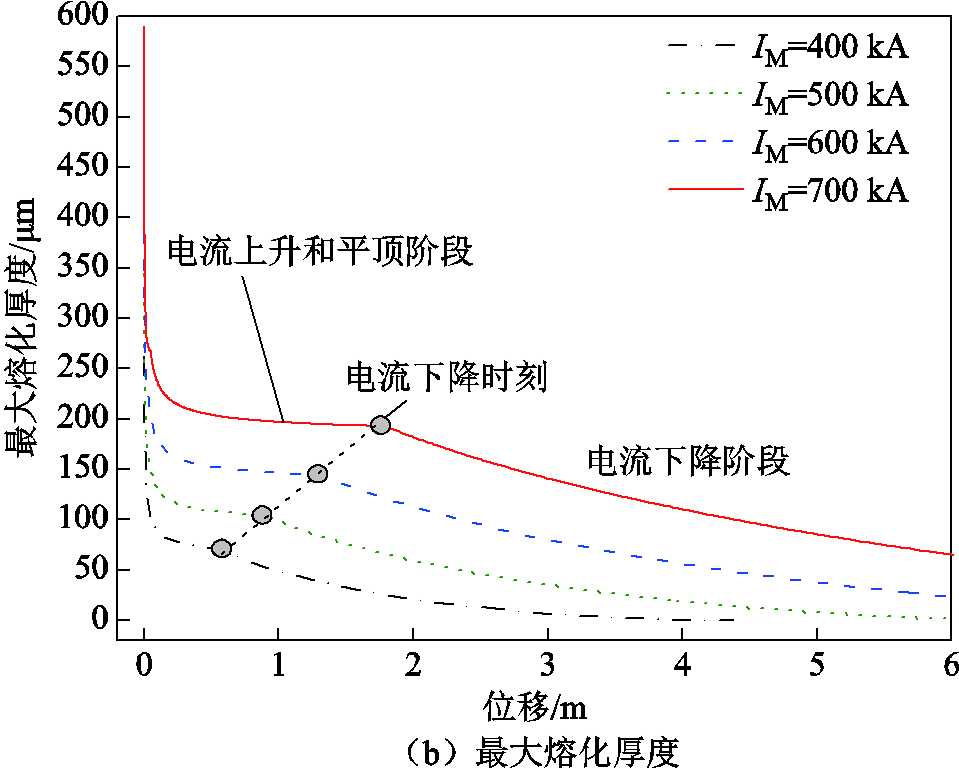
图8 不同电流下沉积层熔化厚度随发射位置变化曲线
Fig.8 Variation curves of deposited layer melting thickness with displacement under different currents
为了分析电枢熔化抑制特性并验证理论分析结果的正确性，本文开展小口径重复发射试验，内膛为20 mm×20 mm方口径，轨道发射长度为2 m，轨道材料为H62铜轨道，电枢采用典型的一体C型电枢，材料为6061铝。典型试验电流波形如图9所示，电流幅值为400 kA。图中电枢速度和位移曲线通过考虑平均滑动摩擦力计算[20]。
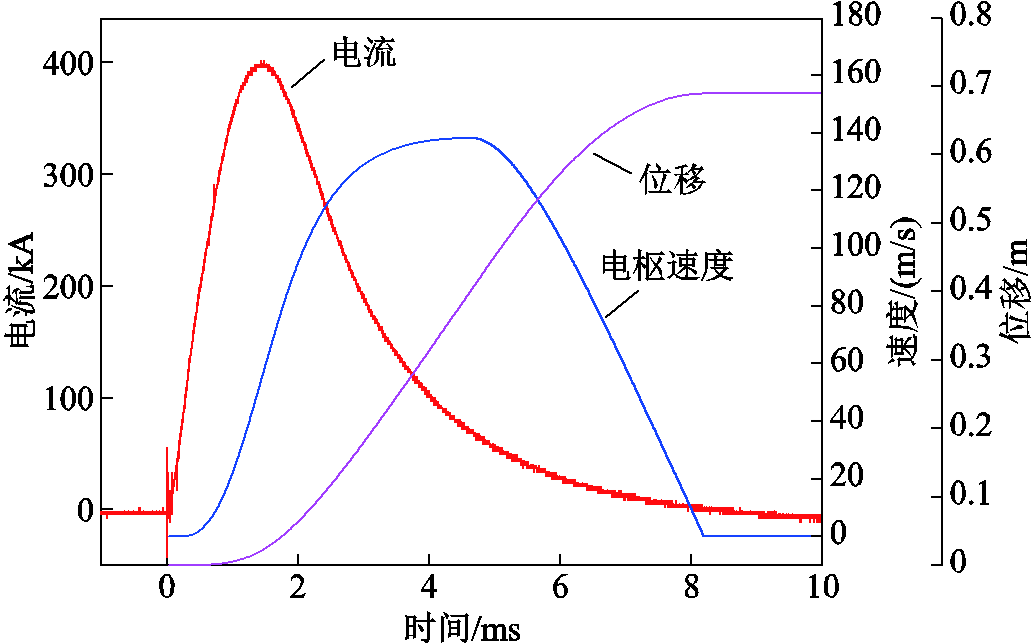
图9 电流、速度、位移曲线
Fig.9 Current, velocity and displacement curves
高速运动情况下，电枢出膛后表面熔化形貌遭到破坏难以完整回收，为了控制电枢出膛速度，采用配重分离方法，在电枢前面放置质量较大的配重金属块，安装示意图如图10所示。由于配重质量较大，可以控制电枢低速运动并在发射后留在膛内，进而完整回收发射后的电枢，观测其熔蚀形貌。
试验采用的C型电枢质量约为22.8 g，配重质量为550 g，保持电流波形和发射质量不变，开展重复发射试验，每次发射后轨道表面沉积层不做处理，保证电枢在沉积层轨道上滑动。每次发射速度约为140 m/s，试验共发射7次。每次试验后回收电枢，其中第1、3、5、7次发射后回收电枢照片如图11所示。
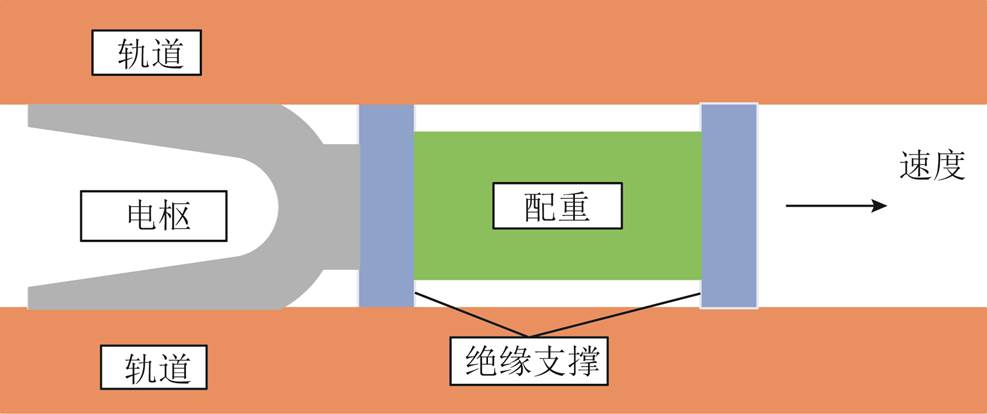
图10 电枢与配重安装示意图
Fig.10 Schematic diagram of armature and payload
图11 回收电枢照片
Fig.11 Photos of recovered armature
三次发射后轨道表面沉积层形貌如图12所示，沉积层主要分布在0～20 cm位置。所以主要针对0～20 cm位置处的沉积层轮廓进行测量。
图12 三次发射后实验轨道照片
Fig.12 Photographs of experimental rail after three shots
每次发射后，取轨道沉积层样本，沿着轨道发射方向，每隔1～2 cm对沉积层横向界面形貌进行测量，其中三次发射后5 cm和14 cm处沉积层截面轮廓曲线如图13所示。
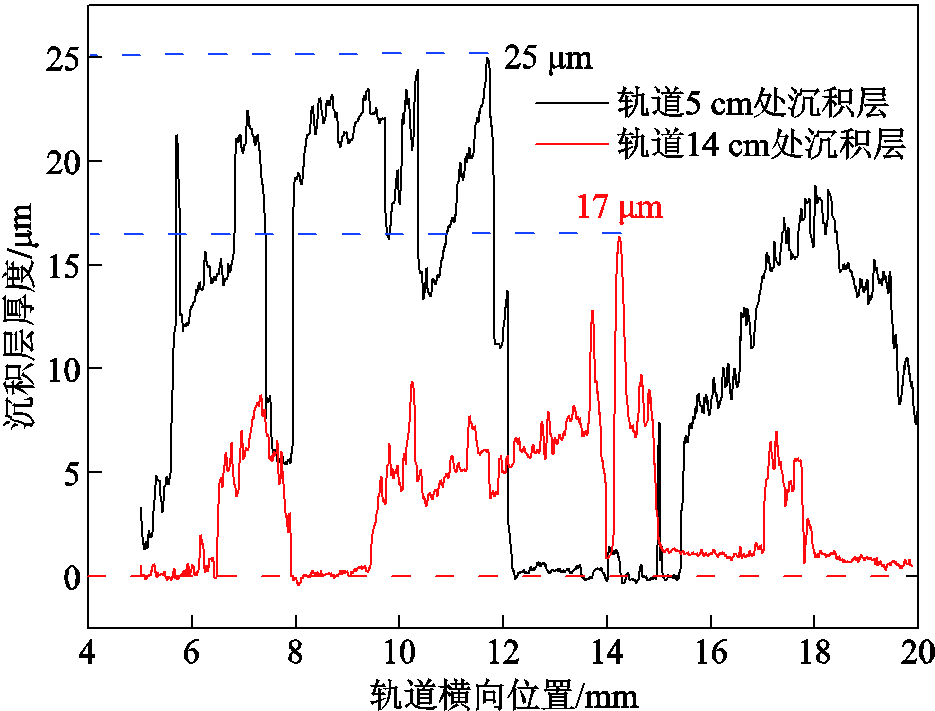
图13 三次发射后沉积层截面轮廓曲线
Fig.13 Cross-sectional profile of the deposited layers after three shots
假设取沉积层横向分布最大值作为该发射位置处的沉积层厚度值，如5 cm处沉积层横向分布最大值为25 μm，14 cm处最大值为17 μm，可以获得不同发射次数下沉积层厚度分布如图14所示。相同发射参数条件下基于计算式（19），可以计算沉积层最小熔化厚度分布曲线如图14中红色虚线所示。可以看到，除了第七发由于测量误差导致的沉积层厚度局部出现在最小熔化厚度之上以外，实际测量的沉积层厚度基本上全部在沉积层最小熔化厚度曲线之下，这说明在这7次重复发射过程中，沉积层均发生了全部熔化，所以本文重复发射条件下沉积层处于全部熔化状态。
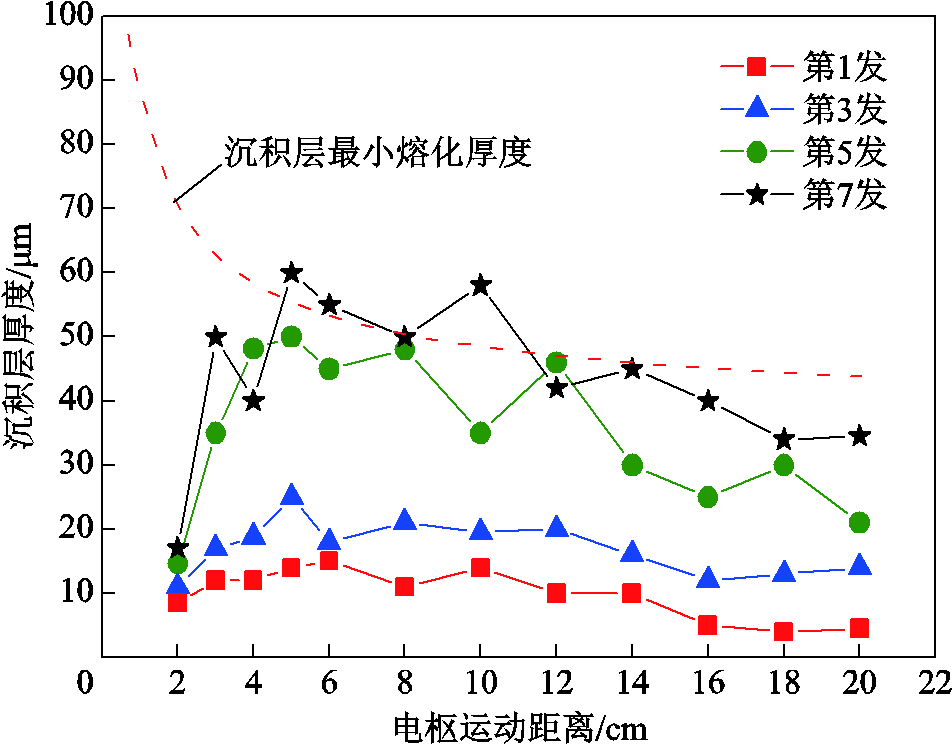
图14 沉积层厚度分布
Fig.14 Thickness distribution of deposited layers
采用轮廓仪对电枢表面轮廓进行测量，电枢表面边缘熔化轮廓曲线如图15所示。第一发时可以看到熔蚀集中在很窄的范围内，说明电流集中在10 cm附近很小的范围内，熔化较为严重。随着发射次数的增加，熔蚀开始向头部移动，使得熔蚀长度变大，并且熔蚀深度也变小。
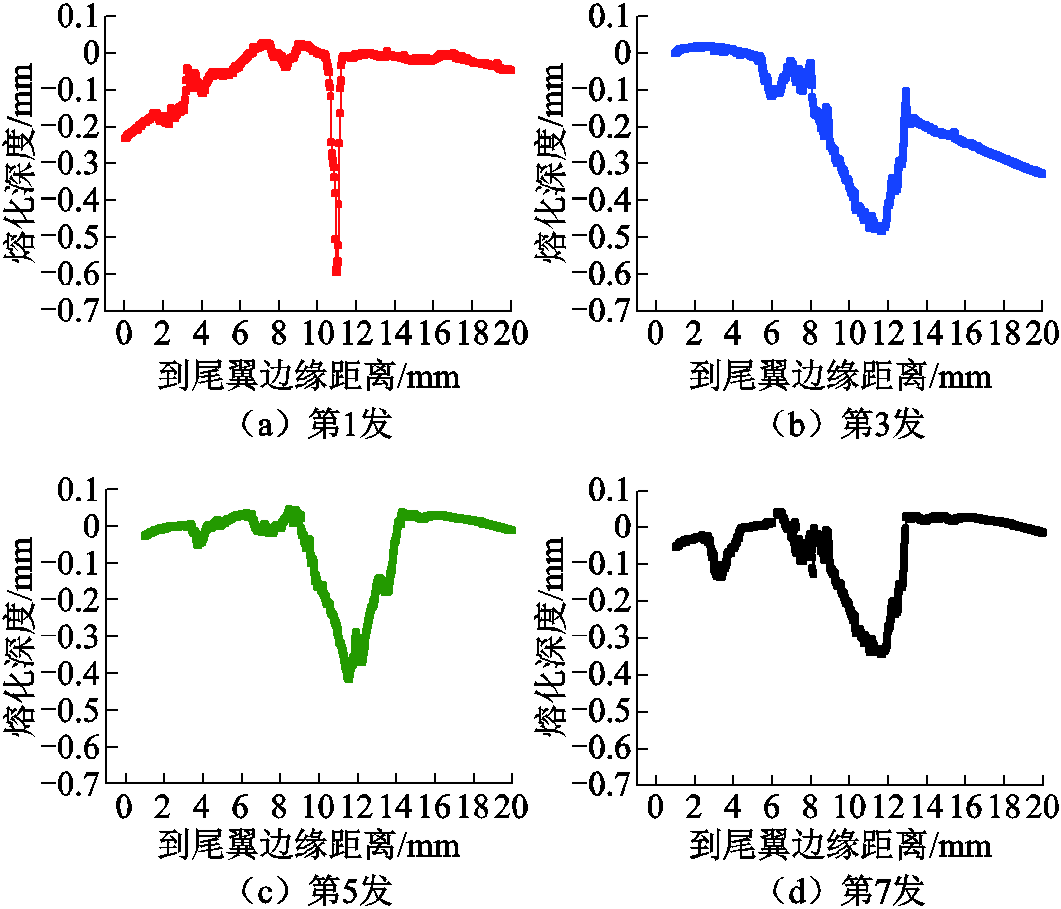
图15 电枢表面边缘熔化轮廓曲线
Fig.15 Melting profile curve of armature surface edge
电枢表面最大熔化深度试验测量结果如图16所示，沉积层最大熔化深度随着发射次数的增加而减小。根据沉积层全部重熔状态下电枢熔化计算模型，可以获得电枢表面平均熔化速度，结合电枢滑动时间可以进一步计算最大熔化深度平均值。模型计算结果如图16中蓝色三角形曲线所示。由于每次发射中沉积层均发生全部熔化，沉积层熔化相比光洁轨道会吸收更多热量，这是因为沉积层厚度随着发射次数逐渐增加，厚度越大沉积层全部熔化吸收的热量越大，对应的电枢熔化越小，即形成电枢熔化深度随发射次数增加而逐渐减小的趋势。模型计算结果变化趋势与试验测量结果变化趋势相同，说明沉积层熔化对电枢熔化有抑制效应。由于本文试验沉积层厚度较小，沉积层一直处于全部熔化状态，电枢熔化随着发射次数逐渐减小。如果试验电流和速度条件足够大，第一发后就产生足够厚的沉积层，沉积层处于部分重熔状态，电枢熔化特性需要进一步的研究分析。
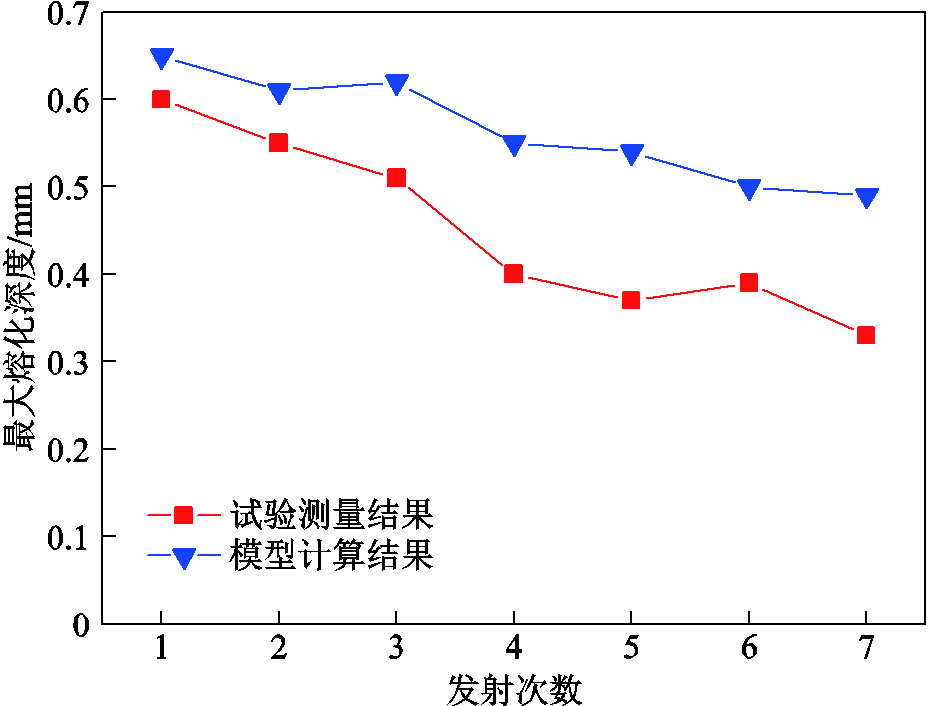
图16 最大熔化深度变化曲线
Fig.16 Variation curves of maximum melting depth
本文基于沉积层受热过程分析，建立了沉积层熔化判断模型，获得了沉积层熔化条件和沉积层熔化厚度。基于沉积层熔化特性，建立了沉积层全部熔化状态下的电枢熔化计算模型，分析了不同电流条件下的沉积层熔化特性，并开展重复发射试验，通过理论分析结合试验验证手段对电枢熔化的抑制特性进行研究。总结如下：
1）电枢载流量对沉积层熔化范围有很大影响，载流量越大，沉积层熔化范围越大，并且启动低速阶段沉积层能够发生熔化，高速阶段沉积层不容易发生熔化。
2）沉积层厚度随着发射次数逐渐增加，沉积层全部熔化状态下，沉积层厚度越大，电枢熔化越小，即电枢最大熔化深度随发射次数增加呈现逐渐减小的趋势。模型计算结果变化趋势与试验测量结果变化趋势相同，说明沉积层熔化对电枢熔化有抑制效应。
参考文献
[1] 马伟明, 鲁军勇, 李湘平. 电磁发射超高速一体化弹丸[J]. 国防科技大学学报, 2019, 41(4): 1-10.
Ma Weiming, Lu Junyong, Li Xiangping. Electro-magnetic launch hypervelocity integrated projectile[J]. Journal of National University of Defense Technology, 2019, 41(4): 1-10.
[2] 马伟明, 鲁军勇. 电磁发射技术的研究现状与挑战[J]. 电工技术学报, 2023, 38(15): 3943-3959.
Ma Weiming, Lu Junyong. Research progress and challenges of electromagnetic launch technology[J]. Transactions of China Electrotechnical Society, 2023, 38(15): 3943-3959.
[3] 胡鑫凯, 鲁军勇, 李白, 等. 瞬态条件下电磁轨道发射装置绝缘体热损伤分析[J]. 电工技术学报, 2023, 38(21): 5673-5681.
Hu Xinkai, Lu Junyong, Li Bai, et al. Thermal damage analysis of insulator in electromagnetic rail launcher under transient conditions[J]. Transactions of China Electrotechnical Society, 2023, 38(21): 5673-5681.
[4] 林庆华, 栗保明. 基于瞬态多物理场求解器的电磁轨道炮发射过程建模与仿真[J]. 兵工学报, 2020, 41(9): 1697-1707.
Lin Qinghua, Li Baoming. Modeling and simulation of electromagnetic railgun launching process based on a transient multi-physical field solver[J]. Acta Armamentarii, 2020, 41(9): 1697-1707.
[5] 张嘉炜, 鲁军勇, 谭赛, 等. 考虑初始接触压力的滑动电接触界面磁扩散模型[J]. 电工技术学报, 2022, 37(2): 488-495.
Zhang Jiawei, Lu Junyong, Tan Sai, et al. A magnetic diffusion model of electromagnetic launcher con-sidering initial contact pressure[J]. Transactions of China Electrotechnical Society, 2022, 37(2): 488-495.
[6] Chen Lixue, Xu Xuan, Wang Zengji, et al. Melting distribution of armature in electromagnetic rail launcher[J]. IEEE Transactions on Plasma Science, 2023, 51(1): 234-242.
[7] Cooper K P, Jones H N, Meger R A. Analysis of railgun barrel material[J]. IEEE Transactions on Magnetics, 2007, 43(1): 120-125.
[8] Watt T, Stefani F. The effect of current and speed on perimeter erosion in recovered armatures[J]. IEEE Transactions on Magnetics, 2005, 41(1): 448-452.
[9] 李白, 鲁军勇, 谭赛, 等. 高速滑动电接触电枢表面动态磨损过程研究[J]. 电工技术学报, 2023, 38(1): 131-139.
Li Bai, Lu Junyong, Tan Sai, et al. Research on dynamic wear process of armature surface in high-speed sliding electric contact[J]. Transactions of China Electrotechnical Society, 2023, 38(1): 131-139.
[10] 徐伟东, 袁伟群, 陈允, 等. 电磁轨道发射器连续发射的滑动电接触[J]. 强激光与粒子束, 2012, 24(3): 668-672.
Xu Weidong, Yuan Weiqun, Chen Yun, et al. Sliding electrical contact performance of electromagnetic launcher system in rapid fire mode[J]. High Power Laser and Particle Beams, 2012, 24(3): 668-672.
[11] 刘传谱, 袁伟群, 严萍, 等. 重复推进滑动电接触的试验研究[J]. 强激光与粒子束, 2010, 22(4): 923-926.
Liu Chuanpu, Yuan Weiqun, Yan Ping, et al. Experimental study of sliding electrical contacts in a multi-shot railgun[J]. High Power Laser and Particle Beams, 2010, 22(4): 923-926.
[12] 姚金明, 傅强. 大电流高速滑动电接触界面热量分配过程[J]. 电工技术学报, 2023: 39(17): 5497-5507.
Yao Jinming, Fu Qiang. Heat Partition process at sliding electrical contact interfaces with high-speed and large current[J]. Transactions of China Electro-technical Society, 2023, 39(17): 5497-5507.
[13] Paek-Spidell G Y. Analysis of heat partitioning during sliding contact at high speed and pressure[D]. Wright-Patterson Air Force Base: Air Force Institute of Technology, 2014.
[14] 汤亮亮. 电磁发射中枢轨接触界面金属液化层特性的实验与理论研究[D]. 武汉: 华中科技大学, 2015.
Tang Liangliang. Experimental and theoretical study on liquid metal film characteristic of armature/rail contact interface in an electromagnetic launching[D]. Wuhan: Huazhong University of Science and Technology, 2015.
[15] Chen Lixue, He Junjia, Xia Shengguo, et al. Some key parameters of different caliber solid-armature railgun related to linear current density[J]. IEEE Transactions on Plasma Science, 2017, 45(7): 1134-1138.
[16] Yao Jinming, Yu Kun, Fu Qiang, et al. Computational method for heat partition at the rail-armature interface based on least squares regression[J]. IEEE Transactions on Plasma Science, 2021, 49(6): 2008-2014.
[17] 温诗铸, 黄平. 摩擦学原理[M]. 4版. 北京: 清华大学出版社, 2013.
[18] Tian Xuefeng, Kennedy F E Jr. Contact surface temperature models for finite bodies in dry and boundary lubricated sliding[J]. Journal of Tribology, 1993, 115(3): 411-418.
[19] 肖铮. 电枢—轨道载流滑动接触面摩擦磨损研究[D]. 武汉: 华中科技大学, 2012.
Xiao Zheng. Friction and wear behavior of armature-rail sliding electrical contact surface[D]. Wuhan: Huazhong University of Science and Technology, 2012.
[20] Yao Jinming, Xia Shengguo, Chen Lixue, et al. Analysis of the melt erosion patterns at rail-armature contact of rail launcher in current range of 10- 20 kA/mm[J]. IEEE Transactions on Plasma Science, 2019, 47(3): 1674-1680.
Abstract Maintaining good sliding electrical contact performance is crucial for achieving high-frequency and high-efficiency operation in electromagnetic rail launch systems. In the environment of high current and high-speed sliding electrical contacts, an aluminum deposited layer appears on the rail surface during the first launch after rail surface cleaning. During repetitive launches, the armature slides on the deposited rail, causing the deposited layer to melt due to heating. Melting state of the deposited layer affects the melting wear process on the armature’s surface, thereby altering the contact state and influencing the sliding electrical contact performance. Therefore, studying armature’s melting characteristics influenced by deposited layer is of great significance for a deeper understanding of interface melting wear mechanisms and for improving sliding electrical contact performance.
Firstly, by analyzing the heating process of the deposited layer, equations for calculating its melting moment and melting thickness were established. Within contact time (tc) between armature and deposited layer, the deposited layer is heated by the interface heat source and undergoes melting. A criterion for determining the melting of the deposited layer was proposed by comparing the contact time with the melting moment. If the heating time (tc) of the deposited layer is greater than melting moment (tm), then melting occurs within the contact time. Analysis of the melting characteristics of the deposited layer under different current conditions reveals that the larger the current load, the larger the melting range of the deposited layer. In addition, the deposited layer is more likely to melt during the low-speed stage and less likely to melt during the high-speed stage. Assuming that the deposited layer completely melts at time tr after the start of contact, the armature and the rail directly engage in heat transfer from time tr onwards. Based on the analysis of the heat balance equation under the condition of complete melting of the deposited layer, a calculation model for the melting wear of the armature under the influence of the deposited layer was established, yielding the melting wear rate of the armature.
Finally, repetitive launch experiments were conducted with a 20 mm square caliber inner bore. Keeping current waveform and launch mass unchanged, each launch had a velocity of approximately 140 m/s, with a total of 7 launches conducted in the experiments. After each experiment, the armature and rail samples were recovered, and a profile gauge was used to measure the maximum melting depth on the armature's surface and the thickness of the deposited layer on the rail's surface. The experimental results show that the thickness of the deposited layer gradually increases with the number of launches, while the maximum melting depth on the armature's surface decreases with the increasing number of launches. By analyzing the thickness distribution curve of the deposited layer in conjunction with the criterion for deposited layer melting, it was found that the deposited layer was in a state of complete remelting under the current launch conditions. Using the armature melting calculation model under the condition of complete deposited layer remelting, the average maximum melting depth was further calculated. The calculated results from the model show the same trend as the experimental measurements, indicating that deposited layer melting has an inhibitory effect on armature melting.
keywords：Repetitive launching, sliding electrical contact, deposited layer melt, armature melt
中图分类号：TM359.4
DOI: 10.19595/j.cnki.1000-6753.tces.231395
国家自然科学基金（52207009, 62073173）和高校科研启动资金（NY219155, NY220192）资助项目。
收稿日期 2023-08-28
改稿日期 2023-11-07
姚金明 女，1989年生，讲师，硕士生导师，研究方向为电磁发射技术等。
E-mail：yaojinming@njupt.edu.cn（通信作者）
孙建东 男，1984年生，高级工程师，研究方向为电磁场数值仿真计算等。
E-mail：sunjiandong@sgepri.sgcc.com.cn
（编辑 李 冰）