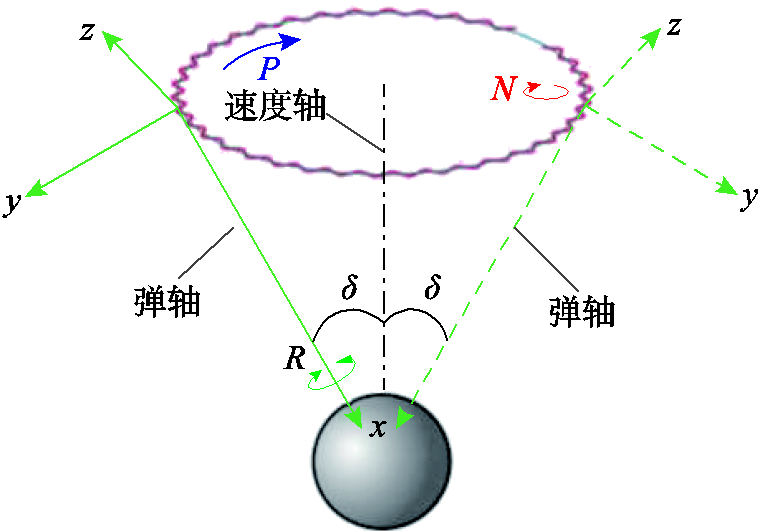
图1 转速闭锁示意图
Fig.1 The diagram of RSL
摘要 针对电磁轨道发射超高速弹丸由于出口扰动、气动不对称等因素引起的转速闭锁现象，从转速闭锁原理、转速闭锁建模、转速闭锁边界分析等方面开展研究，并结合试验数据对转速闭锁模型进行了验证。仿真和试验结果表明：该文建立的转速闭锁模型能够揭示电磁发射超高速弹丸的转速闭锁特性，仿真与试验结果吻合；弹丸初始扰动角速度越大，越不容易产生转速闭锁；存在一个与弹丸俯仰和偏航运动频率相对应的值，当不对称滚转舵控角度越接近这个值时，越容易发生转速闭锁。该文的仿真与分析结果为电磁轨道发射超高速弹丸的转速闭锁设计与控制奠定了理论基础。
关键词：电磁轨道发射 转速闭锁 初始扰动 气动不对称
弹体转速闭锁是指弹体滚转速度与俯仰或者偏航运动频率接近时，攻角较大、诱导滚转力矩和侧向力矩均较大，致使转速不会因为极阻尼力矩减小而维持在一个平衡点，进而产生转速闭锁。转速闭锁问题经常出现在气动不对称的弹体飞行过程中，由于转速闭锁会产生较大的平衡章动角，导致弹体飞行阻力增大，破坏弹体的动态稳定特性，严重时会发生灾难性偏航。因此，在设计时必须避免转速闭锁情况的发生。
电磁发射超高速制导弹采用电磁能发射，具有初速高、射程远、射高高、威力大、精度高等优势，成为近年来国内外各军事强国竞相发展的前沿技术[1-4]。受电磁发射原理的影响，相比火炮发射弹药，电磁发射超高速制导弹出膛扰动更大[5-7]，这是由于电磁发射弹丸在膛内没有膛线约束，且出膛过程中伴随着电枢软化、多体高速碰撞、出口电弧扰动、弹托分离扰动[8]等问题。此外，由于要承受高于传统弹药峰值和持续时间的发射过载，导致弹上部件如舵片、翼片等不可避免地存在变形或错位，从而引起弹丸气动外形的不对称，产生较大攻角和侧滑角，并诱导出滚转力矩。因此，电磁发射弹丸受其发射原理和发射环境的影响，更容易产生转速闭锁现象。目前国内外研究人员针对传统制导炮弹的转速闭锁问题开展了大量研究，得到转速闭锁产生条件，并对转速闭锁后的稳定性进行了分析[9-10]。然而电磁发射制导弹出膛扰动、飞行特性、影响转速闭锁产生的条件更复杂，现有的分析方法和结论不能很好地适用。为了规避电磁发射超高速制导弹转速闭锁问题，发挥其作战优势，迫切需要对其转速闭锁特性进行分析。
本文针对电磁发射超高速制导弹的转速闭锁问题开展研究，首先结合转速闭锁原理和六自由度模型，建立了六自由度转速闭锁模型，得到了转速闭锁的产生条件和特性；其次通过仿真复现了某电磁发射弹丸的转速闭锁现象，验证本文所建转速闭锁模型的正确性；最后分析该弹丸的转速闭锁安全区，为其转速闭锁设计与控制奠定了基础。
弹体转速闭锁是指弹体发生滚转与俯仰和偏航方向的共振运动，进而产生较大的平衡章动角。转速闭锁示意图如图1所示。图中P为绕速度轴旋转速度，N为弹轴摆动角速度，R为绕弹轴旋转速度。由于弹丸自转速度（绕弹轴）和公转速度（绕速度轴）一样，弹丸受到的气动升力一直指向xOy平面，因此z方向加速度和z方向角速度基本为零，且y方向角速度中存在公转角速度在y轴的恒值分量。
图1 转速闭锁示意图
Fig.1 The diagram of RSL
转速闭锁问题经常出现在气动不对称的弹体飞行过程中，其产生原理是由于弹丸存在气动不对称，在攻角作用下产生诱导滚转力矩，导致弹丸形成滚转速度。当滚转速度与俯仰或者偏航运动频率接近时，并且此时攻角较大，诱导滚转力矩和诱导侧向力矩均较大，致使转速不会因为极阻尼力矩减小，而维持在一个平衡点，进而产生转速闭锁。转速闭锁产生的条件为存在一个尾翼面与攻角面的平衡夹角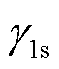
，使得
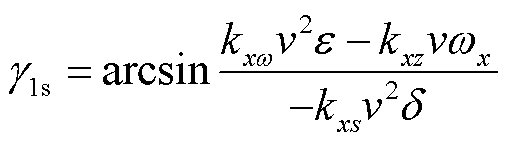（1）
式中，ε和δ分别为尾翼斜置角和攻角；kxs、kxω和kxz分别为诱导滚转力矩系数、导转力矩系数和极阻尼力矩系数；v和ωx分别为弹丸速度和转速。将弹体产生转速闭锁的最小攻角称为转速闭锁临界攻角，临界攻角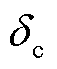
与v、ωx以及kxs、kxω和kxz有关，见式（2），可见转速闭锁发生在某些特定的角度、角速度和速度上。
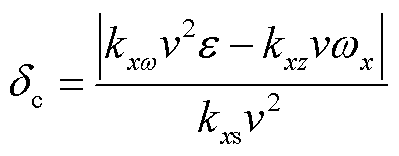（2）
转速闭锁产生的必要条件为攻角大于转速闭锁临界攻角，对于轻微不对称的弹体，其攻角的主要成分是强迫运动攻角，不对称性越大，强迫运动攻角也越大，越容易出现共振。由于弹体的不对称性（加工安装不对称或出膛扰动造成气流不对称）的大小是随机的，因此，即使是同一弹种、相同试验工况，转速闭锁的现象也可能时有时无。
由式（1）和式（2）可知，为了建立转速闭锁模型，首先要建立弹体的飞行外弹道模型。任何自由刚体的运动，都可以看作是刚体的质心运动和围绕质心两种运动的合成，弹体飞行过程中受力示意图如图2所示。其中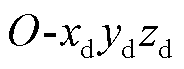
、
、
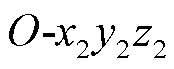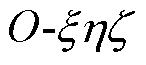分别为平动坐标系、弹道坐标系和第一弹轴坐标系；θ1、α、φ2分别为高低倾角、高低攻角和侧向摆动角[11]。
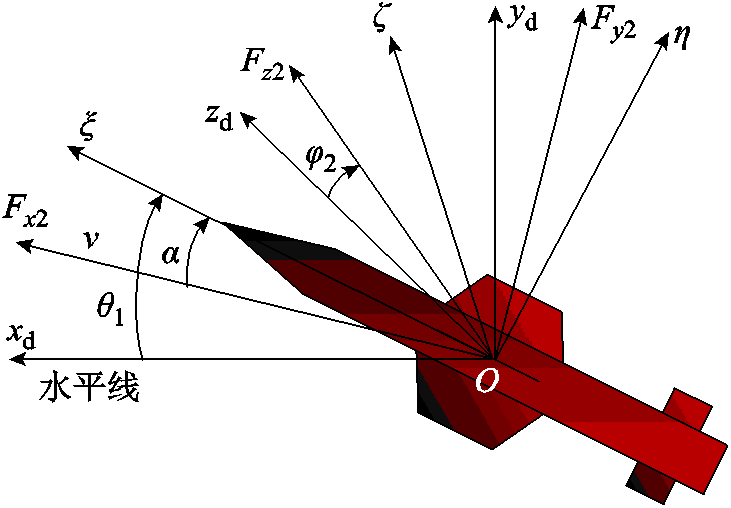
图2 弹体飞行受力示意图
Fig.2 Schematic diagram of the force of a projectile
1）质心动力学和运动学方程
假定弹丸质量均匀分布、弹丸轴对称，由图2可得弹丸的质心动力学方程为
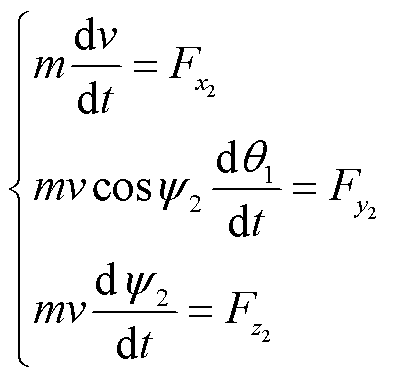（3）
式中，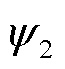
为侧向偏角；
、
、
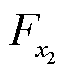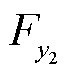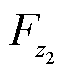分别为外力F（包括重力和气动力）在弹道坐标系三个轴上的分量。
弹丸在地面坐标系下的质点运动学方程为
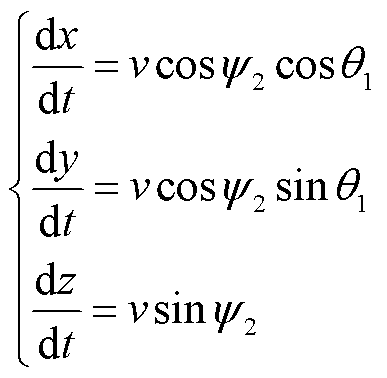（4）
2）绕质心运动的动力学和运动学方程
弹丸绕质心运动的动力学方程为
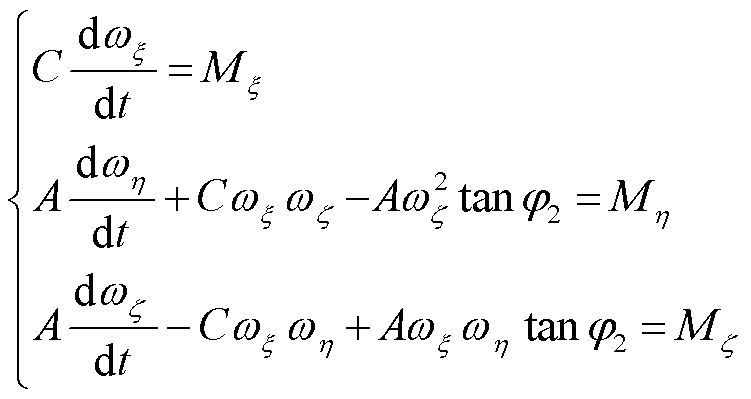（5）
式中，A为赤道转动惯量；C为极转动惯量；ωξ、ωη、ωζ分别为弹丸转动角速度在弹轴坐标系下的三个分量；Mξ、Mη、Mζ分别为弹丸所受外力矩在弹轴坐标系下的三个分量。
弹丸绕质心运动的运动学方程为
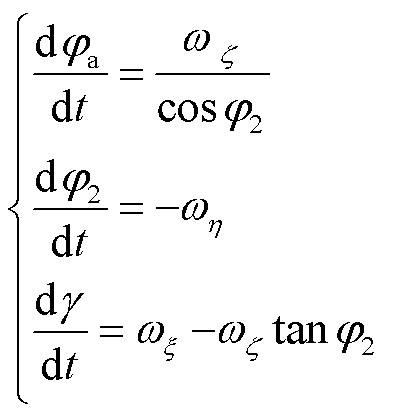（6）
式中，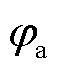
为弹轴高低角；γ为弹体自转角，或称为滚转角。
式（3）～式（6）给出了弹丸外弹道计算方程组，输入量包括弹丸受到的气动力、重力和气动力矩，且这些输入量与弹丸姿态、速度以及所处的外部环境有关，采用实时反馈计算的方法将耗费大量的计算时间，因此工程上一般基于事先求得的弹丸在各个状态下的气动力、气动力矩数据，采用插值拟合的方法得到弹丸外弹道飞行时的各输入量[11]。为便于计算和对比分析，对各气动力和气动力矩采用归一化表示，得到相对应的气动力、力矩系数，见表1。表1中，q为动压，q=0.5ρv2，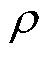
为空气密度；S为弹丸参考截面积；l为参考长度。
表1 气动力和气动力矩系数表达式
Tab.1 Expressions of aerodynamic coefficients
名称公式名称公式 阻力系数压力中心系数 升力系数滚转力矩系数 侧向力系数偏航力矩系数
由转速闭锁的原理可知，弹丸形成转速闭锁的根源在于弹丸出现了由于结构或者气动不对称引起的空气动力学不对称，包括诱导侧向力和滚转力矩两部分。
1）非对称气动力
当流经弹体和尾翼的横流以及压力分布关于攻角面不再镜面对称时，会形成垂直于攻角面的合力Ns，定义指向攻角面左侧的Ns为正，可得其计算公式为
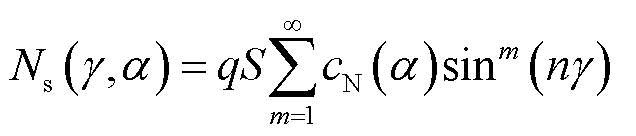（7）
式中，n为弹丸的尾翼数量；cN为法向力系数。
2）非对称气动力矩
弹丸受到的非对称力矩为
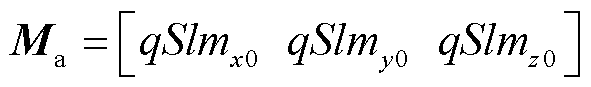（8）
式中，mx0、my0和mz0分别为x、y和z三个方向的非对称空气动力矩系数。压心与固连坐标系的关系如图3所示。图3中，Ma由空气动力对称轴（零升力轴）在固连坐标系里转过αa和βa角来确定，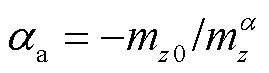
为由空气动力非对称性确定的平衡攻角，
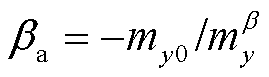为平衡侧滑角。力矩Ma沿x轴的分量为qSlmx0，它既可是随机的，也可是由故意制造的外形不对称所产生的，如由不对称的尾翼（单侧翼）产生的。
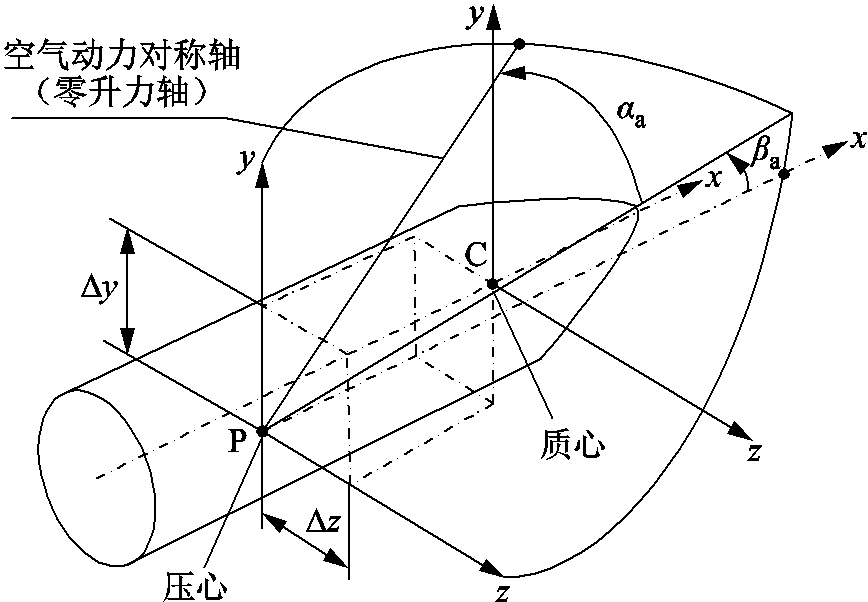
图3 压心与固连坐标系的关系
Fig.3 The relationship of pressure and fixed coordinate system
此外，由于压心偏离固连坐标系也会造成非对称力矩，如图3所示，设压心偏离固连坐标系的xOz平面Δy，偏离xOy平面Δz，则
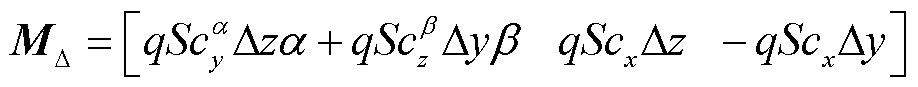（9）
式中，β为侧滑角；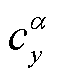
和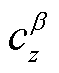
分别为法向力系数导数和侧向力系数导数。上述弹丸受到的非对称力和力矩，可通过在六自由度制导弹道模型中增加攻角和侧滑角零偏角模拟诱导侧向力，增加滚转通道零偏舵角模拟诱导滚转力矩。
基于如图4所示某型弹丸仿真试验数据进行模型验证，弹丸未按照预期弹道飞行。
从如图5所示遥测的惯组数据可以看出，弹丸出膛后有较大的滚转速度，加上此时弹丸有较大的y向加速度（左右）和y向角速度（俯仰），而z向加速度（上下）和z向角速度（偏航）基本为零，综合表现为转速闭锁现象。
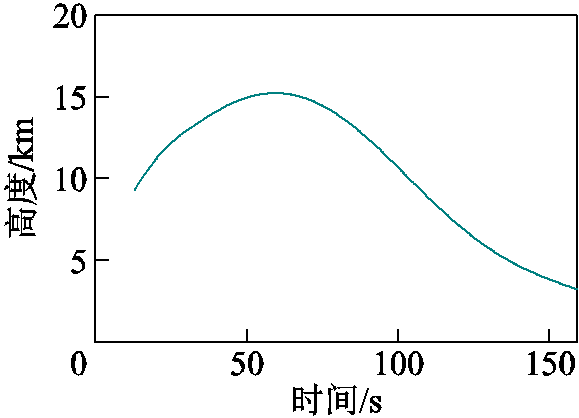
图4 试验弹道曲线
Fig.4 The experimental ballistic curve
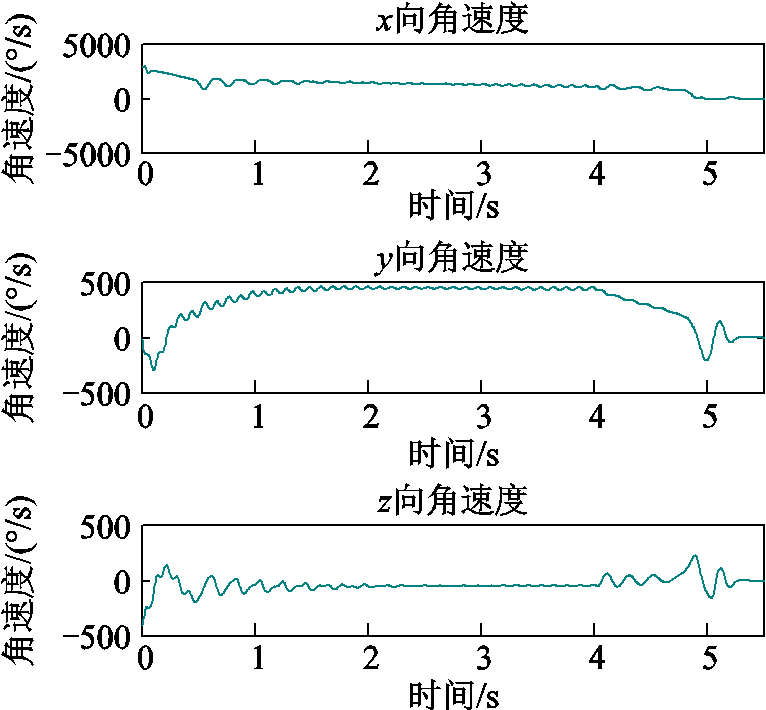
图5 惯组输出数据
Fig.5 The output of inertial measurement unit (IMU)
由上述分析可知，影响转速闭锁的因素包括初始扰动和气动不对称量两部分：初始扰动包括俯仰角速度ωz0和偏航角速度ωy0；气动不对称量包括攻角和侧滑角不对称角度，以及滚转通道的舵控偏差量，分别用Δα、Δβ和Δγ表示。为了复现转速闭锁现象，根据遥测三轴角速度和雷测速度对上述变量进行优化辨识，优化目标为仿真三轴角速度曲线及速度曲线与实测数据吻合度最高。
上述问题属于多目标优化问题，采用数学模型描述为
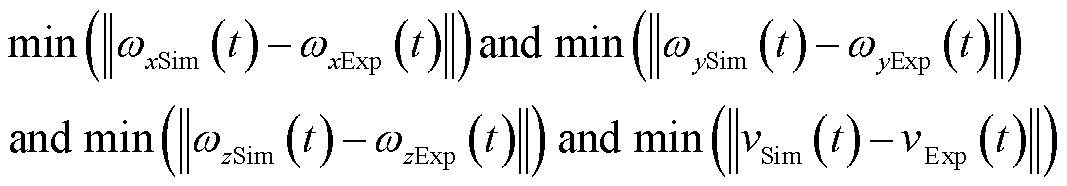（10）
式中，ωxSim、ωySim、ωzSim和vSim分别为仿真的三轴角速度和速度；ωxExp、ωyExp、ωzExp和vExp分别为实测的三轴角速度和速度。为了提高优化速度，根据设计值和以往试验经验，限定优化变量的范围，其中ωz0和ωy0在±30 rad/s以内，Δα和Δβ在±5°以内，Δγ在±1°以内。
对于多变量系统优化问题，遗传算法发挥了重要作用，通过不断迭代逼近最优解，可以实现高度复杂的非线性最优值问题[12-13]。而对于多目标优化问题，通常存在一个解集，这些解集之间就全体目标函数而言无法比较优劣，使得无法仅改进单一目标函数而不削弱其他目标函数，非劣分级排序遗传算法（Non-dominated Sorting in Genetic Algorithms, NSGA）通过在选择算子之前根据个体之间的支配关系进行分层，解决了多目标之间的优化策略权衡问题。此外，为了提高算法的收敛速度，本文采用带有精英策略的NSGA及NSGA-Ⅱ作为初始扰动及非对称参数辨识模型的内核，其优化流程如图6所示。
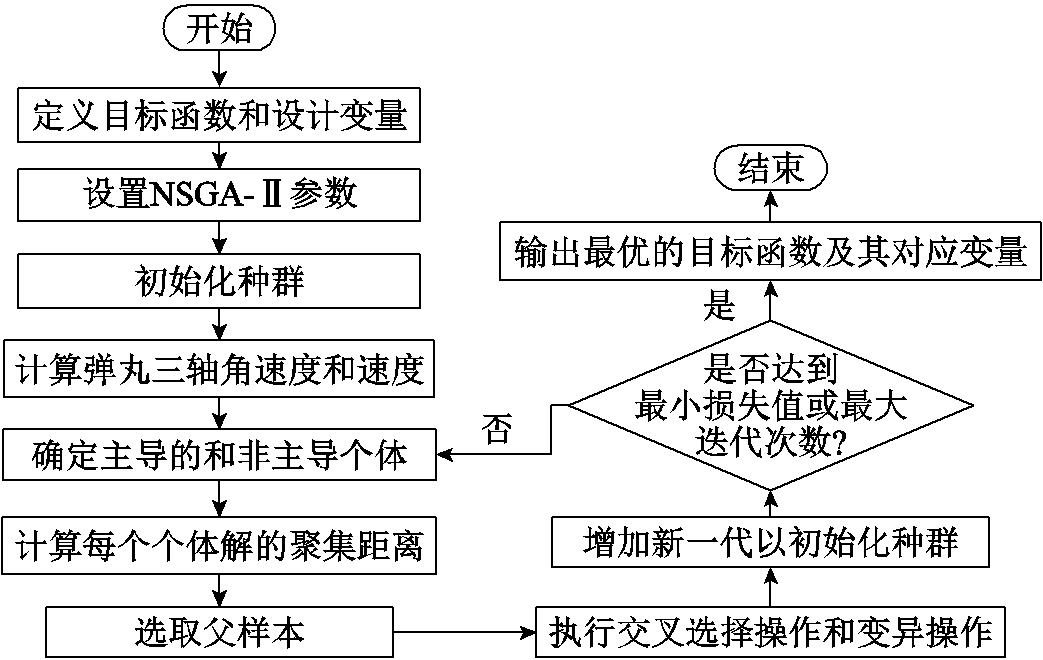
图6 NSGA-Ⅱ优化设计流程
Fig.6 The optimization design process of NSGA-Ⅱ
根据上述多目标函数，采用NSGA-Ⅱ进行多目标优化，其中种群个数为80，交叉因子设为0.9，变异因子设为0.2。选取可行解中各指标和的最小值作为监测量，其值随迭代次数的变化如图7所示，可见收敛较快。最终选取基于NSGA-Ⅱ得到的可行解集中Fx1、Fx2、Fx3和Fx4之和的平均值最小的结果，俯仰和偏航角速度分别为20.2 rad/s和7.59 rad/s，攻角和侧滑角的不对称角度以及滚转通道的舵控偏差量分别为-1.43°、0.70°和 -0.43°。
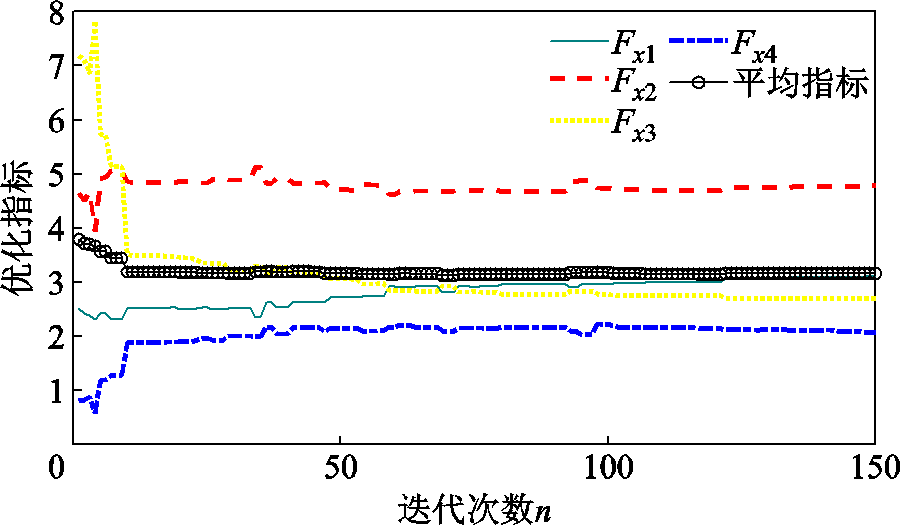
图7 优化迭代过程
Fig.7 The iterative process
将上述辨识得到的初始扰动角速度和气动不对称量代入六自由度模型中，得到弹丸的三轴角速度、加速度，以及攻角和侧滑角曲线如图8所示。可见弹丸出膛后受初始扰动和气动不对称的影响，诱发滚转力矩，导致滚转速度快速增加。出膛3 s后滚转、俯仰、偏航转速，以及攻角和侧滑角基本保持不变，形成转速闭锁。但由于风洞试验气动数据与实际飞行气动数据存在差异，且无法考虑随机风、弹丸结构变形等其他非对称因素的影响，导致仿真结果与实测数据存在差异，但基本复现了转速闭锁现象，从而验证了本文模型的正确性。
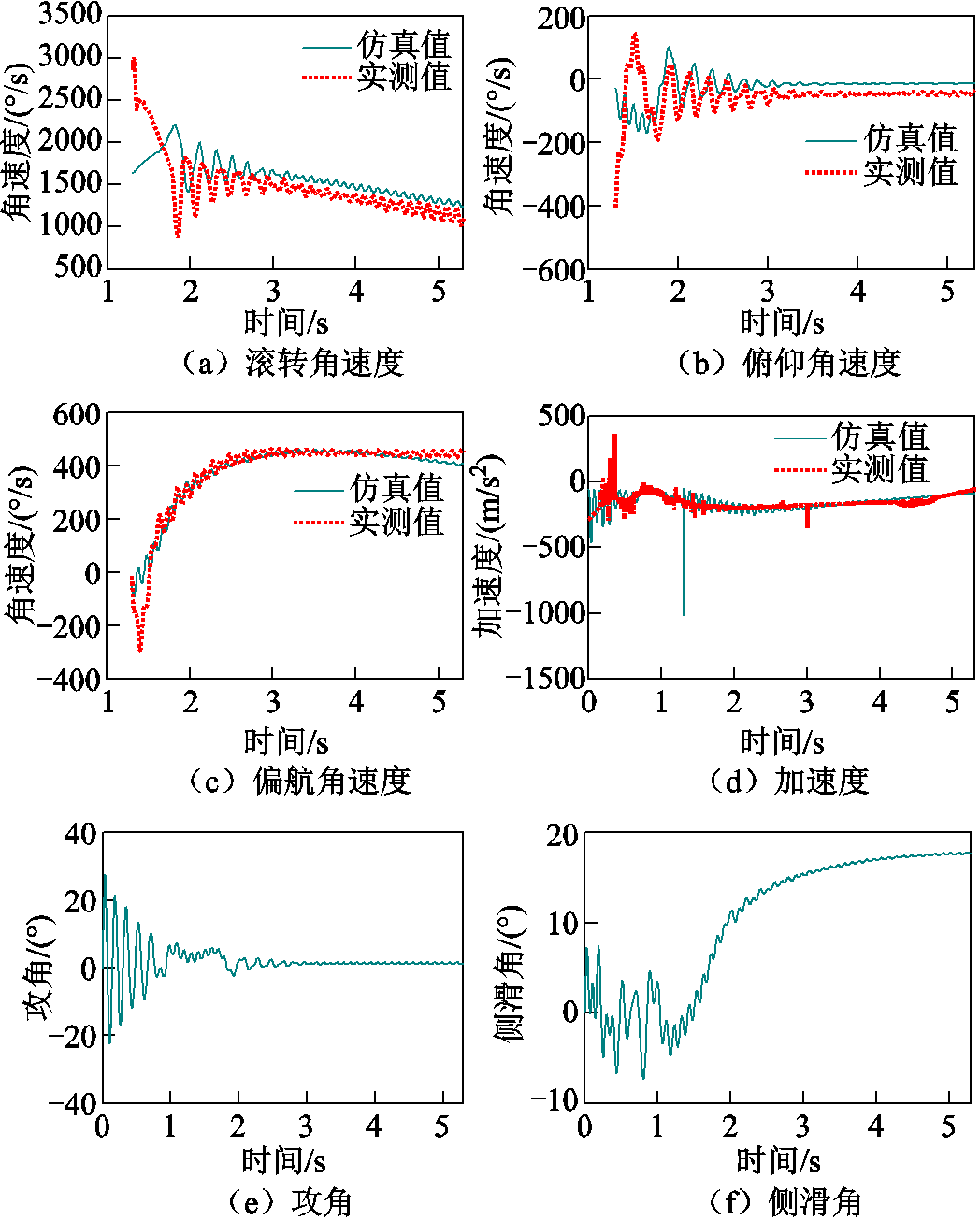
图8 弹丸转速闭锁现象复现
Fig.8 The repetition of RSL phenomenon of projectile
为了彻底规避转速闭锁问题，分析弹丸最大受到多大扰动时，不会出现转速闭锁现象，即转速闭锁边界条件分析。根据转速闭锁的现象，即滚转速度、攻角或侧滑角在一个不为零的数值附近跳动，分析不同扰动角速度（包括俯仰和偏航角速度），以及攻角、侧滑角和滚转通道舵不对称角度下的转速闭锁情况。为便于分析和可视化，对角速度扰动和不对称角度的影响分别进行分析。
假定攻角、侧滑角以及滚转通道舵不对称角度仍然为-1.43°、0.70°和-0.43°，得到不同俯仰和偏航角速度扰动下的转速闭锁分布情况如图9a所示，可见大部分情况下均会发生转速闭锁现象。进一步根据俯仰和偏航扰动角速度的大小划分扰动区域，其中1区表示俯仰和偏航扰动角速度在（0～±10）rad/s，2区表示俯仰和偏航扰动角速度在（±10～±20）rad/s，3区表示俯仰和偏航扰动角速度在（±20～±30）rad/s，统计得到不同扰动区域的转速闭锁占比如图9b所示，1区、2区和3区的占比分别为98%、82%和70%。可见初始扰动越大，越不容易产生转速闭锁，这是由于在一定气动不对称的情况下，初始扰动越大，弹丸诱导的滚转速度越大，滚转频率与俯仰和偏航运动频率相差越大，从而能够避开转速闭锁。
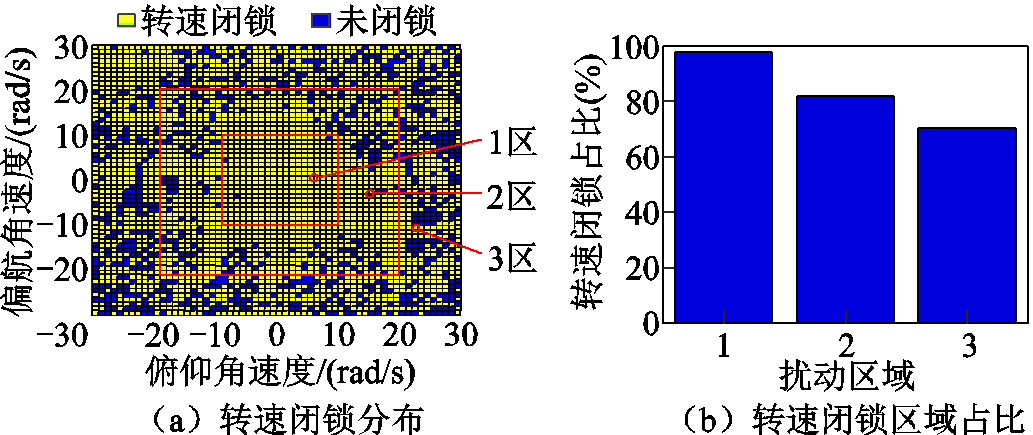
图9 不同初始扰动角速度下的转速闭锁情况
Fig.9 The RSL cases under different initial angular velocity disturbance
以俯仰角速度和偏航角速度都取0 rad/s为例，得到其三轴角速度、速度、攻角和侧滑角如图10所示。可见尽管初始扰动角速度为零，但是由于存在气动不对称情况，导致弹丸产生攻角、侧滑角和滚转速度，在满足式（1）条件时，进入转速闭锁。
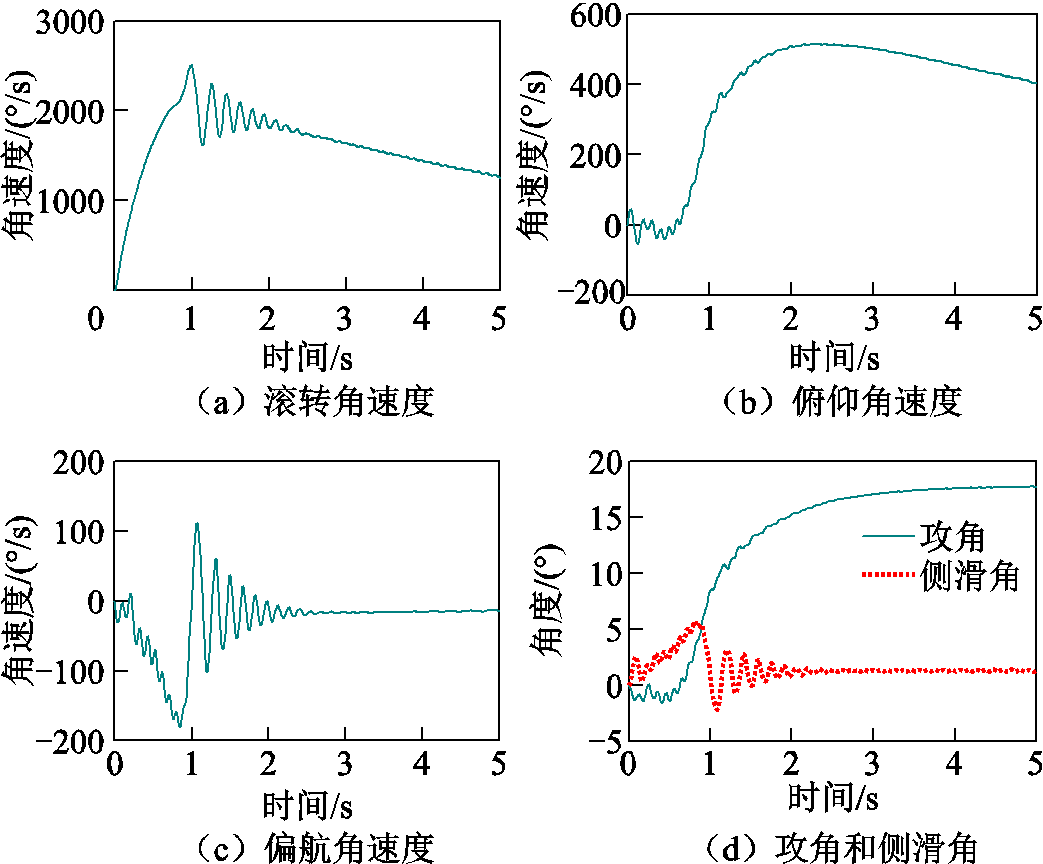
图10 初始不控段转速闭锁情况
Fig.10 The RSL cases during the initial stage of ballistic
假定俯仰和偏航角速度均为9 rad/s（设计指标），得到攻角、侧滑角以及滚转不对称舵控角度下的转速闭锁如图11所示，其中黄色（浅色）代表发生转速闭锁，蓝色（深色）表示未发生转速闭锁。可见滚转舵控角度在某一个值附近时（取决于俯仰和偏航运动频率，此处为±0.2°），容易发生转速闭锁，当远离该角度时，则不易出现转速闭锁，如图11f所示。在零滚转舵控角度下，只有当俯仰或者偏航不对称舵控角度足够大时，才会发生转速闭锁。因此，在进行弹丸设计和加工时，应避免滚转舵控角度的不对称，减少转速闭锁发生的可能性。
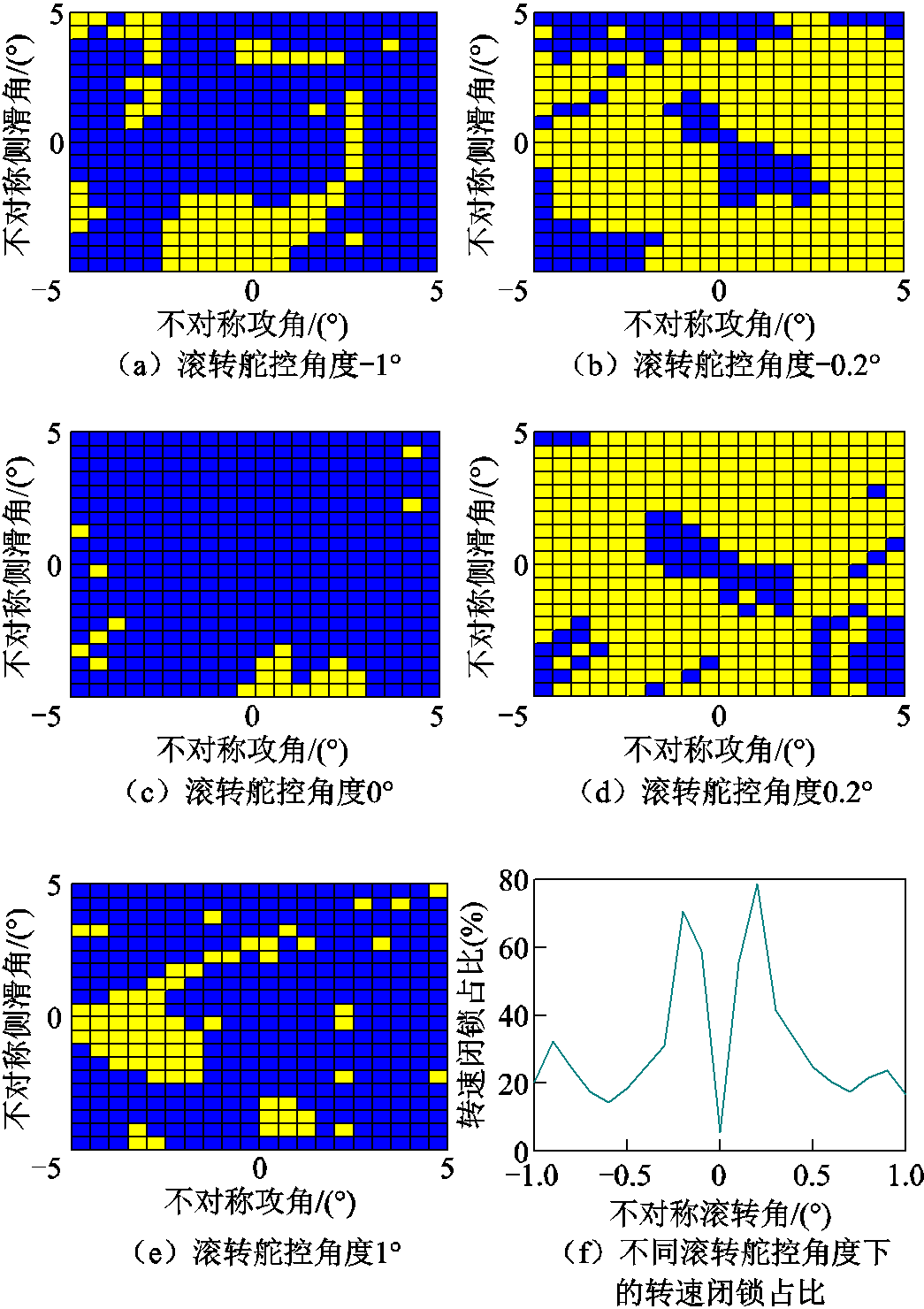
图11 不同不对称舵控角度下的转速闭锁情况
Fig.11 The RSL cases under different asymmetric rudder control angle
转速闭锁问题是外弹道学中的理论难点，也是弹丸设计中要考虑的技术难点。本文针对电磁发射超高速弹丸的转速闭锁问题，首先基于转速闭锁原理和六自由度模型，建立了六自由度转速闭锁模型。其次从电磁发射弹丸的初始扰动特性出发，利用NSGA-Ⅱ辨识了弹丸初始扰动角速度和不对称舵控角，并通过仿真复现了某电磁发射弹丸的转速闭锁现象，仿真结果表明：仿真值与试验结果基本吻合，验证了本文所建转速闭锁模型的正确性。最后分析了该弹丸的转速闭锁安全区，分析结果表明：初始扰动越大，越不容易产生转速闭锁；存在一个与俯仰和偏航运动频率相对应的值，当不对称滚转舵控角度越接近这个值时，越容易发生转速闭锁。本文的仿真与分析结果为电磁发射弹丸的转速闭锁设计与控制奠定了基础。
参考文献
[1] 马伟明, 鲁军勇. 电磁发射技术[J]. 国防科技大学学报, 2016, 38(6): 1-5.
Ma Weiming, Lu Junyong. Electromagnetic launch technology[J]. Journal of National University of Defense Technology, 2016, 38(6): 1-5.
[2] 马伟明, 鲁军勇, 李湘平. 电磁发射超高速一体化弹丸[J]. 国防科技大学学报, 2019, 41(4): 1-10.
Ma Weiming, Lu Junyong, Li Xiangping. Electro-magnetic launch hypervelocity integrated projectile[J]. Journal of National University of Defense Technology, 2019, 41(4): 1-10.
[3] 鲁军勇, 冯军红, 李开, 等. 超高速制导弹丸研究综述[J]. 哈尔滨工程大学学报, 2021, 42(10): 1418-1427.
Lu Junyong, Feng Junhong, Li Kai, et al. Review on guided hypervelocity projectiles[J]. Journal of Harbin Engineering University, 2021, 42(10): 1418-1427.
[4] 马伟明, 鲁军勇. 电磁发射技术的研究现状与挑战[J]. 电工技术学报, 2023, 38(15): 3943-3959.
Ma Weiming, Lu Junyong. Research progress and challenges of electromagnetic launch technology[J]. Transactions of China Electrotechnical Society, 2023, 38(15): 3943-3959.
[5] Du Peipei, Lu Junyong, Feng Junhong, et al. Analysis of the factors influencing the dynamic response of electromagnetic rail launcher[J]. IEEE Transactions on Plasma Science, 2019, 47(5): 2151-2158.
[6] Du Peipei, Lu Junyong, Li Xiangping, et al. Interior ballistic characteristics of electromagnetic rail launcher considering the dynamic characteristics of real launcher[J]. IEEE Transactions on Industrial Electronics, 2021, 68(7): 6087-6096.
[7] Lu Junyong, Du Peipei, Tan Sai, et al. Interior ballistic characteristics of electromagnetic rail launcher under continuous firing[J]. IEEE Transactions on Industry Applications, 2020, 56(5): 4839-4846.
[8] 李湘平, 鲁军勇, 冯军红, 等. 采用动网格技术的弹托分离仿真模型[J]. 国防科技大学学报, 2018, 40(5): 9-13.
Li Xiangping, Lu Junyong, Feng Junhong, et al. Simulation model for sabot discard using dynamic mesh technique[J]. Journal of National University of Defense Technology, 2018, 40(5): 9-13.
[9] 舒敬荣, 张继春, 常思江. 空气动力非对称弹丸大攻角旋转共振运动研究及应用[J]. 兵工学报, 2014, 35(4): 441-447.
Shu Jingrong, Zhang Jichun, Chang Sijiang. Research on large angle-of-attack spin resonance movement of aerodynamic asymmetric projectile[J]. Acta Armamentarii, 2014, 35(4): 441-447.
[10] 孙化东. 制导炮弹动力学特性分析与控制方法研究[D]. 北京: 北京理工大学, 2016.
Sun Huadong. Research on dynamics analysis and control of guided projectiles[D]. Beijing: Beijing Institute of Technology, 2016.
[11] 李湘平, 鲁军勇, 冯军红, 等. 电磁发射弹丸飞行弹道仿真[J]. 国防科技大学学报, 2019, 41(4): 25-32.
Li Xiangping, Lu Junyong, Feng Junhong, et al. Simulation of flight ballistic of electromagnetic launch projectile[J]. Journal of National University of Defense Technology, 2019, 41(4): 25-32.
[12] 李湘平, 鲁军勇, 张晓, 等. 基于NSGA-Ⅱ的过载磁场发生器优化设计[J]. 电工技术学报, 2021, 36(21): 4399-4407.
Li Xiangping, Lu Junyong, Zhang Xiao, et al. Optimization of generator of high overload and strong magnetic field based on NSGA-Ⅱ[J]. Transactions of China Electrotechnical Society, 2021, 36(21): 4399-4407.
[13] 张晓, 鲁军勇, 李湘平, 等. 电磁感应线圈发射子弹系统优化设计[J]. 电工技术学报, 2021, 36(22): 4658-4665.
Zhang Xiao, Lu Junyong, Li Xiangping, et al. System optimization of electromagnetic induction coil launch bullet[J]. Transactions of China Electrotechnical Society, 2021, 36(22): 4658-4665.
Analysis of Rotation Speed Latching of Electromagnetic Launch Hypervelocity Projectile
Abstract The problem of rotational speed lock often occurs in the flight process of the projectile body with asymmetrical pneumatics. Due to rotational speed lock, a large equilibrium nutation angle will be generated, resulting in increased flight resistance of the projectile body, destruction of the dynamic stability characteristics of the projectile body, and catastrophic yaw will occur in severe cases. However, the electromagnetic (EM) launching projectile is more prone to rotational speed lock due to the impact of its launching principle and launching environment. Aiming at the speed lock phenomenon caused by exit disturbance and aerodynamic asymmetry, this paper studies the speed lock principle, speed lock modeling and speed lock boundary analysis, in order to reveal the principle of speed lock and lay a theoretical foundation for its speed lock design and control.
Firstly, based on the principle of speed lock and the six-degree-of-freedom (SDOF) kinematic theory, a SDOF speed lock model considering the asymmetric angle of attack, sideslip angle and zero deflection angle of rolling channel is established. Secondly, based on the data of a live firing test, NSGA-Ⅱ genetic algorithm is used to identify the initial disturbance and non-weighing of the projectile, and the rotational speed locking phenomenon of an EM projectile is simulated and verified the correctness of the rotational speed locking model established in this paper. Finally, based on the identified speed lock influence conditions, the speed lock safety zone of the projectile is analyzed, and the speed lock distribution under different initial disturbance angular velocity and asymmetric angle is given. The simulation and test results show that: (1) The speed locking model established in this paper can reveal the speed locking characteristics of the EM launching ultra-high speed projectile, and the simulation results are in agreement with the test results. (2) The larger the initial disturbance angular velocity of the projectile, the less likely it is to produce speed lock. This is because under certain aerodynamic asymmetry, the larger the initial disturbance, the greater the roll speed induced by the projectile, and the greater the difference between the roll frequency and the pitch and yaw motion frequency, so as to avoid speed lock. (3) There is a value corresponding to the pitch and yaw motion frequency of the projectile, which is ±0.2°. When the asymmetric rolling rudder control angle is closer to this value, the speed lock is more likely to occur; when it is far away from this Angle, the speed lock is not easy to occur.
In this paper, a speed lock modeling method combining equivalent asymmetric moment method and multi-variable and multi-objective genetic algorithm is proposed, which can reproduce the speed lock phenomenon well. However, there is little analysis on the influence mechanism of non-symmetrical weighing on speed lock. Meanwhile, only the safety boundary analysis of speed lock is given, and the control strategy of speed lock is not studied. In the following, the influence mechanism of non-opposite weighing on speed lock is further studied from the kinematic and dynamic equations of projectile, and the control strategy and control effect analysis of speed lock are given.
keywords：Electromagnetic rail launch, rotation speed locking, initial disturbance, aerodynamic asymmetry
中图分类号：TM33; TJ71
DOI: 10.19595/j.cnki.1000-6753.tces.231376
国家自然科学基金资助项目（92266106, 92166205, 52107065, 51925704, 51907203, 51877214）。
收稿日期 2023-08-23
改稿日期 2023-09-28
李湘平 男，1990年生，副教授，硕士生导师，研究方向为电磁发射技术。
E-mail：511422906@qq.com
鲁军勇 男，1978年生，教授，博士生导师，研究方向为直线电机、电磁发射技术和脉冲功率电源等。
Email：Jylu2019@163.com（通信作者）
（编辑 赫 蕾）