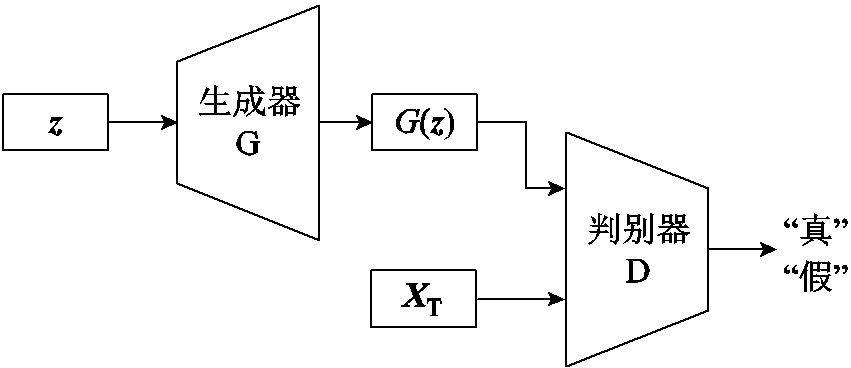
图1 GAN模型结构
Fig.1 GAN model structure
摘要 通过有限元方法计算发射过程中电流密度场，是实现电磁轨道发射器结构精细化设计的必要条件之一，但存在计算时间长、高速计算困难甚至无法计算的问题。该文首先以激励电流、电枢电导率、轨道结构参数和时间t为输入，建立了基于条件生成对抗网络（CGAN）的电流密度场预测模型；然后，为提高对复杂场分布的预测能力，构建ResUnet-Trans网络作为CGAN的特征生成器；最后进行计算验证。以低速电磁轨道发射器实例验证模型内插预测精度，结果表明，模型在测试集上的平均绝对百分比误差（MAPE）小于1.5%；以高速电磁轨道发射器实例验证模型外推预测能力，结果表明，使用由低电导率向高电导率的迁移学习训练策略可以提高模型外推预测精度和泛化能力，在测试集上外推预测MAPE小于2.5%。该文提出的预测方法可实现电流密度场的秒级计算，为高速电磁轨道发射器的优化设计和数字化提供了一种新的思路。
关键词：电磁轨道发射器 电流密度场分布 深度学习 图预测
电磁轨道发射器发射过程中，由于枢轨接触面上的电流分布极不均匀[1]，电流密度接近材料承受极限。电流上升阶段，电流聚集在轨道表面，使轨道表面温度急剧升高，造成材料烧蚀，同时导致轨道机械强度下降，严重影响发射的稳定性和可靠性[2]。因此，分析发射过程中轨道截面和枢轨接触面上的电流分布特性，是控制温升和烧蚀的主要依据，对电磁轨道发射器的结构优化和可靠性设计具有重要意义[3]。
国内外研究团队使用不同数值模拟方法，建立了考虑电枢运动速度影响的三维电磁轨道发射器模型，对低速下场分布、发射特性和高速下电枢运动特性进行了仿真研究[4-6]。文献[4]使用有限元法，通过在电磁场控制方程中添加速度项以考虑电枢运动影响，此时速度反映在方程的对流项中，速度的增大会使单元Peclet数（Pe）增大，当Pe＞1时，求解时可能出现数值解“伪振荡”[7]。文献[5-6]使用Lagrangian坐标系描述的有限元法和有限元/边界元法，此方法会使方程中不显式地出现对流项，而速度反映在运动体的离散网格在每一时间步的位移中。但由于电枢位置与网格变化的联动关系，高速情况下网格的反转和质量下降使计算难以收敛，且存在相对运动区域界面上的网格不匹配问题。电枢高速运动使得电磁轨道发射器的电磁场控制方程计算困难，甚至无法计算。此外，由于三维电磁轨道发射器的数值模拟是一个复杂的非线性多场耦合大型问题，若要获得高精度数值解，需精细化建模，求解一个案例通常需要数小时甚至几天。因此，仅通过数值模拟方法很难甚至无法实现高速下电磁轨道发射器电磁场的精确计算。
除数值模拟方法外，降阶模型通过对偏微分方程降阶，在保证一定精度的条件下，可以降低复杂系统的求解难度，提升建模和求解效率[8]。但传统降阶方法难以应用于电磁轨道发射器这种强非线性、多变量场景，并且降阶过程使得数据点上的物理量失去了空间联系和平移不变性[9]。近年来，人工智能技术得到快速发展。相比于传统机器学习方法，深度学习拥有更加灵活、复杂的网络架构和更强大的非线性表征能力，可为电磁轨道发射器的智能化提供支撑[10]。其可以通过学习数值模拟结果的历史特征，实现数值模拟结果的预测与直接生成[11-14]，极具发展潜力。在电磁轨道发射器领域已有部分学者开展了相应研究，但是主要围绕轨道温升[15]、出口速度[16]等宏观特性预测，为了更科学地指导电磁轨道发射器的优化设计，还需要获取精细化的电流密度场。
为快速获取电流密度场，可以利用深度神经网络强大的特征提取能力[17]，以及学习场的时空变化规律，实现轨道截面和枢轨接触面上电流密度场的高效预测。在时空图像预测领域，常用的方法是将卷积神经网络（Convolutional Neural Network, CNN）和长短期记忆（Long Short-term Memory, LSTM）网络结合，直接从数据中提取时空分布特征[18-20]。但是，一方面这些模型均基于LSTM网络构建，需要前几个时刻的图像作为输入，只能预测特定时间间隔下的图像；另一方面，这些方法只使用均方误差（Mean Square Error, MSE）作为损失函数，MSE对较大误差惩罚力度大，对较小误差则更为容忍，使得训练中部分细节特征丢失，容易导致预测图像模糊，无法满足电磁轨道发射器的高精度预测要求。在图像生成方面，I. J. Goodfellow在2014年提出的生成对抗网络（Generative Adversarial Networks, GAN）由于具有良好的性能表现，目前已成为应用广泛的图像生成模型之一[21]。为解决GAN生成的样本不可控的问题，通过给生成器（Generator, G）和判别器（Discriminator, D）额外增加条件信息y，形成条件生成对抗网络（Condition Generative Adversarial Networks, CGAN），实现了满足条件信息y下的图像生成[22]。文献[23]提出一种CGAN模型，能够根据输入的边界条件，精确预测室内气流场和温度场。文献[24]利用CGAN，直接建立从参数化超临界翼型到其相应的跨音速流场分布的一对一映射，与现有的大多数模型相比，该模型在预测高维流场的效率和准确性方面更优。这些研究表明，CGAN可以实现输入参数到场的直接预测，而生成器G和判别器D的对抗训练可以提高预测结果精度。
由于电磁轨道发射器发射过程中电流密度变化复杂剧烈，对生成器G的特征提取能力具有更高的要求。U-Net在编码器和解码器之间引入了长跳跃连接，可以融合不同尺度的特征，具有更强的细节捕获能力和少样本学习能力[25]。文献[26]在U-Net编码器与解码器中引入残差连接（短残差）[27]构建深度ResUnet，解决了深层网络训练过程中的梯度消失和网络性能退化问题。文献[28]提出基于自注意力机制的Transformer，拥有强大的长距离建模能力和并行计算能力，在自然语言处理领域和计算机视觉领域均得到了广泛应用。
因此，本文提出一种基于CGAN的电流密度场预测方法，以激励电流、电枢电导率、轨道结构参数和时间t作为输入，直接生成相应参数下的电流密度场。为提高对复杂电流分布的特征提取能力，本文进一步构建了基于残差网络、U-Net和Transformer的深度神经网络作为CGAN的生成器，建立了ResUnet-Trans-CGAN模型。
考虑到高速下电磁轨道发射器的数值模拟难以计算，可以将深度神经网络学习到的场时空变化规律泛化至训练集样本空间范围外一定区域内，属于外推预测问题，实现数值模拟无法计算工况的场预测。在外推预测方面，文献[29]提出了融合CNN，建立了圆柱表面压力−速度场模型，以雷诺数范围为70～900的数据作为训练集，测试了模型在雷诺数范围为60～1 100的性能表现。结果表明，模型可以捕捉到流动本质，当测试数据雷诺数在训练集范围外时，虽有一定外推能力，但仍存在较大误差。文献[30]提出一种GAN框架，结合物理损失函数，通过雷诺数范围在100～400的流场数据集，成功预测了雷诺数为500与3 000的流场，但是此方法必须将预测时刻的前几个时刻的流场作为输入信息，不适用于没有初始流场计算结果的情况。文献[31]基于不同电枢电导率下稳定数值模拟数据，提出基于DBN-DNN的电枢电磁推力外推预测的方法，研究了DBN-DNN参数从预测低电导率下电枢电磁推力迁移到基准电导率时的训练策略，实现了电枢电磁推力的高精度外推预测。
因此，为实现电磁轨道发射器高速下电流密度场预测，在本文所提出的ResUnet-Trans-CGAN模型基础上，使用由低电导率向高电导率迁移的学习训练策略，进一步提升模型泛化能力，提高外推预测精度。
GAN由相互竞争的两个神经网络（生成器G和判别器D）组成，如图1所示。G以随机噪声向量z为输入，并尝试生成图像G(z)。D以从训练集中随机抽取的真实图像XT或G生成的“假”图像G(z)为输入，并尝试将接收到的图像分类为“真”或“假”。首先将D的输出代入目标函数计算损失值，根据损失值依次更新G和D的权重参数；然后再次给定新的噪声和训练数据，并不断重复这一过程；最后，G可以生成非常逼真的图像，而D无法再区分真假图像，二者达到纳什平衡，训练结束。此时就不再需要D，只需要给G输入随机噪声z即可生成逼真的图像。GAN的最大优势是无需预先假定具体的数据分布形式，直接从简单随机分布中采样，训练完成后即可生成逼近原始真实数据分布形式的图像，但也因此导致了GAN生成的图像不可控。
图1 GAN模型结构
Fig.1 GAN model structure
CGAN模型结构如图2所示。通过给G和D的输入额外增加条件变量y，约束G必须生成与y相匹配的图像G(z|y)，解决了GAN生成图像不可控的问题。D会接收真实图像XT或G(z|y)，同时根据接收到的y判断图像的真假。训练完成后，只要向G提供条件变量y和噪声输入z，就能生成特定类别的图像。CGAN的目标函数为
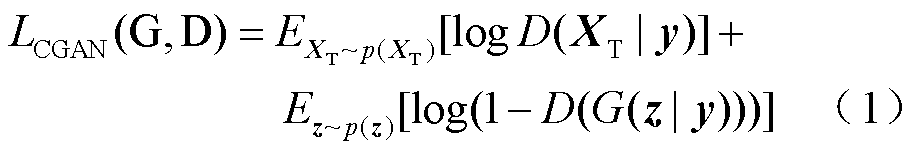
式中，EXT～p(XT)、Ez～p(z)为样本的期望值。
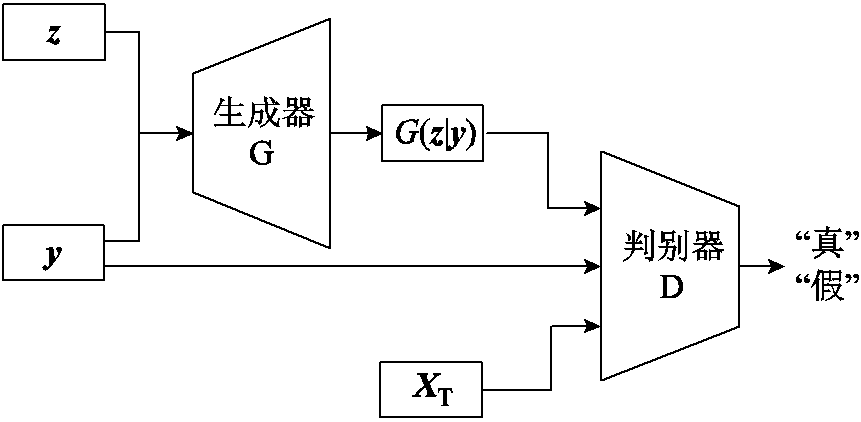
图2 CGAN模型结构
Fig.2 CGAN model structure
ResNet通过引入残差块来学习残差映射，解决了深层神经网络训练时的梯度消失和梯度爆炸问题[27]。残差块由恒等映射h(xl)和残差映射F(xl, ωl)两个分支组成，如图3所示。通过这种方式，网络可以轻松地学习到残差，从而更容易优化和训练。
U-Net模型包括编码器、瓶颈（Bottleneck）模块和解码器，如图4所示。其独特之处在于U形设计，编码器进行下采样，逐渐减小特征图尺寸，同时提取高层次的特征。瓶颈模块用于连接编码器和解码器。解码器进行上采样，逐渐增加特征图的尺寸，并通过跳跃连接（Skip Connections）将下采样路径的特征与上采样路径的特征相连接。跳跃连接将底层特征与更高层特征直接相连，融合不同层次的特征，使得信息能够在网络不同层之间流动，不仅有助于训练过程中的反向传播，而且可以修复编码器阶段因池化操作而丢失的图像细节特征。
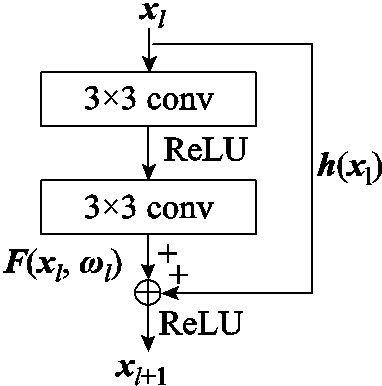
图3 ResNet残差块
Fig.3 ResNet-block
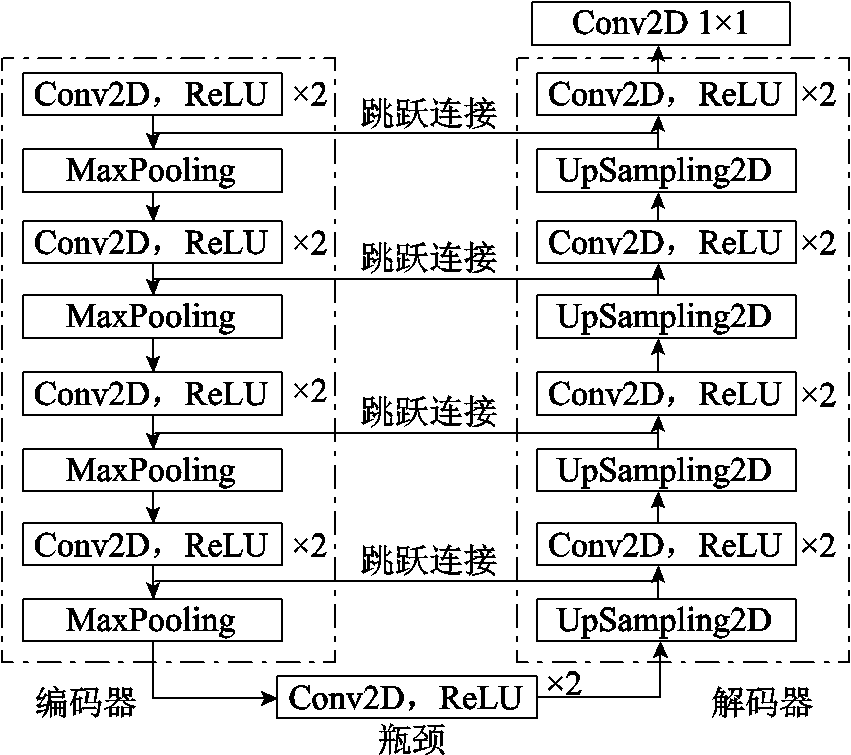
图4 U-Net模型结构
Fig.4 U-Net model structure
Transformer是A. Vaswani等于2017年提出的神经网络架构，突破了传统循环神经网络（Recurrent Neural Network, RNN）和CNN的限制，具有强大的长距离建模能力和并行计算能力，引领了序列建模领域的革命性变革。Transformer的核心创新在于自注意力机制（Self-Attention），这种机制允许模型为输入序列中的每个元素分配不同的权重，从而更好地捕获元素之间的关系，有效地解决了长距离依赖的问题。Transformer另一个重要的组成部分是多头注意力（Multi-Head Attention），通过同时学习多组注意力权重，多头注意力可以在不同位置关注序列的不同部分，从而提升模型的表达能力。因此注意力运算使模型具有了更良好的可解释性[32]。此外，为了处理序列中的位置信息，Transformer引入了位置编码，以便模型了解元素在序列中的位置。整个Transformer架构由编码器和解码器构成，编码器用于编码输入序列信息，解码器用于生成输出序列。由于本文主要使用Transformer对输入数据进行编码，因此只使用编码器部分，如图5所示。
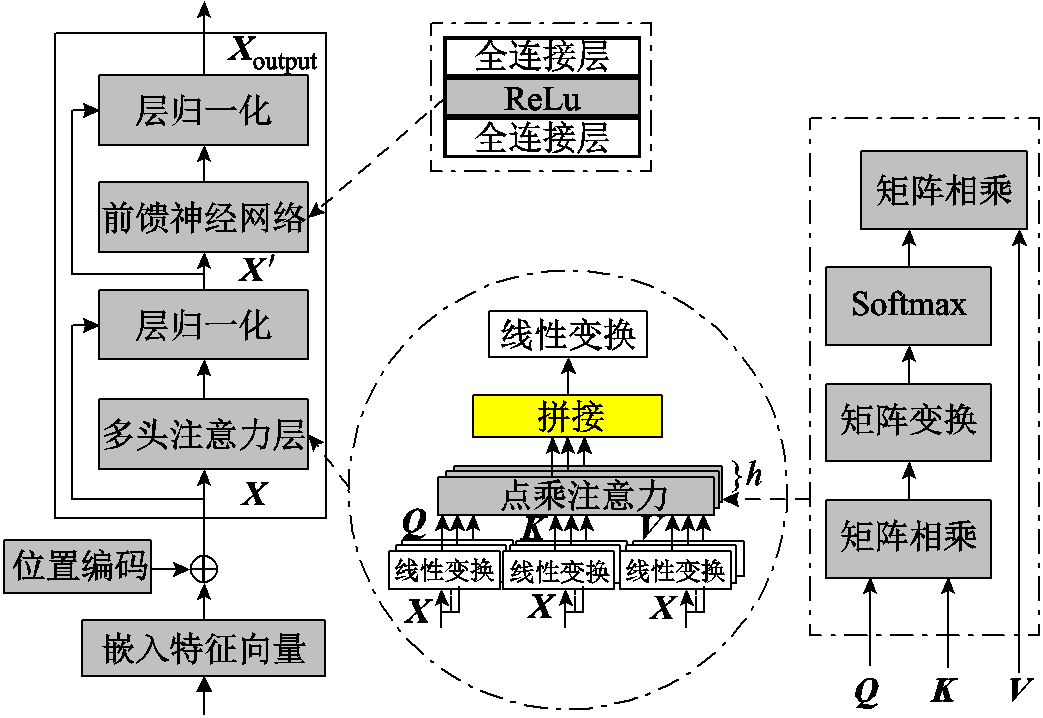
图5 Transformer编码器基本架构
Fig.5 The basic structure of Transformer encoder block
在原始的CGAN模型中，随机噪声z和条件变量y拼接到一起作为G的输入，z的随机性赋予了生成图像之间的差异性，G生成图像的过程可以视为在给定条件变量y约束下的一对多映射。但是本文是要建立激励电流、电枢电导率、轨道结构参数和时间t到对应电流密度场的一对一映射，因此需要去除随机噪声z，G只以条件变量y作为输入。
基于ResUnet-Trans-CGAN的电流密度场预测模型如图6所示，包括训练阶段和测试阶段两部分。在训练阶段，首先将激励电流、电枢电导率、轨道结构参数和时间t拼接组合成为条件变量y，经全连接层进行维度变换后输入G，生成电流密度场G(y)；然后将电流密度数值模拟计算值矩阵化，形成真实图像x，并将条件变量y与生成图像G(y)或者真实图像x拼接组合输入D；最后D对输入数据进行判断，输出图像是真实图像的概率。G和D以对抗的方式进行训练，并交替更新神经网络参数。
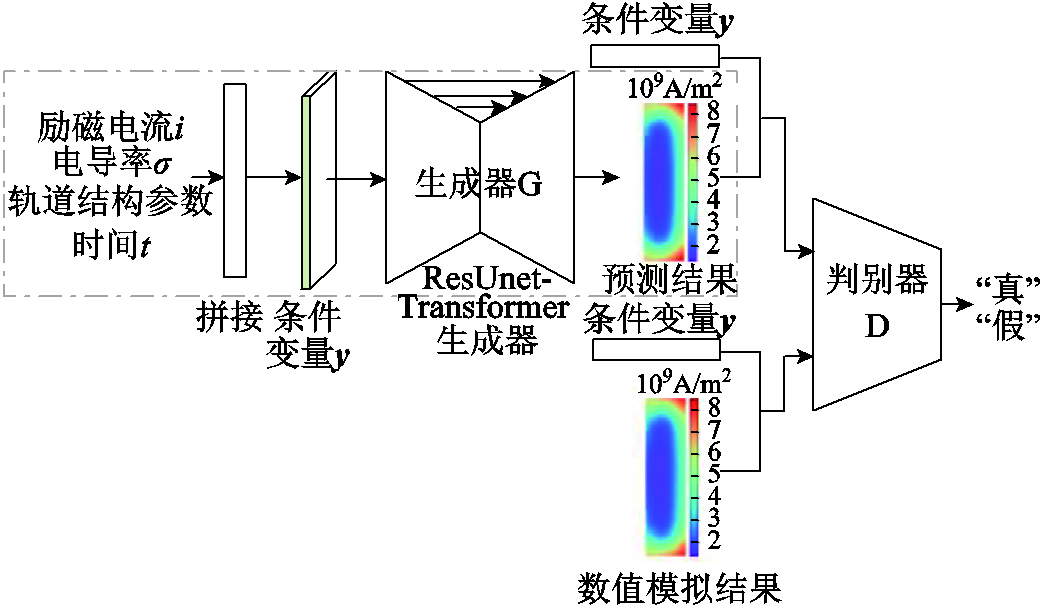
图6 ResUnet-Trans-CGAN电流密度场预测模型
Fig.6 Current density field prediction model based on ResUnet-Trans-CGAN
在测试阶段，抛弃D部分，将激励电流、电枢电导率、轨道结构参数和时间t输入到G，直接生成相应条件下的电流密度场，如图6点画线框中所示。
原始CGAN的生成器为结构简单的全连接神经网络。为提高模型对复杂电流分布的特征提取能力，基于残差网络、U-Net和Transformer，本文建立ResUnet-Transformer生成器，主要结构由编码器、解码器和瓶颈模块组成，如图7所示。
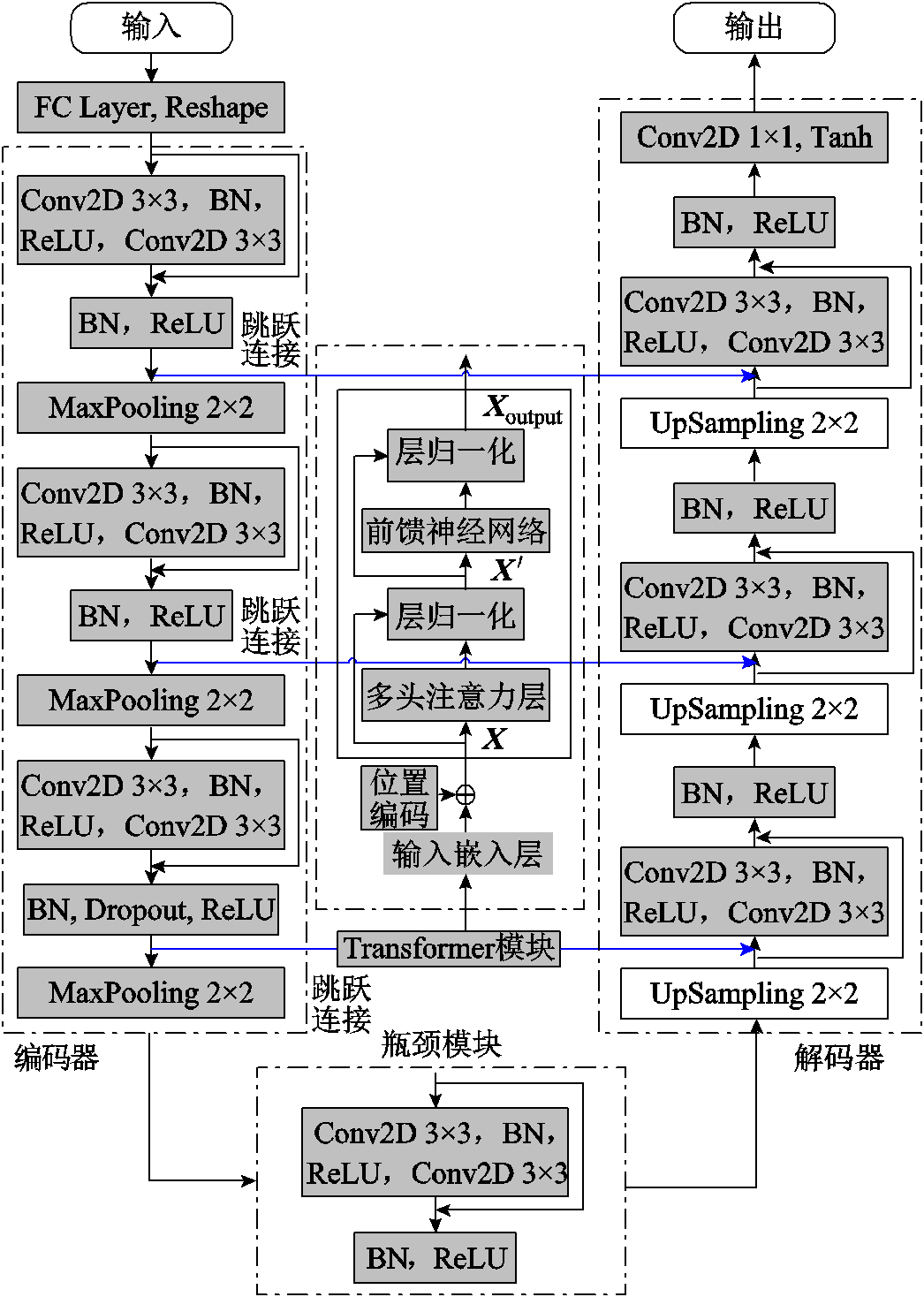
图7 ResUnet-Transformer生成器结构
Fig.7 ResUnet-Transformer generater structure
具体来说，编码器由三个残差块和三个最大池化层组成。在每个残差块中增加批标准化（Batch Normalization, BN）层，提高模型的训练稳定性和收敛速度。首先输入特征图像经过残差块中卷积运算后特征通道数加倍，以提取更丰富的抽象特征。然后使用2×2最大池化层进行下采样，减小特征图像尺寸，增加感受野大小，增强对输入图像干扰的鲁棒性，从而减少过拟合的风险和计算量。
瓶颈模块由一个残差块组成，负责连接编码器和解码器。解码器由三个残差块和三个上采样层组成。通过对图像进行上采样，恢复图像的抽象特征信息，上采样时图像经过残差块后特征通道数量减半。这一过程在解码器中重复三次，将特征解码至原始图像的尺寸。最后使用1×1的卷积层将特征图的通道数量调整为1，并使用tanh激活函数将输出结果限制在（-1, 1）之间。
解码器通过长跳跃连接与编码器每次池化操作前的特征级联，能够直接学习编码器部分提取的特征。这种设计有助于防止由多次池化下采样引起的部分特征丢失，提升预测精度。在编码器第三次池化操作前的长跳跃连接中引入Transformer模块。首先，对输入特征图像的各像素点进行位置编码；然后，通过多头自注意力机制处理特征图像像素点之间的相互关系，重点关注提取的特征图像的空间特征，以增强全局感知能力、避免特征丢失，提高图像预测结果的精细度；最后，使用两个前馈神经网络对特征图像进行维度变换，并与上采样后的特征图像进行融合，从而使融合后的特征图像同时包含高级特征和低级特征。
综上所述，ResUnet-Transformer生成器在原始U-Net模型的基础上进行改进，具有以下优点：①使用ResNet中的残差块替代连续两次的卷积操作，加快了梯度信息的传递，提高了模型表达能力，降低了网络训练难度；②在编码器的第三次池化操作之前的长跳跃连接中引入Transformer模块，可以充分利用Transformer在捕获全局特征方面的优势提升模型的性能。
ResUnet-Trans-CGAN模型的判别器D主要由卷积层组成，其网络结构如图8所示。D的输入为电流密度场和条件变量y，将y维度变换为与电流密度场大小相同的张量（batch×1×256×64），并与电流密度场按通道叠加作为D的输入。输入图像经4次卷积操作进行下采样，每次卷积操作后还进行批标准化操作和LeakyReLU激活。最后使用全连接层将卷积网络输出展开，输出1个标量值，并使用Sigmoid函数将结果限制在（0, 1）之间，表示判断图像为真实图像的概率。
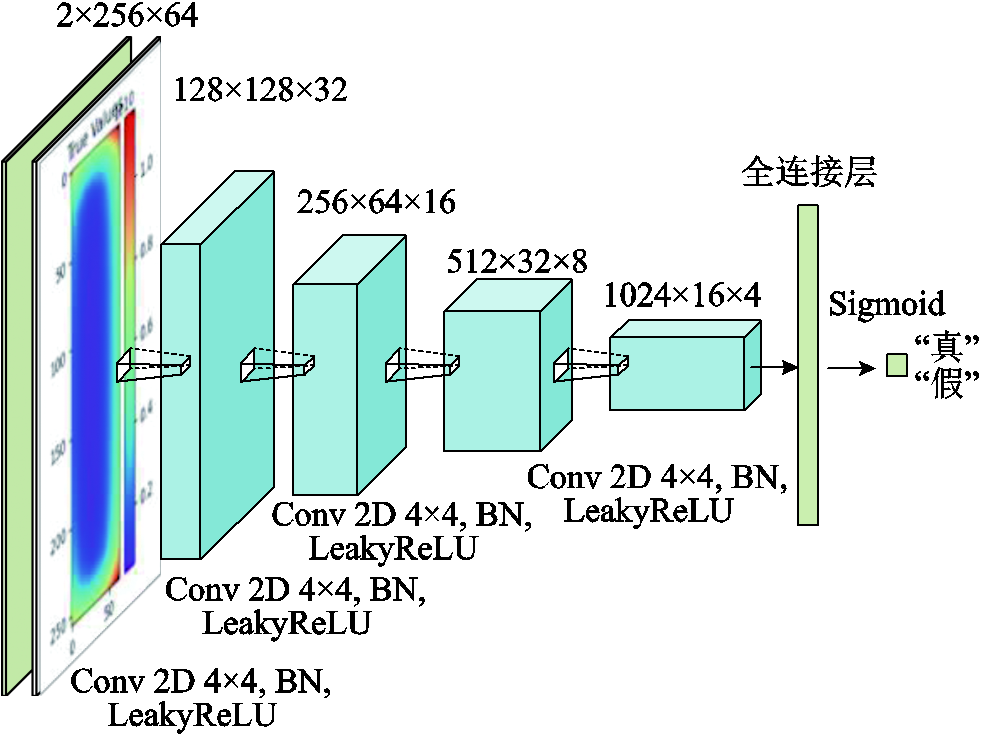
图8 判别器D网络结构
Fig.8 Discriminator network structure
由于生成器G的任务不仅是欺骗判别器D，还要生成接近真实的电流密度场，因此生成器G的损失函数额外增加L1损失函数，表达式为
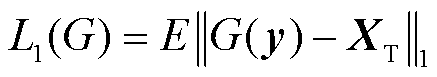（2）
最终整体的目标函数可以写为
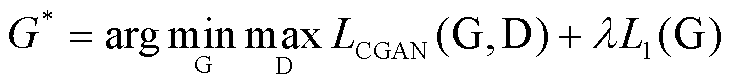（3）
式中，λ为L1损失函数的权重。
电磁轨道发射器的电磁场控制方程为对流扩散方程，速度反映在方程的对流项中。Peclet数是用于衡量对流项在方程中主导程度的无量纲参数，反映该方程数值解稳定性，其计算公式为
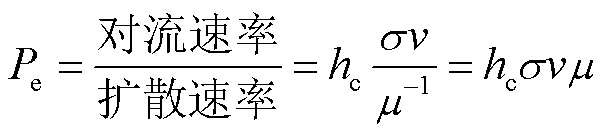（4）
式中，hc为单元网格大小；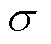
为电导率；v为电枢运动速度；
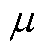为相对磁导率。
由式（4）可知，Pe与网格单元尺寸、速度、电导率和磁导率成正比。随速度增大，Pe逐渐增大。当Pe＞1时，将削弱离散方程组矩阵“主元占优”的特性，导致矩阵出现病态，数值解出现物理上并不存在的“伪振荡”[7]。为避免出现“伪振荡”现象，必须采用非常细密的网格划分。但在高速、高磁导率和高电导率条件下，使Pe＜1的网格划分计算量太大，对于计算机资源的耗费太高，在实际中不可取。
为了获取高速电磁轨道发射器整个发射过程的电流密度场，本文使用深度神经网络提取电流密度场分布特征，学习电流密度分布规律，从而将高速下的电流密度场外推至“伪振荡”阶段。文献[31]以2.20×107 S/m的电枢电导率为基准，证明随着电枢电导率的减小，数值解“伪振荡”出现的时间越来越晚。这为建立充足的数据集提供了基础。
深度神经网络需要大量训练数据，但是在高速电磁轨道发射器基准电导率下能够稳定数值模拟的时间太短，可供训练的数据量不足。因此本文按照100%、80%、60%和40%电枢电导率进行数值模拟，通过降低电枢电导率来延长可稳定数值模拟的时间，从而获取更多训练数据。不同电导率下的预测可被视为求解多个具有相似控制方程的任务，深度神经网络可以从中学习到电流分布随电导率的变化规律，从而提高在基准电导率下的外推预测精度。
因此，本文针对高速情况下存在的数值解“伪振荡”问题，使用不同电导率下的数值模拟数据训练ResUnet-Trans-CGAN，以外推预测基准电导率下“伪振荡”阶段电流密度场。高速下电流密度场外推预测方法如图9所示。
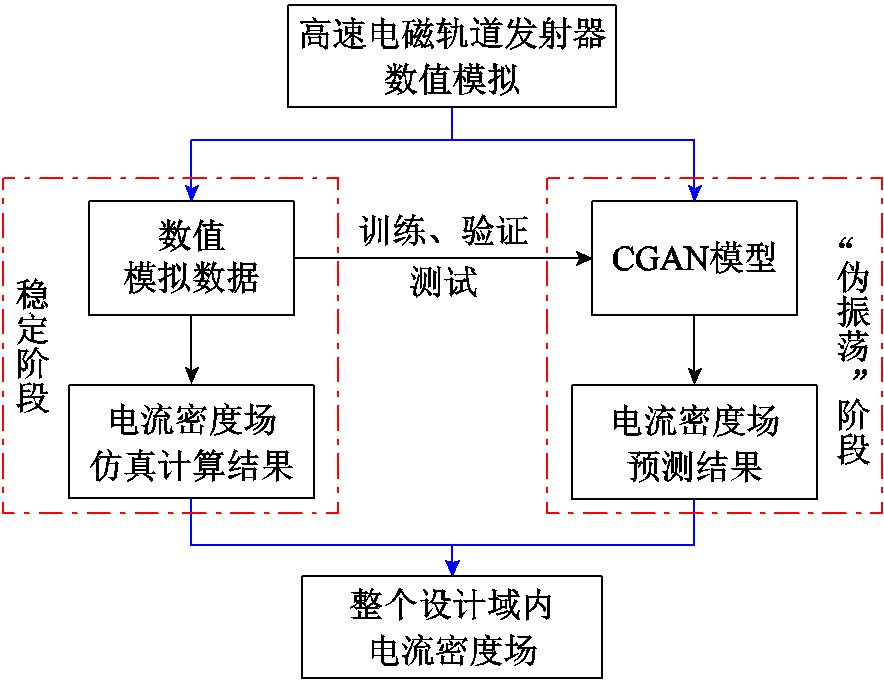
图9 电流密度场外推预测方法
Fig.9 Extrapolation prediction method of current density field
主要步骤如下：
1）数据获取。建立电磁轨道发射器三维有限元仿真模型，计算发射过程中不同电枢电导率下的电流密度场。根据数值解的稳定性，将数值解分为稳定阶段和“伪振荡”阶段。
2）数据预处理。对数据进行最大最小归一化和标准化处理，并划分为训练集和测试集。
3）神经网络模型构建与训练。建立ResUnet-Trans-CGAN模型，使用训练集对模型进行训练。在测试集上测试模型的预测精度，评估模型是否学习到数据中潜在的电流分布规律。
4）外推预测。使用训练好的ResUnet-Trans-CGAN模型，预测基准电导率时高速下“伪振荡”阶段的电流密度场。将数值解稳定阶段数值模拟结果和“伪振荡”阶段预测结果叠加，得到整个发射过程的电流密度场。
考虑电枢运动速度影响时，得到在Eulerian坐标系下的电磁轨道发射器电枢控制方程为[31]
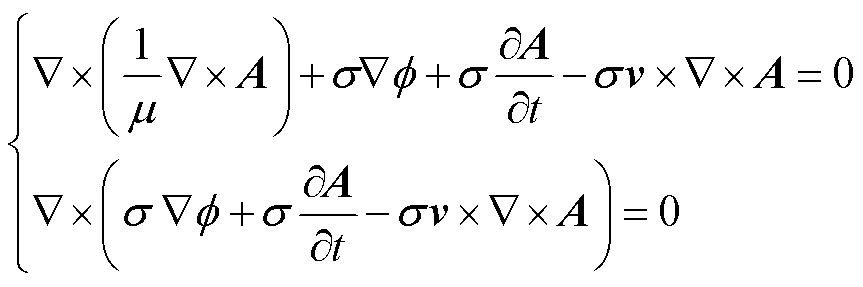（5）
式中，A为矢量磁位；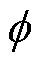
为标量电位。
电枢运动过程中考虑枢轨摩擦阻力和空气阻力的影响，电枢动力学方程为[31]
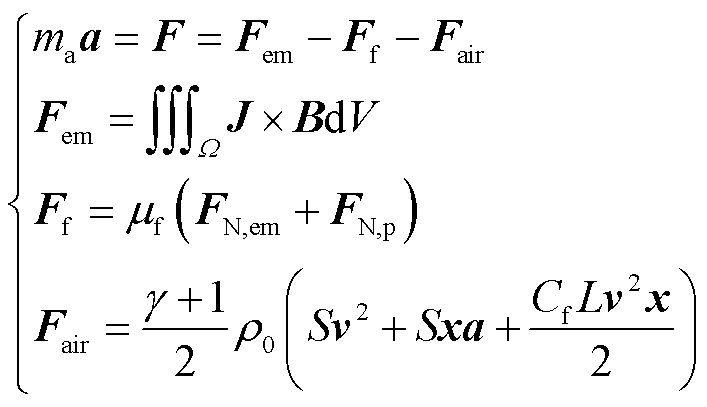（6）
式中，ma、a和x分别为电枢的质量、加速度和位移；Fem为电枢电磁推力，大小与电流密度J和磁通密度B有关；Ω为电枢区域；Ff为枢轨摩擦阻力，大小与摩擦系数μf、电枢电磁接触压力FN,em、电枢机械预紧压力FN,p有关；Fair为空气阻力，大小与电枢运动参数和气动外形有关；γ为空气的比热比；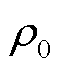
为初始空气密度；S为电枢横截面积；L为电枢截面周长；Cf为黏滞摩擦系数。
在电枢电磁推力、枢轨摩擦阻力和空气阻力的共同作用下，电枢所受合力为F，电枢运动加速度为a。因此，由电枢运动加速度a积分可以得到电枢运动速度为
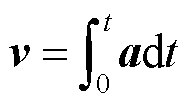（7）
发射速度低的电磁轨道发射器可以完成整个发射过程的数值模拟。因此以低速电磁轨道发射器为计算实例，训练ResUnet-Trans-CGAN模型，并分别预测了轨道截面和枢轨接触面上的电流密度场，检验其对电流时空分布特征的学习能力，以验证本文所提出预测方法的有效性和精确性。
3.2.1 轨道截面电流密度场内插数据集的建立
以美国佛罗里达州实验室公开的电枢测试发射装置（Okaloosa Armature Tester, OAT）和MCA 103电枢为研究对象[33-34]。使用试验编号为SLK 018的发射数据。电枢质量为249.72 g，0～1.0 ms的激励电流，如图10a所示。根据电磁场控制方程、动力学方程、枢轨模型参数和激励电流，使用商业软件建立起理想接触条件下的电磁轨道发射器有限元仿真模型，如图10b所示。考虑到趋肤效应和邻近效应影响，轨道内侧网格更加细致，考虑到枢轨接触面处物理场的变化更加剧烈，对此处网格进行了更加细化的处理，采用瞬态求解器求解。枢轨模型参数见表1。
表1 枢轨模型参数
Tab.1 Parameters of armature and rail model
参数数值 轨道长度/mm220.00 轨道宽度/mm31.75 轨道厚度/mm6.35 轨道间距/mm25.00 轨道电导率σr/(S/m)5.80×107 轨道相对磁导率μr1.00 电枢长度la/mm28.59 电枢宽度ha/mm25.00 电枢电导率σ/(S/m)1.86×107 电枢相对磁导率μ1.00
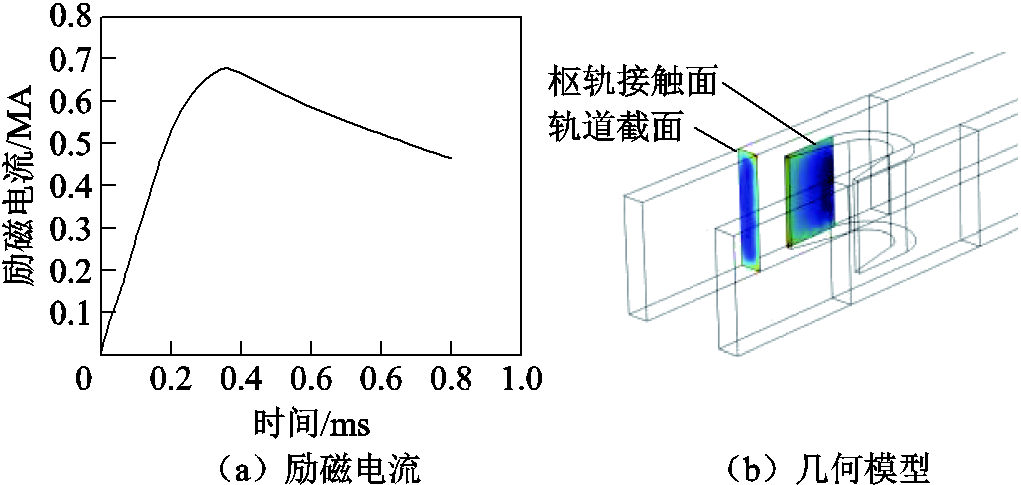
图10 激励电流与电磁轨道发射器几何模型
Fig.10 Excitation current & Geometric model of electromagnetic rail launcher
此案例中电枢加速时间短，出口速度较低，各电导率下数值解均未出现“伪振荡”问题。数值模拟计算出口速度为245.7 m/s，发射试验测量电枢出口速度为247.0 m/s。电枢出口速度数值模拟结果仅比试验测量小0.53%，可以满足实际工程计算需求。由此可见，本文所建立的有限元模型是正确的，可为深度学习模型提供可靠的训练数据。
为验证ResUnet-Trans-CGAN模型对电流密度场时空特征的学习能力，首先考虑激励电流和电导率对电流分布的影响。以图10b所示轨道截面处为观察视角，设定时间步为0.001 ms，以表1中电枢电导率（1.86×107 S/m）为基准，在100%、80%、60%和40%电枢电导率下进行数值模拟。为减少模型参数、降低训练代价，同时又能清晰显示所生成的电流密度场的细节特征，对轨道截面上电流密度数值模拟结果进行插值和矩阵化处理，形成由真实场值构成的单通道云图，分辨率为256×64，最终得到4 000组样本数据。使用蒙特卡罗方法每次抽取激励电流值i、电枢电导率σ、当前时刻t和相应条件下的电流密度场Iiσt，组成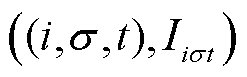
数据对。
模型训练前需对数据进行最大-最小归一化和标准化处理，将数据范围转换到[-1, 1]之间，从而提高模型性能，加快训练时收敛速度。训练集和测试集按照8:2的比例划分。
以MSE和平均绝对百分比误差（Mean Absolute Percentage Error, MAPE）作为模型的性能评价指标，计算公式分别为
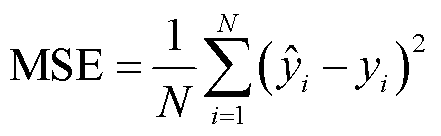（8）
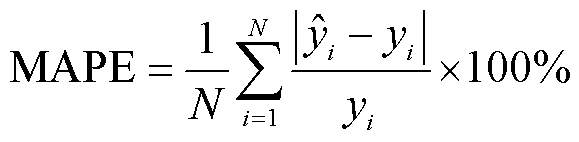（9）
式中，yi和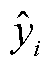
分别为第i个样本的真实值和预测值；N为样本个数。
3.2.2 轨道截面电流密度场内插预测性能分析
本文基于Pytorch深度学习框架构建电磁轨道发射器电流密度场预测模型，使用GPU加速模型训练。硬件配置为：NVIDIA Tesla A800，显存80 GB。
采用常用的自适应矩估计（Adaptive Moment Estimation, Adam）优化器最小化损失函数。为进一步提高模型训练收敛速度，本文在Adam优化器的基础上采用余弦退火算法自适应地调整学习率，使学习率随着训练步数增加逐渐减小，动态变化学习率公式为
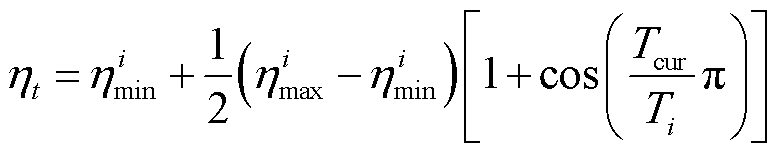（10）
式中，
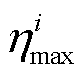和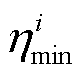
分别为学习率变化的上、下限；
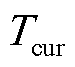为最近一次重启后经历的Epoch数；
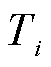为每个调整周期内Epoch总数。
合适的超参数可以加快模型训练速度、防止模型过拟合，提高预测精度。对Epoch、Batch-size、初始学习率、Dropout和L1损失函数权重λ进行超参数调优。按照表2所示超参数取值进行超参数调优，最终确定Epoch为200，Batch-size为4、初始学习率为2×10-4、Dropout为0.5、λ=50时，模型的综合预测性能最好。
表2 超参数变量取值
Tab.2 Values of hyperparameter variables
超参数取值最优值 Epoch[100, 200, 300, 500]200 Batch-size[1, 4, 16, 32]4 初始学习率[2×10-2, 2×10-3, 2×10-4]2×10-4 Dropout[0.1, 0.3, 0.5, 0.6]0.5 损失函数权重λ[10, 30, 50, 80, 100]50
过大的数据集会增加数据处理成本，徒增训练时间，但预测精度并不会得到明显提升。因此，保持模型参数不变，验证数据集大小对模型性能的影响。不同样本数下预测结果见表3。
表3 不同训练集样本数下模型的预测误差和训练时间
Tab.3 Prediction error and training time of the model with different training set samples
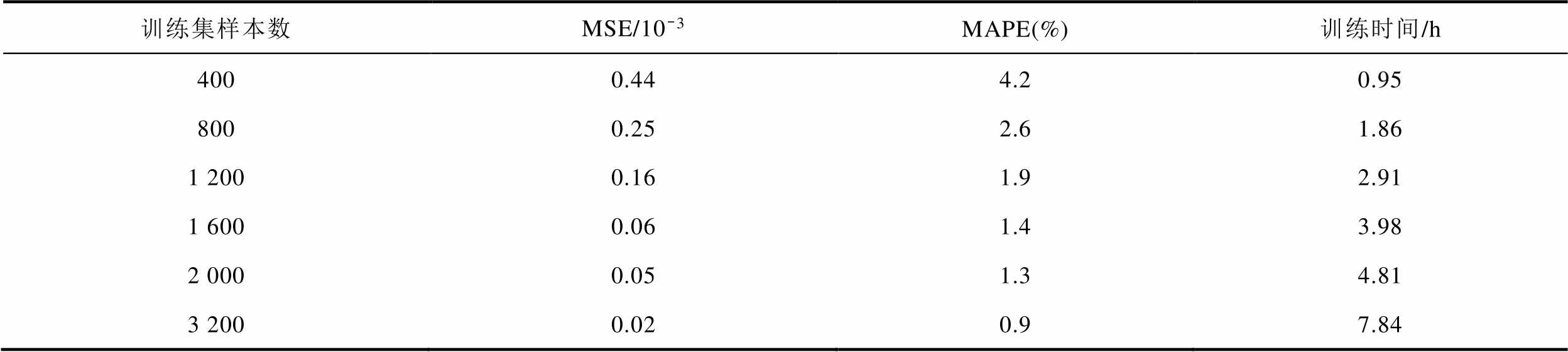
训练集样本数MSE/10-3MAPE(%)训练时间/h 4000.444.20.95 8000.252.61.86 1 2000.161.92.91 1 6000.061.43.98 2 0000.051.34.81 3 2000.020.97.84
当训练集样本数为400和800时，预测效果较差，不满足精度要求。当训练集样本数为1 200、 1 600、2 000时，误差显著减小。但是当样本数从1 600到2 000变化时，误差没有明显减小。当训练集样本数为3 200时，测试集的误差较样本数为2 000时误差进一步降低，电流密度场的MAPE值可以达到0.9%，但训练时间更长。因此，为保证训练速度和预测精度，后续实验均在训练样本数为1 600的情况下进行。
为分析模型结构对预测精度的影响，本文从ResUnet-Transformer生成器的卷积层数、短残差机制、Dropout层、余弦退火算法等方面开展相关实验，预测结果见表4。从实验结果可以看出：①对于卷积层数，并非网络越深，模型的预测效果越好。当生成器G的卷积层数为19层时，预测效果差且训练时间长；当模型的卷积层数降为15层时，预测效果显著提升，训练时间也明显缩短；当模型的卷积层数降为11层时，虽然训练时间进一步缩短，但预测效果变差。②短残差机制能够促进梯度的反向传播，提高预测精度，节省网络的训练时间。③引入Dropout层可以提高模型的泛化能力，提高预测效果，但会略微增加计算量与算法耗时。④余弦退火算法可以使模型训练过程中自适应地调整学习率，提高预测精度。
表4 不同模型结构下电流密度场预测结果
Tab.4 Current density field prediction results under different model structures
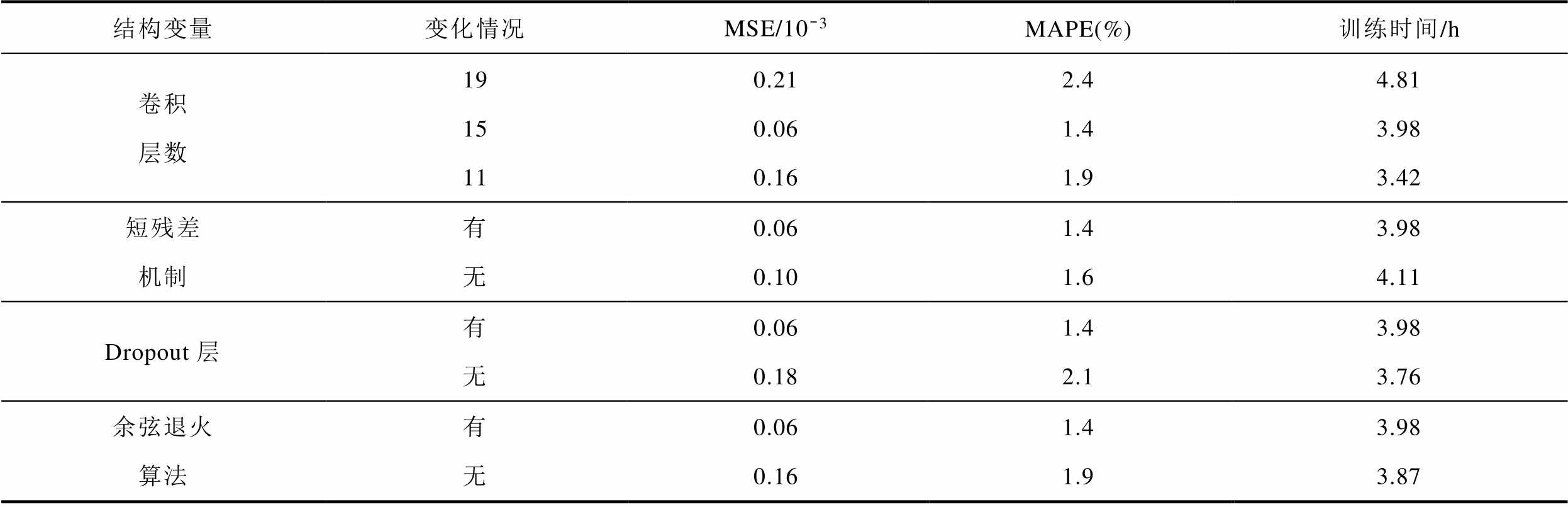
结构变量变化情况MSE/10-3MAPE(%)训练时间/h 卷积层数190.212.44.81 150.061.43.98 110.161.93.42 短残差机制有0.061.43.98 无0.101.64.11 Dropout层有0.061.43.98 无0.182.13.76 余弦退火算法有0.061.43.98 无0.161.93.87
为验证本文提出的ResUnet-Trans-CGAN的先进性，与使用转置卷积网络作为生成器的CGAN和使用U-Net作为生成器的Unet-CGAN对比。为验证对抗损失函数对预测结果的影响，与仅使用MSE损失函数的ResUnet-Transformer对比。使用1 600组训练数据，每个模型的超参数和数据预处理的设置均相同，利用测试集验证模型的泛化能力，各个模型的预测误差和训练时间见表5。
表5 不同算法模型的预测误差和训练时间
Tab.5 Prediction error and training time of different algorithm models
算法模型MSE×10-3MAPE(%)训练时间/h CGAN1.319.32.62 UNet-CGAN0.424.13.12 ResUnet-Transformer0.202.32.87 ResUnet-Trans-CGAN0.061.43.98
通过对比可以发现，使用转置卷积的CGAN模型的结构比较简单，相同样本数下的训练时间最短，但是预测精度最低。UNet-CGAN模型中的长跳跃连接可以融合不同抽象层次的图像特征，预测效果显著提升。相比于ResUnet-Transformer，由于本文所提出的ResUnet-Trans-CGAN模型具有额外的对抗损失函数，因此精度更高。但由于模型更加复杂，因此训练时间也明显增加。
在基准电导率测试集上，使用ResUnet-Trans-CGAN模型，预测不同时刻下的轨道电流密度场，并与数值模拟计算结果对比，其预测结果如图11所示。图中第一行是不同时刻下数值模拟计算结果，第二行是不同时刻下神经网络预测结果，第三行是逐点绝对值误差。受趋肤效应影响，电流首先集中分布于轨道内侧两个尖角处，随着时间增加，电流逐渐向轨道内部扩散，电流密度最大值也从两个尖角处逐渐向轨道内部移动。预测结果表明，本文提出的ResUnet-Trans-CGAN模型能够很好地学习到轨道电流时空分布变化规律，在靠近轨道表面处等电流密度变化率较高处也有很高的预测精度。
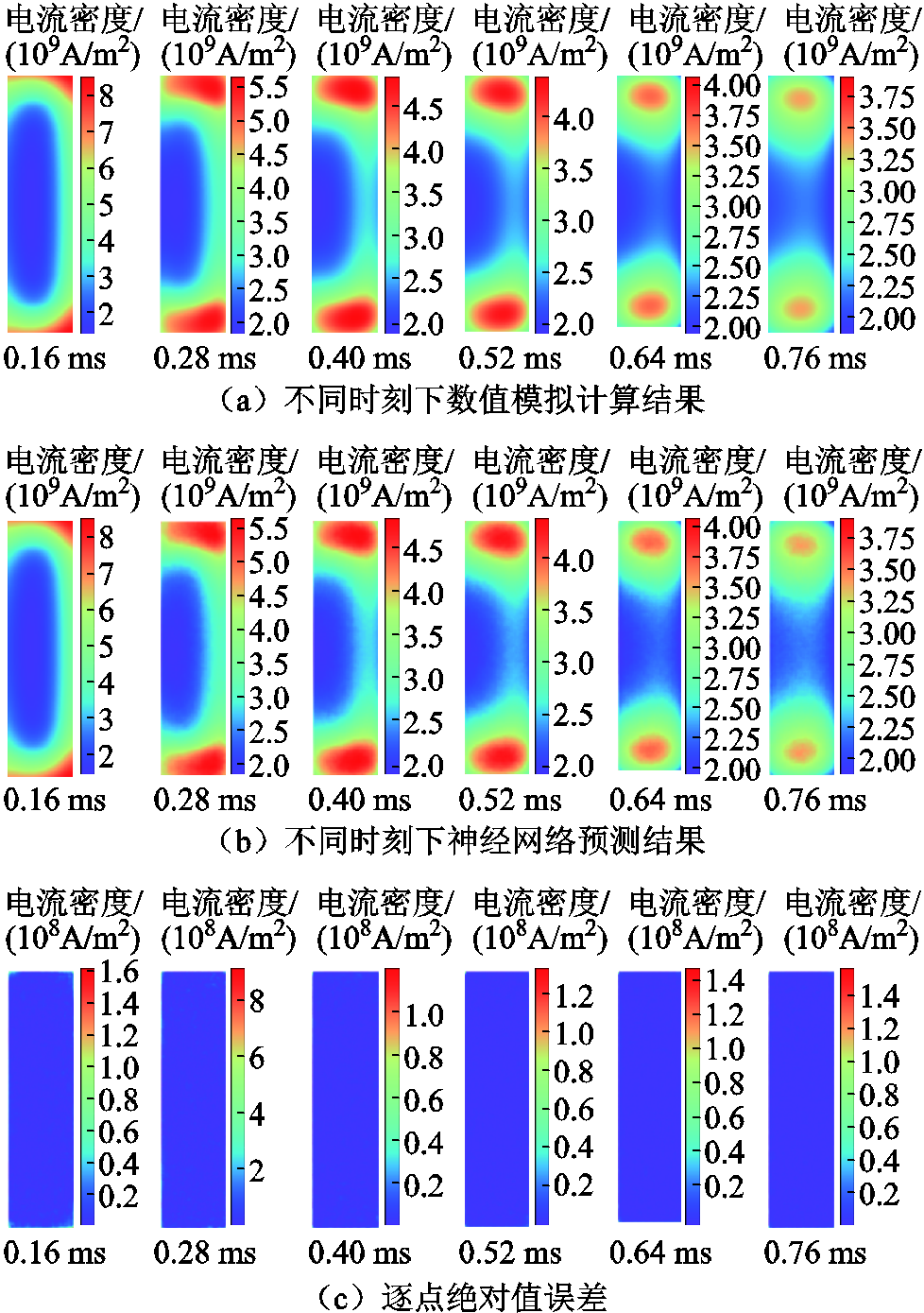
图11 轨道截面电流密度场预测结果
Fig.11 Current density field prediction results on rail cross section
3.2.3 枢轨接触面电流密度场预测
在电磁发射过程中，枢轨接触面工作在极端工况下，其电流分布极不均匀，导致在电流集中分布区域产生更多的焦耳热，造成电枢和轨道的熔蚀损伤，极大影响电磁发射的状态。因此，需进一步对枢轨接触面处的电流分布进行研究，从而优化电流分布，提高电枢和轨道的电流耐受能力。
除激励电流、材料电导率外，枢轨接触面处的电流分布还受枢轨结构参数的影响。因此，为进一步考虑轨道结构参数对电流分布的影响，使用ResUnet-Trans-CGAN模型预测枢轨接触面上的电流分布。
以图10b所示枢轨接触面处为观察视角，设定时间步为0.01 ms，以表6所示轨道结构参数作为变量，以表1中电枢电导率（1.86×107 S/m）为基准，分别在100%、80%、60%和40%电枢电导率下进行数值模拟。提取枢轨接触面处电流密度场，形成分辨率为256×256的单通道云图，组成{(i, σ, h, w, t), Iiσhwt}数据对，最终分别得到每个电枢电导率下各 3 000组样本数据。
表6 轨道结构参数
Tab.6 Parameters of the rail structure
结构参数取值范围步长 轨道宽度h/mm29.75～39.752.00 轨道厚度w/mm5.05～7.650.65
模型训练前需要对生成器的输入层、输出层和判别器的输入层等进行维度调整以适应新的数据集。使用同样的方法进行数据预处理和超参数调优，最终确定Epoch为200，Batch-size为4、Dropout为0.4、初始学习率为2×10-4、λ=80时，模型的综合预测性能最好。
基准电导率测试集上，同一轨道参数设置下不同时刻的预测结果与有限元仿真结果对比，如图12所示。从图12中可以看出，ResUnet-Trans-CGAN模型的预测结果具有很高的精度。随时间的增加，枢轨接触面上电流密度逐渐增加，由于此案例中电枢发射速度低，因此速度趋肤效应对电流分布的影响表现不明显，瞬态趋肤效应占据主导，最大电流密度分布在电枢尾翼两侧，并逐渐向内部扩散。
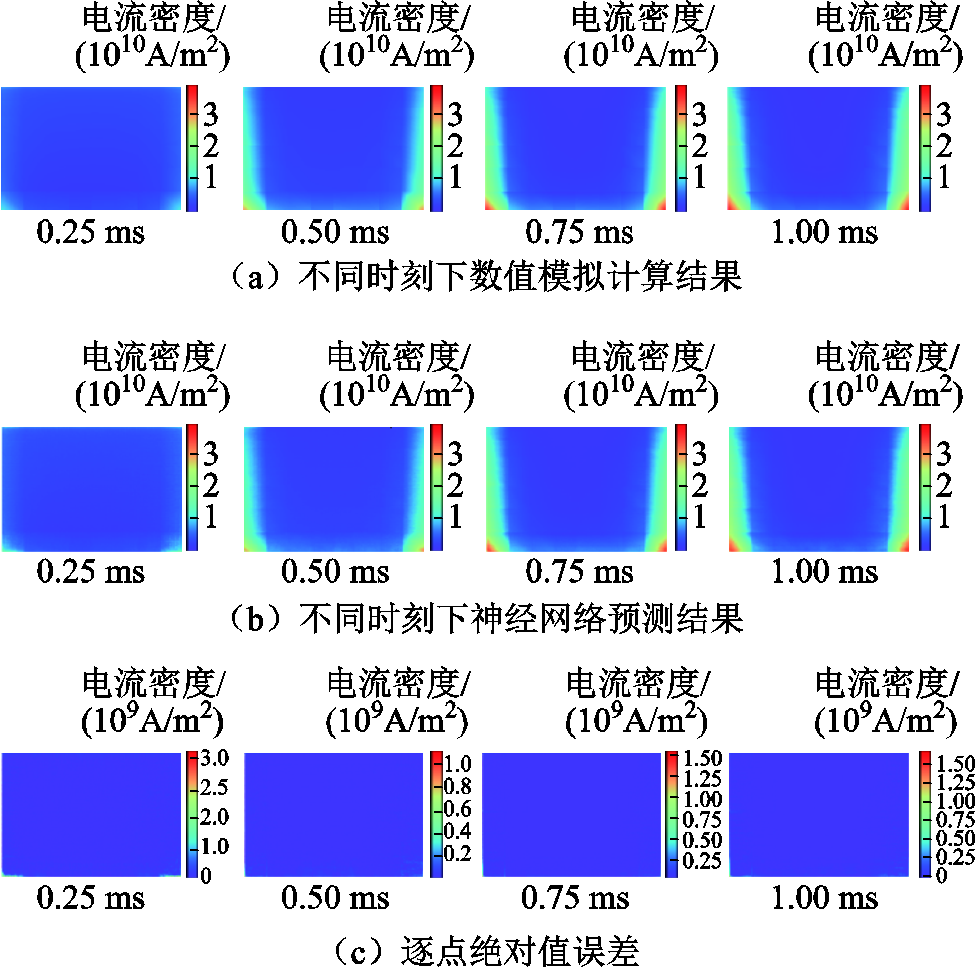
图12 枢轨接触面电流密度场预测结果
Fig.12 Current density field prediction results on armature rail contact surface
在基准电导率测试集上，同一时刻不同轨道结构参数下的预测结果与有限元仿真结果对比，如图13所示，图中每一列分别对应不同的轨道结构参数。从图13中可以观察到，不同轨道结构参数下枢轨接触面处电流均集中于电枢尾翼两侧，但随着轨道厚度和轨道宽度的增加，电流密度最大值减小。因此在设计时适当增加轨道厚度和轨道宽度可以有效地降低通过枢轨接触面的最大电流密度。
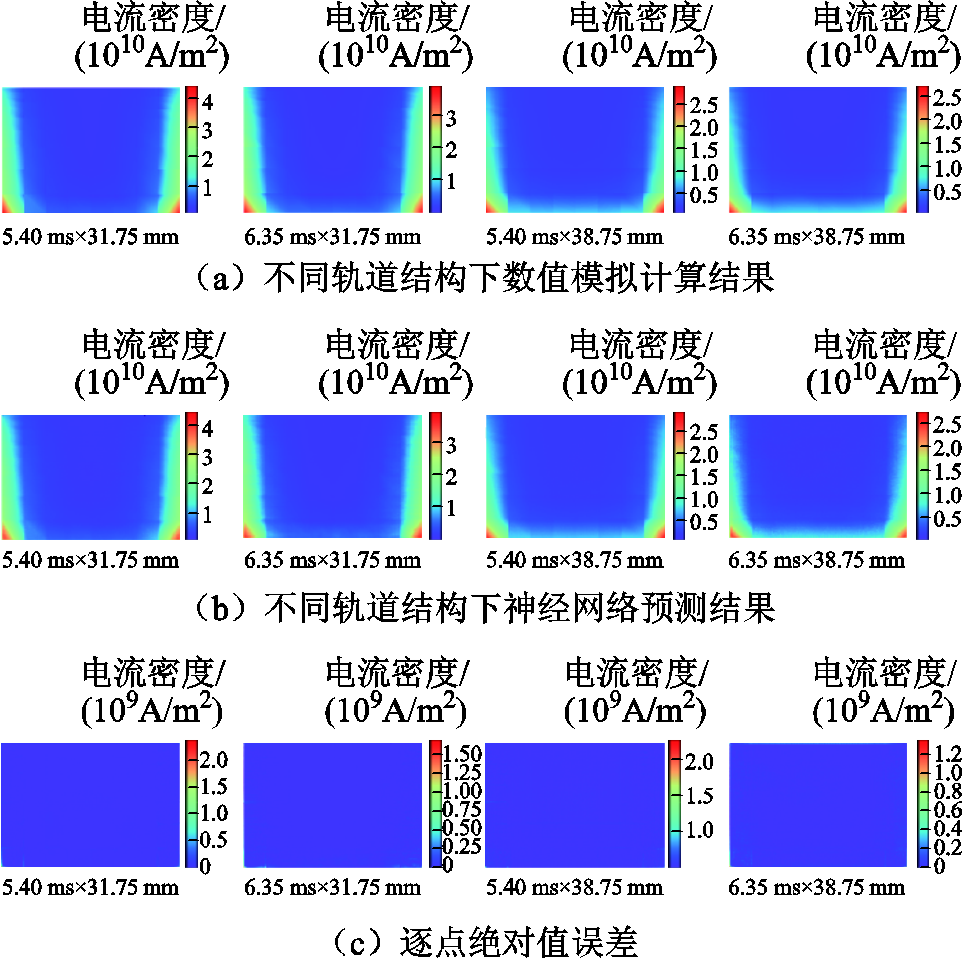
图13 不同轨道结构下枢轨接触面电流密度场预测结果
Fig.13 Current density field prediction results on armature rail contact surface with different rail structure
发射速度高的电磁轨道发射器难以进行高精度稳定数值模拟，因此以高速电磁轨道发射器为计算实例，训练本文提出的ResUnet-Trans-CGAN电流密度场外推预测模型，实现高速下难以稳定数值模拟阶段的电流密度场外推。
3.3.1 外推数据集的建立
以韩国国防发展局（Agency for Defense Development, ADD）研制的40 mm×50 mm中口径轨道发射装置为研究对象[35]。使用试验编号为26的发射数据验证，电枢质量为300 g，出口速度可达 2 000 m/s以上。试验激励电流如图14a所示。
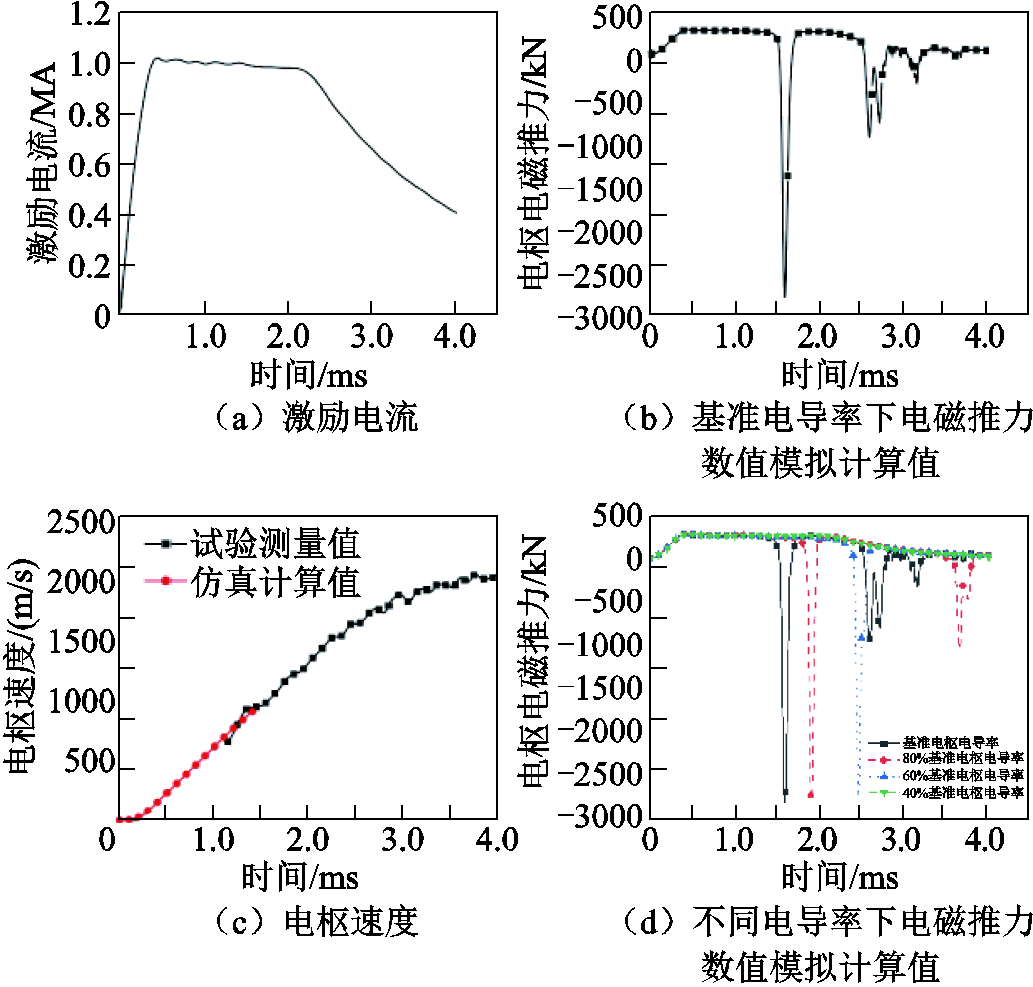
图14 激励电流与数值模拟结果
Fig.14 Excitation current & numerical simulation results
根据发射试验中枢轨模型参数和激励条件，建立电磁轨道发射器有限元仿真模型，设定时间步为0.001 ms。基准电导率下（2.50×107 S/m）电磁推力数值模拟计算值如图14b所示，1.4 ms后出现数值解“伪振荡”现象，此时速度的仿真计算值为901.36 m/s，如图14c所示，比试验测量值928.25 m/s低2.90%，这表明有限元模型的正确性，能够提供可靠的训练数据。经数值模拟，得到不同电枢电导率下的电磁推力和电流密度场数据。不同电枢电导率下电磁推力计算结果如图14d所示，在40%电枢电导率下，可以完整地实现整个发射过程的数值模拟。而在其他电枢电导率下，数值解均出现了不同程度的“伪振荡”现象，导致计算出的电枢电磁推力出现负值。基准电枢电导率下轨道截面不同时刻的电流密度数值模拟结果如图15所示。数值解稳定阶段，轨道截面电流呈规律性变化；数值解“伪振荡”阶段，轨道截面电流分布特征不正常。
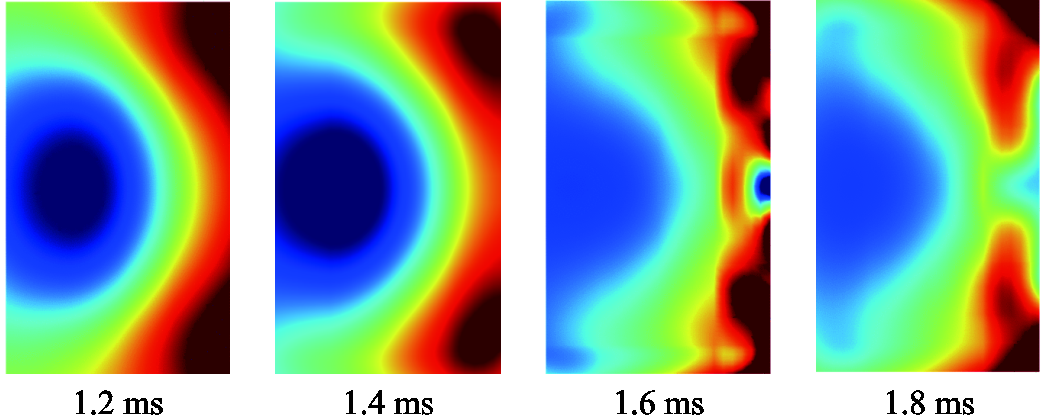
图15 基准电导率下不同时刻电流密度数值模拟结果
Fig.15 Numerical simulation results of current density at different times under reference armature conductivity
经过上述数值模拟，分别得到不同电枢电导率下稳定计算阶段的9 500组样本数据[31]。取每个电枢电导率下稳定数值模拟阶段的前80%数据作为训练集，后20%数据作为外推测试集。模型训练前使用同样的数据预处理方法。
3.3.2 电流密度场外推预测性能分析
模型采用与3.2节实例一中同样的方法进行超参数调优，最终确定Epoch为200，Batch-size为8、Dropout为0.4、初始学习率为2×10-4、λ=80时，模型的综合预测性能最好。选取测试集中1.30 ms和1.35 ms时刻，ResUnet-Trans-CGAN模型预测结果与数值模拟结果对比分别如图16、图17所示。在测试集上，轨道截面处电流密度场预测结果的MAPE平均值为1.83%，枢轨接触面处电流密度场预测结果的MAPE平均值为3.47%，表明模型具有较高的外推预测精度。
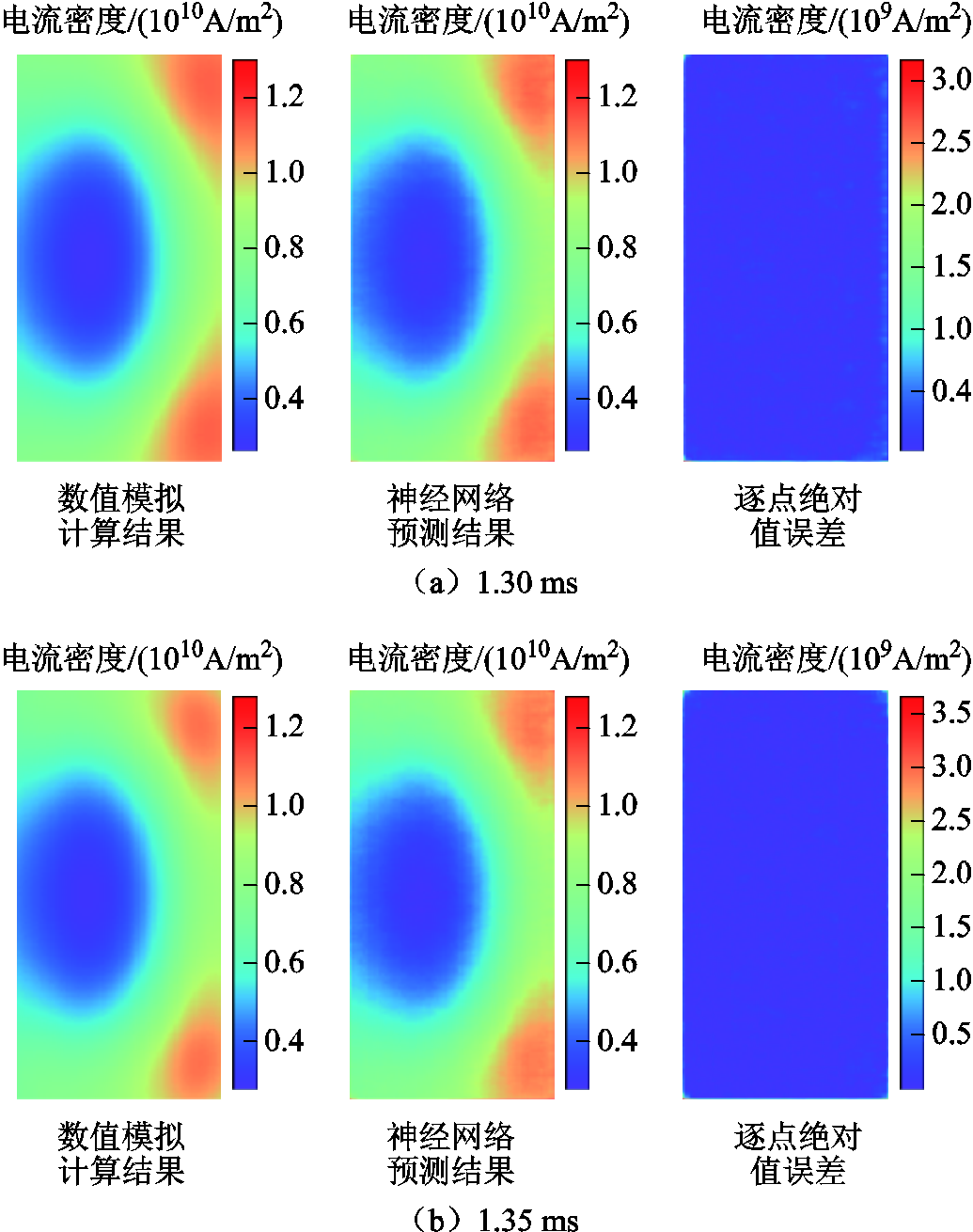
图16 轨道截面处预测结果
Fig.16 Prediction results on rail cross section
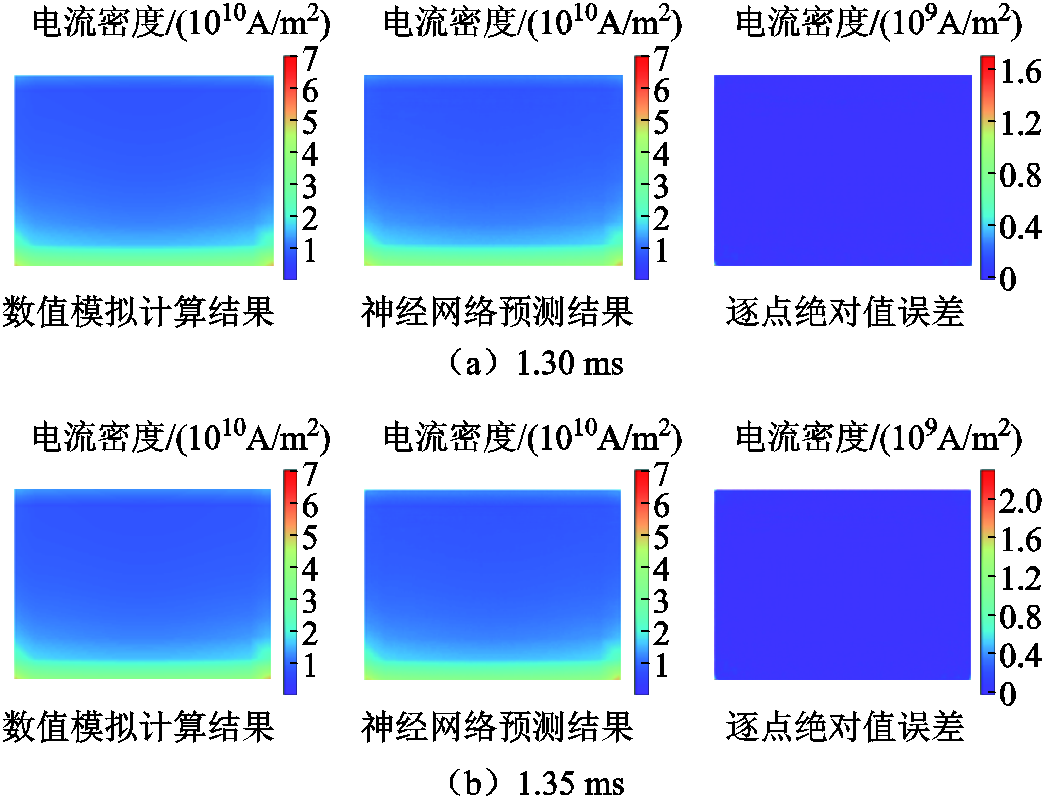
图17 枢轨接触面处预测结果
Fig.17 Prediction results on armature rail contact surface
用训练好的ResUnet-Trans-CGAN模型，对基准电枢电导率下数值解“伪振荡”阶段（1.4～2.0 ms）的电流密度场外推预测。预测得到轨道截面不同时刻的电流密度场如图18所示。由于高速下的稳定数值解难以获得，因此目前尚无法校验预测结果的准确性。对预测结果进行分析可见，数值解“伪振荡”阶段，随着时间和速度的增大，电流分布在动态变化着，电流密度最大值逐渐减小。电流趋向集中分布于轨道内表面的两个尖角处，逐渐向轨道内部扩散。
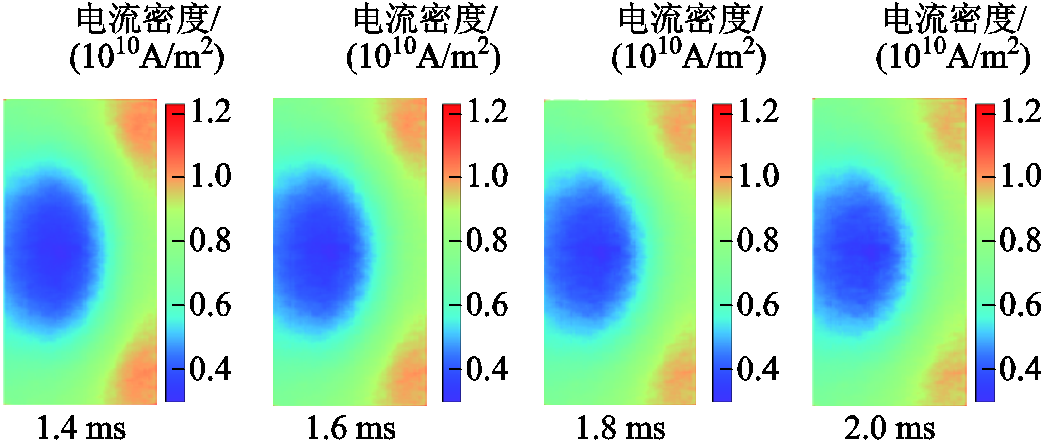
图18 轨道截面电流密度场外推预测结果
Fig.18 Current density field extrapolation prediction results on rail cross section
枢轨接触面电流密度场外推预测结果如图19所示。从图19中可以看出，枢轨接触面上，电流密度变化不明显，电流集中于电枢尾翼末端，这是由于在1.4 ms时，激励电流波形为近似恒定电流阶段，且此时电枢速度的仿真计算值已达901.36 m/s，速度趋肤效应表现明显，因此电枢尾翼末端的电流密度幅值远超头部区域。
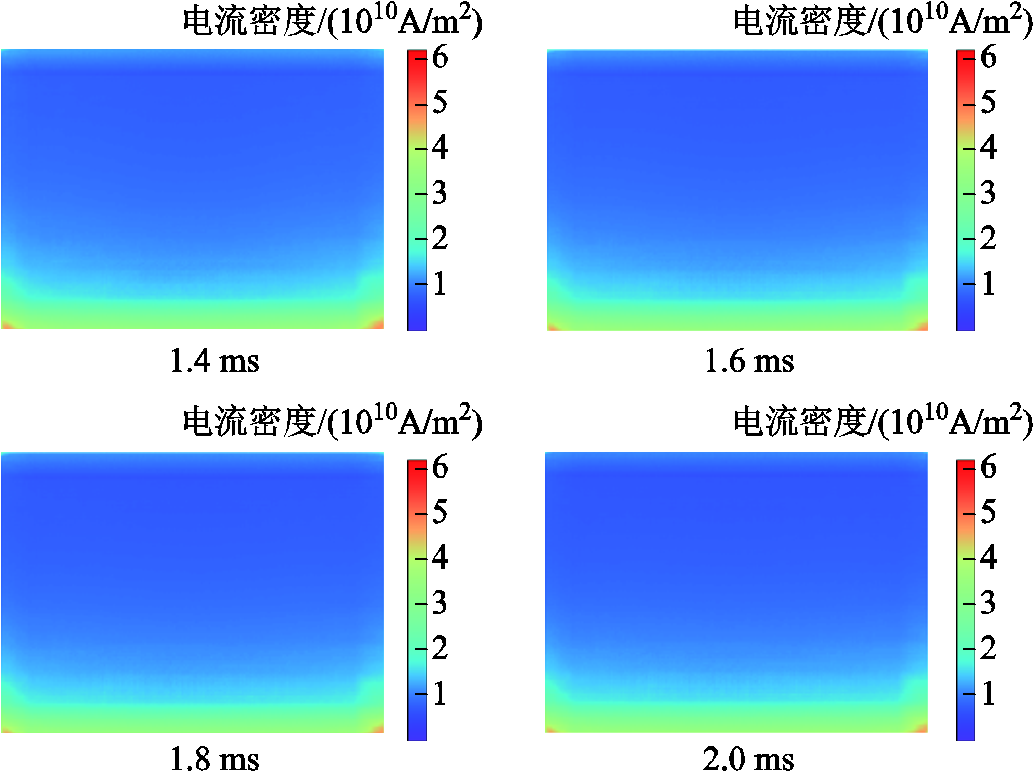
图19 枢轨接触面电流密度场外推预测结果
Fig.19 Current density field extrapolation prediction results on armature rail contact surface
由上述预测结果可知，高速情况下电磁轨道发射器的轨道和枢轨接触面上的电流分布是极不均匀的，这使得强电流部位拥有更高的温升，更容易发生材料的熔化、黏着和剥落，造成的磨损会影响膛内电枢的稳定运行。
3.3.3 训练策略研究
实例一和实例二中使用的是原始训练策略，即基于不同电导率下稳定数值模拟样本数据，共同对模型进行训练，然后对基准电导率下电流密度场外推预测。为提高模型的收敛速度和预测性能，本文进一步引入神经网络模型参数从预测低电导率下电流密度场迁移到基准电导率下的迁移训练策略。具体为：首先基于40%基准电导率下数值模拟数据训练ResUnet-Trans-CGAN，完成训练后保存当前网络参数；然后将其作为60%基准电导率下网络参数的初始值。类似地，将60%基准电导率下训练完成后的网络参数，作为80%基准电枢电导率下网络参数初始值。使用此策略，最终实现基准电枢电导率下电流密度场的外推预测。
对两种训练策略下ResUnet-Trans-CGAN模型预测结果进行对比，结果见表7。由表7可得，对于轨道截面，迁移训练策略比原始训练策略MAPE值分别降低约9.6%和16.9%，预测效果更好。由训练时间对比可得，相比于原始训练策略，迁移训练策略使模型分别提升了13.1%和17.0%的训练速度。对于枢轨接触面，迁移训练策略比原始训练策略MAPE值分别降低约19.0%和30.0%，并分别提升了13.4%和22.1%的训练速度。从总体来看，迁移训练策略能够提高外推预测精度、加快模型训练速度。
表7 不同训练策略下ResUnet-Trans-CGAN模型预测结果
Tab.7 The prediction results of ResUnet-Trans-CGAN model under different training strategies
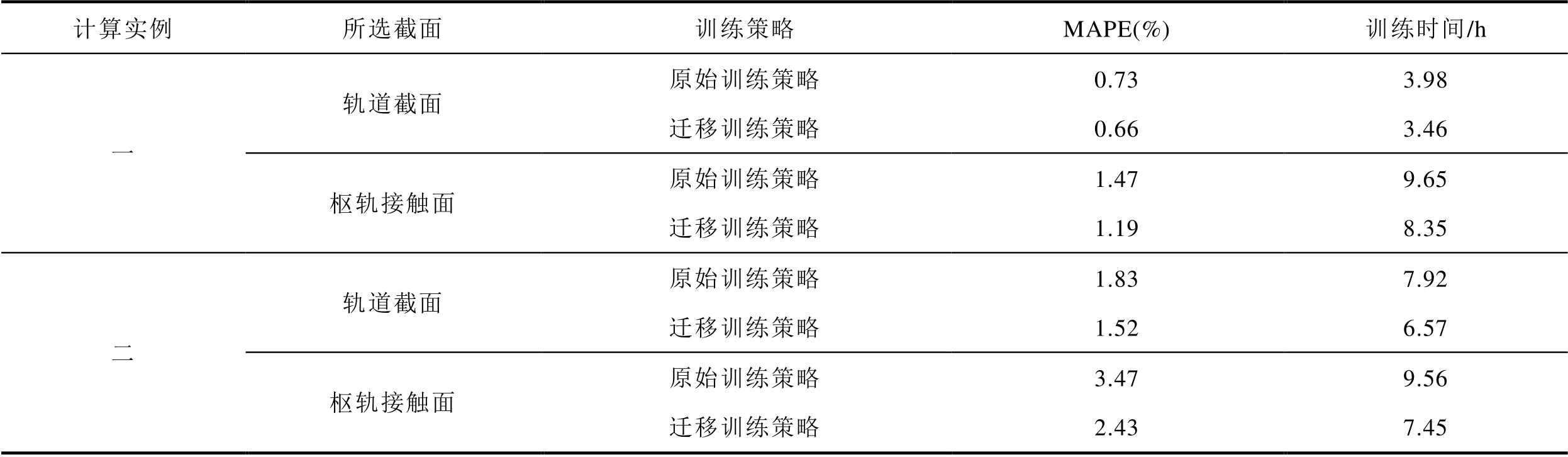
计算实例所选截面训练策略MAPE(%)训练时间/h 一轨道截面原始训练策略0.733.98 迁移训练策略0.663.46 枢轨接触面原始训练策略1.479.65 迁移训练策略1.198.35 二轨道截面原始训练策略1.837.92 迁移训练策略1.526.57 枢轨接触面原始训练策略3.479.56 迁移训练策略2.437.45
在迁移训练策略的ResUnet-Trans-CGAN模型中，不同电导率下的预测可被视为求解多个具有相似控制方程的任务。虽然40%电枢电导率下网络的初始训练误差较高，但之后60%、80%和基准电枢电导率下网络的初始训练误差会逐渐降低。且所需迭代次数随着迁移学习训练过程而减少，加速了网络参数的寻优进程。
针对使用有限元方法计算电磁轨道发射器电流密度场时，存在时间长、高速下难以稳定计算的问题，本文提出了基于ResUnet-Trans-CGAN的高速下电流密度场预测方法。具体结论如下：
1）提出基于CGAN的电流密度场预测方法，以激励电流、电枢电导率、轨道结构参数和时间t作为输入，可直接生成相应参数下的电流密度场。
2）建立残差网络、U-Net和Transformer的生成器，实现ResUnet-Trans-CGAN模型，提高对复杂电流分布的特征提取能力。以低速电磁轨道发射器实例验证模型内插预测精度，结果表明，相比于CGAN、Unet-CGAN和ResUnet-Transformer，本文提出的ResUnet-Trans-CGAN在测试集上电流密度场内插预测MAPE值小于1.5%，具有更高的精度。模型训练完成后能够实现多次调用，可实现设计域内的高效探索。
3）以高速电磁轨道发射器为计算实例，引入由低电导率到高电导率的迁移学习训练策略，进一步提升模型泛化能力，实现更高的外推预测精度。结果表明，使用迁移学习训练策略后，在测试集上ResUnet-Trans-CGAN外推预测电流密度场的误差MAPE由小于3.5%降低至小于2.5%。模型能够实现高速下难以稳定数值模拟阶段的电流密度场直接生成，有助于电磁轨道发射器结构的精细化设计。
由于模型超参数较多，调优复杂费时，下一步将对超参数自动调优开展研究。同时在现有研究基础上，继续基于数值模拟和深度学习方法对磁场、热场和力场等方面开展研究。总之，深度学习方法为电磁轨道发射器的结构优化设计和数字化提供了新的思路和方法，具有广泛的应用前景。
参考文献
[1] 张嘉炜, 鲁军勇, 谭赛, 等. 考虑初始接触压力的滑动电接触界面磁扩散模型[J]. 电工技术学报, 2022, 37(2): 488-495.
Zhang Jiawei, Lu Junyong, Tan Sai, et al. A magnetic diffusion model of electromagnetic launcher considering initial contact pressure[J]. Transactions of China Electrotechnical Society, 2022, 37(2): 488-495.
[2] 古刚, 吴立周, 耿昊, 等. 基于电磁-流场耦合的轨道冷却仿真分析[J]. 电工技术学报, 2020, 35(17): 3601-3608.
Gu Gang, Wu Lizhou, Geng Hao, et al. Simulation and analysis of rail cooling based on electromagnetic and fluid field coupling[J]. Transactions of China Electro-technical Society, 2020, 35(17): 3601-3608.
[3] 阮景煇, 陈立学, 夏胜国, 等. 电磁轨道炮电流分布特性研究综述[J]. 电工技术学报, 2020, 35(21): 4423-4431.
Ruan Jinghui, Chen Lixue, Xia Shengguo, et al. A review of current distribution in electromagnetic railguns[J]. Transactions of China Electrotechnical Society, 2020, 35(21): 4423-4431.
[4] 王增基, 陈立学, 尤彭昊, 等. 考虑速度趋肤效应与接触电阻影响的枢轨界面电流分布特性[J]. 电工技术学报, 2022, 37(19): 5003-5010.
Wang Zengji, Chen Lixue, You Penghao, et al. Current distribution characteristics of armature-rail interface under velocity skin effect and contact resistance[J]. Transactions of China Electrotechnical Society, 2022, 37(19): 5003-5010.
[5] Hsieh K. A Lagrangian formulation for mechanically, thermally coupled electromagnetic diffusive processes with moving conductors[J]. IEEE Transactions on Magnetics, 1995, 31(1): 604-609.
[6] Hsieh K T. Hybrid FE/BE implementation on electromechanical systems with moving conductors[J]. IEEE Transactions on Magnetics, 2007, 43(3): 1131-1133.
[7] 阮江军, 张宇, 张宇娇, 等. 电气设备电磁多物理场数值仿真研究与应用[J]. 高电压技术, 2020, 46(3): 737-756.
Ruan Jiangjun, Zhang Yu, Zhang Yujiao, et al. Numerical simulation research and applications of electromagnetic multiphysical field for electrical equipment[J]. High Voltage Engineering, 2020, 46(3): 737-756.
[8] 胡万君, 刘刚, 朱章宸, 等. 油浸式电力变压器绕组稳态温升降阶计算方法研究[J]. 中国电机工程学报, 2023, 43(16): 6505-6517.
Hu Wanjun, Liu Gang, Zhu Zhangchen, et al. Reduced order calculation method of steady temperature rise of oil immersed power transformer[J]. Proceedings of the CSEE, 2023, 43(16): 6505-6517.
[9] Kutz J N. Deep learning in fluid dynamics[J]. Journal of Fluid Mechanics, 2017, 814: 1-4.
[10] 马伟明, 鲁军勇. 电磁发射技术的研究现状与挑战[J]. 电工技术学报, 2023, 38(15): 3943-3959.
Ma Weiming, Lu Junyong. Research progress and challenges of electromagnetic launch technology[J]. Transactions of China Electrotechnical Society, 2023, 38(15): 3943-3959.
[11] Khan A, Ghorbanian V, Lowther D. Deep learning for magnetic field estimation[J]. IEEE Transactions on Magnetics, 2019, 55(6): 7202304.
[12] Gong Ruohan, Tang Zuqi. Investigation of convolutional neural network U-net under small datasets in transformer magneto-thermal coupled analysis[J]. COMPEL-the International Journal for Computation and Mathematics in Electrical and Electronic Engineering, 2020, 39(4): 959-970.
[13] 金亮, 冯裕霖, 曹佳豪, 等. 基于注意力与长短期记忆网络的变压器代理模型[J]. 电气技术, 2021, 22(7): 65-71, 77.
Jin Liang, Feng Yulin, Cao Jiahao, et al. Transformer surrogate model based on attention and long-short term memory[J]. Electrical Engineering, 2021, 22(7): 65-71, 77.
[14] Jin Liang, Liu Yuankai, Yang Qingxin, et al. Prediction method of motor magnetic field based on improved linknet model[J]. COMPEL: The International Journal for Computation and Mathematics in Electrical and Electronic Engineering, 2023, 42(1): 90-100.
[15] Lu Junyong, Tang Yinyin, Zeng Delin, et al. Fault prediction of electromagnetic launch system based on knowledge prediction time series[J]. IEEE Tran-sactions on Industry Applications, 2021, 57(2): 1830-1839.
[16] Liu J G, Dong Z Q, Ren R, et al. An initial velocity model study of electromagnetic railgun based on back propagation neural network[J]. Journal of Physics: Conference Series, 2020, 1507(7): 072018.
[17] 纪守领, 杜天宇, 邓水光, 等. 深度学习模型鲁棒性研究综述[J]. 计算机学报, 2022, 45(1): 190-206.
Ji Shouling, Du Tianyu, Deng Shuiguang, et al. Robustness certification research on deep learning models: a survey[J]. Chinese Journal of Computers, 2022, 45(1): 190-206.
[18] Han Renkun, Wang Yixing, Zhang Yang, et al. A novel spatial-temporal prediction method for unsteady wake flows based on hybrid deep neural network[J]. Physics of Fluids, 2019, 31(12): 127101.
[19] 王琛, 王颖, 郑涛, 等. 基于ResNet-LSTM网络和注意力机制的综合能源系统多元负荷预测[J]. 电工技术学报, 2022, 37(7): 1789-1799.
Wang Chen, Wang Ying, Zheng Tao, et al. Multi-energy load forecasting in integrated energy system based on ResNet-LSTM network and attention mechanism[J]. Transactions of China Electrotechnical Society, 2022, 37(7): 1789-1799.
[20] 吴鑫, 张艳丽, 王振, 等. 基于深度学习的电工钢片磁畴磁化过程预测与特征量提取[J]. 电工技术学报, 2023, 38(9): 2289-2298.
Wu Xin, Zhang Yanli, Wang Zhen, et al. Prediction of magnetic domains magnetization process and feature extraction of electrical steel sheet based on deep learning[J]. Transactions of China Electrotechnical Society, 2023, 38(9): 2289-2298.
[21] Goodfellow I J, Pouget-Abadie J, Mirza M, et al. Generative adversarial nets[C]//Proceedings of the 27th International Conference on Neural Information Processing Systems, Montreal, Canada, 2014, 2: 2672-2680.
[22] Mirza M, Osindero S. Conditional generative adversarial nets[J]. arXiv: 1411.1784, 2014.
[23] Faulkner C A, Jankowski D S, Castellini J E, et al. Fast prediction of indoor airflow distribution inspired by synthetic image generation artificial intelligence[J]. Building Simulation, 2023, 16(7): 1219-1238.
[24] Wu Haizhou, Liu Xuejun, An Wei, et al. A deep learning approach for efficiently and accurately evaluating the flow field of supercritical airfoils[J]. Computers & Fluids, 2020, 198: 104393.
[25] Ronneberger O, Fischer P, Brox T. U-Net: convolutional networks for biomedical image segmentation[C]//Medical Image Computing and Computer-Assisted Intervention, Freiburg, Germany, 2015: 234-241.
[26] Zhang Zhengxin, Liu Qingjie, Wang Yunhong. Road extraction by deep residual U-net[J]. IEEE Geoscience and Remote Sensing Letters, 2018, 15(5): 749-753.
[27] He Kaiming, Zhang Xiangyu, Ren Shaoqing, et al. Deep residual learning for image recognition[C]//2016 IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 2016: 770-778.
[28] Vaswani A, Shazeer N, Parmar N, et al. Attention is all you need[C]// Proceedings of the 31st International Conference on Neural Information Processing Systems, Red Hook, NY, USA, 2017: 6000-6010.
[29] Jin Xiaowei, Cheng Peng, Chen Wenli, et al. Prediction model of velocity field around circular cylinder over various Reynolds numbers by fusion convolutional neural networks based on pressure on the cylinder[J]. Physics of Fluids, 2018, 30(4): 047105.
[30] Lee S, You D. Data-driven prediction of unsteady flow over a circular cylinder using deep learning[J]. Journal of Fluid Mechanics, 2019, 879: 217-254.
[31] Jin Liang, Gong Dexin, Yan Yingang, et al. Armature electromagnetic force extrapolation prediction method for electromagnetic railgun at high speed[J]. Applied Sciences, 2023, 13(6): 3819.
[32] 房佳姝, 刘崇茹, 苏晨博, 等. 基于自注意力Transformer编码器的多阶段电力系统暂态稳定评估方法[J]. 中国电机工程学报, 2023, 43(15): 5745-5759.
Fang Jiashu, Liu Chongru, Su Chenbo, et al. Multi-stage transient stability assessment of power system based on self-attention transformer encoder[J]. Proceedings of the CSEE, 2023, 43(15): 5745-5759.
[33] Hsieh K T, Kim B K. International railgun modelling effort[J]. IEEE Transactions on Magnetics, 1997, 33(1): 245-248.
[34] Price J H, Yun H D. Design and testing of integrated metal armature sabots for launch of armour penetrating projectiles from electric guns[J]. IEEE Transactions on Magnetics, 1995, 31(1): 219-224.
[35] Yang K S, Kim S H, Lee B, et al. Electromagnetic launch experiments using a 4.8-MJ pulsed power supply[J]. IEEE Transactions on Plasma Science, 2015, 43(5): 1358-1361.
Abstract During the electromagnetic rail launcher's launch process, the current distribution on the rail cross-section and armature-rail contact surfaces exhibits significant inhomogeneity, with current density approaching the material's bearing limit. Calculating the current density field during the launching process is one of the necessary conditions to realize the fine design of its structure. However, due to the complexity of the problem involving multi-field coupling and nonlinearity, refining the modeling and calculations using the finite element method (FEM) is time-consuming, often spanning hours or even days. Affected by the velocity skinning effect, the electromagnetic field control equation is a convection-diffusion equation, which is difficult or even impossible to compute at high speeds. Considering that the deep neural network has a powerful feature extraction ability and can learn the time-space change law of the field from numerical simulation data, this paper proposes a current density field prediction method based on ResUnet-Trans-CGAN at high speed. The dataset is obtained using FEM, and the high-precision interpolation prediction of the current density field and the extrapolation prediction of the difficult-to-stabilize computation stage at high speed can be realized after the training is completed, and the single computation time is within seconds.
First, to realize the direct generation of the current density field, this paper uses the generative adversarial network (GAN), which is currently one of the most widely used image generation models. The conditional generative adversarial network (CGAN) addresses GAN's uncontrollable image generation issue by introducing a conditional variable y to the generator and discriminator. In order to realize the one-to-one mapping from input parameters to current density field, this paper removes the random noise z in the input, and directly inputs the excitation current, armature conductivity, rail structure parameters and time t into the neural network as the conditional variables, and establishes the current density field prediction model based on CGAN. Then, to improve the feature extraction capability for complex current density field distributions, the ResUnet-Trans network is constructed as the feature generator of CGAN. The U-Net structure is used to realize the fusion of different levels of features, short Residuals are introduced to inhibit the deep neural network degradation, and the Transformer is introduced to enhance the model's ability to extract global features. Second, dropout and a cosine annealing algorithm for adaptive learning rate adjustment are introduced in the model to curb overfitting and improve prediction accuracy. Further, a transfer learning training strategy, transitioning from low to high conductivity, is applied during training to improve the model's extrapolation prediction accuracy and generalization ability. Finally, the accuracy of model interpolation and extrapolation prediction is verified with the examples of low-speed and high-speed electromagnetic rail launcher, respectively.
The results show that for interpolation prediction, the ResUnet-Trans-CGAN proposed in this paper has the highest accuracy with the mean absolute percentage error (MAPE) value of current density field prediction less than 1.5% compared to CGAN, Unet-CGAN and ResUnet-Trans. After using the transfer learning training strategy from low to high conductivity, the MAPE is reduced by 9.59% and 19.0% at the rail cross-section and at the armature-rail contact surface, respectively. When extrapolating the prediction at high speeds, the MAPE of the current density field at the rail cross-section is reduced from 1.83% to 1.52% and the training speed is improved by 17.0%, and that at the armature-rail contact surface is reduced from 3.47% to 2.43%, and the training speed is improved by 22.1%, after using the Transfer Learning training strategy of moving from low to high conductivity on the test set. The model can generate the current density field directly at the stage where it is difficult to perform stable numerical simulation at high speed.
keywords：Electromagnetic rail launcher, current density field distribution, deep learning, image prediction
中图分类号：TM359.4
DOI: 10.19595/j.cnki.1000-6753.tces.231549
国家自然科学基金重大研究计划（92066206）、国家自然科学基金面上项目（51977148）和中央引导地方科技发展专项自由探索项目（226Z4503G）资助。
收稿日期 2023-09-20
改稿日期 2023-11-28
金 亮 男，1982年生，教授，博士生导师，研究方向为电磁场数值模拟与智能计算。
E-mail：jinliang_email@163.com（通信作者）
宋居恒 男，1998年生，硕士研究生，研究方向为深度学习在电磁发射领域中的应用。
E-mail：1923671653@qq.com
（编辑 赫 蕾）