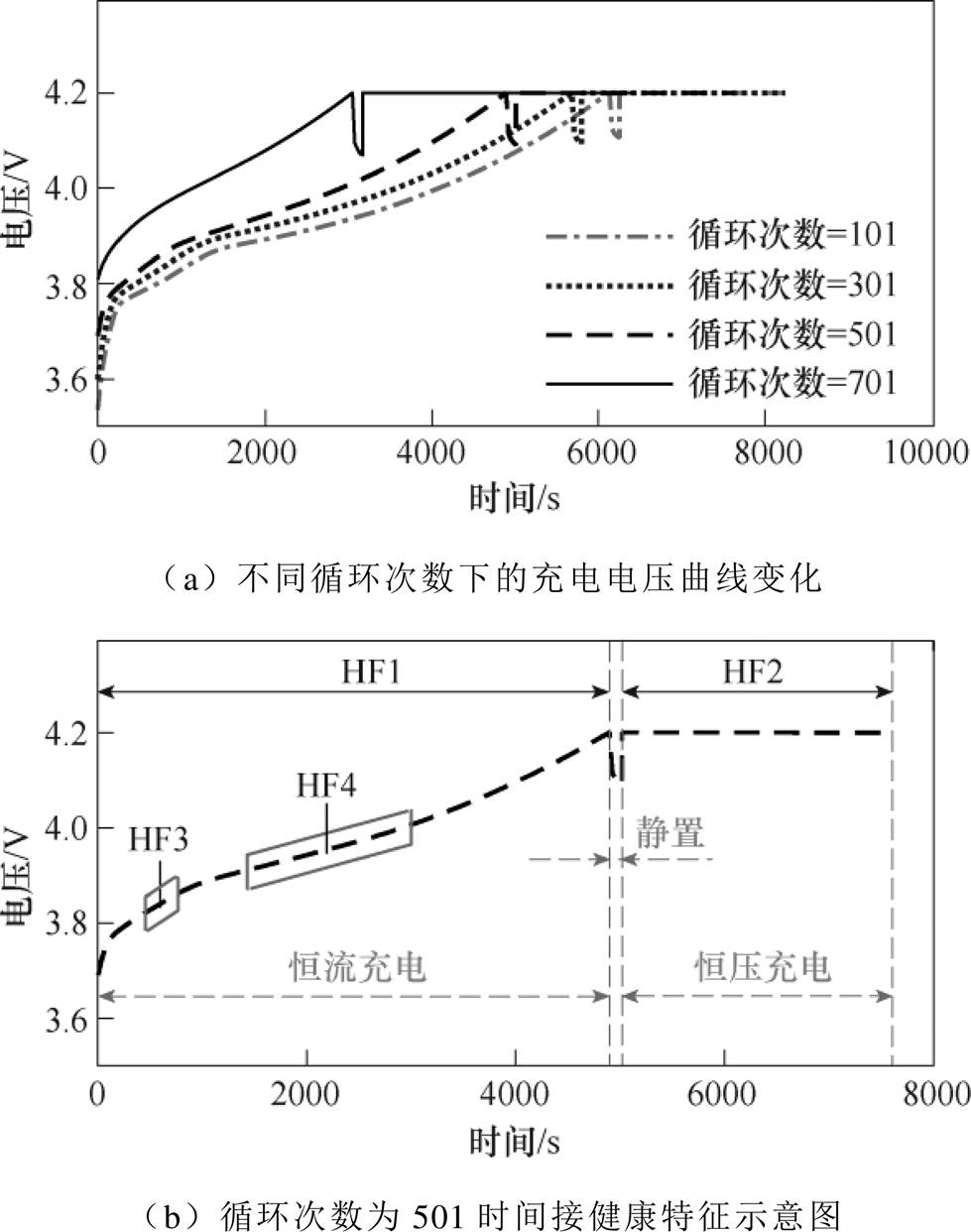
图1 充电电压曲线中间接健康特征选择
Fig.1 Selection of indirect health feature in charging voltage curves
摘要 准确预测锂电池健康状态(SOH)与电池剩余使用寿命(RUL)对提高电池安全性能具有重要意义。而当前针对SOH和RUL的预测,存在着间接健康特征选取困难,以及使用数据驱动方法缺乏不确定性表达的问题。为此,该文提出一种基于间接健康特征优化与多模型融合的锂电池SOH-RUL联合预测方法。首先从充电电压曲线中采集多个健康特征,并通过特征并行融合方法和注意力机制进行优化处理得到间接健康特征(IHF)。然后引入贝叶斯模型平均(BMA)方法来解决预测过程中的不确定性问题,将其与支持向量回归(SVR)和长短期记忆神经网络(LSTM)相结合,构建SVR-BMA融合模型和LSTM-BMA融合模型,并分别进行SOH和RUL预测;通过自适应噪声完备集合经验模态分解(CEEMDAN)方法从SOH预测阶段的容量预测结果中提取出RUL预测的输入特征,以实现SOH和RUL的联合预测。最后利用CALCE数据集进行性能测试,实验结果表明,所提方法能有效提高SOH和RUL预测的准确性和可靠性。
关键词:电池健康状态剩余使用寿命 间接健康特征 贝叶斯模型平均 支持向量回归 长短期记忆神经网络
随着可再生能源的迅速发展和“碳达峰、碳中和”目标的提出,新能源汽车和储能电站的应用前景广阔。而锂电池作为一种电化学储能方式,具有高能量密度、低自放电率、清洁可靠等卓越性能,在动力电池和储能电池技术中占据主导地位[1]。然而,锂电池在充放电循环过程中会因其内部不可逆的电化学反应发生老化,易出现漏液和短路等问题,若无法及时更换或将存在巨大的安全风险[2]。电池管理系统(Battery Management System, BMS)可以通过评估电池的老化状态发出风险预警,并执行电池维护或更换工作,以保证电池安全稳定运行。其中,锂电池健康状态(State of Health, SOH)和剩余使用寿命(Remaining Useful Life, RUL)是BMS中评估电池老化状态的重要指标,其准确预测可以为BMS管理提供参考,实现对电池的预防性维护,对于提高设备安全性能、延长使用寿命等具有重要意义[3]。
电池SOH通常定义为最大可用容量与额定容量之比,通过预测电池容量变化来反映其老化情况。RUL是当前电池老化状态到寿命终止(End of Life, EOL)时的剩余循环次数,EOL可以根据实际应用情况选取,通常设置为SOH降为0.8。与电压、电流等参数不同,SOH和RUL无法直接测量。为此,往往通过寻找具有代表性的间接健康特征(Indirect Health Factors, IHF)来反映电池的老化情况[4]。而IHF与电池老化参数的相关度直接影响电池SOH和RUL的预测结果,如何选取合适的IHF仍是当前面临的一大挑战。Meng Jinhao等[5]通过短期电流脉冲试验,分析出充电电压曲线中的终值和斜率与容量退化规律的关联性,并将其作为IHF进行SOH预测;Yang Duo等[6]分析了充电电压曲线中各参数随循环次数的变化规律,提出了4个与电池容量相关性较强的时间和斜率特征;U. Yayan等[7]则通过采集充电电压与电流等5个IHF,使用长短期记忆网络(Long Short-Term Memory, LSTM)预测SOH。上述研究均利用了IHF的间接预测优势,但未对充电电压中包含的多角度特征信息进行充分挖掘并利用,限制了预测结果的准确度,而使用不同特征堆叠的方式也加重了模型的计算负担。
对于SOH和RUL的准确预测,除电池的IHF选择外,合适的预测方法也尤为关键。在现有研究中,锂电池SOH和RUL预测方法主要分为基于模型的方法和基于数据驱动的方法。基于模型的方法通过建立电化学模型或经验模型,拟合锂电池的老化规律。由于电池内部化学反应复杂多样,电化学模型中的参数辨识十分困难,而经验模型无法解释充放电过程中的容量回升现象,模型精度较低。相比之下,数据驱动方法不需要考虑复杂的电化学特性,而是通过数据学习的方式建立老化预测模型,预测未来的SOH和RUL变化规律[8-12]。其主要包括自回归模型(Autoregressive model, AR)、高斯过程回归(Gauss Process Regression, GPR)、支持向量机回归(Support Vector Regression, SVR)、长短期记忆网络(LSTM)等。J. Park等[10]使用AR预测锂电池容量和SOH,通过动态调整历史数据的输入来拟合未来电池容量和SOH的非线性变化;Zhang Yongzhi等[11]提出了一种基于LSTM的锂电池RUL预测方法,验证了LSTM方法预测电池RUL的有效性和优越性;王萍等[12]提出了一种模型融合的方法,将指数经验模型用于在线SOH预测,并通过GPR校正指数经验模型参数以改善其预测性能。上述方法均基于数据驱动模型对SOH和RUL预测进行了深入探索,但单一的预测模型无法给出预测结果的不确定性表达[13],不利于实现准确的长期老化状态预测。
贝叶斯模型平均(Beyesian Model Averaging, BMA)是一种高效的多模型融合方法。它可以从概率学的角度筛选并融合可靠性高的预测模型,输出多个模型的融合预测结果,从而具备强大的不确定性管理能力,在气候预测、季节性时间序列预测等领域均有广泛应用。研究证明[14-15],使用BMA方法可以获得比任意单一模型更优秀的预测效果。因此,可以将该方法与现有数据驱动方法相结合,构建出相对理想的预测模型,以解决SOH和RUL预测过程中的不确定性问题。
此外,由于SOH和RUL之间密切相关,联合预测有利于真实评估电池的老化状态。然而,在老化过程中,电池容量的回升现象会导致EOL测量值与真实值出现偏差,从而影响锂电池RUL的预测准确度[16]。因此,从电池循环数据中获取有效的输入数据对RUL预测十分重要。现有研究采取了互补集合经验模态分解(Complementary Ensemble Empirical Mode Decomposition, CEEMD)、自适应噪声完备集合经验模态分解(Complete Ensemble Empirical Mode Decomposition with Adaptive Noise, CEEMDAN)等方法进行容量数据去噪[17-18],从预测容量序列中提取出可反映电池RUL变化规律的原始容量,作为RUL的输入特征,以实现其与SOH预测的连接。
因此,为提高SOH和RUL预测的准确性,本文提出一种基于间接健康特征优化与多模型融合的锂电池SOH-RUL联合预测方法,主要从间接健康特征以及预测模型两方面进行优化与改进:
(1)提取充电电压曲线中多个具有代表性的健康特征(Health Factors, HF),结合特征并行融合操作(concat)与注意力机制(attention)对其进行优化,获得强相关的间接健康特征Co-HF。
(2)选取多个锂电池的特征Co-HF,建立相应的SVR子模型,引入BMA融合方法来弥补单一预测模型缺乏不确定性处理能力的缺陷,构建SVR- BMA融合模型预测SOH;将SOH预测结果经CEEMDAN方法进行去噪,获得表征容量单调退化趋势的原始容量,并作为RUL预测输入以去除容量回升现象的影响,结合LSTM和BMA方法构建LSTM-BMA融合模型,进行RUL预测。
本文使用数据均来源于马里兰大学CALCE锂电池数据集。其中,所有电池工况均服从恒流恒压充放电策略,即充电过程包括恒流充电和恒压充电两个阶段,以恒定电流速率0.5C进行充电至电压升至截止电压4.2 V,然后经静置处理,进行恒压充电至充电电流降至0.05 A。大量研究表明[4-12],充电电压曲线随使用时间的推移具有一定的变化规律。以编号为CS236的电池数据为例,图1a为不同循环次数下的充电电压曲线,随着循环次数的增加,到达截止电压的充电时间逐渐缩短,恒压阶段充电时间呈增大的趋势,恒流充电阶段曲线斜率逐渐变陡。除此之外,电池的充电过程较放电过程更为稳定,从中所提取的特征能较好地适应不同工况。故本文从锂电池充电电压曲线中提取4个典型的可测量参数,作为HF:恒流充电时间、恒压充电时间、最佳区间等压升充电时间、最佳区间等时间充电压升,并以HF1~HF4命名。各特征参数在充电电压曲线中所对应的具体含义如图1b所示。

图1 充电电压曲线中间接健康特征选择
Fig.1 Selection of indirect health feature in charging voltage curves
此外,为提取出电压曲线中的片段特征HF3和HF4,本文使用遍历法,通过调整时间与电压间隔遍历充电电压曲线以获得特征HF3、HF4的相关充电区间。使用1.2节的相关性计算方法,将相关系数最大的时间区间和电压区间所对应的特征参数作为目标特征HF3和HF4,最终得出HF3充电时间区间为[300, 450] s,HF4充电电压区间为[3.85, 4.00] V,该遍历过程如图2所示。
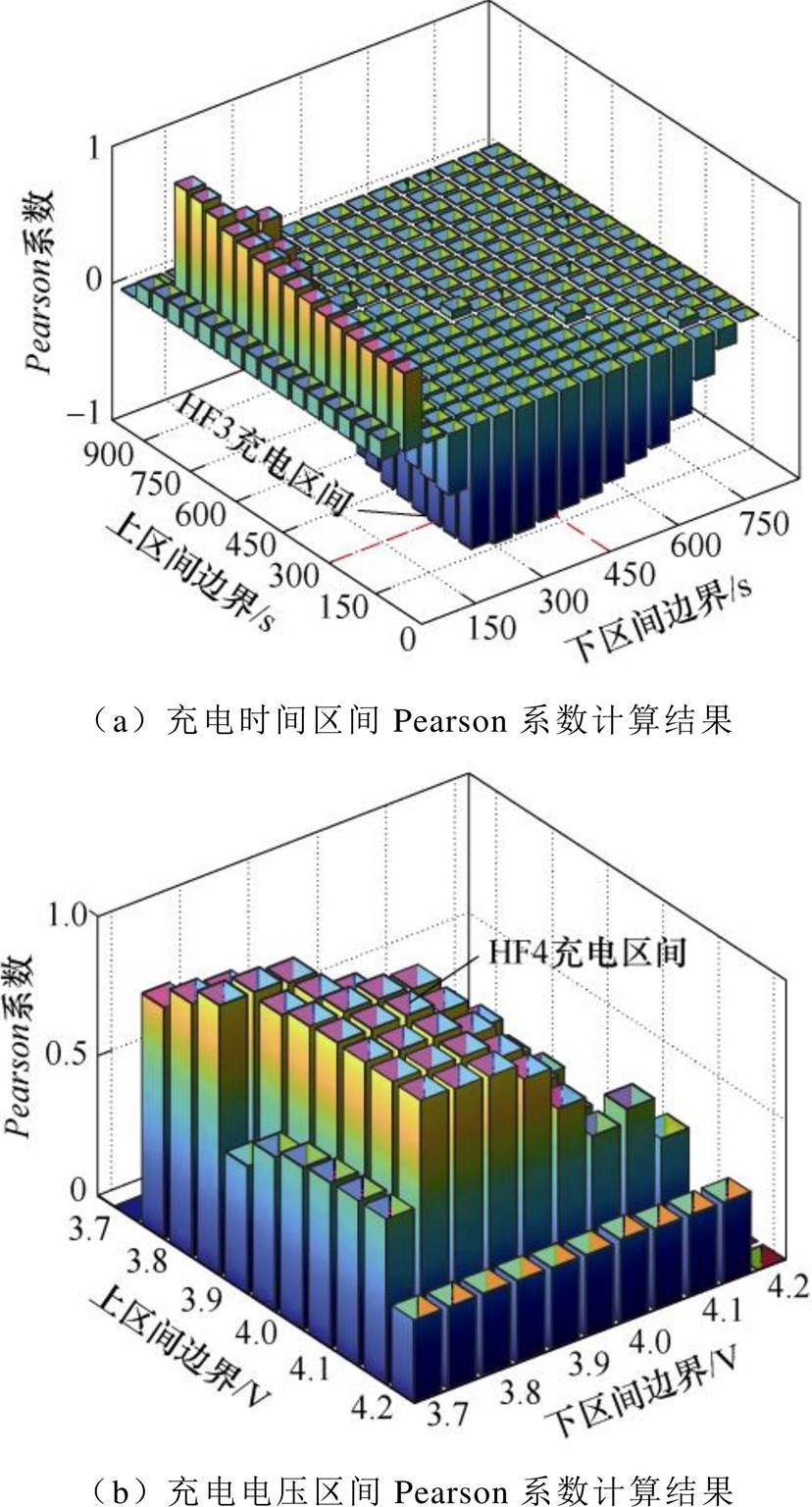
图2 相关充电区间计算
Fig.2 Calculation of relevant charging interval
由图1a可知,所提取的各HF随电池老化的变化规律并不一致,难以直接判断其与容量的相关度。故本文采用Pearson相关系数进一步量化各HF的特征表达能力。Pearson相关系数可以有效分析两个变量之间的线性相关度,其绝对值越大说明两个变量的相关度越高,若绝对值为1则说明二者完全相关。计算表达式为
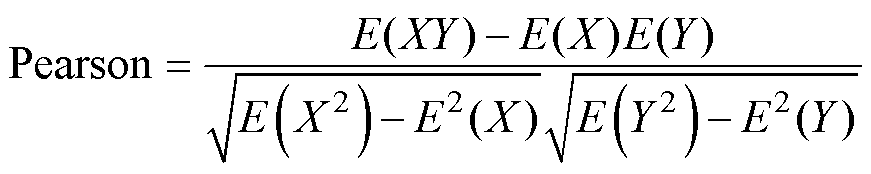 (1)
(1)
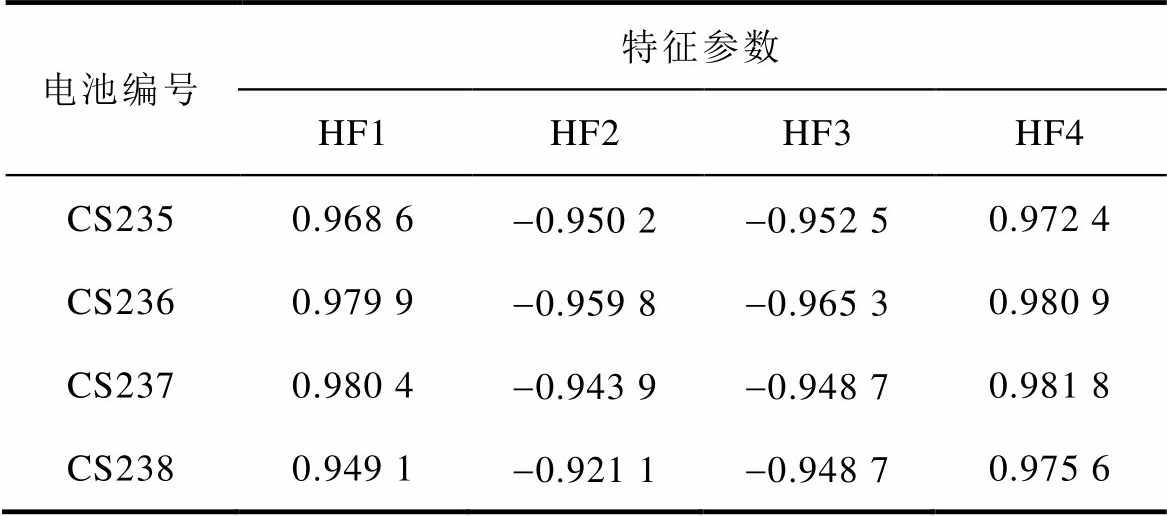
式中,X、Y分别为所提取的特征数据和电池容量数据样本。表1为4个不同电池的各HF与电池容量之间的Pearson相关系数计算结果,证实了所提取的4个特征参数与电池容量之间的相关性。
表1 Pearson相关系数
Tab.1 Pearson correlation coefficient calculation
电池编号特征参数 HF1HF2HF3HF4 CS2350.968 6-0.950 2-0.952 50.972 4 CS2360.979 9-0.959 8-0.965 30.980 9 CS2370.980 4-0.943 9-0.948 70.981 8 CS2380.949 1-0.921 1-0.948 70.975 6
所提取的HF与容量均有较高的相关度,但其相关系数距离完全相关标准1仍有一定偏差。为进一步提升输入特征的表达能力以达到更高的状态监测要求,本文使用特征并行融合操作Concat对所提取HF进行优化,并结合注意力机制计算各HF权重。Concat是实现特征融合的一个经典方法[19],可将同维度的不同输入特征以多通道形式进行组合,实现多特征的优势互补。注意力机制Attention则可以通过动态调节各输入特征的权重,以突出重要特征的影响,增强特征融合效果[20]。该优化过程为
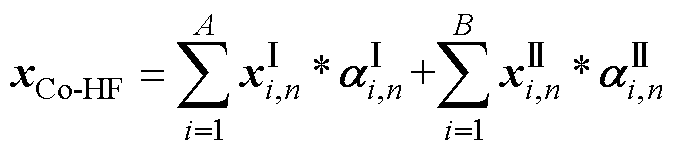 (2)
(2)
式中,xCo-HF为融合特征Co-HF的特征向量;各单项式表示复数域中的两个并行特征通路,其中上标Ⅰ、Ⅱ用以区分各通路中变量,下标n表示循环次数;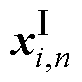 、
、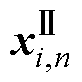 为两通路下的第i个输入特征向量;A、B为各通路的通道数;*表示卷积运算;
为两通路下的第i个输入特征向量;A、B为各通路的通道数;*表示卷积运算;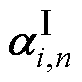 、
、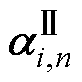 分别为通路特征
分别为通路特征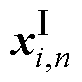 、
、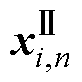 的权重向量,均为1×1×i的卷积核。
的权重向量,均为1×1×i的卷积核。
然后使用注意力得分函数计算权重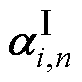 、
、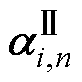 的注意力分布为
的注意力分布为
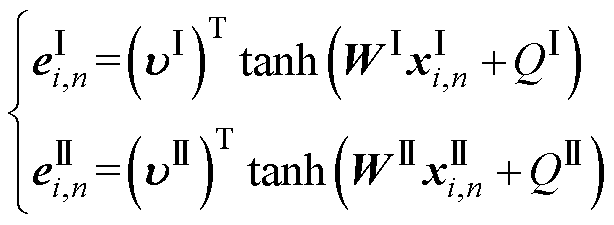 (3)
(3)
式中,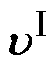 、
、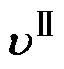 ∈RN和
∈RN和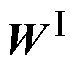 、
、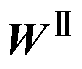 ∈RN×2q为需要学习的权重系数矩阵,其中q为Attention的最后一个隐藏层大小;
∈RN×2q为需要学习的权重系数矩阵,其中q为Attention的最后一个隐藏层大小;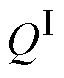 、
、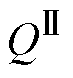 ∈RN为偏置系数。
∈RN为偏置系数。
使用Softmax函数对权重分布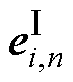 、
、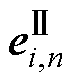 进行归一化处理,得各通道特征权重向量为
进行归一化处理,得各通道特征权重向量为
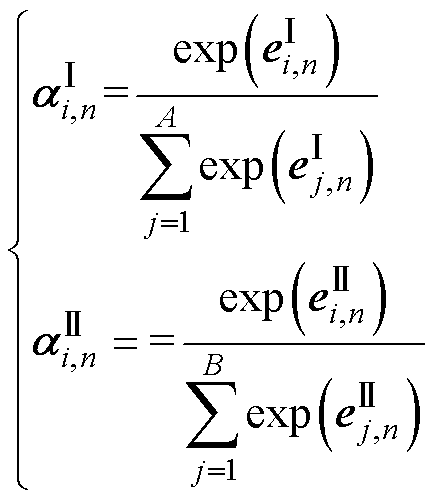 (4)
(4)
根据各HF随电池老化发生的变化特性,本文将与容量衰减变化趋势一致的特征{HF1, HF4}作为通路特征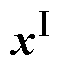 ,变化趋势相反的特征{HF2, HF3}作为通路特征
,变化趋势相反的特征{HF2, HF3}作为通路特征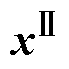 ,由式(2)计算优化后的特征Co-HF。表2展示了其Pearson相关系数的计算结果。
,由式(2)计算优化后的特征Co-HF。表2展示了其Pearson相关系数的计算结果。
表2 Co-HF的Pearson相关系数
Tab.2 Pearson correlation coefficient of Co-HF
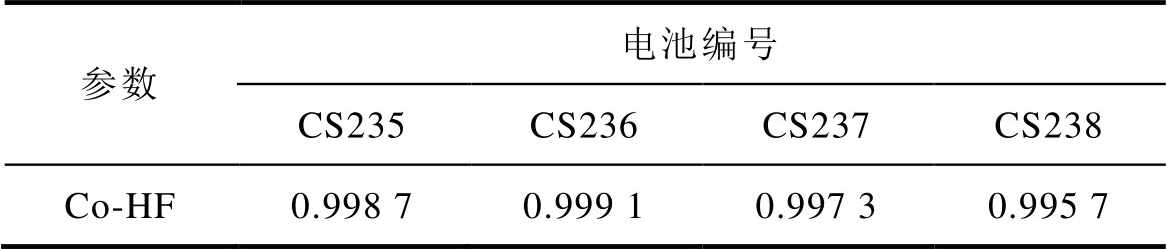
参数电池编号 CS235CS236CS237CS238 Co-HF0.998 70.999 10.997 30.995 7
由此可见,优化后的特征Co-HF在4个锂电池上相关系数均高于0.99,故将其作为本文的IHF,进行SOH和RUL预测。
SVR方法是一种有效的监督学习算法,被广泛应用于时间序列预测领域,能较好地处理小数据样本、非线性及时间序列等问题,且泛化能力较强[21]。
设x为锂电池的IHF输入特征向量。构造SVR回归函数为
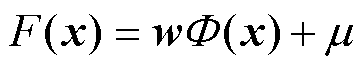 (5)
(5)
式中,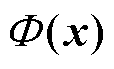 为x在高维特征空间下的映射;w、
为x在高维特征空间下的映射;w、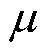 分别为权重向量及截距。
分别为权重向量及截距。
根据统计学理论,通常采用二次规划优化算法来确定SVR回归函数,即
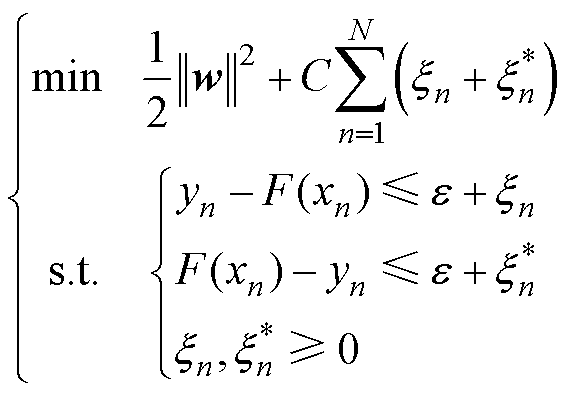 (6)
(6)
式中,C为惩罚因子;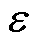 为误差容限;
为误差容限;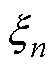 、
、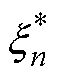 表示两个松弛变量;xn、yn分别为第n次循环下的输入特征及实测容量;N为总循环次数。
表示两个松弛变量;xn、yn分别为第n次循环下的输入特征及实测容量;N为总循环次数。
根据K个训练样本建立K个SVR子模型(SVR- 1,…, SVR-K),并结合BMA方法组合构建SVR- BMA融合模型。BMA方法根据不同子模型预测的后验模型概率对其进行加权,从而生成一个平均模型。其核心在于计算各子模型后验模型概率,即各模型的权重分布。已知本文模型集合中存在K个子模型,设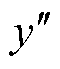 为待预测的容量变量,
为待预测的容量变量,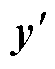 为所有子模型的预测容量集合,其中
为所有子模型的预测容量集合,其中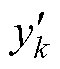 为子模型k的预测容量。基于全概率定律,BMA计算模型可以表示为
为子模型k的预测容量。基于全概率定律,BMA计算模型可以表示为
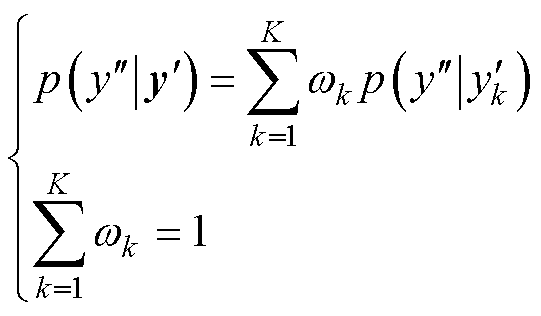 (7)
(7)
式中,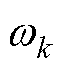 为子模型k为候选模型的后验概率;
为子模型k为候选模型的后验概率;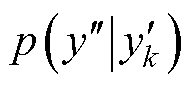 为预测容量
为预测容量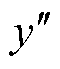 的后验分布,其在BMA中服从高斯随机分布;
的后验分布,其在BMA中服从高斯随机分布;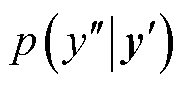 为融合模型的联合概率。
为融合模型的联合概率。
为获得子模型k的权重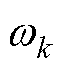 ,使用期望最大化(Expectation Maximization, EM)方法对其进行求解。引入隐变量zk,在第n次循环下,若子模型k在预测时为候选模型,则有zk,n=1;反之,zk,n=0。相关计算步骤为:
,使用期望最大化(Expectation Maximization, EM)方法对其进行求解。引入隐变量zk,在第n次循环下,若子模型k在预测时为候选模型,则有zk,n=1;反之,zk,n=0。相关计算步骤为:
(1) 参数初始化:设置初始期望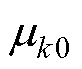 、协方差
、协方差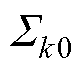 及模型初始权重
及模型初始权重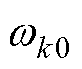 。
。
(2)E步:由当前循环次数n下各参数计算隐变量的后验分布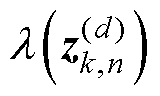 ,其中上标d为迭代次数。
,其中上标d为迭代次数。
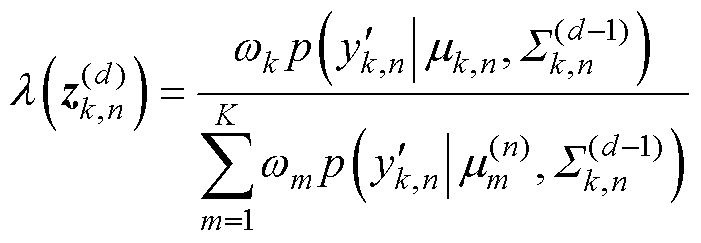 (8)
(8)
(3)M步:极大化数学期望进行参数更新。
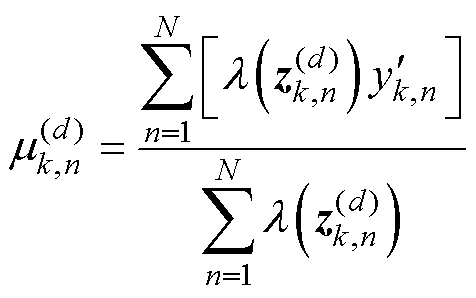 (9)
(9)
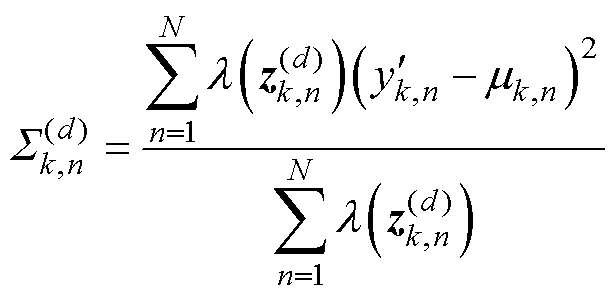 (10)
(10)
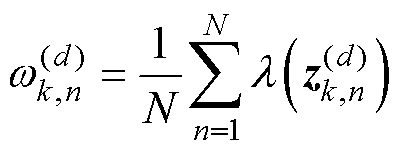 (11)
(11)
由式(8)~式(11)的计算过程求解各子模型权重,经迭代计算将不相关模型权重置为零[14],而后验模型概率较高的子模型将被筛选为候选模型SVRpre参与模型融合。并根据式(7)最终建立SVR-BMA融合模型为
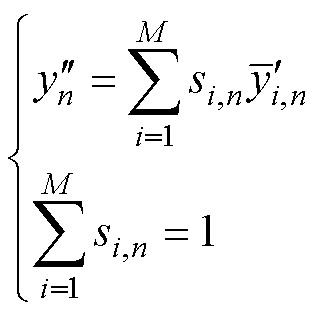 (12)
(12)
式中,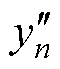 和
和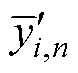 分别为SVR-BMA融合模型和第i个候选模型SVRpre第n次循环的容量预测值;si,n为对应SVRpre模型的权重;M为候选模型个数;i= 1, 2,…, M。
分别为SVR-BMA融合模型和第i个候选模型SVRpre第n次循环的容量预测值;si,n为对应SVRpre模型的权重;M为候选模型个数;i= 1, 2,…, M。
LSTM作为循环神经网络(Rerrent Neural Net- work, RNN)的一种改进结构,可以有效克服网络训练过程中的梯度消失和爆炸现象,从而在记忆时序信息方面具有明显优势[22]。LSTM的基本单元由遗忘门、输入门和输出门三个门机制组成,这使得LSTM具有传递历史信息的能力。设y0n第n次时的原始容量输入,则LSTM的计算过程为
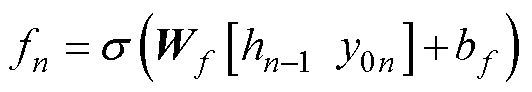 (13)
(13)
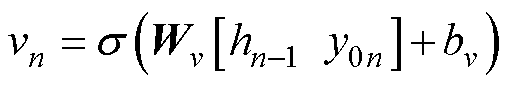 (14)
(14)
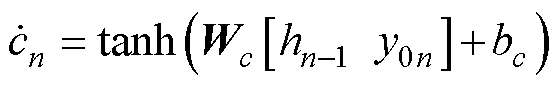 (15)
(15)
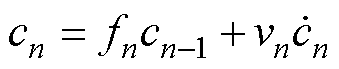 (16)
(16)
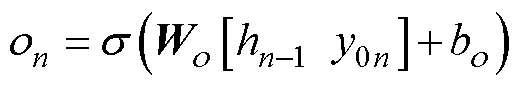 (17)
(17)
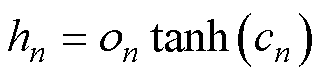 (18)
(18)
式中,fn、vn、on分别为遗忘门、输入门和输出门状态;hn-1为隐藏状态;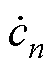 、cn、hn分别为待更新神经元和隐藏状态;Wf、Wv、Wo、Wc和bf、bv、bo、bc分别为各门机制与内部中间状态的权重矩阵和偏置;
、cn、hn分别为待更新神经元和隐藏状态;Wf、Wv、Wo、Wc和bf、bv、bo、bc分别为各门机制与内部中间状态的权重矩阵和偏置; 为激活函数Sigmoid。
为激活函数Sigmoid。
根据K个训练样本所提取的原始容量训练集,建立K个如图3所示的LSTM子模型(LSTM-1,…, LSTM-K)。为减少过拟合,在网络模型中引入Dropout层,经全连接层输出预测结果。
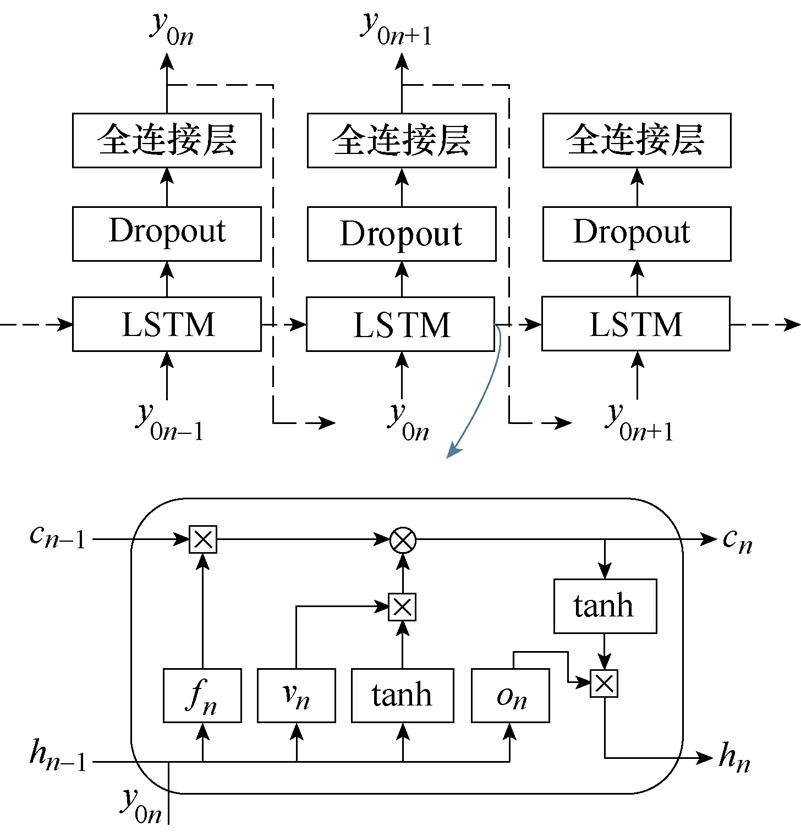
图3 LSTM结构
Fig.3 LSTM structure
引入BMA方法计算各子模型权重,筛选出M个候选模型LSTMpre并对其进行加权平均,具体步骤与式(8)~式(11)计算过程相同。最终建立LSTM-BMA融合模型为
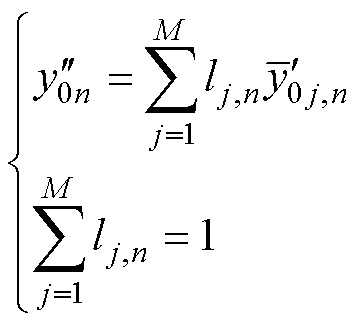 (19)
(19)
式中,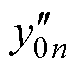 和
和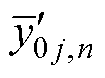 分别为循环次数n下的LSTM-BMA融合模型以及第j个LSTMpre候选模型的原始容量预测值;lj,n为对应LSTMpre模型权重,j=1, 2,…, M。
分别为循环次数n下的LSTM-BMA融合模型以及第j个LSTMpre候选模型的原始容量预测值;lj,n为对应LSTMpre模型权重,j=1, 2,…, M。
结合2.1节和2.2节所构建的模型结构,本文提出了基于间接特征优化与多模型融合的锂电池SOH-RUL联合预测方法。其具体步骤如下:
1)间接健康特征输入
采集充电电压曲线中的相关信息,经间接健康特征优化后,提取各电池的IHF,划分训练集Dp与测试集Dt。
2)SOH预测
利用SVR-BMA融合模型预测SOH:首先由训练集Dp建立各SVR子模型,设置起始预测时间(Starting Point, SP),输入测试集Dt获得各SVR子模型预测的容量序列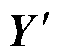 ,使用SVR-BMA融合模型计算各SVRpre的权重,由式(12)输出融合模型的容量预测结果
,使用SVR-BMA融合模型计算各SVRpre的权重,由式(12)输出融合模型的容量预测结果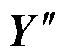 ,进行SOH预测。
,进行SOH预测。
设各SVR子模型起始预测时刻为t0,BMA起始计算时刻为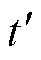 ,则有
,则有
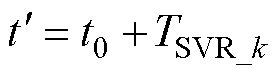 (20)
(20)
式中,TSVR_k为SVR子模型预测所用时长。
3)原始容量提取
为获得用于RUL预测的有效容量数据,根据步骤2)所获得的容量序列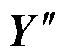 ,使用CEEMDAN方法将初始电池容量数据分解为不同频率范围的本征模态函数(Intrinsic Mode Functions, IMF),从中提取出稳定频率范围内的待测电池原始容量Y0,由此实现容量回升特性的分离。以电池CS236为例,分解后的原始容量如图4所示。
,使用CEEMDAN方法将初始电池容量数据分解为不同频率范围的本征模态函数(Intrinsic Mode Functions, IMF),从中提取出稳定频率范围内的待测电池原始容量Y0,由此实现容量回升特性的分离。以电池CS236为例,分解后的原始容量如图4所示。
该步骤计算时长为
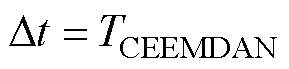 (21)
(21)
式中,TCEEMDAN为CEEMDAN方法计算时长。
4)RUL预测
利用LSTM-BMA融合模型预测RUL:使用CEEMDAN方法,从不同电池容量循环数据中提取出原始容量训练集Dp0,建立各LSTM子模型,输入步骤3)在线预测的原始容量序列Y0,获得预测的原始容量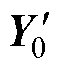 ,由LSTM-BMA融合模型计算各LSTMpre的权重,根据式(19)输出融合模型原始容量预测结果
,由LSTM-BMA融合模型计算各LSTMpre的权重,根据式(19)输出融合模型原始容量预测结果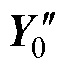 ,进行RUL预测。
,进行RUL预测。
设各LSTM子模型起始预测时刻为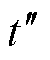 ,BMA模型起始计算时刻为
,BMA模型起始计算时刻为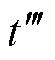 ,则有时间关系式为
,则有时间关系式为
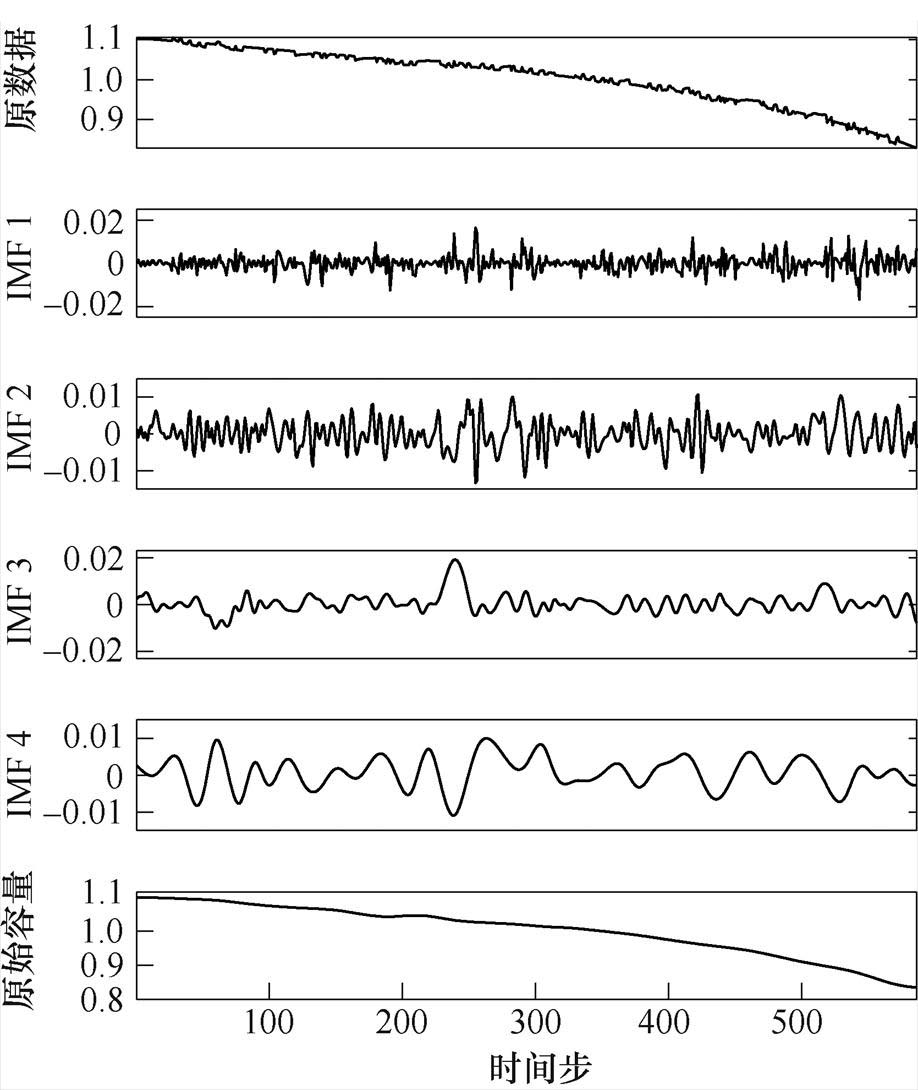
图4 原始容量提取(CS236)
Fig.4 Raw capacity extraction (CS236)
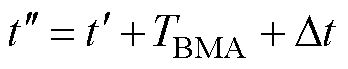 (22)
(22)
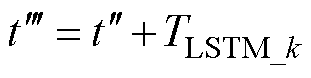 (23)
(23)
式中,TBMA为BMA模型计算时长;TLSTM_k为LSTM子模型预测所用时长。由于输入样本维度一致,故建立的LSTM子模型平行同步预测,预测时长均为TLSTM_k。同理各SVR子模型预测时长均为TSVR_k,各融合模型中BMA方法计算所用时长均为TBMA。则整个预测流程总时长为
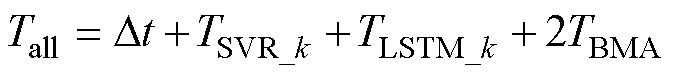 (24)
(24)
经Tall时间后,结束预测。本文所提方法整体预测流程如图5所示。此外,第1节、第2节所提出的各名称缩写以及方法参数的相关定义说明汇总于附录中,便于读者理解。
为验证所提联合预测方法的有效性,本文基于马里兰大学CALCE锂电池数据集进行仿真实验。通过对比分析不同特征以及不同预测模型的预测效果,来检验所提方法的预测优势。另外,实验还通过设置不同的预测起始点来检验预测方法的适应性和鲁棒性,并对不同方法的预测结果进行对比分析,进一步验证所提方法的预测性能。
实验从CALCE数据集中选择4个锂电池CS235、CS236、CS237和CS238进行实验研究。将其中的锂电池CS236数据作为测试集,锂电池CS235、CS237和CS238数据及其组合形式作为训练集。根据BMA原理,训练集中的每个数据样本为一个训练子集,每个子集对应一个预测子模型。建立K=23-1个训练子模型,设置候选模型数量M=3。实验工况与大多数型号电池的实际充放电策略相同,电池以标准恒流恒压模式进行充电,以恒流模式进行放电。为符合大多数工程应用需求,本文将EOL定义为SOH降至0.8时的电池容量。其电池具体参数见表3。
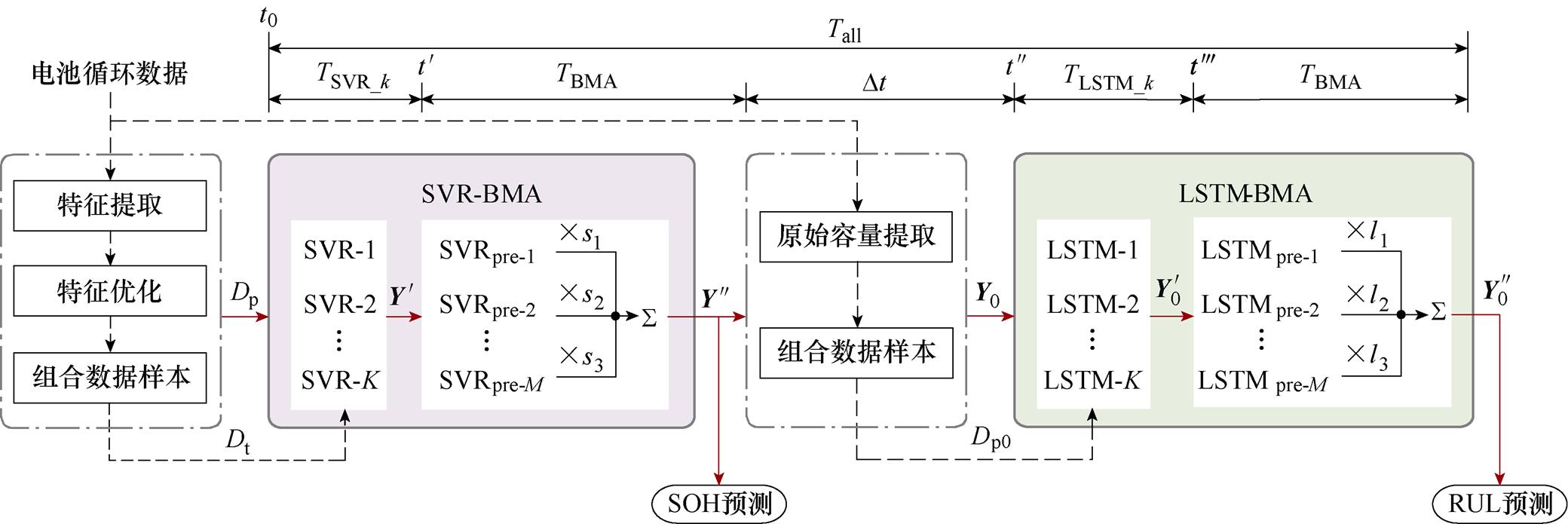
图5 SOH-RUL联合测流程
Fig.5 SOH-RUL joint flow chart measurement
表3 电池参数
Tab.3 Experimental battery parameters

参 数数 值 (型号) 额定容量/(A·h)1.1 电池材料阴极LiCoO2 充电截止电压/V4.2 放电截止电压/V2.7 EOL/(A∙h)0.88
在原始容量提取环节,经CEEMDAN分解后获得电池失效前的有效数据长度不超过800,故隐藏层规模不宜过大。本实验首先使用随机噪声插值扩充电池数据样本,然后建立5层结构的LSTM训练模型,以50为输入单元进行单步预测。由于训练集由同型号锂电池老化数据构成,所建立的SVR子模型和LSTM子模型结构相同。建立SVR子模型时,选择高斯径向基函数(Radial Basis Function, RBF)作为核函数Kernel,并使用交叉验证法确定C参数和g 参数。各子模型的超参数设置见表4。
3.2.1 评价指标
本文使用平均绝对误差(Mean Absolute Error, MAE)和方均根误差(Root Mean Squared Error, RMSE)作为评价指标,对预测结果和算法性能进行定量评价,其表达式为
表4 SVR和LSTM超参数
Tab.4 SVR and LSTM super parameter settings
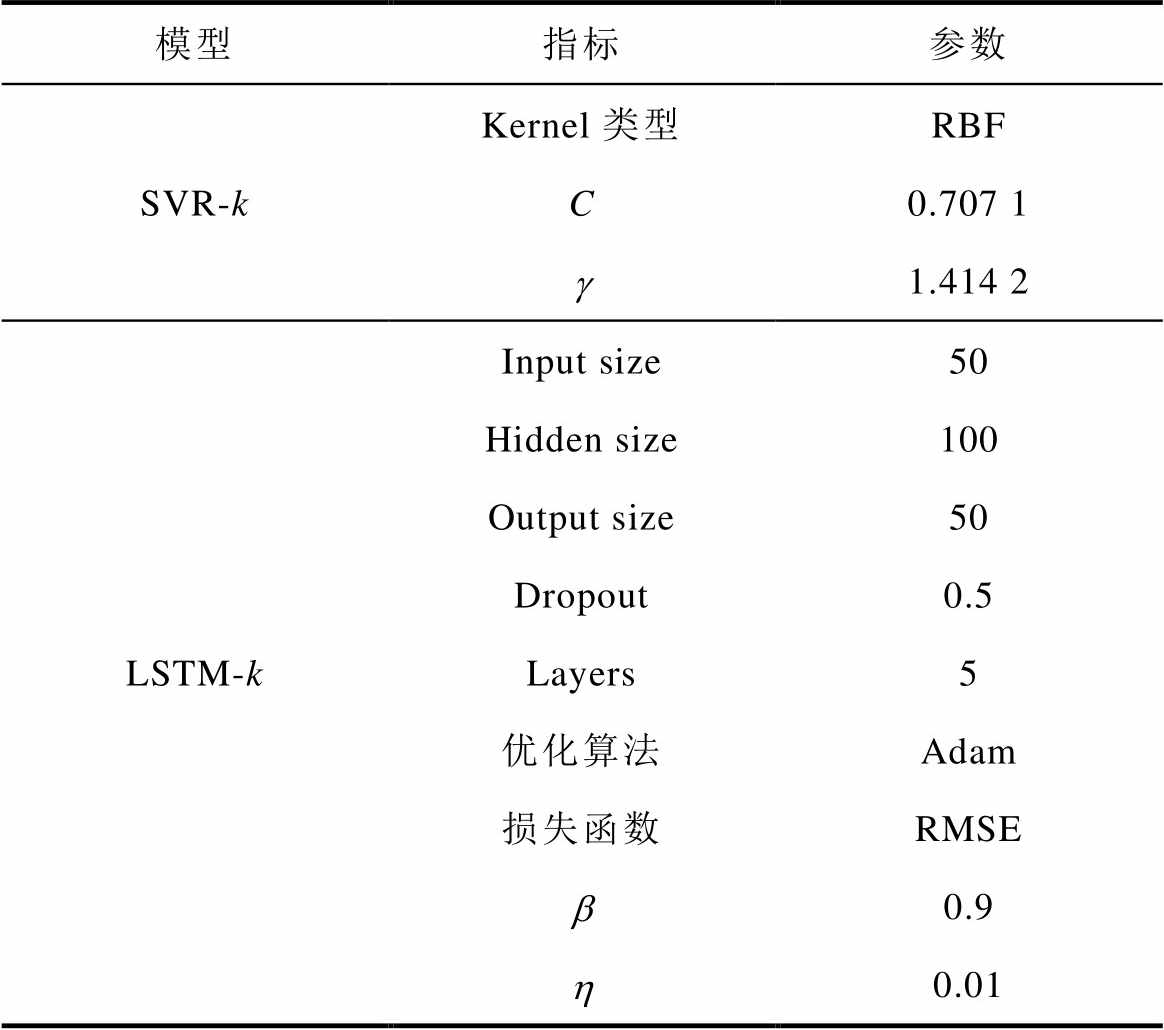
模型指标参数 SVR-kKernel类型RBF C0.707 1 g1.414 2 LSTM-kInput size50 Hidden size100 Output size50 Dropout0.5 Layers5 优化算法Adam 损失函数RMSE b0.9 h0.01
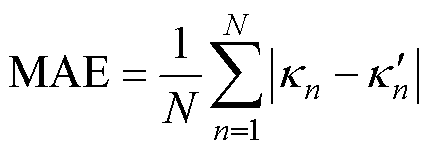 (25)
(25)
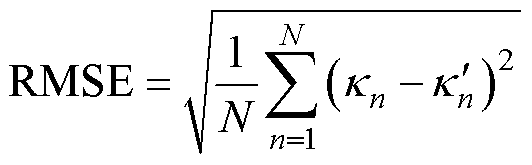 (26)
(26)
式中,n为预测时间步,即电池充放电循环次数;N为预测时间步总长度;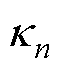 、
、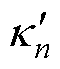 分别为实测值与预测值。
分别为实测值与预测值。
3.2.2 间接健康特征预测对比
间接健康特征与电池容量的相关度将决定预测结果准确度的上限。为检验所提特征Co-HF的预测优势,本文将所提取的4个健康特征{HF1, HF2, HF3, HF4}与优化后的特征Co-HF的容量预测效果进行比较,判断其与容量的相关程度。设置预测起始点SP=300,将4个电池的单特征参数HF和所提特征Co-HF分别作为IHF,输入SOH预测模型预测电池容量,取其局部预测结果进行分析,如图6所示。
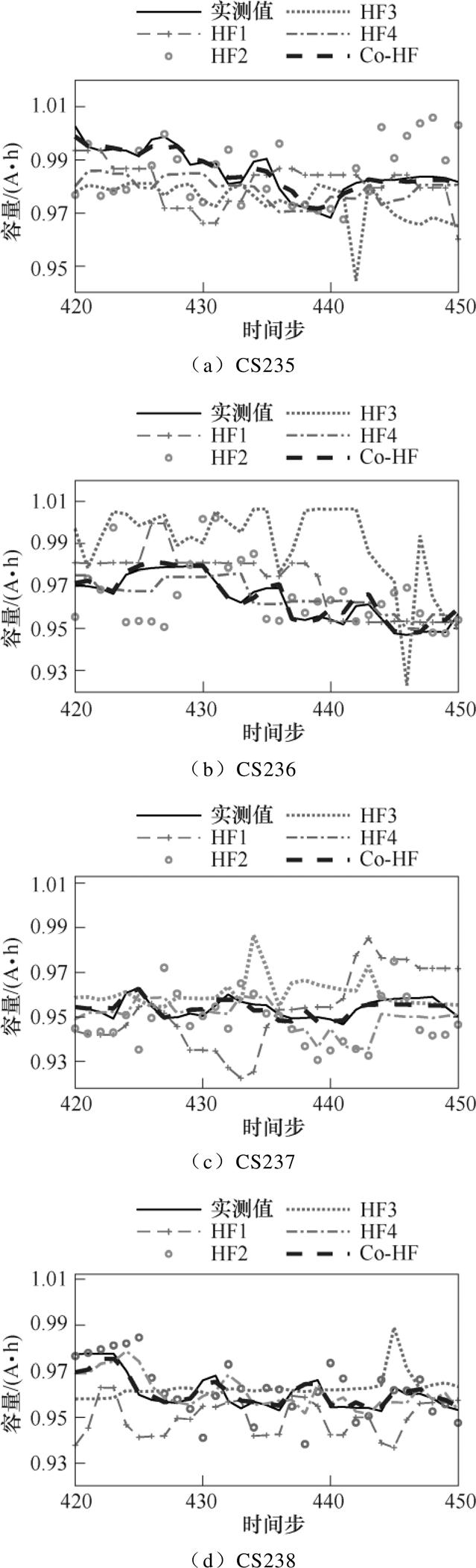
图6 不同间接健康特征预测情况
Fig.6 Comparison of prediction of different indirect characteristics
图6中,实线为电池容量实测值,通过对充满电的电池进行恒流放电至截止电压测得,其余线型或标记则表示不同IHF的容量预测结果。可以看出,特征HF1、HF2的容量预测曲线在大多数预测步下无法对真实退化趋势做到有效跟踪,与实测值偏差较大,且在不同电池上预测效果不一,特征表达能力与适应性不高。特征HF3和特征HF4的预测曲线变化整体接近实测容量曲线,但在局部容量回升区域均出现预测不准的问题,对老化特性的捕捉能力不足。而相比于上述各特征参数,特征Co-HF的预测结果最接近实测值,观察其放大框图可知,使用特征Co-HF的容量预测效果十分稳定,各电池下的预测值均集中在真实值附近,对容量趋势的跟踪效果最为理想。而通过特征并行融合方法对HF进行优化,使特征Co-HF包含4个HF的特征信息。当电池处于容量回升阶段时,若任一特征的相关性表达失效,参与特征融合的其他变量仍能保持其原有的特征表达作用,从而使特征Co-HF与容量的相关度持续在较高的水平,实现多特征的优势互补。由此可见,优化后的特征Co-HF相比于其他IHF具有更强的稳定性与可靠性,更有利于进行后续老化 预测。
3.2.3 SOH预测情况
为验证所提SOH预测方法的有效性,实验提取了锂电池CS236的特征Co-HF样本,分别输入各子模型与SVR-BMA融合模型进行SOH预测,比较待测电池在不同预测模型下的预测结果。设置预测起始点SP=300,并引入95%的置信区间判断预测结果的可靠性,即最大允许误差范围为[-0.05, 0.05]。为便于分析,仅对比3个子模型与SVR-BMA融合模型的预测情况,其中子模型SVR-1、SVR-2、SVR-3分别由锂电池CS235、CS237、CS238的训练子集获得,预测结果如图7所示及见表5。
图7中,各模型预测结果在预测前期均落在置信区间内,但随预测步的增加,3个子模型的预测误差明显增大,其中SVR-2子模型和SVR-3子模型预测曲线超出置信区间,预测后期误差难以收敛。这是因为在锂电池老化过程中,电池内部的结构变化和复杂的电化学过程在容量衰退前期可能不会立即显现,而是在长期循环中具有累积效应。在进行SOH预测时,构成训练集和测试集的4个锂电池遵循该型号电池的普遍老化规律,即电池老化趋势基本相同。在预测早期至中期阶段,各电池老化规律相对单一,各子模型基本都能完成预测任务。然而,实际上每个电池的运行状态及环境难以完全一致,预测中的不确定性因素会对不同电池的老化变化造成影响,并随循环次数增加愈发显著,故而在预测后期,各子模型的SOH预测变得更为困难。而本文通过引入BMA方法来解决预测过程中的不确定性问题,建立了SVR-BMA融合模型进行SOH预测。

图7 SOH预测情况
Fig.7 Comparison of SOH prediction
表5 SOH预测误差
Tab.5 SOH prediction error
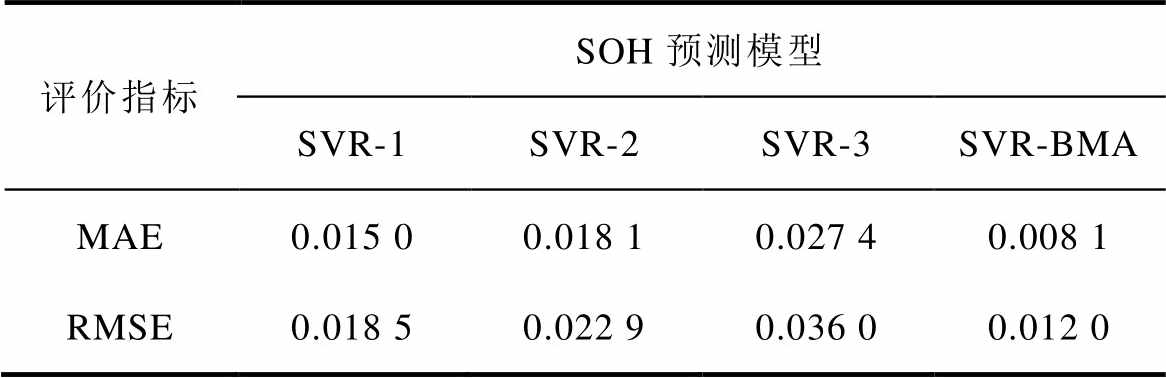
评价指标SOH预测模型 SVR-1SVR-2SVR-3SVR-BMA MAE0.015 00.018 10.027 40.008 1 RMSE0.018 50.022 90.036 00.012 0
由图7可知,当预测步小于200时,其预测误差集中于[-0.01, 0.01],较各子模型预测结果更接近真实值。同时,随着预测步的推进,SVR-BMA融合模型预测结果始终处于置信区间内,误差绝对值均小于0.04,而在要求更高、难度更大的预测后期阶段,该模型的预测结果仍保持着较高的准确度和稳定性,进一步展现了SVR-BMA融合模型的预测优势。此外,表5列出了各模型的MAE和RMSE计算结果,其中SVR-BMA模型的MAE=0.008 1,RMSE=0.012 0,模型预测误差最小。由此可见,该模型的预测精度均优于任一子模型,能够更好地进行SOH预测。
3.2.4 RUL预测情况
RUL预测是针对电池容量衰减到EOL时,剩余循环次数的预测,其更多地体现为电池老化程度的变化趋势。如2.3节所述,在进行RUL预测前,需要将反映容量衰减趋势的原始容量提取出来,作为进行RUL预测的输入参数。本文使用CEEMDAN方法,从SOH预测结果中获得用于RUL预测的输入样本。为验证所提方法的RUL预测准确度,实验选取3个LSTM子模型与LSTM-BMA融合模型的预测结果进行对比,各子模型分别由锂电池CS235、CS237、CS238的训练子集获得,设置SP=300,并引入95%的置信区间。
图8为各子模型与LSTM-BMA融合模型前30次的RUL预测情况。其中,实线为实测值,通过计算当前循环周期距离EOL的循环次数获得,虚线为预测值,填充部分表示95%的置信区间上下边界。可以看出,各子模型的预测曲线均朝着误差增大的方向变化,逐渐偏离实测值,其中LSTM-3模型的预测结果整体超出在置信区间上方,无法准确预测电池RUL的变化规律。这是因为预测过程中的不确定性问题使得不同电池容量的退化存在一定差异,通过CEEMDAN对各电池容量进行模态分解后,这一差异在原始容量上更为明显,且随时间逐渐累积,进而影响各子模型的RUL预测结果。而BMA可以对不确定性问题造成的差异起中和作用,故本文建立LSTM-BMA融合模型进行RUL预测。相比于其他子模型的预测结果,该融合模型的预测曲线与RUL实际值贴合程度更为紧密,误差值不超过2,说明其能精准地追踪RUL的变化趋势,预测准确度较高。
表6为SP=300下各模型的MAE和RMSE计算结果,其中LSTM-BMA融合模型的MAE仅为2.56,RMSE小于5,预测误差明显低于其他预测子模型,这也进一步说明LSTM-BMA融合模型的预测结果更接近RUL的真实情况,具有更高的预测精度。
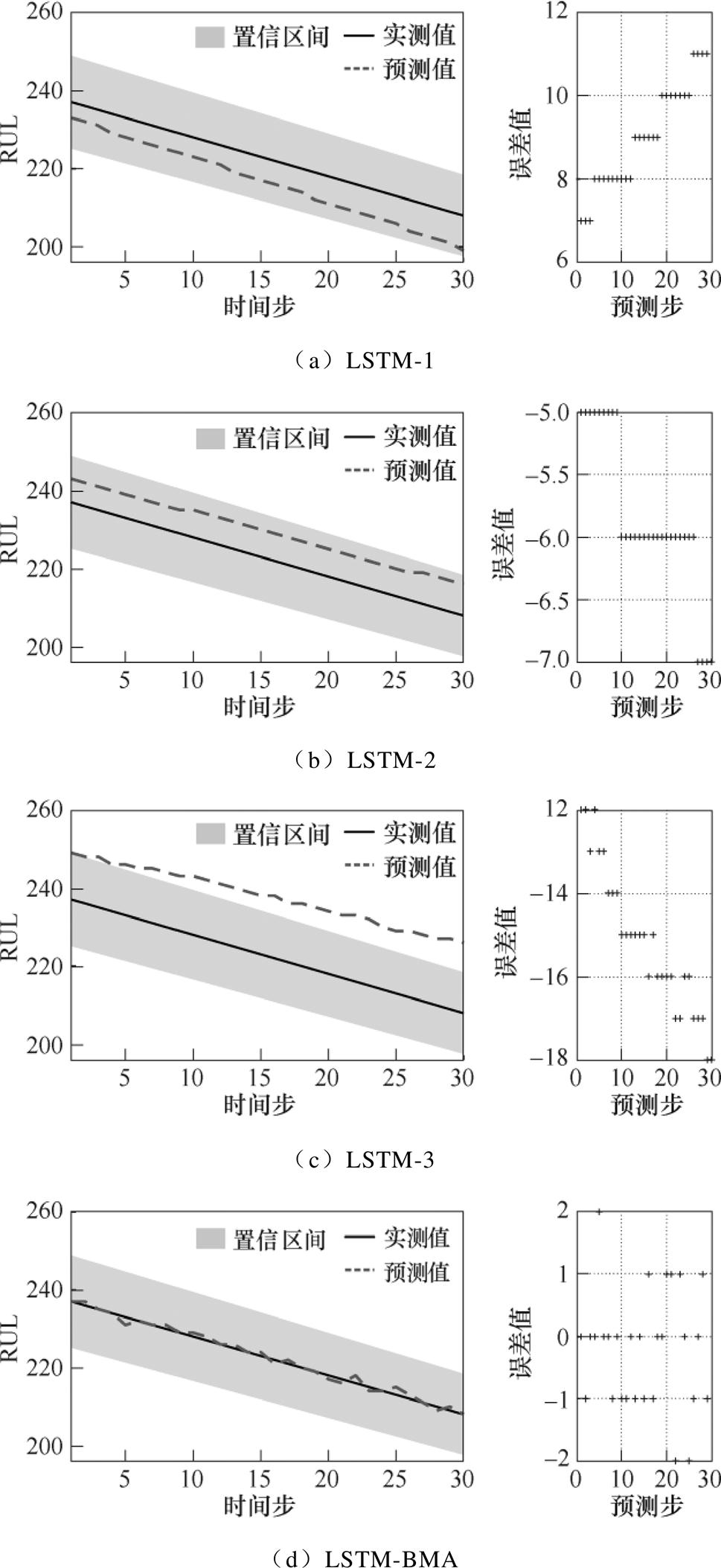
图8 RUL预测情况
Fig.8 Comparison of RUL prediction
表6 RUL预测误差
Tab.6 RUL prediction error
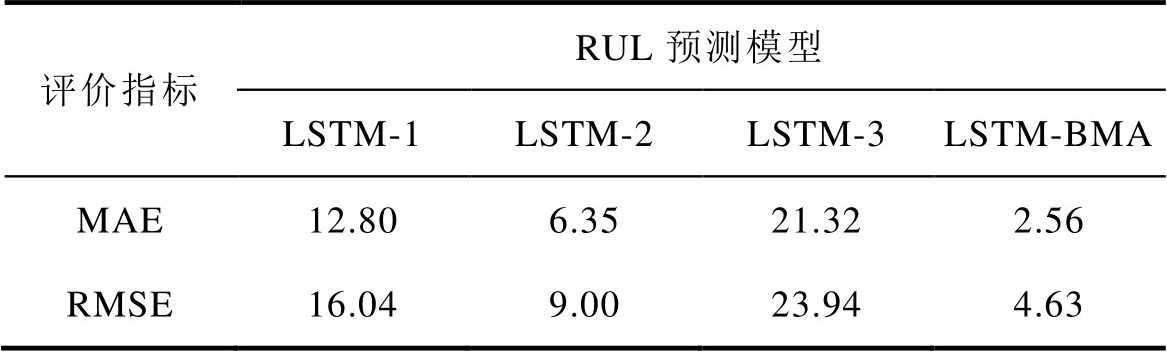
评价指标RUL预测模型 LSTM-1LSTM-2LSTM-3LSTM-BMA MAE12.806.3521.322.56 RMSE16.049.0023.944.63
3.2.5 SOH-RUL联合预测结果
SOH和RUL联合预测可提高电池老化状态估计的有效性。为检验所提方法的SOH和RUL联合预测效果,本文选取待测电池CS236实测容量相近(近似0.946 9)的两次预测结果进行评价,联合预测结果见表7。
表7 SOH-RUL联合预测结果
Tab.7 SOH-RUL combined prediction results
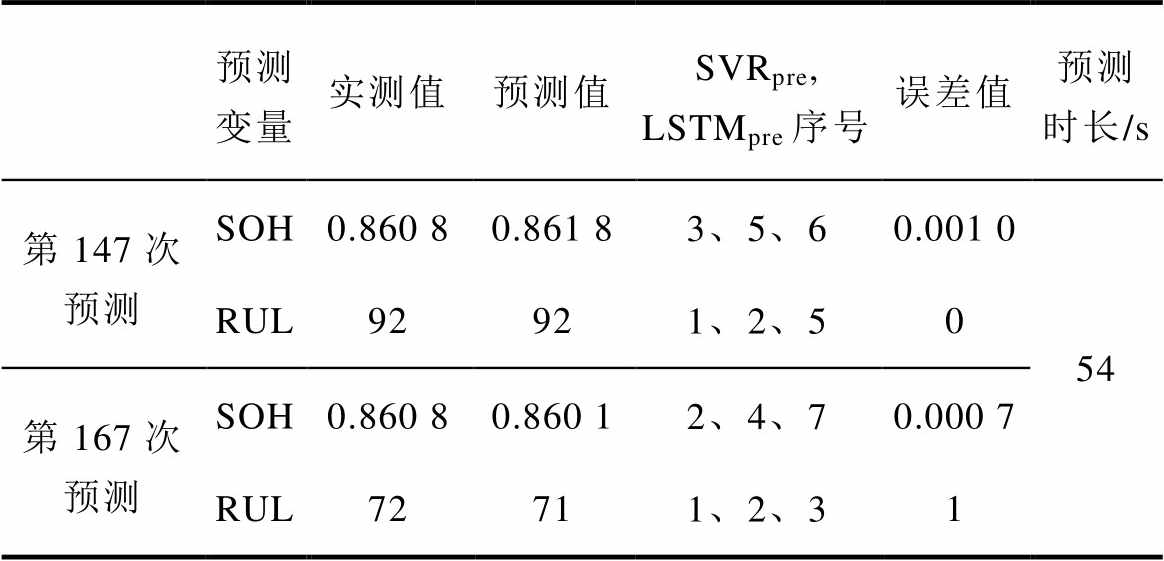
预测变量实测值预测值SVRpre, LSTMpre序号误差值预测时长/s 第147次预测SOH0.860 80.861 83、5、60.001 054 RUL92921、2、50 第167次预测SOH0.860 80.860 12、4、70.000 7 RUL72711、2、31
从表7中可知,两次预测的SOH误差均小于1%,第147次预测的RUL无偏差,第167次预测的RUL误差仅为1次,预测效果较好。此外,本实验记录了实验开始至这两次预测结束的平均所需时长,约为54 s,而评估电池的老化状态需要在充放电循环下进行,该过程往往以小时计,故本方法的时间消耗远低于实际工程应用需求,预测效率较高。而所提SOH和RUL联合预测方法以多个子模型为基础构建融合模型,其中BMA部分以各子模型后验概率为依据筛选出候选模型SVRpre和LSTMpre,这一筛选过程就是BMA在发挥不确定性管理的作用。而本实验所建立的K个训练子集将存在三种形式:单个电池数据、两个电池数据组合或三个电池数据共同组合。每个训练子集对应的子模型均不相同。将“{ }”表示数据集的组合形式,按照电池序号和组合数量递增进行排序,如序号1的训练子集由电池CS235数据构成,序号7的训练子集由{CS235, CS237, CS238}数据构成。以147次预测为例,BMA方法将序号为3、5、6的SVR子模型筛选为SVRpre,其分别由训练子集CS238、{CS235, CS238}、{CS237, CS238}建立;LSTMpre则为序号1、2、3的LSTM子模型,分别由训练子集CS235、CS237、{CS235, CS238}建立。其余预测步下各候选模型与训练子集的对应关系同理。这表明所提方法可以实现候选模型的动态更新,从而获得每个预测步下的最佳预测结果,更有利于实际应用。
3.2.6 预测起始点SP的影响
为检验所提方法的适应性,选择不同的SP进行实验。图9、图10和表8展示了待测电池在SP=100和SP=200下的预测结果。
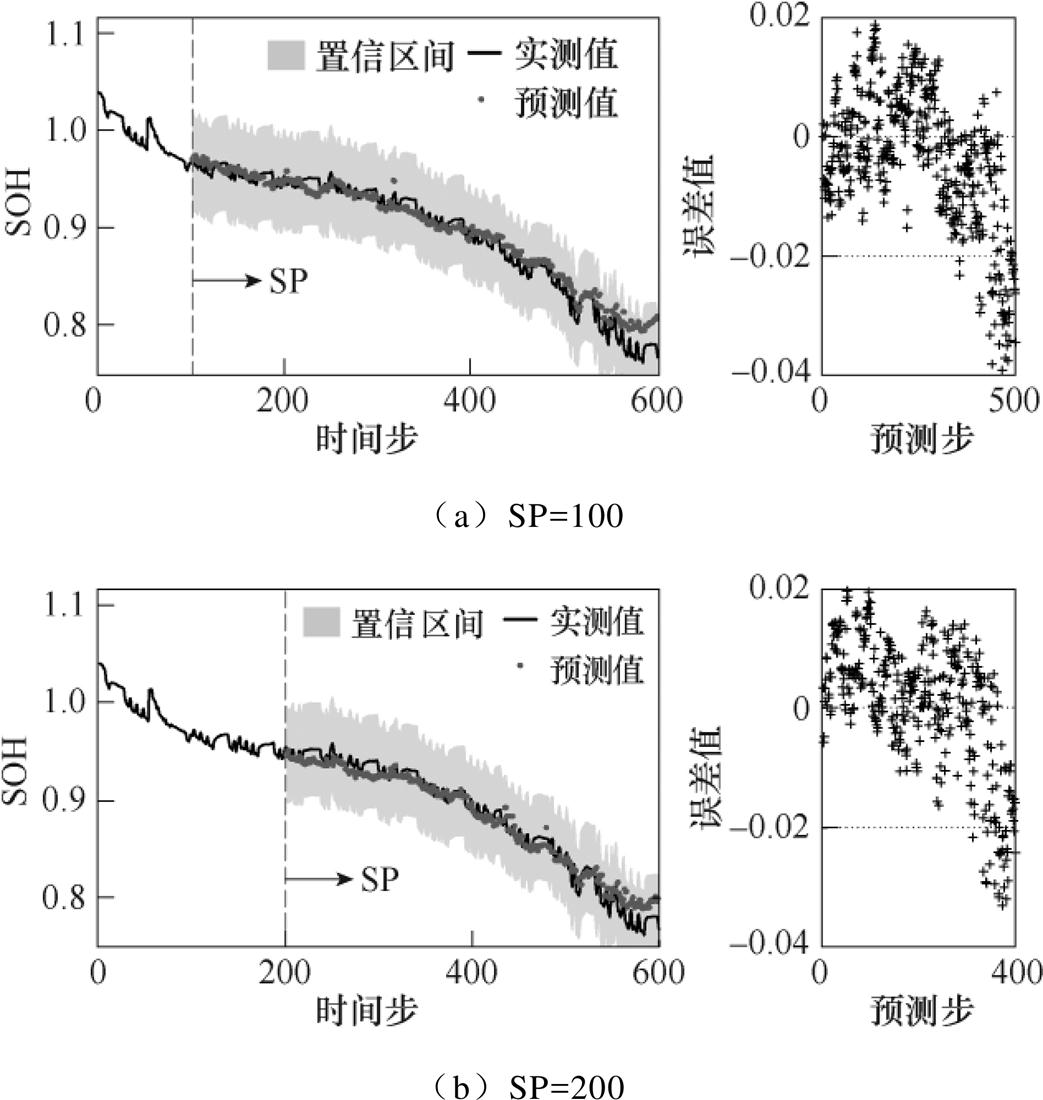
图9 SOH预测结果(SP=100/SP=200)
Fig.9 SOH prediction results (SP=100/SP=200)
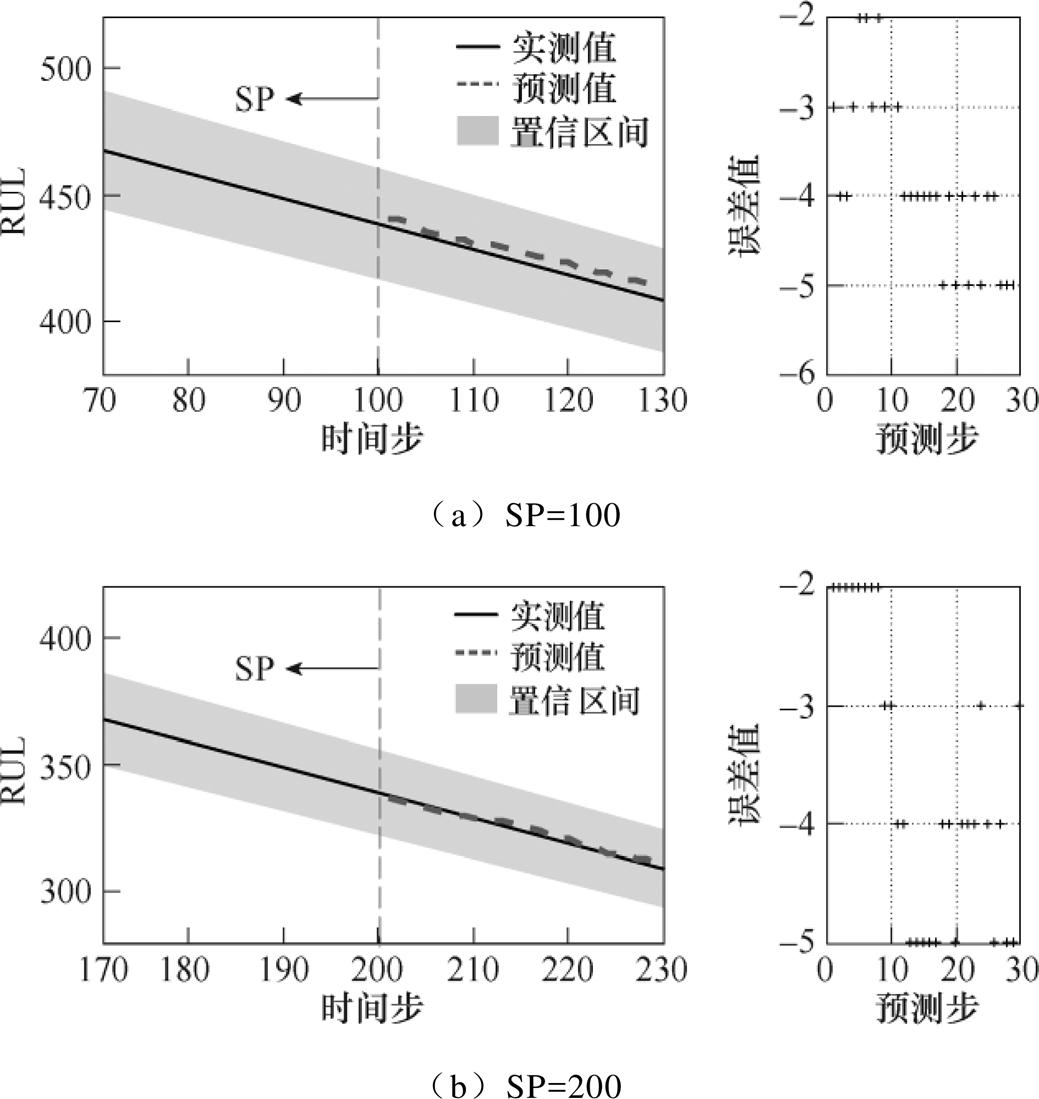
图10 RUL预测结果(SP=100/SP=200)
Fig.10 RUL prediction results (SP=100/SP=200)
从以上的预测结果可知,在不同的预测起始点下预测效果存在一定差异。SP靠后时的预测结果将优于SP靠前的情况。预测起始点后移意味着训练数据的增加,模型可以通过学习更多的循环数据来提高预测性能,同时跟踪趋势则会更趋近于老化曲线。值得一提的是,从不同SP的电池预测结果可以看出,训练数据规模的变动基本未对本方法的预测效果造成影响,3次实验的SOH预测结果的MAE和RMSE均低于0.02,RUL预测结果的MAE和RMSE最大分别为4.75和6.44,这进一步说明了所提出的预测方法精度高且适应性强。
表8 不同SP的预测结果
Tab.8 Prediction results of different SPs
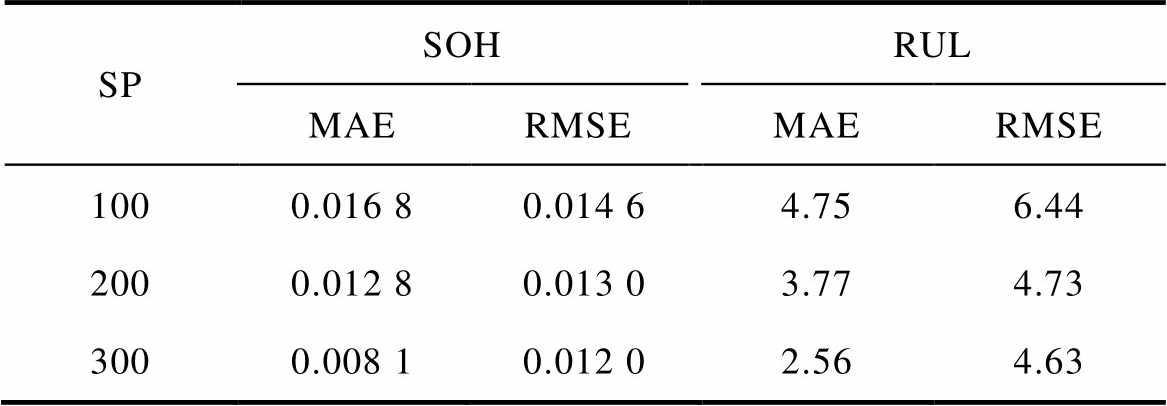
SPSOHRUL MAERMSEMAERMSE 1000.016 80.014 64.756.44 2000.012 80.013 03.774.73 3000.008 10.012 02.564.63
3.2.7 方法对比
为进一步验证本方法的优势,将本方法同现有锂电池SOH-RUL联合预测方法进行对比,结果见表9。
表9 不同方法结果对比
Tab.9 Comparison of results from different methods
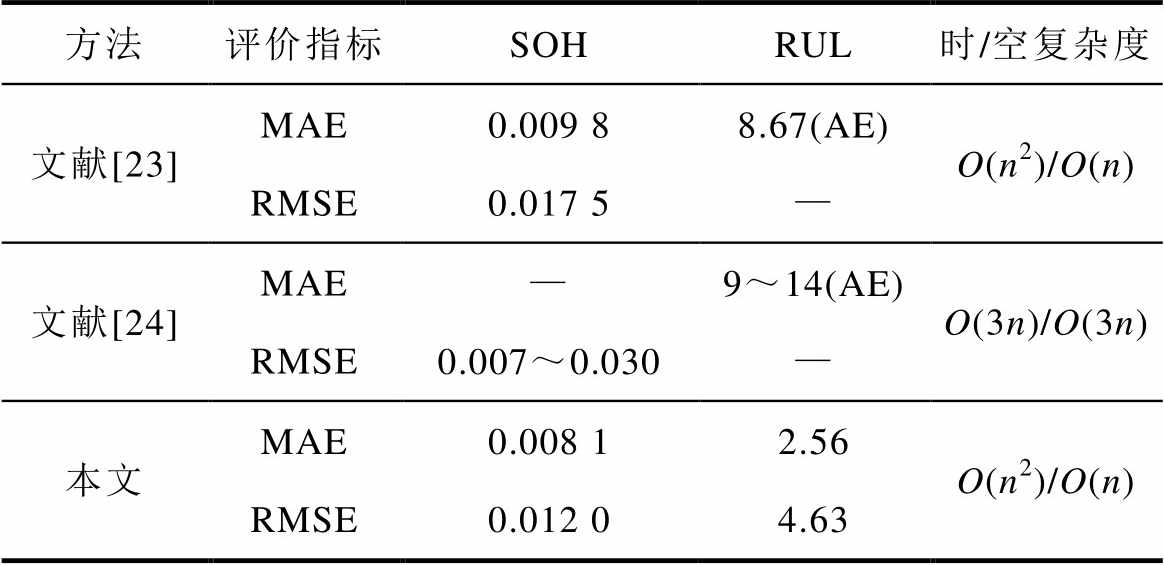
方法评价指标SOHRUL时/空复杂度 文献[23]MAE0.009 88.67(AE)O(n2)/O(n) RMSE0.017 5— 文献[24]MAE—9~14(AE)O(3n)/O(3n) RMSE0.007~0.030— 本文MAE0.008 12.56O(n2)/O(n) RMSE0.012 04.63
本文所对比的方法均使用CALCE数据集进行预测,且预测结果取自相应参考文献。文献[23]利用灰狼优化器对多核相关向量机进行优化,实现SOH的预测,并利用互补集合经验模态分解(CEEMD)提取RUL预测的老化特征,减小了SOH和RUL的预测误差。但是该方法仅针对特定模型进行优化研究,方法选择上存在一定的局限性。文献[24]设计了3层渐进式LSTM预测框架,预测电池SOH与RUL,该方法将先前的预测结果转移到后续预测中,提高了数据驱动模型自身的学习能力。而该方法仅利用了充放电时间特征中的老化特性,使得输入特征中的老化信息并不全面,且联合预测时未考虑容量回升现象,使得预测准确度较低。
表9中,本文采用大O法[18]评估各预测方法的时空复杂度,其中n为预测步长度,即循环次数。由于在联合预测过程中,本方法与文献[23]方法均采取了模态分解算法提取RUL预测特征,时空复杂度与该算法保持一致,均为二次阶O(n2)/线性阶O(n),在相同算法复杂度下,本方法的预测结果较文献[23]方法误差更小,预测效果更为理想;反之,文献[24]方法忽视了原始容量对RUL预测的重要性,尽管预测效率相对较高,但损失了一定的预测精度。同时表9列出了各预测方法的MAE和RMSE计算结果,使用评价指标MAE时,本方法较文献[23]方法在SOH预测上提高了17.34%,使用评价指标RSME时,本方法较文献[23-24]方法分别提高了31.4%、60%(RSME为0.030时);而对于RUL预测,所提方法的MAE与上述两种方法的绝对误差(Absolute Error,AE)位于同一计数等级,且数值明显小于二者预测误差。可以进一步得出,本文提出的联合预测方法在保证较好的运行复杂度基础上,具有更高的精度优势,更适用于新能源汽车和储能电站等预测精度要求严格的应用场景。
为准确地估计电池老化状态,本文提出了一种基于间接健康特征优化与多模型融合的锂电池SOH-RUL联合预测方法。并通过CALCE数据集验证了该方法的预测精度和可靠性,具体结论如下:
1)使用特征并行融合与注意力机制对充电电压曲线上的不同健康特征进行优化,提取出间接健康特征Co-HF。通过与不同健康特征的容量预测效果进行对比,结果表明所提特征Co-HF与电池容量相关度更高,能更全面地反映充电电压中所蕴含的老化信息,更适合作为IHF进行SOH和RUL预测。
2)通过建立SVR-BMA与LSTM-BMA融合预测模型,将多个预测子模型的预测结果进行融合处理,解决数据驱动模型预测的不确定性问题。与单一预测模型相比,该方法明显减少了锂电池SOH与RUL的预测误差,且在相同算法复杂度下,所建立的融合模型较其他方法具有更高的预测精度。
综上所述,本文所提出的基于间接健康特征优化与多模型融合的锂电池SOH-RUL联合预测方法可以有效地提高预测结果的准确性和可靠性,为电池管理和维护提供更有价值的参考信息,从而保障新能源汽车和储能电站等具有储能需求的装置安全稳定运行。然而,该方法尚未在其他电池或更复杂的工况下进行验证,因而在进一步应用时需要对其进行优化,未来的工作将从以下方面进行改进:
1)选取能反映特殊电池容量退化规律的间接健康特征进行实验,如三元锂电池寿命末期可能存在容量跳水现象。
2)采取性能更优的算法对模型参数进行求解。
附录 正文字符定义
附表1 名称缩略词及含义
App.Tab.1 Abbreviated meaning of terms

名称缩写含 义 SOH锂电池健康状态 RUL剩余使用寿命 IHF间接健康特征 SVR支持向量回归 LSTM长短期记忆神经网络 BMA贝叶斯模型平均 CEEMDAN自适应噪声完备集合经验模态分解 BMS电池管理系统 EOL寿命终止 GPR高斯过程回归 EMD经验模态分解 HF健康特征 Concat特征并行融合 Attention注意力机制 EM期望最大化 IMF本征模态函数 SP预测起始点
附表2 流程参数定义
App.Tab.2 Process parameter definition

流程参数定 义 X、Y计算Pearson系数的特征样本、容量样本 Co-HF、xCo-HF优化后的间接健康特征、特征Co-HF的运算向量 下标k表示第k个子模型 下标n表示第n次循环次数 K训练集中训练样本个数 N总循环次数 M候选模型个数 SVR-k、LSTM-kSVR子模型、LSTM子模型 SVRpre、LSTMpreSVR候选模型、LSTM候选模型 xSVR模型输入特征 y实测容量值 子模型容量预测值 SVRpre的容量预测值 SVR-BMA融合模型容量预测值 待测电池原始容量
(续)

流程参数定 义 子模型原始容量预测值 LSTMpre的原始容量预测值 LSTM-BMA融合模型容量预测值 Dp、Dt、Dp0IHF训练集、测试集、原始容量训练集 SVR子模型预测的容量序列, SVR-BMA融合模型预测的容量序列, Y0待测电池原始容量序列, LSTM子模型预测的原始容量序列, LSTM-BMA融合模型预测的原始容量序列,
附表3 方法、参数及定义
App.Tab.3 Method parameter definition

方法参数定义 Concat、Concat两个通路下的输入特征 A、BConcat两个通路下的通道数 *卷积运算 、输入特征、的权重 Attention、输入特征、的注意力分布 、、、得分函数待学习的权重系数 q最后一个隐藏层大小 、得分函数的偏置系数 SVRF(x)xk在高维特征空间下的映射 w、mSVR回归函数的权重、截距 x、x*松弛变量 C惩罚因子 e预测误差容限 BMAwk子模型k的模型权重 、子模型k的后验分布、融合模型的联合概率 mk0、Sk0、wk0和mk、Sk、wk子模型k的初始期望、初始协方差、初始权重以及期望、协方差、权重 zk子模型k的隐变量 隐变量的后验分布,上标(d)表示迭代次数 s、lSVRpre和LSTMpre的模型权重 LSTMfn、vn、on遗忘门、输入门、输出门 、和hn-1、hn内部中间状态和单元隐藏状态 Wf、Wv、Wo、Wc各门机制与内部中间状态的权重矩阵
(续)

方法参数定义 bf、bv、bo、bc各门机制与内部中间状态的偏置 激活函数Sigmoid ⊙向量元素乘积运算
附表4 时间参数定义
App.Tab.4 Time parameter definition
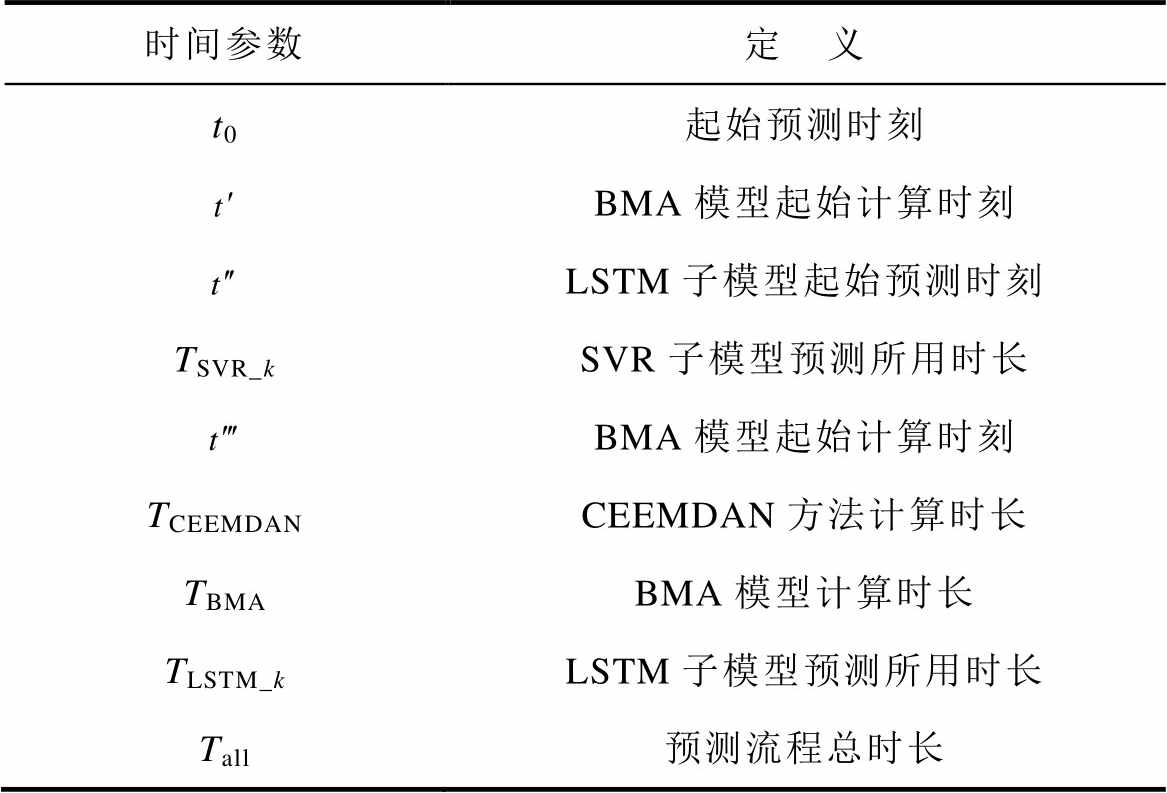
时间参数定 义 t0起始预测时刻 BMA模型起始计算时刻 LSTM子模型起始预测时刻 TSVR_kSVR子模型预测所用时长 BMA模型起始计算时刻 TCEEMDANCEEMDAN方法计算时长 TBMABMA模型计算时长 TLSTM_kLSTM子模型预测所用时长 Tall预测流程总时长
参考文献
[1] 李先锋, 张洪章, 郑琼, 等. 能源革命中的电化学储能技术[J]. 中国科学院院刊, 2019, 34(4): 443- 449.
Li Xianfeng, Zhang Hongzhang, Zheng Qiong, et al. Electrochemical energy storage technology in energy revolution[J]. Bulletin of Chinese Academy of Sciences, 2019, 34(4): 443-449.
[2] 牛志远, 姜欣, 谢镔, 等. 电动汽车过充燃爆事故模拟及安全防护研究[J]. 电工技术学报, 2022, 37(1): 36-47, 57.
Niu Zhiyuan, Jiang Xin, Xie Bin, et al. Study on simulation and safety protection of electric vehicle overcharge and explosion accident[J]. Transactions of China Electrotechnical Society, 2022, 37(1): 36-47, 57.
[3] Hu Xiaosong, Deng Xinchen, Wang Feng, et al. A review of second-life lithium-ion batteries for stationary energy storage applications[J]. Proceedings of the IEEE, 2022, 110(6): 735-753.
[4] Deng Yuanwang, Ying Hejie, Jiaqiang E, et al. Feature parameter extraction and intelligent esti- mation of the state-of-health of lithium-ion batte- ries[J]. Energy, 2019, 176: 91-102.
[5] Meng Jinhao, Cai Lei, Luo Guangzhao, et al. Lithium-ion battery state of health estimation with short-term current pulse test and support vector machine[J]. Microelectronics Reliability, 2018, 88/ 89/90: 1216-1220.
[6] Yang Duo, Zhang Xu, Pan Rui, et al. A novel Gaussian process regression model for state-of-health estimation of lithium-ion battery using charging curve[J]. Journal of Power Sources, 2018, 384: 387-395.
[7] Yayan U, Arslan A T, Yucel H. A novel method for SOH prediction of batteries based on stacked LSTM with quick charge data[J]. Applied Artificial Intel- ligence, 2021, 35(6): 421-439.
[8] 肖迁, 穆云飞, 焦志鹏, 等. 基于改进LightGBM的电动汽车电池剩余使用寿命在线预测[J]. 电工技术学报, 2022, 37(17): 4517-4527.
Xiao Qian, Mu Yunfei, Jiao Zhipeng, et al. Improved LightGBM based remaining useful life prediction of lithium-ion battery under driving conditions[J]. Transactions of China Electrotechnical Society, 2022, 37(17): 4517-4527.
[9] 赵靖英, 胡劲, 张雪辉, 等. 基于锂电池模型和分数阶理论的SOC-SOH联合估计[J]. 电工技术学报, 2023, 38(17): 4551-4563.
Zhao Jingying, Hu Jin, Zhang Xuehui, et al. Joint estimation of the SOC-SOH based on lithium battery model and fractional order theory[J]. Transactions of China Electrotechnical Society, 2023, 38(17): 4551- 4563.
[10] Park J, Lee M, Kim G, et al. Integrated approach based on dual extended Kalman filter and multivariate autoregressive model for predicting battery capacity using health indicator and SOC/SOH[J]. Energies, 2020, 13(9): 2138.
[11] Zhang Yongzhi, Xiong Rui, He Hongwen, et al. Long short-term memory recurrent neural network for remaining useful life prediction of lithium-ion batteries[J]. IEEE Transactions on Vehicular Tech- nology, 2018, 67(7): 5695-5705.
[12] 王萍, 弓清瑞, 张吉昂, 等. 一种基于数据驱动与经验模型组合的锂电池在线健康状态预测方法[J]. 电工技术学报, 2021, 36(24): 5201-5212.
Wang Ping, Gong Qingrui, Zhang Jiang, et al. An online state of health prediction method for lithium batteries based on combination of data-driven and empirical model[J]. Transactions of China Electro- technical Society, 2021, 36(24): 5201-5212.
[13] Liu Kailong, Shang Yunlong, Ouyang Quan, et al. A data-driven approach with uncertainty quantification for predicting future capacities and remaining useful life of lithium-ion battery[J]. IEEE Transactions on Industrial Electronics, 2020, 68(4): 3170-3180.
[14] Vosseler A, Weber E. Forecasting seasonal time series data: a Bayesian model averaging approach[J]. Computational Statistics, 2018, 33(4): 1733-1765.
[15] Yang Jing, Fang Gonghuan, Chen Yaning, et al. Climate change in the Tianshan and northern Kunlun mountains based on GCM simulation ensemble with Bayesian model averaging[J]. Journal of Arid Land, 2017, 9(4): 622-634.
[16] 王萍, 范凌峰, 程泽. 基于健康特征参数的锂离子电池SOH和RUL联合估计方法[J]. 中国电机工程学报, 2022, 42(4): 1523-1534.
Wang Ping, Fan Lingfeng, Cheng Ze. A joint state of health and remaining useful life estimation approach for lithium-ion batteries based on health factor parameter[J]. Proceedings of the CSEE, 2022, 42(4): 1523-1534.
[17] Yu Jianbo. State of health prediction of lithium-ion batteries: multiscale logic regression and Gaussian process regression ensemble[J]. Reliability Engin- eering & System Safety, 2018, 174: 82-95.
[18] 黄凯, 丁恒, 郭永芳, 等. 基于数据预处理和长短期记忆神经网络的锂离子电池寿命预测[J]. 电工技术学报, 2022, 37(15): 3753-3766.
Huang Kai, Ding Heng, Guo Yongfang, et al. Prediction of remaining useful life of lithium-ion battery based on adaptive data preprocessing and long short-term memory network[J]. Transactions of China Electrotechnical Society, 2022, 37(15): 3753- 3766.
[19] Boulahia S Y, Amamra A, Madi M R, et al. Early, intermediate and late fusion strategies for robust deep learning-based multimodal action recognition[J]. Machine Vision and Applications, 2021, 32(6): 121.
[20] 戴俊彦, 夏明超, 陈奇芳. 基于双重注意力机制的电池SOH估计和RUL预测编解码模型[J]. 电力系统自动化, 2023, 47(6): 168-177.
Dai Junyan, Xia Mingchao, Chen Qifang. Encoding and decoding model of state of health estimation and remaining useful life prediction for batteries based on dual-stage attention mechanism[J]. Automation of Electric Power Systems, 2023, 47(6): 168-177.
[21] Zhi Yue, Wang Heqi, Wang Liang. A state of health estimation method for electric vehicle Li-ion batteries using GA-PSO-SVR[J]. Complex & Intelligent Systems, 2022, 8(3): 2167-2182.
[22] Sayah M, Guebli D, Al Masry Z, et al. Robustness testing framework for RUL prediction deep LSTM networks[J]. ISA Transactions, 2021, 113: 28-38.
[23] Lü Zhiqiang, Wang Geng, Gao Renjing. Li-ion battery prognostic and health management through an indirect hybrid model[J]. Journal of Energy Storage, 2021, 42: 102990.
[24] Bak T, Lee S. Accurate estimation of battery SOH and RUL based on a progressive LSTM with a time compensated entropy index[C]//Annual Conference of the PHM Society, Scottsdale, 2019: 2012-2013.
Joint Prediction of Lithium Battery State of Health and Remaining Useful Life Based on Indirect Health Features Optimization and Multi-Model Fusion
Abstract Lithium-ion batteries have become essential for new energy vehicles and energy storage power stations due to their high energy density, low self-discharge rate, and reliable cleanliness. However, lithium batteries gradually age with increasing cycle counts, leading to decreased battery performance. State of health (SOH) and remaining useful life (RUL) are important indicators for evaluating battery aging status, and accurate predictions of these metrics are crucial for the safe operation of energy storage systems. However, choosing suitable indirect health features (IHF) for SOH and RUL predictions is challenging. Data-driven models generate uncertainties, resulting in inaccurate predictions of SOH and RUL. Therefore, this paper proposes a joint prediction method for lithium battery SOH and RUL based on indirect health feature optimization and multi-model fusion.
Firstly, multiple health factors (HF) are extracted from charging voltage curves, and IHF are obtained through feature concatenation and attention mechanism optimization, denoted as feature Co-HF. Then, Bayesian model averaging (BMA) is introduced to address uncertainties in the prediction process. With support vector regression (SVR) and long short-term memory (LSTM), SVR-BMA and LSTM-BMA models are constructed. Additionally, the input features for RUL prediction are extracted from SOH capacity predictions using the complete ensemble empirical mode decomposition with adaptive noise (CEEMDAN) method, enabling joint prediction of SOH and RUL.
The proposed method is validated using the University of Maryland's CALCE lithium battery dataset. Compared with different HFs and predictions of each sub-model, the Co-HF capacity prediction results are closer to the measured values, and the tracking effect of capacity trends is ideal. The mean absolute error (MAE) and root mean squared error (RMSE) of SOH predictions using the proposed fusion model are 0.008 1 and 0.012 0, respectively, and the MAE and RMSE of RUL predictions are 2.56 and 4.63, respectively. The prediction errors are lower than those of each sub-model. In addition, the error tolerance of SOH and RUL predictions is within 5% at SP=100/200/300. Thus, the proposed method significantly reduces the MAE and RMSE of SOH and RUL predictions.
From the experimental analysis, it can be concluded that: (1) the optimized feature Co-HF comprehensively reflects the aging information in lithium battery charging voltage, which is suitable for SOH predictions. (2) The proposed model effectively reduces prediction errors of lithium battery SOH and RUL, improving the accuracy and reliability of predictions. Future work will focus on selecting indirect health features that reflect special battery capacity degradation laws and adopting better algorithms to solve model parameters.
Keywords:State of health, remaining useful life, indirect health factor, bayesian model averaging, support vector regression, long short-term memory
中图分类号:TM912
DOI: 10.19595/j.cnki.1000-6753.tces.231057
湖南省科技创新人才计划科技创新团队资助项目(2021RC4061)。
收稿日期 2023-07-05
改稿日期 2023-07-31
蔡雨思 女,2000年生,硕士研究生,研究方向为锂电池能量管理、状态估计及寿命预测、电池储能系统。
E-mail: cys_0229@163.com
李泽文 男,1975年生,教授,博士生导师,研究方向为储能电池管理技术、现代电力电子技术及电力系统保护与控制等。
E-mail: lzw0917@163.com(通信作者)
(编辑 陈 诚)