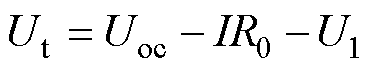 (1)
(1)
摘要 析锂是制约石墨阳极型锂离子电池快充安全与效率的关键问题。为了保障车载电池充电安全、缓解新能源汽车里程焦虑,有必要针对锂离子电池开展无析锂快充研究。鉴于此,该文基于锂离子电池电极等效电路模型,提出一种由阳极电势观测器和充电电流控制器组成的双闭环无析锂快充策略调控方案,实现了锂离子电池的无析锂安全快充。实验结果表明,不同工况下的阳极电势平均观测误差均低于5 mV,最大误差不超过10 mV;在电流调节过程中,阳极电势到达并稳定在设定阈值+1 mV范围内的调节时间为26 s,稳态误差小于0.05 mV,并且无超调和振荡。此外,与1C恒流恒压策略相比,该策略能节省46%的充电时间,充电过程中阳极电势最低为4.8 mV,且将锂离子电池拆解后也未发现析锂,证明该策略能明显缩短充电时间并有效抑制析锂。
关键词:锂离子电池 电极等效电路模型 阳极电势 快充策略
近年来,能源危机与环境污染是世界各国亟须解决的重点问题[1]。为了减少对传统化石能源的依赖,新能源汽车的相关研究受到了越来越多国家的重视[2-3]。锂离子电池具有能量密度高、寿命长、环境友好等优点[4],因此受到了新能源汽车行业的青睐[5]。但随着新能源汽车产业的不断发展,对锂离子电池的能量密度、安全性和寿命等性能提出了更高的要求,使得锂离子电池在新能源汽车上的应用仍然面临许多挑战[6]。其中,安全快速充电问题就是制约锂离子动力电池发展和应用的一大瓶颈[7]。
目前,众多学者对车载电池快速充电方法开展了广泛的研究。在众多充电策略中,最常见的是恒流恒压(Constant Current-Constant Voltage, CC-CV)法,由CC和CV阶段组成。然而,CC-CV充电对
电流和电压的限制过于保守,导致充电时间较长[8]。为了缩短充电时间,相关学者基于CC-CV方法,提出了一些其他的快速充电策略。文献[9]中提出了一种将多级CC与CV相结合的方法。该方法可以减少充电时间,但是难以准确设定每级CC下的充电电流幅值及持续时间。与包含CC和CV阶段的充电模式相比,文献[10]提出一种线性电流衰减(Linear Current Decay, LCD)的充电策略。该策略在初始阶段以高倍率电流对电池充电,然后电流会线性衰减以减少充电时间,但可能导致过充电。此外,脉冲充电(Pulse Charging, PC)可以降低极化现象并提高充电速度[11],但其电流脉冲波形设置具有一定难度。
以上充电策略均是基于锂离子电池运行经验所提出的,尽管这些充电策略在电动汽车电池管理系统(Battery Management System, BMS)中相对容易实现,但充电时没有考虑电池的内部状态,可能会对电池造成损伤[12]。在锂离子电池快充过程中,阳极析锂对电池寿命影响最为严重[13]。在正常充电工况条件下,锂离子从阴极材料中脱离、穿过隔膜并嵌入阳极活性材料中。然而,在低温、高倍率充电、过充电等条件下,阳极电势易达到析锂电势阈值(0 V vs. Li/Li+),从而导致锂离子直接在阳极材料表面发生还原反应,形成析锂[14-15]。析出的锂金属不但易与电解液发生副反应,消耗电池内部可用锂存量,而且部分析出的锂金属会与阳极失去电接触从而转变成“死锂”,加速电池的老化和容量衰减[16]。此外,析出的锂金属在电极表面表现为苔藓状或树枝状等不同的结构。树枝状的金属锂可能会刺破隔膜,导致电池内部短路,从而引发电池热失控等安全事故[17]。
为了解决上述问题,Bernd Epding等[18]基于三电极实验制定了多级CC充电策略,有效避免了析锂反应的发生。除此之外,许多国内外的学者从电池模型角度入手,优化无析锂的充电策略方案。其中,电池模型以电化学模型(Electrochemical Models,EMs)[19]和等效电路模型(Equivalent Circuit Model, ECM)[20]为主。M. Doyle等[21-22]于1993年提出了锂离子电池的伪二维(Pseudo-Two-Dimensional, P2D)模型。该模型由几个耦合非线性偏微分方程组成,是锂离子电池电化学模型的基本框架。虽然该模型能反映电池在运行过程中真实的电化学状态,但其计算成本高,参数辨识困难,因而难以实际应用于电动汽车电池管理系统[23-24]。为此,有学者提出了简化的电化学模型,如单粒子(Single Particle, SP)模型[25]、域分解简化的电化学模型[26]等。S. Tippmann等[27]将电化学模型与热模型相结合,得出了析锂程度随充电速率和电池荷电状态(State of Charge, SOC)变化的曲线。Chu Zhengyu等[28]提出了一种基于简化P2D模型的快速充电算法。该算法由阳极过电位观测闭环和充电电流调节闭环组成,每个闭环均包含一个PID控制器,能够实现预测阳极过电势和自动调节充电电流,具有析锂抑制功能。相较于电化学模型而言,等效电路模型结构简单,需要估计的参数较少[29]。然而,普通等效电路模型无法获知电池内部电极状态信息,因而也无法依据电极电势信息制定相应的无析锂充电策略。因此,Zhao Tongzheng等[30]提出了基于参考电极的半电池等效电路模型,该模型能够用于估计电池的阳极电势,且估计结果与基于P2D模型的估计结果非常接近。R. Drees等[31-33]在此基础上提出了完整的电极等效电路模型,并以模型估算出的阳极电势为边界条件制定了充电策略。但其阳极电势为开环估计,没有考虑实际环境对模型参数产生的影响。在此基础上,Lu Yufang等[34]对比了P2D、SP、ECM和电极等效电路模型的估计精度,提出了基于电极等效电路模型的阳极电势观测算法和基于PID控制的快充算法。但在控制过程中阳极电势与充电电流均存在振荡现象,系统的动态特性不佳。目前针对电极等效电路模型的无析锂快充策略研究较少,充电电流控制方案与模型机理对应不明确,缺乏同时兼顾高精度和高鲁棒性的无析锂快充调控方案。
针对上述问题,本文搭建了基于扩展卡尔曼滤波(Extended Kalman Filter, EKF)算法的阳极电势闭环观测器和具有前置补偿方法的充电电流闭环控制器,二者联合作用构成了锂离子电池无析锂快充策略调控方案,从而实现了阳极电势的在线评估与充电电流的在线平滑控制。首先,搭建了锂离子电池双电极等效电路模型,利用锂离子电池三电极实验完成了多荷电状态条件下模型参数的离线辨识;其次,说明阳极电势闭环观测器和充电电流闭环控制器的联合观测-控制逻辑;最后,论证本文所提锂离子电池无析锂快充策略调控方案的合理性与有 效性。
1.1.1 等效电路模型
常见的等效电路模型由开路电压源、电阻和电容等电气元件组成,能够模拟电池端电压外特性的变化趋势,且具有较高的模型精度和计算效率。文献[35]对比研究了Rint、Thevenin和PNGV等几种常见的等效电路模型结构及其精度,发现Thevenin模型能够兼顾模型复杂度和计算精度。因此,本节以Thevenin模型为例,介绍等效电路模型的建模机理。Thevenin模型的结构如图1所示。该模型的电路方程为
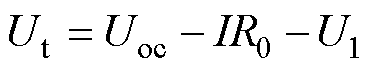 (1)
(1)
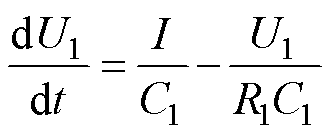 (2)
(2)
式中,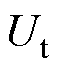 为电池的端电压;
为电池的端电压;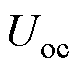 为电池的开路电压;
为电池的开路电压;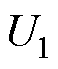 为RC并联支路电压;
为RC并联支路电压;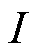 为流过电池的电流,默认电池放电时电流为正;
为流过电池的电流,默认电池放电时电流为正;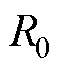 为电池的欧姆内阻;
为电池的欧姆内阻;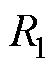 为电池的极化内阻;
为电池的极化内阻;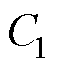 为电池的极化电容。
为电池的极化电容。
假设电池采样时间间隔为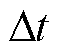 ,根据动态元件的动态时域响应特性,由
,根据动态元件的动态时域响应特性,由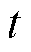 时刻状态计算出
时刻状态计算出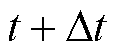 时刻的RC支路的电压响应为
时刻的RC支路的电压响应为
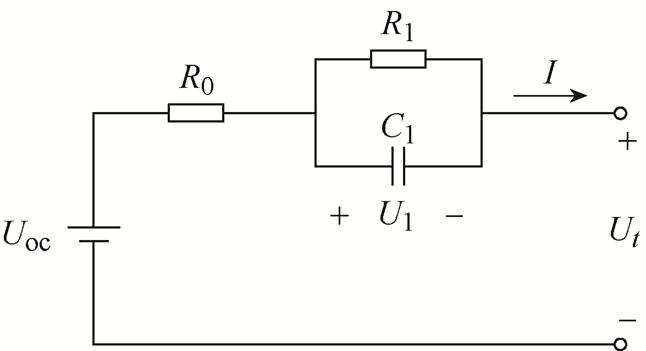
图1 Thevenin模型
Fig.1 Thevenin model
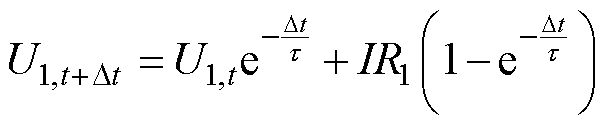 (3)
(3)
式中,t 为电池极化反应的时间常数,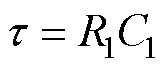 。
。
由模型的电路方程可看出,Thevenin模型能够模拟电池充放电过程中端电压的变化,但是无法反映电极行为和老化特性。
1.1.2 电极等效电路模型
为了解决普通等效电路模型不能获取电池内部电极状态信息的问题,有学者提出了能够模拟电池电极状态的电极等效电路模型(Electrode Equivalent Circuit Model, EECM)。一阶RC-EECM等效电路模型如图2所示,该模型由两个Thevenin模型串联组成,图1中上标ca代表阴极,上标an代表阳极,REF代表参考电极。
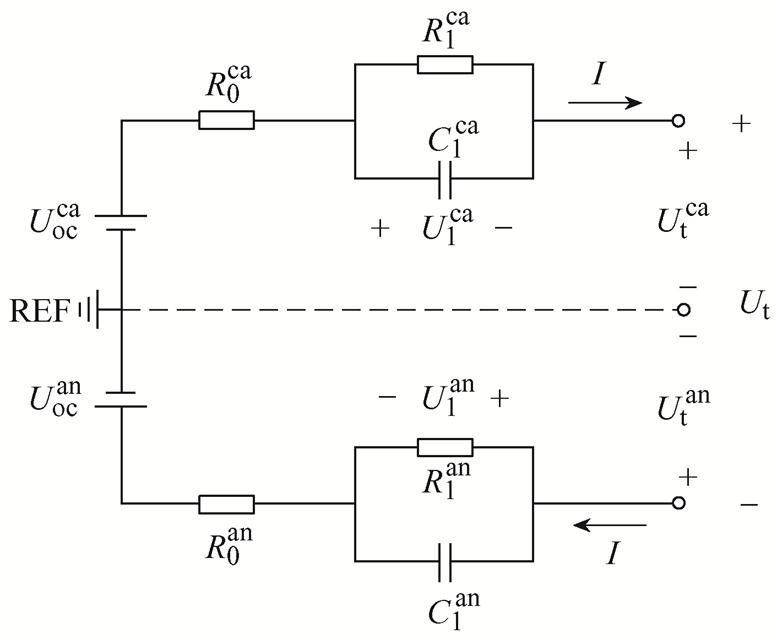
图2 一阶RC电极等效电路模型
Fig.2 First order RC electrode equivalent circuit model
该模型的电路方程以及电极电势关系为
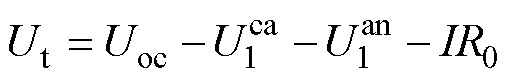 (4)
(4)
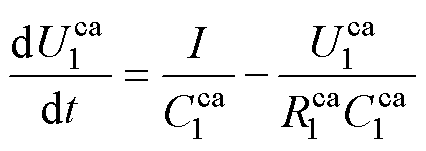 (5)
(5)
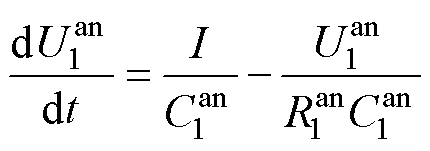 (6)
(6)
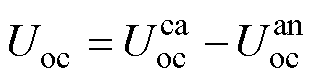 (7)
(7)
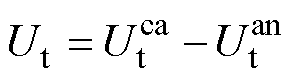 (8)
(8)
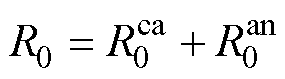 (9)
(9)
式中,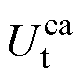 和
和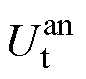 分别为电池的阴极和阳极电势,具体为
分别为电池的阴极和阳极电势,具体为
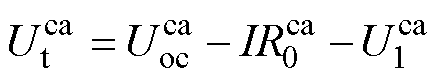 (10)
(10)
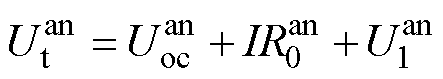 (11)
(11)
设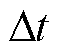 为采样时间,根据动态元件的动态时域响应特性,
为采样时间,根据动态元件的动态时域响应特性,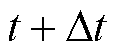 时刻的阴极和阳极RC支路电压分别为
时刻的阴极和阳极RC支路电压分别为
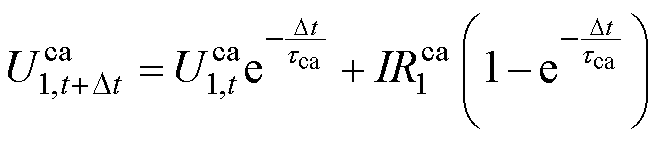 (12)
(12)
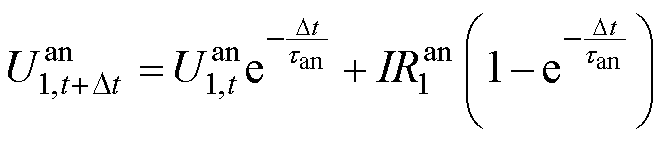 (13)
(13)
其中
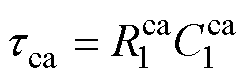
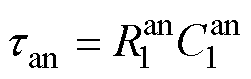
式中,tca、tan分别为阴极和阳极的时间常数。
电池等效电路模型参数可以基于HPPC测试来进行辨识[36]。电极等效电路模型参数辨识,则需要锂离子电池三电极实验测试数据。详细的三电极电池制作方法可参考文献[37]。
本文所用电池容量为0.6 A·h的NCM/石墨型三电极软包锂离子电池,参考电极材料为金属锂,电池叠片顺序、参考电极位置以及三电极锂离子电池实物如图3所示。电池上/下限截止电压阈值分别为4.2 V和3.0 V,且测试环境温度恒为20 ℃。三电极锂离子电池测试平台如图4所示。

图3 三电极锂离子电池测试平台
Fig.3 Three-electrode lithium-ion battery
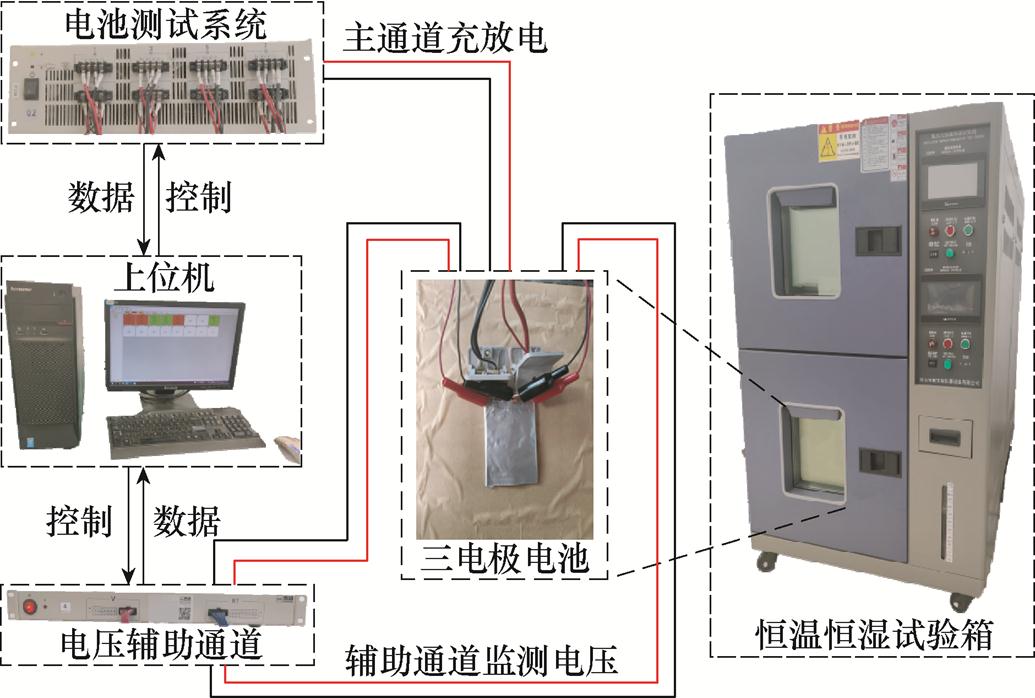
图4 三电极锂离子电池实验测试平台
Fig.4 Three-electrode lithium-ion battery experimental test platform
1.2.1 伪开路电压测试
由式(4)、式(10)~式(13)可知,当流过电池的电流足够小时,可以近似认为电池的端电压等于开路电压。因此采用小倍率电流对电池充电,可近似模拟出电池的开路电压与SOC之间的关系。在电池SOC为0时,用0.05C的小电流对电池进行恒流充电到截止电压4.2 V,即可得到不同SOC下的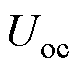 、
、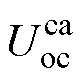 和
和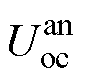 ,辨识结果如图5所示。为方便后续计算,可将开路电压与SOC的关系进行拟合,SOC-OCV曲线的多项式拟合关系为
,辨识结果如图5所示。为方便后续计算,可将开路电压与SOC的关系进行拟合,SOC-OCV曲线的多项式拟合关系为
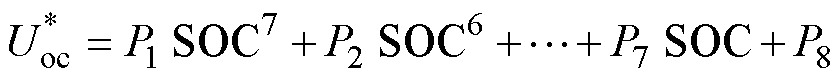 (14)
(14)
式中,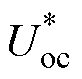 可代表
可代表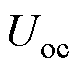 、
、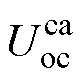 、
、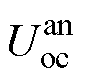 ,
,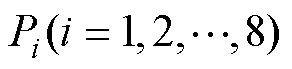 为多项式拟合系数。
为多项式拟合系数。
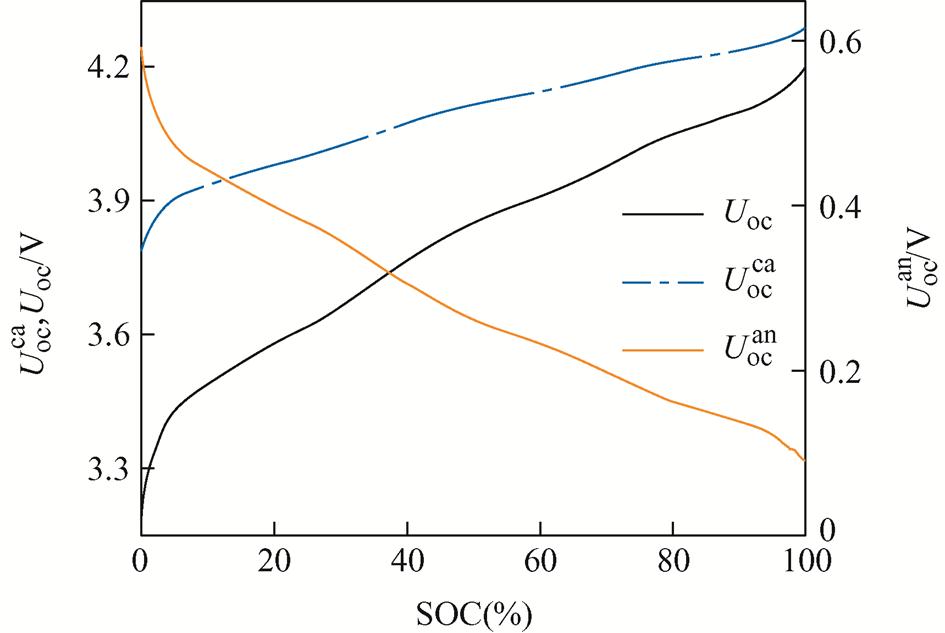
图5 开路电压辨识结果
Fig.5 Open-circuit voltage identification results
1.2.2 变流充电测试
1.2.1节中已经辨识出开路电压参数。一阶RC-EECM中还需要辨识的参数包括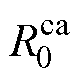 、
、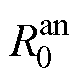 、
、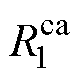 、
、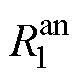 、
、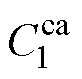 、
、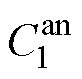 。在后续的算法运行过程中,均使用阴极和阳极的时间常数
。在后续的算法运行过程中,均使用阴极和阳极的时间常数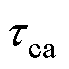 和
和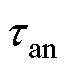 进行迭代计算,故在参数辨识过程中只需辨识
进行迭代计算,故在参数辨识过程中只需辨识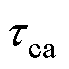 和
和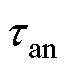 ,无需辨识
,无需辨识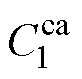 、
、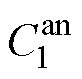 。本节采用一种基于三电极锂离子电池变流充电实验的参数辨识方法,具体实验步骤如下:
。本节采用一种基于三电极锂离子电池变流充电实验的参数辨识方法,具体实验步骤如下:
(1)取SOC=0的三电极锂离子电池。
(2)以0.1C的电流恒流充电1 h。
(3)静置1 h。
(4)重复步骤(2)和步骤(3)直至SOC=90%。
(5)以0.1C的电流恒流充电至截止电压4.2 V。
(6)静置1 h。
通过变流充电实验,即可辨识出阴极、阳极的欧姆内阻和极化内阻。以阴极为例,任取一个步骤(2)和步骤(3)的周期,如图6所示。
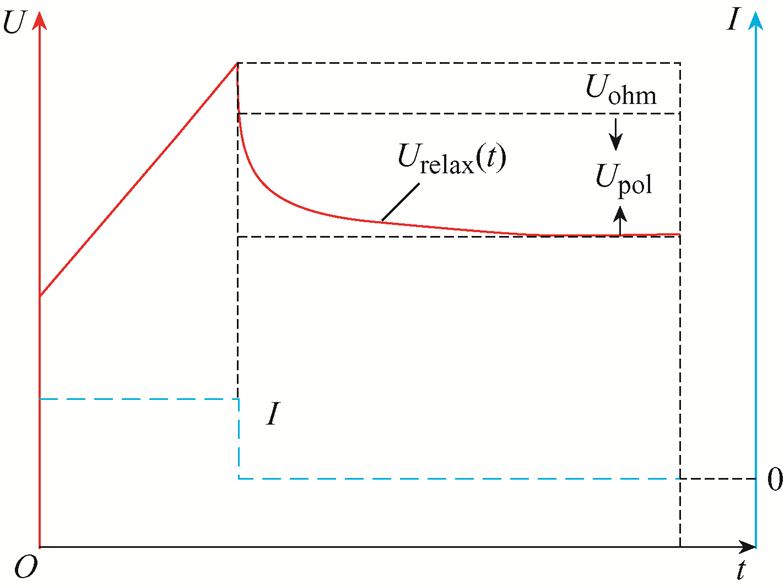
图6 内阻计算方法
Fig.6 Internal resistance calculation method
当前SOC下的欧姆内阻与极化内阻的具体计算式为
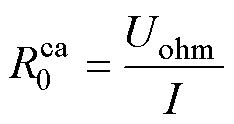 (15)
(15)
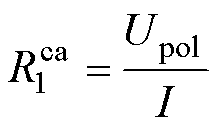 (16)
(16)
式中,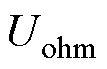 为欧姆压降;
为欧姆压降;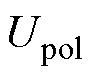 为极化压降;
为极化压降;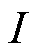 为充电电流值。通过Matlab的拟合工具箱对步骤(3)的电压响应
为充电电流值。通过Matlab的拟合工具箱对步骤(3)的电压响应 进行一阶指数函数拟合,就能得到当前SOC下的阴极的时间常数
进行一阶指数函数拟合,就能得到当前SOC下的阴极的时间常数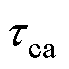 。同理,能得出当前SOC下阳极对应参数
。同理,能得出当前SOC下阳极对应参数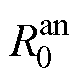 、
、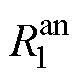 、
、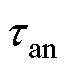 。不同SOC下的
。不同SOC下的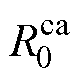 、
、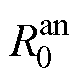 、
、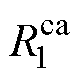 、
、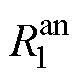 、
、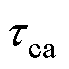 、
、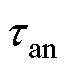 辨识结果如图7所示。阴极、阳极的欧姆内阻和极化内阻随荷电状态的变化而波动,在较低或较高荷电状态时呈现为高阻抗。阴极、阳极的时间常数在高荷电状态时呈现出较大的数值。
辨识结果如图7所示。阴极、阳极的欧姆内阻和极化内阻随荷电状态的变化而波动,在较低或较高荷电状态时呈现为高阻抗。阴极、阳极的时间常数在高荷电状态时呈现出较大的数值。
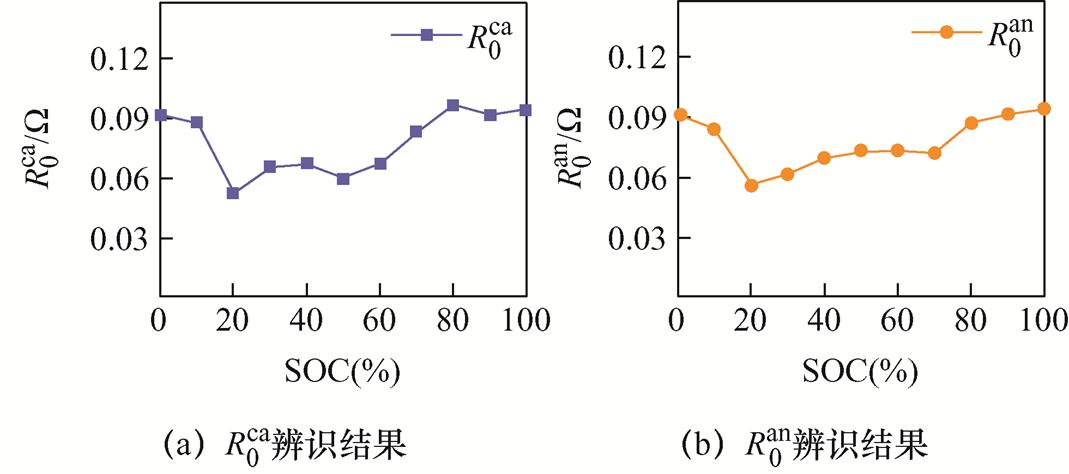
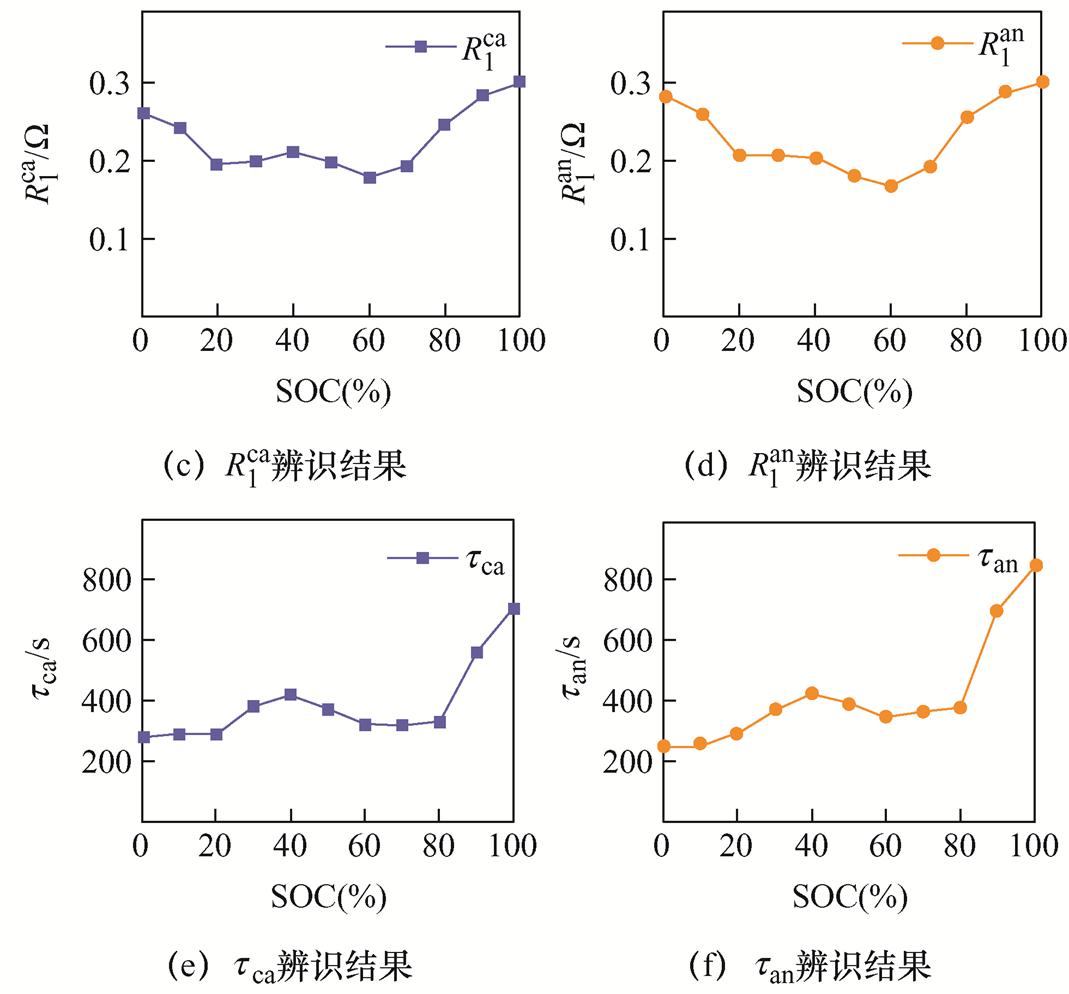
图7 电极等效电路模型参数辨识结果
Fig.7 Results of the identification of the parameters of the electrode equivalent circuit model
安全快速充电的目标是在对电池的损伤最小的情况下尽可能地减少充电时间[29]。锂离子电池在充电过程中,最容易对电池造成损伤的问题就是在阳极发生的金属锂的析出,这就使得想要缩短充电时间并不能一味地提高充电倍率,还要考虑电池的耐受程度。在整个充电过程中,阳极电势应始终保持在0 V(vs. Li/Li+)以上,以避免阳极析锂。
基于电极等效电路模型的锂离子电池无析锂快充流程如下:首先搭建的锂离子电池双电极等效电路模型,利用锂离子电池三电极实验完成多荷电状态下模型参数的离线辨识;其次将阳极电势作为状态变量进行观测;最后划定阳极电势对应的安全充电区域,依据阳极电势的观测值和安全充电区域实现充电电流的在线控制,如图8所示。图中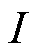 为快充电流,
为快充电流,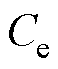 为电池容量。
为电池容量。
本文所提无析锂快充策略调控方案由两个闭环控制器组成,包括阳极电势闭环观测器和充电电流闭环控制器,具体如图9所示。其中,基于EKF算法的阳极电势闭环观测器用于实时观测电池的阳极电势等内部状态,通过把电池端电压作为观测变量,进而提高电池状态观测精度;基于前置补偿方法的充电电流闭环控制器则从模型出发,将观测出的电池阳极状态信息与设定阳极电势阈值建立联系,计算出当前状态下充电电流的最优解,达到调节充电电流的目的,同时对系统进行前置补偿,从而确保阳极电势尽可能地接近设定阈值,且在控制过程中阳极电势不发生超调。图9中,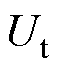 为电池端电压的测量值,
为电池端电压的测量值,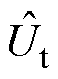 为电池端电压的估计值,
为电池端电压的估计值,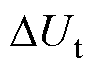 为端电压的估计值与测量值之间的误差,
为端电压的估计值与测量值之间的误差,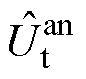 为阳极电势的估计值,
为阳极电势的估计值,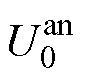 为设定的阳极电势阈值。
为设定的阳极电势阈值。
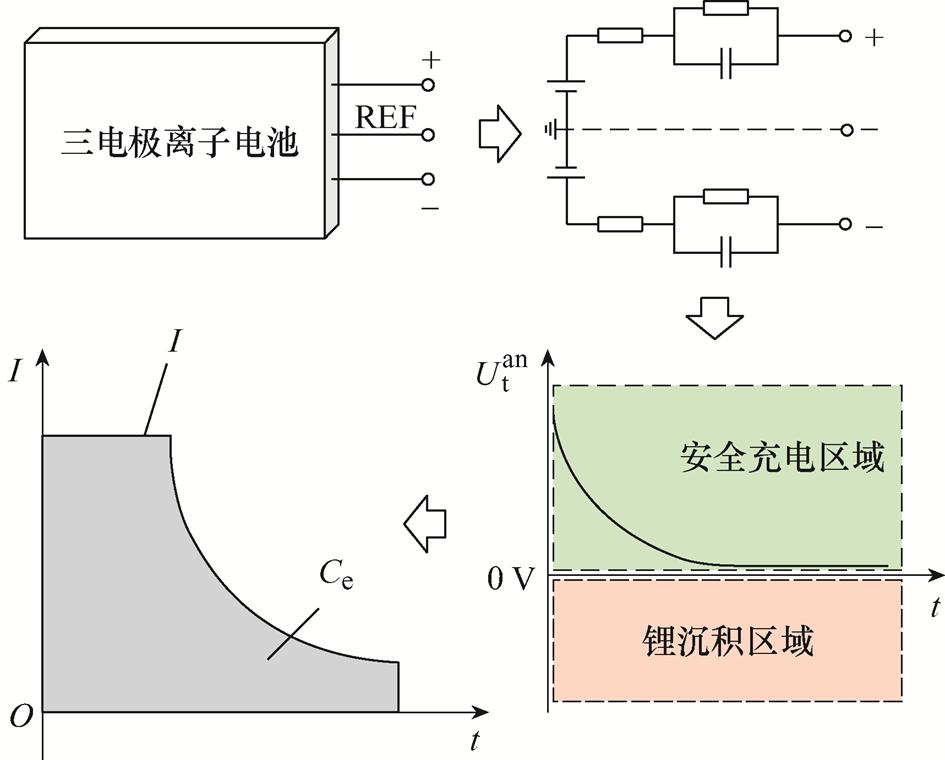
图8 基于EECM的锂离子电池无析锂快充流程
Fig.8 EECM-based fast charging process for lithium-ion batteries without lithium deposition
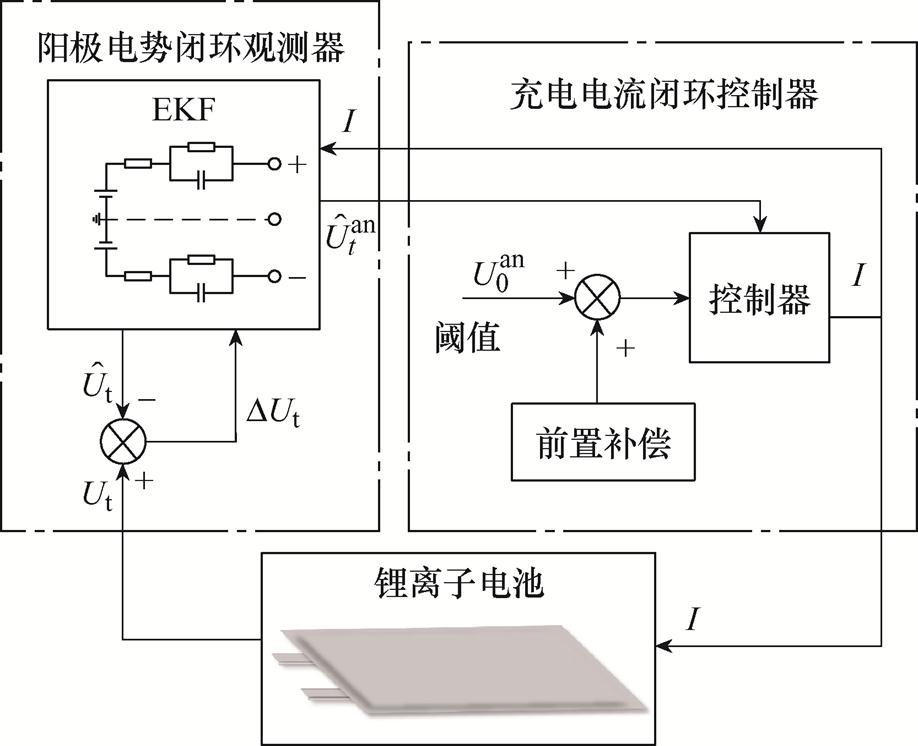
图9 阳极电势闭环观测器和充电电流闭环控制器
Fig.9 Anode potential closed-loop observer and charge current closed-loop controller
相比于ECM,EECM的一大优势就是能观测电池的阳极电势。在电池充电过程中,BMS能实时监测动力电池的端电压和充电电流,结合EECM即可实现动力电池阳极电势的在线监测。但电池所处的环境是非常复杂的,如果直接结合EECM而不引入反馈来观测阳极电势很难满足精度要求。为了提高观测精度以及系统鲁棒性,应该采用闭环控制算法。传统的EKF算法已经应用于传统ECM来进行SOC的估算[38]。在此基础上,本文设计了基于EECM和EKF的阳极电势闭环观测器,从而实现了电池荷电状态和阳极电势的在线观测。EKF算法迭代流程如图10所示。图中P为误差协方差矩阵,Kk为k时刻卡尔曼增益,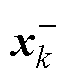 和
和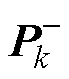 为
为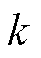 时刻的先验估计值。
时刻的先验估计值。
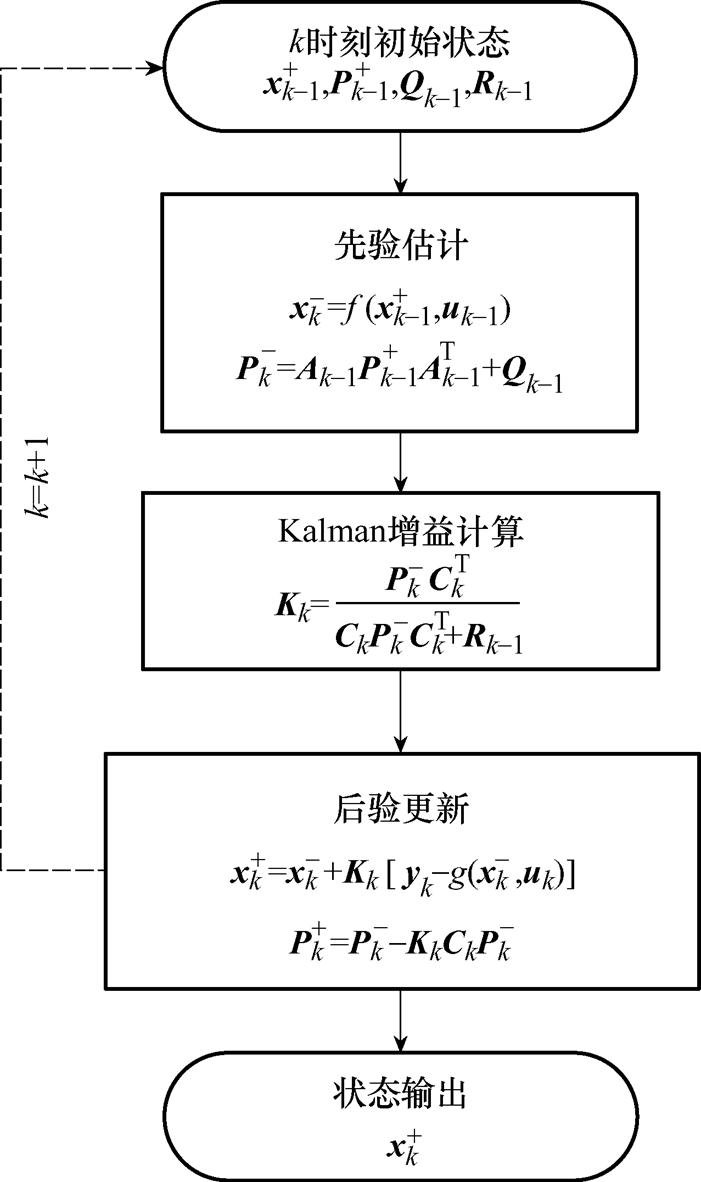
图10 EKF算法流程
Fig.10 EKF algorithm flow
在离散的非线性系统中,系统的状态方程和观测方程为
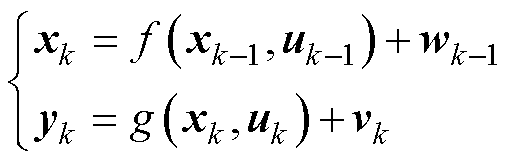 (17)
(17)
式中,非线性函数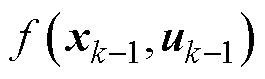 和
和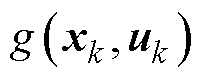 在所有采样点上均可微。
在所有采样点上均可微。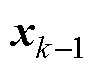 与
与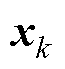 分别为
分别为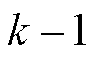 时刻与
时刻与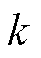 时刻的系统状态向量;
时刻的系统状态向量;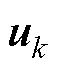 为
为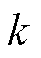 时刻的系统输入量;
时刻的系统输入量;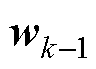 为k-1时刻的过程噪声,其方差表示为
为k-1时刻的过程噪声,其方差表示为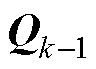 ;
;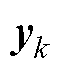 为
为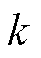 时刻的系统观测信号;
时刻的系统观测信号;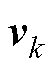 为k时刻的观测噪声,其方差表示为
为k时刻的观测噪声,其方差表示为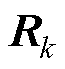 。为了能在非线性系统中实现滤波,EKF将非线性系统线性化的过程,就是将非线性系统状态转移方程
。为了能在非线性系统中实现滤波,EKF将非线性系统线性化的过程,就是将非线性系统状态转移方程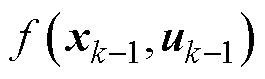 和非线性测量方程
和非线性测量方程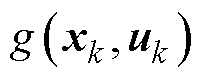 进行泰勒级数展开,省去高次项,留下一次项,从而可以获得一个近似的线性系统。线性化后的系统状态空间方程为
进行泰勒级数展开,省去高次项,留下一次项,从而可以获得一个近似的线性系统。线性化后的系统状态空间方程为
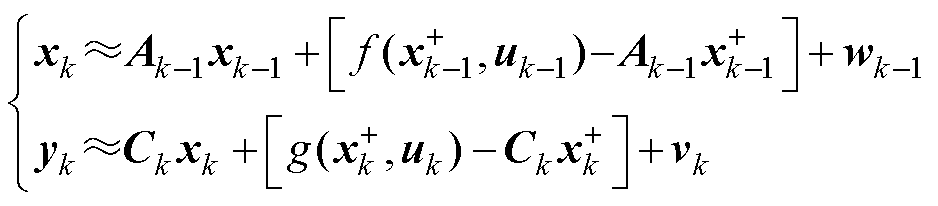 (18)
(18)
式中,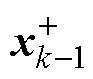 和
和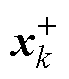 分别为
分别为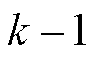 时刻和
时刻和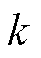 时刻的最优状态估计;
时刻的最优状态估计;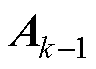 和
和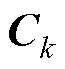 分别为
分别为
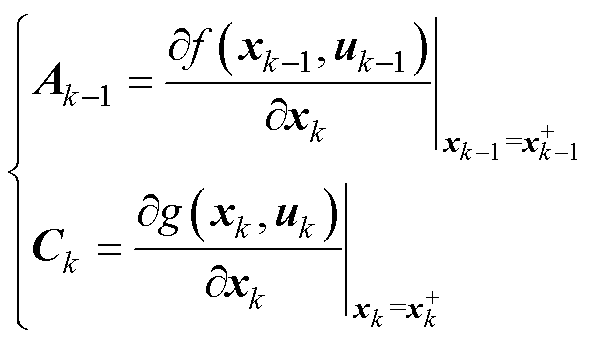 (19)
(19)
在系统状态估计闭环回路即阳极电势观测器中,式(18)对应的系统状态变量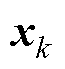 包括电池SOCk、阳极电势
包括电池SOCk、阳极电势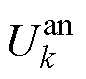 、阴极RC支路电压响应
、阴极RC支路电压响应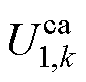 和阳极RC支路电压响应
和阳极RC支路电压响应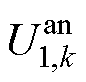 ,系统输入量
,系统输入量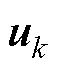 和观测值
和观测值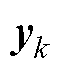 则分别为充电电流
则分别为充电电流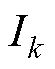 和电池端电压
和电池端电压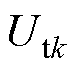 ,具体为
,具体为
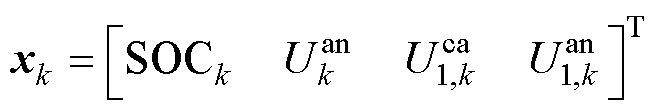 (20)
(20)
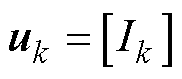 (21)
(21)
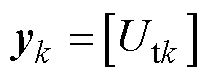 (22)
(22)
式(20)中电池荷电状态可以通过安时积分法估算,具体为
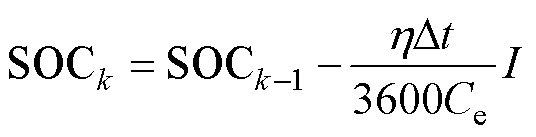 (23)
(23)
式中,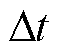 为采样时间间隔,
为采样时间间隔,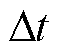 =1 s;
=1 s;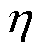 为电池库伦效率,
为电池库伦效率,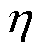 =0.99;本文中取
=0.99;本文中取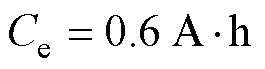 。
。
根据式(4)、式(12)、式(13)、式(23),将系统状态转移方程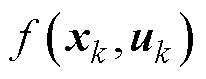 和测量方程
和测量方程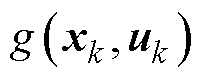 用泰勒公式展开,保留一次项,即可得出
用泰勒公式展开,保留一次项,即可得出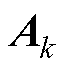 和
和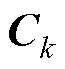 为
为
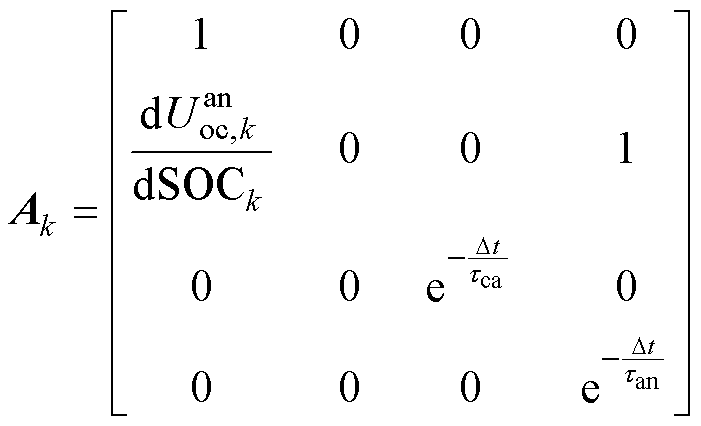 (24)
(24)
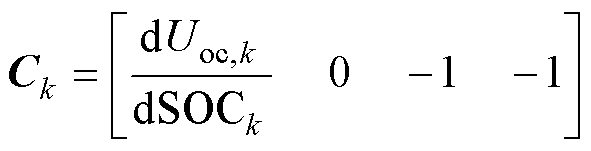 (25)
(25)
在算法运行前,需要对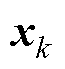 、
、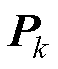 、
、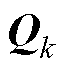 和
和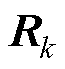 赋初始值。本文中取
赋初始值。本文中取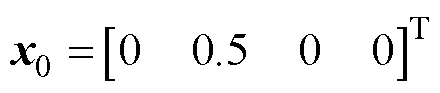 ,
,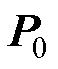 为单位矩阵,
为单位矩阵,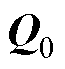 为对角元素为0.001的对角阵,
为对角元素为0.001的对角阵,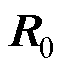 =0.1。结合式(24)、式(25)以及EKF算法流程完成递推,即可对电池荷电状态、阳极电势等状态量进行在线观测。
=0.1。结合式(24)、式(25)以及EKF算法流程完成递推,即可对电池荷电状态、阳极电势等状态量进行在线观测。
2.2.1 电流控制方案
充电电流闭环控制器的基本控制逻辑为,建立当前时刻阳极RC支路电压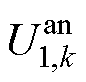 与阳极电势间的联系,约束下一时刻阳极电势到达设定阈值,以此来计算出充电电流的最优解,达到调节充电电流的目的,同时对系统进行前置补偿,从而确保阳极电势尽可能地接近设定阈值,且在控制过程中阳极电势不发生超调。
与阳极电势间的联系,约束下一时刻阳极电势到达设定阈值,以此来计算出充电电流的最优解,达到调节充电电流的目的,同时对系统进行前置补偿,从而确保阳极电势尽可能地接近设定阈值,且在控制过程中阳极电势不发生超调。
在离散系统中,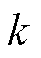 时刻阳极电势与充电电流之间的关系可以描述为
时刻阳极电势与充电电流之间的关系可以描述为
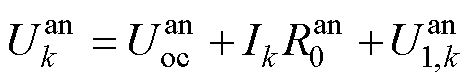 (26)
(26)
同理,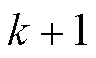 时刻的阳极电势与充电电流之间的关系可以描述为
时刻的阳极电势与充电电流之间的关系可以描述为
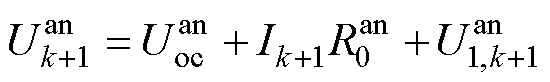 (27)
(27)
假设在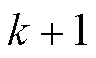 时刻对充电电流进行控制,使得
时刻对充电电流进行控制,使得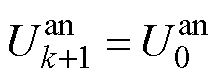 ,那么该时刻经过控制的充电电流为
,那么该时刻经过控制的充电电流为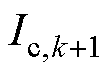 ,此时阳极电势与经控制的充电电流之间的关系满足
,此时阳极电势与经控制的充电电流之间的关系满足
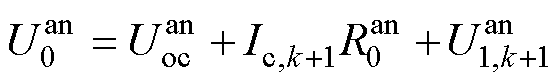 (28)
(28)
式中,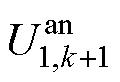 可以由
可以由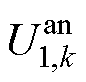 计算得出,即
计算得出,即
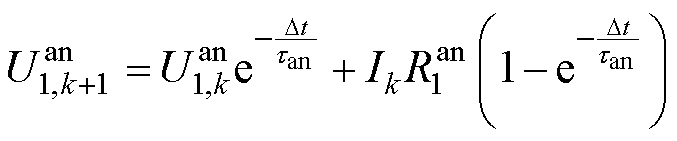 (29)
(29)
由于在BMS中电流采样时间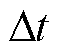 较短,此时
较短,此时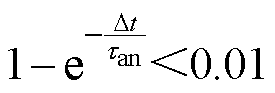 ,可近似认为
,可近似认为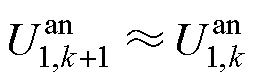 ,故式(28)可以变形为
,故式(28)可以变形为
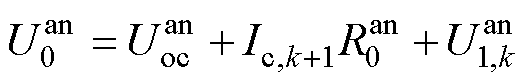 (30)
(30)
根据式(30)即可由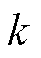 时刻电池状态信息计算出
时刻电池状态信息计算出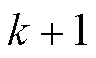 时刻的最优充电电流。但由于观测电池状态与控制充电电流间相差单位采样时间,电流控制存在一定的滞后性,且易产生超调,使得阳极电势低于设定阈值。故本文提出一种前置补偿方法来抑制阳极电势超调。
时刻的最优充电电流。但由于观测电池状态与控制充电电流间相差单位采样时间,电流控制存在一定的滞后性,且易产生超调,使得阳极电势低于设定阈值。故本文提出一种前置补偿方法来抑制阳极电势超调。
2.2.2 抑制超调的前置补偿方法
本文提出一种指数函数前置补偿法来抑制阳极电势超调。其基本思想为,在阳极电势达到设定阈值之前提前对充电电流进行调节,使阳极电势在设定阈值之上缓慢逼近阈值,避免阳极电势超调。具体而言,设定前置补偿指数函数 ,将其叠加到阳极电势阈值
,将其叠加到阳极电势阈值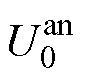 之上,即
之上,即
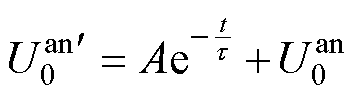 (31)
(31)
式中,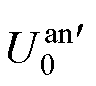 为经过前置补偿的阳极电势阈值;A和τ为待定系数。A的值为指数函数在0时刻的值,可根据阳极电势变化经验取值,本文中取A=0.25。
为经过前置补偿的阳极电势阈值;A和τ为待定系数。A的值为指数函数在0时刻的值,可根据阳极电势变化经验取值,本文中取A=0.25。
对于函数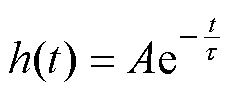 ,时间常数t 的含义为函数值从最大值衰减到最大值的
,时间常数t 的含义为函数值从最大值衰减到最大值的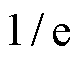 所需要的时间,当
所需要的时间,当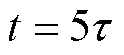 时,函数值衰减为最大值的0.7%。如果能近似估计出阳极电势充电到阈值所需的时间
时,函数值衰减为最大值的0.7%。如果能近似估计出阳极电势充电到阈值所需的时间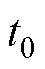 ,利用时间常数的物理特性,可以根据时间
,利用时间常数的物理特性,可以根据时间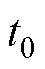 完成对时间常数t 的标定。具体为
完成对时间常数t 的标定。具体为
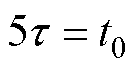 (32)
(32)
电池在低荷电状态下进行充电时,阳极开路电压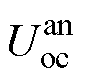 较高,根据式(30)可知,此时
较高,根据式(30)可知,此时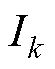 的取值较大,为避免在控制过程中充电电流过大而造成安全事故,设定最大充电电流值为
的取值较大,为避免在控制过程中充电电流过大而造成安全事故,设定最大充电电流值为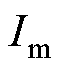 ,使得整个充电过程中的充电电流
,使得整个充电过程中的充电电流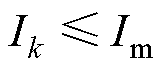 。故在低荷电状态下的充电电流
。故在低荷电状态下的充电电流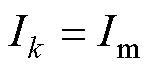 ,此时为恒流充电阶段,电池的阳极电势与充电电流满足关系
,此时为恒流充电阶段,电池的阳极电势与充电电流满足关系
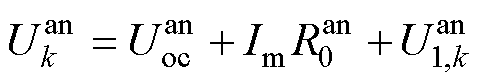 (33)
(33)
当阳极电势降低至所设定阈值时,此时刻为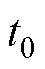 ,该时刻下阳极电势满足关系
,该时刻下阳极电势满足关系
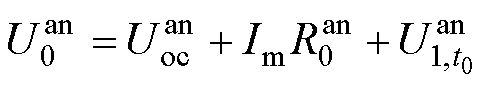 (34)
(34)
式(34)中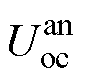 与电池荷电状态存在对应关系,
与电池荷电状态存在对应关系,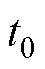 时刻下的SOC和
时刻下的SOC和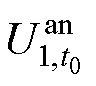 可分别描述为
可分别描述为
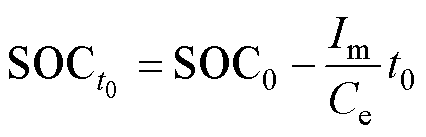 (35)
(35)
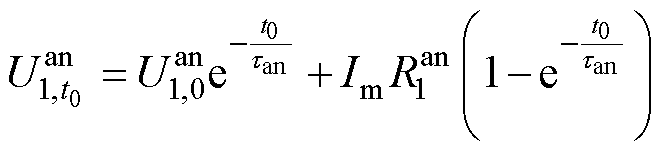 (36)
(36)
式中,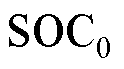 和
和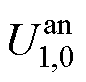 为0时刻的电池荷电状态和阳极RC支路的电压值。为简化计算,将
为0时刻的电池荷电状态和阳极RC支路的电压值。为简化计算,将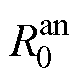 、
、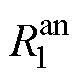 和
和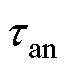 分别取平均值代入,结合
分别取平均值代入,结合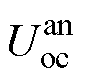 的拟合式(14)与式(34)~式(36),即可估计出阳极电势充电到阈值所需的时间
的拟合式(14)与式(34)~式(36),即可估计出阳极电势充电到阈值所需的时间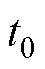 ,进而完成对时间常数t 的标定。
,进而完成对时间常数t 的标定。
在对设定阈值进行前置补偿后,就能在阳极电势达到设定阈值之前提前对充电电流进行调节,使阳极电势缓慢逼近所设定的阳极电势阈值,避免阳极电势超调。
对以上提出的结合前置补偿方法的充电电流控制器与基于EKF的阳极电势观测器递推计算,就可以实现电池内部状态的实时估算和充电电流在线平稳控制,且控制过程中阳极电势无超调,实现锂离子电池无析锂快充策略调控方案的制定。
在2.1节已经详细介绍了阳极电势闭环观测器的设计方案,本节将在0.05C恒流充电、1C恒流恒压充电、变流充电、多级CC-CV工况下验证阳极电势闭环观测器观测效果,并与仅用电气元件连接的开环观测方法进行对比验证,如图11~图14所示。本节中所有仿真均是在Matlab/Simulink环境下进行的。
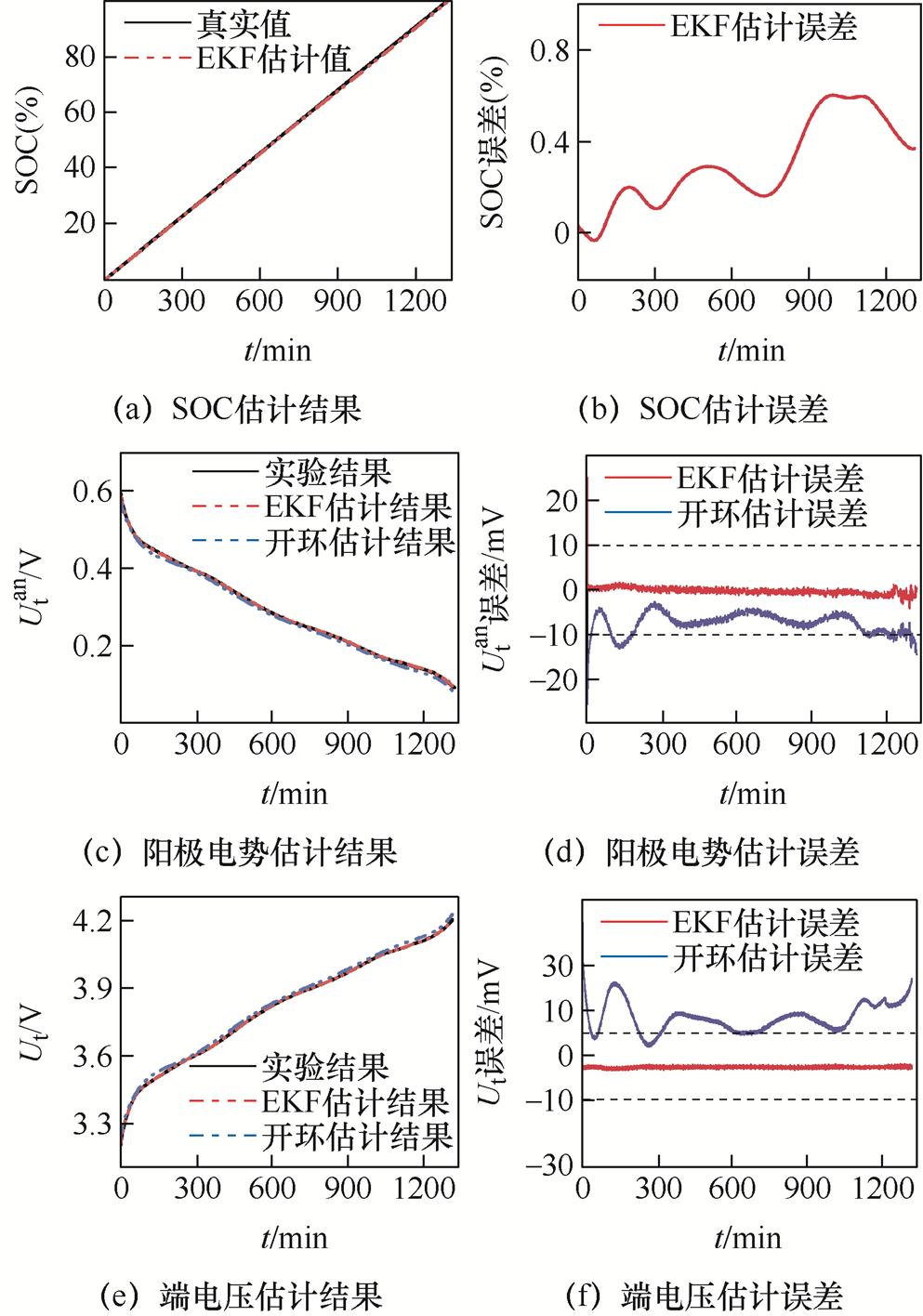
图11 0.05C恒流充电工况验证
Fig.11 0.05C constant current charging condition verification
0.05C恒流充电工况下的SOC、阳极电势、端电压的估计结果及估计误差如图11所示。在该工况下,阳极电势闭环观测器所估计的SOC最大误差为0.6%,平均误差为0.29%;阳极电势最大估计误差为4.11 mV,平均估计误差为0.54 mV;端电压最大估计误差为1.64 mV,平均估计误差为0.27 mV。而阳极电势开环估计最大误差为23.09 mV,平均误差为7.33 mV;端电压开环估计最大误差为44.82 mV,平均误差为14.54 mV。可见在面对小电流响应时,阳极电势闭环观测器与开环估计相比,具有更小的估计误差以及稳定性。
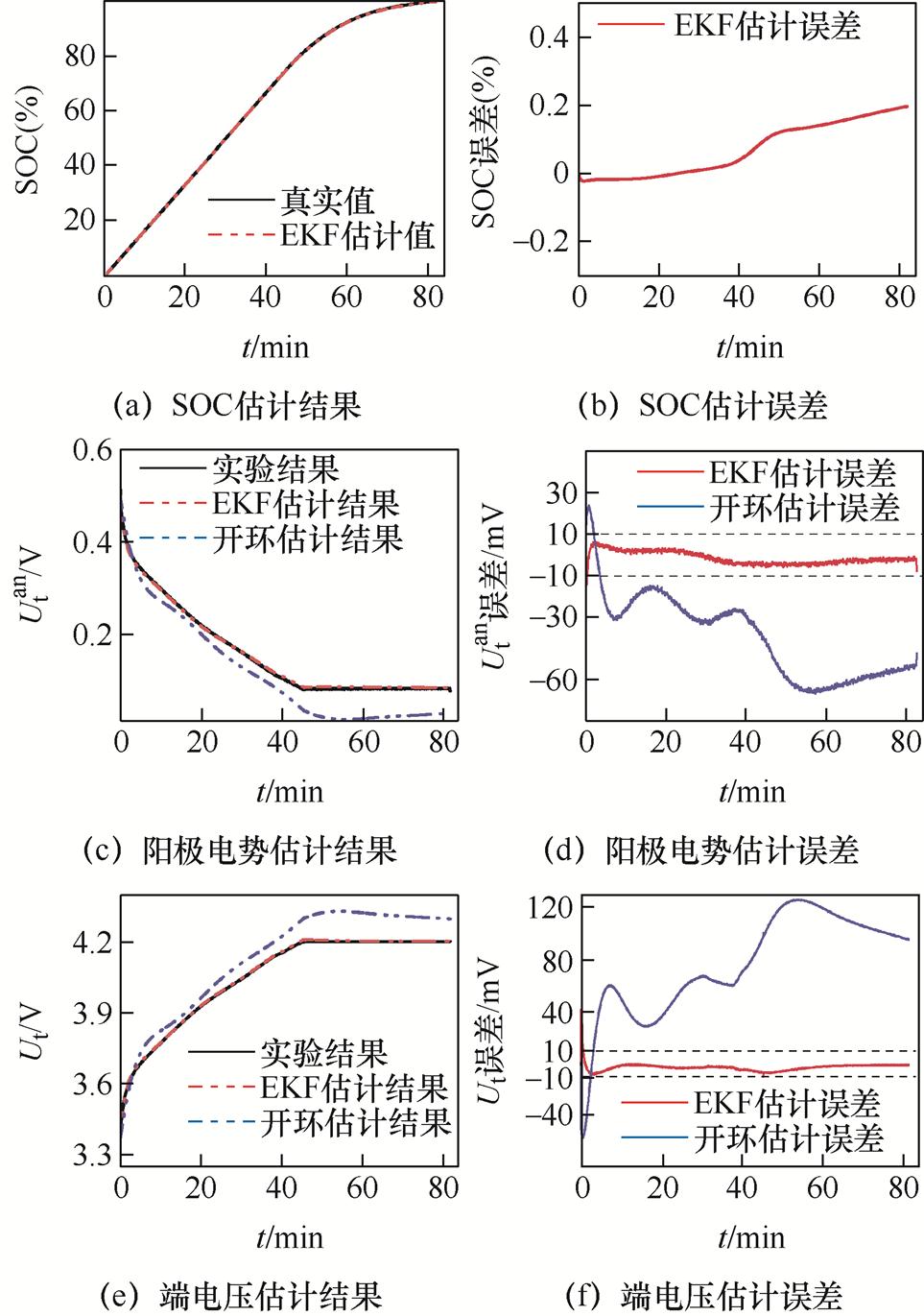
图12 1C恒流恒压充电工况验证
Fig.12 1C constant current charging condition verification
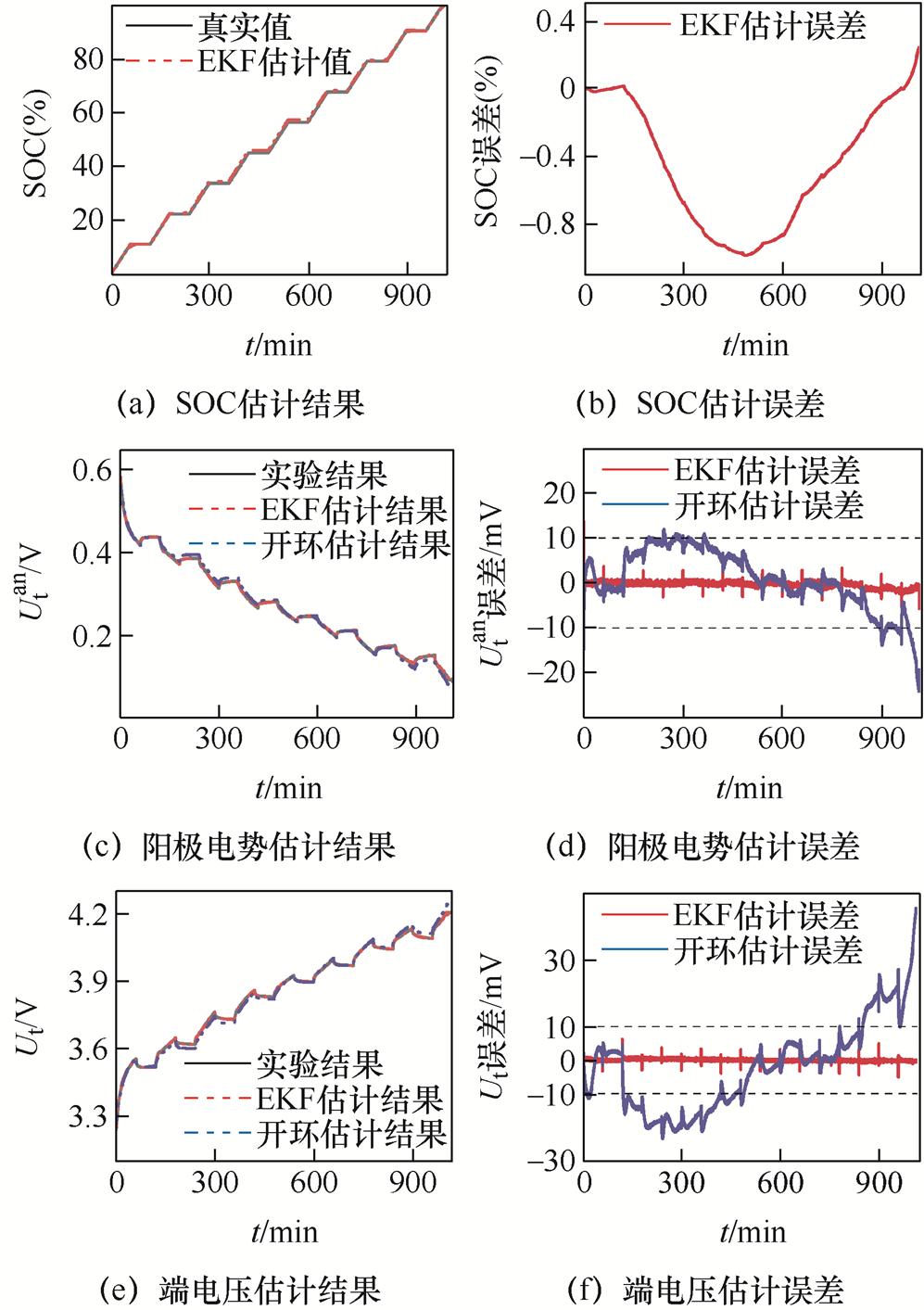
图13 变流充电工况验证
Fig.13 Variable current charging condition verification
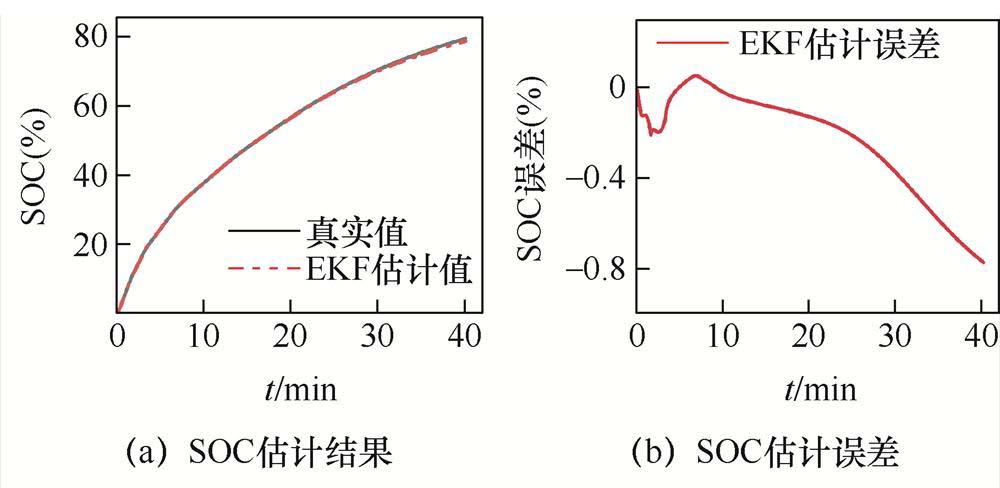
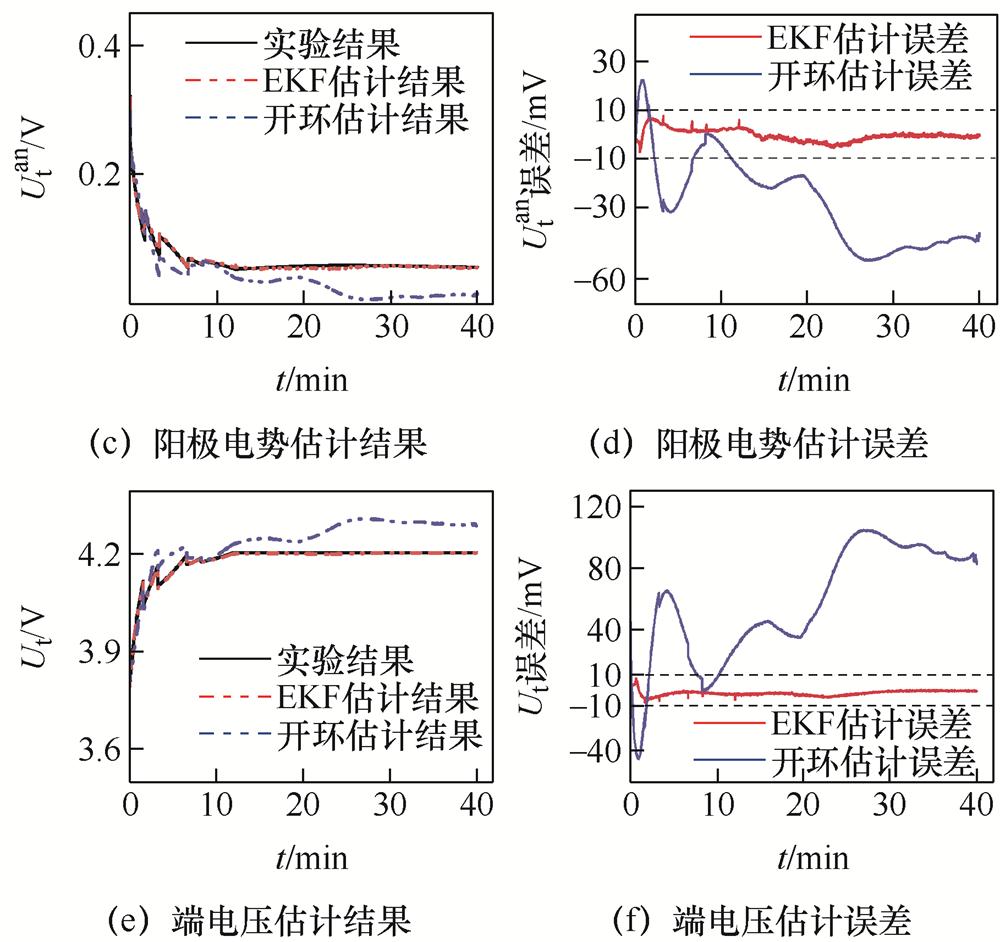
图14 多级CC-CV工况验证
Fig.14 Multistage CC-CV condition verification
1C恒流恒压充电工况下的SOC、阳极电势、端电压的估计结果及误差如图12所示。该工况下阳极电势闭环观测器所估计的SOC最大误差为0.2%,平均误差为0.08%;阳极电势最大估计误差为7.73 mV,平均误差为2.95 mV;端电压最大估计误差为10.10 mV,平均误差为3.13 mV。阳极电势的开环估计最大误差为66.39 mV,平均误差为40.77 mV;端电压开环估计最大误差为126.26 mV,平均误差为79.54 mV。结果表明,在面对常用恒流恒压充电工况时,开环估计结果偏离了真实值,不能满足工程需求;而阳极电势闭环观测器的估计结果能将阳极电势最大估计误差保持在10 mV内,具有较高的精度。
变流充电工况下的SOC、阳极电势、端电压的估计结果及误差如图13所示。在该工况下,阳极电势闭环观测器所估计的SOC最大误差为0.98%,平均误差为0.46%;阳极电势最大估计误差为5.66 mV,平均误差为0.47 mV;端电压最大估计误差为6.18 mV,平均误差为0.22 mV。而阳极电势的开环估计最大误差为24.04 mV,平均误差为5.27 mV;端电压的开环估计最大误差为45.34 mV,平均误差为10.53 mV。结果表明,在面对变流响应时,开环估计在电流变化的瞬间,估计结果会发生跳变,而且很难再次恢复到低误差的稳定状态;而阳极电势闭环观测器在电流发生突变时,能迅速修正估计结果使其接近真实值,将误差控制在较低水平,且在不同SOC条件下均具有较好的性能,证明了阳极电势闭环观测器有较高的观测稳定性。
多级CC-CV工况下的SOC、阳极电势、端电压的估计结果及误差如图14所示。该工况下最大充电电流为4C,阳极电势闭环观测器所估计的SOC最大误差为0.77%,平均误差为0.24%;阳极电势最大估计误差为8.87 mV,平均误差为2.02 mV;端电压最大估计误差为8.0 mV,平均误差为2.08 mV。而阳极电势的开环估计最大误差为52.32 mV,平均误差为29.87 mV;端电压的开环估计最大误差为104.63 mV,平均误差为59.74 mV。结果表明,在面对多级CC-CV响应时,开环估计结果误差很大,偏离了真实值;而阳极电势闭环观测器端电压和阳极电势最大误差都在±10 mV内,且在充电电流改变时仍有较快的响应速度,证明了阳极电势闭环观测器具有较高的鲁棒性。
在面对小电流响应、常用恒流恒压响应、变流响应以及多级CC-CV响应时,开环估计的效果都不稳定,虽然在小电流响应时,开环估计可基本满足低精度要求,但在其他工况下,阳极电势和端电压的估计误差较大,并且误差有较大波动,甚至在常用恒流恒压充电响应下的端电压最大误差达到126.26 mV,平均误差为79.54 mV,这在实际BMS中是不允许的。而阳极电势闭环观测器则具有较好的估计精度,在这几种响应下,SOC的最大估计误差不超过1%,平均估计误差不超过0.5%;阳极电势的最大估计误差不超过10 mV,平均估计误差不超过5 mV。在常用恒流恒压响应下,端电压的最大估计误差虽然为10.10 mV,但其平均估计误差仅有3.13 mV,误差值最大点为恒流阶段转变为恒压阶段的一瞬间,很快就恢复到正常误差水平;在其他几种响应的情况下,端电压的最大估计误差均在10 mV以内,并且在充电电流突变时仍能有较快的响应速度及较好的鲁棒性。
在2.2节已经详细介绍了充电电流闭环控制器的设计方案。在充电过程中,阳极电位闭环观测器能实时观测到电池的阳极电势,根据电池阳极RC支路的电压响应与阳极电势间的关系估算出最优充电电流。同时采用前置补偿方法对阳极电势超调量进行补偿。本节给出了在设定不同条件下的充电电流控制结果,并对控制结果进行分析,验证了所设计的充电电流控制器的有效性。本节中所有仿真验证均是在Matlab/Simulink环境下进行的。
在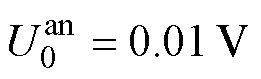 ,
,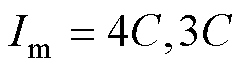 的两种条件下分别对前置补偿效果进行验证,补偿前后的阳极电势如图15所示。加入前置补偿之前,由于系统存在滞后性,阳极电势到达设定阈值之后还会继续减小,产生超调后才开始缓慢回升趋近设定的阳极电势阈值,且随着
的两种条件下分别对前置补偿效果进行验证,补偿前后的阳极电势如图15所示。加入前置补偿之前,由于系统存在滞后性,阳极电势到达设定阈值之后还会继续减小,产生超调后才开始缓慢回升趋近设定的阳极电势阈值,且随着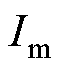 的增加,阳极电势超调量逐渐增加;加入前置补偿之后,阳极电势在到达设定阈值之前提前控制充电电流,使得阳极电势在设定阈值之上逐渐减小,趋近于设定阈值,避免调节初期阳极电势产生超调,证明了所提出的前置补偿方法的有效性。
的增加,阳极电势超调量逐渐增加;加入前置补偿之后,阳极电势在到达设定阈值之前提前控制充电电流,使得阳极电势在设定阈值之上逐渐减小,趋近于设定阈值,避免调节初期阳极电势产生超调,证明了所提出的前置补偿方法的有效性。
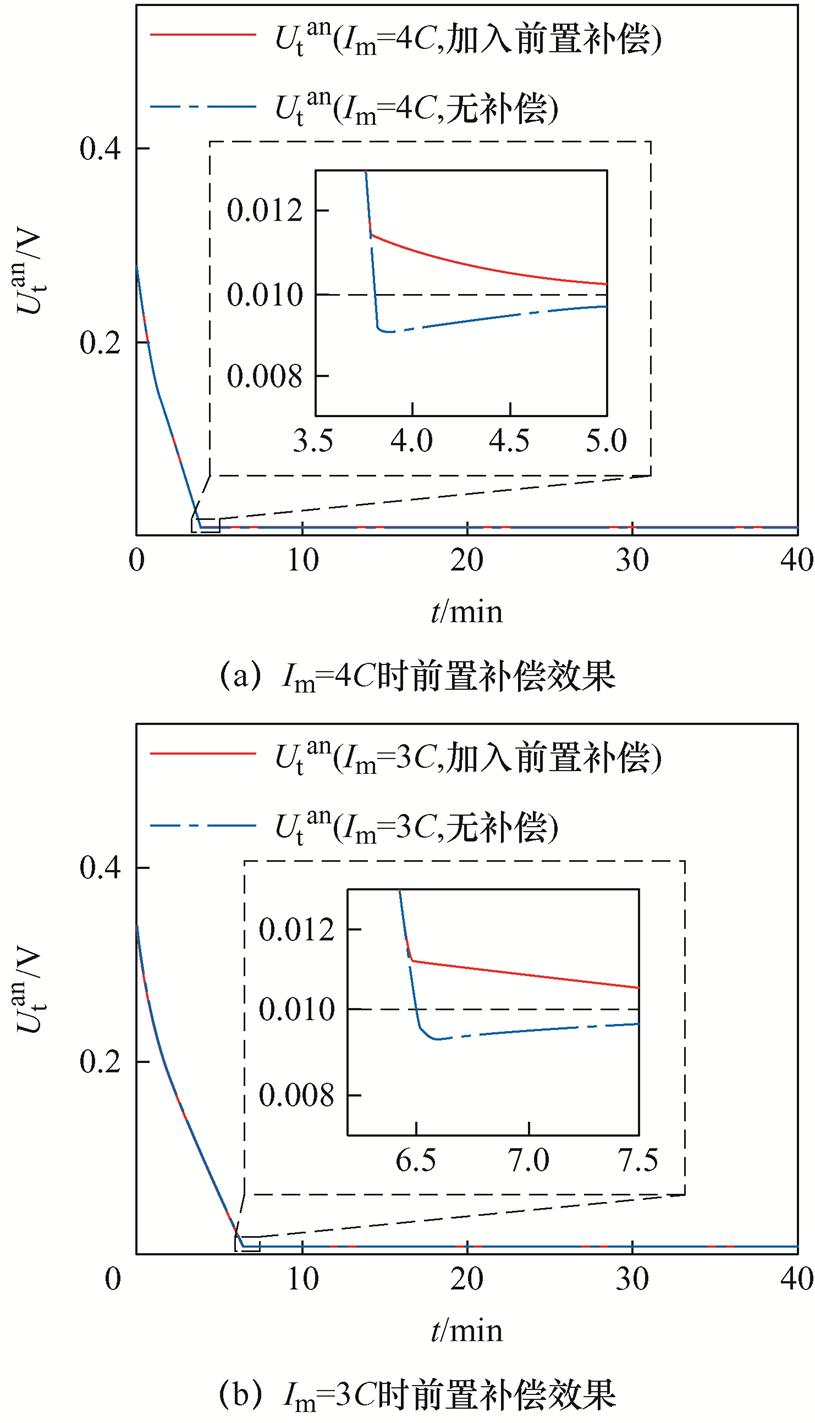
图15 阳极电势前置补偿效果
Fig.15 Anode potential pre-compensation effect
为了验证充电电流闭环控制器的控制效果,本节中设定最大充电电流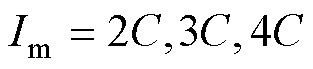 ,阳极电势阈值
,阳极电势阈值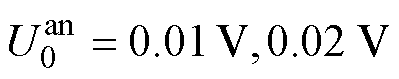 ,在这六组不同的条件下验证闭环充电电流控制器的控制效果,充电过程中阳极电势变化如图16所示。实线和虚线分别代表阳极电势阈值为0.01 V和0.02 V条件下的曲线;用不同的颜色区分最大充电倍率。
,在这六组不同的条件下验证闭环充电电流控制器的控制效果,充电过程中阳极电势变化如图16所示。实线和虚线分别代表阳极电势阈值为0.01 V和0.02 V条件下的曲线;用不同的颜色区分最大充电倍率。
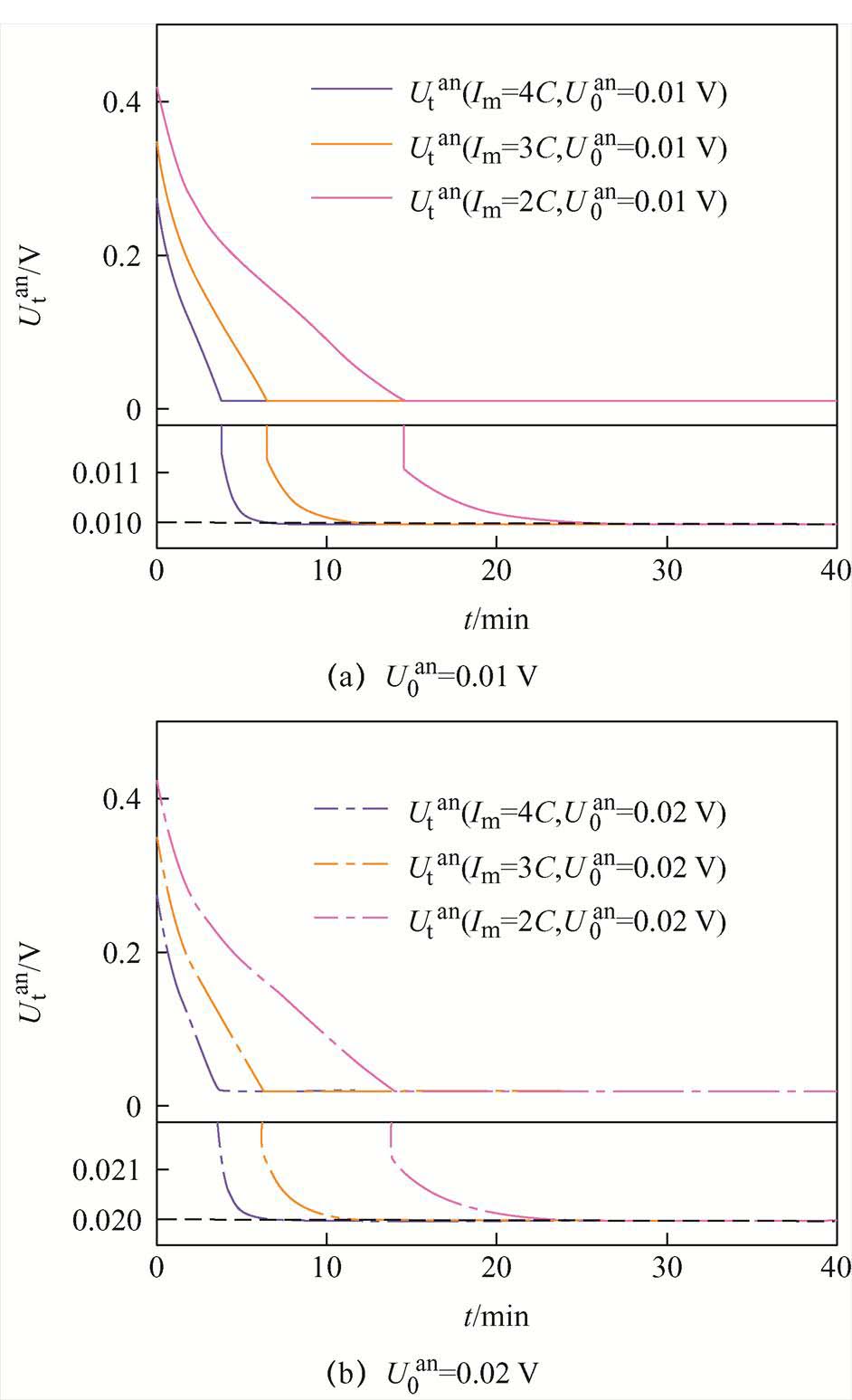
图16 不同设定条件下的阳极电势变化曲线
Fig.16 Curves of anode potential change under different setting conditions
图16a中所示设定的阳极电势阈值为0.01 V,在最大充电电流分别为4C、3C、2C的条件下,阳极电势最低分别为9.96 mV、9.96 mV、9.976 mV,稳态误差分别为0.03 mV、0.03 mV、0.02 mV,到达并保持在设定阈值+1 mV内所需的时间分别为16 s、22 s、23 s;图16b中所示设定的阳极电势阈值为0.02 V,在最大充电电流分别为4C、3C、2C的条件下,阳极电势最低分别为19.962 mV、19.962 mV、19.976 mV,稳态误差分别为0.03 mV、0.03 mV、0.02 mV,到达并保持在设定阈值+1 mV内所需的时间分别为18 s、26 s、26 s。在同一阈值条件下,随着最大充电电流的减小,稳定在固定误差范围内的时间有所延长,原因是充电电流较小时,阳极电势变化较为缓慢,导致趋近阈值所需时间延长。无论是哪种充电条件,当阳极电势不断降低直至接近阈值时,即开始减小充电电流,使得阳极电势在阈值之上缓慢趋近于阈值,且几种条件下的稳态误差均小于0.05 mV,稳定后阳极电势几乎无波动,阳极电势能很好地跟踪设定的阈值,证明了所提出的结合前置补偿方法的充电电流闭环控制器具有较高控制精度及稳定性。
在不同设定条件下,对SOC=0%充电至SOC= 80%所需的充电时间进行分析,该SOC范围为研究快速充电常见的SOC范围。不同条件下的充电SOC曲线以及充电电流曲线如图17所示。在阳极电势阈值为0.01 V的条件下,SOC从0%充电到80%,最大充电电流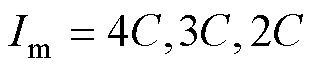 时所需的充电时间分别约为26 min、26.7 min、29.2 min。在阳极电势阈值为0.02 V的条件下,SOC从0%充电到80%,最大充电电流
时所需的充电时间分别约为26 min、26.7 min、29.2 min。在阳极电势阈值为0.02 V的条件下,SOC从0%充电到80%,最大充电电流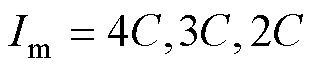 时所需的充电时间分别约为27.2 min、27.9 min、30.2 min。
时所需的充电时间分别约为27.2 min、27.9 min、30.2 min。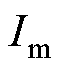 相同时,随着
相同时,随着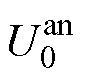 增加所需的充电时间也增加;
增加所需的充电时间也增加;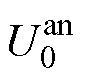 相同时,随着
相同时,随着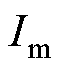 的增加所需充电时间减少。此外,当最大充电倍率增加直至4C时,保持最大电流充电的时间逐步缩短,这是因为充电电流增加时,阳极电势下降更快,使得阳极电势更早地接近设定的阈值。但最大充电电流在3C以上继续增加时,充电时间的减少并不明显。在实际应用中应权衡充电时间和安全性设定合理的最大充电电流值。
的增加所需充电时间减少。此外,当最大充电倍率增加直至4C时,保持最大电流充电的时间逐步缩短,这是因为充电电流增加时,阳极电势下降更快,使得阳极电势更早地接近设定的阈值。但最大充电电流在3C以上继续增加时,充电时间的减少并不明显。在实际应用中应权衡充电时间和安全性设定合理的最大充电电流值。
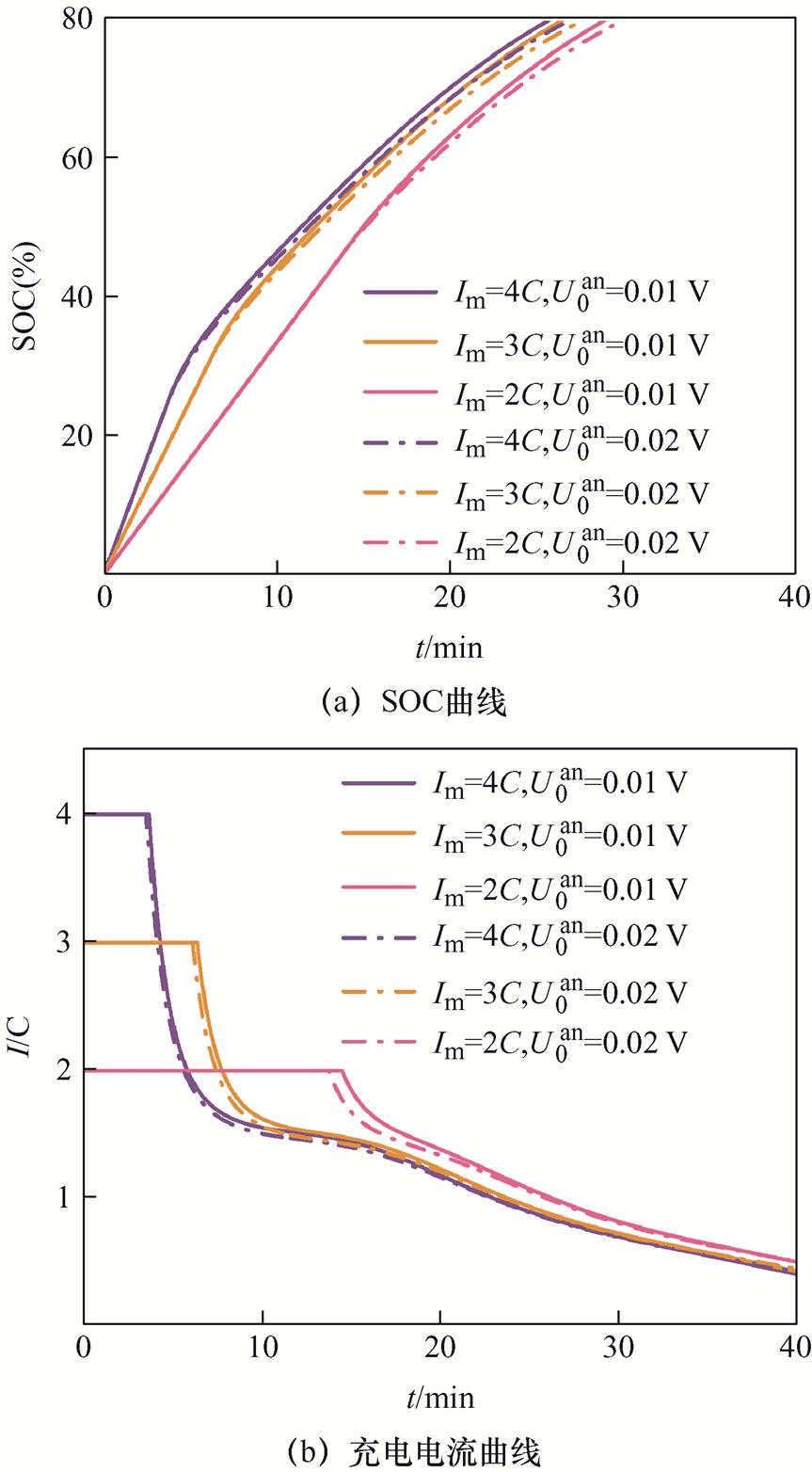
图17 不同条件下充电SOC曲线以及充电电流曲线
Fig.17 Charging SOC curves and charging current curve under different conditions
本文所提出的结合前置补偿方法的充电电流闭环控制器的一大优势就是,能够尽可能地降低所设定的阳极电势阈值,达到减少充电时间的目的。为了验证本文所提快充策略的实际充电效果,综合本文阳极电势观测器的估计精度,将阳极电势阈值设定在0.01 V,在最大充电电流设定为4C和3C两种条件下验证低阈值下快充策略的充电效果,并与1C恒流恒压充电效果进行实验对比验证,结果如图18所示。
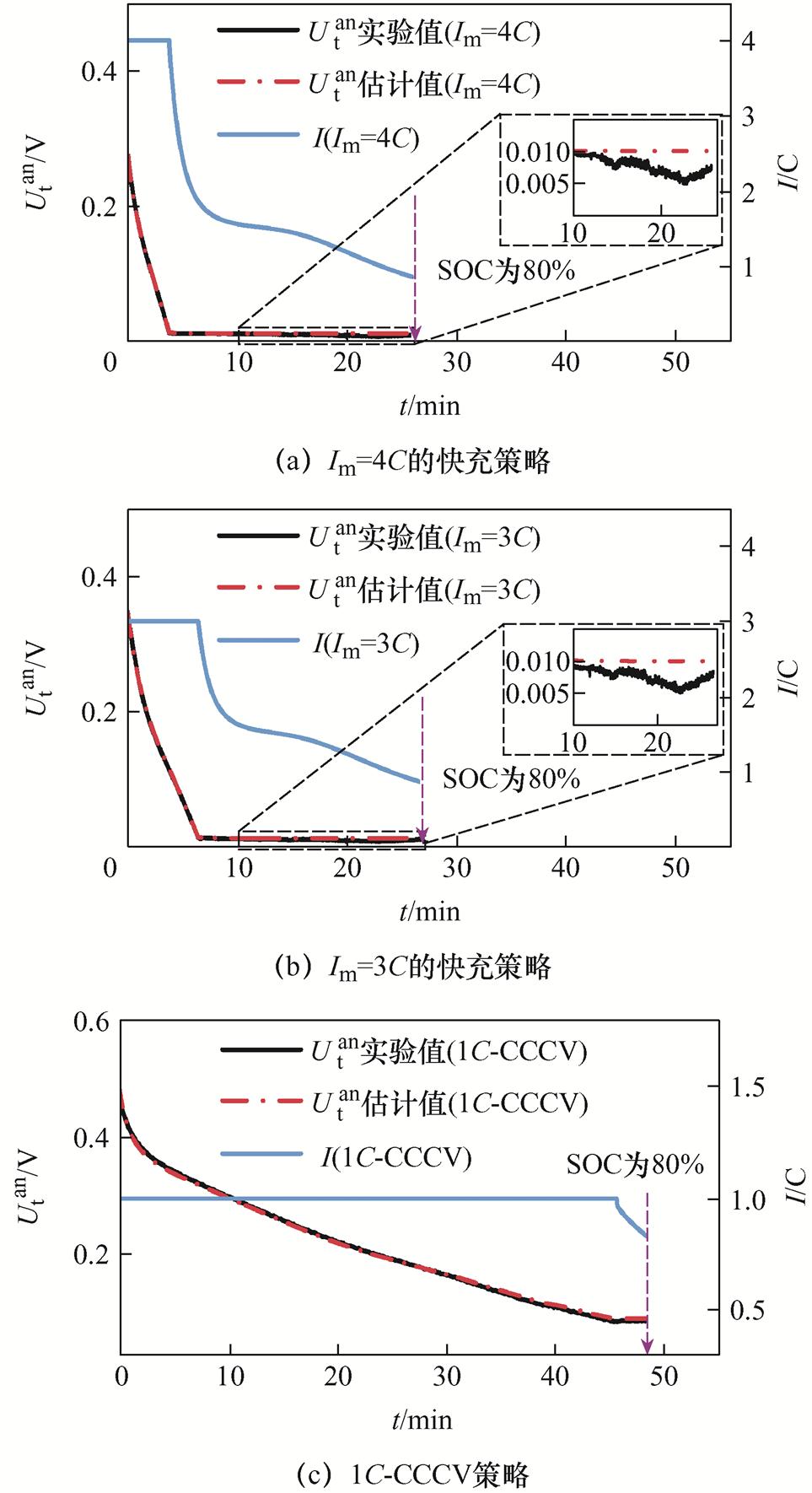
图18 不同条件下的充电效果验证
Fig.18 Verification of charging effect under different conditions
图18a和图18b分别为最大充电电流设定为4C和3C下的快充策略下的验证结果,充电至SOC=80%所需时间分别为26 min和26.7 min,且充电过程中实验测得阳极电势最低值分别为4.8 mV和4.9 mV,阳极电势最大估计误差分别为5.16 mV和5.08 mV,平均误差分别为1.36 mV和1.54 mV;图18c为1C恒流恒压工况下的验证结果,该工况下充电至SOC为80%所需时间为48.2 min,且充电过程中阳极电势最大估计误差为6.22 mV,平均误差为2.82 mV。与1C恒流恒压工况相比,本文所提无析锂快速充电策略能节省约46%的充电时间,且在整个充电过程中阳极电势始终高于金属锂的氧化还原电位,能有效避免金属锂在阳极表面析出。
为了验证该快充策略对析锂的实际抑制效果,分别对该策略和恒流充电策略进行析锂实验验证。设定阳极电势阈值为0.01 V、最大充电电流为4C,以此作为无析锂快充策略的实验条件;恒流充电倍率选取为与该策略充电时间接近的1.85C。在这两种充电条件下,分别对这两种充电策略进行20个充放电循环,循环结束后,将电池进行拆解并观察电池的阳极表面的析锂情况,如图19 所示。

图19 不同策略充电后电池阳极表面
Fig.19 Battery anode surface after charging
图19a所示为经本文所提无析锂快充策略循环后的电池阳极表面,可以看出阳极表面与新电池阳极表面相似,为纯净的黑色表面,且并未发现明显老化现象,这意味着在快充过程中阳极并未发生析锂,延长了电池的使用寿命,保障了电池的充电安全;图19b所示为经过1.85C恒流充电策略循环后的电池阳极表面,相较于图19a老化较为严重,且阳极表面能明显看出灰白色沉积物,表明在恒流充电过程中阳极发生了析锂副反应,灰白色沉积物即为析出的金属锂。电池拆解实验再一次验证了本文所提快充策略的有效性,能够在充电过程中有效的避免阳极析锂。
为了解决锂离子电池在充电过程易发生析锂进而造成安全事故的问题,本文在电极等效电路模型的基础上,提出一种基于EKF算法和前置补偿方法的双闭环无析锂快充策略调控方案,该策略由阳极电势闭环观测器和充电电流闭环控制器组成。具体而言,首先建立锂离子电极等效电路模型,并对模型进行离线参数辨识;然后建立闭环阳极电势观测器用于实时观测SOC、阳极电势等电池状态;最后建立了闭环充电电流控制器,在阳极电势观测的基础上实现充电电流的平稳控制。
仿真及实验结果表明,在小电流充电、常用恒流恒压充电、变流充电、多级CC-CV充电四种不同工况下的阳极电势观测器的估算精度均较高,阳极电势平均估计误差在5 mV以内,最大误差在10 mV以内,并且在充电电流突变时仍能有较快的响应速度及较好的鲁棒性。另外,在设定不同的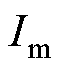 和
和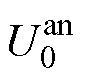 值的情况下对充电电流控制器进行仿真实验分析,结果表明,结合前置补偿方法的充电电流控制器同样具有好的性能,到达并保持在设定阈值+1 mV之内仅需26 s,充电至SOC=80%所需时间为26 min,与1C恒流恒压充电相比,节省了46%的充电时间。并且能够保证电池在快充过程中阳极电势始终保持在金属锂的氧化还原电位(0 V vs. Li/Li+)之上,避免金属锂在阳极表面析出,提高了电池快充的安全性。因此,本文所提锂离子电池无析锂快充策略调控方案是一种精度较高、鲁棒性较好、实用价值较高的无析锂快速充电方法。
值的情况下对充电电流控制器进行仿真实验分析,结果表明,结合前置补偿方法的充电电流控制器同样具有好的性能,到达并保持在设定阈值+1 mV之内仅需26 s,充电至SOC=80%所需时间为26 min,与1C恒流恒压充电相比,节省了46%的充电时间。并且能够保证电池在快充过程中阳极电势始终保持在金属锂的氧化还原电位(0 V vs. Li/Li+)之上,避免金属锂在阳极表面析出,提高了电池快充的安全性。因此,本文所提锂离子电池无析锂快充策略调控方案是一种精度较高、鲁棒性较好、实用价值较高的无析锂快速充电方法。
参考文献
[1] 刘素贞, 陈晶晶, 张闯, 等. 基于区域电压的锂离子电池不均匀发热模型[J]. 电工技术学报, 2022, 37(21): 5627-5636.
Liu Suzhen, Chen Jingjing, Zhang Chuang, et al. Regional voltage-based uneven heating model of lithium-ion battery[J]. Transactions of China Electro- technical Society, 2022, 37(21): 5627-5636.
[2] Zhang Lei, Hu Xiaosong, Wang Zhenpo, et al. Hybrid electrochemical energy storage systems: an overview for smart grid and electrified vehicle applications[J]. Renewable and Sustainable Energy Reviews, 2021, 139: 110581.
[3] 王义军, 左雪. 锂离子电池荷电状态估算方法及其应用场景综述[J]. 电力系统自动化, 2022, 46(14): 193-207.
Wang Yijun, Zuo Xue. Review on estimation methods for state of charge of lithium-ion battery and their application scenarios[J]. Automation of Electric Power Systems, 2022, 46(14): 193-207.
[4] 刘素贞, 袁路航, 张闯, 等. 基于超声时域特征及随机森林的磷酸铁锂电池荷电状态估计[J]. 电工技术学报, 2022, 37(22): 5872-5885.
Liu Suzhen, Yuan Luhang, Zhang Chuang, et al. State of charge estimation of LiFeO4 batteries based on time domain features of ultrasonic waves and random forest[J]. Transactions of China Electrotechnical Society, 2022, 37(22): 5872-5885.
[5] 余佩雯, 郁亚娟, 常泽宇, 等. 相关向量机预测锂离子电池剩余有效寿命[J]. 电气技术, 2023, 24(2): 1-5.
Yu Peiwen, Yu Yajuan, Chang Zeyu, et al. Remain useful life prediction of lithium-ion battery based on relevance vector machine[J]. Electrical Engineering, 2023, 24(2): 1-5.
[6] Sun Bo, Zhang Chuang, Xu Zhicheng, et al. Ultrasonic diagnosis of the nonlinear aging characteristics of lithium-ion battery under high-rate discharge conditions[J]. Journal of Power Sources, 2023, 567: 232921.
[7] 张闯, 孙博, 金亮, 等. 基于声波时域特征的锂离子电池荷电状态表征[J]. 电工技术学报, 2021, 36(22): 4666-4676.
Zhang Chuang, Sun Bo, Jin Liang, et al. Characteri- zation of the state of charge of lithium-ion batteries based on the time-domain characteristics of acoustic waves[J]. Transactions of China Electrotechnical Society, 2021, 36(22): 4666-4676.
[8] Al-Haj Hussein A, Batarseh I. A review of charging algorithms for nickel and lithium battery chargers[J]. IEEE Transactions on Vehicular Technology, 2011, 60(3): 830-838.
[9] Liu Y H, Teng J H, Lin Y C. Search for an optimal rapid charging pattern for lithium-ion batteries using ant colony system algorithm[J]. IEEE Transactions on Industrial Electronics, 2005, 52(5): 1328-1336.
[10] Chung S K, Andriiko A A, Mon’ko A P, et al. On charge conditions for Li-ion and other secondary lithium batteries with solid intercalation electrodes[J]. Journal of Power Sources, 1999, 79(2): 205-211.
[11] Purushothaman B K, Landau U. Rapid charging of lithium-ion batteries using pulsed currents[J]. Journal of the Electrochemical Society, 2006, 153(3): A533.
[12] Sun Bo, Zhang Chuang, Liu Suzhen, et al. Acoustic response characteristics of lithium cobaltate/graphite battery during cycling[J]. Journal of the Electro- chemical Society, 2022, 169(3): 030511.
[13] Anseán D, Dubarry M, Devie A, et al. Operando lithium plating quantification and early detection of a commercial LiFePO4 cell cycled under dynamic driving schedule[J]. Journal of Power Sources, 2017, 356: 36-46.
[14] Liu Qianqian, Du Chunyu, Shen Bin, et al. Under- standing undesirable anode lithium plating issues in lithium-ion batteries[J]. RSC Advances, 2016, 6(91): 88683-88700.
[15] 郭东旭, 杨耕, 冯旭宁, 等. 计及老化路径的锂离子电池加速寿命工况自动生成方法[J]. 电工技术学报, 2022, 37(18): 4788-4797, 4806.
Guo Dongxu, Yang Geng, Feng Xuning, et al. Accelerated aging profile generation method for lithium-ion batteries considering aging path[J]. Transactions of China Electrotechnical Society, 2022, 37(18): 4788-4797, 4806.
[16] Petzl M, Danzer M A. Nondestructive detection, characterization, and quantification of lithium plating in commercial lithium-ion batteries[J]. Journal of Power Sources, 2014, 254: 80-87.
[17] McDowell M T, Lee S W, Nix W D, et al. 25th anniversary article: understanding the lithiation of silicon and other alloying anodes for lithium-ion batteries[J]. Advanced Materials, 2013, 25(36): 4966- 4985.
[18] Bernd Epding, Björn Rumberg, Maximilian Mense, et al. Aging-ptimized fast charging of lithium ion cells based on three-ectrode cell measurements[J]. Energy Technology, 2020, 8(10): 2000457.
[19] Pramanik S, Anwar S. Electrochemical model based charge optimization for lithium-ion batteries[J]. Journal of Power Sources, 2016, 313: 164-177.
[20] Guo Zhen, Liaw B Y, Qiu Xinping, et al. Optimal charging method for lithium ion batteries using a universal voltage protocol accommodating aging[J]. Journal of Power Sources, 2015, 274: 957-964.
[21] Doyle M, Fuller T F, Newman J. Modeling of galvanostatic charge and discharge of the lithium/ polymer/insertion cell[J]. Journal of the Electrochemical Society, 1993, 140(6): 1526-1533.
[22] Doyle M, Newman J, Gozdz A S, et al. Comparison of modeling predictions with experimental data from plastic lithium ion cells[J]. Journal of the Elec- trochemical Society, 2019, 143(6): 1890-1903.
[23] Xiong Rui, Sun Fengchun, Chen Zheng, et al. A data-driven multi-scale extended Kalman filtering based parameter and state estimation approach of lithium-ion polymer battery in electric vehicles[J]. Applied Energy, 2014, 113: 463-476.
[24] 武龙星, 庞辉, 晋佳敏, 等. 基于电化学模型的锂离子电池荷电状态估计方法综述[J]. 电工技术学报, 2022, 37(7): 1703-1725.
Wu Longxing, Pang Hui, Jin Jiamin, et al. A review of SOC estimation methods for lithium-ion batteries based on electrochemical model[J]. Transactions of China Electrotechnical Society, 2022, 37(7): 1703- 1725.
[25] Zhang Dong, Popov B, White R. Modeling lithium intercalation of a single spinel particle under potentiody- namic control[J]. Journal of the Electrochemical Society, 2000, 147: 831-838.
[26] Li Changlong, Cui Naxin, Wang Chunyu, et al. Reduced-order electrochemical model for lithium-ion battery with domain decomposition and polynomial approximation methods[J]. Energy, 2021, 221: 119662.
[27] Tippmann S, Walper D, Balboa L, et al. Low- emperature charging of lithium-ion cells part I: Electrochemical modeling and experimental investi- gation of degradation behavior[J]. Journal of Power Sources, 2014, 252: 305-316.
[28] Chu Zhengyu, Feng Xuning, Lu Languang, et al. Non- destructive fast charging algorithm of lithium-ion batteries based on the control-oriented electrochemical model[J]. Applied Energy, 2017, 204: 1240-1250.
[29] Tomaszewska A, Chu Zhengyu, Feng Xuning, et al. Lithium-ion battery fast charging: a review[J]. eTransportation, 2019, 1: 100011.
[30] Zhao Tongzheng, Zheng Yuejiu, Liu Jinhai, et al. A study on half-cell equivalent circuit model of lithium- on battery based on reference electrode[J]. International Journal of Energy Research, 2021, 45(3): 4155-4169.
[31] Drees R, Lienesch F, Kurrat M. Durable fast charging of lithium-ion batteries based on simulations with an electrode equivalent circuit model[J]. Batteries, 2022, 8(4): 30.
[32] Drees R, Lienesch F, Kurrat M. Fast charging formation of lithium-ion batteries based on real-time negative electrode voltage control[J]. Energy Tech- nology, 2023, 11(5): 2200868.
[33] Drees R, Lienesch F, Kurrat M. Fast charging lithium-ion battery formation based on simulations with an electrode equivalent circuit model[J]. Journal of Energy Storage, 2021, 36: 102345.
[34] Lu Yufang, Han Xuebing, Chu Zhengyu, et al. A decomposed electrode model for real-time anode potential observation of lithium-ion batteries[J]. Journal of Power Sources, 2021, 513: 230529.
[35] Johnson V H. Battery performance models in ADVISOR[J]. Journal of Power Sources, 2002, 110(2): 321-329.
[36] Xu Zhicheng, Wang Jun, Fan Qi, et al. Improving the state of charge estimation of reused lithium-ion batteries by abating hysteresis using machine learning technique[J]. Journal of Energy Storage, 2020, 32: 101678.
[37] Wu M S, Chiang P C J, Lin J C. Electrochemical investigations on advanced lithium-ion batteries by three-electrode measurements[J]. Journal of the Elec- trochemical Society, 2005, 152(1): A47.
[38] Wassiliadis N, Adermann J, Frericks A, et al. Revisiting the dual extended Kalman filter for battery state-of-charge and state-of-health estimation: a use- case life cycle analysis[J]. Journal of Energy Storage, 2018, 19: 73-87.
Optimization of Fast Charging Strategy for Lithium-Ion Batteries without Deposition Based on Electrode Equivalent Circuit Model
Abstract Fast charging is crucial for the application of lithium-ion batteries in electric vehicles. However, traditional fast charging algorithms are prone to causing the anode potential to reach the lithium plating potential threshold (0V vs. Li/Li+). As a result, lithium ions on the anode material surface have a direct reduction reaction, leading to lithium plating, accelerating battery aging, and even causing charging safety incidents. It is necessary to study lithium-plating-free fast charging for lithium-ion batteries. This paper, based on the lithium-ion battery electrode equivalent circuit model, proposes a dual-loop lithium plating-free fast charging strategy control scheme composed of an anode potential closed-loop observer and a charging current closed-loop controller, thereby achieving safe and lithium plating-free fast charging for lithium-ion batteries.
Firstly, a dual-electrode equivalent circuit model for lithium-ion batteries is established. Model parameters under various charge states are identified offline through three-electrode experiments on lithium-ion batteries. Secondly, an anode potential closed-loop observer based on the extended Kalman filter (EKF) algorithm is designed to observe the real-time anode potential, an internal state of the lithium-ion battery. Additionally, a charging current closed-loop controller based on feed forward compensation is designed, enabling online control of the charging current of the lithium-ion battery. The combined observation-control logic of the anode potential closed-loop observer and the charging current closed-loop controller is also explained. Finally, the rationality and effectiveness of the proposed lithium plating-free fast charging strategy control scheme for lithium-ion batteries are demonstrated through simulation and experimentation.
Simulation and experimental results demonstrate that, for the anode potential closed-loop observer, under different operating conditions, the average observed error of the anode potential is less than 5 mV, with a maximum error of no more than 10 mV. Moreover, even during abrupt changes in charging current, the observer can rapidly correct the observed results, keeping the error low. As for the charging current closed-loop controller, during the current adjustment process, the adjustment time for the anode potential to reach and stabilize within the set threshold +1 mV range is 26 s, with a steady-state error of less than 0.05 mV, and without overshooting or oscillation. Furthermore, the charging effect of the proposed fast charging strategy is verified under conditions of two different maximum charging currents. The results indicate that, compared to 1C constant current constant voltage charging, the proposed fast charging strategy can save approximately 46% of the charging time. The minimum anode potential during charging is 4.8 mV. For batteries cycled using the proposed fast charging strategy, no lithium plating is found even after disassembling the battery, affirming that this strategy can significantly reduce charging time and effectively suppress lithium plating. It is a lithium-plating-free fast charging control scheme that simultaneously considers high precision and robustness.
Keywords:Lithium-ion battery, electrode equivalent circuit model, anode potential, fast charging strategy
中图分类号:TM911
DOI:10.19595/j.cnki.1000-6753.tces.230990
国家自然科学基金(52307238)和河北省中央引导地方科技发展专项(216Z4406G)资助项目。
收稿日期 2023-06-26
改稿日期 2023-08-28
赵英杰 男,1998年生,硕士研究生,研究方向为锂离子电池快充策略研究。
E-mail: 202131404107@stu.hebut.edu.cn
徐志成 男,1995年生,讲师,硕士生导师,研究方向为锂离子电池机理建模、状态估计与安全管理等。
E-mail: xzc@hebut.edu.cn(通信作者)
(编辑 郭丽军)