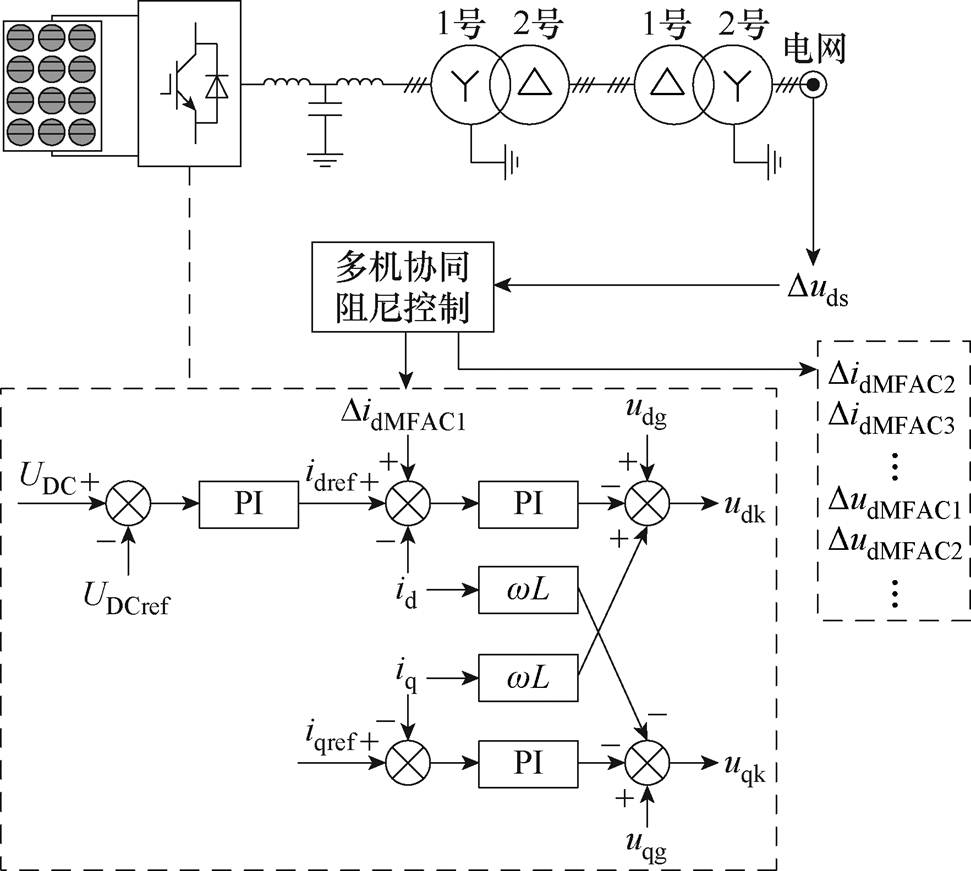
图1 光伏系统的阻尼控制器结构
Fig.1 Damping controller structure for PV
摘要 随着光伏、风电在电网中接入规模的快速增长,电力系统次同步振荡问题逐渐凸显。该文针对包含光伏、双馈风电机组的等效多机新能源场站,提出一种数据驱动的抑制次同步振荡的多机协同阻尼控制方法。首先,结合新能源并网系统的结构与次同步振荡阻尼方法,确定了阻尼控制器信号的输入、输出位置。其次,将次同步振荡场景下的新能源场站等效多机并网系统简化为多输入单输出系统,基于紧格式动态线性化理论,提出了适合光伏、风电多机协同的无模型自适应次同步振荡阻尼控制方法,并对控制参数进行了优化。最后,在IEEE 39节点系统增加新能源接入场景中进行测试,阻抗频率分析与仿真结果均体现出该控制方法能有效提升系统的阻尼。在考虑阻尼控制器投入时间、新能源场站规模、风光出力占比等不同的情况下,验证了该控制方法的有效性和适应性。该控制方法对振荡频率的偏移不敏感,并对系统的大小扰动具有较强的适应能力,体现出良好的次同步振荡阻尼性能。
关键词:无模型自适应阻尼控制 次同步振荡 新能源场站 协同控制 数据驱动
在“双碳”目标驱动的新型电力系统发展背景下,我国对以风电、光伏发电为代表的新能源产业提出了更高的要求,中国2022年新增风电、光电装机约1.25亿kW[1],含高比例可再生能源的交直流混联电网将成为电力系统的典型形态。新能源系统有诸多不确定性,运行方式复杂多变,传统预案式控制模式已难以应对新形态电网的安全需求。与传统电力系统相比,新能源集群送出系统的运行特性发生了深刻变化,近年来已在国内外引发多起振荡脱网事故[2],其中安装双馈感应发电机(Double-Fed Induction Generator, DFIG)的风电机组经串补线路并网易引发次同步振荡(Sub-Synchronous Oscillation, SSO)现象,美国德州南部[3]、明尼苏达西南部[4]、河北沽源地区[5]、哈密东部[2]均发生过新能源并网SSO问题。随着双碳目标的推进,包含多台风电机组、多台光伏(Photovoltaic, PV)的混合新能源场站送出系统成为新能源并网的趋势,在我国宁夏风光火打捆电源基地、哈密电网东部北部片区、张北[2]等地均有风电光伏经汇集后集中外送工程,加强混合新能源场站稳定性问题研究成为大势所趋。
针对新能源场站的SSO问题,现有研究提出了多种机理分析方法,如阻抗分析法[6-7]、特征值法[8]、描述函数法[9]、根轨迹法[10]、路径分析法[11]等。上述理论分析对新能源SSO抑制研究具有指导意义,基于这些建模分析和机理研究,目前最常用的振荡控制方法为附加新能源次同步阻尼控制(Sub- Synchronous Damping Control, SSDC)[12-16],通过增强逆变器在振荡频率处阻尼来提升系统稳定 性[17]。传统SSDC方法属于模型驱动控制方法,依赖精准的系统状态方程进行振荡频率测量、多通道滤波、相位补偿计算、移相等阻尼控制环节。但传统SSDC的滤波器中心频率等控制参数无法实时调整,导致可能无法适用于新的振荡频率[17]。对于工作状态不同的系统,需要根据实际运行情况对每个系统单独地设计阻尼控制器。因此,在混合新能源场站中,传统阻尼策略需要对不同的机组分别配置不同的阻尼控制器及参数,设计较为繁琐,并且适应性有限。
鉴于传统SSDC方法[12-16]的局限性,现有研究采取了自抗扰技术[18-19]、虚拟阻抗技术[20-21]、次同步陷波技术[22-23]、滑模控制技术[24-26]和人工智能方法[27],提升了SSDC策略的控制效果,但这些改进策略仍然未能摆脱对模型的依赖,模型准确性下降则控制效果会降低;也未解决多机系统阻尼策略设计复杂的问题。
含高比例可再生能源的新型电网运行状态复杂多变,数学模型呈现高维、非线性、非连续等复杂特性,动态时间尺度差异大、电气量空间耦合范围广,系统动态规律难以准确刻画。传统新能源SSDC控制器是一种模型驱动的预案式控制,对模型精度和运行方式的匹配性要求高,策略失配风险高,可适用范围有限,难以适应复杂多变的运行工况。
因此,亟须寻找新的策略打破阻尼控制领域的壁垒。文献[17]指出,振荡抑制策略的发展趋势应是“自适应”。目前基于模型驱动的模型预测自适应控制在低频振荡[28-29]、次同步振荡[23, 30-31]阻尼控制领域具有很好的应用前景,但是,这类具有自适应能力的振荡在线阻尼控制中,其中单一模型预测控制对不确定运行状态适应性有限,多模型自适应控制需要对多个系统运行状态构建模型库,模型个数越多,控制性能越好,但系统复杂度和成本大大增加。
尽管模型驱动控制是目前最成熟的控制体系,但对于模型复杂、工况多变的系统,模型驱动控制无法同时兼顾适应性与建模计算量的问题。而数据驱动控制在这方面体现出了不可替代的优势[32]:避免了未建模动态和鲁棒性问题,对不确定性信息的需求少,规避了实际工程中信息量大和干扰多的问题。其中,侯忠生教授等提出的无模型自适应控制(Model-Free Adaptive Control, MFAC)就是一种优秀的数据/响应驱动控制方法[32],MFAC使用系统输入输出数据来等效系统来替代状态方程建模,并在此基础上依靠算法设计实现自适应控制。
相较于模型驱动的传统自适应控制,MFAC仅依赖被控系统的实测输入和输出数据,不需要任何外在的自适应训练过程,计算量小,收敛性与稳定性好,使其更适应实际系统运行工况多变的控制问题,对非预案式场景具有较好的适应能力。
以MFAC为代表的数据驱动控制作为一种新兴控制方式,拥有强适应性的同时,也存在控制性能不易把握的缺点,在电力系统一定范围内进行了成功探索[33-37],但仍未获得广泛应用。在系统工况变化复杂、实时建模难度大的情况下,MFAC等数据驱动控制可作为模型驱动控制的有效补充。
光伏、风电混合新能源场站是风光资源利用的有效方式,其等效多机系统与文献[33-34]中单机系统的运行模式有较大的区别。文献[38]提出新能源多机并网系统中多机存在相近振荡模态,可分析比较不同机组的状态参数从而选择阻尼控制器的机组安装位置,但未对不同机组的控制器进行协调控制。
针对包含光伏、风电的新能源场站经串补并网系统的次同步振荡问题,考虑系统工况变化,本文提出一种适合光伏、风电的多机协同无模型自适应次同步阻尼控制(multi-Machine Cooperative Model- Free Adaptive Control-Sub-Synchronous Damping Control, MC-MFAC-SSDC)策略,这种数据驱动控制策略是一种非预案扰动下的自主协同稳定控制技术,弥补了传统模型驱动阻尼控制方法的缺陷。该控制策略能快速响应并抑制次同步振荡,对振荡频率偏移不敏感,在不同的新能源场站系统测试中均表现出良好的适应性,协同控制效果好、抗扰动能力强,具有较好的工程应用价值。
与传统SSDC方法相比,本文采用的无模型自适应控制算法基于数据驱动,不需要计算振荡频率、滤波、移相等依赖先验知识的阻尼环节[12],在阻尼控制器的输入输出信号选择时仍然需要系统控制器结构的必要信息。算法“无模型”体现在不需要精确的系统状态方程,通过输入输出数据进行系统动态线性化,从而自适应地调整控制器参数。
根据前人的工程经验与分析讨论,本文的新能源场站次同步振荡阻尼控制方案由测量、协同阻尼控制、控制信号输入这三个环节构成。
(1)测量:选取新能源场站的并网电压uds为统一测量信号。
(2)协同阻尼控制:测量信号uds的d轴分量实际值与参考值之差Duds经过多机协同无模型自适应次同步阻尼控制器,生成一组控制信号向量。具体的协同阻尼控制算法将在第2节介绍。
(3)控制信号输入:将控制信号分配到各新能源机组上,控制器生成的不同DidMFAC信号附加到不同PV逆变器内环[12],生成的不同DudMFAC信号附加到不同DFIG转子侧逆变器内环[33]。
本文讨论多PV、多DFIG构成的混合新能源场站,图1和图2分别描述了无模型自适应多机协同阻尼控制在各PV和DFIG并网机组上的实施方法。其中,光伏模型、双馈风电机组模型均来自PSCAD标准模型。控制器生成的不同DidMFAC信号、DudMFAC信号之间的协同控制算法将在第2节展开。

图1 光伏系统的阻尼控制器结构
Fig.1 Damping controller structure for PV
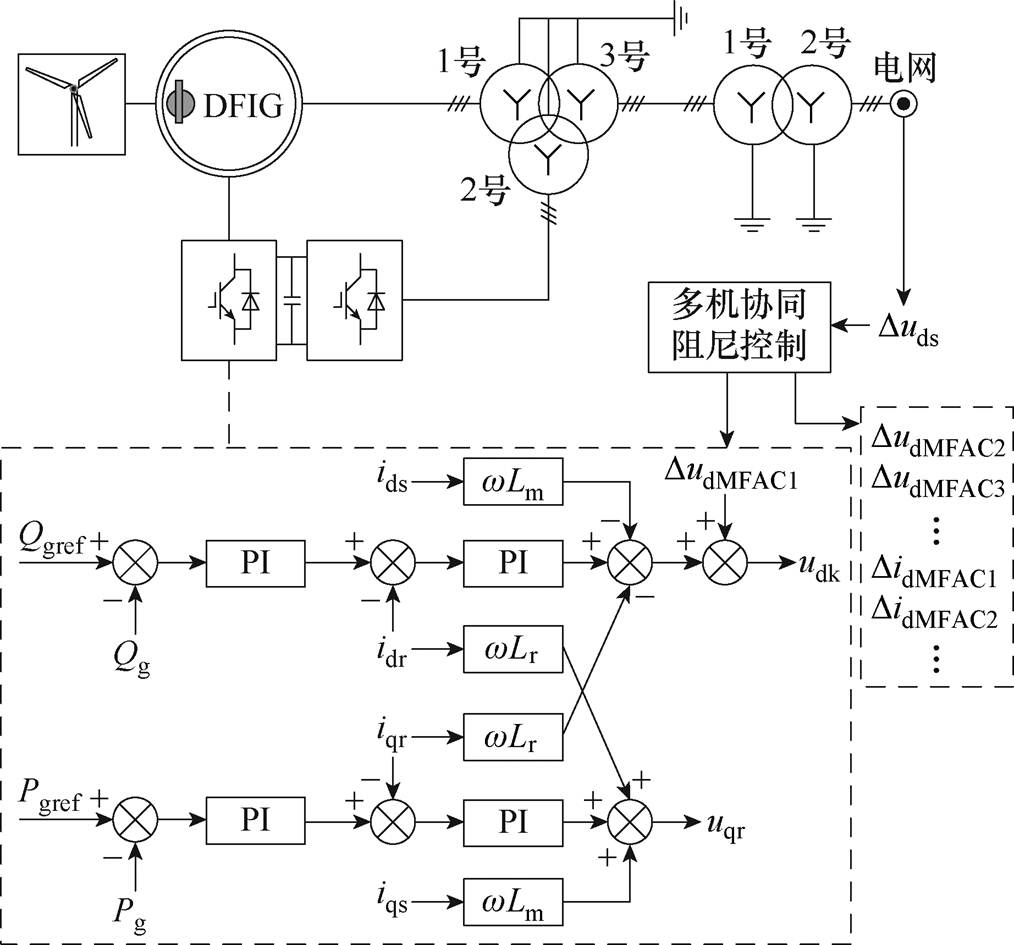
图2 双馈风电机组的阻尼控制器结构
Fig.2 Damping controller structure for DFIG
新能源并网系统作为动态特性复杂的多输入多输出系统,难以量化分析其稳定性问题。在次同步振荡场景下,将其简化为稳定性等价的单输入单输出(Single Input and Single Output, SISO)系统将便于开展稳定性分析与设计控制策略[39]。光伏并网系统[40]、风电机组并网系统[21, 33-34, 41]均可单独等效为SISO系统。
在此基础上,对于含有多光伏电站、多风电机组的新能源场站,在多机协同次同步阻尼控制器设计的过程中,类似地将其等效为多输入单输出(Multiple Input and Single Output, MISO)系统,以场站内各PV、DFIG逆变器内环d轴指令附加量DidMFAC、DudMFAC为输入,新能源场站并网电压d轴分量偏差Duds为输出的MISO系统。
考虑到实际系统中存在采样间隔,因此新能源场站可以视为MISO离散时间非线性系统,描述方程为[32]
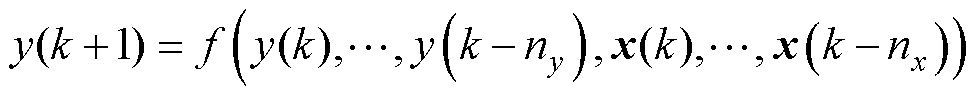 (1)
(1)
式中,x(k)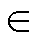 Rm、y(k)
Rm、y(k)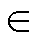 R分别为k时刻的系统输入和输出;nx、ny分别为输入、输出的维数;f( · )代表描述系统的未知非线性函数。
R分别为k时刻的系统输入和输出;nx、ny分别为输入、输出的维数;f( · )代表描述系统的未知非线性函数。
具体地,对上述新能源场站MISO系统,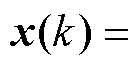
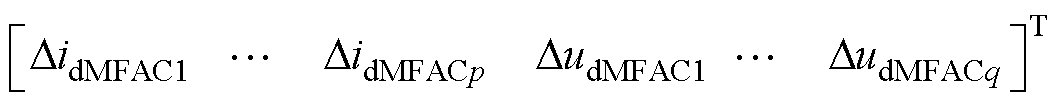 为多机组的阻尼控制信号输入,其中p、q分别为光伏电站、双馈风电机组的台数;y(k)=Duds为阻尼控制器的反馈信号。
为多机组的阻尼控制信号输入,其中p、q分别为光伏电站、双馈风电机组的台数;y(k)=Duds为阻尼控制器的反馈信号。
新能源场站作为实际物理系统,能量输入输出均有界,因此新能源场站并网系统可以采用紧格式动态线性化方法[32],由式(1)得到系统数据模型为
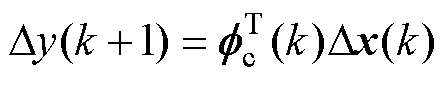 (2)
(2)
其中
Dy(k+1)=y(k+1)-y(k) Dx(k)=x(k)-x(k-1)
式中,Dy(k+1)、Dx(k)分别为相邻时刻的输出变化和输入变化;fc(k)为伪偏导数,与k时刻前输入输出信号有关。Dx(k)=[Dx1(k) Dx2(k) … Dxm(k)]T,fc(k)= [fc1(k) fc2(k) …fcm(k)]T均为向量,m=p+q为输入信号的维数,输入向量中Dxi(k)与伪偏导数向量中fci(k)一一对应,伪偏导数元素决定了其对应的输入元素对系统输出变化造成影响的权重,这是实现协同控制的关键。
需要指出的是,传统线性化方法是将系统状态方程在运行点处进行线性近似,在系统复杂、运行状况多变的情况下,传统线性化方法应用困难;而式(2)的MISO系统紧格式动态线性化模型是基于风光混合场站的输入、输出数据来等效的,系统运行状态发生改变,输入输出数据将反映出相应的变化,动态线性化模型也将随之改变。
对于包含多台图1、图2所示光伏、风电机组接入的复杂新能源电力系统,考虑运行工况的变化,精确建模具有一定挑战性。为此,本文尝试探索数据驱动的阻尼控制方法。
式(2)中,伪偏导数向量fc(k)是本文MISO系统多机协同控制的重要实现途径。向量fc(k)将各个控制分量的伪偏导数综合为近似梯度。相较于基于单一伪偏导数的阻尼控制,采用近似梯度的协同控制期望获得更优的控制效果。
一步向前控制输入准则函数取为
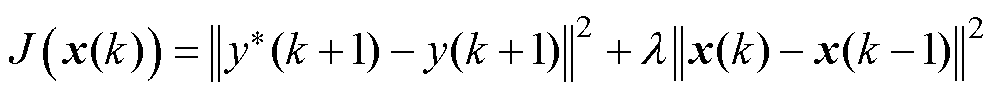 (3)
(3)
式中,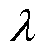 为权重因子,
为权重因子,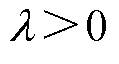 ;
;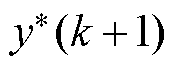 为系统在k+1时刻的期望输出。次同步振荡消失后,并网电压应稳定在参考值,系统输出量Duds的期望值保持为0[33]。
为系统在k+1时刻的期望输出。次同步振荡消失后,并网电压应稳定在参考值,系统输出量Duds的期望值保持为0[33]。
将式(2)代入式(3),对x(k)求导并令其为零,可得到当前时刻的控制输入算法为
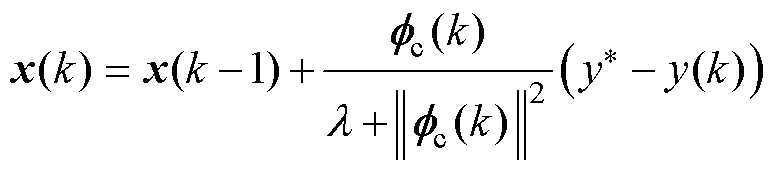 (4)
(4)
由于伪偏导数时变,每一时刻的真值难以获得,因此在设计控制器的算法时引入伪偏导数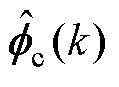 的估计值
的估计值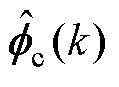 ,预测算法为
,预测算法为
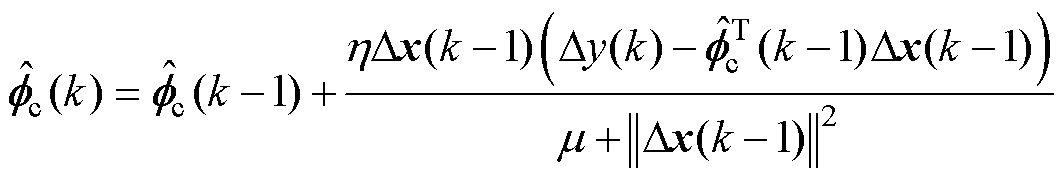 (5)
(5)
式中,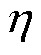 为步长因子,
为步长因子, ;
;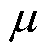 为权重因子,
为权重因子, ;
;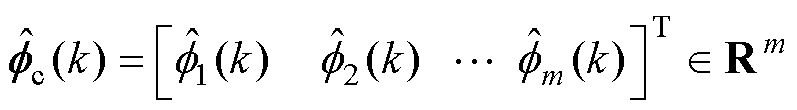 。
。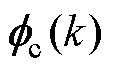 和
和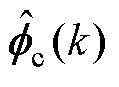 都是有界的多维时变参数[32],
都是有界的多维时变参数[32],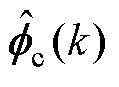 算法处理了对MISO系统多输入向量之间耦合关系。又由式(4),不同的伪偏导数对应各输入信号的不同变化,保证了多控点之间的协同效果[32]。
算法处理了对MISO系统多输入向量之间耦合关系。又由式(4),不同的伪偏导数对应各输入信号的不同变化,保证了多控点之间的协同效果[32]。
为了保证系统可控,当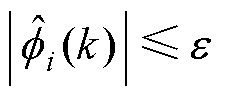 或
或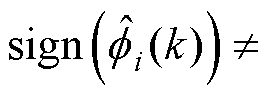
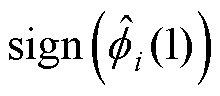 ,对
,对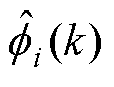 重置,即
重置,即
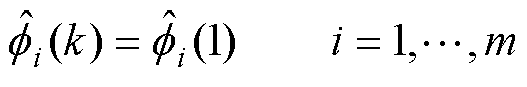 (6)
(6)
式中,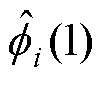 为
为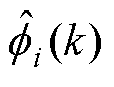 的初值,对于实际工程系统,一般选取
的初值,对于实际工程系统,一般选取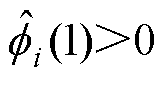 。
。
展开式(2)并更新为含估计值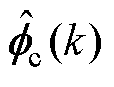 的表达式,即
的表达式,即
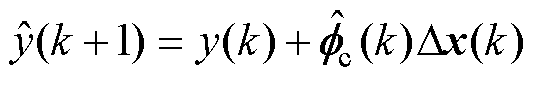 (7)
(7)
记系统输出预测误差为
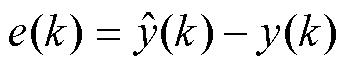 (8)
(8)
为使系统响应速度更快,且更具有一般性,为式(4)引入步长因子系数r0与矩阵r1,并更新为含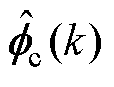 的一步向前预测的控制算法为
的一步向前预测的控制算法为
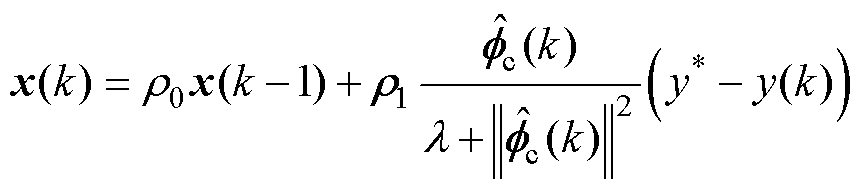 (9)
(9)
式中,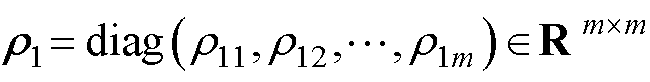 ,
,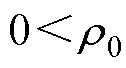 ,
,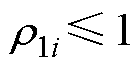 。
。
基于数据驱动的紧格式动态线性化MISO数据模型的MFAC方法,将多个输入信号的作用考虑在整个系统中,通过伪偏导数向量实现了多输入信号之间的协同作用。伪偏导数向量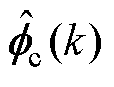 呈现出系统的近似梯度,协同控制使被控量沿着近似梯度方向接近目标值,避免了各控制信号之间负面的相互作用。通过设计合理的伪偏导数初值、各输入向量对应的步长因子,可优化系统控制[42]。
呈现出系统的近似梯度,协同控制使被控量沿着近似梯度方向接近目标值,避免了各控制信号之间负面的相互作用。通过设计合理的伪偏导数初值、各输入向量对应的步长因子,可优化系统控制[42]。
本文的无模型自适应协同阻尼控制算法,无需对新能源并网系统进行状态方程建模,也无需对各新能源机组进行单独的阻尼控制器设计,通过统一格式的算法即可直接得到不同机组对应的控制信号值,并且保证了各控制信号的协同。
结合式(5)、式(6)、式(9),得到新能源场站多机协同无模型自适应次同步阻尼控制方案;式(5)、式(6)为核心关键伪偏导数的预测公式,式(9)为阻尼输入信号的获取方式。综上所述,新能源场站多机协同无模型自适应次同步阻尼控制器的流程如图3所示。
以两光伏两风电的新能源系统为例,输入信号x(k)=[DidMFAC1 DidMFAC2 DudMFAC1 DudMFAC2]T,向量元素为分别注入PV1、PV2、DFIG1、DFIG2的附加阻尼信号;系统输出y(k)=Duds,为新能源场站经串补并网点电压uds的d轴分量实际值与参考值之差。每进行一次完整的控制环节,以该四输入单输出系统为例,该数据驱动多机协同阻尼控制仅需进行24次加(减)法、28次乘(除)法在线运算,逻辑计算时长可忽略,并不考虑额外的控制延时。传统的SSDC策略[12]中每次滤波、移相均需要数据窗周波采样N个点[43],运算量远高于简单代数计算,相位补偿环节增加了控制延时,多机阻尼的计算量又倍增。由此可见,本文设计的多机协同无模型自适应次同步阻尼控制策略计算量远小于传统SSDC,控制算法延时可以忽略。
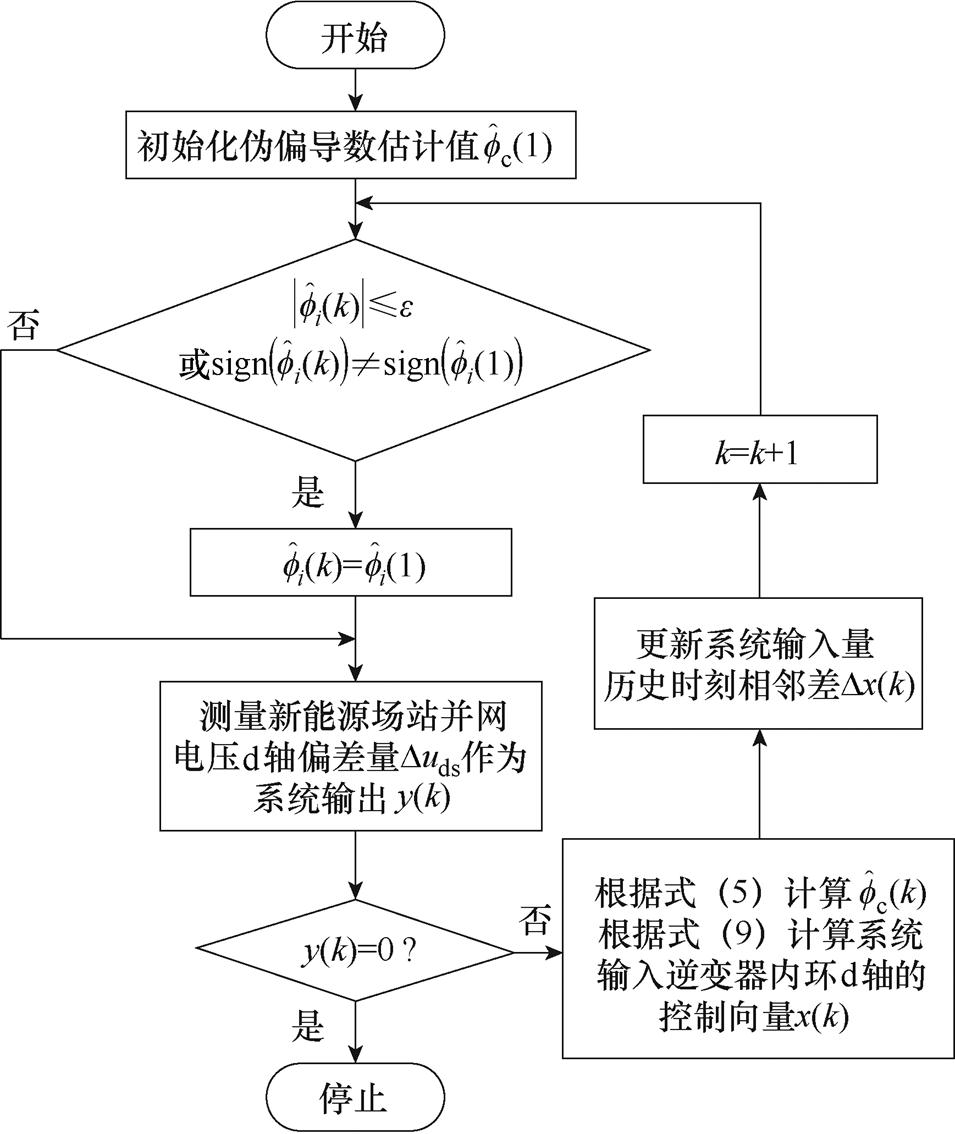
图3 多机协同阻尼控制器算法流程
Fig.3 MC-MFAC-SSDC’s algorithm flow chart
为了进一步验证和分析新能源并网系统的多机协同无模型自适应次同步阻尼控制器性能,本节对传统的IEEE 39节点测试系统进行改造,基于PSCAD/EMTDC平台进行暂态时域仿真分析。
系统接线如图4所示,发电机根据节点位置命名,如节点30接入的发电机命名为G30。在节点9接入容量约163 MW的新能源场站,由两台光伏电站PV1、PV2和两台双馈风电机组DFIG1、DFIG2构成,光伏、双馈风电机组并网模型均采用PSCAD标准模型,仅改变工况与增加本文附加阻尼控制环节。新能源场站风光出力占比为2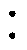 1,场站规模与运行工况见表1。
1,场站规模与运行工况见表1。
图4 新能源场站接入IEEE 39节点系统
Fig.4 Structure of the IEEE 39-node system connected with the new energy station
表1 新能源场站运行工况
Tab.1 Operating conditions of the new energy station
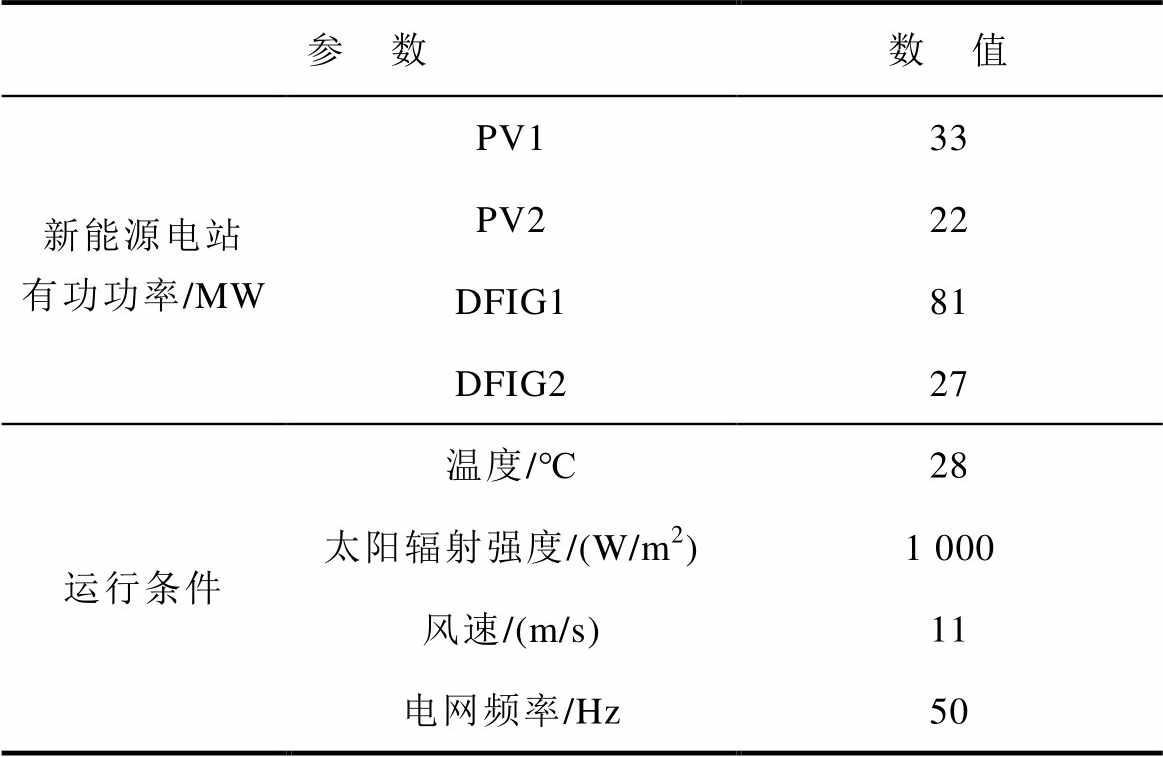
参 数数 值 新能源电站有功功率/MWPV133 PV222 DFIG181 DFIG227 运行条件温度/℃28 太阳辐射强度/(W/m2)1 000 风速/(m/s)11 电网频率/Hz50
本文将多机协同无模型自适应次同步阻尼控制策略应用至含有多光伏、多双馈风电机组的新能源场站并网系统,系统结构复杂,对多维阻尼控制参数的选择提出了更高的要求。
尽管MFAC方法已经具有了基本的理论体系和分析框架,但在应用上仍然处于初始阶段,其中MFAC各种控制器参数的系统整定方法仍然处于研究空白阶段[32]。现在的MFAC应用方式中[33-37],控制器参数的常用取法是通过经验法选取合适的初值,再进行优化调整。
常用的优化方法包括穷举法、黄金分割法、单纯形法、群体智能优化算法。其中,群体智能优化算法擅长解决多目标全局最优化问题,黄金分割法擅长解决单变量函数;对于仅需单目标、多变量的优化对象,单纯形法是一种算法简单、迭代计算少的优化方式[44]。
因此,本文基于PSCAD/EMTDC平台,采用单纯形法对多机协同无模型自适应次同步阻尼控制器参数进行寻优,目标函数选取时间与误差平方乘积的积分函数[44-45]为
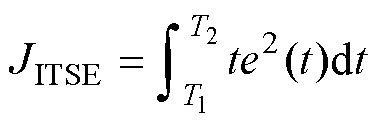 (10)
(10)
式中,T1为控制器投入时刻;T2为仿真结束时刻,对每组寻优程序保持T1、T2相同;误差函数的表达式见式(8)。
对包含两PV、两DFIG的新能源场站,控制输入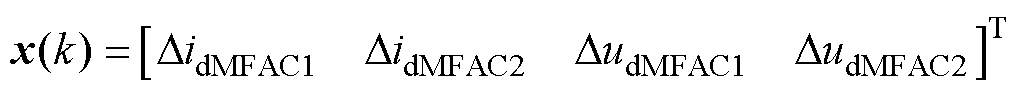 ,控制参数按PV1、PV2、DFIG1、DFIG2的顺序依次排列。在需要选定的参数
,控制参数按PV1、PV2、DFIG1、DFIG2的顺序依次排列。在需要选定的参数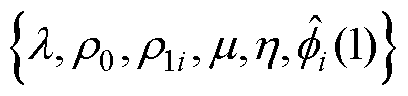 中,权重因子
中,权重因子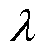 与步长因子
与步长因子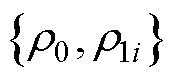 对MFAC控制器的设计起至关重要的作用[32]:
对MFAC控制器的设计起至关重要的作用[32]: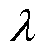 越小,系统闭环反应将变得更快,但其超调也相应地变大;
越小,系统闭环反应将变得更快,但其超调也相应地变大;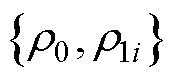 则对输入值起着直观的比例作用,步长因子越大,输入值越大,控制器学习速度也越快,但同样可能引发超调问题。另外,伪偏导数初值的选择会影响系统初始梯度及协同效果,因此,为了体现更好的多机协同效果,需要利用优化算法使协同控制效果更好。
则对输入值起着直观的比例作用,步长因子越大,输入值越大,控制器学习速度也越快,但同样可能引发超调问题。另外,伪偏导数初值的选择会影响系统初始梯度及协同效果,因此,为了体现更好的多机协同效果,需要利用优化算法使协同控制效果更好。
同时,各控制参数的约束条件为
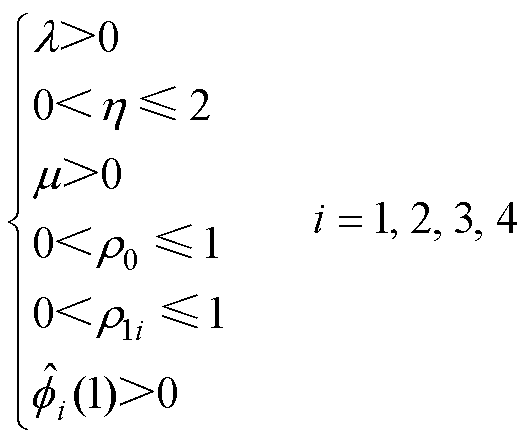 (11)
(11)
考虑在阻尼控制的不同阶段,设计两种不同的工作模式:①在控制器投入前期,以快速抑制振荡为控制目的;②在控制投入后期,以保持稳定、尽量减小超调量为目的。
工作模式①的参数设计时,以目标函数最小为优化目标,在式(11)的可行区域内采用单纯形法对MFAC协同控制器参数进行寻优。文献[32-33]证明了MFAC算法在式(11)可行域内的稳定性与鲁棒性,本文不再重复论证。
利用PSCAD/EMTDC平台进行50组单纯形法参数优化,T1取1.1 s,T2取2 s,设置当目标函数JITSE<50时终止寻优,否则选取50组参数中令目标函数最小的一组控制参数。优化结果为: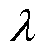 =1.194,
=1.194,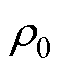 =0.943,
=0.943,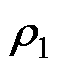 =diag(0.707 7, 0.5077, 1, 1),
=diag(0.707 7, 0.5077, 1, 1),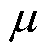 =10.9,
=10.9,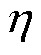 =1,
=1,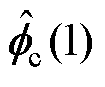 = [0.404 0.404 0.404 0.404]T。工作模式②的参数设计时,在模式①的基础上,适当地增大权重因子并减小步长因子,取
= [0.404 0.404 0.404 0.404]T。工作模式②的参数设计时,在模式①的基础上,适当地增大权重因子并减小步长因子,取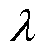 =2,
=2,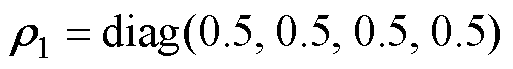 ,其余参数不变。给定一个很小的正数
,其余参数不变。给定一个很小的正数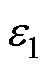 ,当
,当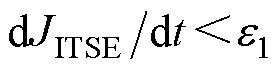 时工作模式由①转入②。限制附加阻尼信号的幅值不超过电压、电流相应参考值的10%,以保证控制器在物理上可以实现。
时工作模式由①转入②。限制附加阻尼信号的幅值不超过电压、电流相应参考值的10%,以保证控制器在物理上可以实现。
基于新能源机组控制策略改进的阻抗重塑方法,是实现振荡抑制的有效措施[2]。为了研究本文数据驱动控制器投入对新能源场站等效电阻的影响,在次同步频率范围内进行频率扫描分析,有、无投入阻尼控制的情况下,新能源场站的正序等效电阻如图5所示。
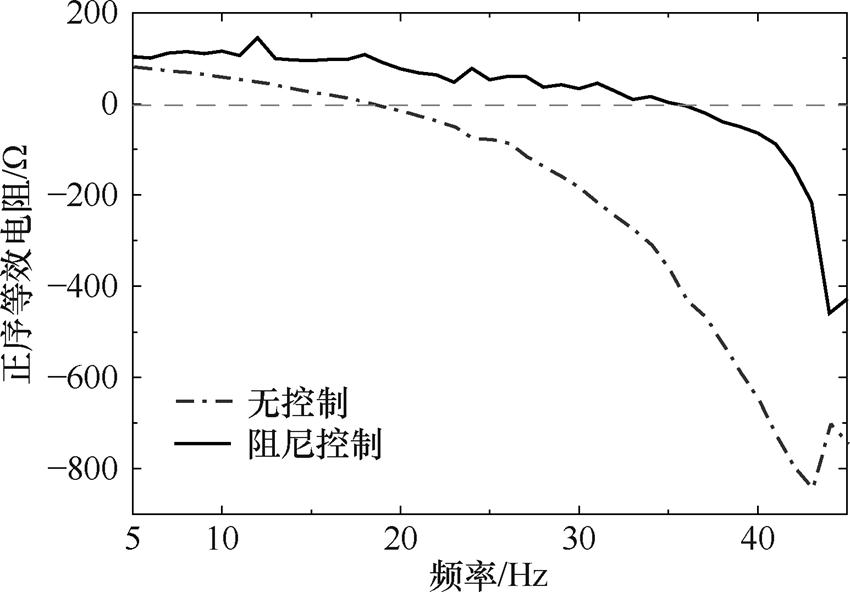
图5 阻尼控制对新能源场站正序等效电阻的影响
Fig.5 Damping control effect on positive-sequence equivalent resistance of the new energy station
由图5可知,在未投入多机协同无模型自适应次同步阻尼控制时,新能源场站在大于19 Hz时呈现出负阻尼;而阻尼控制的投入在次同步频率范围内均显著增大了系统等效电阻,在5~35 Hz范围内呈现出正阻尼,对该频段的次同步振荡具有抑制作用;大于35 Hz的频段内也有效提升了系统等效电阻,削弱了系统次同步振荡的风险。图5从系统阻抗重塑的原理展示了本文阻尼控制器的振荡抑制性能,理论分析表明其对较宽频段的次同步振荡都有控制效果。为更直观地展示阻尼控制器性能,下节将在仿真算例中进一步验证理论分析的结果。
为验证上述分析结果,基于PSCAD/EMTDC平台进行时域仿真。假定t=1 s时投入线路串补,1.1 s投入无模型自适应次同步阻尼协同控制器。当系统发生振荡时,由于有功功率仅包含直流量和振荡分量,能直观地反映振荡强弱。其中,仿真结果显示靠近新能源场站的发电机G31、G39相较其他发电机振荡现象更明显,因此可选取G31、G39和新能源场站的有功功率作为主要的观测对象。
阻尼控制对有功功率和并网点电压的影响如图6和图7所示,在投入多机协同无模型自适应次同步阻尼控制后,系统的次同步振荡得到了快速有效的抑制,发电机与新能源场站的功率迅速趋于平稳,并网电压在约0.5 s的时间内也消除了振荡,并且稳定后的纹波现象基本接近振荡前的情况。
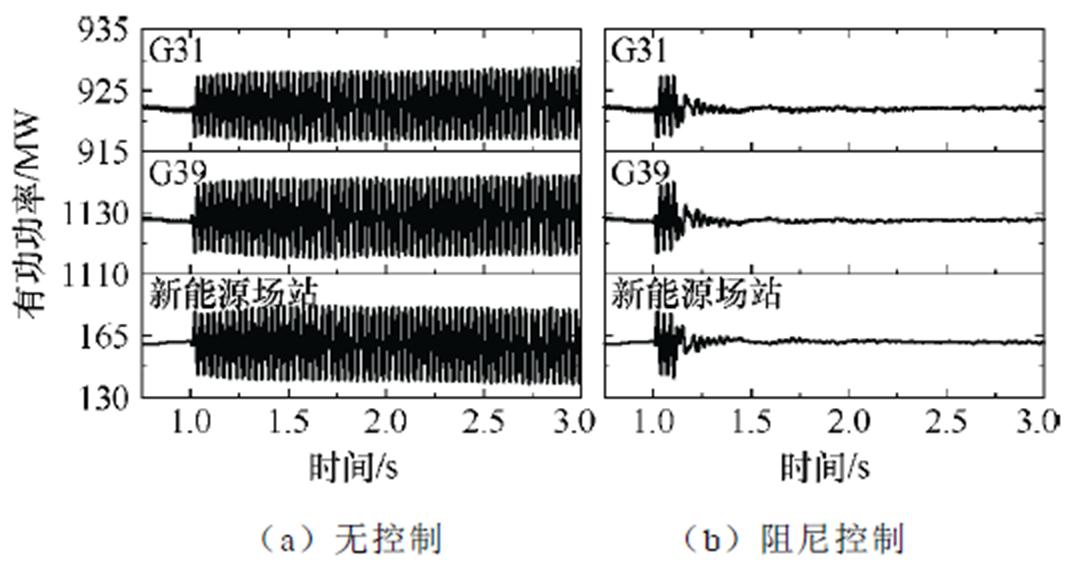
图6 阻尼控制对有功功率的影响
Fig.6 Damping control effect on active power
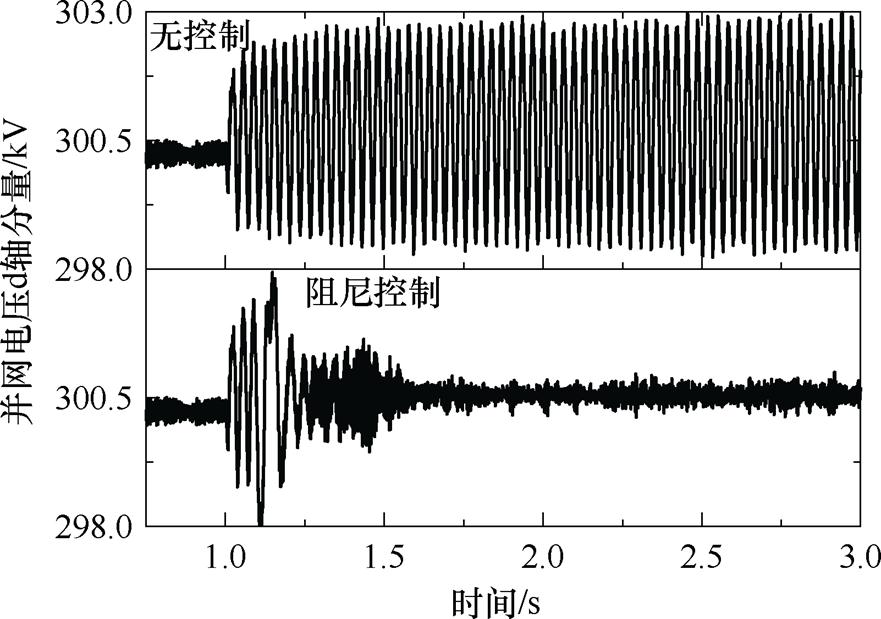
图7 阻尼控制对并网点电压的影响
Fig.7 Damping control effect on grid-connected voltage
以新能源场站的有功功率为例进行振荡频率分析,Prony分析结果表明,未投入阻尼控制时,主导振荡频率为30.732 5 Hz,衰减因子0.129 8,呈发散趋势。其中,Prony阶数选取30阶,其分析结果的信噪比达到51.584 7 dB,认为拟合情况理想[46]。图8给出有、无投入无模型自适应次同步阻尼协同控制的快速傅里叶变换(Fast Fourier Transform, FFT)分析,阻尼控制的投入几乎使主导振荡频率的振荡幅值消失。
图6~图8中t=1.1 s的投入时间考虑了对振荡0.1 s的检测时间,即系统识别振荡信号后迅速投入控制器。此外,图9讨论了多机协同无模型自适应次同步阻尼控制器在其他时间投入对控制效果的影响,其中,t=0 s表示一直投入阻尼控制;t=1.5 s延长了系统对次同步振荡的检测时间;t=2.5 s考虑了更长延时投入阻尼控制的情况。
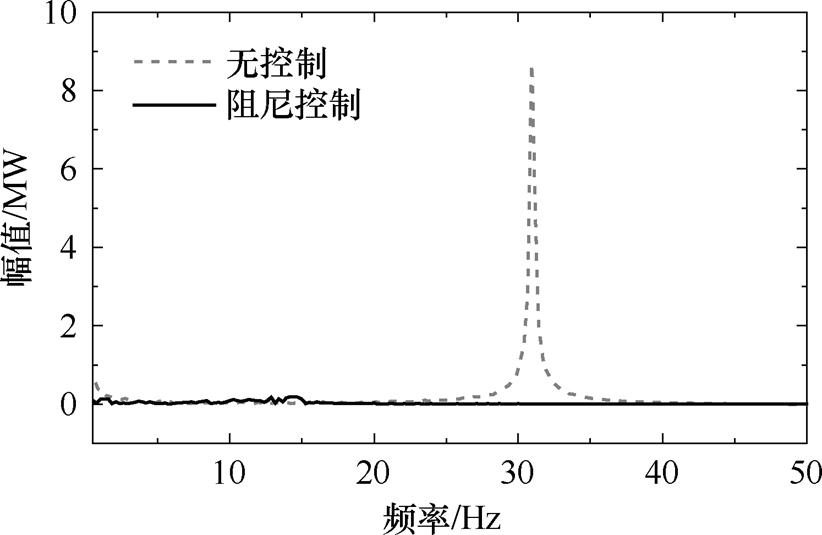
图8 有、无投入阻尼控制时FFT分析结果
Fig.8 FFT analysis results with and without control
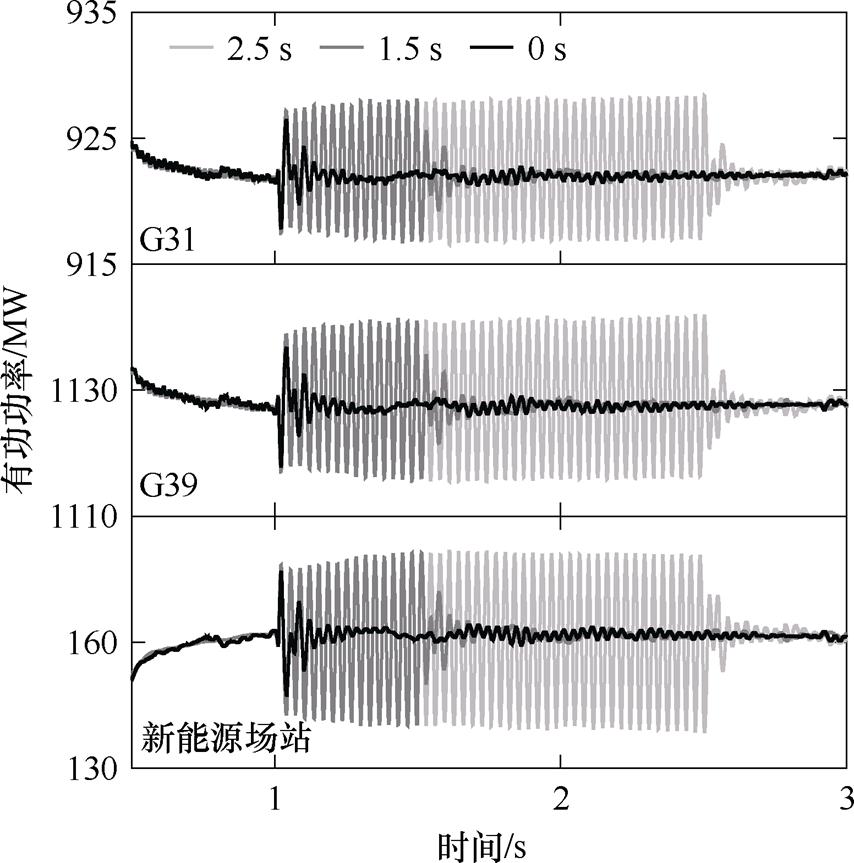
图9 阻尼控制器不同投入时间的控制效果
Fig.9 Control effects with different input time of damping controller
由图9看出,在振荡发展的不同阶段投入阻尼协同控制都能快速抑制振荡,投入时间的延后并不会很明显恶化控制器的控制速度与纹波现象,多机协同无模型自适应次同步阻尼控制器具有显著的控制效果和良好的适应性。
为验证本文多机协同控制策略的有效性,以单机和两机协同效果对比为例,考虑附加阻尼控制的效果对比情况。图10所示新能源场站的并网有功功率曲线,灰色单机曲线为仅考虑DFIG1单独投入无模型自适应附加阻尼控制,黑色双机曲线为考虑DFIG1、DFIG2双机协同的无模型自适应阻尼控制。如图10所示,双机协同控制的效果显著优于单机控制的振荡抑制情况。
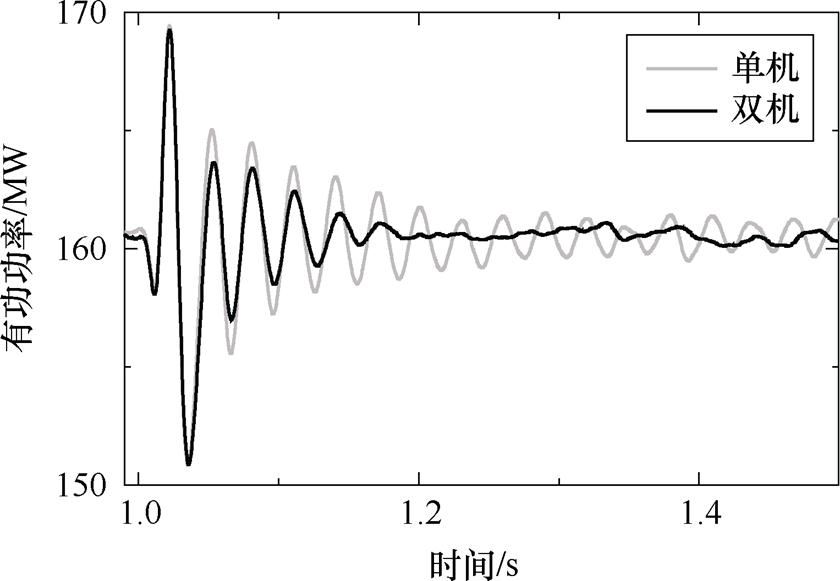
图10 多机协同的阻尼控制效果
Fig.10 Multi-machine damping control effect
上述讨论中,多机协同无模型自适应次同步阻尼控制在3.1节系统参数的算例中体现出良好的控制性能;本节中对新能源场站的规模、风光出力占比及相应的次同步振荡频率进行更广泛的讨论,不同算例中新能源场站参数见表2。图11展示了多机协同无模型自适应次同步阻尼控制在不同算例下的控制效果。阻尼控制在延用3.2节控制参数的情况下,在不同算例中均能迅速有效地抑制住系统振荡。同时,该阻尼控制策略体现出无模型控制的优点,无需根据振荡频率设置控制参数,对30.712 6~33.563 9 Hz的振荡频率偏移不敏感,能够自适应地调整控制信号,从而抑制系统振荡。
表2 不同算例中新能源场站参数
Tab.2 New energy station parameters of different examples
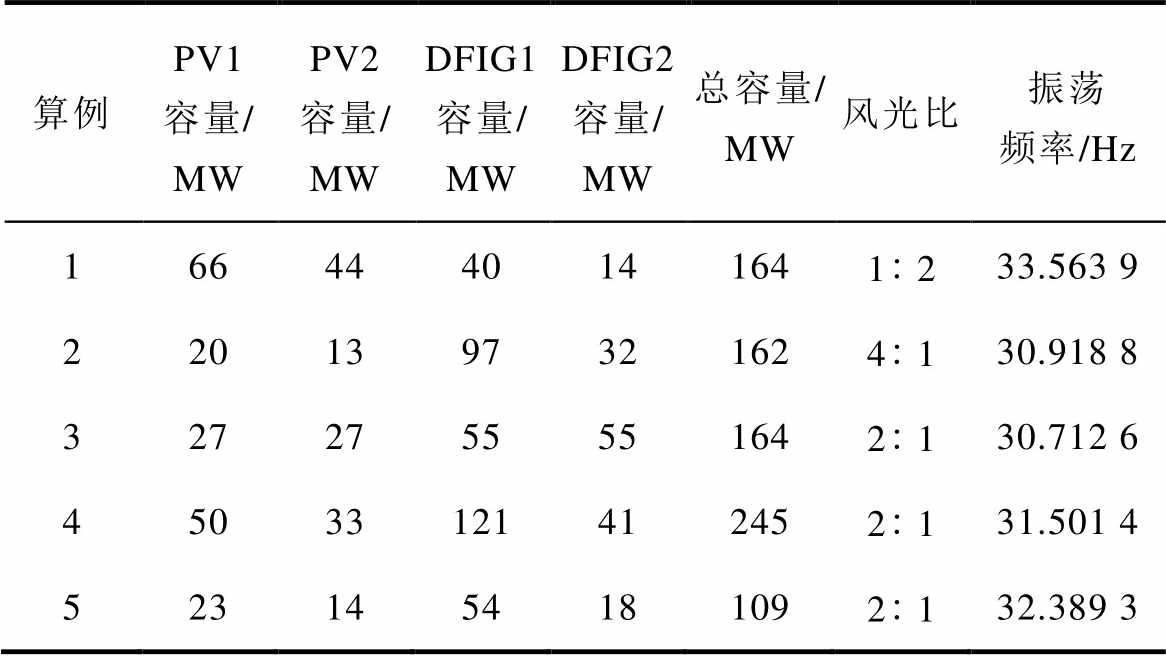
算例PV1容量/MWPV2容量/MWDFIG1容量/MWDFIG2容量/MW总容量/MW风光比振荡频率/Hz 1664440141641233.563 9 2201397321624130.918 8 3272755551642130.712 6 45033121412452131.501 4 5231454181092132.389 3
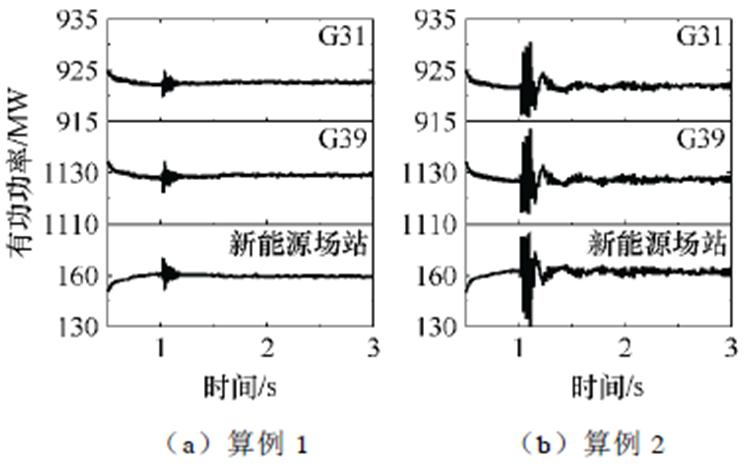
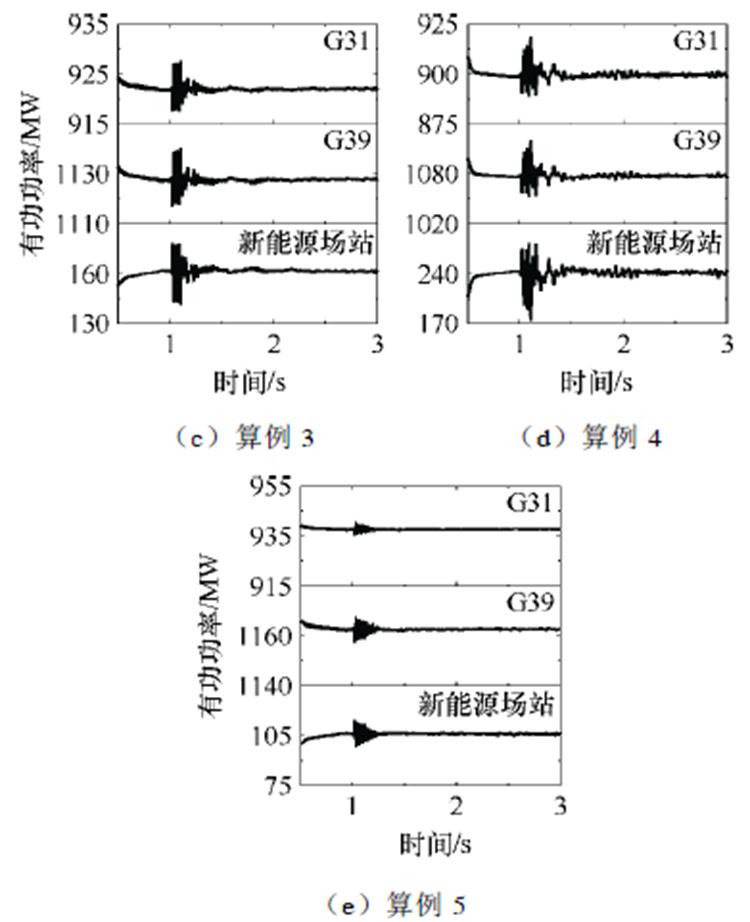
图11 不同新能源场站参数下阻尼控制效果
Fig.11 Damping control effects under different parameters of the new energy station
为进一步验证本文所提控制策略的有效性与适应性,本小节将探讨新能源场站无模型自适应次同步阻尼协同控制对系统扰动的适应能力。根据新能源运行特性,设置自然条件变化的小扰动:①t= 1.5 s风速由11 m/s变为10 m/s,t=1.8 s恢复11 m/s;②t=2 s太阳辐射强度由1 000 W/m2变为1 020 W/m2。根据系统运行模式改变与故障情况,设置切机切负荷的大扰动;③t=2.5 s切除发电机G31;④t=3 s总负荷减载10%。
图12展示了无模型自适应次同步阻尼协同控制对大小扰动的适应能力。在未附加控制的情况下,随着大小扰动的产生,系统中次同步振荡现象有持续发展并继续恶化的趋势,对系统的安全稳定运行造成了严重威胁。在阻尼协同控制下,次同步振荡被迅速抑制住,并且可以克服系统的多次扰动,迅速平稳工作在新的平衡点。本文所提阻尼协同控制策略能适应系统变化的运行工况,鲁棒性良好。
本小节分析本文数据驱动阻尼控制与传统阻尼控制在不同工况下的适应性。为更好地对比两种阻尼策略,本小节对测试系统进行简化,将图4中节点9以外电网部分用无穷大电源代替,保持节点9电压替换前后一致。
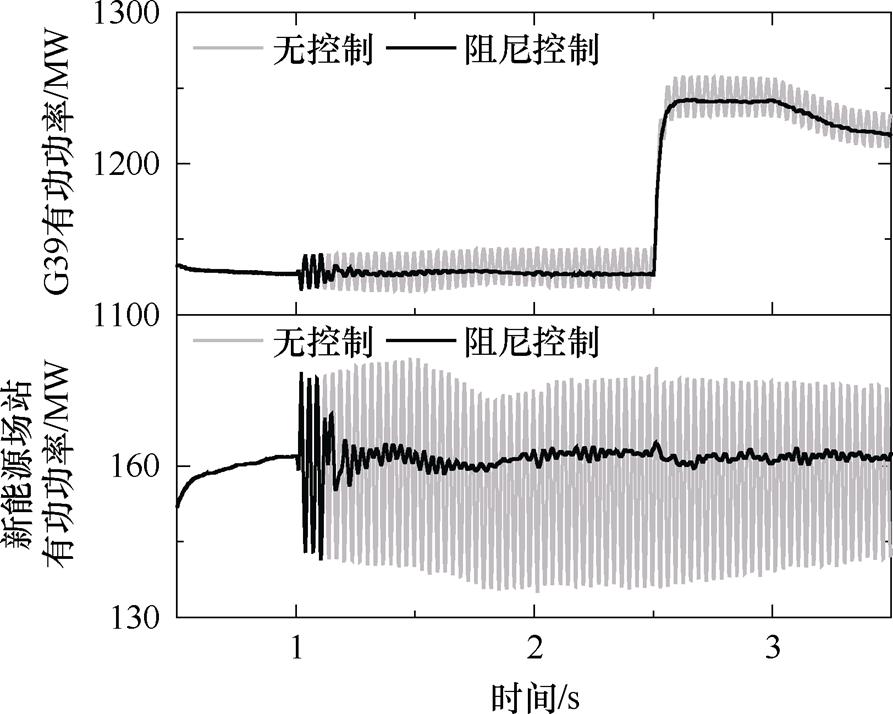
图12 系统扰动下阻尼控制效果
Fig.12 Damping control effect under disturbances
待测试的不同工况运行条件见表3,按工况1对传统阻尼方法进行参数设计。参考传统附加阻尼控制器的设计方法[33],SSDC控制环节按顺序分别为:带通滤波器取中心频率31 Hz、品质因数为20;放大器在DFIG处取增益倍数0.3,在PV处取增益倍数0.1;移相器取相位补偿180°;限幅装置取上、下限幅值0.1(pu)。数据驱动的MFAC阻尼控制器参数及其他系统参数均与前文设置相同。两种阻尼策略的控制效果如图13所示。
表3 不同运行条件
Tab.3 Different operating conditions
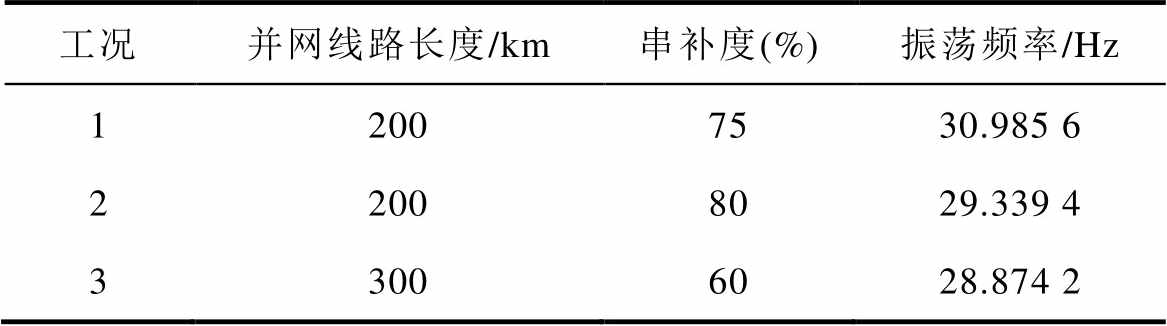
工况并网线路长度/km串补度(%)振荡频率/Hz 12007530.985 6 22008029.339 4 33006028.874 2
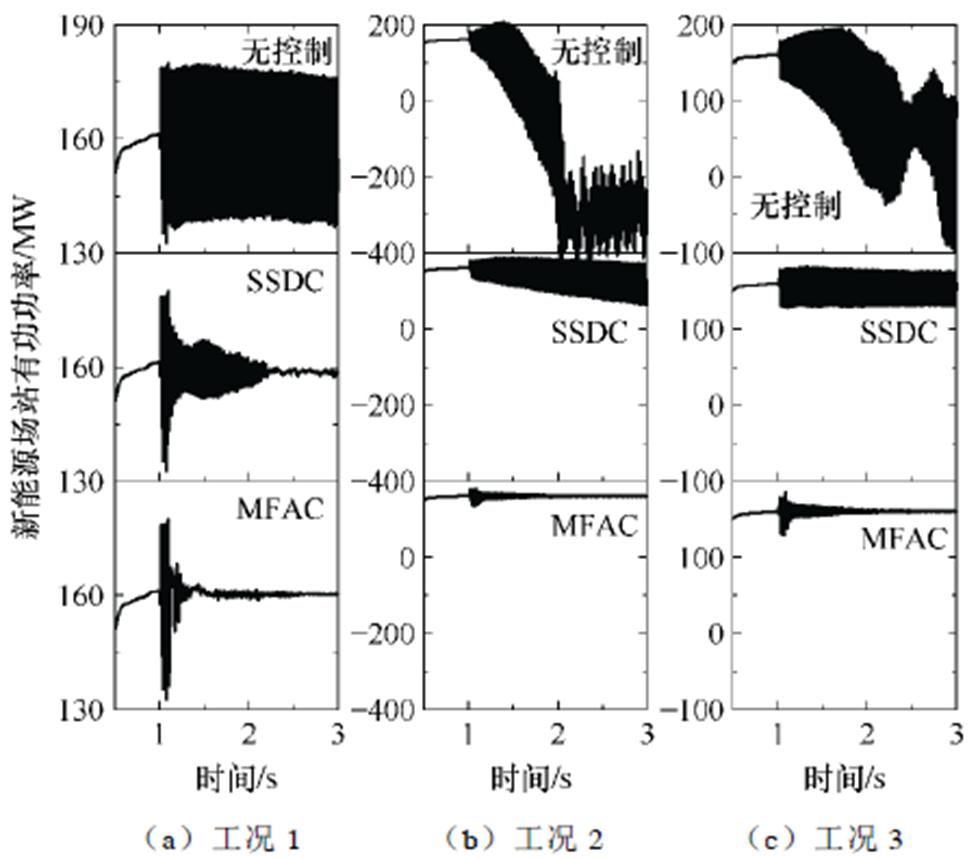
图13 不同工况下两种阻尼控制效果对比
Fig.13 Comparison of two damping control effects under different working conditions
在工况1下,传统SSDC策略与本文MFAC策略均能有效抑制振荡;但是随着系统参数改变,振荡频率发生偏移,传统SSDC策略的振荡抑制能力明显下降,在工况2和工况3下均未能抑制住振荡。而本文MFAC方法在不同工况下均有效地抑制住了次同步振荡,相较传统SSDC策略适应性更好。
针对风、光新能源场站接入系统的次同步振荡问题,本文提出一种数据驱动的多机协同阻尼控制算法,阻抗频率分析与仿真结果验证了所提阻尼控制方法的有效性。主要结论如下:
1)阻抗频率分析表明,该阻尼控制方法能有效重塑新能源场站系统的阻抗,在次同步频率范围内显著提升了系统的正序等效电阻,体现出良好的次同步振荡抑制潜力。
2)算例显示,阻尼控制方法对风电、光伏等效四机系统协同控制效果显著,一次完整的控制过程,仅需进行24次加(减)法、28次乘(除)法运算,计算代价小,易于工程实现。
3)在考虑阻尼控制器投入时间、新能源场站规模、风光出力占比等不同的情况,考虑风速变化、太阳辐射强度变化、切机切负荷等系统大、小扰动的影响,控制器均能有效抑制次同步振荡,同时对振荡频率偏移不敏感。
综上,该数据驱动的多机协同次同步阻尼控制策略对含有多PV、多DFIG的新能源场站适应性良好,兼顾了计算量小、控制效果好的优点,在复杂多机系统的振荡抑制问题中易于实现,具有较强的工程应用潜力。考虑到实际电网中新能源机组众多,下一步将继续研究更多新能源机组的协同控制,使算法更具通用性。
参考文献
[1] 国家能源局. 国家能源局2023年一季度新闻发布会文字实录[EB/OL]. [2023-02-13]. http://www.nea. gov.cn/2023-02/13/c_1310697149.htm.
[2] 王伟胜, 李光辉, 何国庆, 等. 新能源并网系统宽频振荡分析与抑制[M]. 北京: 中国电力出版社, 2022.
[3] IEEE Power & Energy Society. Wind energy systems sub-synchronous oscillations: events and modeling (TR80)[R]. Piscataway, NJ: IEEE PES, 2020.
[4] Narendra K, Fedirchuk D, Midence R. New microprocessor based relay to monitor and protect power systems against sub-harmonics[C]//2011 IEEE Electrical Power and Energy Conference, Winnipeg, 2011: 438-443.
[5] XIE X R, ZHANG X, LIU H K, et al. Characteristic analysis of subsynchronous resonance in practical wind farms connected to series-compensated trans- missions[J]. IEEE Transactions on Energy Conversion, 2017, 32(3): 1117-1126.
[6] 赵书强, 李忍, 高本锋, 等. 光伏并入弱交流电网次同步振荡机理与特性分析[J]. 中国电机工程学报, 2018, 38(24): 7215-7225, 7448.
Zhao Shuqiang, Li Ren, Gao Benfeng, et al. Analysis of mechanism and characteristics in sub synchronous oscillation between PV and weak AC networks[J]. Proceedings of the CSEE, 2018, 38(24): 7215-7225, 7448.
[7] 陈建, 任永峰, 孟庆天, 等. 含UDE附加阻尼支路的构网型直驱永磁同步风电机组次同步振荡抑制策略[J]. 电工技术学报, 2024, 39(7): 1985-2000.
Chen Jian, Ren Yongfeng, Meng Qingtian, et al. Sub-synchronous oscillation suppression strategy for grid-forming direct-drive permanent magnet syn- chronous generator with uncertainty and disturbance estimator supplementary damping branch[J]. Transa- ctions of China Electrotechnical Society, 2024, 39(7): 1985-2000.
[8] 贾祺, 严干贵, 李泳霖, 等. 多光伏发电单元并联接入弱交流系统的稳定性分析[J]. 电力系统自动化, 2018, 42(3): 14-20.
Jia Qi, YanGangui, Li Yonglin, et al. Stability analysis of multiple paralleled photovoltaic power generation units connected to weak AC system[J]. Automation of Electric Power Systems, 2018, 42(3): 14-20.
[9] 刘佳宁, 于淼, 夏杨红, 等. 受弱电网影响光伏并网系统不同频段稳定性分析[J]. 电网技术, 2020, 44(1): 86-95.
Liu Jianing, Yu Miao, Xia Yanghong, et al. Separated frequency stability analysis of grid-connected PV system affected by weak grid[J]. Power System Technology, 2020, 44(1): 86-95.
[10] Fan Lingling, Yin Haiping, Miao Zhixin. On active/ reactive power modulation of DFIG-based wind generation for interarea oscillation damping[J]. IEEE Transactions on Energy Conversion, 2011, 26(2): 513-521.
[11] 高本锋, 王义, 范辉, 等. 基于阻尼路径的新能源经LCC-HVDC送出系统次同步交互作用分析方法[J]. 电工技术学报, 2023, 38(20): 5572-5589.
Gao Benfeng, Wang Yi, Fan Hui, et al. A sub- synchronous interaction analysis method of renewable energy generations integrated with LCC-HVDC system based on damping path[J]. Transactions of China Electrotechnical Society, 2023, 38(20): 5572- 5589.
[12] 汪洋. 大型光伏并网系统的复杂振荡问题研究[D]. 北京: 华北电力大学, 2018.
[13] Yao Jun, Wang Xuewei, Li Jiawei, et al. Sub- synchronous resonance damping control for series- compensated DFIG-based wind farm with improved particle swarm optimization algorithm[J]. IEEE Transactions on Energy Conversion, 2019, 34(2): 849-859.
[14] Zhang Xu, Xie Xiaorong, Liu Hui, et al. Robust subsynchronous damping control to stabilise SSR in series-compensated wind power systems[J]. IET Generation, Transmission & Distribution, 2019, 13(3): 337-344.
[15] 高本锋, 张学伟, 李忍. 大规模风电送出系统的次同步振荡问题研究综述[J]. 电气工程学报, 2015, 10(7): 1-10.
Gao Benfeng, Zhang Xuewei, Li Ren. Studies of sub-synchronous oscillation in system with large- scale wind power transmission[J]. Journal of Elec- trical Engineering, 2015, 10(7): 1-10.
[16] Yan Shuxuan, Zhou Yunpeng, Zhu Jianhang, et al. An improved SSR damping strategy based on SSDC in photovoltaic grid-connected system[C]//2022 IEEE International Power Electronics and Application Conference and Exposition, Guangzhou, 2022: 693- 697.
[17] 姜齐荣, 王玉芝. 电力电子设备高占比电力系统电磁振荡分析与抑制综述[J]. 中国电机工程学报, 2020, 40(22): 7185-7201.
Jiang Qirong, Wang Yuzhi. Overview of the analysis and mitigation methods of electromagnetic oscillations in power systems with high proportion of power electronic equipment[J]. Proceedings of the CSEE, 2020, 40(22): 7185-7200.
[18] 高本锋, 姚磊. 基于改进自抗扰控制的抑制光火打捆经直流送出系统的次同步振荡策略[J]. 电网技术, 2018, 42(2): 533-540.
Gao Benfeng, Yao Lei. Sub-Synchronous oscillation suppression for photovoltaic-thermal-bundled power system based on improved active disturbance rejection control[J]. Power System Technology, 2018, 42(2): 533-540.
[19] 高本锋, 姚磊. 模糊自抗扰附加阻尼控制抑制光火打捆经串补送出的次同步振荡[J]. 电力自动化设备, 2018, 38(7): 121-127.
Gao Benfeng, Yao Lei. Supplementary damping control of SSO based on fuzzy active disturbance rejection control for photovoltaic-thermal-bundled system transmitted by series compensation[J]. Electric Power Automation Equipment, 2018, 38(7): 121-127.
[20] Azghandi M A, Barakati S M. Virtual RL damping and harmonic suppression for current-source inverter- based photovoltaic systems[C]//2019 10th Inter- national Power Electronics, Drive Systems and Technologies Conference, Shiraz, Iran, 2019: 572- 576.
[21] 孙焜, 姚伟, 周毅, 等. 基于SISO序阻抗的直驱风场经柔直输电系统中频振荡机理分析及抑制[J]. 中国电机工程学报, 2023, 43(2): 442-454.
Sun Kun, Yao Wei, Zhou Yi, et al. Mechanism analysis and suppression of medium-frequency oscillation based on the SISO impedance in a PMSG- based wind farm when connected to a VSC-HVDC[J]. Proceedings of the CSEE, 2023, 43(2): 442-454.
[22] 李浩志, 谢小荣, 刘芮彤, 等. 新能源经柔直送出系统的次同步振荡分析与抑制[J]. 中国电机工程学报, 2024, 44(6): 2945-2954.
Li Haozhi, Xie Xiaorong, Liu Ruitong, et al. Analysis and mitigation of the subsynchronous oscillation in renewable energy system connected to the MMC- HVDC[J]. Proceedings of the CSEE, 2024, 44(6): 2945-2954.
[23] 吴熙, 徐珊珊, 冯双, 等. 基于改进自适应陷波的双馈风电场时变次同步振荡抑制策略[J]. 中国电机工程学报, 2024, 44(5): 1836-1849.
Wu Xi, Xu Shanshan, Feng Shuang, et al. Time- varying subsynchronous oscillation mitigation strategy for DFIG wind farms based on improved adaptive notch filter[J]. Proceedings of the CSEE, 2024, 44(5): 1836-1849.
[24] Li Penghan, Xiong Linyun, Wu Fei, et al. Sliding mode controller based on feedback linearization for damping of sub-synchronous control interaction in DFIG-based wind power plants[J]. International Journal of Electrical Power & Energy Systems, 2019, 107(5): 239-250.
[25] Karunanayake C, Ravishankar J, Dong Zhaoyang. Nonlinear SSR damping controller for DFIG based wind generators interfaced to series compensated transmission systems[J]. IEEE Transactions on Power Systems, 2020, 35(2): 1156-1165.
[26] 王智伟, 李鹏瀚, 刘鑫, 等. 基于分数阶滑模控制的双馈风电系统次同步振荡抑制方法[J]. 中国电机工程学报, 2023, 43(19):7519-7530.
Wang Zhiwei, Li Penghan, Liu Xin, et al. Suppression method of subsynchronous oscillation in DFIG-based wind power system based on fractional-order sliding mode control[J]. Proceedings of the CSEE, 2023, 43(19): 7519-7530.
[27] 冯双, 崔昊, 陈佳宁, 等. 人工智能在电力系统宽频振荡中的应用与挑战[J]. 中国电机工程学报, 2021, 41(23): 7889-7905.
Feng Shuang, Cui Hao, Chen Jianing, et al. Appli- cations and challenges of artificial intelligence in power system wide-band oscillations[J]. Proceedings of the CSEE, 2021, 41(23): 7889-7905.
[28] 陈柔伊, 张尧, 钟庆, 等. 抑制区间振荡的自适应模糊广域阻尼控制设计[J]. 中国电机工程学报, 2009, 29(31): 14-20.
Chen Rouyi, Zhang Yao, Zhong Qing, et al. Self-adaptive fuzzy wide-area control design for damping inter-area oscillations[J]. Proceedings of the CSEE, 2009, 29(31): 14-20.
[29] 余希瑞, 周林, 郭珂, 等. 多模型自适应控制应用于大型光伏电站阻尼区间振荡[J]. 中国电机工程学报, 2017, 37(14): 4036-4043, 4282.
Yu Xirui, Zhou Lin, Guo Ke, et al. Application of multiple-model adaptive control for damping inter- area oscillations by large-scale photovoltaic plant[J]. Proceedings of the CSEE, 2017, 37(14): 4036-4043, 4282.
[30] 孙东阳, 孟繁易, 王南, 等. 基于反步自适应准谐振控制的双馈风机次同步振荡抑制策略[J]. 电工技术学报, 2023, 38(9): 2375-2390, 2434.
Sun Dongyang, Meng Fanyi, Wang Nan, et al. DFIG sub-synchronous oscillation suppression strategy based on backstepping adaptive quasi-resonant control[J]. Transactions of China Electrotechnical Society, 2023, 38(9): 2375-2390, 2434.
[31] 苗硕, 李奇南, 查鲲鹏, 等. 基于加窗FFT的风电场自适应振荡抑制策略[J]. 中国电力, 2022, 55(10): 112-123.
Miao Shuo, Li Qinan, Zha Kunpeng, et al. Adaptive oscillation suppression strategy for wind farms based on windowed FFT[J]. Electric Power, 2022, 55(10): 112-123.
[32] 侯忠生, 金尚泰. 无模型自适应控制——理论与应用[M]. 北京: 科学出版社, 2013.
[33] 吴熙, 王梦婷, 施星宇, 等. 基于无模型自适应控制的双馈风机次同步振荡附加阻尼控制方法[J]. 中国电机工程学报, 2022, 42(10): 3601-3614.
Wu Xi, Wang Mengting, Shi Xingyu, et al. SSO supplementary damping control method for DFIG based on model-free adaptive control[J]. Proceedings of the CSEE, 2022, 42(10): 3601-3614.
[34] 杨朋威, 任正, 王新宇, 等. 基于MFAC附加阻尼控制器的次同步振荡抑制方法[J]. 电力系统及其自动化学报, 2023, 35(9): 68-78.
Yang Pengwei, Ren Zheng, Wangxinyu, et al. Sub-synchronous oscillation suppression method based on MFAC sub-synchronous damping con- troller[J]. Proceedings of the CSU-EPSA, 2023, 35(9): 68-78.
[35] 刘国海, 陈仁杰, 张多, 等. 两电机调速系统的神经网络逆无模型自适应鲁棒解耦控制[J]. 中国电机工程学报, 2019, 39(3): 868-874, 965.
Liu Guohai, Chen Renjie, Zhang Duo, et al. Model-free adaptive robust control for two motor drive system based on neural network inversion[J]. Proceedings of the CSEE, 2019, 39(3): 868-874, 965.
[36] 陈宗遥, 卜旭辉, 郭金丽. 基于神经网络的数据驱动互联电力系统负荷频率控制[J]. 电工技术学报, 2022, 37(21): 5451-5461.
Chen Zongyao, Bu Xuhui, Guo Jinli. Neural network based data-driven load frequency control for interconnected power systems[J]. Transactions of China Electrotechnical Society, 2022, 37(21): 5451- 5461.
[37] 曹荣敏, 郑鑫鑫, 侯忠生. 基于改进多入多出无模型自适应控制的二维直线电机迭代学习控制[J]. 电工技术学报, 2021, 36(19): 4025-4034.
Cao Rongmin, Zheng Xinxin, Hou Zhongsheng. An iterative learning control based on improved multiple input and multiple output model free adaptive control for two-dimensional linear motors[J]. Transactions of China Electrotechnical Society, 2021, 36(19): 4025- 4034.
[38] 邵冰冰, 赵峥, 肖琪, 等. 多直驱风机经柔直并网系统相近次同步振荡模式参与因子的弱鲁棒性分析[J] . 电工技术学报, 2023, 38(3): 754-769.
Shao Bingbing, Zhao Zheng, Xiao Qi, et al. Weak robustness analysis of close subsynchronous oscillation modes’ participation factors in multiple direct-drive wind turbines with the VSC-HVDC system[J]. Transactions of China Electrotechnical Society, 2023, 38(3): 754-769.
[39] 宫泽旭, 艾力西尔·亚尔买买提, 辛焕海, 等. 新能源电力系统并网设备小扰动稳定分析(一): 机理模型与稳定判据适用性[J]. 中国电机工程学报, 2022, 42(12): 4405-4419.
Gong Zexü, Yaermaimaiti Ailixier, Xin Huanhai, et al. Small signal stability analysis of equipment in renewable energy power system (part I): mechanism model and adaptation of stability criterion[J]. Proceedings of the CSEE, 2022, 42(12): 4405- 4419.
[40] 高本锋, 邓鹏程, 梁纪峰, 等. 光伏电站与弱交流电网间次同步交互作用路径及阻尼特性分析[J]. 电工技术学报, 2023, 38(24): 6679-6694.
Gao Benfeng, Deng Pengcheng, Liang Jifeng, et al. Analysis of path and damping characteristics of subsynchronous interaction between photovoltaic plant and weak AC grid[J]. Transactions of China Electrotechnical Society, 2023, 38(24): 6679-6694.
[41] 吴天昊, 谢小荣, 姜齐荣. 风电系统次同步等幅振荡的机理与特性分析[J]. 中国电机工程学报, 2023, 43(7): 2689-2699.
Wu Tianhao, Xie Xiaorong, Jiang Qirong. On subsynchronous sustained oscillation issues of wind power systems[J]. Proceedings of the CSEE, 2023, 43(7): 2689-2699.
[42] 柴天佑, 岳恒. 自适应控制[M]. 北京: 清华大学出版社, 2016.
[43] 符玲, 韩文朕, 麦瑞坤, 等. 基于频域动态模型的同步相量测量算法[J]. 中国电机工程学报, 2015, 35(6): 1371-1378.
Fu Ling, Han Wenzhen, Mai Ruikun, et al. Dynamic phasor estimator based on frequency-domain model[J]. Proceedings of the CSEE, 2015, 35(6): 1371-1378.
[44] 韩璞. 现代工程控制论[M]. 北京: 中国电力出版社, 2017.
[45] 冯增喜, 任庆昌, 彭彦平, 等. 基于单纯形法的MFAC参数寻优[J]. 控制工程, 2016, 23(3): 405-410.
Feng Zengxi, Ren Qingchang, Peng Yanping, et al. Optimizing the parameters of MFAC based on the simplex method[J]. Control Engineering of China, 2016, 23(3): 405-410.
[46] 赵成勇, 刘娟. Prony算法在电力系统暂态信号分析中的应用[J]. 电力系统及其自动化学报, 2008, 20(2): 60-64.
Zhao Chengyong, Liu Juan. Analysis of power system transient signal based on Prony algorithm[J]. Proceedings of the CSU-EPSA, 2008, 20(2): 60-64.
Data-Driven Multi-Machine Cooperative Damping Control for Wind and Photovoltaic Plants Restraining Sub-Synchronous Oscillation
Abstract With the rapid growth of photovoltaic and wind power’s access scale in the power grid, the problem of sub-synchronous oscillation (SSO) in the power system has become increasingly prominent. At present, the design scheme of new energy sub-synchronous damping control (SSDC) is mainly based on the model-driven control method, which relies on the accurate system state equation. However, the power system has time-varying and nonlinear characteristics, and the existing SSDC controller for new energy has limited applications, making it difficult to adapt to complex and changeable operating conditions. Therefore, finding a new strategy to break the barriers in damping control is urgent. At the same time, the existing literature has not explored the multi-machine equivalent model with multiple new energy types.
According to previous engineering experience and analysis, the input and output signals of the multi-machine cooperative damping controller are selected. The feedback signal is selected as the grid-connected voltage of the new energy station, and the input position is selected as the inner d-axis of the inverter of the photovoltaic and double-fed wind farms. Then, for a new energy station containing multiple photovoltaic power stations and multiple wind turbines, in the process of designing the SSDC controller, it is similarly equivalent to a multi-input single-output system, and a model-free adaptive control (MFAC) algorithm for multi-machine coordination is designed. The parameters of the simulation system and the controller are designed, and the controller parameters are optimized by the simplex method. Finally, the impedance frequency scan analysis and simulation are carried out in the IEEE 39-node system connected to the new energy station through serial compensation, and the effectiveness of the multi-machine cooperative damping strategy is verified.
The following conclusions can be drawn. (1) Impedance frequency analysis shows that the damping control method can effectively reshape the impedance of the new energy station system and significantly improve the positive sequence equivalent resistance of the system in the range of sub-synchronous frequency, reflecting good SSO suppression potential. (2) The numerical example shows that the damping control method has a significant effect on the cooperative control of the equivalent four-machine system of wind power and photovoltaic. A complete control process only requires 24 addition/subtraction calculations and 28 multiplication/division calculations, reducing calculation costs. (3) Considering the input time of the damping controller, the scale of the new energy station, the proportion of wind power out put to solar power output, and the influence of large and small disturbances of the system (changes in wind speed or radiation intensity, the cutting load of the cutting machine), the controller can effectively suppress the sub-synchronous oscillation and is insensitive to the oscillation frequency deviation. In conclusion, the multi-machine cooperative model-free sub-synchronous damping control strategy is adaptable to new energy stations containing multi-PV and multi-DFIG.
Keywords:Model-free adaptive control, damping control sub-synchronous oscillation, new energy station, cooperative control, data-driven
中图分类号:TM712
DOI: 10.19595/j.cnki.1000-6753.tces.231143
国家重点研发计划资助项目“响应驱动的大电网稳定性智能增强分析与控制技术”(2021YFB2400800)。
收稿日期 2023-07-16
改稿日期 2023-10-07
甄永赞 男,1985年生,博士,副教授,研究方向为新能源电力系统保护与稳定控制。
E-mail: zhenyongzan_001@126.com
狄依容 女,2000年生,硕士研究生,研究方向为新能源电力系统分析与控制。
E-mail: 867783889@qq.com(通信作者)
(编辑 郭丽军)