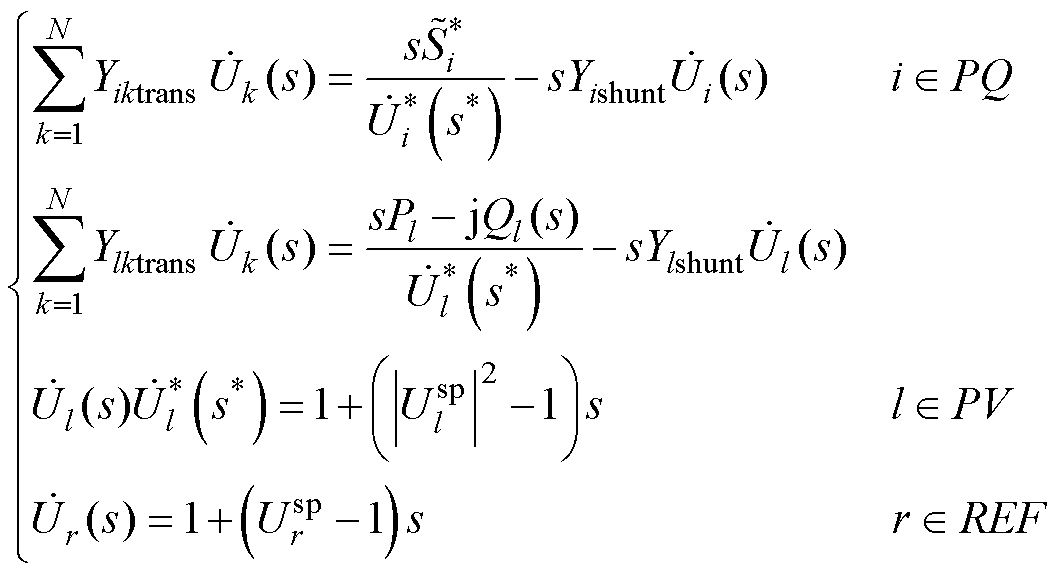 (1)
(1)
摘要 潮流计算是电力系统规划和运行的基础,全纯嵌入潮流计算方法(HELM)因无需初值且具有全局收敛性,因而在电力系统潮流计算中受到极大关注。然而,采用HELM求解大规模电力系统潮流时,高维幂级数系数线性方程组求解和节点电压的幂级数有理的逼近计算量大、耗时久,是制约HELM计算效率提升的关键。为此,该文提出一种基于稳定双正交共轭梯度(BICGSTAB)和Aitken差分的电力系统全纯嵌入潮流并行计算方法,该方法首先采用近似逆预处理的BICGSTAB法并行迭代求解HELM的高维幂级数系数线性方程组,以快速计算节点电压的各阶幂级数系数;其次,借助Aitken差分法实现所有节点电压幂级数有理逼近值的并行计算;然后,基于CPU-GPU异构平台设计所提算法的并行流程,以实现大规模电力系统潮流的快速求解;最后,通过节点在1 354~13 802的不同规模测试系统对所提方法进行分析、验证。结果表明,所提电力系统潮流全纯嵌入并行计算方法可实现电力系统潮流的准确、快速求解。
关键词:全纯嵌入法 潮流计算 Aitken差分法 CPU-GPU异构运算平台 预处理器
电力系统潮流计算是电力系统安全稳定分析与控制的基础,对指导电力系统规划和运行具有重要工程价值[1]。随着新能源大规模并网消纳、交直流互联规模日益扩大、电网结构日趋复杂,电力系统潮流计算效率与鲁棒性面临巨大挑战[2-5]。目前,牛顿-拉夫逊(Newton-Raphson, NR)法仍是电力系统潮流计算使用最广泛的方法,但该方法的收敛性依赖初值选取,不合理的初值将导致潮流计算结果发散。此外,潮流重载时,NR法易出现雅可比矩阵奇异,导致潮流计算结果不收敛,难以满足复杂大规模电力系统对潮流计算效率和鲁棒性的需求[6]。
为克服NR法的不足,文献[7]基于复分析理论提出了一种电力系统潮流计算的全纯嵌入方法(Holomorphic Embedding Load flow Method, HELM)。该方法通过在潮流方程中嵌入复变量构建电压全纯函数和无功功率全纯函数,进而根据全纯函数的展开性质构建高维幂级数系数线性方程组以求解节点电压的各阶幂级数系数,然后根据求得的幂级数系数对节点电压全纯幂级数展开式进行帕德近似(Padé Approximation)获取节点电压的有理逼近值,求得电力系统潮流解[8-9]。基于该理论,文献[10-11]提出了多维全纯嵌入潮流计算方法,并将其应用到电力系统概率潮流计算中;文献[12]进一步将HELM扩展于电力系统交直流潮流计算中。
虽然HELM在电力系统潮流计算中已取得一定进展,但在计算效率方面仍存在以下问题[7]:求解大规模电力系统潮流时,HELM收敛所需幂级数阶数较高,通常需多次求解高维幂级数系数线性方程组,影响了HELM的计算效率;HELM每次求解高维幂级数系数线性方程组得到电压幂级数系数后,需依次对所有节点进行Padé近似获取各节点电压的幂级数有理逼近值,导致HELM的计算效率较低。
目前,针对高维幂级数系数线性方程组,常用的求解方法有直接法[13]和迭代法[14]两大类。直接法通常基于高斯消去思想将线性方程组的系数矩阵转化为上三角矩阵或对角矩阵,进而得到精确解,但当方程组规模增大时,直接法的内存占用率和计算复杂度亦随之增加,导致求解线性方程组的计算耗时较长[15];迭代法为待求变量产生一组向量解,通过对这组向量解的不断修正使之逐步逼近真实解,该方法主要基于矩阵向量间的运算,其内存占用率和计算复杂度较低,在求解大型稀疏线性方程组时具有明显优势。此外,采用迭代法求解线性方程组的过程中各变量间数据关联性弱,可通过并行计算技术进一步提升线性方程组的求解效率[16]。为此,文献[17]通过不完全LU(Incomplete LU decom- position, ILU)分解对潮流雅可比矩阵进行预处理,然后借助图形处理单元(Graphics Processing Unit, GPU)实现修正方程组的并行迭代求解;文献[18]采用雅可比矩阵的近似逆预处理来提升迭代求解修正方程组的收敛性,但雅可比矩阵的不断更新和GPU中预处理器的多次构造制约了该方法求解电力系统潮流的计算效率;文献[19]将预处理共轭梯度迭代与非精确牛顿法相结合,提出一种基于中央处理器(Central Processing Unit, CPU)-GPU异构的电力系统潮流并行计算方法,有效地提升了电力系统潮流的求解效率。综上所述,现有研究已针对NR法中修正方程组的并行求解进行了探索,但针对HELM中高维幂级数系数线性方程组的并行求解目前尚处于空白阶段。
针对节点电压幂级数有理逼近值计算,文献[20]提出了行列式比值法,但该方法所需电压幂级数阶数仍旧较高,难以有效降低电压幂级数的有理逼近次数;文献[21]提出了一种Padé近似变体计算形式,能够提高Padé近似的单次计算速度,但难以保证HELM的全局收敛性。上述针对Padé近似的改进方法旨在提高单次计算速度,但HELM仍需依次计算所有节点电压的幂级数有理逼近值,导致Padé近似的总计算耗时并未显著减少。
针对上述问题,本文提出一种基于稳定双正交共轭梯度(Bi-Conjugate Gradient Stabilized, BICGSTAB)和Aitken差分的电力系统全纯嵌入潮流并行计算方法。该方法首先采用近似逆预处理的BICGSTAB法并行迭代求解高维幂级数系数线性方程组,以获取电压幂级数的各阶系数;然后,借助Aitken差分法实现节点电压幂级数有理逼近值的并行计算;接着,基于CPU-GPU异构计算平台设计所提算法整体并行流程;最后,通过节点规模在1 354~13 802的不同电力系统测试算例对所提电力系统潮流全纯嵌入并行计算方法进行分析、验证。
本节简要介绍了HELM基本原理。不同于NR法采用数值迭代求解电力系统的非线性潮流方程组,HELM求解电力系统潮流的主要思路是在电力系统功率平衡方程中嵌入复变量以构造各类型节点电压和PV节点无功功率的全纯函数,进而借助全纯函数的展开性质实现节点电压的幂级数有理逼近值显式求解,其主要步骤可分为[7]:HELM模型构建、节点电压幂级数系数递归求解和节点电压的幂级数有理逼近值计算。
假设电力系统中共有N个节点,根据电力系统不同类型节点的特点,可在各类型节点功率平衡方程中嵌入复变量s,构造节点电压全纯函数和PV节点无功功率全纯函数,并进一步构造包含PQ节点、PV节点和平衡节点(记为REF)的HELM方程[7]为
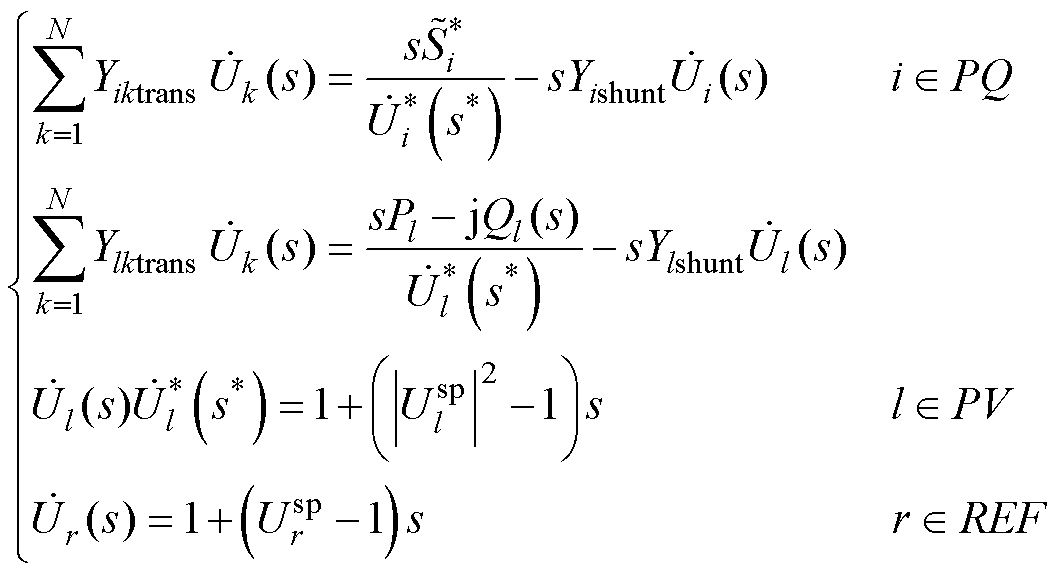 (1)
(1)
式中,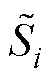 为PQ节点注入功率;
为PQ节点注入功率;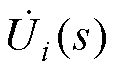 、
、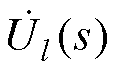 和
和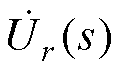 分别为PQ节点、PV节点和平衡节点的电压全纯函数;Yiktrans和Ylktrans分别为不计PQ节点和PV节点对地导纳后的对称部分;Yishunt和Ylshunt分别为节点导纳矩阵中PQ节点和PV节点的对地支路导纳;Pl和Ql分别为PV节点的有功、无功功率;
分别为PQ节点、PV节点和平衡节点的电压全纯函数;Yiktrans和Ylktrans分别为不计PQ节点和PV节点对地导纳后的对称部分;Yishunt和Ylshunt分别为节点导纳矩阵中PQ节点和PV节点的对地支路导纳;Pl和Ql分别为PV节点的有功、无功功率;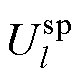 和
和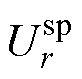 分别为PV节点和平衡节点的电压幅值;“*”为共轭运算符;“j”为虚部符号。
分别为PV节点和平衡节点的电压幅值;“*”为共轭运算符;“j”为虚部符号。
根据全纯函数可在其定义域内进行幂级数展开的性质,可将式(1)中的电压全纯函数和无功功率全纯函数展开,并令嵌入值s=0,以获取节点电压全纯幂级数的零阶项系数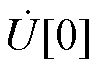 和无功功率全纯幂级数的零阶项系数Ql[0]。附录中详细介绍了零阶项系数
和无功功率全纯幂级数的零阶项系数Ql[0]。附录中详细介绍了零阶项系数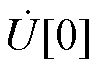 和Ql[0]的求解过程。
和Ql[0]的求解过程。
由附录可知,节点电压全纯幂级数展开式和PV节点无功功率全纯幂级数展开式的零阶项系数可直接通过式(A2)获取。进一步地,为递归计算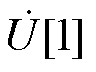 ~
~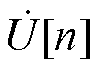 ,将式(A1)所示的全纯幂级数展开式代入式(1),并引入逆幂级数函数构建统一递归求解所有节点电压幂级数系数的高维幂级数系数线性方程组[7],具体过程参见附录。其中,高维幂级数系数线性方程组的系数矩阵Ysys为
,将式(A1)所示的全纯幂级数展开式代入式(1),并引入逆幂级数函数构建统一递归求解所有节点电压幂级数系数的高维幂级数系数线性方程组[7],具体过程参见附录。其中,高维幂级数系数线性方程组的系数矩阵Ysys为
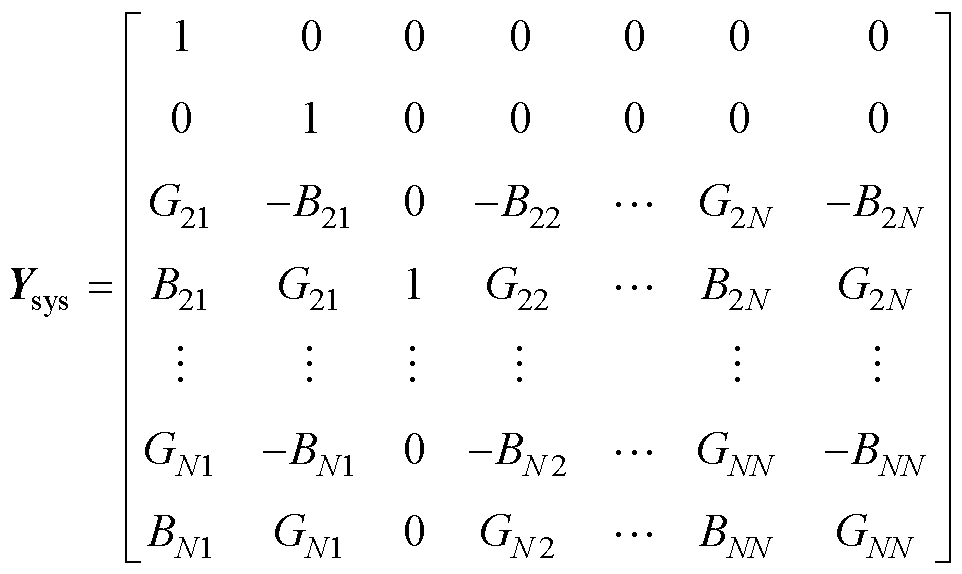 (2)
(2)
式中,G和B分别为电力系统中的电导和电纳,其值在HELM计算过程中不会发生变化,故Ysys具有不变性。
当n=1时,附录中式(A4)的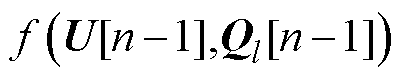 与Ysys均为已知量,求解式(A4)即可获取电压全纯幂级数系数
与Ysys均为已知量,求解式(A4)即可获取电压全纯幂级数系数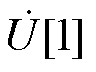 。以此类推,节点电压全纯幂级数的各阶系数
。以此类推,节点电压全纯幂级数的各阶系数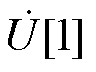 ~
~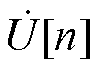 均可通过式(A4)递归计算获得。进一步,可通过式(A3)计算得到各节点电压,进而求得电力系统的潮流解。
均可通过式(A4)递归计算获得。进一步,可通过式(A3)计算得到各节点电压,进而求得电力系统的潮流解。
由附录可知,HELM可通过多次求解高维幂级数系数线性方程组获取计算各节点电压所需的电压级数系数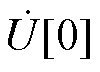 ~
~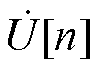 ,进而由附录式(A3)求得各节点电压。然而,在求解大规模电力系统潮流时,HELM所需幂级数系数阶数较高,为此,HELM引入了可扩展电压幂级数收敛域的Padé近似算法替代式(A3)计算节点电压的幂级数有理逼近值,以保证HELM求解电力系统潮流的收敛性。为便于读者理解,附录中简单介绍了Padé近似的基本 思想。
,进而由附录式(A3)求得各节点电压。然而,在求解大规模电力系统潮流时,HELM所需幂级数系数阶数较高,为此,HELM引入了可扩展电压幂级数收敛域的Padé近似算法替代式(A3)计算节点电压的幂级数有理逼近值,以保证HELM求解电力系统潮流的收敛性。为便于读者理解,附录中简单介绍了Padé近似的基本 思想。
由附录可知:为提高电力系统全纯嵌入潮流的计算精度,通常需获取更高阶数的电压幂级数系数,进而多次采用直接法求解式(A4),导致进行HELM计算时内存占用率与计算量较大[22];此外,每次求解高维幂级数系数线性方程组得到电压幂级数系数后,需依次对所有节点进行Padé近似,HELM的计算效率进一步降低。
针对重复多次求解式(A4)和式(A8)导致采用HELM求解大规模电力系统潮流计算效率较低的不足,本节提出了一种基于BICGSTAB和Aitken差分的电力系统全纯嵌入潮流并行计算方法(Parallel computing Holomorphic Embedding Load flow Method based on BICGSTAB and Aitken difference, P-HELM)。该方法首先采用BICGSTAB法迭代求解高维幂级数系数线性方程组,并构造稀疏矩阵近似逆预处理器提升BICGSTAB法求解的收敛效果,进而实现式(A4)的并行求解;然后,借助Aitken差分法实现所有节点电压幂级数有理逼近值的并行计算;最后,设计CPU-GPU异构的P-HELM并行策略,以实现大规模电力系统全纯嵌入潮流的并行求解。
如1.3节所述,采用直接法求解式(A4)所示高维幂级数系数线性方程组的内存占用率与计算复杂度较高,导致HELM计算效率较低。此外,采用直接法求解线性方程组过程中待求变量与已求变量间数据关联性强,难以通过并行计算提升其求解效率。为此,本节根据式(2)中系数矩阵Ysys的稀疏性、非对称性、非正定性,采用Krylov子空间迭代法中的BICGSTAB法求解式(A4)[23],并构造稀疏矩阵近似逆预处理器提升BICGSTAB法的收敛效果,在此基础上实现式(A4)的并行迭代求解,BICGSTAB法特点和计算流程详见文献[23-24]。
2.1.1 系数矩阵预处理
由于采用BICGSTAB法求解线性方程组时,其收敛效果受系数矩阵特征值分布影响较大,而式(2)中系数矩阵Ysys特征值分布较为分散,直接采用BICGSTAB法求解式(A4)的收敛效果并不理想。为此,本节引入系数矩阵预处理技术构造作用于Ysys的预处理器,以改善Ysys特征值的分布区间,提升BICGSTAB法求解高维幂级数系数线性方程组的收敛性。在此过程中,所选预处理器应在计算过程中尽量保持不变以降低预处理器构造的耗时。基于该原则,本节设计了一种基于系数矩阵Ysys的稀疏矩阵近似逆预处理器Fpre。
首先,将系数矩阵Ysys进行因子分解为
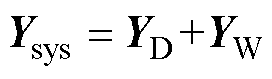 (3)
(3)
式中,YD和YW分别为系数矩阵Ysys的下三角矩阵和上三角矩阵。
YD具体表达形式为
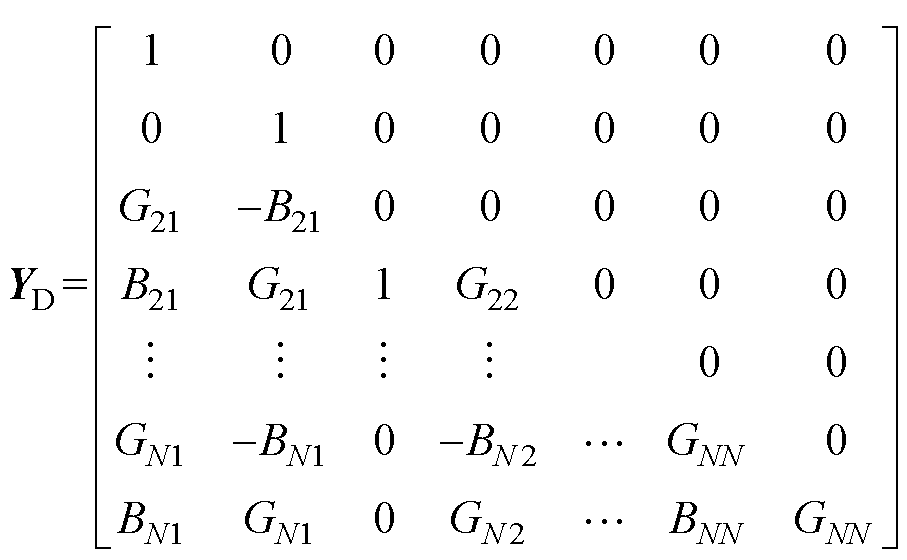 (4)
(4)
YW具体表达形式为
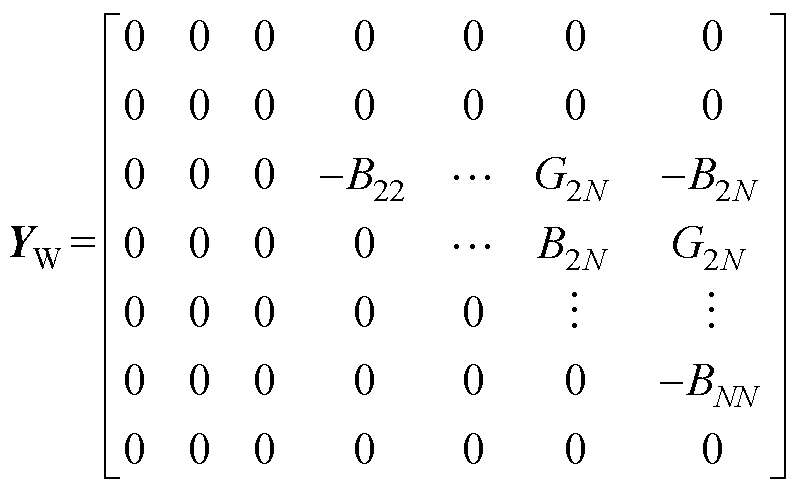 (5)
(5)
进一步地,由YD和YW构造稀疏矩阵近似逆预处理器Fpre为
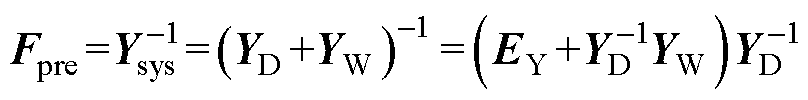 (6)
(6)
式中,EY为与YA维数相同的单位矩阵。
通过预处理器Fpre对Ysys进行预处理后,附录式(A4)可进一步描述为
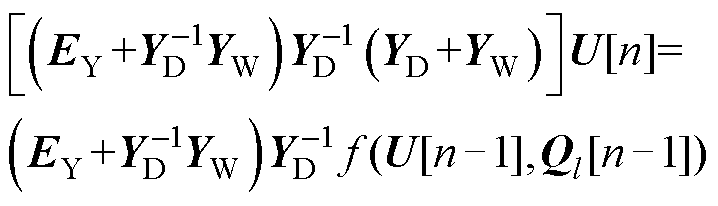 (7)
(7)
对式(7)进一步化简可得
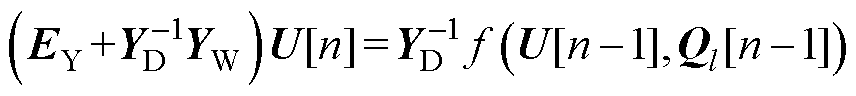 (8)
(8)
式中,预处理后高维幂级数系数线性方程组的系数矩阵可由EY、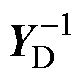 、YW计算得到。
、YW计算得到。
进一步地,参考文献[23-24]中BICGSTAB法的计算流程,可得BICGSTAB第k次迭代下式(8)所示线性方程组的解向量U[k]为
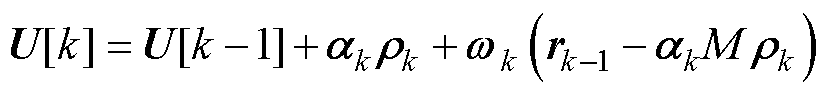 (9)
(9)
式中,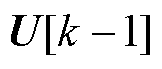 和
和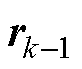 分别为BICGSTAB法第k-1次迭代结果中的解向量和残差向量;
分别为BICGSTAB法第k-1次迭代结果中的解向量和残差向量;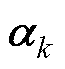 、
、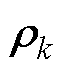 和
和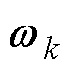 均为BICGSTAB法第k次迭代中需要计算的中间向量。
均为BICGSTAB法第k次迭代中需要计算的中间向量。
相较于求解附录式(A4),P-HELM采用BICGSTAB法求解式(8)仅需1次迭代便可获得较为精确的电压幂级数系数,大幅降低了求解高维幂级数系数线性方程组的计算量。此外,由于系数矩阵Ysys具有不变性,故P-HELM仅需构造1次预处理器即可,有效地降低了系数矩阵Ysys预处理的时间成本。
2.1.2 高维幂级数系数线性方程组的并行求解
本文采用BICGSTAB法迭代求解式(8)可降低采用直接法求解式(A4)的计算耗时。进一步地,由于BICGSTAB法具有较高的并行潜力,因此本文根据文献[23-24]中BICGSTAB法计算流程以及本文构造的预处理器Fpre设计了图1所示并行迭代求解式(8)的策略。
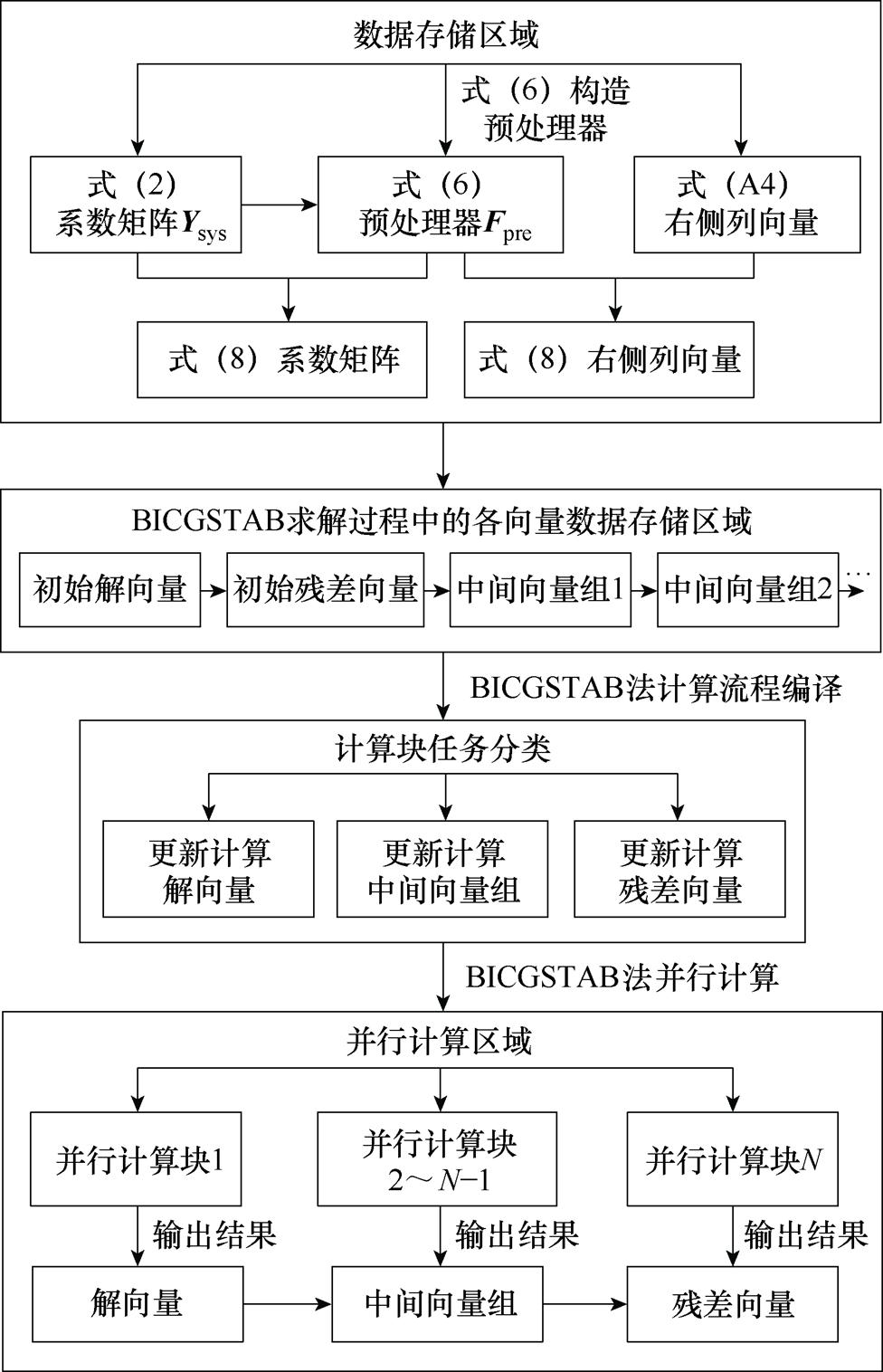
图1 预处理BICGSTAB的并行策略
Fig.1 Parallel strategy for preprocessing BICGSTAB
需要指出的是:式(8)的形成首先需要根据式(3)~式(5)进行系数矩阵Ysys的分解以及式(8)系数矩阵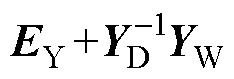 的构造,由于其计算过程较为简便,因此可直接通过串行计算获取并进行数据存储。考虑到BICGSTAB法计算过程中需要利用
的构造,由于其计算过程较为简便,因此可直接通过串行计算获取并进行数据存储。考虑到BICGSTAB法计算过程中需要利用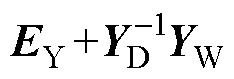 和
和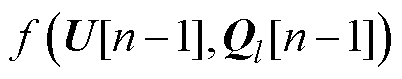 进行多次大规模矩阵向量的乘积计算以获取不同类型的中间向量,可分别针对不同类型向量的计算公式进行计算单元任务编译,进而调用多个计算单元并行计算各节点采用BICGSTAB法求解式(8)时的所有向量,并输出残差向量完成收敛性判断。
进行多次大规模矩阵向量的乘积计算以获取不同类型的中间向量,可分别针对不同类型向量的计算公式进行计算单元任务编译,进而调用多个计算单元并行计算各节点采用BICGSTAB法求解式(8)时的所有向量,并输出残差向量完成收敛性判断。
如2.1节所述,本文所提P-HELM并行计算方法采用预处理BICGSTAB法并行迭代求解式(8)获取各节点电压幂级数系数;进而通过Padé近似依次计算各节点电压幂级数的有理逼近值,进而获得潮流解。然而,该方法需重复多次进行Padé近似计算,导致所提P-HELM计算效率降低。此外,Padé近似过程中分子、分母多项式的各阶系数间数据关联性较强,难以通过并行计算提升Padé近似的计算效率。为此,本节借助计算复杂度较低、并行适应度较好的幂级数加速收敛算法计算电压幂级数有理逼近值并实现并行化,以进一步提高所提P-HELM并行计算方法的计算效率。
2.2.1 基于Aitken差分的电压幂级数有理逼近
Aitken差分法是较Padé近似计算复杂度更低的幂级数加速收敛算法,其计算过程较为简便、各元素间数据关联性较弱,具有较高的并行潜力。需要指出的是,Aitken差分法的计算表达式由s=1时的Padé近似表达式推导得到[25-26]。由于P-HELM采用Padé近似计算电压幂级数有理逼近值时仅关注s=1处的数值解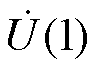 ,因此采用Aitken差分法计算节点电压幂级数有理逼近值时仍能保证P-HELM的收敛性。与Padé近似类似,Aitken差分法需通过求解式(8)所得的各阶电压幂级数系数计算节点电压幂级数有理逼近值。在P-HELM求解过程中,BICGSTAB法并行求解式(8)得到的解向量U[k]中包含了各节点第k阶电压幂级数系数,即
,因此采用Aitken差分法计算节点电压幂级数有理逼近值时仍能保证P-HELM的收敛性。与Padé近似类似,Aitken差分法需通过求解式(8)所得的各阶电压幂级数系数计算节点电压幂级数有理逼近值。在P-HELM求解过程中,BICGSTAB法并行求解式(8)得到的解向量U[k]中包含了各节点第k阶电压幂级数系数,即
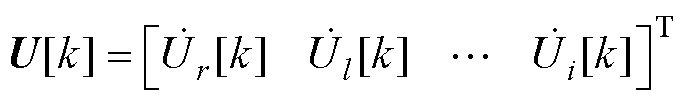 (10)
(10)
式中,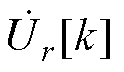 、
、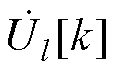 和
和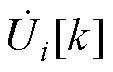 分别为平衡节点、PV节点和PQ节点电压全纯幂级数的第k阶系数。
分别为平衡节点、PV节点和PQ节点电压全纯幂级数的第k阶系数。
因此,采用P-HELM求解式(8)可得各节点在各阶次下的电压幂级数系数为
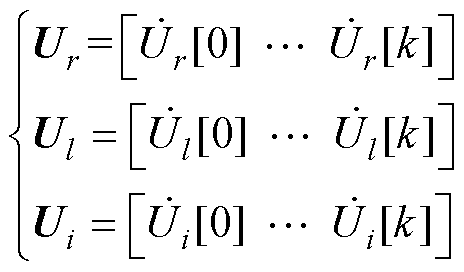 (11)
(11)
式中,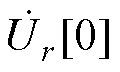 、
、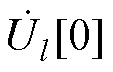 和
和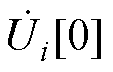 分别为由式(A2)得到的平衡节点、PV节点和PQ节点的电压幂级数零阶项系数;Ur、Ul和Ui分别为包含平衡节点、PV节点和PQ节点的各阶电压幂级数系数的向量。
分别为由式(A2)得到的平衡节点、PV节点和PQ节点的电压幂级数零阶项系数;Ur、Ul和Ui分别为包含平衡节点、PV节点和PQ节点的各阶电压幂级数系数的向量。
参考文献[26]中Aitken差分法的计算表达式,本节基于Aitken差分法构建节点电压幂级数有理逼近形式可分为三部分:①计算不同阶数电压幂级数系数的总和;②计算Aitken差分算子;③计算节点电压的幂级数有理逼近值。
首先,本节通过式(11)向量元素计算不同阶数下电压幂级数系数的和为
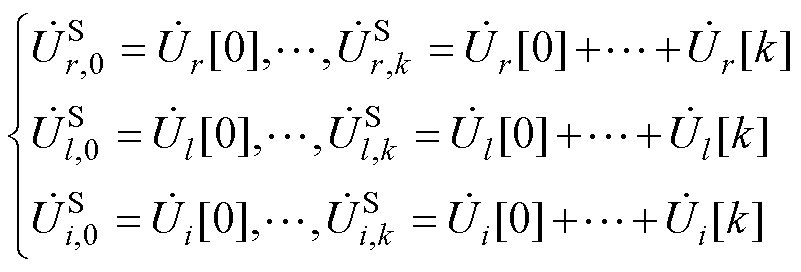 (12)
(12)
式中,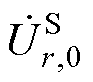 、
、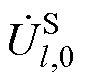 、
、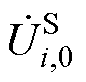 分别为平衡节点、PV节点和PQ节点电压幂级数的零阶项系数;
分别为平衡节点、PV节点和PQ节点电压幂级数的零阶项系数;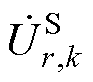 、
、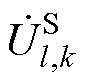 、
、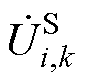 分别为平衡节点、PV节点和PQ节点电压幂级数前k项系数和。
分别为平衡节点、PV节点和PQ节点电压幂级数前k项系数和。
然后,计算Aitken差分算子为
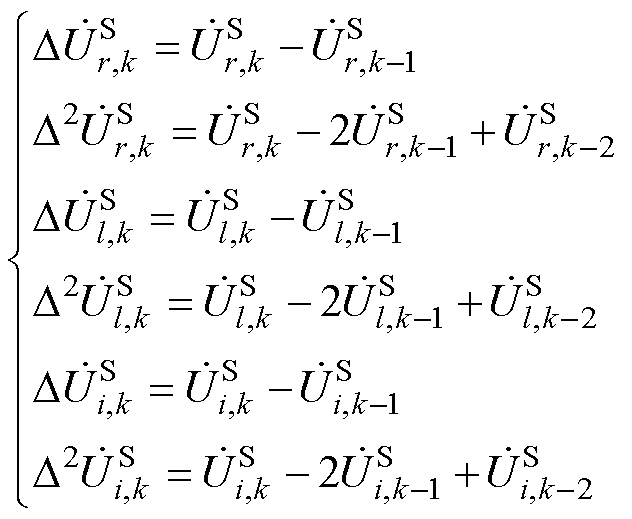 (13)
(13)
式中,“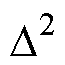 ”为Aitken差分法定义的差分算子,由电压全纯幂级数的前k、k-1和k-2项系数的和计算得到。
”为Aitken差分法定义的差分算子,由电压全纯幂级数的前k、k-1和k-2项系数的和计算得到。
最后,通过Aitken差分公式计算P-HELM中节点电压幂级数的有理逼近值为
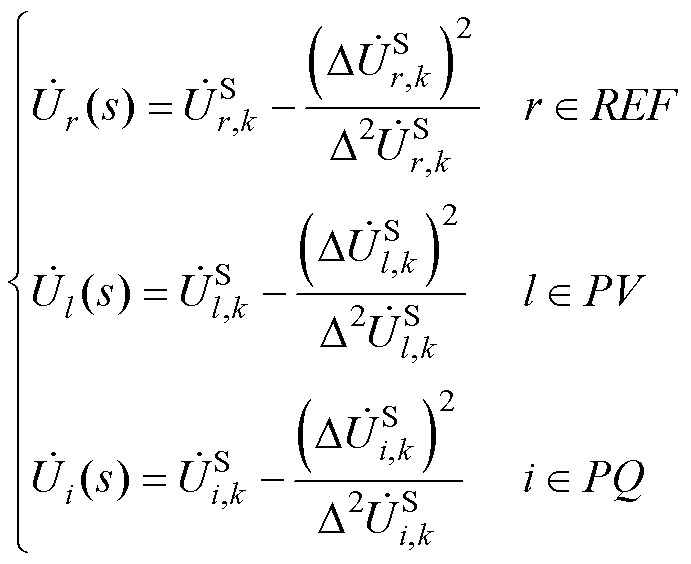 (14)
(14)
式中,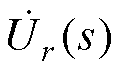 、
、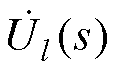 和
和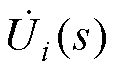 分别为平衡节点、PV节点和PQ节点的电压幂级数有理逼近值。
分别为平衡节点、PV节点和PQ节点的电压幂级数有理逼近值。
如上所示,P-HELM通过式(14)代替Padé近似依次计算所有节点电压幂级数的有理逼近值,进而获得潮流解。相较于Padé近似,式(14)的计算复杂度较低,大幅降低了P-HELM的计算成本。此外,式(14)中各元素间的数据关联性较弱,可进一步通过并行计算技术实现所有节点电压幂级数有理逼近值的并行计算。
2.2.2 电压幂级数有理逼近值的并行计算
如2.2.1节所述,P-HELM通过式(14)降低了电压幂级数有理逼近值的计算成本,且式(14)的并行适应度较高。然而,式(14)计算所需的电压幂级数系数均为双精度浮点型复数,每个系数需占用16字节的存储空间。为降低P-HELM算法的内存占用率以提高P-HELM算法的并行计算效率,本节对式(13)所示的Aitken差分算子进行改进,并基于改进后的Aitken差分算子实现所有节点电压幂级数有理逼近值的并行计算。
将式(13)中Aitken差分算子的实、虚部拆分,以PQ节点为例,有
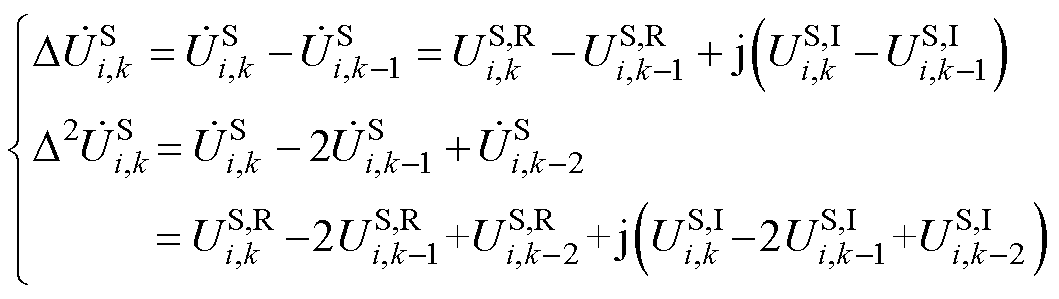 (15)
(15)
式中,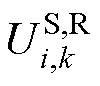 、
、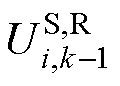 和
和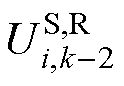 分别为式(12)中
分别为式(12)中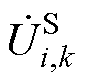 、
、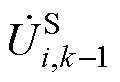 和
和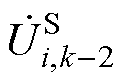 的实部;
的实部;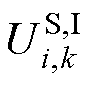 、
、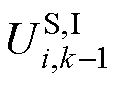 和
和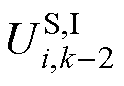 分别为式(12)中
分别为式(12)中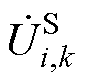 、
、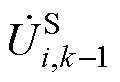 和
和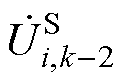 的虚部。
的虚部。
同理,平衡节点和PV节点的Aitken差分算子也可拆分为如上形式。进一步地,将式(15)所示的Aitken差分算子代入式(14)中,得到所有类型节点电压幂级数有理逼近值的统一计算形式为
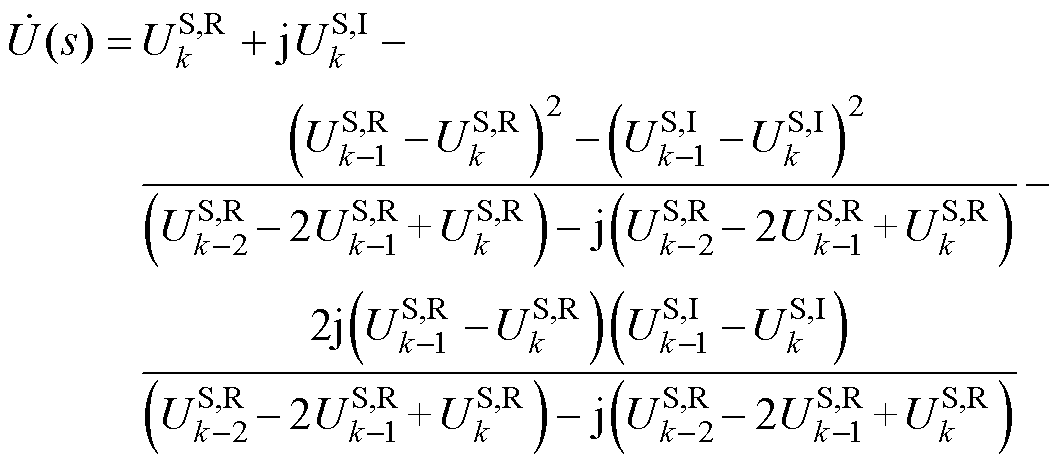 (16)
(16)
如式(16)所示,改进后Aitken差分法所需电压幂级数系数均为双精度浮点型实数,每个系数仅需占用8字节的存储空间,有效地降低了P-HELM并行计算节点电压幂级数有理逼近值时的内存占用率,对并行计算效率提升具有重要意义。
综上所述,所提P-HELM基于式(16)实现了系统所有节点电压幂级数有理逼近值的并行计算,具体策略如图2所示。
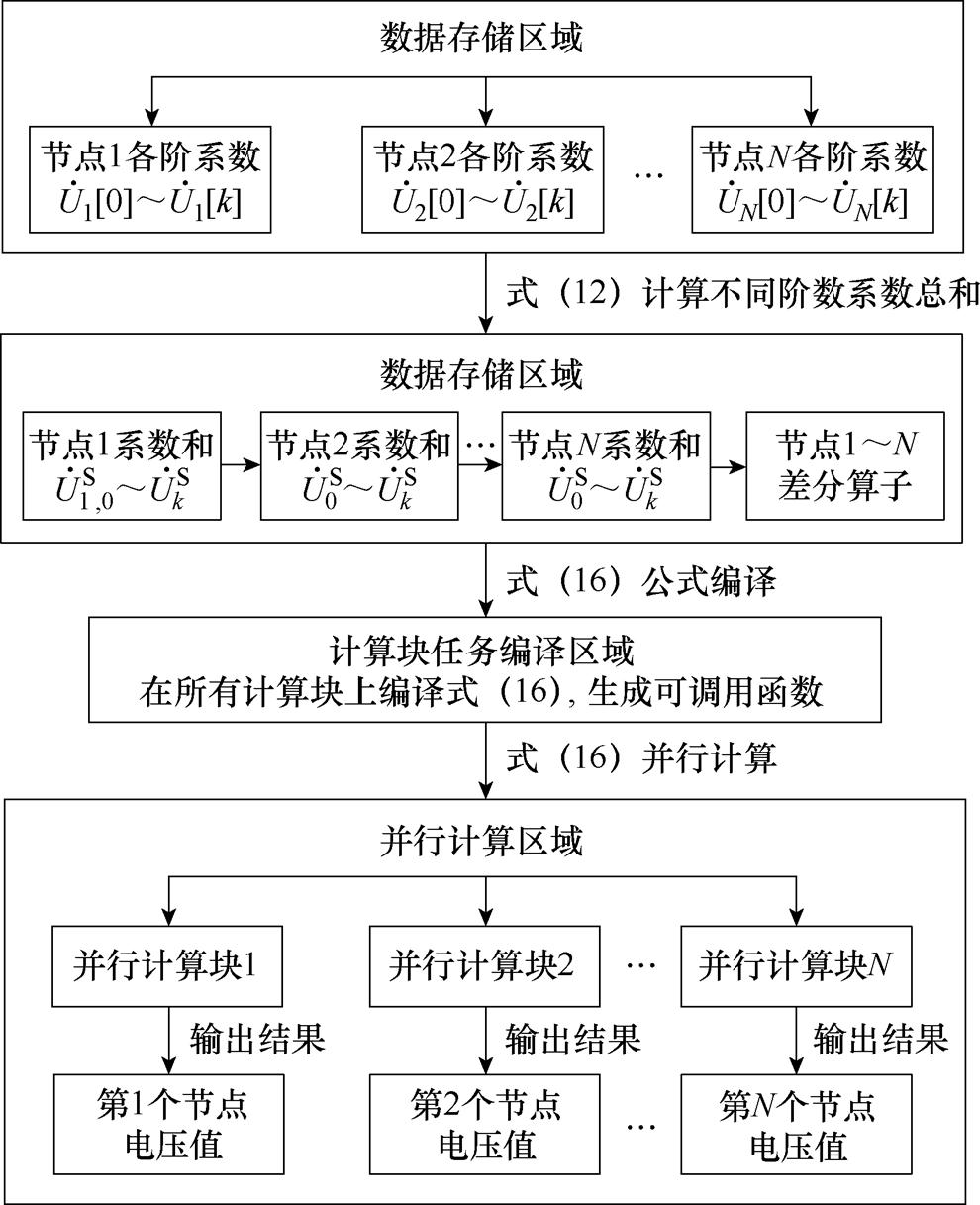
图2 Aitken差分并行计算策略
Fig.2 Parallel computing strategy of Aitken differential
式(16)计算所需的各节点电压幂级数系数均可通过图1所提的预处理BICGSTAB法得到,进而可由式(12)和式(15)分别计算得到各节点电压的幂级数系数及对应的差分算子。由于差分算子计算过程仅涉及简单的加减运算,因此无需进行并行计算;而大规模电力系统节点数量众多,需在计算单元上编译式(16)所示所有类型节点电压幂级数有理逼近的统一计算形式,进一步采用“线程-节点电压”一一对应的自适应线程调用方式,在求解不同规模的电力系统潮流时自动调用与节点数相同的线程数实现所有节点电压幂级数有理逼近值的并行计算。
如2.1节和2.2节所述,所提P-HELM并行计算方法实现了高维幂级数系数线性方程组的并行求解和所有节点电压幂级数有理逼近值的并行计算。为将上述两部分并行计算结合,本节基于CPU-GPU异构计算平台设计了所提P-HELM并行计算方法的整体计算流程。
2.3.1 并行策略设计
在计算机中,GPU是用于处理高度并行化算法的处理器,其大规模数据的计算能力优于CPU,但在逻辑运算方面略逊于CPU。由CPU和GPU组成的CPU-GPU异构计算平台可实现二者之间的协同计算,适用于提升电力系统潮流求解的效率[27-29]。因此,本文基于CPU-GPU异构计算平台设计的P-HELM并行计算策略如图3所示。
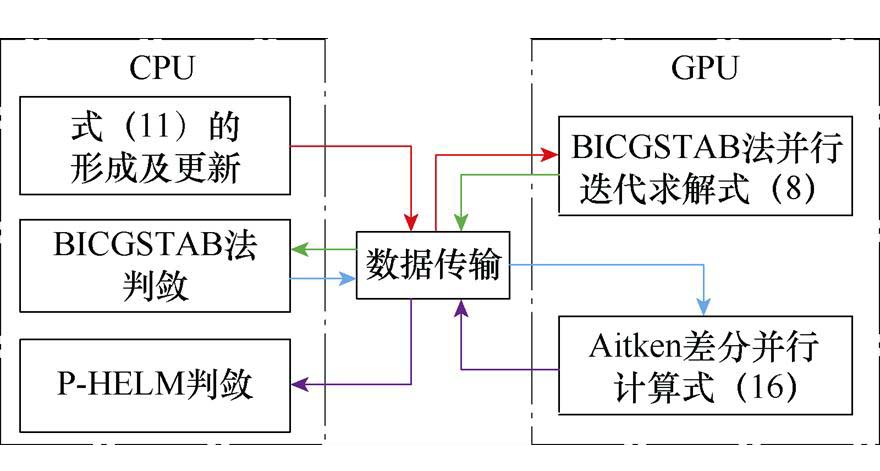
图3 基于CPU-GPU异构运算平台的并行策略
Fig.3 Parallel computing strategy based on CPU-GPU heterogeneous platform
由于在采用BICGSTAB法并行迭代求解式(8)的计算过程中涉及多次大规模矩阵向量的数值计算和逻辑运算,本文所提CPU-GPU异构计算平台不仅能够借助GPU发挥BICGSTAB法在大规模矩阵向量计算中的优势,还能够将求解式(8)得到的解向量快速传输至CPU,完成BICGSTAB法的收敛性判断。此外,根据系数矩阵Ysys不变的特点,P-HELM仅需在CPU中构造1次预处理器Fpre,CPU和GPU间仅需进行1次系数矩阵与预处理器的数据传输,有效控制了CPU与GPU之间的数据交互成本,对提高并行计算效率具有重要意义。
另一方面,在采用Aitken差分法并行计算式(16)过程中存在大规模向量间的计算。本文借助CPU-GPU异构计算平台并行计算式(16)不仅可以发挥GPU强大的数据处理能力以快速实现所有节点电压幂级数有理逼近值的并行计算,还能够将得到的结果快速传输至CPU完成P-HELM的收敛性判断,减少P-HELM的收敛判定时间。
综上所述,本文设计的CPU-GPU异构P-HELM计算策略可同时发挥CPU和GPU的计算优势,提高P-HELM的计算效率。
2.3.2 计算流程
本文所提电力系统潮流的P-HELM计算流程如图4所示,具体步骤如下,其中步骤(7)~步骤(9)为内层循环,旨在并行迭代求解式(8)以快速获得电压幂级数系数;其余步骤为外层循环,旨在并行计算式(16)和逻辑判断:
(1)读取系统的节点数据,得到式(2)中Gij与Bij,构建式(A4)所示方程组。
(2)设置外循环参数:最大误差阈值eeps,迭代次数nite,最大迭代次数Nmax;设置内循环参数:内循环最大误差阈值emin,初始计算阶数i=1,初始解向量xpre。
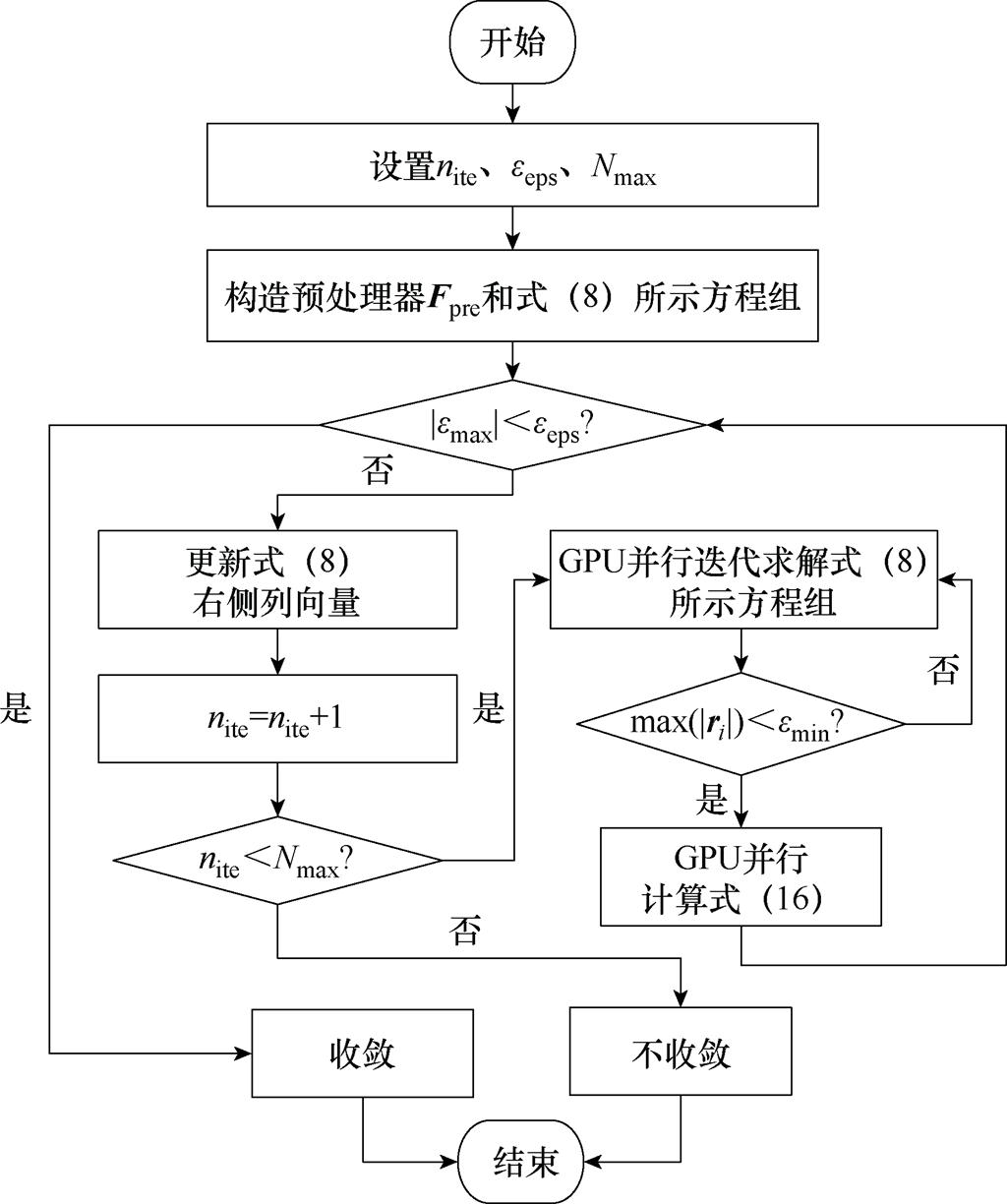
图4 P-HELM算法的并行计算流程
Fig.4 Flowchart of the proposed P-HELM
(3)构造稀疏矩阵近似逆预处理器Fpre,构建式(8)所示线性方程组,并将相应矩阵数据传输至GPU。
(4)基于电压幂级数零阶项系数计算最大失配功率绝对值|emax|,记录误差趋势并转至步骤(5)。
(5)更新式(8)所示线性方程组右侧向量并将其向量数据传输至GPU。
(6)判断nite<Nmax是否成立。若成立,令nite= nite+1,转至步骤(7);反之,算法不收敛。
(7)进行P-HELM算法的内循环。并行迭代求解式(8)所示线性方程组,并利用已传输至GPU中的数据计算BICGSTAB法的中间向量组并输出新的解向量xpre。
(8)更新计算残差向量ri。
(9)进行P-HELM内循环BICGSTAB法误差收敛判定。若max(|ri|)<emin,跳出内循环,转至步骤(10);反之,令i=i+1,转至步骤(7)利用新的残差向量ri更新中间向量组及解向量数据xpre。
(10)采用Aitken差分并行计算式(16)。
(11)将计算所得电压值传回CPU,更新电压幂级数的零阶项系数及最大失配功率绝对值|emax|,判断|emax|<eeps是否成立。若不成立,转至步骤(5)循环计算;若成立,算法收敛,输出P-HELM的潮流计算结果。
本节根据MATPOWER7.1中不同节点规模的测试系统算例对所提P-HELM的计算精度和效率进行分析、验证[30]。测试过程中硬件平台为Dell服务器,CPU为Intel Xeon E5-2620,主频2.10 GHz,内存32 GB;GPU为NVIDIA Tesla P100,拥有3 584个单精度、1 792个双精度核,同时搭配4 096-bit 16 GBHBM2高带宽显存。软件平台采用MatlabR2019a和CUDA10.0。
为验证本文所提P-HELM求解大规模电力系统潮流的准确性,本节首先将P-HELM与NR法进行比较。本节将外循环潮流误差阈值设为10-3、BICGSTAB并行迭代求解式(8)的内循环误差阈值设为10-12、内、外循环的最大循环次数分别设为20和30,在不同规模电力系统测试系统中分别应用上述两种算法计算电力系统潮流,得到最大误差节点的电压幅值和相位分布情况如图5所示。以NR法结果为基准,采用所提P-HELM求解电力系统潮流,最大误差节点绝对误差和相对误差结果见表1。
由图5可知,在不同规模的电力系统中,采用所提P-HELM求解电力系统潮流与采用NR法所得结果的分布情况几乎一致。进一步由表1结果计算可知:不同规模的测试系统中,所提P-HELM相较于NR法的最大相对误差仅为0.003 4%和0.005 3%。该结果表明,P-HELM在求解大规模电力系统潮流时具有与NR法相同的计算精度,能够满足大规模电力系统潮流计算精度要求。
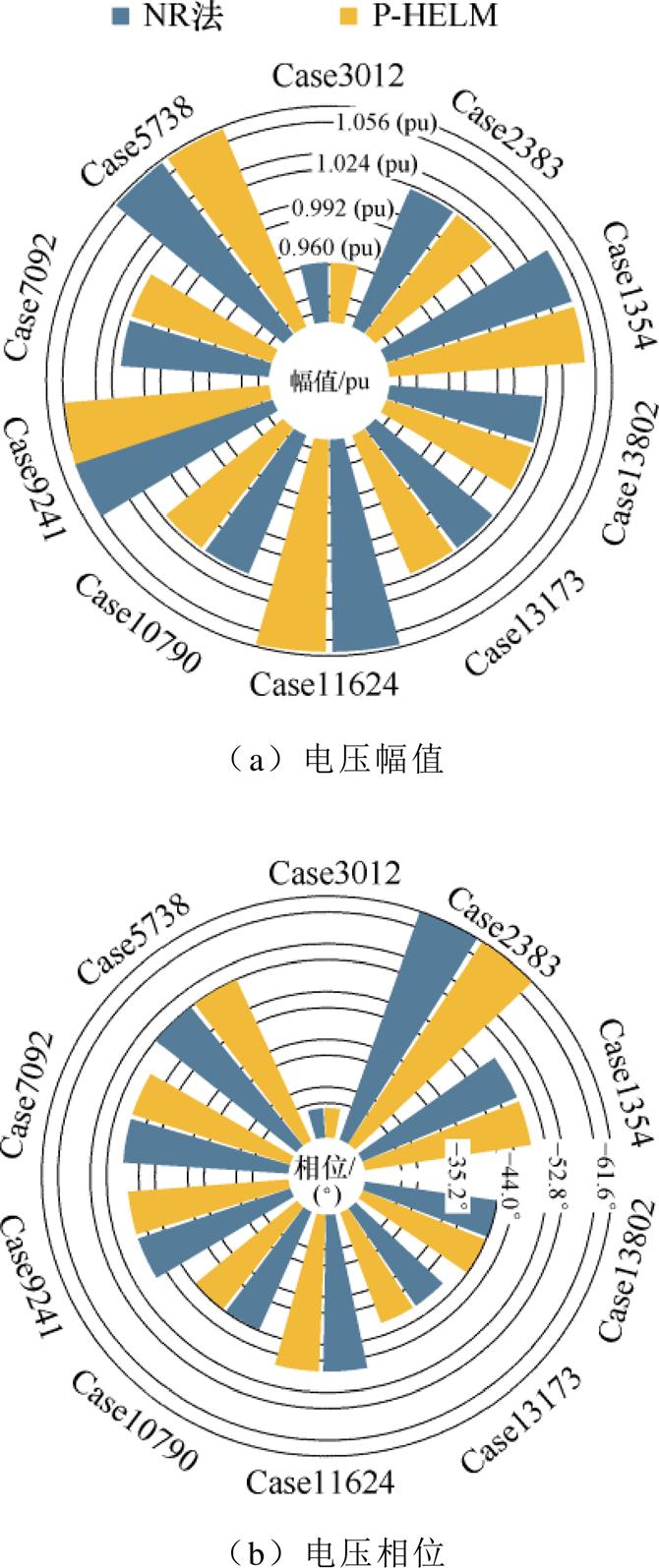
图5 P-HELM与NR法潮流计算结果对比
Fig.5 Power flow comparison between P-HELM and NR
表1 P-HELM相对于NR法的误差百分比
Tab.1 Percentage error of P-HELM relative to NR method
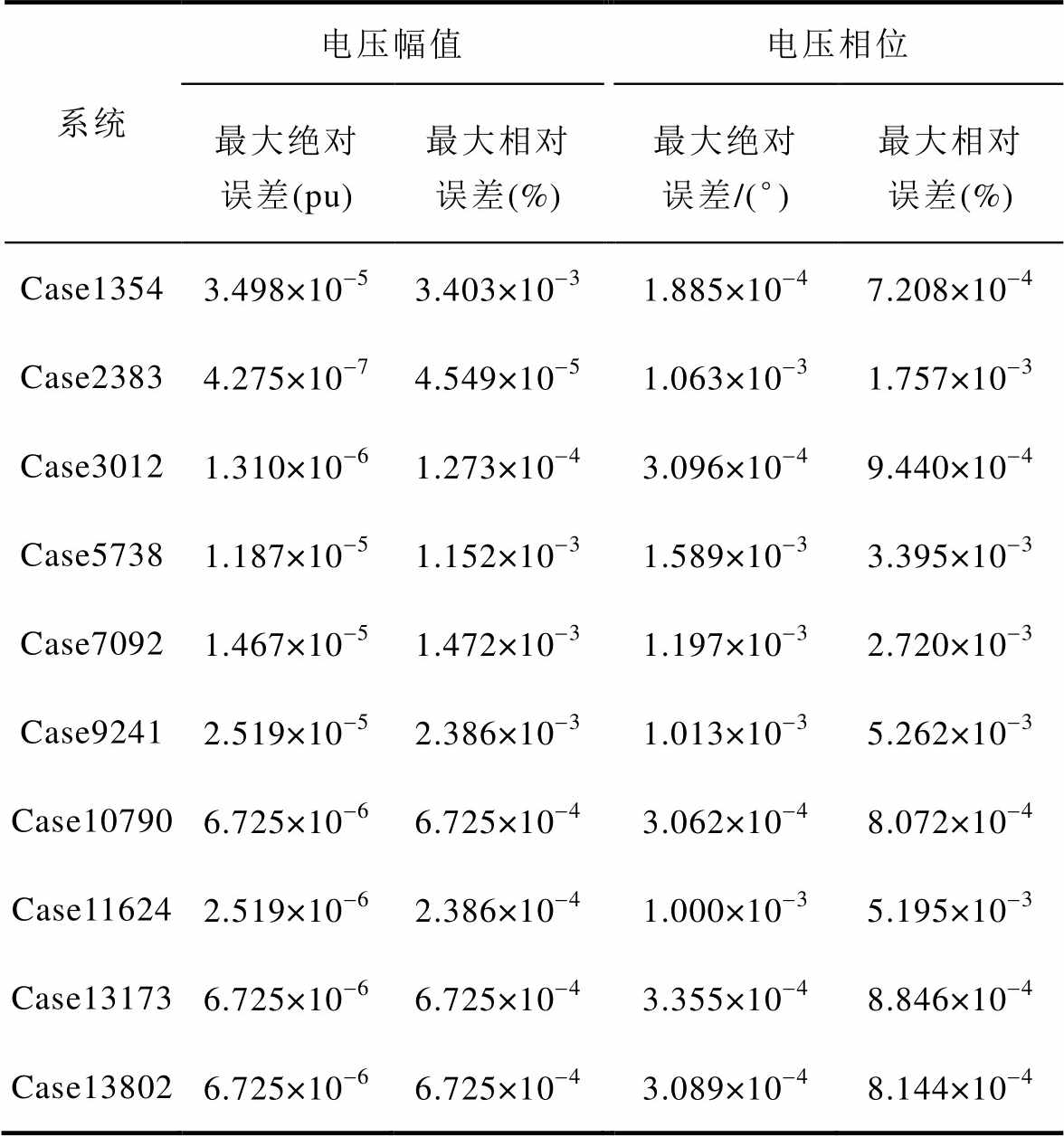
系统电压幅值电压相位 最大绝对误差(pu)最大相对误差(%)最大绝对误差/(°)最大相对误差(%) Case13543.498×10-53.403×10-31.885×10-47.208×10-4 Case23834.275×10-74.549×10-51.063×10-31.757×10-3 Case30121.310×10-61.273×10-43.096×10-49.440×10-4 Case57381.187×10-51.152×10-31.589×10-33.395×10-3 Case70921.467×10-51.472×10-31.197×10-32.720×10-3 Case92412.519×10-52.386×10-31.013×10-35.262×10-3 Case107906.725×10-66.725×10-43.062×10-48.072×10-4 Case116242.519×10-62.386×10-41.000×10-35.195×10-3 Case131736.725×10-66.725×10-43.355×10-48.846×10-4 Case138026.725×10-66.725×10-43.089×10-48.144×10-4
为验证本文所构造预处理器Fpre的有效性,本节对比了BICGSTAB法不采用预处理、采用ILU预处理、采用近似逆预处理时,P-HELM收敛时内、外层循环的平均计算次数,对比结果见表2。
由表2可知,采用BICGSTAB法求解高维幂级数系数线性方程组时,采用ILU或近似逆预处理技术可得到较好的收敛效果。然而,在采用ILU预处理时,BICGSTAB法的内循环次数较多,进而导致BICGSTAB法的求解时间较长。相比之下,基于所提预处理器Fpre的BICGSTAB法仅需1次内循环计算便可输出较为精确的电压幂级数系数,加快了BICGSTAB法收敛速度,在求解高维幂级数系数线性方程组时具有明显优势。
表2 P-HELM内、外层循环的平均计算次数
Tab.2 The number of inner and outer cycles of P-HELM
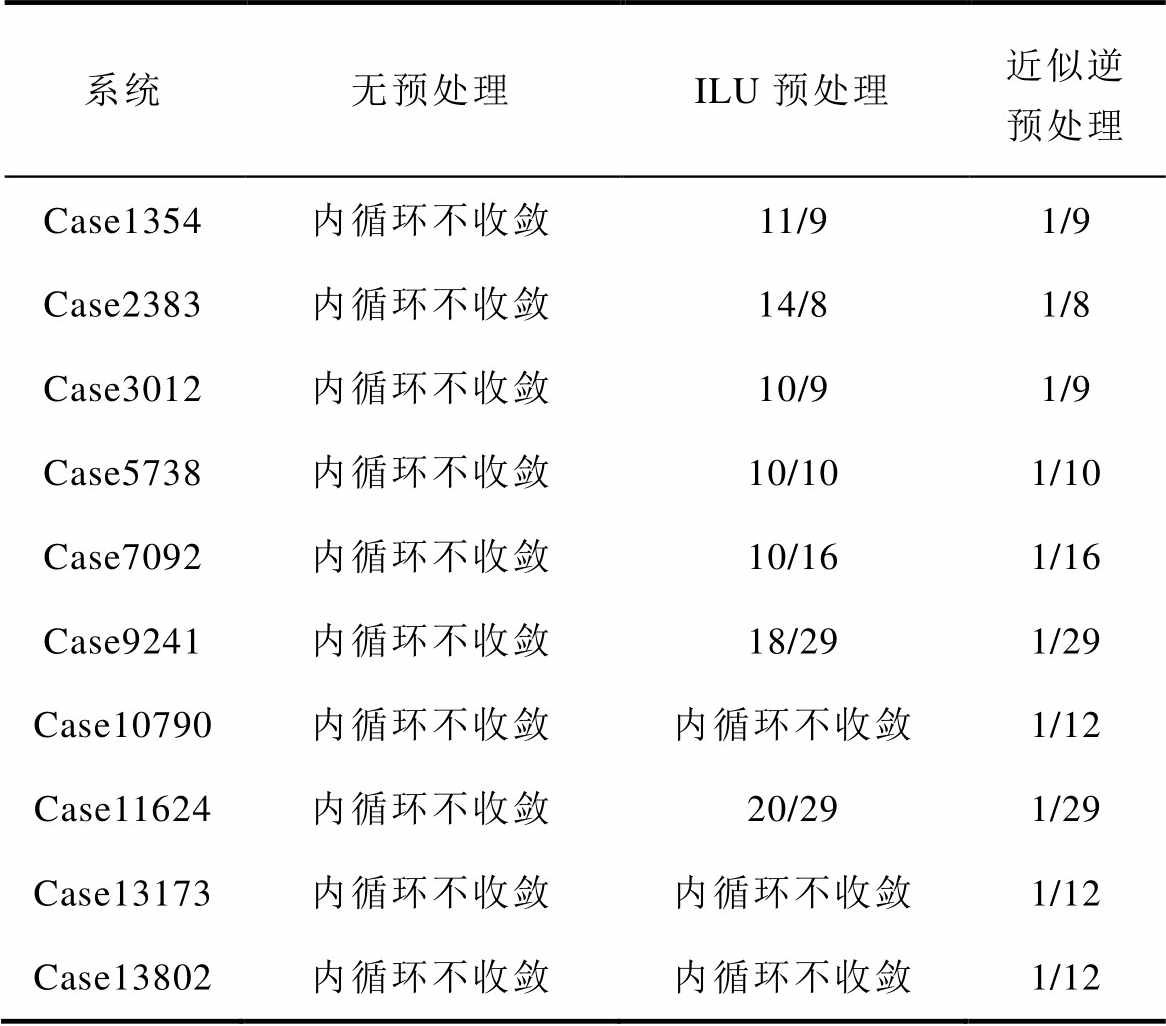
系统无预处理ILU预处理近似逆预处理 Case1354内循环不收敛11/91/9 Case2383内循环不收敛14/81/8 Case3012内循环不收敛10/91/9 Case5738内循环不收敛10/101/10 Case7092内循环不收敛10/161/16 Case9241内循环不收敛18/291/29 Case10790内循环不收敛内循环不收敛1/12 Case11624内循环不收敛20/291/29 Case13173内循环不收敛内循环不收敛1/12 Case13802内循环不收敛内循环不收敛1/12
注:“/”左右分别指P-HELM内循环与外循环的平均计算次数,重复测试十次后取计算次数平均值。
为进一步研究预处理器Fpre对高维幂级数系数线性方程组中系数矩阵的影响,本文以Case1354系统为例,对比了式(2)系数矩阵Ysys和式(8)线性方程组系数矩阵的特征值分布,结果如图6所示。
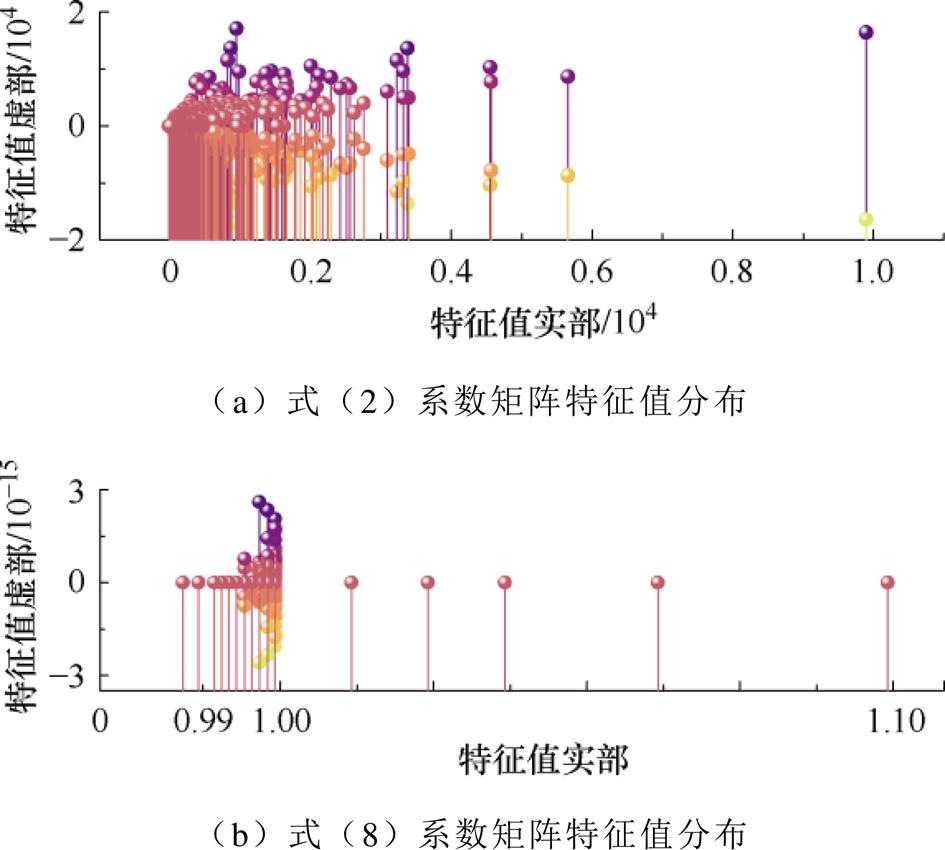
图6 高阶幂级数线性方程组系数矩阵的特征值分布
Fig.6 Eigenvalue distribution of coefficient matrix of the power series linear equations
由图6可知,系数矩阵Ysys的特征值分布呈现出较为分散的特点。其中,特征值实部的分布区间约为0~10 000,特征值虚部的分布区间约为-20 000~20 000。而式(8)所示高维幂级数系数线性方程组的系数矩阵特征值实部的分布区间可降至0.99~1.10,特征值虚部的分布区间降至10-15数量级。由此表明,所提的预处理器构造方式能够显著压缩高维幂级数系数线性方程组中系数矩阵特征值的空间分布,提升BICGSTAB法的收敛效果。
如2.2.1节所述,本文借助Aitken差分法实现节点电压幂级数有理逼近的计算过程较为简便。为验证式(14)计算各节点电压幂级数有理逼近值较Padé近似的高效性,本节对比了采用式(14)和Padé近似计算各节点电压幂级数有理逼近值的计算耗时,结果如图7所示。
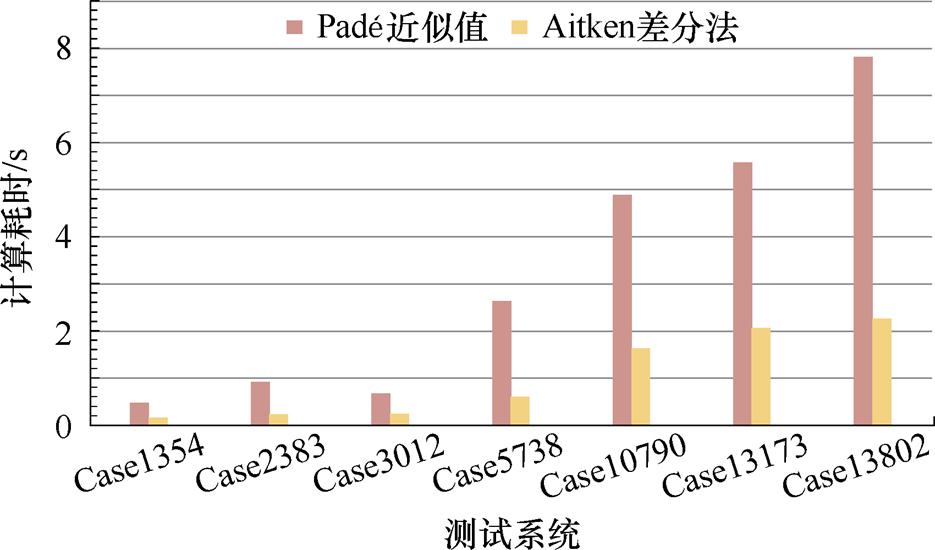
图7 电压幂级数有理逼近值的平均计算时间对比
Fig.7 Computational time comparison between Padé approximation and Aitken difference
由图7可知,采用式(14)计算电压幂级数有理逼近值的耗时较少,与Padé近似相比优势明显。由此表明,本文所提基于Aitken差分法的电压幂级数有理逼近在保证所提算法收敛性和精度的基础上,降低了P-HELM的计算耗时。
由于采用P-HELM求解电力系统潮流的耗时主要集中在并行迭代求解高维幂级数系数线性方程组和并行计算节点电压的幂级数有理逼近值两部分中,因此本节分别对上述两部分并行计算耗时进行对比、分析,并进一步对P-HELM的计算总耗时进行分析。本节中NR法测试程序来源于MATPOWER7.1,内、外循环的相关参数设置与3.1节保持一致,所有测试系统潮流计算耗时均为测试10次所统计的计算时间平均值。
3.4.1 并行迭代求解方程组的高效性验证
为验证本文采用BICGSTAB法并行迭代求解式(8)的计算效率,本节分别统计了Matlab中基于LU分解(LU Decomposition)的多波前线性方程组求解算法、基于LU分解的线性方程组直接法以及预处理BICGSTAB迭代法的计算耗时,结果如图8所示。
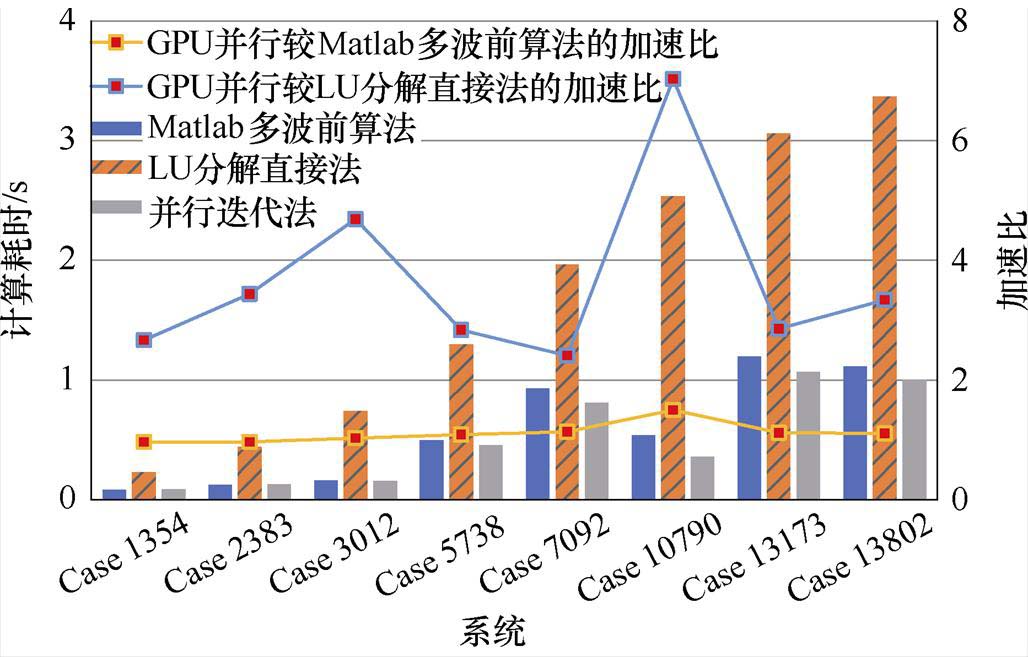
图8 高维幂级数系数线性方程组的计算时间对比
Fig.8 Computational time comparison for solving power series linear equations between different methods
由图8可知,与基于LU的直接法相比,本文采用所提预处理BICGSTAB并行迭代求解式(8)具有较好的加速效果,但与Matlab中基于LU分解的多波前线性方程组求解算法相比计算效率改善效果有限。造成上述现象的主要原因在于采用混合编程时,内、外双循环计算模式下存在CPU与GPU之间的多次数据交互,而大规模数据交互时间在目前的软、硬件条件下仍难以降低,一定程度上限制了并行加速效果的提升。需要指出的是:基于LU分解的多波前线性方程组求解算法是经过了极大程度地优化的,已广泛应用于大规模稀疏线性方程组的求解中。本文所提预处理BICGSTAB并行迭代法仍存在较大的优化空间,可通过优化进一步提高其并行计算效率。
3.4.2 并行计算电压逼近值的计算效率验证
为验证本文所提P-HELM采用式(16)并行计算节点电压幂级数有理逼近值的计算效率,本节针对不同测试系统,分别统计了Padé近似、式(14)中串行Aitken差分法以及式(16)并行Aitken差分法的计算耗时,并计算了并行Aitken差分法与其他两种算法计算耗时的比值即加速比(加速比数值越大表示加速效果越好),测试结果如图9所示及见表3。
由图9及表3可知,P-HELM采用式(16)所示Aitken差分法并行计算节点电压的幂级数有理逼近值耗时较少,相比Padé近似和式(14)的计算耗时加速比较为理想,最高加速比分别可达到58.400和22.999。由此表明,所提P-HELM的节点电压幂级数有理逼近值并行计算效率较高,能够进一步提升P-HELM的计算效率。
3.4.3 并行计算耗时对比
为测试及分析本文所提P-HELM求解大规模电力系统潮流的计算效率,本节首先将基于LU分解直接求解修正方程组的平启动NR法和传统HELM计算耗时作为参考,采用P-HELM求解不同节点规模的电力系统潮流,测试结果见表4。
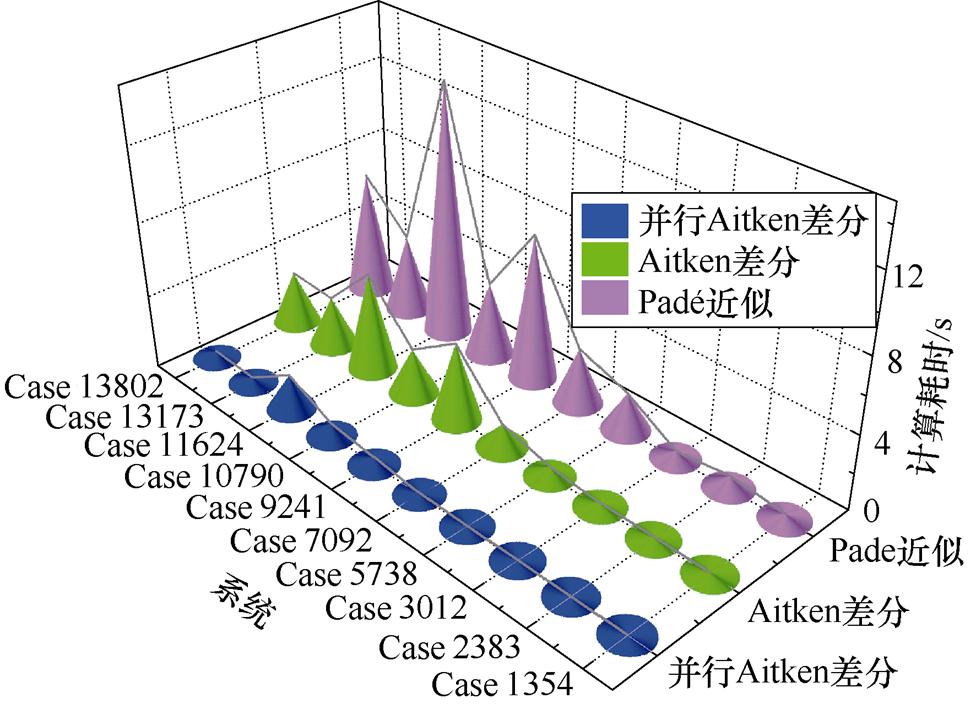
图9 电压幂级数有理逼近值的平均计算时间对比
Fig.9 Computational time comparison for approximating the voltage between different methods
表3 并行Aitken差分法相较Padé近似和串行Aitken差分法的加速比
Tab.3 Acceleration ratio of parallel Aitken difference compared with Padé approximation and serial Aitken difference
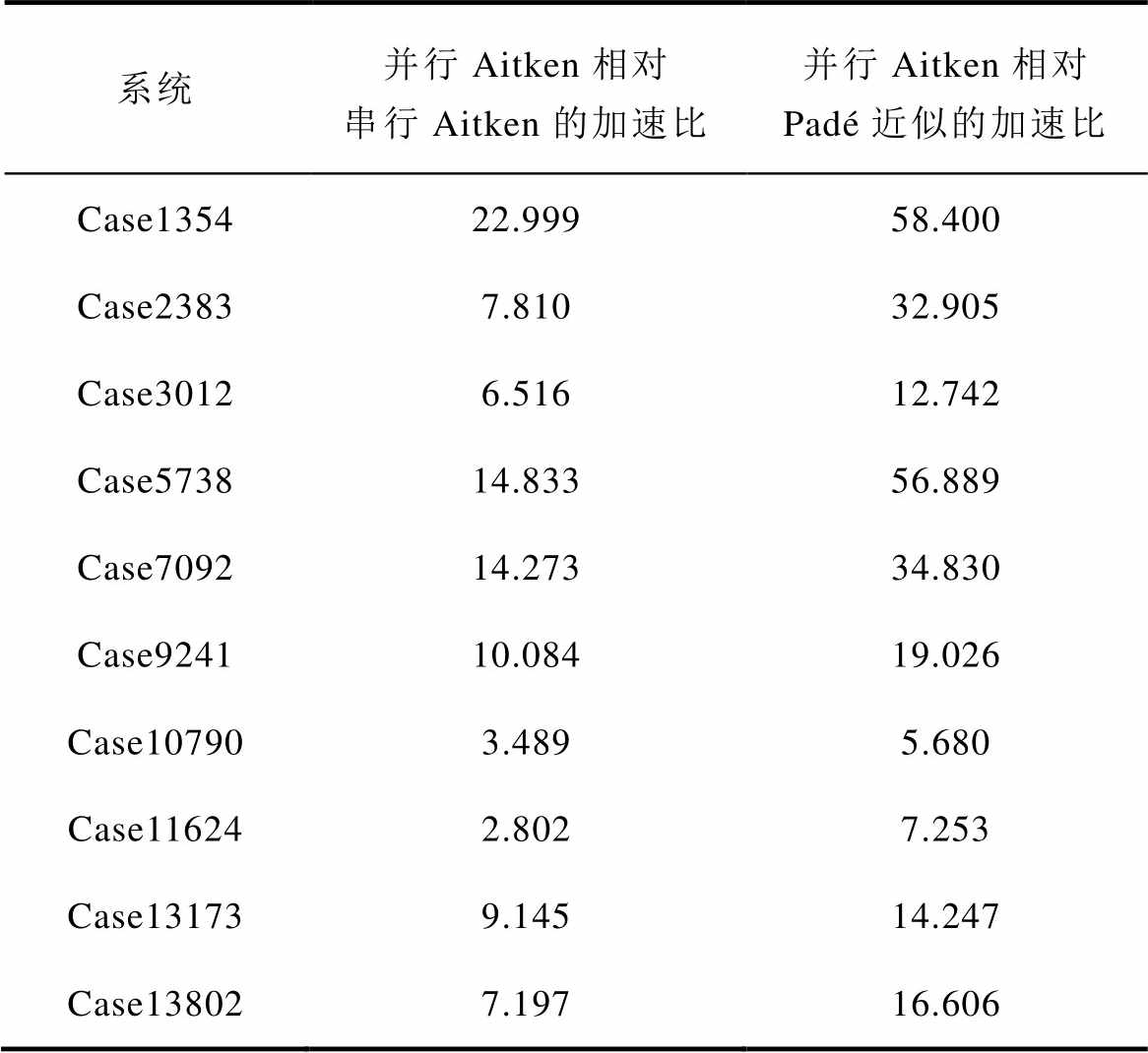
系统并行Aitken相对串行Aitken的加速比并行Aitken相对Padé近似的加速比 Case135422.99958.400 Case23837.81032.905 Case30126.51612.742 Case573814.83356.889 Case709214.27334.830 Case924110.08419.026 Case107903.4895.680 Case116242.8027.253 Case131739.14514.247 Case138027.19716.606
由表4可知,本文所提P-HELM相比于传统HELM,在所有测试系统上均能达到3.40以上的加速比,最高加速比可达到5.64,平均加速比为4.85;与采用LU分解直接求解修正方程组的平启动NR法相比,所提P-HELM的加速比可在54.53以上,最高加速比可达94.96,平均加速比为72.86。
表5进一步对比了基于CPU-GPU异构计算平台,采用平启动NR法和P-HELM并行求解修正方程组的计算耗时。
表4 P-HELM与其他方法的平均计算时间
Tab.4 The average calculation time between P-HELM and other methods (单位: s)
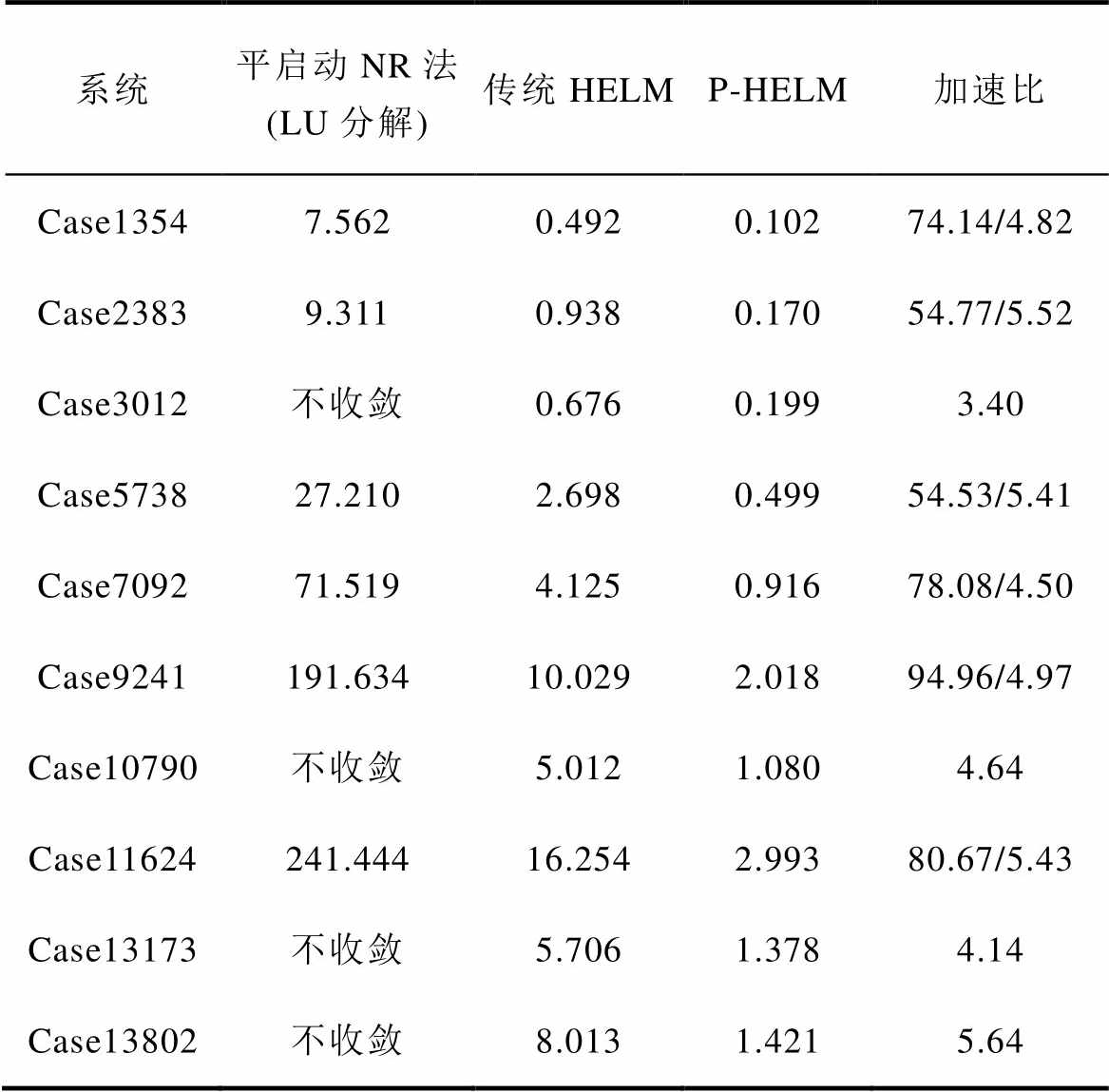
系统平启动NR法(LU分解)传统HELMP-HELM加速比 Case13547.5620.4920.10274.14/4.82 Case23839.3110.9380.17054.77/5.52 Case3012不收敛0.6760.1993.40 Case573827.2102.6980.49954.53/5.41 Case709271.5194.1250.91678.08/4.50 Case9241191.63410.0292.01894.96/4.97 Case10790不收敛5.0121.0804.64 Case11624241.44416.2542.99380.67/5.43 Case13173不收敛5.7061.3784.14 Case13802不收敛8.0131.4215.64
注:“加速比”一栏中,“/”左右分别指P-HELM的平均计算时间相对于基于LU分解直接法求解修正方程组的平启动NR法和传统HELM平均计算时间的加速比。
表5 NR与P-HELM法的平均计算时间
Tab.5 Average calculation time of NR and P-HELM methods (单位: s)
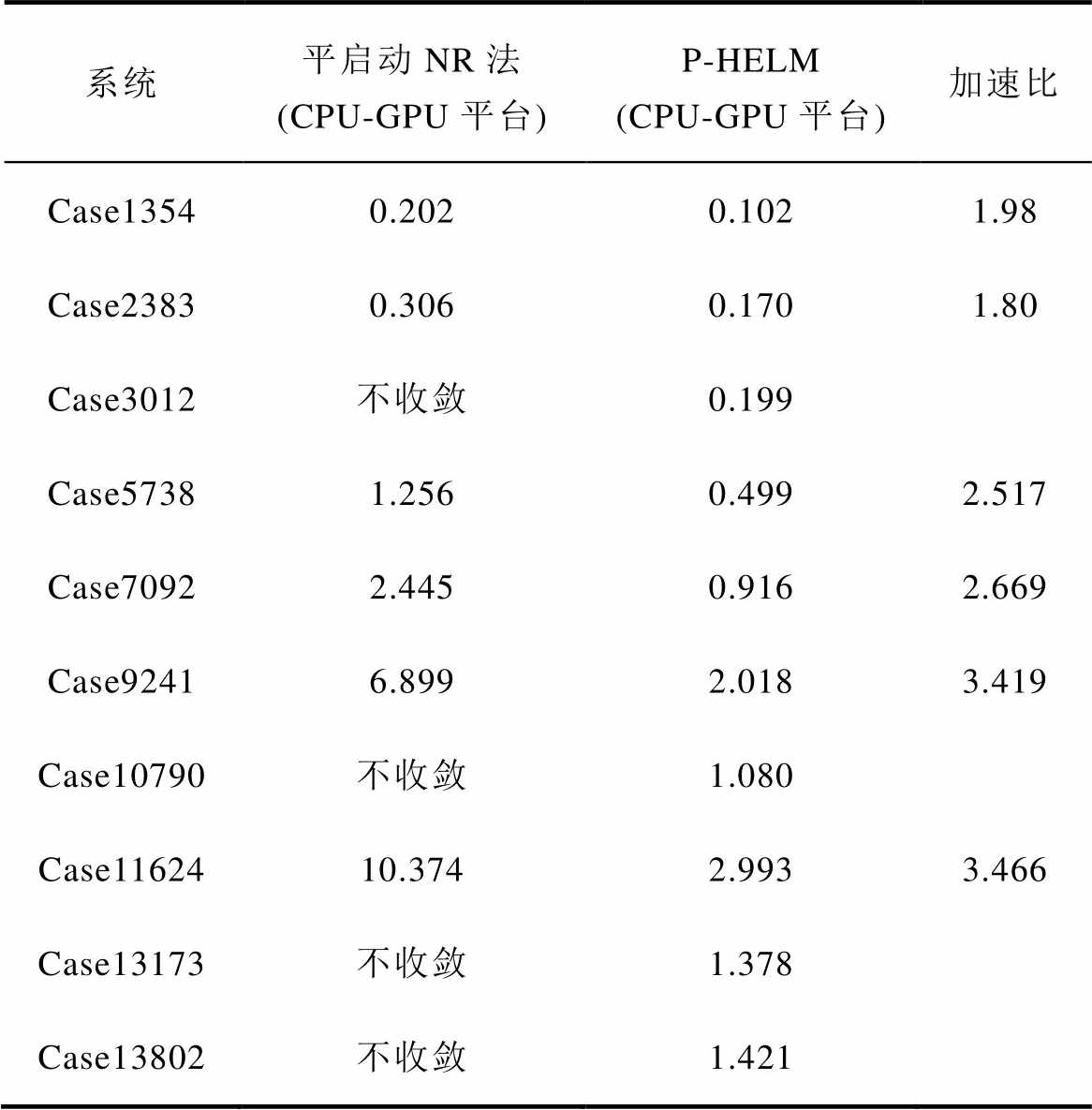
系统平启动NR法(CPU-GPU平台)P-HELM(CPU-GPU平台)加速比 Case13540.2020.1021.98 Case23830.3060.1701.80 Case3012不收敛0.199 Case57381.2560.4992.517 Case70922.4450.9162.669 Case92416.8992.0183.419 Case10790不收敛1.080 Case1162410.3742.9933.466 Case13173不收敛1.378 Case13802不收敛1.421
由表5可知,基于CPU-GPU异构计算平台的NR法计算速度较表4中的NR法有了显著提升,但与P-HELM并行算法相比仍有一定差距,且随着系统规模的扩大,P-HELM在计算效率方面的优势也逐渐增大。此外,对于表5中采用平启动NR法无法收敛的测试系统,P-HELM均能保证收敛性和准确性。由此表明,所提P-HELM不仅具有较高的计算效率,还具有较强的适用性。
综上所述,针对不同规模电力系统的潮流求解问题,P-HELM并行算法均具有较高的计算效率和较强的适用性,能实现电力系统潮流的准确、快速求解。
本文提出了一种基于BICGSTAB和Aitken差分的电力系统全纯嵌入潮流并行计算算法,通过节点规模在1 354—13 802的电力系统测试算例对所提方法进行分析、验证,相关结论如下:
1)所提P-HELM算法适用性强、计算准确性高、计算耗时少,可实现电力系统潮流快速、准确求解。
2)所提P-HELM将BICGSTAB迭代求解法与预处理技术相结合显著提升了高维幂级数系数线性方程组的求解效率。
3)所提P-HELM采用Aitken差分法计算节点电压的幂级数有理逼近值,有效地提升了电力系统潮流求解的计算效率。
4)所提P-HELM分别实现了高维幂级数系数线性方程组的并行求解和节点电压幂级数有理逼近值的并行计算,具有较高的计算效率,与传统HELM和基于LU分解直接法的NR法相比,所提P-HELM在所有测试系统中的平均加速比分别为4.85和72.86,最高加速比分别可达5.64和94.96,计算效率提升显著。
附 录
1. HELM零阶项系数求解
根据全纯函数可在其定义域内进行幂级数展开的性质,可将式(1)中的电压全纯函数和无功功率全纯函数展开为如下通用形式
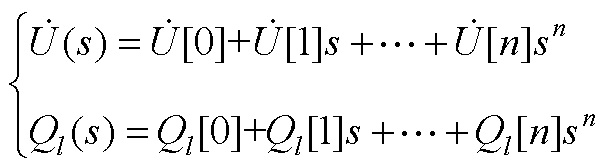 (A1)
(A1)
式中,n为电压幂级数和无功功率幂级数的展开阶数;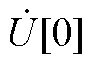 ~
~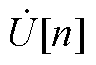 分别为节点电压全纯幂级数的第0, 1,…, n阶系数;
分别为节点电压全纯幂级数的第0, 1,…, n阶系数;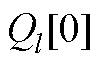 ~
~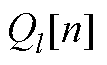 分别为PV节点无功功率全纯幂级数的第0, 1,×…, n阶系数。
分别为PV节点无功功率全纯幂级数的第0, 1,×…, n阶系数。
将式(A1)代入式(1),当嵌入值s=0时,式(1)将转化为仅含变量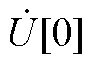 和
和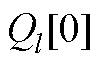 的方程为
的方程为
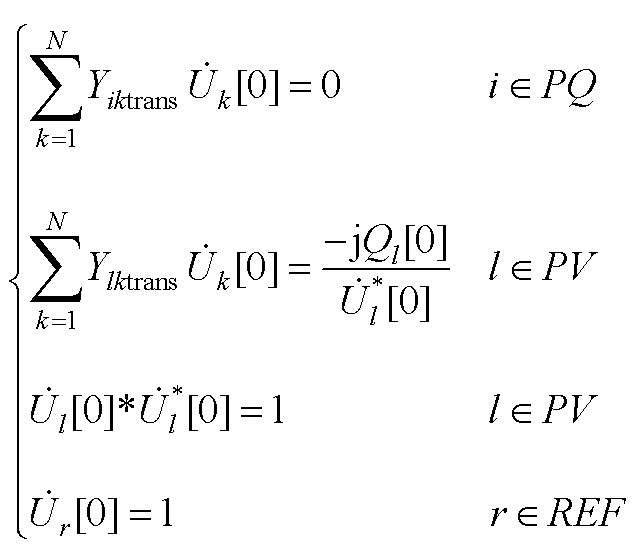 (A2)
(A2)
式中,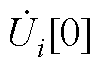 、
、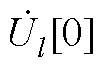 、
、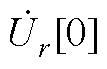 分别为PQ节点、PV节点和平衡节点电压全纯幂级数的零阶项系数;
分别为PQ节点、PV节点和平衡节点电压全纯幂级数的零阶项系数;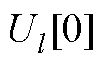 为PV节点无功功率全纯幂级数的零阶项系数。
为PV节点无功功率全纯幂级数的零阶项系数。
当嵌入值s=1时,式(1)与各类型节点的功率平衡方程完全相同,则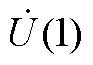 即为节点电压值。此时,式(A1)中待求节点电压表达式为
即为节点电压值。此时,式(A1)中待求节点电压表达式为
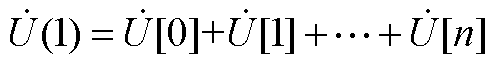 (A3)
(A3)
因此,采用HELM求解电力系统潮流的关键在于求解各节点电压的全纯幂级数系数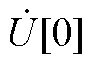 ~
~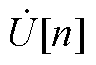 ,进而再根据式(A3)计算各节点电压。
,进而再根据式(A3)计算各节点电压。
与NR法需预设初值不同,由于式(A2)中由Yiktrans和Ylktrans构成的导纳矩阵各行元素之和均为0,因此,当且仅当所有节点电压全纯幂级数的零阶项系数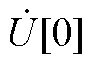 = 1+j0、PV节点无功功率全纯幂级数的零阶项系数
= 1+j0、PV节点无功功率全纯幂级数的零阶项系数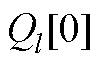 =0时,式(A2)才成立。由此可知:HELM可通过式(A2)直接获取全纯幂级数的零阶项系数
=0时,式(A2)才成立。由此可知:HELM可通过式(A2)直接获取全纯幂级数的零阶项系数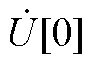 和
和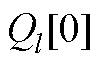 。
。
2. 高维幂级数线性方程组构建
由附录可知,HELM可通过式(A2)直接获取所需的零阶项系数。进一步地,为递归计算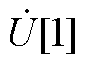 ~
~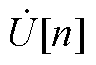 ,HELM将式(A1)所示的全纯幂级数展开式代入式(1),并引入逆幂级数函数构建统一递归求解所有节点电压幂级数系数的高维幂级数系数线性方程组。
,HELM将式(A1)所示的全纯幂级数展开式代入式(1),并引入逆幂级数函数构建统一递归求解所有节点电压幂级数系数的高维幂级数系数线性方程组。
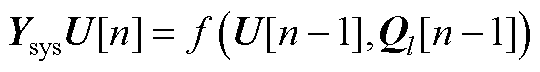 (A4)
(A4)
式中,Ysys为高维幂级数系数线性方程组系数矩阵;n为节点电压和无功功率全纯幂级数的展开阶数;U[n]= 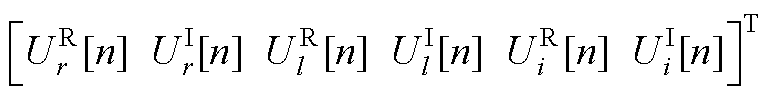 为节点电压的第n阶幂级数系数向量;
为节点电压的第n阶幂级数系数向量;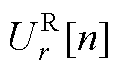 、
、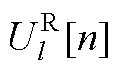 、
、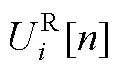 和
和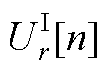 、
、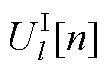 、
、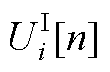 分别为平衡节点、PV节点、PQ节点电压第n阶幂级数系数的实部和虚部;
分别为平衡节点、PV节点、PQ节点电压第n阶幂级数系数的实部和虚部;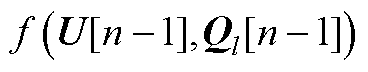 为含第n-1阶电压幂级数系数和无功功率幂级数系数的递归计算表达式。
为含第n-1阶电压幂级数系数和无功功率幂级数系数的递归计算表达式。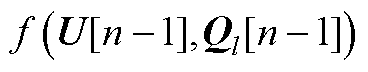 详细表达形式分别为
详细表达形式分别为
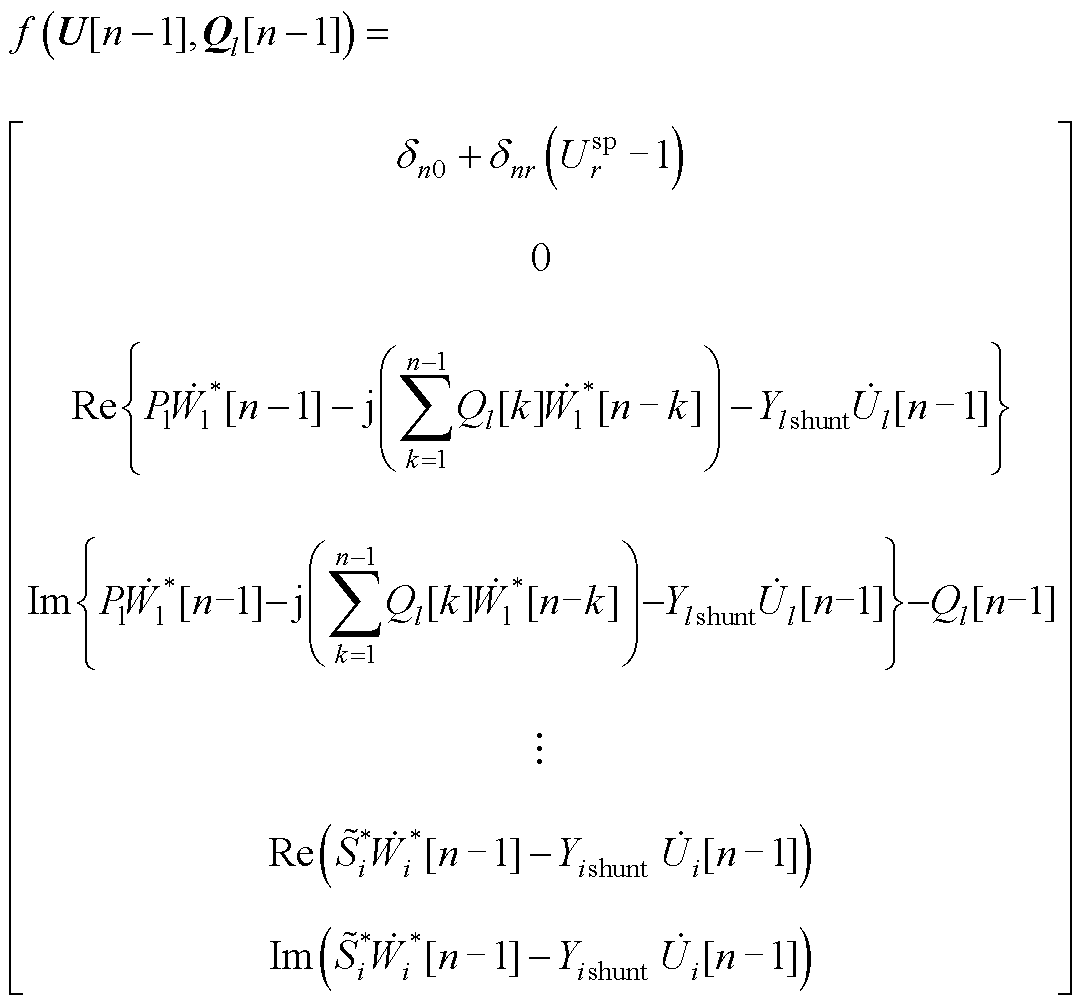 (A5)
(A5)
式中,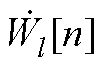 和
和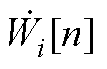 分别为PV节点和PQ节点的第n阶逆幂级数系数;
分别为PV节点和PQ节点的第n阶逆幂级数系数;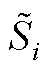 为PQ节点注入功率;Pl和Ql分别为PV节点有功和无功注入;“Re”表示取复数的实部,“Im”表示取复数的虚部;
为PQ节点注入功率;Pl和Ql分别为PV节点有功和无功注入;“Re”表示取复数的实部,“Im”表示取复数的虚部;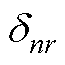 为引入变量,取值为
为引入变量,取值为
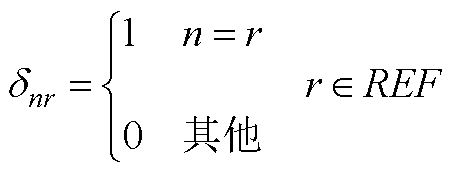 (A6)
(A6)
3. Padé近似基本思想
由电压幂级数系数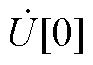 ~
~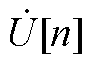 可得式(A3)中节点电压
可得式(A3)中节点电压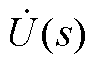 的Padé近似形式为
的Padé近似形式为
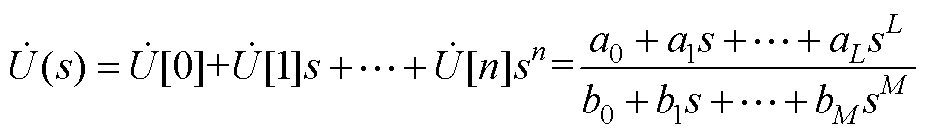 (A7)
(A7)
式中,L和M分别为Padé近似分子和分母多项式中最高次项的幂数,若n为偶数,则L=M=n/2;若n为奇数,则L=(n-1)/2,M=L+1;a0~aL和b0~bM分别为Padé近似表达式中分子和分母多项式中各阶变量的系数,其值可由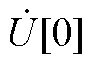 ~
~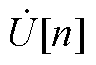 求得。
求得。
计算得到式(A7)中a0~aL和b0~bM后,令s=1即可计算出各节点电压幂级数的有理逼近值为
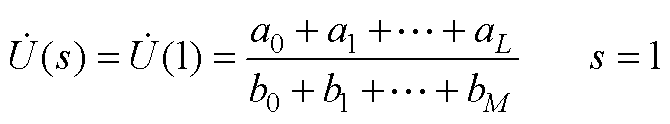 (A8)
(A8)
综上所述,采用HELM求解电力系统潮流的基本流程如附图1所示。
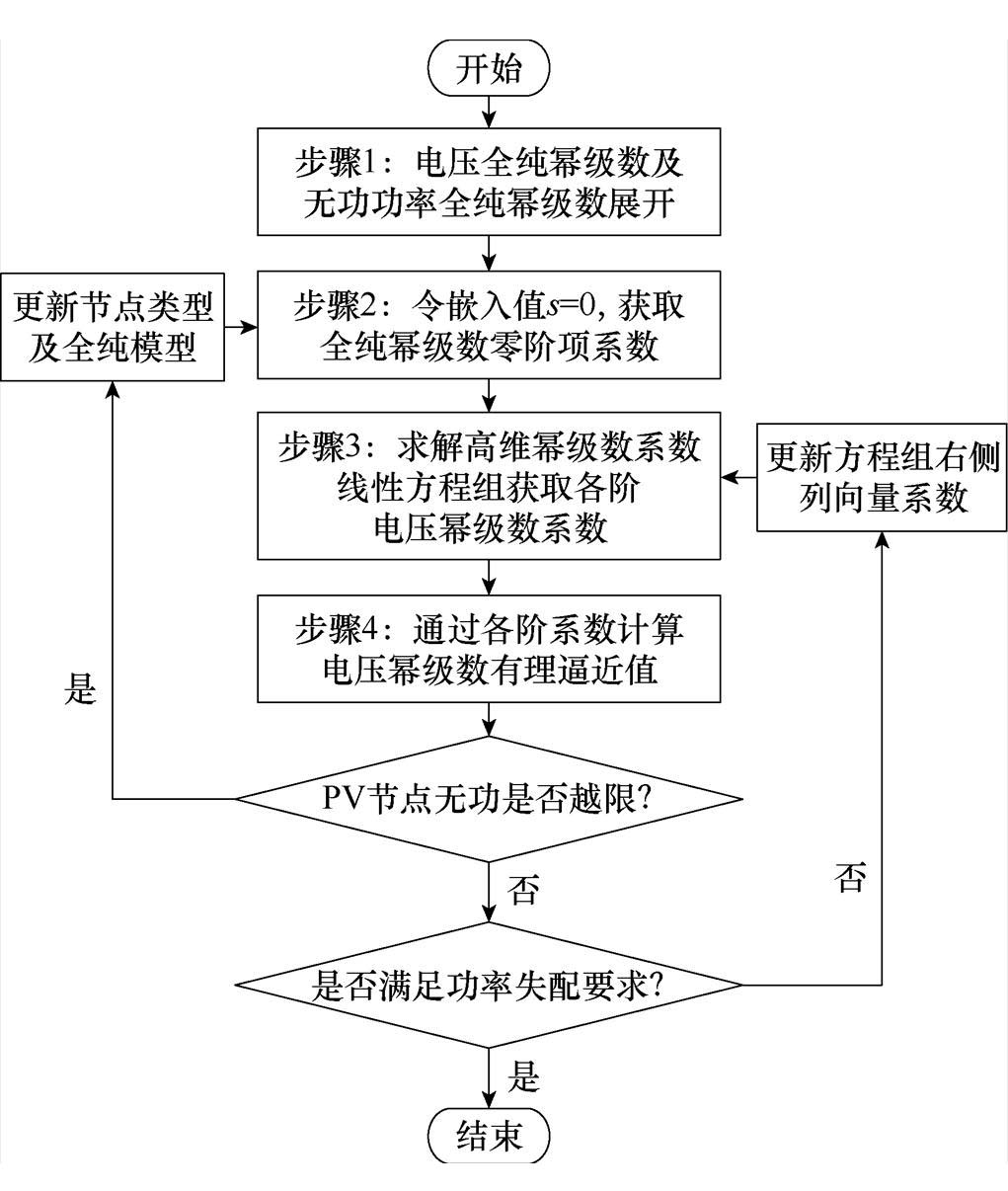
附图1 HELM的求解流程
App.Fig.1 Calculation processing of HELM
[1] 柴润泽, 张保会, 薄志谦. 含电压源型换流器直流电网的交直流网络潮流交替迭代方法[J]. 电力系统自动化, 2015, 39(7): 7-13.
Chai Runze, Zhang Baohui, Bo Zhiqian. Alternating iterative power flow algorithm for hybrid AC/DC networks containing DC grid based on voltage source converter[J]. Automation of Electric Power Systems, 2015, 39(7): 7-13.
[2] 刘洪, 赵晨晓, 葛少云, 等. 基于精细化热网模型的电热综合能源系统时序潮流计算[J]. 电力系统自动化, 2021, 45(4): 63-72.
Liu Hong, Zhao Chenxiao, Ge Shaoyun, et al. Sequential power flow calculation of power-heat integrated energy system based on refined heat network model[J]. Automation of Electric Power Systems, 2021, 45(4): 63-72.
[3] 刘承锡, 徐慎凯, 赖秋频. 基于全纯嵌入法的非迭代电力系统最优潮流计算[J]. 电工技术学报, 2023, 38(11): 2870-2882.
Liu Chengxi, Xu Shenkai, Lai Qiupin. Non-iterative optimal power flow calculation based on holomorphic embedding method[J]. Transactions of China Elec- trotechnical Society, 2023, 38(11): 2870-2882.
[4] 姜涛, 张勇, 李雪, 等. 电力系统交直流潮流的全纯嵌入计算[J]. 电工技术学报, 2021, 36(21): 4429- 4443, 4481.
Jiang Tao, Zhang Yong, Li Xue, et al. A holomorphic embedded method for solving power flow in hybrid AC-DC power system[J]. Transactions of China Electrotechnical Society, 2021, 36(21): 4429-4443, 4481.
[5] 王紫瑶, 廖进贤, 杨家豪, 等. 计及功率控制模式的VSC-MTDC交直流并列运行系统概率潮流计算[J]. 电气技术, 2019, 20(2): 12-17.
Wang Ziyao, Liao Jinxian, Yang Jiahao, et al. Pro- babilistic load flow calculation of VSC-MTDC AC/DC parallel operation system considering power control mode[J]. Electrical Engineering, 2019, 20(2): 12-17.
[6] 李雪, 姚超凡, 姜涛, 等. 基于常项值和先验节点的全纯嵌入潮流计算方法[J]. 电力自动化设备, 2023, 43(2): 142-150.
Li Xue, Yao Chaofan, Jiang Tao, et al. Constant values and priori buses based holomorphic embedding load flow method[J]. Electric Power Automation Equipment, 2023, 43(2): 142-150.
[7] Trias A. The holomorphic embedding load flow method[C]//2012 IEEE Power and Energy Society General Meeting, San Diego, CA, USA, 2012: 1-8.
[8] Liu Chengxi, Wang Bin, Hu Fengkai, et al. Online voltage stability assessment for load areas based on the holomorphic embedding method[C]//2018 IEEE Power & Energy Society General Meeting (PESGM), Portland, OR, USA, 2018: 1.
[9] Wu Dan, Wang Bin. Holomorphic embedding based continuation method for identifying multiple power flow solutions[J]. IEEE Access, 2019, 7: 86843- 86853.
[10] Liu Chengxi, Wang Bin, Xu Xin, et al. A multi- dimensional holomorphic embedding method to solve AC power flows[J]. IEEE Access, 2017, 5: 25270- 25285.
[11] Liu Chengxi, Sun Kai, Wang Bin, et al. Probabilistic power flow analysis using multi-dimensional holomorphic embedding and generalized cumulants[C]// 2019 IEEE Power & Energy Society General Meeting (PESGM), Atlanta, GA, USA, 2019: 1.
[12] 张勇. 含VSC: MTDC的交直流电力系统潮流全纯嵌入计算方法研究[D]. 吉林: 东北电力大学, 2021.
Zhang Yong. Research on pure embedding calculation method of power flow in AC/DC power system with VSC--MTDC[D]. Jilin: Northeast Dianli University, 2021.
[13] 李建斌, 王鹏程, 傅侃, 等. 基于预处理共轭梯度迭代法的电力系统状态估计算法[J]. 电力系统自动化, 2021, 45(14): 90-96.
Li Jianbin, Wang Pengcheng, Fu Kan, et al. State estimation algorithm of power system based on preconditioned conjugate gradient iteration[J]. Auto- mation of Electric Power Systems, 2021, 45(14): 90-96.
[14] 唐灿, 董树锋, 任雪桂, 等. 用于迭代法潮流计算的改进Jacobi预处理方法[J]. 电力系统自动化, 2018, 42(12): 81-86.
Tang Can, Dong Shufeng, Ren Xuegui, et al. Improved Jacobi pre-treatment method for solving iterative power flow calculation[J]. Automation of Electric Power Systems, 2018, 42(12): 81-86.
[15] 刘珊瑕, 靳松, 王文琛, 等. 基于变量相关性分解方法的稀疏线性方程组并行求解算法[J]. 清华大学学报(自然科学版), 2020, 60(4): 312-320.
Liu Shanxia, Jin Song, Wang Wenchen, et al. Parallel algorithm for solving sparse linear equations based on variable correlation decomposition[J]. Journal of Tsinghua University (Science and Technology), 2020, 60(4): 312-320.
[16] 蔡大用, 陈玉荣. 用不完全LU分解预处理的不精确潮流计算方法[J]. 电力系统自动化, 2002, 26(8): 11-14.
Cai Dayong, Chen Yurong. Solving power flow equationswith inexact Newton methodspreconditioned by incomplete LU factorization with partially fill-in[J]. Automation of Electric Power Systems, 2002, 26(8): 11-14.
[17] 唐坤杰, 董树锋, 宋永华. 基于不完全LU分解预处理迭代法的电力系统潮流算法[J]. 中国电机工程学报, 2017, 37(增刊1): 55-62.
Tang Kunjie, Dong Shufeng, Song Yonghua. Power flow algorithm based on an iterative method with incomplete LU decomposition preconditioning[J]. Proceedings of the CSEE, 2017, 37(S1): 55-62.
[18] 林亚君, 陈学军, 陈越. 基于雅可比矩阵逆预处理的快速潮流计算方法[J]. 计算技术与自动化, 2019, 38(2): 72-75.
Lin Yajun, Chen Xuejun, Chen Yue. Fast flow calculation method with Jacobian matrix inverse preconditions[J]. Computing Technology and Auto- mation, 2019, 38(2): 72-75.
[19] Li Xue, Li Fangxing, Yuan Haoyu, et al. GPU-based fast decoupled power flow with preconditioned iterative solver and inexact Newton method[J]. IEEE Transactions on Power Systems, 2017, 32(4): 2695- 2703.
[20] Chiang H D, Wang Tao, Sheng Hao. A novel fast and flexible holomorphic embedding power flow method[J]. IEEE Transactions on Power Systems, 2018, 33(3): 2551-2562.
[21] Trias A, Marín J L. A Padé-Weierstrass technique for the rigorous enforcement of control limits in power flow studies[J]. International Journal of Electrical Power & Energy Systems, 2018, 99: 404-418.
[22] 李雪, 李博, 姜涛, 等. 主动配电网潮流的全纯嵌入计算方法[J]. 中国电机工程学报, 2024, 44(11): 4210-4226.
Li Xue, Li Bo, Jiang Tao, et al. A holomorphic embedding power flow algorithm for active dis- tribution network[J]. Proceedings of the CSEE, 2024, 44(11): 4210-4226.
[23] 宋晓喆, 魏国, 李雪, 等. 基于预处理BICGSTAB法的电力系统潮流并行计算方法[J]. 电力系统保护与控制, 2020, 48(20): 18-28.
Song Xiaozhe, Wei Guo, Li Xue, et al. Parallel power flow computing in power grids based on a preconditioned BICGSTAB method[J]. Power System Protection and Control, 2020, 48(20): 18-28.
[24] 冯金超, 李祎楠, 李哲, 等. 结合预处理BiCGStab和CUDA的BLT快速并行前向方法[J]. 北京工业大学学报, 2017, 43(11): 1658-1665.
Feng Jinchao, Li Yinan, Li Zhe, et al. Fast parallel forward method of BLT combining preconditioned Bi CGStab and CUDA[J]. Journal of Beijing University of Technology, 2017, 43(11): 1658-1665.
[25] Rao S D. Exploration of a scalable holomorphic embedding method formulation for power system analysis applications[D]. Arizona: Arizona State University. 2017.
[26] Rao S D, Tylavsky D J. Theoretical convergence guarantees versus numerical convergence behavior of the holomorphically embedded power flow method[J]. International Journal of Electrical Power & Energy Systems, 2018, 95: 166-176.
[27] 邱智勇, 周越德, 刘中平. CPU+GPU架构下节点阻抗矩阵生成及节点编号优化方法[J]. 电力系统自动化, 2020, 44(2): 215-221.
Qiu Zhiyong, Zhou Yuede, Liu Zhongping. Optimal methods of node impedance matrix construction and node numbering based on CPU and GPU collaborative architecture[J]. Automation of Electric Power Systems, 2020, 44(2): 215-221.
[28] 姜涛, 张道远, 李雪, 等. 基于自适应幂级数初始点的电力系统全纯嵌入潮流并行计算[J]. 电力自动化设备, 2023, 43(10): 208-216.
Jiang Tao, Zhang Daoyuan, Li Xue, et al. Adaptive power series initial points based holomorphic embedding load flow parallel calculation for power system[J]. Electric Power Automation Equipment, 2023, 43(10): 208-216.
[29] 李雪, 张琳玮, 姜涛, 等. 基于CPU-GPU异构的电力系统静态电压稳定域边界并行计算方法[J]. 电工技术学报, 2021, 36(19): 4070-4084.
Li Xue, Zhang Linwei, Jiang Tao, et al. CPU-GPU heterogeneous computing for static voltage stability region boundary in bulk power systems[J]. Transa- ctions of China Electrotechnical Society, 2021, 36(19): 4070-4084.
[30] Zimmerman R D, Murillo-Sánchez C E, Thomas R J. MATPOWER: steady-state operations, planning, and analysis tools for power systems research and education[J]. IEEE Transactions on Power Systems, 2011, 26(1): 12-19.
Parallel Computing Method of Power System Holomorphic Embedded Power Flow
Abstract Power flow calculation is the foundation of power system analysis and control. At present, the Newton-Raphson (NR) method is still the most widely used, and its convergence depends on the initial values election. When the power flow is overloaded, the Jacobian matrix of the NR method is prone to singularity, resulting in divergence of the power flow calculation, making it difficult to meet the efficiency and robustness requirements of complex power flow calculation. Unlike the NR method, the holomorphic embedded power flow (HELM) is a recursive rather than an iterative process. This method fixes the center of the expansion at the initial point and expands the power series term to obtain the target solution. Accordingly, the initial value is no longer to be set, ensuring convergence to the power flow solution and providing a clear signal when there is no power flow solution. However, when solving large-scale power flow, HELM requires multiple solutions to high-dimensional power series coefficient linear equations and Padé approximation, and its computational efficiency is lower than the NR method. Therefore, improving the computational efficiency of HELM is crucial.
This paper proposes a power system holomorphic embedded power flow parallel calculation method based on stable bi-conjugate gradient stabilized (BICGSTAB) and Aitken difference. The BICGSTAB method is used to solve high-dimensional power series coefficient linear equations iteratively. A sparse matrix approximate inverse preprocessor is constructed based on the coefficient matrix of the equation system to improve the convergence effect of the BICGSTAB method and quickly obtain the coefficients of each order of the voltage power series. Then, based on the traditional Aitken difference method, a new Aitken difference calculation for solving voltage is constructed to rapidly calculate rational approximation values of power series of voltage. Next, with the CPU-GPU heterogeneous computing platform, the large-scale matrix vector in the BICGSTAB method is calculated using the GPU, and the logical judgment part of BICGSTAB is achieved using the CPU. Then, an adaptive thread calling method using GPU threads and voltage one-to-one correspondence automatically calls the same thread number as the number of nodes when solving power flow of different scales. Approximation values of voltage power series for all nodes can be calculated in parallel. Furthermore, combined with the above parallel computing based on the CPU-GPU heterogeneous computing platform, the overall parallel computing process is proposed. Finally, the proposed power flow holomorphic embedded parallel calculation method is analyzed and validated through different power system test examples with node sizes ranging from 1 354 to 13 802.
Keywords:Holomorphic embedding method (HEM), power flow calculation, Aitken difference method, CPU-GPU heterogeneous platform, preconditioner
中图分类号:TM744
DOI: 10.19595/j.cnki.1000-6753.tces.231195
国家自然科学基金资助项目(52077029, 52377083, U2066208, U23B20131)。
收稿日期 2023-07-24
改稿日期 2023-08-31
李 雪 女,1986年生,博士,教授,博士生导师,主要研究方向为电力系统安全性与稳定性、电力系统高性能计算、电力市场。
E-mail: xli@neepu.edu.cn
姜 涛 男,1983年生,博士,教授,博士生导师,主要研究方向为电力系统安全性与稳定性、可再生能源集成、综合能源系统。
E-mail: t.jiang@aliyun.com(通信作者)
(编辑 郭丽军)