Ns。摘要 多电平双有源桥直流变换器广泛应用于电压传输范围宽的场合，能够减小功率开关电压应力，并提供更多自由度，优化变换器性能。首先，该文提出基于三电平扩展移相控制的三电平双有源桥直流变换器最小电感电流有效值跟踪控制策略，建立三电平扩展移相控制策略下各工作模式下的数学模型，根据拉格朗日乘数法得到各可行域内部最优极值点处移相比之间的相互关系；然后，分析边界最优点，通过比较内部最优极值点和边界最优点处电感电流有效值，得到全局最优工作点；最后，根据传输功率与全局最优工作点处移相比的变化关系，得到全局最优工作点跟踪控制策略，克服寄生电阻和开关损耗对最优工作点的影响。将三电平扩展移相优化调制策略与两电平扩展移相控制、单移相控制以及峰值电流优化控制进行对比实验，实验结果验证了所提该优化策略能够有效减小电感电流有效值并提高变换效率。
关键词：三电平 扩展移相 双有源桥直流变换器 最小电感电流有效值 跟踪控制
双有源桥（Dual-Active Bridge, DAB）直流变换器具有输入输出电气隔离、高功率密度、能量双向流动等优点，在分布式发电、电动汽车、直流配电网等领域有着广泛的应用[1-4]。当输入输出电压不匹配、两电平DAB采用单移相（Single-Phase-Shift, SPS）控制时，存在着电流应力大、回流功率高、零电压软开关（Zero Voltage Switching, ZVS）难以实现等诸多问题[5-6]。为解决上述问题，国内外学者通过增加变压器一次侧或二次侧桥臂内相移角，提出了扩展移相（Extend Phase-Shift, EPS）控制、双移相（Dual Phase-Shift, DPS）控制和三移相（Triple Phase-Shift, TPS）控制，从减小电流应力、降低回流功率、实现ZVS、偏磁抑制等方面进行优化[7-12]。
增加控制自由度的另一个措施是采用多电平DAB结构[13-14]，不仅能够扩展输入和输出电压范围，而且低耐压的功率器件能够降低装置成本和开关损耗。文献[15-17]研究了二极管钳位与飞跨电容相结合的混合钳位三电平DAB，采用两电平DPS的控制方式，在回流功率最小、实现ZVS、功率开关电压应力均衡等方面对变换器性能进行优化。文献[18]同样采用混合钳位的三电平结构，为了使高压输出情况下能够实现ZVS，在飞跨电容中点与变压器二次绕组中点跨接辅助电感，通过控制辅助电感电流实现ZVS。文献[19]提出了有源中点钳位多电平DAB变换器，分析了实现ZVS的零电压选取方法和飞跨电容电压均衡方法，以电感电流基波分量有效值最小作为最优工作点。文献[20]分析了原二次侧全桥均采用三电平调制方式时电感电流基波和3次谐波最小工作点，得到外移相比确定的情况下电感电流有效值最优工作点，没有考虑其他谐波电流，而且优化结果很复杂。文献[21]分析了混合钳位桥中性点电压自动均衡的原理。文献[19]提出了一种互补小矢量（Complementary Small Vector, CSV）平衡控制方案，每一对互补的小矢量都可以提供相同的电压波形和相反的中点电流方向，根据运行情况，识别出不利的小矢量并将其替换为CSV，实现了中性点电压在小范围内的动态平衡，适用情况更广。文献[23-24]提出了一种利用PI控制器调节Ui/2电平宽度的方案，以实现在单个开关周期内流入中性点的电荷量为零，克服电路中的不平衡因素，实现无静差中性点电压平衡，但受调制波形限制，难以应用于非对称调制波形的情况。以上分析表明，现有的多电平DAB的研究主要集中在扩展ZVS区间、电容电压均衡、电感电流应力优化、谐波分析法进行电感电流有效值优化等方面；且电感电流应力或有效值优化策略方面，通常可得到各功率区段移相比与功率、电压传输比的解析关系，根据输出功率所在区段和电压传输比，选择相应的移相比，这种优化方法没有考虑变换器中存在的杂散电阻损耗和开关损耗，实际工作的最优点将会偏离理想最优点。
本文以一次侧二极管钳位型三电平全桥、二次侧为两电平全桥的三电平DAB（Three Level-DAB, TL-DAB）变换器为研究对象，适合高压输入的场合，采用三电平扩展移相控制策略（3-Level Extend Phase-Shift, 3-EPS），以电感电流有效值最小为优化目标，得到全局最优极值点处移相比之间的相互关系，根据传输功率与最优极值点处移相比之间的变化关系，得到最优极值点跟踪控制策略，克服了杂散电阻和开关损耗对最优极值点的影响，使变换器能够时刻跟踪最优极值点。最后通过实验对所提方案进行了验证。
当输入电压较高时，为减小电压应力，采用如图1所示的三电平DAB变换器拓扑结构，其电路结构由分压电容C1和C2、一次侧二极管钳位三电平全桥、高频储能电感L、高频变压器T、二次侧两电平全桥与输出滤波电容Co依序级联构成。二极管钳位三电平全桥，每个桥臂由4个具有反并联二极管的全控型器件与2个钳位二极管构成。变换器输入电压为Ui，输出电压为Uo，电感电流为iL，高频变压器的匝比为Np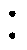Ns。
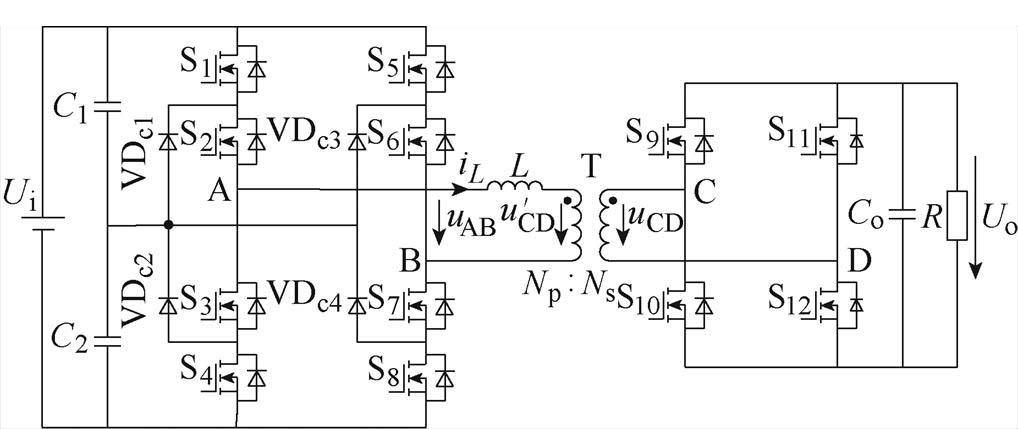
图1 三电平DAB变换器拓扑结构
Fig.1 The topology of TL-DAB converter
uAB、uCD分别为一、二次侧桥臂的输出电压，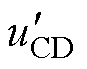
为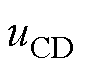
折算到变压器一次侧的电压。定义电压转换比k =Ui/(nUo)，fs为开关频率，Ts为开关周期，Ths为半开关周期。这里只考虑k＞1的情形，当 k＜1时，为减小电压不匹配程度，变换器需要切换到两电平工作模式。
变换器采用三电平扩展移相调制策略时，稳态工作波形如图2a所示。图中，D1、D2为一次侧桥的内移相比，D0为一次、二次侧桥之间的外移相比。各移相比之间满足约束0≤D1≤D2≤1、0≤D0≤1。
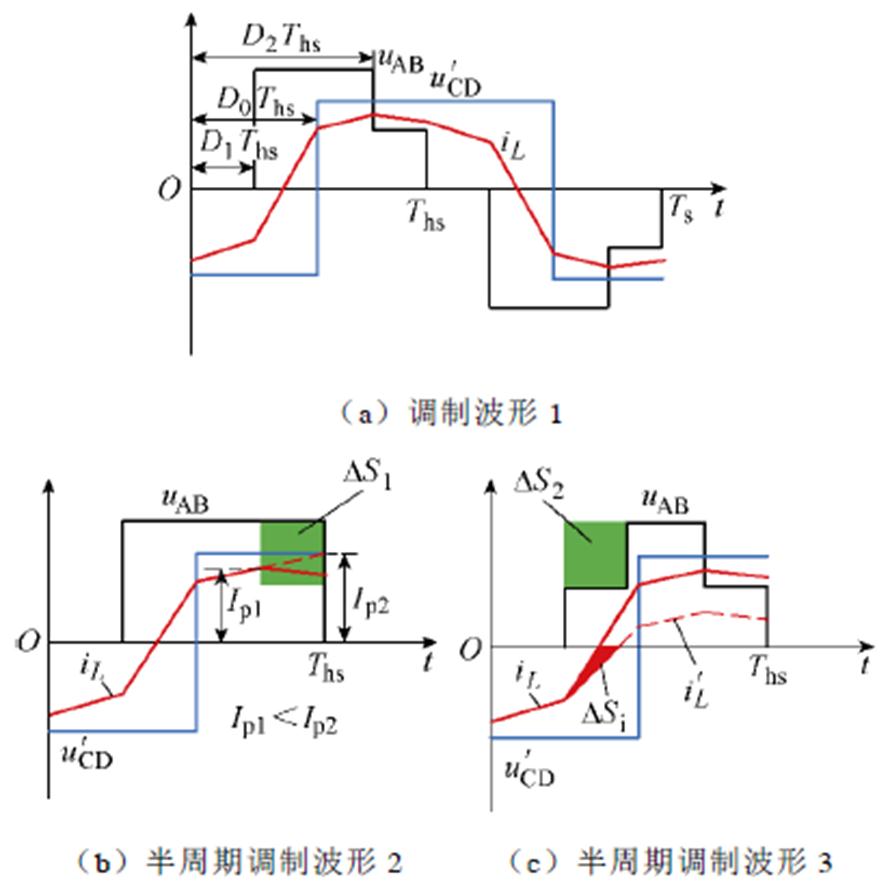
图2 调制波形选择
Fig.2 Selection of modulation waveforms
调制波形1的优越性有：①与图2b所示的两电平EPS控制的调制波形2相比，去除区域∆S1得到的调制波形1，可以获得更小的电流峰值，降低开关管的电流应力；②与图2c所示的左右对称的三电平凸形调制波形3相比，增加区域∆S2得到调制波形1，可以提高此区间的电流变化率，使电感电流过零点前移，增大正向传递功率，减少一次侧的回流功率。
根据变压器二次侧全桥输出电压上升沿与一次侧三电平全桥电压调制波形的对应关系，TL-DAB变换器存在三种工作模式，如图3所示。
设三个控制量D0、D1、D2在三维空间中的坐标为（D0, D1, D2），三个控制量D0、D1、D2相互独立，根据各个工作模式下外移相角D0与内移相角D1、D2的约束关系，三种工作模式下（D0, D1, D2）的定义域如图4所示。需要注意的是，该定义域仅仅是目标函数在模式约束下的定义域，并非目标函数在全空间范围内的可行域，目标函数在全空间范围内的可行域是模式约束空间与功率约束空间的交集。
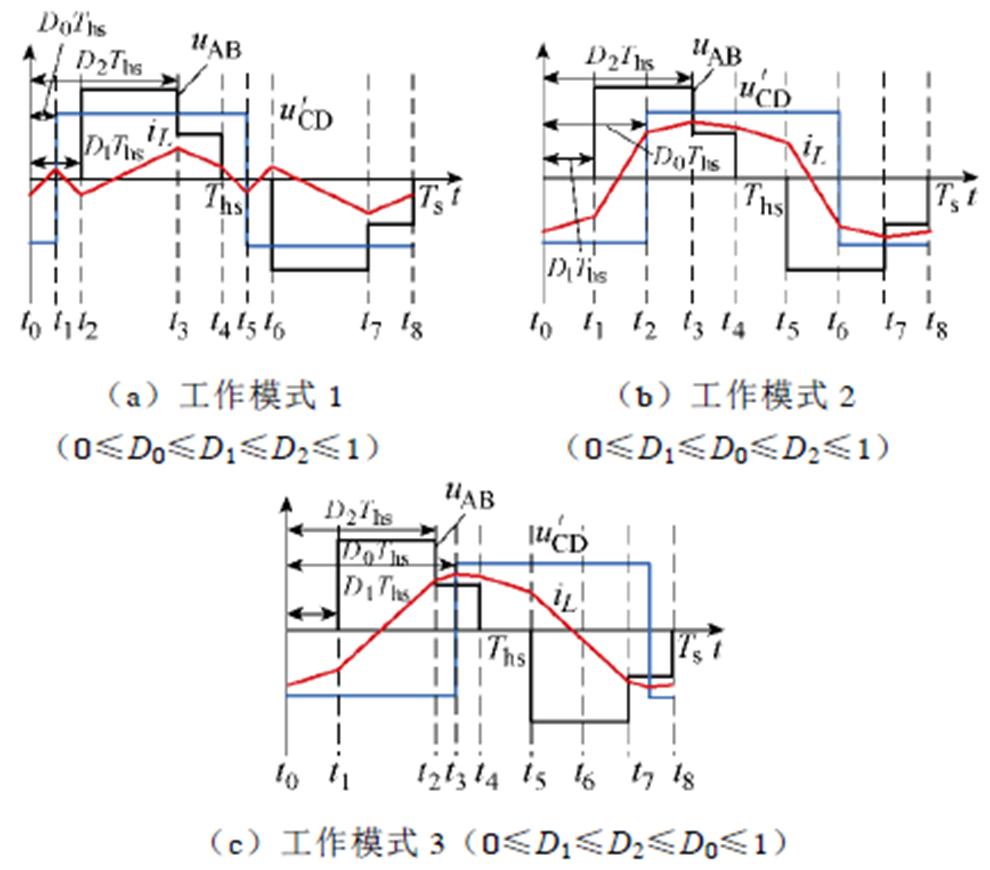
图3 三电平DAB变换器的三种工作模式
Fig.3 Three operating modes of TL-DAB converter
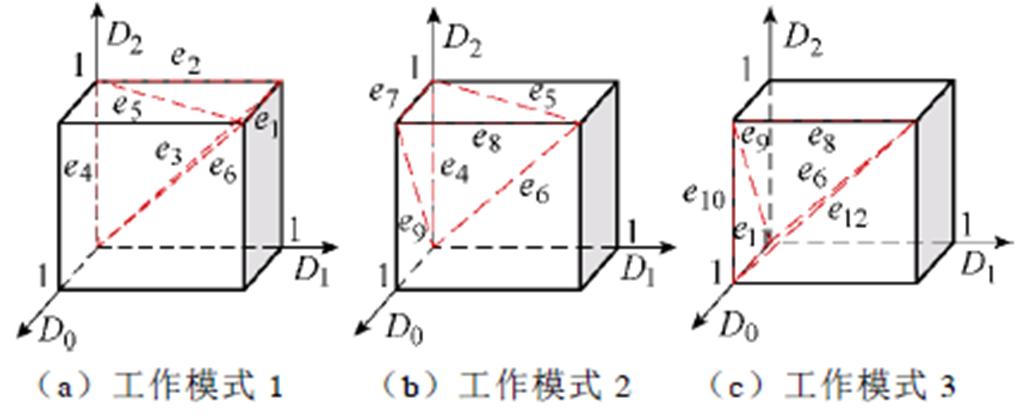
图4 三种模式下的三维空间定义域
Fig.4 3D work area constrained by three modes
由图3可以看出，相比于工作模式1和2，工作模式3下uAB和uCD极性相反的区间更多，在此区间内电感电流在uAB和uCD的作用下急剧增大，但传递到负载的能量有限，因此电感电流应力与有效值更大；而且理论分析优化得到模式3的电流有效值大于其他两种工作模式，因此电感电流有效值优化时不考虑模式3。工作模式1和2下电感电流的表达式见表1。
在不考虑电路损耗的理想状态下，取DAB变换器在一次侧全电平单移相控制下传输的最大功率作为功率的基准值PN，同时，在此功率点，取k=1时电感电流有效值二次方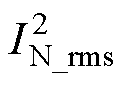
作为电感电流有效值二次方的基准，可得
表1 各工作模式下电感电流时域表达式
Tab.1 Time domain expressions of inductance current in each operating mode
模式电感电流时域表达式 1 2
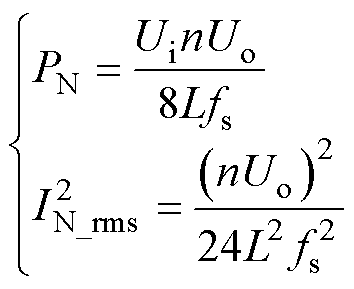（1）
由表1和式（1）可得各工作模式下的传输功率标幺值Pib、电感电流有效值二次方的标幺值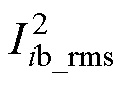
表达式见表2、表3。
由表2和表3可知，传输功率标幺值由坐标（D0, D1, D2）决定；电感电流有效值二次方标幺值由电压转换比k和坐标（D0, D1, D2）共同决定。而当传输功率一定时，有无穷多对坐标（D0, D1, D2）与之对应，不同坐标对应的电感电流有效值不同，总存在一个坐标可以使得电感电流有效值最小。
表2 各工作模式传输功率标幺值
Tab.2 Per unit value of transmitted power in each working mode
模式传输功率标幺值 1 2
表3 各工作模式下电感电流有效值二次方标幺值
Tab.3 Per unit value of the square of the effective value of inductor current in each working mode
模式电感电流有效值二次方的标幺值 1 2
本文以电感电流有效值的二次方最小作为优化目标，可以降低变换器通态损耗，提高变换器效率。当传输功率一定时，此优化问题为
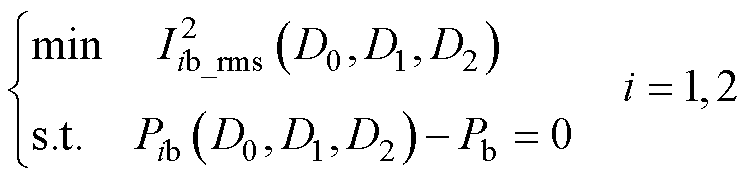（2）
式中，Pb为给定的传输功率的标幺值，本文只考虑功率正向传输即Pb为正的情况。
在某一种工作模式下，式（2）所示的优化问题即为求三元目标函数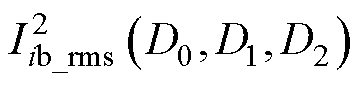
在一个功率等式约束下的最小值点。在可行域内部，求出目标函数在等式约束下的内部极值点，再与最优边界点相比较，其电感电流有效值更小的点就是全局最优工作点。
Lagrange乘数法可用来求目标函数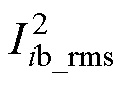在约束条件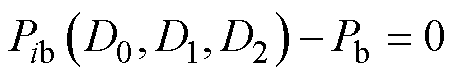
之下的极值点。
模式i（i=1, 2）下的Lagrange函数Li定义如下
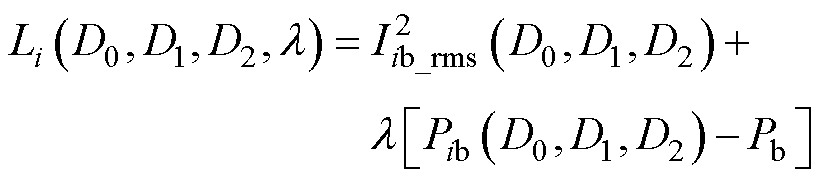（3）
式中，l 为Lagrange乘子。Lagrange函数Li关于D0、D1、D2和l 可微，其可行域内的极值点满足
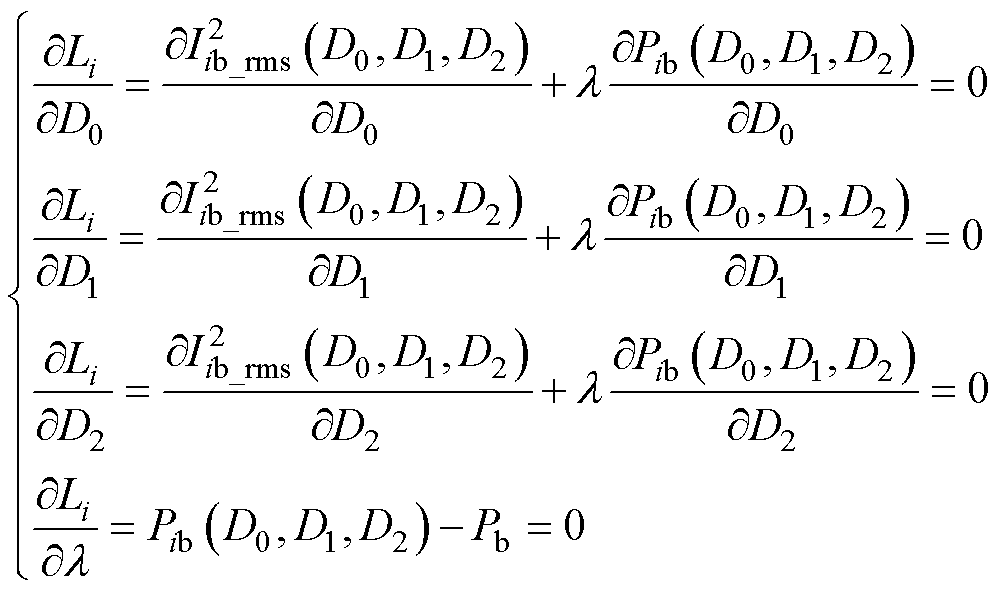（4）
式中，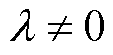
。以l、D0、D1、D2为未知变量，Pb、k为已知变量，无法求得D0、D1、D2与Pb、k的解析关系。通过数值解法，可得到在某一给定功率数值Pb和k下，最优点坐标的数值解，重复这一计算过程，可以得到各个离散数值点 (Pb, k) 对应的最优坐标数值解，这种求解方法计算量很大，实际运用中需要大量存储空间存储线下计算得到的最优数值解，而且没有考虑电路中非理想因素如杂散电阻、开关损耗等对传递功率的影响。
另一方面，如果能够得到极值点处移相比D0、D1与D2的相互关系，进一步得到传输功率Pb与D2的变化关系，可以通过输出电压闭环控制D2跟踪该极值点，能够克服电路中杂散电阻、开关损耗等对传输功率的影响。由l≠0，可知极值点满足
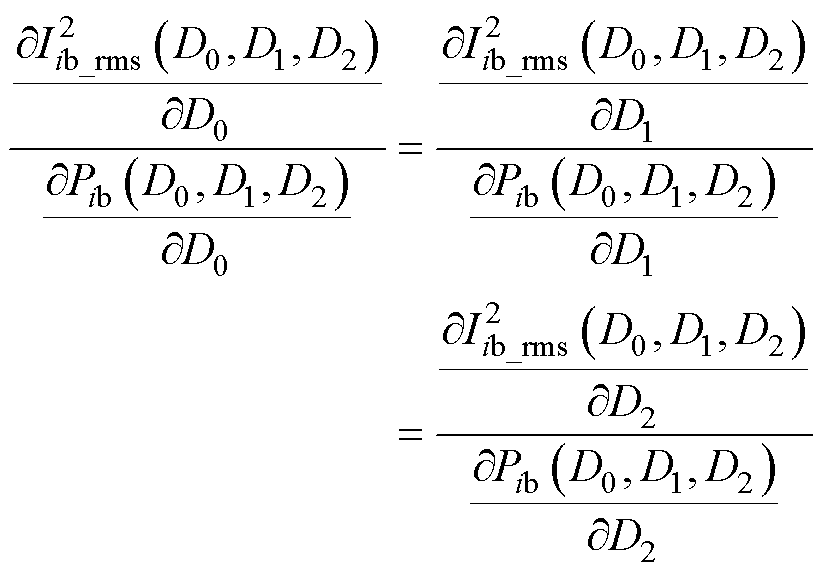（5）
式（5）包含两个独立的方程和三个移相比D0、D1和D2，可以以解析表达式的形式建立极值点处各自由度之间的相互关系；然后，根据该工作模式下需要满足的约束条件排除不满足约束的解，进而得到该工作模式下极值点及其占空比范围和功率范围。
对工作模式1和工作模式2进行上述求解过程并筛选，分别得到两种工作模式下可行域内有效极值点、占空比和功率范围，见表4。
表4 可行域内有效极值点
Tab.4 Effective extremum points in the feasible region
模式可行域内有效极值点适用范围 1解a1 解a2 解a3 2解b1 解b2 解b3
表4所示的极值点处D0、D1和D2的解析关系，其在三维空间中的图像是曲线段，曲线上的每个点都是目标函数在对应于某一功率时的最优点即每条曲线对应一定传输功率范围内的极值点轨迹。表4所示的工作模式1、2可行域内部的部分极值点具有相同的传输功率范围，功率段分布如图5所示，图中，Pb1～Pb5为不同的功率边界。当k＞2时，有2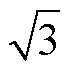＜k＜2+
与k＞2+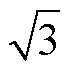两种不同的功率段划分。
由于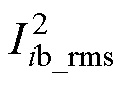表达式很复杂，无法得到最优点处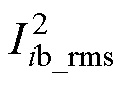与Pb、k的解析关系。这里采用数值法得到不同离散数值点（Pb, k）处最优移相比的数值解，进一步得到其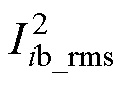数值。当1＜k＜2时，与图5a中对应各功率段不同极值点的
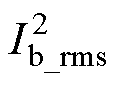的比较如图6所示。
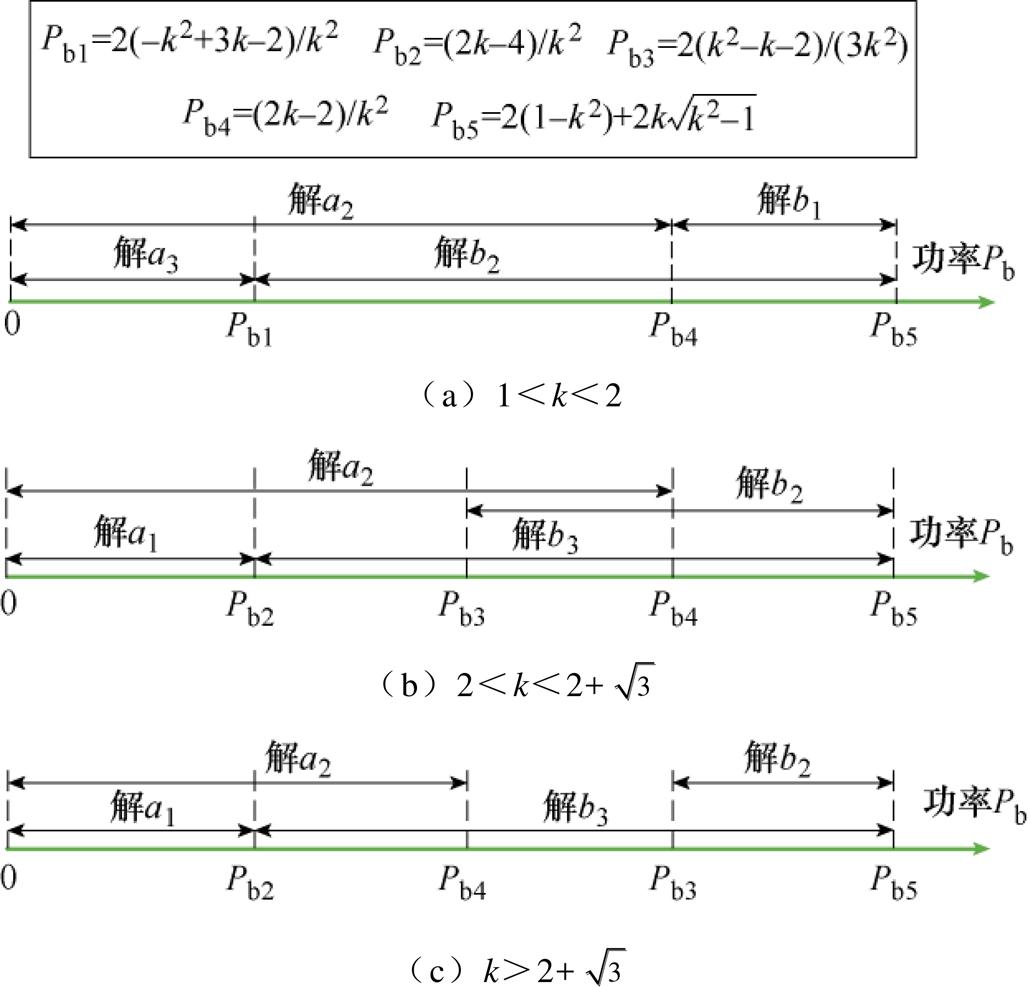
图5 各极值点所能达到的功率段
Fig.5 Power range of each extreme point
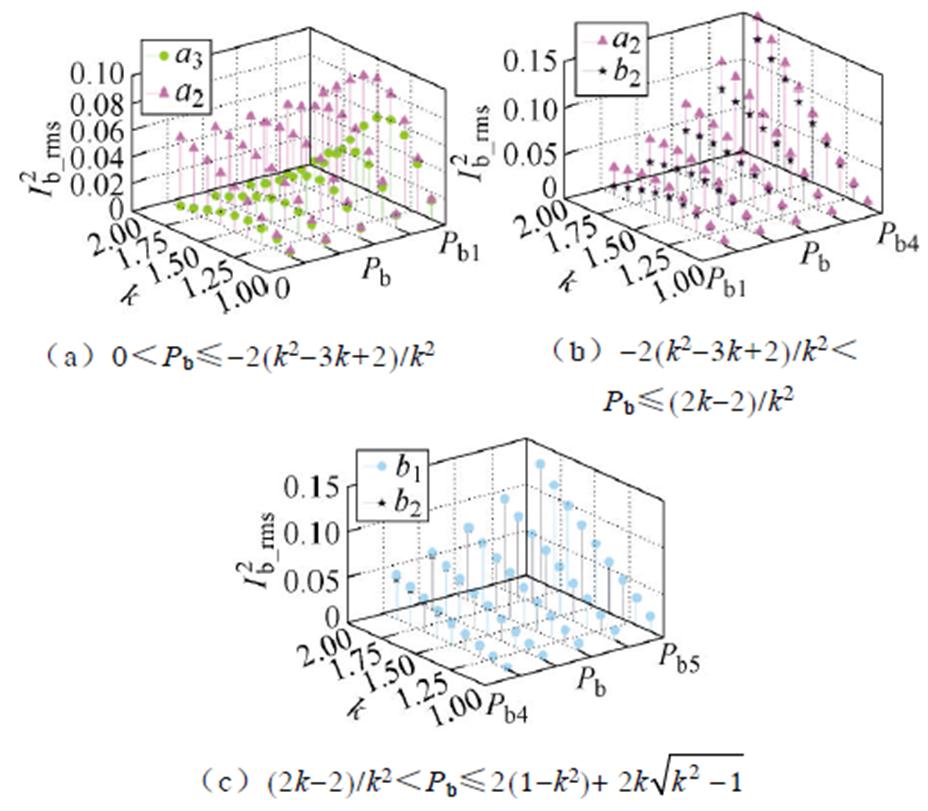
图6 1＜k＜2时的各功率段解的散点对比
Fig.6 Scatter comparison diagram of solutions for each power segment when 1＜k＜2
当2＜k＜2+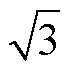时，与图5b中对应各功率段不同极值点的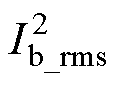的比较如图7所示。
图7 2＜k＜2+
时的各功率段解的散点对比
Fig.7 Scatter comparison diagram of solutions for each power segment when 2＜k＜2+
当k＞2+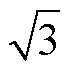时，与图5c中对应各功率段不同极值点的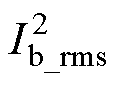的比较如图8所示。
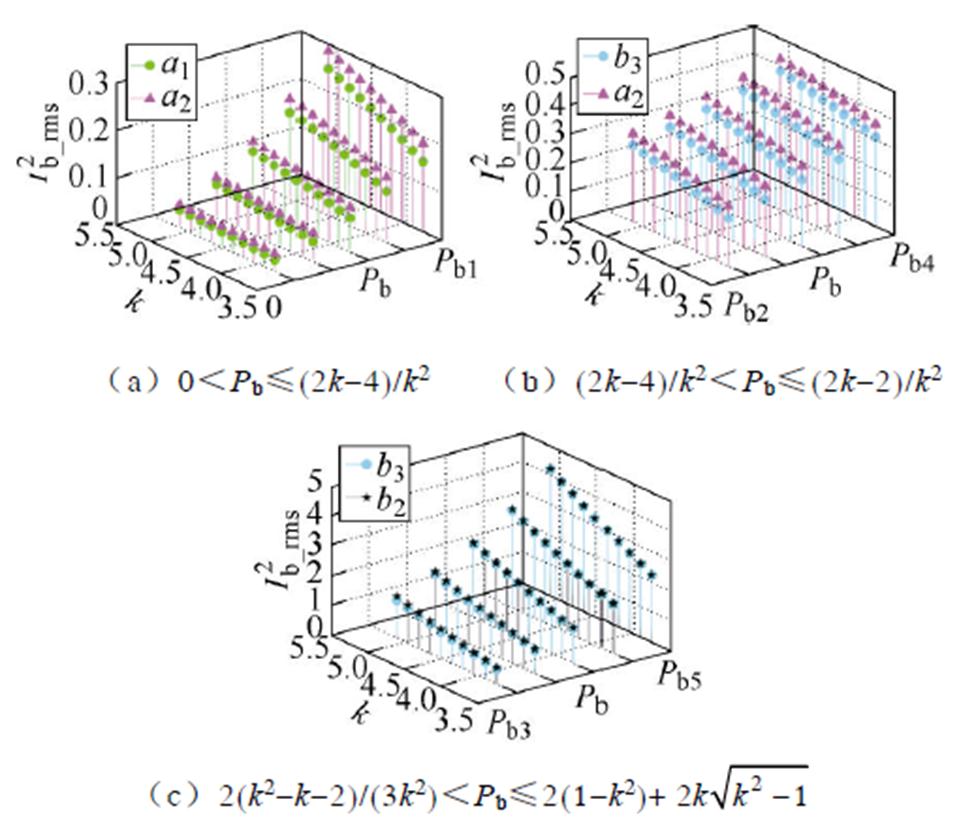
图8 k＞2+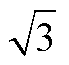时的各功率段解的散点对比
Fig.8 Scatter comparison diagram of solutions for each power segment when k＞2+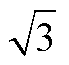
根据图6～图8所示不同k和Pb取值区间，各内部极值点的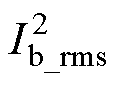的比较，可得每个功率区间的内部最优极值点分布，如图9所示。当1＜k＜2，Pb≤ -2(k2-3k+2)/k2时，解a3最优；Pb≥-2(k2-3k+2)/k2，解b2最优；当k＞2，Pb≤(2k-4)/k2时，解a1最优；Pb≥(2k-4)/k2时，解b3最优。
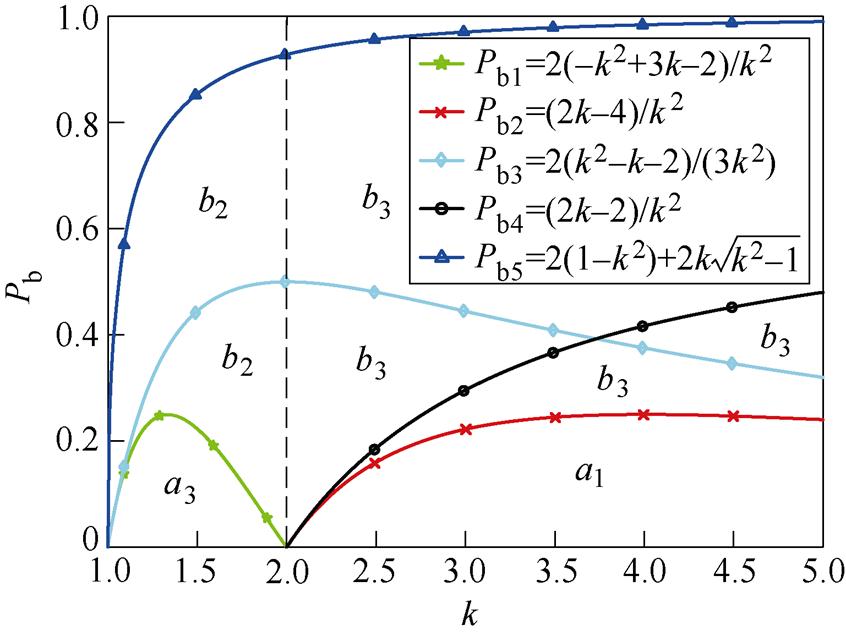
图9 各功率范围段最优极值点
Fig.9 Optimum extremum points of each power range
目标函数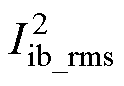
的最小极值点可能出现在目标函数可行域的内部，也可能出现在边界点上，因此需要对目标函数的边界点进行分析。
由图4可知，每个工作模式移相比约束下的定义域均为三棱锥状的空间区域，目标函数的可行域由模式约束和功率约束的定义域共同决定。由功率约束方程可知：若Pb给定，功率约束的定义域在三维空间中是一个等值曲面；当Pb设定在区间（0, 1）范围内变化时，在三维空间中，功率约束的定义域是由无穷多个等值面构成的连续的三维空间区域。这个三维空间区域与图4中模式约束下的三棱锥空间区域的交集就是目标函数真正的可行域。
因此，目标函数可行域的边界点由所有的约束条件共同决定，包括功率约束和模式约束。三元目标函数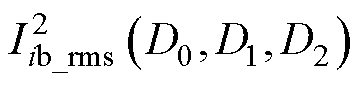共有3个独立的控制自由度，在一个功率等式的约束和两个模式约束共3个约束方程的作用下，目标函数的边界在图4所示三棱锥边界线上，需要对边界线上的功率和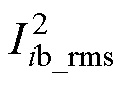进行比较分析。其中，工作模式1和工作模式2共9条边界线e1～e9，其中e1对应变换器一次侧无电压调制波形；e2和e3对应变换器传输反向功率的情况；e8对应的原二次侧桥输出电压无极性相同部分，电感电流应力和有效值大。排除以上无效边界线后，有效边界线及其约束、功率和模式划分见表5。表5中，根据移相比的取值范围的不同将同一条边棱分为两段，对应两种子模式，分别用A、B表示。
表5 各边界线功率表达式及模式划分
Tab.5 Power expression of each boundary line and mode division
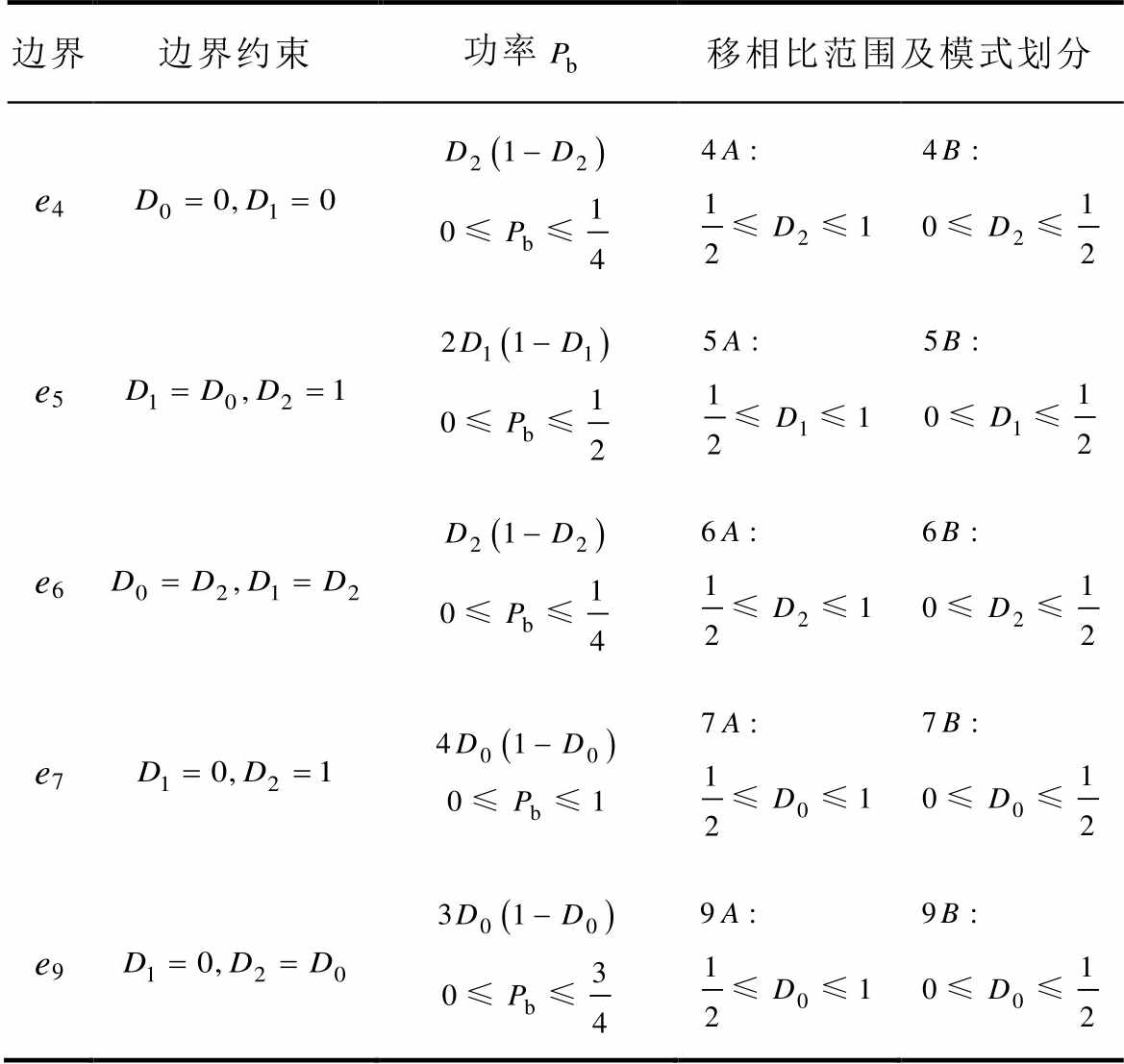
边界边界约束功率移相比范围及模式划分 e4 e5 e6 e7 e9
由于每条棱移相比范围不同所对应的电感电流有效值也不同，则需要分别考虑。首先对各条边界点轨迹在对应功率段下的移相比取值范围进行选取，得到电感电流有效值更小的自由度取值范围。其次对存在功率段交叠的边界点轨迹进行比较，得到功率交叠段电感电流有效值最小的边界点轨迹，从而得到各个功率范围段电感电流有效值最小边界点轨迹。比较过程与内部极值点比较过程类似，可得最优边界点分布，如图10所示，图中，Pb6～Pb9表示不同的功率边界。
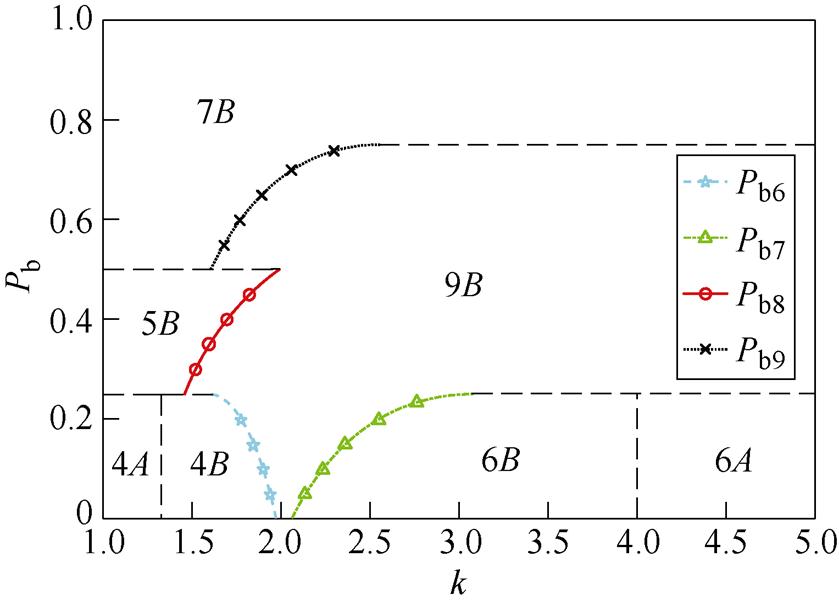
图10 各功率范围段最优边界点
Fig.10 Optimal boundary points of each power range
要得到电感电流有效值最小的全局最优工作点，需要比较可行域内最优极值点和最优边界点处的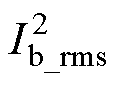，如图11所示。最优边界点对应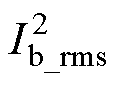均在内部最优极值点对应的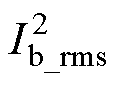之上，说明内部最优极值点的电感电流有效值均低于最优边界点，因此可行域内最优极值点就是全局最优工作点，见表6。
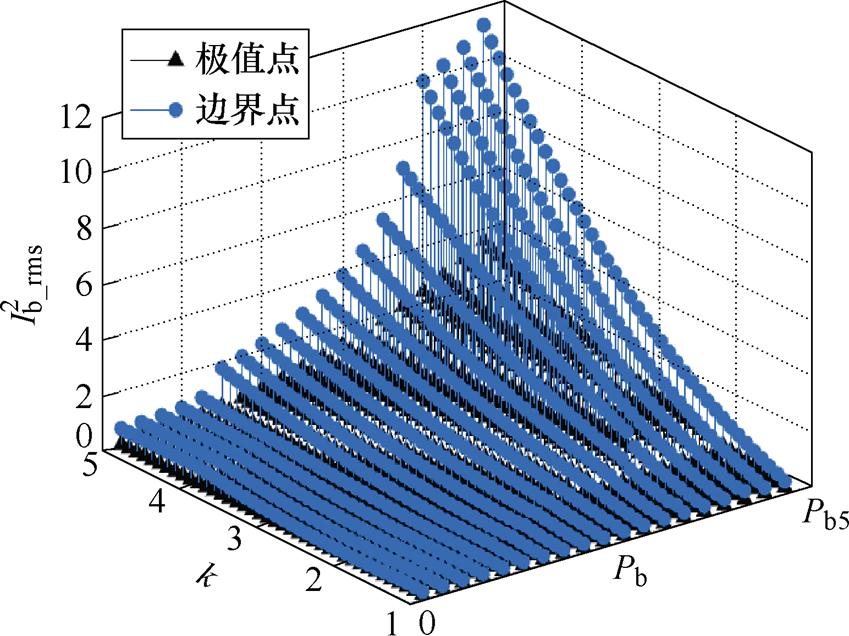
图11 最优极值点与最优边界点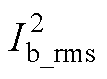
的比较
Fig.11 Comparison of 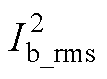of the optimal extreme point and the optimal boundary point
结合各个时刻的电流表达式与各功率开关管的导通顺序，表6中全局最优解在理想情况下的软开关情况见表7，可见大部分工作模式下都可以实现MOSFET的ZVS开通。若考虑切换瞬间电感能量是否足够把结电容上的电荷抽走，则软开关的范围有所减小。
表6 全局最优工作点
Tab.6 Global optimal operating points
k解全局最优极值点 a3 b2 a1 b3
将表6中最优极值点处D0、D1与D2的解析关系代入表2，可得传输功率Pb关于D2与k的解析表达式Pb(k, D2)，在各个最优解对应的 (k, D2) 范围内，求得Pb对D2的偏导数∂Pb(k, D2)/∂D2，其图像如图12所示。
表7 全局最优工作点的软开关情况
Tab.7 Soft switching of the global optimal operating points
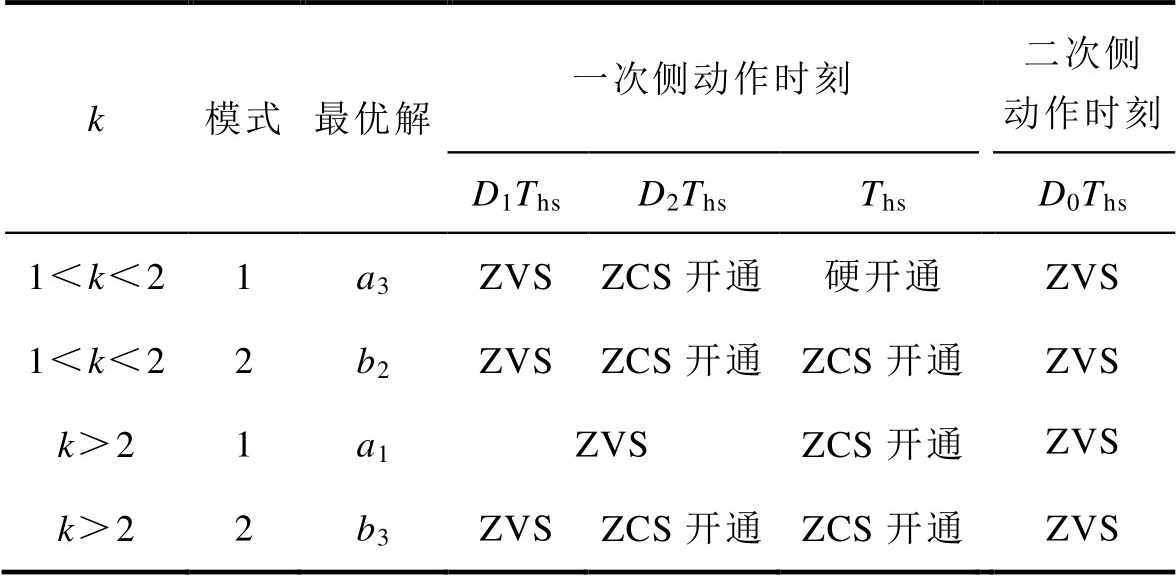
k模式最优解一次侧动作时刻二次侧动作时刻 D1ThsD2ThsThsD0Ths 1＜k＜21a3ZVSZCS开通硬开通ZVS 1＜k＜22b2ZVSZCS开通ZCS开通ZVS k＞21a1ZVSZCS开通ZVS k＞22b3ZVSZCS开通ZCS开通ZVS
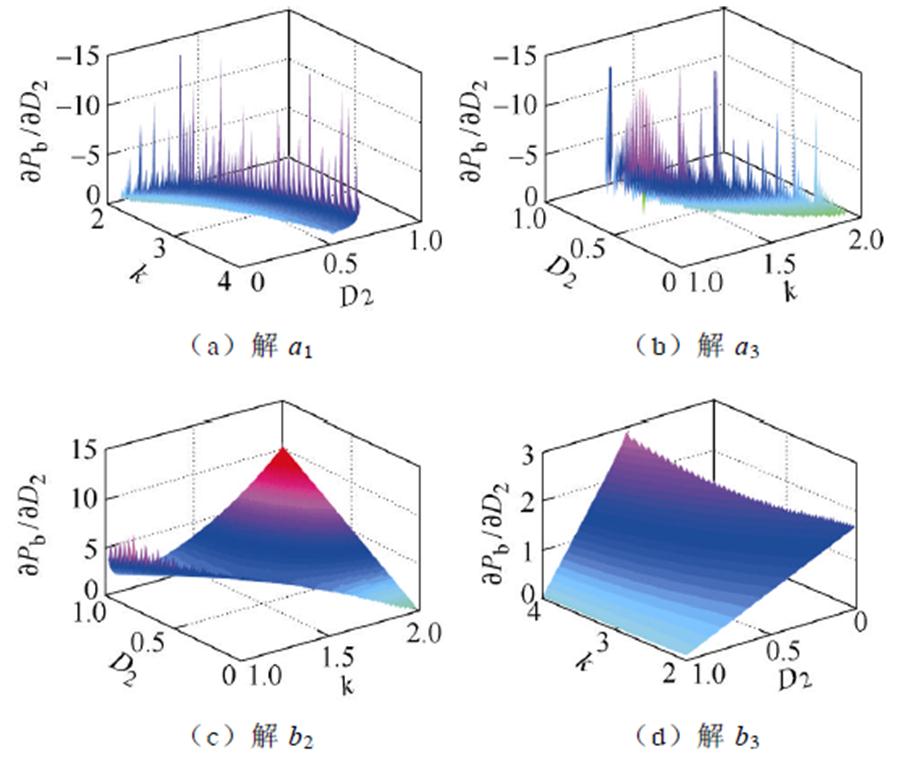
图12 4个最优解对应的∂Pb(k, D2)/∂D2
Fig.12 ∂Pb(k, D2)/∂D2 corresponding to the four optimal solutions
由图12中可以看出，对于解a1和解a3，在对应的 (k, D2) 取值区域内，∂Pb(k, D2)/∂D2＜0，说明在最优解a1和解a3下，Pb与D2呈负相关，解a1和解a3对应的最优解模式应采用负PI进行调节；对于解b2和解b3，在对应的 (k, D2) 取值区域内，∂Pb(k, D2)/∂D2＞0，Pb与D2呈正相关，解b2和解b3对应的最优解模式应采用正PI进行调节。
全局最优工作点跟踪控制框图如图13所示，采样Ui、Uo和Io，得到k、Pb与误差电压ue后，对k和Pb的大小进行判断，得到匹配的最优解模式。将ue通过PI调节器后得到占空比D2，再根据当前工作模式得到D0和D1，实现了最优工作点跟踪。
1＜k＜2时两种最优解模式a3和b2的分界为：D2=(2-k)/k，D0=D1=0；当Pb稍低于临界功率点-2(k2-3k+2)/k2时，考虑杂散电阻损耗和开关损耗，实际传递功率可能大于-2(k2-3k+2)/k2，若工作在a3模式下，D2不断减小，传输功率不断增大，当D2减小到(2-k)/k时，D0=D1=0，需要切换到解b2工作，使传输功率增大。同样地，k＞2时有两种最优解模式a1和b3的分界为D2=(k-2)/k，D0=D1=D2；当Pb稍低于临界功率点(2k-4)/k2时，考虑杂散电阻损耗和开关损耗，实际传递功率可能大于(2k-4)/k2，若工作在a1模式下，D2不断减小，传输功率不断增大，当D2减小到(k-2)/k时，D0=D1=D2，需要切换到解b3工作，使传输功率增大。
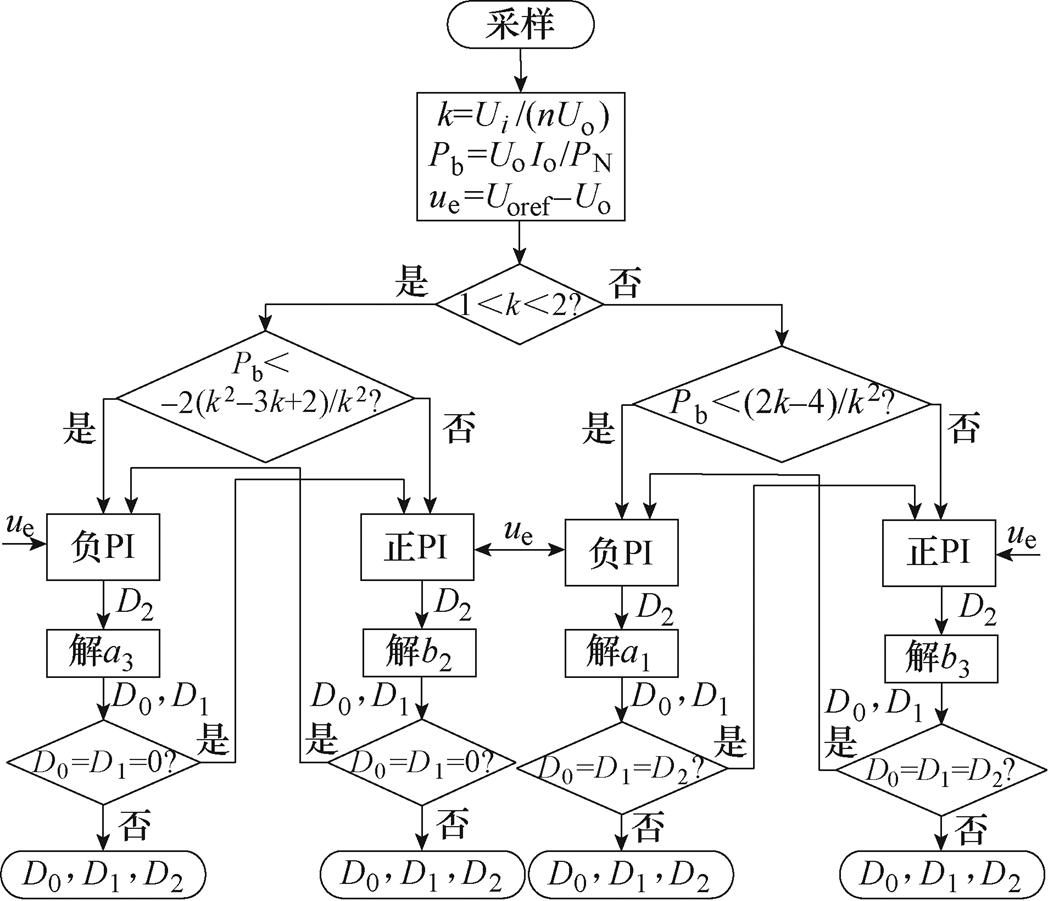
图13 全局最优工作点跟踪控制框图
Fig.13 Control block diagram for tracking global optimal operating points
变换器负载突变时，D0、D1、D2不断改变，当占空比的取值达到临界值而变换器工作状态仍未稳定时，变换器将自动切换至更匹配的最优模式下继续调节，直至变换器稳定工作。
搭建三电平DAB实验平台，采用TMS320F28377为控制系统芯片，开关频率fs=50 kHz，输入电压为200 V，实验平台器件参数与型号见表8。
表8 TL-DAB变换器平台参数
Tab.8 Platform parameters of TL-DAB converter
参 数数 值 (型号) 开关管S1～S12C3M0065090D 二极管VDc1～VDc4C3D20060D 功率电感L/mH96 变压器T匝数比NPNS2613 支撑电容Co, C1, C2/mF680 (450 V)
为验证本文所提的三电平EPS下的电感电流有效值最优控制策略（OPT-3-EPS）的有效性，以SPS控制、两电平EPS下的电感电流有效值最优控制（OPT-2-EPS）和电感电流峰值最小最优控制作为对比实验进行验证。
当k =1.6，Pb=0.1、0.5、0.8时，三种控制策略下的桥臂电压与电感电流的波形如图14～图16 所示。
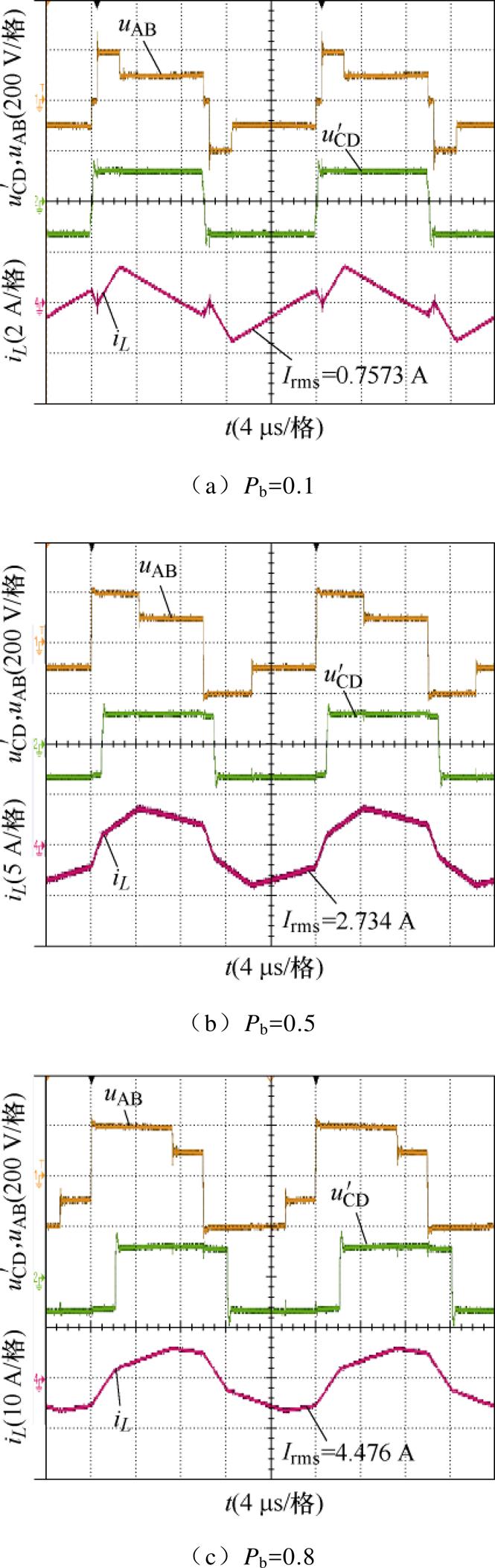
图14 k =1.6时OPT-3-EPS控制策略波形
Fig.14 Waveforms of OPT-3-EPS control strategy at k =1.6
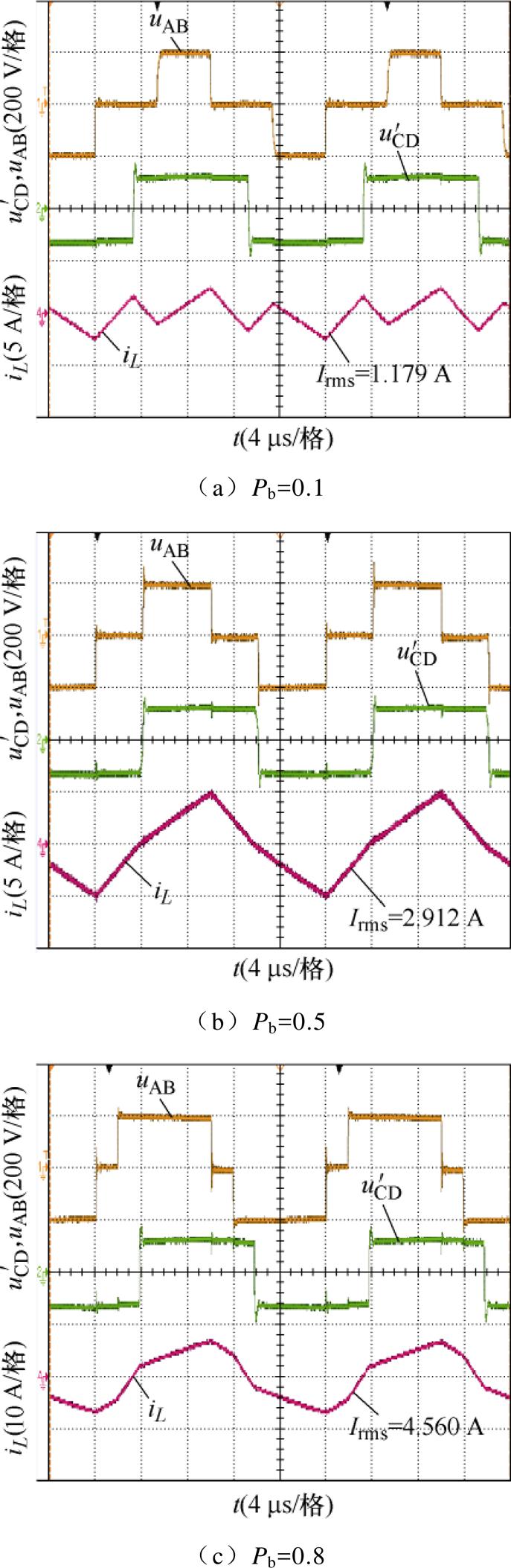
图15 k =1.6时OPT-2-EPS控制策略波形
Fig.15 Waveforms of OPT-2-EPS control strategy at k =1.6
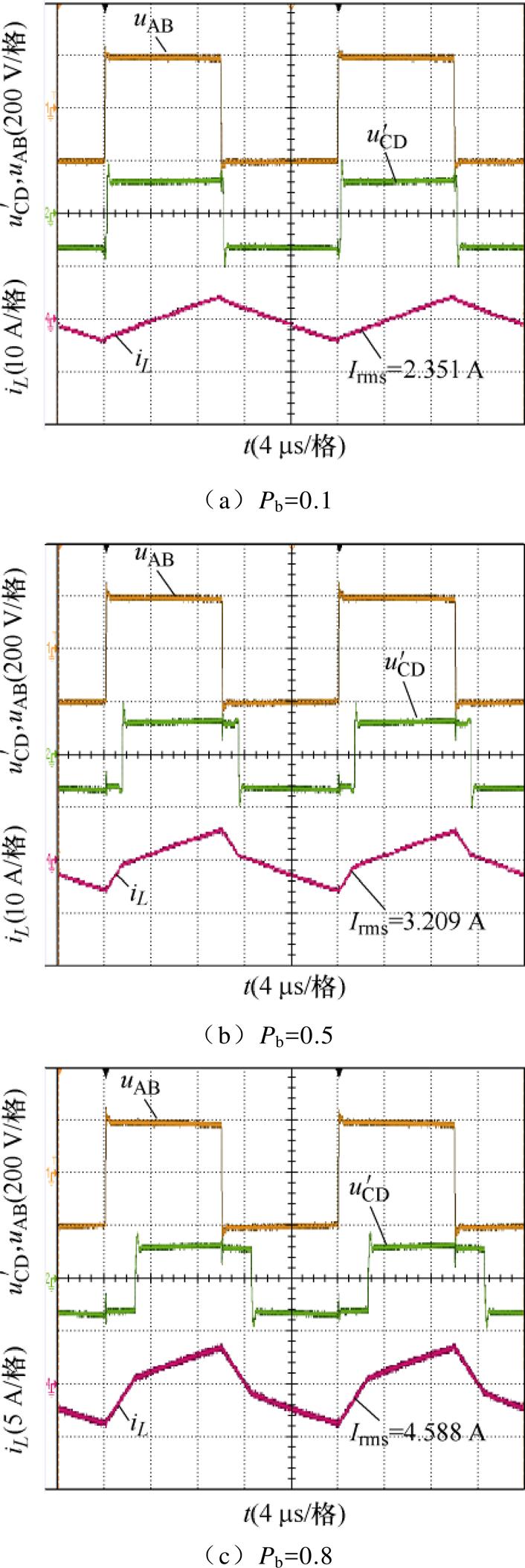
图16 k =1.6时SPS控制策略波形
Fig.16 Waveforms of the SPS control strategy at k =1.6
由图14～图16可以知道，当k =1.6，Pb分别为0.1、0.5、0.8时，OPT-3-EPS控制下的电感电流有效值分别为0.757 3、2.734、4.476 A，OPT-2-EPS控制下的电感电流有效值分别为1.179、2.912、4.560 A，SPS控制下的电感电流有效值分别为2.351、3.209、4.588 A。可以发现，OPT-3-EPS控制下的电感电流有效值为三种控制中的最小。
当k =1.6、Pb改变，三种控制策略下的电感电流有效值与传输效率的对比如图17所示。
由图17可知，当k =1.6时，在所能达到的功率范围内，OPT-3-EPS的电感电流有效值最小，传输效率最高。在中低功率段，OPT-3-EPS明显优于OPT-2-EPS和SPS，当Pb=0.4时，OPT-3-EPS控制下的传输效率达到了最高96.278%，体现了其在中功率段时的优势。随着功率的增大，OPT-3-EPS相比于其他两种控制策略的优势减小，在高功率段内三种控制策略的传输效率基本相当。
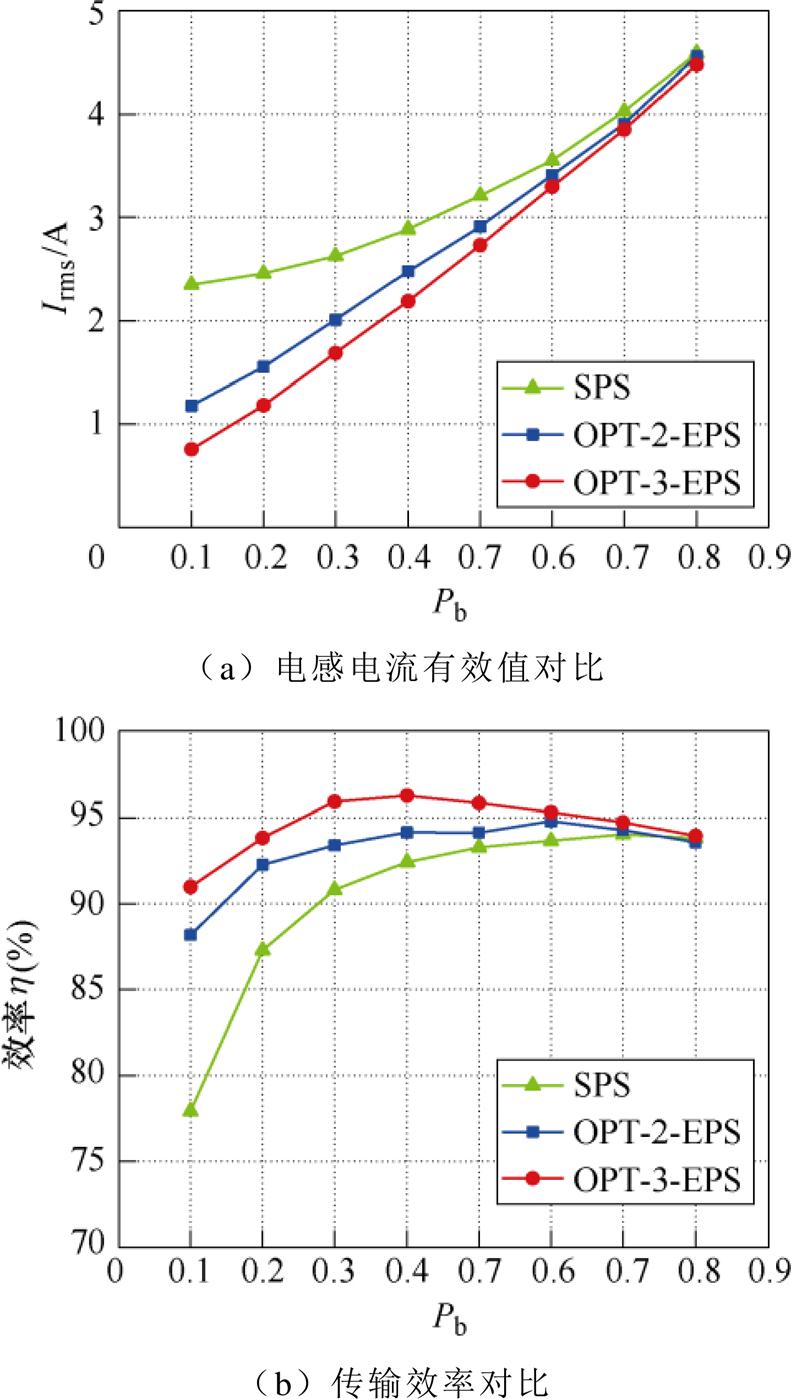
图17 k =1.6、Pb改变的三种控制策略对比
Fig.17 Comparison line chart of three control strategies with k =1.6 but Pb changes
当k =2.6，Pb=0.1、0.5、0.8时，三种控制策略下桥臂电压与电感电流的波形如图18～图20所示。
由图18～图20可知，当k =2.6，Pb分别为0.1、0.5、0.8时，OPT-3-EPS控制下的电感电流有效值分别为0.707 1、2.703、4.285 A，OPT-2-EPS控制下的电感电流有效值分别为1.109、2.975、4.402 A，SPS控制下的电感电流有效值分别为3.811、4.166、4.807 A。OPT-3-EPS控制下的电感电流有效值为三种控制中的最小。
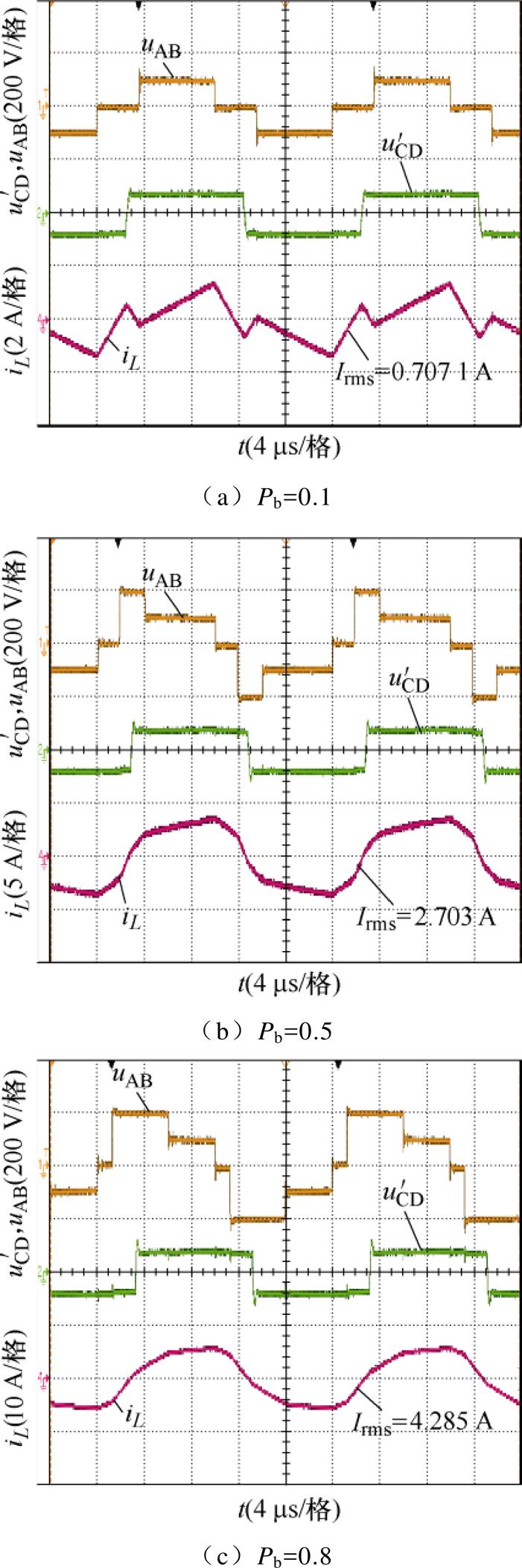
图18 k =2.6时OPT-3-EPS控制策略波形
Fig.18 Waveforms of the OPT-3-EPS control policy when k =2.6
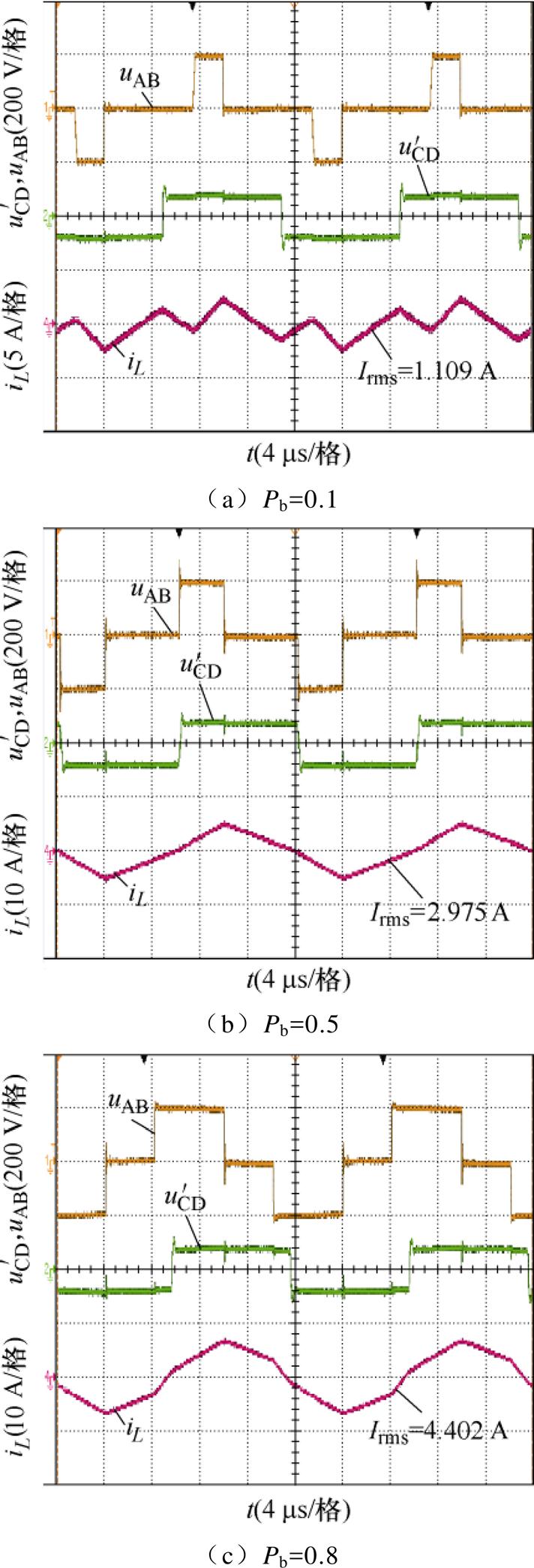
图19 k =2.6时OPT-2-EPS控制策略波形
Fig.19 Waveforms of OPT-2-EPS control strategy at k =2.6
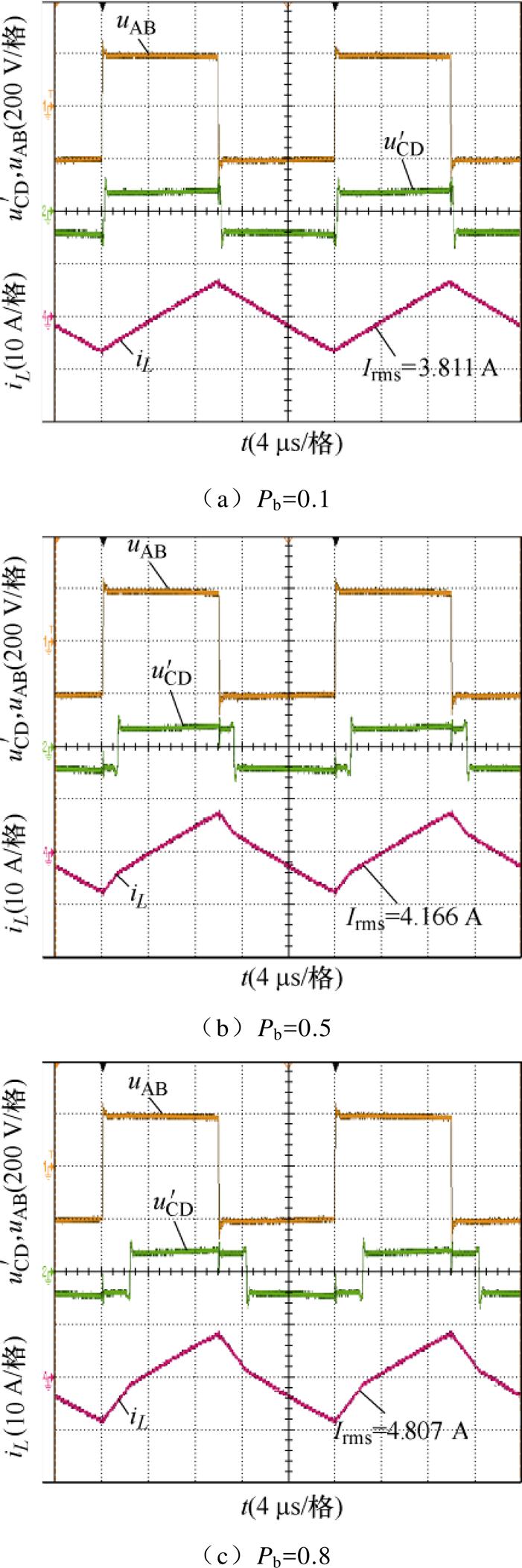
图20 k =2.6时SPS控制策略实验波形
Fig.20 Waveforms of the SPS control strategy at k =2.6
当k =2.6时，传输功率标幺值Pb改变，三种控制策略下的电感电流有效值与传输效率的对比如图21所示。
从图21中可以发现，当k =2.6时，在中低功率范围内，SPS控制的电感电流有效值明显大于其他两种控制策略，传输效率低；OPT-3-EPS电感电流有效值低于OPT-2-EPS，其效率保持在90%以上，但是随着功率的增大，OPT-3-EPS与OPT-2-EPS电流有效值之间的差值逐渐减小。
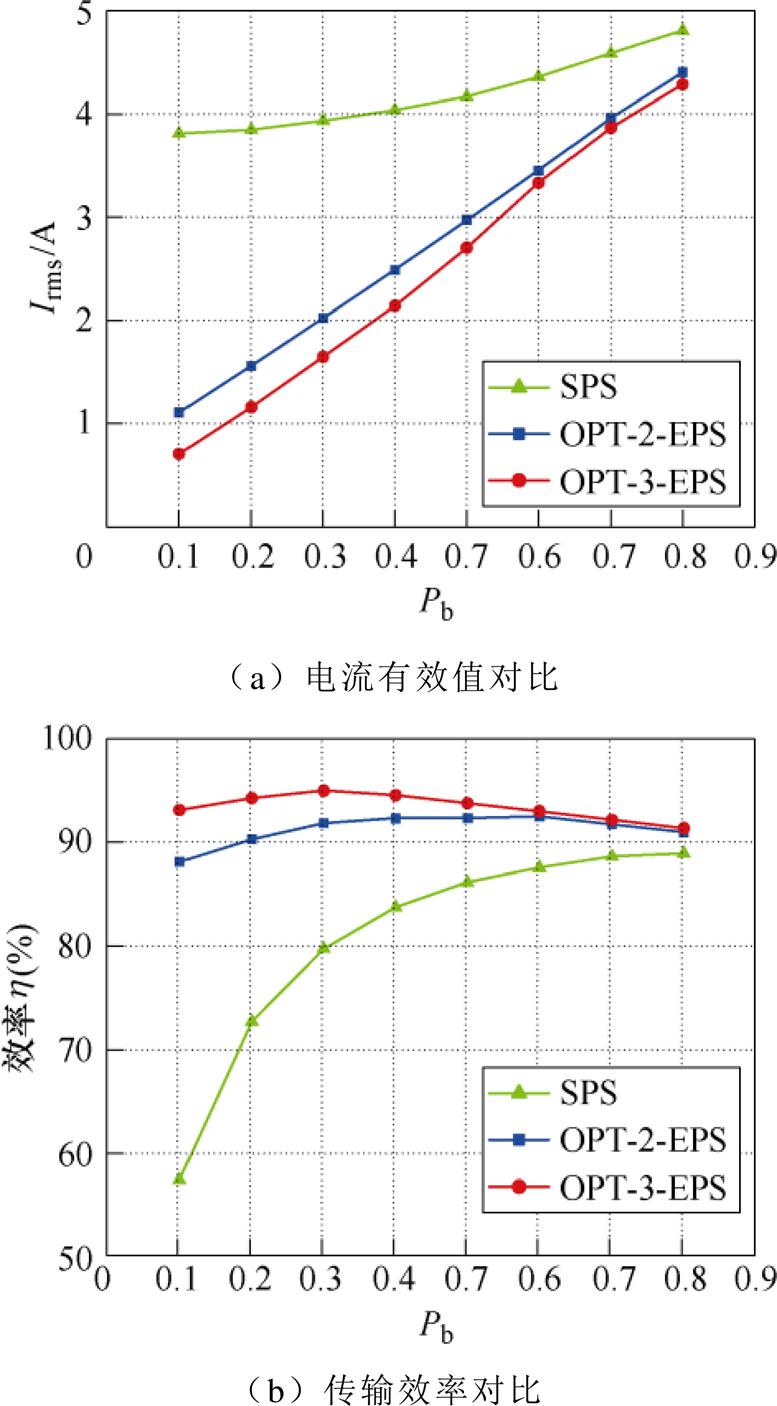
图21 k =2.6、Pb改变时三种控制策略对比
Fig.21 Comparison of three control strategies at k =2.6 with Pb changes
当Pb=0.1与Pb=0.5，k改变时的三种优化策略效率对比如图22、图23所示。由图22和图23可知：
（1）在Pb=0.1，k =1.1时，OPT-3-EPS控制的传输效率略低于OPT-2-EPS控制，这是由于电压匹配度高时，OPT-3-EPS优势不明显，而且此时Pb低，电感电流有效值较小，OPT-3-EPS和OPT-2-EPS的电感电流有效值分别为629.7 mA和758.6 mA，通态损耗比重低，开关损耗所占比重较大。
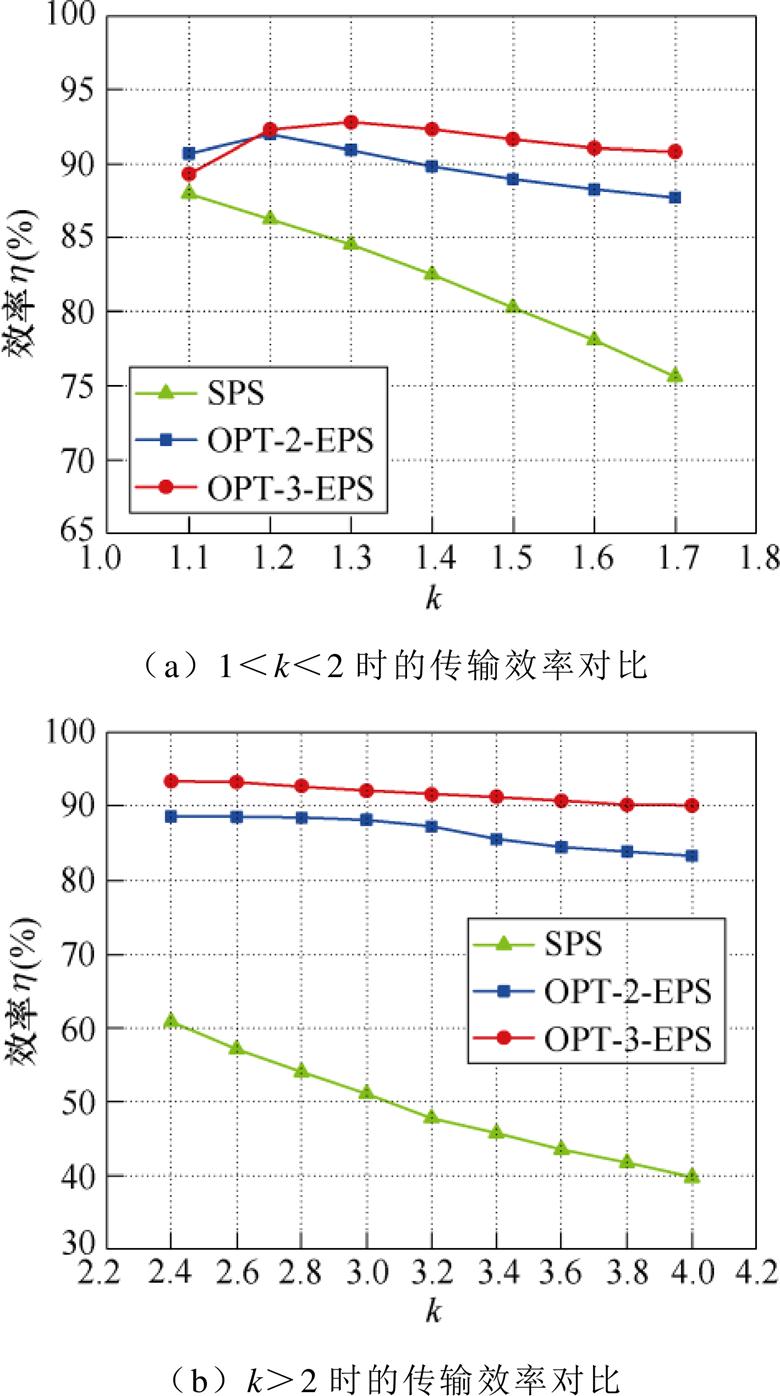
图22 Pb=0.1，k改变时三种控制策略效率对比
Fig.22 Comparison of three control strategies with Pb=0.1 with kchanges
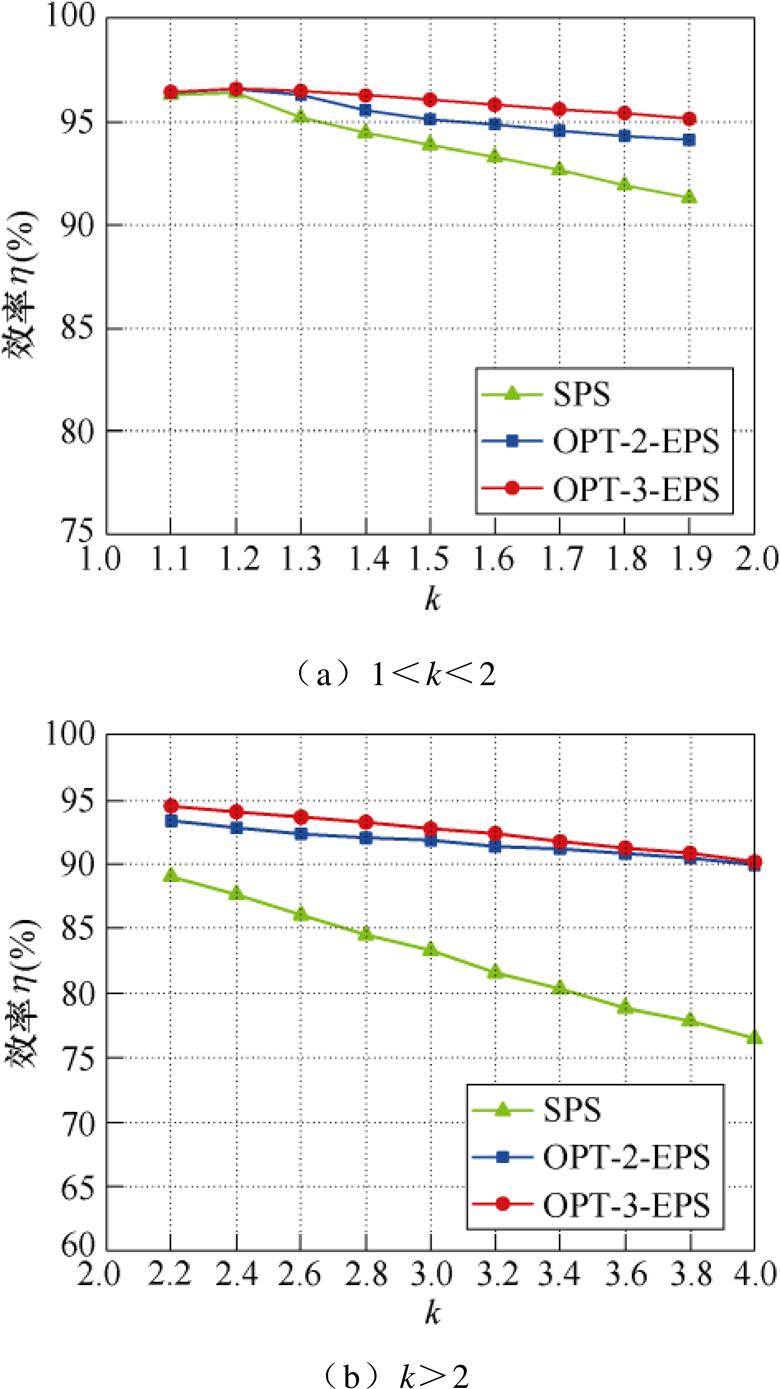
图23 Pb=0.5，k改变时三种控制策略效率对比
Fig.23 Comparison of three control strategies at Pb=0.5 with kchanges
（2） 当1＜k＜2，特别是当k＞1.2时，OPT-3-EPS效率高于OPT-2-EPS；当k＞2时，随着k增大，OPT- 3-EPS相比于OPT-2-EPS的优势在减小，特别是传输功率比较大的时候，当Pb=0.5，k =4时，OPT-3-EPS与OPT-2-EPS效率基本相当。
（3）OPT-3-EPS在电压不匹配度较高的情况下能保持90%以上的传输效率，特别当Pb=0.5，电压转换比1＜k＜2时，OPT-3-EPS控制下的传输效率更是可以始终保持在95%以上。
在调制波形相同的前提下，对电感电流波形的峰值点电流进行优化，得出一套电感电流峰值最小优化控制策略，在此作为有效值优化策略OPT-3- EPS的对比实验。
当k =1.6、k =2.6时，Pb改变时，OPT-3-EPS与电感电流峰值最小优化控制效率对比如图24所示。
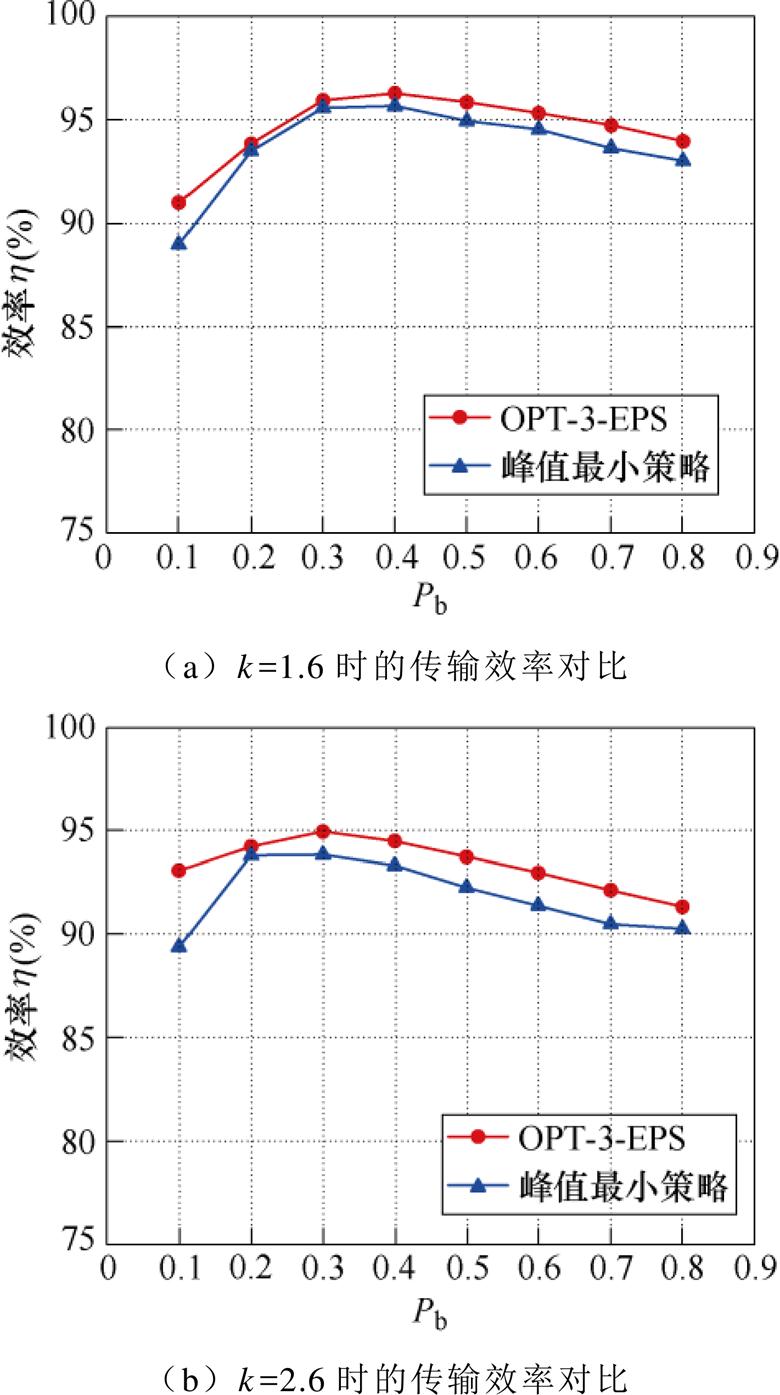
图24 k =1.6或k =2.6、Pb改变时OPT-3-EPS与电感电流峰值最小优化控制效率对比
Fig.24 Comparison of optimal control efficiency between OPT-3-EPS and minimum inductive current peak value when k =1.6 or k =2.6 and Pb change
从图24中可以看出，在k =1.6、k =2.6，Pb改变时，OPT-3-EPS的传输效率始终高于电感电流峰值最小优化控制，可以体现出电感电流有效值最小优化控制策略对比于电感电流峰值最小优化控制策略在提高变换器传输效率方面的优势。
本文基于二极管钳位三电平双有源桥直流变换器三电平扩展移相控制策略，得到电感电流有效值最小的极值点及其所能达到的功率范围，并通过仿真和实验验证优化算法的正确性。得到如下结论：
1）以电感电流有效值为优化目标的OPT-3-EPS控制策略，在宽电压转换比k的情况下都可以实现较低的电感电流有效值，传输效率基本维持在90%以上。
2）当电压转换比k不变时，随着功率的增大，OPT-3-EPS相对于SPS控制和OPT-2-EPS在电感电流有效值方面的优势减小。
3）当功率不变，k越接近于1，OPT-3-EPS的优势不明显；当1.2＜k＜2时，OPT-3-EPS明显优于OPT-2-EPS；当k＞2时，但是当k越大，OPT-3-EPS相比于OPT-2-EPS的优势在减小。
参考文献
[1] Esteban F D, Serra F M, De Angelo C H. Control of a DC-DC dual active bridge converter in DC microgrids applications[J]. IEEE Latin America Transactions, 2021, 19(8): 1261-1269.
[2] 王攀攀, 徐泽涵, 王莉, 等. 基于三重移相的双有源桥DC-DC变换器效率与动态性能混合优化控制策略[J]. 电工技术学报, 2022, 37(18): 4720-4731.
Wang Panpan, Xu Zehan, Wang Li, et al. A hybrid optimization control strategy of efficiency and dynamic performance of dual-active-bridge DC-DC converter based on triple-phase-shift[J]. Transactions of China Electrotechnical Society, 2022, 37(18): 4720-4731.
[3] 樊启高, 卢禹卓, 毕恺韬, 等. 基于倍频采样的两相交错并联三电平双向直流变换器功率均衡解耦控制策略[J]. 电工技术学报, 2022, 37(14): 3654- 3664.
Fan Qigao, Lu Yuzhuo, Bi Kaitao, et al. Decoupled power-balancing control strategy for two-phase interleaved parallel bidirectional DC converter based on frequency-doubling sampling[J]. Transactions of China Electrotechnical Society, 2022, 37(14): 3654- 3664.
[4] 李林柘, 邹旻洋, 吴京驰, 等. 基于周期组合序列调制的三电平双有源桥均压策略[J]. 电工技术学报, 2024, 39(2): 514-524.
Li Linzhe, Zou Minyang, Wu Jingchi, et al. The voltage balance scheme of three level-dual active bridge based on cycle combination sequence modulation[J]. Transactions of China Electrotechnical Society, 2024, 39(2): 514-524.
[5] 蔡逢煌, 石安邦, 江加辉, 等. 结合电流应力优化与虚拟电压补偿的双有源桥DC-DC变换器三重移相优化控制[J]. 电工技术学报, 2022, 37(10): 2559- 2571.
Cai Fenghuang, Shi Anbang, Jiang Jiahui, et al. Triple-phase-shift optimal control of dual-active- bridge DC-DC converter with current stress optimization and virtual voltage compensation[J]. Transactions of China Electrotechnical Society, 2022, 37(10): 2559-2571.
[6] Zhao Biao, Song Qiang, Li Jianguo, et al. Full- process operation, control, and experiments of modular high-frequency-link DC transformer based on dual active bridge for flexible MVDC distribution: a practical tutorial[J]. IEEE Transactions on Power Electronics, 2016, 32(9): 6751-6766.
[7] 竺庆茸. 双有源桥DC-DC的调制方式的研究[J]. 电气技术, 2020, 21(7): 53-56, 68.
Zhu Qingrong. A study of dual active bridge DC-DC modulation mode[J]. Electrical Engineering, 2020, 21(7): 53-56, 68.
[8] 胡钰杰, 李子欣, 赵聪, 等. 基于MOSFET的串联谐振双有源桥死区振荡机理分析及抑制[J]. 电工技术学报, 2022, 37(10): 2549-2558.
Hu Yujie, Li Zixin, Zhao Cong, et al. Mechanism analysis and suppression of oscillation in dead time of series resonant dual active bridge based on MOSFET[J]. Transactions of China Electrotechnical Society, 2022, 37(10): 2549-2558.
[9] 汪涛, 骆仁松, 张茂强, 等. 考虑死区效应的双有源桥直流变压器损耗优化[J]. 电力系统自动化, 2023, 47(6): 197-205.
Wang Tao, Luo Rensong, Zhang Maoqiang, et al. Loss optimization of DC transformer based on dual active bridge considering dead-zone effect[J]. Auto- mation of Electric Power Systems, 2023, 47(6): 197-205.
[10] 杨向真, 王锦秀, 孔令浩, 等. 电压不匹配运行条件下双有源桥变换器的效率优化方法[J]. 电工技术学报, 2022, 37(24): 6239-6251.
Yang Xiangzhen, Wang Jinxiu, Kong Linghao, et al. Efficiency optimization method of DAB converters under wide-voltage operating conditions[J]. Transa- ctions of China Electrotechnical Society, 2022, 37(24): 6239-6251.
[11] 吴春华, 陈修淋, 李智华, 等. 全移相双有源全桥直流变换器的瞬态电流偏置抑制策略[J]. 电工技术学报, 2024, 39(4): 1116-1131.
Wu Chunhua, Chen Xiulin, Li Zhihua, et al. Transient current bias suppression strategy of full phase shifting dual active full bridge DC converter[J]. Transactions of China Electrotechnical Society, 2024, 39(4): 1116- 1131.
[12] 刘子薇, 孙兆龙, 刘宝龙, 等. 基于直接功率控制的双有源桥暂态直流偏置抑制策略[J]. 电工技术学报, 2023, 38(12): 3234-3247
Liu Ziwei, Sun Zhaolong, Liu Baolong, et al. Transient DC bias suppression strategy of dual active bridge based on direct power control[J]. Transactions of China Electrotechnical Society, 2023, 38(12): 3234-3247.
[13] Jin Li, Duan Shanxu. Optimised phase shift control to minimise current stress of three-level dual active bridge DC-DC converter[J]. IET Power Electronics, 2018, 11(15): 2427-2433.
[14] Wang Yi, Wen Huiqing, Zhu Yinxiao, et al. Minimum-current-stress scheme of three-level dual- active-bridge DC-DC converters with the particle swarm optimization[J]. IEEE Transactions on Trans- portation Electrification, 2021, 7(4): 2067-2084.
[15] 金莉, 刘邦银, 段善旭. 三电平双有源全桥DC-DC变换器回流功率最小的移相控制[J]. 电工技术学报, 2018, 33(24): 5864-5873.
Jin Li, Liu Bangyin, Duan Shanxu. Minimum reflux power strategy of three-level dual active bridge DC- DC converter with phase shift control[J]. Transactions of China Electrotechnical Society, 2018, 33(24): 5864-5873.
[16] Jin Li, Liu Bangyin, Duan Shanxu. ZVS soft switching operation range analysis of three-level dual-active bridge DC-DC converter under phase shift control strategy[J]. IEEE Transactions on Industry Applications, 2019, 55(2): 1963-1972.
[17] Liu Peng, Chen Changsong, Duan Shanxu, et al. Dual phase-shifted modulation strategy for the three-level dual active bridge DC-DC converter[J]. IEEE Transactions on Industrial Electronics, 2017, 64(10): 7819-7830.
[18] Guo Zhiqiang, Sun Kai. Three-level bidirectional DC-DC converter with an auxiliary inductor in adaptive working mode for full-operation zero- voltage switching[J]. IEEE Transactions on Power Electronics, 2018, 33(10): 8537-8552.
[19] 高娜, 张宇, 关清心, 等. 基于有源中点钳位五电平电路的双有源桥DC/DC变换器[J]. 中国电机工程学报, 2023, 43(5): 1950-1961.
Gao Na, Zhang Yu, Guan Qingxin, et al. Five-level active neutral point clamed dual active bridge DC/DC converter[J]. Proceedings of the CSEE, 2023, 43(5): 1950-1961.
[20] Liu Peng, Chen Changsong, Duan Shanxu. An optimized modulation strategy for the three-level DAB converter with five control degrees of freedom[J]. IEEE Transactions on Industrial Elec- tronics, 2020,67(1): 254-264.
[21] 刘朋, 陈昌松, 段善旭. 带飞跨电容的三电平全桥直流变换器输入中点电压的自平衡分析[J]. 电工技术学报, 2018, 33(18): 4335-4344.
Liu Peng, Chen Changsong, Duan Shanxu. Self- balance mechanism analysis of the neutral point voltage in three-level full bridge DC-DC converter with flying capacitors[J]. Transactions of China Electrotechnical Society, 2018, 33(18): 4335-4344.
[22] Song Chaochao, Sangwongwanich A, Yang Yongheng, et al. Capacitor voltage balancing control scheme for 2/3-level DAB converters[C]//IECON 2021-47th Annual Conference of the IEEE Industrial Electronics Society, Toronto, ON, Canada, 2021: 1-6.
[23] Filba-Martinez A, Busquets-Monge S, Bordonau J. Modulation and capacitor voltage balancing control of multilevel NPC dual active bridge DC-DC con- verters[J]. IEEE Transactions on Industrial Elec- tronics, 2020, 67(4): 2499-2510.
[24] Filbà-Martínez A, Busquets-Monge S, Bordonau J. Modulation and capacitor voltage balancing control of a three-level NPC dual-active-bridge DC-DC con- verter[C]//IECON 2013-39th Annual Conference of the IEEE Industrial Electronics Society, Vienna, Austria, 2014: 6251-6256.
Optimal Tracking Control Strategy of Inductive Current RMS for Dual-Active Bridge DC Converter with Three-Level Extended Phase-Shift Control
Abstract A two-level dual active bridge (DAB) converter cannot reach high efficiency in wide voltage transmission range occasions. Therefore, a multilevel structure is applied to DAB to optimize converter efficiency and reduce the voltage stress of power switching. A tracking control strategy for minimum inductance current RMS value based on three-level extended phase shift (3-EPS) control is proposed when a large mismatch exists between input and output voltages.
Firstly, the relationship between the phase-shift ratios D0=f0(D2) and D1=f1(D2) at several optimal extreme points in different power regions is obtained by the Lagrange multiplier method. Different extreme points can achieve different power ranges. The inductance current RMS value of each optimal extreme point is compared in the power overlap range, and the global optimum extreme points in different power ranges are obtained. Secondly, the optimal boundary points are analyzed and compared with global optimum extreme points. Because the inductance current RMS values of global optimum extreme points are always smaller than those of boundary points in each power range, the global optimum extreme points are the final global optimal operating points. Finally, the positive PI controller or negative PI controller is chosen based on the partial derivative polarity of the power to D2 to track the global optimal operating points. Besides, based on the switching point current, the zero-voltage switch (ZVS) of most switches can be realized under ideal conditions. However, the ZVS range is compressed, considering that the inductance energy is enough to discharge the parasitic capacitance fully.
Experimental results show that when voltage transmission ratio k equals 1.6 or 2.6, the efficiency of optimal 3-EPS control is higher than optimal two-level extended phase shift (2-EPS) control and single phase shift (SPS) control in low to medium power range. However, the efficiencies of the above three controls are very close when the per unit power reaches 0.8. When per unit power equals 0.5 and k is between 1.1 and 1.2, the advantage of 3-EPS is not apparent. When k is between 1.2 and 2, the advantage is evident again. Compared with 2-EPS, when k is larger than 2, the effect of 3-EPS decreases as k increases. When k equals 4, the efficiencies of 3-EPS and 2-EPS are very close. The efficiency of the minimum inductance current RMS value tracking control strategy is higher than the peak current optimal control.
The following conclusions can be drawn from analysis and experiment results. (1) The optimal control strategy proposed achieves lower inductance current RMS value under a wide input voltage range, and the efficiency is higher than 90% in most power ranges. (2) When k is kept unchanged, compared with 2-EPS and SPS, the effect of 3-EPS decreases as the unitary power increases. (3) When power is kept unchanged, the effect of 3-EPS is not apparent if k is larger than 1 but close to 1 because the mismatch between input and output voltages is minor. When k is between 1 and 2 and away from 1, the effect of 3-EPS is obvious. (4) When k is larger than 2, compared with 2-EPS, the effect of 3-EPS decreases as k increases. When k reaches 4, the effect of 3-EPS is almost vanished.
Keywords：Three-level, extend phase-shift, dual-active bridge DC converter, minimum inductive current RMS value, track control
中图分类号：TM46
DOI: 10.19595/j.cnki.1000-6753.tces.231180
国家自然科学基金资助项目（51537001）。
收稿日期 2023-07-22
改稿日期 2023-09-20
邓丹阳 男，1998年生，硕士研究生，研究方向为新能源发电技术。
E-mail: 1377550372@qq.com
陈艳慧 女，1980年生，博士，副教授，硕士生导师，研究方向为新能源发电技术。
E-mail: cyh_crp@163.com（通信作者）
（编辑 陈 诚）