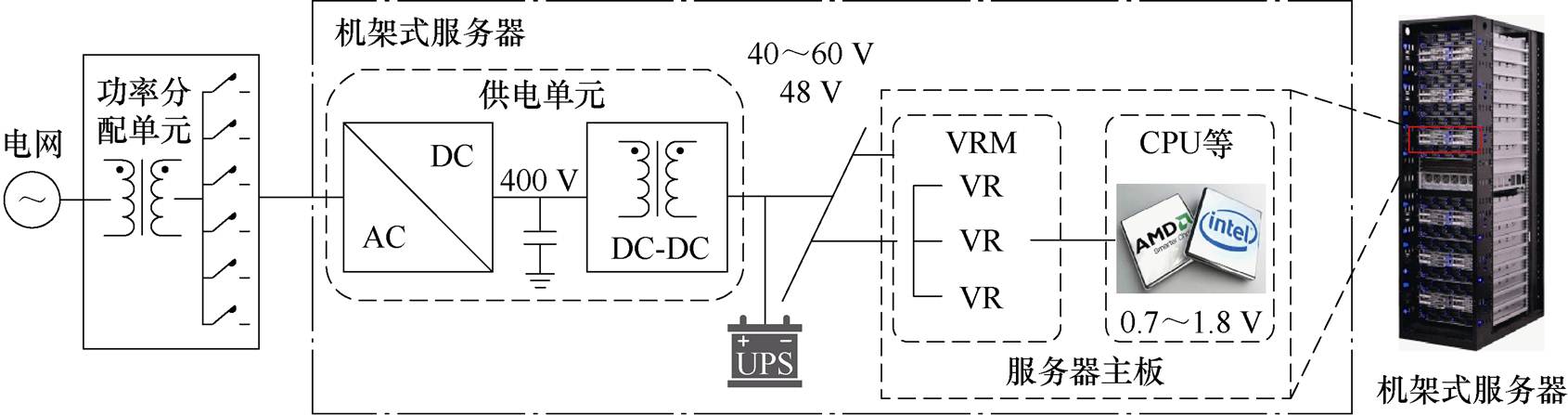
图1 48 V直流母线供电架构
Fig.1 48 V DC bus architecture
摘要 谐振开关电容变换器具有效率高、体积小、质量轻和易集成等优点,是中间母线变换器的理想拓扑,然而其不足之处在于电压比固定以及软开关特性易受谐振参数容差的影响。该文针对这两个问题,将多谐振开关槽式变换器与四开关Buck-Boost变换器进行结合,提出一种基于准并联架构的中间母线变换器,详细分析变换器的工作原理与电压增益特性。通过推导电流时域表达式详细分析谐振参数容差对变换器的影响,并给出参数设计的方法。该文研究一种合适的控制方式,完成环路补偿设计,实现输出电压的闭环控制。通过仿真和实验对上述理论和解决方案进行验证。
关键词:中间母线变换器 谐振开关电容变换器 多谐振开关槽式变换器 准并联架构
数据中心的能耗水平与其供电系统架构有重要关系,目前48 V直流母线供电架构得以广泛应用[1],如图1所示。其服务器主板上的电压调节模块(Voltage Regulator Module, VRM)通常采用中间母线架构(Intermediate Bus Architecture, IBA),由前级中间母线变换器(Intermediate Bus Converter, IBC)与后级的负载点(Point-of-Load, POL)变换器构成[2]。IBC的表现对系统的整体性能具有重要影响,这要求其具有较高的效率和功率密度,同时保持较低的成本。此外,部分应用场合中,前级变换器的输出电压通常具有一定的波动范围,这会使IBC的输入电压不稳。如果IBC作为直流变压器(DC Transformer, DCX)仅采用开环控制,输出电压随负载变化存在较大的波动范围,会导致后级POL的输入电压变化范围较宽,不利于优化POL的效率。这要求中间母线变换器具有一定的闭环调压能力[3]。

图1 48 V直流母线供电架构
Fig.1 48 V DC bus architecture
开关电容变换器(Switched-Capacitor Converter, SCC)[4-7]采用高能量密度的贴片式多层陶瓷电容器(Multi-Layer Ceramic Capacitor, MLCC)作为储能元件[8],在实现高功率密度上有天然优势。谐振开关电容变换器(Resonant Switched-Capacitor Converter, RSCC),在传统的SCC中嵌入适当的电感[9],通过利用电感电容的谐振,可以实现储能电容的“软充放电”,消除开关瞬间的电流电压尖峰,还可以实现开关管的零电流软开关,具有更高的效率,目前已经成功应用在数据中心[10]、移动通信设备[11]、电动汽车[12]及分布式光伏发电[14]等领域。
然而,RSCC也存在一些问题尚待解决。首先,RSCC同SCC一样,电压调节能力较差,劣于基于磁性元件的变换器[13],具体表现有:
(1)采用定频控制时,RSCC电压比只能通过级数扩展实现提升,无法实现增益的线性调节[14]。
(2)采用移相控制时,RSCC可以在一定增益范围内实现输出电压可调,并使部分开关管实现零电压软开关(Zero Voltage Switching, ZVS)[15-17]。但与零电流软开关(Zero Current Switching, ZCS)模式相比,ZVS模式的RSCC仅在轻载时存在效率优势[18]。同时,移相调节电压过程中,相邻谐振开关电容单元间的环流显著增大,也会降低ZVS模式RSCC的工作效率[19]。
(3)采用变频控制时,RSCC都可以实现输出电压线性调节[20],但存在轻载时的调压能力差、开关频率变化范围宽的问题[21]。文献[22]使用了固定开关频率的PWM控制技术,虽然获得一定的调压能力,但会引发RSCC变换器的潜电路状态,牺牲了电路的可靠性与软开关特性。
无源元件参数容差的存在对RSCC的效率与可靠性造成严重威胁,限制了RSCC大规模应用。具体负面影响体现在:
(1)RSCC及其衍生拓扑存在浮地开关管,无源器件参数容差将会造成其电压应力振荡。通过添加合适的死区[23],使得谐振电流在模态切换前尽可能回零,可以削弱一部分负面影响[24]。通过添加额外的电压钳位电路[25],也能消除电压振荡。文献[26]采用电感共用法,将状态相同的基本单元中的电感共用,实现电感耦合回路的解耦。Google公司应用于数据中心的STC变换器中也有体现[27]。
(2)无源元件参数容差会使工作在ZCS模式的RSCC失去软开关特性。针对此问题,可以采用自适应导通时间控制策略[28],在电路中添加额外的检测电路,对谐振电流过零时刻进行检测,保证开关管实现ZCS。这会减小变换器的功率密度,增加生产成本,也使控制变得更加复杂。
本文针对传统谐振开关电容变换器调压能力不足、易受谐振参数容差影响的问题,提出了一种由多谐振开关槽变换器(Multi Resonant Switched Tank Converter, MRSTC)与四开关升降压(Four-Switch Buck-Boost, FSBB)变换器输入串联输出并联构成的准并联变换器,简称为MRSTC-FSBB变换器,通过调节FSBB的占空比实现闭环控制。通过将传统RSCC的串联谐振腔替换为多谐振开关槽,可以使用Ⅱ类陶瓷电容作为谐振元件,降低生产成本,提升变换器对无源参数容差的适应力,通过推导电流时域表达式详细分析了其原理。最后搭建了输入电压48 V(40~60 V),输出12 V/300 W的原理样机,验证了所提方案的可行性及有效性。
基于准并联架构的MRSTC-FSBB变换器由电压比(N+1)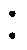 1的MRSTC和FSBB输入串联输出并联组成,其中,MRSTC作为DCX使用,FSBB作为辅助变换器,实现输出稳压。其等效电路如图2所示。针对中间母线架构48~12 V应用场景,可以取N=3
1的MRSTC和FSBB输入串联输出并联组成,其中,MRSTC作为DCX使用,FSBB作为辅助变换器,实现输出稳压。其等效电路如图2所示。针对中间母线架构48~12 V应用场景,可以取N=3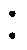 1,4
1,4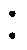 1 MRSTC-FSBB变换器电路如图3所示,Q1a~Q2b为MRSTC的翼侧开关管;Q3a~Q5b为MRSTC整流开关管;Lr1、Cr1、C1和Lr2、Cr2、C2分别是两个谐振单元的谐振参数;CF为钳位电容基本单元的钳位电容;Cin、Co分别为输入、输出滤波电容,RL为负载电阻。各个谐振腔元件参数取值保持一致。
1 MRSTC-FSBB变换器电路如图3所示,Q1a~Q2b为MRSTC的翼侧开关管;Q3a~Q5b为MRSTC整流开关管;Lr1、Cr1、C1和Lr2、Cr2、C2分别是两个谐振单元的谐振参数;CF为钳位电容基本单元的钳位电容;Cin、Co分别为输入、输出滤波电容,RL为负载电阻。各个谐振腔元件参数取值保持一致。
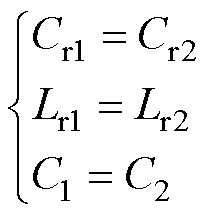 (1)
(1)
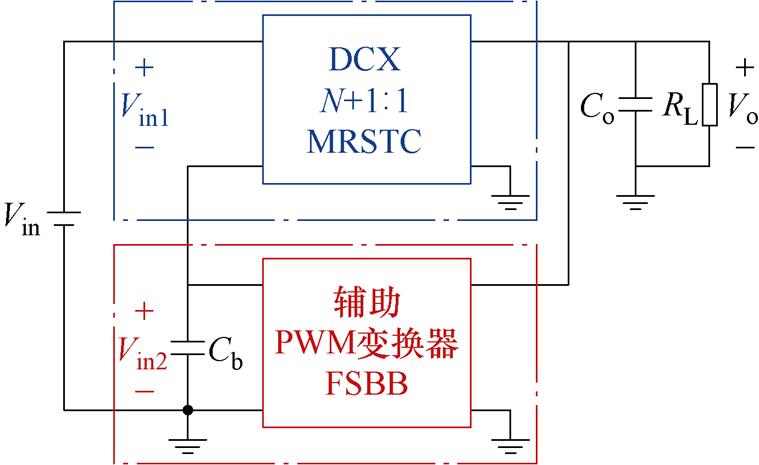
图2 直流等效电路
Fig.2 DC equivalent circuit
由Lr1、Cr1、C1构建的三元件谐振腔有两个谐振频率。其中,电容Cr1和电感Lr1的谐振频率记为fr,电容Cr1、电感Lr1和电容C1的谐振频率记为fr2,二者表达式分别为
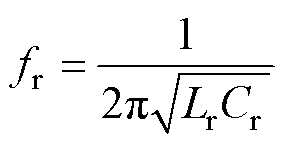 (2)
(2)
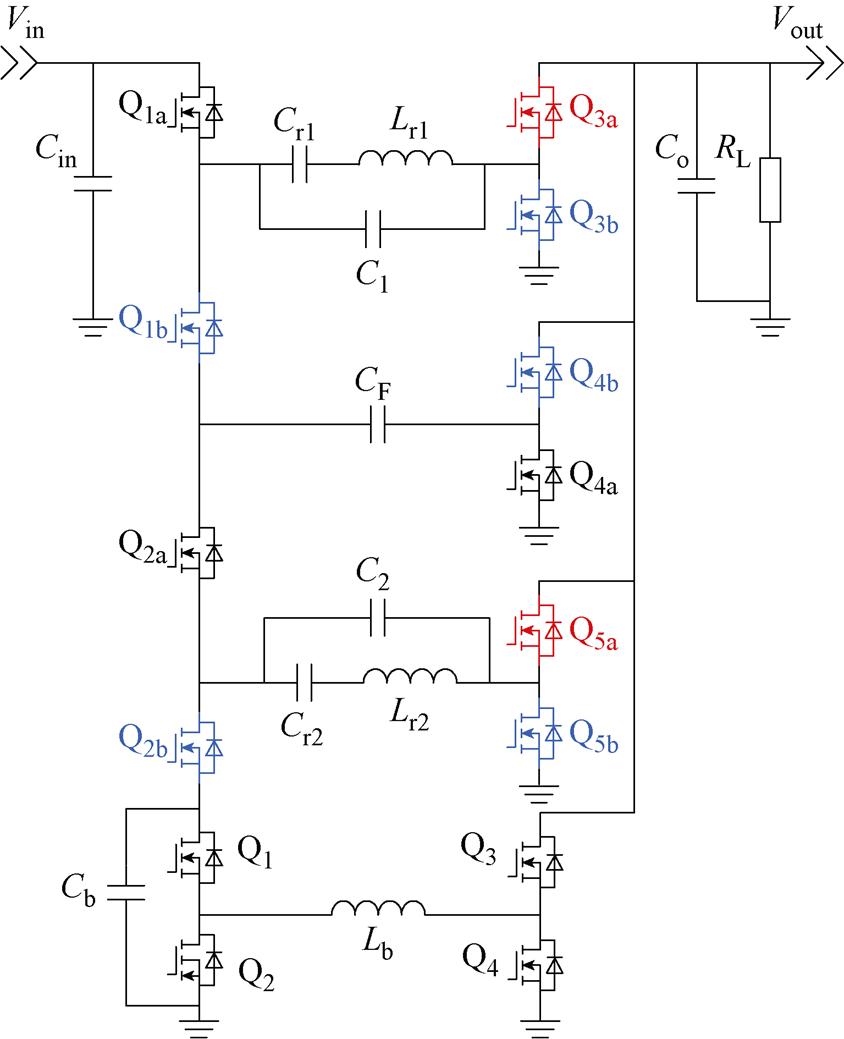
图3 4 1 MRSTC-FSBB变换器电路
1 MRSTC-FSBB变换器电路
Fig.3 The circuit of 4 1 MRSTC-FSBB
1 MRSTC-FSBB
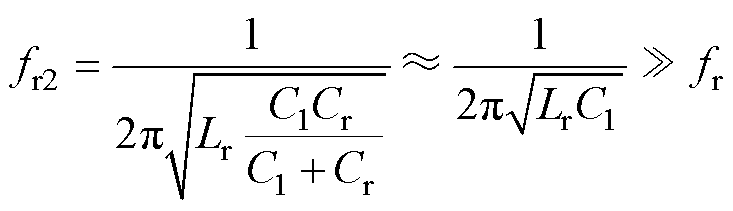 (3)
(3)
式中,fr为串联谐振频率;fr2为陷波谐振频率。当电容C1远小于电容Cr(C1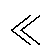 Cr)时,陷波谐振频率fr2可认为仅由电感Lr与电容C1决定。从滤波器角度出发,当输入能量的频率与fr相同时,在忽视寄生电阻的情况下,能量会无损通过谐振腔,谐振腔具有带通特性;当输入能量的频率与fr2相同时,谐振腔的阻抗呈无穷大,阻碍能量向输出侧传递,此时谐振腔具有带阻特性。利用陷波谐振频率fr2的带阻性质,MRSTC可以实现降低变换器对谐振参数容差敏感性的目的。
Cr)时,陷波谐振频率fr2可认为仅由电感Lr与电容C1决定。从滤波器角度出发,当输入能量的频率与fr相同时,在忽视寄生电阻的情况下,能量会无损通过谐振腔,谐振腔具有带通特性;当输入能量的频率与fr2相同时,谐振腔的阻抗呈无穷大,阻碍能量向输出侧传递,此时谐振腔具有带阻特性。利用陷波谐振频率fr2的带阻性质,MRSTC可以实现降低变换器对谐振参数容差敏感性的目的。
MRSTC的控制方式同RSCC一样,所有Qia(i= 1, 2, 3, 4, 5)同步开关,所有Qib同步开关,两组开关管占空比相等,开关周期内存在死区时间。为了减小谐振腔电流的有效值,降低导通损耗,需要令MRSTC的开关频率fs高于串联谐振频率fr(fs>fr)。为了简化分析,视所有器件为理想器件,并假设电路工作于稳态。图4给出了MRSTC第一级谐振单元的关键波形,其各模态的等效电路如图5所示。
(1)模态1 [t0, t1 :t0时刻,Qia导通,Qib截止,第一级谐振单元内输入电压Vin、谐振腔与负载RL三者串联。输入电压Vin与谐振腔串联充电,同时向负载RL供电,谐振电容电压vCr1开始上升。电容C1由于其容值太小(C1
:t0时刻,Qia导通,Qib截止,第一级谐振单元内输入电压Vin、谐振腔与负载RL三者串联。输入电压Vin与谐振腔串联充电,同时向负载RL供电,谐振电容电压vCr1开始上升。电容C1由于其容值太小(C1 Cr),不会影响串联谐振槽的能量传递过程。因此,在导通时间内,电容C1流经的电流iC1可近似为零;三元件谐振腔流经的电流itank1等于谐振电感Lr的电流iLr,也等于输出整流电流IDS,且为正弦波。第三级谐振单元由钳位电容单元供电向负载侧传递能量,波形同第一级一致。
Cr),不会影响串联谐振槽的能量传递过程。因此,在导通时间内,电容C1流经的电流iC1可近似为零;三元件谐振腔流经的电流itank1等于谐振电感Lr的电流iLr,也等于输出整流电流IDS,且为正弦波。第三级谐振单元由钳位电容单元供电向负载侧传递能量,波形同第一级一致。
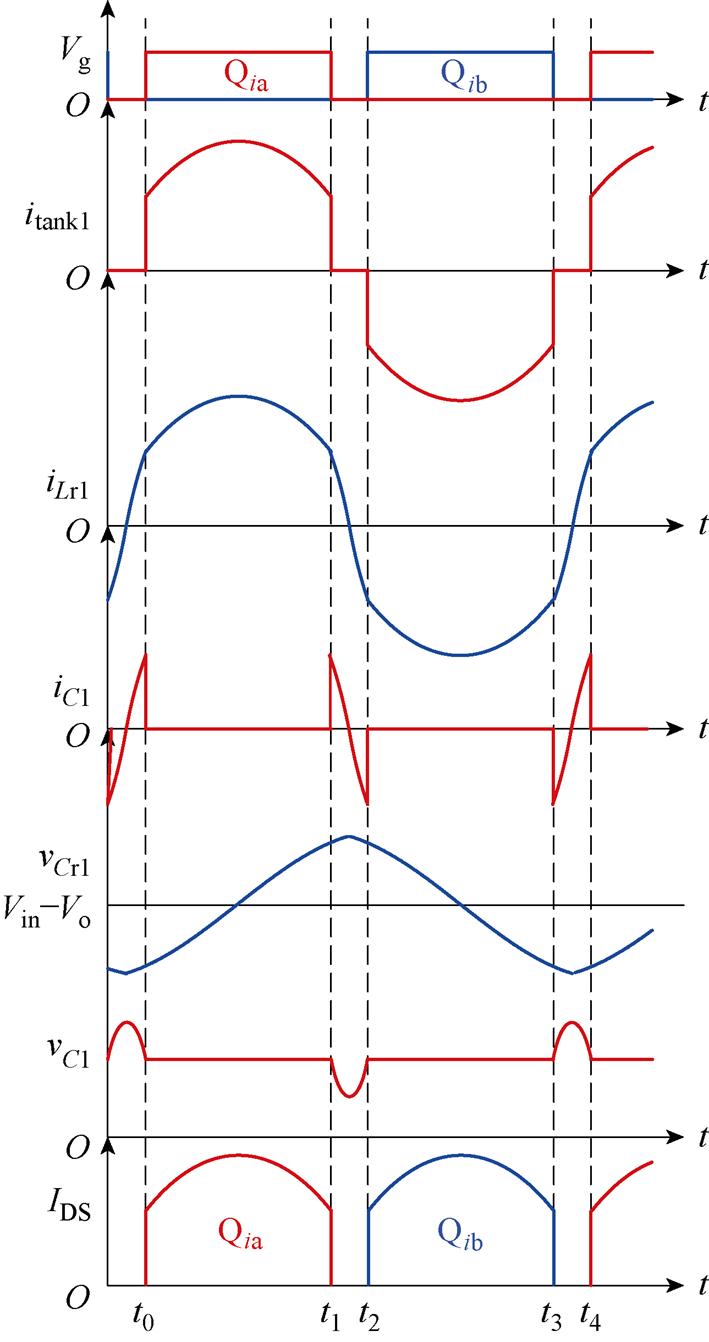
图4 MRSTC的主要波形
Fig.4 Main waveforms of MRSTC
(2)模态2 [t1, t2 :t1时刻,导通时间结束,Qia关断,所有开关管都处于截止状态,谐振腔流出电流itank1瞬间降为零。此模态为死区时间,输入电压Vin与谐振腔均同负载侧断开。电容C1为串联谐振槽内剩余电感电流ILr1提供了流通路径。通过设置死区时间td等于陷波谐振频率fr2的半个谐振周期,能够以无损的方式使得剩余电感电流ILr反向,即
:t1时刻,导通时间结束,Qia关断,所有开关管都处于截止状态,谐振腔流出电流itank1瞬间降为零。此模态为死区时间,输入电压Vin与谐振腔均同负载侧断开。电容C1为串联谐振槽内剩余电感电流ILr1提供了流通路径。通过设置死区时间td等于陷波谐振频率fr2的半个谐振周期,能够以无损的方式使得剩余电感电流ILr反向,即
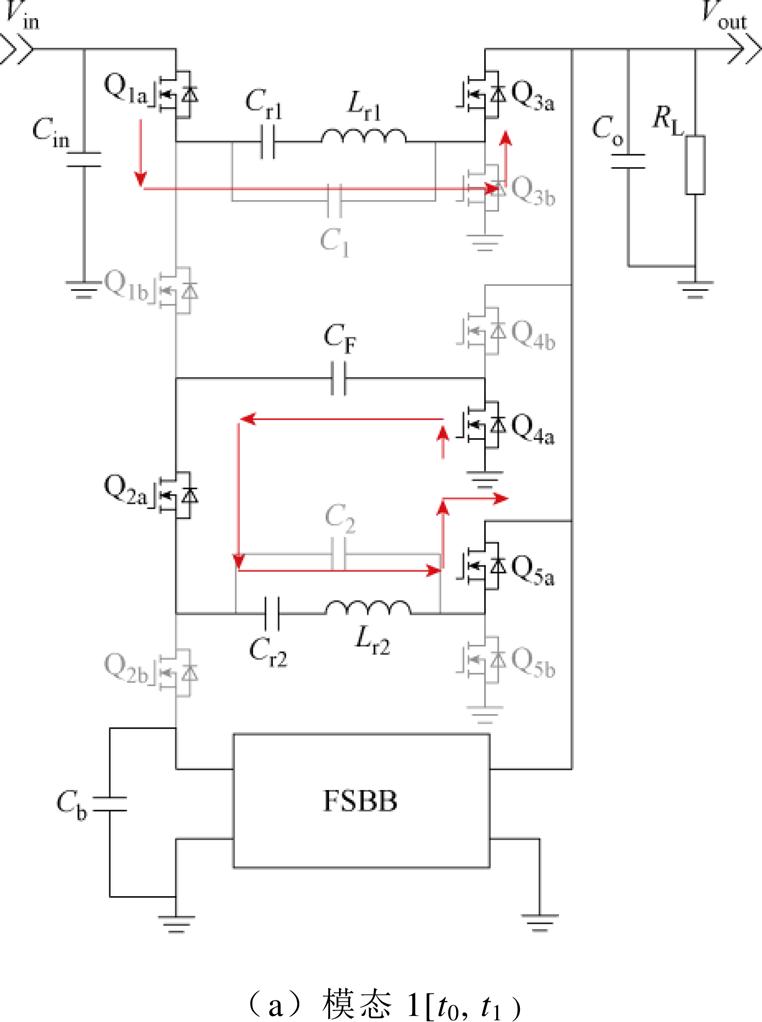
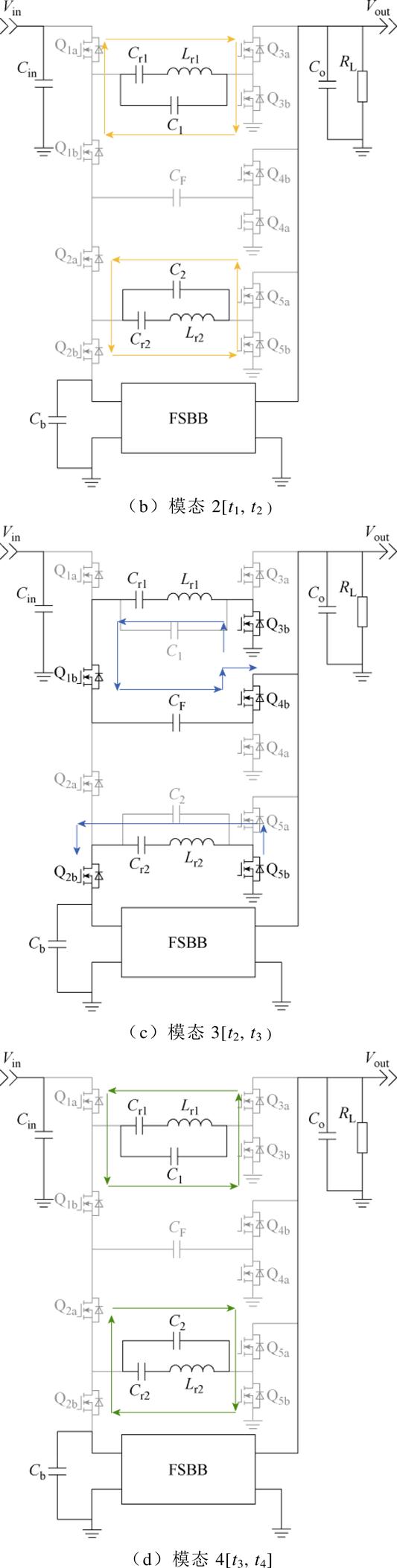
图5 MRSTC的工作模态
Fig.5 Working modes of MRSTC
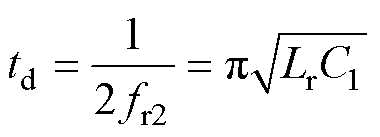 (4)
(4)
(3)模态3 [t2, t3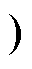 :Qia时刻,剩余电感电流ILr1完成反向,Qib开通,Qia截止。此时输入电压Vin开路。串联谐振槽开始反向谐振,第一级谐振腔向钳位电容供电,第三级向FSBB供电。随着能量流出,谐振电容电压vCr1逐渐降低。与模态1类似。
:Qia时刻,剩余电感电流ILr1完成反向,Qib开通,Qia截止。此时输入电压Vin开路。串联谐振槽开始反向谐振,第一级谐振腔向钳位电容供电,第三级向FSBB供电。随着能量流出,谐振电容电压vCr1逐渐降低。与模态1类似。
(4)模态4 [t3, t4]:此模态为另一段死区时间,与模态2相似,t3时刻,所有开关管都处于截止状态,电流itank1瞬间降为零。串联谐振槽内剩余电流ILr1,流经电容C1,实现无损反向,等待下一个开关周期。
稳态运行时,MRSTC可以实现电压比N 1的降压变换。与RSCC不同的是,MRSTC在死区时间内,利用多谐振电容为串联谐振腔内的剩余电流提供流通路径,在下次导通时间前,完成了剩余电流的无损反向。这种运行机制提升了MRSTC对谐振元件参数容差的适应力。
1的降压变换。与RSCC不同的是,MRSTC在死区时间内,利用多谐振电容为串联谐振腔内的剩余电流提供流通路径,在下次导通时间前,完成了剩余电流的无损反向。这种运行机制提升了MRSTC对谐振元件参数容差的适应力。
根据图2,输入电压Vin与MRSTC变换器的输入电压Vin1和FSBB的输入电压Vin2的关系满足
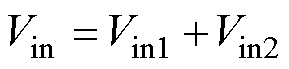 (5)
(5)
电压比为N 1 MRSTC变换器可等效为直流变压器,则Vin1与输出电压Vo满足
1 MRSTC变换器可等效为直流变压器,则Vin1与输出电压Vo满足
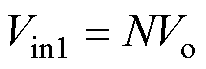 (6)
(6)
辅助变换器FSBB的电压增益M可表示为
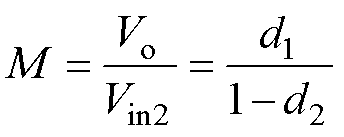 (7)
(7)
式中,d1和d2分别为Q1和Q4的占空比。将式(5)~式(7)联立,可以求得MRSTC-FSBB变换器的电压增益G为
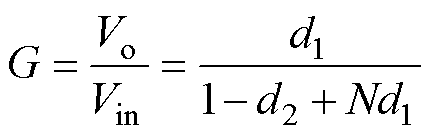 (8)
(8)
为了使得FSBB变换器的Buck单元和Boost单元工作在安全高效的范围内,限定占空比d1和d2的范围为:0.1<d1<0.9,0.1<d2<0.9,可以求出增益的分布曲面如图6所示。
当输入电压Vin存在扰动电压Vjump时,等效电路如图7所示,通过对FSBB增益的调节,可以保持输出电压Vo稳定。由于MRSTC是开环的,保持Vo不变即保持MRSTC的输入电压Vin1不变。输入电压变化的部分由FSBB的输入电容Cb承担,即表征为FSBB的输入电压Vin2发生相应变化。当输出电压Vo与输出电流Io不变时,输入振动也反映为MRSTC与FSBB对应输出电流Io(MRSTC)与Io(FSBB)的改变。输入电压扰动时的电压和功率分配如图8所示。定义FSBB处理的功率PFSBB与总功率Po之比为k,满足
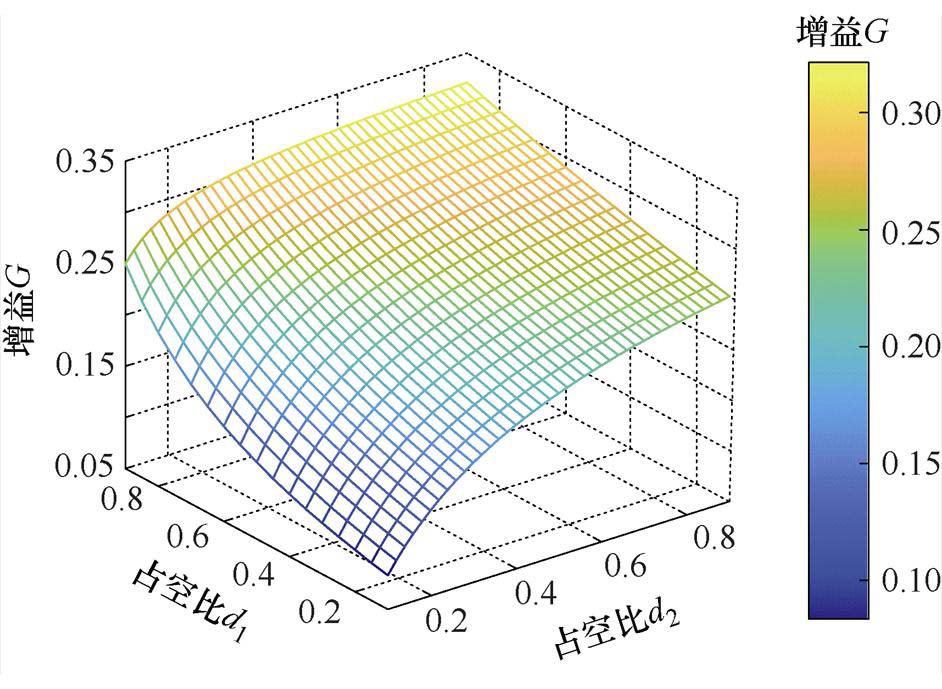
图6 4 1 MRSTC-FSBB电压增益曲线
1 MRSTC-FSBB电压增益曲线
Fig.6 4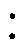 1 MRSTC-FSBB voltage gain surface
1 MRSTC-FSBB voltage gain surface
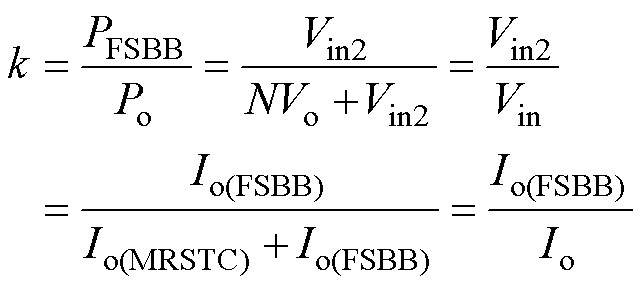 (9)
(9)
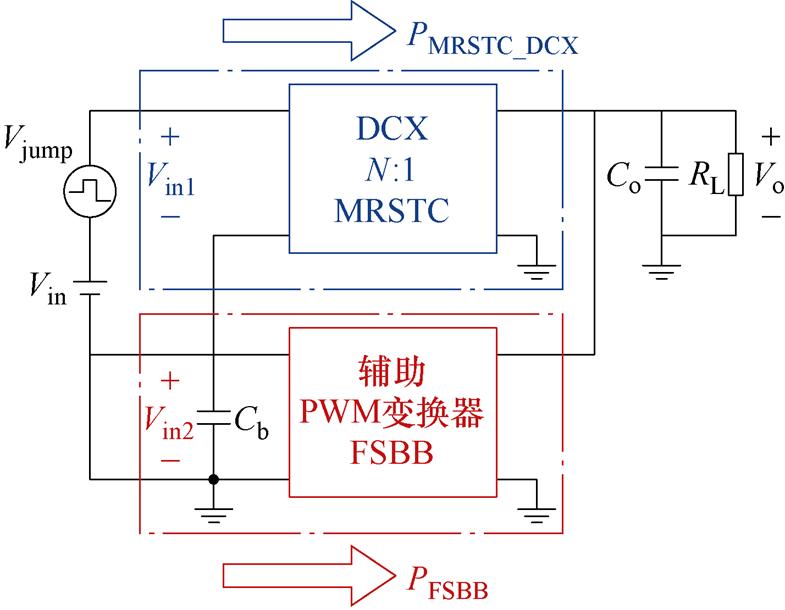
图7 输入电压扰动时的等效电路
Fig.7 Equivalent circuit during input voltage disturbance
实际应用时,由于元件大批量生产导致其参数容差以及长期运行下元件参数发生变化,将导致变换器的开关频率fs与谐振频率fr不可能完全相等。传统RSCC对谐振参数容差十分敏感,会导致软开关特性失效以及导通损耗剧增,而本文所提MRSTC对谐振参数容差适应性较高。
图8 输入电压扰动时的电压和功率分配
Fig.8 Voltage and power distribution during input voltage disturbance
1.3.1 RSCC
RSCC所用串联谐振腔的基本单元如图9所示,当开关频率小于谐振频率(fs<fr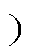 时,谐振电流过零点后会出现反向谐振;而当开关频率大于谐振频率(fs>fr)时,开关管会在谐振电流尚未过零就提前关断。考虑谐振电容存在±20%的偏差,谐振腔电流itank的波形如图10所示。
时,谐振电流过零点后会出现反向谐振;而当开关频率大于谐振频率(fs>fr)时,开关管会在谐振电流尚未过零就提前关断。考虑谐振电容存在±20%的偏差,谐振腔电流itank的波形如图10所示。
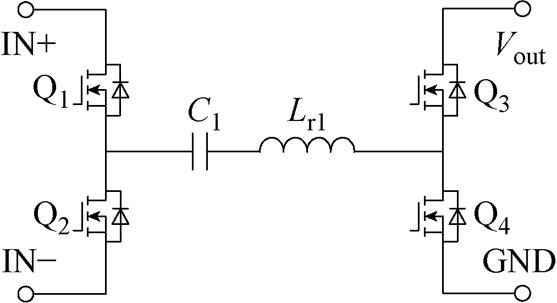
图9 串联谐振腔基本单元
Fig.9 Structure with a series-resonant tank
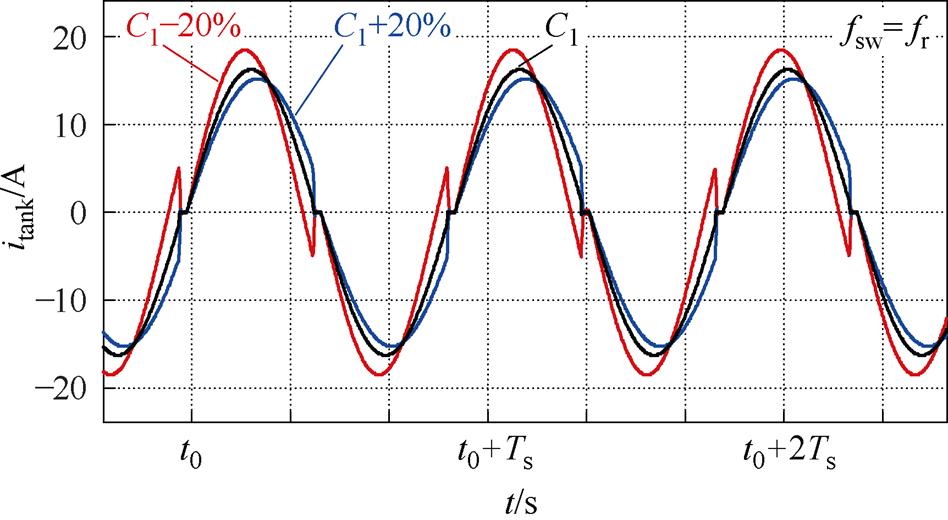
图10 RSCC中谐振腔电流itank的波形
Fig.10 Waveforms of with itank in RSCC
为了进一步研究ZCS失效的影响,可以对电流itank的波形做进一步分析。假设谐振参数误差存在,以fs<fr为例,在模态1 [t0, t1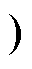 中,谐振腔电流itank将在谐振过零点后,反向谐振一段时间,直至t1时刻硬关断,将其波形重新绘制如图11所示。为了在下一个导通状态开始前使电流itank回零,需要留有一定的死区时间。因此,RSCC的开关周期Ts,可拆分为两个导通时间ton和两个死区时间td,即
中,谐振腔电流itank将在谐振过零点后,反向谐振一段时间,直至t1时刻硬关断,将其波形重新绘制如图11所示。为了在下一个导通状态开始前使电流itank回零,需要留有一定的死区时间。因此,RSCC的开关周期Ts,可拆分为两个导通时间ton和两个死区时间td,即
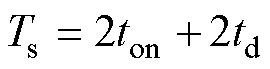 (10)
(10)
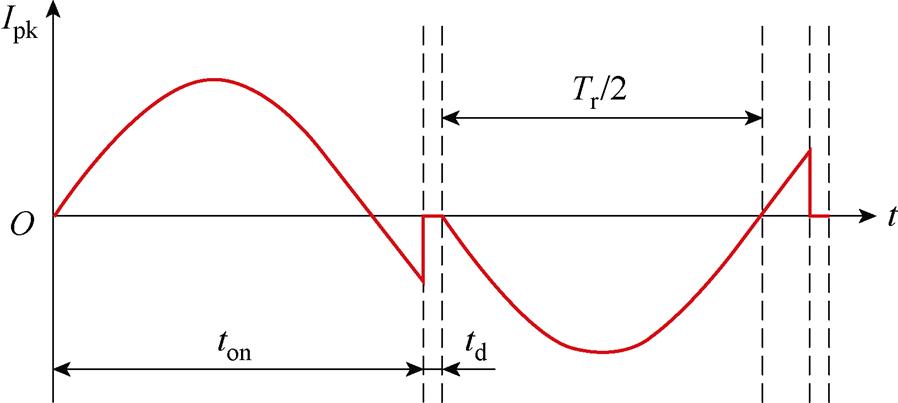
图11 串联谐振腔中itank的波形
Fig.11 Waveforms of itank in a series-resonant tank
半个开关周期内,可将谐振腔电流itank(t)的时域解改写为
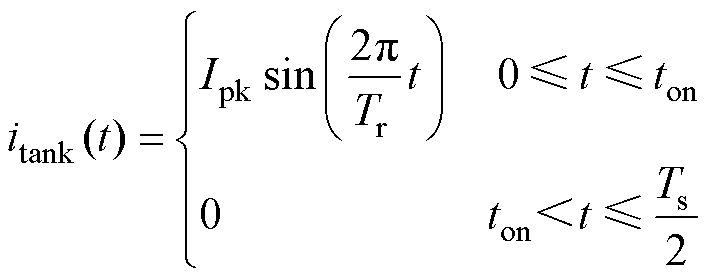 (11)
(11)
式中,Ipk为谐振腔电流itank(t)的峰值。定义中间变量a、l、fn分别为
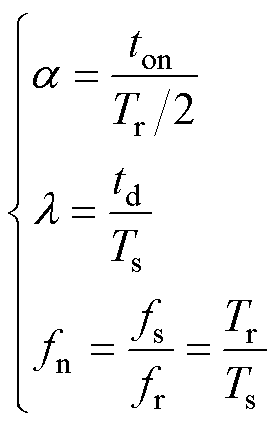 (12)
(12)
谐振腔电流itank的表达式可重写为
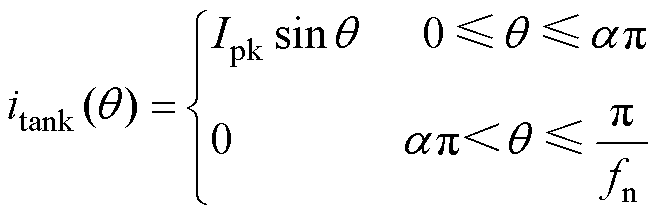 (13)
(13)
半个开关周期内谐振腔电流itank的平均值等于输出电流平均值Io,即
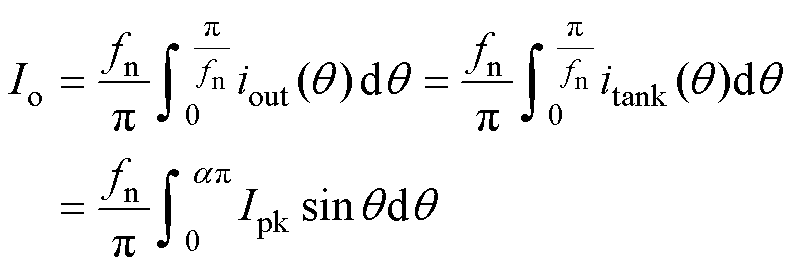 (14)
(14)
得出峰值电流Ipk与输出电流平均值Io的关系为
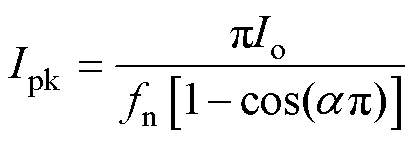 (15)
(15)
假定Rloop为谐振回路的寄生电阻,谐振腔电流的有效值Itrms与itank满足
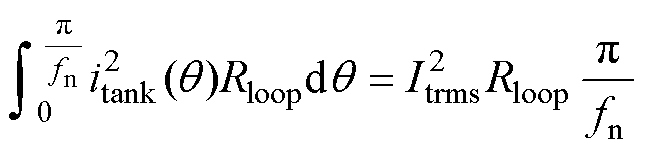 (16)
(16)
求得谐振腔电流的有效值Itrms为
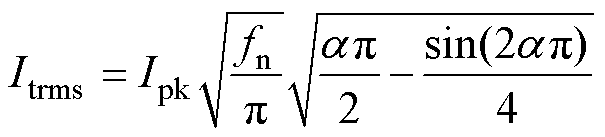 (17)
(17)
定义电流标幺值In为谐振腔电流的有效值Itrms与输出电流平均值Io的比值,即
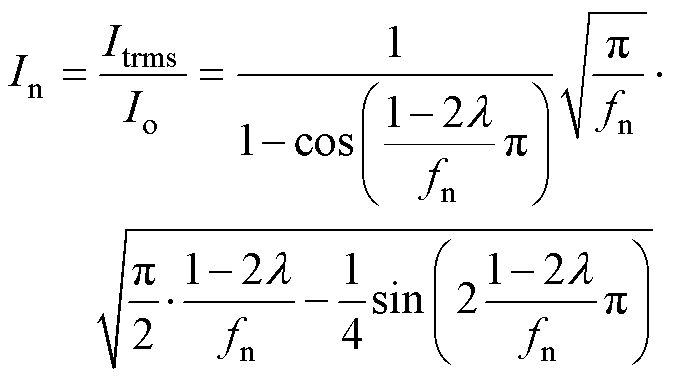 (18)
(18)
1.3.2 MRSTC
MRSTC所用多谐振腔的基本单元如图12所示,参照1.3.1节分析RSCC的方法,对MRSTC的三元件谐振腔流出的电流itank的波形做进一步分析如图13所示。将谐振电感电流iLr1、并联电容的电流iC1、谐振腔流出的电流itank的波形重新绘制如图14所示。
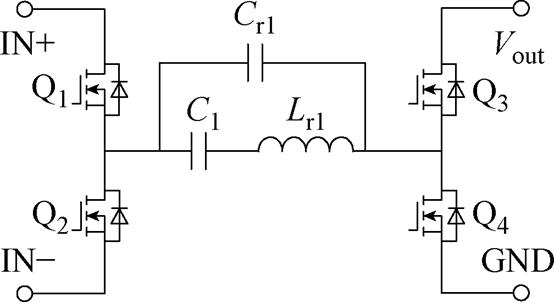
图12 多谐振腔基本单元
Fig.12 Structure with a multi-resonant tank
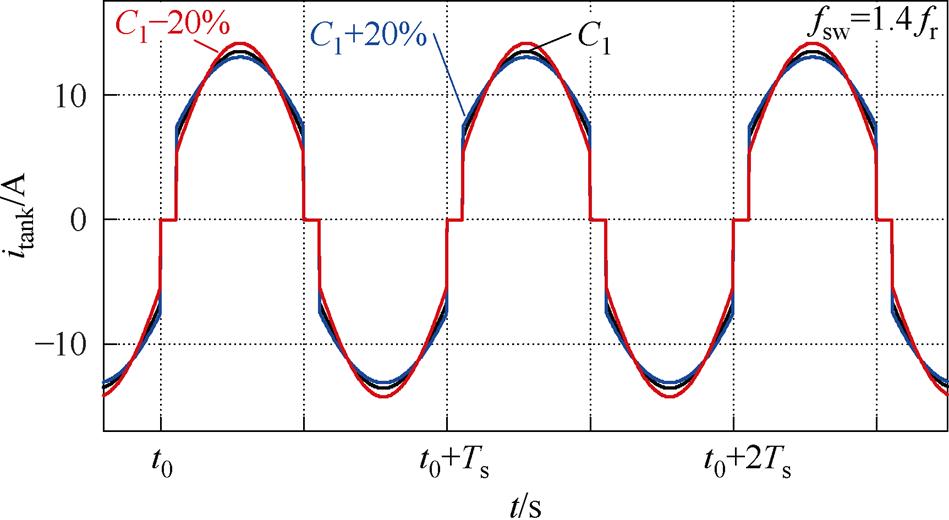
图13 MRSTC中谐振腔电流itank的波形
Fig.13 Waveforms of with itank in MRSTC
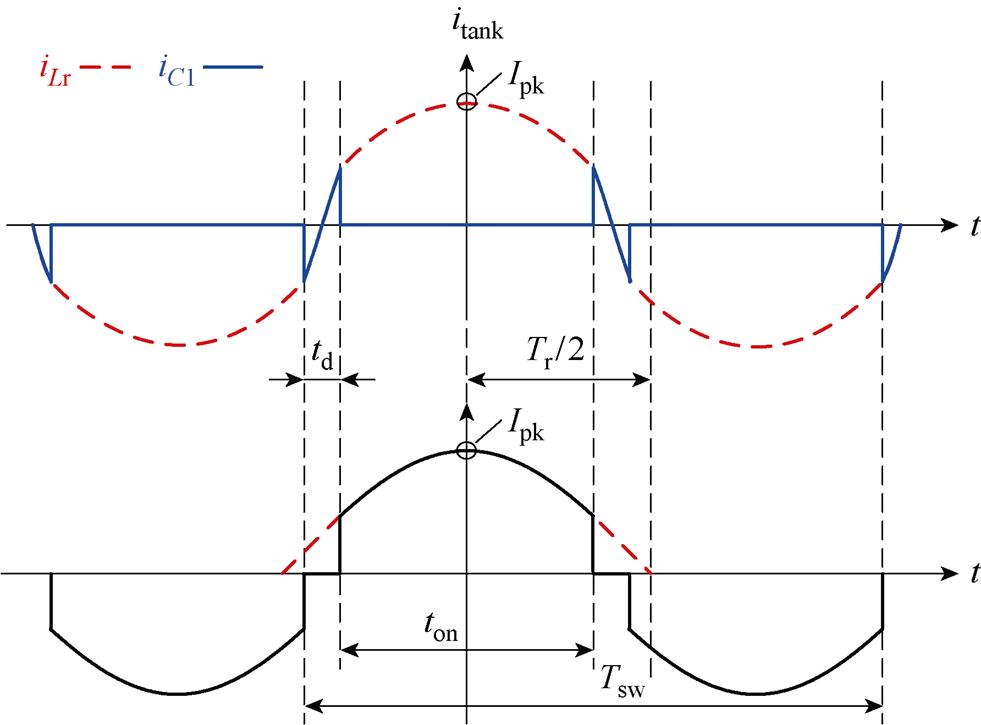
图14 多谐振腔中itank的波形
Fig.14 Waveforms of itank in a multi-resonant tank
半个开关周期内,谐振腔电流itank可用余弦表示为
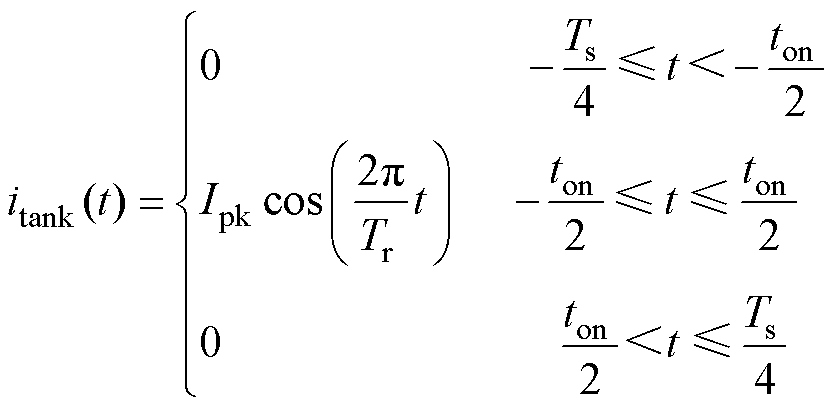 (19)
(19)
引入式(12)所定义的中间变量a、l、fn,谐振腔电流itank可表示为
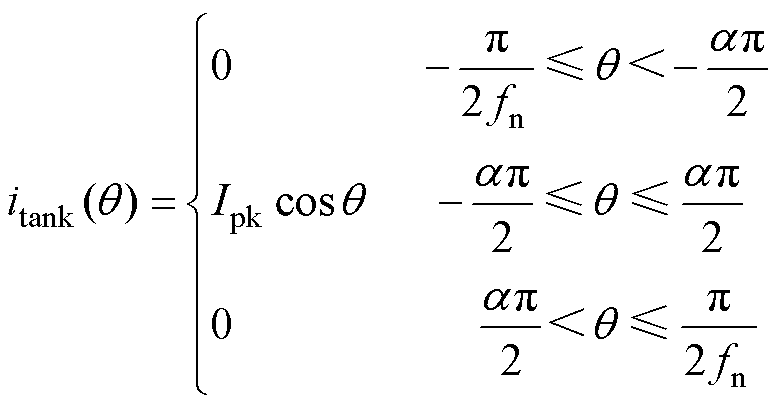 (20)
(20)
同理,可得出峰值电流Ipk与输出电流平均值Io的关系为
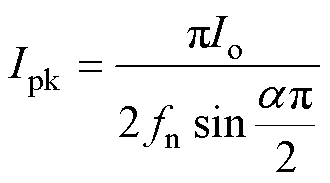 (21)
(21)
求得谐振腔电流的有效值Itrms为
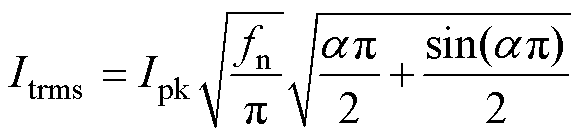 (22)
(22)
可以推导MRSCC的电流标幺值In为
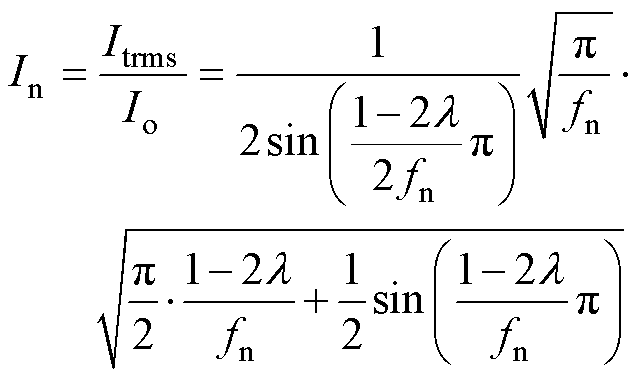 (23)
(23)
根据式(18)和式(23)可分析电流标幺值In、归一化开关频率fn与死区时间td之间的关系。通过取l=0.03,依据式(18)和式(23),绘制RSCC与MRSTC电流标幺值In与归一化开关频率fn的关系,如图15所示,可以作出以下几点分析:
(1)当归一化开关频率fn=1,即fs=fr时,MRSCC与RSCC一样,对应电流标幺值In=1.11(pu),此时MRSTC的导通模态内,电流波形为正弦波。
(2)随着归一化开关频率fn逐渐变大,MRSTC的电流标幺值In呈单调递减的趋势,即开关频率越高,谐振腔电流有效值越接近输出电流平均值,从波形上看,即谐振腔电流更加接近于方波。与正弦波相比,方波可以传递更多的能量。
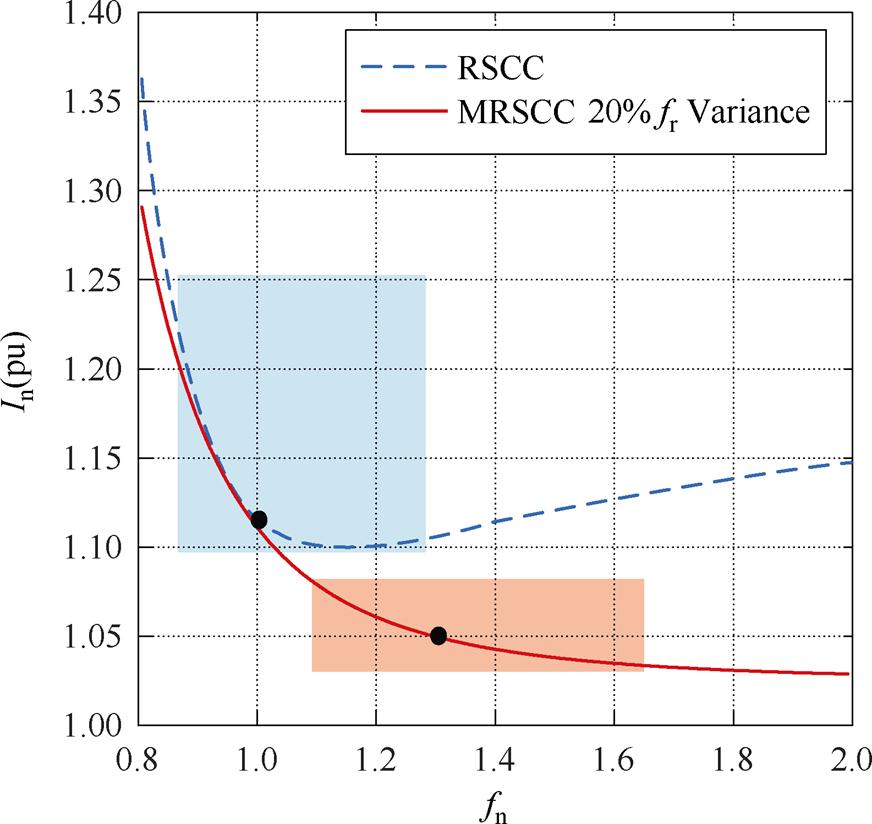
图15 l=0.03时,RSCC与MRSTC Invs.fn
Fig.15 When l=0.03 Invs.fn (RSCC and MRSTC)
(3)通过MRSCC和RSCC电流标幺值In与归一化开关频率fn的关系曲线的对比,可以很明显看出,在同样的谐振参数误差下,MRSCC不仅对应电流标幺值In的值更小,并且对应电流标幺值In的变化范围更小。
(4)图12中的多谐振腔基本单元包含两个谐振频率,在Ton时间内,C1与Lr1串联谐振,由于Cr1容值远小于C1,阻抗较大,所以不会影响串联谐振槽的能量传递过程。而在死区时间td内,C1、Lr1、Cr1构成一个陷波器,其谐振频率为陷波谐振频率fr2,由于Cr1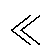 C1,所以陷波谐振频率可认为仅由Cr1和Lr1决定。利用陷波谐振频率的带阻性质,可使谐振腔达到降低变换器对谐振参数容差敏感性的目的。且通过参数设计,使得死区时间td为陷波谐振周期的一半,利用陷波谐振频率的带阻特性在死区时间内翻转谐振电感电流,使其反向。根据上述特性,陷波谐振频率可用其他拓扑实现,同样可以实现降低变换器对谐振参数容差敏感性的目的。
C1,所以陷波谐振频率可认为仅由Cr1和Lr1决定。利用陷波谐振频率的带阻性质,可使谐振腔达到降低变换器对谐振参数容差敏感性的目的。且通过参数设计,使得死区时间td为陷波谐振周期的一半,利用陷波谐振频率的带阻特性在死区时间内翻转谐振电感电流,使其反向。根据上述特性,陷波谐振频率可用其他拓扑实现,同样可以实现降低变换器对谐振参数容差敏感性的目的。
综上所述,通过对RSCC与MRSTC电流标幺值In与归一化开关频率fn的关系进行对比,证明MRSTC具有更低的导通损耗,其谐振腔电流受谐振参数容差的影响更小,对无源元件的参数容差具有更高的适应力。得益于此,MRSCC可以采用Ⅱ类陶瓷电容器,从而降低生产成本。
图16给出了RSCC与MRSCC在谐振频率fr标准与偏高20%情况下的变换器损耗Ploss与输出电流平均值Io的关系。从图16中可以看出,RSCC变换器在失去软开关特性后,随着输出功率的增大,其损耗会明显增加,而MRSCC变换器的损耗受谐振参数容差的影响很小。由于MRSCC本身工作在fs>fr,当fr偏高时,进一步接近fs,变换器开关损耗会降低。考虑到实际运行中电容老化等因素,谐振频率fr偏高是大概率事件。因此MRSCC适合长期运行,而RSCC会由于导通损耗剧增,效率越来越低。由于开关管硬开关及开关频率fs较高的原因,在轻载时,MRSCC损耗高于RSCC,但随着负载增大,导通损耗成为主导损耗,MRSCC更小的电流有效值会使其比RSCC更加高效。
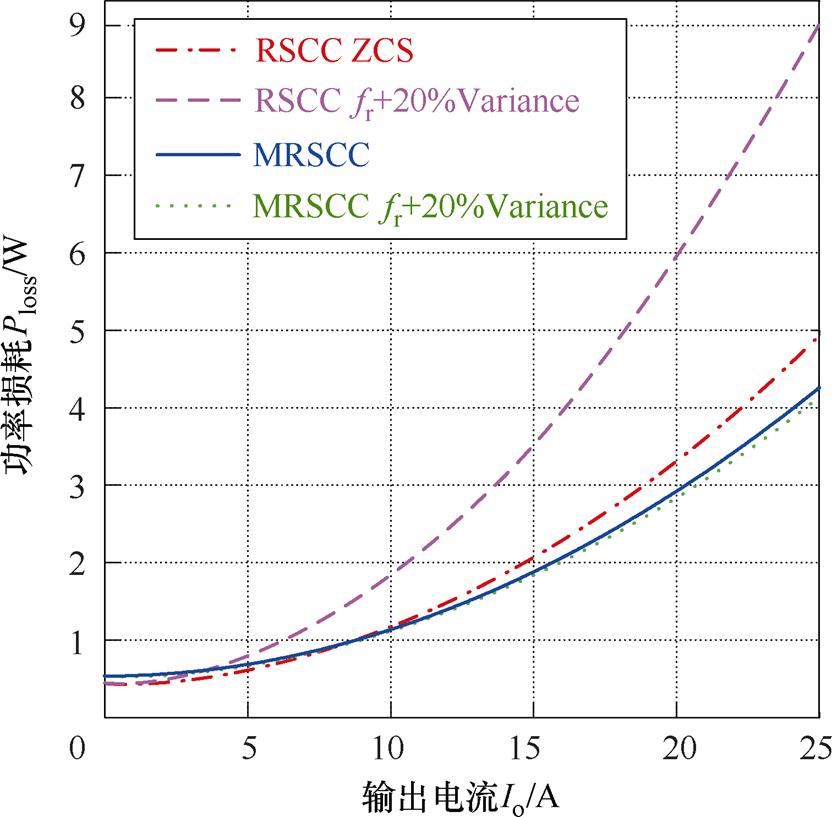
图16 RSCC与MRSCC损耗对比
Fig.16 Comparison of losses between RSCC and MRSCC
目前,FSBB的软开关控制方法已有许多研究成果,但其必要条件都是电感电流iLb可以实现反向流动。但在准并联架构中,这种电流倒灌会使系统不稳定,因此,本节中FSBB采用硬开关控制,通过采用双沿调制[29-30],增加直接功率比重,来提升效率。同时,为了抑制FSBB在输入电压额定值附近反复切换,并提升变换器在输入电压额定值附近的效率,可以采用三模式粗调节的控制方法[25],如图17所示。引入宽度为2DV1的滞环,在区间[40 V, 48 V-DV1]和[48 V+DV1, 60 V]中,FSBB分别以Boost模式和Buck模式工作,在区间[48 V-DV1, 48 V+DV1]内,FSBB工作于滤波模式,等效为一个LC滤波器,而MRSTC-FSBB整体可等效为一个开环的4 1 MRSTC。在本文所提MRSTC-FSBB中,滞环宽度会由于DCX的作用缩小4倍。为了改善滤波模式与Buck模式和Boost模式切换点处的占空比突变问题,可借鉴文献[3]做法,将Boost模式和Buck模式下的输出电压参考值分别设为11.5 V和12.5 V。表1为FSBB在输入电压范围内控制模式的区域划分、驱动信号、输出参考电压以及处理功率比k等信息。
1 MRSTC。在本文所提MRSTC-FSBB中,滞环宽度会由于DCX的作用缩小4倍。为了改善滤波模式与Buck模式和Boost模式切换点处的占空比突变问题,可借鉴文献[3]做法,将Boost模式和Buck模式下的输出电压参考值分别设为11.5 V和12.5 V。表1为FSBB在输入电压范围内控制模式的区域划分、驱动信号、输出参考电压以及处理功率比k等信息。
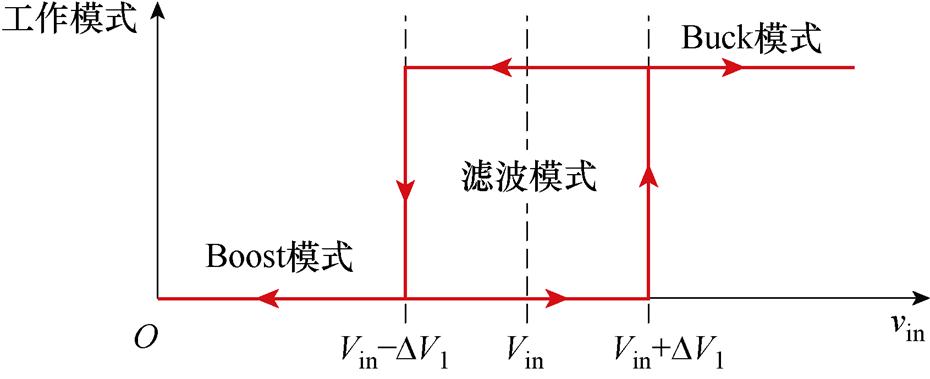
图17 三模式滞环控制
Fig.17 Three mode hysteresis control
表1 FSBB控制模式区域划分
Tab.1 Area division of FSBB control mode
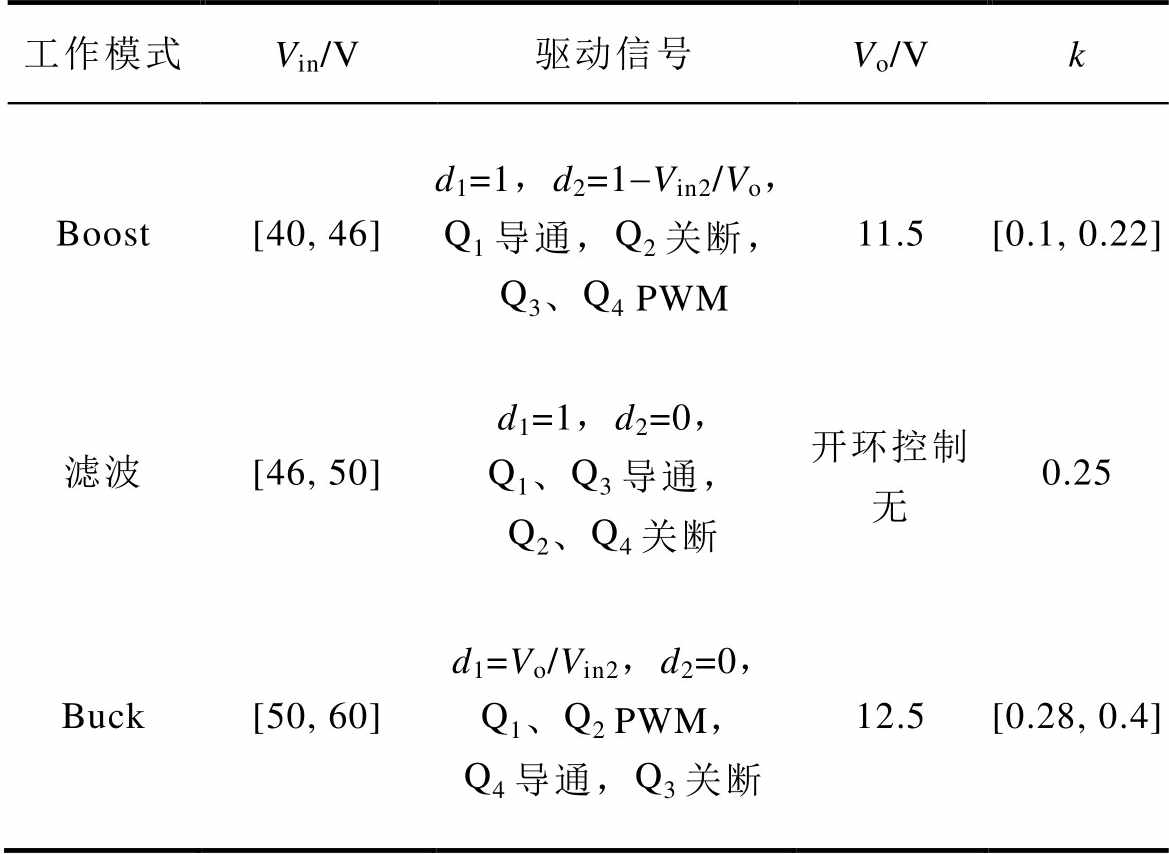
工作模式Vin/V驱动信号Vo/Vk Boost[40, 46]d1=1,d2=1-Vin2/Vo,Q1导通,Q2关断,Q3、Q4 PWM11.5[0.1, 0.22] 滤波[46, 50]d1=1,d2=0,Q1、Q3导通,Q2、Q4关断开环控制无0.25 Buck[50, 60]d1=Vo/Vin2,d2=0,Q1、Q2 PWM,Q4导通,Q3关断12.5[0.28, 0.4]
图18与图19给出了MRSTC-FSBB在Buck模式和Boost模式下的小信号等效电路。式(24)和式(25)为Buck模式输出电压扰动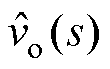 对占空比扰动
对占空比扰动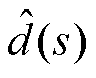 的传递函数Gvd_Buck(s)与电感电流扰动
的传递函数Gvd_Buck(s)与电感电流扰动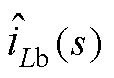 对占空比扰动
对占空比扰动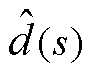 的传递函数Gid_Buck(s),式(26)和式(27)为Boost模式下Gvd_Boost(s)和Gid_Boost(s),式中系数可参见附录。
的传递函数Gid_Buck(s),式(26)和式(27)为Boost模式下Gvd_Boost(s)和Gid_Boost(s),式中系数可参见附录。
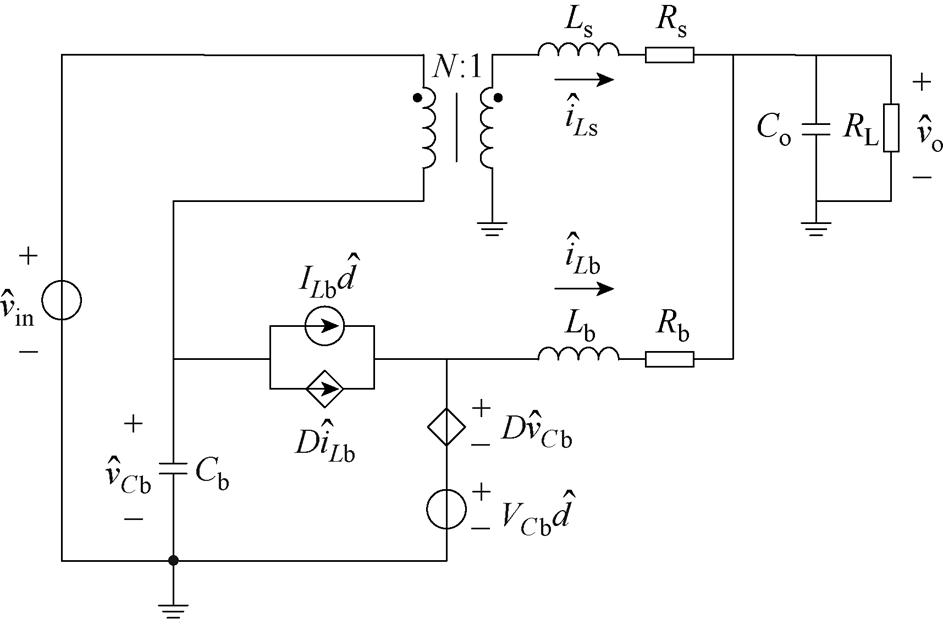
图18 Buck模式下的小信号等效电路
Fig.18 Small signal equivalent circuit in Buck mode
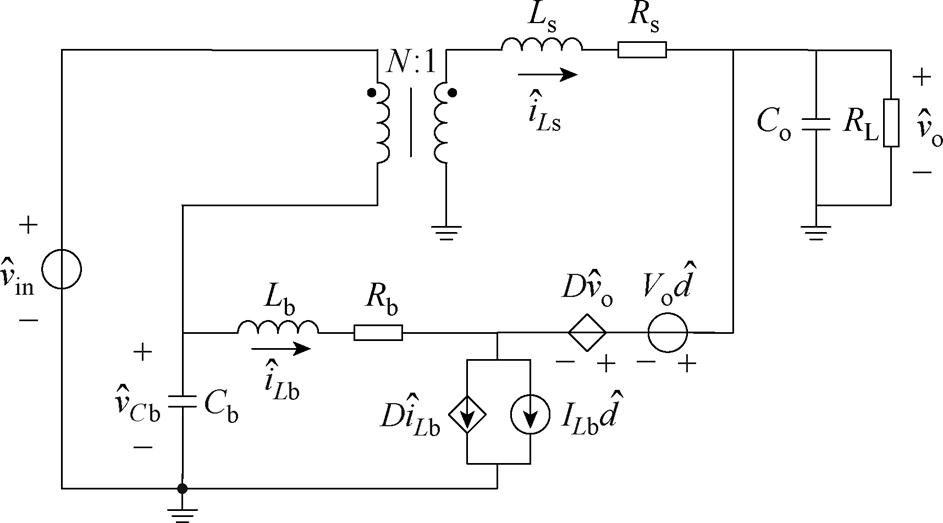
图19 Boost模式下的小信号等效电路
Fig.19 Small signal equivalent circuit in Boost mode
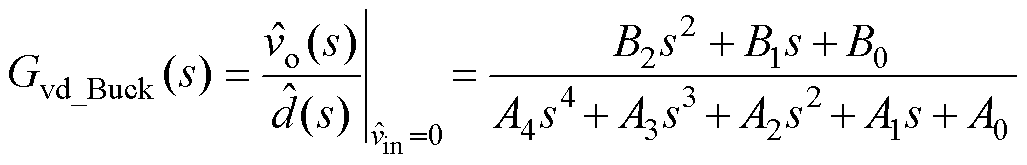 (24)
(24)
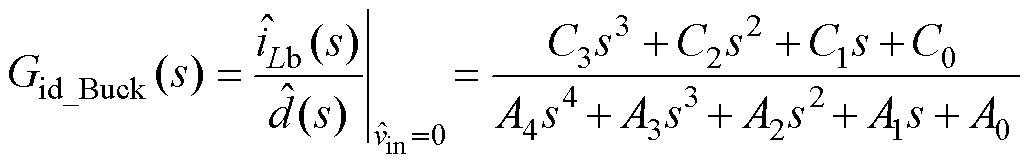 (25)
(25)
 (26)
(26)
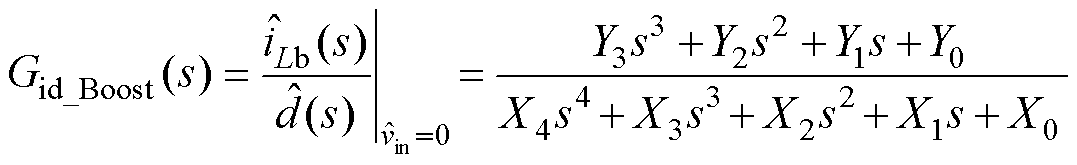 (27)
(27)
根据式(24)~式(27)可以绘制出两模式下Gvd(s)和Gid(s)的伯德图与零极点,如图20~图23所示。可见,在基于准并联架构的MRSTC-FSBB中,无论Buck模式还是Boost模式,其Gid(s)中均包含了右半平面零点,属于非最小相位系统,其对数相频特性曲线均从0°快速跌落至-270°。通过引入电流环控制改善变换器Boost模式下工作性能的想法难以实现。因此本文采用单电压环控制,控制框图如图24所示。图中,Hv(s)为输出电压的反馈系数;GM(s)为PWM的调制函数,可视为一个线性环节,GM(s)=1/VM,VM为PWM的调制电压;Gvc(s)为补偿器。
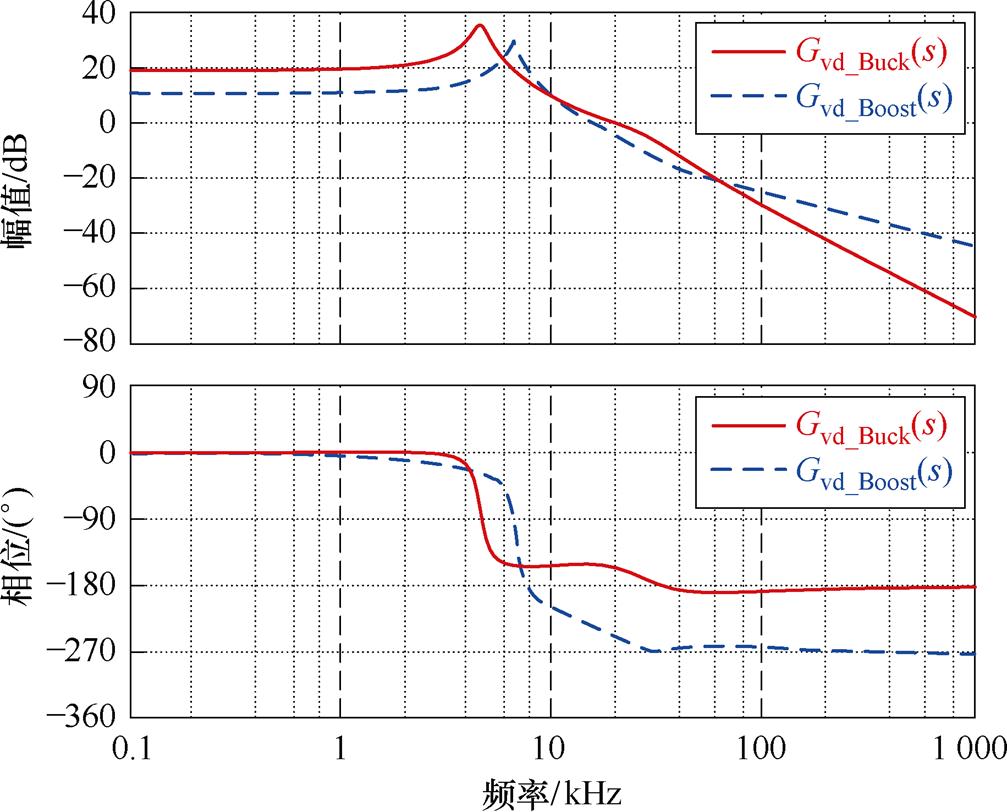
图20 Buck和Boost模式下Gvd(s)伯德图
Fig.20 Bode plots of Gvd(s) in Buck mode and Boost mode
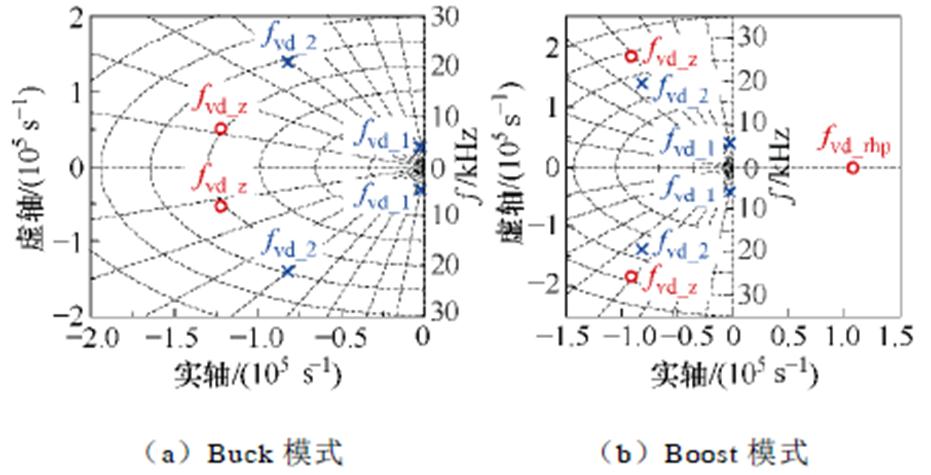
图21 Gvd(s)的零极点分布
Fig.21 Zero pole distribution maps of Gvd(s)
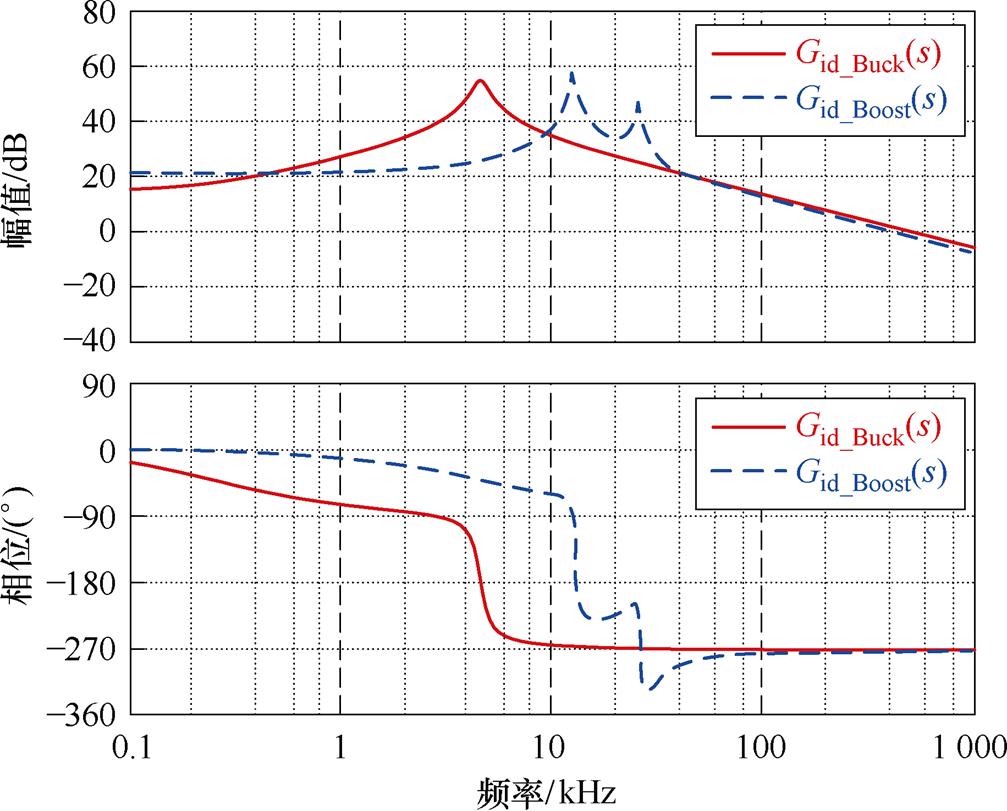
图22 Buck和Boost模式下Gid(s)伯德图
Fig.22 Bode plots of Gid(s) in Buck mode and Boost mode
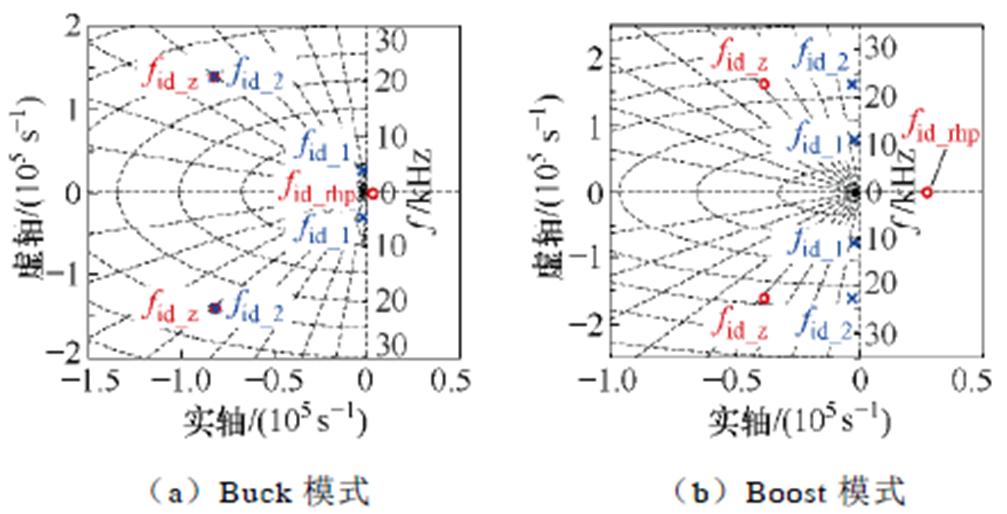
图23 Gid(s)的零极点分布
Fig.23 Zero pole distribution maps of Gid(s)
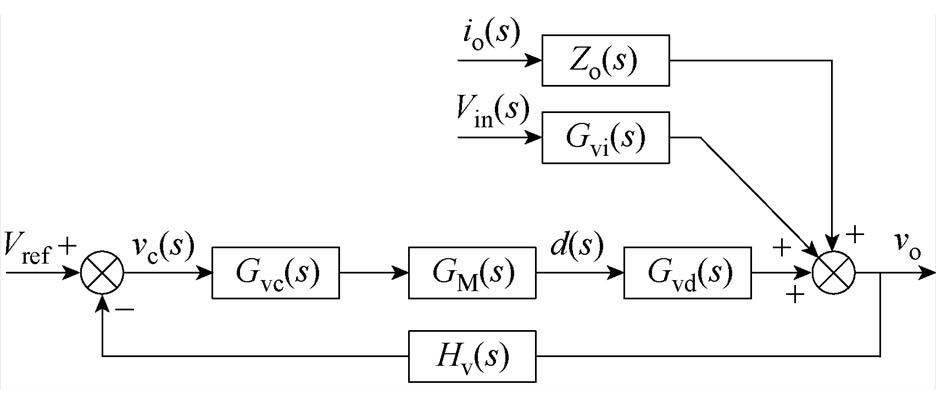
图24 单电压环控制框图
Fig.24 Single voltage loop control block diagram
所设计的两模式Type Ⅲ补偿器的传递函数为
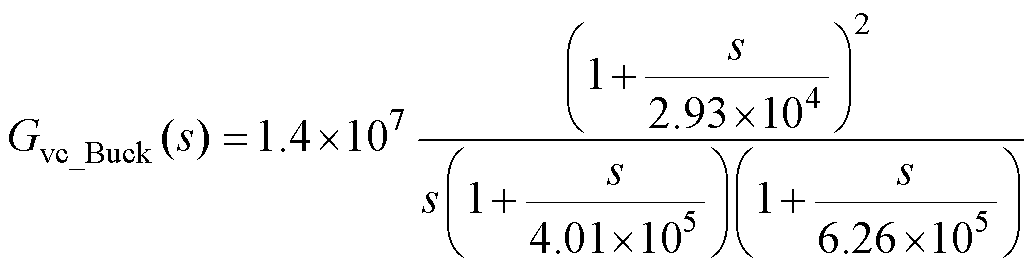 (28)
(28)
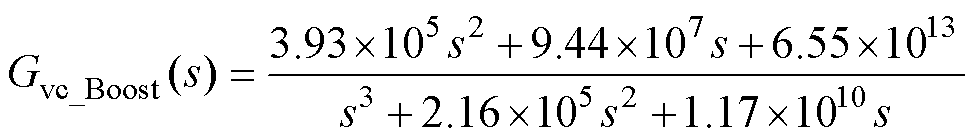 (29)
(29)
图25为两模式下系统补偿前后的伯德图。Buck模式下系统补偿后穿越频率为20 kHz,相位裕度为61°;Boost模式下考虑右半平面零点的影响,穿越频率只能设置在转折频率f1之前,通过在Type Ⅲ补偿器中引入二阶微分环节,消弭了f1处的谐振峰,补偿后穿越频率为3 kHz,系统带宽和稳定裕度均可以满足稳定性设计要求。
为验证所提出变换器的可实施性与理论分析的正确性,搭建了一台输入电压额定48 V(40~60 V),输出电压12 V,额定功率300 W的实验样机,所搭建的样机如图26所示,变换器中各元器件参数及型号见表2、表3。
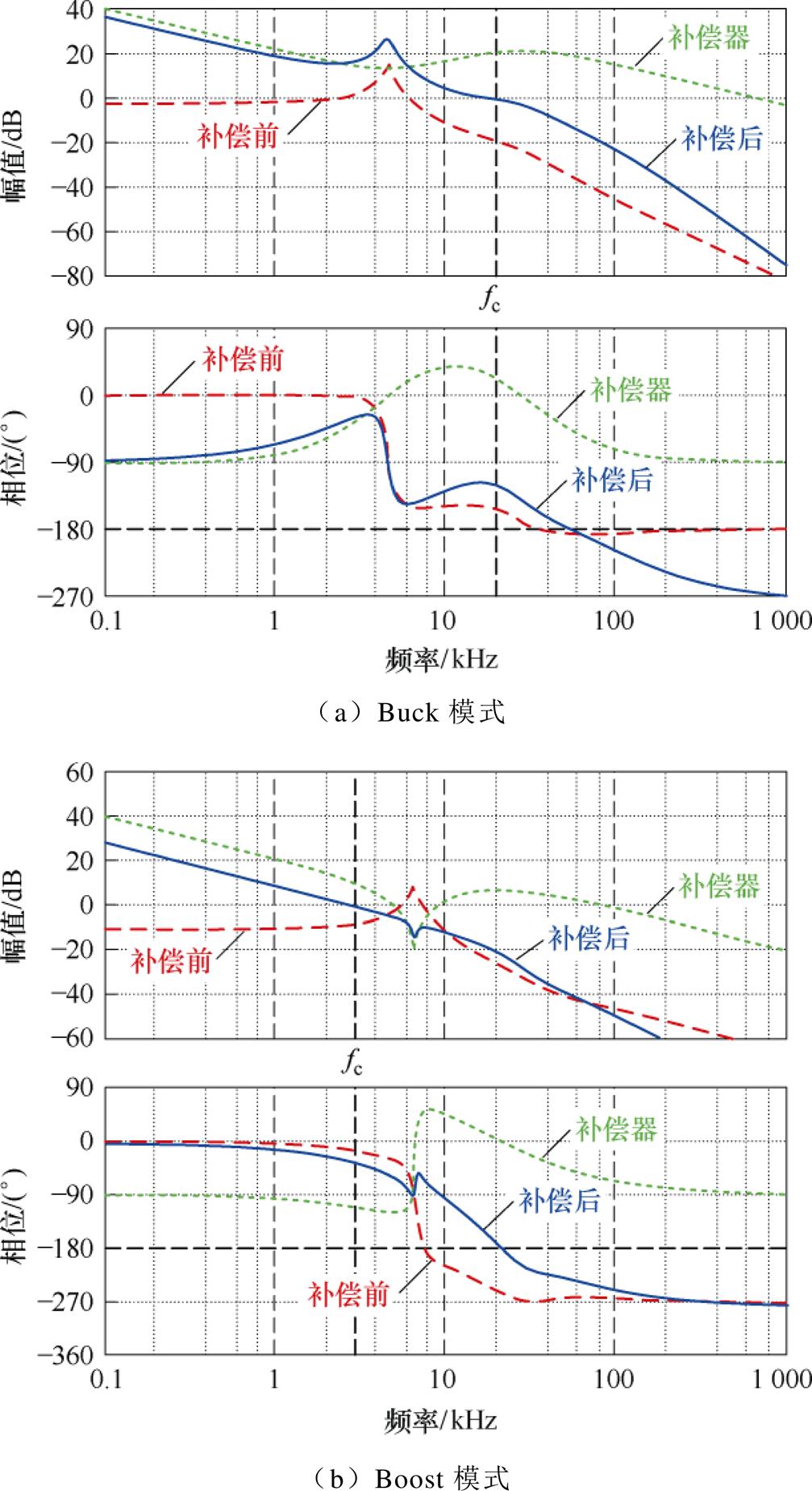
图25 电压调节器Gc(s)补偿前后的伯德图
Fig.25 Bode plots before and after voltage regulator Gc(s) compensation
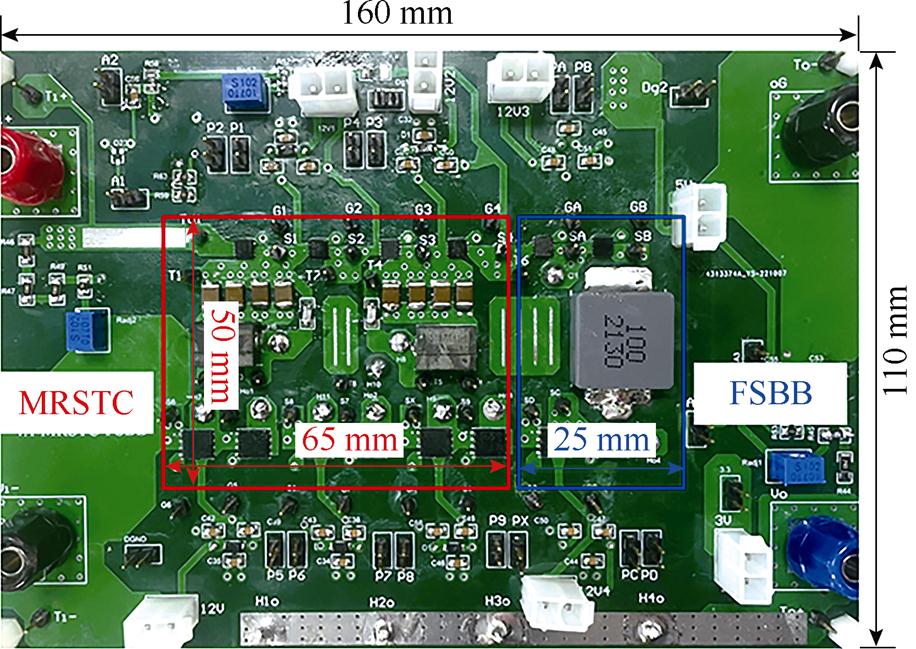
图26 样机
Fig.26 Prototype
表2 MRSTC参数设计与器件选型
Tab.2 Key parameters and selection of MRSTC

参 数型 号 谐振电容Cr160 mF (10 mF×6), X7R, ±10%, 50 V,1812封装, Kemet, C1812C106K3RACTU 钳位电容CF132 mF (22 mF×6), X7R, ±10%, 50 V,1210封装, Kemet, C1210C226K8RACTU 谐振电容Cr219.8 mF (3.3 mF×6), X7R, ±10%, 50 V,1812封装, Kemet, C1812C335K5RACTU 多谐振电容C1, C233 nF, C0G, ±5%, 80 V,1206封装, muRata, GCM3195C1K333JA16D 谐振电感Lr1, Lr2181 nH, ±10%, 0.12 mW, Pulse, PA5187.181HLT 翼侧开关管Q1a, Q2bBSZ018N04LS6, 40 V, 27 A, 1.8 mW 整流开关管Q3a,Q5bBSC009NE2LS5I, 25 V, 40 A, 0.95 mW
表3 FSBB参数设计与器件选型
Tab.3 Key parameters and selection of FSBB

参 数型 号 输入电容Cb132 mF (22 mF×6), X7R, ±10%, 50V1210封装, Kemet, C1210C226K8RACTU 谐振电感Lb10 mH, ±20%, 11.2 mW, 16.8 A,台庆, TMPC1707HP-100MG-D 开关管Q1, Q2BSZ018N04LS6, 40 V, 27 A, 1.8 mW 开关管Q3, Q4BSC009NE2LS5I, 25 V, 40 A, 0.95 mW
3.1.1 基本单元的电流应力
假定所设计的MRSTC,输出电压为Vo,最大输出功率为Po。由于(N+1)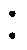 1 MRSTC包含N个基本单元,且第N个单元输入侧也向负载供电,每个基本单元整流侧的输出电流平均值Iox(x=1, 2, 3,…, N)为
1 MRSTC包含N个基本单元,且第N个单元输入侧也向负载供电,每个基本单元整流侧的输出电流平均值Iox(x=1, 2, 3,…, N)为
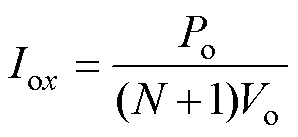 (30)
(30)
与2 1 MRSCC不同的是,(N+1)
1 MRSCC不同的是,(N+1) 1 MRSTC的整流侧仅在一个导通时间ton内向负载侧传递能量,另外一个导通时间ton内,是向相邻基本单元传递能量,故半个开关周期内基本单元内电流itank的平均值是输出电流平均值Io的2倍。对于MRSCC单元,假设各单元参数一致,第x个基本单元的谐振腔电流itankx及其平均值Itankx可分别表示为
1 MRSTC的整流侧仅在一个导通时间ton内向负载侧传递能量,另外一个导通时间ton内,是向相邻基本单元传递能量,故半个开关周期内基本单元内电流itank的平均值是输出电流平均值Io的2倍。对于MRSCC单元,假设各单元参数一致,第x个基本单元的谐振腔电流itankx及其平均值Itankx可分别表示为
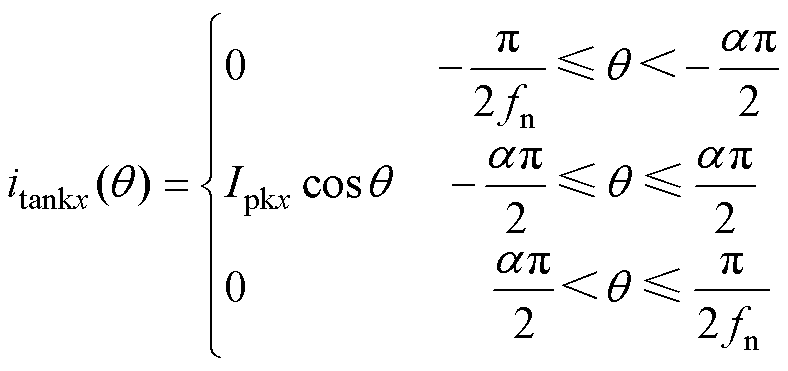 (31)
(31)
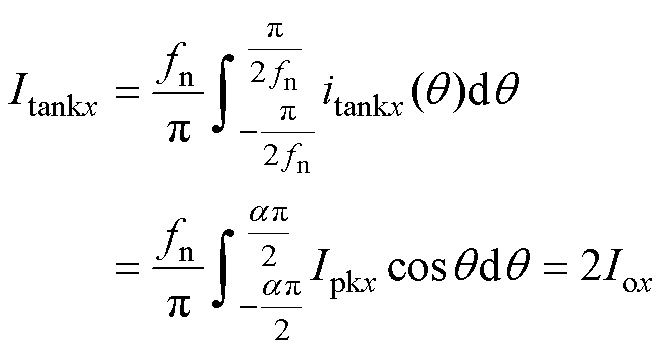 (32)
(32)
依据式(14)和式(30),可以得出第x个基本单元的峰值电流Ipkx与有效值Itrmsx分别与输出电流平均值Iox的关系为
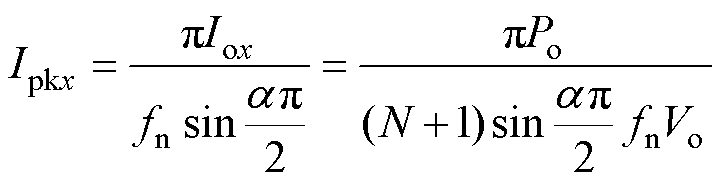 (33)
(33)
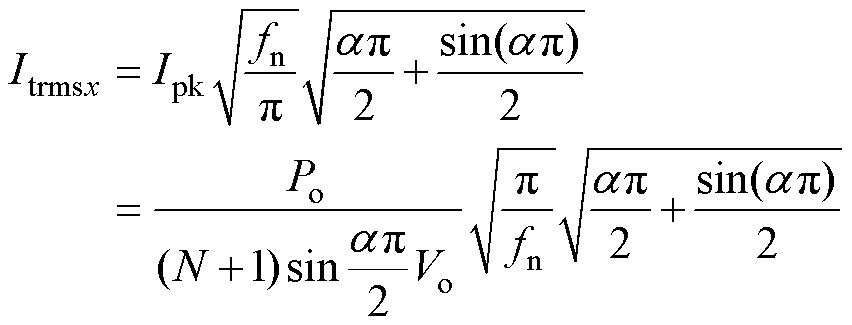 (34)
(34)
式(33)和式(34)为流过谐振电容Crx和谐振电感Lrx的电流峰值和有效值。
3.1.2 三元件谐振槽参数设计
1)谐振电容Crx
谐振电容Crx在半个开关周期内充电电荷DQ为
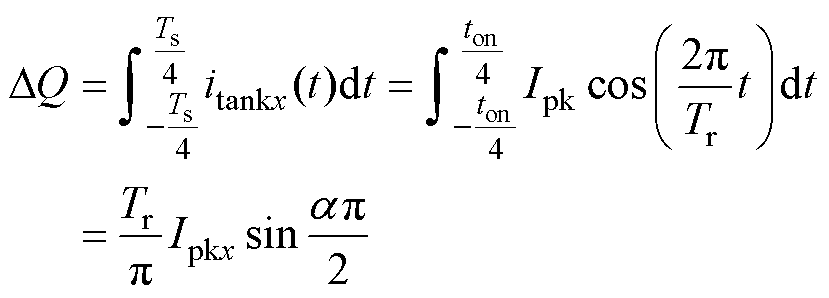 (35)
(35)
根据式(33),可得电荷变化量与额定功率的关系为
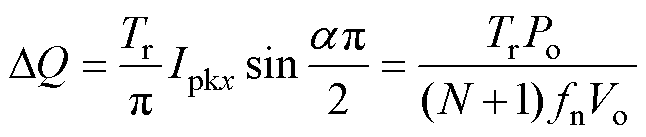 (36)
(36)
谐振电容Crx的电压纹波DVCrx为
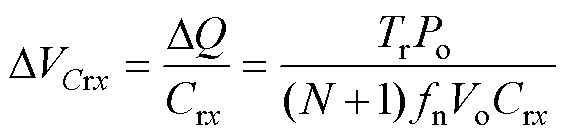 (37)
(37)
为了便于选型和设计,一般各谐振腔选取相同谐振参数,但不同谐振腔单元的直流偏置电压Vbias等级不同,若以高直流偏置电压为基准设计纹波,会导致低Vbias的谐振单元失去正常工作状态。因此要以最小的直流偏置电压Vbias来设计纹波,推荐谐振电容Crx的电压纹波DVCrx控制在输出电压 (20%~60%)Vo。选择具体器件型号时,需考虑谐振电容Crx的直流偏置电压Vbias,要以最高的Vbias值作为选择电容耐压值的基准。如果选择Ⅱ类陶瓷电容,需考虑直流偏置电压以及温升情况下的容值衰减。各谐振电容、多谐振电容与钳位电容的直流偏置电压Vbias见表4,逐级以Vo递减。
表4 (N+1)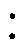 1 MRSTC中各级直流偏置电压
1 MRSTC中各级直流偏置电压
Tab.4 DC bias voltage at all levels in (N+1)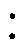 1 MRSTC
1 MRSTC

电 容Vbias Cr1, C1NVo CF2(N-1)Vo Cr3, C3(N-2)Vo CF4(N-3)Vo CrN, C2NVo
2)谐振电感Lrx
选择合适的谐振电容Crx后,根据选定的谐振频率fr和电流应力表达式(33)、式(34),再选择电感值合适的谐振电感Lrx。
3)多谐振电容Cx
为了实现MRSTC对元件参数差异的适应力,选定合适的死区时间td,在满足Cx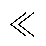 Crx的条件下,再对多谐振电容Cx取值。
Crx的条件下,再对多谐振电容Cx取值。
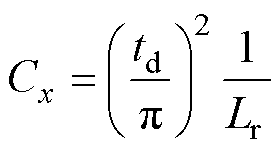 (38)
(38)
选择多谐振电容Cx的具体器件型号时,在耐压方面要考虑其直流偏置电压Vbias,由于有剩余电感电流流入,会存在电压尖峰,耐压裕度要设置高一点。由于死区时间td固定,多谐振电容Cx只能选择Ⅰ类陶瓷电容,从而保证陷波谐振频率fr2的稳定。
3.1.3 钳位电容CF
钳位电容单元中,钳位电容CF在半个开关周期内充电电荷也为DQ,其电压纹波DVCFx为
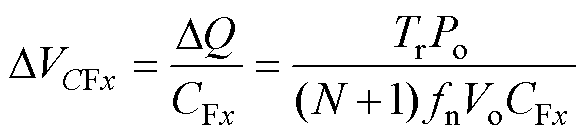 (39)
(39)
为了保证CFx不会影响电容Crx与电感Lrx发生串联谐振,需要设计CFx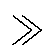 Crx,推荐钳位电容Crx的电压纹波DVCFx控制在输出电压Vo的5%以内。选择具体器件型号时,在耐压值方面要考虑直流偏置电压Vbias,为了节省成本,钳位电容CF一般选用Ⅱ类陶瓷电容。
Crx,推荐钳位电容Crx的电压纹波DVCFx控制在输出电压Vo的5%以内。选择具体器件型号时,在耐压值方面要考虑直流偏置电压Vbias,为了节省成本,钳位电容CF一般选用Ⅱ类陶瓷电容。
图27为输入电压额定且满载时,MRSTC的稳态工作波形。图27a为开关管Q3a的驱动电压Vgs_Q3a,谐振电容电压VCr1、钳位电容电压VCF和谐振电容电压VCr2的波形,各级的直流偏置电压依次为36 V、24 V、12 V,与表3相符。由于谐振腔电流不是完整的正弦波,故谐振电容Cr1、Cr2的充放电波形也不是完美的正弦波,而是包含部分正弦波形的类三角波,但电容依旧实现了软充放电,并且其电压纹波符合设计原则。钳位电容CF的电压VCF,由于直流偏置电压较大且其容值远大于谐振电容,电压纹波并不明显。多谐振电容C1和C2的电压波形如图27b所示,由于其并联于串联谐振腔两侧,直流偏置电压为谐振电容电压与谐振电感电压之和,故谐振电容的充放电纹波并不明显,仅在死区时间内有剩余电感电流流经,存在电压尖峰。
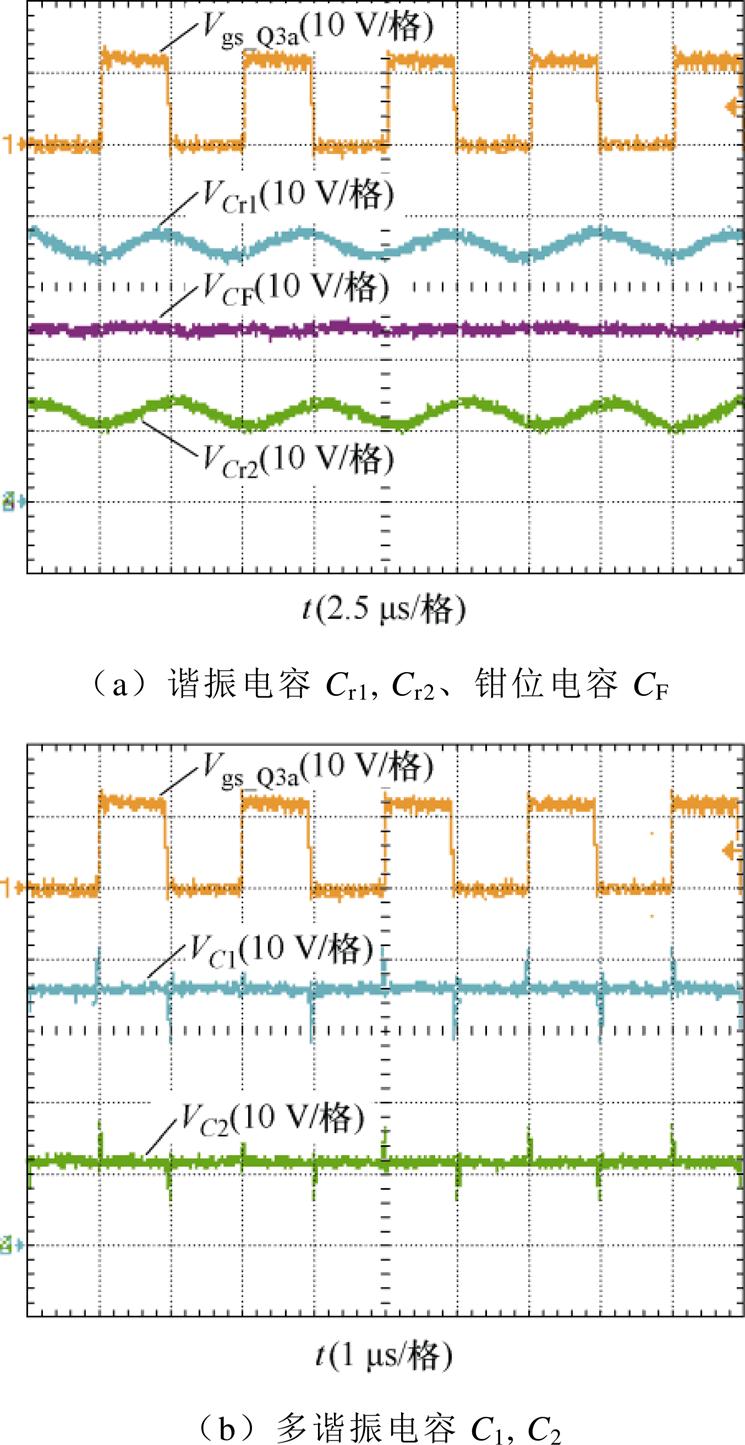
图27 额定输入时,MRSTC稳态时电容电压波形
Fig.27 Rated input, capacitor voltage steady-state waveforms of MRSTC
图28为额定输入时MRSTC稳态时电流波形,图中,两个谐振腔电流itank1和itank3的电流同相位,而钳位电容单元的电流itank2与两者相位相反,本质上钳位电容单元的电流是由相邻谐振腔半个开关周期的电流结合而成的,其电流依旧为谐振电容Cr1、Cr2的充放电电流,钳位电容只起到钳位稳压作用。由于采用Ⅱ类陶瓷电容,无法保证稳态工作时谐振电容Cr1、Cr2在直流偏置电压下的等效容值完全相等,故谐振腔电流itank1和itank3的波形也略有不同。由于模式切换时剩余电流大小不同,也会造成多谐振电容C1和C2死区内的电压尖峰大小不同。如果选用电容不当,可能造成不同单元间存在均流的问题,也可能造成多谐振电容C1和C2被击穿。
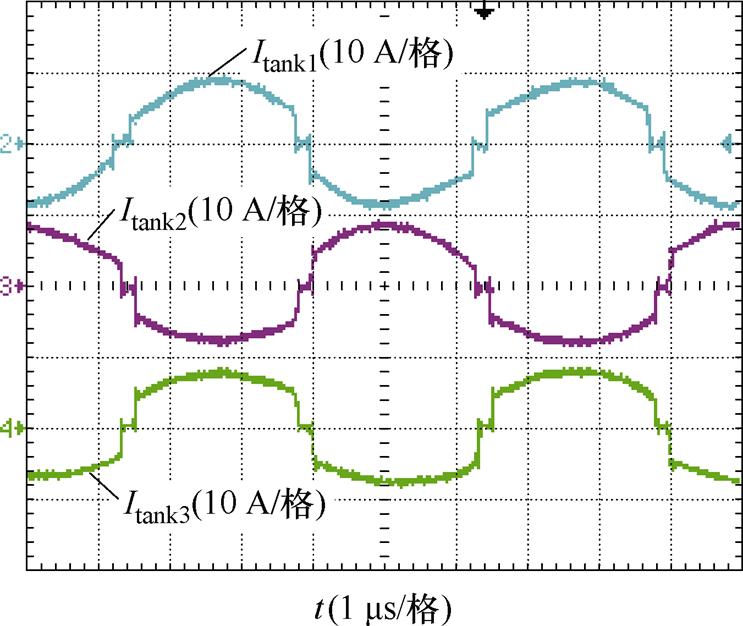
图28 额定输入时,MRSTC稳态时电流波形
Fig.28 Rated input, current steady-state waveforms of MRSTC
图29为额定负载满载下,MRSTC-FSBB中FSBB在不同模式工作时的稳态波形。其中,Vgs_Q1和Vgs_Q3为FSBB直接功率通路中开关管Q1和Q3的驱动电压波形,ILb为电感电流,VCb为FSBB输入电容Cb两端电压。当FSBB工作于滤波模式时,ILb脉动为零,当工作于Buck模式或Boost模式时,电感电流纹波为三角波。对比图29a~图29c可以看出,随着FSBB输入电压的变化,其处理的功率也在变化,滤波模式以及Buck模式下,电感电流ILb的平均值等于FSBB的输出电流平均值,其值随着输入电压的增大而增大,满足式(9)所述功率分配关系。Boost模式下,FSBB也是满足功率分配关系的,只是由于此时电感电流ILb的平均值等于FSBB的输入电流平均值,由于增益关系,ILb会比FSBB的输入电流平均值大,难以从波形中直接看出功率分配的大小关系。

图29 不同模式下,FSBB变换器的关键波形
Fig.29 Main waveforms of FSBB in different modes
图30为MRSTC-FSBB变换器在Buck模式和Boost模式负载跳变时的动态响应曲线,负载由半载切换至满载,可以看出输出电压在加载时无明显跌落,MRSTC的第一级谐振腔输出电流itank1,以及FSBB电感电流都存在一定的波动,Buck模式下,变换器在8 ms内调整完毕,Boost模式要25 ms左右的调节时间恢复到稳态,验证了所设计调节器的有效性。
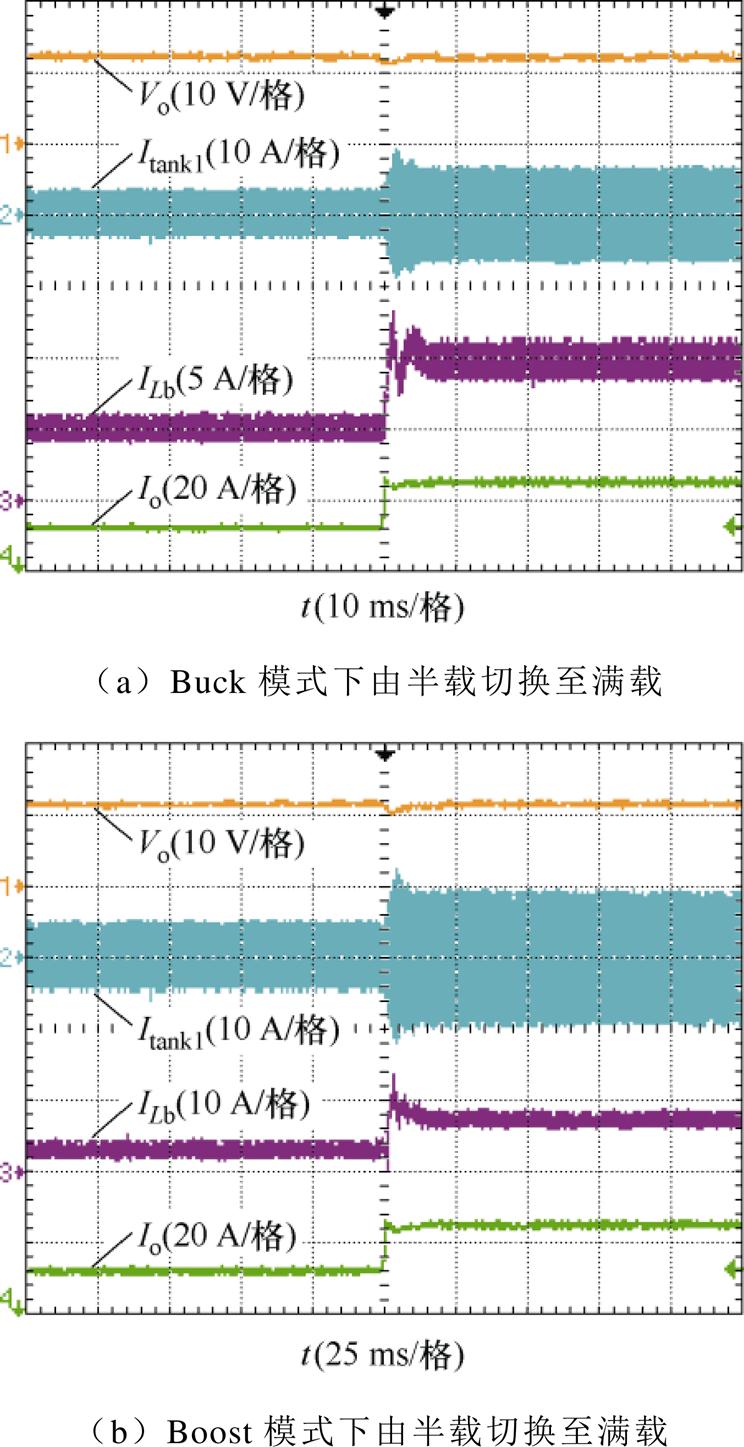
图30 MRSTC-FSBB动态负载波形
Fig.30 MRSTC-FSBB dynamic load waveforms
图31为FSBB输入电压跳变时动态响应曲线,图31a为滤波模式和Buck模式之间的切换,图31b则为滤波模式和Boost模式之间的切换,从中可以看出,模式切换相对平滑,但受限于电压环控制,电感电流依旧存在振荡,造成输出电压有明显超调及跌落。
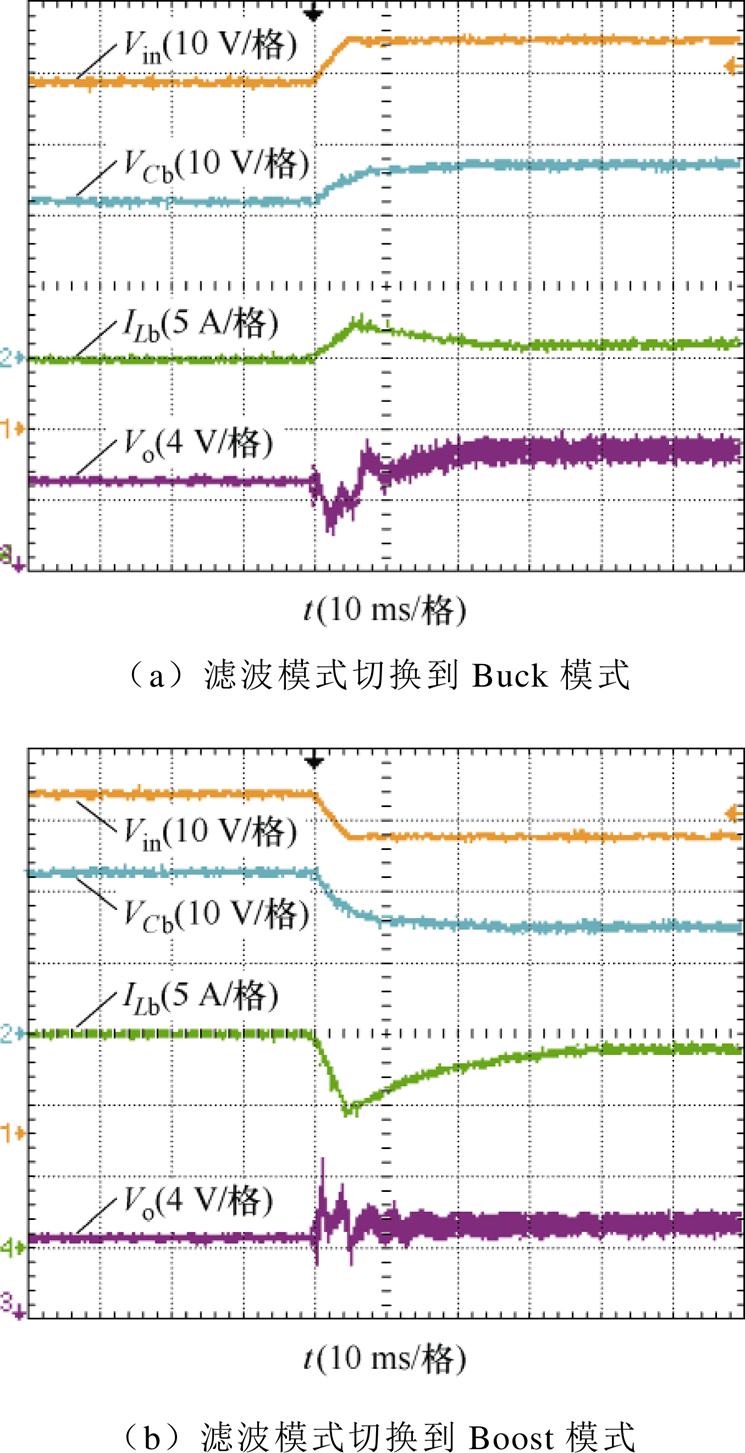
图31 MRSTC-FSBB模式切换波形
Fig.31 MRSTC-FSBB mode switching waveforms
图32给出的是输入电压Vin分别为40、48及60 V时,MRSTC-FSBB变换器在不同负载条件下的效率。当FSBB工作在滤波模式时,变换器整机效率最高,这是由于此时流经FSBB的功率经由直接通路流向负载侧,且没有开关损耗,变换器整体相当于一个4 1的直流变压器在工作,峰值效率为96.4%,满载效率为95.2%。当输入电压发生变化时,Boost模式下变换器的效率要高于Buck模式,这是因为MRSTC和FSBB处理的功率大小之比等于输入电压之比。Boost模式下40 V输入时FSBB处理的功率与总功率之比为k≈0.14,而Buck模式下60 V输入时FSBB处理的功率与总功率之比为k≈0.375,Boost模式下更多的功率经过更高效的MRSTC传递至负载侧,因此整机效率更高。
1的直流变压器在工作,峰值效率为96.4%,满载效率为95.2%。当输入电压发生变化时,Boost模式下变换器的效率要高于Buck模式,这是因为MRSTC和FSBB处理的功率大小之比等于输入电压之比。Boost模式下40 V输入时FSBB处理的功率与总功率之比为k≈0.14,而Buck模式下60 V输入时FSBB处理的功率与总功率之比为k≈0.375,Boost模式下更多的功率经过更高效的MRSTC传递至负载侧,因此整机效率更高。
图33为满载和半载条件下,变换器在不同输入电压下的效率对比。可以看出,FSBB工作在滤波模式时,即输入电压处于[46 V, 50 V]时,变换器的整机效率明显高于Buck模式和Boost模式。原因为在滤波模式时,处于变换器额定输入电压附近,此时d1=1, d2=0,即开关管Q1和Q3保持常开,Q2和Q4保持常关,FSBB等效为一个LC滤波器,而MRSTC- FSBB整体可等效为一个开环的4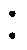 1 MRSTC,消除了FSBB的开关损耗,而FSBB为硬开关,开关损耗较大,所以在滤波模式时其效率更高。在Buck模式内,随着输入电压的不断增大,变换器的效率逐步降低,这是由于FSBB所分配到的功率在随输入电压的上升而增大。通过采用三模式粗调节的方式,有效提升了输入电压在额定值附近时变换器的效率。本文所提出的MRSTC-FSBB变换器与直接采用FSBB在应用场合“输入电压额定48 V(40~60 V),输出电压12 V下”相比,相同功率等级时,FSBB可能要多相交错并联,需要采用更多的开关管,采用的驱动电路更多,造成更多的额外成本。直接采用FSBB时,需要选取的电感值更大,导致体积更大,功率密度减小,电感的等效串联电阻较大。在输出大电流的应用场景下,根据图15,开关频率越高,谐振腔电流有效值越接近输出电流平均值,且MRSTC中只有4个开关管为硬关断,其他开关管实现了ZCS,使得MRSTC-FSBB变换器更有优势。
1 MRSTC,消除了FSBB的开关损耗,而FSBB为硬开关,开关损耗较大,所以在滤波模式时其效率更高。在Buck模式内,随着输入电压的不断增大,变换器的效率逐步降低,这是由于FSBB所分配到的功率在随输入电压的上升而增大。通过采用三模式粗调节的方式,有效提升了输入电压在额定值附近时变换器的效率。本文所提出的MRSTC-FSBB变换器与直接采用FSBB在应用场合“输入电压额定48 V(40~60 V),输出电压12 V下”相比,相同功率等级时,FSBB可能要多相交错并联,需要采用更多的开关管,采用的驱动电路更多,造成更多的额外成本。直接采用FSBB时,需要选取的电感值更大,导致体积更大,功率密度减小,电感的等效串联电阻较大。在输出大电流的应用场景下,根据图15,开关频率越高,谐振腔电流有效值越接近输出电流平均值,且MRSTC中只有4个开关管为硬关断,其他开关管实现了ZCS,使得MRSTC-FSBB变换器更有优势。
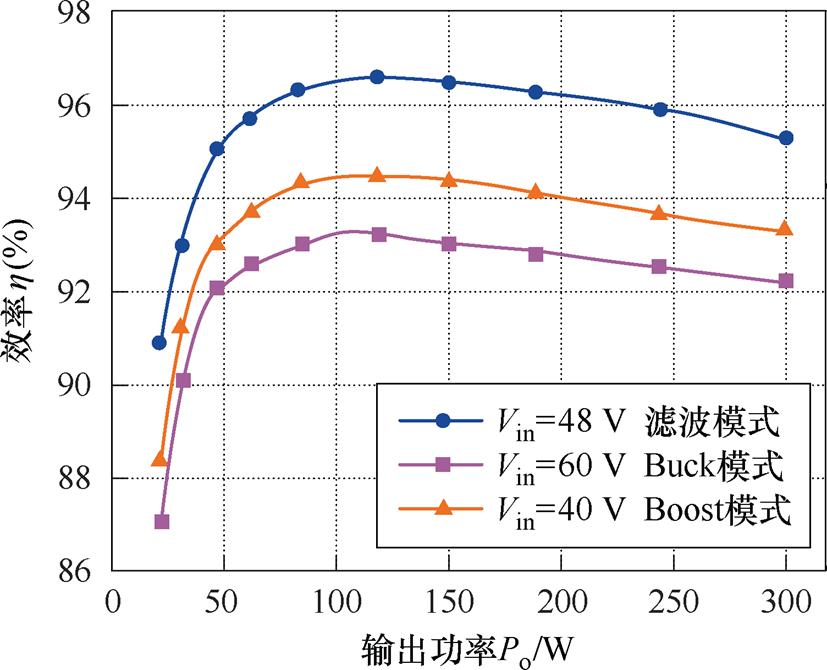
图32 不同负载条件下变换器效率
Fig.32 Converter efficiency under different load conditions
图33 不同输入电压下变换器效率
Fig.33 Converter efficiency under different Vin
针对传统谐振开关电容变换器软开关特性易受谐振参数容差影响与调压能力不足的问题,本文提出了一种基于多谐振开关槽与四开关Buck-Boost电路的准并联架构变换器,详细分析了变换器的工作原理与电压增益特性,基于提高直接功率比重的理念,设计了三模式粗调节的控制方法。在此基础上,推导了变换器的小信号模型和传递函数,完成了环路补偿设计,实现了输出电压的闭环控制。最后,通过仿真和实验对上述理论和解决方案进行验证。实验结果表明,提出的多谐振开关槽对无源元件的参数容差具有较高的适应性和实用性。所设计的中间母线变换器样机实现了输出电压闭环控制的设计目标,在全负载范围内保持了高效率。
附录 传递函数参数
Buck模式下,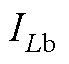 的值可表示为
的值可表示为
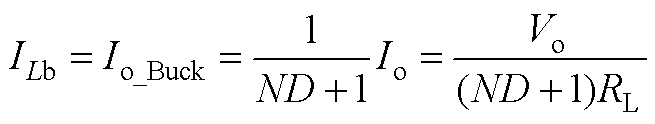
传递函数系数为
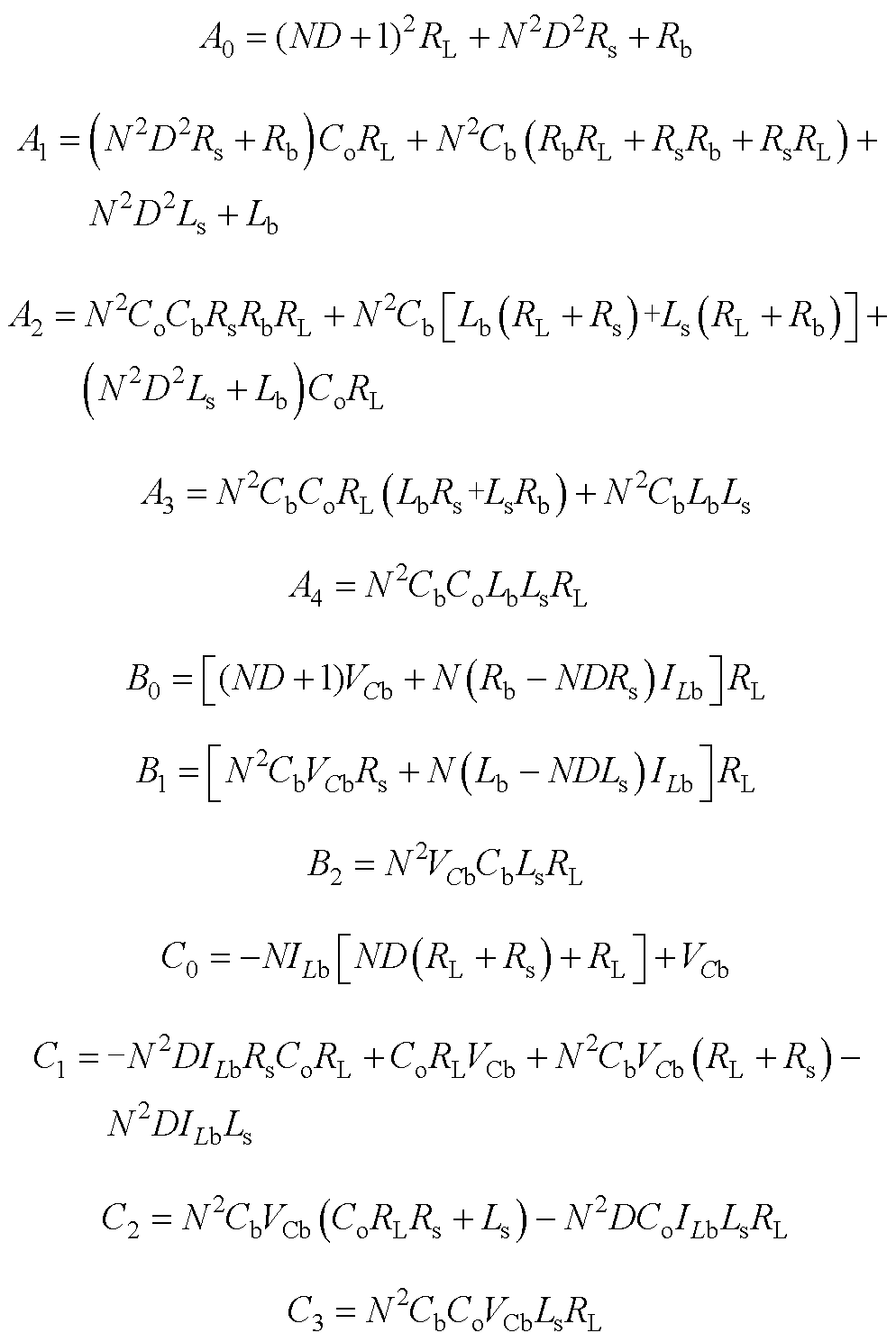
Boost模式下,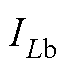 的值可表示为
的值可表示为
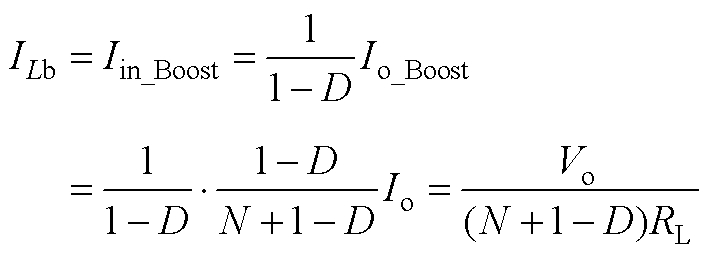
传递函数系数为
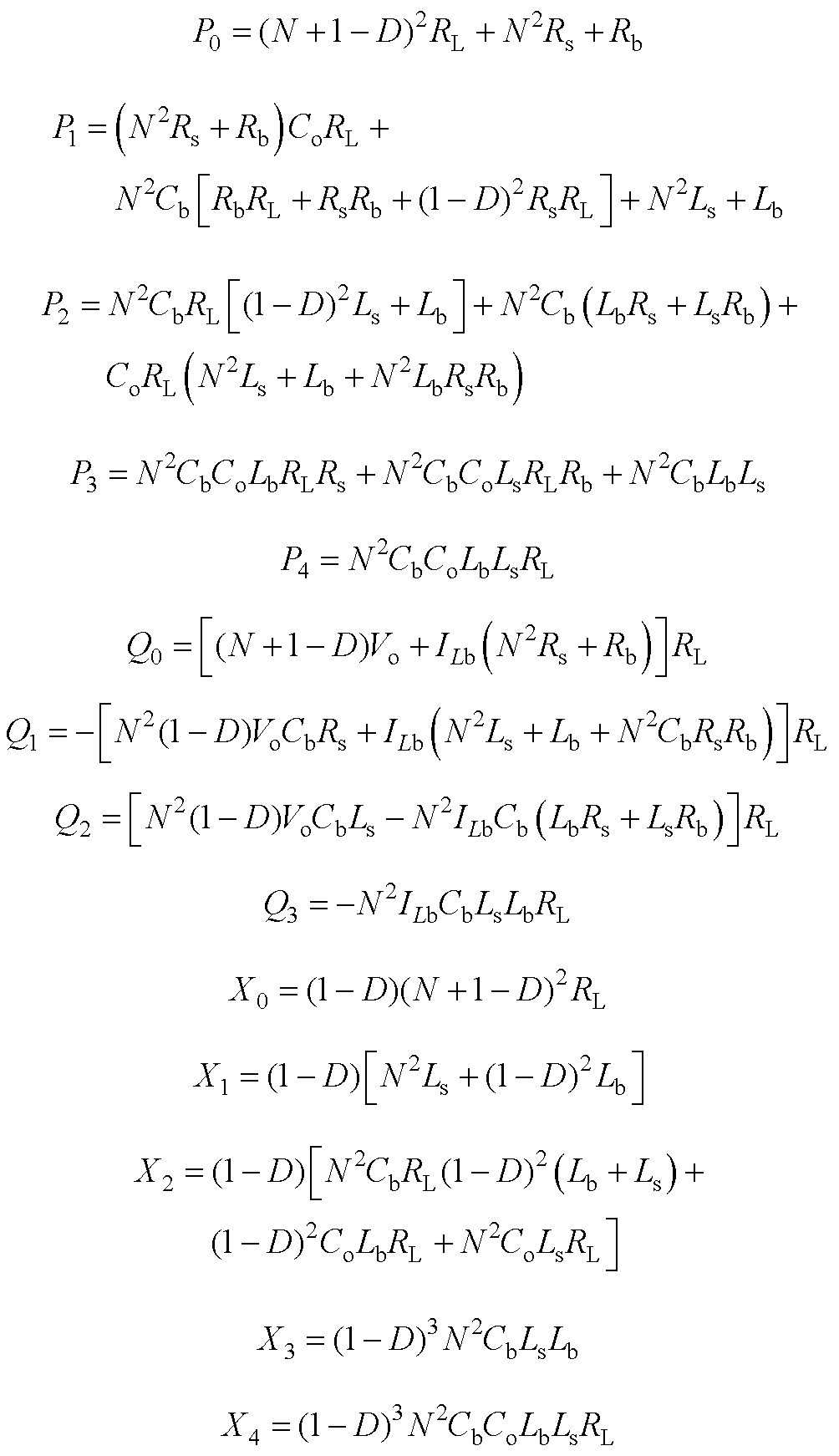
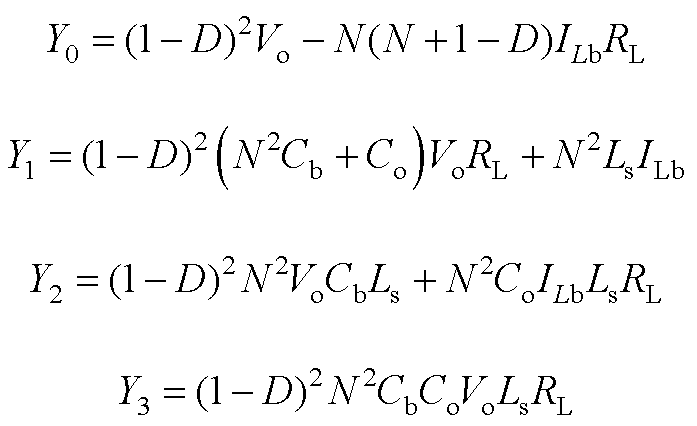
参考文献
[1] 张玉莹, 曾博, 周吟雨, 等. 碳减排驱动下的数据中心与配电网交互式集成规划研究[J]. 电工技术学报, 2023, 38(23): 6433-6450.
Zhang Yuying, Zeng Bo, Zhou Yinyu, et al. Research on interactive integration planning of data centers and distribution network driven by carbon emission reduction[J]. Transactions of China Electrotechnical Society, 2023, 38(23): 6433-6450.
[2] Fei C, Ahmed M H, Lee F C, et al. Two-stage 48V- 12V/6V-1.8V voltage regulator module with dynamic bus voltage control for light-load efficiency improve- ment[J]. IEEE Transactions on Power Electronics, 2017, 32(7): 5628-5636.
[3] 任小永. 高效率高功率密度通信模块电源技术的研究[D]. 南京: 南京航空航天大学, 2008.
Ren Xiaoyong. Research on high efficiency high power density telecom power supply modules[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2008.
[4] 王汝田, 李辉, 刘闯, 等. 基于开关电容与双降压变换器的三相AC-AC变换器[J]. 电工技术学报, 2022, 37(20): 5241-5252.
Wang Rutian, Li Hui, Liu Chuang, et al. A three-phase AC-AC converter based on switched- capacitor and dual-Buck converter[J]. Transactions of China Electrotechnical Society, 2022, 37(20): 5241- 5252.
[5] 陈思哲, 徐梦然, 范元亮, 等. 一种基于开关电容的九电平逆变器[J]. 电工技术学报, 2022, 37(4): 931-941.
Chen Sizhe, Xu Mengran, Fan Yuanliang, et al. A nine-level inverter based on switched-capacitor[J]. Transactions of China Electrotechnical Society, 2022, 37(4): 931-941.
[6] 王要强, 李娜, 赵朝阳, 等. 一种新型多电平逆变器及其模块化分析[J]. 电工技术学报, 2022, 37(18): 4676-4687.
Wang Yaoqiang, Li Na, Zhao Zhaoyang, et al. A new type of multilevel inverter and its modular analysis[J]. Transactions of China Electrotechnical Society, 2022, 37(18): 4676-4687.
[7] 李紫薇, 吴学智, 王静, 等. 谐振开关电容变换器磁集成电感设计[J]. 电工技术学报, 2022, 37(24): 6230-6238.
Li Ziwei, Wu Xuezhi, Wang Jing, et al. Design of magnetic integrated inductor for resonant switched capacitor converter[J]. Transactions of China Elec- trotechnical Society, 2022, 37(24): 6230-6238.
[8] Tang Jun, Guo Tian, Kim J S, et al. A current-mode four-phase synchronous Buck converter with dynamic dead-time control[J]. IEEE Access, 2021, 9: 81078- 81088.
[9] Law K K, Cheng K W E, Yeung Y P B. Design and analysis of switched-capacitor-based step-up resonant converters[J]. IEEE Transactions on Circuits and Systems I: Regular Papers, 2005, 52(5): 943-948.
[10] Ye Zichao, Lei Yutian, Pilawa-Podgurski R C N. The cascaded resonant converter: a hybrid switched- capacitor topology with high power density and efficiency[J]. IEEE Transactions on Power Elec- tronics, 2020, 35(5): 4946-4958.
[11] Li Yongjun, John M, Ramadass Y, et al. AC-coupled stacked dual-active-bridge DC-DC converter for inte- grated lithium-ion battery power delivery[J]. IEEE Journal of Solid-State Circuits, 2019, 54(3): 733- 744.
[12] Li Yanchao, Ni Ze, Liu Chengkun, et al. A 100kW switched-tank converter for electric vehicle appli- cation[C]//2019 IEEE Applied Power Electronics Conference and Exposition (APEC), Anaheim, CA, USA, 2019: 1690-1697.
[13] 管乐诗, 温兆亮, 许晓志, 等. 适用于宽增益范围的可重构单级DC-DC变换器及其磁元件设计[J]. 电工技术学报, 2023, 38(6): 1571-1583.
Guan Yueshi, Wen Zhaoliang, Xu Xiaozhi, et al. A modular reconfigurable single-stage DC-DC converter suitable for wide gain range and its magnetic design[J]. Transactions of China Electrotechnical Society, 2023, 38(6): 1571-1583.
[14] Stauth J T, Kesarwani K, Schaef C. A distributed photovoltaic energy optimization system based on a sub- module resonant switched-capacitor implementation[C]// 2012 15th International Power Electronics and Motion Control Conference (EPE/PEMC), Novi Sad, Serbia, 2012: LS2d.2-1-LS2d.2-6.
[15] Cao Dong, Peng Fangzheng. A family of zero current switching switched-capacitor DC-DC converters[C]// 2010 Twenty-Fifth Annual IEEE Applied Power Electronics Conference and Exposition (APEC), Palm Springs, CA, USA, 2010: 1365-1372.
[16] Li Shouxiang, Liang Shengnan, Li Zhenning, et al. A bidirectional resonant two-switch boosting switched- capacitor converter with phase-shift modulation[C]// 2020 IEEE Applied Power Electronics Conference and Exposition (APEC), New Orleans, LA, USA, 2020: 56-60.
[17] 闫成章, 杨晓峰, 刘妍, 等. 基于移相控制的谐振开关电容变换器占空比优化策略[J]. 电工技术学报, 2021, 36(增刊2): 676-687.
Yan Chengzhang, Yang Xiaofeng, Liu Yan, et al. Duty cycle optimization of phase shift control based on resonant switched capacitor converter[J]. Transa- ctions of China Electrotechnical Society, 2021, 36(S2): 676-687.
[18] Liang Jiawei, Wang Haoyu. Light load efficiency Boost technique for switched tank converters based on hybrid ZVS-ZCS control[C]//2022 International Power Electronics Conference (IPEC-Himeji 2022- ECCE Asia), Himeji, Japan, 2022: 2231-2235.
[19] Li Shouxiang, Liang Shengnan, Li Zhenning, et al. A phase-shift-modulated resonant two-switch boosting switched-capacitor converter and its modulation map[J]. IEEE Transactions on Industrial Electronics, 2023, 70(8): 7783-7795.
[20] 谢文浩. 高功率密度全范围调压的谐振开关电容变换器研究[D]. 哈尔滨: 哈尔滨工业大学, 2021.
Xie Wenhao. Resonant switched-capacitor converters with high power density and full-range regulation[D]. Harbin: Harbin Institute of Technology, 2021.
[21] Li Shouxiang, Zhang Ningning, Zheng Shuhua, et al. A dickson resonant switched-capacitor converter with “indirect” resonant core and continuous conversion ratio[C]//2019 IEEE Applied Power Electronics Conference and Exposition (APEC), Anaheim, CA, USA, 2019: 2218-2222.
[22] 丘东元, 张波, 郑春芳, 等. 谐振开关电容变换器新型PWM控制策略[J]. 中国电机工程学报, 2006, 26(2): 116-120.
Qiu Dongyuan, Zhang Bo, Zheng Chunfang, et al. New PWM control method of resonant switched capacitor DC-DC converter[J]. Proceedings of the CSEE, 2006, 26(2): 116-120.
[23] Li Yanchao, Lü Xiaofeng, Cao Dong, et al. A 98.55% efficiency switched-tank converter for data center application[J]. IEEE Transactions on Industry Applications, 2018, 54(6): 6205-6222.
[24] 吴学智, 祁静静, 刘京斗, 等. 谐振开关电容DC/ DC变换器拓扑研究综述[J]. 中国电机工程学报, 2021, 41(2): 655-666.
Wu Xuezhi, Qi Jingjing, Liu Jingdou, et al. Review of topological research on resonant switched capacitor DC/DC converter[J]. Proceedings of the CSEE, 2021, 41(2): 655-666.
[25] Wei Mengxuan, Li Yanchao, Ni Ze, et al. Zero voltage switching switched-tank modular converter for data center application[C]//2019 IEEE 7th Workshop on Wide Bandgap Power Devices and Applications (WiPDA), Raleigh, NC, USA, 2019: 245-250.
[26] Li B C Y, Lü Xiaofeng, Cao Dong. Single-wing resonant multilevel converter featuring reduced number of resonant inductors[C]//2017 IEEE Energy Conversion Congress and Exposition (ECCE), Cincinnati, OH, USA, 2017: 1733-1738.
[27] Jiang Shuai, Saggini S, Nan Chenhao. Switched tank converters[J]. IEEE Transactions on Power Elec- tronics, 2019, 34(6): 5048-5062.
[28] Sovik G, Urkin T, Masandilov E E, et al. Optimal self-tuning control for data-centers’ 48V-12V ZCS- STC[C]//2020 IEEE Applied Power Electronics Conference and Exposition (APEC), New Orleans, LA, USA, 2020: 455-462.
[29] 任小永, 阮新波, 李明秋, 等. 双沿调制的四开关Buck-Boost变换器[J]. 中国电机工程学报, 2009, 29(12): 16-23.
Ren Xiaoyong, Ruan Xinbo, Li Mingqiu, et al. Dual edge modulated four-switch Buck-Boost converter[J]. Proceedings of the CSEE, 2009, 29(12): 16-23.
[30] 刘妍, 杨晓峰, 闫成章, 等. 考虑寄生电感的谐振开关电容变换器电压尖峰抑制[J]. 电工技术学报, 2021, 36(12): 2627-2639.
Liu Yan, Yang Xiaofeng, Yan Chengzhang, et al. Suppression of voltage spike in resonant switched capacitor converter considering parasitic indu- ctance[J]. Transactions of China Electrotechnical Society, 2021, 36(12): 2627-2639.
A Quasi Parallel Converter Based on Multi Resonant Switched Tank and Buck-Boost Circuit
Abstract With the rapid development of 5G communication, big data, artificial intelligence, and other emerging information technologies, data centers are becoming the critical infrastructure with rapid increases in application scale and power demand. The intermediate bus converter (IBC) is a critical power stage in the power supply architecture. Resonant switched capacitor converters (RSCCs) have the advantages of high efficiency, small size, lightweight, and potential for integration, which are suitable for IBC. This paper investigates an IBC based on the resonant switched capacitor to achieve high efficiency, low cost, and voltage regulation.
Firstly, the conventional 2X step-down RSCC is investigated, and its working principle and voltage gain characteristics for zero-current turn-off operation are analyzed. However, it has shortcomings in the fixed voltage ratio and the susceptibility of the soft switching characteristics to resonant parameters. The simulation shows the resonant frequency drifts due to the tolerance of components, and the switches have hard turning-off problems, thus reducing the efficiency of the converter. The influence of component variation on the converter is analyzed by deducing the time-domain expression of the resonant current.
Therefore, a multi-resonant switched capacitor converter (MRSCC) with high immunity toward component variation is introduced. The converter realizes the lossless reverse of the residual current in the resonant inductor within the dead time using the band-stop characteristic of the notch resonant frequency. The Class II ceramic capacitor can be used as the resonant component, which reduces the production cost. In order to meet different voltage conversion requirements of IBC, the multi-resonant switched tank converter (MRSTC) has been developed, and the basis and procedure for parameter design are proposed.
Regarding the poor voltage regulation capability of convention RSCCs, an IBC based on quasi-parallel is investigated by combining MRSTC with a four-switch Buck-Boost (FSBB) converter. The working principle and voltage gain characteristics of the converter are analyzed. A three-mode rough regulation control strategy is proposed to increase the direct power ratio in FSBB. The small signal model and the transfer functions are deduced. The parameters of the closed-loop control system are designed to enhance the voltage regulation ability, thereby achieving output voltage stability.
The results show that the proposed MRSCC is highly immune to component variation. The designed IBC prototype realizes the closed-loop regulation of output voltage while maintaining high efficiency in the range of input voltage and power.
Keywords:Intermediate bus converter, resonant switched-capacitor converter, multi-resonant switched tank converter, quasi-parallel architecture
中图分类号:TM46
DOI: 10.19595/j.cnki.1000-6753.tces.230918
收稿日期 2023-06-14
改稿日期 2024-01-13
戴瑞然 男,1997年生,硕士研究生,研究方向为电力电子与电力传动。
E-mail: 1410349991@qq.com
马运东 男,1969年生,副教授,硕士生导师,研究方向为电力电子与电力传动。
E-mail: kyleo@nuaa.edu.cn(通信作者)
(编辑 陈 诚)