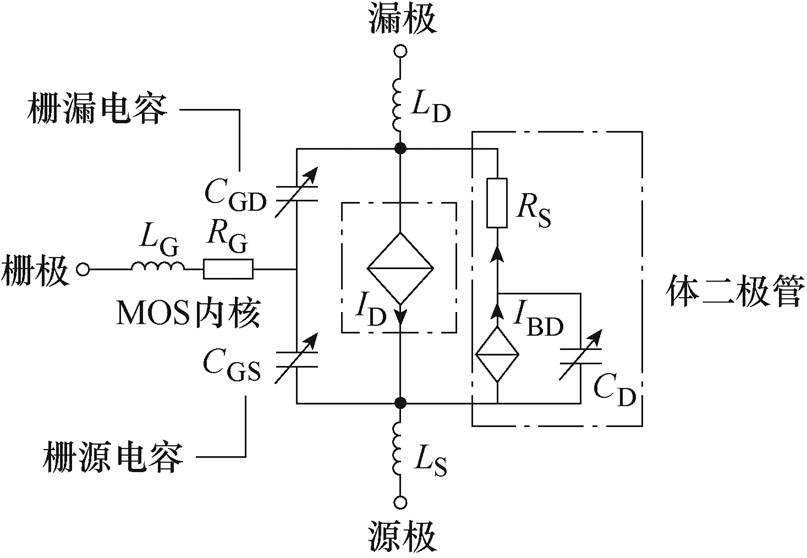
图1 本文建立的SiC MOSFET仿真模型
Fig.1 Simulation model of SiC MOSFET established in this paper
摘要 传统SiC MOSFET模型为提高精度,通常采用分段函数对不同工作区进行建模,但这带来了模型收敛性不足的问题,难以应用于高频仿真电路。该文提出一种连续函数描述的、具有高精度和强收敛性的SiC MOSFET数学模型。构建单一连续函数描述SiC MOSFET在线性区和恒流区内的静态特性;提出带有收敛电阻的非线性电容模型,并针对不同寄生电容构造相应的拟合函数进行建模;此外,体二极管的建模考虑了结温和栅源电压的影响。仿真结果与手册实测数据的对比分析表明,静态模型仿真结果的皮尔逊相关系数大于0.99,寄生电容拟合的平均相关系数达到0.994 8,体二极管模型与实际伏安特性高度匹配。在室温(TJ=25℃)和高温(TJ=150℃)两种条件下基于C2M0025120D进行了300 V/30 A双脉冲实验,对比验证了仿真模型与实验结果在开断特性方面具有良好的一致性。最后将模型应用在级联H桥多电平逆变器,验证了其在复杂电路仿真中的收敛性。
关键词:功率SiC MOSFET 电力电子器件建模 数学模型 收敛模型 高精度
目前,硅(Si)基半导体器件的应用水平已接近材料极限[1]。在新能源等行业日益增长的应用需求背景下,以碳化硅(SiC)器件为代表的宽禁带半导体功率器件成为研究热点,特别是SiC MOSFET因其通态电阻低、热导率高、临界击穿场强大等优点[2-5]正逐渐替代Si基半导体器件。许多学者开始以传统的Si基模型为基础开发SiC MOSFET的仿真模型,但由于Si和SiC功率器件在物理和几何结构上的差异,Si基模型难以准确描述SiC器件的动静态特性[6]。为了对电力电子系统进行评估以提高应用效率并降低成本,亟需建立高精度、强收敛性的SiC MOSFET系统级仿真模型。
尽管部分半导体制造商已经提供了各自的仿真模型,但许多模型仍存在着缺陷[7],例如,模型中缺乏对温度参数的考虑,模型精度不足导致的仿真结果与实际情况存在较大偏差,此外由于模型的不连续和结构的复杂性带来了收敛性不足的问题。
针对这些缺陷,许多研究人员对SiC MOSFET建模方法进行了深入研究。文献[8]考虑了温度参数对饱和电压的影响并进行了拟合,但由于拟合点的不充分,导致模型在驱动电压较小时存在明显的误差;部分模型加入温控电源模拟温度对载流子的影响和雪崩效应等[9-10],但温控电源的函数不易获得,且这样的结构不利于模型收敛。文献[11-12]用MOS LEVEL-3半经验模型,根据实际工作曲线提取SiC MOSFET物理参数,并对不同的工作区分段建模,然而这种模型的精度取决于物理参数提取准确度,且同样存在收敛性不足的问题。为提升模型精度,一些研究人员开始寻找更加适用于SiC MOSFET模型的拟合函数,文献[13]对传统EKV MOSFET模型拟合公式进行了改进,利用两个对数函数的线性组合在两个操作区域之间插值,生成一个单片模型,尽管该模型达到了很高的精度,但模型没有考虑温度参数的影响,限制了其应用价值。
动态模型的研究对象主要是非线性电容的等效电路和寄生电容的拟合函数,传统的建模方法采用西门子的开关模型构建非线性电容,但这种方法需要设置过多的参数,且参数提取方式没有统一标准,建模难度较大[14]。文献[15]采用压控电流源等效寄生电容,模型结构简单且参数提取比较方便,但是该模型存在电压源与电容并联的结构,导致收敛性降低。文献[16-17]为提高拟合的准确性采用了分段拟合的方法,这无疑不利于模型的收敛。除此之外,大多数文献在进行体二极管建模时将二极管视为恒定不变的元件,即二极管模型中没有输入量。事实上,温度会影响二极管载流子扩散速率,因此部分模型考虑了温度对体二极管伏安特性曲线的影 响[17]。另外,栅源电压的改变会影响二极管载流子的浓度,从结果来看,温度与栅源电压的增大会使伏安特性曲线向同一侧偏移,因此栅源电压也是二极管建模中需要考虑的因素,但目前大多文献没有进行相应的建模。
为了提高SiC MOSFET模型的精确性和收敛性,同时进一步拓宽模型的适用工况,本文以CREE公司的C2M0025120D(1 200 V/90 A)为建模对象,以构建描述模型静态特性的连续函数为要点,并提出收敛性良好的动态模型,最终建立高精度、强收敛性的SiC MOSFET模型,模型结构如图1所示。

图1 本文建立的SiC MOSFET仿真模型
Fig.1 Simulation model of SiC MOSFET established in this paper
SiC MOSFET模型的建立流程如图2所示,本文的核心内容如下:
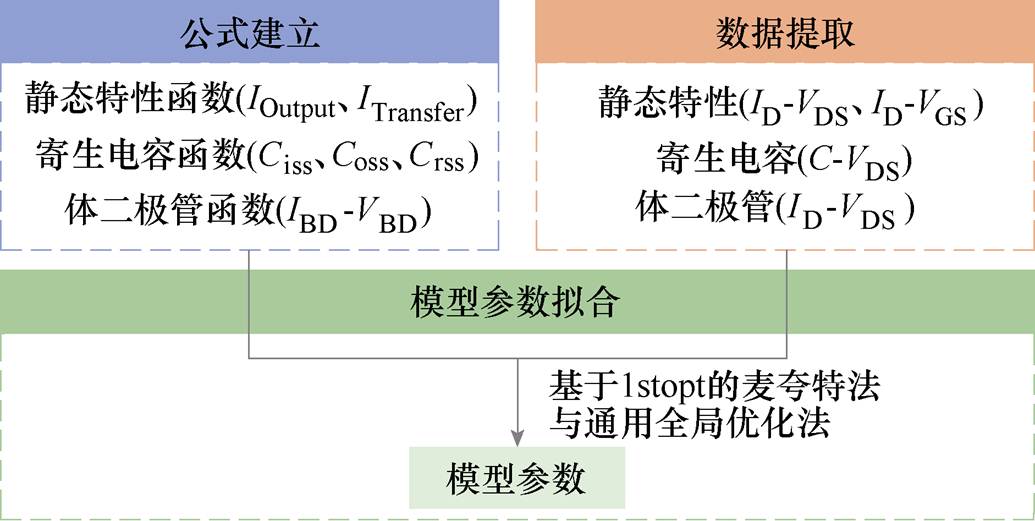
图2 本文的SiC MOSFET建模流程
Fig.2 The SiC MOSFET modeling flow in this paper
(1)构造了用以描述SiC MOSFET漏极电流的MOSFET内核模型,函数的选取充分考虑了静态曲线特征以期望提高精度,其连续性有利于模型的收敛。
(2)提出了一种带有收敛电阻的非线性电容压控电流源模型,使之更有利于复杂电路的仿真收敛;并根据寄生电容曲线特征构建了不同的拟合函数进行建模,进一步提升了仿真精度。
(3)考虑了温度效应和栅源电压对体二极管伏安特性曲线的影响,并基于二极管等效电路对体二极管进行了建模,更适用于不同工况下的电路仿真。
此外,本文设计了300 V/30 A双脉冲实验用以评估模型的开断性能,并通过仿真结果误差的计算和级联H桥七电平逆变器的仿真,对所建模型进行了准确度和收敛性的验证。
MOSFET内核用来表征SiC MOSFET的静态特性,包括输出特性曲线VDS-ID和转移特性曲线VGS-ID。其可以看作是受栅源电压VGS、漏源电压VDS和结温TJ控制的电流源ID,即
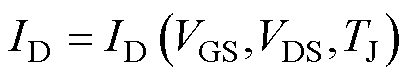 (1)
(1)
根据式(1),MOSFET内核等效为受控电流源,如图3所示。
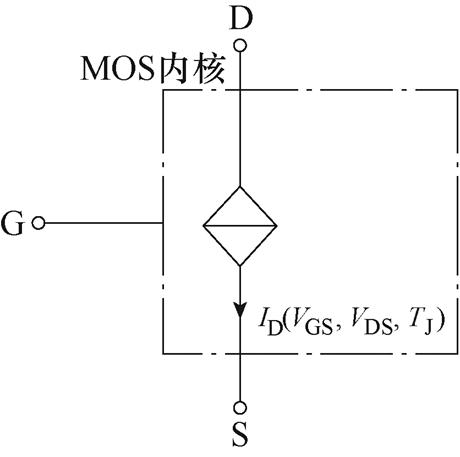
图3 MOSFET内核等效电路
Fig.3 MOSFET core equivalent circuit
传统建模方式将MOSFET线性区和恒流区用分段函数描述,即对于不同的工作区,分别用不同的函数式进行建模。为减少模型分段点数量,本文将这两个工作区用同一个连续函数描述,漏极电流表达式结构可写为
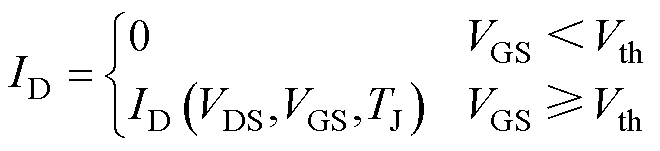 (2)
(2)
式中,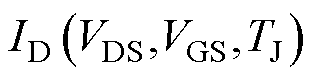 为描述MOSFET线性区和恒流区的函数;Vth为器件的阈值电压,它是关于温度TJ的函数。值得注意的是,传统建模方法一般采用线性函数来拟合阈值电压,但这种拟合形式仅适用于模型温度变化范围有限的情况,为进一步拓宽模型的温度适用范围,本文在此基础上采用三次多项式进行拟合,拟合函数为
为描述MOSFET线性区和恒流区的函数;Vth为器件的阈值电压,它是关于温度TJ的函数。值得注意的是,传统建模方法一般采用线性函数来拟合阈值电压,但这种拟合形式仅适用于模型温度变化范围有限的情况,为进一步拓宽模型的温度适用范围,本文在此基础上采用三次多项式进行拟合,拟合函数为
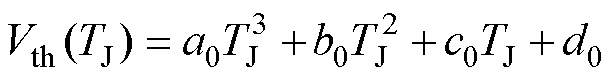 (3)
(3)
式中,a0~d0为拟合参数。
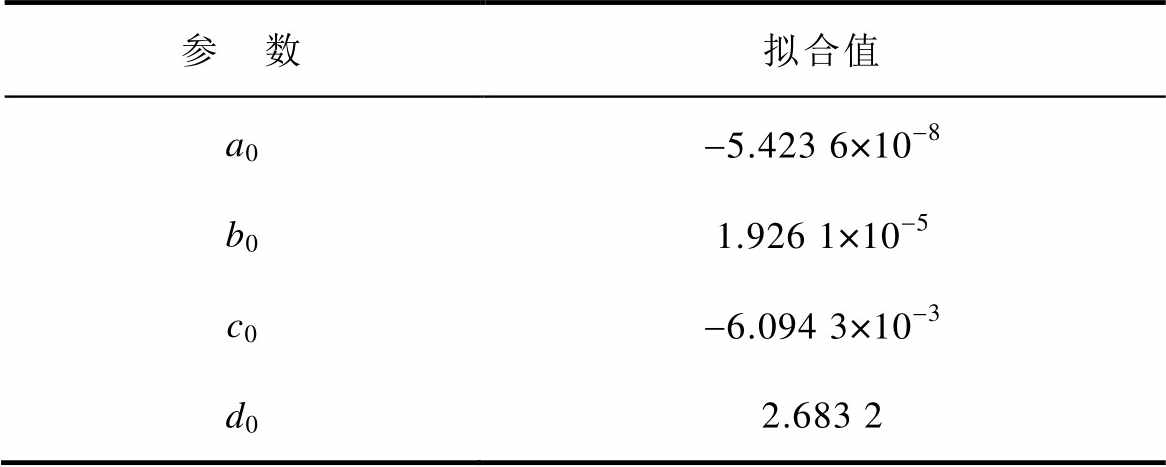
拟合所需要的数据可从C2M0025120D手册中获得,阈值电压的拟合结果见表1。阈值电压拟合如图4所示。
表1 阈值电压拟合参数
Tab.1 Threshold voltage fitting parameters
参 数拟合值 a0-5.423 6×10-8 b01.926 1×10-5 c0-6.094 3×10-3 d02.683 2
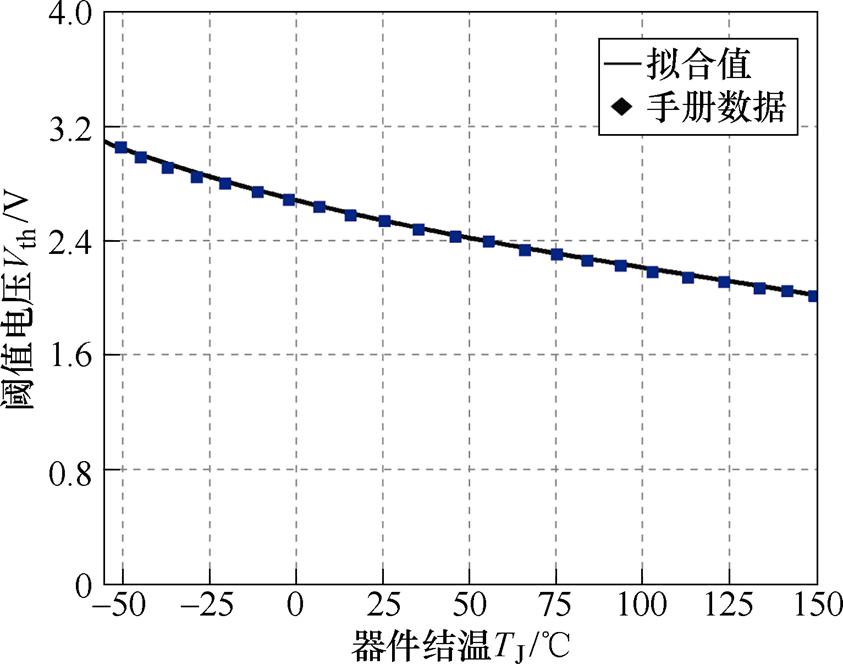
图4 阈值电压拟合
Fig.4 Threshold voltage fitting
漏极电流表达式应同时考虑输出特性和转移特性。因此,本文分别提出并构建输出特性曲线和转移特性曲线所对应的子函数,并取它们的乘积作为拟合的目标函数,如图5所示。该方法得到的目标函数同时包含SiC MOSFET器件的输出特性函数和转移特性函数的特征,因此可以用来描述其静态沟道电流特性。
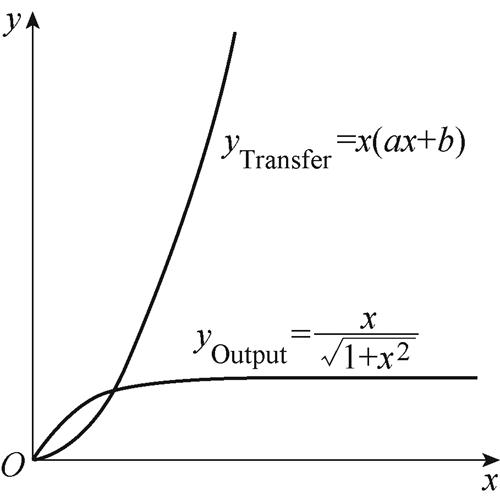
图5 子函数的图像
Fig.5 Image of subfunctions
根据SiC MOSFET静态特性函数图像趋势,本文构建的满足转移特性和输出特性的子函数如式(4)和式(5)所示。它们在趋势上与SiC MOSFET静态特性非常相似,分别用以描述输出特性曲线和转移特性曲线,并且同时满足连续性和收敛性的要求。
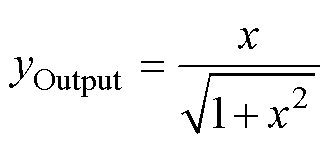 (4)
(4)
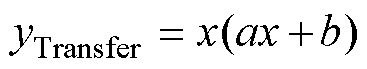 (5)
(5)
为了确保所选函数能够准确描述静态特性,还需对目标函数进行平移、伸缩以及幂运算等。基于以上分析,本文构建的受控电流源表达式为
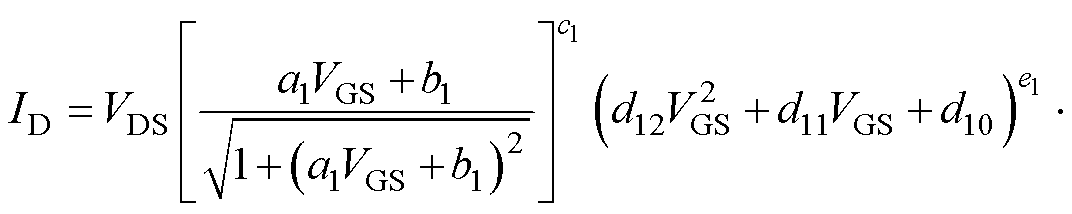
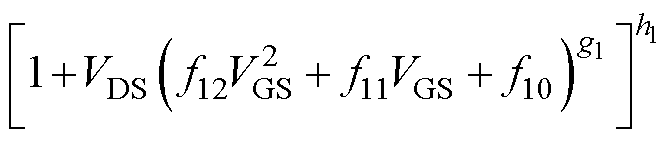 (6)
(6)
式中,a1、b1、c1、d10、d11、d12、e1、f10、f11、f12、g1、h1均为拟合参数,不具备实际物理意义。考虑温度对SiC MOSFET静态特性的影响,这些拟合参数应为温度的函数,本文将其设置为关于温度TJ的一元二次函数,即
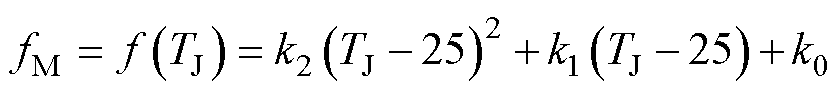 (7)
(7)
式中,k0、k1、k2为温度函数的拟合参数。
在得到漏极电流表达式(6)后,基于麦夸特法与通用全局优化法对所提取的SiC MOSFET输出特性曲线和转移特性曲线数据进行优化拟合,这种方法在使用时无需给出参数的初值,给参数提取带来了极大便利。为加快收敛速度,拟合过程中取的样点不宜过多,同时注意在曲线斜率变化较大的区域应多次取点。经过拟合提取参数后,得到不同结温下的静态特性温度参数值,见表2。
表2 静态特性温度参数
Tab.2 Static characteristic temperature parameters
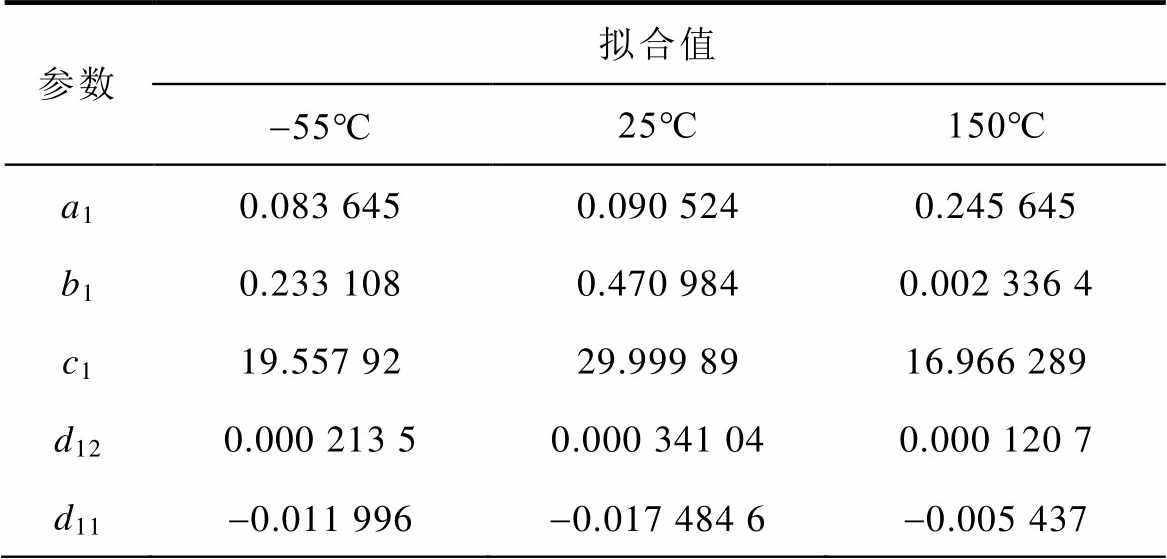
参数拟合值 -55℃25℃150℃ a10.083 6450.090 5240.245 645 b10.233 1080.470 9840.002 336 4 c119.557 9229.999 8916.966 289 d120.000 213 50.000 341 040.000 120 7 d11-0.011 996-0.017 484 6-0.005 437
(续)
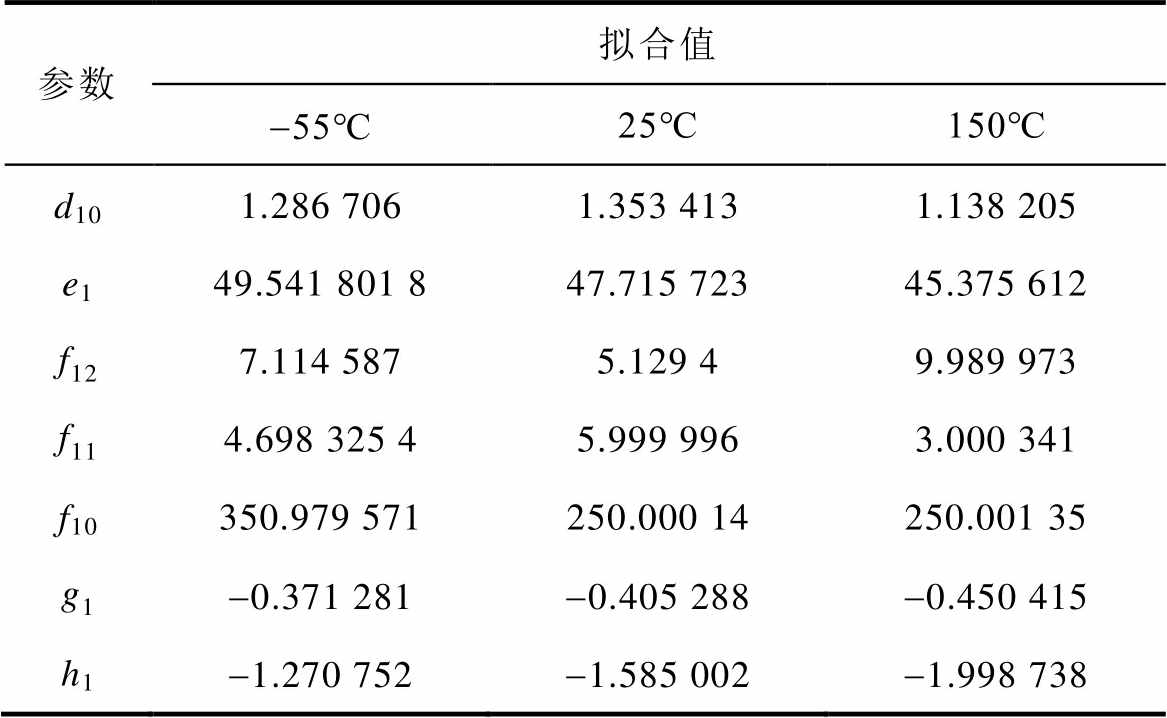
参数拟合值 -55℃25℃150℃ d101.286 7061.353 4131.138 205 e149.541 801 847.715 72345.375 612 f127.114 5875.129 49.989 973 f114.698 325 45.999 9963.000 341 f10350.979 571250.000 14250.001 35 g1-0.371 281-0.405 288-0.450 415 h1-1.270 752-1.585 002-1.998 738
考虑温度对静态参数的影响,基于一元二次函数对各温度参数建立函数关系,结果见表3。
表3 静态参数温度函数系数
Tab.3 Temperature function coefficients of static parameters
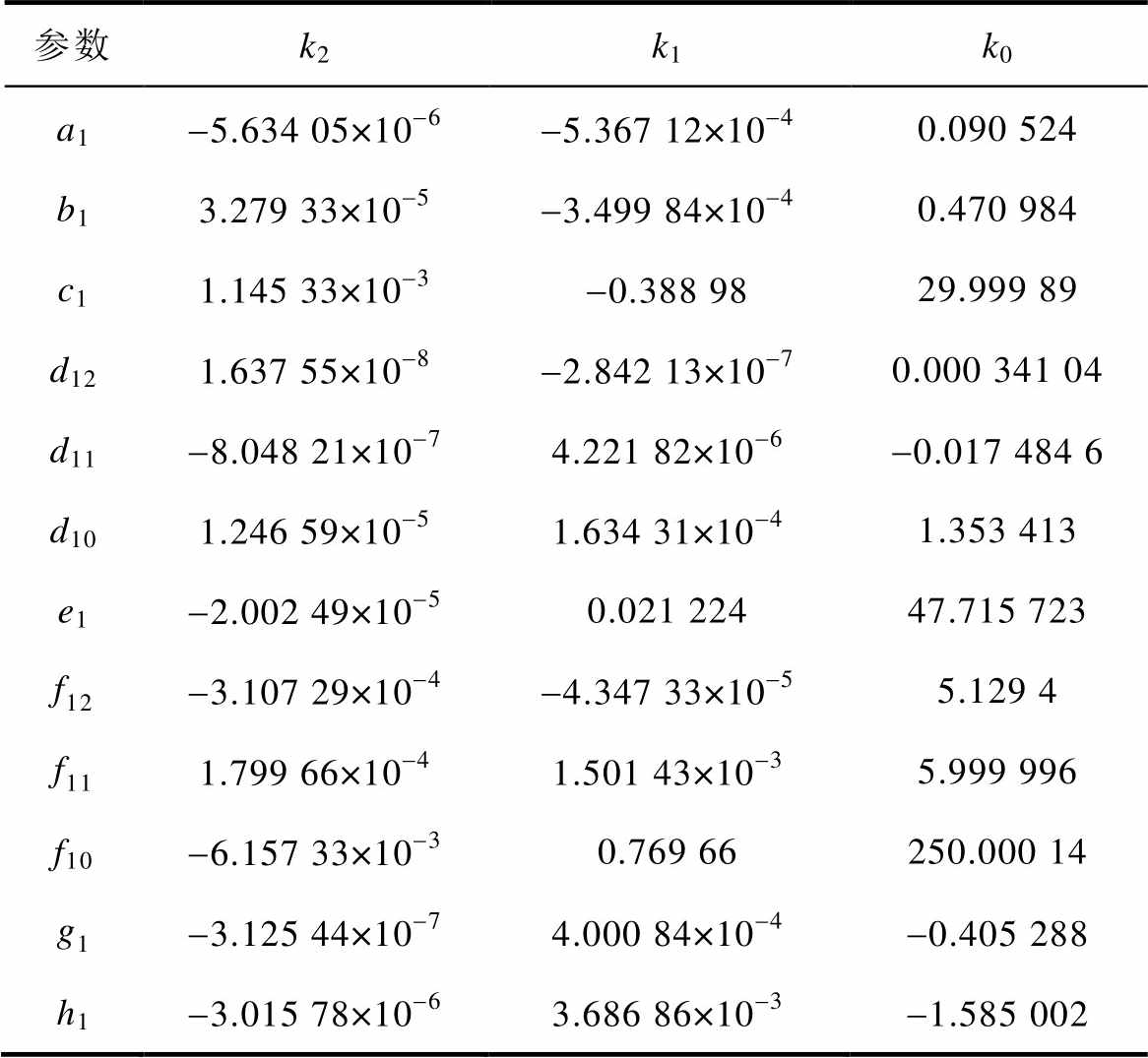
参数k2k1k0 a1-5.634 05×10-6-5.367 12×10-40.090 524 b13.279 33×10-5-3.499 84×10-40.470 984 c11.145 33×10-3-0.388 9829.999 89 d121.637 55×10-8-2.842 13×10-70.000 341 04 d11-8.048 21×10-74.221 82×10-6-0.017 484 6 d101.246 59×10-51.634 31×10-41.353 413 e1-2.002 49×10-50.021 22447.715 723 f12-3.107 29×10-4-4.347 33×10-55.129 4 f111.799 66×10-41.501 43×10-35.999 996 f10-6.157 33×10-30.769 66250.000 14 g1-3.125 44×10-74.000 84×10-4-0.405 288 h1-3.015 78×10-63.686 86×10-3-1.585 002
SiC MOSFET的动态特性主要受寄生电容的影响,而寄生电容具有较强的非线性。本文提出了一种具有良好收敛性的非线性电容压控电流源模型如图6所示。图中,VAB为受控电压源,Cref为参考电容,Rc为收敛电阻,其作用为限制VAB发生突变时回路中产生大电流,提升了模型收敛性。
在该模型中,电流IAB即为电容支路AB的电流IC,电流值受外部电路控制,表达式为
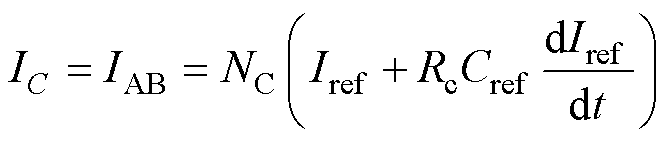 (8)
(8)
由电容元件的伏安关系及基尔霍夫电路定律知
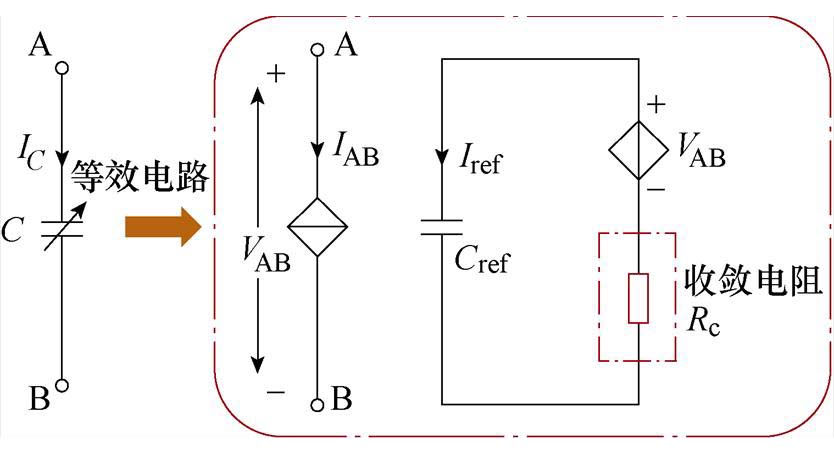
图6 本文提出的非线性电容模型
Fig.6 The nonlinear capacitance model proposed in this paper
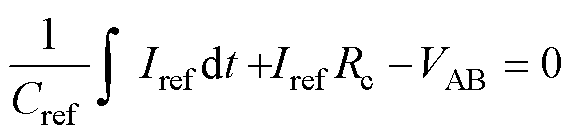 (9)
(9)
对式(9)进一步变形可得
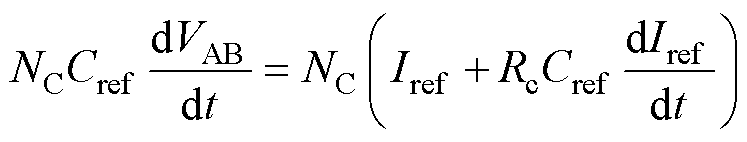 (10)
(10)
结合式(8)和式(10)可知
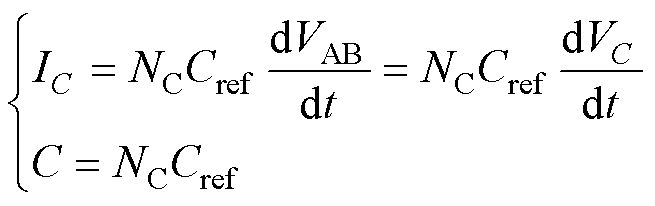 (11)
(11)
式中,VC为电容C两端的电压。
当NC为关于支路电压VAB的函数时,则电容C可等效为由VAB控制的压控电容。为建立寄生电容的模型,还需从寄生电容的C-V曲线中提取数据来构建N的表达式。
通常采用数学拟合的方式对输入电容Ciss、输出电容Coss以及转移电容Crss的变化曲线进行提取,在构建电容模型时,大多数文献采用式(12)进行拟合。
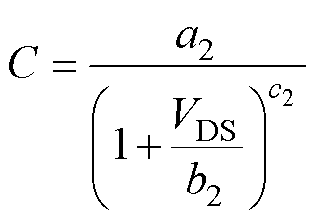 (12)
(12)
式中,a2、b2、c2为拟合参数。然而,该式对寄生电容的拟合精度不高,尤其是在拟合转移电容时,其复杂的物理机制导致转移电容曲线斜率变化非常快[18],使得采用式(12)拟合时误差非常大。为了对拟合电容进行更精确的建模,许多模型采用了分段拟合的方法[16-17],这虽然对精度提升很大,但分段点的引入不利于模型的收敛。
为提高建模精度的同时保证模型收敛性,本文提出了采用多个连续函数对寄生电容进行拟合的策略,根据寄生电容曲线特征选取合适的拟合函数,各寄生电容的表达式为
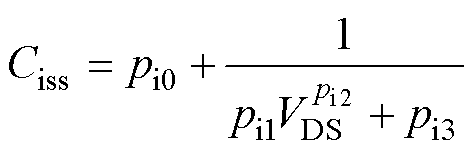 (13)
(13)
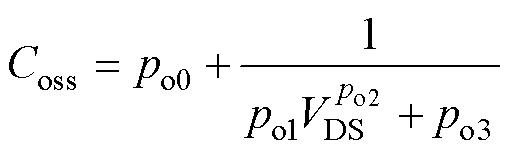 (14)
(14)
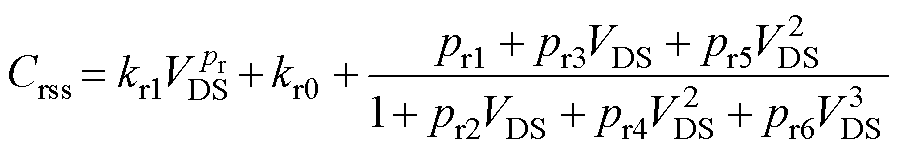 (15)
(15)
式中,pi0~pi3、po0~po3、pr、pr1~pr6、kr0、kr1均为寄生电容的拟合参数。
输入电容和输出电容的表达式在反比例函数的基础上改进得到;转移电容由于其曲线斜率变化迅速,为了提高拟合精度,提出了式(15)所示的拟合函数以减小转移电容的拟合误差。从数据手册中提取拟合点后,得到拟合参数见表4~表6。
表4 寄生电容Crss拟合参数
Tab.4 Parasitic capacitance Crss fitting parameters
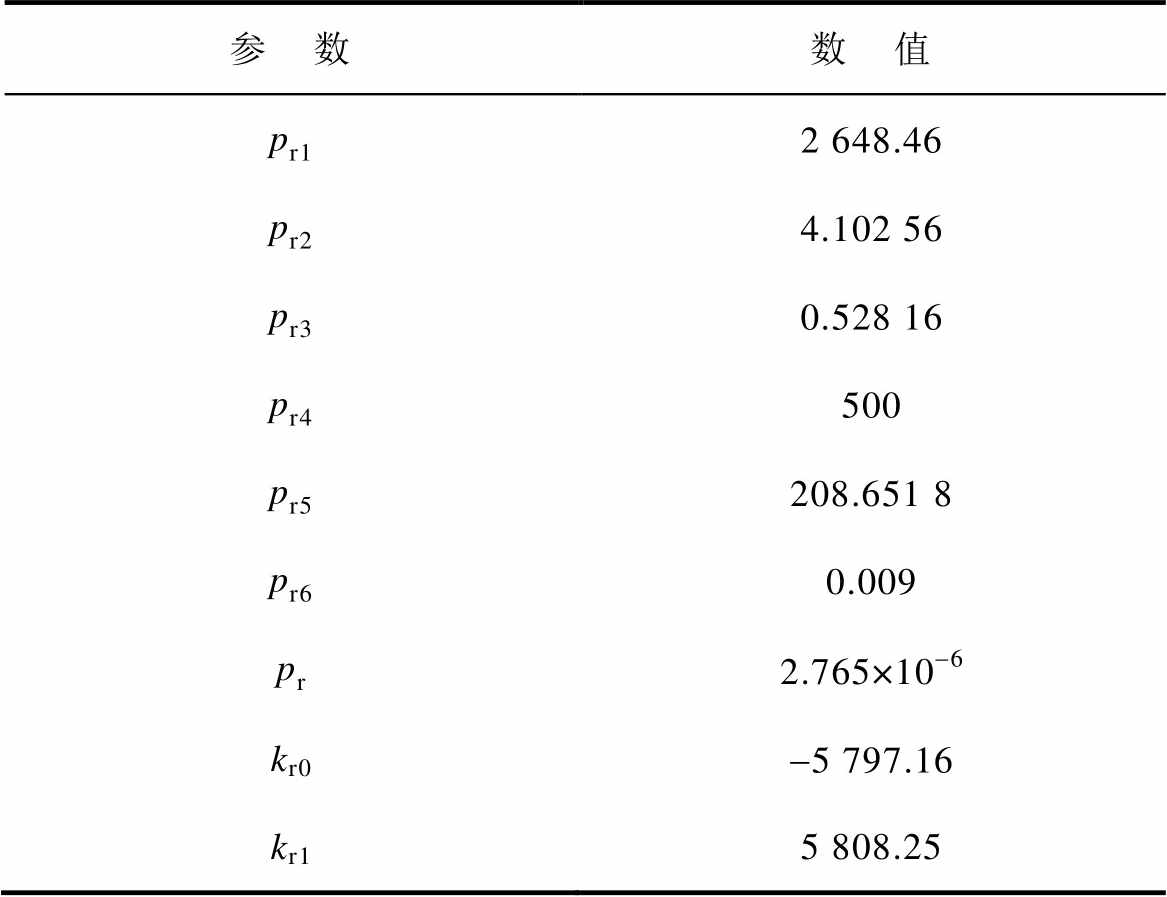
参 数数 值 pr12 648.46 pr24.102 56 pr30.528 16 pr4500 pr5208.651 8 pr60.009 pr2.765×10-6 kr0-5 797.16 kr15 808.25
表5 寄生电容Ciss拟合参数
Tab.5 Parasitic capacitance Ciss fitting parameters

参 数数 值 pi02 954.04 pi11.535 8 pi24.681 5 pi30.001 959
表6 寄生电容Coss拟合参数
Tab.6 Parasitic capacitance Coss fitting parameters

参 数数 值 po0170.01 po14.648 6 po20.943 6 po33.582×10-4
为了对拟合效果进行量化分析,表7给出了拟合结果的相关系数,验证了所提拟合函数的高精度。尤其是对于传统拟合方式难以准确描述的转移电容,其拟合函数相关系数达到了0.988 7。寄生电容拟合结果如图7所示。
表7 寄生电容拟合结果相关系数
Tab.7 Correlation coefficient of parasitic capacitance fitting results

寄生电容相关系数R Ciss0.998 2 Coss0.997 4 Crss0.988 7
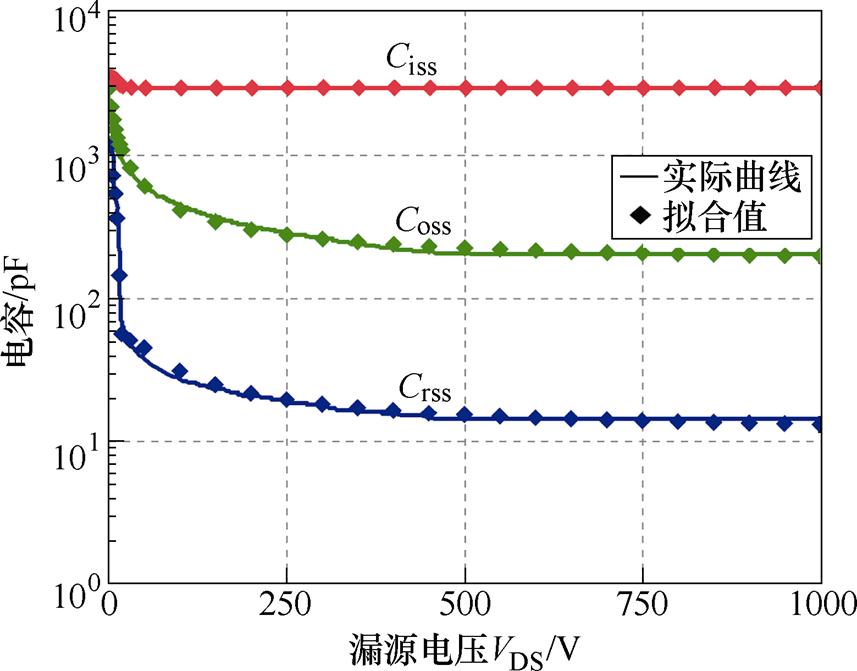
图7 寄生电容拟合结果
Fig.7 Parasitic capacitance fitting results
在得到输入电容、输出电容、转移电容表达式(13)~式(15)后,根据式(16)可分别得到栅漏电容CGD、栅源电容CGS及漏源电容CDS表达式。需要注意的是,栅漏电容根据电压状态的不同具有不同的表达式。在VGD<0时,其值可根据式(16)得到;当VGD>0时,应将其等效为一个恒定电容CGDMAX。
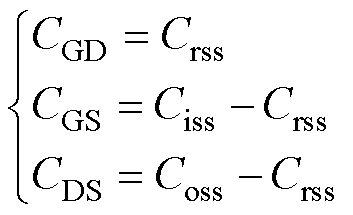 (16)
(16)
传统建模方法对体二极管的建模比较简单,通常采用建模软件(如Model Editor)通过二极管伏安特性曲线提取物理参数进行建模,这种建模方式缺乏对温度和栅源电压等因素的考虑。本文采用图8所示的等效电路来模拟二极管的特性。电流源IBD和串联的电阻RS描述二极管的静态伏安特性;并联电容CD是一个与电路状态相关的可变电容,用来描述二极管开断时的动态行为。
二极管模型中电流源的表达式为
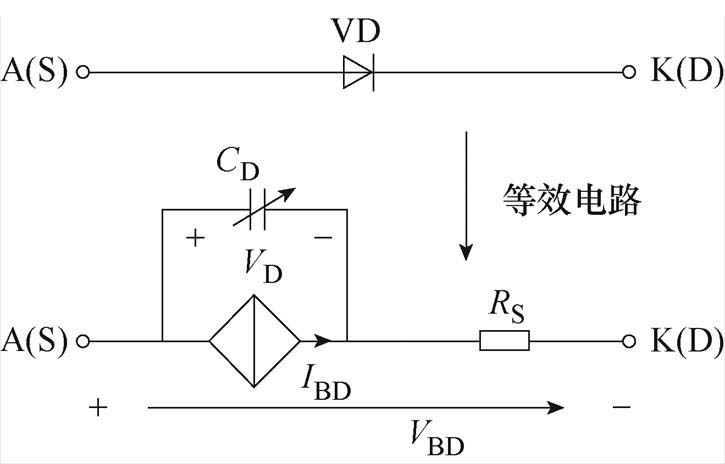
图8 二极管等效电路模型
Fig.8 Diode equivalent circuit model
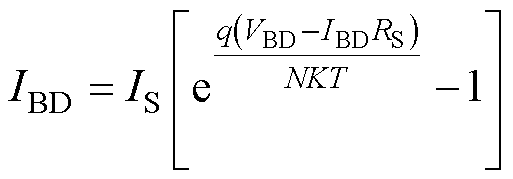 (17)
(17)
式中,IS为二极管反向饱和电流;q为电子电荷;K为玻耳兹曼常数;N为发射系数;RS为欧姆电阻。
为了便于对电流源进行拟合,本文对式(17)进行了简化,简化后得
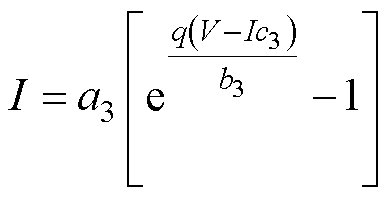 (18)
(18)
式中,a3、b3、c3均为由结温TJ和栅源电压VGS共同决定的拟合参数;V、I分别为体二极管的正向电压和正向电流。为表征结温和栅源电压对体二极管特性的影响,结合二极管伏安特性曲线形状,本文采用二元二次函数fB的形式对参数进行拟合,即
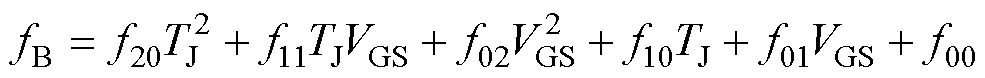 (19)
(19)
在提取SiC MOSFET体二极管特性参数后,采用麦夸特法与通用全局优化法对其进行拟合,得到拟合曲线如图9~图11所示,拟合参数见表8。
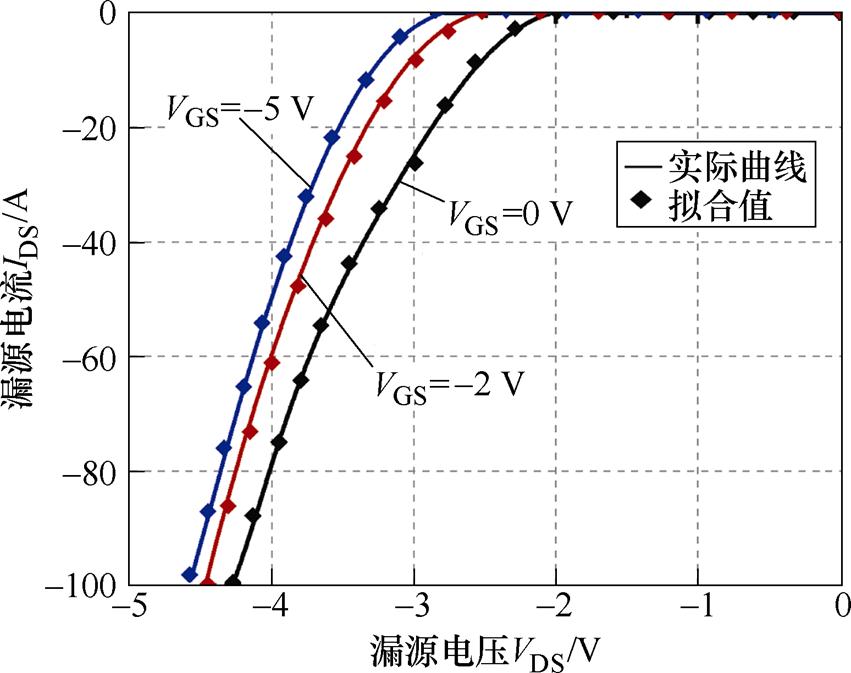
图9 -55℃时体二极管伏安特性曲线
Fig.9 Volt-ampere characteristic curves of body diode at -55℃
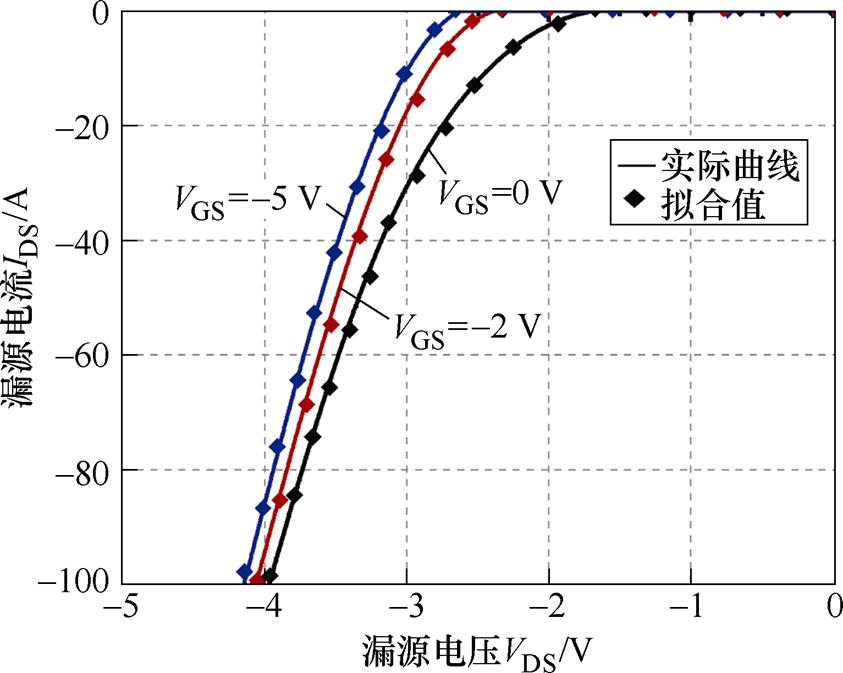
图10 25℃时体二极管伏安特性曲线
Fig.10 Volt-ampere characteristic curves of body diode at 25℃
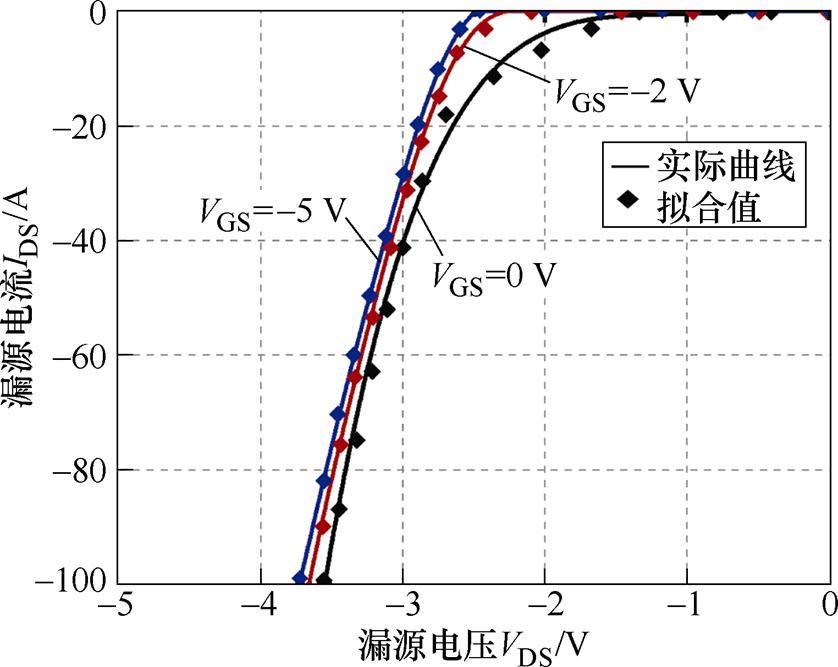
图11 150℃时体二极管伏安特性曲线
Fig.11 Volt-ampere characteristic curves of body diode at 150℃
表8 体二极管拟合参数
Tab.8 Body diode fitting parameters
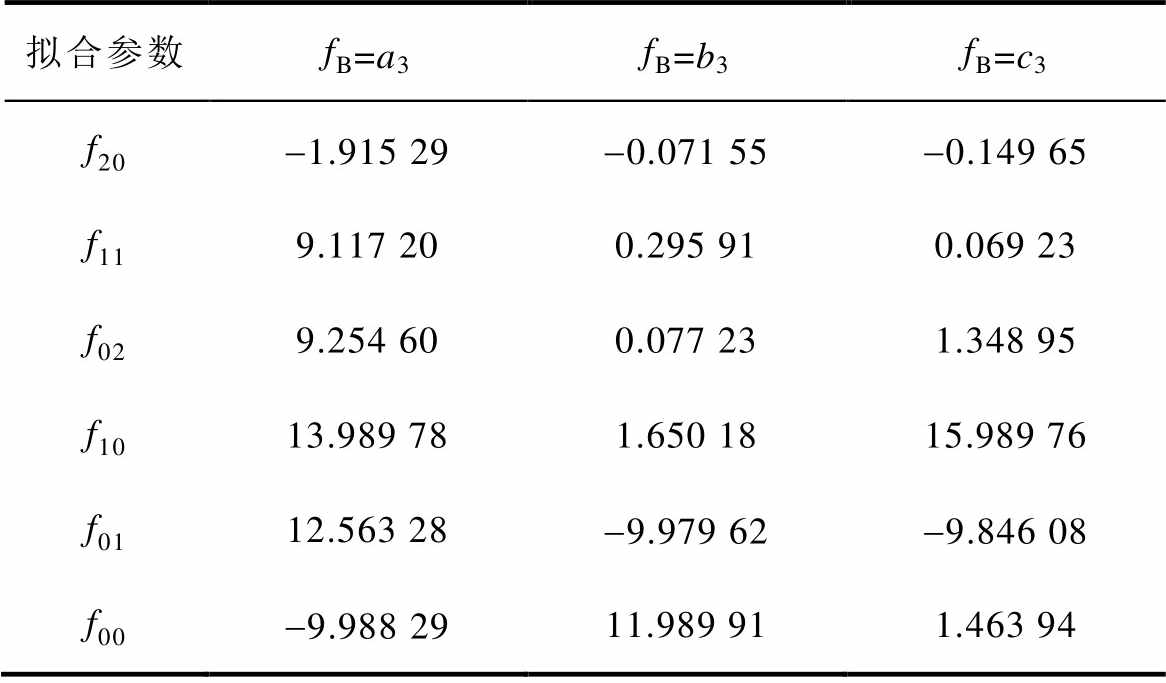
拟合参数fB=a3fB=b3fB=c3 f20-1.915 29-0.071 55-0.149 65 f119.117 200.295 910.069 23 f029.254 600.077 231.348 95 f1013.989 781.650 1815.989 76 f0112.563 28-9.979 62-9.846 08 f00-9.988 2911.989 911.463 94
在二极管动态模型中,需要考虑寄生电容的影响,根据器件的状态用不同的电容表达式来描述。当二极管处于反向偏置时,在PN结上会形成耗尽区,此时形成的势垒电容Cb起主要作用;当二极管正向偏置时,二极管电容主要由多数载流子在扩散过程中积累而形成,此时以扩散电容Cd为主。其中,体二极管势垒电容可等效为SiC MOSFET的极间寄生电容CDS,即当二极管电压VD<0时,有
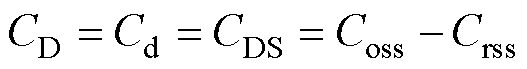 (20)
(20)
当体二极管处于正向偏置时,其电容可以等效为扩散电容Cd,式(21)给出了体二极管正向偏置时的电容近似值表达式。
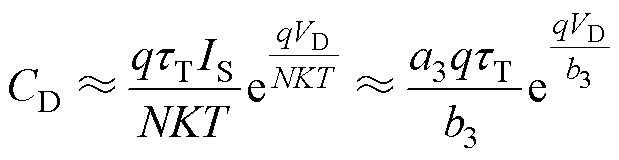 (21)
(21)
式中,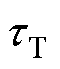 为二极管的渡越时间,在CREE公司提供的C2M0025120D库文件中,渡越时间典型值为15 ns;其余参数可由体二极管伏安特性曲线的拟合结果得到。
为二极管的渡越时间,在CREE公司提供的C2M0025120D库文件中,渡越时间典型值为15 ns;其余参数可由体二极管伏安特性曲线的拟合结果得到。
为验证静态模型的准确性,下面基于C2M0025120D实际工作曲线对模型的输出特性和转移特性进行验证。
在仿真条件的设置方面,本文选取-55℃、25℃和150℃作为测试温度。在测试输出特性曲线时,设置栅源电压为10~20 V,分别对漏源端施加线性电压,并记录电流IDS的变化。测试转移特性曲线时保持漏源电压VDS=20 V,并对栅源端施加线性电压,同时记录漏源电流。验证结果如图12~图15所示,可以看出温度在-55℃、25℃和150℃的条件下,仿真曲线与实际曲线高度吻合。
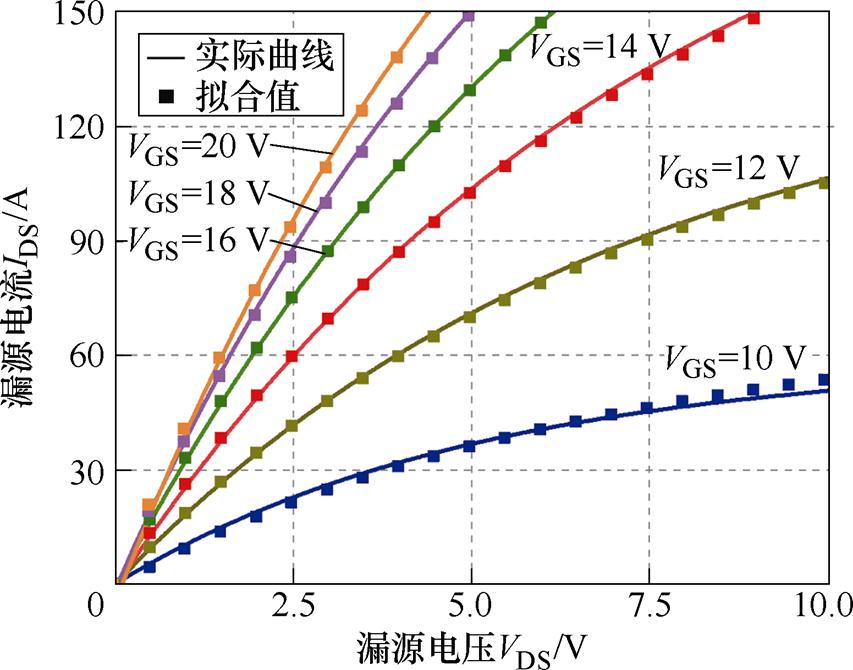
图12 -55℃时输出特性曲线
Fig.12 Output characteristic curves at -55℃
部分模型会存在过拟合的问题,即在数据手册中提供的数据点处拟合效果良好,但在其他点误差较大[8],使得模型在某些工况下的误差较大。为验证本文模型是否存在该问题,图16~图18给出了基于栅源驱动正压偏置下的模型工作曲面,可以看出模型在非拟合点处没有出现过拟合现象。表9为函数模型在阈值电压处的值,验证了模型在阈值电压处的过渡性良好。
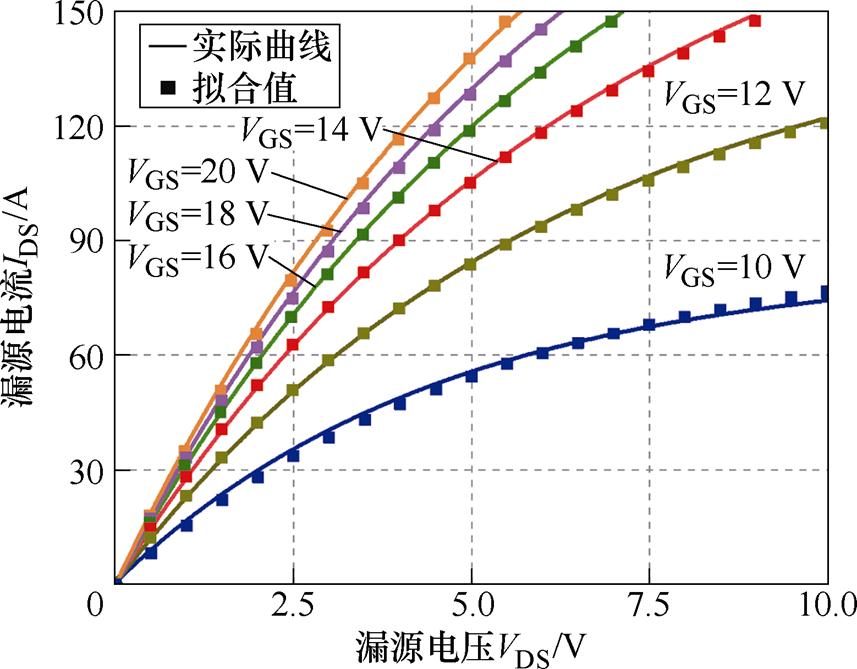
图13 25℃时输出特性曲线
Fig.13 Output characteristic curves at 25℃
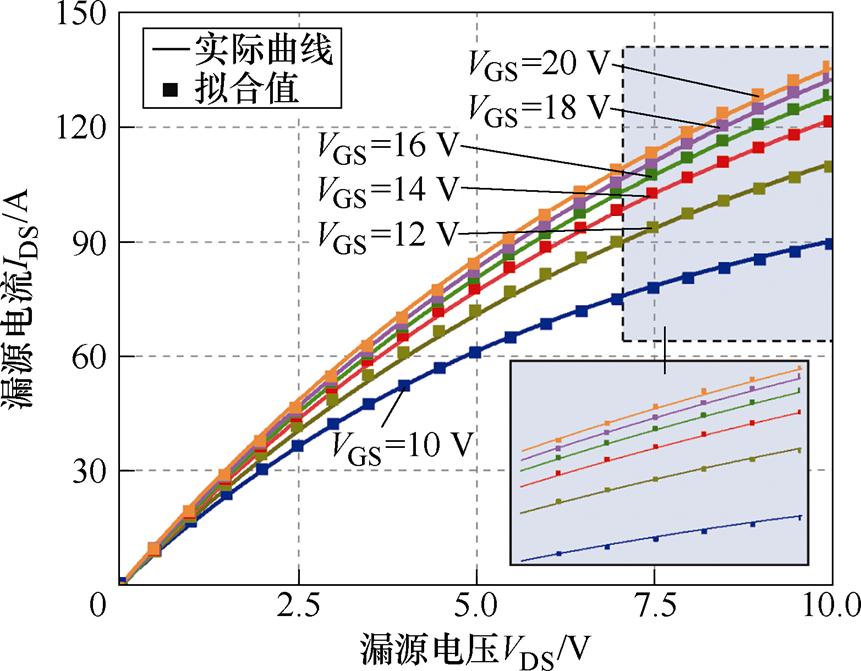
图14 150℃时输出特性曲线
Fig.14 Output characteristic curves at 150℃
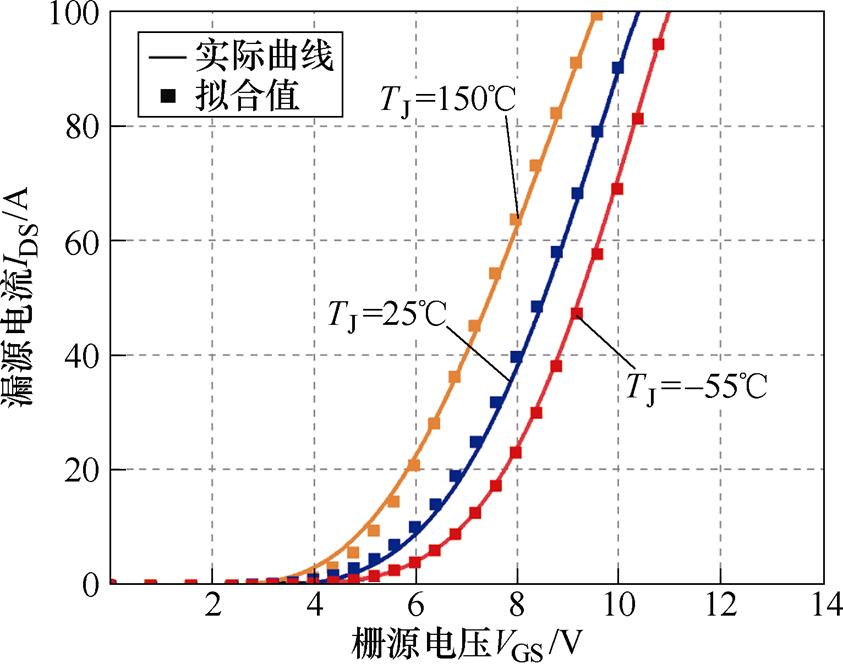
图15 转移特性曲线
Fig.15 Transfer characteristic curves
为计算静态模型的偏差,引入皮尔逊相关系数对模型进行分析计算,计算结果见表10和表11。不同工况下模型的皮尔逊相关系数均为0.99以上,表明所建静态模型满足高精度的要求。
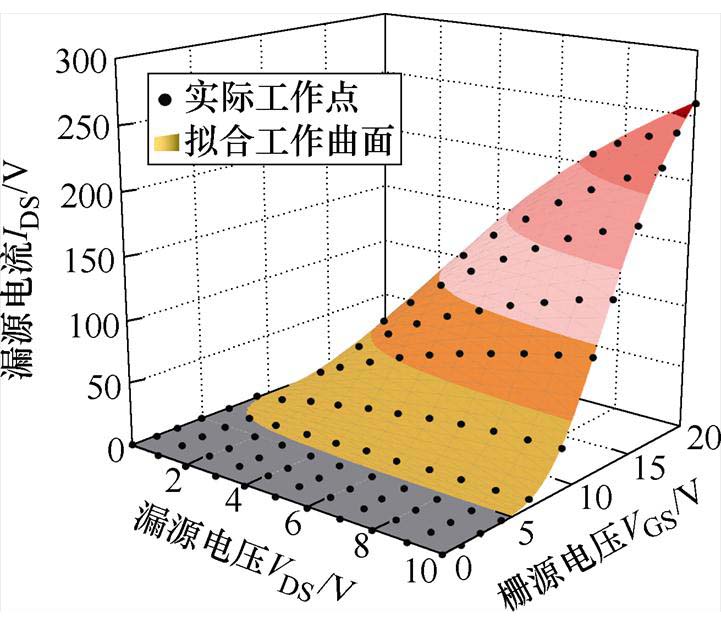
图16 -55℃时SiC MOSFET模型工作曲面
Fig.16 SiC MOSFET model work surface at -55℃
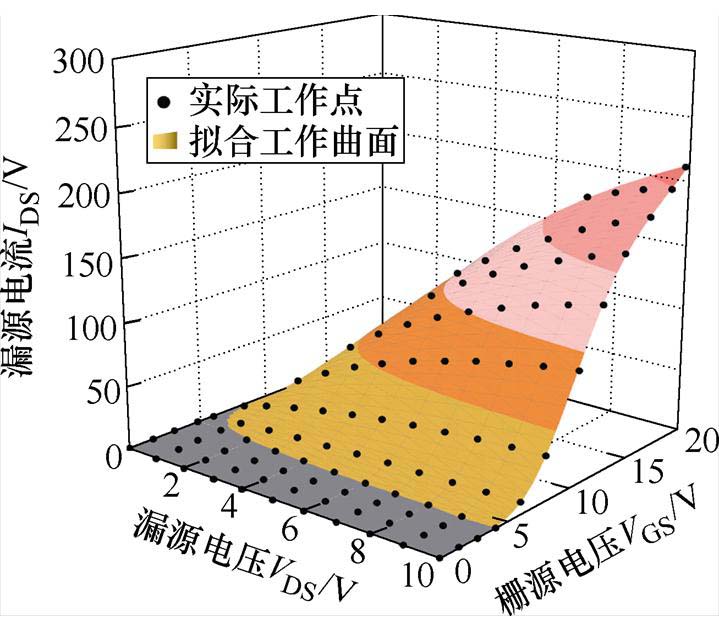
图17 25℃时SiC MOSFET模型工作曲面
Fig.17 SiC MOSFET model work surface at 25℃
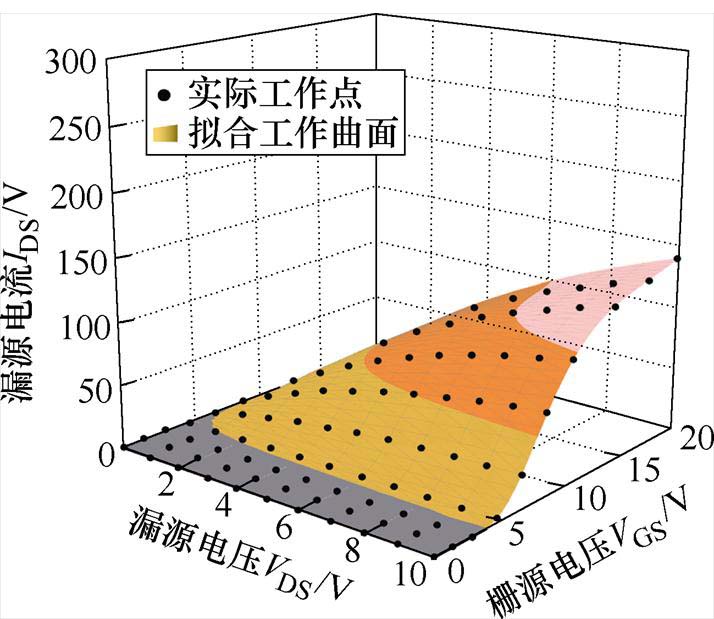
图18 150℃时SiC MOSFET模型工作曲面
Fig.18 SiC MOSFET model work surface at 150℃
表9 漏极电流函数在阈值电压处的函数值
Tab.9 Drain current function at threshold voltage
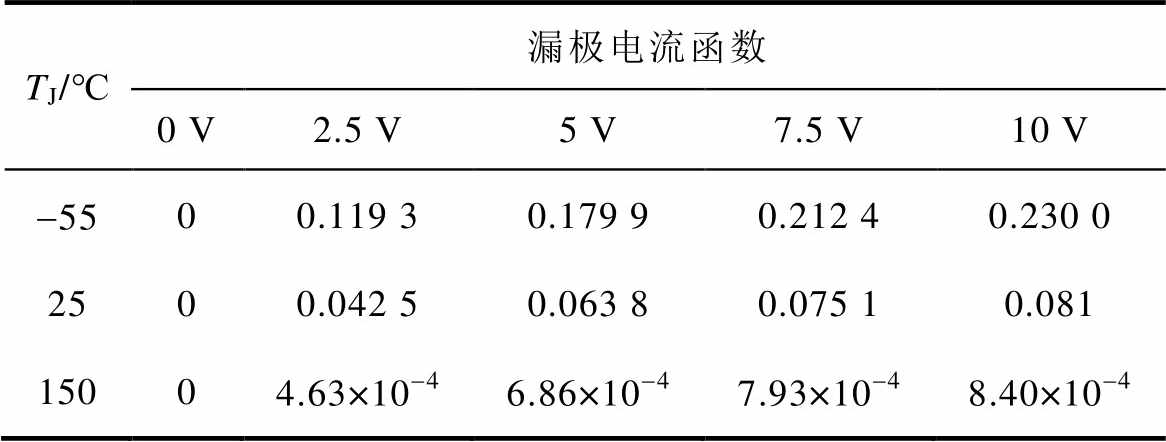
TJ/℃漏极电流函数 0 V2.5 V5 V7.5 V10 V -5500.119 30.179 90.212 40.230 0 2500.042 50.063 80.075 10.081 15004.63×10-46.86×10-47.93×10-48.40×10-4
为验证所搭建动态模型的有效性,本文对所选SiC MOSFET进行了双脉冲实验验证,测试电路和实验平台分别如图19和图20所示。采用IXDD609隔离式栅极驱动器提供驱动信号,选用CYBERTEK知用DP6150B(1 500 V/200 MHz)高压差分探头以及CYBERTEK知用CP9060L柔性线圈电流探头(600 A/12 MHz)对开关的电压电流进行测试,并利用汉邦HPA-1515恒温加热台改变实验温度。基于所建SiC MOSFET模型搭建了相应的仿真电路,器件源极、漏极、栅极的寄生电感采用CREE公司提供的典型值,部分测试条件的参数见表12。
表10 不同温度TJ及栅源极电压VGS下输出特性的皮尔逊相关系数
Tab.10 Pearson correlation coefficient of output characteristics at different temperatures TJ and gate-source voltages VGS
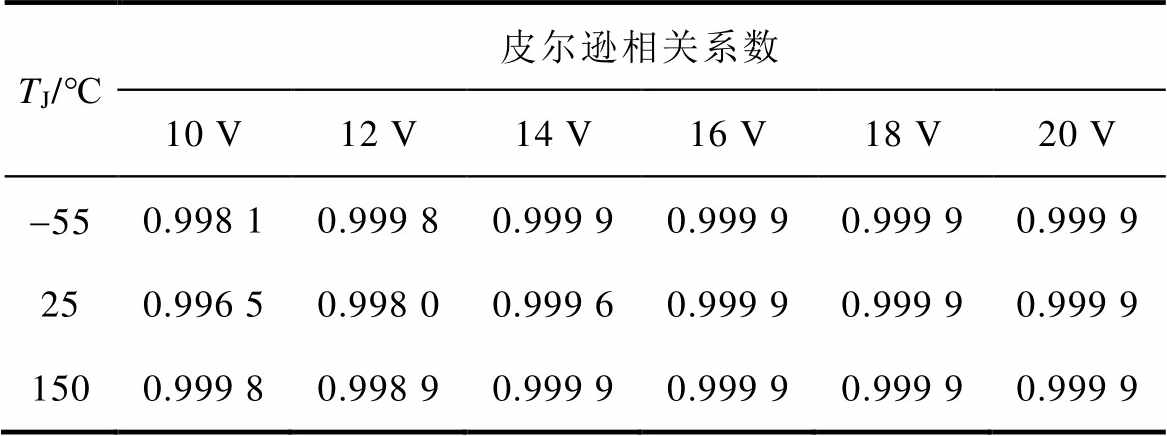
TJ/℃皮尔逊相关系数 10 V12 V14 V16 V18 V20 V -550.998 10.999 80.999 90.999 90.999 90.999 9 250.996 50.998 00.999 60.999 90.999 90.999 9 1500.999 80.998 90.999 90.999 90.999 90.999 9
表11 不同温度TJ下转移特性的皮尔逊相关系数
Tab.11 Pearson correlation coefficients for transfer characteristics at different temperatures TJ

TJ/℃皮尔逊相关系数 -550.999 9 250.997 6 1500.996 8
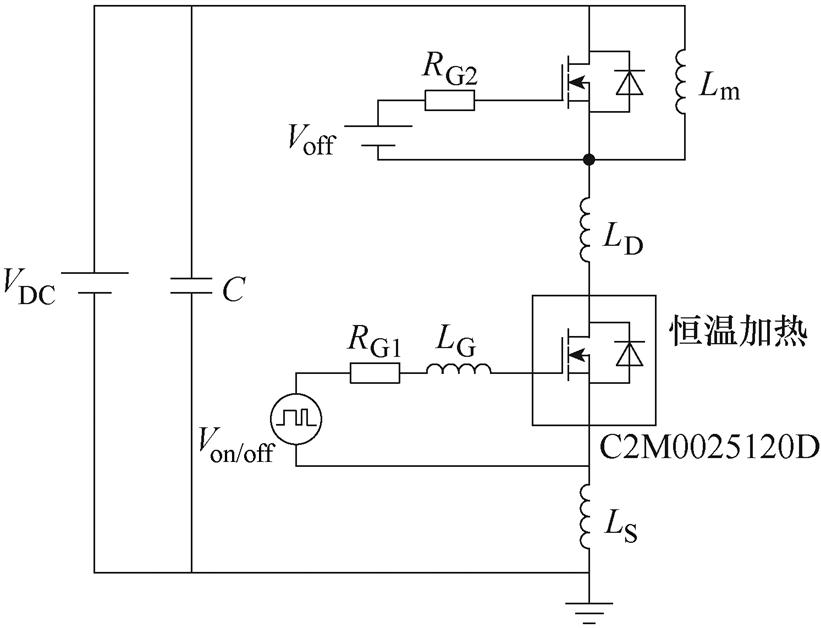
图19 双脉冲测试电路
Fig.19 Double pulse test circuit

图20 双脉冲测试实验平台
Fig.20 Experimental platform for double pulse testing
表12 部分测试条件的参数
Tab.12 Parameters for some test conditions
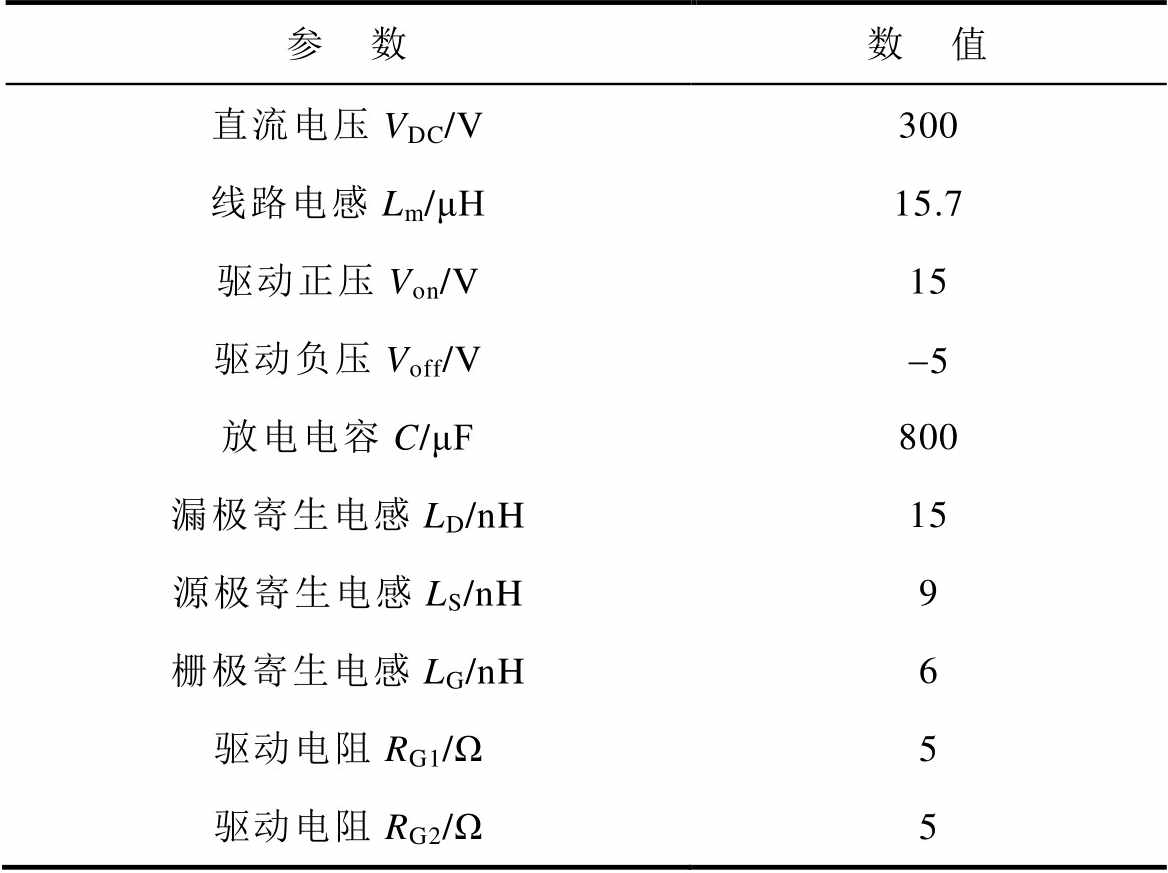
参 数数 值 直流电压VDC/V300 线路电感Lm/μH15.7 驱动正压Von/V15 驱动负压Voff/V-5 放电电容C/μF800 漏极寄生电感LD/nH15 源极寄生电感LS/nH9 栅极寄生电感LG/nH6 驱动电阻RG1/Ω5 驱动电阻RG2/Ω5
图21~图24为SiC MOSFET双脉冲测试第二个脉冲开断过程的实验与仿真波形对比,可以看到在不同温度下仿真的漏源电压、栅源电压以及漏极电流的波形与实验吻合性良好。
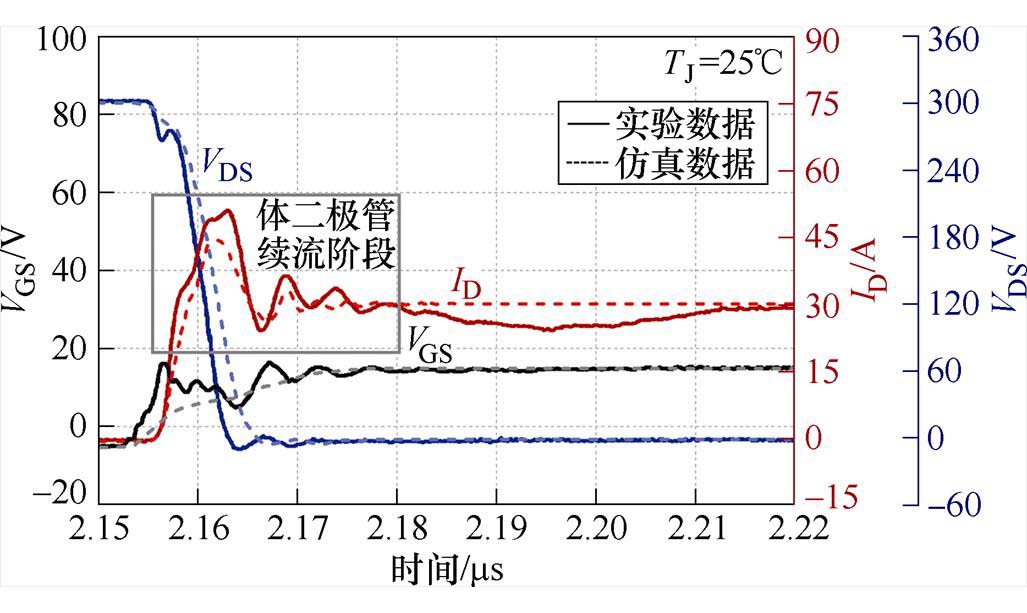
图21 25℃条件下SiC MOSFET开通过程
Fig.21 SiC MOSFET turn-on process at 25℃
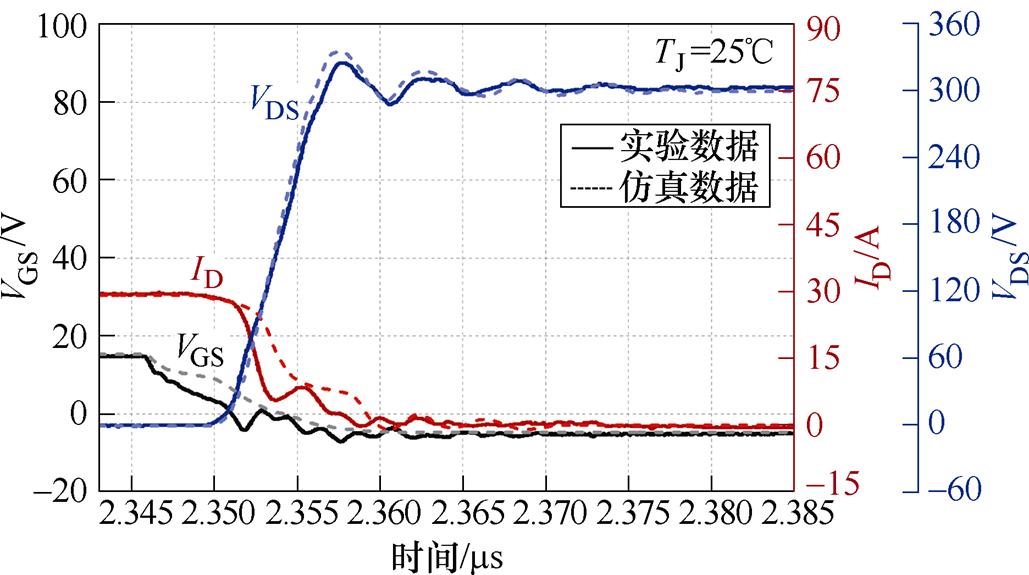
图22 25℃条件下SiC MOSFET关断过程
Fig.22 SiC MOSFET turn-off process at 25℃
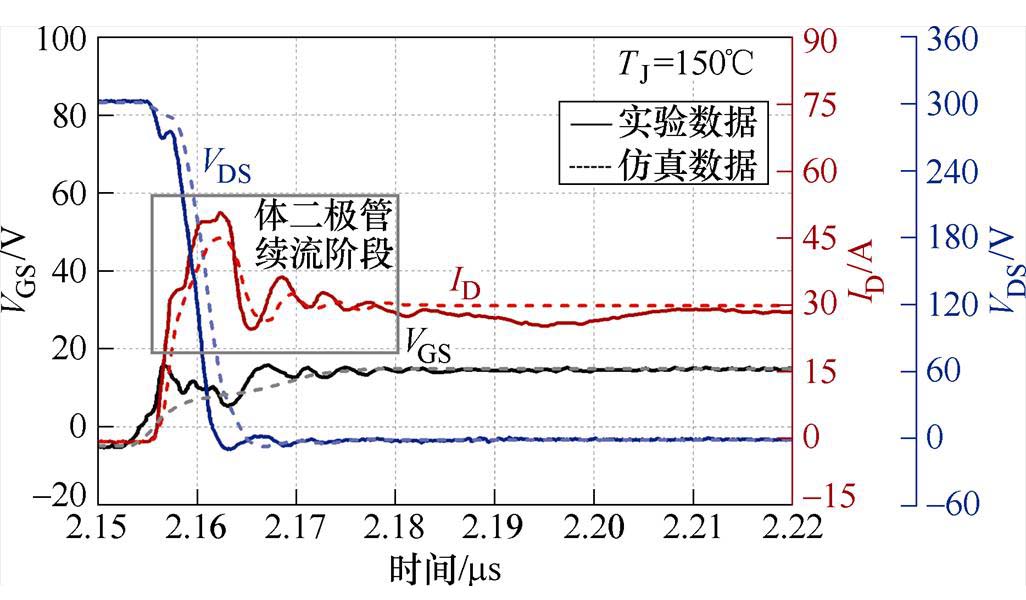
图23 150℃条件下SiC MOSFET开通过程
Fig.23 SiC MOSFET turn-on process at 150℃
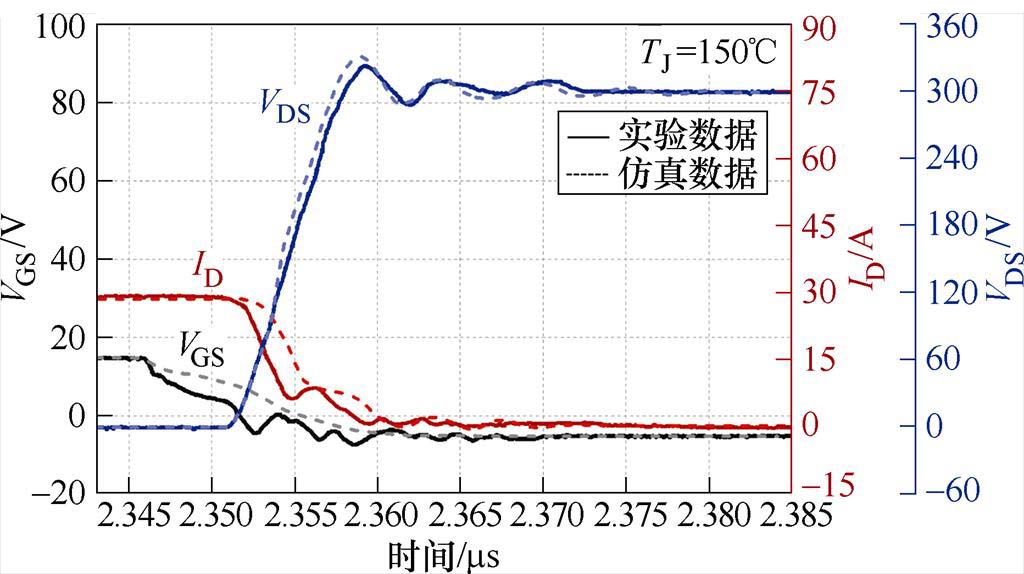
图24 150℃条件下SiC MOSFET关断过程
Fig.24 SiC MOSFET turn-off process at 150℃
对比结果显示,漏源电压VDS和漏极电流ID的仿真与实验测试结果的吻合度非常高,开断波形差异很小,误差在3%左右。由于仿真驱动电路没有考虑实际驱动的各种杂散参数,因此栅源电压VGS的仿真结果相较于另外两个变量来说误差略高,但也在10%以内。在开断速度方面,由于实验采用了高速MOSFET驱动器,实验的开断时间略快于仿真情况。同时随着温度的增加,开通曲线总体向左偏移,关断曲线总体向右偏移,且开断过程变化不明显。由于难以完全考虑电路的杂散参数以及寄生参数等因素,仿真结果与实验存在一定差异,但该模型仍能很好地模拟SiC MOSFET器件的动态特性。
电力电子电路中的SiC MOSFET通常根据设定的开断顺序依次导通关断,在这个过程中MOSFET会在不同的工作状态来回切换,对模型收敛性提出了很高的要求,在高频电路中更是如此。因此,模型的收敛性可以通过检验其在高频电路中的收敛情况来验证[19]。值得说明的是,厂商提供的仿真模型在该电路中不能收敛[20]。本文基于级联H桥七电平逆变器对所建模型进行了收敛性验证,图25展示了逆变器的拓扑结构,逆变器由3个单相H桥级联构成,输出端使用了LC滤波电路,为防止电路发生谐振,在电容上串联了电阻。该逆变器的输出Vout由3个H桥单元叠加而成,其表达式为
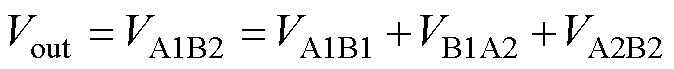 (22)
(22)
式中,右侧的3个电压量为各个子单元输出的电压,每个单元都可以输出三种电平(1 V, 0, -1 V),因此整个逆变器有七种不同的电平(3 V, 2 V, 1 V, 0, -1 V,-2 V, -3 V)。为使逆变器正常工作,需要对各个MOSFET进行高频率的PWM调控。
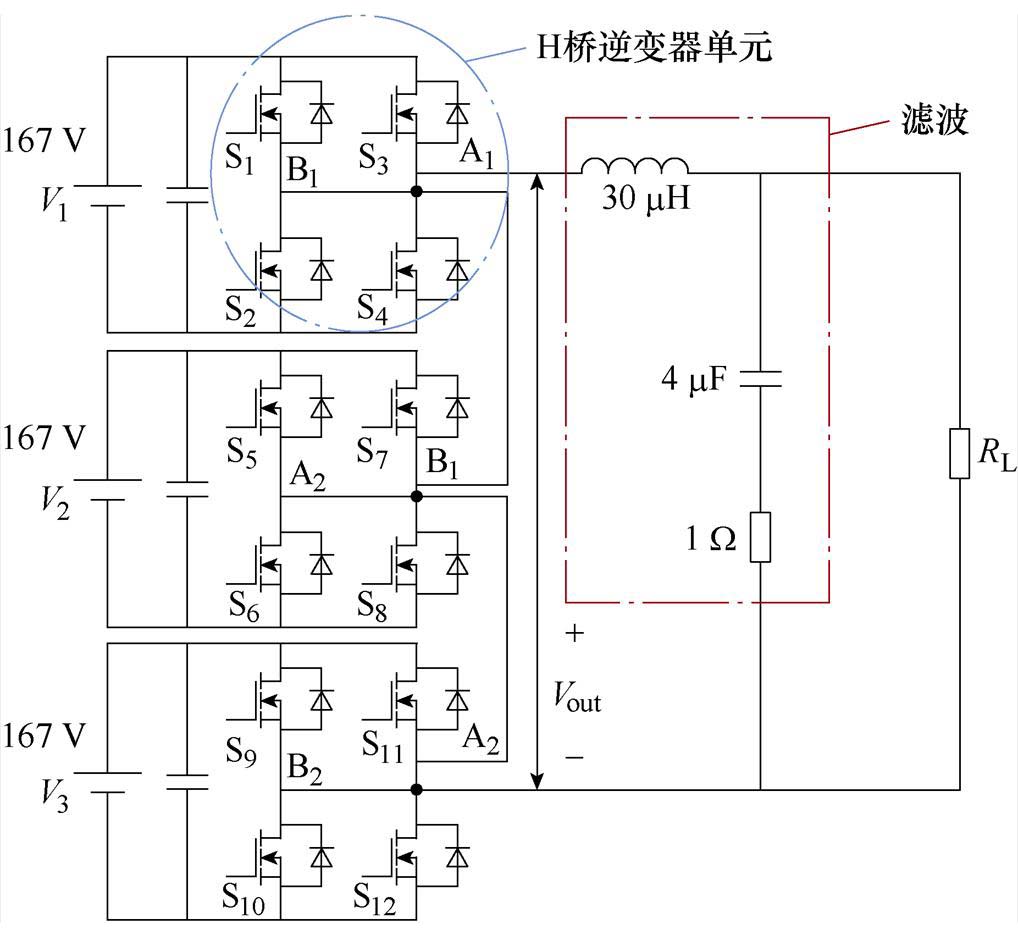
图25 单相级联H桥七电平逆变器
Fig.25 Single-phase cascaded H-bridge seven-level inverter
对于该拓扑PWM的调制策略有很多种,本文采用单极倍频正弦PWM(Sine PWM, SPWM)法对SiC MOSFET驱动信号进行调制,其原理如图26所示。调制波Vr为正弦波,载波Vc为三角波,单极倍频调制的载波频率远高于调制波频率,因此在每一个开关频率中,调制波大小可以认为不变。
驱动信号的类型由调制波和载波的大小决定,以第一个H桥单元为例,表13给出了它们的对应关系。
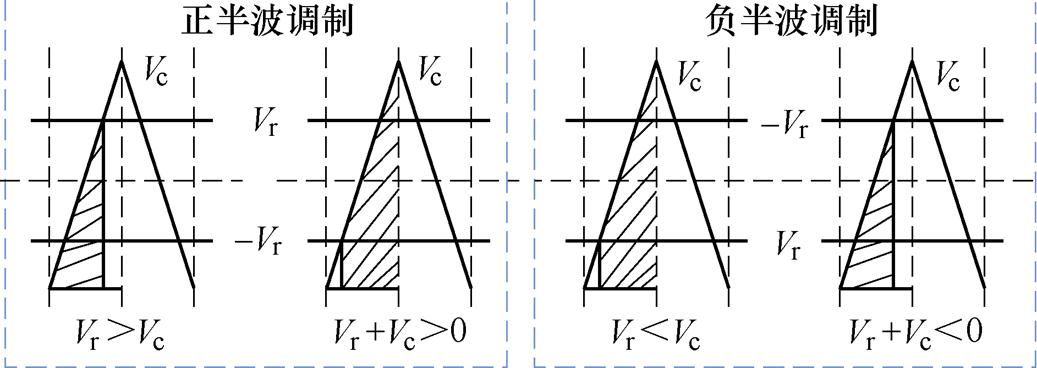
图26 单极倍频SPWM调制原理
Fig.26 Single polarity double frequency SPWM positive modulation principle
表13 调制策略
Tab.13 modulation strategy
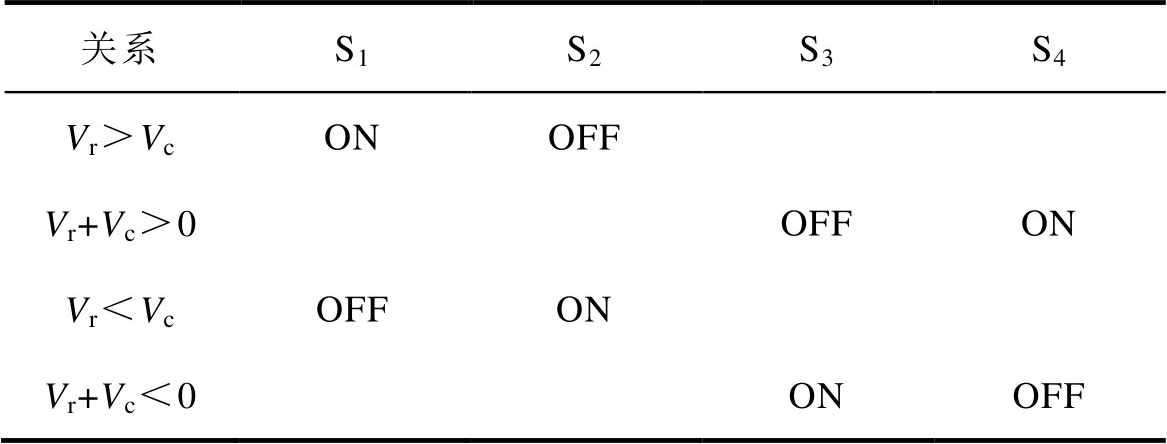
关系S1S2S3S4 Vr>VcONOFF Vr+Vc>0OFFON Vr<VcOFFON Vr+Vc<0ONOFF
通过单极倍频SPWM可生成各个模块的驱动信号,其实现电路如图27所示。
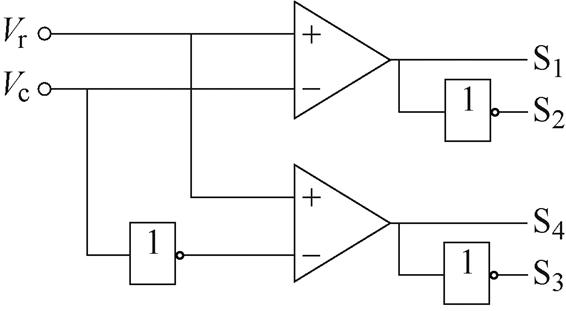
图27 驱动信号发生电路
Fig.27 Drive signal generation circuit
单极倍频SPWM结果如下,这里以第一个H桥单元为例,图28给出了S1~S4四组驱动信号的波形。对于其他H桥的驱动信号,将第一个H桥的载波信号向左平移60°后即可得到下一个H桥的 信号。

图28 驱动信号波形
Fig.28 Drive signal waveforms
为验证本文模型在收敛性方面的提升,首先将CREE官方模型应用于多电平逆变器电路中,该模型采用了三段式分段函数来描述电流特性。仿真结果如图29所示,可以看到该模型在PSpice仿真环境中无法收敛。

图29 CREE模型不收敛实例
Fig.29 Example of CREE model non-convergence
在相同的条件下,用本文所建SiC MOSFET模型替换CREE官方模型进行仿真,结果如图30所示。模型在高频驱动信号下仍能正常收敛,充分验证了其良好的收敛性。
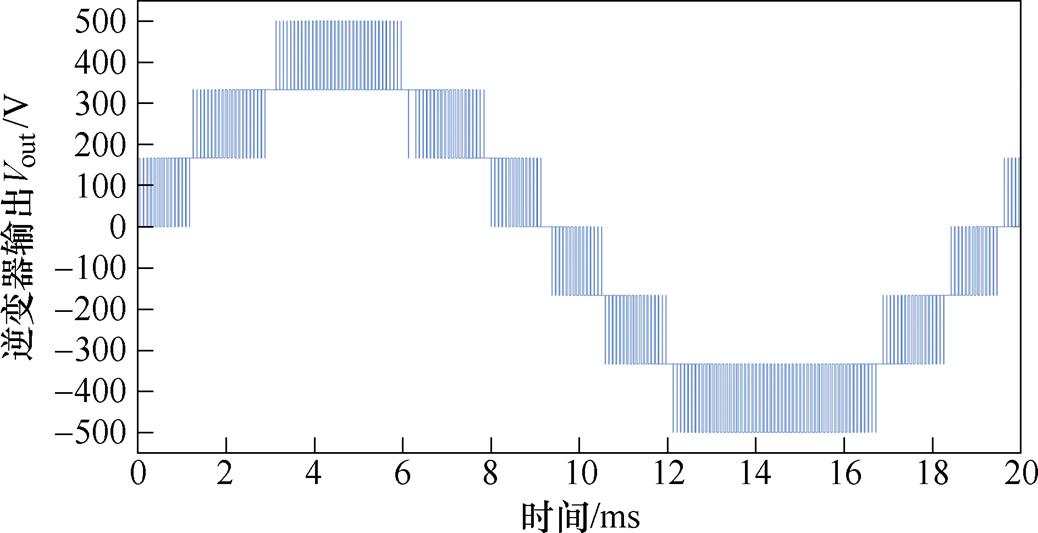
图30 基于SiC MOSFET模型的多电平逆变器仿真输出结果
Fig.30 Simulation output of multilevel inverter based on SiC MOSFET modeling
本文提出了一种满足高精度与强收敛性要求的SiC MOSFET数学建模方法,其核心在于能够精确描述SiC MOSFET特性的连续型拟合函数、收敛性和精度良好的非线性电容模型以及相应的拟合函数。主要结论如下:
1)本文提出的连续型静态拟合函数在不同温度及驱动电压的条件下均能够精确地预测SiC MOSFET工作电流;经验证,静态模型皮尔逊相关系数达到了0.99以上,满足了高精度的要求。
2)对寄生电容采用不同函数分别拟合的方法能够有效地对各个寄生电容进行准确描述,结合引入收敛电阻的寄生电容模型,使得动态模型同时具有精度高和收敛性强两方面的优点。同时体二极管建模基于二极管的电流源等效电路,并考虑了温度和栅源电压的影响,增加了模型在不同工况下的适 用性。
3)完成300 V/30 A双脉冲实验以评估SiC MOSFET模型在室温(TJ=25℃)和高温(TJ=150℃)条件下的开断特性,结果表明,模型在开断波形和开断时间方面与实验结果具有良好的一致性。最后把所建模型应用在级联H桥逆变器中,验证了模型在高频开断的逆变器电路中仍能收敛。
综上所述,本文所提出的SiC MOSFET模型兼顾了精度和收敛性,能够很好地应用于复杂的系统级高频仿真电路中。
参考文献
[1] 文阳, 杨媛, 宁红英, 等. SiC MOSFET短路保护技术综述[J]. 电工技术学报, 2022, 37(10): 2538-2548.
Wen Yang, Yang Yuan, Ning Hongying, et al. Review on short-circuit protection technology of SiC MOSFET[J]. Transactions of China Electrotechnical Society, 2022, 37(10): 2538-2548.
[2] 尚海, 梁琳, 王以建, 等. 6.5kV SiC MOSFET模块加权优化设计与实验研究[J]. 电工技术学报, 2022, 37(19): 4911-4922.
Shang Hai, Liang Lin, Wang Yijian, et al. Weighted optimization design and experimental study of 6.5kV SiC MOSFET module[J]. Transactions of China Electrotechnical Society, 2022, 37(19): 4911-4922.
[3] 薄强, 王丽芳, 张玉旺, 等. 应用于无线充电系统的SiC MOSFET关断特性分析[J]. 电力系统自动化, 2021, 45(15): 150-157.
Bo Qiang, Wang Lifang, Zhang Yuwang, et al. Analysis of turn-off characteristics of SiC MOSFET applied to wireless charging system[J]. Automation of Electric Power Systems, 2021, 45(15): 150-157.
[4] 张少昆, 孙微, 范涛, 等. 基于分立器件并联的高功率密度碳化硅电机控制器研究[J]. 电工技术学报, 2023, 38(22): 5999-6014.
Zhang Shaokun, Sun Wei, Fan Tao, et al. Research on high power density silicon carbide motor controller based on parallel connection of discrete devices[J]. Transactions of China Electrotechnical Society, 2023, 38(22): 5999-6014.
[5] 林弘毅, 伍梁, 郭潇, 等. 高功率密度SiC静止无功补偿器强迫风冷散热综合建模及优化设计方法[J]. 电工技术学报, 2021, 36(16): 3446-3456.
Lin Hongyi, Wu Liang, Guo Xiao, et al. A com- prehensive model of forced air cooling and optimal design method of high power density SiC-static var generator[J]. Transactions of China Electrotechnical Society, 2021, 36(16): 3446-3456.
[6] Xie Yue, Chen Cai, Yan Yiyang, et al. Investigation on ultralow turn-off losses phenomenon for SiC MOSFETs with improved switching model[J]. IEEE Transactions on Power Electronics, 2021, 36(8): 9382-9397.
[7] Yang Tongtong, Li Xianbing, Yin Sen, et al. A datasheet-driven nonsegmented empirical SPICE model of SiC MOSFET with improved accuracy and convergence capability[J]. IEEE Transactions on Electron Devices, 2023, 70(1): 4-12.
[8] Jin Miaoxin, Gao Qiang, Wang Yijie, et al. A temperature-dependent SiC MOSFET modeling method based on MATLAB/Simulink[J]. IEEE Access, 2017, 6: 4497-4505.
[9] Wang Jun, Zhao Tiefu, Li Jun, et al. Characterization, modeling, and application of 10-kV SiC MOSFET[J]. IEEE Transactions on Electron Devices, 2008, 55(8): 1798-1806.
[10] 孙凯, 陆珏晶, 吴红飞, 等. 碳化硅MOSFET的变温度参数建模[J]. 中国电机工程学报, 2013, 33(3): 37-43, 17.
Sun Kai, Lu Juejing, Wu Hongfei, et al. Modeling of SiC MOSFET with temperature dependent parame- ters[J]. Proceedings of the CSEE, 2013, 33(3): 37-43, 17.
[11] Arribas A P, Shang Fei, Krishnamurthy M, et al. Simple and accurate circuit simulation model for SiC power MOSFETs[J]. IEEE Transactions on Electron Devices, 2015, 62(2): 449-457.
[12] Wei Yuqi, Mantooth A. Subcircuit based modelling of SiC MOSFET in Matlab/Simulink[C]//2021 IEEE 12th Energy Conversion Congress & Exposition-Asia (ECCE-Asia), Singapore, 2021: 2339-2344.
[13] Yang Xin, Wang Ziru, Ding Yifei, et al. Improved simulation modelling and its verification for SiC MOSFET[J]. IET Power Electronics, 2022, 15(8): 728-737.
[14] Sun Kai, Wu Hongfei, Lu Juejing, et al. Improved modeling of medium voltage SiC MOSFET within wide temperature range[J]. IEEE Transactions on Power Electronics, 2014, 29(5): 2229-2237.
[15] Leonardi C, Raciti A, Frisina F, et al. A new PSpice power MOSFET model with temperature dependent parameters: evaluation of performances and com- parison with available models[C]//IAS '97. Conference Record of the 1997 IEEE Industry Applications Conference Thirty-Second IAS Annual Meeting, New Orleans, LA, USA, 2002: 1174-1181.
[16] 余秋萍, 赵志斌, 孙鹏, 等. 基于分段拟合的SiC MOSFET模型优化方法[J]. 半导体技术, 2021, 46(11): 866-874.
Yu Qiuping, Zhao Zhibin, Sun Peng, et al. SiC MOSFET model optimization method based on piecewise fitting[J]. Semiconductor Technology, 2021, 46(11): 866-874.
[17] Li Hong, Zhao Xingran, Sun Kai, et al. A non- segmented PSpice model of SiC MOSFET with temperature-dependent parameters[J]. IEEE Transa- ctions on Power Electronics, 2019, 34(5): 4603- 4612.
[18] 李鑫, 罗毅飞, 史泽南, 等. 一种基于物理的SiC MOSFET改进电路模型[J]. 电工技术学报, 2022, 37(20): 5214-5226.
Li Xin, Luo Yifei, Shi Zenan, et al. An improved physics-based circuit model for SiC MOSFET[J]. Transactions of China Electrotechnical Society, 2022, 37(20): 5214-5226.
[19] Rashid A U, Hossain M M, Emon A I, et al. Datasheet-driven compact model of silicon carbide power MOSFET including third-quadrant behavior[J]. IEEE Transactions on Power Electronics, 2021, 36(10): 11748-11762.
[20] Wang Ning, Zhang Jianzhong, Deng Fujin. Improved SiC MOSFET model considering channel dynamics of transfer characteristics[J]. IEEE Transactions on Power Electronics, 2023, 38(1): 460-471.
Abstract An accurate and effective SiC MOSFET device model forms the foundation for engineering circuit pre-design and analysis. Currently, most well-developed MOSFET models are based on Si. Due to the differences in their physical structures, Si-based modeling approaches are only partially suitable for SiC MOSFET modeling and often encounter convergence issues. It is noted that most manufacturers' simulation models are comparatively basic and significantly deviate from the genuine features of SiC MOSFETs. This paper proposes a high-precision SiC MOSFET simulation model described by continuous functions to improve accuracy and convergence simultaneously. Additionally, the required data for modeling can be obtained directly from the datasheet, reducing modeling complexity.
A method for constructing a continuous function for SiC MOSFET static drain current is proposed based on the shape characteristics of the static characteristic curves. Sub-functions of the model are considered separately based on output and transfer characteristic curve features, and a target function for the model is obtained through mathematical methods. The continuous function model ensures the convergence of the model. Traditional parasitic capacitance fitting functions are improved to address significant slope variations in the transfer capacitance curve that are difficult to fit. An equivalent circuit model for parasitic capacitance with a convergence resistor is proposed. Parameterization is applied to the diode model current source expression, considering temperature and gate-source negative voltage. All these model parameter extraction methods are based on the Levenberg-Marquardt algorithm and a general global optimization method. In addition, accurate extraction of the SiC MOSFET datasheet’s operating curves is required.
Comparisons with the operating curves in the datasheet verify the accuracy of the static model. Experimental results from a 300 V/30 A dual-pulse test for C2M0025120D at different operating temperatures (25℃ and 150℃) confirm the consistency between the dynamic model and the actual dynamic characteristics. Furthermore, the developed model is successfully applied in a cascaded H-bridge seven-level inverter using PSpice simulation, confirming the model’s convergence.
In conclusion, the following findings can be drawn: (1) The model obtained through the proposed static modeling method can accurately describe the actual static characteristics of SiC MOSFET devices. The Pearson correlation coefficient for the static model exceeds 0.99. (2) Introducing the convergence resistor in the parasitic capacitance model effectively improves the model’s convergence. (3) The improved transfer capacitance fitting function can accurately describe the transfer capacitance characteristics, reducing fitting errors. The Pearson correlation coefficient of the fitting is 0.988 7. (4) The body diode model considering junction temperature and gate-source negative voltage can enhance model accuracy and applicability. (5) The turn-on errors of the drain-source voltage and drain current are approximately 3%, while the gate-source voltage error is around 8%.
Keywords:Power SiC MOSFET, power electronics modelling, mathematical model, convergence model, high accuracy
中图分类号:TN386
DOI: 10.19595/j.cnki.1000-6753.tces.231170
国家重点研发计划资助项目(2018YFB2100100)。
收稿日期 2023-07-22
改稿日期 2023-11-25
谭亚雄 男,1990年生,博士,副教授,硕士生导师,研究方向为应用超导电力技术、直流开断技术等。
E-mail: yxtan@cqu.edu.cn(通信作者)
张梦洋 男,1999年生,硕士研究生,研究方向为功率半导体器件的建模与应用等。
E-mail: 774321691@qq.com
(编辑 陈 诚)