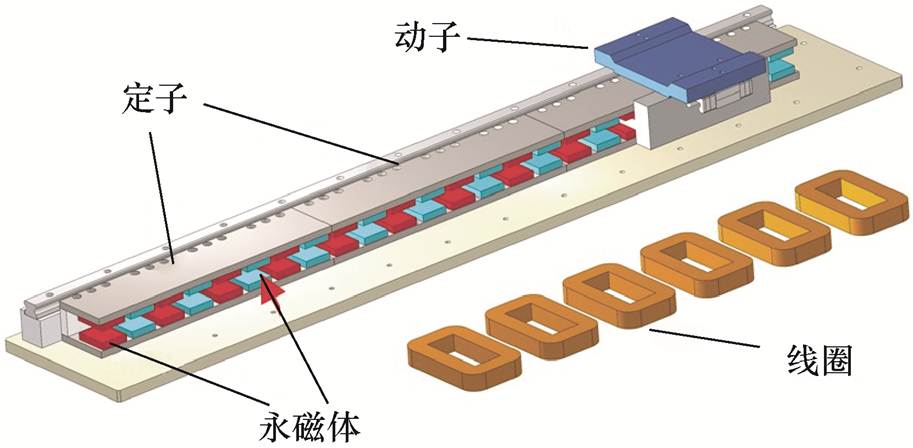
图1 永磁同步直线电机三维拓扑结构
Fig.1 3D topological structure of PMSLM
摘要 该文提出一种基于杂散磁通密度信号立体螺旋曲线投影面变换与ResNeXt-18深度学习框架相结合的方法，以实现永磁同步直线电机（PMSLM）偏心故障的非侵入式诊断。首先，建立PMSLM有限元模型，分析静态和动态偏心故障下的电机内部与杂散磁场分布。采用隧道磁阻效应（TMR）传感器并设计连接件，实现传感器与电机动子一体化设计，对电机外部杂散磁通密度信号进行实时非接触式测量。其次，引入立体螺旋曲线变换（TDSCT）信号处理算法，对电机偏心故障下的外部杂散磁通密度一维信号进行三维调制，并通过对多视角下二维投影面图像的拼接融合，实现故障特征的可视化增强。然后，引用深度学习ResNeXt-18分类框架，通过对杂散磁通密度信号二维投影面数据集的训练学习，实现偏心故障的定量精细化诊断，精度高达99.4%。与Xception，ResNet-18，GoogLeNet和CNN的对比实验表明，ResNeXt-18具有更高的诊断精度和鲁棒性。最后，搭建PMSLM样机实验平台，验证了该文所提方法的有效性。
关键词：永磁同步直线电机 偏心故障诊断 外部杂散磁场信号 立体螺旋曲线变换ResNeXt-18
永磁同步直线电机（Permanent Magnet Syn- chronous Linear Motor, PMSLM）具有传动效率高、推力品质高、定位精度高等优点[1-4]，被广泛应用于线性直驱的工业场景，如高精密机床、并联机器人等[5-7]。由于PMSLM运行工况复杂、机械装配误差、导轨变形等原因，会导致偏心故障的产生，引起电机推力波动增大、定位精度降低等问题，甚至会造成电机系统的报废。因此，需要对PMSLM偏心故障进行精准识别分类，保障其高效稳定运行。
在PMSLM偏心故障诊断研究中，有两个难点值得研究：①如何使用非侵入式方法获取偏心故障信号，并提取有效故障特征；②如何建立智能分类识别模型，实现偏心故障定量精细化诊断。
在电机偏心故障信号获取和特征提取方面：文献[8]通过获取感应电机定子线圈电流信号，使用Wigner Distribution频域分析提取故障信号的频谱信息，提取感应电机动态偏心与负载转矩振荡的故障特征；文献[9]通过离散小波变换获取三相笼型感应电机中的一相定子电流的频域信息，并应用能量频谱密度提取需要的频域故障特征；文献[10]通过分析大型三相感应电机框架振动信号的谐波频率分量，实现对偏心故障的特征获取；文献[11]通过提取四极或六极感应电机声音信号的主要频域特征信息，实现了对电机偏心故障的诊断。基于定子电流信号的故障诊断方法可能会受到控制器故障[12-13]的影响，而基于振动信号、声音信号的诊断方法易受环境噪声的干扰[14]。同时，文献[15]通过霍尔效应传感器获取电机内部气隙磁通密度信号，通过分析转子角度与内部气隙磁通密度谐波的关系，实现偏心故障的特征提取；文献[16]通过探测线圈传感器获取感应电机偏心故障状态下的时域气隙磁通密度信号，并通过短时傅里叶变换获取频域故障特征；文献[17]使用气隙磁通探头传感器获取涡轮发电机的时域气隙磁通密度信号，并通过分析所测磁通密度信号与转子旋转位置的位置关系，实现对电机转子线圈短路故障的诊断；文献[18]使用磁致伸缩传感器测量永磁旋转电机内部的气隙磁通密度信号，并通过分析信号的脉冲变化，获取电机的退磁故障特征，以上研究需要在电机内部安装传感器，属于侵入式测量诊断[19]。
在电机偏心故障的智能识别分类方面：文献[20]使用支持向量机实现了电机转子断条和偏心故障诊断；文献[21]利用k-近邻算法分析涡轮式发电机线圈电流信号特征向量，实现了对涡轮式发电机的线圈短路与偏心故障的诊断；文献[22]利用随机森林算法分析起动永磁同步电机的多组时域特征，实现了对动子断条故障的诊断，以上方法属于机器学习分类模型，但面对本文中故障类型多、训练样本量较大的分类任务，对深度特征的提取能力稍弱[23-24]。文献[25]利用多层感知结构的神经网络分析感应电机杂散磁通的频域特征，实现了感应电机电压不平衡故障诊断；文献[26]通过卷积神经网络（Convolutional Neural Network, CNN）分类网络分析多分段一维时域信号合成的灰度图像，获取电机轴承的故障特征；文献[27]提出一种基于前馈神经网络分析杂散磁通密度信号时频特征的感应电机偏心故障诊断方法，但以上方法随着网络层数的增加可能会发生梯度弥散或退化的问题。
为了解决上述问题，本文提出了一种新型非侵入式PMSLM偏心故障诊断方法，具体工作如下：首先，根据PMSLM拓扑结构约束，提出采用隧道磁阻效应（Tunnel Magnetoresistance, TMR）传感器测量PMSLM外部杂散磁通密度信号作为偏心故障诊断的有效信号，通过与电机动子的一体化设计，对PMSLM外部杂散磁通密度信号进行实时非接触式测量。其次，引入立体螺旋曲线变换（Three-Dimensional Spiral Curve Transformation, TDSCT）信号处理方法，将一维磁通密度信号调制为三维曲线，并通过多视角投影图像拼接融合生成二维图像，实现PMLSM偏心故障特征的增强。然后，引入ResNeXt-18分类模型，解决了传统CNN模型训练中的退化问题，实现了PMSLM偏心故障的精准定量化诊断。对比实验表明，该方法具有较高的精度和鲁棒性。最后，搭建PMSLM偏心故障诊断实验平台，验证了本文所提方法的有效性和优越性。
永磁同步直线电机的三维拓扑结构如图1所示。
图1 永磁同步直线电机三维拓扑结构
Fig.1 3D topological structure of PMSLM
该电机为U形动圈式结构，由永磁定子和线圈动子组成。定子部分由上、下对称的定子铁轭和N、S交错排列的贴片式钕铁硼永磁体组成，动子主要由线圈绕组与滑动平台组成。主要部件和结构参数见表1。
表1 PMSLM主要部件及结构参数
Tab.1 Structural parameters of PMSLM stator
参 数数值 (型号) 永磁体长×宽×高/(mm×mm×mm)30×24×6.5 永磁体材料NdFeB 线圈长度/mm61 磁体间距/mm30 磁体气隙宽度/mm9 极距/mm30 剩磁/T1.31
偏心故障是旋转电机中常见的故障类型，主要可分为静态故障、动态故障两种[19]，如图2所示。
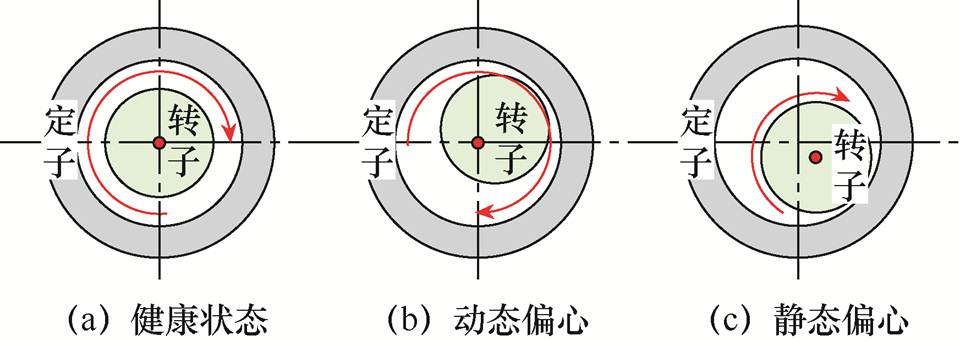
图2 旋转电机偏心故障类型
Fig.2 Different types eccentricity faults of rotary motor
与旋转电机相似，双定子永磁直线电机的偏心故障类型主要分为四大类，如图3所示，包括：①右动态偏心故障（上定子背板右端翘起）；②左动态偏心故障（上定子背板左端翘起）；③上静态偏心故障（上定子背板上扬）；④下静态偏心故障（上定子背板下倾）。
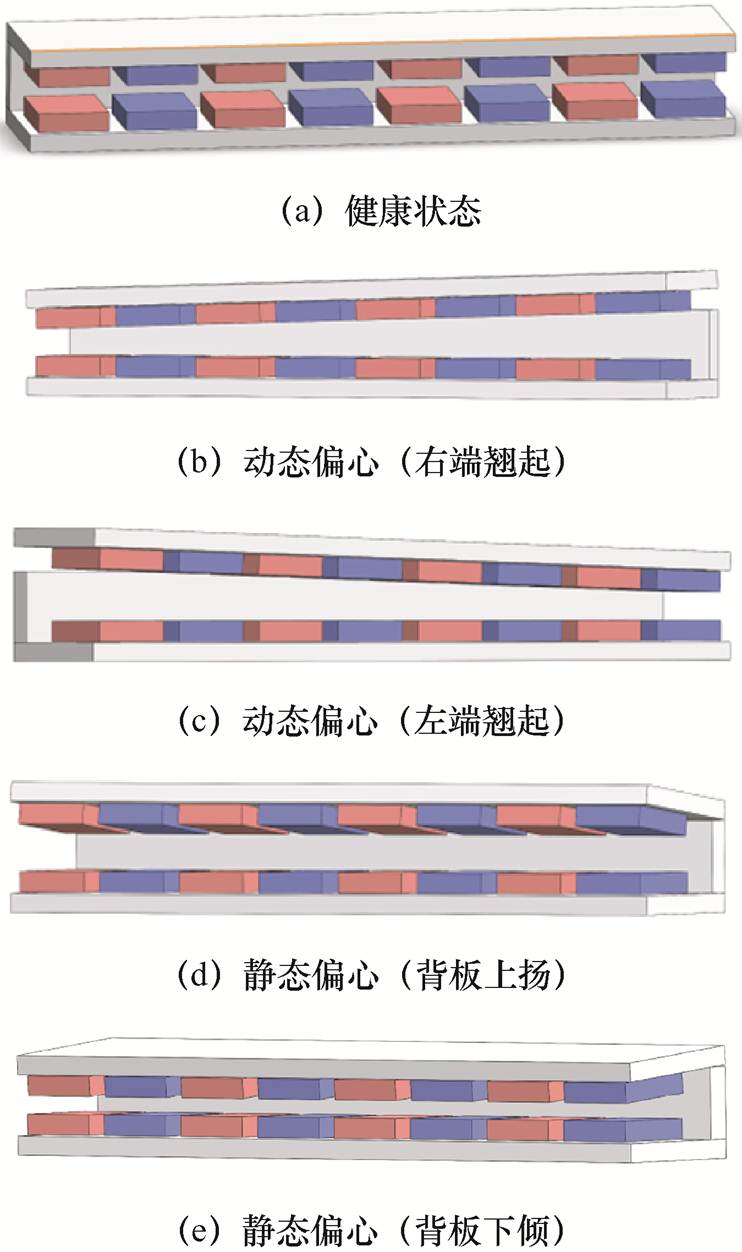
图3 PMSLM偏心故障类型
Fig.3 Different types eccentricity faults of PMSLM
本文采用JMAG有限元仿真软件，建立PMSLM健康和偏心故障状态下的有限元模型，直线电机磁通分布如图4所示。
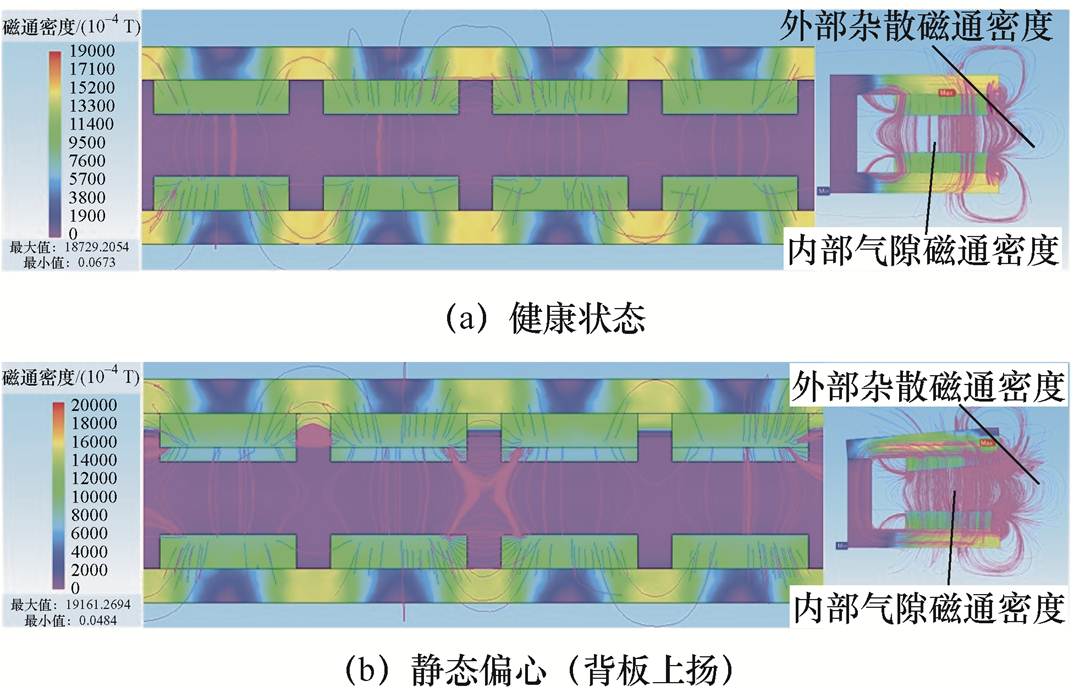
图4 直线电机磁通分布
Fig.4 Flux distribution of linear motor
图4中，当PMSLM发生偏心故障时，电机内部气隙磁通密度和外部杂散磁通密度都会发生明显变化。由于电机拓扑结构的约束，气隙的宽度通常较小（mm级），难以在不拆解电机的前提下，在气隙空间内部安装传感器并进行磁通密度测量。因此，本文选择PMSLM外部杂散磁场信号作为偏心故障诊断的有效信号。
为了获取直线电机偏心故障下的样本信号数据，为后续的故障识别分类奠定基础，本文对电机进行不同类型的故障预设，见表2。
表2 直线电机偏心故障预设
Tab.2 Setting of PMSLM eccentricity fault degree
故 障偏心故障程度/mm 动态右端翘起0.05～4.95 动态左端翘起0.05～4.95 静态背板上扬0.05～4.95 静态背板下倾0.05～4.95
每隔0.01 mm的偏心故障程度，仿真计算获取一条外部杂散磁通密度信号曲线。图5a～图5d分别展示了图3所示的四类故障下，五种不同严重程度的杂散磁通密度信号曲线。
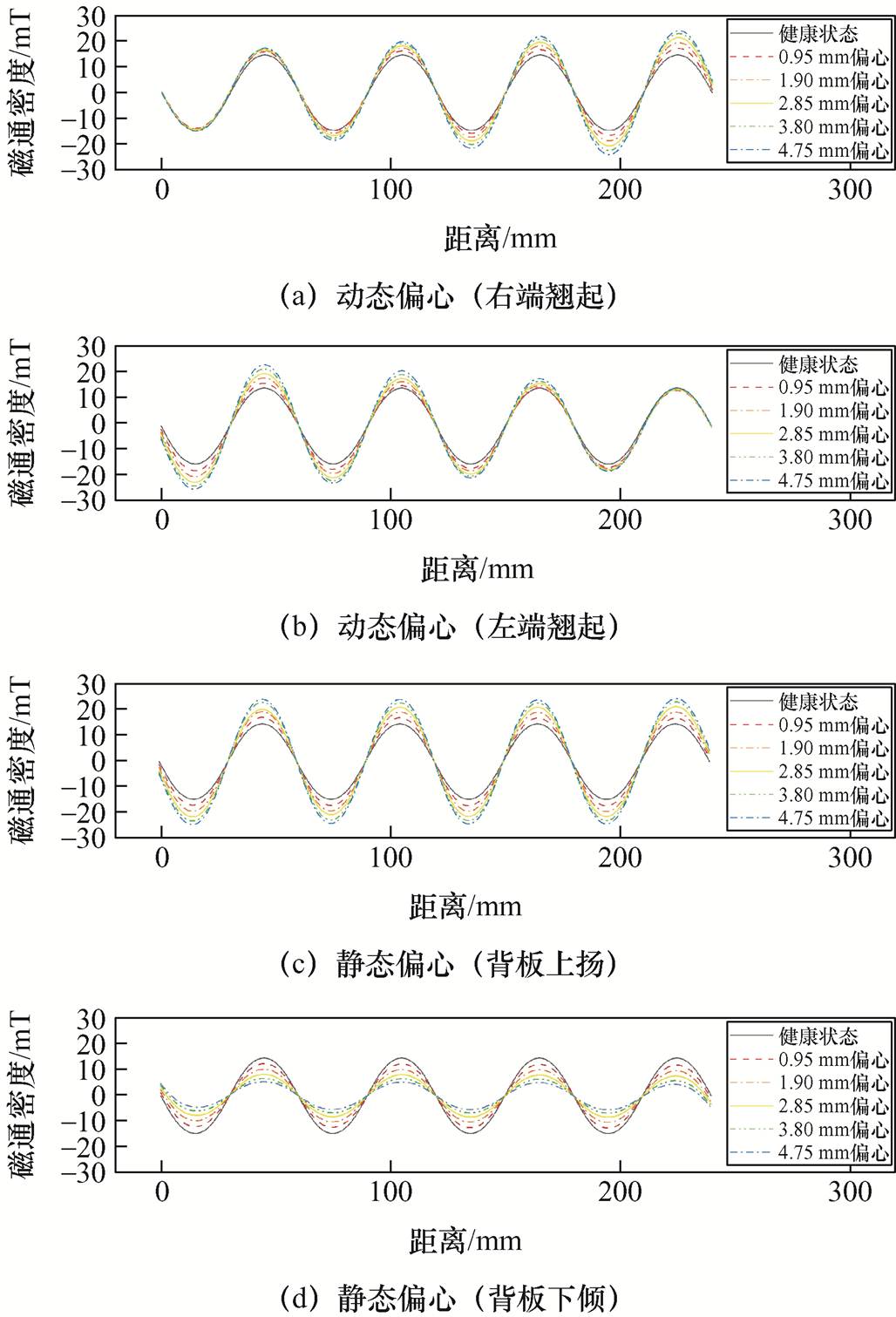
图5 偏心故障下杂散磁通密度信号曲线
Fig.5 Stray magnetic density under eccentricity faults
如图5所示，四种典型的直线电机偏心故障的磁通密度信号曲线形态各不相同，且随着故障程度的变化而明显改变，表明外部杂散磁通密度信号可以有效反映直线电机偏心故障的信息，且需进一步进行信号处理和特征提取，为后续精细定量化故障识别奠定基础。
TMR传感器是一种基于隧道磁阻效应的传感器，具有磁阻效应大、灵敏度高等优点，已被成功用于电车充电线圈偏移检测[27]与电机转子位置测量[28]。本文创新性地引入TMR传感器，并根据PMSLM拓扑结构设计连接件，用于样机实验中外部杂散磁场的感知与测量，其测量原理如图6所示。
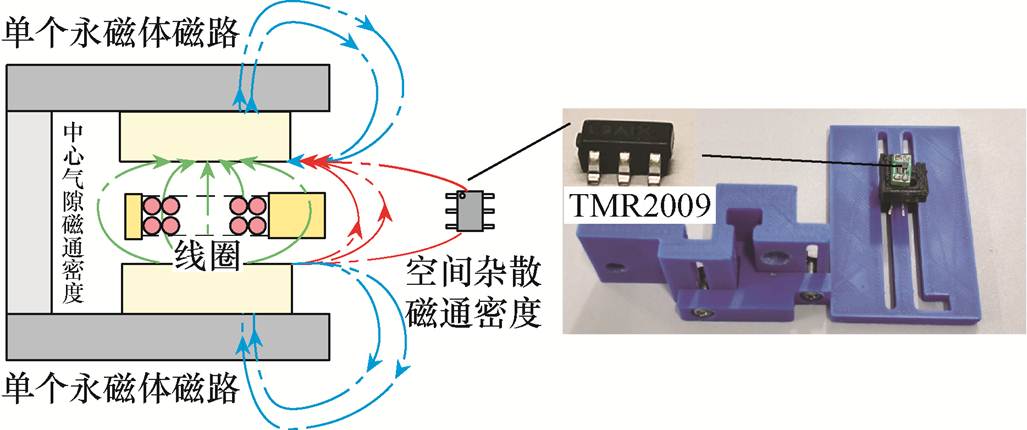
图6 基于TMR传感器的PMSLM杂散磁通密度测量原理
Fig.6 Measurement principle of spatial stray magnetic density of PMSLM based on TMR sensor
TDSCT是一种新型的信号处理方法，已应用于电能质量扰动[29]领域。本文引入该算法，以实现电机偏心故障特征的增强显示。
二维平面上的任意一条曲线都可以被描述为[x(t), y(t)]，而在三维空间中可被表达为[x(t), y(t), z(t)]，其中，t为曲线在各个维度上函数的时间变量。文献[27]中提出了一种具有N层重叠对称性的立体曲线，满足
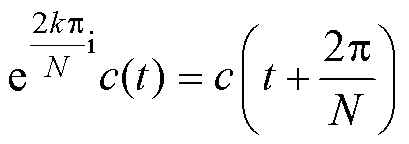（1）
式中，c(t)为空间曲线；k为2π相位的任意整数倍数；N为曲线重叠层数；k和N为互质数。
同时，任何的复数在极坐标中可以表示为
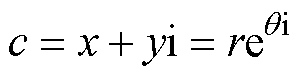（2）
式中，r与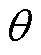
分别为极坐标中复数的幅值与相位。为了获取立体螺旋曲线的性质，c(t)被表述为
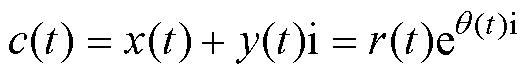（3）
式中，x(t)与y(t)分别为曲线c(t)沿x轴的实部分量与沿y轴的虚部分量；r(t)与θ(t)分别为曲线c(t)在极坐标中复数的幅值与相位。
将式（1）修改为
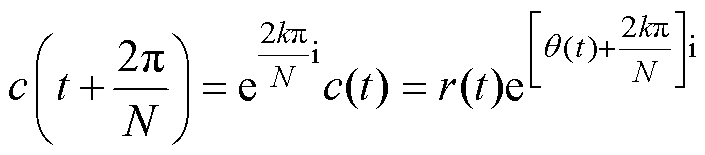（4）
由式（2）可得
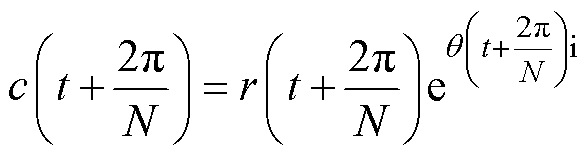（5）
对比式（4）和式（5），可得
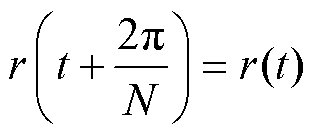（6）
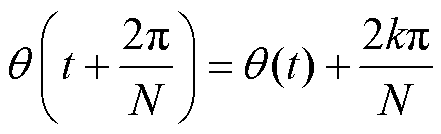（7）
式（6）表示r(t)是一个周期为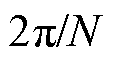
的函数，式（7）表示
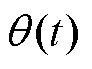是一个线性函数与周期函数之和。这里不难看出，螺旋曲线变换可以通过替换c(t)实现将周期函数的幅值r(t)与相位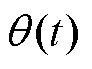解耦从而获得。复数在xy平面上被描述为
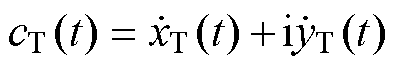。基于这种极坐标形式下，以
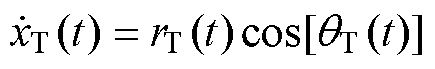表示实部，以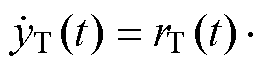
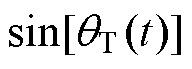表示虚部，实现对曲线
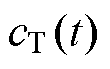频域下的描述。
直线电机外部杂散磁通密度曲线作为幅值与频率变化的周期函数，可以通过螺旋曲线变换突出其变化的特征。这种以r(t)表征幅值变化，以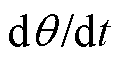
表征即刻频率的信号频域变换自然地关联到希尔伯特变换（Hilbert Transform, HT）。HT在复杂的时域变换中表现出色，常应用于处理非线性非平稳信号[30]。HT可以视作一个冲激响应为
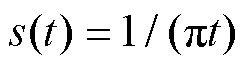的线性系统，处理后的信号各个频率分量的幅值不变化，对正频率分量滞后
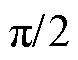，而负频率分量超前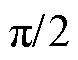。HT为
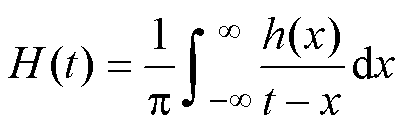（8）
由变换所得的复数结果的实部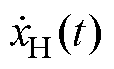
为原本的实部，而虚部
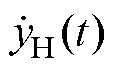则为实际的希尔伯特变换。式（3）也可表示为
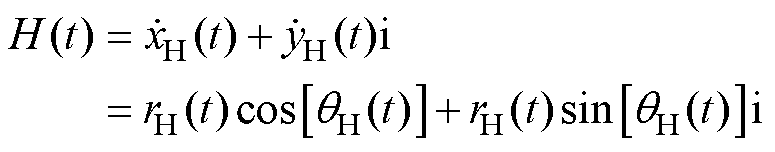（9）
式中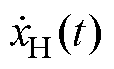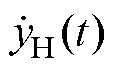，、分别为信号在希尔伯特变换后所得的实部与虚部；
、
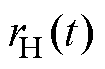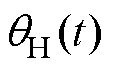分别为信号的幅值与相位。由式（7）、式（8），可得基于HT的立体螺旋曲线在三维空间中的函数表达为
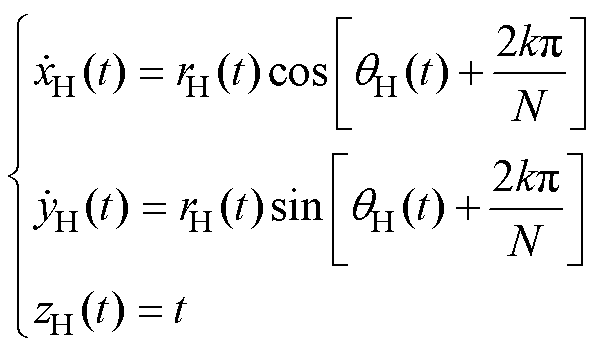（10）
本文引入TDSCT对PMSLM杂散磁通密度信号数据进行三维映射转换，对其正视、侧视和俯视视角进行二维投影和重组融合，如图7所示。
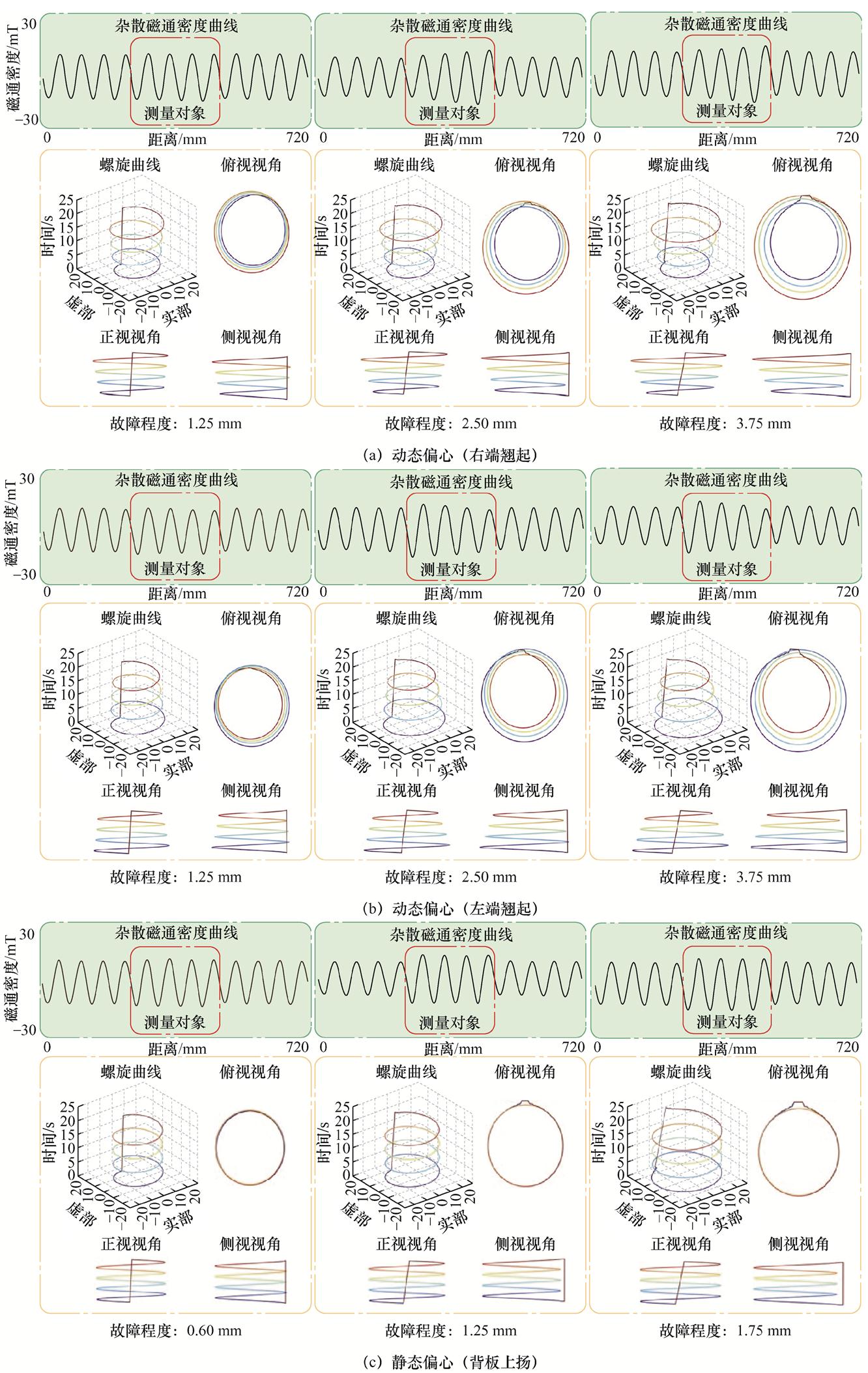
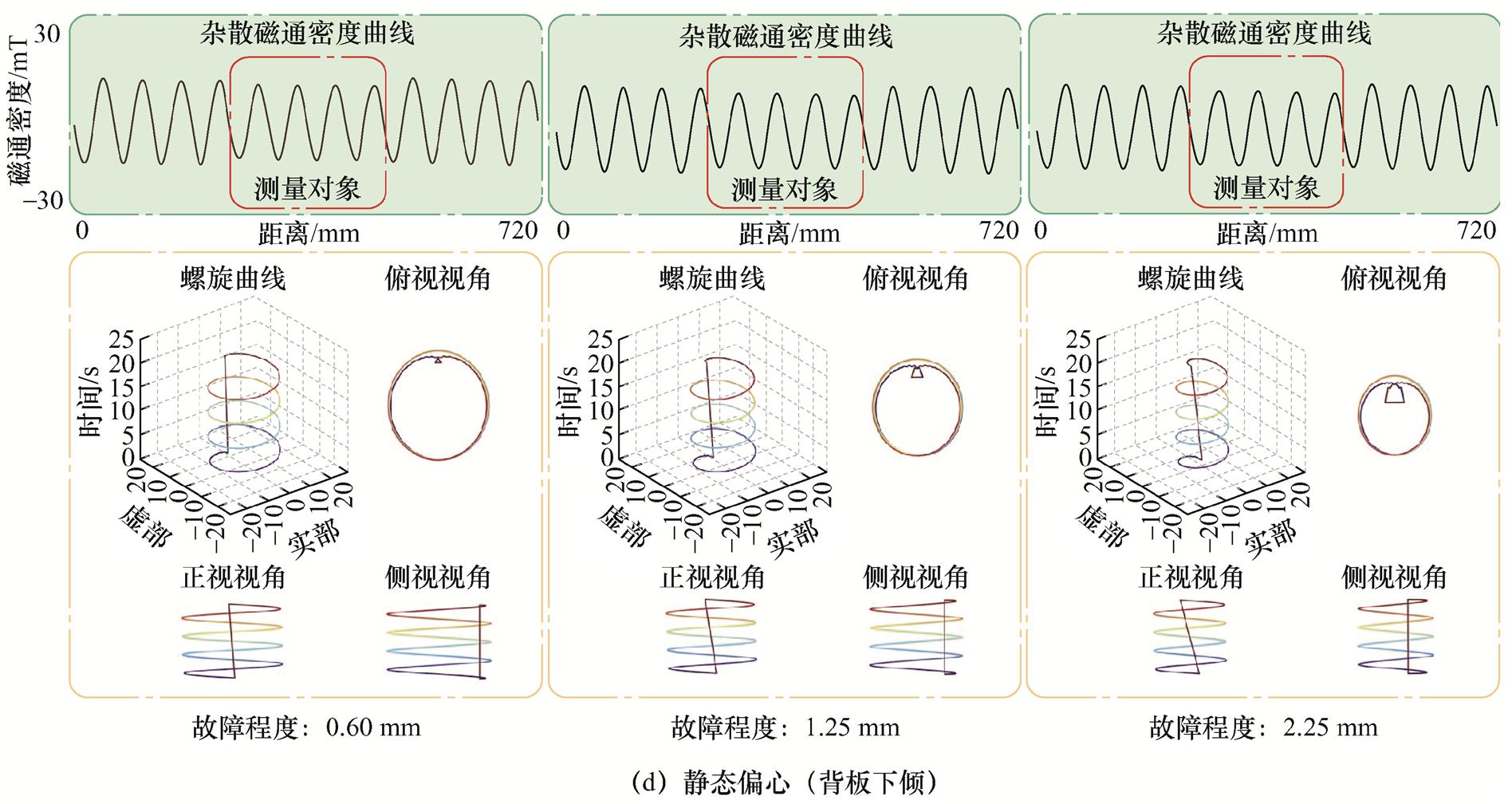
图7 基于TDSCT的静态偏心故障信号变换
Fig.7 Static eccentricity fault signal conversion based on TDSCT
分析可得：①图7a所示的动态偏心故障右端翘起的类型，其磁通密度信号的立体螺旋曲线中心均发生了明显的偏移，且故障程度越严重，曲线中心向右偏移越明显，曲线呈圆台状；对于动态偏心左端翘起，则反之。②图7c所示的静态偏心故障背板上扬的类型，其磁通密度信号立体螺旋曲线随着故障程度变大，呈现直径逐渐变大的趋势；对于背板下倾，则反之。
PMSLM偏心故障样本数据集设置为四组，分别为俯视、正视、侧视以及多视角拼接融合图，PMSLM偏心故障数据集属性见表3。根据偏心故障严重程度的不同，可将其分为：①轻度（0.05～1.65 mm）；②中度（1.70～3.30 mm）；③重度（3.35～4.95 mm）。PMSLM偏心数据集标签见表4。
表3 PMSLM偏心故障数据集属性
Tab.3 Parameters of the PMSLM eccentricity fault datasets
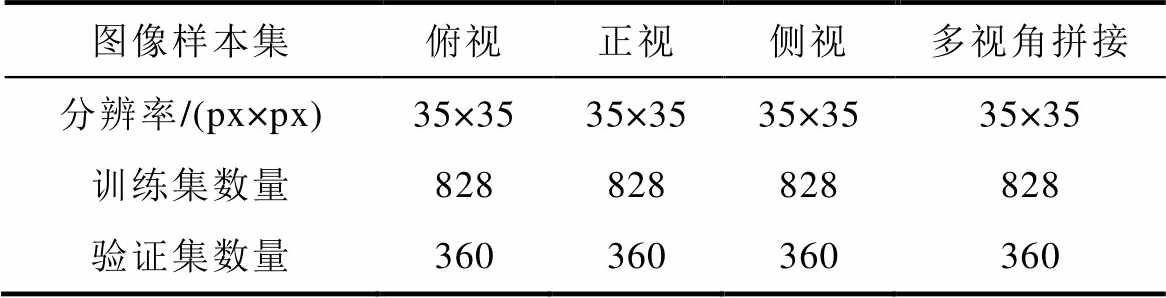
图像样本集俯视正视侧视多视角拼接 分辨率/(px×px)35×3535×3535×3535×35 训练集数量828828828828 验证集数量360360360360
表4 PMSLM偏心数据集标签
Tab.4 Labels of the PMSLM eccentricity fault datasets
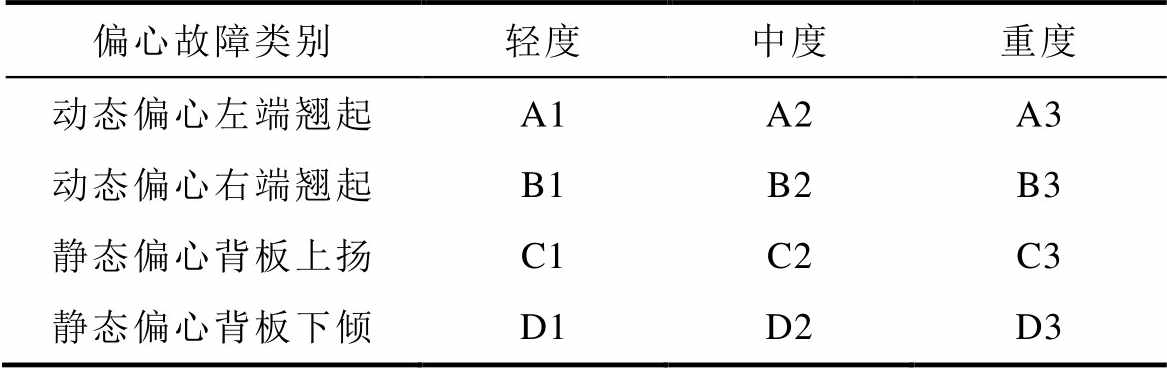
偏心故障类别轻度中度重度 动态偏心左端翘起A1A2A3 动态偏心右端翘起B1B2B3 静态偏心背板上扬C1C2C3 静态偏心背板下倾D1D2D3
ResNet是一种深度学习残差模型[31]，可以有效规避传统深度学习因深度增加所导致的退化问题，已成功用于图像物体检测[32]、永磁同步电机退磁故障诊断[33]与轴承故障诊断[34]。其表达式为
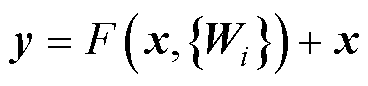（11）
式中，y与x分别为输出与输入；函数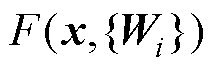
为所需学习的残差映射；
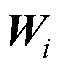为第i块中的卷积运算。式（11）可以改写为
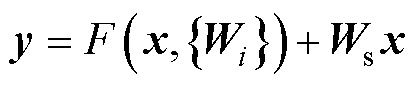（12）
式中，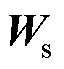
用于维度匹配。而由浅层l到深层L的学习特征为
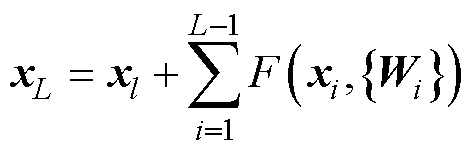（13）
式中，xL与xl分别为深层L与浅层l的学习特征；xi为第i层的输入特征。
ResNeXt模型是在ResNet基础上结合了Inception模型的分割-变换-合并的策略，进行改进增强得到的新方法[35]，解决了深度和宽度的增加无法为传统ResNet带来性能提升的问题，已成功用于语音识别[36]及肿瘤分类[37]。本文引入ResNeXt分类算法，实现直线电机偏心故障的精准分类，其结构如图8所示。
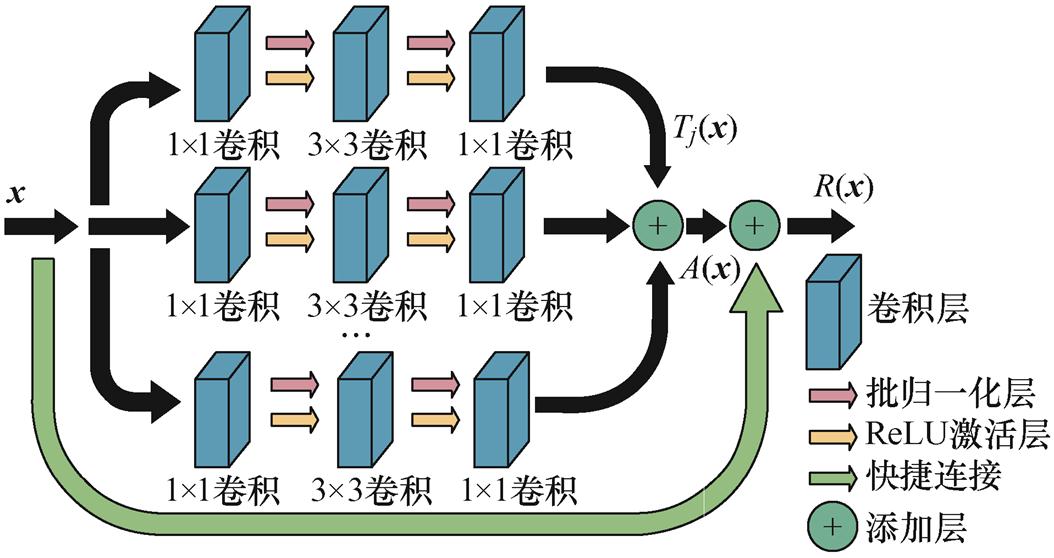
图8 ResNeXt块的拓扑结构
Fig.8 Topological structure of ResNeXt block
ResNeXt将传统的ResNet残差块中的权重层以多分支的集合转换架构替代，其表示为
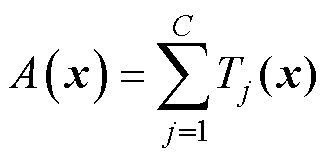（14）
式中，Tj(x)为第j个将输入x投射入一个更低维度的特征；C为一个模块中集合转换的数量。由式（12）与式（14）可得，一个ResNeXt模块R(x)可表示为
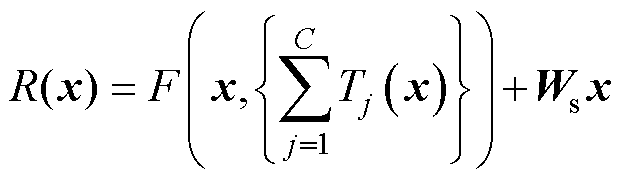（15）
基于ResNeXt-18的偏心故障诊断流程如图9所示。
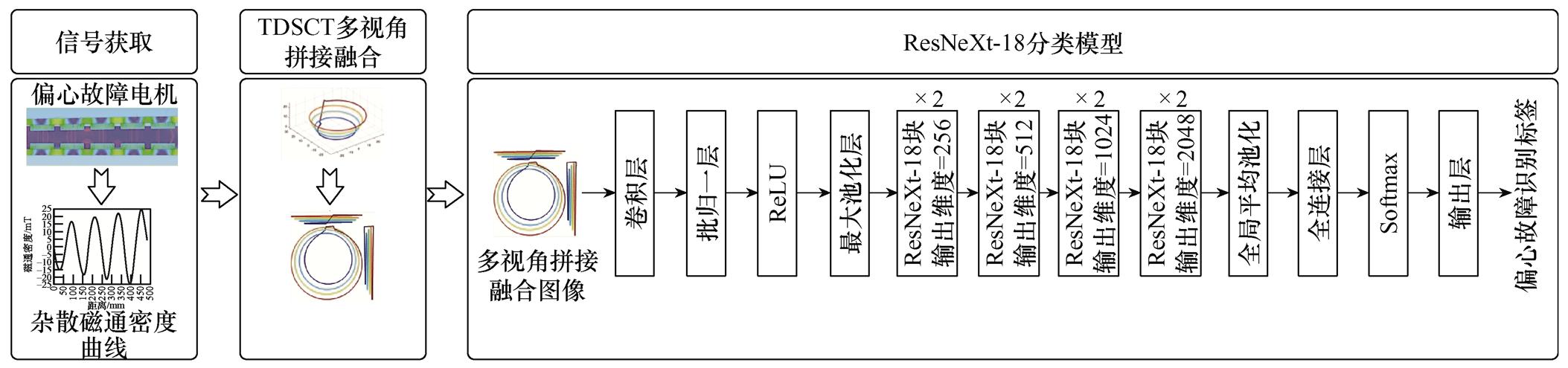
图9 基于直线电机偏心故障识别分类流程
Fig.9 Eccentricity fault identification and classification flow chart of PMSLM based on ResNeXt-18
为了验证本文所提方法的有效性，进行了不同数据集和不同分类算法的对比验证，具体如下：
（1）二维投影面数据集优选对比实验。为了论证本文的TDSCT的优越性和多视角拼接融合的有效性，将有限元仿真得到的一维磁通密度信号数据集（未进行信号处理变换）、三个不同视角（俯视、侧视、正视）下的TDSCT二维投影面数据集，以及多视角拼接融合得到的二维投影面数据集输入至CNN分类模型，以验证不同数据集对分类精度的 影响。
分类结果如图10所示，分析可得以下结论：①采用TDSCT得到的二维投影面数据集，其分类精度普遍高于一维磁通密度信号数据集，说明TDSCT可以有效实现偏心故障特征的增强。②三视角融合拼接视图数据集的分类识别率相比单一视角数据集分别提升了3.4%、3.7%和6.2%，表明拼接融合后的视图可以有效提高单一视角下的故障特征信息互补性，有效提升识别精度。
（2）不同分类方法识别分类效果对比实验。将多视角拼接融合数据集输入ResNeXt-18分类模型中，迭代训练结果如图11所示，ResNeXt-18各层参数见表5。
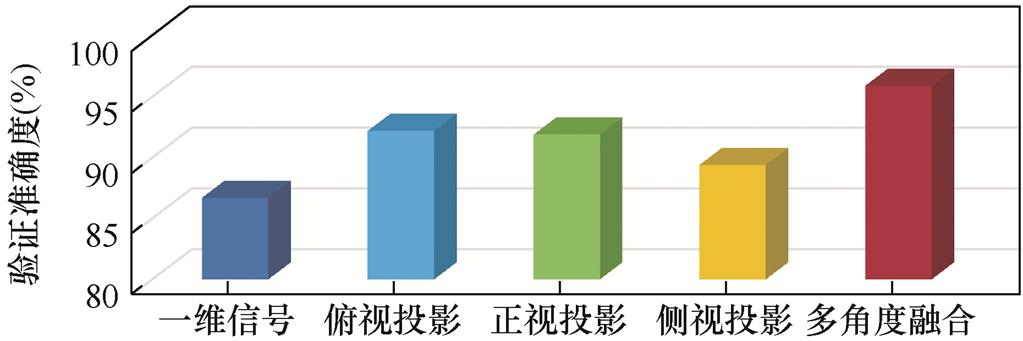
图10 不同数据集对偏心故障分类精度的影响
Fig.10 Influence of different data sets on the classification accuracy of eccentricity faults
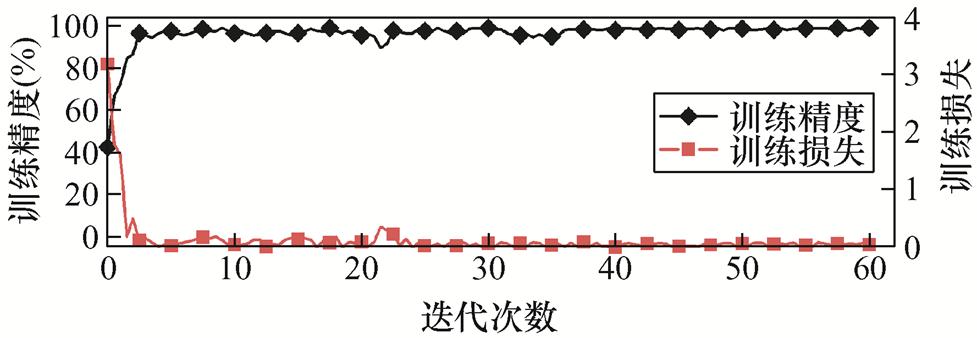
图11 ResNeXt-18训练损失与精度
Fig.11 Training loss and accuracy of the ResNeXt-18
此外，为了进一步对比验证ResNeXt-18性能的优越性，引入四种流行的分类模型（Xception、ResNet-18、GoogLeNet、CNN）进行对比，以证明本文使用的ResNeXt-18的优越性，具体结果如图12、图13所示。
表5 ResNeXt-18的各层参数
Tab.5 The layer parameters of the ResNeXt-18
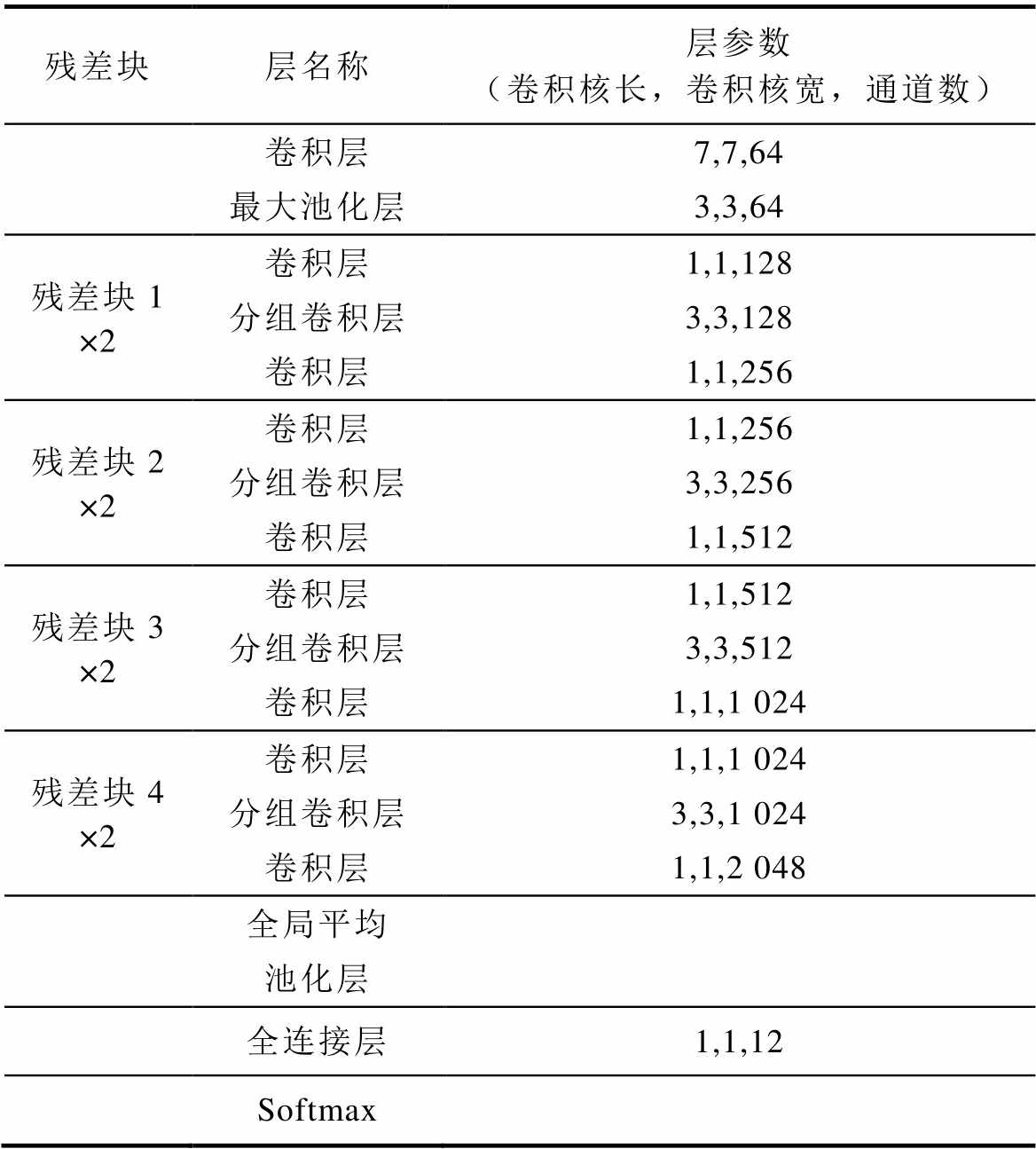
残差块层名称层参数（卷积核长，卷积核宽，通道数） 卷积层7,7,64 最大池化层3,3,64 残差块1×2卷积层1,1,128 分组卷积层3,3,128 卷积层1,1,256 残差块2×2卷积层1,1,256 分组卷积层3,3,256 卷积层1,1,512 残差块3×2卷积层1,1,512 分组卷积层3,3,512 卷积层1,1,1 024 残差块4×2卷积层1,1,1 024 分组卷积层3,3,1 024 卷积层1,1,2 048 全局平均 池化层 全连接层1,1,12 Softmax
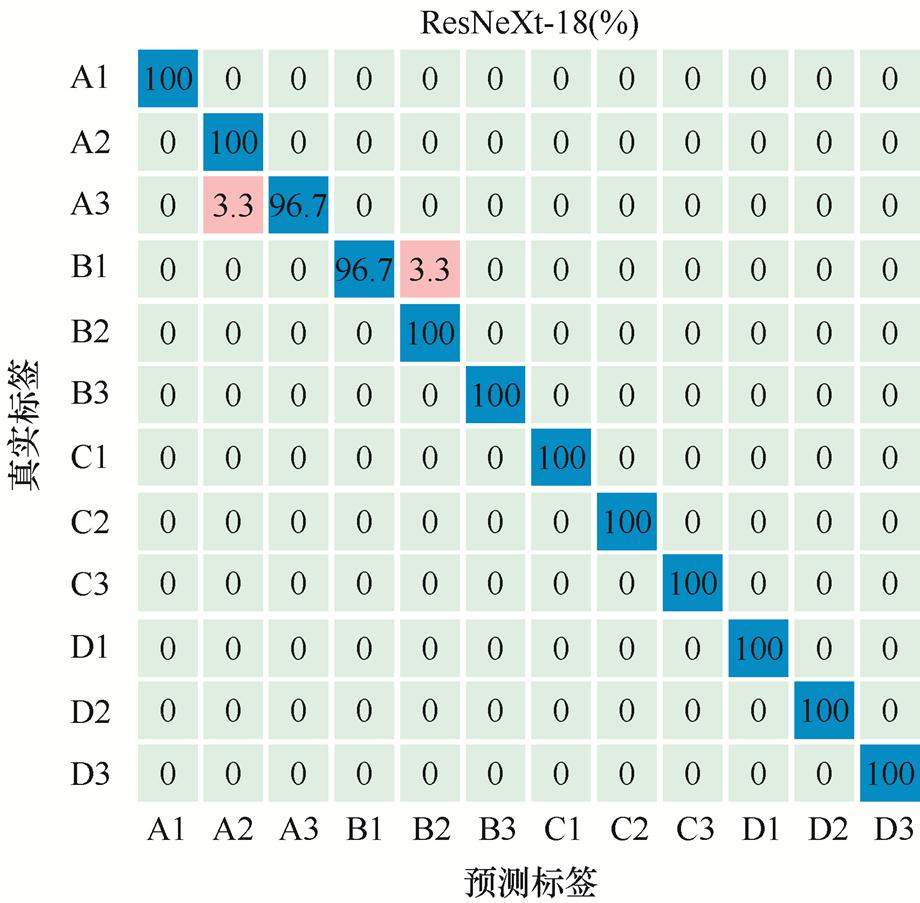
图12 ResNeXt-18的混淆矩阵
Fig.12 The confusion matrix of the ResNeXt-18
如图12、图13所示，ResNeXt-18对于直线电机偏心故障诊断的识别精度，分别较Xception、ResNet-18、GoogLeNet、CNN方法提高了1.3%、1.6%、1.3%、3.8%。主要原因有：①ResNeXt-18模型中采用的类似多头注意力机制策略[38]使得模型相较于ResNet具有更强的表征能力；②随着Cardinality维度增加，使得卷积核提取的特征更加稀疏，显著降低子模型[39]的复杂度，相比于ResNet，过拟合的风险也大大降低。
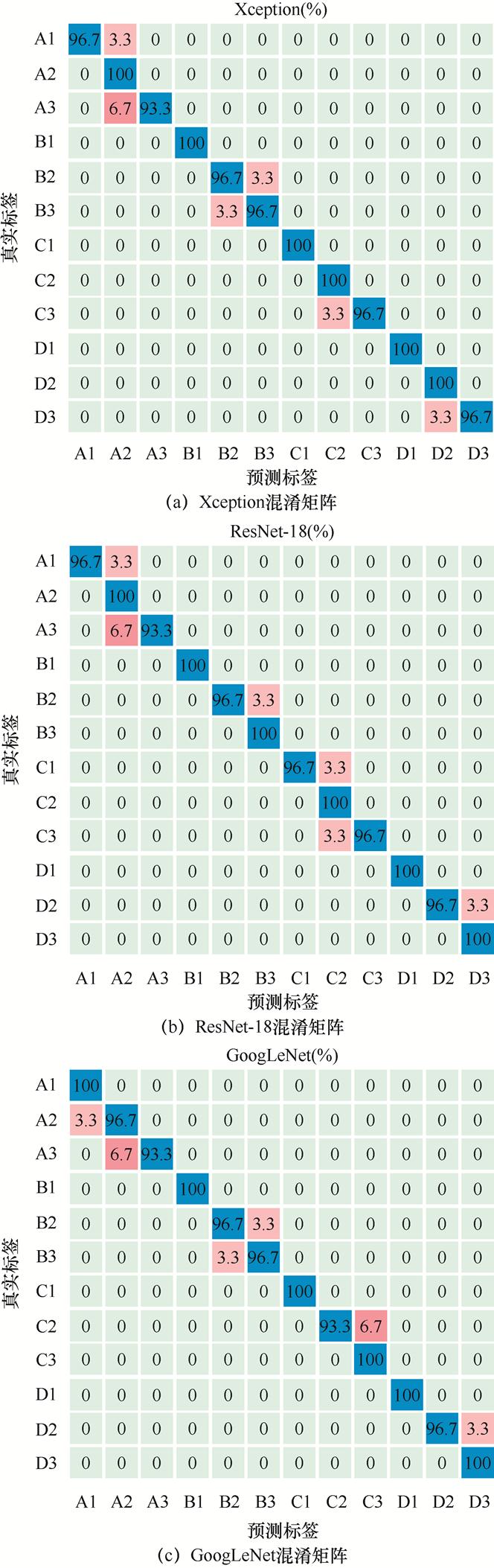
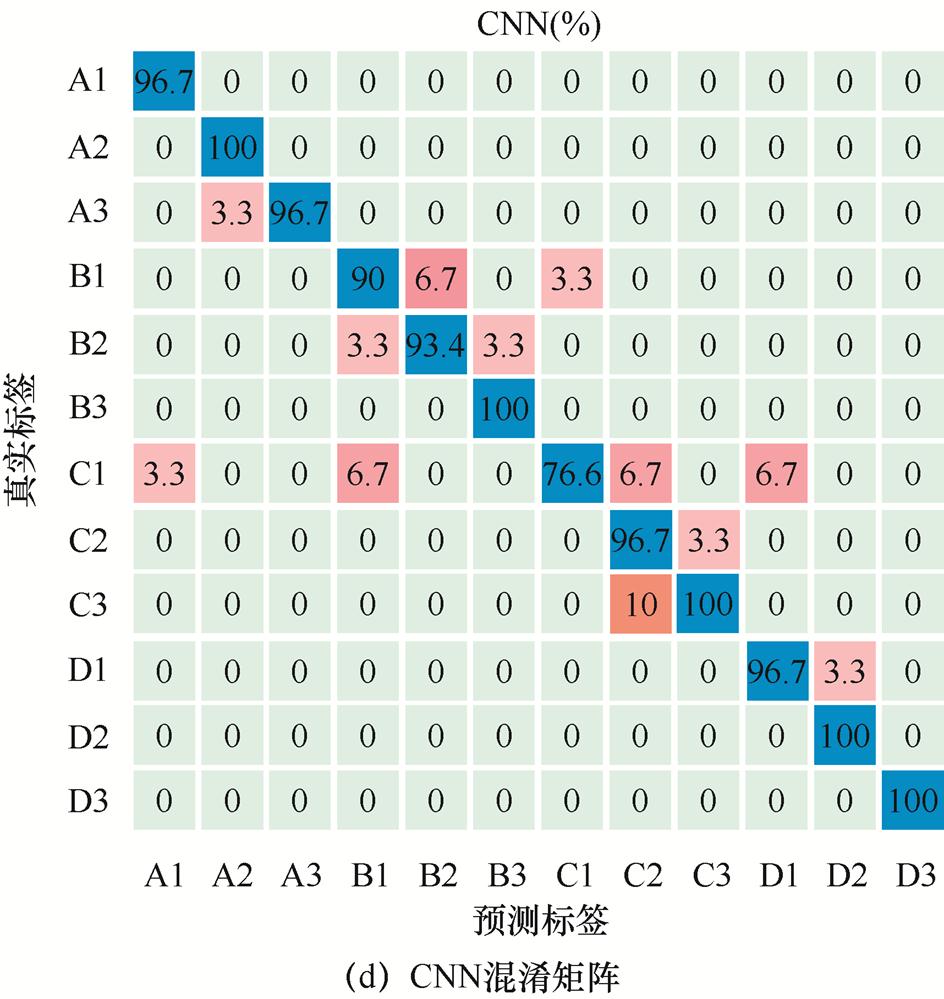
图13 不同分类方法对比混淆矩阵
Fig.13 The confusion matrixes of different methods
为了进一步论证本文使用的分类模型的鲁棒性，分别将30 dB和40 dB的高斯噪声引入生成的仿真数据并生成视角拼接图作为样本集，以验证ResNeXt-18相较于其他模型的抗噪能力和鲁棒性。噪声环境下的各模型验证准确度见表6和图14。
表6 噪声环境下的各模型验证准确度
Tab.6 Validation accuracy of each model under noise （%）
模型无噪声SNR=40 dBSNR=30 dB ResNeXt-1899.498.998.9 Xception98.197.596.7 ResNet-1898.196.795.8 GoogLeNet97.895.892.5 CNN95.694.292.8
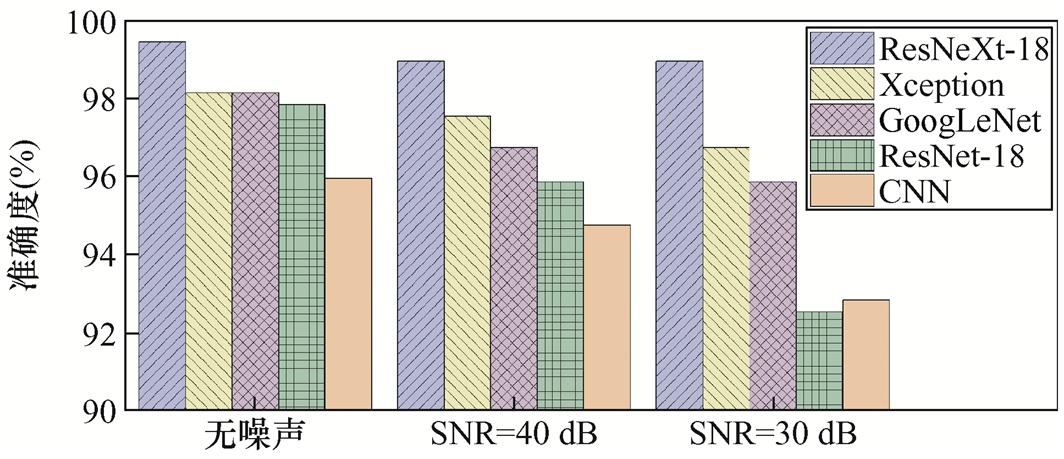
图14 噪声环境下的各模型验证准确度
Fig.14 Validation accuracy of each model under noise
由表6与图14可知，除本文中使用的ResNeXt- 18模型外，其他的对比对象在面对40 dB与30 dB噪声时，验证准确度均出现了不同程度的下降，分析可得以下结论：①40 dB噪声下，Xception、GoogLeNet、ResNet-18、CNN分别下降了1.4%、2.3%、5.3%与2.9%；30 dB的高斯噪声下，对比模型验证准确度分别降低0.6%、1.4%、2.0%与1.4%。②ResNeXt-18在30 dB与40 dB噪声下均下降0.5%，相较于其他模型展现出了更优的鲁棒性。
本文对直线电机的定子模块进行不同类型的偏心故障预设，如图15所示。
图15 PMSLM偏心故障预设
Fig.15 Eccentricity fault presets of PMSLM
搭建的PMSLM偏心故障诊断实验平台如图16所示。实验平台组成：①PMSLM样机（参数见表1）；②具有偏心故障的电机定子模块；③TMR2009传感器；④3D打印的传感器连接件；⑤基于AD620芯片的杂散磁场信号硬件放大电路；⑥NI USB- 4431数据采集卡；⑦计算机。
图16 直线电机偏心故障诊断实验平台
Fig.16 Eccentricity fault diagnosis platform for PMSLM
具体实验步骤如下：
（1）对直线电机的定子模块进行偏心故障预设，通过塞入不同厚度的塞尺人为制造PMSLM的动态与静态偏心故障（见图15），故障设置见表7。
表7 直线电机偏心故障预设
Tab.7 Eccentricity fault presets of linear motor （单位: mm）
故障类型动态偏心右端翘起动态偏心左端翘起静态偏心背板上扬静态偏心背板下倾 程度10.40.41.30.9 程度21.51.52.03.0 程度34.23.14.03.8
（2）将TMR传感器通过连接件固定在电机动子上，控制电机动子沿直线方向进行运动。此时，TMR传感器伴随电机动子进行同步运动，并将采集到的PMSLM外部杂散磁通密度信号传输给硬件放大电路，再通过NI数据采集卡采集传输至计算机。
（3）实测数据处理过程。使用TDSCT对实测的电机定子外部杂散磁通密度信号进行处理与变换，生成拼接融合图像数据集，如图17所示。
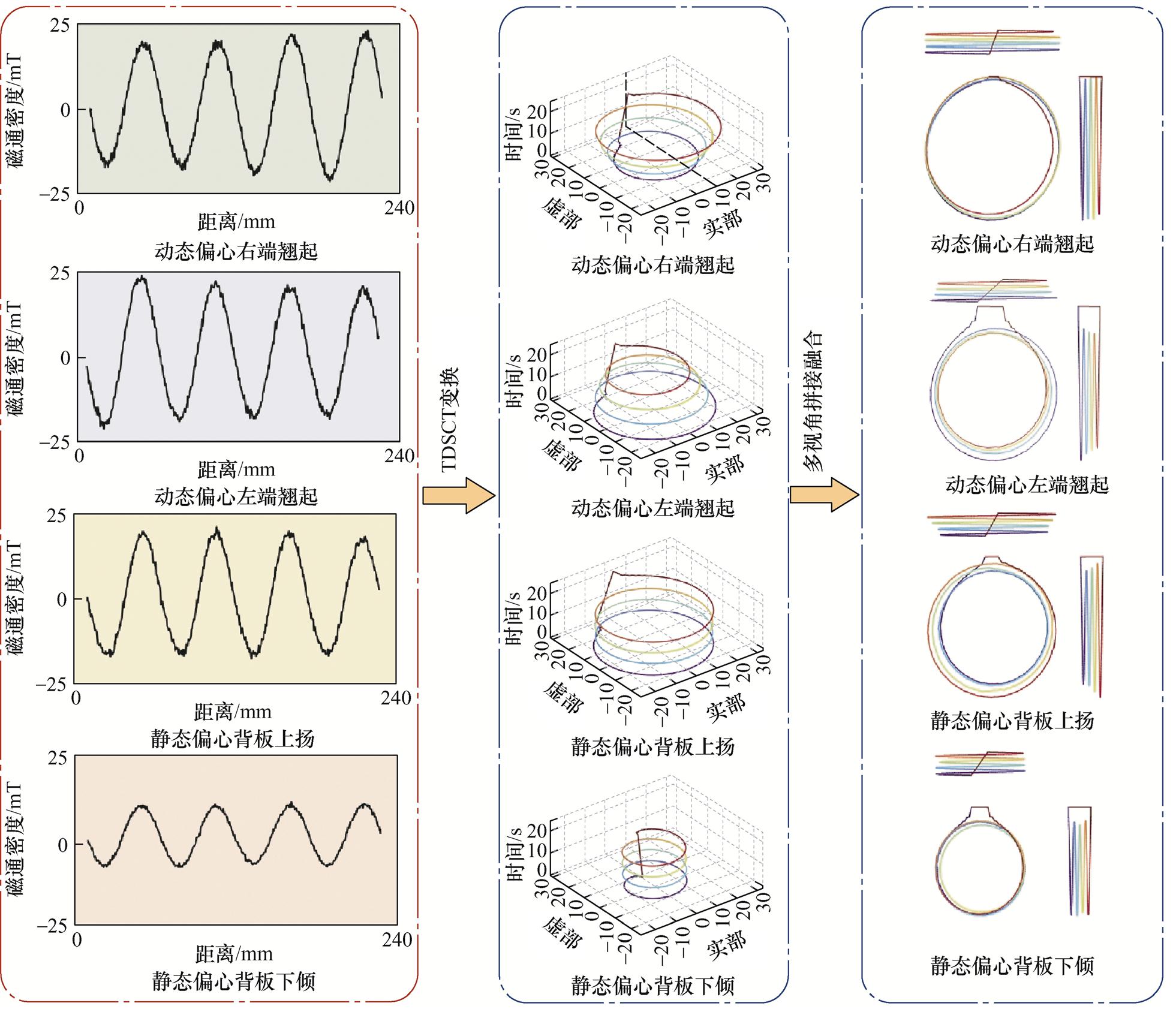
图17 实验数据立体曲线多视角拼接图像变换
Fig.17 Multi-view splicing image transformation of three-dimensional spiral curve of experiment data
（4）分类模型性能验证。将生成的测试集图像输入ResNeXt-18分类模型中，并添加30 dB与40 dB高斯噪声。噪声环境状态下与无噪声环境下，各分类模型的分类效果见表8。模型分类结果与有限元仿真故障分类结果相似，有效地证明了ResNeXt-18优越的分类准确度与鲁棒性，同时证明了本文所提方法的有效性。
表8 预设偏心故障识别率
Tab.8 Preset eccentricity fault validation accuracy （%）
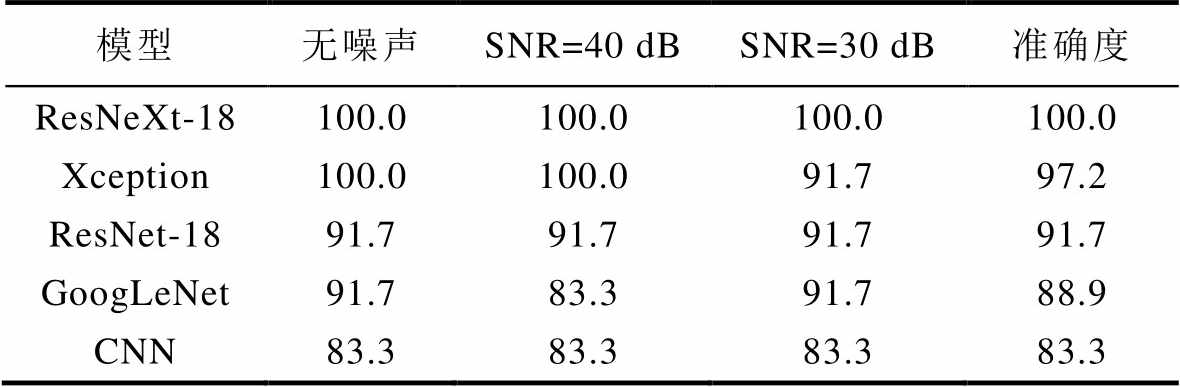
模型无噪声SNR=40 dBSNR=30 dB准确度 ResNeXt-18100.0100.0100.0100.0 Xception100.0100.091.797.2 ResNet-1891.791.791.791.7 GoogLeNet91.783.391.788.9 CNN83.383.383.383.3
本文针对PMSLM偏心故障，提出了一种基于杂散磁通密度信号立体螺旋曲线投影面变换与ResNeXt-18深度学习框架相结合的故障诊断新方法，通过仿真和实验可得以下结论：
1）采用TMR传感器，并与电机动子进行一体化设计，对PMSLM外部杂散磁通密度进行测量，有效解决了传统信号在电机偏心故障诊断时的缺点，为PMSLM非侵入式偏心故障诊断奠定了基础。
2）创新性地提出立体螺旋曲线投影面变换方法用于PMSLM偏心故障信号处理中，将一维的外部杂散磁通密度信号转换为立体螺旋曲线，并通过多视角投影融合，实现了偏心故障特征的增强显示。
3）引入了一种ResNeXt新型分类模型，具有结构简单、高精度和易于模型移植的优点，有效解决了传统ResNet深度学习表征能力较弱、易过拟合的缺点，该方法具有更高的分类精度和鲁棒性。
参考文献
[1] 许孝卓, 封海潮, 艾立旺, 等. U型永磁凸极直线电机结构及电磁特性[J]. 电工技术学报, 2021, 36(6): 1179-1189.
Xu Xiaozhuo, Feng Haichao, Ai Liwang, et al. Structure and electromagnetic characteristics of U-shaped permanent magnet salient pole linear motor[J]. Transactions of China Electrotechnical Society, 2021, 36(6): 1179-1189.
[2] 沈燚明, 卢琴芬. 初级励磁型永磁直线电机研究现状与展望[J]. 电工技术学报, 2021, 36(11): 2325- 2343.
Shen Yiming, Lu Qinfen. Overview of permanent magnet linear machines with primary excitation[J]. Transactions of China Electrotechnical Society, 2021, 36(11): 2325-2343.
[3] 王明杰, 贾宛英, 张志艳, 等. 永磁直线同步电机空载反电动势和推力的解析计算[J]. 电工技术学报, 2021, 36(5): 954-963.
Wang Mingjie, Jia Wanying, Zhang Zhiyan, et al. Analytical calculation of no-load eletromotive force and thrust in permanent magnet linear synchronous motors[J]. Transactions of China Electrotechnical Society, 2021, 36(5): 954-963.
[4] 郭科宇, 李耀华, 史黎明. 分段供电双三相永磁同步直线电机电流解耦与扰动抑制[J]. 电工技术学报, 2022, 37(24): 6332-6344.
Guo Keyu, Li Yaohua, Shi Liming. Current decoupling and force disturbance suppression of dual three-phase permanent magnet linear synchronous motors with section power supply[J]. Transactions of China Electrotechnical Society, 2022, 37(24): 6332- 6344.
[5] 张洪彬, 徐志科, 金龙, 等. 混合叠压圆筒型永磁直线振荡电机电磁特性分析[J]. 电工技术学报, 2023, 38(19): 5090-5100, 5140.
Zhang Hongbin, Xu Zhike, Jin Long, et al. Electromagnetic characteristics analysis of tubular permanent magnet linear oscillation actuator with hybrid lamination[J]. Transactions of China Electro- technical Society, 2023, 38(19): 5090-5100, 5140.
[6] 苏光靖, 李红梅, 李争, 等. 永磁同步直线电机无模型电流控制[J]. 电工技术学报, 2021, 36(15): 3182-3190.
Su Guangjing, Li Hongmei, Li Zheng, et al. Research on model-free current control of permanent magnet synchronous linear motor[J]. Transactions of China Electrotechnical Society, 2021, 36(15): 3182-3190.
[7] 张春雷, 张辉, 叶佩青. 高霍尔位置检测精度的圆筒型永磁同步直线电机设计[J]. 电工技术学报, 2022, 37(10): 2481-2490.
Zhang Chunlei, Zhang Hui, Ye Peiqing. Design of tubular permanent magnet synchronous linear motor by reliability-based robust design optimization[J]. Transactions of China Electrotechnical Society, 2022, 37(10): 2481-2490.
[8] BlodtM, Regnier J, Faucher J. Distinguishing load torque oscillations and eccentricity faults in induction motors using stator current wigner distributions[C]// Conference Record of the 2006 IEEE Industry Applications Conference Forty-First IAS Annual Meeting, Tampa, FL, USA, 2006: 1549-1556.
[9] Agah G R, Rahideh A, Khodadadzadeh H, et al. Broken rotor bar and rotor eccentricity fault detection in induction motors using a combination of discrete wavelet transform and teager-kaiser energy operator[J]. IEEE Transactions on Energy Conversion, 2022, 37(3): 2199-2206.
[10] Cameron J R, Thomson W T, Dow A B. Vibration and current monitoring for detecting airgap eccentricity in large induction motors[J]. IEE Proceedings B Electric Power Applications, 1986, 133(3): 155.
[11] Ellison A J, Yang S J. Effects of rotor eccentricity on acoustic noise from induction machines[J]. Proceedings of the Institution of Electrical Engineers, 1971, 118(1): 174.
[12] 张丹, 赵吉文, 董菲, 等. 基于概率神经网络算法的永磁同步直线电机局部退磁故障诊断研究[J]. 中国电机工程学报, 2019, 39(1): 296-306, 344.
Zhang Dan, Zhao Jiwen, Dong Fei, et al. Partial demagnetization fault diagnosis research of per- manent magnet synchronous motors based on the PNN algorithm[J]. Proceedings of the CSEE, 2019, 39(1): 296-306, 344.
[13] 张晓虎, 赵吉文, 王立俊, 等. 基于自适应互联扩展卡尔曼观测器的永磁同步直线电机高精度抗干扰在线多参数辨识[J]. 中国电机工程学报, 2022, 42(12): 4571-4581.
Zhang Xiaohu, Zhao Jiwen, Wang Lijun, et al. High precision anti-interference online multiparameter estimation of PMSLM with adaptive interconnected extend Kalman observer[J]. Proceedings of the CSEE, 2022, 42(12): 4571-4581.
[14] Dorrell D G, Salah A, Kayani O. The detection and suppression of unbalanced magnetic pull in wound rotor induction motors using pole-specific search coils and auxiliary windings[C]//2015 IEEE Energy Conversion Congress and Exposition (ECCE), Montreal, QC, Canada, 2015: 277-284.
[15] Mirzaeva G, Saad K I. Advanced diagnosis of stator turn-to-turn faults and static eccentricity in induction motors based on internal flux measurement[J]. IEEE Transactions on Industry Applications, 2018, 54(4): 3961-3970.
[16] Park Y, Choi H, Shin J, et al. Airgap flux based detection and classification of induction motor rotor and load defects during the starting transient[J]. IEEE Transactions on Industrial Electronics, 2020, 67(12): 10075-10084.
[17] ŠašićM, Lloyd B, Elez A. Finite element analysis of turbine generator rotor winding shorted turns[J]. IEEE Transactions on Energy Conversion, 2012, 27(4): 930-937.
[18] Mohammed A, MelecioJI, Djurović S. Electrical machine permanent magnets health monitoring and diagnosis using an air-gap magnetic sensor[J]. IEEE Sensors Journal, 2020, 20(10): 5251-5259.
[19] Gurusamy V, Capolino G A,Akin B, et al. Recent trends in magnetic sensors and flux-based condition monitoring of electromagnetic devices[J]. IEEE Transactions on Industry Applications, 2022, 58(4): 4668-4684.
[20] Dias C G, da da Silva L C, Chabu I E. Fuzzy-based statistical feature extraction for detecting broken rotor bars in line-fed and inverter-fed induction motors[J]. Energies, 2019, 12(12): 2381.
[21] Biet M. Rotor faults diagnosis using feature selection and nearest neighbors rule: application to a turbogenerator[J]. IEEE Transactions on Industrial Electronics, 2013, 60(9): 4063-4073.
[22] Quiroz J C, Mariun N, Mehrjou M R, et al. Fault detection of broken rotor bar in LS-PMSM using random forests[J]. Measurement, 2018, 116: 273-280.
[23] Chandra M A, Bedi S S. Survey on SVM and their application in imageclassification[J]. International Journal of Information Technology, 2021, 13(5): 1-11.
[24] Taunk K, De S, Verma S, et al. A brief review of nearest neighbor algorithm for learning and classification[C]//2019 International Conference on Intelligent Computing and Control Systems (ICCS), Madurai, India, 2019: 1255-1260.
[25] Bacha K, Henao H, Gossa M, et al. Induction machine fault detection using stray flux EMF measurement and neural network-based decision[J]. Electric Power Systems Research, 2008, 78(7): 1247-1255.
[26] Wen Long, Li Xinyu, Gao Liang, et al. A new convolutional neural network-based data-driven fault diagnosis method[J]. IEEE Transactions on Industrial Electronics, 2018, 65(7): 5990-5998.
[27] Zamudio-Ramírez I, Osornio-Ríos R A, Antonino- Daviu J A, et al. Smart-sensor for the automatic detection of electromechanical faults in induction motors based on the transient stray flux analysis[J]. Sensors (Basel, Switzerland), 2020, 20(5): E1477.
[28] Liu Xuyang, Liu Chunhua, Han Wei, et al. Design and implementation of a multi-purpose TMR sensor matrix for wireless electric vehicle charging[J]. IEEE Sensors Journal, 2019, 19(5): 1683-1692.
[29] Narayanaswami R, Sundaresan D, Ranjan Prema V. The mystery curve: a signal processing based power quality disturbance detection[J]. IEEE Transactions on Industrial Electronics, 2021, 68(10): 10078-10086.
[30] Hao Yongqi, Wang Qian, Li Yanan, et al. An intelligent algorithm for fault location on VSC-HVDC system[J]. International Journal of Electrical Power & Energy Systems, 2018, 94: 116-123.
[31] He Kaiming, Zhang Xiangyu, Ren Shaoqing, et al. Deep residual learning for image recognition[C]// 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 2016: 770-778.
[32] Haque M F, Lim H Y, Kang D S. Object detection based on VGG with ResNet network[C]//2019 International Conference on Electronics, Information, and Communication (ICEIC), Auckland, New Zealand, 2019: 1-3.
[33] 高彩霞, 李炳锟, 陈昊, 等. 基于半周反电势残差的永磁同步电机局部退磁故障诊断[J]. 电机与控制学报, 2023, 27(7): 183-194.
Gao Caixia, Li Bingkun, Chen Hao, et al. Local demagnetization fault diagnosis of permanent magnet synchronous motor based on half-period back EMF residual[J]. Electric Machines and Control, 2023, 27(7): 183-194.
[34] 李峰, 陈皖皖, 杨义. 基于稀疏自适应S变换和深度残差网络的轴承故障诊断方法[J]. 电机与控制学报, 2022, 26(8): 112-119.
Li Feng, Chen Wanwan, Yang Yi. Research on bearing fault diagnosis based on sparse adaptive S-transform and deep residual network[J]. Electric Machines and Control, 2022, 26(8): 112-119.
[35] Xie Saining, Girshick R, Dollár P, et al. Aggregated residual transformations for deep neural networks[C]// 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 2017: 5987-5995.
[36] Zhou Tianyan, Zhao Yong, Wu Jian. ResNeXt and Res2Net structures for speaker verification[C]//2021 IEEE Spoken Language Technology Workshop (SLT), Shenzhen, China, 2021: 301-307.
[37] Koné I, Boulmane L. Hierarchical ResNeXt models for breast cancer histology image classification[C]// 2018 International Conference on Image Analysis and Recognition (ICIAR), Póvoa de Varzim, Portugal, 2018: 796-803.
[38] Vaswani A, Shazeer N, Parmar N, et al. Attention is all you need[C]//2017 Conference on Neural Infor- mation Processing Systems (NIPS), Long Beach, CA, USA, 2017: 5998-6008.
[39] Szegedy C, Ioffe S,Vanhoucke V, et al. Inception-v4, inception-ResNet and the impact of residual connections on learning[C]//Proceedings of the Thirty-First AAAI Conference on Artificial Intelligence, San Francisco, California, USA, 2017: 4278-4284.
Eccentricity Fault Diagnosis of Permanent Magnet Linear Motor Based on Spiral Curve Transformation of Stray Magnetic Field Signal and ResNeXt-18
Abstract Permanent magnet synchronous linear motor (PMSLM) has the advantages of high transmission efficiency, high thrust quality and high positioning accuracy. It is widely used in industrial scenarios with linear direct drive such as high-precision machine tools, parallel robots, etc. In actual industrial applications, PMSLM may produce eccentricity faults due to complex operating conditions, mechanical assembly errors and other factors. The traditional eccentricity fault diagnosis method based on electrical signal is very easy to be affected by environmental noise, operating conditions and other factors, and it is still not enough to directly reflect the state of the motor eccentricity fault. In recent years, some fault diagnosis methods for motor eccentricity based on magnetic density signal which can directly reflect the state of the motor eccentricity fault have been proposed, but most of them exist some drawbacks, such as cumbersome sensor installation steps, insufficient sensor sensitivity and incomplete fault information feature extraction.
To solve the above problems, this paper proposes eccentricity fault diagnosis of permanent magnet linear motor based on three-dimensional spiral curve transformation of stray magnetic field signal and ResNeXt-18. Firstly, finite element simulation models under healthy state and eccentricity fault state of PMSLM are established to obtain the external stray magnetic density signal of PMSLM. Secondly, the eccentricity fault feature enhancement signal processing method based on three-dimensional spiral curve transformation (TDSCT) is applied to transform the external stray magnetic density signal into two-dimensional eccentricity fault feature imagein order to realize fault feature enhancement display. Thirdly, the dataset is input into the deep learning ResNeXt-18 classification framework, through which various fault signal characteristics are obtained and accurate fault diagnosis is achieved. In simulation experiments, the validation accuracy of ResNeXt-18 improves 1.3%, 1.3%, 1.6% and 3.8% compared with Xception, GoogLeNet, ResNet-18 and CNN, respectively. Under Gaussian noise of 40 dB, the validation accuracy of comparison model is reduced by 1.4%, 2.3%, 5.3% and 2.9%, respectively, and that decreased by 0.6%, 1.4%, 2.0% and 1.4% respectively under Gaussian noise of 30 dB. The ResNeXt-18 decreases by 0.5% under Gaussian noise of both 30 dB and 40 dB, which show better robustness compared to other models.
This work establishes PMSLM prototype experimental platform with different eccentricity faults to conduct verification experiments, and the excellent performances of this proposed method is verified. The conclusions of this work are as follows: (1) Using TMR sensor and integrated design with rotor, the measurement of the external stray magnetic density of PMSLM effectively solves the shortcomings of traditional signals in the motor eccentricity fault diagnosis, and build a foundation for the non-invasive eccentricity fault diagnosis of PMSLM. (2) An innovative three-dimensional spiral curve transformation with multi-view projection fusion method is proposed for PMSLM eccentricity fault signal processing. One-dimensional external stray magnetic density signal is converted into 3D spiral curve, and the enhanced vision features of eccentricity fault is realized through multi-view projection fusion. (3) A new classification model of ResNeXt is introduced, which has the advantages of simple structure, high precision and easy model transplantation, and effectively solves the shortcomings of traditional ResNet deep learning network, which is weak in representation ability and easy to overfit. This method has higher classification accuracy and robustness.
Keywords：Permanent magnet synchronous linear motor (PMSLM), eccentricity fault diagnosis, externalstray magnetic field, three-dimensional spiral curve transformation (TDSCT), ResNeXt-18
中图分类号：TM359.4
DOI: 10.19595/j.cnki.1000-6753.tces.231021
国家自然科学基金面上项目（52075002）、国家自然科学基金青年项目（52207036）、安徽省自然科学基金青年项目（2208085QE167）和安徽省教育厅自然科学重点项目（KJ2021A0018）资助。
收稿日期 2023-06-30
改稿日期 2023-10-16
钱 龙 男，2000年生，硕士，研究方向为直线电机状态监测与故障诊断。
E-mail: z22201010@stu.ahu.edu.cn
宋俊材 男，1992年生，讲师，硕士生导师，研究方向为电机故障诊断、直线电机优化设计。
E-mail: songjuncai@ahu.edu.cn（通信作者）
（编辑 崔文静）