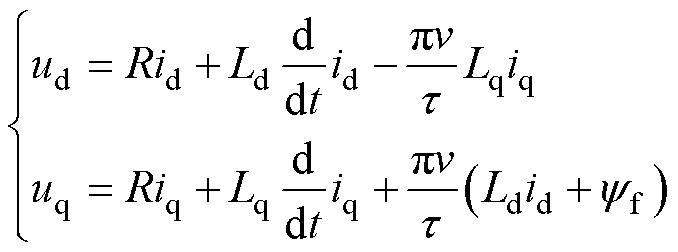（1）
摘要 为了提高永磁同步直线电机在载荷变化工况下的伺服性能，该文提出了一种基于非线性时间延迟扰动估计的无模型鲁棒位置控制策略。首先，建立一种新型的动力学阶次模型，消除了传统动力学模型中的电机参数和非线性项；其次，引入终端吸引因子设计了期望非线性误差动力学，确保位置跟踪误差的高精度有限时间收敛；然后，采用时间延迟扰动估计技术在线估计载荷变化引起的不确定性并前馈补偿到控制回路，同时结合非线性阻尼项克服时间延迟扰动估计的误差，利用李雅普诺夫理论分析了闭环控制器的稳定性和有限时间收敛性；最后，在不同工况下与传统的比例微分控制和滑模控制进行对比，仿真和实验结果验证了所提方法的有效性和优越性。
关键词：永磁同步直线电机 伺服性能 阶次模型 非线性时间延迟扰动估计 李雅普诺夫
区别于传统旋转电机与滚轴丝杠或齿轮齿条相结合的直线伺服模式，永磁同步直线电机（Permanent Magnet Synchronous Linear Motors, PMSLMs）驱动的伺服系统消除了中间机械环节，实现了零传动和高带宽的直线伺服。得益于这一优点，PMSLM驱动的直线伺服系统已广泛应用于各类高精度工业场合，如数控机床、医疗设备和工业机器人等[1-3]。然而，在实际应用过程中，有效载荷时变引起的不确定性，如惯量失配和非线性摩擦，会导致伺服系统的跟踪精度大大降低。因此，亟须设计一种鲁棒的位置控制器克服上述不确定性，进而实现PMSLM伺服系统的高精度位置跟踪。
针对上述问题，目前采用的控制策略主要分为两大类：线性控制策略和非线性控制策略。其中，线性控制策略应用最广泛的为PID控制[4-5]。PID结构简单易实现，且通过零极点法可以实现无静差跟踪，但零极点法依赖精确的电机参数。此外，诸如模型预测控制[6]、迭代学习控制[7]、智能控制[8]和滑模控制[9-10]等非线性控制策略也随着数字处理器的发展而得到进一步应用。其中，模型预测控制基于离散的电机数学模型和系统历史信息，在线滚动优化向前预测控制输出，拓展了直线电机位置环带宽。迭代学习控制通过生成近似模型逆动力学的前馈控制作用，有效地抑制了直线电机往复运动中的周期性扰动，实现了对参考轨迹的完全跟踪。滑模控制通过不连续切换项提高了系统对不确定性和扰动的鲁棒性。上述方法都在一定程度上提升了直线电机的伺服性能，但实现过程中或多或少都依赖电机的精确模型和参数。然而，PMSLM是一个多变量和强耦合的非线性系统，通常情况下很难建立其精确的数学模型[11]。
为了减小对电机系统模型的依赖，文献[12-13]采用模糊或神经网络等智能算法得到了电机动力学的“黑箱”模型。但是这些方法往往引入了许多不确定的增益或参数，有时需要开发复杂的算法来调整这些参数。因此，在数字处理器上实现这些智能算法是相当占用计算资源的。此外，“黑箱”模型由于算法的复杂性和增益调优的难度，一般只有专业的控制工程师才能使用。无模型控制作为一种基于数据驱动的方案，可以消除物理参数对模型精度的影响，具有较强的鲁棒性[14]。无模型思想与其他控制策略结合的复合控制，如无模型自适应控制[15]、无模型预测控制[16]和无模型滑模控制[17]等，可以在保持原有性能的基础上，增强系统的鲁棒性。选择合适的数据驱动结构是无模型控制获得高品质控制性能的核心。法国学者M. Fliess提出了基于超局部思想的无模型控制概念[18]，并通过代数辨识方法估计系统的不确定项，提高了非线性系统的鲁棒性和控制性能。目前，基于超局部思想的无模型控制在电机系统中也得到了部分应用，但大部分集中在电流环和速度环[19-22]，对位置环的研究较少。文献[19-21]将预测控制和无模型控制相结合，有效减小了电机参数失配下的电流跟踪误差。文献[22]基于超局部模型分别设计了永磁同步电机转速环滑模控制器和观测器，有效提高了电机的调速性能。此外，采用代数辨识法和观测器法估计超局部模型中的不确定项相对复杂且未考虑估计误差的影响。
基于上述分析，本文旨在提出一种更为简单、鲁棒和通用的无模型位置控制方法，以提高PMSLM在载荷变化下的伺服跟踪性能。首先，根据系统输入输出关系建立一种新型的动力学阶次模型，避免原始精确动力学中的复杂非线性项；其次，引入终端吸引因子设计期望非线性误差动力学，驱动跟踪误差在有限时间内收敛到零；再次，采用时间延迟扰动估计技术在线补偿载荷变化引起的不确定性，并结合非线性阻尼项吸收时间延迟扰动估计误差带来的剩余能量；最后，通过仿真和实验验证了本文方法的正确性和有效性。
在交直轴同步旋转坐标系下，PMSLM的电压电流方程[11]表示为
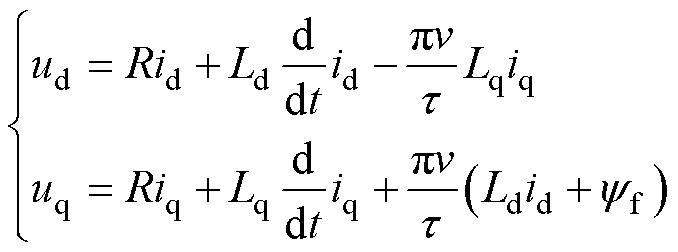（1）
式中，ud, uq、id, iq和Ld, Lq分别为交直轴动子电压、电流和电感；R为绕组相电阻；v为电机动子线速度；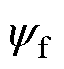
为永磁体磁链；t 为极距。
考虑到本文的研究对象为表贴式PMSLM，可以近似认为交直轴电感相等[19]，即Ld=Lq。那么，PMSLM的电磁推力可以表示为
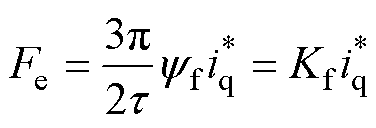（2）
式中，Kf为电磁推力系数；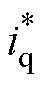
为电流指令值。因此，PMSLM的机械运动方程可以表示为
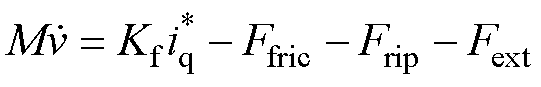（3）
式中，M为动子质量；Ffirc为非线性摩擦力；Frip为推力波动；Fext为包括负载推力和线缆拉力的外部扰动力。
进一步考虑PMSLM运动过程中发生的载荷变化，式（3）中的动力学模型可以重新写为
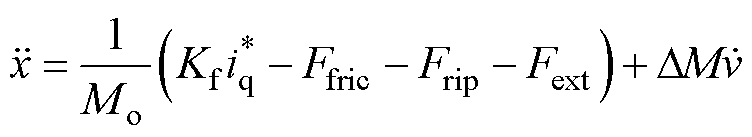（4）
式中，x为电机动子位移；Mo为标称的动子质量；DM为载荷变化引起的动子质量的变化值。根据式（4）易知，PMSLM伺服系统是一个二阶系统。只考虑系统阶数这一基本性质，将式（4）中包含不同参数的电机精确模型等效为单输入单输出的同阶模 型[14]，如图1所示。阶次模型的输入u和输出y对应原始模型中的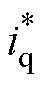和x。
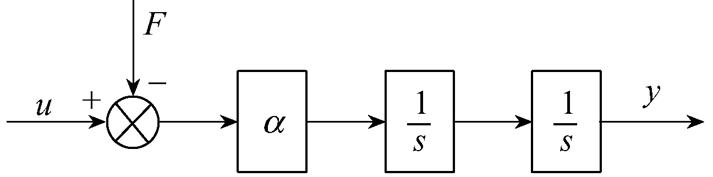
图1 等效的PMSLM动力学阶次模型
Fig.1 Equivalent PMSLM dynamic order model
根据图1，等效后的PMSLM动力学阶次模型可以表示为
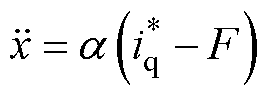（5）
式中，a 为待设计的非物理参数；F为PMSLM中的非线性项和各种不确定性的集总，不再需要对其作任何区别。相比于式（4）中的动力学模型，重构后的动力学模型不再包含任何电机参数，是一个无模型的单输入单输出结构。如果进一步估计出集总不确定性F并将估计值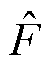
前馈补偿到控制输入中，如图2所示，系统将具有较强的抗扰动性能。
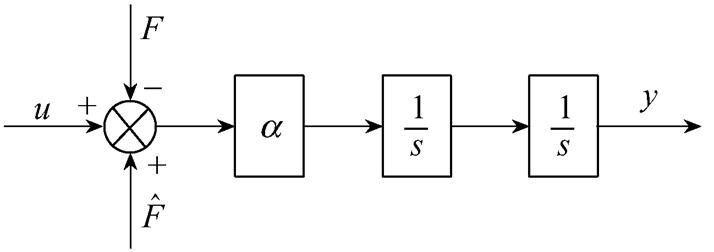
图2 补偿后的PMSLM动力学阶次模型
Fig.2 Compensated PMSLM dynamic order model
本节提出了一种基于非线性时间延迟扰动估计的PMSLM无模型位置控制器，主要包括期望的非线性误差动力学、时间延迟扰动估计和非线性阻尼的设计，整体控制框图如图3所示。
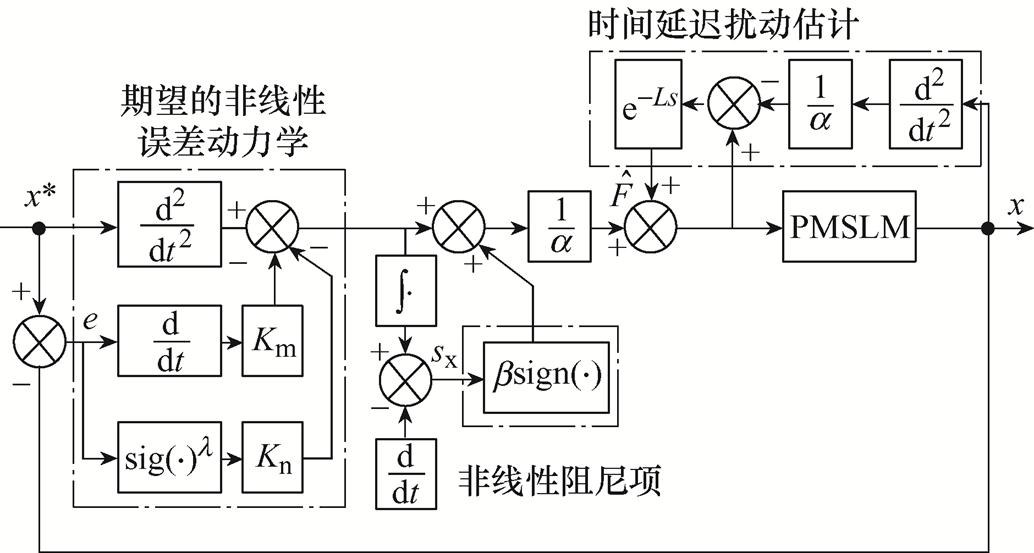
图3 基于非线性时间延迟扰动估计的无模型位置控制框图
Fig.3 Block diagram of model-free position control based on nonlinear time delay disturbance estimation
定义位置跟踪误差为
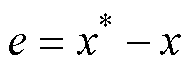（6）
式中，x*为位置指令值。将式（5）代入式（6）得到PMSLM位置跟踪误差的动力学为
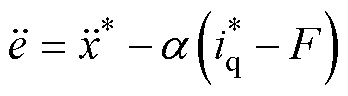（7）
为了实现位置跟踪误差的高精度快速收敛，引入终端吸引因子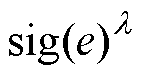
设计期望的非线性误差动力学，表示为
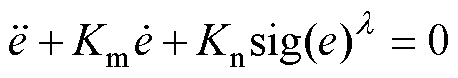（8）
其中
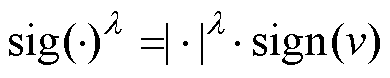
式中，Km、Kn和l 为待设计参数，满足Km＞0，Kn＞0，0＜l＜1。
通过对式（8）积分，得到滑模变量为
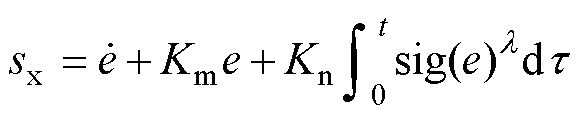（9）
从式（9）可以看出，当系统状态远离滑模面时，误差的收敛速度主要取决于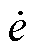
=-Kme，并且收敛速度是指数的。当系统状态接近滑模面时，收敛速度主要由终端吸引因子项
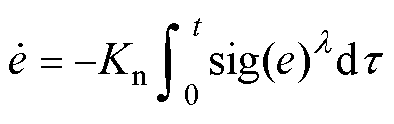起主导作用。因此，在终端吸引因子的作用下，跟踪误差可以在有限时间内收敛（详细证明请参考附录）。
在忽略系统集总不确定性的情况下，将式（7）
代入式（9），并令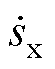
=0，可得滑模等效控制率为
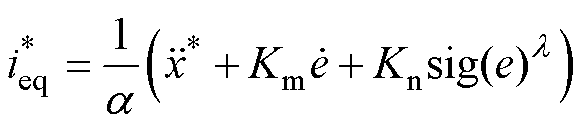（10）
为了实现集总不确定性F的估计，本文拟采用时间延迟扰动估计方法。假设F是连续或者分段连续的，可以认为F在一段足够小的时间L内是保持不变的[21]，即
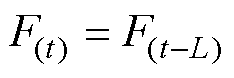（11）
将PMSLM动力学阶次模型式（5）前推一个延时时间L，可以得到
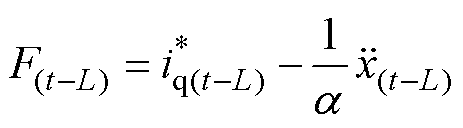（12）
结合式（11）和式（12），可得集总不确定性项F的估计值为
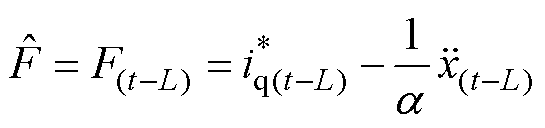（13）
将式（10）和式（13）代入式（6），可得PMSLM实际的跟踪误差动力学为
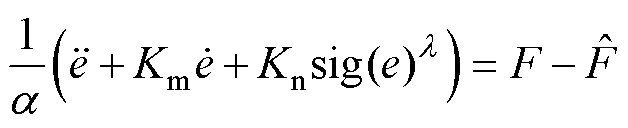（14）
不难发现，如果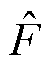=F，式（14）就完全等价于式（8）。这意味在控制律式（10）和式（13）的作用下，PMSLM系统可以实现期望的误差动力学。然而，在实际的伺服驱动过程中，PMSLM的速度突然反向、传感器测量噪声和有限的采样时间都会影响延时估计的估计精度，导致
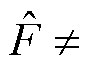F。在该情况下，式（14）可以进一步改写为
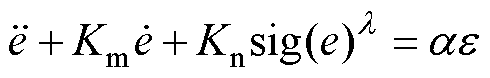（15）
其中
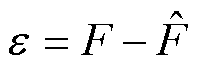
式中，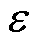
为时间延迟扰动估计的估计误差。
为了克服延时估计误差的影响，设计非线性阻尼项为
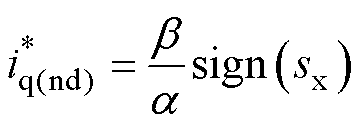（16）
式中，b 为非线性阻尼项的系数，b ＞0。
综上所述，基于非线性时间延迟扰动估计的无模型位置控制律为
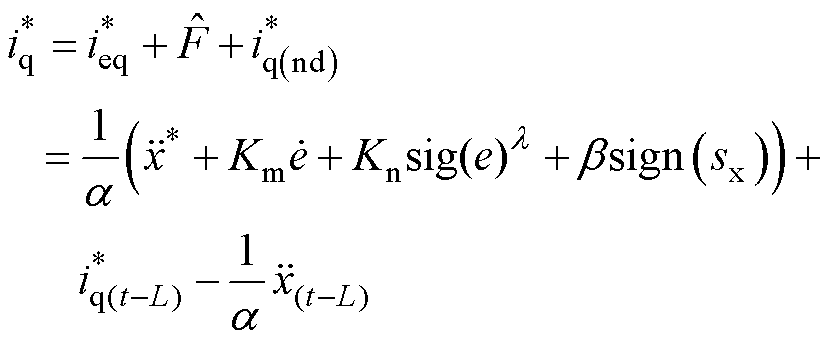（17）
将式（17）代入式（6），可得PMSLM伺服系统的闭环误差动力学为
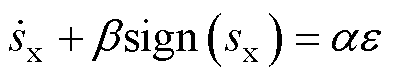（18）
由文献[23]易知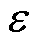，和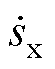可以等效为稳态一阶滤波器的输入与输出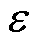，对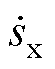的影响比式（15）减弱。因此，非线性阻尼项可以有效吸收时间延迟扰动估计误差带来的能量，驱动闭环误差动力学无限接近所设计的期望动力学。
与现有的相关工作相比，本文所提出的控制方法具有以下显著特点：①相比于传统比例微分（Pro- portional-Derivative, PD）控制中的线性误差动力学，本文通过引入终端吸引因子构建的非线性误差动力学，可以实现系统的有限时间收敛，响应速度更快；②相比于传统的扰动观测器，本文提出的延时扰动估计方法不仅不依赖电机的精确模型，还具有等效低通滤波器的效果，避免了额外的滤波器设计；③基于滑模面的非线性阻尼项可以有效抑制延时扰动补偿带来的估计误差，提高系统的控制精度。
为了验证闭环系统的稳定性，首先分析时间延迟扰动估计误差的有界性。根据式（17），将时间延迟扰动估计误差写为
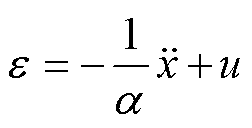（19）
其中
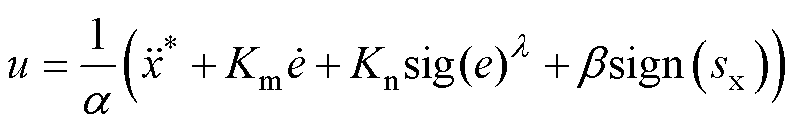
将式（19）代入式（4），可得PMSLM系统关于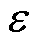的动力学为
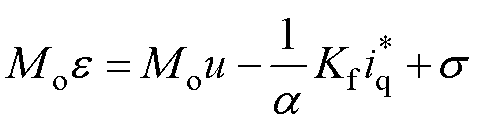（20）
其中
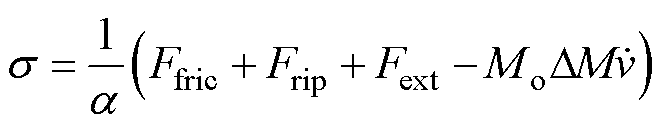
将控制律式（17）代入式（20），可得
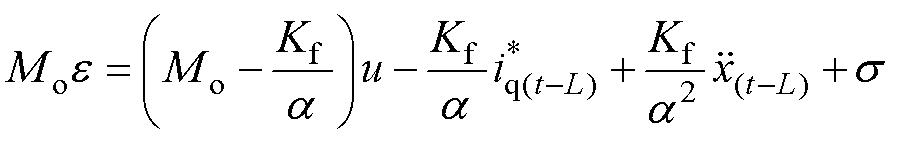（21）
进一步将
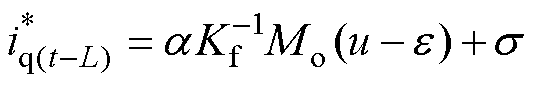和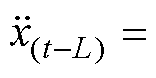
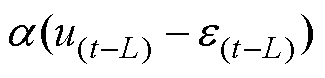代入式（21），可得
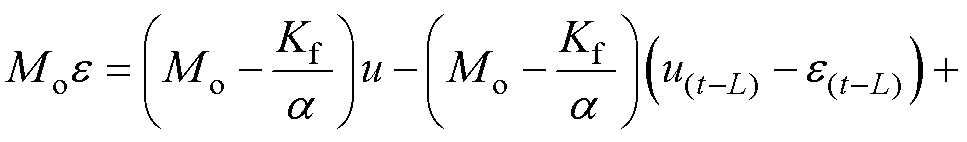
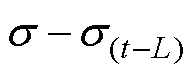（22）
为了便于分析，可将式（22）重写为
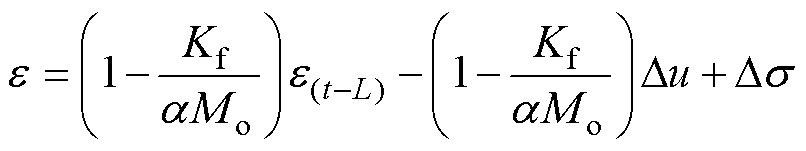（23）
其中
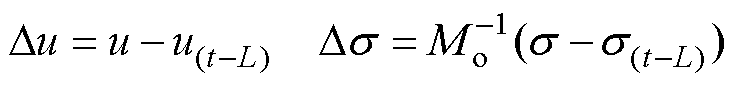
相应地，式（23）的离散形式表示为
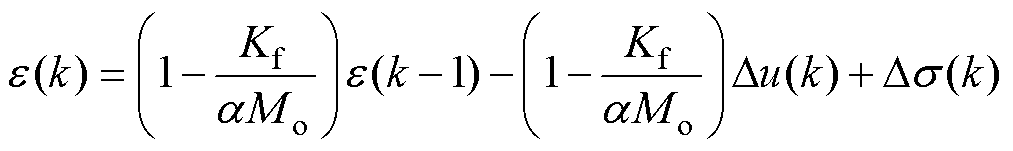（24）
式中，k为采样周期。
根据BIBO稳定理论[24]，为了保证式（24）中的一阶离散方程渐进收敛，a 需要满足
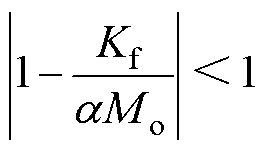（25）
同时，时间时延估计误差将收敛到有界区域。
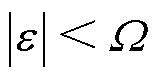（26）
式中，W 为一个正数。
在此基础上，定义李雅普诺夫函数为
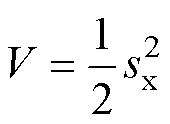（27）
对V求导，可得
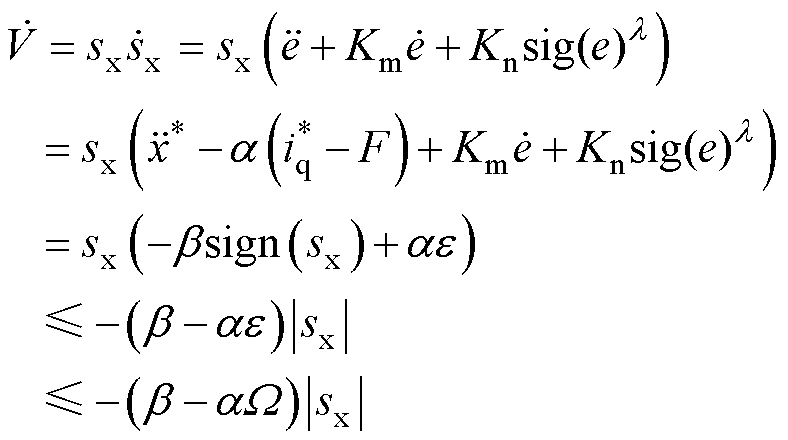（28）
从式（28）可以看出，只要非线性阻尼项的系数b ＞aW，就可以保证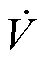
＜0，系统就会在有限时间内收敛到零[23]。至此，就完成了闭环系统稳定性证明。在仿真环境中设置参考位置为0.1sin(6.28t) m，外部扰动力为5sin(10t) N，a =10。根据图4a中的扰动估计误差上界分别设置b =0.005＜aW和b =0.15＞aW，两种条件下的位置响应结果如图4b和图4c所示。可以看出，在满足稳定条件b ＞aW时，系统可以跟踪上参考位置信号；相反，当b ＜aW时，系统发散，无法跟踪上参考位置信号。上述结果与稳定性理论分析的结果一致。
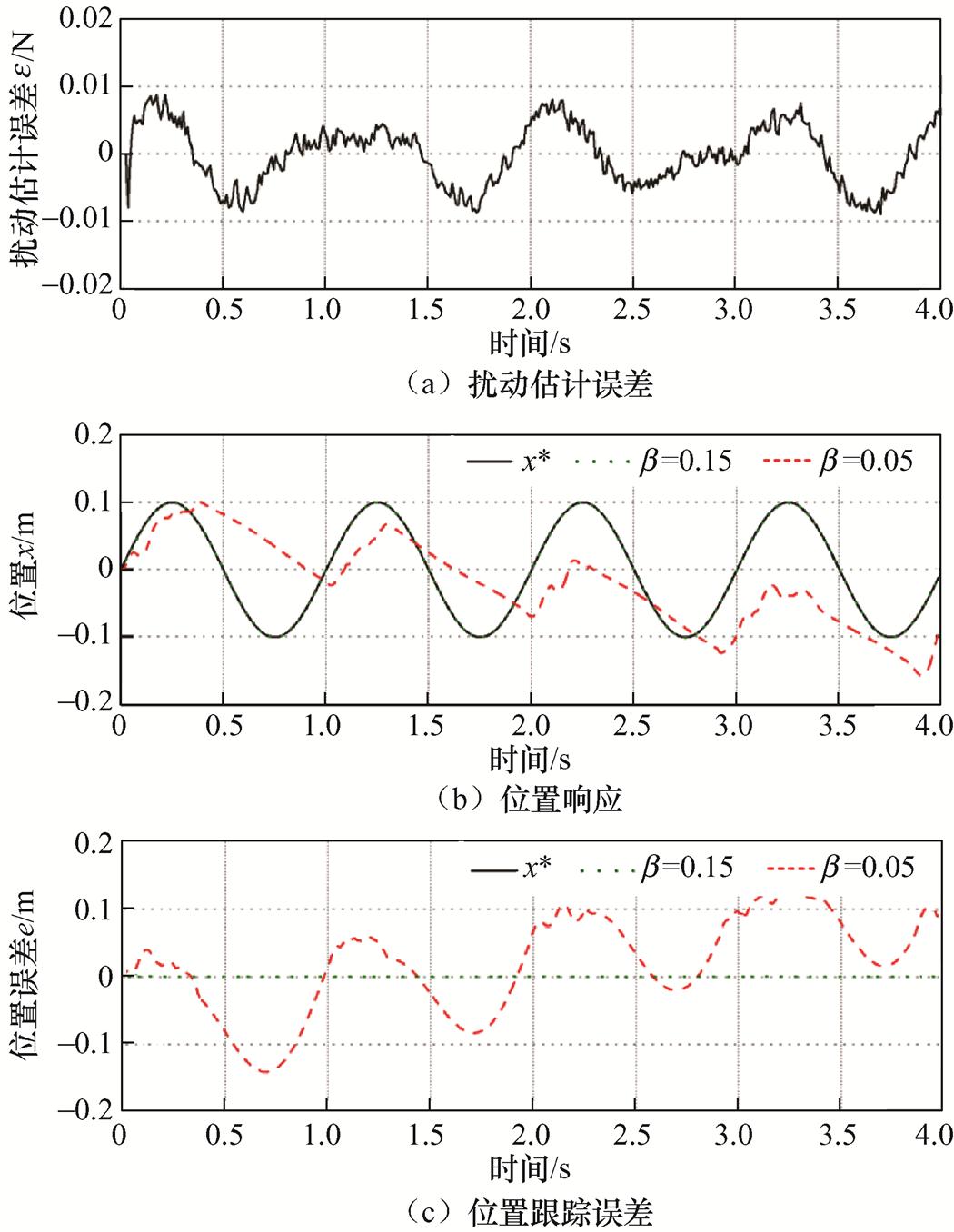
图4 不同b 下的位置响应结果
Fig.4 Position response under various b
在实际的应用中，控制器参数的合理选择对PMSLM系统的伺服性能至关重要。为了保证系统在集总不确定性下的快速收敛和高精度跟踪，可以使用以下参数选取准则作为参考。
（1）a 的整定准则。首先，a 的选择应满足式（25）来保证系统的稳定性。此外，a 是系统跟踪精度和噪声抑制之间的权重因子。具体分析如下，将式（17）改写为
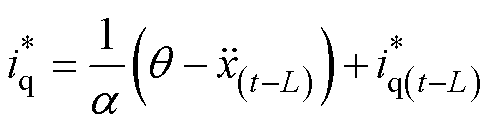（29）
其中
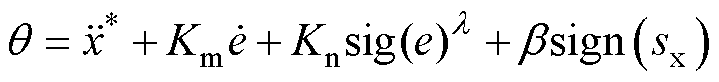
如果引入一个额外的数字低通滤波器，控制律可以重新推导为
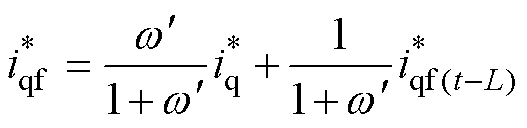（30）
其中
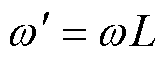
式中，w 为低通滤波器的截止频率；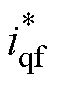
为滤波器的输出。将式（29）代入式（30），可得
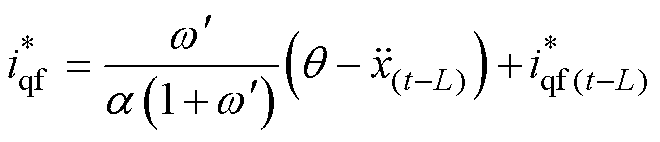（31）
从式（31）可以看出，较大的a 可以等效为低通滤波器的效果，进而抑制加速度项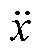
带来的噪声。另一方面，从式（20）可以看出，较小的a 可以减小系统的跟踪误差。因此，在实际调试过程中可以从较小的a 逐渐增加直到满足工程需求。
（2）Km、Kn和l 的整定准则。Km影响系统的收敛速度，较大的Km可以提高系统的动态响应，但是过大的Km可能导致输入饱和。Kn影响滑模面的带宽，Kn越大带宽越高，系统的收敛速度和跟踪精度越高。l 作为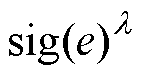连续控制(l→1)和切换控制(l→0)之间的桥梁，决定了系统的抖振程度和鲁棒性，较大的l 可以平滑控制信号，但是相应的鲁棒性也会降低。
（3）b 的整定准则。非线性阻尼项系数b 在满足b ＞aW的情况下尽可能选择较小的值。较大的b会由于符号函数sign的存在而带来严重的抖振。因此，实际应用中，可以从一个较小的值逐渐增大，直到调试效果满足工程要求。
首先在Matlab/Simulink中搭建如图5所示的位置电流双闭环控制模型，电机参数见表1。本文方法的控制参数选为：a =15、Km=50、Kn=100、l =0.08和b =0.1。为了突出本文方法的优越性，选择比例微分（PD）控制和滑模控制（Sliding Mode Control, SMC）作为对比。对比工况选择如下三种：①标称条件下的正弦位置跟踪，以验证所提方法的稳态性能；②不同载荷下的正弦位置跟踪，以验证所提方法的鲁棒性能；③阶跃位置跟踪，以验证所提方法的动态响应性能。
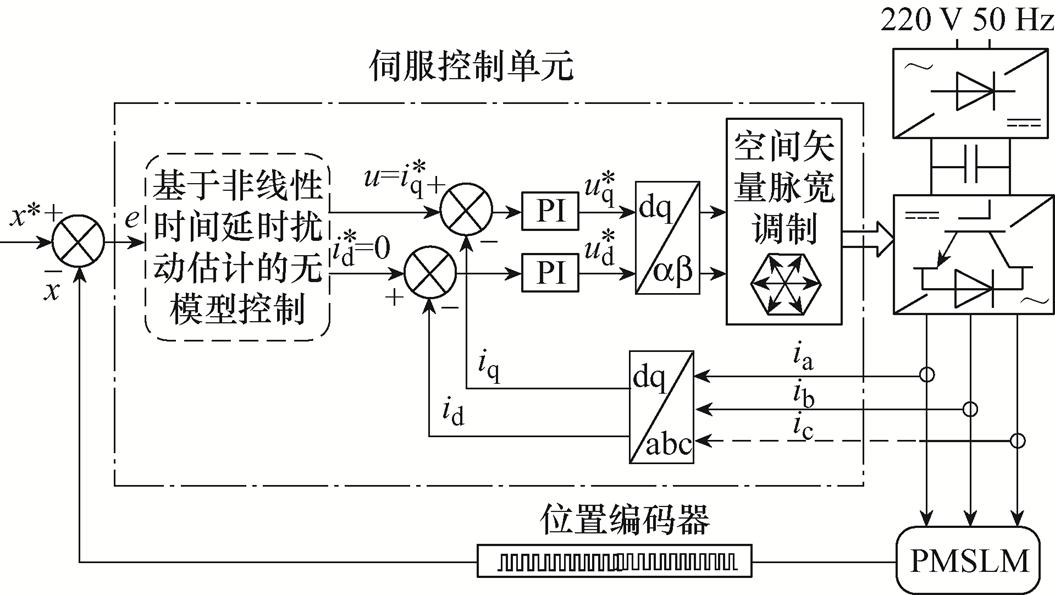
图5 基于非线性时间延迟扰动估计的无模型位置控制框图
Fig.5 Block diagram of model-free position control based on nonlinear time delay disturbance estimation
表1 直线电机参数
Tab.1 Parameters of the PMSLM
参 数数 值 动子质量/kg1.88 交直轴电感/H0.004 永磁体磁链/Wb0.092 4 相电阻/W3.62 极距/m0.023 7 粘滞摩擦系数/(N·s/m)9.36
（1）工况1。在标称条件（载荷DM=0）下给定周期为1 s、幅值为0.1 m的正弦位置轨迹，三种方法的跟踪结果如图6～图8所示。从图6和图7可以看出，三种方法基本都可以跟踪上给定信号，传统PD控制的稳态跟踪误差最大，其稳态下的最大误差边界（Tracking Error Bound, TEB）达到2.77 mm。相比之下，SMC的TEB减小到了0.72 mm，这得益于SMC的切换控制律可以在一定程度上抑制推力波动和非线性摩擦等不确定性的影响。本文的方法更是在SMC的基础进一步将TEB减小到了0.064 mm，取得了最优的跟踪效果，这是因为本文方法中的时间延迟扰动估计项有效补偿了系统存在的集总扰动，同时所设计的滑模变量中的积分项可以进一步减小系统稳态误差。此外，从图8可以看出，PD的控制输入电流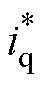最为平滑，而SMC的控制输入电流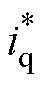抖振现象严重，这是因为SMC的控制律中包含了不连续符号函数项，且需要设置足够大的切换增益克服系统不确定性，这一现象不仅影响跟踪精度的进一步提升，还会带来较大的电机工作噪声。相比于SMC，本文方法的控制输入电流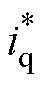抖振现象明显减弱，但相比于PD控制，本文方法的控制输入电流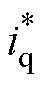包含了更多的噪声，这是控制律中的加速项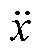引起的。但得益于时间延迟扰动估计的等效低通滤波作用，这一噪声并未进一步劣化和影响PMSLM伺服系统的跟踪性能。
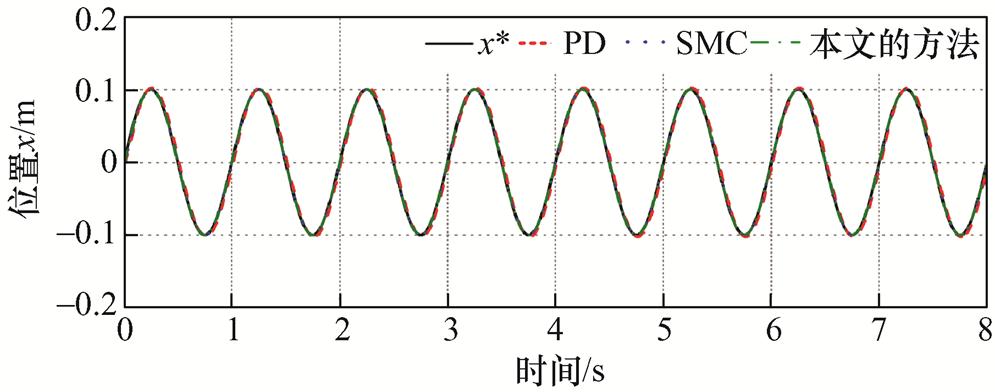
图6 标称条件下的位置响应曲线
Fig.6 Position response curves under nominal condition
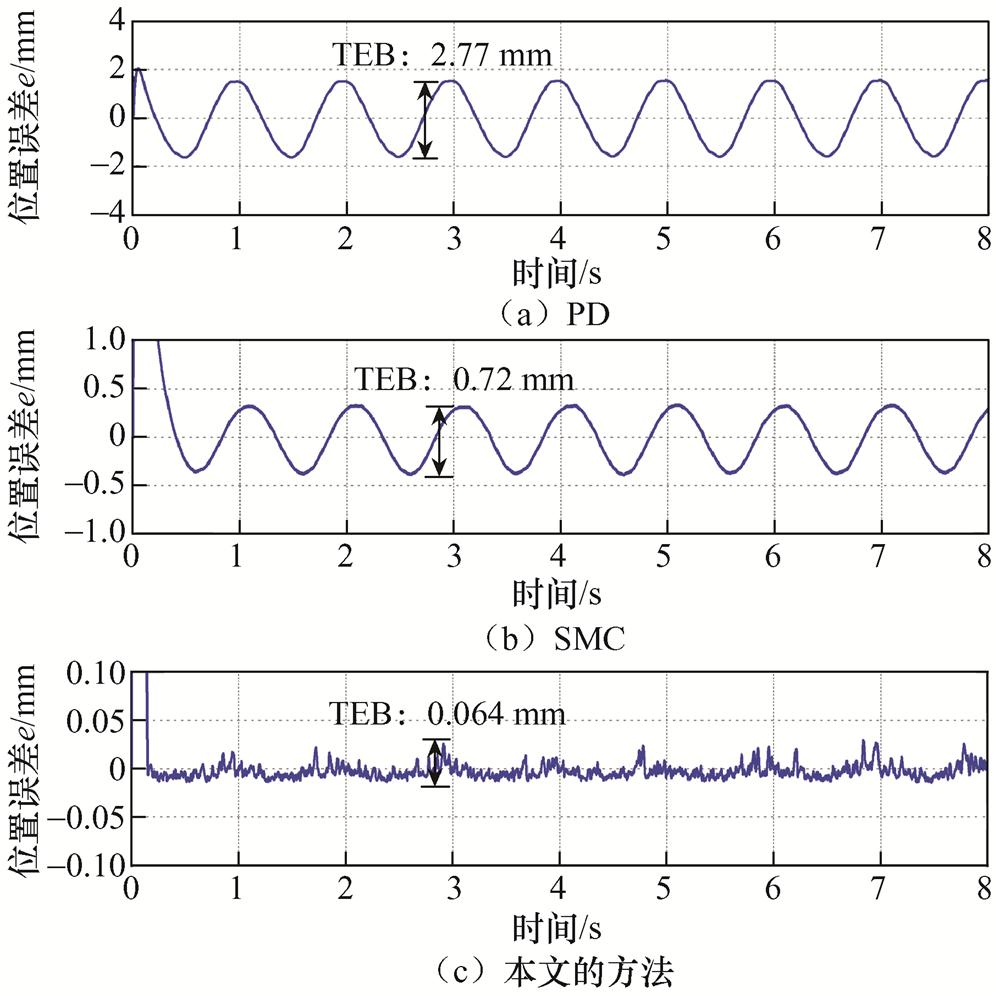
图7 标称条件下的位置跟踪误差
Fig.7 Position tracking error under nominal condition
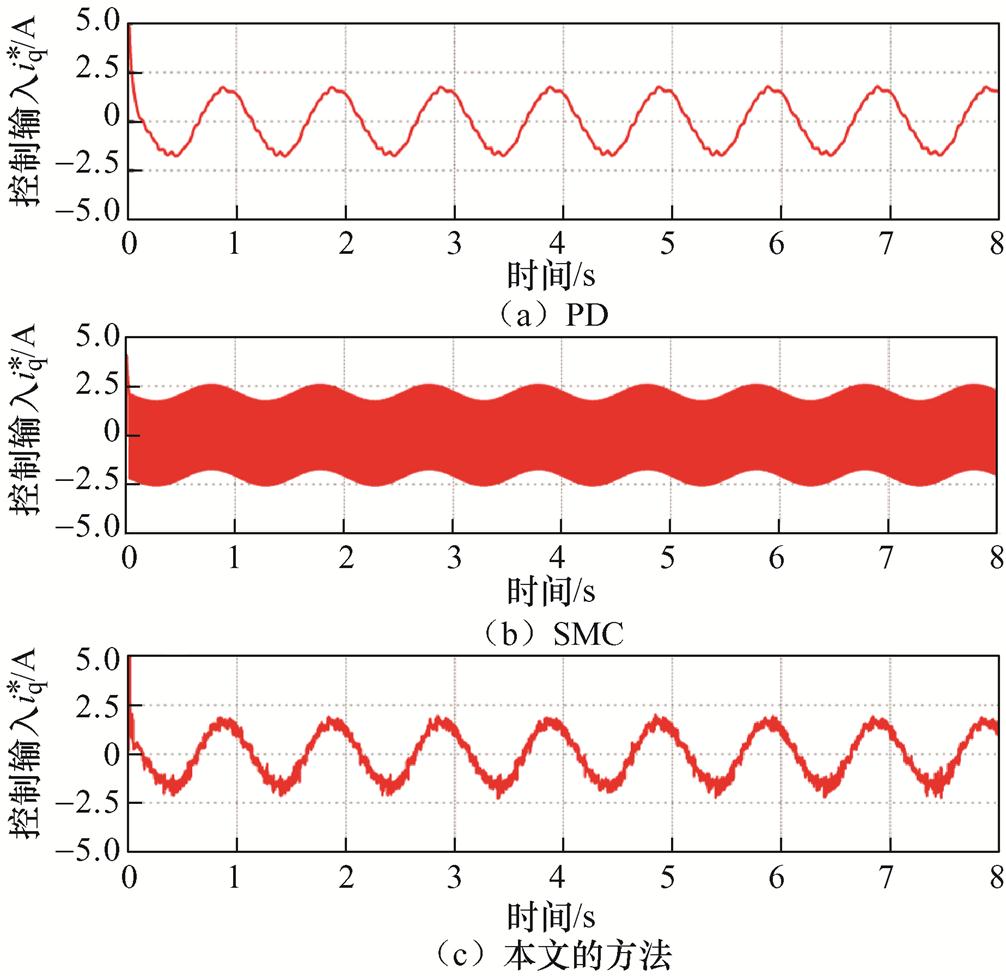
图8 标称条件下的控制输入电流
Fig.8 Control input current under nominal condition
（2）工况2。通过改变仿真模型中的电机质量模拟不同载荷条件，即0～8 s，载荷DM=Mo；8～16 s，载荷DM=2Mo；16～24 s，载荷DM=3Mo。三种方法的跟踪结果如图9～图11所示。从图9可以看出，PD控制和SMC的位置响应曲线随着载荷的增加，逐渐偏离给定位置轨迹。具体而言，在0～8 s之间，PD的稳态TEB为3.99 mm，在8～16 s之间，TEB增加到5.43 mm，而在16～24 s，TEB更是增加到6.95 mm。这是因为单一的PD参数无法适应不同载荷工况。相比之下，SMC在0～8 s、8～16 s和16～24 s之间的稳态TEB分别为0.74 mm、1.06 mm和1.26 mm，远小于PD在不同载荷下的TEB，可见SMC对载荷变化引起的额外不确定性具有一定的鲁棒性。与工况1中的控制输入电流类似，SMC的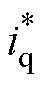具有严重的抖振，如图11所示。而本文的方法取得了最好的跟踪效果，在不同载荷条件下的TEB分别为0.045 mm、0.047 mm和0.050 mm。与此同时，控制输入电流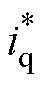也相对平滑。
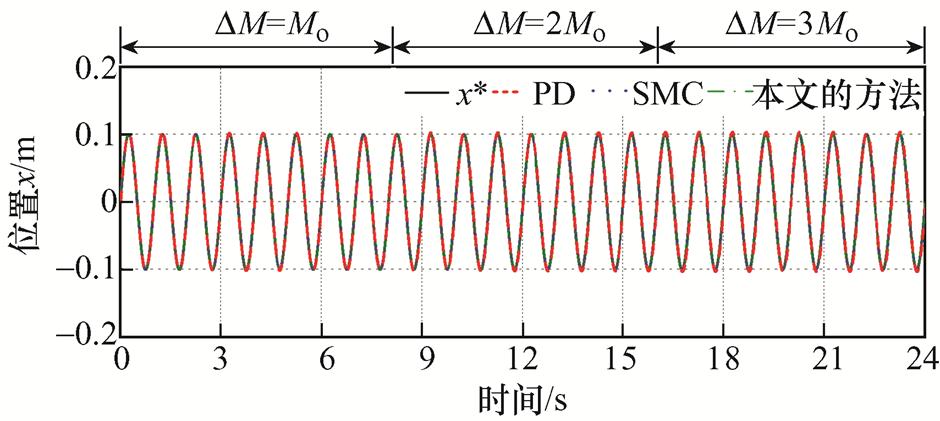
图9 不同载荷条件下的位置响应曲线
Fig.9 Position response curves under various payload conditions
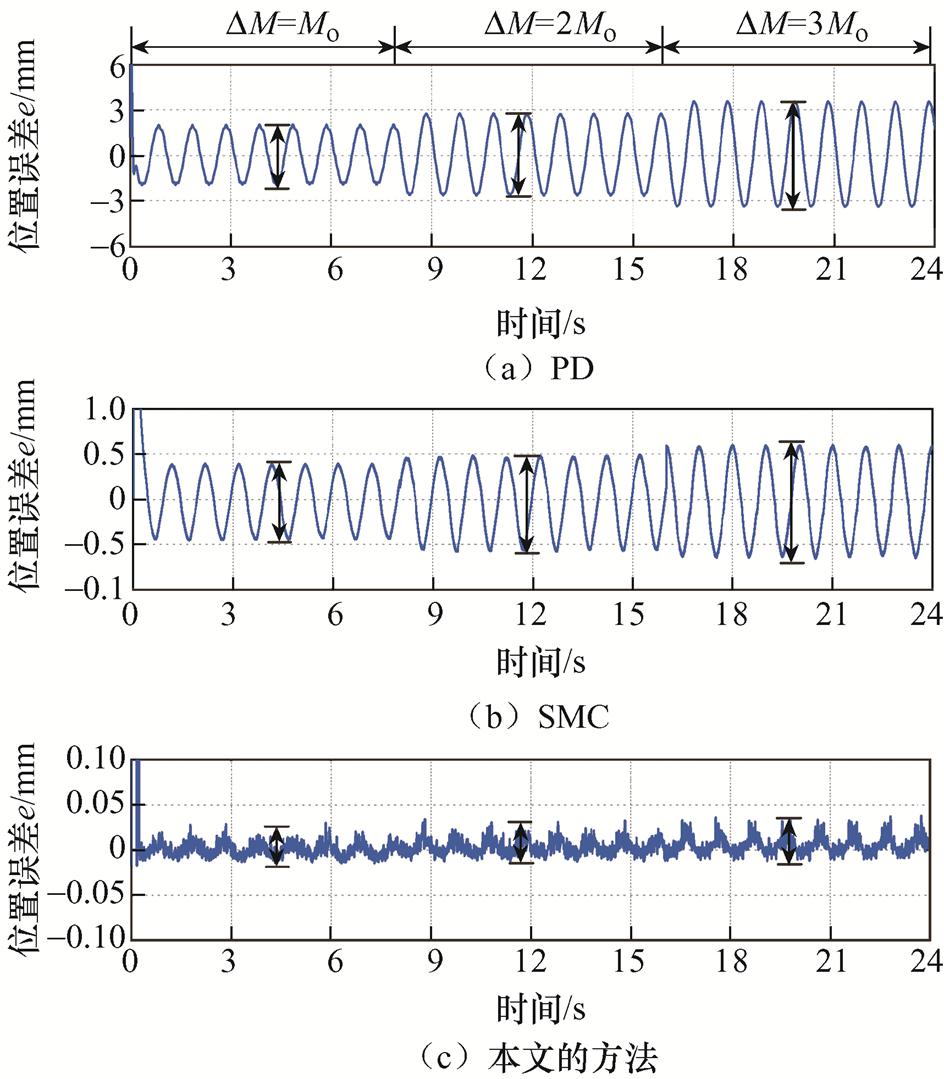
图10 不同载荷条件下的位置跟踪误差
Fig.10 Position tracking error under various payload conditions
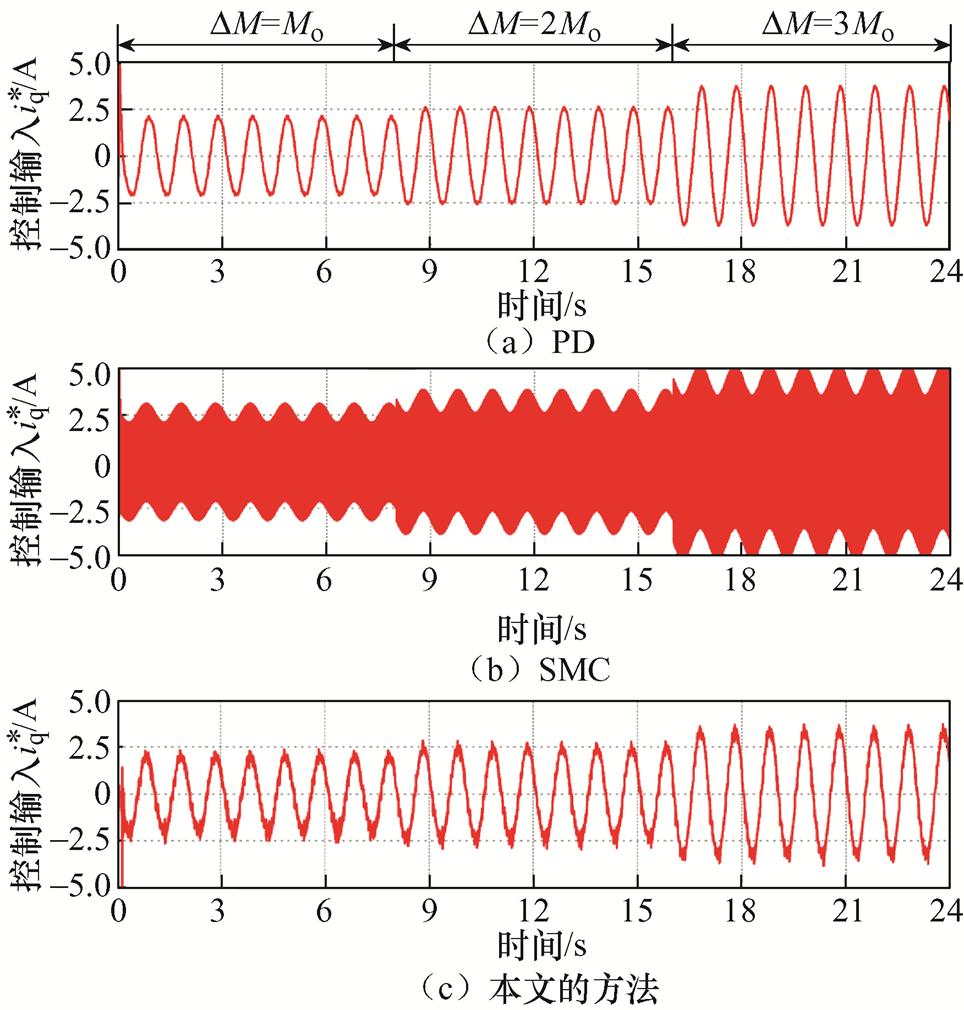
图11 不同载荷条件下的控制输入电流
Fig.11 Control input current under various payload conditions
（3）工况3。为了进一步验证本文方法的动态性能，给定幅值为0.1 m的位置阶跃信号，三种方法的响应结果如图12和图13所示。从图12可以看出，PD、SMC及本文方法三种方法的响应时间分别为0.163 s、0.132 s和0.114 s，很明显本文的方法动态响应能力更好，这主要得益于所设计的期望非线性误差动力学可以保证系统的有限时间收敛，而PD和SMC只能保证跟踪误差的渐进收敛。
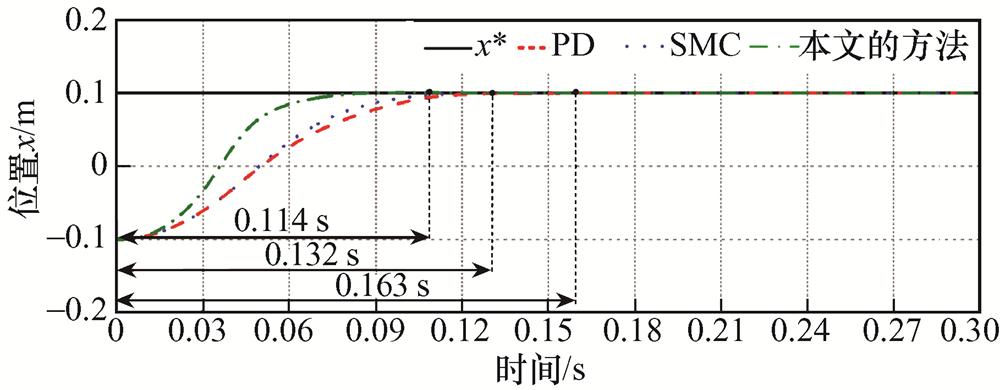
图12 位置阶跃响应曲线
Fig.12 Position step response curves
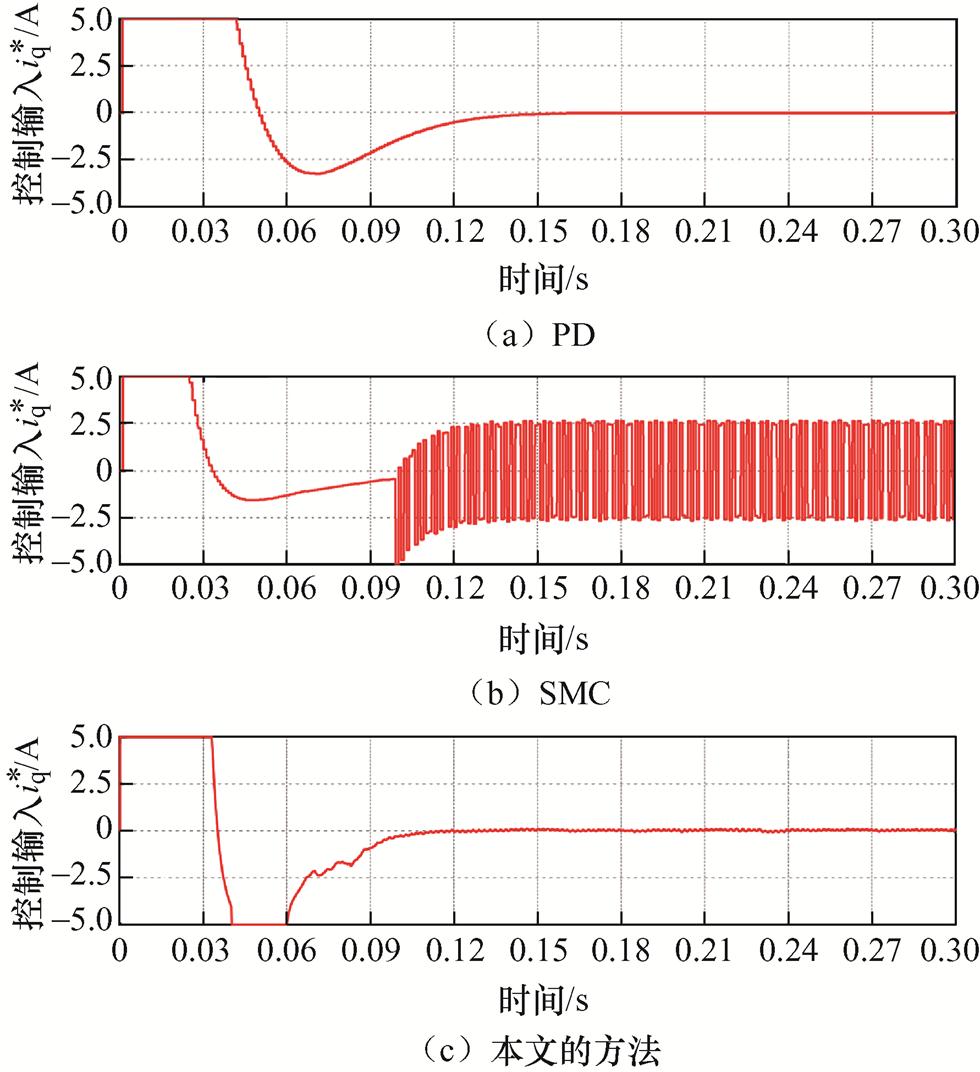
图13 阶跃响应下的控制输入电流
Fig.13 Control input current under step response
为了进一步验证本文所提方法的可行性和优越性，搭建了如图14所示的PMSLM实验平台并开展了相关的实物实验。其中，位置编码器采用精度为5 mm的线性磁栅，并且与电机导轨平行安装，来实现电机位置信息的反馈，两个霍尔传感器用于采集电机相电流，半实物AD5435系统用于执行控制算法、增强正交编码器解码和空间矢量脉宽调制等，逆变电路由智能功率模块驱动，开关频率为10 kHz，电机动子工作台上可放置载荷，电机参数与表1一致。
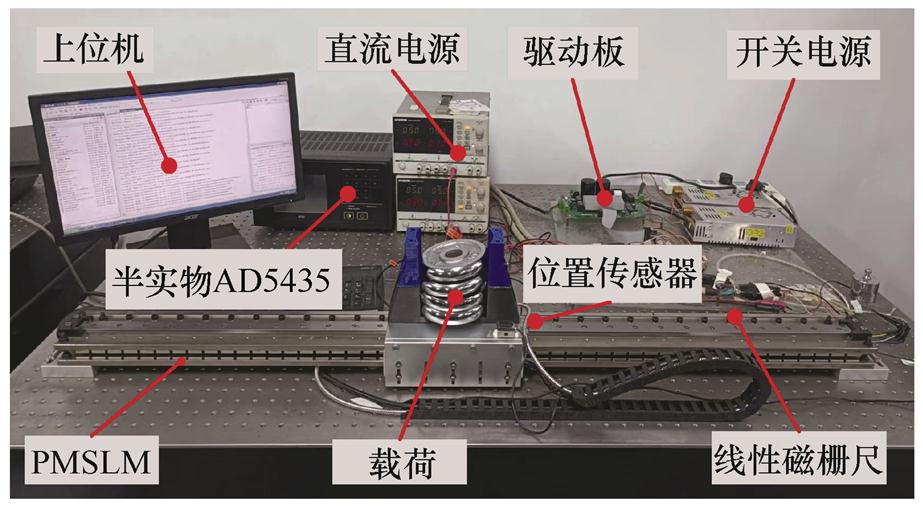
图14 实验平台
Fig.14 Experimental platform
考虑到Matlab/Simulink中的电机模型相对理想，与实际的电机模型存在一定的差异。因此，需要对控制器的参数进行重新调试。根据2.3节的控制器参数选取准则和实际的响应结果，实验中的控制参数设置为：a =10、Km=25、Kn=20、l =0.7和b =2。对比方法仍为传统的PD控制策略和SMC策略，实验工况与仿真中的工况一致，包括标称条件下的正弦位置跟踪、不同载荷条件下的正弦位置跟踪和阶跃响应位置跟踪。
（1）工况1。三种方法在标称条件（载荷DM=0）下的正弦位置跟踪响应结果如图15所示。从图15a可以看出，三种方法基本都可以跟踪上给定轨迹。为了更加清晰地体现所提方法的优越性，采用TEB、误差平均值（Mean value, MEA）和误差最小标准差（Minimum Standard Deviation, MSD）三个指标来定量分析三种方法的跟踪性能，相应的结果总结在表2中。显然，本文方法的TEB、MEA和MSD都是最小的，这意味着本文的方法具有最优的稳态跟踪性能。此外，从图15c可以看出，与仿真结果类似，PD的控制输入电流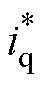最为平滑，而SMC的控制输入电流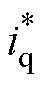抖振现象严重，本文方法的控制输入电流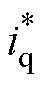由于加速项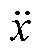的存在包含一定的噪声，但得益于时间延迟扰动估计的等效低通滤波作用，这一噪声并未进一步劣化和影响系统跟踪性能。
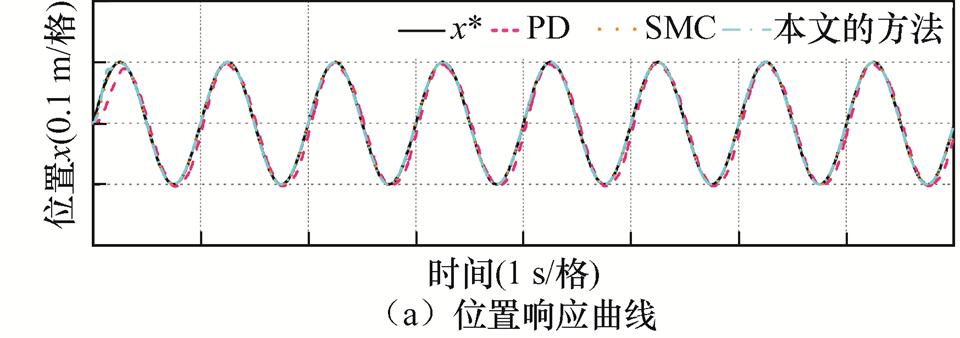
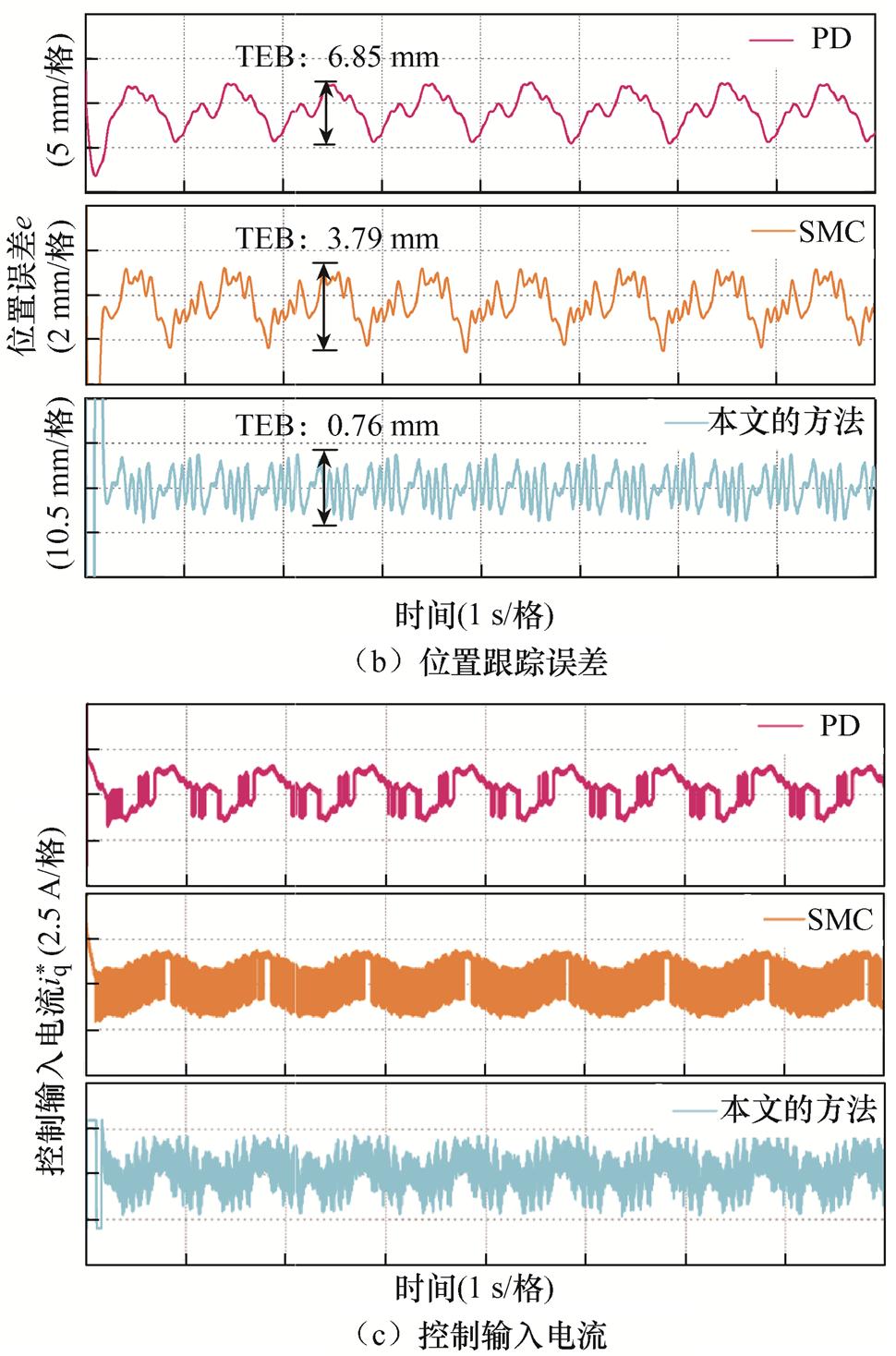
图15 标称条件下的正弦位置跟踪
Fig.15 Sinusoidal position tracking under nominal condition
表2 标称条件下三种方法的稳态跟踪性能对比
Tab.2 Comparison of steady-state tracking performance of three methods under nominal condition （单位: mm）
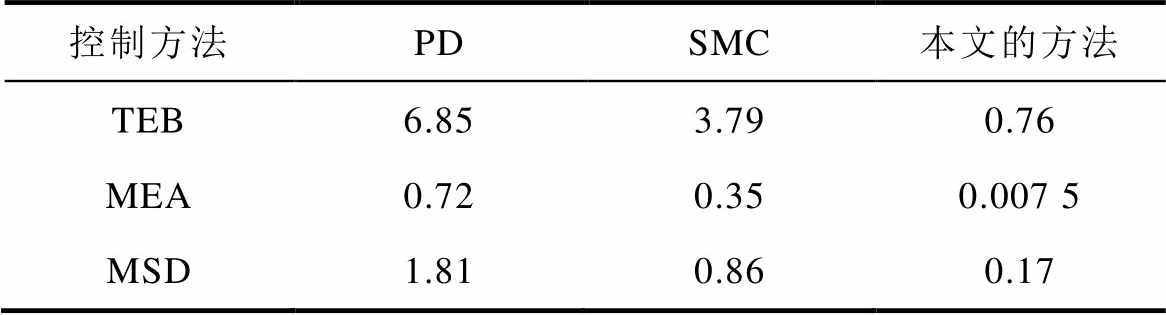
控制方法PDSMC本文的方法 TEB6.853.790.76 MEA0.720.350.007 5 MSD1.810.860.17
（2）工况2。当电机处于静止状态时，分别在动子工作台上放置Mo、2Mo和3Mo的载荷，并将三种载荷下的稳态实验结果组合，如图16所示。从图16a可以看出，不同载荷条件下PD和SMC的位置响应曲线已经开始偏离给定位置轨迹，且载荷越大，偏离程度越明显。相比之下，本文的方法则始终能准确跟踪给定位置轨迹。三种方法跟踪误差的TEB、MEA和MSD统计见表3。显然，无论是在0～8 s之间载荷为Mo，还是在8～16 s之间载荷为2Mo或者在16～24 s之间载荷为3Mo，本文的方法相比于PD和SMC，都具有更小的TEB、MEA和MSD。这充分说明本文的方法即使在电机载荷发生变化时，也保持着优异的稳态跟踪性能，这在高精密直线伺服场合具有重要意义。从图16c可以看出，这三种方法的控制输入电流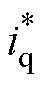在载荷变大时也相应增加，以产生足够的推力驱使直线电机保持良好的跟踪性能。此外，本文方法的控制输入电流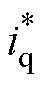在实验环境中的抖振相比于仿真环境中更大，其主要原因是实验中的a 取值更小，削弱了控制律的滤波效果。
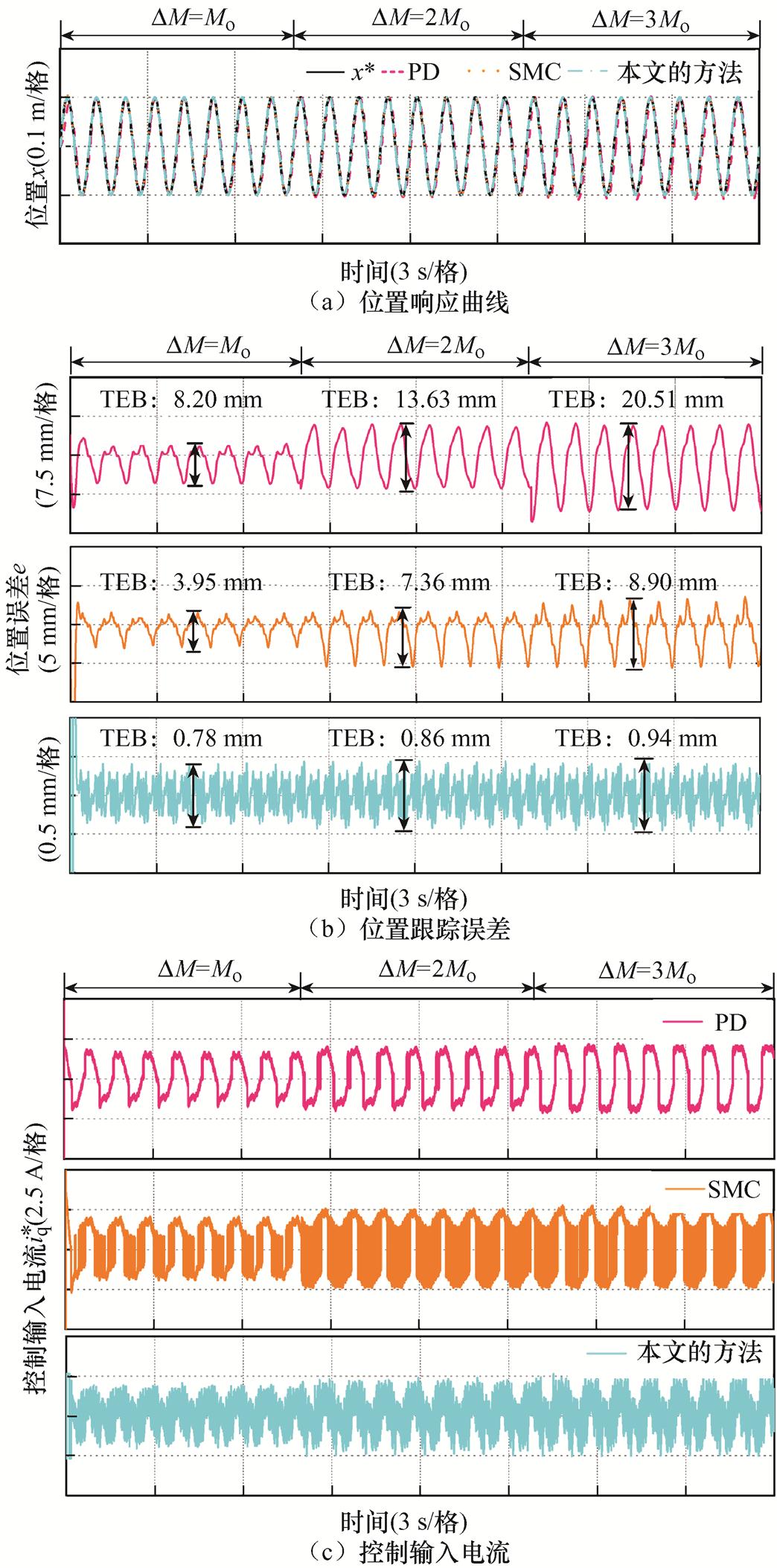
图16 不同载荷条件下的正弦位置跟踪
Fig.16 Sinusoidal position tracking under various payload conditions
（3）工况3。为了进一步验证本文方法的动态性能，给定幅值为0.1 m的位置阶跃信号，三种方法的响应结果如图17所示。从图17a可以看出，本文方法的响应时间为0.202 s，明显小于PD的0.312 s和SMC的0.273 s。这表明本文的方法拥有更快的动态响应能力，也充分验证了所设计的期望非线性误差动力学的有限时间收敛的优越性。另一方面，三种方法的控制输入电流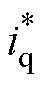结果与正弦稳态跟踪下的结果类似，PD的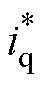最为平滑，SMC的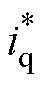抖振最严重，本文方法的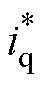相对平滑，但包含一定的噪声。
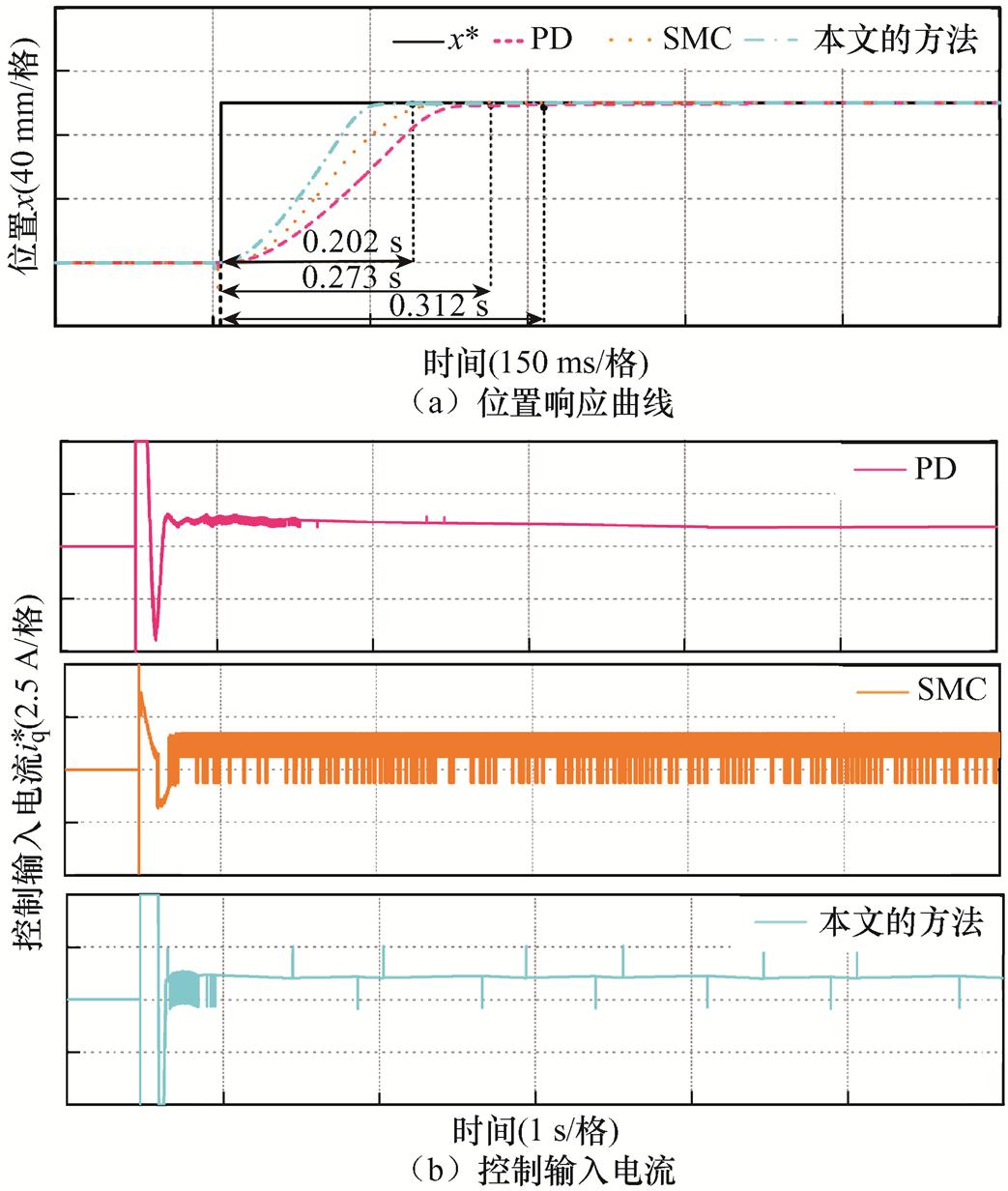
图17 阶跃指令位置跟踪
Fig.17 Step command position tracking
表3 不同载荷下三种方法的稳态跟踪性能对比
Tab.3 Comparison of steady-state tracking performance of three methods under various payload conditions（单位: mm）
控制方法PDSMC本文的方法 DM=MoDM=2MoDM=3MoDM=MoDM=2MoDM=3MoDM=MoDM=2MoDM=3Mo TEB8.2013.6320.513.957.368.900.780.860.94 MEA1.070.281.670.501.171.130.005 70.008 60.014 MSD2.264.207.431.562.903.320.1720.1840.189
（4）工况4。为了进一步验证位置采样扰动对本文方法的影响，在反馈位置信号中加入幅值为0.1 mm的随机噪声，三种方法的响应结果如图18所示。从图18b可以看出，在位置噪声的影响下，PD和SMC的TEB分别为8.85 mm和3.96 mm，相比于标称条件下都有所增加。本文方法的控制律由于具有低通滤波器的作用，可以削弱采样噪声的影响，仍保持最小的跟踪误差。
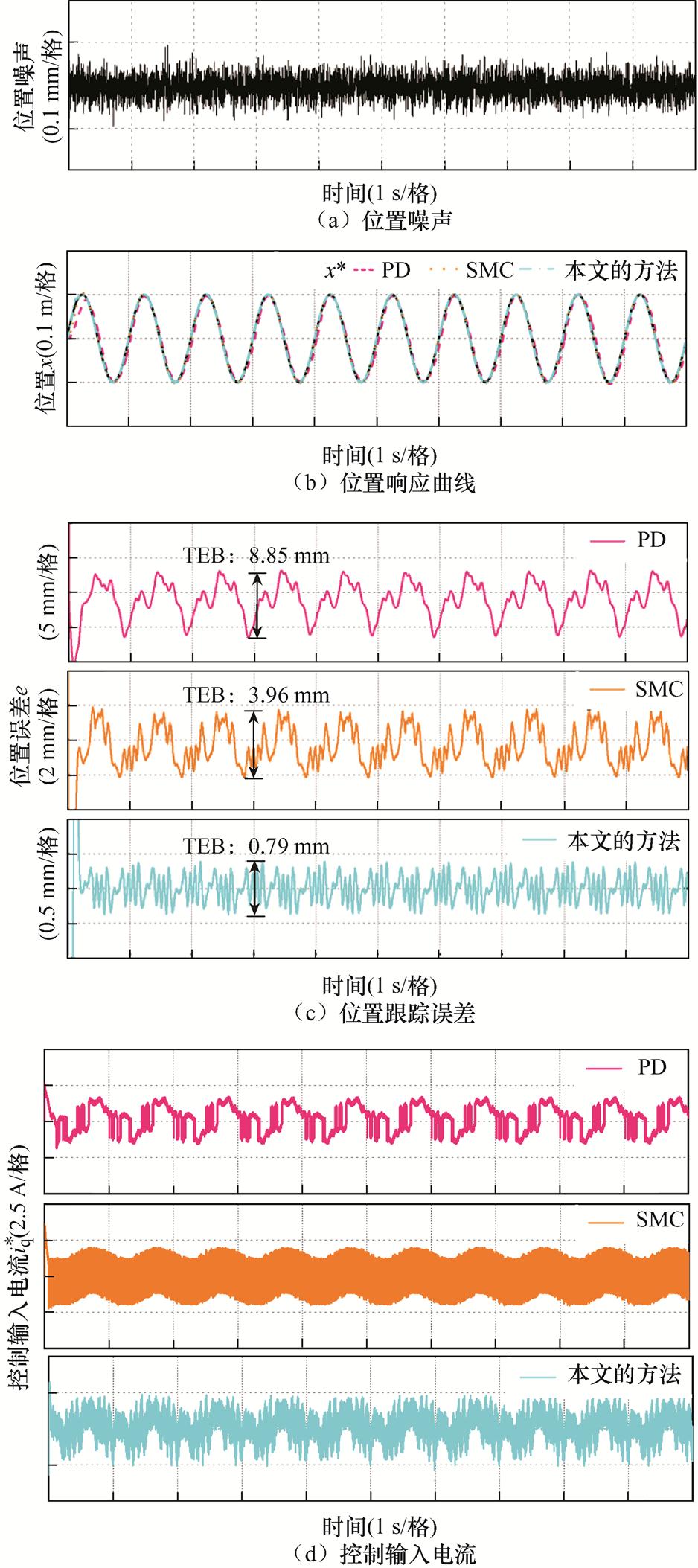
图18 位置采样噪声下的正弦位置跟踪
Fig.18 Sinusoidal position tracking under position sampling noise
针对载荷变化对永磁同步直线电机伺服性能的影响，本文提出了一种基于非线性时间延迟扰动估计的无模型位置控制策略。通过建立一种新型的动力学阶次模型，消除了传统动力学模型中的电机参数和非线性项。在此基础上，设计了由期望误差动力学、时间延迟扰动估计和非线性阻尼项组成的无模型位置控制器。相比于现有的PD控制和SMC，本文的方法不仅可以保证系统的有限时间收敛，还能有效抑制载荷变化等引起的不确定性。仿真和实验结果都表明，本文的方法无论是在标称条件还是在不同载荷条件下都表现出更优异的稳态跟踪性能，同时还兼顾更快的动态性能。
所提控制律中涉及的增益a 是恒定的，很难在每个工况下保证控制性能达到最优。在未来的研究工作中，将开发一种模型增益的在线自校正算法，以满足PMLSM伺服系统的多种工况要求。
附 录
跟踪误差收敛性证明。定义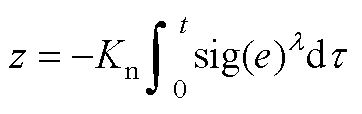
，当系统到达滑模面时，有
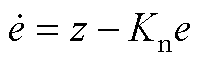。根据文献[25]易知，可以建立一个绝对连续函数满足
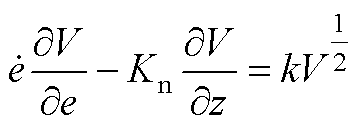（A1）
并选择w(e, z)和q(e, z)为
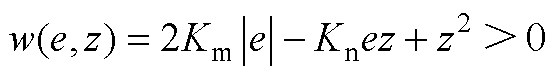（A2）
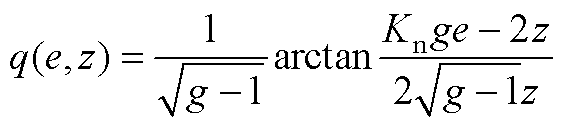（A3）
其中
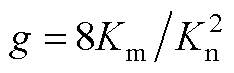
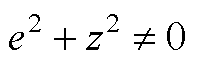
然后，李雅普诺夫函数V(e, z)可以建立为
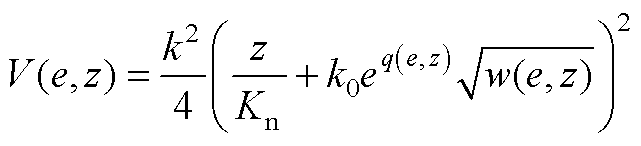（A4）
其中
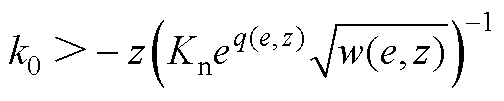
因此，V(e, z) 关于时间的微分满足
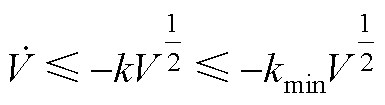（A5）
其中
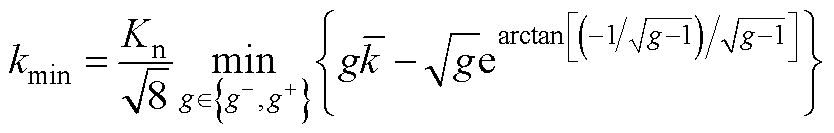
根据文献[26]中的定理1，可得系统跟踪误差收敛到零的有限时间满足
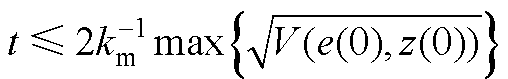（A6）
参考文献
[1] Boldea I, Tutelea L N, Xu Wei, et al. Linear electric machines, drives, and MAGLEVs: an overview[J]. IEEE Transactions on Industrial Electronics, 2018, 65(9): 7504-7515.
[2] 方馨, 王丽梅, 张康. 基于扰动观测器的永磁直线电机高阶非奇异快速终端滑模控制[J]. 电工技术学报, 2023, 38(2): 409-421.
Fang Xin, Wang Limei, Zhang Kang. High order nonsingular fast terminal sliding mode control of permanent magnet linear motor based on disturbance observer[J]. Transactions of China Electrotechnical Society, 2023, 38(2): 409-421.
[3] Wang Mingyi, Li Liyi, Pan Donghua, et al. High- bandwidth and strong robust current regulation for PMLSM drives considering thrust ripple[J]. IEEE Transactions on Power Electronics, 2016, 31(9): 6646-6657.
[4] Thomsen S, Hoffmann N, Fuchs F W. PI control, PI-based state space control, and model-based predictive control for drive systems with elastically coupled loads-a comparative study[J]. IEEE Transactions on Industrial Electronics, 2011, 58(8): 3647-3657.
[5] 孙强, 张为堂. 磁通切换永磁电机模糊自适应PI控制策略[J]. 中国电机工程学报, 2017, 37(22): 6611-6618, 6773.
Sun Qiang, Zhang Weitang. An adaptive-fuzzy PI control strategy for flux-switching permanent magnet motors[J]. Proceedings of the CSEE, 2017, 37(22): 6611-6618, 6773.
[6] Huang Sudan, Cao Guangzhong, Xu Junqi, et al. Predictive position control of long-stroke planar motors for high-precision positioning applications[J]. IEEE Transactions on Industrial Electronics, 2021, 68(1): 796-811.
[7] Song Fazhi, Liu Yang, Xu Jianxin, et al. Iterative learning identification and compensation of space-periodic disturbance in PMLSM systems with time delay[J]. IEEE Transactions on Industrial Electronics, 2018, 65(9): 7579-7589.
[8] 王璨, 李国冲, 杨桂林, 等. 基于生物智能环状耦合的嵌入式永磁同步直线电机高精度位置协同控制研究[J]. 电工技术学报, 2021, 36(5): 935-943.
Wang Can, Li Guochong, Yang Guilin, et al. Research on position cooperative control of high-precision embedded permanent magnet synchronous linear motor based on biological intelligence loop coupling[J]. Transactions of China Electrotechnical Society, 2021, 36(5): 935-943.
[9] Cupertino F, Naso D, Mininno E, et al. Sliding-mode control with double boundary layer for robust compensation of payload mass and friction in linear motors[J]. IEEE Transactions on Industry Applications, 2009, 45(5): 1688-1696.
[10] 付东学, 赵希梅. 永磁直线同步电机自适应非奇异快速终端滑模控制[J]. 电工技术学报, 2020, 35(4): 717-723.
Fu Dongxue, Zhao Ximei. Adaptive nonsingular fast terminal sliding mode control for permanent magnet linear synchronous motor[J]. Transactions of China Electrotechnical Society, 2020, 35(4): 717-723.
[11] Wang Lijun, Zhao Jiwen, Yang Xing, et al. Robust deadbeat predictive current regulation for permanent magnet synchronous linear motor drivers with parallel parameter disturbance and load observer[J]. IEEE Transactions on Power Electronics, 2022, 37(7): 7834-7845.
[12] Chen S Y, Chiang H H, Liu T S, et al. Precision motion control of permanent magnet linear synchronous motors using adaptive fuzzy fractional- order sliding-mode control[J]. IEEE/ASME Transactions on Mechatronics, 2019, 24(2): 741-752.
[13] Zeman V, Patel R V, Khorasani K. Control of a flexible-joint robot using neural networks[J]. IEEE Transactions on Control Systems Technology, 1997, 5(4): 453-462.
[14] Li Wanrong, Yuan Huawei, Li Sinan, et al. A revisit to model-free control[J]. IEEE Transactions on Power Electronics, 2022, 37(12): 14408-14421.
[15] 姚文龙, 裴春博, 池荣虎, 等. 基于无模型自适应控制的船舶微电网二次调频控制策略[J]. 电机与控制学报, 2023, 27(3): 135-146.
Yao Wenlong, Pei Chunbo, Chi Ronghu, et al. Secondary frequency modulation control strategy of ship microgrid with model-free adaptive control[J]. Electric Machines and Control, 2023, 27(3): 135-146.
[16] 尹政, 胡存刚, 芮涛, 等. LC滤波型电压源逆变器无模型预测电压控制策略[J]. 电工技术学报, 2023, 38(14): 3723-3732.
Yin Zheng, Hu Cungang, Rui Tao, et al. Model-free predictive voltage control strategy for LC-filtered voltage source inverter[J]. Transactions of China Electrotechnical Society, 2023, 38(14): 3723-3732.
[17] Kang Jinsong, Huang Xiayi, Xia Chang, et al. Ultralocal model-free adaptive supertwisting nonsingular terminal sliding mode control for magnetic levitation system[J]. IEEE Transactions on Industrial Electronics, 2024, 71(5): 5187-5194.
[18] Fliess M, Join C. Model-free control[J]. International Journal of Control, 2013, 86(12): 2228-2252.
[19] Zhang Yongchang, Jin Jialin, Huang Lanlan. Model- free predictive current control of PMSM drives based on extended state observer using ultralocal model[J]. IEEE Transactions on Industrial Electronics, 2021, 68(2): 993-1003.
[20] Zhou Yanan, Li Hongmei, Zhang Hengguo. Model-free deadbeat predictive current control of a surface-mounted permanent magnet synchronous motor drive system[J]. Journal of Power Electronics: A Publications of the Korean Institute of Power Electronics, 2018, 18(1): 103-115.
[21] 苏光靖, 李红梅, 李争, 等. 永磁同步直线电机无模型电流控制[J]. 电工技术学报, 2021, 36(15): 3182-3190.
Su Guangjing, Li Hongmei, Li Zheng, et al. Research on model-free current control of permanent magnet synchronous linear motor[J]. Transactions of China Electrotechnical Society, 2021, 36(15): 3182-3190.
[22] Gao Siyu, Wei Yanjun, Zhang Di, et al. Model-free hybrid parallel predictive speed control based on ultralocal model of PMSM for electric vehicles[J]. IEEE Transactions on Industrial Electronics, 2022, 69(10): 9739-9748.
[23] Franklin G F, Powell J D. Digital control of dynamic systems[M]. New Jersey:Addison-Wesley Publishing Company, 1980.
[24] Jin M, Kang S H, Chang P H. Robust compliant motion control of robot with nonlinear friction using time-delay estimation[J]. IEEE Transactions on Industrial Electronics, 2008, 55(1):258-269.
[25] Slotine J J E. The robust control of robot manipu- lators[J]. The International Journal of Robotics Research, 1985, 4(2): 49-64.
[26] Polyakov A, Poznyak A. Reaching time estimation for “super-twisting” second order sliding mode controller via Lyapunov function designing[J]. IEEE Transactions on Automatic Control, 2009, 54(8): 1951-1955.
Model-Free Robust Position Tracking Control of Permanent Magnet Synchronous Linear Motor Based on Nonlinear Time Delay Disturbance Estimation
Abstract In practical permanent magnet synchronous linear motor (PMSLM) servo drive applications, uncertainties arising from time-varying payloads, such as mismatched inertia and nonlinear friction, can significantly degrade the tracking accuracy of the servo system. Traditional robust control techniques can enhance the servo performance of linear motors but often rely on the motor’s precise models and parameters. To diminish reliance on the motor system model, a model-free control approach grounded in the ultra-local model concept has been introduced in recent years. Nevertheless, the uncertainty estimation within the ultra-local model typically involves complex algebraic identification and observer methods, which are intricate and fail to account for the effects of estimation errors. This paper presents a model-free robust position control strategy predicated on nonlinear time delay estimation, streamlining the implementation process and enhancing its universality.
Firstly, a dynamic order model for PMSLM is constructed on the foundation of the ultra-local concept. This model eliminates motor parameters and nonlinear terms in dynamic models, furnishing a framework for model-free control. Secondly, the terminal sliding mode attraction factor is introduced to design the expected nonlinear error dynamics, ensuring high-precision finite-time convergence of position tracking errors. Then, the uncertainty caused by payload changes is estimated online using the time-delay disturbance estimation technology, and feedforward is compensated to the control loop. Meanwhile, nonlinear damping terms are integrated to counteract the time-delay disturbance estimation error. Finally, the stability of the closed-loop controller is examined via Lyapunov theory, and guidelines for controller parameter selection are articulated.
The simulation and experimental results of the position step response are 0.114 s and 0.202 s with the proposed method, 0.163 s and 0.392 s with the traditional proportional-derivative (PD) control, and 0.132 s and 0.273 s with the sliding mode control (SMC). In addition, the control input current 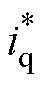of PD is the smoothest, while the 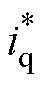of SMC exhibits a severe jitter phenomenon. The 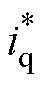of the proposed method contains noises due to the presence of the acceleration term. Regarding the payload variation, the position response curves of both PD and SMC begin to diverge from the designated positioning trajectory, with great loads leading to more pronounced deviations. In contrast, the tracking error bounds (TEBs) measured by the proposed method are 0.78 mm, 0.86 mm, and 0.94 mm, consistently ensuring accurate tracking of the positioning trajectory. Random noise with an amplitude of 0.1mm is added to the feedback position signal to further verify the impact of position sampling disturbance on the proposed method. The results indicate that the impact of these noises is not significant.
The conclusions are as follows. (1) Compared with PD and SMC controls, the proposed method guarantees finite-time convergence of the system and effectively mitigates uncertainties from payload fluctuations. (2) The time-delay disturbance estimation technique is independent of the motor's precise model and intrinsically serves as an equivalent low-pass filter. Thus, an additional filter design is optimal. (3) Incorporating a nonlinear damping term founded on the sliding mode surface curtails estimation errors associated with delayed disturbance compensation, thereby enhancing the control precision of the system.
Keywords：Permanent magnet synchronous linear motor, servo performance, order model, nonlinear time delay disturbance estimation, Lyapunov
中图分类号：TM351
DOI: 10.19595/j.cnki.1000-6753.tces.231048
国家自然科学基金资助项目（51837001，52177038）。
收稿日期 2023-07-04
改稿日期2023-12-14
王立俊 男，1994年生，博士研究生，研究方向为直线电机驱动控制。
E-mail: 2020010033@mail.hfut.edu.cn
赵吉文 男，1973年生，教授，博士生导师，研究方向为直线电机本体优化设计、驱动控制、机器视觉与机器人等。
E-mail: ustczjw@hfut.edu.cn（通信作者）
（编辑 崔文静）