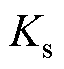 和阻尼系数
和阻尼系数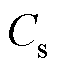 ,当弹性连接装置发生扭转形变时,会产生转矩
,当弹性连接装置发生扭转形变时,会产生转矩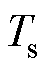 。电机侧的电磁转矩
。电机侧的电磁转矩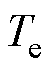 和弹性连接装置转矩
和弹性连接装置转矩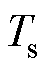 共同作用于电机转轴,弹性连接装置转矩
共同作用于电机转轴,弹性连接装置转矩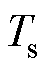 和负载转矩
和负载转矩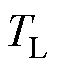 作用于执行机构。
作用于执行机构。摘要 针对双惯量弹性伺服系统存在的机械谐振问题,提出一种基于锁相环型扩张状态观测器(PLL-ESO)的机械谐振抑制策略。与常规ESO相比,PLL-ESO方法在相同的极点配置情况下具有更高带宽和更大相位裕度,有助于提高机械谐振的抑制动态特性和稳定性。实验结果表明,所提PLL-ESO方法可以有效地抑制机械谐振,且相比陷波滤波器和常规ESO方法具有更快的谐振抑制速度和更高的抑制精度。同时,实验还对观测器无阻尼固有频率和系统参数鲁棒性进行了分析,验证了PLL-ESO在宽无阻尼固有频率范围内都能抑制机械谐振,且输入参数摄动会影响谐振抑制的快速性和稳态精度。
关键词:双惯量弹性伺服系统 机械谐振 锁相环型扩张状态观测器(PLL-ESO) 谐振频率
伺服系统一般由伺服电动机通过联轴器、变速箱等传动机构连接负载,是一个典型的双惯量系 统[1]。传动机构是伺服系统中的重要组成部分,是动力传递的纽带[2]。然而,由于传动机构并非完全刚性,其弹性特性会导致系统出现速度振荡,即机械谐振。随着伺服系统的动态性能不断地提升,忽略弹性环节所带来的影响也越发显著[3-7]。对于存在机械谐振的系统,会导致其控制性能恶化,调节时间变长,速度环带宽降低,并可能引起系统机械结构损伤,甚至会发生断轴现象,对系统及人身安全造成极大威胁[8-9]。因此,在弹性伺服系统中,通常需要采取一些机械谐振抑制措施。
传统的双惯量弹性系统机械谐振的抑制主要通过改变传动机构,如增加阻尼器,该方法可以增加系统阻尼,减小振荡幅度,从而抑制系统谐振[10]。然而,加入阻尼器会增加成本,使机械结构复杂化,降低系统的动态性能,无法满足高动态性能的需求。
目前,对于伺服系统的机械谐振主要分为两类方法,即被动式和主动式。被动式主要利用陷波滤波器对特定频率信号起到强衰减作用,而对其他的频段信号几乎不产生影响的特性,实现对机械谐振有效抑制[11]。该方法的优点在于原理简单、易实现,是目前应用于工业伺服抑制机械谐振最常用的方法,但是需要获得准确的谐振频率,频率不够准确会导致抑制性能变差。因此,高性能伺服系统对于机械谐振抑制的需求是寻找一种对谐振频率变化不敏感的抑制方法。
主动式主要有利用极点配置设计PI控制器、PI控制结合状态反馈、基于状态观测器的反馈控制和高级控制算法[12-20]。①针对利用极点配置设计PI控制器方法,主要通过配置系统的闭环传递函数零极点位置,整定速度控制器参数;但当速度控制器出现饱和时,该方法无法对机械谐振进行有效的抑制。并且速度控制器仅存在两个参数,设计能力受到限制,无法同时满足系统的抑制性能和动态性能的要求[15]。②PI结合状态反馈方法在理论上可通过极点进行自由的配置,反馈状态可包括电机侧信息和负载侧信息,因而有着较大的自由度。但是,该方法结构较为复杂,并且需要测量负载侧的转速信息,增加了系统成本和体积,使得方法的应用存在较大局限性。文献[16]推导和分析了不同状态结构,给出了不同的状态反馈结构参数计算的表达式,但是该方法会增加系统的传递函数的阶数。③基于状态观测器方法以其通用性强、谐振抑制效果好等优点,成为谐振抑制研究的热门方向。观测器可以有效解决扰动不易测量的问题。因此,可以通过对扰动的实时观测及补偿进而抑制机械谐振。文献[17]提出了一种基于分数阶状态反馈观测器的方法,抑制机械谐振所产生的速度振荡,并增强系统抗干扰能力。但是,分数阶方法不便于离散化,使得其在数字控制系统中实现变得困难。文献[18]采用自适应观测器估计状态和参数,虽然有良好的机械谐振抑制效果,但该观测器的结构较为复杂。文献[19]提出了基于扰动观测器的滑模控制器的谐振控制方法,通过对位置信号进行滤波操作,再根据不变流形原理设计了观测器,整体结构包含了滤波算法、滑模控制器和未知扰动观测器部分,但是控制结构变得较复杂。④高级控制算法包含神经网络控制、准时间最优控制、模糊控制、鲁棒控制、H∞控制等。文献[20]提出了一种自适应模糊逻辑的高级算法,并基于反步法设计了自适应模糊控制器,对抑制伺服系统的机械谐振抑制取得了较好的效果。然而,对于机械谐振抑制,高级控制算法过于复杂,不便应用于实际的工业现场,因而高级算法不能被普遍推广应用。在实际应用中,对于机械谐振抑制需要简单、易于实现,且具有良好的鲁棒性的抑制方法。
为解决双惯量弹性伺服系统机械谐振抑制问题以及所提到抑制方法的不足,本文提出锁相环型扩张状态观测器的谐振抑制方法。所提方法利用PLL- ESO的高带宽和大相位裕度特点,提升谐振抑制效果,并与陷波滤波器方法和ESO谐振抑制方法进行实验对比,同时通过理论和实验分析了参数选择对PLL-ESO谐振抑制性能的影响。
双惯量弹性系统模型如图1所示。双惯量弹性系统由弹性连接装置、伺服电动机和执行机构构成。弹性连接装置具有刚度系数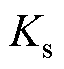 和阻尼系数
和阻尼系数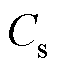 ,当弹性连接装置发生扭转形变时,会产生转矩
,当弹性连接装置发生扭转形变时,会产生转矩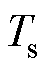 。电机侧的电磁转矩
。电机侧的电磁转矩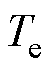 和弹性连接装置转矩
和弹性连接装置转矩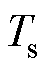 共同作用于电机转轴,弹性连接装置转矩
共同作用于电机转轴,弹性连接装置转矩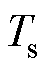 和负载转矩
和负载转矩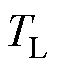 作用于执行机构。
作用于执行机构。
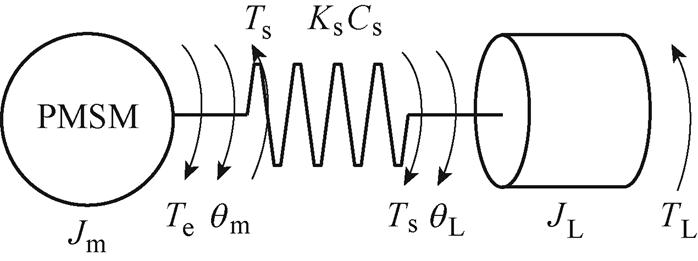
图1 双惯量弹性系统模型
Fig.1 A two-inertia elastic system model
通常情况下,可以忽略弹性连接的惯量,根据分析,可以得到以下数学模型。


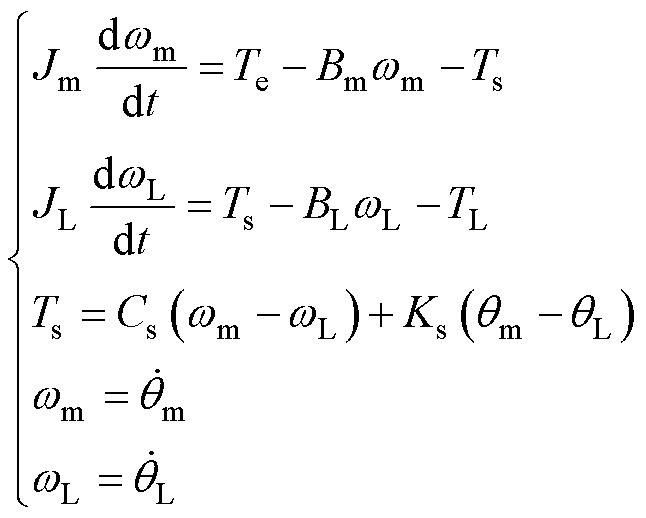 (1)
(1)
式中,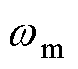 为电机角速度;
为电机角速度;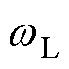 为负载角速度;
为负载角速度;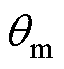 为电机机械角度;
为电机机械角度;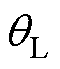 为负载机械角度;
为负载机械角度;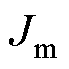 和
和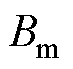 分别为电机转动惯量和摩擦系数;
分别为电机转动惯量和摩擦系数;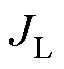 和
和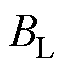 分别为负载侧等效转动惯量和摩擦系数。
分别为负载侧等效转动惯量和摩擦系数。
弹性连接装置的阻尼系数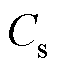 一般情况下较小,可忽略不计,对上述微分方程组进行Laplace变换,可得
一般情况下较小,可忽略不计,对上述微分方程组进行Laplace变换,可得
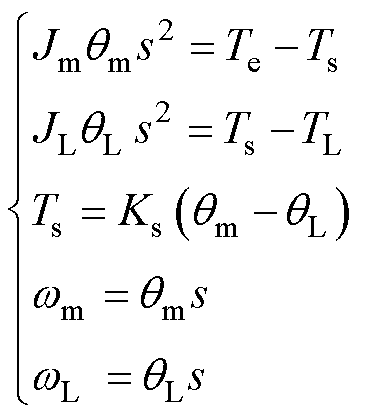 (2)
(2)
将数学表达式等效为双惯量系统等效框图,如图2所示。
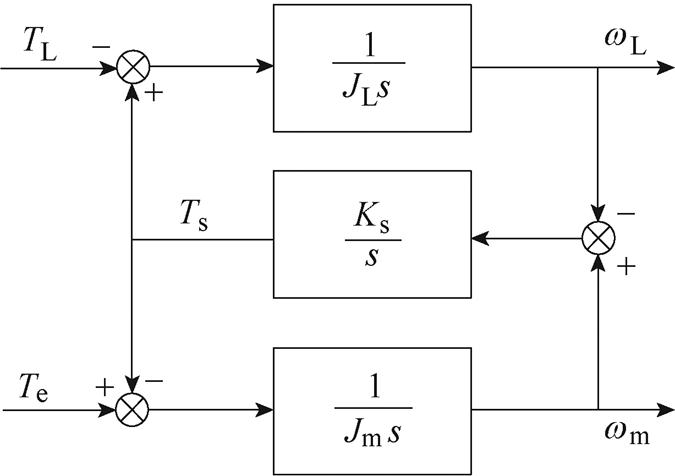
图2 双惯量弹性系统等效框图
Fig.2 Equivalent block diagram of a two-inertia elastic system
通过双惯量系统等效框图推导出电机角速度与电磁转矩之间的传递函数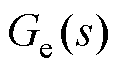 为
为
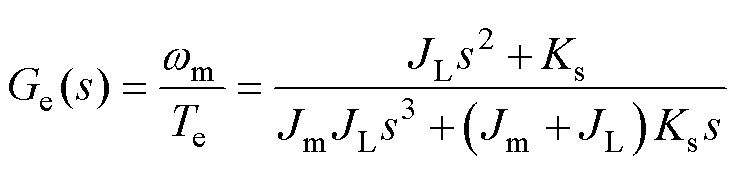 (3)
(3)
从式(3)中可以得出,弹性环节的存在使系统的整体传递函数引入了一对共轭的零点和极点,这组零极点均位于虚轴上。共轭零点为系统的反谐振频率(Antiresonance Frequency, ARF);共轭极点为系统的自然振荡频率(Natural Torsional Frequency, NTF),也为双惯量弹性系统的机械谐振频率点。整理计算得到相应的谐振频率 和反谐振频率
和反谐振频率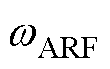 分别为
分别为
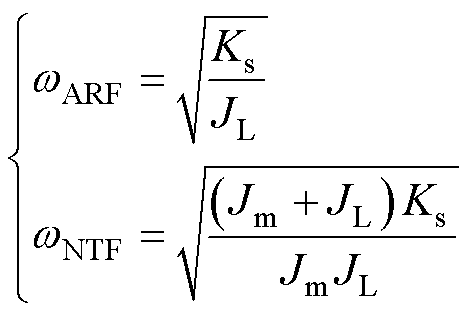 (4)
(4)
根据式(4)可以观察到,双惯量弹性系统的谐振频率和反谐振频率主要与系统的机械参数有关。
双惯量弹性系统的频率特性曲线如图4所示,频率特性曲线中存在谐振频率点与反谐振频率点,谐振频率是双惯量弹性系统固有的特性,当输入信号的频率接近谐振频率时,系统的响应幅值会急剧 变大。
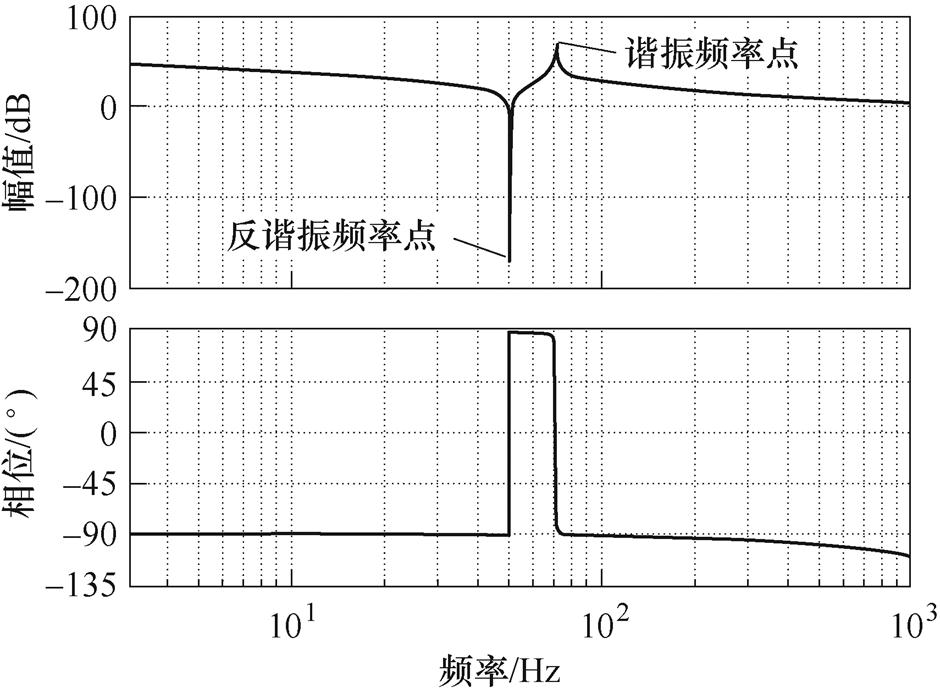
图3 双惯量弹性系统频率特性曲线
Fig.3 Frequency characteristic curves of a two-inertia elastic system
弹性连接装置的引入使得系统电机角速度与电磁转矩之间的传递函数存在一对位于虚轴的谐振极点。然而,引入陷波滤波器能够抵消该谐振极点对系统的影响。陷波滤波器传递函数为
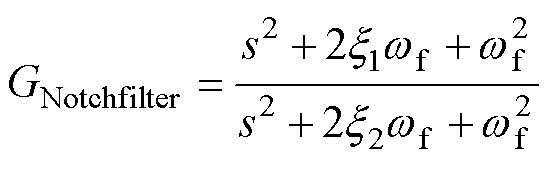 (5)
(5)
式中,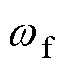 为陷波频率;
为陷波频率;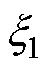 和
和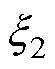 为阻尼系数。
为阻尼系数。
陷波滤波器的频率特性曲线如图4所示。
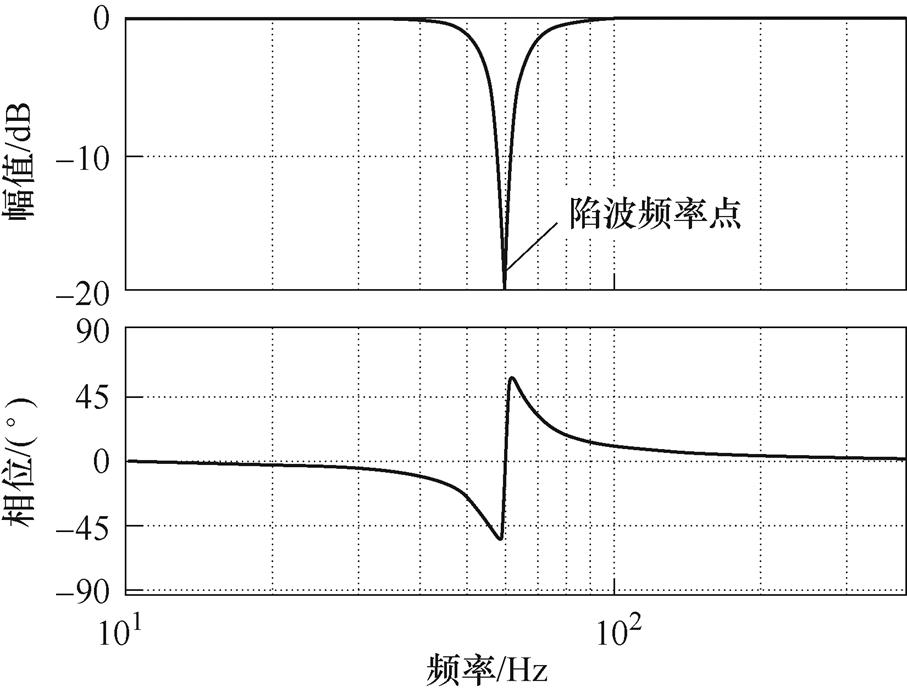
图4 陷波滤波器频率特性曲线
Fig.4 Frequency characteristic curves of the notch filter
尽管应用陷波滤波器是一种有效的方法,但陷波滤波器需要准确的陷波频率。陷波滤波器的频率设置不正确会导致陷波失败,同时随着机械装置的工作,机械参数会发生变化,进而导致机械谐振频率偏移,给陷波滤波器的使用带来巨大的挑战[21]。
本小节主要对ESO和PLL-ESO两种谐振抑制方法进行分析[22]。
电机侧的机械方程为
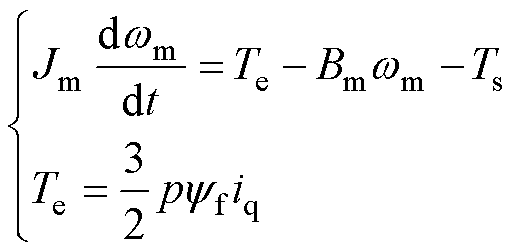 (6)
(6)
式中,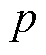 为电机极对数;
为电机极对数;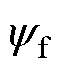 为电机转子磁链;iq为电机q轴电流。
为电机转子磁链;iq为电机q轴电流。
对电机侧机械方程进行整理得到
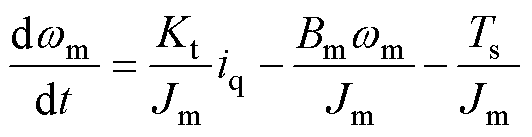 (7)
(7)
其中
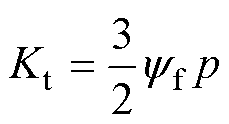
对式(7)进行改写得到
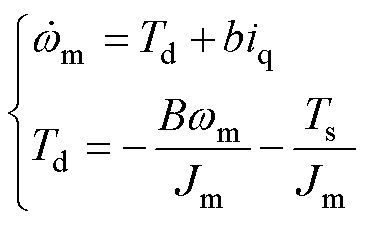 (8)
(8)
其中
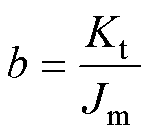
式中,Td为总扰动转矩。
对机械方程改写,得到ESO的状态方程式为
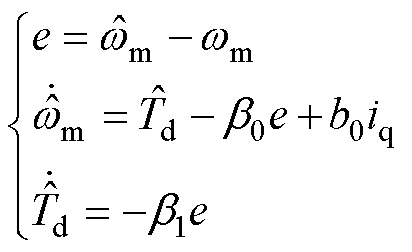 (9)
(9)
式中,ESO状态变量为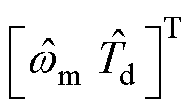 ;
;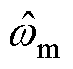 为电机角速度的估计;
为电机角速度的估计;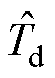 为扰动转矩的估计;
为扰动转矩的估计;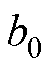 为
为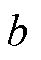 的估计量;
的估计量;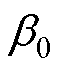 和
和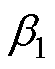 为观测器参数。ESO结构如图5所示。
为观测器参数。ESO结构如图5所示。
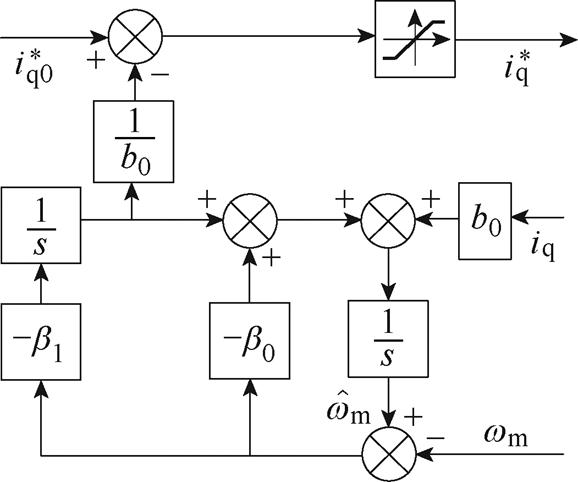
图5 ESO结构
Fig.5 Structure diagram of the ESO
ESO通过对外部总体扰动实时估计,包括弹性环节所产生的转矩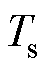 ,并进行前馈补偿,从而抑制谐振。
,并进行前馈补偿,从而抑制谐振。
根据电机机械方程设计PLL-ESO,和ESO基本原理一致,用扩张状态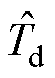 对扰动进行估计。
对扰动进行估计。
根据机械方程设计PLL-ESO状态方程为
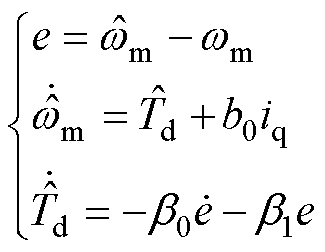 (10)
(10)
PLL-ESO结构如图6所示。
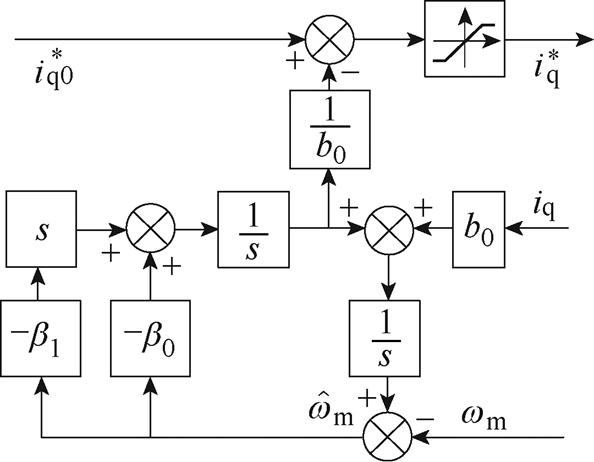
图6 PLL-ESO结构
Fig.6 Structure diagram of the PLL-ESO
对比式(9)和式(10)发现,PLL-ESO在扩张状态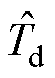 的估计中引入了误差的导数,这将对PLL- ESO产生什么影响,下面会具体分析。
的估计中引入了误差的导数,这将对PLL- ESO产生什么影响,下面会具体分析。
3.2.1 PLL-ESO稳定性分析
将式(8)写成方程组为
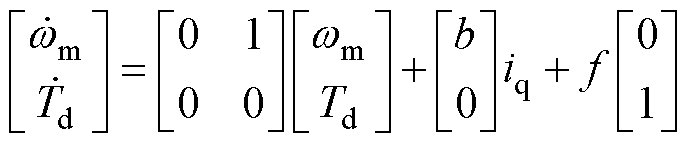 (11)
(11)
式中,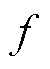 为
为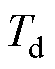 的导数。
的导数。
将PLL-ESO同样写成方程组,有
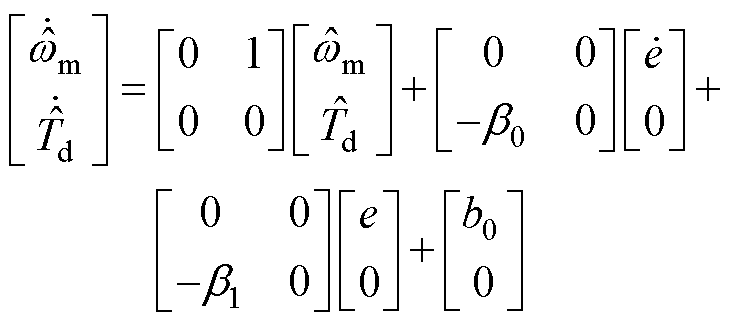 (12)
(12)
将式(11)与式(12)相减可得到误差的状态矩阵方程为
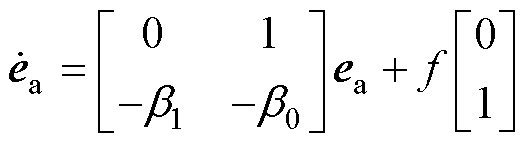 (13)
(13)
其中
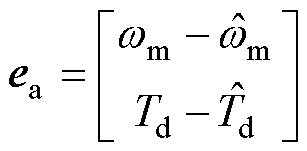
求取状态误差矩阵方程的特征方程为
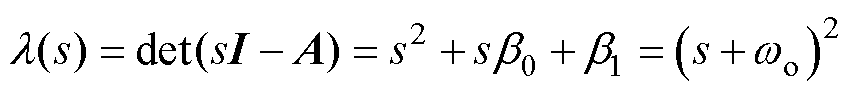 (14)
(14)
其中
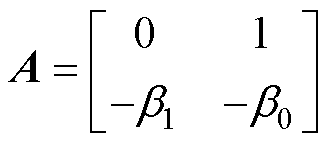
式中,I为单位矩阵;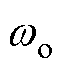 为无阻尼固有角频率,
为无阻尼固有角频率,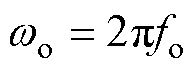 ,
,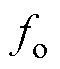 为无阻尼固有频率。
为无阻尼固有频率。
通过式(14)参数之间的关系可得
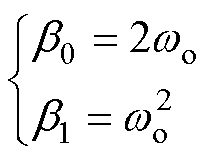 (15)
(15)
式中,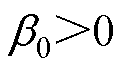 、
、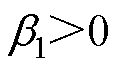 ,因此证明了观测器稳定。
,因此证明了观测器稳定。
3.2.2 PLL-ESO跟踪性能分析
将式(10)进行Laplace变换可得
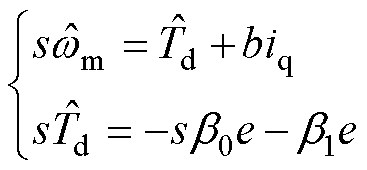 (16)
(16)
将式(16)和机械方程进行整理可得
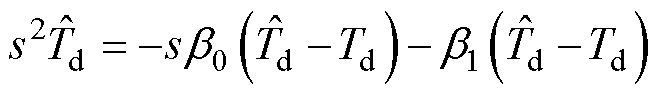 (17)
(17)
根据式(17)整理得到估计扰动和实际扰动之间的传递函数为
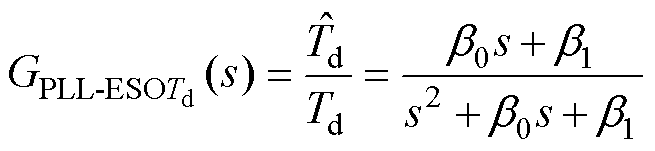 (18)
(18)
同上述方法推导出ESO的估计扰动和实际扰动的传递函数为
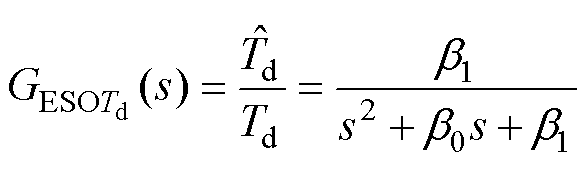 (19)
(19)
根据扰动传递函数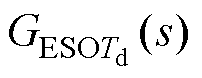 和
和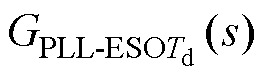 得到频率特性曲线,如图7所示,PLL-ESO的相位裕度优于ESO。当
得到频率特性曲线,如图7所示,PLL-ESO的相位裕度优于ESO。当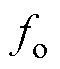 =50 Hz时,PLL-ESO的相位裕度相较于ESO大15°。在幅值为-3 dB时,若
=50 Hz时,PLL-ESO的相位裕度相较于ESO大15°。在幅值为-3 dB时,若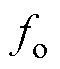 同都为50 Hz,ESO的截止频率为32 Hz,而PLL-ESO为110 Hz。PLL-ESO的截止频率更高,因此PLL- ESO有着高动态性能。但是,随着
同都为50 Hz,ESO的截止频率为32 Hz,而PLL-ESO为110 Hz。PLL-ESO的截止频率更高,因此PLL- ESO有着高动态性能。但是,随着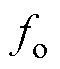 的增加,观测器的跟踪性能变好,但过大的
的增加,观测器的跟踪性能变好,但过大的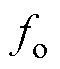 会引入高频噪声,使系统稳定性受到影响。
会引入高频噪声,使系统稳定性受到影响。
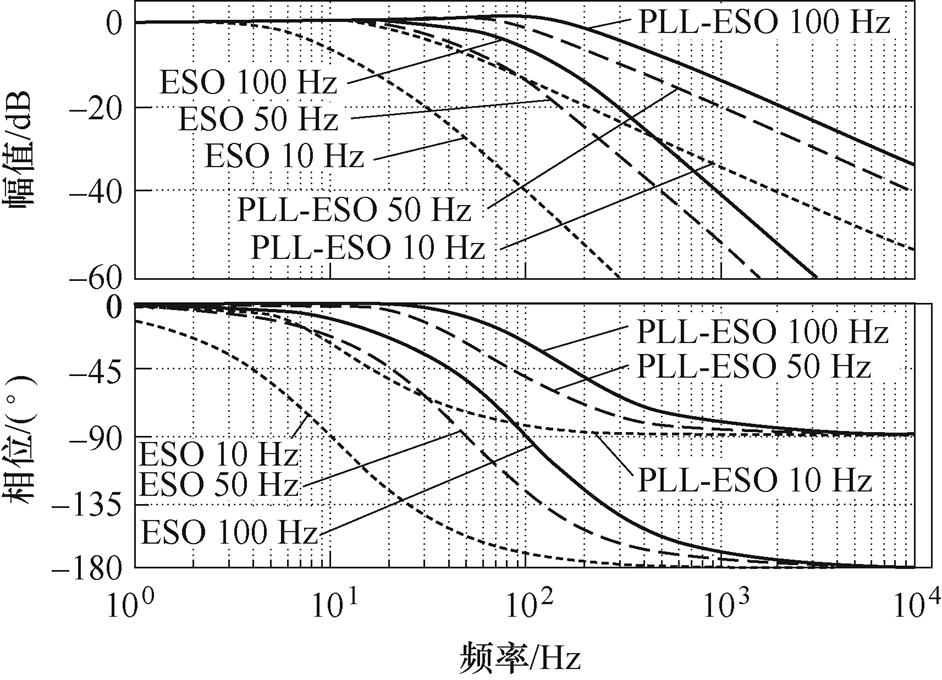
图7 ESO和PLL-ESO扰动传递函数频率特性曲线
Fig.7 Frequency characteristic curves of perturbation transfer functions of the ESO and the PLL-ESO
双惯量弹性伺服系统的整体控制框图如图8所示。在应用PLL-ESO抑制方法时,速度环控制器采用比例控制[23],PLL-ESO通过观测总扰动并补偿到q轴电流环输入,从而实现对机械谐振抑制。
图9为双惯量伺服系统实验平台,左右两侧为同型号的永磁同步电机,一台为被测电机,另一台为加载电机,中间采用弹性联轴器连接。驱动器控制芯片为TMS320F28335数字信号处理器,采用被测电机的光电编码器作为位置反馈,实现电机矢量控制。该编码器线数为2 500线。实验平台电气和机械参数见表1。
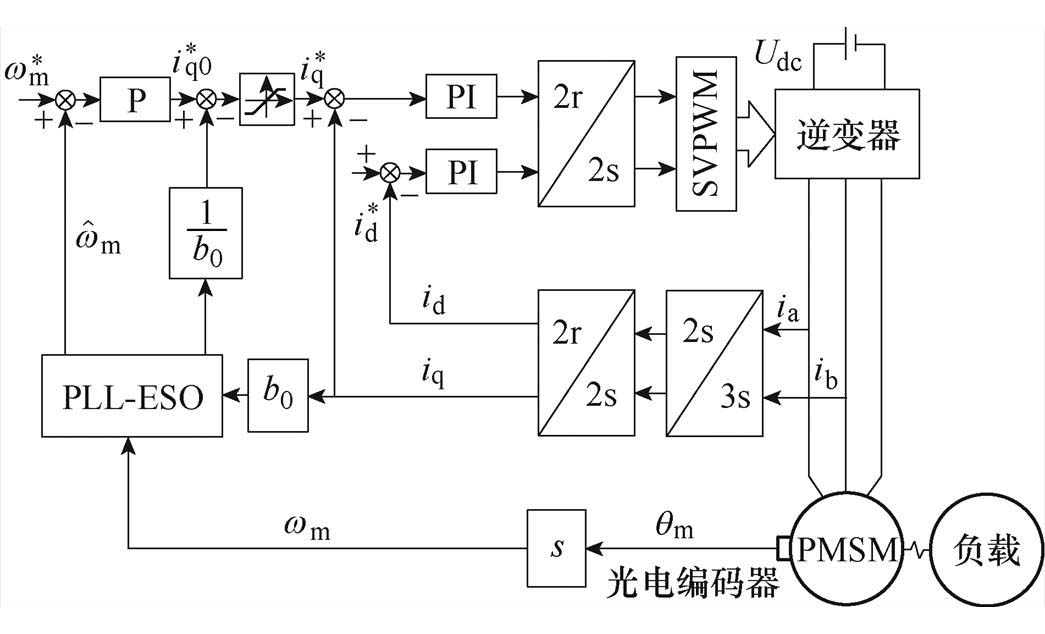
图8 双惯量弹性伺服系统整体控制框图
Fig.8 Overall control block diagram of the two-inertia elastic servo system

图9 双惯量弹性伺服系统实物图
Fig.9 Platform of the two-inertia elastic servo system
表1 双惯量弹性伺服系统实验参数
Tab.1 Parameters of the two-inertia elastic servo system
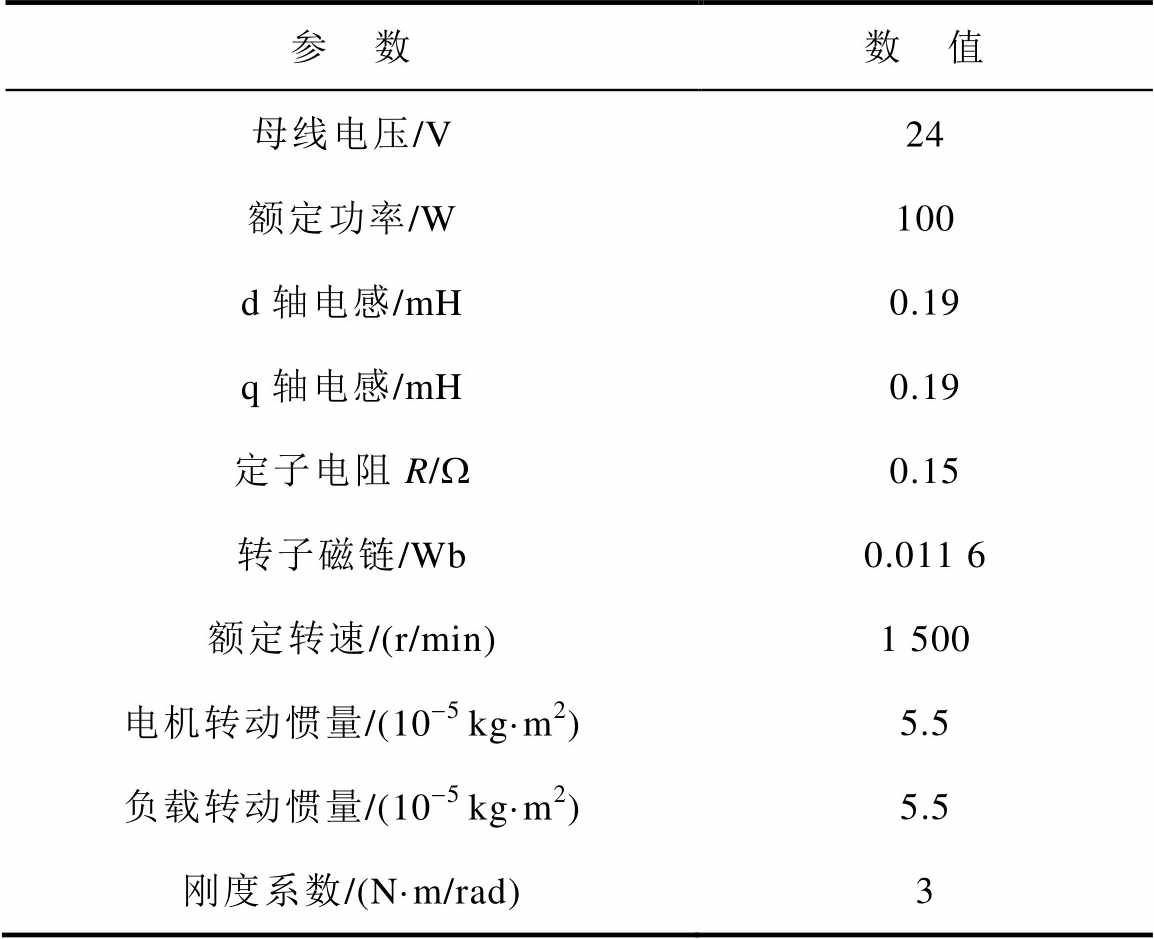
参 数数 值 母线电压/V24 额定功率/W100 d轴电感/mH0.19 q轴电感/mH0.19 定子电阻R/W0.15 转子磁链/Wb0.011 6 额定转速/(r/min)1 500 电机转动惯量/(10-5 kg·m2)5.5 负载转动惯量/(10-5 kg·m2)5.5 刚度系数/(N·m/rad)3
为了验证双惯量弹性系统机械谐振的存在,通过施加正弦扫频信号至电流环给定,对系统的谐振频率进行离线辨识[24],输出速度与实际q轴电流曲线如图10所示。将速度输出曲线和实际q轴电流曲线进行快速傅里叶分析得到系统幅频特性曲线,如图11所示。
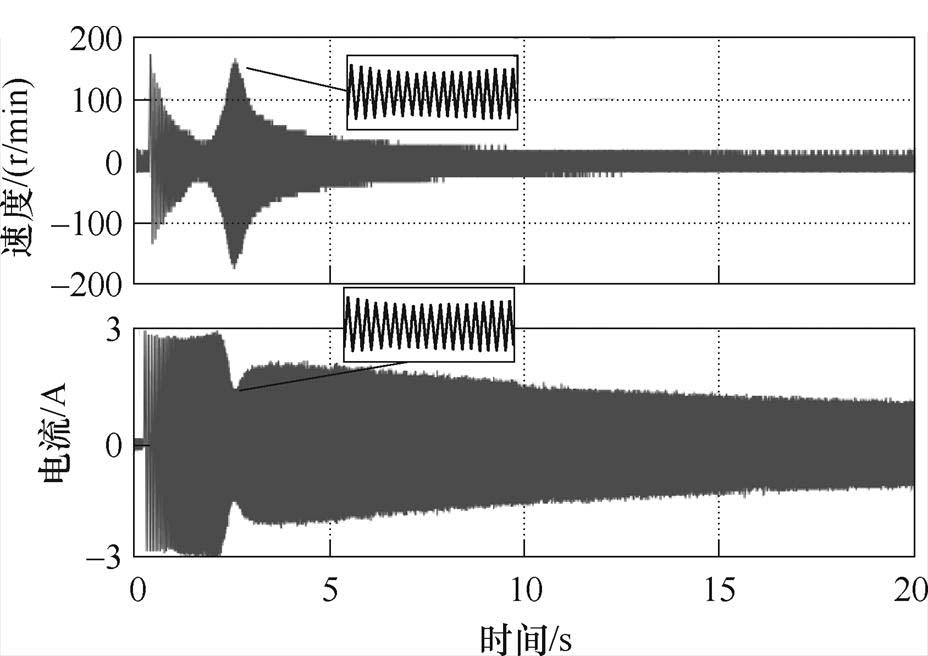
图10 辨识过程电机速度和q轴电流曲线
Fig.10 Motor speed and q-axis current curves during the identification period
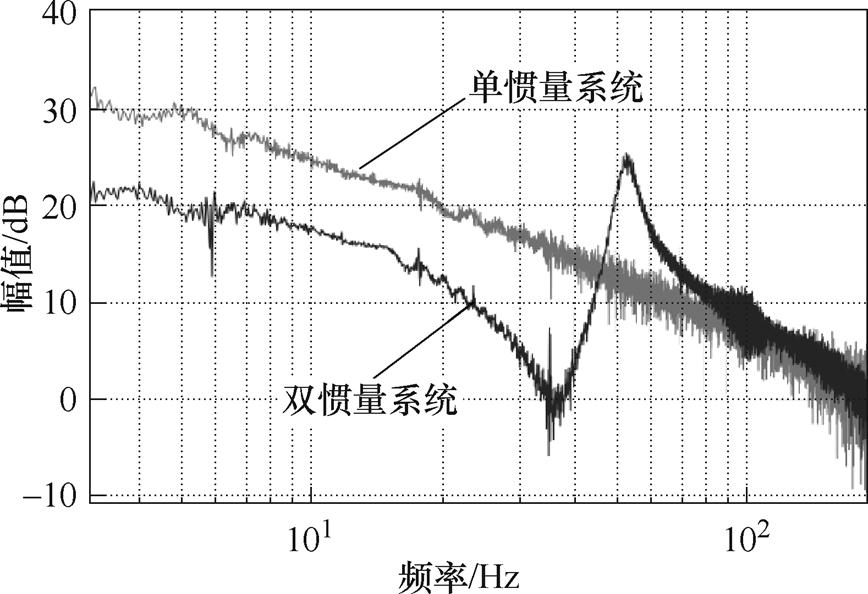
图11 双惯量弹性系统与单惯量系统幅频特性曲线
Fig.11 Amplitude-frequency characteristic curves of the two-inertia servo system and the single-inertia servo system
图11同时展示了单惯量伺服系统(仅被测电机)和双惯量伺服系统的幅频特性曲线,可以明显观察到双惯量伺服系统存在机械谐振现象,而单被测电机则不存在机械谐振。该幅频响应在52 Hz处为谐振频率点,在36 Hz处为反谐振频率点。实验中,谐振频率点为陷波滤波器设计的陷波频率,即52 Hz,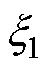 和
和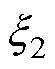 阻尼系数分别为0.01、0.5。
阻尼系数分别为0.01、0.5。
在实验中给定额定速度1 500 r/min,分析空载的情况下采用不同抑制方法的双惯量弹性系统响应曲线。
图12a为未采用任何机械谐振抑制方法的双惯量弹性系统响应曲线。在加速阶段,可以明显观察到速度振荡现象,到达稳态时间为75 ms,再次证明了双惯量弹性系统机械谐振的存在。图12b为陷波滤波器机械谐振抑制方法的系统响应曲线,陷波滤波器加在速度环输出和q轴电流输入之间。在加速阶段的速度振荡得到有效抑制,与未加抑制方法相比,到达稳态的时间基本不变,但是在加速开始阶段速度仍有微小振荡。
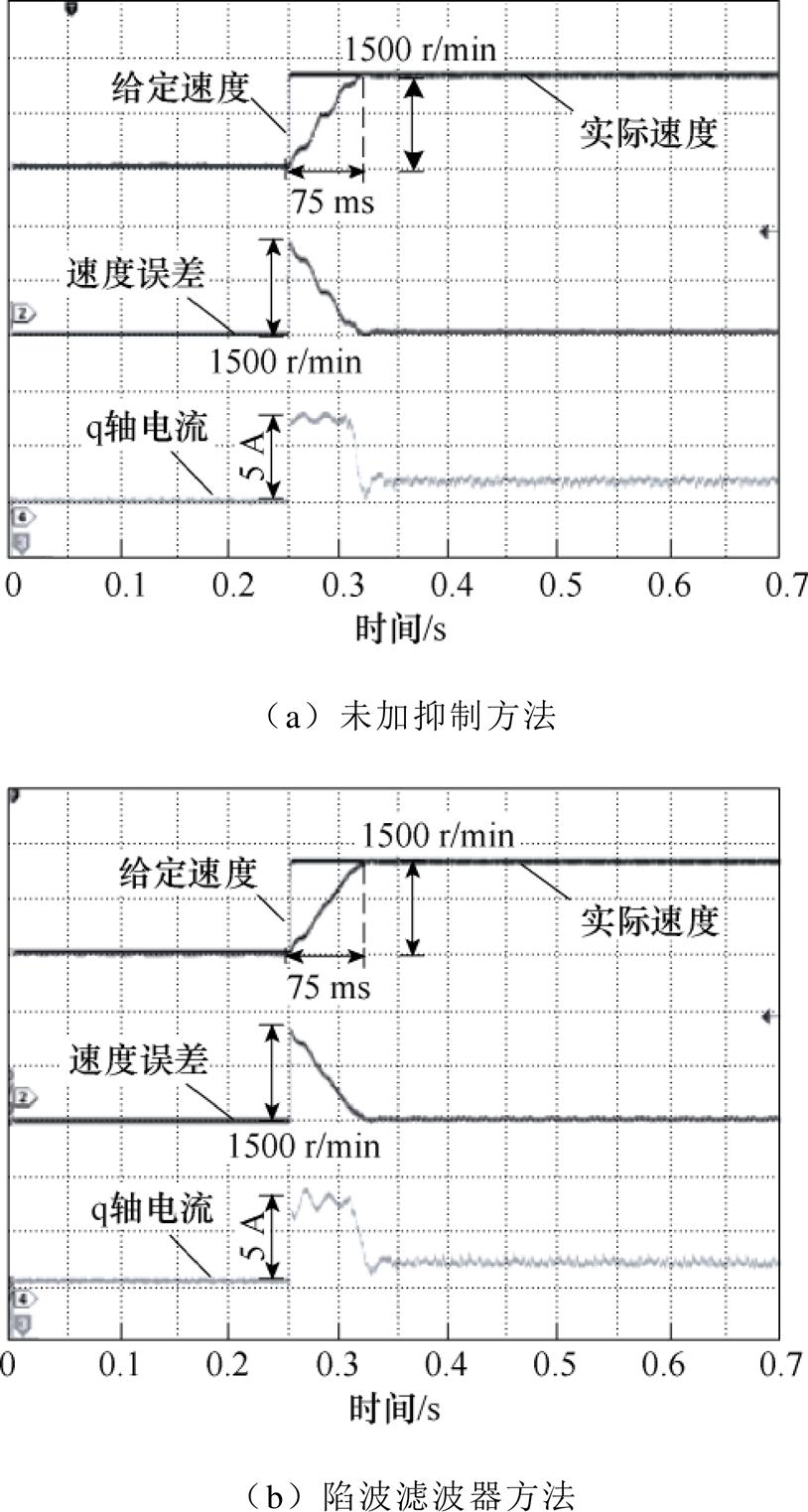
图12 未加抑制和陷波滤波器方法空载速度响应曲线
Fig.12 System response curves without resonant suppression strategy and with the notch filter method under no load
在与图12相同的测试条件下,ESO和PLL-ESO观测器的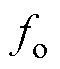 均设定为50 Hz进行实验对比。图13a为ESO方法的系统响应曲线,加速到达稳态的时间为90 ms,速度没有出现振荡;图13b为PLL-ESO方法的系统响应曲线,加速过程速度无振荡,加速时间为75 ms,抑制速度快于陷波滤波器。通过空载实验对比,可以得出两种方法均能够有效地抑制机械谐振,且PLL-ESO方法动态方面更加优越,加速时间更短,抑制精度(加速度过程中速度的波动)更高。
均设定为50 Hz进行实验对比。图13a为ESO方法的系统响应曲线,加速到达稳态的时间为90 ms,速度没有出现振荡;图13b为PLL-ESO方法的系统响应曲线,加速过程速度无振荡,加速时间为75 ms,抑制速度快于陷波滤波器。通过空载实验对比,可以得出两种方法均能够有效地抑制机械谐振,且PLL-ESO方法动态方面更加优越,加速时间更短,抑制精度(加速度过程中速度的波动)更高。
进一步验证上述方法在加载情况下的谐振抑制效果,图14、图15分别为无谐振抑制和陷波滤波器方法、ESO和PLL-ESO方法,在额定负载下进行加速实验,得到不同方法的系统响应曲线。
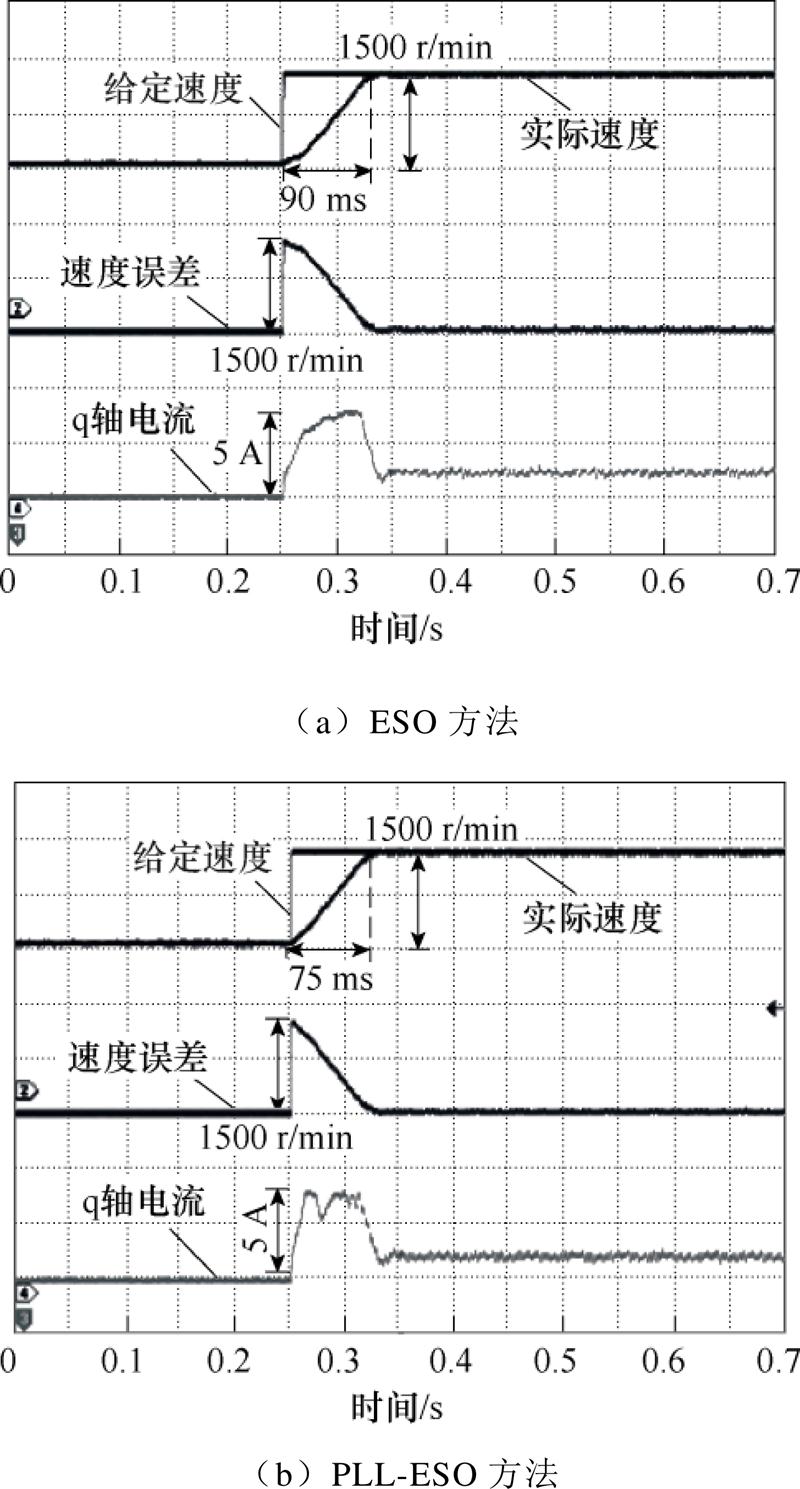
图13 ESO方法和PLL-ESO方法空载下系统响应曲线
Fig.13 System response curves of the ESO and the PLL-ESO strategies under no load
图14a为未加入谐振抑制方法系统负载响应,可以看到,在加速阶段速度出现明显的速度振荡,且负载条件下,振荡时间变长,加速到稳态的时间增至160 ms。图14b为陷波滤波器方法的系统负载响应,可以观察到,加速过程中出现较明显的速度振荡,机械谐振并未得到很好的抑制,这表明陷波滤波器方法在加载情况下并不能起到很好的谐振抑制效果。
图15a为ESO方法的系统负载响应曲线,到达稳态的时间200 ms,加速过程速度没有出现大幅度振荡。图15b为PLL-ESO方法的响应曲线,加速到达稳态的时间为160 ms,且加速过程速度平稳、无振荡。并且从实际q轴电流响应曲线看,PLL-ESO方法q轴电流增长速度快于ESO方法。因此,上述空载和加载实验结果表明,相比ESO方法,在速度振荡都得到较好抑制的情况下,PLL-ESO方法的响应速度更快,为高动态伺服系统快速谐振抑制提供了更好的选择。
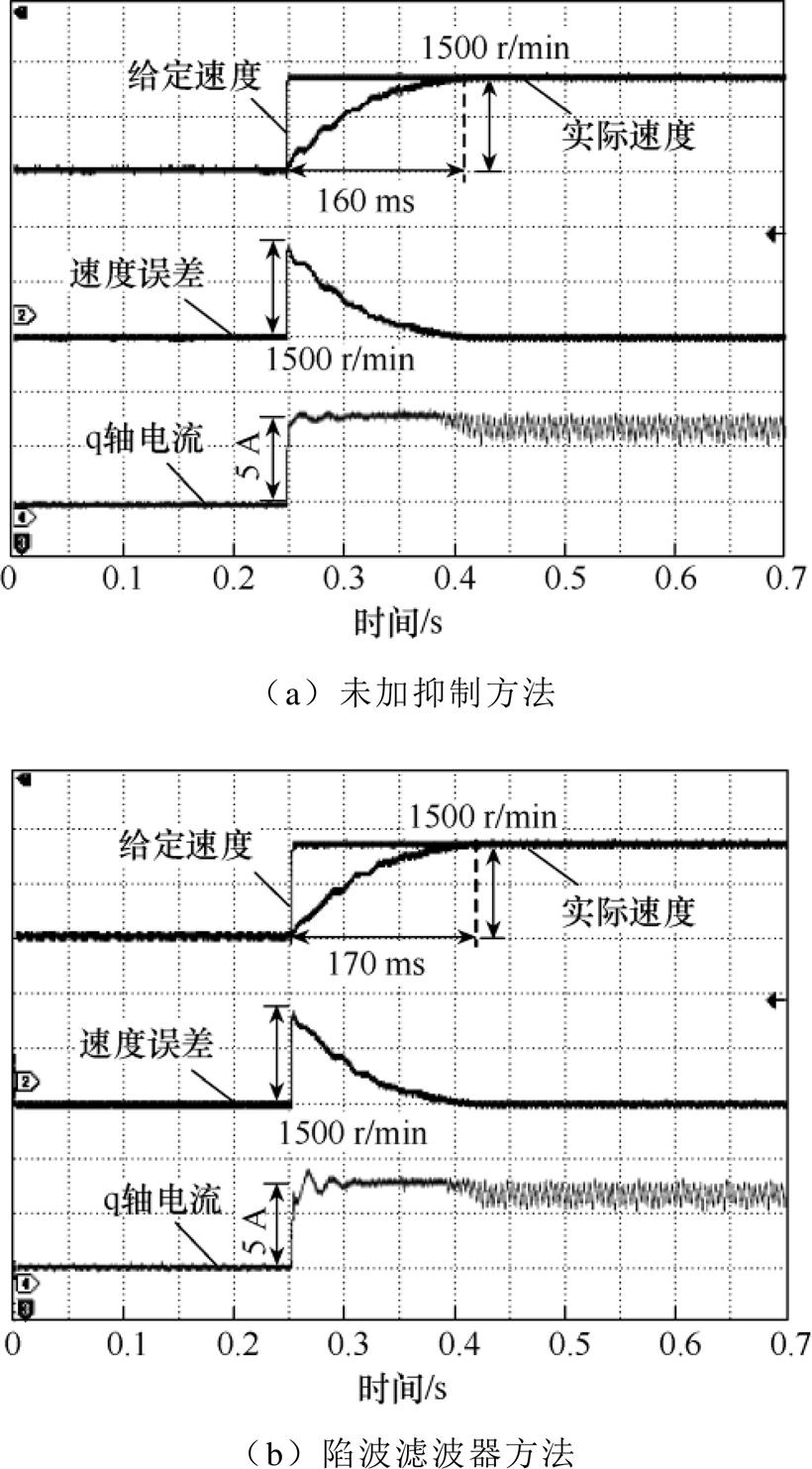
图14 未加抑制方法和陷波器方法额定负载下响应曲线
Fig.14 System response curves without resonant suppression strategy and with the notch filter method under the rated load
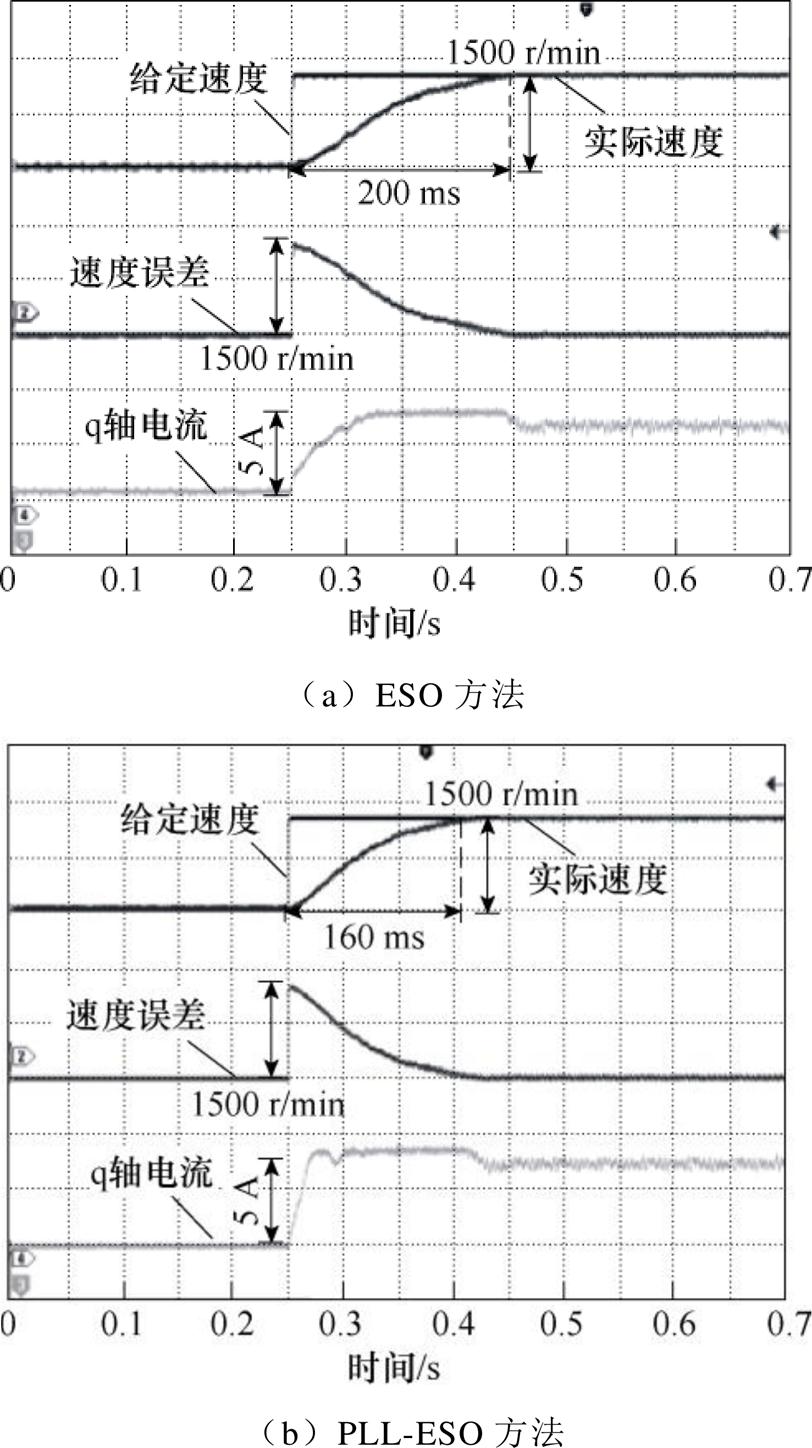
图15 ESO和PLL-ESO方法加载响应曲线
Fig.15 System response curves of the ESO and the PLL-ESO strategies under the rated load
 比较实验波形
比较实验波形为了进一步验证所提方法的适用性,下面实验分析不同 对机械谐振抑制效果的影响。
对机械谐振抑制效果的影响。
图16为ESO和PLL-ESO不同的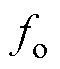 时的系统空载响应曲线,其中观测器的
时的系统空载响应曲线,其中观测器的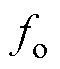 分别为10、100 Hz。如图16a所示,ESO的
分别为10、100 Hz。如图16a所示,ESO的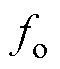 =10 Hz,可以观察到,在加速阶段出现了较明显的速度振荡,加速时间为100 ms,q轴电流上升缓慢,说明降低
=10 Hz,可以观察到,在加速阶段出现了较明显的速度振荡,加速时间为100 ms,q轴电流上升缓慢,说明降低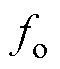 会削弱ESO方法对机械谐振的抑制效果;如图16b所示,PLL-ESO的
会削弱ESO方法对机械谐振的抑制效果;如图16b所示,PLL-ESO的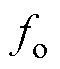 =10 Hz,相比ESO方法,PLL-ESO仍能够较好地抑制机械谐振,速度曲线没有出现振荡现象,表明抑制精度更高,另外加速时间为80 ms,比ESO方法快20 ms。图16c中,ESO的
=10 Hz,相比ESO方法,PLL-ESO仍能够较好地抑制机械谐振,速度曲线没有出现振荡现象,表明抑制精度更高,另外加速时间为80 ms,比ESO方法快20 ms。图16c中,ESO的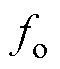 =100 Hz,能够较好抑制机械谐振,说明增大
=100 Hz,能够较好抑制机械谐振,说明增大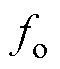 会使得到达稳态的时间变短。图16d为PLL-ESO的
会使得到达稳态的时间变短。图16d为PLL-ESO的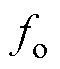 =100 Hz的系统的响应曲线,完整的运行过程速度没有出现明显的振荡。上述实验结果表明,当设计的观测器无阻尼固有频率低于系统谐振频率时,如图7所示,PLL-ESO相比ESO具有更高的幅频增益,即幅值衰减更小,这会带来更好的谐振抑制效果。另外,随着观测器无阻尼固有频率增加,谐振抑制能力基本不变,且加速时间还略有缩短。实际系统中,系统谐振频率会随着机械磨损等原因而发生偏移,由上述结果可以推知,PLL-ESO等观测方法对谐振点偏移不敏感。
=100 Hz的系统的响应曲线,完整的运行过程速度没有出现明显的振荡。上述实验结果表明,当设计的观测器无阻尼固有频率低于系统谐振频率时,如图7所示,PLL-ESO相比ESO具有更高的幅频增益,即幅值衰减更小,这会带来更好的谐振抑制效果。另外,随着观测器无阻尼固有频率增加,谐振抑制能力基本不变,且加速时间还略有缩短。实际系统中,系统谐振频率会随着机械磨损等原因而发生偏移,由上述结果可以推知,PLL-ESO等观测方法对谐振点偏移不敏感。
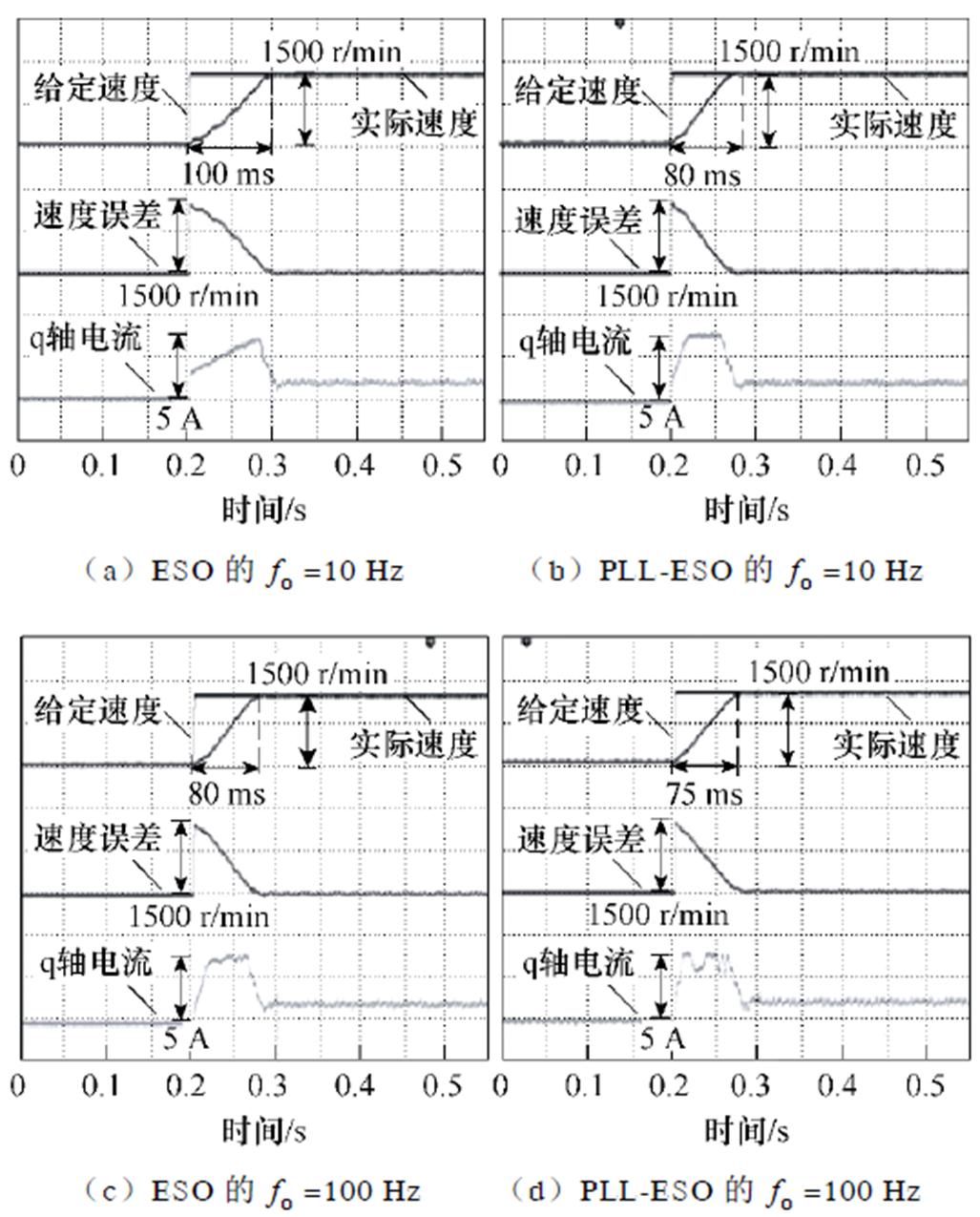
图16 空载情况下,ESO和PLL-ESO的 分别为10、100 Hz时系统响应曲线
分别为10、100 Hz时系统响应曲线
Fig.16 System response curves of the ESO and the PLL-ESO methods at 10 and 100 Hz undamped natural frequency under no load
图17为ESO和PLL-ESO中参数b0变化时系统响应曲线。图17a为ESO的b0改为真值的0.5倍时,系统的动态响应会大幅度下降,q轴电流不能建立到最大值,但可以更好地抑制机械谐振;图17b为b0变为2倍时,对动态响应影响较小,但速度出现微小振荡,系统的抑制性能变弱;图17c为PLL- ESO的b0改为真值的0.5倍时,系统的动态响应降低,相比于ESO方法到达稳态时间减少15 ms,但可以抑制机械谐振;图17d为b0变为2倍时,动态响应未发生变化,但仍然能够削弱机械谐振产生的速度振荡。
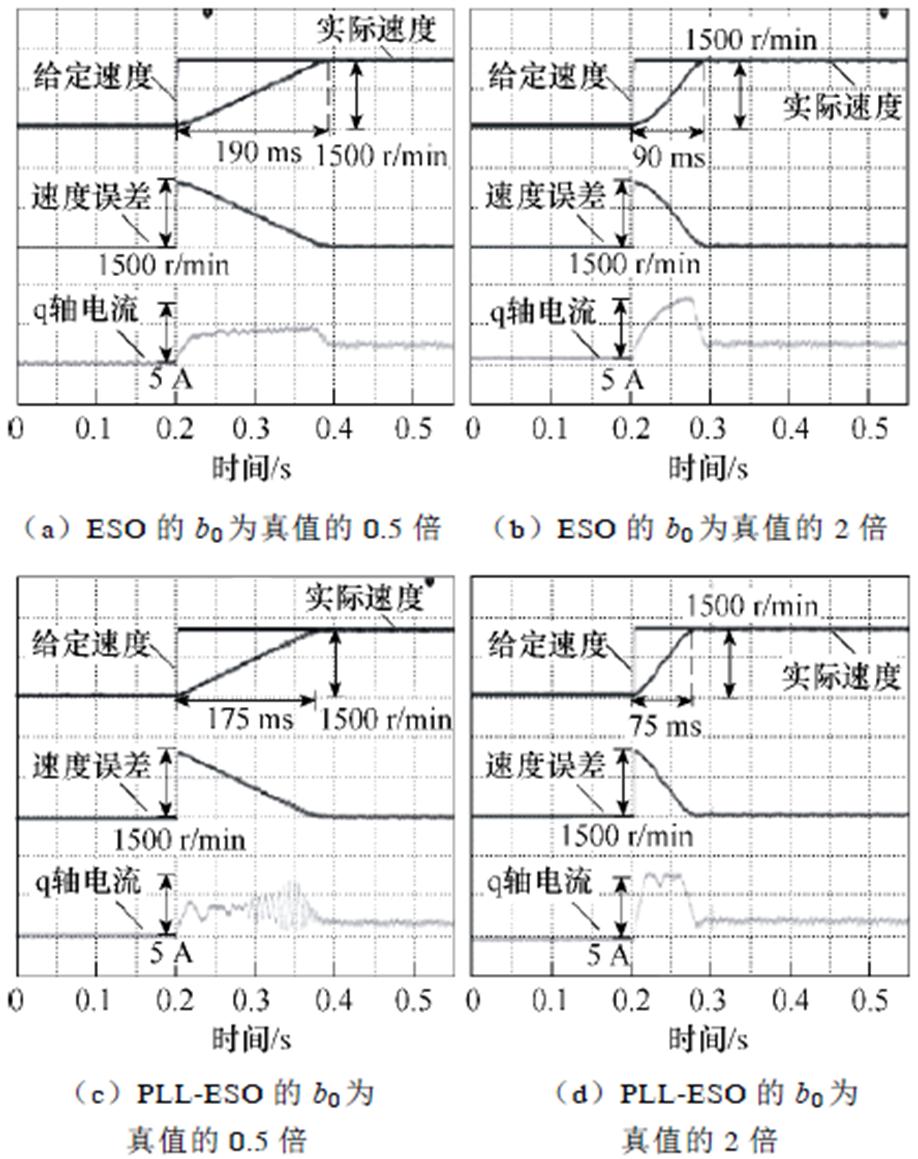
图17 ESO和PLL-ESO观测器参数b0变化系统响应曲线
Fig.17 System response curves of the ESO and PLL-ESO methods with different parameter b0 under no load
针对双惯量弹性伺服系统的机械谐振抑制方法中,常规陷波滤波器方法需要准确获得系统谐振频率,ESO观测补偿方法性能受观测器参数影响敏感等问题,提出一种基于PLL-ESO观测的谐振抑制方法,充分利用该观测器的高带宽和大相位裕度等优点,实现更好的谐振抑制。通过理论分析和充分的实验验证,得到的如下结论:
1)在双惯量弹性系统实验中,陷波滤波器需要准确的谐振频率,在空载下能够有效地抑制机械谐振,但在负载情况下,仍然出现了振荡;ESO能够进行机械谐振有效抑制,但观测器动态响应较差;PLL-ESO有着较优的动态性能,同时抑制速度和精度都优于陷波滤波器。在负载的情况下,PLL-ESO方法到达稳态的时间相比于陷波滤波器和ESO分别提高了10 ms和40 ms。另外,相比固定频率陷波滤波器方法,观测器方法对于实际系统的谐振点偏移有更强的抑制能力。
2)对PLL-ESO和ESO的不同的无阻尼固有频率进行实验,表明PLL-ESO有着更宽的无阻尼固有频率选择,能够有效减少因获得机械谐振频率不准确所带来的影响,同时对于机械谐振的抑制性能更加优越。在低无阻尼固有频率情况下,PLL-ESO同样有较快的动态性能和更高的抑制精度。
3)PLL-ESO中参数b0减小会降低系统的动态响应速度,但是对谐振仍有较好抑制作用;b0增大虽然动态响应影响较小,但是对系统的机械谐振抑制能力变弱。
但是,在观测器设计中,需要使用电机参数,例如转动惯量、转矩常数等。如果这些参数偏差过大,会降低观测器对扰动估计精度,削弱谐振抑制效果。因此,强鲁棒性的PLL-ESO设计是未来研究的方向。
参考文献
[1] Tian Minghe, Wang Bo, Yu Yong, et al. Adaptive active disturbance rejection control for uncertain current ripples suppression of PMSM drives[J]. IEEE Transactions on Industrial Electronics, 2024, 71(3): 2320-2331.
[2] 杨明, 刘铠源, 陈扬洋, 等. 基于PI-Lead控制的永磁同步电机双环位置伺服系统[J]. 电工技术学报, 2023, 38(8): 2060-2072.
Yang Ming, Liu Kaiyuan, Chen Yangyang, et al. Permanent magnet synchronous motor dual-loop position servo system based on PI-lead control[J]. Transactions of China Electrotechnical Society, 2023, 38(8): 2060-2072.
[3] 卜飞飞, 郭子韬, 顾毅君, 等. 基于改进型降阶观测器的永磁直驱伺服电动机转矩扰动抑制策略[J]. 电工技术学报, 2022, 37(16): 4104-4115.
Bu Feifei, Guo Zitao, Gu Yijun, et al. Torque disturbance suppression strategy of permanent magnet direct drive servo motor based on improved reduced order observer[J]. Transactions of China Electro- technical Society, 2022, 37(16): 4104-4115.
[4] Chen Yangyang, Yang Ming, Sun Yongping, et al. A modified Bi-quad filter tuning strategy for mechanical resonance suppression in industrial servo drive systems[J]. IEEE Transactions on Power Electronics, 2021, 36(9): 10395-10408.
[5] 杨帆, 赵希梅, 金鸿雁, 等. 基于GPI观测器的永磁同步电机鲁棒谐振预测电流控制[J/OL]. 电工技术学报, 2023, DOI: 10.19595/j.cnki.1000-6753.tces. 230331.
Yang Fan, Zhao Ximei, Jin Hongyan, el al. Robust resonant predictive current control based on GPI observer for permanent magnet synchronous motor[J/OL]. Transactions of China Electrotechnical Society, 2023, DOI: 10.19595/j.cnki.1000-6753.tces. 230331.
[6] 王璨, 李国冲, 杨桂林, 等. 基于生物智能环状耦合的嵌入式永磁同步直线电机高精度位置协同控制研究[J]. 电工技术学报, 2021, 36(5): 935-943.
Wang Can, Li Guochong, Yang Guilin, et al. Research on position cooperative control of high-precision embedded permanent magnet synchronous linear motor based on biological intelligence loop coupling[J]. Transactions of China Electrotechnical Society, 2021, 36(5): 935-943.
[7] 东野亚兰, 杨淑英, 王奇帅, 等. 基于增强型扩张状态观测器的永磁同步电机低抖振高抗扰二阶终端滑模电流控制[J]. 电工技术学报, 2024, 39(8): 2434-2448.
Dong-Ye Yanlan, Yang Shuying, Wang Qishuai, el al. Enhanced extended state observer based second order terminal sliding mode current control for permanent magnet synchronous machine with low chattering and improved disturbance rejection[J]. Transactions of China Electrotechnical Society, 2024, 39(8): 2434- 2448.
[8] 刘军, 周飞航, 刘飞. 永磁同步风电机组传动轴振动分析与抑制[J]. 电工技术学报, 2018, 33(4): 930-942.
Liu Jun, Zhou Feihang, Liu Fei. Analysis and restraining of permanent magnet synchronous wind turbine shaft vibration[J]. Transactions of China Electrotechnical Society, 2018, 33(4): 930-942.
[9] Fuentes E, Kalise D, Kennel R M. Smoothened quasi-time-optimal control for the torsional torque in a two-mass system[J]. IEEE Transactions on Industrial Electronics, 2016, 63(6): 3954-3963.
[10] Chen Yangyang, Yang Ming, Long Jiang, et al. Analysis of oscillation frequency deviation in elastic coupling digital drive system and robust Notch filter strategy[J]. IEEE Transactions on Industrial Elec- tronics, 2019, 66(1): 90-101.
[11] 龚文全, 罗炳章. 基于自适应陷波滤波器的伺服系统谐振频率估计及抑制[J]. 电机与控制应用, 2019, 46(11): 37-42, 93.
Gong Wenquan, Luo Bingzhang. Resonance frequ- ency estimation and suppression of servo system based on adaptive Notch filter[J]. Electric Machines & Control Application, 2019, 46(11): 37-42, 93.
[12] 杨影, 张杰鸣, 徐国卿, 等. 转速负反馈在伺服系统机械谐振抑制中的应用研究[J]. 电工技术学报, 2018, 33(23): 5459-5469.
Yang Ying, Zhang Jieming, Xu Guoqing, et al. Application research on speed negative feedback in mechanical resonance suppression in servo system[J]. Transactions of China Electrotechnical Society, 2018, 33(23): 5459-5469.
[13] Thomsen S, Hoffmann N, Fuchs F W. PI control, PI-based state space control, and model-based predictive control for drive systems with elastically coupled loads-a comparative study[J]. IEEE Transa- ctions on Industrial Electronics, 2011, 58(8): 3647- 3657.
[14] 王璨, 杨明, 栾添瑞, 等. 双惯量弹性伺服系统外部机械参数辨识综述[J]. 中国电机工程学报, 2016, 36(3): 804-817.
Wang Can, Yang Ming, Luan Tianrui, et al. A review of external mechanical parameter identification of two-mass elastic servo systems[J]. Proceedings of the CSEE, 2016, 36(3): 804-817.
[15] Zhang G, Furusho J. Speed control of two-inertia system by PI/PID control[J]. IEEE Transactions on Industrial Electronics, 2000, 47(3): 603-609.
[16] Szabat K, Orlowska-Kowalska T. Vibration supper- ssion in a two-mass drive system using PI speed controller and additional feedbacks-comparative study[J]. IEEE Transactions on Industrial Electronics, 2007, 54(2): 1193-1206.
[17] 郎志, 杨明, 徐殿国. 双惯量弹性系统负载扰动观测器设计研究[J]. 电工技术学报, 2016, 31(增刊2): 84-91.
Lang Zhi, Yang Ming, Xu Dianguo. Research on design of load disturbance observer for double inertia elastic system[J]. Transactions of China Electro- technical Society, 2016, 31(S2): 84-91.
[18] 赵寿华, 毛永乐, 许翠翠, 等. 基于自适应观测器和线性二次型调节器的高性能伺服系统谐振抑制[J]. 电工技术学报, 2016, 31(6): 108-117.
Zhao Shouhua, Mao Yongle, Xu Cuicui, et al. Torsional vibration suppression based on adaptive observer and linear quadratic regulator in high performance servo drives[J]. Transactions of China Electrotechnical Society, 2016, 31(6): 108-117.
[19] 王树波, 李冬伍, 任雪梅. 基于未知动态观测器双惯量伺服系统低频主动谐振抑制[J]. 控制理论与应用, 2020, 37(12): 2535-2542.
Wang Shubo, Li Dongwu, Ren Xuemei. Low frequency active resonance suppression based on unknown dynamics estimator for dual inertia servo systems[J]. Control Theory & Applications, 2020, 37(12): 2535-2542.
[20] 杜仁慧, 陶春荣, 张伟, 等. 伺服系统机械谐振抑制的自适应模糊控制方法[J]. 电机与控制学报, 2017, 21(10): 116-122.
Du Renhui, Tao Chunrong, Zhang Wei, et al. Adaptive fuzzy control method for mechanical resonance suppression of servo systems[J]. Electric Machines and Control, 2017, 21(10): 116-122.
[21] Xia Jiakuan, Guo Zhiyan, Li Zexing. Optimal online resonance suppression in a drive system based on a multifrequency fast search algorithm[J]. IEEE Access, 2021, 9: 55373-55387.
[22] Singh J K, Prakash S, Al Jaafari K, et al. Active disturbance rejection control of photovoltaic three- phase grid following inverters under uncertainty and grid voltage variations[J]. IEEE Transactions on Power Delivery, 2023, 38(5): 3155-3168.
[23] 倪刚, 金辉宇, 兰维瑶. 基于Ziegler-Nichols规则的一阶线性自抗扰控制参数整定[C]//第三十九届中国控制会议论文集, 沈阳, 中国, 2020: 1097-1101.
[24] 杨明, 郝亮, 徐殿国. 双惯量弹性负载系统机械谐振机理分析及谐振特征快速辨识[J]. 电机与控制学报, 2016, 20(4): 112-120.
Yang Ming, Hao Liang, Xu Dianguo. Analysis of mechanical resonance mechanism and fast identi- fication of resonance characteristic for 2-mass system with elastic load[J]. Electric Machines and Control, 2016, 20(4): 112-120.
Abstract In a two-inertia servo system, mechanical resonance is generated due to an elastic part in the connection device between a motor and a load. Consequently, suppressing mechanical resonance has become a focus for achieving high-performance servo control. One effective strategy is notch filters, which can attenuate the magnitude of the resonance frequency. Nevertheless, the design of the notch filter requires accurate knowledge of the mechanical resonance frequency, which is a complex task. As a result, the use of the notch filter is limited due to the difficulties in obtaining an accurate mechanical resonance frequency.
The observer-based method for suppressing mechanical resonance does not require identifying the mechanical resonance frequency. Present studies adopt the observer method for mechanical resonance suppression, where the observer estimates and compensates in real time. According to the extended state observer (ESO), a new approach named the phase-locked loop type ESO (PLL-ESO) is proposed. The state equations of the PLL-ESO are designed based on the system’s kinetic equations, and the stability of the PLL-ESO is verified based on the pole location of state equations. A comparative analysis assesses the resonance suppression performance of the ESO and the PLL-ESO. The theoretical analysis indicates that the PLL-ESO method exhibits a larger phase margin of stabilization and faster dynamic performance than the ESO method.
The experiment aims to evaluate the effectiveness of PLL-ESO in suppressing mechanical resonance compared with notch filters and the ESO. The resonance frequency is identified by applying a sinusoidal sweep signal to the q-axis current reference. A fast Fourier transform (FFT) analysis of the q-axis current response and the real speed are performed on the sampled data to obtain the frequency characteristics of the two-inertia system. It confirms that an elastic connection causes mechanical resonance. A design procedure is established for implementing a resonance suppression strategy. Experiments are conducted under no load and rated load conditions. The results show that the notch filter method can effectively suppress mechanical resonance under no load but cannot wholly succeed in the rated load condition. The ESO method successfully suppresses mechanical resonance under no load and rated load conditions. However, its performance does not satisfy a fast dynamic response requirement. The PLL-ESO method demonstrates superior dynamic performance and achieves faster suppression. Under no load and rated load conditions, the PLL-ESO method reduces transient time by 10 ms and 40 ms to reach steady states compared with the ESO method. Additionally, experiments with different undamped natural frequencies of the PLL-ESO and the ESO reveal that the PLL-ESO method owns high bandwidth and large phase margin for the same pole configuration. Therefore, the PLL-ESO has vast frequency range choices of suitable undamped natural frequencies, especially in addressing inaccurate system parameters and shifted resonance frequencies. The impact of parameter b0 on the performance of the PLL-ESO is also analyzed. It is observed that decreasing b0 slows down the system’s dynamic response while maintaining effective resonance suppression. Conversely, increasing b0 has a weak effect on dynamic response but reduces the suppression of mechanical resonance. In conclusion, compared with the notch filter and ESO methods, the proposed PLL-ESO-based method effectively suppresses mechanical resonance.
Keywords:Two-inertia elastic servo system, mechanical resonance, phase locked loop-type extended state observer (PLL-ESO), resonant frequency
中图分类号:TM921.2
DOI: 10.19595/j.cnki.1000-6753.tces.231093
国家自然科学基金(52007169)和浙江省自然科学基金(LY23E070004)资助项目。
收稿日期 2023-07-11
改稿日期 2023-09-26
吴 春 男,1987年生,博士,副教授,研究方向为电机控制。
E-mail: wuchun@zjut.edu.cn(通信作者)
王 超 男,1998年生,硕士研究生,研究方向为电机控制。
E-mail: wangchao5166a@outlook.com
(编辑 崔文静)