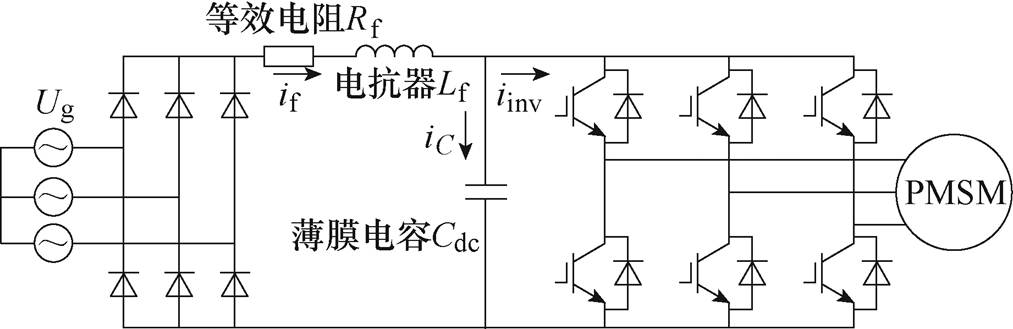
图1 三相小电容PMSM驱动系统主电路拓扑
Fig.1 Topology of three-phase small capacitor PMSM drive system
摘要 直流母线采用小电容永磁同步电机驱动系统具有降低成本和延长运行寿命的优势。但在系统运行时网侧电流中存在大量的谐波,这将会影响网侧电流质量。为了改善小电容永磁同步电机(PMSM)驱动系统的网侧电能质量,该文提出一种基于阻抗重塑的有源阻尼控制方法,以抑制网侧电流谐波。通过对驱动系统进行建模,分析影响网侧电流谐波的因素,建立母线电流与网侧电流的数学关系。采用有源阻尼控制方法,提取母线电压谐波信号,以最优电压补偿的方式构建反馈回路,重塑驱动系统的特定频率处的等效阻抗,以实现网侧电流谐波的改善。同时,为了抑制电压补偿模块对电流内环扰动的影响,设计电流环级联双频陷波器,并通过系统极点图进行了稳定性分析。仿真结果和实验分析验证了所提控制方法的有效性。
关键词:小电容电机驱动 网侧电流谐波 阻抗重塑 双频陷波器 电流环
永磁同步电机(Permanent Magnet Synchronous Motor, PMSM)因功率密度和效率等方面的优势,已广泛应用于家用电器、轨道牵引和其他工业场 合[1-4]。为了保持母线电压恒定,PMSM驱动系统直流侧通常需要配备一个大型电解电容器。然而,在这种拓扑中,逆变器故障很大一部分归因于电解电容器[5]。此外,大容量电解电容会降低变换器的功率密度。为了避免大型直流母线电容的使用带来的问题,近年来,直流侧小容量薄膜电容电机驱动已成为研究的热点[6-9]。
虽然小容量薄膜电容电机驱动器具有可靠性高、成本低和电能质量优等特点,但由于小电容能量缓冲能力降低,可能导致驱动系统不稳定。同时,直流环节小电容电机驱动系统中,功率因数校正电路也被取消,可能导致网侧电流出现较大的谐波。而网侧或直流侧电感和直流侧小电容形成的LC电路,会进一步加剧谐振频率处的谐波,如果谐振幅度太大,会导致过电压或过电流故障,并显著缩短电容器和开关管的寿命[10-12]。因此,在采用小容量薄膜电容代替大电解电容的电机驱动系统中,必须先解决这些问题。现有的方案主要包括基于硬件电路改进的控制方案和基于算法的控制策略[13-16]。
文献[17]采用在网侧级联附加电阻的方法直接减小谐振,并在直流电容两端并联LC谐振电路,调谐谐振频率以匹配直流母线电压的波动频率,进而改善驱动系统稳定性。而文献[18-20]则应用功率因数校正拓扑,有效地改善了电网输入性能。然而,此类方法由于引入了额外的电阻、电感和电容,增加了系统的成本和体积,同时降低了功率密度。因此,更有效的方法是通过阻尼控制方法提高驱动系统的稳定性,抑制网侧电流谐波。
文献[21]研究了一种基于直流母线电压反馈的主动阻尼方法。该方法首先通过高通滤波器直接提取阻尼电流,然后将其注入到dq轴电压参考中,有效地抑制了网侧电流谐波。文献[22]基于有源阻尼控制思想,通过母线电压波动量进行阻尼控制,然而,该方法不能调控特定频率谐波。文献[23]将电机负载等效为负阻抗特性,采用有源阻尼控制来降低网侧电流总谐波畸变率(Total Harmonic Distortion, THD),从而抑制网侧电流谐波。该方法不依赖系统参数,但需要对源电压进行采样,增加了硬件成本。考虑到电机侧特性,文献[24]基于系统模型提出了一种固有谐波阻抗整形的谐振抑制策略。该策略通过设计谐振频率附近固有谐波的阻抗,可以减少电机侧功率干扰,降低网侧电流THD,进而改善网侧电流谐波。以上是基于增加系统阻尼的概念,提出了多种方法来抑制小电容电机驱动系统中的LC谐振,这是电力电子中谐振抑制有效且通用的解决方案。然而,考虑到网侧三相输入小电容电机驱动系统的特性,这些方法需要进一步改进,以适应特定的驱动器特性。
本文从驱动系统模型出发,提出了一种基于阻抗重塑有源阻尼控制的固有谐波抑制方法。相较于传统方法,本文研究的策略是针对特定频率谐波进行控制的,不需要额外的传感器,更易于工业应用。首先,对小电容PMSM驱动系统进建模,阐明影响网侧电流总谐波的因素,采用一种基于母线电压最优补偿的有源阻尼控制方法,以实现网侧电流谐波的改善。同时,为了抑制电压补偿对电流内环扰动的影响,设计了电流环级联双频陷波器,并通过系统极点图进行了稳定性分析。最后,仿真和实验结果验证了所提控制方法的有效性。
三相交流供电小电容PMSM驱动系统主电路拓扑如图1所示,该系统由网侧经三相二极管整流电路供电,并通过LC滤波器滤波。Ug为网侧电压;Rf、Lf分别为直流侧等效电阻和滤波电感;Cdc为直流侧电容。

图1 三相小电容PMSM驱动系统主电路拓扑
Fig.1 Topology of three-phase small capacitor PMSM drive system
由图1可知,直流侧母线电流if可以表示为
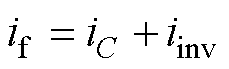 (1)
(1)
式中,iC和iinv分别为电容电流和流入逆变器的电流。
忽略逆变器的功率损耗,流入逆变器的电流可以表示为
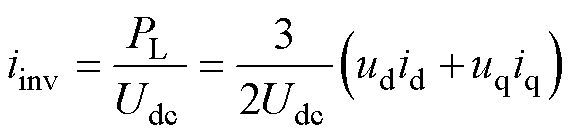 (2)
(2)
式中,PL为负载功率;Udc为直流母线电压;ud、uq和id、iq分别为d、q轴电压和电流。
母线电容电流为
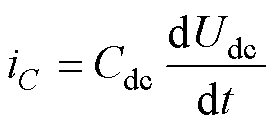 (3)
(3)
将式(2)、式(3)代入式(1)中,可表示为
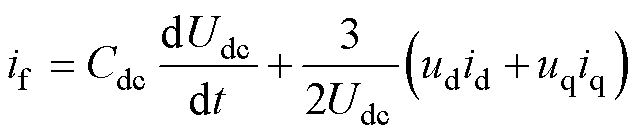 (4)
(4)
由式(4)可以看出,直流母线电流if与dq轴电压有关。
为了便于分析影响网侧电流的因素,根据图1,图2给出了小电容驱动系统s域电路模型。图中,Ug(s)、Ig(s)、IC(s)和Iinv(s)分别为复频域网侧电压、网侧电流、电容电流和流入到逆变器侧电流。Udc(s)和Es(s)分别为复频域直流侧电压和负载侧等效电压。
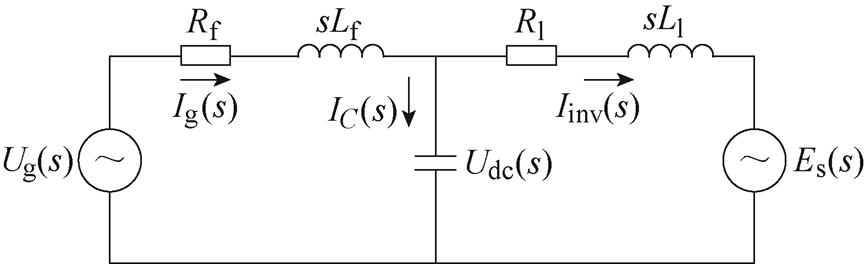
图2 小电容驱动系统s域电路模型
Fig.2 s-domain model of small capacitor drive system
由图2所示的s域模型,根据KVL,可得
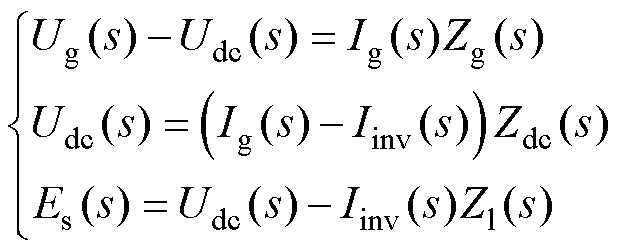 (5)
(5)
式中,Zg(s)=Lfs+Rf;Zdc(s)=1/(Cfs);Zl(s)=Lls+Rl。
由式(5),可求解出网侧电流Ig(s)为
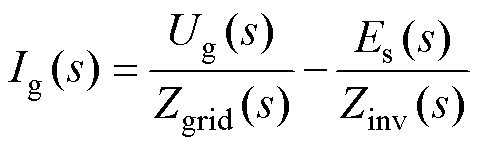 (6)
(6)
式中,Zgrid(s)为网侧阻抗;Zinv(s)为逆变器侧阻抗,分别表示为
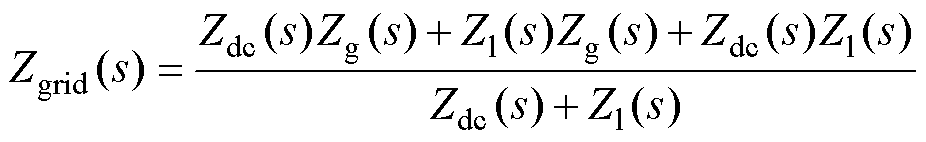 (7)
(7)
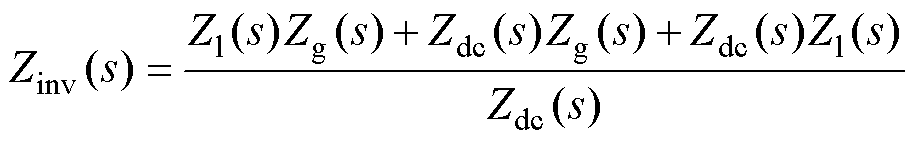 (8)
(8)
由式(6)可知,驱动系统的网侧电流由两部分决定:一部分由网侧电压和网侧阻抗决定;另一部分由等效电压和逆变器侧阻抗决定。假如相应谐波频率处的网侧阻抗不够大,则网侧电流THD很可能超出谐波标准,产生较大的谐波污染。通过适当增大网侧谐波频率处的网侧阻抗可以减小谐波电流。同时,为了保证驱动系统正常输送功率,基波频率处的阻抗应尽可能保持不变。
考虑到母线电流的交流分量和直流分量,直流母线电流的一般表达式为
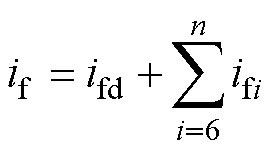 (9)
(9)
式中,ifd为母线电流的直流分量;ifi为母线电流的i次谐波分量。
与母线电流包含的谐波分量类似,交流侧任意相电流(以a相为例)ia包括平滑母线电流ifd产生的电流iad,和由注入整流器电路的总谐波电流在交流电路中感应的电流Din。即
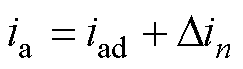 (10)
(10)
通过式(10)可知,减小母线电流n次谐波分量可以有效地改善网侧电流谐波。为进一步量化网侧电流THD的影响因素,需建立母线电流谐波含量与网侧电流THD的关系。母线电流谐波主要包含六倍频和十二倍频分量,则网侧电流a相电流[14]可表示为
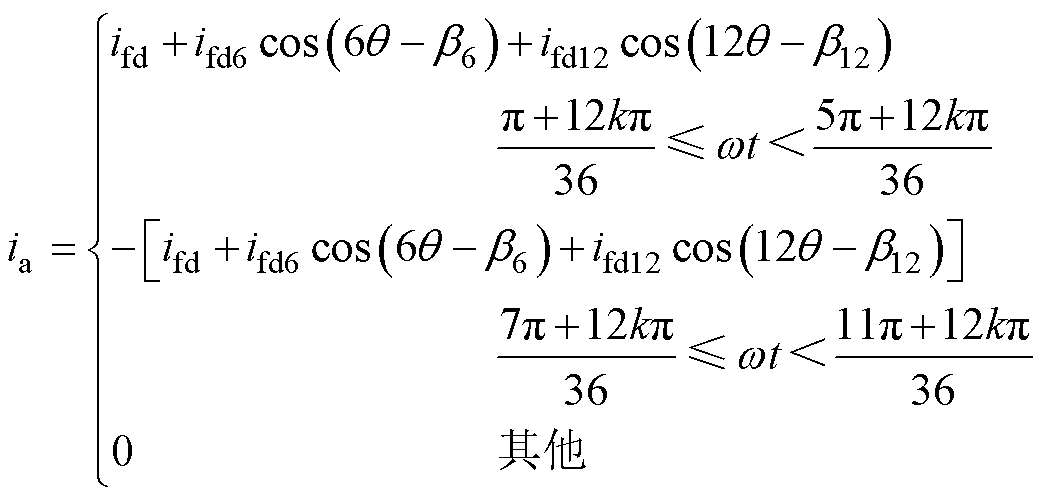 (11)
(11)
式中,k为正整数;ifd6、ifd12分别为母线电流六倍频和十二倍频分量的幅值;q、q6、q12分别为基波、6次谐波、12次谐波电流初始相位。
母线电流中含有的六倍频和十二倍频谐波分量将会对网侧性能产生较大的影响。因此,若能有效地降低直流母线电流中的六倍频和十二倍频分量,则可以降低网侧电流THD,改善网侧电流质量。图3给出了理想母线电流iidc、实际母线电流if和网侧a相电流ia的仿真波形。
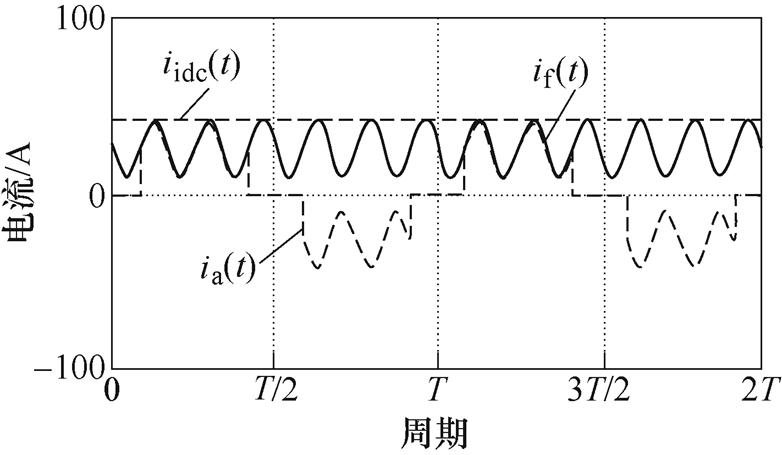
图3 母线电流和网侧电流的仿真波形
Fig.3 Simulation waveforms of DC current and grid side current
由图3可以看到,直流侧母线电流呈现6次、12次谐波成分。理想的母线电流不包含任何波动成分,如果母线电流的波动成分被消除,那么将被塑造成理想的母线电流参考。由于消除母线电流中的所有波动成分非常困难,因此,本文选择消除主要的谐波成分。
基于以上分析,本文通过重塑驱动系统阻抗来改善网侧电流,采用一种基于虚拟阻抗的有源阻尼控制方法,由于该阻抗不是一个物理电阻,具体实现方式是注入额外的电流以达到在母线电容两端产生并联虚拟阻抗的效果。该方法可以提高驱动系统对特定频率交流分量阻抗,进而降低网侧电流THD。在电容两端并联虚拟阻抗的等效电路如图4a所示,Zvi为产生阻尼效果的等效阻抗,图4b为产生虚拟阻抗的等效控制框图。
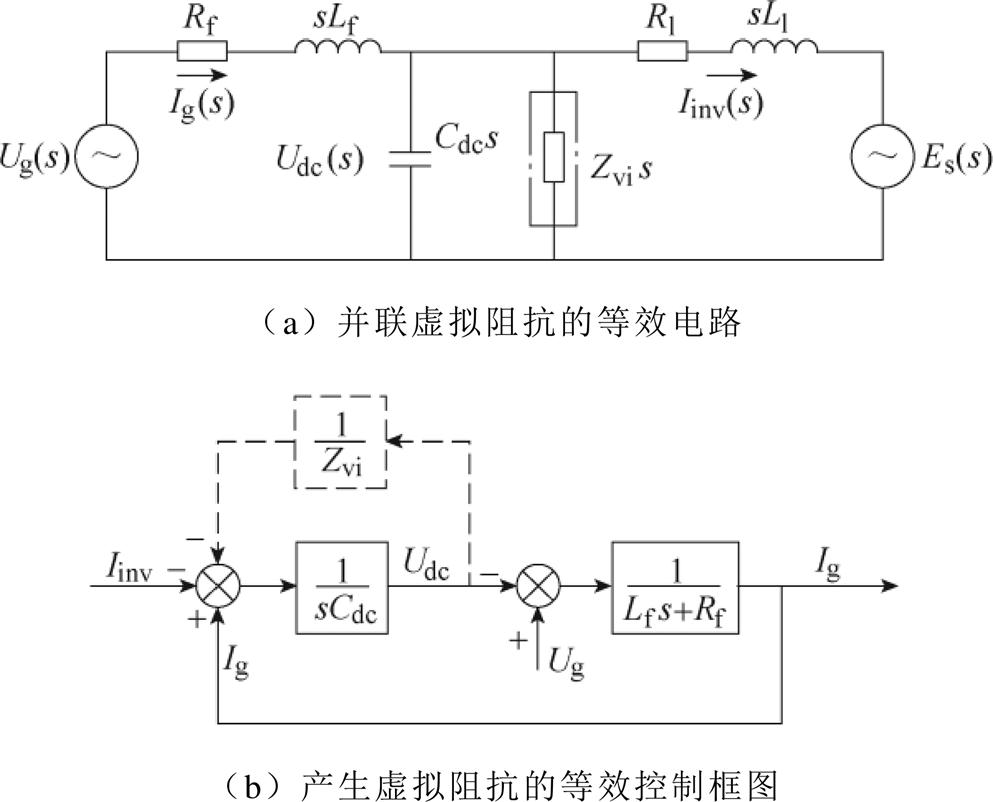
图4 所提阻抗重塑方案
Fig.4 Proposed impedance reshaping strategy
根据图4a阻抗重塑的驱动系统等效电路,带有虚拟阻抗的驱动系统特征多项式表示为
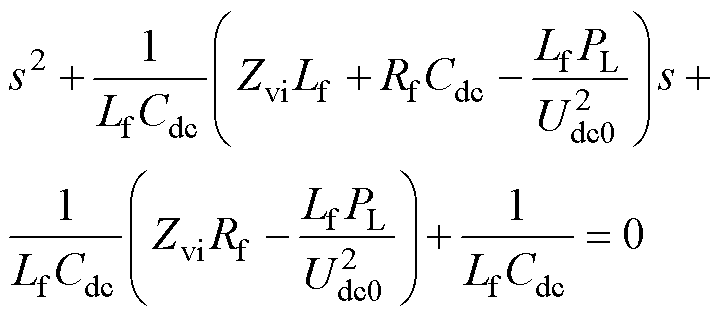 (12)
(12)
根据高阶多项式的劳斯-赫尔维茨判据,若使驱动系统稳定,需满足
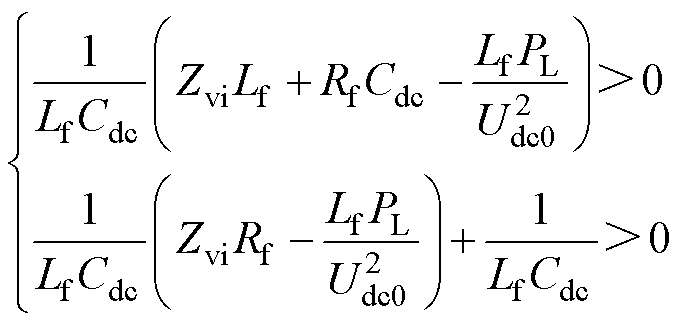 (13)
(13)
为了评估驱动系统的稳定性,根据本文驱动系统实验样机的参数,式(13)中应用的劳斯-赫尔维茨判据准则确定了系统稳定时Zvi的最小值,图5给出了带有虚拟阻抗的驱动系统极点。从图5可以看出,当Zvi>0.08时,系统变得稳定。
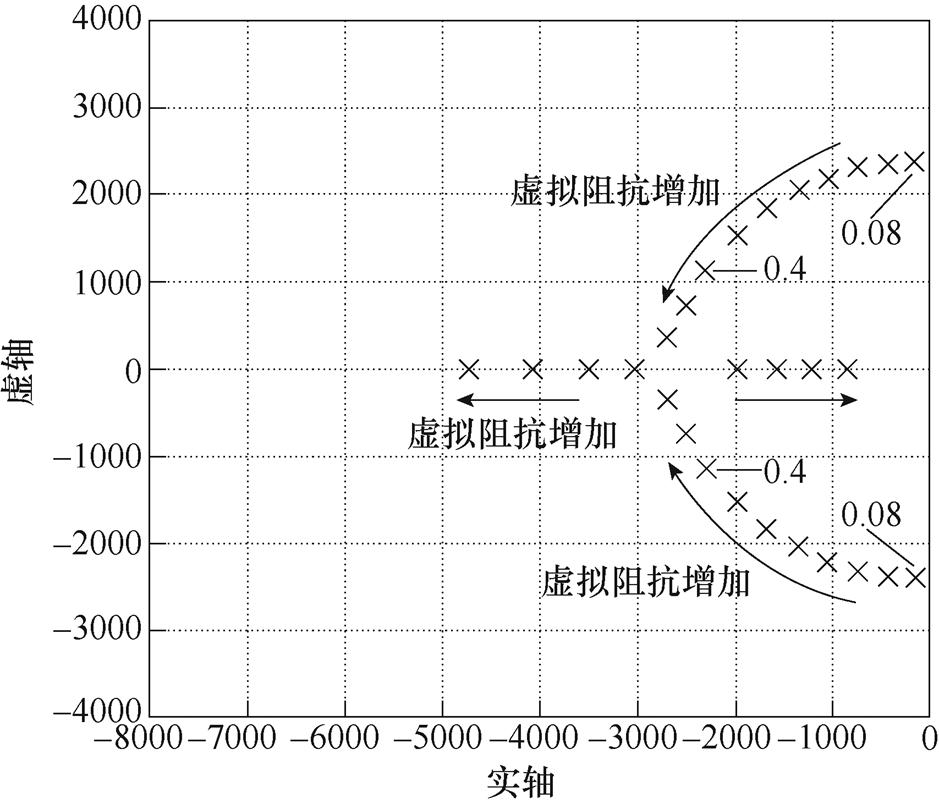
图5 带有虚拟阻抗的驱动系统极点
Fig.5 Pole diagram of the drive system with virtual impedance
在图4a中,由于与直流侧电容并联的虚拟阻抗难以精确产生和控制。因此,实现虚拟阻抗的解决方案可以转换为产生等效阻尼功率Pdamp,该等效阻尼功率由逆变器功率产生,可表示为
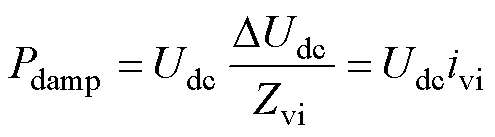 (14)
(14)
式中,DUdc为直流母线电压交流量;ivi为流经虚拟阻抗Zvi的虚拟电流。
所提方法的控制框图如图6所示。虚拟阻抗电流ivi可以由直流母线电压经过带通滤波器和比例环节获得。获得的阻抗电流ivi与Udc相乘生成阻尼功率Pdamp,由于与电流补偿相比,基于电压补偿的方案可以避免电流控制器带宽的限制,所以本文选择电压补偿方式,最终生成补偿到dq轴的电压Dud和Duq。所提出的方法不影响系统双闭环控制结构。
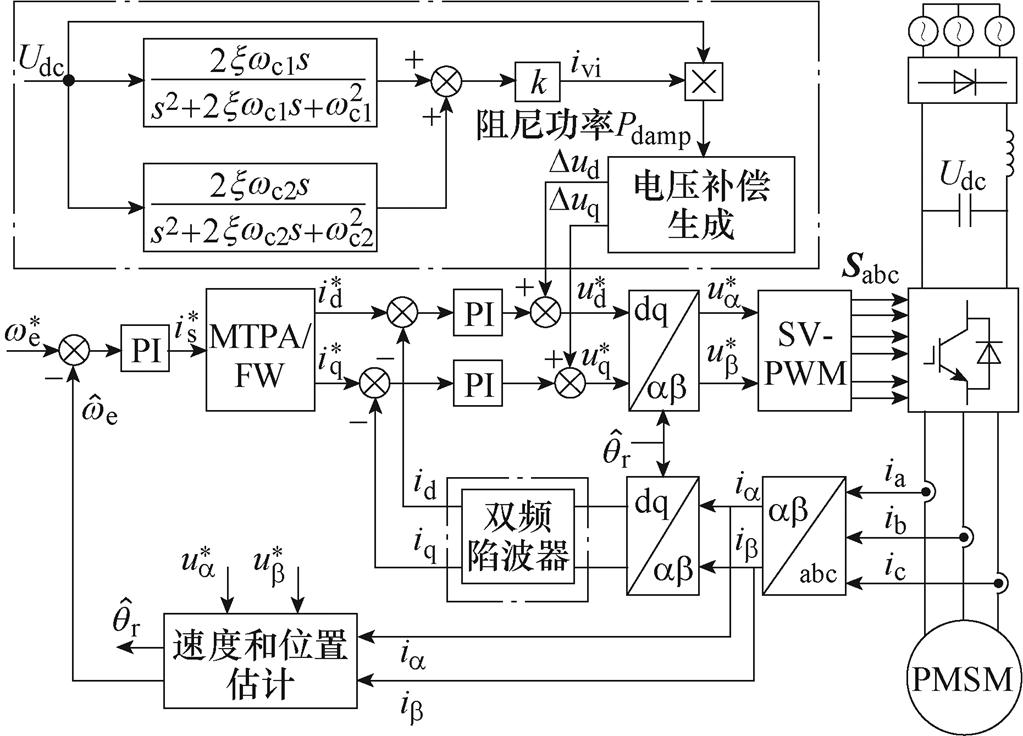
图6 所提方法的控制框图
Fig.6 Block diagram of the proposed control method
忽略逆变器功率损耗,由功率守恒,有
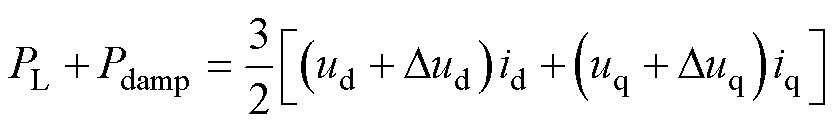 (15)
(15)
其中
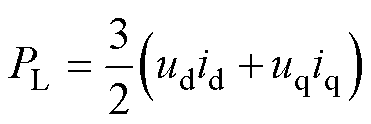 (16)
(16)
式中,Dud和Duq分别为补偿到d、q轴的电压。
对于电机内环电流控制来说,补偿到dq轴的电压又可视为扰动分量。在电压补偿生成模块中,应考虑电压补偿对驱动系统的影响最小,并且电压矢量的大小应尽可能小。最优电压补偿如图7所示,补偿电压的可能方向是无限的,所有这些都可以产生相同的阻尼功率Pdamp。从图7中可以看出,当补偿电压矢量方向与电流矢量方向一致时,补偿电压幅值最小,这可以减少电压指令对驱动系统的影响。因此,基于阻尼功率Pdamp产生补偿到dq轴的电压命令。
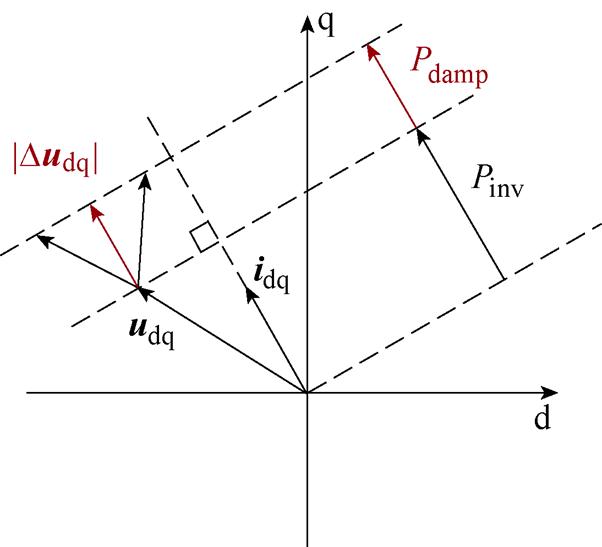
图7 最优电压补偿
Fig.7 Diagram of optimal compensation voltage
联立式(14)、式(15),可得到最小补偿电压的模为
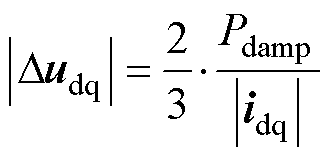 (17)
(17)
按dq轴方向分解,则dq轴补偿电压分量为
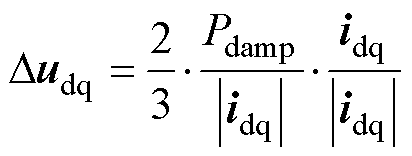 (18)
(18)
在上述分析中,给出了最优补偿电压的设计,但仍需进一步对扰动分量进行抑制。仅对某一频率的谐波信号实现陷波的称为单频陷波器(Single Frequency Notch Filter, SFNF),其传递函数可以表示为
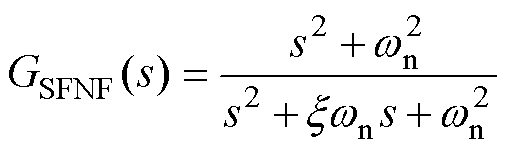 (19)
(19)
式中,wn为陷波频率;x 为陷波因子。
在电压补偿过程中提取了直流侧电压六倍频和十二倍频谐波,因此需要对两种不同频率的谐波信号同时抑制,本文设计级联SFNF,级联后的陷波器可称为双频陷波器(Dual Frequency Notch Filter, DFNF),其传递函数为
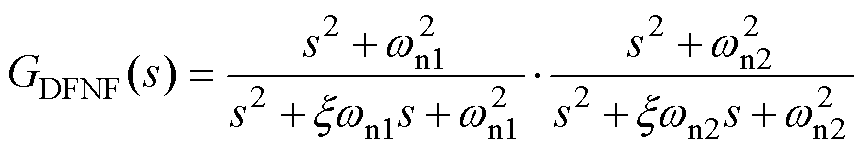 (20)
(20)
式中,wn1、wn2为陷波频率,wn1=1 885 rad/s,wn2= 3 770 rad/s。
图8给出了双频陷波器的伯德图。从图8中可以看出,改变x 的大小可以调节陷波宽度和陷波深度。当双频陷波频率为1 885 rad/s(300 Hz)和3 770 rad/s(600 Hz)时,即六倍频次和十二倍频次波动频率时,选取不同x 值,幅度都有明显的改变,而其他频率处的幅度几乎不受影响。综合考虑幅度和相位的变化,x 选为0.3。
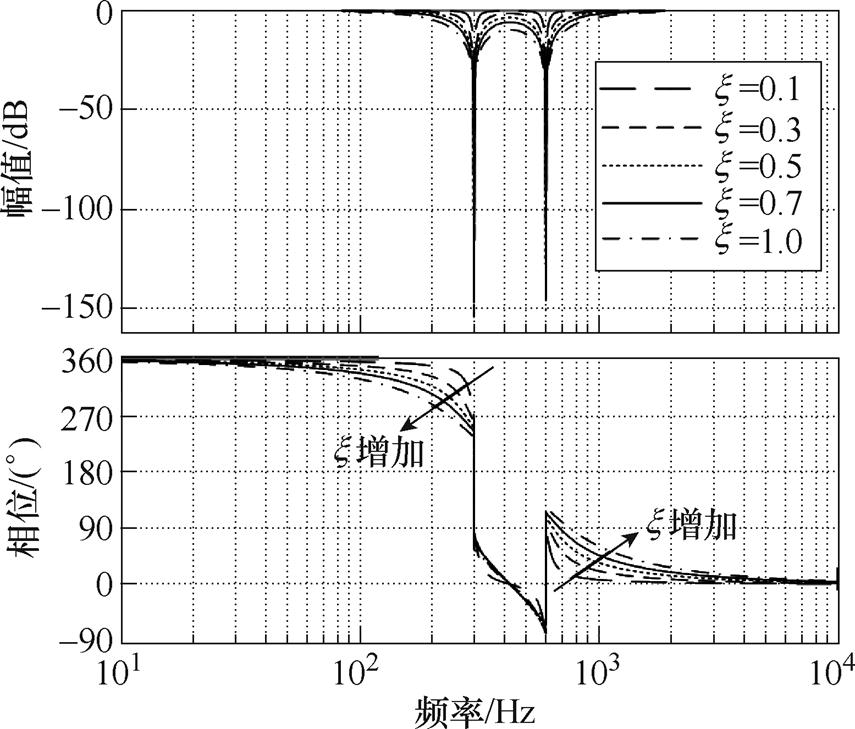
图8 双频陷波器的频域特性
Fig.8 Characteristic curves of dual frequency notch filter
为分析加入电压补偿后电流内环的稳定性,图9给出了电流环在电压补偿下的动态结构。
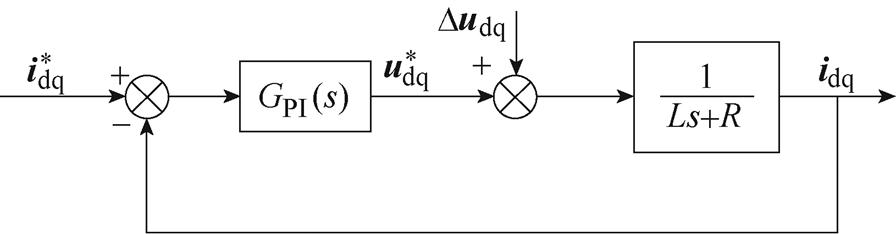
图9 基于电压补偿的电流内环控制结构
Fig.9 Diagram of current inner loop control with voltage compensation
因d轴控制结构与q轴类似,这里以q轴为例进行分析。电流内环q轴传递函数可以表示为
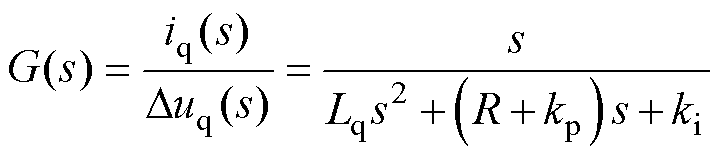 (21)
(21)
式中,Lq、R、kp和ki分别为q轴电感、定子电阻和q轴电流比例积分控制器的增益。将这些参数代入式(21),经过计算可以得到,G(s)的幅值相对小,这意味着电压命令对电机运行几乎没有影响。因此,系统在Dudq引起的扰动下降是稳定的。
为进一步分析加入双频陷波器后系统的稳定性,图10给出了基于双频陷波器的电流内环控制 结构。
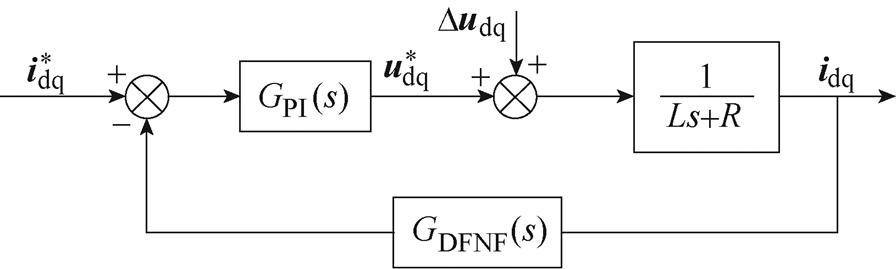
图10 基于双频陷波器的电流内环控制结构
Fig.10 Diagram of current inner loop control with dual frequency notch filter
根据图10,电流内环q轴闭环传递函数为
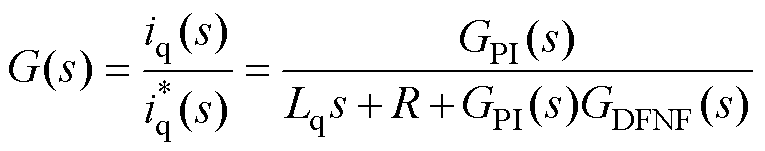 (22)
(22)
图11给出了加入双频陷波器前后电流内环极点。从图11中可以看出,加入双频陷波器后的极点在不同电流内环带宽均在系统左半平面,表明系统一直是稳定的。
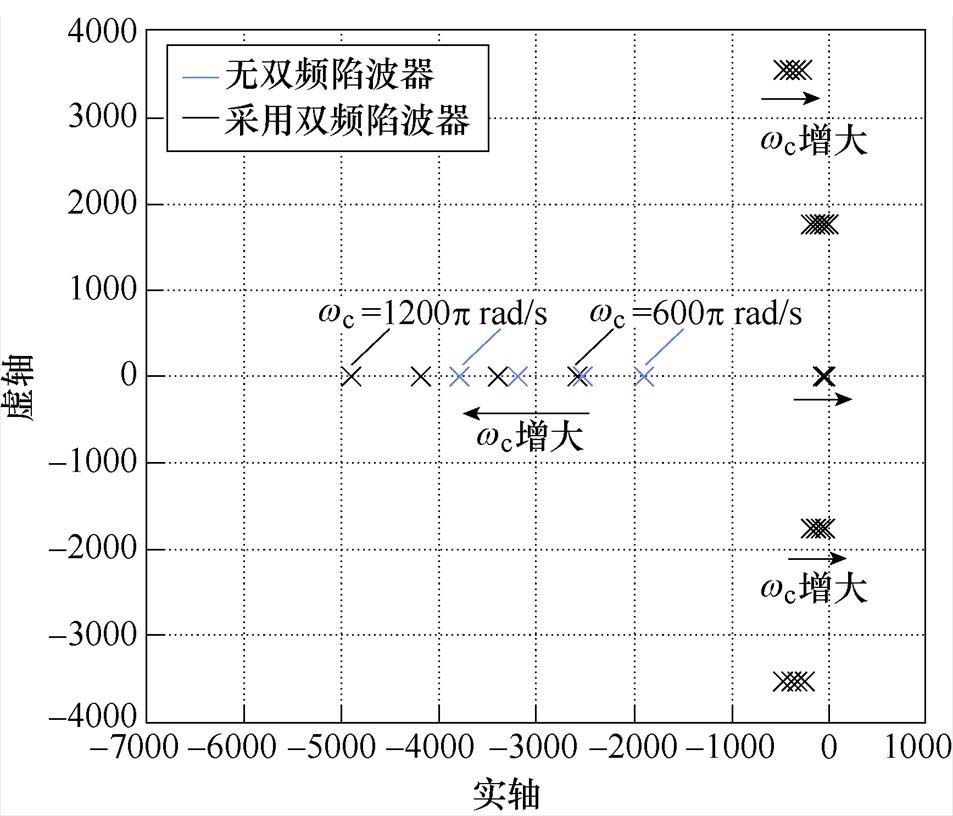
图11 电流内环极点
Fig.11 Pole diagram of current inner loop
为了验证所提控制方法的有效性,在Matlab/ Simulink模块中搭建了系统模型进行仿真分析。驱动系统主要参数见表1。
表1 驱动系统主要参数
Tab.1 Main parameters of the drive system
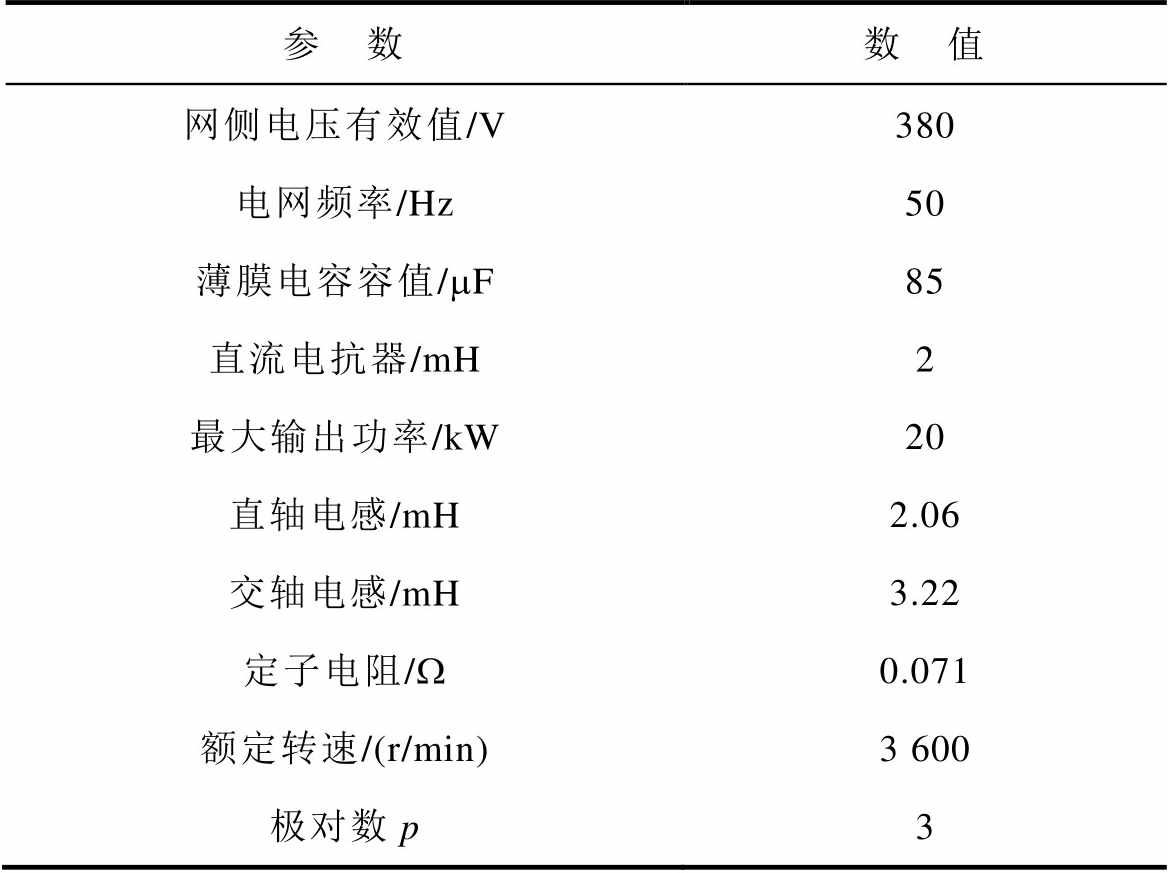
参 数数 值 网侧电压有效值/V380 电网频率/Hz50 薄膜电容容值/mF85 直流电抗器/mH2 最大输出功率/kW20 直轴电感/mH2.06 交轴电感/mH3.22 定子电阻/W0.071 额定转速/(r/min)3 600 极对数p3
图12给出了电机运行频率270 Hz、负载转矩20 N·m时采用所提控制方法前后的仿真结果。图中所有波形从上到下依次为网侧电流、直流母线电压纹波和电机电流波形。图12a为采用所提控制方法前后的整体波形,图12b、图12c和图12d依次为未采用所提控制方法、采用所提电压补偿和扰动滤除的局部放大波形,图12e为网侧电流频谱。

图12 电机运行频率270 Hz、负载转矩20 N·m时采用所提方法控制前后对比结果
Fig.12 Comparison results of motor operating frequency of 270 Hz and load torque of 20 N·m without and with the proposed control method
从图12b、图12c和图12d中可以看出,采用所提控制方法后,网侧输入电流最大值逐渐减小,直流母线电压纹波由最初的156 V减小到120 V,最终降低到65 V,与未采用所提控制方法相比,降低了58.3%。在图12e中,通过对未采用本文所提方法和加入本文所提补偿电压、扰动滤除后的网侧电流进行谐波分析得出,网侧电流THD从52.2%减小到36.6%,最后降低到32.7%。与未采用所提控制方法相比,网侧电流THD最终降低了37.38%,网侧电流谐波得到了明显的改善。
为了验证所提控制策略的动态性能,图13a、图13b分别给出了加减载和加减速的动态仿真波形。图13a中,在某一时刻负载转矩由20 N·m增加至25 N·m,经历2.5 s后负载转矩再突变至20 N·m。由图13a可见,动态过程中采用所提方法的直流母线电压会有微小跌落,网侧电流和电机电流均平滑增加,在经历短暂的瞬态过程后均趋于稳定。图13b中,负载转矩为20 N·m,在某一时刻给定转速由5 400 r/min动态增加到6 600 r/min,在经历1.5 s后减小到5 400 r/min。从图13b中可知,转速上升、下降过程平滑,网侧电流和直流母线电压变化平稳,电机电流有略微的振荡。整体来看,当转速或负载变化时,所提控制策略的动态性能良好。
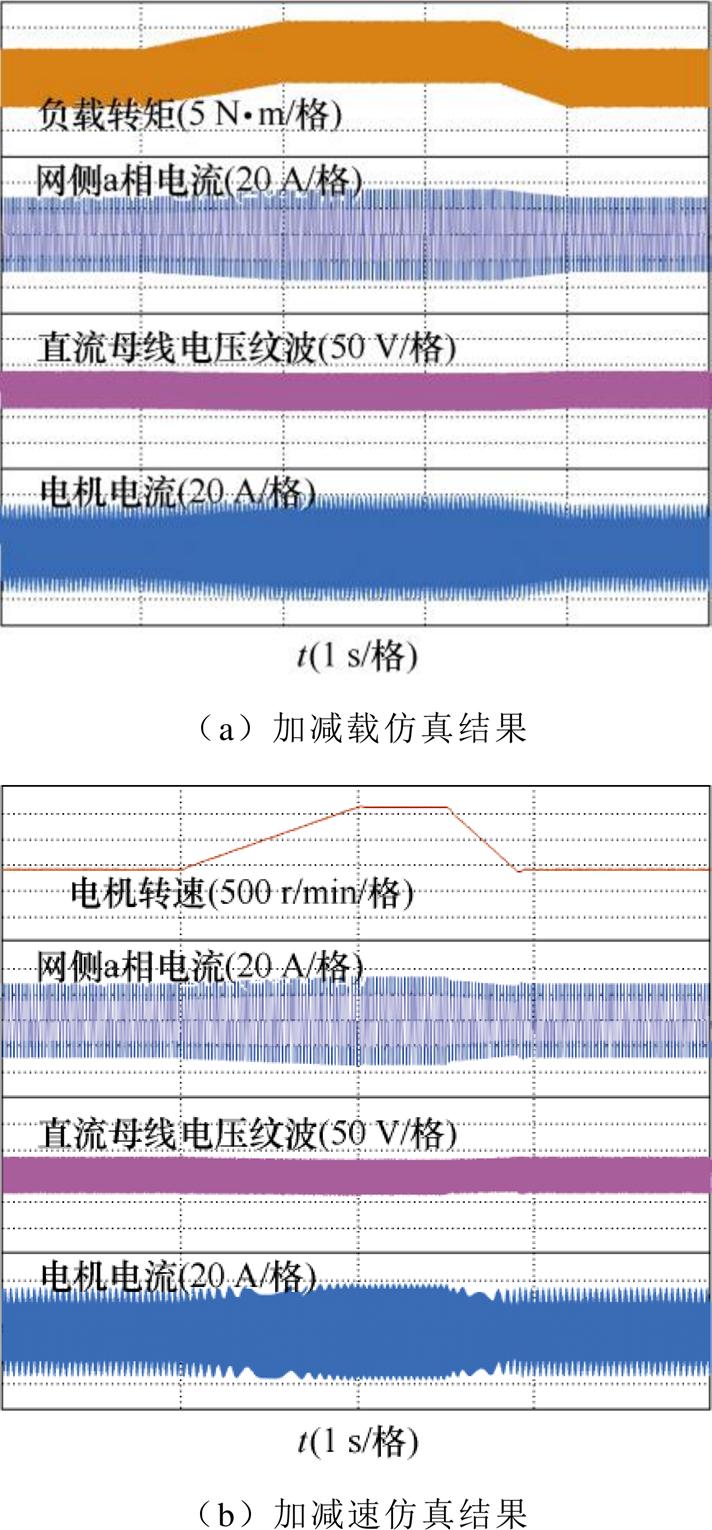
图13 动态实验工况下的仿真结果
Fig.13 Simulation results under dynamic experimental conditions
为了进一步比较和验证所提控制方法与传统有源阻尼控制方案的控制性能,搭建了空调压缩机驱动系统整机实验平台,如图14所示。系统的整个控制算法由数字信号处理器TMS320F28062芯片实现,开关频率为6.5 kHz,系统参数与仿真参数一致。

图14 直流小电容空调压缩机驱动系统实验平台
Fig.14 Experimental platform of small DC-link capacitor air-conditioning compressor drive system
图15给出了当电机运行在270 Hz时采用传统有源阻尼控制方法前后的实验结果,与本文所提控制方法作对比分析。图15a、图15b和图15c分别为采用传统有源阻尼控制方法前后整体实验结果、未采用传统有源阻尼控制方法和采用传统有源阻尼控制方法的局部放大实验结果。图中所有波形从上到下依次为网侧电流、直流母线电压纹波和电机电流波形。
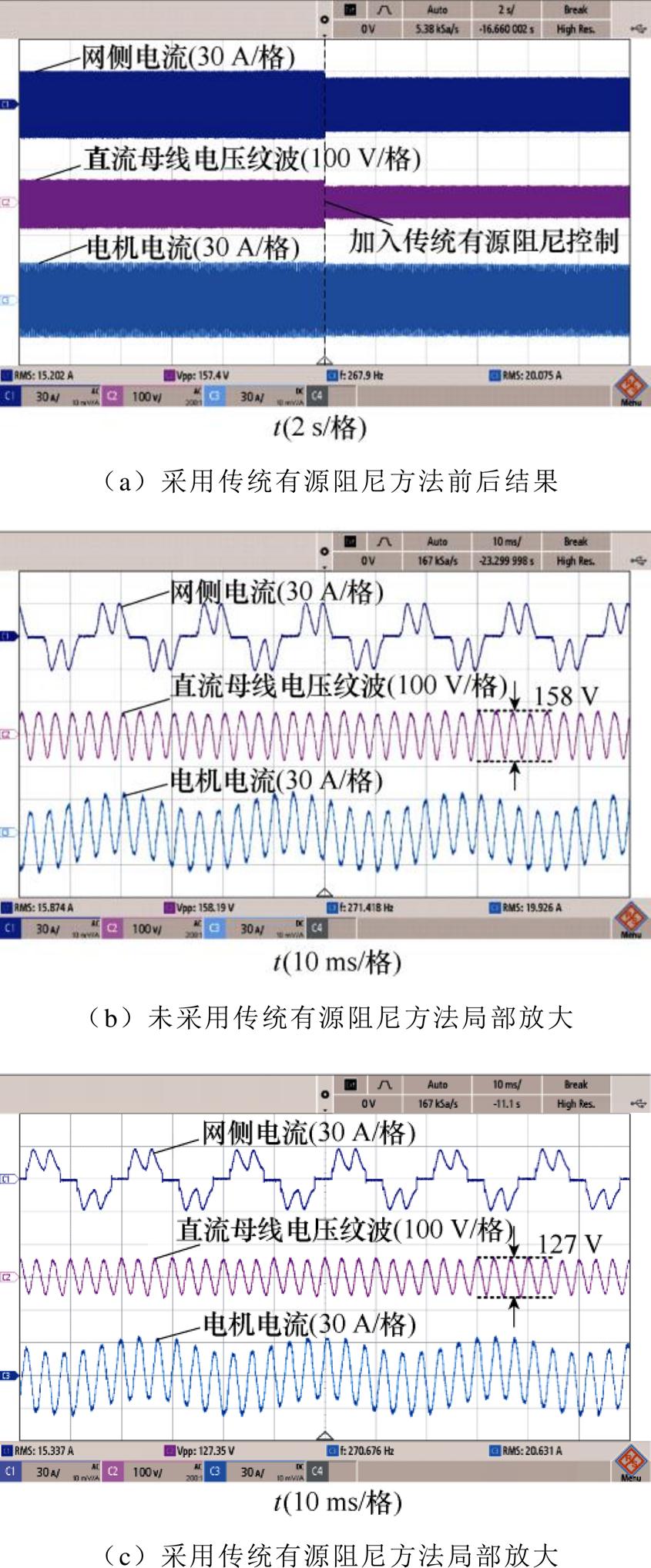
图15 电机运行在270 Hz采用传统有源阻尼控制前后实验结果
Fig.15 Experimental results without and with traditional active damping control for motor operation at 270 Hz
从图15中可以看出,采用传统有源阻尼控制方法后的网侧电流波形有一定的改善,同时,直流母线电压纹波由158 V降低到127 V,降低了约20%。
图16给出了电机运行在270 Hz时采用本文所提控制方法前后的实验对比结果。图16a、图16b和图16c分别为采用本文所提方法前后的整体实验结果、采用本文所提电压补偿和扰动滤除的局部放大实验结果。
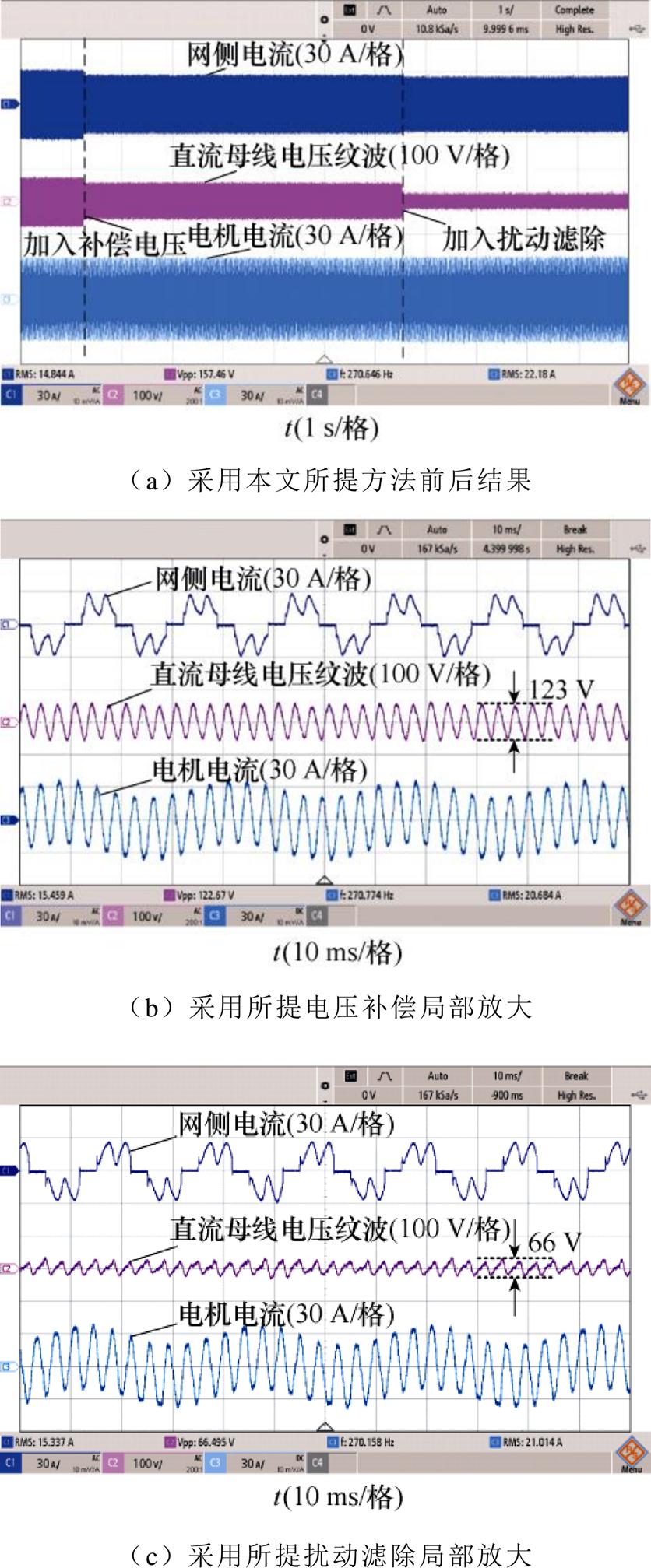
图16 电机运行在270 Hz采用本文所提控制方法前后的实验结果
Fig.16 Experimental results without and with the proposed control method when the motor operates at 270 Hz
从图16b、图16c中可以看出,采用本文所提电压补偿后的网侧电流波形有一定的改善,经过扰动滤除后网侧电流波形得到了进一步的改善。同时,直流母线电压纹波由158 V降低到123 V,最终降低到66 V,与未采用本文所提方法之前直流母线电压纹波相比,降低了约58%,与图15c中采用传统有源阻尼控制方法相比,直流母线电压纹波降低了约48%。验证了所提控制策略对六倍、十二倍频谐波有明显的抑制效果。
为了更加直观地对比所提控制方法与传统有源阻尼控制方法在网侧电流谐波抑制方面的效果,图17给出了未采用任何方法、采用传统有源阻尼控制方法、采用本文所提电压补偿以及扰动滤除控制方法的网侧a相电流频谱。
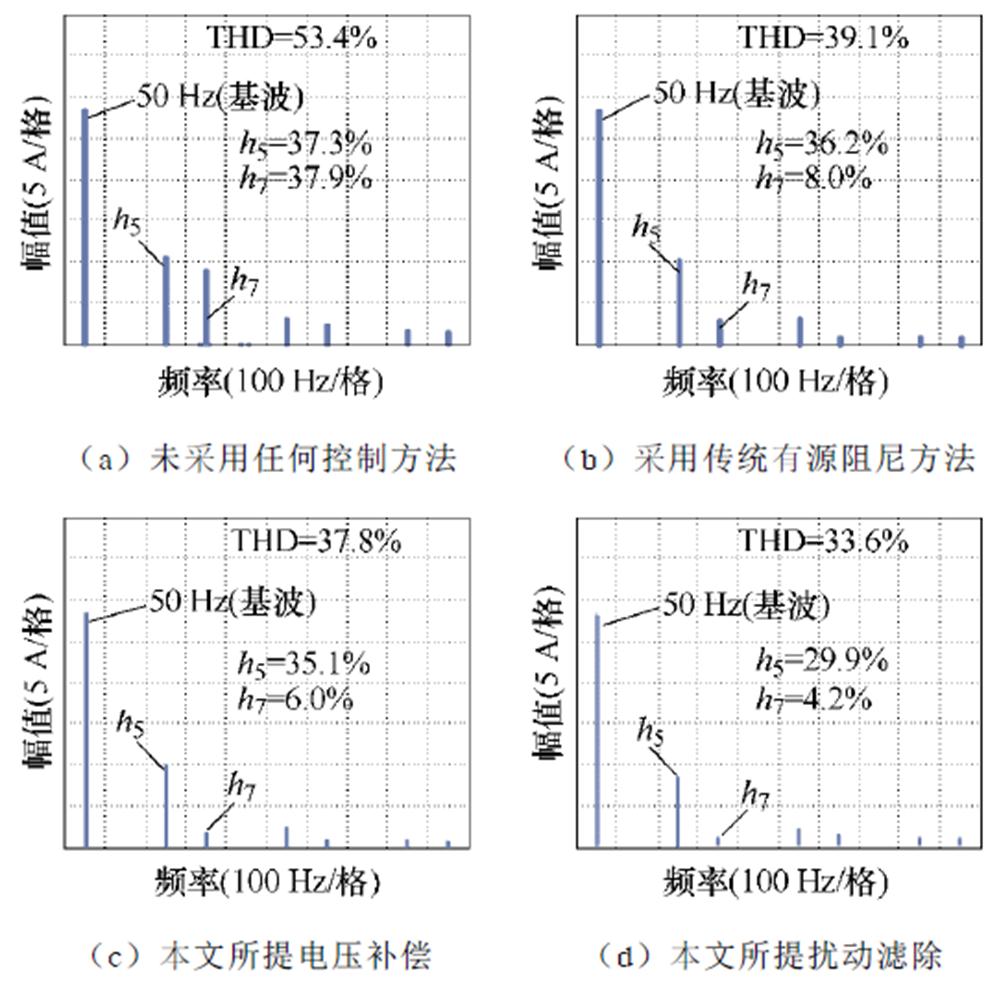
图17 网侧a相电流频谱
Fig.17 FFT analysis of a-phase grid side current
从图17中可有看出,未采用任何方法之前网侧a相电流THD为53.4%,采用传统有源阻尼控制方法的a相电流THD为39.1%,降低了26.8%,5次谐波变化不明显,但7次谐波降低了78.8%。采用本文所提电压补偿的a相电流THD为37.8%,5次谐波和7次谐波分别降低了5.8%和84.3%;当进一步采用本文所提扰动滤除后,a相电流THD降低到33.6%,降低了37.1%,5次谐波和7次谐波分别降低了19.8%和88.8%。验证了本文所提控制方法性能更优。
表2给出了电机运行在不同工况下,采用传统有源阻尼控制策略和本文所提控制策略网侧电流THD实验统计结果。从表2中可以看出,电机运行在不同工况时,采用本文所提控制方法的网侧电流THD均有一定的降低,且与传统有源阻尼控制方法相比,网侧电流改善效果更加明显,验证了所提控制策略的有效性。
表2 不同运行工况下传统有源阻尼控制和本文所提方法的实验统计结果对比
Tab.2 Comparison of experimental statistical results between traditional active damping control and the proposed method under different load operating conditions
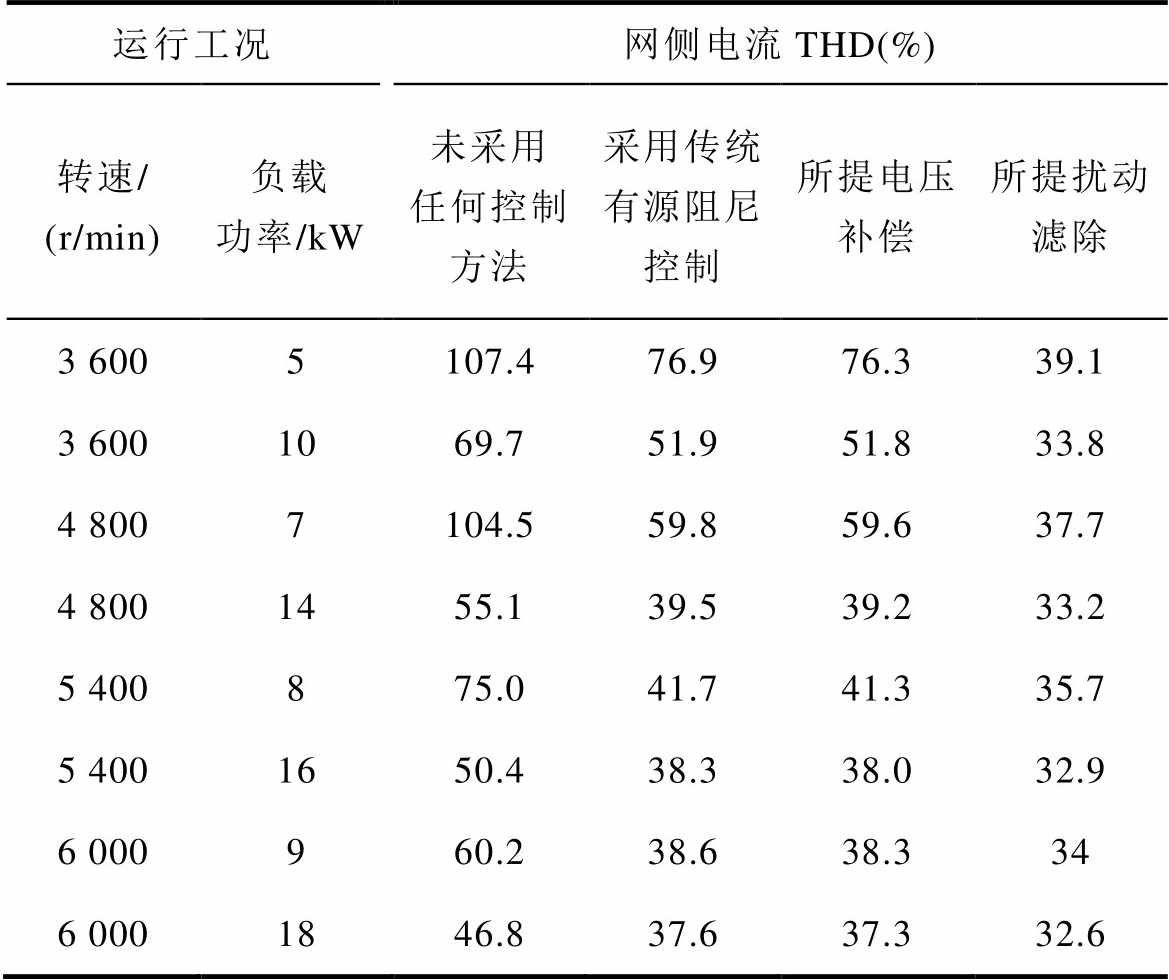
运行工况网侧电流THD(%) 转速/(r/min)负载功率/kW未采用任何控制方法采用传统有源阻尼控制所提电压补偿所提扰动滤除 3 6005107.476.976.339.1 3 6001069.751.951.833.8 4 8007104.559.859.637.7 4 8001455.139.539.233.2 5 400875.041.741.335.7 5 4001650.438.338.032.9 6 000960.238.638.334 6 0001846.837.637.332.6
为了更好地验证所提方法的使用价值,分别对传统有源阻尼控制策略和本文所提控制策略在电机不同运行频率下进行了实验测试。根据实验数据计算得到各种频率工况下采用不同控制策略的母线电压利用率见表3。
从表3中可以看出,电机运行在不同频率时,采用传统有源阻尼控制策略的母线电压利用率和本文所提有源电压补偿时几乎一致,当电机运行在高频时采用扰动滤除后的母线电压利用率略微降低,对逆变器的输出带载能力略有影响。
表3 不同运行频率下传统有源阻尼控制策略和本文所提控制策略的母线电压利用率
Tab.3 DC-link voltage utilization of traditional active damping control strategy and the control strategy proposed in this paper under different operating frequencies
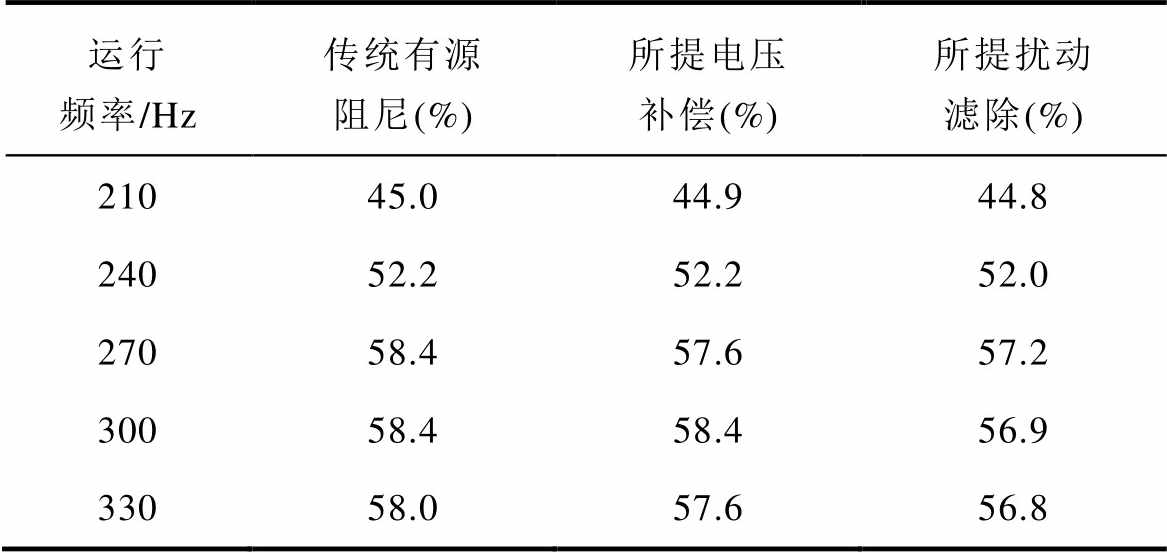
运行频率/Hz传统有源阻尼(%)所提电压补偿(%)所提扰动滤除(%) 21045.044.944.8 24052.252.252.0 27058.457.657.2 30058.458.456.9 33058.057.656.8
加减速过程的实验结果如图18所示,以验证瞬态过程中所提控制策略的有效性。在图18中,给定转速在某一时刻由5 400 r/min突增到6 600 r/min,稳定一段时间后再突减至5 400 r/min。从图18中可以看出,网侧电流、直流母线电压纹波、电机电流动态变化过程平稳,验证了所提控制策略具有良好的动态性能。

图18 给定转速动态变化的实验结果
Fig.18 Experimental results under dynamic changes in given speed
本文针对直流母线小电容电机驱动系统提出了一种基于阻抗重塑的有源阻尼控制策略以改善网侧电流质量。通过理论研究和仿真、实验验证,可以得到以下结论:
1)直流母线电流中含有的谐波分量会对网侧电流产生较大影响;适当增大网侧谐波频率处的阻抗可以减小谐波电流。
2)本文所提基于阻抗重塑的有源阻尼电压补偿和扰动滤除控制相结合的方法,不改变系统的控制结构,实现简单且无需额外的硬件。
3)与传统有源阻尼控制策略相比,电机运行在不同工况下,采用本文所提控制策略均可更加显著地降低网侧电流THD,改善驱动系统网侧电流质量,同时也能有效地降低直流母线电压纹波。
参考文献
[1] 王菁, 颜建虎, 季国东, 等. 一种基于双位置观测器的永磁同步电机低速无位置传感器控制方法[J]. 电工技术学报, 2023, 38(2): 375-386.
Wang Jing, Yan Jianhu, Ji Guodong, et al. A sensor- less control method for permanent magnet syn- chronous machine based on dual position observers at low speed[J]. Transactions of China Electrotechnical Society, 2023, 38(2): 375-386.
[2] 郑长明, 董萱萱, 肖子语, 等. 基于虚拟电阻有源阻尼的LC滤波型永磁同步电机系统预测电流控制[J]. 电工技术学报, 2023, 38(22): 6059-6069.
Zheng Changming, Dong Xuanxuan, Xiao Ziyu, et al. Virtual resistance active damping based predictive current control of LC-filtered permanent magnet synchronous motor system[J]. Transactions of China Electrotechnical Society, 2023, 38(22): 6059-6069.
[3] Selvaraj G, Rajashekara K, Ramachandran Potti K R. Minimization of DC-link capacitance for a DC-link- based variable speed constant frequency aircraft power system[J]. IEEE Transactions on Industry Applications, 2022, 58(4): 5068-5080.
[4] 徐奇伟, 熊德鑫, 陈杨明, 等. 基于新型高频纹波电流补偿方法的内置式永磁同步电机无传感器控制[J]. 电工技术学报, 2023, 38(3): 680-691.
Xu Qiwei, Xiong Dexin, Chen Yangming, et al. Research on sensorless control strategy of IPMSM based on new high frequency ripple current com- pensation method[J]. Transactions of China Electro- technical Society, 2023, 38(3): 680-691.
[5] 霍军亚, 王高林, 赵楠楠, 等. 无电解电容电机驱动系统谐振抑制控制策略[J]. 电工技术学报, 2018, 33(24): 5641-5648.
Huo Junya, Wang Gaolin, Zhao Nannan, et al. Resonance suppression control strategy of electrolytic capacitor-less motor drives[J]. Transactions of China Electrotechnical Society, 2018, 33(24): 5641-5648.
[6] Huang Xinze, Ruan Xinbo, Fang Jie, et al. A virtual impedance based control scheme for modular elec- trolytic capacitor-less second harmonic current com- pensator[J]. IEEE Transactions on Industrial Elec- tronics, 2021, 68(1): 198-209.
[7] Ding Dawei, Zhao Nannan, Wang Gaolin, et al. Suppression of beat phenomenon for electrolytic capacitorless motor drives accounting for sampling delay of DC-link voltage[J]. IEEE Transactions on Industrial Electronics, 2022, 69(2): 1167-1176.
[8] Yang Zezhou, Sun Jianjun, Tang Yi, et al. An integrated dual voltage loop control for capacitance reduction in CHB-based regenerative motor drive systems[J]. IEEE Transactions on Industrial Elec- tronics, 2019, 66(5): 3369-3379.
[9] 姚绪梁, 罗兴鸿, 马赫, 等. 小电容双PWM调速系统直流母线电压波动抑制策略[J]. 电工技术学报, 2022, 37(12): 2971-2981.
Yao Xuliang, Luo Xinghong, Ma He, et al. DC bus voltage fluctuation suppression strategy for small capacitance dual-PWM speed regulating system[J]. Transactions of China Electrotechnical Society, 2022, 37(12): 2971-2981.
[10] Maheshwari R, Munk-Nielsen S, Lu Kaiyuan. An active damping technique for small DC-link capacitor based drive system[J]. IEEE Transactions on Indu- strial Informatics, 2013, 9(2): 848-858.
[11] Gu B G, Nam K. A DC-link capacitor minimization method through direct capacitor current control[J]. IEEE Transactions on Industry Applications, 2006, 42(2): 573-581.
[12] Bao Danyang, Pan Xuewei, Wang Yi, et al. Integrated- power-control-strategy-based electrolytic capacitor- less back-to-back converter for variable frequency speed control system[J]. IEEE Transactions on Indu- strial Electronics, 2020, 67(12): 10065-10074.
[13] Shin H, Son Y, Ha J I. Grid current shaping method with DC-link shunt compensator for three-phase diode rectifier-fed motor drive system[J]. IEEE Transa- ctions on Power Electronics, 2017, 32(2): 1279-1288.
[14] 赵楠楠, 周峰, 丁大尉, 等. 永磁电机无电解电容驱动系统网侧电流谐波抑制策略[J]. 中国电机工程学报, 2022, 42(3): 1145-1154.
Zhao Nannan, Zhou Feng, Ding Dawei, et al. Suppression strategy of grid-side current harmonics for electrolytic capacitor-less permanent magnet motor drives[J]. Proceedings of the CSEE, 2022, 42(3): 1145-1154.
[15] Li Ke, Sun Tianfu, Li Huiyun, et al. Grid current quality improvement for three-phase diode rectifier- fed small DC-link capacitance IPMSM drives[J]. IEEE Transactions on Energy Conversion, 2022, 37(4): 2310-2320.
[16] 林宏民, 宋文祥, 赵凌云. 小电容电机驱动系统的直流母线电压稳定性分析与控制[J]. 中国电机工程学报, 2020, 40(18): 5997-6006.
Lin Hongmin, Song Wenxiang, Zhao Lingyun. Analysis and control of DC-link voltage stabilization in small capacitor motor drive system[J]. Proceedings of the CSEE, 2020, 40(18): 5997-6006.
[17] Mathe L, Török L, Wang Dong, et al. Resonance reduction for AC drives with small capacitance in the DC link[J]. IEEE Transactions on Industry Appli- cations, 2017, 53(4): 3814-3820.
[18] Meng Linghui, Ma Lan, Zhu Weiwei, et al. Control strategy of single-phase UPQC for suppressing the influences of low-frequency DC-link voltage ripple[J]. IEEE Transactions on Power Electronics, 2022, 37(2): 2113-2124.
[19] Jung H S, Chee S J, Sul S K, et al. Control of three-phase inverter for AC motor drive with small DC-link capacitor fed by single-phase AC source[J]. IEEE Transactions on Industry Applications, 2013, 50(2): 1074-1081.
[20] Zheng Bining, Cao Yanfei, Li Xinmin, et al. An improved DC-link series IGBT chopping strategy for brushless DC motor drive with small DC-link capa- citance[J]. IEEE Transactions on Energy Conversion, 2021, 36(1): 242-252.
[21] Lee K, Jahns T M, Lipo T A, et al. Impact of input voltage sag and unbalance on DC-link inductor and capacitor stress in adjustable-speed drives[J]. IEEE Transactions on Industry Applications, 2008, 44(6): 1825-1833.
[22] Li Haichun, Yin Quan, Wang Qingyi, et al. A novel DC-link voltage feedback active damping control method for IPMSM drives with small DC-link capacitors[J]. IEEE Transactions on Industrial Elec- tronics, 2022, 69(3): 2426-2436.
[23] Lee W J, Sul S K. DC-link voltage stabilization for reduced DC-link capacitor inverter[J]. IEEE Transa- ctions on Industry Applications, 2014, 50(1): 404- 414.
[24] Ding Dawei, Zhang Guoqiang, Wang Gaolin, et al. Impedance reshaping for inherent harmonics in PMSM drives with small DC-link capacitor[J]. IEEE Transactions on Power Electronics, 2022, 37(12): 14265-14279.
Harmonic Suppression Strategy of Grid Side Current for DC-Link Small Capacitor Permanent Magnet Synchronous Motor Drive System
Abstract Traditional permanent magnet synchronous motor (PMSM) drive systems often use large- capacity electrolytic capacitors to keep the dc-link voltage constant. However, DC-link electrolytic capacitors have disadvantages of short life and large volume, leading to drive system failure. The small-capacity film capacitor instead of the dc-link large electrolytic capacitor is a trend to reduce the size and enhance system reliability. However, due to the substantial reduction of the dc-link capacitance, the energy coupling between the input side of the grid and the output side of the inverter is severe. When the system operates normally, the grid-side current generates a large number of harmonics, affecting the power quality of the grid side. This paper proposes an active damping control method based on impedance reshaping to suppress grid-side current harmonics.
Firstly, the small-capacity PMSM drive system is modeled, and the factors affecting the grid-side current are obtained by analyzing the drive system impedance. Secondly, the harmonic characteristics of the grid-side current are analyzed, and the mathematical relationship between the dc-link current and the grid-side current is established. Then, an active damping control method based on virtual impedance is adopted, and a band-pass filter is used to extract the harmonic signal of the DC-link voltage. The feedback loop is constructed as optimal voltage compensation, the equivalent impedance at a specific frequency of the drive system is reshaped, and the grid-side current harmonics are improved. Finally, a cascaded dual-frequency notch filter for the current loop is designed to suppress the voltage compensation module’s influence on current inner loop disturbances.
The simulation analysis shows that when the motor runs at 270 Hz and the load torque is 20 N·m, the grid side current THD decreases from 52.2% to 36.6%, finally decreasing to 32.7%. At the same time, the dc-link voltage ripple is reduced by 58.3%. The performance of the proposed control strategy is still good when the speed and load torque change dynamically. Based on the air-conditioning compressor drive system, the THD of a-phase current using the traditional active damping control method is 39.1%, the 5th harmonic has no apparent change, and the 7th harmonic is reduced by 78.8%. In contrast, the THD of a-phase current using the proposed voltage compensation is 37.8%, and the 5th and 7th harmonics are reduced by 5.8% and 84.3%, respectively. Using the proposed disturbance filtering, the a-phase current THD is reduced to 33.6 %, and the 5th and 7th harmonics are decreased by 19.8% and 88.8%, respectively.
The following conclusions can be drawn from the simulation analysis and experimental verification: (1) The harmonic components in the dc-link current greatly affect the grid-side current. Increasing the impedance at the grid-side harmonic frequency can reduce the harmonic electric current. (2) Combined with the active damping voltage compensation and disturbance filtering control, the proposed method does not change the control structure of the system and is simple to implement. (3) Compared with the traditional active damping control method, the proposed control strategy significantly reduces the grid-side current THD and the dc-link voltage ripple.
Keywords:Small capacitor motor drive, grid side current harmonic, impedance reshaping, dual frequency notch filter, current inner loop
中图分类号:TM351
DOI: 10.19595/j.cnki.1000-6753.tces.231005
收稿日期 2023-06-29
改稿日期 2023-08-04
宋 健 男,1993年生,博士研究生,研究方向为永磁同步电机驱动控制技术。
E-mail: songjianjy@163.com
宋文祥 男,1973年生,教授,博士生导师,研究方向为电力电子变换、电机驱动控制及应用。
E-mail: wxsongshu@126.com(通信作者)
(编辑 陈 诚)