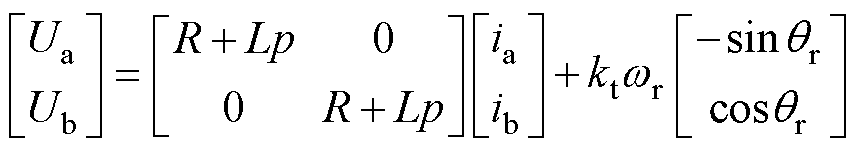 (1)
(1)
摘要 针对混合式步进电机阻尼系数较小引起的振荡以及失步问题,提出一种主动式阻尼闭环控制方法提高步进电机的控制品质。首先,该方法基于同步旋转dq坐标系下的电机模型,将电流id控制恒为额定电流,利用转速误差调节电流iq生成瞬时转矩,改善电机运行时存在的振荡现象。其次,为实现转速闭环,提出一种扩展滑模反电动势观测器(ESMO)与双锁相环(DPLL)相结合的无传感器控制方法,ESMO改善了传统滑模观测器的抖振问题,DPLL能消除加减速过程中的稳态误差。最后,通过实验验证了所提方法的有效性。
关键词:混合式步进电机 闭环控制 主动式阻尼控制 锁相环 滑模观测器
混合式步进电机(Hybrid Stepper Motor, HSM)因其定位精准、运行可靠、结构简单等优点,受到广泛关注,被应用于数控机床、计算机外围设备、印刷设备等[1]。混合式步进电机通常以开环方式运行,但由于机械结构特殊,所以电机的粘滞阻尼系数很小,在实际运行过程中容易引起抖振和失步问题,严重限制了混合式步进电机的应用场景。
为了解决上述问题,必须通过外加或控制的方式来增大电机阻尼。外加阻尼的方法分为机械式和电子式,如文献[2]中,在电机轴与端盖之间放置一个阻尼胶圈,利用胶圈与转轴间的摩擦力来增大阻尼。但是机械阻尼存在安装空间,且阻尼使用过久会造成阻尼参数改变的问题。电子式阻尼通常采用电阻或电容等无源元件来解决步进电机阻尼系数过小的缺陷,但此方法会降低电机的输出转矩。微步进(micro-stepping)控制[3]也可有效减小因阻尼系数过小引起的振荡,但这种方法只降低了振荡幅度,并未改变阻尼大小。除上述方法外,以闭环控制方式改变电机阻尼参数,也可以有效地提高步进电机的性能[4]。文献[5]在电机闭环控制过程中,根据实际值与估测值之间的误差调节生成补偿电流,解决电机的振荡问题。但此方法计算需基于电机参数且闭环控制由光学编码器实现。文献[6]提出了一种利用人工神经网络改善电机共振现象的阻尼控制器,但此控制器只适用于电机低速运行,且相关电机转子信息通过编码器进行反馈。外加编码器会增加系统成本[7],并且当温度变化或是处于恶劣环境时,编码器会降低电机控制系统的可靠性,而无传感器控制方式可以有效避免出现上述问题。
无传感器电机控制方法一般可以分为两类,即低速时的高频信号注入法和中高速时的反电动势观测法。文献[8]利用脉振高频信号注入法,将高频正弦信号注入d轴,利用磁饱和效应构造“饱和凸极”,并通过此凸极提取转子位置信息。高频信号注入法虽然不受电机参数变化的影响,但其缺点是需要外加信号并且信号处理过程复杂,电机动稳态特性不理想。目前,主流方法为反电动势观测法,通过对反电动势观测和处理来获取电机的转子信息。目前,主要的反电动势观测法有卡尔曼观测器法、滑模观测器法、状态观测器法[9]等。文献[10]采用自适应陷波滤波器与锁相环相结合的方法来消除特定次谐波,但剩余的谐波仍会影响电机转子位置的精度。文献[11]通过扩展卡尔曼滤波器估计电机转速,但此方法计算复杂且实时性较差。文献[12]针对步进电机中高速运行阶段,通过龙伯格观测器获得反电动势信息,利用锁相环对反电动势进行处理得到转子位置。传统锁相环虽然可以避免微分运算引起的噪声影响,但当电机转速发生变化时其动态性能较差。文献[13]提出基于滑模观测器的无传感器速度控制,并通过李雅普诺夫函数分析确定观测器的增益。滑模观测器法不依赖精确的电机数学模型,且对外部扰动具有较强鲁棒性,一定程度上解决了系统参数变化及扰动带来的影响。但传统滑模观测器容易导致系统发生抖振现象[14],并且外加低通滤波器会引起相位滞后,降低了滑模观测器的观测精度。
综上所述,为有效抑制步进电机实际运行过程中的振荡问题,本文提出了一种基于ESMO-DPLL的混合式步进电机主动式阻尼控制方法。首先,该方法基于同步旋转dq坐标系下的电机模型,将电流id控制恒为电流额定值,利用转速误差产生调节电流iq主动增加电机阻尼,以达到抑制振荡、减少稳定时间的目的。其次,主动式阻尼控制需要获取转速信息,提出一种将扩展滑模反电动势观测器(Extended Sliding Mode Observer, ESMO)与双锁相环(Dual Phase Locked Loop, DPLL)相结合的无传感器控制方法。ESMO将反电动势作为扩展状态变量,并利用饱和函数代替传统符号函数,削弱抖振的同时实现反电动势的精确估测。DPLL可以消除传统锁相环在电机加减速时存在的稳态误差,实现电机转速的精确辨识。最后,通过实验验证了本文方法的有效性。
在固定坐标系中,两相混合式步进电机的数学模型[15]表示为
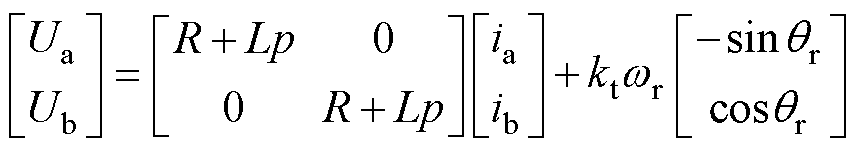 (1)
(1)
式中,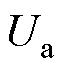 和
和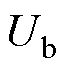 分别为
分别为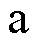 、
、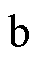 轴电压;
轴电压;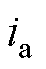 、
、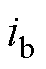 分别为
分别为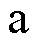 、
、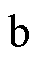 轴电流;p为微分算子;
轴电流;p为微分算子;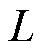 和
和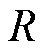 分别为定子绕组电感和电阻;
分别为定子绕组电感和电阻;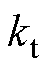 为转矩系数;
为转矩系数;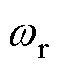 为转子电角速度;
为转子电角速度;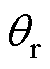 为转子电角度。
为转子电角度。
本文采用同步坐标电流控制,利用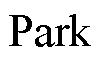 变换将固定坐标系转化为与定子电流保持同步旋转的dq坐标系,两坐标系之间的矢量图如图1所示。图中,qe为定子电流角度。
变换将固定坐标系转化为与定子电流保持同步旋转的dq坐标系,两坐标系之间的矢量图如图1所示。图中,qe为定子电流角度。
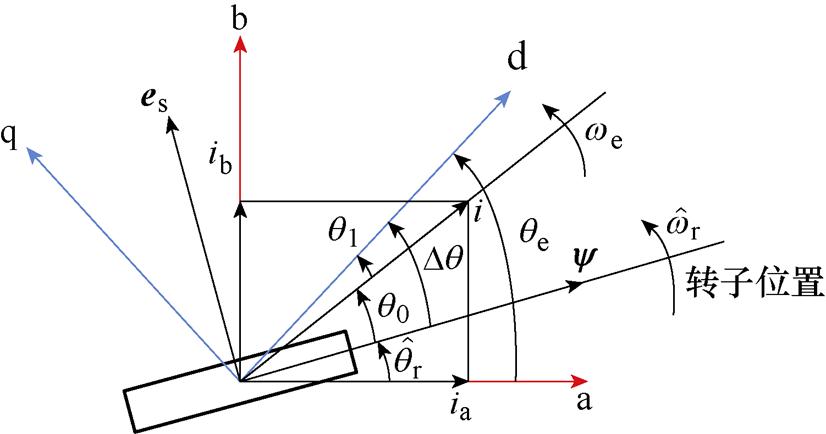
图1 坐标轴关系矢量图
Fig.1 Coordinate axis vector diagram
转换至同步dq坐标系的电机数学模型表示为
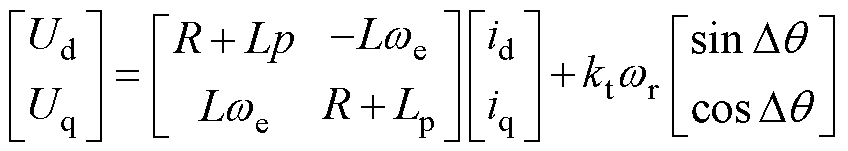 (2)
(2)
式中,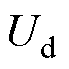 和Uq分别为
和Uq分别为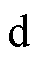 、
、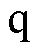 轴电压;
轴电压;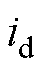 、iq分别为
、iq分别为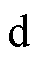 、
、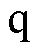 轴电流;
轴电流;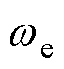 为定子电流转速;
为定子电流转速;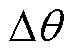 为电机负载角,
为电机负载角,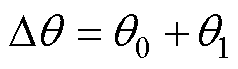 ,其中,
,其中,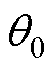 为稳态分量,
为稳态分量,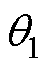 为暂态分量。
为暂态分量。
同步dq坐标系下的电机输出转矩方程为
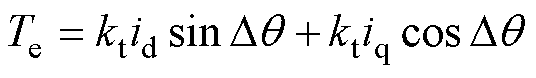 (3)
(3)
步进电机的机械运动方程[16]为
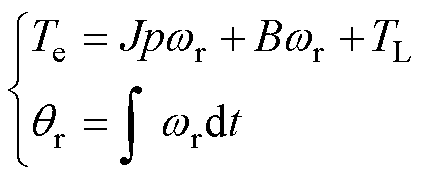 (4)
(4)
式中,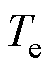 为输出转矩;
为输出转矩;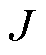 为转动惯量;
为转动惯量;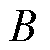 为粘滞摩擦系数;
为粘滞摩擦系数;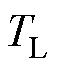 为负载转矩。
为负载转矩。
为有效抑制混合式步进电机运行过程中的振荡现象,需对电机的阻尼进行控制。本文提出了一种主动式阻尼闭环控制方案,结构框图如图2所示,设计阻尼增益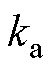 用于调节指令
用于调节指令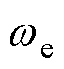 与估计的电机转速
与估计的电机转速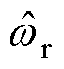 之间的误差。
之间的误差。
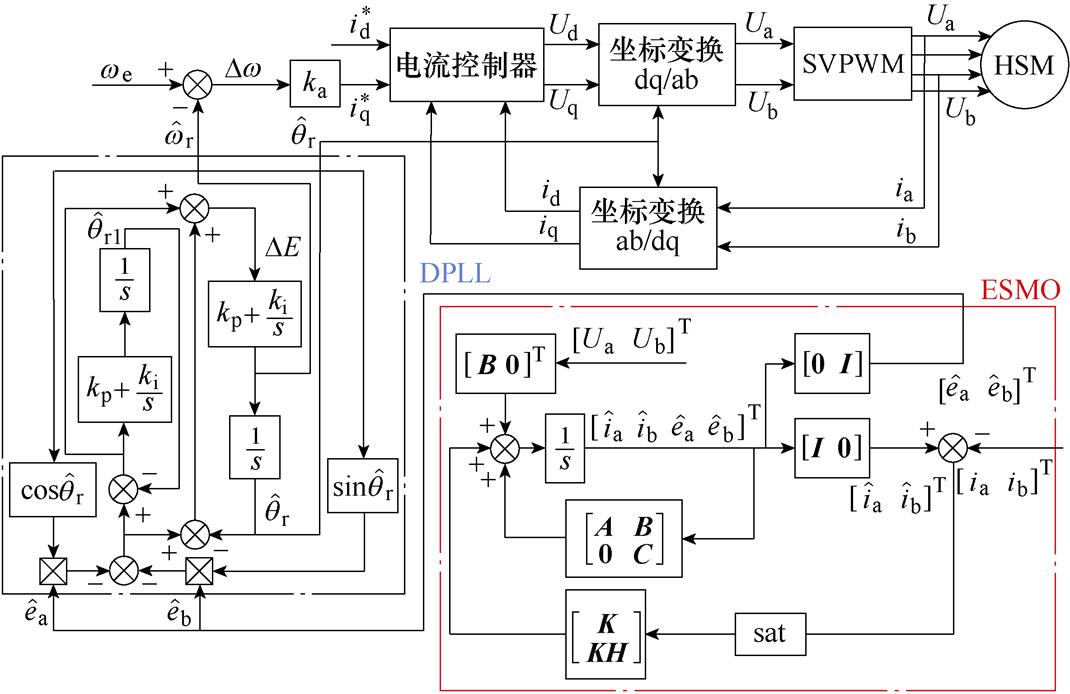
图2 基于ESMO-DPLL的HSM无传感器控制框图
Fig.2 Block diagram of HSM sensorless control based on ESMO-DPLL
本文设计的主动式阻尼控制方法,通过控制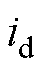 恒为额定电流,利用转速误差产生调节电流iq主动式增加电机阻尼,以达到抑制振荡、减少稳定时间的目的。当步进电机稳态运行时,输出转矩仅由电流
恒为额定电流,利用转速误差产生调节电流iq主动式增加电机阻尼,以达到抑制振荡、减少稳定时间的目的。当步进电机稳态运行时,输出转矩仅由电流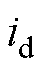 产生,当负载不超过
产生,当负载不超过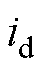 单独所能产生的最大保持转矩时,电机的电流矢量和转子保持同步旋转。但当电机发生振荡时,转子位置会超前或滞后于电流矢量,此时根据定子电流转速
单独所能产生的最大保持转矩时,电机的电流矢量和转子保持同步旋转。但当电机发生振荡时,转子位置会超前或滞后于电流矢量,此时根据定子电流转速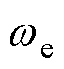 与转子观测转速
与转子观测转速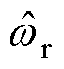 之间的误差调节生成电流iq,以抑制振荡现象。
之间的误差调节生成电流iq,以抑制振荡现象。
由图2可得
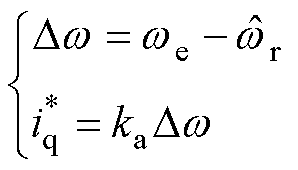 (5)
(5)
式中,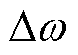 为定子电流转速
为定子电流转速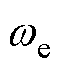 与转子观测转速
与转子观测转速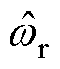 之间的误差;
之间的误差;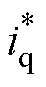 为q轴指令电流;
为q轴指令电流;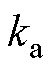 为阻尼增益。
为阻尼增益。
将式(5)代入式(3)和式(4)可得
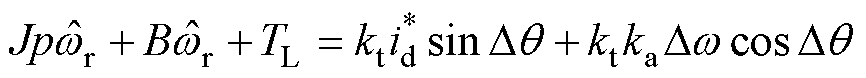 (6)
(6)
式中,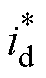 为d轴指令电流。
为d轴指令电流。
由于
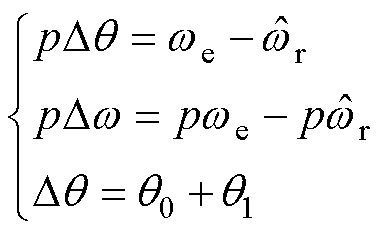 (7)
(7)
式(6)两边同时求导后,将式(7)代入可得
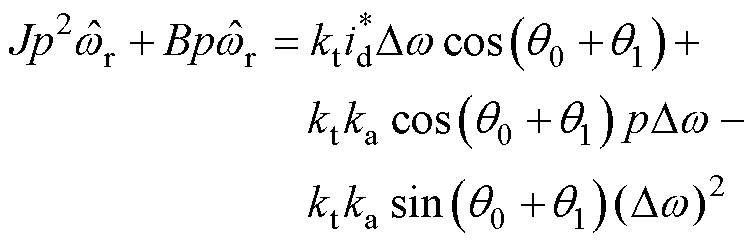 (8)
(8)
电机稳态运行时定子电流转速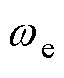 与观测转速
与观测转速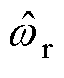 基本保持同步,因此
基本保持同步,因此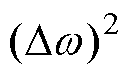 值很小,可忽略。同时,调控生成的电流
值很小,可忽略。同时,调控生成的电流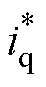 值为极小的暂态值,即电流
值为极小的暂态值,即电流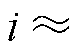
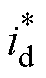 ,根据q1=arctan(
,根据q1=arctan(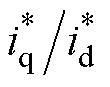 )可得暂态分量q1角度很小,即
)可得暂态分量q1角度很小,即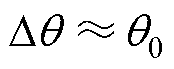 。因此,由式(8)可得传递函数为
。因此,由式(8)可得传递函数为
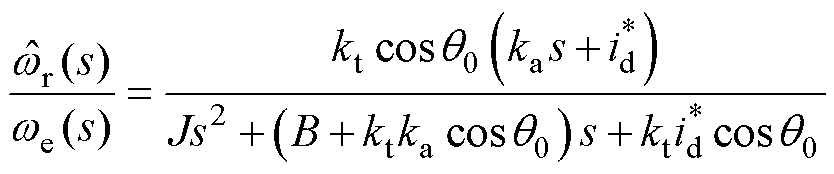 (9)
(9)
将式(9)和标准二阶系统的传递函数相比,自然频率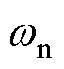 和阻尼比
和阻尼比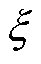 分别为
分别为
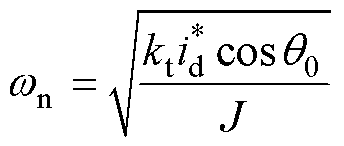 (10)
(10)
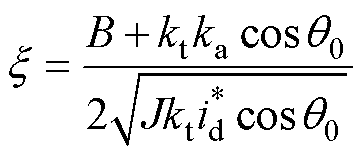 (11)
(11)
由式(11)可知,改变阻尼增益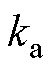 可以有效调节系统阻尼比大小,抑制步进电机运行过程中存在的振荡现象。但式(11)同时表明,负载角的变化会对阻尼比产生影响,为明确其影响对系统进行根轨迹分析,q0变化时系统根轨迹图如图3所示。
可以有效调节系统阻尼比大小,抑制步进电机运行过程中存在的振荡现象。但式(11)同时表明,负载角的变化会对阻尼比产生影响,为明确其影响对系统进行根轨迹分析,q0变化时系统根轨迹图如图3所示。
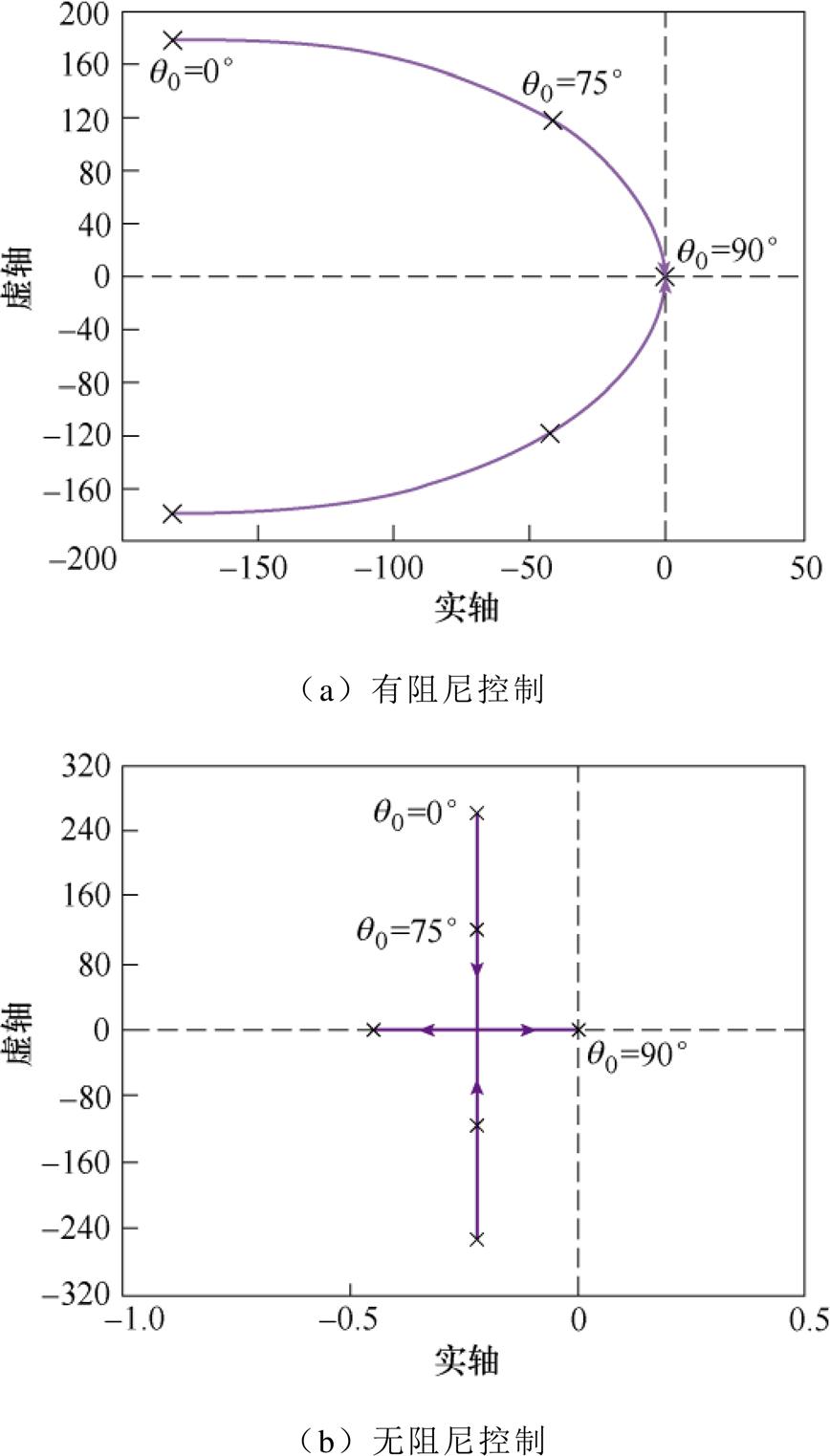
图3 q0变化时系统根轨迹图
Fig.3 System root trajectory diagram when q0 varies
图3a为带主动式阻尼控制时,通过调节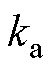 值使阻尼比
值使阻尼比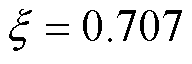 ,
,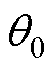 从0~90°的根轨迹图。可知,当电机以小于90°的负载角运行时,控制系统是稳定的。图3b为无阻尼控制即
从0~90°的根轨迹图。可知,当电机以小于90°的负载角运行时,控制系统是稳定的。图3b为无阻尼控制即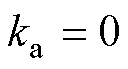 时的根轨迹图,可知,此时根轨迹非常靠近虚轴,容易导致系统响应振荡。
时的根轨迹图,可知,此时根轨迹非常靠近虚轴,容易导致系统响应振荡。
为实现步进电机主动式阻尼控制,还需获取电机转子信息作为反馈完成闭环。传统滑模观测器获得的信号中包含较多谐波成分,而外加滤波器会导致相位滞后且容易降低系统性能,因此本文设计了一种扩展滑模反电动势观测器,结构如图4所示。
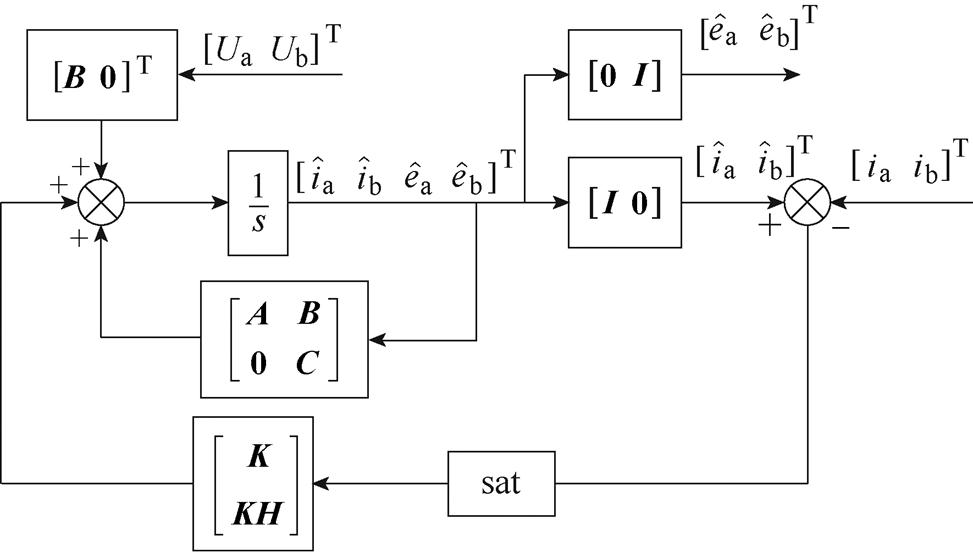
图4 扩展滑模观测器结构
Fig.4 Block diagram of ESMO
将式(1)中的电流和反电动势作为系统的状态变量,可得步进电机的扩展状态方程为
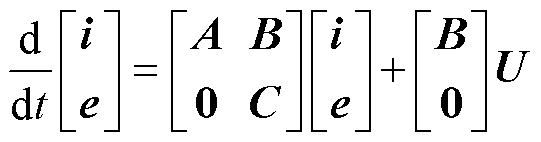 (12)
(12)
其中
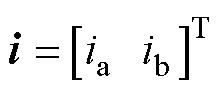
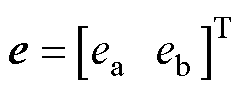
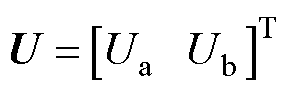
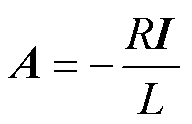
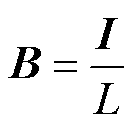
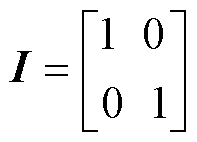
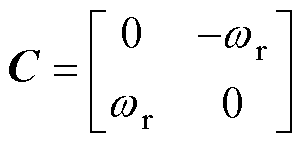
式中,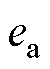 和
和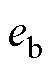 分别为反电动势
分别为反电动势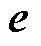 的
的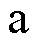 、
、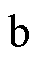 轴分量。
轴分量。
根据式(12)状态方程,建立扩展滑模反电动势观测器为
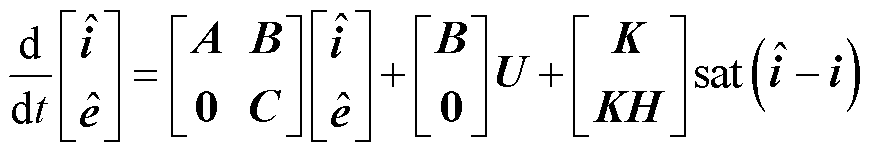 (13)
(13)
其中
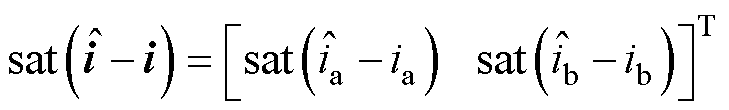
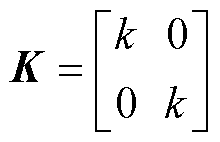
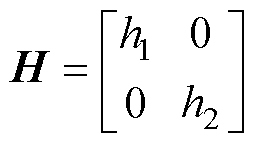
式中,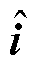 为电流
为电流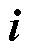 的观测值;
的观测值;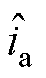 和
和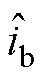 分别为电流
分别为电流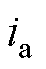 与
与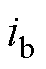 的观测值;
的观测值;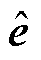 为反电动势
为反电动势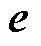 的观测值;
的观测值;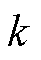 、
、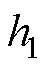 、
、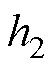 为增益系数;
为增益系数;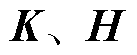 为滑模增益矩阵;
为滑模增益矩阵; 为饱和函数,本文采用的饱和函数表示为
为饱和函数,本文采用的饱和函数表示为
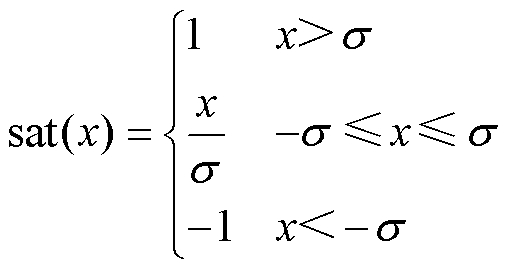 (14)
(14)
式中, 为边界层厚度。
为边界层厚度。
选取滑模面为
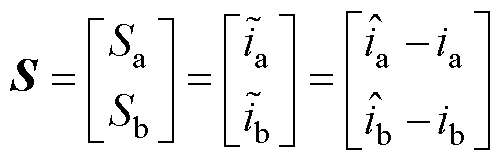 (15)
(15)
式中,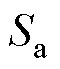 、
、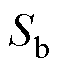 为滑模面
为滑模面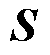 的分量;
的分量;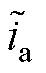 、
、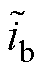 为电流观测误差分量。
为电流观测误差分量。
将式(13)减去式(12)可得观测器误差方程为
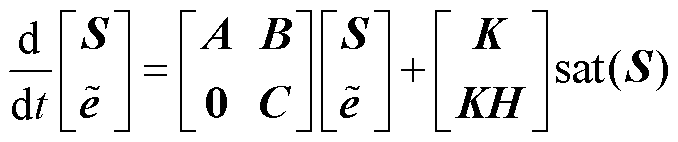 (16)
(16)
其中
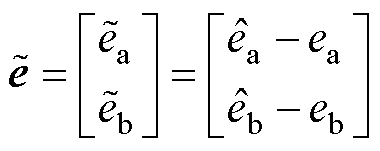
式中,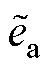 、
、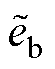 为反电动势观测误差
为反电动势观测误差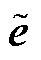 的分量;
的分量;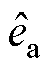 和
和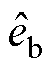 分别为反电动势分量
分别为反电动势分量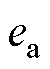 与
与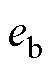 的观测值。
的观测值。
为了证明滑模观测器的稳定性,定义李雅普诺夫函数为
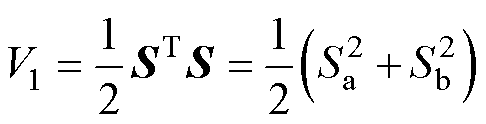 (17)
(17)
对式(17)进行求导并将式(16)代入可得
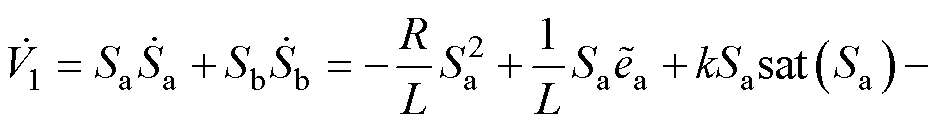
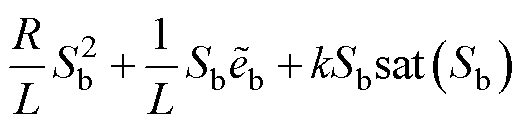 (18)
(18)
由式(18)可知,为满足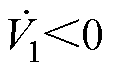 ,有
,有
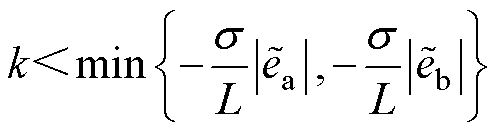 (19)
(19)
依据滑模控制理论,当系统状态进入滑动模态时,式(20)[17]成立。
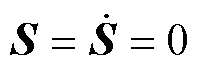 (20)
(20)
将式(20)代入式(16)可得
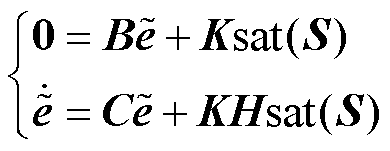 (21)
(21)
取李雅普诺夫函数为
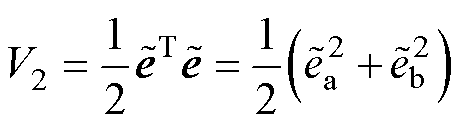 (22)
(22)
对式(22)求导,并将式(21)代入可得
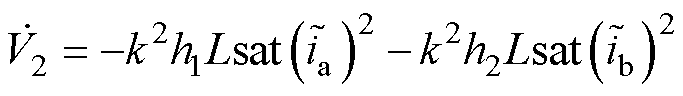 (23)
(23)
为满足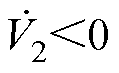 ,可得条件为
,可得条件为
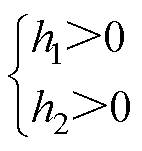 (24)
(24)
对反电动势观测器得到的反电动势进行反正切计算,可以得到转子位置为
 (25)
(25)
对转子位置信息进行微分可得转子速度,但微分运算将放大高频噪声,会降低电机转子信息的观测精度。反电动势信号输出后利用锁相环对其进行处理,能避免微分运算引起的噪声影响[18-19]。
基于文献[20]中设计的传统锁相环(PLL),通过对其分析可得电机转速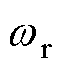 与观测转速
与观测转速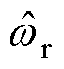 间的传递函数为
间的传递函数为
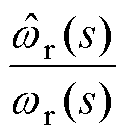
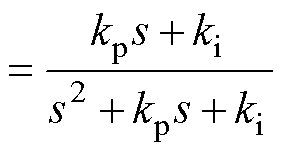 (26)
(26)
式中,kp为PI调节器的比例系数;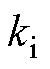 为PI调节器的积分系数。
为PI调节器的积分系数。
此时PLL实际转速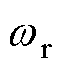 与观测转速
与观测转速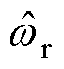 之间的误差
之间的误差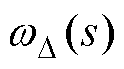 表示为
表示为
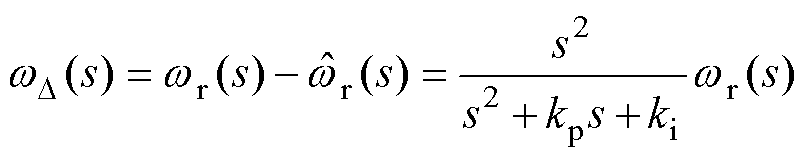 (27)
(27)
利用终值定理分析电机在恒定速度(Case Ⅰ)以及加减速状态(Case Ⅱ)下的稳态误差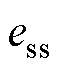 分别为
分别为
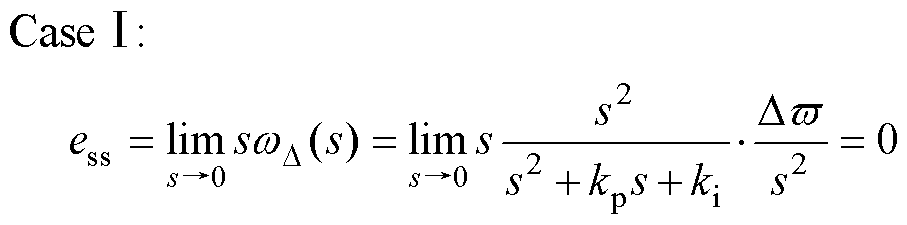 (28)
(28)
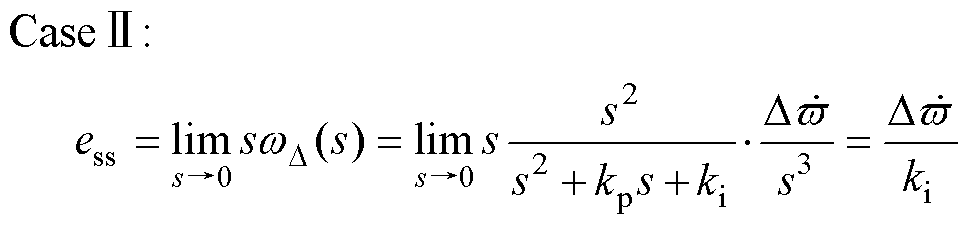 (29)
(29)
式中,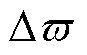 为电机加减速状态下的速度变化率。由式(29)可得,基于传统锁相环(PLL)的步进电机在加速或减速状态下存在稳态误差
为电机加减速状态下的速度变化率。由式(29)可得,基于传统锁相环(PLL)的步进电机在加速或减速状态下存在稳态误差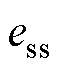 。针对此问题,本文设计了一种双锁相环(DPLL)以消除稳态误差,结构框图如图5所示。
。针对此问题,本文设计了一种双锁相环(DPLL)以消除稳态误差,结构框图如图5所示。
传统锁相环开环传递函数G(s)表示为
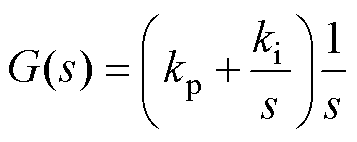 (30)
(30)
由式(30)及图5可得PLL-1的闭环传递函数为
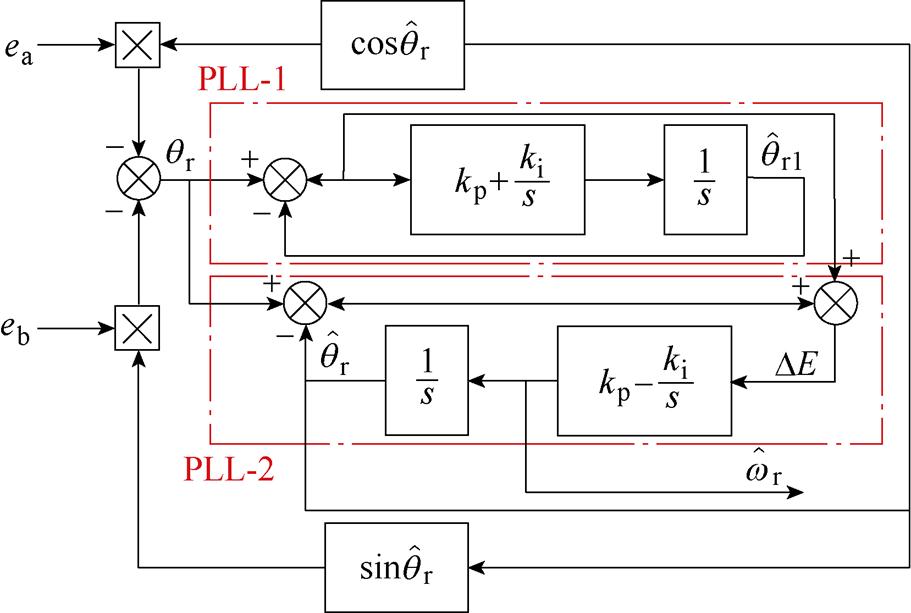
图5 三阶锁相环结构框图
Fig.5 Block diagram of third-order PLL
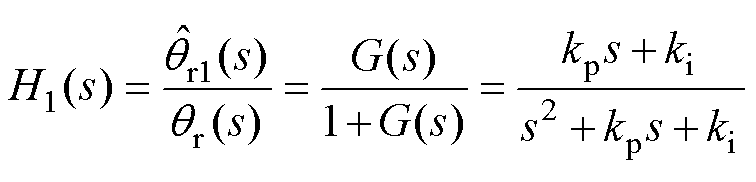 (31)
(31)
式中,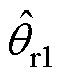 为PLL-1中转子电角度
为PLL-1中转子电角度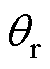 的观测值。
的观测值。
PLL-2中转子电角度观测值表示为
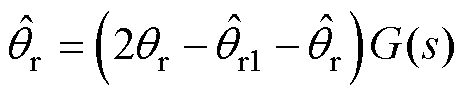 (32)
(32)
由式(31)、式(32)可得双锁相环系统的闭环传递函数为
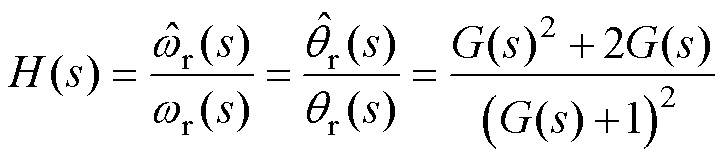 (33)
(33)
根据式(33)可得误差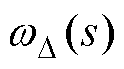 表示为
表示为
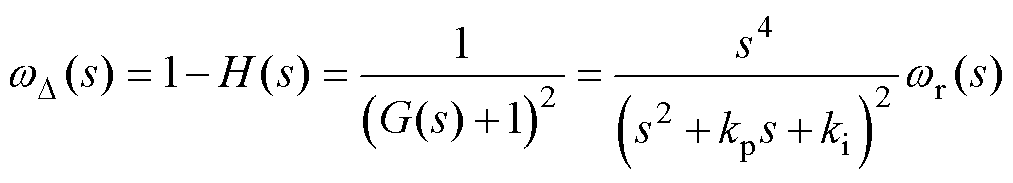 (34)
(34)
此时电机在恒定速度(Case Ⅰ)以及加减速(Case Ⅱ)状态下的稳态误差分别为
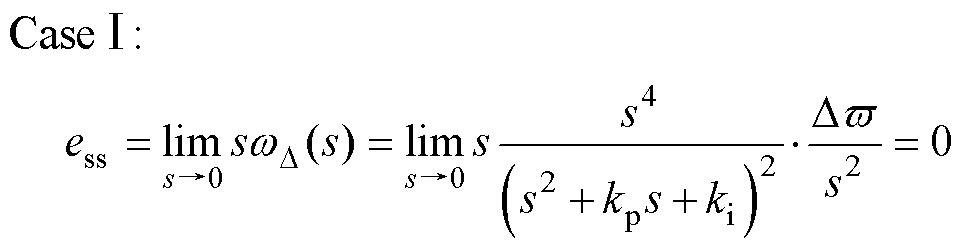 (35)
(35)
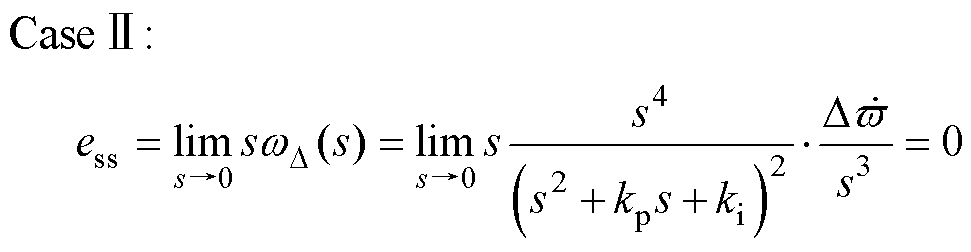 (36)
(36)
将式(36)和式(29)对比分析可得,DPLL可以有效消除电机的稳态误差,在加减速状态下将稳态误差降为零。
为验证基于ESMO-DPLL的主动式阻尼控制方法的可靠性和有效性,对57BYG250型混合式步进电机进行实验研究,电机参数见表1。基于STM32F407开发板的步进电机实验装置如图6所示,负载转矩为额定值1.2 N×m,同时采用N38-06-N型600线增量型旋转编码器,编码器用来测量电机真实转速,以对比验证转速观测器的有效性。
表1 混合式步进电机参数
Tab.1 Parameters of HSM
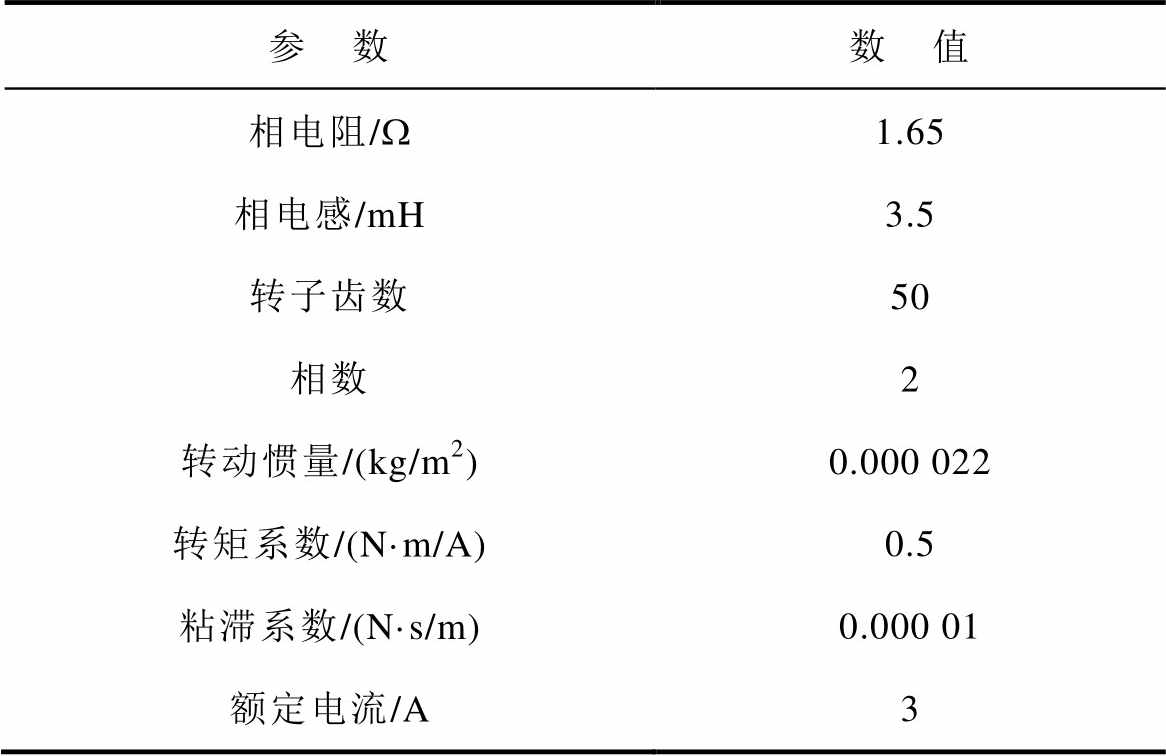
参 数数 值 相电阻/W1.65 相电感/mH3.5 转子齿数50 相数2 转动惯量/(kg/m2)0.000 022 转矩系数/(N·m/A)0.5 粘滞系数/(N·s/m)0.000 01 额定电流/A3

图6 实验系统实物
Fig.6 Photograph of experimental system
为验证本文提出的观测器方法的有效性,分别利用传统滑模观测器和扩展滑模观测器对反电动势进行观测,实验结果如图7、图8所示。
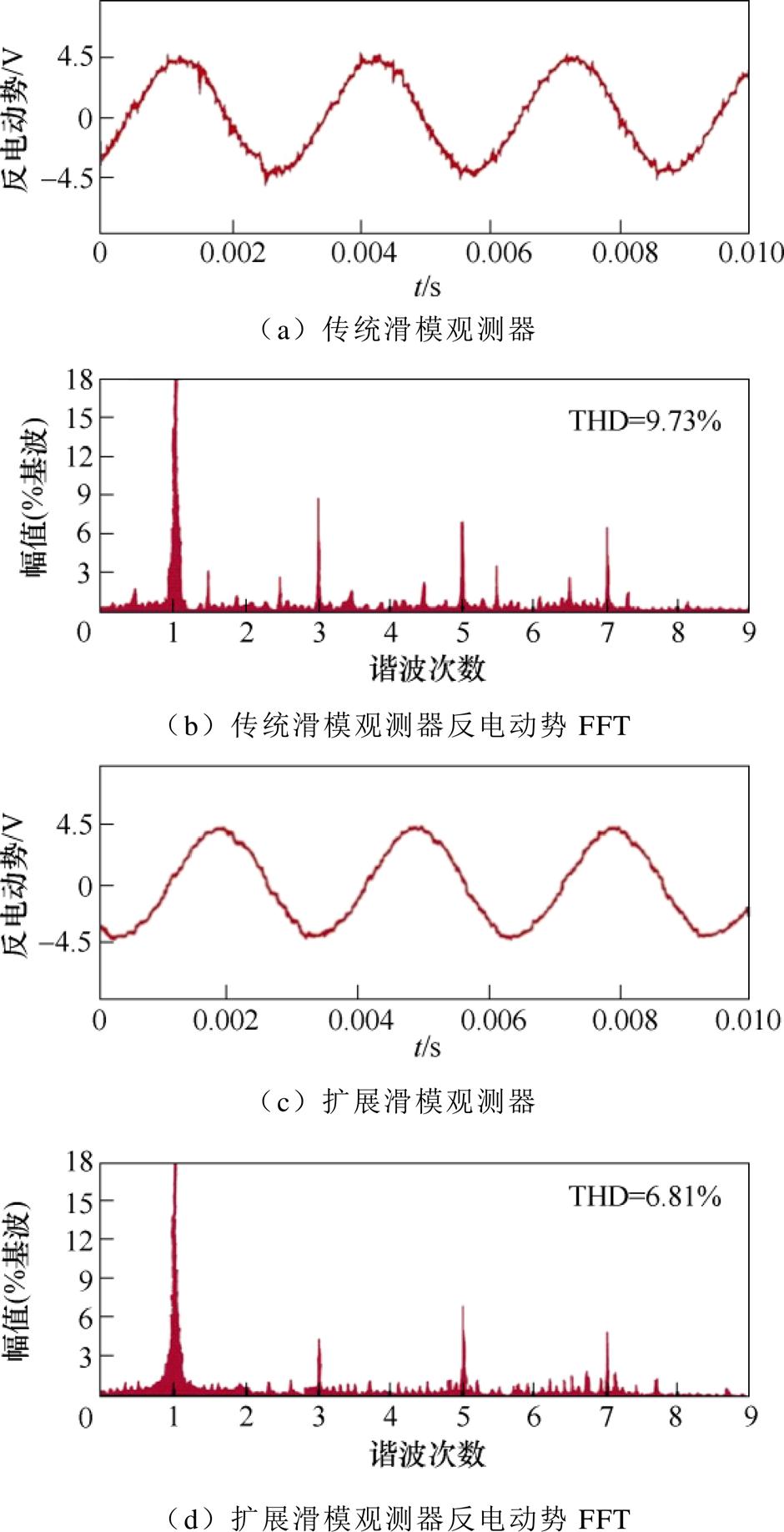
图7 we=300 Hz时的实验结果
Fig.7 Experimental results at we=300 Hz
图7为转速为300 Hz时,两种观测器输出的反电动势及快速傅里叶变换(Fast Fourier Transformation,FFT)分析。图7a中,传统滑模观测器获得的反电动势信号发生明显畸变,存在抖振现象。相比于图7a,图7c中扩展滑模观测器获得的反电动势信号波形更加平滑。对比两种观测器输出的反电动势傅里叶分析图7b与图7d可知,由扩展滑模观测器获得的反电动势谐波含量更小,总谐波畸变率(Total Harmonic Distortion, THD)由9.73%降低为6.81%。
图8为电机转速为500 Hz时的反电动势及傅里叶分析。将图8a与图8c对比可得,扩展滑模观测器输出的反电动势信号正弦度明显提高。对比两种观测器输出的反电动势傅里叶分析图8b与图8d可知,由扩展滑模观测器获得的反电动势谐波含量更小,总谐波畸变率明显降低。由此可得,扩展滑模观测器能有效解决传统滑模观测器的抖振问题,获取更加精确的反电动势估测值。
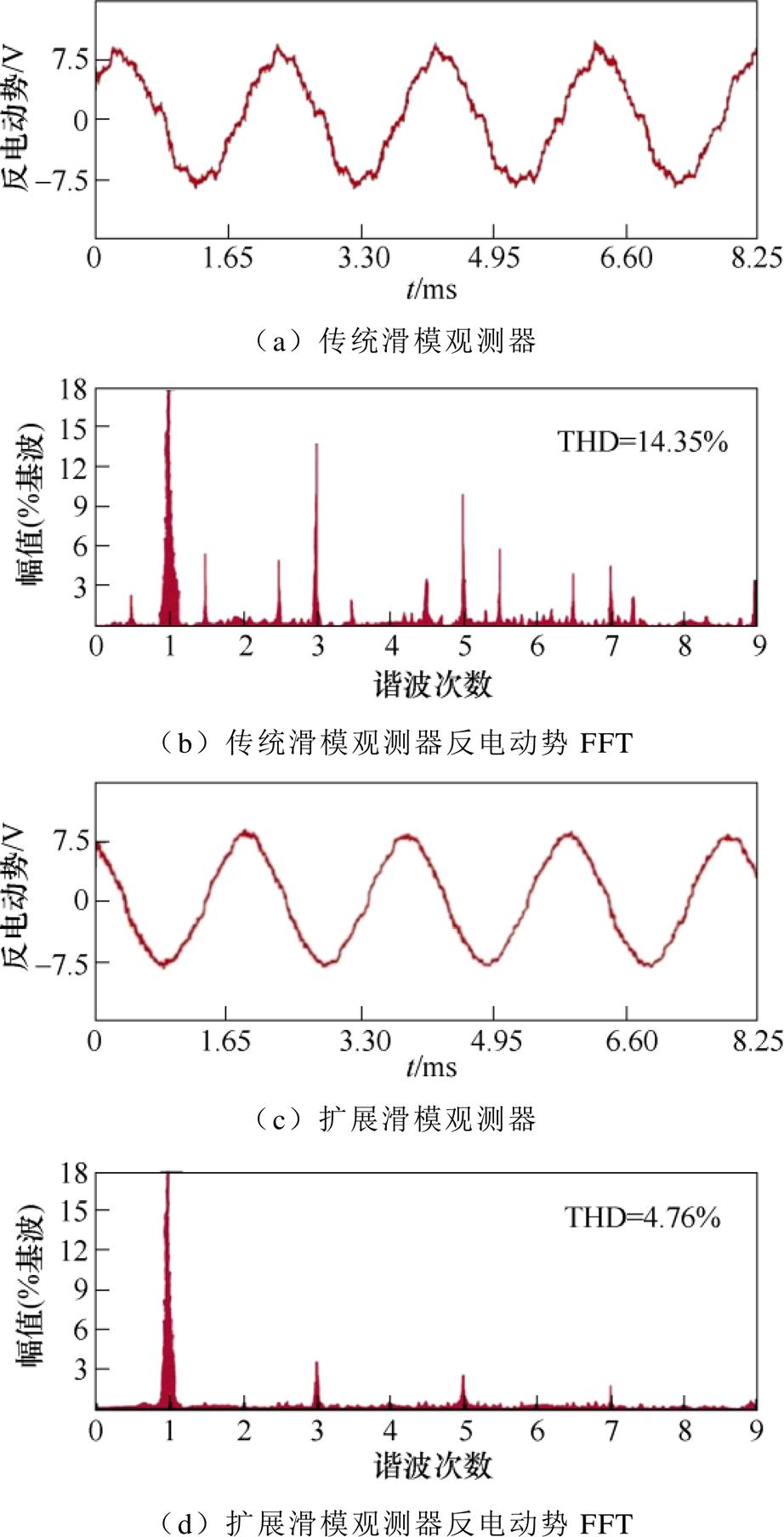
图8 we=500 Hz时的实验结果
Fig.8 Experimental results at we=500 Hz
在不同转速下,验证基于ESMO-DPLL的混合式步进电机闭环主动式阻尼控制对系统振荡抑制的有效性。
图9、图10分别为电机从静止状态加速至10 Hz,最后减速到0 Hz的实验结果。由图9可得,采用无阻尼控制时,实际转速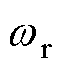 和估测转速
和估测转速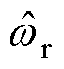 曲线均有较大振荡,最大观测转速误差约为5 Hz,指令转速
曲线均有较大振荡,最大观测转速误差约为5 Hz,指令转速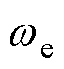 和实际转速
和实际转速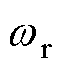 之间的最大实际转速误差约为6 Hz。图10为带主动式阻尼控制时的结果,实际转速
之间的最大实际转速误差约为6 Hz。图10为带主动式阻尼控制时的结果,实际转速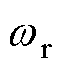 与估测转速
与估测转速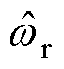 间最大观测转速误差减小至4 Hz,最大实际转速误差约为5 Hz。相比于无阻尼控制,带主动式阻尼控制时转速曲线的振荡幅度减小。由上述实验结果证明,在电机低速运行时,本文提出的主动式阻尼控制能抑制电机运行过程中的振荡现象。
间最大观测转速误差减小至4 Hz,最大实际转速误差约为5 Hz。相比于无阻尼控制,带主动式阻尼控制时转速曲线的振荡幅度减小。由上述实验结果证明,在电机低速运行时,本文提出的主动式阻尼控制能抑制电机运行过程中的振荡现象。
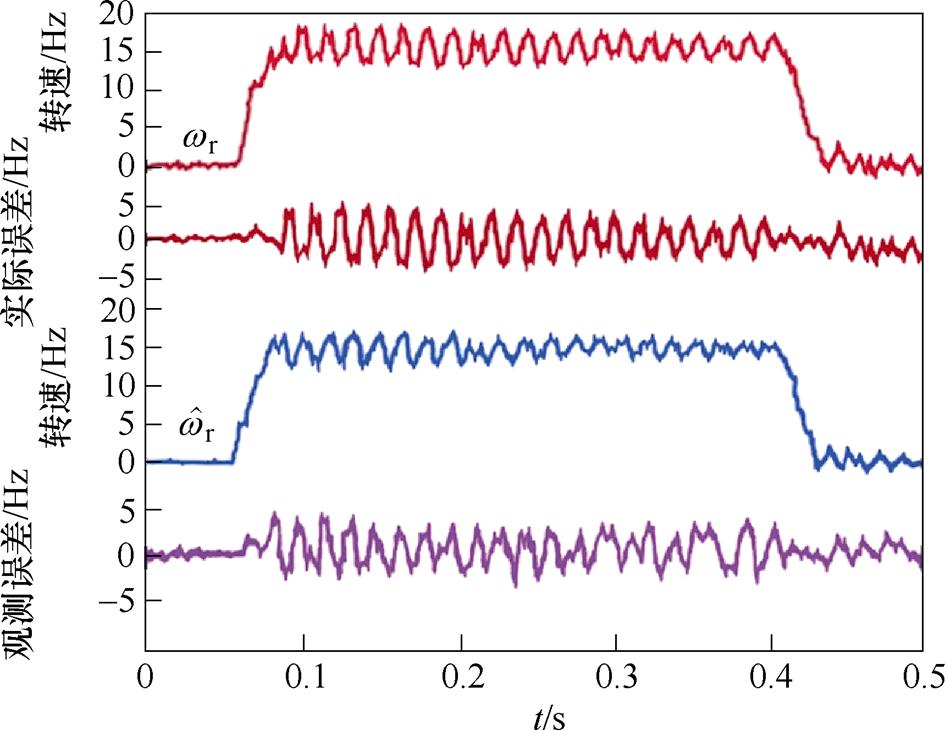
图9 无阻尼控制时转速响应及误差波形,we=10 Hz
Fig.9 Velocity response and error waveforms without damping control,we=10 Hz
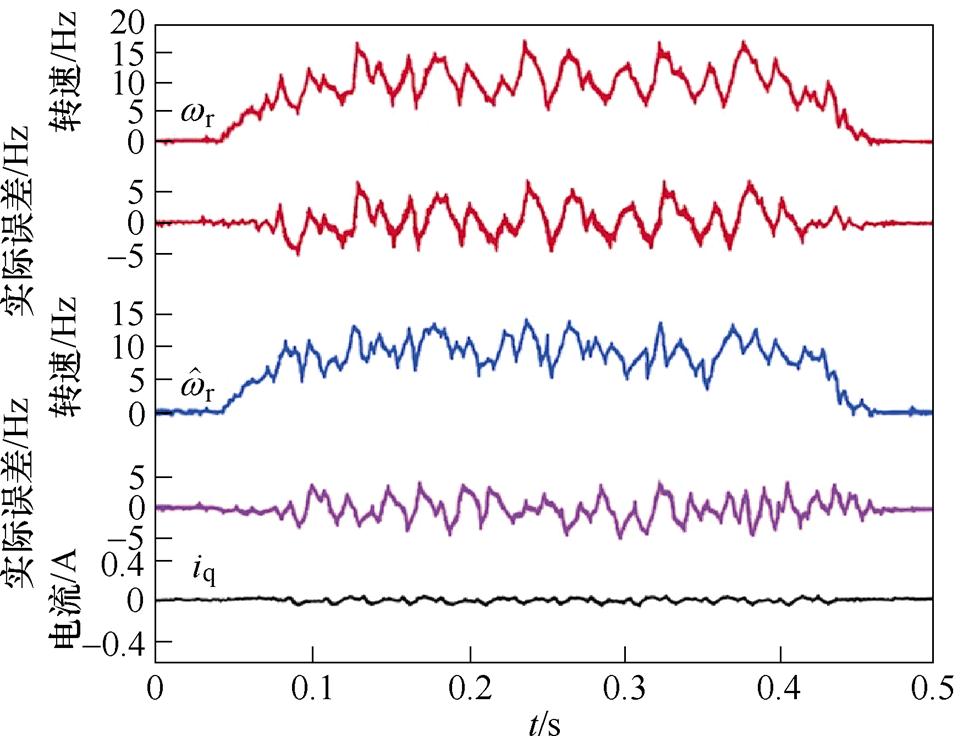
图10 有阻尼控制时转速响应及误差波形,we=10 Hz
Fig.10 Velocity response and error waveforms with damping control, we=10 Hz
图11、图12为电机从静止状态加速至300 Hz最后再变为静止状态的实验波形。图11为无阻尼控制时的结果,图12为采用主动式阻尼控制的实验结果。图11波形中电机实际转速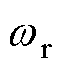 与估测转速
与估测转速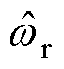 之间的最大观测误差约为75 Hz,指令转速
之间的最大观测误差约为75 Hz,指令转速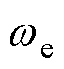 和实际转速
和实际转速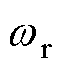 之间的最大实际转速误差约为80 Hz,而带主动式阻尼控制时实际转速曲线更加平滑,振荡幅度明显减小,最大观测转速误差约为30 Hz左右。图12中观测器输出的估测转速
之间的最大实际转速误差约为80 Hz,而带主动式阻尼控制时实际转速曲线更加平滑,振荡幅度明显减小,最大观测转速误差约为30 Hz左右。图12中观测器输出的估测转速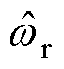 曲线也更为平稳,估测转速与实际转速值基本吻合,最大实际转速误差约为30 Hz。图12和图10对比可得,在电机转速较大时,主动式阻尼控制方法能有效抑制电机振荡。
曲线也更为平稳,估测转速与实际转速值基本吻合,最大实际转速误差约为30 Hz。图12和图10对比可得,在电机转速较大时,主动式阻尼控制方法能有效抑制电机振荡。
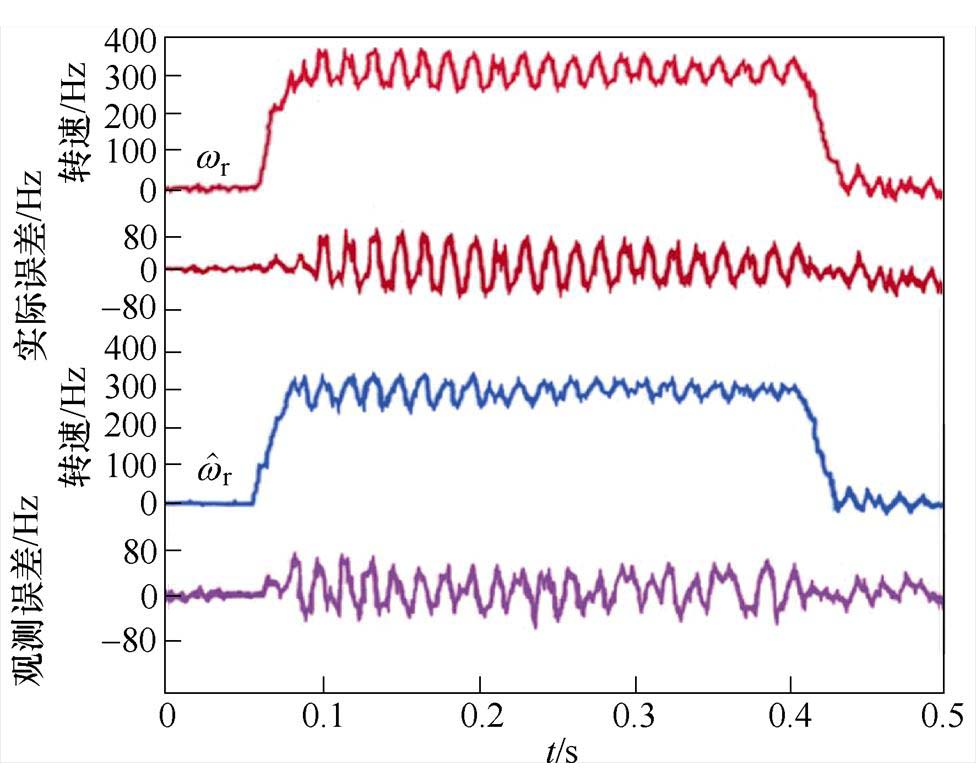
图11 无阻尼控制时转速响应及误差波形,we=300 Hz
Fig.11 Velocity response and error waveforms without damping control,we=300 Hz
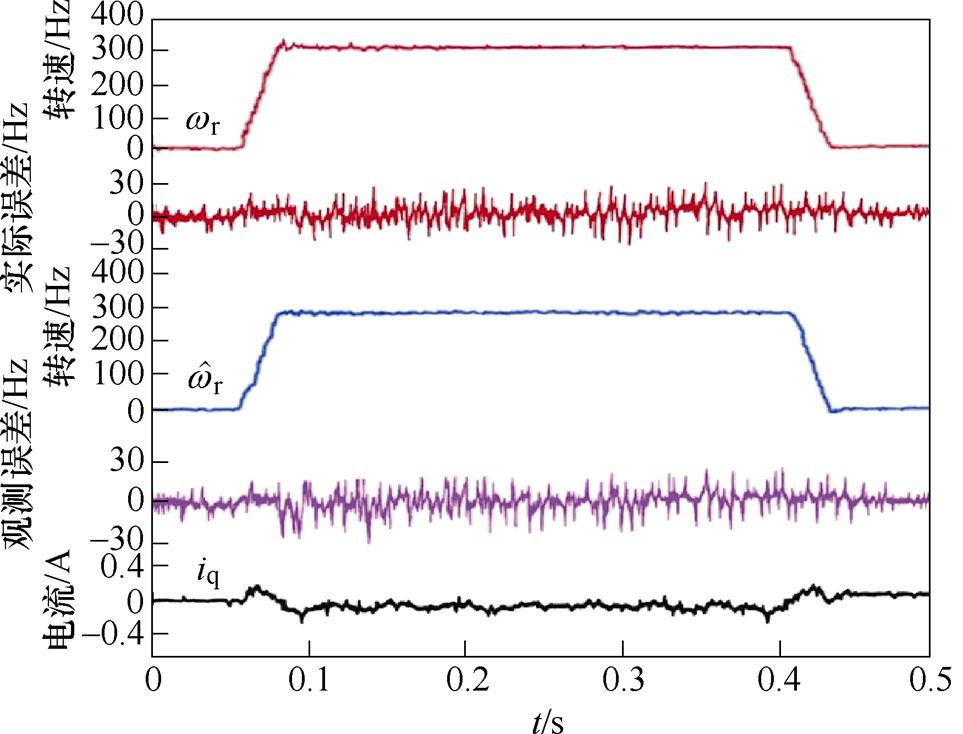
图12 有阻尼控制时转速响应及误差波形,we=300 Hz
Fig.12 Velocity response and error waveforms with damping control, we=300 Hz
图13、图14为电机从0 Hz加速至500 Hz后减速至静止状态的实际转速、估测转速和转速误差的实验波形。图13无阻尼控制时电机转速波形存在明显振荡,实际转速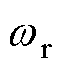 与估测转速
与估测转速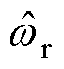 间的观测误差约为65 Hz,指令转速
间的观测误差约为65 Hz,指令转速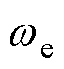 和实际转速
和实际转速 之间的最大实际转速误差约为80 Hz。图14带主动式阻尼控制时观测转速误差明显减小,观测误差维持在一个较小范围内,电机转速曲线平滑,最大实际转速误差约为28 Hz,实际转速与观测器输出的转速曲线相近,观测器能较好地实现对实际值的跟踪。由此实验可得,在高速运行时,主动式阻尼控制能够有效抑制实际运行过程中的振荡现象。将图14与图12、图10对比,电机在中高速运行时,主动式阻尼控制的效果更为明显。
之间的最大实际转速误差约为80 Hz。图14带主动式阻尼控制时观测转速误差明显减小,观测误差维持在一个较小范围内,电机转速曲线平滑,最大实际转速误差约为28 Hz,实际转速与观测器输出的转速曲线相近,观测器能较好地实现对实际值的跟踪。由此实验可得,在高速运行时,主动式阻尼控制能够有效抑制实际运行过程中的振荡现象。将图14与图12、图10对比,电机在中高速运行时,主动式阻尼控制的效果更为明显。
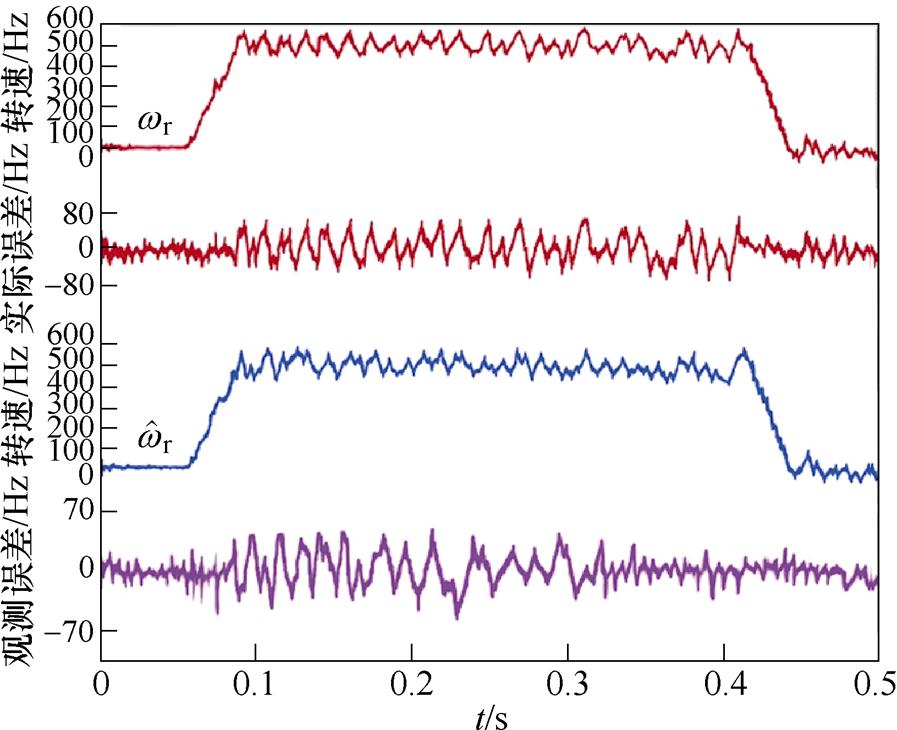
图13 无阻尼控制时转速响应及误差波形,we=500 Hz
Fig.13 Velocity response and error waveforms without damping control,we=500 Hz
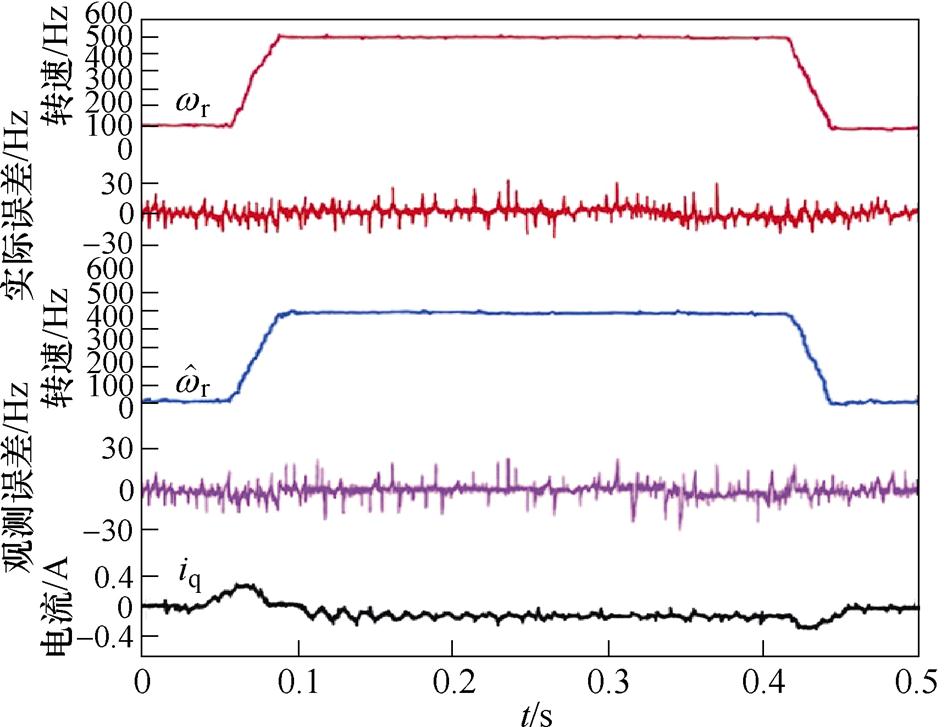
图14 有阻尼控制时转速响应及误差波形,we=500 Hz
Fig.14 Velocity response and error waveforms with damping control, we=500 Hz
本文提出了一种基于ESMO-DPLL的混合式步进电机主动式阻尼控制方法。通过定子电流转速与观测转速间的误差产生调节电流可以有效增大电机阻尼,达到抑制振荡的目的。同时设计扩展滑模观测器与双锁相环相结合的方法获取电机转速信息实现闭环控制。ESMO将电流和反电动势作为状态变量,采用饱和函数代替传统符号函数,减少系统抖振的同时实现对反电动势的精确估测,DPLL可以消除传统锁相环在电机加减速时存在的稳态误差,实现电机转速的精确辨识。实验结果表明,本文提出的控制方案可以有效抑制混合式步进电机实际运行过程中的振荡现象,使电机平稳运行。
参考文献
[1] 王春雷, 曹东兴. 两相混合式步进电机全速范围无位置传感器速度控制[J]. 电机与控制学报, 2022, 26(3): 41-48.
Wang Chunlei, Cao Dongxing. Wide-speed-range sensorless speed control of two-phase hybrid stepper motors[J]. Electric Machines and Control, 2022, 26(3): 41-48.
[2] Yang Shengming, Kuo Eilang. Damping a hybrid stepping motor with estimated position and velo- city[J]. IEEE Transactions on Power Electronics, 2003, 18(3): 880-887.
[3] 陈学军. 步进电机细分驱动控制系统的研究与实现[J]. 电机与控制应用, 2006, 33(6): 48-50.
Chen Xuejun. Research and realization of subdivided driving system of stepping motor[J]. Electric Machines & Control Application, 2006, 33(6): 48-50.
[4] Schweid S A, Lofthus R M, McInroy J E, et al. Hybrid step motor position estimation from back EMF[C]// Proceedings of International Conference on Control Applications, Albany, NY, USA, 2002: 774-778.
[5] Le K M, Van Hoang H, Jeon J W. An advanced closed-loop control to improve the performance of hybrid stepper motors[J]. IEEE Transactions on Power Electronics, 2017, 32(9): 7244-7255.
[6] Le Q N, Jeon J W. Neural-network-based low-speed- damping controller for stepper motor with an FPGA[J]. IEEE Transactions on Industrial Electronics, 2010, 57(9): 3167-3180.
[7] 葛扬, 宋卫章, 杨洋. 基于扩张式主从自适应陷波滤波器与动态频率跟踪的永磁同步电机无传感器控制[J]. 电工技术学报, 2023, 38(14): 3824-3835.
Ge Yang, Song Weizhang, Yang Yang. PMSM sensorless control based on extended master-slave adaptive Notch filter and dynamic frequency tracking[J]. Transactions of China Electrotechnical Society, 2023, 38(14): 3824-3835.
[8] 孙明阳, 和阳, 邱先群, 等. 随机频率三角波注入永磁同步电机无位置传感器降噪控制[J]. 电工技术学报, 2023, 38(6): 1460-1471.
Sun Mingyang, He Yang, Qiu Xianqun, et al. Random-frequency triangular wave injection based sensorless control of PMSM drives for audible noise reduction[J]. Transactions of China Electrotechnical Society, 2023, 38(6): 1460-1471.
[9] Xu Wei, Jiang Yajie, Mu Chaoxu, et al. Improved nonlinear flux observer-based second-order SOIFO for PMSM sensorless control[J]. IEEE Transactions on Power Electronics, 2019, 34(1): 565-579.
[10] Yin Guiliang, Guo Lei, Li Xiangnan. An amplitude adaptive Notch filter for grid signal processing[J]. IEEE Transactions on Power Electronics, 2013, 28(6): 2638-2641.
[11] 刘宁, 夏长亮, 周湛清, 等. 基于比例增益补偿的永磁同步电机转速平滑控制[J]. 电工技术学报, 2018, 33(17): 4007-4015.
Liu Ning, Xia Changliang, Zhou Zhanqing, et al. Smooth speed control for permanent magnet syn- chronous motor using proportional gain compen- sation[J]. Transactions of China Electrotechnical Society, 2018, 33(17): 4007-4015.
[12] 陈乾, 陈敏祥, 王宗培. 混合式电机无传感器控制的研究[J]. 机电工程, 2019, 36(6): 642-646.
Chen Qian, Chen Minxiang, Wang Zongpei. Sensor- less control for hybrid motor[J]. Journal of Mechanical & Electrical Engineering, 2019, 36(6): 642-646.
[13] Saadaoui O, Khlaief A, Abassi M, et al. A sliding- mode observer for high-performance sensorless control of PMSM with initial rotor position detection[J]. International Journal of Control, 2017, 90(2): 377-392.
[14] 武志涛, 李帅, 程万胜. 基于扩展滑模扰动观测器的永磁直线同步电机定结构滑模位置跟踪控制[J]. 电工技术学报, 2022, 37(10): 2503-2512.
Wu Zhitao, Li Shuai, Cheng Wansheng. Fixed structure sliding mode position tracking control for permanent magnet linear synchronous motor based on extended sliding mode disturbance observer[J]. Transactions of China Electrotechnical Society, 2022, 37(10): 2503-2512.
[15] Wang Chunlei, Cao Dongxing. New sensorless speed control of a hybrid stepper motor based on fuzzy sliding mode observer[J]. Energies, 2020, 13(18): 4939.
[16] 战家治, 崔皆凡. 基于神经网络的两相混合式步进电机反步控制[J]. 电机与控制应用, 2022, 49(1): 28-33, 55.
Zhan Jiazhi, Cui Jiefan. Backstepping control of two-phase hybrid stepping motor based on neural network[J]. Electric Machines & Control Application, 2022, 49(1): 28-33, 55.
[17] 梅三冠, 卢闻州, 樊启高, 等. 基于滑模观测器误差补偿的永磁同步电机无位置传感器控制策略[J]. 电工技术学报, 2023, 38(2): 398-408.
Mei Sanguan, Lu Wenzhou, Fan Qigao, et al. Sensorless control strategy of permanent magnet synchronous motor based on error compensation estimated by sliding mode observer[J]. Transactions of China Electrotechnical Society, 2023, 38(2): 398-408.
[18] 王光宇, 付立军, 胡祺, 等. 计及电压环影响的虚拟同步发电机低频振荡阻尼分析与控制[J]. 电力系统自动化, 2022, 46(14): 177-184.
Wang Guangyu, Fu Lijun, Hu Qi, et al. Analysis and control of low-frequency oscillation damping of virtual synchronous generator considering influence of voltage loop[J]. Automation of Electric Power Systems, 2022, 46(14): 177-184.
[19] 章春娟, 王慧贞, 刘伟峰, 等. 基于宽频带同步基频提取滤波器的永磁同步电机转子位置与转速估计[J]. 电工技术学报, 2022, 37(4): 882-891.
Zhang Chunjuan, Wang Huizhen, Liu Weifeng, et al. Rotor position and speed estimation of permanent magnet synchronous motor based on wideband syn- chronous FundamentalFrequency extraction filter[J]. Transactions of China Electrotechnical Society, 2022, 37(4): 882-891.
[20] Liu Gang, Zhang Haifeng, Song Xinda. Position- estimation deviation-suppression technology of PMSM combining phase self-compensation SMO and feed-forward PLL[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2021, 9(1): 335-344.
Active Damping Control of Hybrid Stepper Motor Based on ESMO-DPLL
Abstract Hybrid stepper motors (HSM) have gained significant attention in the motor control field due to their ability to achieve energy conversion with high reliability, efficiency, and affordability. However, the mechanical structure of the stepper motor often results in undesired jitter vibration and out-of-step problems during operation because it relies on open-loop control. This paper introduces an active damping control method for hybrid stepper motors based on ESMO-DPLL.
The method is based on the motor model under the synchronous rotating coordinate system. The control of the current id is kept constant at the current rating, while the current iq is adjusted according to the speed error to enhance motor damping and suppress oscillation during operation. Combined with an extended sliding mode observer (ESMO) and a dual phase locked loop (DPLL), a sensorless control method is introduced to achieve closed-loop speed control. ESMO employs the inverse potential as an extended state variable and replaces the traditional state variable with a saturation function.
To verify the effectiveness of the ESMO observation method, the motor speed is set to be constant at 300 Hz and 500 Hz, respectively, and the experimental results of the inverse electromotive force obtained by the traditional SMO and ESMO methods are compared. The results demonstrate that the ESMO observation method effectively addresses the jitter problem of the traditional sliding mode observer and provides a more accurate estimate of the inverse electromotive force.
Furthermore, the effectiveness of the ESMO-DPLL-based closed-loop active damping control for hybrid stepper motors in suppressing system oscillations is verified by comparing speed curves between undamped and damped control at different speeds. The motor is accelerated from a standstill to 10 Hz and then decelerated to 0 Hz. In undamped control, the maximum actual speed error between the actual speed and the estimated speed is approximately 5 Hz, while in damped control, it is reduced to 4 Hz. Similarly, when the motor accelerates from a standstill to 300 Hz and decelerates back to the standstill, the undamped control exhibits significant speed oscillations with a maximum actual speed error of about 75 Hz. With damping control, the motor's oscillation amplitude is noticeably reduced, and the maximum speed error is around 30 Hz. Likewise, when the motor accelerates from 0 Hz to 500 Hz and then decelerates to a standstill, the undamped control results in pronounced speed oscillations with a maximum actual speed error of about 65 Hz. The damping control significantly suppresses motor speed oscillation, reducing the maximum actual speed error to approximately 30 Hz.
The experimental results have demonstrated that the proposed ESMO-DPLL-based active damping control method effectively suppresses oscillation during the operation of hybrid stepper motors, enabling smooth motor operation. Overall, this control scheme successfully addresses the damping shortcomings of stepper motors and effectively inhibits oscillation during actual operation.
Keywords:Hybrid stepper motor, closed-loop control, active damping control, phase locked loop, sliding mode observer
中图分类号:TM383.6
DOI: 10.19595/j.cnki.1000-6753.tces.231049
辽宁省自然科学基金计划(2022-KF-14-03)和特种电机与高压电器教育部重点实验室开放课题项目(KFKT202104)资助。
收稿日期 2023-07-04
改稿日期 2023-09-18
施 雨 女,1997年生,硕士研究生,研究方向为混合式步进电机的控制。
E-mail: sshhiyu@163.com
武志涛 男,1981年生,博士,副教授,研究方向为直线电机伺服驱动技术。
E-mail: aswzt@163.com(通信作者)
(编辑 崔文静)