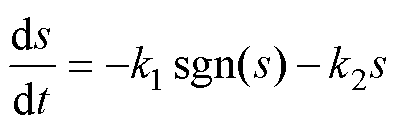 (1)
(1)
摘要 针对开关磁阻电机运行时存在的转矩波动大与外部干扰下电机运行不稳定等问题,该文提出了一种基于自抗扰滑模控制的开关磁阻电机转矩分配控制策略。由于传统滑模控制中趋近律采用的符号函数引起系统振荡频率高,造成被控对象抖振大,该文采用新型滑模趋近律,用平滑函数代替符号函数,并引入状态变量,同时提升了响应速度并降低抖振;此外,为了解决开关磁阻电机外部干扰对电机运行带来的稳定性问题,该文设计了一种自抗扰扩张状态观测器,这种观测器可以实现对负载扰动的实时观测,将观测值作为滑模速度控制器的前馈补偿,减小电机固有参数不确定对控制系统的影响。最后,通过仿真和实验验证了所提出的方案能够有效地改进控制系统在不同工况下的动态性能。
关键词:开关磁阻电机 转矩分配控制 新型滑模趋近律 自抗扰扩张状态观测器
目前,新能源汽车逐渐受到大众的青睐,电机作为电动系统中至关重要的部件,其使用效率、成本和输出功率等性能是评估的关键[1]。开关磁阻电机(Switched Reluctance Motor, SRM)具有调速范围广、可靠性高、易于控制等多方面的优点,在电动汽车领域具有很强的竞争力[2-4]。但是由于SRM的双凸极结构影响,导致SRM的磁路非线性和强耦合,很难建立理想的数学模型,在实际应用中有较大的转矩波动,限制了SRM在高精度领域的推广[5-8]。如果采用传统的比例积分(Proportional Integral, PI)控制策略,可以在一定的条件下满足控制要求,但是针对电机固有参数不确定和系统易受外部干扰的情况,PI控制很难满足控制精度的需求[9]。
随着现代控制理论的研究深入,一些非线性控制方法的应用从不同方面提高了SRM控制系统的动态性能,目前应用于SRM调速系统的前馈智能控制策略有PI控制、自适应控制、预测控制、滑模控制(Sliding Mode Control, SMC)等。其中,PI控制操作简单,适用于不同的控制对象,但是无法完全消除系统的稳态误差,且可能会出现被控对象的超调现象[10];自适应控制不需要精确的系统模型,但是对参数的依赖性较高,如果超出参数的阈值,会导致控制系统的振荡[11];预测控制可以预测系统未来的状态并做出调整,可是受模型准确度的影响较大[12];SMC通过设计的滑模面和趋近律使系统运动点趋近于滑模面,并在滑模面上运动[13],在系统数学模型非线性的场合中体现出较好的鲁棒性,且响应速度快,有良好的研究前景。文献[14-15]利用神经网络算法设计滑模控制器,减少了系统运动点趋近于滑模面的时间,且提高了系统的鲁棒性,但是神经网络算法需要大量的数据支撑,在线运算量大,对控制器的要求较高;文献[16]通过引入系统状态变量来设计滑模趋近律,有效减小了稳态误差,但是在趋近律中由于使用的符号函数切换频率高,会造成较大的系统抖振,降低了趋近运动到滑模面的动态品质;文献[17-18]利用非奇异快速终端滑模控制来设计控制器,提升了系统的响应速度,保证跟踪误差在有效时间收敛,但是算法的复杂性对控制器的精度要求高,当出现外部干扰时可能会造成系统不稳定。为了进一步提升SMC的性能,本文设计了一种新型滑模趋近律,提高了系统的响应速度,且在干扰较小时对抑制抖振有较好的效果。
文献[19]采用了饱和函数来设计趋近律,进一步抑制了转矩波动,但是对于扰动较大或扰动上限不确定的场合,为了保证系统的响应速度,需要设置趋近律增益为足够大,这样会导致系统的抖振变大。如果开关增益设置得较小,则会降低系统的抗干扰和快速反应的能力。为了解决这个问题,文献[20]设计了负载转矩观测值自适应律,减小了算法的复杂性,但是在系统非线性的情况下要达到稳定状态,对自适应律的取值要求较高,在一定程度上降低了系统的鲁棒性。因此,本文引入了扩张状态观测器(Extended State Observer, ESO)来整定系统扰动。ESO估计了系统集总扰动,即内部扰动和外部扰动,此方法不需要精确的被控对象模型,就能对系统的不确定性进行较好的整定,适合固有参数不确定的非线性系统[21]。本文利用ESO整定SRM全速工况下的负载转矩,作为滑模速度控制器的前馈补偿,提高系统的稳定性。
转矩分配函数法(Torque Sharing Function, TSF)是SRM的一种转矩控制策略,TSF利用编写的最佳转矩分配函数输出各相的转矩参考值,再经过转矩滞环比较器控制各相的开关[22-23]。本文提出一种基于自抗扰滑模控制(Active Disturbance Rejection Sliding Mode Control, ADRSMC)的开关磁阻电机转矩分配控制策略,将自抗扰扩张状态观测器和滑模速度控制器复合控制作用在速度环,旨在加快控制系统的响应速度,抑制转矩波动,增强系统的抗干扰性。
在滑模控制中,趋近律的品质决定了系统的动态性能,传统指数趋近律可表示为
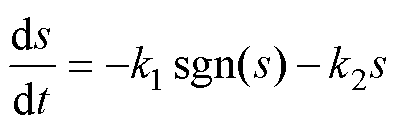 (1)
(1)
式中,ds/dt为滑模面函数关于时间的变化率;k1、k2为趋近律正系数;t为时间;s为滑模面;sgn(s)为符号函数。
对式(1)两边从t=0时刻到系统到达滑模面的时间ta积分,可从数学方面求得系统到达滑模面所需的时间,其中,s(ta)=0。
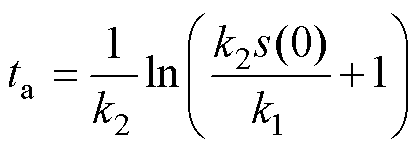 (2)
(2)
式中,s(0)为初始滑模面位置。
根据图1所示的滑模控制轨迹可以观察到,系统运动点的轨迹可分为两个主要阶段:系统从当前状态运动至滑模面的趋近运动和在滑模面上的滑动模态运动,且选取的趋近律会直接影响趋近运动的时间。
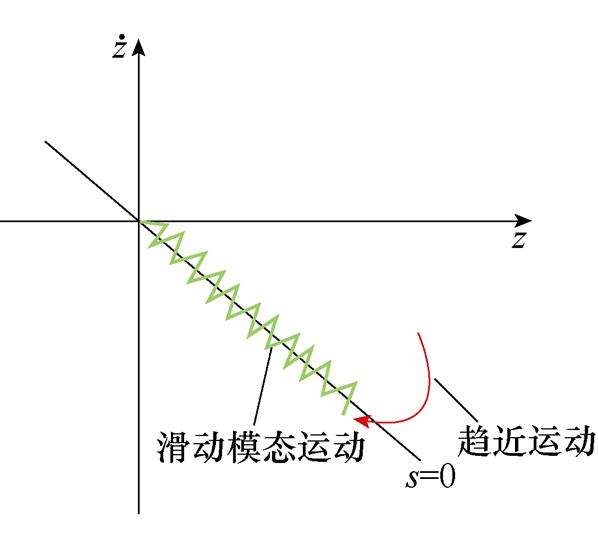
图1 滑模控制轨迹
Fig.1 Trajectory of sliding mode control
传统指数趋近律由等速趋近项和指数趋近项组成,其中,符号函数sgn(s)导致了系统的切换频率高,造成抖振较大,因此,可以利用平滑曲线来克服sgn(s)函数造成的滞后性。此外,当系统的初始状态和预期状态相差较大时,趋近律仍是固定的开关增益,造成了系统响应的延迟,本文引入状态变量,可以随着系统状态的改变来调节增益大小。
本文提出的新型滑模趋近律有以下的优势:
(1)引入系统状态变量,可以随着系统运动点的变化调整状态变量的值,提升系统的动态性能。
(2)用平滑函数H(s)代替传统指数趋近律中的符号函数sgn(s),减小较大的切换频率带来的系统抖振,H(s)的表达式为
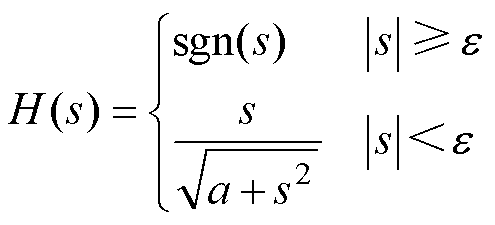 (3)
(3)
式中,参数a为H(s)的补偿系数;e 为函数分段点。
将式(3)代入新型滑模趋近律,有
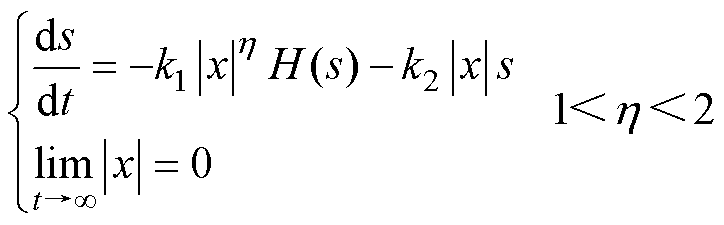 (4)
(4)
式中,x为系统状态变量,代表系统状态点到滑模面的距离;h 为状态变量的幂次项。
H(s)函数使运动点平滑快速地运动到达滑模面,当系统运动点远离滑模面时,状态变量x以较大的值保证运动点能快速趋近滑模面;当系统运动点即将到达滑模面时,状态变量x逐渐减小,达到抑制抖振的效果。
传统指数趋近律采用符号函数sgn(s),如图2a所示。新型滑模趋近律利用H(s)函数的平滑特性改善了传统指数趋近律由于切换频率高造成系统抖振大的问题。其中,参数a决定了H(s)函数的平滑连续性,假设e=20,当|s|≤e 时,H(s)函数如图2b所示。
从图2b可以看出,当a=0.1时,H(s)在趋近于0时发生了曲折;当a=10时,H(s)的幅值较小,趋近速度较慢,为了兼顾H(s)的平滑性和运动速度,本文取a=1,可以减少系统抖振,且保证系统的响应速度。
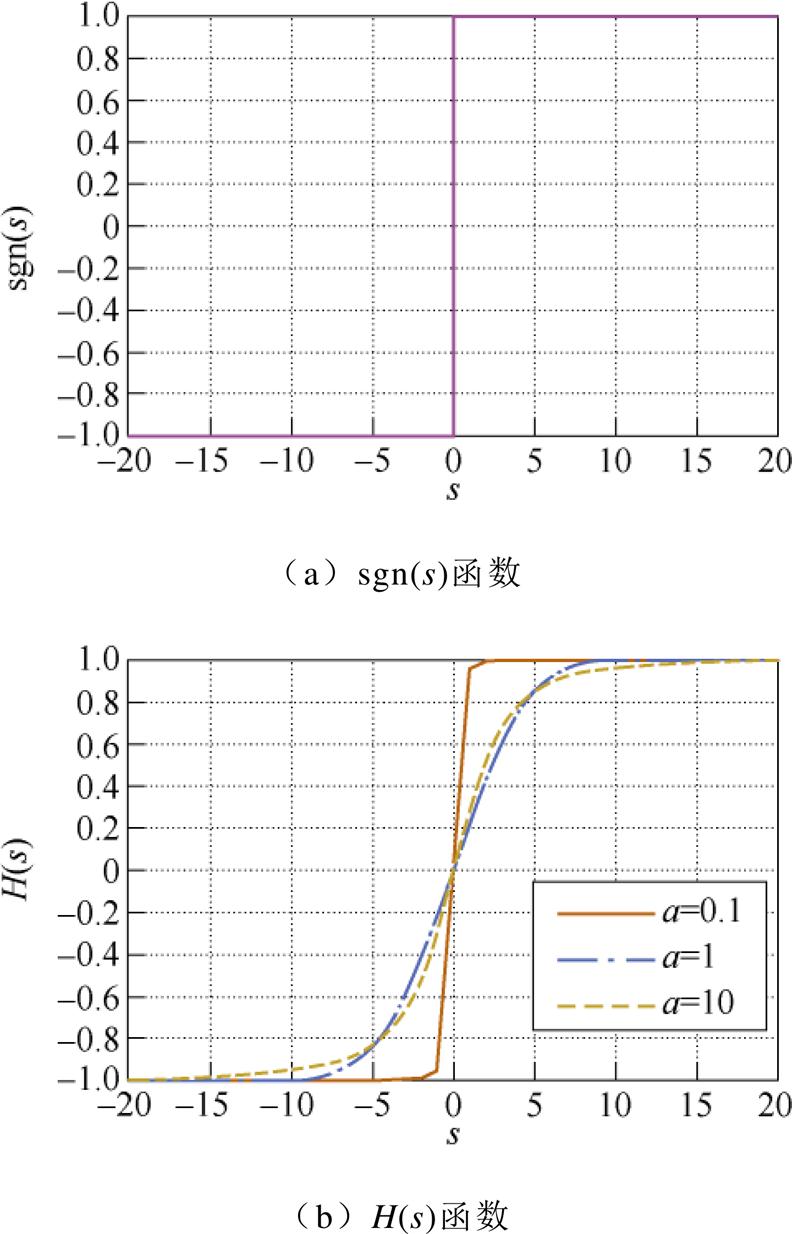
图2 sgn(s)和H(s)的函数曲线
Fig.2 Function curves of sgn(s) and H(s)
为了说明设计的滑模趋近律的稳定性,选择李雅普诺夫函数
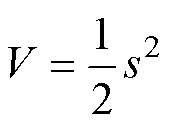 (5)
(5)
对式(5)求导,得到
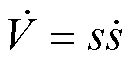 (6)
(6)
为了满足稳定性,新型滑模趋近律需要满足
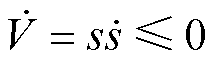 (7)
(7)
将式(4)代入式(6)中,有
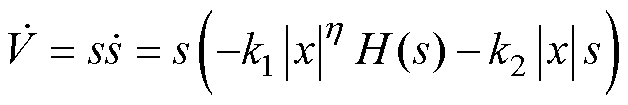 (8)
(8)
根据图2b可以看出,当s>0时,H(s)的任意值都为正,且所用的系数都为正,所以式(8)中的k1|x|hH(s)项为正,且k2|x|s项也为正,可以得到s关于时间t的一阶导数的任意值为负,满足s和s关于时间t的一阶导数的任意值异号;同理,当s<0时,s关于时间t的一阶导数的任意值为正,满足s和s关于时间t的一阶导数的任意值异号;当s=0时,H(s)的任意值都为0,则s关于时间t的一阶导数的任意值为0。综上,新型滑模趋近律满足
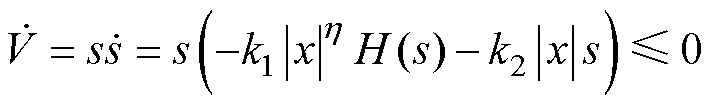 (9)
(9)
即设计的滑模速度控制器是稳定的。
但是,李雅普诺夫函数往往只用于评估系统运动的稳定性,而不能用于体现动态性能的优越性。下面简单验证了新型滑模趋近律的动力学性能。
当|s|≥e 时,|x|≥1,根据数学方程的推导,将式(4)两边对时间进行积分,表示为
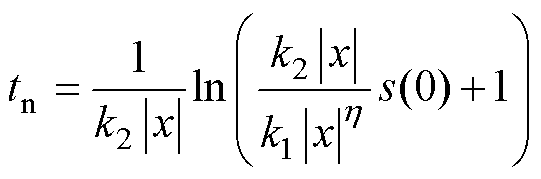 (10)
(10)
式中,tn为采用新型滑模趋近律的系统运动点到达滑模面的时间。
根据式(2)可知,采用传统指数趋近律下系统运动点到达滑模面的时间为ta,对式(10)进行不等式的放缩,可得
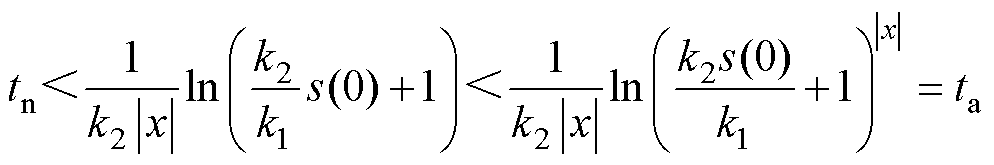 (11)
(11)
进一步可说明
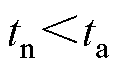 (12)
(12)
当|s|<e 时可以得到相同的结论。因此,可以说明新型滑模趋近律的趋近速度快于传统指数趋近律。
SRM的机械运动方程表达式为
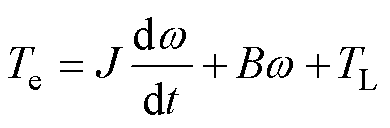 (13)
(13)
式中,w 为电机机械角速度;J为电机转动惯量;B为黏性摩擦因数;Te为总电磁转矩;TL为负载转矩。
图3为12/8的SRM静态转矩。
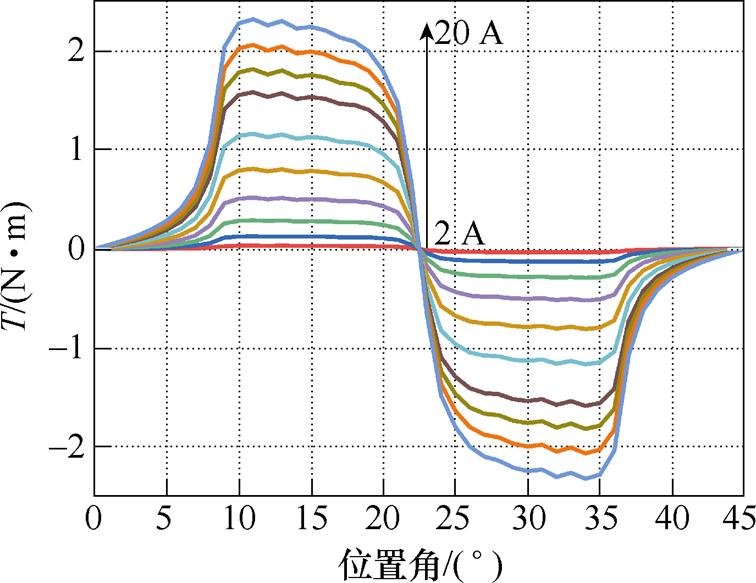
图3 12/8 SRM静态转矩
Fig.3 Static torque diagram of 12/8 SRM
三相SRM总电磁转矩为
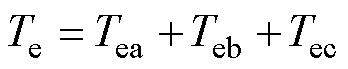 (14)
(14)
式中,Tea、Teb、Tec分别为A、B、C三相的电磁转矩。
本文采用正弦型转矩分配函数,其中,第i相转矩的正弦型分配函数表示为
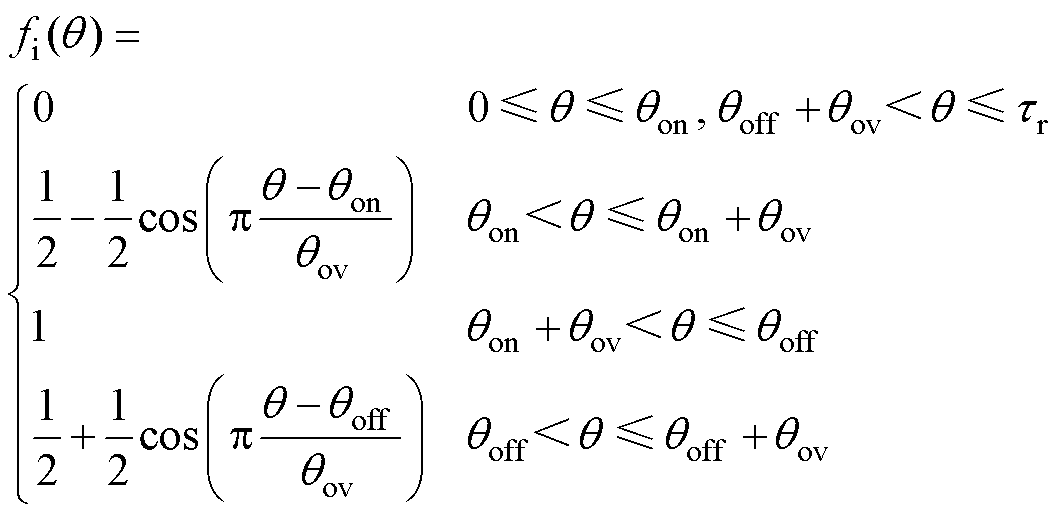 (15)
(15)
式中,q 为各相的转子位置角;qon和qoff分别为开通角度和关断角度;qov为换相重叠角度;tr为转子角度周期。
图4为传统SMC的三相12/8 SRM控制框图,采用SMC控制器作为TSF的输入,外环为速度环,内环为转矩环,通过TSF模块输出各相转矩参考值,与各相实际转矩滞环比较后输出开关信号。
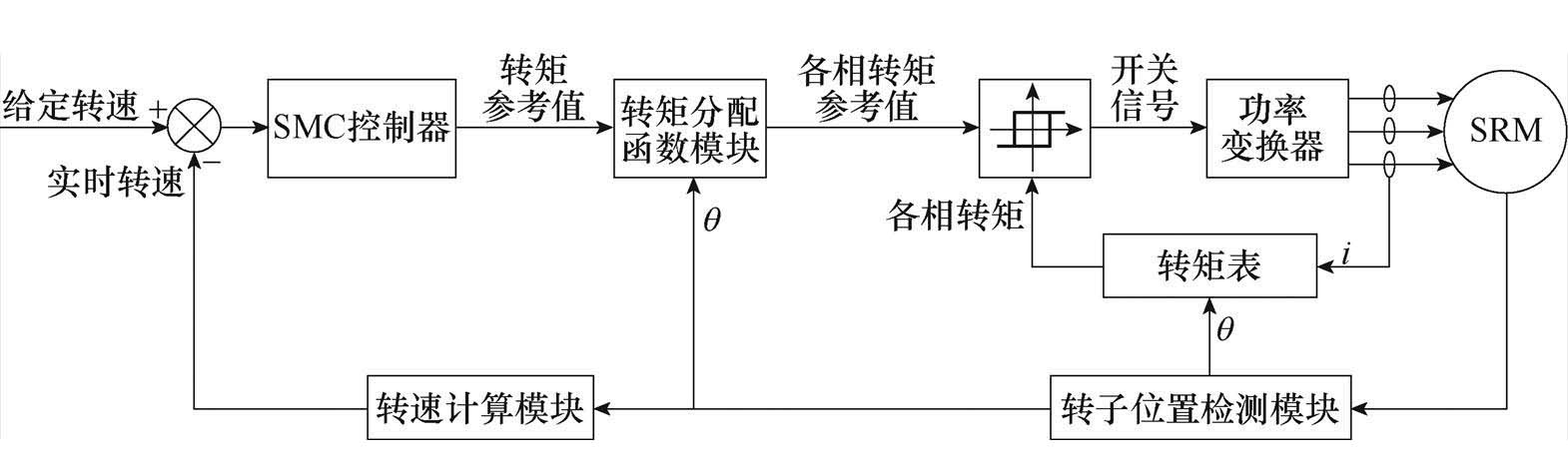
图4 传统SMC的三相SRM 控制框图
Fig.4 Three-phase SRM control block diagram of traditional SMC
由于SMC策略中采用的传统指数趋近律会造成参数随系统状态变化不灵敏和稳态抖振较大的问题,为了有效降低跟踪误差,实现对电机给定转速的精确跟踪,本节介绍了基于新型滑模趋近律的滑模速度控制器设计。
根据式(13),得到电机实时转速的一阶导数为
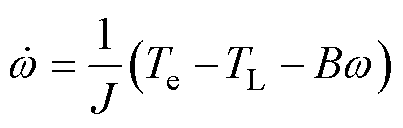 (16)
(16)
式中,w 为电机实时转速。
速度控制器必须满足电机实时转速能跟踪电机给定的转速,将速度误差定义为
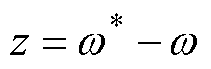 (17)
(17)
式中,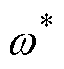 为电机给定转速;z为电机给定转速和实时转速的偏差量。
为电机给定转速;z为电机给定转速和实时转速的偏差量。
滑模速度控制器的设计分为两个步骤:首先是设计合适的滑模面;其次是基于新型滑模趋近律设计滑模速度控制器。
对比传统的线性滑模面,传统的积分滑模面能有效减小系统抖振,其中,比例项用于修正状态偏差,积分项用于抑制系统的稳态偏差,但是如果采用固定的积分项增益,系统的收敛效果较差,因此将式(4)中的系统状态变量代入传统的积分滑模面,以提高系统的收敛效果。本文结合电机转速对控制器的直接影响,将式(17)中的电机转速偏差量z代入改进的积分滑模面,有
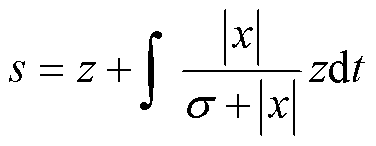 (18)
(18)
式中,s 为积分项的补偿系数。
令式(18)等于0,得到
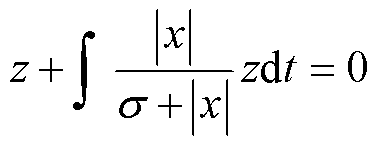 (19)
(19)
对式(19)两边求导,得到
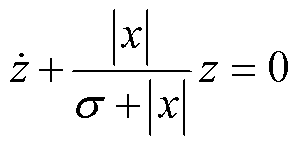 (20)
(20)
通过解微分方程,可得出转速误差z和时间t的关系式为
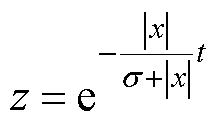 (21)
(21)
根据式(21)能看出,可以通过改变系统状态变量来调节系统的运动速率,当系统做滑动模态运动时,系统的运动速率随状态变量的变小而减慢,提高系统的收敛性。
将式(17)代入式(18)中,并求导得到
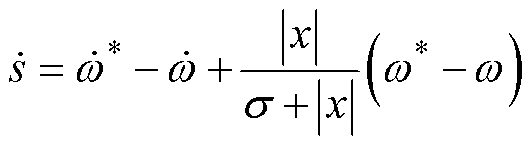 (22)
(22)
考虑到SRM的机械方程,将式(16)代入式(22)中,得到
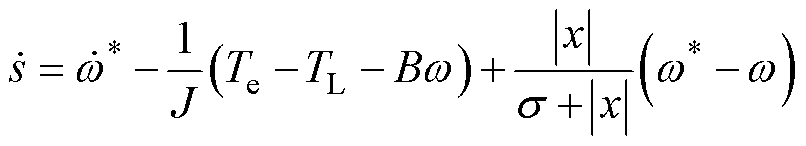 (23)
(23)
引入所设计的新型滑模趋近律,将式(4)代入式(23)中,得到
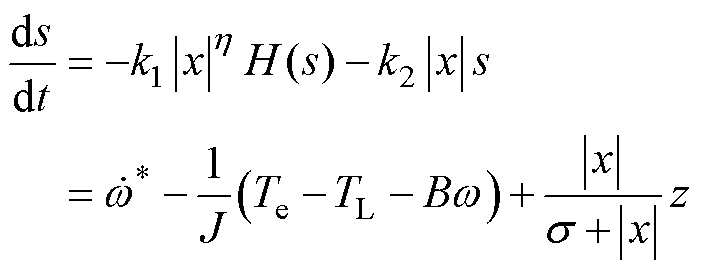 (24)
(24)
最后,基于新型滑模趋近律的滑模速度控制器输出的电磁转矩参考值为
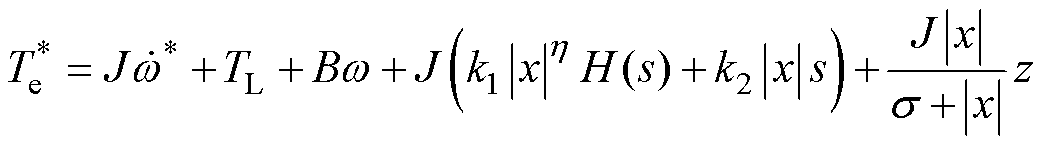 (25)
(25)
式中,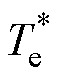 为电机电磁转矩参考值。
为电机电磁转矩参考值。
图5为滑模速度控制器的控制框图,由改进的积分滑模面和新型滑模趋近律组成,可以通过Matlab/Simulink在仿真中搭建算法模型。
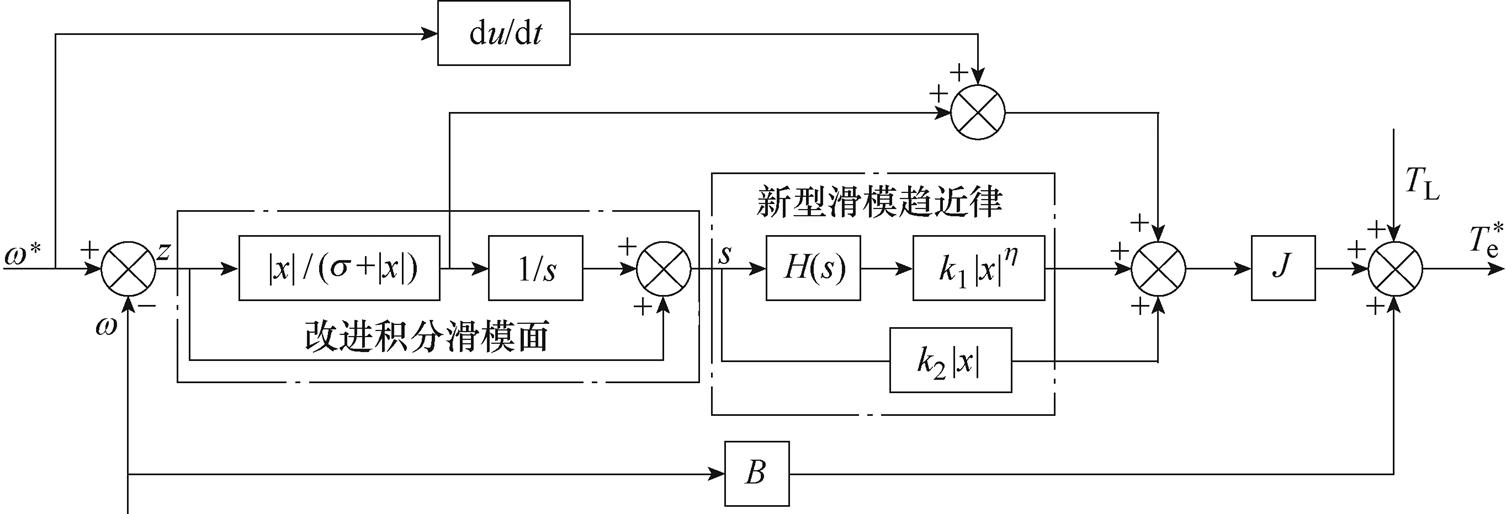
图5 滑模速度控制器设计
Fig.5 Design diagram of sliding mode speed controller
SMC本质是一种开关控制,为了提高响应速度,SMC的开关增益通常选择较大的值,会降低系统的稳定性,且SRM运行时由于负载扰动的影响会造成系统在变速变载时产生转速波动。为了进一步提高SRM控制器的抗干扰性能,本文采用自抗扰扩张状态观测器在线估计控制系统的集总扰动,作为滑模速度控制器的前馈补偿,提高系统稳定性。
将参数不确定的因素考虑进式(16)中,可得
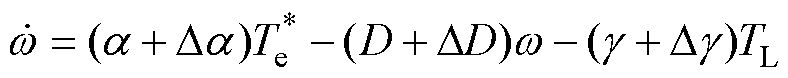 (26)
(26)
其中
a =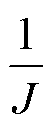 D=
D=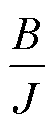 g =
g =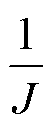
式中,Da、DD和Dg 分别为对应参数的变化量。
将式(26)进行拆分,可得
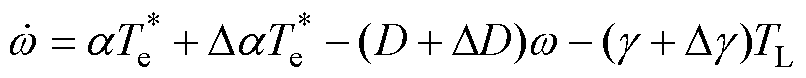 (27)
(27)
引入参数r、d,有
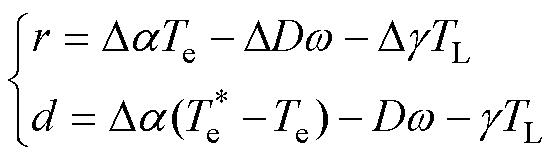 (28)
(28)
式中,r为不确定参数适应值;d为系统总扰动量。
将式(28)代入式(27)中,得到
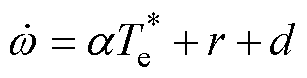 (29)
(29)
引入二阶单输入单输出的系统方程为
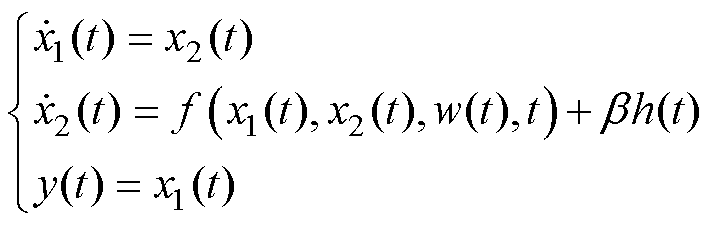 (30)
(30)
式中,y(t)为控制输出函数;x1(t)为过渡函数;x2(t)为控制输出关于时间的导函数;f(x1(t), x2(t), w(t), t)为系统状态和外部干扰关于时间的非线性扰动函数;w(t)为外部干扰;系数b 为补偿因子;h(t)为控制输入函数。
根据式(29)和式(30),将d看作新的集总扰动,h1(t)代替x2(t),h2(t)代表d的观测值,重构自抗扰扩张状态观测器方程为
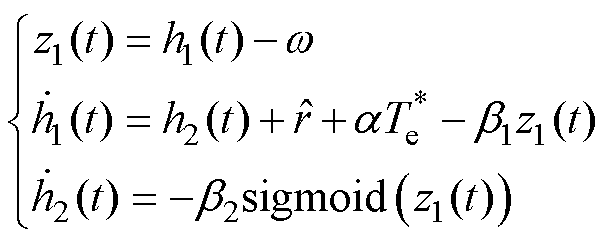 (31)
(31)
式中,z1(t)为误差关于时间的函数;b1、b2为自抗扰扩张状态观测器的增益;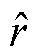 为不确定参数适应值的观测量;h1(t)为速度反馈信号观测量;h2(t)为系统总扰动观测量。
为不确定参数适应值的观测量;h1(t)为速度反馈信号观测量;h2(t)为系统总扰动观测量。
其中,sigmoid(z1(t))函数表示为
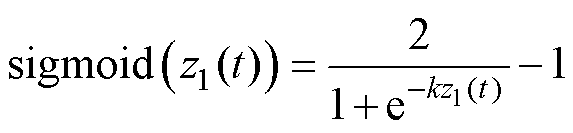 (32)
(32)
式中,k为自变量正系数。
引入式(17)的电机转速偏差量z,式(31)中不确定参数适应值r的观测量随时间的一阶导数表示为
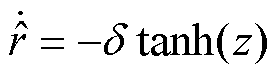 (33)
(33)
式中,d 为补偿因子。
根据式(17)和式(29),可以将电机速度偏差量z的一阶导数表示为
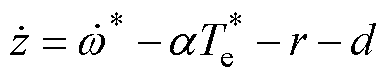 (34)
(34)
结合式(4)、式(18)和式(34),可得到基于自抗扰扩张状态观测器的开关磁阻电机滑模速度控制器输出为
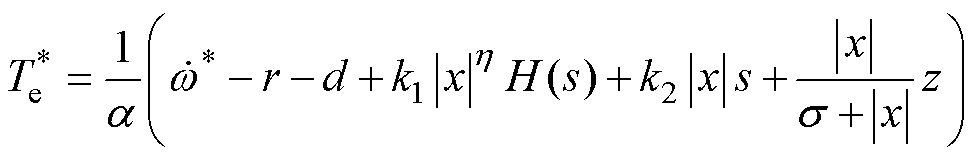 (35)
(35)
基于ADRSMC策略的控制器原理如图6所示。自抗扰扩张状态观测器估计系统扰动,作为滑模速度控制器的前馈补偿,提高系统的稳定性。
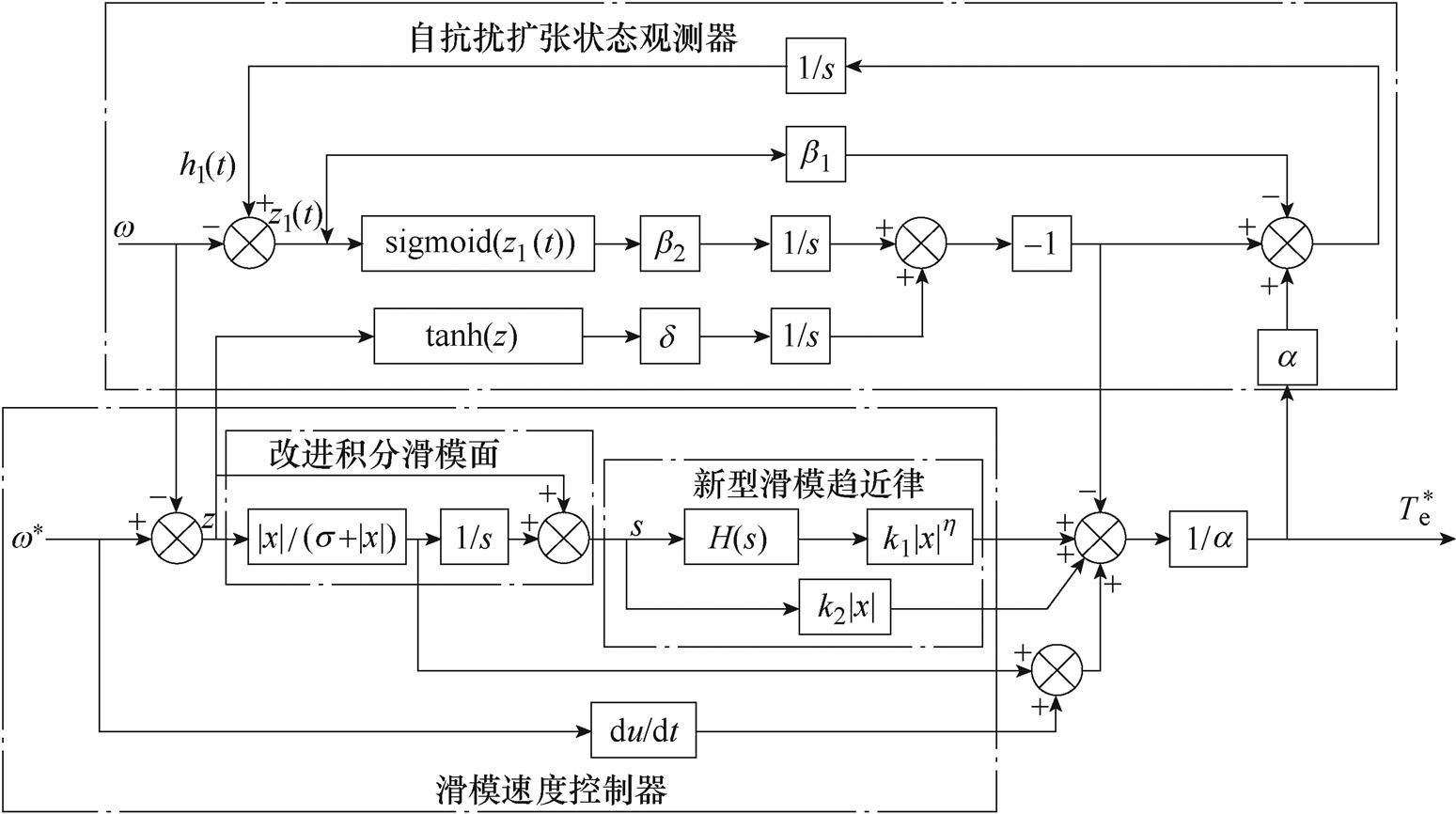
图6 ADRSMC策略原理
Fig.6 Schematic diagram of ADRSMC strategy
为了保证系统的稳定运行,下面对控制系统在自抗扰滑模控制器作用下的稳定性进行分析。
系统扰动误差定义为系统实际扰动和系统扰动观测值的差,即
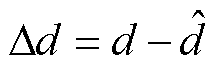 (36)
(36)
式中,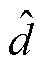 为系统扰动观测值。
为系统扰动观测值。
由于控制系统驱动器通常使用的采样周期为100~200 ms,即系统扰动随时间的一阶导数为0。
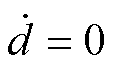 (37)
(37)
选取李雅普诺夫函数为
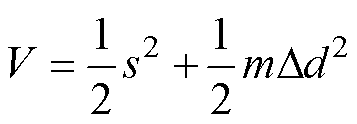 (38)
(38)
式中,m为干扰估计误差Dd的增益,设计[24]为
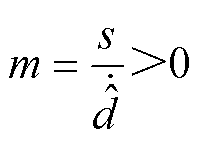 (39)
(39)
结合式(9)、式(22)、式(29)、式(37)和式(39),将式(38)求导可得
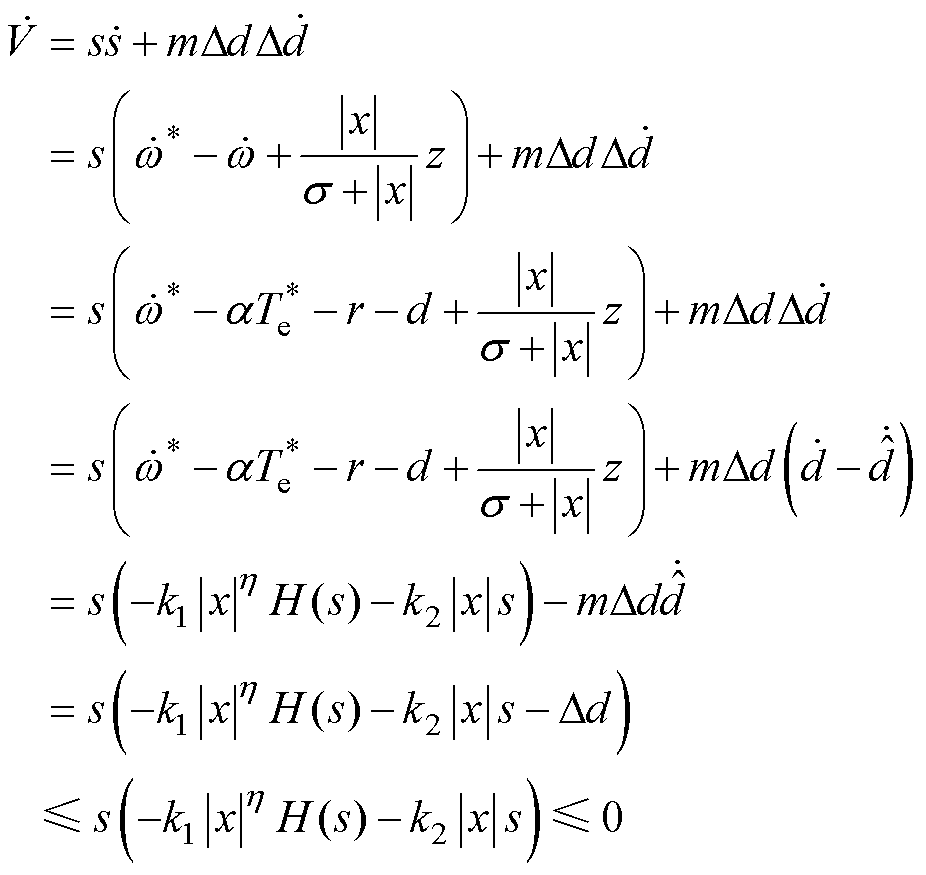 (40)
(40)
由式(40)可知,所设计的自抗扰扩张状态观测器和滑模速度控制器复合作用的控制系统满足李雅普诺夫稳定性理论,验证了基于ADRSMC策略的控制系统可以在有限时间内趋于稳定。
图7为ADRSMC策略的三相SRM控制框图,采用自抗扰滑模速度控制器作为TSF的输入。
根据图7所示原理,以三相12/8结构SRM的TSF控制系统为基础,在Matlab/Simulink中搭建SRM调速系统仿真,在起动、变速、变载工况下分别对PI控制策略、SMC策略和ADRSMC策略下的系统性能进行分析。三相12/8结构SRM的开通角和关断角分别设置为0°和19.5°,负载转矩分别为0.2 N·m和0.5 N·m。其中,PI控制策略参数分别设定为kp=0.05,ki=0.5;SMC策略参数分别设定为k1=1,k2=0.8;ADRSMC策略中滑模控制器参数分别设定为k1=5,k2=2,h=1.2,e=0.8,s=2,a=1,自抗扰扩张状态观测器参数分别设定为b1=150,b2=0.02,k=2,d=50,a=0.05。
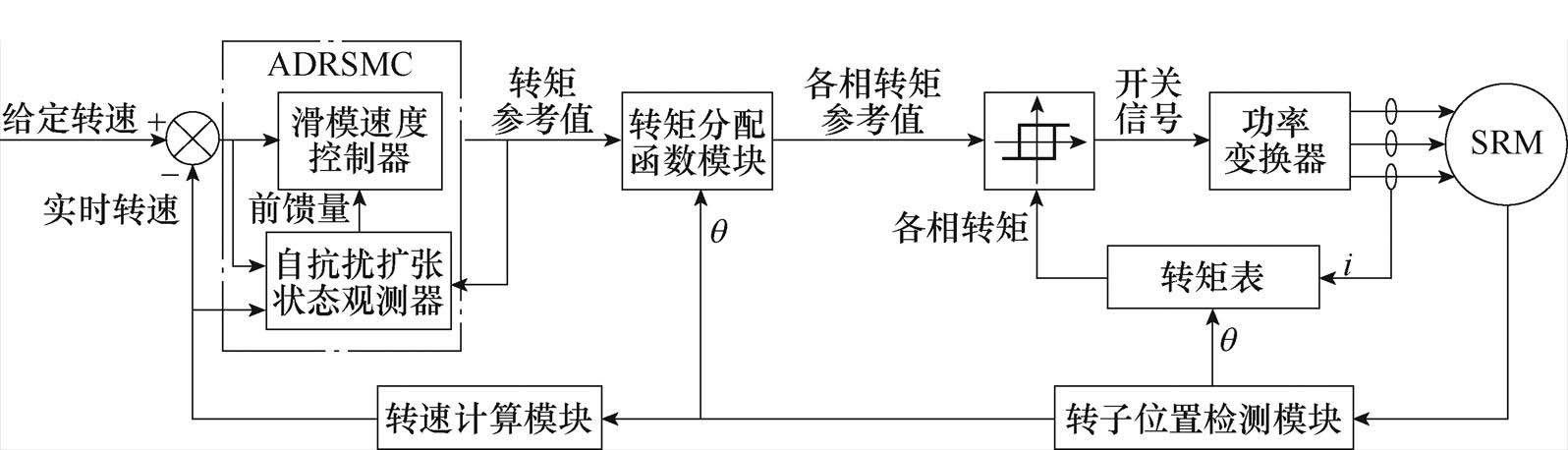
图7 ADRSMC策略的三相SRM 控制框图
Fig.7 Three-phase SRM control block diagram of ADRSMC strategy
图8为负载转矩为0.5 N·m,设定转速分别为500 r/min和1 000 r/min的工况下,SRM处于稳态时的三相电流和转矩波形。可以看出,相较于PI控制策略和SMC策略,采用ADRSMC策略下SRM的转矩波动更小,有效抑制了转矩脉动,且三相电流更加稳定,控制效果有明显的优越性。
在电机稳态运行时,SRM的转矩脉动系数定义为
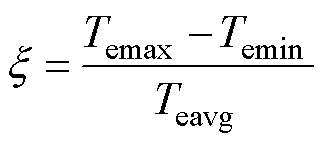 (41)
(41)
式中,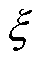 为转矩脉动系数;Temax为转矩最大值;Temin为转矩最小值;Teavg为平均转矩。
为转矩脉动系数;Temax为转矩最大值;Temin为转矩最小值;Teavg为平均转矩。

图8 0.5 N·m的500 r/min和1 000 r/min稳态波形
Fig.8 Steady state waveforms at 500 r/min and 1 000 r/min under 0.5 N·m
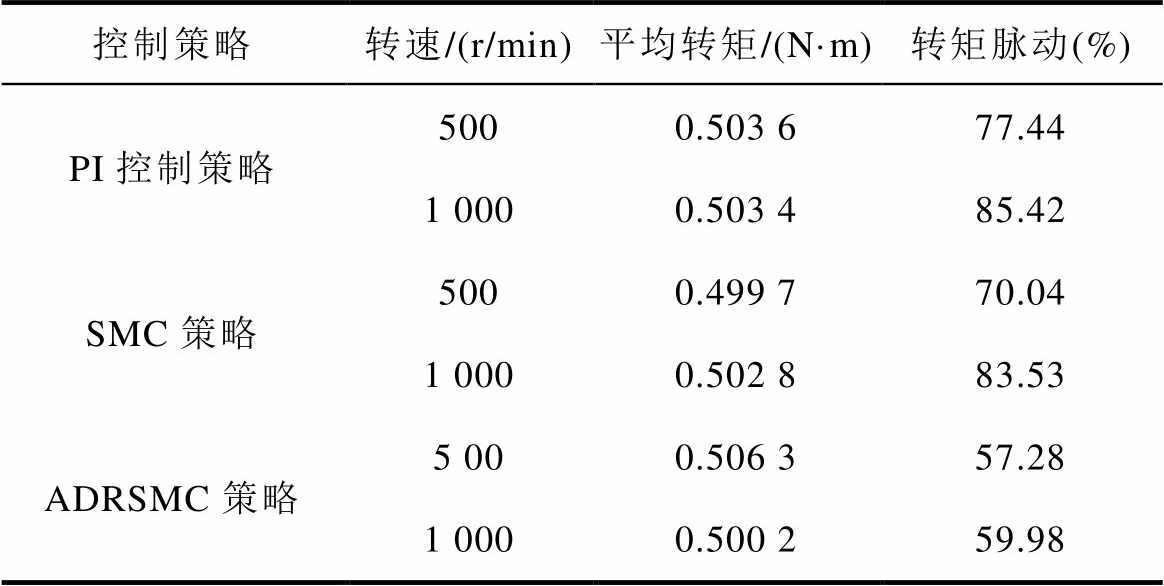
表1给出了负载为0.5 N·m,设定转速分别为500 r/min和1 000 r/min的工况下三种控制策略的电机平均转矩和转矩脉动两个参数,可以看出,采用ADRSMC策略的SRM调速系统有更好的转矩脉动抑制效果。
表1 负载0.5 N·m的电机稳态运行对比
Tab.1 Comparison of steady state motor operation under 0.5 N·m
控制策略转速/(r/min)平均转矩/(N·m)转矩脉动(%) PI控制策略5000.503 677.44 1 0000.503 485.42 SMC策略5000.499 770.04 1 0000.502 883.53 ADRSMC策略5 000.506 357.28 1 0000.500 259.98
图9和图10给出了电机在负载分别为0.2 N·m和0.5 N·m工况下转速突变的波形。首先可以看出电机从起动到稳定在设定转速,采用ADRSMC策略的系统能有效抑制转速的超调,更快趋近于预期转速,体现出良好的动态性能。从图9a和图9b中可看出,当负载转矩为0.2 N·m,转速从500 r/min突变至1 000 r/min,采用PI控制策略和SMC策略分别所用的响应时间为0.44 s和0.12 s;从图9c中可以看出,相较于PI控制策略和SMC策略,采用ADRSMC策略下电机从500 r/min达到1 000 r/min的响应时间为0.08 s。从图10a和图10b中可看出,当负载转矩为0.5 N·m,采用PI控制策略和SMC策略下电机从500 r/min达到1 000 r/min分别所用的响应时间为0.68 s和0.18 s;从图10c可以看出,采用ADRSMC策略下电机从500 r/min达到1 000 r/min的响应时间为0.11 s,相较于PI控制策略和SMC策略,分别缩短了0.57 s和0.07 s。
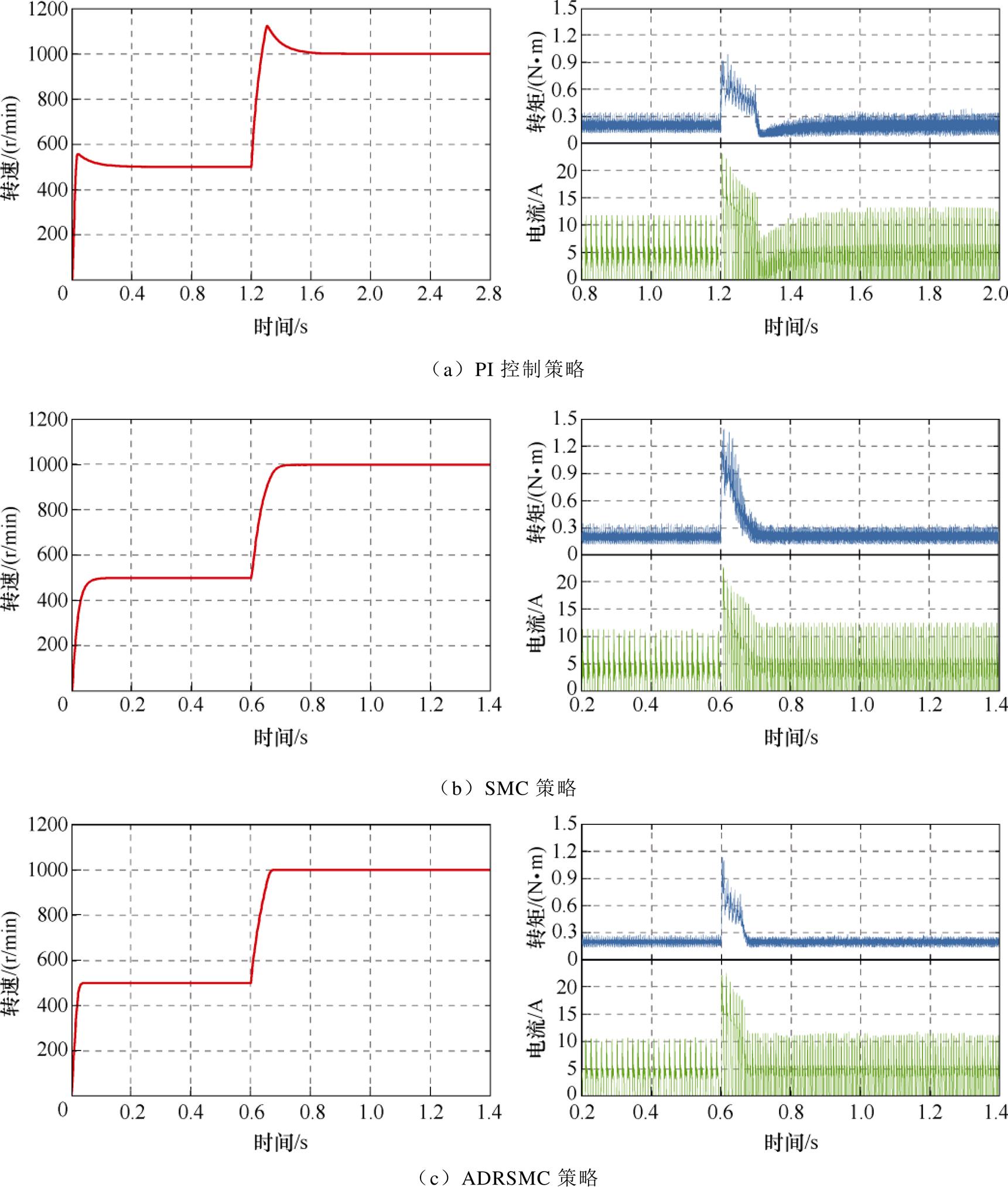
图9 0.2 N·m、变速工况下的波形
Fig.9 Waveforms under 0.2 N·m and variable speed conditions
图11和图12分别给出了SRM在设定转速为500 r/min和1 000 r/min下负载转矩从0.2 N·m突变至0.5 N·m的波形。对比波形可以观察到,当电机负载转矩发生突变时,三种控制策略下的系统都能回到原来的转速。在图11a和图12a中,采用PI控制策略时电机转速下降波动较大,相较图11b和图12b采用的SMC策略,图11c和图12c采用的ADRSMC策略在负载转矩发生突变时,电机能在更短的时间内回到原来的状态,说明基于ADRSMC策略的系统引入的自抗扰扩张状态观测器能有效对负载转矩估计值进行观测,降低负载变化对系统运行的干扰,这进一步证实了该方法能提高系统的鲁棒性。

图10 0.5 N·m、变速工况下的波形
Fig.10 Waveforms under 0.5 N·m and variable speed conditions

图11 500 r/min、变载工况下的波形
Fig.11 Waveforms under 500 r/min and variable load conditions
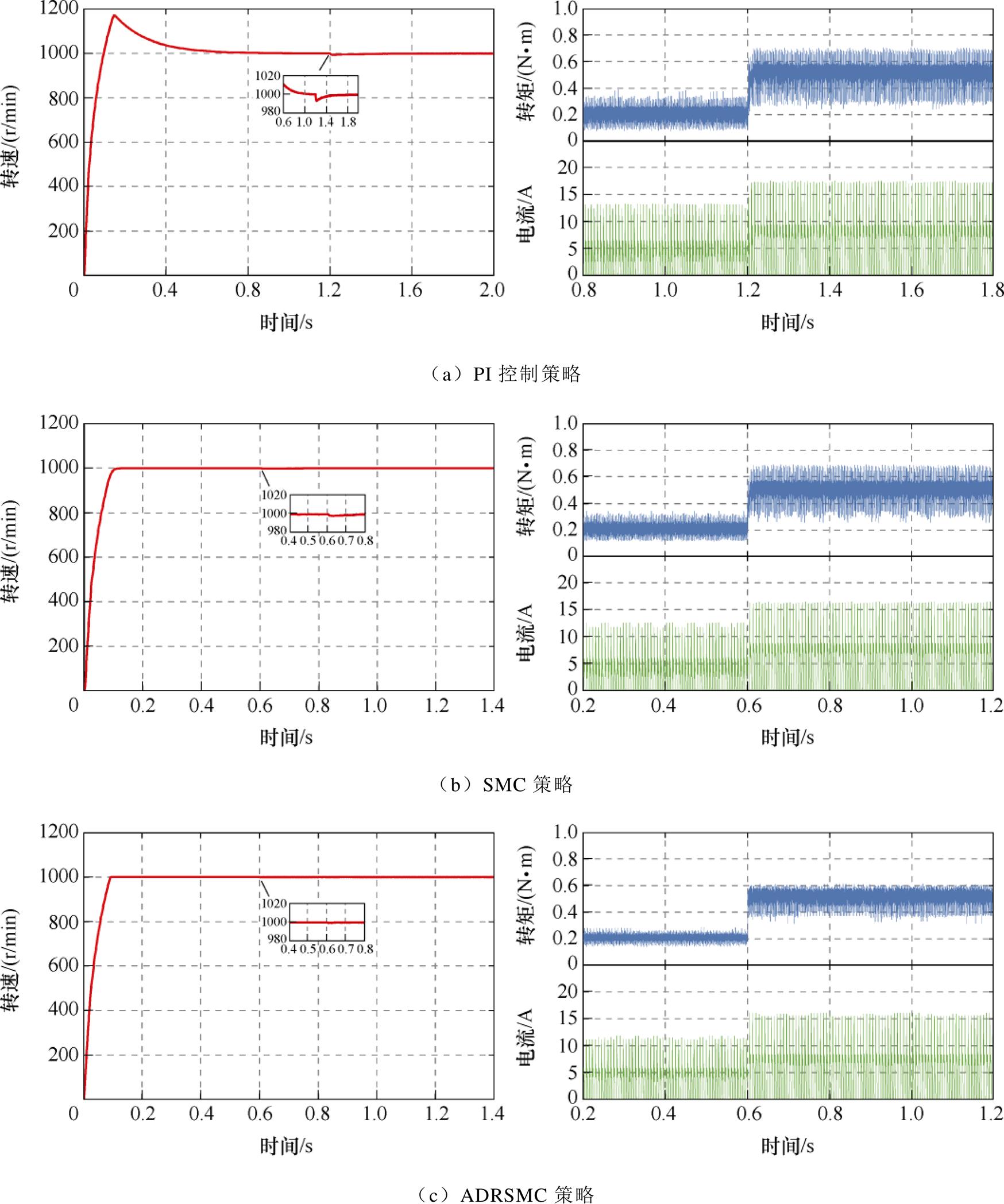
图12 1 000 r/min、变载工况下的波形
Fig.12 Waveforms under 1 000 r/min and variable load conditions
为了验证该方法的有效性,搭建了三相12/8的SRM实验平台,如图13所示。其中,采用一台12/8三相开关磁阻电机,采用三相不对称半桥功率变换器,主控制器为TMS320F28335最小系统板,采样芯片采用AD7606。实验参数和仿真参数一致,表2为所用的开关磁阻电机的主要参数。
图14为负载转矩0.5 N·m工况下电机给定转速分别为500 r/min和1 000 r/min的三相电流和转矩波形。从图14可以看出,采用ADRSMC策略下电流波形展现的效果更好,转矩的波动幅度较小,说明该控制下的电机转速更加稳定,有效抑制了转矩脉动,体现出仿真和实验的对应性。

图13 开关磁阻电机实验平台
Fig.13 Experimental platform of SRM
表2 电机参数
Tab.2 Motor parameters

参 数数 值 电机相数3 定子极数12 转子极数8 额定功率/W100 额定负载/(N·m)0.6 额定转速/(r/min)1 500
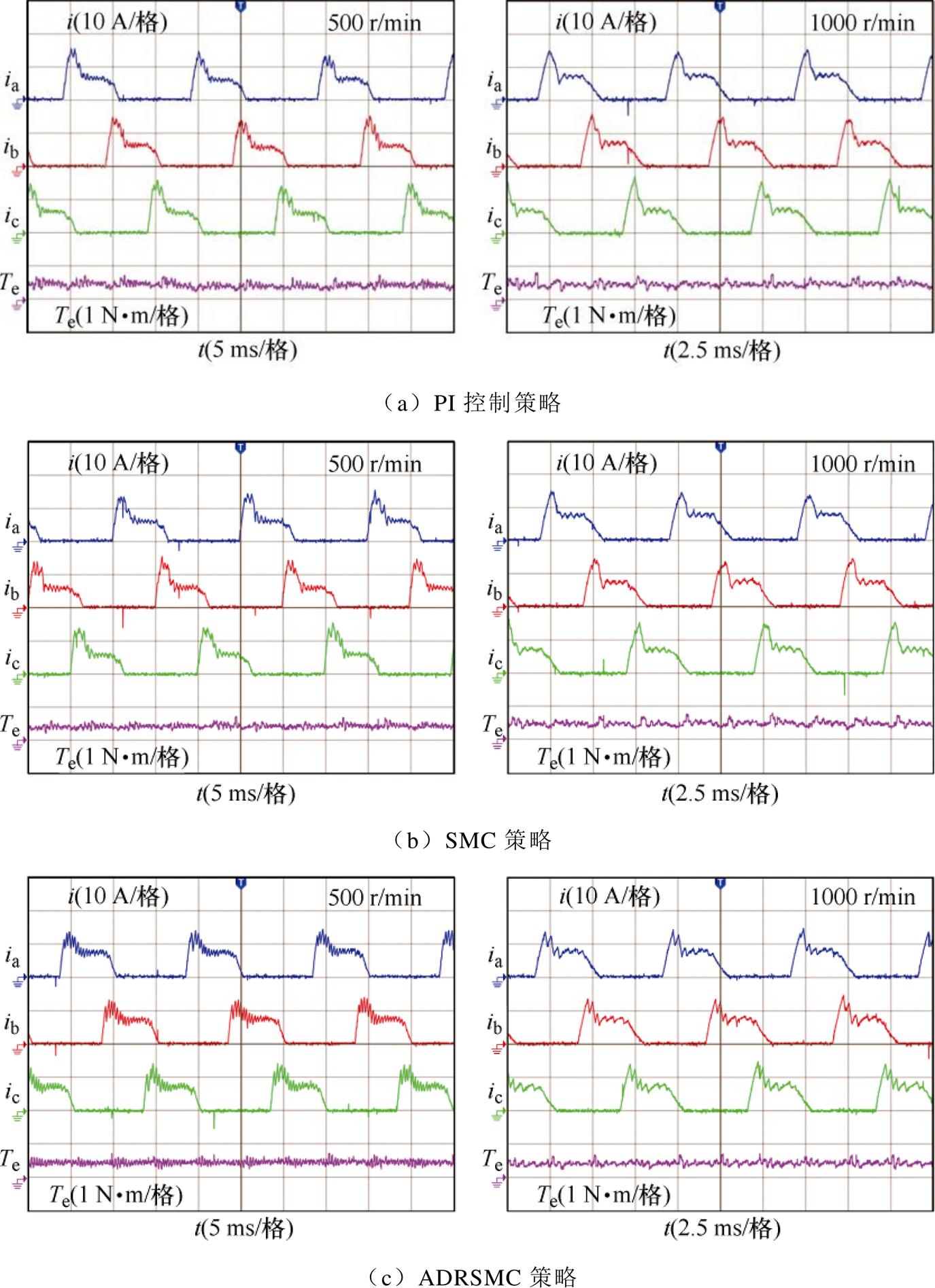
图14 负载0.5 N·m的电机稳态波形
Fig.14 Steady state waveforms of motor at 0.5 N·m
图15给出了SRM在负载转矩为0.2 N·m和0.5 N·m工况下转速突变的波形。可以看出采用ADRSMC策略下电机在起动阶段能快速地跟随预期转速。当负载转矩为0.2 N·m,采用PI控制策略和SMC策略下电机转速从500 r/min突变至1 000 r/min分别所用的时间为0.65 s和0.28 s,采用ADRSMC策略的响应时间为0.1 s。当负载转矩为0.5 N·m,采用PI控制策略和SMC策略下电机转速从500 r/min突变至1 000 r/min分别所用的响应时间为0.73 s和0.5 s,采用ADRSMC策略的响应时间为0.13 s,相较于PI控制策略和SMC策略,分别缩短0.6 s和0.37 s,说明在转速发生突变时,滑模控制策略下的系统克服了PI控制策略超调的影响,且基于ADRSMC策略下电机所用的响应时间更短,减小了电机的抖振对转速的影响,验证了该方法的响应性能的优越性。
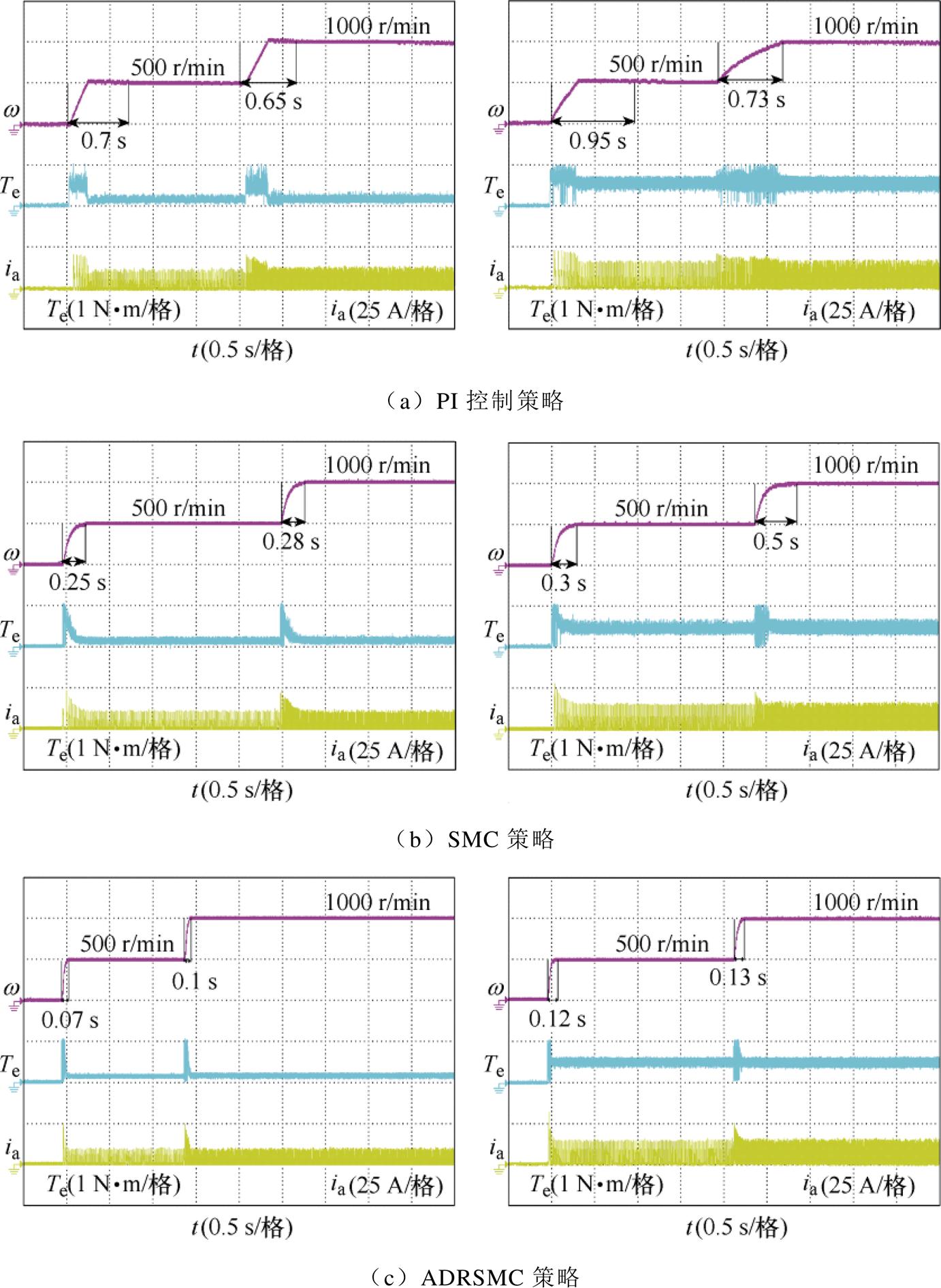
图15 负载0.2 N·m和0.5 N·m的转速突变波形
Fig.15 Speed burst waveforms for loads of 0.2 N·m and 0.5 N·m
图16给出了SRM在设定转速为500 r/min和1 000 r/min下负载转矩从0.2 N·m突变至0.5 N·m的波形。对比波形可以观察到,当电机负载发生突变时,三种控制策略下系统都可以在一定的时间内趋于原来的状态。采用ADRSMC策略时,电机在500 r/min转速下突变负载,电机在0.03 s后回到原来的转速,在1 000 r/min转速下突变负载后回到原来的转速用了0.08 s,相较于PI控制策略和SMC策略,采用ADRSMC策略下突变负载对电机转速的波动影响较小,且能在较短时间内趋于电机原来的状态,这进一步证实了ADRSMC策略具有较好的抗干扰能力。
表3分别给出了PI控制策略、SMC策略和ADRSMC策略下电机运行的性能对比。表中,t为电机响应时间。可以看出,在负载为0.5 N·m,设定转速分别为500 r/min和1 000 r/min的工况下,采用ADRSMC策略有效抑制了电机的转矩脉动,且在变速变载的工况下,相较于PI控制策略和SMC策略,采用ADRSMC策略下电机展现出更快的响应速度。
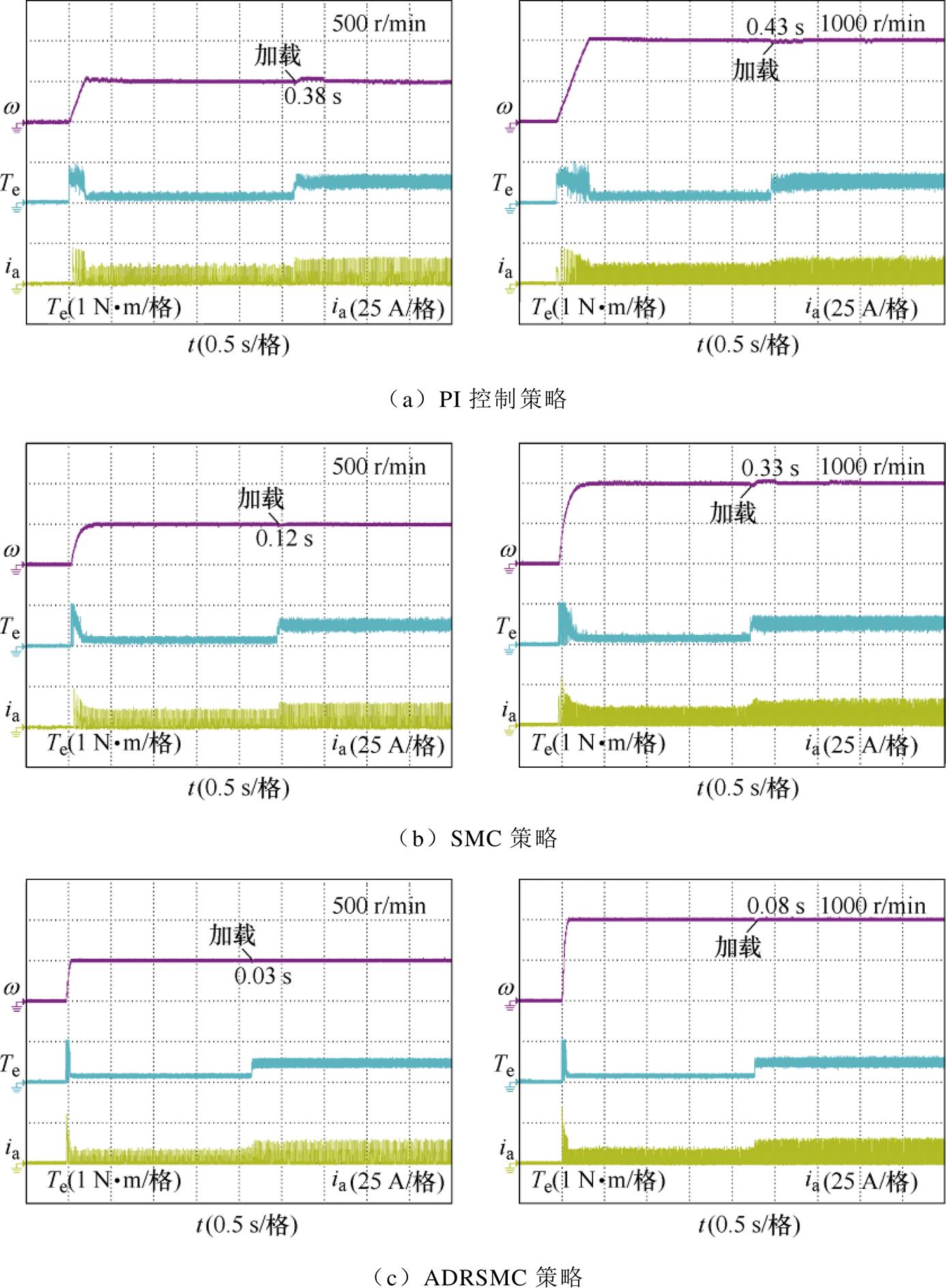
图16 转速500 r/min和1 000 r/min的负载突变波形
Fig.16 Load burst waveforms for speeds of 500 r/min and 1 000 r/min
表3 三种控制策略的性能对比
Tab.3 Performance comparison of three control strategies
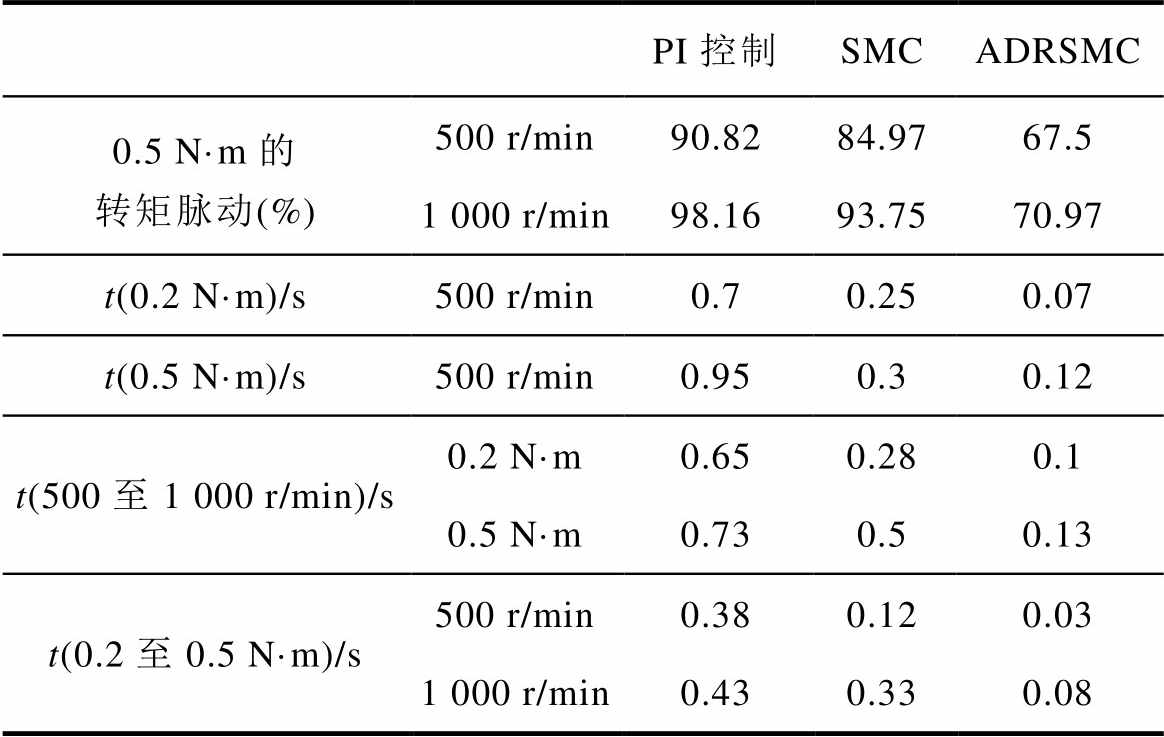
PI控制SMCADRSMC 0.5 N·m的转矩脉动(%)500 r/min90.8284.9767.5 1 000 r/min98.1693.7570.97 t(0.2 N·m)/s500 r/min0.70.250.07 t(0.5 N·m)/s500 r/min0.950.30.12 t(500至1 000 r/min)/s0.2 N·m0.650.280.1 0.5 N·m0.730.50.13 t(0.2至0.5 N·m)/s500 r/min0.380.120.03 1 000 r/min0.430.330.08
表4给出了四种控制策略的性能对比,本文提出的ADRSMC策略优化了滑模控制的性能,且引入了自抗扰观测器来保证电机在复杂工况下的稳定性。
表4 四种滑模控制策略的优化对比
Tab.4 Optimization comparison of four SMC strategies
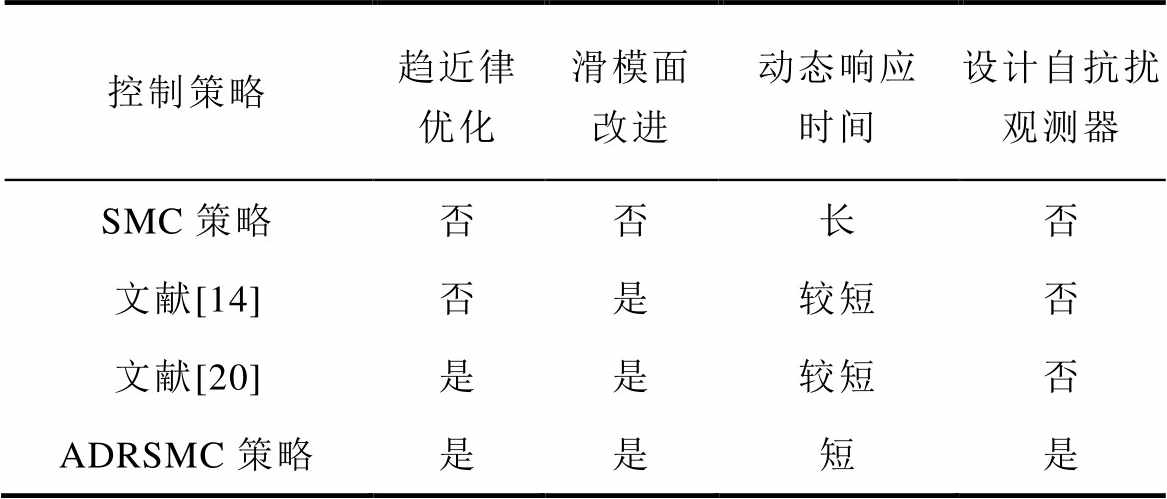
控制策略趋近律优化滑模面改进动态响应时间设计自抗扰观测器 SMC策略否否长否 文献[14]否是较短否 文献[20]是是较短否 ADRSMC策略是是短是
本文提出了一种基于自抗扰滑模控制的开关磁阻电机转矩分配控制策略。首先,针对传统SMC存在的抖振大和动态响应较慢等问题,将传统指数趋近律中的符号函数用平滑函数H(s)代替,并引入了系统状态变量,在趋近阶段使得系统运动点能快速地运动至滑模面,在滑动模态阶段系统随着状态变量的减小而减慢运动速度,抑制了电机的转矩波动,且利用改进的积分滑模面提高了系统的收敛性。同时,由于开关磁阻电机数学模型的非线性,且考虑到外部扰动会降低控制系统的稳定性,本文引入了自抗扰扩张状态观测器观测系统扰动,并作为滑模速度控制器的前馈补偿,平衡新型滑模趋近律增益的取值,提高了系统的抗干扰性。最后,通过仿真和实验验证了ADRSMC策略在提高系统响应速度和抑制转矩波动方面的优越性和有效性。
参考文献
[1] Sun Xiaodong, Cao Junhao, Lei Gang, et al. Speed sensorless control for permanent magnet synchronous motors based on finite position set[J]. IEEE Transa- ctions on Industrial Electronics, 2020, 67(7): 6089- 6100.
[2] 李孟秋, 高天, 朱慧玉, 等. 基于转矩分配函数的开关磁阻电机预测转矩控制[J]. 电力系统及其自动化学报, 2021, 33(9): 123-129.
Li Mengqiu, Gao Tian, Zhu Huiyu, et al. Predictive torque control of switched reluctance motor based on torque sharing function[J]. Proceedings of the CSU- EPSA, 2021, 33(9): 123-129.
[3] 闫文举, 陈昊, 刘永强, 等. 一种用于电动汽车磁场解耦型双定子开关磁阻电机的新型功率变换器[J]. 电工技术学报, 2021, 36(24): 5081-5091.
Yan Wenju, Chen Hao, Liu Yongqiang, et al. A novel power converter on magnetic field decoupling double stator switched reluctance machine for electric vehicles[J]. Transactions of China Electrotechnical Society, 2021, 36(24): 5081-5091.
[4] 方成辉, 陈昊, Galina Demidova, 等. 开关磁阻电机无电流传感器控制方法[J]. 电工技术学报, 2023, 38(2): 365-374.
Fang Chenghui, Chen Hao, Demidova G, et al. Current sensorless control method of switched reluctance motors[J]. Transactions of China Elec- trotechnical Society, 2023, 38(2): 365-374.
[5] 卿龙, 王惠民, 葛兴来. 一种高效率开关磁阻电机转矩脉动抑制方法[J]. 电工技术学报, 2020, 35(9): 1912-1920.
Qing Long, Wang Huimin, Ge Xinglai. A high efficiency torque ripple suppression method for switched reluctance motor[J]. Transactions of China Electrotechnical Society, 2020, 35(9): 1912-1920.
[6] 丁文, 李可, 付海刚. 一种12/10极模块化定子混合励磁开关磁阻电机分析[J]. 电工技术学报, 2022, 37(8): 1948-1958.
Ding Wen, Li Ke, Fu Haigang. Analysis of a 12/10-pole modular-stator hybrid-excited switched reluctance machine[J]. Transactions of China Electro- technical Society, 2022, 37(8): 1948-1958.
[7] 孙玉坤, 袁野, 黄永红, 等. 磁悬浮开关磁阻电机及其关键技术发展综述[J]. 电工技术学报, 2015, 30(22): 1-8.
Sun Yukun, Yuan Ye, Huang Yonghong, et al. Development of the bearingless switched reluctance motor and its key technologies[J]. Transactions of China Electrotechnical Society, 2015, 30(22): 1-8.
[8] 许爱德, 任萍, 陈加贵, 等. 基于电感特殊位置点的开关磁阻电机转子位置检测及误差补偿[J]. 电工技术学报, 2020, 35(8): 1613-1623.
Xu Aide, Ren Ping, Chen Jiagui, et al. Rotor position detection and error compensation of switched reluctance motor based on special inductance position[J]. Transactions of China Electrotechnical Society, 2020, 35(8): 1613-1623.
[9] 左月飞, 刘闯, 张捷, 等. 永磁同步电动机转速伺服系统PI控制器的一种新设计方法[J]. 电工技术学报, 2016, 31(13): 180-188.
Zuo Yuefei, Liu Chuang, Zhang Jie, et al. A novel design method of PI controller for permanent magnetic synchronous motor speed servo system[J]. Transactions of China Electrotechnical Society, 2016, 31(13): 180-188.
[10] 王喜莲, 许振亮. 基于PI参数自适应的开关磁阻电机调速控制研究[J]. 中国电机工程学报, 2015, 35(16): 4215-4223.
Wang Xilian, Xu Zhenliang. Speed regulation control of switched reluctance motors based on PI parameter self-adaptation[J]. Proceedings of the CSEE, 2015, 35(16): 4215-4223.
[11] 黄仁志, 全相军, 吴在军, 等. 基于多重谐振控制器的参考值前馈自适应控制[J]. 电工技术学报, 2022, 37(16): 4212-4224.
Huang Renzhi, Quan Xiangjun, Wu Zaijun, et al. A multiple resonant based on reference feedforward adaptive voltage control of three-phase inverter[J]. Transactions of China Electrotechnical Society, 2022, 37(16): 4212-4224.
[12] Liu Huixian, Li Shihua. Speed control for PMSM servo system using predictive functional control and extended state observer[J]. IEEE Transactions on Industrial Electronics, 2012, 59(2): 1171-1183.
[13] Sun Xiaodong, Feng Liyun, Diao Kaikai, et al. An improved direct instantaneous torque control based on adaptive terminal sliding mode for a segmented-rotor SRM[J]. IEEE Transactions on Industrial Electronics, 2021, 68(11): 10569-10579.
[14] 魏惠芳, 王丽梅. 永磁直线同步电机自适应模糊神经网络时变滑模控制[J]. 电工技术学报, 2022, 37(4): 861-869.
Wei Huifang, Wang Limei. Adaptive fuzzy neural network time-varying sliding mode control for permanent magnet linear synchronous motor[J]. Transactions of China Electrotechnical Society, 2022, 37(4): 861-869.
[15] 王天鹤, 赵希梅, 金鸿雁. 基于递归径向基神经网络的永磁直线同步电机智能二阶滑模控制[J]. 电工技术学报, 2021, 36(6): 1229-1237.
Wang Tianhe, Zhao Ximei, Jin Hongyan. Intelligent second-order sliding mode control based on recurrent radial basis function neural network for permanent magnet linear synchronous motor[J]. Transactions of China Electrotechnical Society, 2021, 36(6): 1229- 1237.
[16] Xu Bo, Zhang Lei, Ji Wei. Improved non-singular fast terminal sliding mode control with disturbance observer for PMSM drives[J]. IEEE Transactions on Transportation Electrification, 2021, 7(4): 2753- 2762.
[17] 付东学, 赵希梅. 永磁直线同步电机自适应非奇异快速终端滑模控制[J]. 电工技术学报, 2020, 35(4): 717-723.
Fu Dongxue, Zhao Ximei. Adaptive nonsingular fast terminal sliding mode control for permanent magnet linear synchronous motor[J]. Transactions of China Electrotechnical Society, 2020, 35(4): 717-723.
[18] 方馨, 王丽梅, 张康. 基于扰动观测器的永磁直线电机高阶非奇异快速终端滑模控制[J]. 电工技术学报, 2023, 38(2): 409-421.
Fang Xin, Wang Limei, Zhang Kang. High order nonsingular fast terminal sliding mode control of permanent magnet linear motor based on disturbance observer[J]. Transactions of China Electrotechnical Society, 2023, 38(2): 409-421.
[19] 夏长亮, 李莉, 谷鑫, 等. 双永磁电机系统转速同步控制[J]. 电工技术学报, 2017, 32(23): 1-8.
Xia Changliang, Li Li, Gu Xin, et al. Speed synchronization control of dual-PMSM system[J]. Transactions of China Electrotechnical Society, 2017, 32(23): 1-8.
[20] 韩国强, 陆哲, 吴孟霖, 等. 基于改进滑模控制策略的开关磁阻电机直接瞬时转矩控制方法[J]. 电工技术学报, 2022, 37(22): 5740-5755.
Han Guoqiang, Lu Zhe, Wu Menglin, et al. Direct instantaneous torque control method for switched reluctance motor based on an improved sliding mode control strategy[J]. Transactions of China Electro- technical Society, 2022, 37(22): 5740-5755.
[21] Han Jingqing. From PID to active disturbance rejection control[J]. IEEE Transactions on Industrial Electronics, 2009, 56(3): 900-906.
[22] 贲彤, 聂恒, 陈龙, 等. 一种正弦补偿型转矩分配函数的SRM转矩脉动抑制策略[J]. 电机与控制学报, 2022, 26(8): 100-111.
Ben Tong, Nie Heng, Chen Long, et al. SRM torque ripple suppression strategy based on sinusoidal compensation torque sharing function[J]. Electric Machines and Control, 2022, 26(8): 100-111.
[23] Xia Zekun, Fang Gaoliang, Xiao Dianxun, et al. An online torque sharing function method involving current dynamics for switched reluctance motor drives[J]. IEEE Transactions on Transportation Elec- trification, 2023, 9(1): 534-548.
[24] Qu Lizhi, Qiao Wei, Qu Liyan. Active-disturbance- rejection-based sliding-mode current control for permanent-magnet synchronous motors[J]. IEEE Transa- ctions on Power Electronics, 2021, 36(1): 751-760.
Torque Sharing Function Control Strategy for Switched Reluctance Motor Based on Active Disturbance Rejection Sliding Mode Control
Abstract The research of new energy electric vehicles is currently a hot topic. Switched reluctance motors (SRM) are applied in electric vehicles due to their simple structure, robust fault tolerance, and ease of control. Among them, motor torque ripple and system response speed are critical indicators to measure the performance of motor drive systems. Sliding mode control is a nonlinear algorithm with the advantages of fast response speed and strong robustness, including sliding mode approach law and sliding mode surface. The sign function used in the traditional exponential approach law can cause system oscillation and large chattering in the control system. The smooth function is used instead of the sign function, and the system state variable is introduced to improve control flexibility. At the same time, an improved integral sliding surface is proposed to improve the convergence of the traditional integral sliding surface. Because of the nonlinearity, the motor’s load torque and inherent parameters significantly affect the operation of the motor under variable speed and load conditions. Therefore, the active disturbance rejection extended state observer (ADRESO) is used as a feedforward compensation for the sliding mode speed controller to adjust the uncertain parameters and load torque of the motor. The design of the ADRESO does not require an accurate mathematical model of the motor, and it can ensure the stability of the system under complex operating conditions and has strong robustness.
Experimental results of an actual switched reluctance motor show that under steady-state operating conditions, when the motor load is 0.5 N·m and the set speeds are 500 r/min and 1 000 r/min, the proposed active disturbance rejection sliding mode control (ADRSMC) results in smaller motor pulsation. Under variable speed conditions, when the load torque is 0.2 N·m, the starting time of the system using PI control and traditional sliding mode control is 0.7 s and 0.25 s, and the variable speed response time is 0.65 s and 0.28 s. The starting time of the system with the proposed ADRSMC is 0.07 s, and the variable speed response time is 0.1 s. When the load torque is 0.5 N·m, the starting time of the system using PI control and traditional sliding mode control is 0.95 s and 0.3 s, and the variable speed response time is 0.73 s and 0.5 s. The starting time of the system with the proposed ADRSMC is 0.12 s, and the variable speed response time is 0.13 s. The proposed method reduces motor speed fluctuations under stable operation. Under variable load conditions, when the set speed is 500 r/min, the time for the system to return to the original state with PI control and traditional sliding mode control is 0.38 s and 0.12 s. The response time of the system with the proposed ADRSMC is 0.03 s. When the set speed is 1 000 r/min, the time for the system to return to the original state using PI control and traditional sliding mode control is 0.43 s and 0.33 s. The system’s response time with the proposed ADRSMC is 0.08 s, indicating that the proposed ADRSMC can approach the original speed in a relatively short period.
It can be concluded that the proposed control strategy can effectively reduce the torque ripple of the motor, improve the response time of the system, and enhance the stability of the speed.
Keywords:Switched reluctance motor, torque sharing function control, new type of sliding mode reaching law, active disturbance rejection extended state observer (ADRESO)
中图分类号:TM352
DOI: 10.19595/j.cnki.1000-6753.tces.231277
深圳市协同创新专项计划国际合作研究项目(GJHZ20220913144400001)和深圳市基础研究专项重点项目(JCYJ20220818100000001)资助。
收稿日期 2023-08-08
改稿日期 2023-09-04
李宗霖 男,1999年生,硕士研究生,研究方向为开关磁阻电机系统及其控制。
E-mail: lizonglin_binary@163.com
陈 昊 男,1969年生,教授,博士生导师,研究方向为开关磁阻电机系统及其控制。
E-mail: hchen@cumt.edu.cn(通信作者)
(编辑 崔文静)