基于参数辨识的永磁辅助同步磁阻电机电流无差拍控制
许爱德1 刘 鑫2 李新宇2 胡士迈1
(1. 大连海事大学信息科学技术学院 大连 116026 2. 大连海事大学船舶电气工程学院 大连 116026)
摘要 针对永磁辅助同步磁阻电机电感参数失配引起传统无差拍预测电流控制器受扰动的问题,该文提出一种电感参数自适应的无差拍预测电流控制方案。所提算法利用模型参考自适应系统对电感参数进行在线辨识,并将辨识结果代替控制器中的原始电感模型参数,以确保控制器的模型参数和电机实际参数相匹配,进而增强无差拍预测电流控制系统的鲁棒性。根据永磁辅助同步磁阻的数学模型,对电机本体进行了建模,以实现对所提算法的仿真验证。最后在以TMS320F28335控制器为核心的实验平台上进行了实验验证。仿真和实验结果均表明,当电机参数与模型参数不匹配时,所提算法相较于传统的无差拍预测电流控制算法在电流波动峰峰值、电流跟踪静差及系统鲁棒性方面都有明显的改善。
关键词:永磁辅助同步磁阻电机 参数辨识 无差拍预测电流控制 模型参考自适应
0 引言
21世纪以来,我国煤、天然气、石油等不可再生资源消耗巨大,环境污染问题日益严重,全世界都在关注环境气候的变化,科技和经济都向着节能、低碳的方向发展,而电机作为一种常用的能量转换设备被广泛应用在国民经济的各个领域。目前,大多数电机采用的是价格较高的稀土钕铁硼永磁体电机[1],虽然有较好的性能,但是其稀土用量较大,带来了较高的使用成本且对环境的破坏较为严重。因此,开发对环境友好且成本较低的高性能电机已成为了近年来的研究热点。永磁辅助同步磁阻电机(Permanent Magnet Assisted Synchronous Reluctance Motor, PMA-SynRM)作为一种特殊的内置式永磁同步电机被提出,但其与内置式永磁同步电机在结构特性和控制方式上有所不同[2-4]。在输出转矩的分配上,PMA-SynRM以磁阻转矩为主、永磁转矩为辅,往往采用最大转矩电流比(Maximum Torque Per Ampere, MTPA)的控制方式[5]。而内置式永磁同步电机以磁阻转矩为辅,永磁转矩为主,因此可以忽略磁阻转矩,采用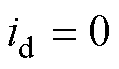 的控制方式。在电感特性上,内置式永磁同步电机电感随电流及转子位置变化较小,而PMA-SynRM电感随电流及转子位置变化较大。此外,PMA-SynRM相较于永磁同步电机具有更少的永磁体用料,成本较低。以上这些区别和特点使PMA-SynRM成为了符合当下社会发展需要的高性能电机。但是,目前国内外学者对PMA-SynRM的研究主要集中在电机的本体设计方面[6-9],对电机的高性能控制算法的研究还处于起步阶段,其特有的高凸极比特性使其对电流环性能要求更高,因此设计高性能的电流环控制器对其广泛应用有着至关重要的意义。
的控制方式。在电感特性上,内置式永磁同步电机电感随电流及转子位置变化较小,而PMA-SynRM电感随电流及转子位置变化较大。此外,PMA-SynRM相较于永磁同步电机具有更少的永磁体用料,成本较低。以上这些区别和特点使PMA-SynRM成为了符合当下社会发展需要的高性能电机。但是,目前国内外学者对PMA-SynRM的研究主要集中在电机的本体设计方面[6-9],对电机的高性能控制算法的研究还处于起步阶段,其特有的高凸极比特性使其对电流环性能要求更高,因此设计高性能的电流环控制器对其广泛应用有着至关重要的意义。
目前,国内外对PMA-SynRM的高性能电流环的控制研究主要集中在MTPA控制和传统PI控制方面。文献[10]将定子绕组电流约束成固定不变的量,进而求解出电磁转矩的最大值,最后推导出PMA-SynRM的最大转矩电流比最佳电流角的计算公式,并利用观测器对电机的电感参数进行在线辨识,并将得到的电感参数应用于电流指令的计算中。文献[11]提出了一种转矩预测控制,在MTPA和弱磁运行时发挥了较好的动稳态性能。文献[12]针对新型磁链增强永磁辅助同步磁阻电机,应用基于MTPA的直接转矩控制,并对转矩脉动进行了研究,在抑制转矩脉动方面取得了较好的效果。文献[13]介绍了PMA-SynRM在不同开相故障下的最大转矩电流比控制。
无差拍控制在永磁辅助同步磁阻电机中的应用相对较少,文献[14]针对永磁辅助同步磁阻电机直接转矩控制转矩脉动较大的问题,研究了基于PMA-SynRM的无差拍直接转矩控制方案,有效地降低了电机的转矩脉动。文献[15]针对永磁同步电机电流谐波问题,设计了谐波采集器,对谐波电流进行提取,最后采用无差拍电流预测控制(Deadbeat Predictive Current Control, DBPCC)策略生成补偿电压用于抑制谐波电流。文献[16]为了增强电流无差拍控制系统的鲁棒性,将永磁同步电机的铁损考虑在控制的过程中。
对于PMA-SynRM而言,电机的d、q轴电感参数会随着电流变化而改变,进而反过来影响电流。要想使高性能的电流环控制器发挥应有的控制效果,准确的电机参数至关重要。因此,参数辨识是实现高性能控制的重要一环。文献[17]利用在线辨识的方法对PMA-SynRM的电感参数进行辨识,并且将辨识结果代入改进自寻优控制策略与模型预测电流控制中,以提高控制性能。文献[18]提出了一种自适应的模型预测控制,将永磁同步电机的电感作为辨识对象,以减小因参数失配引起的电流失真和转矩脉动较大的问题。文献[19]在充分考虑电压源逆变器非线性的前提下,提出了一种基于神经网络的参数在线辨识方法来提高永磁同步电机无差拍控制器的抗扰动能力。文献[20]提出了一种基于电流注入扰动观测器的参数识别方法,以实现对永磁同步电机的电阻和电感进行辨识。文献[21]在永磁同步电机上应用改进粒子群算法对电机电感和磁链进行在线辨识。文献[22]介绍了一种基于电路模型的永磁同步电机参数在线辨识技术,并采用牛顿迭代法来求解辨识的非线性方程组。然而,考虑可变参数的无差拍控制在PMA-SynRM中较少应用。
本文首先详细地分析了d、q轴电感参数失配对最大转矩电流比控制器电流角精度以及对电流无差拍控制器稳定性的影响。其次提出了一种基于模型参考自适应系统(Model Reference Adaptive System, MRAS)的d、q轴电感参数在线辨识的电流无差拍控制算法,优化了由于电感参数失配对传统无差拍控制带来的电流角精度下降以及电流无差拍控制器失稳的问题。最后通过仿真和实验结果表明,所提算法相较于传统电流无差拍控制算法有更优的电流控制效果,系统的整体鲁棒性能更好。
1 PMA-SynRM的数学模型
本实验研究所用电机为6极36槽铁氧体永磁辅助同步磁阻电机,图1为PMA-SynRM的转子结构示意图以及d、q轴坐标的位置定义。
为了简化分析,假设PMA-SynRM满足以下理想情况:①忽略电机的铁心饱和;②不计涡流和磁滞损耗;③忽略电流谐波。
在基于以上假设的前提下,可以列写永磁辅助同步磁阻电机d、q轴坐标系的电压、磁链、电磁转矩方程分别为
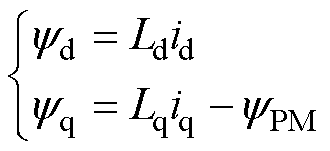 (2)
(2)
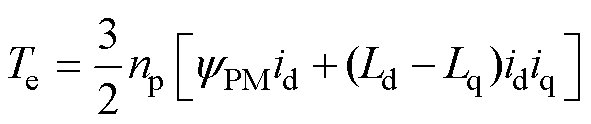 (3)
(3)
式中,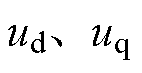 分别为定子电压矢量的d、q轴分量;
分别为定子电压矢量的d、q轴分量;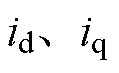 分别为定子电流矢量的d、q轴分量;
分别为定子电流矢量的d、q轴分量;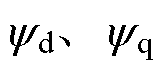 分别为定子的d、q轴磁链;
分别为定子的d、q轴磁链;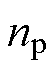 为电机极对数;
为电机极对数;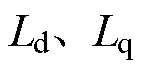 分别为电机定子绕组的d、q轴电感;
分别为电机定子绕组的d、q轴电感;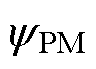 为永磁体产生的磁链;
为永磁体产生的磁链;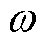 为电机的电角速度;
为电机的电角速度;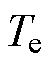 为电磁转矩;
为电磁转矩;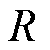 为绕组相电阻。
为绕组相电阻。
本文所采用的MTPA计算方法是以固定定子电流为约束条件,进而求解出当输出转矩最大时的电流角,因此将式(3)中的电磁转矩的表达式改写为
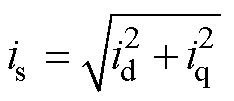 (5)
(5)
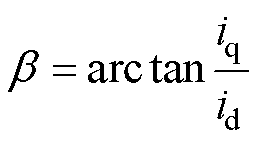 (6)
(6)
式中,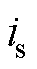 为定子电流幅值;
为定子电流幅值;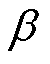 为定子电流与d轴的夹角。
为定子电流与d轴的夹角。
2 传统无差拍预测电流控制策略分析
2.1 MTPA的基本原理
最大转矩电流比控制的核心思想就是在保证电机输出转矩恒定的前提下,使每单位的电枢电流产生的电磁转矩达到最大值。在图1所示的建模条件下,电流角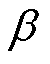 的计算公式为
的计算公式为
2.2 PMA-SynRM无差拍预测电流控制公式推导
选择d、q轴电流作为状态变量,可以得到关于电机电流的状态方程为
通常情况下,控制系统的采样频率极高,因此可以将式(8)左边进行一阶泰勒离散化处理,可得
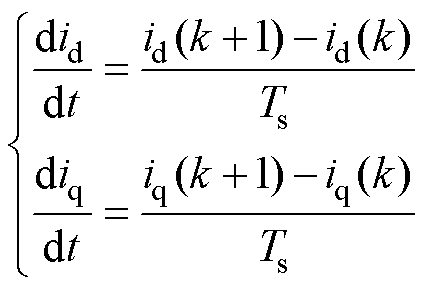 (9)
(9)
式中,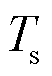 为离散化采样时间。
为离散化采样时间。
将式(9)代入式(8)中,可以得到永磁辅助同步磁阻电机的离散化电压的矩阵表现形式为
其中
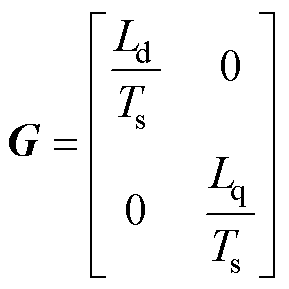
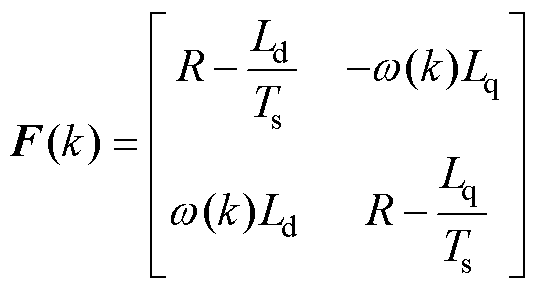
式中,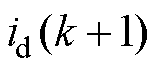 、
、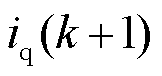 分别为
分别为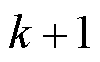 时刻d、q轴电流预测值;
时刻d、q轴电流预测值;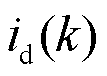 、
、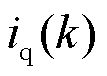 分别为
分别为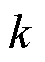 时刻的d、q轴电流;
时刻的d、q轴电流;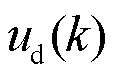 、
、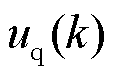 分别为
分别为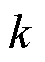 时刻的d、q轴电压;
时刻的d、q轴电压;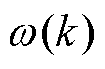 为
为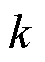 时刻电机的电角速度。
时刻电机的电角速度。
为了使无差拍预测电流控制器有较好的控制效果,应该使预测的下一拍电流跟随最大转矩电流比控制器输出的d、q轴参考电流,因此将MTPA控制器输出的参考电流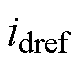 和
和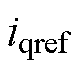 分别取代式(10)中的
分别取代式(10)中的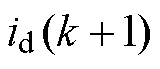 ,
,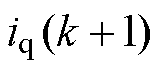 即可得到PMA-SynRM无差拍预测电流控制系统的参考电压为
即可得到PMA-SynRM无差拍预测电流控制系统的参考电压为
2.3 控制原理及问题分析
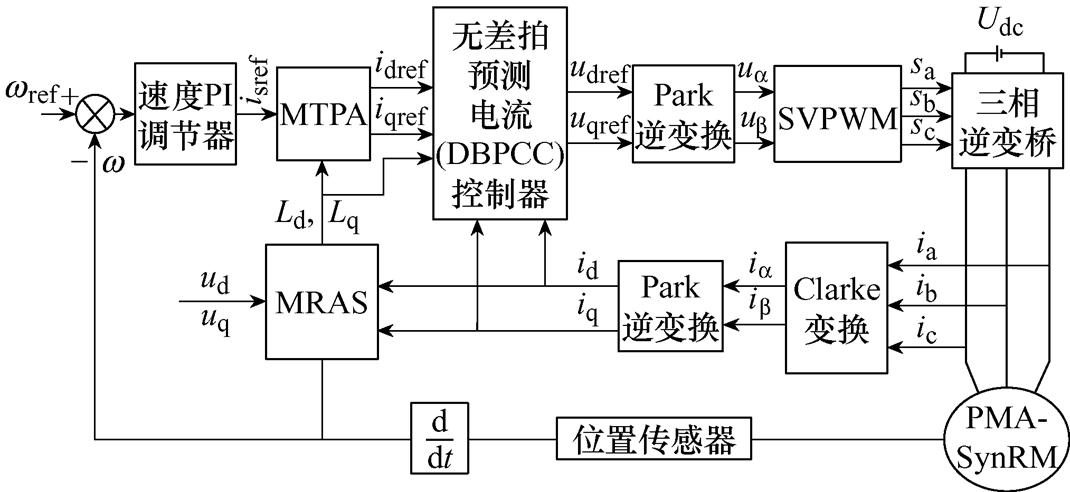
如图2所示为固定参数的MTPA-DBPCC策略原理框图。功率变换器采用的是三相全桥逆变电路。传统的控制策略由速度环PI调节器求得参考的定子电流,并将参考的定子电流传递给MTPA,以求得d、q轴的参考电流,令DBPCC控制器预测的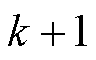 时刻d、q轴电流跟随MTPA输出的参考电流,进而生成参考的d、q轴电压矢量,最后通过空间电压矢量调制的方式生成控制脉冲以驱动功率变换器的开关器件导通,进而对电机进行闭环控制。
时刻d、q轴电流跟随MTPA输出的参考电流,进而生成参考的d、q轴电压矢量,最后通过空间电压矢量调制的方式生成控制脉冲以驱动功率变换器的开关器件导通,进而对电机进行闭环控制。
根据传统的控制策略原理结合式(7)和式(11)可以看出,传统的MTPA-DBPCC是基于控制器精确模型参数的一种控制方式,其控制效果依赖于控制器模型参数的准确性,但由于永磁辅助同步磁阻电机的高凸极比特性,使得其在不同工况运行下参数会随电流的波动发生较大变化,其中d、q轴电感随电流变化尤为明显,这会使基于固定参数的控制器难以发挥其优越的控制性能,因此分析MTPA电流角和无差拍预测电流控制系统对电感参数变化的敏感性是至关重要的。
首先,分析无差拍预测电流控制系统对d、q轴电感参数变化的敏感程度。在实际的控制系统中,可以算出k时刻电机d、q轴电压的实际值,有
其中
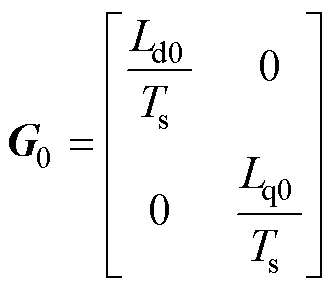
式中,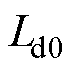 、
、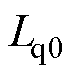 分别为电机铭牌标称的d、q轴电感。
分别为电机铭牌标称的d、q轴电感。
令式(12)左侧与式(11)左侧相等,由于本文只分析d、q轴电感参数的变化情况,默认为磁链和电阻在电机实际运行中保持恒定值不变,不做考虑。此外,实际的控制系统的电流环采样频率一般在10 kHz以上,故采样周期很短,因此可以求解出当无差拍控制器和实际电机参数不匹配时,电机实际反馈电流和给定参考电流之间的关系。
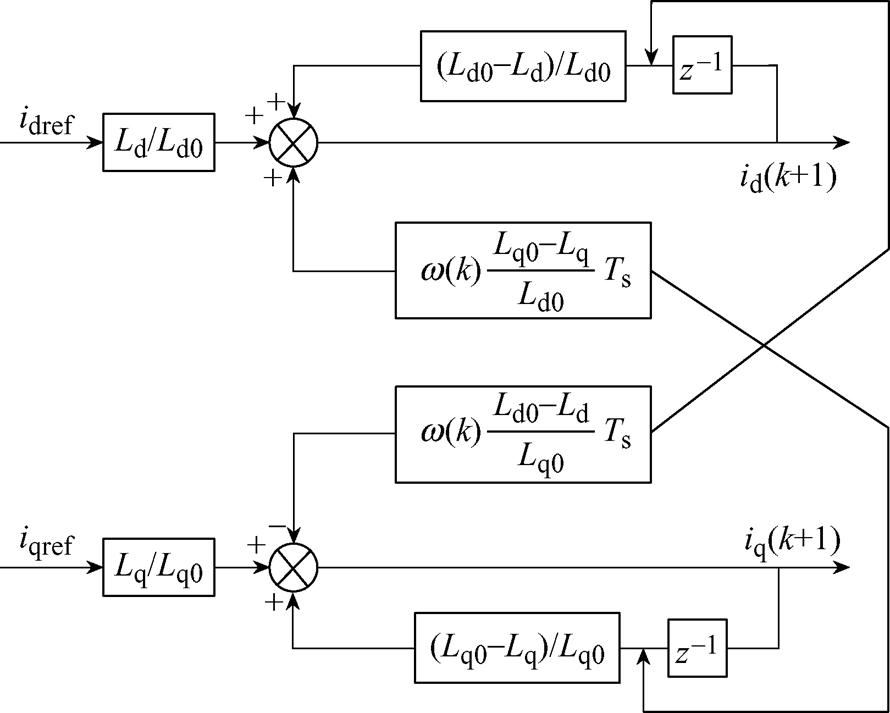
由于电机在实际运行的过程中,电机转速变化的时间常数相对于电流变化的时间常数更大,故电机转速的变化相较于电流变化来说非常缓慢,因此可以将式(13)中含有的项作为扰动量并对其进行Z变换。系统的闭环传递函数框图如图3所示。
因此,可以列写离散域传递函数为
当系统的闭环极点都位于Z平面的单位圆内时,则系统保持稳定。因此,根据式(14)可以得到DBPCC控制器的稳定条件为
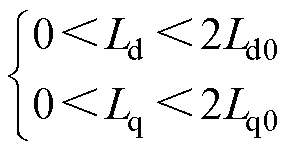 (15)
(15)
通过不等式式(15)可以看出,当控制器中d、q轴电感参数大于电机电感参数的两倍时,系统将不再满足稳定性条件,可能会影响系统的稳定运行。接下来分析当无差拍控制器中d、q轴电感大于电机实际电感两倍时,对电机的d、q轴电流产生的影响。在进入到稳态运行之后,可以近似认为两个相邻周期内d、q轴电流的参考值和反馈值分别相等,即
将式(16)代入式(13)中,可以将式(13)简化为
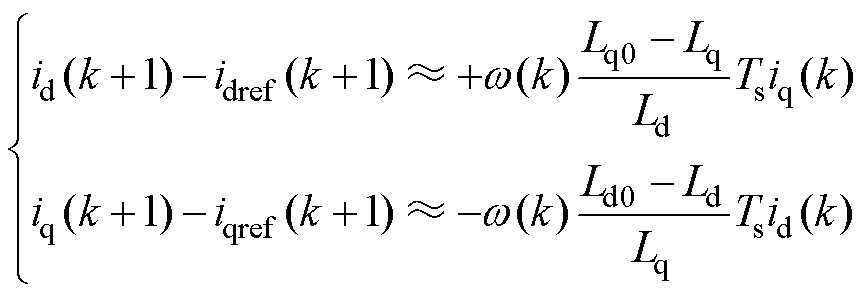 (17)
(17)
从式(17)可以看出,当无差拍控制器中d、q轴电感参数与电机实际的电感参数相匹配时,式(17)的右侧等于0,即表示下一时刻电流准确跟踪参考电流且跟踪电流静差为零。但当d、q轴电感参数偏离准确值时,d、q轴电流的跟踪静差将不再为零。当无差拍控制器中q轴电感参数大于电机标称电感参数时,d轴产生负的电流跟踪误差,小于时则产生正的电流跟踪误差;当无差拍控制器中d轴电感参数大于电机标称电感参数时,q轴产生正的电流跟踪误差,小于时将产生负的电流跟踪误差。
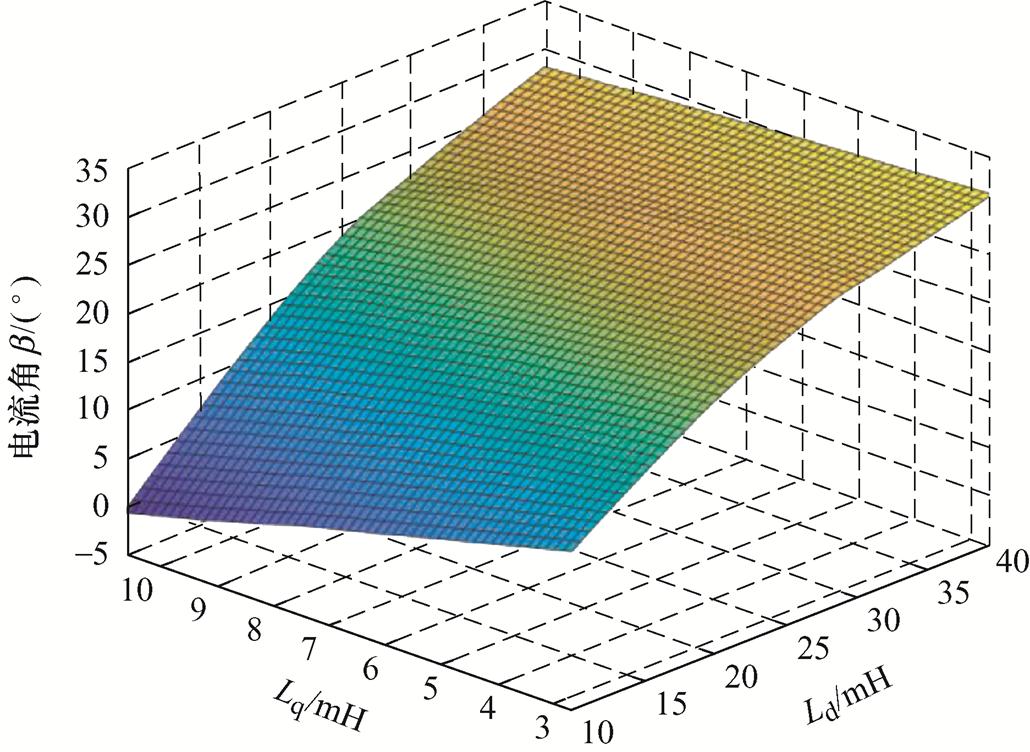
同样地,d、q轴电感参数的变化对MTPA控制器的电流角计算也有一定的影响,在相同转速和负载条件下,根据MTPA控制器中的模型电感参数与电机实际电感偏差的不同程度,可以拟合出电流角和dq轴电感参数的三维曲面图如图4所示。
根据图4,当电机的实际电感和模型电感参数失配时,MTPA控制器所计算的最佳电流角也会有所不同,这会使MTPA控制器输出的参考电流不同。当电感偏差过大时,甚至出现了负的电流角,这个角度对应的q轴电流也是负值,根据式(3)可以发现,此时磁阻转矩是制动转矩,影响了电机输出电磁转矩的大小,却增加了电机的损耗。
3 参数自适应无差拍控制器设计
3.1 基于MRAS的电感辨识器设计
第2节分析了PMA-SynRM实际电感和模型电感参数失配时对MTPA控制器和电流无差拍控制器的影响,为了解决这个问题,本节提出了一种基于MRAS的电感参数在线辨识算法,并利用辨识结果去更新MTPA和电流无差控制器的模型电感参数值,以确保模型参数和电机实际参数保持匹配,从而使控制算法发挥应有的控制效果。
以实际电机为参考模型,即参考模型为
其中
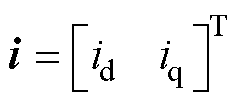
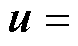
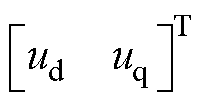
式中,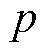 为其中微分算子。
为其中微分算子。
设计电机的可调模型为
其中
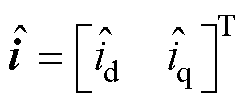
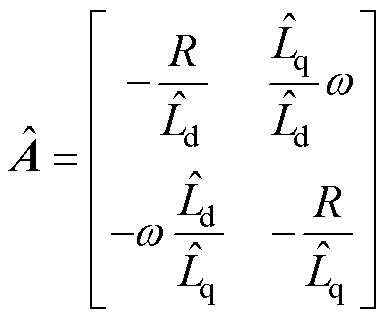
用参考模型减去可调模型,有
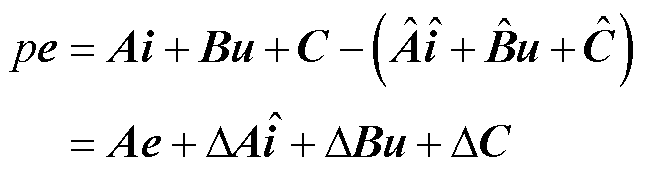 (20)
(20)
其中
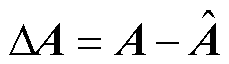
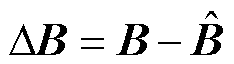
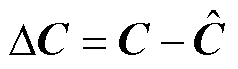
令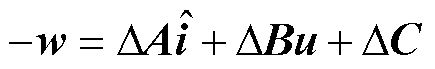 ,则有
,则有
式中,I为单位矩阵。
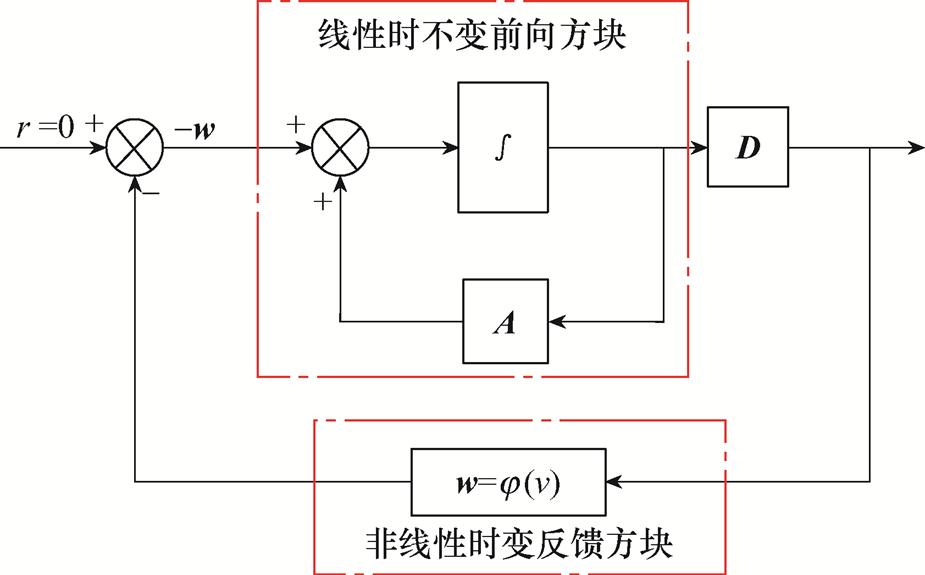
根据以上方程,MRAS可以等效为线性时不变部分和非线性时变部分共同组成的非线性反馈系统,系统框图如图5所示。
根据Popov超稳定性理论,若要使这个反馈系统保持稳定,前向通道必须是正实的。同时,需要确保非线性反馈通道满足Popov积分不等式。即可列写线性定常前向方块的状态方程为
存在正定矩阵P和Q,使得式(23)成立,则可证明控制系统的线性定常前向方块是严格正实的。
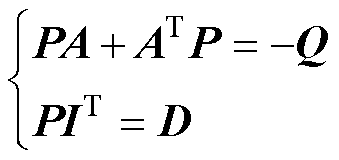 (23)
(23)
本文取P为单位矩阵,对应的补偿矩阵D也为单位矩阵。考虑A为负定矩阵,则必存在正定对称Q使得线性定常前向方块严格正实,其次设计参数自适应律来保证非线性反馈回路满足Popov积分不等式,有
式中,g0为有限正常数。
将v、w的值代入Popov积分不等式并求解可计算出d、q轴电感的自适应律分别为
式中,kp、ki分别为比例、积分常数。
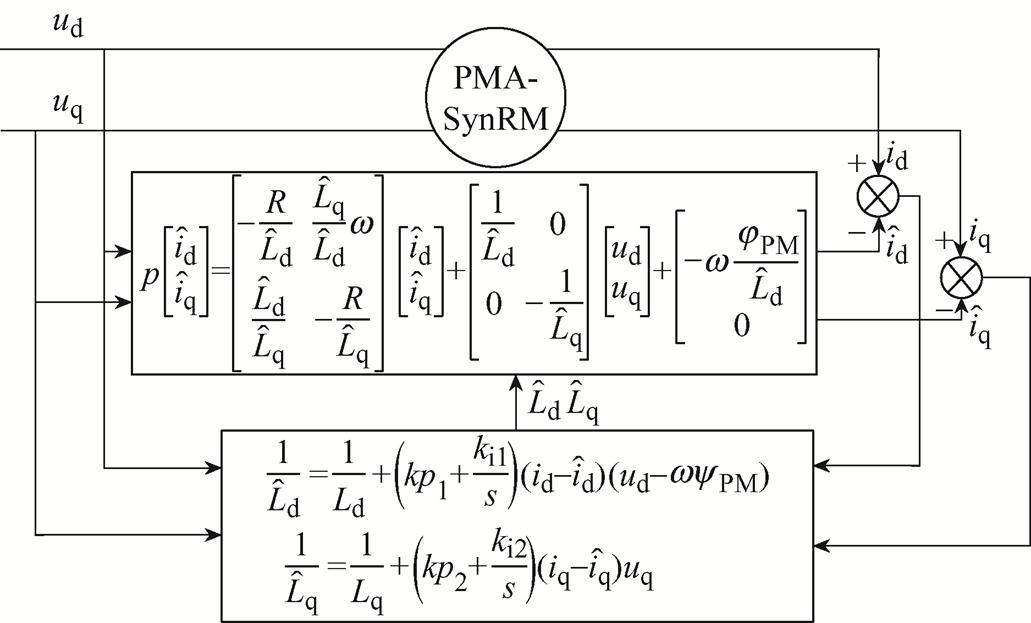
综上所述,PMA-SynRM的d、q轴电感的模型参考自适应参数辨识系统的结构框图如图6所示。
3.2 可变参数的MTPA-DBPCC控制器设计
利用辨识所得到的d、q轴电感参数值代替传统MTPA-DBPCC控制器中的电感参数可以得到基于参数辨识的最大转矩电流比计算公式和无差拍预测电流的计算公式为
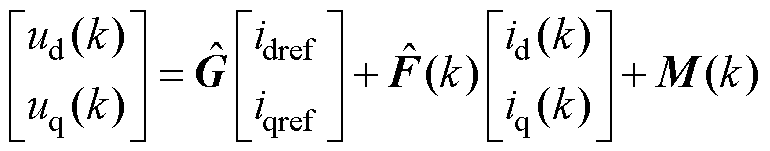 (27)
(27)
其中
基于参数辨识的无差拍预测电流控制算法框图如图7所示。
4 仿真分析
为了验证本文提出的基于参数辨识的电流无差拍控制算法的有效性,在Matlab/Simulink环境下搭建了PMA-SynRM的本体和控制器的仿真模型。由于参数失配对MTPA的影响是最佳电流角的计算,在图4中已予以说明,因此本节主要验证参数变化对无差拍控制器的影响,分别对DBPCC中d、q轴电感失配时进行动稳态仿真分析。本文所用PMA- SynRM参数见表1。
表1 PMA-SynRM参数
Tab.1 Parameters of PMA-SynRM prototype
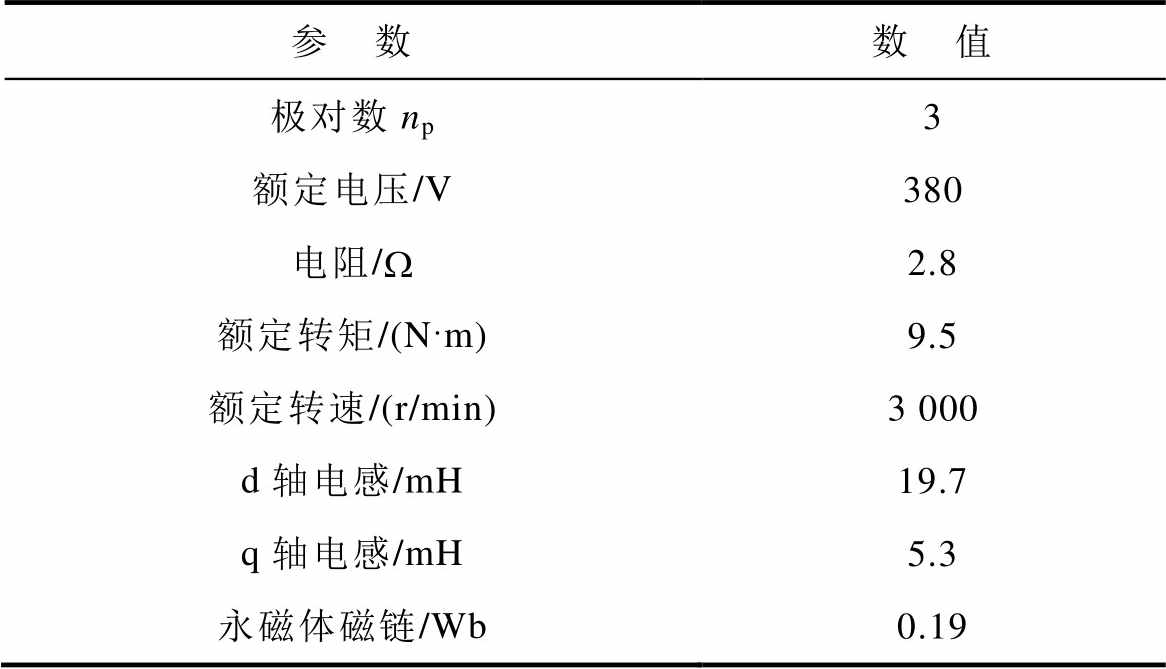
参 数数 值 极对数np3 额定电压/V380 电阻/W2.8 额定转矩/(Nm)9.5 额定转速/(r/min)3 000 d轴电感/mH19.7 q轴电感/mH5.3 永磁体磁链/Wb0.19
4.1 参数辨识算法动稳态仿真验证
仿真条件为给定参考转速1 500 r/min,负载转矩在0.05 s由2 Nm突变至5 Nm。d、q轴电感辨识动稳态仿真波形如图8所示。从仿真结果可以看出,d、q轴电感的辨识值在0.03 s左右基本收敛到参考值附近,收敛误差在3%以内。在0.05 s转矩突变时,由于d、q轴电流会相应突变,因此导致电感也会发生一定的波动,但是很快重新收敛到参考值附近,可见在转矩突变时,辨识算法依旧具有良好的收敛性。
4.2 电流无差拍控制稳态仿真验证
仿真条件为给定转速1 500 r/min,恒定负载5 Nm,开关频率10 kHz。定义电流波动误差为
式中,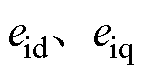 分别为d、q轴电流跟踪误差。
分别为d、q轴电流跟踪误差。
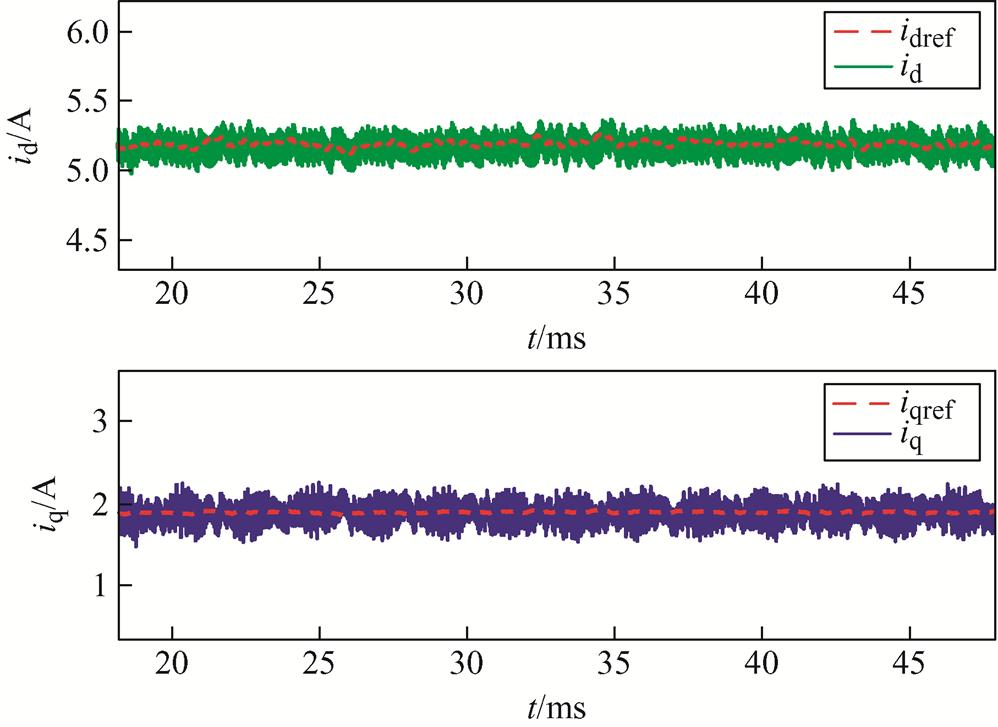
参数匹配时d、q轴电流稳态波形如图9所示。由图9可知,当电机进入稳定状态且参数匹配时,d、q轴电流波动较平稳,d轴实际电流与参考电流的误差仅为-18 mA,q轴实际电流与参考电流的误差仅为-28 mA。可见,参数匹配时无差拍预测电流控制系统稳态电流波动较小,几乎不产生电流跟踪静差,控制器对闭环系统电流的控制效果较好。
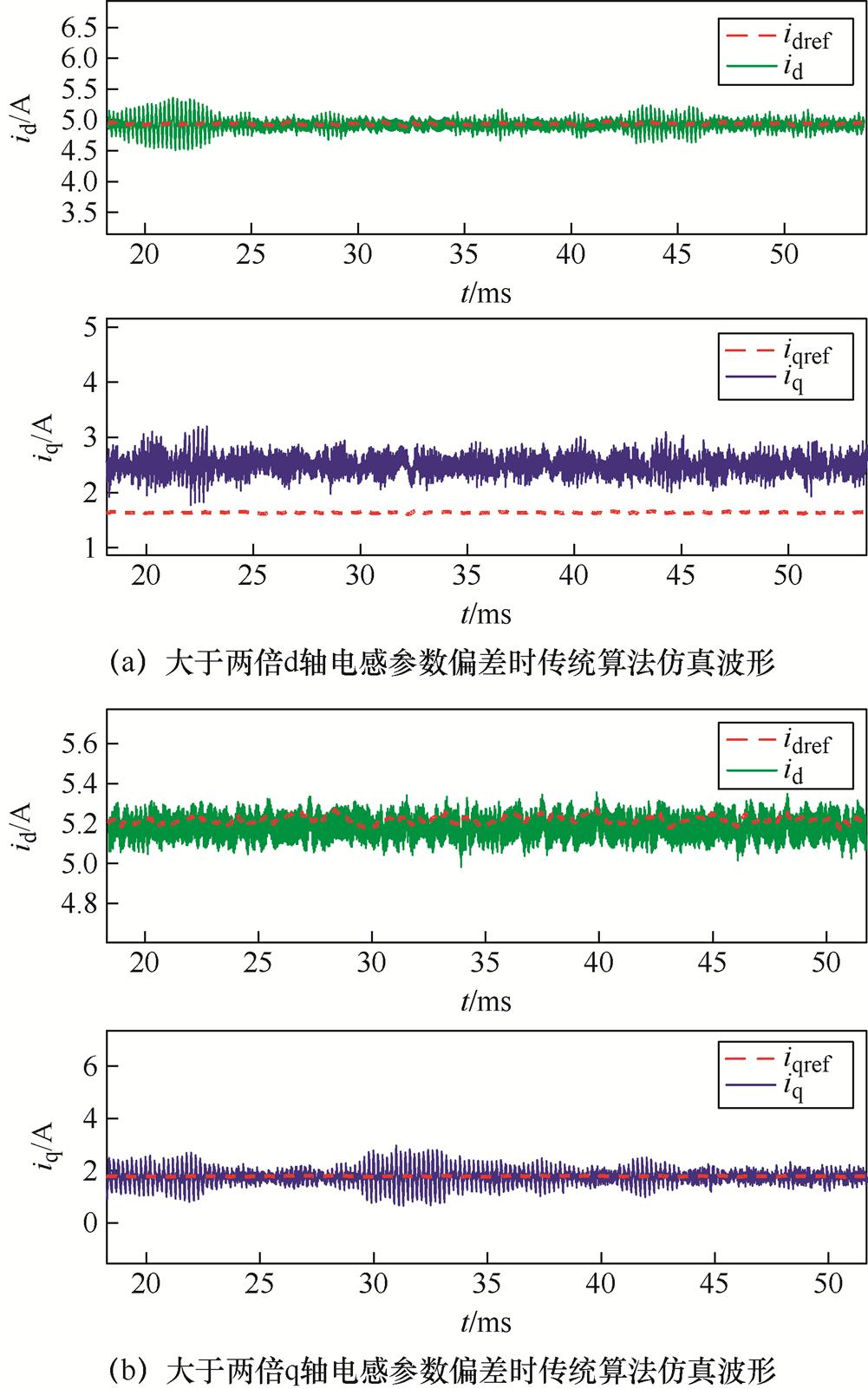
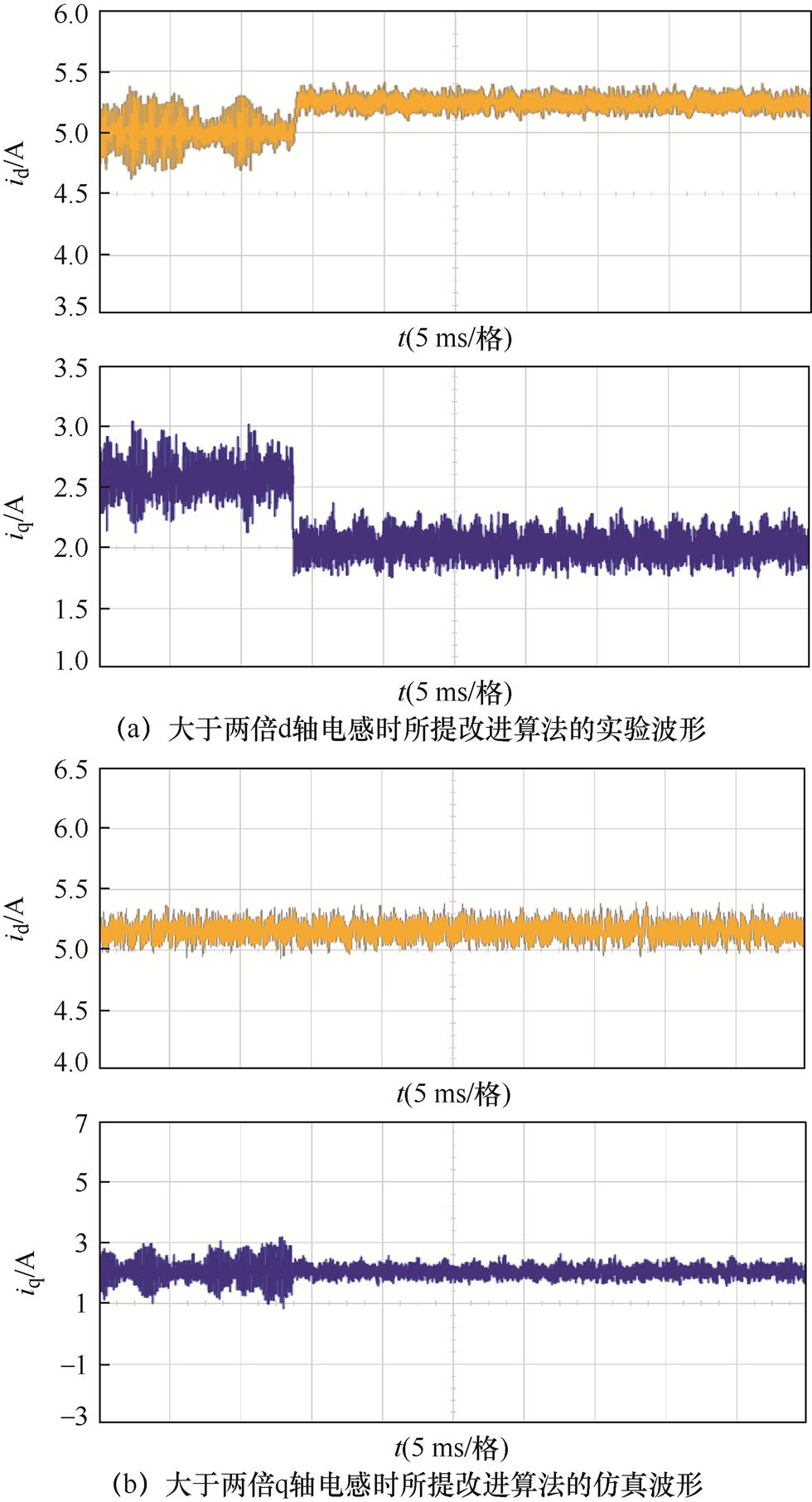
当控制器内的d、q轴电感参数分别大于电机模型电感参数两倍时,d、q轴电流实际值与参考值的仿真波形如图10所示。
根据图10a,由于无差拍预测电流控制器d轴电感模型参数失配大于两倍,控制器处于不稳定状态,d、q轴电流开始出现纹波且电流波动峰间变大。电流跟踪误差相较于参数匹配时更大,且d轴电流出现了负的跟踪误差,q轴出现了正的跟踪误差。
而图10b反映了q轴电感失配时的情况,这时也不满足系统的稳定条件。从仿真图中可以看出,d轴电流波动峰间变大,而q轴电流出现纹波且电流波动峰间变大,且d、q轴电流同时出现了负的跟踪误差,以上结论与分析式(17)所得出来的结论相符。表2给出了具体的仿真数据对比。
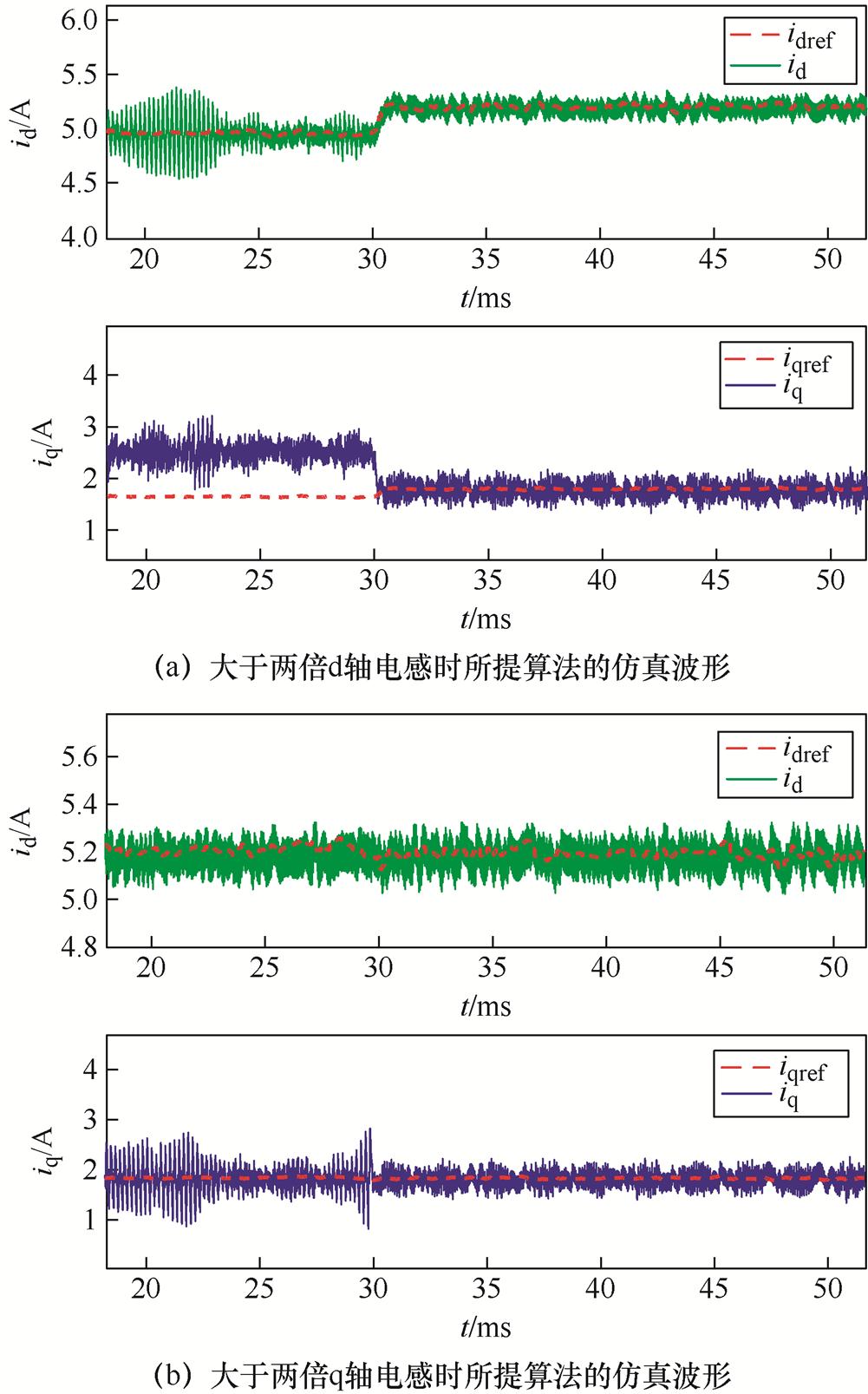
4.3 所提算法稳态仿真验证
在同样的仿真条件下,对所提控制算法进行仿真验证,仿真结果如图11所示。仿真开始时,由于无差拍控制器的模型参数失配,导致d、q轴电流波动幅度较大且出现了纹波,但当0.03 s时辨识系统将电感参数准确辨识出来并修正无差拍控制器中初始电感参数后,d、q轴电流波动幅值明显降低,振荡及纹波现象消失,系统重新回到与参数匹配时相同的收敛性。
表2 电流结果对比
Tab.2 Current result comparison
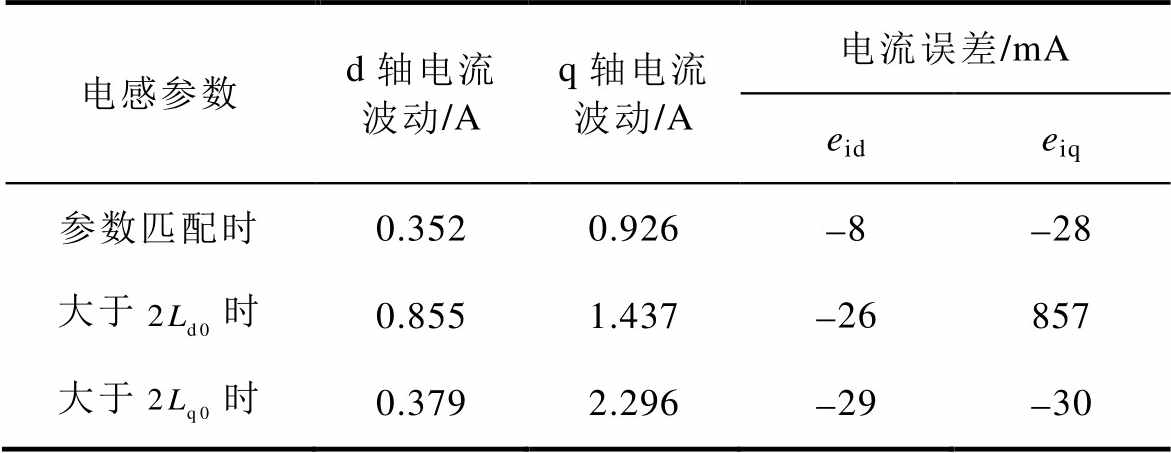
电感参数d轴电流波动/Aq轴电流波动/A电流误差/mA eideiq 参数匹配时0.3520.926-8-28 大于时0.8551.437-26857 大于时0.3792.296-29-30
4.4 所提算法动态仿真验证
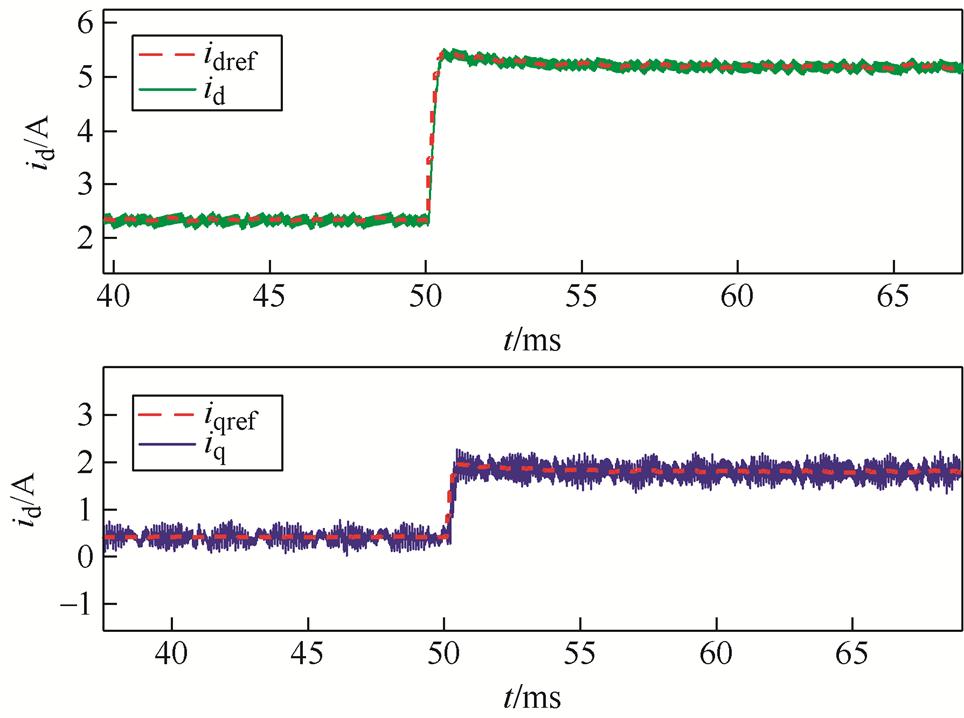
对所提算法进行转矩跳变动态仿真验证,仿真条件为给定转速1 500 r/min,负载转矩在0.05 s由2 Nm突变至5 Nm。大于两倍参数偏差时所提算法的动态仿真波形如图12所示。
根据图12,当转矩发生突变时,所提算法依旧具有较好的鲁棒性能,d轴反馈电流与参考电流之间的误差仅为17 mA,q轴反馈电流与参考电流之间的误差仅为26 mA,系统跟踪精度较高。
4.5 所提算法转速响应仿真验证
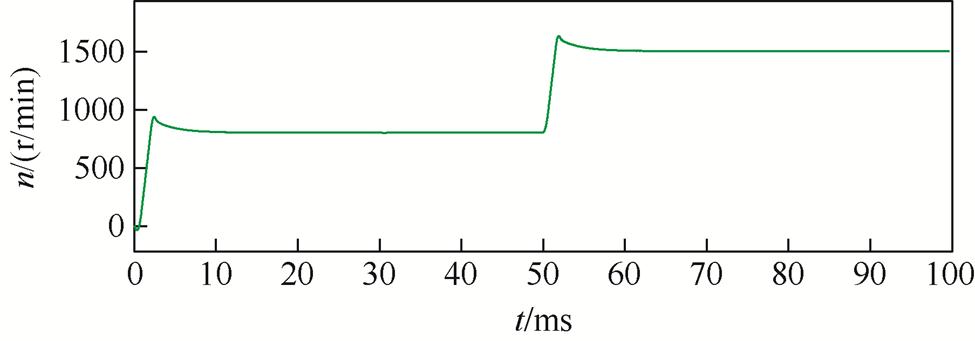
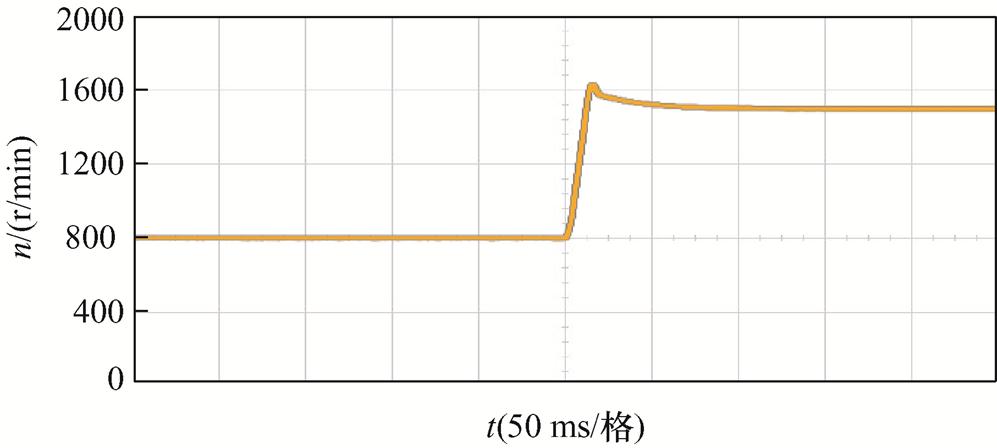
对所提算法进行转速跳变动态仿真验证,仿真条件为初始给定转速800 r/min,在0.05 s时跳变至1 500 r/min。所提算法的转速动态响应仿真波形如图13所示。
根据图13,d、q轴参数失配对转速波形的影响较小,一开始只经过15 ms便收敛到一条平滑的直线,在50 ms的时刻转速突变至1 500 r/min,经过短暂时间便跟随上给定的参考值,系统抗扰性能良好。
5 实验结果
为了验证所提改进算法的可行性,所用PMA- SynRM控制实验平台如图14所示,该平台用智能功率模块搭建三相全桥功率变换器,以TMS320F28335芯片为控制核心,一台6极36槽的PMA-SynRM为控制对象。
1)参数辨识实验验证
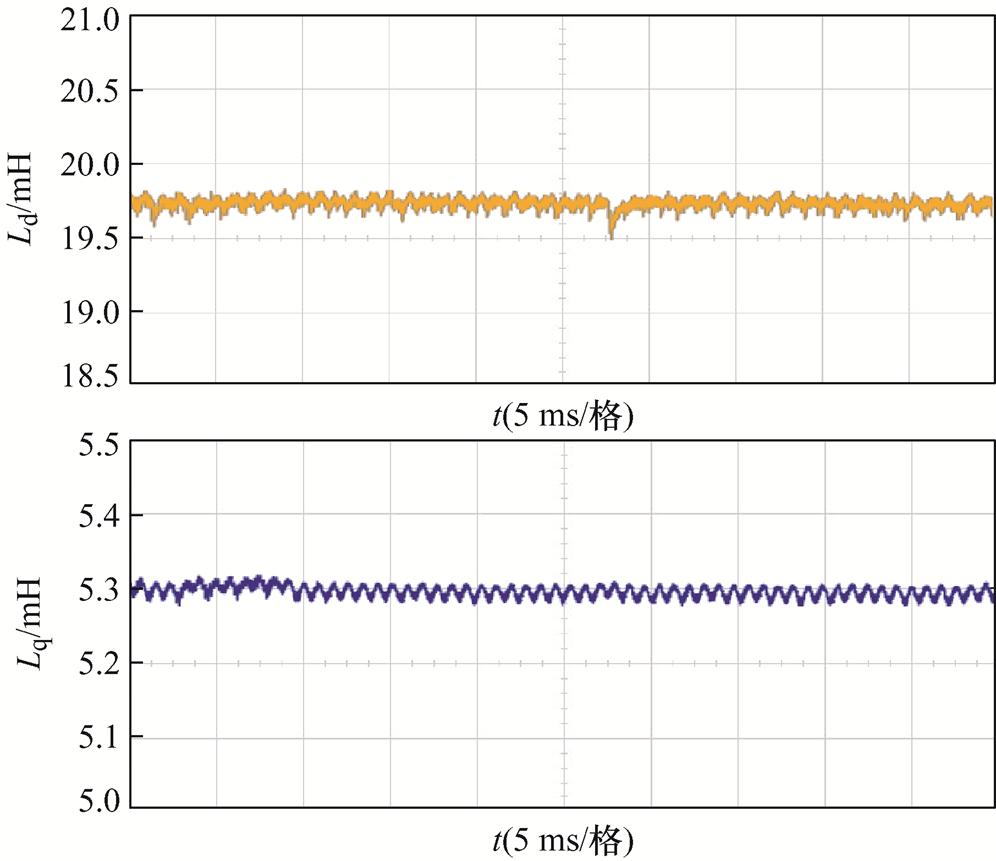
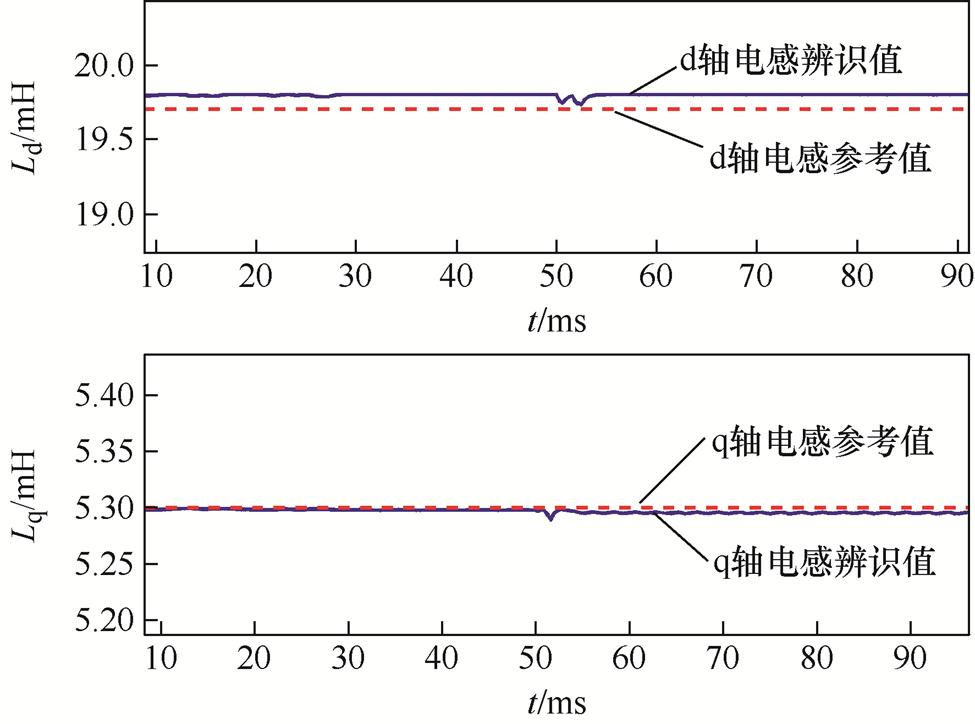
实验条件为给定参考转速1 500 r/min,负载转矩在0.05 s由2 Nm突变至5 Nm。d、q轴电感辨识实验波形如图15所示。
根据图15实验波形可以看出,d、q轴电感的辨识值在0.03 s左右基本收敛到参考值附近,收敛误差在3%以内。在0.05 s转矩突变时,辨识电感值很快又跟随上模型电感参数值。
2)所提改进算法稳态实验验证
实验条件为给定参考转速1 500 r/min,负载转矩在恒定5 Nm,开关频率为10 kHz。参数失配时所提算法实验波形如图16所示。实验开始时,由于无差拍控制器的模型参数与电机的实际参数不匹配,导致d、q轴电流波动幅度增大且出现了纹波,因为q轴电感较小,因此,当q轴电感两倍失配时,波动和纹波相较于d轴小。然而,当0.03 s时辨识系统将电感参数准确辨识出来并修正无差拍控制器中初始电感参数后,这种波动峰间增大和纹波的现象得以改善。
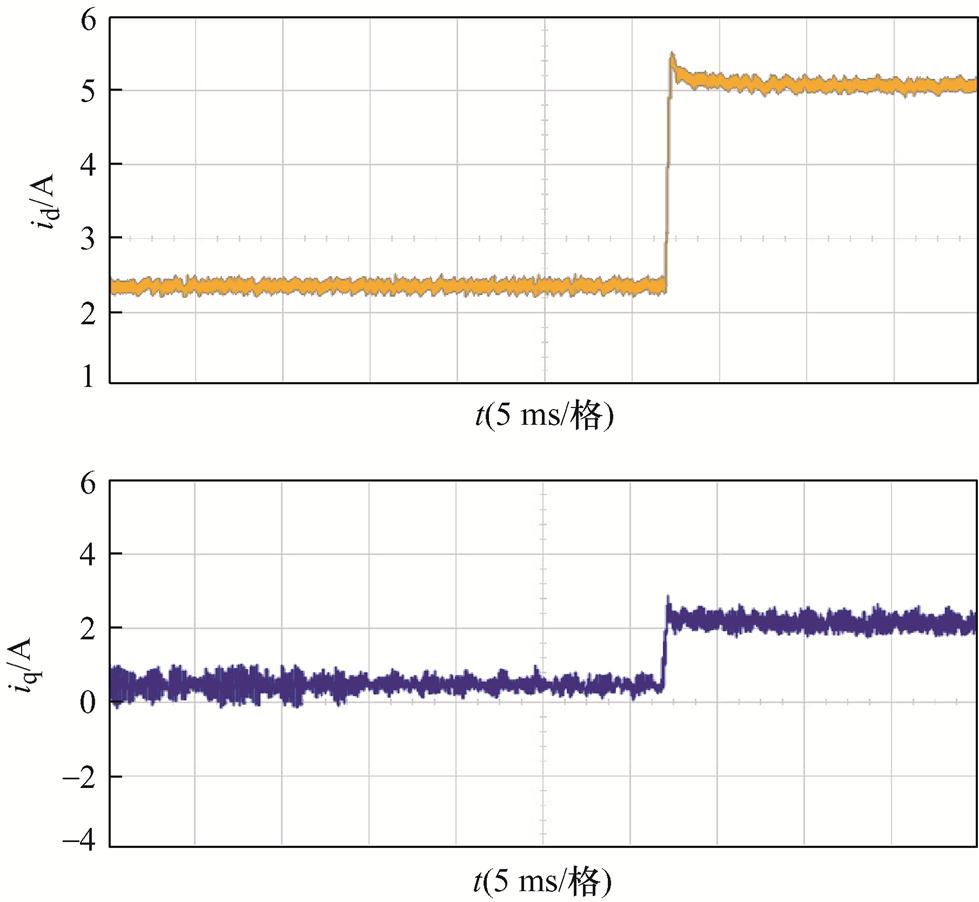
3)所提改进算法动态实验验证
对所提算法进行转矩跳变动态实验验证,实验条件为给定转速1 500 r/min,负载转矩在0.05 s由2 Nm突变至5 Nm,开关频率为10 kHz。大于两倍参数偏差时所提算法的动态实验波形如图17所示。当转矩发生突变时,所提算法依旧具有较快的动态响应性能,在转矩跳变的过程中系统依旧能保持良好的稳定性。
4)所提改进算法转速响应实验验证
实验条件为初始给定转速800 r/min,在0.5 s时跳变至1 500 r/min。所提算法的转速动态响应实验波形如图18所示。
根据图18,在0.5 s时转速由800 r/min跳变至1 500 r/min,由实验波形发现,参数失配对转速的影响不大,但是会使电流产生振荡,进而导致功率器件发热,严重时甚至损坏。
6 结论
以3 kW永磁辅助式同步磁阻电机为研究对象,本文针对电感参数失配会导致MTPA控制器电流角计算不准确和无差拍电流预测控制的稳定性差问题,提出一种参数自适应的无差拍预测电流控制算法,通过仿真和实验验证分析可以得到以下结论:
1)电机参数失配会对最大转矩电流比控制和无差拍电流预测控制产生一定的影响,主要包括电流角计算不准确、鲁棒性差、稳态电流波动大和跟踪静差大。
2)通过模型参考自适应系统设计出d、q轴电感参数在线辨识的方法,仿真和实验证明了此方法的收敛时间在30 ms左右,收敛误差在3%以内,具有较快的辨识速度和较高的辨识精度。
3)将上述得到的参数辨识结果传递到MTPA控制器和无差拍电流预测控制器中,可以有效地抑制参数失配带来的影响,减小了因参数失配带来的系统振荡和电流纹波的问题。当d轴电感大于两倍失配时,d、q轴电流波动峰峰值分别减小约142%和55%;当q轴电感大于两倍失配时,d、q轴电流波动峰峰值分别减小约7.6%和147%,因此提高了系统的鲁棒性。
参考文献
[1] Dieterle O, Greiner T, Heidrich P. Control of a PMSM with quadruple three-phase star-connected windings under inverter short-circuit fault[J]. IEEE Transactions on Industrial Electronics, 2019, 66(1): 685-695.
[2] Jia Shaofeng, Zhang Ping, Liang Deliang, et al. Design and comparison of three different types of IE4 efficiency machines[C]//2019 22nd International Conference on Electrical Machines and Systems (ICEMS), Harbin, China, 2019: 1-4.
[3] 曹恒佩, 艾萌萌, 王延波. 永磁辅助同步磁阻电机研究现状及发展趋势[J]. 电工技术学报, 2022, 37(18): 4575-4592.
Cao Hengpei, Ai Mengmeng, Wang Yanbo. Research status and development trend of permanent magnet assisted synchronous reluctance motor[J]. Transa- ctions of China Electrotechnical Society, 2022, 37(18): 4575-4592.
[4] 黄辉, 胡余生. 永磁辅助同步磁阻电机设计与应用[M]. 北京: 机械工业出版社, 2017.
[5] Niazi P, Toliyat H A, Goodarzi A. Robust maximum torque per ampere (MTPA) control of PM-assisted SynRM for traction applications[J]. IEEE Transa- ctions on Vehicular Technology, 2007, 56(4): 1538- 1545.
[6] 狄冲, 鲍晓华, 潘晋, 等. 基于Elmer开源有限元平台的铁氧体辅助同步磁阻电机的建模和分析[J]. 电工技术学报, 2022, 37(5): 1136-1144.
Di Chong, Bao Xiaohua, Pan Jin, et al. Modelling and analysis of a ferrite assisted synchronous reluctance machine based on the open-source platform Elmer[J]. Transactions of China Electrotechnical Society, 2022, 37(5): 1136-1144.
[7] 杨晨, 白保东, 陈德志, 等. 可变磁通永磁辅助同步磁阻电机设计与性能分析[J]. 电工技术学报, 2019, 34(3): 489-496.
Yang Chen, Bai Baodong, Chen Dezhi, et al. Design and analysis of a variable flux permanent magnet assisted synchronous motor[J]. Transactions of China Electrotechnical Society, 2019, 34(3): 489-496.
[8] Li Changbin, Wang Xiuhe, Liu Feng, et al. Analysis of permanent magnet-assisted synchronous reluctance motor based on equivalent reluctance network model[J]. CES Transactions on Electrical Machines and Systems, 2022, 6(2): 135-144.
[9] 孙毅, 蔡顺, 林迎前, 等. 永磁辅助同步磁阻电机顶层优化设计[J]. 电工技术学报, 2022, 37(9): 2306- 2318.
Sun Yi, Cai Shun, Lin Yingqian, et al. Top-level design pattern of PM-assisted synchronous reluctance machines[J]. Transactions of China Electrotechnical Society, 2022, 37(9): 2306-2318.
[10] 解正宵. 永磁辅助同步磁阻电机控制策略研究[D].杭州:浙江大学, 2021.
Xie Zhengxiao. Research on control strategies of permanent magnet-assisted synchronous reluctance motor[D]. Hangzhou: Zhejiang University, 2021.
[11] 方磊, 谭国俊, 刘娜, 等. 永磁辅助式同步磁阻电机转矩预测控制方法[J]. 电机与控制应用, 2018, 45(5): 1-7.
Fang Lei, Tan Guojun, Liu Na, et al. Torque predictive control method for permanent magnet assisted synchronous reluctance motor[J]. Electric Machines & Control Application, 2018, 45(5): 1-7.
[12] Huynh T A, Le N D, Hsieh M F, et al. A modified of DTC control applied to novel FI-PMA-SynRM for torque ripple reduction[C]//2019 IEEE 4th International Future Energy Electronics Conference (IFEEC), Singapore, 2019: 1-7.
[13] Arafat A, Haque M S, Islam M Z, et al. Performance comparison at maximum torque per ampere control between rare earth and rare earth free five-phase PMa-SynRM under open phase faults[C]//2018 IEEE Energy Conversion Congress and Exposition (ECCE), Portland, OR, USA, 2018: 784-789.
[14] 翁子恺, 储剑波. 基于定子磁场定向的永磁辅助同步磁阻电机无差拍直接转矩控制[J]. 电机与控制应用, 2022, 49(5): 20-26.
Weng Zikai, Chu Jianbo. Deadbeat direct torque control of PMASynRM based on stator field orientation[J]. Electric Machines & Control Appli- cation, 2022, 49(5): 20-26.
[15] 谷鑫, 鲁金月, 王志强, 等. 基于无差拍电流预测控制的永磁同步电机谐波电流抑制策略[J]. 电工技术学报, 2022, 37(24): 6345-6356.
Gu Xin, Lu Jinyue, Wang Zhiqiang, et al. Harmonic current suppression strategy for permanent magnet synchronous motor based on deadbeat current predi- ction control[J]. Transactions of China Electrotech- nical Society, 2022, 37(24): 6345-6356.
[16] Ba Xin, Wang Peng, Zhang Chengning, et al. Improved deadbeat predictive current control to enhance the performance of the drive system of permanent magnet synchronous motors[J]. IEEE Transactions on Applied Superconductivity, 2021, 31(8): 0603004.
[17] 邱建琪, 曾汉, 史涔溦. 永磁辅助式同步磁阻电机自寻优控制及参数辨识[J]. 电机与控制学报, 2022, 26(6): 1-8.
Qiu Jianqi, Zeng Han, Shi Cenwei. Self-optimizing control and parameters identification for permanent magnet assisted synchronous reluctance motor[J]. Electric Machines and Control, 2022, 26(6): 1-8.
[18] An Xingke, Liu Guohai, Chen Qian, et al. Adjustable model predictive control for IPMSM drives based on online stator inductance identification[J]. IEEE Transactions on Industrial Electronics, 2022, 69(4): 3368-3381.
[19] Wang Zitan, Chai Jianyun, Xiang Xuewei, et al. A novel online parameter identification algorithm designed for deadbeat current control of the permanent-magnet synchronous motor[J]. IEEE Transactions on Industry Applications, 2022, 58(2): 2029-2041.
[20] Yao Yu, Huang Yunkai, Peng Fei, et al. An improved deadbeat predictive current control with online parameter identification for surface-mounted PMSMs[J]. IEEE Transactions on Industrial Electronics, 2020, 67(12): 10145-10155.
[21] 李婕, 杨淑英, 谢震, 等. 基于有效信息迭代快速粒子群优化算法的永磁同步电机参数在线辨识[J]. 电工技术学报, 2022, 37(18): 4604-4613.
Li Jie, Yang Shuying, Xie Zhen, et al. Online parameter identification of permanent magnet synchronous motor based on fast particle swarm optimization algorithm with effective information iterated[J]. Transactions of China Electrotechnical Society, 2022, 37(18): 4604-4613.
[22] Ma Xiaojun, Bi Chao. A technology for online parameter identification of permanent magnet syn- chronous motor[J]. CES Transactions on Electrical Machines and Systems, 2020, 4(3): 237-242.
Current Deadbeat Control of Permanent Magnet-Assisted Synchronous Reluctance Motor Based on Parameter Identification
Xu Aide1 Liu Xin2 Li Xinyu2 Hu Shimai1
(1. School of Information and Science Technology Dalian Maritime University Dalian 116026 China 2. School of Electrical Engineering of Ships Dalian Maritime University Dalian 116026 China)
Abstract The permanent magnet-assisted synchronous reluctance motor, which combines the characteristics of permanent magnet synchronous motor and synchronous reluctance motor, has received more and more attention from many scholars because of its characteristics of less permanent magnet usage, high efficiency and high torque density. Deadbeat predictive control is widely used in modern motor control schemes. However, the control effect of deadbeat predictive control depends on the accuracy of the model, and in the actual operation of PMA-SynRM characterized by a high convex pole ratio, the motor parameters will be changed greatly with the change of operating conditions, which is more obvious in the motor inductance parameters. When the motor inductance parameter varies greatly, it leads to a decrease in the calculation accuracy of the current angle of the maximum torque per ampere controller and a decrease in the control effect of the deadbeat controller. Therefore, a parametric online identification method for the d and q axis inductance parameters of permanent magnet assisted synchronous reluctance motors is adopted in this paper. In order to improve the control effect of deadbeat predictive current control system, the identification value is used to replace the initial model inductance parameters in MTPA controller and deadbeat predictive current controller.
First, this paper defines the position of the d and q axis in the rotor structure and derives a mathematical model of a permanent magnet-assisted synchronous reluctance motor. Secondly, according to the voltage equation of permanent magnet-assisted synchronous reluctance motor, the mathematical equation of traditional deadbeat predictive current control is deduced, and the parameter sensitivity of inductance parameters in traditional deadbeat predictive current control scheme is analyzed. According to the stability condition of closed-loop transfer function in discrete domain, the fluctuation range of d and q axis inductance which can keep the deadbeat predictive current controller stable is given. The controller is in an unstable state when the d and q axis inductance is greater than two times the nominal model inductance. Finally, the parameter adaptive rate of the model reference adaptive motor parameter identification system is designed according to Popov's super stability theory, and the inductance parameter online identification scheme of PMA-SynRM is given to complete the design of the variable parameter MTPA-DBPCC controller.
In order to verify the effectiveness of the deadbeat predictive current control strategy based on parameter identification, the algorithm is simulated and verified in Matlab/Simulink environment, and the experiment is carried out on the experimental platform with TMS320F28335 controller as the core. The simulation and experimental results show that the deadbeat predictive current control scheme based on parameter identification can effectively suppress the system oscillation and current ripple caused by inductance parameter mismatch. When the d axis inductance is greater than two times the parameter mismatch, the peak values of d and q axis current fluctuations are reduced by about 142% and 55%, respectively; when the q axis inductance is greater than two times the parameter mismatch, the peak values of d and q axis current fluctuations are reduced by about 7.6% and 147%, respectively, thus the robustness of the system is improved.
Keywords:Permanent magnet-assisted synchronous reluctance motor, parameter identification, deadbeat predictive current control, model reference adaptive system
中图分类号:TM352
DOI: 10.19595/j.cnki.1000-6753.tces.231197
国家自然科学基金资助项目(51407021, 52377037)。
收稿日期 2023-07-25
改稿日期 2023-11-09
作者简介
许爱德 女,1974年生,教授,硕士生导师,研究方向为电力电子技术及现代电气传动、电机先进控制、预测控制与智能控制等。
E-mail: aidexu@dlmu.edu.cn(通信作者)
刘 鑫 男,1999年生,硕士研究生,研究方向永磁辅助同步磁阻电机控制。
E-mail: xliu9942@163.com
(编辑 崔文静)
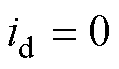 的控制方式。在电感特性上,内置式永磁同步电机电感随电流及转子位置变化较小,而PMA-SynRM电感随电流及转子位置变化较大。此外,PMA-SynRM相较于永磁同步电机具有更少的永磁体用料,成本较低。以上这些区别和特点使PMA-SynRM成为了符合当下社会发展需要的高性能电机。但是,目前国内外学者对PMA-SynRM的研究主要集中在电机的本体设计方面[6-9],对电机的高性能控制算法的研究还处于起步阶段,其特有的高凸极比特性使其对电流环性能要求更高,因此设计高性能的电流环控制器对其广泛应用有着至关重要的意义。
的控制方式。在电感特性上,内置式永磁同步电机电感随电流及转子位置变化较小,而PMA-SynRM电感随电流及转子位置变化较大。此外,PMA-SynRM相较于永磁同步电机具有更少的永磁体用料,成本较低。以上这些区别和特点使PMA-SynRM成为了符合当下社会发展需要的高性能电机。但是,目前国内外学者对PMA-SynRM的研究主要集中在电机的本体设计方面[6-9],对电机的高性能控制算法的研究还处于起步阶段,其特有的高凸极比特性使其对电流环性能要求更高,因此设计高性能的电流环控制器对其广泛应用有着至关重要的意义。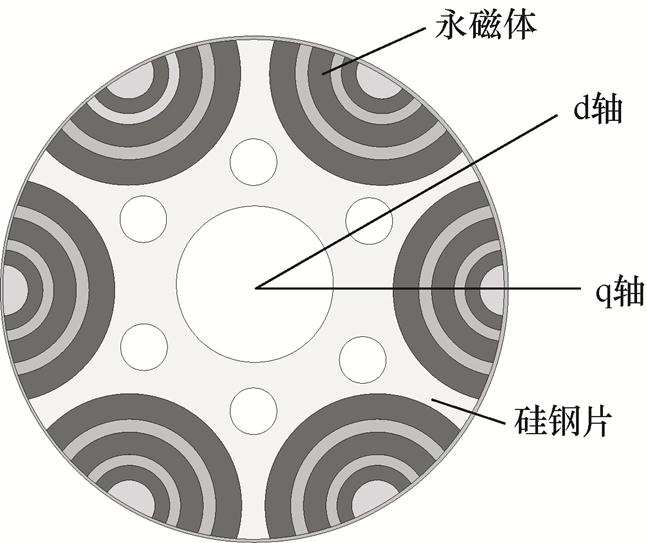
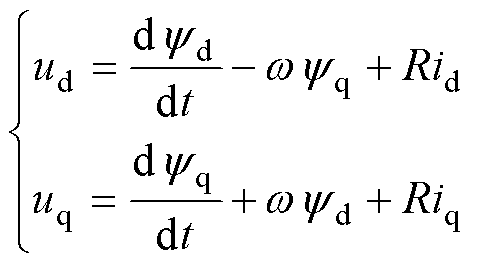 (1)
(1)
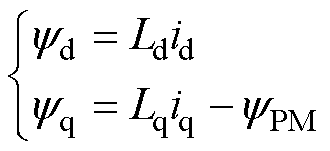 (2)
(2)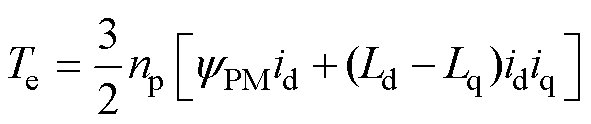 (3)
(3)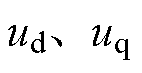 分别为定子电压矢量的d、q轴分量;
分别为定子电压矢量的d、q轴分量;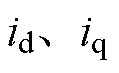 分别为定子电流矢量的d、q轴分量;
分别为定子电流矢量的d、q轴分量;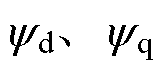 分别为定子的d、q轴磁链;
分别为定子的d、q轴磁链;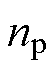 为电机极对数;
为电机极对数;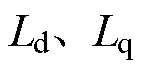 分别为电机定子绕组的d、q轴电感;
分别为电机定子绕组的d、q轴电感;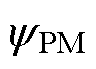 为永磁体产生的磁链;
为永磁体产生的磁链;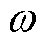 为电机的电角速度;
为电机的电角速度;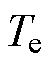 为电磁转矩;
为电磁转矩;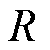 为绕组相电阻。
为绕组相电阻。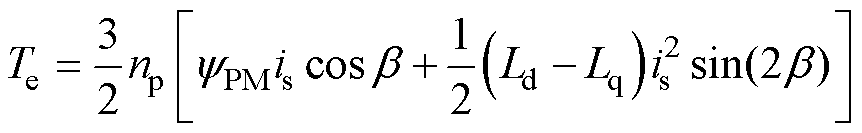 (4)
(4)
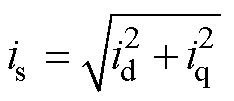 (5)
(5)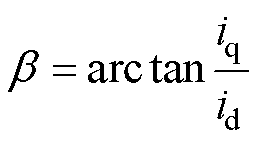 (6)
(6)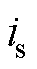 为定子电流幅值;
为定子电流幅值;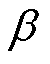 为定子电流与d轴的夹角。
为定子电流与d轴的夹角。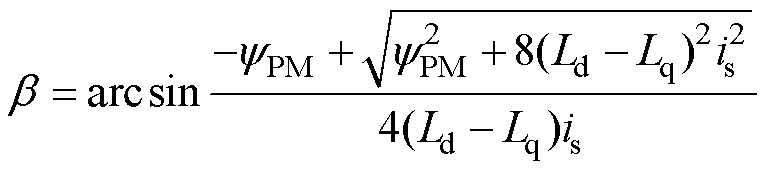 (7)
(7)
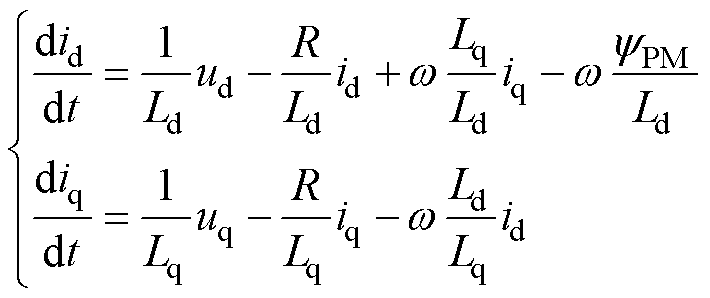 (8)
(8)
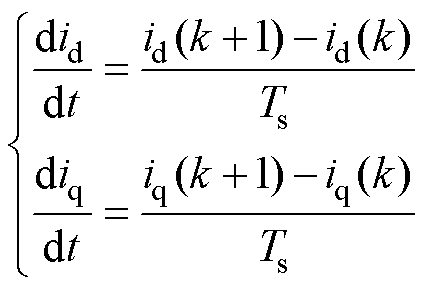 (9)
(9)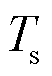 为离散化采样时间。
为离散化采样时间。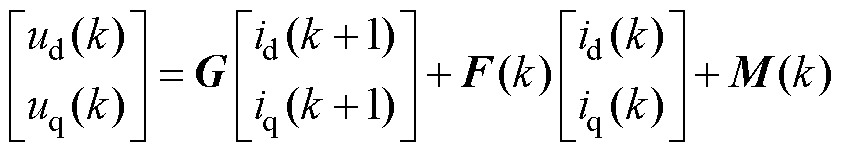 (10)
(10)
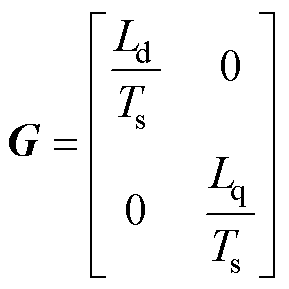
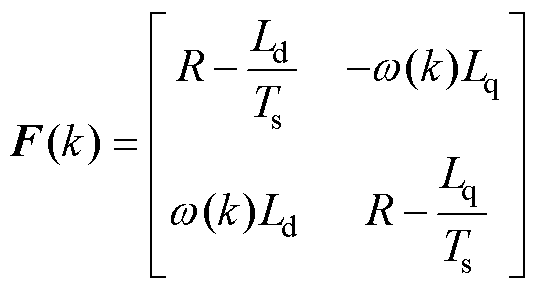
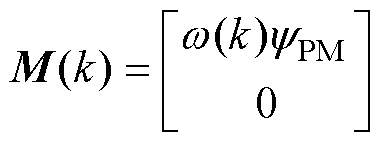
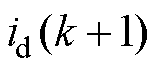 、
、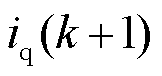 分别为
分别为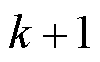 时刻d、q轴电流预测值;
时刻d、q轴电流预测值;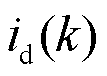 、
、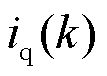 分别为
分别为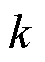 时刻的d、q轴电流;
时刻的d、q轴电流;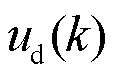 、
、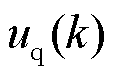 分别为
分别为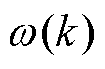 为
为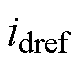 和
和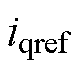 分别取代式(10)中的
分别取代式(10)中的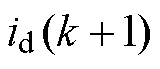 ,
,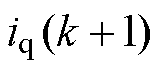 即可得到PMA-SynRM无差拍预测电流控制系统的参考电压为
即可得到PMA-SynRM无差拍预测电流控制系统的参考电压为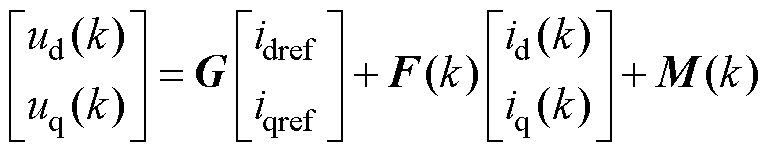 (11)
(11)
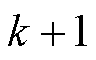 时刻d、q轴电流跟随MTPA输出的参考电流,进而生成参考的d、q轴电压矢量,最后通过空间电压矢量调制的方式生成控制脉冲以驱动功率变换器的开关器件导通,进而对电机进行闭环控制。
时刻d、q轴电流跟随MTPA输出的参考电流,进而生成参考的d、q轴电压矢量,最后通过空间电压矢量调制的方式生成控制脉冲以驱动功率变换器的开关器件导通,进而对电机进行闭环控制。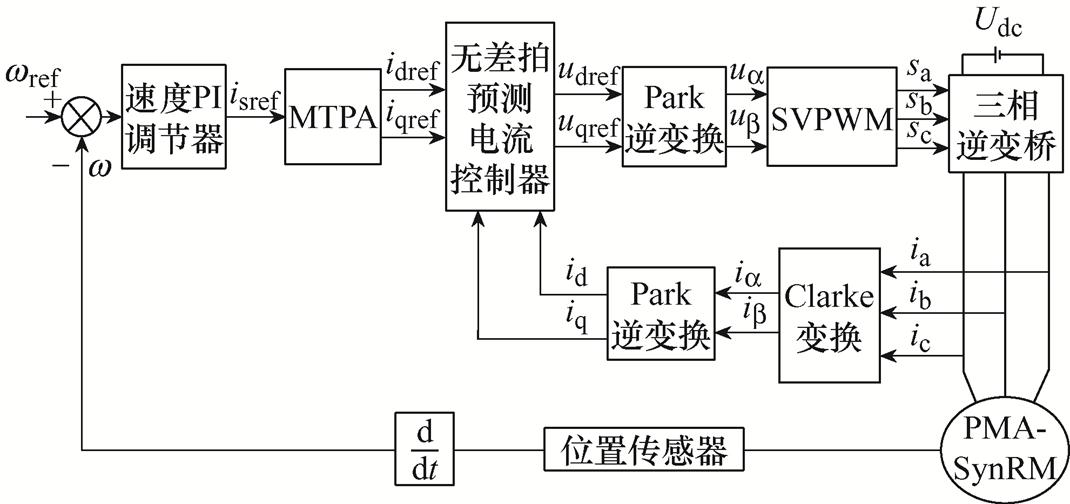
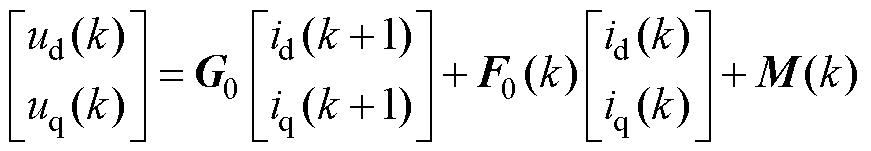 (12)
(12)
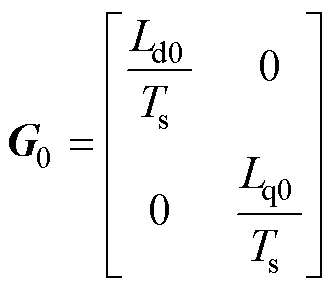
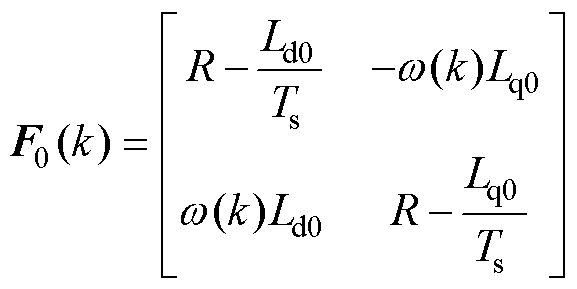
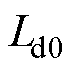 、
、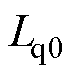 分别为电机铭牌标称的d、q轴电感。
分别为电机铭牌标称的d、q轴电感。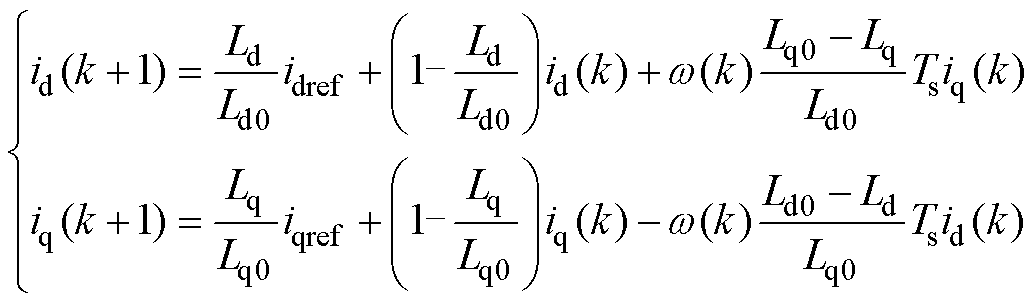 (13)
(13)
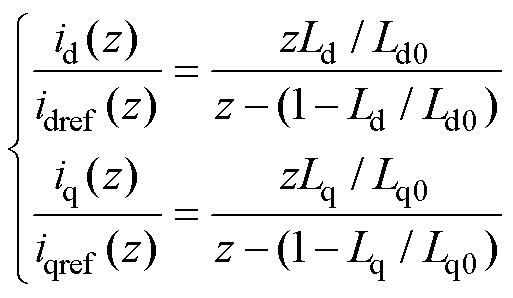 (14)
(14)
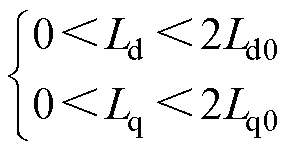 (15)
(15)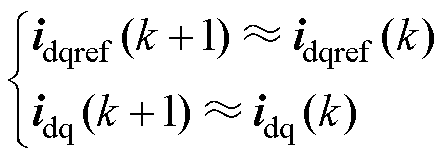 (16)
(16)
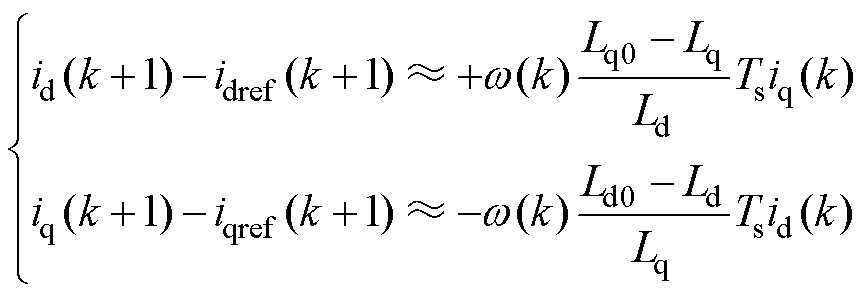 (17)
(17)
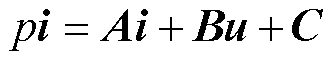 (18)
(18)
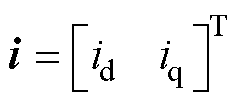
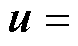
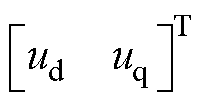
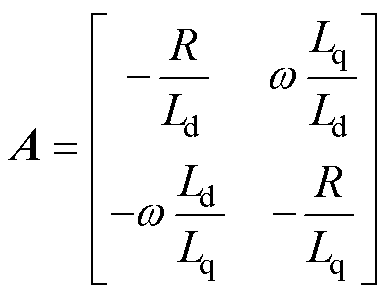
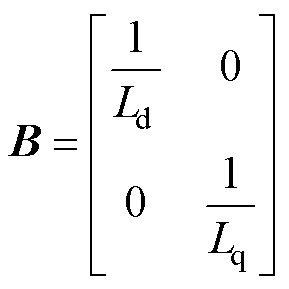
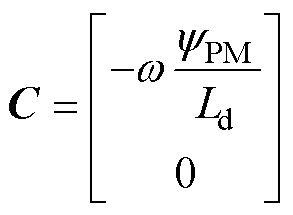
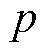 为其中微分算子。
为其中微分算子。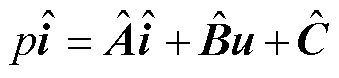 (19)
(19)
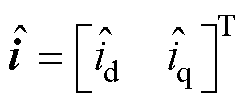
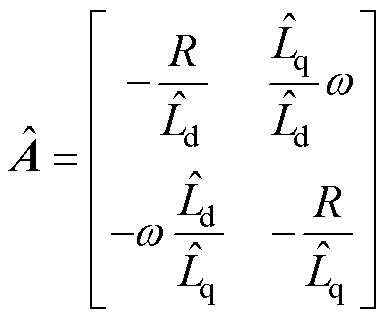
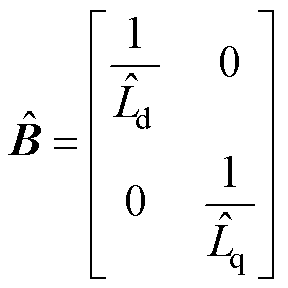
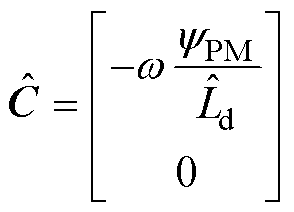
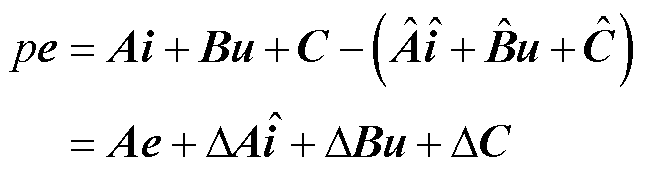 (20)
(20)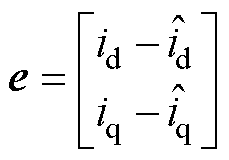
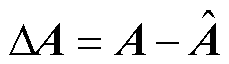
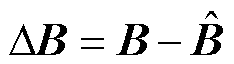
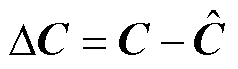
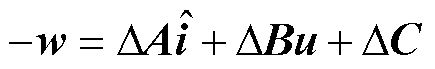 ,则有
,则有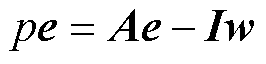 (21)
(21)
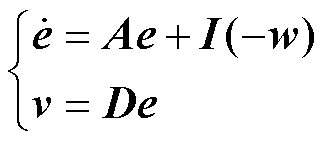 (22)
(22)
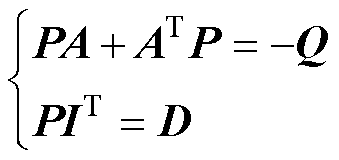 (23)
(23)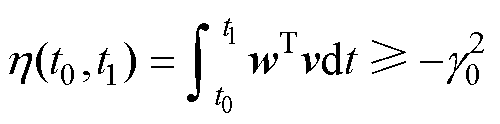
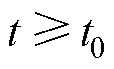 (24)
(24)
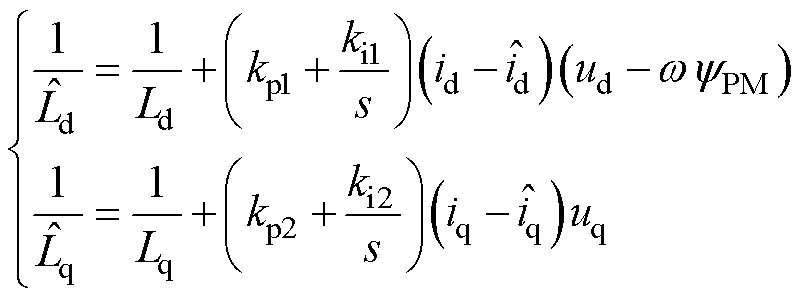 (25)
(25)
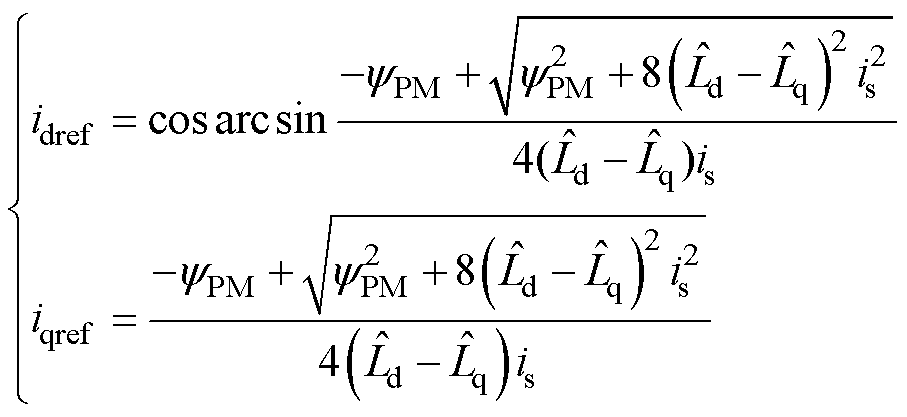 (26)
(26)
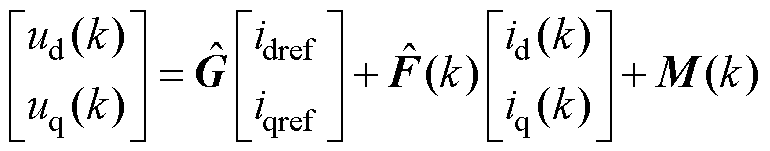 (27)
(27)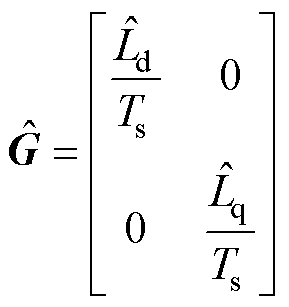
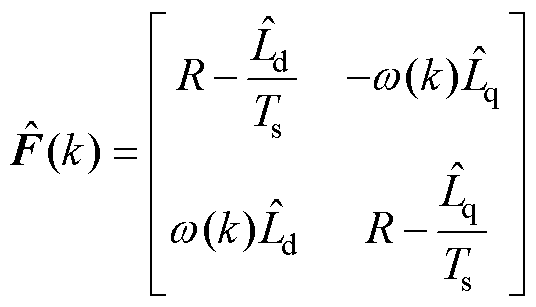

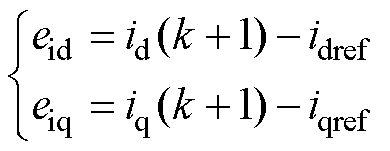 (28)
(28)
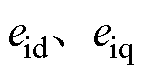 分别为d、q轴电流跟踪误差。
分别为d、q轴电流跟踪误差。