表1 系统规格
Tab.1 System specification
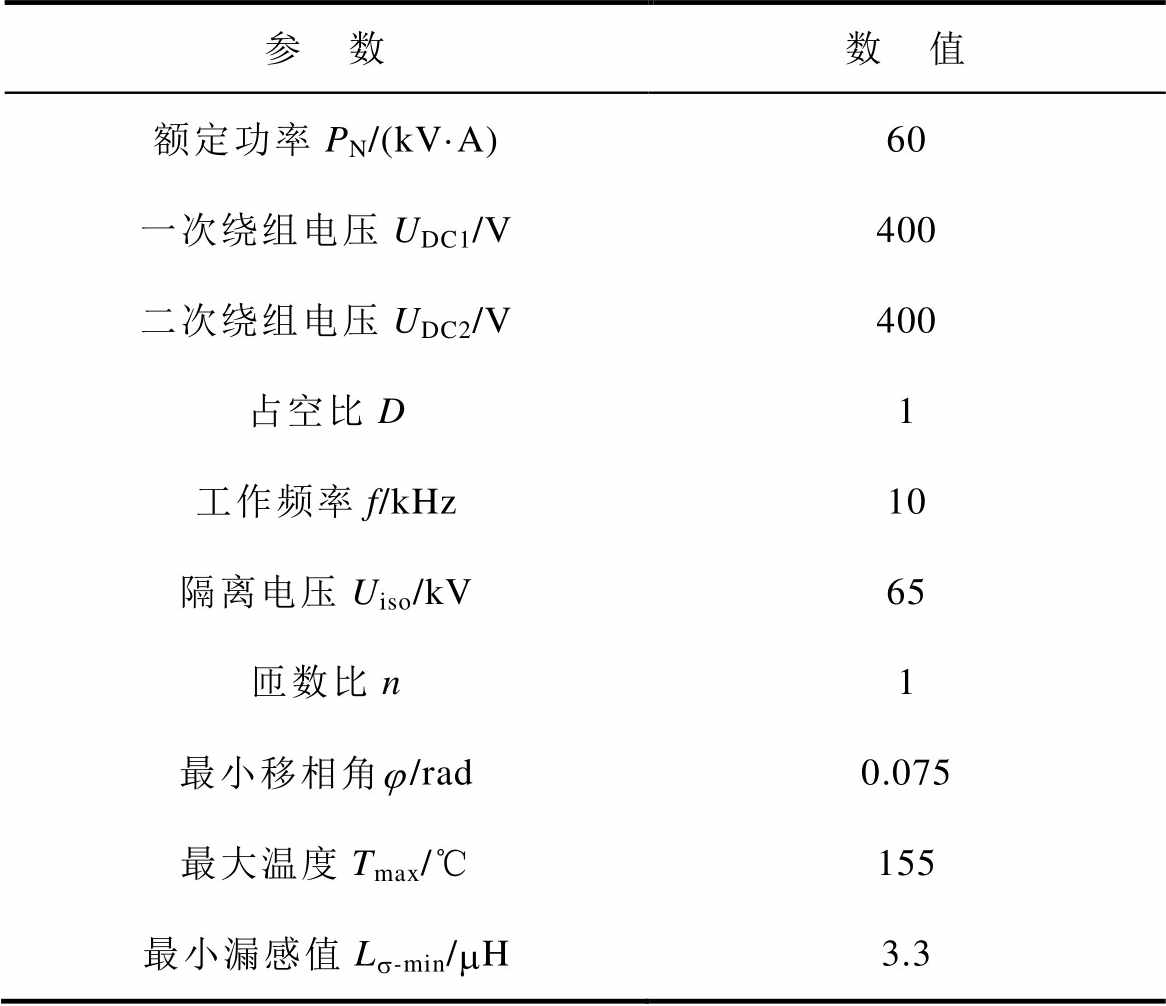
参 数数 值 额定功率PN/(kV·A)60 一次绕组电压UDC1/V400 二次绕组电压UDC2/V400 占空比D1 工作频率f/kHz10 隔离电压Uiso/kV65 匝数比n1 最小移相角j/rad0.075 最大温度Tmax/℃155 最小漏感值Ls-min/mH3.3
摘要 高频变压器(HFT)作为电力电子变换器等功率变换装备的核心部件,其优化设计是实现高功率密度、高效率和高可靠性的重要环节。为有效解决高频条件下显著的涡流效应和复杂紧凑的结构使变压器损耗难以准确计算、针对绝缘设计裕量不足的问题,本文提出计及高频效应和结构效应的电磁场建模方法,构建了高频变压器多目标协同优化设计方案。首先建立了低成本与高效率兼备的磁心损耗计算模型。其次,根据面积等效原理推导了考虑绕组结构效应的近似 Dowell 模型,实现绕组损耗的高精度计算。然后提出了考虑绕组端部效应和频率影响的漏感计算模型,减小漏感对于结构和频率的依赖性。在此基础上,采用一种新型多重绝缘结构,提高绕组间的绝缘耐压水平。最后,基于改进的非支配排序遗传算法(INSGA-Ⅱ)和自由参数扫描法建立了高频变压器的优化设计流程,根据筛选的最优设计方案研制了一台高频变压器样机。
关键词:高频变压器 自由参数扫描法 改进的非支配排序遗传算法(INSGA-Ⅱ) 优化设计 结构效应
随着电力电子变换器在中高压交直流输电网中应用的不断深入,对高频变压器(High Frequency Transformer, HFT)的开发与研究方兴未艾。精准有效的高频变压器设计不仅能够提高工作效率和功率密度,还能够保证其工作的可靠性与稳定性[1]。开关器件性能的提高与纳米晶等新型磁性材料的广泛应用[2-3],使得电力电子装置越来越朝着高频化与高功率密度的方向发展。如今,高频变压器已成为交直流混合配电网、电力牵引和电力电子变换器等功率变换领域的核心部件,起着电压转换与隔离等非常关键的作用[4],并广泛应用于光伏发电、海上风电等新能源直流汇集系统和铁路电气牵引系统,因而对全面评估损耗、绝缘、漏感等指标提出了更加严苛的要求。由于高频变压器通常工作在非正弦激励条件下,各优化目标之间相互冲突、难以平衡。因此,高频变压器的优化设计是一个需要考虑诸多因素影响的多目标优化过程。
目前,国内外许多研究机构对高频变压器的优化设计已取得一定成果。在电场建模方面,文献[5]采用一种特殊的磁心和绕组结构,利用自由参数扫描法设计了一台200 kW/30 kHz的风冷多绕组中频变压器样机,效率可达99.18%,但在设计过程中没有考虑绝缘结构。文献[6]基于网格搜索和重复网格细化的参数扫描法对一台166 kW/20 kHz的水冷高频变压器进行优化,功率密度为44 kW/dm3,效率为99.4%,该团队使用氮化铝优化了冷却系统结构,但同样没有对绝缘材料的填充和绝缘结构的设计作具体说明。磁场建模主要包括对磁心损耗、绕组损耗和漏感计算模型的研究。大多数文献使用斯坦梅兹公式(Improved Generalized Steinmetz Equation,IGSE)计算磁心损耗,该公式中含有计算成本高昂的数值积分,迭代次数较多时会造成计算时间延长。文献[7-8]采用理想的一维Dowell模型计算绕组损耗,该模型仅适用于宽箔绕组和单匝绕组变压器,对于利兹线绕组来说,在高频下使用该模型会产生较大误差。文献[9]基于自由参数扫描法,设计了一台15 kW/5 kHz、500 V/500 V的纳米晶合金大功率中频三相变压器,但文中没有考虑绕组端部的横向磁场分量对于漏感解析方法的影响。文献[10]提出了一种基于最佳磁通密度的优化设计方法,使总损耗达到最小,设计了一台10 kV/0.5 MW的变压器样机,然而计算漏感时没有考虑频率的影响。
对高频变压器的电磁场建模完成后,还需要结合智能优化算法,对各项电磁和结构参数进行全局寻优。目前使用较为广泛的是遗传算法和自由参数扫描法。文献[11-13]基于遗传算法优化设计了相应的高频变压器样机,但是该算法会出现种群分布不均、容易陷入局部收敛等问题。查尔姆斯理工大学的团队基于自由参数扫描法,将在较宽范围内扫描得到的参数集应用于设计流程图中以找到最佳参数集,设计制造了两台50 kW、1/3 kV、5 kHz的缩小版中频变压器样机[14-16],但当优化参数和优化目标较多时,参数扫描产生的有效设计方案较多,难以筛选最优设计方案。洛桑联邦理工学院的学者以效率、功率密度和温升作为目标函数,在使用参数扫描技术的基础上,使用性能过滤函数对产生的设计进行交互过滤,通过放松和收紧相应约束选取最符合要求的一组解,最终设计了一款100 kW/10 kHz的N87铁氧体堆叠磁心的中频变压器[16]。
此外,高频条件下显著的涡流效应和复杂紧凑的结构使得变压器损耗难以准确计算、绝缘设计裕量不足,这给高频变压器的电磁设计带来了严峻挑战。因此本文提出基于高频效应和结构效应分析的电磁场建模方法,构建了高频变压器多目标协同优化的设计方案。首先,通过拟合高频非正弦激励波形下IGSE中的复杂积分函数,建立了低成本与高效率兼备的磁心损耗计算模型。其次,为实现绕组损耗的高精度计算,本文考虑了绕组的结构效应和涡流效应,推导了适用于利兹线绕组的近似Dowell模型。然后,提出了考虑绕组端部效应和频率影响的漏感计算模型,减小漏感对于结构和频率的依赖性。在此基础上,采用考虑长短期介电强度的新型多重绝缘结构,提升高频变压器绕组间的绝缘耐压水平。最后,引入动态聚集距离(Dynamic Clustering Distance, DCD)和算术交叉算子对非支配排序遗传算法(Nondominated Sorting Genetic Algorithm, NSGA-Ⅱ)进行改进,利用ZDT1和ZDT3函数进行测试,并结合自由参数扫描法建立高频变压器的优化设计流程,制作了一台高频变压器样机,通过有限元仿真、空载试验和温升测量验证了最优设计方案。
在高频变压器的整个优化设计过程中,首先需要设定设计空间,包括磁心材料、磁心结构、绕组形式的确定以及绝缘材料的填充,然后根据表1中双有源桥(Dual Active Bridge, DAB)变换器的系统规格,对选取的磁心、绕组和绝缘材料的固定参数进行计算。综合高频变压器的电磁场计算模型,基于自由参数扫描法和改进的非支配排序遗传算法(Improved NSGA-Ⅱ, INSGA-Ⅱ)完成高频变压器的多目标优化设计。
表1 系统规格
Tab.1 System specification

参 数数 值 额定功率PN/(kV·A)60 一次绕组电压UDC1/V400 二次绕组电压UDC2/V400 占空比D1 工作频率f/kHz10 隔离电压Uiso/kV65 匝数比n1 最小移相角j/rad0.075 最大温度Tmax/℃155 最小漏感值Ls-min/mH3.3
本文建立的满足要求的高频变压器优化设计流程如图1所示。
DAB变换器[17-18]具有易于实现软开关、双向功率传输以及模块化、结构对称的特点,被越来越多地应用于大功率场合,成为直流配电网的重要组成部分。DAB变换器的等效电路及稳态下产生的电压和电流波形如图2所示。
图2a中的串联电感可集成为高频变压器的漏电感,以减少元件数量,实现更高的功率密度。变换器一次电流IT1为分段线性波形,其有效值表达式为
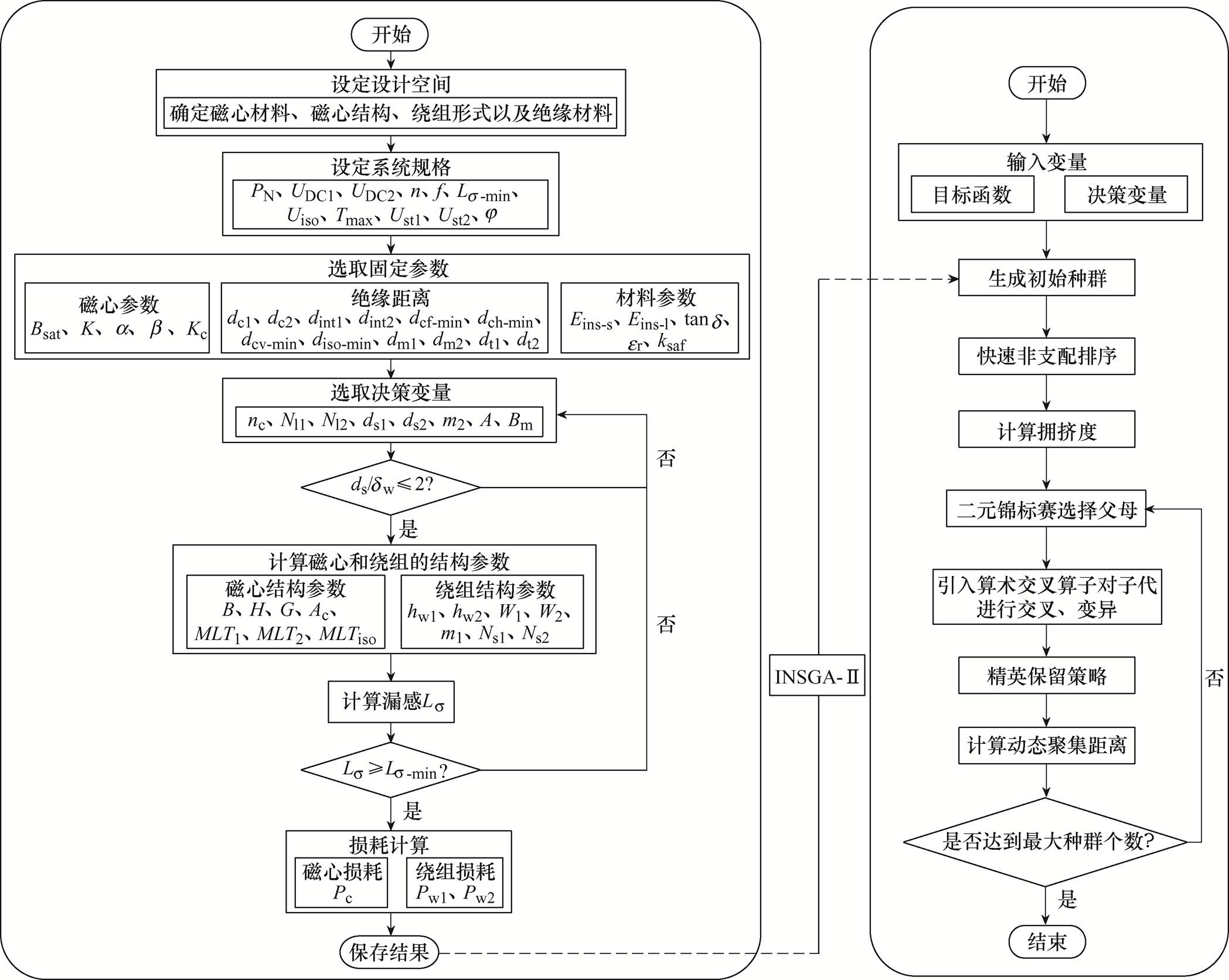
图1 高频变压器的优化设计流程
Fig.1 Optimization design flow chart of high frequency transformer
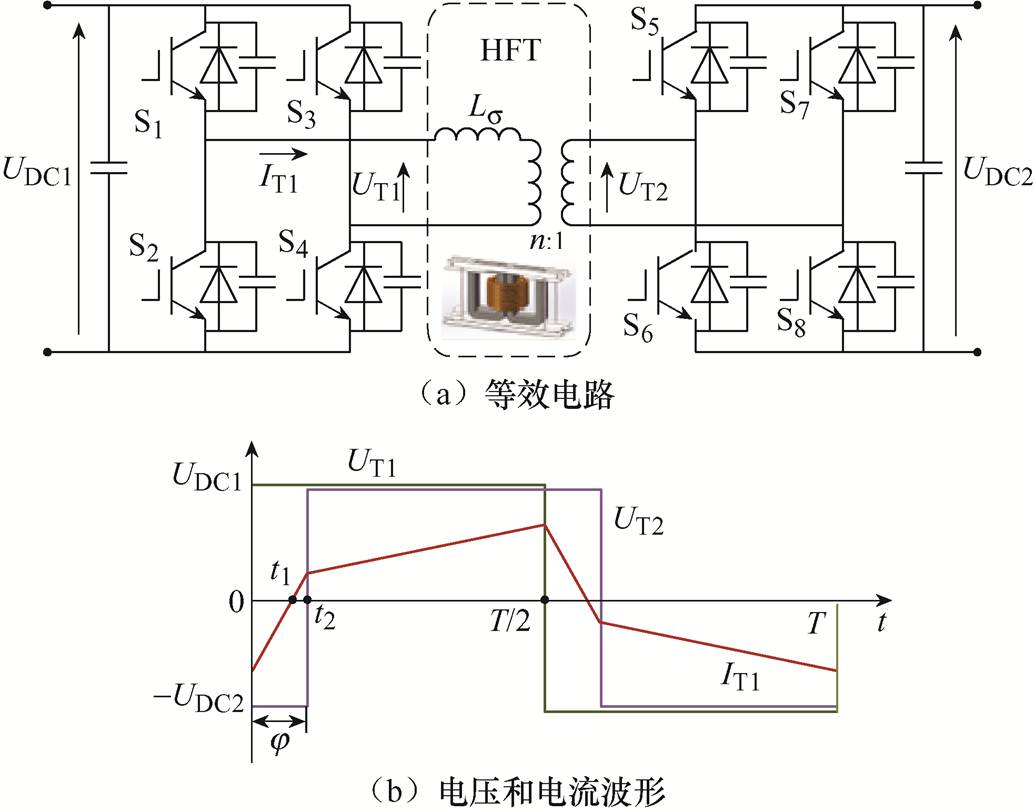
图2 DAB变换器的等效电路及稳态下产生的电压和电流波形
Fig.2 Equivalent circuit diagram of the DAB converter and the voltage and current waveforms generated at steady state
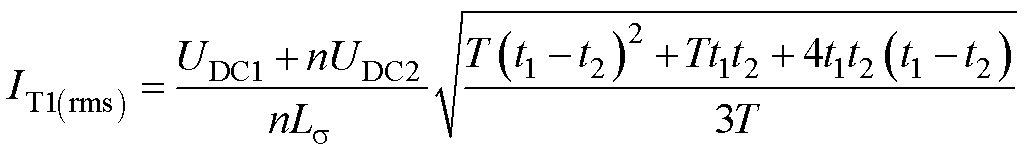 (1)
(1)
式中,t1、t2分别为IT1、UT2第一次过零的时间;T为采样周期。
为实现高频变压器小型化、轻量化的设计要求,减小高频下涡流效应的影响,本文采用方形利兹线绕组和集成良好的壳式磁心结构,所建立的高频变压器结构设计方案如图3所示。对磁心窗口内的所有结构尺寸参数化处理,并按照文献[19]中的设计理论进行推导计算。
由于改进的通用IGSE在工作范围内准确性高、贴合性好,且只需要三个经验系数,是高频非正弦激励波形下计算磁心损耗更适合的表达式。IGSE修正前的公式[20]为
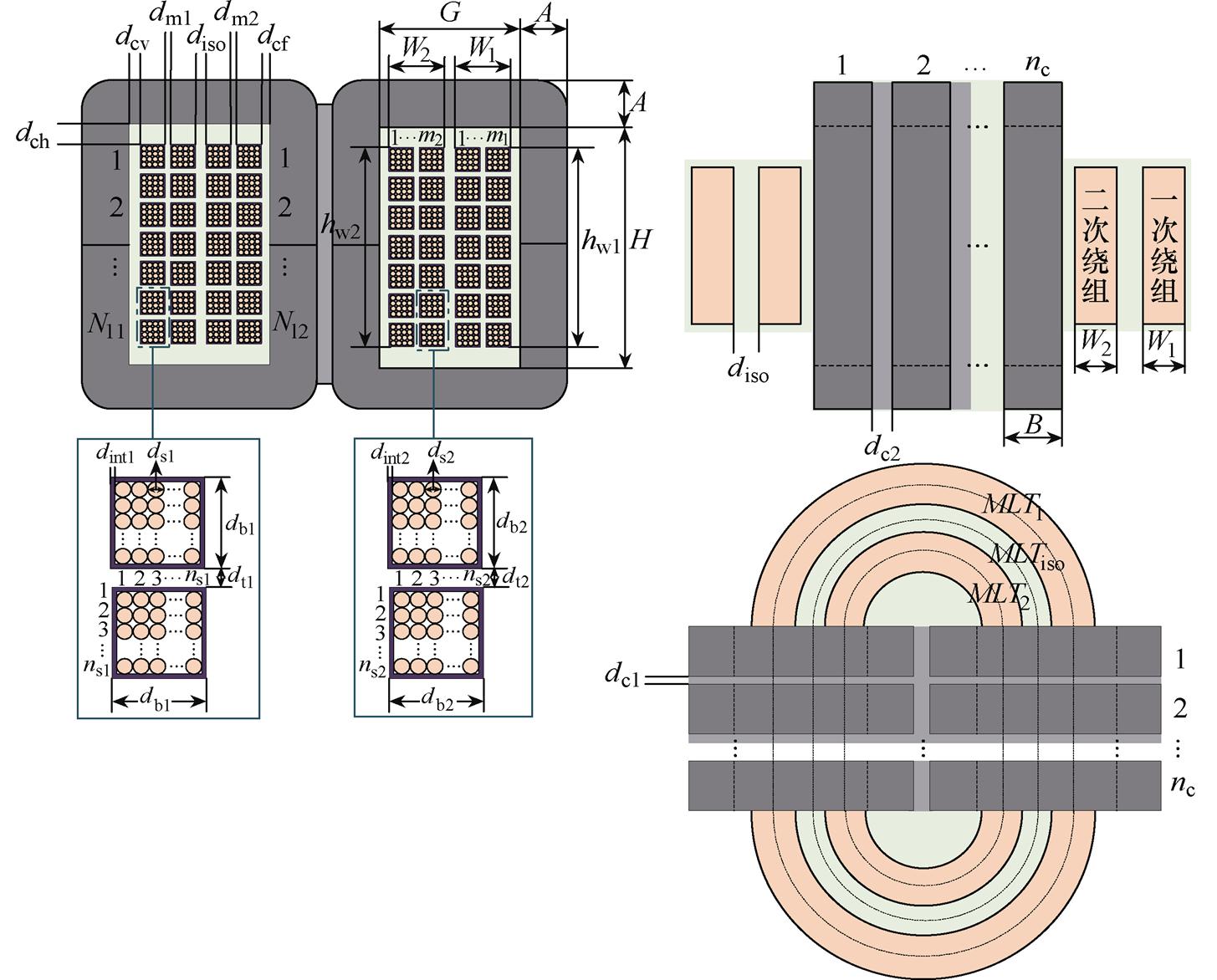
图3 高频变压器结构的设计方案
Fig.3 Design sketch of structure of HFT
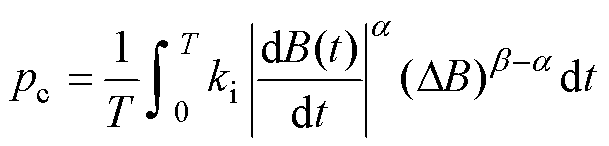 (2)
(2)
其中
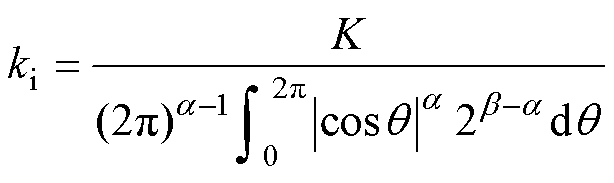 (3)
(3)
式中,B为磁通密度;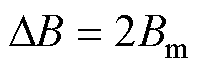 。
。
为避免IGSE中的复杂积分函数增加计算成本,本文依据图4并参考文献[21]中的方法对该公式进行修正。修正后的IGSE表达式为
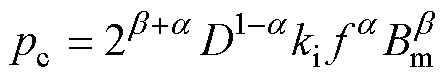 (4)
(4)
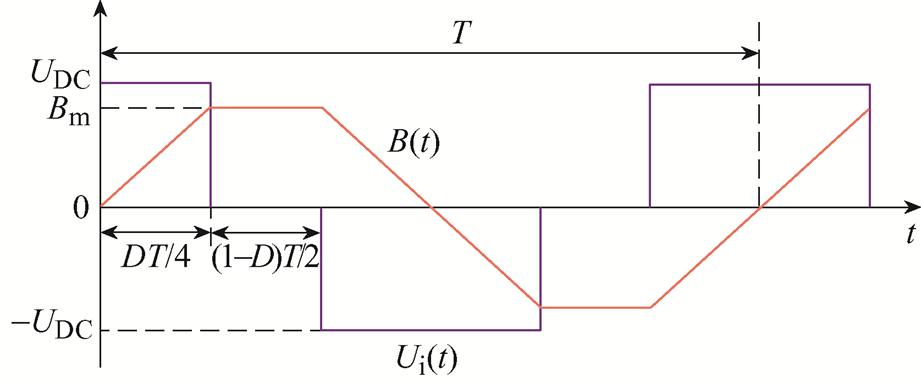
图4 电压和磁通密度波形
Fig.4 Voltage and flux density waveforms
在磁心选材方面,纳米晶合金具有更高的磁导率,饱和磁通密度较高,且热稳定性好,更适合作为本文的磁心材料。磁心选材完成后,搭建纳米晶磁环损耗数据的测量平台,如图5所示。通过测量正弦感应波形下纳米晶磁环的损耗数据,拟合得到IGSE的经验系数见表2。

图5 纳米晶磁环损耗数据测量平台
Fig.5 The loss data measurement platform of nanocrystalline magnetic rings
表2 IGSE的经验系数
Tab.2 Empirical coefficients of IGSE

经验系数数 值 a1.397 b2.296 K4.229×10-5
同时,在方波激励下测量不同频率的纳米晶磁环的损耗数据,如图6所示。可以看出,在小于饱和磁通密度的区域内,频率较低时磁滞损耗占主要部分,涡流损耗不明显,磁环损耗的增势较慢;随着频率的升高,磁环内涡流损耗越来越大,损耗曲线越来越陡。因此,选取合适的频率和磁通密度对高频变压器的优化设计具有重要意义。
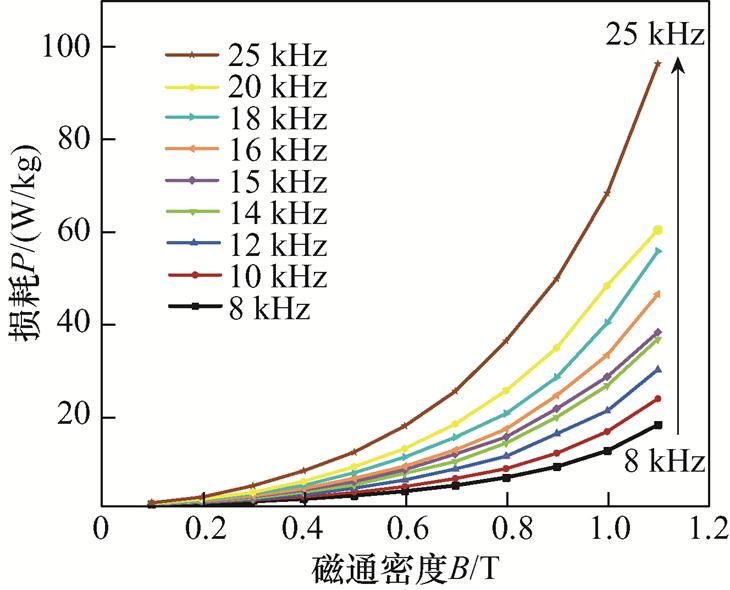
图6 不同频率的方波下测量的纳米晶磁环的损耗曲线
Fig.6 Loss curves of nanocrystalline magnetic rings measured under square wave of different frequencies
绕组损耗作为高频变压器的主要损耗之一,是影响磁性元件体积、效率和温升的关键参数。然而利兹线绕组绞合结构复杂,采用理想的Dowell模型难以准确计算绕组损耗[22]。因此本文在面积等效[23]的基础上推导了一种适用于利兹线绕组的近似Dowell模型,以快速准确计算绕组损耗。利兹线绕组等效过程如图7所示。
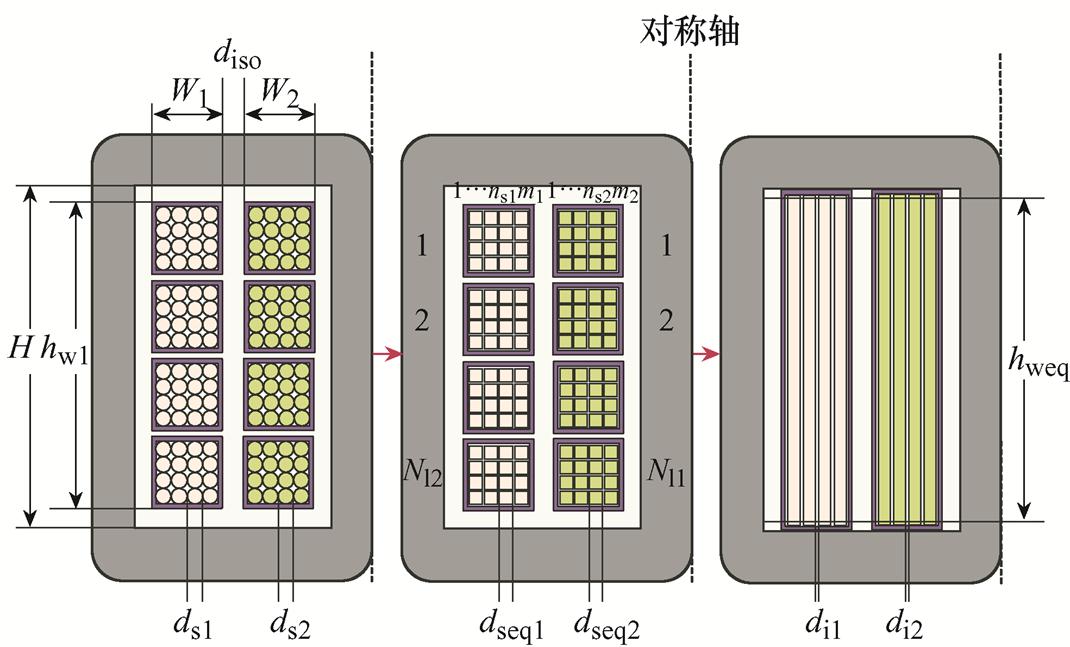
图7 利兹线绕组的等效过程
Fig.7 Equivalent process of Litz wire windings
首先在利兹线绕组的匝数和层数不变的条件下用方形股线替代圆形股线,等效的方形股线边长dseq为
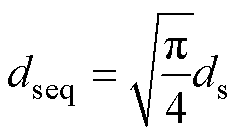 (5)
(5)
然后将方形股线绕组等效为箔式绕组。但这种等效改变了绕组的有效导电横截面积,为确保绕组的直流导电性相同,引入孔隙率h以修正绕组的电导率,即
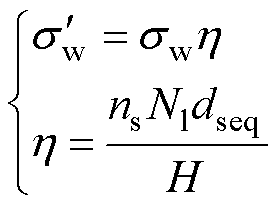 (6)
(6)
式中,H为磁心窗口高度;ns为绕组单匝利兹线子行数;Nl为每层绕组的匝数。
箔片间的绝缘距离为
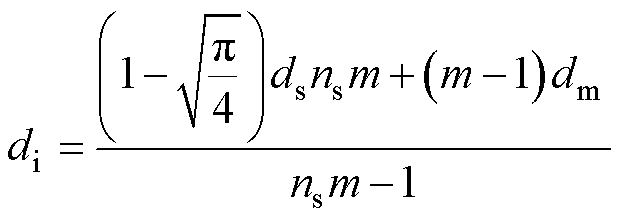 (7)
(7)
式中,m为绕组层数;dm为绕组层间距。
为验证利兹线绕组等效过程的有效性和准确性,对实际磁心窗口结构与等效磁心窗口结构进行二维涡流场有限元仿真,仿真结果如图8所示。可以看出,等效磁心窗口结构的磁场强度和磁能明显小于实际的磁心窗口结构,且磁场强度和磁能分布也更加均匀,趋肤效应与邻近效应不明显。
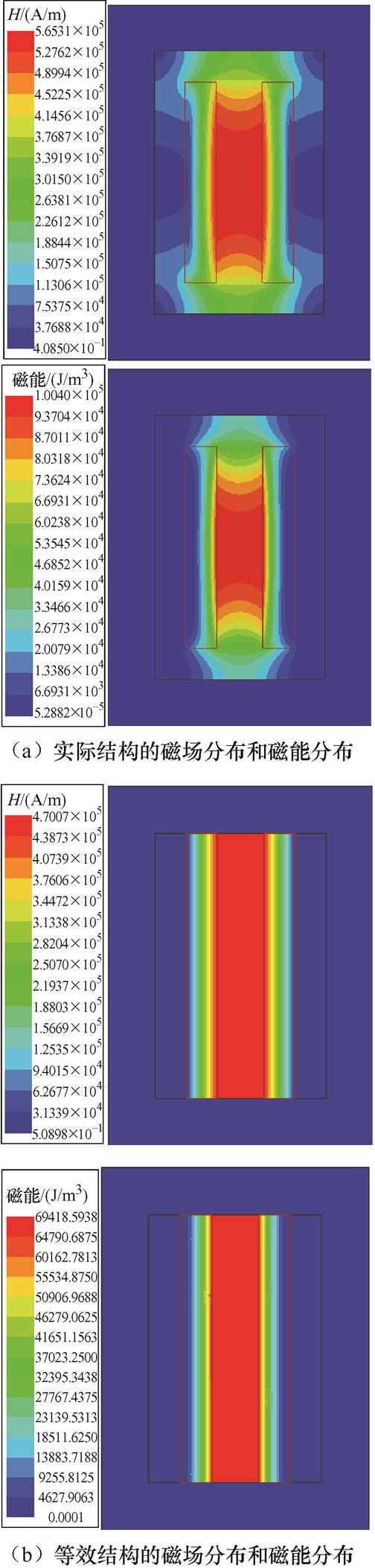
图8 磁心窗口内二维有限元涡流场仿真
Fig.8 Simulation of two-dimensional finite element eddy current field within the core window
DAB变换器中包含大量高次谐波,在计算绕组损耗时应考虑所有谐波下的损耗。高频变压器的绕组损耗计算式为
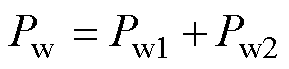 (8)
(8)
其中
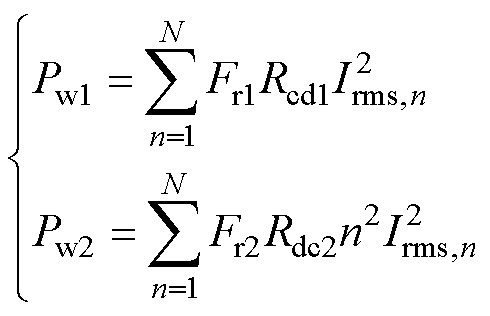 (9)
(9)
绕组的交流电阻系数Fr为
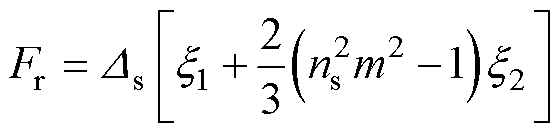 (10)
(10)
式中,Ds为绕组穿透率;x1、x2分别为绕组的趋肤修正因子和邻近修正因子。
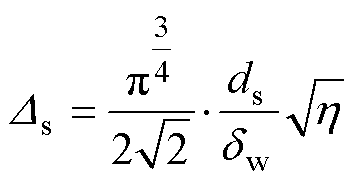 (11)
(11)
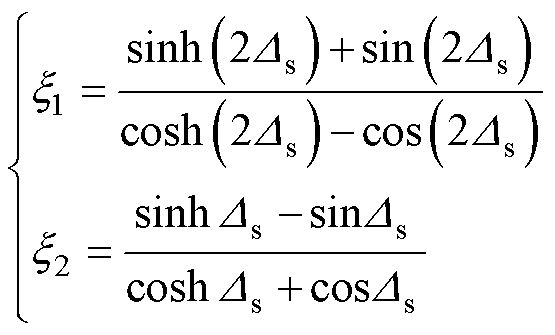 (12)
(12)
式中,dw为绕组在运行频率下的趋肤深度,即
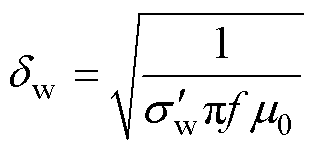 (13)
(13)
式中,m0为真空磁导率。
一次绕组与二次绕组导线的直流电阻为
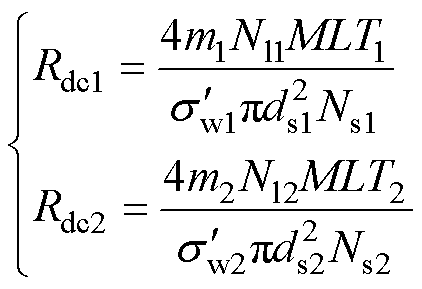 (14)
(14)
式中,MLT为绕组的平均匝长;Ns为绕组单匝利兹线股线数。
n次谐波下变压器一次侧的激励电流为
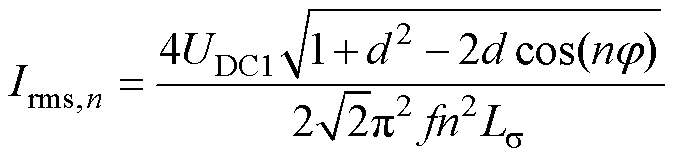 (15)
(15)
式中,d为直流变换比。
由于高频条件下涡电流的感应,绕组的趋肤效应和邻近效应增强,电流密度分布不均,交流电阻系数Fr随之增大。为在高频时实现方形利兹线绕组计算更准确的,本文将Dowell模型中的复杂函数线性化[24],得到Fr的近似表达式为
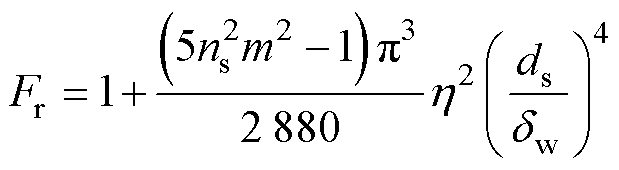 (16)
(16)
采用有限元法对高频变压器方形利兹线绕组的交流电阻进行仿真计算。110 kHz时绕组的电流密度分布如图9所示。利兹线的股线直径为0.1 mm,股数为100股。可见在高频条件下,利兹线的电流密度分布均匀,趋肤效应不明显。
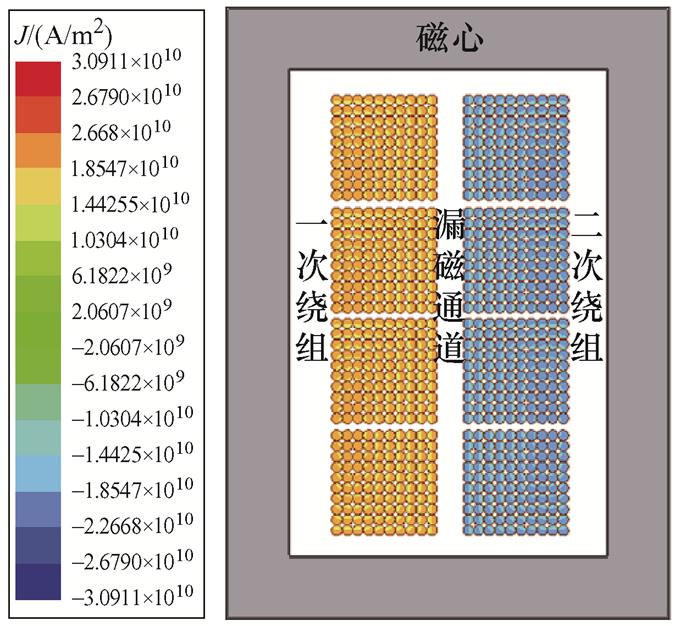
图9 110 kHz下方形利兹线绕组的电流密度分布
Fig.9 Current density distribution of rectanguar Litz wire windings at 110 kHz
图10显示了近似Dowell模型和有限元仿真获得的宽频带一次绕组的交流电阻系数曲线。可以看出,利用近似Dowell模型计算的交流电阻系数与仿真结果吻合较好,可以将该模型用于高频变压器的优化设计。
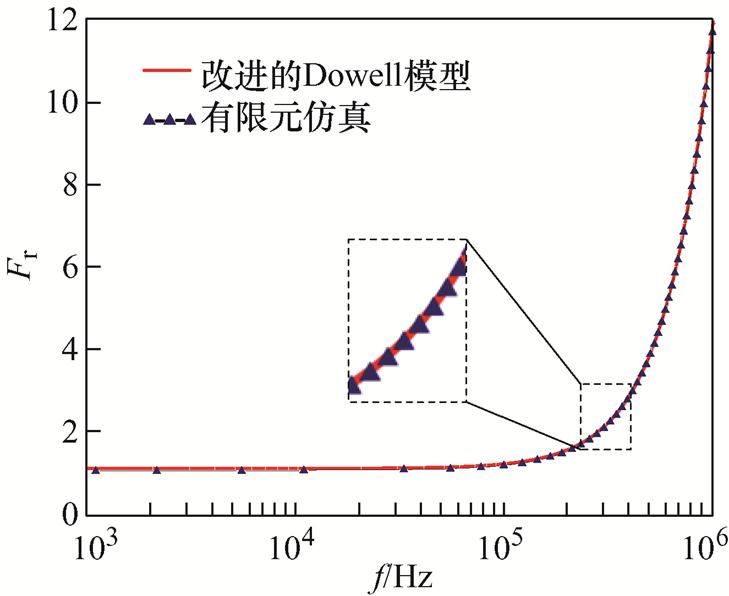
图10 由近似Dowell模型和有限元仿真获得的一次绕组交流电阻系数曲线的比较
Fig.10 Comparison of AC resistance coefficient curves of primary winding obtained from approximate Dowell model and finite element simulation
为探究绕组的趋肤深度对绕组损耗的影响,使绕组层数m在1~20范围内变化,孔隙率h=0.8,得到Fr关于ds/dw变化的曲线如图11a所示,其中实线表示Dowell模型,虚线表示近似Dowell模型。然后保持绕组层数m=3不变,使孔隙率h 在0.6~1范围内变化,得到Fr关于ds/dw变化的曲线如图11b所示。
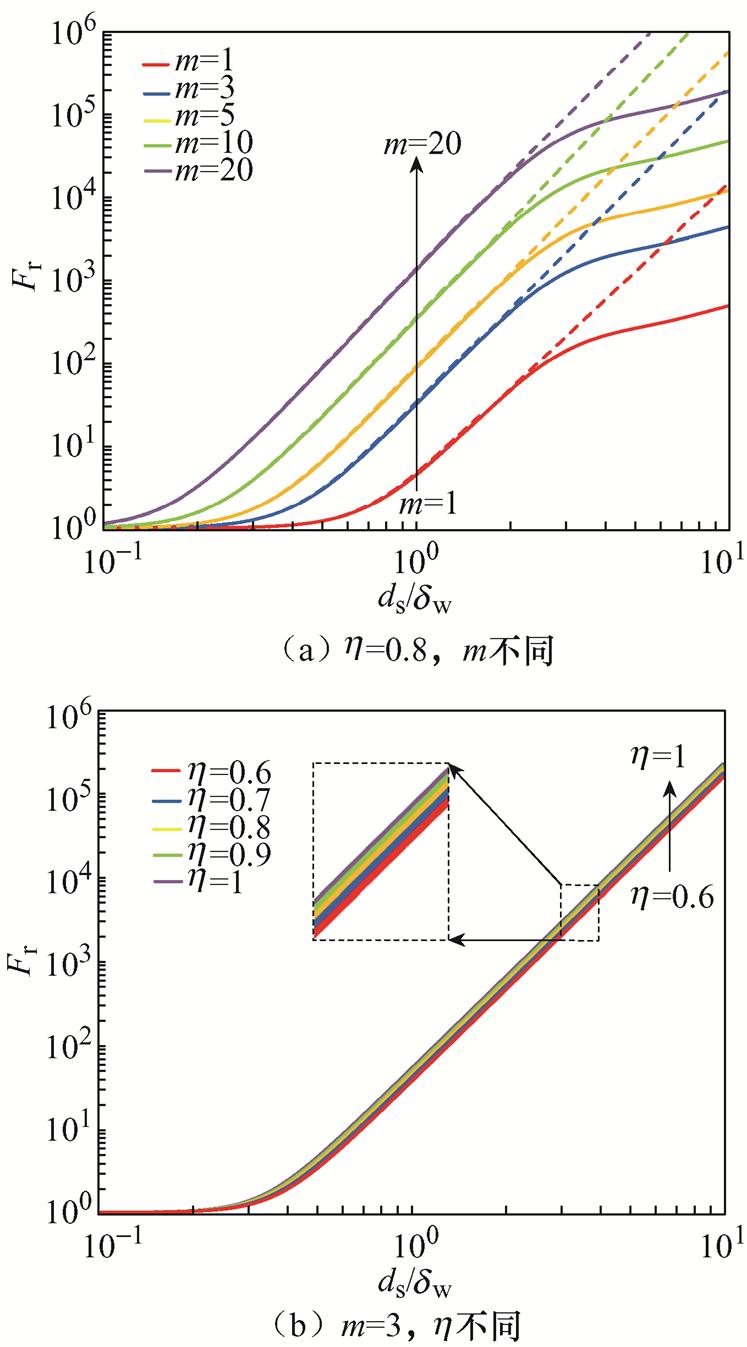
图11 方形利兹线绕组的交流电阻系数Fr关于ds/dw变化的曲线
Fig.11 The curves of AC resistance coefficient Fr of rectanguar Litz wire windings with respect to the variation of ds/dw
从图11中可得出以下结论:
(1)随着ds/dw的增大,绕组的趋肤效应和邻近效应逐渐明显,电流密度分布不均匀,从而造成绕组的交流电阻增大。
(2)从图11b可以看出,当h 变化时,由近似Dowell模型计算的交流电阻系数Fr没有明显差别,可见该模型在计算绕组损耗时减少了对于绕组结构的依赖性。
(3)当ds/dw>2时,影响交流电阻系数的主要是邻近效应,趋肤效应的变化不明显,导线利用率不足致使Dowell模型中Fr的增势变缓。
综上所述,在设计高频变压器的过程中,为使近似Dowell模型计算的绕组损耗与Dowell模型的计算结果误差较小,要尽量使ds/dw≤2。
由于实际磁心窗口结构中绕组与磁心间存在一定的绝缘距离,使绕组端部出现横向磁场分量,工作频率越高,端部效应越明显,造成漏感的计算结果偏低。因此,本文提出了考虑绕组端部效应和频率影响的漏感计算模型。
为考虑通过空气路径的磁通对于高频变压器漏感的影响,本文引入Rogowski因子KR[25],通过校正磁场路径长度对绕组高度进行修正,减小磁场强度和磁能分布对绕组结构的依赖性。
绕组的等效高度为
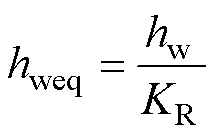 (17)
(17)
与直接应用Dowell模型相比,这种修正允许适当考虑绝缘间距,在设计高频变压器时能够更加准确地计算各参数值。
在计算漏感时将其分为图12的两部分,一部分是频率相关区域,用蓝色表示,即绕组所在区域的漏感Lsb;另一部分是频率不相关区域,用黄色表示,即绕组层间绝缘区域和漏磁通道区域的漏感Lsy。
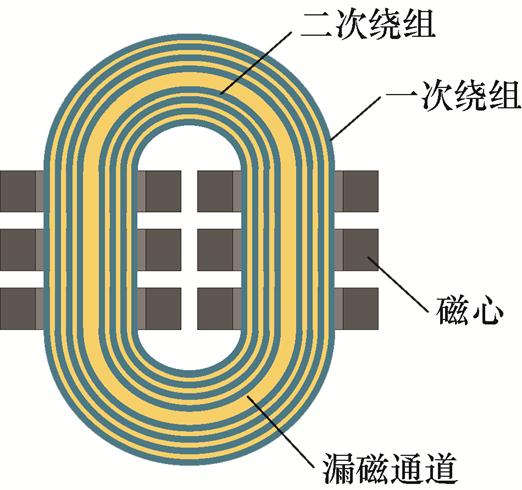
图12 高频变压器磁心窗口的俯视剖面图
Fig.12 Top view cross-sectional drawn of the core window of HFT
对于蓝色区域所表示的频率相关部分的漏感,引入考虑了绕组结构效应的频率相关因子kf,则Lsb计算式为
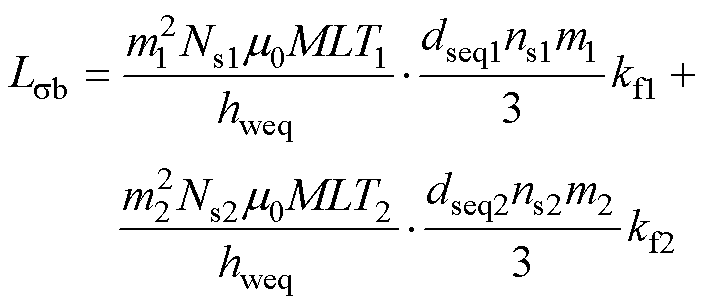 (18)
(18)
式中
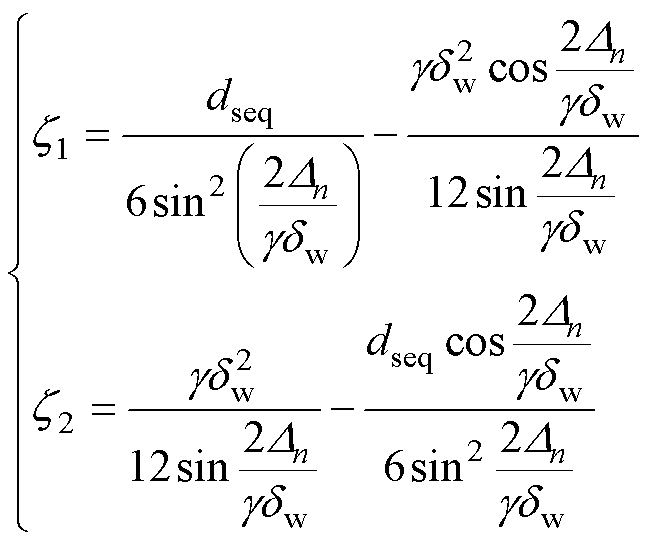 (19)
(19)
式中,g 为传导系数,g=(1+j)/dw。
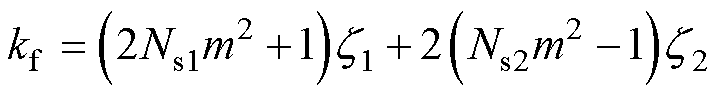 (20)
(20)
Lsy的计算表达式为
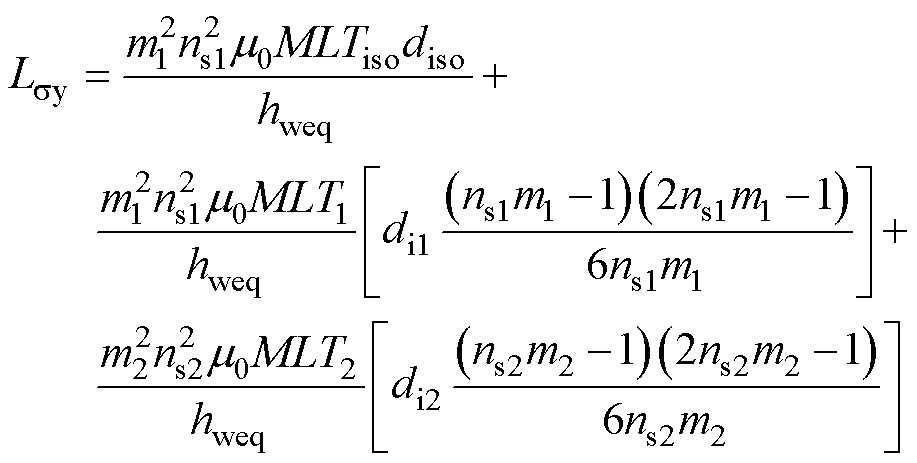 (21)
(21)
图13显示了110 kHz时磁心窗口内漏磁场的有限元仿真结果。从图中可以看出,最大磁场强度位于一次绕组与二次绕组之间的漏磁通道处。因此,若想求得漏感的准确值,需要合理设计漏磁通道的宽度diso。
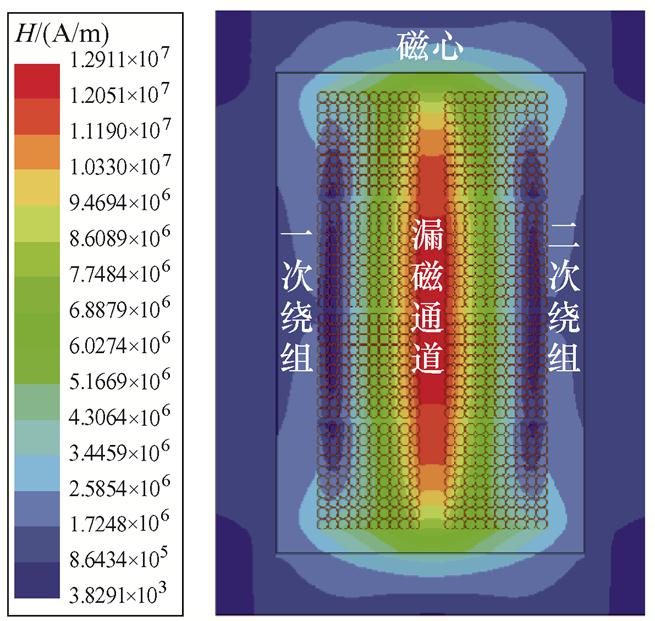
图13 110 kHz时磁心窗口内漏磁场的有限元仿真结果
Fig.13 Finite element simulation results of leakage magnetic field in the magnetic core window at 110 kHz
由解析法和有限元仿真得到的漏感曲线结果如图14所示。可以看出在频率高于200 kHz时,解析法计算得到的漏感略低于有限元仿真结果,但仍在误差允许范围内,可以将该模型用于高频变压器的优化设计。
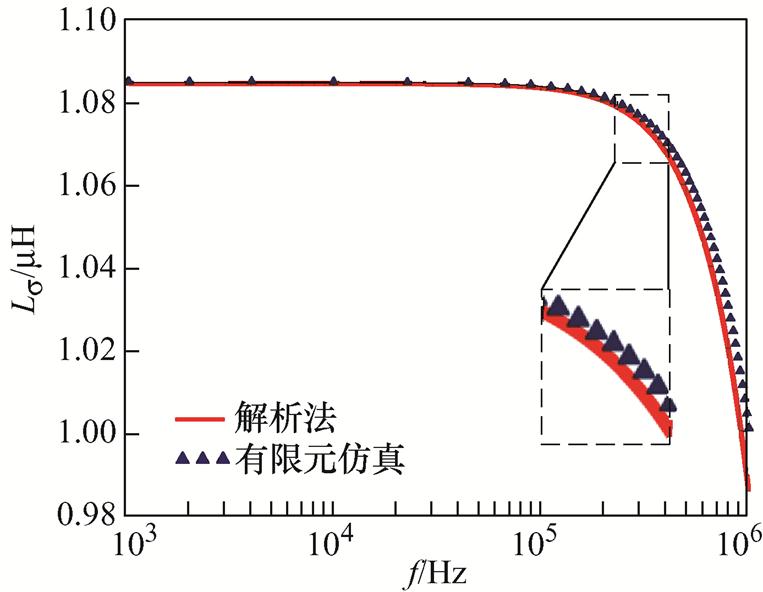
图14 由解析法和有限元仿真获得的漏感的比较
Fig.14 Comparison of leakage inductance obtained by analytical method and finite element simulation
为降低高频变压器运行过程中热老化等问题造成绝缘可靠性下降的风险程度,提高绕组间的绝缘耐压水平,本文采用一种新型多重绝缘结构,如图15所示。在磁心和绕组外层刷半导体漆,以增强结构强度,降低噪声;在磁心窗口内部浇注介电性能优异的环氧树脂,使所需的绝缘距离与空气绝缘相比大幅减少;单股导线使用聚氨酯薄膜缠绕,利兹线采用双层绝缘设计[26],内层绕包聚酰亚胺薄膜,外层绕包Nomex T410绝缘纸,将电应力束缚在主绝缘层内,既可以避免绝缘层外空气中电场强度过高发生的局部放电问题,又可以柔化主绝缘层电 应力。
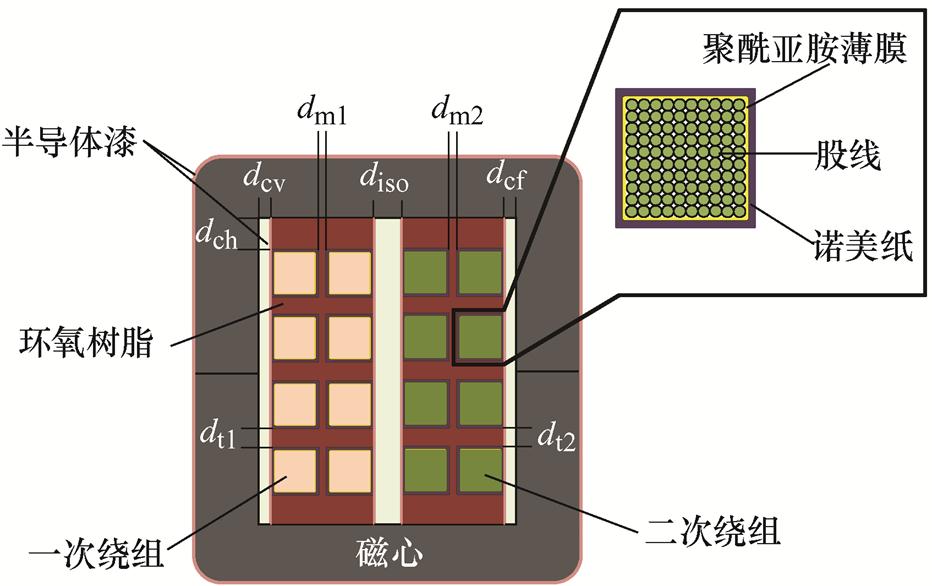
图15 新型多重绝缘结构
Fig.15 Novel multilayer dielectric structure
图15中各种绝缘材料的绝缘特性可参考文献[27],各个绝缘距离[28-29]计算如下:
一次绕组与二次绕组的最小绝缘距离为
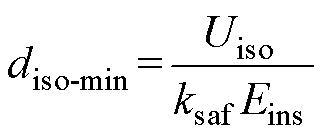 (22)
(22)
为保证能够实现DAB变换器的零电压软开关,安全系数ksaf =30%。
绕组与上、下磁轭间的水平和垂直绝缘距离为
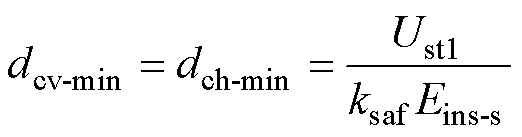 (23)
(23)
式中,Ust1为一次绕组对地短期工频耐受电压;Eins-s为短期介电强度,即在工频时的击穿电场强度。
二次绕组与磁心中心柱间的绝缘距离为
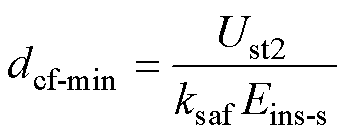 (24)
(24)
式中,Ust2为二次绕组对地短期工频耐受电压。
绕组匝间绝缘、层间绝缘尺寸仅与匝间绝缘材料在高频方波电压下的击穿场强有关,可计算为
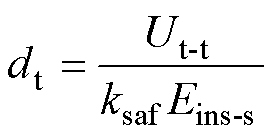 (25)
(25)
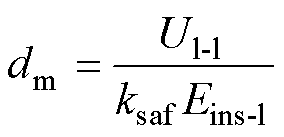 (26)
(26)
式中,Eins-l为长期介电强度,即绝缘材料在高频方波电压下的击穿场强;Ut-t为长期高频方波电压下绕组的匝间电压;Ul-l分别为长期高频方波电压下绕组的层间电压。
使用Ansys软件中的静电场求解器对高频变压器磁心窗口内的静电场进行有限元仿真,获得电场强度的分布,如图16所示,可以看出最大电场强度出现在一次绕组第一匝的上轮廓处,与环氧树脂的介电强度相比,安全系数为89.01%。
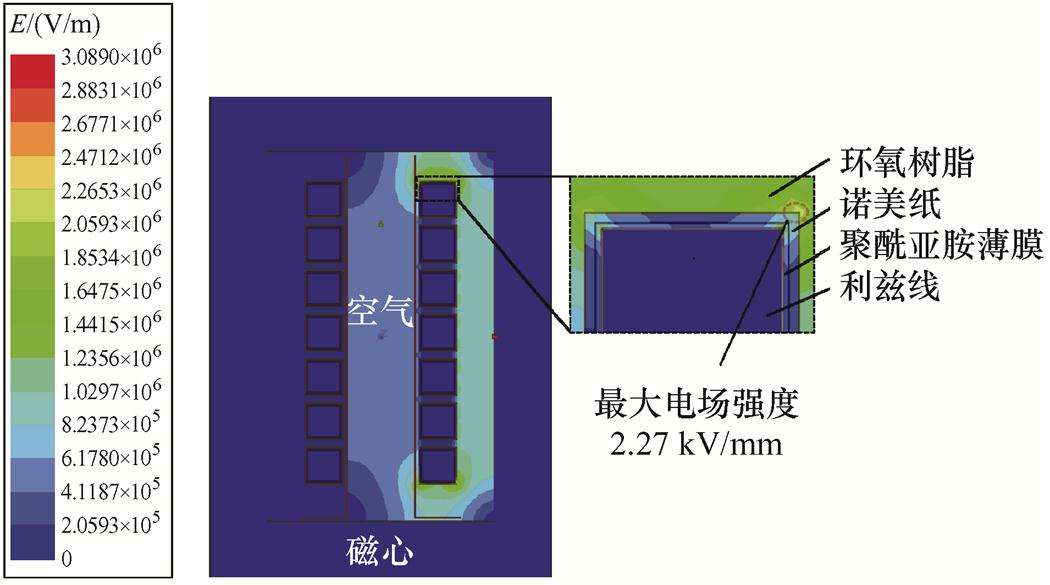
图16 磁心窗口内电场的有限元仿真
Fig.16 FEM simulation for electric field distribution in core window area
决策变量的选择是优化算法的一个重要方面,取决于优化目标和约束条件。要进行高频变压器的设计,必须在广泛范围内定义大量的电气和结构参数。当优化参数较多时,计算成本高、效率低,因此本文采用灵敏度分析法[30-31]仅选取了对设计结果影响较大的决策变量。灵敏度分析法可以全面评估各变量对优化目标的影响程度,是实现高效优化的方法之一。该方法通过控制变量和有限元仿真,分析交流电阻系数对磁心窗口内各个结构因子的敏感程度,选择敏感程度较高的结构因子作为决策变量。
本文选取的8个决策变量为:磁心堆叠的块数nc,磁心横截面的侧边长A,一次绕组和二次绕组的股线直径ds1、ds2,二次绕组层数m2,一次绕组和二次绕组的匝数Nl1、Nl2以及最大磁感应强度Bm,其上边界由材料的饱和磁通密度Bsat设定。为防止不必要的磁通密度波动使磁心发生饱和,在Bm和Bsat之间引入20%的安全裕度。
目标函数1:高频变压器的磁心损耗、绕组损耗最小,实现效率最大化。
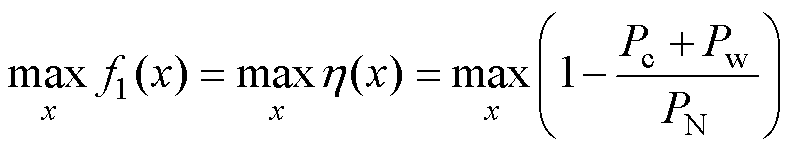 (27)
(27)
目标函数2:高频变压器的体积最小,实现功率密度最大化。
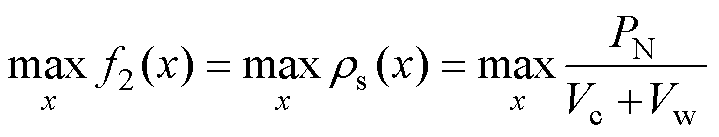 (28)
(28)
在能承受最小绝缘电压水平Uiso的条件下,为保证能够实现零电压软开关,漏感应大于能够满足最小隔离要求的最小漏感值Lσ-min,因此本文选取的约束条件为
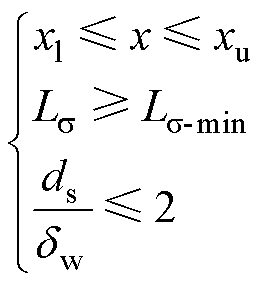 (29)
(29)
式中,xl为决策变量的下界;xu为决策变量的上界。
采用自由参数扫描法在所有决策变量的范围内进行58万次参数扫描,产生26万个更通用的有效设计方案,得出10 Hz~100 kHz范围内的体积功率密度和效率的分布云图,如图17所示。其中每一个点代表一种有效设计方案,并将其作为INSGA-Ⅱ中的初始种群进行迭代计算。
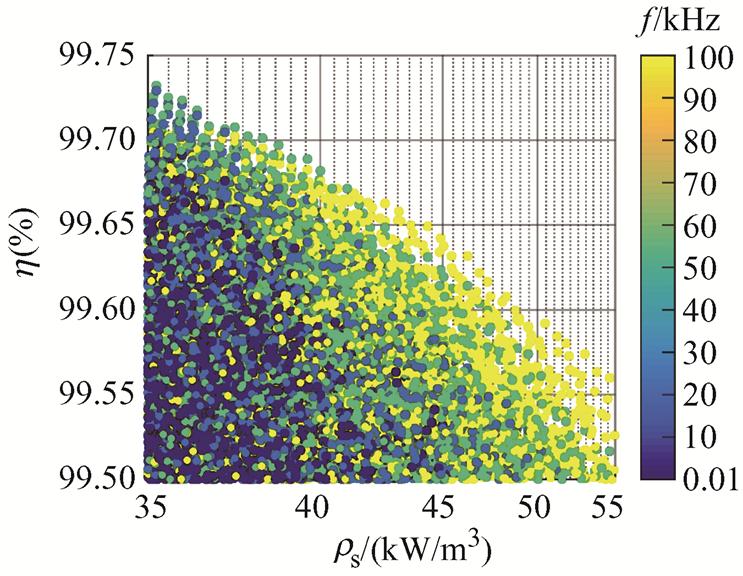
图17 10 Hz~100 kHz范围内高频变压器体积功率密度和效率的分布
Fig.17 Distribution of volume power density and efficiency of HFT from 10 Hz to 100 kHz
由于NSGA-Ⅱ在高频变压器优化设计的过程中仍存在种群分布不均匀、容易陷入局部收敛等问题,为使该算法具有更好的全局搜索能力,本文引入DCD和算术交叉算子对NSGA-Ⅱ进行改进,提升种群分布的广度和均匀性,提高全局寻优效率。
4.1.1 算术交叉算子
相比于模拟二进制交叉算子,算术交叉算子能够更好地保持种群的多样性,其表达式为
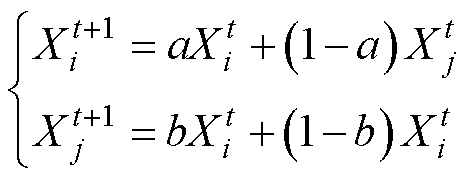 (30)
(30)
式中,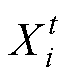 、
、 分别为第t代的两个个体交叉点处对应的决策变量的实数值编码;a、b分别为[0, 1]上均匀分布的随机数。
分别为第t代的两个个体交叉点处对应的决策变量的实数值编码;a、b分别为[0, 1]上均匀分布的随机数。
4.1.2 动态聚集距离
个体i的动态聚集距离计算如下。
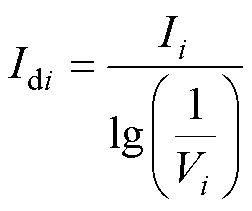 (31)
(31)
其中
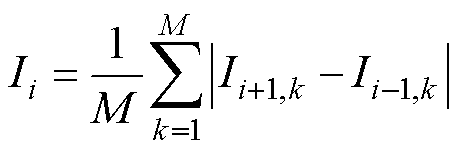 (32)
(32)
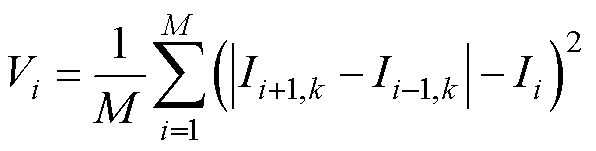 (33)
(33)
式中,Ii为个体i的聚集距离;M为目标维数,Ii,k为第i个个体在第k维目标上排序后的聚集距离。
利用Matlab调试改进后的算法,使用ZDT1和ZDT3函数进行测试。NSGA-Ⅱ和INSGA-Ⅱ中的种群规模Np=100,代数Gen=200,测试次数tr=8,交叉概率pc=0.8,变异概率pm=1/nv(nv是决策变量的个数),交叉分布指数mu=80,变异分布指数mum= 20。通过比较图18中NSGA-Ⅱ改进前后测试函数的Pareto前沿,可以看出INSGA-Ⅱ的Pareto前沿曲线更加平滑,解的分布更加均匀,所以INSGA-Ⅱ更适合应用于高频变压器的多目标优化设计。
根据高频变压器的优化设计流程,分别使用NSGA-Ⅱ和INSGA-Ⅱ对自由参数扫描后获得的所有有效设计方案进行全局寻优,得到高频变压器的功率密度-效率的Pareto前沿如图19所示。可以看出,NSGA-Ⅱ的Pareto前沿大多集中于效率较高但功率密度较小的区域,局部收敛性很强;而INSGA- Ⅱ的Pareto前沿曲线更加平滑,种群分布更加均匀,能获得更准确的全局最优解,从而验证了改进算法的有效性。根据功率密度最大化原则寻找一个全局最优设计方案,并在图19b中用红色星号表示。
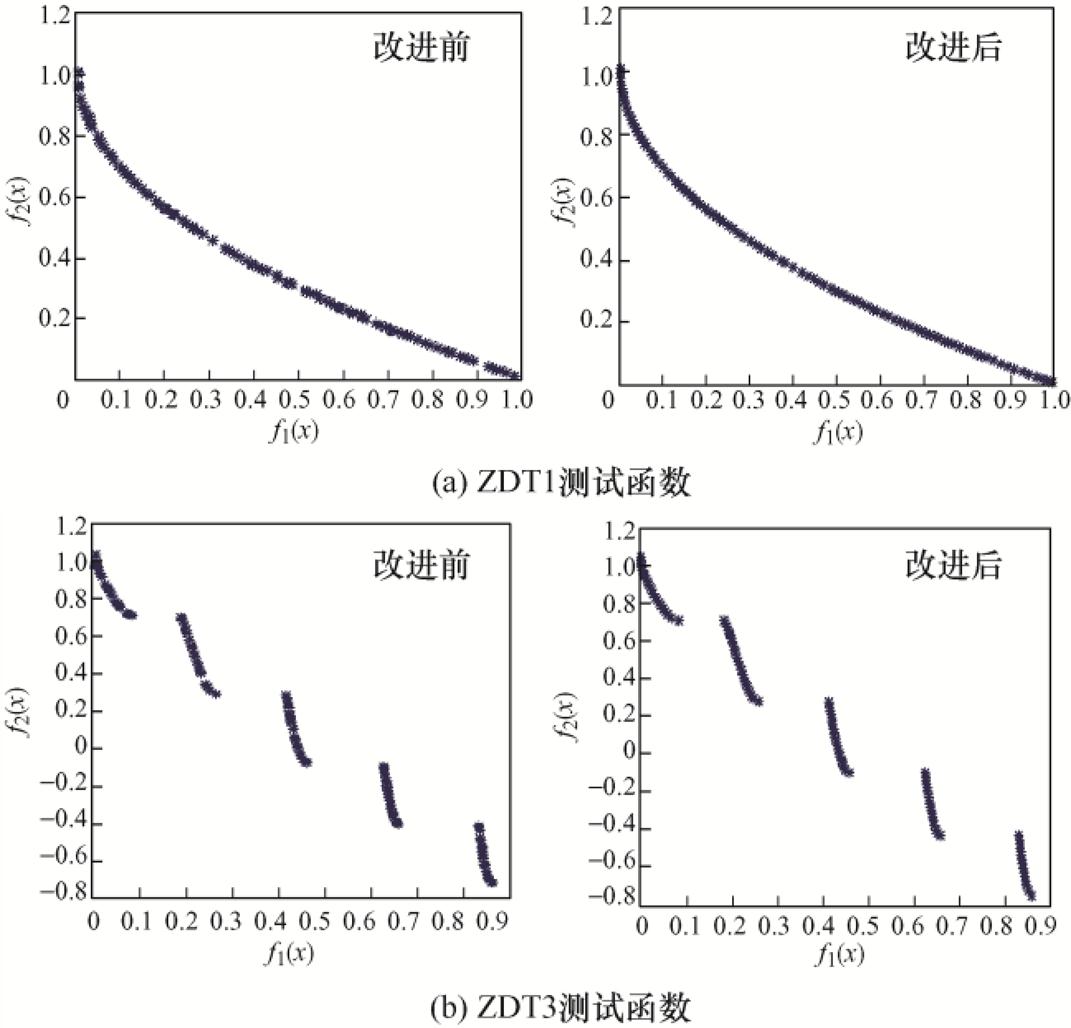
图18 NSGA-Ⅱ改进前后测试函数的Pareto前沿
Fig.18 Pareto fronts of test functions before and after the improvement of NSGA-Ⅱ
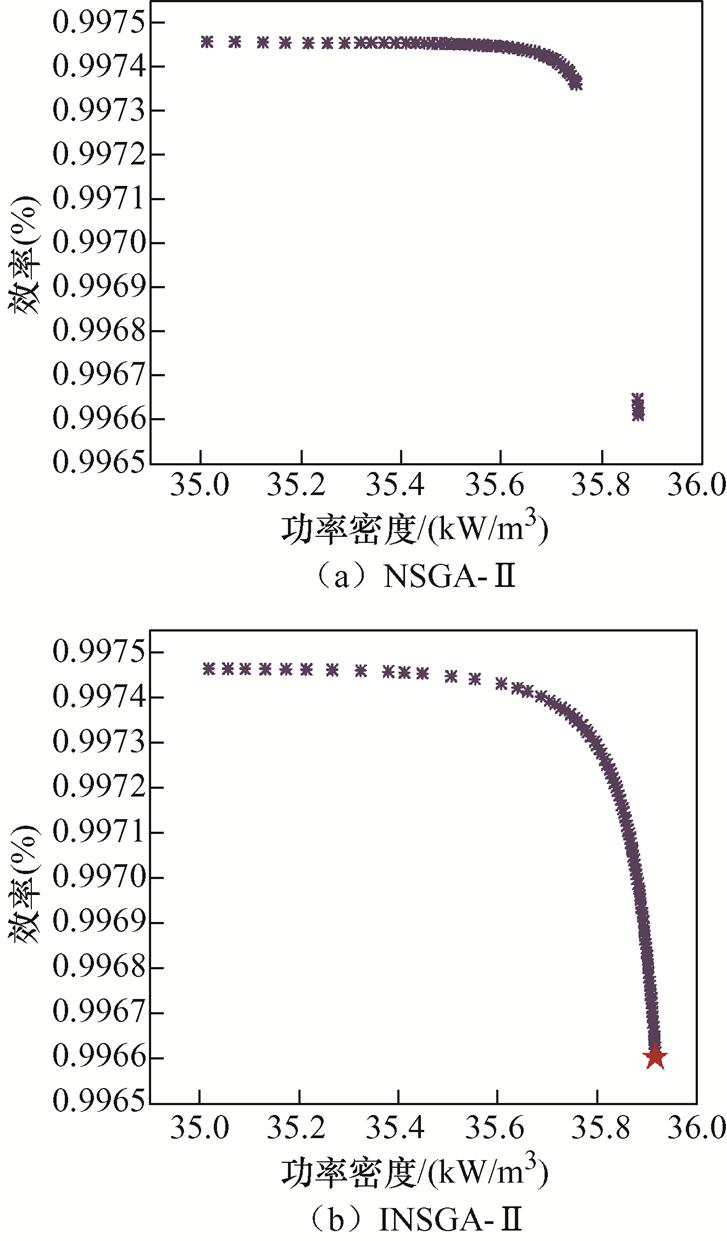
图19 功率密度-效率的Pareto前沿
Fig.19 The Pareto fronts of power density-efficiency
表3总结了高频变压器设计过程中所需要的设计参数。
利用4.1节中获得的全局最优设计方案制造一台高频变压器样机,其三维结构和样机图片如图20所示。
表3 设计参数
Tab.3 Design parameters

参 数数 值 磁心叠片系数Kc0.8 并排磁心间距dc1/mm10 一次绕组与二次绕组导线的自绝缘厚度dint1, dint2/mm0.15 一次绕组与二次绕组的匝间绝缘距离dt1, dt2/mm1.7 二次绕组与磁心中心柱间的绝缘距离dcf-min/mm10 一次绕组与上下磁轭间的水平绝缘距离dch-min/mm10 一次绕组与上下磁轭间的垂直绝缘距离dcv-min/mm10 一次、二次绕组间绝缘距离diso/mm10 归算至一次侧的漏感值Ls/mH8.1

图20 高频变压器的三维结构图及样机图片
Fig.20 3D structure diagram and prototype image of HFT
对于制成的高频变压器样机,磁心使用安泰科技的Antainano纳米晶材料,规格为:CN-(窗口长度)154 mm×(窗口宽度)87 mm×(磁心叠厚)28 mm×(磁心高度)35 mm。方形利兹线绕组的股线直径均为0.1 mm,利兹线结构为16×137股,即将2 192股线依次扭转成16个子束,每个子束137股线,再将16个子束绞合成一匝利兹线。单匝利兹线的尺寸为11.65 mm×11.65 mm,绝缘厚度为0.3 mm。磁心上磁轭前后使用Z型不锈钢夹板连接,下磁轭前后使用U型不锈钢板作为结构的夹件,并通过螺杆连接,使整体结构紧固成形。
通过Tonghui TH2840B阻抗分析仪测量高频变压器样机的漏感和交流电阻,测量过程中将高频变压器样机二次绕组短路,一次绕组开路,忽略励磁电感的影响。漏感测量结果为7.92 mH,与归算至一次侧的漏感值相比,误差为2.2%。交流电阻的测量结果为3.1 mW,并根据测量的交流电阻值以及额定谐波电流的方均根值计算绕组损耗的测量值。
在实际制作过程中,高频变压器的骨架尺寸和绝缘距离与设计值相比存在一定差异,造成漏感和绕组损耗的测量值与设计值不能完全保持一致。
搭建如图21所示的空载试验平台。激励源是带有NF4520A功率放大器的WF1974信号发生器,产生幅值为400 V的方波电压,工作频率为10 kHz,同时二次绕组保持开路。使用LMG500功率分析仪读取电压、电流和磁心损耗的值,同时使用NAPUL TP230X温度记录仪记录各热点温度。图22显示了空载条件下高频变压器一次电压和一次电流波形以及磁心对应的磁滞回线。

图21 空载试验平台
Fig.21 No-load experimental platform
在Solid Works2020软件中建立高频变压器的三维模型,并导入Ansys软件中对磁心和绕组分别进行有限元仿真,频率为10 kHz。将磁心损耗与绕组损耗的计算值和测量值与仿真值进行对比,得到的误差结果见表4。
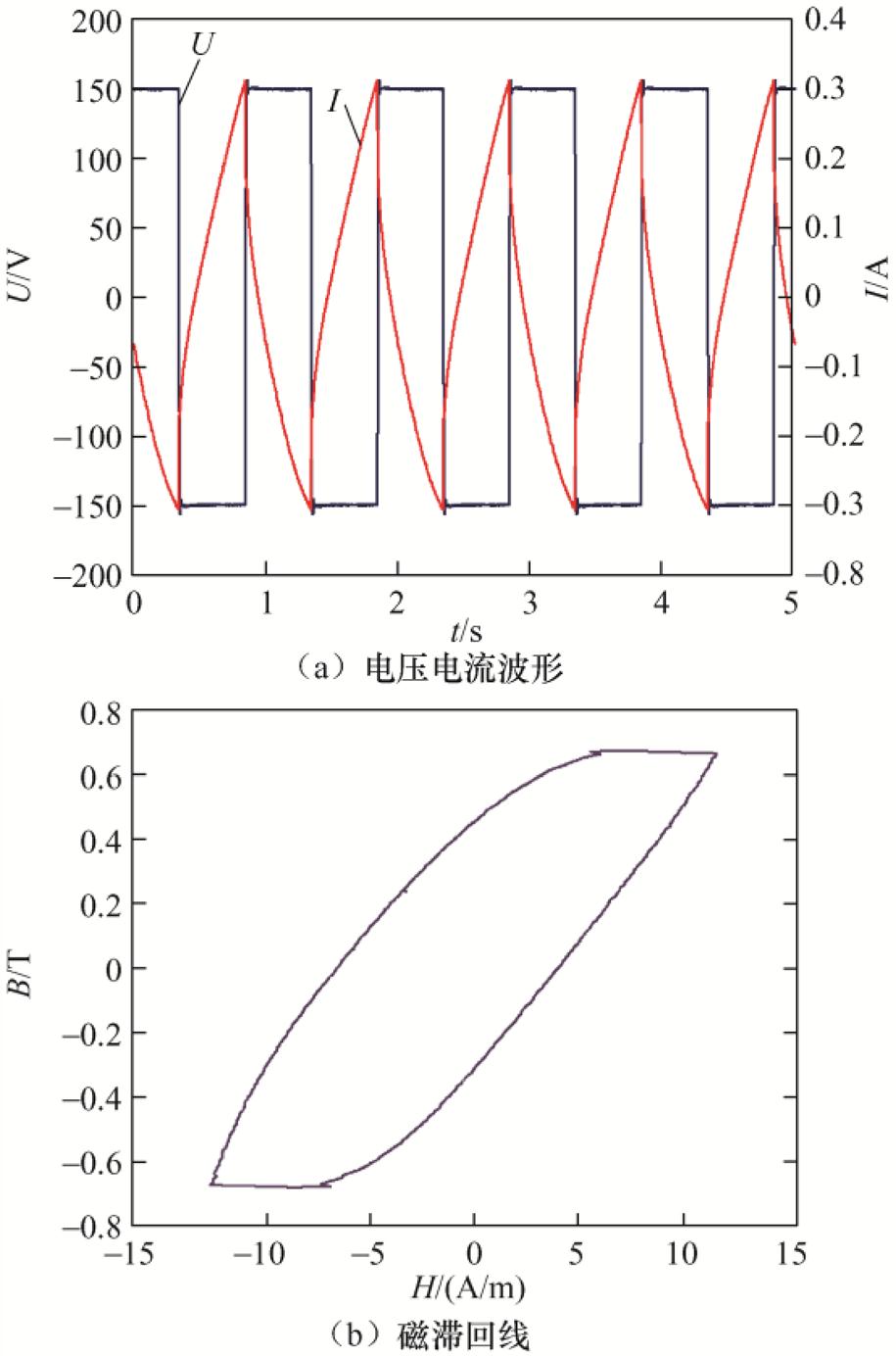
图22 10 kHz下高频变压器一次电压、电流波形及磁心对应的磁滞回线
Fig.22 Voltage and current waveforms on the primary side of HFT at 10 kHz and the corresponding hysteresis returns of the core
表4 高频变压器磁心损耗、绕组损耗的比较
Tab.4 Comparison of core loss and winding loss of high frequency transformer conditions
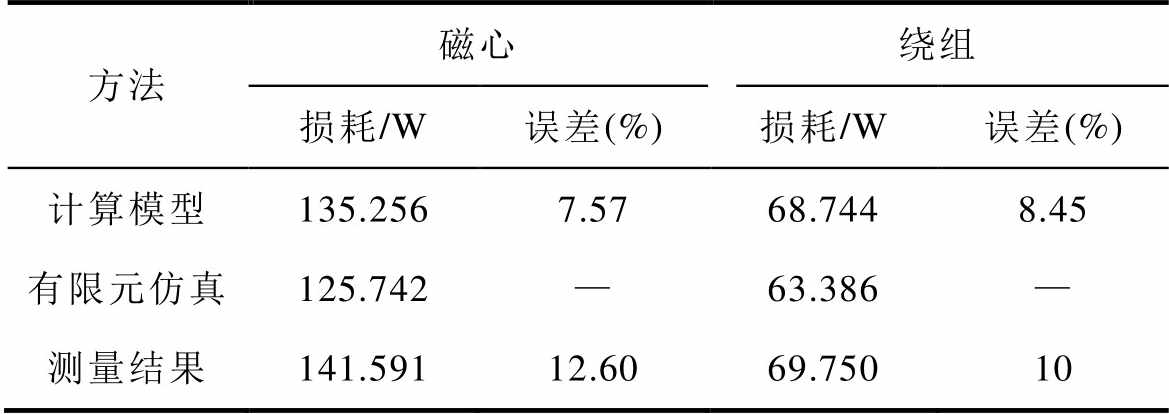
方法磁心绕组 损耗/W误差(%)损耗/W误差(%) 计算模型135.2567.5768.7448.45 有限元仿真125.742—63.386— 测量结果141.59112.6069.75010
为验证所设计高频变压器样机的热特性,使高频变压器样机在空载、额定电压激励下热运行5 h,直至达到稳定状态,环境温度为20℃,各热点温度的测量结果如图23a所示。图23b显示了FLUKE Ti32红外热成像仪拍摄的高频变压器稳态运行时的热成像。由于空载条件下绕组主要通过热耦合加热,绕组内磁化电流较低,从而绕组温度较低。此时高频变压器内主要存在的是磁心损耗,可以看出磁心温度最高,稳定运行状态下温度可达135.7℃,但仍在安全运行范围内,温升符合预期设计要求。
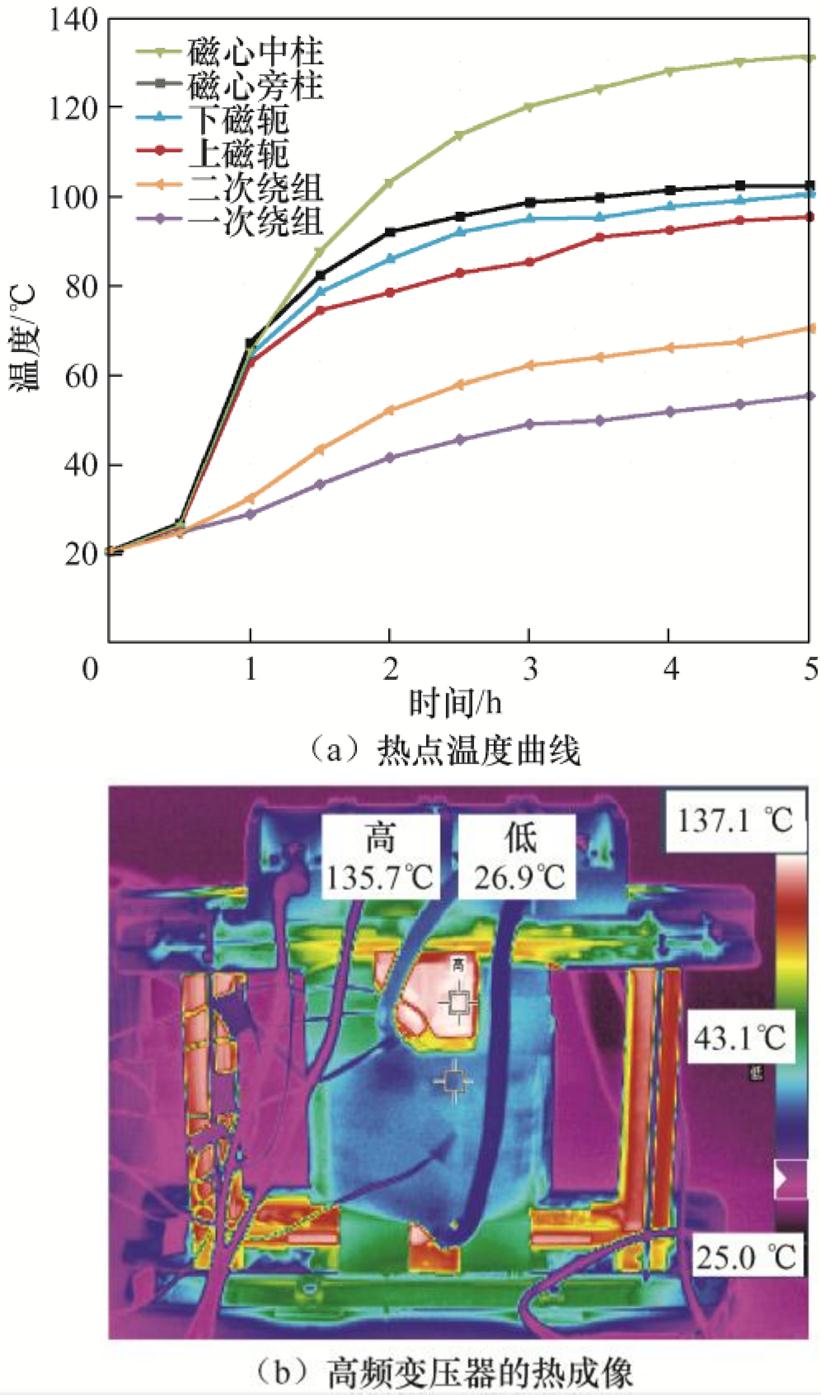
图23 5 h热运行期间测量的热点温度曲线及空载稳态下高频变压器的热成像
Fig.23 Hot spot temperature profile measured during 5 hours of hot operation and thermal imaging of HFT at no-load steady state
本文依据考虑了高频效应和结构效应的电磁场计算模型,基于INSGA-Ⅱ和自由参数扫描法设计制作了一台高频变压器样机。
1)通过拟合高频非正弦激励波形下IGSE中的复杂积分函数,减少了计算成本,提高了计算效率。该模型的磁心损耗计算结果与有限元仿真结果基本吻合。
2)推导了弱化绕组结构对绕组损耗影响的近似Dowell模型,实现了绕组损耗的高精度计算。该模型的绕组损耗计算结果和测量结果与有限元仿真结果相比,误差均在可接受范围内。
3)提出了考虑绕组端部效应和结构效应的漏感计算模型,减少了漏感对于结构和频率的依赖性,并对该模型进行详细的电磁有限元分析、推导和实验验证,结果表明该模型能够准确计算高频变压器的总漏感。
4)采用一种考虑长短期介电强度的新型多重绝缘结构,提升绕组间的绝缘耐压水平。通过有限元仿真验证了最大电场强度在可靠安全裕度内。
5)空载条件下,对样机的磁心损耗和温升进行测量,实验结果表明,磁心损耗的测量结果与仿真结果的误差较小,温升符合预期设计要求,无热运行问题。
参考文献
[1] 骆仁松, 汪涛, 文继峰, 等. 大功率高频变压器三维温升计算及优化设计方法[J]. 电工技术学报, 2023, 38(18): 4994-5005, 5016.
Luo Rensong, Wangtao, Wen Jifeng, et al. Three- dimensional temperature calculation and optimization design method for high power high-freguency transformer[J]. Transactions of China Electrotechnical Society, 2023, 38(18): 4994-5005, 5016.
[2] Bahmani M A, Thiringer T, Rabiei A, et al. Comparative study of a multi-MW high-power density DC transformer with an optimized high-frequency magnetics in all-DC offshore wind farm[J]. IEEE Transactions on Power Delivery, 2016, 31(2): 857- 866.
[3] Villar I, Mir L, Etxeberria-Otadui I, et al. Optimal design and experimental validation of a Medium- Frequency 400 kVA power transformer for railway traction applications[C]//2012 IEEE Energy Conversion Congress and Exposition (ECCE), Raleigh, NC, USA, 2012: 684-690.
[4] 孙凯, 卢世蕾, 易哲嫄, 等. 面向电力电子变压器应用的大容量高频变压器技术综述[J]. 中国电机工程学报, 2021, 41(24): 8531-8546.
Sun Kai, Lu Shilei, Yi Zheyuan, et al. A review of high-power high-frequency transformer technology for power electronic transformer applications[J]. Proceedings of the CSEE, 2021, 41(24): 8531-8546.
[5] 王佳宁, 邹强, 胡嘉汶, 等. 一种中压绝缘大功率中频变压器的优化设计方法[J]. 电工技术学报, 2022, 37(12): 3048-3060.
Wang Jianing, Zou Qiang, Hu Jiawen, et al. An optimal design method for medium-voltage insulated high-power medium-frequency transformer[J]. Transactions of China Electrotechnical Society, 2022, 37(12): 3048-3060.
[6] Czyz P, Guillod T, Zhang Daifei, et al. Analysis of the performance limits of 166 kW/7 kV air-and magnetic-core medium-voltage medium-frequency Transformers for 1: 1-DCX applications[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2022, 10(3): 2989-3012.
[7] 温志伟, 熊斌, 程自然. 强化液冷牵引变压器电磁结构设计及优化[J]. 电工技术学报, 2021, 36(增刊2): 460-466.
Wen Zhiwei, Xiong Bin, Cheng Ziran. Design and optimization of electromagnetic structure of reinforced liquid-cooled traction transformer[J]. Transactions of China Electrotechnical Society, 2021, 36(S2): 460- 466.
[8] 律方成, 郭云翔, 李鹏. 大功率中频变压器多目标参数优化设计[J]. 高电压技术, 2017, 43(1): 210- 217.
Lü Fangcheng, Guo Yunxiang, Li Peng. Optimization design for multiple target parameters of high power medium frequency transformer[J]. High Voltage Engineering, 2017, 43(1): 210-217.
[9] 陈彬, 梁旭, 唐波, 等. 大功率中频三相变压器优化设计方法[J]. 中国电机工程学报, 2021, 41(8): 2877-2890.
Chen Bin, Liang Xu, Tang Bo, et al. Optimization method of high-power medium-frequency three-phase transformer[J]. Proceedings of the CSEE, 2021, 41(8): 2877-2890.
[10] Huang Pei, Mao Chengxiong, Wang Dan, et al. Optimal design and implementation of high-voltage high-power silicon steel core medium-frequency transformer[J]. IEEE Transactions on Industrial Electronics, 2017, 64(6): 4391-4401.
[11] 曹小鹏, 陈武, 宁光富, 等. 基于多目标遗传算法的大功率高频变压器优化设计[J]. 中国电机工程学报, 2018, 38(5): 1348-1355.
Cao Xiaopeng, Chen Wu, Ning Guangfu, et al. Optimization design of high-power high-frequency transformer based on multi-objective genetic algorithm[J]. Proceedings of the CSEE, 2018, 38(5): 1348-1355.
[12] Zhang Ke, Chen Wu, Cao Xiaopeng, et al. Optimization design of high-power high-frequency transformer based on multi-objective genetic algorithm[C]//2018 IEEE International Power Electronics and Application Conference and Exposition (PEAC), Shenzhen, China, 2018: 1-5.
[13] Liu Xiaojing, Wang Tingting, Hu Lian, et al. Design and optimization of high frequency transformer with nanocrystalline core[C]//2019 4 th International Conference on Intelligent Green Building and Smart Grid (IGBSG), Hubei, China, 2019: 246-249.
[14] Bahmani M A, Thiringer T, Kharezy M. Design methodology and optimization of a medium-frequency transformer for high-power DC-DC applications[J]. IEEE Transactions on Industry Applications, 2016, 52(5): 4225-4233.
[15] Bahmani M A. Design considerations of medium- frequency power transformers in HVDC applications[C]// 2017 Twelfth International Conference on Ecological Vehicles and Renewable Energies (EVER), Monte Carlo, Monaco, 2017: 1-6.
[16] Leibl M, Ortiz G, Kolar J W. Design and experimental analysis of a medium-frequency transformer for solid- state transformer applications[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2017, 5(1): 110-123.
[17] 杨向真, 王锦秀, 孔令浩, 等.电压不匹配运行条件下双有源桥变换器的效率优化方法[J]. 电工技术学报, 2022, 37(24): 6239-6251.
Yang Xiangzhen, Wang Jinxiu, Kong Linghao, et al. Efficiency optimization method of DAB converters under wide-voltage operating conditions[J]. Transa- ctions of China Electrotechnical Society, 2022, 37(24): 6239-6251.
[18] 陈彬, 李琳, 赵志斌, 等. 电感集成式大容量高频变压器精细化设计方法[J]. 中国电机工程学报, 2018, 38(5): 1356-1368.
Chen Bin, Li Lin, Zhao Zhibin, et al. Design method of Inductor-integrated high-power high-frequency transformers[J]. Proceedings of the CSEE, 2018, 38(5): 1356-1368.
[19] Bahmani M A, Thiringer T, Kharezy M. Optimization and experimental validation of medium-frequency high power transformers in solid-state transformer applications[C]//2016 IEEE Applied Power Electronics Conference and Exposition (APEC), Long Beach, CA, USA, 2016: 3043-3050.
[20] Venkatachalam K, Sullivan C R, Abdallah T, et al. Accurate prediction of ferrite core loss with nonsinusoidal waveforms using only Steinmetz parameters[C]//2002 IEEE Workshop on Computers in Power Electronics, 2002. Proceedings, Mayaguez, PR, USA, 2002: 36-41.
[21] Mogorovic M, Dujic D. 100 kW, 10 kHz Medium- frequency transformer design optimization and experimental verification[J]. IEEE Transactions on Power Electronics, 2019, 34(2): 1696-1708.
[22] Reatti A, Kazimierczuk M K. Comparison of various methods for calculating the AC resistance of inductors[J]. IEEE Transactions on Magnetics, 2002, 38(3): 1512- 1518.
[23] Mogorovic M, Dujic D. Medium frequency trans- former leakage inductance modeling and experimental verification[C]//2017 IEEE Energy Conversion Congress and Exposition (ECCE), Cincinnati, OH, USA, 2017: 419-424.
[24] Wojda R P, Kazimierczuk M K. Winding resistance and power loss of inductors with Litz and solid-round wires[J]. IEEE Transactions on Industry Applications, 2018, 54(4): 3548-3557.
[25] Kulkarni S V, Khaparde S. Transformer engineering: design and practice[M]. New York Basel: Marcel Dekker Inc., 2004.
[26] 陈彬, 曹红霞, 王帅兵, 等. 基于响应面法的多绕组中频变压器绝缘结构优化设计[J]. 绝缘材料, 2023, 56(4): 68-76.
Chen Bin, Cao Hongxia, Wang Shuaibing, et al. Optimization design of insulation structure of multi- winding medium frequency transformer based on response surface method[J]. Insulating Materials, 2023, 56(4): 68-76.
[27] 尚星宇,庞磊,卜钦浩,等.大功率高频变压器绝缘问题研究综述[J].中国电机工程学报, 2024, 44(8): 3306-3326.
Shang Xingyu, Pang Lei, Bu Qinhao, et al. Research review on insulation issues of high-power high- frequency transformers[J]. Proceedings of the CSEE, 2024, 44(8): 3306-3326.
[28] 王威望, 李睿喆, 何杰峰, 等. 快速陡脉冲重复电场下高频变压器绝缘介质损耗与冲击能量积聚特性[J]. 电工技术学报, 2023, 38(05): 1206-1216.
Wang Weiwang, Li Ruizhe, He Jiefeng, et al. Dielectric loss and lmpact energy accumulation of high frequency transformer insulation under rapidly repetitive pulsed voltages[J]. Transactions of China Electrotechnical Society, 2023, 38(5): 1206-1216.
[29] Chen Bin, Liang Xu, Wan Nina. Design methodology for inductor-integrated Litz-wired high-power medium- frequency transformer with the nanocrystalline core material for isolated DC-link stage of solid-state transformer[J]. IEEE Transactions on Power Electronics, 2020, 35(11): 11557-11573.
[30] 陈彬, 陈健, 唐波, 等. 高频变压器漏电感参数灵敏度分析及其半经验模型[J]. 电机与控制学报, 2021, 25(10): 97-111.
Chen Bin, Chen Jian, Tang Bo, et al. Sensitivity analysis and semiempirical model of leakage inductance parameters of high frequency transformer[J]. Electric Machines and Control, 2021, 25(10): 97-111.
[31] 王晨旭, 唐飞, 刘涤尘, 等. 基于双层代理模型的概率-区间潮流计算及灵敏度分析[J]. 电工技术学报, 2022, 37(5): 1181-1193.
Wang Chenxu, Tang Fei, Liu Dichen, et al. Probabilistic-interval power flow and sensitivity analysis using double layer surrogate method[J]. Transactions of China Electrotechnical Society, 2022, 37(5): 1181-1193.
Optimization Design of Electromagnetic Structure of High Frequency Transformer Based on Intelligent Optimization Algorithm
Abstract As a core component in power conversion fields such as power electronic transformers (PET), the optimal design of high-frequency transformers (HFT) has become essential to achieving high power density, high efficiency, and high reliability. However, the significant eddy current effect and complex and compact structure under high-frequency conditions make it challenging to accurately calculate transformers’ losses and insufficient insulation design margins. Meanwhile, the multiple optimization objectives of HFT are mutually constrained yet difficult to balance, which brings severe challenges to electromagnetic design. Therefore, an electrical and magnetic field modeling method based on the analysis of high-frequency and structure effects is proposed, and a design scheme for multi-objective collaborative optimization of HFT is constructed.
A core loss calculation model with low cost and high efficiency is established by fitting the complex integral function in IGSE under high-frequency non-sinusoidal excitation waveform. The calculation results of the magnetic core loss are consistent with the finite element simulation results. To achieve high-precision calculation of winding losses, an approximate Dowell model, which takes account of the structure effect and eddy current effect of windings, is derived according to the equivalence principle of area, and the impact of winding structure on winding losses is weakened. Compared with the finite element simulation results, the errors in the calculation and measurement results of winding losses of this model are all within acceptable ranges.A leakage inductance calculation model is presented considering the winding edge effect and frequency effect to reduce the dependence of leakage inductance on structure and frequency. Detailed electromagnetic finite element analysis, derivation, and experimental verification are conducted on this model, indicating that this model can accurately calculate the total leakage inductance of high-frequency transformers. To reduce the risk of insulation reliability degradation caused by thermal aging and other issues during the operation of high-frequency transformers, a novel multiple dielectric structure upgrades the insulation to withstand voltage levels between windings, considering long-term and short-term dielectric strength. At the same time, the maximum electric field strength is verified to be within a reliable safety margin through finite element simulation.The algorithm of NSGA-Ⅱ is improved by introducing dynamic clustering distance and arithmetic crossover operator, which is tested using ZDT1 and ZDT3 functions. The effectiveness of the improved scheme is verified using a mathematical model for high-frequency transformer optimization design.
Finally, combined with the INSGA-Ⅱ with the free parameter scanning method, the optimization design process of HFT is established, and an HFT prototype is manufactured based on the selected optimal design. Under no-load conditions, the magnetic core loss and temperature rise of the prototype are measured. The experimental results show that the error between the measurement and simulation results of the magnetic core loss is small, and the temperature rise meets the expected design requirements without thermal operation problems.
Keywords:High frequency transformer, free parameter scanning method, improved nondominated sorting genetic algorithm, optimization design, structure effect
中图分类号:TM433
DOI: 10.19595/j.cnki.1000-6753.tces.231062
国家自然科学基金资助项目(52077053,52377008)。
收稿日期 2023-07-04
改稿日期 2023-11-12
赵志刚 男,1981年生,教授,博士生导师,主要研究方向为电工磁材料磁性能模拟与工程电磁场数值仿真及应用方面的研究工作。
E-mail: zhaozhigang@hebut.edu.cn
白若南 女,1997年生,硕士研究生,主要研究方向为电工磁材料磁性能模拟与工程电磁场数值仿真及应用方面的研究工作。
E-mail: 2209064082@qq.com(通信作者)
(编辑 郭丽军)