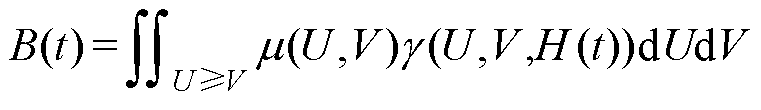 (1)
(1)
摘要 铁磁材料的磁滞、涡流和驰豫效应对电力变压器铁心的非线性特性和功率损耗有显著的影响。为了研究电磁暂态过程中电力变压器的时域响应行为,需要准确计及铁心的动态磁化特性,在电路仿真中对电力变压器铁心进行精细建模。为此,该文首先采用考虑可逆分量的解析Preisach模型表征铁磁材料的静态磁滞效应,通过磁导-电容类比法建立了铁心的回转器-磁导模型,构建铁心静态电磁模型。其次,基于传统损耗统计理论和场分离理论,在静态电磁模型的基础上引入恒定磁阻和受控磁动势源,分别用于表征铁磁材料的涡流效应和弛豫效应对磁滞效应和损耗效应的影响,构建基于传统损耗统计理论的铁心动态电磁模型。最后,运用R-L分数阶导数对涡流损耗表达式进行修正,采用受控磁动势源表示涡流效应,对传统的铁心动态电磁模型进行改进。基于电工钢测量系统测量了硅钢铁心在不同频率、不同磁通密度下的动态磁滞回线,与实验相比改进模型的平均相对误差为6.59%,验证了所提出的改进动态模型的正确性。
关键词:电力变压器 涡流效应 Preisach模型 分数阶导数 磁导-电容类比法
当电力系统发生故障或进行操作时,变压器内部将产生电磁暂态过程,造成铁心饱和、励磁电流畸变、铁心损耗增加的问题[1]。为了研究电磁暂态对系统稳定性和效率的影响程度,准确预估过电压和过电流大小,需要建立精确的变压器电磁暂态模型[2-3]。铁磁材料的磁滞效应、动态涡流和驰豫效应与变压器运行过程中的非线性特性和铁心损耗密切相关[4]。因此,针对铁心的非线性磁滞特性及动态损耗特性建立准确的动态磁滞模型[5],对变压器电磁暂态模型的建立具有重要意义。
目前变压器电磁模型主要有以下三种方法: ①基于电路理论的非线性电感模型;②磁路模型及其对偶变换后的电路模型;③基于磁导-电容类比法的回转器-磁导模型。F. de Leon等将铁心用一个Cauer等效电路表示,采用电感充当磁通通道,电阻表征涡流损耗,利用等效电路模拟了铁心的的涡流损耗[6],但是该模型未能体现铁心的非线性特性。P. Holmberg、J. G. Zhu等采用电阻、电感构成的梯式网络建立了铁心模型,该模型考虑了磁滞效应和动态效应,但是所建模型直观性差并且难以推广到复杂的铁心结构[7-8]。重庆大学邹密基于磁路理论建立了三相变压器的磁路模型,并通过电磁对偶原理将磁性元件等效为电路元件,建立了三相变压器的电磁暂态模型[9]。该模型考虑了铁心的非线性特性,并且能够很好地模拟铁心的励磁涌流等暂态现象,但是该模型无法同时反映电路、磁路的信息,无法充分了解变压器和电路部分的工作状态。
D. C. Hamill基于磁导-电容类比法,提出了铁心的回转器-电容模型[10-11],将变压器模型分为磁路部分和电路部分,变压器的绕组等效为一个LC回转器,铁心磁导用电容代替,以回转器为媒介实现了电路和磁路的耦合。回转器-电容模型的建模方法能够用于PLECS、Saber等电路仿真软件,Luo Min等将磁导-电容类比法引入铁磁材料的电磁建模并将模型使用于系统级电力电子仿真软件PLECS,基于解析Preisach模型构建可变磁导,用于模拟铁心的静态磁滞特性,但是仅适用于低频条件,并未考虑高频条件下涡流损耗和剩余损耗两个动态项的影 响[12]。相比于J-A模型和Energetic模型,基于洛伦兹等拟合函数的解析Preisach模型具有显式表达式,不需要进行微分求导运算,具有形式简便、易于编程实现、参数辨识难度低等特点[13-15],更适合于变压器铁心磁滞建模。文献[16]结合高频下涡流分布特点,将硅钢片沿厚度方向不均匀划分为若干层,每层对应一个恒定电阻,以此考虑高频涡流的影响,但是该方法精度低并且无法准确反映高频条件下铁心的动态过程。
随着大量非线性负荷引入电力系统,变压器更加频繁地工作于高频,铁磁材料在高频条件下表现出很强的频率依赖性。由于Bertotti提出的传统损耗统计理论中的涡流损耗表达式,已经无法考虑频率对涡流效应的影响。为了解决上述问题,B. Ducharne等将分数阶导数对传统涡流损耗表达式进行修正[17],在高频下实现了磁滞回线的精确模拟;在此基础上,B. Zhang、D. C. Jiles、Liu Ren等学者运用改进的涡流损耗项与传统静态JA、Preisach、Energetic模型相结合[18-20],精确模拟了铁磁材料的动态磁滞回线。文献[21-22]通过寻优算法对分数阶导数参数进行全局寻优,准确预测了铁磁材料的动态损耗。上述R-L分数阶模型为铁心轭高频涡流损耗建模提供了一个思路。
为了准确建立变压器的铁心模型,精确分析变压器在各种电磁暂态下端口的电压、电流特性,本文使用磁导-电容类比法建立了硅钢铁心的回转器-磁导模型,采用考虑可逆分量的解析Preisach模型表征铁磁材料的静态磁滞特征,基于损耗统计理论和场分离技术,在静态模型的基础上引入动态项表征铁磁材料的涡流损耗和剩余损耗,运用R-L分数阶导数对涡流损耗表达式进行修正并改进动态模型。最后,利用电工钢测量系统测量了硅钢铁心在不同频率、不同磁通密度下的动态磁滞回线,并与模型进行对比,验证了本文提出的动态模型的正确性。
经典Preisach模型是一种唯象数学模型,认为铁磁材料的磁滞特性是无数个具有矩形磁滞特性的磁滞算子的叠加,其表达式为
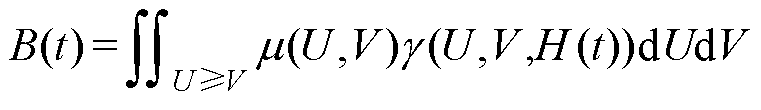 (1)
(1)
式中,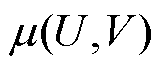 为分布函数;
为分布函数;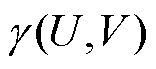 为磁滞算子;H(t)为t时刻的磁场强度;U和V分别为磁滞算子上、下输入的开关阈值。
为磁滞算子;H(t)为t时刻的磁场强度;U和V分别为磁滞算子上、下输入的开关阈值。
经典Preisach磁滞模型的输出可以根据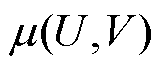 分布函数取值进行求解[15]。图1为Preisach磁滞模型的积分区域S,可以分为S+和
分布函数取值进行求解[15]。图1为Preisach磁滞模型的积分区域S,可以分为S+和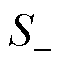 两个区域,在S+区域中磁滞算子值为+1,
两个区域,在S+区域中磁滞算子值为+1,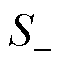 区域中磁滞算子值为-1。当磁场强度增大时,阶梯线L垂直于U轴向右移动;当磁场强度减小时,阶梯线垂直于V轴向下移动。图1中,Hs为铁磁材料的饱和磁场强度。
区域中磁滞算子值为-1。当磁场强度增大时,阶梯线L垂直于U轴向右移动;当磁场强度减小时,阶梯线垂直于V轴向下移动。图1中,Hs为铁磁材料的饱和磁场强度。
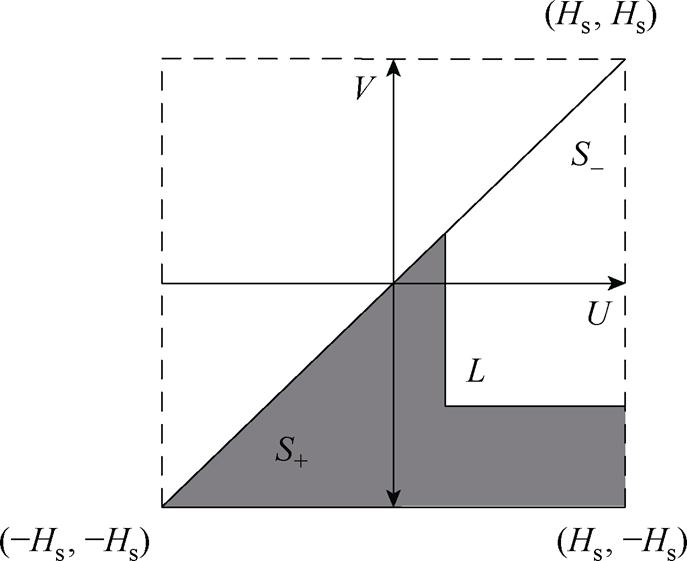
图1 分布函数取值域
Fig.1 The range of values of the distribution function
经典Preisach模型分布函数的辨识是模型应用的难点,通过提取一阶回转曲线求解分布函数的方法存在计算时间长、精度低等问题,有学者通过引入Everett函数的方法来对分布函数进行计算,但是在实际工程应用中存在计算过程复杂、计算难度大等问题。为了兼顾准确性和计算速度,本文采用洛伦兹函数近似代替分布函数。洛伦兹函数解析式[23]为
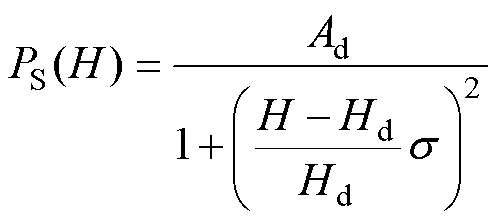 (2)
(2)
式中,H为磁场强度;Ad、 、
、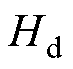 为洛伦兹函数参数。
为洛伦兹函数参数。
参数Ad可根据 、
、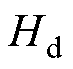 算出,计算式[23]为
算出,计算式[23]为
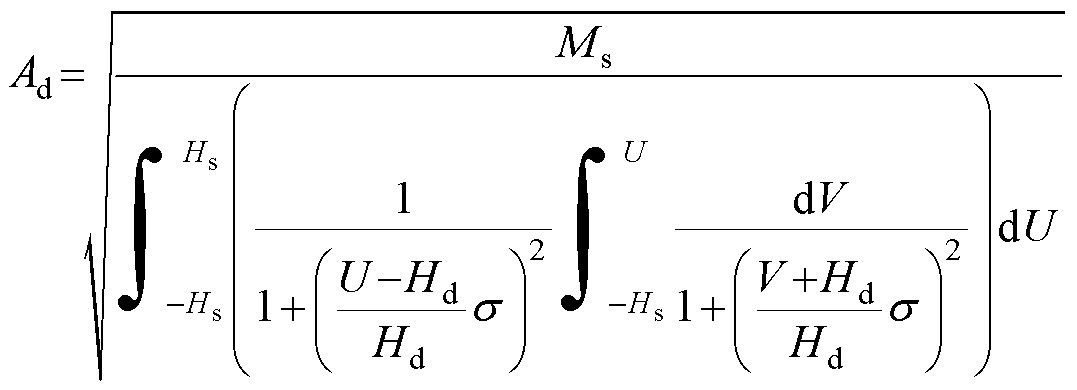 (3)
(3)
式中,Ms为饱和磁化强度;Hs为饱和磁场强度。
基于洛伦兹函数解析式,Preisach模型分布函数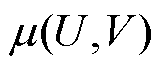 可以表示为
可以表示为
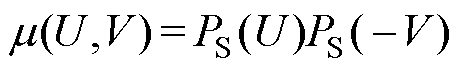 (4)
(4)
将式(2)、式(4)代入式(1)并结合铁磁材料磁滞回线饱和点(Hs, Bs)可得,以H为输入、B为输出的磁滞回线上升支和下降支的表达式[21]分别为
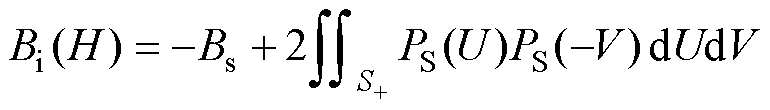 (5)
(5)
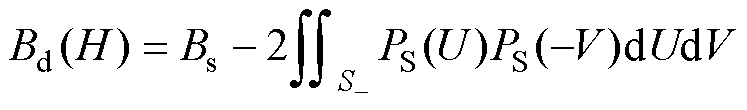 (6)
(6)
将式(5)和式(6)对H求导,可以得到上升支和下降支的磁导率分别为
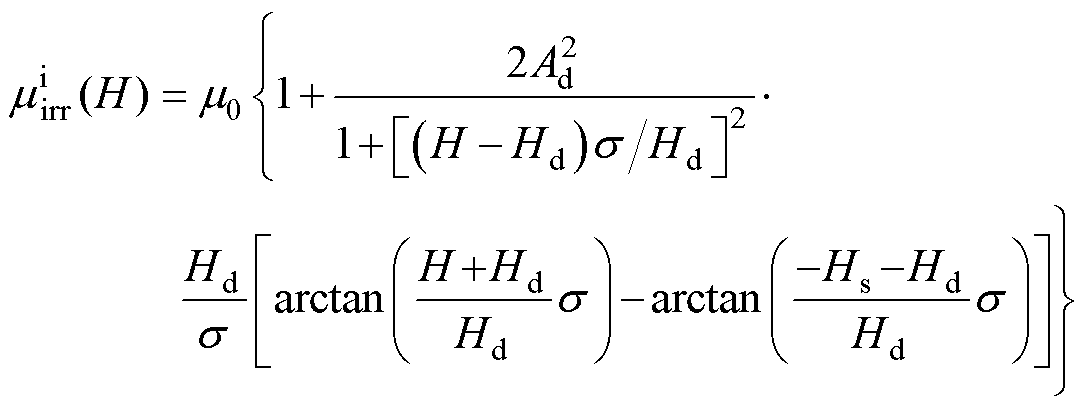
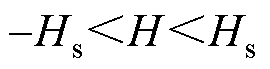 (7)
(7)
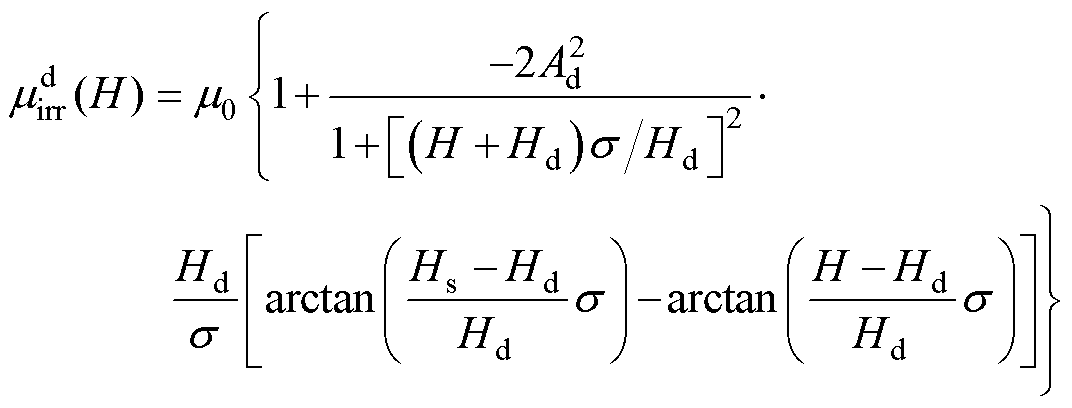
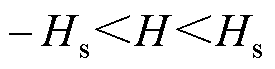 (8)
(8)
虽然经典Preisach模型能够较为准确地重现铁磁材料中的剩磁和磁顽力,但是经典Preisach模型及其改进模型均存在基于矩形磁滞回环来描述磁滞特性的问题,没有考虑磁化过程中的可逆磁化分量,进而影响了磁滞回线模拟的准确度。为了准确模拟铁磁材料的静态磁滞特性,在经典Preisach模型上引入可逆分量表达式[23],其中可逆磁化分量与磁化过程中磁畴壁的弯曲对应,而不可逆磁化分量与磁化过程中磁畴壁的位移对应[24]。总磁通密度等于可逆磁化分量Brev(H)和不可逆磁化分量Birr(H)之和,计算式为
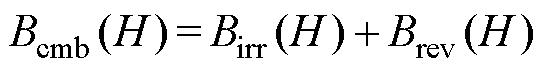 (9)
(9)
总磁导率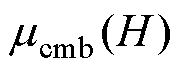 等于不可逆分量磁导率
等于不可逆分量磁导率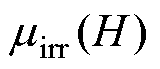 和可逆分量磁导率
和可逆分量磁导率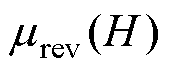 之和,计算式为
之和,计算式为
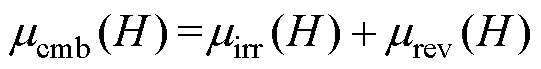 (10)
(10)
其中,可逆分量磁导率mrev(H)计算公式为
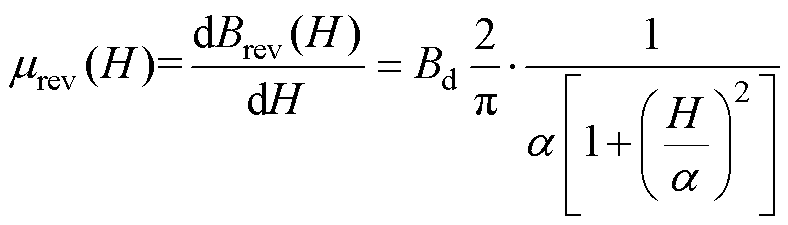 (11)
(11)
式中,Bd和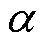 为磁导率计算参数。
为磁导率计算参数。
基于磁导-电容类比法,D. C. Hamill提出了回转器-电容模型(Gyrator-Capacitor model, G-C)。G-C模型包括电路部分和磁路部分,磁路的磁动势F、磁通变化率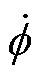 和磁导p分别类比为电路的电压v、电流i和电容C,绕组则被类比于回转器,成为连接电路和磁路的接口[10-11]。图2给出了硅钢变压器的回转器-电容模型,其磁路部分等效为一个非线性磁导,回转器电路侧和磁路侧物理量满足
和磁导p分别类比为电路的电压v、电流i和电容C,绕组则被类比于回转器,成为连接电路和磁路的接口[10-11]。图2给出了硅钢变压器的回转器-电容模型,其磁路部分等效为一个非线性磁导,回转器电路侧和磁路侧物理量满足
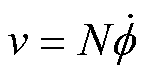 (12)
(12)
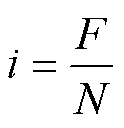 (13)
(13)
式中,v和i分别为电路侧的电压和电流;N为绕组匝数;F为绕组的磁动势;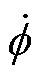 为磁通的变化率。
为磁通的变化率。
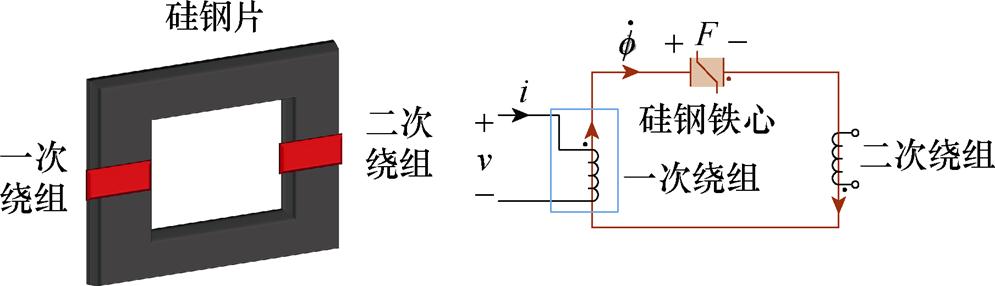
图2 硅钢变压器的回转器-电容模型
Fig.2 Gyro-capacitor model of silicon steel transformer
磁导两端的磁动势F、磁通变化率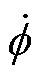 满足
满足
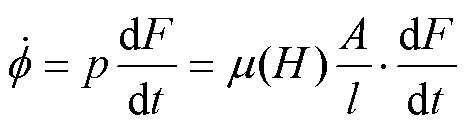 (14)
(14)
式中,A为硅钢变压器铁心横截面积;l为磁路长度;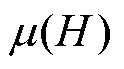 为可变磁导率,根据实时输入磁场强度进行更新。
为可变磁导率,根据实时输入磁场强度进行更新。
采用PLECS系统级电力电子仿真软件进行磁滞磁导建模。为了考虑铁心非线性磁化特性,磁导模块可以根据输入的磁场强度信号实时调整磁导率大小更新磁导取值。含不可逆分量的铁心磁路段模块如图3所示。采用磁动势探针实时提取的磁导两端的磁动势F(t),将F(t)除以磁路长度l,得到磁场强度瞬时值H(t),H(t)作为PLECS中C-Script可编程模块的输入量,按照静态解析Preisach模型计算并输出微分磁导率,磁导率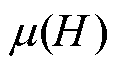 乘以A/l作为磁导输入可变磁导模块。
乘以A/l作为磁导输入可变磁导模块。
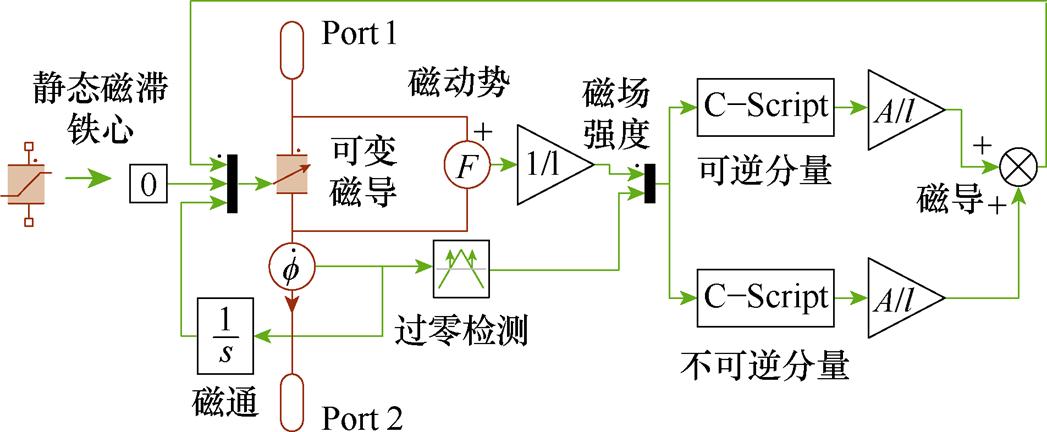
图3 含不可逆分量的铁心磁路段模块
Fig.3 Core segment module with irreversible component
图4显示了Preisach模型初始磁化曲线的实现过程:假设t1=0为仿真的起始点,对应于B-H坐标系的原点位置(点1)。此时铁磁材料处于完全退磁状态,Preisach三角平面上正向算子(S+)和负向算子数量(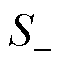 )相等,即Preisach输出的磁感应强度B为0。当电路中励磁电流i增加,磁场强度H逐渐增大,正向算子(S+)所占的面积逐渐增大,负向算子(
)相等,即Preisach输出的磁感应强度B为0。当电路中励磁电流i增加,磁场强度H逐渐增大,正向算子(S+)所占的面积逐渐增大,负向算子(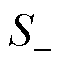 )的所占面积逐渐减小,输出的磁通密度B逐渐增加,沿着点1和点2之间的初始磁化曲线移动,此时输出的磁通密度计算式为
)的所占面积逐渐减小,输出的磁通密度B逐渐增加,沿着点1和点2之间的初始磁化曲线移动,此时输出的磁通密度计算式为
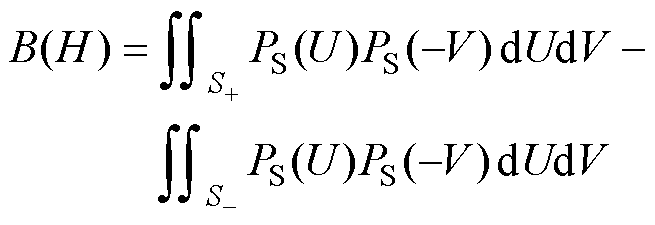 (15)
(15)
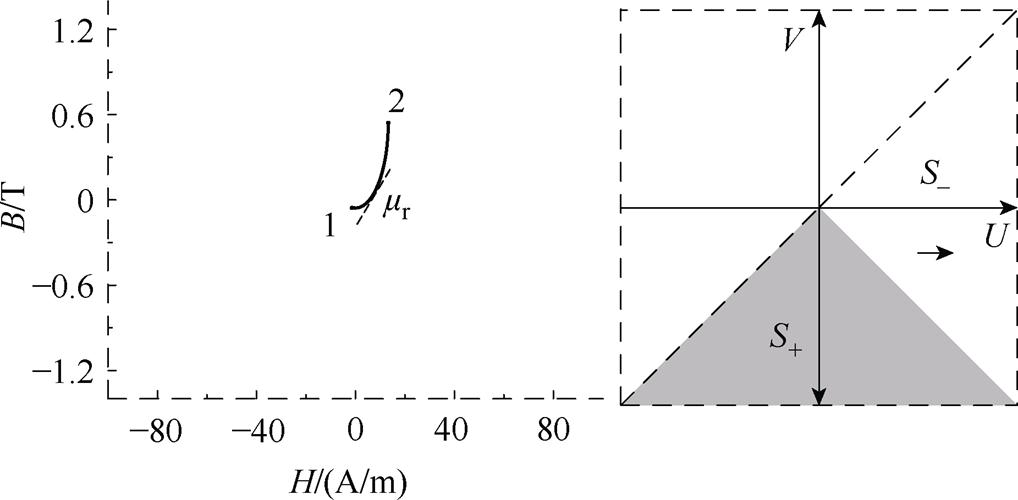
图4 初始磁化曲线实现过程示意图
Fig.4 Schematic diagram of the implementation process of the initial magnetization curve
在B-H曲线上,此时的初始磁导率计算为
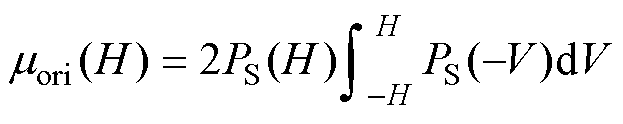 (16)
(16)
PS(H)为式(2)给出的洛伦兹函数,式(16)可以计算为
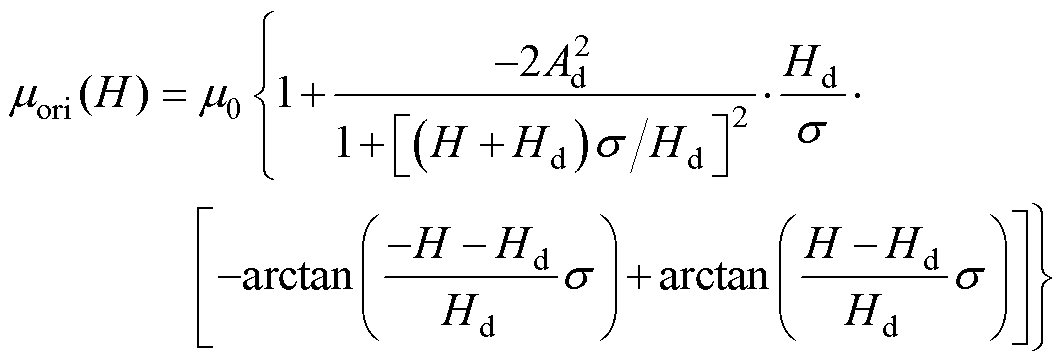
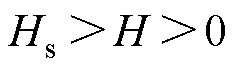 (17)
(17)
由于式(17)为显性表达式,磁场强度H为输入变量,可将式(14)中的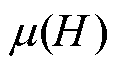 替换为式(17)直接赋值给可变磁导模块。
替换为式(17)直接赋值给可变磁导模块。
下降支曲线实现过程示意图如图5所示。在t2时刻(见图5中点3),电流达到峰值后逐渐减小,磁场强度H开始下降,正向算子(S+)所占的面积由最大逐渐减小,负向算子(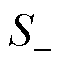 )的所占面积逐渐增大,输出磁通密度B开始减小,沿点3和点4之间的磁滞回线下降支移动,此时Hs为点3对应的磁场强度,可以根据
)的所占面积逐渐增大,输出磁通密度B开始减小,沿点3和点4之间的磁滞回线下降支移动,此时Hs为点3对应的磁场强度,可以根据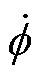 符号变化进行过零检测得到该点,此时磁导率计算为
符号变化进行过零检测得到该点,此时磁导率计算为
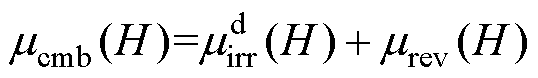 (18)
(18)
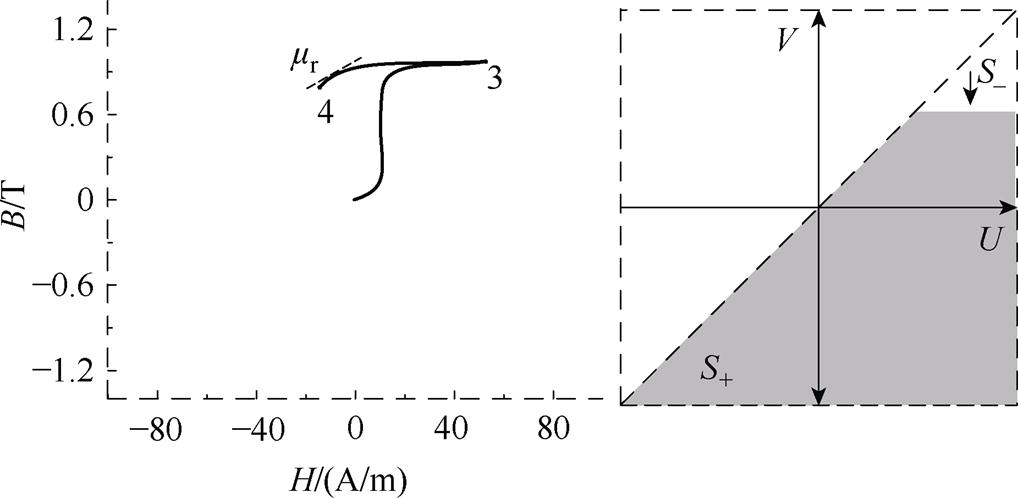
图5 下降支曲线实现过程示意图
Fig.5 Schematic diagram of the implementation process of the descending branch curve
上升支曲线实现过程示意图如图6所示。当达到下降支翻转点(见图6中点5)时,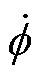 由负变为正,H开始增加,正向算子(S+)所占的面积由0逐渐增大,负向算子(
由负变为正,H开始增加,正向算子(S+)所占的面积由0逐渐增大,负向算子(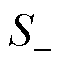 )的所占面积由最大逐渐减小,HS被更新,磁通密度B沿点5和点6之间的磁滞回线上升支移动,在位置6上,此时磁导率计算为
)的所占面积由最大逐渐减小,HS被更新,磁通密度B沿点5和点6之间的磁滞回线上升支移动,在位置6上,此时磁导率计算为
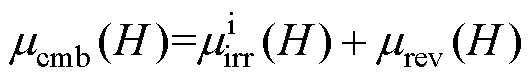 (19)
(19)
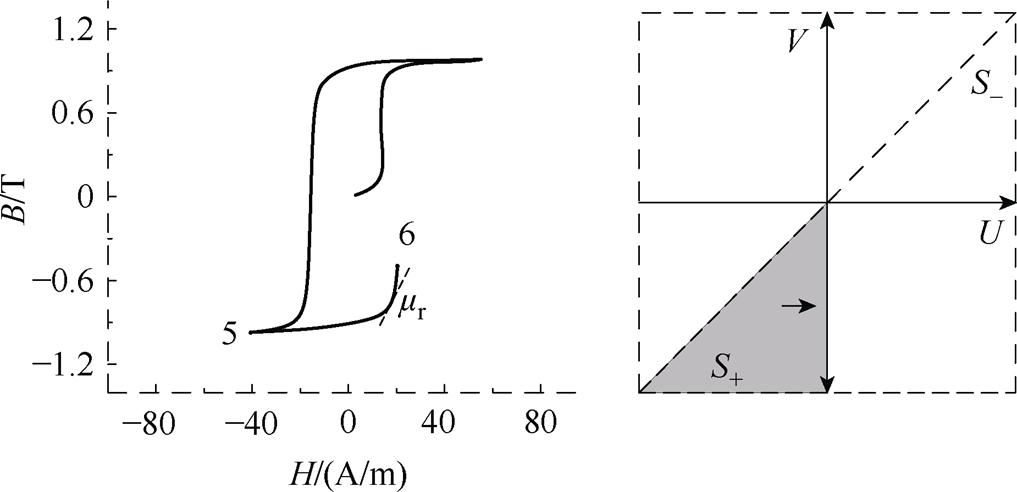
图6 上升支曲线实现过程示意图
Fig.6 Schematic diagram of the implementation process of the upper and lower branch curve
基于损耗统计理论[5],铁磁材料的损耗不仅有静态磁滞损耗Wh,还包括涡流损耗Wcl与剩余损耗Wex,铁磁材料的总损耗表示为
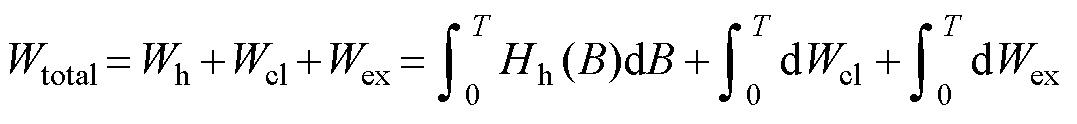
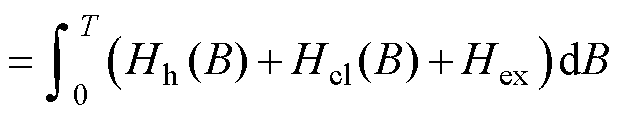 (20)
(20)
式中,Hh、Hcl、Hex分别为静态磁滞损耗、涡流损耗和剩余损耗对应的磁场强度分量,Hcl、Hex的表达式分别为
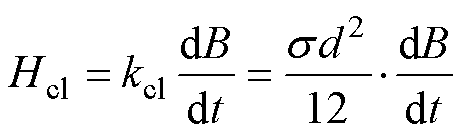 (21)
(21)
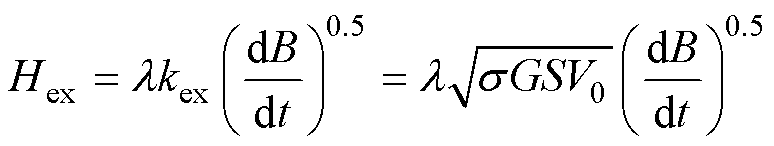 (22)
(22)
式中,kcl、kex分别为前文提出的涡流损耗磁场强度Hcl和剩余损耗磁场强度Hex表达式的前置系数;d为铁磁材料厚度;s 为电导率;G为无量纲数,G= 0.135 6;S为铁磁材料横截面积;V0为统计系数,与铁磁材料局部磁场分布有关;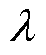 为符号函数,当
为符号函数,当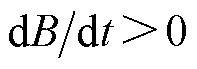 时,
时,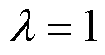 ;当
;当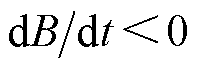 时,
时,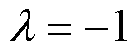 。
。
因此,铁磁材料的磁场强度Htotal可以视为三个磁场强度的叠加,即
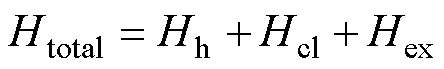 (23)
(23)
为了与磁路建立联系,将式(23)结合磁路长度l得到铁磁材料的总磁动势Ftotal为
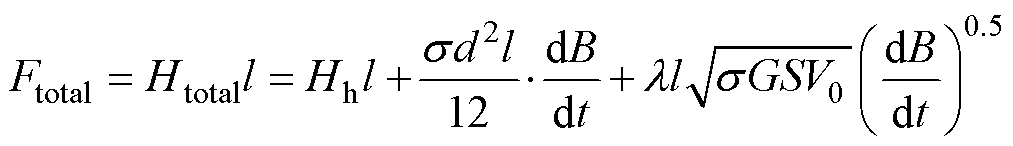 (24)
(24)
根据式(21)~式(24),可以在PLECS上搭建出传统的动态磁滞磁导模型,如图7所示。式(24)中第一项为静态磁滞损耗相关的磁动势,根据式(14)对时间t进行积分。第二项为涡流损耗相关的磁动势Fcl,由磁阻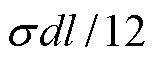 乘以磁通变化率
乘以磁通变化率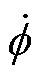 表示。第三项为剩余损耗相关的磁动势,由受磁通变化率
表示。第三项为剩余损耗相关的磁动势,由受磁通变化率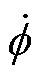 控制的受控磁动势表示,
控制的受控磁动势表示,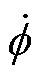 作为输入变量输入剩余损耗模块,在可编程模块C-Script根据式(22)进行计算,乘以磁路长度l后输出Fex。在图7绕组两端接入正弦电压源,提取传统动态模型两端磁场强度H和磁通密度B,得到硅钢变压器铁心的动态磁滞回线,图8显示了时域仿真中动态磁滞回线的叠加过程。
作为输入变量输入剩余损耗模块,在可编程模块C-Script根据式(22)进行计算,乘以磁路长度l后输出Fex。在图7绕组两端接入正弦电压源,提取传统动态模型两端磁场强度H和磁通密度B,得到硅钢变压器铁心的动态磁滞回线,图8显示了时域仿真中动态磁滞回线的叠加过程。
传统模型计算涡流损耗是基于铁磁材料内部磁通均匀分布的前提,但在高频条件下,铁磁材料内部磁通由于趋肤效应通常非均匀分布,因此式(21)计算高频涡流损耗具有一定误差,随着频率增大,误差也逐渐增大,因此需要对传统模型进行改进以适应高频条件。
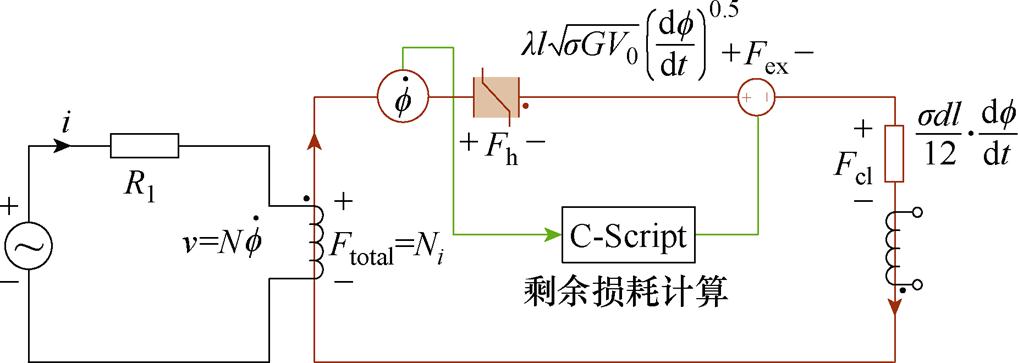
图7 基于传统损耗统计理论的动态磁滞磁导模型
Fig.7 Dynamic hysteresis permeance model based on traditional loss statistical theory
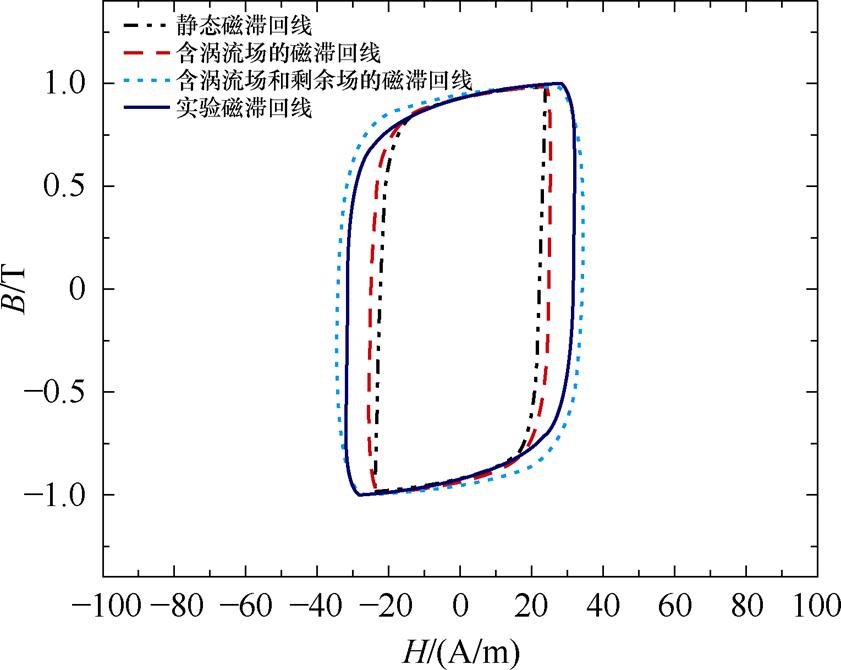
图8 硅钢铁心动态磁滞回线各场强叠加示意图
Fig.8 Schematic diagram of superposition of each field strength of the dynamic hysteresis loop of silicon steel core
传统涡流损耗表达式中含有磁通密度对时间的整数阶导数,但整数阶导数无法揭示铁磁材料涡流损耗存在的非局部、频率、历史等依赖性过程[17],为了解决上述问题,本文引入分数阶导数,对传统涡流损耗公式进行改进,以实现高频状态下铁磁材料的电磁建模。
分数阶导数将传统导数的阶数n由整数推广至非整数和复数。目前常用的分数阶导数算子有Grünwald-Letnikov(G-L)型与Riemann-Liouville(R-L)型分数阶导数,相比于G-L分数阶导数,R-L分数阶导数运用范围更广泛[25]。因此,本文选用R-L分数阶导数对涡流分量进行修正,R-L型分数阶导数算子表达式为
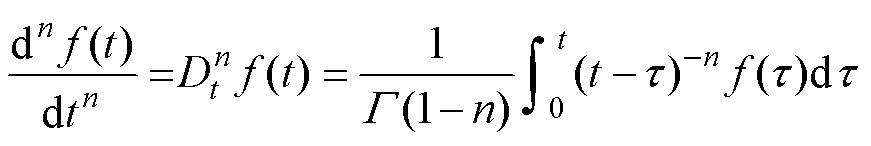 (25)
(25)
式中,n为分数阶导数的阶数,通常n的取值范围为(0,1);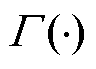 为欧拉伽马函数。
为欧拉伽马函数。
将式(25)引入式(21),可以实现对传统损耗统计理论中的涡流场分量的改进,有
 (26)
(26)
式中,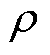 为改进后的涡流分量阻尼系数。
为改进后的涡流分量阻尼系数。
在正弦激励下,计算式(26)可进一步表示为
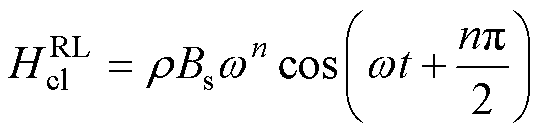 (27)
(27)
式中,Bs为最大磁通密度;w 为角频率。
基于分数阶导数的改进涡流损耗表达式为
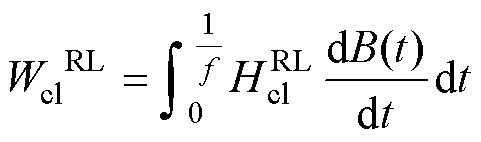 (28)
(28)
改进涡流损耗后铁磁材料总磁动势F为
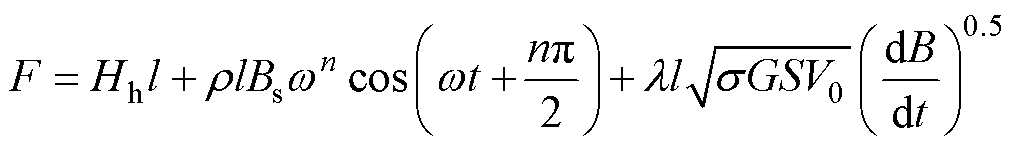 (29)
(29)
根据式(29)在PLECS搭建改进动态磁滞磁导模型,如图9所示。改进模型采用受控磁动势源表示涡流损耗,t为仿真计算时间,作为输入变量输入涡流损耗C-Script模块,并根据式(28)计算得到改进后的涡流磁场强度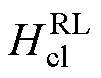 ,乘以磁路长度l后得到改进后的涡流磁动势
,乘以磁路长度l后得到改进后的涡流磁动势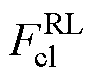 。基于磁导-电容类比法及R-L分数阶导数,建立的改进动态磁滞磁导模型的实现流程如图10所示。首先初始化磁导率
。基于磁导-电容类比法及R-L分数阶导数,建立的改进动态磁滞磁导模型的实现流程如图10所示。首先初始化磁导率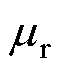 、仿真时间t0,在t0时刻根据p=
、仿真时间t0,在t0时刻根据p=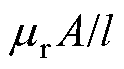 ,得到磁导p,对于回转器的电路侧而言,回转器将磁路磁导等效为动态电感,可以计算出回转器两端的电流和电压,进而计算各磁动势并更新磁导率。
,得到磁导p,对于回转器的电路侧而言,回转器将磁路磁导等效为动态电感,可以计算出回转器两端的电流和电压,进而计算各磁动势并更新磁导率。
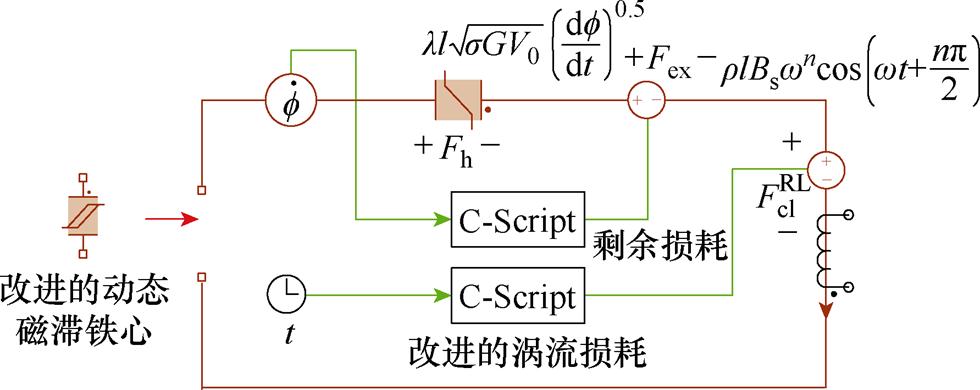
图9 改进的动态磁滞磁导模型
Fig.9 Improved dynamic hysteresis permeance model
利用BROCKHAUS-MPG-200D电工钢测量系统对超薄取向硅钢片进行实验[5]。硅钢长度、宽度、厚度分别为300、30、0.079 45mm,硅钢横截面积为2.383 4 mm2,质量密度7 190 kg/m3,电导率为2.17×106 S/m,激励线圈和感应线圈的匝数均为200匝。通过测量系统测量材料在不同频率、不同峰值磁通密度下的准静态和动态磁滞回线,如图11所示。通过式(30)可以计算出硅钢片中的总损耗。
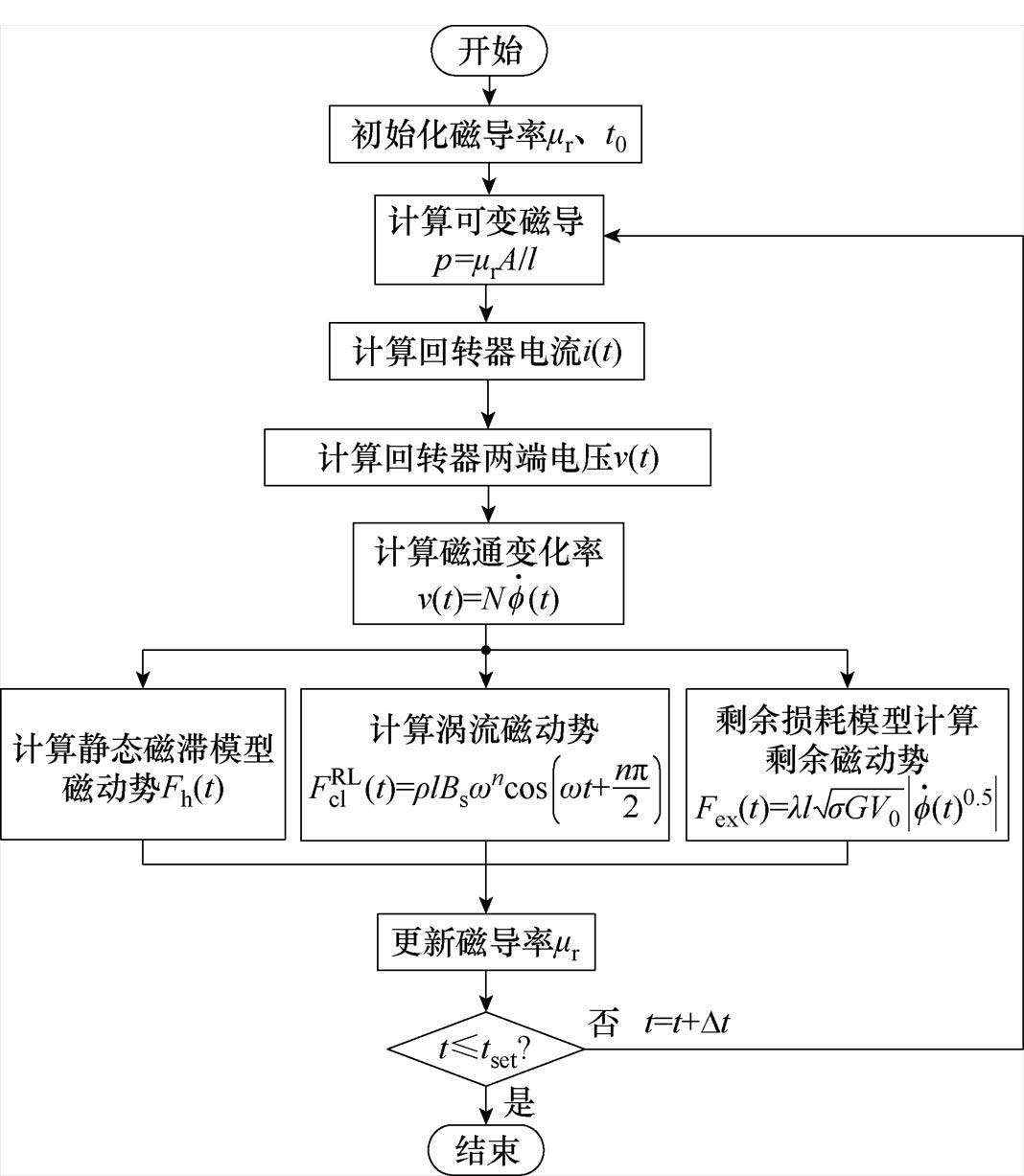
图10 改进的动态磁滞磁导模型实现流程
Fig.10 Flowchart of improved dynamic hysteresis permeance model
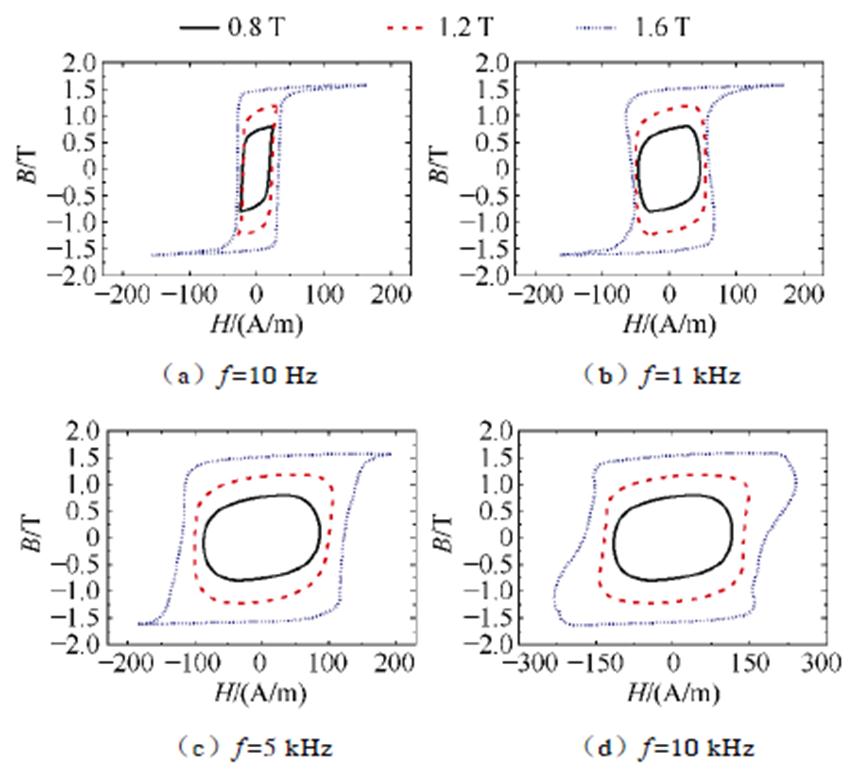
图11 不同频率和不同磁通密度下磁滞回线实验值
Fig.11 Experimental values of hysteresis loops at different frequencies and magnetic densities
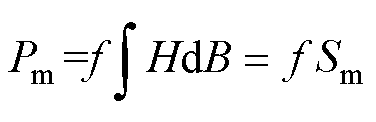 (30)
(30)
式中,Sm为频率f下动态磁滞回线面积。
通过文献[23]提出的全局粒子群算法对静态Preisach模型的各项参数进行辨识。首先根据磁滞回线下降支的拐点(Hmax, Bmax)来确定式(11)可逆分量中的Bd和a 的参数。然后用磁滞回线实验值减去可逆分量得到不可逆分量实验值。以不可逆分量的实验值磁通密度与Preisach模型理论计算磁通密度之间的方均根误差作为目标函数,来计算参数s、Hd的最优值。方均根误差表达式为
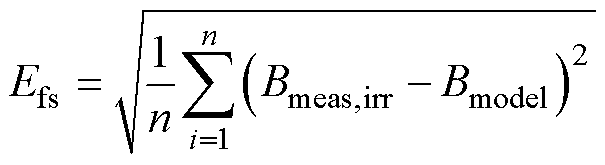 (31)
(31)
式中,Efs为实验值与计算值之间的方均根误差;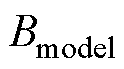 为基于式(5)与式(6)的理论计算值;
为基于式(5)与式(6)的理论计算值;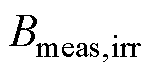 为实验测量的不可逆分量值。
为实验测量的不可逆分量值。
粒子群算法具体步骤如下:
(1)初始化粒子群:设置粒子数量为20,设置s 和Hd的取值范围为[0, 20]、[0, 50],并初始化粒子群的速度为[0.2, 0.5]。
(2)初始化最优值:初始化个体最优值矩阵和群体最优值矩阵,根据式(31)求粒子与目标值的误差,保存每次迭代后生成的最优值矩阵。
(3)开始迭代:根据用迭代后的粒子(s, Hd)计算目标函数Ef,如果误差更小则更新个体最优值矩阵和群体最优值矩阵。
(4)判断是否达到最大迭代数,满足条件计算结束;否则,继续下一步运算。
(5)更新粒子的速度和位置,迭代次数加1,返回步骤(3)。达到最大迭代数后,迭代停止,输出最优值s、Hd。图12为不同磁通密度下方均根误差随迭代次数变化,表1为不同磁通密度下静态解析Preisach磁滞模型参数取值。
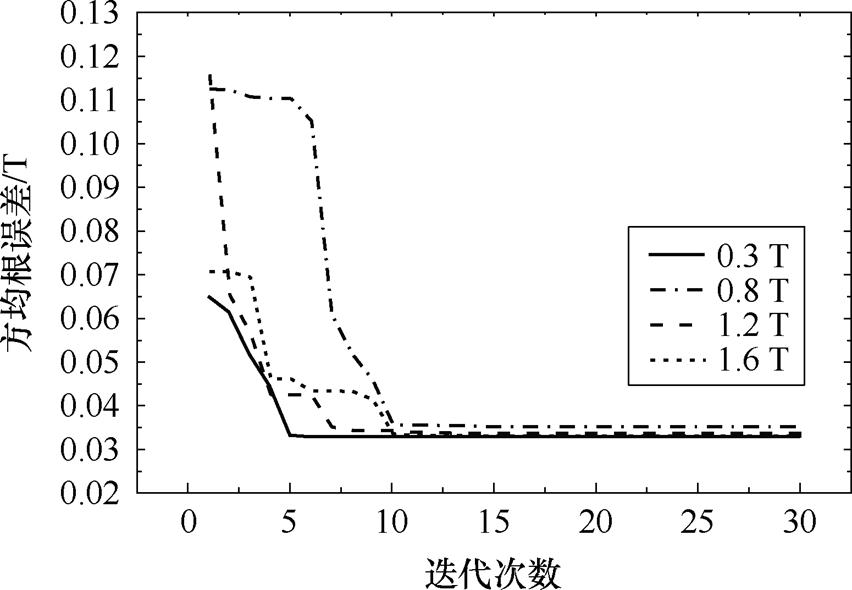
图12 不同磁通密度下方均根误差随迭代次数变化
Fig.12 Root-mean-square deviation versus iteration number under different magnetic densities
表1 不同磁通密度下静态Preisach磁滞模型参数取值
Tab.1 Parameter values of static Preisach hysteresis model under different magnetic densities
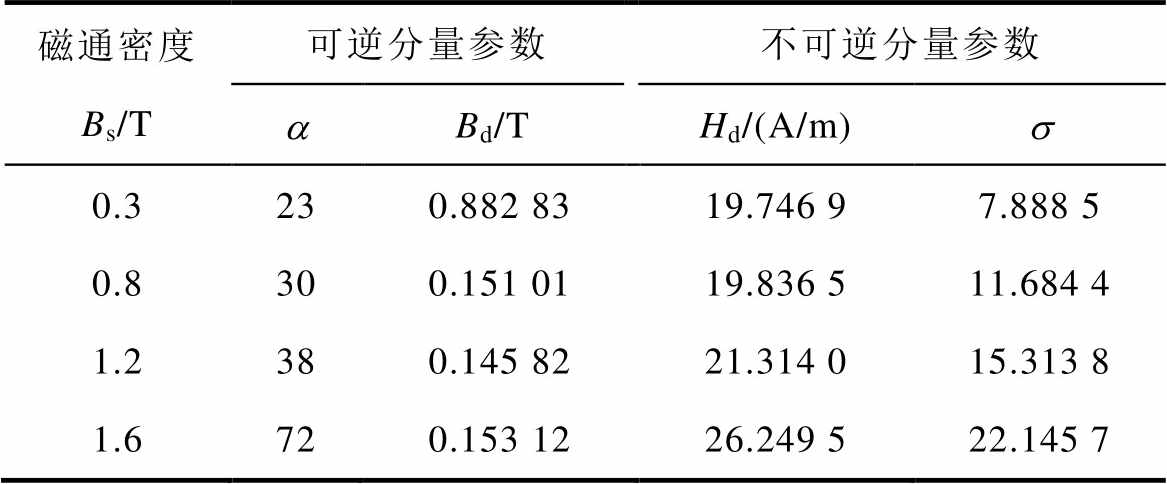
磁通密度Bs/T可逆分量参数不可逆分量参数 aBd/THd/(A/m)s 0.3230.882 8319.746 97.888 5 0.8300.151 0119.836 511.684 4 1.2380.145 8221.314 015.313 8 1.6720.153 1226.249 522.145 7
通过文献[21]提出的量子遗传算法对式(26)中R-L分数阶参数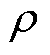 、
、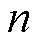 进行辨识。量子遗传算法通过每次迭代,对染色体进行更新,使其不断靠近最优值。根据式(20)计算铁磁材料的总损耗,其中涡流损耗为基于式(28)的R-L分数阶损耗计算值。直接运用损耗测量值与总损耗计算值之间的方均根误差作为优化算法的目标函数为
进行辨识。量子遗传算法通过每次迭代,对染色体进行更新,使其不断靠近最优值。根据式(20)计算铁磁材料的总损耗,其中涡流损耗为基于式(28)的R-L分数阶损耗计算值。直接运用损耗测量值与总损耗计算值之间的方均根误差作为优化算法的目标函数为
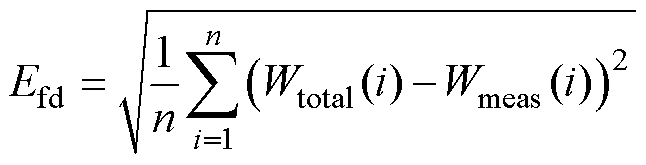 (32)
(32)
式中,Wtotal为基于式(20)与式(28)的理论计算值;Wmeas为实验测量的损耗值。
剩余损耗中的参数V0可以通过低频条件下的总损耗测量值Wmeas来确定,此时趋肤效应可以忽略。将总损耗测量值Wmeas减去式(21)得到的涡流损耗计算值Wcl,可以得一个频率区间内不同峰值磁通密度对应的静态磁滞损耗Wh和剩余损耗Wex随着f0.5的变化曲线,如式(33)所示。V0可以通过计算该曲线的斜率得到,图13为参数V0随最大磁通密度变化曲线。
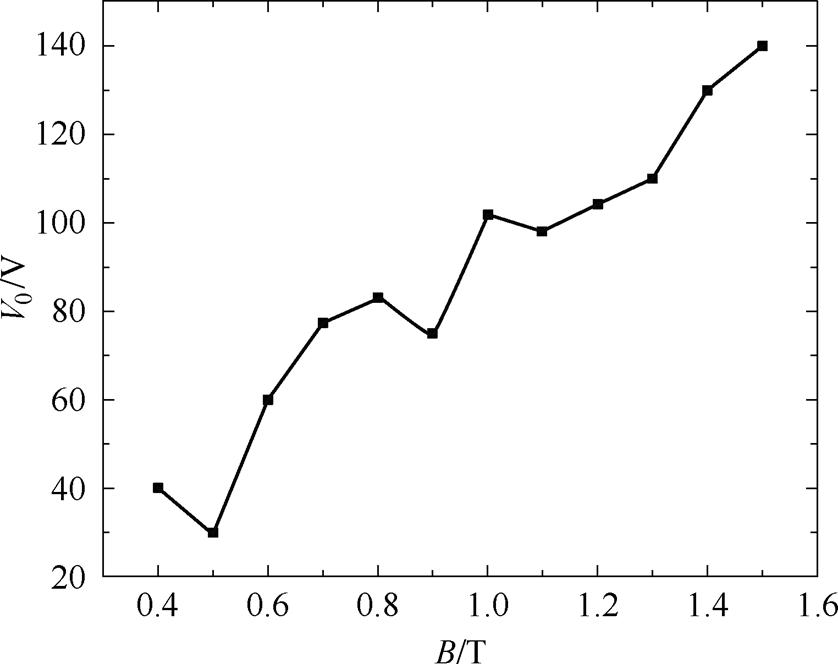
图13 V0随最大磁通密度变化曲线
Fig.13 Curve of V0 variation with maximum magnetic density
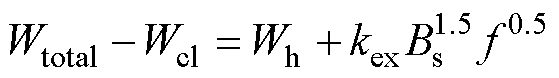 (33)
(33)
式中,kex为剩余损耗拟合系数,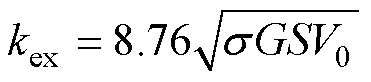 。
。
获得V0之后,利用量子遗传算法可以得到分数阶导数参数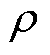 和
和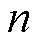 。
。
量子遗传算法基本步骤如下:
(1)种群初始化:利用算法函数生成量子比特并应用于染色体编码矩阵。
(2)初始化最优值:对初始种群的每个个体进行测量,得到对应的解集。
(3)适应度评估:基于目标函数式(32)对每个个体的解进行适应度评估,并记录最优个体及其适应度。
(4)迭代更新:对步骤(3)进行循环迭代,更新最优值,选择适应度更小的个体进行更新。
(5)终止条件判断:判断是否达到结束条件,本文为最大迭代次数。
(6)迭代次数加1,返回步骤(3)进行下一轮迭代。
最终,采用量子遗传算法辨识出的分数阶导数参数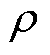 和
和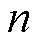 分别为0.005 2和0.812,分数阶导数参数方均根误差随迭代次数变化如图14所示。
分别为0.005 2和0.812,分数阶导数参数方均根误差随迭代次数变化如图14所示。
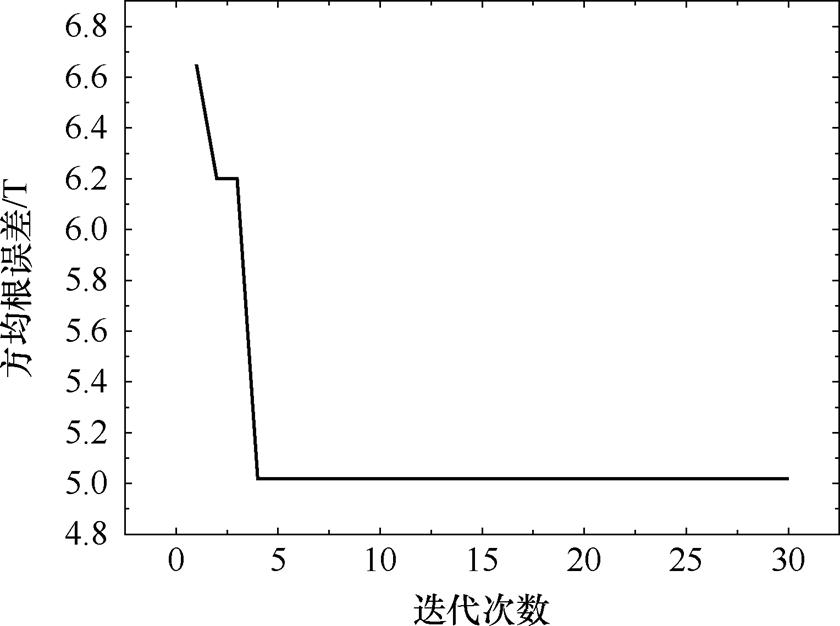
图14 分数阶导数参数方均根误差随迭代次数变化
Fig.14 Root-mean-square deviation of fractional derivative parameter versus iteration number
图15为验证静态磁滞磁导模型的电路,在磁滞铁心模块一端通入电压激励,另一端开路,R1为电源内阻,提取组合磁滞铁心模型中的磁场强度H、磁感应强度B,绘制B-H曲线。图16为最大磁通密度分别为0.8、1.2、1.6 T时实验测量的静态B-H曲线与仿真结果的对比,由图16可知,仿真结果与实验结果吻合良好。
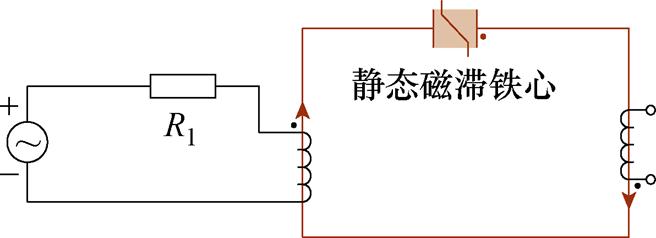
图15 静态磁滞磁导模型验证电路
Fig.15 Static hysteresis permeance model verification circuit
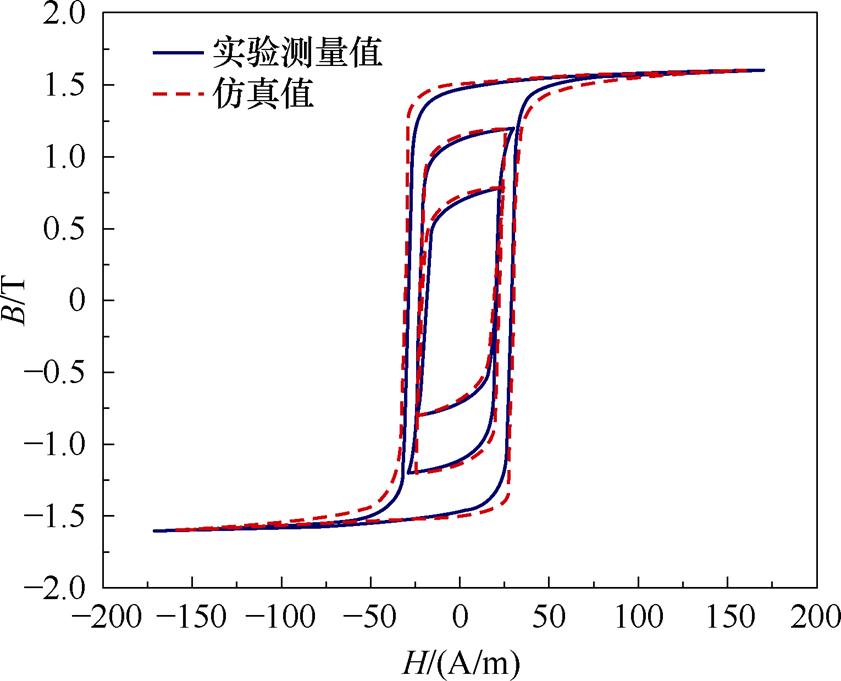
图16 硅钢铁心静态磁滞回线实验值与仿真值
Fig.16 Experimental values and simulated values of static hysteresis loop of silicon steel core
根据第2.1节的基于传统损耗统计理论的动态磁滞磁导模型,以及第2.2节的改进动态磁滞磁导模型,搭建图17所示的验证电路。对1~10 kHz激励频率下,最大磁通密度分别为0.8、1.2、1.6 T时的动态磁滞回线进行仿真并与实验进行对比。在一次绕组输入电压激励,测量一次绕组电流和二次绕组电压,仿真波形与实验波形如图18所示。通过测量模型两端的磁场强度H与磁通密度B,图19显示了传统模型、改进的动态模型和实验测量B-H曲线。由图19可知,相比于传统模型,改进的模型更接近实验测量值,并且随着频率增大,改进的模型误差更小。
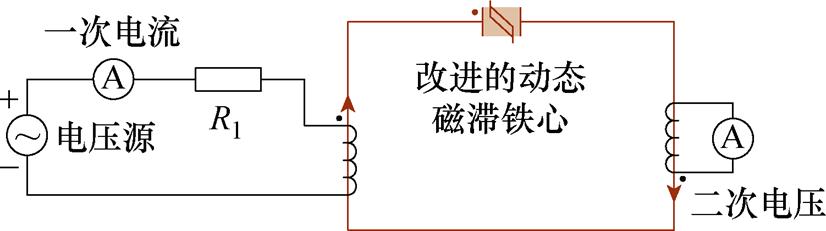
图17 动态磁滞磁导模型验证电路
Fig.17 Dynamic hysteresis permeance model verification circuit
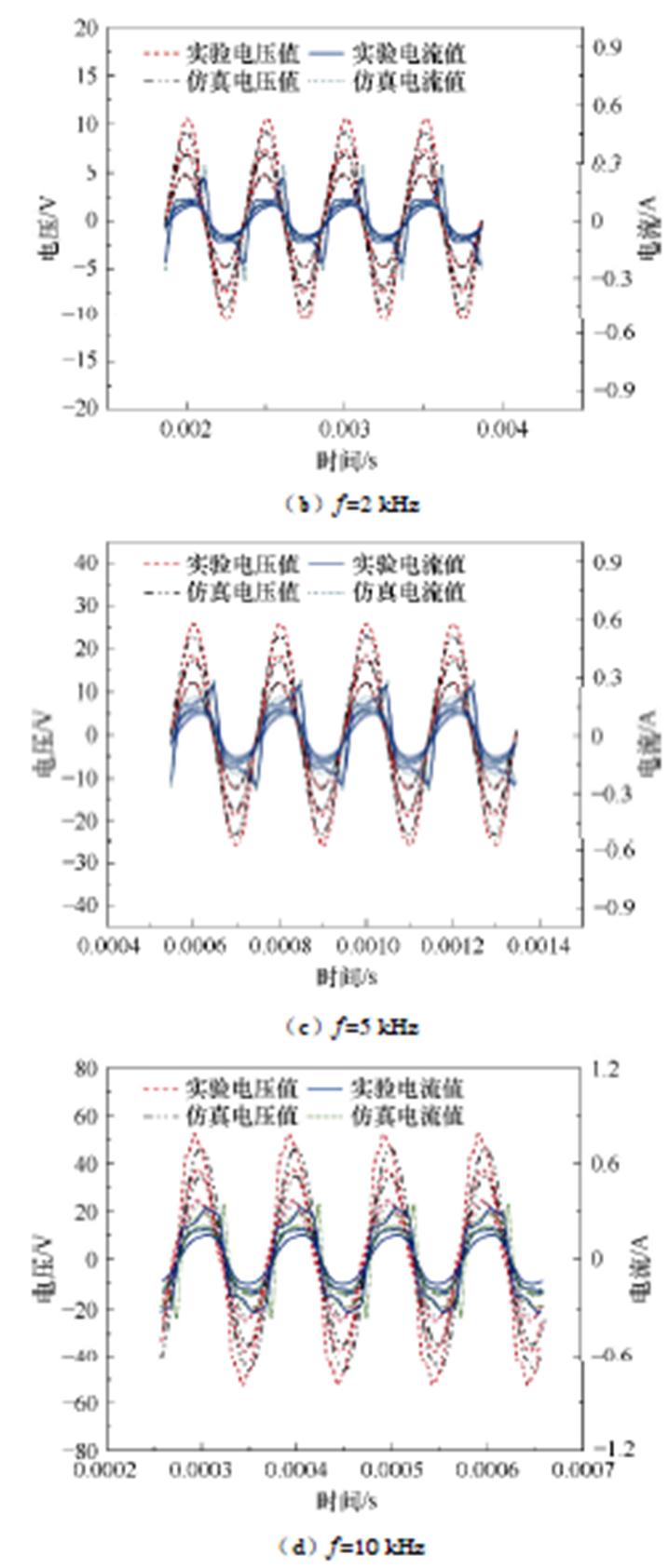
图18 不同频率和不同磁通密度下的电压、电流波形
Fig.18 Voltage and current waveforms at different frequencies and magnetic densities
为了评估模型建立的准确性,本文根据式(34)计算了实验测量损耗值与模型仿真损耗值,并引入平均相对误差对于模型进行评估,平均相对误差的表达式为
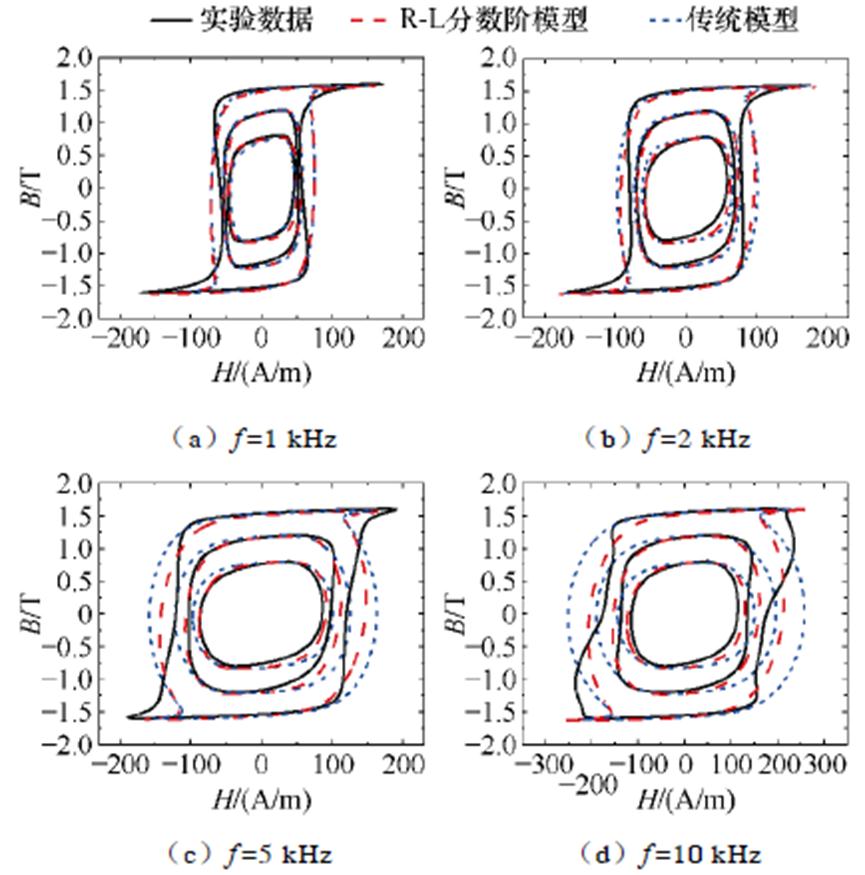
图19 不同频率和不同磁通密度下磁滞回线仿真值与实验值
Fig.19 Simulation and experimental values of hysteresis loops under different frequencies and magnetic densities
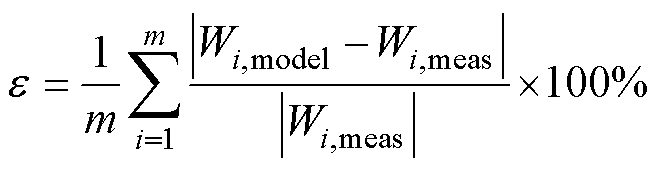 (34)
(34)
式中,m为不同磁通密度下1~10 kHz范围内的测量频点数目,本文中m=10;Wi,model为硅钢变压器时域仿真下的总损耗;Wi,meas为第i个测量频点实验测量的损耗值。图20给出了不同频率、不同磁通密度下的实验测量损耗值与传统模型、R-L分数阶模型的计算值对比,根据结果,传统模型的相对平均误差为14.04%,R-L分数阶模型的相对平均误差为6.59%。
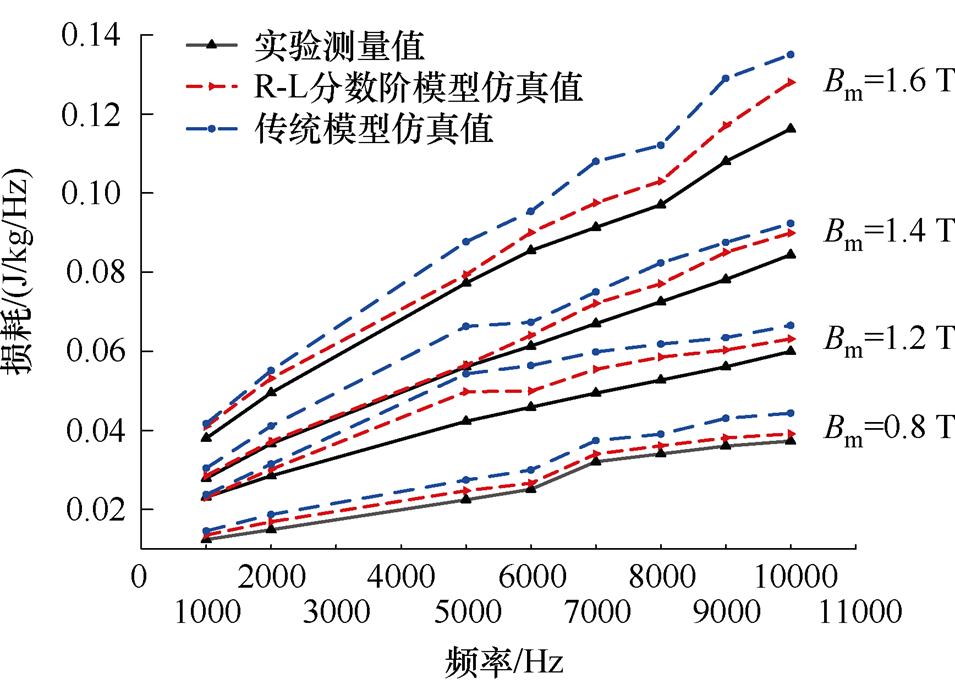
图20 不同频率和不同磁通密度下动态损耗仿真值与实验值
Fig.20 Simulation and experimental values of dynamic losses under different frequencies and magnetic densities
为了精确分析变压器在各种电磁暂态下端口的电压电流特性,并且准确模拟变压器的铁心损耗,必须详细考虑铁心的动态磁化特性。本文采用了磁导-电容类比法进行铁磁材料的电磁建模,在电路分析软件中实现了动态磁滞磁导模块的构建。采用基于洛伦兹分布函数的解析Preisach磁滞模型,建立了静态磁滞磁导模块,用于模拟静态磁滞效应,该磁滞模型结构简便、参数易于获取。基于损耗统计理论和场分离理论,引入受控磁动势源表征铁心的涡流损耗和剩余损耗。为了考虑趋肤效应对涡流磁场强度的影响,运用R-L分数阶导数对传统的涡流场表达式进行修正,并利用量子遗传算法得到分数阶导数参数。改进的铁心动态磁滞磁导模型可以有效地模拟绕组激励电压和电流波形,损耗计算结果的平均误差可控制在6.59%。
参考文献
[1] 杨庆, 崔浩楠, 揭青松, 等. 基于对偶性原理的配电变压器高频电磁暂态模型[J]. 高电压技术, 2022, 48(4): 1498-1509.
Yang Qing, Cui Haonan, Jie Qingsong, et al. High frequency electromagnetic transient model of distribution transformer based on duality principle[J]. High Voltage Engineering, 2022, 48(4): 1498-1509.
[2] 赵玉顺, 戴义贤, 庄加才, 等. 基于热固耦合的中频变压器绝缘材料性能参数优化配合方法[J]. 电工技术学报, 2023, 38(4): 1051-1063.
Zhao Yushun, Dai Yixian, Zhuang Jiacai, et al. Optimization of insulation material performance parameters for medium frequency transformers based on thermosolid coupling[J]. Transactions of China Electrotechnical Society, 2023, 38(4): 1051-1063.
[3] 王威望, 刘莹, 何杰峰, 等. 高压大容量电力电子变压器中高频变压器研究现状和发展趋势[J]. 高电压技术, 2020, 46(10): 3362-3373.
Wang Weiwang, Liu Ying, He Jiefeng, et al. Research status and development of high frequency transformer used in high voltage and large capacity power electronic transformer[J]. High Voltage Engineering, 2020, 46(10): 3362-3373.
[4] Luo Min, Dujic D, Allmeling J. Modeling frequency- dependent core loss of ferrite materials using permeance-capacitance analogy for system-level circuit simulations[J]. IEEE Transactions on Power Electronics, 2019, 34(4): 3658-3676.
[5] 陈彬, 秦小彬, 万妮娜, 等. 基于R-L型分数阶导数与损耗统计理论的铁磁材料高频损耗计算方法[J]. 电工技术学报, 2022, 37(2): 299-310.
Chen Bin, Qin Xiaobin, Wan Nina, et al. Calculation method of high-frequency loss of ferromagnetic materials based on R-L type fractional derivative and loss statistical theory[J]. Transactions of China Electrotechnical Society, 2022, 37(2): 299-310.
[6] de Leon F, Semlyen A. Time domain modeling of eddy current effects for transformer transients[J]. IEEE Transactions on Power Delivery, 1993, 8(1): 271-280.
[7] Holmberg P, Bergqvist A, Engdahl G. Modelling eddy currents and hysteresis in a transformer laminate[J]. IEEE Transactions on Magnetics, 1997, 33(2): 1306- 1309.
[8] Zhu J G, Hui S Y R, Ramsden V S. A dynamic equivalent circuit model for solid magnetic cores for high switching frequency operations[J]. IEEE Transa- ctions on Power Electronics, 1995, 10(6): 791-795.
[9] 邹密. 计及磁滞效应的变压器低频电磁暂态模型及其在铁磁谐振中的应用[D]. 重庆: 重庆大学, 2018.
Zou Mi. Low-frequency transformer model con- sidering hysteresis behavior and its application in ferroresonance[D]. Chongqing: Chongqing University, 2018.
[10] Hamill D C. Lumped equivalent circuits of magnetic components: the gyrator-capacitor approach[J]. IEEE Transactions on Power Electronics, 1993, 8(2): 97- 103.
[11] Hamill D C. Gyrator-capacitor modeling: a better way of understanding magnetic components[C]//Proceedings of 1994 IEEE Applied Power Electronics Conference and Exposition-ASPEC'94, Orlando, FL, USA, 1994: 326-332.
[12] Luo Min, Dujic D, Allmeling J. Modelling hysteresis of soft core materials using permeance-capacitance analogy for transient circuit simulations[C]//2017 19th European Conference on Power Electronics and Applications (EPE'17 ECCE Europe), Warsaw, Poland, 2017: 1-10.
[13] 刘任, 杜莹雪, 李琳, 等. 解析逆Preisach磁滞模型[J]. 电工技术学报, 2023, 38(10): 2567-2576.
Liu Ren, Du Yingxue, Li Lin, et al. Analytical inverse Preisach hysteresis model[J]. Transactions of China Electrotechnical Society, 2023, 38(10): 2567-2576.
[14] 李岱岩, 张艳丽, 荆盈, 等. 基于J-A模型的电工钢片磁致伸缩特性模拟与实验[J]. 电工技术学报, 2022, 37(20): 5081-5091.
Li Daiyan, Zhang Yanli, Jing Ying, et al. Modeling of magnetostrictive characteristics in an electrical steel sheet based on the J-A model and its experimental verification[J]. Transactions of China Electro- technical Society, 2022, 37(20): 5081-5091.
[15] 陈昊, 李琳, 刘洋. 基于Energetic模型的机械应力作用下电工钢片磁滞特性模拟[J]. 电工技术学报, 2023, 38(12): 3101-3111.
Chen Hao, Li Lin, Liu Yang. Simulation of magnetic hysteresis characteristics of electrical steel sheet under mechanical stress based on Energetic model[J]. Transactions of China Electrotechnical Society, 2023, 38(12): 3101-3111.
[16] Luo Min, Dujic D, Allmeling J. Permeance based modeling of magnetic hysteresis with inclusion of eddy current effect[C]//2018 IEEE Applied Power Electronics Conference and Exposition (APEC), San Antonio, TX, USA, 2018: 1764-1771.
[17] Ducharne B, Sebald G, Guyomar D, et al. Fractional model of magnetic field penetration into a toroidal soft ferromagnetic sample[J]. International Journal of Dynamics and Control, 2018, 6(1): 89-96.
[18] Zhang B, Gupta B, Ducharne B, et al. Preisach’s model extended with dynamic fractional derivation contribution[J]. IEEE Transactions on Magnetics, 2018, 54(3): 6100204.
[19] Jiles D C, Atherton D L. Theory of ferromagnetic hysteresis[J]. Journal of Magnetism and Magnetic Materials, 1986, 61(1/2): 48-60.
[20] Liu Ren, Li Lin. Analytical prediction model of energy losses in soft magnetic materials over broadband frequency range[J]. IEEE Transactions on Power Electronics, 2021, 36(2): 2009-2017.
[21] 陈彬, 王斐然, 陈睿, 等. 基于R-L型分数阶导数的动态解析逆Preisach模型[J]. 高电压技术, 2023, 49(9): 3918-3926.
Chen Bin, Wang Feiran, Chen Rui, et al. Dynamic analytical inverse Preisach model based on R-L fractional derivative[J]. High Voltage Engineering, 2023, 49(9): 3918-3926.
[22] 陈彬, 秦小彬, 唐波, 等. 基于R-L分数阶导数的动态J-A磁滞模型及其特征参数辨识算法[J]. 中国电机工程学报, 2022, 42(12): 4590-4603.
Chen Bin, Qin Xiaobin, Tang Bo, et al. Dynamic J-A hysteresis model based on R-L fractional derivative and its characteristic parameter identification algorithm[J]. Proceedings of the CSEE, 2022, 42(12): 4590-4603.
[23] 陈彬, 王斐然, 万妮娜, 等. 考虑可逆分量的解析Preisach磁滞模型及其特征参数辨识算法[J]. 高电压技术, 2023, 49(11): 4766-4774.
Chen Bin, Wang Feiran, Wan Nina, et al. Analytical Preisach hysteresis model considering reversible component and its characteristic parameter identi- fication algorithm[J]. High Voltage Engineering, 2023, 49(11): 4766-4774.
[24] 刘任, 李琳. 基于损耗统计理论与J-A磁滞模型的直流偏磁下磁性材料损耗计算方法[J]. 高电压技术, 2019, 45(12): 4062-4069.
Liu Ren, Li Lin. Loss prediction of magnetic material under DC bias based on the statistical theory of losses and Jiles-Atherton hysteresis model[J]. High Voltage Engineering, 2019, 45(12): 4062-4069.
[25] 陈文, 孙洪广, 李西成, 等. 力学与工程问题的分数阶导数建模[M]. 北京: 科学出版社, 2010.
Abstract With the introduction of a large number of nonlinear loads into the power system, transformers work more frequently at high frequencies, and ferromagnetic materials show strong frequency dependence under high-frequency conditions. Therefore, this paper establishes an electromagnetic loss model considering the eddy current effect and relaxation effect of ferromagnetic materials, which can simulate the voltage and current characteristics at both ends of the transformer and predict the core loss of the transformer.
Firstly, the Lorentz function replaces the distribution function of the classical Preisach model. The ascending and descending branch expressions are derived with the input of the magnetic field strength Hand the output of the magnetic induction intensity B. The reversible component expression is introduced in the classical Preisach model to simulate the static hysteresis characteristics of ferromagnetic materials accurately. The characteristic parameters of the Preisach model are obtained according to static hysteresis loop data from experimental measurements and particle swarm optimization algorithm. Based on the permeance-capacitance analogy method and the analytical Preisach model, the static hysteresis permeance model of the core is established in the simulation software PLECS, which can adjust the permeance value in real-time according to the change of magnetic field strength H. According to the experimental data, the static hysteresis permeance model can simulate the static hysteresis loop of the core.
Secondly, based on the traditional loss statistical theory and field separation theory, the loss of ferromagnetic materials is divided into hysteresis loss, eddy current loss, and residual loss. Constant magnetoresistive and controlled magnetomotive force sources are introduced to characterize the eddy current loss and residual loss of ferromagnetic materials. The traditional core dynamic hysteresis permeance model is established. Based on the electrical steel measurement system, the hysteresis loop and loss value of silicon steel core at different frequencies and magnetic densities aremeasured. Under high-frequency conditions, the internal magnetic flux of ferromagnetic materials is not uniformly distributed due to the skin effect. As a result, the average error of the traditional dynamic hysteresis permeance model is 14.04% compared with the experimental data.
Finally, to consider the non-local, frequency, historical, and other dependent processes of eddy current loss of ferromagnetic materials, the R-L fractional derivative is used to modify the eddy current loss expression, and its parameters are extracted according to the experimental loss value and quantum genetic algorithm. The controlled magnetomotive force source characterizes the eddy current effect, and an improved core dynamic hysteresis permeability model is established. The average relative error of the improved model is 6.59%, which verifies that the improved model can shorten the error.
Keywords:Power transformer, eddy current effect, Preisach model, fractional derivative, permeance- capacitance analogy method
中图分类号:TM433
DOI: 10.19595/j.cnki.1000-6753.tces.231113
国家自然科学基金青年科学基金项目(52107006)和湖北省自然科学基金面上项目(2021CFB149)资助。
收稿日期 2023-07-12
改稿日期 2023-08-29
陈 彬 男,1989年生,副教授,博士生导师,研究方向为电力装备电磁特性模拟与测量技术、电工新材料综合磁特性模拟与测量技术。
E-mail: chenbin@ctgu.edn.cn(通信作者)
王川源 男,1997年生,硕士研究生,研究方向为磁性元件建模和优化设计。
E-mail: 1035078352@qq.com
(编辑 郭丽军)