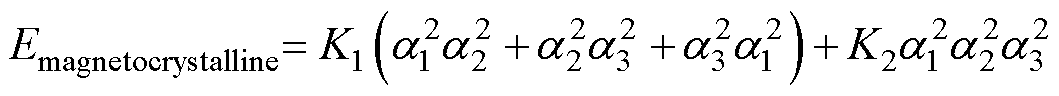（1）
摘要 磁致伸缩材料工作在应力激励条件下的输出特性在很大程度上取决于偏置条件（预应力、偏置磁场）和激励频率。为指导磁致伸缩材料在动态应力驱动下的应用，需要建立一个能够适应各种操作条件的动态磁滞模型。该文结合Armstrong能量模型和J-A磁滞模型，建立了磁致伸缩材料的静态维拉里磁滞模型，通过引入频率相关时间常数的一阶微分方程将静态模型拓展为考虑动态损耗的动态非线性维拉里磁滞模型。利用粒子群遗传优化算法通过三个递进步骤提取模型参数。实验数据与模型计算数据的对比结果表明，该模型不仅能够充分描述预应力和偏置磁场对准静态维拉里效应的影响，而且能够反映在不同频率动态应力下磁通密度-应力（B-s）动态小环和主环的变化趋势，该模型可为磁致伸缩材料器件在应力条件下的应用提供理论指导。
关键词：磁致伸缩材料 维拉里效应 压磁系数 Armstrong能量模型 粒子群遗传优化算法
磁致伸缩材料是一类新型智能材料，能够实现磁能与机械能的相互转化，这种磁-力耦合特性导致了两种独特的行为：焦耳效应（磁致伸缩效应）和维拉里效应（逆磁致伸缩效应）[1]。焦耳效应是指材料在磁场激励下体积发生变化，已被广泛应用于换能器[2]、致动器[3]等领域。维拉里效应是指材料在受到机械应力时本身的磁化状态发生变化，已被应用于传感[4-5]、避震[6]和能量收集[7-8]等领域。在过去几年中，基于维拉里效应的能量收集设备受到了越来越多的关注，由于磁致伸缩材料具有明显的非线性、各向异性、滞后和饱和等特性，其输出特性还显示出强的偏置条件（偏置磁场、预应力）依赖性[9-10]，当磁致伸缩材料工作在高频条件下涡流效应是不可避免的[11]，这降低了能量收集的转化效率。因此为了使电磁器件能够工作在最优偏置条件下，并考虑涡流效应对材料特性的影响，开发和建立能够描述动态应力条件下的磁致伸缩材料本构模型具有研究意义。
目前最简单的本构模型是假设应力和磁化线性相关[12]，这种方法在小幅值应力条件下是准确的，但它不包含材料的滞后和非线性特性，因此在更高频率的应用中会有很大的限制。J-A模型基于具有钉扎效应的畴壁运动模拟了材料的磁化过程，该模型有助于描述畴壁运动中的磁滞行为，通过一个简单的五参数一阶微分方程对磁滞现象进行了数值模拟，计算过程简单但参数确定较为复杂，而且对于不同工况下的参数需要重新确定[13]。基于能量的本构模型，如Armstrong能量模型[14]，通过最小化自由能，量化了磁场和应力输入下的材料磁化和磁致伸缩响应，作者利用该模型定性描述了恒定单轴应力下外加磁场过程中铽镝铁合金的磁化特性。J. Atulasima等[15]基于Armstrong能量模型，通过玻耳兹曼分布的热力学平方均程计算了铁镓合金的磁化和应变。模拟结果与实验结果在准静态区域非常吻合，但作者未考虑材料的磁滞现象。U. Ahmed等[16]基于亥姆霍兹自由能提出了一个能量密度函数来表征磁机械耦合现象，通过将能量密度函数与测量的磁化曲线拟合来确定模型参数，模型计算结果较好地模拟了原型能量收集装置的实验结果。但忽略了涡流效应的影响，在高频激励下会导致输出误差较大。文献[17]提出了基于微观磁畴旋转的二维模型与混合有限元方法相结合，用来描述Galfenol的非线性行为，但运用的分析方法较为复杂，且未考虑预应力和激励频率对材料特性的影响。文献[18]开发了一个包含J-A模型和二维轴对称磁场扩散的集总参数模型。该模型在2 kHz以下的频率范围内使用Terfenol-D致动器进行了验证，但该集总参数模型仅限于二维轴对称几何形状。文献[19]利用分数阶导数在静态J-A磁滞模型的基础上，引入压应力及涡流损耗相关项对模型参数进行了修正，得到了高频动态磁滞模型，在1～9 kHz交流磁场下对铁镓合金进行实验测试与模型验证，该模型对磁致伸缩效应进行了较好的表征但无法描述动态应力条件下的材料特性。
本文首先基于Armstrong能量模型推导了无磁滞磁化方程，并结合J-A模型的基本思想将无磁滞磁化强度分解为可逆磁化强度与不可逆磁化强度，从而得到了应力驱动下考虑磁滞现象的准静态本构模型。针对高频应力驱动情况，利用具有频率相关时间常数的一阶微分方程来描述材料磁化的动态行为，得到与外施应力频率相关的动态磁滞模型。最后利用粒子群优化-遗传算法（Particle Swarm Optimization-Genetic Algorithm, PSO-GA），通过三个递进步骤对模型参数进行识别，对不同实验条件下的Galfenol输出特性进行了预测，验证了本文所建立模型的有效性。该方法有助于理解和预测磁致伸缩材料的磁化行为，可为相关领域的应用提供理论参考。
Armstrong能量模型[14]描述了基于能量加权平均方案的材料非线性建模过程。该模型的构建由磁晶各向异性能量（Emagnetocrystalline）、磁弹性能（Emagnetoelastic）和磁场能（Emagnetic）组成。
对于三维立方晶体系统，磁晶各向异性能量可以用各向异性常数K1和K2以及磁化强度M对应的方向余弦（a1, a2,a3）来表示，即
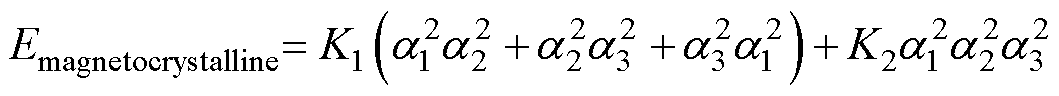（1）
三维立方晶体系统的磁弹性能可以利用[1 0 0]和[1 1 1]取向上的磁致伸缩常数l100和l111、大小为s和方向余弦为（b1, b2, b3）的应力以及磁化强度M对应的方向余弦（a1, a2, a3）来表示。
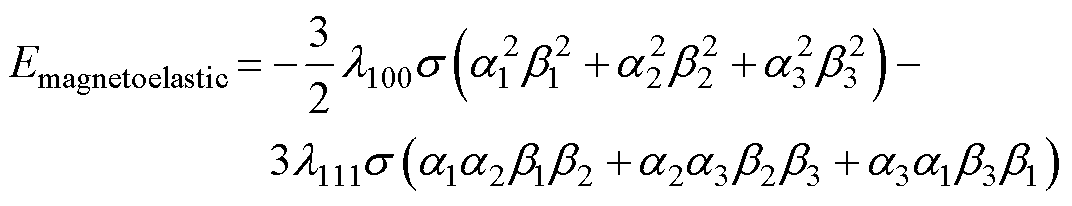（2）
磁场能取决于磁场强度H、饱和磁化强度Ms以及磁场强度H和磁化强度M之间夹角的余弦值，H与M之间夹角的余弦值利用两者方向余弦的点积表示。
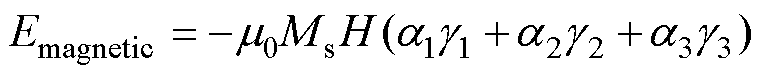（3）
式中，（g1, g2, g3）代表磁场强度H的方向余弦。
在外施激励（应力s 和磁场强度H）下，磁畴的总自由能可以表示为
（4）
式中，g 为引入的矫正系数[15]，用于缩放磁弹性能量对于总能量的影响，以准确捕捉应力对磁机械耦合行为的影响。由于对该参数的物理含义尚不明确，因此将其描述为一个无量纲的经验参数。
磁致伸缩材料在微观尺寸是由大量等效磁畴单元组成，每个等效磁化单元具有特定的磁化取向，其概率取决于该取向对应的能量。Armstrong假设在磁畴之间不存在相互作用且当前磁畴的取向与其先前状态无关的条件下（即不考虑磁滞行为），可以合理地认为磁畴的取向遵循玻耳兹曼分布。引入玻耳兹曼函数来描述大量微观磁畴在宏观尺度下的行为，因此，Armstrong假设只能描述无磁滞的磁化行为[14]。
基于以上假设，x轴方向的宏观无磁滞磁化强度Manx可以表示为
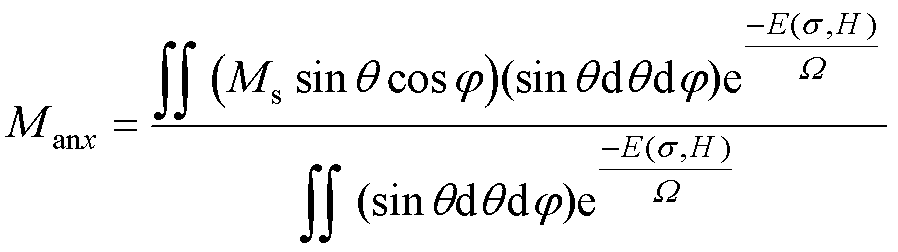（5）
式中，j、q 分别为球坐标系下的方位角与极角；W为平滑系数，该系数可以使B-s 曲线具有所需的平滑性。Many和Manz可以进行类似Manx的计算；Manx、Many、Manz分别对应于沿[1 0 0]、[0 1 0]和[0 0 1]方向的宏观无磁滞磁化强度。
对于其他任意方向的无磁滞磁化强度ManR可以表示为
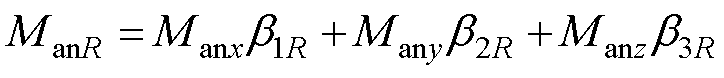（6）
式中，（b1R, b2R, b3R）为任意方向的方向余弦。
考虑到基于维拉里效应的磁致伸缩器件的大部分应用场景为施加应力与偏置磁场作用于材料的 [1 0 0]方向[8, 15-16]即(b1, b2, b3)=(1, 0, 0)、(g1, g2, g3)= (1, 0, 0)。因此对上述方程进行降维弱化，得到针对[1 0 0]方向的无磁滞磁化方程组为
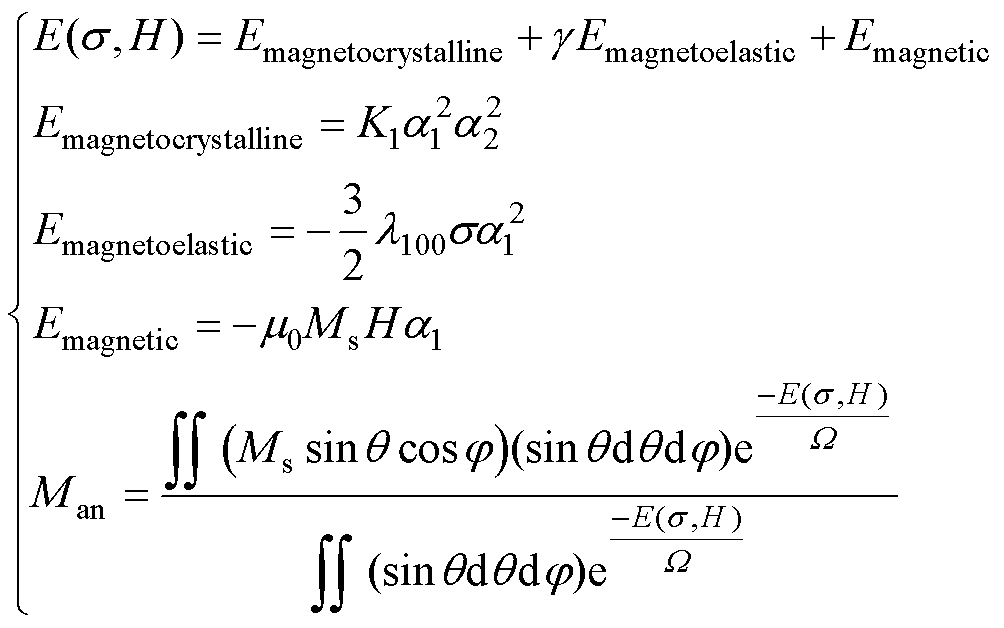（7）
式中，球坐标系下方向余弦与方位角和极角的关系如下：a1=sinqcosj，a2=sinqsinj。
在1.1节中假设不考虑磁滞的建模过程中，磁化过程是由于磁畴旋转引起的，这是完全可逆的。然而，铁磁材料中的非磁性夹杂物或晶体结构中的错位会导致磁畴壁的钉扎效应，需要外部能量来改变磁畴壁从固定状态到非固定状态。钉扎位置能量损失是准静态磁滞损失的主要来源，因此为了模拟材料的磁滞现象，本节将借助J-A模型的思想建立静态磁滞模型。
J-A模型是基于铁磁材料畴壁理论建立起来的描述外加磁场与磁化强度关系的磁滞模型。该模型通过考虑钉扎效应下的磁畴壁运动来模拟磁化过程，将静态磁化强度M分解为由畴壁弯曲引起的可逆磁化分量Mrev和畴壁取代引起的不可逆磁化分量Mirr。J-A模型中Man、Mrev、Mirr、M满足[13]
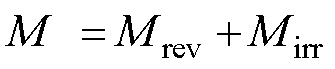（8）
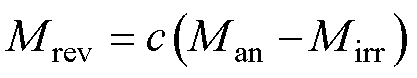（9）
式中，c为可逆磁化系数；Man为式（7）定义的无磁滞磁化强度。将式（9）代入式（8）得到
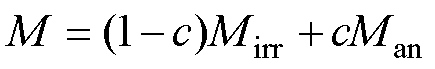（10）
J-A模型当中的输入量H与输出量M的滞回特性来源于不可逆磁化强度Mirr关于有效磁场He的微分方程[13]，即
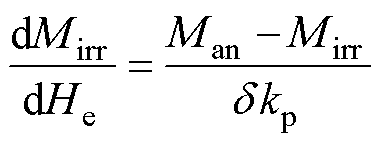（11）
式中，kp为钉扎系数，用于量化材料中钉扎位点的密度；d 为方向系数，当ds/dt≥0时，d =1；当ds/dt＜0时，d=-1。
本节为建立描述应力驱动下磁致伸缩材料的维拉里磁滞现象本构模型，类比式（11）得到了Mirr关于应力s 的微分方程为
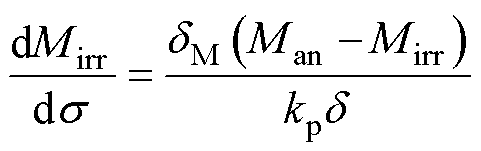（12）
式中，dM为为了防止出现非物理解而定义的方向系数，即
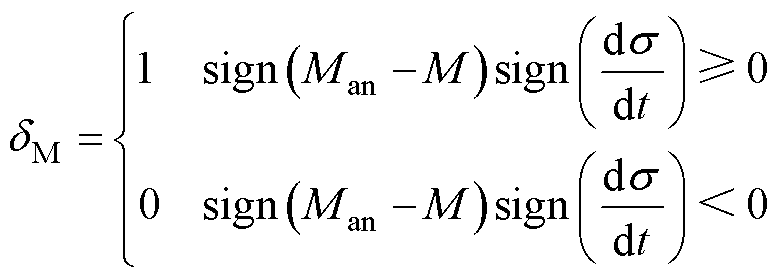（13）
对式（10）关于应力s 求导并结合式（12）推导得到以应力s 作为输入量的磁滞模型为
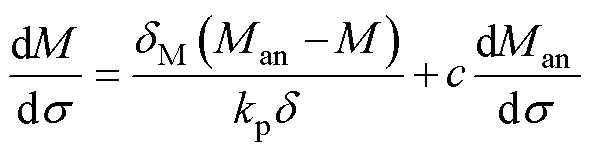（14）
静态磁通密度Bs定义为
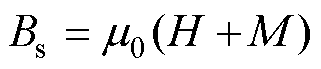（15）
由于应力诱导的磁畴运动，动态力的输入会导致磁感应强度的动态变化，涡流损耗作为动态磁感应强度Bd的响应会进一步导致材料的能量损失，具体体现为随输入应力s 频率的增加，材料内部的涡流损耗会相应增加，导致迟滞现象增强，B-s 回环发生畸变。对于时变的输入应力，本文利用包含频率相关时间常数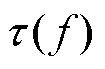
的一阶微分方程表示动态磁化强度Md与静态磁化强度M之间的非线性关系为
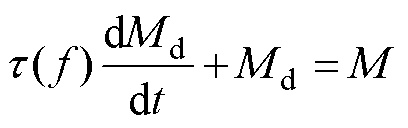（16）
动态磁通密度Bd定义为
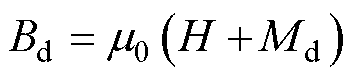（17）
式中，时间常数t 与驱动频率f近似幂函数关系，将在下文中提到。描述t 与f之间的数值关系为
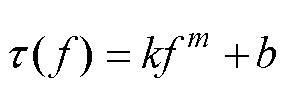（18）
Armstrong能量模型（见式（7））结合J-A模型（见式（8）～式（14））和一阶微分方程（见式（16））构成了本文考虑磁滞效应、涡流效应的非线性动态维拉里效应磁滞模型，其可用于模拟磁致伸缩材料在动态应力驱动下的动态响应。该模型中有8个参数需要识别，分别是K1、l100、Ms、g、W、c、kp、t。其中，K1、l100、Ms、g、W、c、kp为静态参数，t 为动态参数。
粒子群优化（PSO）算法是一种基于种群行为模拟鸟群或鱼群等自然群体行为的智能优化算法，该算法参数少，原理简单易于实现，粒子在每次迭代中不断更新速度和位置进行搜索，以获取最优粒子，具有较强的局部搜索能力。速度更新和位置更新公式可表示为
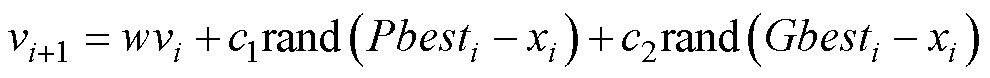（19）
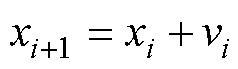（20）
式中，xi为粒子位置；vi为粒子移动速度；w为惯性权重；c1为个体学习因子；c2为社会学习因子；Pbesti和Gbesti分别为当前粒子位置最优值与所有粒子的最优值。
遗传算法（GA）是一种基于达尔文适者生存进化论的非梯度并行优化算法，它广泛适用于非线性、非连续、多模态问题的优化，具有很强的全局寻优能力，但局部寻优能力较弱，容易产生早熟，有时难以找到精确值。
粒子群优化-遗传算法（PSO-GA）综合了粒子群优化算法（PSO）和遗传算法（GA）的优点，通过模拟群体中粒子的行为和遗传算法的进化操作来进行优化问题的求解。该算法兼具全局搜索能力、局部搜索能力、记忆能力和多样性保持能力，在多参数优化问题中可以取得良好的效果，本文基于该算法对模型参数进行识别，算法流程如图1所示。
对于上述模型中的8个参数，分为静态参数K1、l100、Ms、g、W、c、kp与动态参数t，动态参数t 会随激励频率发生改变且需要在已知静态参数的基础上进行识别。基于以上特点，本文采取了如图2所示的三个递进步骤来提取模型参数。
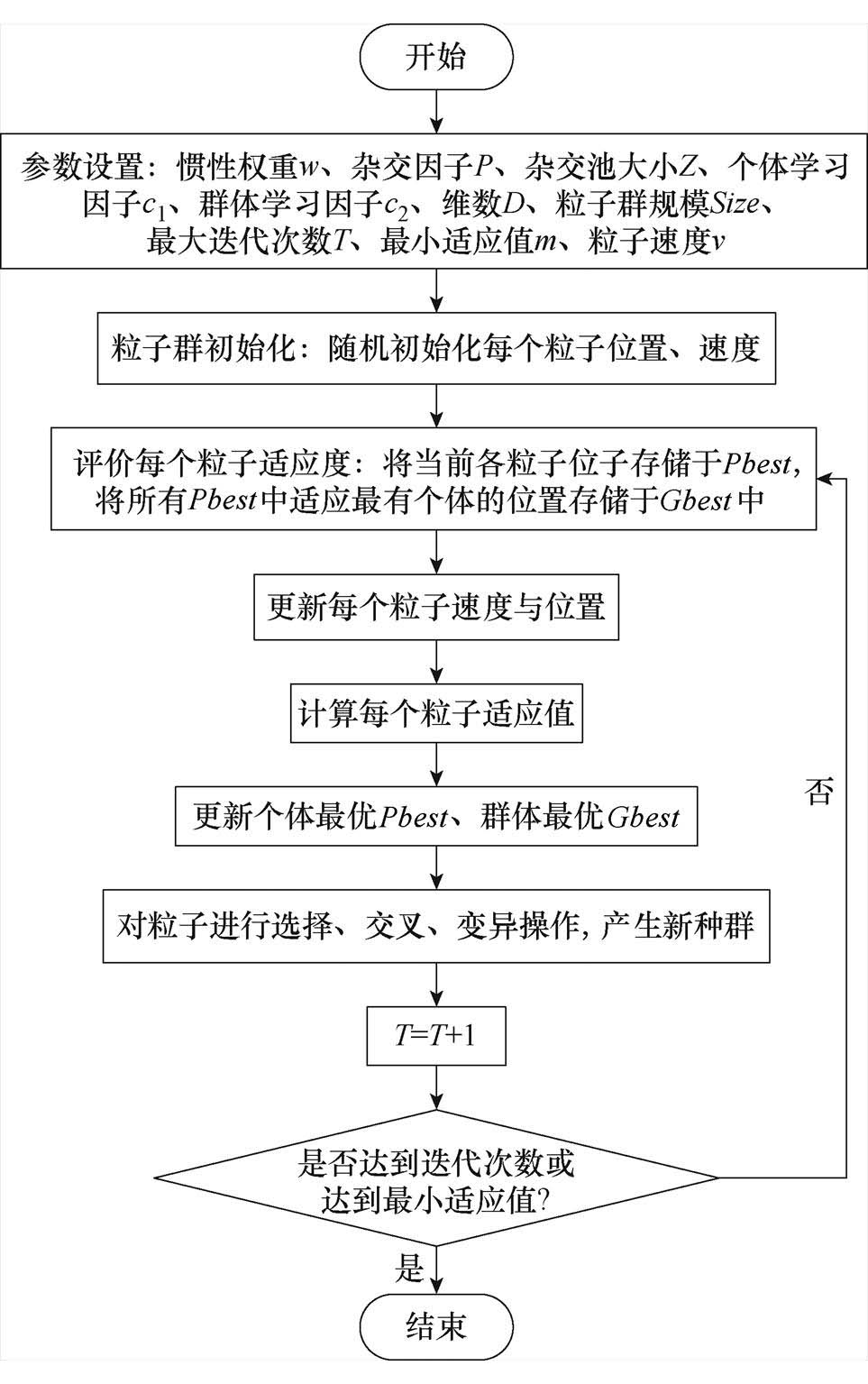
图1 PSO-GA流程
Fig.1 PSO-GA flow chart
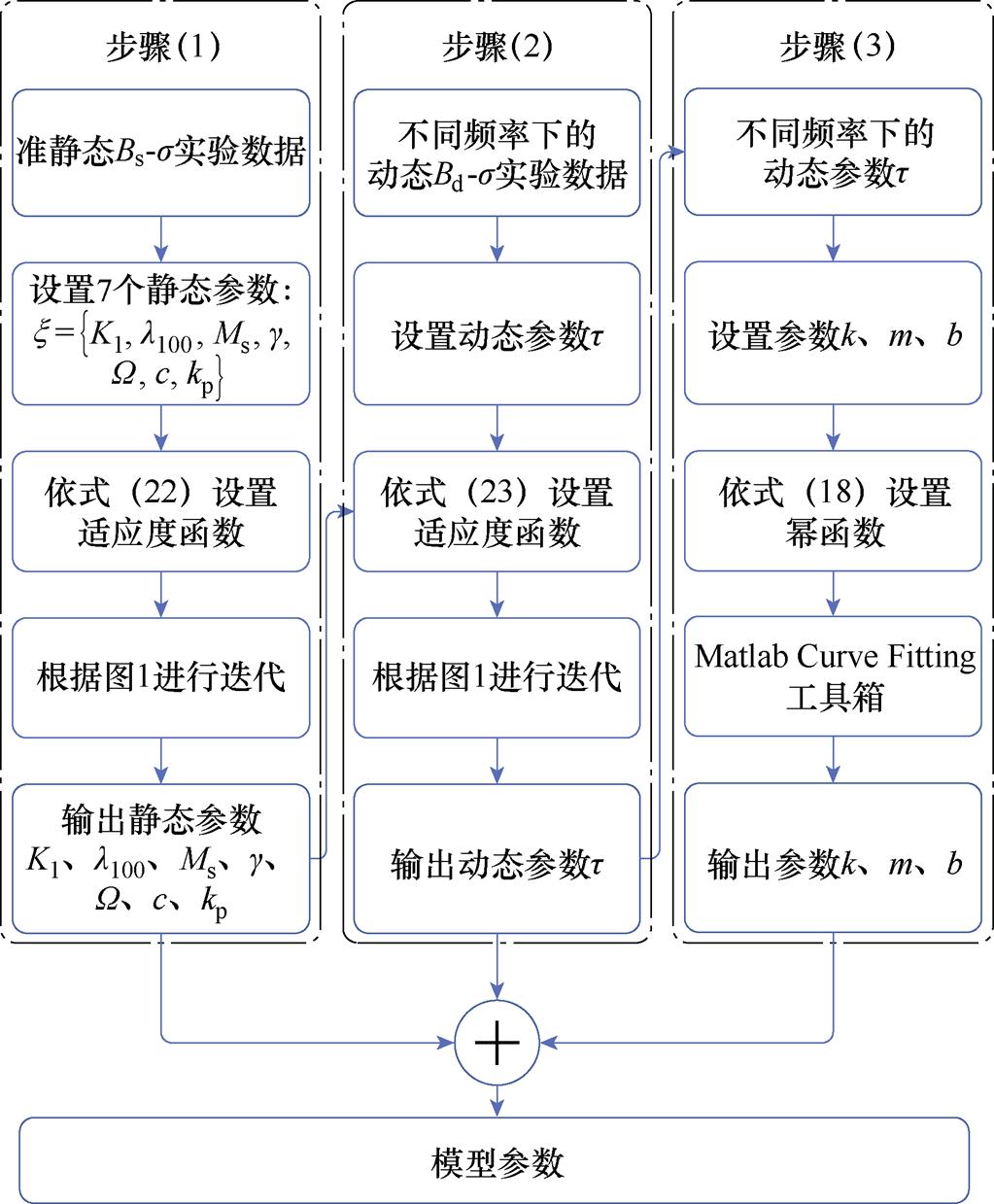
图2 模型参数辨识过程
Fig.2 Model parameter identification process diagram
步骤（1）：提取静态参数K 1、l100、Ms、g、W、c、kp的值。在准静态条件（f=1 Hz）下利用不同偏置磁场条件下的B-s 回线来提取静态参数，该条件下动态损耗可以忽略不计，仅用式（7）和式（14）即可描述准静态条件下的B-s 回线。设置待辨识参数为
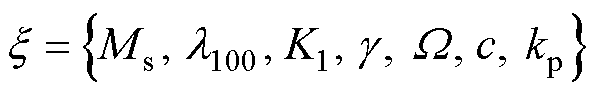（21）
式（7）、式（14）、式（15）用于模拟不同偏置磁场下准静态应力驱动的磁通密度，并表示为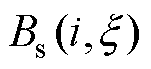
，实验测量的静态磁通密度表示为
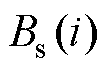。本文采用实测静态磁通密度值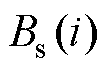与模型计算磁通密度值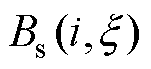的方均根误差作为目标函数，即
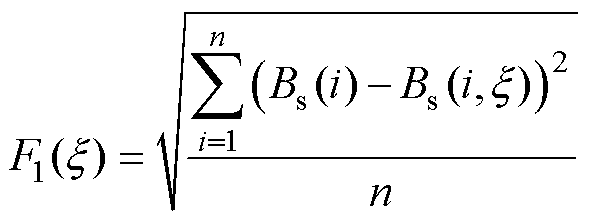（22）
式中，n为数据点总数；i为第i个数据点。
静态参数通过第（1）步识别获得。
步骤（2）：在静态参数的基础上确定不同应力频率下的动态参数t。式（16）和式（17）用于模拟的不同频率的应力驱动下的磁通密度，表示为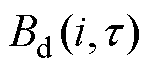
，实验测量的动态磁通密度表示为
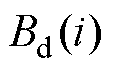，适应度函数设置为
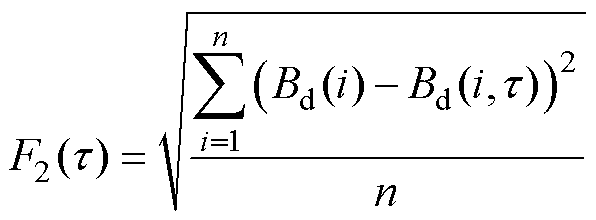（23）
步骤（3）：将辨识得到的不同频率下的动态参数t 与对应频率数据导入到Matlab软件Curve Fitting工具箱中根据式（18）进行拟合。
在本文提出的参数提取过程中，静态参数的识别使用了三组不同偏置磁场（3.88、5.50、7.17 kA/m）下的准静态Bs-s 回线作为数据集，偏置磁场的磁场强度为0.73、1.42、2.41、8.84、10.51、12.19、13.76 kA/m的实验数据用于验证静态参数的有效性。动态Bd-s 主环及动态Bd-s 小环动态参数的识别各使用了四组不同应力频率（10、50、100、200 Hz）下的动态Bd-s 回线作为数据集，应力频率为400 Hz、600 Hz下的实验数据用于验证动态参数的有效性。
文献[21]利用MTS831.50高频动态力加载装置对[1 0 0]取向的多晶Galfenol（Fe81.6Ga18.4）棒材在应力驱动下的响应进行了测量，该棒材由ETREMA Products公司生产，棒材直径为6.27 mm，长度为76.2 mm，偏置磁场经直流线圈产生并由图3所示的对称磁路施加到样品上。
图3 实验装置图[21]
Fig.3 Diagram of the experimental setup[21]
文献[21]中对[1 0 0]取向的Galfenol棒材在应力驱动下的响应进行了准确的测量，准静态条件下应力幅值为31.4 MPa，预应力为-31.9 MPa，以1 Hz的频率循环施加到Galfenol棒材的长度方向，偏置磁场范围为0.73～13.76 kA/m。
图4显示了Galfenol棒材在偏置磁场分别为0.73、1.42、2.41、3.88、5.50、7.17、8.84、10.51、12.19、13.76 kA/m下的准静态Bs-s 主环实验数据。
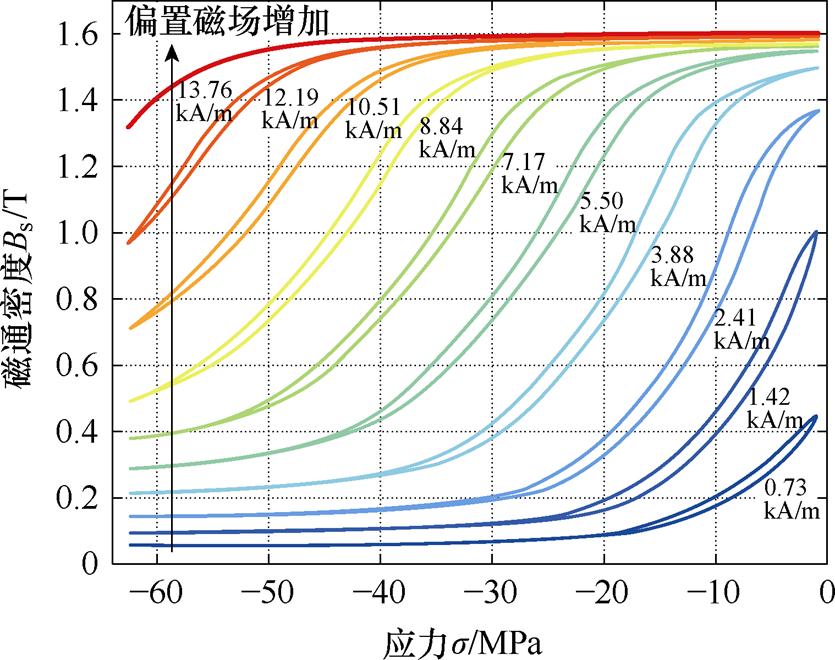
图4 不同偏置磁场下准静态Bs-s 主环实验数据
Fig.4 Experimental data of quasi-static Bs-s majorloops with different biased magnetic fields
本文以偏置磁场为3.88、5.50、7.17 kA/m下的实验数据为数据集，分别确定了对应的静态参数x，见表1。图5显示了用于参数辨识过程的模型计算数据与实验数据的对比结果。
表1中不同偏置磁场下静态参数x 相对于平均值最大变化范围为1.8%，这很大程度上是由于PSO-GA的随机性造成[20]。取偏置磁场3.88、5.50、7.17 kA/m下的静态参数x 的平均值x0作为最终的静态模型参数。利用x0对0.73、1.42、2.41、3.88、5.50、7.17、8.84、10.51、12.19、13.76 kA/m偏置磁场下的准静态主要Bs-s 磁滞回线进行计算，计算数据与实验数据的对比如图6所示，随着偏置磁场的增加，Bs-s 回线由蓝色变为红色。
表1 静态参数辨识值
Tab.1 Static parameter identification values
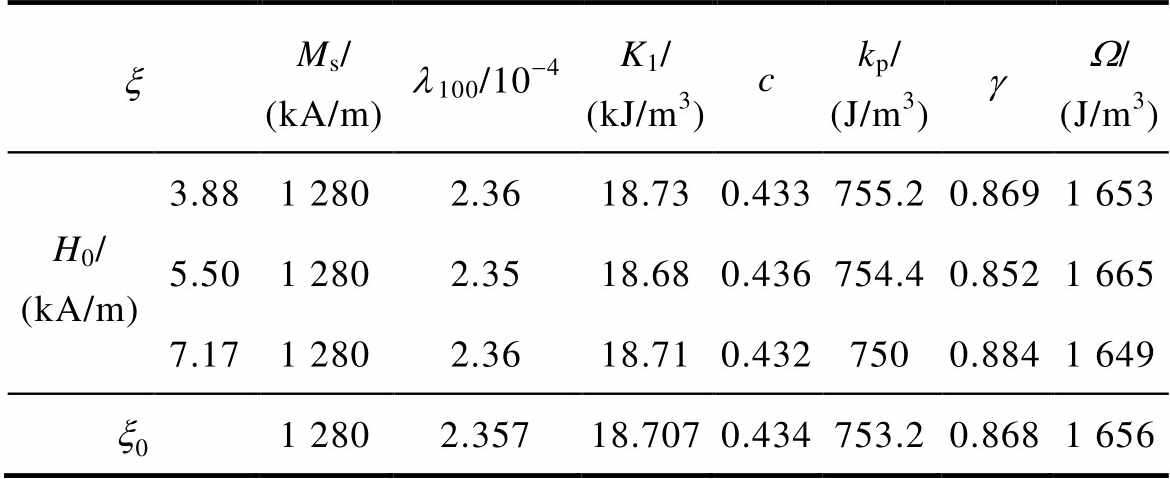
xMs/ (kA/m)l100/10-4K1/ (kJ/m3)ckp/ (J/m3)gW/ (J/m3) H0/ (kA/m)3.881 2802.3618.730.433755.20.8691 653 5.501 2802.3518.680.436754.40.8521 665 7.171 2802.3618.710.4327500.8841 649 x01 2802.35718.7070.434753.20.8681 656
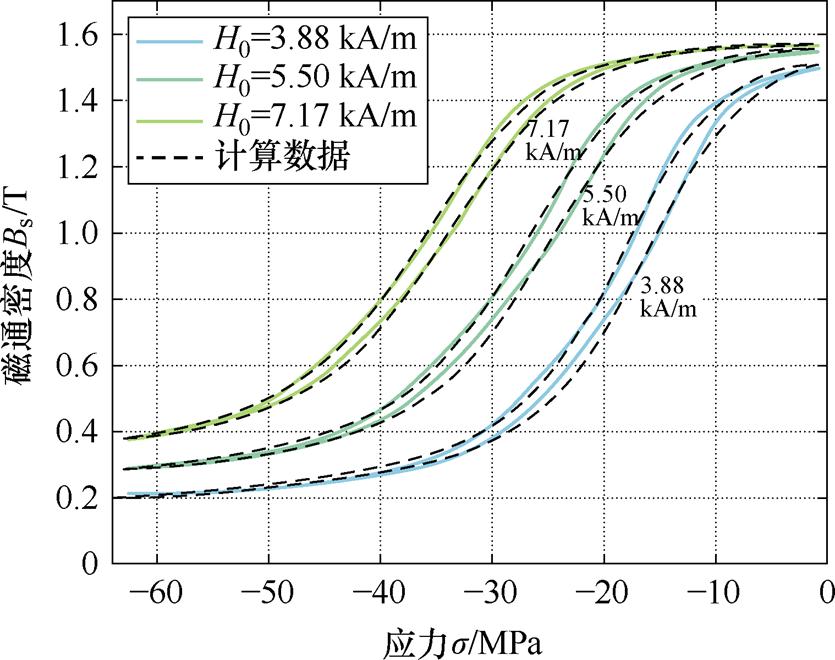
图5 静态参数辨识计算数据与实验数据对比
Fig.5 Comparison of calculation data and experimental data for static parameter identification
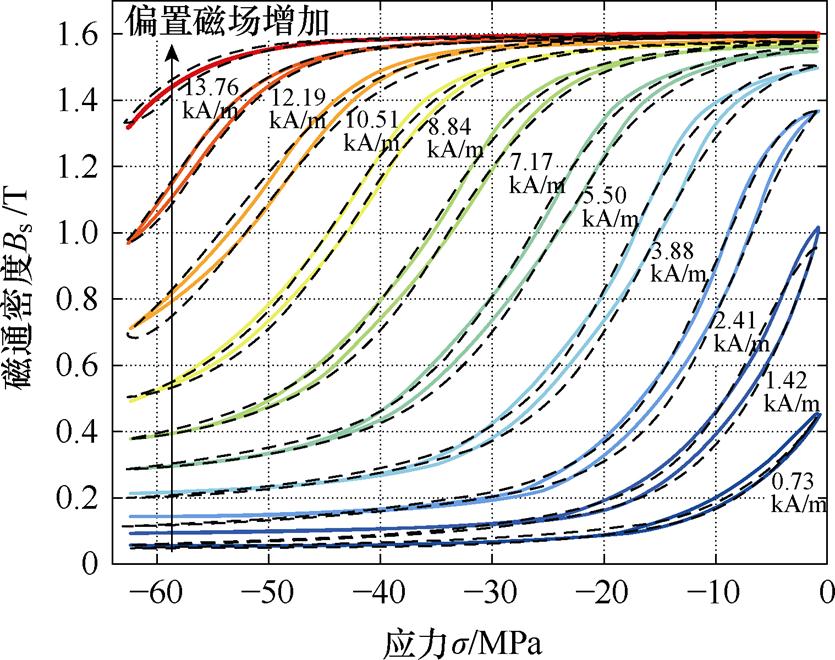
图6 基于平均静态参数x0的准静态Bs-s 主环计算数据（虚线）与实验数据（彩色实线）对比
Fig.6 Comparison of quasi-static Bs-smajorloops calculation data (dashed line) with experimental data (colored solid line) based on average static parameter x0
为表示模型的准确度，本文定义误差量E为
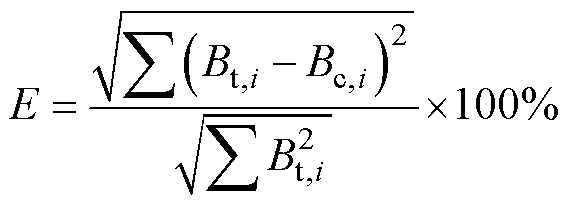（24）
式中，Bt,i、Bc,i分别为相同应力与偏置磁场下的实验数据与计算数据；下标i为第i个数据点参数。结果表明，基于平均静态参数x0，本文所建立的模型能够很好地拟合不同偏置磁场下的准静态Bs-s 主要磁滞回线，实验数据与模型计算数据的平均误差量为2.37%。
为验证静态参数是否对于准静态Bs-s 小环具有适用性，模拟准静态Bs-s 小环所使用的参数仍为3.1节辨识得到的平均静态模型参数x0。
图7显示了Galfenol棒材在不同偏置磁场（0.73、1.42、2.41、3.88、5.50、7.17、8.84、10.51、12.19和13.76 kA/m）和偏置应力（-5.73、-12.9、-20.1、-27.2、-34.4和-41.6 MPa）条件下的准静态Bs-s 小环的模型计算结果，应力幅值为2.88 MPa，频率为1 Hz。随偏置磁场的增加，小环由蓝色变为红色。
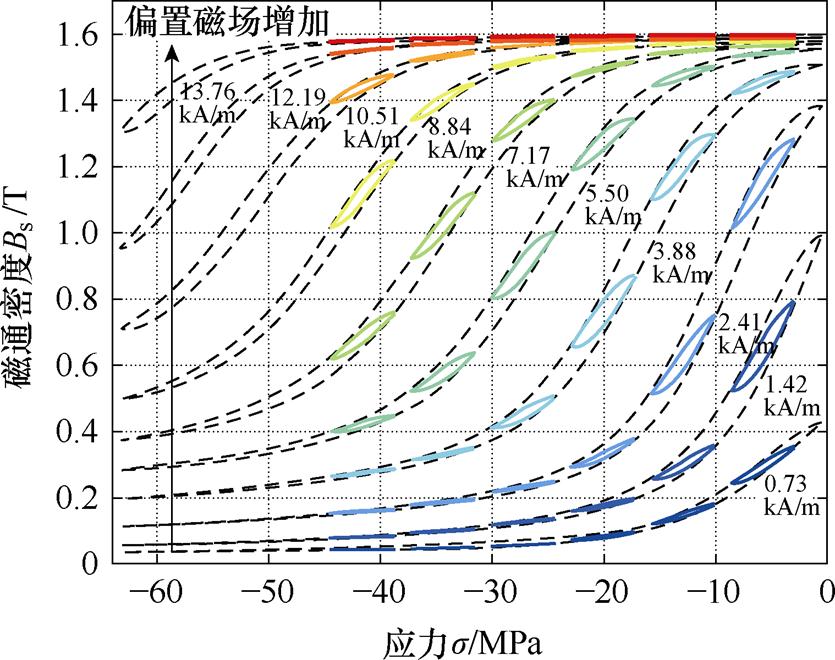
图7 基于平均静态参数x0的准静态Bs-s 小环计算数据
Fig.7 Quasi-static Bs-s minorloops calculation data based on average static parametersx0
结果表明，基于平均静态参数x0，本文所提出的模型能够较好地拟合不同偏置磁场下的准静态Bs-s 小环，与文献[21]的实验结果一致。静态小环与静态主环叠加绘制，显示静态小环位于静态主环内。通过曲线的比较可以看出，小环在轨迹上跟随大环，但静态小环的应力灵敏度略低于静态主环，这一现象也与文献[21]的实验数据相符。
压磁系数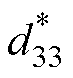
能够反映Galfenol材料的压力灵敏度，是传感器、能量收集器设计的基础参数。其计算公式为
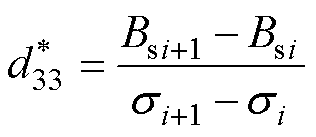（25）
式中，i和i+1对应Bs和s 的连续值。
准静态主环的压磁系数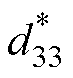随应力变化曲线如图8所示。通过将主环划分上下两个部分，分别对应应力压缩与应力释放过程，取回路上下部分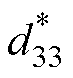的计算平均值得到主环的压磁系数。其中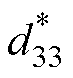最大值（91.8 T/GPa）对应的偏置条件为H0=1.42 kA/m，s0=-1.65 MPa，说明本文所建立的模型能够预测材料的最佳偏置点，可为相关器件设计提供数据支撑。
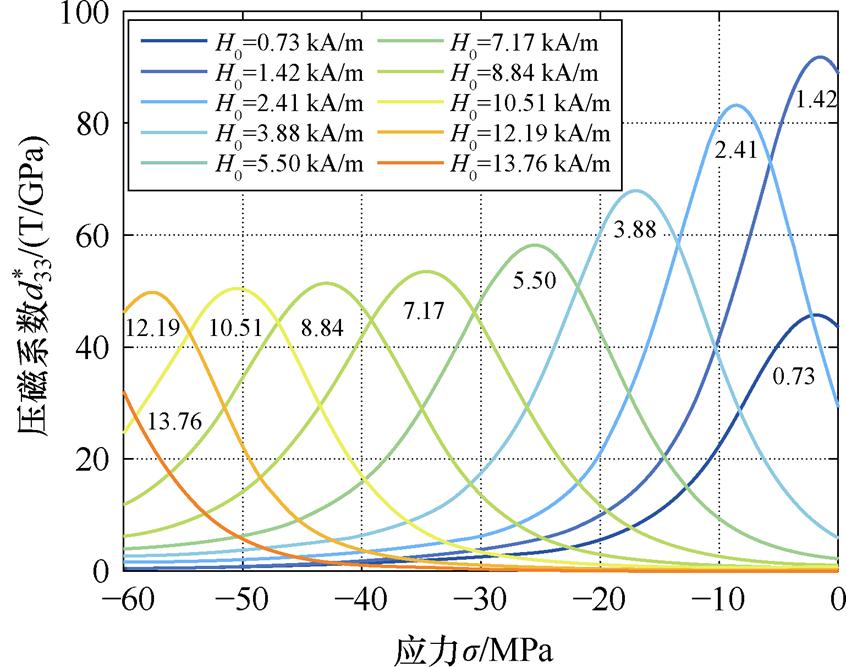
图8 不同偏置磁场下准静态Bs-s 主环压磁系数
Fig.8 The quasi-static Bs-s majorloops piezomagnetic coefficient with different bias magnetic fields
图9给出了在1.42、3.88和7.17 kA/m偏置磁场下，根据准静态Bs-s 主环和小环计算的压磁系数与应力的关系曲线。由于小环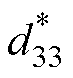的变化幅值较小，本文将其表述为定值，横坐标由偏置应力决定，用圆点标记在图中。小环压磁系数始终低于主环，例如，当偏置磁场为1.42 kA/m时，在相同应力（-5.73 MPa）下主环压磁系数为73.4 T/GPa，而小环压磁系数为47.9 T/GPa，减小34.7%。
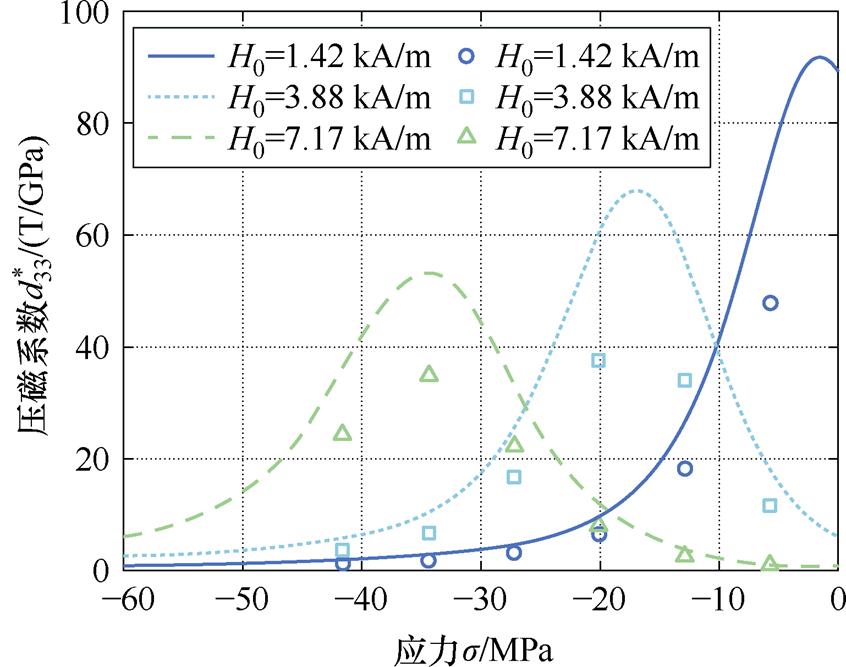
图9 不同偏置磁场下准静态Bs-s 主环（线图）与准静态Bs-s 小环（点图）压磁系数对比
Fig.9 Comparison of piezomagnetic coefficients of quasi-static Bs-s majorloops (line) and quasi-static Bs-sminorloops (dots) with different bias magnetic fields
本节基于文献[21]中不同应力频率下的动态Bd-s 主环实验数据对本文所建立的计及应力频率的动态模型进行了验证。
图10显示了Galfenol棒材在偏置磁场为2.46 kA/m，应力幅值为31.4 MPa，预应力为-31.9 MPa，频率为10、50、100、200、400、600 Hz条件下的动态Bd-s 主环的测量数据。不同频率下的应力幅值波动是由于高频机械载荷下的惯性力导致的[21]。
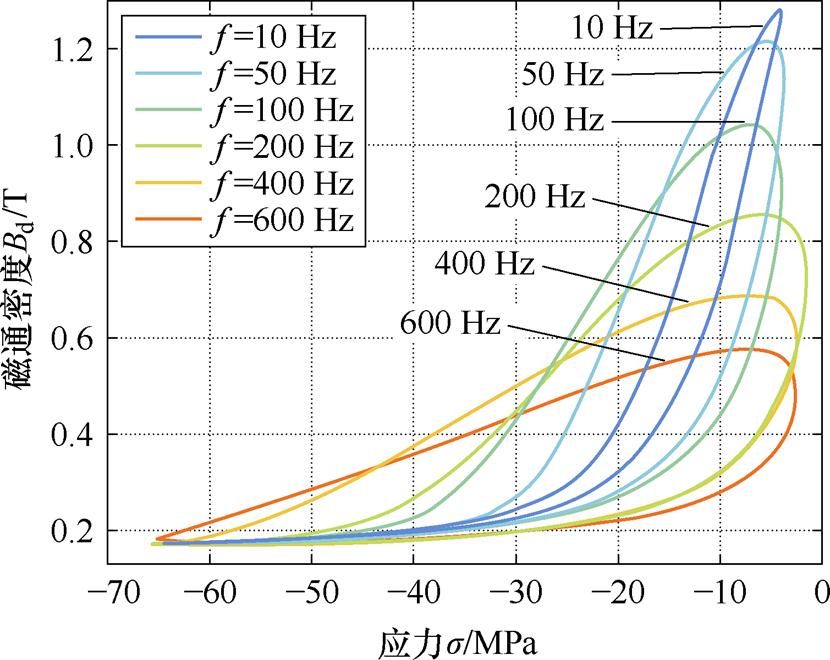
图10 不同频率下动态Bd-s 主环实验数据
Fig.10 Experimental data of dynamic Bd-s majorloops at different frequency
在动态参数辨识过程中本文利用动态Bd-s 主环10、50、100、200 Hz下的实验数据作为数据集，得到了对应频率下动态Bd-s 主环的动态参数tp的辨识值，见表2。图11所示为用于参数辨识过程的数据集与计算数据的对比结果，平均误差量为5.47%。表明本文所建立的动态模型，可以反映Galfenol材料在应力频率改变时的动态主环响应。
表2 动态参数辨识值
Tab.2 Dynamic parameter identification values
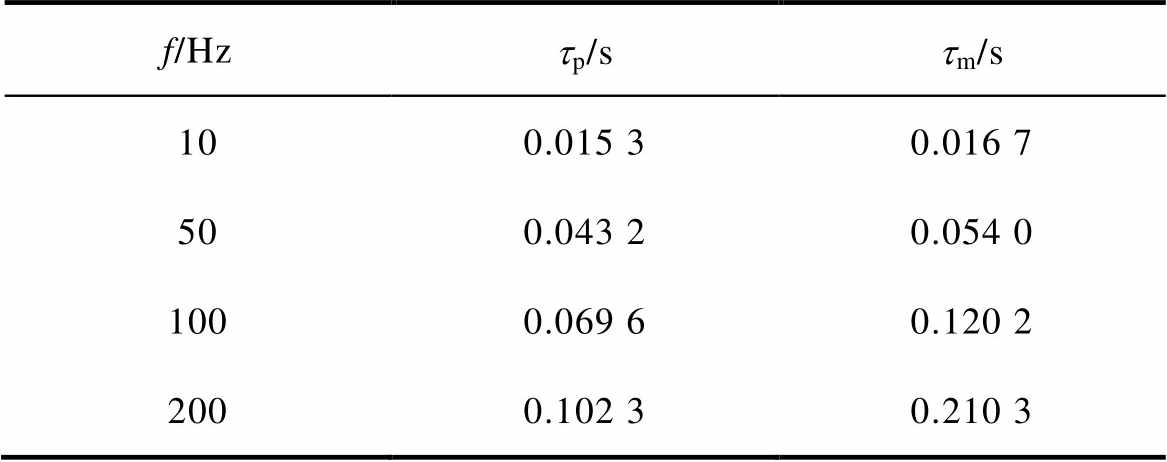
f/Hztp/stm/s 100.015 30.016 7 500.043 20.054 0 1000.069 60.120 2 2000.102 30.210 3
动态参数tp与驱动频率f之间具有明显的幂函数关系，基于式（18）利用Matlab软件中的Curve Fitting工具箱，拟合得到
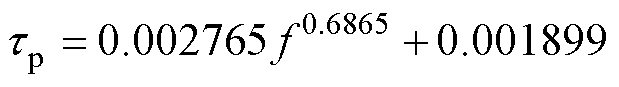（26）
该式拟合度为99.85%，为验证式（26）在更高驱动频率下的准确性，由式（26）计算得到了400、600 Hz下的动态参数tp的预测值，代入动态模型中进行计算。图12显示了400、600 Hz频率下动态Bd-s 主环的实验数据与计算数据的对比情况。结果表明：基于式（26）预测的动态参数tp准确地反映了动态磁通密度与应力的滞回关系及变化趋势，平均误差为6.28%。
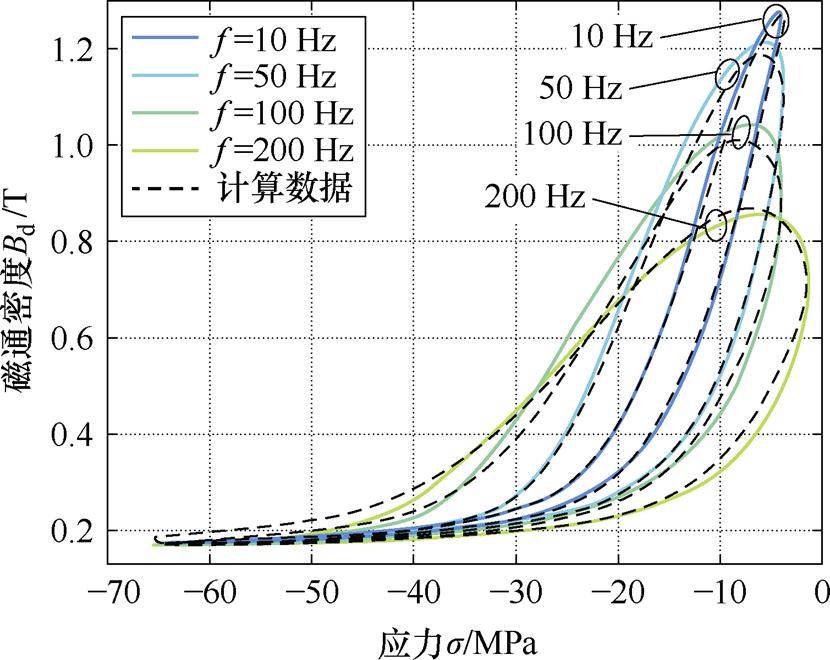
图11 动态参数辨识计算数据与实验数据对比
Fig.11 Comparison of calculation data and experimental data for dynamic parameter identification
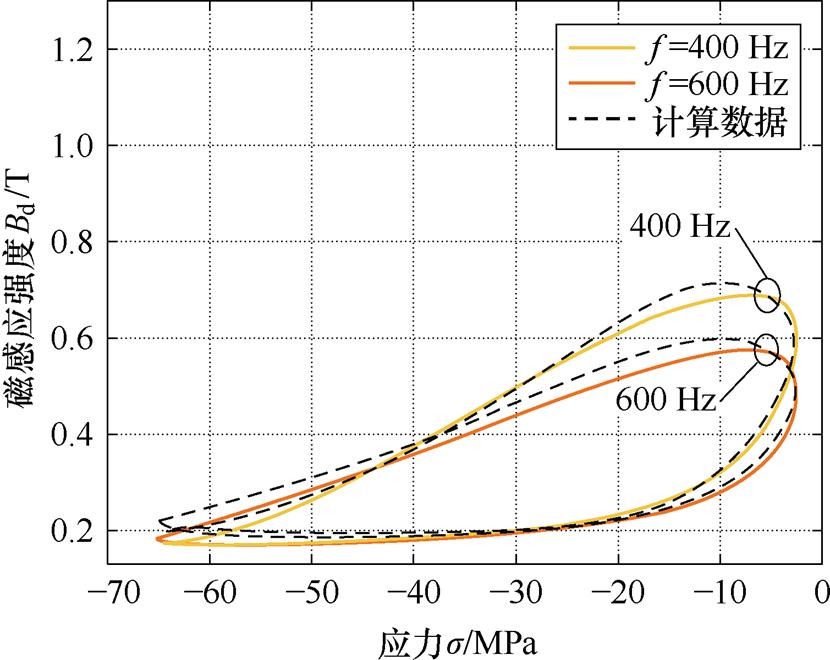
图12 基于tp预测值的计算数据与实验数据对比
Fig.12 Comparison between calculation data and experimental data based on predicted value of tp
随应力频率上升，涡流损耗增加导致材料的动态响应更加线性，压力敏感性降低。当频率增加到100 Hz以上时，Bd-s 主环在低压应力状态下的尖锐部分逐渐消失，这些趋势表明在高频激励下磁畴旋转在Galfenol棒材中受到抑制。
由于Galfenol的非线性特性，实际应用环境中通常在较小的应力范围内工作[12]。动态Bd-s 小环有助于指导Galfenol材料在特定环境下的应用。图13显示了Galfenol棒材在偏置磁场为2.46 kA/m，应力幅值为2.88 MPa，预应力为-7.96 MPa，频率为10、50、100、200、400、600 Hz条件下的动态Bd-s 小环的实验数据[21]。
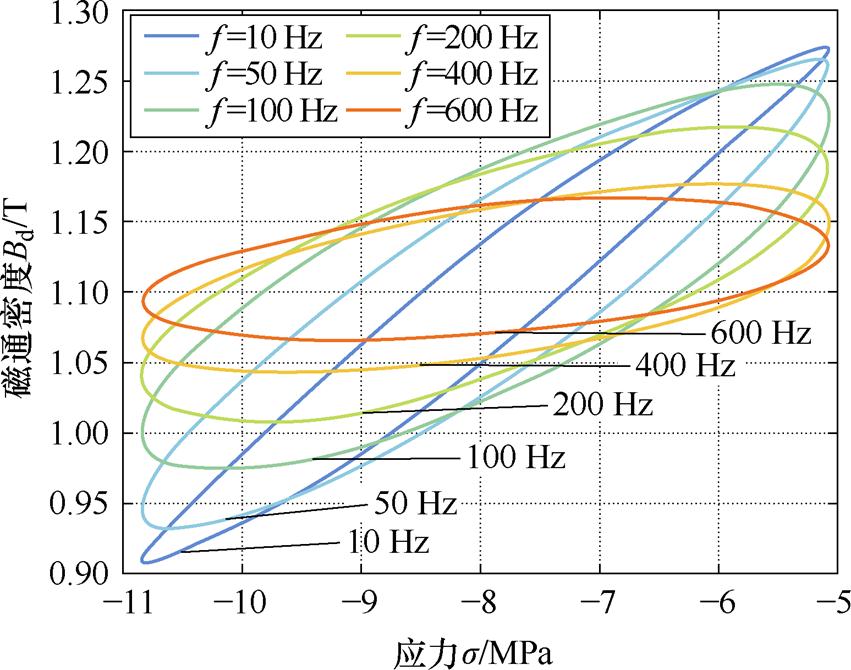
图13 不同频率下动态Bd-s 小环实验数据
Fig.13 Experimental data of dynamic Bd-s minorloops at different frequency
利用动态Bd-s 小环10、50、100、200 Hz下的实验数据作为数据集，得到了对应频率下动态Bd-s 小环的动态参数tm的辨识值，见表2。图14显示了用于参数辨识过程的数据集与计算数据的对比结果，平均误差量为3.23%。结果表明，本文所建立的动态模型可以反映Galfenol材料在应力频率改变时的动态小环响应。
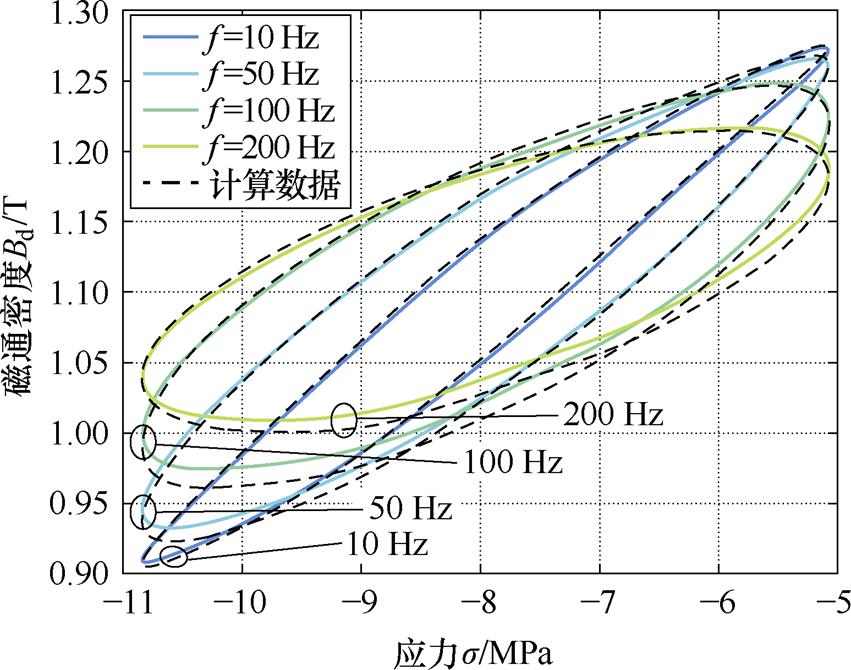
图14 动态参数辨识计算数据与实验数据对比
Fig.14 Comparison of calculation data and experimental data for dynamic parameter identification
利用幂函数式（18）对动态参数tm与驱动频率f的关系进行表征，由Matlab软件中的Curve Fitting工具箱，拟合得到
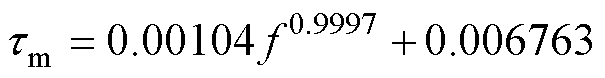（27）
式（27）拟合度为99.95%，为验证式（27）在更高驱动频率下的准确性，由式（27）计算得到了400、600 Hz下的动态参数tm的预测值，代入动态模型中进行计算。
图15显示了400、600 Hz频率下动态Bd-s 小环的实验数据与计算数据的对比情况。结果表明：基于式（27）预测的动态参数tm准确地反映了磁通密度与应力的滞回关系与变化趋势，平均误差量为3.58%。
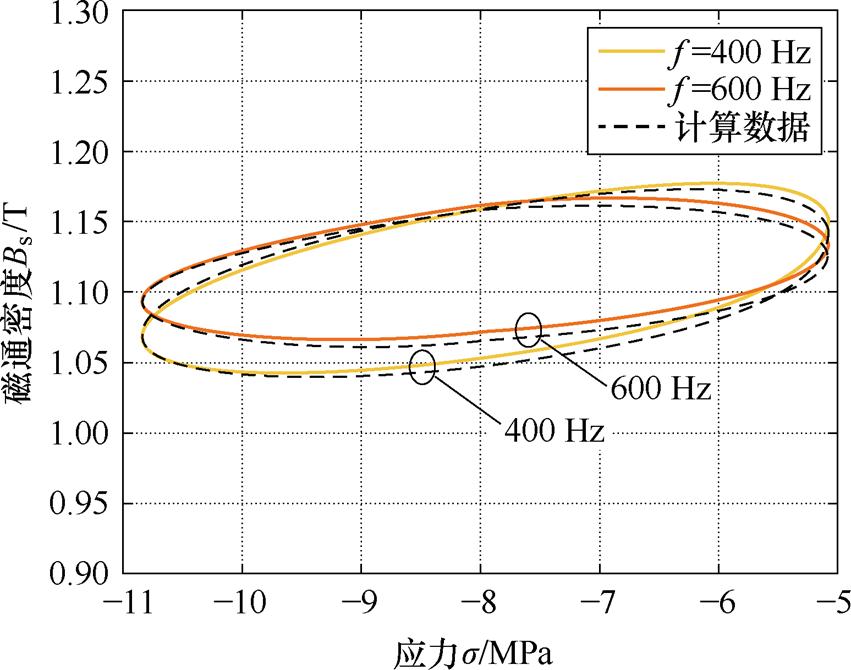
图15 基于tm预测值的计算数据与实验数据对比
Fig.15 Comparison between calculation data and experimental data based on predicted value of tm
结合Armstrong能量模型和J-A磁滞模型的基本思想，本文提出了一种用于表征磁致伸缩材料维拉里效应的静态磁滞模型，然后考虑动态损耗利用频率相关时间常数的一阶微分方程将静态模型拓展为计及应力频率的动态磁滞模型，该模型可描述偏置磁场、预应力、应力幅值和应力驱动频率对材料动态响应的影响。在实验数据的基础上，基于PSO-GA算法通过三个递进步骤对模型参数进行 提取。
通过对比实验数据与模型的计算结果验证了模型的有效性。结果表明，本文建立的模型可以合理地预测Galfenol材料在0.73～13.76 kA/m偏置磁场下的准静态滞回过程，并在10～600 Hz激励频率下的动态滞回过程中取得了良好的预测效果。此外，该模型还能够预测产生最大压磁系数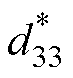所需的预应力和偏置磁场。
本文的研究工作可有效地预测Galfenol材料在外界压应力变化时的磁特性响应。面向实际工程应用，可为磁致伸缩能量收集器、传感器以及阻尼器等电磁器件的优化设计及性能调控提供理论支持。
参考文献
[1] Ekreem N B, Olabi A G, Prescott T, et al. An overview of magnetostriction, its use and methods to measure these properties[J]. Journal of Materials Processing Technology, 2007, 191(1/2/3): 96-101.
[2] Li Pengyang, Liu Qiang, Li Shujuan, et al. Design and numerical simulation of novel giant magnetostrictive ultrasonic transducer[J]. Results in Physics, 2017, 7: 3946-3954.
[3] Zhao Tianyu, Yuan Huiqun, Pan Honggang, et al. Study on the rare-earth giant magnetostrictive actuator based on experimental and theoretical analysis[J]. Journal of Magnetism and Magnetic Materials, 2018, 460: 509-524.
[4] Yang Huiwen, Weng Ling, Wang Bowen, et al. Design and characterization of high-sensitivity magnetostrictive tactile sensor array[J]. IEEE Sensors Journal, 2022, 22(5): 4004-4013.
[5] Yang Huiwen, Weng Ling, Wang Bowen, et al. Magnetostrictive tactile sensor array based on L-shaped Galfenol wire and application for tilt detection[J]. IEEE Sensors Journal, 2022, 22(13): 12645-12655.
[6] 贲彤, 王进, 陈龙, 等. 考虑磁致伸缩逆效应的非晶合金开关磁阻电机减振方法[J]. 电工技术学报, 2023, 38(10): 2648-2660.
Ben Tong, Wang Jin, Chen Long, et al. Vibration reduction method of switched reluctance motor with amorphous alloy cores based on inverse- magnetostriction effect[J]. Transactions of China Electrotechnical Society, 2023, 38(10): 2648-2660.
[7] Clemente C S, Davino D, Loschiavo V P. Analysis of a magnetostrictive harvester with a fully coupled nonlinear FEM modeling[J]. IEEE Transactions on Magnetics, 2021, 57(6): 4001204.
[8] 黄文美, 刘泽群, 郭万里, 等. 磁致伸缩振动能量收集器的全耦合非线性等效电路模型[J]. 电工技术学报, 2023, 38(15): 4076-4086.
Huang Wenmei, Liu Zequn, Guo Wanli, et al. Fully coupled nonlinear equivalent circuit model for magnetostrictive vibration energy harvester[J]. Transactions of China Electrotechnical Society, 2023, 38(15): 4076-4086.
[9] 翁玲, 梁淑智, 王博文, 等. 考虑预应力的双励磁线圈铁镓换能器输出特性[J]. 电工技术学报, 2019, 34(23): 4859-4869.
Weng Ling, Liang Shuzhi, Wang Bowen, et al. Output characteristics of double-excited coil Fe-Ga trans- ducer considering pre-stress[J]. Transactions of China Electrotechnical Society, 2019, 34(23): 4859-4869.
[10] 黄文美, 郭萍萍, 郭万里, 等. 直流偏置对磁致伸缩材料高频动态损耗及磁特性的影响分析[J]. 电工技术学报, 2022, 37(22): 5765-5775.
Huang Wenmei, Guo Pingping, Guo Wanli, et al. Impact analysis of DC bias on high-frequency dynamic loss and magnetic characteristics for magnetostrictive materials[J]. Transactions of China Electrotechnical Society, 2022, 37(22): 5765-5775.
[11] Chen Yunshuai, Li Pengyang, Sun Jian, et al. Loss- based structures and frequency dependencies of giant magnetostrictive materials for rotary ultrasonic machining applications[J]. Journal of Science: Advanced Materials and Devices, 2023, 8(3): 100609.
[12] 孟爱华, 杨剑锋, 蒋孙权, 等. 柱棒式超磁致伸缩能量收集器的设计与实验[J]. 振动与冲击, 2017, 36(12): 175-180.
Meng Aihua, Yang Jianfeng, Jiang Sunquan, et al. Design and experiments of a column giant mag- netostrictive energy harvester[J]. Journal of Vibration and Shock, 2017, 36(12): 175-180.
[13] 郑加驹, 王洪礼, 曹淑瑛. 超磁致伸缩驱动器频率相关的动态磁滞模型[J]. 机械工程学报, 2008, 44(7): 38-44.
Zheng Jiaju, Wang Hongli, Cao Shuying. Frequent- dependent dynamic hysteresis model of giant magnetostrictive actuator[J]. Chinese Journal of Mechanical Engineering, 2008, 44(7): 38-44.
[14] Armstrong W D. Magnetization and magnetostriction processes in Tb(0.27-0.30)Dy(0.73-0.70)Fe(1.9-2.0)[J]. Journal of Applied Physics, 1997, 81(5): 2321-2326.
[15] Atulasima J, Flatau A B, Cullen J R. Energy-based quasi-static modeling of the actuation and sensing behavior of single-crystal iron-gallium alloys[J]. Journal of Applied Physics, 2008, 103(1): 014901.
[16] Ahmed U, Jeronen J, Zucca M, et al. Finite element analysis of magnetostrictive energy harvesting concept device utilizing thermodynamic magneto- mechanical model[J]. Journal of Magnetism and Magnetic Materials, 2019, 486: 165275.
[17] Sathish Kumar R, Jayabal K. Micromechanically motivated constitutive model embedded in two- dimensional polygonal finite element framework for magnetostrictive actuators[J]. Journal of Applied Physics, 2019, 125(19): 194101.
[18] Sarawate N N, Dapino M J. A dynamic actuation model for magnetostrictive materials[J]. Smart Materials and Structures, 2008, 17(6): 065013.
[19] 黄文美, 陶铮, 郭萍萍, 等. 变压应力条件下铁镓合金棒材高频磁特性测试与模型构建[J]. 电工技术学报, 2023, 38(14): 3769-3778.
Huang Wenmei, Tao Zheng, Guo Pingping, et al. Analysis and modeling of high frequency magnetic properties of rod gallium iron alloy under variable compressive stress[J]. Transactions of China Elec- trotechnical Society, 2023, 38(14): 3769-3778.
[20] Garg H. A hybrid PSO-GA algorithm for constrained optimization problems[J]. Applied Mathematics and Computation, 2016, 274: 292-305.
[21] Scheidler J J, Asnani V M, Deng Zhangxian, et al. Dynamic characterization of Galfenol[C]//SPIE Smart Structures and Material Systems+Nondestructive Evaluation and Health Monitoring, San Diego, United States, 2015.
Abstract The Villari effect describes the magnetization change of magnetostrictive materials induced by mechanical loading. Magnetostrictive devices based on the Villari effect can realize electrical energyconverted from mechanical energy to harvest vibration energy in the environment. The output characteristics of magnetostrictive materials under stress excitation conditions depend on the bias conditions (prestress, bias magnetic field) and excitation frequency. Previous studies establishthe Villari effect model according to linear piezomagnetic equations, ignoring the material’s nonlinearity, hysteresis properties, and eddy current effects.
This paper uses the Armstrong energy model to derive a hysteresis-free magnetization strength equation of magnetostrictive materials under stress. The hysteresis-free equation is expanded into a static hysteresis model combined with the basic ideologies of the J-A hysteresis model. Then, considering the eddy current effect inside the material under high-frequency stress, the static model is expanded into a dynamic nonlinear Villari hysteresis model by introducing a first-order differential equation with a frequency-dependent time coefficient. The particle swarm and genetic optimization algorithms extract the model parameters through 3 progressive steps. The particle swarm genetic algorithm calculates the average static model parameter values for the quasi-static B-smajor loops of the Galfenol bar with 3.88～7.17 kA/m bias magnetic fields under 31.4 MPa stress amplitude, 1 Hz frequency, and -31.9 MPa prestress. The values of the quasi-static B-smajor and minor loops with bias magnetic fields of 0.73～13.76 kA/m are simulated using the average static model parameter values, which agree with experimental data. The bias conditions of the maximum piezo magnetic coefficient of the quasi-static B-smajor loop are -1.65 MPa prestress and 1.42 kA/m bias magnetic field. Based on the average static model parameter values, the dynamic parameter values tp for the dynamic B-smajor loops are extracted with 2.46 kA/m bias magnetic field under 31.4 MPa stress amplitude, 10～200 Hz frequency, and -31.9 MPa prestress. The dynamic parameter values tm for the dynamic B-sminor loops are extracted with 2.46 kA/m bias magnetic field under 2.88 MPa stress amplitude, 10～200 Hz frequency, and -7.96 MPa prestress. The dynamic parameters tp, tm, and the stress frequency are distributed according to a power function law. The model calculation values of the dynamic major loop and minor loops under 400 Hz and 600 Hz stress frequencies are obtained. The maximum error is 6.28%, which verifies the accuracy of the proposed dynamic model.
The results show that the nonlinear dynamic Villari hysteresis model can effectively predict the magnetic property response of magnetostrictive materials when the external compressive stress changes. It can provide a reference for the optimal design and performance regulation of electromagnetic devices, such as magnetostrictive energy harvesters, sensors, and dampers.
Keywords：Magnetostriction materials, Villari effect, piezomagnetic coefficient, Armstrong energy model, particle swarm optimization-genetic algorithm (PSO-GA)
中图分类号：TM274
DOI: 10.19595/j.cnki.1000-6753.tces.231174
国家自然科学基金资助项目（51777053, 52077052）。
收稿日期 2023-07-22
改稿日期 2023-11-22
黄文美 女，1969年生，博士，教授，研究方向为磁性材料与器件、电机电器及其控制。
E-mail: huzwm@hebut.edu.cn（通信作者）
冯晓博 男，1999年生，硕士研究生，研究方向为磁性材料与器件、电机电器及其控制。
E-mail: eio3690@qq.com
（编辑 郭丽军）