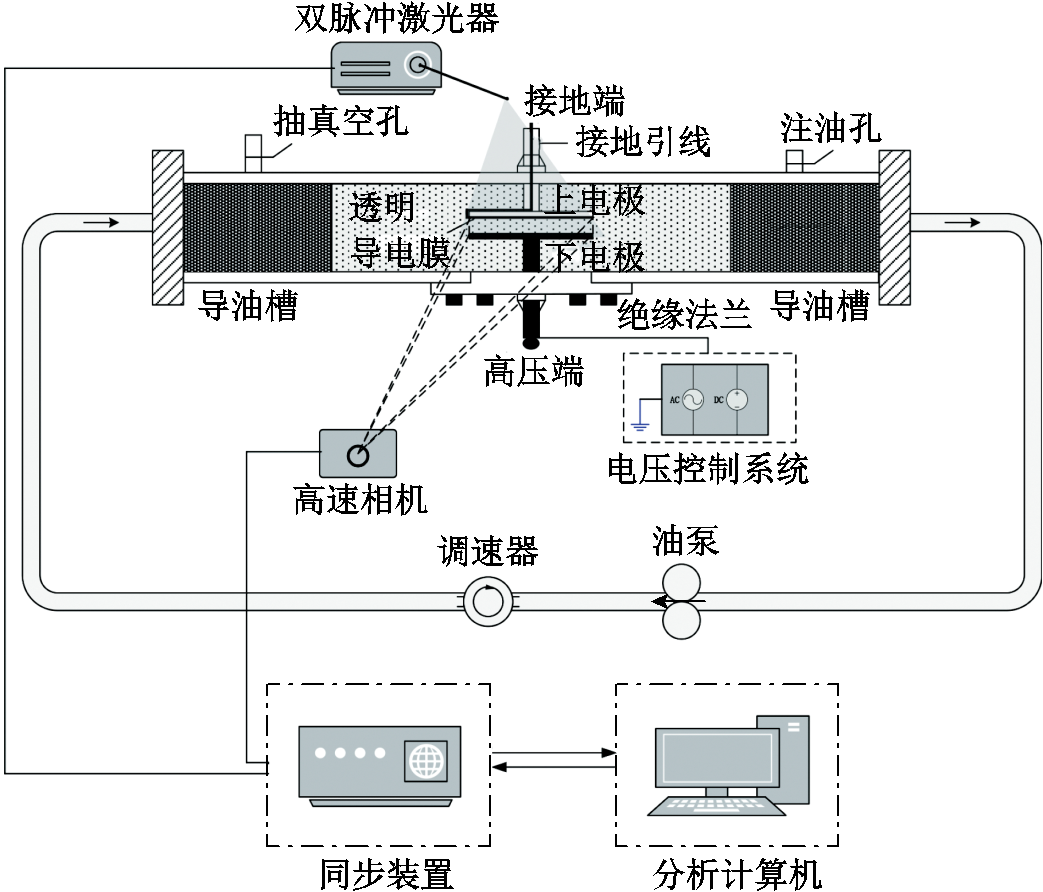
图1 实验平台示意图
Fig.1 Schematic diagram of the experimental platform
摘要 绝缘油中金属颗粒的荷电量分布是研究颗粒运动特性以及绝缘油中局部放电与击穿行为的关键。该文搭建了油道模拟观测系统，采用动力学分析的方法，构建了液固耦合系统中金属颗粒的运动模型，并在此基础上提出通过粒子图像测速（PIV）来计算颗粒荷电量；分析了不同油流速度、电压等级以及电压类型对颗粒荷电量的分布影响以及作用机理。结果表明，基于PIV计算出的油中颗粒的荷电量与传统模型的计算结果数量级相近，绝缘油中金属颗粒荷电量占比分布曲线接近高斯分布，这是由于颗粒与颗粒之间碰撞也会发生电荷转移或中和。在直流电压下流速增加会阻碍颗粒之间的电荷传递，增加颗粒与极板碰撞概率，导致颗粒荷电量减小。电压等级增加则会使颗粒群的流线由平缓变为振荡，颗粒荷电量普遍增加。相比于直流电压，在交流电压下，荷电量大的颗粒占比较多。
关键词：粒子图像测速 金属颗粒 绝缘油 液固耦合 荷电分布
绝缘油由于其良好的电气性能及热力学性能而被广泛应用于各种电力设备中[1-3]。然而，在电力设备的制造、运输、安装、运行及维护过程中，容易导致绝缘油中混入金属、纤维等各种固体杂质颗粒，随着电力设备长期运行，被污染的油形成具有液固两相流动特性的耦合系统。在电场与流场的共同作用下，两相流中的杂质颗粒会荷电并在油中运动，携带的电荷也会随之迁移，在造成电场畸变的同时将引发油中的局部放电从而破坏电力设备的绝缘平衡[4-5]。而相比于非金属颗粒，金属颗粒对油的局部放电和电弧击穿影响更大[6]。因此，有必要对金属颗粒在绝缘油中的荷电分布与运动特性进行研究，以揭示颗粒对绝缘油中的放电与击穿行为的影响机理。
目前的研究方向主要是通过数字仿真与实验的方式对杂质颗粒在绝缘介质中的荷电与运动特性进行研究与分析。黄宇辰等对纤维颗粒在交直流电压下的运动特性进行了仿真研究，结果表明，在流速较高及交流电场情况下颗粒不易碰撞，从而降低了颗粒之间的电荷转移概率[7]。孙继星等结合仿真与实验对直流电压下金属颗粒的带电量进行了估算与碰撞分析，结果表明，随着金属颗粒尺寸的增大，金属颗粒的碰撞频率逐渐减小，向接地电极与高压电极运动的时间差逐渐增加[8]。董曼玲等研究了金属颗粒放电特性和聚集特性之间的关联性，结果表明，颗粒之间聚集的紧密程度以及与电极碰撞的概率是影响局部放电的主要因素[9]。骆仲泱等研究细颗粒物在直流电晕放电下的荷电特性得出，直径小于0.2 μm时荷电方式主要是扩散荷电，直径大于0.2 μm时则是场致荷电，颗粒荷电量随着粒径与直流电压的增大而增大[10]。但敏等通过使用高速相机记录光学图像的方式研究了纤维颗粒成桥与运动特性，结果表明，在直流电压下，相比于天然酯，纤维颗粒在矿物油中运动速度更快，更容易成桥，并且矿物油中的桥呈现细圆柱状，天然酯中的桥呈三角锥形[11]。A. Khayari等研究了直流电压下均匀电场中金属颗粒的荷电机理，结果表明，当颗粒接触电极时产生放电，外部记录电流脉冲的电荷比从电极转移到球上的电荷量小一个数量级[12]。R. Sarathi等研究了高频交流电压和谐波交流电压下变压器油中颗粒运动引起的局部放电，结果表明，外施电压增大到颗粒悬浮电压以上时，由于颗粒运动而形成的超高频信号幅度增加，与电源电压频率无关[13]。
综上所述，当前的研究主要是通过实验的方式定性地分析影响颗粒荷电过程与运动行为的相关因素，并通过数字模拟和仿真的方式加以验证。研究过程中尚存在忽略绝缘介质流动的作用，仅通过传统的荷电模型来解释流-电耦合场中颗粒的荷电机理与运动行为的情况，并且未能统计颗粒荷电量的分布。
因此，本文主要研究了液-固两相耦合系统中颗粒的荷电与运动特性，首先搭建了油中颗粒实验观测平台，基于粒子图像测速（Particle Image Velocimetry, PIV）对含有大量金属颗粒的绝缘油颗粒群流速进行了测定；其次，在离散颗粒模型的基础上提出了一种通过分析颗粒受力模型推导出颗粒荷电量的方法；最后，分析了电场强度、电压类型及流场速度对金属颗粒荷电分布的影响，对更加深入地研究金属颗粒放电特性、运动行为及击穿机理具有一定的参考价值。
以电力变压器为例，为了切合变压器油道环境，并对杂质金属颗粒的运动轨迹及速度进行观测，搭建了油道模拟观测系统，实验平台示意图如图1所示。实验平台主要由油流循环装置、电极和电压源、PIV测量系统组成。其中，油流循环装置包括油泵、调速器、连接管以及有机玻璃制成的矩形观察管。通过调速器控制油速，油速最大可以调节至1 m/s。此外，平板电极位于观测管线的中心，上电极采用圆柱形有机玻璃板，下表面粘贴一层透明导电膜，并通过导线接地。而下电极则由与上电极尺寸相同的铜板制成，通过金属棒与高压源相连接，可以通过调节下极板的高度来改变极板间距。此外，可以从高压源向平板电极施加最大值为60 kV的负极性直流电压或100 kV的交流电压。
图1 实验平台示意图
Fig.1 Schematic diagram of the experimental platform
PIV测量系统由双脉冲激光器、高速相机、同步装置和分析计算机组成。为了获得尽可能好的观测结果，使双脉冲激光垂直于电极，发射1 mm厚的片状光束，并将高速相机的图像捕获方向设置为垂直于光束。PIV观测示意图如图2所示。
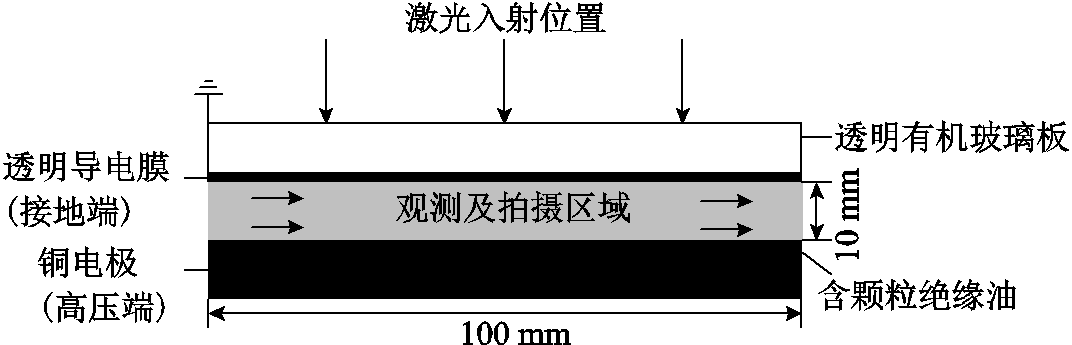
图2 PIV观测示意图
Fig.2 Schematic diagram of PIV observation
在实验中，通过同步装置的周期性TTL（transistor-transistor logic）信号实现高速相机和激光器的时间同步后，高速相机连续拍摄电极间隙中的流场图像。拍摄过程中，在相机镜头上安装了一个特殊的玻璃滤光片（可见光的透射率为10%），以减少噪声和强光反射对相机造成的损坏。PIV系统参数见表1。
表1 PIV系统参数
Tab.1 PIV system parameters
设备名称参数数值 高速相机分辨率2 456×2 056 像素/μm3.45 采集速率/(帧/s)16 PIV模式最小曝光间隔/ns≤500 双脉冲激光源波长/nm532 脉冲宽度/ns6～8 工作频率/Hz5 同步装置时间精度/ns0.25
拍摄过程中，时间步长（跨帧时间）的选择对于准确量化流场速度尤为重要。根据分析软件计算网格的大小，将颗粒在时间步长内的最大位移限制在8个像素左右。当流速和施加的电压改变时，需要设置不同的时间步长以满足颗粒的有限位移。
为了避免实验中所用颗粒在油箱底部快速沉积进而改变实验过程中颗粒物的浓度，本次实验选取金属铝颗粒作为示踪颗粒，形状选择为球形以保证图像清晰度与计算精度。绝缘油中的金属颗粒直径一般满足Rosin-Rammler分布，并且直径范围为5～100 μm，因此，选取平均直径为50 μm的颗粒作为样品[14-15]。本次实验使用电力设备中常用的25号变压器油，具体参数见表2。
表2 变压器油与颗粒参数
Tab.2 Transformer oil and particle parameters
参数25号变压器油铝颗粒 密度/(kg/m3)8752 700 黏度/[kg/(m·s)]9.88×10-3— 直径/μm—50 相对介电常数2.2—
在注入油箱之前需要对变压器油进行处理，首先使用0.1 μm的滤网对油进行多次过滤以滤除油中的固体杂质颗粒，之后将油放入真空干燥箱内24 h进行干燥、脱气以去除油中的气体与水分。使用分析天平称量一定质量的金属铝颗粒，通过磁力搅拌器将油与颗粒混合均匀后加入油箱，确保颗粒质量浓度保持在0.062 5 g/L，对应于NAS1638颗粒污染分类标准的10～11水平。
每次观测实验开始之前需要提前开启油泵使油循环10 min，以确保颗粒在油中的均匀分布以及油流的稳定。实验过程中通过示波器监测输出电压，在PIV测量系统记录图像时，每600个图像记为一组数据，每次实验记录三组数据以减小实验过程中的误差，最后在MicroVec中计算具体流场参数。
计算金属颗粒在流动绝缘油下的荷电分布状况时，首先应该在考虑电场和流场共存的状态下对其建立液-固两相流的模型。而液-固两相流研究中主要应用两种方法[16]，即拉格朗日法和欧拉法。
2.1.1 拉格朗日法
拉格朗日法以流体中的某一流体质点作为研究对象，通过研究这一质点在流场中发生位移时运动参数的变化规律，再对其他质点进行分析，最终得出一定空间内所有流体质点的运动规律。其中的单个质点位置坐标是时间t的函数，流体质点的运动方程可以表示为
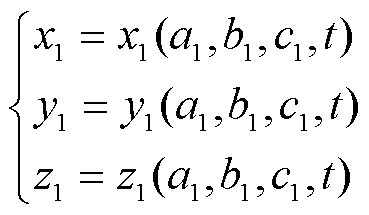（1）
式中，(a1, b1, c1)为流体质点的初始坐标；(x1, y1, z1)为质点位置坐标。
2.1.2 欧拉法
拉格朗日法通过描述质点的位置坐标从而得到速度与加速度。而欧拉法并不直接追究质点的运动过程，而是以流体质点流经流场中各空间点的运动作为研究对象，通过研究各个时刻质点在流场中的运动规律，最后综合足够多的空间点来反映流体的运动情况。
按照NAS1638颗粒污染分类标准的10～11水平，金属颗粒的体积分数远远小于10%，而根据液-固两相流中的基础理论[17]，在这种情况下应该将固相在拉格朗日坐标下进行描述，即通过拉格朗日法对单一金属颗粒建立动力学方程进行分析。
考虑到金属颗粒受到流场和电场的共同作用，颗粒的主要受力包括电场力、介电泳力、流体曳力、重力、浮力、Saffman升力、Magnus升力、附加质量惯性力及压力梯度力等附加力[18]。而在本次实验中，颗粒位于平板电极下，电场分布均匀，因此不受介电泳力的影响；又由于颗粒粒径在50 μm左右且为球形，颗粒周围流速相差不大，而Saffman升力与Magnus升力都是由颗粒四周流速不同而产生的，故可以忽略；在稳定的流体中，当颗粒粒径较小时，压力梯度力及Basset力可以忽略不计[19-21]。因此，在油流中的y方向上可以得到颗粒的运动方程为
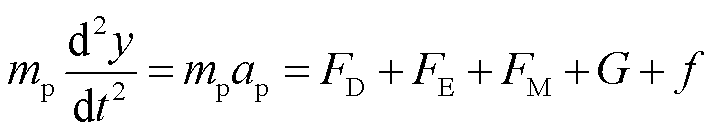（2）
式中，mp为每个颗粒的质量，kg；ap为颗粒在垂直方向上的加速度，m/s2；FD为流体曳力，N；FE为电场力，N；FM为附加质量惯性力，N；G为重力，N；f为浮力，N。
由于在垂直方向上流场近似不存在，则可以在垂直方向上建立颗粒的受力方程（正方向为y方向向上）[22]。
流体曳力为
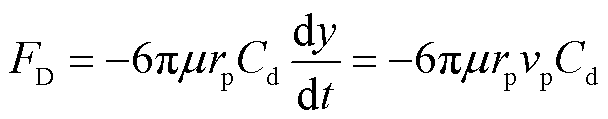（3）
式中，vp为颗粒垂直方向上的速度，m/s；rp为颗粒的半径；μ为油的运动黏度，Pa·s；Cd为曳力系数，本实验中取0.56。
电场力为
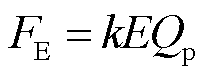（4）
式中，k为镜像电荷引起的修正系数，本实验中为1；E为电场强度，V/m；Qp为颗粒荷电量，C。
附加惯性质量力为
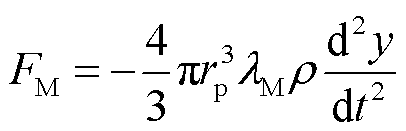（5）
式中，ρ为油的密度，kg/m3；λM为由电极引起的校正系数，本实验中为0.5。
重力与浮力之和为
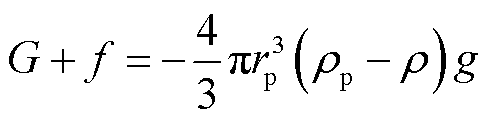（6）
式中，ρp为颗粒的密度，kg/m3；g为重力加速度，m/s2。
由式（2）～式（6）可以得出
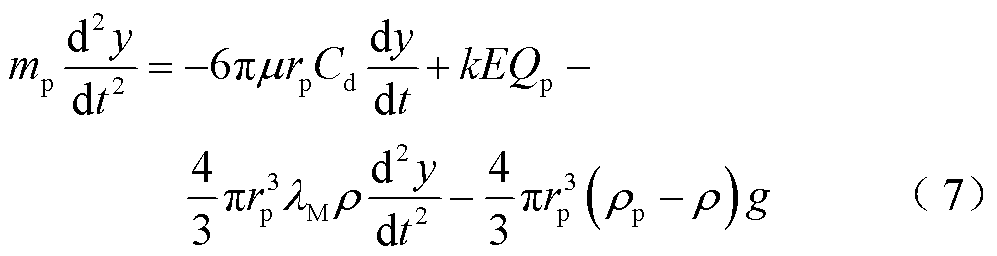
由式（7）可得
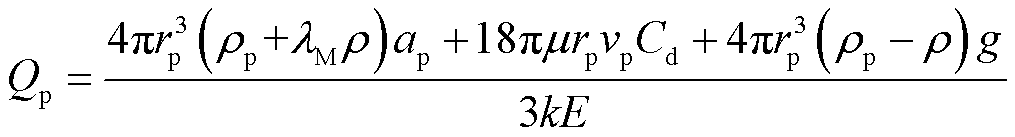（8）
由式（8）可得，除vp与ap以外，其余的量均已知，则测量出颗粒的速度并计算出加速度即可得出颗粒的荷电量Qp。
选取多组实验数据中一组典型的颗粒群速度云图与流线如图3所示。
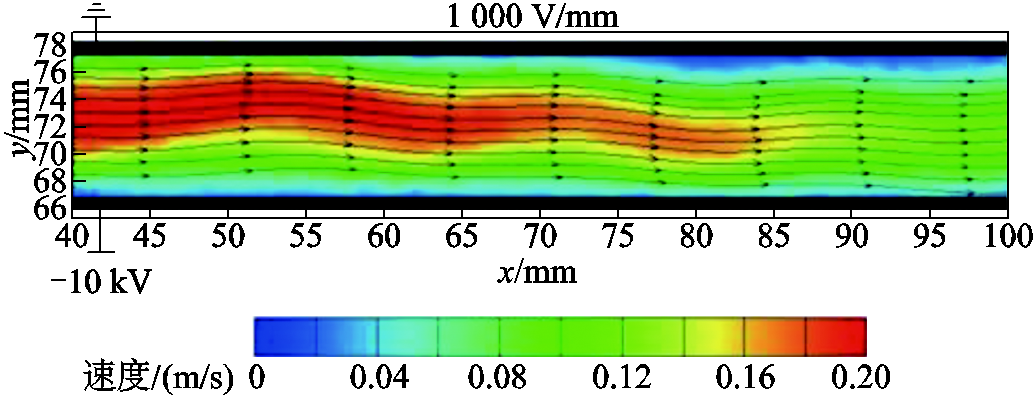
图3 平板电极下颗粒群的速度云图与流线（v=0.15 m/s, U=DC-10 kV）
Fig.3 Velocity cloud and streamline of particle swarm under a flat electrode (v=0.15 m/s, U=DC-10 kV)
图3中上下黑色条框分别表示接地的上电极以及连接高压电源的下电极，下电极所加电压为-10 kV，整体流速控制在0.15 m/s左右，电极间不同的颜色代表此处速度的大小，电极间均匀分布的黑色线条为流场的流线，流线上的箭头显示出流场的方向。电极的直径为100 mm，但由于40～100 mm区间的流场较为均匀稳定，因此选定该区域计算加速度及电荷量的分布。
由于流场的变化是连续的，而颗粒的流场在短时间内具有准稳态特性，因此可以认为在极小距离内颗粒沿着流线运动[23]。在电极间均匀地取10条流线，PIV测量系统能够在60 mm的区域中的一条流线上测量出近420个点的速度与位置数据。由于相邻两点的间距较小，平均水平距离为0.14 mm左右，因此可以根据有限差分法[24]，将连续的加速度变化函数离散为每条流线上选定节点的差分方程。此时假定液-固两相流中颗粒在相邻两点中由点1运动到点2时，垂直方向上的加速度在[t, t+Δt]时间段内为一恒量，则有
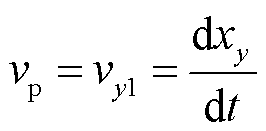（9）
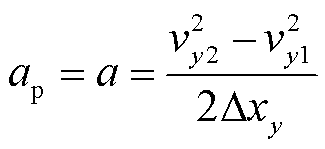（10）
式中，vy1为颗粒位于点1时垂直方向上的速度；vy2为颗粒位于点2时垂直方向上的速度；xy为颗粒在垂直方向上的位移；Δxy为相邻选定节点在垂直方向上的距离。其中vy1、vy2及Δxy的具体数值可以通过PIV测量系统获得。则由式（10）可以计算出两点间的加速度a，代入式（8）即可计算出颗粒在该点处所携带的电荷量。本文统计了图3所示区域的颗粒荷电量分布，如图4所示。从图4中可以看出，颗粒的荷电量主要分布在-0.05～0.05 pC之间。
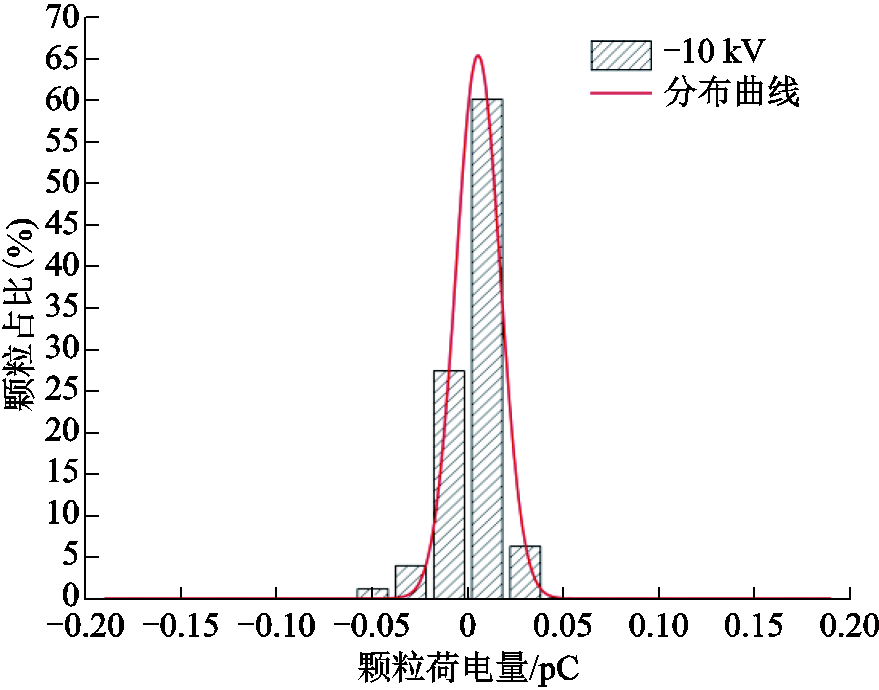
图4 金属颗粒荷电量分布（v=0.15 m/s, U=DC-10 kV）
Fig.4 Proportion of metal particle charge distribution (v=0.15 m/s, U=DC-10 kV)
按照经典荷电理论[25]，即当半径为rp的金属颗粒进入电场强度为E的均匀电场中与电极发生碰撞之后，颗粒的荷电量为
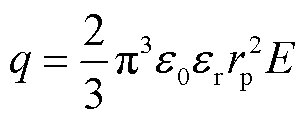（11）
式中，ε0为真空介电常数；εr为金属颗粒的相对介电常数。
则在同样实验条件下（颗粒粒径为50 μm，电场强度为1 000 V/mm），通过式（11）可以计算出颗粒的荷电理论值q=2.515×10-13 C，与图4中计算出的最大荷电量对比可以发现，传统模型计算出的颗粒荷电量偏大，但仍然与本文计算出的最大荷电量在近似数量级。这可能是由于传统模型只考虑了单个颗粒与电极发生碰撞而导致颗粒荷电的情况，并未考虑实际情况中颗粒较多时，绝缘介质流动导致荷电量不同的金属颗粒之间碰撞而发生电荷转移的情况。
并且金属颗粒在与极板碰撞时，可能导致极板表面电离，使得绝缘油中的自由电子增多[26]，大量自由电子的迁移和扩散也会使得金属颗粒荷电量改变。由此可见，本文所提出的模型及相应的计算方法较为合理。
为了进一步研究绝缘介质流动对金属颗粒荷电量的影响，在外施直流电压为-30 kV时分别对入口处流速为0.15 m/s与0.3 m/s的颗粒群流场进行了拍摄，结果如图5所示。
图5 不同流速时颗粒群的速度云图与流线
Fig.5 Velocity cloud and streamline of particle swarm at different flow rates
从图5中可以看出，速度较大的颗粒主要分布在电极中部区域。同时对比图5a与图5b可以发现，当油流速度增大时，颗粒的流线明显趋于平稳，颗粒在垂直方向上的速度分量减小，即油速的增加减小了外施电场对颗粒运动的影响程度。
此时使用前文所述计算方法对颗粒荷电量进行计算，统计之后得到颗粒具体荷电量分布如图6所示。
图6 不同流速时颗粒荷电量分布
Fig.6 Distribution of particle charge proportion at different flow rates
由图6可知，颗粒荷电量分布所拟合出的曲线在电荷量为零时到达最高峰，并且左右对称，接近于高斯分布，而不同于传统模型与电极碰撞后所有相同粒径的颗粒荷电量为一恒量。这种现象可以解释为：一部分颗粒与上电极碰撞之后形成带正电的颗粒团，在电场力的作用下向下运动时与同样原因带负电的颗粒团发生碰撞，导致颗粒之间发生电荷转移与中和。
此外，球形颗粒之间发生碰撞后失去或者得到的电荷量Q12为[27]
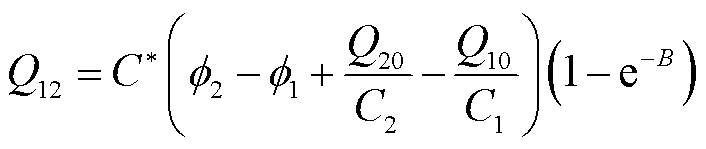（12）
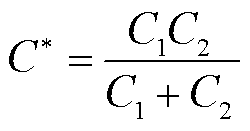（13）
式中，C*为颗粒之间的相对电容；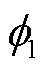
与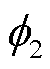
分别为两个颗粒的功函数；Q10与Q20分别为两个颗粒相互碰撞前的电荷量；C1与C2分别为两个颗粒的电容；B为与颗粒相关的常数。
球形均质颗粒的电容为
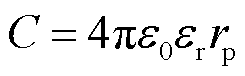（14）
从式（14）中可以看出，在颗粒粒径都为50 μm左右，并且同样是金属颗粒时，C1与C2相近；又由于功函数的大小只与颗粒本身材质相关，因此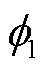=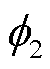，则式（12）变为
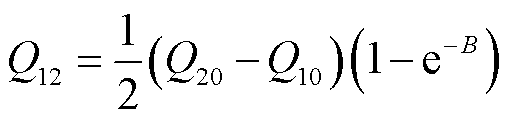（15）
由于B为正的常数[27]，则由式（15）可得，当不同荷电量的两个颗粒之间碰撞时，它们各自得到或者失去的电荷量不超过两者之间电荷量差值的一半。而当荷电量相同的两个颗粒之间发生碰撞时，两者之间并不会发生电荷的迁移，两者之间电荷量不发生改变。
由图6可知，在油流速为0.15 m/s时，颗粒最大荷电量为0.17 pC，荷电量绝对值大于0.01 pC的颗粒占比为36%；而在油流速为0.3 m/s时，颗粒最大荷电量为-0.13 pC，荷电量绝对值大于0.01 pC的颗粒占比为29%。可以接受的解释是，由于流场主要作用于x方向，当油流速增大时，颗粒受到的水平拖曳力增大，使颗粒群流经电场区域的时间缩短。而油流中颗粒群的荷电具有时间特性，需要一定时间才能完成电荷积累，颗粒群在平板电极间的电场中运动时间的缩短将不利于这一过程的进行。另外，流速的增大使颗粒在y方向上的偏移量减小，导致颗粒与电极的碰撞次数以及参与碰撞的颗粒数都减少。同时，整体流场的水平速度变大，使得已荷电的颗粒更加迅速地逸出平板电极之间的区域，则极板附近区域荷电量较大的颗粒与离极板较远区域的颗粒发生碰撞时，传递电荷的概率也会相对变小。因此，油流速越大，对颗粒群的荷电过程影响越大，颗粒群的荷电量就越少。
当入口处油流速为0.15 m/s，外施直流电压分别为10、20、30 kV时，颗粒群的速度云图与流线如图7所示。对比图7中的流线可以发现，随着外施电压等级的提升，颗粒的流线逐渐开始振荡，两电极中部区域流体的流速明显减小，流线的方向逐渐由近似水平变化为倾斜向下，即电场的增强导致颗粒在y方向上运动更加剧烈。
图7 不同电压等级下颗粒群的速度云图与流线
Fig.7 Velocity cloud and streamline of particle swarm under different voltage levels
当入口处油体流速为0.15 m/s，外施直流电压分别为10、20、30 kV时，颗粒荷电量的分布如图8所示。再将图8中所拟合出的不同电压等级的荷电量分布曲线作对比，结果如图9所示。
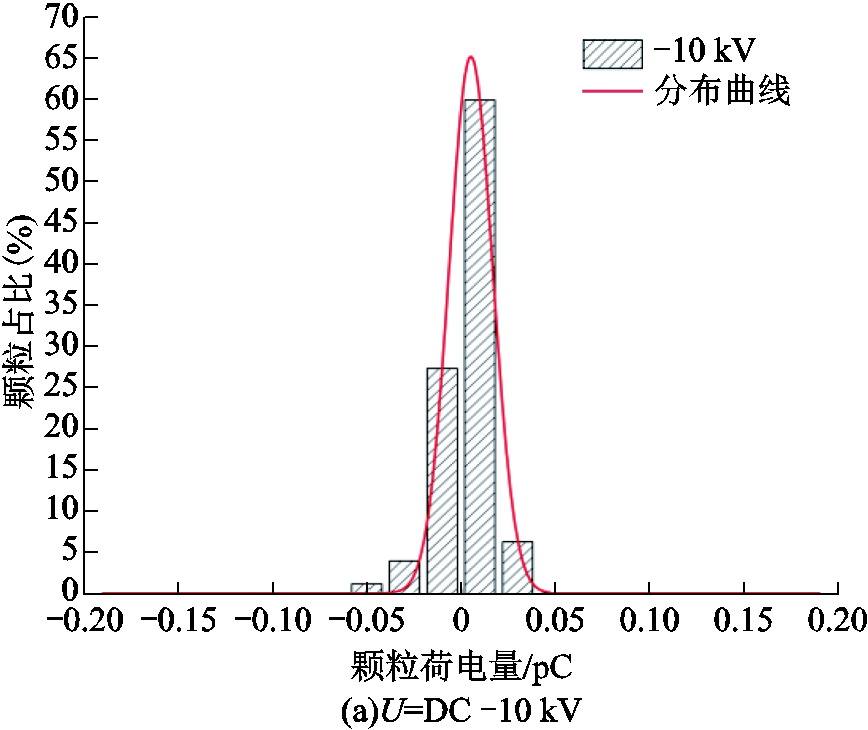
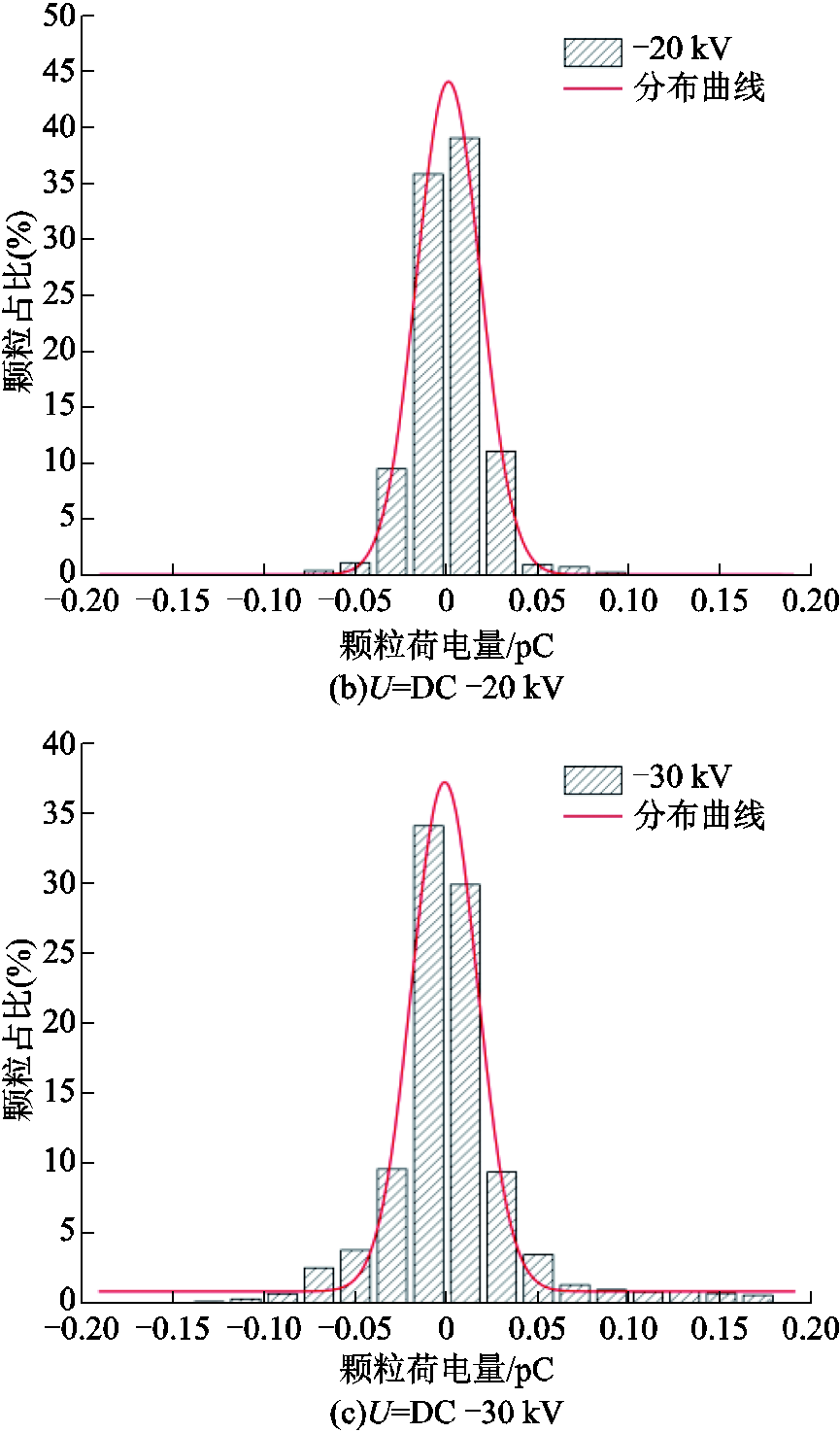
图8 不同直流电压等级下颗粒荷电量分布
Fig.8 Particle charge distribution curve under different DC voltage levels
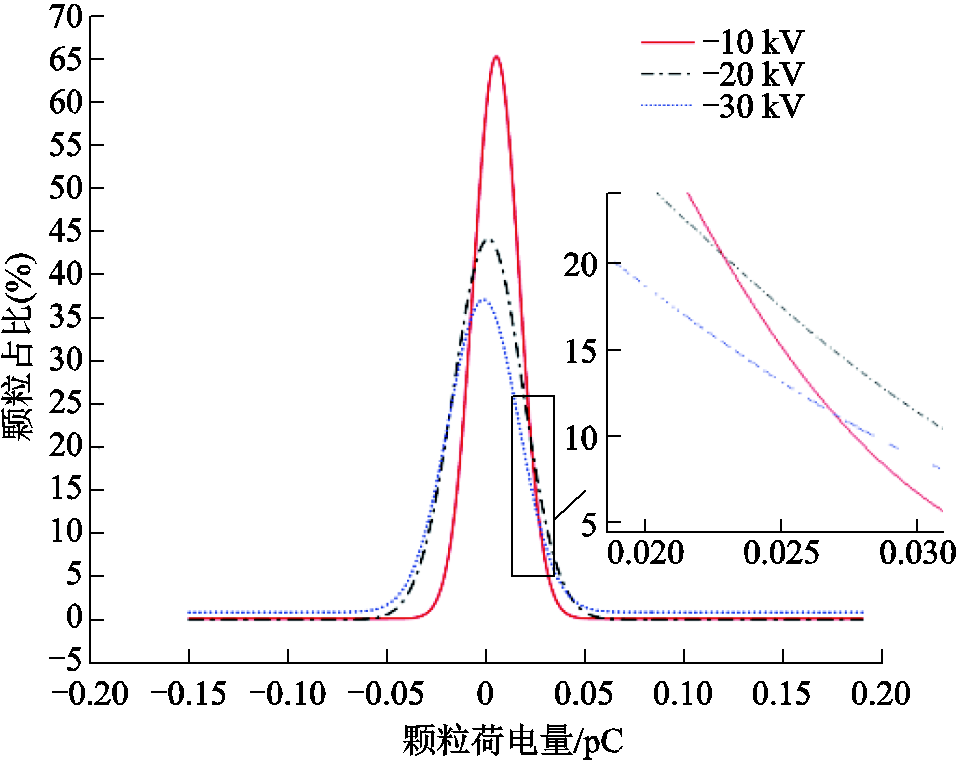
图9 不同直流电压等级下颗粒荷电量分布曲线对比
Fig.9 Comparison of particle charge distribution curves under different DC voltage levels
由图8可知，在电压为-10 kV时，颗粒最大荷电量为0.05 pC，荷电量绝对值大于0.01 pC的颗粒占比为12%；在电压为-20 kV时，颗粒最大荷电量为0.09 pC，荷电量绝对值大于0.01 pC的颗粒占比为25%；在电压为-30 kV时，颗粒最大荷电量为0.17 pC，荷电量绝对值大于0.01 pC的颗粒占比为36%。
结合图9可以明显看出，随着外施直流电压等级的不断提高，荷电量接近于零的颗粒占比逐渐减小，颗粒的最大荷电量变大，荷电量较大的颗粒占比增多。从式（11）可以看出，电场强度的增大会使得金属颗粒的最大荷电量增加，而由式（4）可以看出，颗粒所受电场力将会大幅度增强，这会导致颗粒在y方向上的速度分量变大，颗粒在y方向上的运动更加剧烈，从而与电极碰撞的概率增大，颗粒与电极之间的放电变得更加频繁，则会有更多的与电极碰撞而荷电的颗粒出现，并且颗粒之间电荷传递的过程变得较为容易。
工程实际中，外施电压的类型（直流/交流）也会对杂质颗粒的荷电状况产生影响[28]。因此当入口处油流速度为0.15 m/s、分别施加幅值为30 kV的工频交流电压及直流电压时，PIV系统测得的颗粒群速度云图与流线如图10所示。
图10 不同电压类型下颗粒群速度云图与流线
Fig.10 Velocity cloud and streamline of particle swarm under under different voltage types
由图10可知，在外施电压为交流的情况下，颗粒在垂直方向上的速度分量较小，流线较为水平，流场整体分布较为均匀。对图10所示流场中颗粒的荷电量进行计算与统计，结果如图11所示。从图11中可以看出，荷电量绝对值大于0.01 pC的颗粒占比为10%左右，颗粒最大荷电量为0.03 pC。结合颗粒群流场分析，这可能是由于当外施电压为交流时，大部分颗粒沿x方向运动，y方向的交变电场导致颗粒在小范围内做往复运动，很难与电极发生碰撞。
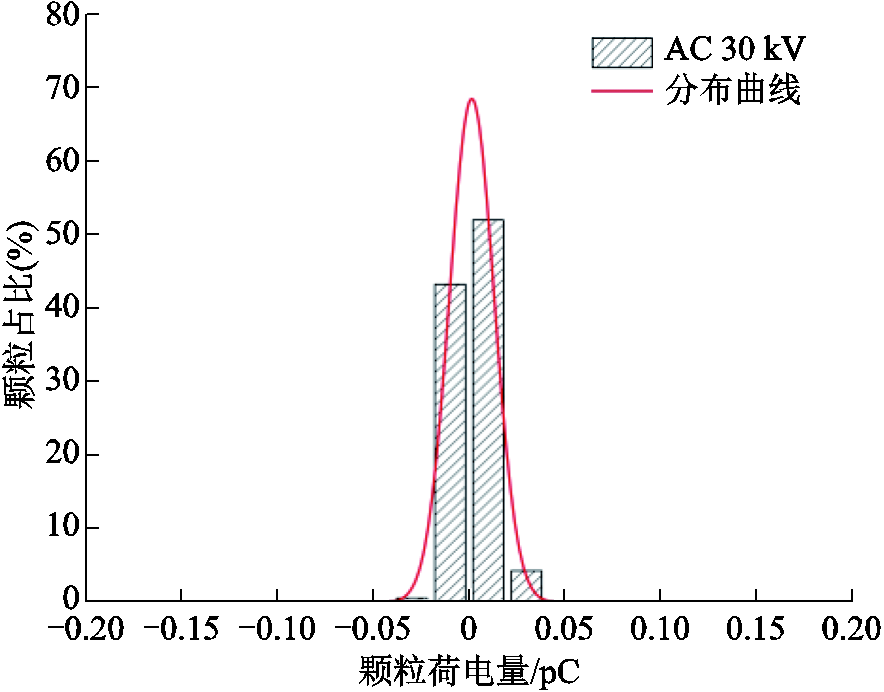
图11 金属颗粒荷电量分布占比（v=0.15 m/s, U=AC 30 kV）
Fig.11 Proportion of metal particle charge distribution (v=0.15 m/s, U=AC 30 kV)
图12为外施幅值为30 kV的交流电压与直流电压时颗粒荷电量分布曲线对比情况。可见直流和交流电压下荷正电的颗粒与荷负电的颗粒占比接近，说明外施电压类型不影响颗粒电荷量的极性。
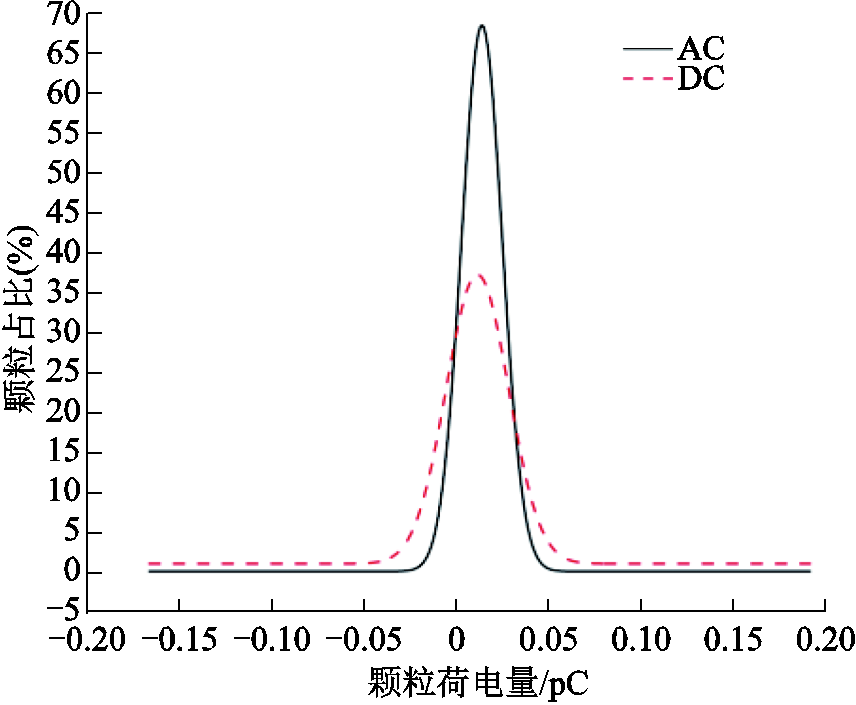
图12 不同电压类型时颗粒荷电量分布曲线对比
Fig.12 Comparison of particle charge distribution curves under different voltage types
当外施电压类型为交流时，荷电量较高的颗粒占比明显减少，这可以解释为由于在工频交流电场中，电场强度呈现正弦曲线变化，当电场强度较小时，由式（11）可得与电极碰撞而荷电的颗粒的电荷量较小。又由于外施电压为交流时，除了靠近电极表面区域的颗粒可以与电极发生碰撞外，其他位置的颗粒与极板碰撞的概率较低，这就导致相比于直流电压下，交流电场中荷电量多的颗粒占比较少。另外，一些颗粒在与电极碰撞荷电后，由于交流电场的存在，半个周期的运动时间不足以使颗粒迁移至离电极较远的区域，进一步弱化了垂直方向上电荷的传递过程。
综上所述，多种因素的影响导致交流电场下金属颗粒群在电极间流动时整体的荷电量偏小。
1）通过建立金属颗粒受力模型反推出荷电量的计算公式，代入PIV系统测得的流场参数计算出的颗粒最大荷电量与传统模型在相近数量级，但颗粒荷电量分布曲线接近高斯分布，这表明：金属颗粒在绝缘油流中的荷电方式并非只有颗粒与电极碰撞荷电，也可能是颗粒之间碰撞导致电荷转移与中和。
2）绝缘油流速增加使得颗粒群在电极间电场中的运动时间减少，降低了不同区域的颗粒之间发生碰撞传递电荷的概率，导致未与电极发生碰撞的颗粒占比增多。
3）外施电场强度的增加使颗粒群的流线发生振荡，颗粒在y方向上的速度分量增加，并且颗粒与电极的碰撞变得频繁，电荷容易在颗粒之间传递，致使颗粒的荷电量普遍增高。
4）外施电压类型不影响颗粒荷电量的极性分布，当外施电压为交流时，颗粒群流线平缓，由于交流电场强度在一个周期的大部分时间内数值较小，使得荷电量大的颗粒占比较少。
参考文献
[1] 刘道生, 周春华, 丁金, 等. 变压器纳米改性油纸复合绝缘研究综述[J]. 电工技术学报, 2023, 38(9): 2464-2479, 2490.
Liu Daosheng, Zhou Chunhua, Ding Jin, et al. Research overview of oil-paper composite insulation modified by nano particles for transformer[J]. Transactions of China Electrotechnical Society, 2023, 38(9): 2464-2479, 2490.
[2] 张宁, 刘士利, 郝建, 等. 变压器油中气泡杂质相局部放电特性研究综述[J]. 电工技术学报, 2023, 38(10): 2757-2776.
Zhang Ning, Liu Shili, Hao Jian, et al. Review on partial discharge characteristics of bubble impurity phase in transformer oil[J]. Transactions of China Electrotechnical Society, 2023, 38(10): 2757-2776.
[3] 谢小荣, 贺静波, 毛航银, 等. “双高”电力系统稳定性的新问题及分类探讨[J]. 中国电机工程学报, 2021, 41(2): 461-475.
Xie Xiaorong, He Jingbo, Mao Hangyin, et al. New issues and classification of power system stability with high shares of renewables and power electronics[J]. Proceedings of the CSEE, 2021, 41(2): 461-475.
[4] 王有元, 吴俊锋, 徐海鹰. 电力设备局部放电超高频信号检测用新型微带天线[J]. 电工技术学报, 2016, 31(10): 136-144.
Wang Youyuan, Wu Junfeng, Xu Haiying. A new microstrip antenna used for detecting the ultra-high frequency signal caused by the partial discharge in power equipments[J]. Transactions of China Electrotechnical Society, 2016, 31(10): 136-144.
[5] 张国治, 闫伟阳, 王堃, 等. 流动绝缘油中纤维杂质颗粒运动特性仿真研究[J]. 电工技术学报, 2023, 38(9): 2500-2509.
Zhang Guozhi, Yan Weiyang, Wang Kun, et al. Simulation research on movement characteristics of fiber impurity particles in flowing insulating oil[J]. Transactions of China Electrotechnical Society, 2023, 38(9): 2500-2509.
[6] 骆欣瑜. 换流变压器油道中带电自由金属微粒运动规律和局部放电特性研究[D]. 重庆: 重庆大学, 2020.
Luo Xinyu. Transformers particles in the oil channel of converter characteristics of free charged metallic investigations on motion behaviors and PD[D]. Chongqing: Chongqing University, 2020.
[7] 黄宇辰, 房俊龙, 闫伟阳. 不同电压类型下油流中纤维杂质颗粒运动特性仿真研究[J]. 高电压技术, 2022, 48(12): 4817-4828.
Huang Yuchen, Fang Junlong, Yan Weiyang. Simulation research on the motion characteristics of fiber impurity particles in oil flow under different voltage types[J]. High Voltage Engineering, 2022, 48(12): 4817-4828.
[8] 孙继星, 陈维江, 李志兵, 等. 直流电场下运动金属微粒的带电估算与碰撞分析[J]. 高电压技术, 2018, 44(3): 779-786.
Sun Jixing, Chen Weijiang, Li Zhibing, et al. Charge estimation and impact analysis of moving metal particle under DC electric field[J]. High Voltage Engineering, 2018, 44(3): 779-786.
[9] 董曼玲, 寇晓适, 姚德贵, 等. 交直流复合电压下变压器油中金属微粒聚集特性和局部放电特性研究[J]. 绝缘材料, 2022, 55(10): 74-79.
Dong Manling, Kou Xiaoshi, Yao Degui, et al. Aggregation behaviors and partial discharge characteristics of metal particles in transformer oil under AC/DC composite voltage[J]. Insulating Materials, 2022, 55(10): 74-79.
[10] 骆仲泱, 江建平, 赵磊, 等. 不同电场中细颗粒物的荷电特性研究[J]. 中国电机工程学报, 2014, 34(23): 3959-3969.
Luo Zhongyang, Jiang Jianping, Zhao Lei, et al. Research on the charging of fine particulate in different electric fields[J]. Proceedings of the CSEE, 2014, 34(23): 3959-3969.
[11] 但敏, 郝建, 廖瑞金, 等. 直流电压下矿物油和天然酯中纤维颗粒运动及成桥特性的差异[J]. 电网技术, 2018, 42(2): 665-672.
Dan Min, Hao Jian, Liao Ruijin, et al. Different motion and bridging characteristics of fiber particles in mineral oil and natural ester under DC voltage[J]. Power System Technology, 2018, 42(2): 665-672.
[12] Khayari A, Perez A T. Charge acquired by a spherical ball bouncing on an electrode: comparison between theory and experiment[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2002, 9(4): 589-595.
[13] Sarathi R, Archana M. Investigation of partial discharge activity by a conducting particle in transformer oil under harmonic AC voltages adopting UHF technique[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2012, 19(5): 1514-1520.
[14] Wei Chao, Wang Shengquan, Lu Yuncai, et al. Influence of metallic particles on the breakdown voltage of insulating oil at AC and DC voltage[C]//2016 IEEE Electrical Insulation Conference (EIC), Montreal, QC, Canada, 2016: 280-283.
[15] 尹克宁. 变压器设计原理[M]. 北京: 中国电力出版社, 2003.
[16] 于萍. 工程流体力学[M]. 2版. 北京: 科学出版社, 2015.
[17] Gouesbet G, Berlemont A. Eulerian and Lagrangian approaches for predicting the behaviour of discrete particles in turbulent flows[J]. Progress in Energy and Combustion Science, 1999, 25(2): 133-159.
[18] 麻守孝, 唐炬, 张明君, 等. 牵引变压器中运动金属颗粒群的分布状态及影响因素仿真研究[J]. 高电压技术, 2015, 41(11): 3628-3634.
Ma Shouxiao, Tang Ju, Zhang Mingjun, et al. Simulation study on distribution and influence factors of metal particles in traction transformer[J]. High Voltage Engineering, 2015, 41(11): 3628-3634.
[19] 贺博, 王鹏, 吴锴, 等. 多物理场中染污绝缘油内杂质相动力学行为研究综述[J]. 电工技术学报, 2022, 37(1): 266-282.
He Bo, Wang Peng, Wu Kai, et al. Reviews on impurity phase dynamics in contaminated insulating oil under multi-physical field conditions[J]. Transactions of China Electrotechnical Society, 2022, 37(1): 266-282.
[20] 刘刚, 王晓晗, 马永强, 等. 基于控制体—迎风有限元法的变压器绕组二维流体场—温度场耦合计算方法研究[J]. 高压电器, 2021, 57(6): 1-9.
Liu Gang, Wang Xiaohan, Ma Yongqiang, et al. Study on coupled calculation method of two dimensional fluid and temperature field of transformer winding based on control volume-upstream FEM[J]. High Voltage Apparatus, 2021, 57(6): 1-9.
[21] 李维仲, 姜远新. 小木球在固液两相流中上升规律研究及Magnus力测量[J]. 大连理工大学学报, 2011, 51(5): 653-657.
Li Weizhong, Jiang Yuanxin. Research on rising motion rule of wooden ball in solid-liquid two-phase flow and its Magnus force measurement[J]. Journal of Dalian University of Technology, 2011, 51(5): 653-657.
[22] 张国强, 吴家鸣. 流体力学[M]. 北京: 机械工业出版社, 2006.
[23] 刘大有. 二相流体动力学[M]. 北京: 高等教育出版社, 1993.
[24] Bermúdez A, Rodríguez R. Finite element computation of the vibration modes of a fluid—solid system[J]. Computer Methods in Applied Mechanics and Engineering, 1994, 119(3/4): 355-370.
[25] Wang L K, Pereira N C, Hung Y T. Air Pollution Control Engineering[M]. New Jersey: Humana Press, 2004.
[26] 程林, 李兴兴, 唐炬, 等. 不同温度下含金属微粒的流动液体绝缘介质放电形成过程与机理分析[J]. 高电压技术, 2018, 44(9): 2917-2925.
Cheng Lin, Li Xingxing, Tang Ju, et al. Discharge process and its mechanism analysis in flowing liquid dielectric containing metal particles at different temperatures[J]. High Voltage Engineering, 2018, 44(9): 2917-2925.
[27] Cheng L, Soo S L. Charging of dust particles by impact[J]. Journal of Applied Physics, 1970, 41(2): 585-591.
[28] 申南轩, 苏子寒, 张远航, 等. 湿度对悬浮液滴荷电特性及离子流场特性的影响[J]. 电工技术学报, 2022, 37(13): 3422-3430, 3452.
Shen Nanxuan, Su Zihan, Zhang Yuanhang, et al. Influence of humidity on the charge characteristics of suspension droplets and the characteristics of ion flow field[J]. Transactions of China Electrotechnical Society, 2022, 37(13): 3422-3430, 3452.
Study on the Charge Calculation and Influencing Factors of Metal Particle Groups in Fluid-Electric Coupling Field
Abstract In the life cycle of power equipment, the insulating oil is easy to mix with various solid impurity particles such as metal and fiber, which will cause electric field distortion and insulation balance failure of equipment. Therefore, considering that compared with non-metallic particles, metal particles have a greater impact on partial discharge and arc breakdown of oil, this paper proposes a method to derive the charge of particles by analyzing the force model of metal particles on the basis of discrete particle model, and reveals the influence of electric field intensity, voltage type and flow velocity on the charge distribution of metal particles.
Firstly, the internal oil channel environment of power transformer was simulated and the experimental observation platform for particles in oil was built. Secondly, the force model of metal particles in the fluid electric coupling system was established combined with fluid dynamics. The formula for calculating the charge of metal particles under experimental conditions was derived through the formula. Thirdly, the particle image velocimetry (PIV) system was used to capture the cloud picture of particle swarm velocity and streamline, and the velocity and acceleration of metal particles were calculated through the streamline of particles and the finite difference method, so as to calculate the charge of particles, which was close to the charge of particles calculated by the traditional model. Finally, by changing the applied voltage, oil flow rate and voltage type, the charge value and distribution of metal particles in the oil flow were calculated and counted.
The experimental results show that when the flow rate of insulating oil is 0.15 m/s, the maximum charge of particles is 0.17 pC, and the proportion of particles with the absolute value of charge greater than 0.01 pC is 36%, while when the flow rate is 0.3 m/s, the maximum charge of particles is -0.13 pC, and the proportion of particles with the absolute value of charge greater than 0.01 pC is 29%, which may be due to the increase of horizontal drag force on particles when the flow rate of oil increases. The time of particles flowing through the electric field region is shortened. When the voltage is -10 kV, the maximum charge of particles is 0.05 pC, and the proportion of particles whose absolute value of charge is greater than 0.01 pC is 12%. When the voltage is -20 kV, the maximum charge of particles is 0.09 pC, and the proportion of particles whose absolute value of charge is greater than 0.01pC is 25%. When the voltage is -30 kV, the maximum charge of particles is 0.17 pC, and the proportion of particles whose absolute value of charge is greater than 0.01 pC is 36%. The acceptable explanation is that the increase of electric field intensity leads to the increase of collision probability between particles and electrodes. When the applied voltage is AC, the proportion of particles with the absolute value of charge greater than 0.01 pC is about 10%, and the maximum charge of particles is 0.03 pC.
Through the above analysis, it can be concluded that: (1) The maximum charge of particles is in the same order of magnitude as the traditional model, but the distribution curve of the charge proportion of particles is close to the Gaussian distribution. (2) With the increase of insulating oil flow rate, the movement time of particles in the electric field between electrodes is reduced, resulting in the reduction of the probability of particles colliding with electrodes in the same time interval, and the proportion of particles not colliding with electrodes is increased. (3) The velocity component of particles in the vertical direction increases, the collision between particles and electrodes becomes frequent, and the charge of particles generally increases. (4) When the applied voltage is AC, the particles with large charge account for less.
keywords：Particle image velocimetry, metal particles, insulating oil, liquid solid coupling, charge distribution
中图分类号：TM855
DOI: 10.19595/j.cnki.1000-6753.tces.231050
国家自然科学基金资助项目（51977170）。
收稿日期 2023-07-05
改稿日期 2023-09-13
张 宁 男，2000年生，硕士研究生，研究方向为绝缘介质特性以及电力设备绝缘结构仿真。
E-mail：zi1213123321456@stu.xjtu.edu.cn
贺 博 男，1976年生，教授，博士生导师，研究方向为高电压与绝缘技术领域的基础理论、电力设备绝缘性能分析与绝缘结构优化设计、复合电介质形态结构与性能关系等。
E-mail：hebo@mail.xjtu.edu.cn（通信作者）
（编辑 李 冰）