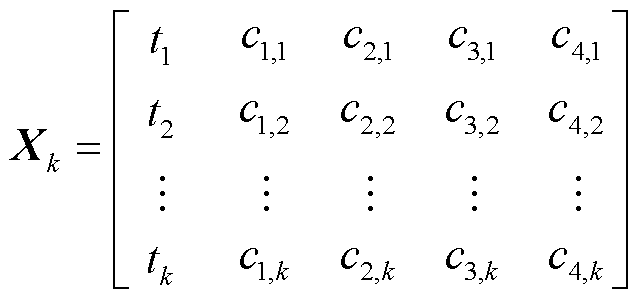（1）
摘要 高质量传感数据是驱动新型电力系统数字化和智能化发展的基础，而由于传感器性能退化、传输中断或其他干扰因素，数据时常出现错误和异常值，造成数据利用率低等问题。针对在役电力变压器油中溶解气体在线监测数据，该文提出了基于COPOD、孤立森林（IForest）与Grubbs的联合方法提升油中溶解气体数据的价值。首先，通过COPOD和IForest筛选出包含离群点的数据集，再采用Grubbs对其进行检验，有效识别离群值。进一步地，采用掩码方式优化训练Transformer神经网络模型，填补空缺值重构油中溶解气体数据序列。在相同气体数据序列上，所提算法正确识别点数、正确识别离群点数和受试者工作特征曲线平均面积相比于传统K-近邻算法分别提升了3.5%、29.4%和5.0%。对于数据填补，对比双向缩放算法，填补后的数据与实际数据的方均根误差均值为7.29 μL/L，平均绝对误差均值为2.7 μL/L，性能分别提升了9.7%和9.2%，有效地提高了数据的质量和利用率。最后，通过11台500 kV变压器油中溶解气体数据分析，有力支撑了变压器状态评价和设备数字化管理。
关键词：电力变压器 油中溶解气体 联合检测方法 离群点检测 数据重构技术
作为电力系统中最重要的设备之一，高电压等级油浸式电力变压器的健康状态对电网的安全可靠运行有着重要意义。油中溶解气体分析（Dissolved Gases Analysis, DGA）作为变压器评估绝缘状态的关键指标，尤其在设备数字化管理和状态检修[1-2]的趋势下，其数据质量和积累对变压器健康指数分析、设备管理甚至智能电网建设[3-4]具有重要价值。
变压器DGA数据一般通过传感器在线获取，但在线监测设备运行过程中的数据质量难以保证，主要原因包括：①传感器性能退化：传感器由于长期工作不可避免地会出现老化，导致检测精度下降；②通信故障：数据传输过程中可能遭遇传输系统故障、停电等情形，导致通信中断或传输错误，采集到大量零值或离群值；③其他因素干扰：高温、电磁辐射等带来的干扰，会影响采集数据准确度；④数据误差大：行业标准通常允许的数据范围在±15%之内即可，使数据本身就带有一定的随机性。因此，DGA数据中难免出现离群值、空缺值等，导致无法充分地发挥在线监测数据的作用[5-6]，降低了基于数据驱动的变压器状态评价和寿命评估的效果，甚至出现错误的评价结果，影响设备的运维和检修，带来资源浪费和经济损失。
DGA本身作为最有效的检测技术[7]，如何提高DGA的数据质量而广受关注。离群值识别是DGA数据质量提升的关键环节，目前主要采用统计参量、基于靠近关系的聚类分析和时间序列的机器学习三种方法[5]。基于统计学的典型离群值识别方法有箱型图、直方图[8]、盒图、Grubbs检验[9]等，此类方法简单但不适用于高维空间和分布模型未知的数据集。在基于靠近关系的聚类分析方法中，K-means算法[10]被广泛使用，其可实现大规模数据离群值的快速检测，但对初始值较为敏感，且无法给出离群值具体位置；Liu Hang等[11]采用基于密度的聚类（Density-Based Spatial Clustering of Applications with Noise, DBSCAN）算法，结合产气速率构建了二维序列用于聚类分析，可以实现有效的离群点识别，但聚类半径需要人工确定。在机器学习的方法研究中，严英杰等[12]采用自回归滑动平均（Autoregression Moving Average, ARMA）模型实现离群点的识别，该方法可以保留序列中的有用信息，但对数据的平稳性、线性程度有一定的要求；相比而言，支持向量机（Support Vector Machine, SVM）对非线性数据处理能力更强，但其对参数较为敏感，可通过智能寻优算法改进SVM[13]，提高其泛化能力，然而仍存在计算复杂、训练时间长等问题。总体而言，在离群点检测研究方法中，多数检测算法仍属于监督或半监督学习，依赖人工调参，泛化能力弱，变压器个体差异性难以体现。
DGA离群点的剔除或原有空缺值的存在会带来时间序列不连续的问题，影响数据分析，有必要填补空缺值进一步重构数据[14]。关于空缺值的填补，可以采用局部平均值插值、线性插值[15]、回归分析[16]等拟合进行插值，但人为改变了原始数据的分布。为避免这一影响，张若愚等[17]提出了基于马尔可夫状态转移模型的空缺值填补方法，但其填补精度依赖区间划分步长，空缺值连续时，评价状态也恒定。另一类方法是采用时间序列神经网络填补空缺值，如递归神经网络（Recurrent Neural Network, RNN）[18]、生成对抗式神经网络（Generative Adversarial Network, GAN）[19]等，其核心是采用预测值填补空缺值。例如，文献[20]采用一种基于自注意力的生成对抗式网络（Self-Attention Generative Adversarial Networks, SA-GAN）来填补电力设备在线监测的缺失数据。神经网络虽然在时间序列填补中有着优秀的表现，但对历史数据的质量要求较高，需要对数据预先进行清洗，以确保模型的训练和预测效果。因此，亟待深入开展DGA数据的高质量清洗与重构，从而有效支撑电力变压器绝缘状态的差异化准确评估。
针对现场实际DGA在线监测数据质量差且离群点识别方法泛化能力弱的难题，本文提出基于COPOD（Copula based outlier detection）、孤立森林（Isolation Forest, IForest）和Grubbs的联合检测方法，在保留有效数据的前提下，实现在线监测数据离群点的自动识别；进一步对剔除离群点后的在线监测数据，采用掩码训练的Transformer模型进行DGA空缺值填补，实现在线监测数据质量的提升；最终将生成的仿真数据与实际变压器DGA数据进行分析，并与现有成熟方法对比，论证了所提方法的有效性和先进性。
本文针对11台长时间在役运行的500 kV电力变压器构建了DGA数据库，分别来自五个省份（江苏、浙江、河北、四川、山东），选取记录条目较多的H2、总烃（Total Dissolved Combustible Gases, TDCG）、CO、CO2作为分析对象。
为保证目标序列的顺利构造以及后续分析的一致性，首先对原始数据进行以下处理：①如果一天内存在多条监测数据，取非零值的平均作为对应的记录值；②对于超范围值，直接通过3σ法则删除并标记为空缺值；③对于缺失值，用缺失前后的有效值进行拼接并标记。经过上述处理后，可以将变压器对应的气体含量序列Xk表示为
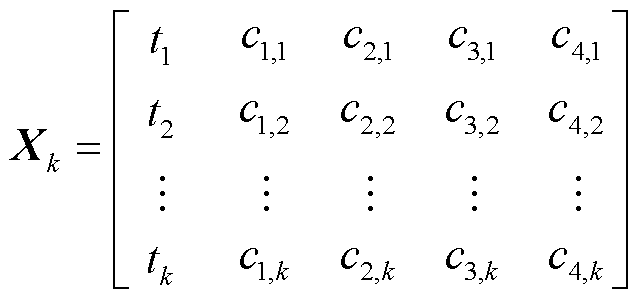（1）
式中，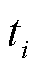
为监测点i对应的时间，i=1, 2,…, k，k为总监测点数，且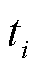不连续；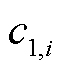
、
、
、
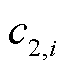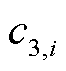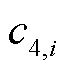分别为ti时H2、TDCG、CO、CO2所对应的监测记录。
由于DGA的趋势性，对原始序列直接进行离群值检测，识别出的离群点会集中在序列首尾两端，使检测算法无效化。同时，若离群点连续出现，则会相互遮掩，导致检测的结果准确率较低。
为解决上述问题，本文引入气体产气速率作为辅助变量，在每个监测点构建气体含量-正向产气速率（r+）-逆向产气速率（r-）三维向量，构建方法为
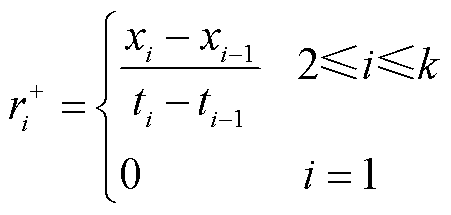（2）
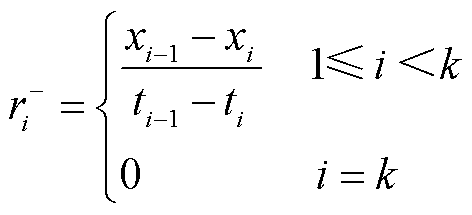（3）
式中，xi为气体含量第i个监测点的监测数据；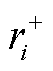
和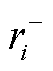
分别为第i个监测点对应的正向产气速率和逆向产气速率。设气体含量原始序列经过扩展后，形成的目标矩阵为Cj（j=1, 2, 3, 4），可表示为
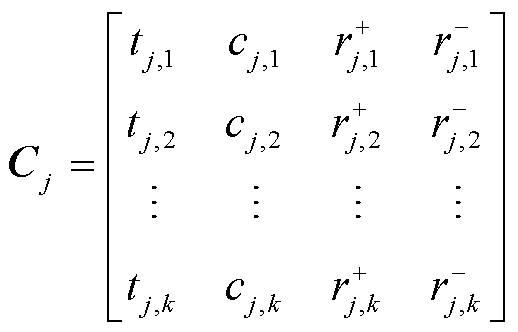（4）
式中，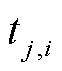
、
、
、
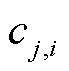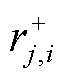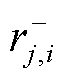分别为第j种气体的第i条记录点对应的时间、气体含量、正向产气速率和逆向产气速率；
即为在监测时间点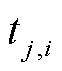时构建的三维目标向量。
由于直接对Cj的全部数据进行离群点检测会出现局部特征被掩盖现象，故本文采用滑动窗的方式对Cj进行检测，以保证局部特征的有效利用，具体检测流程示意图如图1所示。设序列中有1个离群点，以长度为6、滑动步长为3的滑动窗进行检测。通过滑动窗的移动，在每个数据点上可以得到两次检测结果，两次结果的交集认定为离群点。
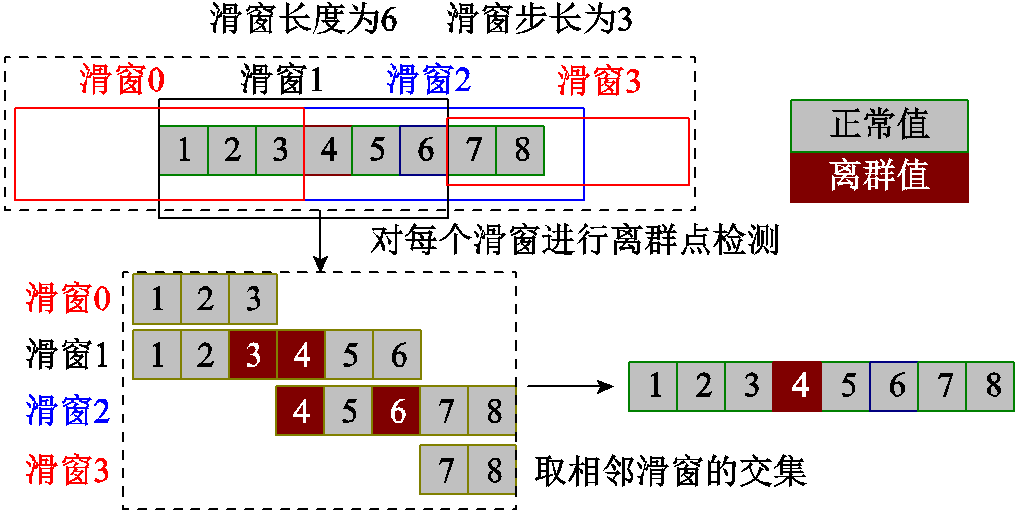
图1 滑动窗识别离群点流程示意图
Fig.1 Outlier detection process by sliding window
在实际应用中，由于离群点检测算法的原理和主要用途不同，在检测上存在不同的优缺点。COPOD算法的优点是可以处理多维、高维和大规模数据集，但对于密集数据集的检测效果较差；IForest算法对于密集数据集的检测效果较好。因此，可将COPOD和IForest算法结合优势互补，从而更准确地检测离群点。然而COPOD和IForest算法的实际检测结果为异常分数，需要在异常分数的基础上人工设定阈值进行离群点判断，阈值的大小会影响最终的检测效果。因此可以结合COPOD和IForest两个算法，通过设定较高阈值标记出较多的离群点，对目标向量进行初步检验。
由于设置了较高阈值，初步检验出的离群值中混杂着部分正常DGA数据。为了能够进一步提高离群值识别的准确性，引入了Grubbs检验。Grubbs检验是一种用于检测离群值的统计方法，其灵敏度高、适用性广，但在单次检验中只能检测一个离群值。当数据集很大时，存在离群值较多，由于DGA具有一定的趋势性，若对所有数据集进行检验，两端的值容易被判断为离群点，带来较大的误差，并且Grubbs检验在小样本中的表现性能更好。因此，先通过初步检验获得一个小的可疑离群点数据集；再通过Grubbs检验对其进行二次检验，将误识别的正常数据从检测结果中排除；最终将离群点剔除后再通过Transformer神经网络进行填补。本文提出的离群点检测和数据重构流程如图2所示。
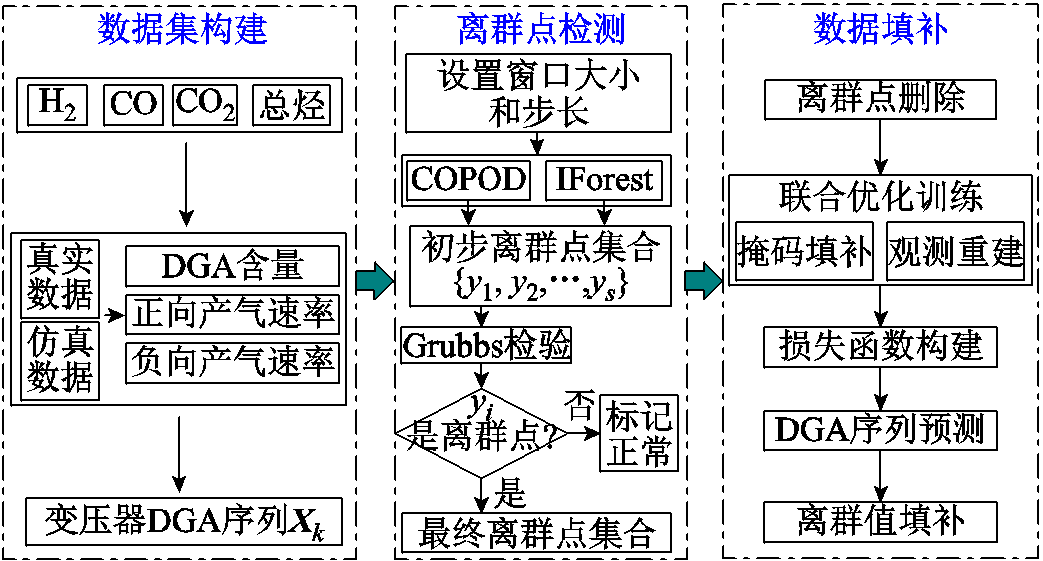
图2 基于多方法联合的离群点检测和数据重构流程
Fig.2 Outlier detection and data reconstruction process based on multi-method joint
COPOD算法是一种基于概率的检测方法，其理论基础为Copula函数[21]。DGA数据是具有相关性的随机变量，而Copula（连接函数）是一类将随机变量边缘概率分布与联合概率分布建立联系的函数，表示多个随机变量之间的关联或依赖性[22-23]，因此可以使用Copula函数对DGA数据进行分析。然后通过估计每种油中溶解气体数据的尾端概率，便可以对异常情况进行评估。
IForest算法[24]是基于树结构的离群点检测方法，其基本思想是通过构建一棵随机树来检测离群点。IForest算法的优点是无监督、效率高[25]，可以快速处理高维数据和大规模数据集，并且对于密集数据集的检测效果较好，其基本流程可参考文献[26]。
Grubbs检验由F. Grubbs提出，又称为最大归一化残差测试，是一种统计测试方法，用于检测假设的单变量数据集中的异常值，可以应用于标准差未知时的离群值检测[27-28]。在一组DGA数据中，当某个气体数据的残差与标准差的比值大于Grubbs临界值时，可以判断该DGA数据存在较大误差，将其视作“可疑值（偏离值）”，并从数据集中删除该异常值，然后重新计算期望方差或迭代测试直到没有检测到异常值。
通过离群值的识别与剔除，经过处理的DGA数据序列中包含一定的缺失值，影响设备状态评价和基于数据驱动的DGA故障预测分析，为此本文采用Transformer神经网络模型进行数据填补。
2017年，Google公司首次提出Transformer模型[29]，该模型以自注意力机制取代了常见的RNN网络，使得Transformer具备并行训练的能力。
Transformer最初的应用场景是语言翻译任务，而时间序列同样属于序列的一种，因此在时间序列数据预测上，Transformer也具有不俗的表现。Transformer模型的结构如图3所示，该模型包括编码模块和解码模块两个部分[30]。
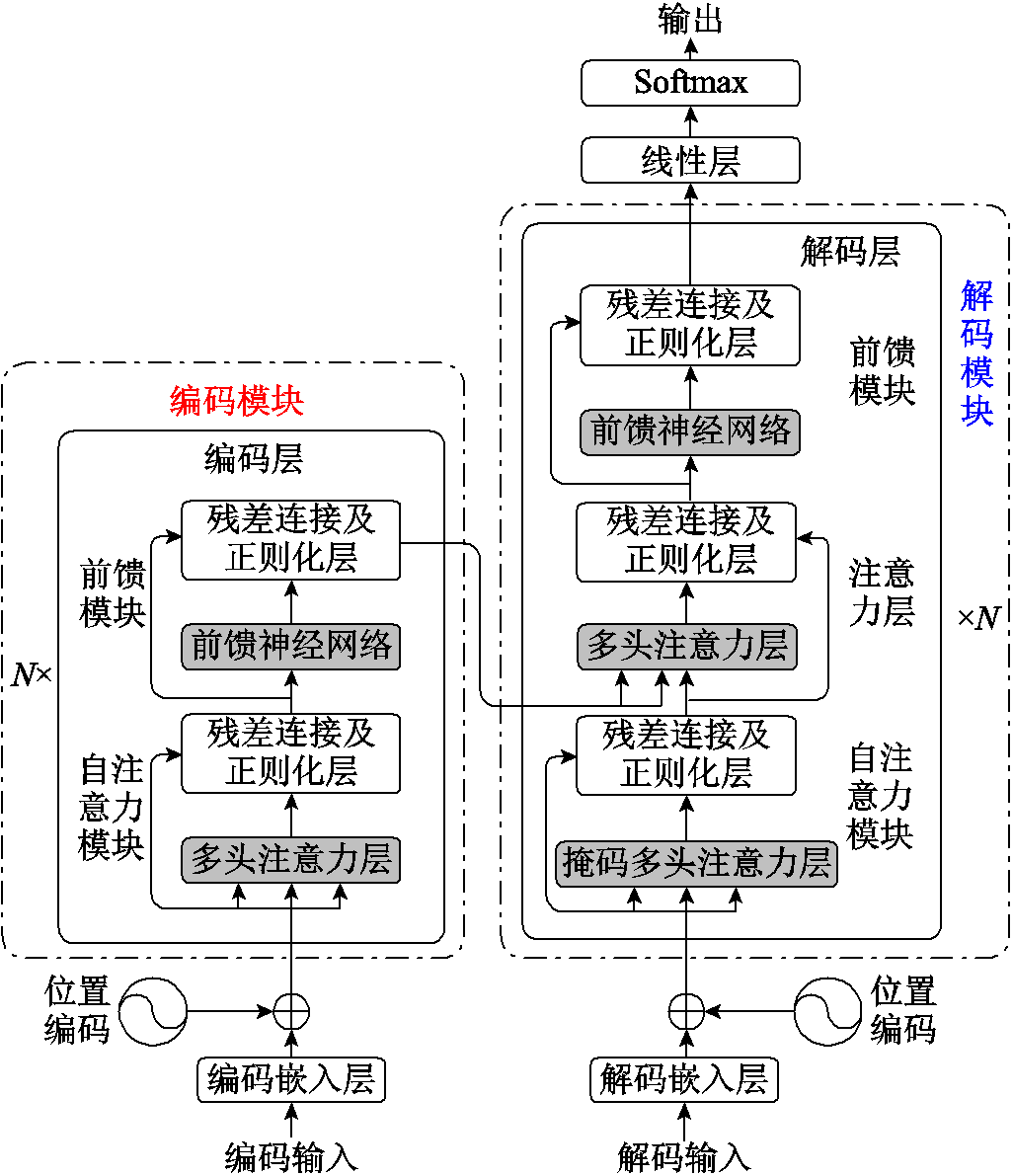
图3 Transformer神经网络模型基本结构
Fig.3 Basic structure of Transformer neural network
可以看出，编码模块和解码模块均可以视为N个相应的编码层/解码层堆叠形成。其中，编码层包括自注意力模块和前馈模块两个部分，而解码层相较于编码层多了一层注意力层。编码层和解码层中均包含多头注意力层，多头注意力层以自注意力机制为基础。多头注意力机制和自注意力机制如图4所示。
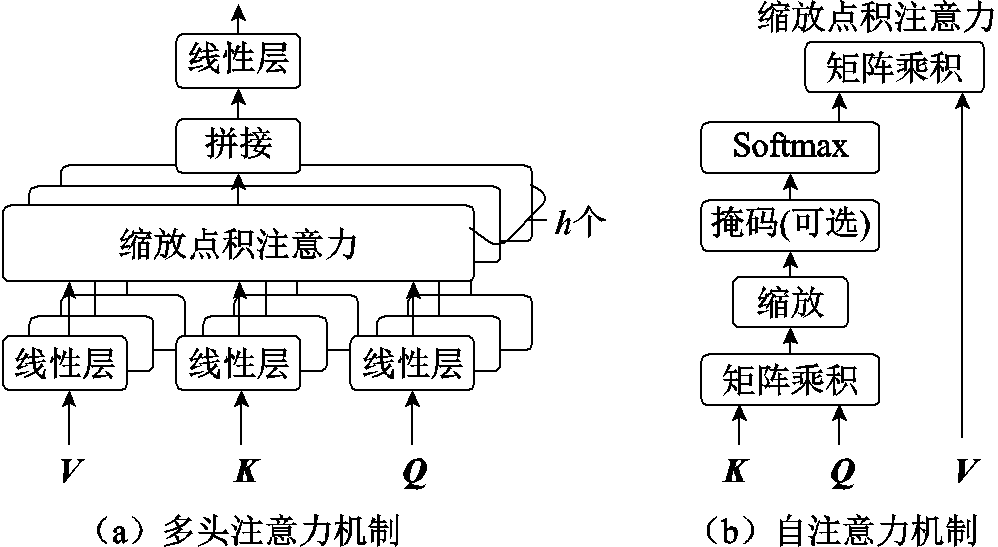
图4 多头注意力机制与自注意力机制
Fig.4 Multi-head attention and self-attention mechanism
为有效提升Transformer模型在DGA序列插值上的性能，本文采取两项优化训练任务[31]：掩码填补（Masked Imputation Task, MIT）和观测重建（Observed Reconstruction Task, ORT）。设目标DGA序列X={x1, x2,…, xn}为一维序列，则可以根据X得到实际标记序列M={m1, m2,…, mn}为
（5）
类似地，通过在X中随机标记，得到人工空缺值标记序列I={i1, i2,…, in}为
（6）
进而，可以将训练任务描述为：
1）掩码填补（MIT）。根据I将X中的数据进行二次标记，模型填补结果中I对应的数据重构误差应尽可能地小，此时，损失函数可以表示为
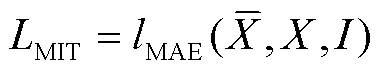（7）
式中，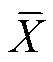
为模型填充后的完全序列；lMAE(·)为平均绝对误差（Mean Absolute Error, MAE）损失函数。
2）观测重建（ORT）。将模型填充得到的完全序列中的标记值，与实际标记序列M进行对比，其填补数据的重构误差也应该尽可能地小，对应的损失函数可以表示为
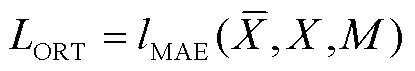（8）
设填充序列为xest={xest1, xest2,…, xestn}，目标真实序列为xtar={xtar1, xtar2,…, xtarn}，标记序列为mmask= {mmask1, mmask2,…, mmaskn}，MAE损失函数lMAE(xest, xtar, mmask)的表达式为
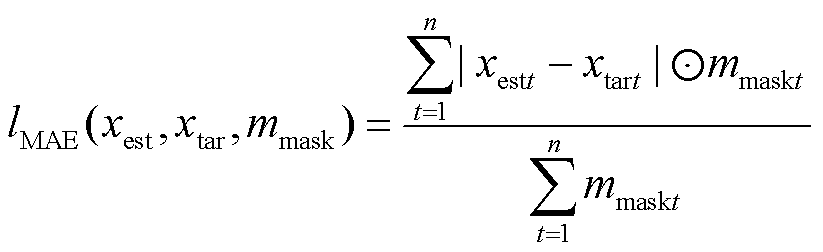（9）
式中，
代表序列中对应元素相乘。
针对DGA含量插值，采用的损失函数定义为
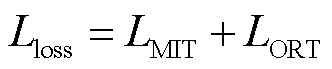（10）
在训练神经网络的过程中，通过上述过程人为地制造空缺值并将其部分遮掩构造损失函数，不断减小反向误差，达到提高模型预测精度的作用。
本文采用11台500 kV在运变压器在线监测数据作为分析对象，变压器型号为ODFS-334000/500，包含在线监测得到的CO、CO2、H2、总烃四种气体数据，共计18 495条，采集时间间隔不等，约为1条/天。同时，为证明所提出的检测方法的有效性和先进性，根据真实数据的统计特征生成了模拟数据集，在模拟数据集上验证离群点识别和空缺值填补算法的性能。
Grubbs检验是在正态分布的假设下开发的，但是在实践中，它可以用于少数偏离正态分布的样本。已有研究分析表明DGA数据分布服从威布尔分布[32-33]，而威布尔分布和正态分布之间存在着相应的转换关系。
Q-Q图（Quantile-Quantile plot）是一种用于检验数据是否服从某种特定分布的图形方法。它通过将数据的分位数与理论分布的分位数进行比较，以帮助科研人员确定数据是否符合某种分布。为了避免单台变压器数据的随机性，采用11台变压器的所有在线监测数据，分别绘制各个气体含量的Q-Q图，如图5所示。
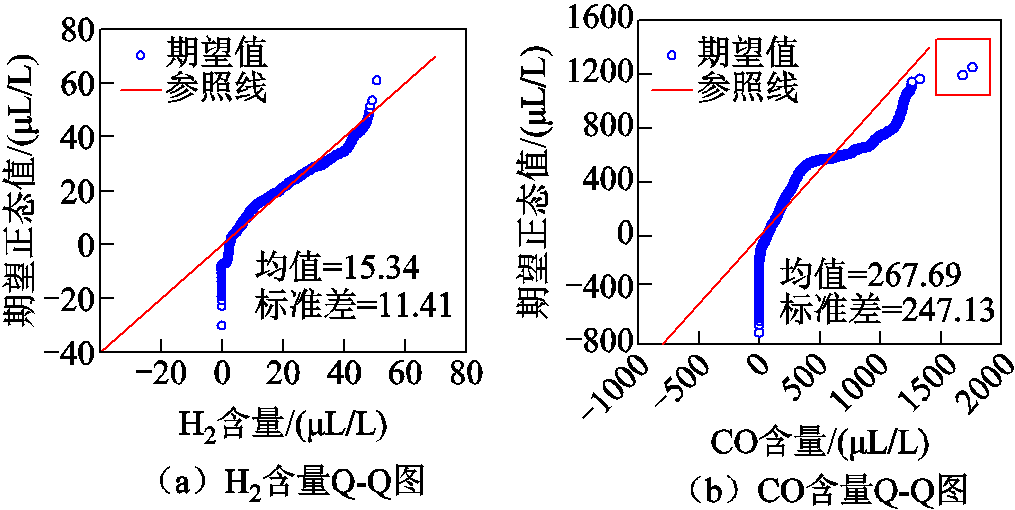
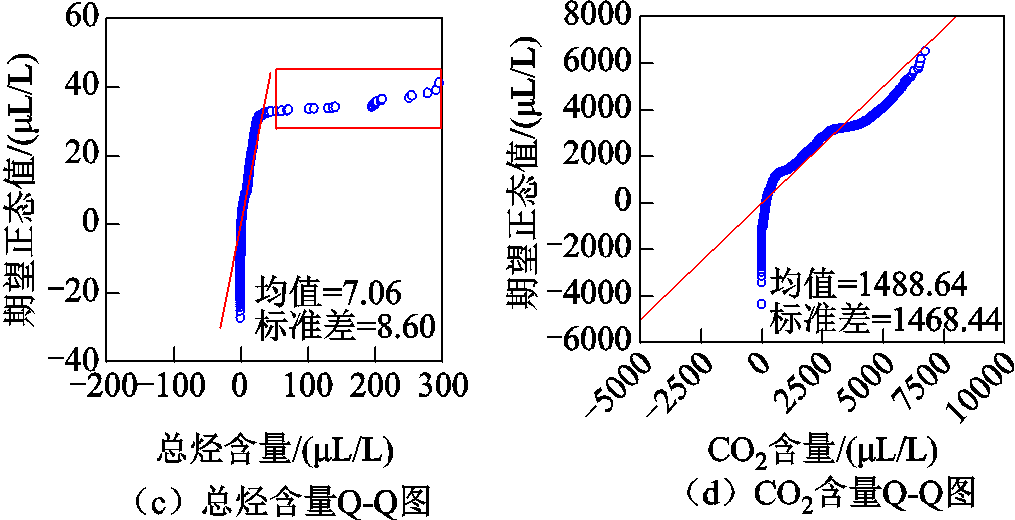
图5 所有变压器油中溶解气体含量Q-Q图
Fig.5 Q-Q plot of dissolved gas in all transformer oils
由图5可见，各气体DGA数据分布与参照线重合或者平行，证明了DGA数据较为符合正态分布。为了能更加直观地表示DGA数据的分布情况，将所有气体含量以及对应的正向产气率绘制成气体含量-正向产气率散点图，如图6所示。
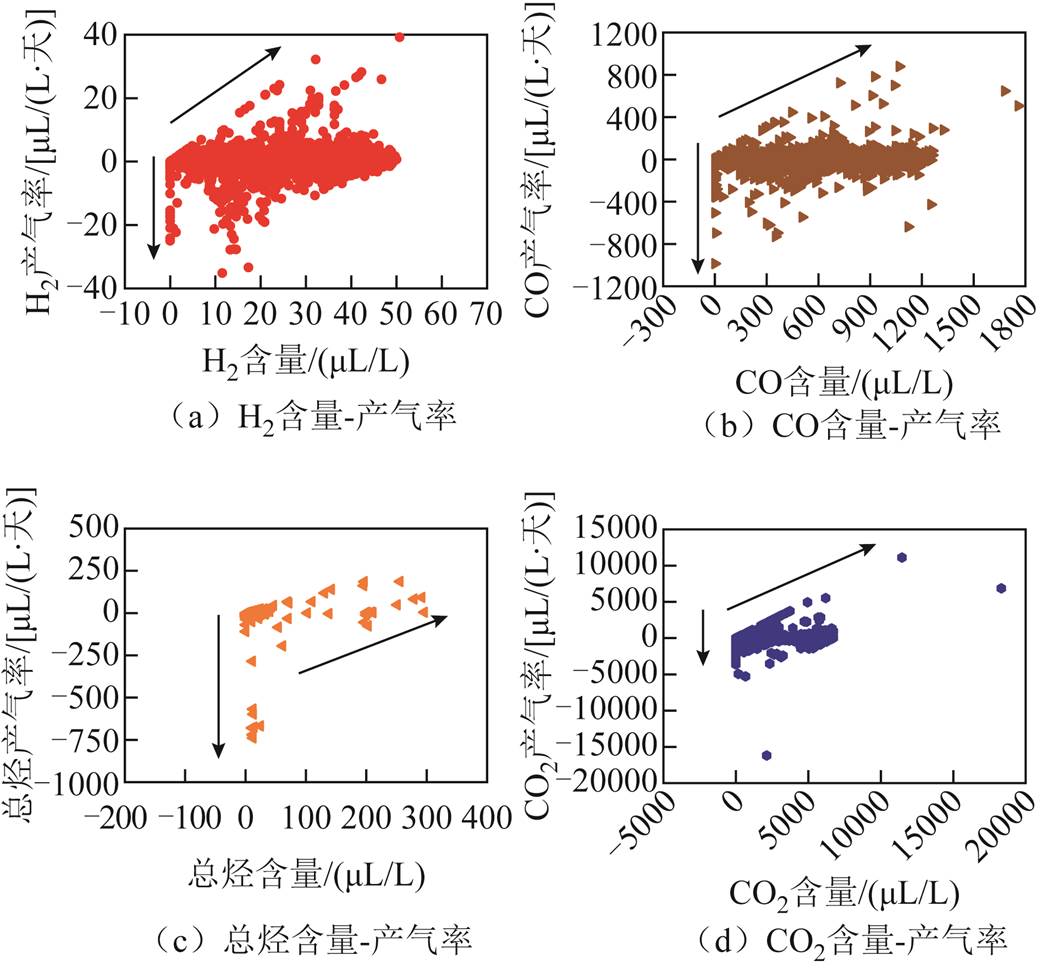
图6 所有变压器DGA气体含量-正向产气速率散点图
Fig.6 DGA content-forward gas production rate of all transformers
从图6可以看出，所有气体的正向产气率均值集中在0 μL/(L·天)附近，即正常运行中气体含量的总体趋势是保持不变的。而在气体含量-正向产气率散点图上出现了明显的两条线（如图6中箭头所示）：①垂直于气体含量为0 μL/L的直线；②以45°向右上延伸的直线。原因是在DGA序列中存在零值，这些零值对应的产气速率各不相同，体现在散点图上为垂直于气体含量为0 μL/L的直线；而这些零值之后的正常值点，对应的产气速率在数值上与其含量相等，体现在散点图上为以45°向右上延伸的直线。
为方便后续说明，本文从11台变压器中选取了一台变压器T1作为实际案例进行分析。变压器T1于2018年8月投运，运行1 085天，总记录数据为1 055条，数据长度适中；且变压器T1的离群值较为明显，易于对比离群点识别及空缺值填补前后DGA数据的差异。
所选变压器在线监测的气体含量原始数据如图7所示，对应的气体含量-正向产气率散点图如图8所示。可以看出，该变压器所有DGA含量均呈现上升的趋势，同时存在着部分明显的“突刺”，其中CO2离群值最为明显，体现在散点图上为数据点明显偏离主体部分。
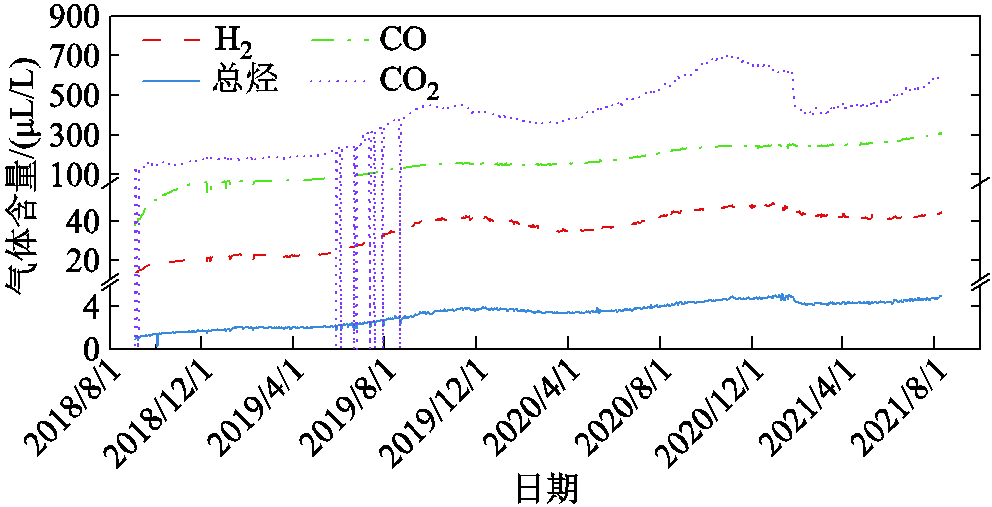
图7 变压器T1油中溶解气体含量实际数据
Fig.7 Field data of DGA content in Transformer T1
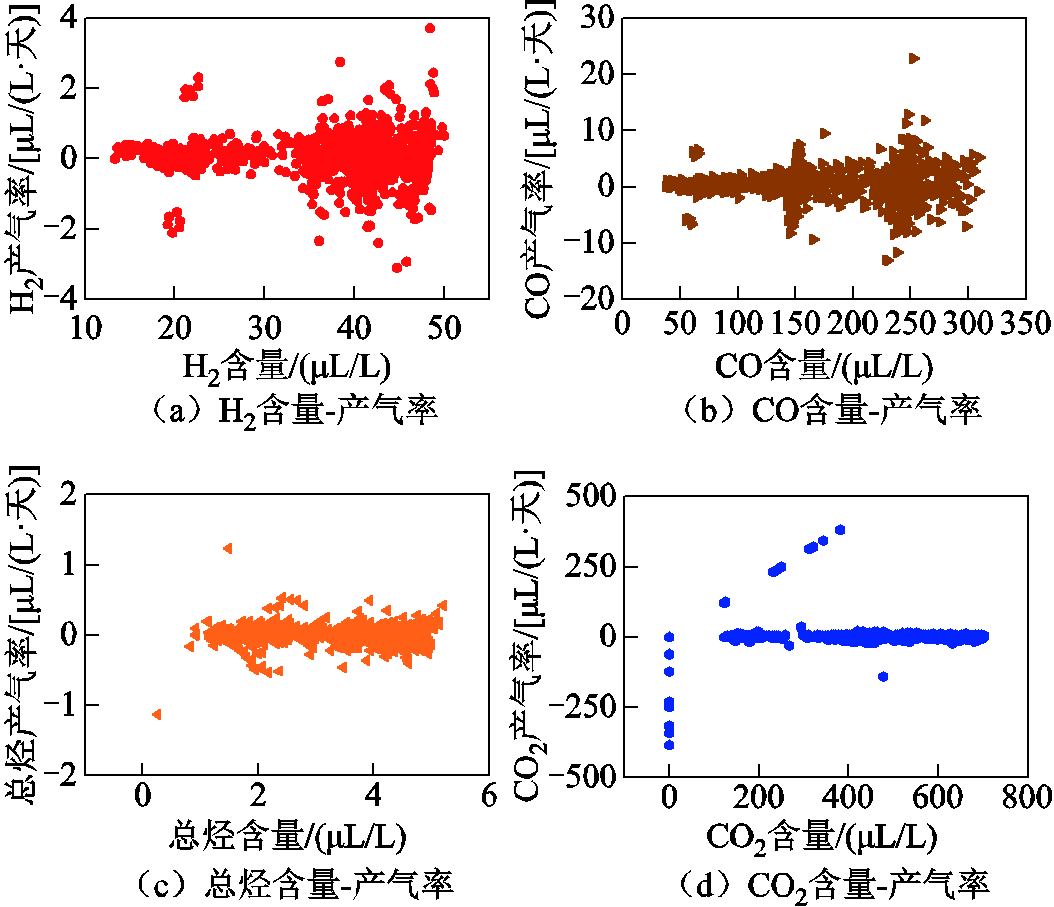
图8 变压器T1 DGA气体含量-正向产气速率散点图
Fig.8 Scattering plot of DGA gas content- forward gas production rate in selected Transformer T1
由于实际DGA数据没有离群值标签，难以验证算法的准确性。因此，本文模拟DGA数据统计特征生成了10组带离群值标签的数据，每组数据长度均为200，这10组数据的生成方式如下：
1）设定数据点总数n=200，污染率c=0.2。
2）设定第一组正态分布的期望μ1和标准差σ1，生成200个随机数，即为序列X1。
3）对序列X1求累计和，得到基准序列X2。
4）设定第二组和第三组正态分布的期望μ2=μ3=0和标准差σ2＞5σ1、σ3＞10σ1分别生成n1和n2个随机数，记为X1,1和X1,2，使得n1+n2=nc=40。
5）将X1,1和X1,2随机叠加至X2，记录相应的位置，标记为离群值点，得到生成的气体含量序列X和离群值标签序列L。
6）对序列X和X的逆序列X -做差分运算，得到产气率序列x和逆向产气率序列x-。
生成的DGA含量和产气率散点图（其中1组）分别如图9a和图9b所示。为说明所生成的数据的统计特征，绘制了相应的Q-Q图，如图9c所示。可以看出，数据在中间部分平行于参考线且主要部分均处于上下限之间，而两端偏差较大，与实际DGA分布规律图5相似，能够模拟DGA数据用来验证算法的可行性和准确性。
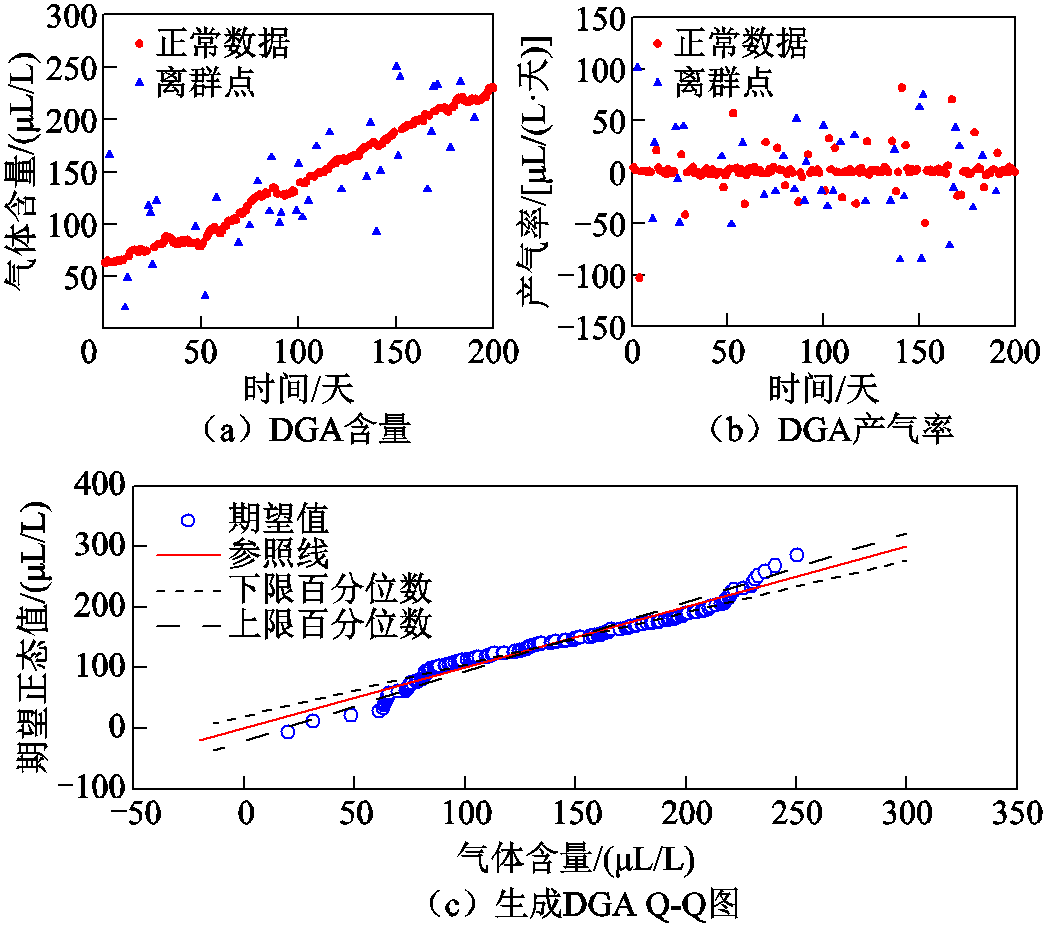
图9 生成数据的气体含量图
Fig.9 Gas content maps of data generated
为验证本文提出离群点检测流程在DGA数据离群值检测上的有效性，本文对比了常见的离群点检测算法见表1。
表1 本文所选用于对比的检测算法
Tab.1 The algorithm used for comparison in this paper
模型名称模型缩写污染率 基于连接函数的离群点检测COPOD0.2 孤立森林IForest 主成分分析PCA 基于聚类的本地异常因子CBLOF
（续）
模型名称模型缩写污染率 K-近邻KNN0.2 基于角度的离群点检测ABOD 轻型异常在线检测器LODA 支持向量机SVM
对于不同算法的参数设置，由于IForest仅需要确定决策树个数，其太小容易欠拟合，太大不能显著提升模型识别离群点的准确率，本文选择经验数值20。对于COPOD和IForest算法还需要确定阈值，均设定为较高的0.2；设置滑动窗口为90，通过COPOD和IForest算法得到可疑数据集，由于滑动窗口限制了可疑数据集的数量，其数量大小一般为几十个，能够满足Grubbs算法的使用条件，也能够体现数据分布的整体规律。
为量化分析在不同情况下不同算法的性能，本文采用三个指标作为评价标准：①正确识别的数据点数，包括正常数据和离群点；②正确识别的离群点数；③受试者工作特征（Receiver Operating Characteristic, ROC）曲线所围成的面积（Area Under the Curve, AUC）。对检测性能进行对比，结果如图10～图12所示。
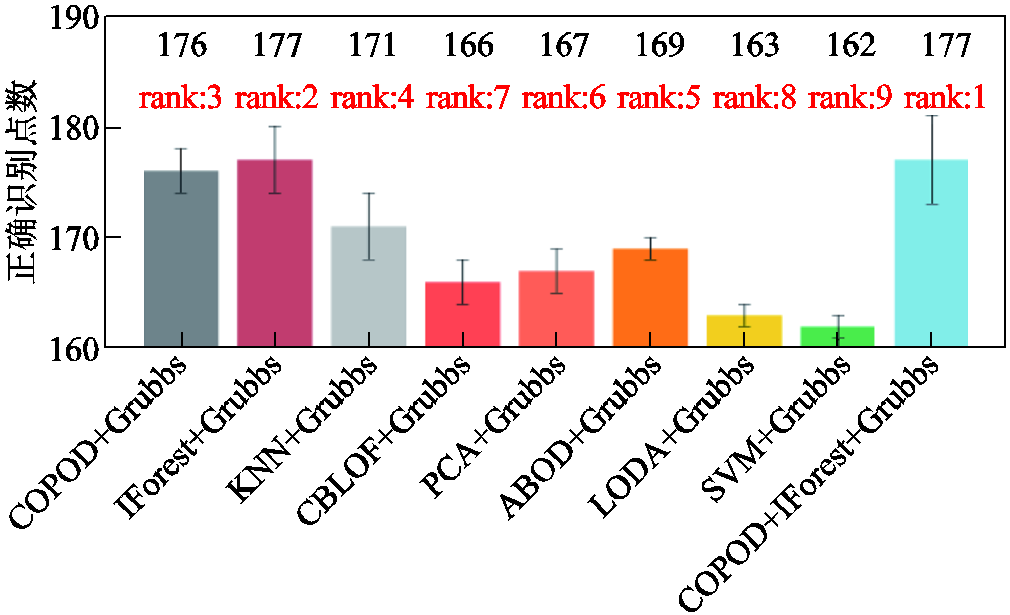
图10 正确识别的数据点数排名
Fig.10 Rank of correctly identified data spot
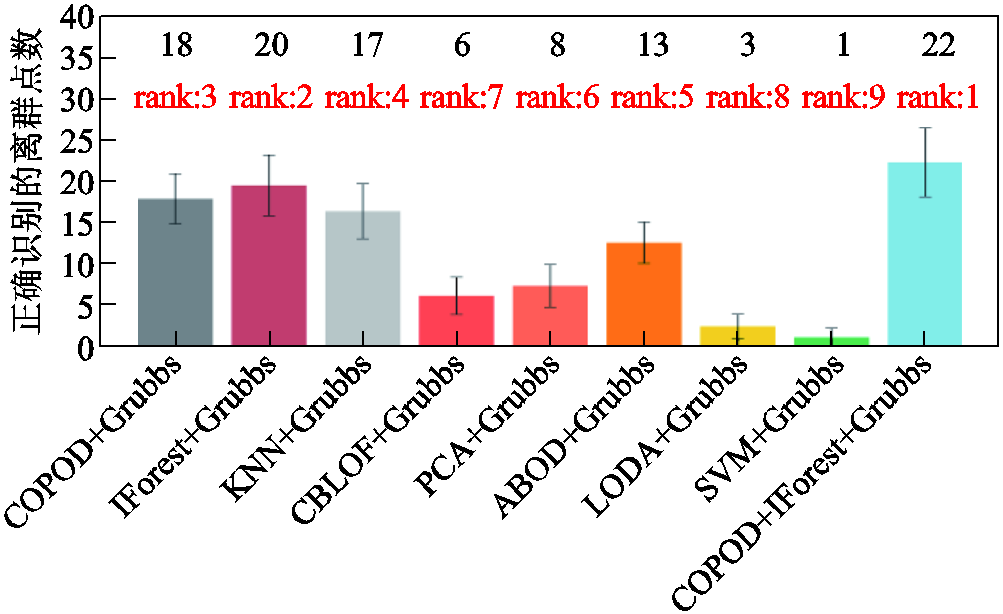
图11 正确识别的离群点数排名
Fig.11 Rank of the number of correctly identified outliers
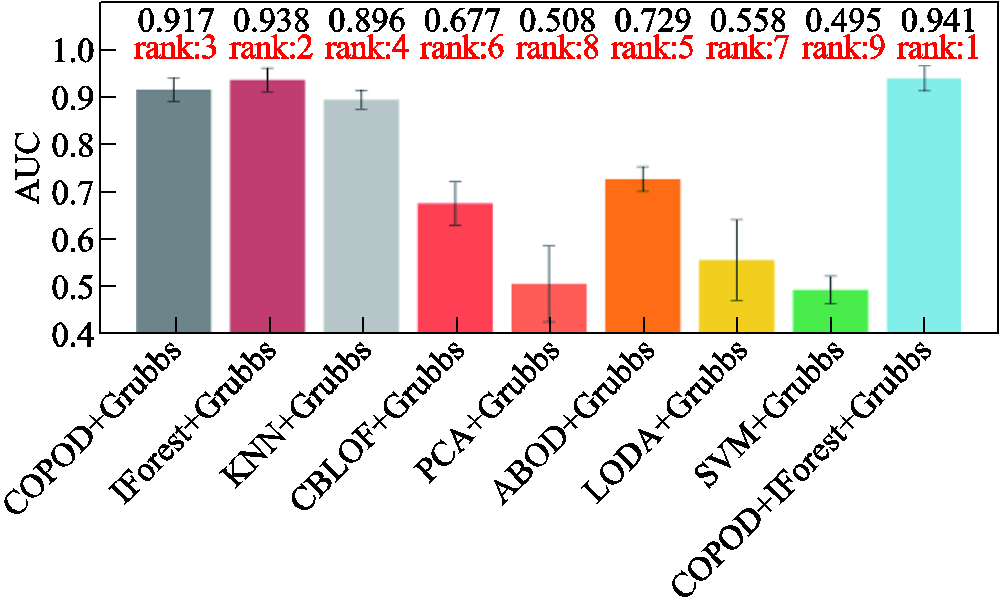
图12 AUC大小排名
Fig.12 Rank of AUC
本文方法在10组生成数据上正确识别的数据点数平均值为177，与IForest+Grubbs相当，但正确识别的离群点数平均值22优于IForest+Grubbs的20。如图12所示，本文方法的AUC为0.941，相比于排名第二的IForest+Grubbs方法提高了0.003；相比于常见的KNN算法，所提出算法的正确识别点数、正确识别离群点数、ROC曲线平均面积分别提升了3.5%、29.4%和5.0%。综上所述，在所有对比模型中，本文所提出的DGA离群点检测算法在正确识别点数、正确识别离群值点数以及AUC排名上都有着优秀的性能表现，提高了离群点检测的性能。
传统KNN和PCA算法的时间复杂度都服从幂函数，随着样本量的增加，易出现梯度爆炸的问题。而IForest算法不需要计算距离或密度度量，也不需要构建完全的模型，具备线性复杂度，复杂度相对较低，适用于实际生产中较大规模的数据。因此本文所提的联合方法时间复杂度不高，拓展了模型的普适性，有利于实际工程的应用。
为说明本文所提出算法的空缺值填补性能，采用KNN、链式方程多重填补（Multiple Imputation by Chained Equations, MICE）、双向缩放（Bidirectional Scaler, BiScaler）[34]、时间序列的双向递归插补（Bidirectional Recurrent Imputation for Time Series, BRITS）[35]方法进行对比。为验证各模型空缺值的填补性能，采用上述的数据生成流程，生成10组数据不包含离群点的数据，每组数据长度为3 000，并随机标记其中500个数据为空缺值。
生成的其中1组数据的局部数值如图13所示。可见生成的气体数据处于一定的趋势下并带有随机的波动，比较符合实际变压器DGA的变化规律。
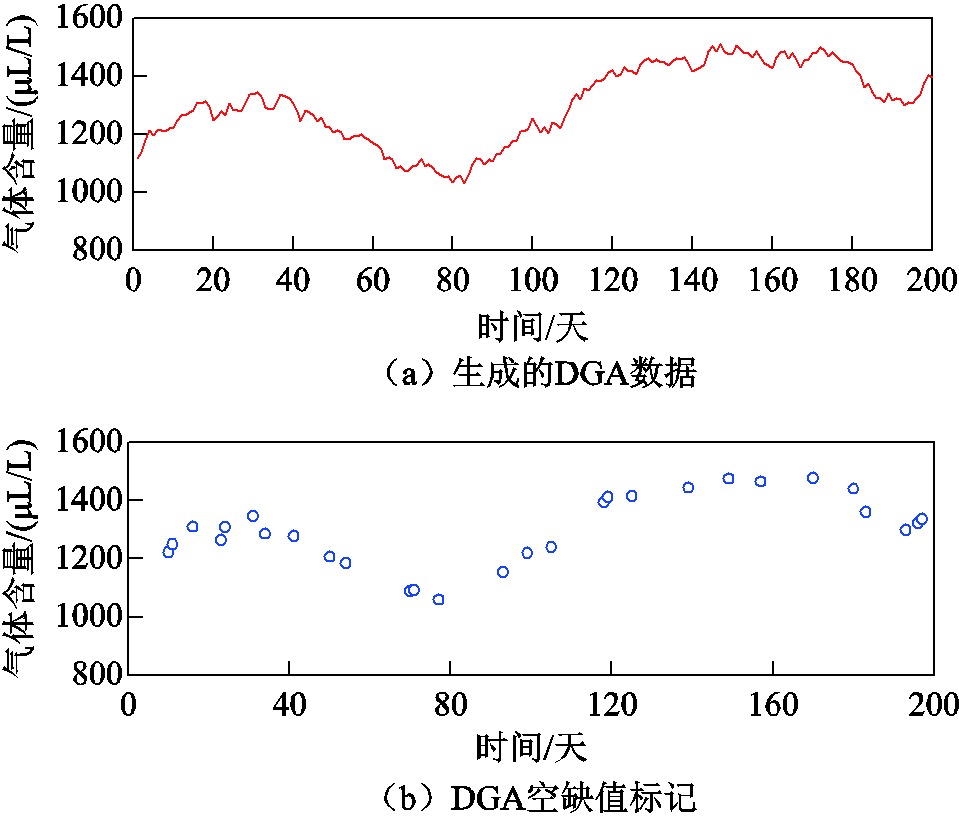
图13 所生成的数据图概览
Fig.13 An overview of the generated data graph
对于填补结果，采用方均根误差（Root Mean Square Error, RMSE）均值和平均绝对误差（MAE）均值作为评价指标，结果分别如图14和图15所示。可以看出，在生成的10组数据集上，Transformer模型的填补后数据与实际数据的方均根误差均值为7.29 μL/L，平均绝对误差均值为2.66 μL/L，与BiScaler算法对比，性能分别提升了9.7%和9.2%，填补效果最好。
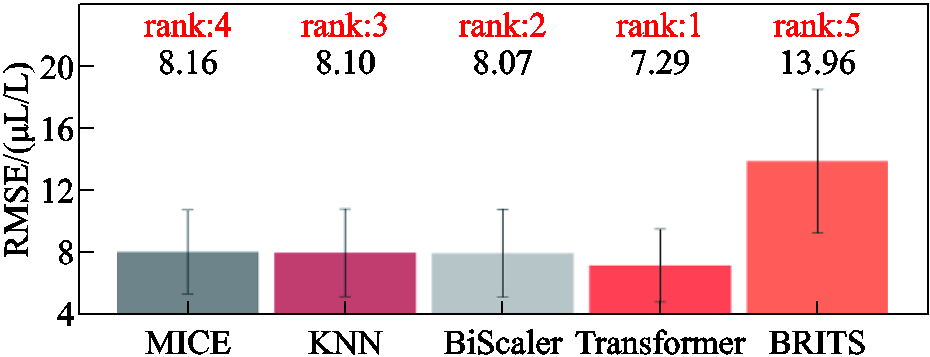
图14 各模型在10组数据上RMSE均值对比
Fig.14 The mean RMSE values comparation of each model on 10 groups of data
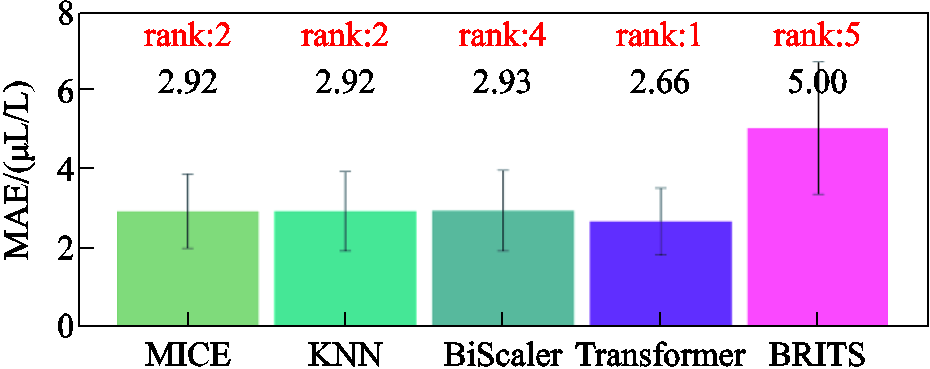
图15 各模型在10组数据上MAE均值对比
Fig.15 The mean MAE values comparation of each model on 10 groups of data
生成的某组DGA数据在局部（2 400～2 500天）的数据填补情况如图16所示。从整体上空缺值的填补情况来看，Transformer模型填补与实际气体数据最为接近，其误差最小，准确度最高。
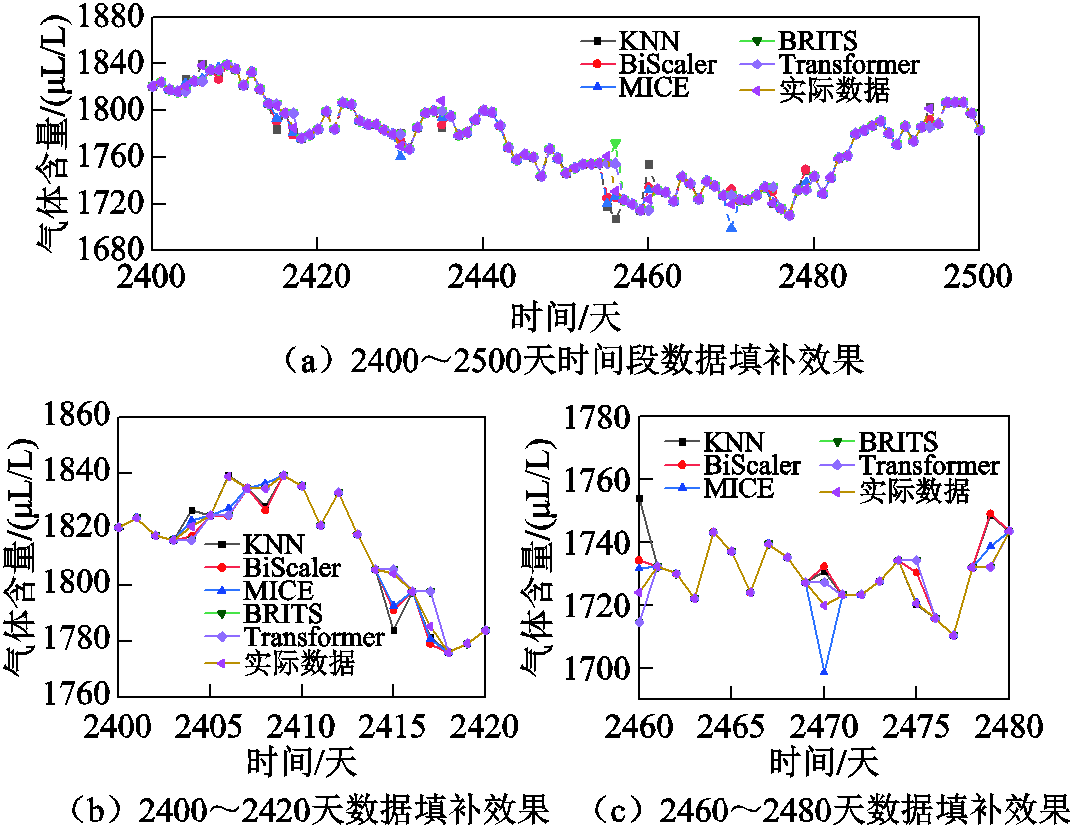
图16 生成数据中某段数据填补效果对比
Fig.16 Comparison of data filling effect in generated data
以变压器T1的DGA数据为例，其气体空缺值填补后序列如图17所示。在完成空缺值填补后，仍存在少部分偏离主体部分的数据，这部分数据是由于对应的气体含量在该点前后发生了较大的突变，如CO2在2021年4月突然降低，是因为该变压器在该月进行了停电检修。
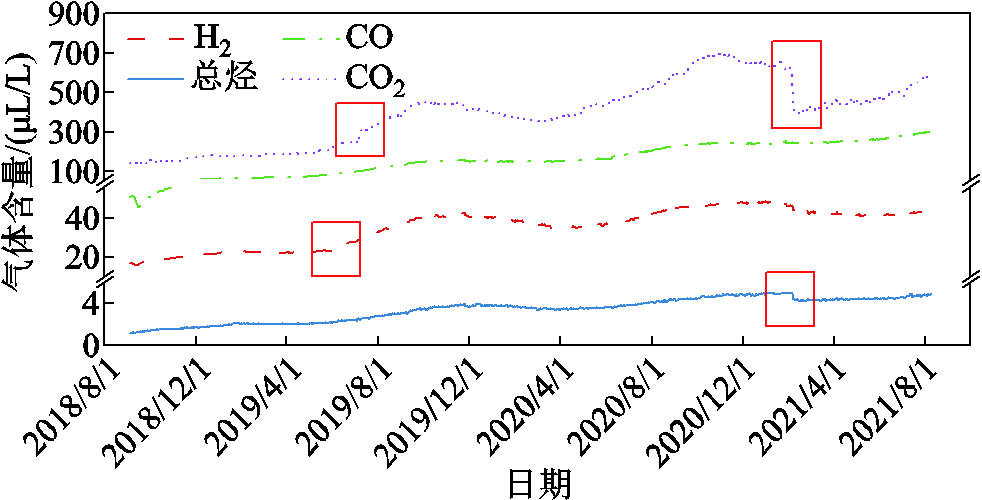
图17 变压器T1 DGA在完成空缺值填补后的序列图
Fig.17 Sequence diagram of Transformer T1 DGA after filling the vacancy value
为对比空缺值填补后对数据特征的影响，绘制了空缺值填补后气体含量的Q-Q图如图18所示。空缺值填补前后各气体含量的Q-Q图形状（分布特征）基本没有发生变化。相比于数据清洗前（见图5），图18的CO和总烃离群数据（图5红色方框处）被剔除，H2标准差减小0.28 μL/L，CO标准差减小7.50 μL/L，总烃标准差减小3.04 μL/L，CO2标准差减小0.03 μL/L，说明数据清洗和填补后变压器整体的DGA分布趋势更加集中，质量显著提高。
威布尔分布的参数和形状可作为数据清洗和填补前后特征是否变化的一个判断依据，变压器T1中CO2数据清洗填补前后概率密度分布变化如图19所示。
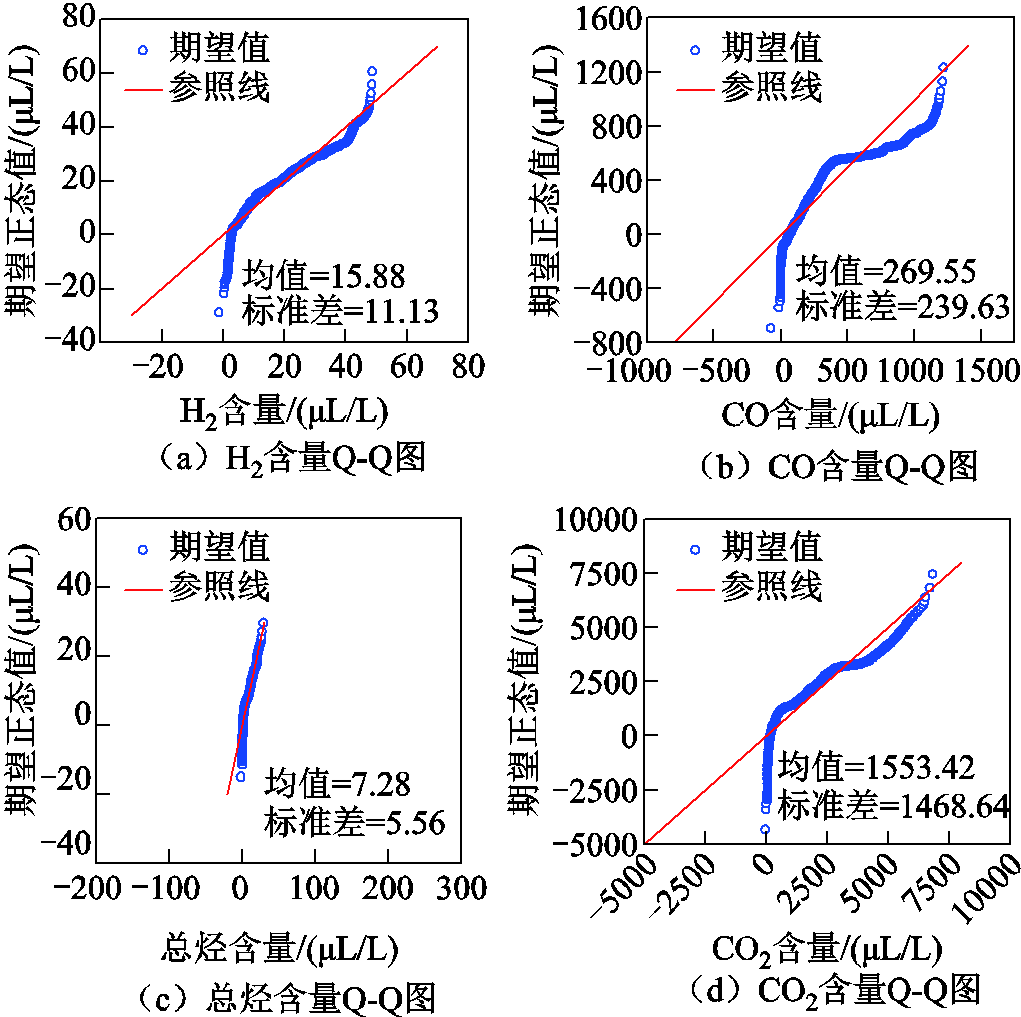
图18 11台变压器各气体完成空缺值填补后Q-Q图
Fig.18 Q-Q plot of 11 transformers DGA after filling the vacancy value
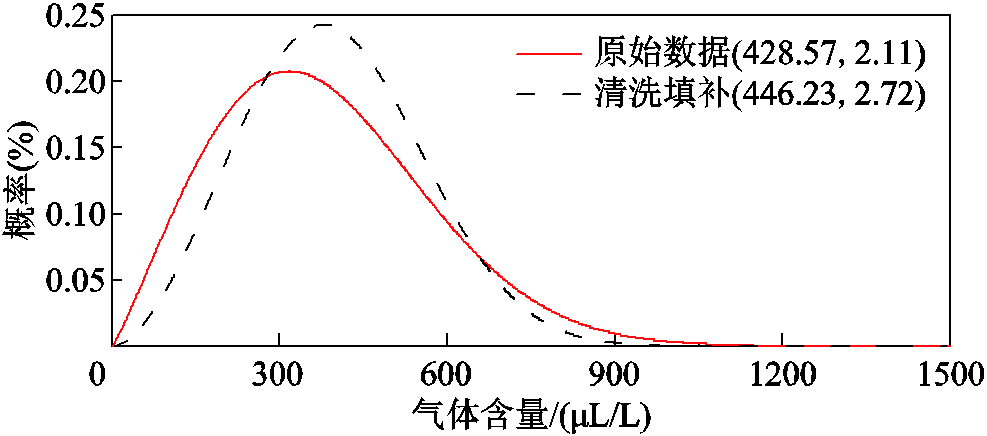
图19 变压器T1中CO2数据威布尔分布
Fig.19 Weibull distribution of CO2 data in Transformer T1
由图19可见，数据清洗和填补后其威布尔分布的整体形状略向右上偏移，变得更加“瘦高”。观察其分布参数的变化，尺度参数从428.57 μL/L增大到446.23 μL/L，原因是剔除的离群值都比较小；其形状参数从2.11增加到2.72，表明数据更加集中，即在保持数据整体的分布特征大体不变的情况下，数据质量得到了提高。进一步补充数据清洗和填补后时间序列指标[17]，对补全效果进行综合评估，见表2。
表2 CO2数据补全结果综合评估
Tab.2 Comprehensive evaluation of CO2 data completion results
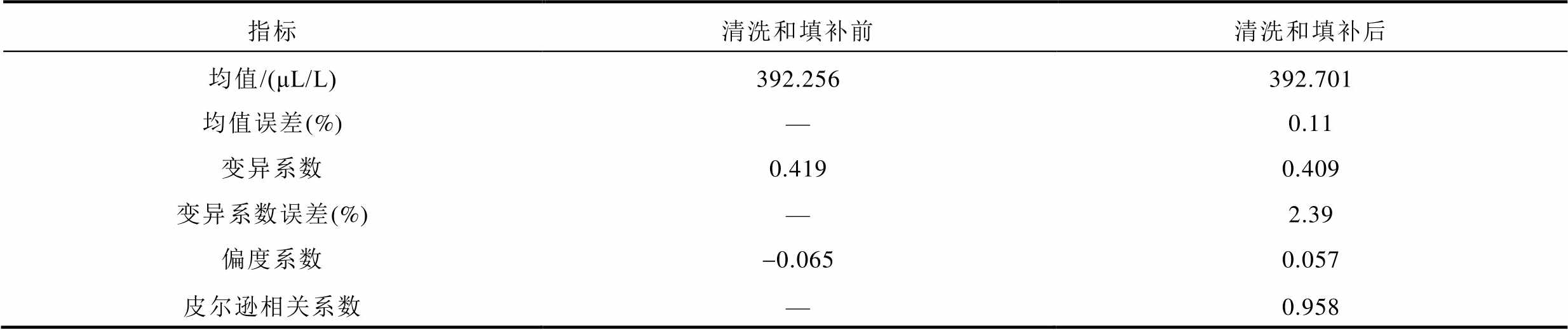
指标清洗和填补前清洗和填补后 均值/(μL/L)392.256392.701 均值误差(%)—0.11 变异系数0.4190.409 变异系数误差(%)—2.39 偏度系数-0.0650.057 皮尔逊相关系数—0.958
可见，变压器T1的CO2数据在清洗和填补前后，其数据均值和变异系数误差分别为0.11%和2.39%，表明数据的平均水平和离散程度均未发生较大的改变。皮尔逊相关系数为0.958，十分接近于1，也证明了数据清洗和填补前后两个数据具有较强的相关性，接近程度较高。而偏度系数从处理前的-0.065变为处理后的0.057，这表明数据分布从轻微的左偏变为右偏，也可以从图19中威布尔分布形状变化得出，其原因是剔除了较小的离群值。
通过生成的模拟数据与真实变压器DGA数据离群值识别和数据填补的案例分析，并与现有方法进行对比，得到以下结论：
1）本文提出了先识别后检验的COPOD、IForest和Grubbs联合算法应用于变压器DGA在线数据离群值识别，在相同气体数据序列上进行分析，所提出的算法正确识别点数、正确识别离群点数、ROC曲线平均面积相比于常见的KNN算法分别提升了3.5%、29.4%和5.0%。在实际应用中，面对大量变压器在线监测数据，提高了离群点检测的准确性，改善了数据质量。
2）通过优化训练的Transformer神经网络对DGA空缺值进行填补，解决了实际应用中由于缺乏训练离群点数据标签导致训练效果差的问题。对比双向缩放算法，填补后数据与实际数据的方均根误差均值为7.29 μL/L，平均绝对误差均值为2.66 μL/L，性能分别提升了9.7%和9.2%。通过多种时间指标对数据清洗填补前后进行了对比，表明数据具有较强的相似性，提高了数据的完整性和利用率。
3）通过本文方法对变压器DGA数据进行填补后，可在不改变数据整体分布的情况下，使数据更加集中，质量显著提高。本文方法复杂度适中，可靠性高，可有效地支撑变电设备的健康趋势预测、状态评价及数字孪生等高阶应用。
参考文献
[1] 杨童亮, 胡东, 唐超, 等. 基于SMA-VMD-GRU模型的变压器油中溶解气体含量预测[J]. 电工技术学报, 2023, 38(1): 117-130.
Yang Tongliang, Hu Dong, Tang Chao, et al. Prediction of dissolved gas content in transformer oil based on SMA-VMD-GRU model[J]. Transactions of China Electrotechnical Society, 2023, 38(1): 117-130.
[2] Walker C, Al Rashdan A, Agarwal V. Transformer health monitoring using dissolved gas analysis: a technical brief[J]. International Journal of Prognostics and Health Management, 2022, 13(2): 1-8.
[3] 谢庆, 蔡扬, 谢军, 等. 基于ALBERT的电力变压器运维知识图谱构建方法与应用研究[J]. 电工技术学报, 2023, 38(1): 95-106.
Xie Qing, Cai Yang, Xie Jun, et al. Research on construction method and application of knowledge graph for power transformer operation and maintenance based on ALBERT[J]. Transactions of China Electrotechnical Society, 2023, 38(1): 95-106.
[4] 池源, 郭莹霏, 孟庆昊, 等. 主动配电网储能应用新形态：虚拟配电变压器与馈线[J]. 电力系统自动化, 2023, 47(12): 163-175.
Chi Yuan, Guo Yingfei, Meng Qinghao, et al. New form of energy storage application in active distribution network: virtual distribution transformers and feeders[J]. Automation of Electric Power Systems, 2023, 47(12): 163-175.
[5] 吴瞻宇, 董明, 王健一, 等. 基于模糊关联规则挖掘的电力变压器故障诊断方法[J]. 高压电器, 2019, 55(8): 157-163.
Wu Zhanyu, Dong Ming, Wang Jianyi, et al. Fault diagnosis of power transformer based on fuzzy association rules mining[J]. High Voltage Apparatus, 2019, 55(8): 157-163.
[6] 刘文君, 贺馨仪, 王彬, 等. 基于异常检测集成算法的油色谱在线监测数据质量评价体系[J]. 电网与清洁能源, 2022, 38(8): 16-23.
Liu Wenjun, He Xinyi, Wang Bin, et al. Online monitoring data quality evaluation system for oil chromatography based on anomaly detection integrated algorithm[J]. Power System and Clean Energy, 2022, 38(8): 16-23.
[7] 王文森, 杨晓西, 刘阳, 等. 基于层次聚类分析的变压器油中溶解气体在线监测数据异常检测[J]. 高压电器, 2023, 59(1): 142-147.
Wang Wensen, Yang Xiaoxi, Liu Yang, et al. Anomaly detection of online monitoring data of dissolved gases in transformer oil based on hierarchical cluster analysis[J]. High Voltage Apparatus, 2023, 59(1): 142-147.
[8] 吴睿涵, 何亚倩, 江军, 等. 变压器油中溶解乙炔光热干涉检测系统的温度和压强特性[J]. 电力工程技术, 2023, 42(5): 30-36.
Wu Ruihan, He Yaqian, Jiang Jun, et al. Temperature and pressure characteristics of dissolved acetylene in transformer oil based on photothermal interference detection system[J]. Electric Power Engineering Technology, 2023, 42(5): 30-36.
[9] Adikaram K K L B, Hussein M A, Effenberger M, et al. Data transformation technique to improve the outlier detection power of Grubbs’ test for data expected to follow linear relation[J]. Journal of Applied Mathematics, 2015, 2015: 1-9.
[10] 韩崇, 袁颖珊, 梅焘, 等. 基于K-means的数据流离群点检测算法[J]. 计算机工程与应用, 2017, 53(3): 58-63.
Han Chong, Yuan Yingshan, Mei Tao, et al. Data stream outlier detection algorithm based on K-means[J]. Computer Engineering and Applications, 2017, 53(3): 58-63.
[11] Liu Hang, Wang Youyuan, Chen Weigen. Anomaly detection for condition monitoring data using auxiliary feature vector and density‐based clustering[J]. IET Generation Transmission & Distribution, 2019, 14(1): 108-118.
[12] 严英杰, 盛戈皞, 陈玉峰, 等. 基于时间序列分析的输变电设备状态大数据清洗方法[J]. 电力系统自动化, 2015, 39(7): 138-144.
Yan Yingjie, Sheng Gehao, Chen Yufeng, et al. Cleaning method for big data of power transmission and transformation equipment state based on time sequence analysis[J]. Automation of Electric Power Systems, 2015, 39(7): 138-144.
[13] 顾仲翔, 马宏忠, 张勇, 等. 基于VMD与优化SVM的变压器绕组松动缺陷振动信号诊断方法[J]. 高压电器, 2023, 59(1): 117-125.
Gu Zhongxiang, Ma Hongzhong, Zhang Yong, et al. Vibration signal diagnosis method of transformer winding looseness defect based on VMD and optimized SVM[J]. High Voltage Apparatus, 2023, 59(1): 117-125.
[14] 朱倩雯, 叶林, 赵永宁, 等. 风电场输出功率异常数据识别与重构方法研究[J]. 电力系统保护与控制, 2015, 43(3): 38-45.
Zhu Qianwen, Ye Lin, Zhao Yongning, et al. Methods for elimination and reconstruction of abnormal power data in wind farms[J]. Power System Protection and Control, 2015, 43(3): 38-45.
[15] 赵厚翔, 沈晓东, 吕林, 等. 基于GAN的负荷数据修复及其在EV短期负荷预测中的应用[J]. 电力系统自动化, 2021, 45(16): 143-151.
Zhao Houxiang, Shen Xiaodong, Lü Lin, et al. Load data restoration based on generative adversarial network and its application in short-term load forecasting of electric vehicle[J]. Automation of Electric Power Systems, 2021, 45(16): 143-151.
[16] Khoury R, Harder D W. Numerical Methods and Modelling for Engineering[M]. Cham: Springer, 2016.
[17] 张若愚, 齐波, 张鹏, 等. 面向电力变压器状态评价的油中溶解气体监测数据补全方法[J]. 电力自动化设备, 2019, 39(11): 181-187.
Zhang Ruoyu, Qi Bo, Zhang Peng, et al. Method for interpolating monitoring data of dissolved gas in oil for power transformer state assessment[J]. Electric Power Automation Equipment, 2019, 39(11): 181-187.
[18] Che Zhengping, Purushotham S, Cho K, et al. Recurrent neural networks for multivariate time series with missing values[J]. Scientific Reports, 2018, 8: 6085.
[19] Luo Yonghong, Cai Xiangrui, Zhang Ying, et al. Multivariate time series imputation with generative adversarial networks[C]//Proceedings of the 32nd International Conference on Neural Information Processing Systems, Montréal, Canada, 2018: 1603-1614.
[20] 周远翔, 林孟龙, 陈健宁, 等. 基于自注意力生成对抗网络的电力设备在线监测缺失数据填补[J]. 高电压技术, 2023, 49(5): 1795-1809.
Zhou Yuanxiang, Lin Menglong, Chen Jianning, et al. Missing data imputation for online monitoring of power equipment based on self-attention generative adversarial networks[J]. High Voltage Engineering, 2023, 49(5): 1795-1809.
[21] 李阳, 沈小军, 张扬帆, 等. 基于速度-关联约束的风电机组风速感知异常数据识别方法[J]. 电工技术学报, 2023, 38(7): 1793-1807.
Li Yang, Shen Xiaojun, Zhang Yangfan, et al. Cleaning method of wind speed outliers for wind turbines based on velocity and correlation constraints[J]. Transactions of China Electrotechnical Society, 2023, 38(7): 1793-1807.
[22] 郭慧军, 李永亭, 齐咏生, 等. 两阶段CP-Copula的风电机组异常数据清洗算法[J]. 计算机仿真, 2022, 39(11): 85-91.
Guo Huijun, Li Yongting, Qi Yongsheng, et al. A two-stage CP-Copula algorithm for clearing abnormal data of wind turbine[J]. Computer Simulation, 2022, 39(11): 85-91.
[23] 陈雨鸽, 陈昌铭, 张思, 等. 考虑时空耦合的小水电富集型虚拟电厂优化调度策略[J]. 电力系统自动化, 2022, 46(18): 90-98.
Chen Yuge, Chen Changming, Zhang Si, et al. Optimal dispatching strategy of small hydropower enriched virtual power plant considering temporal-spatial coupling[J]. Automation of Electric Power Systems, 2022, 46(18): 90-98.
[24] 唐立, 郝鹏, 任沛阁, 等. 基于改进孤立森林算法的无人机异常行为检测[J]. 航空学报, 2022, 43(8): 326789.
Tang Li, Hao Peng, Ren Peige, et al. UAV abnormal behavior detection based on improved IForest algorithm[J]. Acta Aeronautica et Astronautica Sinica, 2022, 43(8): 326789.
[25] 徐东, 王岩俊, 孟宇龙, 等. 基于Isolation Forest改进的数据异常检测方法[J]. 计算机科学, 2018, 45(10): 155-159.
Xu Dong, Wang Yanjun, Meng Yulong, et al. Improved data anomaly detection method based on isolation forest[J]. Computer Science, 2018, 45(10): 155-159.
[26] 李新鹏, 高欣, 阎博, 等. 基于孤立森林算法的电力调度流数据异常检测方法[J]. 电网技术, 2019, 43(4): 1447-1456.
Li Xinpeng, Gao Xin, Yan Bo, et al. An approach of data anomaly detection in power dispatching streaming data based on isolation forest algorithm[J]. Power System Technology, 2019, 43(4): 1447-1456.
[27] Ding Kun, Zhang Jingwei, Ding Hanxiang, et al. Fault detection of photovoltaic array based on Grubbs criterion and local outlier factor[J]. IET Renewable Power Generation, 2020, 14(4): 551-559.
[28] Vaswani A, Shazeer N, Parmar N, et al. Attention is all you need[C]//Proceedings of the 31st International Conference on Neural Information Processing Systems, Long Beach, California, USA, 2017: 6000-6010.
[29] 黄飞虎, 赵红磊, 弋沛玉, 等. 一种改进Transformer的电力负荷预测方法[J]. 现代电力, 2023, 40(1): 50-58.
Huang Feihu, Zhao Honglei, Yi Peiyu, et al. An improved power load forecasting method based on Transformer[J]. Modern Electric Power, 2023, 40(1): 50-58.
[30] 叶林, 李奕霖, 裴铭, 等. 寒潮天气小样本条件下的短期风电功率组合预测[J]. 中国电机工程学报, 2023, 43(2): 543-555.
Ye Lin, Li Yilin, Pei Ming, et al. Combined approach for short-term wind power forecasting under cold weather with small sample[J]. Proceedings of the CSEE, 2023, 43(2): 543-555.
[31] Du Wenjie, Côté D, Liu Yan. SAITS: self-attention-based imputation for time series[J]. Expert Systems With Applications, 2023, 219: 119619.
[32] 张鹏, 齐波, 刘娟, 等. 电力变压器油中溶解气体数据的分布特征参数快速计算方法[J]. 中国电机工程学报, 2022, 42(5): 2001-2012.
Zhang Peng, Qi Bo, Liu Juan, et al. Fast calculation method for distribution characteristic parameters of dissolved gas data in power transformer oil[J]. Proceedings of the CSEE, 2022, 42(5): 2001-2012.
[33] Qi Bo, Zhang Peng, Rong Zhihai, et al. Differentiated warning rule of power transformer health status based on big data mining[J]. International Journal of Electrical Power & Energy Systems, 2020, 121: 106150.
[34] Hastie T, Mazumder R, Lee J D, et al. Matrix completion and low-rank SVD via fast alternating least squares[J]. Journal of Machine Learning Research, 2015, 16: 3367-3402.
[35] Cao Wei, Wang Dong, Li Jian, et al. BRITS: bidirectional recurrent imputation for time series[C]// Proceedings of the 32nd International Conference on Neural Information Processing Systems, Montréal, Canada, 2018: 6776-6786.
Abstract Transformer plays a vital role of power transmission and voltage conversion in power system, and its health is of great significance to the safe operation and reliability of the whole power grid. Dissolved gas analysis (DGA) in oil is an important indicator for transformer condition evaluation and health evaluation, especially in the process of power equipment condition maintenance and the promotion of digital power grid. Its data quality and data accumulation are of great value for transformer health index analysis, equipment management and even smart grid development. However, due to the degradation of performance, transmission interruption or other interference factor during the operation of the on-line sensors, the monitoring data occur errors and outliers, which greatly affects the use of data, and results in a waste of resources.
Considering that Copula based outlier detection (COPOD) algorithm could handle multidimensional, high and large-scale data sets, and isolation forest (IForest) algorithm had a better detection effect on dense data sets, the two algorithms were combined to mark more outliers by setting a higher detection threshold as preliminary test. To reduce the influence of both ends of data on the detection algorithm caused by the trend of data, the method of sliding window was used to detect outliers by the two algorithms respectively, and the intersection of the results was taken as the outlier data set. Due to the high threshold, the suspect outlier data set were mixed with some normal DGA data. Further, Grubbs test with high sensitivity, wide applicability and suitable for single detection was introduced, and its performance is better in small samples. Then the suspect outlier data was tested twice through Grubbs method for improving the accuracy of outlier identification, and the misidentified normal data was excluded from the detection results. After the outliers are removed, Transformer neural network is used to fill in the outliers. Mask filling and observation reconstruction were adopted to optimize the loss function and train the network structure. Finally, the predicted values using neural network were used to fill in the data to construct DGA data.
Simulation data and actual online monitoring data of 11 500 kV oil-immersed transformers in operation were used to verify the performance of the algorithm. Results show that, the number of correct identification points, the number of correct identification outlier points and the average area of the receiver operating characteristic (ROC) curve of the proposed algorithm are improved by 3.5%, 29.4% and 5.0% on the same gas series compared with the traditional K-nearest neighbors (KNN). For data filling, compared with the bidirectional scaling (BiScaler) algorithm, the mean of root mean square error (RMSE) is 7.29 μL/L, and the mean of mean absolute error (MAE) is 2.66 μL/L. The performance is improved by 9.7% and 9.2% respectively, effectively improving the quality and utilization of data.
The following conclusions can be drawn from the simulation analysis:(1) The combined algorithm of COPOD, IForest and Grubbs, which is used to identify outliers in transformer DGA online data, is more accurate than the traditional algorithm KNN, the misidentification of outliers is also reduced. (2) By optimizing the loss function using mask filling and observation reconstruction, the Transformer neural network is trained to improve the prediction performance and effectively complete the data filling task. (3) After the transformer DGA data is filled, the data is more concentrated and the quality is significantly improved without changing the overall data distribution. This method has moderate complexity and high reliability，and it is suitable for large-scale data preprocessing in practical applications.
keywords：Power transformer, dissolved gases in oil, joint detection method, outlier detection, data reconstruction technique
中图分类号：TM411
DOI: 10.19595/j.cnki.1000-6753.tces.231033
国家自然科学基金（52177150）和南京航空航天大学科研与实践创新计划（xcxjh20220314）资助项目。
收稿日期 2023-07-03
改稿日期 2023-07-31
江 军 男，1988年生，博士，研究员，研究方向为面向电力设备及航空航天电气装备的状态监测与故障诊断。
E-mail: jiangjun0628@163.com（通信作者）
张文乾 男，1997年生，硕士研究生，研究方向为电气设备状态检测与故障诊断。
E-mail: hnzzzwq123@163.com
（编辑 李 冰）