图1 液态金属桥拉伸断裂过程中三种电弧燃烧模式[17]
Fig.1 Three arc regimes in the process of the breakup of a stretched liquid-metal bridge[17]
摘要 构建流体仿真模型可以有效地分析液桥拉伸断裂过程中的流体动力学特性，为基于液态金属桥拉伸断裂过程的电弧开断性能调控提供指导。已有的液桥仿真模型基于动网格或其他网格变形方法，无法仿真液桥的大范围拉伸形变和几何断裂。为此，该文提出了一种不依赖网格形变的液桥拉伸断裂有限元仿真方法。该方法对液体设置极大黏度值，以不可流动液体区域对固体进行近似，同时通过极大黏度值界线的移动配合计算域内液体的流出来等效液桥的拉伸，实现了对液桥拉伸断裂过程的仿真。基于该仿真模型探究了液桥体积、拉伸速度等对液桥拉伸断裂过程的影响，获得了全拉伸速度范围内液桥拉伸断裂特性的转变规律。最终，结合实验结果分析了液桥拉伸断裂特性转变对于电弧燃烧模式的影响，给出了全拉伸速度范围内电弧燃烧模式转变相图，为液桥式开关的电弧开断性能调控提供了依据。该文研究内容对微型继电器、接触器等基于液桥断裂原理的微型开关研发具有指导意义。
关键词：电弧和电接触 液态金属桥 机械开关 直流开断 有限元仿真 流体仿真
传统机械式开关采用一对固体金属片作为导电触点实现开关操作。从微观上来看，固体电极实际上是通过表面微凸起构成的接触斑点来实现物理接触[1-2]。固体金属导电斑点的存在导致接触电阻增大[3-4]、闭合触点间产生电动斥力[5-6]以及分断电流时产生开关电弧[7-9]等一系列电接触稳定性问题，严重影响了机械式开关的使用寿命。由于接触斑点是固体电接触的本质属性，无论是对开关本身进行结构优化还是对固体金属进行材料改性都难以从根本上解决机械式开关的触点电接触退化问题。考虑到继电器、小型断路器等传统微型开关触点体积小、分断速度慢等固有特点[10-13]，上述电接触问题对这一类开关设备影响尤其显著。在微型机械式开关固体触点中嵌入液态金属（镓铟锡合金（GaInSn））桥构建自愈性的室温液体导电触点，有望从根本上消除接触斑点的存在，解决传统机械式开关中的电接触稳定性问题[14-16]。
针对拉伸微型液态金属桥实现电弧开断的新型开关原理，文献[17]结合高速摄影和电测量手段揭示了液桥拉伸断裂过程中的电弧燃烧特性及其开断性能，展示了微尺度液态金属桥在安培级电流快速开断中的应用潜力。在220 V直流阻性电路中开断安培级电流时，微型液态金属桥在拉伸断裂过程中呈现出三种特征迥异的电弧燃烧模式，如图1所示。由图1可知，粘附在两固体金属电极（直径3 mm）之间的液态金属液滴（18 μL）受到上电极拉伸时，可在表面张力作用下形成两端粗、中间细的液桥。液桥上无断口出现时，电流可经两端固体电极和中间液态金属完成传导，开关处于闭合状态。当液态金属桥被进一步拉伸发生断裂时，断口的出现将引燃电弧。燃弧模式一发生在初始开断电流I0比较小的情况下，如图1a所示，当电路中电流小于0.75 A时，液桥下端收缩断裂之后在中间液丝与底部液滴之间形成单一的电弧燃烧，并随着液丝收缩与电弧伸长完成电流开断。随着初始电流增大，下端断口之间的单电弧燃烧将不足以开断电路。如图1b所示，随着外部机构的继续拉伸，液桥中间的细丝将在与顶部液滴的连接处发生第二次收缩断裂并随之引燃第二段电弧。此后，上下两段电弧通过中间液丝的串联相向扩展直至完成电流开断，这种情况被称为模式二，发生在初始电流为0.75～3 A的参数范围之内。该燃弧模式下，在液桥发生第二次断裂的时刻，上端断口与底部液滴顶端之间的距离被定义为断裂距离Rd，中间液丝底端与底部液滴顶端之间的距离被定义为底部距离Bd。在图1c所示的电弧燃烧模式三中可以看到，当初始开断电流增大到一定程度，即I0＞3 A时，双电弧串联依旧不足以完成电流开断。中间液丝两端的双电弧会跨过一段长度为跨越距离Ld的液态金属丝重新融合为一段电弧，并随着外部机构的拉伸继续扩展，最终完成电路开断。这种燃弧模式被命名为双电弧“串联-合并”燃烧。图2给出了图1c模式三情况下液桥拉伸断裂过程中电弧的“电压-电流”开断波形，更好地揭示了液桥电弧燃烧时电学参数的变化。t1时刻，液桥下端断口以及第一段电弧的产生带来第一对近极压降的建立，在波形图上体现为约17 V的电压上升台阶以及0.25 A左右的电流下降台阶；t2时刻，液桥上断口以及第二段电弧的产生带来第二对近极压降的建立，在波形图上体现为第二个电压上升台阶和电流下降台阶，同时，电压上升率和电流下降率也在t2时刻之后明显增大；t3时刻，随着双电弧的相向扩展拉伸，电弧电压继续增大，电流继续减小；在双电弧跨越融合的瞬间，一对近极压降的消失对应了t4时刻电压的陡降和电流的陡升，同时双电弧融合之后也降低了电弧扩展拉伸的总速度。
图1 液态金属桥拉伸断裂过程中三种电弧燃烧模式[17]
Fig.1 Three arc regimes in the process of the breakup of a stretched liquid-metal bridge[17]
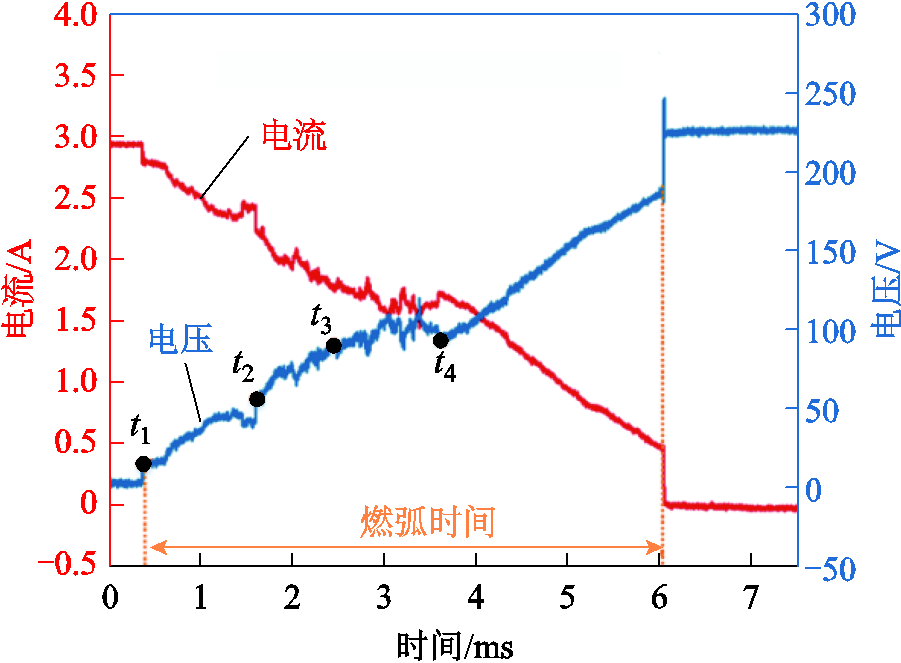
图2 液桥电弧开断波形（与图1c过程对应）
Fig.2 The waveform of arc interruption enabled by a liquid-metal bridge (corresponding to Fig.1c)
进一步地，文献[17]的研究结果还指出，液桥式开关的电弧开断性能，即燃弧时间的长短，随着燃弧模式的变化存在一定的波动，其中模式二时性能最佳。这是因为模式二下双电弧串联独立拉伸时一对近极压降的增加和第二段电弧扩展带来的额外拉弧速度都对电弧的限流开断发挥了正向作用。此外，文献[17]还指出，液桥拉伸断裂过程中流体动力学特征（诸如断裂距离Rd、底部距离Bd等）与电流大小、电弧长度等电学特征的匹配决定了燃弧模式的转变。更长的断裂距离和底部距离都可以延迟电弧模式的转变，提升设备的电弧开断性能。因此，研究液桥拉伸断裂过程的流体动力学原理和流体特征转变规律，对于液桥式开关电弧开断性能的调控至关重要。
由于实验能够创造的条件有限且费时费力，构建流体仿真模型，通过数值模拟的手段研究液桥拉伸断裂的流体动力学过程显得尤为必要。文献[18]基于动网格的方法探究了拉伸速度、流体物性参数及流体体积等对液桥拉伸断裂过程的影响。受限于动网格本身的应用条件，该模型仅能针对液桥断裂之前的流体过程进行计算，不能仿真带有流体几何断裂的收缩断裂过程。文献[19]将水平集方法与一种可调控的网格拉伸、收缩算法相结合，仿真了液桥从拉伸、收缩到断裂过程的毛细收缩行为，仿真结果与实验结果获得了较高的一致性。这种方法不需要重新划分网格，节省了计算资源。但是考虑到网格的过度拉伸会影响计算的准确性，该方法仅能应用于拉伸速度不高、液桥形变程度较小的情况。针对高速、大形变情况下的液桥拉伸断裂仿真模型还有待开发。
鉴于此，本文提出了在流体仿真中通过对液体设置极大黏度值，以不可流动液体区域实现对固体材料近似的“极大黏度法”，以及通过向区域外抽取液态金属来等效液桥拉伸效果的“抽液近似法”。基于以上两种近似方法，首先，在多物理场仿真软件COMSOL Multiphysics中建立了液桥高速拉伸断裂过程的有限元仿真模型，获得了与实验数据一致的计算结果；其次，探究了液桥体积、拉伸速度等因素对液桥断裂距离和底部距离的影响，并从流体动力学角度阐明了其中的动力学原理，同时将流体特性的变化落脚到对电弧燃烧模式的影响上；最后，基于仿真结果提出了全拉伸速度范围内液桥燃弧模式的预测相图。本文研究内容对于液桥拉伸断裂过程的仿真方法开发和液桥式开关的电弧性能调控具有重要意义。
实验系统示意图如图3a所示。为了防止液态金属氧化，液桥及其拉伸操动机构整体布置于手套箱内部。外部电路以及控制、测试设备通过密封接口实现与液桥及机构的电气连接。在液桥闭合及电路连通状态下，运动控制器控制操动机构拉伸液桥，完成液桥断裂及电弧开断。与此同时，高速相机和示波器通过观察窗及电气接口记录流体运动过程和电压电流波动。图3b给出了液桥及其拉伸操动机构的三维结构。液桥位于上电极柱与下电极柱之间，直线滑台和电磁铁可带动上电极柱上下移动来实现液桥的拉伸断裂和主回路电流开断。
图3 实验原理说明
Fig.3 Explanation of experimental principle
液桥拉伸断裂模型如图4所示，其中，图4a为实验过程中获得的高速摄影图片，图4b给出了根据实验参数建立的几何模型及仿真基本设置。作为世界上已知表面张力最大的室温液体（张力系数大于0.5 N/m）[20]，粘附在两固体表面之间的镓铟锡合金可以在尽可能大的尺度上依靠表面张力形成毛细液态金属桥。外部机构以速度vs拉伸上电极向上运动时液桥被随之拉长，并在表面张力作用下形成凹形液颈。液颈凹液面上每一点都受到垂直于气、液界面指向液桥内部的附加压力，即拉普拉斯压力，表示为
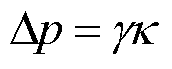（1）
式中，γ为液态金属表面张力系数；κ为界面上该点的主曲率[21-22]。当液桥被拉伸至表面曲率和拉普拉斯压力足够大时，液态金属就会在该附加压力作用下产生从液颈最细处向液桥两侧快速的自发流动，直至发生断裂。由于重力作用导致的液桥形变和表面张力作用的不对称性，液桥会在中间液丝的下端和上端先后发生两次断裂。这就是液桥拉伸断裂的基本原理和物理模型。
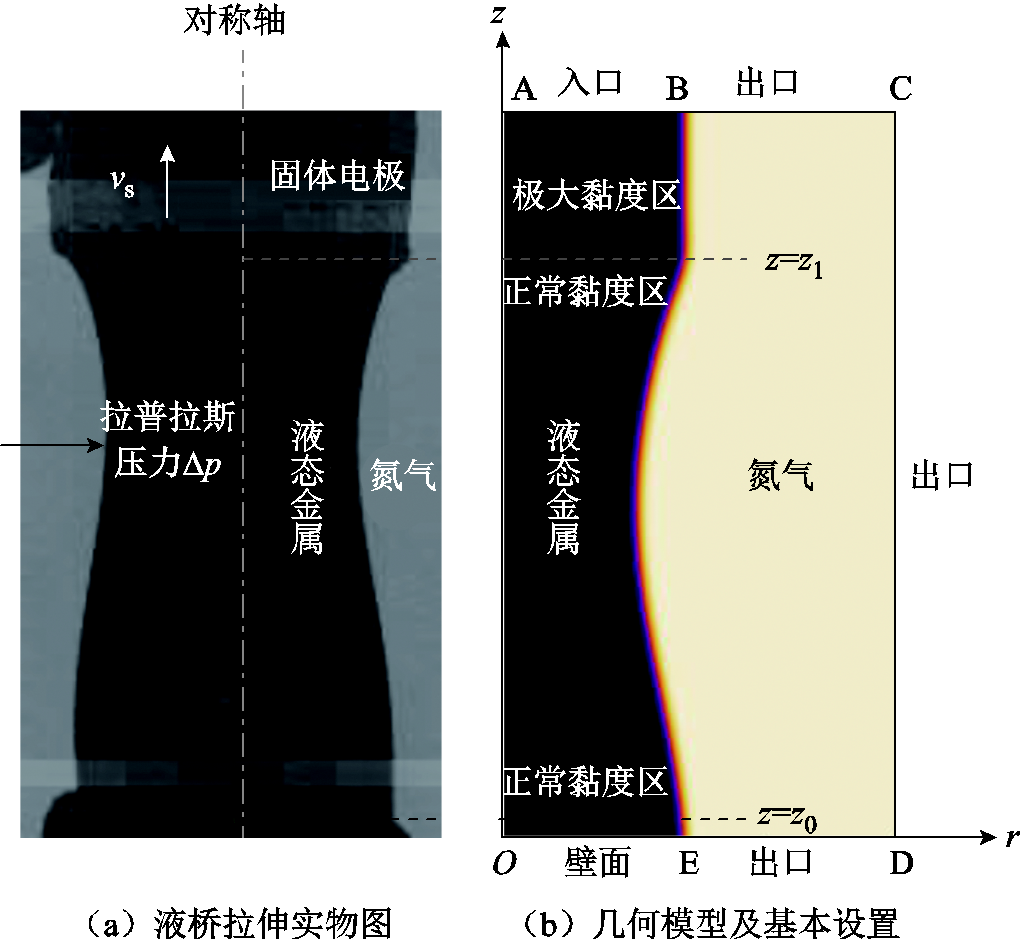
图4 液桥拉伸断裂模型
Fig.4 Model of the stretch-induced breakup of a liquid bridge
实验结果显示，当施加竖直向上的拉伸速度时，液桥的收缩断裂基本上是一个关于竖直中心线对称的过程。为了节约计算资源，在建模时以竖直对称轴为z轴，以液桥底部半径为r轴，选取液桥的1/2竖直切面及外围氮气域作为仿真对象。液桥底面半径按照实际尺寸1.5 mm设置，气体域宽度与液体区相同，整个计算域竖直高度依据仿真中的拉伸高度进行动态调整。此外，图4b中还给出了边界条件等其他模型基本设置，详细内容参见后文。
1）液态金属桥的拉伸断裂过程仅从断口和近极压降的产生、弧柱数量、电弧扩展速度和扩展空间等宏观参数上单向作用于电弧发展和电流开断过程。实验中燃弧电流小于10 A（能量小）且开断过程发生在敞开空间。因此，该模型的建立不考虑电弧烧蚀对液态金属表面张力、黏度等材料属性的影响，也不研究等离子体物性参数和温度、压强分布等微观效应对流体过程的影响。模型仅对液桥拉伸断裂的纯流体过程进行分析。
2）液态金属在流动过程中，其密度和体积不随压力和温度发生变化，并且在自收缩过程中气体介质也始终处于低速流动状态，因此液态金属和周边氮气两种流体均为不可压缩流体。
3）液桥的拉伸断裂问题涉及液态金属桥、氮气介质以及固定液桥所需要的固体电极，是一个典型的三相流问题。可以考虑将固体电极区的液态金属黏度设置为极大值进行固体等效近似，从而将模型简化为液体与气体两相流进行处理。
4）取流体流速为电极拉伸速度0.5 m/s，特征长度为液桥底面半径1.5 mm，GaInSn运动黏性系数υ=3.9×10-7 m2/s，计算可得雷诺数为1 923，可以采用层流模型进行建模。
5）液桥拉伸过程中认为液态金属是锚定在固体电极表面的，不考虑接触角的变化，假定固液接触线是固定不动的。
1.3.1 三相流简化为两相流
在本文研究的流动问题中，固体与液体、气体的区别本质上是黏度的差别。在仿真过程中可将固体区域等效为黏度极大的液体区域来简化仿真模型[23-24]，即通过将顶部和底部电极区域对应的液态金属黏度设置为极大值的形式将三相流问题简化为“液态金属-氮气”两相流问题。
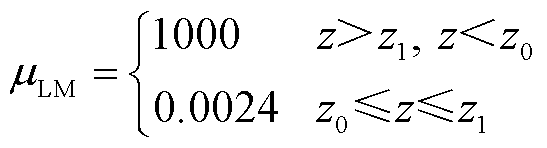（2）
式中，μLM为液态金属相的黏度值，Pa·s；z0、z1分别为液态金属与下、上电极区域的交界面。其中，z0取固定值0.5 mm，代表液桥与固体电极接触的 0.5 mm范围是黏度极大、不可流动的物质，同样的结论也适用于z1以上的范围。式（2）中，0.002 4 Pa·s表示镓铟锡合金的实际黏度值；1 000 Pa·s为用于近似固体效果的极大黏度值。相关区域的具体分配形式如图4b所示。本文将这种方法定义为“极大黏度法”。
1.3.2 “抽液近似法”模拟外部拉伸
由于动网格法在遇到流体几何断裂时无法继续计算，这就意味着动网格法不能仿真液桥断裂之后的流体行为。为了计算液桥断裂之后形成的断裂距离Rd和底部距离Bd，以及探究液桥断裂特性的影响，需要对液桥从拉伸到形变再到收缩断裂的过程进行建模仿真。为了实现对液桥拉伸效果的模拟，建模中通过在液桥顶端设置入口条件配合极大黏度边界的移动来等效固体电极的拉伸。模型计算过程中，固、液边界（极大黏度区和正常黏度区的边界）随着液体的减少而等效移动，本文将这种方法定义为“抽液近似法”。具体设置液态金属域顶端入口条件为
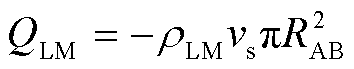（3）
式中，QLM为液态金属的抽液质量流率，kg/s；ρLM为液态金属密度，取值6 440 kg/m3；vs为机构拉伸速度；RAB为电极及液桥顶部半径。与此对应，随着液态金属被抽走，极大黏度与正常黏度区域的边界也随之移动对应的距离，即
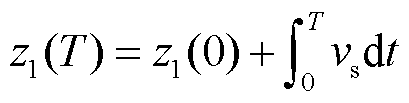（4）
式中，z1(T)为仿真中z1在T时刻的实时值；z1(0)为仿真中z1的初始值。
如此一来，就可以在不使用动网格的前提下等效机构拉伸带来的液桥上边界的实时移动。
1.3.3 水平集方法追踪两相流界面
经过简化之后，该模型变成了包含液态金属相和氮气相的两相流模型。模型使用水平集方法追踪气、液两相分界面，从而确定液态金属桥的动态轮廓。水平集方法通过定义一个变量φ来描述相界面。该变量数值在气相（或液相）中为0，在液相（或气相）中为1，在两相分界面上为0.5，在分界面附近从0～1连续变化。变量φ的数值通过求解水平集方程获得。
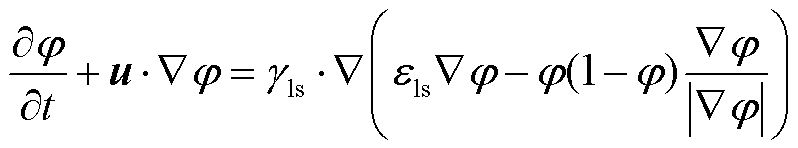（5）
式中，u为流场速度；γls为重新初始化速度值；εls为界面厚度控制参数。
通过求解式（5）和φ=0.5等值线可以确定液态属桥的动态轮廓。水平集变量除了确定两相分界面外，还可以用来定义流场中的材料物性参数。例如，流场中流体的密度ρ可以表示为
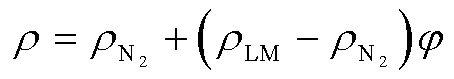（6）
式中，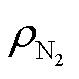
为氮气的密度。
此外，基于水平集变量，模型还定义了一个单位脉冲函数，表示为
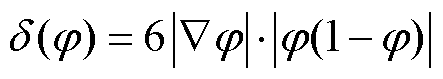（7）
该函数仅在两相分界面处为非零值，可以用来施加与两相流分界面相关的计算条件。
1.3.4 流场控制方程
由于本文所研究的液桥断裂过程属于层流问题，仅采用斯托克斯方程即可求解该二维流场。
连续性方程为
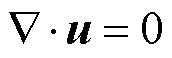（8）
动量守恒方程为
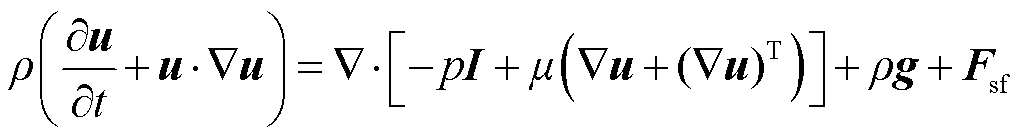（9）
式中，p为流场中的压力；I为单位矩阵；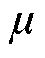
为流体黏度；g为重力加速度；Fsf为两相界面上的界面张力，表达式为
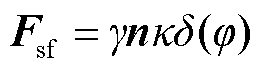（10）
式中，n为相分界面的法向量。
图4b中已经对模型各个边界上的条件进行了简单标注。液桥上底面AB设置入口条件，通过式（3）的定义可以将液态金属从AB边界按照上电极移动的瞬时速度所对应的质量流率抽出；氮气环境所对应的自由边界BC、CD、DE均设置为自由出口，赋予压力边界条件p=p0，p0为大气压；液桥的下底面EO设置壁面边界条件，即速度u=0。
模型输入主要有两个：一个是初始液桥的几何形状，可以通过图像处理的方法将实验拍摄得到的液态金属桥的轮廓以数学坐标的形式给出；另一个是电极的拉伸速度曲线，也可以通过图像处理的方法对大量连续的高速摄影图片进行液桥边缘定位和位置读取实现。图5给出了某次仿真初始时刻液桥轮廓的获取过程：先将原始灰度图片二值化，在二值化图片上对黑、白像素的边缘进行识别可以确定出液桥轮廓；再根据像素尺寸进行对应的尺度变化即可获取液桥轮廓的数值曲线。采用同样的方法对连续的高速摄影图片进行处理可以获取实验中的液桥高度，即液桥上边界的运动曲线，如图6所示。
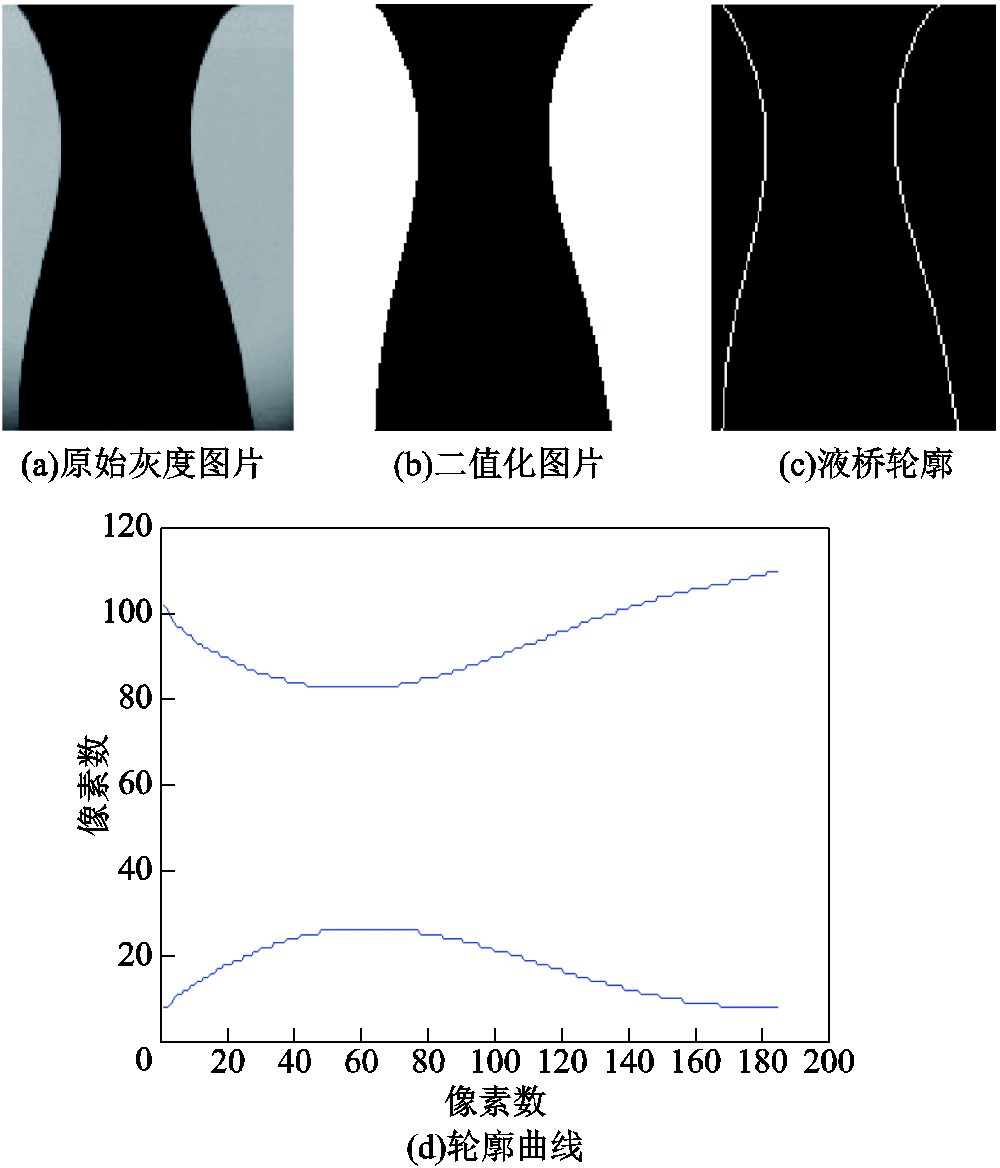
图5 仿真初始时刻液桥轮廓曲线的获取
Fig.5 Extracting the profile curve of a liquid bridge corresponding to the initial simulation time
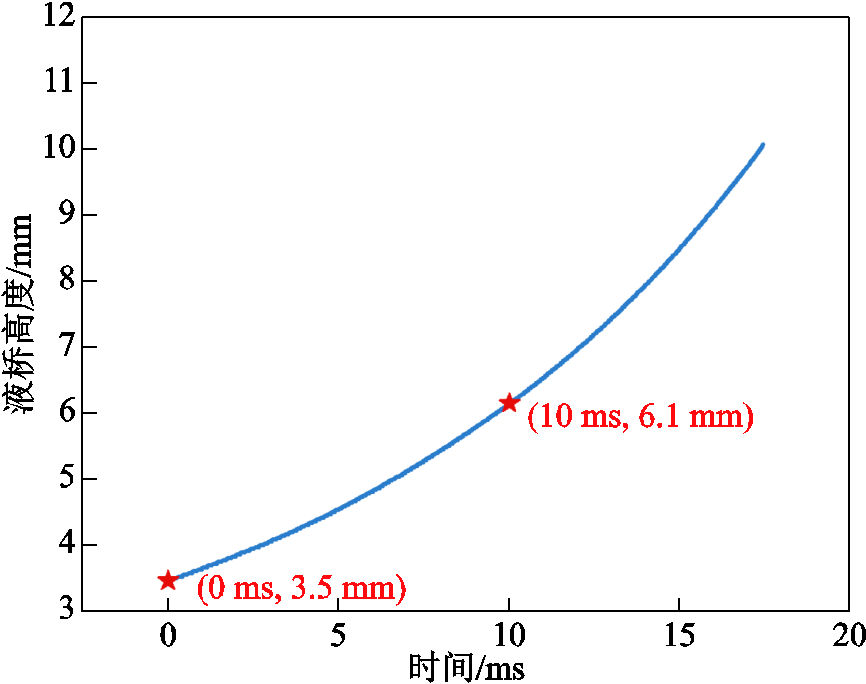
图6 从实验结果中获取得液桥高度变化曲线
Fig.6 Height variations of a liquid bridge extracted from the experimental results
将建立好的模型在COMSOL Multiphysics 5.4有限元仿真软件包中进行网格划分和求解。模型网格划分采用自由三角形网格，网格尺寸采用软件包内置的“超细化”设置。在3 mm×8 mm的计算域内共剖分出三角形网格49 572个，网格顶点25 122个。
模型求解采用基于后向差分公式的瞬态求解器，求解器步长采用软件包内置的“自适应变步长”选项。在一台3 GHz主频、16 GB RAM的计算机上，求解时间在1 h以内。
图7给出了仿真中t=0和t=10 ms两个时刻计算区域的黏度分布和气体体积分数分布。对比图6可以看出，仿真结果中极大黏度区与正常黏度区的分界线可以准确追踪实验过程中的液桥高度变化，即液桥的上边界运动。同时，极大黏度区的液态金属可以依靠黏度的耗散作用克服表面张力驱动下的流体运动，从而保持近乎标准的圆柱形状。而正常黏度区的液态金属会在表面张力作用下发生形变，符合液桥拉伸运动的实际情况。本文提出的“极大黏度法”与“抽液近似法”相结合可以有效跟踪液桥高度和边界的实时变化，在不需要进行网格拉伸的情况下将液桥拉伸断裂的三相流问题合理简化为两相流问题。
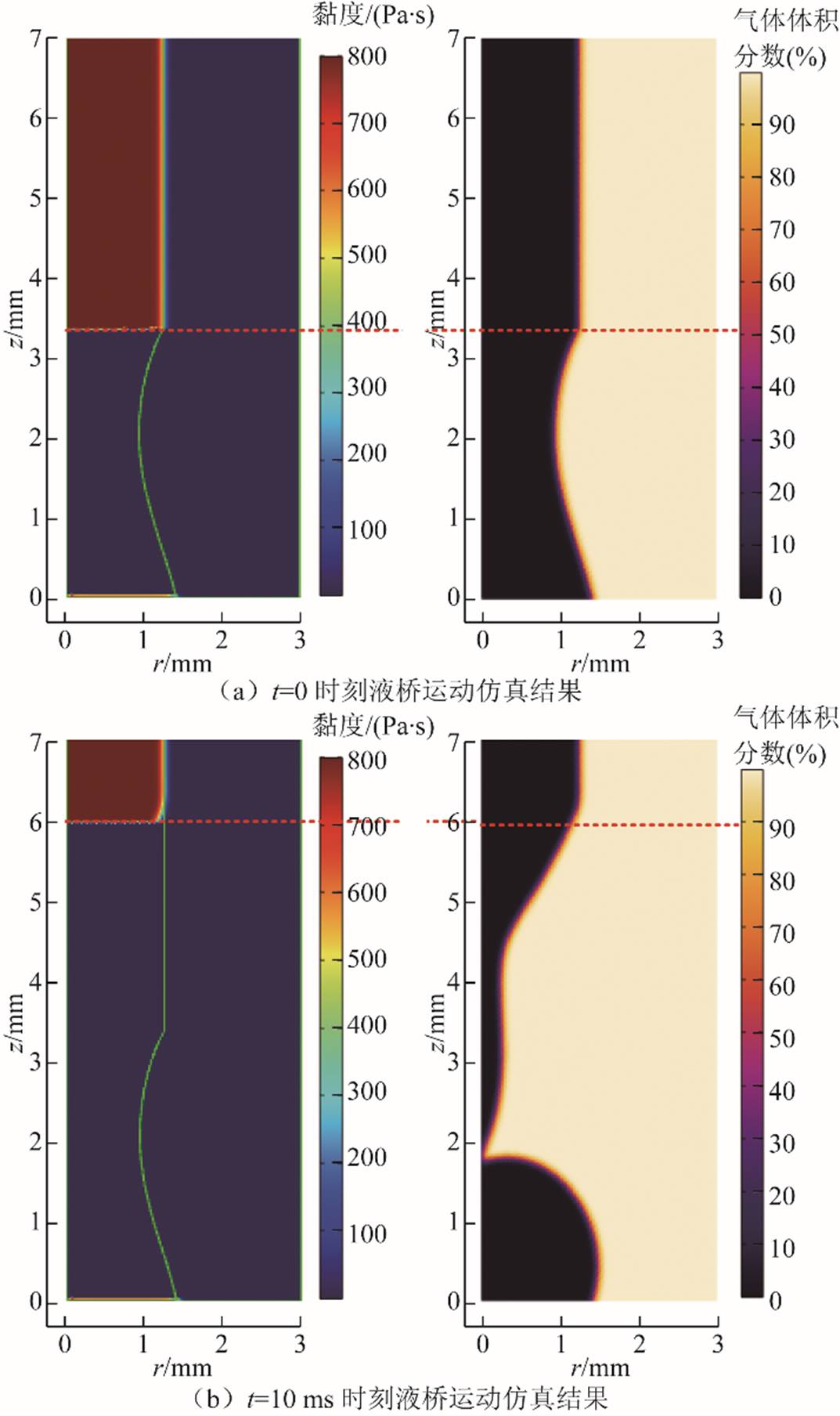
图7 液桥上边界追踪的仿真结果
Fig.7 Simulation results of tracking of the liquid bridge’s upper boundary
图8给出了一组仿真结果与实验结果的对照图，图中每一时刻的照片都是由一半仿真结果（右半边）与一半实验结果（左半边）拼接合成。除了t=0时刻仿真结果中液态金属桥的轮廓是由仿真初始时刻手动导入外，其他均是由模型计算而来。从图8可以看出，模型所得液桥流形仿真结果与实验结果在时间尺度和几何形状上具有较高的吻合度，该模型可以有效地预测液桥拉伸断裂的流体动力学特性。仿真结果的准确性验证了本文所建立流体拉伸模型的合理性。值得注意的是，在t=10～11.45 ms这段时间内，尽管液桥的上边界移动很少，液桥却完成了液丝上端的二次断裂并形成了较大的底部距离。这也印证了液桥的断裂本质上是拉普拉斯压力驱动下的自收缩过程。
图8 液桥拉伸断裂过程的实验结果与仿真结果对照
Fig.8 Comparison of the experimental and simulated results of the process of liquid metal bridge’s breakup induced by stretch
根据文献[17]的研究结果，断裂距离Rd对于液桥电弧开断性能和燃弧模式转变的影响最大。本文首先研究了液桥体积对于拉伸断裂过程中Rd形成的影响。在仿真模型中构建体积分别为8、13、 18 μL的圆柱形初始液桥，随后以0.1 m/s的速度匀速拉伸各个液桥直至发生二次断裂，记录Rd形成时刻的液桥形状，仿真结果如图9所示。对比可知，液桥断裂过程中的断裂距离随着液桥体积的增大而增大。
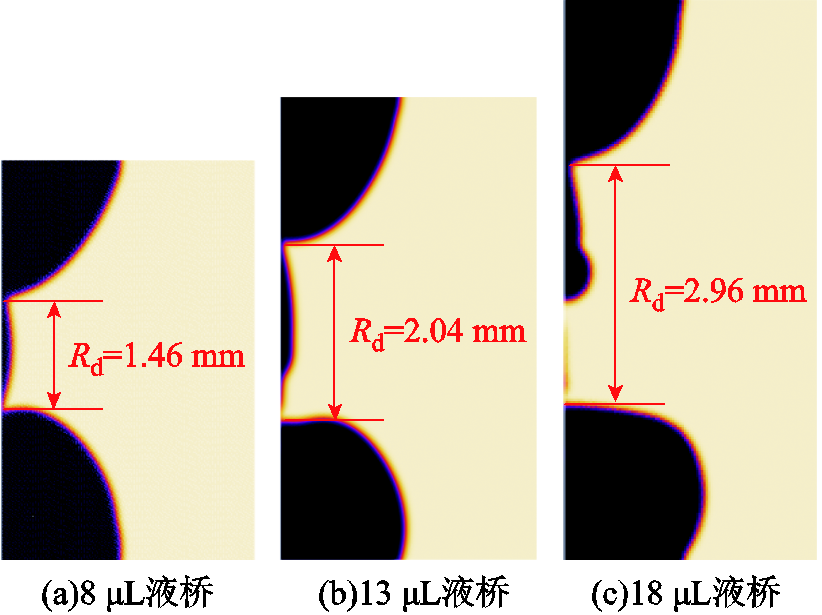
图9 不同体积液桥Rd的对比
Fig.9 Comparison of Rd in LM bridges of different volumes
液桥体积影响断裂距离的相关机理可以从液桥形变程度和附加拉普拉斯压力的角度进行解释。图10给出了不同体积液桥在被拉伸相同距离（2.7 mm）后表面曲率的分布。尽管被拉伸了同样的距离，不同体积液桥表面的曲率分布差别较大。具体来说，8 μL液桥中间液颈最细处的曲率在3 300 m-1左右，液桥表面其他地方曲率在几百到3 000 m-1不等。作为对比，13 μL液桥液颈最细处的曲率约为1 500 m-1，18 μL液桥液颈最细处的曲率约为1 300 m-1，液桥表面其他部分的曲率则更小。由式（1）可知，更大的曲率可以产生更大的拉普拉斯压力，从而使液桥尽早进入附加压力主导的快速自收缩断裂阶段。也就是说，大体积液桥对于外界的拉伸效果具有更强的形变耐受度，需要被拉伸到更大的长度以完成两次自收缩断裂，从而导致更大断裂距离的形成。
图10 不同体积液桥拉伸相同距离下的表面曲率对比
Fig.10 Comparison of surface curvature in LM bridges of different volumes, under the same extended distance
为了获得拉伸速度对液桥断裂过程的影响，本文在仿真中对三种不同体积的液桥施加0.1～1 m/s的均匀拉伸速度，获取液桥的拉伸断裂过程。图11给出了8 μL液桥在不同拉伸速度下发生二次断裂时刻的仿真截图序列。在这一速度范围内，仿真结果相比于图1中的实验结果，液桥的流体动力学特性变化更为丰富。当拉伸速度小于0.5 m/s时，液桥的断裂距离随着拉伸速度的增大而增大。液桥呈现出与实验结果类似的两次断裂，第一次断裂出现在液丝与下液滴之间，第二次断裂出现在液丝与上液滴之间。当拉伸速度在0.5 m/s左右时，液桥上、下两端同时断裂，呈现出对称特征。拉伸速度继续增大，液桥的断裂距离随之增加，同时，液桥开始出现新的二次断裂特征：液丝两个断裂点发生的时间先后顺序出现翻转，即液丝先在与上液滴的连接处断裂，随后在与下液滴的连接处断裂，本文将该现象称为“二次断裂翻转”。与之对应，本文也将液桥出现上、下两端同时对称断裂时的外部机构拉伸速度定义为临界翻转速度。此后，随着液桥拉伸速度的增加，断裂距离持续增大，但液桥始终维持上端先断、下端后断的二次断裂模式。
图11 不同拉伸速度下的液桥（8 μL）断裂
Fig.11 Breakup and rupture of a LM bridge (8 μL) under different stretching velocities
拉伸速度的增大不仅会导致断裂距离增加，还会导致中间液丝变长。当液丝变长到一定程度之后，液丝收缩过程中会在表面张力作用下发生三次断裂。在实际应用中，如果此时电路尚未断开，液丝的三次断裂将会引燃第三段电弧，并新增第三对电弧近阴极区、近阳极区和对应的近极压降[25]；随着液丝的进一步收缩和断裂，甚至还有可能产生第四段、第五段电弧以及相应的近极压降，这对于电路的开断过程无疑是十分有利的。受限于样机的拉伸速度，文献[17]的实验研究中并没有能够观察到这种情况，但从理论上看这是必然可以发生的一种情形，本文将其命名为“模式二Plus”。图12给出了“模式二Plus”情况下可能存在的液桥电弧拉伸示意图。结合示意图分析可知，假如此时中间的液态金属丝断裂形成了n段独立的液态金属液丝并且电弧尚未熄灭，那么将会有n+1段电弧串联燃烧，从而带来n+1对近极压降以及n个附加的液丝收缩拉弧速度vc。毫无疑问，这对于电弧的快速熄灭是十分有利的。
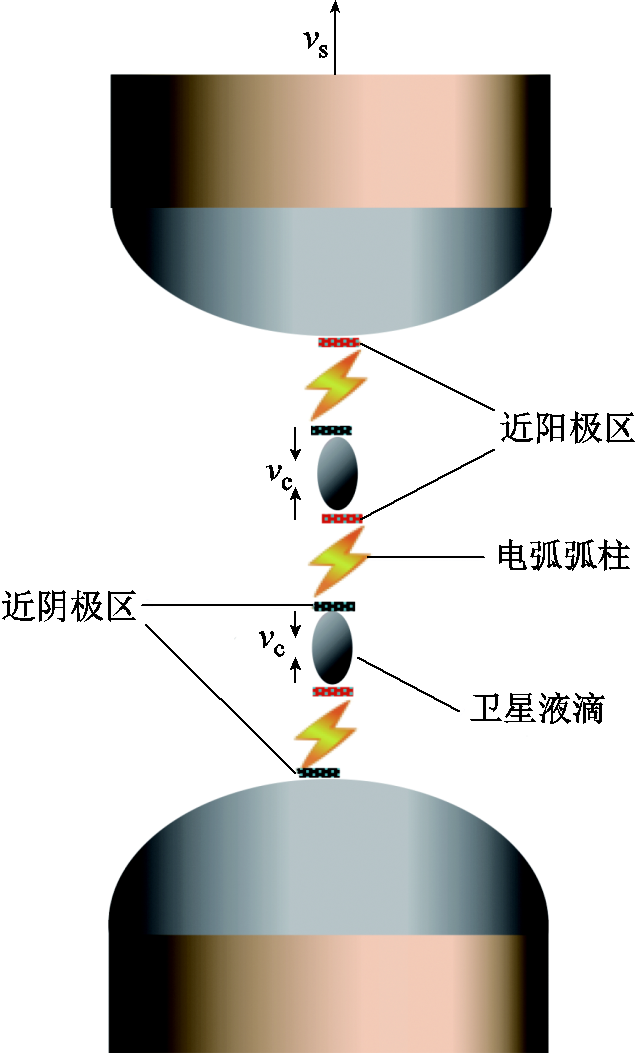
图12 “模式二Plus”液桥电弧拉伸示意图
Fig.12 Schematic of electrical arcs’ elongation in “Regime Ⅱ Plus”
液桥收缩断裂过程中断裂距离的变化及二次断裂翻转可以结合流体动力学的作用效果进行解释。液桥在拉伸断裂及毛细收缩过程中主要受到四个作用效果的影响：表面张力、重力、外部机构的拉伸及流体本身的黏性耗散。表面张力以拉普拉斯压力的形式维持液颈的自收缩，提供液桥断裂的动力来源。在此基础上，重力的效果是使流体微元趋于下坠，从而造成液丝下端更大的压差以及更早的断裂。与重力的作用方向相反，外部机构对液桥的拉伸则通过向上的惯性效应对抗张力的收缩，起到稳定液丝结构的作用。该作用效果通过一个无量纲速度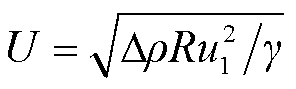
来衡量[18]。其中，Δρ为液体与周围气体的密度差，R为液桥底面半径，u1为液桥的实际拉伸速度。随着拉伸速度的增大，无量纲速度U，即拉伸速度作用在液丝上的惯性力和稳定效应增强，最终导致液丝长度及断裂距离也增大。液桥的二次断裂翻转则可以通过重力的下坠作用与拉伸带来的惯性效应的竞争来解释。当拉伸速度很小时，重力的下坠作用明显，液桥首先在液丝下端发生断裂；当拉伸速度增大到一定程度之后，惯性力与重力作用相平衡，液桥只在张力作用下收缩，发生对称断裂；拉伸速度继续增大，向上的惯性力效应超过向下的重力作用，液丝上端将率先发生断裂。作为对照，本文还对无拉伸以及无重力作用下凹形液桥的断裂过程进行了仿真，结果如图13所示。这种情况下液桥仅在表面张力作用下发生对称的毛细收缩断裂，这与前面的理论分析是一致的。
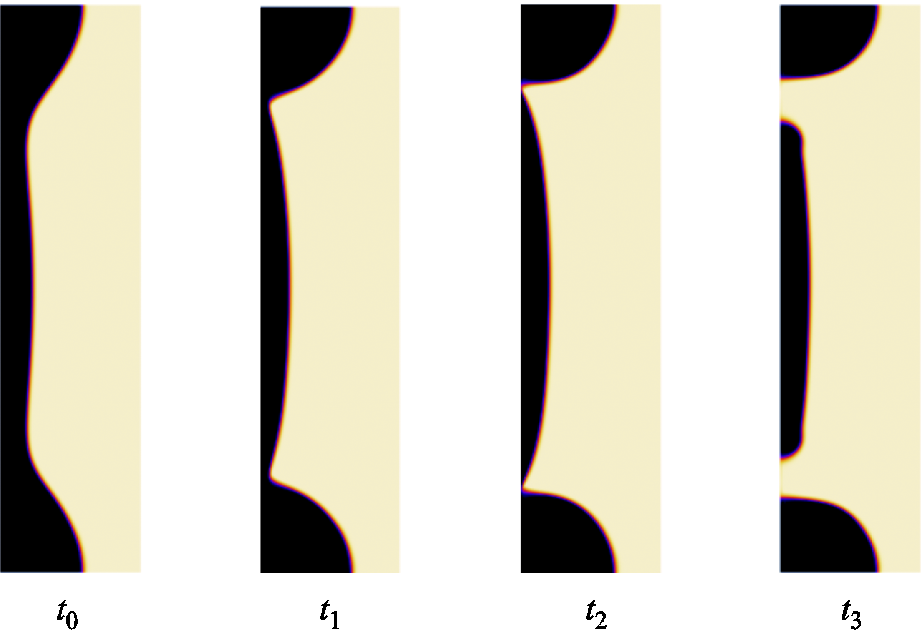
图13 无重力、无拉伸作用下的液桥断裂
Fig.13 Breakup of a LM bridge without the effect of gravity or stretching
图11以8 μL液桥为例分析了拉伸速度对于液桥断裂流体动力学特性的影响。实际上，随着液桥体积的增大，其拉伸断裂过程也会展现出更加丰富的流体动力学变化。18 μL液桥在不同拉伸速度下的断裂变化如图14所示，可见其与8 μL液桥有两个明显不同之处：①断裂距离随拉伸速度的增加不再保持单调变化，0.34 m/s时的断裂距离相比 0.3 m/s时略有下降；②液桥会发生多次二次断裂翻转，分别以0.19、0.34、0.5 m/s作为临界翻转速度，拉伸速度超过0.5 m/s以后断裂位置不再翻转。对于这两个新特征，本文推断是由于随着液桥体积的增大，中间液丝的质量增加明显，液丝的重力对于液桥的断裂过程产生了新的不可忽略的影响。
图14 不同拉伸速度下的液桥（18 μL）断裂
Fig.14 Breakup and rupture of a LM bridge (18 μL) under different stretching velocities
图15总结了三种不同体积液桥在0.1～1 m/s匀速拉伸速度范围内断裂距离的变化情况。当拉伸速度较小时，惯性力的作用相对于重力和表面张力较弱，液桥断裂距离与拉伸速度和液桥体积成正比。随着拉伸速度的增大，惯性力开始发挥作用，液桥的断裂位置开始发生翻转。不同体积液桥断裂时的翻转速度和翻转次数都不尽相同，断裂距离与拉伸速度不再是单调的正比关系。当拉伸速度继续增大以后，表面张力和重力相对于惯性力的作用可以忽略，断裂距离再次随着拉伸速度的增大而增大。
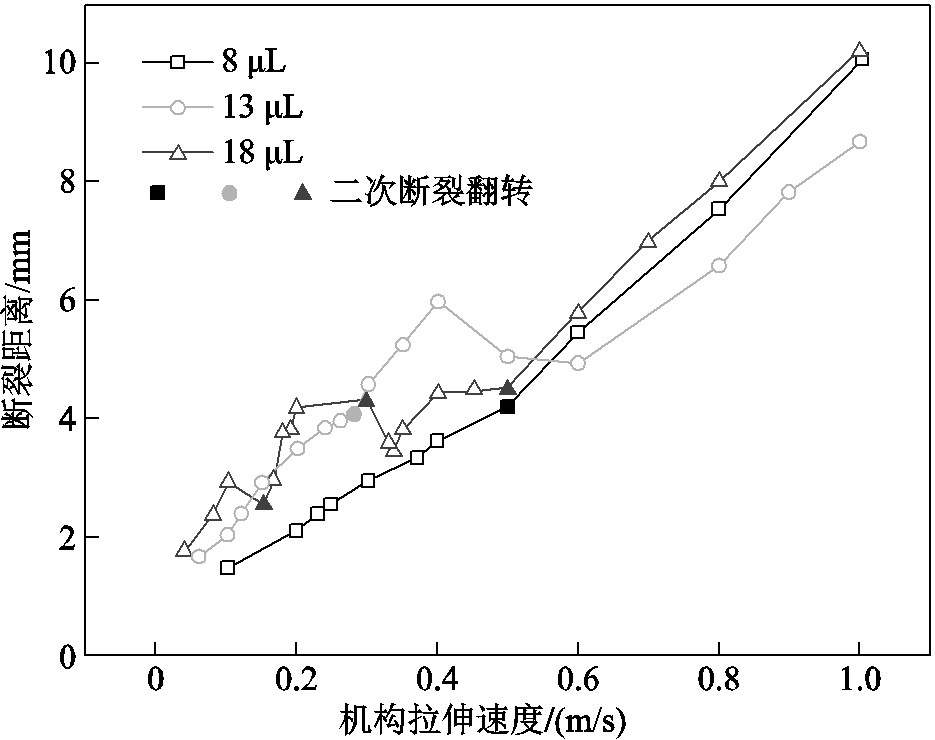
图15 不同体积液桥断裂距离随拉伸速度的变化
Fig.15 Rupture distance versus stretching velocities of LM bridges with different volumes.
图16给出了不同体积液桥的底部距离Bd在不同拉伸速度下的变化。在液桥二次断裂翻转之前，液桥的底部距离先增加后减小，不同体积液桥的底部距离均在一定范围内波动。从流体动力学角度来看，底部距离是由外部机构的拉伸速度、液丝的收缩速度以及液丝两次断裂的时间间隔综合决定的。在液桥断裂位置发生翻转之前，机构拉伸速度的增加一方面有利于在一定的断裂时间间隔内增大底部距离，另一方面也因为缩短了两次断裂的间隔时间而抑制了底部距离的生长。因此，在这个区间内，底部距离只是在一定范围内波动。而当机构拉伸速度增大到一定程度之后，底部距离则主要取决于外部拉伸速度，随着外部拉伸速度的增大而增大。图16中还以液桥的“二次断裂翻转”为界将底部距离进行了正、负区分。当液桥在临界翻转位置时，液丝在与顶部和底部液滴连接处同时、对称断裂，此时底部距离Bd=0；当液丝下端先发生断裂时，底部距离由液丝底端与下液滴顶端的位置确定，为正值；当液丝上端先发生断裂时，底部距离由液丝顶端与上液滴底端的位置确定，为负值。
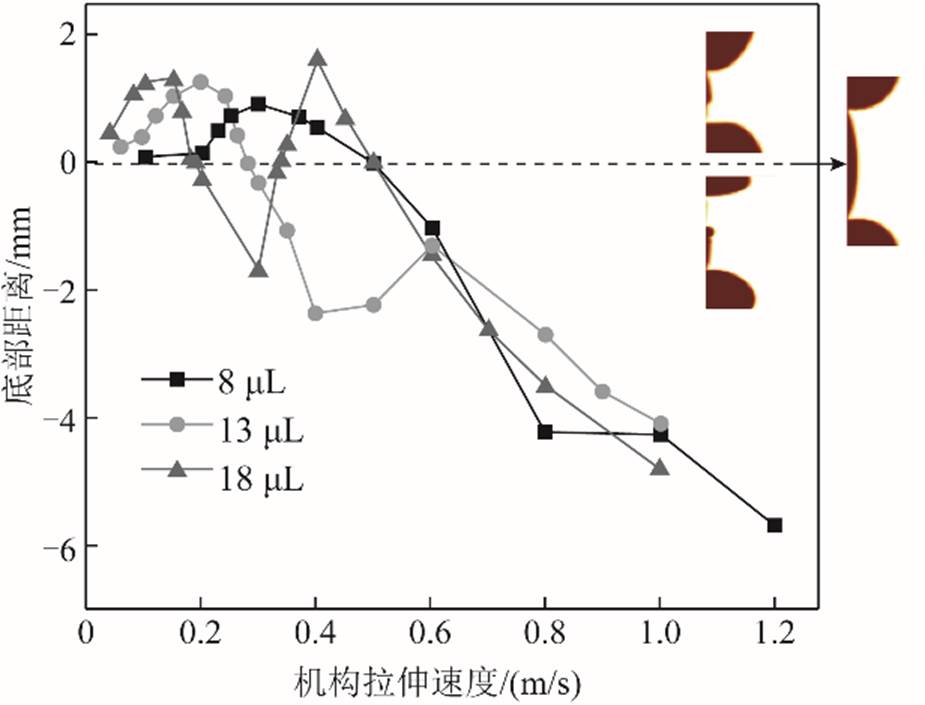
图16 不同体积液桥底部距离随拉伸速度的变化
Fig.16 Bottom distance versus stretching velocities of LM bridges with different volumes
综合以上分析可知，在一定的范围内提高液桥的拉伸速度总体上来看可以增加液桥的断裂距离和底部距离。结合文献[17]的研究结论可知，断裂距离和底部距离的增加将为单电弧燃烧或双电弧串联燃烧提供更多的发展空间，从而延迟液桥燃弧模式三的到来，缩短燃弧时间，提升液桥的电弧开断性能。
受限于实验条件的限制，文献[17]仅给出了较低拉伸速度条件下的三种液桥燃弧模式及其随着初始开断电流增大时的模式转变规律。本文的仿真模型在较大的拉伸速度范围内获得了更为一般性的结论，结合文献[17]中的实验结果可以推广得到全拉伸速度范围内液态金属电弧燃烧的模式转变相图，如图17所示。在全拉伸速度范围下，液桥燃弧模式的转变将存在不同的转变路线。拉伸速度较小时，液桥燃弧模式的转变遵从文献[17]和本文图1中的实验结果分析，即随着开断初始电流的增大，电弧燃烧遵从“模式一→模式二→模式三”的转变方式；当拉伸速度到达二次断裂翻转位置临界值附近时，液桥上下两端对称断裂，液桥燃弧不再存在模式一，而是遵从“模式二→模式三”的转变路线；对于具有较大体积的液桥，其具有多个临界翻转速度，因此这种模式转变路线可能会随着拉伸速度的增大交替出现多次；最后，拉伸速度的增大会导致更长的液丝以及液丝的多次断裂，从而使液桥燃弧出现“模式一→模式二→模式二Plus”这种转变路线。参考图17，可以对液桥式开关的电弧燃弧模式及其转变路线进行调控。
图17 全速度范围液桥燃弧模式转变相图
Fig.17 Arc regimes transition of a LM bridge among the whole-range stretching velocities
针对液态金属桥从拉伸形变到收缩断裂的流体运动过程，本文提出了一种不需要网格拉伸的有限元仿真方法。该方法对液体设置极大黏度值，以不可流动液体对固体材料进行近似，通过向计算域外抽取液体配合极大黏度边界的移动来模拟液桥拉伸。模型仿真结果与实验结果的对比验证了该方法的有效性。同时，本文还通过改变仿真条件分析了液桥拉伸断裂流体动力学特性的转变规律及其影响因素。最后，结合相关实验结果对液态金属桥的电弧燃烧特性进行了推广和预测。相关研究内容对于微型继电器、接触器等微型开关的研发具有指导意义。本文得到的主要结论如下：
1）“极大黏度法”与“抽液近似法”相结合可以有效地模拟液态金属桥从拉伸形变到收缩断裂的流体运动过程。相比常规的网格拉伸方法，该仿真方法具有更宽广的适用范围，可以用于带有流体拓扑断裂和计算域高速、大范围拉伸情况下的仿真计算。
2）液桥断裂过程的不对称性是由重力和外界拉伸的作用效果共同决定的。当重力作用效果占优时，液桥下端先发生断裂；反之，则上端先发生断裂；当两者作用效果相当时，液桥发生上、下两端的对称断裂。较大体积的液桥会发生多次断裂翻转。
3）大体积液桥对于外界拉伸效果具有更高的曲率耐受度，可以发展出更大的断裂距离。增大液桥的拉伸速度总体上可以增大断裂距离和底部距离，为液桥的单电弧和双电弧串联燃烧创造更大的发展空间，缩短燃弧时间，提升开断性能。
4）全拉伸速度范围下液桥的燃弧模式转换路线更加丰富。临界翻转速度下液桥将直接进入双电弧串联燃烧模式；更大拉伸速度下会发生液桥多次断裂导致的“模式二Plus”。这两种情况下的液桥电弧开断性能较佳。
参考文献
[1] Slade P G. Electrical Contacts: Principles and Applications[M]. 2nd ed. Boca Raton: CRC Press, 2014.
[2] 陈忠华, 李兵红, 陈明阳, 等. 弓网滑动电接触电磁热力耦合效应研究进展[J]. 电工技术学报, 2023, 38(10): 2777-2793.
Chen Zhonghua, Li Binghong, Chen Mingyang, et al. Research advances in electrical-magnetic-thermal-mechanical coupling effects of electric contact between pantograph and catenary[J]. Transactions of China Electrotechnical Society, 2023, 38(10): 2777-2793.
[3] 王召斌, 翟国富, 黄晓毅. 电磁继电器贮存期接触电阻增长的动力学模型[J]. 电工技术学报, 2012, 27(5): 205-211.
Wang Zhaobin, Zhai Guofu, Huang Xiaoyi. Kinetic model of contact resistance increment of electromagnetic relay in storage[J]. Transactions of China Electrotechnical Society, 2012, 27(5): 205-211.
[4] 任万滨, 武剑, 陈宇, 等. 电触点材料接触电阻高精密测量技术[J]. 电工技术学报, 2014, 29(1): 31-36.
Ren Wanbin, Wu Jian, Chen Yu, et al. Precision measuring technique for contact resistance of contact materials[J]. Transactions of China Electrotechnical Society, 2014, 29(1): 31-36.
[5] Li Xingwen, Chen Degui. 3-D finite element analysis and experimental investigation of electrodynamic repulsion force in molded case circuit breakers[J]. IEEE Transactions on Components and Packaging Technologies, 2005, 28(4): 877-883.
[6] 于国飞, 袁仲林, 郑翔. 高压直流继电器触头间电动斥力分析[J]. 电器与能效管理技术, 2020(9): 13-17.
Yu Guofei, Yuan Zhonglin, Zheng Xiang. Analysis of electric-dynamic repulsion force between contacts of high voltage DC relay[J]. Electrical & Energy Management Technology, 2020(9): 13-17.
[7] 汪倩, 陈思磊, 孟羽, 等. 低压直流系统故障电弧检测技术研究综述[J]. 高压电器, 2023, 59(5): 93-103.
Wang Qian, Chen Silei, Meng Yu, et al. Review of research on DC arc fault detection technology in low voltage DC system[J]. High Voltage Apparatus, 2023, 59(5): 93-103.
[8] 陈默, 陆宁懿, 翟国富. 基于电弧磁流体仿真的DC 1500 V两极塑壳断路器气道优化设计[J]. 电工技术学报, 2023, 38(8): 2222-2232.
Chen Mo, Lu Ningyi, Zhai Guofu. Arc chamber optimization of DC 1 500 V two-pole circuit breakers based on arc magneto hydro dynamics simulation[J]. Transactions of China Electrotechnical Society, 2023, 38(8): 2222-2232.
[9] 马飞越, 姚晓飞, 刘志远, 等. 2/3匝线圈式纵磁触头大开距真空断路器分闸速度设计[J]. 电工技术学报, 2024, 39(13): 4139-4152.
Ma Feiyue, Yao Xiaofei, Liu Zhiyuan, et al. Design of opening velocities for large-gap vacuum circuit breakers with 2/3 coil-type axial magnetic field contacts[J]. Transactions of China Electrotechnical Society, 2024, 39(13): 4139-4152.
[10] 薄凯. 直流继电器触点熔焊仿真分析与实验研究[D]. 哈尔滨: 哈尔滨工业大学, 2019.
Bo Kai. Simulation and experimental researchon contacts welding for DC relay[D]. Harbin: Harbin Institute of Technology, 2019.
[11] 鲍光海, 王金鹏, 王毅龙. 磁保持继电器多物理场耦合模型设计与触头弹跳影响因素分析[J]. 电工技术学报, 2023, 38(3): 828-840.
Bao Guanghai, Wang Jinpeng, Wang Yilong. Design of multi-physical field coupling model of magnetic latching relay and analysis of influencing factors of contact bounce[J]. Transactions of China Electro-technical Society, 2023, 38(3): 828-840.
[12] 薄凯, 周学, 翟国富, 等. 智能电表用磁保持继电器短路电流条件下触头斥开机理仿真研究[J]. 中国电机工程学报, 2018, 38(17): 5238-5245, 5321.
Bo Kai, Zhou Xue, Zhai Guofu, et al. Simulation on contact repelling mechanism under short-circuit currents of magnetic latching relays for intelligent watt-hour meters[J]. Proceedings of the CSEE, 2018, 38(17): 5238-5245, 5321.
[13] 何志鹏, 赵虎. 微型断路器电寿命评估[J]. 电工技术学报, 2022, 37(4): 1031-1040.
He Zhipeng, Zhao Hu. Electrical lifespan evaluation of miniature circuit breakers[J]. Transactions of China Electrotechnical Society, 2022, 37(4): 1031-1040.
[14] Zhu Xiaonan, Yang Fei, Zhao Siyuan, et al. Liquid-metal capillary switch for electrical power application [J]. Applied Physics Letters, 2020, 117(26): 263701.
[15] Zhu Xiaonan, Yang Fei, Wang Haoran, et al. Robust electrical contacts integrating a liquid metal bridge for mechanical switches[J]. Journal of Physics D: Applied Physics, 2022, 55(14): 145002.
[16] Sen P, Kim C J C. Microscale liquid-metal switches—a review[J]. IEEE Transactions on Industrial Electronics, 2009, 56(4): 1314-1330.
[17] Zhu Xiaonan, Yang Fei, Wang Haoran, et al. Power-level electrical switch enabled by a liquid-metal bridge[J]. ACS Applied Electronic Materials, 2022, 4(6): 2859-2868.
[18] Zhuang Jinda, Ju Y S. A combined experimental and numerical modeling study of the deformation and rupture of axisymmetric liquid bridges under coaxial stretching[J]. Langmuir, 2015, 31(37): 10173-10182.
[19] Deganello D, Williams A J, Croft T N, et al. Level-set method for the modelling of liquid bridge formation and break-up[J]. Computers & Fluids, 2011, 40(1): 42-51.
[20] 尚超, 阳倦成, 张杰, 等. 镓铟锡液滴撞击泡沫金属表面的运动学特性研究[J]. 力学学报, 2019, 51(2): 380-391.
Shang Chao, Yang Juancheng, Zhang Jie, et al. Experimental study on the dynamic characteristics of galinstan droplet impacting on the metal foam surface[J]. Chinese Journal of Theoretical and Applied Mechanics, 2019, 51(2): 380-391.
[21] 方涌. 对弯曲液面的附加压强的推导[J]. 物理通报, 2000(8): 11-13.
[22] Eggers J, Villermaux E. Physics of liquid jets[J]. Reports on Progress in Physics, 2008, 71(3): 036601.
[23] Bo Kai, Zhou Xue, Zhai Guofu. Investigation on arc dwell and restriking characteristics in DC high-power relay[J]. IEEE Transactions on Plasma Science, 2017, 45(6): 1032-1042.
[24] Courtois M, Carin M, Le Masson P, et al. Guidelines in the experimental validation of a 3D heat and fluid flow model of keyhole laser welding[J]. Journal of Physics D: Applied Physics, 2016, 49(15): 155503.
[25] Hemmi R, Yokomizu Y, Matsumura T. Anode-fall and cathode-fall voltages of air arc in atmosphere between silver electrodes[J]. Journal of Physics D: Applied Physics, 2003, 36(9): 1097-1106.
Simulation Analysis of Stretch Induced Breakup of a Liquid-Metal Bridge for the Development of Micro-Switches
Abstract Traditional mechanical switches use a pair of solid-metal sheets as conductive contacts to achieve switch operations. Existence of conductive spots leads to a series of electrical contact stability problems such as the increase of contact resistance, electrodynamic repulsion force between closed contacts and the generation of switching arcs in current breaking, which seriously affect the service life of mechanical switches, especially microswitches like relays and miniature circuit breakers. Stretching a liquid-metal bridge to breakup could realize rapid arc breaking of low-voltage DC ampere-level currents, thereby eliminating the above electrical contact problems caused by solid conductive spots. Constructing a simulation model can effectively analyze the fluid dynamics of a liquid-metal bridge during the stretch induced breakup, providing guidance for the regulation of the liquid-metal bridge’s arc breaking performance. Most existed models for liquid bridge’s breakup simulation are based on moving mesh or other mesh deformation methods, which cannot simulate the wide range deformation or geometric rupture of a liquid bridge.
To address the above issue, a finite element simulation method that doesn’t rely on grid deformation for liquid bridge’s breakup is proposed here. This method approximates solids by setting a maximum viscosity for liquids, and simulates the liquid bridge’s stretch process by moving the boundary of the maximum viscosity area cooperating with the liquid mass flowing out of the calculating domain. Fluid variations of the liquid bridge obtained from the model are in good agreement with experimental results, in terms of time scale and geometric shape. The model could be used to accurately track the boundary movement and profile development of a liquid bridge during the whole breakup process. Based on this model, fluid dynamics of a liquid bridge during stretch induced breakup could be accurately predicted.
Based on the model, the effects of liquid metal volume and stretching speed on the breakup characteristics of a liquid bridge are explored. Transition law of a liquid bridge’s breakup characteristics within the full stretching speed range is also obtained. Liquid bridges with a larger volume have higher curvature tolerance towards external stretching effect, thus could develop larger rupture distances. Increasing the stretching speed can generally increase the rupture distance and bottom distance of a liquid bridge, which helps to create larger space for the development of single arc and double arc in series, shortening the arcing time and improving the breaking performance in the end. The stretching speed also affects the order of two times ruptures of the liquid bridge through competition with the effect of gravity. As the stretching speed increases, two times ruptures of the liquid bridge follow a transition pattern of firstly rupturing at the lower end, simultaneous rupturing at both ends, and firstly rupturing at the upper end.
Combined with experimental results, the influence of liquid bridge breakup characteristics’ transition on the arc regimes was analyzed, and the phase diagram of the arc regimes’ transition within the full stretching speed range was given, providing a basis for regulating the arc breaking performance of the liquid bridge-based switch. Within the full stretching speed range, electrical arc regimes’ transition routes of the liquid bridge are more diverse. At the critical transition speed, breakup of the liquid bridge will directly give birth to the Regime Ⅱ where two electrical arcs elongate in series. At higher stretching speeds, “Regime Ⅱ Plus” of electrical arcs emerge due to multiple breakups of the liquid bridge. In the above two situations, electrical arc breaking performance of the liquid bridge is superior.
This study has strong reference significance for the study of both fluid simulation methods for liquid bridge breakup and the development of liquid bridge-based microswitches such as relays and contactors.
keywords：Electric arc and electrical contacts, liquid-metal bridge, mechanical switches, DC interruption, finite element simulation, fluid simulation
中图分类号：TM501
DOI: 10.19595/j.cnki.1000-6753.tces.231132
国家自然科学基金（52077172）和陕西省三秦创新团队“先进直流电力装备关键技术及其产业化示范创新团队”资助项目。
收稿日期 2023-07-17
改稿日期 2023-09-13
朱晓楠 男，1995年生，博士，工程师，研究方向为装备电气性能综合测试技术和多物理场仿真分析。
E-mail：zxnxjtu@163.com
杨 飞 男，1982年生，教授，博士生导师，研究方向为直流电力开关设备、电力设备数字化设计与智能制造、开关器件新原理及其应用等。
E-mail：yfei2007@mail.xjtu.edu.cn（通信作者）
（编辑 李 冰）