
图1 轨道表面沉积层
Fig.1 Deposition layer on the rail’s surface
摘要 大电流高速滑动电接触环境下,多次发射后轨道表面出现铝沉积现象。电枢与铝沉积层在界面热源作用下发生熔化磨损会改变接触状态,严重影响滑动电接触性能。界面热源在电枢和沉积层轨道间的热分配特性是研究界面材料熔化磨损的基础,因此有必要对滑动电接触界面热量分配过程进行研究。该文首先建立了电枢和沉积层轨道热传递模型,获得了电枢和沉积层轨道温度分布方程。根据界面温度连续性,推导热分配控制方程,应用最小二乘估计法优化误差函数,提出了基于最小二乘估计法的界面热分配数值计算模型。基于热分配数值计算模型,研究分析了材料热参数、速度对热分配特性的影响规律,结果表明:材料热参数影响热分配曲线的初始值,速度影响热分配曲线的衰减速率,速度越大热分配随时间衰减越快。最后,通过理论分析探讨了枢轨界面热分配过程的物理机制,理论分析结果与数值计算结果一致。研究成果可以为界面热过程提供更加深入的理解,为界面材料熔化磨损特性的研究提供技术支持。
关键词:高速滑动电接触 界面热源 热分配计算模型 最小二乘估计
电磁轨道发射(Electromagnetic Launch, EML)依靠脉冲大电流形成强磁场,推动载流电枢在轨道表面高速滑动。维持良好的滑动电接触性能是实现EML高频率和高效率工作的重要保证[1-5]。
电枢在轨道上高速滑动的过程中,电枢和轨道通过表面凸起斑点接触,界面接触电阻较大,电流流过会产生巨大的界面焦耳热[6]。同时,电枢高速滑动会在界面产生接触摩擦热,界面焦耳热和摩擦热共同构成界面总热源[7]。总的接触热源在电枢和轨道侧动态分配,一部分热量流入电枢的接触表面,另一部分热量流入轨道侧的接触表面。除了受接触热作用外,枢轨接触材料本体流过电流,由于自身体电阻还会产生体电阻焦耳热[8]。枢轨接触材料在自身体电阻焦耳热和界面接触热的共同作用下产生温升、发生熔化。接触材料自身体焦耳热可以通过电磁场模块计算获得并添加到热传导方程中[9],而接触热的作用只能通过加载热通量边界条件的形式体现。定义电枢侧热分配系数为流入电枢表面的热量与界面总热量的比值,热分配系数值决定了流入电枢和轨道侧接触表面热通量的大小,进而影响界面材料熔化磨损的程度。熔化磨损引起的接触状态改变会对枢轨滑动电接触性能产生重要影响[10-11]。因此,研究热分配的变化过程,对深入理解界面熔化磨损机理,提高滑动电接触性能具有重要意义。
文献[12]开发了EMAP 3D有限元编码程序,联合电磁、传热交叉研究,获得了界面电流、轨道温度分布的瞬态特性。研究关注界面电流和轨道温度的分布区域与轨道损伤的关系,但由于保密原因,并未对界面热通量边界条件的处理给予明确说明。
文献[13]建立了一种包含电路、电磁场、热场和结构场等瞬态多物理场求解器,获得了电枢瞬态温度场分布特性,模型为了简化计算,忽略了界面接触电阻焦耳热和摩擦热,仅考虑材料本体焦耳热,并未考虑界面接触热源的影响。文献[14]假设界面接触热全部传给轨道,采用灰色系统分析方法研究了轨道的温度分布。文献[15]基于均匀面热源滑过半有限固体时最大闪温求解原理,通过假设轨道保持电枢熔点为最大温度,给出了电枢熔化后流入轨道的热通量边界条件,但是无法确定界面材料熔化前流入轨道的热量,也未对界面热分配变化特性进行分析。文献[16]通过理论分析和数值仿真对高速滑动电接触电枢表面动态磨损过程进行研究,在处理轨道侧热通量时沿用文献[15]给定的近似表达式,但未涉及热分配变化特性研究。
鉴于此,考虑实际发射过程界面热源和速度动态变化特性,建立了电枢和沉积层轨道热传递模型,获得了电枢和沉积层轨道温度分布方程,并基于界面温度连续性特点,获得热分配控制方程。实际电磁发射过程中电枢运动速度、界面焦耳热和摩擦热均随时间动态变化,此情况下热分配方程存在多重积分及奇异函数,无法获得解析解。最小二乘估计法因最优解唯一、求解方便及具有较好的解析性质,广泛应用在非线性方程求解过程,尤其是热传导方程的非线性问题。通过将最小二乘估计法应用于热分配方程的求解过程,获得了实际发射过程中接触热源在界面上的动态热分配特性。
电磁轨道发射依靠脉冲大电流形成强磁场,推动载流电枢在轨道表面高速滑动,滑动电接触界面产生焦耳热和摩擦热。由于界面接触电阻产生的焦耳热远远大于电枢轨道自身焦耳热,轨道自身焦耳热产生的本体温升可以忽略,认为界面焦耳热仅由接触电阻产生。
接触电阻产生的界面焦耳热和高速滑动摩擦产生的界面摩擦热一起构成界面热源。在滑动过程中,界面热源持续加热接触界面,界面热源相对于电枢为静止热源;相对于轨道来说,只有接触区域存在热源,所以是运动热源。多次发射后轨道表面覆盖一层薄薄的沉积层,沉积层主要成分为铝。试验后轨道表面沉积层如图1所示。

图1 轨道表面沉积层
Fig.1 Deposition layer on the rail’s surface
多次发射过程中,电枢与轨道侧铝沉积层直接接触,由于滑动时间较短,热量在接触界面的透入深度远小于电枢和轨道侧沉积层的尺寸,电枢和沉积层轨道可以看作半无限大固体[17],并且初始温度分布均为室温。
电枢-沉积层轨道热分配示意图如图2所示。由于电枢滑动时间较短,与空气的对流换热可以忽略不计,热量传递方式仅为热传导形式。假设不考虑界面上的热量损失,认为界面热源全部被沉积层轨道和电枢吸收。图2中,α(0≤α≤1)为电枢侧热分配系数值,定义为电枢侧吸收的热量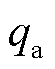 占总热量q的比值,则1-α就是沉积层轨道侧的热分配系数值。为方便分析,认为界面热源均匀分布在接触区域,并且在滑动过程中接触区域面积保持不变。若驱动电流为I,接触面积为A,枢轨接触面间的接触电阻为Rc[16],则单位面积上产生的焦耳热流速率可以写为
占总热量q的比值,则1-α就是沉积层轨道侧的热分配系数值。为方便分析,认为界面热源均匀分布在接触区域,并且在滑动过程中接触区域面积保持不变。若驱动电流为I,接触面积为A,枢轨接触面间的接触电阻为Rc[16],则单位面积上产生的焦耳热流速率可以写为
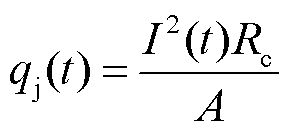 (1)
(1)
单位面积上界面摩擦热流速率为
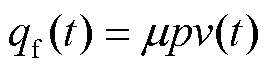 (2)
(2)
式中,p为枢轨接触压强;v为电枢滑动速度;μ为动摩擦系数,μ≤0.1,在本文中取μ=0.1。
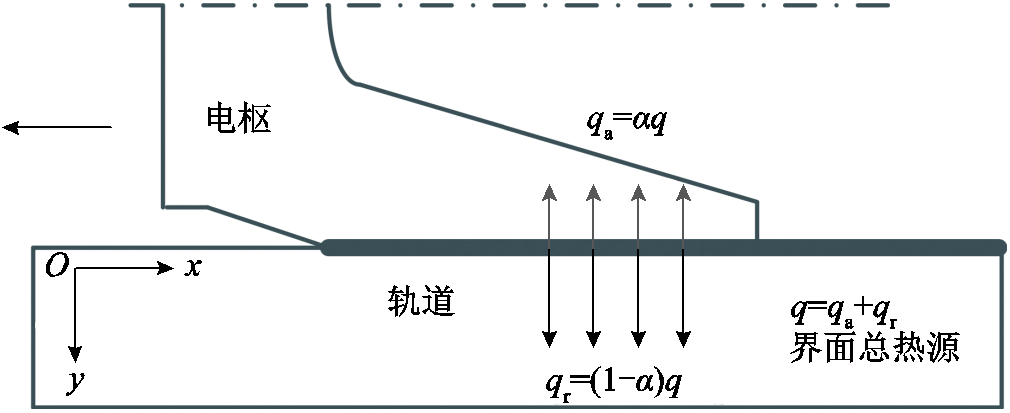
图2 电枢-沉积层轨道热分配示意图
Fig.2 Schematic diagram of heat partition in armature-deposited rail
一体C形电枢尾翼提供的电磁接触压力示意图如图3所示。流经电枢尾翼的电流I在电流产生的磁场B作用下产生电磁力F,电磁力垂直于轨道的分力即为电枢/轨道电磁接触压力FEM。假设电枢后部炮膛中的磁场均匀分布,并且轨道电流从电枢尾翼端部流入电枢内部,可以得到电枢尾翼电磁接触压力为
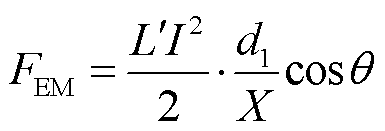 (3)
(3)
式中,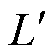 为电感梯度;d1为电枢尾翼长度;X为轨道间距;θ为尾翼倾角。
为电感梯度;d1为电枢尾翼长度;X为轨道间距;θ为尾翼倾角。
若考虑枢轨接触压强由电磁横向分力提供,则单位面积单位时间内界面产生的摩擦热为
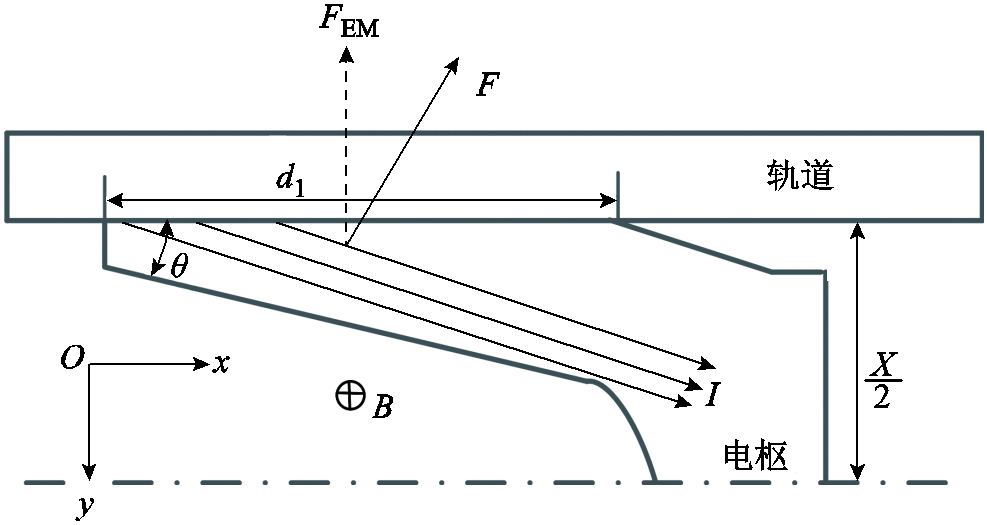
图3 电枢/轨道电磁接触压力示意图
Fig.3 Schematic diagram of armature/rail electromagnetic contact pressure
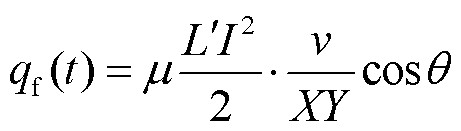 (4)
(4)
式中,Y为电枢宽度。
总的界面热流量q(t)由焦耳热和摩擦热共同组成,表示为
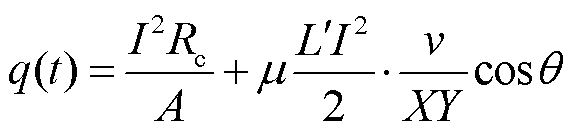 (5)
(5)
则αq(t)为流入电枢的热流量,(1-α)q(t)为流入沉积层轨道侧的热流量。高速情况下,接触区域表面中心线上的温度分布在三维情况下与二维情况基本相同,因此可以建立二维热传递模型研究电枢轨道界面热特性[18]。
实际发射中电枢在轨道上滑动,电枢坐标系与轨道坐标系的关系可用图4进行描述,轨道固定不动,电枢以v(t)的速度向左运动。xa为运动电枢坐标的位置,xr为固定轨道坐标的位置,运动t*时间后,电枢沿着轨道坐标运动的距离为
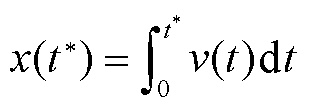 (6)
(6)
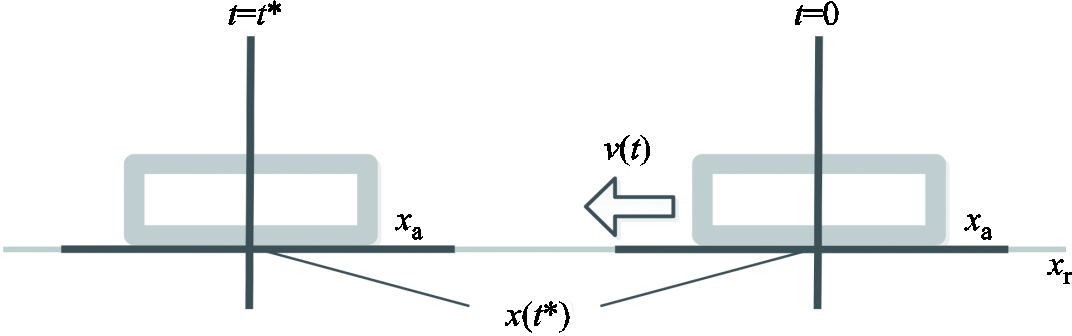
图4 电枢和轨道坐标
Fig.4 Armature and rail coordinate system
在建立热传递方程时,假定电枢坐标固定,轨道坐标相对电枢为运动坐标。相对于电枢坐标,对轨道坐标进行伽利略变换得到
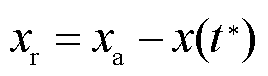 (7)
(7)
若Ta、Tr分别为电枢和轨道的温度分布,坐标变换后,电枢坐标系统下的电枢和轨道二维热传递方程分别为
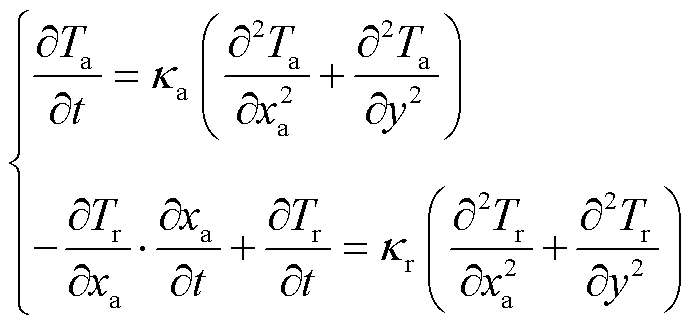 (8)
(8)
式中,下标a、r分别表示电枢和轨道;κ为热扩散系数,定义为κ=k/(cρ),其中k为热导率,c为比热容,ρ为密度。
电枢和轨道的偏微分方程可以转换成无量纲形式,引入无量纲变量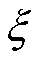 、
、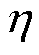 和
和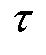 ,有
,有
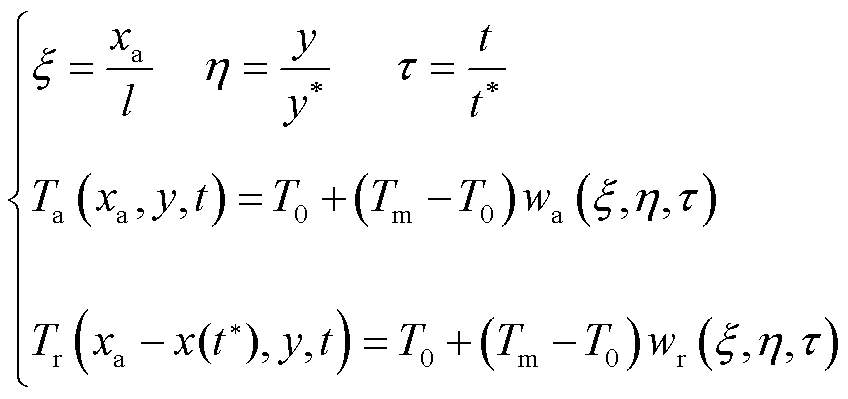 (9)
(9)
式中,l为电枢长度的1/2;t*为总作用时间;y*为热扩散深度,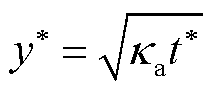 ;T0为初始室温;Tm为电枢熔化温度;wa为电枢温度无量纲形式;wr为轨道温度无量纲形式。为了简化方程,定义ε = y*/l、γ=κr/κa、
;T0为初始室温;Tm为电枢熔化温度;wa为电枢温度无量纲形式;wr为轨道温度无量纲形式。为了简化方程,定义ε = y*/l、γ=κr/κa、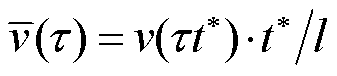 ,将无量纲变量式(9)代入电枢和轨道二维热传递方程式(8),可以得到电枢和轨道二维热传递方程的无量纲形式分别为
,将无量纲变量式(9)代入电枢和轨道二维热传递方程式(8),可以得到电枢和轨道二维热传递方程的无量纲形式分别为
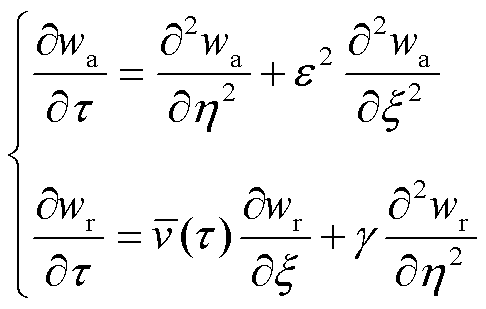 (10)
(10)
电枢和轨道初始温度均为室温,为了求解上述电枢和轨道温度偏微分方程式(10),还需要确定边界条件。由于电枢和轨道均为半无限大固体,当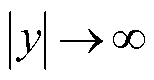 时,轨道和电枢均为室温T0。已知电枢接触长度为2l,在滑动过程中电枢固定不动,认为仅在-l≤xa≤l区间内接触区域产生热源q,电枢和轨道各自的边界如图5所示。图中,B1和B3为轨道外边界,B2和B5为轨道和电枢的接触边界,B4和B6分别为电枢的前边界和后边界。
时,轨道和电枢均为室温T0。已知电枢接触长度为2l,在滑动过程中电枢固定不动,认为仅在-l≤xa≤l区间内接触区域产生热源q,电枢和轨道各自的边界如图5所示。图中,B1和B3为轨道外边界,B2和B5为轨道和电枢的接触边界,B4和B6分别为电枢的前边界和后边界。
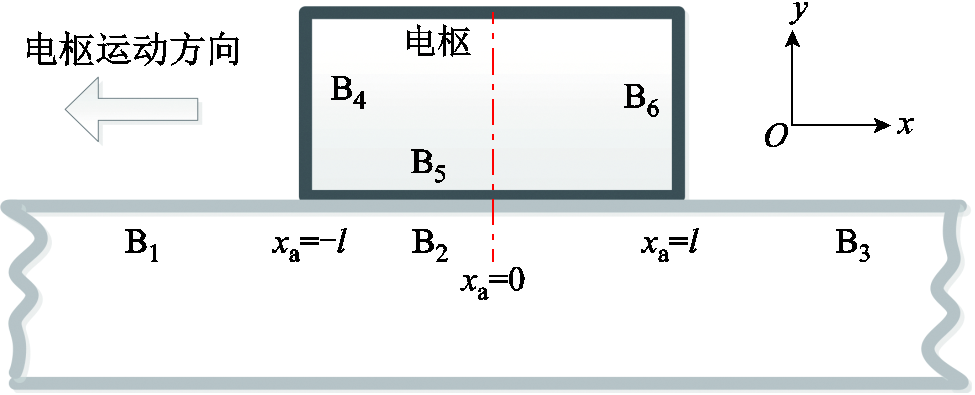
图5 电枢和轨道边界
Fig.5 Armature and rail boundaries
忽略导体与周围空气的热交换,仅考虑导体间的热传导,认为热量仅在接触区域进行传导,并且对外绝热,所以在电枢边界B4和B6以及轨道边界B1和B3处均有
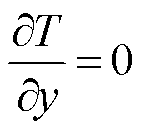 (11)
(11)
由于在-l≤xa≤l接触区域内存在界面热源q,假设流入电枢热量为αq,流入轨道的热量为(1-α)q,则在电枢接触边界B5处有
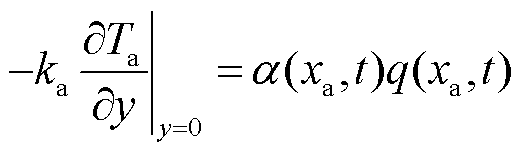 (12)
(12)
轨道侧接触边界B2处有
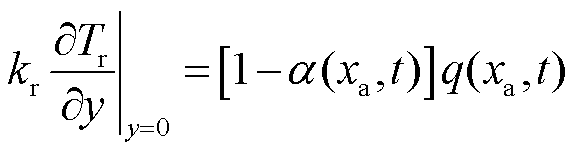 (13)
(13)
统一转换成无量纲形式,初始条件变为
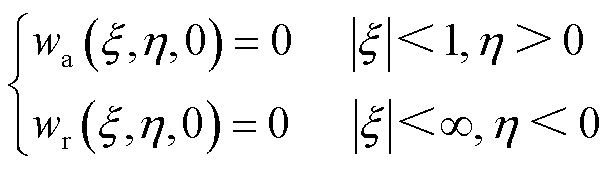 (14)
(14)
无穷远边界条件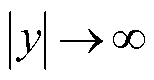 无量纲形式为
无量纲形式为
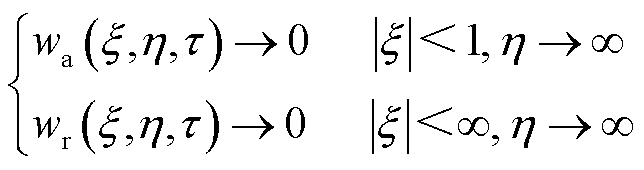 (15)
(15)
电枢y=0界面处边界条件无量纲形式为
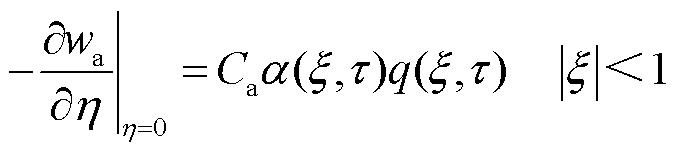 (16)
(16)
轨道y=0界面处边界条件无量纲形式为
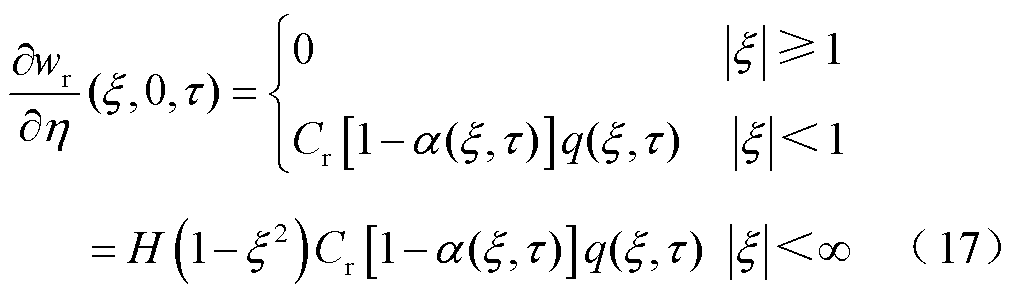
其中
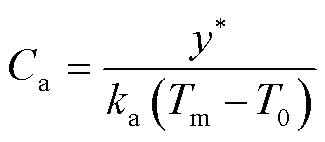
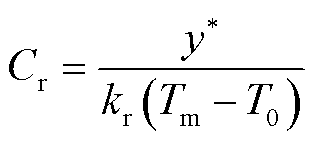
式中,H(·)为赫维赛德阶跃函数。
根据以上初始条件和边界条件,采用拉普拉斯变换和逆变换、傅里叶变换和逆变换对电枢和轨道二维热传递方程式(10)进行求解,可以分别求得电枢和轨道的温度分布方程。电枢温度分布的无量纲形式为
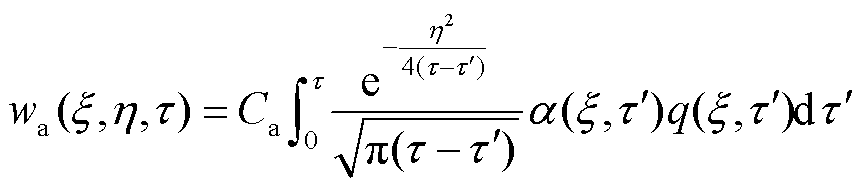 (18)
(18)
轨道温度分布的无量纲形式为
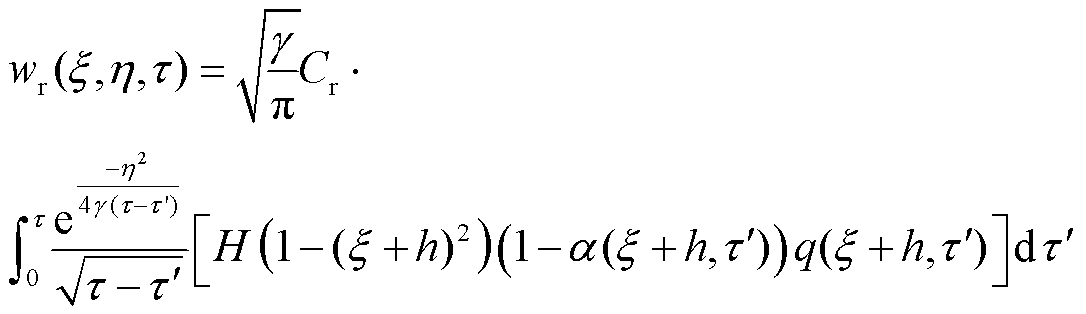 (19)
(19)
式中,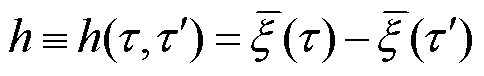 ,
,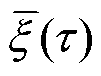 为电枢在τ时刻所处位置,
为电枢在τ时刻所处位置,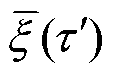 为
为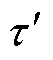 时刻电枢在轨道上所处位置。由于界面热源只存在于轨道和电枢接触界面,所以有
时刻电枢在轨道上所处位置。由于界面热源只存在于轨道和电枢接触界面,所以有
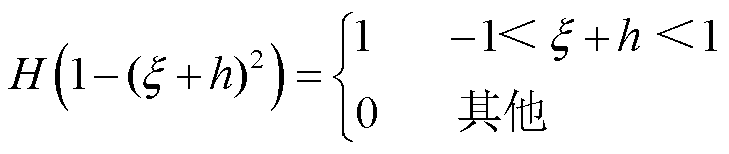 (20)
(20)
轨道和电枢在界面处(即η=0)的温度分布分别为
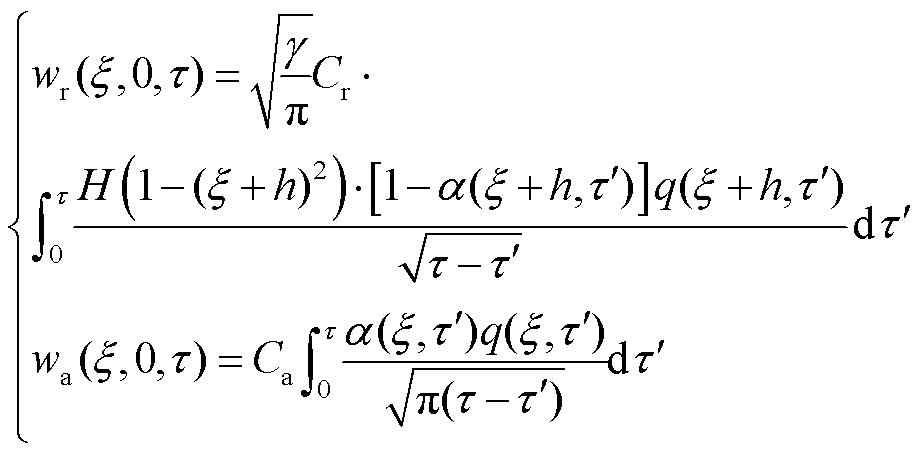 (21)
(21)
为了求解界面热分配系数,假设电枢和轨道在界面处的平均温度分布相等[19]。并且进一步假设界面热分配系数和界面热源在界面上为均匀分布,仅与滑动时间有关,即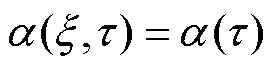 ,
,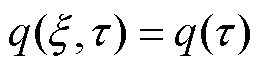 。则电枢侧界面温度平均值为
。则电枢侧界面温度平均值为
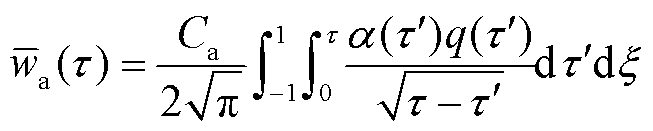 (22)
(22)
轨道侧界面平均温度可以写为
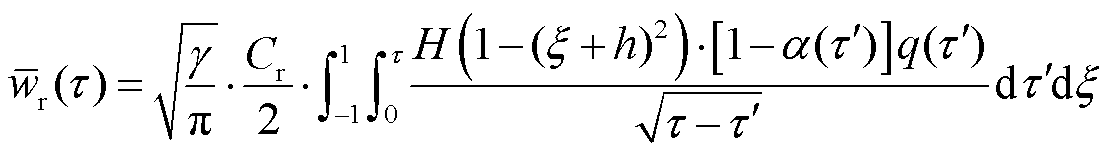 (23)
(23)
令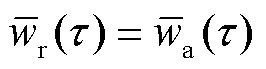 ,热分配系数的控制方程可以写为
,热分配系数的控制方程可以写为
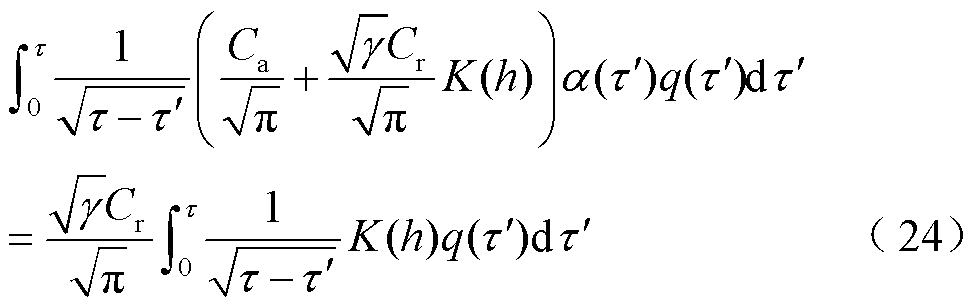
其中
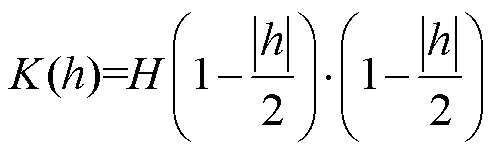
由于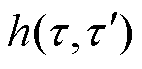 表征了
表征了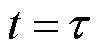 时刻和
时刻和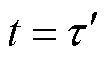 时刻电枢在轨道上的无量纲位置之差,这意味着赫维赛德阶跃函数是关于速度v(t)的函数,如果v(t)随时间而变化,将导致式(24)无法得到解析解,只能用数值方法求解。
时刻电枢在轨道上的无量纲位置之差,这意味着赫维赛德阶跃函数是关于速度v(t)的函数,如果v(t)随时间而变化,将导致式(24)无法得到解析解,只能用数值方法求解。
本文采用回归分析估算实际的热分配系数。实际热分配系数可以写为
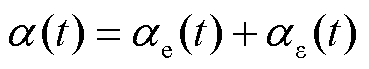 (25)
(25)
式中,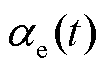 为估算的热分配系数;
为估算的热分配系数; 为由于估算产生的误差函数。热分配估算函数可以写为关于时间t的多项式函数,对应的实际热分配系数的多项式表达形式为
为由于估算产生的误差函数。热分配估算函数可以写为关于时间t的多项式函数,对应的实际热分配系数的多项式表达形式为
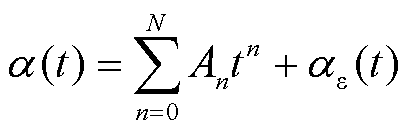 (26)
(26)
式中,n为多项式次数;N为多项式展开的序数;An为对应的多项式系数。将上述多项式形式的实际热分配函数代入式(24)得
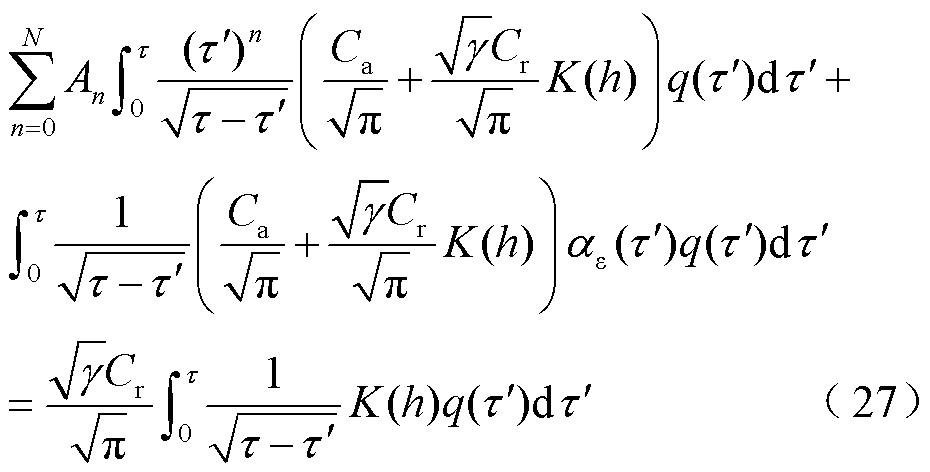
基于最小二乘估计法,把滑动时间区间离散成多个时间点ti,定义误差的平方和为E2,则
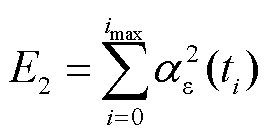 (28)
(28)
式中,imax为时间点总数。通过对E2求导,获取当误差项为最小值时的系数An,进而获得实际热分配系数估计值。
电枢启动前热分配系数值不随时间变化,等于热分配初始值,若速度为0,则K(h)=1。热分配系数不随时间变化时,根据式(24)可以求得电枢热分配系数初始值解析表达式为
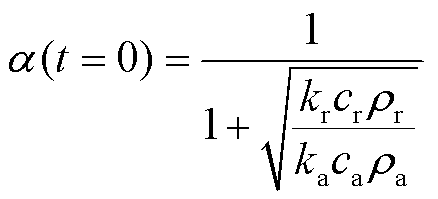 (29)
(29)
定义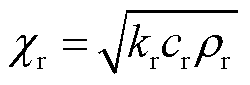 为轨道侧材料吸热系数,
为轨道侧材料吸热系数,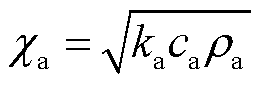 为电枢侧吸热系数,吸热系数表示物体向与接触的高温物体吸热的能力。令
为电枢侧吸热系数,吸热系数表示物体向与接触的高温物体吸热的能力。令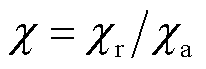 为吸热比例系数,定义为轨道侧与电枢侧材料吸热系数之比,
为吸热比例系数,定义为轨道侧与电枢侧材料吸热系数之比,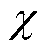 越大表示轨道侧材料吸热系数越大,相应的电枢侧热分配系数就越小。轨道侧材料分别取钢、镍、铁、铝、铜,基于解析表达式(29),不同材料参数对应的热分配系数初始值见表1。由表1可知,不同材料对应的热分配系数初始值不同。固定电枢材料为铝,当轨道侧材料吸热系数越大时,其相应的热分配系数初始值越小。比如吸热系数最大的铜轨道,其相应的热分配系数初始值最小为0.35。
越大表示轨道侧材料吸热系数越大,相应的电枢侧热分配系数就越小。轨道侧材料分别取钢、镍、铁、铝、铜,基于解析表达式(29),不同材料参数对应的热分配系数初始值见表1。由表1可知,不同材料对应的热分配系数初始值不同。固定电枢材料为铝,当轨道侧材料吸热系数越大时,其相应的热分配系数初始值越小。比如吸热系数最大的铜轨道,其相应的热分配系数初始值最小为0.35。
表1 不同轨道材料对应热分配系数初始值
Tab.1 Initial values of heat partition coefficients corresponding to different rail materials
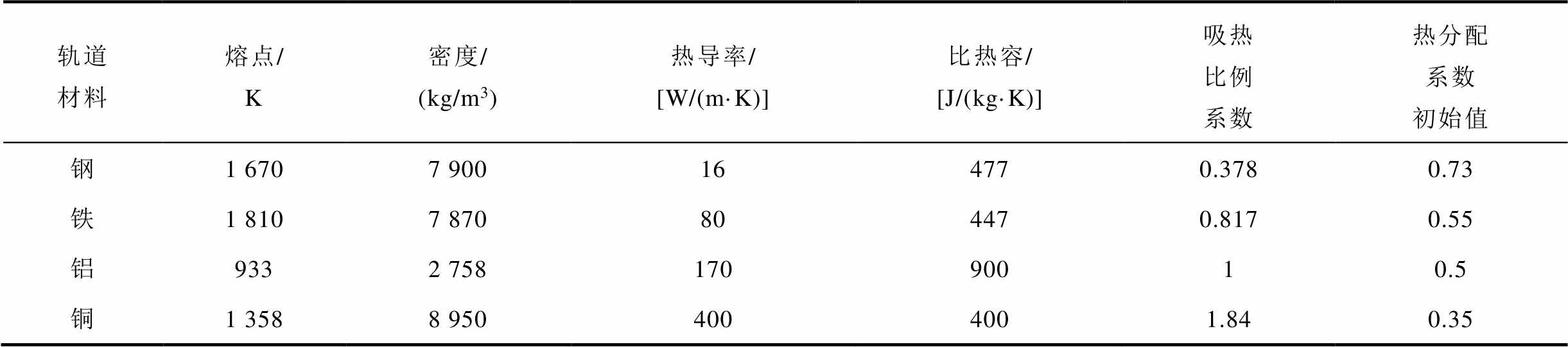
轨道材料熔点/K密度/(kg/m3)热导率/[W/(m·K)]比热容/[J/(kg·K)]吸热比例系数热分配系数初始值 钢1 6707 900164770.3780.73 铁1 8107 870804470.8170.55 铝9332 75817090010.5 铜1 3588 9504004001.840.35
为了方便分析材料参数的影响,假设电枢滑动速度保持400 m/s匀速运动,基于最小二乘估计法计算不同材料参数情况下热分配系数随时间的变化曲线如图6所示。由图6可知,基于最小二乘估计的热分配数值计算模型初始值计算结果与热分配初始值解析表达式(29)计算结果一致。
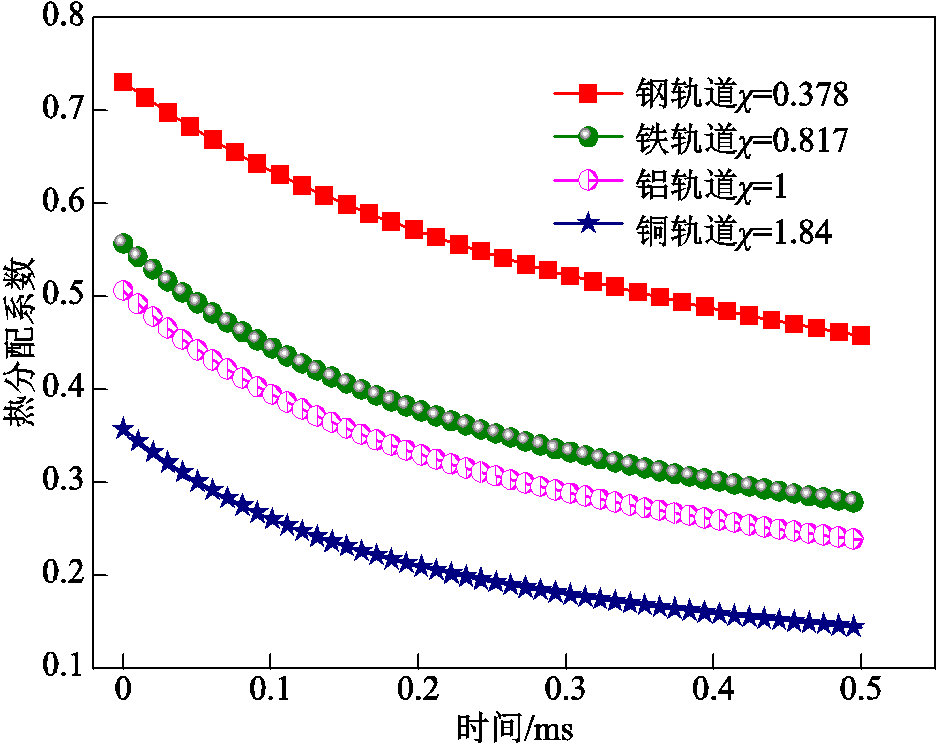
图6 不同材料下的热分配系数变化曲线
Fig.6 Heat partition coefficient curves with different materials
从图6可以看出,吸热比例系数越大,热分配系数初始值越小,随着时间的推进,热分配系数值逐渐衰减,但是不同材料下其衰减速率基本不变。对应的不同材料下热分配衰减速率变化曲线如图7所示,可见衰减速率变化曲线几乎重合,即材料热特性仅改变热分配系数初始值,不改变衰减速率。
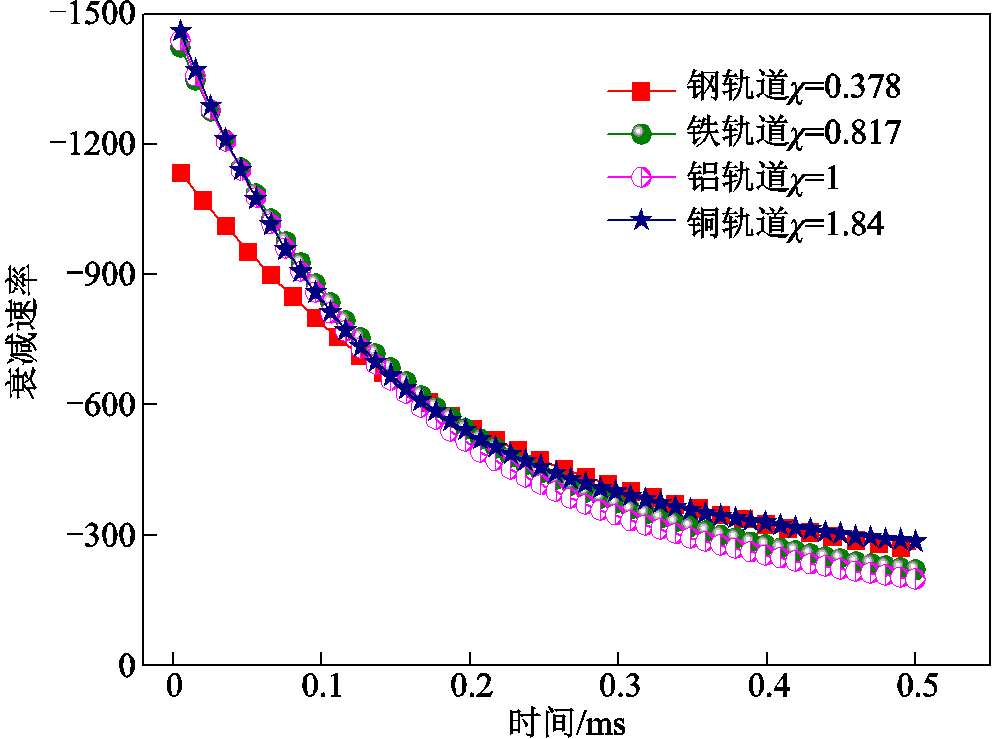
图7 衰减速率变化曲线
Fig.7 Decay rate curves
采用铜轨道时电枢侧吸收热量较小,熔化磨损也相对较小,所以实际发射时,为了减小电枢的熔化磨损,可以选用导热能力较好的轨道材料,目前常采用铜轨道。铜轨道条件下,重复发射时,轨道表面形成沉积层,由于沉积层材料与电枢铝材料相近,相当于轨道材料变成了铝,热分配系数相比光洁的铜轨道要大,即沉积层轨道情况下,如果不考虑沉积层重熔,仅从材料传热能力大小的角度分析,相比于光洁轨道,沉积层轨道会使得电枢熔化量更多。
在实际电磁发射过程中,由于电枢过盈设计,电枢和轨道之间巨大的静摩擦力使电枢存在一个启动时间。设铜铝间的静摩擦系数μ0=0.4,动摩擦系数μ=0.1。电流波形如图8所示,电流幅值IM为600 kA,上升沿时间为0.5 ms,电枢口径为 20 mm×20 mm,尾翼长度d1=20 mm,尾翼倾角θ=15°,过盈预压力为2.2 kN。
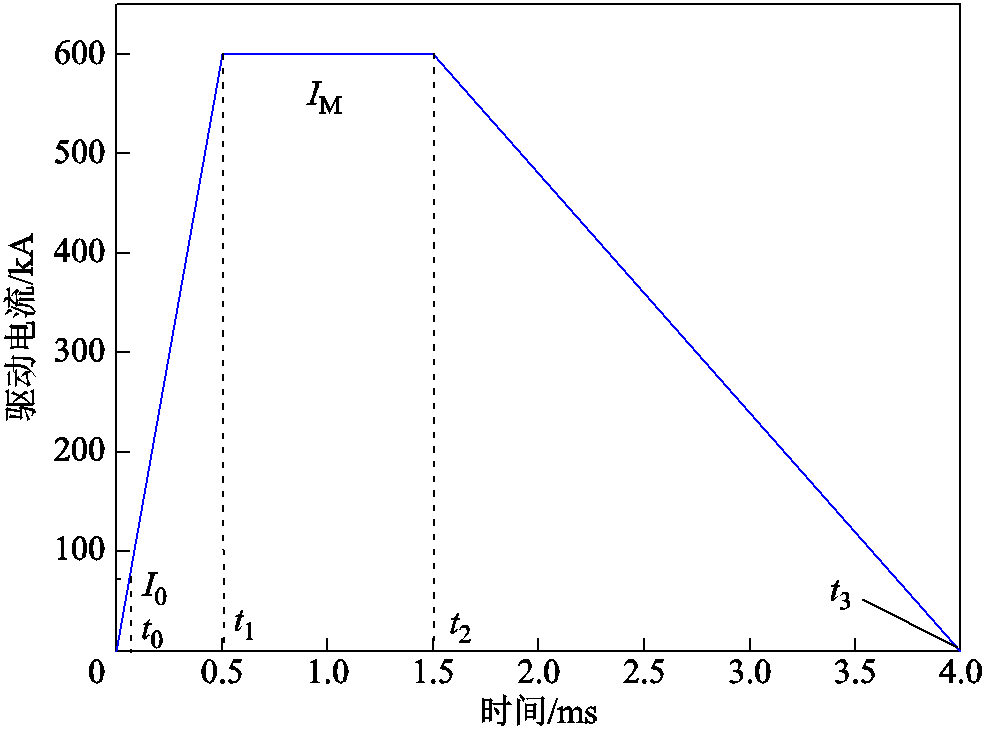
图8 电流波形
Fig.8 Current waveform
脉冲电流作用下电枢总推力[9]为
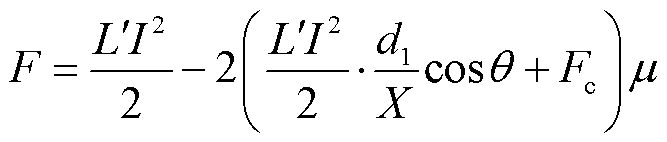 (30)
(30)
式中,Fc为过盈预压力,文中取2.2 kN。
当电流值达到I0时电枢开始运动,即
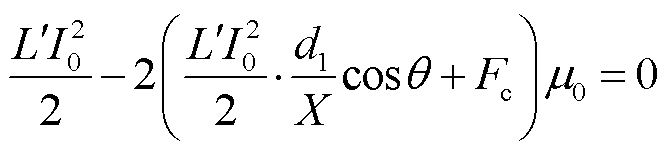 (31)
(31)
则启动时刻t0可以表示为
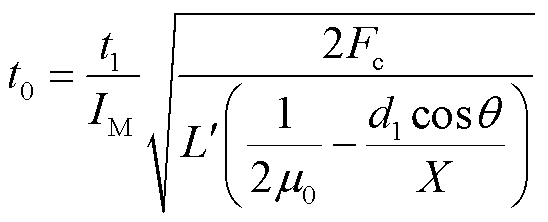 (32)
(32)
若电枢发射质量为M,电枢在启动时刻t0下的发射速度[11]为
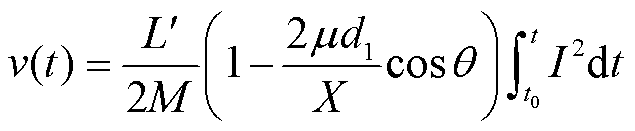 (33)
(33)
电枢发射位移计算表达式[11]为
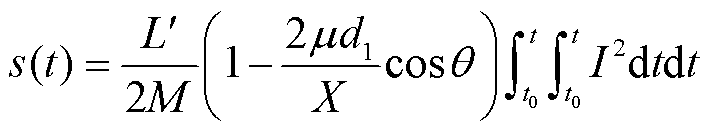 (34)
(34)
由发射速度和发射位移表达式可知,通过改变发射质量的大小可以调整发射速度。为了方便对比分析不同发射速度情况下的热分配变化特性,保持电流幅值和其他参数不变,分别调整发射质量M=30 g和M=50 g,对应电枢速度和位移曲线如图9所示。由图9可知,电枢启动时刻为0.164 ms,两种质量电枢到达上升沿时刻0.5 ms时对应的速度分别为300 m/s和225 m/s。
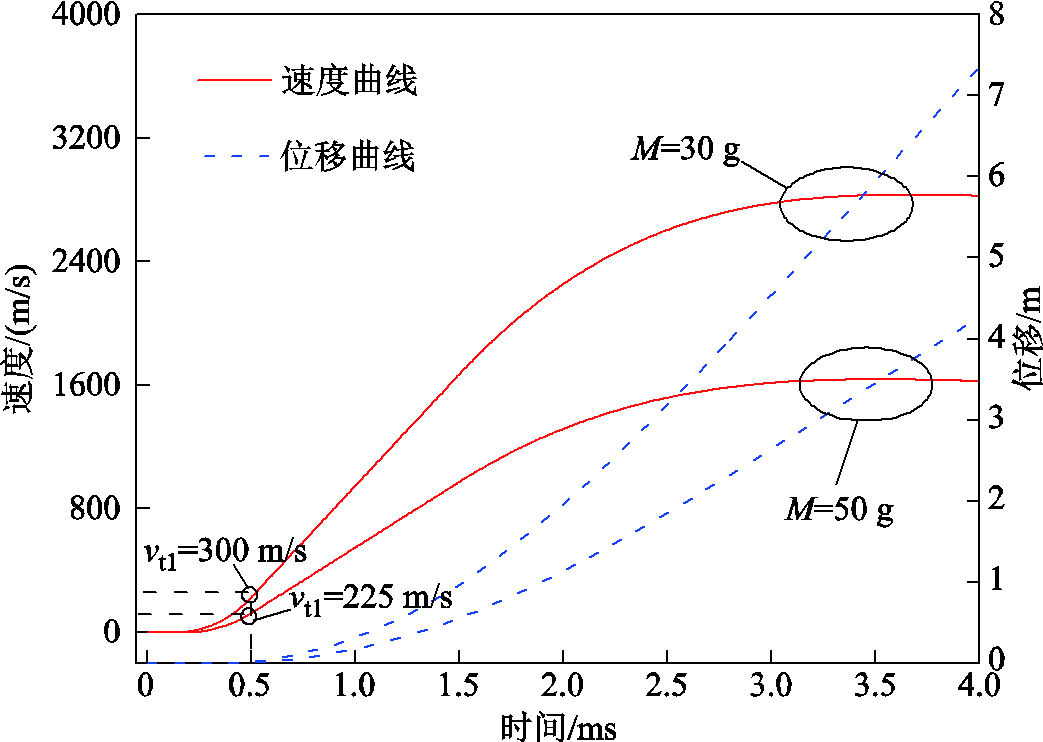
图9 电枢运动速度和位移曲线
Fig.9 Armature’s velocity and displacement curves
启动之前电枢速度为零,根据上文分析,对应的热分配系数值仅与材料特性有关。考虑重复发射后轨道表面存在一定厚度的沉积层,沉积层主要材料为铝,与电枢材料一致,基于热分配初始值解析表达式(29),电枢启动前热分配系数应该为0.5。采用最小二乘估计法计算不同发射速度下热分配变化曲线如图10所示。启动阶段热分配值均为0.5左右,与解析解计算结果一致;电枢启动后到上升沿时刻,随着速度的缓慢增加,刚开始由于速度极小,热分配系数曲线变化不明显,当速度增加到一定值,电枢热分配系数值开始明显下降。图10中红色方形曲线对应发射质量M=30 g、上升沿时刻电枢速度vt1=300 m/s;蓝色三角形曲线对应发射质量M=50 g、上升沿时刻电枢速度vt1=225 m/s,发射质量越小发射速度越大,对应的电枢侧热分配曲线也衰减得越快。
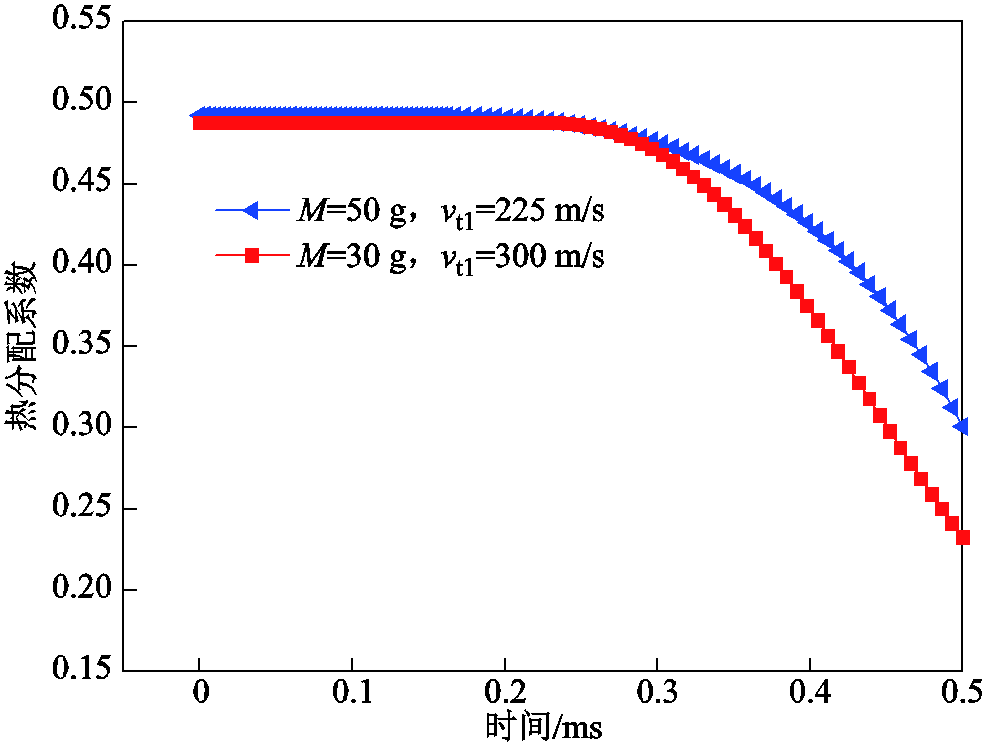
图10 不同发射速度下热分配特性
Fig.10 Heat partition characteristics at different speed
为了研究运动形式对热分配特性的影响,将实际发射速度情形与匀速、匀加速情况进行对比。假设三种运动形式在0.5 ms时的速度均达到300 m/s,三种速度曲线如图11所示,对应的热分配变化曲线如图12所示。三种速度在上升沿时刻均为300 m/s,可以发现,实际变加速运动时,热分配系数最大,启动阶段热分配系数变化较小几乎不变;匀速运动时热分配值最小。电枢在刚开始启动时,匀速情况下的速度最大,热分配值也减小得最快,但是随着速度的增加,实际变加速情况热分配系数衰减幅度最大。这说明速度变化曲线决定热分配系数变化曲线的走势,速度越大热分配系数越小,加速度越大热分配系数下降得越快。但是相同时间下,电枢速度相等时,热分配系数也近似相等,如匀速、匀加速、实际变加速情况均在0.5 ms达到300 m/s,即0.5 ms时刻三种运动形式下热分配系数值均为0.25左右。
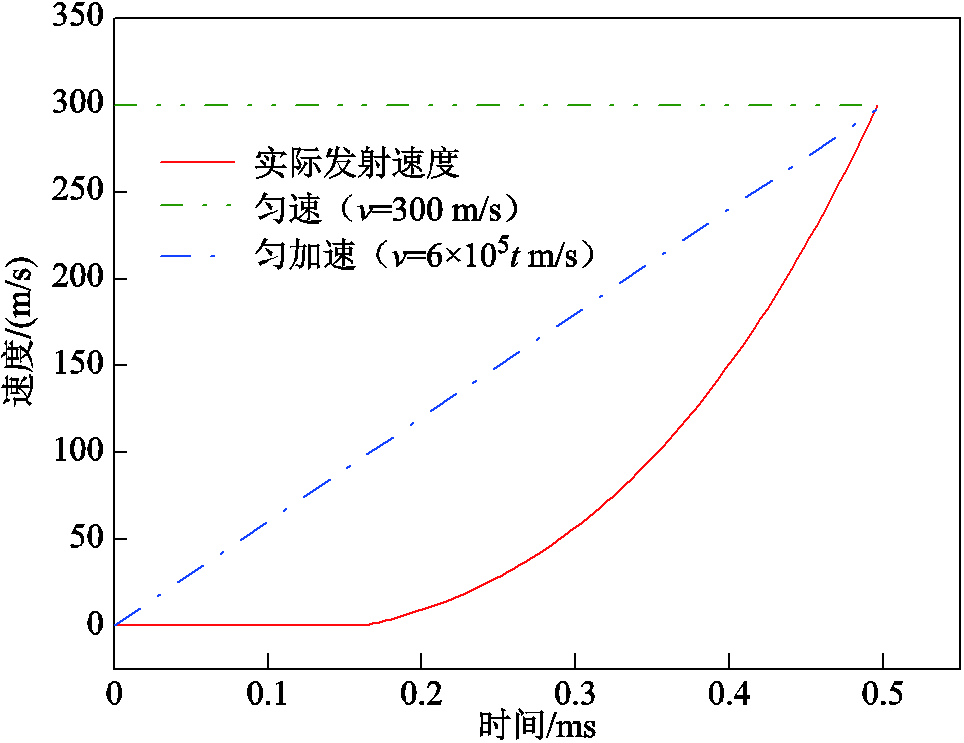
图11 三种速度曲线
Fig.11 Three speed curves
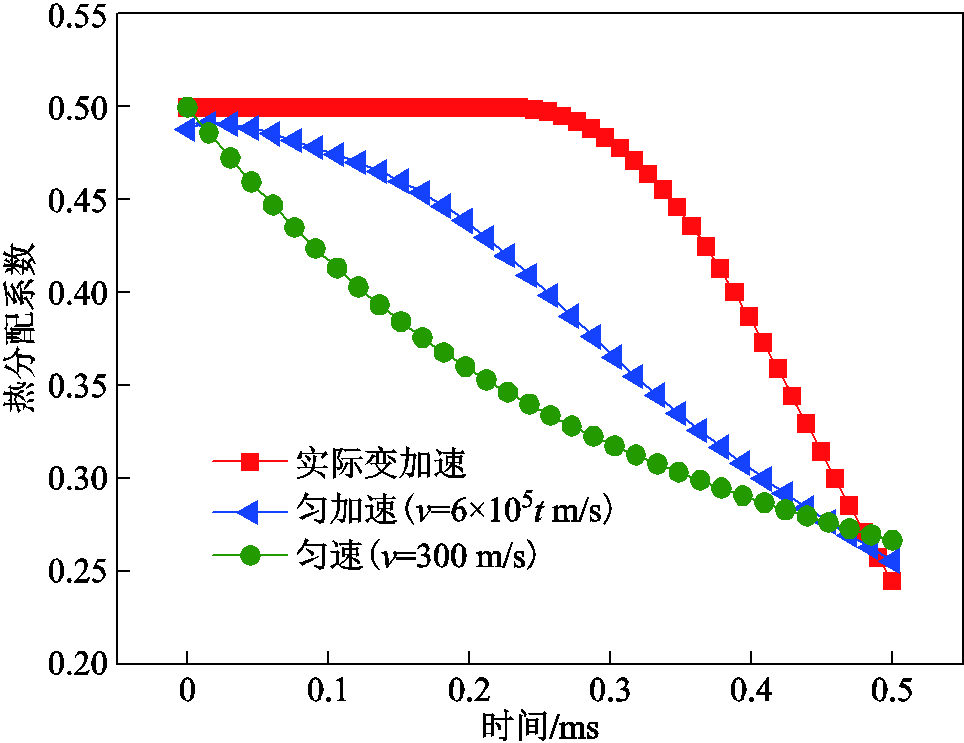
图12 不同运动状态下电枢热分配曲线
Fig.12 Armature’s heat partition curves at different speeds
无沉积的铜轨道情况下,其材料参数见表1。保持发射电流和速度曲线不变,电流幅值为600 kA,电枢质量为30 g,计算实际发射过程中铜轨道和沉积层轨道对应的热分配系数随时间变化曲线如图13所示。为了对比分析,匀速情况下的热分配曲线也绘于图13中。由图13可以看出,铝电枢-铜轨道热分配初始值约为0.35,铝电枢-沉积层轨道热分配初始值约为0.5,与电枢热分配系数初始值解析表达式(29)计算结果一致。铜轨道和沉积层轨道热分配值随时间增加均逐渐减小,并且沉积层轨道热分配值要大于铜轨道,意味着沉积层轨道中的电枢从界面吸收的热量较多,电枢熔化得越快。铝电枢-铜轨道情况下,速度对热分配值曲线的影响规律与铝电枢-沉积层轨道情况下一致,即速度变化曲线决定热分配系数变化曲线的走势,速度越大热分配系数越小,相同时间下,电枢速度相等时,热分配值也近似相等。
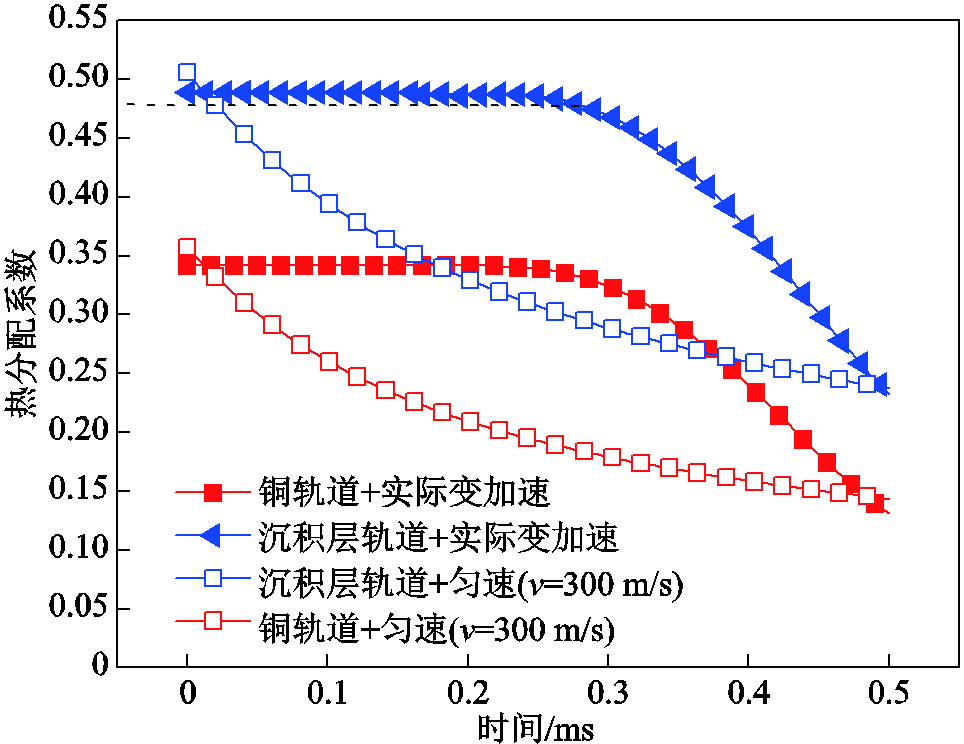
图13 铜轨道和沉积层轨道热分配系数
Fig.13 Heat partition of copper rail and deposited rail
实际变加速情况对应的界面平均温度变化曲线如图14所示。由图14可知,铜轨道电枢界面平均温度在tm=0.33 ms时达到熔点Tm并开始熔化,而沉积层轨道在tm=0.276 ms时就已经达到熔点。沉积层作用下,由于其热导率相比铜轨道大大减小,导致电枢热分配值变大,使电枢提前发生熔化。但是由于沉积层熔点低于铜轨道,沉积层也会发生重熔,重熔液会减少启动时间。
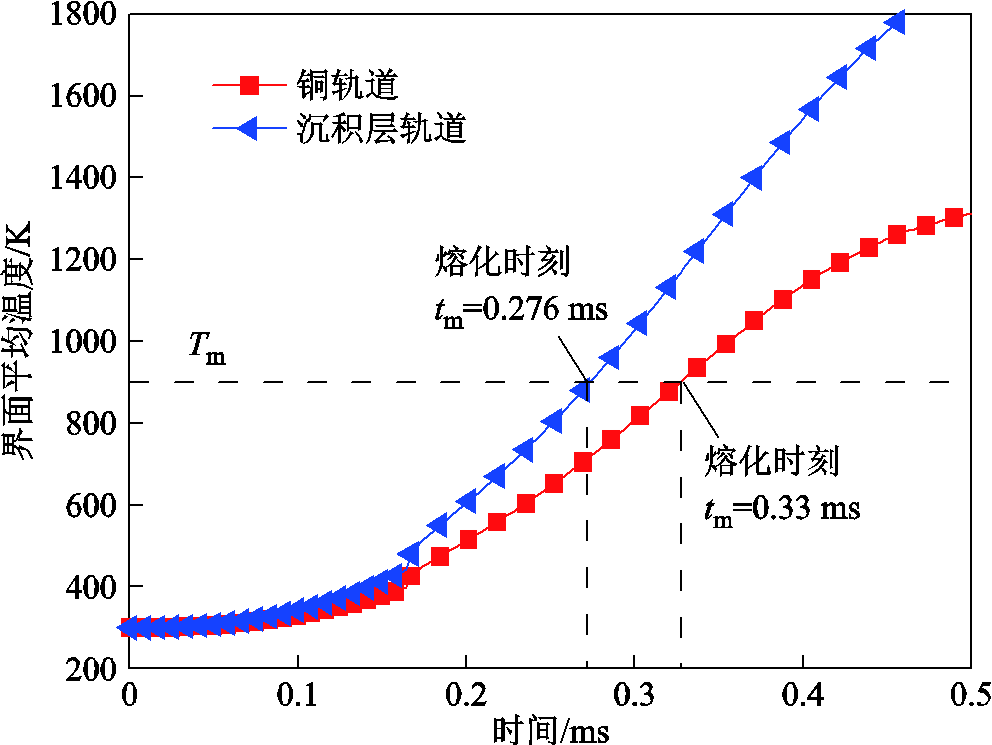
图14 界面平均温度
Fig.14 Average interface temperature
根据以上分析可知,界面热分配值与枢轨材料热参数、电枢运动速度和滑动时间有关。在材料和速度不变的情况下,电枢热分配值随时间变化呈衰减趋势,材料热参数影响热分配衰减的初始值,速度影响其衰减速率,速度越大,热分配值越小,衰减速率越大。在材料热参数、电枢运动速度和滑动时间均相等的情况下,热分配值也相等。可以从传热物理机制的角度对以上结论进行论证分析。界面热传导物理过程如图15所示,界面热源分别向电枢和轨道传递,流入电枢表面的热流量为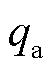 ,轨道表面流入的热流量为
,轨道表面流入的热流量为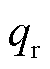 。
。
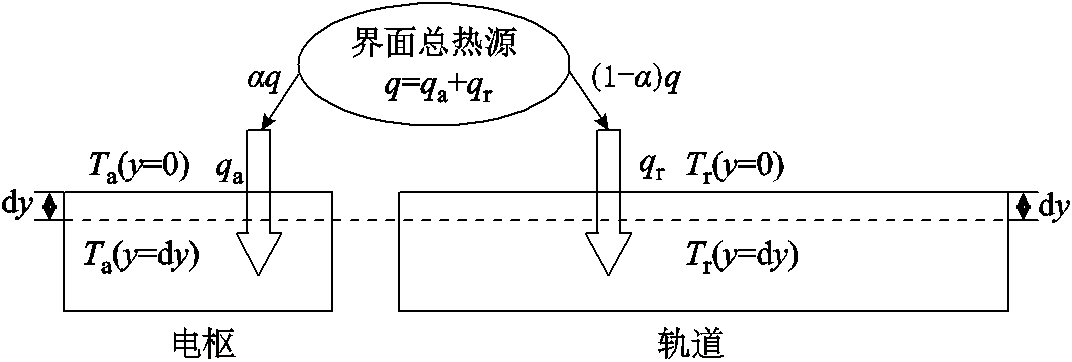
图15 界面热传导物理过程
Fig.15 Physical process of heat conduction at the interface
电枢侧热分配系数为
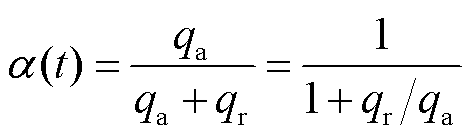 (35)
(35)
即热分配系数值与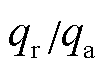 成反比。而电枢和轨道表面热流量与表面温度梯度有关。假设在电枢和轨道表面分别取相等微元位移dy,dy足够小,则电枢表面热流量可以写为
成反比。而电枢和轨道表面热流量与表面温度梯度有关。假设在电枢和轨道表面分别取相等微元位移dy,dy足够小,则电枢表面热流量可以写为
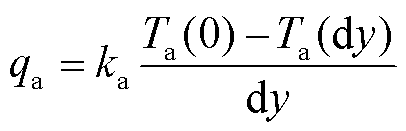 (36)
(36)
由于dy处的温度与电枢材料热特性、滑动时间、电枢表面温度成正比,即电枢导热能力越好、滑动时间越长、电枢表面温度越大,dy处的温度也越高。所以随着时间的推进,电枢体积温度和表面温度均逐渐升高,电枢表面发生熔化。假设熔化后材料立即被轨道带走,电枢表面仍然与轨道表面直接接触,接触界面温度保持熔化温度Tm不变,当dy处的体积温度逐渐升高,电枢表面温度梯度逐渐减小,最终热量几乎全部进入轨道,仅有少量热量传导进入电枢用于电枢材料温升熔化。文献[11]通过实验测量也发现整个发射过程中最终有90%热量进入轨道。将电枢材料热特性用βa表示,滑动时间为t,则有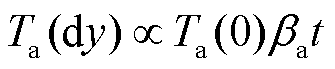 。为方便分析,dy处的温度可以写为
。为方便分析,dy处的温度可以写为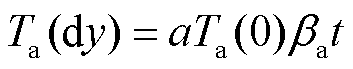 ,其中a为常系数。
,其中a为常系数。
特征时间内轨道侧热流量可以写为
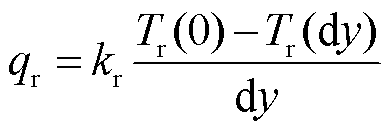 (37)
(37)
其中,dy处的温度与轨道材料热特性βr、轨道表面温度、特征时间tc成正比。若枢轨接触长度为la,接触时间内电枢平均速度为U,特征时间为tc=la/U。如果界面发生熔化,轨道表面温度被限制在熔点Tm,随着速度的增加,电枢与轨道接触特征时间内,传热时间较短,dy处的温度越来越小,轨道表面温度梯度越来越大,即轨道侧热分配系数越来越大,当dy处的温度接近室温时,轨道热分配系数则趋于稳定。dy处的轨道温度可以写为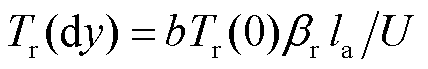 ,其中b为常系数。
,其中b为常系数。
由于温度的连续性,可认为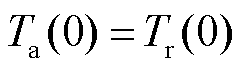 ,则轨道与电枢表面热流量之比可以化简为
,则轨道与电枢表面热流量之比可以化简为
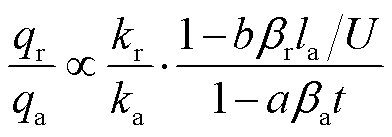 (38)
(38)
电枢侧热分配系数可以化简为
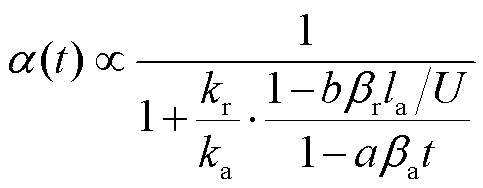 (39)
(39)
由式(39)可以看出,界面热分配系数仅与材料热参数、速度、接触长度、时间有关,即在速度、材料参数和接触长度不变的情况下,时间越大,热分配系数越小,热分配系数随时间变化呈衰减趋势;材料参数和接触长度一定时,速度越大,热分配系数值越小,即衰减速率越快。理论分析结果与采用最小二乘法获得的分析结果一致。
电枢轨道滑动电接触界面的热分配问题是研究界面熔化过程和温度分布的基础,其应用框图如图16所示。热分配值决定了流入电枢和轨道侧接触表面热通量的大小,流入电枢的热量使得电枢表面材料发生熔化;流入轨道侧的热量会使沉积层发生熔化、轨道产生温升,沉积层熔化特性与电枢熔化特性相互作用共同影响界面熔化过程。本文建立的计算模型和分析结果可为界面熔化机理的研究提供基础支撑,进一步为界面结构设计、热管理设计及沉积层控制技术提供理论指导,对提高重复发射滑动电接触性能具有重要意义。
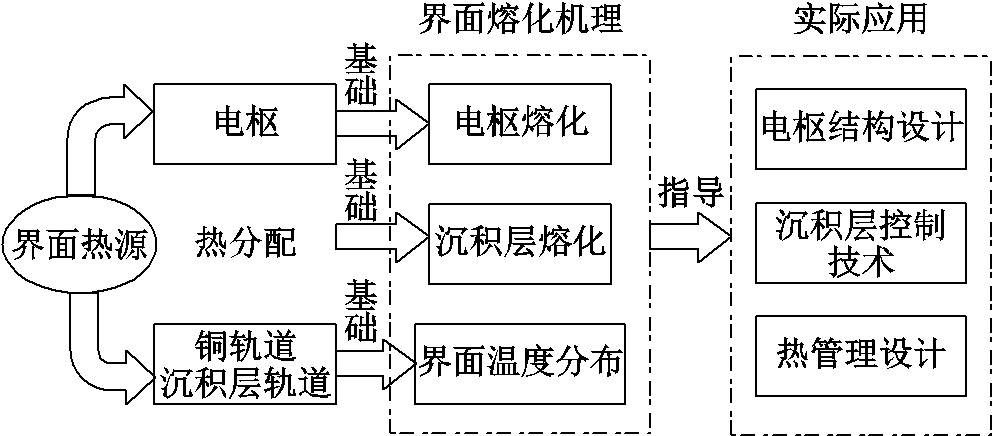
图16 热分配研究的应用框图
Fig.16 Application diagram of heat partition study
本文基于最小二乘估计法建立了枢轨界面热分配计算模型,研究了速度、材料热参数对热分配系数的影响规律,并通过理论分析进一步揭示了界面热分配过程物理机制。得到结论如下:
1)热分配系数值与发射速度、接触材料热参数、接触长度、发射时间有关。材料热参数影响热分配系数随时间变化曲线的初始值,不改变热分配系数随时间变化的衰减速率。
2)速度影响热分配系数随时间变化衰减的速率,速度越大热分配系数随时间衰减越快。相同时刻和速度条件下,热分配系数值相等。
3)在整个发射过程中,随着速度的不断增加,热分配系数逐渐减小,当速度达到很高时,热分配系数趋于稳定值,界面大部分热量最终都传入轨道。
参考文献
[1] 马伟明, 鲁军勇, 李湘平. 电磁发射超高速一体化弹丸[J]. 国防科技大学学报, 2019, 41(4): 1-10.
Ma Weiming, Lu Junyong, Li Xiangping. Electromagnetic launch hypervelocity integrated projectile[J]. Journal of National University of Defense Technology, 2019, 41(4): 1-10.
[2] 马伟明, 鲁军勇. 电磁发射技术的研究现状与挑战[J]. 电工技术学报, 2023, 38(15): 3943-3959.
Ma Weiming, Lu Junyong. Research progress and challenges of electromagnetic launch technology[J]. Transactions of China Electrotechnical Society, 2023, 38(15): 3943-3959.
[3] 胡鑫凯, 鲁军勇, 李白, 等. 瞬态条件下电磁轨道发射装置绝缘体热损伤分析[J]. 电工技术学报, 2023, 38(21): 5673-5681.
Hu Xinkai, Lu Junyong, Li Bai, et al. Thermal damage analysis of insulator in electromagnetic rail launcher under transient conditions[J]. Transactions of China Electrotechnical Society, 2023, 38(21): 5673-5681.
[4] Fair H D, Schmidt E E. The science and technology of electric launch: a US perspective[J]. IEEE Transactions on Magnetics, 1999, 35(1): 11-18.
[5] 阮景煇, 陈立学, 夏胜国, 等. 电磁轨道炮电流分布特性研究综述[J]. 电工技术学报, 2020, 35(21): 4423-4431.
Ruan Jinghui, Chen Lixue, Xia Shengguo, et al. A review of current distribution in electromagnetic railguns[J]. Transactions of China Electrotechnical Society, 2020, 35(21): 4423-4431.
[6] 张嘉炜, 鲁军勇, 谭赛, 等. 考虑初始接触压力的滑动电接触界面磁扩散模型[J]. 电工技术学报, 2022, 37(2): 488-495.
Zhang Jiawei, Lu Junyong, Tan Sai, et al. A magnetic diffusion model of electromagnetic launcher considering initial contact pressure[J]. Transactions of China Electrotechnical Society, 2022, 37(2): 488-495.
[7] Chen Lixue, He Junjia, Xiao Zheng, et al. Experimental study of armature melt wear in solid armature railgun[J]. IEEE Transactions on Plasma Science, 2015, 43(5): 1142-1146.
[8] Chen Lixue, Xu Xuan, Wang Zengji, et al. Melting distribution of armature in electromagnetic rail launcher[J]. IEEE Transactions on Plasma Science, 2023, 51(1): 234-242.
[9] Yao Jinming, Xia Shengguo, Chen Lixue, et al. Analysis of the melt erosion patterns at rail-armature contact of rail launcher in current range of 10–20 kA/mm[J]. IEEE Transactions on Plasma Science, 2019, 47(3): 1674-1680.
[10] 李白, 鲁军勇, 谭赛, 等. 滑动电接触界面粗糙度对电枢熔化特性的影响[J]. 电工技术学报, 2018, 33(7): 1607-1615.
Li Bai, Lu Junyong, Tan Sai, et al. Effect of interfacial roughness of sliding electrical contact on the melting characteristics of armature[J]. Transactions of China Electrotechnical Society, 2018, 33(7): 1607-1615.
[11] 汤亮亮. 电磁发射中枢轨接触界面金属液化层特性的实验与理论研究[D]. 武汉: 华中科技大学, 2015.
Tang Liangliang. Experimental and theoretical study on liquid metal film characteristic of armature/rail contact interface in an electromagnetic launching[D]. Wuhan: Huazhong University of Science and Technology, 2015.
[12] Hsieh K T. Numerical study on groove formation of rails for various materials[J]. IEEE Transactions on Magnetics, 2005, 41(1): 380-382.
[13] 林庆华, 栗保明. 基于瞬态多物理场求解器的电磁轨道炮发射过程建模与仿真[J]. 兵工学报, 2020, 41(9): 1697-1707.
Lin Qinghua, Li Baoming. Modeling and simulation of electromagnetic railgun launching process based on a transient multi-physical field solver[J]. Acta Armamentarii, 2020, 41(9): 1697-1707.
[14] 李松乘, 鲁军勇, 程龙, 等. 基于灰色模型的电磁轨道发射装置温度研究[J]. 国防科技大学学报, 2020, 42(5): 90-97.
Li Songcheng, Lu Junyong, Cheng Long, et al. Research on temperature of electromagnetic rail launcher based on gray model[J]. Journal of National University of Defense Technology, 2020, 42(5): 90-97.
[15] Balić E E. Melt wear control of metals in high-speed sliding contacts[D]. Troy: Rensselaer Polytechnic Institute, 2008.
[16] 李白, 鲁军勇, 谭赛, 等. 高速滑动电接触电枢表面动态磨损过程研究[J]. 电工技术学报, 2023, 38(1): 131-139.
Li Bai, Lu Junyong, Tan Sai, et al. Research on dynamic wear process of armature surface in high-speed sliding electric contact[J]. Transactions of China Electrotechnical Society, 2023, 38(1): 131-139.
[17] Paek-Spidell G Y. Analysis of heat partitioning during sliding contact at high speed and pressure[D]. Wright-Patterson Air Force Base: Air Force Institute of Technology, 2014.
[18] Kennedy T C, Plengsaard C, Harder R F. Transient heat partition factor for a sliding railcar wheel[J]. Wear, 2006, 261(7/8): 932-936.
[19] Jaeger J C. Moving sources of heat and the temperature at sliding contacts[J]. Journal and Proceedings of the Royal Society of New South Wales, 1943, 76(3): 203-224.
Abstract Aluminum deposition phenomenon occurs on rail’s surface after a multishot at high-speed sliding electrical contact with a large current. The melt-wear of armature and deposited aluminum at the interface due to huge heat source’s thermal effect can change contact condition, significantly affecting sliding electrical contact performance. The heat partition characteristics at interface between armature and deposited rail are crucial for investigating melting and wear of interface materials. Therefore, it is necessary to study the heat partition process at sliding electrical contact interface. Initially, this study established a thermal transfer model to derive the temperature distribution equations for armature and deposited rail. Control equation for heat partition is obtained by utilizing the principle of interface temperature continuity. Applying the least squares estimation method to optimize error function, a numerical calculation model for interface heat partition is proposed.
Heat partition curves are calculated for varying material parameters based on numerical model for heat partition. Numerical results for heat partition’s initial value are consistent with analytical solution. The results show that: the larger the heat absorption coefficient, the smaller the heat partition’s initial value. As time progresses, the heat partition value is gradually decaying. While maintaining constant velocity, the heat partition decaying curves closely coincide across different material parameters. In order to study the effect of velocity on heat partition value, the actual launching velocity is compared with uniform velocity and uniform acceleration, assuming that three forms of motion reach 300 m/s at 0.5 ms. It can be found that heat partition is maximum for actual variable acceleration motion and is minimum for uniform velocity. At started-up stage for armature, velocity is maximum under uniform velocity and the heat partition curve decays faster, but as the velocity increases, the heat partition curve decays fastest in the actual variable acceleration case. It shows that the velocity curve determines the change trend for heat partition curve, the larger the velocity the smaller the heat partition, and the larger the acceleration the faster the heat partition decays. However, the heat partition values are also approximately equal when armature velocity are equal at the same moment. For example, if uniform velocity, uniform acceleration, and actual variable acceleration all reach 300 m/s at 0.5 ms, the heat partition values in the three forms of motions at the moment of 0.5 ms are all around 0.25.
In the end, physical mechanism of the heat partition process at the interface between the armature and rail is discussed theoretically. It is found that the theoretical analysis results are consistent with the numerical calculation results. The following conclusions can be drawn from above analysis:(1) Heat partition value is related to launching velocity, material thermal parameters, contact length, and launching time. Material thermal parameters affect initial value of the heat partition curve and does not change its decaying rate. (2) Launching velocity affects the heat partition’s decay rate, the larger the velocity the faster the heat partition decays with time. Under the same moment and velocity conditions, the heat partition value is equal. (3) During the entire launching process, the heat partition decreases with increasing velocity, and when the velocity reaches a very high level, the heat partition tends to a stable value, and most of the heat at the interface is finally transferred into the rail.
keywords:High-speed sliding electrical contact, heat source, calculation model for heat partition, least squares estimation method
中图分类号:TM359.4
DOI: 10.19595/j.cnki.1000-6753.tces.231136
国家自然科学基金(52207009)和高校科研启动资金(NY219155)资助项目。
收稿日期 2023-07-17
改稿日期 2023-08-24
姚金明 女,1989年生,讲师,硕士生导师,研究方向为电磁发射技术等。
E-mail:yaojinming@njupt.edu.cn(通信作者)
傅 强 女,1985年生,高级工程师,研究方向为配网运行与控制、电磁发射混合储能技术等。
E-mail:304573164@qq.com
(编辑 李 冰)