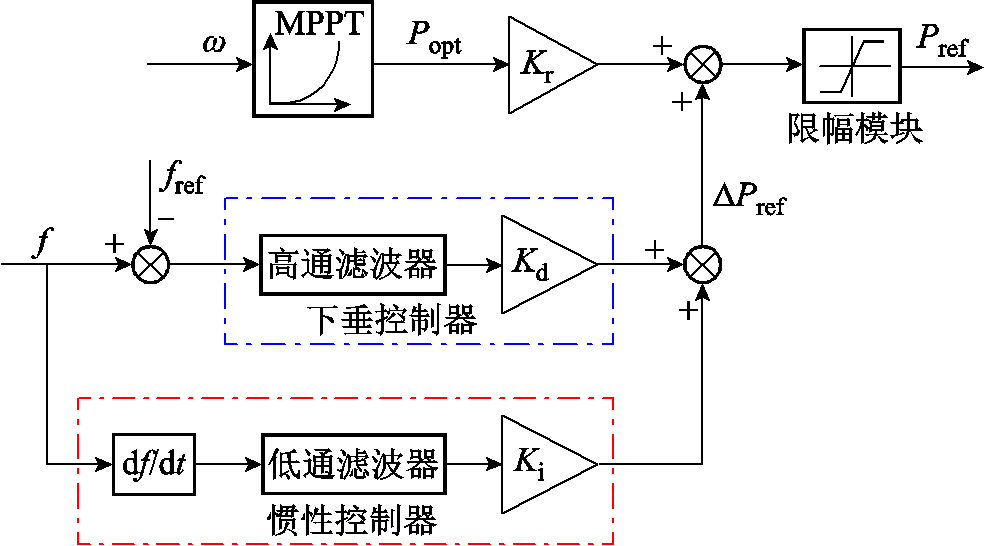
图1 附加频率调节措施
Fig.1 Additional frequency regulation measures
摘要 新能源发电类型、渗透率及控制方式的不同会影响电力系统实时惯量，评估惯量水平有助于提高电力系统抗扰动能力。该文在分析风电、光伏的虚拟惯性响应特性及其对电力系统频率稳定性影响的基础上，考虑负荷静态电压特性，提出一种基于量测数据的新能源电力系统区域等效惯量实时评估方法。评估结果计及发电机惯量、新能源虚拟惯量和负荷等效惯量。为了减小因扰动后频率分布特性造成的误差，从加权平均数的角度提出频率采样点的选取及区域频率的计算方法，解决了量测数据众多且获取困难的问题。通过算例验证了所提方法对传统电力系统及新能源电力系统区域等效惯量评估均具有可行性和有效性。
关键词：新能源电力系统 区域等效惯量评估 量测数据 联络线功率 虚拟惯性控制 负荷静态电压特性
随着风电、光伏等可再生能源的大规模开发和利用，新能源渗透率逐渐增高[1]。高比例新能源并网使电力系统低惯量问题日益突出，频率问题更加严峻。当电力系统出现功率缺额时，惯量支撑不足会引起机组低频减载动作，造成大面积停电，如澳大利亚“9·28”和英国“8·9”事故[2-3]。因此，为提高现代电力系统的稳定运行能力，完善频率稳定控制体系，充分发挥源网荷侧非同步机组调频资源的调节能力，有必要开展电力系统等效惯量提升及新能源虚拟惯量控制策略的研究，并对系统惯量水平进行评估与分析[4-5]。
目前，基于大扰动数据的惯量评估是最广泛应用的评估方法，采用扰动发生后的功率和频率量测数据进行计算[6]，评估精度受采样点选取位置、测量装置精度、量测数据处理方式等因素影响。区域惯量分布不均会影响扰动传播速度，进而影响系统频率的分布，因此频率采样点的选取对惯量评估结果至关重要。文献[7]基于惯量图心的概念确定频率采样点，但该方法需要获取系统的拓扑结构、支路参数和运行状态，所需参数众多，计算过程复杂。文献[8]选取电网空间分布尽可能多的不同采样点，计算采样点频率变化率（Rate of Change of Frequency, RoCoF）的平均值，快速估计电网转动惯量。
实际电力系统由多个区域构成，各区域惯量来源、网络结构和拓扑参数等不完全相同，评估区域惯量水平有助于分析各区域频率支撑能力，进而制定相应的频率调节策略。现有的大扰动方法评估惯量水平大都集中在系统层面，惯量区域分布不均的特性考虑较少。文献[9]选取各区域中参与因子较大的机组频率作为评估所需的计算数据，但并未考虑负荷静态特性对系统不平衡功率的影响。文献[10]利用同步相量测量单元（Phasor Measurement Units, PMUs）采集发电机转子频率，计算扰动发生时刻的频率变化率评估区域等效惯量。实际中，受测量装置精度的影响，计算得到的RoCoF往往包含振荡分量，发电机转子角频率参数也难以获取，这给准确评估系统惯量水平造成了一定的困难[7]。惯性的时间特性表现为惯量对同一节点频率的支撑能力随时间发生变化[11]。文献[9-10]认为区域等效惯量恒为常值，采用不同时刻的量测数据差值计算得到惯性时间常数表达式，这种方法不适用于等效惯量时变的新能源电力系统。
对于新能源电力系统的惯量评估研究，文献[12]采用扰动发生后1 s的频率值对采用虚拟同步发电机（Virtual Synchronous Generators, VSG）控制的光伏。文献[13]推导了时域下的风电场等效虚拟惯量表达式，发现含虚拟惯性控制的风电场等效惯量可用一条具有3阶段时变特性的曲线描绘，然而这种方法需要获取所有风电机组的内部参数，给系统惯量评估带来了困难。文献[14]利用受控自回归模型以及含有遗忘因子的递推最小二乘算法对含虚拟惯性响应的风电场等效惯量进行评估。虽然基于系统辨识方法的惯量评估不需要获取风电机组内部参数，但需要对高阶模型进行降阶，从而影响惯量评估精度。文献[15]采用量测数据求取风电场等效惯量，避免了因辨识模型降阶带来的误差。
针对上述问题，本文通过分析新能源虚拟惯性响应特性、负荷等效惯量和区域惯量评估原理，提出了一种采用有功功率、频率和电压量测数据的区域等效惯量评估方法。该方法考虑了惯量区域分布特性和频率分布特性的影响，所需量测数据少且易于获取，减少了数据处理步骤，对新能源机组内部参数未知的情况同样适用。通过算例验证了所提方法的有效性和优越性，分别对含虚拟惯性控制的风电（辅助调频控制）、光伏（VSG控制）系统等效惯量进行评估，比较分析了二者参与系统调频的效果及经济性。
现代电力系统要求新能源发电设备尽可能具备类似于常规电源的频率调节能力[16]，通过虚拟惯性控制、下垂控制、虚拟同步机技术等为系统提供惯量支撑[17-19]。风机转子动能法通过附加一定的频率控制环节将转子部分存储动能转换为电磁功率参与系统频率调节[20]，使风电机组提供远比实际惯量大的“虚拟惯量”，因此称为虚拟惯量控制。目前风电机组主要有四类机型：恒速恒频异步风机、转子电阻型异步风机、双馈异步风机、永磁直驱风机[21]。常见的风电机组有双馈式机组和直驱式机组，二者均可在最大功率点跟踪（Maximum Power Point Tracking, MPPT）控制基础上附加频率调节措施实现虚拟惯性控制[22-23]，如图1所示。
图1 附加频率调节措施
Fig.1 Additional frequency regulation measures
将频率控制环节附加在风机MPPT输出功率参考值上，综合使用惯性控制器与下垂控制器控制有功输出。在大扰动条件下，惯性控制能提高系统暂态响应性能，下垂控制能提高系统稳态响应性能[24]。风机虚拟惯量控制的调频辅助功率由两部分构成：一部分模拟同步发电机惯性响应特性，系统频率下降时，机组释放转子中储存的动能，增发与频率变化率df/dt呈比例关系的有功出力；另一部分模拟同步发电机组的有功-频率静态特性，通过一次调频响应系统频率变化，增发与频率偏差∆f呈比例关系的有功出力，即
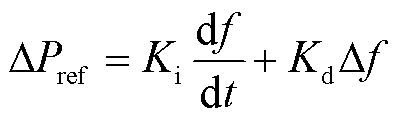（1）
式中，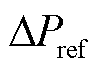
为调频辅助功率；Kd和Ki分别为惯性参数与下垂参数。本文不考虑下垂系数对惯量评估的影响，设定Kd =0。
为了保障风电机组安全运行，需要考虑其实际出力限制及转子频率越限问题，包括以下两点：
1）虚拟惯量控制所提供的支撑功率不得越限。机组调频过程中应满足功率约束[17,22]，功率限幅模块确保机组输出电磁功率不超过额定功率限制，即
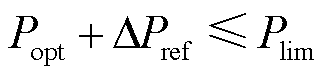（2）
式中，Popt为最大跟踪功率；Plim一般为机组额定功率。对于不同类型的风电机组，Plim还应考虑实际逆变器的额定容量限制，双馈异步电机的变流器容量远远小于风机容量，一般是在30%左右；永磁直驱机组电机的能量完全通过变流器，变流器容量与风机容量相似。
2）调频过程中转子转速不得越限。变速风机的转子转速运行范围一般为0.7(pu)～1.2(pu)[17]。风电机组在MPPT运行方式下参与调频，转子速度下降，若机组没有多余的备用容量，转子速度降到最小值时没有多余的动能用来提供支撑功率。为了避免风电机组调频致使转子转速低于最小值，增加转速保护控制模块[19]。当转速低于0.7(pu)时机组暂时退出虚拟惯量控制，不再参与调频，此时设定ΔPref=0。
以双馈风电机组（Doubly-Fed Wind Turbine, DFIG）并网为例，附加惯性控制器参与系统频率调节，大扰动情况下惯性参数Ki对系统频率、风机输出功率和转子频率的影响如图2～图4所示。
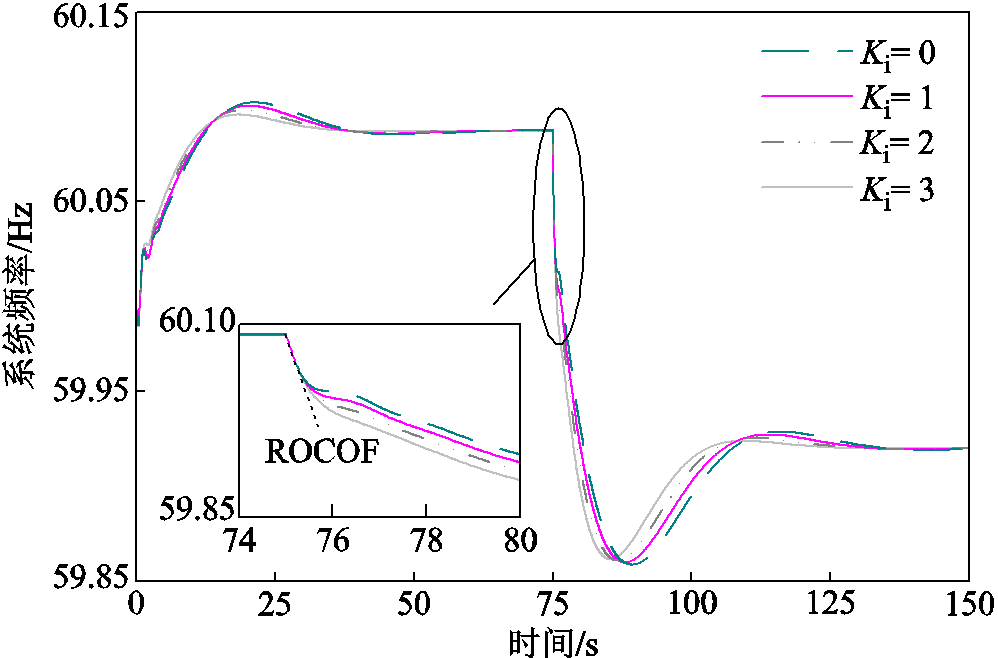
图2 系统频率
Fig.2 System frequency
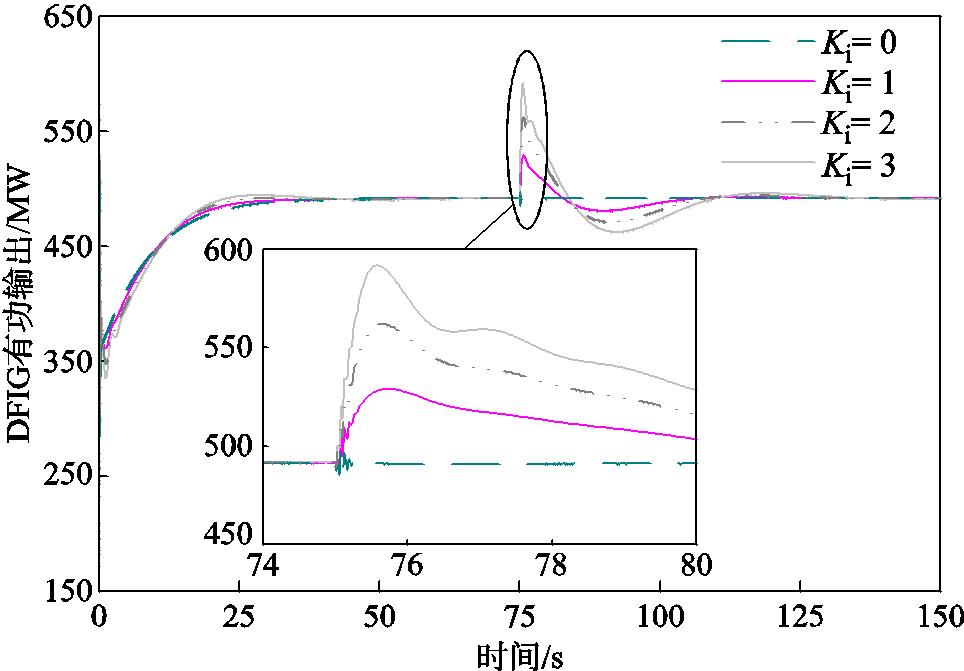
图3 DFIG有功输出
Fig.3 Active output of DFIG
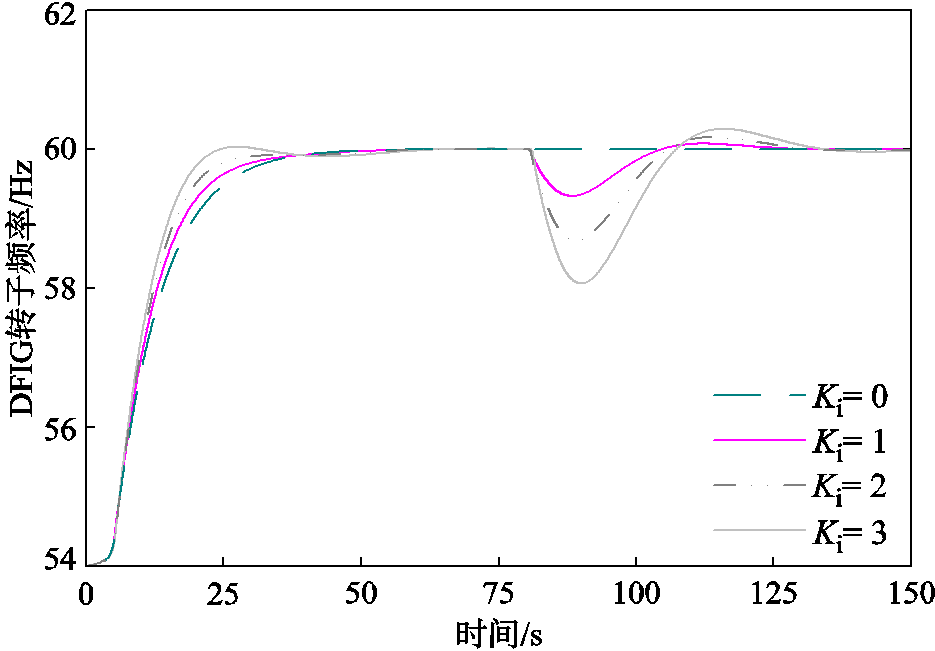
图4 DFIG转子频率
Fig.4 Rotor frequency of DFIG
如图2所示，惯性参数Ki越大，扰动发生时刻附近的RoCoF越小，阻碍频率变化的能力越强，说明系统惯量水平越高。可见，引入惯性参数Ki可提高系统应对故障情况下的频率支撑能力，为一次调频留有足够的调节时间，避免触发第三道防线造成大面积停电。
由图3和图4可知，随着Ki的增大，扰动发生后风电机组的有功输出增加，转子频率偏差增大，风机转子释放动能弥补系统出现的功率缺额。当Ki=0时，扰动发生后的系统频率变化对风机输出功率和转子频率几乎没有影响，两者基本保持稳态时的状态，此时风电机组不提供系统不平衡功率支撑，这是由于电力电子装置将风力发电设备与电力系统解耦，使其无法快速响应系统频率变化，因而无法对系统扰动提供惯性支撑。风电系统虚拟惯量来源于风电机组自身动能的变化，发生扰动时，系统频率从f(t0)变化到f(t)，机组转子转速将相应地从ωr(t0)变化到ωr(t)，则单台风机转子吸收或释放的旋转动能为
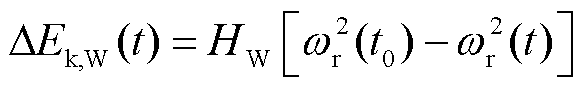（3）
式中，HW为风电机组固有惯性时间常数；ωr(t0)、ωr(t)分别为扰动发生前t0时刻、扰动发生后t时刻风电机组转子角速度。其中，t介于扰动发生时刻与一次调频开始动作时刻之间。
由于惯量响应过程中一次调频未动作，因此认为风电机组所捕获的机械能为0。根据能量守恒原理，该过程中风电机组自身动能变化量与输出电能变化量处于动态平衡状态[15]，即
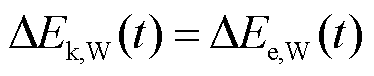（4）
式中，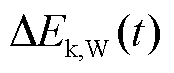
、
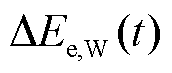分别为扰动发生后t时刻风电机组的动能变化量、输出电能变化量。其中，输出电能变化量用电磁功率变化量的积分表示，即
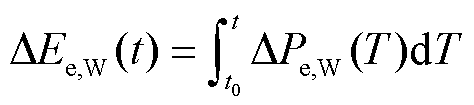（5）
式中，DPe,W为风电机组电磁功率变化量，可通过测量公共连接点（Point of Common Coupling, PCC）母线处的功率变化获取。
当风电机组附加频率调节措施时，发电机转子频率与系统频率相耦合，式（3）可从另一个角度表示为
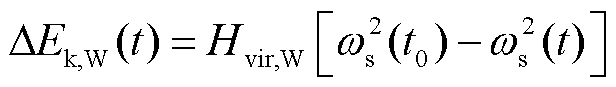（6）
式中，Hvir,W为风电机组等效虚拟惯性时间常数；ωs(t0)、ωs(t)分别为扰动发生前t0时刻、扰动发生后t时刻PCC母线处的频率。
由式（3）～式（6）可得风电等效虚拟惯性时间常数如式（7）所示，通过文献[15-16]可知，Hvir,W具有时变特性。
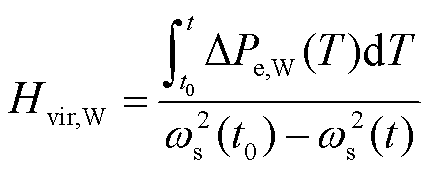（7）
光伏系统因内部无旋转部件，因此无法利用自身动能变化提供虚拟惯量，但为了应对光伏系统存在的低惯量问题，基于逆变器并网的VSG控制策略可使系统输出的总功率、频率和电压输出模拟同步发电机的外特性[25]。当光伏功率波动和负载变化时，在暂态过程中引入惯性和阻尼参与电网的调频和调压，以维持系统频率与电压稳定，提高新能源电力系统稳定性及消纳能力。
光伏虚拟同步发电机通常由变流器、储能单元和控制部件三部分组成[26]。光储VSG系统相当于一个可控的电源，当储能的荷电状态处于较高水平时，有足够的能量平衡光伏出力的峰谷变化且可参与电网调频，并网逆变器能够按照指定功率进行有功输出。采用VSG控制的光储系统中，由于光伏按MPPT运行，不具有功率调节能力，所需功率支撑完全由储能单元实时提供，同时储能还能承担光伏功率与逆变器并网功率之间的平抑和缓冲作用[27]。VSG输入的有功功率由两部分组成，如图5所示，一是整个光储并网发电系统的指令Pref，二是由于频率偏差引起的有功变化量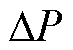
，即
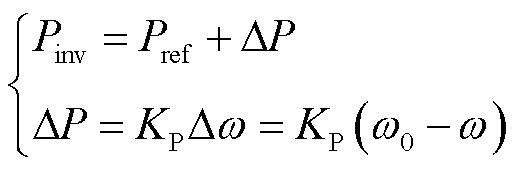（8）
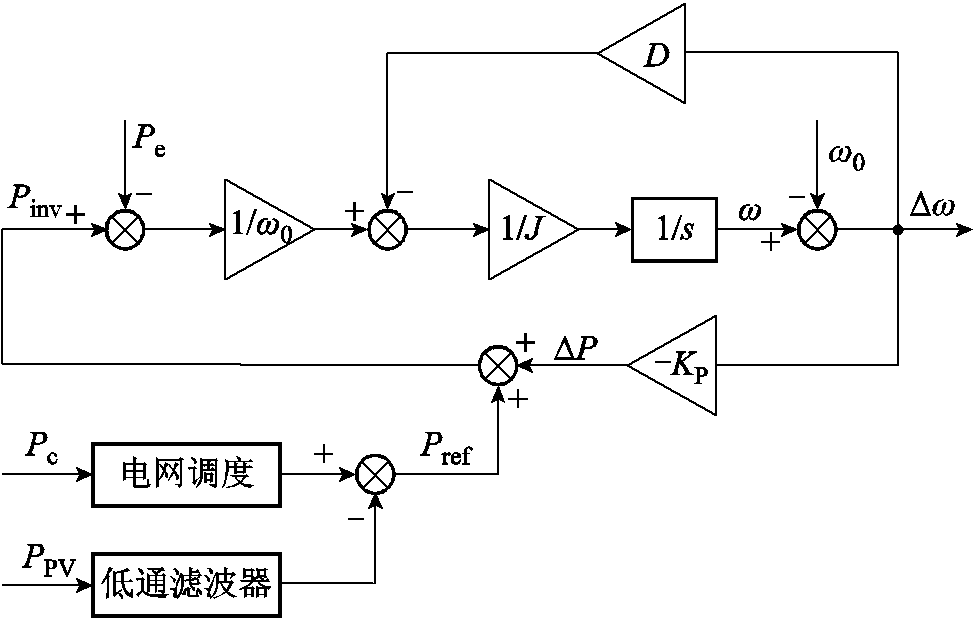
图5 VSG的有功-频率控制框图
Fig.5 The diagram of P-ω control of VSG
式中，Pref为并网指令由上层调度控制中心按经济调度原则确定的功率指令Pc与光伏阵列按MPPT策略输出的有功功率PPV的差值；DP模拟同步发电机有功-频率的下垂静态特性；w为电网实际角速度；w0为额定角速度；KP为有功-频率下垂系数。本文不考虑下垂系数对惯量评估的影响，设定KP=0。
与风电系统虚拟惯量响应过程分析类似，光伏等效虚拟惯性时间常数Hvir,PV计算公式为
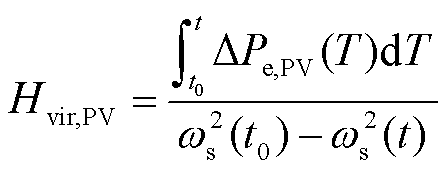（9）
式中，DPe,PV为光伏系统电磁功率变化量。
同样地，采用虚拟同步发电机控制的光储系统提供功率支撑需要考虑其实际出力限制。根据《光伏发电站设计规范（征求意见稿）》条文说明，光伏电站额定容量即光伏发电站中安装的逆变器的额定有功功率之和，通常情况下逆变器输出功率不能达到所对应的组件的安装容量值，在光伏发电系统设计时应考虑光伏组件安装容量相对逆变器额定容量超配的要求。因此，采用VSG控制的光储系统在实际应用中需要考虑逆变器容量配比的问题。
电力系统惯性是系统频率稳定的重要保障，惯性的大小可以用惯量衡量[28]。当电力系统受到扰动时，系统中机械功率与电磁功率不平衡，同步发电机通过惯性响应过程抵消不平衡功率，从而在一定程度上保持系统频率稳定。不考虑同步发电机自身阻尼，单台发电机惯性时间常数为[7]
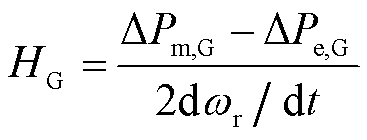（10）
式中，DPm,G为发电机机械功率变化量，且有DPm,G≈0；DPe,G为发电机电磁功率变化量；ωr为发电机转子角速度。
在实际电网中，由于同步发电机转子角速度参数获取困难，一般采用PMU测量其出口母线频率ωs近似代替转子角频率ωr。对式（10）两端进行积分，则单台发电机惯性时间常数为
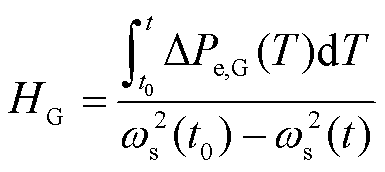（11）
通过类比式（7）、式（9）、式（11）可以发现，新能源机组虚拟惯性时间常数与同步发电机惯性时间常数表达式相同，故可将不同类型发电设备视为同一类型机组，对新能源电力系统等效惯量进行整体评估。
以图6所示含n个区域的新能源电力系统说明惯量评估原理，区域间通过联络线相连，分别对各区域求取惯性时间常数。
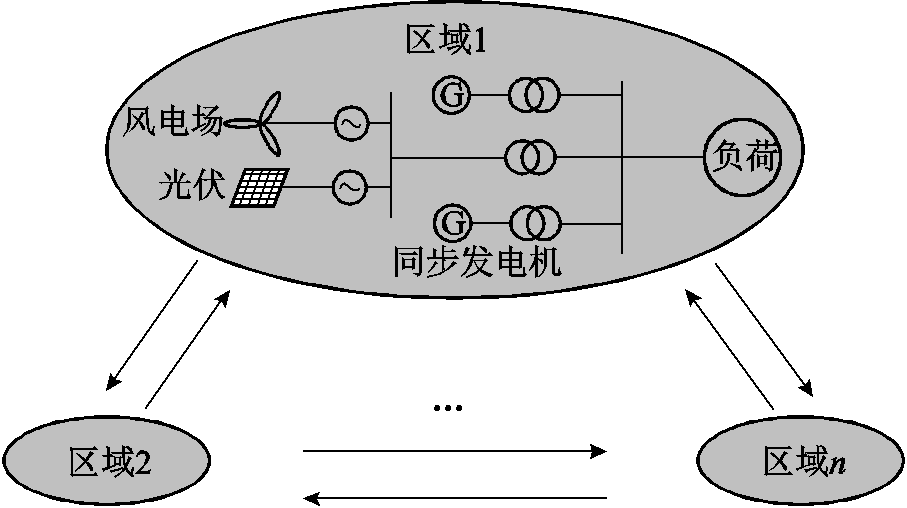
图6 多区域新能源电力系统
Fig.6 Multi-area new energy power system
将式（11）推广得到区域惯性时间常数Harea为
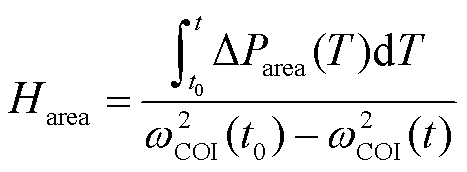（12）
式中，ωCOI为区域惯量中心频率；DParea为区域不平衡功率。
若扰动发生在区域j，则故障区域j的不平衡功率为扰动功率与该区域联络线功率变化量的和，非故障区域k的不平衡功率为该区域联络线功率变化量的和，如式（13）和式（14）所示。
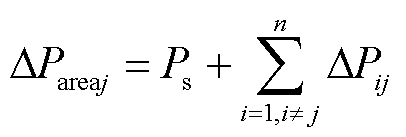（13）
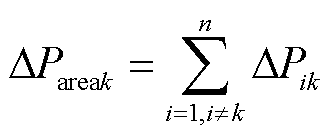（14）
式中，Ps为扰动功率；DPij、DPik分别为故障区域j、非故障区域k联络线功率变化量。
结合式（12）～式（14）得到各区域等效惯性时间常数为
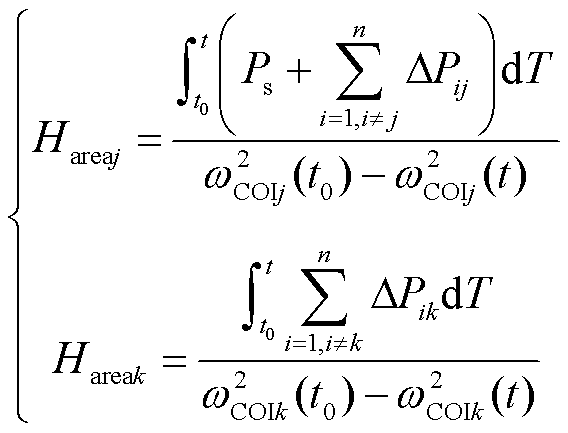（15）
分析式（15）可知，获取扰动发生前后各区域联络线功率及电源出口母线频率，便可利用量测数据评估区域惯量水平，因而不需要获取新能源机组内部参数及控制参数，同时避免了因计算dωs/dt含有振荡分量而导致评估结果受到影响的问题，减少了数据处理步骤，同时提高了评估精度。
负荷等效惯量主要体现在其静态电压特性上。系统发生大规模功率缺额故障时，电压跌落较大，此时电压变化对负荷的影响不能忽略[8]。负荷的静态电压特性[29]为
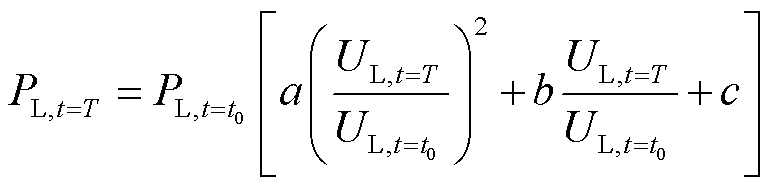（16）
式中，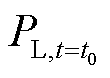
、
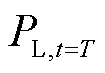分别为扰动发生前t=t0时刻、扰动发生后t=T时刻负荷的有功功率；
、
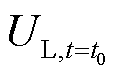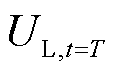分别为扰动发生前t=t0时刻、扰动发生后t=T时刻负荷节点瞬时电压；a、b、c分别为恒阻抗、恒电流、恒功率类型负荷所占的成分比例，且a+b+c=1。
扰动前后负荷的有功差DPL为
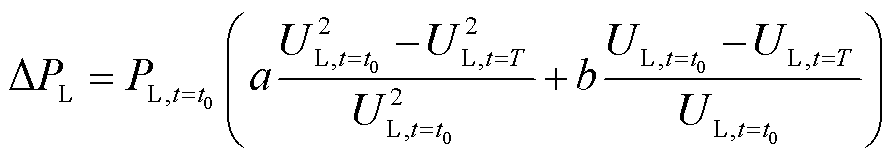（17）
计及负荷静态电压特性后对式（13）和式（14）进行修正，故障区域j和非故障区域k的不平衡功率为
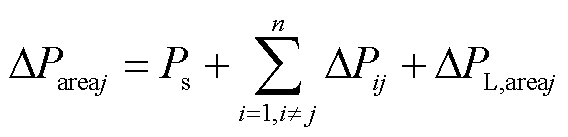（18）
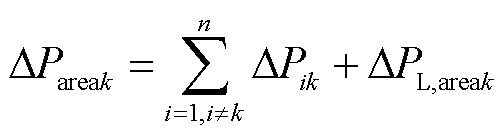（19）
由于电网频率的动态变化从扰动发生位置向四周传播，存在一定延时，不同时刻和不同节点的动态频率特征不同，因此惯量对不同时刻与不同节点频率的阻碍作用也不同。取单个节点的频率估计惯量时会导致误差增大，通常采用惯量中心频率ωCOI来代表整个系统的频率，惯量中心频率被描述为所有发电机的动态行为参数以惯性时间常数为权重的加权平均值[30]，有
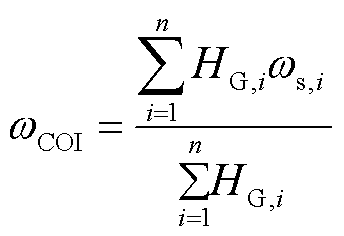（20）
式中，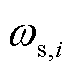
、
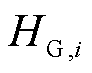分别为第i台发电机的母线频率和惯性时间常数。
各台同步发电机组惯性时间常数通常从数据采集与监视控制（Supervisory Control and Data Acquisition, SCADA）系统中获取[31]，有
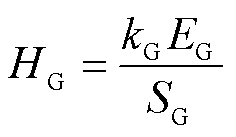（21）
式中，EG为发电机转子动能；kG为机组启停状态，kG=1代表开机状态，kG=0代表停机状态；SG为发电机容量。
惯量中心频率的计算需要获取所有运行发电机的频率数据，所需量测数据多且计算量大。为了解决这个问题，从加权平均数的角度分析式（20），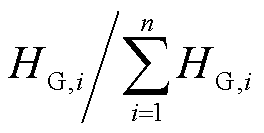
相当于ωs,i对应的权数，权数对其在平均数中的影响起着权衡轻重的作用，加权平均数的大小更倾向于受到具有较大权重的数值的影响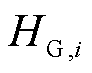，越大意味着发电机i对ωCOI的贡献越大。因此，在获取系统频率时可以只计及数值较大的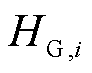，采集对应的ωs,i，从而减少量测量与计算量。
基于上述分析，提出一种频率采样点的选取及区域频率的计算方法，具体步骤如下。
1）根据式（21），从实时惯量监测结果中选取各区域惯性时间常数较大的同步发电机组，将其出口母线作为该区域的频率采样点。其中，选取的机组数量应由实际区域电网规模、网络结构等因素综合确定。对于含虚拟惯性控制的风电系统，常在风机虚拟惯性控制的设计上增加一阶惯性环节[15]，使得风电输出功率不会立即响应系统频率变化，因而不适合将风电场PCC作为频率采样点。
2）利用PMU获取扰动发生后采样点的动态频率数据。
3）计算各区域频率ωareaj和ωareak。通过式（20）计算故障区域j和非故障区域k惯量评估所需的区域频率。
根据上述分析，评估区域等效惯量所需的量测数据见表1。
表1 区域等效惯量评估所需量测数据
Tab.1 Measurement data required for regional equivalent inertia assessment
采样时间采样点频率联络线功率负荷节点电压负荷功率 扰动前√√√√ 扰动后√√√
由表1可知，评估区域等效惯量需要采集扰动发生前后2个时刻的量测数据。由于扰动发生时电力系统各状态量变化有一定延时，因此t0取扰动发生时刻，通过去趋势波动分析（Detrended Fluctuation Analysis, DFA）从量测数据中判定惯量评估中的扰动发生时刻[10,15]。
由于PMU采集到的数据含有一定程度的噪声干扰，因此采用低通滤波器对量测数据进行预处理。为了减小某一时刻量测中的偶然误差，采用滑动窗口技术进行数据处理，取一个时间窗内对应量测数据的平均值，从而降低一次调频对惯量评估精度的影响。扰动数据时间窗如图7所示，A为采样点个数，W为窗口数，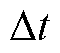
为两个采样点之间的时间间隔，A=5，W=2。
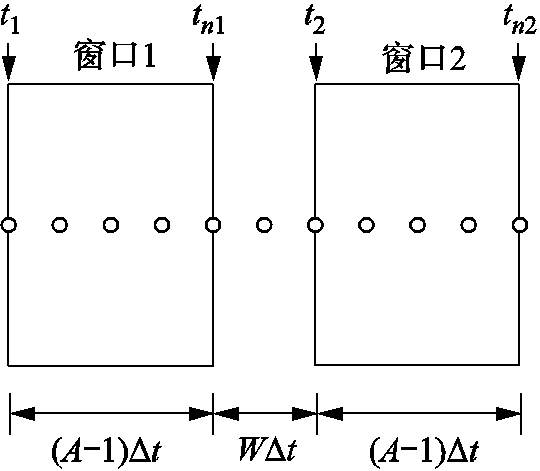
图7 扰动数据时间窗
Fig.7 Time window of disturbance data
综上所述，本文所提新能源电力系统区域等效惯量评估流程如图8所示。
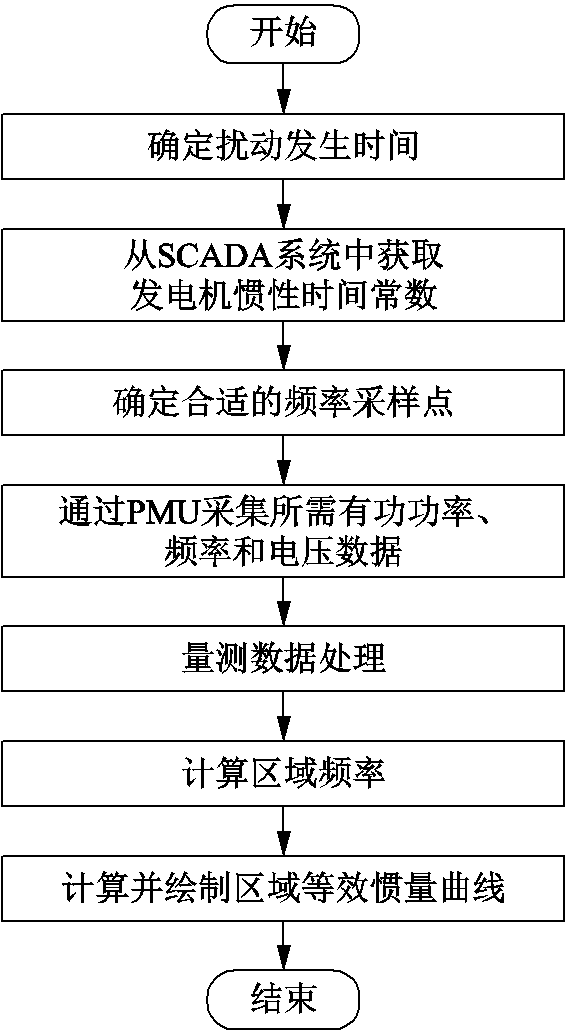
图8 评估流程
Fig.8 Evaluation process
在Matlab/Simulink中搭建图9所示的4机2区域系统。区域1包含2台同步发电机组G1、G2，区域2包含2台同步发电机组G3、G4，机组额定容量均为900 MV∙A，额定电压均为20 kV，负荷均为电压敏感型。设置t0=75 s时母线B7处负荷突然增加200 MW，仿真时间为150 s。扰动前系统电源和负荷平衡，同步发电机均处于开机状态。
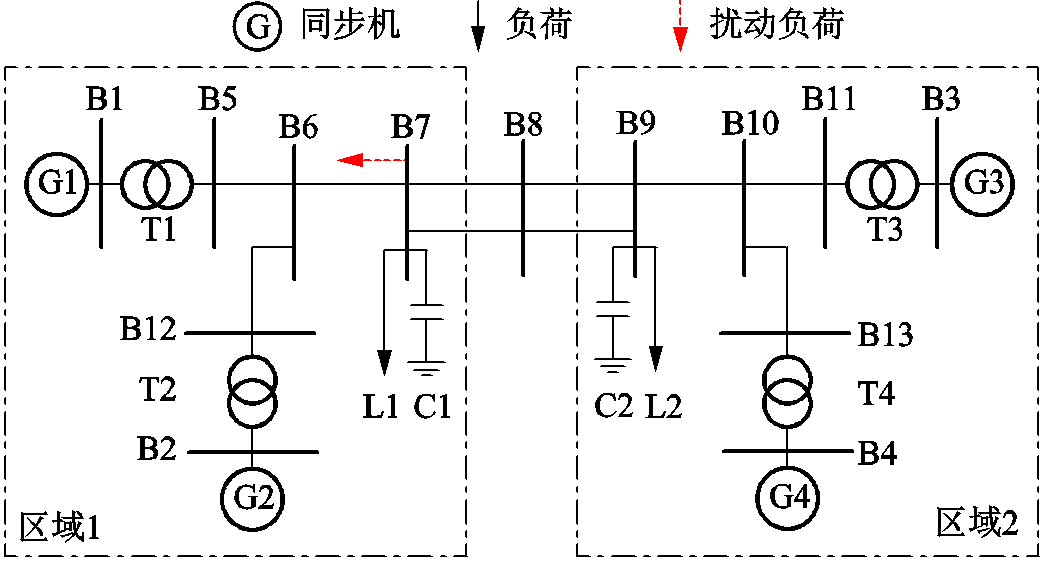
图9 算例系统
Fig.9 Test system
算例部分主要进行以下研究内容：
1）与文献[7]采样点选取方法进行对比分析，验证本文所提频率采样点选取方法的可行性；基于所选采样点计算区域频率，与惯量中心频率及实际频率作比较，验证本文所提区域频率计算方法的可行性。
2）与文献[10]区域惯量评估方法进行对比分析，分析其不足之处并揭示原因，进一步表明本文所提评估方法的优越性。
3）验证本文所提惯量评估方法在传统电力系统和新能源电力系统中的有效性，同时研究新能源虚拟惯性控制参数、不同类型新能源的出力占比对区域等效惯量大小的影响。
4）基于算例分别对含虚拟惯性控制的风电（辅助调频控制）、光伏（VSG控制）系统等效惯量进行评估，比较分析二者参与系统调频的效果及经济性。
同步发电机典型惯性时间常数为2～9 s[32]。考虑电力系统网络结构、支路参数及发电机惯性时间常数等因素对惯量中心位置的影响，设置两种场景，不同场景下的发电机惯性时间常数见表2。
表2 不同场景下的发电机惯性时间常数 （单位：s）
Tab.2 Generator inertia time constant in different scenarios
场景HG1HG2HG3HG4 场景16.56.56.1756.175 场景22938
由于算例系统规模较小，故选取各区域内惯性时间常数最大的同步发电机出口母线作为频率采样点，由此确定两种场景下的采样点见表3。
表3 不同场景下的频率采样点
Tab.3 Frequency sampling points in different scenarios
场景区域1区域2 场景1B1或B2B3或B4 场景2B2B4
考虑到频率分布特性对惯量评估结果的影响，文献[7]通过惯量图心的概念，选取FE最小值节点作为整个电力系统的频率采样点，采用该方法求取两种场景下各个节点的FE值，结果如图10所示。
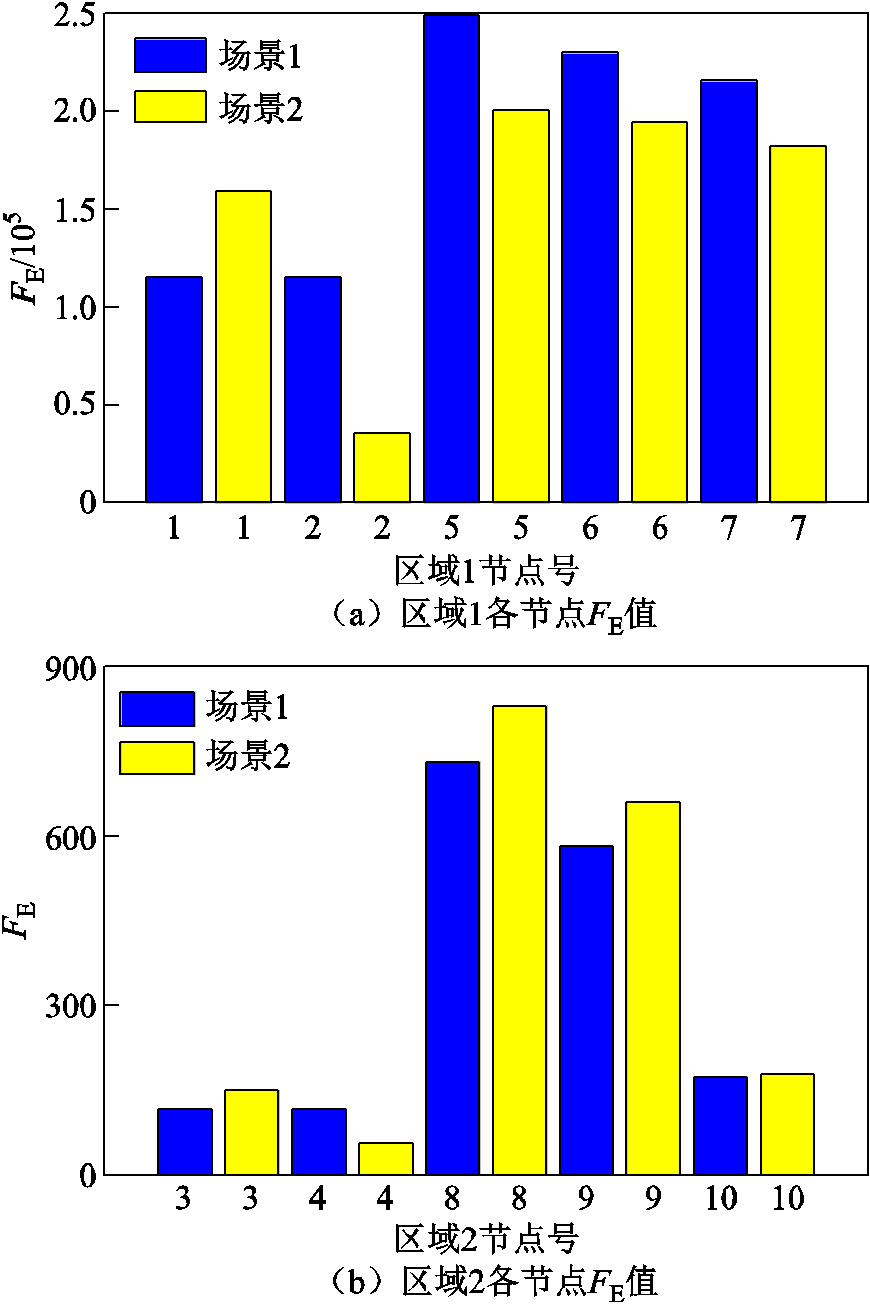
图10 各个节点的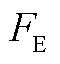
值
Fig.10 Value of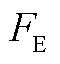 for each bus
如图10所示，采用文献[7]方法选取的频率采样点与表3结果一致，验证了本文所提频率采样点选取方法的可行性。相比于文献[7]，本文所提方法利用SCADA系统直接选取惯性时间常数较大的同步发电机出口母线作为频率采样点，简单方便，可以避免大规模计算。
为进一步验证区域频率获取方法的有效性，基于场景1比较各区域频率、惯量中心频率及实际频率曲线。区域1和区域2频率分别取采样点B1和B3处的频率。各区域频率响应情况如图11所示。
由图11可知，各区域采样点频率与惯量中心频率及实际频率曲线总体非常相近，频率扰动的动态过程吻合度较高，可用于评估区域等效惯量。由此证明所提区域频率计算方法的有效性，可进一步应用于传统电力系统及新能源电力系统区域等效惯量评估。
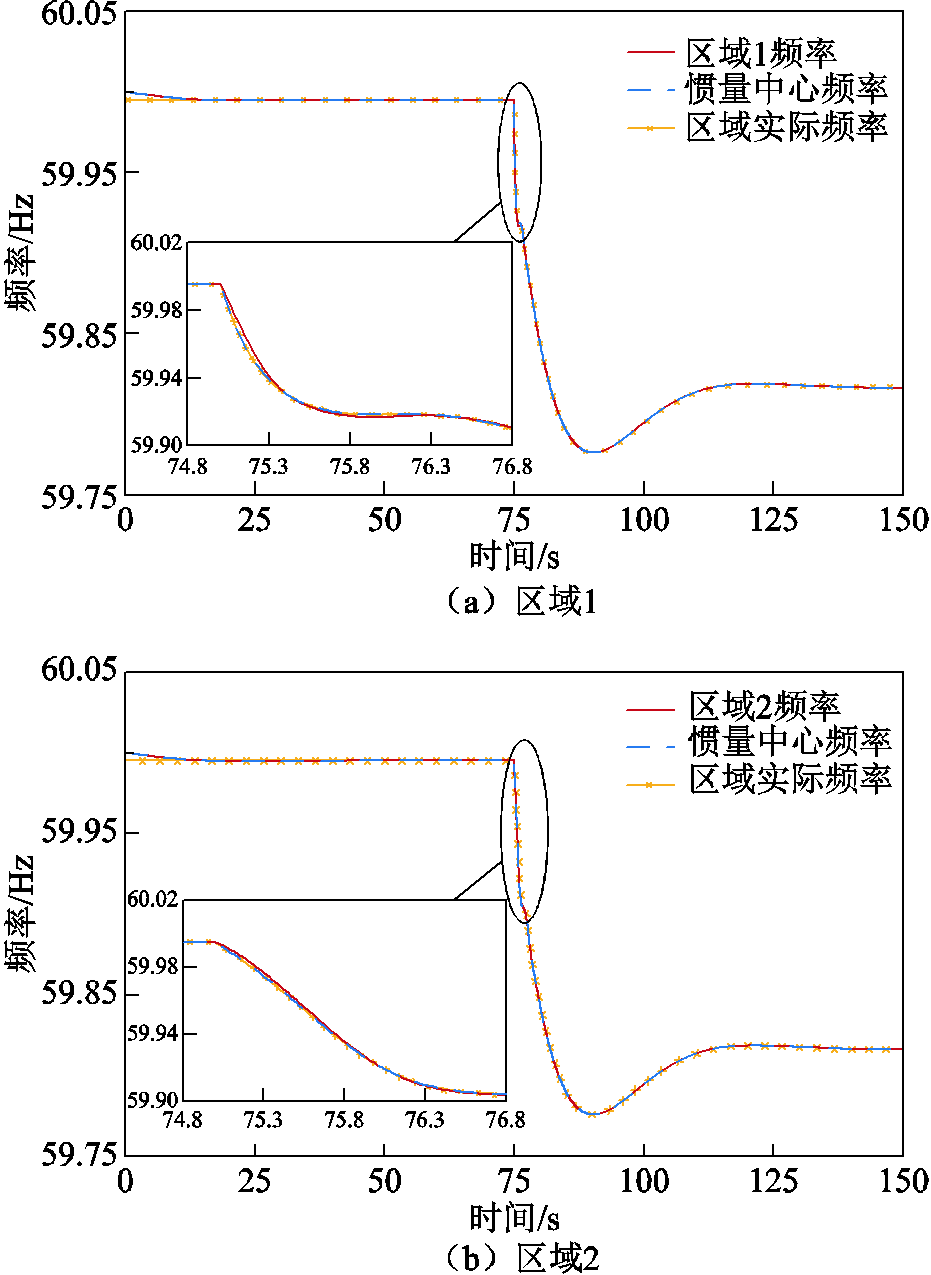
图11 各区域频率响应情况
Fig.11 Frequency response of each area
文献[10]没有考虑负荷静态特性因素，利用大扰动下两个采样时刻的联络线功率-频率数据进行区域惯量评估，采用该方法和本文所提方法进行对比，场景1下各区域等效惯量评估曲线如图12所示。观察图12中采用本文方法得到的评估结果可知，在一次调频动作时刻t=75.5 s时，各区域等效惯量评估值减小至理论值附近，随后趋于稳定，选取该时刻评估结果的相对误差作为衡量标准，误差均在5%以内，表明本文所述评估方法的准确性。而采用文献[10]所述方法得到的评估结果与理论值相差较大，是因为没有计及负荷等效惯量。同时，由图12b可观察到，采用文献[10]方法计算得到区域2等效惯量曲线与理论值有且仅有1个交点，因此采用该方法准确评估等效惯量对采样时刻t的选取要求较高。
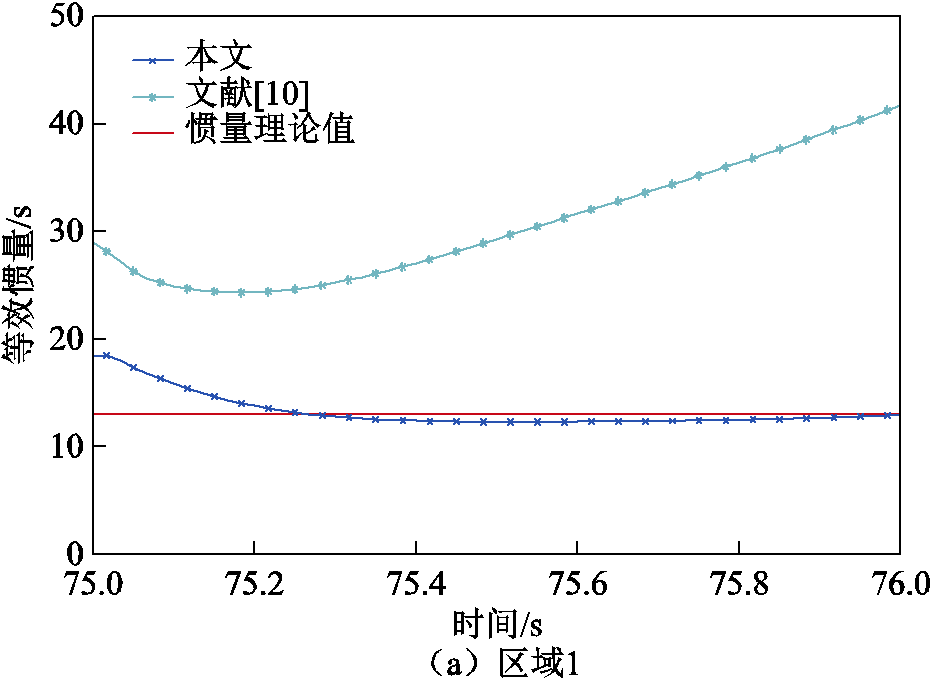
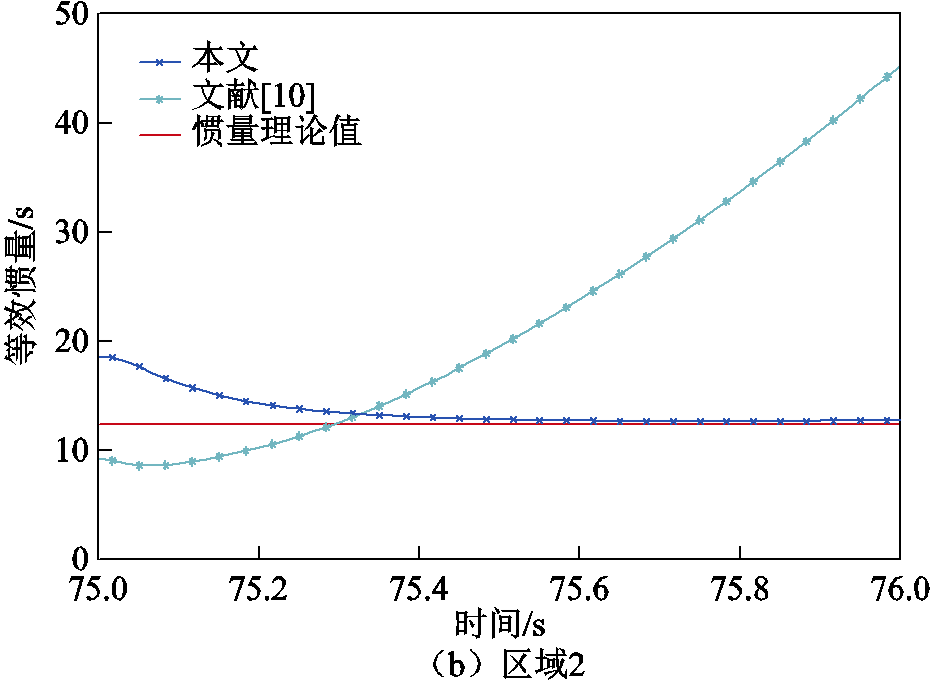
图12 不同评估方法下各区域等效惯量
Fig.12 Equivalent inertia of each area under different assessment methods
测试系统中，风电与光伏一同取代同步发电机G4，为系统负荷提供等效功率输出。风机初始转子转速为0.9(pu)，风速为10 m/s，辐照度为1 000 W/m²。风电惯性时间常数为2～6 s[33]，这里设置风机固有惯性时间常数为5.04 s。通过调节风机台数与光伏电池个数改变二者出力占比，设置表4所示三种场景验证本文所提评估方法的有效性。其中，风电机组采用以下两种控制方法做对比，分别为：①无附加控制（Ki=0）；②惯性控制（Ki=1, 2, 3）。各区域等效惯量评估结果如图13所示。
表4 新能源出力比例
Tab.4 Proportion of new energy output
场景风电出力(%)光伏出力(%) 场景13070 场景25050 场景37030
如图13a～图13c所示，区域1等效惯量在t=75.5 s左右达到最小值，随后由于一次调频作用的影响而缓慢上升。不同惯性参数Ki对各区域等效惯量的影响见表5，评估结果最小值相对误差均在10%以内。通过对表5分析可知，随着惯性参数Ki和风电出力的增加，区域1等效惯量评估最小值相对误差增大，说明采用本文所提方法进行惯量评估时，风电机组出力及虚拟惯性控制参数对系统中其他区域惯量评估结果精度有一定的影响。
如图13d～图13f所示，无惯性控制时区域2等效惯量恒为发电机G3的固有惯量值。含风电惯性控制的等效惯量具有3阶段时变特性，扰动时刻附近区域2惯量由同步机提供，在一次调频动作时刻附近达到最大值。可见变速风力发电机组在转子动能控制下能虚拟出比自身固有惯量大很多倍的等效惯量，给系统频率稳定提供更有效的支撑。随着采样时刻的推移，系统频率恢复，区域2等效惯量逐渐减小，与文献[15]风电场等效惯量时变特征一致。扰动发生时刻附近，区域2等效惯量没有突增，这是由于风电虚拟惯性控制措施中的一阶惯性环节使风机输出功率得到缓冲，此时风电机组还未提供虚拟惯量，区域等效惯量仍为同步发电机组G3固有惯量。
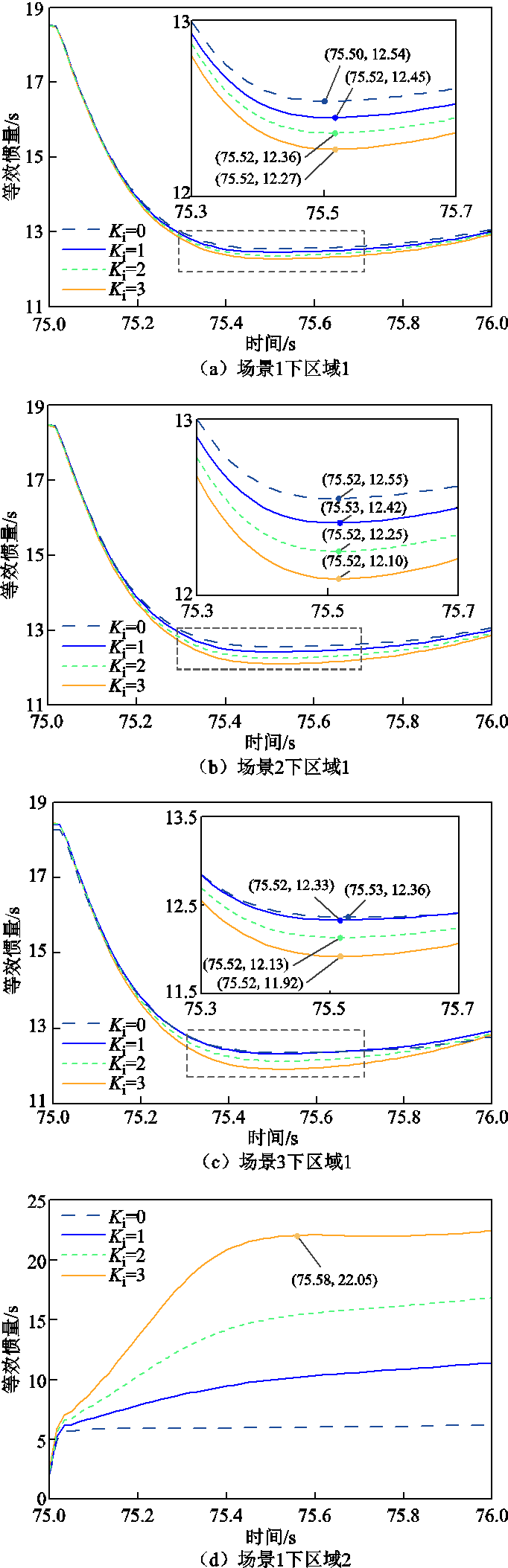
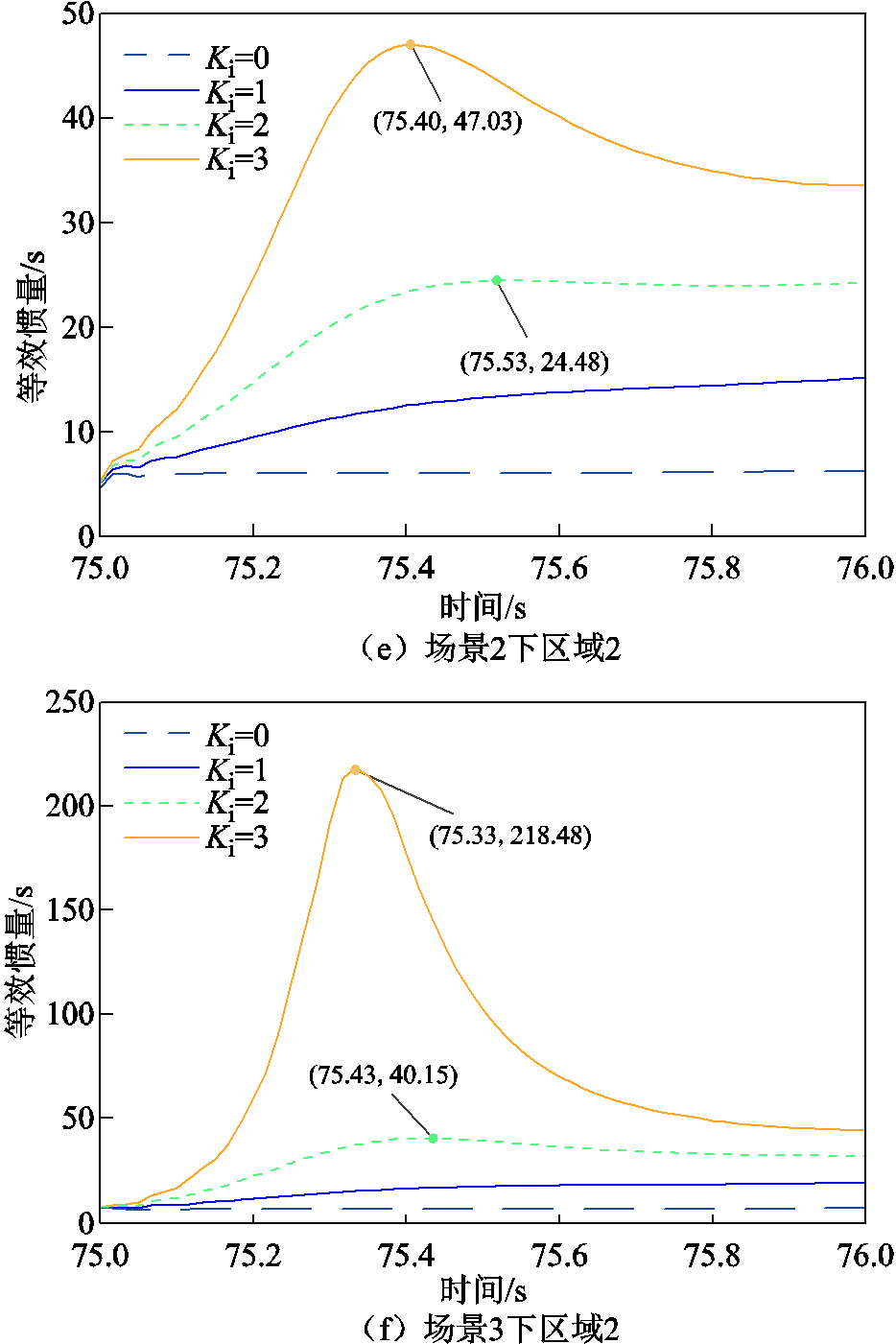
图13 不同场景下的区域等效惯量
Fig.13 Equivalent inertia of each area in different scenarios
表5 区域1等效惯量误差
Tab.5 Equivalent inertia error in Area 1
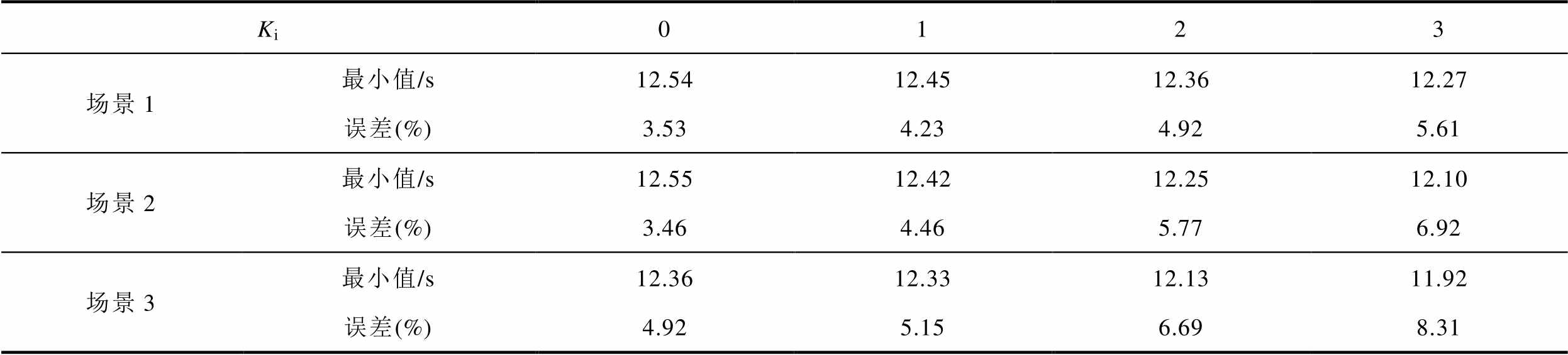
Ki0123 场景1最小值/s12.5412.4512.3612.27 误差(%)3.534.234.925.61 场景2最小值/s12.5512.4212.2512.10 误差(%)3.464.465.776.92 场景3最小值/s12.3612.3312.1311.92 误差(%)4.925.156.698.31
当Ki=1和Ki=2时，图13d中区域2等效惯量不存在最大值，是因为风电提供的惯性支撑功率较少，虚拟惯性响应较慢，在达到惯量最大值时刻前一次调频已经介入。如图13e和图13f所示，随着惯性参数Ki和风电出力的增加，区域2惯量最大值提高，且达到该值所用时间减少，说明风电机组能更快地响应系统频率变化。
下面讨论光伏采用VSG控制参与调频的情况。风光储并网发电系统结构如图14所示。
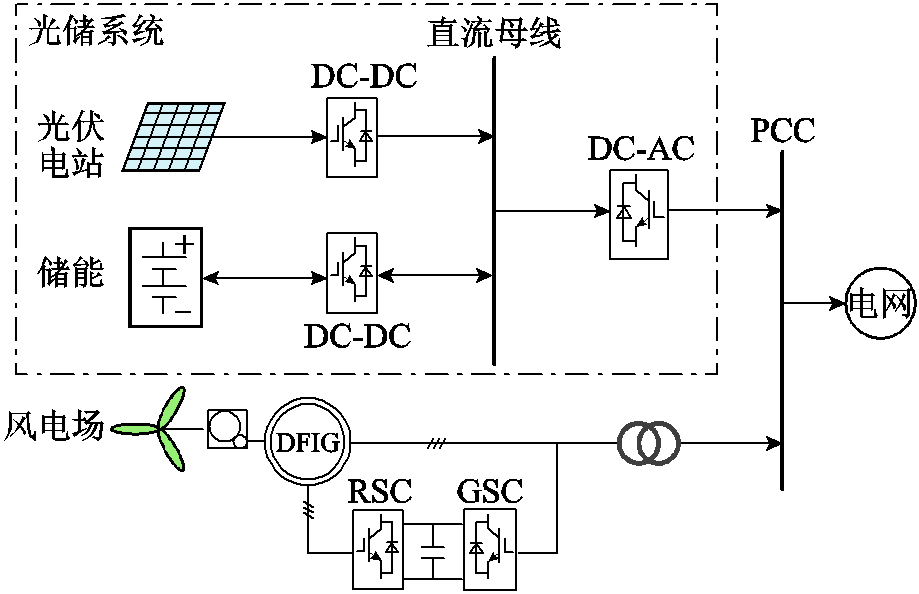
图14 风光储并网系统结构
Fig.14 The structure of the wind-solar-storage grid-connected system
光伏电站和储能单元并联在直流母线上，通过逆变器并入电网。蓄电池通过充放电维持直流母线电压，平衡光伏发电与负载功率之间的差额。其中，光伏发电系统采用最大功率跟踪控制；储能系统采用蓄电池电压电流双闭环稳压控制；并网逆变器实现电压型VSG控制策略。为比较分析风机辅助调频控制与光伏VSG控制参与系统调频的效果及经济性，在风电和光伏出力均为30%的条件下，设置以下两种情况。
情况1：基于表4中的场景3，光储系统采用定功率VSG控制参与系统调频，风电不参与调频。稳态时，给定整个光储并网发电系统的指令Pref= 200 MW，设置t0=75 s时Pref阶跃至230 MW，储能荷电状态SOC=100%。
情况2：基于表4中的场景1，风电采用辅助调频控制参与系统调频（Ki =3），光伏不参与调频。
有功功率如图15所示。扰动发生前光伏系统按MPPT运行出力206 MW，不具有功率调节能力，储能不出力，VSG按调度指令输出功率为200 MW。扰动发生后，光伏输出功率保持不变，调度指令要求增发的30 MW功率支撑完全由储能单元实时提供，VSG输出有功功率为230 MW。
不同情况下的区域频率如图16所示。情况1下各区域最大频率偏差和频率变化率RoCoF均比情况2小，这是因为采用VSG控制的光储系统可快速跟随功率指令变化提供不平衡功率支撑。同时，由于采用辅助调频控制的风电机组惯性响应时间较短，因此情况1稳态频率恢复值比情况2大。由此可见，采用VSG控制的光储系统相较于采用辅助调频控制的风电机组出力更灵活，调节速度更快，调频效果更好。
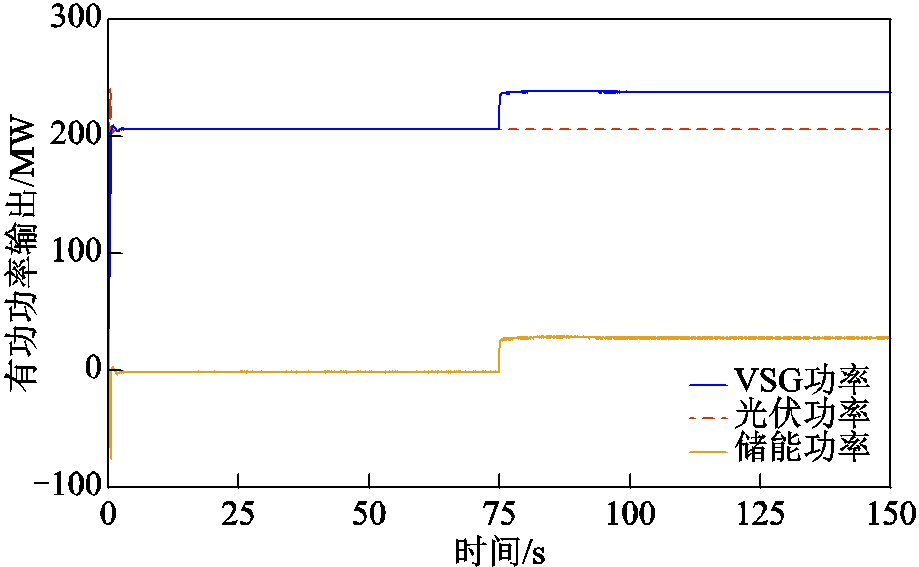
图15 有功功率
Fig.15 Active power
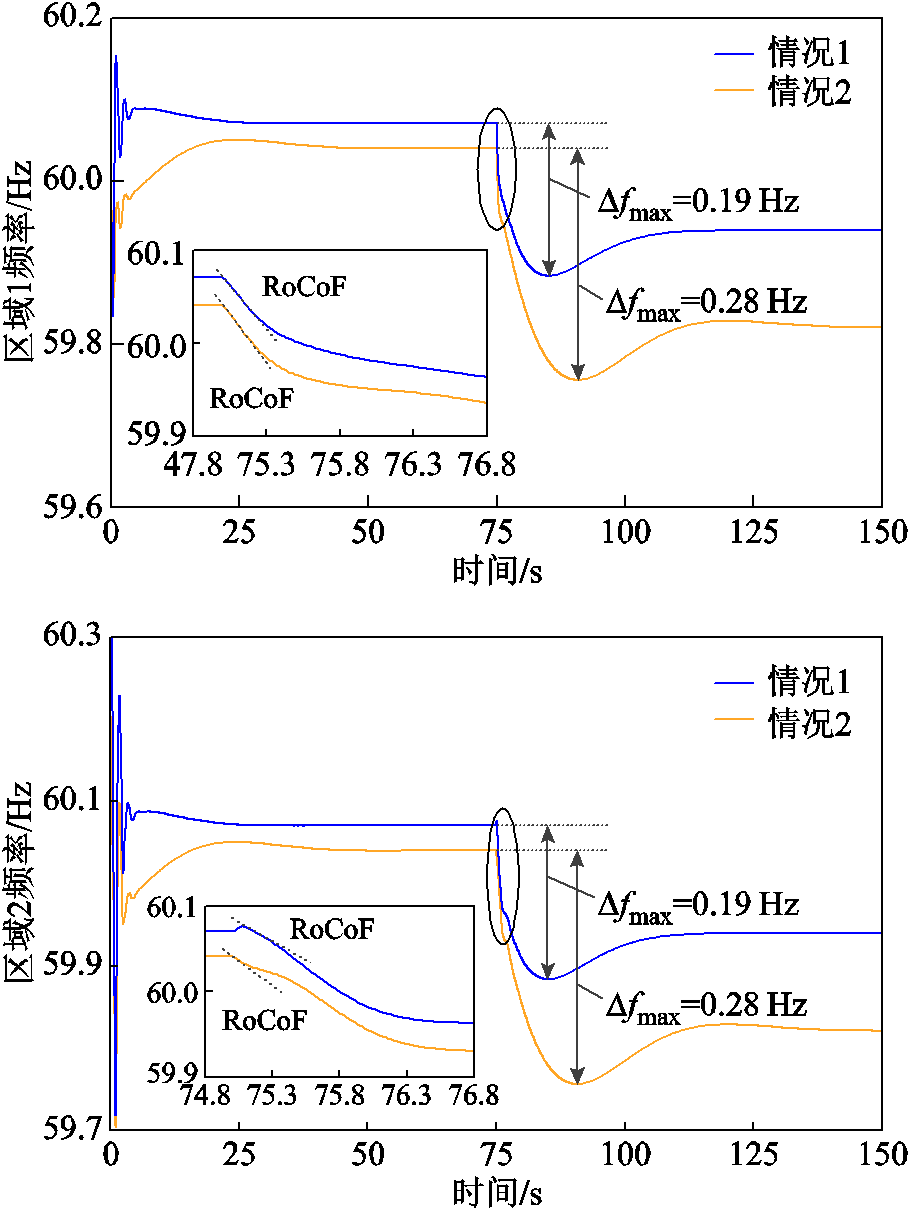
图16 不同情况下的区域频率
Fig.16 Regional frequency in different cases
情况1下区域1等效惯量如图17所示，在t=75.22 s达到最小值24.20 s，情况2下区域1等效惯量在t=75.52 s时刻（见图13a）达到最小值12.45 s。由此可知，情况1下区域1等效惯量最小值不再是同步发电机组固有惯性时间常数，且最小值出现的时间也较一次调频时间提前，这是因为扰动发生后，储能单元能够立即响应调度指令，提供功率支撑，说明采用VSG控制的光储系统并网对系统中其他区域等效惯量水平也具有提高作用。
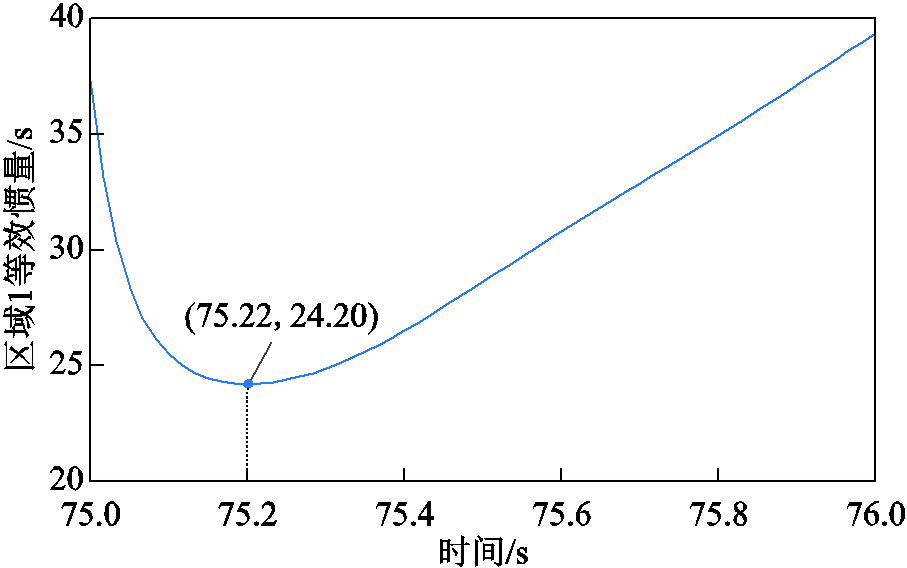
图17 情况1下区域1等效惯量
Fig.17 Equivalent inertia of Area 1 in Case 1
情况1下区域2等效惯量如图18所示，在t=75.17 s达到最大值468.57 s后迅速下降，随着时间的推移趋近于稳定值；情况2下区域2等效惯量在t=75.58 s达到最大值22.05 s（见图13d）。对比分析可知，采用VSG控制的光储系统在扰动发生后能够快速响应系统频率变化，提供所需功率支撑，而风电机组由于一阶惯性环节的影响，响应系统频率变化的速度较慢，且由于风电机组转子转速和输出功率的限制，其虚拟惯性响应时间短，所能提供的等效惯量也有限。
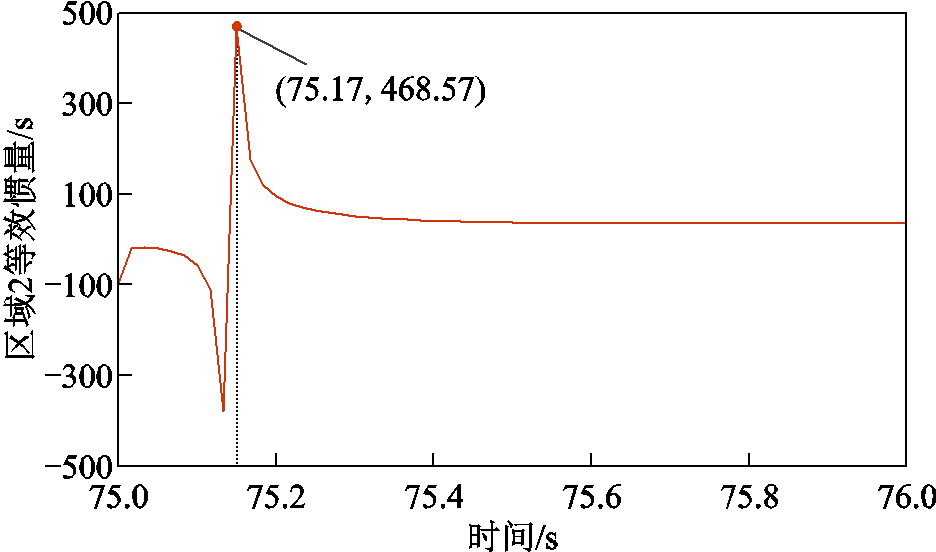
图18 情况1下区域2等效惯量
Fig.18 Equivalent inertia of Area 2 in Case 1
综合仿真分析结果可以看出：本文所提方法能够较为准确地评估传统电力系统及新能源电力系统区域等效惯量，对机组内部参数未知的情况下仍然适用。此外，采用VSG控制的光伏虚拟惯性响应速度快，时间长，出力灵活，调频效果优于风机辅助调频控制。
随着大规模新能源并网，响应“双碳”目标的同时也带来了电网消纳问题，配置一定的储能设施成为新能源发电渗透率进一步提升的必然选择。储能单元能够“削峰填谷”，将系统多余的功率储存起来或对系统功率缺额进行补偿。当系统负荷突然发生变化时，VSG并网系统在调频过程中所需要的惯量由储能单元提供，不但保证了新能源发电的灵活性，同时保证了系统运行的稳定性。
然而高比例配置储能增大了投资，并不具有经济性。根据2023年《河北省风电、光伏发电年度开发建设方案拟安排项目情况公示》的要求，冀北电网新能源按20%/2 h配置储能。目前储能变流器的价格约为0.3元/W，锂电池的价格约为1.2元/(W∙h)。按照本文算例，运营一个200 MW的光伏电站，依照政策要求，需要配置储能40 MW/40 MW∙h，即40 MW的储能变流器和40 MW∙h的储能电池，光伏电站总造价将增加6 000万元，按照循环寿命 3 000次计算，度电成本增加0.5元/(kW∙h)。目前光伏上网电价为0.32元/(kW∙h)左右，为光伏电站配置大容量储能不但无法从光伏电站中获得发电收益，还可能面临亏损的风险。
如何平衡经济性与惯量水平是提高新能源等效惯量需要解决的主要问题，可以从以下两方面进行考虑。
1）调度方面。文献[34]采用单位虚拟惯量增补价格近似表征增配储能及增加新能源虚拟惯量等补充手段下，增加单位系统惯量所付出的成本。当虚拟惯量增补价格低于最小临界价格时，优先考虑采用补充手段满足系统最小惯量需求，不考虑调度手段；当虚拟惯量增补价格在临界价格之间时，同时考虑补充手段与调度手段参与调节；当虚拟惯量增补价格高于最大临界价格时，先穷尽调度手段带来的惯量支撑，再考虑补充手段增加新能源虚拟惯量。
2）新能源类型方面。与常规光伏相比，采用VSG控制的光伏参与系统频率调节，需要将传统逆变器控制算法进行升级，并增加储能单元。风机也可采用虚拟同步发电机控制参与系统调频，但由于电化学电池成本较高，不能单独、长时间地给电网提供频率支持，且会导致风电机组的结构和控制变得复杂，不建议风机VSG中配置储能。因此多采用辅助频率控制的风机，且相较于常规风机仅需要对控制软件进行升级[26]。然而风力发电采用转子动能法，惯性响应时间较短，转子转速不能长时间维持在降速状态，随着转子转速的恢复，有可能造成系统频率的二次降低[35]。
综上所述，从技术经济性的角度考虑，当系统惯量不足时，首先考虑调度手段带来的功率支撑，若采用新能源发电设备提供功率支撑时，优先考虑利用风机转子动能控制提供虚拟惯量，当风机实际出力及转子转速不满足要求时，再考虑为光伏或风机配置储能设施提供功率支撑[17]。
本文通过分析新能源虚拟惯性响应特性及区域惯量评估原理，提出了一种含大规模新能源并网的电力系统区域等效惯量评估方法，能够较为准确地评估各区域等效惯量，通过理论分析和算例验证得出以下结论：
1）提出了根据量测数据实时评估惯量的方法，评估结果计及发电机惯量、新能源虚拟惯量和负荷静态电压特性的影响，所提方法解决了量测数据众多且获取困难的问题，同时提高了评估结果的精度。
2）新能源出力占比及虚拟惯性控制参数会影响其所在区域的等效惯量水平，同时对系统中其他区域的等效惯量和评估结果有一定的影响。
3）附加虚拟惯性控制有利于提高等效惯量，采用VSG控制的光伏虚拟惯性响应时间长，出力更加灵活，调频效果更好，但大规模光伏并网参与电力系统调频需要配置大容量储能，经济效益不好。采用辅助调频控制的风电系统不需要配置储能，一次投资小，但随着转子转速的恢复，有可能造成电力系统频率的二次降低。因此如何平衡经济性与新能源出力是需要进一步研究的问题。
附 录
表1 算例系统参数取值
App.Tab.1 Parameter values of test system
参数数值 风机额定容量SN/(MV∙A)1.5 额定电压UN/V575 定子电阻RS(pu)0.007 06 定子电感LS(pu)0.171 转子电阻Rr(pu)0.005 转子电感Lr(pu)0.156 励磁电感Lm(pu)2.9 固有惯量HW/s5.04 光伏辐照度/(W/m2)1 000 电池效率(%)10 温度/℃25 发电机SN/(MV∙A)900 UN/kV20 xd(pu)1.8 xq(pu)1.7
（续）
参数数值 发电机0.3 0.55 0.25 0.25 8 0.4 0.03 0.05 D(pu)0
参考文献
[1] 滕贤亮, 谈超, 昌力, 等. 高比例新能源电力系统有功功率与频率控制研究综述及展望[J]. 电力系统自动化, 2023, 47(15): 12-35.
Teng Xianliang, Tan Chao, Chang Li, et al. Review and prospect of research on active power and frequency control in power system with high proportion of renewable energy[J]. Automation of Electric Power Systems, 2023, 47(15): 12-35.
[2] 曾辉, 孙峰, 李铁, 等. 澳大利亚“9·28”大停电事故分析及对中国启示[J]. 电力系统自动化, 2017, 41(13): 1-6.
Zeng Hui, Sun Feng, Li Tie, et al. Analysis of “9·28” blackout in South Australia and its enlightenment to China[J]. Automation of Electric Power Systems, 2017, 41(13): 1-6.
[3] 樊陈, 姚建国, 张琦兵, 等. 英国“8·9”大停电事故振荡事件分析及思考[J]. 电力工程技术, 2020, 39(4): 34-41.
Fan Chen, Yao Jianguo, Zhang Qibing, et al. Reflection and analysis for oscillation of the blackout event of 9 August 2019 in UK[J]. Electric Power Engineering Technology, 2020, 39(4): 34-41.
[4] 贾焦心, 颜湘武, 李铁成, 等. 基于改进RoCoF测量方法的储能辅助光伏机组快速调频策略[J]. 电工技术学报, 2022, 37(增刊1): 93-105.
Jia Jiaoxin, Yan Xiangwu, Li Tiecheng, et al. Fast frequency regulation strategy of PV power system assisted by energy storage based on improved measurement method of RoCoF[J]. Transactions of China Electrotechnical Society, 2022, 37(S1): 93-105.
[5] 孙华东, 王宝财, 李文锋, 等. 高比例电力电子电力系统频率响应的惯量体系研究[J]. 中国电机工程学报, 2020, 40(16): 5179-5192.
Sun Huadong, Wang Baocai, Li Wenfeng, et al. Research on inertia system of frequency response for power system with high penetration electronics[J]. Proceedings of the CSEE, 2020, 40(16): 5179-5192.
[6] 李兆伟, 方勇杰, 吴雪莲, 等. 频率紧急控制中动作时延和措施量对低惯量系统控制有效性的影响分析[J/OL]. 电工技术学报, 2023: 1-13. https://doi.org/ 10.19595/j.cnki.1000-6753.tces.231175.
Li Zhaowei, Fang Yongjie, Wu Xuelian, et al. Influence of action delay and amount on the control effectiveness of low inertia systems in frequency emergency control[J/OL]. Transactions of China Electrotechnical Society, 2023: 1-13. https:// doi.org/ 10.19595/j.cnki.1000-6753.tces.231175.
[7] 李东东, 张佳乐, 徐波, 等. 考虑频率分布特性的新能源电力系统等效惯量评估[J]. 电网技术, 2020, 44(8): 2913-2921.
Li Dongdong, Zhang Jiale, Xu Bo, et al. Equivalent inertia assessment in renewable power system considering frequency distribution properties[J]. Power System Technology, 2020, 44(8): 2913-2921.
[8] 曾辉, 苏安龙, 葛延峰, 等. 考虑负荷特性的区域电网在线转动惯量快速估计算法[J]. 电网技术, 2023, 47(2): 423-436.
Zeng Hui, Su Anlong, Ge Yanfeng, et al. Fast estimation algorithm for on-line moment of inertia of regional power grid considering load characteristics[J]. Power System Technology, 2023, 47(2): 423-436.
[9] 刘方蕾, 胥国毅, 王凡, 等. 基于差值计算法的系统分区惯量评估方法[J]. 电力系统自动化, 2020, 44(20): 46-53.
Liu Fanglei, Xu Guoyi, Wang Fan, et al. Assessment method of system partition inertia based on differential calculation method[J]. Automation of Electric Power Systems, 2020, 44(20): 46-53.
[10] 刘方蕾, 毕天姝, 闫家铭, 等. 基于PMU同步测量的分区惯量估计方法[J]. 华北电力大学学报(自然科学版), 2020, 47(3): 19-26.
Liu Fanglei, Bi Tianshu, Yan Jiaming, et al. Area inertia estimation based on PMU synchronous measurements[J]. Journal of North China Electric Power University (Natural Science Edition), 2020, 47(3): 19-26.
[11] 曾繁宏, 张俊勃. 电力系统惯性的时空特性及分析方法[J]. 中国电机工程学报, 2020, 40(1): 50-58, 373.
Zeng Fanhong, Zhang Junbo. Temporal and spatial characteristics of power system inertia and its analysis method[J]. Proceedings of the CSEE, 2020, 40(1): 50-58, 373.
[12] 李东东, 郭天洋, 刘庆飞, 等. 计及光伏发电的新能源电力系统惯量评估[J]. 太阳能学报, 2021, 42(5): 174-179.
Li Dongdong, Guo Tianyang, Liu Qingfei, et al. Inertia estimation of renewable power system considering photovoltaics[J]. Acta Energiae Solaris Sinica, 2021, 42(5): 174-179.
[13] 李世春, 宋秋爽, 薛臻瑶, 等. 含风电虚拟惯性响应的新能源电力系统惯量估计[J]. 电力工程技术, 2023, 42(2): 84-93.
Li Shichun, Song Qiushuang, Xue Zhenyao, et al. Inertia estimation of new energy power system with virtual inertia response of wind power[J]. Electric Power Engineering Technology, 2023, 42(2): 84-93.
[14] 李世春, 徐松林, 李惠子, 等. 风电场等效虚拟惯量快速估计方法[J]. 电网技术, 2021, 45(12): 4683-4692.
Li Shichun, Xu Songlin, Li Huizi, et al. Rapid estimation of equivalent virtual inertia of wind farm[J]. Power System Technology, 2021, 45(12): 4683-4692.
[15] 安军, 盛帅, 周毅博, 等. 基于量测数据的风电场等效虚拟惯量评估方法[J]. 电网技术, 2023, 47(5): 1819-1829.
An Jun, Sheng Shuai, Zhou Yibo, et al. Evaluation of equivalent virtual inertia of wind farm based on measured data[J]. Power System Technology, 2023, 47(5): 1819-1829.
[16] 王博, 杨德友, 蔡国伟. 高比例新能源接入下电力系统惯量相关问题研究综述[J]. 电网技术, 2020, 44(8): 2998-3007.
Wang Bo, Yang Deyou, Cai Guowei. Review of research on power system inertia related issues in the context of high penetration of renewable power generation[J]. Power System Technology, 2020, 44(8): 2998-3007.
[17] 张祥宇, 胡剑峰, 付媛, 等. 风储联合系统的虚拟惯量需求与协同支撑[J]. 电工技术学报, 2024, 39(3): 672-685.
Zhang Xiangyu, Hu Jianfeng, Fu Yuan, et al. Virtual inertia demand and collaborative support of wind power and energy storage system[J]. Transactions of China Electrotechnical Society, 2024, 39(3): 672-685.
[18] 张冠锋, 杨俊友, 王海鑫, 等. 基于虚拟同步机技术的风储系统协调调频控制策略[J]. 电工技术学报, 2022, 37(增刊1): 83-92.
Zhang Guanfeng, Yang Junyou, Wang Haixin, et al. Coordinated frequency modulation control strategy of wind farm-storage system based on virtual synchronous generator technology[J]. Transactions of China Electrotechnical Society, 2022, 37(S1): 83-92.
[19] 胡正阳, 高丙团, 张磊, 等. 风电机组双向支撑能力分析与自适应惯量控制策略[J]. 电工技术学报, 2023, 38(19): 5224-5240.
Hu Zhengyang, Gao Bingtuan, Zhang Lei, et al. Bidirectional support capability analysis and adaptive inertial control strategy of wind turbine[J]. Transactions of China Electrotechnical Society, 2023, 38(19): 5224-5240.
[20] 王科, 秦文萍, 张宇, 等. 双馈风机等效惯量控制比例系数对系统功角首摆稳定的影响机理分析[J]. 电工技术学报, 2023, 38(3): 741-753.
Wang Ke, Qin Wenping, Zhang Yu, et al. Mechanism analysis of effect of equivalent proportional coefficient of inertia control of DFIG on stability of first swing of power angle[J]. Transactions of China Electrotechnical Society, 2023, 38(3): 741-753.
[21] 张旭, 陈云龙, 岳帅, 等. 风电参与电力系统调频技术研究的回顾与展望[J]. 电网技术, 2018, 42(6): 1793-1803.
Zhang Xu, Chen Yunlong, Yue Shuai, et al. Retrospect and prospect of research on frequency regulation technology of power system by wind power[J]. Power System Technology, 2018, 42(6): 1793-1803.
[22] 陈宇航, 王刚, 侍乔明, 等. 一种新型风电场虚拟惯量协同控制策略[J]. 电力系统自动化, 2015, 39(5): 27-33.
Chen Yuhang, Wang Gang, Shi Qiaoming, et al. A new coordinated virtual inertia control strategy for wind farms[J]. Automation of Electric Power Systems, 2015, 39(5): 27-33.
[23] 王鑫, 杨德健. 基于变系数PI控制的双馈风电机组自适应转速恢复策略[J]. 电工技术学报, 2023, 38(15): 4120-4129.
Wang Xin, Yang Dejian. Adaptive speed recovery strategy of doubly-fed induction generator based on variable PI control coefficient[J]. Transactions of China Electrotechnical Society, 2023, 38(15): 4120-4129.
[24] 蔡葆锐, 杨蕾, 黄伟. 基于惯性/下垂控制的变速型风电机组频率协调控制方法[J]. 电力系统保护与控制, 2021, 49(15): 169-177.
Cai Baorui, Yang Lei, Huang Wei. Frequency coordination control of a variable speed wind turbine based on inertia/droop control[J]. Power System Protection and Control, 2021, 49(15): 169-177.
[25] 陈文倩, 辛小南, 程志平. 基于虚拟同步发电机的光储并网发电控制技术[J]. 电工技术学报, 2018, 33(增刊2): 538-545.
Chen Wenqian, Xin Xiaonan, Cheng Zhiping. Control of grid-connected of photovoltaic system with storage based on virtual synchronous generator[J]. Transactions of China Electrotechnical Society, 2018, 33(S2): 538-545.
[26] 吕志鹏, 盛万兴, 刘海涛, 等. 虚拟同步机技术在电力系统中的应用与挑战[J]. 中国电机工程学报, 2017, 37(2): 349-360.
Lü Zhipeng, Sheng Wanxing, Liu Haitao, et al. Application and challenge of virtual synchronous machine technology in power system[J]. Proceedings of the CSEE, 2017, 37(2): 349-360.
[27] 杨晓楠, 李洋, 史梁, 等. 光-储虚拟同步机多模式运行控制与改善储能系统寿命的选择性投退策略[J]. 太阳能学报, 2022, 43(4): 66-74.
Yang Xiaonan, Li Yang, Shi Liang, et al. Multi-mode operating control of optical-storage virtual synchronizer and selectively plug in/out strategy for improving energy storage system lifetime[J]. Acta Energiae Solaris Sinica, 2022, 43(4): 66-74.
[28] 秦晓辉, 苏丽宁, 迟永宁, 等. 大电网中虚拟同步发电机惯量支撑与一次调频功能定位辨析[J]. 电力系统自动化, 2018, 42(9): 36-43.
Qin Xiaohui, Su Lining, Chi Yongning, et al. Functional orientation discrimination of inertia support and primary frequency regulation of virtual synchronous generator in large power grid[J]. Automation of Electric Power Systems, 2018, 42(9): 36-43.
[29] Kundur P, Balu N J, Lauby M G. Power system stability and control[M]. New York: McGraw-Hill, 1994.
[30] Cepeda J C, Rueda J L, Colomé D G, et al. Real-time transient stability assessment based on centre-of-inertia estimation from phasor measurement unit records[J]. IET Generation, Transmission & Distribution, 2014, 8(8): 1363-1376.
[31] 王宝财, 孙华东, 李文锋, 等. 考虑动态频率约束的电力系统最小惯量评估[J]. 中国电机工程学报, 2022, 42(1): 114-127.
Wang Baocai, Sun Huadong, Li Wenfeng, et al. Minimum inertia estimation of power system considering dynamic frequency constraints[J]. Proceedings of the CSEE, 2022, 42(1): 114-127.
[32] Wall P, Terzija V. Simultaneous estimation of the time of disturbance and inertia in power systems[J]. IEEE Transactions on Power Delivery, 2014, 29(4): 2018-2031.
[33] Morren J, Pierik J, de Haan S W H. Inertial response of variable speed wind turbines[J]. Electric Power Systems Research, 2006, 76(11): 980-987.
[34] 叶畅, 柳丹, 杨欣宜, 等. 基于最小惯量评估的高比例新能源电力系统优化运行策略[J]. 电网技术, 2023, 47(2): 502-516.
Ye Chang, Liu Dan, Yang Xinyi, et al. Optimal operation strategy of high proportion new energy power system based on minimum inertia evaluation[J]. Power System Technology, 2023, 47(2): 502-516.
[35] 唐西胜, 苗福丰, 齐智平, 等. 风力发电的调频技术研究综述[J]. 中国电机工程学报, 2014, 34(25): 4304-4314.
Tang Xisheng, Miao Fufeng, Qi Zhiping, et al. Survey on frequency control of wind power[J]. Proceedings of the CSEE, 2014, 34(25): 4304-4314.
Assessment Method of Regional Equivalent Inertia of New Energy Power System Based on Measured Data
Abstract The high proportion of new energy connected to the grid makes the problem of low inertia of the power system increasingly prominent, and the frequency problem more frequency problem is more serious. In order to improve the stable operation ability of the new energy power system, it is necessary to evaluate the level of system inertia and analyze the influence of new energy power generation type, permeability and virtual inertia control mode on the real-time inertia of the system At present, the most widely used evaluation methods have the problem of a large number of measurement data and difficulty in obtaining them. The evaluation accuracy is affected by the selection of frequency sampling points, measurement devices, and the processing methods of measurement data. To address these issues, this paper proposes a method for assessing the regional equivalent inertia of new energy system based on measured data. The active power, frequency, and voltage data are used to accurately calculate the inertia, measurement data are few and easy to obtain, which reduces the data processing steps and is still applicable when the internal parameters of the new energy units are unknown.
Firstly, the virtual inertia response characteristics of wind power and photovoltaic power and their influence on the frequency stability of the system are analyzed. Secondly, on the basis of analyzing the principle of regional equivalent inertia assessment, the expression of regional equivalent inertia of new energy system is derived by considering the load voltage characteristics. Finally, in order to reduce the error caused by the frequency distribution characteristics, the selection of sampling points and the calculation method of regional frequency are proposed from the perspective of weighted average. Sampling points are determined according to the real-time inertia monitoring results of the SCADA system, which saves the installation cost of PMUs (phasor measurement units) and avoids large amount of calculations. In addition, the low-pass filter and sliding window technology are used to process the measurement data, which improves the accuracy of the inertia assessment results.
The simulation results show that the proposed method can accurately assess the regional equivalent inertia of both traditional and new energy power system. Wind power system with additional frequency control can provide virtual inertia much larger than the actual inertia, but due to the limitation of actual speed and output, its virtual inertia response time is short, and the support power can be limited. The virtual inertia response time of the PV system controlled by VSG (virtual synchronous generators) is fast, and can provide support power according to the dispatching needs, but it needs to be equipped with large energy storage devices.
The following conclusions can be drawn from the simulation analysis: (1) Changing the new energy output and virtual inertia control parameters will cause a change in the equivalent inertia and results. (2) The PV virtual inertia control using VSG has a long response time, more flexible output, and better frequency regulation effect, but it requires large-capacity energy storage, the economic benefits are not good. The wind power system with additional frequency control does not need energy storage, and the primary investment is small, but with the recovery of rotor speed, it is possible to cause a secondary reduction in system frequency. (3) From the perspective of technical economy, when the system inertia is insufficient, the power support brought by dispatching means should be considered first, if new energy power is used to provide power support, priority should be given to the use of wind turbine rotor kinetic energy control, when the actual output and rotor speed do not meet the requirements, then consider the configuration of energy storage for photovoltaic or wind turbine.Therefore, how to balance the economy and the output of new energy is a problem that needs further research.
keywords：New energy power system, regional inertia assessment, measurement data, tie-line power, virtual inertial control, load static voltage characteristics
中图分类号：TM73; TM61
DOI: 10.19595/j.cnki.1000-6753.tces.231250
国家自然科学基金资助项目（52277100）。
收稿日期 2023-08-03
改稿日期 2023-12-11
马燕峰 女，1978年生，博士，副教授，研究方向为电力系统分析、运行与控制等。
E-mail：ma_yanfeng01@163.com
李金媛 女，1998年生，硕士研究生，研究方向为新能源电力系统运行与控制。
E-mail：1833310564@qq.com（通信作者）
（编辑 赫 蕾）