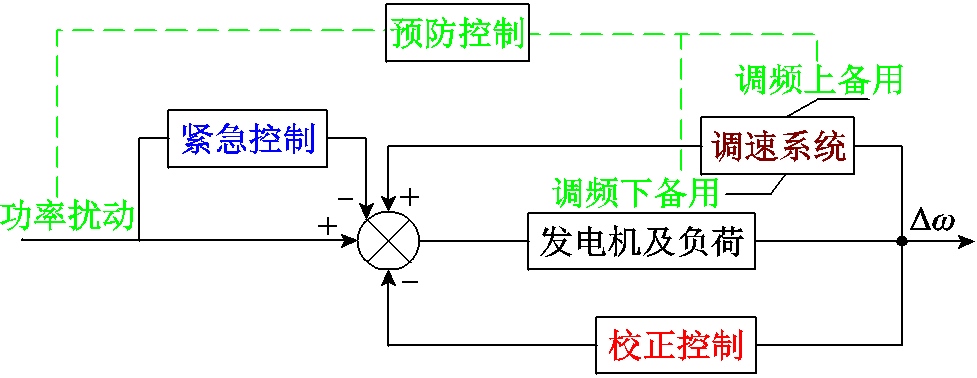
图1 考虑三道防线的系统频率分析模型示意图
Fig.1 Schematic diagram of system frequency analysis model considering three defense lines
摘要 频率紧急控制是保障电网故障后频率安全的第二道防线，通常由基于事件触发的稳控系统实现，已成为支撑特高压直流安全送电的标配。随着高比例新能源的快速发展，系统调频能力和惯量水平不断下降，电网故障后的频率响应特性出现跌落深度大、速度快的新特征，紧急控制能否有效是关系系统频率安全的关键因素。该文首先建立了计及频率紧急控制的高比例新能源电力系统频率响应模型和传递函数；其次从永久性扰动和短时性扰动两方面，详细分析了系统频率响应特性以及频率紧急控制动作时延和措施量的有效性，并给出了紧急控制有效时新能源接入比例的限值；最后结合实际电网仿真模型开展了时域仿真验证，指出低惯量电力系统短路故障引起的连锁短时性功率扰动将成为频率安全防御的关键和难点。
关键词：新能源 频率安全 频率紧急控制 低惯量电力系统 短时性功率扰动 新能源低电压穿越
为实现2030年“碳达峰”、2060年“碳中和”能源战略目标，我国正积极构建以新能源为主体的新型电力系统。随着大规模新能源发电并网、跨区直流输电容量快速增长，传统同步电源占比逐渐减小，系统（等效）惯量水平不断下降，频率抗扰动能力和调节能力日益下降，以电网故障后最大频率偏差为关键指标的暂态频率安全已经成为制约新型电力系统发展的瓶颈问题。2019年英国“8·9”[1-2]、2016年澳洲“9·28”[3]等停电事故以及2015年我国华东电网“9·19”锦苏直流双极闭锁事件[4]，均是由偶发故障造成的新能源无序脱网或直流大功率损失导致的大频差事件。此外，电力电子器件设备的耐压耐流能力较弱，交直流故障时新能源低电压穿越、直流换相失败等造成的短时性功率冲击也会导致电网频率大幅值跌落[5-6]。
我国电力系统已经建立了较为完备的频率控制体系。一次调频、二次调频等网源协调技术是电源接入电力系统必备的基本能力[7]，主要面向电网稳态频率控制，应对电网正常负荷或电源波动时的频率偏移问题；面向电网故障后的频率控制，主要依靠电网故障防御三道防线[8]。三道防线是我国电力系统安全稳定运行的重要实践，深刻影响着电网故障扰动后的频率特性。
目前关于高比例新能源电力系统的频率特性分析，已有的文献较少考虑三道防线的作用，多集中在不同新能源渗透率下的频率特性变化，从加强新能源一次调频、虚拟惯量能力等方面开展研究[9-13]，通常需要新能源预留有功备用或配置储能加以实现。大容量特高压直流闭锁故障等场景主要依靠频率紧急控制系统[14-16]和低频减载、高频切机等组成的频率校正控制防线[17]，其中紧急控制由于应对场景明确、响应速度快、控制后影响范围有限等特点，是优先考虑的故障后控制措施，各个大区电网的系统保护均将频率紧急控制作为主要功能，近年来的研究重点主要在于如何挖掘更多的控制资源，通过多资源协调紧急控制保证系统频率安全[18-20]。但紧急控制基于稳控系统实现，虽然通过专用通信通道进行信息快速传输，但一般工程上考虑故障发生至控制完成仍有不超过300 ms的延时；同时紧急控制的控制量一般依赖于所监测故障事件，如直流闭锁故障时，直流功率损失量可由监测装置获取，实际控制量与监测的损失量密切相关。对于新能源高占比的弱惯量系统，随着频率变化速度加快、扰动形式复杂化，紧急控制动作延时及措施量在低惯量电力系统中不同故障扰动下的有效性需要深入研究。
本文首先建立了计及频率紧急控制的高比例新能源电力系统频率响应模型和传递函数；其次从永久性扰动和短时性扰动两方面分析了低惯量系统的频率响应特性以及频率紧急控制的适应性；最后结合实际电网仿真模型开展了时域仿真验证，指出低惯量电力系统短路故障引起的连锁短时性功率扰动是未来新型电力系统频率安全防御的关键问题。
从我国当前的频率防御体系来看，第一道防线中的预防控制，主要包括合理安排电网运行方式、保证电网具有合理的惯量水平和调频备用、避免出现超出电网承受能力的扰动功率等。对暂态频率安全起作用的主要是s级时间尺度响应的一次调频备用和系统的惯量，通常与电网调频机组的开机容量密切相关。第二道防线的紧急控制，是由电网发生的特定故障扰动事件触发，匹配预先整定的策略表，在300 ms内执行切机、切负荷或直流功率控制等措施，属于前馈控制。第三道防线的校正控制，由分散布置的装置就地检测频率触发，按照提前制定的策略分轮次执行，主要包括低频减载、高频切机、低频解列等措施，属于反馈控制。故障防御三道防线深刻影响着电力系统初始状态、故障后系统承受的不平衡功率。考虑三道防线的系统频率分析模型示意图如图1所示。
图1 考虑三道防线的系统频率分析模型示意图
Fig.1 Schematic diagram of system frequency analysis model considering three defense lines
根据我国目前三道防线的配置现状，忽略电网频率的分布特性，不考虑电压对负荷特性影响、调速器限幅等非线性环节，可以得到系统频率响应的简化聚合模型如图2所示。
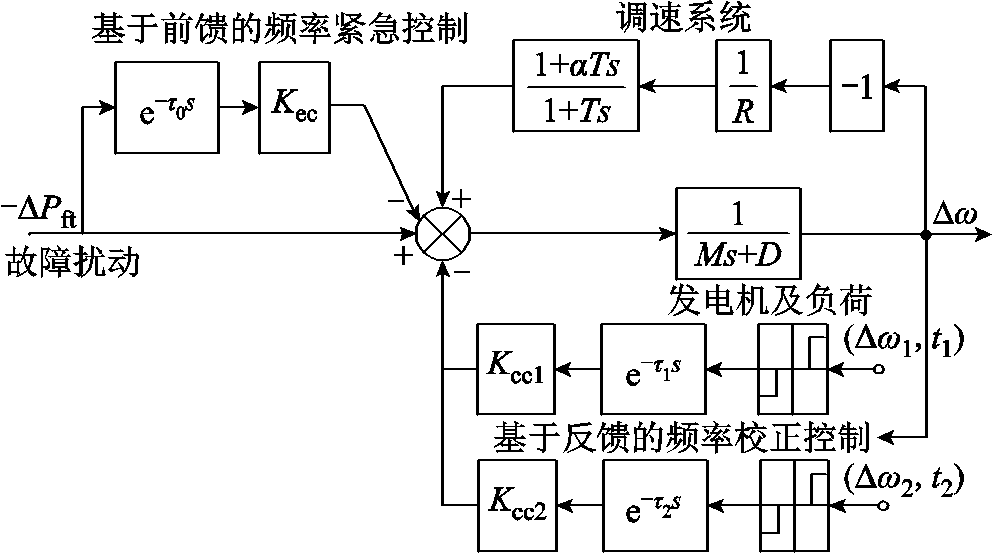
图2 考虑频率稳定控制的系统频率响应聚合模型
Fig.2 A system frequency response aggregation model considering frequency stability control
图2中，M为系统的等效惯性时间常数；D为包含负荷有功频率响应系数的系统等效阻尼；T为涡轮机的等效时间常数；R为调速器的调差率；α为涡轮机特征系数；τ0为紧急控制的固有延时，包括故障识别、策略表搜索、开关跳闸等，通常小于300 ms；Kec为紧急控制量比例系数，与电网的不平衡功率承受能力相关，通常小于1；τ1、τ2为频率校正控制不同轮次的延时，基础轮次延时一般为200～300 ms，特殊轮次延时一般为10～30 s；Δω1、Δω2为频率校正控制不同轮次的频率偏差阈值； Kcc1、Kcc2为频率校正控制不同轮次的切负荷比例；ΔPft为系统承受的功率扰动。
目前，电网暂态频率安全通常以电网受到交直流故障扰动冲击后，频率偏差及持续时间不超过第三道防线首轮的频率阈值为标准，以避免电网出现大规模不可控停电事故[21]。因此，在分析暂态频率安全时，可忽略校正控制环节，但需要确保紧急控制动作后频率最大偏差在合理范围内。为计及新能源大规模接入对系统惯量及调频能力的影响，假定新能源发电占比的提升是以替代常规电源机组实现，记常规同步机组发电系数[11]为
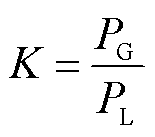（1）
式中，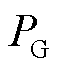
为常规同步机组的发电总出力；
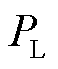为系统总负荷。
假设所有新能源按频率下垂控制参与系统一次调频，且采用快速电力电子控制技术，忽略传统同步发电机的涡轮机动态过程，可以得到大规模新能源接入后考虑频率紧急控制的系统简化聚合模型如图3所示。图3中，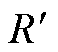
为新能源一次调频的调差率。考虑频率紧急控制的系统频率响应聚合等效模型如图4所示。
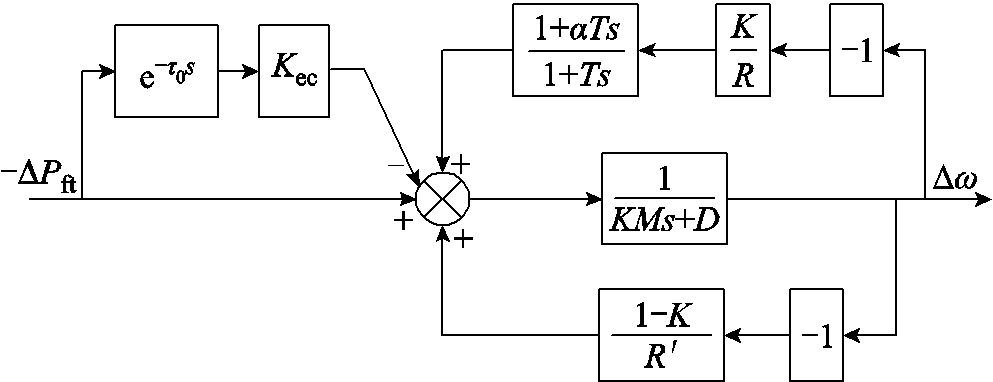
图3 考虑频率紧急控制的系统频率响应聚合模型
Fig.3 A system frequency response aggregation model considering frequency emergency control
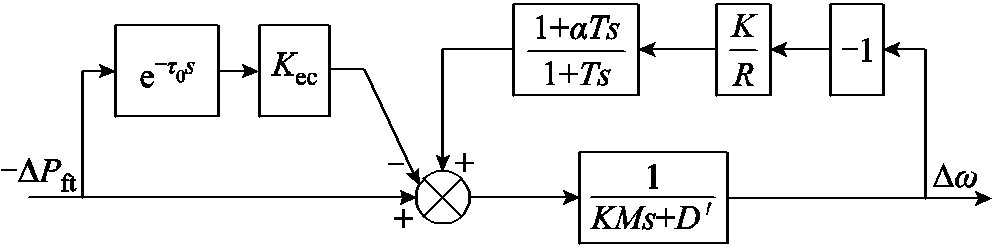
图4 考虑频率紧急控制的系统频率响应聚合等效模型
Fig.4 A system frequency response aggregation equivalent model considering frequency emergency control
图4中，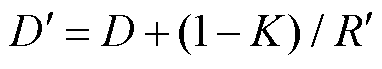
，新能源按下垂控制参与一次调频等效于提高了系统阻尼。
当τ0很小时，延时环节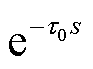
可以简化为式（2）所示的一阶惯性环节。
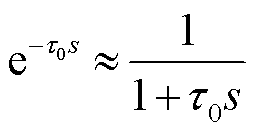（2）
由图2可得系统的闭环传递函数为
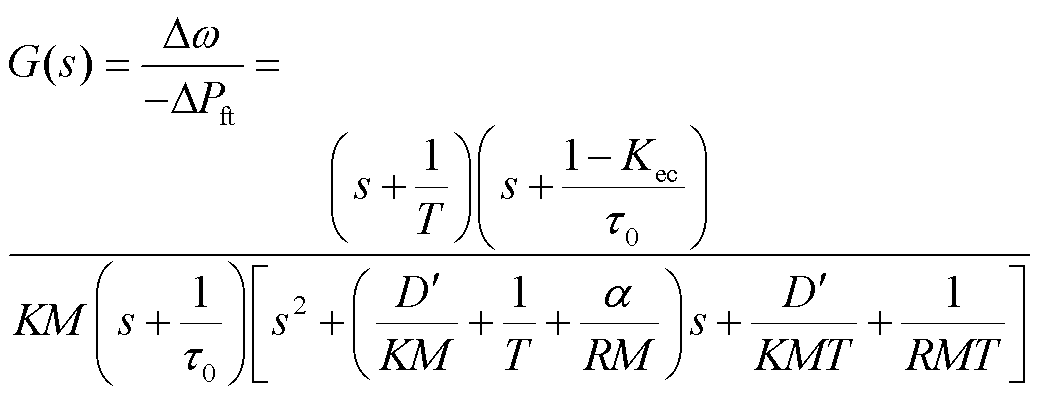（3）
进一步整理可得
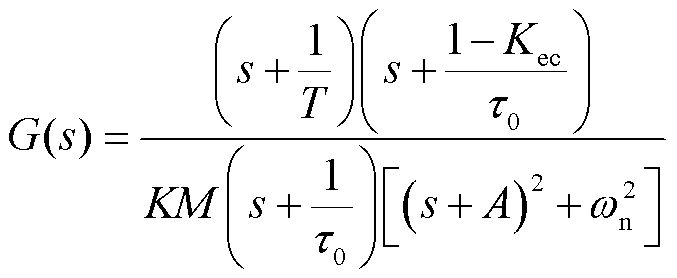（4）
其中
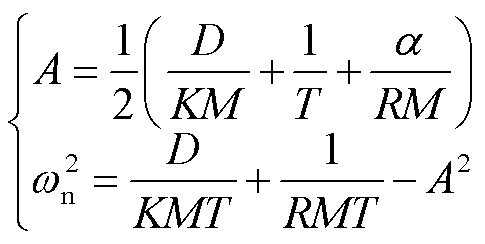（5）
与文献[11]相比，计及紧急控制的闭环控制系统增加了一个闭环零点（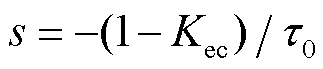
）和闭环极点（
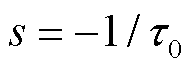），增加的闭环极点位于虚轴左半平面，不会改变闭环系统的稳定性；增加的闭环零点，会使系统最大频率偏差时间提前，在同样的功率扰动下有利于改善暂态频率安全。当满足A＞0时，闭环系统稳定，即需要满足
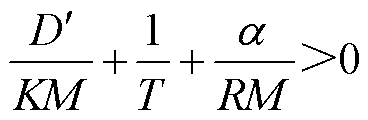（6）
对于新能源大规模接入火电系统，通常α＞0，当同步机组发电系数K＞0时，满足上述稳定条件。对于新能源大规模接入水电系统，由于水锤效应的存在，通常α＜0[22]，为满足闭环系统稳定条件，需要满足
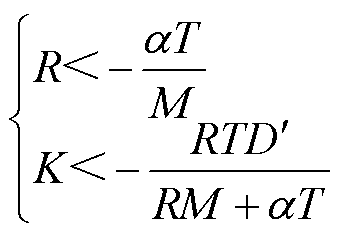（7）
为分析高比例新能源电网故障后的频率响应特性，本文着重考虑两大类扰动：永久性不平衡功率扰动和短时性功率扰动。永久性功率扰动以直流闭锁、机组跳闸、新能源脱网等故障为代表[23]，即在暂态频率的时间尺度上，故障造成的扰动功率无法快速恢复，类比于永久性短路故障会跳开故障线路；短时性功率扰动以新能源低电压穿越（不脱网）[5]、常规直流换相失败、柔性直流低电压穿越[24]等为代表，即在暂态频率的时间尺度上，扰动功率仅在较短时间内起作用，通常是由电网短路故障引起连锁过程，随着电网故障消失或被隔离，该扰动功率逐渐消失，类比于瞬时性短路故障，故障消失后无需跳开故障线路。下文将详细分析两种类型扰动下频率紧急控制的有效性。
永久性不平衡功率扰动在频域上可用阶跃函数表达，假设扰动功率为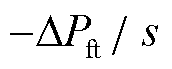
，根据式（4）给出的系统的闭环传递函数，系统频率偏差的频域表达式为
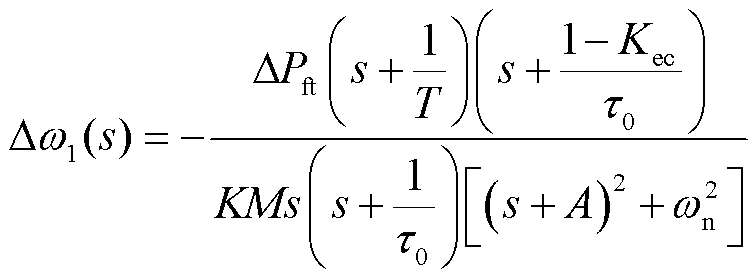（8）
根据终值定理，阶跃扰动下频率偏差的稳态响应为
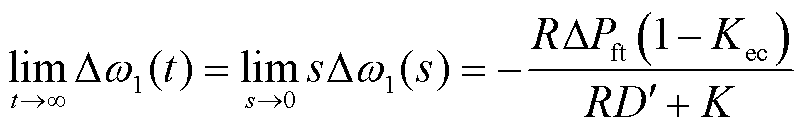（9）
可见，永久性功率扰动下，系统的频率稳态响应除了与扰动功率、系统发电和负荷的频率调节特性相关外，与同步机组发电系数K也密切相关，随着K系数的降低，系统稳态频率偏差呈变大的趋势。同时，频率紧急控制可以减小故障扰动给系统造成的不平衡功率，有助于减小系统暂态和稳态频率偏差，紧急控制的响应速度对稳态偏差无影响。
将永久性功率扰动函数作为输入，代入图4所示的传递框图，并根据拉普拉斯反变换，可以得到计及紧急控制的系统频率响应的时域表达式为
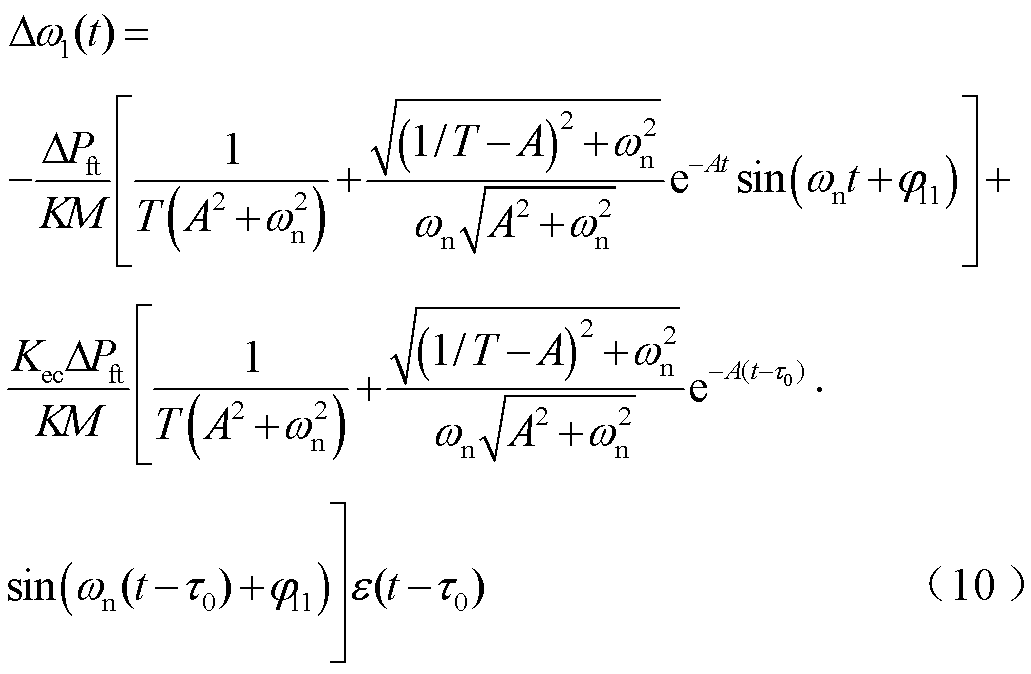
式中，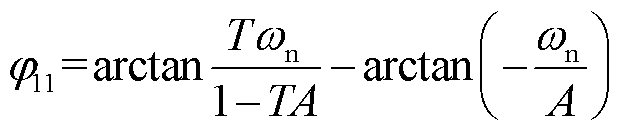
。
根据式（10）可见，考虑紧急控制后，系统的频率时域响应由两部分时域响应叠加而成。前半部分为故障扰动影响下的时域响应，后半部分为紧急控制造成的功率突变下的时域响应。由于涡轮机的惯性时间常数T通常为s级[22]，相比紧急控制的固有延时τ0大1个数量级，简单推导可知，紧急控制的影响总是与故障扰动相反，即紧急控制总能改善扰动后的频率恢复特性。但从系统暂态频率安全的角度，紧急控制能否解决大扰动下故障扰动后的暂态频率不安全风险，取决于紧急控制后的系统偏差是否达到低频减载或高频切机的控制阈值。
分析式（10）前半部分故障扰动影响下的频率响应，可知，当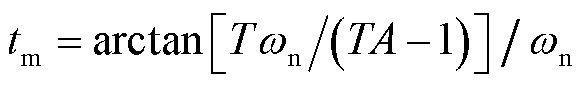
时，频率偏差达到最大值，只有紧急控制时刻τ0＜tm时，才会改善系统频率的最大偏差。紧急控制动作后，系统频率是否继续下跌取决于紧急控制量与系统当前的功率缺额量的大小。
在紧急控制动作之前，任意时刻系统频率的变化率为
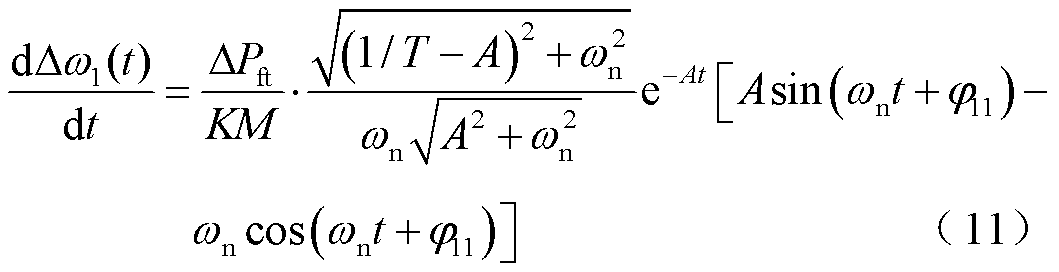
根据同步机的转子运动方程可知，系统在紧急控制动作时刻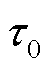
的有功功率不平衡量为
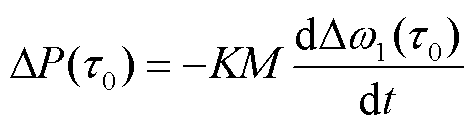（12）
为确保紧急控制动作后，系统频率不再继续下跌，即紧急控制动作后的瞬间，系统的频率变化率大于或等于零，则需要的最小紧急控制系数为
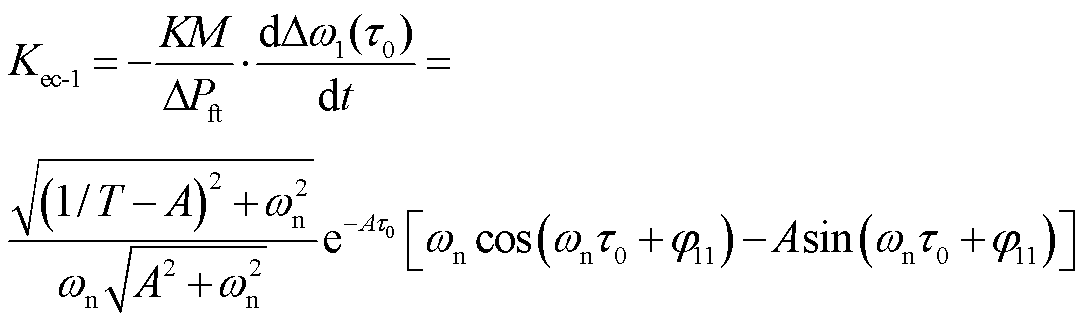（13）
此时系统的最低频率为
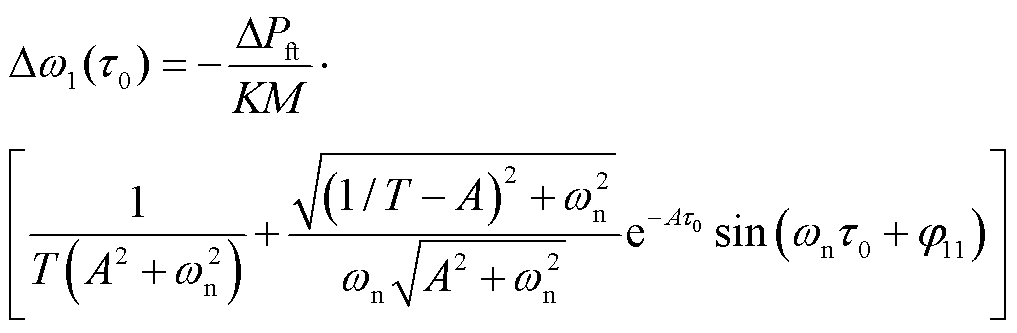（14）
当紧急控制系数大于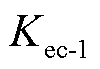
时，系统的最低频率即为
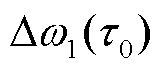，若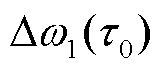为可承受的，则系统暂态频率安全，紧急控制系数越大，后续的频率恢复速度越快，但紧急控制系数过大会引起系统暂态高频的风险。当紧急控制系数小于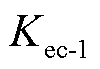时，系统频率将继续下跌，系统最低频率需要对式（10）的分段函数求导，由紧急控制措施量、延时、系统调频能力、同步系数等共同决定。工程中，应对系统低频的紧急控制的资源比较紧缺，尤其切负荷的应用容易影响民生用电，需要统筹紧急控制措施量与系统可承受的暂态频率偏差。对于典型系统参数[22]，系统的等效惯性时间常数M=12 s，系统等效阻尼D=2.0，涡轮机的等效时间常数T=6 s，涡轮机特征系数α=0.333，调速器的调差率R=0.05，新能源一次调频调差率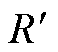=0.1，紧急控制的固有延时τ0=0.2 s，常规同步机组发电系数K=0.8；系统承受的功率扰动ΔPft=0.3。扰动后不同紧急控制系数下的系统频率响应曲线如图5所示。
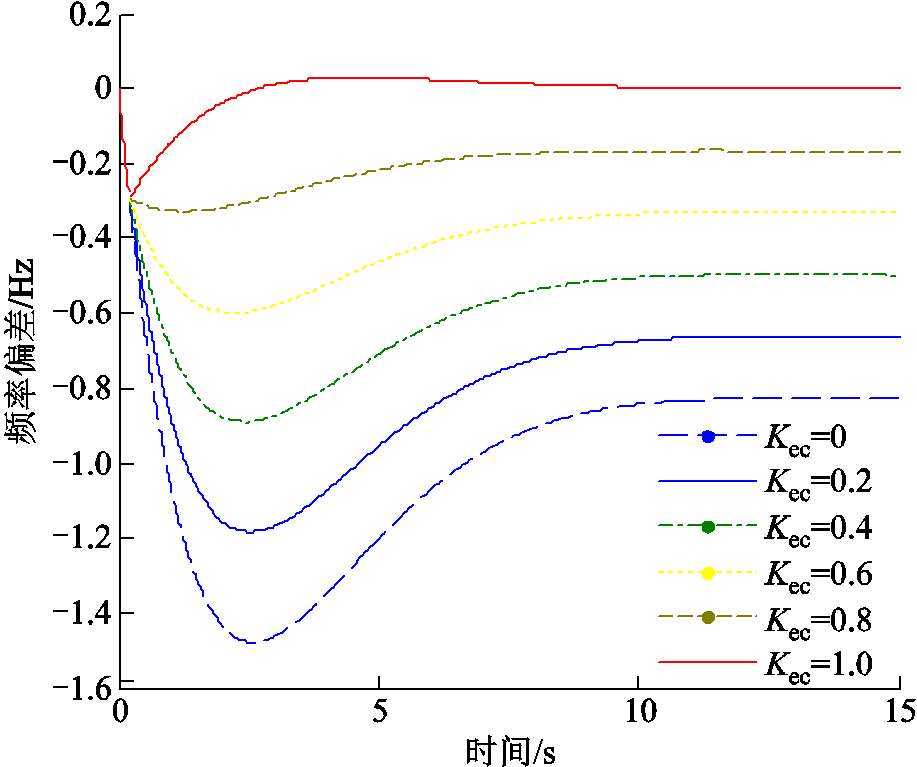
图5 不同控制量下的频率响应特性曲线
Fig.5 Frequency response characteristic curves under different control quantities
当紧急控制系数一定时，随着紧急控制延时增加，系统最低频率呈下降趋势。当紧急控制的延时大于系统最低频率出现时刻时，紧急控制无法改善系统的最大频率偏差。不同的紧急控制量下，系统的最低频率随紧急控制的延时曲线如图6所示。
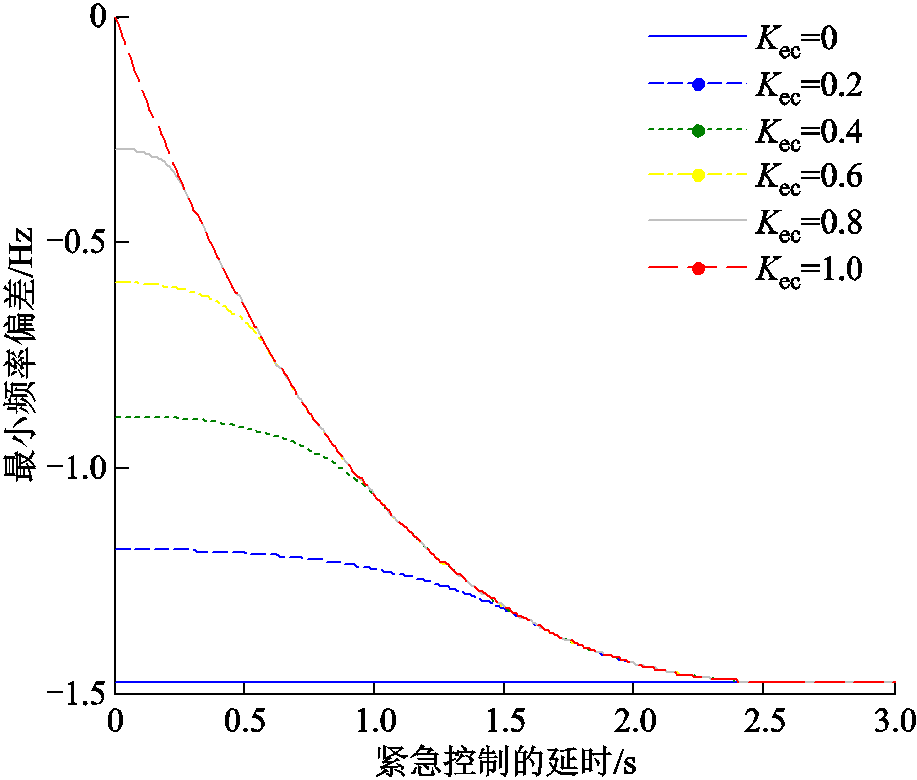
图6 不同紧急控制延时下的频率响应特性曲线
Fig.6 Frequency response characteristic curves under different emergency control delays
随着新能源大规模接入导致同步机发电系数的下降，系统低惯量特征越发明显，频率下跌的速度加快。当紧急控制从事件检测、信息通信到动作实施的总响应延时大于系统频率下跌至第三道防线第一轮动作时间时，不可控停电事故的风险会大大增加。
由于涡轮机的时间常数T通常比紧急控制的固有延时τ0大得多，故障后τ0时刻之前的系统频率可进一步可简化为
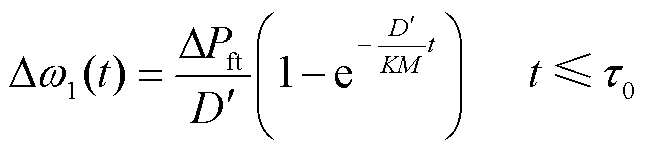（15）
根据式（15），对于给定的系统可接受的最大频率偏差，紧急控制的最大允许延时与同步机发电系数为
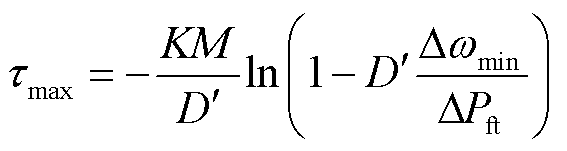（16）
对于低频减载启动门槛值49 Hz，以紧急控制能够避免第三道防线启动为边界，假设可用的紧急控制量充足，紧急控制的延时与系统可承受的最小发电系数K的关系如图7所示。
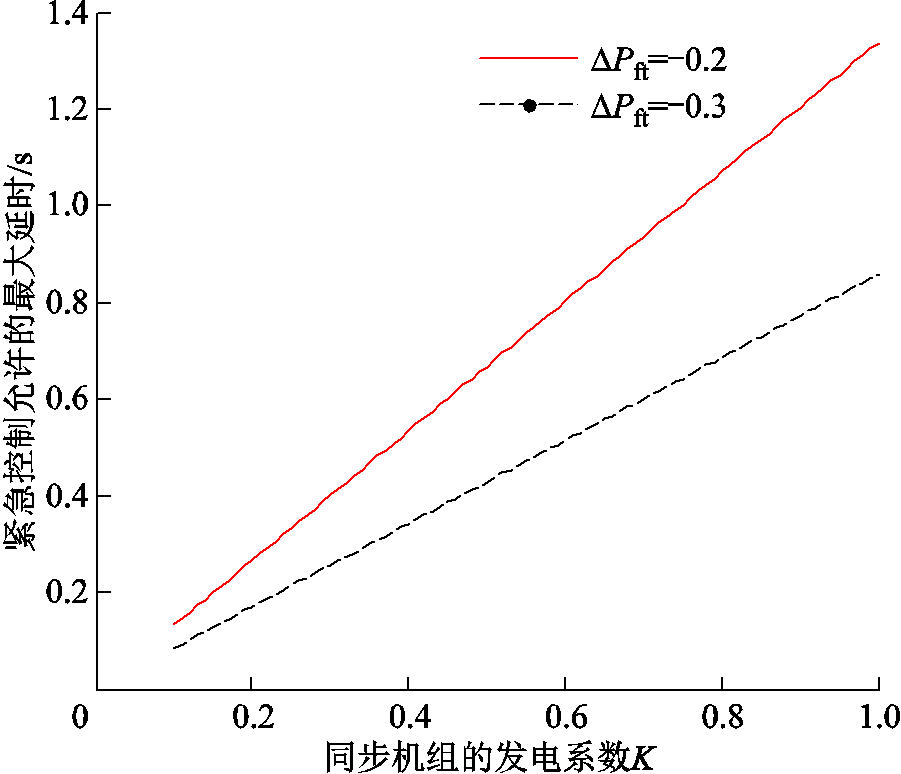
图7 紧急控制延时与系统最小发电系数的关系
Fig.7 The relationship between emergency control delay and the minimum power generation coefficient
由上述响应曲线可知，在一定的功率扰动下，随着新能源发电占比的增加，为了避免第三道防线动作，对紧急控制的响应时间和控制量要求越来越高。但紧急控制的固有延时，使得紧急控制适用的场景受到限制。如对于目前技术水平下紧急控制延时按300 ms考虑[25]，若发生30%负荷容量的永久性功率扰动，同步机组的发电系数不能小于35%，即新能源出力的极限值为系统总负荷的65%。为了给紧急控制争取时间，需要采取措施减缓系统频率下降速度，如电力电子设备的“虚拟惯量”、更加快速的一次调频能力，利用分散式的低代价控制资源，弥补频率紧急控制的不足，避免低频减载等传统第三道防线动作。
短时性不平衡功率扰动以新能源低电压穿越造成的典型扰动为例，《光伏发电站接入电力系统技术规定》（GB/T 19964—2012）要求对电力系统故障期间没有脱网的光伏发电站以至少每秒30%额定功率的功率变化率恢复至正常发电状态，《风电场接入电力系统技术规定》（GB/T 19963.1—2021）要求故障清除后风电场至少以每秒20%额定功率的速度恢复至正常发电状态。由于不同厂家新能源低电压穿越后的特性略有差异，不失一般性，考虑新能源低电压穿越至功率恢复期间，功率扰动形式呈现阶跃下降，持续一段时间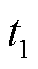
后，再以一定的斜率缓慢恢复至初始值（持续时间
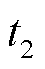），在频域上的扰动功率函数可以表示为
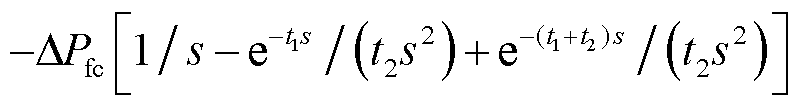。由于在新能源等电力电子设备故障穿越期间，其正常的频率、电压控制策略均无效，因此本文在分析其影响时忽略电力电子设备的快速调节性能，即在分析频率最大偏差时忽略新能源的一次调频作用，为避免触发低频减载动作，考虑故障事件触发的频率紧急控制改善暂态频率特性。
将短时性功率扰动函数作为输入，代入图4所示的传递框图，可以得到系统频率偏差的频域表达式为
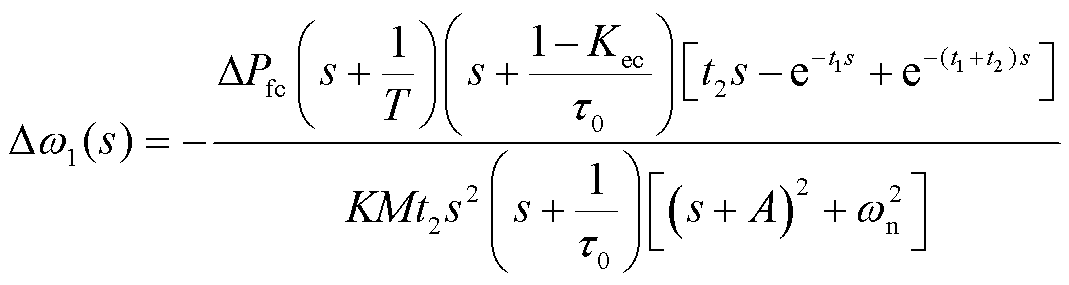（17）
根据拉普拉斯反变换，可以得到系统频率响应的时域表达式为
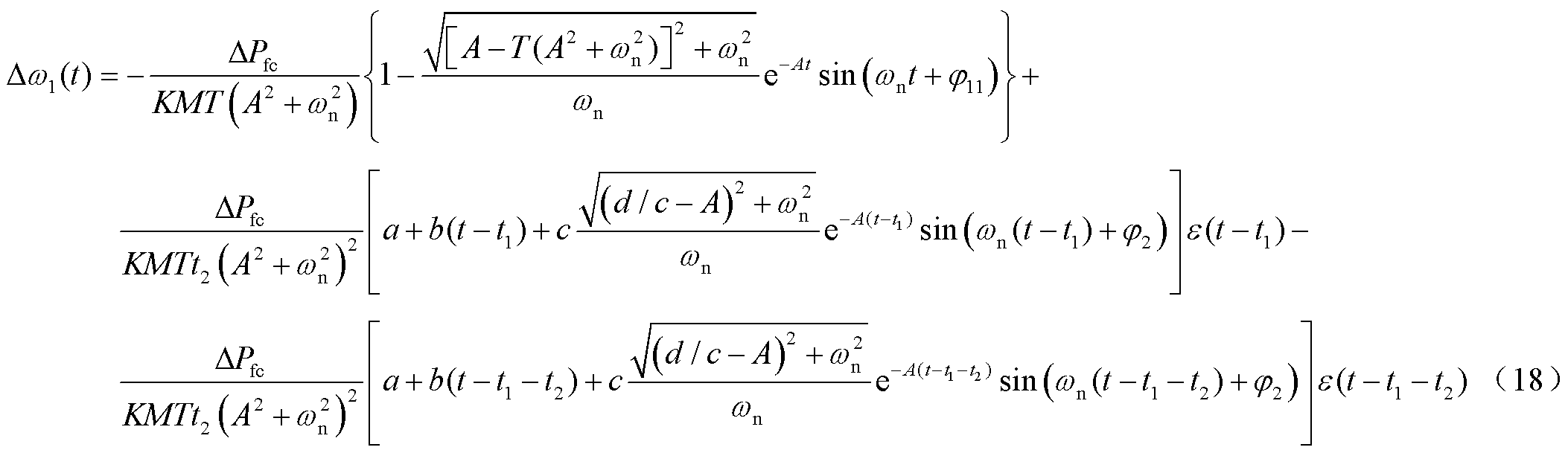
式中，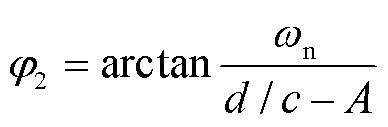
，
，
，
，
。
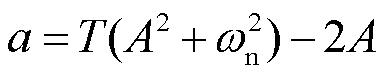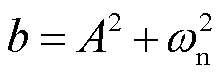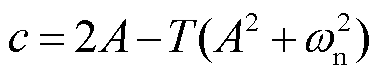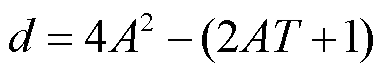
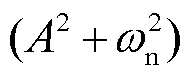对于2.2节中给定的系统参数，考虑常规同步机组发电系数K=0.3，系统承受的功率扰动ΔPfc=0.2，阶跃扰动持续时间t1=0.2 s，斜坡恢复持续时间t2=2.5 s，新能源在低电压穿越期间无法参与一次调频，即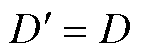
，系统频率响应曲线响应曲线如图8所示。
短时性不平衡功率扰动下，不考虑紧急控制作用，系统的频率稳态响应与扰动功率持续时间、系统发电和负荷的频率调节特性均无关，稳态频率偏差为零。随着新能源、直流等电力电子电源相对负荷占比的不断提升，短时性功率扰动量将不断增加，严重情况下也会造成系统暂态频率越过不安全的边界，虽然扰动消失后系统稳态频率逐渐恢复正常，但对现行的频率校正控制防线适应性造成巨大影响[19]，需要提前研究应对措施，值得电力系统生产运行单位关注。
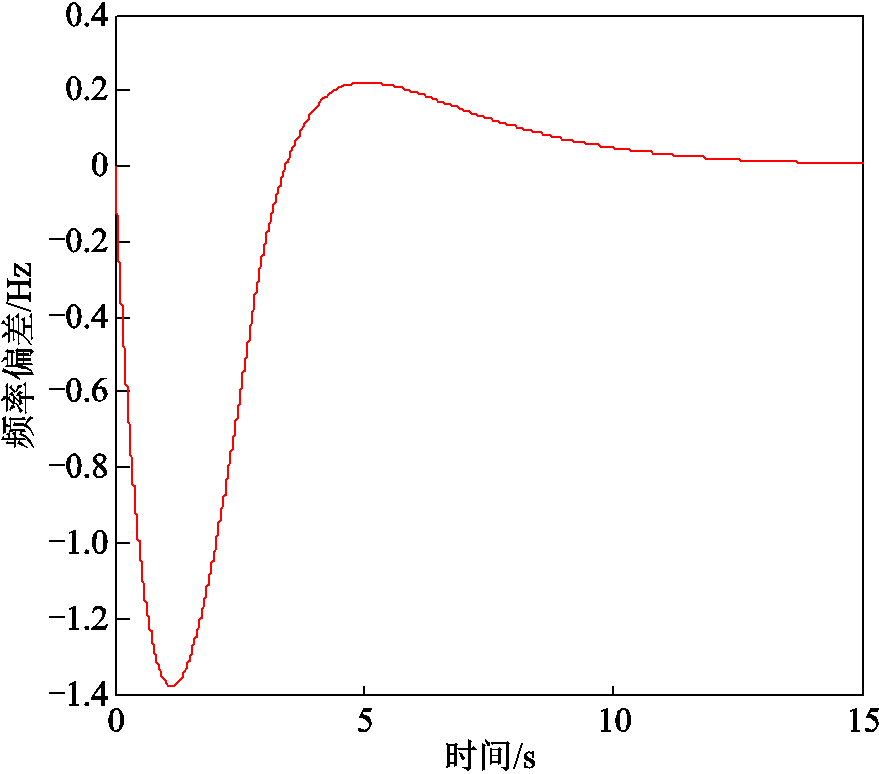
图8 典型短时性功率扰动下的频率响应
Fig.8 Frequency response under typical short-term power disturbances
由于系统频率响应的时域表达式为非连续可导的分段函数，难以直接解析求取极值，对典型的短时性功率扰动进行简化，分析其对大电网频率特性的影响，如图9所示典型新能源低电压穿越功率扰动曲线中的虚线部分，不影响结论的一般性，其中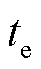
为等效的恢复时间。
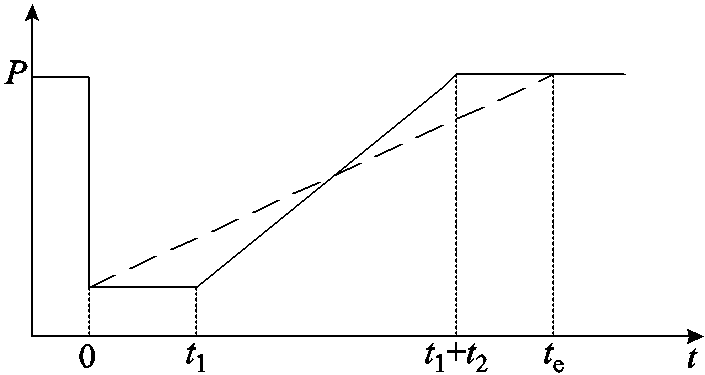
图9 典型新能源低电压穿越功率扰动曲线
Fig.9 Typical power disturbance curve during new energy low voltage ride through
上述短时性功率扰动形式在频域上可以表示为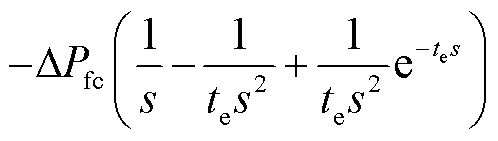
，由于系统的最低频率出现的时刻必然早于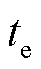，当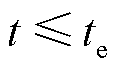
时，系统频率偏差的频域表达式为
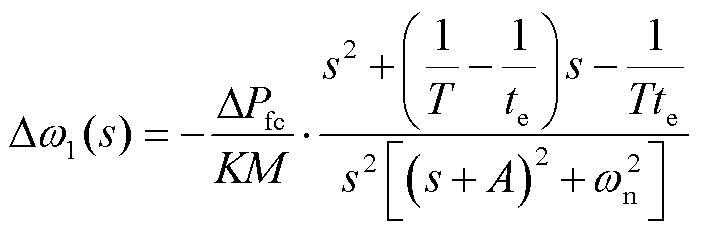（19）
可以得到不计及紧急控制的系统频率响应的时域表达式为
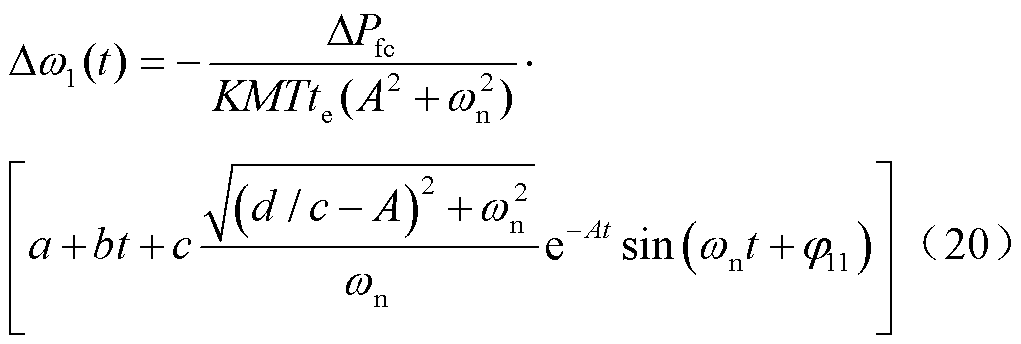
其中
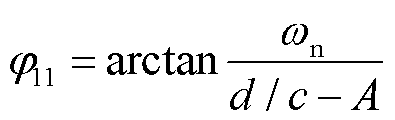
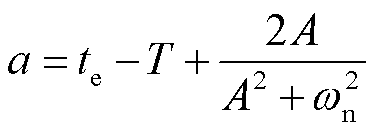
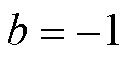
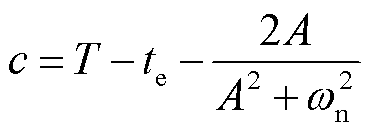
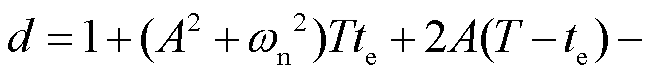
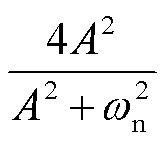
对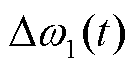
求导，可以得到频率达到最低点的时刻
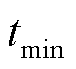满足
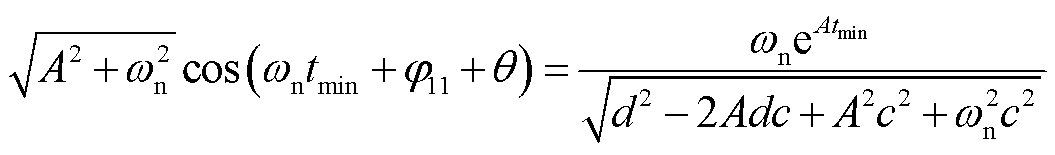（21）
式中，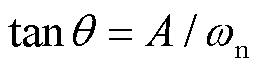
。
考虑以改善最大频率偏差为目标的紧急控制，需要确保在最低时刻之前响应，即满足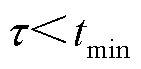
。
不同等效的恢复时间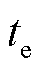
下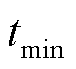，的响应曲线如图10所示。
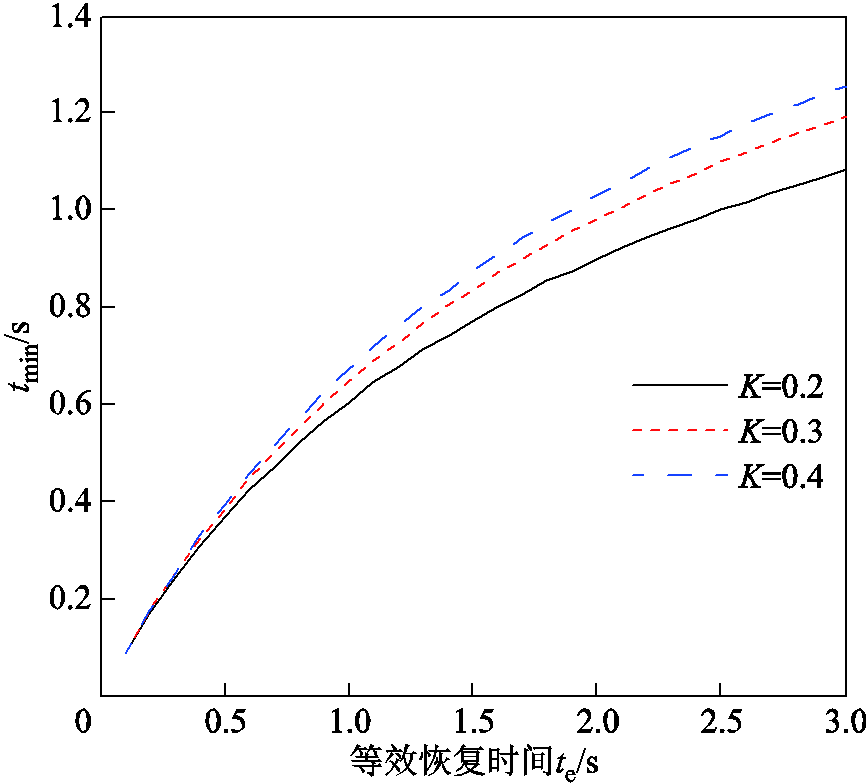
图10 不同等效恢复时间下系统最低频率时刻
Fig.10 The lowest frequency moment under different equivalent recovery times
可以看出，频率跌落至最小值的时间与扰动功率的恢复时间密切相关，且同步机的占比越大，频率跌落至极值的延时越长，对紧急控制的响应时间要求越低。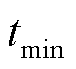时刻对应的最低频率如图11所示。
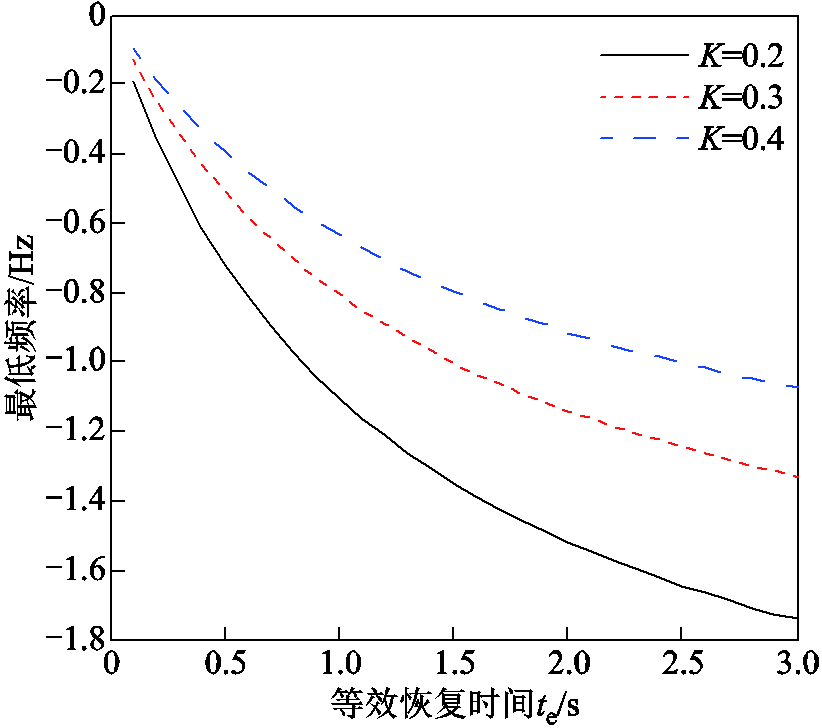
图11 不同等效恢复时间下系统最低频率
Fig.11 The lowest frequency under different equivalent recovery times
随着同步机占比的减小，系统因转动惯量减小导致可释放的动能减小，在相同的功率扰动下，系统的最低频率逐渐降低至第三道防线动作的门槛值，对紧急控制的动作量要求越来越高。
虽然及时的紧急控制能够改善最低频率，避免触发低频减载动作，但随着新能源功率的恢复，过量的紧急控制可能导致高频切机风险。
以低频减载启动门槛值49 Hz和高频切机启动门槛值50.5 Hz为例，对于2.2节中给定的系统参数，考虑常规同步机组发电系数K=0.3，系统承受的功率扰动ΔPfc=0.2，等效的扰动持续时间te=2.72 s，控制量与扰动功率的比例系数Kec=0.15。
以紧急控制能够同时避免第三道防线低频切负荷与高频切机启动为边界，系统允许的紧急控制量与系统的同步发电系数K的关系如图12所示。其中，黑色虚线上方对应的控制量才能避免触发低频减载，红色实线下方对应的控制量才能避免触发高频切机。
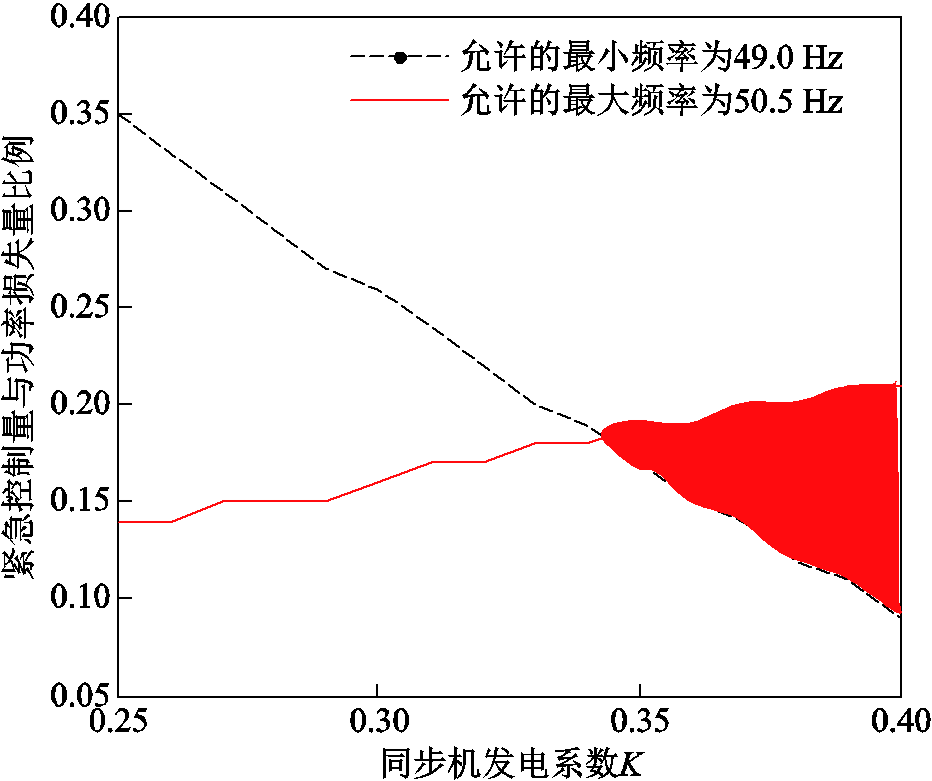
图12 不同同步发电系数下的紧急控制有效域
Fig.12 Feasibility region of emergency control under different synchronous generation coefficients
从图12可以看出，随着同步机发电系数的逐渐减小，可采取的合理紧急控制量区间逐渐减小。当K＜0.34时（即新能源出力占比达到66%以上），在给定的短时性扰动边界下，不能单纯依赖传统一次性动作的紧急控制，同时避免触发低频减载和高频切机。可见，随着新能源占比的不断提升，电力电子设备弱抗扰性带来的短时性功率冲击给现有频率安全防线带来了巨大的挑战，需要统筹考虑新能源接入容量、新能源涉网性能及电网故障防御三道防线技术及策略。
华东电网是我国典型的特高压直流多馈入受端电网，频率安全问题较为突出[4]。近年来，包括分布式光伏、沿海风电的快速发展，新能源装机容量迅速提升。截至2022年底，华东电网共馈入直流13回，额定容量7 976万kW，新能源装机已达到1.02亿kW（其中光伏6 392万kW，风电3 972万kW）。按照规划，十四五期间华东电网的风电装机容量将达到7 000万kW，光伏1.1亿kW，系统等效惯量将不断下降。本节针对华东电网规划的大规模新能源与直流大容量多馈入场景开展交直流故障仿真分析，并与前面的分析结论进行比较。
目前，华东电网频率安全风险主要来自特高压直流双极闭锁故障造成的永久性功率缺额，以及特高压线路短路故障下大规模新能源低电压穿越和多回直流同时换相失败造成的短时性功率缺额。
某规划典型方式下，系统总负荷为1.82亿kW，同步机组出力为0.85亿kW，留取旋转备用为0.35亿kW，常规同步机组发电系数K=0.47，即新能源与直流等电力电子接口电源占比达到53%，系统的等效惯性时间常数M=12 s，等效阻尼D约为1.2。
1）永久性功率缺额仿真
宾金直流双极闭锁故障下，功率扰动为530万kW，系统承受的功率扰动ΔPft约为2.9%。若假设系统允许的最大频率偏差为49.5 Hz，根据式（16），可以估算出紧急控制的延时最大为3.36 s，由式（13）可知，最小控制量为功率扰动量的59.94%。基于华东电网详细模型的时域仿真计算，该故障下系统的最低频率为49.35 Hz，按59.94%功率扰动量设置控制量，考虑紧急控制不同延时下系统的频率响应仿真曲线如图13所示，其中3 s后采取紧急控制下系统最低频率约为49.5 Hz，与理论分析基本相符。
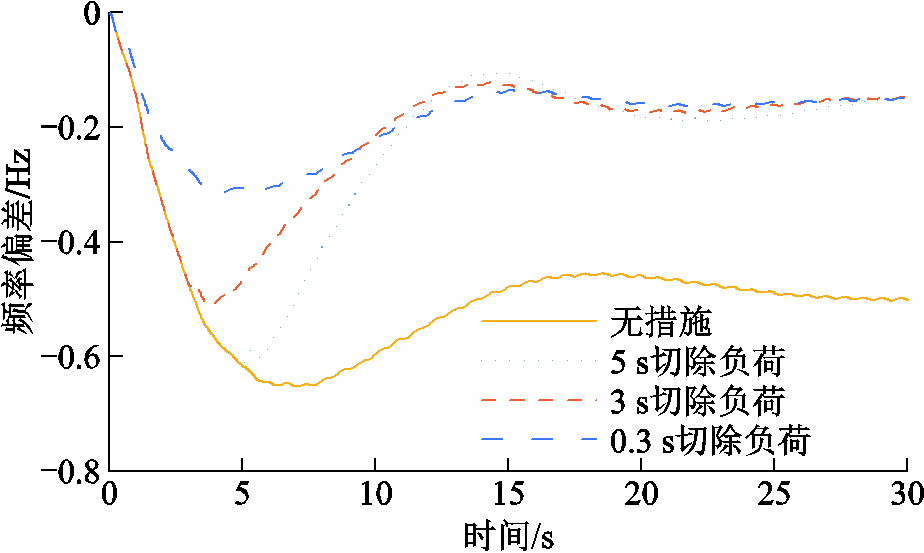
图13 不同紧急控制延时下的频率响应曲线
Fig.13 Frequency response curves under different emergency control delays
2）短时性功率缺额仿真
1 000 kV等级线路芜湖-安吉安吉侧三永N-1故障，造成大规模新能源进入低电压穿越和多回直流同时换相失败，暂态最大功率扰动量约为0.33亿kW，占负荷比例高达18.1%，经1.4 s暂态功率扰动平息。根据式（21）可知，估算系统频率达到最低的时刻为1.26 s。
利用华东电网详细模型进行仿真计算，芜湖-安吉安吉侧三永N-1故障下，不考虑采取紧急控制措施，系统的最低频率为49.34 Hz；考虑故障后0.3 s触发紧急控制，不同控制量下系统的频率响应曲线如图14所示。可以看出，为确保系统的最高频率小于50.5 Hz，紧急控制最大措施量为暂态最大功率扰动量10.61%，但此时又无法确保系统的最低频率在49.5 Hz以上。
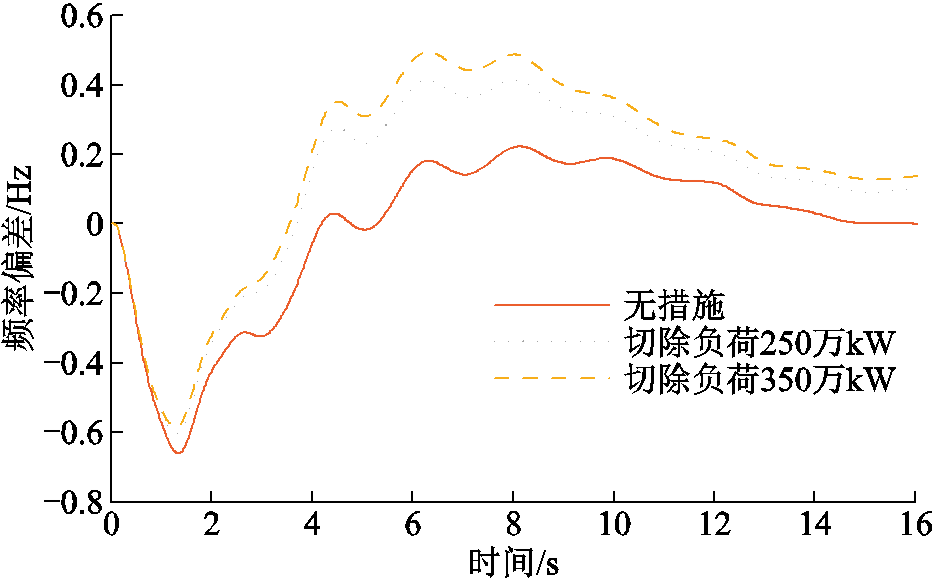
图14 不同紧急控制量下的频率响应曲线
Fig.14 Frequency response curves under different emergency control quantities
由上述仿真结果可知，随着大规模新能源接入华东电网，华东电网频率响应特性呈现恶化趋势，除了直流闭锁等永久性功率缺额外，短路故障引起的新能源低电压穿越、直流换相失败等短时性功率扰动尤其值得关注。由于短路故障下的短时功率扰动量巨大，远远超出系统一次调频的能力，频率在极短时间内到达最低点，速度相比典型永久性扰动加快80%，且已达到华东电网频率协调紧急控制系统的就地控制功能动作阈值[26]。在应对永久性功率缺额故障时，华东电网现有的紧急控制措施能够保障电网暂态频率安全。关于短时性功率扰动，理论和仿真分析表明紧急控制在改善最低频率的效果方面较弱，且极易引起电网连锁高频，未来随着华东电网新能源并网容量和跨区直流输电规模的进一步增长，将成为华东电网频率安全稳定控制要解决的关键问题。
频率紧急控制是保障电网故障后频率安全的重要防线，随着高比例新能源接入，电网承受的功率扰动形式更加多样，频率响应特性也随之变化，围绕频率紧急控制的适应性，有以下结论：
1）大规模新能源替换传统同步电源，导致电网惯量水平与调频能力下降，频率跌落速度加快是影响紧急控制适应性的重要原因。
2）高比例新能源电网中，交流短路故障引起的大规模新能源低电压穿越、常规直流换相失败、柔性直流低电压穿越，会产生巨量的短时性功率扰动，相比传统的单回直流闭锁故障，可能造成系统频率“闪降”，容易诱发电网中的频率校正控制防线动作。频率紧急控制在应对时，既要满足系统低频控制要求，又要避免控制实施后连锁高频问题，适应难度大。
大规模新能源低电压穿越等短时性功率扰动给电网频率安全防御体系带来巨大挑战，如何结合电网实际需求，从新能源涉网性能提升、电网惯量能力建设、频率紧急和校正控制策略优化等方面值得进一步研究。
参考文献
[1] 方勇杰. 英国“8·9”停电事故对频率稳定控制技术的启示[J]. 电力系统自动化, 2019, 43(24): 1-5.
Fang Yongjie. Reflections on frequency stability control technology based on the blackout event of 9 August 2019 in UK[J]. Automation of Electric Power Systems, 2019, 43(24): 1-5.
[2] 孙华东, 许涛, 郭强, 等. 英国“8·9”大停电事故分析及对中国电网的启示[J]. 中国电机工程学报, 2019, 39(21): 6183-6192.
Sun Huadong, Xu Tao, Guo Qiang, et al. Analysis on blackout in great Britain power grid on August 9th, 2019 and its enlightenment to power grid in China[J]. Proceedings of the CSEE, 2019, 39(21): 6183-6192.
[3] 曾辉, 孙峰, 李铁, 等. 澳大利亚“9·28”大停电事故分析及对中国启示[J]. 电力系统自动化, 2017, 41(13): 1-6.
Zeng Hui, Sun Feng, Li Tie, et al. Analysis of “9·28” blackout in South Australia and its enlightenment to China[J]. Automation of Electric Power Systems, 2017, 41(13): 1-6.
[4] 李兆伟, 吴雪莲, 庄侃沁, 等. “9·19”锦苏直流双极闭锁事故华东电网频率特性分析及思考[J]. 电力系统自动化, 2017, 41(7): 149-155.
Li Zhaowei, Wu Xuelian, Zhuang Kanqin, et al. Analysis and reflection on frequency characteristics of East China grid after bipolar locking of “9·19” jinping-sunan DC transmission line[J]. Automation of Electric Power Systems, 2017, 41(7): 149-155.
[5] 刘洋, 王聪颖, 夏德明, 等. 电网故障导致大面积风电低电压穿越对电网频率的影响分析及措施[J]. 电网技术, 2021, 45(9): 3505-3514.
Liu Yang, Wang Congying, Xia Deming, et al. Influence of large area wind power low voltage ride-through on power grid frequency caused by power grid faults[J]. Power System Technology, 2021, 45(9): 3505-3514.
[6] 花赟玥, 吴琛, 黄伟, 等. 考虑风电低电压穿越过程的频率最低点量化及其提升方法[J]. 电力系统自动化, 2023, 47(1): 126-134.
Hua Yunyue, Wu Chen, Huang Wei, et al. Quantification and enhancement method for frequency nadir considering low voltage ride-through process of wind power[J]. Automation of Electric Power Systems, 2023, 47(1): 126-134.
[7] 国家能源局. 电力系统网源协调技术规范: DL/T 1870—2018[S]. 北京: 中国电力出版社, 2018.
[8] 国家质量监督检验检疫总局, 中国国家标准化管理委员会. 电力系统安全稳定控制技术导则: GB/T 26399—2011[S]. 北京: 中国标准出版社, 2011.
[9] 文云峰, 杨伟峰, 林晓煌. 低惯量电力系统频率稳定分析与控制研究综述及展望[J]. 电力自动化设备, 2020, 40(9): 211-222.
Wen Yunfeng, Yang Weifeng, Lin Xiaohuang. Review and prospect of frequency stability analysis and control of low-inertia power systems[J]. Electric Power Automation Equipment, 2020, 40(9): 211-222.
[10] 杨德健, 王鑫, 严干贵, 等. 计及调频死区的柔性风储联合频率控制策略[J]. 电工技术学报, 2023, 38(17): 4646-4656.
Yang Dejian, Wang Xin, Yan Gangui, et al. Flexible frequency regulation scheme of DFIG embed battery energy storage system considering deadbands[J]. Transactions of China Electrotechnical Society, 2023, 38(17): 4646-4656.
[11] 张剑云, 李明节. 新能源高渗透的电力系统频率特性分析[J]. 中国电机工程学报, 2020, 40(11): 11, 3498-3506.
Zhang Jianyun, Li Mingjie. Analysis of frequency characteristics of power system with high permeability of new energy[J]. Proceedings of the CSEE, 2020, 40(11): 11, 3498-3506.
[12] 闵勇, 陈磊, 刘瑞阔, 等. 电力系统频率动态中惯量与惯量响应特性辨析[J]. 中国电机工程学报, 2023, 43(3): 853-867.
Min Yong, Chen Lei, Liu Ruikuo, et al. Analysis on characteristics of inertia and inertial response in power system frequency dynamics[J]. Proceedings of the CSEE, 2023, 43(3): 853-867.
[13] 王科, 秦文萍, 张宇, 等. 双馈风机等效惯量控制比例系数对系统功角首摆稳定的影响机理分析[J]. 电工技术学报, 2023, 38(3): 741-753.
Wang Ke, Qin Wenping, Zhang Yu, et al. Mechanism analysis of effect of equivalent proportional coefficient of inertia control of DFIG on stability of first swing of power angle[J]. Transactions of China Electrotechnical Society, 2023, 38(3): 741-753.
[14] 陈国平, 李明节, 许涛. 特高压交直流电网系统保护及其关键技术[J]. 电力系统自动化, 2018, 42(22): 2-10.
Chen Guoping, Li Mingjie, Xu Tao. System protection and its key technologies of UHV AC and DC power grid[J]. Automation of Electric Power Systems, 2018, 42(22): 2-10.
[15] 罗亚洲, 陈得治, 李轶群, 等. 华北多特高压交直流强耦合大受端电网系统保护方案设计[J]. 电力系统自动化, 2018, 42(22): 11-18, 68.
Luo Yazhou, Chen Dezhi, Li Yiqun, et al. Design of system protection scheme for North China multi-UHV AC and DC strong coupling large receiving-end power grid[J]. Automation of Electric Power Systems, 2018, 42(22): 11-18, 68.
[16] 柯德平, 冯帅帅, 刘福锁, 等. 新能源发电调控参与的送端电网直流闭锁紧急频率控制策略快速优化[J]. 电工技术学报, 2022, 37(5): 1204-1218.
Ke Deping, Feng Shuaishuai, Liu Fusuo, et al. Rapid optimization for emergent frequency control strategy with the power regulation of renewable energy during the loss of DC connection[J]. Transactions of China Electrotechnical Society, 2022, 37(5): 1204-1218.
[17] 孙诚斌, 李兆伟, 李碧君, 等. 电化学储能参与电网低频第三道防线的控制策略[J]. 电力工程技术, 2021, 40(3): 27-34.
Sun Chengbin, Li Zhaowei, Li Bijun, et al. A control strategy for the low frequency third defense line of power grid containing the electrochemical energy storage[J]. Electric Power Engineering Technology, 2021, 40(3): 27-34.
[18] 李兆伟, 方勇杰, 李威, 等. 电化学储能应用于电网频率安全防御三道防线的探讨[J]. 电力系统自动化, 2020, 44(8): 1-7.
Li Zhaowei, Fang Yongjie, Li Wei, et al. Discussion on application of electrochemical energy storage in three defense lines of power grid frequency[J]. Automation of Electric Power Systems, 2020, 44(8): 1-7.
[19] 许涛, 吴雪莲, 李兆伟, 等. 改善系统频率稳定性的多直流功率紧急支援协调控制策略[J]. 电力系统自动化, 2018, 42(22): 69-77, 143.
Xu Tao, Wu Xuelian, Li Zhaowei, et al. Coordinated control strategy of multi-DC emergency power support to improve frequency stability of power systems[J]. Automation of Electric Power Systems, 2018, 42(22): 69-77, 143.
[20] 李兆伟, 方勇杰, 黄慧, 等. 系统保护中跨区直流频率调制与紧急功率支援的协调控制[J]. 电力系统自动化, 2020, 44(22): 31-36.
Li Zhaowei, Fang Yongjie, Huang Hui, et al. Coordinated control of cross-region DC frequency control and emergency power support in system protection[J]. Automation of Electric Power Systems, 2020, 44(22): 31-36.
[21] 电力安全事故应急处置和调查处理条例[M]．北京: 中国电力出版社, 2011.
[22] Kundur P, Balu N J, Lauby M G. Power system stability and control[M]. New York: McGraw-Hill, 1994.
[23] 李明节. 大规模特高压交直流混联电网特性分析与运行控制[J]. 电网技术, 2016, 40(4): 985-991.
Li Mingjie. Characteristic analysis and operational control of large-scale hybrid UHV AC/DC power grids[J]. Power System Technology, 2016, 40(4): 985-991.
[24] 赵畹君. 高压直流输电工程技术[M]. 2版. 北京: 中国电力出版社, 2011.
[25] 李德胜, 罗剑波. 特高压直流配套安全稳定控制系统的典型设计[J]. 电力系统自动化, 2016, 40(14): 151-157.
Li Desheng, Luo Jianbo. Typical design of security and stability control system for UHVDC transmission[J]. Automation of Electric Power Systems, 2016, 40(14): 151-157.
[26] 许涛, 励刚, 于钊, 等. 多直流馈入受端电网频率紧急协调控制系统设计与应用[J]. 电力系统自动化, 2017, 41(8): 98-104.
Xu Tao, Li Gang, Yu Zhao, et al. Design and application of emergency coordination control system for multi-infeed HVDC receiving-end system coping with frequency stability problem[J]. Automation of Electric Power Systems, 2017, 41(8): 98-104.
Abstract Frequency emergency control (FEC) is the second defense line to ensure frequency safety after power grid failures, usually triggered by event of fault, and has become a standard configuration of ultra-high voltage DC (UHVDC). With the rapid development of high proportion of new energy (NE), the frequency regulation ability and system inertia are continuously decreasing. The frequency response characteristics after power grid faults have some new characteristics of large drop depth and fast speed. The effectiveness of emergency control is a key factor related to the frequency safety.
This article first establishes frequency response model and transfer function of a high proportion NE power system considering FEC. To analyze the effectiveness of emergency control, this article focuses on two types of disturbances: permanent power disturbances (PPD) and short-term power disturbances (STPD). PPD are represented by faults such as DC blocking, unit tripping, and NE disconnection; STPD are represented by low voltage ride through (LVRT, without disconnection) of NE or flexible DC, DC commutation failure.
According to the derivation, the time-domain expression of the system frequency response considering FEC under PPD can be obtained. FEC may not always solve the transient frequency insecurity risk depending on whether the system deviation reaches the control threshold of under-frequency load shedding (UFLS) or over-frequency generator tripping (OFGT) after FEC. When FEC action delay τ0 is less the time when the frequency reaches its lowest point tm, the maximum frequency deviation will be improved. But excessive emergency control amount can cause the risk of transient high-frequency in the system. When the delay of FEC is greater than the moment when the system's minimum frequency occurs, FEC cannot improve the maximum frequency deviation. For the current technical level, the emergency control delay is considered as 300ms.If a PPD of 30% load capacity occurs, the limit value for NE access is 65% of the load.
Under STPD the steady-state frequency deviation is zero. With the continuous increase of NE, DC and other power electronic power sources, the amount of STPD will continue to increase. In severe cases, it can also cause the system's transient frequency to cross unsafe boundaries, which may lead to the current frequency corrective control line action and lead to power outages. As the proportion of synchronous machines decreases, the released kinetic energy decreases due to the rotational inertia. So that under the same STPD, the lowest frequency of the system gradually decreases to the threshold value of the third defense such as UFLS, and the demand for FEC is becoming increasingly high. Although timely FEC can improve the minimum frequency and avoid triggering UFLS, excessive FEC may lead to risks of OFGT. As the proportion of synchronous machines gradually decreases, the range of reasonable amounts of FEC that can be taken gradually decreases. When the proportion of synchronous machines is less than 34% of load, under a given STPD boundary, FEC cannot solely rely on traditional one-time actions to avoid triggering UFLS and OFGT.
The following conclusions can be drawn. (1) The large-scale replacement of traditional synchronous power sources with NE has led to a decrease in the inertia and frequency regulation ability of the power grid, and the increased ROCOF is an important reason for affecting the adaptability of FEC. (2) In a high proportion of NE grids, large-scale LVRT of NE and flexible DC, conventional DC commutation failure caused by AC short circuit faults can generate significant STPD. Compared to traditional DC blocking faults, it may cause system frequency "flicker" and easily trigger UFLS. When responding to FEC, it is necessary to not only meet the low-frequency control requirements, but also avoid interlocking high-frequency after control implementation, which becomes more and more difficult to adapt to.
STPD such as large-scale LVRT of NE pose significant challenges to the frequency security defense system. Further research is needed on how to improve the grid performance of NE, build grid inertia capacity, optimize FEC and corrective control strategies based on the actual needs of the power grid.
Keywords：New energy, frequency safety, frequency emergency control, low inertia power system, short term power disturbance, low voltage ride through of new energy
中图分类号：TM76
DOI: 10.19595/j.cnki.1000-6753.tces.231175
国家自然科学基金重点项目（61933005）和国家电网公司科技项目（5100-202240026A-1-1-ZN）资助。
收稿日期 2023-07-23
改稿日期 2023-09-09
李兆伟 男，1985年生，博士研究生，研究方向电力系统安全稳定分析与控制。
E-mail：lizhaowei1@sgepri.sgcc.com.cn（通信作者）
方勇杰 男，1964年生，研究员级高级工程师，博士生导师，研究方向为电力系统安全稳定分析与控制。
E-mail：fangyongjie@sgepri.sgcc.com.cn
（编辑 赫 蕾）