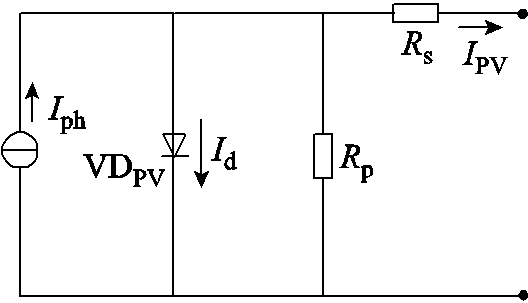
图1 光伏电池等效电路模型
Fig.1 Equivalent circuit model of photovoltaic cells
摘要 对新能源低压直流配电系统开展暂态实时仿真研究对优化其运行控制具有重要作用。由于现场可编程门阵列(FPGA)内部集成了大量具有不同功能的电路,FPGA正成为电力系统暂态实时仿真领域主要的计算载体之一。该文面向新能源低压直流配电系统的暂态实时仿真需求,开发了一种基于FPGA的包含小型分布式风力发电、光伏发电以及蓄电池储能单元的新能源低压直流配电系统暂态实时仿真器。首先,研究构建了分布式发电单元和典型控制回路的计算模块,利用FPGA的并行计算特性并结合“算法-结构-有效匹配(AAA)”理念建立了底层模块串并联混合求解结构;然后,在节点分析法的框架下,建立了一种结合矩阵LDU分解和有向无环图(DAG)的电气系统节点电导矩阵并行求解方法;最后,在建立电气系统与控制系统并行求解架构的基础上,开发了一种基于FPGA的新能源低压直流配电系统暂态实时仿真器,通过将其仿真结果与PSCAD/EMTDC离线仿真平台的计算结果进行对比,验证了所开发暂态实时仿真器的有效性和准确性。
关键词:现场可编程门阵列(FPGA) 实时仿真 分布式发电 低压直流配电系统 并行计算
新能源低压直流配电系统相比于传统低压交流配电系统具有节省换流环节、可控性更好等诸多优势,因此,低压直流配电系统及其相关技术的发展备受关注[1-5]。有效的仿真工具和方法是探究新能源低压直流配电系统动态特征,分析其内部运行机理乃至为其规划设计和优化调度过程提供技术支撑的重要基础。当前,新能源低压直流配电系统可依托的仿真工具主要有离线仿真工具(PSCAD/EMTDC、Matlab/Simulink和ATP(alternative transient program)等)与实时仿真装置(HYPERSIM[6]、RTDS(real time digital simulation system)[7-8]、ADPSS(advanced digital power system simulator)[9]、RT-LAB[10]和PLECS[11]等)。相比于离线仿真工具,实时仿真装置既具备在计算过程中保证仿真时刻与外部时钟精确同步的能力,也具有强大且灵活的建模仿真能力和多种类型的外部接口。因此,新能源低压直流配电系统实时仿真装置一方面可以为系统中的各种保护与控制等二次装置提供高度模拟现场实际的测试环境;另一方面也可以为系统中的分布式发电装置和多类型电力电子装置,以及其他不同类型硬件设施的先进建模方法提供可靠的模型校验途径[11-13]。此外,随着数字控制技术的进步,具有更小设备体积、更低实现成本及更高系统集成度的新能源低压直流配电系统实时仿真装置还可以被嵌入到控制回路中,为高层级优化求解器完成状态观测或预测等功能,以提升其性能[14]。
就电力系统实时仿真装置的具体实现而言,当前有许多依托不同实时仿真装置或程序的研究。文献[6]提出一种基于HYPERSIM平台的柔性直流输电系统数模混合仿真建模方法,该方法在传统仿真方法的基础上接入了实际柔性直流输电工程的控制保护装置,取得了较好的仿真效果。文献[7]依托RTDS平台提出了一种适用于电力系统电磁暂态和机电暂态并行计算情况下的实时接口电路和接口数据交换方式,推动了实时仿真技术的进一步发展。文献[9]结合ADPSS平台和实际物理仿真平台开发了一种针对交直流电网且具有较高建模速度和仿真灵活度的功率连接接口装置。文献[10]在建立一种基于RT-LAB的光伏系统模型的基础上,建立了电压源变换器控制器的离散模型,提升了仿真系统的可靠性。文献[11]建立了一种基于PLECS的包含多种类型电源的交流微电网实时仿真模型,同时验证了对应控制回路的有效性。上述实时仿真装置或程序基本是以CPU或DSP(digital signal processing)为底层计算载体,而CPU和DSP本质上是串行计算单元,在面对规模较大的仿真系统时,实时仿真装置的计算效率和经济性都面临着很大挑战。
现场可编程门阵列(Field Programmable Gate Array, FPGA)是一种专用集成电路(Application Specific Integrated Circuit, ASIC),能够以类似片上系统的方式为应用程序的计算、内存和电源需求的开发提供最适合的电路架构[15-16]。相比于商业化的实时仿真平台,FPGA本身集成了包括片上物理处理器、软处理器、专用DSP硬件及多类型存储器等支撑结构,这使得FPGA除了具有强大的并行计算性能之外,还具备经过二次配置后成为任何一种具有特定计算功能的功能块的能力。考虑到其强大的计算能力,FPGA已经应用到部分商业实时仿真平台中完成一定的功能,如RT-LAB和PLECS等。而在以FPGA为主要计算平台的电力系统实时仿真领域,国内外许多学者也做了很多工作。文献[17]考虑到模块化多电平换流器(Modular Multilevel Converter, MMC)对于直流电力系统运行的重要性,建立了基于FPGA的MMC硬件模型,实现了MMC的仿真步20 μs的实时仿真,建立模型的过程中采用IGBT的动态曲线拟合模型,考虑了影响其瞬态性能的因素,使功率损耗和结温等器件级行为可以准确地再现在功率变换器的电磁热模拟中,以便用于其设计评估。文献[18]介绍了一种基于FPGA的针对级联静止无功补偿器的实时仿真模型,以减小步长和提高仿真精度为目的,提出一种基于改进开关函数法的仿真方法,在一定程度上简化了仿真模型,减少了仿真计算量。文献[19]为满足电力牵引传动系统高速实时仿真的需求,基于FPGA平台建立了电力牵引传动系统的小步长硬件在环仿真装置,实现了微秒级实时仿真。文献[20]在FPGA器件上开发了一种不同于传统全数字锁相环的可变模全数字锁相环。该锁相环中心频率可变,具有锁相范围大、锁相速度高及输出抖动减小的优势。文献[21-22]介绍了一种小规模传统交流配电系统基于FPGA的暂态实时仿真器的计算求解框架。文献[23]用FPGA实现了对一种单相并网电压源变换器的实时功率分析和控制。文献[24]针对交直流电力系统的实时仿真问题,构建了由异构硬件组成的实时协同仿真器,可实现交直流电力系统的微秒级实时仿真计算,其中FPGA用于进行电磁暂态计算,为网络层提供近乎连续的瞬时波形。
在上述工作中,FPGA主要用于实体装置或小规模电力网络的实时仿真计算,在计算过程中引入并行结构来提升仿真系统的计算效率。但当仿真规模较大时,这样的计算结构会导致FPGA内部有限硬件资源占用率的大幅升高,从而影响FPGA性能的充分发挥。而在新能源低压直流配电系统中常集成大量多种类型能源形式和多种时间尺度装置,并且各种信息耦合程度也更高,这就对FPGA的计算结构和方式有更高要求,特别是在该实时仿真装置被嵌入到控制回路中充当系统的状态观测器或预测器时,高效地利用FPGA内部的硬件资源有助于提升实时仿真装置的系统集成度和其在面对较大规模仿真系统时对高维线性方程组的求解能力。
鉴于此,本文面向新能源低压直流配电系统的暂态实时仿真需求,依托节点分析框架,研究建立了一种基于FPGA的包含多种分布式电源的新能源低压直流配电系统暂态实时仿真器。首先,为了提升FPGA内部的硬件资源利用率,在底层基础功能模块中,充分利用FPGA的并行计算特性并结合“算法-结构-有效匹配(Algorithm Architecture Adequation, AAA)”理念建立了一种串并联混合的硬件计算结构;然后,为了确保仿真计算过程中数据流动的高效性,设计了一种结合矩阵LDU分解和有向无环图(Directed Acyclic Graph, DAG)的电气系统节点电导矩阵并行求解方法;最后,在建立电气系统和控制系统的并行求解架构的基础上开发了一种基于FPGA的新能源低压直流配电系统暂态实时仿真器,通过和PSCAD/EMTDC离线平台的对比实验,验证了所开发的暂态实时仿真器的可靠性和有效性。
光伏阵列的基本组成单元为光伏电池,本文采用光伏电池的等效电路模型,其等效电路模型如图1所示。对于大规模的光伏阵列来说,只需要在此模型的基础上改变参数即可。

图1 光伏电池等效电路模型
Fig.1 Equivalent circuit model of photovoltaic cells
光伏电池的数学模型可表示为
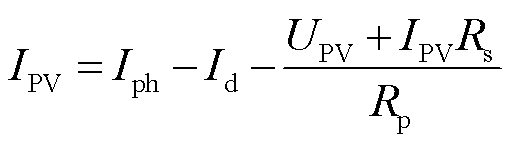 (2)
(2)
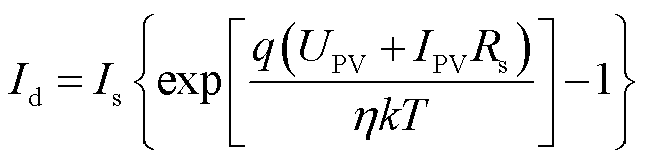 (3)
(3)
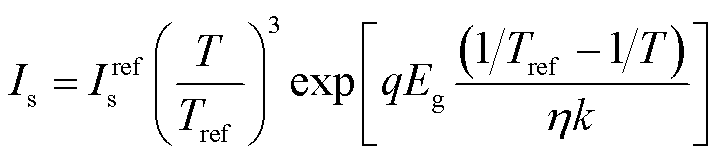 (4)
(4)
式中,S和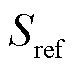 分别为实际和标准条件下的光照强度,lx;
分别为实际和标准条件下的光照强度,lx;![]() 和
和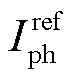 分别为实际和标准条件下的光生电流值,A;
分别为实际和标准条件下的光生电流值,A;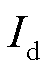 为二极管电流,A;Rp和Rs分别为内部并联和串联电阻,Ω;
为二极管电流,A;Rp和Rs分别为内部并联和串联电阻,Ω;![]() 为温度系数;T为实际温度,K;
为温度系数;T为实际温度,K;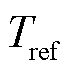 为标准条件下的温度,K;
为标准条件下的温度,K;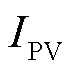 为光伏电池输出电流,A;
为光伏电池输出电流,A;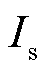 为二极管反向饱和电流,A;q为单个电子电量,q=1.602×10-19 C;k为玻尔兹曼常数,k=1.381×10-23 J/K;
为二极管反向饱和电流,A;q为单个电子电量,q=1.602×10-19 C;k为玻尔兹曼常数,k=1.381×10-23 J/K;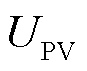 为断路电压;
为断路电压;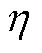 为拟合系数,A/K;
为拟合系数,A/K;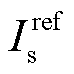 为标准条件下的反向饱和电流,A;
为标准条件下的反向饱和电流,A;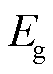 为禁带宽度,eV。
为禁带宽度,eV。
在小型分布式风力发电领域应用越来越广泛的直驱型永磁同步风力发电机型有结构简单、易维护和高风能利用率等优势,其结构如图2所示[25]。
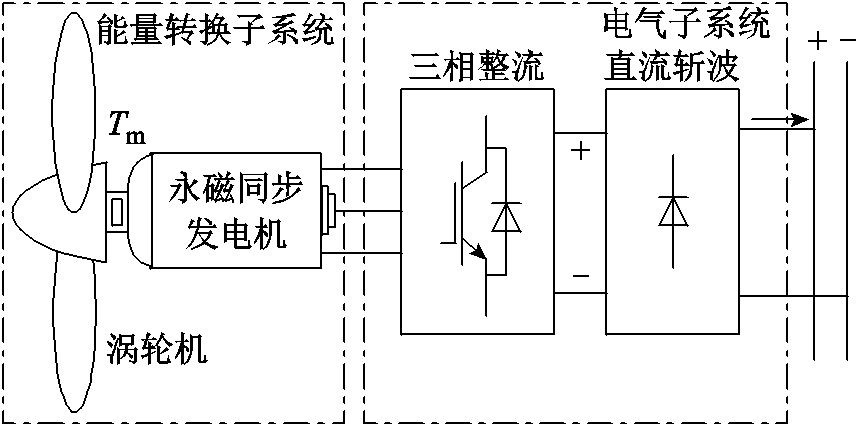
图2 小型分布式风力发电系统模型
Fig.2 Model of small-scale distributed wind power system
从整体上来看,该风力发电系统主要包括能量转换子系统和电气子系统两部分。能量转换子系统负责捕获并转换风能,主要包括风力涡轮机和发电机;电气子系统负责调制能量转换子系统输出的电能,主要包括三相全桥整流器和直流斩波电路。其中,风力涡轮机及传动系统的数学模型可表示为
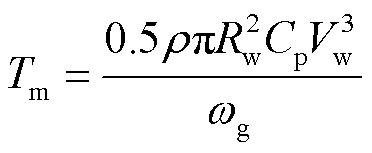 (5)
(5)
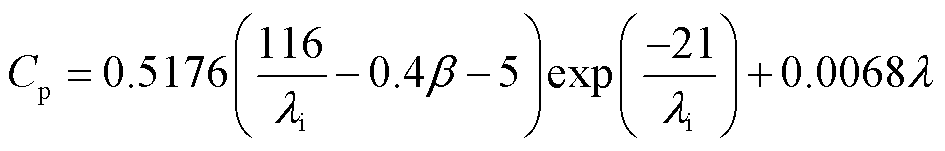 (6)
(6)
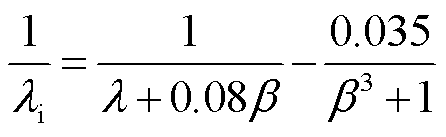 (7)
(7)
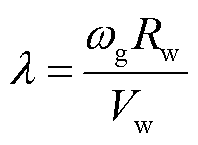 (8)
(8)
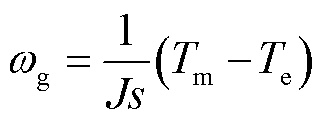 (9)
(9)
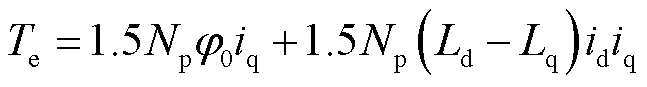 (10)
(10)
式中,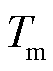 为风力涡轮机输出机械转矩,N·m;
为风力涡轮机输出机械转矩,N·m;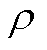 为空气密度,kg/m3;
为空气密度,kg/m3;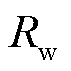 为叶片半径,m;
为叶片半径,m;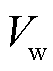 为风速,m/s;
为风速,m/s;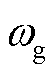 为机械转速,rad/s;
为机械转速,rad/s;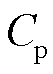 为风能利用系数;
为风能利用系数;![]() 为叶片桨距角,º;
为叶片桨距角,º;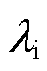 为中间变量;
为中间变量;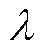 为叶尖速比;s为微分算子;
为叶尖速比;s为微分算子;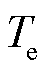 为发电机内部电磁转矩;J为转动惯量;
为发电机内部电磁转矩;J为转动惯量;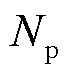 为发电机极对数;
为发电机极对数;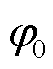 为永磁体的磁链;
为永磁体的磁链;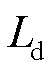 为d轴电感;
为d轴电感;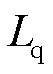 为q轴电感;
为q轴电感;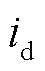 和
和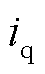 分别为d轴和q轴电流。
分别为d轴和q轴电流。
永磁同步发电机(Permanent Magnet Synchronous Generator, PMSG)的等效电路模型如图3所示[26]。
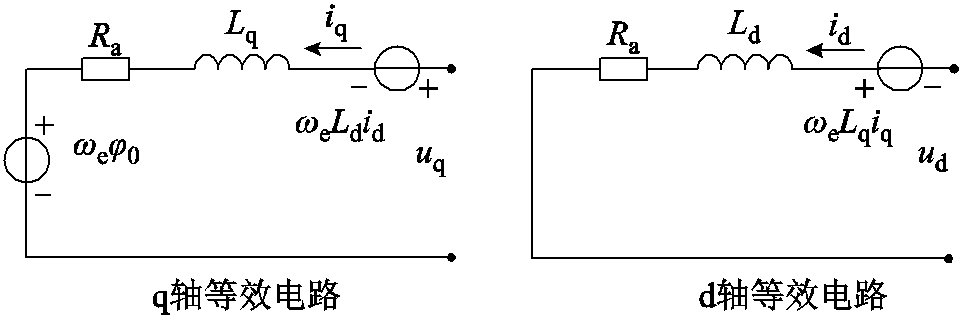
图3 永磁同步发电机等效电路模型
Fig.3 PMSG equivalent circuit model
经过转换后其s域模型可以表示为
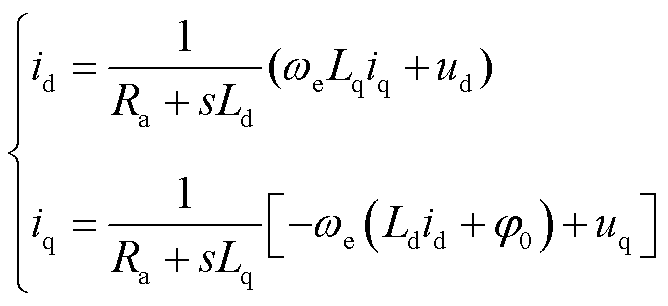 (11)
(11)
式中,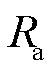 为定子电阻;
为定子电阻;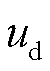 和
和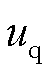 分别为发电机d轴和q轴电压; we为发电机电磁转速,
分别为发电机d轴和q轴电压; we为发电机电磁转速,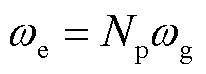 。
。
蓄电池戴维南等效电路模型如图4所示。
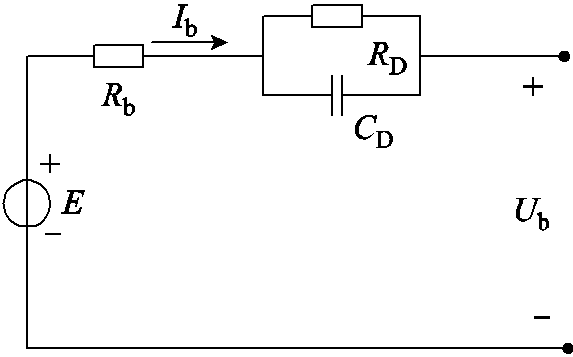
图4 蓄电池戴维南等效电路模型
Fig.4 Thevenin equivalent circuit model of the battery
蓄电池储能单元的数学模型可以表示为
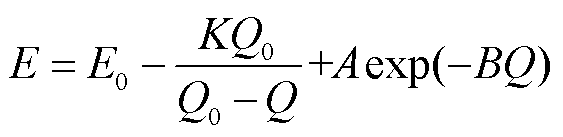 (12)
(12)
式中,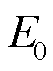 为蓄电池内电势,V;K为极化电压,V;
为蓄电池内电势,V;K为极化电压,V;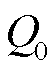 为蓄电池总容量,A·h;Q为实际蓄电池容量,
为蓄电池总容量,A·h;Q为实际蓄电池容量,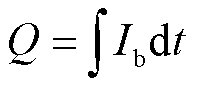 ,A·h;A为指数区域幅值;B为指数区域时间常数的倒数。
,A·h;A为指数区域幅值;B为指数区域时间常数的倒数。
在新能源低压直流配电系统中,电气系统是由基本RLC电路及整流器、斩波器等电力电子装置组成的,其基本组成元件是电阻、电容、电感及电力电子开关器件。在建立仿真系统的过程中,重点是建立有效的电力电子开关器件暂态仿真模型。本文采用相关离散电路法(Associated Discrete Circuit, ADC)模拟电力电子开关器件的动态行为,即在开关闭合时用电感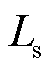 模拟,而在开关断开时用电阻串联电容(
模拟,而在开关断开时用电阻串联电容(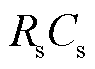 )的组合元件模拟,具体模拟方式如图5所示。不同于常用的双电阻法[27],在采用ADC法时,可以通过选取适当的
)的组合元件模拟,具体模拟方式如图5所示。不同于常用的双电阻法[27],在采用ADC法时,可以通过选取适当的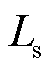 、
、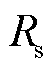 和
和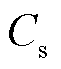 满足
满足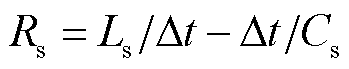 ,即可以使系统节点导纳矩阵在开关状态切换前后保持不变,从而避免系统节点导纳矩阵的在线求逆运算。
,即可以使系统节点导纳矩阵在开关状态切换前后保持不变,从而避免系统节点导纳矩阵的在线求逆运算。
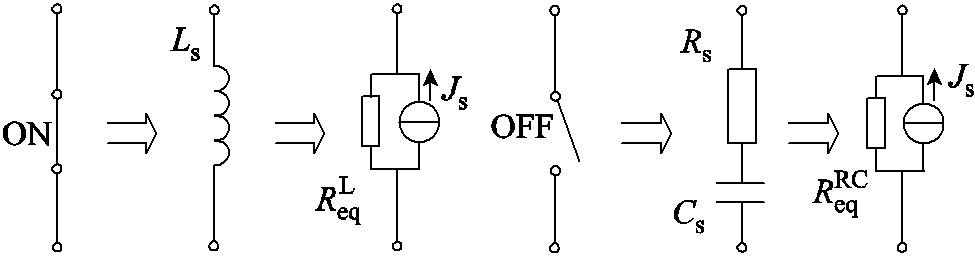
图5 不同开关状态的ADC等效电路
Fig.5 ADC equivalent circuits for different switching states
实时仿真系统的时序分配如图6所示,其中,实时仿真系统总体上被分为控制系统和电气系统两部分,控制系统和电气系统依托FPGA内部配置的嵌入式RAM完成数据交互。因控制系统中存在数据输入输出关系的环节较多,所以通常控制系统的计算时长大于电气系统的解算时长,因此,有时在控制系统的计算周期内电气系统可以解算多次。本文为了保证实时性,设定控制系统和电气系统的计算时长相同,当计算时长较短的电气系统完成解算过程后,其数据推迟至控制系统完成计算的时刻,这样持续下去即可完成整个系统的暂态仿真计算。
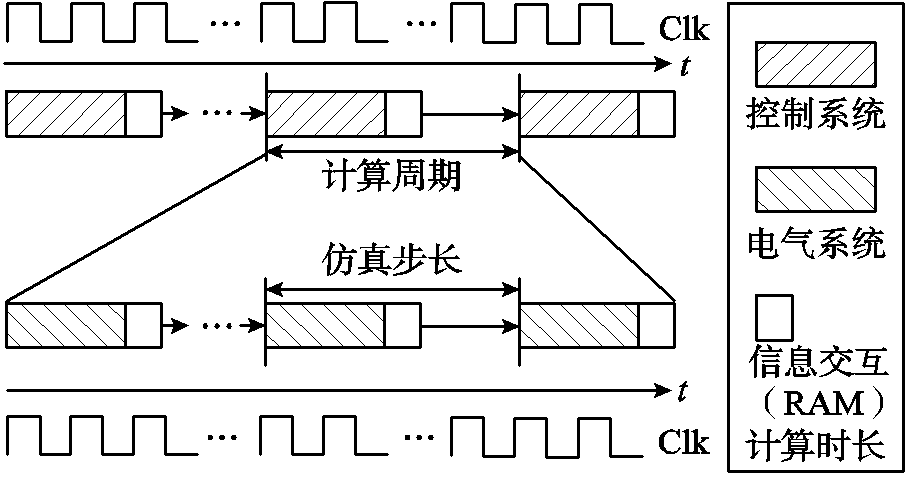
图6 仿真系统时序分配
Fig.6 Timing allocation of the simulation system
2.2.1 基于AAA方法的计算结构
新能源低压直流配电系统中包含大量具有随机性和波动性的分布式电源,实时仿真装置可以充当状态观测器或预测装置嵌入控制回路中,为高层级优化求解器实时呈现或预测系统的运行状态,以提升控制系统性能,这对基于FPGA的实时仿真装置内部硬件资源利用率提出了新的要求。
本文依托AAA理念建立了一种串并联混合计算结构以提升FPGA内部硬件资源的利用率。在该方法中,仿真系统的整体运算过程可以被分解为多个子运算,这些子运算在数据流层面有的具有数据依赖关系,而有的在空间上是完全独立的不存在任何数据依赖关系。在进行硬件结构设计的过程中充分考虑算法结构,针对已经分解的算法的硬件执行结构主要有:①两个具有数据依赖关系的子运算可以由同一运算符按照既定的数据流向以顺序求解的方式进行计算;②两个不具有数据依赖关系的子运算可以由同一运算符以任意顺序计算,也可以由不同的运算符同时计算。在上述过程中应使所设计的算法和硬件结构相匹配,才能够使所设计系统的计算性能达到最优。在设计硬件执行结构时,当采用同一运算符执行不同子运算的硬件结构时,就会形成局部串行计算的结构,会在一定程度上降低算法的计算效率,但该方式可以显著降低FPGA内部硬件资源的占用率;当使用不同的运算符同时执行不同子运算的计算方式时,可以提升系统的并行计算程度,从而提升算法的执行效率,但该方式是以牺牲FPGA内部资源占用率来换取相对较短的计算时长。因此,在建立基于FPGA的实时仿真器的过程中,应在满足可用资源上限和符合解算时长限制的分解水平之间建立一个折中方案,这就要求在该过程中做到算法与硬件协同设计,以有机结合的方式并行设计算法结构和硬件执行结构,从中找到算法和硬件执行结构的最佳结合点,通过综合分析系统算法和硬件功能以及现有资源,协同设计算法和硬件执行结构,使系统效率最佳。为具体说明AAA理念的应用方式,以控制系统中常见的PI环节为例,其s域通用形式可表示为
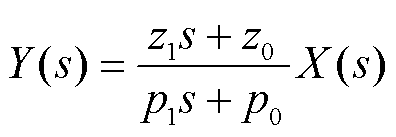 (13)
(13)
经过双线性变换后的时域表达形式为
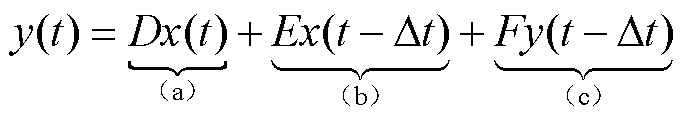 (14)
(14)
其中
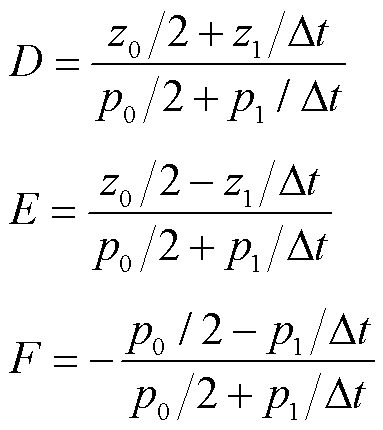
PI环节硬件执行结构如图7所示。PI环节计算过程中的浮点数运算被完全分解,底层硬件电路的执行时序由图8所示的基于有限状态机(Finite State Machine, FSM)的序列发生器在系统时钟信号的驱动下进行控制。在完成相应的计算后,其结果存储至寄存器中,以便进行下一步计算。
结合图7和图8可知,式(14)中的(a)、(b)和(c)三个乘法运算以流水线的形式由同一乘法运算符完成,其计算结果各相差一个时钟周期,相比于完全并行计算方式,在一定程度上降低了计算效率,但该计算过程节省了两个乘法运算符,提升了FPGA内部硬件资源的利用率。
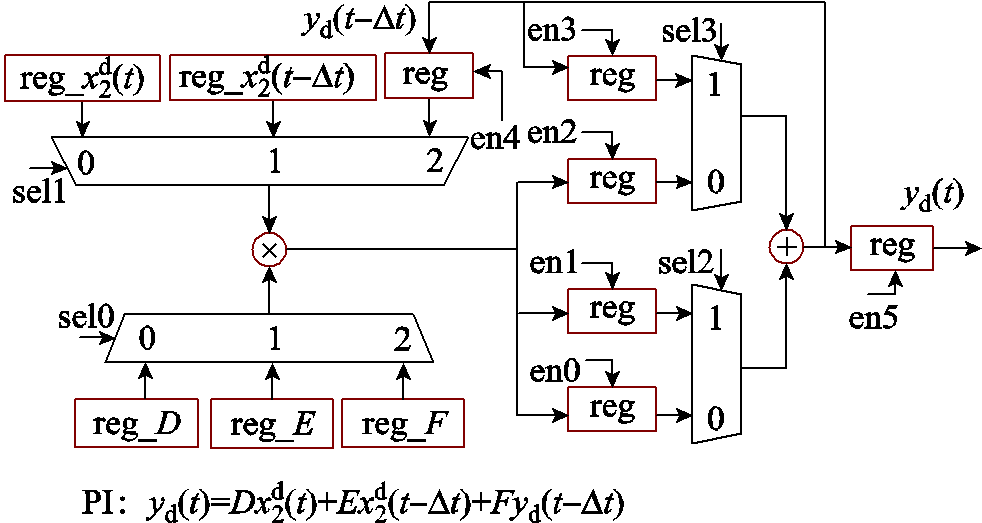
图7 PI环节硬件执行结构
Fig.7 PI unit hardware execution structure
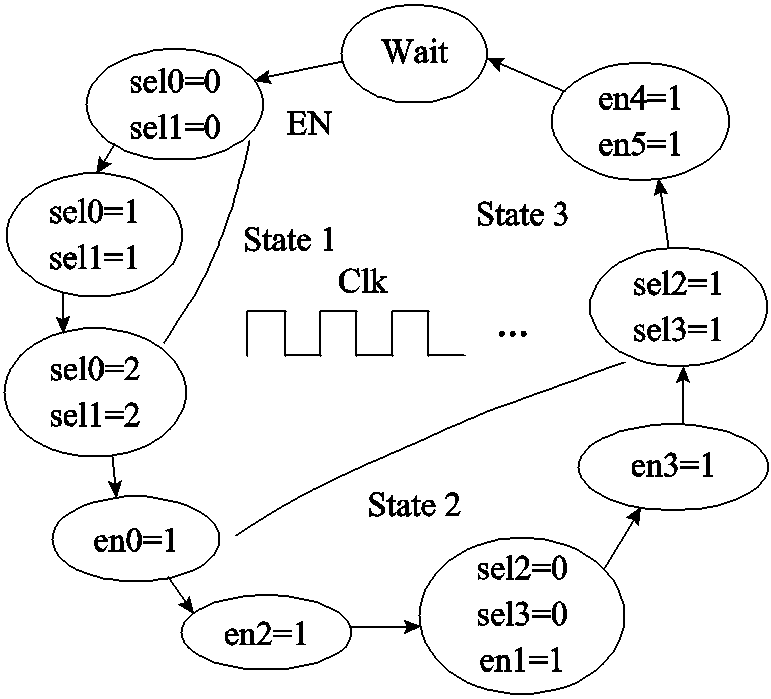
图8 基于FSM的PI环节序列发生器
Fig.8 Sequencer of PI unit based on FSM
2.2.2 节点电导矩阵计算结构
在节点分析法的框架下,电气系统节点电导矩阵实时解算器是核心模块之一。在每个仿真步长内,该解算器都要求解由节点电导矩阵G、节点电压向量u和支路电流向量i形成的线性方程组,其求解速度和求解精度制约着实时仿真器仿真性能的提高,而逐步增加的仿真对象系统规模对线性方程组的求解能力提出了更高的要求。
考虑电力系统节点电导矩阵G具有稀疏性,为了充分利用FPGA的并行计算性能的同时降低片上存储资源的占用率,本文设计了一种基于LDU分解的节点电导矩阵并行求解方法,其数学表示如式(15)所示。
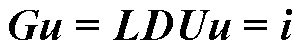 (15)
(15)
式中,L、D和U分别为矩阵G经分解后得到的下三角矩阵、对角矩阵和上三角矩阵。
求解过程主要包括线下预处理与线上实时求解两个阶段,其解算器结构如图9所示,其中预处理阶段在上位机中完成,目的是降低FPGA线上实时求解任务的难度,从而提升线上实时求解的效率。
主要步骤有:
1)系统电导矩阵G主元重新选取,避免在进行数据分解的过程中出现误差过大的现象;主元重新选取的基本方法是通过初等变换将矩阵元素进行重新排列,使矩阵对角线元素为矩阵每列(或每行)绝对值最大的值。对于给定的电导矩阵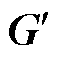 ,其主元选取过程可表示为
,其主元选取过程可表示为
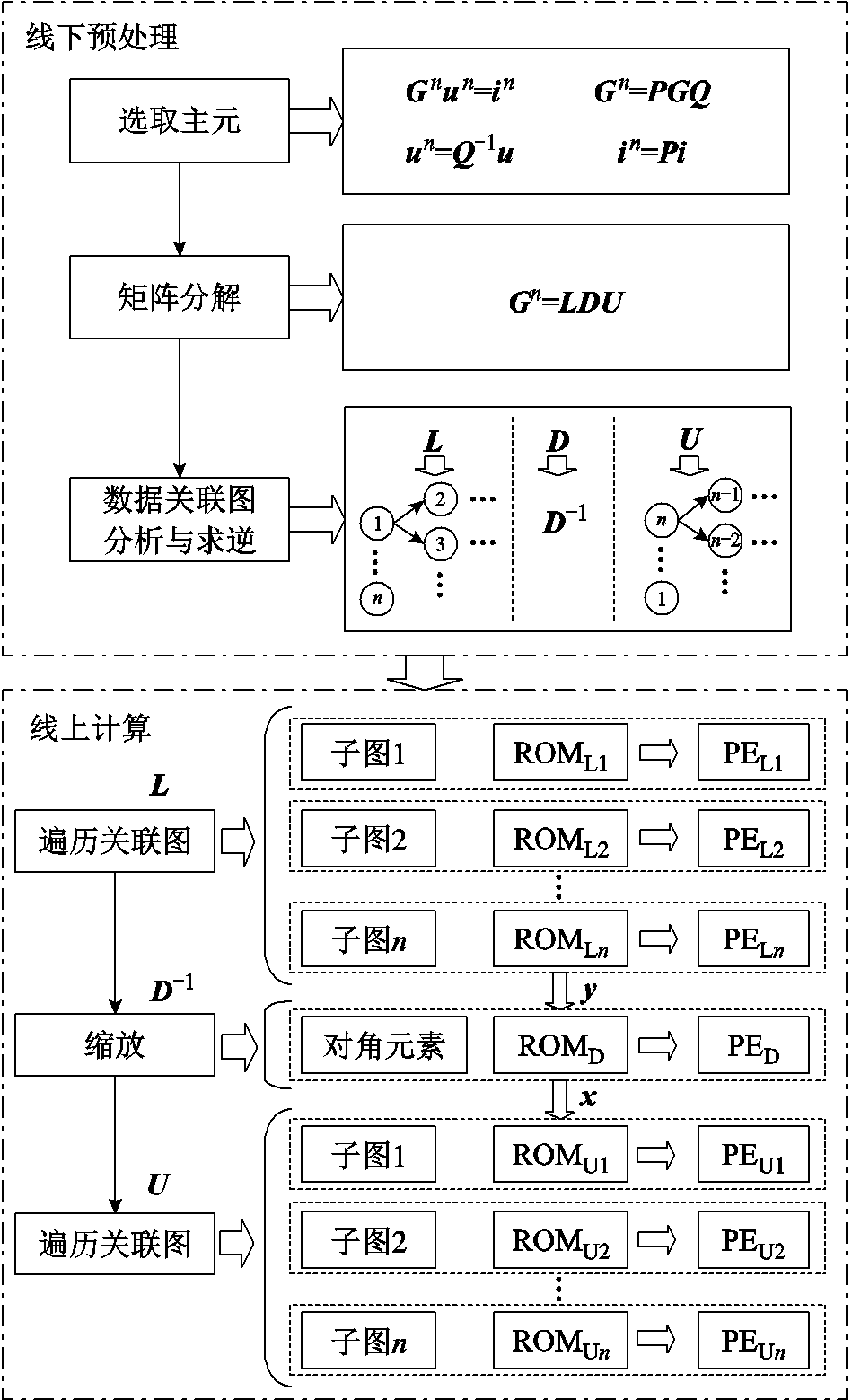
图9 实时解算器的求解框架
Fig.9 Solving framework for the real-time solver
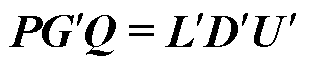 (16)
(16)
式中,P和Q分别为行变换和列变换矩阵。经过主元选取之后,系统的节点电导矩阵方程可表示为
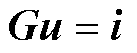 (17)
(17)
式中,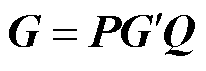 为主元重新选取之后的节点电导矩阵;u和i分别为元素重新排序后的节点电压和输入电流向量,其具体形式可表示为
为主元重新选取之后的节点电导矩阵;u和i分别为元素重新排序后的节点电压和输入电流向量,其具体形式可表示为
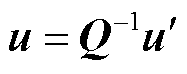 (18)
(18)
在线下预处理阶段,节点电导矩阵、节点电压和输入电流向量进行了重新排序,在FPGA完成线上实时计算之后,存储的节点电压输入电流向量的地址向量也需要重新排序,以保证求解过程稳定性。其地址重新排序方式与式(18)和式(19)相对应。
2)电导矩阵G的LDU分解,将G分解为单位下三角矩阵L、对角矩阵D和上三角矩阵U三个矩阵相乘的形式。
3)对L与U进行内部数据关联图分析并求取对角矩阵D的逆矩阵。首先,将求解过程中L与U内部数据之间的依赖关系以有向无环图(DAG)的形式表示;然后,存储其中的非零元素到片上ROM中,而在存储D时存储的是D-1,这样可以在实时计算时变资源消耗较大的除法运算为相对较小的乘法运算,提升计算能效。
经过LDU分解后,节点电导矩阵方程的求解过程可表示为
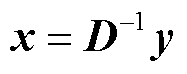 (21)
(21)
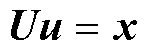 (22)
(22)
矩阵L与U的主对角线为1并且具有稀疏性,其求解顺序关联性可用基于DAG的数据关联图G(V, E)表示,其中V是所有节点的集合,E为体现矩阵中非零元素的有向边的集合,集合中的每条有向边表示相邻节点i和节点j之间具有求解依赖关系。例如,矩阵L中的非零元素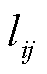 表示的节点i和节点j之间的求解依赖关系为:在计算节点i的过程中需要预先计算节点j的具体数值,即节点j是节点i的前驱变量,节点i是节点j的后继变量。以公式(20)的求解为例,假定L的维数为9,其具体形式及其求解数据关联图如图10所示。
表示的节点i和节点j之间的求解依赖关系为:在计算节点i的过程中需要预先计算节点j的具体数值,即节点j是节点i的前驱变量,节点i是节点j的后继变量。以公式(20)的求解为例,假定L的维数为9,其具体形式及其求解数据关联图如图10所示。
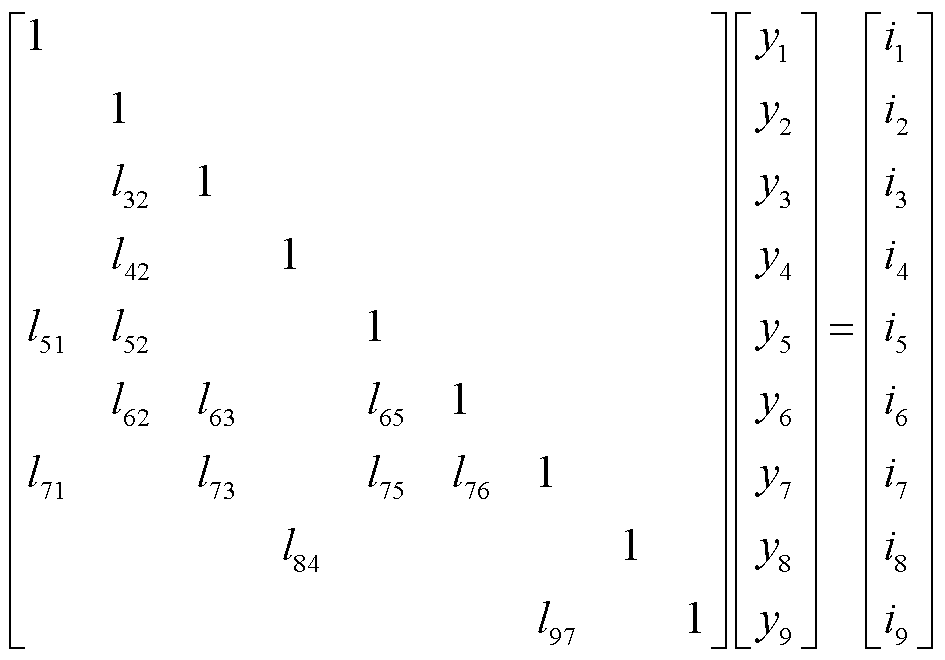
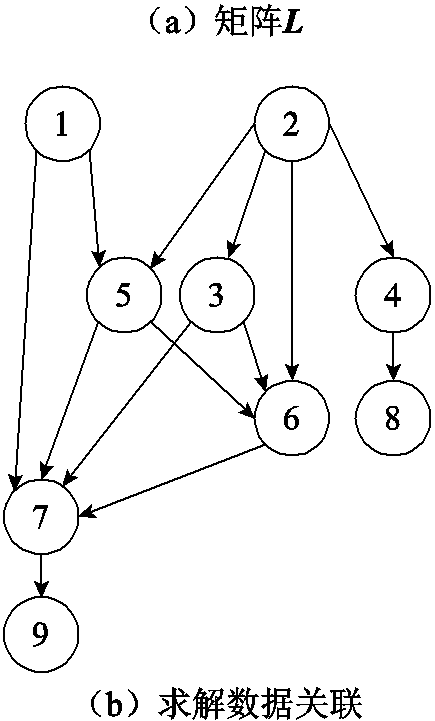
图10 矩阵L及其求解数据关联图
Fig.10 Matrix L and its solution data correlation diagram
经过整理可得向量y中变量的计算公式为
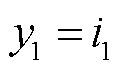 (23)
(23)
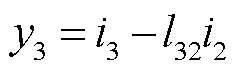 (25)
(25)
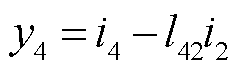 (26)
(26)
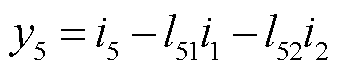 (27)
(27)
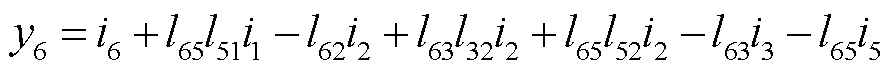 (28)
(28)
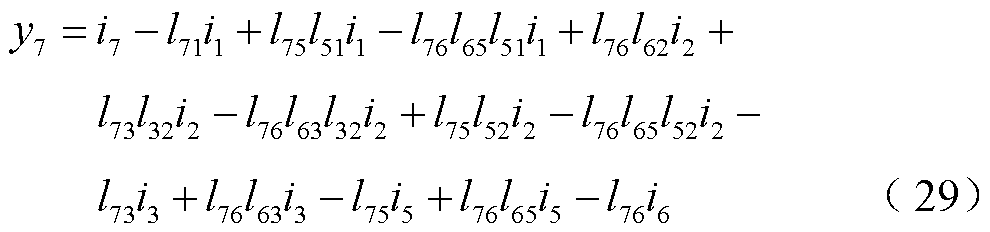
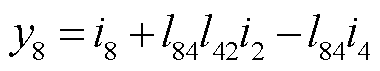 (30)
(30)
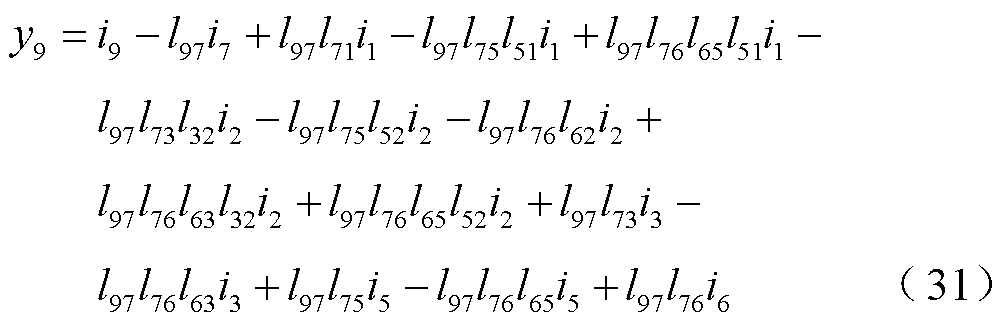
通过观察可知,向量y中的变量计算公式的首项为向量i中的对应项,而其他项可表示为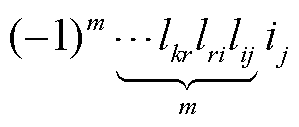 。
。
结合上述变量计算公式可以将图10中所示的总求解顺序关联图分解为向量i中的对应项为根节点,其他后续节点作为子节点,数量为节点总数的多个子图,并且每个子图可按照节点分布和计算顺序划分为多个计算层级。
考虑到FPGA线上实时求解是由各硬件处理单元(Processing Element, PE)以并行方式遍历预处理阶段构建的DAG,并顺序求解式(20)~式(22)完成。而当仿真系统的规模很大时,得到的各独立子图中所包含的节点数目和计算层级可能相差悬殊,若将各独立子图直接分配给各PE处理,可能会导致并行PE之间计算负荷的严重不平衡。当计算负荷较小的PE完成计算任务之后需要等待其他计算负荷较大的PE,这样会导致整体并行计算效能的下降和硬件资源的浪费,因为每调用一个PE都会占用一定的硬件资源。因此,有必要对分解后的子图进行重新整合,在FPGA内部形成多个求解计算区域,各区域的计算任务大致平衡从而降低FPGA内部硬件资源占用率。综合考虑上述所有因素之后,计算子图及求解区域的划分情况如图11所示。每个子图可按照节点分布和计算顺序划分为多个计算层级,同时计算子图中的具有多个扇入项的子节点被分解为数量为扇入项数目的多个分节点,其后续节点也被分解为相同数目的多个分节点,如在子图1中节点7的扇入项为3,所以子节点7被分解为7a、7b和7c三个分节点,并且其后续子节点9也被分解为9a、9b和9c三个分节点,分解后的分节点作为对应子节点的部分值被分别存储用以计算向量y。其中,每条有向边连接的不同节点之间的数据依赖关系可表示为
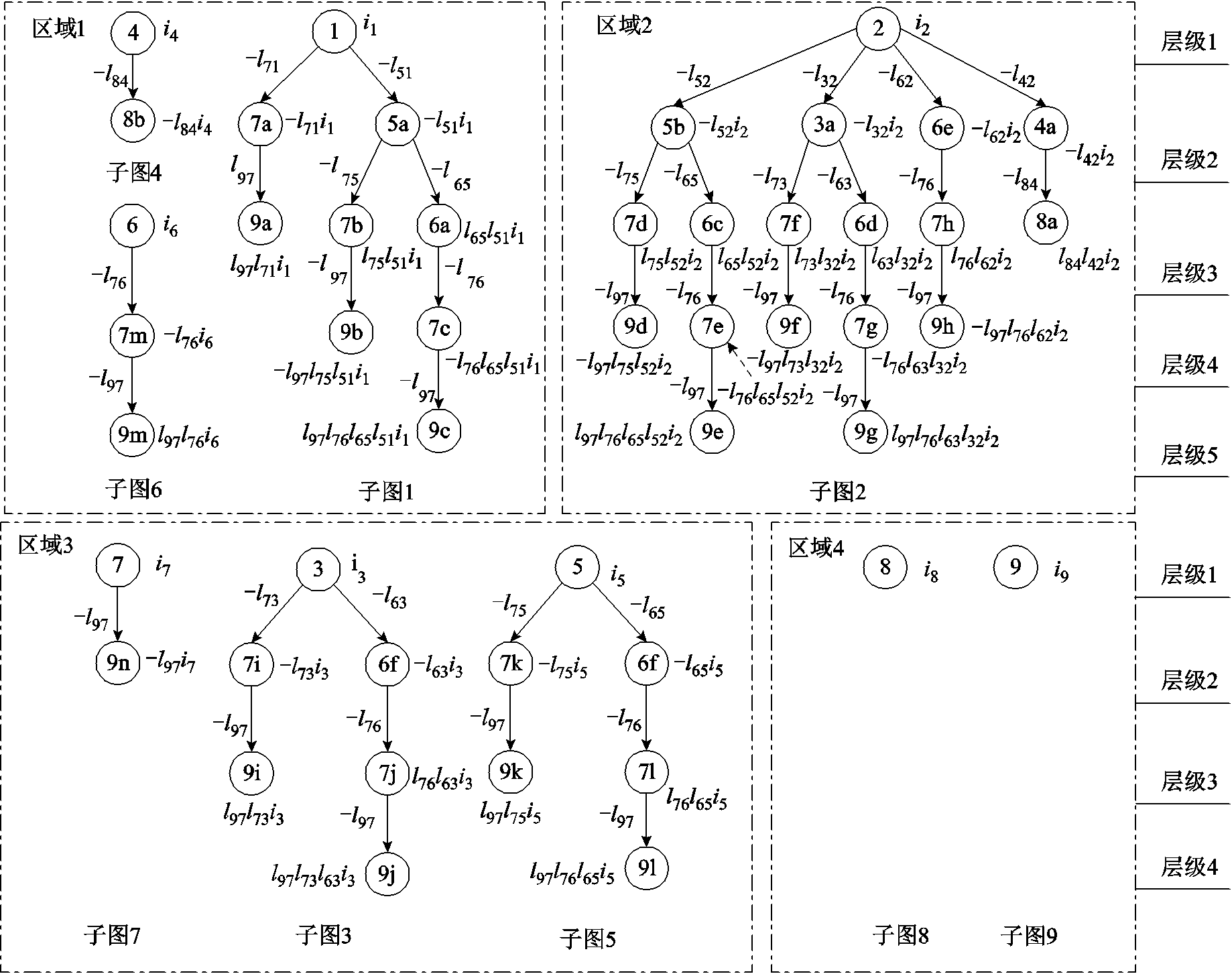
图11 FPGA求解区域划分图
Fig.11 Diagram of the solution area division of the FPGA
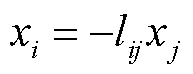 (32)
(32)
重组后的区域1、3和4中包含多个原子图,其中区域4中只包含两个根节点,在FPGA进行实时计算的过程中并不会分配PE,而是直接将数据存储,其他区域会在FPGA内部单独分配PE,按照计算层级逐层进行实时计算。
计算区域重新划分之后,矩阵中的非零数据以列压缩存储形式存储于FPGA的片上ROM中以供调用。当计算过程完成后,便会得到新计算周期的各节点电压值。基于FPGA的实时求解模块硬件结构和完成浮点数运算的PE的通用结构如图12所示。其中,PE的种类有完成乘法运算的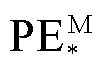 和加法运算的
和加法运算的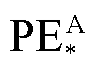 两种,其上标M和A分别指代乘法和加法运算,其下标“*”除体现矩阵运算的环节之外还表明了该环节所包含的PE的总数。在计算
两种,其上标M和A分别指代乘法和加法运算,其下标“*”除体现矩阵运算的环节之外还表明了该环节所包含的PE的总数。在计算![]() 和
和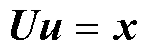 环节中,PE的总数分别为X和Y,而X和Y分别表示的是在求解顺序关联子图重新划分后形成的计算区域的数量,而在计算
环节中,PE的总数分别为X和Y,而X和Y分别表示的是在求解顺序关联子图重新划分后形成的计算区域的数量,而在计算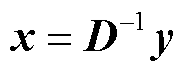 过程中,PE的总数可根据系统对模块计算时长和资源消耗等具体要求进行设定,本文选定其总数为系数矩阵的维数N。在每个PE中,除了包含浮点数运算符之外,还包括一定数目的寄存器和多路数据选择器,其中寄存器负责寄存中间数据,多路数据选择器根据计算顺序对运算符的输入端赋值。计算开始时预先存储在ROM中的数据在全局控制器的调度下由数据分配器经“memory bus” 总线分配给各个PE以完成相应的浮点数运算。每一级PE完成计算之后所得数据需经各级“memory bus”总线分配给下一级PE,在所有PE完成计算之后,所得数据需经过“u memory bus”总线实现电压向量u的寻址和重排序后,方可输出到其余模块用于更新节点电压和支路电流。
过程中,PE的总数可根据系统对模块计算时长和资源消耗等具体要求进行设定,本文选定其总数为系数矩阵的维数N。在每个PE中,除了包含浮点数运算符之外,还包括一定数目的寄存器和多路数据选择器,其中寄存器负责寄存中间数据,多路数据选择器根据计算顺序对运算符的输入端赋值。计算开始时预先存储在ROM中的数据在全局控制器的调度下由数据分配器经“memory bus” 总线分配给各个PE以完成相应的浮点数运算。每一级PE完成计算之后所得数据需经各级“memory bus”总线分配给下一级PE,在所有PE完成计算之后,所得数据需经过“u memory bus”总线实现电压向量u的寻址和重排序后,方可输出到其余模块用于更新节点电压和支路电流。
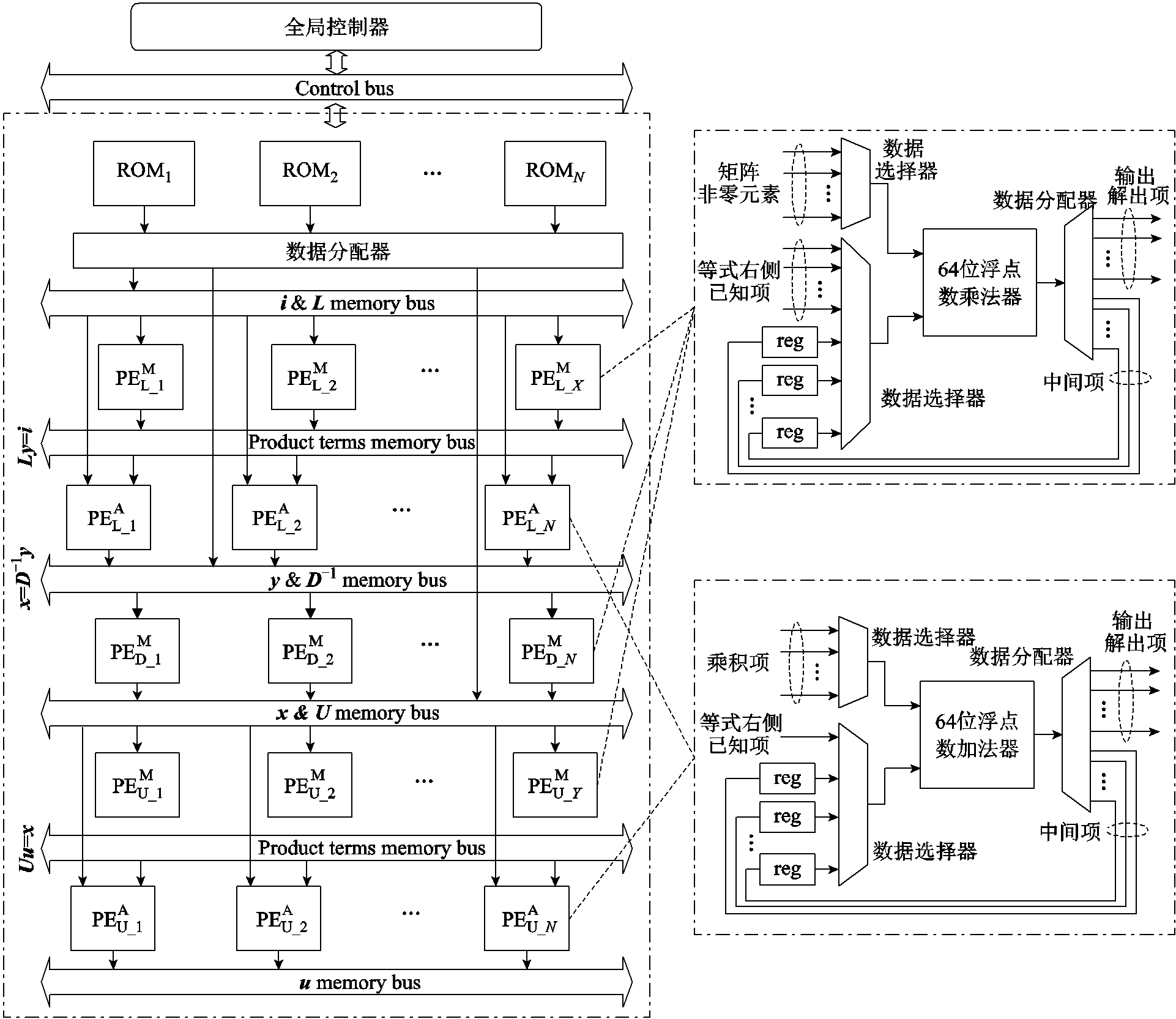
图12 基于FPGA的实时求解模块硬件设计
Fig.12 FPGA-based real-time solution module hardware design
本文采用的是Altera Stratix V系列的5SGSM- D5K2F40C2N及其配套开发板,低压直流配电系统的主体结构如图13所示。其中,小型分布式风力发电系统、蓄电池储能系统及分布式光伏发电系统通过电能转换装置并联在直流母线上,同时直流母线经网联转换器与交流母线连接,所有参数取值具体见表1。分布式光伏发电系统和小型分布式风力发电系统工作在最大功率跟踪模式,储能系统负责维持母线电压。母线电压参考值为750 V,负载额定功率为19 kW,光伏发电系统最大功率为9.3 kW,小型分布式风力发电系统容量为11 kW,中间母线电压参考值为200 V,初始磁链为 0.475 Wb,蓄电池初始荷电状态(State of Charge, SOC)为0.8,中间电压参考值为550 V。FPGA仿真器的时钟频率为140 MHz,其仿真步长和PSCAD/EMTDC仿真步长均为2 μs,仿真时长均定为3 s。此外,本文中的PSCAD/EMTDC软件所依托的上位机计算核心为Intel core (TM) i5-3210M CPU @2.50 GHz,内存为6 GB RAM。
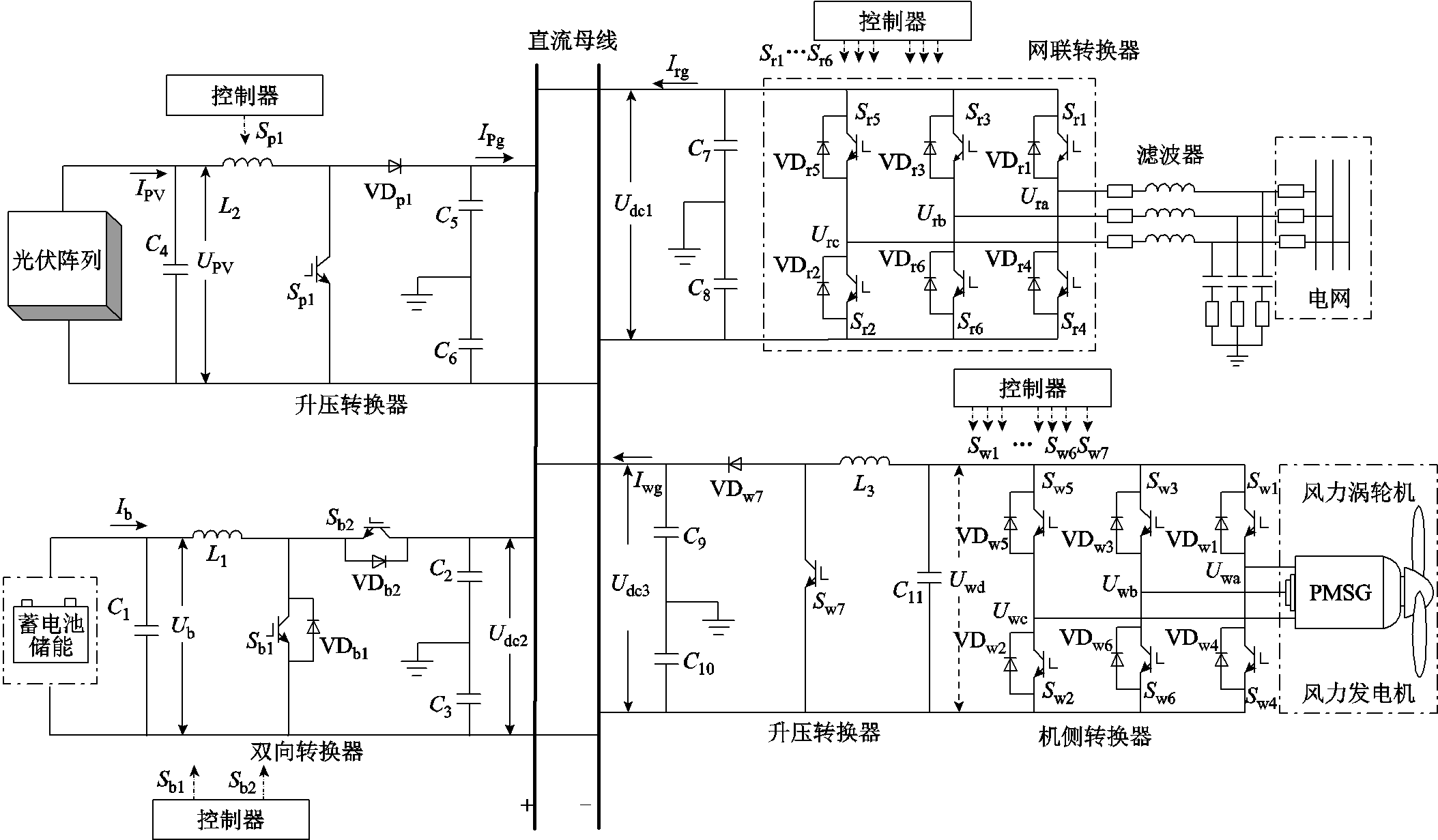
图13 风/光/储低压直流配电系统主体结构
Fig.13 Structure of wind/solar/storage low-voltage DC distribution system
表1 系统参数取值
Tab.1 The values of system parameters
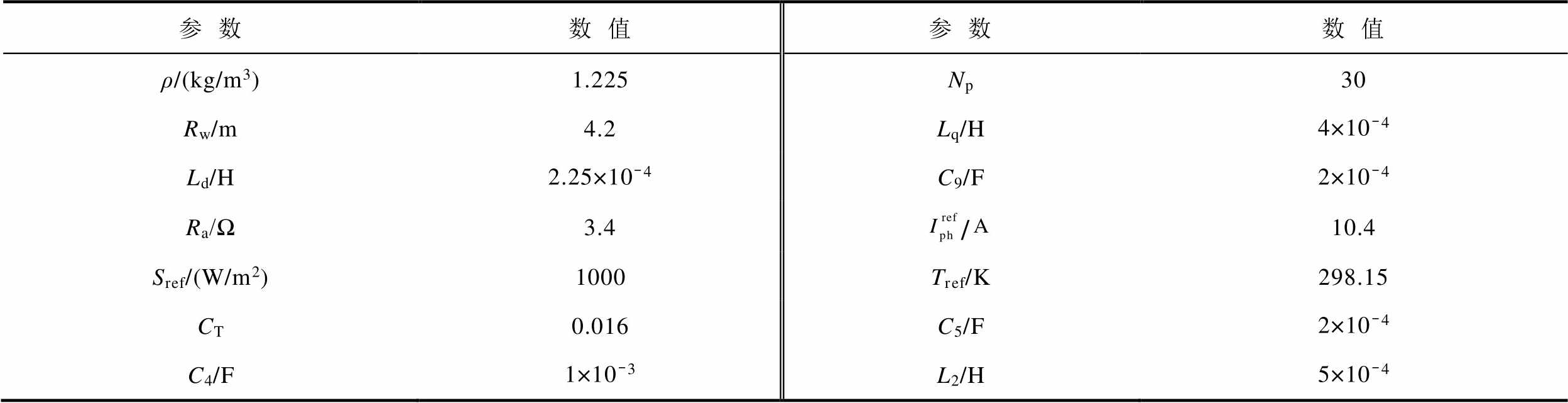
参数数值参数数值 ρ/(kg/m3)1.225Np30 Rw/m4.2Lq/H4×10-4 Ld/H2.25×10-4C9/F2×10-4 Ra/Ω3.410.4 Sref/(W/m2)1000Tref/K298.15 CT0.016C5/F2×10-4 C4/F1×10-3L2/H5×10-4
(续)
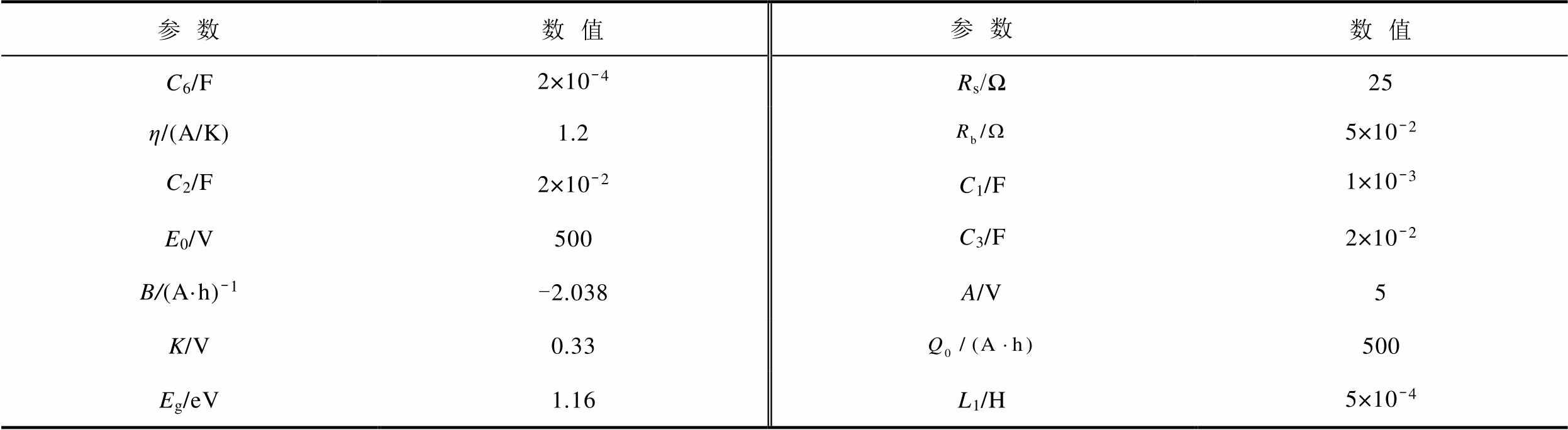
参数数值参数数值 C6/F2×10-4Rs/Ω25 η/(A/K)1.25×10-2 C2/F2×10-2C1/F1×10-3 E0/V500C3/F2×10-2 B/(A·h)-1-2.038A/V5 K/V0.33500 Eg/eV1.16L1/H5×10-4
1)测试了实时仿真装置在光照条件改变时的计算性能,假定系统运行到2.0 s时,光照强度由初始值1 kW/m2降为600 W/m2,FPGA与仿真软件PSCAD/EMTDC的运行结果如图14所示。由图14所示的结果可知,在光伏发电系统输出电流降低时,直流母线电压随之降低,而蓄电池增大电流输出以维持母线电压稳定。FPGA与PSCAD/EMTDC的仿真测试结果基本一致,验证了所建立的实时仿真装置的准确性。此外,在该暂态场景中,FPGA的仿真计算时间和物理时钟严格同步为3 s,而经统计PSCAD/EMTDC的仿真计算时长为82.5 s。
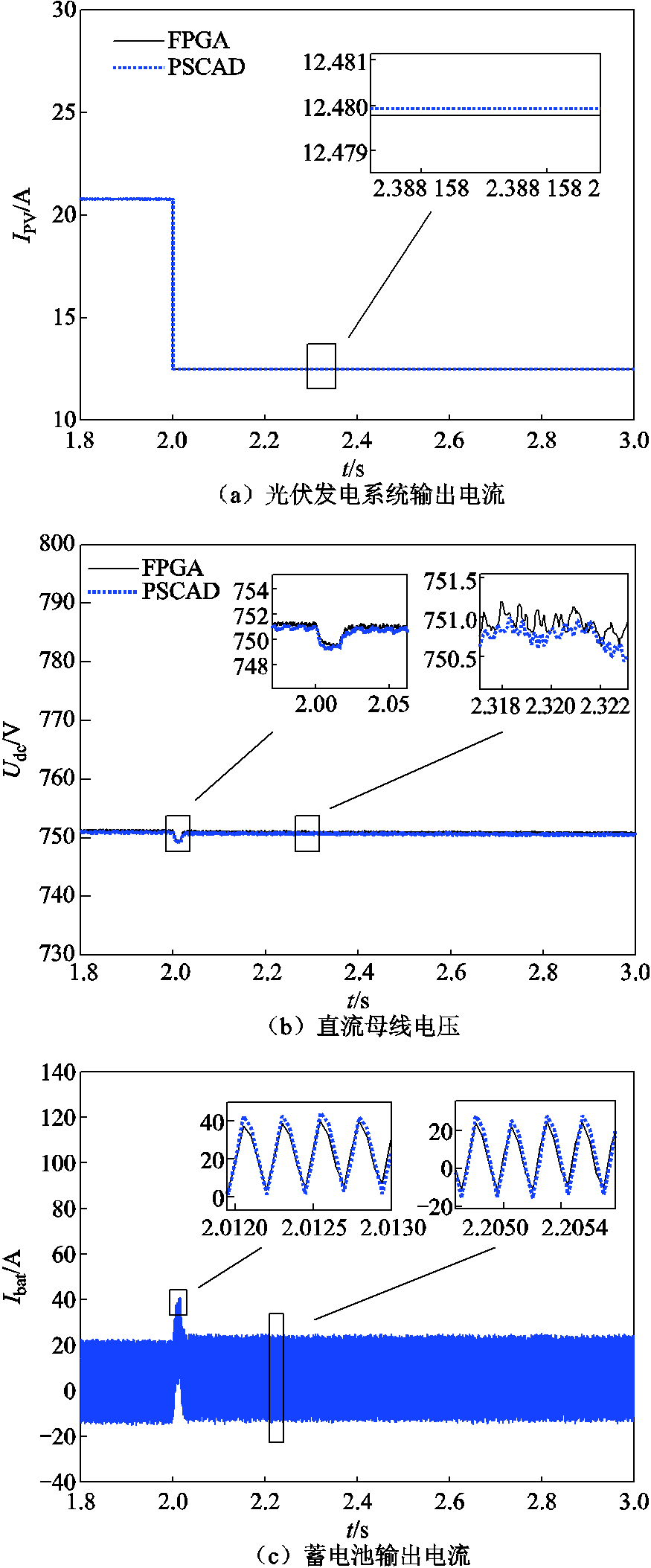
图14 FPGA与PSCAD运行结果对比
Fig.14 Comparison of FPGA and PSCAD operating results
2)测试了仿真系统在外部风速改变时的仿真性能,设定风力机的工作风速在2 s时由9 m/s降低至8 m/s,FPGA与商业软件PSCAD/EMTDC的仿真结果如图15所示。由图15可知,在外部风速降低时,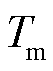 随之降低,风力发电系统输出电流幅值降低,减少功率输出。因此,直流母线电压
随之降低,风力发电系统输出电流幅值降低,减少功率输出。因此,直流母线电压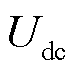 也随之降低。在该场景中,FPGA与PSCAD/EMTDC的仿真测试结果基本一致,且相对误差在0.2%以内,进一步验证了所建立的FPGA模型和实时仿真系统的准确性。此外,在该暂态场景中,FPGA的仿真计算时间为3 s,而经统计PSCAD/EMTDC的仿真计算时长为85.7 s。
也随之降低。在该场景中,FPGA与PSCAD/EMTDC的仿真测试结果基本一致,且相对误差在0.2%以内,进一步验证了所建立的FPGA模型和实时仿真系统的准确性。此外,在该暂态场景中,FPGA的仿真计算时间为3 s,而经统计PSCAD/EMTDC的仿真计算时长为85.7 s。
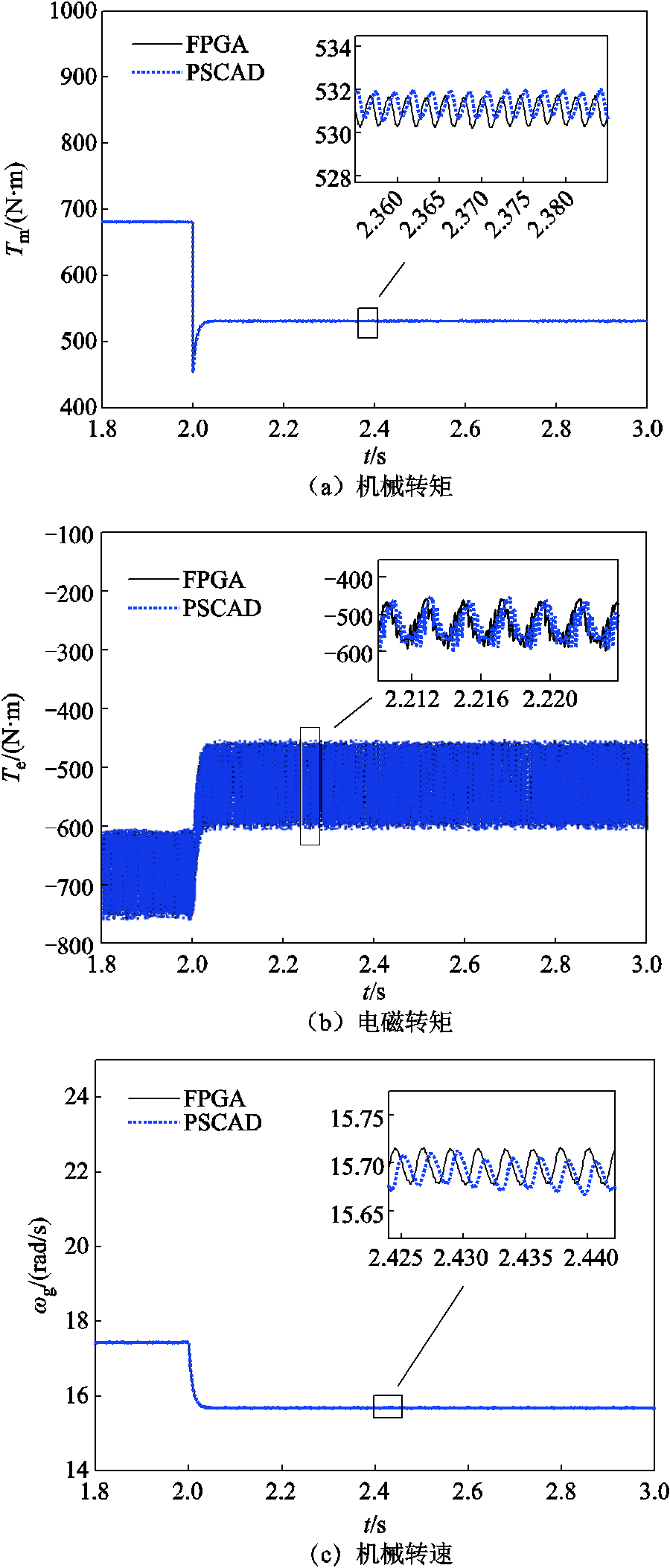

图15 FPGA与PSCAD运行结果对比
Fig.15 Comparison of FPGA and PSCAD operating results
3.2.1 内部硬件资源消耗
直流配电系统算例集成了多种分布式发电系统,本文所提硬件计算结构与传统全并行硬件计算结构的FPGA内部资源占用情况见表2。相比于传统结构设计,本文所提出的硬件计算结构节约了FPGA内部约21%的逻辑资源、37%的DSP 18×18专用乘法器资源和7%的存储器资源。相比于传统计算结构来说节省了大量的计算资源,大幅提升了其利用率,尤其是较为稀少的DSP模块,这主要得益于在AAA计算方法中对FPGA内部的运算符的高效利用。此外,此仿真系统依托半定制集成电路,具有设计灵活、可重构的优势,降低了仿真成本。
表2 内部资源消耗情况对比
Tab.2 Comparison of internal resource consumption (%)

硬件设计逻辑资源(172 600)DSP模块(1 590)存储资源(41 246 720) 本文设计511738 传统设计725445
3.2.2 时钟消耗情况
在仿真步长均设定为2 μs时,本文所提的硬件计算结构与传统全并行硬件计算结构的时钟消耗情况对比见表3。相比于电气系统,控制系统中数据存在依赖关系的运算较多,所以控制系统消耗的时钟数也较多。当采用传统并行计算结构时,仿真计算过程中不存在数据依赖关系的运算可通过调用不同的运算符以并行的方式完成,从而可以在一定程度上降低对系统时钟的消耗。结合表2可知,虽然本文所提的计算结构因在局部采用了串行的计算方式,从而在一定程度上导致所需系统时钟数量的升高,但直接大幅降低了FPGA内部硬件资源的占用率,尤其是总数稀少的DSP资源。因为FPGA内部的各类运算资源的总数是有限的,所以对其内部硬件资源的高效利用就显得十分重要。本文所提的硬件计算结构提升了对FPGA内部硬件资源的使用效率,以及实时仿真装置的系统集成度和其在面对较大规模仿真系统时对高维线性方程组的求解能力。
表3 时钟消耗情况对比
Tab.3 Comparison of clock consumption

硬件设计控制系统消耗时钟周期个数电气系统消耗时钟周期个数 本文设计276208 传统设计255173
为保障新能源低压直流配电系统的安全高效运行,开发高精度、小步长的实时仿真工具成为了必然趋势。本文面向新能源低压直流配电系统的暂态实时仿真需求,基于FPGA硬件计算平台,开发了一种包含小型分布式风力发电、光伏发电及蓄电池储能单元的新能源低压直流配电系统暂态实时仿真器,所得结论如下:
1)建立了分布式发电单元和典型控制回路实时仿真模块,在充分利用FPGA的并行计算特性的同时结合AAA理念建立了底层模块串并联混合求解结构,相比于传统全并行计算设计节约了FPGA内部约19%的逻辑资源、37%的DSP 18×18专用乘法器资源和7%的存储器资源,提升了所开发的实时仿真装置在仿真规模上的优势。
2)在节点分析法的框架下,建立了一种结合矩阵LDU分解和DAG的电气系统节点电导矩阵并行求解方法,提升了FPGA的动态计算效率和对高维线性方程组的求解能力。
3)建立了仿真器内部电气系统和控制系统的全并行求解架构,开发了基于FPGA的新能源低压直流配电系统暂态实时仿真器。该实时仿真结构为集成更多种类分布式电源的直流配电系统小步长实时仿真奠定了基础。
参考文献
[1] 江道灼, 郑欢. 直流配电网研究现状与展望[J]. 电力系统自动化, 2012, 36(8): 98-104.
Jiang Daozhuo, Zheng Huan. Research status and developing prospect of DC distribution network[J]. Automation of Electric Power Systems, 2012, 36(8): 98-104.
[2] 庄莹, 裴玮, 刘子奇, 等. 提升低压直流配电稳定性的时滞模型预测附加控制[J]. 电工技术学报, 2023, 38(12): 3248-3263.
Zhuang Ying, Pei Wei, Liu Ziqi, et al. Time-delay model predictive additional control strategy to improve the stability of low-voltage DC distribution system[J]. Transactions of China Electrotechnical Society, 2023, 38(12): 3248-3263.
[3] 李博通, 刘涛, 杨昕陆, 等. 故障自清除型直流配电网新型双极短路故障元件识别方法[J]. 电工技术学报, 2022, 37(17): 4423-4434.
Li Botong, Liu Tao, Yang Xinlu, et al. New fault element identification method of bipolar short-circuit fault in DC distribution network with fault self-clearing[J]. Transactions of China Electrotechnical Society, 2022, 37(17): 4423-4434.
[4] 郭慧, 汪飞, 顾永文, 等. 基于电压分层控制的直流微电网及其储能扩容单元功率协调控制策略[J]. 电工技术学报, 2022, 37(12): 3117-3131.
Guo Hui, Wang Fei, Gu Yongwen, et al. Coordinated power control strategy for DC microgrid and storage expansion unit based on voltage hierarchical control[J]. Transactions of China Electrotechnical Society, 2022, 37(12): 3117-3131.
[5] 林莉, 范米, 林雨露, 等. 基于不确定与扰动估计器的直流配电网电压鲁棒控制[J]. 电工技术学报, 2023, 38(17): 4657-4671.
Lin Li, Fan Mi, Lin Yulu, et al. Uncertainty and disturbance estimator-based control for voltage robust controller in DC distribution network[J]. Transactions of China Electrotechnical Society, 2023, 38(17): 4657-4671.
[6] 杨立敏, 朱艺颖, 郭强, 等. 基于HYPERSIM的柔性直流输电系统数模混合仿真建模及试验[J]. 电网技术, 2020, 44(11): 4055-4062.
Yang Limin, Zhu Yiying, Guo Qiang, et al. Modelling and validation of digital-analog hybrid simulation for VSC-HVDC system based on HYPERSIM[J]. Power System Technology, 2020, 44(11): 4055-4062.
[7] 杨玲. 基于RTDS的大规模交直流电力系统仿真建模研究[D]. 保定: 华北电力大学, 2010.
Yang Ling. Research on simulation and modeling of large scale AC/DC power systems based on RTDS[D]. Baoding: North China Electric Power University, 2010.
[8] 张建伟, 张然, 龚栋梁, 等. 基于RTDS的配电网单相接地选线方法验证[J]. 电气技术, 2018, 19(10): 40-43, 49.
Zhang Jianwei, Zhang Ran, Gong Dongliang, et al. The verification based on RTDS of fault line selection method for distribution power system[J]. Electrical Engineering, 2018, 19(10): 40-43, 49.
[9] 胡涛, 朱艺颖, 张星, 等. 全数字实时仿真装置与物理仿真装置的功率连接技术[J]. 电网技术, 2010, 34(1): 51-55.
Hu Tao, Zhu Yiying, Zhang Xing, et al. Power connection technology for full-digital real-time simulator and analogue simulator[J]. Power System Technology, 2010, 34(1): 51-55.
[10] Khazaei J, Miao Zhixin, Piyasinghe L, et al. Real-time digital simulation-based modeling of a single-phase single-stage PV system[J]. Electric Power Systems Research, 2015, 123: 85-91.
[11] Srinivasan A, Moirangthem J, Panda S K, et al. Hardware-in-loop control of a standalone microgrid[C]//2019 IEEE International Conference on Sustainable Energy Technologies and Systems (ICSETS), Bhubaneswar, India, 2019: 365-370.
[12] 付浩, 李鹏, 富晓鹏, 等. 面向多FPGA实时仿真器的资源优化配置方法[J]. 电力系统自动化, 2023, 47(11): 88-100.
Fu Hao, Li Peng, Fu Xiaopeng, et al. Optimal resource allocation method for real-time simulator based on multiple field programmable gate arrays[J]. Automation of Electric Power Systems, 2023, 47(11): 88-100.
[13] 李子润, 徐晋, 汪可友, 等. 电力电子换流器离散小步合成实时仿真模型[J]. 电工技术学报, 2022, 37(20): 5267-5277.
Li Zirun, Xu Jin, Wang Keyou, et al. A discrete small-step synthesis real-time simulation model for power converters[J]. Transactions of China Electrotechnical Society, 2022, 37(20): 5267-5277.
[14] Dagbagi M, Hemdani A, Idkhajine L, et al. ADC-based embedded real-time simulator of a power converter implemented in a low-cost FPGA: application to a fault-tolerant control of a grid-connected voltage-source rectifier[J]. IEEE Transactions on Industrial Electronics, 2016, 63(2): 1179-1190.
[15] Vanderbauwhede W, Benkrid K. High-Performance Computing Using FPGAs[M]. New York, NY: Springer, 2013.
[16] Lee J S, Choi G. Modeling and hardware-in-the-loop system realization of electric machine drives—a review[J]. CES Transactions on Electrical Machines and Systems, 2021, 5(3): 194-201.
[17] Lin Ning, Dinavahi V. Dynamic electro-magnetic-thermal modeling of MMC-based DC–DC converter for real-time simulation of MTDC grid[J]. IEEE Transactions on Power Delivery, 2018, 33(3): 1337-1347.
[18] 朱建鑫, 胡海兵, 陆道荣, 等. 应用于级联STATCOM的高精度低成本全FPGA实时仿真模型研究[J]. 电工技术学报, 2019, 34(4): 777-785.
Zhu Jianxin, Hu Haibing, Lu Daorong, et al. The research on fully FPGA-based real-time simulation with high fidelity and low cost for the cascaded STATCOM[J]. Transactions of China Electrotechnical Society, 2019, 34(4): 777-785.
[19] 郝琦, 葛兴来, 宋文胜, 等. 电力牵引传动系统微秒级硬件在环实时仿真[J]. 电工技术学报, 2016, 31(8): 189-198.
Hao Qi, Ge Xinglai, Song Wensheng, et al. Microsecondhardware-in-the-loop real-time simulation of electrical traction drive system[J]. Transactions of China Electrotechnical Society, 2016, 31(8): 189-198.
[20] 肖帅, 孙建波, 耿华, 等. 基于FPGA实现的可变模全数字锁相环[J]. 电工技术学报, 2012, 27(4): 153-158.
Xiao Shuai, Sun Jianbo, Geng Hua, et al. FPGA based ratio changeable all digital phase-locked-loop[J]. Transactions of China Electrotechnical Society, 2012, 27(4): 153-158.
[21] 王成山, 丁承第, 李鹏, 等. 基于FPGA的配电网暂态实时仿真研究(一): 功能模块实现[J]. 中国电机工程学报, 2014, 34(1): 161-167.
Wang Chengshan, Ding Chengdi, Li Peng, et al. Real-time transient simulation for distribution systems based on FPGA, part I: module realization[J]. Proceedings of the CSEE, 2014, 34(1): 161-167.
[22] 王成山, 丁承第, 李鹏, 等. 基于FPGA的配电网暂态实时仿真研究(二): 系统架构与算例验证[J]. 中国电机工程学报, 2014, 34(4): 628-634.
Wang Chengshan, Ding Chengdi, Li Peng, et al. Real-time transient simulation for distribution systems based on FPGA, part Ⅱ: system architecture and algorithm verification[J]. Proceedings of the CSEE, 2014, 34(4): 628-634.
[23] Cardenas A, Guzman C, Agbossou K. Development of a FPGA based real-time power analysis and control for distributed generation interface[J]. IEEE Transactions on Power Systems, 2012, 27(3): 1343-1353.
[24] Duan Tong, Cheng Tianshi, Dinavahi V. Heterogeneous real-time co-emulation for communication-enabled global control of AC/DC grid integrated with renewable energy[J]. IEEE Open Journal of the Industrial Electronics Society, 2020, 1: 261-270.
[25] Nasiri M, Milimonfared J, Fathi S H. Modeling, analysis and comparison of TSR and OTC methods for MPPT and power smoothing in permanent magnet synchronous generator-based wind turbines[J]. Energy Conversion and Management, 2014, 86: 892-900.
[26] 尹明, 李庚银, 张建成, 等. 直驱式永磁同步风力发电机组建模及其控制策略[J]. 电网技术, 2007, 31(15): 61-65.
Yin Ming, Li Gengyin, Zhang Jiancheng, et al. Modeling and control strategies of directly driven wind turbine with permanent magnet synchronous generator[J]. Power System Technology, 2007, 31(15): 61-65.
[27] Pejovic P, Maksimovic D. A method for fast time-domain simulation of networks with switches[J]. IEEE Transactions on Power Electronics, 1994, 9(4): 449-456.
[28] 宋丽翠. 大规模稀疏线性系统的并行求解方法研究[D]. 北京: 华北电力大学, 2019.
Song Licui. Research on parallel solving of large scale sparse linear systems[D]. Beijing: North China Electric Power University, 2019.
Research on Transient Real-Time Simulation of New Energy Low-Voltage DC Distribution System Based on Field Programmable Gate Array
Abstract New energy low-voltage direct current (DC) distribution system is closely connected with the power consumers and has advantages of low construction cost, high operation efficiency and high compatibility of power electronic devices. However, the new energy generation systems that have fluctuating and intermittent characteristics directly affect the stability and reliability of the low-voltage DC distribution system operation. A real-time simulation device of the low-voltage DC distribution system can reproduce its dynamic characteristics in real time to help each device in the system complete hardware-in-loop test so as to improve the stability and reliability of the entire system. As an application-specific integrated circuit, field programmable gate array (FPGA), which integrates various functional circuits, has the advantages of small size, low cost and outstanding parallel computing capabilities. But one factor that must be considered is that FPGA only has limited hardware resources, which determines the operation of the simulator. As a result, in the development of FPGA-based simulator, both the real-time performance of simulation calculation and the operating efficiency of internal hardware resources should be taken into account. After considering these issues, this paper develops an FPGA-based real-time simulator of low-voltage DC distribution system containing a variety of distributed new energy sources.
Firstly, the characteristics of different types of distributed power supply are analyzed and the corresponding simulation method based on FPGA is designed. The simulation method of the switching components of power electronics is obtained by using the associated discrete circuit method. Secondly, an FPGA-based simulation architecture of the new energy low-voltage DC distribution system is presented. In this architecture, the electrical system and the control system operate in parallel to improve the computational efficiency and are further decomposed into smaller functional blocks. The internal floating-point operations are factorized by introducing the methodology of "algorithm architecture adequation (AAA)" to reduce the occupancy of hardware resources inside FPGA. Then, under the framework of nodal analysis method, a parallel solution method for the electrical system nodal conductance matrix combining matrix LDU decomposition and directed acyclic graph (DAG) is established. In this method, after obtaining the triangular matrices L and U, the data dependencies in solving the corresponding equations are expressed in the form of DAG. The DAG is further decomposed and reorganized to multiple new computational areas with relatively balanced computational load so as to improve the computational efficiency of the hardware processing elements (PEs), which are operated in parallel online. Finally, an FPGA-based real-time simulator of new energy low-voltage DC distribution system is developed. The experiment results under different transient scenarios are obtained and compared with the calculation results of PSCAD/EMTDC to verify the effectiveness and accuracy of the developed real-time simulator.
The experiments lead to these conclusions: (1) The comparative experimental results show that the relative error of the real-time simulator constructed in this paper is within the allowable range. (2) The proposed series-parallel hybrid computing architecture established by introducing AAA methodology effectively reduces the occupancy of FPGA internal hardware resources. (3) The proposed real-time solution method of electrical system node conductance matrix combining matrix LDU decomposition and DAG improves the dynamic calculation efficiency of FPGA and the ability to solve high-dimensional linear equations.
Keywords:Field programmable gate array (FPGA), real-time simulation, distributed generation, low-voltage DC distribution system, parallel computing
中图分类号:TM743
DOI: 10.19595/j.cnki.1000-6753.tces.231035
国家自然科学基金资助项目(52077149)、国家自然科学基金重点支持项目、智能电网联合基金(U2166202)资助。
收稿日期 2023-07-03
改稿日期 2023-12-06
王守相 男,1973年生,教授,博士生导师,研究方向为分布式发电、微网与智能配电网等。
E-mail:sxwang@tju.edu.cn
赵倩宇 女,1990年生,讲师,研究方向为分布式发电与配电网优化与控制等。
E-mail:zhaoqianyu@tju.edu.cn(通信作者)
(编辑 赫 蕾)