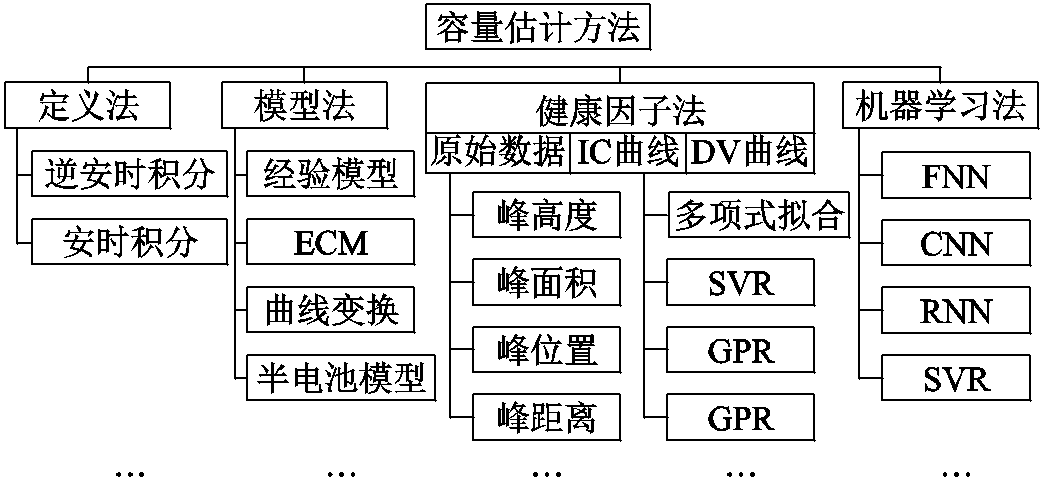
图1 典型的容量估计方法
Fig.1 Typical capacity estimation methods
摘要 锂离子电池关键材料的持续突破和规模化应用是我国双碳目标实现的重要技术路径。然而，电池具有即用即衰性和老化特性的复杂性，准确的老化分析和容量估计极其困难。为此，该文发现了电池容量增量曲线半峰面积与寿命衰减的映射关系，提出了基于充电容量增量曲线特征峰半峰面积的最大可用容量估计方法，明确了可用锂损耗为电池主要容量衰退模式，通过采用递推更新算法在线计算曲线特征峰半峰面积实施电池容量在线估计。考虑环境温度和充电倍率对容量估计算法的影响，进一步建立了基于环境温度、充电倍率的容量优化估计算法，不同老化状态和电池的验证结果表明最大可用容量估计误差小于3%。
关键词：锂离子电池 容量估计 老化模式 容量增量分析
大力发展新能源汽车和电化学储能是解决能源短缺和环境污染的重要举措，也是实现“双碳”目标的有力抓手。其中，锂离子电池具有电压高、比能量高、循环寿命长、环境友好、兼具良好的能量密度和功率密度等优点，得到了广泛的应用。然而，电池每用即衰、每用必衰，容量衰退伴随电池性能的退化，其安全性和可靠性也会降低。容量是分析电池老化行为的重要指标，对容量的精确估计是动力电池全寿命周期高效、安全管理的基础。然而对于实际应用中的电池系统开展满充满放的实时容量标定试验可行性不高，容量估计算法研究成为电池管理系统的关键。电池常用容量估计方法如图1所示。
1）定义法：定义法包括安时积分法与逆安时积分法。其中，安时积分法基于可用容量定义对单体多次满充满放求均值获取容量，只能在离线条件下开展，通常作为评估其他容量估计方法的参考值；逆安时积分法则通过计算电量变化量与荷电状态（State of Charge, SOC）变化量的比值估计容量[1]，此类方法为开环方法，受SOC精度、电流噪声等影响较大，估计结果并不稳定且SOC和容量估计误差互相耦合。
图1 典型的容量估计方法
Fig.1 Typical capacity estimation methods
2）模型法：基于模型的容量估计方法相比则具有更好的鲁棒性和稳定性。依据容量估计原理的差异，基于模型的方法还可进一步细分。其中经验模型通过大量离线测试构建容量与温度、静置时间、充放电倍率、充放电深度等老化条件之间的函数关系，例如I. Bloom等[2]通过加速日历和循环寿命测试，提出了如下的容量衰退经验模型：
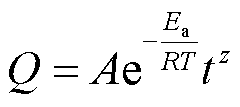（1）
式中，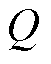
为容量衰减量；
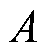为常数；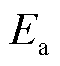
为活化能；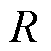
为气体常数；
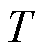为温度；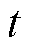
为时间；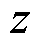
为时间指数。该类模型依赖大量离线测试，而实验室环境难以完全模拟电池复杂多变的老化条件，当实际应用环境与测试条件不符时该类模型存在失效的风险。基于ECM[3]、电化学模型[4]和分数阶模型[5]等自适应模型的容量估计方法则将容量作为模型参数之一，将容量估计转换为优化问题求解，优化目标通常为模型端电压输出误差最小。该类方法本质上利用了电池参数会随老化变化的特性，例如电池SOC-OCV曲线[6]。但是该类方法的估计精度取决于模型的精度，且多个电池参数耦合造成的模型输出误差难以解耦，使得该类方法在实际应用中的适用性较差。
3）健康因子（Health Indicator, HI）法：基于原始充放电曲线或通过微分、差分等运算变换后获得的容量增量（Incremental Capacity, IC）曲线[7]、差分电压（Differential Voltage, DV）曲线[8]作为HI，并构建HI与容量的映射关系，在线应用时通过计算HI得到容量估计结果。健康因子法的原理如图2所示。可见，HI的选择与提取方法以及HI和容量映射关系的构建方法是该类容量估计方法的主要研究方向。例如，Tang Xiaopeng等[9]通过开展四种电池的循环实验，发现IC曲线峰面积与容量呈线性关系，基于此构建的容量估计器的误差小于2.5%；Wang Limei等[10]则基于中心最小二乘法获取DV曲线，利用DV曲线两个拐点之间的距离作为HI进行容量估计，误差在2.5%以内。可见，基于HI的容量估计方法计算总体较为简单，在车端具有良好的应用前景。
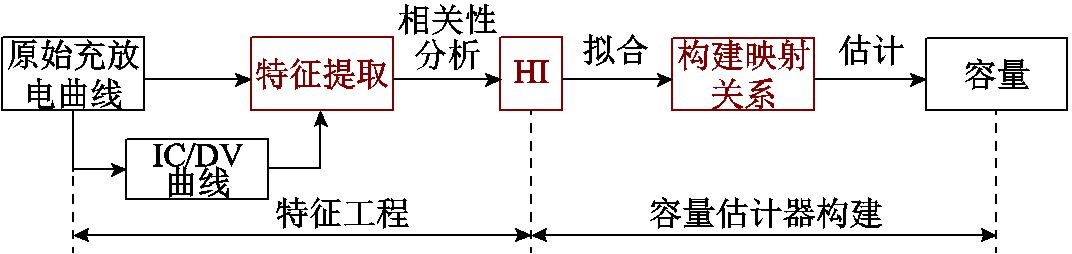
图2 基于健康因子的容量估计方法原理
Fig.2 Principle of capacity estimation method based on health factor
但现有研究主要面向实验室测试场景，在固定温度或应用工况下进行算法开发，未考虑实际应用时温度和充放电工况等对算法的影响。目前相关研究过度依赖数据驱动和相关性分析的方法，缺乏从容量衰退模式和机理角度对方法的合理性进行系统性论证。所以，如何提取与容量衰退机理相符且强相关的HI，以及如何在实车宽温度范围、多倍率条件下均能够实现高精度容量估计仍有待进一步研究。
4）机器学习法：该类方法常与健康因子法结合，使用先进机器学习算法提取特征因子——健康因子开展容量估计，减少人工提取HI的工作量，甚至可以实现“端到端”的容量估计，从而完全避免了特征工程。例如，Xiong Rui等[11]提出了一种基于深度卷积神经网络的容量估计方法，通过充电时采集的300个点的数据即可预测完整充电曲线，从而获取容量估计结果。但上述方法仍依赖大量有标签数据，针对云端无标签数据的应用仍然存在较大挑战。
为此，本文提出了以半峰面积作为健康因子的电池容量估计方法，通过分析容量衰退模式确定老化特征区间，利用递推更新法计算充电容量增量曲线的半峰面积，实施车端有限计算和存储资源条件下健康因子的在线提取，从而实现了宽温域、多倍率条件下通用化容量估计。
为开展动力电池测试，首先搭建测试平台如图3所示。包括充放电测试设备、可程控式温箱、可编程上位机以及待测电池单体等。其中，电池单体充放电测试设备为ARBIN-BT2000，负责对动力电池施加上位机发出的激励信息，进行相应充放电操作；动力电池置于可程控式温箱中，模拟电池所处的不同温湿度环境；上位机用于控制充放电测试设备的工作模式，并能实时记录和保存电池电流、电压、温度等状态数据。
图3 动力电池测试平台
Fig.3 Power battery testing platform
以某商用磷酸铁锂电池（LiFePO4, LFP）为研究其对象，基本规格参数见表1。为了获取不同测试条件下的数据，同时避免不一致性对测试结果造成的影响，使用了5只电芯开展测试，分别标号为LFP1～5。
电池测试包括容量标定测试、OCV标定测试、不同温度和倍率条件下的恒流充电测试以及老化循环测试。总体流程如图4所示。
表1 电池基本规格参数
Tab.1 Basic specifications of the battery cell
参数数值 标准容量/(A·h)202 电池内阻/mΩ0.16±0.05 充电温度范围/℃0～60 标准放电倍率0.5C 工作电压范围/V2.5～3.65
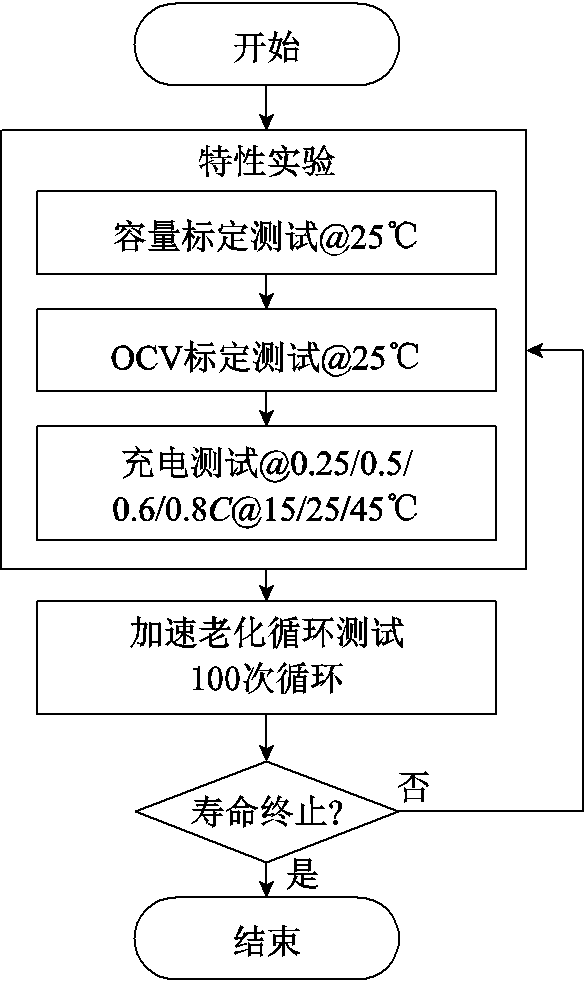
图4 电池测试总体流程
Fig.4 Overall process of battery test
图4中，容量标定测试流程如下：
（1）调整温度至25℃，静置2 h。
（2）以标准放电倍率放电至下截止电压。
（3）以0.05C恒流放电至下截止电压。
（4）静置2 h。
（5）以标准实车快充策略充电，分别以0.5C和0.05C恒流充电至上截止电压。
（6）静置2 h。
（7）重复步骤（2）～（6）三次，以充电容量均值作为容量标定结果。
OCV标定测试的流程如下：
（1）静置5 min。
（2）以标准实车快充策略充电，分别以0.5C和0.05C恒流充电至上截止电压。
（3）静置2 h。
（4）以0.025C恒流放电至下截止电压。
（5）以0.025C恒流充电至上截止电压。
（6）静置2 h。
考虑到LFP电池循环寿命一般较长，为减少总体测试时间，老化循环测试在45℃条件下以1C的充放电倍率进行。
电池具有即用即衰的特性，其容量在充放电循环、静置过程中自放电、温度或机械应力冲击等条件下均会衰减，因此明确磷酸铁锂电池的容量衰退模式和机理是进行全寿命周期容量估计的前提。图5展示了锂离子动力电池常见的三种容量衰退模式，分别为可用锂离子损失（Loss of Lithium-ion Inventory, LLI）、负极活性材料损失（Loss of Active Material in the Negative Electrode, LAMNE）和正极活性材料损失（Loss of Active Material in the Positive Electrode, LAMPE）。
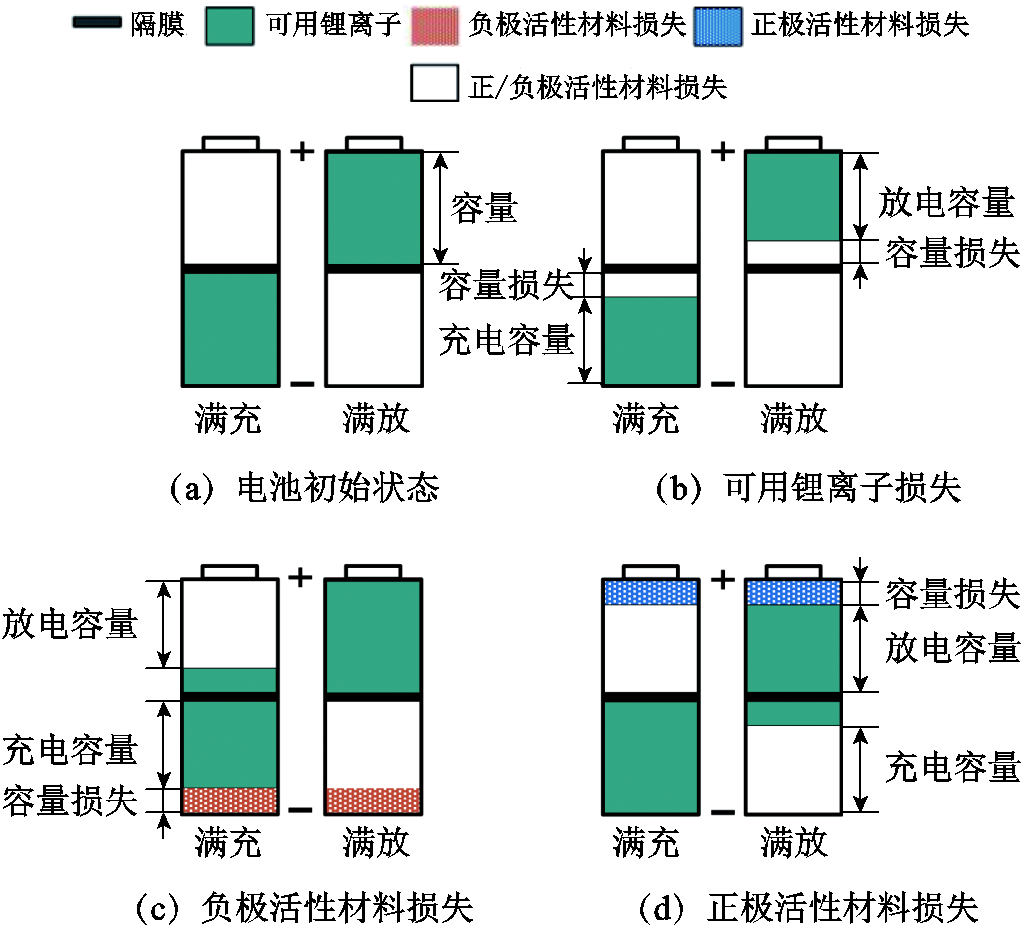
图5 不同容量衰退模式示意图
Fig.5 Schematic diagram of different capacity fading modes
图5a为电池的初始状态，充电时锂离子完全嵌入负极活性材料，而放电时锂离子从负极活性材料中完全脱出，通过隔膜进入正极活性材料，因此电池初始容量如图所示，即等于可用锂离子量。需要说明的是，商用锂电池初始状态下正负极活性材料量并不一致，以此为正负电极材料中易于老化的一方提供老化余量，也在一定程度上起到避免完全嵌锂或脱锂的保护作用，从而延长使用寿命。此外，LAM通常伴随着LLI，二者耦合共同造成容量损失。为便于说明，此处假定初始时刻正负极活性材料最大可嵌入锂离子数均等于可用锂离子数，且只考虑单一衰退模式对容量的影响。由图5b可见，当发生LLI时，满充或满放时动力电池正负极活性材料均未完全嵌锂，由此造成了实际充放电容量小于初始容量。而当负极发生LAM时，由图5c可见，满充时虽然负极材料完全嵌锂，但负极可用活性材料减少导致充电过程中锂离子未被完全利用，实际最大充电容量减少。同理，正极LAM也会使得放电过程中锂离子无法从负极中完全脱出，从而造成容量损失。
实际应用中造成上述衰退模式的因素众多，且高度耦合。以常见的石墨负极电池为例，其不同容量衰退模式的常见衰退机理如图6所示[12]。
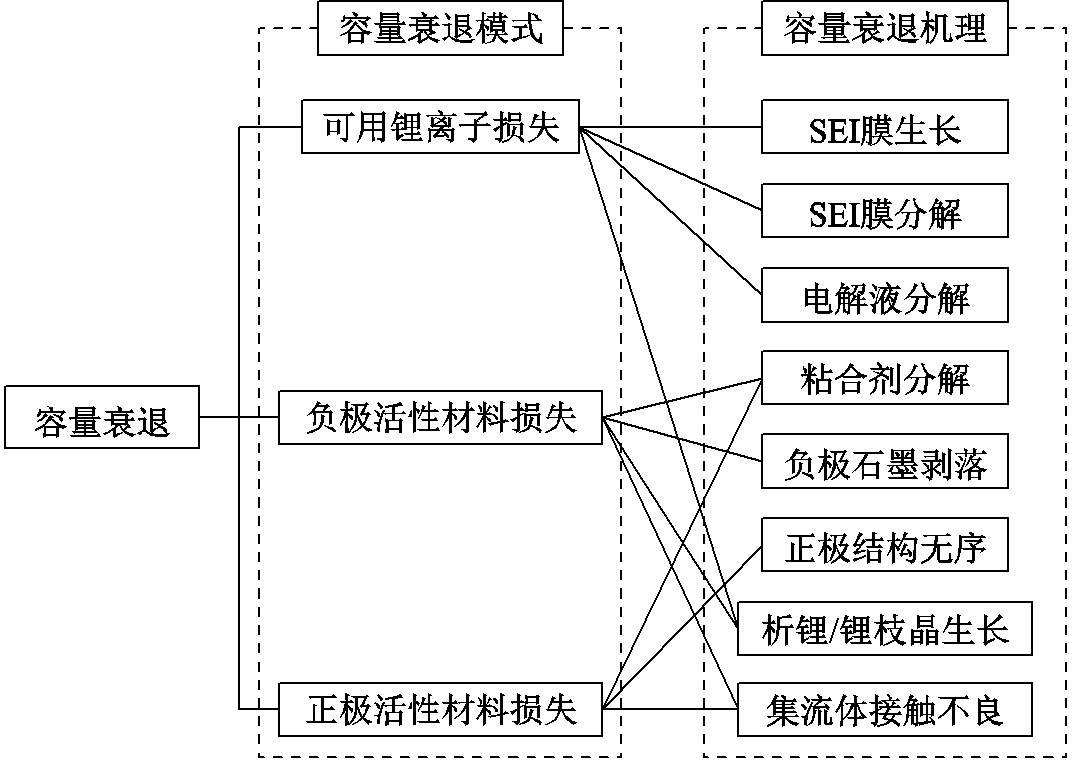
图6 不同容量衰退模式的衰退机理
Fig.6 Fading mechanism of different capacity fading modes
对于LLI，在初始充放电循环中锂离子在负极表面与电解液中的有机溶剂反应生成固体电解质界面（Solid Electrolyte Interface, SEI）膜覆盖于石墨表面，从而造成初始LLI[13]。而随着充放电循环次数的增加，SEI膜因为温度冲击、负极电极体积变化产生的机械应力等影响出现破裂、分解，从而导致SEI膜不断再生，消耗锂离子形成持续性的LLI[14-15]。此外，在低温、大倍率充电等条件下，锂离子因无法及时嵌入石墨负极而是以金属锂的形式在石墨表面析出，也会造成不可逆的LLI[16-17]。可见上述过程均会导致LLI，这也是造成容量衰退的最主要原因。除此之外，有机溶剂透过SEI膜与负极发生反应造成石墨剥落[18]、电极活性材料体积变化或因被钝化膜覆盖导致与集流体接触不良[14]、黏合剂腐蚀分解等原因均会造成实际参与电化学反应的正负极活性材料减少，这也是导致容量衰退的可能因素。综上可见，某一衰退模式可能由多种衰退机理导致，同时单一衰退机理也会造成多种不同的衰退模式，进而产生容量衰退的不同表现形式。
为了分析电池容量衰退的演变过程，在电化学研究中常利用扫描电镜等方法对动力电池进行拆解测试。但这显然并不适用于车载在线应用场景，且商用动力电池状态估计算法开发过程中通常难以开展拆解等破坏性测试，因此多采用原位分析方法。容量增量分析（Incremental Capacity Analysis, ICA）是一种常用的原位分析方法，其通过对恒流充放电曲线进行微分获取IC曲线[19]。恒流曲线的不同电压平台对应于IC曲线的不同峰区，因此IC曲线能够将恒流曲线平台区正负极相变过程随老化变化的差异进行放大。通过分析IC曲线不同峰随老化变化的特征即可获取电池内部的衰减情况。
以本文使用的LFP5电池为例，利用其不同老化状态下OCV标定测试数据中的充电部分提取IC曲线并分析衰退模式，从而指导容量估计。由于LFP电池存在电压平台，对充电曲线进行微分计算难以实施，因此此处利用概率密度函数（Probability Density Function, PDF）法获取IC曲线[20]。LFP5电池不同老化状态下的充电IC曲线如图7所示。
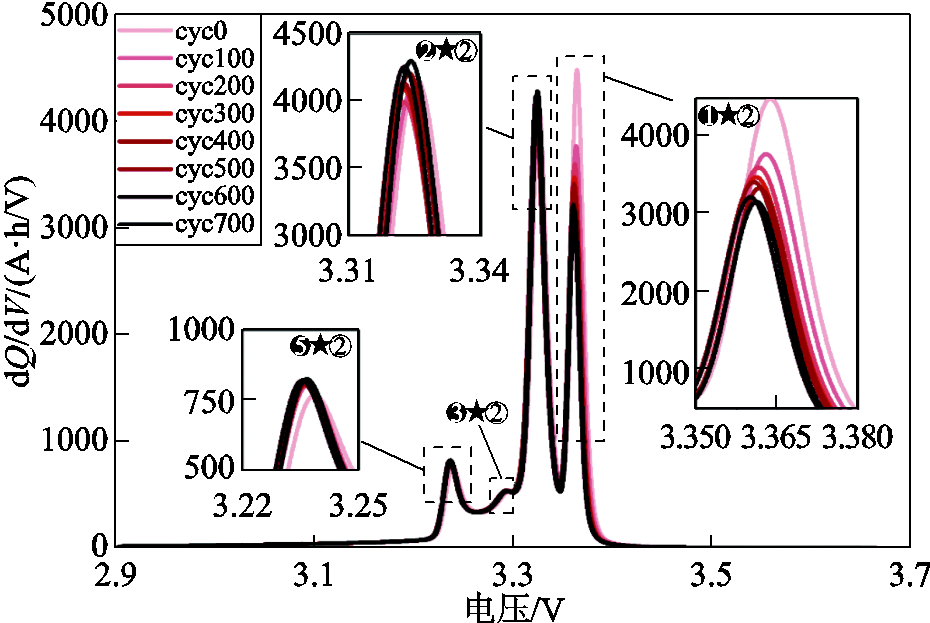
图7 LFP5电池不同老化状态下的充电IC曲线
Fig.7 Charging IC curves of LFP batteries under different aging states
在图中共可观察到四个峰，分别对应文献[21]中的❶★②、❷★②、❸★②和❺★②峰，其中❸★②峰并不明显，与文献[22]测试结果相似。对于LFP电池，其充电过程中正极由LiFePO4变为FePO4，是一个两相相变过程；而负极由C逐渐变为LiC6过程中存在5个不同的相变过程[23-24]。正负极在每个相变过程中其开路电势（Open Circuit Potential, OCP）曲线均会生成一个电势平台。上述❶、❷、❸和❺分别表示负极材料相变不同阶段的OCP平台对应的IC峰，而k表示正极材料相变时OCP平台对应的IC峰。全电池OCV等于正极与负极的电势差，因此全电池OCV的电压平台实际为正负极OCP平台的叠加。由于LFP电池正极OCP平台占正极完整OCP曲线的95%以上[21]，因此其为观察负极OCP变化提供了良好的参考，负极OCP曲线的变化能够在全电池OCV曲线上被完整地展现。相应的❶★②、❷★②、❸★②和❺★②即表示负极各峰与正极k峰叠加得到的全电池IC峰。
由图7可见，该动力电池❷★②、❸★②和❺★②峰高度随老化没有显著变化，说明正负极几乎不存在LAM。然而，❶★②峰随着老化出现了明显降低，表明该单体的LLI随着循环数的增加而不断增加[11, 23-24]，这与文献中描述的LFP电池容量衰减的主要影响因素是LLI而非LAM的规律相符[14-15]。其中0～100循环中由于初始SEI膜生成过程额外消耗了部分可用锂离子，造成LLI明显大于其他老化循环。当初始SEI膜生成后，❶★②峰衰减速率趋于稳定。此外，各峰的位置并没有明显变化，说明该单体的内阻随老化没有明显变化。由于大容量电池通常内阻小，欧姆极化对充电曲线和IC曲线的影响很小，在小电流条件下可以忽略。
通过上述分析可知，IC曲线的❶★②峰反映了实际的LLI，可以很好地表征动力电池的不同老化状态。因此可以基于❶★②峰的老化特征提取健康因子（HI），并构建HI与容量的映射关系，在线应用时通过计算HI即可实现车端容量估计。基于上述思路，针对本文使用的LFP电池，本节提出了基于充电IC曲线半峰面积的容量估计方法。
对于车载电池管理系统（Battery Management System, BMS）应用场景，采用式（2）的离散形式计算IC曲线上各点值。
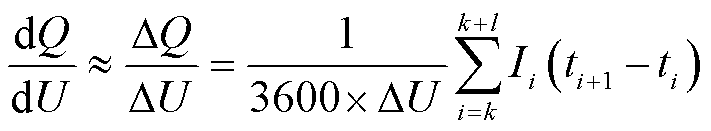（2）
式中，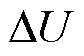
为计算电压步长，为算法的一个超参数；
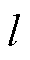为从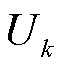
～
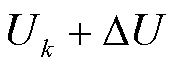过程中的采样点个数。设置较大的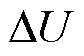可以得到更光滑的IC曲线，但是可能会丢失与老化相关的重要特征；而设置过小的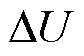则可能造成IC曲线出现过多波动。针对本文使用的LFP电池和测试环境，通过试错法确定的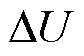=1 mV。需要说明的是，实车采样数据通常含有测量噪声，会对IC曲线形状造成影响，因此在线应用时可以利用滑动平均、高斯滤波等方法进行滤波，文献[25-26]等对此已有研究，在此不再赘述。
HI的选取是基于IC曲线进行容量估计的关键，常见的HI包括峰位置、峰高度、峰距离和峰面积等。其中以峰位置、峰高度和峰距离作为HI均需要获取峰值点的准确位置，然而实车采样数据易受噪声和采样漂移的影响使得获取准确峰值点较为困难[27]，且提取IC曲线所用的滤波算法、充电初始极化状态差异等也会对峰高度和峰位置造成影响，因此基于峰位置、峰高度和峰距离作为HI进行容量估计在实车应用时的稳定性较差。而基于峰面积的容量估计结果则具有更好的稳定性，其以IC曲线峰值点附近区间的面积作为HI，等价于融合了峰值点附近的多个特征点信息，从而避免了仅依赖单个峰值点可能造成的误差。实际上，以峰高度作为HI是以峰面积作为HI的一个特例，当计算峰面积的区间宽度趋近于0时二者相等。但是，实车充电时无法提前预测IC峰的起始和终止位置，为了获取峰面积，需要先存储完整充电曲线再进行离线计算，这对于车载BMS有限的存储空间提出了挑战。对此，本节提出以半峰面积作为HI，并利用递推更新法进行在线提取，从而大幅减少了对嵌入式系统存储空间的需求。半峰面积的定义如图8所示，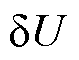
表示半峰宽度，为算法的超参数。在半峰宽度约束的区间内IC曲线与横轴围成区域的面积即为半峰面积。
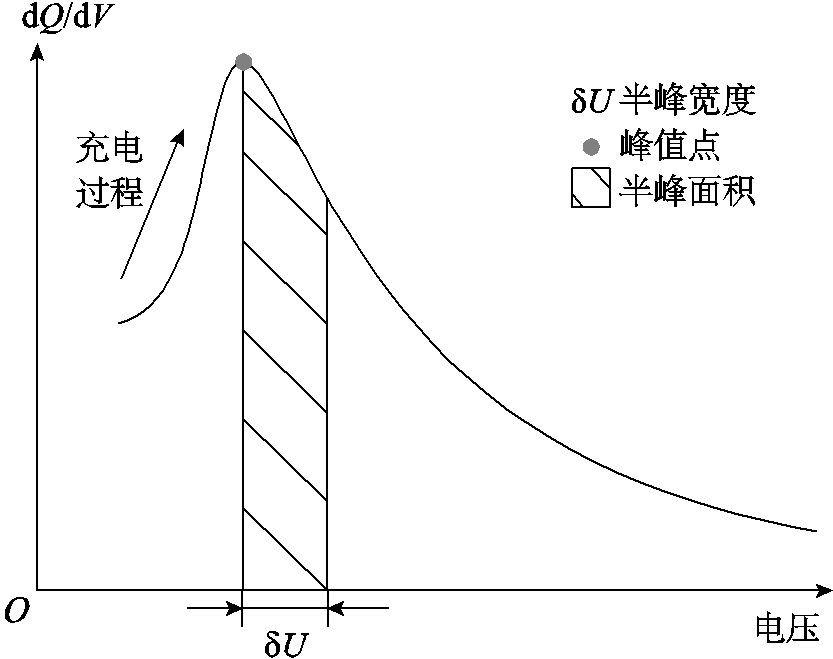
图8 半峰面积的定义
Fig.8 Definition of half peak area
利用递推更新法确定❶★②峰对应半峰面积的具体流程如图9所示。充电过程中，基于式（2）在线计算容量增量计算单元当前的IC值。IC峰值判断单元则用于判断当前IC值是否为峰值。若当前IC值大于或等于前一IC值，则说明此时处于IC峰左侧上升阶段并未进入半峰区间，记录当前时刻的电压Upeak，作为临时峰值点电压，并将半峰面积计算结果置0。继续充电并不断更新Upeak，直至某一时刻IC值小于前一IC值时，表明当前充电过程进入IC峰右侧下降阶段，之前记录的Upeak即为求得的IC峰值。此时半峰面积计算单元开始对充入电量进行连续积分直至电压超出半峰区间范围，求得的电量积分值即为半峰面积。需要注意的是，由于IC曲线存在多个峰值，因此充电过程中利用递推更新法会获得多个半峰面积。但因为❶★②峰所在的电压范围最高，充电至❶★②峰时其半峰面积计算结果会将之前峰的计算结果覆盖，所以最终输出结果仍为❶★②峰的半峰面积。对于不完整充电过程则需要通过SOC或电压判断充电过程是否包含❶★②峰对应的大致区间，若充电曲线不包含❶★②峰区间，则认定此次充电过程无法提取有效HI。实际上并非每次充电均能够获得有效HI，但是由于动力电池容量衰退是一个长时间尺度过程，因此在若干次充电过程中只需获取一次有效HI即可对容量估计结果进行更新。需要说明的是，对于实车多阶恒流充电过程，通常第一阶段即会以恒定电流充电至上截止电压附近，因此只需用第一个充电阶段的数据提取HI。
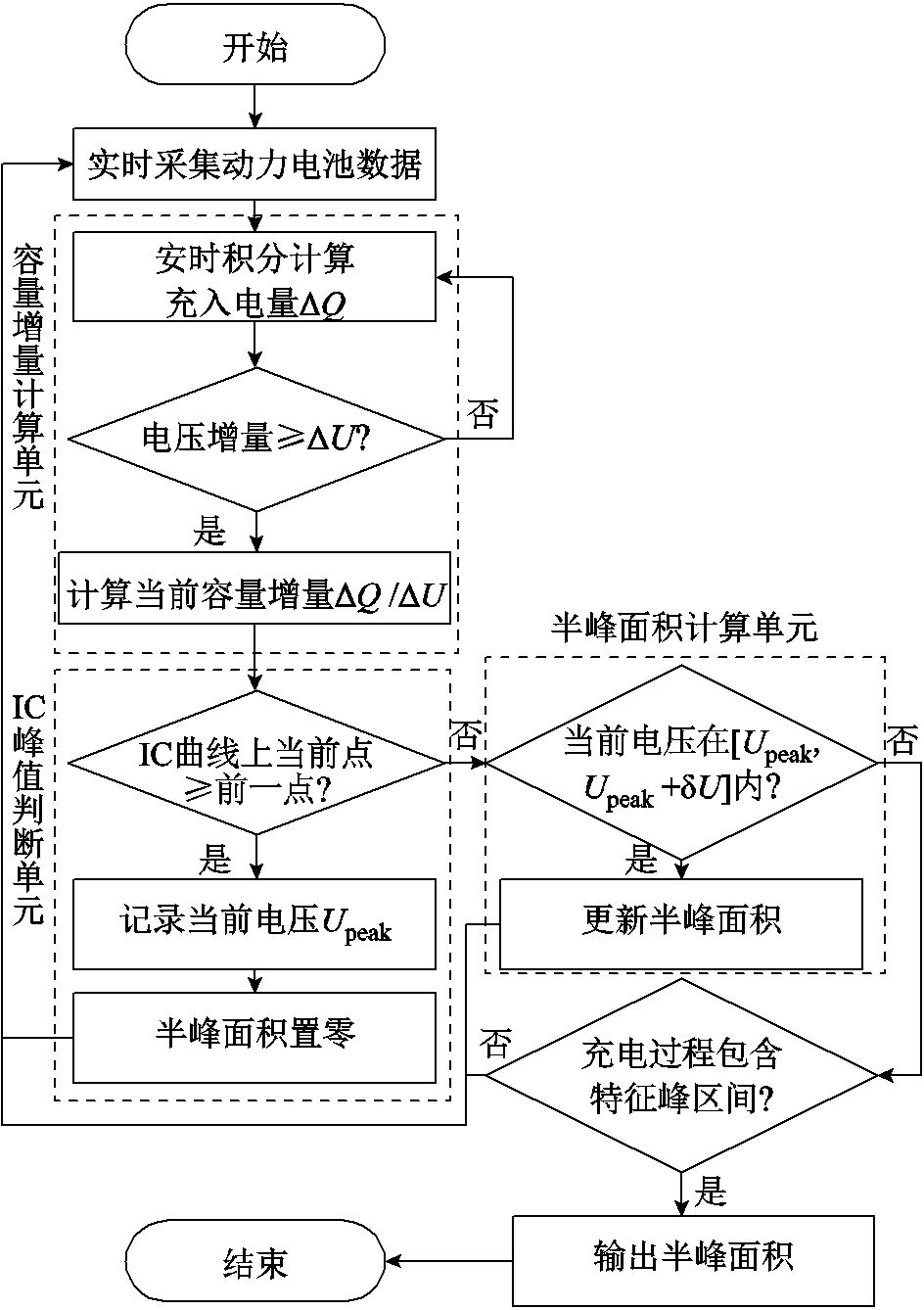
图9 半峰面积递推更新计算方法
Fig.9 Half-peak area recursive update calculation method
HI提取完成后即可构建与容量的映射关系。以本文使用的LFP5电池为例，设置半峰宽度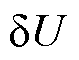为 20 mV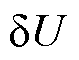，通过试错法确定，利用其不同老化状态的充电OCV测试数据提取HI，其与容量的关系如图10a所示。可见所提取的HI与容量满足良好的二次关系，利用多项式式（3）即可构建HI与容量的映射关系式，决定系数达到了0.998 0。
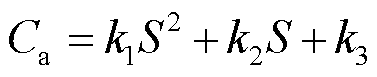（3）
式中，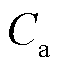
为估计的容量；
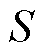为利用递推更新法在线求得的半峰面积；
、
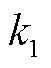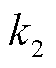和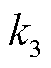
为拟合系数。
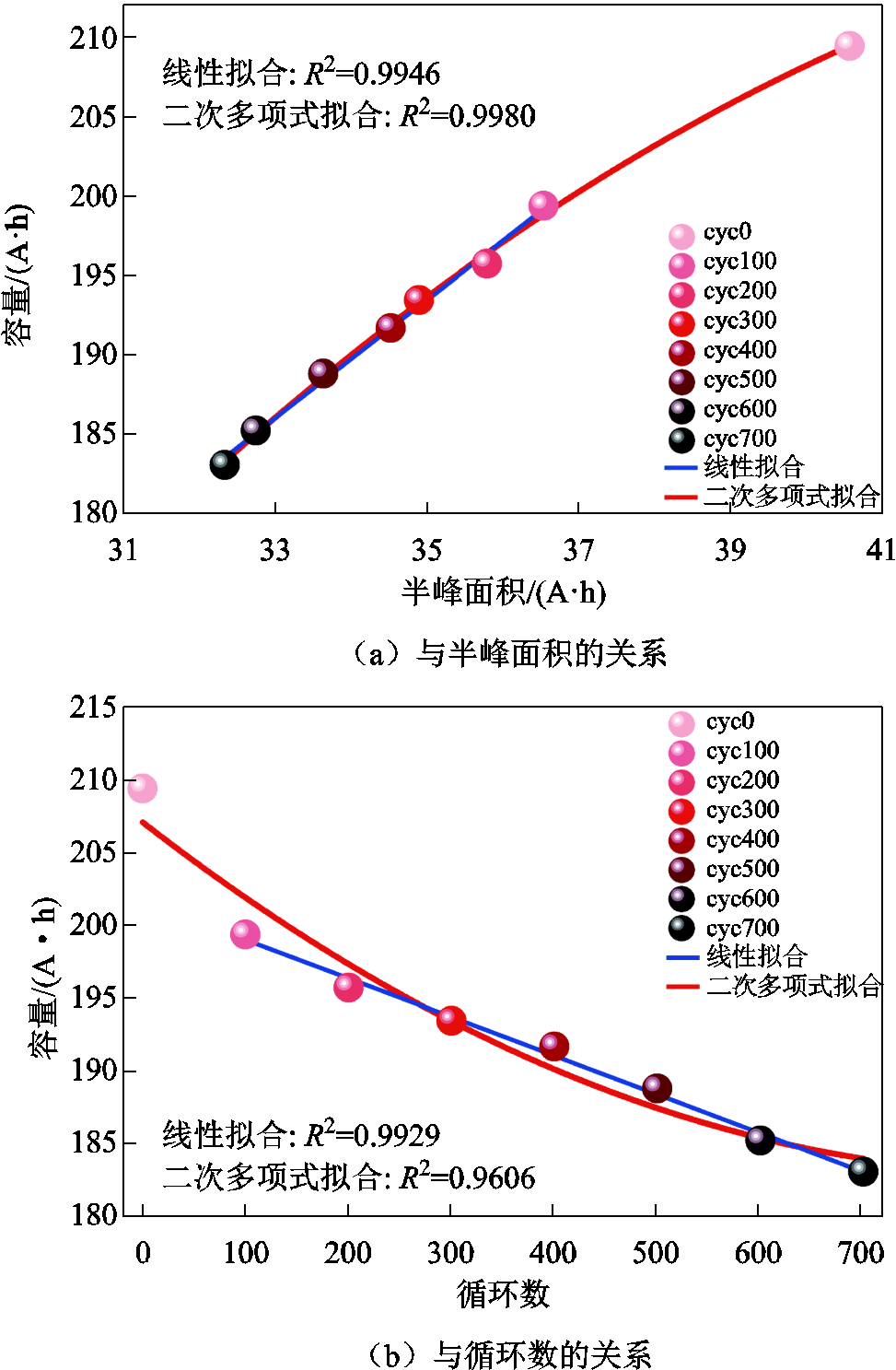
图10 容量与半峰面积、循环数的关系
Fig.10 Relationship of capacity, half-peak area and cycle
充电过程中在线获取HI后，即可利用式（3）得到容量估计结果。需要说明的是，此处得到的拟合关系式是基于25℃、0.025C的充电数据构建的，但是实车充电倍率范围通常为0.1C～1C，且充电温度并不固定，因此实际应用时还需考虑温度和倍率的影响，这将在下节进行讨论。此外，在图10a中还可以发现，除0老化循环的新电芯测试结果外，其他老化点的半峰面积与容量具有良好的线性相关性，线性拟合的决定系数达到了0.994 6。而由图10b可见，随循环数增加容量衰退轨迹与图10a呈现相似规律，即除了初始点以外，容量呈线性衰退的趋势。文献[28]指出，LLI造成容量线性衰退，而LAM则可能使得容量呈现幂型或指数型衰退。因此可以推断LLI是造成该动力电池容量衰减的主要因素。而初始SEI膜生成过程中负极的LAM导致初始容量衰退轨迹中耦合了幂型衰退分量，因而使得0～700次老化循环容量衰退的整体轨迹呈现二次函数形式。上述推断与前述容量衰退模式分析结果一致。综上可见，本节提出的半峰面积与容量衰退强相关，且能够在一定程度上表征电池内部的容量衰退模式，十分适合作为车端容量估计的HI。
鉴于25℃、0.025C条件下IC曲线半峰面积与容量具有强相关性，但实车难以获取小电流充电数据，快充、慢充倍率并不相同且实际充电电流还受限于充电桩最大可输出功率，充电时的环境温度也并不固定，因此需要对不同温度和倍率进行改进。
实际上温度和充电倍率对HI的影响具有耦合性，为研究单一变量对HI的影响规律，分别利用LFP2电池固定倍率和固定温度的充电测试数据进行分析。由图11a可见，IC曲线整体随着温度的升高而向低电压区间移动，且各峰的高度随着温度的升高而增加，这主要是由动力电池内阻随着温度升高而降低导致的。相应地，由图11b可见半峰面积也随着温度的升高而增加，可用二次多项式进行拟合。
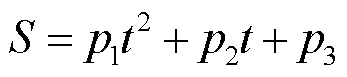（4）
式中，S为半峰面积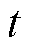；为半峰区间内的平均温度；
、
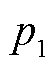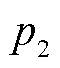和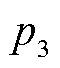
表示温度拟合系数。以25℃作为基准，则在其他温度利用相同倍率充电时获取的HI可利用式（5）进行修正，从而得到同倍率下25℃充电时的HI为
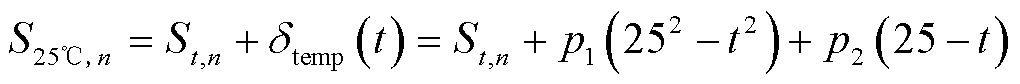（5）
式中，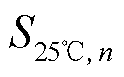
为25℃条件下以倍率nC充电得到的HI；
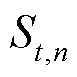为同老化状态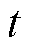条件下以倍率nC充电得到的HI；
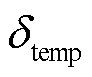为温度修正量。
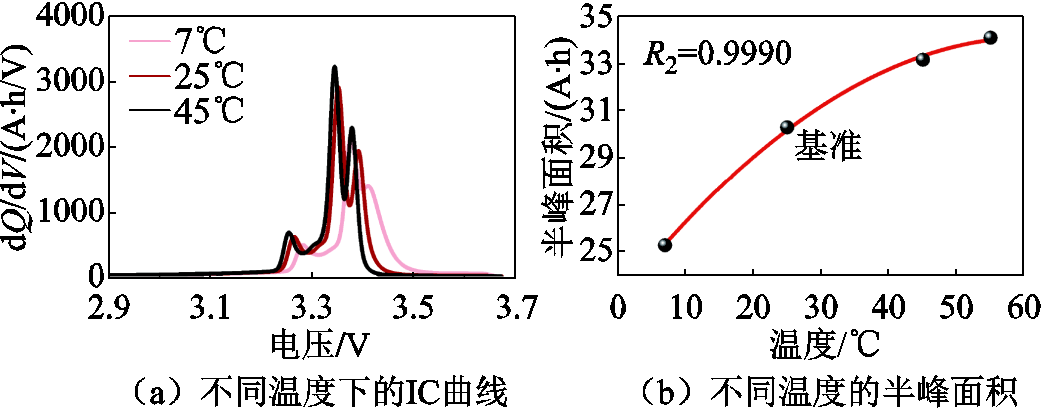
图11 温度对IC曲线和HI的影响
Fig.11 Effect of temperature on IC curve and HI
相似地，利用LFP2电池25℃恒定环境温度下不同倍率恒流充电测试数据分析倍率对HI的影响。由于动力电池在大倍率下生热造成温度偏离25℃，因此求得的HI实际包含倍率和温度的耦合影响。为了实现解耦，需要先利用式（5）对不同倍率下的HI进行温度修正，去除温度对HI造成的影响。分别基于25℃充电OCV曲线和以标准实车快充倍率充电获得的充电曲线提取IC曲线，结果如图12a所示。可见随着充电倍率的增大，极化电压增大导致IC曲线整体向高电压区间移动，且各峰高度均有所下降但峰的宽度有所增加。相应地，由图12b可见，半峰面积也随着充电倍率的增加而减少，可利用如下二次多项式进行拟合。
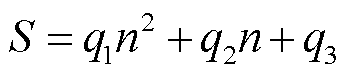（6）
式中，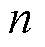
为充电倍率；
、
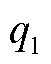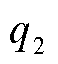和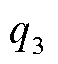
为倍率拟合系数。以充电OCV测试中设定的0.025C作为基准，则可利用式（7）将以任意倍率充电时求得的HI转化为同温度下以0.025C充电所对应的HI。
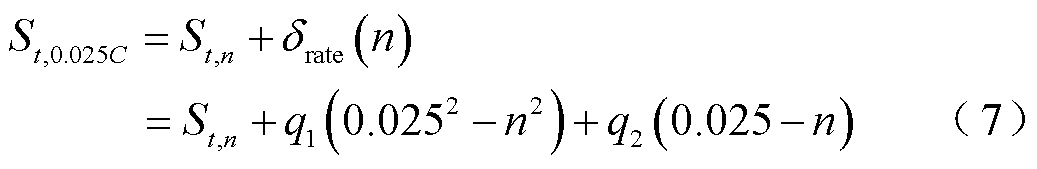
式中，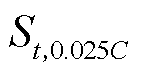
为在温度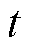条件下以0.025C充电得到的HI；
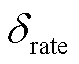为倍率修正量。
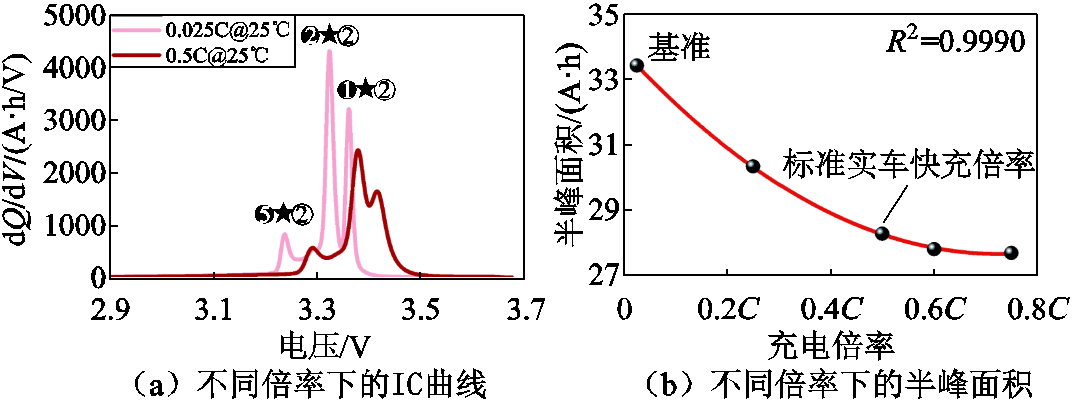
图12 充电倍率对IC曲线和HI的影响
Fig.12 Effect of charge rate on IC curve and HI
综合上述式（5）和式（7）可知，基于任意温度和倍率充电数据计算得到的HI，可利用式（8）转换为同老化状态下基于25℃、0.025 C充电曲线提取得到的HI。
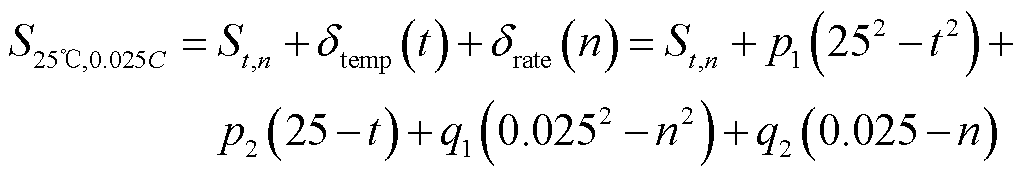（8）
再将转换后得到的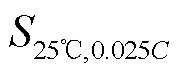
代入式（3），即可得到容量估计结果。可见，基于温度、充电倍率，本节对基准HI进行修正，实现了算法在宽温度范围和宽倍率范围的应用。
选择LFP1、LFP3和LFP4单体开展不同倍率和温度的充电测试，对本文提出的容量估计方法进行验证。测试温度包括15℃、25℃和45℃，测试的充电倍率包括0.025C、0.25C、0.5C、0.6C和0.8C。利用LFP5单体不同老化点的充电OCV数据提取HI，并基于式（3）构建HI与容量的映射关系。以此为基准，再基于式（8）利用LFP4电池不同温度和倍率条件下的充电测试数据构建温度、倍率修正函数。
首先利用开发完成的容量估计算法对LFP4单体充电数据进行验证，评估指标为估计相对误差，LFP4单体真实容量为197.87 A×h，测试结果见表2。可见在车端动力电池常用温度区间范围内最大容量估计误差为1.79%，而当以该动力电池车端标准快充倍率0.5C进行充电时最大容量估计误差仅为0.69%。
表2 LFP4单体容量估计测试结果
Tab.2 LFP4 cell capacity estimation test results
温度/℃误差（%） 0.025C0.25C0.5C0.6C0.8C 15——0.11—— 250.301.040.450.440.73 45—0.940.691.041.79
为了测试建立的容量估计算法对不同单体的适用性和在不同老化状态的估计精度，进一步利用LFP1和LFP3单体进行了测试。开展本节验证测试时LFP1和LFP3单体的真实容量分别为191.34 A·h和194.52 A·h。不同温度、不同倍率的验证测试结果分别见表3和表4。可见基于LFP5和LFP4单体数据构建的算法应用于LFP1和LFP3单体时也能够取得良好的精度，在不同温度和充电倍率条件下的最大容量估计误差均小于3%。实车应用时，通过对多次充电过程的容量估计结果取均值，将有望进一步降低估计误差。综上可见，本文提出的容量估计方法在宽温度范围和多倍率条件下均能够取得良好的估计精度。
表3 LFP1单体容量估计测试结果
Tab.3 LFP1 cell capacity estimation test results
温度/℃误差（%） 0.025 C0.25 C0.5 C0.6 C0.8 C 15——0.11—— 250.301.040.450.440.73 45—0.940.691.041.79
表4 LFP3单体容量估计测试结果
Tab.4 LFP3 cell capacity estimation test results
温度/℃误差（%） 0.025 C0.25 C0.5 C0.6 C0.8 C 15——0.72—— 250.311.222.021.411.54 45—0.711.612.950.41
锂离子电池容量的精确在线估计是其安全高效应用的基础，本文提出了一种基于充电曲线半峰面积的电池容量估计方法，主要结论如下：
1）厘清了锂离子电池主要的容量衰退模式和衰退机理，基于磷酸铁锂电池测试数据和容量增量曲线分析了容量衰退模式，明确了可用锂离子损失是造成其容量衰退的主要原因。
2）提出了一种基于容量增量曲线半峰面积的锂离子电池容量在线估计方法，在充电过程中应用递推更新算法在线计算容量增量曲线特征峰的半峰面积，降低算法对嵌入式系统存储空间的需求。
3）提出了温度、倍率修正函数，对在线提取的健康因子进行修正，从而实现了在宽温度范围和多倍率条件下的通用性。基于不同温度和倍率电池数据的验证结果表明：容量估计最大绝对误差小于3%。
4）该算法对硬件设备的计算和存储能力要求低，可实现宽温度、多倍率条件下锂离子电池最大可用容量在线估计，有望在新能源汽车车端控制器以及电网储能电站的边缘侧得到应用。
参考文献
[1] Shen Ping, Ouyang Minggao, Lu Languang, et al. The co-estimation of state of charge, state of health, and state of function for lithium-ion batteries in electric vehicles[J]. IEEE Transactions on Vehicular Technology, 2018, 67(1): 92-103.
[2] Bloom I, Cole B W, Sohn J J, et al. An accelerated calendar and cycle life study of Li-ion cells[J]. Journal of Power Sources, 2001, 101(2): 238-247.
[3] 王榘, 熊瑞, 穆浩. 温度和老化意识融合驱动的电动车辆锂离子动力电池电量和容量协同估计[J]. 电工技术学报, 2020, 35(23): 4980-4987.
Wang Ju, Xiong Rui, Mu Hao. Co-estimation of lithium-ion battery state-of-charge and capacity through the temperature and aging awareness model for electric vehicles[J]. Transactions of China Electrotechnical Society, 2020, 35(23): 4980-4987.
[4] 武龙星, 庞辉, 晋佳敏, 等. 基于电化学模型的锂离子电池荷电状态估计方法综述[J]. 电工技术学报, 2022, 37(7): 1703-1725.
Wu Longxing, Pang Hui, Jin Jiamin, et al. A review of SOC estimation methods for lithium-ion batteries based on electrochemical model[J]. Transactions of China Electrotechnical Society, 2022, 37(7): 1703-1725.
[5] Tian Jinpeng, Xiong Rui, Yu Quanqing. Fractional-order model-based incremental capacity analysis for degradation state recognition of lithium-ion batteries[J]. IEEE Transactions on Industrial Electronics, 2019, 66(2): 1576-1584.
[6] Pattipati B, Balasingam B, Avvari G V, et al. Open circuit voltage characterization of lithium-ion batteries[J]. Journal of Power Sources, 2014, 269: 317-333.
[7] 杨胜杰, 罗冰洋, 王菁, 等. 基于容量增量曲线峰值区间特征参数的锂离子电池健康状态估算[J]. 电工技术学报, 2021, 36(11): 2277-2287.
Yang Shengjie, Luo Bingyang, Wang Jing, et al. State of health estimation for lithium-ion batteries based on peak region feature parameters of incremental capacity curve[J]. Transactions of China Electrotechnical Society, 2021, 36(11): 2277-2287.
[8] Afshari S S, Cui S, Xu X, et al. Remaining Useful Life Early Prediction of Batteries Based on the Differential Voltage and Differential Capacity Curves[J]. IEEE Transactions on Instrumentation and Measurement, 2022, 71: 1-9.
[9] Tang Xiaopeng, Zou Changfu, Yao Ke, et al. A fast estimation algorithm for lithium-ion battery state of health[J]. Journal of Power Sources, 2018, 396: 453-458.
[10] Wang Limei, Pan Chaofeng, Liu Liang, et al. On-board state of health estimation of LiFePO4 battery pack through differential voltage analysis[J]. Applied Energy, 2016, 168: 465-472.
[11] Tian Jinpeng, Xiong Rui, Shen Weixiang, et al. Deep neural network battery charging curve prediction using 30 points collected in 10 Min[J]. Joule, 2021, 5(6): 1521-1534.
[12] Birkl C R, Roberts M R, McTurk E, et al. Degradation diagnostics for lithium ion cells[J]. Journal of Power Sources, 2017, 341: 373-386.
[13] 孙丙香, 任鹏博, 陈育哲, 等. 锂离子电池在不同区间下的衰退影响因素分析及任意区间的老化趋势预测[J]. 电工技术学报, 2021, 36(3): 666-674.
Sun Bingxiang, Ren Pengbo, Chen Yuzhe, et al. Analysis of influencing factors of degradation under different interval stress and prediction of aging trend in any interval for lithium-ion battery[J]. Transactions of China Electrotechnical Society, 2021, 36(3): 666-674.
[14] Aurbach D, Zinigrad E, Cohen Y, et al. A short review of failure mechanisms of lithium metal and lithiated graphite anodes in liquid electrolyte solutions[J]. Solid State Ionics, 2002, 148(3/4): 405-416.
[15] Aurbach D. Review of selected electrode–solution interactions which determine the performance of Li and Li ion batteries[J]. Journal of Power Sources, 2000, 89(2): 206-218.
[16] Mei Wenxin, Jiang Lihua, Liang Chen, et al. Understanding of Li-plating on graphite electrode: detection, quantification and mechanism revelation[J]. Energy Storage Materials, 2021, 41: 209-221.
[17] 严康为, 龙鑫林, 鲁军勇, 等. 高倍率磷酸铁锂电池简化机理建模与放电特性分析[J]. 电工技术学报, 2022, 37(3): 599-609.
Yan Kangwei, Long Xinlin, Lu Junyong, et al. Simplified mechanism modeling and discharge characteristic analysis of high C-rate LiFePO4 battery[J]. Transactions of China Electrotechnical Society, 2022, 37(3): 599-609.
[18] Zhang Sheng shui. A review on electrolyte additives for lithium-ion batteries[J]. Journal of Power Sources, 2006, 162(2): 1379-1394.
[19] Dubarry M, Svoboda V, Hwu R, et al. Incremental capacity analysis and close-to-equilibrium OCV measurements to quantify capacity fade in commercial rechargeable lithium batteries[J]. Electrochemical and Solid-State Letters, 2006, 9(10): A454-A457.
[20] Feng Xuning, Li Jianqiu, Ouyang Minggao, et al. Using probability density function to evaluate the state of health of lithium-ion batteries[J]. Journal of Power Sources, 2013, 232: 209-218.
[21] Dubarry M, Liaw B Y, Chen M S, et al. Identifying battery aging mechanisms in large format Li ion cells[J]. Journal of Power Sources, 2011, 196(7): 3420-3425.
[22] 韩雪冰. 车用锂离子电池机理模型与状态估计研究[D]. 北京: 清华大学, 2014.
Han Xuebing. Study on Li-ion Battery Mechanism Model and State Estimation for Electric Vehicles[D]. Beijing: Tsinghua University, 2014.
[23] Dubarry M, Truchot C, Cugnet M, et al. Evaluation of commercial lithium-ion cells based on composite positive electrode for plug-in hybrid electric vehicle applications. Part I: Initial characterizations[J]. Journal of Power Sources, 2011, 196(23): 10328-10335.
[24] Dubarry M, Truchot C, Liaw B Y, et al. Evaluation of commercial lithium-ion cells based on composite positive electrode for plug-in hybrid electric vehicle applications. Part II. Degradation mechanism under 2 C cycle aging[J]. Journal of Power Sources, 2011, 196(23): 10336-10343.
[25] Li Xiaoyu, Yuan Changgui, Li Xiaohui, et al. State of health estimation for Li-Ion battery using incremental capacity analysis and Gaussian process regression[J]. Energy, 2020, 190: 116467.
[26] Li Yi, Abdel-Monem M, Gopalakrishnan R, et al. A quick on-line state of health estimation method for Li-ion battery with incremental capacity curves processed by Gaussian filter[J]. Journal of Power Sources, 2018, 373: 40-53.
[27] 张谦, 邓小松, 岳焕展, 等. 计及电池寿命损耗的电动汽车参与能量-调频市场协同优化策略[J]. 电工技术学报, 2022, 37(1): 72-81.
Zhang Qian, Deng Xiaosong, Yue Huanzhan, et al. Coordinated optimization strategy of electric vehicle cluster participating in energy and frequency regulation markets considering battery lifetime degradation[J]. Transactions of China Electrotechnical Society, 2022, 37(1): 72-81.
[28] Honkura K, Takahashi K, Horiba T. Capacity-fading prediction of lithium-ion batteries based on discharge curves analysis[J]. Journal of Power Sources, 2011, 196(23): 10141-10147.
Online Capacity Estimation Method Based on Half Peak Area of Lithium-Ion Battery Capacity Increment Curve
Abstract The development of electric vehicles is my country's national strategy and a powerful starting point to achieve the goal of "carbon neutrality and carbon peaking". The rapid growth of electric vehicles has led to the rapid development of the lithium-ion battery industry. Lithium-ion batteries (LiBs) are widely used in electric vehicles and energy storage fields because of their advantages such as high voltage, long cycle life, environmental friendliness, and high energy and power density. However, LiBs decay immediately after use, and capacity fading leads to performance degradation. For example, safety and reliability gradually decline with aging. Accurate estimation of battery capacity is the basis for efficient and safe management of the entire life cycle of LiBs. However, it is not feasible to conduct real-time capacity calibration testing of full charge and discharge of the battery system in practical applications. Therefore, the research on capacity estimation algorithms has become the key to battery management systems. To this end, this manuscriptproposes a battery capacity estimation method that uses a half-peak area as a health factor. The aging characteristic interval is determined by analyzing the capacity decline mode, and the half-peak area of the charging capacity increment curve is calculated using the recursive update method, and limited calculation is implemented on the vehicle side. Online extraction of health factors under storage resource conditions enables universal capacity estimation under a wide temperature range and multi-rate conditions.
First, a lithium-ion power battery test platform was built to conduct capacity calibration tests, open circuit voltage tests, and accelerated aging tests on the five commercial LiFePO4 batteries. In this way, we can obtain battery multi-temperature and multi-rate characteristic data, which are helpful for the development of lithium-ion power battery maximum available capacity estimation algorithm and algorithm effect verification.Secondly, by analyzing the change of the characteristic peak of the incremental capacity curve with the number of aging cycles, it was found that there is almost no loss of active material in the positive and negative electrodes during the aging process of these batteries. In contrast, the loss of lithium ions continues as the number of cycles increases. It is concluded that the main factor affecting the capacity fading of these LiFePO4 batteries is the loss of lithium ions rather than the loss of active materials. The loss of lithium ions corresponds to the characteristic peak ❶★②. Finally, the half-peak area of the characteristic peak of the incremental capacity curve is extracted as the health factor, and an online estimation algorithm for lithium-ion power battery capacity is developed. Considering the influence of ambient temperature and charging current rate on the calculation of half-peak area, temperature, and rate correction functions are proposed to correct the health factor extracted online to achieve versatility under a wide temperature range and multiple rate conditions. It was verified based on battery data at different temperatures and rates, and the results showed that the maximum absolute error in capacity estimation was less than 3%. Considering engineering applications, the maximum available capacity estimation algorithm of lithium-ion batteries proposed in this article can online extract the characteristic peak half-peak area of the incremental capacity curve to implement capacity estimation. It has low requirements for the computing and storage capabilities of hardware equipment. It is expected to be used in new energy vehicles and the edge side of grid energy storage power stations.
keywords：Lithium-ion battery, capacity estimation, aging model, incremental capacity analysis
中图分类号：TM912
DOI: 10.19595/j.cnki.1000-6753.tces.231248
国家重点研发计划（2021YFB2402002）和中国南方电网有限责任公司科技项目（STKJXM20210097）资助。
收稿日期 2023-08-01
改稿日期 2023-08-17
李乐卿 男，1986年生，工程师，研究方向为抽水蓄能电厂电气设备检修及电池储能技术。
E-mail：raul223@126.com
熊 瑞 男，1985年生，教授，博士生导师，研究方向为动力/储能电池管理与控制。
E-mail：rxiong@bit.edu.cn（通信作者）
（编辑 郭丽军）