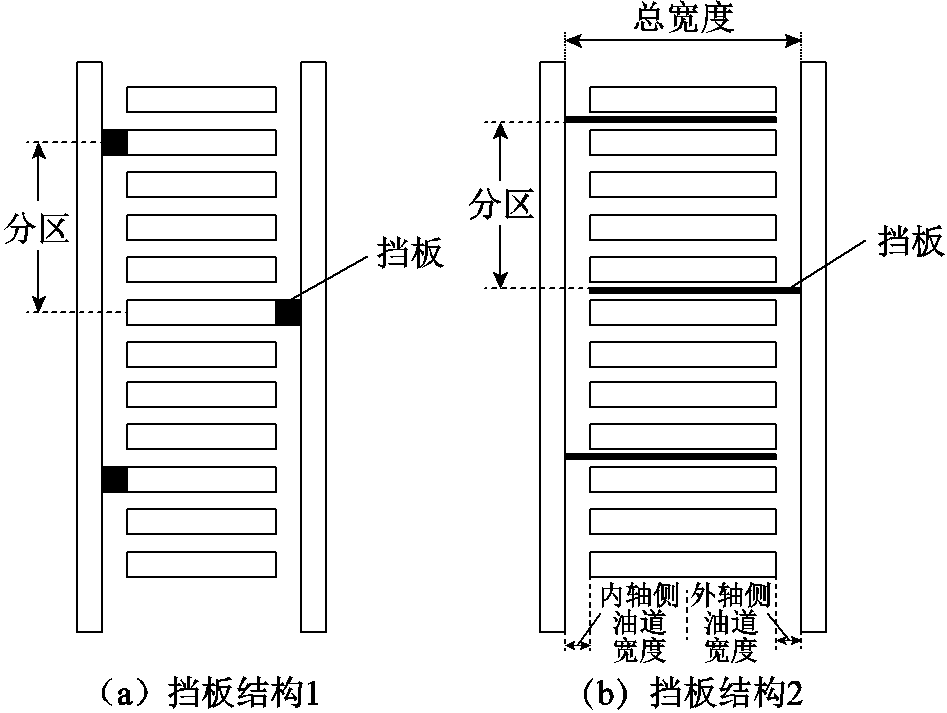
图1 油浸式变压器挡板结构
Fig.1 Structure of oil immersed transformer block washers
摘要 热点温度过高会严重影响变压器运行稳定性，为提高变压器运行的稳定性，该文以降低变压器绕组热点温度为优化目标，采用径向基函数（RBF）响应面模型优化变压器绕组挡板尺寸，改善油流分布以实现更好的散热。为提高RBF响应面模型的拟合精度，该文采用鲸鱼优化算法（WOA）对径向基函数的超参数值进行优化，并与传统网格搜索（GS）寻优方法和定参RBF模型进行对比。对比结果表明对于超参数优化问题，在拟合精度占优的前提下，WOA优化效率是GS寻优方法的3.13倍。在此基础上，该文基于WOA-RBF响应面模型对绕组挡板结构尺寸进行优化，优化后的热点温度相较于初始结构的热点温度降低了3.81℃，相对于全场域的最大温升降低了13.42%，并有效地降低了绕组整体温升。同时将所提算法与遗传算法（GA）优化结果进行对比，在保证精度的同时，WOA-RBF响应面模型优化效率是GA的13.41倍。根据上述结果分析可知，所提算法具有很好的优化性能，同时相比于遗传算法，可以在保证优化精度的同时，显著地提高优化效率。
关键词：响应面方法 径向基函数 热点温度 鲸鱼优化算法 油浸式变压器 挡板结构优化
变压器绕组热点温度是影响变压器使用寿命的关键参数之一[1-2]。油浸式变压器依靠变压器油在绕组间流动进行散热，绕组间油道的分布会影响绕组的散热能力，而油道分布情况最主要的影响因素是绕组各分区间的挡板结构[3-4]，因此进行挡板尺寸优化，即优化各分区间油道的尺寸，对降低变压器温升热点，提高变压器运行可靠性具有重要意义。
变压器绕组中挡板的主要作用是将变压器绕组及其对应油道进行分区，在各分区间约束油流流向，来帮助油流更充分地与绕组接触，以达到更好散热的目的[3]。目前变压器挡板结构主要有如图1所示两种形式。E. Rahimpour等对如图1a所示油浸式变压器油道中影响绕组温升的参数进行了研究，分析由于挡板的存在而提高了导热系数，有效降低了变压器热点温度，同时对不同挡板数量下的热点温度进行对比，选取了热点最低的方案作为最优设计方案[3]。图1a所示挡板结构虽然简单，但其挡板紧贴绕组，在该侧堵住了全部油流通道，绕组该侧散热明显变差，容易引起绕组温度分布不均匀，引起局部过热现象；而采用图1b中所示挡板结构，保留了一定的油道间隙，在加入挡板的同时没有完全封住绕组两侧油道，更好地提高了绕组内部的散热性能。谭又博等针对图1b所示挡板结构进行了研究，通过对挡板数量和轴向、径向油道尺寸进行优化，有效地降低了绕组的最大温升和平均温升[5]。
图1 油浸式变压器挡板结构
Fig.1 Structure of oil immersed transformer block washers
上述有关挡板结构的研究当中，主要针对挡板数量进行优化设计，未考虑对挡板尺寸进行优化。对于图1a所示挡板结构，由于挡板需封住整个油道端口，故其尺寸固定，无法进行优化；而对于图1b所示挡板结构，挡板尺寸的可调范围十分宽泛，挡板尺寸的改变也意味着相邻分区间油道结构的改变，从理论上说这会对绕组的散热水平产生较为显著的影响，因此对于图1b所示的挡板结构[6-8]，在确定分区数量的前提下，针对挡板尺寸进行优化对于降低变压器绕组温升水平具有十分重要的意义。
变压器结构优化属于典型的“黑箱问题”，对于不同的结构参数和不同的优化指标，很难用合适的经验性解析公式将两者之间复杂的隐性关系准确表达[9]。此时全局优化算法[10-13]和响应面方法[9,14-17]便是解决这类“黑箱问题”行之有效的两种方法。但全局优化算法在处理黑箱优化问题时，由于需大量调用有限元模型来获取训练及寻优样本，造成其优化效率低下[9, 16]。而响应面方法只需计算一定数目的数据集样本，便可将一个黑箱问题拟合成一个明确表达式的形式，再对相应表达式进行优化将大大提高优化效率。
在响应面方法中，径向基函数（Radial Basis Function, RBF）响应面模型以其兼顾计算精度和效率的优势而被广泛使用[18-20]。文献[21]利用RBF响应面模型对涡轮集气腔结构进行多目标优化，以更好地降低冷气流动损失和出流不均匀度。但传统的RBF响应面模型中具有一些待定的参数，这些参数通常都是经验选取[9]或网格搜索（Grid Search, GS）寻优[22]来获得。经验选取获得的超参数值可靠性较低；GS方法是一种离散的插值寻优，无法保证全局优化而且还需要花费较大的计算成本；而智能优化算法可以通过有效的设计达到全局优化，且对于具有明确表达式的模型，智能优化算法优化效率极高。陈伟根等利用遗传算法（Genetic Algorithm, GA）对支持向量机（Support Vector Machine, SVM）模型超参数进行优化，并与GS方法进行对比，结果表明GA获得的模型参数拟合效果更优，验证了智能优化算法在超参数优化领域的可行性[23]。因此本文考虑引入智能优化算法和RBF响应面模型结合以确定最优超参数，使模型实现更好的拟合优化效果。
文献[24]采用鲸鱼优化算法（Whale Optimization Algorithm, WOA）对SVM的超参数进行优化，并与基于GA和粒子群优化（Particle Swarm Optimization, PSO）的SVM做对比，验证了WOA-SVM方法的有效性。结合上述研究，同时考虑到WOA算法结构简单、优化效率高的特点[25-27]，对于RBF响应面模型这样的双参量优化问题尤为适用，因此本文考虑采用基于WOA-RBF响应面模型对变压器绕组挡板尺寸进行优化。
本文以一台强迫油循环的油浸式电力变压器的二维八分区绕组模型为优化对象，以降低绕组温升热点为优化目标，将各分区间的七个挡板尺寸作为优化变量，提出采用WOA-RBF响应面方法对其进行优化。首先，基于Workbench仿真平台提出了八分区绕组及各分区挡板的参数化建模方法；其次，在样本空间内采用拉丁超立方采样（Latin Hyper cube Sampling, LHS）方法获取数据集，通过Matlab和Workbench相互调用计算对应响应值，并对数据集进行交叉验证，以获得拟合性能最好的训练集和测试集组合；然后，通过训练得到的WOA-RBF响应面模型对变压器挡板尺寸进行优化；最后，以绕组热点温度为优化目标，将优化结果与原始挡板尺寸下流场-温度场分布和基于遗传算法的优化结果进行对比，以验证本文所提方法的有效性。同时，本文还从超参数优化的角度，将WOA与GS寻优方法进行了对比分析。
本文的研究对象为一台强迫油循环的油浸式变压器，考虑其绕组轴对称结构特点建立了二维变压器绕组八分区不分匝模型，并将分区间挡板长度进行参数化，以方便后续获取响应面模型的训练集和测试集的输出响应（即各组挡板尺寸下的热点温度）。
本文采用一台大型变压器绕组发热冷却实验模型进行试验，试验装置和绕组外观如图2所示。
图2 试验装置及绕组外观
Fig.2 Test device and winding appearance
文献[7]将试验绕组等效为一个八分区绕组分匝模型，如图3a所示。试验绕组共有8个分区，由上至下分别为分区1～8。其中分区1～3中有线饼7个，分区4～8有线饼9个，总计66个线饼；每个线饼均由15匝导线组成，每匝导线由2根铜导线并绕而成。由于本文需要进行绕组挡板结构优化，获取训练集和测试集过程中每次更新挡板尺寸都需要重新进行网格剖分，为了提高建模和仿真的效率，采用不分匝模型（见图3b），通过等效导热系数考虑匝间绝缘的影响，以减少网格剖分数量，提高计算效率，图3c给出了一个分区内不分匝绕组及油道的相关尺寸，其中挡板厚为1.5 mm。采用文献[8]中对八分区不分匝绕组等效导热系数的研究，选取其利用最小热阻法则计算得到的等效导热系数，其中轴向导热系数为1.624 8 W/(m·K)，径向导热系数为0.781 3 W/(m·K)，相关材料物性参数列于表1中。采用有限元软件Fluent 18.0进行变压器流-热耦合计算。
图3 变压器绕组八分区结构示意图
Fig.3 Schematic diagram of transformer winding eight zone structure
表1 材料物性参数
Tab.1 Material property parameters
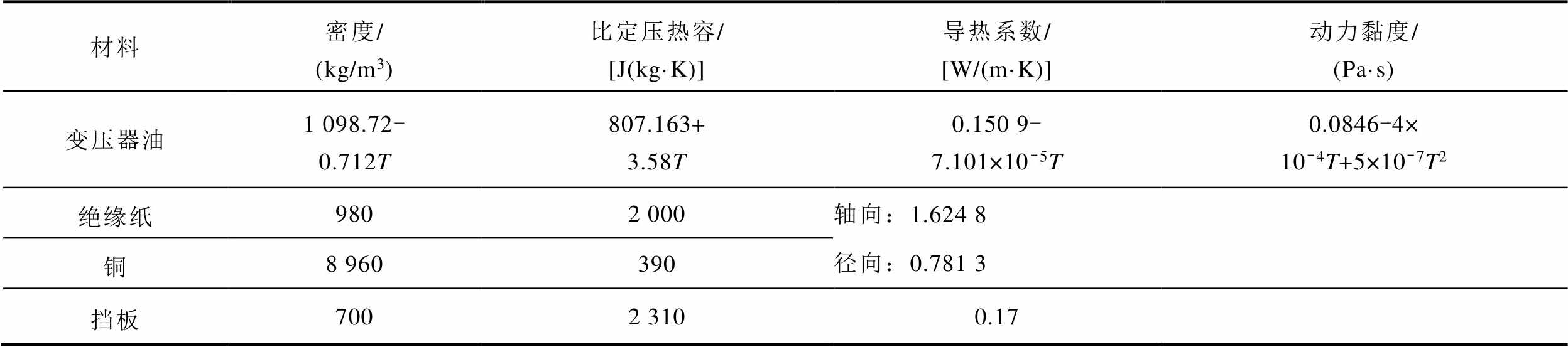
材料密度/(kg/m3)比定压热容/[J(kg·K)]导热系数/[W/(m·K)]动力黏度/(Pa·s) 变压器油1 098.72-0.712T807.163+3.58T0.150 9-7.101×10-5T0.0846-4×10-4T+5×10-7T2 绝缘纸9802 000轴向：1.624 8径向：0.781 3 铜8 960390 挡板7002 3100.17
由于Fluent 18.0本身不具有建模和导出热点温度的功能，因此为了做到自动更新挡板尺寸并获得相应尺寸下的热点情况，本文采用Workbench 18.0来实现模型的建立、剖分、计算和结果导出的操作，具体界面如图4所示。
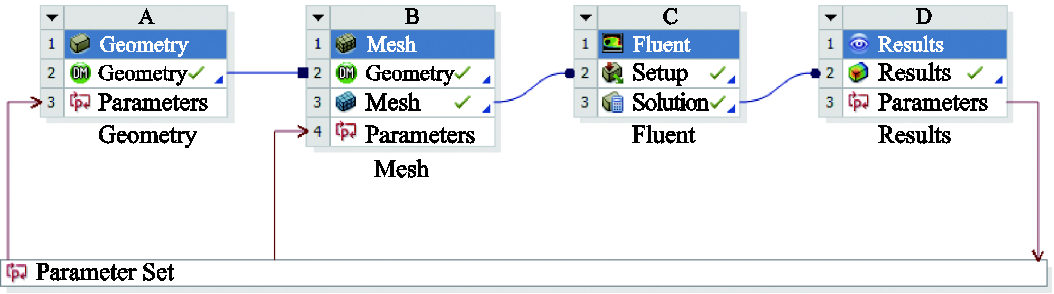
图4 Workbench模块搭建界面
Fig.4 Workbench module building interface
实际计算过程中，利用Matlab和Workbench之间的相互调用来获取训练集和测试集的热点温度响应值，二者之间的联系通过记录Workbench操作过程的Gui命令脚本来实现，图5为相互调用获取数据的过程。
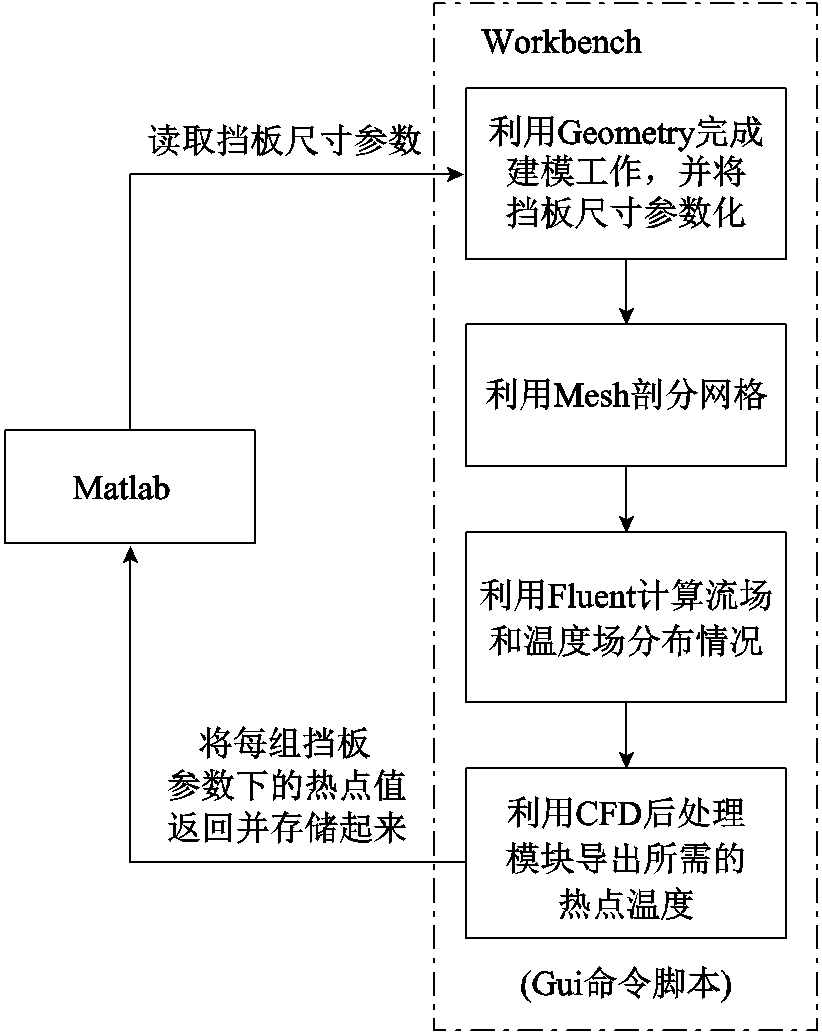
图5 Matlab和Workbench相互调用过程
Fig.5 Mutual call process between Matlab and Workbench
本文所使用Matlab版本为Matlab r2018a，所用设备型号为：CPU：12th Gen Intel(R) Core(TM) i9-12900KF 3.20 GHz；内存：128 GB。
1.2.1 流动方程
由于变压器油的密度变化很小，所以可认为变压器油是不可压缩流体，从而其流动状态可用相应的质量守恒方程和动量守恒方程来描述[8]，分别为
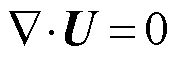（1）
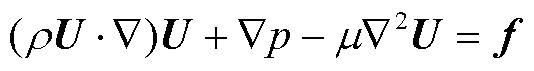（2）
式中，U为油的速度矢量；ρ为流体密度；p为流体压力；μ为流体动力黏度系数；f为外力密度矢量。
1.2.2 传热方程
流体和固体的传热过程可用统一格式的能量守恒方程加以描述，其中方程左端的第一项为热对流项，第二项为热传导项，右端为热源项[8]，即
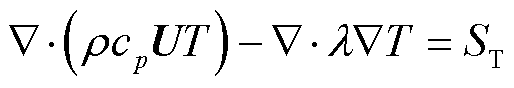（3）
式中，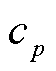
为比定压热容；λ为导热系数；ST为单位体积内热源的产热率；T为温度。
对于固体传热，由于固体内部速度U为0，从而所满足的控制方程对流项也为0，即
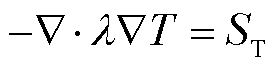（4）
1.2.3 边界条件
试验所采用运行工况为：入口流量经测量为14.15 m3/h，假设入口流速是均匀分布的，则流速可视为流量与入口截面积之比，进而换算出流速为0.105 2 m/s，入口温度经测量为62.31℃；出口设置为压力边界条件，压力为0 Pa·m2；绝缘筒和挡板设置为无滑移的壁面边界条件，根据文献[7]，将油箱壁面设置为绝热边界。热源为绕组损耗，功率分析仪测得功率为40 kW。
基于上述条件本文分别建立了八分区分匝模型和基于等效导热系数的不分匝模型，通过分匝模型与不分匝模型之间热点、全域温度场、全域流体场分布的对比，以验证不分匝模型的有效性。将两种模型流场和温度场的计算结果进行对比，如图6所示。
根据图6可以看出，不分匝模型与分匝模型在流场、温度场分布上几乎一致，其中分匝模型最大流速为0.191 3 m/s、热点为90.4℃，不分匝模型最大流速为0.191 2 m/s、热点为90.7℃，热点上二者仅相差0.3℃，满足误差允许要求，不分匝模型热点计算结果准确。上述两个模型的网格剖分情况为：分匝模型单元数为723 314，不分匝模型单元数为703 756（所选用模型均已通过网格无关性检验），采用不分匝模型在保证热点计算准确的同时减少了网格剖分量，提高了模型的计算效率，因此将其应用在以降低热点为目标的变压器绕组结构优化研究中是合适的。
图6 不分匝模型与分匝模型的流-热结果对比
Fig.6 Comparison of flow heat results between non-split turn model and turn model
径向基函数（RBF）是一类以未知点与已知数据点之间的欧氏距离作为自变量的函数。以径向函数为基函数，通过线性组合构造出的模型即为径向基函数模型。其基本形式为[9]
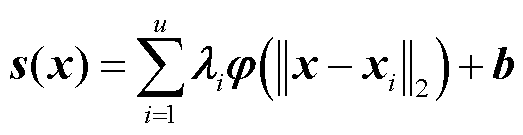（5）
式中，φ为径向函数；r=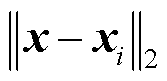
为坐标点到点的径向距离；λi为权系数；b为输出的截距向量；u为已知样本点的个数。常用的径向函数有线性函数、三次函数、薄板样条函数、高斯函数和多二次函数等。其中，高斯函数因其非线性拟合能力强而被广泛使用，因此本文也采用高斯函数作为径向基函数。
代入高斯函数，则第j个输出可写为通式，即
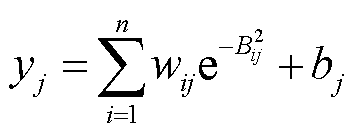（6）
其中
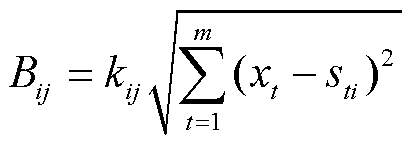
式中，m为输入变量个数；n为测试集数量，即隐含层数；j为第j个输出变量；wij为第i个隐含层到第j个输出层的权重；sti为第i组测试集的第t个输入变量对应的值；xt为第t个输入变量；kij为第i个隐含层到第j个输出的阈值；bj为第j个输出的截距。本文选取newrb函数来构建RBF响应面模型，上述各参数均可通过net.相关命令来获得[9]。
newrb函数在使用过程中，除训练集外还需要输入4个相关参数：goal（期望误差）、spread（扩展速度）、MN（神经元最大数目）和DF（两次显示之间所添加的神经元数目）。4个参数中期望误差goal应提前给定，为保证精度，常选取为零；DF主要影响构造网络的速度，对模型拟合效果几乎无影响，故期望误差虽然选取为零，但模型对测试集的拟合效果还要取决于剩余的两个超参数，即超参数spread和MN会对RBF响应面模型预测优化准确性起着至关重要的作用。目前已有的研究中[9,21]，对于超参数的选取都是给定一个经验数值作为后续预测优化过程所使用的参数，但这样的处理无法保证所使用的超参数值是适配模型精度最好的值。
网格搜索寻优法是一种十分常用的超参数优化方法[22,28]，但该方法需要人为设定调整步长，若步长设置过大，搜索精度无法保证；若步长设置过小，搜索时间成本又较高，无法保证可以高效准确地获取最优超参数值。为解决上述问题，本文决定引入鲸鱼优化算法，以测试集预测结果方均根误差最小为目标，获取径向基函数的最优超参数组合，以高效获得拟合效果最好的RBF响应面模型。
根据前文所述，建立RBF响应面模型需要确定两个超参数，超参数组合选取的合理性将对模型的预测优化结果准确性产生很大影响。为使本文所使用的RBF响应面模型具有最优的性能，本文采用鲸鱼优化算法对RBF响应面模型的超参数进行寻优。
鲸鱼优化算法是一种源于座头鲸群体捕食行为的算法，通过模仿鲸鱼的游走搜索、包围收缩、螺旋捕食三种策略进行迭代寻优，其算法的优点在于原理简单、寻优能力强且调整参数少。对于径向基函数响应面模型的超参数优化问题，由于仅有两个待优化超参数，采用鲸鱼优化算法正相适合[25]。
座头鲸是在逐渐缩小的圆圈内沿螺旋线轨迹绕着猎物进行游动的。为了模拟这种行为，假设某一种群中最优鲸鱼的位置为目标猎物的位置，同时认为选择搜寻包围或螺旋线气泡网的捕食方式更新优化过程中鲸鱼位置的概率各为50%。即有一个[0,1]之间的随机数r1。
当r1≥0.5时，采用螺旋线气泡网的捕食方式进行位置更新，位置更新为
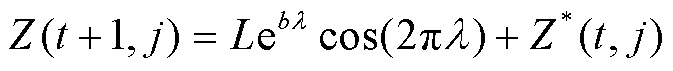（7）
式中，Z(t, j)为第t代种群的j维变量下的鲸鱼位置；Z*(t, j)为第t代种群内取得全局最优解的鲸鱼j变量对应的位置；L为鲸鱼到猎物之间的距离，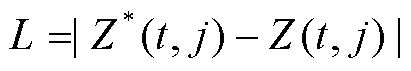
；b为控制对数螺旋形状的常数；λ为[-1,1]上的一个随机数。
当p＜0.5时，采用搜寻包围的捕食方式进行位置更新，并根据系数向量A的模值来确定究竟是猎物搜寻阶段还是包围阶段。
当|A|＜1时，进入猎物包围阶段，位置更新为
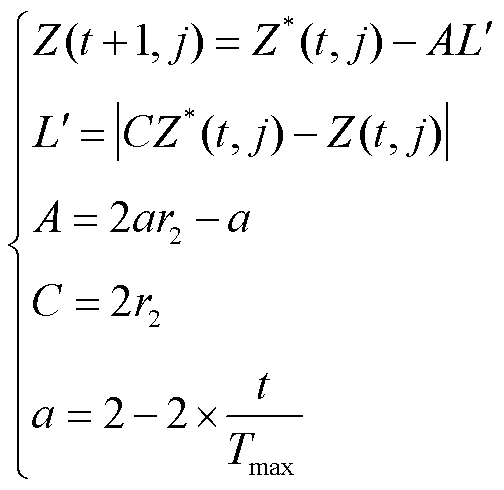（8）
式中，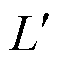
为包围步长；A和C分别为系数向量；
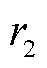r为[0,1]间的随机数；a为收敛因子，随迭代次数的增加从2线性减小至0；Tmax为最大迭代次数。
当|A|≥1时，进入猎物搜寻阶段，位置更新为
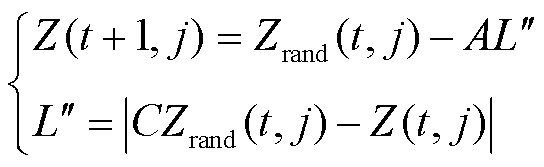（9）
式中，Zrand(t)为从当前种群中随机选择的一个个体j变量的位置；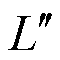
为搜寻步长。
变压器绕组挡板结构优化流程如图7所示。首先要确定优化变量，前述研究中已将绕组确定为八分区，故挡板数量和位置均已固定，仅需对挡板尺寸进行优化，由于7个挡板的厚度均远远小于其长度，故将优化变量选取为挡板的长度，变量个数为7。
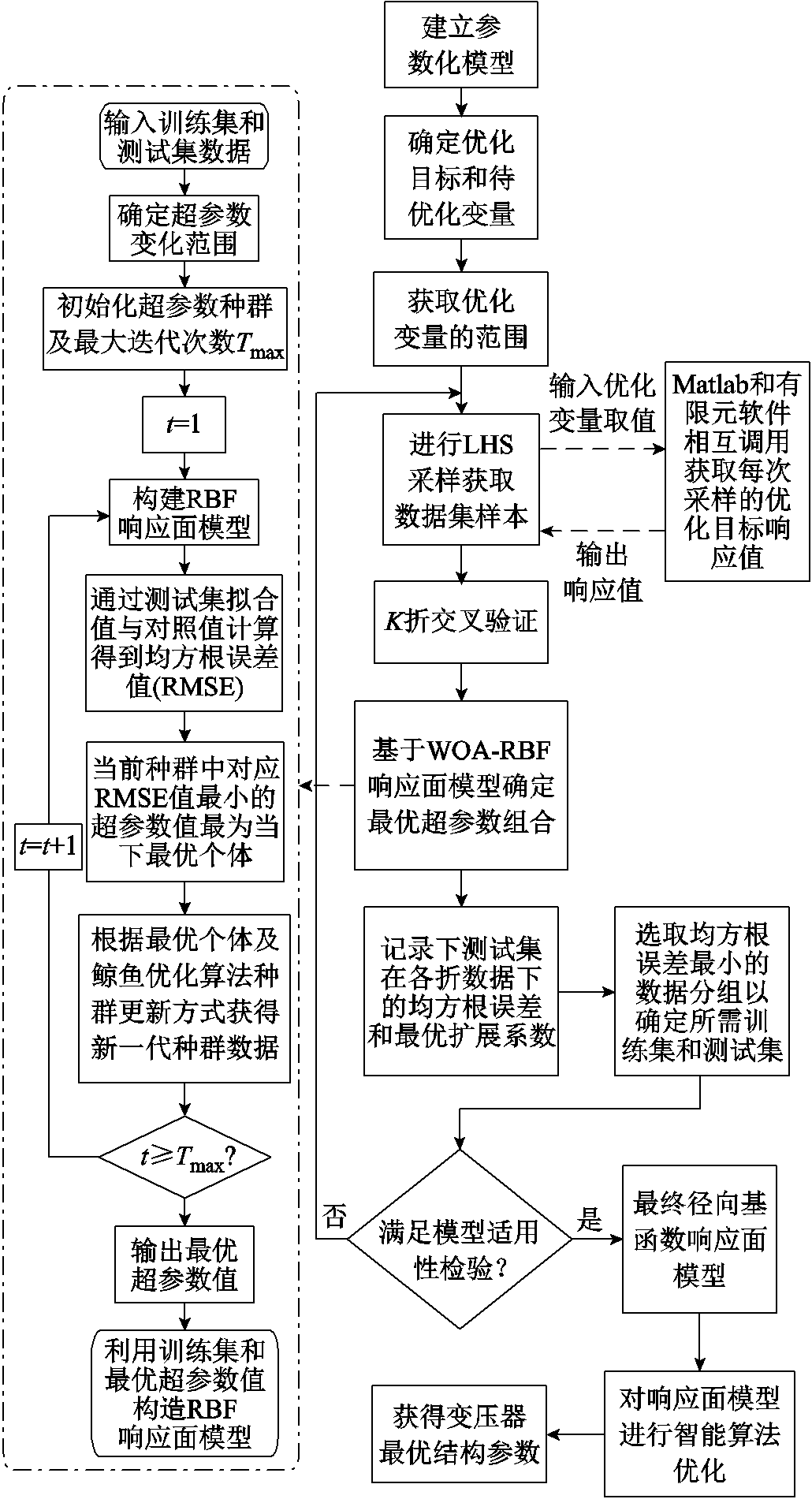
图7 变压器绕组挡板结构优化流程
Fig.7 Optimization process of transformer winding block washer structure
之后要确定优化变量的取值范围，考虑到挡板的作用是进行油道分区，不能太长封死某一分区，也不能太短起不到分区导向的作用，为避免出现油流死区，经过综合考量选取挡板尺寸变化范围为相邻侧竖直油道宽度到该宽度加上138 mm（绕组宽度）。将各挡板长度由上至下分别命名为D1、D2、D3、D4、D5、D6、D7，如图3b所示。其中D1、D3、D5、D7的长度变化范围为[10 mm, 148 mm]； D2、D4、D6的长度变化范围为[8 mm, 146 mm]。图3b中各挡板结构长度为[D1, D2, D3, D4, D5, D6, D7] = [148 mm, 146 mm, 148 mm, 146 mm, 148 mm, 146 mm, 148 mm]。
根据变量个数和变量变化范围采用拉丁超立方采样（LHS）进行试验设计，获取数据集的样本分布，通过Matlab和Workbench相互调用来获取数据集的响应值（热点温度），利用交叉验证思想并结合鲸鱼优化算法确定使测试集方均根误差（Root-Mean-Square Error, RMSE）最小的训练集、测试集组合及相应的最优扩展系数值。利用训练集和最优扩展系数生成最终的RBF响应面模型，如式（6）所示，对式（6）采用智能算法进行优化以获取绕组热点温度最低的挡板尺寸参数。
本文利用拉丁超立方采样方法获取200组数据集，通过交叉验证方法，将数据分组，将每组数据分别作为测试集、其余数据作为训练集建立RBF响应面模型，选取其中拟合效果最好的一组训练集和测试集开展后续工作。
每组作为测试集开展模型有效性验证时，均结合WOA算法以确定对应的最优超参数值。经研究发现，扩展系数spread值超过500时训练集无法完全拟合所选定的模型；神经元最大数目MN最大取值应与训练集数目一致。同时newrb函数规定扩展系数和最大神经元数目必须为正，过小也会引起欠拟合。因此扩展系数spread的变化范围设定为[1, 500]，最大神经元数目MN的变化范围设定为 [1, num_train]。每代种群规模为40，最大迭代次数为200次。
考虑到不同训练集和测试集的选取对获取最优超参数的影响，本文对该数据集进行K折交叉验证（K-fold Cross Validation, K-CV），在不同组训练集、测试集下，以方均根误差作为适应度函数，对采用WOA超参数优化方法、网格搜索（Grid Search, GS）寻优法和固定超参数的RBF模型进行对比。交叉验证的初始化分组为10，即训练集180组、测试集20组。固定超参数选取为常见经验值数据，即(spread, MN)=(50, 180)。超参数spread的变化范围为[1, 500]，MN的变化范围为[1, 180]，步进大小分别为1.995和2，判断终止条件为相邻两次迭代最优值相对误差在10-4以内，对比结果见表2。其中，K为10折数据中测试集所在那一折。根据表2绘制各组测试集和数据集下取最优超参数组合时的方均根误差如图8所示。
根据图8可以看出，不同数据分组情况下给定超参数组合的RBF响应面模型的方均根误差最大。采用鲸鱼优化算法和网格搜索寻优方法进行最优寻参对比：根据表2数据，WOA-RBF的十折交叉验证的方均根误差平均值更小，GS-RBF和定参RBF的平均RMSE分别是WOA-RBF的1.12倍和4.52倍；根据放大图来看，GS-RBF的RMSE曲线整体包裹着WOA-RBF的RMSE曲线。因此WOA-RBF响应面模型具有更好的全局拟合精度。
表2 不同方法获得超参数组合下各类结果对比
Tab.2 Comparison of various results obtained by different methods under hyper parameter combinations
参数方法K=1K=2K=3K=4K=5K=6K=7K=8K=9K=10平均值 最优参数组合WOA-RBF(145.8, 124)(124.5, 122)(114.8, 132)(234, 49)(223.6, 136)(220.3, 71)(277.4, 42)(166.1, 37)(139.6, 130)(232.2, 47) GS-RBF(144.9, 98)(144.9, 112)(108.9, 146)(252.9, 96)(270.9, 130)(396.8, 92)(153.9, 98)(162.9, 118)(117.9, 106)(198.9, 98) RBF(50, 180) RMSE/℃WOA-RBF0.143 10.316 50.147 40.162 40.155 50.188 30.218 70.201 50.167 30.226 00.192 7 GS-RBF0.164 90.330 90.157 80.179 30.189 10.253 50.243 20.228 00.173 60.241 50.216 2 RBF0.939 40.802 70.648 40.270 60.819 31.031 30.619 30.583 52.1280.869 50.871 2 优化误差（%）WOA-RBF1.081.21.070.383.34.311.311.550.810.251.53 GS-RBF3.875.981.162.564.612.30.582.030.841.592.55 RBF4.886.196.393.442.382.190.391.664.756.93.92 优化结果/℃WOA-RBF87.2387.3887.1886.8988.0789.6587.648886.9286.9587.59 GS-RBF89.7891.9486.9187.2788.0487.2586.8987.2186.9887.5287.98 RBF90.6392.0491.9289.7588.188.186.9587.789.0492.4589.67 时间/sWOA-RBF2 840.82 678.32 392.42 646.42 681.92 441.92 296.82 480.92 059.82 009.62 452.9 GS-RBF7 648.27 605.47 756.37 654.57 644.17 689.67 674.87 742.57 666.77 612.97 669.5 RBF47.7647.7149.2646.3250.4249.850.5650.4547.2447.8548.74
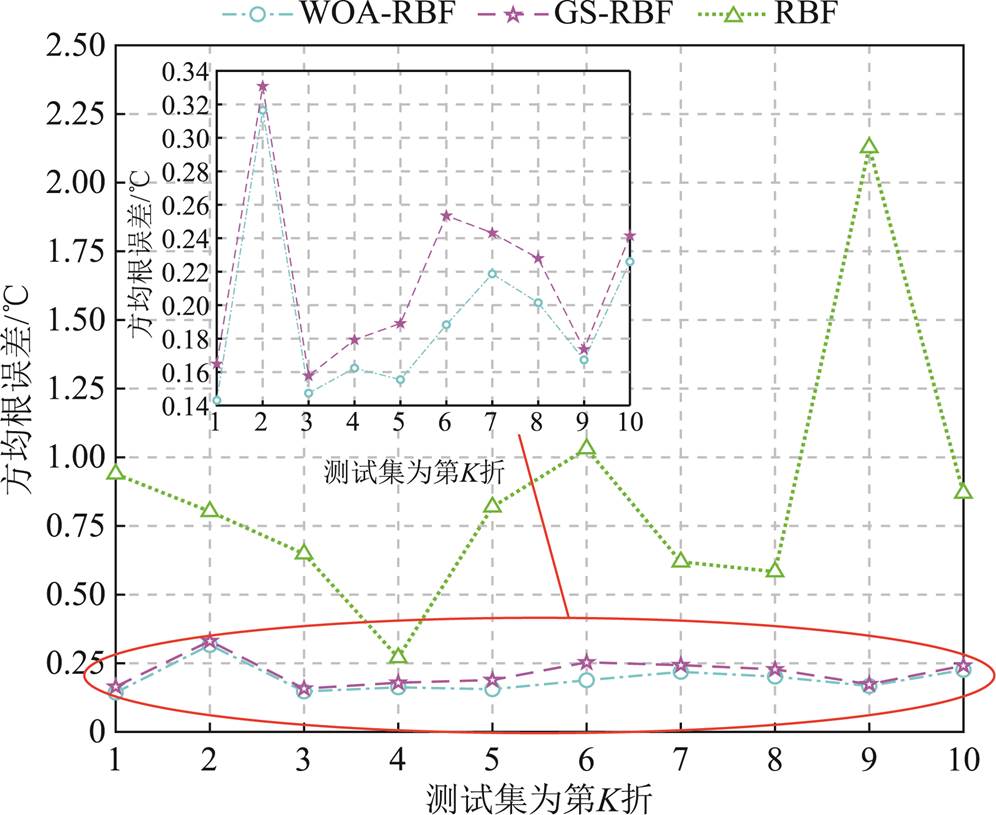
图8 各数据分组下最优参数对应方均根误差值
Fig.8 RMSE values corresponding to the optimal parameters for each group of data classification
根据表2可以发现WOA-RBF方法十折试验下优化后的热点平均值更小，相比于GS-RBF方法和定参RBF模型，优化后热点温度平均值分别降低了0.39℃和2.08℃。关注于优化精度，GS-RBF方法和定参RBF模型的平均优化误差分别是WOA-RBF方法的1.67倍和2.56倍；根据图9，针对每一折下的优化误差来看，除了测试集为第5～7折这三种数据情况外，其余情况下WOA-RBF方法的优化误差都是最小的，并且在测试集为第4折数据情况下，获得最小的热点温度为86.89℃。
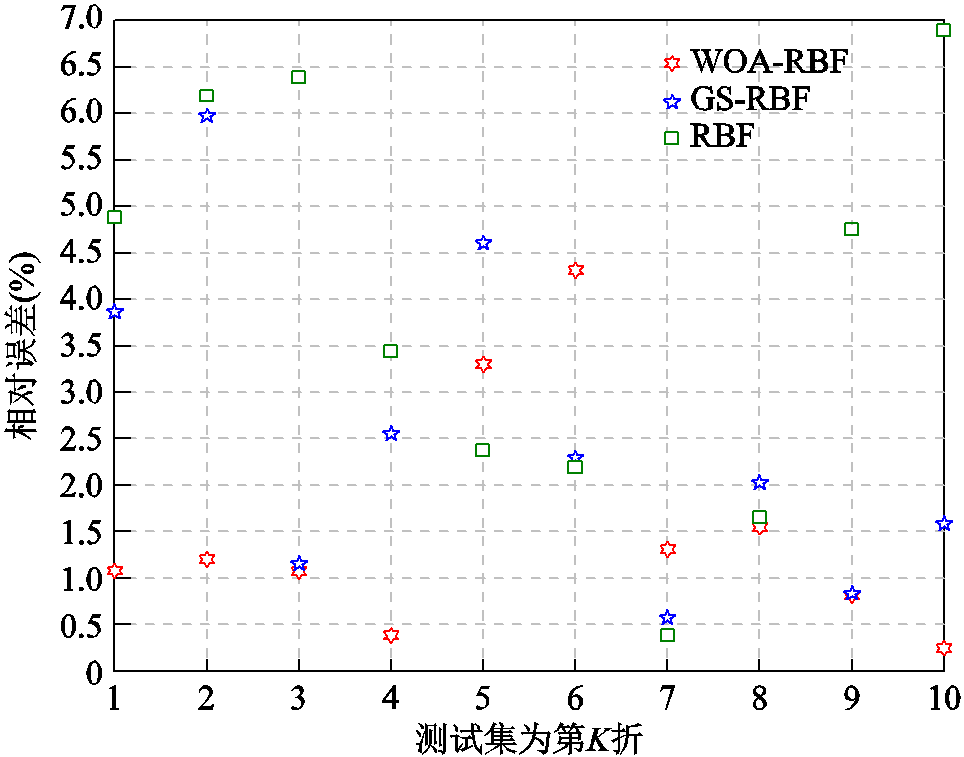
图9 各数据分组下最优参数优化结果相对误差值
Fig.9 Relative error values corresponding to the optimal parameters for each group of data classification
最后根据表2对计算时间进行比较，十折交叉试验下GS-WOA方法的平均时间是WOA-RBF方法的3.13倍，因此采用WOA算法进行超参数优化在保证优化精度的同时也大大提高了参数优化效率，验证了WOA优化方法对RBF响应面模型最优寻参的有效性。
根据表2数据可知，综合考量全局拟合能力、优化精度和优化能力三个指标，以RMSE=0.162 4、优化相对误差为0.38%、取到十折交叉试验下最小热点温度86.89℃的第4折数据为测试集，其余数据作为训练集的数据分组将作为本文的后续数据处理情况。对应的最优扩展系数spread为234，神经元最大数目为49，在(234, 49)的超参数组合下构建可以预测变压器绕组热点的RBF响应面模型。
将20组测试集数据代入模型进行适用性检验，得到测试集的预测值与对照值对比如图10所示（对照值为利用Fluent计算出的热点值）。
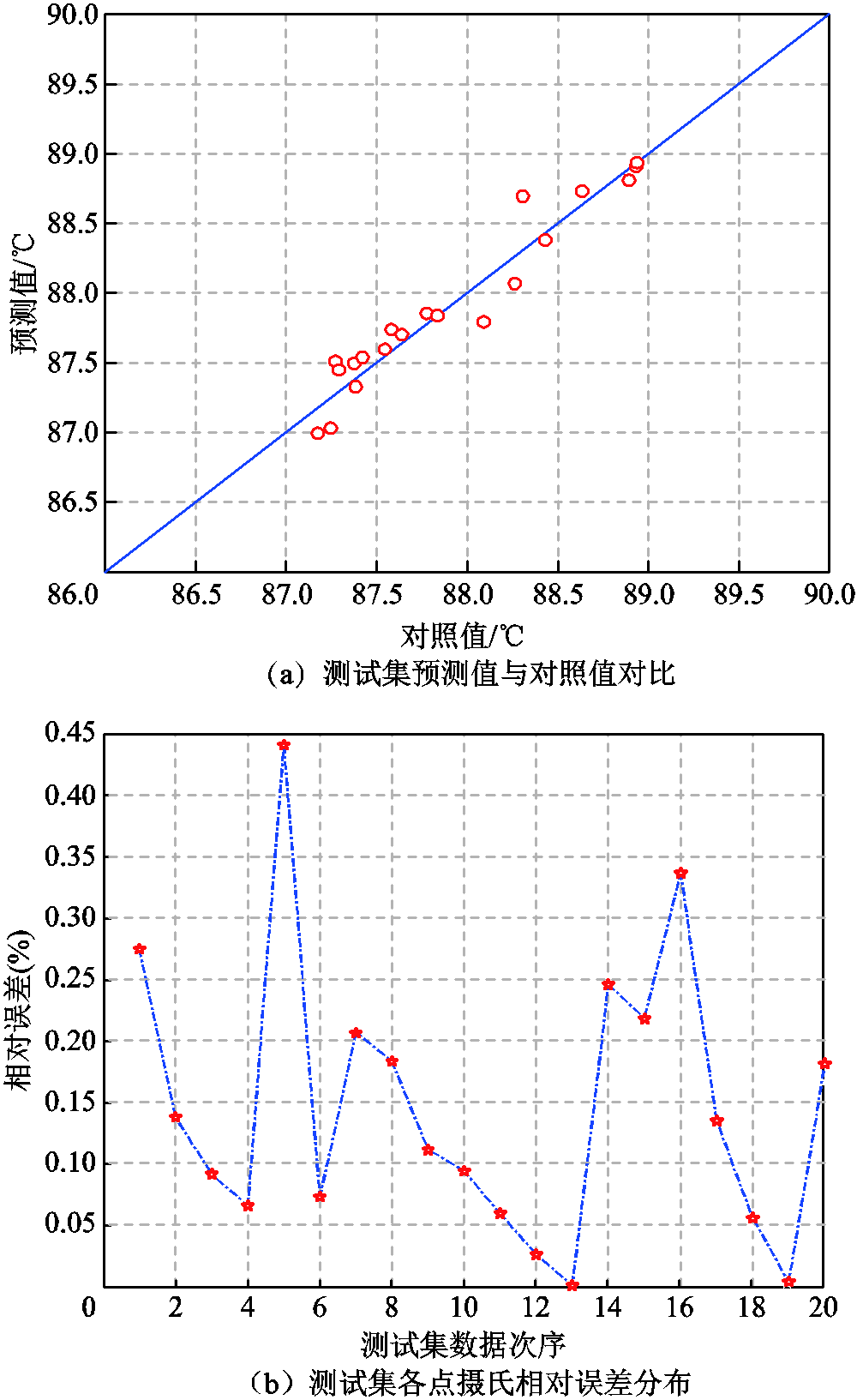
图10 RBF响应面模型适用性检验
Fig.10 Applicability test of RBF RSM
根据图10可知，预测值与对照值的整体拟合效果趋于y=x直线，测试集数据最大误差出现在第5组，即预测值数据为88.69℃，对照值数据为88.31℃，最大相对误差为0.440 9%，满足误差要求，因此，所建立的WOA-RBF响应面模型满足了模型的适用性检验。
根据训练好的响应面模型，利用文献[9]中给出的Matlab相关命令获取所需参数，得到如式（6）的表达形式，采用遗传算法对其进行优化，以获取变压器绕组最小热点温度及其对应挡板尺寸。遗传算法优化过程中，初始种群数量为40个，代沟为0.8，变异概率为0.03，交叉概率为0.7，种群迭代次数为1 000代。
最终求解结果如图11所示，得到最小热点温度为86.56℃，对应7个挡板尺寸由上到下分别为D1=111.62 mm、D2=111.5 mm、D3=79 mm、D4=39.79 mm、D5=148 mm、D6=8 mm、D7=148 mm，用时47.23 s。
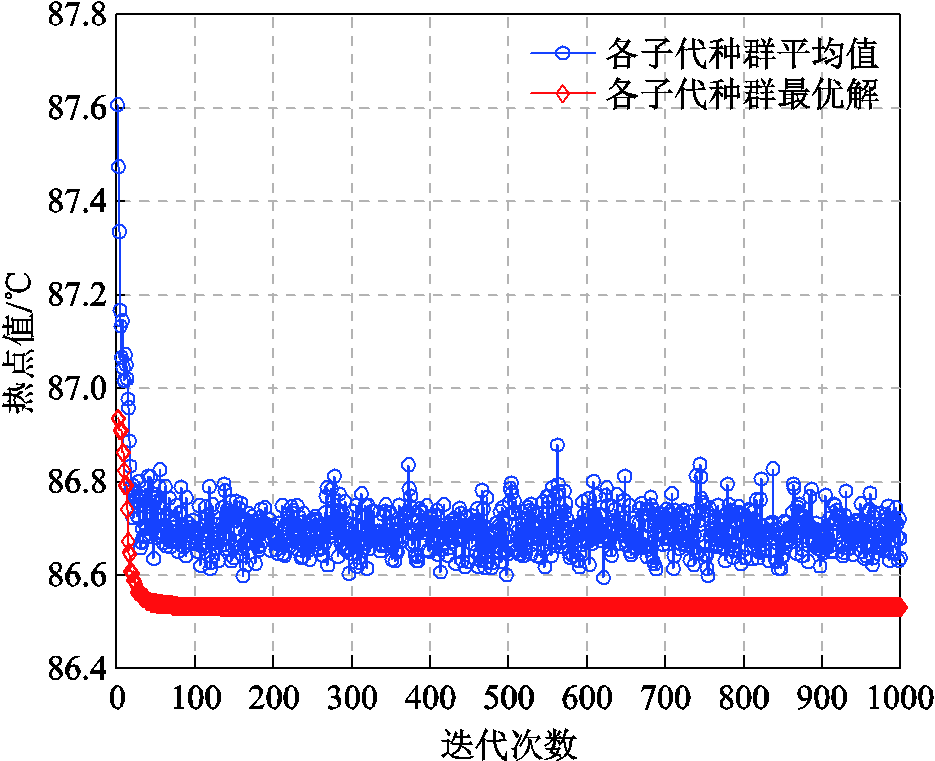
图11 遗传算法优化过程
Fig.11 Genetic algorithm optimization process
利用Fluent计算出对应挡板尺寸模型热点值为86.89℃，将该热点值作为优化结果的对照值，基于WOA-RBF响应面模型获得的最小热点温度与对照值之间仅相差0.33℃，相对误差为0.38%，优化结果满足精度要求，证明了基于WOA-RBF响应面模型优化结果的准确性。优化过程总用时393 453.4 s，约为109.29 h，其中包括200组数据集温升热点计算用时390 807 s，以及超参数寻优和和模型优化用时2 646.4 s。
考虑到工程实际制造能力，将优化后的挡板尺寸取整列于表3中。
表3 优化结果对比
Tab.3 Comparison of Optimization Results
尺寸D1/mmD2/mmD3/mmD4/mmD5/mmD6/mmD7/mm热点值/℃ 原始14814614814614814614890.7 优化后1121127940148814886.89
表3中列出了优化前后挡板尺寸下的热点值，经过优化后的绕组挡板结构使热点值有效降低了3.81℃，同时入口温度为62.31℃，则原始结构下最大温升为28.39℃，优化后的最大温升为24.58℃，最大温升减小了13.42%。根据各组流场温度场结果进行分析，得到优化前后挡板结构流-热分布如图12所示。
图12 优化前后挡板结构流-热分布对比
Fig.12 Comparison of flow heat distribution between optimized block washer structure and initial block washer structure
根据图12a可以发现，优化前各分区最高温度均出现在相邻下一分区挡板上侧的线饼上，图中标出了各分区出现局部温升较大线饼的标号，而在优化后的挡板尺寸下，这些局部温升较大区域均出现了改善，尤其是前四分区的7、14、21和30号线饼。因此优化后的挡板结构不仅降低了绕组热点温度，也有效地抑制了各分区下的局部温升过大现象，是一种全域温度改善方法，验证了优化后挡板尺寸在改善变压器绕组温度场分布的有效性。对优化前后流体场进行对比，分析产生上述改善效果的原因，如图12b所示。可以发现在优化前两分区间相隔挡板与上一分区的最后一个线饼间的油道（已在图中标出）几乎没有油流流过，而优化后由于挡板尺寸的减小，油流可以在一定程度上绕过挡板与上一分区相邻线饼进行接触，有油流流过就会带来更好的散热效果，所以在温度场上对于各分区最后一个线饼的温度改善效果最为明显。
为验证响应面方法所获优化结果是否达到最优，本文采用全局优化算法——遗传算法进行优化对比。需要说明的是，4.2节中采用遗传算法求解是对式（6）所示的径向基响应面模型表达式进行的，而本节是将挡板结构优化看作“黑箱问题”，用遗传算法进行优化求解。
遗传算法参数设置如下：取每代种群数量为40，代沟为0.8，变异概率为0.01，最大迭代次数为100。为加快计算速度，本文采用距离法对遗传算法相邻两代中个体进行筛选，筛选出未变异的个体，不再重复计算，节约计算时间。遗传算法的结果优化过程如图13所示。
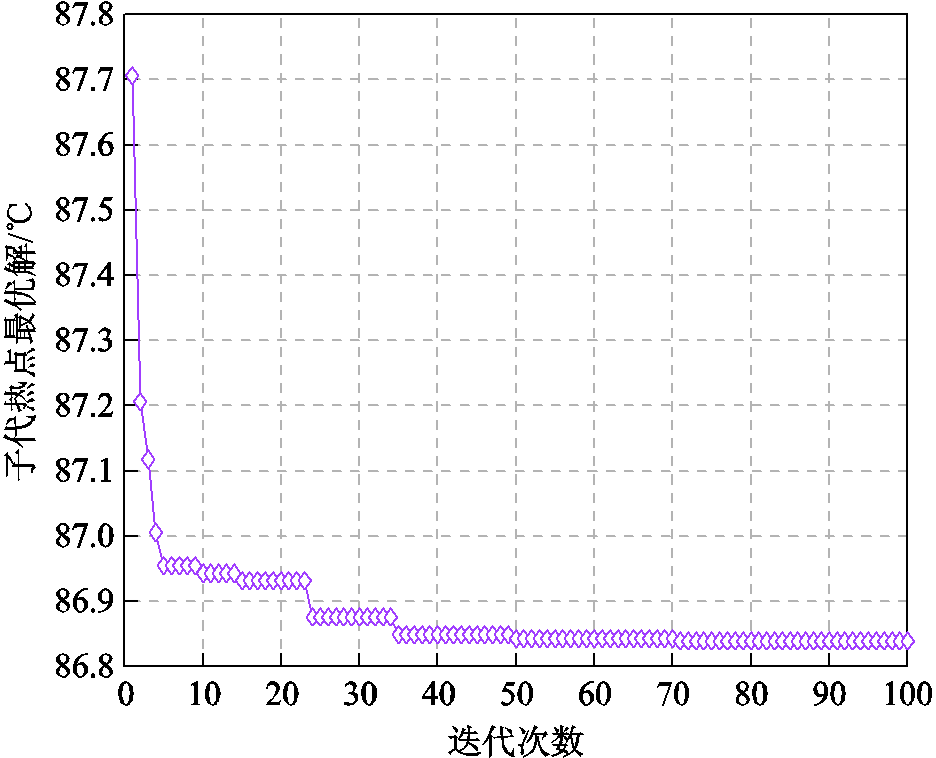
图13 遗传算法优化过程
Fig.13 Genetic algorithm optimization process
图13给出了遗传算法迭代100次时子代种群热点最优解的变化曲线，热点最优解在第50代左右达到了最小值，并稳定在86.84℃，获得的优化变量取值见表4。
表4 不同优化方法结果对比
Tab.4 Comparison of results of different optimization methods
优化方法D1/mmD2/mmD3/mmD4/mmD5/mmD6/mmD7/mm热点优化结果/℃计算用时/h RBF112 112 79 40148814886.89109.29 GA113 114 71 4511015 126 86.841 465.2
根据表4，遗传算法优化后挡板尺寸虽然与RBF响应面模型不完全相同，但各组变量取值趋势是一致的，且优化后最小热点值相差0.05℃，相对误差仅为0.06%，满足误差要求。再对两种方法所得挡板尺寸优化结果进行详细对比，在前四个挡板尺寸下两组解是十分接近的，尺寸优化结果的差异主要体现在后面三个挡板上。而根据图12a有关挡板尺寸对温度场的改善结果可以发现，前四个挡板之上的分区区域温度改善较为明显，而下面四个分区优化前后温度场分布变化不大。其原因是下方油流没有充分受热，油流的散热效果会更好，所以在下面四个分区所存在的三个挡板尺寸对该区域的温度改善起的作用不大。因此根据前四个挡板尺寸优化情况，认为RBF响应面模型与GA优化结果可以相互验证，即挡板结构优化属于一个多解问题，RBF响应面模型与GA优化结果是多解问题的两个可信解。响应面模型所得挡板尺寸可以视为全局最优解之一，验证了RBF响应面模型优化结果的可靠性。且GA的计算用时是RBF响应面模型的13.41倍，说明RBF响应面模型是一种可以兼顾优化精度和效率的方法，更适合应用于工程实际。
本文基于WOA-RBF响应面模型实现了对一台大型油浸式变压器的八分区绕组挡板尺寸的优化，得到了有效降低热点温度对应的挡板尺寸设计方案，并得到如下结论：
1） 采用WOA优化RBF响应面模型的超参数，并与GS寻优方法和定参RBF模型进行对比，GS-RBF和定参RBF的平均RMSE分别是WOA-RBF的1.12倍和4.52倍；GS-RBF方法和定参RBF模型的平均优化误差分别是WOA-RBF方法的1.67倍和2.56倍。在拟合和优化精度都较优的情况下，WOA优化效率是GS方法的3.13倍，验证了WOA应用于超参数优化设计的可行性，为后续进行动态径向基函数响应面模型优化策略的高效计算做好了准备。
2）提出采用WOA-RBF响应面模型对变压器绕组挡板尺寸进行优化，与原始挡板尺寸相比，优化后热点温度下降了3.81℃，最大温升减小了13.42%，同时有效抑制了各分区下的局部温升较大现象。本文所提方法不仅可以降低热点温度，也可以作为一种全域温度场的改善措施，具有一定的实际应用价值。
3）为验证WOA-RBF响应面方法优化结果的可靠性，将其与遗传算法优化结果进行对比，二者最优解趋势一致，且最优热点值仅相差0.05℃，两种方法优化所得挡板尺寸是多解问题对应最优值下取到的两个可信解，响应面法所得优化结果的可靠性得到验证；同时响应面法的优化效率是遗传算法的13.41倍，表明本文所提方法在保证优化精度的同时可以更高效地解决变压器绕组挡板结构优化问题。
参考文献
[1] Abdali A, Abedi A, Mazlumi K, et al. Novel hotspot temperature prediction of oil-immersed distribution transformers: an experimental case study[J]. IEEE Transactions on Industrial Electronics, 2023, 70(7): 7310-7322.
[2] Tan Youbo, Yu Xiaoling, Ji Shengchang, et al. Parametric study and optimization of a full-scale converter transformer winding[J]. International Journal of Heat and Mass Transfer, 2021, 181: 121861.
[3] Rahimpour E, Barati M, Schäfer M. An investigation of parameters affecting the temperature rise in windings with zigzag cooling flow path[J]. Applied Thermal Engineering, 2007, 27(11/12): 1923-1930.
[4] Torriano F, Campelo H, Quintela M, et al. Numerical and experimental thermofluid investigation of different disc-type power transformer winding arrangements[J]. International Journal of Heat and Fluid Flow, 2018, 69: 62-72.
[5] Tan Youbo, Yu Xiaoling, Wang Xiaolin, et al. Interaction analysis and multi-response optimization of transformer winding design parameters[J]. International Communications in Heat and Mass Transfer, 2022, 137: 106233.
[6] 刘刚, 郝世缘, 胡万君, 等. 基于子循环自适应串行交错时间匹配算法的油浸式变压器绕组瞬态温升计算[J]. 电工技术学报, 2024, 39(4): 1185-1197.
Liu Gang, Hao Shiyuan, Hu Wanjun, et al. Transient temperature rise calculation of oil immersed transformer winding based on sub cyclic adaptive staggered time matching algorithm[J]. Transactions of China Electrotechnical Society, 2024, 39(4): 1185-1197.
[7] 武卫革, 杜振斌, 刘刚, 等. 大型油浸式变压器绕组温度场仿真及验证[J]. 华北电力大学学报(自然科学版), 2020, 47(6): 68-74.
Wu Weige, Du Zhenbin, Liu Gang, et al. Simulation and verification of winding temperature field for large oil immersed transformer[J]. Journal of North China Electric Power University (Natural Science Edition), 2020, 47(6): 68-74.
[8] 王晓晗. 基于等效导热系数法的油浸式电力变压器绕组流—热耦合分析[D]. 保定: 华北电力大学, 2021.
Wang Xiaohan. Analysis of Flow-thermal coupling of oil-immersed power transformer windings based on equivalent thermal conductivity method[D]. Baoding: North China Electric Power University, 2021.
[9] 刘刚, 高成龙, 胡万君, 等. 基于改进的连续局部枚举采样和径向基函数响应面法的变压器静电环结构优化设计[J]. 电工技术学报, 2023, 38(23): 6266-6278.
Liu Gang, Gao Chenglong, Hu Wanjun, et al. Optimized design of transformer electrostatic ring based on radial basis function response surface method with enhanced successful local enumeration sampling[J]. Transactions of China Electrotechnical Society, 2023, 38(23): 6266-6278.
[10] 温志伟, 熊斌, 程自然. 强化液冷牵引变压器电磁结构设计及优化[J]. 电工技术学报, 2021, 36(增刊02): 460-466.
Wen Zhiwei, Xiong Bin, Cheng Ziran. Electromagnetic design and optimization of enhanced liquid-cooling traction transformer[J]. Transactions of China Electrotechnical Society, 2021, 36(S02): 460-466.
[11] Ding Zheshi, Fan Xianhao, Song Boshu, et al. NSGA-Ⅱ model-based dielectric frequency response parameters for aging and moisture analysis of transformer insulation[J]. IEEE Transactions on Instrumentation and Measurement, 2022, 71: 3518710.
[12] Zhou Lei, Yang Dingye, Zhai Xiaolin, et al. GA-STT: human trajectory prediction with group aware spatial-temporal transformer[J]. IEEE Robotics and Automation Letters, 2022, 7(3): 7660-7667.
[13] 刘道生, 魏博凯, 蔡昌万, 等. 基于混沌自适应遗传算法的非晶合金干式变压器优化设计[J]. 高压电器, 2022, 58(10): 40-47.
Liu Daosheng, Wei Bokai, Cai Changwan, et al. Optimization design of amorphous alloy metal dry-type transformer based on chaotic adaptive genetic algorithm[J]. High Voltage Apparatus, 2022, 58(10): 40-47.
[14] 陈彬, 曹红霞, 王帅兵, 等. 基于响应面法的多绕组中频变压器绝缘结构优化设计[J]. 绝缘材料, 2023, 56(4): 68-76.
Chen Bin, Cao Hongxia, Wang Shuaibing, et al. Optimization design of insulation structure of multi-winding medium frequency transformer based on response surface method[J]. Insulating Materials, 2023, 56(4): 68-76.
[15] 赵玉顺, 戴义贤, 庄加才, 等. 基于热固耦合的中频变压器绝缘材料性能参数优化配合方法[J]. 电工技术学报, 2023, 38(4): 1051-1063.
Zhao Yushun, Dai Yixian, Zhuang Jiacai, et al. Optimization of insulation material performance parameters for medium frequency transformers based on thermosolid coupling[J]. Transactions of China Electrotechnical Society, 2023, 38(4): 1051-1063.
[16] 刘刚, 刘西娅, 刘尧, 等. 基于响应面法的变压器静电环绝缘优化设计[J]. 高电压技术, 2022, 48(10): 4163-4171.
Liu Gang, Liu Xiya, Liu Yao, et al. Optimal design of transformer electrostatic ring insulation based on response surface method[J]. High Voltage Engineering, 2022, 48(10): 4163-4171.
[17] 宁倩, 李桥, 高兵, 等. 电—磁—机—声多场边界下的超磁致伸缩Ⅳ型弯张换能器设计方法[J]. 电工技术学报, 2023, 38(12): 3112-3121.
Ning Qian, Li Qiao, Gao Bing, et al. Design of giant magnetostrictive class Ⅳ flextensional transducer under electrical-magnetic-mechanical-acoustic multi-field boundaries[J]. Transactions of China Electrotechnical Society, 2023, 38(12): 3112-3121.
[18] 彭磊, 刘莉, 龙腾. 基于动态径向基函数代理模型的优化策略[J]. 机械工程学报, 2011, 47(7): 164-170.
Peng Lei, Liu Li, Long Teng. Optimization strategy using dynamic radial basis function metamodel[J]. Journal of Mechanical Engineering, 2011, 47(7): 164-170.
[19] 陈鑫. 高超声速飞行器气动—热—结构建模及模型降阶研究[D]. 北京: 北京理工大学, 2015.
Chen Xin. Studies on aerodynamic—structural—thermal modeling and reduced order modeling of hypersonic vehicles[D]. Beijing: Beijing Institute of Technology, 2015.
[20] Jin Ruichen, Chen Wei, Simpson T. Comparative studies of metamodeling techniques under multiple modeling criteria[C]//8th Symposium on Multidis-ciplinary Analysis and Optimization, Long Beach, CA, USA, 2000: 4801.
[21] 王振宇, 王春华, 张靖周. 涡轮集气腔结构参数优化研究[J]. 中南大学学报(自然科学版), 2022, 53(7): 2756-2765.
Wang Zhenyu, Wang Chunhua, Zhang Jingzhou. Research on structural parameter optimization of turbine coolant collection/distribution plenum[J]. Journal of Central South University (Science and Technology), 2022, 53(7): 2756-2765.
[22] 袁发庭, 施文菀, 王玥, 等. 基于多物理场仿真的油浸式变压器温度特性分析及散热器优化[J]. 高电压技术, 2024, 50(1): 221-231.
Yuan Fating, Shi Wenyu, Wang Yue, et al. Temperature characteristic analysis and radiator optimization of oil-immersed transformer based on multi-physical field simulation[J]. High Voltage Engineering, 2024, 50(1): 221-231.
[23] 陈伟根, 滕黎, 刘军, 等. 基于遗传优化支持向量机的变压器绕组热点温度预测模型[J]. 电工技术学报, 2014, 29(1): 44-51.
Chen Weigen, Teng Li, Liu Jun, et al. Transformer winding hot-spot temperature prediction model of support vector machine optimized by genetic algorithm[J]. Transactions of China Electrotechnical Society, 2014, 29(1): 44-51.
[24] 李英顺, 阚宏达, 王德彪, 等. 一种基于KPCA-WOA-SVM火控系统故障诊断方法[J]. 火炮发射与控制学报, 2023, 44(4): 14-19.
Li Yingshun, Kan Hongda, Wang Debiao, et al. A fault diagnosis method for fire control systems based on KPCA-WOA-SVM[J]. Journal of Gun Launch & Control, 2023, 44(4): 14-19.
[25] 冯增喜, 李嘉乐, 葛珣, 等. 融合多策略改进鲸鱼优化算法及其应用[J/OL]. 计算机集成制造系统, 2023: 1-23[2023-04-25]. http:///kns.cnki.net/kcms/ detail/11. 5946.tp.20230104.1215.014.html.
Feng Zengxi, Li Jiale, Ge Jun, et al. Integrating multiple strategies to improve the whale optimization algorithm and its application[J/OL]. Computer Integrated Manufacturing Systems, 2023: 1-23[2023-04-25]. http://kns.cnki.net/kcms/detail/11.5946.tp.20230104.1215.014.html.
[26] 李畸勇, 张伟斌, 赵新哲, 等. 改进鲸鱼算法优化支持向量回归的光伏最大功率点跟踪[J]. 电工技术学报, 2021, 36(9): 1771-1781.
Li Jiyong, Zhang Weibin, Zhao Xinzhe, et al. Global maximum power point tracking for PV array based on support vector regression optimized by improved whale algorithm[J]. Transactions of China Electrotechnical Society, 2021, 36(9): 1771-1781.
[27] 安国庆, 史哲文, 马世峰, 等. 基于RF特征优选的WOA-SVM变压器故障诊断[J]. 高压电器, 2022, 58(2): 171-178.
An Guoqing, Shi Zhewen, Ma Shifeng, et al. Fault diagnosis of WOA-SVM transformer based on RF feature optimization[J]. High Voltage Apparatus, 2022, 58(2): 171-178.
[28] 刘会兰, 常庚垚, 赵书涛, 等. 溯源弹簧形变过程的断路器振动信号递归量化分析辨识方法[J]. 电工技术学报, 2024, 39(8): 2567-2577.
Liu Huilan, Chang Gengyao, Zhao Shutao, et al. Recursive quantification analysis and identification method for circuit breaker vibration signal tracing spring deformation process[J]. Transactions of China Electrotechnical Society, 2024, 39(8):
Abstract High hot spot temperature (HST) can seriously affect the stability of transformer operation. The structure of the transformer winding block washers plays a key role in the distribution of oil flow between windings, indirectly affecting the heat dissipation capacity of the windings. In order to improve the stability of transformer operation, this article takes reducing the winding HST as the optimization objective, and uses radial basis function (RBF) response surface model (RSM) to optimize the size of winding block washers, improve oil flow distribution, and achieve better heat dissipation. To the problem of empirical selection of hyper-parameters in the construction of traditional RBF RSM, this paper introduces the whale optimization algorithm (WOA) to determine the optimal hyper-parameters of the RBF RSM. The WOA-RBF RSM is proposed to optimize the size of winding block washers to improve the fitting accuracy and optimization ability of the RSM.
Firstly, use the Workbench platform to parameterize the block washers’ size with a two-dimensional eight-zone winding with non-split turn model based on an actual large oil immersed transformer. Secondly, the optimization variable was determined to be the lengths of 7 block washers. The range of changes in block washers’ length was determined, aiming to avoid oil flow dead zones. Use Latin hypercube sampling (LHS) to obtain the data set, and obtain the corresponding HST response values of the relevant data set through mutual calls between Matlab and Workbench, forming the final sample set. Thirdly, based on the existing sample set, a RBF RSM was established using the newrb function provided by Matlab. Combining WOA and cross validation ideas, hyper-parameters were optimized for the two hyper-parameters in the newrb function: spread (expansion speed) and MN (maximum number of neurons). Finally, the final RBF RSM was constructed based on the optimal hyper-parameters, and intelligent algorithms were used to obtain the optimal block washers’ size scheme and the corresponding minimum HST.
The effectiveness of the non-split turn model used was verified by comparing the flow and temperature results of the split and the non-split turn model. The optimized results based on the WOA-RBF RSM were compared with those before optimization. The HST decreased by 3.81℃ and the maximum temperature rise decreased by 13.42%. Moreover, the optimized block washers’ size not only reduced the HST, but also effectively ameliorated the phenomenon of excessive local temperature rise in winding various zones. To verify the accuracy of the optimization results by WOA-RBF, the results were compared with the optimization results of the genetic algorithm (GA). The optimal solution trends of the two methods were consistent, and the optimal HST value difference was only 0.05℃. The block washers’ sizes obtained by the two methods were the two optimal credible solutions of the multi-solution problem. The reliability of the optimization results obtained by WOA-RBF was verified. Meanwhile, the efficiency of WOA-RBF is 13.41 times that of GA, indicating that the WOA-RBF method is an accurate and efficient method to solve the optimization problem of winding block washers’ size. Simultaneously, this article also compared the WOA with grid search (GS) optimization method and fixed hyper-parameter method from the perspective of hyper-parameter optimization. The average root mean square error (RMSE) and average optimization error of GS-RBF and fixed parameter RBF are 1.12 times, 4.52 times and 1.67 times, 2.56 times higher than those of WOA-RBF, respectively. In the case of superior fitting and optimization accuracy, the optimization efficiency of WOA was 3.13 times than that of GS method, which verified the feasibility of applying WOA to hyper-parameter optimization design.
Keywords：Response surface method (RSM), radial basis function (RBF), hot spot temperature (HST), whale optimization algorithm (WOA), oil immersed transformer, block washer structural optimization.
中图分类号：TM403.2
DOI: 10.19595/j.cnki.1000-6753.tces.231064
国家重点研发计划（2021YFB2401700）和中央高校基本科研业务费专项资金（2022MS073）资助项目。
收稿日期 2023-07-04
改稿日期 2023-08-07
刘 刚 男，1985年生，副教授，硕士生导师，研究方向为电气设备多物理场建模及仿真、电力系统时域仿真和电磁场理论及其应用。
E-mail：liugang_em@163.com（通信作者）
高成龙 男，1999年生，硕士研究生，研究方向为多物理场理论及其应用优化。
E-mail：cg_01041024@163.com
（编辑 郭丽军）